15 简谐振动 旋转矢量法ppt课件
合集下载
(优选)简谐振动旋转矢量法

初相位 : 也叫初位相或初相.
t=0时的相位, 描述初始时刻的 振动状态, 与初始条件有关.
相位差ΔΦ : 相位的差值.
单位: 弧度(rad)
4. 求解振幅和初相
设 t =0 时
x0 Acos , v0 Asin
x2 0
v2 0
2
A2 (sin 2 cos2 )
A2
振幅:
A
x0
2
v0
6cm x
解: A=12cm, T=2s, x0=6cm
(1)
2π π s1
x
x
o
to
o
t
t
相位差为 2 整数倍: 同步
相位差为 或 奇数倍: 反相
3. 用旋转矢量图画简谐运动的x t
例2: 一质点沿x轴作简谐运动 的振幅为12cm, 周期为2s. 当 t = 0 时, 位移为6cm, 且沿 x 轴 正方向运动. 求: (1) 振动表达式; (2) t = 0.5s时, 质点的位置, 速 度和加速度; (3) 如果在某时刻质点位于 x=-6cm, 且沿 x 轴负方向运 动, 求从该位置回到平衡位置 所需要的最短时间.
振子沿 x 轴负方向运动 2. 比较各振动之间的相位关系 不同振动同一时刻的相位差
x1 Acos( t ) x2 Acos(t )
x1 Acos( t1 ) x2 Acos( t2 ) Φ (t2 ) (t1 )
(t2 t1) ( ) t
Φ 2 1
Φ 0 同步
x
0 超前 Φ π反相 Φ 0 落后
v d x 0.24sin 6.0t dt
sin 6.0t 1 cos2 6.0t
1
1
2
3
2 2
t=0时的相位, 描述初始时刻的 振动状态, 与初始条件有关.
相位差ΔΦ : 相位的差值.
单位: 弧度(rad)
4. 求解振幅和初相
设 t =0 时
x0 Acos , v0 Asin
x2 0
v2 0
2
A2 (sin 2 cos2 )
A2
振幅:
A
x0
2
v0
6cm x
解: A=12cm, T=2s, x0=6cm
(1)
2π π s1
x
x
o
to
o
t
t
相位差为 2 整数倍: 同步
相位差为 或 奇数倍: 反相
3. 用旋转矢量图画简谐运动的x t
例2: 一质点沿x轴作简谐运动 的振幅为12cm, 周期为2s. 当 t = 0 时, 位移为6cm, 且沿 x 轴 正方向运动. 求: (1) 振动表达式; (2) t = 0.5s时, 质点的位置, 速 度和加速度; (3) 如果在某时刻质点位于 x=-6cm, 且沿 x 轴负方向运 动, 求从该位置回到平衡位置 所需要的最短时间.
振子沿 x 轴负方向运动 2. 比较各振动之间的相位关系 不同振动同一时刻的相位差
x1 Acos( t ) x2 Acos(t )
x1 Acos( t1 ) x2 Acos( t2 ) Φ (t2 ) (t1 )
(t2 t1) ( ) t
Φ 2 1
Φ 0 同步
x
0 超前 Φ π反相 Φ 0 落后
v d x 0.24sin 6.0t dt
sin 6.0t 1 cos2 6.0t
1
1
2
3
2 2
简谐运动的旋转矢量描述法

π
4
A g a'*
h' * g'* *
t f O b*' T T f'* 3T T 5T
e
c' 4* 2*e' 4
4
-A
d*'
T 2 (旋转矢量旋转一周所需的时间)
用旋转矢量图画简谐运动的 x t 图
T 2π (旋转矢量旋转一周所需的时间)
二、旋转矢量法对相位的表示
若某时刻t,测得质点的位移为x =A/2,向OX轴负方
简谐运动的旋转 矢量表示法
一、简谐运动的旋转矢量表示法
P
t=t
t+
o
A t=0
A
x·
x
x Aco(s t )
x Aco(s t )
旋 转 矢量 A的
x 端点在
轴上的投
影点的运
动为简谐
运动.
x Acos(t )
用旋转矢量图画简谐运动的 x t 图
x
Ah
a
bO
c -Ad
x
x Acos(t )
向运动
M
A
O 3P
X
M
三、旋转矢量法对相位差的表示
A2
A1
O
相位差 2 1 2kπ
x
(k 0,1, 2,)
两个振动同相,步调相同
A1
O
A2
相位差 2 1 (2k 1)π
x
(k 0,1,)
两个振动反相,步调相反
例题 两个同方向、同频率的谐振动,频率为2s-1,
当第一个振子从平衡位置向正向运振动的相位差。
解:
2 1
A 2
t
o
简谐振动旋转矢量法讲课文档

机械振动, 电磁振荡 机械波, 电磁波 德布罗意波——几率波
振动学是波动学的基础
第5章 机械振动
振动: 任何一个物理量(物体的位置, 电 流强度, 电场强度, 磁场强度等)在某一 固定值附近作往复变化. 机械振动: 物体在固定位置(平衡位置) 附近作来回往复的运动. 简谐运动: 是最基本, 最简单的振动.
ω 6π 6
第18页,共20页。
§ 5.3 单摆
O
l T
mg
小球受力矩:
Mmg siln
根据转动定律
M J
mgslinm2ldd2t2
化简得:
d2
dt2
gsin
l
0
当θ 很小时, sin
d2
dt2
g l
0
结论: 单摆振动是简谐运动
0 cos t
g
l
T 2π l g
θ为振动角位移,θ0叫做角振幅
第19页,共20页。
例3: 一简谐振动曲线如图所示, 则振动周期
x(m 4) 2
1
t(s)
2 4 cos
0 4cos
3
32
5
6
T 2 12 5
(A)2.62 s (B)2.40 s (C)0.42 s (D)0.382 s
答案: B
第20页,共20页。
v d x 0.24sin 6.0t dt
sin 6.0t 1 cos2 6.0t
1
1
2
3
2 2
依题意, v<0
v 0.24 3 0.208 m s1 2
第11页,共20页。
§5.2 简谐运动的旋转矢量 表示法
5.2.1 旋转矢量表示法
振动学是波动学的基础
第5章 机械振动
振动: 任何一个物理量(物体的位置, 电 流强度, 电场强度, 磁场强度等)在某一 固定值附近作往复变化. 机械振动: 物体在固定位置(平衡位置) 附近作来回往复的运动. 简谐运动: 是最基本, 最简单的振动.
ω 6π 6
第18页,共20页。
§ 5.3 单摆
O
l T
mg
小球受力矩:
Mmg siln
根据转动定律
M J
mgslinm2ldd2t2
化简得:
d2
dt2
gsin
l
0
当θ 很小时, sin
d2
dt2
g l
0
结论: 单摆振动是简谐运动
0 cos t
g
l
T 2π l g
θ为振动角位移,θ0叫做角振幅
第19页,共20页。
例3: 一简谐振动曲线如图所示, 则振动周期
x(m 4) 2
1
t(s)
2 4 cos
0 4cos
3
32
5
6
T 2 12 5
(A)2.62 s (B)2.40 s (C)0.42 s (D)0.382 s
答案: B
第20页,共20页。
v d x 0.24sin 6.0t dt
sin 6.0t 1 cos2 6.0t
1
1
2
3
2 2
依题意, v<0
v 0.24 3 0.208 m s1 2
第11页,共20页。
§5.2 简谐运动的旋转矢量 表示法
5.2.1 旋转矢量表示法
简谐振动 旋转矢量法共60页

1、不要轻言放弃,否则对不起自己。
2、要冒一次险!整个生命就是一场冒险。走得最远的人,常是愿意 去做,并愿意去冒险的人。“稳妥”之船,从未能从岸边走远。-戴尔,回味起来却有 久久不会退去的余香。
简谐振动
旋转矢量法 4、守业的最好办法就是不断的发展。 5、当爱不能完美,我宁愿选择无悔,不管来生多么美丽,我不愿失 去今生对你的记忆,我不求天长地久的美景,我只要生生世世的轮 回里有你。
40、学而不思则罔,思而不学则殆。——孔子
谢谢!
36、自己的鞋子,自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢,但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何,且尽全力做你应该做的事吧。——美华纳
2、要冒一次险!整个生命就是一场冒险。走得最远的人,常是愿意 去做,并愿意去冒险的人。“稳妥”之船,从未能从岸边走远。-戴尔,回味起来却有 久久不会退去的余香。
简谐振动
旋转矢量法 4、守业的最好办法就是不断的发展。 5、当爱不能完美,我宁愿选择无悔,不管来生多么美丽,我不愿失 去今生对你的记忆,我不求天长地久的美景,我只要生生世世的轮 回里有你。
40、学而不思则罔,思而不学则殆。——孔子
谢谢!
36、自己的鞋子,自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢,但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何,且尽全力做你应该做的事吧。——美华纳
简谐振动的旋转矢量图示.ppt
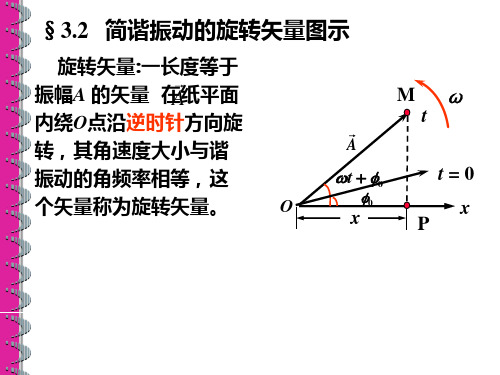
角频率ω
A 与参考方向x 的夹角
振动相位ωt+φ0
3、两个谐振动的相位差
x1 A1 cos(t 1 ) x2 A2 cos(t 2 )
相位差为 (t 2 ) (t 1) 2 1
采用旋转矢量表示为:
A2
2
A1
1
O
x
例1、两个同频率的谐振动,它们都沿x轴振动,且振
幅相等,当t =0时质点1在x=A/2处向左运动,另一质点
F kx m 2x
(0.01kg)(π s1)2 (0.069m) 1.70103 N
2
(2)由起始位置运动到 x 0.04m 处所需要
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
解法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04m (0.08m) cos[(π s1)t π ]
x 0.12cos( 0.5 ) 0.104 m
3
v 0.12 sin( 0.5 ) 0.18 m/s
3 a 0.12 2 cos( 0.5 ) 1.03 m/s2
3
在t =T/4=0.5s时,可得
可得x 0.12cos( 0.5 ) 0.104 m
3
v 0.12 sin( 0.5 ) 0.18 m/s
sin0 0
0
3
简谐振动表达式 x 0.12cos( t ) m
3
因为
(2)由简谐振动的运动方程 x 0.12cos( t ) m
3
可得
v dx 0.12 sin( t ) m/s
dt
3
a dv 0.12 2 cos( t ) m/s2
§3.2 简谐振动的旋转矢量图示【VIP专享】
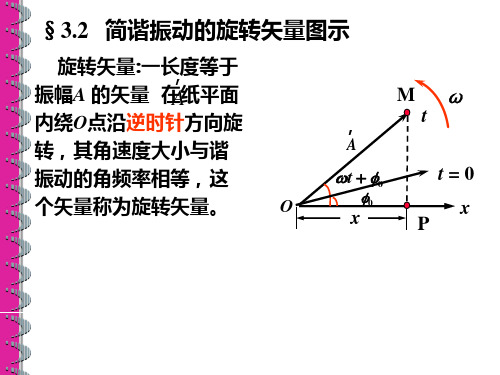
F kx m 2x
(0.01kg)(π s1)2 (0.069m) 1.70103 N
2
(2)由起始位置运动到 x 0.04m 处所需要
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
解法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04m (0.08m) cos[(π s1)t π ]
sin0 0
0
3
简谐振动表达式 x 0.12cos( t ) m
3
因为
(2)由简谐振动的运动方程 x 0.12cos( t ) m
3
可得
v dx 0.12 sin( t ) m/s
dt
3
a dv 0.12 2 cos( t ) m/s2
dt
3
在t =T/4=0.5s时,可得
x (0.08m) cos[(π s1)t π ] 3
2
3
v0 0
π
3
A
π3
x/m
0.08 0.04 o 0.04 0.08
x (0.08m) cos[(π s1)t π ]
2
3
m 0.01kg
v
x/m
0.08 0.04 o 0.04 0.08
t 1.0s 代入上式得 x 0.069m
2
3
v
x/m
0.08 0.04 o 0.04 0.08
cos( t ) 1
23 2
t 2 或 4
233 3
又因为第一次到达- 0.04m处时,v 0
即v A sin(t ) 0
23
所以t 2
23 3
t 2s 3
(0.01kg)(π s1)2 (0.069m) 1.70103 N
2
(2)由起始位置运动到 x 0.04m 处所需要
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
解法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04m (0.08m) cos[(π s1)t π ]
sin0 0
0
3
简谐振动表达式 x 0.12cos( t ) m
3
因为
(2)由简谐振动的运动方程 x 0.12cos( t ) m
3
可得
v dx 0.12 sin( t ) m/s
dt
3
a dv 0.12 2 cos( t ) m/s2
dt
3
在t =T/4=0.5s时,可得
x (0.08m) cos[(π s1)t π ] 3
2
3
v0 0
π
3
A
π3
x/m
0.08 0.04 o 0.04 0.08
x (0.08m) cos[(π s1)t π ]
2
3
m 0.01kg
v
x/m
0.08 0.04 o 0.04 0.08
t 1.0s 代入上式得 x 0.069m
2
3
v
x/m
0.08 0.04 o 0.04 0.08
cos( t ) 1
23 2
t 2 或 4
233 3
又因为第一次到达- 0.04m处时,v 0
即v A sin(t ) 0
23
所以t 2
23 3
t 2s 3
简谐振动-旋转矢量法

简谐振动的运动学函数应是复数 z 的实部
即
x Re[ Aei( t ) ]
用复数表示振动,有时在处理复杂振动过程中很方 便;最终只取实部(可观察物理量只可能是实量)。
复数法在光学、电工学等专业领域中被广泛运用
四、旋转矢量法
旋转矢量法
当t 0 时
A
o
x0 x
x0 Acos
t t 时
o
A
t
x
x
A1 o
o
A
A2
A A1 A2
Tt
结论
A A12 A22 2A1 A2 cos(2 1 )
若两分振动同相Байду номын сангаас:
2 1 2k k 0,1, 2,
A A1 A2
若两分振动反相位:
两分振动相互加强
2 1 (2k 1) k 0,1, 2,
A A1 A2
两分振动相互减弱
再若 A1= A2 , 则 A= 0
简谐振动的描述方法有多种∶代数法、曲线表 示法、旋转矢量法、复数法等等。
一、代数法
x Acos(t )
振幅 系统固有角频率 相位 初相位 其中,振幅、角频率、初相是简谐振动的特征量
二、图示法: (振动曲线)
x Acos(t 0 )
三、复数法
z Aei( t )
由欧拉公式 ei cos i sin
sin2 (2 1)
y
2) 2 1 π
y A2 x A1
3)2 1 π 2
x A2
o A1
x2 A12
y2 A22
1
x A1 cost
y
A2
cos(t
π) 2
A2 y
简谐振动 旋转矢量法
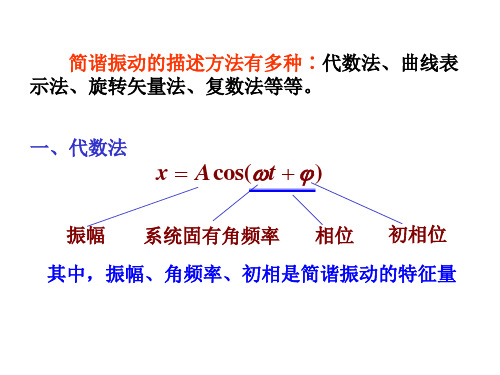
( 1) 2 1 0, 称同相; (2) 2 1 , 称反相; (3) 2 1 0, 称振动2超前, 振动1落后; (4) 1 2 0, 称振动1超前, 振动2落后.
对于沿 x 轴振动的两个同频率的简谐振动:
用旋转矢量表示相位关系 同相位 反相位
2 1
A2 A1
A2 A1
A2
x
x
x
A1
例题1 : 确定以下几种情况的初相位 0 x0 A x0 A
普通物理学教案
x0 A / 2 正向运动 x0 A / 2 正向运动
解: 作参考圆
/ 4
2 / 3
例题2 :
普通物理学教案
A
P x
注意:旋转矢量在第 2 象限 速度v < 0
M
A
P x
注意:旋转矢量在第 2 象限 速度v < 0
M P
A
x
注意:旋转矢量在第 2 象限 速度v < 0
M
P
A
x
注意:旋转矢量在第 3 象限 速度v 0
P M
A
<
x
注意:旋转矢量在第 3 象限 速度v 0
P x M
A
<
注意:旋转矢量在第 3 象限 速度v 0
2 1 2 2
x2
1
x1
A1
A A A 2 A1 A2 cos( 2 1 )
A1 sin 1 A2 sin 2 tan A1 cos 1 A2 cos 2
两个同方向同频 率简谐运动合成 后仍为简谐运动
讨论
1)相位差
对于沿 x 轴振动的两个同频率的简谐振动:
用旋转矢量表示相位关系 同相位 反相位
2 1
A2 A1
A2 A1
A2
x
x
x
A1
例题1 : 确定以下几种情况的初相位 0 x0 A x0 A
普通物理学教案
x0 A / 2 正向运动 x0 A / 2 正向运动
解: 作参考圆
/ 4
2 / 3
例题2 :
普通物理学教案
A
P x
注意:旋转矢量在第 2 象限 速度v < 0
M
A
P x
注意:旋转矢量在第 2 象限 速度v < 0
M P
A
x
注意:旋转矢量在第 2 象限 速度v < 0
M
P
A
x
注意:旋转矢量在第 3 象限 速度v 0
P M
A
<
x
注意:旋转矢量在第 3 象限 速度v 0
P x M
A
<
注意:旋转矢量在第 3 象限 速度v 0
2 1 2 2
x2
1
x1
A1
A A A 2 A1 A2 cos( 2 1 )
A1 sin 1 A2 sin 2 tan A1 cos 1 A2 cos 2
两个同方向同频 率简谐运动合成 后仍为简谐运动
讨论
1)相位差
简谐运动的物理矢量描述课件高中物理竞赛(共20张PPT)
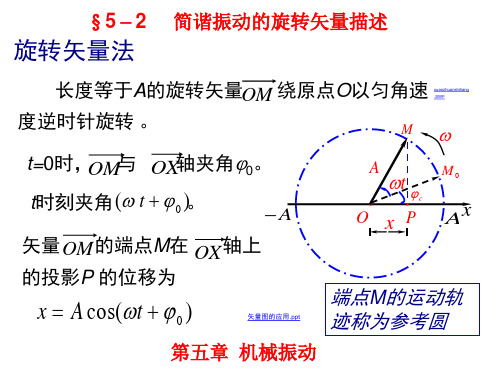
A
t
M0
c
O x P Ax
端点M的运动轨 迹称为参考圆
第五章 机械振动
§5-2
振动曲线
简谐振动的旋转矢量描述
mm m
oA x x00<=x0A0< A(伸长量)
x A
= /2
=0
1.S WF
3.SWF
o
ωt
-A
ωT=2π
>0
第五章 机械振动
§5-2 简谐振动的旋转矢量描述
两个同振幅同频率,不同周相的简谐振动的位移时间曲线
速度共振:当驱动力角频率等于系统固有频率时,速度幅值达到最大值。
t时刻夹角
。
解:船静浮时,浮力与重力平衡
两个同振幅同频率,不同周相的简谐振动的位移时间曲线
1 1 2 2 2 的位置取静浮时水面P点来代表,则船在任一位置y时,船受合力为
小号发出的声波足以使酒杯破碎
m A sin (t ) k A cos (t ) 解:船静浮时,浮力与重力平衡
§5-2 简谐振动的旋转矢量描述
两个同振幅同频率,不同周相的简谐振动的位移时间曲线
x A cost M
x
x
M
ON
3
O
2
xN
A cos(t
3)
2
t
3
2
第五章 机械振动
§5-2 简谐振动的旋转矢量描述
两个同振幅同频率,不同周相的简谐振动的位移时间曲线
x A cos(t 0) M
xM
x
N2
O
o
xN
A cos(t
1)
2
2
t
第五章 机械振动
§5-3 几种常见的简谐振动
大学物理(9.1.2)--简谐振动旋转矢量

东北大学 理学院 物理系
大学物理 第九单元 振动
三 相位差
第一讲 简谐振动 旋转矢量
表示两个相位之差
( 1 )对同一简谐运动,相位差可以给出两
运动状态间变化所需的时间.
x1 A cos(t1 + j ) x2 A cos(t2 + j )
j (t2 + j) (t1 + j)
第一讲 简谐振动 旋转矢量
受迫振动
无阻尼自由振 动
自由振动
阻尼自由振动
简谐振动
无阻尼自由谐振动
无阻尼自由非谐振 动
东北大学 理学院 物理系
大学物理 第九单元 振动
第一讲 简谐振动 旋转矢量
壹.简谐振动 一物理量随时间的变化规律遵从
余弦函数关系,则称该物理量作
简谐振动。 谐振子 作简谐运动的物体
1 、 弹簧振子的振动
t
t2
t1
j
东北大学 理学院 物理系
大学物理 第九单元 振动
第一讲 简谐振动 旋转矢量
求 : a , b 两点的时间差 , 周期为
x
A A2
a
b
T.
t
o
A
v
A o
tb
j x A ta A
2
j
π 3
t
t2
t1
j
t
π 2
第一讲 简谐振动 旋转矢量
振动有各种不同的形式
机械振动 电磁振动
广义振动:任一物理量 ( 如位移、电流、电压
、密度、压强、场强等 ) 随时间的周期性变化。 包括行星的运动、生态的循环、股指的振荡。
简谐振动的旋转矢量图示法PPT课件

3
v 0.12 sin( 0.5 ) 0.18 m/s
3 a 0.12 2 cos( 0.5 ) 1.03 m/s2
3
SUCCESS
THANK YOU
2019/7/30
(3) 当x = -0.06m时,该时刻设为t1,得
cos(
t1
5 t 6 5 0.83 s
6
例3、一弹簧振子 k 0.72N/m, m 20g (1)将物体从平衡位置向右拉到 x=0.05m 处释放,求谐振
动方程. (2)求物体第一次经过A/2 处时速度大小。 (3)如果物体在x=0.05m处速度大小为 v 0.30m/s ,且向
§3.2 简谐振动的旋转矢量图示法
旋转矢量:一长度等
于振幅A 的矢量 A 在纸平
Mω
t
面内绕O点沿逆时针方向
A
旋转,其角速度大小与谐
振动的角频率相等,这个
t 0
t=0
矢量称为旋转矢量。
O
0
x
x P
M 点在 x 轴上投影点(P点)的运动规律:
x Acos(t 0 )
说明: 1、旋转矢量的方向: 逆时针方向
一长度等于振幅a的矢量在纸平面内绕o点沿逆时针方向旋转其角速度大小与谐振动的角频率相等这个矢量称为旋转矢量m点在x轴上投影点p点的运动规律振动相位t0逆时针方向的长度振幅a角频率旋转的角速度与参考方向x的夹角说明1旋转矢量的方向2旋转矢量和谐振动的对应关系相位之差为采用旋转矢量表示为3两个谐振动的相位差例1两个同频率的谐振动它们都沿x轴振动且振幅相等当t0时质点1在xa2处向左运动另一质点2在xa2处向右运动试用旋转矢量法求两质点的相位差解oxa例2一
v 0.12 sin( 0.5 ) 0.18 m/s
3 a 0.12 2 cos( 0.5 ) 1.03 m/s2
3
SUCCESS
THANK YOU
2019/7/30
(3) 当x = -0.06m时,该时刻设为t1,得
cos(
t1
5 t 6 5 0.83 s
6
例3、一弹簧振子 k 0.72N/m, m 20g (1)将物体从平衡位置向右拉到 x=0.05m 处释放,求谐振
动方程. (2)求物体第一次经过A/2 处时速度大小。 (3)如果物体在x=0.05m处速度大小为 v 0.30m/s ,且向
§3.2 简谐振动的旋转矢量图示法
旋转矢量:一长度等
于振幅A 的矢量 A 在纸平
Mω
t
面内绕O点沿逆时针方向
A
旋转,其角速度大小与谐
振动的角频率相等,这个
t 0
t=0
矢量称为旋转矢量。
O
0
x
x P
M 点在 x 轴上投影点(P点)的运动规律:
x Acos(t 0 )
说明: 1、旋转矢量的方向: 逆时针方向
一长度等于振幅a的矢量在纸平面内绕o点沿逆时针方向旋转其角速度大小与谐振动的角频率相等这个矢量称为旋转矢量m点在x轴上投影点p点的运动规律振动相位t0逆时针方向的长度振幅a角频率旋转的角速度与参考方向x的夹角说明1旋转矢量的方向2旋转矢量和谐振动的对应关系相位之差为采用旋转矢量表示为3两个谐振动的相位差例1两个同频率的谐振动它们都沿x轴振动且振幅相等当t0时质点1在xa2处向左运动另一质点2在xa2处向右运动试用旋转矢量法求两质点的相位差解oxa例2一
简谐振动 旋转矢量法

2 1 2 2
2 1 2k π (k 0 , 1, 2,)
x
x
A
A2
A1
o
o
T
t
A A 1 A 2
A A A 2 A1 A2 cos( 2 1 ) 2)相位差 2 1 (2k 1)π (k 0 , 1, )
A
P x
注意:旋转矢量在第 2 象限 速度v < 0
M
A
P x
注意:旋转矢量在第 2 象限 速度v < 0
M P
A
x
注意:旋转矢量在第 2 象限 速度v < 0
M
P
A
x
注意:旋转矢量在第 3 象限 速度v 0
P M
A
<
x
注意:旋转矢量在第 3 象限 速度v 0
P x M
A
<
注意:旋转矢量在第 3 象限 速度v 0
( 1) 2 1 0, 称同相; (2) 2 1 , 称反相; (3) 2 1 0, 称振动2超前, 振动1落后; (4) 1 2 0, 称振动1超前, 振动2落后.
对于沿 x 轴振动的两个同频率的简谐振动:
用旋转矢量表示相位关系 同相位 反相位
对应关系
t
用旋转矢量图画简谐运动的
x t
图
T 2π (旋转矢量旋转一周所需的时间)
A
P
M
x
注意:旋转矢量在第 1 象限 速度v < 0
A
P
M
x
注意:旋转矢量在第 1 象限 速度v < 0
A
P
M x
2 1 2k π (k 0 , 1, 2,)
x
x
A
A2
A1
o
o
T
t
A A 1 A 2
A A A 2 A1 A2 cos( 2 1 ) 2)相位差 2 1 (2k 1)π (k 0 , 1, )
A
P x
注意:旋转矢量在第 2 象限 速度v < 0
M
A
P x
注意:旋转矢量在第 2 象限 速度v < 0
M P
A
x
注意:旋转矢量在第 2 象限 速度v < 0
M
P
A
x
注意:旋转矢量在第 3 象限 速度v 0
P M
A
<
x
注意:旋转矢量在第 3 象限 速度v 0
P x M
A
<
注意:旋转矢量在第 3 象限 速度v 0
( 1) 2 1 0, 称同相; (2) 2 1 , 称反相; (3) 2 1 0, 称振动2超前, 振动1落后; (4) 1 2 0, 称振动1超前, 振动2落后.
对于沿 x 轴振动的两个同频率的简谐振动:
用旋转矢量表示相位关系 同相位 反相位
对应关系
t
用旋转矢量图画简谐运动的
x t
图
T 2π (旋转矢量旋转一周所需的时间)
A
P
M
x
注意:旋转矢量在第 1 象限 速度v < 0
A
P
M
x
注意:旋转矢量在第 1 象限 速度v < 0
A
P
M x
高二物理竞赛课件:简谐振动的旋转矢量投影表示法

初位相确定简谐振动在初始时刻的运动状态。 l
位相 (t) = t + —物体在任一时刻的位相。
位相确定简谐振动在任意时刻的运动状态。
周期T —物体完成一次全振动所用的时间。
频率 — 单位时间内物体完成全振动的次数。
说明:
1.周期、频率和角频率(圆频率)三者关系: T 1 2
2. 一个系统自由振动的周期和频率完全由这个系统本 身的性质决定,该频率称为固有频率。 3. 频率的单位是赫兹 (Hz),角频率的单位与角速度相 同,均为弧度/秒(rad/s),周期的单位是秒 (s).
/ )2
A2
A
x
2 0
v0
2
②/①有:tg v0 / A v0
x0 / A
x 0
(周期为 )
在 0—2 之间有两个解,但只有一个解符合要求,
为此要根据初始条件 x0、v0 的正负来判断和取舍。
二、简谐振动的旋转矢量法
在平面上作坐标轴OX, 由原点O作长度等于振幅的矢量 A.
t = 0, 矢 量与坐标轴夹角等于初相 0 = .
A2
x2 A2 cos(t 2 )
x A1
(t 2 ) (t 1) A 0
A
2 1
0同步 x
o
t
1
2
2
超前
π 反相
为其它
落后
x
o
1 0
x
A/ 2
o
2
1
3
或
1
5 3
t
t
2 0, 振动2比振动1超前4 / 3
或 0, 振动2比振动1落后2 / 3
例1. 计算下列情况的初位相
应用
(1) 用旋转矢量法确定谐振动的初位相 .
位相 (t) = t + —物体在任一时刻的位相。
位相确定简谐振动在任意时刻的运动状态。
周期T —物体完成一次全振动所用的时间。
频率 — 单位时间内物体完成全振动的次数。
说明:
1.周期、频率和角频率(圆频率)三者关系: T 1 2
2. 一个系统自由振动的周期和频率完全由这个系统本 身的性质决定,该频率称为固有频率。 3. 频率的单位是赫兹 (Hz),角频率的单位与角速度相 同,均为弧度/秒(rad/s),周期的单位是秒 (s).
/ )2
A2
A
x
2 0
v0
2
②/①有:tg v0 / A v0
x0 / A
x 0
(周期为 )
在 0—2 之间有两个解,但只有一个解符合要求,
为此要根据初始条件 x0、v0 的正负来判断和取舍。
二、简谐振动的旋转矢量法
在平面上作坐标轴OX, 由原点O作长度等于振幅的矢量 A.
t = 0, 矢 量与坐标轴夹角等于初相 0 = .
A2
x2 A2 cos(t 2 )
x A1
(t 2 ) (t 1) A 0
A
2 1
0同步 x
o
t
1
2
2
超前
π 反相
为其它
落后
x
o
1 0
x
A/ 2
o
2
1
3
或
1
5 3
t
t
2 0, 振动2比振动1超前4 / 3
或 0, 振动2比振动1落后2 / 3
例1. 计算下列情况的初位相
应用
(1) 用旋转矢量法确定谐振动的初位相 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
振 幅A:x02 v0022 x00.0m 4
依题意, v<0
1
1
2
2
3 2
arctavn0 0 x0
v 0.24 3 0 .20 m s 8 1
(为什么 不取π ?)
2
P.9/35
§5.2 简谐运动的旋转矢量表示法 5.2.1 旋转矢量表示法
t
x P
• 旋转矢量 的模A即为简谐运动的振幅.
第5章 机械振动
• 旋转矢量 与xA轴的夹角(t+)即为简谐
运动的相位.
• 旋转矢量 角频率.
的A 角速度 即为振动的
• t =0时, 初相.
与xA 轴的夹角即为简谐振动的
• 旋转矢量 动.
旋A 转一周, P点完成一次全振
周期: T 2 π
结论: 投影点的运动为简谐运动
xAcost()
P.10/35
第三篇 机械振动&机械波
第五章 机械振动
为何讨论的重点是简谐运动 复杂振动可分解为若干简谐运动 振动的运动学规律
简谐振动的动力学特征
振动能量的周期性特征
第5章 机械振动
P.2/35
振动和波动的关系: 波动——振动的传播 振动——波动的源头
机械振动, 电磁振荡 机械波, 电磁波 德布罗意波——率波
(1) 振动表达式; (2) t = 0.5s时, 质点的位置, 速度和加速 度; (3) 如果在某时刻质点位于 x=-6cm, 且沿 x 轴负方向运动, 求从 该位置回到平衡位置所需要的最短时 间.
P.5/35
第5章 机械振动
xAcots()
x xt图
A
T 2π 取 0
vA si n t ()
o
A
A v
T
vt 图
o
T
t
t
Acost(π) A
2
a at图
a A 2co t s() A2
o
Tt
A 2cots(π)A2
P.6/35
简谐运动的运动方程
第5章 机械振动
xAcost()Acost(2)
(t2t1)()
t
P.12/35
第5章 机械振动
Φ21
Φ0同步
x
Φπ反相
x
0 超前
Φ
落后
0
x
o
o
o
t
t
t
2 相位差为 整数倍: 同步
相位差为 或 奇数倍: 反相
P.13/35
3. 用旋转矢量图画简谐运动的
xt
第5章 机械振动
P.14/35
例2: 一质点沿x轴作简谐运动的振幅为 12cm, 周期为2s. 当 t = 0 时, 位移为6cm, 且沿 x 轴正方向运动. 求:
v0
2
初相:
arctan(v0 ) x0
A 和 完全由初始条件决定.
的取值不唯一, 并与坐标正方向的选 取有关.
P.8/35
第5章 机械振动
例1: 轻弹簧一端固定, 另一端连接一个物 块. 整个系统位于水平面内, 系统的角频率
得x: 0 .0c4o 6 .0 tsm
为6.0s-1. 将物体沿水平向右拉到 x0= 0.04 m 处再释放, 试求: (1)简谐运动表达式; (2)
物 体 从 初 始 位 置 起 第 一 次 经 过 A/2 处 时 的
(2) 由(1)中结果
0.0 20.0c 4o 6.0 s t
速度.
cos6.0t 1
2
vdx0.2s4i6 n.0t
dt
解: (1)
si6 n.0t1co26s.0t
x 0 0m .,0 v 0 4 0 , 6 .0 s 1
( )t ( )
若两个振动的频率相同, 则 相位差为
A
A
x
Φ
同一振动不同时刻的相位差
振子沿 x 轴负方向运动 2. 比较各振动之间的相位关系 不同振动同一时刻的相位差
x1A co ts ()
x2A co ts ()
x1A co ts1 ()
x2A co ts2 ()
Φ (t2 ) (t1 )
圆(角)频率 : 2 秒内振动的次数.
2 单位: 弧度/秒(rad/s)
周期, 频率与角频率关系:
k
m
T 1 2π 只取决于系统本身.
P.7/35
简谐运动的运动方程
xAcots()
3. 初相位, 相位和相位差 相位ωt + : 也叫位相或周相. 一个周期 当中, 相位与振子的运动状态(包括位置, 速度, 加速度)一一对应.
P.3/35
§5.1 简谐运动
第5章 机械振动
5.1.1 简谐运动的特征及其运动方程
弹簧振子——理想模型
简谐运动的受力
f kx
始终指向平衡位置(有心力)
简谐运动的动力学方程
单
摆
m d2x k x
dt 2
P.4/35
简谐运动动力学方程
m d2x k x 令 dt 2
2 k m
d2x dt2
2x
第5章 机械振动
y vm t π
t an
2 A
vm A
an A2
0
a
v
x
vAcost(π)
xAcots()
2
aA 2cots ()
远离 x,v0 接近 x,v0
P.11/35
5.2.2 旋转矢量图的应用
1. 求初相位
振子沿 x 轴正方向运动
x x
第5章 机械振动
Φ ( t ) ( t )
初相位 : 也叫初位相或初相. t=0时的 相位, 描述初始时刻的振动状态, 与初始 条件有关.
相位差ΔΦ : 相位的差值. 单位: 弧度(rad)
第5章 机械振动
4. 求解振幅和初相
设 t =0 时
x0Acos, v0Asi n
x0 2 v0 2 2A2(s2in co2s)A2
振幅:
A
x02
振动学是波动学的基础
第5章 机械振动
第5章 机械振动 振动: 任何一个物理量(物体的位置, 电流强度, 电 场强度, 磁场强度等)在某一固定值附近作往复变 化. 机械振动: 物体在固定位置(平衡位置)附近作来回 往复的运动. 简谐运动: 是最基本, 最简单的振动.
复杂振动 = ∑简谐振动 研究目的 —— 利用, 减弱 or 消除
xAcots()
5.1.2 简谐运动方程中的三个基本 物理量
Acos(t2))
T 2
频率 : 单位时间内完成的振动次数.
1. 描述振动强弱的物理量 振幅 A : 离开平衡位置的最远距 离.
单位: m 2. 描述振动快慢的物理量 周期 T : 往复振动一次所经历的 时间.
单位: s
1 T
单位: 赫兹(Hz, 1/s)
0
微分方程的解(运动方程)
简谐运动的速度与加速度
第5章 机械振动
v d x A si nt ()
a
dt dv
vmcos(tπ2)
2Acost ()
v
d t a m co ts (π) a
xAcots()
简谐运动: 某个物理量随时间的变 化规律满足简谐运动方程, 或遵从 余(正)弦规律, 一般来说, 这一物理 量就作简谐运动.
依题意, v<0
1
1
2
2
3 2
arctavn0 0 x0
v 0.24 3 0 .20 m s 8 1
(为什么 不取π ?)
2
P.9/35
§5.2 简谐运动的旋转矢量表示法 5.2.1 旋转矢量表示法
t
x P
• 旋转矢量 的模A即为简谐运动的振幅.
第5章 机械振动
• 旋转矢量 与xA轴的夹角(t+)即为简谐
运动的相位.
• 旋转矢量 角频率.
的A 角速度 即为振动的
• t =0时, 初相.
与xA 轴的夹角即为简谐振动的
• 旋转矢量 动.
旋A 转一周, P点完成一次全振
周期: T 2 π
结论: 投影点的运动为简谐运动
xAcost()
P.10/35
第三篇 机械振动&机械波
第五章 机械振动
为何讨论的重点是简谐运动 复杂振动可分解为若干简谐运动 振动的运动学规律
简谐振动的动力学特征
振动能量的周期性特征
第5章 机械振动
P.2/35
振动和波动的关系: 波动——振动的传播 振动——波动的源头
机械振动, 电磁振荡 机械波, 电磁波 德布罗意波——率波
(1) 振动表达式; (2) t = 0.5s时, 质点的位置, 速度和加速 度; (3) 如果在某时刻质点位于 x=-6cm, 且沿 x 轴负方向运动, 求从 该位置回到平衡位置所需要的最短时 间.
P.5/35
第5章 机械振动
xAcots()
x xt图
A
T 2π 取 0
vA si n t ()
o
A
A v
T
vt 图
o
T
t
t
Acost(π) A
2
a at图
a A 2co t s() A2
o
Tt
A 2cots(π)A2
P.6/35
简谐运动的运动方程
第5章 机械振动
xAcost()Acost(2)
(t2t1)()
t
P.12/35
第5章 机械振动
Φ21
Φ0同步
x
Φπ反相
x
0 超前
Φ
落后
0
x
o
o
o
t
t
t
2 相位差为 整数倍: 同步
相位差为 或 奇数倍: 反相
P.13/35
3. 用旋转矢量图画简谐运动的
xt
第5章 机械振动
P.14/35
例2: 一质点沿x轴作简谐运动的振幅为 12cm, 周期为2s. 当 t = 0 时, 位移为6cm, 且沿 x 轴正方向运动. 求:
v0
2
初相:
arctan(v0 ) x0
A 和 完全由初始条件决定.
的取值不唯一, 并与坐标正方向的选 取有关.
P.8/35
第5章 机械振动
例1: 轻弹簧一端固定, 另一端连接一个物 块. 整个系统位于水平面内, 系统的角频率
得x: 0 .0c4o 6 .0 tsm
为6.0s-1. 将物体沿水平向右拉到 x0= 0.04 m 处再释放, 试求: (1)简谐运动表达式; (2)
物 体 从 初 始 位 置 起 第 一 次 经 过 A/2 处 时 的
(2) 由(1)中结果
0.0 20.0c 4o 6.0 s t
速度.
cos6.0t 1
2
vdx0.2s4i6 n.0t
dt
解: (1)
si6 n.0t1co26s.0t
x 0 0m .,0 v 0 4 0 , 6 .0 s 1
( )t ( )
若两个振动的频率相同, 则 相位差为
A
A
x
Φ
同一振动不同时刻的相位差
振子沿 x 轴负方向运动 2. 比较各振动之间的相位关系 不同振动同一时刻的相位差
x1A co ts ()
x2A co ts ()
x1A co ts1 ()
x2A co ts2 ()
Φ (t2 ) (t1 )
圆(角)频率 : 2 秒内振动的次数.
2 单位: 弧度/秒(rad/s)
周期, 频率与角频率关系:
k
m
T 1 2π 只取决于系统本身.
P.7/35
简谐运动的运动方程
xAcots()
3. 初相位, 相位和相位差 相位ωt + : 也叫位相或周相. 一个周期 当中, 相位与振子的运动状态(包括位置, 速度, 加速度)一一对应.
P.3/35
§5.1 简谐运动
第5章 机械振动
5.1.1 简谐运动的特征及其运动方程
弹簧振子——理想模型
简谐运动的受力
f kx
始终指向平衡位置(有心力)
简谐运动的动力学方程
单
摆
m d2x k x
dt 2
P.4/35
简谐运动动力学方程
m d2x k x 令 dt 2
2 k m
d2x dt2
2x
第5章 机械振动
y vm t π
t an
2 A
vm A
an A2
0
a
v
x
vAcost(π)
xAcots()
2
aA 2cots ()
远离 x,v0 接近 x,v0
P.11/35
5.2.2 旋转矢量图的应用
1. 求初相位
振子沿 x 轴正方向运动
x x
第5章 机械振动
Φ ( t ) ( t )
初相位 : 也叫初位相或初相. t=0时的 相位, 描述初始时刻的振动状态, 与初始 条件有关.
相位差ΔΦ : 相位的差值. 单位: 弧度(rad)
第5章 机械振动
4. 求解振幅和初相
设 t =0 时
x0Acos, v0Asi n
x0 2 v0 2 2A2(s2in co2s)A2
振幅:
A
x02
振动学是波动学的基础
第5章 机械振动
第5章 机械振动 振动: 任何一个物理量(物体的位置, 电流强度, 电 场强度, 磁场强度等)在某一固定值附近作往复变 化. 机械振动: 物体在固定位置(平衡位置)附近作来回 往复的运动. 简谐运动: 是最基本, 最简单的振动.
复杂振动 = ∑简谐振动 研究目的 —— 利用, 减弱 or 消除
xAcots()
5.1.2 简谐运动方程中的三个基本 物理量
Acos(t2))
T 2
频率 : 单位时间内完成的振动次数.
1. 描述振动强弱的物理量 振幅 A : 离开平衡位置的最远距 离.
单位: m 2. 描述振动快慢的物理量 周期 T : 往复振动一次所经历的 时间.
单位: s
1 T
单位: 赫兹(Hz, 1/s)
0
微分方程的解(运动方程)
简谐运动的速度与加速度
第5章 机械振动
v d x A si nt ()
a
dt dv
vmcos(tπ2)
2Acost ()
v
d t a m co ts (π) a
xAcots()
简谐运动: 某个物理量随时间的变 化规律满足简谐运动方程, 或遵从 余(正)弦规律, 一般来说, 这一物理 量就作简谐运动.
