三角、反三角函数图像与性质与三角公式
最全三角函数概念公式、图像大全完整版.doc

初等函数的图形幂函数的图形指数函数的图形各三角函数值在各象限的符号sinα·cscα cosα·secα tanα·cotα三角函数的性质反三角函数的图形反三角函数的性质三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinBtan(A+B) =tanAtanB -1tanBtanA +tan(A-B) =tanAtanB 1tanBtanA +-cot(A+B) =cotA cotB 1-cotAcotB +cot(A-B) =cotAcotB 1cotAcotB -+倍角公式tan2A =Atan 12tanA2- Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a)sin(2A )=2cos 1A -cos(2A)=2cos 1A +tan(2A)=A A cos 1cos 1+-cot(2A )=A A cos 1cos 1-+tan(2A )=A A sin cos 1-=A A cos 1sin +和差化积sina+sinb=2sin2b a +cos 2ba - sina-sinb=2cos 2b a +sin 2ba -cosa+cosb = 2cos 2b a +cos 2ba -cosa-cosb = -2sin 2b a +sin 2ba -tana+tanb=ba b a cos cos )sin(+积化和差sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)]sinacosb = 21[sin(a+b)+sin(a-b)]cosasinb = 21[sin(a+b)-sin(a-b)]sin(-a) = -sina cos(-a) = cosasin(2π-a) = cosacos(2π-a) = sinasin(2π+a) = cosacos(2π+a) = -sinasin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosatgA=tanA =aacos sin万能公式sina=2)2(tan 12tan2aa + cosa=22)2(tan 1)2(tan 1aa+- tana=2)2(tan 12tan2aa -a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=ab ] a•sin(a)-b•cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=ba ] 1+sin(a) =(sin2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a)2其他非重点三角函数csc(a) =a sin 1 sec(a) =acos 1双曲函数sinh(a)=2e -e -aacosh(a)=2e e -aa +tg h(a)=)cosh()sinh(a a公式一设α为任意角,终边相同的角的同一三角函数的值相等: sin (2kπ+α)= sinα cos (2kπ+α)= cosα tan (2kπ+α)= tanα cot (2kπ+α)= cotα设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)= -cosαtan(π+α)= tanαcot(π+α)= cotα公式三任意角α与-α的三角函数值之间的关系:sin(-α)= -sinαcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tanαcot(π-α)= -cotα公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)= -sinαcos(2π-α)= cosαtan(2π-α)= -tanαcot(2π-α)= -cotα2π±α及23π±α与α的三角函数值之间的关系:sin (2π+α)= cosαcos (2π+α)= -sinαtan (2π+α)= -cotαcot (2π+α)= -tanαsin (2π-α)= cosαcos (2π-α)= sinαtan (2π-α)= cotαcot (2π-α)= tanαsin (23π+α)= -cosαcos (23π+α)= sinαtan (23π+α)= -cotαcot (23π+α)= -tanαsin (23π-α)= -cosαcos (23π-α)= -sinαtan (23π-α)= cotαcot (23π-α)= tanα(以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin)cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明(全部)公式表达式乘法与因式分解a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2) 三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b|a-b|≥|a|-|b|-|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注:韦达定理判别式b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/6 13+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3 正弦定理a/sinA=b/sinB=c/sinC=2R注:其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB注:角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r >0扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注:其中,S'是直截面面积,L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h-------------------------------------------------------------------------------------------- 三角函数积化和差和差化积公式记不住就自己推,用两角和差的正余弦:cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB这两式相加或相减,可以得到2组积化和差:相加:cosAcosB=[cos(A+B)+cos(A-B)]/2相减:sinAsinB=-[cos(A+B)-cos(A-B)]/2sin(A+B)=sinAcosB+sinBcosAsin(A-B)=sinAcosB-sinBcosA这两式相加或相减,可以得到2组积化和差:相加:sinAcosB=[sin(A+B)+sin(A-B)]/2相减:sinBcosA=[sin(A+B)-sin(A-B)]/2这样一共4组积化和差,然后倒过来就是和差化积了不知道这样你可以记住伐,实在记不住考试的时候也可以临时推导一下正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负.3.三角形中的一些结论:(不要求记忆)(1)anA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1 ...........................已知sinα=m sin(α+2β), |m|<1,求证tan(α+β)=(1+m)/(1-m)tanβ解:sinα=m sin(α+2β)sin(a+β-β)=msin(a+β+β)sin(a+β)cosβ-cos(a+β)sinβ=msin(a+β)cosβ+mcos(a+β)sinβ sin(a+β)cosβ(1-m)=cos(a+β)sinβ(m+1)tan(α+β)=(1+m)/(1-m)tanβ赠送以下资料《二次函数的应用》中考题集锦10题已知抛物线222(0)y x mx m m =+-≠.(1)求证:该抛物线与x 轴有两个不同的交点;(2)过点(0)P n ,作y 轴的垂线交该抛物线于点A 和点B (点A 在点P 的左边),是否存在实数m n ,,使得2AP PB =?若存在,则求出m n ,满足的条件;若不存在,请说明理由.答案:解:(1)证法1:22229224m y x mx m x m ⎛⎫=+-=+- ⎪⎝⎭,当0m ≠时,抛物线顶点的纵坐标为2904m -<, ∴顶点总在x 轴的下方.而该抛物线的开口向上,∴该抛物线与x 轴有两个不同的交点.(或者,当0m ≠时,抛物线与y 轴的交点2(02)m -,在x 轴下方,而该抛物线的开口向上,∴该抛物线与x 轴有两个不同的交点.)证法2 :22241(2)9m m m ∆=-⨯⨯-=,当0m ≠时,290m >,∴该抛物线与x 轴有两个不同的交点. (2)存在实数m n ,,使得2AP PB =.设点B 的坐标为()t n ,,由2AP PB =知,①当点B 在点P 的右边时,0t >,点A 的坐标为(2)t n -,且2t t -,是关于x 的方程222x mx m n +-=的两个实数根.2224(2)940m m n m n ∴∆=---=+>,即294n m >-.且(2)t t m +-=-(I ),2(2)t t m n -=--(II )由(I )得,t m =,即0m >.将t m =代入(II )得,0n =.∴当0m >且0n =时,有2AP PB =.②当点B 在点P 的左边时,0t <,点A 的坐标为(2)t n ,,且2t t ,是关于x 的方程222x mx m n +-=的两个实数根.2224(2)940m m n m n ∴∆=---=+>,即 294n m >-.且2t t m +=-(I ),222t t m n =--(II )由(I )得,3mt =-,即0m >. 将3m t =-代入(II )得,2209n m =-且满足294n m >-.∴当0m >且2209n m =-时,有2AP PB =第11题一人乘雪橇沿如图所示的斜坡笔直滑下,滑下的距离S (米)与时间t (秒)间的关系式为210S t t =+,若滑到坡底的时间为2秒,则此人下滑的高度为( )A.24米 B.12米C.米 D.6米答案:B第12题我市英山县某茶厂种植“春蕊牌”绿茶,由历年来市场销售行情知道,从每年的3月25日起的180天内,绿茶市场销售单价y (元)与上市时间t (天)的关系可以近似地用如图(1)中的一条折线表示.绿茶的种植除了与气候、种植技术有关外,其种植的成本单价z (元)与上市时间t (天)的关系可以近似地用如图(2)的抛物线表示.关系式;(2)求出图(2)中表示的种植成本单价z (元)与上市时间t (天)(0t >)的函数关系式;(3)认定市场销售单价减去种植成本单价为纯收益单价,问何时上市的绿茶纯收益单价最大?(说明:市场销售单价和种植成本单价的单位:元/500克.))图(1)图(2)天)答案:解:(1)依题意,可建立的函数关系式为:2160(0120)380(120150)220(150180)5t t y t t t ⎧-+<<⎪⎪=<⎨⎪⎪+⎩,,. ≤ ≤≤ (2)由题目已知条件可设2(110)20z a t =-+. 图象过点85(60)3,,2851(60110)203300a a ∴=-+∴=.. 21(110)20300z t ∴=-+ (0)t >. (3)设纯收益单价为W 元,则W =销售单价-成本单价. 故22221160(110)20(0120)3300180(110)20(120150)3002120(110)20(150180)5300t t t W t t t t t ⎧-+---<<⎪⎪⎪=---<⎨⎪⎪+---⎪⎩,,. ≤ ≤≤ 化简得2221(10)100(0120)3001(110)60(120150)3001(170)56(150180)300t t W t t t t ⎧--+<<⎪⎪⎪=-+<⎨⎪⎪--+⎪⎩,,. ≤ ≤≤①当21(10)100(0120)300W t t =--+<<时,有10t =时,W 最大,最大值为100; ②当21(110)60(120150)300W t t =--+<≤时,由图象知,有120t =时,W 最大,最大值为2593;③当21(170)56(150180)300W t t =--+≤≤时,有170t =时,W 最大,最大值为56. 综上所述,在10t =时,纯收益单价有最大值,最大值为100元.第13题如图,足球场上守门员在O 处开出一高球,球从离地面1米的A 处飞出(A 在y 轴上),运动员乙在距O 点6米的B 处发现球在自己头的正上方达到最高点M ,距地面约4米高,球落地后又一次弹起.据实验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.(1)求足球开始飞出到第一次落地时,该抛物线的表达式. (2)足球第一次落地点C距守门员多少米?(取7=)(3)运动员乙要抢到第二个落点D,他应再向前跑多少米?(取5=)答案:解:(1)(3分)如图,设第一次落地时, 抛物线的表达式为2(6)4y a x =-+. 由已知:当0x =时1y =. 即1136412a a =+∴=-,. ∴表达式为21(6)412y x =--+.(或21112y x x =-++)(2)(3分)令210(6)4012y x =--+=,.212(6)4861360x x x ∴-===-<.≈,(舍去). ∴足球第一次落地距守门员约13米.(3)(4分)解法一:如图,第二次足球弹出后的距离为CD根据题意:CD EF =(即相当于将抛物线AEMFC 向下平移了2个单位)212(6)412x ∴=--+解得1266x x =-=+1210CD x x ∴=-=. 1361017BD ∴=-+=(米). 解法二:令21(6)4012x --+=.解得16x =-,2613x =+.∴点C 坐标为(13,0).设抛物线CND 为21()212y x k =--+.将C 点坐标代入得:21(13)2012k --+=.解得:11313k =-(舍去),2667518k =+++=.21(18)212y x =--+ 令210(18)212y x ==--+,0.118x =-,21823x =+. 23617BD ∴=-=(米). 解法三:由解法二知,18k =, 所以2(1813)10CD =-=, 所以(136)1017BD =-+=. 答:他应再向前跑17米.第14题荆州市“建设社会主义新农村”工作组到某县大棚蔬菜生产基地指导菜农修建大棚种植蔬菜.通过调查得知:平均修建每公顷大棚要用支架、农膜等材料费2.7万元;购置滴灌设备,这项费用(万元)与大棚面积(公顷)的平方成正比,比例系数为0.9;另外每公顷种植蔬菜需种子、化肥、农药等开支0.3万元.每公顷蔬菜年均可卖7.5万元. (1)基地的菜农共修建大棚x (公顷),当年收益(扣除修建和种植成本后)为y (万元),写出y 关于x 的函数关系式.(2)若某菜农期望通过种植大棚蔬菜当年获得5万元收益,工作组应建议他修建多少公项大棚.(用分数表示即可)(3)除种子、化肥、农药投资只能当年受益外,其它设施3年内不需增加投资仍可继续使用.如果按3年计算,是否修建大棚面积越大收益越大?修建面积为多少时可以得到最大收益?请帮工作组为基地修建大棚提一项合理化建议.答案:(1)()227.5 2.70.90.30.9 4.5y x x x x x x =-++=-+. (2)当20.9 4.55x x -+=时,即2945500x x -+=,153x =,2103x =从投入、占地与当年收益三方面权衡,应建议修建53公顷大棚. (3)设3年内每年的平均收益为Z (万元)()()2227.50.90.30.30.3 6.30.310.533.075Z x x x x x x x =-++=-+=--+(10分)不是面积越大收益越大.当大棚面积为10.5公顷时可以得到最大收益.建议:①在大棚面积不超过10.5公顷时,可以扩大修建面积,这样会增加收益. ②大棚面积超过10.5公顷时,扩大面积会使收益下降.修建面积不宜盲目扩大.③当20.3 6.30x x -+=时,10x =,221x =.大棚面积超过21公顷时,不但不能收益,反而会亏本.(说其中一条即可)第15题一家用电器开发公司研制出一种新型电子产品,每件的生产成本为18元,按定价40元出售,每月可销售20万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价1元,月销售量可增加2万件.(1)求出月销售量y (万件)与销售单价x (元)之间的函数关系式(不必写x 的取值范围);(2)求出月销售利润z (万元)(利润=售价-成本价)与销售单价x (元)之间的函数关系式(不必写x 的取值范围);(3)请你通过(2)中的函数关系式及其大致图象帮助公司确定产品的销售单价范围,使月销售利润不低于480万元.答案:略.第16题一座隧道的截面由抛物线和长方形构成,长方形的长为8m ,宽为2m ,隧道最高点P 位于AB 的中央且距地面6m ,建立如图所示的坐标系(1)求抛物线的解析式;(2)一辆货车高4m ,宽2m ,能否从该隧道内通过,为什么?(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么?答案:(1)由题意可知抛物线经过点()()()024682A P B ,,,,,设抛物线的方程为2y ax bx c =++ 将A P D ,,三点的坐标代入抛物线方程. 解得抛物线方程为21224y x x =-++ (2)令4y =,则有212244x x -++=解得1244x x =+=-212x x -=>∴货车可以通过.(3)由(2)可知21122x x -=>∴货车可以通过.第17题如图,在矩形ABCD 中,2AB AD =,线段10EF =.在EF 上取一点M ,分别以EM MF ,为一边作矩形EMNH 、矩形MFGN ,使矩形MFGN ∽矩形ABCD .令MN x =,当x 为何值时,矩形EMNH 的面积S 有最大值?最大值是多少?答案:解:矩形MFGN ∽矩形ABCD ,MN MFAD AB∴=. 2AB AD MN x ==,,2MF x ∴=.102EM EF MF x ∴=-=-. (102)S x x ∴=-2210x x =-+ 2525222x ⎛⎫=--+ ⎪⎝⎭.∴当52x =时,S 有最大值为252.第18题某企业信息部进行市场调研发现:信息一:如果单独投资A 种产品,则所获利润A y (万元)与投资金额x (万元)之间存在正比例函数关系:A y kx =,并且当投资5万元时,可获利润2万元.信息二:如果单独投资B 种产品,则所获利润B y (万元)与投资金额x (万元)之间存在二次函数关系:2B y ax bx =+,并且当投资2万元时,可获利润2.4万元;当投资4万元时,可获利润3.2万元.(1)请分别求出上述的正比例函数表达式与二次函数表达式;(2)如果企业同时对AB ,两种产品共投资10万元,请你设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少?B A D MF答案:解:(1)当5x =时,12250.4y k k ===,,, 0.4A y x ∴=,当2x =时, 2.4B y =;当4x =时, 3.2B y =.2.4423.2164a ba b =+⎧∴⎨=+⎩解得0.21.6a b =-⎧⎨=⎩∴20.2 1.6B y x x =-+.(2)设投资B 种商品x 万元,则投资A 种商品(10)x -万元,获得利润W 万元,根据题意可得220.2 1.60.4(10)0.2 1.24W x x x x x =-++-=-++ 20.2(3) 5.8W x ∴=--+当投资B 种商品3万元时,可以获得最大利润5.8万元,所以投资A 种商品7万元,B 种商品3万元,这样投资可以获得最大利润5.8万元.第19题如图所示,图(1)是一座抛物线型拱桥在建造过程中装模时的设计示意图,拱高为30m ,支柱3350m A B =,5根支柱1122334455A B A B A B A B A B ,,,,之间的距离均为15m ,1515B B A A ∥,将抛物线放在图(2)所示的直角坐标系中. (1)直接写出图(2)中点135B B B ,,的坐标; (2)求图(2)中抛物线的函数表达式; (3)求图(1)中支柱2244A B A B ,的长度.答案:(1)1(30)B -,0,3(030)B ,,5(300)B ,; (2)设抛物线的表达式为(30)(30)y a x x =-+,把3(030)B ,代入得(030)(030)30y a =-+=.B 图(1)图(2)l130a =-∴. ∵所求抛物线的表达式为:1(30)(30)30y x x =--+. (3)4B ∵点的横坐标为15, 4B ∴的纵坐标4145(1530)(1530)302y =--+=. 3350A B =∵,拱高为30,∴立柱44458520(m)22A B =+=. 由对称性知:224485(m)2A B A B ==。
三角反三角函数公式

三角反三角函数公式三角函数是数学中的基本函数之一,它们包括正弦函数、余弦函数和正切函数。
而反三角函数则是用来求解一些特定角度的函数值的反函数。
本文将详细介绍三角反函数的定义、图像、主要性质以及它们与三角函数之间的关系。
1. 反正弦函数(arcsin或sin-1):反正弦函数用于求解正弦函数的反函数。
它的定义域是[-1,1],值域是[-π/2,π/2]。
该函数的图像是一个关于直线y=x的对称图像。
反正弦函数的主要性质如下:-反正弦函数是单调递增的,它的导数是1/√(1-x²)。
- 反正弦函数的奇偶性与正弦函数相同,即arcsin(-x)=-arcsin(x)。
-反正弦函数在定义域内是连续且可导的。
-反正弦函数的导数是定义域内的凸函数。
2. 反余弦函数(arccos或cos-1):反余弦函数用于求解余弦函数的反函数。
它的定义域是[-1,1],值域是[0,π]。
该函数的图像是一个关于直线y=x的对称图像。
反余弦函数的主要性质如下:-反余弦函数是单调递减的,它的导数是-1/√(1-x²)。
- 反余弦函数的奇偶性与余弦函数相同,即arccos(-x)=π-arccos(x)。
-反余弦函数在定义域内是连续且可导的。
-反余弦函数的导数是定义域内的凹函数。
3. 反正切函数(arctan或tan-1):反正切函数用于求解正切函数的反函数。
它的定义域是(-∞,+∞),值域是(-π/2,π/2)。
该函数的图像是一个关于原点对称的S型曲线。
反正切函数的主要性质如下:-反正切函数是单调递增的,它的导数是1/(1+x²)。
- 反正切函数的奇偶性与正切函数相同,即arctan(-x)=-arctan(x)。
-反正切函数在定义域内是连续且可导的。
-反正切函数的导数是定义域内的凸函数。
三角函数和反三角函数之间有一些重要的关系:1. 正弦函数和反正弦函数、余弦函数和反余弦函数、正切函数和反正切函数是互为反函数关系,即sin(arcsin(x))=x, cos(arccos(x))=x, tan(arctan(x))=x。
三角函数及反三角函数图像性质、知识点总结
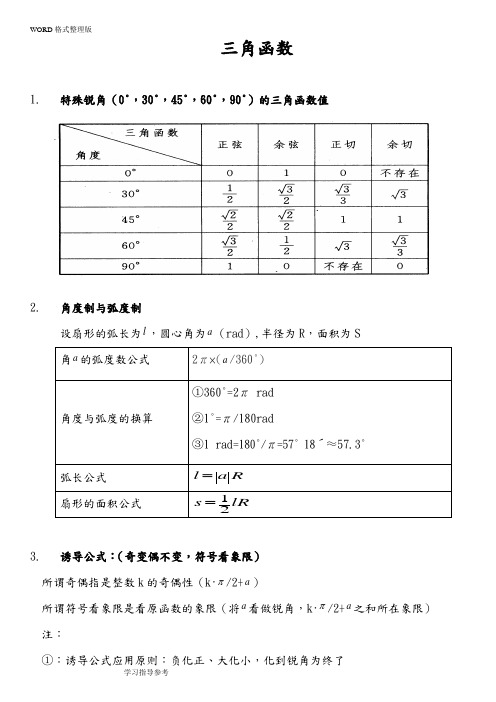
三角函数 1. 特殊锐角(0°,30°,45°,60°,90°)的三角函数值2.角度制与弧度制设扇形的弧长为l ,圆心角为a (rad ),半径为R ,面积为S 角a 的弧度数公式 2π×(a /360°)角度与弧度的换算①360°=2π rad ②1°=π/180rad③1 rad=180°/π=57° 18′≈57.3°弧长公式 l a R =扇形的面积公式 12s lR =3.诱导公式:(奇变偶不变,符号看象限)所谓奇偶指是整数k 的奇偶性(k ·π/2+a )所谓符号看象限是看原函数的象限(将a 看做锐角,k ·π/2+a 之和所在象限) 注:①:诱导公式应用原则:负化正、大化小,化到锐角为终了4. 三角函数的图像和性质:(其中z k ∈)①:三角函数x y sin = x y cos =x y tan = cot y x=函 数 图 象定义域 R R 2x k ππ≠+x k π≠值域 [-1,1][-1,1]RR周期 2π2πππ奇偶性 奇偶奇非奇非偶单 调 性 2,222k k ππππ⎡⎤-+↑⎢⎥⎣⎦2,222k k ππππ⎡⎤-+↑⎢⎥⎣⎦[]2,2k k πππ-↑ []2,2k k πππ+↓,22k k ππππ⎡⎤-+↑⎢⎥⎣⎦[],k k πππ+↓对 称 性 :2x k ππ=+对称轴对称中心:(,0)k π:x k π=对称轴:对称中心(+,0)2k ππ:对称中心(,0)2k π零值点 πk x =2ππ+=k xπk x =2ππ+=k x最 值 点2ππ+=k x ,1max=y2ππ-=k x ,1min-=yπk x 2=,1max =y ;2y k ππ=+,1min -=y②:函数)sin(ϕω+=x A y 的图像与性质:(1) 函数)sin(ϕω+=x A y 和)cos(ϕω+=x A y 的周期都是ωπ2=T(2) 函数)tan(ϕω+=x A y 和)cot(ϕω+=x A y 的周期都是ωπ=T5.三角函数尺度变换sin y x =经过变换变为sin y x ϖϕ=+A ()的步骤(先平移后伸缩): 1sin sin sin sin y x y x y x y x ϖϕϖϖϖϕϖϕ=−−−−−−−→=−−−−−→=+−−−−−−−→=+横坐标变为原来的倍向左或向右纵坐标不变平移个单位纵坐标变为原来的A 倍横坐标不变()A ()6.三角函数的对称变换:① )()(x f y x f y -=→=) 将)(x f y =图像绕y 轴翻折180°(整体翻折) (对三角函数来说:图像关于x 轴对称)② )()(x f y x f y -=→=将)(x f y =图像绕x 轴翻折180°(整体翻折) (对三角函数来说:图像关于y 轴对称)③ )()(x f y x f y =→= 将)(x f y =图像在y 轴右侧保留,并把右侧图像绕y 轴翻折到左侧(偶函数局部翻折)④ )()(x f y x f y =→=保留)(x f y =在x 轴上方图像,x 轴下方图像绕x 轴翻折上去(局部翻动)7.反三角函数的图像与性质:名称y=arsinx y=arccosx y=arctanx y=arccotx定义y=sinx((,))22xππ∈-的反函数,叫做反正弦函数y=cosx((0,))xπ∈的反函数,叫做反余弦函数y=tanx((,))22xππ∈-的反函数,叫做反正切函数y=cotx((0,))xπ∈的反函数,叫做反余切函数性质图像定义域[-1,1][-1,1](-∞,+∞)(-∞,+∞)值域[-2π,2π][0,π](-2π,2π) (0,π) 单调性[]1,1-增函数[]1,1-减函数(),-∞+∞增函数(),-∞+∞减函数奇偶性arcsin()arcsinθθ-=-arccos()arccosθπθ-=-arctan()arctanθθ-=-arccot()arccotθπθ-=-周期性非周期函数非周期函数非周期函数非周期函数7.三角函数公式:(1)倒数关系: (2)平方关系:tan cot 1sin csc 1cos sec 1αααααα⋅=⋅=⋅= 222222sin cos 11tan sec 1cot csc αααααα+=+=+=(3)三角和与差公式:sin()sin cos cos sin cos()cos cos sin sin tan tan tan()1tan tan αβαβαβαβαβαβαβαβαβ+=++=-++=- sin()sin cos cos sin cos()cos cos sin sin tan tan tan()1tan tan αβαβαβαβαβαβαβαβαβ-=--=+--=+(4)二倍角公式:()22222sin 22sin cos cos 2cos sin 2cos 112sin 2tan tan 21tan ααααααααααα==-=-=-=-升幂公式 22221cos 2sin 1cos 22sin 2(1cos 21cos 22cos cos 2αααααααα-⎫=⎪⎧-=⎪⎪⇒⎬⎨++=⎪⎩⎪=⎪⎭降幂公式) (5)三角函数的和差化积公式 (6)三角函数的积化和差公式sin sin 2sin cos22sin sin 2cos sin22cos cos 2cos cos22cos cos 2sin sin22αβαβαβαβαβαβαβαβαβαβαβαβ+-+=⋅+--=⋅+-+=⋅+--=-⋅ [][][][]1sin cos sin()sin()21cos sin sin()sin()21cos cos cos()cos()21sin sin cos()cos()2αβαβαβαβαβαβαβαβαβαβαβαβ⋅=++-⋅=+--⋅=++-⋅=-+-- 六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
三角和反三角函数图像+公式

三角和反三角函数图像+公式-CAL-FENGHAI.-(YICAI)-Company One1三角、反三角函数图像六个三角函数值在每个象限的符号:sinα·cscα cosα·secα tanα·cotα三角函数的图像和性质:1-1y=sinx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoyx1-1y=cosx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoyx y=tanx3π2ππ2-3π2-π-π2oyxy=cotx3π2ππ22π-π-π2oyx函数y=sinx y=cosx y=tanx y=cotx定义域R R{x|x∈R且x≠kπ+2π,k∈Z}{x|x∈R且x≠kπ,k∈Z}值域[-1,1]x=2kπ+2π时y max=1x=2kπ-2π时y min=-1[-1,1]x=2kπ时y max=1x=2kπ+π时y min=-1R无最大值无最小值R无最大值无最小值周期性周期为2π周期为2π周期为π周期为π奇偶性奇函数偶函数奇函数奇函数单调性在[2kπ-2π,2kπ+2π]上都是增函数;在[2kπ+2π,2kπ+32π]上都是减函数(k∈Z)在[2kπ-π,2kπ]上都是增函数;在[2kπ,2kπ+π]上都是减函数(k∈Z)在(kπ-2π,kπ+2π)内都是增函数(k∈Z)在(kπ,kπ+π)内都是减函数(k∈Z).反三角函数:arcsinx arccosxarctanx arccotx名称反正弦函数 反余弦函数 反正切函数反余切函数 定义y=sinx(x ∈〔-2π,2π 〕的反函数,叫做反正弦函数,记作x=arsiny y=cosx(x ∈〔0,π〕)的反函数,叫做反余弦函数,记作x=arccosy y=tanx(x ∈(-2π, 2π)的反函数,叫做反正切函数,记作x=arctanyy=cotx(x ∈(0,π))的反函数,叫做反余切函数,记作x=arccoty理解arcsinx 表示属于[-2π,2π] 且正弦值等于x 的角arccosx 表示属于[0,π],且余弦值等于x 的角 arctanx 表示属于(-2π,2π),且正切值等于x 的角 arccotx 表示属于(0,π)且余切值等于x 的角性质 定义域 [-1,1] [-1,1] (-∞,+∞) (-∞,+∞) 值域 [-2π,2π] [0,π] (-2π,2π) (0,π)单调性在〔-1,1〕上是增函数在[-1,1]上是减函数 在(-∞,+∞)上是增数在(-∞,+∞)上是减函数 奇偶性 arcsin(-x)=-arcsinx arccos(-x)=π-arccosx arctan(-x)=-arctanxarccot(-x)=π-arccotx 周期性都不是同期函数 恒等式sin(arcsinx)=x(x ∈[-1,1])arcsin(sinx)=x(x ∈[-2π,2π]) cos(arccosx)=x(x ∈[-1,1]) arccos(cosx)=x(x ∈[0,π])tan(arctanx)=x(x ∈R)arctan(tanx)=x (x ∈(-2π,2π)) cot(arccotx)=x(x ∈R)arccot(cotx)=x(x ∈(0,π))互余恒等式 arcsinx+arccosx=2π(x ∈[-1,1]) arctanx+arccotx=2π(X ∈R)。
高三数学 反三角函数概念、图像和性质,反三角函数的运算,简单的三角方程 知识精讲

高三数学 反三角函数概念、图像和性质,反三角函数的运算,简单的三角方程 知识精讲一. 反三角函数的概念,图像和性质 1. 反三角函数的定义 函数y x x =∈-sin ([])ππ22, y x x y x x y x x =∈=∈-=∈c o s ([])tan (())cot (()),,,,,,,,0220ππππ的反三角函数分别为:y x x y x x y x x R y a r c x x R =∈-=∈-=∈=∈a r c s i n ([])arccos ([])arctan ()cot (),,,,,,11112. 反三角函数的性质(1)奇偶性y x y x y x y arc x ====arcsin arccos arctan cot 在定义域内为奇函数;在定义域内为非奇非偶函数;在定义域内为奇函数;在定义域内为非奇非偶函数。
(2)反三角函数的单调性y x y x y x y a r c x ====a r c s i n a r c c o s a r c t a n cot 在定义域内单调递增;在定义域内单调递减;在定义域内单调递增;在定义域内单调递减。
3. 三角函数的图像二. 反三角函数的运算:1. 掌握三角函数的反三角运算,反三角函数的三角运算,熟悉常见的一些恒等式。
三角函数的反三角运算a r c s i n (s i n )[]a r c c o s (c o s )[]a r c t a n (t a n )()o t (c o t )()x x x x x x x x x a r c x x x =∈-=∈=∈-=∈,,,,,,,,ππππππ220220 反三角函数的三角运算 s i n (a r c s i n )[]x x x =∈-,,11c o s (a r c c o s )[]t a n (a r c t an )c o t (o t )x x x x x x R a r c x x x R=∈-=∈=∈,,,,11反三角函数间的互余关系 a r c s i n a r c c o s a r c t a n o t x x x a r c x +=+=ππ22,反三角函数的性质a r c s i n ()a r c s i n a r c t a n ()a r c t a n a r c c o s ()a r c c o s c o t ()cot -=--=--=--=-x x x x x x arc x arc x,,ππ在使用上面的概念和公式要特别注意的是,必须在变量的指定范围内,否则结果就是错误的。
三角函数与反三角函数的基本公式与性质

三角函数与反三角函数的基本公式与性质三角函数与反三角函数是高等数学中重要的概念,它们在许多数学和科学领域的计算中起着重要作用。
本文将介绍三角函数与反三角函数的基本公式与性质,以帮助读者更好地理解和应用这些概念。
I. 三角函数的基本公式与性质1. 正弦函数(sin)正弦函数是三角函数中的一种,用于描述一个角的对边与斜边的比值。
它的基本公式如下:sinθ = 对边 / 斜边,其中θ为角度,sinθ为对应角度的正弦值。
正弦函数的性质如下:(1)定义域:由于斜边为斜边上的点与圆心的连线,所以定义域为实数集。
(2)值域:正弦函数的值域为[-1, 1]。
(3)周期性:正弦函数的周期为2π,即sin(θ+2π) = sinθ。
(4)奇偶性:正弦函数是奇函数,即sin(-θ) = -sinθ。
2. 余弦函数(cos)余弦函数也是描述角的函数之一,用于表示一个角的邻边与斜边的比值。
它的基本公式为:cosθ = 邻边 / 斜边,其中θ为角度,cosθ为对应角度的余弦值。
余弦函数的性质如下:(1)定义域:与正弦函数相同,定义域为实数集。
(2)值域:余弦函数的值域也为[-1, 1]。
(3)周期性:余弦函数同样具有周期性,即cos(θ+2π) = cosθ。
(4)偶函数:余弦函数是偶函数,即cos(-θ) = cosθ。
3. 正切函数(tan)正切函数用于表示一个角的对边与邻边的比值。
它的基本公式为:tanθ = 对边 / 邻边,其中θ为角度,tanθ为对应角度的正切值。
正切函数的性质如下:(1)定义域:由于邻边不为0,所以定义域为实数集中除去点π/2 + kπ(k为整数)的集合。
(2)值域:正切函数的值域为整个实数集R。
(3)周期性:正切函数的周期为π,即tan(θ+π) = tanθ。
(4)奇函数:正切函数是奇函数,即tan(-θ) = -tanθ。
II. 反三角函数的基本公式与性质1. 反正弦函数(arcsin)反正弦函数是正弦函数的反函数,用于求解一个角的度数。
三角函数与反三角函数的图像与性质

在每个[-亍十2k兀,y+2k兀]上递增
在每个H+2^ι,-+2^ ]上递减
2 2
"Z
在每个[-兀+2kτc,2kτc]上递增 在每个[2k兀,兀+2k兀]上递减
"Z
奇偶性
奇函数
偶函数
周期性
是周期函数,2皿为最小正周期
是周期函数,2兀为最小正周期
对称性
对称中心(gθ),
对称轴:x =±+k兀,(k^z)
三角函数与反三角函数的图像与性质
一、三角函数的图像和性质
1.正弦与余函数的图像与性质
函数
y = sin X
y = CoSX
图像
K.必
1∖/、
厂f∖/、
≡∖"/晋a'J
∖√
-t
定域义
R
R
值域
1-1,1]
1-1,1]
最值
x=^∙+2k兀时,y最大=1,k^Z
X^-+2k兀时,y最小=—1, kEZ 2
x = 2k^时,y最大=1, ^Z χ = n+2k兀时,y最小=_1,Z
是y =sinχ,的反函数
1 2 2J
反余弦函数y = arccos X
是y =cosx, X壬[0,兀]的反函数
图像
I I
I
I
I||
I
I
I
I
I
I
I
I
4
2
y
πk
!2
V= ≡WC CoSX
—1 I
厂
μ:!
I
I
I
V
I
」O
三角、反三角函数图像(实用)
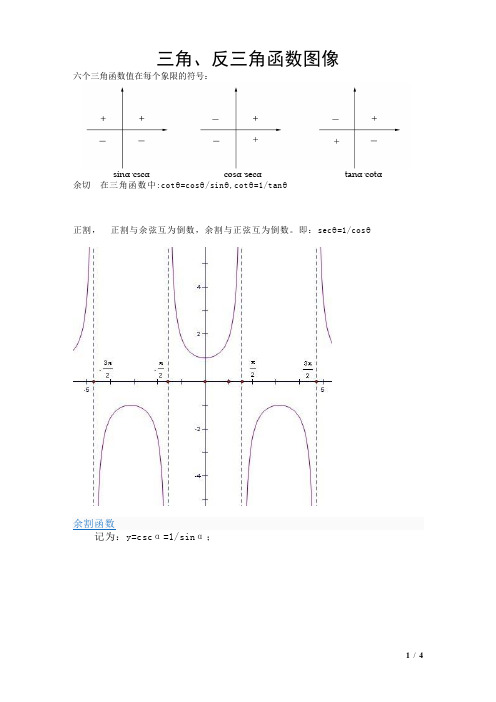
三角、反三角函数图像六个三角函数值在每个象限的符号:sinα·cscα cosα·secα tanα·cotα余切在三角函数中:cotθ=cosθ/sinθ,cotθ=1/tanθ正割,正割与余弦互为倒数,余割与正弦互为倒数。
即:secθ=1/cosθ余割函数记为:y=cscα=1/sinα;三角函数的图像和性质:1-1y=sinx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoy x1-1y=cosx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoy xy=tanx3π2ππ2-3π2-π-π2oyxy=cotx3π2ππ22π-π-π2oyx函数 y=sinx y=cosx y=tanx y=cotx 定义域RR{x |x ∈R 且x≠kπ+2π,k ∈Z } {x |x ∈R 且x≠kπ,k ∈Z }值域[-1,1]x=2kπ+2π时y max =1x=2kπ-2π时y min =-1[-1,1] x=2kπ时y max =1x=2kπ+π时y min =-1R 无最大值 无最小值R无最大值 无最小值 周期性 周期为2π周期为2π周期为π周期为π奇偶性奇函数偶函数奇函数奇函数单调性在[2kπ-2π,2kπ+2π]上都是增函数;在[2kπ+2π,2kπ+32π]上都是减函数(k∈Z)在[2kπ-π,2kπ]上都是增函数;在[2kπ,2kπ+π]上都是减函数(k∈Z)在(kπ-2π,kπ+2π)内都是增函数(k∈Z)在(kπ,kπ+π)内都是减函数(k∈Z).反三角函数:arcsinx arccosxarctanx arccotx名称反正弦函数反余弦函数反正切函数反余切函数定义y=sinx(x∈〔-2π,2π〕的反函数,叫做反正弦函数,记作x=arsinyy=cosx(x∈〔0,π〕)的反函数,叫做反余弦函数,记作x=arccosyy=tanx(x∈(-2π,2π)的反函数,叫做反正切函数,记作x=arctanyy=cotx(x∈(0,π))的反函数,叫做反余切函数,记作x=arccoty理解arcsinx表示属于[-2π,2π]且正弦值等于x的角arccosx表示属于[0,π],且余弦值等于x的角arctanx表示属于(-2π,2π),且正切值等于x的角arccotx表示属于(0,π)且余切值等于x的角性质定义域[-1,1][-1,1](-∞,+∞)(-∞,+∞)值域[-2π,2π][0,π](-2π,2π) (0,π)单调性在〔-1,1〕上是增函数在[-1,1]上是减函数在(-∞,+∞)上是增数在(-∞,+∞)上是减函数奇偶性arcsin(-x)=-arcsinx arccos(-x)=π-arccosxarctan(-x)=-arctanx arccot(-x)=π-arccotx周期性都不是同期函数恒等式sin(arcsinx)=x(x∈cos(arccosx)=x(tan(arctanx)=x(x∈cot(arccotx)=x(x[-1,1])arcsin(sinx)=x(x ∈[-2π,2π]) x ∈[-1,1]) arccos(cosx)=x(x ∈[0,π])R)arctan(tanx)=x (x ∈(-2π,2π)) ∈R)arccot(cotx)=x(x ∈(0,π))互余恒等式 arcsinx+arccosx=2π(x ∈[-1,1]) arctanx+arccotx=2π(X ∈R)反三角函数其他公式arcsin(-x)=-arcsinx ; arccos(-x)=π-arccosx ; arctan(-x)=-arctanx ; arccot(-x)=π-arccotx ;arcsinx+arccosx=π/2=arctanx+arccotx ;sin(arcsinx)=cos(arccosx)=tan(arctanx)=cot(arccotx)=x ; 当 x ∈[-π/2, π/2] 有arcsin(sinx)=x ; x ∈[0,π], arccos(cosx)=x ; x ∈(-π/2, π/2), arctan(tanx)=x ; x ∈(0, π), arccot(cotx)=x ;。
三角函数与反三角函数公式大全

三角函数与反三角函数公式大全三角函数和反三角函数是高中数学中的重要内容,也是数学和物理学中广泛应用的数学工具。
下面我们将介绍一些常用的三角函数和反三角函数的公式。
1. 正弦函数(sin)和余弦函数(cos)的关系:sin^2x + cos^2x = 12. 正切函数(tan)与正弦函数(sin)和余弦函数(cos)的关系:tanx = sinx / cosx3. 余切函数(cot)和正弦函数(sin)和余弦函数(cos)的关系:cotx = cosx / sinx4. 正弦函数(sin)和余弦函数(cos)的周期性:sin(x + 2π) = sinxcos(x + 2π) = cosx5. 正弦函数(sin)和余弦函数(cos)的奇偶性:sin(-x) = -sinxcos(-x) = cosx6. 正切函数(tan)和余切函数(cot)的奇偶性:tan(-x) = -tanxcot(-x) = -cotx7. 正弦函数(sin)和余弦函数(cos)的对称性:sin(π - x) = sinxcos(π - x) = -cosx8. 正切函数(tan)和余切函数(cot)的对称性:tan(π - x) = -tanxcot(π - x) = -cotx9. 正弦函数(sin)和余弦函数(cos)的双角和差公式:sin(x ± y) = sinxcosy ± cosxsinycos(x ± y) = cosxcosy ∓ sinxsiny10. 正切函数(tan)和余切函数(cot)的双角和差公式:tan(x ± y) = (tanx ± tany) / (1 ∓ tanxtany)cot(x ± y) = (cotxcoty ∓1) / (coty ± cotx)11. 正弦函数(sin)和余弦函数(cos)的和差化积公式:sinx + siny = 2sin[(x + y) / 2]cos[(x - y) / 2]sinx - siny = 2sin[(x - y) / 2]cos[(x + y) / 2]cosx + cosy = 2cos[(x + y) / 2]cos[(x - y) / 2]cosx - cosy = -2sin[(x + y) / 2]sin[(x - y) / 2] 12. 正切函数(tan)和余切函数(cot)的和差化积公式:tanx + tany = (tanx + tany) / (1 - tanxtany)tanx - tany = (tanx - tany) / (1 + tanxtany)cotx + coty = (cotx + coty) / (cotxcoty - 1)cotx - coty = (cotx - coty) / (cotxcoty + 1)13. 正弦函数(sin)和余弦函数(cos)的倍角公式:sin2x = 2sinxcosxcos2x = cos^2x - sin^2x = 2cos^2x - 1 = 1 - 2sin^2x14. 正弦函数(sin)和余弦函数(cos)的半角公式:sin(x/2) = ±√[(1 - cosx) / 2]cos(x/2) = ±√[(1 + cosx) / 2]15. 反正弦函数(arcsin)和反余弦函数(arccos)的范围:-π/2 ≤ arcsinx ≤ π/20 ≤ arccosx ≤ π16. 反正弦函数(arcsin)和反余弦函数(arccos)的负值关系:arcsin(-x) = -arcsinxarccos(-x) = π - arccosx17. 反正弦函数(arcsin)和反余弦函数(arccos)的和、差关系:arcsin(x) ± arccos(x) = π/2这些公式是三角函数和反三角函数的基本关系,掌握它们对于理解和解决三角函数相关的问题非常重要。
三角函数与反三角函数总结 简洁版

二、反三ቤተ መጻሕፍቲ ባይዱ函数:
函数 反正弦 反余弦 反正切 反余切 反正割 反余割
表示(与三角函数一一对应) 若 x sin y ,则 y arc sin x 若 x cos y ,则 y arc cos x 若 x tan y ,则 y arc tanx 若 x cot y ,则 y arc cotx 若 x sec y ,则 y arcsec x 若 x cscy ,则 y arccscx
tan( ) tan tan 1 tan tan
tan( ) tan tan 1 tan tan
5、二倍角公式:
sin 2 2sin cos cos 2 cos 2 sin 2 2cos 2 1 1 2sin 2
tan 2 2 tan 1 tan 2
6、降幂公式:
三角函数与反三角函数
一、三角函数:
1、定义:
名称
正弦
定
sin
义
对边 斜边
y r
余弦
cos
邻边 斜边
x r
正切
tan
对边 邻边
y x
余切
cot
邻边 对边
x y
正割
sec
斜边 邻边
r x
余割
csc
斜边 对边
r y
2、正六边形法则:
图形结构:
上弦、中切、下割; 左正、右余、中间 1
图形关系:
tan cot 1 (1)倒数关系: SinCsc 1
2
sin
1 cos 2
2
2
cos
1
cos 2
2
7、辅助角公式:
a sin x b cos x a2 b2 sin(x )
三角函数及反三角函数公式大全

三角函数是数学中的一种基本函数,它可以描述角度与直角三角形的边长之间的关系。
而反三角函数则是三角函数的逆运算,它可以用来求解角度或直角三角形的边长。
在数学和物理等领域中,三角函数和反三角函数广泛应用,包括圆的运动、波的传播、信号处理等。
本文将介绍三角函数及反三角函数的定义、性质和公式,希望能够对读者有所帮助。
一、三角函数的定义与性质1. 正弦函数(sin)正弦函数可以用来描述直角三角形中某个角的正弦值,定义为对边与斜边的比值。
正弦函数的性质包括周期性、奇偶性、界值等,它在数学和物理中有着重要的应用。
2. 余弦函数(cos)余弦函数是描述直角三角形中某个角的余弦值的函数,定义为邻边与斜边的比值。
余弦函数也具有周期性、奇偶性、界值等性质,它与正弦函数有着密切的关系。
3. 正切函数(tan)正切函数可以用来描述直角三角形中某个角的正切值,定义为对边与邻边的比值。
正切函数的性质包括周期性、奇偶性、界值等,它在数学和工程中有着广泛的应用。
4. 余切函数(cot)余切函数是描述直角三角形中某个角的余切值的函数,定义为邻边与对边的比值。
余切函数也具有周期性、奇偶性、界值等性质,它与正切函数有着密切的关系。
5. 正割函数(sec)正割函数可以用来描述直角三角形中某个角的正割值,定义为斜边与邻边的比值。
正割函数的性质包括周期性、奇偶性、界值等,它在数学和物理中有着重要的应用。
6. 余割函数(csc)余割函数是描述直角三角形中某个角的余割值的函数,定义为斜边与对边的比值。
余割函数也具有周期性、奇偶性、界值等性质,它与正割函数有着密切的关系。
二、反三角函数的定义与性质1. 反正弦函数(arcsin)反正弦函数是正弦函数的逆运算,可以用来求解某个数值的角度。
反正弦函数的定义域和值域、奇偶性、单调性等性质是求解问题时需要考虑的重要因素。
2. 反余弦函数(arccos)反余弦函数是余弦函数的逆运算,可以用来求解某个数值的角度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角、反三角函数图像( 附:资料全部来自网络, 仅对排版做了改动, 以方便打印及翻阅, 其中可能出现错误,阅者请自行注意。
)1. 六个三角函数值在每个象限的符号:sin α· csc α cos α· sec αtan α· cot α2. 三角函数的图像和性质:y=sinxy-5- 2 12-7o -4-3-2 -3 -2-1237 25223 422xy=cosxy-5- 2 1-32- -4-7-2 -3o 22-1yy=tanx3 3 7 2225 422yy=cotxx-3-- 22o322x-- 2o3 2x22函数y=sinx y=cosxy=tanx{ x | x ∈ R 且定义域RRx ≠ k π+,k ∈ Z }[ -1,1]2[ -1,1]x=2k π+ 时x=2k π时 y max =12Ry max =1x=2k π +π时值域无最大值y min =-1无最小值 x=2k π-时 y min =-12y=cotx{ x | x ∈ R 且x ≠ k π∈,kZ }R无最大值无最小值周期性 周期为 2π 周期为 2π 周期为 π 周期为 π奇偶性奇函数偶函数奇函数奇函数1 / 5在[ 2kπ-,2kπ+ ]在[ 2kπ-π,2kπ]在 (k π- ,在 (k π,kπ+π)内上都是增函数;都是减函数22在[ 2kπ,2kπ+π]2(k ∈ Z)上都是增函数;在单调性2上都是减函数k π+ )内都是增[ 2kπ+,2k(k ∈ Z)2π+ π]函数 (k ∈ Z)23上都是减函数(k ∈Z)3.反三角函数的图像和性质:arcsinx arccosxarctanx名称反正弦函数y=sinx(x ∈〔-,〕的反函2 2定义数,叫做反正弦函数,记作 x=arsinyarcsinx 表示属于理解[ -,]22x 的且正弦值等于角定义域[ -1, 1]值域[ -,]性22单调性在〔 -1, 1〕上是增质函数奇偶性arcsin(-x)=-arcsinx 周期性都不是周期函数反余弦函数y=cosx(x ∈〔0, π〕)的反函数,叫做反余弦函数,记作x=arccosyarccosx 表示属于[ 0,π],且余弦值等于 x 的角[-1, 1][0,π]在[ -1,1]上是减函数arccos(- x)= π-ar ccosxarccotx反正切函数反余切函数y=tanx(x ∈ (-,y=cotx(x ∈(0, π ))的反函数,叫做2反余切函数,记2)的反函数,叫作 x=arccoty做反正切函数,记作x=arctanyarctanx表示属于arccotx 表示属于(-,),且正切值(0,π)且余切值等于 x 的角22等于 x 的角(-∞,+∞)(-∞, +∞)(-,)(0,π)2 2在(-∞, +∞)上是增在(-∞,+∞)上是数减函数arctan(-x)=-arctanx arccot(- x)= π-arc cotx2/ 5sin(arcsinx)=x(x ∈cos(arccosx)=x([ -1,x∈[ -1,1] )恒等式1] )arcsin(sinx)=x(arccos(cosx)=x(x∈[ - ,] )x∈[ 0, π] )22互余恒等式arcsinx+arccosx=(x∈[ -1,1] )2tan(arctanx)=x(x ∈cot(arccotx)=x(x R)arctan(tanx)=x∈ R)( x∈ (-, ))arccot(cotx)=x(x∈ (0, π))22arctanx+arccotx=(X ∈R)2arcsin(-x)=-arcsinx arccos(-x)=π-arccosxarctan(-x)=-arctanx arccot(-x)=π-arccotxarcsinx+arccosx=arctanx+arccotx=π/2sin(arcsinx)=cos(arccosx)=tan(arctanx)=cot(arccotx)=x当 x ∈[- π /2,π/2]arcsin(sinx)=xx∈[0, π]arccos(cosx)=xx∈(- π/2,π/2)arctan(tanx)=xx∈(0,π)arccot(cotx)=x3/ 5三角公式总表1.正弦定理 :a=bc= 2R ( R 为三角形外接圆半径)=sin A sin B sin C2.余弦定理:a 2=b 222 2 2 -2ac cosB c22 2+c -2bc cos A b =a +c =a +b -2ab cosCcos Ab 2c 2a 22bc3. S ⊿= 1 a h a = 1 ab sin C = 1 bc sin A = 1 ac sin B =abc=2R2sin A sin B sin C2 22 24Ra 2 sin B sin Cb 2 sin Asin Cc 2 sin Asin B=pr=p( p a)( pb)( pc)=2sin A==2sinC2sin B(其中 p1(a bc) , r 为三角形内切圆半径 )24. 同角关系:⑴商的关系:① tg= sin= sinsec② ctgcos coscsccossin③ sincostg④ sec1 tgcsccos⑤ cossinctg⑥ csc1 ctgsecsin⑵倒数关系: sin csccos sec tg ctg 1⑶平方关系: sin 2 cos 2sec 2tg 2csc 2ctg 21⑷ a sinb cosa 2b 2 sin() (其中辅助角与点( a,b )在同一象限,且tgb )a5. 和差角公式① sin( ) sin cos cos sin② cos( ) coscos sin sin③ tg ()tg tg④ tg tgtg ()(1 tg tg )1 tgtg⑤ tg (tg tgtg tg tgtg)tgtgtgtgtg其中当 A+B+C= π时 ,有:1tgi). tgAtgB tgCtgA tgB tgCii). tg AtgBtg A tg Ctg B tg C12 2 22 224 / 56. 二倍角公式: ( 含万能公式 )① sin 2 2sin cos2tg1 tg 2② cos22sin 22cos 21 12sin 21 tg 2cos1 tg 2③ tg 22tg1 tg 2④ sin 2tg 2 1 cos 2⑤ 21 cos21 tg22cos27. 半角公式:(符号的选择由所在的象限确定)2① sin1 cos② sin 21 cos2222③ cos1 cos④ cos 21 cos2222 ⑤ 1 cos2 sin 2⑥ 1 cos2 cos 222⑦ 1sin(cos sin ) 2cossin2 222⑧ tg 1 cossin1 cos21 cos1 cossin8. 积化和差公式:① sincos1 sin( ) sin()2② cossin 1 sin( ) sin()2③ coscos1cos() cos()2④ sinsin1) coscos(29. 和差化积公式:① sinsin 2 sincos22② sinsin2 cossin22③ coscos2 coscos22④ coscos2sinsin225 / 5。
