2.1.1指数函数与指数幂的运算
2019A新高中数学必修第一册:2.1.1 指数与指数幂的运算

1 3
);
x-
1 2
y
2 3
)(-4
x
1 4
y
2 3
);
(7)
(2
x
1 2
+
3
y-
1 6
)(2
x
1 2
-
3
y
- 16
);
(8)
4
x
1 4
(-3
x
1 4
y-
1 3
)
(-6
x
- 12
y-
2 3
).
解:
(1)
13 7
a 3a4a12
=
a
13+
3 4
+172
=
a
5 3
.
(2)
23
a3a4
5
a6
=
a
32+
43-
3. 分数指数幂
我们将下面根式变形:
10
a>0 时, 5 a10 = 5 ( a2 )5 = a2 = a 5 .
12
a>0 时, 4 a12 = 4 ( a3 )4 = a3 = a 4 .
m
规定: a n = n am (a 0, m, nN *. 且n1).
a-
m n
=
1
m
(a 0,
m,
解:
(1)
原式
=
x3
y2(-
27
1 x3
y31)
=
-
1 27 y
.
(2) 原式 = 4(- 32)a2-(-1)b-1-(-1)= -6a3.
(3)
原式
2016-2017学年人教A版高一数学必修一书本讲解课件:第二章 2.1 2.1.1 第1课时 根

第二十三页,编辑于星期五:十五点 三十六分。
课时作业
第二十四页,编辑于星期五:十五点 三十六分。
解析:4 0.062 5+
245-
3
27 8
=4 0.54+ 2 522- 3 323=12+52-32=32. 答案:32
第二十二页,编辑于星期五:十五点 三十六分。
4.化简:( a-1)2+ 1-a2+3 1-a3. 解析:由题得 a≥1, ∴( a-1)2+ 1-a2+3 1-a3 =a-1+|1-a|+1-a =a-1.
原式=[a
2 3
·(a-3)
1 2
]
1 3
·(a
5 2
·a
13 2
)
1 2
=a
2 9
·a
1 2
·a
5 4
·a
13 4
=a
5 18
·a-2=a
41 18
=
1
.
a2·18 a5
第十九页,编辑于星期五:十五点 三十六分。
[易错警示]
错误原因
纠错心得
避免错误的方法是先将根式化
错解中主要是在进行化简时,根 为分数指数幂,然后按分数指数
C.1 或 2a-1
D.0
(2)当 a、b∈R 时,下列各式总能成立的是( )
A.(6 a-6 b)6=a-b
8 B.
a2+b28=a2+b2
4 C.
a4-4
b4=a-b
D.10 a+b10=a+b
第十二页,编辑于星期五:十五点 三十六分。
[解析] (1)a+4 1-a4=a+|1-a|=1 或 2a-1,故选 C. (2)取 a=0,b=1,A 不成立. 取 a=0,b=-1,C、D 不成立. ∵a2+b2≥0,∴B 正确,故选 B. [答案] (1)C (2)B
高一数学必修一第二章基本初等函数知识点总结
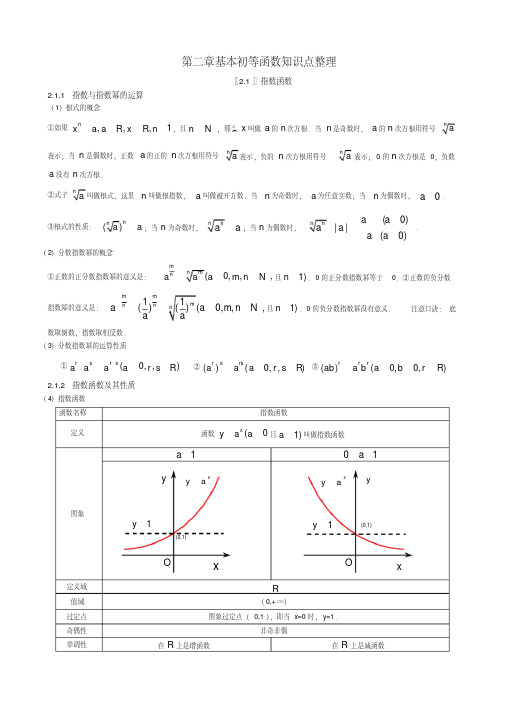
在 R 上是减函数
函数值的 变化情况
a 变化对
图象的影 响
y>1(x > 0), y=1(x=0), 0 < y<1(x < 0)
y> 1(x < 0), y=1(x=0), 0 < y< 1(x > 0)
在第一象限内, a 越大图象越高,越靠近 y 轴; 在第一象限内, a 越小图象越高,越靠近 y 轴; 在第二象限内, a 越大图象越低,越靠近 x 轴. 在第二象限内, a 越小图象越低,越靠近 x 轴.
y
f ( x) 中反解出 x
1
f ( y) ;
③将 x f 1( y ) 改写成 y f 1 ( x) ,并注明反函数的定义域.
( 8)反函数的性质
①原函数 y
f (x) 与反函数 y
1
f ( x) 的图象关于直线 y
x 对称.
②函数 y f ( x) 的定义域、值域分别是其反函数 y f 1 (x ) 的值域、定义域. ③若 P(a,b) 在原函数 y f (x ) 的图象上,则 P' (b, a) 在反函数 y f 1(x ) 的图象上.
③根式的性质: (n a )n a ;当 n 为奇数时, n an
a ;当 n 为偶数时, n an | a |
a (a 0)
.
a (a 0)
( 2)分数指数幂的概念
m
①正数的正分数指数幂的意义是: a n n a m (a 0, m, n N , 且 n 1) . 0 的正分数指数幂等于 0.②正数的负分数
设一元二次方程 ax 2 bx c 0( a 0) 的两实根为 x1, x2 ,且 x1 x2 .令 f ( x) ax 2 bx c ,从以下四个方
面来分析此类问题:①开口方向: a ②对称轴位置: x
2.1 指数函数

2.1 指数函数【2.1.1】指数与指数幂的运算(1)根式的概念①如果,,,1n x a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a 的n 当n 是偶数时,正数a 的正的n 示,负的n 次方根用符号0的n 次方根是0;负数a 没有n 次方根.n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数时,0a ≥.③根式的性质:n a =;当n 为奇数时,a =;当n 为偶数时,(0)|| (0)a a a a a ≥⎧==⎨-<⎩. (2)分数指数幂的概念①正数的正分数指数幂的意义是:0,,,m na a m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是: 1()0,,,m m nn aa m n N a -+==>∈且1)n >.0的负分数指数幂没有意义. 注意口诀:底数取倒数,指数取相反数.(3)分数指数幂的运算性质①(0,,)rsr sa a aa r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r rab a b a b r R =>>∈【2.1.2】指数函数及其性质(4)指数函数当堂训练[基础训练A组]一、选择题1.计算122[(]-的结果是().A. D.-2.对任意实数x,下列等式恒成立的是().A.211332()x x= B.211332()x x= C.311535()x x= D.131355()x x--= 3.化简(21)(21)2222k k k-+----+等于().A.22k- B.(21)2k-- C.(21)2k-+- D.24.下列函数中指数函数的个数是().①23xy=⋅②13xy+=③3xy=④3y x=A.0 B.1 C.2 D.35.方程135108x x x-⋅=的解集是().A.{}1,4 B.14⎧⎫⎨⎬⎩⎭C.11,4⎧⎫⎨⎬⎩⎭D144⎧⎫⎨⎬⎩⎭,6.函数()(0,1)xf x a a a=>≠且对任意正实数,x y都有().A.()()()f xy f x f y= B.()()()f xy f x f y=+C .()()()f x y f x f y +=D .()()()f x y f x f y +=+ 二、填空题1.化简:1114424111244()a b ba ab --=- . 2.计算:120.750311(0.064)(16()23---÷÷-= .3.若239x=,3x-= .4.985316,8,4,2,2从小到大的排列顺序是 . 5.若函数()11x mf x a =+-是奇函数,则m 为 . 三、解答题1.化简下列各式: (1)11122()()x x x x x --++-;(2)222222223333x y x y xyxy--------+--+-;(3)3333441()()[(1)()]a a a a a a a a ----+-÷++-.2.计算下列各式:(1)1020.5231(2)2(2)(0.01)54--+⋅-;(2)20.520371037(2)0.1(2)392748π--++-+.3.已知2212213333334,3,3a b x a a b y b a b +==+=+,求2233()()x y x y ++-的值.4. 比较下列各组数的大小:(1)0.1()4-和 0.2-; (2)163()4和154()3-; (3)2(0.8)-和125()3- .5.家用电器(如冰箱等)使用的氟化物的释放破坏了大气上层的臭氧层,臭氧含量Q 呈指数函数型变化,满足关系式0.00250t Q Q e -=,其中0Q 是臭氧的初始量. (1)随时间的增加,臭氧的含量是增加还是减少? (2)多少年以后将会有一半的臭氧消失?[基础训练B 组] 一、选择题1.设全集为R ,且22{|0},{|1010}x x A x B x -=≤==,则()R A B ð为( ). A .{2} B .{1}- C .{|2}x x ≤ D .∅2.函数y x =3与y x =--3的图像关于下列那种图形对称( ). A .x 轴 B .y 轴 C .直线y x = D .原点中心对称3.函数11x x e y e -=+的值域是( ).A .(1,1)-B .[1,1]-C .(0,1)D .(,)e e - 4.已知集合{}11M =-,,11242x N x x +⎧⎫=<<∈⎨⎬⎩⎭Z ,,则M N = ( ). A .{}11-,B .{}1-C .{}0D .{}10,1-,5.函数11()()3x f x -=在区间[2,1]--上的最大值是( )A .1B .3C .9D .276.设1x ,2x 是函数()(1)x f x a a =>定义域内的两个变量,且12x x <,设121()2m x x =+.那么下列不等式恒成立的是( ). A .12|()()||()()|f m f x f x f m ->-B .12|()()||()()|f m f x f x f m -<-C .12|()()||()()|f m f x f x f m -=-D .212()()()f x f x f m > 二、填空题1.若集合{11|,|x A y y B x y -⎧⎫====⎨⎬⎩⎭,则集合A B = _________.2.方程33131=++-xx的解是_____________. 3.若1122a a-+=1114421124___________1111aaaa+++=+-++. 4.化简11410104848++的值等于__________. 5.若关于x 的方程12220x x a -++=有两个实数解,则实数 的取值范围是_______. 6.对于函数f (x )定义域中任意的x 1,x 2(x 1≠x 2),有如下结论:①)()()(2121x f x f x x f ⋅=+; ②)()()(2121x f x f x x f +=⋅;③0)]()([)(2121<-⋅-x f x f x x ; ④2)()()2(2121x f x f x x f +<+ 当xx f -=2)(时,上述结论正确结论的序号是 .(写出全部正确结论的序号) 三、解答题1.求函数11()()142xxy =-+在[]3,2x ∈-上的值域.2.求函数241(),[0,5)3x xy x -=∈的值域.3.解方程:(1)192327xx ---⋅= (2)649x x x +=.4.已知11()(),(0)212x f x x x =+≠-, (1)判断()f x 的奇偶性; (2)证明()0f x >.5.在工程技术中经常用到一类所谓的双曲函数,定义如下:双曲正弦,2x xe e shx --=;双曲余弦,2x x e e chx -+=;双曲正切,x xx xe e thx e e---=+,请证明: (1)()sh x y shxchy chxshy +=+;(2)()1thx thyth x y thxthy++=+.同步提升一、选择题(12*5分) 1.(369a )4(639a )4等于( )(A )a 16 (B )a 8(C )a 4(D )a 22.函数f (x )=(a 2-1)x在R 上是减函数,则a 的取值范围是( ) (A )1>a (B )2<a (C )a<2 (D )1<2<a3.下列函数式中,满足f(x+1)=21f(x)的是( ) (A)21(x+1) (B)x+41 (C)2x (D)2-x4.已知a>b,ab 0≠下列不等式(1)a 2>b 2,(2)2a>2b,(3)ba 11<,(4)a 31>b 31,(5)(31)a <(31)b 中恒成立的有( )(A )1个 (B )2个 (C )3个 (D )4个5.函数y=121-x 的值域是( ) (A )(-1,∞) (B )(-,∞0)⋃(0,+∞) (C )(-1,+∞) (D )(-∞,-1)⋃(0,+∞) 6.下列函数中,定义域为R 的是( ) (A )y=5x-21 (B )y=(31)1-x(C )y=1)21(-x(D )y=x 21- 7.下列关系中正确的是( )(A )(21)32<(51)32<(21)31 (B )(21)31<(21)32<(51)32(C )(51)32<(21)31<(21)32 (D )(51)32<(21)32<(21)318.若函数y=3·2x-1的反函数的图像经过P 点,则P 点坐标是( )(A )(2,5) (B )(1,3) (C )(5,2) (D )(3,1)9.函数f(x)=3x +5,则f -1(x)的定义域是( ) (A )(0,+∞) (B )(5,+∞) (C )(6,+∞) (D )(-∞,+∞)10.已知函数f(x)=a x+k,它的图像经过点(1,7),又知其反函数的图像经过点(4,0),则函数f(x)的表达式是( )(A)f(x)=2x +5 (B)f(x)=5x +3 (C)f(x)=3x +4 (D)f(x)=4x+311.已知0<a<1,b<-1,则函数y=a x+b 的图像必定不经过( ) (A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限12.一批设备价值a 万元,由于使用磨损,每年比上一年价值降低b%,则n 年后这批设备的价值为( )(A )na(1-b%) (B )a(1-nb%) (C )a(1-(b%)n ) (D )a(1-b%)n二、填空题(4*4分) 13.若a 23<a2,则a 的取值范围是 。
指数函数与幂函数运算

指数幂的形式呢?
2. 分数指数幂:
能否把下列根式写为:
2
3 a 2 a 3 ( a > 0),
1
b b 2 ( b > 0),
5
4 c5 c 4 ( c > 0 ).
如果可以,那么整数指数幂的运算性质 (ak )n akn
式子 n a 叫根式,
n 叫根指数 ,a 叫被开方数.
问:(n a)n a成立吗? n an a 成立吗?
答: 根据 n 次方根的意义, (n a)n a成立.
n an a 不一定成立.
当n为奇数时,n a n a.
当n为偶数时,n
an
|
a
|
a a
(a 0), (a 0).
归纳:
(1)若xn a,
那么 x 叫做 a 的 n 次方根 .
记作xn a(n为奇数,或 )n a(a0,n为偶数. )
例如:
3 27 3 , 5 32 2 , 3 a 6 a 2 , 4 16 2 .
正数的奇次方根是正数,负数的奇次方根
是负数,用符号 n a 表示.
正数的偶次方根是两个互为相反数的数,用 符号 n a (a0) 表示. 负数没有偶次方根. 0的任何次方根都是0, 记作n 00.
(3) 4 34 3 3;
(4) ab2 a b ab(ab).
2. 分数指数幂:
请大家看下列式子:
5
a10
5
(a2 )5
a2
10
a5
(a > 0),
3 a12
3
12
(a 4 ) 3 a4 a 3
2.1.1 指数与指数幂的运算

(
1
6000
) 5730
,
2
(
1
10000
) 5730
,
2
(
1
100000
) 5730
,
.
2
(3)由以上的实例来推断关系式应该是什么?
P
(
1 2
)
t 5730
.
考古学家根据上式可以知道, 生物死亡t年 后,体内碳14的含量P的值.
(4)我们已经知道 1 2,1 22,1 23, ...是正整数指
二、分数指数
• 规定: 1、正数的正分数指数幂的意义为:
m
a n n am (a 0, m, n N *, n 1)
2、正数的负分数指数幂的意义与负整数幂的意义相同
即:a
m n
1
m
an
1 n am
(a 0, m, n N *, n 1)
3、0的正分数指数幂等于0,0的负分数指数幂无意义
我们可以先来考虑这样的问题:
(1)当生物体死亡了5730, 5730×2, 5730×3,… 年后,它体内碳14的含量P分别为原来的多少?
1,
( 1 )2 ,
2
2
(
1 2
)3
,
.
(2) 当 生 物 体 死 亡 了 6000 年 ,10000 年 ,100000 年 后,它体内碳14的含量P分别为原来的多少?
………………………………………… 通过类比方法,可得n次方根的定义.
2n = a xn =a
2叫a的n次方根; x叫a的n次方根.
1.方根的定义 如果xn=a,那么x叫做 a 的n次方根(n th root),
2.1.1 指数幂及其运算

先将根式化为分数指数幂的形式,再运用分数指数幂的运算性
质进行化简.
11
11
7
【解析】(1)原式=a3 ·a4 =a3 +4 =a12 .
111
111
7
(2)原式=a2 ·a4 ·a8 =a2 +4 +8 =a8 .
23
23
13
(3)原式=a3 ·a2 =a3 +2 =a 6 .
1
1
2 13
213
73
了灵活运用运算法则外还要关注条件中的字母是否有隐含的条
件.
1
【正解】由(-a)2 知-a≥0,故 a-1<0.
11
∴(1-a)[(a-1)-2(-a)2 ]2
=(1-a)(1-a)-1·(-a)14=(-a)14 .
【警示】在利用指数幂的运算性质时,要关注条件中有无
隐含条件,在出现根式时要注意是否为偶次方根,被开方数是
(1)4 2+1·23-2 2·64-3 ;
11
(2)
a-b
1
1
-a+b1-2a21 ·b2
a2 +b2
a2 -b2
【解析】(1)原式=22 2+2·23-2 2·2-4=21=2.
1
1
1
1
1
1
(2)原式=a2
+b2 ·a2 a21+b12
-b2
-a21 a2
-b2
1
-b2
2
1
=a2
1
-b2
- a 1 2
方法二:a2+a-2=a2+2aa-1+a-2-2aa-1
=(a+a-1)2-2=25-2=23.
1
1
(2)∵(a2 -a-2 )2=a+a-1-2=5-2=3,
(学习方略)高中数学 2.1.1指数与指数幂的运算课件 新人教A版必修1

A
28
【解】 当n为奇数时, 原式=a-b+a+b=2a; 当n为偶数时,∵a<b<0, ∴原式=|a-b|+|a+b|=b-a+(-a-b)=-2a. 综上知, n a-bn+n a+bn=2-a2an为n奇 为数 偶数 ,.
A
29
规律技巧 为使开偶次方不出现符号错误,先用绝对值保 留开方的结果,然后根据题设条件化去绝对值符号,没给条件 的要分情况讨论.
A
7
2.根式的性质
(1)当n为奇数时, n an =________,当n为偶数时, n an = ________.
(2)负数没有偶次方根,零的任何次方根都是________.
A
8
3.分数指数幂的意义
(1)设a>0,m,n∈N*,n>1,则将 n am 表示为a的分数指数
幂的形式为____________,a-
A
10
1.(1)xn=a 根式 根指数 被开方数 a
(2)负数 n a n a -n a ±n a
自 2.(1)a |a|=a a≥0 -a a<0 我 (2)0
校
m1
3.(1)a n m
对
an
(2)0 没有意义
4.ar+s ars arbr
A
11
思考探究 在有理数指数幂的运算性质中,为什么要规定
A
32
规律技巧 本题ab与a-b互为倒数,抓住这一点,已知和 所求分别平方很快得出答案,这里运用了公式变形a-b2=a +b2-4ab.
A
33
变式训练4
已知a
1 2
+a-
1 2
=m,求a2+a 1的值.
指数与指数幂的运算优秀教案

2.1.1 指数与指数幂的运算( 2 课时)第一课时根式教案目标:1.理解n 次方根、根式、分数指数幂的概念;2.正确运用根式运算性质和有理指数幂的运算性质;3.培养学生认识、接受新事物和用联系观点看问题的能力。
教案重点:根式的概念、分数指数幂的概念和运算性质教案难点:根式概念和分数指数幂概念的理解教案方法:学导式教案过程:(I)复习回顾引例:填空(1)0=1(a 0) ;0=1(a0) ;n * )a a a n N(; an a个a n1na(a 0, n N *)(2) m n m n m nmn n n na a a (m,n∈Z);(a ) a(m,n∈Z);(ab ) a b (n∈Z)(3)9 _____ ;- 9 _____ ;0 ______ (4)( a)2 _____( a 0) ;a2 ________(II )讲授新课1 / 151.引入:(1)填空(1),(2)复习了整数指数幂的概念和运算性质(其中:因为m na a可看作m na a ,所以m n m na a a 可以归入性质m n m na a a ;又因为an( ) 可看作bm na a ,所以na an n n n( ) 可以归入性质( ab) a b (n∈Z)),这是为下面学习分nb b数指数幂的概念和性质做准备。
为了学习分数指数幂,先要学习n 次根式(n N* )的概念。
(2)填空(3),(4)复习了平方根、立方根这两个概念。
如:22=4 ,(-2)2=4 2,-2 叫4 的平方根23=8 2 叫8 的立方根;(-2)3=-8 -2 叫-8 的立方根25=32 2 叫32 的 5 次方根⋯2n=a 2 叫 a 的 n 次方根2=4,则2叫4 的平方根;若23=8,2 叫做 8 的立方根;若25=32,则分析:若 22 叫做 32 的 5次方根,类似地,若2n=a,则2叫a 的n 次方根。
由此,可有:2.n次方根的定义:(板书)一般地,如果nx a ,那么 x 叫做 a的 n 次方根(n th root),其中n 1,且n N 。
高中数学第二章基本初等函数(Ⅰ)2.1指数函数2.1.1指数与指数幂的运算(3)教案数学教案
指数与指数幂的运算(3)导入新课思路1.同学们,既然我们把指数从正整数推广到整数,又从整数推广到正分数到负分数,这样指数就推广到有理数,那么它是否也和数的推广一样,到底有没有无理数指数幂呢?回顾数的扩充过程,自然数到整数,整数到分数(有理数),有理数到实数.并且知道,在有理数到实数的扩充过程中,增添的数是——实数.对无理数指数幂,也是这样扩充而来.既然如此,我们这节课的主要内容是:教师板书本堂课的课题(指数与指数幂的运算(3))之无理数指数幂.思路2.同学们,在初中我们学习了函数的知识,对函数有了一个初步的了解,到了高中,我们又对函数的概念进行了进一步的学习,有了更深的理解,我们仅仅学了几种简单的函数,如一次函数、二次函数、正比例函数、反比例函数、三角函数等,这些远远不能满足我们的需要,随着科学的发展,社会的进步,我们还要学习许多函数,其中就有指数函数,为了学习指数函数的知识,我们必须学习实数指数幂的运算性质,为此,我们必须把指数幂从有理数指数幂扩充到实数指数幂,因此我们本节课学习:指数与指数幂的运算(3)之无理数指数幂,教师板书本堂课的课题.推进新课新知探究提出问题①我们知道2=1.414 213 56…,那么1.41,1.414,1.414 2,1.414 21,…,是2的什么近似值?而1.42,1.415,1.414 3,1.414 22,…,是2的什么近似值?③你能给上述思想起个名字吗?④一个正数的无理数次幂到底是一个什么性质的数呢?如52,根据你学过的知识,能作出判断并合理地解释吗?⑤借助上面的结论你能说出一般性的结论吗?活动:教师引导,学生回忆,教师提问,学生回答,积极交流,及时评价学生,学生有困惑时加以解释,可用多媒体显示辅助内容:问题①从近似值的分类来考虑,一方面从大于2的方向,另一方面从小于2的方向.问题②对图表的观察一方面从上往下看,再一方面从左向右看,注意其关联.问题③上述方法实际上是无限接近,最后是逼近.问题④对问题给予大胆猜测,从数轴的观点加以解释.问题⑤在③④的基础上,推广到一般的情形,即由特殊到一般.讨论结果:①1.41,1.414,1.414 2,1.414 21,…这些数都小于2,称2的不足近似值,而1.42,1.415,1.414 3,1.414 22,…,这些数都大于2,称2的过剩近似值.②第一个表:从大于2的方向逼近2时,52就从51.5,51.42,51.415,51.4143,51.41422,…,即大于52的方向逼近52.第二个表:从小于2的方向逼近2时,52就从51.4,51.41,51.414,51.414 2,51.414 21,…,即小于52的方向逼近52.从另一角度来看这个问题,在数轴上近似地表示这些点,数轴上的数字表明一方面52从51.4,51.41,51.414,51.414 2,51.414 21,…,即小于52的方向接近52,而另一方面52从51.5,51.42,51.415,51.4143,51.41422,…,即大于52的方向接近52,可以说从两个方向无限地接近52,即逼近52,所以52是一串有理数指数幂51.4,51.41,51.414,51.414 2,51.414 21,…,和另一串有理数指数幂51.5,51.42,51.415,51.4143,51.41422,…,按上述变化规律变化的结果,事实上表示这些数的点从两个方向向表示52的点靠近,但这个点一定在数轴上,由此我们可得到的结论是52一定是一个实数,即51.4<51.41<51.414<51.414 2<51.41421<…<52<…<51.41422<51.4143<51.415<51.42<51.5.充分表明52是一个实数.③逼近思想,事实上里面含有极限的思想,这是以后要学的知识. ④根据②③我们可以推断52是一个实数,猜测一个正数的无理数次幂是一个实数.⑤无理数指数幂的意义:一般地,无理数指数幂a α(a>0,α是无理数)是一个确定的实数.也就是说无理数可以作为指数,并且它的结果是一个实数,这样指数概念又一次得到推广,在数的扩充过程中,我们知道有理数和无理数统称为实数.我们规定了无理数指数幂的意义,知道它是一个确定的实数,结合前面的有理数指数幂,那么,指数幂就从有理数指数幂扩充到实数指数幂. 提出问题(1)为什么在规定无理数指数幂的意义时,必须规定底数是正数?(2)无理数指数幂的运算法则是怎样的?是否与有理数指数幂的运算法则相通呢? (3)你能给出实数指数幂的运算法则吗?活动:教师组织学生互助合作,交流探讨,引导他们用反例说明问题,注意类比,归纳. 对问题(1)回顾我们学习分数指数幂的意义时对底数的规定,举例说明.对问题(2)结合有理数指数幂的运算法则,既然无理数指数幂a α(a>0,α是无理数)是一个确定的实数,那么无理数指数幂的运算法则应当与有理数指数幂的运算法则类似,并且相通. 对问题(3)有了有理数指数幂的运算法则和无理数指数幂的运算法则,实数的运算法则自然就得到了.讨论结果:(1)底数大于零的必要性,若a=-1,那么a α是+1还是-1就无法确定了,这样就造成混乱,规定了底数是正数后,无理数指数幂a α是一个确定的实数,就不会再造成混乱. (2)因为无理数指数幂是一个确定的实数,所以能进行指数的运算,也能进行幂的运算,有理数指数幂的运算性质,同样也适用于无理数指数幂.类比有理数指数幂的运算性质可以得到无理数指数幂的运算法则: ①a r ·a s =a r+s(a>0,r,s 都是无理数).②(a r )s =a rs(a>0,r,s 都是无理数).③(a·b)r =a r b r(a>0,b>0,r 是无理数).(3)指数幂扩充到实数后,指数幂的运算性质也就推广到了实数指数幂. 实数指数幂的运算性质:对任意的实数r,s,均有下面的运算性质: ①a r ·a s =a r+s(a>0,r,s∈R ).②(a r )s =a rs(a>0,r,s∈R ).③(a·b)r =a r b r(a>0,b>0,r∈R ). 应用示例思路1例1利用函数计算器计算.(精确到0.001) (1)0.32.1;(2)3.14-3;(3)3.143;(4)33.活动:教师教会学生利用函数计算器计算,熟悉计算器的各键的功能,正确输入各类数,算出数值,对于(1),可先按底数0.3,再按键,再按幂指数2.1,最后按,即可求得它的值; 对于(2),先按底数3.14,再按键,再按负号键,再按3,最后按即可;对于(3),先按底数3.1,再按键,再按34,最后按即可;对于(4),这种无理指数幂,可先按底数3,其次按键,再按键,再按3,最后按键.有时也可按或键,使用键上面的功能去运算.学生可以相互交流,挖掘计算器的用途.答案:(1)0.32.1≈0.080;(2)3.14-3≈0.032; (3)3.143≈2.336;(4)33≈6.705.点评:熟练掌握用计算器计算幂的值的方法与步骤,感受现代技术的威力,逐步把自己融入现代信息社会;用四舍五入法求近似值,若保留小数点后n 位,只需看第(n+1)位能否进位即可.例2求值或化简. (1)3224ab ba -(a>0,b>0); (2)(41)21-213321)()1.0()4(---b a ab (a>0,b>0);(3)246347625---+-.活动:学生观察,思考,所谓化简,即若能化为常数则化为常数,若不能化为常数则应使所化式子达到最简,对既有分数指数幂又有根式的式子,应该把根式统一化为分数指数幂的形式,便于运算,教师有针对性地提示引导,对(1)由里向外把根式化成分数指数幂,要紧扣分数指数幂的意义和运算性质,对(2)既有分数指数幂又有根式,应当统一起来,化为分数指数幂,对(3)有多重根号的式子,应先去根号,这里是二次根式,被开方数应凑完全平方,这样,把5,7,6拆成(3)2+(2)2,22+(3)2,22+(2)2,并对学生作及时的评价,注意总结解题的方法和规律.解:(1)3224ab ba -=2224b a -(a 31b 32)21=a -2ba 61b 31=a611-b 34=61134ab .点评:根式的运算常常化成幂的运算进行,计算结果如没有特殊要求,就用根式的形式来表示.(2)(41)21-2133231)()1.0()4(---b a ab =223211044•a 23a 23-b 23-b 23=254a 0b 0=254.点评:化简这类式子一般有两种办法,一是首先用负指数幂的定义把负指数化成正指数,另一个方法是采用分式的基本性质把负指数化成正指数.(3) 246347625---+- =222)22()32()23(---+- =3-2+2-3-2+2=0.点评:考虑根号里面的数是一个完全平方数,千万注意方根的性质的运用.例3已知x=21(5n 1-5n 1-),n∈N *,求(x+2x 1+)n 的值.活动:学生思考,观察题目的特点,从整体上看,应先化简,然后再求值,要有预见性,5n1与5n1-具有对称性,它们的积是常数1,为我们解题提供了思路,教师引导学生考虑问题的思路,必要时给予提示.x 2=41(5n 1-5n 1-)2=41(5n 2-2·50+5n 2-)=41(5n 2+2+5n 2--4) =41(5n 1+5n 1-)2-1. 这时应看到1+x 2=1+41(n 1-5n 1-)2=41(5n 1+5n 1-)2,这样先算出1+x 2,再算出2x 1+,带入即可.解:将x=21(5n 1-5n 1-)代入1+x 2,得1+x 2=1+41(5n 1-5n 1-)2=41(5n 1+5n 1-)n ,所以(x+2x 1+)n=[21(5n 1-5n 1-)+211)55(41n n-+]n=[21(5n 1-5n 1-)+21(5n 1+5n 1-)]n =(5n 1)n=5.点评:运用整体思想和完全平方公式是解决本题的关键,要深刻理解这种做法.思路2 例1计算:(1)105432)(0625.0833416--+++π;(2)12532+(21)-2+34331-(271)31-;(3)(-2x 41y31-)(3x 21y 32);(4)(x 21-y 21)÷(x 41-y 41).活动:学生观察、思考,根式化成分数指数,利用幂的运算性质解题,另外要注意整体的意识,教师有针对性的提示引导,对(1)根式的运算常常化成幂的运算进行,对(2)充分利用指数幂的运算法则来进行,对(3)则要根据单项式乘法和幂的运算法则进行,对(4)要利用平方差公式先因式分解,并对学生作及时的评价. 解:(1)105432)(0625.0833416--+++π =(425)21+(827)31+(0.062 5)41+1-21=(25)2×21+(23)313⨯+(0.5)414⨯+21 =25+23+0.5+21 =5;(2)12532+(21)-2+34331-(271)31-=(53)32+(2-1)-2+(73)31-(3-3)31-=5323⨯+2-2×(-1)+7313⨯-3)31(3-⨯-=25+4+7-3=33; (3)(-2x 41y 31-)(3x 21y 32)=(-2×3)(x 41x 21·y31-y 32)=323121416+-+•-yx=-6x 43y 31=3436y x-;(4)(x 21-y 21)÷(x 41-y 41)=((x 41)2-(y 41)2)÷(x 41-y 41) =(x 41+y 41)(x 41-y 41)÷(x 41-y 41) =x 41+y 41.点评:在指数运算中,一定要注意运算顺序和灵活运用乘法公式.例2化简下列各式: (1)323222323222--------+--++yxy x yxy x ;(2)(a 3+a -3)(a 3-a -3)÷[(a 4+a -4+1)(a-a -1)].活动:学生观察式子的特点,特别是指数的特点,教师引导学生考虑题目的思路,这两题要注意分解因式,特别是立方和和立方差公式的应用,对有困难的学生及时提示:对(1)考查x 2与x 32的关系可知x 2=(x 32)3,立方关系就出来了,公式便可运用,对(2)先利用平方差,再利用幂的乘方转化为立方差,再分解因式,组织学生讨论交流. 解:(1)原式=323222323222--------+--++yxy x yxy x=])())(()[()()(23232322322323232232--------++-+-yyx x yy x x=343234343234)()(---------+-yxy xy xy x=xyxy xy 3322)(2-=--; (2)原式=[(a 3)2-(a -3)2]÷[(a 4+a -4+1)(a-a -1)]=))(1()()(1442222----++-a a a a a a =))(1()1)((1444422-----++++-a a a a a a a a =1212)(----a a a a =a+a -1.点评:注意立方和立方差公式在分数指数幂当中的应用,因为二项和、差公式,平方差公式一般在使用中一目了然,而对立方和立方差公式却一般不易观察到,a 23=(a 21)3还容易看出,对其中夹杂的数字m 可以化为m·a 21a 21-=m,需认真对待,要在做题中不断地提高灵活运用这些公式的能力.知能训练课本P 59习题2.1A 组 3.利用投影仪投射下列补充练习: 1.化简:(1+2321-)(1+2161-)(1+281-)(1+241-)(1+221-)的结果是( )A.21(1-2321-)-1B.(1-2321-)-1C.1-2321- D.21(1-2321-) 分析:根据本题的特点,注意到它的整体性,特别是指数的规律性,我们可以进行适当的变形. 因为(1+2321-)(1-2321-)=1-2161-,所以原式的分子分母同乘以(1-2321-),依次类推,所以321212121)21)(21(----+-=32112121----=21(1-2321-)-1. 答案:A2.计算(297)0.5+0.1-2+(22710)32--3π0+9-0.5+490.5×2-4.解:原式=(925)21+100+(6427)32-3+4921×161=53+100+169-3+31+167=100.3.计算1212--+-+a a a a (a≥1). 解:原式=|11|11)11()11(22--++-=--++-a a a a (a≥1).本题可以继续向下做,去掉绝对值,作为思考留作课下练习.4.设a>0,x=21(a n 1-a n 1-),则(x+2x 1+)n 的值为_______.分析:从整体上看,应先化简,然后再求值,这时应看到解:1+x 2=1+41(a n 1-a n 1-)2=41(a n 1+a n 1-)2.这样先算出1+x 2,再算出2x 1+,将x=21(a n 1-a n 1-)代入1+x 2,得1+x 2=1+41(a n 1-a n 1-)2=41(a n 1+a n 1-)2.所以(x+2x 1+)n=[21(a n 1-a n 1-)+41(a n 1+a n 1-)2]n=[21(a n 1-a n 1-)+21(a n 1+a n 1-)]n=a.答案:a 拓展提升参照我们说明无理数指数幂的意义的过程,请你说明无理数指数幂32的意义.活动:教师引导学生回顾无理数指数幂52的意义的过程,利用计算器计算出3的近似值,取它的过剩近似值和不足近似值,根据这些近似值计算32的过剩近似值和不足近似值,利用逼近思想,“逼出”32的意义,学生合作交流,在投影仪上展示自己的探究结果.我们把用2作底数,3的不足近似值作指数的各个幂排成从小到大的一列数 21.7,21.72,21.731,21.7319,…,同样把用2作底数, 3的过剩近似值作指数的各个幂排成从大到小的一列数: 21.8,21.74,21.733,21.7321,…,不难看出3的过剩近似值和不足近似值相同的位数越多,即3的近似值精确度越高,以其过剩近似值和不足近似值为指数的幂2α会越来越趋近于同一个数,我们把这个数记为32. 即21.7<21.73<21.731<21.7319<…<32<…<21.7321<21.733<21.74<21.8.也就是说32是一个实数,32=3.321 997 …也可以这样解释:当3的过剩近似值从大于3的方向逼近3时,32的近似值从大于32的方向逼近32; 当3的不足近似值从小于3的方向逼近3时,32的近似值从小于32的方向逼近32.所以32就是一串有理指数幂21.7,21.73,21.731,21.7319,…,和另一串有理指数幂21.8,21.74,21.733,21.7321,…,按上述规律变化的结果,即32≈3.321 997.课堂小结(1)无理指数幂的意义.一般地,无理数指数幂a α(a>0,α是无理数)是一个确定的实数. (2)实数指数幂的运算性质:对任意的实数r,s,均有下面的运算性质: ①a r ·a s =a r+s(a>0,r,s∈R ).②(a r )s =a rs(a>0,r,s∈R ).③(a·b)r =a r b r(a>0,b>0,r∈R ).(3)逼近的思想,体会无限接近的含义. 作业课本P 60习题2.1 B 组 2.设计感想无理数指数是指数概念的又一次扩充,教学中要让学生通过多媒体的演示,理解无理数指数幂的意义,教学中也可以让学生自己通过实际情况去探索,自己得出结论,加深对概念的理解,本堂课内容较为抽象,又不能进行推理,只能通过多媒体的教学手段,让学生体会,特别是逼近的思想、类比的思想,多作练习,提高学生理解问题、分析问题的能力.。
高中数学人教版A版必修一课时作业及解析:第二章2-1指数函数

∴原式=--24x1-≤2x<3 -3<x<1 .
12.解
1
1
1
原式=
a3
2
a 8b
1
2
a3
2b3
1
1
×a3
4b3 2a3 a 3
a3
13.解 ∵x- xy-2y=0,x>0,y>0, ∴( x)2- xy-2( y)2=0, ∴( x+ y)( x-2 y)=0, 由 x>0,y>0 得 x+ y>0, ∴ x-2 y=0,∴x=4y, ∴y2+x-2 xxyy=8yy+-42yy=65.
6
1
-32>0, 33
<0,C
选项错.故选
D.]
6.B [①中,当 a<0 时,
a2
3 2
a2
1 2
3
=(-a)3=-a3,
∴①不正确;
②中,若 a=-2,n=3,
则3 -23=-2≠|-2|,∴②不正确;
x-2≥0, ③中,有3x-7≠0,
即 x≥2 且 x≠73,
故定义域为[2,73)∪(73,+∞),∴③不正确; ④中,∵100a=5,10b=2, ∴102a=5,10b=2,102a×10b=10,即 102a+b=10.
1 2
3
xy
1 2
·(xy)-1
12
= x3 ·y 3
1
x6
y
1 6
x
1 2
y
1 2
=x1 3·x1 31, =-1,x<0
x>0
.
(2)原式= 1 + 1 + 2+1-22 22
=2 2-3.
指数函数与指数幂的运算(优秀经典导学案)

必修一 第二章基本初等函数(Ι) 2. 1指数函数 2. 1. 1 指数与指数幂的运算第1课时 根式一、课时目标:1. 理解n 次方根及根式的概念.(重点)2.正确运用根式的运算性质进行根式运算.(重点、难点)预习案阅读教材P 48~P 50例1的有关内容,完成下列问题: 1.如果 ()*∈>Nn n ,1,那么x 叫做a 的n 次方根.2.式子n a 叫做 ,这里n 叫做 ,a 叫做 . 3.根式的性质:(1)n 0= (n ∈N *,且n >1); (2) ()nnaN n 时,*∈= ; (3) n a n=⎪⎩⎪⎨⎧为偶数)(为奇数)(n a n a .自测练习1.(1)若x 3=8,则x =________; (2)若x 2=4,则x =________. 2. 判断正误 (正确的打“√”,错误的打“×”):(1)(-2)2=-2 ( ) (2)(3a 3)=a ( ) (3)(416)=±2 ( ) 3.化简()()33233--+x x 得()A .6B .x 2C .6或-x 2D .-x 2或6或x 24.化简下列各式: (1)()332-; (2)327-; (3)()()4433238-+-; (4)()44b a -.互动探究例1.求下列各式的值.(1)(5)2; (2)(3-3)3; (3)4(-2)4; (4)(3-π)2.[变式训练1] 已知4(a +1)4=-a -1,则实数a 的取值范围是________.例2 . 若代数式2x -1+2-x 有意义,化简4x 2-4x +1+24(x -2)4.[变式训练2] 设9612,3322++-+-<<-x x x x x 求的值.课堂检测1.481的运算结果是( )A .3B .-3C .±3D .以上都不对2.m 是实数,则下列式子中可能没有意义的是( )A .4m 2B .5mC .6m D .5-m3.下列说法:①16的4次方根是2;②416的运算结果是±2;③当n 为大于1的奇数时,na 对任意a ∈R 有意义;④当n 为大于1的偶数时,na 只有当a ≥0时才有意义.其中正确的是( ) A .①③④ B .②③④ C .②③ D .③④ 4.计算下列各式的值:(1)(3-5)3=________; (2)(-b )2=________. 5.当8< x <10时,化简:(x -8)2+(x -10)2.6.写出使下列各式成立的x 的取值范围. (1) 3⎝⎛⎭⎫1x -33=1x -3; (2) (x -5)(x 2-25)=(5-x )x +5.第2课时 指数幂及运算学校:澜沧一中 学科:数学 年级:高一 主备教师:沈琼梅 参与教师:刘英华、单祖培、尹继叶、王丝然、张露平、樊明文审定教师:沈琼梅一、课时目标:1. 理解分数指数幂的含义.(难点)2.掌握根式与分数指数幂的互化.(重点、易错点)3.掌握有理数指数幂的运算性质.(重点) 分数指数幂的意义预习案阅读教材P 50~P 53“思考”的有关内容,完成下列问题:1.(1)规定正数的正分数指数幂的意义是:nm a = ()1,0>∈>*n N m n a ,且、;(2)规定正数的负分数指数幂的意义是:nm a -= = ()1,0>∈>*n N m n a ,且、; (3)0的正分数指数幂为 ,0的负分数指数幂 . 2.有理数指数幂的运算性质:(1)=s r a a ()Q s r a ∈>、,0; (2)()=s ra ()Q s r a ∈>、,0;(3)()=rab ()Q r b a ∈>>,0,0.3. 一般地,无理数指数幂a α (a >0,α是无理数) 是一个确定的 , 的运算性质同样适用于无理数指数幂.自测练习1.用根式表示下列各式 (式中a 均为正数):(1) 31a =________; (2) 54a =________; (3) 23-a =________.2. 化简: (1) 12743aa ⋅=________; (2)b 2b=________; (3) 331)(ab =________.互动探究例1.将下列根式化成分数指数幂的形式:(1)a a (a >0); (2) 3252)(1x x ( x >0 ); (3) 32432)(--b( b >0 ).[变式训练1] (1)用根式表示下列各式:53x ,53-x ;(2)用分数指数幂表示下列各式:a 2a ,a . (式中a 均为正数)例2. 化简下列各式 (其中字母均表示正数): (1) 2175.034303101.016])2[()87()064.0(-++-+-----; (2))3(6)(2(656131212132b a b a b a -÷-.[变式训练2] 化简:4xy yx x 3234461)3(-÷⋅-⋅.例3. 已知21a +21-a=3,求下列各式的值:(1)a +a -1; (2)a 2+a -2; (3) 21212323----aa a a .[变式训练3] 已知21a +21-a =3,在题设条件不变的情况下,求a 2 -a-2的值.课堂检测1.下列运算正确的是( )A .a ·a 2= a 2B .(ab )3=ab 3C .(a 2)3=a 6D .a 10÷a 2=a 5 2.233可化为( )A . 2B .33C .327D .273. 41)62581(-的值是________. 4.化简下列各式 (a >0,b >0):(1)3a ·4a ; (2)a a a ; (3)3a 2·a 3; (4)(3a )2·ab 3.5.已知x +y =12,x y =9,且x < y ,求21212121yx y x +-的值.2.1.2 指数函数及其性质 第1课时 指数函数的图象和性质学校:澜沧一中 学科:数学 年级:高一主备教师:沈琼梅 参与教师:刘英华、单祖培、尹继叶、王丝然、张露平、樊明文 审定教师:沈琼梅一、课时目标:1. 理解指数函数的概念和意义.(重点)2.能借助计算器或计算机画出指数函数的图象.(难点) 3.初步掌握指数函数的有关性质.(重点、难点)预习案阅读教材P 54~P 56的有关内容,完成下列问题:1.一般地,函数 叫做指数函数,其中x 是自变量,函数的定义域为 . 2.完成下表:a >1 0<a <1自测练习1.下列以x 为自变量的函数中,是指数函数的是( )A .(4)xy =- B .xy π= C .4xy =- D .2x y a +=()10≠>a a ,且2. 判断正误(正确的打“√”,错误的打“×”)(1)函数x y 2=的定义域为(0,+∞).( ) (2)函数xy -=2在定义域内是增函数.( )(3)函数x y 3=y =3x 与x y )31(=的图象关于y 轴对称.( )互动探究当底数a 大小不定时,必须分“a >1”和“0< a < 1”两种情形讨论.指数函数y =a x 的图象如图所示,由指数函数y =a x 的图象与x =1相交于点(1,a )可知:图中的底数的大小关系为0 < a 4 < a 3 < 1 < a 2 < a 1 .①在y 轴右侧,图象从上到下相应的底数由大变小,即当a >1时,底越大,图象越靠近y 轴; ②在y 轴左侧,图象从下到上相应的底数由大变小,即当0< a < 1时,底越小,图象越靠近y 轴. 例1.若指数函数f (x )的图象经过点(2, 9),求f (x )及f (-1).[变式训练1] 若函数y =(a 2-3a +3)·a x 是指数函数,则实数a =________.例2. 若函数y =a x +b -1 (a >0,且a ≠1) 的图象经过第二、三、四象限,则一定有( )A .0< a < 1,且b >0B .a >1,且b >0C .0< a < 1,且b < 0D .a >1,且b <0[变式训练2] 函数y =a x +3+2 (a >0,且a ≠1) 的图象过定点________.例3. 求下列函数的定义域与值域:(1) 114.0-=x y ; (2) 153-=x y ; (3) y =2x +1.[变式训练3] 求下列函数的定义域和值域:(1) 4-12x y =; (2) 2)31(-=x y .课堂检测1.下列函数是指数函数的是( )A .y =(-2)xB .y =x 3C .y =-2xD .y =2x 2.指数函数y =a x 与y =b x 的图象如图所示,则( )A .a <0,b <0B .a <0,b >0C .0<a <1,b >1D .0<a <1,0<b <13.函数y =a x +1 (a >0且a ≠1) 恒过定点 ________.4.下列函数是指数函数吗?分别求函数的定义域、值域:(1)y =165+x ; (2)y =x 3)21(; (3)y =x 17.0; (4)y =π-x ; (5)y =xa )12(- ⎝⎛⎭⎫a >12且a ≠1.第2课时 指数函数及其性质的应用学校:澜沧一中 学科:数学 年级:高一 主备教师:沈琼梅 参与教师:刘英华、单祖培、尹继叶、王丝然、张露平、樊明文审定教师:沈琼梅一、课时目标:1. 理解指数函数单调性与底数a 的关系,能运用指数函数的单调性解决一些问题.(重点、难点) 2.会解指数函数型的应用题.(重点) 3.掌握指数函数的图象变换.(易错点)预习案 阅读教材P 57~P 58的有关内容,完成下列问题:1.a >10<a <1R2.如图是指数函数 ①y =a x ,②y =b x ,③y =c x ,④y =d x 的图象,则a ,b ,c ,d 的大小关系是( )A .a <b <1<c <dB .b <a <1<d <cC .1<a <b <c <dD .a <b <1<d <c自测练习1.画出函数115,3,(),()35x x x x y y y y ====的图象,说出底数与函数图象的位置关系.2. 指数函数增长模型:原有量N ,平均最长率P ,则经过时间x 后的总量y = .3. 形如 (01a a >≠且)的函数是一种 ,这是非常有用的函数模型.互动探究例1.比较下列各组数的大小:(1)1.52.5和1.53.2; (2)0.6-1.2和0.6-1.5; (3)1.70.2和0.92.1; (4)0.60.4和0.70.4.[变式训练1] 已知a =5-12,函数f (x )=a x ,若实数m ,n 满足f (m ) > f (n ),则m ,n 的大小关系为________.例2. 如果a -5x > a x +7(a > 0且a ≠1),求x 的取值范围.[变式训练2] 若a x +1> x a35)1(- (a >0,且a ≠1),求x 的取值范围.例3. 已知函数f (x )=a -12x +1(x ∈R ). (1)用定义证明:不论a 为何实数,f (x )在(-∞,+∞)上为增函数;(2)若f (x )为奇函数,求a 的值; (3)在(2)的条件下,求f (x )在区间 [1,5] 上的最小值.[变式训练3] 已知函数f (x )=3x -13x +1.(1)证明:f (x )为奇函数. (2)判断f (x )的单调性,并用定义加以证明. (3)求f (x )的值域.课堂检测1.若a =21)5.0(,b =31)5.0(,c =41)5.0(,则a ,b ,c 的大小关系是( )A .a >b >cB .a <b <cC .a >c >bD .b <c <a 2.若函数f (x )=x x -+33与g (x )=x x --33的定义域均为R ,则( )A .f (x )与g (x )均为偶函数B .f (x )为偶函数,g (x )为奇函数C .f (x )与g (x )均为奇函数D .f (x )为奇函数,g (x )为偶函数 3.函数f (x )=x )21(在区间 [-1,2] 上的最大值是________.4.画出函数y =12+x 的图象,并根据图象指出它的单调区间.2.2 对数函数 2.2.1 对数与对数运算第1课时 对数学校:澜沧一中 学科:数学 年级:高一 主备教师:沈琼梅 参与教师:刘英华、单祖培、尹继叶、王丝然、张露平、樊明文 审定教师:沈琼梅一、课时目标:1. 理解对数的概念,能进行指数式与对数式的互化.(重点) 2.理解对数的底数和真数的范围.(易混点) 3.掌握对数的基本性质及对数恒等式.(难点)预习案阅读教材P 62~P 63的有关内容,完成下列问题:1.定义:一般地,如果 (0,1)a a >≠,那么x 叫做 ,记作 ,其中a 叫做对数的 ,N 叫做 .2. 定义: 我们通常将以10为底的对数叫做 , 并把常用对数 简记作 ;在科学技术中常使用以无理数e = 2.71828……为底的对数,以e 为底的对数叫 ,并把自然对数 简记作 .3.指数与对数间的关系: 当0,1a a >≠时, ⇔ .4.对数的性质: ⑴ 没有对数; ⑵ ; ⑶ =a a log .自测练习1.(1) 2x =3,则x =________; (2) 10x =5,则x =________; (3)4log 3=b a ,则 . 2. 判断正误 ( 正确的打“√”,错误的打“×”)(1)(-2)3=-8可化为log (-2)(-8)=3( ) (2)对数运算的实质是求幂指数( ) 3. (1)2713=x 的对数表达式为 ,x = ;(2) x =16log 2的指数表达式为 ,x = .4.计算:21log 16= , 2.5log 2.5= ,0.4log 1= . 互动探究例1.求下列各式中x 的值:(1) 2327log =x ; (2) 32log 2-=x ; (3) 91log 27=x ; (4) 16log 21=x .[变式训练1] 求下列各式中x 的值:(1) log x 81=2; (2) x =log 8 4; (3) lg x =-2; (4) 5 lg x =25.例2. 求下列各式中x 的值:(1) log 2 (log 5 x )=0; (2) log 3 (lg x )=1; (3) x =+-2231log )12(.[变式训练2] 若lg (ln x )=1,则x =________.课堂检测1.下列指数式与对数式互化不正确的一组是( )A .010=1与lg1=0 B .312731=-与3131log 27-= C .9log 3=2与219=3 D .5log 5=1与51=5 2.在b =log 3 (m -1) 中,实数m 的取值范围是( )A .RB .(0,+∞)C .(-∞,1)D .(1,+∞)3.ln e + lg 1=____ ____.4.若312log 19x-=,则x = .5.求下列各式的值:(1) log 3 27; (2) 1)3-2()32(log -+.第2课时 对数的运算学校:澜沧一中 学科:数学 年级:高一主备教师:沈琼梅 参与教师:刘英华、单祖培、尹继叶、王丝然、张露平、樊明文 审定教师:沈琼梅一、课时目标:1. 理解并掌握对数的运算性质,并能运用运算性质进行对数的有关运算.(重点) 2.能用换底公式将一般对数化成自然对数或常用对数解题.(难点)预习案阅读教材P 64~P 67“思考”的有关内容,完成下列问题: 1.对数的运算性质:如果0,0,1,0>>≠>N M a a ,那么(1)a log (MN)= ; (2)aMlog =N; (3)n a log M = . 2. 换底公式: (1) = log c b log c a (a >0,且a ≠1;c >0,且c ≠1); (2)log log m n a a nb b m =;(3) log a b ·log b a = (a >0,且a ≠1;b >0,且b ≠1).自测练习1.判断正误 (正确的打“√”,错误的打“×”):(1)log a (-2)+log a (-4) =log a 8 ( ) (2)log a b 2 =2log a b ( )(3)log a (M +N ) =log a M +log a N ( ) (4)log a M N=log a M ÷log a N ( )2. 若lg 2=a ,lg 3=b ,则log 2 3=________.互动探究 例1.求下列各式的值:(1)2log 32-log 3329+log 38-5 log 53; (2)lg 25+23lg 8+lg 5·lg 20+(lg 2)2.[变式训练1] 计算:(1)2log 122+log 123; (2)lg 500-lg 5; (3)已知lg 2=0.301 0,lg 3=0.477 1,求lg 45.例2. 已知log 189=a ,18b =5,则a ,b 表示log 3645的值.[变式训练2] (1) (log 29)·(log 34)=( )A .14B .12C .2D .4(2) 已知2m =5n =10,则1m +1n=________.例3. 一种放射性物质不断变化为其他物质,每经过一年剩余的质量约是原来的75%,估计约经过多少年,该物质的剩余量是原来的13(结果保留1个有效数字) (lg 2≈0.301 0,lg 3≈0.477 1)?[变式训练3] 抽气机每次抽出容器内空气的60%,要使容器内的空气少于原来的0.1%,则至少要抽几次?(lg 2≈0.301 0).课堂检测1.log 23·log 32的值为( )A .1B .-1C .2D .-2 2.设a >0,a ≠1,且x > y >0,n ≥2,n ∈N *,考虑下列等式:①(log a x )n =n log a x ; ②log a (xy )=(log a x )(log a y ); ③log a x y =log a x log a y ; ④log a nx =1nlog a x ; ⑤a log a x =x ;⑥log a (x +y )=log a x +log a y ; ⑦log a x -y x +y =-log a x +yx -y.其中正确等式的个数为( )A .2B .3C .4D .5 3.若3a =2,则2log 36-log 38=________.4.求下列各式的值:(1)lg 25+lg 2·lg 5+lg 2; (2)12lg 3249-43lg 8+lg 245; (3)log 535+2log 122-log 5150-log 514.2. 2. 2 对数函数及其性质 第1课时 对数函数的图象及性质学校:澜沧一中 学科:数学 年级:高一 主备教师:沈琼梅 参与教师:刘英华、单祖培、尹继叶、王丝然、张露平、樊明文 审定教师:沈琼梅一、 课时目标:1. 理解对数函数的概念.(易错点)2. 掌握对数函数的图象及性质.(重点、难点)预习案阅读教材P 70~P 71的有关内容,完成下列问题:1. 一般地,函数 叫做对数函数,其中x 是自变量,函数的定义域为 . 2 a >1 0< a<1定义域为 ,值域为 .自测练习1.下列函数中,是对数函数的是________(1) y =log a x (a >0,且a ≠1); (2) y =log 2 x +2; (3) y =8log 2 (x +1); (4) y =log x 6 (x >0,且x ≠1); (5) y =log 6x .2. 判断正误 (正确的打“√”,错误的打“×”): (1)若f (x )是对数函数,则f (1)=0 ( ) (2)函数y =log 2 x 在R 上是增函数 ( )(3)函数y =log a x (a >0,且a ≠1) 的图象一定位于y 轴的右侧 ( )互动探究当底数a 大小不定时,必须分“a >1”和“0< a < 1”两种情形讨论.对数函数y =log a x 的图象如图所示,由对数函数y =log a x 的图象与y =1相交于点(a ,1)可知:图中的底数的大小关系为0 < c < d < 1 < a < b .① 在x 轴上侧,图象从右到左相应的底数由大变小,即当a >1时,底越大,图象越靠近x 轴;② 在x 轴下侧,图象从下左到右相应的底数由大变小,即当0< a < 1时,底越小,图象越靠近x 轴. 例1.求下列函数的定义域:(1) y =lg (2-x ); (2) y =1log 3(3x -2); (3) y =log (2x -1) (-4x +8).y=log b x y=log c x[变式训练1] 函数y =lg (x +1)x -1的定义域是( )A .(-1,+∞)B .[-1,+∞)C .(-1,1)∪(1,+∞)D .[-1,1)∪(1,+∞) 例2. 画出下列函数的图象,并根据图象写出函数的定义域、值域以及单调区间:(1) y =log 3(x -2); (2) y =|x 21log |.[变式训练2] (1) 函数y =log 2|x |的图象大致是( )(2) 函数y=log a (2x -3)+1的图象恒过定点P ,则点P 的坐标是________.课堂检测1.下列函数是对数函数的是( )A .y =log a (2x ) (a >0,且a ≠1)B .y =log a (x 2+1) (a >0,且a ≠1)C .y =x a1log (a >0,且a ≠1) D .y =2lg x2.图中曲线是对数函数y =log a x 的图象,已知a 取3,43,35,110,则相应于曲线C 1,C 2,C 3,C 4的a 值依次为( )A .3,43,35,110B .3,43,110,35C . 43,3,35,110D . 43,3,110,353.函数y =log a (x -2) (a >0,且a ≠1)的图象恒过定点________. 4.求下列函数的定义域:(1) f (x )=lg (4-x )x -3; (2) y =log 0.1(4x -3).第2课时 对数函数及其性质的应用学校:澜沧一中 学科:数学 年级:高一 主备教师:沈琼梅 参与教师:刘英华、单祖培、尹继叶、王丝然、张露平、樊明文审定教师:沈琼梅一、课时目标:1. 了解指数函数y =a x (a >0,且a ≠1)与对数函数y =log a x (a >0,且a ≠1)互为反函数.(易混点) 2.理解并掌握对数函数的性质.(重点、难点)预习案 阅读教材P 72~P 73的有关内容,完成下列问题:1.对数函数log (0,1)a y x a a =>≠且和指数函数(0,1)x y a a a =>≠且互为 . 特点是: .2. 互为反函数的两个函数的图象关于直线 对称.3. 若函数y =f (x )图象上有一点 (a ,b ), 则 (b ,a ) 必在其反函数图象上.反之,若 (b ,a ) 在反函数图象上,则 (a ,b ) 必在原函数图象上.自测练习 1.(1)y =10x 的反函数是________; (2)y =x )54(的反函数是________; (3)y =x 31log 的反函数是________; (4)y =log 2 x 的反函数是________.2.若函数x y lg =与函数y =x a 的图象关于直线x y =对称,则a =______.互动探究例1.比较下列各组数的大小.(1)log 1245与log 1267; (2)log 123与log 153; (3)log a 2与log a 3; (4)log 120.4与log 40.6.[变式训练1] 设a =log 32,b =log 52,c =log 23,则( )A .a >c >bB .b >c >aC .c >b >aD .c >a >b例2. 解下列不等式:(1) log 2 (2x +3) > log 2 (5x -6); (2) log x 12 >1.[变式训练2] 若实数a 满足log a 23< 1,求a 的取值范围.例3. 已知函数f (x )=log a 1-mxx -1(a >0,且a ≠1,m ≠1) 是奇函数.(1)求实数m 的值; (2)探究函数f (x )在 (1,+∞) 上的单调性; (3)若a =2,试求函数f (x )在 [3,5] 上的值域.[变式训练3] 若函数f (x )=log a x (a >0,且a ≠1) 在区间 [a ,2a ] 上的最大值是最小值的3倍,求a 的值.课堂检测1.函数y =x 21log (x >0)的反函数是( )A .y =21x ,x >0 B .y =x )21(,x ∈R C .y =x 2,x ∈R D .y =2x ,x ∈R 2.函数y =log 3 x (1≤ x ≤ 9) 的值域为( )A .[0,+∞)B .RC .(-∞,2]D .[0,2]3.比较下列各组数的大小:(1)log 22________log 23; (2)log 32________1;(3)log 134________0;(4)log 43________log 34.4.若log a 25< 1 (a >0,且a ≠1),求a 的取值范围.2. 3 幂函数学校:澜沧一中 学科:数学 年级:高一 主备教师:沈琼梅 参与教师:刘英华、单祖培、尹继叶、王丝然、张露平、樊明文审定教师:沈琼梅一、课时目标:1. 了解幂函数的概念.(易错点)2.结合函数y =x ,y =x 2,y =x 3,y =x -1,y =21x 的图象,了解它们的变化情况.(重点)预习案阅读教材P 77~P 78的有关内容,完成下列问题:1.幂函数的概念:形如 的函数称为幂函数,其中 是自变量, 是常数.2321-1y =x3.(1)幂函数的图象不过第 象限,都过点 ; (2)当α>0时,幂函数在上是 ;当α< 0时,幂函数在上是 ;(3)当时,幂函数是 ;当时,幂函数是 .自测练习1.下列函数是幂函数的是________.①y =2x 2 ②y =2x ③y =x 3 ④y =x -1 2.如图所示是幂函数αx y =在第一象限的图象, 比较1,,,,,04321αααα的大小( )A .102431<<<<<ααααB .104321<<<<<αααα C .134210αααα<<<<< D .142310αααα<<<<< 互动探究例1.已知函数y =(m 2+2m -2) x m +2+2n -3是幂函数,求m ,n 的值.[变式训练1] 已知函数f (x )=(m 2+2m )xm 2+m -1,m 为何值时,f (x )是:(1)正比例函数? (2)反比例函数? (3)二次函数? (4)幂函数?例2. 已知幂函数的图象过点P ⎝⎛⎭⎫12,4. 讨论y =f (x )的定义域、值域、奇偶性、单调性,并画出草图.[0,)+∞(0,)+∞2,2α=-11,1,3,3α=-α[变式训练2] 已知函数y =32x .(1)求定义域; (2)判断奇偶性;(3)已知该函数在第一象限的图象如图所示,试补全图象,并由图象确定单调区间.例3. 比较下列各组数中两个数的大小.(1)5.0)52(与5.0)31(; (2) 1)32(--与1)53(--; (3) 43)32(与32)43(.[变式训练3] 比较大小:(1) 535.1________537.1; (2)0.71.5________0.61.5; (3) 32-2.2________32-8.1; (4)0.15-1.2________0.17-1.2;(5)0.20.6________0.30.4;(6) 87-9________76)98(.课堂检测1.下列函数中是幂函数的是( )A .y =x 2xB .y =2xC .y =x 2D .y =3x +22.函数y =35x 的图象大致是图中的( )3.下列结论中,正确的是( )A .幂函数的图象都通过点(0,0),(1,1)B .幂函数的图象可以出现在第四象限C .当幂指数α取1,3,12时,幂函数y =x α是增函数 D .当幂指数α=-1时,幂函数y =x α在定义域上是减函数4.比较下列各题中数值的大小:(1)1.33,1.43; (2)0.26-1,0.27-1; (3)(-5.2)2,(-5.3)2; (4)2,3,0.72.。
人教版高一数学必修一2.指数与指数幂的运算第一、二、三课时

2.当根式的被开方数的指数不能被根指数整除 时,根式也可以写成分数指数幂的形式.
2
如: 3 a2 a3;
1
5
b b 2 (b 0); 4 c 5 c 4 (c 0).
分数指数幂
2.1.1 指数与指数幂的运算
1)规定正数的正分数指数幂的意义:
m
a n n a m (a 0, m`n N ,且n 1)
生 物 体 内 碳14含 量 与 死 亡 年 数t之 间 的 关 系
P
(
1
)
t 5730
由 此 可 知 2:
当 生 物 死 亡 了1年 ,2年 ,10年 , ,10000年 后 , 该
生 物 体 内 碳14的 含 量P的 值 分 别 是
P
(
1
)
1 5730
,
2
P
(
1
)
2 5730
,
2
P
(
1
)
10 5730
3.求下列各式的值 : (1)6 ( x y)6 ; (2)3 (27); (3) ( 2 3)2 ; (4) x6 .
4.下 列 各 式 中,正 确 的 是( C )
A.6 (2)2 3 2 B.4 (3 )4 3
C .(3 2 )3 2 D.6 (2a 1)6 2a 1
讨论:5 2的结果?
2.1.1 指数与指数幂的运算
由上表不难发现: 当 2的不足近似值从小于 2的方向逼近 2时,
5 2的近似值从小于5 2的方向逼近5 2; 当 2的过剩近似值从大于 2的方向逼近 2时,
5 2的近似值从大于5 2的方向逼近5 2.
结论:一般地,无理指数幂a (a 0,是无理数)是一个确定
2.1.1有理指数幂教案

第二章 基本初等函数(Ⅰ)2.1指数函数2 .1.1 指数与指数幂的运算一.教学目标:1.知识与技能:(1)理解分数指数幂和根式的概念; (2)掌握分数指数幂和根式之间的互化; (3)掌握分数指数幂的运算性质;(4)培养学生观察分析、抽象等的能力. 2.过程与方法:通过与初中所学的知识进行类比,分数指数幂的概念,进而学习指数幂的性质. 3.情态与价值(1)培养学生观察分析,抽象的能力,渗透“转化”的数学思想;(2)通过运算训练,养成学生严谨治学,一丝不苟的学习习惯; (3)让学生体验数学的简洁美和统一美. 二.重点、难点1.教学重点:(1)分数指数幂和根式概念的理解; (2)掌握并运用分数指数幂的运算性质; 2.教学难点:分数指数幂及根式概念的理解 三.学法与教具1.学法:讲授法、讨论法、类比分析法及发现法2.教具:多媒体 四、教学设想:第一课时一、复习提问:什么是平方根?什么是立方根?一个数的平方根有几个,立方根呢?归纳:在初中的时候我们已经知道:若2x a =,则x 叫做a 的平方根.同理,若3x a =,则x 叫做a 的立方根.根据平方根、立方根的定义,正实数的平方根有两个,它们互为相反数,如4的平方根为2±,负数没有平方根,一个数的立方根只有一个,如―8的立方根为―2;零的平方根、立方根均为零. 二、新课讲解类比平方根、立方根的概念,归纳出n 次方根的概念.n 次方根:一般地,若nx a =,则x 叫做a 的n 次方根(throot ),其中n >1,且n ∈N*,当n 为偶数时,a 的n 次方根中,正数用n a 表示,如果是负数,用n a -表示,n a 叫做根式.n 为奇数时,a 的n 次方根用符号n a 表示,其中n 称为根指数,a 为被开方数. 类比平方根、立方根,猜想:当n 为偶数时,一个数的n 次方根有多少个?当n 为奇数时呢?n nn a n aa n a n a⎧⎪⎨±⎪⎩为奇数, 的次方根有一个,为为正数:为偶数, 的次方根有两个,为n n a n aa n a n ⎧⎪⎨⎪⎩为奇数, 的次方根只有一个,为为负数:为偶数, 的次方根不存在.零的n 次方根为零,记为00n =举例:16的次方根为2±,527527--的次方根为等等,而27-的4次方根不存在. 小结:一个数到底有没有n 次方根,我们一定先考虑被开方数到底是正数还是负数,还要分清n 为奇数和偶数两种情况.根据n 次方根的意义,可得:()n n a a =()n n a a =肯定成立,n n a 表示a n 的n 次方根,等式n n a a =一定成立吗?如果不一定成立,那么n na 等于什么?让学生注意讨论,n 为奇偶数和a 的符号,充分让学生分组讨论. 通过探究得到:n 为奇数,n na a =n 为偶数,,0||,0nn a a a a a a ≥⎧==⎨-<⎩如34334(3)273,(8)|8|8-=-=--=-=小结:当n 为偶数时,nna 化简得到结果先取绝对值,再在绝对值算具体的值,这样就避免出现错误:例题:求下列各式的值(1)33(1)(8)- 2(2)(10)- 44(3)(3)π-2(4)()a b -分析:当n 为偶数时,应先写||nna a =,然后再去绝对值. 思考:()nn nn a a =是否成立,举例说明. 课堂练习:1. 求出下列各式的值473473(1)(2)(2)(33)(1)(3)(33)a a a --≤-2.若2211,a a a a -+=-求的取值范围. 3.计算343334(8)(32)(23)-+---三.归纳小结:1.根式的概念:若n >1且*n N ∈,则n ,x a x a n 是的次方根,n 为奇数时,=n 为偶数时,n x a =±;2.掌握两个公式:(0),||(0)nnna a n a n a a a a ≥⎧==⎨-<⎩n为奇数时,()为偶数时,3.作业:课后习题2.1 A 组 第1题第二课时提问:1.习初中时的整数指数幂,运算性质?00,1(0),0n a a a a a a a =⋅⋅⋅⋅⋅=≠无意义1(0)n na a a -=≠;()m n m n m n mn a a a a a +⋅== (),()n m mn n n n a a ab a b ==什么叫实数?有理数,无理数统称实数.2.观察以下式子,并总结出规律:a >0 ① 1051025255()a a a a === ②884242()a a a a ===③1212343444()a a a a === ④5105102525()a a a a ===小结:当根式的被开方数的指数能被根指数整除时,根式可以写成分数作为指数的形式,(分数指数幂形式).根式的被开方数不能被根指数整除时,根式是否也可以写成分数指数幂的形式.如:2323(0)a a a ==> 12(0)b b b ==>5544(0)c c c ==>即:*(0,,1)m nmna a a n N n =>∈> 为此,我们规定正数的分数指数幂的意义为:*(0,,)m n m na a a m n N =>∈正数的定负分数指数幂的意义与负整数幂的意义相同.即:*1(0,,)m nm na a m n N a-=>∈规定:0的正分数指数幂等于0,0的负分数指数幂无意义.说明:规定好分数指数幂后,根式与分数指数幂是可以互换的,分数指数幂只是根式的一种新的写法,而不是111(0)n m m m ma a a a a =⋅⋅⋅⋅>由于整数指数幂,分数指数幂都有意义,因此,有理数指数幂是有意义的,整数指数幂的运算性质,可以推广到有理数指数幂,即:(1)(0,,)rsr sa a aa r s Q +⋅=>∈(2)()(0,,)r S rsa a a r s Q =>∈ (3)()(0,0,)rr ra b a b Q b r Q ⋅=>>∈若a >0,P 是一个无理数,则P 该如何理解?为了解决这个问题,引导学生先阅读课本P 62——P 62.即:2的不足近似值,从由小于2的方向逼近2,2的过剩近似值从大于2的方向逼近2.所以,当2不足近似值从小于2的方向逼近时,25的近似值从小于25的方向逼近25.当2的过剩似值从大于2的方向逼近2时,25的近似值从大于25的方向逼近25,(如课本图所示)所以,25是一个确定的实数.一般来说,无理数指数幂(0,)pa a p >是一个无理数是一个确定的实数,有理数指数幂的性质同样适用于无理数指数幂.无理指数幂的意义,是用有理指数幂的不足近似值和过剩近似值无限地逼近以确定大小.思考:32的含义是什么?由以上分析,可知道,有理数指数幂,无理数指数幂有意义,且它们运算性质相同,实数指数幂有意义,也有相同的运算性质,即:(0,,)r s r s a a a a r R s R +⋅=>∈∈ ()(0,,)r s rs a a a r R s R =>∈∈ ()(0,)r r r a b a b a r R ⋅=>∈3.例题 (1).(P 60,例2)求值 解:① 2223323338(2)224⨯====② 1112()21222125(5)555--⨯--====③ 5151(5)1()(2)2322----⨯-===④334()344162227()()()81338-⨯--=== (2).(P 60,例3)用分数指数幂的形式表或下列各式(a >0) 解:117333222.a a a a a a+=⋅== 22823222333a a a a aa+⋅⋅⋅==31442133332()aa a a a a a =⋅===分析:先把根式化为分数指数幂,再由运算性质来运算. 课堂练习:课后练习 第 1,2,3,4题 补充练习:1. 计算:122121(2)()248n n n ++-⋅的结果 2. 若13107310333,384,[()]n a a a a a -==⋅求的值小结:1.分数指数是根式的另一种写法. 2.无理数指数幂表示一个确定的实数.3.掌握好分数指数幂的运算性质,其与整数指数幂的运算性质是一致的. 作业: 习题 2.1 第2题第三课时一.教学目标1.知识与技能:(1)掌握根式与分数指数幂互化;(2)能熟练地运用有理指数幂运算性质进行化简,求值. 2.过程与方法:通过训练点评,让学生更能熟练指数幂运算性质. 3.情感、态度、价值观(1)培养学生观察、分析问题的能力;(2)培养学生严谨的思维和科学正确的计算能力. 二.重点、难点:1.重点:运用有理指数幂性质进行化简,求值. 2.难点:有理指数幂性质的灵活应用. 三.学法与教具:1.学法:讲授法、讨论法. 2.教具:投影仪 四.教学设想:1.复习分数指数幂的概念与其性质2.例题讲解 例1.(课本例4)计算下列各式(式中字母都是正数)(1)211511336622(2)(6)(3)a b a b a b -÷- (2)31884()m n - (先由学生观察以上两个式子的特征,然后分析、提问、解答)分析:四则运算的顺序是先算乘方,再算乘除,最后算加减,有括号的先算括号的. 整数幂的运算性质及运算规律扩充到分数指数幂后,其运算顺序仍符合我们以前的四则运算顺序.我们看到(1)小题是单项式的乘除运算;(2)小题是乘方形式的运算,它们应让如何计算呢?其实,第(1)小题是单项式的乘除法,可以用单项式的运算顺序进行.第(2)小题是乘方运算,可先按积的乘方计算,再按幂的乘方进行计算.解:(1)原式=211115326236[2(6)(3)]a b+-+-⨯-÷-=04ab =4a (2)原式=318884()()m n -=23m n - 例2.(课本例5)计算下列各式 (1)34(25125)25-÷ (2)232(.a a a a>0)分析:在第(1)小题中,只含有根式,且不是同类根式,比较难计算,但把根式先化为分数指数幂再计算,这样就简便多了,同样,第(2)小题也是先把根式转化为分数指数幂后再由运算法则计算.解:(1)原式= 111324(25125)25-÷= 231322(55)5-÷ = 2131322255---= 1655- = 655-(2)原式=12522652362132a aa a a a--===⋅小结:运算的结果不强求统一用哪一种形式表示,但不能同时含有根号和分数指数,也不能既有分母,又含有负指数. 课堂练习:化简:(1)52932232(9)(10)100-÷ (2)322322+-- (3)a aa a归纳小结:1. 熟练掌握有理指数幂的运算法则,化简的基础.2.含有根式的式子化简,一般要先把根式转化为分数指数幂后再计算. 作业:课后 习题2.1A 组 第4题B 组 第2题。
人教A版数学必修一2.1.1指数与指数幂的运算

② 3-2 2 + 3 (1- 2)3 + 4 (1- 2)4 = _____2_-__1.
2.1.1 │ 考点类析
[解析] ①8 (x-3)8=|x-3|,当 x≥3 时,原式=x-3; 当 x<3 时,原式=3-x.
所以8 (x-3)8=x3--3x,,xx≥<33. , ②因为 3-2 2=2-2 2+1=( 2)2-2 2+1=( 2-1)2, 所 以 3-2 2 + 3 (1- 2)3 + 4 (1- 2)4 = ( 2-1)2+ 3 (1- 2)3+ 4 (1- 2)4= 2-1+1- 2+ 2-1= 2-1.
2.1.1 │ 考点类析
[小结] 有理指数幂运算的基本原则和常规方法: (1)基本原则:式子里既有分数指数幂又有根式时,
一般把根式统一化为分数指数幂的形式,再用有理指数 幂的运算性质化简.
(2)常规方法:①化负指数幂为正指数幂;②化根式 为分数指数幂;③化小数为分数.
2.1.1 │ 考点类析
考点四 条件求值 重点探究型 [导入] 已知 x+1x=a(a≥2),如何求 x2+x12的值?
[ 解 析 ] (1)① 4 (-8)4 = | - 8| = 8 ;
②3 (-8)3=-8.
6 (2)①
1-π3 6=1-π3 =π3 -1;② 5
1-π3 5
=1-π3 .
2.1.1 │ 考点类析
(3)计算下列各式的值:
①8
x-3,x≥3,
(x-3)8=_3_-__x_,_x_<_3,
2.1.1 │ 考点类析
【变式】 (1)设 10m=2,10n=3,则 10-2m-10-n=_-_1_12_____.
[解析] 由 10m=2 得 10-2m=(101m)2=14,10 -n=110n=13, 所以 10-2m-10-n=14-13=-112.
最新-2021高中数学必修1课件:2.1.1 指数与指数幂的运算 第1课时 根式 精讲优练课型 精品

【典例】已知x∈[1,2],化简
=_______.
( 4 x 1)4 6 (x2 4x 4)3
【失误案例】
【错解分析】分析解题过程,你知道错在哪里吗? 提示:错误的根本原因是化简偶次根式 不是恒等变形.忽视了条件
6 x 26
1≤x≤2的限制.
【自我矫正】因为x∈[1,2],所以 ( 4 x 1)4 6 (x2 4x 4)3
(1)已知x6=2013,则x=
.
(2)已知x5=-2013,则x=
.
【解析】(1)由于6为偶数,所以x=±
(2)由于5为奇数,所以
6 2 013.
答案:
x 5 2 013 5 2 013.
1 6 2 0132 5 2 013
类型二 根式的化简与求值
【典例】化简:
1 1.
【解题探究】典例3 (中2 对于5)3分母( 3中2 含有5 )3根号的式子应如何进行化简?
【方法技巧】根式化简或求值的注意点 (1)解决根式的化简或求值问题,首先要分清根式为奇次根式还是偶次 根式,然后运用根式的性质进行化简或求值. (2)对于根式的运算还要注意变式,整体代换,以及平方差、立方差和 完全平方、完全立方公式的运用,做到化繁为简,必要时进行讨论.
【补偿训练】1.求下列各式的值:
=|3.14-π|+|33..1144 + π2|+=2π3..14 2
(2)原式=|m-n|+(m-n)=
2m n,m n,
0,
m<n.
类型三 有限制条件的根式运算
【典例】1.若x<0,则x+|x|+ x2 =______.
2.若代数式
有意义,x化简
2x 1+ 2 x
4x2 4x 1+24 x 24 .
指数与指数幂的运算习题

课外作业:课本P60B组第2题,《名师一号》 P43例4,变式4,P44第9,10题
指数式的计算与化简
2.1.1 指数与指数幂的运算
指数式的计算与化简,除了掌握定义、法则外,还 要掌握一些变形技巧.根据题目的不同结构特征,灵 活运用不同的技巧,才能做到运算合理准确快捷.
一、巧用乘法公式 回顾 (1)(a b)2 a2 2ab b2
基本 (2)a2 b2 (a b)(a b)
由于引入 负指数及分数 指数幂后,初 中的平方差、 立方差、完全 平方公式等, 有了新特征:
公式 (3)a3 b3 (a b)(a2 ab b2 )
如 : (a a1 )2 a2 2 a2;
1
11
1
a b (a 2 b 2 )(a 2 b 2 );
“整体代入”的办法
小结
2.1.1 指数与指数幂的运算
ห้องสมุดไป่ตู้
1、本节的化简、求值问题,要注意整体代 换,注意平方差、立方差、立方和等公式 的运用。 2、将指数合理拆分,进而因式分解是指数 运算中的常用技巧。 3、单项式乘以单项式、多项式乘以多项式 以及多项式除以单项式、多项式除以多项 式的运算都没有改变。
1
12
11
2
a b (a 3 b 3 )(a 3 a 3b 3 b 3 )等.
二、能力训练
2.1.1 指数与指数幂的运算
例1
1
已知 a 2
1
a 2
3,求下列各式的值
(1)a a1;
答案:
(2)a2 a2;
3
3
a2 a 2
(3) 1 1 .
a2 a 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3 n n n n n n n
a, a ≥ 0 −a, a < 0
(3) (−2)4 ;
4
(4) (3 − π)2
二.实数指数幂: (1)分数指数幂:
m
a n n a m (a>0,m,n∈N*,且 n>1)
王新敞
奎屯
新疆
要注意两点: 一是分数指数幂是根式的另一种表示形式; 二是根式与分数指数幂可以进行互 化.
a m a n a m n (m, n Q) (a m ) n a mn (m, n Q) (ab) a b (n Q )
n n n
王新敞
奎屯 新疆
说明:若 a>0,P 是一个无理数,则 a p 表示一个确定的实数,上述有 理指数幂的运算性质,对于无理数指数幂都适用 三、讲解例题:
1−a −1
1 −1
C. 6
D.2
例 5:计算:
-
1+ 2 −a 2
2
例 1:求值: 8 3 ,100 2 , ( ) 3 , ( ) 4 . 例 2:用分数指数幂的形式表示下列各式:
a2 a, a3 3 a2 , a a
3
1
1 4
16 81
3
(式中 a>0)
3
4
王新敞
奎屯
新疆
例 3:计算: (1 + 2) + (1 − 2)
4
例 4:已知x 2 +x −2 =2 2,且 x> 1,则x 2 -x −2 =() A.2 或-2 B.-2
(2).规定:(1) a
m n
1 a
m n
(a>0,m,n∈N*,且 n>1)
王新敞
奎屯
新疆
(2)0 的正分数指数幂等于 0.(3)0 的负分数指数幂无意义. 规定了分数指数幂的意义以后, 指数的概念就从整数推广到有理
数指数.当 a>0 时,整数指数幂的运算性质,对于有理指数幂也同样 适用.即对于任意有理数 r,s,均有下面的运算性质. (3).有理指数幂的运算性质:
