期末试卷2
八年级(下)数学期末试卷(2)

八年级(下)数学期末试卷(2)一.选择题(共11小题,满分33分,每小题3分)1.(3分)“漏壶”是一种古代计时器,如图所示.在壶内盛一定量的水,水从壶底的小孔漏出,壶内壁画有刻度,人们根据壶中水面的位置计算时间.用x表示漏水时间,y表示壶底到水面的高度,不考虑水量变化对压力的影响,下列图象能表示y与x对应关系的是()A.B.C..D.2.(3分)在一篇文章中,“的”、“地”、“得”三个字共出现100次.已知“的”和“地”的频率之和是0.7,那么“得”字出现的频数是()A.28B.30C.32D.343.(3分)甲、乙、丙、丁四位同学五次数学测验成绩统计如表.如果从这四位同学中,选出一位平均成绩较高且状态稳定的同学参加数学比赛,那么应选()甲乙丙丁平均数80858580方差42455459 A.甲B.乙C.丙D.丁4.(3分)下列二次根式中属于最简二次根式的是()A.B.C.D.5.(3分)下列各式中,无意义的是()A.B.C.D.6.(3分)若x+y=6,x2+y2=20,求xy的值是()A.6B.8C.26D.207.(3分)下列命题中,真命题是()A.任何数的零次幂都等于1B.对角线相等且垂直的四边形是正方形C.有一条边相等的两个等腰直角三角形全等D.有两直角边对应相等的两个直角三角形全等8.(3分)如图,将一副直角三角尺重叠摆放,使得60°角的顶点与等腰直角三角形的直角顶点重合,且DE⊥AB于点D,与BC交于点F,则∠DCF的度数为()A.20°B.15°C.30°D.45°9.(3分)如图,点E是Rt△ABC、Rt△ABD的斜边AB的中点,AC=BC,∠DBA=25°,则∠DCE的度数是()A.20°B.30°C.35°D.40°10.(3分)顺次联结四边形ABCD各边中点所形成的四边形是矩形,那么四边形ABCD是()A.平行四边形B.矩形C.菱形D.等腰梯形11.(3分)函数y=2x+3的图象可能是()A .B .C .D .二.填空题(共4小题,满分12分,每小题3分)12.(3分)小华在整理平行四边形、矩形、菱形、正方形的性质时,发现它们的对角线都具有同一性质是.13.(3分)在平行四边形ABCD 中,AB=3,BC=4,则平行四边形ABCD的周长等于.14.(3分)有5位教师和一群学生一起去公园,教师的全票票价是每人7元,学生票收半价.如果买门票共花费206.5元,那么学生有多少人?设学生有x人,填写下表:人数/人票价/元总票价/元教师学生根据题意,得方程,所以学生有人.15.(3分)直线y=﹣x+m与y=nx+4n(n≠0)的交点的横坐标为﹣2,则关于x的不等式﹣x﹣nx>4n﹣m的解集为.三.解答题(共4小题,满分30分)16.(11分)计算:(1);(2).17.(6分)如图,A,B,H是直线上的三个点,AC⊥l于点A,BD⊥l于点B,HC=HD,AB=5,AC=2,BD=3,求AH的长.18.(6分)如图,任意四边形ABCD中,AB=CD,M、N分别为BC、AD的中点.说明∠1与∠2的大小关系.19.(7分)排球垫球是体育中考的项目之一,下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.运动员甲测试成绩表测试序号12345678910成绩(分)7687758787(1)运动员甲测试成绩的众数为;运动员乙测试成绩的中位数为;运动员丙测试成绩的平均数为;(2)经计算三人成绩的方差分别为S甲2=0.8,S乙2=0.4,S丙2=0.6,如果在他们三人中选择一位垫球成绩较为稳定的接球能手作为自由人,则运动员更合适;(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)四.解答题(共3小题,满分23分)20.(7分)如图,四边形ABCD的对角线AC⊥BD于点E.点F为四边形ABCD外一点,且∠FCA=90°,BC平分∠DBF,∠CBF=∠DCB.(1)求证:四边形DBFC是菱形;(2)若AB=BC,∠F=45°,BD=2,则AC=.21.(8分)计算:(1)(+)÷﹣6;(2)﹣(1+)(2﹣).22.(8分)某城市有一类出租车,在5时到23时的时间段内运营,计费规定如下:行驶里程不超过3千米付费14元,超过3千米且不超过15千米的部分每千米付费2.50元;总里程超过15千米的部分每千米付费3.80元(等候时间管不计费).(1)该类出租车起步价为多少元?在多少千米内只收起步价?(2)某人乘该类出租车行驶了x千米,试写出当x(千米)超过3(千米)但不超过15(千米)时,乘车费用y(元)关于里程数x(千米)的函数解析式,并求当所付费用为26元时出租车行驶的里程数.(3)当乘车费用为82元时,出租车行驶了多少千米?五.解答题(共2小题,满分22分)23.(10分)(1)【探究发现】如图①,已知矩形ABCD的对角线AC的垂直平分线与边AD,BC分别交于点E,F.求证:四边形AFCE是菱形;(2)【类比应用】如图②,直线EF分别交矩形ABCD的边AD,BC于点E,F,将矩形ABCD沿EF翻折,使点C的对称点与点A重合,点D的对称点为D',若AB=3,BC=4,求四边形ABFE的周长;(3)【拓展延伸】如图③,直线EF分别交平行四边形ABCD的边AD,BC于点E,F,将平行四边形ABCD沿EF翻折,使点C的对称点与点A重合,点D的对称点为D',若,BC=4,∠C=45°,求EF的长.24.(12分)已知:在矩形ABCD中,AB=6,AD=2,P是BC边上的一个动点,将矩形ABCD折叠,使点A与点P重合,点D落在点G处,折痕为EF.(1)如图1,当点P与点C重合时,则线段EB=,EF=;(2)如图2,当点P与点B,C均不重合时,取EF的中点O,连接并延长PO与GF的延长线交于点M,连接PF,ME,MA.①求证:四边形MEPF是平行四边形;②当tan∠MAD=时,求四边形MEPF的面积.。
北师大版八年级(下)数学期末试卷(2)
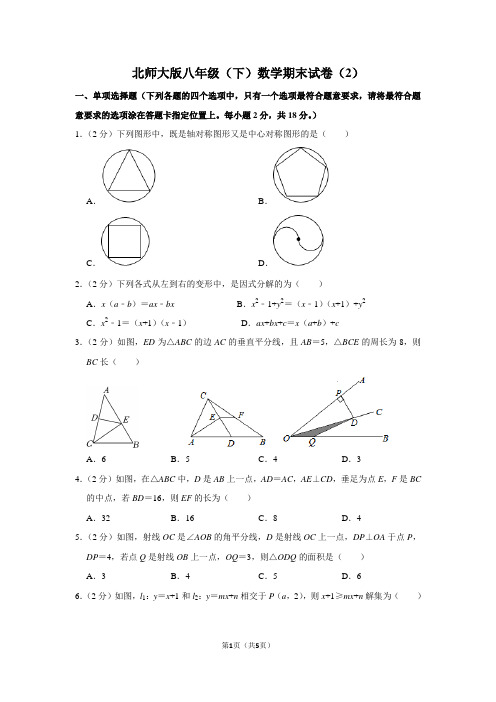
北师大版八年级(下)数学期末试卷(2)一、单项选择题(下列各题的四个选项中,只有一个选项最符合题意要求,请将最符合题意要求的选项涂在答题卡指定位置上。
每小题2分,共18分。
)1.(2分)下列图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.2.(2分)下列各式从左到右的变形中,是因式分解的为()A.x(a﹣b)=ax﹣bx B.x2﹣1+y2=(x﹣1)(x+1)+y2C.x2﹣1=(x+1)(x﹣1)D.ax+bx+c=x(a+b)+c3.(2分)如图,ED为△ABC的边AC的垂直平分线,且AB=5,△BCE的周长为8,则BC长()A.6B.5C.4D.34.(2分)如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为点E,F是BC 的中点,若BD=16,则EF的长为()A.32B.16C.8D.45.(2分)如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P,DP=4,若点Q是射线OB上一点,OQ=3,则△ODQ的面积是()A.3B.4C.5D.66.(2分)如图,l1:y=x+1和l2:y=mx+n相交于P(a,2),则x+1≥mx+n解集为()A.x>﹣1B.x<1C.x≥1D.x>a7.(2分)下列分式变形正确的是()A.B.C.D.8.(2分)若分式的值为正数,则x的取值范围是()A.x>﹣2B.x<1C.x>﹣2且x≠1D.x>19.(2分)已知2x﹣y=1,xy=2,则4x3y﹣4x2y2+xy3的值为()A.﹣2B.1C.﹣1D.2二、填空题(每题2分,共18分)10.(2分)多项式x2+mx+5因式分解得(x+5)(x+n),则m=.11.(2分)已知分式,当x=1时,分式无意义,则a=.12.(2分)已知一个多边形的内角和是外角和的3倍,则这个多边形为边形.13.(2分)如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=10,将△ABC沿CB 方向向右平移得到△DEF,若四边形ABED的面积为20,则平移距离为.14.(2分)如图,在▱ABCD中,DE平分∠ADC,交BC于点E,若AD=8,BE=3,则ABCD的周长是.15.(2分)已知关于x的不等式组有且仅有三个整数解,则a的取值范围是.16.(2分)一次函数y=(2m﹣1)x+2﹣m的图象经过第一、二、四象限,则m的取值范围为.17.(2分)如果关于x的方程﹣=1的解为负数,则m的取值范围是.18.(2分)如图,将两个全等的等腰直角三角形摆成如图所示的样子,其中AB=AC=AG =FG,AF、AG分别与BC交于D、E两点,将△ACE绕着点A顺时针旋转90°得到△ABH,①BH⊥BC;②DA平分∠HDE;③若BD=3,CE=4.则AB=6;④若AB=BE,S△ABD=S△ADE,其中正确的序号有.三、解答题(19题10分;20题10分;21题8分;22题8分;23题8分;24题10分;25题10分;)19.(10分)(1)因式分解:﹣8ax2+16axy﹣8ay2;(2)解不等式组.20.(10分)(1)解分式方程:=+1;(2)先化简(﹣)÷,然后从2,0,﹣1三个数中选一个合适的数代入化简后的结果中进行求值.21.(8分)如图,等腰直角△ABC中,∠ABC=90°,点P在AC上,将△ABP绕顶点B 沿顺时针方向旋转90°后得到△CBQ.当AB=4,AP=时,求PQ的大小.22.(8分)某村计划对面积为1600m2的农场进行数字化硬件改造升级,经投标由甲、乙两个工程队来完成.已知甲队每天能完成改造的面积是乙队每天能完成改造面积的3倍,如果两队各自独立完成面积为720m2区域的改造时,甲队比乙队少用8天.(1)求甲、乙两工程队每天各能完成多少面积的改造;(2)若甲队每天改造费用是2.7万元,乙队每天改造费用为0.8万元,要使这次改造的总费用不超过22万元,则至少应安排乙工程队改造多少天?23.(8分)如图,已知点A、B、C、D在一条直线上,BF、CE相交于O,AE=DF,∠E =∠F,OB=OC.(1)求证:△ACE≌△DBF;(2)如果把△DBF沿AD折翻折使点F落在点G,连接BE和CG.求证:四边形BGCE 是平行四边形.24.(10分)甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价的八折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价的九折优惠.设顾客预计累计购物x元(x>300).(1)请用含x的代数式分别表示顾客在两家超市购物所付的费用.(2)试比较顾客到哪家超市购物更优惠?说明你的理由.25.(10分)(1)【问题发现】小明遇到这样一个问题:如图1,△ABC是等边三角形,点D为BC的中点,且满足∠ADE=60°,DE交等边三角形外角平分线CE所在直线于点E,试探究AD与DE的数量关系.小明发现,过点D 作DF∥AC,交AB于点F,通过构造全等三角形,经过推理论证,能够使问题得到解决,请直接写出AD与DE的数量关系:;(2)【类比探究】如图2,当点D是线段BC上(除B,C外)任意一点时(其它条件不变),试猜想AD与DE之间的数量关系,并证明你的结论.(3)【拓展应用】当点D在线段BC的延长线上,且满足CD=BC(其它条件不变)时,请直接写出△ABC与△ADE的面积之比.。
北师版数学六年级上学期期末真题试卷2(含答案)

一、认真审题,正确填写1.在同一个圆中,所有半径都小学数学六年级上期期末考试()。
2.学生体质健康调研最新最新数据表明,全国小学生近视眼发病率为22.8%,22.8%表示()占()的22.8%。
3.晚上,淘气竖立拿着一根竹竿走在街道上,海气离街边的路灯越近,竹竿在灯下的影子就越()。
(填“短”“长”)4.()()()()() 3=0.75=%=6=: 4÷=折。
5.0.4∶0.12化简为最简单的整数比是(),比值是()。
6.一瓶饮料的净含量是600毫升,它的30%是()毫升。
7.如图中涂色部分的面积是6cm 2,那么整个圆的面积是()cm 2。
8.在一场篮球比赛中,甲队全场共得了98分,上半场和下半场所得分数的比是3∶4,甲队下半场得了()分。
9.用200粒种子做发芽试验,发芽率是92%,有()粒种子没有发芽。
10.学校操场地面上画了一个周长是31.4m 的圆,六(1)班全体同学站在圆上做游戏,老师站在圆内,他和每个同学之间的距离都相等。
老师和每个同学之间的距离是()m 。
11.《九章算术》是我国古代一部数学专著,它给出了相当完整的分数运算法则。
该书所介绍的分数除法的运算方法采用了先将两个分数通分、再使分子相除的方法,称之为“经分”。
即:a c ad bc adb d bd bd bc÷=÷=按照上述方法计算()()()()()()4375÷=÷=。
12.如图,自行车的链条每节长为2.5cm ,每两节链条相连接部分重叠的圆的直径为0.8厘米,这段链条共有50节。
则这段链条总长度为()厘米。
期末复习与测试二、精心挑透。
填对序号。
13.某班上女生人数占全班人数的817,女生人数与全班人数的比是()。
A.8∶17B.9∶17C.8∶9D.9∶814.如下图,圆心的位置是()4,4,下面四句话()是错误的。
A.点()4,3在圆周内B.点()1,4在圆周上C.点()6,7在圆周外D.点()7,6在圆周上15.周长相等的正方形、长方形、正三角形、圆,()的面积最大。
五年级(下)期末数学试卷2

五年级(下)期末数学试卷一、选择题(每题2分,共30分)1.(2分)下面算式的结果比小的是()A.B.C.D.2.(2分)在、、0.66、这四个数中,最小的数是()A.B.C.0.66D.3.(2分)在长方体(不包括正方体)的6个面中,最多有()个面是正方形。
A.2B.3C.4D.54.(2分)如图是由8个小正方体拼成的,如果拿走一个小正方体,它的表面积和原来相比()A.变小了B.变大了C.没有变化D.无法确定5.(2分)一个正方体的棱长总和是72厘米,它的底面积是()平方厘米。
A.6B.24C.36D.2166.(2分)下面说法正确的是()A.0的倒数是0B.假分数一定大于1C.0.25和4互为倒数D.分母为5的真分数有5个7.(2分)淘气看到洗发水瓶的包装上印有“净含量500mL”的字样,这个“500mL”是指()A.洗发水瓶的体积B.洗发水瓶内洗发水的体积C.洗发水瓶的容积D.洗发水的质量8.(2分)图书馆在公园西偏南30°的方向,那么公园在图书馆()的方向。
A.南偏西30°B.东偏北30°C.北偏东30°D.南偏西60°9.(2分)一个正方体的棱长扩大为原来的3倍,体积扩大为原来的()倍。
A.6B.9C.12D.2710.(2分)下面的图形能折成正方体的是()A.B.C.D.11.(2分)在一次单元测试中,笑笑语文、数学和英语三科的平均成绩是94分,语文和数学的平均成绩是92.5分、笑笑的英语成绩是()分。
A.93B.94C.96D.9712.(2分)在中,最简分数有()个。
A.1B.2C.3D.413.(2分)淘气要统计深圳和北京去年的1~6月份气温变化情况,用()统计图比较合适。
A.条形B.折线C.复式条形D.复式折线14.(2分)将四个长10cm,宽5cm,高3cm的长方体盒子用彩纸包在一起,最省包装纸的方法是()A.B.C.D.15.(2分)把米长的绳子平均分成6段,每段长()A.米B.米C.米D.二、填空题(每空1分,共18分)16.(2分)在横线上填上合适的单位名称。
浙江省杭州市六年级下学期数学期末试卷(二)及答案

浙江省杭州市六年级下学期数学期末试卷(二)一、基础知识填空题1.2022年亚运主场馆奥体博览城核心区占地A5B3C00平方米,A为最小非零自然数,B为最小合数,C既是奇数又是合数,这七位数是,四舍五入到万位约为万平方米.2.÷75=()=40%=16:=成()3.3小时45分=小时 1.6万千克=吨4.世界人均粮食占有量为360公斤,约为我国人均粮食占有量的45,我国的人均粮食占有量为公斤;世界人均粮食占有量比我国人均水平少%.5.一个长方形广场长是200m,在设计图上长5cm,这幅图的比例尺为,图上长方形面积为20cm2,实际有m2.6.现在微信支付简单便捷,下面是童童爸爸2月份的零钱收支明细,2月份爸爸一共支出了元,零钱比上个月多了元.日期2月5日2月14日2月19日2月23日2月26日收支明细/元+200.00﹣80.00﹣9.80+2.40+18.807.观察如图,第6个图有个圆点,第n个图比它前一个图多个圆点。
图序1234……点群……圆点数151430……8.有一些相同的小正方体构成的几何体,从前面和右边看都是,则相同的小正方体最多有个,最少有个.9.一个长方体的长宽高分别为8cm,4cm,4cm,把它分成两个棱长为4cm的正方体,总表面积比原来(填“增加”或“减少”)了cm2.10.9个完全相同的小长方形围成一个大长方形(如图),那么小长方形长和宽的比是,大长方形长和宽的比是.二、判断题11.一个商品降价20%,就是打二折出售.()12.比例中,两内项互为倒数,则两外项之积一定是1.()13.2019=3×673,所以,2019的最大因数是673.()14.长、宽、高为10cm,8cm,1cm长方体刚好可放10个棱长为2cm的正方体.()15.小明吃了一个蛋糕的四分之一,小亮吃了剩下的25%,他们吃的一样多.()三、选择题16.一个三角形的三个内角的度数比是2:a:5,当a为()它是一个直角三角形.A.2B.5C.2或5D.3或717.把6支铅笔放入3个笔筒,错误的是()A.存在1个笔筒至少有2支铅笔B.可能有1笔筒有4支铅笔C.总有1个笔筒至少有3支铅笔D.可能会有2个笔筒均有1支铅笔18.把一个体积为9.42立方分米的圆锥放入底面半径为4分米的圆柱形装水容器中(水浸没且无溢出),水面上升了多少分米,列式正确的是()A.9.42÷3÷(3.14×4×4)B.9.42÷(3.14×4×4)C.9.42×3÷(3.14×4×4)D.9.42×9÷(3.14×4×4)19.如图,正方形ABCD和长方形BDFE哪个面积更大()A.长方形B.正方形C.一样大D.无法比较20.图中能作为圆柱侧面展开图的有()个A.1B.2C.3D.4四、基本技能21.直接写出得数2019﹣128=10﹣0.86=20×0.8=100÷20%=10÷0.5=58﹣0.375=59×0.81=52﹣32=0.125×5×0.8=13÷91= 3.14×8= 4.5﹣4.5÷15=6﹣2920=23×98=45÷32%=34×8÷34×8=22.递等式计算(1)828﹣828÷23(2)18÷45+40×0.35(3)(0.52+725)÷23﹣1423.简便计算(要求写出简算过程)(1)25−0.27+85−0.13(2)817÷23+123×917(3)2017÷2018201924.求未知数x(1)x﹣25%x=1.25(2)34(x﹣8)=32(3)56:x=225:1.8五、操作题25.(1)A点的位置为(,),画出绕A点逆时针旋转90°后得到的图形.(2)按1:2的比画出原三角形变化后的图形.26.在如图的长方形中画一个最大的半圆,并涂上阴影,再计算空白部分的面积.六、图形计算27.分别绕AB和AC边旋转得到的圆锥体积相差多少.28.正方形边长8cm,求阴影部分面积.七、看图填空29.如图是打国际长途电话所需付的电话费与通话时间之间的关系图.(1)打2分钟需要元电话费,3分钟以上每分钟元.(2)打6分钟需要元,10.4元打了分钟.八、综合应用30.修一条全长2400米的小路,前6天完成了75%,每天完成多少米?31.明明读一本书,每天读20页,15天读完.如果每天读25页,可提前几天看完?32.2019年1月2日,中国自行研造的“复兴号”动车首次实现时速350千米自动驾驶功能,从杭州到上海共210km,比以前乘坐200km/h的动车,可节约多少小时?33.要从含盐12.5%的盐水40千克中蒸去多少水分才能制出含盐20%的盐水?34.红领巾是少先队员的标志.小号红领巾是底边和腰长分别为1m和0.6m的等腰三角形,大号红领巾是小号红领巾按一定的比例放大,已知大号红领巾底边长1.2m,求腰长?(用比例解)35.足球,2019年纳入杭州市体测项目了!根据表中文件说明,测试距离(起点线至终点)为多少米?36.一个圆锥形的沙堆,底面直径是4米、高1.5米.用这堆沙子铺在宽10米,厚5厘米的路上,能铺多长?37.自2019年起,个人所得税又有新政策了,除了扣除5000元的个人免征额后,淙淙爸爸还可享受专项附加扣除项(如图),如果他1月份工资为11000元,根据新政策,他又可少缴纳多少个人所得税(剩余部分按3%税率交税)?附加扣除子女教育赡养老人额度1000元2000元38.氧气占空气含量的21%,人呼吸时吸进氧气,呼出二氧化碳等废气,每分钟大约消耗氧气1.2L.把一个人关在1立方米的密闭空间内,1小时后氧气浓度为百分之几?39.王大伯准备用12米长的篱笆围成一面靠墙的长方形菜地(如图,长和宽均取整数),这块菜地最大可以有多少平方米?请写出思考过程.答案解析部分1.【答案】1543900;154【解析】【解答】2022年亚运主场馆奥体博览城核心区占地A5B3C00平方米,A为最小非零自然数,B为最小合数,C既是奇数又是合数,这七位数是1543900,四舍五入到万位约为154万平方米。
2021-2022学年部编版六年级下册期末考试语文试卷2

……装…………○_______姓名__________班……订…………○…………绝密★启用前 2021-2022学年部编版六年级下册期末考试语文试卷2 试卷副标题 注意事项: 1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上 第I 卷(选择题) 请点击修改第I 卷的文字说明 第II 卷(非选择题) 请点击修改第II 卷的文字说明 一、书写 1.看拼音,写词语。
láo dāo kū qì tī chú dǎo méi hè nián wū yā tūn yàn bǎi tān 二、信息匹配 2.在加点字的正确读音下画“____”。
汤匙.(chí shí) 唾.沫(tuò chuí) 肿.胀(zhǒng zǒng ) 嘟囔.(náng nang ) 搁.板(gē gé) 黄焖.鸡(mēn mèn ) 3.选词填空。
A .闲在 B .自在 (1)靠南墙根种了半圈南瓜,一棵棵像绿色的龙蛇,蔓儿( )地顺着木棍爬到墙上,向墙外伸头探脑。
(2)腊月和正月,在农村正是大家最( )的时候。
A .何况 B .奈何 (3)桌上那大青花瓷碗中的半碗陈腊肉,八儿的爹同妈也都( )它下不来。
(4)从古以来的先贤圣人,还需要勤奋学习,( )是普通之人呢! 三、填空题4.比一比,再组词。
便( ) 嚷( ) 搂( ) 展( ) 鞭( ) 壤( ) 篓( ) 碾( ) 5.把下列词语补充完整,并选词填空。
势不( )( ) 心( )肉( ) ( )( )不安 自作( )( ) 不假( )( ) ( )( )澎湃 (1)小强不小心打碎了玻璃窗,见老师来了,立即( )起来。
(2)这次篮球联赛,红队在最后关头转败为胜,( )。
6.根据课文内容填空。
1.《腊八粥》这篇课文围绕着_________展开故事情节,通过对八儿与母亲的描写,充分体现了八儿对腊八粥的______与_______,字里行间流露着浓浓的________,为人们展现了一幅淳朴、和睦、温馨的图景。
广东省佛山市2022-2023学年三年级上学期语文期末试卷(含答案)2

广东省佛山市2022-2023学年三年级上学期语文期末试卷一、识字加油站。
(20分)1.读拼音,写词语。
chūxiàhuāng yěbào yǔkělián xiéyáng2.比一比,再组词。
露装烈惜霜袋列蜡3.填空“圈”用部首查字法查字典,应先查部首,再查画。
它有两个读音,读“quān”时可组词,读“juàn”时可组词。
二、词句段运用。
(28分)4.我能把词语补充完整,再按要求填空。
(1)一正大一七八四八红张舞窗明目睹赤(2)我发现第一行的成语都含有数字,我能写出一个带“百”的成语:(3)形容房间明亮,陈设整洁的词语是5.按要求完成句子(1)照样子,写句子。
例:王老师急得直跺脚。
那机器的声音大得。
(2)请你用修改符号修改病句。
陈老师让我把不正确的错别字改正过来。
(3)今天的雨下得真大!(围绕开头,写一段话。
)6.日积月累。
(1),有礼者敬人。
——《孟子》(2)二人同心,。
(3)停车坐爱枫林晚,。
(4)叶绍翁看到篱笆下的灯火,想起了童年夜捉蟋蟀的美好时光,便吟诵“,。
”(5)金秋的阳光,酒在树叶上,洒在花瓣上...秋天来了,例如秋高气爽、、,还想起了苏轼的那句“一年好景君须记,。
”三、阅读与鉴赏。
(22分)阅读读不完的大书(节选)我最喜爱的,是我家屋后的两丛竹子和一株棕榈。
竹子长得快,雨后春笋,没几天就长得和我一样高了。
微风吹来,沙沙的竹叶声,大蒲扇似的叶子在风中摇摆,一副超凡脱俗的样子。
在秋高气爽的日子里,它倒映在池塘的水中。
小鱼在倒影间游玩,又是另一种境界。
7.这段话是围绕哪句话写的?请用横线画出来。
8.请从文中找出能概括竹子和棕榈特点的词语,填在横线上。
竹子:棕榈:9.文中画“——”的句子中,“它”指的是。
小鱼在“它”的倒影间游玩,多有趣啊!10.“微风吹来,沙沙的竹叶声,如同温柔的细语。
”这句话运用了的修辞手法,把比作,写出了竹叶声音的轻柔,表达了作者对竹子的之情。
2022-2023学年辽宁省沈阳市三年级下册数学期末检测试卷(卷二)含解析

2022-2023学年辽宁省沈阳市三年级下册数学期末检测试卷(卷二)一、判断对错。
(对的打“√”,错的打“×”)(5分)1.(1分)40×56与560×4的积相等。
2.(1分)读作:五分之八..3.(1分)1吨=1000千克..4.(1分)边长是4dm的正方形,周长和面积相等.5.(1分)分母相同的两个分数,分子大的那个分数比较大。
二、选一选。
(将正确答案的字母涂黑)(10分)6.(2分)估算6□×3□的积是()A.三位数B.四位数C.可能是三位数或四位数7.(2分)一个正方形的边长是5分米,它的面积是()平方分米。
A.10B.20C.258.(2分)一只母鸡大约重2()A.克B.千克C.吨9.(2分)如图,涂色部分占整个长方形的()A.B.C.10.(2分)下面汉字,()组都是轴对称图形。
A.丰田B.儿童C.春天三、填空。
(第7题2分,其余每空1分,共20分)11.(2分)4000平方分米=平方米5千克﹣250克=克12.(2分)□83÷5,要使商是两位数,□里填,要使商是三位数,□里最小填。
13.(2分)把一个蛋糕平均分成8份,每份是这个蛋糕的,5份是这个蛋糕的。
14.(4分)在横线上填合适的单位。
(1)一颗葡萄大约重4(2)淘气朗读一篇课文用了3(3)数学书封面的面积约500(4)教室门的面积约215.(1分)爸爸驾车从博罗出发,到广州大学城要2时30分,如果爸爸想要9:00到达,他最迟就要出发。
16.(2分)一个长方形的周长是36厘米,它的长是12厘米,宽是厘米,它的面积是平方厘米。
17.(2分)在横线上填“>”“<”或“=”。
(1)4090克44千克(2)25×4040×25(3)800dm 280m 2(4)18.(2分)□÷6=14……〇,〇里是,这时的□是。
19.(2分)钟面上的分针的运动属于现象,拉动抽屉的运动属于现象。
部编版二年级语文下册期末试卷 附答案 (2)

部编版二年级语文下册期末教学质量检测试卷温馨提示:请注意书写工整,卷面整洁。
卷面分4分将计入总分。
一、读拼音,写字词。
(13分)x ún zh ǎo w ēn nu ǎn tu án yu án b ì k ōng r ú x ǐyu àn y ì s ài p ǎo h ài p à w áng y áng b ǔ l áom ào y óu j ú b āng zh ù 雷锋叔叔 着大雨,跑到 ,把钱寄给灾区需要 的人。
二、字词乐园。
(19分)1.圈出每组加点字中读音不同的一个词语。
(3分)◎漂.泊 漂.浮 漂.移 漂.亮 ◎尽.管 尽.兴 尽.头 山穷水尽.◎倒.下 倒.立 倒.退 倒.背如流 2.读一读,连一连。
(8分)3.选字组词,在正确的字上画“√”。
(8分)(沟 钩)子 (源 原)头 (张 涨)潮 (体 休)息(梅 海)花 (仙 灿)烂 (坟 蚊)墓 (平 苹)果三、字词句运用。
(25分)年迈的晶莹的弯弯的奔腾的 露珠 江河 大娘 小路 滋润 迎接 饲养 播撒 大地 鸽子 草籽 客人四、 1.把你积累的词语写下来。
(9分)(1)形容生气:、、(2)形容高兴:、、(3)形容难过:、、2.查字典,按要求填空。
(8分)3.把下面的每组词语连成一句话(只写序号),并加上标点。
(4分)①拿着②公文包③爸爸④上班⑤去公司①小泡泡②一连串的③鱼儿④轻轻地⑤吐出了4.照样子,写句子。
(4分)例:门前开着鲜花。
门前开着一大片五颜六色的鲜花。
(1)树林里飞来了鸟。
树林里飞来了鸟。
(2)小河里游着鱼。
小河里游着鱼。
例:最后一个太阳害怕极了....地躲进了大海里。
....,慌慌张张(3)小红高兴极了....,跑进了教室。
(4)中午回到家,我很饿..,端起碗就吃起来。
浙江省杭州市2021-2022学年四年级上学期语文期末试卷(含答案)2

浙江省杭州市2021-2022学年四年级上学期语文期末试卷一、积累与运用(30分)1.研学标语。
学校电子屏滚动播放着:“博学之,审问之,慎思之,明辨之,笃行之。
——《礼记》”请你将它抄写在下面的空白书签中,做到正确、端正、整洁。
◎字的中心要在横格的中线上,保持水平。
◎字距要差不多,标点符号和字之间也要保持一定的距离。
◎注意提高书写的速度。
____________________________________________________________________________________________ 2.研学倡议。
周一升旗仪式上,校长宣读了研学倡议书,请你根据拼音在括号里写出相应的词语。
亲爱的同学们:研学旅行就是探索世界的ào mì 。
以自然为师,领略qí guān 之瑰丽;以历史为师,树立jiān dìng 的理想bào fù ;以伟人为师,huò dé 精神之gǔwǔ ……也许一路奔波会让我们jīng pí lì jié ,别怕!成长的道路就是用汗水guàn gài成的,让我们带着yīn qiè 的希望一路探索,一路chuàng zào 吧!爱你们的校长2022年1月1日3.本次研学活动的开幕式,平时默默无闻的小明____地____,担任了主持人的角色。
”填入句子合适的一项是()A.开绿灯挑大梁B.破天荒打头阵C.开绿灯占上风D.破天荒挑大梁4.“为了筹集更多的研学基金,学校组织了‘研学义卖’活动,同学们,想出了很多办法招揽顾客。
”句子中成语运用合适的一项是()A.神机妙算B.威风凛凛C.各显神通D.容光焕发5.同学们纷纷为自己的研学小组取了名字,下列选项中读音和字形完全正确一项是()A.花卉研究组(huì)攀登者小队B.花蕊小队(xīn)爬山虎小队C.田埂探秘组(gěn)豌豆侠小队D.韭菜观测组(jiǔ)水蹈实验组6.植物园里,芬芳艳丽的玫瑰园旁是一片不起眼但有药用价值的金银花,大家不禁感叹道:“____。
七年级数学上册期末考试试题2(含答案)

人教版七年级上数学期末试卷(时间:90分钟,满分100分)一、认真填一填(每题3分,共30分)1.实施西部大开发是党中央面向21世纪的重大战略决策,我国西部地区的面积为6400000平方千米,可用科学记数法将这个数字表示为 平方千米.2.下表是我国几个城市某年一月份的平均气温:把它们的平均气温按从高到低的顺序排列为: .3.绝对值大于1而小于4的整数有 . 4.9时45分时,时钟的时针与分针的夹角是 .5.如下图已知线段AD=16cm,线段AC=BD=10cm,E,F 分别是AB,CD 的中点,则EF 长为 .6.如果x=2是方程mx-1=2的解,那么m= . 7.如下图,从点A 到B 有a ,b ,c 三条通道,最近的一条 通道是 ,这是因为 .8. 某校女生占全体学生会数的52%,比男生多80人。
若设这个学校的学生数为x ,那么可出列方程 .9. 202135,3o αα'''∠=∠=则 . 10. 若=+=++-b a b a 那么,02)1(2 .二、仔细选一选(每题3分,共15分)请将正确答案的代号字母填入题后的括号内.11.F E BC DA B12.有下列四种说法:①锐角的补角一定是钝角;②一个角的补角一定大于这个角;③如果两个角是同一个角的补角,那么它们相等;④锐角和钝角互补.其中正确的是( )A .①② B. ①③ C. ①②③ D. ①②③④ 13. 如果n 是正整数,那么])1(1[n n --的值( )A .一定是零 B.一定是偶数 C.一定是奇数 D.是零或偶数 14.如果a,b 互为相反数,x,y 互为倒数,则()1742a b xy ++的值是( )A .2 B. 3 C. 3.5 D. 415.右下图反映的是地球上七大洲的面积占陆地总面积的百分比,某同学根据右下图得出下列四个结论:①七大洲中面积最大的是亚洲;②南美洲、北美洲、非洲三大州面积的和 约占陆地总面积的50%;③非洲约占陆地总面积的20%; ④南美洲面积是大洋洲面积的2倍. 你认为上述四个结论中正确的为( )A .①② B. ①④ C. ①②④ D. ①②③④ 三、用心做一做16.(6分)22138(3)2()42()423-÷⨯-++÷-17.(6分)解方程2151136x x +--=29.3%20.2%北美洲16.1%南美洲南极洲18.(8分)请你来做主:小明家搬了新居要购买新冰箱,小明和妈妈在商场看中了甲、乙两种冰箱.其中,甲冰箱的价格为2100元,日耗电量为1度;乙冰箱是节能型新产品,价格为2220元,日耗电量为0.5度,并且两种冰箱的效果是相同的.老板说甲冰箱可以打折,但是乙冰箱不能打折,请你就价格方面计算说明,甲冰箱至少打几折时购买甲冰箱比较合算?(每度电0.5元,两种冰箱的使用寿命均为10年,平均每年使用300天)19.(10分)画图说明题 (1) 作∠AOB=90;(2) 在∠AOB 内部任意画一条射线OP ; (3) 画∠AOP 的平分线OM ,∠BOP 的平分线ON ; (4) 用量角器量得∠MON= . 试用几何方法说明你所得结果的正确性.20.( 8分)将连续的奇数1,3,5,7,9…,排成如下的数表: (1)十字框中的五个数的平均数与15有什么关系?(2)若将十字框上下左右平移,可框住另外的五个数,这五个数的和能等于315吗?若能,请求出这五个数;若不能,请说明理由.353121119121.(9分)牛奶加工厂现有鲜奶8吨,若在市场上直接销售鲜奶(每天可销售8吨),每吨可获利润500元;制成酸奶销售,每加工1吨鲜奶可获利润1200元;制成奶片销售,每加工1吨鲜奶可获利润2000元.该厂的生产能力是:若制酸奶,每天可加工3吨鲜奶;若制奶片,每天可加工1吨鲜奶;受人员和设备限制,两种加工方式不可同时进行,受气温条件限制,这批牛奶必须在4天内全部销售或加工完毕.请你帮牛奶加工厂设计一种方案,使这8吨鲜奶既能在4天内全部销售或加工完毕,又能获得你认为最多的利润.22.(8分)观察下图,回答下列问题:(1)在∠AOB 内部画1条射线OC ,则图中有 个不同的角; (2)在∠AOB 内部画2条射线OC ,OD ,则图中有 个不同的角; (3)在∠AOB 内部画3条射线OC ,OD ,OE 则图中有 个不同的角; (4)在∠AOB 内部画10条射线OC ,OD ,OE …则图中有 个不同的角; (5)在∠AOB 内部画n 条射线OC ,OD ,OE …则图中有个不同的角;(1) (2) (3)B B七年级上数学参考答案及评分意见一、认真填一填(每题3分,共30分)1.6.4×1062.13.1>3.8>2.4>-4.6>-19.4 3.±2,±3 4.22.5° 5.10cm 6.327.b ,两点之间线段最短 7.2 8. 80)52.01(52.0=--x x 9. 616'45'' 10.-1 二、仔细选一选(每题3分,共15分)11. A 12. B 13. D 14. C 15. D 三、用心做一做16.解: 22138(3)2()42()423-÷⨯-++÷-4339()44()928=⨯⨯-++⨯- ………………………………………………(3分)3642322=-+-=--72=- …………………………………………………………………………(6分)17.解:2151136x x +--= 去分母,得 2(21)(51)6x x +--=, ………………………………………(2分) 去括号,得 42516x x +-+=, ……………………………………………(4分) 移项及合并,得 3x -=,系数化为1,得 3x =-. ……………………………………………………(6分) 18.解:设甲冰箱至少打x 折时购买甲冰箱比较合算,依题意,得2100×10x+10×300×1×0.5=2220+10×300×0.5×0.5, 解这个方程,得 x=7.答:设甲冰箱至少打7折时购买甲冰箱比较合算.……………………………(8分) 19.画图说明题(1)略.………………………………………………………………………………(1分) (2)略.………………………………………………………………………………(3分)(3)略.………………………………………………………………………………(5分)(4)45°. …………………………………………………………………………(7分)下面用几何方法说明所得结果的正确性:因为∠POB+∠POA=∠AOB=90°,∠POM=12∠POB,∠PON=12∠POA,……………………………………(8分)所以∠POM+∠PON=12(∠POB+∠POA)=12∠AOB=12×90°=45°. ………(10分)20.(1)十字框中的五个数的平均数为15;………………………………………(2分)(2)十字框框住的五个数的和能等于315.……………………………………(3分)观察可知,同一行左右相邻两个数相差为2,同一列上下相邻两个数相差为10,因此,若设十字框中间的数为x,则十字框框住的五个数的和为:(x-2)+x+(x+2)+(x-10)+(x+10)=5x即十字框框住的五个数的和一定能被5整除。
人教版六年级数学上册期末试卷 附答案 (2)

人教版六年级数学上册期末综合素质达标一、填空。
(第5题2分,其余每空1分,共25分) 1. 57×( )=( )×12=29÷( )=0. 25×( )=1 2.将8 cm ∶3.2 dm 化成最简整数比是( ),如果将这个最简整数比的前项加上3,要使比值不变,后项应加上( )。
3.在○里填上“>”“<”或“=”。
78×910○910 47÷89○47 89÷23○150%×89 1320÷14○1320÷4 4.比5 m 多15是( )m ;24 t 比( )t 多20%;比200 kg 少25%是( )kg ;一个数增加它的14是200,这个数减少它的30%是( )。
5. 小玲从家出发,先向( )偏( )( )°方向走( )m 到商场,再向( )偏( )( )°方向走( )m 到书店。
6.学校将360本作业本按3∶5分给四年级和六年级,四年级分得这些作业本的( )%,六年级比四年级多分到( )本。
7.在一个周长是16厘米的正方形内画一个最大的圆,圆规两脚叉开的距离是( )厘米,圆的周长是( )厘米,面积是( )平方厘米。
8.一项工程,甲、乙两队合作需要10天完成,甲队单独做需要15天完成。
两队合作6天后,余下的甲队独做,还需要( )天完成任务。
9.张师傅加工一批零件,在已加工的80个零件中,经查验有8个不合格,已经加工的零件合格率是( )%。
后来改进方法,他又加工了140个零件,这时加工的全部零件合格率达到95%,后来加工的零件中不合格的有( )个。
10.瑞士数学教师巴尔末成功地从光谱数据95、1612、2521、3632、…中得到巴尔末公式,从而打开了光谱奥妙的大门。
按照这种规律写出的第7个数是( )。
二、选择。
(将正确答案的字母填在括号里)(每题1分,共8分)1.一批货物,第一次运走总量的14,第二次运走余下的12,哪次运走的多些?( )。
部编版五年级语文下册期末试卷 附答案 (2)

部编版五年级语文下册期末试卷积累与运用(39分)1.根据拼音写词语,做到规范、端正、整洁。
(5分)2022年春节,我区出现了新冠肺炎确诊病例,在这万分jǐn jí ()的时刻,医护人员和志愿者逆行而上,bēn fù()抗疫前线,他们为人民筑起了安全pínɡ zhànɡ(),让病患尽快huī fù()了健康。
全区人民tuán jié()一心,每个人都为抗击疫情贡献着自己的力量。
2.先补充词语,再选词填空,将序号写在句中横线上。
(10分)①摩拳()掌①手()眼快①风平浪()①情不自()①跃跃()试①哭()不得①一针见()①出谋划()第1句:在神舟十三号航天员翟志刚、王亚平、叶光富顺利出舱的那一刻,人们地欢呼起来。
第2句:足球比赛进入到白热化阶段,只见对方球员拔脚怒射,我方守门员地扑住了这个险球。
3.选择。
(18分)(1)下面词语中,加点字读音完全正确的一项是()。
A.调.度(tiáo)养尊处.优(chǔ)B.难堪.(kān)船艄.(xiāo)C.由衷.(zhōnɡ)簇.拥(cù)D.停泊.(pō)吆.喝(yāo)(2)下面词语中,书写完全正确的一项是()。
A.蚂蚱武艺锻练喉咙B.衔接放肆遮掩桅杆C.欺负诚认慈祥熟练D.引荐笼罩享乐姆指(3)下列每组词语中,加点字的意思不同的是()。
A.吾盾之坚.坚.固B.道.旁李道.路C.陷.子之盾缺陷.(4)爷爷写了两幅扇面送给属虎的儿孙:他用()写“生龙活虎”祝小明充满活力;用()写“如虎添翼”祝小明爸爸的公司引进人才后实力倍增。
A.小篆B.隶书C.楷书(5)本学期,同学们积累了三个与“看”有关的词语,请为下面三句话选择恰当的词语。
A.瞄准B.审视C.远眺第1句:负责丰台站改造项目的总工程师()着眼前的施工图纸,生怕忽视了某个细节。
第2句:出游赏秋、登高()、观赏菊花、吃重阳糕、饮菊花酒等,都是重阳节的习俗。
二年级下册数学期末试卷附完整答案【历年真题】-(2)

北师大版二年级下册数学期末试卷一.选择题(共6题, 共12分)1.小明刷牙大约要用3〔〕。
A.小时B.分C.秒2.比699大1的数是〔〕。
A.698B.600C.7003.80-〔27+36〕=〔〕A.17B.53C.89D.634.28个人去旅游, 有6辆小轿车, 每辆小轿车可以做4个人, 请问剩下〔〕个人无法做小轿车。
A.4B.14C.8D.25.31÷7的余数与下面〔〕中的余数相同。
A.40÷7B.47÷8C.39÷66.12-3×4的得数是〔〕。
A.0B.63C.36二.判断题(共6题, 共18分)1.55÷8=7……1。
〔〕2.□×7<45, □里只能填6。
〔〕3.12+35÷7=19。
〔〕4.验算有余数的除法, 可以用商乘除数再加上余数。
〔〕5.把3+5=8和8×4=32改成一道两步计算的算式是〔3+5〕×4。
〔〕6.49÷8=5……9。
〔〕三.填空题(共6题, 共15分)1.填上适当的数。
〔〕÷6=8……〔〕〔〕÷〔〕=4 (7)2.分一分, 填一填。
〔1〕13个, 每人分5个, 可以分给〔〕人, 还剩〔〕个。
〔2〕13个, 平均分给6人, 每人分到〔〕个, 还剩〔〕个。
3.□÷9=4……○, 当○最大时, □应该是〔〕。
4.括号内最大能填几?5×〔〕<38 〔〕×9<60 50>7×〔〕5.在括号内填上>、<或=。
46+72÷9〔〕6×8+727÷3+36〔〕3×2×76.世界上海拔最高的山峰是我国的珠穆朗玛峰, 约8848米。
读作:〔〕。
四.计算题(共3题, 共21分)1.计算。
19÷4=〔〕…… 〔〕17÷3=〔〕…… 〔〕15÷2=〔〕…… 〔〕21÷6=〔〕…… 〔〕2.脱式计算。
2022-2023学年北京大学附属中学高二上学期期末考复习数学试卷(2)含详解

期末复习二一、选择题(共10小题,每小题4分,共40分,在每小题列出的四个选项中,选出符合题目要求的一项)1.已知a R ∈,()13ai i i +=+,(i 为虚数单位),则=a ()A .1- B.1C.3- D.32.已知直线20l y ++=,下列说法中正确的是()A.直线l 的倾斜角为120︒B.(是直线l 的一个方向向量C.直线lD.)1-是直线l 的一个法向量3.的是()A.22142x y += B.221x y -= C.2213y x -= D.24y x=4.设a R ∈,则“a =1”是“直线ax+y-1=0与直线x+ay+1=0平行”的A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分也不必要条件,5.若直线l :0x y m --=经过抛物线28y x =的焦点,且与抛物线交于A ,B 两点,则下列说法中错误的是()A.抛物线的焦点为()2,0B.2m =C.抛物线的准线为4x =- D.16AB =6.下列关于圆C :22(1)4x y +-=的说法中正确的个数为()①圆C 的圆心为(0,1)C ,半径为2②直线l :3410x y -+=与圆C 相交③圆C 与圆1C :22(1)(2)9x y ++-=相交④过点2)作圆C 50y --=A.1B.2C.3D.47.公元前4世纪,古希腊数学家梅内克缪斯利用垂直于母线的平面去截顶角分别为锐角、钝角和直角的圆锥,发现了三种圆锥曲线.之后,数学家亚理士塔欧、欧几里得、阿波罗尼斯等都对圆锥曲线进行了深入的研究.直到3世纪末,帕普斯才在其《数学汇编》中首次证明:与定点和定直线的距离成定比的点的轨迹是圆锥曲线,定比小于、大于和等于1分别对应椭圆、双曲线和抛物线.已知,A B 是平面内两个定点,且|AB |=4,则下列关于轨迹的说法中错误的是()A.到,A B 两点距离相等的点的轨迹是直线B.到,A B 两点距离之比等于2的点的轨迹是圆C.到,A B 两点距离之和等于5的点的轨迹是椭圆D.到,A B 两点距离之差等于3的点的轨迹是双曲线8.已知正方体ABCD ﹣A 1B 1C 1D 1的棱长为1,若点P 满足1311534AP AB AD AA =++,则点P 到直线AB 的距离为()A.25144 B.512C.1320D.159.已知椭圆1C :222116x y m +=和双曲线2C :22214x yn-=有公共的焦点F 1(−3,0),F 2(3,0),点P 是C 1与C 2在第一象限内的交点,则下列说法中错误的个数为()①椭圆的短轴长为;②双曲线的虚轴长为③双曲线C 2的离心率恰好为椭圆C 1离心率的两倍;④ PF 1F 2是一个以PF 2为底的等腰三角形.A.0B.1C.2D.310.已知动圆C 经过点1(0)F ,,并且与直线1y =-相切,若直线50l y -+=与圆C 最多有一个公共点,则圆C 的面积()A.有最小值为16π9B.有最大值为16π9C.有最小值为16πD.有最大值为16π二、填空题(共6小题,每小题4分,共24分)11.若直线l 与直线2x-y-1=0垂直,且不过第一象限,试写出一个直线l 的方程:________.12.与双曲线224312y x -=有相同焦点,且长轴长为6的椭圆标准方程为_________.13.已知椭圆C :22221x y a b+=(0a b >>)中,1F ,2F 为椭圆的左、右焦点,1B ,2B 为椭圆的上、下顶点,若四边形1122F B F B 是一个正方形,则椭圆的离心率为__________.14.过点()2,5作圆22:(1)4C x y +-=的切线,则切线方程为__________.15.已知O 为坐标原点,抛物线的焦点F 在x 轴上,且过点(1,2)-,P 为抛物线上一点,||3PF =,则抛物线的标准方程为___________,OPF △的面积为_____________.16.若点()2,0到直线l 的距离小于1,则在下列曲线中:①28y x =;②()2234x y -+=;③22195x y +=;④2213y x -=;与直线l 一定有公共点的曲线的序号是_________.(写出你认为正确的所有序号)三、解答题(共3题,共36分,解答应写出文字说明,演算步骤或证明过程)17.如图,在四棱锥P ABCD -中,底面ABCD 为正方形,PA ⊥平面ABCD ,,M N 分别为棱,PD BC 的中点,2PA AB ==.(1)求证://MN 平面PAB ;(2)求直线MN 与平面PCD 所成角的正弦值.18.已知椭圆()2222:10x y C a b a b+=>>的左、右顶点分别为,A B ,且AB 4=,离心率为12,O 为坐标原点.(1)求椭圆C 的方程;(2)设P 是椭圆C 上不同于,A B 的一点,直线,PA PB 与直线4x =分别交于点,M N .证明:以线段MN 为直径作圆被x 轴截得的弦长为定值,并求出这个定值.19.已知抛物线2:4C y x =,O 为坐标原点,过焦点F 的直线l 与抛物线C 交于不同两点,A B .(1)记AFO V 和BFO V 的面积分别为12,S S ,若212S S =,求直线l 的方程;(2)判断在x 轴上是否存在点M ,使得四边形OAMB 为矩形,并说明理由.期末复习二一、选择题(共10小题,每小题4分,共40分,在每小题列出的四个选项中,选出符合题目要求的一项)1.已知a R ∈,()13ai i i +=+,(i 为虚数单位),则=a ()A.1-B.1C.3- D.3C【分析】首先计算左侧的结果,然后结合复数相等的充分必要条件即可求得实数a 的值.【详解】()213ai i i ai i a a i i +=-=-+=++=,利用复数相等的充分必要条件可得:3,3a a -=∴=-.故选:C.2.已知直线20l y ++=,下列说法中正确的是()A.直线l 的倾斜角为120︒B.(是直线l 的一个方向向量C.直线lD.)1-是直线l 的一个法向量A【分析】先根据方程得斜率,进而得到直线的倾斜角,以及方向向量和方法向量,从而判断各选项.【详解】因为直线:20l y ++=,所以斜率k =120︒,故A 正确,C 不正确;因为直线l 经过点()0,2A -,()B ,所以直线l 的一个方向向量为()AB =,因向量(与()AB =不共线,故(不是直线l 的一个方向向量,故B 不正确;又因为)13360AB -⋅=--=-≠,所以)1-不是直线l 的一个法向量,故D 不正确.故选:A.3.的是()A.22142x y += B.221x y -= C.2213y x -= D.24y x=B【分析】根据标准方程逐个求出离心率,即可得到.【详解】对于A :22142x y +=中2,a b c ===22c e a ==,所以A 错误;对于B :221x y -=中1,1,a b c ====,则ce a==B 正确;对于C :2213y x -=中1,2a b c ===,则2c e a ==,所以C 错误;对于D :24y x =中1e =,所以D 错误;故选:B4.设a R ∈,则“a =1”是“直线ax+y-1=0与直线x+ay+1=0平行”的A.充分不必要条件 B.必要不充分条件C.充分必要条件 D.既不充分也不必要条件,C【详解】若直线ax+y-1=0与直线x+ay+1=0平行,则21a =,且11a-≠解得1a =故选C点睛:这是一道关于充分条件和必要条件判断的题目.考查的主要是充分条件,必要条件,熟练掌握掌握充分条件和必要条件的判定方法.本题中,利用直线平行的条件是解决问题的关键.5.若直线l :0x y m --=经过抛物线28y x =的焦点,且与抛物线交于A ,B 两点,则下列说法中错误的是()A.抛物线的焦点为()2,0B.2m =C.抛物线的准线为4x =-D.16AB =C【分析】求出抛物线的焦点坐标、准线方程,将焦点坐标代入直线方程求出实数m ,将直线方程与抛物线方程联立,求出焦点弦长,依次判断选项即可.【详解】设抛物线方程为22y px =(0p >),则焦点坐标为,02p F ⎛⎫ ⎪⎝⎭,准线方程为2px =-,∵抛物线方程为28y x =,∴4p =,22p=,∴抛物线的焦点坐标()2,0F ,准线方程为2x =-,将焦点()2,0F 代入直线l 的方程:0x y m --=得200m --=,∴2m =,∴直线l 的方程为20x y --=,设直线l 与抛物线28y x =两交点坐标为()11,A x y ,()22,B x y ,点A ,B 到准线的距离分别为A d ,B d ,由2820y x x y ⎧=⎨--=⎩消去y ,化简得21240x x -+=(0∆>),∴1212x x +=,∴由抛物线的定义,12A p AF d x ==+,22B p BF d x ==+,∴1212416AB AF BF x x p =+=++=+=.对于A ,抛物线的焦点坐标()2,0F ,选项A 正确;对于B ,实数m 的值为2m =,选项B 正确;对于C ,抛物线的准线方程为2x =-,选项C 错误;对于D ,弦长16AB =,选项D 正确,故以上说法中,错误的是C 选项.故选:C.6.下列关于圆C :22(1)4x y +-=的说法中正确的个数为()①圆C 的圆心为(0,1)C ,半径为2②直线l :3410x y -+=与圆C 相交③圆C 与圆1C :22(1)(2)9x y ++-=相交④过点2)作圆C 50y --=A.1 B.2C.3D.4C【分析】对于①,根据圆的标准方程求出圆心坐标和半径,可知①正确;对于②,根据圆心到直线的距离小于半径,可知②正确;对于③,根据圆心距与两圆半径之间的关系,可知③正确;对于④,点2)在圆C ,可知点2)在圆C ,求出切线的斜率,根据点斜式可求出切线方程,可知④不正确.【详解】对于①,由22(1)4x y +-=可知,圆心为(0,1)C ,半径为2,故①正确;对于②,圆心(0,1)C 到直线3410x y -+=的距离35d ==2<,所以直线l :3410x y -+=与圆C 相交,故②正确;对于③,圆1C :22(1)(2)9x y ++-=的圆心1(1,2)C -,半径为3,因为圆心距1||CC ==,且3232-<<+,所以圆C 与圆1C :22(1)(2)9x y ++-=相交,故③正确;对于④,因为点2)在圆C :22(1)4x y +-=上,所以点2)为切点,所以切点与圆心C3=,所以切线的斜率为,所以切线方程为:2y x -=-50y +-=,故④不正确.故选:C7.公元前4世纪,古希腊数学家梅内克缪斯利用垂直于母线的平面去截顶角分别为锐角、钝角和直角的圆锥,发现了三种圆锥曲线.之后,数学家亚理士塔欧、欧几里得、阿波罗尼斯等都对圆锥曲线进行了深入的研究.直到3世纪末,帕普斯才在其《数学汇编》中首次证明:与定点和定直线的距离成定比的点的轨迹是圆锥曲线,定比小于、大于和等于1分别对应椭圆、双曲线和抛物线.已知,A B 是平面内两个定点,且|AB |=4,则下列关于轨迹的说法中错误的是()A.到,A B 两点距离相等的点的轨迹是直线B.到,A B 两点距离之比等于2的点的轨迹是圆C.到,A B 两点距离之和等于5的点的轨迹是椭圆D.到,A B 两点距离之差等于3的点的轨迹是双曲线D【分析】判断到,A B 两点距离相等的点的轨迹是,A B 连线的垂直平分线,判断A;建立平面直角坐标系,求出动点的轨迹方程,可判断B;根据椭圆以及双曲线的定义可判断C,D .【详解】对于A ,到,A B 两点距离相等的点的轨迹是,A B 连线的垂直平分线,正确;对于B ,以AB 为x 轴,AB 的中垂线为y 轴建立平面直角坐标系,则()()2,0,2,0A B -,设动点(,)P x y ,由题意知||2||PA PB =,2=,化简为221064(39x y -+=,即此时点的轨迹为圆,B 正确;对于C ,不妨设动点P 到,A B 两点距离之和等于5,即5PA PB +=,由于54>,故到,A B 两点距离之和等于5的点的轨迹是以,A B 为焦点的椭圆,C 正确;对于D ,设动点P 到,A B 两点距离之差等于3,即||||3-=PA PB ,由于34<,故到,A B 两点距离之差等于3的点的轨迹是双曲线靠近B 侧的一支,D 错误,故选:D8.已知正方体ABCD ﹣A 1B 1C 1D 1的棱长为1,若点P 满足1311534AP AB AD AA =++,则点P 到直线AB 的距离为()A.25144 B.512C.1320D.10515B【分析】过P 作PM ⊥平面ABCD 于点M ,过M 作NM AB ⊥于点N ,连接PN ,则PN 即为所求,【详解】解:如图,过P 作PM ⊥平面ABCD 于点M ,过M 作NM AB ⊥于点N ,连接PN ,则PN 即为所求,因为满足1311534AP AB AD AA =++,所以35AN =,13MN =,14MP =,所以512PN ==,故选:B .【点睛】本题考查了求点到直线的距离的方法,属于基础题.9.已知椭圆1C :222116x y m +=和双曲线2C :22214x yn-=有公共的焦点F 1(−3,0),F 2(3,0),点P 是C 1与C 2在第一象限内的交点,则下列说法中错误的个数为()①椭圆的短轴长为;②双曲线的虚轴长为③双曲线C 2的离心率恰好为椭圆C 1离心率的两倍;④ PF 1F 2是一个以PF 2为底的等腰三角形.A.0 B.1C.2D.3A【分析】根据椭圆1C :222116x y m +=和双曲线2C :22214x yn-=有公共的焦点F 1(−3,0),F 2(3,0),求得m ,n ,再逐项判断.【详解】解:因为椭圆1C :222116x y m +=和双曲线2C :22214x yn-=有公共的焦点F 1(−3,0),F 2(3,0),所以2216949m n ⎧-=⎨+=⎩,解得m n ⎧=⎪⎨=⎪⎩则①椭圆的短轴长为,故正确;②双曲线的虚轴长为③双曲线C 2的离心率32e =,椭圆C 1离心率的34e =,故正确;④由22221167145x y x y ⎧+=⎪⎪⎨⎪-=⎪⎩,解得833P ⎛ ⎝⎭,则16PF =,211222,6PF a PF F F =-==,所以 PF 1F 2是一个以PF 2为底的等腰三角形,故正确.故选:A10.已知动圆C 经过点1(0)F ,,并且与直线1y =-相切,若直线50l y -+=与圆C 最多有一个公共点,则圆C 的面积()A.有最小值为16π9B.有最大值为16π9C.有最小值为16πD.有最大值为16πD【分析】已知直线:50l y -+=与圆C 最多有一个公共点,则直线l 与圆相切或相离,而圆C 经过点1(0)F ,,并且与直线1y =-相切,则直线l 与圆相切时圆最大,直线l 与圆相离时圆最小,数形结合求出半径即可得到圆C 的面积.【详解】解:已知直线50l y -+=与圆C 最多有一个公共点,则直线l 与圆相切或相离,当直线l 与圆相离时圆最小,满足经过点1(0)F ,,并且与直线1y =-相切的圆如图所示,此时以原点O 为圆心,1为半径,圆C 的面积2min π1πS =⋅=,故A ,C 选项错误;当直线l 与圆相切时圆最大,满足经过点1(0)F ,,并且与直线1y =-相切的圆如图所示,此时直线l 与直线1y =-为圆2C 的公切线,则圆心需在两直线所成角的角平分线上,因为直线l 60︒,所以角平分线的倾斜角为30︒,斜率为33,联立501y y -+==-⎪⎩,可得63,13A ⎛⎫-- ⎪ ⎪⎝⎭所以角平分线的方程为133y x ⎛⎫+=+ ⎪ ⎪⎝⎭,即13y x =+,恰好点1(0)F ,在角平分线上,则222r AF r =+,所以222224r r r r ===+,解得24r =,圆C 的面积2max π416πS =⋅=,故B 选项错误;故选:D.二、填空题(共6小题,每小题4分,共24分)11.若直线l 与直线2x-y-1=0垂直,且不过第一象限,试写出一个直线l 的方程:________.112y x =--(答案不唯一)【详解】由直线l 与直线210x y --=垂直,设直线l 的方程为12y x c =-+∵直线l 不经过第一象限∴0c ≤∴可令1c =-,即直线l 的方程为112y x =--故答案为112y x =--(答案不唯一).12.与双曲线224312y x -=有相同焦点,且长轴长为6的椭圆标准方程为_________.22129x y +=【分析】双曲线化为标准形式,求出焦点,即可由共焦点进一步求出椭圆短半轴,即可求得标准方程.【详解】224312y x -=即22134y x -=,焦点为(0,,椭圆长轴26a =,即3a =,故短半轴b ==22129x y +=.故答案为:22129x y +=.13.已知椭圆C :22221x y a b+=(0a b >>)中,1F ,2F 为椭圆的左、右焦点,1B ,2B 为椭圆的上、下顶点,若四边形1122F B F B 是一个正方形,则椭圆的离心率为__________.22【分析】四边形1122F B F B 是个正方形,则其对角线12F F 与12B B 相等,即22c b =,由此结合a ,b ,c 的关系,即可求出离心率.【详解】∵四边形1122F B F B 是一个正方形,∴正方形1122F B F B 的对角线相等,1212F F B B =,∵焦距122F F c =,短轴长122B B b =,∴22c b =即c b =,∴a ===,∴离心率22c e a ===.故答案为:2.14.过点()2,5作圆22:(1)4C x y +-=的切线,则切线方程为__________.2x =或34140x y -+=【分析】当斜率不存在时,检验即可;当斜率存在时,设出直线,利用圆心到直线的距离等于半径列方程求解即可.【详解】圆22:(1)4C x y +-=的圆心为()0,1,半径2r =过点()2,5的直线,当斜率不存在时,直线方程为2x =,符合与圆C 相切;当斜率存在时,设直线方程为()25y k x =-+,即250kx y k --+=,2=,解得34k =,此时直线方程为34140x y -+=.故答案为:2x =或34140x y -+=.15.已知O 为坐标原点,抛物线的焦点F 在x 轴上,且过点(1,2)-,P 为抛物线上一点,||3PF =,则抛物线的标准方程为___________,OPF △的面积为_____________.①.24y x =②.【分析】设抛物线方程为22y ax =(0)a ≠,将点(1,2)-代入求出a ,可得抛物线的标准方程;设00(,)P x y ,根据||3PF =以及抛物线的定义求出0x 和0y ,根据三角形的面积公式可求出结果.【详解】依题意,设抛物线方程为22y ax =(0)a ≠,因为抛物线过点(1,2)-,所以2(2)2a -=,所以2a =,所以抛物线的标准方程为:24y x =.由24y x =可知,准线方程为:=1x -,设00(,)P x y ,则0||1PF x =+,因为||3PF =,所以013x +=,即02x =.所以2004428y x ==⨯=,所以0||y =,所以OPF △的面积为:011||||122OF y ⋅=⨯⨯=.故答案为:24y x =.16.若点()2,0到直线l 的距离小于1,则在下列曲线中:①28y x =;②()2234x y -+=;③22195x y +=;④2213y x -=;与直线l 一定有公共点的曲线的序号是_________.(写出你认为正确的所有序号)①②③④【分析】将问题转化为直线l 必经过圆()2221x y -+=的内的点,分别作出每个选项与圆()2221x y -+=的图象,根据包含关系可确定结果.【详解】若点()2,0到直线l 的距离小于1,则直线l 必经过以()2,0为圆心,1为半径的圆的内部,即直线l 必经过圆()2221x y -+=的内的点;对于①,作出28y x =与()2221x y -+=图象如下图所示,则过圆()2221x y -+=内的点的所有直线与28y x =都有交点,①正确;对于②,作出()2234x y -+=与()2221x y -+=图象如下图所示,则过圆()2221x y -+=内的点的所有直线与()2234x y -+=都有交点,②正确;对于③,作出22195x y +=与()2221x y -+=图象如下图所示,则过圆()2221x y -+=内的点的所有直线与22195x y +=都有交点,③正确;对于④,作出2213y x -=与()2221x y -+=图象如下图所示,则过圆()2221x y -+=内的点的所有直线与2213y x -=都有交点,④正确.故答案为:①②③④.【点睛】关键点点睛:本题考查圆锥曲线中各种曲线图象之间的关系,解题关键是能够将问题转化为经过圆内部的点的直线与曲线永远有公共点,从而根据曲线方程作出图象,根据图象包含关系来确定结果.三、解答题(共3题,共36分,解答应写出文字说明,演算步骤或证明过程)17.如图,在四棱锥P ABCD -中,底面ABCD 为正方形,PA ⊥平面ABCD ,,M N 分别为棱,PD BC 的中点,2PA AB ==.(1)求证://MN 平面PAB ;(2)求直线MN 与平面PCD 所成角的正弦值.(1)证明见解析;(2)1010.【分析】(1)证明线面平行,用线面平行的判定定理,在面PAB 内找一条直线与MN 平行;(2)建立空间直角坐标系,利用向量法求线面角.【详解】(1)在四棱锥P ABCD -中,取PA 的中点E ,连接EB 、EM ,因为M 是PD 的中点,所以EM AD ,且12EM AD =.又因为底面ABCD 是正方形,N 是BC 的中点,所以BN AD ∥,且12=BN AD ,所以EM BN ∥且=EM BN ,所以四边形MNBE 是平行四边形.所以MN BE ∥.由于EB ⊂平面PAB ,MN ⊄平面PAB ,所以//MN 平面PAB .(2)因为底面ABCD 是正方形,所以AB ⊥AD .又因为PA ⊥平面ABCD ,所以可以以点A 为坐标原点,AB 、AD 、AP 分别为x 、y 、z 轴,如图建立空间直角坐标系,则(0,0,0)A ,(2,2,0)C ,(0,2,0)D ,(0,0,2)P ,(0,1,1)M ,(2,1,0)N .(2,2,2),(2,0,0)PC CD →→=-=-,设平面PCD 的法向量为(,,)m x y z =,有:0,0,m PC m CD ⎧⋅=⎨⋅=⎩即0,0,x y z x +-=⎧⎨=⎩,令1y =,则=1z ,所以(0,1,1)m = .(2,0,1)MN =- ,设直线MN 与平面PCD 所成角为θ,有:sin cos ,MN m θ= =MN m MN m⋅⋅10.所以直线MN 与平面PCD 所成角的正弦值为1010.【点睛】立体几何解答题的基本结构:(1)第一问一般是几何位置关系的证明,通常用判定定理;(2)第二问是计算,求角或求距离(求体积通常需要先求距离),通常可以建立空间直角坐标系,利用向量法计算.18.已知椭圆()2222:10x y C a b a b+=>>的左、右顶点分别为,A B ,且AB 4=,离心率为12,O 为坐标原点.(1)求椭圆C 的方程;(2)设P 是椭圆C 上不同于,A B 的一点,直线,PA PB 与直线4x =分别交于点,M N .证明:以线段MN 为直径作圆被x 轴截得的弦长为定值,并求出这个定值.(1)22143x y +=(2)证明见解析,定值为6【分析】(1)根据24AB a ==、离心率和椭圆,,a b c 之间关系可直接求得结果;(2)设(),P m n ,可得直线,PA PB 方程,进而确定,M N 两点坐标,设椭圆右焦点为F ,利用平面向量数量积的坐标运算可证得FM FN ⊥,可知以MN 为直径的圆过点()1,0F ,由此可确定线段MN 为直径作圆被x 轴截得的弦长.【小问1详解】由题意知:24AB a ==,解得:2a =,又离心率12c e a ==,1c ∴=,2223b a c ∴=-=,∴椭圆C 的方程为:22143x y +=.【小问2详解】由(1)得:()2,0A -,()2,0B ,设(),P m n ,则223412m n +=,即224123n m =-;直线():22n PA y x m =++,直线():22n PB y x m =--,M ∴点纵坐标62M n y m =+,N 点纵坐标22N n y m =-,即64,2n M m ⎛⎫ ⎪+⎝⎭,24,2n N m ⎛⎫ ⎪-⎝⎭,又椭圆右焦点为()1,0F ,63,2n FM m ⎛⎫∴= ⎪+⎝⎭ ,23,2n FN m ⎛⎫= ⎪-⎝⎭,()()22222231239412999990444m m n FM FN m m m --∴⋅=+=+=+=-=--- ,即FM FN ⊥,∴以MN 为直径的圆过点()1,0F ,又圆心横坐标为4,∴以MN 为直径的圆被x 轴截得的弦长为()2416⨯-=.即以线段MN 为直径作圆被x 轴截得的弦长为定值6.【点睛】关键点点睛:本题考查直线与椭圆综合应用中的定值问题的求解,本题求解定值问题的关键是能够利用平面向量数量积的坐标运算说明椭圆右焦点即为所求圆与x 轴的其中的一个交点,由圆的对称性可确定定值.19.已知抛物线2:4C y x =,O 为坐标原点,过焦点F 的直线l 与抛物线C 交于不同两点,A B .(1)记AFO V 和BFO V 的面积分别为12,S S ,若212S S =,求直线l 的方程;(2)判断在x 轴上是否存在点M ,使得四边形OAMB 为矩形,并说明理由.(1)440x -=;(2)不存在,理由见详解.【分析】(1)设直线l 方程为1x ty =+,()()1122,,,A x y B x y ,利用韦达定理及212y y =-计算可得答案;(2)假设存在点M ,使得四边形OAMB 为矩形,根据抛物线的性质推出OA OB ⊥不成立,则可得不存在点M ,使得四边形OAMB 为矩形.【小问1详解】设直线l 方程为1x ty =+,()()1122,,,A x y B x y 联立241y x x ty ⎧=⎨=+⎩,消去x 得2440y ty --=,得124y y t +=①,124y y =-②,又因为212S S =,则212y y =-③由①②③解得24t =±,即直线l 的方程为14x y =±+,即440x ±-=【小问2详解】假设存在点M ,使得四边形OAMB 为矩形,则,OM AB 互相平分所以线段AB 的中点在x 上,则AB x ⊥轴,此时()()1,2,1,2A B -41OA OB k k ∴=-≠-则OA OB ⊥不成立.故在x 轴上不存在点M ,使得四边形OAMB 为矩形。
三年级上册数学期末试卷(2)题目及解析

2020-2021学年三年级上册数学期末试卷(二)一.选择题(共8小题)1.如图中大正方形的周长是小正方形周长的多少倍?()A.2倍B.4倍C.6倍D.8倍2.1吨减去60千克()500千克+1000克.A.>B.<C.=3.800×5积的末尾有()个0。
A.1 B.2 C.3 D.44.下面的汉字中,从上剪下来的是()A.B.C.5.小丽、小红和小刚到超市买蛋糕.小丽用68元买了4块巧克力蛋糕,小红用104元钱买了8块豆沙蛋糕,小刚用84元钱买了6块奶油蛋糕.哪种蛋糕每块的价钱最贵?()A.巧克力蛋糕B.豆沙蛋糕C.奶油蛋糕6.算式72÷(3×3)应先算()A.除法B.乘法C.同时计算7.写数和读数时,要从()位起.A.个B.高C.百8.桌上有1张纸,第一次把它剪成3块放回桌上;第二次从桌上拿起1块剪成3块后放回桌上;….进行了这样的8次操作后,桌上一共有()块纸.A.24 B.21 C.19 D.17二.填空题(共8小题)9.如图,四个小动物排座位,一开始,小鼠坐在第1号座位,小猴坐在第2号座位,小兔坐在第3号座位,小猫坐在第4号座位.以后它们不断地交换位子.第一次上下两排交换,第二次在第一次交换后左右两列交换.第3次再上下两排交换,第4次再左右两列交换…这样下去,第十四次交换座位后,小兔在第号座位上.10.从墙上的镜子中,看到钟表(指针式,无数字)指示时间是9:20,此时的实际时间为.11.24×0÷8=6×;75﹣36=18+.12.在除法算式“□08÷6=?”中,要想使商是三位数,那么□里最小填,要想使商是两位数,□里最大填.13.120的4倍是,是60的6倍。
14.70000千克=吨.15.在一个长是12米,宽是6米的长方形花坛周围围上栏杆,栏杆的总长度是米;一个正方形的周长是328厘米,它的边长是厘米。
16.最大的四位数是,最小的三位数是,它们的和是.三.判断题(共5小题)17.10×20÷5+20的得数是0..(判断对错)18.一个长方形的长增加5厘米,宽减少5厘米,它的周长不变..(判断对错)19.三位数除以一位数,商一定是三位数.(判断对错)20.从上剪下来的是图案。
安徽省2023年八年级下学期期末考试数学试卷 (2)

安徽省八年级下学期期末考试数学试卷一、精心选一选,慧眼识金(每小题3分,共30分)1.(3分)下列各式是最简二次根式的是()A.B.C.D.考点:最简二次根式.专题:常规题型.分析:先根据二次根式的性质化简,再根据最简二次根式的定义判断即可.解答:解:A、=3,故不是最简二次根式,故A选项错误;B、是最简二次根式,符合题意,故B选项正确;C、=2,故不是最简二次根式,故C选项错误;D、=,故不是最简二次根式,故D选项错误;故选:B.点评:本题考查了对最简二次根式的定义的理解,能理解最简二次根式的定义是解此题的关键.2.(3分)下列各组数中,能构成直角三角形的是()A.4,5,6 B.1,1,C.6,8,11 D.5,12,23考点:勾股定理的逆定理.专题:计算题.分析:根据勾股定理逆定理:a2+b2=c2,将各个选项逐一代数计算即可得出答案.解答:解:A、∵42+52≠62,∴不能构成直角三角形,故A错误;B、∵12+12=,∴能构成直角三角形,故B正确;C、∵62+82≠112,∴不能构成直角三角形,故C错误;D、∵52+122≠232,∴不能构成直角三角形,故D错误.故选:B.点评:此题主要考查学生对勾股定理的逆定理的理解和掌握,要求学生熟练掌握这个逆定理.3.(3分)已知一次函数y=kx+b的图象如图所示,则k、b的符号是()A.k<0,b<0 B.k>0,b<0 C.k<0,b>0 D.k>0,b>0考点:一次函数图象与系数的关系.专题:数形结合.分析:由图可知,一次函数y=kx+b的图象经过二、三、四象限,根据一次函数图象在坐标平面内的位置与k、b的关系作答.解答:解:由一次函数y=kx+b的图象经过二、三、四象限,当k<0时,直线必经过二、四象限,故k<0,直线与y轴负半轴相交,故b<0.故选:A.点评:本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.解答本题注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限;k<0时,直线必经过二、四象限;b>0时,直线与y轴正半轴相交;b=0时,直线过原点;b<0时,直线与y轴负半轴相交.4.(3分)(•潍坊)在某校“我的中国梦”演讲比赛中,有9名学生参加比赛,他们决赛的最终成绩各不相同,其中的一名学生要想知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的()A.众数B.方差C.平均数D.中位数考点:统计量的选择.分析:9人成绩的中位数是第5名的成绩.参赛选手要想知道自己是否能进入前5名,只需要了解自己的成绩以及全部成绩的中位数,比较即可.解答:解:由于总共有9个人,且他们的分数互不相同,第5的成绩是中位数,要判断是否进入前5名,故应知道中位数的多少.故选:D.点评:此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.5.(3分)连接对角线互相垂直的四边形的四边中点,所构成的四边形一定是()A.矩形B.菱形C.正方形D.梯形考点:中点四边形.专题:探究型.分析:根据中位线的与对角线平行的性质,因此顺次连接四边中点可以得到一个相邻的边互相垂直的四边形,根据矩形的定义,邻边垂直的四边形为矩形.解答:已知:AC⊥BD,E、F、G、H分别为各边的中点,连接点E、F、G、H.求证:四边形EFGH是矩形.证明:∵E、F、G、H分别为各边的中点,∴EF∥AC,GH∥AC,EH∥BD,FG∥BD,(三角形的中位线平行于第三边)∴四边形EFGH是平行四边形,(两组对边分别平行的四边形是平行四边形)∵AC⊥BD,EF∥AC,EH∥BD,∴∠EMO=∠ENO=90°,∴四边形EMON是矩形(有三个角是直角的四边形是矩形),∴∠MEN=90°,∴四边形EFGH是矩形(有一个角是直角的平行四边形是矩形).故选:A.点评:本题考查的是矩形的判定方法,常用的方法有三种:①一个角是直角的平行四边形是矩形.②三个角是直角的四边形是矩形.③对角线相等的平行四边形是矩形.6.(3分)若的整数部分为x,小数部分为y,则的值是()A.B.C.1D.3考点:二次根式的加减法.专题:计算题.分析:因为的整数部分为1,小数部分为﹣1,所以x=1,y=﹣1,代入计算即可.解答:解:∵的整数部分为1,小数部分为﹣1,∴x=1,y=﹣1,∴=﹣(﹣1)=1.故选:C.点评:关键是会表示的整数部分和小数部分,再二次根式的加减运算,即将被开方数相同的二次根式进行合并.7.(3分)将直线y=﹣2x向右平移2个单位所得直线的解析式为()A.y=﹣2x+2 B.y=﹣2x﹣4 C.y=﹣2x﹣2 D.y=﹣2x+4考点:一次函数图象与几何变换.分析:根据“左加右减”的平移规律可由已知的解析式写出新的解析式.解答:解:将直线y=﹣2x向右平移2个单位所得直线的解析式为y=﹣2(x﹣2),即y=﹣2x+4.故选:D.点评:本题考查了一次函数图象与几何变换,掌握解析式“左加右减”的平移规律是解题的关键.8.(3分)某班50名学生身高测量结果如下表:身高 1.51 1.52 1.53 1.54 1.55 1.56 1.57 1.58 1.59 1.60 1.64人数 1 1 3 4 3 4 4 6 8 10 6该班学生身高的众数和中位数分别是()A.1.60,1.56 B.1.59,1.58 C.1.60,1.58 D.1.60,1.60考点:众数;中位数.专题:图表型.分析:找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.解答:解:表图为从小到大排列,数据1.60出现了10次,出现最多,故1.60为众数;1.58和1.58处在第25、26位,其平均数1.58,故1.58为中位数.所以本题这组数据的中位数是1.58,众数是1.60.故选:C.点评:本题属于基础题,考查了确定一组数据的中位数和众数的能力.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求.如果是偶数个则找中间两位数的平均数.9.(3分)(•南昌)某人驾车从A地上高速公路前往B地,中途在服务区休息了一段时间.出发时油箱中存油40升,到B地后发现油箱中还剩油4升,则从出发后到B地油箱中所剩油y(升)与时间t(小时)之间函数的大致图象是()A.B.C.D.考点:函数的图象.专题:图表型.分析:根据某人驾车从A地上高速公路前往B地,中途在服务区休息了一段时间,休息时油量不再发生变化,再次出发油量继续减小,即可得出符合要求的图象.解答:解:某人驾车从A地上高速公路前往B地,油量在减小;中途在服务区休息了一段时间,休息时油量不发生变化;再次出发油量继续减小;到B地后发现油箱中还剩油4升;只有C符合要求.故选:C.点评:本题考查了利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.10.(3分)(1998•内江)能判定四边形是平行四边形的条件是()A.一组对边平行,另一组对边相等B.一组对边相等,一组邻角相等C.一组对边平行,一组邻角相等D.一组对边平行,一组对角相等考点:平行四边形的判定.专题:证明题.分析:平行四边形的判定:①两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③两组对角分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;⑤一组对边平行且相等的四边形是平行四边形.根据判定定理进行推导即可.解答:解:如图所示,若已知一组对边平行,一组对角相等,易推导出另一组对边也平行,两组对边分别平行的四边形是平行四边形.故根据平行四边形的判定,只有D符合条件.故选:D.点评:此题主要考查学生对平行四边形的判定的掌握情况.在应用判定定理判定平行四边形时,应仔细观察题目所给的条件,仔细选择适合于题目的判定方法进行解答,避免混用判定方法.二、耐心填一填,一锤定音(每小题3分,共21分)11.(3分)(•襄阳)使代数式有意义的x的取值范围是x≥且x≠3.考点:二次根式有意义的条件;分式有意义的条件.专题:计算题.分析:根据被开方数大于等于0,分母不等于0列式进行计算即可得解.解答:解:根据题意得,2x﹣1≥0且3﹣x≠0,解得x≥且x≠3.故答案为:x≥且x≠3.点评:本题考查的知识点为:分式有意义,分母不为0;二次根式的被开方数是非负数.12.(3分)请你写出同时具备下列两个条件的一次函数的表达式(写出一个即可)y=﹣x ﹣6.(1)y随x的增大而减小;(2)图象经过点(2,﹣8)考点:一次函数的性质.专题:开放型.分析:由题可知,需求的一次函数只要满足k<0且经过点(2,﹣8)即可.解答:解:设函数关系式是y=kx+b(k≠0)由y随着x的增大而减小得k<0可设k=﹣1,将(2,﹣8)代入函数关系式,得b=﹣6因此一次函数表达式为y=﹣x﹣6.(此题答案不唯一)故答案为:y=﹣x﹣6.点评:本题考查了一次函数的性质.此类题要首先运用待定系数法确定k,b应满足的一个确定的关系式,再根据条件确定k的值,进一步确定b的值,即可写出函数关系式.13.(3分)已知,则x3y+xy3=10.考点:二次根式的化简求值.专题:计算题.分析:由已知得x+y=2,xy=1,把x3y+xy3分解因式再代入计算.解答:解:∵,∴x+y=2,xy=1,∴x3y+xy3=xy(x2+y2)=xy[(x+y)2﹣2xy]=(2)2﹣2=10.点评:解题时注意,灵活应用二次根式的乘除法法则,切忌把x、y直接代入求值.14.(3分)已知一组数据为:10;8,10,10,7,则这组数据的方差是 1.6.考点:方差.专题:计算题.分析:结合方差公式先求出这组数据的平均数,然后代入公式求出即可.解答:解:平均数为:(10+8+10+10+7)÷5=9,S2=[(10﹣9)2+(8﹣9)2+(10﹣9)2+(10﹣9)2+(7﹣9)2],=(1+1+1+1+4),=1.6,故答案为:1.6.点评:此题主要考查了方差的有关知识,正确的求出平均数,并正确代入方差公式是解决问题的关键.15.(3分)已知一次函数y=2x+1,则它的图象与坐标轴围成的三角形面积是.考点:一次函数图象上点的坐标特征.专题:数形结合.分析:求得函数与坐标轴的交点,然后根据三角形的面积公式即可求得三角形的面积.解答:解:一次函数的关系式是y=2x+1,当x=0时,y=1;当y=0时,x=﹣,它的图象与坐标轴围成的三角形面积是:×1×|﹣|=.故答案是:.点评:本题主要考查了一次函数图象上点的坐标特征.求线段的长的问题一般是转化为求点的坐标的问题解决.16.(3分)一个三角形的三边长分别为15cm、20cm、25cm,则这个三角形最长边上的高是12cm.考点:勾股定理的逆定理.专题:数形结合.分析:过C作CD⊥AB于D,根据勾股定理的逆定理可得该三角形为直角三角形,然后再利用三角形的面积公式即可求解.解答:解:如图:设AB=25是最长边,AC=15,BC=20,过C作CD⊥AB于D,∵AC2+BC2=152+202=625,AB2=252=625,∴AC2+BC2=AB2,∴∠C=90°,∵S△ACB=AC×BC=AB×CD,∴AC×BC=AB×CD15×20=25CD,∴CD=12(cm);故答案为:12.点评:本题考查勾股定理的逆定理和三角形的面积公式的应用.根据勾股定理的逆定理判断三角形为直角三角形是解答此题的突破点.17.(3分)如图,在直角坐标系中,正方形A1B1C1O、A2B2C2C1、A3B3C3C2、…A n B n C n C n 的顶点A1、A2、A3、…、A n均在直线y=kx+b上,顶点C1、C2、C3、…、C n在x轴上,﹣1若点B1的坐标为(1,1),点B2的坐标为(3,2),那么点B4的坐标为(15,8).考点:一次函数图象上点的坐标特征;正方形的性质.专题:规律型.分析:首先利用待定系数法求得直线A1A2的解析式,然后分别求得B1,B2,B3…的坐标,可以得到规律:B n(2n﹣1,2n﹣1),据此即可求解.解答:解:∵B1的坐标为(1,1),点B2的坐标为(3,2),∴正方形A1B1C1O边长为1,正方形A2B2C2C1边长为2,∴A1的坐标是(0,1),A2的坐标是:(1,2),代入y=kx+b得:,解得:,则直线A1A2的解析式是:y=x+1.∵A1B1=1,点B2的坐标为(3,2),∴点A3的坐标为(3,4),∴A3C2=A3B3=B3C3=4,∴点B3的坐标为(7,4),∴B1的纵坐标是:1=20,B1的横坐标是:1=21﹣1,∴B2的纵坐标是:2=21,B2的横坐标是:3=22﹣1,∴B3的纵坐标是:4=22,B3的横坐标是:7=23﹣1,∴B n的纵坐标是:2n﹣1,横坐标是:2n﹣1,则B n(2n﹣1,2n﹣1).∴B4的坐标是:(24﹣1,24﹣1),即(15,8).故答案为:(15,8).点评:此题主要考查了待定系数法求函数解析式和坐标的变化规律.此题难度较大,注意正确得到点的坐标的规律是解题的关键.三、用心做一做,马到成功(本大题共49分)18.(15分)计算(1)(﹣4)﹣(3﹣2);(2)(﹣)2+2×3;(3)5•(﹣4)(a≥0,b≥0).考点:二次根式的混合运算.专题:计算题.分析:(1)先把各二次根式化为最简二次根式,然后去括号后合并即可;(2)先利用完全平方公式和二次根式的乘法法则运算,然后合并即可;(3)利用二次根式的乘法法则运算.解答:解:(1)原式=4﹣﹣+=3;(2)原式=2﹣2+3+×3=5﹣2+2=5;(3)原式=﹣20=﹣20a2b.点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.19.(8分)如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?用你学过的方法进行解释.考点:翻折变换(折叠问题);勾股定理.专题:几何图形问题.分析:根据矩形的性质得AB=CD=8,BC=AD=10,∠B=∠C=90°,再根据折叠的性质得AF=AD=10,DE=EF,在Rt△ABF中,利用勾股定理计算出BF=6,则CF=BC﹣BF=4,设CE=x,则DE=EF=8﹣x,在Rt△CEF中利用勾股定理得到∴42+x2=(8﹣x)2,然后解方程即可.解答:解:∵四边形ABCD为矩形,∴AB=CD=8,BC=AD=10,∠B=∠C=90°,∵长方形纸片ABCD折纸,顶点D落在BC边上的点F处(折痕为AE),∴AF=AD=10,DE=EF,在Rt△ABF中,AB=8,AF=10,∴BF==6,∴CF=BC﹣BF=4,设CE=x,则DE=EF=8﹣x,在Rt△CEF中,∵CF2+CE2=EF2,∴42+x2=(8﹣x)2,解得x=3,即EC的长为3cm.点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质和勾股定理.20.已知:如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交于BE的延长线于点F,且AF=DC,连接CF.(1)求证:D是BC的中点;(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.考点:矩形的判定;全等三角形的判定与性质;等腰三角形的性质;平行四边形的性质.专题:证明题.分析:(1)可证△AFE≌△DBE,得出AF=BD,进而根据AF=DC,得出D是BC中点的结论;(证法2:可根据AF平行且相等于DC,得出四边形ADCF是平行四边形,从而证得DE是△BCF的中位线,由此得出D是BC中点)(2)若AB=AC,则△ABC是等腰三角形,根据等腰三角形三线合一的性质知AD⊥BC;而AF与DC平行且相等,故四边形ADCF是平行四边形,又AD⊥BC,则四边形ADCF是矩形.解答:(1)证明:∵E是AD的中点,∴AE=DE.∵AF∥BC,∴∠FAE=∠BDE,∠AFE=∠DBE.在△AFE和△DBE中,,∴△AFE≌△DBE(AAS).∴AF=BD.∵AF=DC,∴BD=DC.即:D是BC的中点.(2)解:四边形ADCF是矩形;证明:∵AF=DC,AF∥DC,∴四边形ADCF是平行四边形.∵AB=AC,BD=DC,∴AD⊥BC即∠ADC=90°.∴平行四边形ADCF是矩形.点评:此题主要考查了全等三角形的判定和性质,等腰三角形的性质,平行四边形、矩形的判定等知识综合运用.21.(9分)在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港.最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图.(1)填空:A、C两港口间的距离为120km,a=4;(2)请分别求出y1、y2与x的函数关系式,并求出交点P的坐标;(3)若两船的距离不超过10km时能够相互望见,求甲、乙两船经过多长时间正好相距10千米?考点:一次函数的应用.专题:综合题;分类讨论.分析:(1)从图中可以看出A、B两港是30km,B、C两港是90km,A、C两港口间的距离为30+90=120km,根据路程÷时间求出甲的速度,进而求出a的值;(2)利用待定系数法求出y1=,y2=15x(0≤x≤6),解方程组,即可求出点P的坐标.(3)先根据一次函数的图象求出乙的速度,再根据甲在乙船前和乙船后,及甲船已经到了而乙船正在行驶,三种情况进行解答即可.解答:解:(1)从图中可以看出A、B两港是30km,B、C两港是90km,所以A、C两港口间的距离为30+90=120(km);甲的速度为:30÷1=30(km/h),a=120÷30=4.故答案为:120,4;(2)当0≤x≤1时,由点(0,30),(1,0)求得y1=﹣30x+30;当1<x≤4时,由点(1,0),(4,90)求得y1=30x﹣30;即y1与x的函数关系式为y1=;由点(6,90)求得,y2=15x(0≤x≤6),即y2与x的函数关系式为y2=15x(0≤x≤6);由图象可知,交点P的横坐标x>1,此时y1=y2,解方程组,得,所以点P的坐标为(2,30);(3)由函数图象可知,乙船的速度为:90÷6=15(km/m).①甲在乙后10km,设行驶时间为xh,则x<2.如果0≤x≤1,那么(﹣30x+30)+15x=10,解得x=,不合题意舍去;如果1≤x<2,那么15x﹣(30x﹣30)=10,解得x=,符合题意;②甲超过乙后,甲在乙前10km,设行驶时间为xh,则x>2.由题意,得30x﹣30﹣15x=10,解得x=,符合题意;③甲船已经到了而乙船正在行驶,则4≤x<6.由题意,得90﹣15x=10,解得x=,符合题意;即甲、乙两船经过小时或小时或小时,正好相距10千米.点评:本题考查的是一次函数的图象及一次函数的应用,解答此题时要注意运用分类讨论的思想,不要漏解.22.(9分)如图,在线段AE的同侧作正方形ABCD和正方形BEFG(BE<AB),连接EG 并延长交DC于点M,作MN⊥AB,垂足为N,MN交BD于点P,设正方形ABCD的边长为1.(1)证明:四边形MPBG是平行四边形;(2)设BE=x,四边形MNBG的面积为y,求y关于x的函数关系式,并写出自变量x的取值范围;(3)如果按题设作出的四边形BGMP是菱形,求BE的长.考点:四边形综合题;平行线的判定.专题:几何综合题.分析:(1)分别证得DB∥ME和MN∥CB后利用两组对边分别相等的四边形是平行四边形即可证得结论;(2)根据正方形BEFG,从而可得CM=1﹣x,然后得y=(BG+MN)•BN即可.(3)由已知易得四边形BGMP是平行四边形,要使四边形BGMP是菱形则BG=MG,可得x=(1﹣x),解得x即可.解答:证明:(1)∵ABCD、BEFG是正方形∴∠CBA=∠FEB=90°,∠ABD=∠BEG=45°,∴DB∥ME(同位角相等,两直线平行).∵MN⊥AB,CB⊥AB,∴MN∥CB.∴四边形MPBG是平行四边形;(2)∵正方形BEFG,∴BG=BE=x.∵∠CMG=∠BEG=45°,∴CG=CM=BN=1﹣x.∴y=(GB+MN)•BN=(1+x)(1﹣x)=﹣x2(0<x<1);(3)∵四边形BGMP是菱形,∴BG=MG,∴x=(1﹣x),∴x=2﹣,∴BE=2﹣.点评:此题考查了四边形的综合知识,较复杂,但充分利用题目所给的条件,根据四边形性质列出方程即可解答.解答此题,不要局限于一种方法,可以多试几种方法,以提高解题的“含金量”.教师的职务是‘千教万教,教人求真’;学生的职务是‘千学万学,学做真人’。
山西省长治市二年级语文下学期期末试卷(2)A卷

山西省长治市二年级语文下学期期末试卷(2)A卷姓名:________ 班级:________ 成绩:________同学们,经过一段时间的学习,你一定长进不少,让我们好好检验一下自己吧!一、拼音,识字 (共5题;共24分)1. (5分)拼一拼,写一写。
shàn zi yù jiàn tóu tònɡān xīn zuì hǎo________________________________________2. (4分)按要求完成练习。
(1)下列字形和读音完全正确的一组是()A . 几呼(jī hū)B . 答应(dā ying)C . 切开(qiè kāi)D . 稍息(shāo xī)(2)“诲”读“huì”,这个字和下列哪个意思有关?()A . 教导B . 后悔C . 时间D . 说话3. (7分)选择题。
(1)下列加点字的读音有误的一项是()。
A . 恳求(kěn)筛选(shāi)B . 梭子(suō)监狱(yù)C . 酝酿(niàng)瞌睡(kē)D . 稀罕(hān)拘束(jū)(2)下列带“儿”的词语,读法与其他三项不同的一项是()。
A . 小曲儿B . 一块儿C . 女儿D . 伴儿(3)给加点字选择正确的读音。
我昨晚睡觉落________枕了,脖子一动就疼。
早上我因为着急赶去学校,一疏忽又把书落________在家里了。
唉!今天的心情真是一落________千丈。
A.luò B.là C.lào D.luō4. (3分)读拼音,写句子。
zhōng qiū jié dào le,wǒ hěn gāo xìng.________bà ba zài chuáng shàng kàn shū.________tiān shàng yǒu yí gè jīn sè de tài yáng.________5. (5分)我家有个好习惯:晚上,爸爸妈妈常常为我念好听的故事。
2023八年级下学期期末考试语文试卷2

2023-2023八年级下学期期末考试语文试卷2023-2023八年级下学期期末考试语文试卷2023-2023八年级下学期期末考试语文试卷1 一、选择题〔题文〕以下词语中加点字的注音完全正确的一组是〔〕A、翘望〔qiáo〕嫉妒〔jí〕箴言〔zhēn〕拈轻怕重〔niān〕B、摒弃〔bìng〕遴选〔lián〕粗糙〔cāo〕锲而不舍〔qiè〕C、精华〔suí〕雕镂〔lòu〕吮吸〔shǔn〕鳞次栉比〔zhì〕D、抽噎〔yē〕踮脚〔diǎn〕叱咤〔chà〕半身不遂〔suí〕以下各句中,加点的成语使用不恰当的一项为哪一项〔〕A、这位教师教学有方,经常在课堂上故弄玄虚,以启发学生,收到了深化浅出的效果。
B、罕见雪灾袭向神州大地,一个个雪中送炭的场面立马再现。
C、就目前而言,南水北调工程正在如火如荼地进展,地方间跨流域调水也变得屡见不鲜。
D、这虽是几句无稽之谈,但他听后却很快乐,拼命地钻研《美国十大富豪传》,找发财致富的门径。
选择以下对课文描绘有错误的一项〔〕A.《白杨礼赞》,是现代作家茅盾的作品,文章以象征的手法,讴歌了中国____领导下的北方抗日军民以及中华民族的精神和意志。
B.《马说》、《陋室铭》,文体即题目所说的“说”“铭”,它们的作者分别是唐朝的韩愈、宋朝的刘禹锡。
C.《沙漠里的奇怪现象》是一篇科学小品文,文章由现象到本质,诠释了“魔鬼的海”和鸣沙原理;蒲松龄的《山市》那么着重表现了山市空虚缥缈、瞬息万变的特点。
D.《人的高贵在于灵魂》,作者周国平运用了比喻、引用等论证方法,说明了“人的高贵在于灵魂”的道理,提倡人们在生活中应该保持纯粹的精神追求。
以下句子顺序排列正确的一项为哪一项〔〕。
①有一些微生物发现,牛的胃是它们生长的乐园。
②于是,这些小家伙纷纷光临这里,居住下来。
③自然界存在着各种各样的微生物,它们总是各就各位,在适宜它们生长的地方安家落户。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
期末测试卷2一、选择题1.计算机网络中的共享资源主要指硬件、软件和()。
A.网络B.程序C.传输介质D.数据2.OSI参考模型的()负责建立、维护和管理应用程序之间的会话。
A.传输层B.会话层C.应用层D.表示层3.数据只能沿一个固定方向传输的的通信方式是()。
A.单工B.半双工C.全双工D.混合4.双绞线中共有()根铜导线。
A.2 B.4 C.6 D.85.当两种类型相同但使用不同通信协议的网络进行互联时,需要使用()。
A.中继器B.集线器C.路由器D.网桥6.光缆的光束是在()内传输。
A.玻璃纤维B.透明橡胶C.同轴电缆D.网卡7.一台计算机已经加入了某个域,如果该计算机的管理员在该计算机上进行了本机登录,则该域的管理员可以进行的操作是()。
A.可以同时管理该计算机与该计算机的本地管理员B.无法管理该计算机,也无法管理该计算机的本地管理员C.可以管理该计算机,但不可以管理该计算机的本地管理员D.可以管理该计算机的本地管理员,但不可以管理该计算机。
8.将一台与DC分属两个网段的计算机加入域时,不正确的理解为()。
A.当前的计算机名在此域中必须是唯一的B.当前计算机必须配置有正确的DNS服务器IP地址C.在“隶属于”对话框中必须输入当前域的DNS全名而非NetBIOS名D.加入过程中必须提供域内置管理员administrator的用户名及其口令9.Windows Server 2003用户中,不需要密码就可以进入系统的是()用户。
A.Administrator B.Power user C.User D.Guest10.Windows Server 2003的DNS不允许建立的区域类型是()。
A.主要区域B.辅助区域C.传送区域D.存根区域11.如果不希望其他人使用自己计算机上的资源,可以取消本机资源的()。
A.权限B.共享属性C.用户数的限制D.缓存12.在OSI模型中,第N层和其上的N+1层的关系是()。
A.N层为N+1层提供服务B.N+1层将从N层接的信息增加了一个头C.N层利用N+1层提供的服务D.N层对N+1层没有任何作用13.OSI模型中从高到低排列的第五层是()。
A.会话层B.数据链路层C.网络层D.表示层14.CSMA/CD是IEEE802.3所定义的协议标准,它适用于()。
A.令牌环网B.令牌总线网C.网络互联D.以太网15.下列关于TCP和UDP的描述正确的是()。
A.TCP和UDP均是面向连接的B.TCP和UDP均是无连接的C.TCP是面向连接的,UDP是无连接的D.U DP是面向连接的,TCP是无连接的16.目前局域网中最常用的网线是()。
A.STP B.细缆C.粗缆D.UTP17.双绞线中的线成对扭绞旨在()。
A.易辨认B.使电磁射和外部电磁干扰减到最小C.加快数据传输速度D.便于与网络设备连接18.网络中的传输距离超过一定长度,传输介质中的数据信号就会衰减。
如果需要加大传输距离,就需要安装()。
A.中继器B.集线器C.路由器D.网桥19.当连接两个结构不同的网络时,必须使用()。
A.中继器B.集线器C.路由器D.网关20.建立计算机网络的主要目标是()。
A.实现资源共享B.增强计算机处理能力C.浏览新闻D.提高计算机运行能力二、填空题1.IP地址和主机物理地址之间的转换由IP协议提供的和实现。
2.测试网络连通性所采用方法是使用系统提供的命令。
3.对等网络中共享资源的使用方法可以归纳为、和通过对等网开展广播、网络电话、视频、邮件服务等3种。
6.带有网关的无线AP有一个以太网接口,支持和两种管理方式。
7.交换机的配置方式主要有以下4种:、、、。
8.网络资源平台设计主要包括、、网络应用系统三个方面。
9.Windows Server 2003目录服务的基本管理单位是____________。
10.安装DNS组件过程中,打开Windows组件向导对话框,需要单击______________________按钮11.Windows Server 2003的域的内置账号有__________和__________。
12.DNS协议的基本功能是_____________________________。
13.利用IIS的向导建立FTP服务器过程中,需将路径指向Windows Server 2003系统光盘的__________目录。
14.Windows Server 2003网络监视器的主界面主要由4个平铺窗口组成,分别为_____、_____、_____、_____。
15.Windows 系统中内置的常用网络测试工具有IP测试工具_____、测试TCP/IP配置工具_____、网络协议统计工具_____。
三、名词解释1.资源共享2. 数据通信3. 网络适配器4.单模光纤SMF(Single mode fiber)5. 网络通信协议6. 管理进程:7. 管理信息库:8. 网管代理四、简答题1.计算机网络由哪几部分组成?主要有哪些功能?2.局域网常用拓扑结构有哪些?各有什么特点?3.冗余拓扑结构会引发哪些问题?4.网络安全设计需要遵守哪些原则?5.请简述Sniffer软件的工作原理?6.防火墙技术有什么功能?其体系结构有哪些?7.交换机常见的故障有哪些?8. 什么是广域网?9. 网络通信三要素?10.网络管理模式有哪几种?11.SNMP的基本组成部分有哪些?12.什么是管理信息库?它有哪些作用?13.简述DHCP的主要功能。
参考答案一、选择题(每题1分,共20分)D B A D C A C D D CB ACD C D B A D A二、填空题(每空1分,共30分)1.地址解析协议ARP、反向地址解析协议RARP2.ping3.直接使用网络资源、通过映射网络驱动器共享资源6.软件、Web7.通过Console端口配置交换机、通过Telnet方式配置交换机、通过Web方式配置交换机、通过网管软件方式配置交换机8.服务器、服务器子网连接方案9.域10.添加/删除Windows组件11.Administrator、Guest12.在主机名与IP地址间建立映射关系13.i38614.图表窗口、会话统计窗口、机器统计窗口、捕获统计窗口15.Ping、ipconfig、netstat三、名词解释(每题5分,共15分)1.资源共享“资源”指的是网络中所有的软件资源、硬件资源、数据资源和通信信道资源。
“共享”指的是网络中的用户都能够部分或全部地享受这些资源。
2. 数据通信数据通信是用来快速传送计算机与终端、计算机与计算机之间的各种信息,包括文字信息、新闻消息、咨询信息、图片资料、报纸版面等。
3. 网络适配器网络适配器又称网络接口卡NIC(Network Interface Card),简称为网卡。
在局域网中用于将用户计算机与网络相连的接口设备,大多数局域网采用以太(Ethernet)网卡,但也可以采用NE2000网卡、PCMCIA卡、D-Link网卡。
4.单模光纤SMF(Single mode fiber)单模光纤又称为细光纤,或称为轴路径光纤。
细光纤的工作原理是,光束是沿光纤的轴径进行传播(轴路径传播方式)的。
由于光束是沿直线传播的原故,致使单模光纤的信息传输量有限,但它却能进行远距离的传输,单段单模光纤的有效距离最长可达100KM。
5. 网络通信协议通俗的说,通信协议就是在网络信息传输过程中,数据通信格式的约定。
6. 管理进程:管理进程是一个或一组软件程序,一般运行在网络管理站(网络管理中心)的主机上,它可以在SNMP的支持下命令管理代理执行各种管理操作。
7. 管理信息库:管理信息库用于记录网络中管理对象的信息。
例如:状态类对象的状态代码、参数类管理对象的参数值等。
8. 网管代理网管代理是一个软件模块,它驻留在被管设备上。
四、简答题(每题5分,35分)1.计算机网络由硬件系统和软件系统两大部分组成。
计算机网络的硬件系统主要由网络服务器、网络工作站、网络连接设备和网络连接线组成:服务器是网络控制的核心;工作站是网络中各用户的工作场所;,计算机网络中的连接设备主要负责网络中各计算机的互连、数据信息的转发及数据格式的转换等;网络传输介质是网络中传输数据、连接各网络站点的实体。
计算机网络软件系统主要包含三部分:网络操作系统是网络的心脏和灵魂,是向网络计算机提供服务的特殊操作系统;网络通信协议为不同的计算机提供沟通的桥梁;网络管理软件主要用于监视和控制网络的运行。
2.总线型拓扑结构是一种共享通路的物理结构,这种结构安装容易,扩充或删除一个节点很容易,但是由于信道共享,连接的节点不宜过多,并且总线自身的故障可能导致系统的崩溃;星型拓扑结构传输速度快,容易在网络中增加新的站点,结构简单,费用低,缺点是可靠性低,一旦中心节点出现故障则会全网瘫痪;环型拓扑结构安装容易、费用较低,电缆故障容易查找和排除,但是当节点发生故障时,整个网络就不能正常工作。
3.采用冗余拓扑结构虽然保证了当设备或链路故障时提供备份设备或链路,从而不影响正常的通信。
但是,如果网络设计不合理,这些冗余设备及链路构成的环路将会引发以下问题:1)广播风暴2)单帧的多次递交3)桥接表的不稳定4.在设计网络方案时,应该遵守以下原则:(1)网络信息系统安全与保密的“木桶原则”。
(2)网给安全系统的整体性原则。
(3)网络安全系统的有效性与实用性原则。
(4)网络安全系统的“等级性”原则。
(5)设计为本原则。
(6)自主和可控性原则。
(7)安全有价原则。
5.Sniffer软件是NAI公司推出的功能强大的协议分析软件,具有捕获网络流量进行详细分析、实时监控网络活动、利用专家分析系统诊断问题、收集网络利用率和错误等功能。
在以太网中发送数据帧时其他计算机都能够收到该数据帧,不管该数据帧是否是发送给自己。
数据帧中包含有目的主机的MAC地址,一般情况下只有具有数据帧中目的MAC地址的主机才会接收这个数据帧。
可以通过在计算机上设置网卡的接收模式来决定是否接收不是发送给本机的数据帧。
网络嗅探工具Sniffer软件工作时,一般将网卡设置为混杂模式,在混杂模式下的网卡能够接收一切通过它的数据,而不管该数据是否是传给它的。
6.防火墙的主要功能:(1)强化网络安全策略(2)对网络存取和访问进行监控审计(3)防止内部信息外泄防火墙的体系结构主要有:(1)筛选路由式体系结构(2)双宿主主机体系结构(3)屏蔽主机式体系结构(4)屏蔽子网式体系结构7.1)100M的网卡连到交换机上时通信不正常。
故障现象:装有10M网卡的计算机连接10/100M自适应的交换机上通信正常,但是将装有100M网卡的计算机连到该交换机上时显示红灯,通信不正常。
