天体距离
天文学计量单位。

天文学计量单位。
天文学中常用的计量单位包括:
1.天文单位(Astronomical Unit,AU):定义为地球和太阳之间的平均距离,约为1.496 ×10^8 公里,用于表示太阳系内天体之间的距离。
2.光年(Light-year,ly):光年是光在真空中传播一年的距离,约等于9.461 ×10^12 公里,常用于表示星际距离。
3.阿斯特罗米特(Astronomical Unit of Length,AUL):定义为地球和太阳之间的平均距离,约为1.496 ×10^11 米,是国际标准单位制中的一个单位。
4.角秒(arcsecond):角秒是天文学中角度的单位,1角秒等于1/360 0 角度,常用于表示天体的视直径或视距离。
5.太阳质量(Solar Mass,M☉):太阳质量是天文学中用来表示天体质量的单位,等于太阳的质量,约为2 ×10^30 千克。
这些天文学计量单位在研究天体运动、距离、质量等方面都有重要的应用。
天体距离

不同的天体距离要有不同的方法,摘抄如下:天体测量方法2.2.2光谱在天文研究中的应用人类一直想了解天体的物理、化学性状。
这种愿望只有在光谱分析应用于天文后才成为可能并由此而导致了天体物理学的诞生和发展。
通过光谱分析可以:(1)确定天体的化学组成;(2)确定恒星的温度;(3)确定恒星的压力;(4)测定恒星的磁场;(5)确定天体的视向速度和自转等等。
2.3天体距离的测定人们总希望知道天体离我们有多远,天体距离的测量也一直是天文学家们的任务。
不同远近的天体可以采不同的测量方法。
随着科学技术的发展,测定天体距离的手段也越来越先进。
由于天空的广袤无垠,所使用测量距离单位也特别。
天文距离单位通常有天文单位(AU)、光年(ly)和秒差距(pc)三种。
2.3.1月球与地球的距离月球是距离我们最近的天体,天文学家们想了很多的办法测量它的远近,但都没有得到满意的结果。
科学的测量直到18世纪(1715年至1753年)才由法国天文学家拉卡伊(caille)和他的学生拉朗德(Larand)用三角视差法得以实现。
他们的结果是月球与地球之间的平均距离大约为地球半径的60倍,这与现代测定的数值(384401千米)很接近。
雷达技术诞生后,人们又用雷达测定月球距离。
激光技术问世后,人们利用激光的方向性好,光束集中,单色性强等特点来测量月球的距离。
测量精度可以达到厘米量级。
2.3.2太阳和行星的距离地球绕太阳公转的轨道是椭圆,地球到太阳的距离是随时间不断变化的。
通常所说的日地距离,是指地球轨道的半长轴,即为日地平均距离。
天文学中把这个距离叫做一个“天文单位”(1AU)。
1976年国际天文学联合会把一个天文单位的数值定为1.49597870×1011米,近似1.496亿千米。
太阳是一个炽热的气体球,测定太阳的距离不能像测定月球距离那样直接用三角视差法。
早期测定太阳的距离是借助于离地球较近的火星或小行星。
先用三角视差法测定火星或小行星的距离,再根据开普勒第三定律求太阳距离。
主要深空天体一览表及介绍
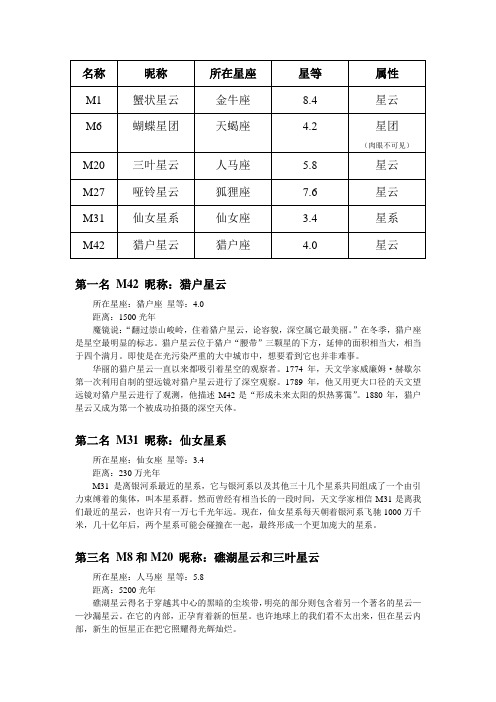
名称昵称所在星座星等属性M1 蟹状星云金牛座8.4 星云M6 蝴蝶星团天蝎座 4.2 星团(肉眼不可见)M20 三叶星云人马座 5.8 星云M27 哑铃星云狐狸座7.6 星云M31 仙女星系仙女座 3.4 星系M42 猎户星云猎户座 4.0 星云第一名M42 昵称:猎户星云所在星座:猎户座星等:4.0距离:1500光年魔镜说:“翻过崇山峻岭,住着猎户星云,论容貌,深空属它最美丽。
”在冬季,猎户座是星空最明显的标志。
猎户星云位于猎户“腰带”三颗星的下方,延伸的面积相当大,相当于四个满月。
即使是在光污染严重的大中城市中,想要看到它也并非难事。
华丽的猎户星云一直以来都吸引着星空的观察者。
1774年,天文学家威廉姆·赫歇尔第一次利用自制的望远镜对猎户星云进行了深空观察。
1789年,他又用更大口径的天文望远镜对猎户星云进行了观测,他描述M42是“形成未来太阳的炽热雾霭”。
1880年,猎户星云又成为第一个被成功拍摄的深空天体。
第二名M31 昵称:仙女星系所在星座:仙女座星等:3.4距离:230万光年M31是离银河系最近的星系,它与银河系以及其他三十几个星系共同组成了一个由引力束缚着的集体,叫本星系群。
然而曾经有相当长的一段时间,天文学家相信M31是离我们最近的星云,也许只有一万七千光年远。
现在,仙女星系每天朝着银河系飞驰1000万千米,几十亿年后,两个星系可能会碰撞在一起,最终形成一个更加庞大的星系。
第三名M8和M20 昵称:礁湖星云和三叶星云所在星座:人马座星等:5.8距离:5200光年礁湖星云得名于穿越其中心的黑暗的尘埃带,明亮的部分则包含着另一个著名的星云——沙漏星云。
在它的内部,正孕育着新的恒星。
也许地球上的我们看不太出来,但在星云内部,新生的恒星正在把它照耀得光辉灿烂。
对于M20来说,“三叶星云”这个名称实在是很形象。
透过小型天文望远镜,你就会发现,M20的明亮区域是明显分为三个部分的,就像三片树叶拼在一起。
天体距离的测量方法

的单位 ,它们的关系是
m - M = - 5 + log10 d 。
(4)
视星等 m 由观测确定 ,关键是确定恒星的绝对星等
M 。方法是 ,先拍摄距离我们较近的恒星光谱 ,恒
星的光谱和它的表面温度有关 ,按光谱的种类和强
度可以把光谱归纳为几种类型 ,分别是 O 、B 、A 、F 、
G、K、M 型 ;另一方面 ,利用视差法求出恒星的实际
离是几百万光年 ,银河系与仙女星云之间的距离 ,一 般来说 ,大约等于众星系之间的平均距离 。
图 3 赫罗图
银河系有多大呢 ? 通过测量 ,其直径约为 105 光年 ,厚度约为 104 光年 。银河系像一个扁平的盘 , 太阳系位于从圆盘中心到边缘一半的地方 。银河系 里恒星间的平均距离大约为 10 光年的数量级 ,据此 可粗略算出银河系内有大约 500 亿颗星的数量级 。
是宇宙膨胀学说 。1929 年哈勃用 215 米大型望远
镜观测到了更多星系 ,同时发现星系离我们越远 ,其
退行速度 (星系离开我们的速度) 越大 。退行速度
V 和距离 D 成正比 ,即
V = H·D 。
(5)
这就是著名的哈勃定律 , H 为哈勃常数 ,其数值约
为 50~80 千米/ (秒·兆秒差距) 。将星系中特定原
可以通过安放在地球上 A 、B 两点的两个望远镜同
时测得对 C 的两个角度 A 和 B ,算出视差 (视差为 C
对 A 、B 两点的张角) ,再测出 A 、B 两点的距离 ———
基线 ,利用三角知识就可求出人造卫星的高度 。这
·54 ·
种测量距离的方法叫三角视差法 。
在天文测量中 ,通常取地球绕太阳公转的轨道
(ly) 和秒差距 (pc) 。太阳与地球间的平均距离叫做
太阳地球月亮直径和距离的关系

太阳、地球和月亮是我们太阳系中最重要的天体。
它们之间存在着复杂的相互作用和引力关系,这些关系决定了它们之间的距离和大小关系。
下面我们将从太阳、地球和月亮的直径和距离的关系展开探讨。
1. 太阳的直径和距离太阳是我们太阳系中最大的天体,它的直径约为1.39 million km。
太阳到地球的平均距离为约1.496×10^8 公里,这个距离被定义为一个天文单位(AU)。
太阳的直径和距离关系遵循着开普勒定律,根据这个定律我们可以计算出太阳和地球之间的引力加速度。
2. 地球的直径和距离地球是我们生活的星球,它的直径约为xxx.2 km。
地球和太阳之间的平均距离为一个天文单位。
地球的大小和距离决定了它所接受的太阳辐射量,从而影响了地球的气候和生态环境。
3. 月亮的直径和距离月亮是我们太阳系中的卫星,它的直径约为3476 km。
月亮和地球之间的平均距离约为xxx km。
月亮的大小和距离决定了它的视觉大小和引力对地球的影响。
4. 太阳、地球和月亮的相互关系太阳、地球和月亮之间的直径和距离关系决定了它们之间的引力相互作用和天体运动。
太阳通过引力控制着地球和月亮的运动轨道,地球受到太阳的引力影响绕着太阳运动,月亮受到地球的引力影响围绕地球运动。
5. 结论太阳、地球和月亮之间的直径和距离关系是我们太阳系中非常重要的天文参数,它们影响了天体之间的引力相互作用和运动轨道。
了解太阳、地球和月亮的直径和距离关系有助于我们更深入地理解它们之间的复杂关系,也有助于我们对太阳系的形成和演化过程有更深刻的认识。
希望我们今天的探讨能给大家带来一些新的启发和思考。
6. 太阳系的结构和规律太阳、地球和月亮之间的直径和距离关系是太阳系中众多天体之间相互作用的一部分。
太阳系是由太阳和围绕太阳运动的行星、卫星、小行星、彗星等组成的,它们之间存在着复杂的引力相互作用和运动规律。
除了太阳系中的行星和卫星,还有一些介于行星和小行星之间的天体,它们称为“矮行星”和“小行星”等。
天体运动公式周期

天体运动公式周期
太阳系的行星的运动是一个精彩的现象,他们绕着太阳公转,其周期都不同。
通过运动公式,我们可以算出不同行星的周期。
首先,太阳系中最接近太阳的行星是水星,它距离太阳的距离大约是57.91×10^6公里,公转周期为87.969天。
其次是金星,它距离太阳的距离是108.2×10^6公里,其公转周期为224.7天。
地球距离太阳的距离是149.6×10^6公里,其公转周期为365天。
最后是火星,它距离太阳的距离是227.9×10^6公里,其公转周期为686.9天。
以上就是太阳系行星的公转周期,它们是形成太阳系的基础,毛泽东曾经说过:“宇宙中无论有多少星,每一颗星,每一颗行星都受到其他星的影响作用。
”的确。
我们需要如何共同合作才能把我们的世界加以保护和发展,就像行星是如何围绕太阳公转,形成宇宙内其他星辰群的一部分。
不管太阳系行星如何运动,这些运动公式给了我们一个关于宇宙规律的重要体现。
研究公式有助于人类了解宇宙的结构,以此有助于开展更深入的研究,带来更多有益的研究成果。
星等计算公式范文

星等计算公式范文星等的计算公式有很多种,具体的计算方法取决于所考虑的因素和应用的领域。
下面简要介绍几种常见的星等计算公式:1.绝对星等公式绝对星等是指一个天体在10秒差距(pc)距离上的视星等。
绝对星等与视星等之间的关系可以通过以下公式计算:m-M=5log(d/10)其中,m为视星等,M为绝对星等,d为天体距离。
2.真实星等公式真实星等是指一个天体在地球大气影响下的视星等。
真实星等与绝对星等之间的关系可以通过以下公式计算:m-M=5log(d/10)+ A其中,A为大气消光系数,考虑大气的吸收和散射等效应。
3.距离模数公式距离模数是指一个天体的视星等与其距离的对数的差别。
距离模数与距离之间的关系可以通过以下公式计算:m-M=5log(d/10)其中,m为视星等,M为绝对星等,d为天体距离。
4.偏红移公式偏红移是指一个天体的光谱中的谱线向长波段移动的现象。
偏红移与星等之间的关系可以通过以下公式计算:m-M=5log(d/10)+ z其中,m为视星等,M为绝对星等,d为天体距离,z为红移值。
5.其他公式除了以上常见的公式之外,还有很多其他的星等计算公式,根据应用的需要可以选择不同的公式。
例如,天体的表面亮度和角直径可以用千秒差距(kpc)来计算星等,天体的温度和半径可以通过色温和绝对星等之间的关系计算。
总之,星等的计算公式是根据天体的视星等、绝对星等、距离、红移等因素通过数学关系得出的。
不同的公式适用于不同场景和领域的应用,需要根据实际情况来选择合适的公式进行计算。
在实际应用中,还需要考虑到测量误差、数据精度等因素,以获得更准确的结果。
第5章 天文学距离测量法

l 秒差距约等于3.26光年或30万亿公里 距离(秒差距)= l/视差(角秒)
织女星的视差为 0′′.12 距离=8.1秒差距
哥白尼在创立日心学说时 曾尝试测量恒星视差以证明地球围绕太阳运
转(未成功)。 哥白尼之后经过了三百来年的 努力,1838年由德国天文学家贝塞尔才测量出 恒星的视差。地动说真正确立。
三, 不同方法测定的天体距离分类
1.几何距离 2.光度距离 3.尺度距离 4.速度距离 5.宇宙学距离 6.距离的绝对测定和相对测定
天文学上的常用距离单位
天文单位:地球到太阳的平均距离, 约为1亿5千万公里。
光年:光线在真空中一年时间内经过的 距离,约为10万亿公里。
秒差距 (pc):对地球公转轨道半长径的 张角为 1″处的天体的距离。 1pc=3.26光年
4.速度距离
设天体的运动角速度为ω,相应的 线速度为v,根据转动的运动学规律,则 有
v=ω·D 角速度ω是可观测量,要是能知道 与ω相应的v,由上式可求得距离, 称为速度距离。
5.宇宙学距离
哈勃定律为(观测发现的) Vr=DH0
H0为已知的哈勃常数,Vr为天体视向速 度,由此求得的就是宇宙学距离。
上式只能用于远距离天体。如果Vr 接近光速,还要考虑相对论性改正。 哈勃定律的简单解释是宇宙正在膨胀。
星系团:由几十个到几千个星系构成的更为庞 大的恒星集团。星系团的尺度可达 5Mpc。宇宙中约有85%的星系构成 大小不等的星系团。
5.光度函数
光度---描述恒星自身的辐射功率, 单位:尔 格/秒; 适用于光学,红外、紫外、射电、Χ及γ 射线波段。
一群天体(恒星,星团,星系团等等)中,由 不同光度天体所占的比例而构成的函数。观测 到的光度函数是离散型的,理论上的光度函数 由解析式表示。
2太阳系天体距离的规律性

太阳系天体距离的规律性内容提要文章叙述了提丢斯-波得定则和目前人们关于太阳系天体距离规律性的普遍看法(β为与行星质量有关的常数)。
根据太阳系天文观测资料提出太阳系天体距离规律的客观性。
详细探讨了太阳系行星距离规律性,木星系统卫星距离规律性,土星系统卫星距离规律性和天王量系统卫星距离规律性。
并对太阳系天体距离规律性进行了理论解释。
目录1 太阳系天体距离规律性的目前理论1.1提丢斯-波得定则1.2 普遍看法2太阳系天体距离的规律性2.1太阳系天体观测资料2.2太阳系天体距离的规律性2.3太阳系行星距离规律性2.4木星系统卫星距离规律性2.5土星系统卫星距离规律性2.6天王星系统卫星距离规律性3 太阳系天体距离规律性的理论解释1 太阳系天体距离规律性的目前理论1.1 提丢斯-波得定则1766年由德国的J.D.提丢斯首先提出经验关系,1772年德国的J.E.波得公开发表所总结的公式(1)(1) 式称为提丢斯-波得定则,式中是以天文单位表示的第颗行星离太阳的平均距离,是离太阳由近及远的次序(但水星为例外)。
1781年发现的天王星正符合的位置上,因而促使人们去寻找的天体,1801年果然发现了小行星(与相符)。
但波得的公式物理意义不明,而且1846年发现的海王星、1930 年发现的冥王星与该式的偏离很大,因此许多人至今对提丢斯-波得定则持否定态度。
认为充其量不过是帮助记忆的经验公式。
该定则的物理意义还有待进一步的探讨。
表1列出了按照提丢斯-波得定则计算的结果。
表1 按照提丢斯-波得定则计算的结果1.2 普遍看法目前,人们普遍认为的太阳系行星距离规律性是(2)上式中β近似等于常数,β与行星质量有关。
在卫星系统中,规则卫星也同样存在着类似关系。
表2列出了相邻行星和卫星的值比率表2 相邻行星和卫星的值比率行星卫星卫星卫星水星火卫一火卫二2.51土卫十天卫五金星 1.87 土卫一1.77天卫一1.48地球 1.38 木卫五土卫二1.28天卫二1.39火星 1.52 木卫一 2.33 土卫三1.24天卫三1.64(小行星) (1.77) 木卫二 1.59土卫四1.28天卫四1.34木星 1.92 木卫三 1.59 土卫五1.24土星 1.83 木卫四 1.76 土卫六2.32海卫一海卫二15.7天王星2.02木卫十三、六、七、十、6.11土卫七1.21海王星1.57土卫八2.40冥王星1.31 木卫十二、十一、八、九2.02土卫九3.54太阳系天体距离的规律性是天体力学的重要内容。
哪颗星星更遥远?天体距离测量方法浅谈

哪颗星星更遥远?天体距离测量方法浅谈对物体真实大小认识的准确性,取决于对距离远近认识的准确性。
对古人来说,太阳和月亮比高山的顶峰高不了多少。
因此,太阳和月亮就不会被认为是太大的物体。
现代人认识到太阳到地球的距离为公里(km),也就不难意识到太阳是很大很大的。
我们看到天空中的太阳只有足球大小,并不能得出太阳的大小和足球差不多的结论。
在这里距离的信息是十分重要的。
当我们想测量空间中两点的距离时,如果我们能从一点移动到另一点,测量是很容易的。
只要我们把量尺首尾相接的连续截取连接两点的线段,我们就可以得到两点的距离。
当我们不能从一点移动到另一点时,我们必须想别的办法来测。
一、视觉测量、声波或光波的传播时间一般说来,人们从日常经验可以粗略估计物体距离,房屋和人的高度是比较均匀的,如果我们知道房屋和成人在不同距离时的视觉形象大小,我们从房屋和成人的视觉形象大小可以推出其大致距离。
用几何学的方法,如三角函数和相似三角形等方法,即使我们不能从一点移动到另一点,我们仍然可以测量两点之间的距离。
如图8-14所示,我们想测量AB的距离,而我们又到不了B点。
从三角函数我们知道,AB/AC=tgθ,通过测量AC的距离和∠ACB的角度θ,我们可以得出距离AB=AC·tgθ。
在空气和水中测量两点之间的距离,我们可以用定向性很好的超声束(在空气中衰减很快,长距离不实用)来测量距离。
用声速乘以发射和接收波的时间差的一半来确定距离。
跟踪潜艇的声纳系统和海洋深度的测量就是用这一方法。
在较远的距离上用光的发射和接收反射波的时间差来测量距离也是可行的,把反射镜放到月球上,可以用激光束的发射和接收时间差来测量地球和月球之间的距离。
这一办法不能用于更远的星体,原因有以下几点:1.很难把反射镜放到更远的天体上。
2.即使天体不需反射镜,激光束的能量太弱,到达遥远天体再返回后,信号太弱不能再被检测到。
3.即使反射回的激光束能被检测,对于十几万光年或几十亿光年外的天体,一次测量的时间可能超过人类的可能存在时间,并无现实意义。
天体距离测量方法

天体距离测量方法郭鹏波 PB12203103摘要:研究了几种常用的天文学测量恒星距离的方法,包括对近距离以及对远距离的星体测量方法,区分了各种方法的适用范围,以及对星系的测量方法和最近对于哈勃常数测定的最新进展。
关键词:天体;测量;距离引言天体距离测定是天文学中最重要的工作之一,包括探究银河系结构和运动学以及宇宙大尺度结构在内的一些重要天体物理研究领域,都离不开对恒星、星系和星系团距离的尽可能准确测定。
为此,长期以来天文学家始终为多途径测定各类天体的距离而不懈努力。
测定天体的距离可有两条途径,即绝对测定和相对测定。
所谓“绝对测定”,是指无需借助其他方法就能直接测定天体的距离,如利用周年视差位移测定恒星的几何距离便是一种最基本的绝对测定方法。
而相对测定必须借助对标距天体或标距关系的“绝对定标”才能推算出天体的距离,如利用周光关系测定变星及其寄主星系的距离。
1恒星距离测定在恒星距离的测定中,不断观测天体总结规律. 当地球在 A 点时,看到某恒星在天空的A′点,当地球运动到B 点时,看同一颗恒星在B′点,这样,在1 年之内,这些描出的位点一般构成椭圆,它的长轴与黄道平行,半长轴所张的角等于恒星的周年视差,也有些特殊位置的恒星可成圆或一段直线. 我们以太阳到恒星的距离r 为弦,以地球和太阳的平均距离a 为最短边所构成的直角三角形的最小角α为周年视差,如图1所示. 恒星的周年视差可由相隔半年的 2 次恒星位置的测定计算出来. 由于恒星离太阳很远,周年视差很小,若α用弧度表示, a 用天文单位表示,则r , a ,α三者关系为r = aα.只要测出周年视差,就可以算出恒星距离r ,这种通过测周年视差来求恒星距离的方法叫做周年视差法. 测定周年视差的方法有很多,下面分别研究几种测周年视差的方法.1.1 三角视差法在天文测量中,通常取地球绕太阳公转的轨道半径(115×108km)为基线,当被测天体的视差为1角秒时(1角秒=1/3600度),该天体的距离叫做1秒差距(1pc)。
人类距离月球有多远?

人类距离月球有多远?随着人类科学技术的进步,人们对于宇宙的探索也日渐深入。
而其中,距离我们最近的天体——月球,更是引起了人们的巨大兴趣。
那么,人类距离月球到底有多远呢?接下来,就让我们一起通过本文,去探索这个问题吧。
1. 月球的距离有多远?如果准确地问起:人类距离月球的实际距离是多少,一般会得到一个近似“38万千米”的答案。
但是,事实上,这个距离是在月球和地球的距离最短时(即“近月点”)所测得的距离。
而在月球和地球的最远距离(即“远月点”)时,这个距离则会变成约40.6万千米。
因此,我们一般用月球到地球中心的平均距离,即约38.4万千米来描述月球和地球的距离。
2. 为什么月球和地球的距离会发生变化?月球和地球之间的距离并非不变的,而是会因两者绕行轨道不同而发生变化。
这是因为,月球是绕着地球运行的,而且轨道是椭圆形的,所以在运行的过程中,月球会有慢和快、近和远的轨道运行状态,因而与地球的距离也会有所不同。
3. 来自不同国家的探空任务如何?自从人类踏上月球之后,各国也纷纷进行了数次月球探险任务。
其中,苏联成功地向月球发射了世界上第一颗人造卫星,也是人类历史上第一次无人机探测月球,并在1966年成功着陆月球,取得了许多科学数据。
而美国也在其登月计划中成功将人类送上月球,并为月球的探险工作做出了极大的贡献。
此外,中国也成功发射了嫦娥探月工程,开启了中国探月的历程。
4. 月球对于人类探索的意义自古以来,月亮一直是人类心目中的神秘而美丽的存在。
而随着科技的进步,人类对月球的探索也变得越来越深入。
月球作为人类探索宇宙的重要目标之一,不仅能够揭示太阳系的起源和演化,还有着广阔的实用价值。
例如,月球可以作为建造空间基地的理想地点,也可作为太空旅游的重要目的地。
此外,月球还有丰富的矿产资源,其对于解决人类能源和资源短缺的问题也有着重要的作用。
5. 结论总的来说,人类距离月球的距离约为38.4万千米。
而该距离的变化,是由于月球和地球绕行轨道不同导致的。
恒星周年视差名词解释

恒星周年视差名词解释恒星周年视差是一项关键的天文观测参数,用于测量天体距离。
在本文中,我们将探讨恒星周年视差的定义、计算方法以及其在天文学中的应用。
恒星周年视差的定义恒星周年视差是指在地球公转一周的时间内,观测者从两个不同位置观测同一个天体所得到的视差。
这个视差是由于观测者在地球轨道上运动而产生的,因此称为周年视差。
恒星周年视差的计算方法恒星周年视差的计算需要知道天体的视差和其距离。
视差是指天体在地球上观测时的视角直径,通常用角秒(arcsecond)表示。
视差越大,说明天体离地球越近。
天体的距离可以通过视差计算得到。
根据三角函数的定义,视差和距离之间的关系可以表示为:d = 1/p其中,d表示天体距离,p表示视差。
在实际观测中,我们通常使用毫角秒(milliarcsecond,mas)作为视差的单位。
这是因为大多数天体的视差非常小,通常只有几毫角秒。
恒星周年视差的应用恒星周年视差是测量天体距离的重要参数,因此在天文学中有着广泛的应用。
下面我们将介绍几个典型的应用。
1. 确定星系距离通过测量银河系中恒星的周年视差,天文学家可以确定星系的距离。
这是因为恒星的距离和周年视差之间有着确定的关系,可以使用上文提到的公式计算得到。
2. 确定恒星的质量恒星周年视差还可以用来确定恒星的质量。
这是因为恒星的质量和其亮度之间有着确定的关系,而亮度可以通过测量恒星的表面温度和表面积得到。
如果我们知道了恒星的距离,就可以通过测量其亮度和周年视差来确定其质量。
3. 探测行星恒星周年视差还可以用来探测行星。
当行星绕恒星公转时,会对恒星的位置和速度产生微小的影响,从而导致恒星的周年视差发生变化。
通过测量这种变化,我们可以推断出行星的存在和轨道参数。
总结恒星周年视差是测量天体距离的重要参数,可以通过测量天体的视差和使用三角函数计算得到。
恒星周年视差在天文学中有着广泛的应用,包括确定星系距离、恒星质量和探测行星等。
第五讲+天体的运动与距离

d=1.3 pc(4.3 ly)
• 限制 – 由于受到地球大气扰动的影响,周年视差的 精确测量受到限制 – 地面望远镜的角分辨本领一般不超过0.01″ – Hipparcos卫星(1989年8月发射) 的测量分辨率达到0.001″,100pc内的测量 误差小于10%。测量了约12万颗恒星的距离
• 地内行星在一个会合周期内, 所经历的过程为:上合→ (顺行)→东大距→(顺行) →留→(逆行)→下合→ (逆行)→留→(顺行)→ 西大距→(顺行)→上合
• 相位变化和凌日
地外行星的运动
• 合、冲、东方照和西 方照
• 地外行星在一个会合 周期中视运动所经历 的过程为:合→(顺 行)→ 西方照→(顺 行)→ 留→(逆行) → 冲→(逆行)→ 留→(顺行)→ 东方 照→(顺行)→ 合
银川0.99(19时15分) 北京0.92*(19时10分)
全食可观测时间 ≤2分钟
2009年7月22日日全食, 印度,中国,大平洋
昆明0.88(9时08分) 成都1.00(9时12分)
武汉1.03(9时26分) 南京0.99(9时34分)
上诲1.0l(0时38分)
杭州1.02(9时36分)
全食可观测时间 ≤6分钟
倾角 0.01 177.36 23.45 25.19 3.13 26.73 97.77 28.32
月球的视运动
• 黄白交角:5°8′43.42″ • 地月距离:356400 – 406700公里 • 1恒星月 = 27.321661天 • 1朔望月 = 29.530588天 • 月相变化:朔 – 新月(娥眉月) - 上弦月 –
第五讲 天体的运动与距离
• 行星与卫星的运动特征 • 行星运动定律 • 几个基本概念 • 天体距离的测定
测量天体距离的方法

测量天体距离的方法测量天体距离是天文学中的一个重要问题,有许多不同的方法可以用来估算天体的距离。
在下面的文章中,我们将介绍10种常用的方法,并对每一种方法进行详细的描述。
1. 星差法星差法是一种古老但有效的方法,可以用来测量距离较近的星系的距离。
它基于天文学家观察太阳系内各个行星和彗星的位置并计算它们的运动。
通过比较在两个不同时间点观测到的星系位置的差异,可以测量它们与地球的距离。
2. 视差法视差法也是一种测量星系距离的方法,但它使用不同的技术。
这种方法基于地球绕太阳的运动,相机或望远镜拍摄的星系在两个不同时间点呈现的位置差异,测量恒星与地球之间的距离。
更近的星系视差变化更大。
3. 恒星颜色指数法恒星的颜色也可以用来确定它们的距离。
这种方法基于恒星发出的光的频率与它们的温度和距离之间的关系。
比较恒星的可见光和红外线光谱可以测量它们的颜色指数,从而确定恒星相对于地球的距离。
4. 间接测量法有些天体的距离可以间接测量。
恒星和行星周围经过的彗星和小行星,如果它们的轨道知道得足够准确,可以测量它们的角直径并通过三角法确定距离。
5. 恒星发光度法恒星的亮度和表面温度之间有一个明显的关系,这意味着恒星表面温度越高,它的亮度就越高。
这个关系可以用斯特凡-玻尔兹曼定律来表述,并用来估算恒星与地球之间的距离。
6. 脉冲星测距法脉冲星是极度稳定的天体,它们发出规律的射电信号,这些信号可以被用来确定它们的距离。
每发出一个射电信号,脉冲星就像一个闹钟一样,它会在地球上留下一个特定的时间印记。
通过测量这些脉冲的时间和频率,可以确定信号是从何处来的以及它来自哪个射电星系。
7. 巨星振荡法这种方法利用恒星的内部振荡模式测量距离。
恒星的尺寸和质量同时影响到它的振荡模式,这些模式的频率可以用来确定恒星与地球的距离,并揭示出恒星的内部结构。
8. 引力透镜引力透镜是相对论基础上的一种测量距离的方法。
说得简单些就是代替太阳重力场产生一个替代的重力场,这样它会扭曲背后的星光,形成一个光环。
天体距离的测量方法

天体距离的测量方法
1 历史上测量天体距离的方法
人类了解太阳系的起源和结构,依赖于测量其中各天体之间的距离。
历史上有很多方法用来测量太阳系天体之间的距离,具体的方法
有视差角、年差角、黄赤交角、光行差法。
1.1 视差角
视差角是指两个天体从地球的视角看到的角度,通过观测两个天
体的大小和视差角,可以精确的计算出两个天体之间的距离,它是许
多很详细的距离测量方法中的一种,一般用它来测量木星、金星和火
星之间的距离。
1.2 年差角
年差角测量方法基于太阳系内绝对位置可以改变的事实,它是基
于一年内太阳系对象的相对位置变化的,也就是在一年中不断改变的
太阳系的各个物体的位置,这些变化现象与物体之间的实际距离有关。
通过观察他们的运行位置,可以精确表示它们之间的距离。
1.3 黄赤交角
黄赤交角是一个基于天体天体间相对位置的概念,它可以帮助我
们计算出天体到地球的距离。
这个方法基于天文学观测点的差异,即
黄道和赤道的位置,当观测一个天体时,我们可以计算出它与另一个
天体的角距离。
1.4 光行差法
光行差法是基于物体的星光的时间差的原理,它可以让我们以小
的时间间隔来观测星体的相对位置,根据物体星光的行进时间的差异,我们可以计算出它们之间的距离。
说明:以上就是历史上用来测量天体距离的四种方法,它们可以
帮助我们测算出太阳系天体之间的准确距离,从而帮助我们更好的理
解太阳系的结构与发展状况。
测量天体空间距离的方法

测量天体空间距离的方法
测量天体空间距离的方法可以分为几种不同的技术和方法。
以下是一些常用的方法:
1. 视差测量:这是最常用且基本的方法之一。
视差是指由于地
球在公转运动中,观测同一个星体时所得到的观测位置的微小差异。
通过测量这种微小的视差,并结合基线长度,可以计算出星体与地球的距离。
这种方法适用于较近的天体,如太阳系内的星体。
2. 原动测量:原动是指恒星的自行运动。
通过观测恒星在天空
中的位置随时间的变化,可以计算出其自行运动的大小和方向,并进一步推断出其距离。
这种方法适用于较近的恒星。
3. 光度测量:根据恒星的亮度和光谱信息,可以推断出其绝对
亮度和表面温度。
通过比较观测到的亮度和推断的绝对亮度,可以计算出恒星的距离。
这种方法主要适用于较远的恒星。
4. 小行星雷达测量:利用雷达技术,可以测量小行星与地球之
间的距离。
这种方法在测量太阳系内小天体的距离时非常有效。
5. 基于星系红移的测量:根据宇宙膨胀的观测事实,远离我们
的星系会由于多普勒效应而出现红移。
通过测量星系的红移,可以推断出其与我们的距离。
这种方法适用于较远的星系。
这些方法常常需要结合使用,并且在不同距离范围内各有适用性。
科学家们不断探索和改进这些方法,以便更准确地测量天体空间距离。
极距名词解释

极距名词解释极距(PolarDistance)是天文学中一个重要的概念,通常用于描述一个天体与极点之间的距离,也可以用于描述两个天体之间的距离。
在天文学中,极距通常是指一个天体与北极或南极之间的距离。
这个距离通常以角度的形式来表示,单位是度(°),分(′)和秒(″)。
例如,地球的极距是23°26′13″。
极距的计算通常需要使用天球坐标系。
天球坐标系是一种以地球为中心的坐标系,用于描述天体在天空中的位置。
在天球坐标系中,天空被划分为若干个区域,每个区域都对应着一个特定的坐标系。
其中最常用的是赤道坐标系和黄道坐标系。
在赤道坐标系中,天球被划分为两个半球,赤道将这两个半球分成了北半球和南半球。
赤道上的点被定义为天球的赤道极点,它们与地球的赤道相交。
赤道极点是赤道坐标系的原点,它们的位置可以用赤经和赤纬来表示。
赤经是从春分点开始,沿着赤道向东测量的角度,范围是0°到360°。
赤纬是从赤道开始,向天顶或向天底测量的角度,范围是-90°到90°。
在黄道坐标系中,天球被划分为两个半球,黄道将这两个半球分成了北半球和南半球。
黄道上的点被定义为天球的黄道极点,它们与地球的黄道相交。
黄道极点是黄道坐标系的原点,它们的位置可以用黄经和黄纬来表示。
黄经是从春分点开始,沿着黄道向东测量的角度,范围是0°到360°。
黄纬是从黄道开始,向天顶或向天底测量的角度,范围是-90°到90°。
在天文学中,极距还可以用于描述两个天体之间的距离。
例如,两颗恒星之间的极距可以用它们的视差来计算。
视差是一个天体在地球上两个不同位置上所观测到的位置差异,通常用角秒(″)来表示。
视差越大,两个天体之间的距离就越小。
总之,极距是天文学中一个重要的概念,用于描述一个天体与极点之间的距离,也可以用于描述两个天体之间的距离。
它的计算需要使用天球坐标系,通常以角度的形式来表示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
天体距离distance of celestial bodies
早在古代,人们通过粗略的观测已建立起天体的相对距离的初步概念。
公元前三世纪,古希腊阿利斯塔克推算出日、月到地球的距离的近似比值。
公元前二世纪,喜帕恰斯求得月球的距离为地球直径的倍。
1751~1753年,法国拉卡伊和拉朗德第一次用三角测量法精确测定了月球的距离。
1672年,G.D.卡西尼精确测定了太阳的距离。
1837~1839年,В.Я.斯特鲁维、贝塞耳和T.亨德森几乎同时分别利用三角视差法相当精确地测定了织女星(即天琴座α)、天鹅座61和南门二(即半人马座α)三颗近距星的距离(见视差)。
测量天体距离的最经典的方法是三角视差法,此外还有许多方法。
每种方法都有一定的适用范围。
下面按照天体的从近到远的距离分为三类,分别叙述各种测量方法。
太阳系内的天体三角测量法用于测定月球、行星的周日地平视差,由此可以求得它们的距离。
根据天体力学的理论,利用行星的周日地平视差,可以求得太阳的周日地平视差(即太阳视差),由此可以求得地球和太阳之间的平均距离。
这是二十世纪六十年代以前测定太阳距离的常用方法。
雷达测距法通过向月球和大行星(如金星、火星、水星等)发射无线电脉冲,然后接收从它们表面反射的回波,并将电波往返的时间精确地记录下来,便能推算出天体的距离。
雷达测距法目前已成为测量太阳系内某些天体的基本方法之一。
1946年首次用这一方法成功地测定了月球的距离,1957年月距的测定精度已优于一公里。
自1961年起,对金星、火星和水星等多次进行雷达测距。
对大行星的雷达测距还为测定地球和太阳间平均距离提供了最优的方法。
根据对金星的雷达测距求得的日地间平均距离的数值是迄今最精确的(见雷达天文方法)。
激光测距法它比雷达测距法更精确。
但目前只适用于很近的天体,如人造卫星和月球。
它的工作原理与雷达测距法相似。
太阳系外较近的天体三角视差法对离太阳100秒差距范围以内的近距星,都可利用三角视差法测定它们的距离。
但对距离超过50秒差距的天体,此法所测得的距离已不够准确。
三角视差法迄今仍是测定太阳系外天体距离的最基本方法。
用其他方法测得的距离都要用三角视差法来校准。
分光视差法分析恒星谱线以测定恒星距离的一种方法。
以秒差距为单位的恒星距离r与它的视星等m(见星等)和绝对星等M之间存在下列关系:5lgr=m-M +5。
根据恒星谱线的强度或宽度差异,估计恒星的绝对星等,再从观测得到恒星的视星等,由上式求得恒星的距离。
由于星际消光对M和m有影响,用分光视差法测定恒星的距离必须计及星际消光这个很复杂的因素。
威尔逊-巴普法1957年,O.C.威尔逊和巴普两人发现,晚型(G、K和M型)恒星光谱(见恒星光谱分类)中电离钙的反转发射线宽度的对数与恒星的绝对星等之间存在着线性关系。
对这条谱线进行光谱分析,便可得到晚型恒星的距离。
星际视差法在恒星的光谱中出现有星际物质所产生的吸收线。
这些星际吸收线的强度与恒星的距离有关:星越远,星和观测者之间存在的星际物质越多,星际吸收线就越强。
利用这个关系可测定恒星的距离。
常用的星际吸收线是最强的电离钙的K线和中性钠的D双线。
不过这个方法只适用于O型和早B型星,因为其他恒星本身也会产生K线和D线,这种谱线同星际物质所产生的同样谱线混合在一起无法区分。
由于星际物质分布不均匀,一般说来,用此法测得的距离,精度是不高的。
力学视差法目视双星的相对轨道运动遵循开普勒第三定律,即伴星绕主星运转的轨道椭圆的半长径的立方与绕转周期的平方成正比。
设主星和伴星的质量分别为m1和m2,以太阳质量为单位表示,绕转周期P以恒星年(见年)为单位表示,轨道的半长径的线长度A以天文单位表示,这种双星在观测者处所张的角度α以角秒表示,则其周年视差π为:,
式中α和P可从观测得到。
因此,如果知道双星的质量,便可按上述公式求得该双星的周年视差。
如果不知道双星的质量,则用迭代法解上式,仍可求得较可靠的周年视差。
周年视差的倒数就是该双星以秒差距为单位的距离。
星群视差法移动星团的成员星都具有相同的空间速度。
由于透视作用,它们的自行会聚于天球上的一点或者从某点向外发散,这个点称为“辐射点”。
知道了移动星团的辐射点位置,并从观测得到n个成员星的自行μk 和视向速度V 噰(k=1,2,…,n),则该星团的平均周年视差为:
式中θk为第k个成员星和辐射点的角距,堸为n个成员星的空间速度的平均值。
这样求得的周年视差的精度很高。
但目前此法只适用于毕星团。
其他移动星团因距离太远,不能由观测得到可靠的自行值。
统计视差法根据对大量恒星的统计分析资料,知道恒星的视差与自行之间有相当密切的关系:自行越大,视差也越大。
因此对具有某种共同特征并包含有相当数量恒星的星群,可以根据它们的自行的平均值估计它们的平均周年视差。
这样得到的结果是比较可靠的。
自转视差法银河系的较差自转(即在离银河系核心的距离不同处,有不同的自转速率)对恒星的视向速度有影响。
这种影响的大小与星群离太阳的距离远近有关,因此可从视向速度的观测中求出星群的平均距离。
这个方法只能应用于离太阳不太远,距离大约在1,200秒差距以内的恒星。
太阳系外的远天体利用天琴座RR型变星这类变星的特点是:尽管光变周期长短不同,而它们的光度是相同的,绝对星等差不多都在+0.5等左右。
因此,先通过观测得到它们的视星等,再把视星等同上述绝对星等数值作比较,便可求得含有这类变星的球状星团的距离。
这类变星由于光度大,光变周期为0.05~1.5天,显得特别引人注目,所以可作为相当理想的“距离指示器”。
利用造父变星这类变星的光变周期长,而且它们的光度和光变周期之间有一种确定的周光关系,即光度越大,光变周期越长。
应用这种关系,便可根据观测得到的光变周期计算它们的绝对星等,再将算出的绝对星等同视星等作比较,就可求得这类变星及其所在星团或较近的河外星系的距离。
利用角直径假如各个球状星团或星系的线直径D(以天文单位表示)大致是相等的,则通过观测得到它们的角直径d(以角秒为单位),就可求得星团或星系的距离r(以秒差距为单位):。
但实际上,无论是球状星团,还是各类星系,它们的线直径相差不小,而且要确定它们的角直径也很困难,所以用这个方法求得的距离是很粗略的。
主星序重叠法这个方法的出发点是:认为所有主序星都具有相同的性质,同一光谱型的所有主序星都具有相同的绝对星等。
可以把待测星团的赫罗图(以色指数为横坐标,视星等为纵坐标)同太阳附近恒星的赫罗图(以色指数为横坐标,以绝对星等为纵坐标)相比较,使这两个图的主星序重叠。
根据纵坐标读数之差即星团的主序星的视星等和绝对星等之差,可算出该星团的距离。
也可以把待测星团的主星序同已知距离的比较星团的主星序相重叠,则纵坐标读数之差就是两星团的主序星的视星等之差,由此可以求得这两个星团的相对距离。
根据比较星团的已知距离,便得到所测星团的距离。
这是测定银河星团和球状星团的距离的一种有效方法。
利用新星和超新星新星和超新星的光度变化都具有这样一个特征:在不长的时间内光度便达到极大值,而且所有新星或属同一类型的超新星的最大绝对星等变化范围不大。
因此,可先取它们的平均值作为一切新星或属同一类型的超新星的最大绝对星等,再把它同观测到的最大视星等相比较,便可定出该新星或超新星所在星系的距离。
利用亮星对于河外星系,可以认为它们所包含的亮星的平均绝对星等与银河系里属于同一类型星的平均绝对星等是相同的。
因此,可以先通过观测得到这些亮星的视星等,然后把它们同上述平均绝对星等作比较,以求得河外星系的距离。
利用累积星等球状星团的累积星等变化范围不大,可先取其平均值作为所有球状星团的累积绝对星等,再从观测得到所测星团的累积视星等,便可算出该球状星团的距离。
此法也可用于河外星系,但必须考虑到星系的形态类型,不同类型星系的累积平均绝对星等应取不同的数值。
利用谱线红移观测表明,在目前光学望远镜和射电望远镜所及的空间范围内,河外星系的谱线都有红移现象,而且红移量同星系的距离成正比。
以r表示星系的距离,c表示光速,λ表示波长,Δλ表示波长的变化量,则:,
式中Δλ/λ为红移量,哈勃常数H=50公里/(秒·百万秒差距)。
因此,只要测量出星系的谱线红移量,便可推算出星系的距离。
测定天体的距离是天体测量最重要的研究课题之一,尽管方法很多,但要得到可靠的结果是不容易的。
因此,对于某一天体,应尽可能采用几种方法分别测定它的距离,然后相互校核,才能得到可靠的结果。
