第2章 极限与连续
(完整版)赵树嫄微积分第四版第二章极限与连续

x从右侧无限趋近x0 , 记作x x0 (或x x0 0 ) .
左极限:
0, 0,使当x0 x x0时, 恒有 | f ( x) A | .
记作 lim f ( x) A 或 x x0
f ( x0 0) A .
x0
x0
x
左极限:
0, 0,使当x0 x x0时, 恒有 | f ( x) A | .
定义无限接近于无限增大时sinlimsinlim为中心线直线图形完全落在以函数lim不存在arctanlim不存在lim的一条水平渐近线就是那么的距离趋于零这时我们称直线lim的一条水平渐近线就是那么为常数二自变量趋于有限点处时函数的极限问题
第二章 极限与连续
本章介绍极限的概念、性质和运算法则,以及与极 限概念密切相关的,并且在微积分运算中起重要作 用的无穷小量的概念和性质。此外还给出了两个极 其有用的重要极限。随后,运用极限引入了函数的 连续性概念,它是客观世界中广泛存在的连续变化 这一现象的数学描述,微积分学中讨论的函数主要 是连续函数。
x
x
故 lim ex 不存在. x
o
x
一条伸展到无穷远的曲线 y f ( x) ,当点P( x, f ( x)) 沿 曲线无限远离原点时,点 P 到直线 y A 的距离趋于零, 这时我们称直线 y A 是曲线 y f ( x) 的水平渐近线.
如果 lim f ( x) A 或 lim f ( x) A ( A 为常数),
性质2 有界性
对于数列{an } ,如果存在常数 M 0 ,使对一切 n,有
| an | M , 则称数列{an } 是有界的。
定理2 收敛的数列必定有界。 注1 有界性是数列收敛的必要条件,不是充分条件。
二章极限与连续

得证。
大学数学教研室 2024年4月25日6时7分
12
首页 上页 下页 后页 返回
例3 证明 lim C C n
事实上: 任给 0
CC 0
(C为常数)
恒成立
故
lim C C
n
得证。
大学数学教研室 2024年4月25日6时7分
13
首页 上页 下页 后页 返回
二.函数的极限
数列极限是考察数列在n →∞ 这一过程中的变化 总趋势(即有无极限). 而对于函数y=ƒ(x), 当考察它的 变化总趋势时, 因自变量的连续变化过程有许多情况, 如x→∞, x →-∞, x →0, x →x0+, x →x0- 等.
•
••
N
n
•
大学数学教研室 2024年4月25日6时7分
11
首页 上页 下页 后页 返回
例2 利用定义证明 lim 2n 1 2
n n
证明:要使
2n 1 2 1
n
n
,只须
n 1
故:任给
0
,总存在
N
1
,当 n N 时,
2n 1 2 1
n
n
恒成立,因此
lim 2n 1 2 n n
3、 lin 2n n
解:1、 lin 1 0
n n
lin (1 1 ) 2、 n n
4、
lin 1 1n
n 2
2、 lin (1 1 ) 1
n
n
2 3、
lin n 不存在
n
1 1n
4、
lin n 2
不存在
大学数学教研室 2024年4月25日6时7分
7
首页 上页 下页 后页 返回
高等数学-第2章--极限与连续

第二章 极限与连续极限是高等数学中最主要的概念之一,也是研究微积分的重要工具,如导数、定积分、重积分等定义都需要用极限来定义,因此,掌握极限的思想和方法是学好微积分学的基本前提.第一节 极限的定义教学目的:1.理解极限的概念,理解函数左极限与右极限的概念,以及极限存在与左、右极限之间的关系。
2.理解无穷小、无穷大的概念,掌握无穷小的比较方法,会用等价无穷小求极限。
教学重难点:1.极限的概念和左极限与右极限概念及应用;2.无穷小及无穷小的比较;本节将在中学学习过的数列的极限的基础上学习函数的极限、极限性质、无穷小的定义及性质、无穷大的定义及其与无穷小的关系.一、数列的极限定义 对于数列{}n x ,如果当n 无限增大时)(∞→n ,n x 无限趋近于一个确定的常数A , 则称A 为数列{}n x 的极限.记作=∞→n n x lim A 或 A x n →(n ∞→). 亦称数列{}n x 收敛于A ;如果数列{}n x 没有极限,就称数列{}n x 是发散的.数列极限的运算法则为:如果∞→n lim =n x A , ∞→n lim =n y B ,那么 法则1 ∞→n lim (n x ±n y ) ∞→=n lim n x ±∞→n lim =n y A ±B ;法则2 ∞→n lim (nx n y ) ⋅=∞→n n x lim n n y ∞→lim AB =;法则3 ∞→n lim lim n n n Cx C x →∞==CA (C 是常数); 法则4∞→n lim B A y x y x nn n n n n ==∞→∞→lim lim ()0≠B . 以上法则1,法则2可以推广到有限个数列的和与积的情形.二、函数的极限1.当∞→x 时,函数)(x f 的极限定义 如果当x 的绝对值无限增大(即∞→x )时,函数)(x f 无限趋近于一个确定的常数A ,那么A 称为函数)(x f 当∞→x 时的极限,记为 A x f x =∞→)(lim 或 当∞→x 时,A x f →)(. 如图1-5(b )所示, 函数xx f 1)(=当x 的绝对值无限增大时, 函数xx f 1)(=的图象无限接近于x 轴.也就是,当∞→x 时,)(x f 无限地接近于常数零,即01lim=∞→xx . 在上述定义中,自变量x 的绝对值无限增大指的是既取正值无限增大(记为+∞→x ),同时也取负值而绝对值无限增大(记为-∞→x ).但有时自变量的变化趋势只能或只需取这两种变化的一种情形,为此有下面的定义:定义 如果当+∞→x (或-∞→x )时,函数)(x f 无限趋近于一个确定的常数A ,那么A 称为函数)(x f 当+∞→x (或-∞→x )时的极限,记为 lim ()x f x A →+∞=或当x →+∞时,()f x A →; lim ()x f x A →-∞=或当x →-∞时,()f x A →. 由图1-5(b )可以看出,01lim=+∞→xx 及01lim =-∞→x x ,这两个极限与01lim =∞→x x 相等,都是0.由图1-11(b )可以看出,2arctan lim π=+∞→x x ,2arctan lim π-=-∞→x x .由于当+∞→x 和-∞→x 时,函数x y arctan =不是无限趋近于同一个确定的常数,所以x x arctan lim ∞→不存在.由上面的讨论,我们得出下面的定理: 定理 A x f x =∞→)(lim 的充要条件是: )(lim x f x +∞→A x f x ==-∞→)(lim .(证明略)2.当0x x →时,函数)(x f 的极限定义 设函数()y f x =在点0x 的某个近旁(点0x 本身可以除外)内有定义,如果当x 趋于0x (但0x x ≠)时,函数)(x f 无限趋近于一个确定的常数A ,那么A 称为函数)(x f 当0x x →时的极限,记为A x f xx =→)(lim 0或 当0x x →时,A x f →)(.例1 考察极限C x x 0lim → (C 为常数)和x xx 0lim →. 解 因为当0x x →时,)(x f 的值恒为C ,所以=→)(lim 0x f x x C C xx =→0lim . 因为当0x x →时,()x ϕx=的值无限接近于x ,所以lim ()x x x ϕ→=00lim x x xx =→. 3.当0x x →时,)(x f 的左、右极限因为0x x →有左右两种趋势,而当x 仅从某一侧趋于0x 时,只需讨论函数的单边趋势,于是有下面的定义:定义 如果当x 从0x 左侧趋近0x (记为0x x -→)时,函数)(x f 无限趋近于一个确定的常数A ,那末A 称为函数)(x f 当0x x →时的左极限,记为 0lim ()x x f x A -→=.如果当x 从0x 右侧趋近0x (记为0x x +→)时,函数)(x f 无限趋近于一个确定的常数A ,那末A 称为函数)(x f 当0x x →时的右极限,记为 0lim ()x x f x A +→=定理 A x f xx =→)(lim 0的充要条件是: 0lim ()lim ()x x x x f x f x A -+→→==. (证明略)例2 讨论函数10()0010x x f x x x x -<⎧⎪==⎨⎪+>⎩当0→x 时的极限.解 观察图2-1可知:0lim ()x f x -→1)1(lim 0-=-=-→x x ,0lim ()x f x +→1)1(lim 0=+=+→x x .因此,当0→x 时,)(x f 的左右极限存在但不相等,由定理2知,极限 )(lim 0x f x →不存在. 例3 研究当x →0时, x x f =)(的极限.解 观察图2-2可知:⎩⎨⎧≥<-==0)(x x x x x x f 由于)(lim 0x f x -→0)(lim 0=-=-→x x ,=+→)(lim 0x f x 0lim 0=+→x x .所以当x 0→时,)(x f 的左, 右极限都存在且相等.由定理2知x →0时, x x f =)(的极限存在,且等于0.三、无穷小量实际问题中,常有极限为零的变量.例如,电容器放电时,其电压随着时间的增加而逐渐减小并趋近于零.对于这样的变量,有下面的定义:1.无穷小量的定义定义 极限为零的变量称为无穷小量,简称为无穷小. 如果0lim ()0x x x α→=,则变量()x α是0x x →时的无穷小,如果lim ()0x x β→∞=,则称()x β是x →∞时的无穷小,类似的还有0x x +→,0x x -→,x →+∞,x →-∞等情形下的无穷小.根据定义可知,无穷小是一种变化状态,而不是一个量的大小,无论多么小的一个数都不是无穷小,只有零是唯一的一个可作为无穷小的常数,无穷小是有极限变量中最简单而最重要的一类,在数学史上,很多数学家都致力于“无穷小分析”.2.无穷小量的性质定理 有限个无穷小的代数和为无穷小.(证明略)注意,无穷个无穷小之和未必是无穷小,如n →∞时,21n ,22n ,2nn 都是无穷小,但是222212(1)2n n n n n n n +++⋅⋅⋅+=,当n →∞时2(1)122n n n +→,所以不是无穷小.定理 有界函数与无穷小的积为无穷小. (证明略) 推论1 常数与无穷小的乘积是无穷小. (证明略)图2-1图2-2推论2 有限个无穷小的积为无穷小.(证明略) 例4 求极限01lim sin x x x→. 解 因为x 是当0→x 时的无穷小,而x1sin 是一个有界函数,所以1lim sin0x x x→=. 3.函数极限与无穷小的关系 设A x f xx =→)(lim 0,即0x x →时()f x 无限接近于常数A ,有()f x A -就接近于零,即()f x A -是0x x →时的无穷小,若记()()x f x A α=-,于是有 定理 3 (极限与无穷小的关系)A x f xx =→)(lim 0的充分必要条件是()()f x A x α=+,其中()x α是0x x →的无穷小.例如11x x +→当()x →∞时,有111x x x +=+,其中1x就是()x →∞时的无穷小.四、 无穷大量 1.无穷大的定义定义 6 若当0x x →(x →∞)时,函数()f x 的绝对值无限增大,则称函数()f x 为当0x x →(或x →∞)时的无穷大.函数()f x 当0x x →(或x →∞)时为无穷大,它的极限是不存在的,但为了便于描述函数的这种变化趋势,我们也说“函数的极限为无穷大”,并记为lim ()x x f x →=∞ 或 lim ()x f x →∞=∞. 例如,当0→x 时,x1是一个无穷大,又例如, 当x →+∞时,x e 是一个无穷大.注意,说一个函数()f x 是无穷大,必须指明自变量x 的变化趋向;无穷大是一个函数,而不是一个绝对值很大的常数.2.无穷大与无穷小的关系我们知道,当2x →时,2x -是无穷小,12x -是无穷大;当x →∞时,x 是无穷大,1x是无穷小.一般地,在自变量的同一变化过程中,如果)(x f 为无穷大,则)(1x f 是无穷小;反之,如果)(x f 为无穷小,且)(x f 0≠,则)(1x f 是无穷大. 利用这个关系,可以求一些函数的极限.例5 求极限13lim1-+→x x x . 解 因为031lim1=+-→x x x ,由无穷大与无穷小的关系,所以∞=-+→13lim 1x x x .五、无穷小量比较 由无穷小的性质,我们知道两个无穷小的和、差及乘积仍是无穷小.但两个无穷小的商却会出现不同的情况.例如,当0x →时, x 2、2x 、x sin 均为无穷小,而02lim 20=→x x x ,∞=→202lim x x x ,1sin lim 0=→xx x .两个无穷小之比的极限的不同情况,反映了不同的无穷小趋向于零的“快慢”程度.一般地,对于两个无穷小之比有下面定义:定义 设α和β都是同一过程的两个无穷小量,即lim 0α=,lim 0β=,1.若lim0αβ=,则称α是β的高阶无穷小量;记作()o αβ=,此时也称β是α的低阶无穷小量.2.若lim 0C αβ=≠,则称α与β是同阶的无穷小量.记作()O αβ=.3.若lim 1αβ=,则称α与β是等价无穷小量.记作βα~.例16 当1x →时,比较无穷小1x -与31x -的阶. 解 由于 0)1(lim 1=-→x x ,0)1(lim 31=-→x x ,且 3111limx x x --→3111lim 21=++=→x x x , 所以当1x →时,1x -与31x -是同阶无穷小.例17 当0→x 时,证明x cos 1-与22x 等价.解 由于 0)cos 1(lim 0=-→x x ,02lim20=→x x ,且=-→2cos 1lim 20xx x 122sin 2lim 220=→x xx .所以,当0→x 时,x cos 1-与22x 为等价无穷小.习题训练1.利用函数图像,观察函数的变化趋势,并写出其极限: (1)21limx x →∞; (2)lim 2x x →-∞; (3)1lim ()10x x →+∞; (4)1lim(2)x x→∞+;(5)2lim(45)x x →-; (6)2lim sin x x π→. 2.设2,1()1,1x x f x x ⎧≥-=⎨<-⎩,作出它的图象,求出当1-→x 时,()f x 的左极限、右极限,并判断当1-→x 时,()f x 的极限是否存在?3.设1()1x f x x -=-,求(10)f -和 (10)f +,并判断()f x 在1→x 时的极限是否存在?4.设21()1x f x x-=-,求0lim ()x f x →,1lim ()x f x →. 5.下列函数在自变量怎样变化时是无穷小?无穷大? (1)31y x = ; (2)211y x=+;(3) ln y x =;(4)y =6.求下列函数的极限:(1) sin limx x x →∞; (2)01lim cos x x x→; (3) 1lim1x xx →-; (4)32222lim (2)x x x x →+-.第二节 极限的运算教学目的:1.掌握极限的性质及四则运算法则;2.掌握利用两个重要极限求极限的方法。
极限与连续

第2章 极限与连续2.1 数列的极限1. 数列及其极限一、数列极限的描述性定义1.依照某种规律排列的一串数叫做数列。
数列中的每一个数叫做数列的项。
数列中的一般项称为通项,用x n 表示。
2.看几个数列的实例: 1,4,9,16,25,…,n 2,… 1,0,-1,0,1,0,-1,0,1,…3.数列可以看成为自变量取正整数值n 的函数 即:x n =f(n)4.数列的极限对于数列x 1,x 2,x 3,…,x n ,…,当项数n 无限增大时,它的通项x n 无限趋近于某一个常数a ,则称a 为数列{x n }的极限。
记作a x n n =+∞→lim 或x n →a(n →+∞) 5.具有极限的数列称为收敛数列,没有极限的数列称为发散数列 例如:⑴ ,21,,41,21,11-n ⑵ ,1)1(,,45,34,23,2n n n+--- ⑶ ,1,,43,32,21+n n⑷ 1,-4,9,-16,25,-36,…,(-1)n+1n 2,… 其中,⑴⑶是收敛数列,⑵⑷是发散数列。
[几点说明]1.数列的收敛与否与这个数列的增减性无关例如上面的收敛数列中,⑴是递减数列,⑶是递增数列。
常数列一定是收敛数列。
2.收敛的数列一定有界,但有界的数列不一定收敛。
3.收敛数列的极限有的可以达到,有的不能达到。
例如,常数列可以达到它的极限,但上面的例子都不能达到它们的极限。
二、数列极限的精确定义 1.无限趋近于a 的意义是指:⑴随着n 的增大,数列的项x n 与a 之间的距离越来越小⑵只要n 足够大,数列的项x n 与a 之间的距离可以小于给定的任何正数 ⑶无论你给定一个多小的正数,都一定可以在数列中找到一项x N ,使这一项后面所有的项与a 之间的距离小于你给定的那个正数。
定义2.1对于给定的无论怎样小的正数ε,总存在一个自然数N ,使得当n >N 时,不等式|x n -a|<ε成立,那么,就称a 是数列{x n }的极限。
高等数学第二章极限与连续

第二章第二章 极限与连续极限与连续一、本章提要 1.基本概念函数的极限,左极限,右极限,数列的极限,无穷小量,无穷大量,等价无穷小,在一点连续,连续函数,间断点,第一类间断点(可去间断点,跳跃间断点),第二类间断点,第二类间断点. .2.基本公式 (1) 1sin lim0=®口口口,(2) e )11(lim 0=+®口口口(口代表同一变量代表同一变量).). 3.基本方法⑴ 利用函数的连续性求极限;利用函数的连续性求极限; ⑵ 利用四则运算法则求极限;利用四则运算法则求极限; ⑶ 利用两个重要极限求极限;利用两个重要极限求极限; ⑷ 利用无穷小替换定理求极限;利用无穷小替换定理求极限;⑸ 利用分子、分母消去共同的非零公因子求形式的极限;形式的极限; ⑹ 利用分子,分母同除以自变量的最高次幂求¥¥形式的极限;形式的极限;⑺ 利用连续函数的函数符号与极限符号可交换次序的特性求极限;利用连续函数的函数符号与极限符号可交换次序的特性求极限; ⑻ 利用“无穷小与有界函数之积仍为无穷小量”求极限利用“无穷小与有界函数之积仍为无穷小量”求极限. .4.定理左右极限与极限的关系,单调有界原理,夹逼准则,极限的惟一性,极限的保号性,极限的四则运算法则,极限与无穷小的关系,无穷小的运算性质,无穷小的替换定理,无穷小与无穷大的关系,初等函数的连续性,闭区间上连续函数的性质小与无穷大的关系,初等函数的连续性,闭区间上连续函数的性质. .二、要点解析问题1 如果如果如果 A x f x x =®)(lim 0存在,那么函数)(x f 在点0x 处是否一定有定义处是否一定有定义? ?解析 A x f x x =®)(lim 0存在与)(x f 在0x 处是否有定义无关.例如1sin lim0=®xxx ,而)(x f =xx sin 在0=x 处无定义;又如0lim 20=®x x ,而2)(x x f =在0=x 处有定义处有定义..所以,)(lim 0x f x x ®存在,不一定有)(x f 在0x 点有定义点有定义. .问题2 若若A x f x g x x =×®)()(lim 0存在,那么)(lim 0x g x x ®和)(lim 0x f x x ®是否一定存在?是否一定有)(lim 0x g x x ®·)(x f =)(lim 0x g x x ®·)(lim 0x f x x ®?解析 )(lim 0x g x x x x ®·A x f =)(存在,并不能保证)(lim 0x g x x x x ®与)(lim 0x f x xx x ®均存在均存在..例如0lim 1lim 020==®®x x x x x ,而x x 1lim 0®不存在不存在..又因为只有在)(lim 0x g x x ®与)(lim 0x f x x ®均存在的条件下,才有)(lim 0x g x x ®·)(x f =)(lim 0x g x x ®·)(lim 0x f x x ®,所以)(lim 0x g x x ®·)(x f 存在,不能保证)(lim 0x g x x ®·)(x f =)(lim 0x g x x ®·)(lim 0x f x x ®.问题3 +¥=®xx 1e lim 是否正确,为什么是否正确,为什么? ?解析 不正确不正确..尽管+¥=+®xx 10e lim ,而0e1lim elim e lim 101010===---®-®®xx xx xx .这说明这说明,,0®x 时,x1e 不是无穷大不是无穷大. .三、例题精解 例1 求下列极限求下列极限求下列极限: :(1) ))(cos sin (lim tan 2224πx x x x x ++®;(2) 1)1232(lim +¥®++x x x x ;(3) 3111limxxx --®;(4) )1sin sin (lim 0xx x x x ++®; (5) )2sin(lim x x x -++¥®;(6) xx x x1sin53lim 2-¥®. 解 (1)(1)由于讨论函数由于讨论函数xx x x x f tan222)(cos sin )(++=在4π=x 处有定义,而且在4π=x 处连续,所以有处连续,所以有 ])(cos sin [lim tan 2224πx x x x x ++®4πtan222)4π(cos )4π(sin )4π(++=222)22()22(16π++= 116π2+=. (2)123lim()21x x x x +®¥++1212lim()21x x x x +®¥++=+ 12lim(1)21x x x +®¥=++ (这是¥1型,设法将其化为口口)口(11lim +¥®)11221lim(1)12x x x ++®¥=++2121)2111(lim )2111(lim ++×++=¥®+¥®x x x x x212121)]2111(lim [)2111(lim ++++=¥®+¥®+x x x x x211e ×=e =.(3) 311lim 1x xx®-- (这是(这是00型未定式)23323331(1)(1)1()lim (1)1()(1)x x x x x x x x x ®éù-+++ëû=éù-+++ëû2331(1)1()lim (1)(1)x x x x x x ®éù-++ëû=-+ (分子、分母均含非零因子1-x ) 23311()lim 1x x x x®++=+ 32=. (4))1s i ns i n(l i m 0x x x x x ++®x x x x x x 1sin lim sin lim 00++®®+= 01+=1=.需要注意,01sin lim 0=+®x x x 是由于x 为+®0x 时的无穷小量,x 1sin ≤1,即x 1si n 为有界函数,所以x x1sin为+®0x 时的无穷小时的无穷小.. (5)lim sin(2)x x x ®+¥+-sin lim (2)x x x ®+¥=+- ( (函数符号与极限符号交换函数符号与极限符号交换函数符号与极限符号交换)) (2)(2)sin lim2x x x x x x x®¥+-++=++(分子有理化)2sin lim2x x x®+¥=++0s i n = 0=. (6)235lim1sinx x x x®¥-(35)lim11(sin )x x xx x ®¥-= (适当变形) lim (35)11lim (sin )x x x x x x®¥®¥-= (利用商的极限公式)105lim (3)111lim (sin )x xx x x ®¥®-= (利用重要极限1sin lim 0=®口口口)3=例2 设ïîïíì<+>=,0,,0,1sin )(22x x a x x x x f 问a 为何值时)(lim 0x f x ®存在,并求此极限值存在,并求此极限值. . 解解 对于分段函数,对于分段函数,讨论分段点处的极限讨论分段点处的极限..由于函数在分段点两边的解析式不同,所以,一般先求它的左、右极限一般先求它的左、右极限. .01sin lim )(lim 200==++®®xx x f x x ,a x a x f x x =+=--®®)(lim )(lim 20.为使为使)(lim 0x f x ®存在,必须即),(lim )(lim 0x f x f x x -+®®=0=a . 因此,因此,0=a 时,)(lim0x f x ®存在且0)(lim 0=®x f x . 例3 设ïïîïïíì<--³+=,0,,0,2cos )(x x x a a x x x x f 问当a 为何值时,0=x 是)(x f 的间断点? ? 是什么间断点是什么间断点是什么间断点? ?解0lim ()lim x x a a xf x x--®®--=0()()lim ()x a a x a a x x a a x -®--+-=+- 0lim ()x x x a a x -®=+-01limx a a x -®=+-12a=,212cos lim )(lim 0=+=++®®x x x f x x ,当ax f x f x x 2121)(lim )(lim 0¹¹-+®®,即,亦即1¹a 时,0=x 是)(x f 的间断点;由于a 为大于0的实数,故)0()0(-+f f 与均存在,只是)0()0(-+¹f f ,故0=x 为)(x f 的跳跃间断点的跳跃间断点. .例 4 已知已知 011lim 2=÷÷øöççèæ--++¥®b ax x x x ,求b a ,的值的值. . 解 因为因为 )11(lim 2b ax x x x --++¥®2(1)()1lim1x a x a b x bx ®¥--++-=+0=,由有理函数的极限知,上式成立,必须有2x 和x 的系数等于0,0,即即îíì=+=-01b a a ,于是1,1-==b a .四、练习题⒈ 判断正误⑴ 若函数)(x f 在0x 处极限存在,则)(x f 在0x 处连续处连续. ( . ( . ( ×× ) 解析 函数在一点连续,函数在一点连续,函数在一点连续,要求函数在该点极限存在,要求函数在该点极限存在,要求函数在该点极限存在,且极限值等于该点函数值.且极限值等于该点函数值.且极限值等于该点函数值.如函数如函数îíì=¹=,0,1,0,)(x x x x f 0lim )(lim 00==®®x x f x x ,即函数)(x f 在0=x 处极限存在;但1)0(0)(lim 0=¹=®f x f x ,所以函数îíì=¹=0,1,0,)(x x x x f 在0=x 处不连续.处不连续. ⑵分段函数必有间断点⑵分段函数必有间断点. ( . ( . ( ×× )解析 分段函数不一定有间断点.如函数îíì<-³=0,,0,)(x x x x x f 是分段函数,()0lim )(lim 0=-=--®®x x f x x ,0lim )(lim 0==++®®x x f x x ,所以0)(lim 0=®x f x ;又因为0)0(=f ,即)0()(lim 0f x f x =®,所以函数)(x f 在0=x 处连续,无间断点.处连续,无间断点.⑶x 3tan 与x 3sin 是0®x 时的等价无穷小时的等价无穷小. ( . ( . ( √√ ) 解析 13cos 1lim3sin 3tan lim 00==®®xxx x x ,由等价无穷小的定义,x 3tan 与x 3sin 是0®x 时的等价无穷小.的等价无穷小.⑷无界函数不一定是无穷大量⑷无界函数不一定是无穷大量. ( . ( . ( √√ ) 解析 无穷大必无界,但反之不真.如函数无穷大必无界,但反之不真.如函数x x x f cos )(=,当¥®x 时是无界函数;但若取2ππ2+=n x ,¥®x (¥®n )时0cos )(==x x x f ,不是无穷大量.,不是无穷大量. 2.选择题⑴下列极限存在的是⑴下列极限存在的是( B ) ( B )(A) xx 4lim ¥®; (B) 131lim 33-+¥®x x x ; (C)x x ln lim 0+®; (D) 11sin lim 1-®x x . 解析 (A)04lim =-¥®x x ,+¥=+¥®x x 4lim , 所以所以xx 4lim ¥®不存在;不存在;(B)311311lim 131lim 3333=-+=-+¥®¥®x x x x x x ,极限存在;,极限存在;(C)-¥=+®x x ln lim 0,所以x x ln lim 0+®不存在;不存在; (D)1®x 时,01®-x ,¥®-11x ,所以,所以11sinlim 1-®x x 不存在.不存在. ⑵已知615lim =-+¥®x ax x ,则常数=a ( C ).(A) 1(A) 1;; (B) 5 (B) 5 ;; (C) 6 (C) 6 ;; (D) -1.解析611515lim ==-+=-+¥®a xx a x ax x ,所以,所以6=a . ⑶xx f 12)(=在0=x 处 ( C ).(A) (A) 有定义;有定义;有定义; (B) (B) 极限存在;极限存在;极限存在; (C) (C) 左极限存在;左极限存在;左极限存在; (D) (D) 右极限存在右极限存在右极限存在. . 解析 因xx f 12)(=,在0=x 处无定义,处无定义,02lim )(lim 1==--®®xx x x f ,即xx f 12)(=在0=x 处左极限存在,处左极限存在,+¥==++®®x x x x f 102lim )(lim ,即xx f 12)(=在0=x 处右极限不存在,处右极限不存在,由极限存在的充要条件,可知函数xx f 12)(=在0=x 处的极限不存在.处的极限不存在. ⑷当⑷当+¥<<x 0时,xx f 1)(=( D ).(A) (A)有最大值与最小值有最大值与最小值有最大值与最小值; ; (B)(B)有最大值无最小值有最大值无最小值有最大值无最小值; ;(C)(C)无最大值有最小值无最大值有最小值无最大值有最小值; ; (D)(D)无最大值无最小值无最大值无最小值无最大值无最小值. . 解析 xx f 1)(=在()+¥,0上是连续函数,图形如下:上是连续函数,图形如下:所以当+¥<<x 0时,xx f 1)(=无最大值与最小值.无最大值与最小值. 3.填空题Oyxx1(1) (1)已知已知b a ,为常数,3122lim2=-++¥®x bx ax x ,则=a 0 0 ,,=b 6 6 ;; 解 ¥®x 时极限值存在且值为3,则分子、分母x 的最高次幂应相同,所以0=a ,那么那么 32122lim 122lim 122lim 2==-+=-+=-++¥®¥®¥®b xx b x bx x bx ax x x x ,所以6=b .(2)23)(2+-=x x x f 的连续区间是(][)¥+¥-,21, ;解 由0232³+-x x ,知函数)(x f 的定义区间为(][)¥+¥-,21, .又因为初等函数在其定义区间上连续,所以23)(2+-=x x x f 的连续区间是(][)¥+¥-,21, .(3)0=x 是xx x f sin )(=的 可去可去可去 间断点间断点间断点; ;解 0=x 时,函数xx x f sin )(=无定义,但1sin lim0=®xxx ,极限存在,所以0=x 是xx x f sin )(=的可去间断点.的可去间断点.(4)(4)若若a x x =¥®)(lim j (a 为常数为常数)),则=j ¥®)(elim x x ae.解 由复合函数求极限的方法,ax x x x e eelim )(lim )(==j j ¥®¥®.4.解答题⑴ qq q q sin cos 1lim 0-®; 解一 qq q q sin cos 1lim 0-®2cos2sin 22sin 2lim 2q q q qq ®=2cos2122sinlim 0qqqq ×=®2cos 21lim 10q q ®×=21=.解二 无穷小量的等价代换,由于无穷小量的等价代换,由于0®q 时,2~cos 1,~sin 2q q q q -,所以所以 q q q q sin cos1lim 0-®q q q q ×=®2lim 2021= .⑵ 设x x f ln )(=,求,求 1)(lim1-®x x f x ; 解由无穷小量的等价代换,1®x 即01®-x 时,()[]1~11ln ln )(--+==x x x x f ,所以所以 111lim 1ln lim 1)(lim 111=--=-=-®®®x x x x x x f x x x .⑶ x xx sin e lim -+¥®;解 +¥®x 时,x-e 是无穷小量,x sin 是有界变量.是有界变量. 因为有界变量乘无穷小量仍是无穷小量,所以因为有界变量乘无穷小量仍是无穷小量,所以 0sin e lim =-+¥®x xx .⑷ 设îíì>-£=,1,56,1,)(x x x x x f 试讨论)(x f 在1=x 处的连续性,写出)(x f 的连续区间;解 1lim )(lim 11==--®®x x f x x ,()156lim )(lim 11=-=++®®x x f x x ,所以1)(lim 1=®x f x .且1)1(=f ,即)1()(lim 1f x f x =®,所以函数)(x f 在1=x 处连续.处连续.又因为当1£x 时函数x x f =)(连续,当1>x 时函数56)(-=x x f 也连续,也连续,所以函数所以函数)(x f 的连续区间为()¥+¥-,.⑸ 设ïïîïïíì>=<=,0,sin ,0,1,0,e )(xx x x x x f x求)(lim ),(lim 00x f x f x x +-®®,并问)(x f 在0=x 处是否连续;处是否连续;e 1xe 1e 11=--xxe 1e 1e 1111=-=---++xx xxe 1e 11+-=xx 的跳跃间断点.的跳跃间断点. xx 2sin )1ln(lim0+;212lim 2sin )1ln(lim00=+x x x x .。
高等数学第二章极限与连续

上页 下页 返回
注:数列极限的定义没有给出求极限的方法,但可
利用定义证明数列的极限
lim
n
an
A
例1、证明 lim n
0,N 0,当n (1)n1
1.
N时,有 an
A
.
n
证明:任给
0,
n 要使
n
(1)n1
1
1
,
n
n
只要n 1 ,
取N
[1],
则当n N时,
有 n (1)n1 1 , 故 lim n (1)n1 1.
A B 0, A B. 故唯一性得证.
(设 A B 0,取 A B 0,
4
A B 2 A B A B 矛盾,故 A B 0.)
4
2
上页 下页 返回
定理2[有界性]:收敛数列必有界.
lim
n
an
A,
lim
n
an
B,
则
0,
N1 0,当n N1时, 有 an A .
N2 0,当n N2时, 有 an B .
取N maxN1 , N2, 则当n N时, 有
an A , an B ,
A B ( A an ) (an B)
an A an B 2 .
二、数列极限
1、极限思想 (1) 割圆术 “割之弥细,所失弥少,割之又割,以至于不可割, 则与圆周合体而无所失矣” ——刘徽
正六边形的面积 S1
正十二边形的面积 S2
R
正6 2n1形的面积 Sn
S1 , S2 , S3 , , Sn ,
S
上页 下页 返回
(2)截丈问题
“一尺之棰,日截其半,万世不竭”
第2章极限与连续

2.5.1 连续的概念和性质
2.5.2 初等函数的连续性
1. 连续函数的运算
由极限性质可得到连续函数的如下性质。
总结以上,所有的基本初等函数在定义 域内连续。
由于初等函数是由基本初等函数经有 限次四则运算和复合得到的,因而所有的初 等函数在定义区间内连续。
定义区间是指包含在定义域内的区间。 有些函数的定义域为孤立点,不能形成 区间,因而函数在该点没有极限也就无法连续。
该极限的正确求法为
2.5 函数的连续性
许多自然现象和社会现象都是不断变化 的,例如树木生长、四季更迭、水滴石穿等。
这些变化都具有一定的连续性,即在很短 的时间内现象的变化也很微小。
这一特性在数学上称为函数的连续性, 即自变量变化很小时,函数的变化量也很小。
本节介绍函数连续的概念、间断点的分 类、初等函数的连续性以及闭区间上连续函 数的性质。
以上讨论的3个数列有共同的特性:当n 无限增大时,其通项都无限接近某个常数。
把这种特性抽象出来,就形成了极限的 定义。
2. 数列的极限概念
定义2 设{xn} 为一数列,如果存在常数a, 当n 无限增大时,xn 无限接近常数a,则称常 数a 是数列{xn} 的极限,或者说数列{xn} 收 敛于a,记为
定理2(收敛数列的有界性) 如果数列 {xn} 收敛,则数列{xn} 必有界。
由定理2可知,有界是数列收敛的必要 条件。
我们常用该定理判断数列发散。
例如,{(-1)nn}的通项的绝对值(-1)nn =n, 故{(-1)nn}无界,所以{(-1)nn}必发散。
注意,有界数列不一定收敛。 例如,数列{(-1)n} 的通项xn ≤1,是有界 数列,但该数列发散。
f(ξ)=0 如图2-10所示,函数y =f(x)对应的曲线 由 x 轴的下侧连续地变化到上侧,至少要经过x 轴一次。
2极限与连续

如果数列没有极限,就说数列是发散的或不收敛.
例如
lim
n
n
n
1
=
1,
lim
n
1 2n
=
0,
lim
n
n (-1)n-1 n
=.
而{2n},{ (-1)n1},是发散的.
例2(P49)、数列趋向于∞的定义见P50
对无限接近的刻划:
“当n无限增大时,xn无限接近于a” 等价于:当n 无限增大时,|xn-a |无限接近于0;或者说,要|xn-a |有多小,只要n足够大, |xn-a |就能有多小.
x1=f(1),x2=f(2),x3=f(3),x4=f(4),...,xn=f(n)
2. 数列的极限的通俗定义:
对于数列{xn},如果当n 无限增大时,数列的一般
项xn无限地接近于某一确定的数值a ,则称数列{xn}收
敛, a 是数列{xn}的极限,或称数列{xn}收敛于a .记为
lim
n
xn=a.
2. 无穷大定义:
如果当x x0(或x )时,对应的函数值的绝对 值|f (x)|无限增大,就说函数f (x)当x x0 (或x )时 为无穷大,记为
lim f (x)= (或lim f (x)= ).
x x0
x
应注意的问题:
当x x0(或x )时为无穷大的函数f(x),按函数 极限定义来说,极限是不存在的.但为了便于叙述函
那么函数 f (x)叫做x x0(或x )时的无穷小. 例如 因为 lim(x -1) = 0 ,
x1
所以函数x-当x1时为无穷小.
无穷小与极限的关系:
定理1 在自变量的同一变化过程x x0(或x ) 中,具有极限的函数等于它的极限与一个无穷小之和; 反之,如果函数可表示为常数与无穷小之和,那么该 常数就是这函数的极限.(P66)
第二章 极限与连续 《经济数学》PPT课件

值无限趋近于一个确定的常数A,则称常数A为函数在自变量x趋向于无穷大时的
极限.记做:
Lim(x→∞)f(x)=A 或 f(x)→A (x→∞)
• 当自变量x大于0而绝对值无限增大时,如果函数y=f(x)的对应值无限趋近于一个
确定的常数A,则称常数A为函数在自变量x趋向于正无穷大时的极限.记做:
lim (x→+∞)f(x)=A 或 f(x)→A (x→+∞)
形的面积时,实际上采用的就是求极限的办法.而我国魏晋时期的大数学家刘徽(公元3世纪)就曾 用圆的内接正多边形来逼近圆的方法,计算的圆周率精确到小数点后4位的数值:3.1416. • 设有一圆,首先作内接正六边形,把它的面积记为A1;再作内接正十二边形,其面积记为A2;再作内 接正二十四边形,其面积记为A3;循此下去,每次边数加倍,一般地,把内接正6×2n-1边形的面积记 为An(n∈N).这样,就得到一系列内接正多边形的面积: • A1,A2,A3,…,An,…
2.1.2 无穷小与无穷大
3)无穷小的阶 ➢ 有限个无穷小的代数和与积仍是无穷小,但是两个无穷小的商则
会出现不同的情况.例如,当x→0时,2x,x2,sin x都是无穷小,但它 们两两之比的极限会出现各种不同情况,这反映了不同的无穷小 趋向于零的快慢程度.由于两个无穷小之商一般不能立刻判断其 极限是否存在,所以我们通常称这种极限为未定式极限.
高等数学西财社版第二章极限与连续

二、无穷大量
有时,无穷大量具有确定的符号:在x的某种变化趋势下,若f(x)恒为正且无限增大,则称f(x) 为正无穷大量,并用+∞表示;若f(x)恒为负且其绝对值无限增大,则称f(x)为负无穷大量, 并用-∞表示.
注意 无穷大量是一个函数,而不是一个很大的数.函数为无穷大量,是函数极限不存在的一种 特殊情况.但为了叙述方便,仍然说成函数的极限是无穷大.任意常数都不是无穷大 量.
二、函数的极限
1.当x→∞时,函数f(x)的极限
观察函数f(x)= 1 可以发现,x无论取正数还是取负数,只要|x|无限增大,函数值就会无限
x
趋近于0,如图2-4所示.
定义5 设函数f(x)当|x|>a时有定义(a为某个常数), 如果当x的绝对值无限增大时,相应的函数值f(x)无限趋 近于一个确定的常数A,则称A为当x趋于无穷大时函数 f(x)的极限,记作
二、函数的极限
1.当x→∞时,函数f(x)的极限
定义7 设函数f(x)在(-∞,a)内I有定义(a为某个常数),如果当x无限减小(或x无限增大)
时,相应的函数值f(x)无限趋近于一个确定的常数A,则称A为当x趋于负无穷大时函数f(x)的极 限,记作
二、函数的极限
2.当x→x0时,函数f(x)的极限
三、无穷小量与无穷大量的关系
定义3 设α(x)与β(x)均为自变量在同一变化趋势下的无穷小.
二、复合函数的极限运算法则
二、复合函数的极限运算法则
二、复合函数的极限运算法则
三、知识拓展
第三节
两个重要极限
问题情境
伴随着汽车普及程度的提高和汽车消费观念的不断成熟,人们对于二手车的接受程度 也在不断地提高,从而带来了二手车市场的蓬勃发展.据中国汽车流通协会统计,2018 年全国二手车累积交易1 382.19万辆,累计同比增长11.46%.预计到2020 年,我国二 手车交易规模将达到2 920万辆,新车与二手车交易规模比例将接近1∶1.但由于影响二 手车价格的因素比较多,因此消费者在对二手车进行估价时往往不知道从何下手.
高等数学第二章极限与连续

x1 ≥ x2 ≥ x3 ≥ ≥ xn ≥ xn+1 ≥
那么称数列为单调递减数列. 那么称数列为单调递减数列 单调递减数列
xn
x 4 x 3 x 2 x1
x
单调递增和单调递减数列统称为单调数列 单调递增和单调递减数列统称为单调数列. 单调数列
二,有界性
如果存在M>0,对于任何正整数 ,恒有 对于任何正整数n 如果存在 对于任何正整数 那么称数列 {xn }为有界的;否则称为无界的. 有界的 否则称为无界 无界的 如果数列所有的项都不超过某一个常数,即 如果数列所有的项都不超过某一个常数,
x2 4 x2 4 lim =2 或 →2 x → 2 2( x 2) 2( x 2)
(x →2).
3 2 1 -4 -3 -2 -1 0 -1 -2 -3
x2 4 f ( x) = 2( x 2)
x →2 ← x
4
定义3 的某个去心邻域有定义, 定义 设函数在点 x 0的某个去心邻域有定义,如果当 x源自xn = n ,3
1,8, ,, n 3 , (1) 27
1 1 1 1 , , , , n , 2 4 8 2
1 xn = n , 2
(2)
xn = (1)
n 1 xn = n
n1
1 , n
1 1 n 1 1 1, , , , ( 1 ) , 2 3 n
(3) (4) (5)
x n = (1)
x → +∞
lim f ( x) = A 或 f ( x) → A ( x → +∞).
例如,由函数 的图形可见, 例如 由函数 f ( x) = arctanx 的图形可见 y
π
2
y = arctan x
微积分第2章极限与连续

2. 用定义只能验证极限,不能求极限.
第二章 极限与连续
7
三、数列极限的运算法则 (课本p.66§2.5 )
定理 设
则
会应用
证明
特别地,
第二章 极限与连续
8
例2 求极限:
注意: 极限四则运算只适用于 有限项运算,且各项极限存在!
(上下同除以n3)
例3 设函数
(先求括号内各项之和)
,求极限 (考研题)
例4 证明方程 x3 - 4x2 + 1=0 在 (0,1) 内至少有一个根.
函数极限的计算方法
1. 图像观察 2. 按定义验证 3. 四则运算(拆分后各部分极限应存在) 4. 夹逼准则 5. 两个重要极限及其应用 6. 无穷小、无穷大的性质 7. 无穷小等价代换 8. f 在连续点 x0 处的极限为 f(x0) 9. 多重复合函数,遇连续函数,极限符号可向内移位 10. 变量替换
例2 比较 x→0 时下列各无穷小量的阶:
1) sinx 与 x, tanx 与 x;
等价
2)
与 x;
同阶
3)
与 x (x→0+) ;
4) 1-cos x 与 x2/2;
等价
x→0 时常用等价无穷小量
要记
x ~ sin x ~ tan x ~ arcsin x ~ arctan x ~ ln(1+x) ~ ex -1
一、无穷小量 二、无穷大量 三、无穷小量的阶 四、无穷小量等价代换
一、无穷小量
定义 若
,则称 f(x) 为当x→X 时的无穷小量.
若 f(x) 在 X 某邻域内有界,则称 f(x) 为x→X 时的有界量.
例: x2, sinx, 0 是 x→0 时的无穷小量;
高等数学 第二章 极限与连续

lim
x x0
f
(x) 的值等于该点的函数值
f
(x0 )
如果
lim
xx
0
f (x)
f (x0 )
(或 lim
xx
0
f (x)
f (x0 )
一、函数极限的概念 二、函数极限的性质
一、函数极限的概念
1)自变量趋于有限值时函数的极限
设函数 f (x) 在点 x0 的去心邻域内有定义,如
果在 x x0 的过程中,对应的函数值 f (x) 无限接
近 于 确 定 的 数 值 A , 那 么 称 A 是 函 数 f (x) 当
x
x0
时的极限,记作
性质 1 有限个无穷小的代数和仍为无穷小. 性质 2 有界函数与无穷小的乘积仍是无穷小. 推论 1 常数与无穷小的乘积仍是无穷小. 推论 2 有限个无穷小的乘积仍是无穷小
定理 lim f (x) A的充分必要条件是 f (x) A , x x0
其中 为当 x x0 时的无穷小.
二、无穷大
性质 1 (极限的唯一性) 如果数列{yn} 有极 限(或收敛),那么它的极限是唯一的.
性质 2 (收敛数列的有界性) 如果数列{yn} 有极限,那么数列{yn} 一定有界.
性质 3(收敛数列的保号性)如果给定数列
{
y
n
}
,且
lim
n
yn
a ,a
0(或 a
0) 那么从某一项
起,都有 yn 0 (或 yn 0 ).
yn
AB;
(3)
lim xn n yn
lim
n
xn
lim
n
yn
A B
《数学研究》第二章极限与连续
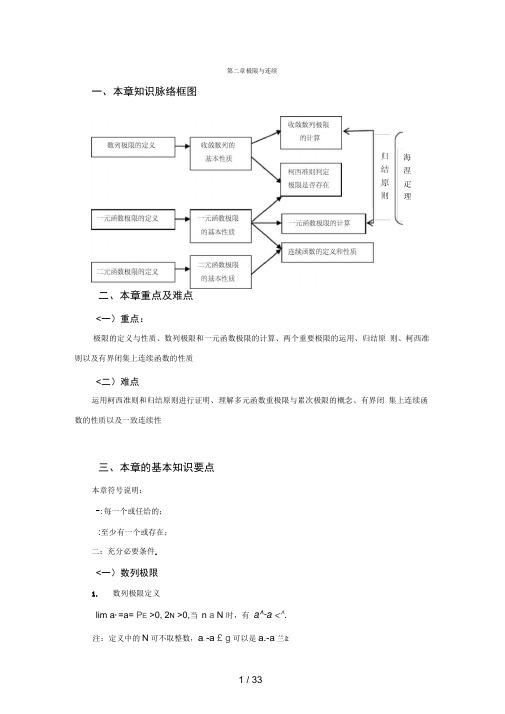
第二章极限与连续一、本章知识脉络框图海涅疋理二、本章重点及难点<一)重点:极限的定义与性质、数列极限和一元函数极限的计算、两个重要极限的运用、归结原则、柯西准则以及有界闭集上连续函数的性质<二)难点运用柯西准则和归结原则进行证明、理解多元函数重极限与累次极限的概念、有界闭集上连续函数的性质以及一致连续性三、本章的基本知识要点本章符号说明:-:每一个或任给的;:至少有一个或存在;二:充分必要条件.<一)数列极限1.数列极限定义lim a* =a= P E>0, 2N >0,当n a N 时,有a^-a <^.注:定义中的N可不取整数,a. -a £ g可以是a.-a兰&定理:增加、改变或去掉数列的有限项,不影响数列的收敛性和极限.重排不改变数列敛散性.数列极限的等价定义(1> W呂a0,三N >0,当n a N时有a.—a<k名,其中k为某个正数(2>\/0 VE c c,2N n0,当n >N时有a. —a <k w,其中c与k为某个正数.2.收敛数列的性质(1>唯一性定理:每个收敛的数列只有一个极限(2>有界性定理:收敛的数列必定有界.(3>保号性定理:若lim a.二a,则对任意r ::: a(或r • a), T N, -n • N,有a. r (或a. :r>.(4>保不等式性定理:若1 i ma. , l ibm都存在,且N, -门• N有a.辽»则lim a.冬lim b..._丿.—几(5>迫敛性定理:设.im a.二.im b.二a.数列{c.}满足:N,-. • N 有a. _ c. _ b.,则数列{c.}收敛,且lim c. =a.(6>四则运算法则:设lim a.二a,lim b.二b,则i) lim(a. _b.)二a _b;n—ii) lim a. b.二a b;n—iii) lim 旦'二色,其中bn=O,b = O.F b. b(7>与子列的关系:数列{a.}收敛二数列{a.}的任何非平凡子列都收敛3.数列极限存在的条件递增数列:冃乞a2 川一a. ^a. 1 二1 II;递减数列:日一a2 川a. -a. 1 III.(1>单调有界定理:在实数系中,有界的单调数列必有极限.(2> 柯西收敛准则:一;・0, N,-"n, m - N,|a.-a m卜:;.<二)函数极限1.函数极限和非正常极限概念函数极限定义(通过对比加以理解>:(x) =A= - ; 0, k ■ 0,当 x k 时,恒有 | f(x)- 列:::;.(2> lim f (x) = A= W E >0,三k >0,当x c —k 时,恒有 f(x) — A c& x —严 (3> l i m f (x) = A u W E >0, 2k >0,当 | x> k 时,恒有 | f (x) - A (4> lim f (x) = A=>0,萊 A 0,当 0vx_x 0|c 5 时,恒有 f(x)-AcE.1(5> lim f (x) = Au Fg 》0,a 0,当—6 vx —x 0v0 时,恒有 | f(x) — A cg . (6> lim*f (x) = Au Fg 》0,为=0,当0vx — x0C 毎时,恒有 |f(x)—Av& 上述左极限lim f (x)和右极限lim f (x)也可以写成f (x^ -0)和f(x ) 0).X 吋JX Q ■定理:lim f (x)二 A= f (x 0 - 0) = f (x 0 0) = A.非正常极限定义 <只列出2个,其余可以类似写出):(1> lim f(x) = -::u - M 0,工心〉0,当 0 ::|x - x 01 ::、时,恒有 f(x)::-M. (2> lim f(x)=^ =于M >0,弓k 》0,当 |x|Ak 时,恒有f (x) > M .x_^c2. 函数极限的基本性质下面只以lim f (x)为代表来说明,其余类型极限的性质可以类似写出X 的 (1>唯一性定理:若lim f (x)存在,则极限唯一.(2>局部有界性定理:若lim f(x)存在,则f (x)在x0的某个空心邻域 U 0(x 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
lim f (x ) 不存在.
x0
图2-5
由极限定义可以推算出下述两个结论:
x x0
lim x x0
, (C 为常数)
lim C C ,
2.1.3
1.无穷小量的定义
无穷小量
定义 2.5 极限为零的变量称为无穷小量,简称无穷小,记 为 .
1 1 例如 lim =0,所以函数 当 x 时是无穷小. x x x
x
π lim ( arctan x )=- . x 2
(2) x x0 时, 函数的极限
邻域的概念: 设实数 x0 ,
且 >0,数集{x x0 x x0 }. 叫点
x0 的 邻域,记作U ( x0 , ) .即U ( x0 , ) {x x0 x x0 }.
左,右极限统称单侧极限.
x, x 0; 例5 求函数 f ( x) 当x 0 时的左极限 f ( x0 ) 和右 1, x 0.
极限 f ( x0 ) .
y
y x
1
解 这是一个分段函数,如 图 2-4 所示,由图可直观看到, f ( x0 ) = lim f (x) = lim ( x) =0
O
x
1 解 由图 2-1 可知 lim =0, x x 1 1 lim =0 . 所以lim =0. x x x x
图2-1
例3 讨论当 x 时候,函数 y arctan x 的极限.
π 解 由于 lim (arctan x) , x 2 所以 lim arctan x 不存在.
是无穷小.
即 lim f ( x) A lim 0 , f ( x) A .
3. 无穷小的运算性质 性质1 性质2 性质3 性质4 有限个无穷小的代数和是无穷小. 有限个无穷小的积是无穷小. 有界函数与无穷小的积是无穷小. 常数与无穷小的积是无穷小.
例8
1 求 lim x sin x 0 x
如果对于自变量 x 所对应的变量 y 值是正的(或负的) ,则 记作 lim y , lim y .) (
2. 无穷大的性质
定理2.5 在自变量的同一变化过程中 (1) 有限个无穷大的乘积仍是无穷大; (2) 无穷大与有界量的和仍是无穷大.
注意: (1) 有限个无穷大的代数和不一定是无穷大; (2) 无穷大与有界量的乘积也不一定是无穷大. 3. 无穷小与无穷大的关系
函数 f (x ) 在点x0 的右半邻域内有定义, 当自变量在此半邻 域内无限接近于 x0 时,函数 f (x ) 无限接近于常数 A,则称 A 为函数 f (x ) 在 x0 点的右极限,记作 lim f ( x ) A 或 f ( x ) A
x x0
x x0 )或 f ( x0 ) A (
x 0 x 0 f ( x0 ) = lim f (x) = lim 1=1 x 0 x 0
y 1
x
O
图2-4
x 1, x 0; 例6讨论函数 f ( x) 0, x 0; 当 x 0 时的极限 lim f (x ) . x0 x 1, x 0. y
lim f (x) =A,或 f ( x ) A( x ) .
x
f (x) 无
定理 2.2
lim f (x) = A的充要条件是
x x
lim f (x) = lim f ( x) A
x
y
1 y x
1 例 2 设函数 y ,考察当 x x 趋于无穷时的极限.
点 x0 叫邻域的中心, 叫邻域的半径.
因 为 x x0 相 当 于
x x0 , 即 x0 x x0 , 所以在几何上, 邻域 U ( x0 , ) 表示以点x0 为
中心,长为 2 的开区间( x0 , x0 ) .如图 2-2
n 这种数列通常也形式地记作 lim yn =lim 2 = + n n
2. 函数的极限
(1) x 时, 函数的极限 定义 2.2 设函数 f (x) ,如果当 x 的绝对值无限增大时,函数
f (x) 无限趋于一个确定的常数 A,则称当 x 趋于无穷时,函数
f (x) 以 A 为极限,记作 lim f (x) =A,或 f (x) A ( x ).
1 解ห้องสมุดไป่ตู้因 lim x 0, sin 1, 故由无穷小性质 3 有 x 0 x 1 lim x sin 0 x 0 x
2.1.4
极限的性质
性质1(唯一性)函数若有极限,则其极限必唯一. 性质2(有界性)有极限的变量是有界变量.
性质 3 (保号性) 若在 U ( x0 , ) 内, 恒有 f (x) ≥0 (或 ≤0)且 lim f ( x) A ,则 A≥0(或 A≤0).
观察如上 4 个数列在n 无限增大时的变化趋势, 可以看到数 n 1 n 1 1 列 和 (1) 无限接近于常数 无限接近于 0,数列 n n n 1 1,而数列2n 随着 n 的增大,数列中的项也越来越大,不会靠 近一个确定的常数,我们给出数列极限的定义.
又如 lim( x 1) =0,所以函数x 1 当 x 1时是无穷小.
x 1
注意: (1)无穷小是一个变量,是在变化过程中绝对值越来越小, 并且无限地趋于零的变量. (2)绝不能将其与很小的常量相混淆,数零是唯一可作为 无穷小的常数, (3)由于无穷小表达的是量的变化状态,因此说一个函数
x2 1 例4讨论函数 y f ( x) 当 x 无限趋近于 1 时的变化趋势. x 1 解 当 x 从 1 的左侧无限接近 1 时,对应函数值变化如下:
该函数的图像是直线 y x 1上除去点(1,2)以外的部分, 如图 2-3,从图 2-3 可以看到,此函数在 x =1 处虽然没有定义, 但是当 x 从 x =1 处的左右两边分别越来越接近 1 时,函数 x2 1 y f ( x) 的值越来越趋 x 1 x2 1 y 2 近于 2,于是,按定义 2.3, x 1 2 x 1 函数 f ( x) 当 x 1时 x 1 1 x2 1 以 2 为极限 即 lim =2. x1 x 1 x 1 O
定义 2.1
n 设数列 yn ,若当 无限增大时, 趋于一 yn
n
个确定的常数 A,则称 A 为数列 yn 的极限,记作 limyn =
n A,或 yn A( )亦称数列 yn 收敛于 A.
有极限的数列称为收敛数列,没有极限的数列称为发散数列.
按上述定义,表示例 1 中数列(1)(2)(4)的极限分别为: , , n 1 1 lim =0; lim lim (-1) n1 =0. =1; n n n n 1 n n 数列(3)的极限不存在,当 n 时, yn 越来越大趋于 ,
定理 2.6 在同一变化过程中 1 (1) 若 y 是无穷大,则 是无穷小; y 1 (2) 若 y 是无穷小,且 y ≠0,则 是无穷大. y
2.1.6
1
2 3 4 5
小结
函数的极限
左极限与右极限 无穷小量 极限的性质 无穷大量
例 1 看下面的例子 1 1 1 1 (1) :1, , ,„, ,„; 2 3 n n n n 1 2 3 (2) ,„; : , , ,„, n 1 n 1 2 3 4 n 21 ,22 ,23 ,„, n ,„; 2 (3) 2 :
1 1 1 n 1 1 n 1 1 (4) (1) ,„. :1,- , ,- ,„, (1) n n 2 3 4 等等都是数列.
x
如果 x >0 且 x 无限增大(记作 x )时, 函数 f (x) 无限趋 近于一个确定的常数 A,可得 lim f ( x) A ,或 f ( x) A
x
( x ) .
如果 x<0 且 x 无限增大 (记作 x ) 函数 时, 限趋近于一个确定的常数 A,可得
解 如图 2-5 所示 lim f (x ) = lim ( x 1) 1;
x 0 x 0
y x 1
1
x 0
lim f (x ) = lim ( x 1) 1;
x 0
x 0
O
x
因 故
lim f (x ) ≠ lim f (x )
x 0
y x 1
2
(3) 因 lim 2 x =0,故当 x 时, 2 x 为无穷小;
x
1 x 1 x (4) 因 lim ( ) =0,故当 x 时, ( ) 为无穷小. x 4 4
2. 极限与无穷小的关系
定理 2.4 lim f ( x) A 的充要条件是 f ( x) A ,其中
x x0
0
f (x)
若 lim f ( x) A ,且 A>0(或 A<0 ) ,则当 充分小时,
x x0
在U ( x0 , ) 内,恒有 f ( x) 0 (或 f ( x ) 0 ).
0
性质 4(夹逼准则) x∈U ( x0 , ) 时, h(x) ≤ f (x) ≤g (x) 若 有 且 则
第2章
2.1 2.2 2.3 2.4
极限与连续
极 限 极限的运算 函数的连续性 闭区间上连续函数的性质
第2章
2.1
2.1.1
极限与连续
极 限
函数的极限
2.1.2 左极限与右极限 2.1.3 无穷小量 2.1.4 极限的性质
2.1.5
2.1.6
无穷大量
小结
2
2.1.1
1. 数列的极限
