首师大附中培训班试题7：圆的学问

合集下载

圆的知识点及训练题

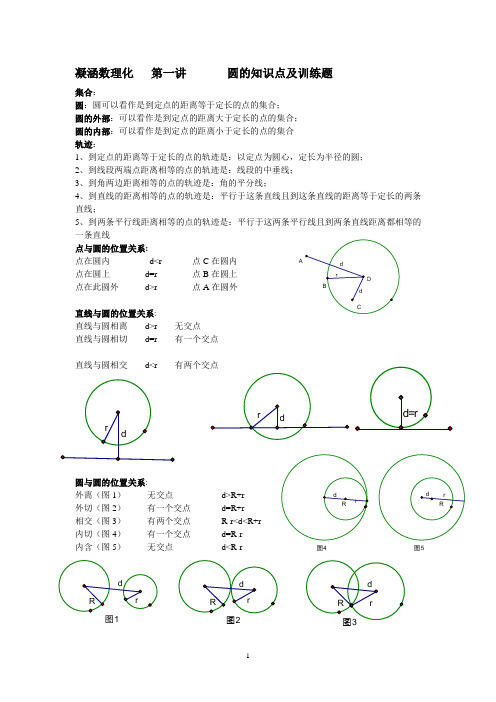
A图1图2图4图5凝涵数理化第一讲圆的知识点及训练题集合：圆：圆可以看作是到定点的距离等于定长的点的集合；圆的外部：可以看作是到定点的距离大于定长的点的集合；圆的内部：可以看作是到定点的距离小于定长的点的集合轨迹：1、到定点的距离等于定长的点的轨迹是：以定点为圆心，定长为半径的圆；2、到线段两端点距离相等的点的轨迹是：线段的中垂线；3、到角两边距离相等的点的轨迹是：角的平分线；4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线点与圆的位置关系:点在圆内d<r 点C在圆内点在圆上d=r 点B在圆上点在此圆外d>r 点A在圆外直线与圆的位置关系:直线与圆相离d>r 无交点直线与圆相切d=r 有一个交点直线与圆相交d<r 有两个交点圆与圆的位置关系:外离（图1）无交点d>R+r外切（图2）有一个交点d=R+r相交（图3）有两个交点R-r<d<R+r内切（图4）有一个交点d=R-r内含（图5）无交点d<R-rB ABAO 垂径定理：垂直于弦的直径平分弦且平分弦所对的弧推论1：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧以上共4个定理，简称2推3定理：此定理中共5个结论中，只要知道其中2个即可推出其它3个结论，即：①AB 是直径 ②AB ⊥CD ③CE=DE ④ ⑤ 推论2：圆的两条平行弦所夹的弧相等。

即：在⊙O 中，∵AB ∥CD圆周角定理：同一条弧所对的圆周角等于它所对的圆心的角的一半即：∵∠AOB 和∠ACB 是所对的圆心角和圆周角 ∴∠AOB=2∠ACB 圆周角定理的推论：推论1：同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧是等弧即：在⊙O 中，∵∠C 、∠D 都是所对的圆周角∴∠C=∠D推论2：半圆或直径所对的圆周角是直角；所对的弦是直径即：在⊙O 中，∵AB 是直径或∵∠C=90° ∴∠C=90° ∴AB 是直径推论3：三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形即：在△ABC 中，∵OC=OA=OB ∴△ABC 是直角三角形或∠C=90°注：此推论实是初二年级几何中矩形的推论：在直角三角形中斜边上的中线等于斜边的一半的逆定理。

第二十四章圆知识点及练习题(附答案)

《圆》章节知识点复习和练习附参考答案一、圆的概念集合形式的概念： 1、圆可以看作是到定点的距离等于定长的点的集合； 2、圆的外部：可以看作是到定点的距离大于定长的点的集合； 3、圆的内部：可以看作是到定点的距离小于定长的点的集合轨迹形式的概念：1、圆：到定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆；（补充）2、垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）； 3、角的平分线：到角两边距离相等的点的轨迹是这个角的平分线；4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线。

二、点与圆的位置关系1、点在圆内 ⇒ d r < ⇒ 点C 在圆内；2、点在圆上 ⇒ d r = ⇒ 点B 在圆上；3、点在圆外 ⇒ d r > ⇒ 点A 在圆外；三、直线与圆的位置关系1、直线与圆相离 ⇒ d r > ⇒ 无交点；2、直线与圆相切 ⇒ d r = ⇒ 有一个交点；3、直线与圆相交 ⇒ d r < ⇒ 有两个交点；四、圆与圆的位置关系外离（图1）⇒ 无交点 ⇒ d R r >+；外切（图2）⇒ 有一个交点 ⇒ d R r =+；相交（图3）⇒ 有两个交点 ⇒ R r d R r -<<+；内切（图4）⇒ 有一个交点 ⇒ d R r =-；内含（图5）⇒ 无交点 ⇒ d R r <-；A五、垂径定理垂径定理：垂直于弦的直径平分弦且平分弦所对的弧。

推论1：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧以上共4个定理，简称2推3定理：此定理中共5个结论中，只要知道其中2个即可推出其它3个结论，即：①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧AD中任意2个条件推出其他3个结论。

北京市海淀区首师大附中2025届高三英语第一次调研考试试题含解析

Several months later, on Christmas morning, my sister and I each found a $20 bill in our stockings. I was just putting it into my pocket_____12_____Kathleen tapped me on the shoulder.
I_____15_____to believe that a $10 loan could more than double so quickly. Much to my_____16_____, my sister got her pencil and tablet and showed me exactly how it all_____17_____.
5. A. shorterB. moreC. longerD. less
6. A. cashB. debtC. noteD. saving
7. A. totalB. costC. numberD. bill
8. A. encouragedB. shockedC. satisfiedD. confused
20. A. unfairB. worthlessC. painfulD. decisive
【答案】1. A 2. D 3. A 4. B 5. C 6. B 7.A 8. D 9. D 10. B 11. B 12. B A 20. C
16. A. reliefB. delightC. annoyanceD. regret
17. A. added upB. showed upC. turned upD. sped up
18. A. turnedB. hurtC. stuckD. nodded

2023北京首都师大附中初一(下)期中数学试卷含答案

2023北京首都师大附中初一（下）期中数学一、选择题（本题共10小题，每小题3分，共30分）1．“会飞的饺子皮”刷爆朋友圈，卡塔尔世界杯吉祥物“拉伊卜”刷爆网络！下面是“拉伊卜”的形象图片，在下面的四个图形中，能由左图经过平移得到的图形是（）A．B．C．D．2．81的平方根是（）A．9B．±9C．±3D．33．下列命题是真命题的是（）A．同位角相等B．内错角相等C．同旁内角互补D．邻补角互补4．在平面直角坐标系中，下列点一定在第二象限内的点是在（）A．（﹣m，1）B．（﹣2，1）C．（﹣2，m）D．（2，﹣1）5．如图，PN⊥OB于点N，且PM∥OB，∠OPM＝30°，则∠OPN的度数为（）A．70°B．60°C．50°D．45°6．我国民间流传一道数学名题．其题意为：一群老者去赶集，半路买了一堆梨，一人一个多一个，一人两个少两个．请问君子知道否，几个老者几个梨？设有老者x人，有梨y个，则可列二元一次方程组为（）A．B．C．D．7．如图，面积为7的正方形ABCD的顶点A在数轴上，且点A表示的数为1，若点E在数轴上，（点E在点A的右侧）且AB＝AE，则点E所表示的数为（）A．B．C．D．8．若方程组的解x与y相等，则a的值等于（）A．0B．﹣1C．1D．29．如图，平遥古城是我国唯一以整座古城成功申报世界文化遗产的古县城，其主要景点有县衙、市楼、日升昌、城隍庙、清虚观、文庙等，若景点A“日升昌”的坐标为（1，1），景点B“清虚观”的坐标为（4，2），则景点C“文庙”的坐标可能是（）A．（4，3）B．（﹣4，3）C．（﹣4，﹣3）D．（4，﹣3）10．中国结是一种手工编织工艺品，因为其外观对称精致，可以代表汉族悠久的历史，符合中国传统装饰的习俗和审美观念，故命名为中国结，中国结的意义在于它所显示的情致与智慧正是汉族古老文明中的一个侧面，也是数学奥秘的游戏呈现，它有着复杂曼妙的曲线，却可以还原成最单纯的二维线条，其中的八字结对应着数学曲线中的双扭线在平面直角坐标系中如图所示，则下列结论中正确的有（）①双扭线围成的面积小于6；②双扭线内部（包含边界）包含11个整数点（横坐标、纵坐标都是整数的点）；③双扭线上任意一点到原点的距离不超过3；④假设点P为双扭线上的一个点，A，B为双扭线与x轴的交点（如图所示），则满足S△P AB＝3的P点有4个．A．①②③B．②③C．②③④D．①②③④二、填空题（本题共8小题，每小题2分，共16分）11．（2分）请写一个比3小的无理数（答案不唯一）．12．（2分）如图，在马路旁有一个村庄，现要在马路l上设立一个核酸检测点为方便该村村民参加核酸检测，核酸检测点最好设在点C处，理由是垂线段最短．13．（2分）已知点A坐标为（m+2，2m），且点A在y轴上，则m＝﹣2．14．（2分）若二元一次方程组的解为，则a﹣b＝．15．（2分）如图，直线a∥b，将一直角三角形的直角顶点置于直线b上，若∠1＝29°，则∠2的度数是119°．16．（2分）如果a，b是2023的两个平方根，那么a+b﹣ab＝4046．17．（2分）已知点M（a，b）在第二象限，点M到x轴的距离等于它到y轴距离的2倍，且点M到两坐标轴的距离之和为9，则点M的坐标为（﹣3，6）．18．（2分）甲、乙、丙三人做游戏：有三张背面完全一样，正面分别写有正整数a、b、c的卡片，且a＜b ＜c，洗匀卡片之后分发给三人，每人一张，并按每人所得卡片上的数字发相应颗数的糖果，然后收回卡片再洗匀，所得的糖果由每人自己保存，这样洗卡片、发卡片、发糖果的游戏至少进行两次，已知游戏结束时甲、乙、丙三人分别获得糖果17颗、9颗、7颗，且乙在最后一次游戏中得到c颗糖果，则：（1）a+b+c＝11；（2）丙在第一次游戏中得到的糖果的准确数量是3颗．三、解答题（本大题共9小题，共54分，第19～20题，每题6分，第21、22题，每题5分，第23~25题，每题6分，第26~27题，每题7分)19．（6分）计算：（1）﹣+|﹣3|；（2）．20．（6分）解下列方程组：（1）；（2）．21．（5分）自由下落物体的高度h（单位：m）与下落时间t（单位：s）的关系是h＝4.9t2，如图，有一个物体从49m高的建筑物上自由落下，到达地面需要多长时间（结果四舍五入取整数）？22．（5分）如图，已知线段AB与线段AC，点O为AB上一点，∠A＝60°．（1）按要求完成下列画图：在AB下方画射线BE，使∠OBE＝60°连接CO并延长交射线BE于点D．（2）求证：∠C＝∠CDB．证明：∵∠A＝60°，∠OBD＝60°，∴∠A＝∠OBD∴AC∥BD（内错角相等，两直线平行）∴∠C＝∠CDB（两直线平行，内错角相等）．23．（6分）在平面直角坐标系xOy中，如图，已知三角形ABC，将三角形ABC向上平移m个单位，向右平移n个单位后，得到三角形OB′C′，其中点A的对应点为原点O．（1）画出平移后得到的三角形OB′C′；（2）m+n＝7；（3）在x轴上存在一点D，使O，B′，C′，D所围成的四边形的面积为6，直接写出点D的坐标．24．（6分）如图，已知四边形ABCD中，点E为AB上一点，AC与DE交于点F，ED∥BC．（1）若∠ACB ＝84°，求∠AFD的度数；（2）若∠BCD+∠AED＝180°，AC平分∠BAD，∠ADC＝4∠ACD，求∠ACD．25．规定：关于x，y的二元一次方程mx+ny＝p有无数组解，每组解记为P（x，y），称P（x，y）为“成德点”，将这些“成德点”连接得到一条直线，称这条直线是“成德点”的“达才线”，回答下列问题：（1）已知P1（﹣1，3），P2（4，﹣1），P3（1，2），则是“达才线”x+y＝2的“成德点”的是P1（﹣1，3）．（2）若A（1，1），B（4，﹣1）是“达才线”（a2+1）x+by＝5的“成德点”，求a，b的值．（3）已知h，t是实数，且，若是“达才线”6x﹣2y＝s的一个“成德点”，用等式表示s与h之间的关系，并求出s的最小值．26．（7分）已知，AB∥CD，直线l分别交AB、CD于点E，F，∠EFC＝60°，点P在直线AB的左侧，射线EK平分∠PEF．（1）如图1，若∠AEP＝20°，直接写出∠AEF与∠KEF的度数；（2）点M在直线CD的左侧，∠AEP＝2∠CFM，∠MFH＝90°，直线PE与直线FH相交于点H．①如图2，当点P在直线l上方时，设∠CFM＝α，用含α的式子分别表示∠EHF与∠BEK；②若2∠EHF＝∠BEK+80°，请直接写出此时∠CFM的度数．27．（7分）在平面直角坐标系xOy中，已知点P（a，b），k＞0，对点P进行如下操作：第一步：若a≥0，则向右平移k|a|个单位，若a＜0，则向左平移k|a|个单位；第二步：若b≥0，则向上平移k|b|个单位，若b＜0，则向下平移k|b|个单位；得到点P′，则称点P′为点P的“k倍距点”，例：点Q（2，﹣1）的“1倍距点”为Q′（4，﹣2）．若图形W上存在一点R，且点R的“k倍距点”R′恰好也在图形W上，则称图形W为“k倍距图形”．（1）点M（1，2）的“1倍距点”为（2，4）；若点N的“3倍距点”为（﹣8，12），则点N的坐标为（﹣2，3）；（2）已知点A（0，3），点B（3，0），若点与线段AB组成的图形是“2倍距图形”，求点C 的坐标．（3）已知n＞0，点D（0，1），E（0，1+n），F（n，1+n），G（n，1）组成一个正方形DEFG，它是一个“n倍距图形”，将该正方形水平方向移动t个单位后，仍然是“n倍距图形”．①t的最大值为1；②t的最小值为﹣n2（用含n的式子表示）．参考答案一、选择题（本题共10小题，每小题3分，共30分）1．【答案】D【分析】根据平移的定义“平移是指在同一平面内，将一个图形整体按照某个方向移动一定的距离，这样的图形运动叫做图形的平移运动，简称平移”．【解答】解：根据平移的性质可知，平移只改变图形的位置，而图形的形状及大小不变，所以图形平移后得到的是D选项，故选：D．2．【答案】B【分析】依据平方根的定义求解即可．【解答】解：∵（±9）2＝81，∴81的平方根是±9．故选：B．3．【答案】D【分析】根据同位角，内错角，同旁内角，邻补角的定义进行判断即可．【解答】解：A、两直线平行，同位角相等，故本选项错误；B、两直线平行，内错角相等，故本选项错误；C、两直线平行，同旁内角互补，故本选项错误；D、邻补角互补，故本选项正确．故选：D．4．【答案】B【分析】根据各个象限点的坐标特征判断．【解答】解：A．当m≤0时，点（﹣m，1）不在第二象限，故本选项不符合题意；B．点（﹣2，1），故本选项符合题意；C．当m≤0时，点（﹣2，m）不在第二象限，故本选项不符合题意；D．（2，﹣1）在第四象限，故本选项不符合题意；故选：B．5．【答案】B【分析】根据平行线的性质得到∠BOC＝∠OPM＝30°，根据直角三角形的性质求解即可．【解答】解：∵PM∥OB，∠OPM＝30°，∴∠BOC＝∠OPM＝30°，∵PN⊥OB于点N，∴∠ONP＝90°，∴∠OPN+∠BOC＝90°，∴∠OPN＝60°．故选：B．6．【答案】B【分析】题意中涉及两个未知数：几个老头几个梨．两组条件：一人一个多一梨，一人两个少二梨，可列出二元一次方程组．【解答】解：依题意得．故选：B．7．【答案】A【分析】根据正方形面积公式求出边长，表示点E即可．【解答】解：∵正方形ABCD的面积为7，∴AB2＝7，∴AB＝，∴AE＝AB＝，∵点A表示的数为1，∴点E表示的数为1+．故选：A．8．【答案】D【分析】把x＝y代入4x+3y＝7中，求出x，y的值，再将x，y的值代入ax+（a﹣1）y＝3，求出a的值即可．【解答】解：由题意，得：x＝y，把x＝y代入4x+3y＝7，得：4y+3y＝7，解得：y＝1，∴x＝y＝1，把x＝y＝1代入ax+（a﹣1）y＝3，得：a+（a﹣1）＝3，解得：a＝2．故选：D．9．【答案】D【分析】根据“日升昌”“清虚观”的坐标建立平面直角坐标系，以此即可得到“文庙”的坐标．【解答】解：∵“日升昌”的坐标为（1，1），“清虚观”的坐标为（4，2），∴可以建立如图所示的平面直角坐标系，∴“文庙”的坐标可能是（4，﹣3）．故选：D．10．【答案】C【分析】由题得，点ABPQMN都在双扭线上，计算△OPB的面积，观察图形，即可判断各个结论．【解答】解：如图，连接OP，BP，得S△OPB＝，4×＝6，∴双扭线围成的面积大于6，故①不正确；由图得，双扭线内部包含4个整数点，边界上有7个整数点，共11个，故②正确；由图得，点A、B与原点距离最大为3，故③正确；设△P AB的高为h，∵S△P AB＝3，且AB＝6，∴h＝1，由图得，点P、Q、M、N均满足题意，故④正确，故选：C．二、填空题（本题共8小题，每小题2分，共16分）11．【答案】（答案不唯一）．【分析】根据无理数的定义写出一个比3小的无理数即可．【解答】解：写出一个比3小的无理数是（答案不唯一）．故答案为：（答案不唯一）．12．【答案】垂线段最短．【分析】由垂线段最短即可进行判断．【解答】解：∵垂线段最短，∴核酸检测点最好设在点C处，理由是垂线段最短．故答案为：垂线段最短．13．【答案】﹣2．【分析】直接利用y轴上点的坐标特点得出m+2＝0，进而得出答案．【解答】解：∵点A（m+2，2m）在y轴上，∴m+2＝0，解得：m＝﹣2．故答案为：﹣2．14．【答案】见试题解答内容【分析】将代入原方程组，可得出关于a，b的二元一次方程组，解之可得出a，b的值，再将其代入a﹣b中，即可求出结论．【解答】解：将代入原方程组得：，解得：，∴a﹣b＝﹣＝．故答案为：．15．【答案】119°．【分析】依据AB∥CD，即可得出∠2＝∠ABC＝∠1+∠CBE．【解答】解：如图，∵AB∥CD，∴∠2＝∠ABC＝∠1+∠CBE＝29°+90°＝119°，故答案为：119°．16．【答案】4046．【分析】根据平方根的性质可知a、b互为相反数，再根据相反数的性质即可求出结果．【解答】解：∵a，b是2023的两个平方根，∴a+b＝0，ab＝﹣2023，∴a+b﹣2ab＝0﹣2×（﹣2023）＝4046．故答案为：4046．17．【答案】（﹣3，6）．【分析】根据点到x轴的距离是纵坐标的绝对值，点到y轴的距离是点的横坐标的绝对值，可得答案．【解答】解：因为点M（a，b）在第二象限，所以a＜0，b＞0，又因为点M（a，b）在第二象限，点M到x轴的距离等于它到y轴距离的2倍，且点M到两坐标轴的距离之和为9，所以，解得，所以点M的坐标为（﹣3，6）故答案为：（﹣3，6）．18．【答案】（1）11；（2）3．【分析】分游戏进行两次，三次，四次三种情况讨论，由题意列出不等式，先求出a和c的取值，分类讨论求出b的值，即可求解（1）和（2）．【解答】解：∵正整数a、b、c，且a＜b＜c，∴a≥1，b≥2，c≥3，若游戏只进行了两次，∵甲、乙、丙三人分别获得糖果17颗、9颗、7颗，∴2c＞17，c＜9，∴＜c＜9，∵c为正整数，∴不存在c，若游戏只进行了三次，∵甲、乙、丙三人分别获得糖果17颗、9颗、7颗，∴3c＞17，2c＜17，3a≤7，∴＜c＜，1≤a≤，∵a，c为正整数，∴c＝6或7或8，a＝1或2，当c＝8时，8+1+1＞9，不合题意舍去，当c＝7，a＝1时，7+1+1＝9，即乙第一，第二，第三次游戏分别得到糖果的数量为1颗，1颗，7颗；∵丙三次只获得7颗糖果，∴丙不能得到c卡片，∴2×7+b＝14，∴b＝3，∴甲第一，第二，第三次游戏分别得到糖果的数量为7颗，7颗，3颗；∴丙第一，第二，第三次游戏分别得到糖果的数量为3颗，3颗，1颗；当c＝7，a＝2时，7+2+2＞9，不合题意舍去，当c＝6，a＝1时，则6+b+1＝9，∴b＝2，∵2c+b＝14＜17，∴不合题意舍去；当c＝6，a＝2时，则6+b+2＝9，∴b＝1＜a，∴不合题意舍去；当游戏只进行了四次时，∵甲、乙、丙三人分别获得糖果17颗、9颗、7颗，∴4c＞17，c＜9，4a≤7，∴＜c＜9，1≤a≤，∵a，c为正整数，∴c＝5或6或7或8，a＝1，∵乙、丙两人分别获得糖果9颗、7颗，∴乙只获得c卡片1次，丙不能获得c卡片，∴甲获得c卡片3次，∴3c＜17，∴c＜，∴c＝5，∴b＝2，∴甲四次分别获得糖果数量分别为5，5，5，2；乙四次分别获得糖果数量分别为1，1，2，5；丙四次分别获得糖果数量分别为2，2，1，2；∵四次游戏只能产生4张b卡，∴不合题意舍去．综上所述：甲第一，第二，第三次游戏分别得到糖果的数量为7颗，7颗，3颗；乙第一，第二，第三次游戏分别得到糖果的数量为1颗，1颗，7颗；丙第一，第二，第三次游戏分别得到糖果的数量为3颗，3颗，1颗．∴（1）a+b+c＝1+3+7＝11．故答案为：11；（2）丙在第一次游戏中得到的糖果的准确数量是3颗．故答案为：3．三、解答题（本大题共9小题，共54分，第19～20题，每题6分，第21、22题，每题5分，第23~25题，每题6分，第26~27题，每题7分)19．【答案】（1）2﹣；（2）5﹣3．【分析】（1）首先计算开平方、开立方和绝对值，然后从左向右依次计算，求出算式的值即可；（2）首先计算乘法，然后从左向右依次计算，求出算式的值即可．【解答】解：（1）﹣+|﹣3|＝3﹣4+（3﹣）＝3﹣4+3﹣＝2﹣．（2）＝2﹣3+3＝5﹣3．20．【答案】（1）；（2）．【分析】（1）利用加减消元法进行求解即可；（2）利用加减消元法进行求解即可．【解答】解：（1），①×2得：2x﹣8y＝18③，②﹣③得：5y＝﹣11，解得：y＝﹣，把y＝﹣代入①得：x+＝9，解得：x＝，故原方程组的解是：；（2），①×4得：2x﹣6y＝﹣4③，②﹣③得：7y＝7，解得：y＝1，把y＝1代入②得：2x+1＝3，解得：x＝1，故原方程组的解是：．21．【答案】3s．【分析】根据题意列出方程，根据算术平方根的概念解方程即可．【解答】解：当h＝49m时，49＝4.9t2，解得t1≈3，t2≈﹣3（舍去）．答：物体从49m高的建筑物上自由落下，到达地面需要3s．22．【答案】（1）作图见解答；（2）内错角相等，两直线平行；两直线平行，内错角相等．【分析】（1）根据几何语言画出对应的几何图形；（2）先根据内错角相等，两直线平行证明AC∥BD，然后根据平行线的性质得到∠C＝∠CDB．【解答】（1）解：如图，（2）证明：∵∠BAC＝60°，∠OBD＝60°，∴∠A＝∠OBD，∴AC∥BD（内错角相等，两直线平行），∴∠C＝∠CDB（两直线平行，内错角相等）．故答案为：内错角相等，两直线平行；两直线平行，内错角相等．23．【答案】（1）见解析；（2）7；（3）D（3，0）或（﹣3，0）．【分析】（1）如图所示，△OB′C′即为所求；（2）根据图形得出平移路径即可得出m、n的值，即可求解；（3）设D（a，0），根据题意得出，求出a的值即可求解．【解答】解：（1）如图所示，△OB′C′即为所求；（2）由图形可知，将三角形ABC向上平移3个单位，向右平4个单位后，得到三角形OB′C′，∴m+n＝3+4＝7，故答案为：7；（3）设D（a，0），则，∴a＝3或﹣3，∴D（3，0）或（﹣3，0）．24．【答案】（1）96°；（2）30°．【分析】（1）根据平行线的性质以及平角的定义进行计算即可；（2）利用角平分线的定义，平行线的性质以及三角形内角和定理进行计算即可．【解答】解：（1）∵ED∥BC．∴∠AFE＝∠ACB＝84°，∴∠AFD＝180°﹣84°＝96°，答：∠AFD＝96°；（2）∵DE∥BC，∴∠AED＝∠ABC，∵∠BCD+∠AED＝180°，∴∠BCD+∠ABC＝180°，∴CD∥BE，∴∠BAC＝∠ACD，∵AC平分∠BAD，∴∠BAC＝∠CAD，∴∠CAD＝∠ACD，∵∠ADC＝4∠ACD，∠CAD+∠ACD+∠ADC＝180°，∴6∠ACD＝180°，即∠ACD＝30°．25．【答案】（1）P1（﹣1，3）；（2）a＝±1，b＝3；（3）s与h之间的关系为＝s﹣1，s的最小值是1．【分析】（1）判断P1（﹣1，3），P2（4，﹣1），P3（1，2）的坐标是否满足x+y＝2即可；（2）根据“成德点”和“达才线”的定义，得出二元一次方程组求解即可；（3）根据“成德点”和“达才线”的定义，得出关于h、t、s的两个二元一次方程，再消掉t即可，再根据算术平方根的定义得出s的取值范围即可．【解答】解：（1）由于点P1（﹣1，3）是二元一次方程x+y＝2的解，而P2（4，﹣1），P3（1，2）不是二元一次方程x+y＝2的解，所以“达才线”x+y＝2的“成德点”的是点P1（﹣1，3），故答案为：P1（﹣1，3）；（2）因为A（1，1），B（4，﹣1）是“达才线”（a2+1）x+by＝5的“成德点”，所以，解得或，答：a＝±1，b＝3；（3）∵是“达才线”6x﹣2y＝s的一个“成德点”，∴6﹣2t＝s，∵，∴＝s﹣1，∵≥0，即s﹣1≥0，∴s≥1，因此s的最小值为1，答：s与h之间的关系为＝s﹣1，s的最小值是1．26．【答案】（1）∠AEF＝120°，∠KEF＝70°．（2）①∠EHF＝90°+α，∠BEK＝120°+α．②∠CFM＝20°．【分析】（1）根据平行线的性质，两直线平行，同旁内角互补，求出∠PEF的度数，再根据角平分线的定义求出∠KEF度数即可；（2）①根据题意表示出∠EFM和∠EFH，再根据三角形内角和定理求解即可．②将∠EHF与∠BEK代入2∠EHF＝∠BEK+80°中即可求解．【解答】解：（1）∵AB∥CD，∴∠AEF+∠EFC＝180°，又∵∠EFC＝60°，∴∠AEF＝120°，∵∠AEP＝20°，∴∠PEF＝∠AEP+∠AEF＝140°，∵射线EK平分∠PEF，∴∠KEF＝＝70°．答：∠AEF＝120°，∠KEF＝70°．（2）①已知∠CFM＝α，且∠AEP＝2∠CFM，∴∠AEP＝2α，又∵∠EFC＝60°，∴∠EFM＝∠EFC﹣∠CFM＝60°﹣α，∵∠MFH＝90°，∴∠EFH＝∠MFH﹣∠EFM＝30°+α，∵∠PEA+∠AEF+∠FEH＝180°，∴∠FEH＝180°﹣2α﹣120°＝60°﹣2α，根据三角形内角和定理，∴∠EHF＝180°﹣（60°﹣2α）﹣（30°+α）＝90°+α，故∠EHF＝90°+α；由（1）知，∠AEF＝120°，∠KEF＝，∵∠PEF＝∠AEP+∠AEF＝120°+2α，∴∠KEF＝α+60°，∴∠BEK＝∠BEH+∠FEH+∠KEF＝2α+60°﹣2α+60°+α＝120°+α，故∠BEK＝120°+α．②∵2∠EHF＝∠BEK+80°，∴2（90°+α）＝120°+α+80°，∴α＝20°，∴∠CFM＝20°．27．【答案】（1）（2，4），（﹣2，3）；（2）（，）或（，）（3）①1；②﹣n2．【分析】（1）根据“k倍距点”的概念直接得出结论即可；（2）先求出直线AB的解析式，然后根据C点的“2倍距图形”在线段AB上求出C点的坐标即可；（3）①当t＞0时，写出平移后DEFG对应点D'E'F'G'的坐标，当D'点的“n倍距点”是F'点时，t有最大值，求出此时的t的值即可；②当t＜0时，写出平移后DEFG对应点D“E“F“G“的坐标，当F“点的“n倍距点”是D“点时，t有最小值，求出此时的t的值即可．【解答】解：（1）由题意知，将M点先向右平移1个单位，再向上平移2个单位，得到点M（1，2）的“1倍距点”为（2，4），设N点的坐标为（a，b），由题意知，a+3a＝﹣8，b+3b＝12，解得a＝﹣2，b＝3，即点N的坐标为（﹣2，3），故答案为：（2，4），（﹣2，3）；（2）设直线AB的解析式为y＝kx+b，代入点A（0，3），点B（3，0）的坐标得，解得，∴直线AB的解析式为y＝﹣x+3，①若点的“2倍距点”C'在线段AB上，则C'（，y+2y），即﹣+3＝3y，解得y＝；②线段AB上一点C“的“2倍距点”为点，则C“（，），即﹣+3＝，解得y＝，∴C点的坐标为（，）或（，）；（3）①当t＞0时，若平移后对应点为D'E'F'G'，当D'点的“n倍距点”是F'点时，t有最大值，此时，D'（t，1），E'（t，1+n），F'（n+t，1+n），G'（n+t，1），当D'点的“n倍距点”是F'点时，t+nt＝n+t，解得t＝1，故答案为：1；②当t＜0时，若平移后DEFG对应点为D“E“F“G“，当F“点的“n倍距点”是D“点时，t有最大值，此时，D“（t，1），E“（t，1+n），F“（n+t，1+n），G“（n+t，1），当G“点的“n倍距点”是E“点时，n+t+n（n+t）＝t+nt，解得t＝﹣n2，故答案为：﹣n2．。

32【提高】圆的基本概念和性质(培优课程讲义例题练习含答案)

圆的基本概念和性质—知识讲解（提高）【学习目标】1．知识目标：理解圆的有关概念和圆的对称性；2．能力目标：能应用圆半径、直径、弧、弦、弦心距的关系，•圆的对称性进行计算或证明；3．情感目标：养成学生之间发现问题、探讨问题、解决问题的习惯.【要点梳理】要点一、圆的定义及性质1.圆的定义(1)动态：如图，在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转所形成的图形叫做圆，固定的端点O叫做圆心，线段OA叫做半径. 以点O为圆心的圆，记作“⊙O”，读作“圆O”．要点诠释：①圆心确定圆的位置，半径确定圆的大小；确定一个圆应先确定圆心，再确定半径，二者缺一不可；②圆是一条封闭曲线.(2)静态：圆心为O，半径为r的圆是平面内到定点O的距离等于定长r的点的集合.要点诠释：①定点为圆心，定长为半径；②圆指的是圆周，而不是圆面；③强调“在一个平面内”是非常必要的，事实上，在空间中，到定点的距离等于定长的点的集合是球面，一个闭合的曲面.2.圆的性质①旋转不变性：圆是旋转对称图形，绕圆心旋转任一角度都和原来图形重合；圆是中心对称图形，对称中心是圆心；②圆是轴对称图形：任何一条直径所在直线都是它的对称轴.或者说，经过圆心的任何一条直线都是圆的对称轴.要点诠释：①圆有无数条对称轴；②因为直径是弦，弦又是线段，而对称轴是直线，所以不能说“圆的对称轴是直径”，而应该说“圆的对称轴是直径所在的直线”.3.两圆的性质两个圆组成的图形是一个轴对称图形，对称轴是两圆连心线（经过两圆圆心的直线叫做两圆连心线）.要点二、与圆有关的概念1.弦弦：连结圆上任意两点的线段叫做弦.直径：经过圆心的弦叫做直径.弦心距：圆心到弦的距离叫做弦心距.要点诠释：直径是圆中通过圆心的特殊弦，也是圆中最长的弦，即直径是弦，但弦不一定是直径.为什么直径是圆中最长的弦？如图，AB是⊙O的直径，CD是⊙O中任意一条弦，求证：AB≥CD.证明：连结OC、OD∵AB=AO+OB=CO+OD≥CD(当且仅当CD过圆心O时，取“=”号)∴直径AB是⊙O中最长的弦.2.弧弧：圆上任意两点间的部分叫做圆弧，简称弧.以A、B为端点的弧记作，读作“圆弧AB”或“弧AB”.半圆：圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆；优弧：大于半圆的弧叫做优弧；劣弧：小于半圆的弧叫做劣弧.要点诠释：①半圆是弧，而弧不一定是半圆；②无特殊说明时，弧指的是劣弧.3.同心圆与等圆圆心相同，半径不等的两个圆叫做同心圆.圆心不同，半径相等的两个圆叫做等圆.同圆或等圆的半径相等.【高清ID号：356996 关联的位置名称（播放点名称）：概念、性质的要点回顾】4.等弧在同圆或等圆中，能够完全重合的弧叫做等弧.要点诠释：①等弧成立的前提条件是在同圆或等圆中，不能忽视；②圆中两平行弦所夹的弧相等.【典型例题】类型一、圆的定义1．已知：如图，矩形ABCD的对角线AC与BD相交于点O，求证：点A、B、C、D在以点O为圆心的同一个圆上.【答案与解析】∵四边形ABCD是矩形，∴OA=OC，OB=OD，AC=BD，∴OA=OC=OB=OD，∴点A、B、C、D在以点O为圆心、OA为半径的圆上.【总结升华】要证几个点在同一个圆上，只能依据圆的定义，去说明这些点到平面内某一点的距离相等. 举一反三：【变式】平行四边形的四个顶点在同一圆上，则该平行四边形一定是（）A.正方形B.菱形C.矩形D.等腰梯形【答案】C.2．爆破时，导火索燃烧的速度是每秒0.9cm，点导火索的人需要跑到离爆破点120m以外的安全区域。

北京市首都师范大学附属中学九年级数学上册第四单元《圆》检测卷(包含答案解析)

一、选择题1．如图，AC 为半圆的直径，弦3AB =，30BAC ∠=︒，点E 、F 分别为AB 和AC 上的动点，则BF EF +的最小值为（）A ．3B ．332C ．3D ．332+ 2．如图，在ABC 中，90ACB ∠=︒，过B ，C 两点的O 交AC 于点D ，交AB 于点E ，连接EO 并延长交O 于点F ．连接BF ，CF ，若135EDC ∠=︒，2AE =，4BE =，则CF 的值为（）．A ．10B ．22C ．23D ．33．如图，一块直角三角板的30°角的顶点P 落在O 上，两边分别交圆O 于A ，B 两点，若O 的直径为6，则弦AB 的长为（）A ．3B ．2C 2D 34．如图，AB 是⊙O 的弦，AO 的延长线交过点B 的⊙O 的切线于点C ，如果∠ABO =30°，则∠C 的度数是（）A ．70°B ．45°C ．30°D ．20°5．如图，一条公路的拐弯处是一段圆弧AB ，点O 是这段弧所在的圆的圆心，20cm AB =，点C 是AB 的中点，点D 是AB 的中点，且5cm CD =，则这段弯路所在圆的半径为（）A ．10cmB ．12.5cmC ．15cmD ．17cm 6．给出下列说法：①圆是轴对称图形，对称轴是圆的每一条直径；②三角形的外心到三角形各顶点的距离相等；③经过三个点一定可以画一个圆；④平分弦的直径垂直于弦；⑤垂直于弦的直径平分弦，并且平分弦所对的两条弧．正确的有（）A ．4B ．3C ．2D ．17．如图，在ABC 中，90C ∠=︒，7AB =，4AC =，以点C 为圆心、CA 为半径的圆交AB 于点D ，求弦AD 的长为（）A 433B ．327C ．337D ．1678．若圆锥的底面半径为5cm ，侧面积为265cm π，则该圆锥的高是（） A ．13cm B ．12cm C ．11cm D ．10cm 9．如图，⊙O 的直径12CD =，AB 是⊙O 的弦，AB CD ⊥，垂足为P ，:1:2CP PO =，则AB 的长为（）A ．45B ．215C ．16D ．8 10．已知O 的半径为4，点P 在O 外，OP 的长可能是（） A ．2 B ．3 C ．4D ．5 11．如图，PA 、PB 、CD 是O 的切线，切点分别是A 、B 、E ，CD 分别交PA 、PB 于C 、D 两点，若60APB ∠=︒，则COD ∠的度数（）A ．50°B ．60°C ．70°D ．75° 12．一个圆锥的底面直径为4 cm ，其侧面展开后是圆心角为90°的扇形，则这个圆锥的侧面积等于（）A ．4πcm 2B ．8πcm 2C ．12πcm 2D ．16πcm 2第II 卷（非选择题）请点击修改第II 卷的文字说明参考答案二、填空题13．如图，在扇形AOB 中，90AOB ∠=︒正方形CDEF 的顶点C 是弧AB 的中点，点D 在OB 上，点E 在OB 的延长线上，当正方形CDEF 的边长为2时，阴影部分的面积为_______．14．如图，点A ，B ，C 在圆O 上，54ACB ∠=︒，则ABO ∠的度数是______．15．如图，PA ，PB 是O 的切线，A ，B 为切点，AC 是O 的直径，35BAC ∠=︒，则P ∠的度数为________.16．如图，四边形ABCD 是O 的内接四边形，对角线AC ，BD 交于点E ，且AC BD AB ==，若70AEB ∠=︒，则AOB ∠等于______︒．17．在ABC 中，90,3,4C AC BC ∠===，则ABC 的内切圆的周长为___________．18．如图，已知BD 是⊙O 的直径，点A ，C 在⊙O 上，58AOB ∠=，B 是弧AC 的中点，则BDC ∠的度数为___________．19．如图，已知AD 为半圆形O 的直径，点B ，C 在半圆形上，AB BC =，30BAC ∠=︒，8AD =，则AC 的长为________．20．如图，AB 是O 的直径，CD AB ⊥于E ，24CD =，8BE =，则AB =__________．三、解答题21．在平面直角坐标系中，ABC 的三个顶点分别为()5,2A -，()1,2B -，()4,5C -．（1）画出ABC 关于原点成中心对称的图形111A B C △，并写出点1B 的坐标；（2）将ABC 绕点B 顺时针旋转90°，求旋转过程中点A 走过的路径长．22．对于平面直角坐标系xOy 中的点P 和C ，给出如下定义：如果C 的半径为r ，C 外一点P 到C 的切线长小于或等于2r ，那么点P 叫做C 的“离心点”．（1）当C 的半径为1时，①在点())12313,0,2,5,02P P P ⎛- ⎝⎭中，C 的“离心点”是_____________； ②点P(m ，n)在直线3y x =-+上，且点P 是O 的“离心点”，求点P 横坐标m 的取值范围；（2）C的圆心C在y轴上，半径为2，直线132y x=-+与x轴．y轴分别交于点A、B．如果线段AB上的所有点都是C的“离心点”，请直接写出圆心C纵坐标的取值范围．23．如图，在边长为1个单位长度的小正方形组成的网格中，点A，B在小正方形的顶点上，将线段AB绕着点O顺时针方向旋转90°，得到线段A1B1．（1）在网格中画出线段A1B1（2）计算线段AB在变换到A1B1的过程中扫过的区域的面积（重叠部分不重复计算）24．如图，在Rt△OAB中，∠OAB=90°，且点B的坐标为（4，2）．（1）画出△OAB关于绕着点O逆时针旋转180°得到的△OA1B1，并写出点B1的坐标；（2）点A旋转到点A1所经过的路径长为__________（结果保留π）．25．如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为16cm2，求大正方形的面积．26．如图，OA、OB、OC分别是⊙O的半径，且AC=CB，D、E分别是OA、OB的中点．CD与CE相等吗？为什么？【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【分析】作B点关于直径AC的对称点B′，过B′点作B′E⊥AB于E，交AC于F，如图，利用两点之间线段最短和垂线段最短可判断此时FB＋FE的值最小，再判断△ABB′为等边三角形，然后计算出B′E的长即可．【详解】解：作B点关于直径AC的对称点B′，过B′点作B′E⊥AB于E，交AC于F，如图，则FB＝FB′，∴FB＋FE＝FB′＋FE＝B′E，此时FB＋FE的值最小，∵∠BAC＝30°，∴∠B′AC＝30°，∴∠BAB′＝60°，∵AB＝AB′，∴△ABB′为等边三角形，∵B′E⊥AB，∴AE＝BE＝32，∴B′E3＝332，即BF＋EF 33．故选：B．【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．也考查了等腰三角形的性质．2．A解析：A【分析】由四边形BCDE 内接于⊙O 知∠EFC=∠ABC=45°，据此得AC=BC ，由EF 是⊙O 的直径知∠EBF=∠ECF=∠ACB=90°及∠BCF=∠ACE ，再根据四边形BECF 是⊙O 的内接四边形知∠AEC=∠BFC ，从而证△ACE ≌△BCF 得AE=BF ，根据Rt △ECF 是等腰直角三角形知EF 2=20，继而可得答案．【详解】∵四边形BCDE 内接于O ，且135EDC ∠=︒， ∴18045EFC ABC EDC ︒∠=∠=-∠=︒， ∵90ACB ∠=︒，∴ABC 是等腰三角形，∴AC BC =，又∵EF 是O 的直径， ∴90EBF ECF ACB ∠=∠=∠=︒，∴BCF ACE ∠=∠，∵四边形BECF 是O 的内接四边形，∴AEC BFC ∠=∠，∴()ACE BFC ASA ≅△△，∴AE BF =，Rt BEF △中，22222224220EF BF BE BE AE =+=+=+=，Rt ECF △中，45EFC ∠=︒，∴CE CF =，∴2222220CE CF CF EF +===，∴210CF =， ∴CF =故选:A ．【点睛】本题主要考查圆周角定理，解题的关键是掌握圆内接四边形的性质、圆周角定理、全等三角形的判定与性质及勾股定理．3．A解析：A【分析】连接AO 并延长交O 于点D ，连接BD ；根据同弦所对的圆周角相等可得30D P ∠=∠=︒；再说明AD=6,然后根据在直角三角形中30°所对的直角边为斜边的一半．【详解】解：如图：连接AO 并延长交O 于点D ，连接BD ，30P ∠=︒，30D P ∴∠=∠=︒，∵AD 是O 的直径，6AD =，90ABD ∠=︒，132AB AD ∴==．故答案为A ．【点睛】本题考查了圆周角定理以及直角三角形的性质，掌握直径所对的圆周角为直角是解答本题的关键．4．C解析：C【分析】由BC 是⊙O 的切线，OB 是⊙O 的半径，得到∠OBC =90°，根据等腰三角形的性质得到∠A =∠ABO =30°，由外角的性质得到∠BOC =60°，即可求得∠C =30°．【详解】∵BC 是⊙O 的切线，OB 是⊙O 的半径，∴∠OBC =90°，∵OA =OB ，∴∠A =∠ABO =30°，∴∠BOC =60°，∴∠C =30°．故选：C ．【点睛】本题考查了切线的性质，等腰三角形的性质，三角形的外角性质，解题的关键是灵活运用所学知识解决问题．5．B解析：B【分析】根据题意，可以推出AD ＝BD ＝10，若设半径为r ，则OD ＝r ﹣5，OA ＝r ，结合勾股定理可推出半径r 的值．【详解】解：∵OC⊥AB，AB＝20，∴AD＝DB＝10，在Rt AOD中，OA2＝OD2+AD2，设半径为r得：r2＝（r﹣5）2+102，解得：r＝12.5，∴这段弯路的半径为12.5，故选：B．【点睛】本题主要考查垂径定理的应用、勾股定理的应用，关键在于设出半径为r后，用r表示出OD、OA的长度．6．C解析：C【分析】根据对称轴是一条直线，即可判断①；根据外心的性质即可判断②；利用确定圆的条件即可判断③；根据弦不是直径时，平分弦的直径才垂直于弦，即可判断④；根据垂径定理的推论，即可判断⑤．【详解】∵圆是轴对称图形，直径所在直线是它的对称轴，∴①错误；∵三角形的外心到三角形的三个顶点的距离相等，∴②正确；∵经过不在同一直线上的三点确定一个圆，∴③错误；∵平分弦（弦不是直径）的直径垂直于弦，∴④错误；∵垂直于弦的直径平分弦，且平分弦所对的弧，∴⑤正确；综上，正确的是②⑤，共2个，故选：C．【点睛】本题考查了垂径定理及其推论，三角形的外接圆与外心等知识点的应用，正确把握相关定义是解题关键．7．B解析：B【分析】过C作CF⊥AB于F，根据垂径定理得出AD=2AF，根据勾股定理求BC，根据三角形面积公式求出CF，根据勾股定理求出AF即可．【详解】过C作CF⊥AB于F，∵CF⊥AB，CF过圆心C，∴AD=2AF．∵△ABC中，∠ACB是直角，AC=4，AB=7，∴由勾股定理得：22227433AB AC-=-=由三角形的面积公式得：AC×BC=AB×CF，即33=7CF，∴433在△AFC中，由勾股定理得：222243316477 AC CF⎛⎫-=-=⎪⎪⎝⎭，∴AD=2AF=327．故选：B．【点睛】本题考查了勾股定理，垂径定理，三角形的面积等知识点的应用，关键是求出AF的长．8．B解析：B【分析】先根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形面积公式得到12•2π•5•OA=65π，可求出OA=13，然后利用勾股定理计算圆锥的高．【详解】解：根据题意得12•2π•5•OA=65π，解得：OA=13，所以圆锥的高2213512．故选：B．【点睛】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．9．A解析：A【分析】连接OA，先根据⊙O的直径CD＝12，CP：PO＝1：2求出CO及OP的长，再根据勾股定理可求出AP的长，进而得出结论．【详解】连接OA，∵⊙O的直径CD＝12，CP：PO＝1：2，∴CO＝6，PO=4，∵AB⊥CD，∴22OA OP-2264-5，∴AB＝2AP＝22545⨯=故选：A．【点睛】本题考查了垂径定理和勾股定理的应用，解决与弦有关的问题时，往往需构造以半径、弦心距和弦长的一半为三边的直角三角形，若设圆的半径为r，弦长为a，这条弦的弦心距为d，则有等式2222ar d⎛⎫=+⎪⎝⎭成立，知道这三个量中的任意两个，就可以求出另外一个．10．D解析：D【分析】根据题意可以求得OP的取值范围，从而可以解答本题．【详解】解：∵O的半径为4，点P在⊙O外，∴OP＞4，故选：D．【点睛】本题考查点和圆的位置关系，解答本题的关键是明确题意，求出OP的取值范围．11．B解析：B【分析】连接AO ，BO ，OE 由切线的性质可得90PAO PBO ︒∠=∠=，结合已知条件和四边形的内角和为360°可求出AOB 的度数，再由切线长定理即可求出COD 的度数.【详解】如图，连接AO ，BO ，OE ，∵PA 、PB 是O 的切线，∴∠PAO =∠PBO =90∘，∵60APB ∠=︒，∴36029060120AOB ∠=︒-⨯︒-︒=︒，∵PA 、PB 、CD 是⊙O 的切线，∴∠ACO =∠ECO ，∠DBO =∠DEO ，∴∠AOC =∠EOC ，∠EOD =∠BOD ， ∴1602COD COE EOD AOB ∠=∠+∠=∠=︒，故选B.【点睛】本题考查了切线的性质及切线长定理，解答本题的关键是熟练掌握：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线，平分两条切线的夹角.12．D解析：D【分析】设展开后的圆半径为r ，根据圆锥性质可知底面周长就等于展开后扇形的弧长，然后算出展开后扇形的半径，进而计算出扇形的面积．【详解】解：设展开后的扇形半径为r ，由题可得：4π=2r π解得r =8∴S 扇形=14π×82 =16π故选：D【点睛】此题主要考查了圆锥的计算，正确理解圆锥侧面展开图与各部分对应情况是解题关键．二、填空题13．π﹣2【分析】连结OC 根据勾股定理可求OC 的长根据题意可得出阴影部分的面积＝扇形BOC 的面积﹣三角形ODC 的面积依此列式计算即可求解【详解】解：连接OC ∵在扇形AOB 中∠AOB ＝90°正方形CDEF解析：π﹣2【分析】连结OC ，根据勾股定理可求OC 的长，根据题意可得出阴影部分的面积＝扇形BOC 的面积﹣三角形ODC 的面积，依此列式计算即可求解．【详解】解：连接OC ，∵在扇形AOB 中，∠AOB ＝90°，正方形CDEF 的顶点C 是弧AB 的中点，∴∠COD ＝45°，∴OC ＝2CD ＝22，∴阴影部分的面积＝扇形BOC 的面积﹣三角形ODC 的面积＝245(22)360π⨯⨯﹣12×22 ＝π﹣2．故答案为：π﹣2．．【点睛】本题考查了扇形面积的计算以及正方形的性质，解题的关键是得到扇形半径的长度． 14．36°【分析】根据圆周角定理可得再利用等腰三角形的性质即可求解【详解】解：∵∴∵∴故答案为：36°【点睛】本题考查圆周角定理掌握圆周角定理是解题的关键解析：36°【分析】根据圆周角定理可得2108AOB ACB ∠=∠=︒，再利用等腰三角形的性质即可求解．【详解】解：∵54ACB ∠=︒，∴2108AOB ACB ∠=∠=︒，∵OA OB =，∴()1180362ABO BAO AOB ∠=∠=︒-∠=︒，故答案为：36°．【点睛】本题考查圆周角定理，掌握圆周角定理是解题的关键．15．70°【分析】根据题意可以求得∠OAP 和∠OBP 的度数然后根据∠BAC ＝35°即可求得∠P 的度数【详解】解：连接OB ：∵PAPB 是⊙O 的两条切线AB 是切点AC 是⊙O 的直径∴∠OAP ＝∠OBP ＝90°解析：70°【分析】根据题意可以求得∠OAP 和∠OBP 的度数，然后根据∠BAC ＝35°，即可求得∠P 的度数．【详解】解：连接OB ：∵PA 、PB 是⊙O 的两条切线，A 、B 是切点，AC 是⊙O 的直径，∴∠OAP ＝∠OBP ＝90°，∵∠BAC ＝35°，OA ＝OB ，∴∠BAC ＝∠OBA ＝35°，∴∠PAB ＝∠PBA ＝55°，∴∠P ＝180°−∠PAB−∠PBA ＝70°，即∠P 的度数是70°，故答案为：70°．【点睛】本题考查切线的性质，解答此类问题的关键是明确题意，找出所求问题需要的条件，利用切线的性质解答问题．16．125【分析】根据题意先求出∠ABE=∠BAE=55°然后由等腰三角形的定义和三角形的内角和定理求出∠C=625°即可求出的度数【详解】解：根据题意∵在圆中有∴∴∴在△ABE 中∴在等腰△ABC 中则∴解析：125【分析】根据题意，先求出∠ABE=∠BAE=55°，然后由等腰三角形的定义和三角形的内角和定理，求出∠C=62.5°，即可求出AOB ∠的度数．【详解】解：根据题意，∵在圆中，有AC BD AB ==，∴AC BD =，∴AD BC =，∴ABD BAC ∠=∠，在△ABE 中，70AEB ∠=︒， ∴1(18070)552ABD BAC ∠=∠=⨯︒-︒=︒，在等腰△ABC 中，AC AB =则1(18055)62.52C ∠=⨯︒-︒=︒， ∴2125AOB C ∠=∠=︒；故答案为：125．【点睛】本题考查了圆内接四边形的性质，圆周角定理，三角形的内角和定理，等腰三角形的定义，解题的关键是熟练掌握所学的知识，正确的进行解题．17．【分析】先根据勾股定理求出斜边AB 的长再根据直角三角形内切圆的半径公式求出半径再算出周长【详解】解：根据勾股定理内切圆半径内切圆周长故答案是：【点睛】本题考查三角形的内切圆解题的关键是掌握直角三角形解析：2π【分析】先根据勾股定理求出斜边AB 的长，再根据直角三角形内切圆的半径公式求出半径，再算出周长．【详解】解：根据勾股定理，5AB ==，内切圆半径345122AC BC AB +-+-===，内切圆周长22r ππ==．故答案是：2π．【点睛】本题考查三角形的内切圆，解题的关键是掌握直角三角形内切圆半径的求解方法． 18．29°【分析】先由是弧的中点可得再根据圆周角定理可得结果【详解】解：连接OC ∵是弧的中点∴∴∠BOC=∠AOB=58°∴∠BDC==29°故答案为29°【点睛】本题考查了圆周角定理掌握圆周角定理是解解析：29°【分析】先由B 是弧AC 的中点，可得AB BC = ，再根据圆周角定理可得结果．【详解】解：连接OC ，∵B 是弧AC 的中点，∴AB BC =．∴∠BOC=∠AOB=58°∴∠BDC=1582⨯︒=29°．故答案为29°．【点睛】本题考查了圆周角定理，掌握圆周角定理是解题的关键．19．【分析】连接CD 由已知可以得到∠B=120°所以∠D=60°然后在Rt △ACD 中计算AC 即可【详解】解：如图所示连接CD ∵∴∠B=120°∴∠D=60°∵AD 为直径∴∠ACD=90°∴CD=4∴AC解析：43【分析】连接CD ，由已知可以得到∠B=120°，所以∠D=60°，然后在Rt △ACD 中计算AC 即可．【详解】解：如图所示，连接CD∵AB BC =，30BAC ∠=︒∴∠B=120°∴∠D=60°∵AD 为直径∴∠ACD=90°∴CD=4∴3【点睛】本题主要考查圆的内接四边形对角性质，掌握直径所对的圆周角是90°和圆的内接四边形对角互补是解题的关键．20．【分析】连接OD 设的半径为r 则OE=r-8再根据勾股定理求出r 最后根据直径和半径的关系即可解答【详解】解：如图：设的半径为r 则OE=r-8∵AB ⊥CD 于E 且CD=24∴DE=CD=12在Rt △ODE解析：26【分析】连接OD ，设O 的半径为r ，则OE=r-8，再根据勾股定理求出r ，最后根据直径和半径的关系即可解答．【详解】解：如图：设O 的半径为r ，则OE=r-8，∵AB ⊥CD 于E ，且CD=24，∴DE=12CD=12，在Rt △ODE 中，OD=r ，OE=r-8，DE=12，∴OE 2+DE 2=OD 2，∴（r-8）2+122=r 2，解得r=13∴AB=2r=26．故答案为26．【点睛】本题主要考查了垂径定理，正确作出辅助线、构造出直角三角形是解答本题的关键．三、解答题21．（1）见解析，点1B 的坐标为()1,2-；（2）2π【分析】（1）根据中心对称的定义即可求解；（2）根据弧长公式即可求解．【详解】解：（1）111A B C △如图所示点1B 的坐标为()1,2-（2）∵()5,2A -，()1,2B -∴4AB =∴ABC 绕点B 顺时针旋转90°过程中，点A 走过的路径长为：9042180ππ⨯⨯=．【点睛】本题考查中心对称的定义、弧长公式，掌握以上基本概念是解题的关键．22．（1）①23,P P ；②12m ≤≤；（2）圆心C 的纵坐标满足34y <≤或1515y -≤<-【分析】(1) ①分别计算123OP OP OP ，，的长，判断P 到C 的切线长是否小于或等于2r ，即可解题；②设(),3P m m -+，根据题意，当过点P 的切线长为2时，OP=5，列出相应的一元二次方程，解方程即可；(2) 分类讨论，当C 在y 轴的正半轴上时，当点C 在y 轴的负半轴上时，当圆C 与直线112y x =-+相切时，画出相应的图形，结合全等三角形的判定与性质解题．【详解】 ①())12313,0,2,5,02P P P ⎛- ⎝⎭ 1231,2,5OP OP OP ===所以点1P 不在圆上，不符合题意；因为过点2P 的切线长为2213=-=，32<所以2P 是圆的离心点因为过3P 的切线长为5122=-==所以3P 是离心点；故答案为23,P P ；②如图设(),3P m m -+当过点P 的切线长为2时，OP=5，所以22(3)5m m +-+=解得m=1或m=2观察图像得12m ≤≤（2）如图2，当C 在y 轴的正半轴上时，经过点B(1，0)，A(2，0) 当AC=25，点A 是离心点，此时C(0，4)；观察图像知圆的纵坐标满足34y <≤，线段AB 上所有的点都是离心点；如图3，当点C 在y 轴的负半轴上时，5BC =B 是离心点，此时C(0， 125-)如图4，当圆C 与直线112y x =-+相切时，设切点为N ，如图，由题意得CNB AOB ∆≅∆5CB NB ==，()0,15C ∴-，观察图像得当圆C 的纵坐标满足12515y -≤<-，线段AB 上的所有点都是离心点；综上所述,圆C 的纵坐标满足34y <≤或12515y -≤<-．【点睛】本题考查直线与圆的位置关系、切线等知识，是重要考点，难度中等，掌握相关知识是解题关键．23．（1）见解析；（2）2π．【分析】（1）分别连接AO 、BO ，均以O 为圆心顺时针旋转90°，找到对应点连接即可；（2）根据图形可知11AOA BOB S S S =-扫过扇形面积扇形计算即可．【详解】解：（1）见图：（2）根据图形可知OA 13OB 5∴1AOA S 扇形＝2n 360r π＝9013360π＝134π 1BOB S 扇形＝2n 360r π＝905360π＝54π ∴S 扫过面积＝134π－54π＝2π 【点睛】本题主要考查图形的旋转的性质、勾股定理、扇形的面积、割补法求面积、画图等．解题关键是正确画出图形，再根据图形的进行计算，利用大扇形的面积减去小扇形的面积可得．24．（1）作图见解析，B 1（-4，-2）；（2）4π．【分析】（1）将点A 和点B 分别绕点O 逆时针旋转90°后所得对应点，再顺次连接即可得；（2）根据弧长公式计算可得．【详解】解：（1）∴△OA 1B 1即为所求作三角形，如图，点B 1（-4，-2）．（2）∵OA ＝4，∠1AOA ＝180°，∴点A 旋转到点A 1所经过的路径长为1804180π⋅=4π．【点睛】本题主要考查作图−旋转变换，解题的关键是熟练掌握旋转变换的定义与性质，并据此得出变换后的对应点，及弧长公式．25．64cm 2【分析】连接OA 、OB 、OE ，证Rt △ADO ≌Rt △BCO ，推出OD=OC ，设AD=a ，则OD=12a ，由勾股定理求出5a ，求出EF=FC=4cm ，在△OFE 中由勾股定理求出a ，即可求出答案．【详解】解：连接OA 、OB 、OE ，∵四边形ABCD 是正方形，∴AD=BC ，∠ADO=∠BCO=90°，∵在Rt △ADO 和Rt △BCO 中∵OA OB AD BC =⎧⎨=⎩， ∴Rt △ADO ≌Rt △BCO ，∴OD=OC ，∵四边形ABCD 是正方形，∴AD=DC ，设AD=acm ，则OD=OC=12DC=12AD=12acm ，在△AOD 中，由勾股定理得：5acm ， ∵小正方形EFCG 的面积为16cm 2，∴EF=FC=4cm ，在△OFE 中，由勾股定理得：5a)2=42+(12a+4)2，解得：a=-4（舍去），a=8，∴正方形面积为264cm故答案为：64cm²．【点睛】本题考查了全等三角形的性质和判定，勾股定理的应用，主要考查学生运用定理进行计算的能力，用的数学思想是方程思想．26．CD=CE ．见解析．【分析】由题意易得OD=OE ，由等弧所对的圆心角相等可得DOC EOC ∠=∠，进而由全等三角形的判定证得△CDO ≌△CEO ，进而求证结论．【详解】CD=CE ．∵ D 、E 分别是OA 、OB 的中点， ∴12OD OA ，12OE OB =， ∴OD=OE ，∵AC CB =．∠=∠，∴DOC EOC又∵OC=OC，∴△CDO≌△CEO，∴CD=CE．【点睛】本题主要考查圆圆周角定理、全等三角形的判定和性质，解题的关键是由等弧所对的圆心∠=∠．角相等求得DOC EOC。

新初中数学圆的知识点训练附答案

新初中数学圆的知识点训练附答案一、选择题1．已知⊙O的直径CD=10cm，AB是⊙O的弦，AB=8cm，且AB⊥CD，垂足为M，则AC的长为（）A．25cm B．45 cm C．25cm或45cm D．23cm或43cm【答案】C【解析】连接AC，AO，∵O的直径CD=10cm，AB⊥CD，AB=8cm，∴AM=12AB=12×8=4cm,OD=OC=5cm,当C点位置如图1所示时，∵OA=5cm，AM=4cm，CD⊥AB，∴OM=222254OA AM-=-=3cm，∴CM=OC+OM=5+3=8cm，∴AC=22224845AM CM+=+=cm；当C点位置如图2所示时，同理可得OM=3cm，∵OC=5cm，∴MC=5−3=2cm，在Rt△AMC中,AC=22224225AM CM+=+=cm.故选C.2．如图，在平行四边形ABCD中，BD⊥AD，以BD为直径作圆，交于AB于E，交CD于F，若BD=12，AD：AB=1：2，则图中阴影部分的面积为（）A．3B．36ππC．312πD．48336ππ【答案】C【解析】【分析】易得AD 长，利用相应的三角函数可求得∠ABD 的度数，进而求得∠EOD 的度数，那么一个阴影部分的面积=S △ABD -S 扇形DOE -S △BOE ，算出后乘2即可．【详解】连接OE ，OF ．∵BD=12，AD ：AB=1：2，∴AD=43 ，AB=83，∠ABD=30°，∴S △ABD =×43×12=243,S 扇形=603616,633933602OEB S ππ⨯==⨯⨯=V ∵两个阴影的面积相等，∴阴影面积=()224369330312ππ⨯--=- .故选：C【点睛】本题主要是理解阴影面积等于三角形面积减扇形面积和三角形面积．3．如图，圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上．已知铁片的圆心为O ，三角尺的直角顶点C 落在直尺的10cm 处，铁片与直尺的唯一公共点A 落在直尺的14cm 处，铁片与三角尺的唯一公共点为B ，下列说法错误的是（）A ．圆形铁片的半径是4cmB ．四边形AOBC 为正方形 C ．弧AB 的长度为4πcmD ．扇形OAB 的面积是4πcm 2【答案】C【解析】【分析】【详解】解：由题意得：BC ，AC 分别是⊙O 的切线，B ，A 为切点，∴OA ⊥CA ，OB ⊥BC ，又∵∠C=90°，OA=OB ，∴四边形AOBC 是正方形，∴OA=AC=4，故A ，B 正确；∴»AB 的长度为：904180π⨯=2π，故C 错误； S 扇形OAB =2904360π⨯=4π，故D 正确．故选C ．【点睛】本题考查切线的性质；正方形的判定与性质；弧长的计算；扇形面积的计算．4．如图，正方形ABCD 内接于⊙O ，AB=22，则»AB 的长是（）A ．πB ．32πC ．2πD ．12π 【答案】A【解析】【分析】连接OA 、OB ，求出∠AOB=90°，根据勾股定理求出AO ，根据弧长公式求出即可．【详解】连接OA 、OB ，∵正方形ABCD 内接于⊙O ，∴AB=BC=DC=AD ，∴»»»»AB BCCD DA ===， ∴∠AOB=14×360°=90°，在Rt △AOB 中，由勾股定理得：2AO 2=（2）2，解得：AO=2，∴»AB 的长为902180π´=π，故选A ．【点睛】本题考查了弧长公式和正方形的性质，求出∠AOB的度数和OA的长是解此题的关键．5．已知下列命题：①若a＞b，则ac＞bc；②若a=1，则a=a；③内错角相等；④90°的圆周角所对的弦是直径．其中原命题与逆命题均为真命题的个数是（）A．1个B．2个C．3个D．4个【答案】A【解析】【分析】先对原命题进行判断，再判断出逆命题的真假即可．【详解】解:①若a＞b，则ac＞bc是假命题，逆命题是假命题；②若a=1，则a=a是真命题，逆命题是假命题；③内错角相等是假命题，逆命题是假命题；④90°的圆周角所对的弦是直径是真命题，逆命题是真命题；其中原命题与逆命题均为真命题的个数是1个；故选A．点评：主要考查命题与定理，用到的知识点是互逆命题的知识，两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两个命题叫做互逆命题．其中一个命题称为另一个命题的逆命题，判断命题的真假关键是要熟悉课本中的性质定理．6．如图，点I为△ABC的内心，AB=4，AC=3，BC=2，将∠ACB平移使其顶点与I重合，则图中阴影部分的周长为（）A．4.5 B．4 C．3 D．2【答案】B【解析】【分析】连接AI、BI，因为三角形的内心是角平分线的交点，所以AI是∠CAB的平分线，由平行的性质和等角对等边可得：AD=DI，同理BE=EI，所以图中阴影部分的周长就是边AB 的长．【详解】连接AI、BI，∵点I为△ABC的内心，∴AI平分∠CAB，∴∠CAI=∠BAI，由平移得：AC∥DI，∴∠CAI=∠AID，∴∠BAI=∠AID，∴AD=DI，同理可得：BE=EI，∴△DIE的周长=DE+DI+EI=DE+AD+BE=AB=4，即图中阴影部分的周长为4，故选B．【点睛】本题考查了三角形内心的定义、平移的性质及角平分线的定义等知识，熟练掌握三角形的内心是角平分线的交点是关键．7．如图，小明随意向水平放置的大正方形内部区域抛一个小豆子，则小豆子落在小正方形内部及边界（阴影）区域的概率为（）A．34B．13C．12D．14【答案】C【解析】【分析】算出阴影部分的面积及大正方形的面积，这个比值就是所求的概率．【详解】解：设小正方形的边长为1，则其面积为1．Q圆的直径正好是大正方形边长，∴22，∴2，222=，则小球停在小正方形内部（阴影）区域的概率为12．故选：C．【点睛】概率=相应的面积与总面积之比，本题实质是确定圆的内接正方形和外切正方形的边长比．设较小吧边长为单位1是在选择填空题中求比的常见方法.8．如图，四边形ABCD为⊙O的内接四边形．延长AB与DC相交于点G，AO⊥CD，垂足为E，连接BD，∠GBC=50°，则∠DBC的度数为（）A．50°B．60°C．80°D．90°【答案】C【解析】【分析】根据圆内接四边形的性质得：∠GBC=∠ADC=50°，由垂径定理得：··=，则∠CM DMDBC=2∠EAD=80°．【详解】如图，∵四边形ABCD为⊙O的内接四边形，∴∠GBC=∠ADC=50°．∵AE⊥CD，∴∠AED=90°，∴∠EAD=90°﹣50°=40°，延长AE交⊙O于点M．∵AO⊥CD，∴··=，∴∠DBC=2∠EAD=80°．CM DM故选C．【点睛】本题考查了圆内接四边形的性质：圆内接四边形的任意一个外角等于它的内对角，还考查了垂径定理的应用，属于基础题．9．如图，已知AB是⊙O的直径，点C在⊙O上，过点C的切线与AB的延长线交于点P，连接AC，若∠A=30°，PC=3，则⊙O的半径为（）A．3B．23C．32D．233【答案】A【解析】连接OC，∵OA=OC，∠A=30°，∴∠OCA=∠A=30°，∴∠COB=∠A+∠ACO=60°，∵PC是⊙O切线，∴∠PCO=90°，∠P=30°，∵PC=3，∴OC=PC•tan30°=3，故选A10．如图，用半径为12cm，面积272cm的扇形无重叠地围成一个圆锥，则这个圆锥的高为（）A．12cm B．6cm C．6√2 cm D．3【答案】D【解析】【分析】先根据扇形的面积公式计算出扇形的圆心角，再利用周长公式计算出底面圆的周长，得出半径．再构建直角三角形，解直角三角形即可．【详解】72π=212360n π⨯ 解得n=180°，∴扇形的弧长=18012180π⨯=12πcm ．围成一个圆锥后如图所示：因为扇形弧长=圆锥底面周长即12π=2πr解得r=6cm ，即OB=6cm根据勾股定理得OC=22126=63-cm ，故选D ．【点睛】本题综合考查了弧长公式，扇形弧长=用它围成的圆锥底面周长，及勾股定理等知识，所以学生学过的知识一定要结合起来．11．一个圆锥的侧面展开图是半径为1的半圆，则该圆锥的底面半径是（） A ．13 B ．12 C ．34 D ．1【答案】B【解析】【分析】根据侧面展开图的弧长等于圆锥的底面周长，即可求得底面周长，进而即可求得底面的半径长．【详解】圆锥的底面周长是：π；设圆锥的底面半径是r ，则2πr=π．解得：r=12．故选B ．【点睛】本题考查了圆锥的计算，正确理解理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．12．下列命题中哪一个是假命题（）A ．8的立方根是2B ．在函数y ＝3x 的图象中，y 随x 增大而增大C ．菱形的对角线相等且平分D ．在同圆中，相等的圆心角所对的弧相等【答案】C【解析】【分析】利用立方根的定义、一次函数的性质、菱形的性质及圆周角定理分别判断后即可确定正确的选项．【详解】A 、8的立方根是2，正确，是真命题；B 、在函数3y x =的图象中，y 随x 增大而增大，正确，是真命题；C 、菱形的对角线垂直且平分，故错误，是假命题；D 、在同圆中，相等的圆心角所对的弧相等，正确，是真命题，故选C ．【点睛】考查了命题与定理的知识，能够了解立方根的定义、一次函数的性质、菱形的性质及圆周角定理等知识是解题关键．13．如图，已知某圆锥轴截面等腰三角形的底边和高线长均为10cm ，则这个圆锥的侧面积为（）A ．50cm 2B ．50πcm 2C ．52D ．5cm 2【答案】D【解析】【分析】根据勾股定理求出圆锥的母线长，求出底面圆周长，根据扇形面积公式计算即可．【详解】解：如图所示，∵等腰三角形的底边和高线长均为10cm ， 22105+＝55，圆锥底面圆半径为5，∴这个圆锥的底面圆周长=2×π×5=10π，即为侧面展开扇形的弧长，圆锥的侧面积＝12×10π×55＝255πcm2，故选：D．【点睛】本题考查了圆锥的计算，解题的关键是弄清楚圆锥的侧面积的计算方法，特别是圆锥的轴截面是等腰三角形，勾股定理的应用，以及圆锥的底面周长等于圆锥的侧面扇形的弧长．14．如图，点A、B、C、D、E、F等分⊙O，分别以点B、D、F为圆心，AF的长为半径画弧，形成美丽的“三叶轮”图案．已知⊙O的半径为1，那么“三叶轮”图案的面积为（）A．π+33B．π-33C．33π+D．33π-【答案】B【解析】【分析】连接OA、OB、AB，作OH⊥AB于H，根据正多边形的中心角的求法求出∠AOB，根据扇形面积公式计算．【详解】连接OA、OB、AB，作OH⊥AB于H，∵点A、B、C、D、E、F是⊙O的等分点，∴∠AOB=60°，又OA=OB，∴△AOB是等边三角形，∴AB=OB=1，∠ABO=60°，∴OH=2211()2-=3， ∴“三叶轮”图案的面积=（2601360π⨯⨯-12×1×3）×6=π-33，故选B ．【点睛】本题考查的是正多边形和圆、扇形面积的计算，掌握正多边形的中心角的求法、扇形面积公式是解题的关键．15．如图，若干全等正五边形排成环状．图中所示的是前3个正五边形，则要完成这一圆环还需．．（）个这样的正五边形A ．6B ．7C ．8D ．9【答案】B【解析】【分析】【详解】如图，∵多边形是正五边形，∴内角是15×（5-2）×180°=108°， ∴∠O=180°-（180°-108°）-（180°-108°）=36°， 36°度圆心角所对的弧长为圆周长的110，即10个正五边形能围城这一个圆环，所以要完成这一圆环还需7个正五边形.故选B.16．若正六边形的半径长为4，则它的边长等于（）A．4 B．2 C．23D．43【答案】A【解析】试题分析：正六边形的中心角为360°÷6=60°，那么外接圆的半径和正六边形的边长将组成一个等边三角形，故正六边形的半径等于4，则正六边形的边长是4．故选A．考点：正多边形和圆．17．我们研究过的图形中，圆的任何一对平行切线的距离总是相等的，所以圆是“等宽曲线”.除了圆以外，还有一些几何图形也是“等宽曲线”，如勒洛三角形(如图1)，它是分别以等边三角形的每个顶点为圆心，以边长为半径，在另两个顶点间画一段圆弧，三段圆弧围成的曲边三角形. 图2是等宽的勒洛三角形和圆形滚木的截面图.图1图2有如下四个结论：①勒洛三角形是中心对称图形②图1中，点A到BC上任意一点的距离都相等③图2中，勒洛三角形的周长与圆的周长相等④使用截面是勒洛三角形的滚木来搬运东西，会发生上下抖动上述结论中，所有正确结论的序号是（）A．①②B．②③C．②④D．③④【答案】B【解析】【分析】逐一对选项进行分析即可.【详解】①勒洛三角形不是中心对称图形，故①错误；②图1中，点A到BC上任意一点的距离都相等，故②正确；③图2中，设圆的半径为r∴勒洛三角形的周长=12032180rrππ⨯=g g圆的周长为2rπ∴勒洛三角形的周长与圆的周长相等，故③正确；④使用截面是勒洛三角形的滚木来搬运东西，不会发生上下抖动，故④错误故选B【点睛】本题主要考查中心对称图形，弧长公式等，掌握中心对称图形和弧长公式是解题的关键.18．如图，⊙O过点B、C，圆心O在等腰直角△ABC的内部，∠BAC＝90°，OA＝1，BC＝6，则⊙O的半径为（）A．23B．13C．4 D．32【答案】B【解析】【分析】如下图，作AD⊥BC，设半径为r，则在Rt△OBD中，OD=3－1，OB=r，BD=3，利用勾股定理可求得r.【详解】如图，过A作AD⊥BC，由题意可知AD必过点O，连接OB；∵△BAC是等腰直角三角形，AD⊥BC，∴BD=CD=AD=3；∴OD=AD-OA=2；Rt△OBD中，根据勾股定理，得：22+BD OD13故答案为：B.【点睛】本题考查了等腰直角三角形的性质和勾股定理的应用，解题关键是利用等腰直角三角形ABC判定点O在AD上.19．如图，⊙O的直径CD＝10cm，AB是⊙O的弦，AB⊥CD，垂足为M，OM：OC＝3：5，则AB的长为（）A．91cm B．8cm C．6cm D．4cm【答案】B【解析】【分析】由于⊙O的直径CD＝10cm，则⊙O的半径为5cm，又已知OM：OC＝3：5，则可以求出OM＝3，OC＝5，连接OA，根据勾股定理和垂径定理可求得AB．【详解】解：如图所示，连接OA．⊙O的直径CD＝10cm，则⊙O的半径为5cm，即OA＝OC＝5，又∵OM：OC＝3：5，所以OM＝3，∵AB⊥CD，垂足为M，OC过圆心∴AM＝BM，在Rt△AOM中，22AM=5-3=4，∴AB＝2AM＝2×4＝8．故选：B．【点睛】本题考查了垂径定理和勾股定理的应用，构造以半径、弦心距和弦长的一半为三边的直角三角形，是解题的关键.20．如图所示，AB为⊙O的直径，点C在⊙O上，且OC⊥AB，过点C的弦CD与线段OB 相交于点E，满足∠AEC＝65°，连接AD，则∠BAD等于()A．20°B．25°C．30°D．32.5°【答案】A【解析】【分析】连接OD，根据三角形内角和定理和等边对等角求出∠DOB＝40°，再根据圆周角定理即可求出∠BAD的度数．【详解】解：连接OD，∵OC⊥AB，∴∠COB＝90°，∵∠AEC＝65°，∴∠OCE＝180°﹣90°﹣65°＝25°，∵OD＝OC，∴∠ODC＝∠OCD＝25°，∴∠DOC＝180°﹣25°﹣25°＝130°，∴∠DOB＝∠DOC﹣∠BOC＝130°﹣90°＝40°，∴由圆周角定理得：∠BAD＝12∠DOB＝20°，故选：A．【点睛】本题考查了圆和三角形的问题，掌握三角形内角和定理、等边对等角、圆周角定理是解题的关键．。

圆的全章练习题大全(非常全)精编版

圆的基础学习教案一姓名分数家长评价在一次上时间管理的课上，教授在桌子上放了一个装水的罐子。

然後又从桌子下面拿出一些正好可以从罐口放进罐子里的鹅卵石。

当教授把石块放完后问他的学生道：“你们说这罐子是不是满的？”“是。

”所有的学生异口同声地回答说。

“真的吗？”教授笑着问。

然后再从桌底下拿出一袋碎石子，把碎石子从罐口倒下去，摇一摇，再加一些，再问学生：“你们说，这罐子现在是不是满的？”这回他的学生不敢回答得太快。

最后班上有位学生怯生生地细声回答道：“也许没满。

”“很好！”教授说完后，又从桌下拿出一袋沙子，慢慢的倒进罐子里。

倒完后，于是再问班上的学生：“现在你们再告诉我，这个罐子是满的呢？还是没满？”“没有满。

”全班同学这下学乖了，大家很有信心地回答说。

“好极了！”教授再一次称赞这些“孺子可教也”的学生们。

称赞完了后，教授从桌底下拿出一大瓶水，把水倒在看起来已经被鹅卵石、小碎石、沙子填满了的罐子。

当这些事都做完之后，教授正色问他班上的同学：“我们从上面这些事情得到什麽重要的功课？”班上一阵沈默，然後一位自以为聪明的学生回答说：“无论我们的工作多忙，行程排得多满，如果要逼一下的话，还是可以多做些事的。

”这位学生回答完後心中很得意地想：“这门课到底讲的是时间管理啊！”教授听到这样的回答後，点了点头，微笑道：“答案不错，但并不是我要告诉你们的重要信息。

”说到这里，这位教授故意顿住，用眼睛向全班同学扫了一遍说：“我想告诉各位最重要的信息是，如果你不先将大的鹅卵石放进罐子里去，你也许以後永远没机会把它们再放进去了。

”感悟：第一节圆的概念1.圆的定义: ,圆心: , 半径: .2.圆的面积公式：。

圆的周长公式：。

3.圆的记号:以点O 为圆心的圆,记作"________",读作"_______".4.点与圆的位置关系1、点在圆内 ⇒ ⇒ 点C 在圆内；2、点在圆上 ⇒ ⇒ 点B 在圆上；3、点在圆外 ⇒ ⇒ 点A 在圆外5.在平面上，经过给定两点的圆有个。

《数圆的学问》练习题

《数圆的学问》练习题
数圆的学问练题
1. 圆的定义和基本性质
1.1 请简要说明圆的定义和特点。

1.2 如果一条线段的两个端点都在同一圆上，那么这条线段被称为什么？
2. 圆的边界和内部
2.1 圆的边界由什么构成？请描述每个组成部分的特点。

2.2 圆的内部由什么构成？
3. 圆的弧
3.1 请简要解释什么是圆的弧。

3.2 圆心角和圆上的弧之间有什么关系？
4. 圆的唯一性质
4.1 圆的内部有哪个唯一性质？
4.2 圆的边界上有哪个唯一性质？
5. 圆的测量
5.1 请解释下列测量单位：半径、直径、周长、面积。

5.2 给定一个圆的直径，如何计算它的周长和面积？
5.3 给定一个圆的周长，如何计算它的直径和面积？
5.4 给定一个圆的面积，如何计算它的半径和周长？
6. 圆的双重角
6.1 请简要解释什么是圆的双重角。

6.2 圆的双重角的度数有什么特点？
7. 圆的切线和切点
7.1 什么是圆的切线和切点？
7.2 圆心角与切线之间有什么关系？
8. 圆的正割和余割
8.1 请简要解释什么是圆的正割和余割。

8.2 圆的正割和余割的度数有什么特点？
9. 圆的弦
9.1 请简要解释什么是圆的弦。

9.2 圆心角与弦之间有什么关系？
10. 圆的扇形
10.1 请简要解释什么是圆的扇形。

10.2 扇形的度数与弧长之间有什么关系？
以上是《数圆的学问》的练题，请认真回答每个问题。

祝你研究愉快！。

2020年人大附中初三数学基础练习25-圆(1)(教师版)

练习25 圆（1）知识点一：圆的概念1．在以下所给的命题中.①直径是弦； ②弦是直径； ③半圆是弧，但弧不一定是半圆； ④半径相等的两个半圆是等弧； ⑤长度相等的弧是等弧．正确的个数为（）A ．1B ．2C ．3D ．4 【答案】C【详解】解：根据直径和弦的概念，知①正确，②错误；根据弧和半圆的概念，知③正确；根据等弧的概念，半径相等的两个半圆一定能够重合，是等弧，④正确；长度相等的两条弧不一定能够重合，⑤错误．故选：C ．知识点二：垂径定理2．如图，AB 是⊙O 的直径，弦CD ⊥AB ，垂足为M ，下列结论不成立的是（）A ．CM ＝DMB ．CB⌒＝DB ⌒ C ．∠ACD ＝∠ADC D ．OM ＝MB【答案】D【详解】解：∵AB 是⊙O 的直径，弦CD ⊥AB ，∴CM ＝DM ，CB ⌒＝DB ⌒，AC ⌒＝AD ⌒，∴∠ACD ＝∠ADC ．故选：D ．3．如图，⊙O 的直径为10，AB 为弦，OC ⊥AB ，垂足为C ，若OC ＝3，则弦AB 的长为（）A ．8B ．6C ．4D ．10 【答案】A【详解】解：连接OA ，∵OA ∴AC ＝2222534OA OC -=-=， ∵OC ⊥AB ，∴AB ＝2AC ＝2×4＝8．故选：A ．4．如图，AB 是⊙O 的一条弦，OD ⊥AB 于点C ，交⊙O 于点D ，连接OA ．如果AB ＝8，CD ＝2，那么⊙O 的半径为．【答案】5【详解】解：设⊙O 的半径为r ，则OC ＝r －2，∵OD ⊥AB ，DOAC B∴AC＝12AB＝4，在Rt△AOC中，OA2＝OC2+AC2，即r2＝(r－2)2+42，解得，R＝5，故答案为：5．5．如图，⊙O的半径等于4，如果弦AB所对的圆心角等于120°，那么圆心O到弦AB的距离等于．【答案】2【解答】解：如图，∵圆心角∠AOB＝120°，OA＝OB，∴△OAB是等腰三角形，∵OC⊥AB，∴∠ACO＝90°，∠A＝30°，∴OC＝12OA＝2，故答案为：26．如图，AB是⊙O的直径，BC是弦，E是BC⌒的中点，OE交BC于点D．连接AC，若BC＝6，DE＝1，则AC的长为．【答案】8【解答】解：连接OC，如图所示．∵点E是BC⌒的中点，∴∠BOE＝∠COE．∵OB＝OC，∴OD⊥BC，BD＝DC．∵BC＝6，∴BD＝3．设⊙O的半径为r，则OB＝OE＝r．∵DE＝1，∴OD＝r－1．∵OD⊥BC即∠BDO＝90°，∴OB2＝BD2+OD2．∵OB＝r，OD＝r－1，BD＝3，∴r2＝32＋(r－1)2．解得：r＝5．∴OD＝4．∵AO＝BO，BD＝CD，∴OD＝12 AC．∴AC＝8．DCOB AOA7．如图，将⊙O 沿着弦AB 翻折，劣弧恰好经过圆心O ．如果弦AB ＝43，那么⊙O 的半径长度为（）A ．2B ．4C ．23D ．43 【答案】B【解答】解：作OD ⊥AB 于D ，连接OA ．∵OD ⊥AB ，AB ＝43，∴AD ＝12AB ＝23，由折叠得：OD ＝12AO ，设OD ＝x ，则AO ＝2x ，在Rt △OAD 中，AD 2＋OD 2＝OA 2， (23)2＋x 2＝(2x )2，x ＝2，∴OA ＝2x ＝4，即⊙O 的半径长度为4；故选：B ．8．为了测量一个铁球的直径，将该铁球放入工件槽内，测得的有关数据如图所示（单位：cm ），则该铁球的直径为（） A ．12 cmB ．10 cmC ．8 cmD ．6 cm 【答案】B【详解】解：连接AB ，CD 交于点D ，由题意得，OC ⊥AB ，则AD ＝DB ＝12AB ＝4，设圆的半径为R cm ，则OD ＝(r －2)cm ，在Rt △AOD 中，OA 2＝AD 2＋OD 2，即R 2＝42＋(r －2)2，解得，R ＝5，则该铁球的直径为10cm ，故选：B ．9．筒车是我国古代发明的一种水利灌溉工具，彰显了我国古代劳动人民的智慧，图1，点P 表示筒车的一个盛水桶．如图2，当筒车工作时，盛水桶的运行路径是以轴心O 为圆心，5 m 为半径的圆，且圆心在水面上方．若圆被水面截得的弦AB 长为8m ，求筒车工作时，盛水桶在水面以下的最大深度．OABC82OBA（图1）（图2）【答案】解：作OD ⊥AB 于E ，交⊙O 于点D ，∴AE ＝21AB ． ∵AB ＝8， ∴AE ＝4．在Rt △AEO 中，AO ＝5， ∴OE 223OA AE =-=． ∴ED ＝2．∴筒车工作时，盛水桶在水面以下的最大深度为2m.。

【北师大版圆的认识练习题】

【北师大版圆的认识练习题】圆的认识数字电视小测学号：姓名：成绩一．填空。

（2×20=40分）1．圆中心的一点叫做（），用字母（）表示，它到圆上初始值常量一点的距离都（）。

2．圆心到（）叫做半径，用字母（）表示。

通过（）并且两端都在（）的线段叫做直径，用字母（）表示。

3．圆是轴对称图形，它有（）条对称轴，（）都是它的对称轴。

4．在一个圆里，有（）条半径、有（）条直径。

5．（）确定圆的位置，（）确定圆的大小。

6．在一个直径是8分米的圆里，半径是（）厘米。

7．画圆时，圆规两脚彼此间的距离是圆的( )。

8．在同一圆内，所有的（）都相等，所有的（）也相等。

（）的长度等于（）长度的2倍。

二．判断。

（2×4=8分）1．半径间距都是直径的一半。

（）2．同一个圆中，直径都相等。

（）3．在交汇点圆上任意两点的线段中，直径最长。

（）4．画一个直径是a厘米的圆，圆规两脚应叉开a厘米。

（）三、选择题。

（2×3=6分）1．圆是平面上的（），而三角形、长方形、正方形、平行四边形、梯形都是（）。

① 直线图形② 曲线图形③ 无法确定2．圆中两端几乎在圆上的线段，（）。

① 一定是圆的半径② 一定是圆的直径③ 无法确定是不是直径。

3．一个圆的半径有（）条。

① 1 ② 2 ③ 无数四．按要求画圆。

（3×2=6分）1．半径是1.5厘米。

2．直径是4厘米。

五．用字母标出圆心、半径和直径，并量出像半径和直径的长度。

（3×2=6分）六．找出圆的圆心与直径，用字母标出来。

（2八．在下列图形中，你能画几条对称轴？请画出来。

（6分）BEOJ九．填一填。

（14分）0 12 3 4 5 6 7 8 9 10 11 12 13 14 151.用数对表示每个中点的位置：圆1（，）圆2（，）圆3（，）2.要让圆1移动到圆3的位置，要先向（）平移（）格，再向（）平移（3.把圆2向左平移6格，再向上平移2格，画出平移后的图形，并标出圆心O2。

人大附中圆知识总结

圆知识总结
一、基本概念
内容
备注
圆
圆、圆心、半径
在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆，固定的端点O叫做圆心，线段OA叫做半径
1．“圆”指圆周，不是圆面；
2．圆心决定圆的位置，半径长度决定圆的大小；
3．表示为⊙O
圆心为O，半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合
2
相交
圆圆
0
外离
－两圆圆心的距离；
、－两圆的半径长（）
内含
1
外切
内切
2
相交
内容
图形
符号表示
备注
切线的性质
圆的切线垂直于过切点的半径
有切线时，常用“连接圆心和切点”的辅助线
切线的判定
经过半径外端并且垂直于这条半径的直线是圆的切线
证切线时，常用“连半径，证垂直”或“作垂直，证半径”的方法
切线长
从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角
2．外心可能在三角形的内部、边上或外部，内心只能在三角形的内部
与三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心是三角形三条角平分线的交点，叫做这个三角形的内心
正多边形的中心、半径、中心角、边心距
一个正多边形的外接圆的圆心叫做这个正多边形的中心，外接圆的半径叫做正多边形的半径，正多边形每一边所对的圆心角叫做正多边形的中心角，中心到正多边形的一边的距离叫做正多边形的边心距
等弧
能够互相重合的弧叫做等弧
等弧不仅指弧的长度相等，而且指弧所在的圆的半径也相等
圆心角
顶点在圆心的角叫做圆心角
圆周角
顶点在圆上，并且两边都与圆相交的角叫做圆周角

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第七讲圆的学问
训练巩固
1.一块正方形的草地，边长为4米，在两个相对的角上各有一棵树，树上各拴一只羊，绳子长4米，问两只羊都能吃到草的草地面积有多大?
2.AB是圆的直径，C、D是AB上两点且AC=CD=DB=a厘米．求阴影部分的面积。

3.下图是三个半圆（单位：cm)，其阴影部分的周长是多少?
4.有七根直径5厘米的塑料管，用一根橡皮筋把它们勒紧一捆（如左下图），此时橡皮筋的长度是多少厘米?
60，弓形的高(弓形弧的中点到弦的垂直线段的长)是2厘米，5.在半径是8厘米的圆中，弓形弧的度数为o
求弓形的面积。

6.求下图中阴影部分的面积（单位：cm）。

拓展提高
1．下图中四个圆的半径都是5厘米，求阴影部分的面积。

2．草场上有一个长20米、宽10米的关闭着的羊圈，在羊圈的一角用长30米的绳子拴着一只羊(见下图)。

问：这只羊能够活动的范围有多大?
3．直角三角形ABC 放在一条直线上，斜边AC 长20厘米，直角边BC 长10厘米。

如下图所示，三角形由位置I 绕A 点转动，到达位置II ，此时B ，C 点分别到达1B ，1C 点；再绕1B 点转动，到达位置III ，此时A ，1C 点分别到达2A ，2C 点。

求C 点经1C 到2C 走过的路径的长。

4.图中阴影部分的面积是2.28厘米2
，求扇形的半径。