2018届九年级数学下学期第八周辅导精练《相似三角形判定》(pdf) 新人教版
人教版初三数学下册三角形相似的性质与判定
相似三角形的判定复习(一)教学案例
【学习目标】
1.掌握三角形相似的判定方法。
2.会用相似三角形的判定方法和性质来判断及计算
【学习重点】三角形相似的判定性质及其应用。
【学习难点】三角形相似的判定和性质的灵活运用。
相似是解决数学中图形问题的重要的工具,也是初中数学的重点内容,因此也是中考的重要考查内容。
【学法指导】设置问题、探究讨论、展示讲解、小组讨论。
【导学过程】
【复习案】
一、知识点回顾:
相似三角形的判定方法
二、随堂练习:
1.已知,△ABC中,DE‖BC,AD=2,BD=3,DE=1,求BC=。
2.已知,DE‖BC,DE=2,BC=4,BD=9,求AD=。
3.如图,AB与CD交于点E,∠A=∠C,AD=2,BC=3,AE=1,DE=4,求EC= 。
三、例题讲解:
1.如图,锐角三角形ABC的边AB和AC上的高线CE和BF相交于点D.
求证(1)△AEC ∽△ABF
(2)AE·AB=AF·AC
2.如图,弦AB、CD相交于点P,试证明:AP·PC=CP·PD
3..如图,△ABC内接于⊙O,AD是△ABC的边BC上的高,AE是⊙O的直径,
求证:AB·AC=AD·AE
6. 过平行四边形A B C D 的一个顶点A 作一直线分别交对角线B D ,边B C , 边D C 的延长线于E 、
F 、
G . 求证:E A 2 = E F · E G .
四、小结:。
2018年春人教版数学九年级下册27.2 相似三角形

27.2.1 相似三角形的判定学习目标、重点、难点【学习目标】1.掌握两个三角形相似的判定条件(三个角对应相等,三条边的比对应相等,则两个三角形相似)——相似三角形的定义,和三角形相似的预备定理(平行于三角形一边的直线和其它两边相交,所构成的三角形与原三角形相似).2.掌握“两组对应边的比相等且它们的夹角相等的两个三角形相似”的判定方法;掌握“两角对应相等,两个三角形相似”的判定方法.3.会运用“两个三角形相似的判定条件”和“三角形相似的预备定理”解决简单的问题.【重点难点】1.相似三角形的定义与三角形相似的预备定理.2.运用三角形相似的条件解决简单的问题.知识概览图 定义及表示方法两个三角形的三组对应边的比相等两个三角形的两组对应边的比相等,并且它们的夹角相等 两个三角形有两对对应角相等相似三角形的性质:对应角相等,对应边的比相等 新课导引【生活链接】 小明为了迎接世界中学生数学大会的召开,制作了一个如右图所示形状的花束,三边长分别是35 cm ,40 cm ,50 cm ,小丽也想制作一个这样形状的花束,但她手中只有一根长100 cm 的木条,她应该怎么制作呢?【问题探究】 如果两个多边形满足对应角相等,对应边的比相等,那么这两个多边形相似,但是定义中条件较多,过于苛刻,你能减少定义中的条件来判断两个三角形相似吗? 教材精华知识点1 相似三角形相似三角形是形状相同的三角形,它们的对应角都相等,对应边的比都相等.如图27—10所示,△ABC 与△DEF 的形状相同,大小不同,这两个三角形相似,所以∠A =∠D ,∠B =∠E ,∠C=∠F ,AB BC AC DE EF DF==· 拓展 相似三角形的定义既是最基本的判定方法,也是最重要的性质.知识点2 相似三角形的表示方法△ABC 与△DEF 相似,可以写成△ABC ∽△DEF ,也可以写成△DEF ∽△ABC ,读作“△ABC 相似于△DEF ”或“△DEF 相似于△ABC ”.拓展 用“∽”这个符号表示两个图形相似时,对应的顶点应该写在对应的位置上,如图27-10所示,表示△ABC 与△DEF 相似,∠A 的对应角是∠D ,∠B 的对应角是∠E ,∠C 的对应角是∠F ,即△ABC ∽△DEF ,而不要写成△ABC ∽△EFD ,如果把△ABC 写成△BAC ,那么就应该记作△BAC ∽△EDF ,这样做的目的是为了指明对应角、对应边.相似三角形相似三角形的判定知识点3 三角形的相似比两个三角形相似,对应边的比叫做相似比.例如:若△ABC ∽△DEF ,则AB BC CA DE EF FD ==.设比值为k ,于是AB BC CA DE EF FD===k ,即△ABC 与△DEF 的相似比为k .拓展 这时△DEF 与△ABC 的相似比为1k .若BC =6,EF =8,则△ABC 与△DEF 的相似比为6384=,△DEF 与△ABC 的相似比为43. 探究交流 如果两个三角形的相似比k =1,那么这两个三角形有怎样的关系?点拨 当两个三角形相似,且相似比为1时,这两个三角形全等,也就是说,这两个三角形的对应角都相等,对应边都相等,这两个三角形能够重合.三角形全等是三角形相似的特例.知识点4 平行线分线段成比例定理三条平行线截两条直线,所得的对应线段的比相等.把这个定理应用到三角形中,可以得到:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段的比相等. 知识点5 相似三角形的判定定理判定定理1:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.如图27—11所示,在△ABC 中,过AB 上一点D 作DE ∥BC 交AC 于点E ,求证△ADE ∽△ABC .证明:∵DE ∥BC ,∴∠ADE =∠ABC ,∠AED =∠ACB .连接DC ,BE ,∵S △EBC =S △DBC ,∴S △ABE =S △ACD .∵同高的两个三角形面积的比等于底边的比, ∴,ADE ADE ABE ACD S S AD AE S AB S AC==△△△△. ∵,ADE ADE ABE ACD S S AD AE S S AB AC=∴=△△△△. 如图27-12所示,过点D 作DF ∥AC 交BC 于点F . 易证.BD BF AB BC= 又∵BD =AB -AD ,BF =BC -F C =BC -DE ,∴AB AD BC DE AB BC --=,即AD DE AB BC=. ∴AD AE DE AB AC BC==. 又∵∠A =∠A ,∠ADE =∠ABC ,∠AED =∠ACB ,∴△ADE ∽△ABC .判定定理2:如果两个三角形的三组对应边的比相等,那么这两个三角形相似.如图27-13所示,在△ABC 和△A ′B ′C ′中,AB BC AC A B B C A C=='''''',求证△ABC ∽△A ′B ′C ′.证明:在线段A ′B ′(或它的延长线)上截取A ′D =AB ,过点D 作DE ∥B ′C ′交A ′C ′于点E ,∴△A ′DE ∽△A ′B ′C ′,∴A D DE A E A B B C A C ''==''''''. 又∵AB BC AC A B B C A C =='''''',A ′D =AB , ∴A E AC A C A C '=''''.∴A ′E =AC ,同理DE =BC , ∴△A ′DE ≌△ABC (SSS),∴△ABC ∽△A ′B ′C ′.例如:在△ABC 与△A ′B ′C ′中,AB =4 cm ,BC =6 cm ,AC =8 cm ,A ′B ′=12 cm ,B ′C ′=18 cm ,A ′C ′=24 cm ,此时41123AB A B =='',61183BC B C =='',81243AC A C =='',∴AB BC AC A B B C A C =='''''',∴△ABC ∽△A ′B ′C ′. 书写格式:在△ABC 与△A ′B ′C ′中,∵AB BC AC A B B C A C=='''''',∴△ABC ∽△A ′B ′C ′. 判定定理3:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.如图27-14所示.书写格式:在△ABC 与△A ′B ′C ′中,∵AB AC A B A C ='''',∠A =∠A ′,∴△ABC ∽△A ′B ′C ′.判定定理4:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.如图27—15所示,在△ABC 与△A ′B ′C ′中,∠A =∠A ′,∠B =∠B ′,求证△ABC ~△A ′B ′C ′.证明:在△ABC 的边AB 上截取AD =A ′B ′,过点D 作DE ∥BC 交AC 于点E ,∴△ADE ≌△A ′B ′C ′,且△ADE ~△ABC ,∴△ABC ∽△A ′B ′C ′.书写格式:在△ABC 与△A ′B ′C ′中,∵∠A =∠A ′,∠B =∠B ′,∴△ABC ~△A ′B ′C ′.规律方法小结 判定三角形相似的方法主要有以下几种:(1)定义;(2)平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似;(3)如果两个三角形的三组对应边的比相等,那么这两个三角形相似;(4)如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似;(5)如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似;(6)直角三角形被斜边上的高分成的两个直角三角形都与原三角形相似(此知识常用,但有时需要证明);(7)若两个直角三角形满足一个锐角对应相等,或两组直角边的比相等,则这两个直角三角形相似.知识点6 相似三角形的性质相似三角形对应角相等,对应边的比相等.拓展 相似三角形的性质可用于有关角的计算、线段的计算以及三角形的周长和面积的计算等,还可以用于证明两角相等、两条线段相等.规律方法小结 运用转化思想把要求证的线段间的关系逐步转化为易证的线段间的关系,即由未知向已知转化.当两个三角形相似,但又没有指明对应的情况时,应进行分类讨论.课堂检测基本概念题1、所有的直角三角形都相似吗?所有的等腰直角三角形呢?为什么?2、根据下列条件判定△ABC与△A′B′C′是否相似,并说明理由.(1)∠A=120°,AB=7 cm,AC=14 cm,∠A′=120°,A′B′=3 cm,A′C′=6 cm;(2)AB=4 cm,BC=6 cm,AC=8 cm,A′B′=12 cm,B′C′=18 cm,A′C′=21 cm.基础知识应用题3、如图27-17所示,根据下列情况写出各组相似三角形的对应边的比例式.(1)△ABC∽△ADE,其中DE∥BC;(2)△OAB∽△OA′B′,其中A′B′∥AB;(3)△ABC∽△ADE,其中∠ADE=∠B.4、如图27-18所示,已知AB∥CD∥EF,那么下列结论正确的是 ( )A.AD BCDF CE= B.BC DFCE AD=C.CD BCEF BE= D.CD ADEF AF=5、如图27-19所示,△ABD∽△ACE,求证△ABC∽△ADE.6、如图27-20所示,在不等边三角形ABC中,P是AB边上一点,过点P作一条直线,使截得的三角形与△ABC相似,则满足条件的直线一共有多少条?请画出图形.7、如图27—22所示,在Rt△ABC中,∠C=90°,△ABC中有一个内接正方形DEF C,连接AF交DE于G,AC=15,BC=10,求GE的长.综合应用题8、如图27-23所示,从ABCD的顶点C向AB和AD的延长线引垂线CE和C F,垂足分别为E,F,求证AB·AE+AD·AF=AC2.9、如图27-24所示,小明为了测量一楼房MN的高度,在离N点20 m的A处放了一个平面镜,小明沿NA后退到C点,正好从镜子中看到楼顶M点,若AC=1.5 m,小明的眼睛离地面的高度为1.6 m,请你帮助小明计算一下楼房的高度.(结果保留小数点后一位)探索与创新题10、如图27—25所示,在直角梯形ABCD中,∠D=90°,AD=7,AB=2,DC=3,P为AD上一点,以P,A,B为顶点的三角形与以P,D,C为顶点的三角形相似,那么这样的点P 一共有多少个?为什么?体验中考1、如图27-28所示,已知△ABC是边长为6 cm的等边三角形,动点P,Q同时从A,B 两点出发,分别沿AB,BC匀速运动,其中点P运动的速度是1 cm/s,点Q运动的速度是2 cm/s,当点Q到达点C时,P,Q两点都停止运动,设运动时间为t s,解答下列问题.(1)当t=2时,判断△BPQ的形状,并说明理由;(2)设△BPQ的面积为S cm2,求S与t的函数关系式;(3)作QR∥BA交AC于点P,连接PR,当t为何值时,△APR∽△PRQ?2、如图27-29所示,在ABCD中,E在DC上,若DE:EC=1:2,则BF:BE= .学后反思附: 课堂检测及体验中考答案课堂检测1、分析 由相似三角形的定义可知,所有的直角三角形不都相似,而所有的等腰直角三角形都相似.解:所有的直角三角形不都相似.如图27—16所示的两个直角三角形中的两个锐角显然不相等,因此这两个直角三角形不相似.所有的等腰直角三角形都相似.因为任意一个等腰直角三角形的三个内角分别为45°,45°,90°,三条边的比为1:1因此所有的等腰直角三角形都相似.【解题策略】 所有的直角三角形中不满足对应角都相等,因此所有的直角三角形不都相似.2、分析 根据判断两个三角形相似的判定定理3与判定定理2来判定.解:(1)∵73AB A B ='',14763AC A C =='',∴AB AC A B A C=''''. 又∵∠A =∠A ′,∴△ABC ∽△A ′B ′C ′. (2) 41123AB A B =='', 61183BC B C =='',821AC A C ='',∴AB BC AC A B B C A C =≠''''''. 即△ABC 与△A ′B ′C ′的三组对应边的比不相等,所以它们不相似.【解题策略】 此类题主要考查相似三角形的判定定理.3、分析 要写出比例式,关键应明确哪些边是对应边,而要找到对应边,比较好的方法是找到对应角(或对应的顶点).以(2)为例,由于A ′B ′∥AB ,∴∠A =∠A ′,∠B =∠B ′,∠A ′OB ′=∠AOB ,因此点A 与点A ′是对应点,点B 与点B ′是对应点,另一个公共点O 是两个三角形的对应点.解:(1) .AD AE DE AB AC BC== (2)AO BO AB A O B O A B ==''''. (3) .AD AE DE AB AC BC== 【解题策略】 两个三角形相似,在找对应角和对应边时应按照对应字母来找.4、分析 如图27-18所示,把直线AD 向右平移,且使点A 与点B 重合.容易证明:AD =BD ′,DF =D ′F ′,由比例线段的特点知BC BD AD CE D F DF'==''.故选A .5、分析 由于△ABD ∽△ACE ,所以∠BAD =∠CAE ,所以∠BAC=∠DAE.又AB ACAD AE=,所以问题得证.证明:∵△ABD∽△ACE,∴∠BAD=∠CAE,∴∠BAD+∠DAC=∠CAE+∠DAC,即∠BAC=∠DAE.又∵△ABD∽△ACE,∴AB AD AC AE=,即AB ACAD AE=,∴△ABC∽△ADE.【解题策略】解决此类问题的关键是熟练掌握相似三角形的判定方法.6、分析可利用“如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似”和“平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似”来画直线,故过点P分别作BC,AC的平行线,或过点P作与∠C相等的角,从而得到相似三角形.解:满足条件的直线一共有四条,如图27-21所示.【解题策略】本题考查相似三角形的识别方法,通过构造“两角对应相等”使两个三角形相似.7、分析根据相似三角形的判定方法和性质列出比例式,从而求得GE的长.解:∵在Rt△ABC中,∠C=90°,正方形DEF C为其内接正方形,∴△ADE∽△ACB,△AGE∽△AF B,∴AD DE AE AC CB AB==.设正方形DEF C的边长为x,则151510x x-=,∴x=6.∵△AGE∽△AFB,∴AE GEAB FB=.又∵1569315155AE ADAB AC-====,∴35GEFB=,即31065GE=-,∴GE=125.【解题策略】利用比例式求线段的长度是求线段的一种重要方法,主要是根据相似的关系列出比例式,再由比例式列出方程,从而通过解方程求得线段的长.8、分析等式左边的两项均为两条线段之积,而右边为AC2,故应设法将AC2拆成两条线段乘积的形式,由图中可知AC2=AC(AG+GC)=AC·AG+AC·GC,从而只需证AC·AG和AC·GC 与所证等式的左端两项分别相等即可.证明:过B作BG⊥AC于G,∵∠BGA=∠CE A=90°,∠3=∠3,∴△ABG ∽△ACE ,∴AG AB AE AC=, ∴AC ·AG =AB ·AE .①又∵BC ∥AD ,C F ⊥AF ,∴∠1=∠2,∠CG B =∠AF C =90°,∴△CBG ∽△ACF ,∴CB CG AC AF=, ∴AC ·CG =CB ·AF .②由①+②得AC (AG +CG )=AB ·AE +CB ·AF .又∵CB =AD ,∴AB ·AE +AD ·AF =AC 2.【解题策略】 一般地,要证形如ab =cd +ef 的线段关系,常常在a (或b )上取一点P ,使ab 转化为两项.9、分析 根据物理学中的反射定律可知:光线的反射角等于入射角,即∠BAP =∠MAP ,从而∠BAC =∠M A N ,这样就可以得到△MNA ∽△BCA ,再利用相似三角形的性质即可求出MN . 解:∵BC ⊥CA ,MN ⊥AN ,∴∠BCA =∠MNA =90°,又∵∠BAP =∠MAP ,∴∠BAC =∠M A N ,∴△BCA ∽△MN A ,∴MN :BC =A N :AC ,即MN :1.6=20:1.5,∴MN =1.6201.5⨯≈21.3(m), ∴楼房的高度约为21.3 m .【解题策略】 利用相似三角形的对应边成比例,列出比例式求线段的长是常用的方法.10、分析 △PAB 与△PDC 中各有一个直角,两边对应成比例,所以应分两种情况进行讨论,即∠APB =∠DPC 和∠APB =∠PCD ,分别求解即可.解:设AP =x ,则PD =7-x .①当△PAB ∽△PDC ,即∠A =∠D =90°,∠APB =∠DPC 时, 273x x =-,∴x =145. ②当△PAB ∽△CDP ,即∠A =∠D =90°,∠APB =∠DCP 时, 237x x=-,∴x 1=1,x 2=6. 因此AP 的值有三个,也就是这样的点P 一共有三个.【解题策略】 本题中△PAB 与△PDC 相似,由于没有指明两个三角形的对应点(除点A 和点D 外),所以要分类讨论.体验中考1、分析 (1)∠B =60°,只要判断出BQ 与BP 的关系即可.(2)用含t 的代数式分别表示BP 和BP 边上的高,因此需过点Q 作BP 边上的高;(3)找出使△APR ∽△PRQ 成立的条件即可.解:(1)△BPQ 是等边三角形,理由如下:当t =2时,AP =2×1=2,BQ =2×2=4,∴BP =AB -AP =6-2=4 .∴BQ =BP .又∵∠B =60°,∴△BPQ 是等边三角形.(2)过点Q 作QE ⊥AB ,垂足为点E .由QB =2t ,得QE =2t ·sin 60.由AP =t ,得PB =6-t .∴S △BPQ =12BP ·QE =12(6-t )t 2. (3)∵QR ∥BA ,∴∠QR C =∠A =60°,∠RQC =∠B =60°.又∵∠C =60°,∴△QRC 是等边三角形,∴QR =RC =QC =6-2t .∵BE =BQ ·cos 60°=2t ×12=t , ∴EP =AB -AP -BE =6-t -t =6-2t .∴EP =QR ,又∵EP ∥QR ,∴四边形EPRQ 是平行四边形,∴PR =EQ .又∵∠PEQ =90°,∴∠APR =∠PRQ =90°.∵△APR ∽△PRQ ,∴∠QPR =∠A =60°.∴tan 60°=QRPR t =65. ∴当t =65s 时,△APR ∽△PRQ . 【解题策略】 分析动点问题时,要抓住动点的起点、运动方向、速度、时间、距离等要素.2、分析 ∵DE :EC =1:2,∴设DE =x ,则EC =2x ,∴AB =3x .由△ABF ∽△CEF ,得3,2BF AB FE CE ==∴BF :BE =3:5.故填3:5.27.2.2 相似三角形应用举例学习目标、重点、难点【学习目标】1.进一步巩固相似三角形的知识.2.能够运用三角形相似的知识,解决不能直接测量物体的长度和高度(如测量金字塔高度问题、测量河宽问题、盲区问题)等的一些实际问题.3.通过把实际问题转化成有关相似三角形的数学模型,进一步了解数学建模的思想,培养分析问题、解决问题的能力.【重点难点】1.运用三角形相似的知识计算不能直接测量物体的长度和高度.2.灵活运用三角形相似的知识解决实际问题(如何把实际问题抽象为数学问题). 知识概览图相似三角形的应用:灵活把握题意,把实际问题转化为数学问题,运用数学建模思想和数形结合思想灵活地解决问题.新课导引【生活链接】 王芳同学跳起来把一个排球打在离她2 m 远的地上,然后球反弹碰到墙上,如果王芳跳起击排球时的高度是1.8m ,排球落地点离墙的水平距离是6m ,假设排球一直沿直线运动,那么排球能碰到墙上离地多高的地方?【问题探究】 由题意可得到如右图所示的图形.已知AB =1.8 m ,AP =2 m ,P C =6 m ,PQ ⊥AC ,那么如何求DC 的长呢?由已知可证Rt △APB ∽Rt △C PD ,由相似三角形的性质可知AB AP DC PC =,即1.826DC =,所以DC =5.4(m).利用相似三角形的知识还能解决许多实际问题. 教材精华知识点 应用相似三角形的知识解决实际问题相似三角形的知识在实际生产和生活中有着广泛的应用,这一应用是建立在数学建模思想和数形结合思想的基础上,把实际问题转化为数学问题,通过求解数学问题达到解决实际问题的目的.拓展 求线段的长度时,可根据已知条件并利用相似建立未知线段的比例关系式,从而求出所求线段的长.运用数学建模思想把生活中的实际问题抽象为数学问题,通过求解数学问题达到解决实际问题的目的.课堂检测基础知识应用题1、如图27—38所示,为了估算河的宽度,我们可以在河对岸选定一个目标P ,在近岸取点Q 和S ,使点P ,Q ,S 共线且直线PS 与河垂直,接着在过点S 且与PS 垂直的直线a 上选择适当的点T ,确定PT 与过点Q 且垂直PS 的直线b 的交点R ,如果测得QS =45 m ,ST =90 m ,QR =60 m ,求河的宽度PQ .2、古代一位数学家想出了一种测量金字塔高度的方法,如图27-39所示,为了测量金字塔的高度OB,先竖起一根已知长度的木棒O′B′,比较木棒的影长A′B′与金字塔的影长AB,即可近似地算出金字塔的高度OB且已知O′B′=1米,A′B′=2米,AB=274米,求金字塔的高度OB.综合应用题3、如图27-40所示,△ABC是一块锐角三角形余料,边BC=240 mm,高AD=160mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,则这个正方形零件的边长是多少?4、如图27—41所示,在Rt△ABC中,∠B=90°,BC=4 cm,AB=8 c m,D,E,F分别为AB,AC,BC边的中点,P为AB边上一点,过P作PQ∥BC交AC于Q,以PQ为一边,在点A的另一侧作正方形PQMN,若AP=3 c m,求正方形PQMN与矩形EDBF的公共部分的面积.探索与创新题5、教学楼旁边有一棵树,课外数学兴趣小组的同学在阳光下测得一根长为1 m的竹竿的影长为0.9 m,在同一时刻他们测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,如图27-42所示,经过一番争论,该小组的同学认为继续测量也可以求出树高,他们测得落在地面上的影长为2.7 m,落在墙壁上的影长为1.2 m,请你计算树高为多少.体验中考小明在一次军事夏令营活动中,进行打靶训练,在用枪瞄准目标点B时,要使眼睛O、准星A、目标B在同一条直线上,如图27-45所示,在射击时,小明有轻微的抖动,致使准星A偏离到A′,若OA=0.2 m,OB=40 m,AA′=0.0015 m,则小明射击到的点B′,偏离目标点B的长度BB′为 ( )A.3 m B.0.3 m C.0.03 m D.0.2 m学后反思附:课堂检测及体验中考答案课堂检测1、分析可利用三角形相似的性质来求解.解:∵∠PQR=∠PST=90°,∠P=∠P,∴Rt△PQR∽Rt△PST,∴PQ QR PS ST=,即PQ QRPQ QS ST=+,∴604590PQPQ=+,PQ×90=(PQ+45)×60,解得PQ=90.故河宽大约为90 m.【解题策略】利用相似三角形的性质能够测量不方便到达的两点间的距离.2、分析要求OB的长度,可以通过证明△OAB∽△O′A′B′,从而得到比例式OB AB O B A B='''',进而求解. 解:∵太阳光是平行光线,∴∠OAB =∠O ′A ′B ′.又∵∠ABO =∠A ′B ′O ′=90°,∴△OAB ∽△O ′A ′B ′,∴OB :O ′B ′=AB :A ′B ′,∴OB =27412AB O B A B ''⨯='' =137(米). 故金字塔的高度为137米.【解题策略】 本题重点考查阅读理解能力和知识的迁移运用能力,从而计算出不能直接测量的物体的高度.3、分析 若四边形PQMN 为正方形,则AE ⊥PN ,这样△APN 的高可以写成AD -ED =AD -PN ,再由△APN ∽△ABC ,即可找到PN 与已知条件之间的联系.解:设正方形PQMN 为加工成的正方形零件,边QM 在BC 上,顶点P ,N 分别在AB ,AC上,△ABC 的高AD 与正方形PQMN 的边PN 相交于E ,设正方形的边长为x mm .∵PN ∥BC ,∴△APN ∽△ABC ,∴AE PN AD BC=, ∴160160x -=240x ,解得x =96(mm), ∴加工成的正方形零件的边长为96 mm .【解题策略】 本题中相似三角形的知识有了一个实际意义,所以在解题时要善于把生活中的问题转化为数学问题来解决.4、分析 由于PQ ∥BC ,所以PQ AP BC AB=,从而可求出PQ 的长,而四边形PQMN 是正方形,所以PN 的长及DN 的长都可以求出来.由于正方形FQMN 与矩形EDBF 的公共部分是矩形,故只要求出DN ,MN 的长,就可以求出矩形的面积.解:在Rt △ABC 中,∠B =90°,AB =8 cm ,BC =4 cm ,D ,E ,F 分别为AB ,AC ,BC 边的中点,则AD =4 c m ,DE ∥BC ,DE ⊥AB .又∵PQ ∥BC ,∴△APQ ∽△ABC ,∴AP PQ AB BC =,即384PQ =,∴PQ =32. 由四边形PQMN 是正方形,得PN =32, ∴A N =92,DN =AN -AD =12, ∴正方形PQMN 与矩形EDBF 的公共部分的面积为:DN ·MN =DN ·PQ =12×32=34(cm 2). 【解题策略】 本题考查了直角三角形、正方形与相似三角形知识的综合应用,要熟练掌握每一种几何图形的性质.5、分析 首先根据题意画出示意图(如图27-43所示),把实际问题抽象成数学问题,从而利用△PQR ∽△DEC ,△PQR ∽△ABC 求出树高AB .解:如图27-43(1)所示,延长AD ,BE 相交于C ,则CE 是树的影长的一部分.由题意可得△PQR ∽△DEC ,∴PQ QR DE EC=, 即10.91.2CE=,∴CE =1.08(m), ∴BC =BE +CE =2.7+1.08=3.78(m).又∵△PQR ∽△ABC ,∴PQ QR AB BC=, 即10.93.78AB =,∴AB =4.2(m), 故树高为4.2 m .体验中考分析 由三角形相似可得OA AA OB BB '=',∴BB ′=OB AA OA ' =400.00150.2⨯=0.3(m).故选B. 【解题策略】 解决此题的关键是根据AA ′∥BB ′,从而判定两个三角形相似.27.2.3 相似三角形的周长与面积学习目标、重点、难点【学习目标】1.理解并初步掌握相似三角形周长的比等于相似比,面积的比等于相似比的平方.2.能用三角形的性质解决简单的问题.【重点难点】1.相似三角形的性质与运用.2.相似三角形性质的灵活运用,及对“相似三角形面积的比等于相似比的平方”性质的理解,特别是对它的反向应用的理解,即对“由面积比求相似比”的理解.知识概览图 相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比 相似三角形周长的比等于相似比(相似多边形周长的比等于相似比) 相似三角形面积的比等于相似比的平方(相似多边形面积的比等于相似比的平方)新课导引【生活链接】 如果两个三角形相似,那么它们的周长之间有什么关系?它们的面积之间有什么关系?两个相似多边形呢?【问题探究】 前面我们已经学习了相似图形的性质:相似图形的对应角相等,对应边相似三角形的周长与面积的比相等.那么相似图形的周长与面积又具有怎样的性质呢?教材精华知识点1 相似三角形对应高的比等于相似比如图27-57所示,如果△ABC ∽△A ′B ′C ′,且AB A B ''=k ,那么△ABC 与△A ′B ′C ′的相似比为k ,过A 作AD ⊥BC ,过A ′作A ′D ′⊥B ′C ′,垂足分别为D ,D ′,在△ABD 与△A ′B ′D ′中,∠B =∠B ′,∠ADB =∠A ′D ′B ′=90°,所以Rt △ABD∽Rt △A ′B ′D ′,所以AD AB A D A B =''''=k ,即相似三角形对应高的比等于相似比k .知识点2 相似三角形对应中线的比、对应角平分线的比都等于相似比如图27-58所示,在△ABC 和△A ′B ′C ′中,AD ,A ′D ′分别为△ABC 和△A ′B ′C ′的中线,BE ,B ′E ′分别为△ABC 和△A ′B ′C ′的角平分线,若△ABC ∽△A ′B ′C ′,则AD AB A D A B=''''=k . 知识点3 相似三角形周长的比等于相似比如果△ABC ∽△A ′B ′C ′,并且△ABC 与△A ′B ′C ′的相似比为k ,那么AB BC AC A B B C A C ==''''''=k ,则AB =k ·A ′B ′,BC =k ·B ′C ′,AC =k ·A ′C ′,因此()ABC AB BC CA kA B kB C kA C k A B B C C A k A B C A B B C C A A B B C C A A B B C C A ''''''''''''++++++===='''''''''''''''''''''++++++△的周长△的周长,即相似三角形周长的比等于相似比.例如:已知△ABC ∽△A ′B ′C ′,它们的周长分别为60 cm 和72 cm ,且AB =15 cm ,B ′C ′=24 cm ,则这两个三角形的相似比为605726=,且56AB BC ABBC =='''',因为AB =15 cm ,B ′C ′=24 cm ,所以A ′B ′=18 c m ,BC =20 c m ,所以AC =60-15-20=25(cm),A ′C ′=72-18-24=30(cm).知识点4 相似多边形周长的比等于相似比如果多边形A 1A 2…A n 与多边形A 1′A 2′…A n ′相似,并且多边形A 1A 2…A n 与多边形A 1′A 2′…A n ′的相似比为k ,则2311212231n n A A A A A A A A A A A A ==''''''…=k ,∴A 1A 2=kA 1′A 2′,A 2A 3=kA 2′A 3′,…,A n A 1=kAn ′A 1′,∴A 1A 2+A 2A 3+…+A n A 1=k (A 1′A 2′+A 2′A 3′+…+A n ′A 1′),∴1223112231n n A A A A A A A A A A A A+++''''''+++……=k ,即相似多边形周长的比等于相似比. 知识点5 相似三角形面积的比等于相似比的平方若△ABC ∽△A ′B ′C ′,△ABC 与△A ′B ′C ′的相似比是k ,AD ,A ′D ′分别是BC 与B ′C ′边上的高,则1212ABCA B C BC AD S BC AD S B CA DBC AD '''==='''''''' △△ =k ·k =k 2,即相似三角形面积的比等于相似比的平方.知识点6 相似多边形面积的比等于相似比的平方对于两个相似的四边形,可以把它们分成两对相似的三角形,可以得出这两个四边形面积的比等于相似比的平方.对于两个相似的多边形,用类似的方法,可以把它们分成若干对相似的三角形,从而得出相似多边形面积的比等于相似比的平方.规律方法小结 (1)如果两个三角形相似,那么它们对应高的比、对应角平分线的比、对应中线的比、对应周长的比都等于相似比.(2)相似三角形的面积比等于相似比的平方.(3)类比相似三角形的性质可知,相似多边形的周长比等于相似比,面积比等于相似比的平方.(4)本节内容中求相似三角形对应边的比和面积的比的问题可以互相转化,对于没有指明对应顶点的相似三角形仍然要分类讨论.课堂检测基本概念题1、(1)若两个相似三角形的面积比为1:2,则它们的相似比为;(2)若两个相似三角形的周长比为3:2,则它们的相似比为;(3)若△ABC∽△A′B′C′,且AB=5,A′B′=3,△A′B′C′的周长为12,则△ABC 的周长为 .基础知识应用题2、如图27-59所示,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,△ABC的周长是24,面积是48,求△DEF的周长和面积.3、如图27-60所示,在锐角三角形ABC中,AD,CE分别为BC,AB边上的高,△ABC 和△BDE的面积分别为18和2,DE=2,求AC边上的高.4、如图27-61所示,在△ABC与△CAD中,AD∥BC,CD交AB于点E,且AE:E B=1:2,EF∥BC交AC于点F,且S△ADE=1,求S△BCE和S△AEF.5、如图27-62所示,AD是△ABC的角平分线,BH⊥AD于点H,CK⊥AD于点K,求证AB·DK=AC·DH.综合应用题6、如图27-63所示,在梯形ABCD中,对角线AC,BD相交于点O,若△COD的面积为a2,△AOB的面积为b2,其中a>0,b>0,求梯形ABCD的面积S.探索与创新题7、如图27-64所示,ABCD的对角线AC,BD相交于点O,E是AB延长线上一点,OE 交BC于点F,AB=a,BC=b,BE=c,求BF的长.8、如图27-65所示,在△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB 相交于点E,EC与AD相交于点F.(1)求证△ABC∽△FCD;(2)若S△FCD =5,BC =10,求DE 的长体验中考1、已知△ABC 与△DEF 相似且面积比为4:25,则△ABC 与△DEF 的相似比为 .2、如图27-67所示,在△ABC 中,BC >AC ,点D 在BC 上,且DC =AC ,∠ACB 的平分线CF 交AD 于F ,点E 是AB 的中点,连接EF .(1)求证EF ∥BC ;(2)若四边形BDFE 的面积为6,求△ABD 的面积.学后反思附: 课堂检测及体验中考答案课堂检测1、分析 (1)∵两个相似三角形的面积比等于相似比的平方,∴k 2=12,且k >0,∴k.(2)∵相似三角形的周长比等于相似比,且周长比为3:2,∴相似三角形的相似比为3:2.(3)∵相似比5:3,∴53ABC A B C ='''△的周长△的周长.又∵△A ′B ′C ′的周长为12,∴12ABC △的周长=53,∴△ABC 的周长为20.答案: 2 (2)3:2 (3)20【解题策略】 解决此类题时,可直接应用相似三角形的周长比、面积比与相似比的。
下册相似三角形的判定人教版九年级数学全一册课件1

第4课时 相似三角形的判定(3)
学习目标
1.熟练掌握判定三角形相似的定理 4:两角分别相等的两个 三角形相似. 2.会选择恰当的方法判定两个三角形相似.
知识要点
知识点一:复习回顾 相似三角形的判定定理 1(相似∥): 如图 1, ∵ DE∥BC, ∴ △ADE∽△ABC.
(2)相似三角形的判定定理 2(相似 SSS):
下册相似三角形的判定人教版九年级 数学全 一册课 件1
下册相似三角形的判定人教版九年级 数学全 一册课 件1
(1)证明:∵AB⊥BC,ED⊥CD, ∴∠B=∠D=90°.∴∠A+∠1=90°. 又∵∠1+∠2=90°,∴∠A=∠2,∴△ABC∽△CDE. (2)解:∵△ABC∽△CDE,∴CADB=DBCE,
知识点二:相似三角形的判定定理 4(相似 AA) 两角分别相等的两个三角形 相似.
几何语言: 如图,∵ ∠A=∠A′, ∠B=∠B′ , ∴ △ABC∽△A′B′C′ .
2.如图,根据所给条件证明图中三角形相似.
证明:在△ABC 和△DFE 中, ∵∠C=180°-∠A-∠B=50°,∴∠C=∠E, 又∵∠A=∠D,∴△ABC∽△DFE.
下册相似三角形的判定人教版九年级 数学全 一册课 件1
解:底角相等的两个等腰三角形相似;证明如下:
∵∠B=∠C=∠B′=∠C′, ∴△ABC∽△A′B′C′.
下册相似三角形的判定人教版九年级 数学全 一册课 件1
下册相似三角形的判定人教版九年级 数学全 一册课 件1
4.【例 2】如图,BE,CD 相交于点 A,连接 BC,DE,下列 条件中不能判断△ABC∽△ADE 的是( C )
(1)求证:△ACD∽△ABC; (2)求证:AC2=AD·AB.
人教版九年级数学下册《相似三角形的判定》说课稿

人教版九年级数学下册《相似三角形的判定》说课稿一、说教材相似三角形的知识是在全等三角形知识的基础上的拓广和发展,相似三角形承接全等三角形,从特殊的相等到一般的成比例予以深化,学好相似三角形的知识,为今后进一步学习三角函数及有关的比例线段等知识打下良好的基础。
本节课是为学习相似三角形的判定定理做准备的,因此学好本节内容对今后的学习至关重要。
二、说教学目标和要求1.知识目标:理解相似三角形的概念,掌握判定三角形相似的预备定理。
2.能力目标:培养学生探究新知识,提高分析问题和解决问题的能力,增进发放思维能力和现有知识区向最近发展区迁延的能力。
3.情感目标:加强学生对知识探究的兴趣,渗透几何中理性思维的思想。
三、说教学的重点和难点1.教学重点:相似三角形和相似比的概念及平行线分线段成比例定理。
2.教学难点:相似三角形的定义和平行线分线段成比例定理。
四、说教法与学法采用直观、类比的方法,以多媒体手段辅助教学,引导学生预习教材内容,养成良好约自学才惯,启发学生发现问题、思考问题,培养学生逻辑思维能力。
逐步设疑,引导学生积极参与讨论,肯定成绩,使其具有成就感,提高他们学习的兴趣和学习的积极性。
五、说教学过程本节课分为六个环节:复习提问—创设情境,引入新知—合作交流,学习新知—应用拓展培养能力—课堂小结回顾反馈—布置作业巩固知识。
1.关于相似三角形定义的学习,是在前面学习了相似多边形后,学生自已看书总结得出的,培养学生观察归纳的思维方法。
指明具有这两个特性的两个三角形就叫做相似三角形。
这一段教学方法的设计是要培养学生的动手能力和观察能力。
并逐步培养从具体到抽象的归纳思维能力。
将所截得的三角形移出记为△ABC,原三角形记为△A'B'C'。
因此,如果有:∠A=∠A',∠B=∠B',∠C=∠C',那么△ABC与△A'B'C'是相似的.。
以此来加强两个三角形相似定义的认识。
人教版九年级下册 27.2.1_相似三角形的判定 学案(PDF版含答案与解析)

初中九年级数学下册第二十七章:相似——27.2.1:相似三角形的判定解析一:知识点讲解知识点一:相似三角形的定义概念:三个角分别相等,三条边成比例的三角形叫做相似三角形。
表示:相似用符号“∽”来表示,读作“相似于”。
应注意,用“∽”表示相似时,对应顶点写在对应的位置上。
相似比:相似三角形对应边的比叫做相似比,通常用“k”表示。
✧相似比有顺序✧全等是相似的特殊情况,相似比等于1性质:相似三角形的对应角相等,对应边成比例。
注意:关键要找准对应边和对应角。
图例:有关三角形相似的基本图形:✧平行线型:✧斜交型:✧旋转型:例1:如右图所示,△ABC ∽△ADE ,则∠ABC =∠ADE ,∠ACB =∠AED ,BC ∥DE ,=AB ADACAE =BCDE 。
知识点二:平分线分线段成比例基本事实:两条直线被一组平行线所截,所得的对应线段成比例。
由3l ∥4l ∥5l ,得EF DE BC AB =,DF DE AC AB =,DFEFAC BC =应用:平行于三角形一边的直线截其他两边(或两边的延长线)。
所得的对应线段成比例。
由DE ∥BC ,得ACAEAB AD =例2:如右图,直线a ∥b ∥c ,直线1l 、2l 与这三条平行线分别交于点A 、B 、C 和点D 、E 、F 。
若AB ∶BC =1∶2,DE =3,则EF 的长为6。
知识点三:相似三角形的判定方法——“平行定理”内容:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。
类别:✧“A ”字型DE 与AB ,AC 相交DE 与AB ,AC 的延长线相交✧“X ”字型:DE 与AB ,AC 的反向延长线相交例3:如下图,在□ABCD 中,点E 、F 分别在边AD 、BC 上,且EF ∥CD ,G 为边AD 延长线上一点,连接BG ,则图中与△ABG 相似的三角形有(D )△EGN 、△FBN 、△DGM 、△CBMA.1个B.2个C.3个D.4个知识点四:相似三角形的判定方法——“三边定理”文字语言:三边成比例的两个三角形相似。
九年级数学下册知识讲义-27相似三角形的判定与性质(附练习及答案)-人教版
一、考点突破1. 理解相似三角形的定义,掌握平行线分线段成比例定理、相似三角形的判定方法和性质,能够运用三角形相似的条件和性质解决简单的问题。
2. 全等是相似的特例,是相似比为1的情况,因此在学习相似三角形时,应对照全等三角形来学,从而发现知识的内在结构、区别与联系,这对学透、学活知识是有很大帮助的。
二、重难点提示重点:掌握相似三角形的判定方法,会利用相似三角形解决简单的问题。
难点:准确运用两个三角形相似的条件,来判定三角形是否相似。
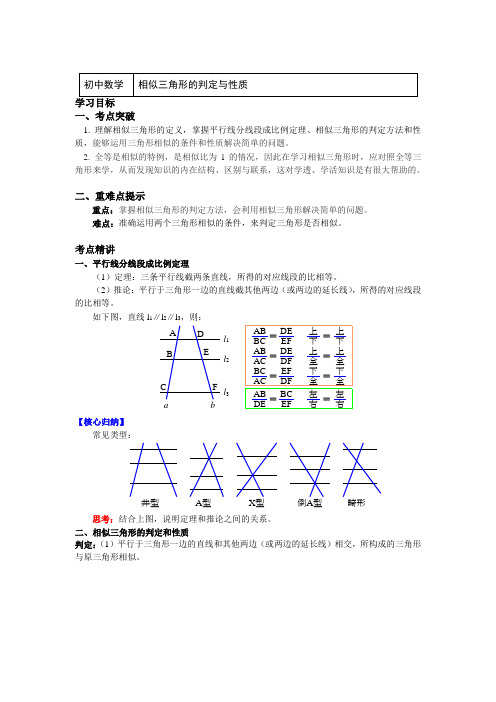
考点精讲一、平行线分线段成比例定理(1)定理:三条平行线截两条直线,所得的对应线段的比相等。
(2)推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段的比相等。
如下图,直线l1∥l2∥l3,则:a b l1 l2l3A BC DEFABBCDEEF上下ABACDEDF上全BCACEFDF下全ABDEBCEF左右========上下上全下全左右【核心归纳】常见类型:井型A型X型倒A型畸形思考:结合上图,说明定理和推论之间的关系。
二、相似三角形的判定和性质判定:(1)平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
(2)如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
简单说:两角对应相等,两三角形相似。
若则(3)两边对应成比例且夹角相等,两三角形相似。
若:则(4)三边对应成比例,两三角形相似。
若:则(5)两个直角三角形,如果斜边与一条直角边对应成比例,则两直角三角形相似。
若:则性质:相似三角形的对应角相等,对应边成比例。
【规律总结】特殊三角形的相似:①所有的全等三角形都相似;②所有的等边三角形都相似;③所有的等腰直角三角形都相似。
典例精讲例题1在研究相似问题时,甲、乙两同学的观点如下:甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似。
九年级数学下册相似三角形的判定(第1课时)相似三角形的判定(1)课件(新版)新人教版

关闭
答案
1
2
3
4
4.
如图,把△OAB沿x轴向右平移得到△CDE,CD交AB于点F,则△OAB △CFB.
关闭
由平移得到CF∥OA, 故△OAB∽△CFB.
关闭
∽
解析 答案
27.2.1
相似三角形的判定
第1课时
相似三角形的判定(1)
1.在相似多边形中,最简单的就是 相似三角形 . 2.在△ABC和△A'B'C'中,如果 ∠A=∠A',∠B=∠B',∠C=∠C', 别 相等 相似于 ,三条边 成比例 相似 △A'B'C' 作“
������������ ������'������'
1.平行线分线段成比例的基本事实的运用
������������ ������ ������������
【例 1】 如图,l1∥l2∥l3,������������ = ������ ,求证:������������ = ������+������.
������
分析先根据平行线分线段成比例的基本事实,得到线段 AB,BC,DE,EF的比例式,再根据比例的性质对比例式变形就得到要 求的结果.
C.10
������������
解析:∵EF∥AB,∴△DEF∽△DAB. ∴������������ = ������������.而������������ = 3,∴������������ = 2.
������������ ������������ ������������ ∴ ������������ ������������+������������ ������������ 3 5 =1+ =1+ = . ������������ ������������ 2 2 2 ������������ ������������ 2 = ,即 = = . 5 ������������ ������������ 5 4 2 EF=4,∴������������ = 5,∴CD=AB=10,故应选
人教版九年级数学下册:相似三角形的判定【精品课件】

例1 根据下列条件,判断△ABC与 △A'B'C'是否相似,并说明理由:
(1)AB=4cm, BC=6cm, AC=8cm, A'B'=12cm, B'C'=18cm, A'C'=24cm;
(2)∠A=120°, AB=7cm, AC=14cm, ∠A'=120°, A'B'=3cm, A'C'=6cm.
△ADE∽ △ABC
证明: DE∥BC,∠E=∠C,∠B=∠D,
过E作EF∥BD交CB的延长线于F,
∵DE∥BC,EF∥BD,∴AACE
AD AB
ቤተ መጻሕፍቲ ባይዱ
BF AE BC AC
又∵四边形BDEF是平行四边形,∴DE=BF
∴
AE AC
AD AB
DE BC
∴△ADE∽△ABC
练习
1.如图,在△ABC中,DE∥BC,且AD=3,
A' B' B' C ' A' C '
又
AB A' B'
BC B' C'
AC A' C '
, A'D=AB
∴ DE BC , A' E AC
B' C ' B' C ' A' C ' A' C '
∴DE=BC, A'E =AC ∴△A'DE≌△ABC
∴△ABC∽△A'B'C' △ A'DE是证明的中介,它把
两个等腰三角形不一定相似
两个等边三角形一定相似
(人教版)九年级下册数学《相似三角形的判定》教学课件共33页

1
0
、
倚
南
窗
以
寄
傲
,
安
。
46、我们若已接受最坏的,就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们引入最美好的社会,使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首,不会作诗也会吟。——孙洙 50、谁和我一样用功,谁就会和我一样成功。——莫扎特
(人教版)九年级下册数学《相似三角 形的判定》教学课件
6
、
露
凝
无
游
氛
,
天
高
风
景
澈
。
7、翩翩新 来燕,双双入我庐 ,先巢故尚在,相 将还旧居。
8
、
吁
嗟
身
后
名
,
于
我
若
浮
烟
。
9、 陶渊 明( 约 365年 —427年 ),字 元亮, (又 一说名 潜,字 渊明 )号五 柳先生 ,私 谥“靖 节”, 东晋 末期南 朝宋初 期诗 人、文 学家、 辞赋 家、散
