平面与圆柱面的截线
2.2-2.3 平面与圆柱面的截线 平面与圆锥面的截线 课件(人教A选修4-1)

返回
[悟一法]
借助条件中已经建立的直角坐标系,通过相关平面图 形转换确定椭圆的长、短轴的长是关键.
返回
[通一类] 1.平面内两个定点的距离为8,动点M到两个定点的距离 的和为10,求动点M的轨迹方程.
解:以两点的连线段所在的直线为 x 轴,线段的中垂线 为 y 轴建立直角坐标系,则由椭圆的定义知,动点的轨 x2 y2 迹是椭圆,设所求椭圆方程为 2+ 2=1. a b ∵2a=10,2c=8,∴a=5,c=4.则 b2=9. x2 y2 故所求椭圆的方程为 + =1. 25 9
返回
[研一题]
[例1] 已知圆柱底面半径为,平面β与圆柱母线夹
角为60°,在平面β上以G1G2所在直线为横轴,以 G1G2中点为原点,建立平面直角坐标系,求平面β与
圆柱截口椭圆的方程.
返回
分析:本题考查平面与圆柱面的截线.解答本题需要根
据题目条件确定椭圆的长轴和短轴.
解:过 G1 作 G1H⊥BC 于 H. ∵圆柱底面半径为 3, ∴AB=2 3. ∵四边形 ABHG1 是矩形, ∴AB=G1H=2 3. G1H 2 3 在 Rt△G1G2H 中,G1G2= = =4. sin∠G1G2H 3 2 又椭圆短轴长等于底面圆的直径 2 3, x2 y2 ∴椭圆的标准方程为 + =1. 4 3
曲线的形状,尤其是焦点的确定更加不容易,但可以采 用与上节中定理1的证明相同的方法,即Danelin双球法, 这时较容易确定椭圆的焦点,学生也容易入手证明,使 问题得到解决.
返回
[通一类] 2.在空间中,取直线l为轴,直线l′与l相交于O点,夹角
为α,l′围绕l旋转得到以O为顶点,l′为母线的圆锥面,任
2 解:由题意知,椭圆的长半轴长 a= =2 2, sin 45° 短半轴长 b=2,则半焦距 c= a2-b2= 8-4=2. 所以焦距 2c=4.
平面与圆柱面的截线平面与圆锥面的截线课件人教A选修21

截线的一般形式和几何意义
截线的一般形式:平面与圆柱面、圆锥面的交线
几何意义:截线是平面与圆柱面、圆锥面的公共部分 截线的性质:截线是平面与圆柱面、圆锥面的交线,具有平面和圆柱面、 圆锥面的共同性质 截线的应用:截线在工程、建筑、机械等领域有广泛应用
03
平面与圆锥面的截 线
截线的定义和性质
截线:平面与圆锥面相交形成的曲线 性质:截线是圆锥面的一部分,具有圆锥面的性质 截线的形状:取决于平面与圆锥面的相对位置 截线的长度:取决于平面与圆锥面的交角大小
截线的分类和特点
截线类型:平面与圆锥面的截线可以分为直线、曲线和点
直线截线:当平面与圆锥面相交时,如果平面与圆锥面的轴线平行, 则截线为直线
课件特点:图文并茂,易于理 解,便于记忆,适合学生自学
课件内容:包括平面与圆柱面、 圆锥面的截线定义、性质、应 用等,以及相关例题和练习题
课件形式:PPT课件,便于教 师讲解和学生自学,支持多媒 体播放和互动操作
课件使用方法和技巧
课件内容: 包括平面与 圆柱面、圆 锥面的截线 定义、性质、 应用等
内容:包括平面与圆柱面、 圆锥面的截线、截线的性质、
截线的应用等
教学方法:采用直观教学法, 通过图形的直观展示来理解
截线的性质和应用
教材使用方法和技巧
阅读教材:认真阅读教材中的内容,理解平面与圆柱面、圆锥面的截线原理。 动手实践:通过动手实践,加深对平面与圆柱面、圆锥面的截线原理的理解。 思考问题:思考教材中的问题,尝试自己解答,提高解决问题的能力。 交流讨论:与同学、老师交流讨论,分享自己的理解和想法,互相学习,共同进步。
课件形式: PPT演示文 稿,包含文 字、图片、 动画等元素
课件操作: 使用演示文 稿软件,熟 悉基本操作 和功能
平面与圆柱面的截线 课件

2.如图乙所示,AB、CD是两个等圆的直径,AB∥CD, AD、BC与两圆相切,作两圆的公切线EF,切点分别为点F1、 F2,交BA、DC的延长线于点E、F,交AD于点G1,交BC于点 G2.设EF与BC、CD的交角分别为φ、θ.
图乙
图丙
(1)G2F1+G2F2______AD.
(2)G1G2______AD. (3) G2F1 ______cos φ______sin θ.
AA 2 (2)所求截面为矩形 AA′B′B,面积等于 2 2 cm2. (3)点 O 到截面的距离即 OO′到截面的距离,也是点 O′ 到截面的距离为 2 cm.
2
的面积.
如果椭圆的长轴长为2a,短轴长为2b,求椭圆
解析:如图所示,设椭圆是由半径为 r 的圆柱面的斜截
面截得的,且斜截面与母线所成角为,则 b=r,a= r . sin
5.一平面与圆柱面的母线成45°角,平面与圆柱面的截
32
线椭圆的长轴为6,则圆柱面的半径为____2 __.
6.已知平面δ斜截一准线半径为r的圆柱面,轴线与平面δ
所成的角为α,求证:存在圆柱面的内切球与平面δ相切.
证明:作一平面δ∥平面α,且平面δ与平面α的距离等于
圆柱面准线的半径r,则平面δ与圆柱面的轴线相交于一点C. 以点C为圆心,r为半径作球,则球C(C,r)为圆柱面的
内切球. 过点C作CC′⊥平面δ,则C′∈δ,CC′=r. 又∵球的半径为r, ∴C′在球面上. 又∵过球的半径的外端与半径垂直的平面与球只有唯一
公共点, ∴球C(C,r)与平面δ只有一个公共点. ∴球C(C,r)与平面相切. ∴存在圆柱面的内切球C(C,r)与平面δ相切
7.已知一个平面垂直于圆柱的轴,截圆柱所得为半径为2 的圆,另一平面与圆柱的轴成30°角,求截线的长轴,短轴和 离心率.
平面与圆柱面的截线 课件

1.定理 1 圆柱形物体的斜截口是椭圆. 温馨提示 (1)内切球:圆柱面与球面相切,该球叫 做圆柱的内切球.(2)焦球:设平面 m 截割圆柱面,与平 面 m 相切的圆柱面的内切球叫截割平面 m 的焦球.
圆柱的截割面的两侧各有一个焦球.若截割面是圆柱 面的直截面时,两焦球与直截面切于同一点,即截线圆的 圆心;若截割面是圆柱面的斜截面时,两焦球与斜截面的 切点恰好是截线椭圆的两个焦点,此时称两焦球为丹德林 (Dandelin)双球.
类型 2 椭圆性质的应用
[典例 2] 如图所示,已知球 O1、O2 分 别切平面 β 于点 F1、F2.G1G2=2a,Q1Q2=2b, G1G2 与 Q1Q2 与垂直平分, 求证:F1F2=2 a2-b2.
证明:连接 AB,作 G1H⊥BG2,H 为垂足,则四边形
ABHG1 是矩形.
所以 G1H=AB. 因为 Q1、Q2 分别是 P1、P2 的平行射影,所以 P1Q1 綊 P2Q2.
所以四边形 P1Q1Q2P2 是平行四边形. 所以 Q1Q2=P1P2,
即 Q1Q2 等于底面圆直径. 所以 G1H=AB=Q1Q2=2b. 又由切线长定理,G1A=G1F1=G2F2,G2F1=G2B, 所以 G2F1-G2F2=G2B-G1A. 又 G1A=BH,所以 G2F1-G2F2=G2B-BH. 所以 F1F2=G2H.
反之,如果根据所给条件能确定斜截面与已知圆柱母 线的夹角,也可以确定两焦球的球所示,F1、F2 叫做椭圆的焦点, F1F2 叫做椭圆的焦距,AB 叫做椭圆的长轴, CD 叫做椭圆的短轴.
3.椭圆的性质 (1)如果长轴为 2a,短轴长为 2b,那么 2c=2___a_2_-__b_2 . (2)准线:底面与截面的交线.
平面与圆柱面的截线(超链接)

平面与圆柱面的截线
教材分析 学情分析 教学目标
教学重难点
教学过程
教材分析
(1)高中数学选修4-1第三讲第二节
(2)更好地把握椭圆与其他几何图形的关系
(3)蕴含了丰富的思想方法,对于学生的数 学学习意义深远
学情分析
(1)有利因素:掌握一定基本知识 具备空间想象能力、几何直观能力
重点:平面与圆柱面的斜截线是椭圆 难点:定理的探究及证明过程
教学过程
生活情景 数学猜想 探究过程 得出结论
情境引入
提出猜想
合作探究
获得新知
课堂小结
情境引入
提出猜想
合作探究
获得新知
课堂小结
猜想:平面与圆柱面的斜截线是椭圆
平面与圆柱面的截线
探究一:寻找定点
F1
O1
另一个定点? 焦点关于短 轴对称
定理:平面与圆柱面的斜截线是椭圆。
例题:一圆柱底面半径为4,截面与轴成30°角, 从该截面上、下放入圆柱的两个内切球,使它们 都与截面相切,求这两个切点之间的距离。
30°
作业布置
必做题:习题3.2
谢
谢
2
如图,把模型 顺时针旋180°
F2
F1
O1
F2 O2
O2
探究二:确定定长
定长
A O P
B
定长
O1 K1
切线长定理的空间推广
O2 K2
(定值)
所以平面与圆柱面的斜截线是椭圆
情境引入
提出猜想
合作探究
获得新知
课堂小结
定理:平面与圆柱面的斜截线是椭圆
情境引入
提出猜想
ቤተ መጻሕፍቲ ባይዱ
平面与圆柱面的截线平面与圆锥面的截线课件人教A选修13

02 直 、 倾 斜 b . 截 线 性 质 : 长 度 、 角 度 、 面 积
a. 截线类型:平行、垂直、倾斜 b. 截线性质:长度、角度、面积
内容二:平面与圆锥面的截线 a. 截线类型:平行、垂
03 直 、 倾 斜 b . 截 线 性 质 : 长 度 、 角 度 、 面 积
截线的性质
截线是平面与圆柱面、圆锥面的 交线
截线的形状取决于平面与圆柱面、 圆锥面的相对位置
添加标题
添加标题
截线可以是直线、曲线或点
添加标题
添加标题
截线的长度、方向和位置可以通 过几何关系计算得出
截线与圆柱面的关系
截线与圆柱面的切线:截线 与圆柱面相切时,会产生一 条切线。
截线与圆柱面的交点:截线 与圆柱面相交时,会产生一 个交点。
05
人教A选修(22)介绍
人教A选修(22)简介
教材名称:人教A选修(22) 教材内容:平面与圆柱面、圆锥面的截线 教材特点:理论与实践相结合,注重培养学生的动手能力和创新能力 教材适用范围:高中数学选修课程,适用于对数学有兴趣的学生
人教A选修(22)内容概述
平面与圆柱面、圆锥面的截线:介绍平面与圆柱面、圆锥面的截线及其性质 截线方程:介绍截线的方程及其求解方法 截线与平面、圆柱面、圆锥面的关系:介绍截线与平面、圆柱面、圆锥面的关系及其应用 截线与平面、圆柱面、圆锥面的交点:介绍截线与平面、圆柱面、圆锥面的交点及其性质
YOUR LOGO
20XX.XX.XX
平面与圆柱面、圆锥面的截线
,
汇报人:
目 录
01 单 击 添 加 目 录 项 标 题
02 平 面 与 圆 柱 面 的 截 线
最新人教版高中数学选修4-1《平面与圆柱面的截线》预习导航

预习导航请沿着以下脉络预习:1.圆柱形物体的斜截口是椭圆.2.如图,椭圆中,F 1、F 2是焦点,B 1B 2是F 1F 2的中垂线,则A 1A 2叫做椭圆的长轴,B 1B 2叫做椭圆的短轴,F 1F 2叫做椭圆的焦距.若长轴为2a ,短轴为2b ,则焦距2c =2a 2-b 2.3.椭圆上任一点到焦点F 1的距离与到直线l 1的距离之比为定值cos φ,则直线l 1叫做椭圆的一条准线.4.若e =cos φ,则e 叫做椭圆的离心率.1.如果椭圆的两个焦点将长轴分成三等份,那么,这个椭圆的两准线间的距离是焦距的( ).A .9倍B .4倍C .12倍D .18倍答案:A解析:设椭圆的长轴长,短轴长,焦距分别为2a,2b,2c ,由已知,得2a 3=2c ,即a =3c , ∴两准线间的距离为2a 2c =18c 2c=18C . 2.下列说法不正确的是( ).A .圆柱面的母线与轴线平行B .圆柱面的某一斜截面的轴面总是垂直于直截面C .圆柱面与斜截面截得的椭圆的离心率与圆柱面半径无关,只与母线和斜线面的夹角有关D .平面截圆柱面的截线椭圆中,短轴长即为圆柱面的半径答案:D解析:显然A 正确,由于任一轴面过轴线,故轴面与圆柱的直截面垂直,B 正确,C 显然正确,D 中短轴长应为圆柱面的直径长,故不正确.3.已知椭圆两准线间的距离为8,离心率为12,则Dandelin 球的半径是__________. 答案: 3解析:由题意知⎩⎨⎧ a 2c =4,c a =12,解得⎩⎪⎨⎪⎧a =2,c =1, ∴b =a 2-c 2= 3.∴Dandelin 球的半径为 3.4.已知平面α与一圆柱的底面成60°角,则该平面与圆柱截口图形的离心率是__________. 答案:32解析:平面与圆柱面截口图形为椭圆,其离心率e =sin 60°=32. 5.已知一平面截圆柱面所得的截口椭圆的离心率为35,长轴长是20,求该圆柱的底面圆半径.解:设该椭圆半焦距为c ,短半轴长为b ,长半轴长为a ,则a =10,e =c a =35.∴c =35×10=6. ∴圆柱的底面圆半径r =b =a 2-c 2=102-62=8.。
平面与圆柱面的截线 课件

(2a)2 -(2b)2 =2 a2 -b 2 ,
1.圆柱形物体的截口是(
)
A.双曲线
B.圆
C.抛物线
D.椭圆或圆
解析:当截面与圆柱的底面平行时,截口是圆,否则是椭圆.
答案:D
2.若一条直线与过平面的一条斜线在此平面上的射影垂直,则这条直线与
这条斜线的位置关系是(
)
A.垂直
B.异面
C.相交
D.不能确定
我们把 A1A2 叫做椭圆的长轴,B1B2 叫做椭圆的短轴,F1F2 叫做椭圆的
焦距.如果长轴为 2a,短轴为 2b,那么焦距 2c=2 a2 -b 2 .
(3)Dandelin 双球探究椭圆性质:如图所示,设球 O1,O2 与圆柱的交线(圆)
所在的平面分别为 α,γ,椭圆所在的斜截面 β 与它们的交线分别为 l1,l2,α,γ 与
PQ
P1
PQ
=
φ=定值.
②椭圆上任意一点到焦点 F1 的距离与到直线 l1 的距离之比为定值 cos
φ.我们把直线 l1 叫做椭圆的一条准线.
③椭圆上任意一点到焦点 F2 的距离与到直线 l2 的距离之比也为定值
cos φ,所以 l2 是椭圆的另一条准线.
④记 e=cos φ,我们把 e 叫做椭圆的离心率.
其截平面的关系,综合应用切线长定理、三角形的相似与全等,解直角三角
形,以及平行射影的性质.
【典型例题 2】 如图所示,已知球 O1,O2 分别切平面 β 于点 F1,F2,P1P2
为☉O1 的一条直径,Q1,Q2 分别为 P1,P2 在平面 β 内的平行射
影,G1 G2=2a,Q1Q2=2b,G1 G2 与 Q1Q2 垂
直平分,求证:F1F2=2 a2 -b2 .
高一数学试题答案及解析
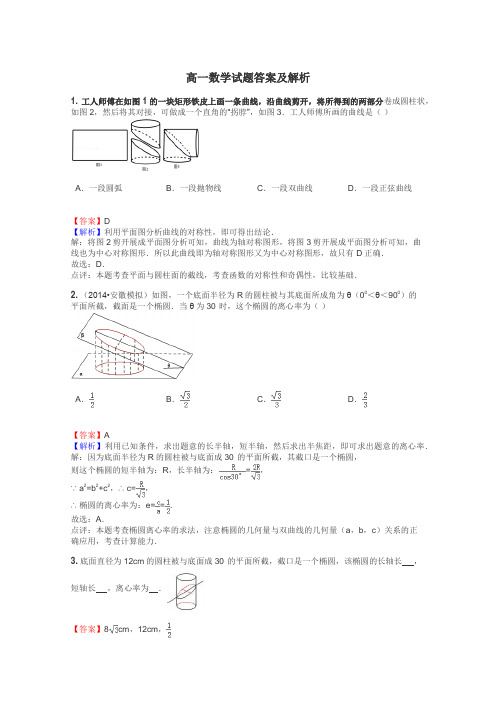
高一数学试题答案及解析1.工人师傅在如图1的一块矩形铁皮上画一条曲线,沿曲线剪开,将所得到的两部分卷成圆柱状,如图2,然后将其对接,可做成一个直角的“拐脖”,如图3.工人师傅所画的曲线是()A.一段圆弧B.一段抛物线C.一段双曲线D.一段正弦曲线【答案】D【解析】利用平面图分析曲线的对称性,即可得出结论.解:将图2剪开展成平面图分析可知,曲线为轴对称图形,将图3剪开展成平面图分析可知,曲线也为中心对称图形.所以此曲线即为轴对称图形又为中心对称图形,故只有D正确.故选:D.点评:本题考查平面与圆柱面的截线,考查函数的对称性和奇偶性,比较基础.2.(2014•安徽模拟)如图,一个底面半径为R的圆柱被与其底面所成角为θ(00<θ<900)的平面所截,截面是一个椭圆.当θ为30°时,这个椭圆的离心率为()A.B.C.D.【答案】A【解析】利用已知条件,求出题意的长半轴,短半轴,然后求出半焦距,即可求出题意的离心率.解:因为底面半径为R的圆柱被与底面成30°的平面所截,其截口是一个椭圆,则这个椭圆的短半轴为:R,长半轴为:=,∵a2=b2+c2,∴c=,∴椭圆的离心率为:e==.故选:A.点评:本题考查椭圆离心率的求法,注意椭圆的几何量与双曲线的几何量(a,b,c)关系的正确应用,考查计算能力.3.底面直径为12cm的圆柱被与底面成30°的平面所截,截口是一个椭圆,该椭圆的长轴长,短轴长,离心率为.【答案】8cm,12cm,【解析】根据平面与圆柱面的截线及椭圆的性质,可得圆柱的底面直径为12cm,截面与底面成30°,根据截面所得椭圆长轴、短轴与圆柱直径的关系,我们易求出椭圆的长轴长和短轴长,进而得到椭圆的离心率.解:∵圆柱的底面直径d为12cm,截面与底面成30°∴椭圆的短轴长2b=d=12cm椭圆的长轴长2a==8cm根据得,椭圆的半焦距长C=2cm则椭圆的离心率e===故答案为:8cm,12cm,点评:若与底面夹角为θ平面α截底面直径为d圆柱,则得到的截面必要椭圆,且椭圆的短轴长等于圆柱的底面直径,长轴长等于.4.工人师傅在如图1的一块矩形铁皮的中间画了一条曲线,并沿曲线剪开,将所得的两部分卷成圆柱状,如图2,然后将其对接,可做成一个直角的“拐脖”,如图3.对工人师傅所画的曲线,有如下说法:(1)是一段抛物线;(2)是一段双曲线;(3)是一段正弦曲线;(4)是一段余弦曲线;(5)是一段圆弧.则正确的说法序号是.【答案】③④【解析】利用平面图分析曲线的对称性,即可得出结论.解:将图2剪开展成平面图分析可知,曲线为轴对称图形,将图3剪开展成平面图分析可知,曲线也为中心对称图形.所以此曲线即为轴对称图形又为中心对称图形,故只有③④正确.故答案为:③④.点评:本题考查平面与圆柱面的截线,考查函数的对称性和奇偶性,比较基础.5.平行投影与中心投影之间的区别是.【答案】平行投影的投影线互相平行,而中心投影的投影线交于一点【解析】平行投影与中心投影之间的区别是平行投影的投影线互相平行,而中心投影的投影线交于一点.主要从形成投影的光线来比较两者的区别.解:平行投影与中心投影之间的区别是平行投影的投影线互相平行,而中心投影的投影线交于一点,故答案为:平行投影的投影线互相平行,而中心投影的投影线交于一点点评:本题考查平行投影和中心投影,是一个概念性问题,这种问题不用运算,只要理解两种投影形成的不同之处就可以.6.如图,PA、PB、DE分别与⊙O相切,若∠P=40°,则∠DOE等于()度.A.40B.50C.70D.80【答案】C【解析】连接OA、OB、OP,由切线的性质得∠AOB=140°,再由切线长定理求得∠DOE的度数.解:连接OA、OB、OP,∵∠P=40°,∴∠AOB=140°,∵PA、PB、DE分别与⊙O相切,∴∠AOD=∠POD,∠BOE=∠POE,∴∠DOE=∠AOB=×140°=70°.故选C.点评:本题考查了弦切角定理和切线长定理,是基础知识,要熟练掌握.7.如图,△ABC内接于圆⊙O,CT切⊙O于C,∠ABC=100°,∠BCT=40°,则∠AOB=()A.30°B.40°C.80°D.70°【答案】C【解析】由圆周角定理知,欲求∠AOB,需求出∠ACB的度数;在△ABC中,已知∠ABC的度数,而根据弦切角定理,可得出∠CAB的度数;再,由三角形内角和定理,可求出∠ACB的度数,由此得解.解:∵CT切⊙O于C∴∠BAC=∠BCT=40°;在△ABC中,∠BAC=40°,∠ABC=100°,∴∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣40°﹣100°=40°,∴∠AOB=2∠ACB=2×40°=80°.故选C.点评:此题考查的是三角形的内角和定理、圆周角角及弦切角定理,是中学阶段的基本题目.8.如图所示,圆O的直径AB=6,C为圆周上一点,BC=3过C作圆的切线l,过A作l的垂线AD,垂足为D,则∠DAC=()A.15°B.30°C.45°D.60°【答案】B【解析】根据所给的圆的直径和BC的长,得到三角形的一个锐角是30°,根据同弧所对的圆周角等于弦切角,得到另一个直角三角形的角的度数,即为所求.解:∵圆O的直径AB=6,C为圆周上一点,BC=3∴∠BAC=30°,∠B=60°,∵过C作圆的切线l∴∠B=∠ACD=60°,∵过A作l的垂线AD,垂足为D∴∠DAC=30°,故选B.点评:本题考查弦切角,本题解题的关键是同弧所对的圆周角和弦切角相等和含有30°角的直角三角形的应用,本题是一个基础题.9.(2010•崇文区一模)如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么点P与O间的距离是()A.16B.20C.D.【答案】C【解析】作辅助线,连接OA,OP,根据切线长定理可知:∠OPA=∠APB,由PA与⊙O相切,可知:OA⊥AP,根据已知条件可将OP的长求出.解:连接OA,OP∵PA,PB是⊙O的切线,∠APB=60°,∴∠OPA=∠APB=30°,OA⊥OP,∴OP===,∴点P与O间的距离是.故选C.点评:本题主要考查切线长和特殊三角函数值的运用和计算.属于基础题.10.(2014•咸阳一模)(选修4﹣1 几何证明选讲)如图,两个等圆⊙O与⊙O′外切,过O作⊙O′的两条切线OA,OB,A,B是切点,点C在圆O′上且不与点A,B重合,则∠ACB= .【答案】60°【解析】连接OO′,AO′,B0′,设圆的半径为r,根据切线的性质可得AO′⊥AO,BO′⊥BO,由两圆相外切可得,OO′=2r,AO′=BO′=r,从而有∠AOO′=∠BOO′=30°,∠AO′B=2×60°=120°,由圆周角定理可得,可求解:连接OO′,AO′,B0′,设圆的半径为r根据切线的性质可得AO′⊥AO,BO′⊥BO由两圆相外切可得,OO′=2r,AO′=BO′=r∴∠AOO′=∠BOO′=30°,∠AO′B=2×60°=120°由圆周角定理可得,=60°故答案为:60°点评:本题主要考查了圆的切线的性质、两圆相外切的性质、圆周角定理的综合应用,解题的关键是发现,(圆周角定理).11.(2014•海珠区一模)如图,过圆O外一点P分别作圆的切线和割线交圆于A,B,且PB=9,C是圆上一点使得BC=4,∠BAC=∠APB,则AB= .【答案】6【解析】根据同弧所对的圆周角与弦切角相等,得到∠C=∠BAP,根据所给的两个角相等,得到两个三角形相似,根据相似三角形对应边成比例,得到比例式,代入已知的长度,求出结果.解:∵∠BAC=∠APB,∠C=∠BAP,∴△PAB∽△ACB,∴∴AB2=PB•BC=9×4=36,∴AB=6,故答案为:6.点评:本题考查圆的切线的性质的应用,考查同弧所对的圆周角等于弦切角,考查三角形相似的判断和性质,本题是一个综合题目.12.(2014•泸州三模)在△ABC中,O是其外接圆的圆心,其两条中线的交点是G,两条高线的交点是H,设OG=λGH,则λ的值为.【答案】【解析】取特殊值,假设△ABC是直角三角形,∠ABC=90°,由重心性质得OG=GH,又OG=λGH,所以λ=.解:取特殊值,假设△ABC是直角三角形,∠ABC=90°,如图,AC边的中点O是其外接圆的圆心,两条中线BO,AD交于点G,则G是△ABC的重心,两条高线AB,CB交于H,H与B重合,则由重心性质得OG=GH,又OG=λGH,所以λ=.故答案为:.点评:本题考查实数值的求法,是基础题,解题时要认真审题,注意特殊值法的合理运用.13.(2012•和平区模拟)如图,已知AB为圆O的直径,AC与圆O相切于点A,CE∥AB交圆O于D、E两点,若AB=6,BE=2,则线段CD的长为.【答案】【解析】设CD=x,则CE=6﹣x,利用切割线定理和勾股定理即可得出AD,再利用同圆的等弧所对的弦相等即可得出.解:设CD=x,则CE=6﹣x.∵AC与圆O相切于点A,∴AC⊥AB,AC2=CD•CE=x(6﹣x).∴AD2=AC2+CD2=6x.∵CE∥AB,∴AD=BE,∴6x=4,∴x=.故答案为:.点评:熟练掌握矩形和圆的性质、切割线定理和勾股定理、同圆的等弧所对的弦相等是解题的关键.14.如图所示,l1∥l2∥l3,下列比例式正确的是()A.=B.=C.=D.=【答案】D【解析】根据平行线分线段成比例定理得出相应的线段对应成比例,进而逐一判断四个答案的正误,可得答案.解:∵直线l1∥l2∥l3,∴=,故A错误;=,故B错误;=,故C错误;=,故D正确;故选:D点评:本题考查了平行线分线段成比例定理,注意:一组平行线截两条直线,所截的线段对应成比例.15.如图,在梯形ABCD中,AB∥CD∥EF,若AB=5,CD=2,EF=4,则梯形ABFE与梯形EFDC的面积比是()A.B.C.D.【答案】D【解析】过D作DG∥BC交AB于G,交EF于H,根据平行四边形的性质先求出BG=FH=CD,从而得到EH,AG的长,再根据平行线分线段成比例定理可求出梯形ABFE与梯形EFDC的高的比,即可求出梯形ABFE与梯形EFDC的面积比.解:过D作DG∥BC交AB于G,交EF于H.则BG=FH=CD=2,∴EH=EF﹣FH=2,AG=3,∵AB∥EF,∴DE:AE=2:1,∴梯形ABFE与梯形EFDC的高的比为1:2,∴梯形ABFE与梯形EFDC的面积比是=故选:D.点评:本题考查平行线分线段成比例定理,考查梯形的面积公式是一个基础题,解题的时候容易出的一个错误是把两个梯形看成相似梯形,根据相似多边形的面积之比等于相似比的平方.16.(2011•宝山区二模)如图,在梯形ABCD中,AD∥BC,AC、BD相交于O,记△BCO、△CDO、△ADO的面积分别为S1、S2、S3,则的取值范围是.【答案】(2,+∞)【解析】根据三角形相似的引理,我们易判断△AOD∽△COB,然后根据三角形相似的性质得到对应边成比例,而根据同高的两个三角形面积之比等于底边长之比,结合基本不等式即可求出的取值范围.解:∵AD∥BC,∴△AOD∽△COB∴∴==≥2=2当且仅当时,即BO=DO时,即O为BD中点时取等;又∵四边形ABCD为梯形,故O不可能为BD的中点,故>2即的取值范围(2,+∞)故答案为:(2,+∞)点评:本题考查的知识点是相似三角形的判定及基本不等式,其中根据梯形的性质,判断O不可能为BD的中点易被忽略而错解为[2,+∞)17.(2010•广东)如图,在直角梯形ABCD中,DC∥AB,CB⊥AB,AB=AD=a,CD=,点E,F分别为线段AB,AD的中点,则EF=.【答案】【解析】要求EF的长,关键是关键是构造一个三角形,使EF位于该三角形,解三角形即可求解:解:连接DE,∵四边形ABCD为直角梯形,AB=AD=a,CD=,CB⊥AB,点E,F分别为线段AB,AD的中点∴△AED为直角三角形.则EF是RT△AED斜边上的中线,由直角三角形斜边上的中线等于斜边的一半得,EF=DE=AB=.故答案为:点评:连接DE,构造含有线段EF的直角三角形是解答本题的关键,由此可得,解决平面几何的求值和证明问题,辅助线的添加是基础.18.如图,矩形纸片ABCD,AB=8,AD=6,折叠纸片使AD边与对角线BD重合,点A在BD上的落点为点A′,折痕为DG,则AG的长为.【答案】3【解析】根据勾股定理可得BD=5,由折叠的性质可得△ADG≌△A'DG,则A'D=AD=6,A'G=AG,则A'B=10﹣6=4,在Rt△A'BG中根据勾股定理求AG的即可.解:在Rt△ABD中,AB=8,AD=BC=6,∴BD=10,由折叠的性质可得,△ADG≌△A'DG,∴A'D=AD=6,A'G=AG,∴A'B=BD﹣A'D=10﹣6=4,设AG=x,则A'G=AG=x,BG=8﹣x,在Rt△A'BG中,x2+42=(8﹣x)2解得x=3,即AG=3.故答案为:3.点评:此题主要考查折叠的性质,综合利用了勾股定理的知识.认真分析图中各条线段的关系,也是解题的关键.19.(2009•广州二模)如图所示,在四边形ABCD中,EF∥BC,FG∥AD,则= .【答案】1【解析】根据两条直线平行,得到平行线所截的对应线段成比例,得到两个比例式,把要求的两个比值的变化为同一条直线上的线段之间的关系,合并同类项得到一个分子和分母相等的分式,得到结果.解:∵EF∥BC,∴∵FG∥AD,∴,∴==故答案为:1点评:本题考查平行线等分线段定理,考查等量代换,考查分式的整理方法,是一个基础题,这种题目是几何证明中的典型题.20.若直线m被两平行线l1:x﹣y+1=0与l2:x﹣y+3=0所截得的线段的长为,则m的倾斜角可以是①15°②30°③45°④60°⑤75°其中正确答案的序号是(写出所有正确答案的序号)【答案】①或⑤【解析】先求两平行线间的距离,结合题意直线m被两平行线l1与l2所截得的线段的长为,求出直线m与l1的夹角为30°,推出结果.解:两平行线间的距离为,由图知直线m与l1的夹角为30°,l1的倾斜角为45°,所以直线m的倾斜角等于30°+45°=75°或45°﹣30°=15°.故填写①或⑤故答案为:①或⑤点评:本题考查直线的斜率、直线的倾斜角,两条平行线间的距离,考查数形结合的思想.。
2.2-2.3 平面与圆柱面的截线 平面与圆锥面的截线 课件(人教A选修4-1)

返回
点击下图进入“创新演练”
返回
返回
2.平面与圆锥面的截线
(1)如图,AD是等腰三角形底边BC上的高,∠BAD=α,
直线l与AD相交于点P,且与AD的夹角为β(0<β<),则: ① β>α ,l与AB(或AB的延长线)、AC相交; ② β=α ③ β<α ,l与AB不相交; ,l与BA的延长线、AC都相交.
返回
(2)定理2:在空间中,取直线l为轴,直线l′与l相交于O 点,夹角为α,l′围绕l旋转得到以O为顶点,l′为母线的圆锥 面.任取平面π,若它与轴l的交角为β(当π与l平行时,记β=
返回
[研一题] [例2] 证明:定理2的结论(1),即β>α时,平面π与圆 锥的交线为椭圆. 分析:本题考查平面与圆锥面的截线.解答本题需要 明确椭圆的定义,利用椭圆的定义证明.
返回
证明:如图,与定理1的证明相同,在圆锥内部嵌入 Dandelin双球,一个位于平面π的上方,一个位于平面π的 下方,并且与平面π及圆锥均相切.
所以PF1+PF2=PQ1+PQ2=Q1Q2. 由正圆锥的对称性,Q1Q2的长度等于两圆S1、S2所在平行平 面间的母线段的长度而与P的位置无关,由此我们可知在β>α时, 平面π与圆锥的交线是以F1、F2为焦点的椭圆.
返回
[悟一法]
由平面中,直线与等腰三角形两边的位置关系拓广
为空间内圆锥与平面的截线之后,较难入手证明其所成
曲线的形状,尤其是焦点的确定更加不容易,但可以采 用与上节中定理1的证明相同的方法,即Danelin双球法, 这时较容易确定椭圆的焦点,学生也容易入手证明,使 问题得到解决.
数学人教A版选修4-1素材:教材习题点拨 第三讲二 平面

教材习题点拨探究1解:由教材图35,根据切线长定理有G 2F 1=G 2B ,G 2F 2=G 2C ,于是G 2F 1+G 2F 2=G 2B +G 2C =BC =AD .又∵G 1G 2=G 1F 2+F 2G 2,由切线长定理知G 1F 2=G 1D ,F 2G 2=G 2C ,∴G 1G 2=G 1D +G 2C .连接F 1O 1,F 2O 2,容易证明△EF 1O 1≌△FF 2O 2.∴EO 1=FO 2.又∵O 1A =O 2C ,∴EA =FC .于是可证得△FCG 2≌△EAG 1.∴G 1A =G 2C .∴G 1G 2=G 1D +G 1A =AD .在Rt △G 2EB 中,cos φ=G 2B G 2E =G 2F 1G 2E, ∴G 2F 1=G 2E cos φ.又∵φ=90°-θ,∴G 2F 1=G 2E cos φ=G 2E sin θ.由此得到结论:(1)G 2F 1+G 2F 2=AD ;(2)G 1G 2=AD ;(3)G 2F 1G 2E=cos φ=sin θ. 思考解:猜想,两个焦点可能在两个球与斜截面的切点上,即过球心O 1,O 2分别作斜截面的垂线,其垂足F 1,F 2就可能是焦点.探究2解:当点P 与G 2重合时,有G 2F 1+G 2F 2=AD .当点P 不在端点时,连接PF 1,PF 2,则PF 1,PF 2分别是两个球面的切线,切点为F 1,F 2.过P 作母线,与两球面分别相交于K 1,K 2,则PK 1,PK 2分别是两球面的切线,切点为K 1,K 2.根据切线长定理的空间推广,知PF 1=PK 1,PF 2=PK 2,所以PF 1+PF 2=PK 1+PK 2=AD .由于AD 为定值,故点P 的轨迹是椭圆.习题3.2图(1)图(2)证明:图(1)的轴截面如图(2)所示.∵F 1F 2=2c ,G 1G 2=2a ,∴G 2B =G 2F 1=a +c ,G 1A =G 1F 1=a -c .∵△EAG 1∽△EBG 2, ∴EG 1EG 2=G 1A G 2B ,即EG 1EG 1+2a =a -c a +c,解得EG 1=a (a -c )c . ∵在Rt △PK 1Q 中,∠K 1PQ =φ,∴cos φ=PK 1PQ =PF 1PQ. 又∵在Rt △G 2BE 中,∠BG 2E =φ,∴cos φ=G 2B EG 2. ∴PF 1PQ =G 2B EG 2=a +c a (a -c )c+2a =c a , 即P 到F 1的距离PF 1与到l 1的距离PQ 之比等于c a.。
平面与圆柱面圆锥面的截面课件
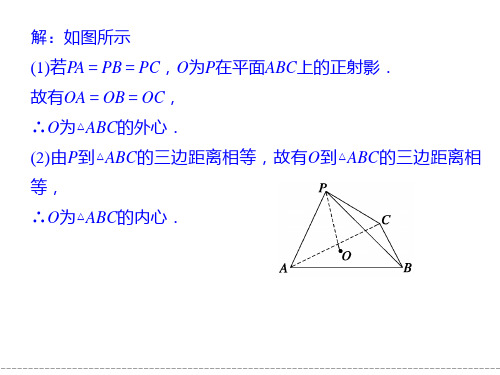
(3)PO⊥平面ABC、PA⊥PB,PA⊥PC, ∴PA⊥平面PBC, ∴PA⊥BC, ∴OA⊥BC,同理OB⊥AC,OC⊥AB, ∴O为△ABC的垂心. 【反思感悟】 根据射影的性质,可以确定点在一个平面内射 影的位置.
知识点三 定 理
在空间给定一个圆锥面S,轴线与母线 的夹角为α,任取一个不通过S的顶点 的平面δ,设其与轴线的夹角为β(β与 轴线平行时,规定β=0),则 (1)当β>α时,平面σ与圆锥面的交线为 椭圆; (2)当β=α时,平面σ与圆锥面的交线 为抛物线; (3)当β<α时,平面σ与圆锥面的交线为 双曲线.
【探究学习】 对射影与垂直关系的探究
【例6】如果椭圆的长轴长为2a,短轴长为2b,求椭圆的面积.
解:如图所示,设椭圆是由半径为 r 的圆柱面的斜截面截得的, 且斜截面与母线所成角为 α, 则 b=r,a=sinr α. 取圆柱面一直截面,则其面积 S 圆=πr2, 直截面与斜截面的夹角为π2-α,由面积射 影定理有 S 椭圆=cosSπ2圆-α=sπinr2α=π·r·sinr α=πab. 即为椭圆的面积. 【反思感悟】 注意图形面积和其射影面积关系的应用.
【例5】已知一平面垂直于轴线截一圆柱面所得的截线为一个半径 为3的圆,另一截面与圆柱轴线所成角为60°,求椭圆截线的 两个焦点之间的距离.
解:由斜截面与圆ห้องสมุดไป่ตู้轴线成 60°, 即与圆柱母线成 60°角,故椭圆 的长半轴 a=sinr φ=sin360°=2 3, 又椭圆的短半轴 b=r=3. 故椭圆的焦距 2c=2 a2-b2=2 3. 即为截线的两个焦点间的距离.
湘教版选修4《平面和圆柱面的截线》评课稿

湘教版选修4《平面和圆柱面的截线》评课稿导言本文是对湘教版选修4《平面和圆柱面的截线》课程进行评课的文稿。
评课的目的是对该课程的教学内容、教学方法、教学效果等各个方面进行细致的分析和评价,以期对教学过程进行合理的改进和优化,提高学生的学习效果和兴趣。
一、课程概述湘教版选修4《平面和圆柱面的截线》是一门高中数学选修课程,主要内容是探究平面和圆柱面的截线性质和应用。
通过本门课程的学习,学生可以深入了解平面和圆柱面的截线的数学性质,并将其运用到实际问题中去。
二、教学目标在湘教版选修4《平面和圆柱面的截线》课程中,教学目标主要包括:1.理解平面和圆柱面的截线的概念和性质;2.能够掌握计算平面和圆柱面的截线的方法;3.学会应用截线的性质解决现实问题;4.培养学生的数学思维和推理能力。
三、教学内容湘教版选修4《平面和圆柱面的截线》课程的教学内容包括以下几个方面:1.平面和圆柱面的基本概念介绍;2.平面和圆柱面的截线性质和特点;3.计算平面和圆柱面的截线;4.截线在几何问题中的应用。
四、教学方法在湘教版选修4《平面和圆柱面的截线》课程的教学过程中,可以采用以下教学方法:1.讲授法:通过讲解基本概念、截线性质和计算方法,引导学生对知识点的理解和掌握;2.演示法:通过实际的几何图形演示,展示平面和圆柱面的截线性质和特点,增加学生的直观感受;3.实践操作:设计一些实际的应用问题,让学生通过实践操作,巩固和应用所学内容;4.小组讨论:设置小组讨论环节,让学生在小组内进行交流和合作,提高学生的思维能力和团队合作精神。
五、教学设计为了达到教学目标,可以设计以下教学环节和内容:1. 导入部分通过引入一个生活实例,如“修建隧道时如何计算隧道截面的形状”,激发学生对截线问题的兴趣,引导学生思考和探索。
2. 知识讲解首先,通过讲解基本概念和定义,如平面、圆柱面和截线等,让学生对课程内容有一个初步的认识和理解。
然后,针对截线的性质和特点,以及计算截线的方法,进行详细的讲解和演示。
平面与圆柱面的截线优秀教学设计

平面与圆柱面的截线
【教学目标】
1.知识与内容:
(1)通过观察平面截圆锥面的情境,体会定理1 (2)利用Dandelin 双球证明定理1
(3)通过探究,得出椭圆的准线和离心率,加深对椭圆结构的理解 2.过程与方法:
利用现代计算机技术,动态地展现Dandelin 两球的方法,帮助学生利用几何直观进行思维,培养学生的几何直观能力,重视直觉的培养和训练,直觉用于发现,逻辑用于证明。
3.情感态度价值观:
通过亲历发现的过程,提高对图形认识能力,重视合情推理和演绎推理的启发、应用和培养,让学生辩证地观察、分析问题。
【教学重难点】
重点:定理1的证明;椭圆准线和离心率的探究 难点:椭圆准线和离心率的探究
【教学准备】
模型
【教学方法】
探究 讨论
【教学过程】
1.平面与圆柱面的截线
探究讨论:如图,AB ,CD 是两个等圆的直径,AB//CD ,AD 、BC 均与两圆相切。
作公切线EF ,切点分别为F 1和F 2 ,交BA ,DC 的延长线与E ,F ,交AD 于G 1 ,交BC 于G 2 ,设EF 与BC ,CD 的交角分别为φ,θ。
AD )1(2212=+F G F G 21G G AD )2(=
定理1.圆柱形物体的斜截口是椭圆。
课后小结
1
G 2。
第三讲平面和圆柱面截

置 时,过P作l1的 垂 线, 垂
K2
足 为Q,过P作 平 面的
图3 8
垂 线, 垂 足 为K1 , 连 接K1Q, 得
RtPK1Q,则QPK1 .从 而 有PF1 PK1 cos 定 值.
PQ PQ
所以, 椭圆上任意一点到焦点F1的距离与到直
线l1的距离之比为定值cos .我们把直线l1叫做
的 点 的 轨 迹 叫 做 椭 圆.
1
2
图3 2
我们分析一下图3 22中的
D H
水平面的结构.如图3 3, 水平 G
面的图形可看成是以杯子
A E
Q F C
圆柱的母线为投影方向, 杯
P
口圆在水平面所在平面上的
射影.其中,点A的投影为点E, 点D的投影为F.显然EF AD.
椭圆的一条准 线. 同理, 椭圆上任意一点到焦点F2的距离与到直
线l2的距离之比也为定值cos .所以l2是椭圆的
另 一 条 准 线.
记e cos,我们把e叫做椭圆的离心率.
将 两 个 球 嵌 入 圆 柱 内, 使 它 们 分 别 位 于 斜 截 面 的 上 方 和 下 方,并 且 与 圆 柱 面 和 斜 截 面均 相 切, 这 是 证 明 定 理 的 关 键.这 种 方 法 是 数 学 家Dan dlin创 立 的, 故 将 嵌 入 的 双 球 称 为Dandlin双 球.
我们还是从特殊情况
开 始 探 究 这 种 关 系 .由 前 面 对 图3 5的 探 究
E l1 A Q
O1 K1
B
可 知, 对 于 椭 圆 的 长 轴
G1 F1
端 点G2 , 有
G2 F1 cos 定 值.
平面与圆柱面的截线

PF1 PK1 cos 定值 PQ PQ
点P在椭圆的任意位置
椭圆上任意一点到焦点F1的距离与到直线l1的 距离之比为定值cos. 同样,椭圆上任意一点到焦点F2的距离与到直 线l2的距离之比为定值cos.
l1,l2 椭圆的准线 椭圆的离心率
∴G2F1+G2F2=G2B+G2C=BC=AD
又∵G1G2=G1F2+F2G2
由切线长定理知 G1F2=G1D,F2G2=G2C,
∴G1G2=G1D+G2C
连接F1O1,F2O2,容易证明
△EF1O1≌△FF2O2
∴EO1=FO2
又∵O1A=O2C, ∴ EA=FC 于是可证得△FCG2≌△EAG1 ∴G1A=G2C ∴G1G2=G1D+G1A=AD 在Rt△G2EB中
你能猜想这个椭圆的两个焦 点的位置吗?
猜想:两个焦点为两个球与 斜截面的切点上,即过球心 O1、O2分别作斜截面的垂 线,其垂足F1、F2就可以 能是焦点。
对截口上任一点P, 证明 PF 1 + PF 2 = 定值
当点P与G2重合时,有
G2F1+G2F2=AD 当点P不在端点时,连接PF1,PF2,则 PF1,PF2分别是两个球面的切线,切 点为F1,F2. 过P作母线,与两球面分别相交于 K1,K2,则PK1,PK2分别是两球面的 切线,切点为K1,K2
PF1=PK1,PF2=PK2,
PF1+PF2=PK1+PK2=AD
定理1 圆柱形物体的斜截口是椭圆 焦点 F1、F2 B1B2是F1F2的中垂线
长轴 A1A2
短轴 B1B2 焦距 F1F2
2a
ቤተ መጻሕፍቲ ባይዱ
2.2-2.3 平面与圆柱面的截线 平面与圆锥面的截线 课件(人教A选修4-1)

返回
在 Rt△PBQ1 中,PB=PQ1cos α. PQ1 cos β ∴ = . PA cos α PF1 又∵PQ1=PF1,α=β,∴ =1, PA 即 PF1=PA, 动点 P 到定点 F1 的距离等于它到定直线 m 的距 离,故当 α=β 时,平面与圆锥的交线为抛物线.
返回
本课时考点在高考中很少考查.2012年梅州模拟以
返回
[读教材·填要点]
1.平面与圆柱面的截线
(1)椭圆组成元素: F1,F2 叫椭圆的焦点; F1F2 叫椭圆 的焦距;AB叫椭圆的 长轴 ;CD叫椭圆 的 短轴 .
如果长轴为2a,短轴为2b,那么焦 2 a2-b2 . 距2c=
返回
(2)如图(1),AB、CD是两个等圆的直径,AB∥CD,
AD、BC与两圆相切,作两圆的公切线EF,切点分别为F1、 F2,交BA、DC的延长线于E、F,交AD于G1,交BC于G2. 设EF与BC、CD的交角分别为φ、θ.
返回
①G2F1+G2F2= AD;②G1G2= AD; G2F1 =cosφ=sinθ. ③ G2E (3)如图(2),将两个圆拓广为球面,将矩形 ABCD 看 成是圆柱面的轴截面,将 EB、DF 拓广为两个平面 α、β, EF 拓广为平面 γ,则平面 γ 与圆柱面的截线是 椭圆 .即 得定理 1:圆柱形物体的斜截口是椭圆.
返回
[研一题] [例2] 证明:定理2的结论(1),即β>α时,平面π与圆 锥的交线为椭圆. 分析:本题考查平面与圆锥面的截线.解答本题需要 明确椭圆的定义,利用椭圆的定义证明.
返回
证明:如图,与定理1的证明相同,在圆锥内部嵌入 Dandelin双球,一个位于平面π的上方,一个位于平面π的 下方,并且与平面π及圆锥均相切.
平面与圆柱面的截线-高中数学知识点讲解(含答案)
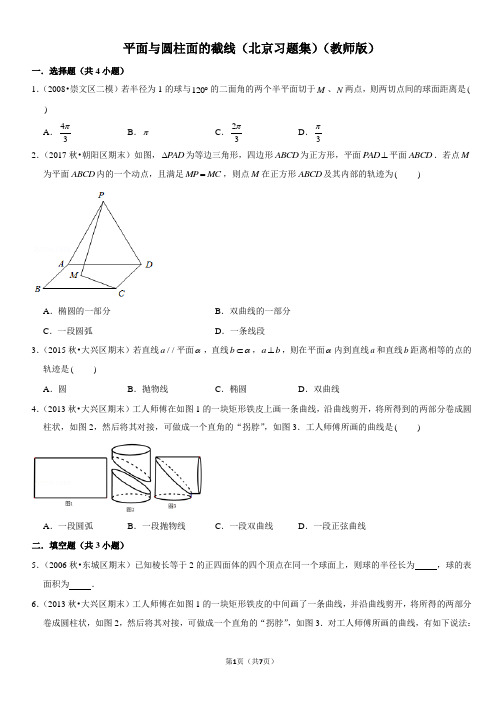
平面与圆柱面的截线(北京习题集)(教师版)一.选择题(共4小题)1.(2008•崇文区二模)若半径为1的球与120︒的二面角的两个半平面切于M、N两点,则两切点间的球面距离是( )A.43πB.πC.23πD.3π2.(2017秋•朝阳区期末)如图,PAD∆为等边三角形,四边形ABCD为正方形,平面PAD⊥平面ABCD.若点M 为平面ABCD内的一个动点,且满足MP MC=,则点M在正方形ABCD及其内部的轨迹为()A.椭圆的一部分B.双曲线的一部分C.一段圆弧D.一条线段3.(2015秋•大兴区期末)若直线//a平面α,直线bα⊂,a b⊥,则在平面α内到直线a和直线b距离相等的点的轨迹是()A.圆B.抛物线C.椭圆D.双曲线4.(2013秋•大兴区期末)工人师傅在如图1的一块矩形铁皮上画一条曲线,沿曲线剪开,将所得到的两部分卷成圆柱状,如图2,然后将其对接,可做成一个直角的“拐脖”,如图3.工人师傅所画的曲线是()A.一段圆弧B.一段抛物线C.一段双曲线D.一段正弦曲线二.填空题(共3小题)5.(2006秋•东城区期末)已知棱长等于2的正四面体的四个顶点在同一个球面上,则球的半径长为,球的表面积为.6.(2013秋•大兴区期末)工人师傅在如图1的一块矩形铁皮的中间画了一条曲线,并沿曲线剪开,将所得的两部分卷成圆柱状,如图2,然后将其对接,可做成一个直角的“拐脖”,如图3.对工人师傅所画的曲线,有如下说法:(1)是一段抛物线;(2)是一段双曲线;(3)是一段正弦曲线;(4)是一段余弦曲线;(5)是一段圆弧.则正确的说法序号是.7.(2003•北京)如图,已知底面半径为r的圆柱被一个平面所截,剩下部分母线长的最大值为a,最小值为b,那么圆柱被截后剩下部分的体积是.平面与圆柱面的截线(北京习题集)(教师版)参考答案与试题解析一.选择题(共4小题)1.(2008•崇文区二模)若半径为1的球与120︒的二面角的两个半平面切于M 、N 两点,则两切点间的球面距离是()A .43πB .πC .23πD .3π 【分析】画出图形,圆O 是球的一个大圆,MAN ∠是二面角的平面角,AM 、AN 是圆O 的切线,欲求两切点间的球面距离即求圆O 中劣弧MN 的长,将立体几何问题转化为平面几何问题解决.【解答】解:画出图形,如图,在四边形OMNA 中,AM 、AN 是球的大圆的切线,AM OM ∴⊥,AN ON ⊥,12060MAN MON ∠=︒∴∠=︒∴两切点间的球面距离是33MN OM ππ=⨯=.故选:D .【点评】空间几何体的主要元素往往集中在某一特征截面上,这个特征截面是一个平面图,从而将立体几何问题转化为平面几何问题.从特征截面入手加以剖析,实现转化是解题的关键.2.(2017秋•朝阳区期末)如图,PAD ∆为等边三角形,四边形ABCD 为正方形,平面PAD ⊥平面ABCD .若点M为平面ABCD 内的一个动点,且满足MP MC =,则点M 在正方形ABCD 及其内部的轨迹为( )A.椭圆的一部分B.双曲线的一部分C.一段圆弧D.一条线段【分析】在空间中,过线段PC中点,且垂直线段PC的平面上的点到P,C两点的距离相等,此平面与平面ABCD 相交,两平面有一条公共直线.【解答】解:在空间中,存在过线段PC中点且垂直线段PC的平面,平面上点到P,C两点的距离相等,记此平面为α平面α与平面ABCD有一个公共点,则它们有且只有一条过该点的公共直线.故点M在正方形ABCD及其内部的轨迹为一条线段.故选:D.【点评】本题是轨迹问题与空间线面关系相结合的题目,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.3.(2015秋•大兴区期末)若直线//⊥,则在平面α内到直线a和直线b距离相等的点的a平面α,直线bα⊂,a b轨迹是()A.圆B.抛物线C.椭圆D.双曲线【分析】设a到α距离为d,在α内的射影为c,则在α内以b为x轴,c为y轴建立坐标系.设(,)P x y,根据平面α内的动点P到b与到a的距离相等,即可得出.【解答】解:设a到α距离为d,在α内的射影为c,则在α内以b为x轴,c为y轴建立坐标系.设(,)P x y,则平面α内的动点P到b的距离与到a的距离相等,22∴=+||y x d222∴-=,y x d∴点P的轨迹是双曲线.故选:D.【点评】本题考查了双曲线的标准方程及其性质、两点之间的距离公式、空间线面位置关系,考查了推理能力,属于中档题.4.(2013秋•大兴区期末)工人师傅在如图1的一块矩形铁皮上画一条曲线,沿曲线剪开,将所得到的两部分卷成圆柱状,如图2,然后将其对接,可做成一个直角的“拐脖”,如图3.工人师傅所画的曲线是()A.一段圆弧B.一段抛物线C.一段双曲线D.一段正弦曲线【分析】利用平面图分析曲线的对称性,即可得出结论.【解答】解:将图2剪开展成平面图分析可知,曲线为轴对称图形,将图3剪开展成平面图分析可知,曲线也为中心对称图形.所以此曲线即为轴对称图形又为中心对称图形,故只有D正确.故选:D.【点评】本题考查平面与圆柱面的截线,考查函数的对称性和奇偶性,比较基础.二.填空题(共3小题)5.(2006秋•东城区期末)已知棱长等于2的正四面体的四个顶点在同一个球面上,则球的半径长为6,球的表面积为.【分析】将正四面体补成正方体,再将正方体放在一个球体中,利用它们之间的关系求解.【解答】解:如图,将正四面体补形成一个正方体,正四面体为2,∴2又球的直径是正方体的对角线,设球半径是R,2236R∴==6R∴=,球的表面积为6π.故填:62;6π. 【点评】巧妙构造正方体,利用正方体的外接球的直径为正方体的对角线,从而将问题巧妙转化.若已知正四面体V ABC -的棱长为a ,求外接球的半径,我们可以构造出一个球的内接正方体,再应用对角线长等于球的直径可求得.6.(2013秋•大兴区期末)工人师傅在如图1的一块矩形铁皮的中间画了一条曲线,并沿曲线剪开,将所得的两部分卷成圆柱状,如图2,然后将其对接,可做成一个直角的“拐脖”,如图3.对工人师傅所画的曲线,有如下说法:(1)是一段抛物线;(2)是一段双曲线;(3)是一段正弦曲线;(4)是一段余弦曲线;(5)是一段圆弧.则正确的说法序号是 ③④ .【分析】利用平面图分析曲线的对称性,即可得出结论.【解答】解:将图2剪开展成平面图分析可知,曲线为轴对称图形,将图3剪开展成平面图分析可知,曲线也为中心对称图形.所以此曲线即为轴对称图形又为中心对称图形,故只有③④正确.故答案为:③④.【点评】本题考查平面与圆柱面的截线,考查函数的对称性和奇偶性,比较基础.7.(2003•北京)如图,已知底面半径为r 的圆柱被一个平面所截,剩下部分母线长的最大值为a ,最小值为b ,那么圆柱被截后剩下部分的体积是 21()2r a b π+ .【分析】用补形法:两个相同的几何体,倒立一个,对应合缝,恰好形成一个圆柱体.求出总体积的一半即可.【解答】解:取两个相同的几何体,倒立一个,对应合缝,恰好形成一个圆柱体.所求几何体的体积:2211()()22r a b r a b ππ⨯⨯+=+故答案为:21()2r a b π+ 【点评】本题考查几何体的体积,考查转化思想,是基础题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E l1 A Q
O1 K1
B
G1
F1
P
F2
G2
D
O2
C
l2 F
K2
图7
大兴安岭实验中学 杨丽英
由切线长定理知G1F2 G1D, F2G2 G2C,
A E G1
O1
B
F1
F2 G2
D
F O2 C
图2
所以G1G2 G1D G2C. 连接F1O1, F2O2, 容易证明EF1O1 FF2O2.
所以EO1 FO2.又因为O1 A O2C,所以EA FC. 于是可证得FCG2 EAG1.所以G1 A G2C .
G2 E
将图3 中的两个圆拓广
为球面, 将矩形A B CD看成 是 A O1 B 圆柱面的轴截面 , 将 EB、DF G1 F1 K1
拓广为两个平面 、 , EF 拓
广为平面 ,得到图4.显然,平 面与圆柱面的截线是椭圆 .根 D
据上面的结论, 你能猜想这个
P F2
O2
G2 C
K2
椭圆的两个焦点的位置吗 ?
所以G1G2 G1D G1 A AD.
在RtG2EB中, cos G2B
G2 E
A E G1
O1
B
F1
G2F1 ,即G2F1 G2E cos
G2 E
F2 G2
D
F O2 C
又因为 900 ,
所以G2F1 G2E cos G2E sin.
图3
由此得到结论:
1G2F1 G2F2 AD; 2G1G2 AD ; 3 G2F1 cos sin .
则PK 、PK 分别是两球面的切线 ,ห้องสมุดไป่ตู้切点为
1
2
K 、K .根据切线长定理的空间 推广, 知
1
2
PF PK , PF PK ,
1
1
2
2
所以PF PF PK PK AD.
1
2
1
2
由于AD为定值, 故点P的轨迹是椭圆.
A
O1
B
G1 F1
K1
P F2
D
O2
G2 C
K2
图6
我们知道椭圆存在 离心率和准线,你 能结合图7估计椭 圆的准线是那两条 吗?
图1
1 G2 F1 G2 F2与AD有什么关系? 相等
2 AD的长与G1G2的长有什么关系? 相等
3 G F 与G E有什么关系?
21
2
G2F1 cos sin .
G2 E
由图 2, 根据切线长定理有 G2F1 G2B, G2F2 G2C, 所以G2F1 G2F2 G2B G2C BC AD. 又因为G1G2 G1F2 F2G2 ,
图4
我们猜想, 两个焦点可能在
两个球与斜截 面的切点上, 即过球心 O1、O2 分别作斜 截面的垂线,其垂足 F1、F2 就可能是焦点.为此, 我们需 要证明: 对于截口上任意一 点P,有PF1 PF2 定值.
A
O1
B
G1 F1
K1
P F2
D
O2
G2 C
K2
探究 如图5,当点P与G2
重合时,可以得到什么结论 ?
图5
当点P在其他位置时, 还有这个结论吗 ?
由于图5 就是图6 经过母线 AD、
BC的轴截面,由前面已有的结论 ,当点
P与G 重合时, 有G F G F AD.
2
21
22
当点P不在端点时, 连接PF、PF ,则PF、
1
2
1
PF 分别是两个球的切线 2
,
切点为
F、F
1
2
.
过P作母线, 与两球面分别相交于 K 、K , 2 1
大兴安岭实验中学 杨丽英
探究 : 如图1, AB、CD是
两个等圆的直径 AB // CD ,
A E G1
O1
B
AD、BC与两圆相切.作两圆的公切线EF, F1
切点分别为F 、F , 交BA、DC的延长线于
F2
G2
12
D
E、F , 交 AD于G , 交 BC于G .设EF与BC
F O2 C
1
2
、CD的交角分别为、 .
