武汉理工matlab作业
武汉理工大学-计算机仿真实验作业答案

五、(10分)已知系统的传递函数为6168682)(232+++++=s s s s s s G 。
语言建立系统传递函数模型,并求:⑴ 该系统的单位阶跃响应;(2分)⑵ 输入函数为u(t)时的响应;(3分)(u(t)正弦信号,周期2秒,仿真时间8秒,采样周期0.1);(3) 输入函数为u(t)时的响应;(3分)(u(t)方波输入信号,周期10秒,仿真时间20秒,采样周期0.05)(4) 绘出系统的波德图(Bode )。
(2分)解答:num=[2 8 6];den=[1 8 16 6];sys=tf(num,den);t=0:0.1:8;y1=step(sys,t);u=sin(t*pi);y2=lsim(sys,u,t);subplot(2,2,1);plot(t,y1);grid;title('阶跃响应曲线');xlabel('响应时间');ylabel('响应值');hold on;subplot(2,2,2);plot(t,y2);grid on ;title('对sin(t)的响应曲线');xlabel('响应时间');ylabel('响应值');t=0:0.05:20u=square(pi/5*t)y3=lsim(sys,u,t);subplot(2,2,3);plot(t,y3)grid on ;title('对方波信号的响应曲线');xlabel('响应时间');ylabel('响应值');subplot(2,2,4);bode(sys);grid ;title('bode 图');运行结果:六、(10分)设二阶动力学系统的传递函数如下,假设将无阻尼固有频率固定为ωn =1 rad/s ,将阻尼比的值分别设置成ζ=0,0.1,0.2,0.3,…,MATLAB 语言编程,分析在这些阻尼比ζ的取值下该系统的阶跃响应。
matlab大作业实验报告,《Matlab程序设计》期末实验报告-大作业2015.doc

matlab⼤作业实验报告,《Matlab程序设计》期末实验报告-⼤作业2015.doc《MATLAB程序设计》实验报告学院: 学号: 姓名:⼀、题⽬:1、(10分)已知矩阵,⽤Matlab代码实现以下要求:(1)将矩阵赋给变量A,并在屏幕上显⽰A;(2)将A按列进列逆序重排,重排后的矩阵赋给变量B,并在屏幕上显⽰B;(3)⽤reshape命令将A重排为⼀个2⾏6列矩阵并赋给变量C;(4)将A重排为⼀个列向量,将其赋给变量D,求D的平均值,在屏幕上显⽰D和它的平均值;(5)⽤命令查看变量A的维数,并显⽰运⾏结果。
2、(10分)写代码实现以下要求:构造菜单项‘Plot’,菜单项Plot有两个⼦菜单项Plot sin(选择此项后执⾏画出曲线,线型为虚线,线条颜⾊为红⾊)和Plot cos(选择此项后执⾏画出曲线 ,线型为实线,线条宽度为2)。
3、(20分)已知,实现下列操作:(1)在同⼀个图形窗⼝,同⼀坐标系下⽤不同的颜⾊和线型绘制三条曲线,并添加图例来区分三条曲线(5分)。
(2)⽤subplot命令,以⼦图的⽅式绘制三条曲线,图形排列⽅式为三⾏⼀列(5分)。
(3) 分别⽤直⽅图(bar)、棒状图(stem)和填充图(fill)绘制三条曲线,以⼦图⽅式绘制,排列⽅式为3⾏3列,共9幅⼦图(10分)。
4、(10分)⽤surf命令绘制曲⾯图形,⽤shading interp命令进⾏插值着⾊处理并添加垂直颜⾊棒。
5、(15分)⾃2011年9⽉1⽇起,我国实⾏新的个⼈所得税征收办法,起征点为3500元,请⽤If-else if-else-end结构实现⼈⼯输⼊⽉收⼊后能计算出个⼈所得税的缴纳额并显⽰⽉收⼊10000元时应缴纳的税款。
级数应纳税所得额x(元)税率备注1x<=15003%x指⽉收⼊扣除起征点3500元之后的余额;215008000045%同上6. (10分)⽤while-end循环结构计算级数和的值,输⼊n值,能计算出f的值,并显⽰结果。
武汉理工大学电路MATLAB仿真基础强化训练报告
训练目的:1.掌握Matlab基本语法结构及调试方法;2.熟悉Matlab函数调用,熟练其用于电工电子的一些计算;3.学会用Matlab/Simulink进行简单电路的仿真。
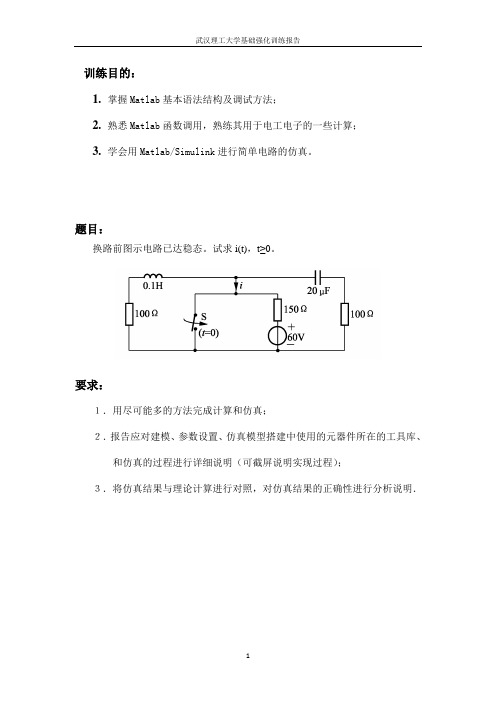
题目:换路前图示电路已达稳态。
试求i(t),t≥0。
要求:1.用尽可能多的方法完成计算和仿真;2.报告应对建模、参数设置、仿真模型搭建中使用的元器件所在的工具库、和仿真的过程进行详细说明(可截屏说明实现过程);3.将仿真结果与理论计算进行对照,对仿真结果的正确性进行分析说明.目录摘要 2 1.电路模型求解 3 1.1 初始值的求解 3 1.2 利用微分方程求解 31.3 利用拉普拉斯求解 42. 利用MATLAB计算和仿真 5 2.1 用微分方程设计程序 5 2.2 用微分方程建立仿真模型 62.3 用拉普拉斯变换设计程序 93.仿真结果与理论值的比较 104.总结与体会 115.参考文献 11摘要本次基础强化训练的问题是求一电路的零输入响应,并且通过matlab的编程计算或matlab的simulink工具箱进行仿真.我先通过基础电路当中所学的电路知识,通过两种方法进行求解:一种方法是通过微分方程求解,另一种方法是通过拉普拉斯变换及其逆变换,得到相应的零输入响应.求解电路完之后,我再利用matlab编程和matlab中的simulink工具箱进行仿真,仿真中也采用三种方法进行仿真:一种是利用微分方程设计程序计算,一种是利用微分方程进行simulink 仿真,另一种是利用拉普拉斯变换设计程序计算,得到仿真图形,与实际理论值进行比较。
关键字:simulink工具箱;微分方程;拉普拉斯变换基础强化训练论文1.电路模型求解:试求下图电路的零输入响应i(t),t≥0。
1.1初始值的求解图 1-1由图1-1,用KVL 定律,易求得 (0)(0)24c c u u V+-== 11(0)(0)0.24i i A+-==-1.2利用微分方程求解图1-2 KVL 电压与电流定律图形由KVL 电压定律,得到如下表达式:1110di L R di dt += .....................( 1 )20c c du R C u dt += ...................... ( 2 )又由于22c u R i = 代入2式得2220di R Ci dt += ...................... ( 3 )初始值:1(0)0.24i A+=- ...................... ( 4 )22(0)24(0)0.24100c u i A R ++=== .................... ( 5 )代入数值到1式和3式得到:111000di i dt =- ...................... ( 6 )22500di i dt =- ..................... ( 7 )分析电路易知:12i i i =+ .................... ( 8 )做到这一步之后,我已经基本解决了该问题,剩下的是通过高等数学的微分方程知识来求解该微分方程:从而解得微分方程得到:5001000()0.240.24t ti t e e --=- (t≥0)1.2 利用拉普拉斯变换来求解该模型:在电路中我们学习过利用拉普拉斯来求解电路响应,首先要将电路转化为拉普拉斯变换的形式,再通过相应的电路定律来求解电路.我通过电路转化,得到如下的拉普拉斯电路形式:图1-3 拉普拉斯变换电路图形同理,我利用KVL 电压定律有得到下面的拉普拉斯方程:111()(0)()0s L I s L i R Is --+= ..........................( 9 )222(0)1()()0u I s R I s sC s -++= ...........................( 10 )12()()()I s I s I s =- .........................( 11 )解得 ,66()25250002512500I s s s -=+++ ...........................( 12 )得到所需求响应的拉普拉斯形式之后,再利用拉普拉斯逆变换来求得响应的时间域响应形式,得到下面的表达式:5001000()0.240.24t ti t e e --=- (t≥0)2.电路仿真:2.1利用微分方程设计程序搭建微分方程: 111000di i dt =-22500dii dt =-12i i i =+M 程序为: i1=dsolve('Di1=-1000*i1','i1(0)=-0.24');i2=dsolve('Di2=-500*i2','i2(0)=0.24'); i0=char(i1+i2);ezplot(i0,[0,0.01])得到仿真图像为:图2-12.2利用微分方程搭建电路仿真模型有:搭建微分方程:111000 dii dt=-22500diidt=-12i i i=+图2-2 微分方程模型图Gain的参数设置为:图2-3Gain1的参数设置为:图2-4 Gain1参数设置图Step1和Step2的参数设置均为:图2-5 step参数设置图通过上面的参数设置之后,我得到了关于时间t与i(t)的图像,下面就是仿真图像:图2-6 i(t)仿真图形2.3利用拉普拉斯变换设计程序:拉普拉斯变换得到的最后结果为:2120()1500500000I s s s =++M 程序为: syms s; b=[120];a=[1,1500,500000];is=poly2sym(b,s)/poly2sym(a,s); it=ilaplace(is); ezplot(it,[0,0.01])得到图像为:图2-73.仿真结果与理论值的比较:通过1中的理论计算和2中的仿真运用,我们可以看到仿真结果与理论计算比较吻合,能够很好的反应出理论值,因此我可以认为仿真结果是正确的.不过,仿真的缺点是不能到达时间为无穷远处,只能仿真出在有限时间内的图形.同时为了能够更好的得到仿真结果与理论值的比较,我根据所求得的理论表达式得到理论图形如图2-1和图2-7。
MATLAB作业

MATLAB作业⼀、必答题:1. MATLAB系统由那些部分组成?答:MATLAB系统主要由开发环境、MATLAB语⾔、MATLAB数学函数库、图形功能和应⽤程序接⼝五个部分组成。
2. 如何启动M⽂件编辑/调试器?答:在操作界⾯上选择“建⽴新⽂件”或“打开⽂件”操作时,M⽂件编辑/调试器将被启动。
在命令窗⼝中键⼊“edit”命令也可以启动M⽂件编辑/调试器。
3. 存储在⼯作空间中的数组能编辑吗?如何操作?答:存储在⼯作空间的数组可以通过数组编辑器进⾏编辑:在⼯作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输⼊修改内容即可。
4. 在MATLAB中有⼏种获得帮助的途径?答:在MATLAB中有多种获得帮助的途径:(1)帮助浏览器:选择view菜单中的Help菜单项或选择Help菜单中的MATLAB Help菜单项可以打开帮助浏览器;(2)help命令:在命令窗⼝键⼊“help” 命令可以列出帮助主题,键⼊“help 函数名”可以得到指定函数的在线帮助信息;(3)lookfor命令:在命令窗⼝键⼊“lookfor 关键词”可以搜索出⼀系列与给定关键词相关的命令和函数(4)模糊查询:输⼊命令的前⼏个字母,然后按Tab键,就可以列出所有以这⼏个字母开始的命令和函数。
5. 有⼏种建⽴矩阵的⽅法?各有什么优点?答:(1)以直接列出元素的形式输⼊;(2)通过语句和函数产⽣;(3).在m⽂件中创建矩阵;(4)从外部的数据⽂件中装⼊。
6. 命令⽂件与函数⽂件的主要区别是什么?答:命令⽂件: M⽂件中最简单的⼀种,不需输出输⼊参数,⽤M ⽂件可以控制⼯作空间的所有数据。
运⾏过程中产⽣的变量都是全局变量。
运⾏⼀个命令⽂件等价于从命令窗⼝中顺序运⾏⽂件⾥的命令,程序不需要预先定义,只要依次将命令编辑在命令⽂件中即可。
函数⽂件:如果M⽂件的第⼀个可执⾏⾏以function开始,便是函数⽂件,每⼀个函数⽂件定义⼀个函数。
汽车理论课后习题MATLAB编程-武汉理工版

汽车理论课后习题MATLAB编程1.3 确定一轻型货车的动力性能(货车可装用4挡或5挡变速器,任选其中的一种进行整车性能计算):1)绘制汽车驱动力与行驶阻力平衡图。
2)求汽车最高车速,最大爬坡度及克服该坡度时相应的附着率。
3)绘制汽车行驶加速度倒数曲线,用图解积分法求汽车用2档起步加速行驶至70km/h的车速-时间曲线,或者用计算机求汽车用2档起步加速行驶至70km/h的加速时间。
解:(1) 求汽车驱动力与行驶阻力平衡图和汽车最高车速:n=[600:10:4000];Tq=-19.313+295.27*(n/1000)-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/10 00).^4;m=3880;g=9.8;nmin=600;nmax=4000;G=m*g;ig=[5.56 2.769 1.644 1.00 0.793];nT=0.85;r=0.367;f=0.013;CDA=2.77;i0=5.83;L=3.2;a=1.947;hg=0.9;If=0.218;Iw1=1.798;Iw2=3.598;Ft1=Tq*ig(1)*i0*nT/r;Ft2=Tq*ig(2)*i0*nT/r;Ft3=Tq*ig(3)*i0*nT/r;Ft4=Tq*ig(4)*i0*nT/r;Ft5=Tq*ig(5)*i0*nT/r;ua1=0.377*r*n/ig(1)/i0;ua2=0.377*r*n/ig(2)/i0;ua3=0.377*r*n/ig(3)/i0;ua4=0.377*r*n/ig(4)/i0;ua5=0.377*r*n/ig(5)/i0;ua=[0:5:120];Ff=G*f;Fw=CDA*ua.^2/21.15;Fz=Ff+Fw;plot(ua1,Ft1,ua2,Ft2,ua3,Ft3,ua4,Ft4,ua5,Ft5,ua,Fz);title('驱动力-行驶阻力平衡图');xlabel('ua(km/s)');ylabel('Ft(N)');gtext('Ft1'),gtext('Ft2'),gtext('Ft3'),gtext('Ft4'),gtext('Ft5'),gtext('Ff+Fw');zoom on;[x,y]=ginput(1);zoom off;disp('汽车最高车速=');disp(x);disp('km/h');汽车最高车速=99.3006km/h(2)求汽车最大爬坡度程序:n=[600:10:4000];Tq=-19.313+295.27*(n/1000)-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/10 00).^4;m=3880;g=9.8;nmin=600;nmax=4000;G=m*g;ig=[5.56 2.769 1.644 1.00 0.793];nT=0.85;r=0.367;f=0.013;CDA=2.77;i0=5.83;L=3.2;a=1.947;hg=0.9;If=0.218;Iw1=1.798;Iw2=3.598;Ft1=Tq*ig(1)*i0*nT/r;ua1=0.377*r*n/ig(1)/i0;Ff=G*f;Fw1=CDA*ua1.^2/21.15;Fz1=Ff+Fw1;Fi1=Ft1-Fz1;Zoom on;imax=100*tan(asin(max(Fi1/G)));disp('汽车最大爬坡度=');disp(imax);disp('%');汽车最大爬坡度=35.2197%(3)求最大爬坡度相应的附着率和求汽车行驶加速度倒数曲线程序:clearn=[600:10:4000];Tq=-19.313+295.27*(n/1000)-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/10 00).^4;m=3880;g=9.8;nmin=600;nmax=4000;G=m*g;ig=[5.56 2.769 1.644 1.00 0.793];nT=0.85;r=0.367;f=0.013;CDA=2.77;i0=5.83;L=3.2;a=1.947;hg=0.9;If=0.218;Iw1=1.798;Iw2=3.598;Ft1=Tq*ig(1)*i0*nT/r;Ft2=Tq*ig(2)*i0*nT/r;Ft3=Tq*ig(3)*i0*nT/r;Ft4=Tq*ig(4)*i0*nT/r;Ft5=Tq*ig(5)*i0*nT/r;ua1=0.377*r*n/ig(1)/i0;ua2=0.377*r*n/ig(2)/i0;ua3=0.377*r*n/ig(3)/i0;ua4=0.377*r*n/ig(4)/i0;ua5=0.377*r*n/ig(5)/i0;Fw1=CDA*ua1.^2/21.15;Fw2=CDA*ua2.^2/21.15;Fw3=CDA*ua3.^2/21.15;Fw4=CDA*ua4.^2/21.15;Fw5=CDA*ua5.^2/21.15;Ff=G*f;deta1=1+(Iw1+Iw2)/(m*r^2)+(If*ig(1)^2*i0^2*nT)/(m*r^2);deta2=1+(Iw1+Iw2)/(m*r^2)+(If*ig(2)^2*i0^2*nT)/(m*r^2);deta3=1+(Iw1+Iw2)/(m*r^2)+(If*ig(3)^2*i0^2*nT)/(m*r^2);deta4=1+(Iw1+Iw2)/(m*r^2)+(If*ig(4)^2*i0^2*nT)/(m*r^2);deta5=1+(Iw1+Iw2)/(m*r^2)+(If*ig(5)^2*i0^2*nT)/(m*r^2);a1=(Ft1-Ff-Fw1)/(deta1*m);ad1=1./a1;a2=(Ft2-Ff-Fw2)/(deta2*m);ad2=1./a2;a3=(Ft3-Ff-Fw3)/(deta3*m);ad3=1./a3;a4=(Ft4-Ff-Fw4)/(deta4*m);ad4=1./a4;a5=(Ft5-Ff-Fw5)/(deta5*m);ad5=1./a5;plot(ua1,ad1,ua2,ad2,ua3,ad3,ua4,ad4,ua5,ad5);axis([0 99 0 10]);title('汽车的加速度倒数曲线');xlabel('ua(km/h)');ylabel('1/a');gtext('1/a1');gtext('1/a2');gtext('1/a3');gtext('1/a4');gtext('1/a5');a=max(a1);af=asin(max(Ft1-Ff-Fw1)/G);C=tan(af)/(a/L+hg*tan(af)/L);disp('假设后轮驱动,最大爬坡度相应的附着率=');disp(C);假设后轮驱动,最大爬坡度相应的附着率=0.4219(4) >>clearnT=0.85;r=0.367;f=0.013;CDA=2.77;i0=5.83;If=0.218;Iw1=1.798;Iw2=3.598;L=3.2;a=1.947;hg=0.9;m=3880;g=9.8;G=m*g; ig=[5.56 2.769 1.644 1.00 0.793];nmin=600;nmax=4000;u1=0.377*r*nmin./ig/i0;u2=0.377*r*nmax./ig/i0;deta=0*ig;for i=1:5deta(i)=1+(Iw1+Iw2)/(m*r^2)+(If*(ig(i))^2*i0^2*nT)/(m*r^2);endua=[6:0.01:99];N=length(ua);n=0;Tq=0;Ft=0;inv_a=0*ua;delta=0*ua;Ff=G*f;Fw=CDA*ua.^2/21.15;for i=1:Nk=i;if ua(i)<=u2(2)n=ua(i)*(ig(2)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000)^2+40.874*(n/1000)^3-3.8445*(n/100 0)^4;Ft=Tq*ig(2)*i0*nT/r;inv_a(i)=(deta(2)*m)/(Ft-Ff-Fw(i));delta(i)=0.01*inv_a(i)/3.6;elseif ua(i)<=u2(3)n=ua(i)*(ig(3)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000)^2+40.874*(n/1000)^3-3.8445*(n/100 0)^4;Ft=Tq*ig(3)*i0*nT/r;inv_a(i)=(deta(3)*m)/(Ft-Ff-Fw(i));delta(i)=0.01*inv_a(i)/3.6;elseif ua(i)<=u2(4)n=ua(i)*(ig(4)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000)^2+40.874*(n/1000)^3-3.8445*(n/100 0)^4;Ft=Tq*ig(4)*i0*nT/r;inv_a(i)=(deta(4)*m)/(Ft-Ff-Fw(i));delta(i)=0.01*inv_a(i)/3.6;elsen=ua(i)*(ig(5)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000)^2+40.874*(n/1000)^3-3.8445*(n/100 0)^4;Ft=Tq*ig(5)*i0*nT/r;inv_a(i)=(deta(5)*m)/(Ft-Ff-Fw(i));delta(i)=0.01*inv_a(i)/3.6;enda=delta(1:k);t(i)=sum(a);endplot(t,ua);axis([0 80 0 100]);title('汽车2档原地起步换挡加速时间曲线');xlabel('时间t(s)');ylabel('速度ua(km/h)');>> ginputans =25.8223 70.073725.7467 70.0737所以汽车2档原地起步换挡加速行驶至70km/h的加速时间约为25.8s2.7已知货车装用汽油发动机的负荷特性与万有特性。
武汉理工matlab实验报告

学生实验报告书实验课程名称数学软件与数学实验开课学院指导教师姓名学生姓名学生专业班级2012-- 2013学年第二学期实验教学管理基本规范实验是培养学生动手能力、分析解决问题能力的重要环节;实验报告是反映实验教学水平与质量的重要依据。
为加强实验过程管理,改革实验成绩考核方法,改善实验教学效果,提高学生质量,特制定实验教学管理基本规范。
1、本规范适用于理工科类专业实验课程,文、经、管、计算机类实验课程可根据具体情况参照执行或暂不执行。
2、每门实验课程一般会包括许多实验项目,除非常简单的验证演示性实验项目可以不写实验报告外,其他实验项目均应按本格式完成实验报告。
3、实验报告应由实验预习、实验过程、结果分析三大部分组成。
每部分均在实验成绩中占一定比例。
各部分成绩的观测点、考核目标、所占比例可参考附表执行。
各专业也可以根据具体情况,调整考核内容和评分标准。
4、学生必须在完成实验预习内容的前提下进行实验。
教师要在实验过程中抽查学生预习情况,在学生离开实验室前,检查学生实验操作和记录情况,并在实验报告第二部分教师签字栏签名,以确保实验记录的真实性。
5、教师应及时评阅学生的实验报告并给出各实验项目成绩,完整保存实验报告。
在完成所有实验项目后,教师应按学生姓名将批改好的各实验项目实验报告装订成册,构成该实验课程总报告,按班级交课程承担单位(实验中心或实验室)保管存档。
6、实验课程成绩按其类型采取百分制或优、良、中、及格和不及格五级评定。
实验课程名称:《数学软件与数学实验》4.根据网址为/military/html/784/index.html。
武汉理工大学过程仿真与建模作业

实验一 面向方程的数值积分方法仿真一 、实验目的:加深理解四阶龙格---库塔法的原理及其稳定性二、 实验内容 对下列系统进行仿真 A . 线性定常系统'24(0)1u μμ=-⎧⎨=⎩ (01)t <≤B . 非线性系统()()()()()()()()dx t rx t ax t y t dtdy t sy t bx t y t dt⎧=-⎪⎪⎨⎪=-+⎪⎩其中:1. r=0.001,a=2*104, s=0.015, b=10-4; x(0)=1200, y(0)=6002. r=0.001,a=2*10-6, s=0.01, b=10-6; x(0)=12000, y(0)=6000三、实验要求:1. 为保证稳定性,分析系统(1)的最大仿真步长(方法自选)2. 设计MatLab 、Fortran 或C 程序,用四阶龙格---库塔法进行仿真计算,改变参数及仿真步长,观察实验结果,寻找最合宜的仿真步长和临界仿真步长;四、实验报告1. 实验所用程序清单2. 实验结果及分析1.分析系统A 的最大仿真步长,寻找临界仿真步长1.1四阶阶龙格—库塔的稳定性四阶龙格—库塔格式为:11234(22)6n n hu u K K K K +=++++ 其中1(,)n n K f t u = 2112(,)2n n hK f tu K +=+ 3122(,)2n n hK f tu K +=+ 413(,)n n K f t u hK +=+ 由于'24u u =-,则有2233411(63)64n n n h u u h h h u λλλλ+=++++为保证龙格—库塔的稳定性,则有1n n u u +≤,从而可以得223341(63)64n n n h u h h h u u λλλλ++++≤1.2通过编程求最大稳定步长clear allsyms K1 K2 K3 K4 y h y1=-24*y;y1=inline(y1); K1=y1(y);K2=y1(y+1/2*K1*h); K3=y1(y+1/2*K2*h); K4=y1(y+h*K3);R1=K1+2*K2+2*K3+K4; R11=inline(R1); R=solve(R1,'h'); R=eval(R); p=R==real(R); R=R(p);fprintf('保证稳定性的最大仿真步长为%0.5f\n',R) 结果显示为:1.3改变参数及仿真步长,观察实验结果MATLAB编写程序作图以步长h=0.025为例:clear allsyms K1K2K3K4y hy1=-24*y;y1=inline(y1);K1=y1(y);K2=y1(y+1/2*K1*h);K3=y1(y+1/2*K2*h);K4=y1(y+h*K3);R1=K1+2*K2+2*K3+K4;R11=inline(R1);h=0.025f=1;for ii=1:10t=0.1*ii;tt(ii)=t;n=(t-0)/h;for i=1:nf=f+1/6*h*R11(h,f) ;endff(ii)=f;endplot(tt,ff,'o-')hold ona=legend('步长h为0.025',1)xlabel('t')ylabel('u')1.31寻找临界步长分别取步长h为0.025、0.05、0.075、0.01、0.0125,用MATLAB作出图像0.10.20.30.40.50.60.70.80.9100.010.020.030.040.050.060.070.080.090.1t u步长h 为0.025图1,步长h 为0.025时,u 的值0.10.20.30.40.50.60.70.80.9100.020.040.060.080.10.12tu步长h 为0.05图2,步长h 为0.05时,u 的值0.10.20.30.40.50.60.70.80.9100.050.10.150.20.250.30.35tu步长h 为0.075图3,步长h 为0.075时,u 的值0.10.20.30.40.50.60.70.80.9100.10.20.30.40.50.60.7tu步长h 为0.1图4,步长h 为0.1时,u 的值0.10.20.30.40.50.60.70.80.9100.511.522.533.5x 105tu步长h 为0.125图5,步长h 为0.125时,u 的值由图1-5可知,临界步长在0.1~0.125之间 为了方便分析,计算A 方程的真实值,并作图 clear all t=0.1:0.1:1 u=exp(-24*t) plot(t,u,'o-') legend('真实值',1) xlabel('t') ylabel('u') 运行得到图6:0.10.20.30.40.50.60.70.80.9100.010.020.030.040.050.060.070.080.090.1t u真实值图6,u 的真实值在0.1~0.125附近步长,得到图7如下:图7 比较真实值和0.1附近步长可以得出结论,最合适仿真步长如果太大,结果不精确。
汽车理论课后习题MATLAB编程-武汉理工版

汽车理论课后习题MATLAB编程1.3 确定一轻型货车的动力性能(货车可装用4挡或5挡变速器,任选其中的一种进行整车性能计算):1)绘制汽车驱动力与行驶阻力平衡图。
2)求汽车最高车速,最大爬坡度及克服该坡度时相应的附着率。
3)绘制汽车行驶加速度倒数曲线,用图解积分法求汽车用2档起步加速行驶至70km/h的车速-时间曲线,或者用计算机求汽车用2档起步加速行驶至70km/h的加速时间。
解:(1) 求汽车驱动力与行驶阻力平衡图和汽车最高车速:n=[600:10:4000];Tq=-19.313+295.27*(n/1000)-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/10 00).^4;m=3880;g=9.8;nmin=600;nmax=4000;G=m*g;ig=[5.56 2.769 1.644 1.00 0.793];nT=0.85;r=0.367;f=0.013;CDA=2.77;i0=5.83;L=3.2;a=1.947;hg=0.9;If=0.218;Iw1=1.798;Iw2=3.598;Ft1=Tq*ig(1)*i0*nT/r;Ft2=Tq*ig(2)*i0*nT/r;Ft3=Tq*ig(3)*i0*nT/r;Ft4=Tq*ig(4)*i0*nT/r;Ft5=Tq*ig(5)*i0*nT/r;ua1=0.377*r*n/ig(1)/i0;ua2=0.377*r*n/ig(2)/i0;ua3=0.377*r*n/ig(3)/i0;ua4=0.377*r*n/ig(4)/i0;ua5=0.377*r*n/ig(5)/i0;ua=[0:5:120];Ff=G*f;Fw=CDA*ua.^2/21.15;Fz=Ff+Fw;plot(ua1,Ft1,ua2,Ft2,ua3,Ft3,ua4,Ft4,ua5,Ft5,ua,Fz);title('驱动力-行驶阻力平衡图');xlabel('ua(km/s)');ylabel('Ft(N)');gtext('Ft1'),gtext('Ft2'),gtext('Ft3'),gtext('Ft4'),gtext('Ft5'),gtext('Ff+Fw');zoom on;[x,y]=ginput(1);zoom off;disp('汽车最高车速=');disp(x);disp('km/h');汽车最高车速=99.3006km/h(2)求汽车最大爬坡度程序:n=[600:10:4000];Tq=-19.313+295.27*(n/1000)-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/10 00).^4;m=3880;g=9.8;nmin=600;nmax=4000;G=m*g;ig=[5.56 2.769 1.644 1.00 0.793];nT=0.85;r=0.367;f=0.013;CDA=2.77;i0=5.83;L=3.2;a=1.947;hg=0.9;If=0.218;Iw1=1.798;Iw2=3.598;Ft1=Tq*ig(1)*i0*nT/r;ua1=0.377*r*n/ig(1)/i0;Ff=G*f;Fw1=CDA*ua1.^2/21.15;Fz1=Ff+Fw1;Fi1=Ft1-Fz1;Zoom on;imax=100*tan(asin(max(Fi1/G)));disp('汽车最大爬坡度=');disp(imax);disp('%');汽车最大爬坡度=35.2197%(3)求最大爬坡度相应的附着率和求汽车行驶加速度倒数曲线程序:clearn=[600:10:4000];Tq=-19.313+295.27*(n/1000)-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/10 00).^4;m=3880;g=9.8;nmin=600;nmax=4000;G=m*g;ig=[5.56 2.769 1.644 1.00 0.793];nT=0.85;r=0.367;f=0.013;CDA=2.77;i0=5.83;L=3.2;a=1.947;hg=0.9;If=0.218;Iw1=1.798;Iw2=3.598;Ft1=Tq*ig(1)*i0*nT/r;Ft2=Tq*ig(2)*i0*nT/r;Ft3=Tq*ig(3)*i0*nT/r;Ft4=Tq*ig(4)*i0*nT/r;Ft5=Tq*ig(5)*i0*nT/r;ua1=0.377*r*n/ig(1)/i0;ua2=0.377*r*n/ig(2)/i0;ua3=0.377*r*n/ig(3)/i0;ua4=0.377*r*n/ig(4)/i0;ua5=0.377*r*n/ig(5)/i0;Fw1=CDA*ua1.^2/21.15;Fw2=CDA*ua2.^2/21.15;Fw3=CDA*ua3.^2/21.15;Fw4=CDA*ua4.^2/21.15;Fw5=CDA*ua5.^2/21.15;Ff=G*f;deta1=1+(Iw1+Iw2)/(m*r^2)+(If*ig(1)^2*i0^2*nT)/(m*r^2);deta2=1+(Iw1+Iw2)/(m*r^2)+(If*ig(2)^2*i0^2*nT)/(m*r^2);deta3=1+(Iw1+Iw2)/(m*r^2)+(If*ig(3)^2*i0^2*nT)/(m*r^2);deta4=1+(Iw1+Iw2)/(m*r^2)+(If*ig(4)^2*i0^2*nT)/(m*r^2);deta5=1+(Iw1+Iw2)/(m*r^2)+(If*ig(5)^2*i0^2*nT)/(m*r^2);a1=(Ft1-Ff-Fw1)/(deta1*m);ad1=1./a1;a2=(Ft2-Ff-Fw2)/(deta2*m);ad2=1./a2;a3=(Ft3-Ff-Fw3)/(deta3*m);ad3=1./a3;a4=(Ft4-Ff-Fw4)/(deta4*m);ad4=1./a4;a5=(Ft5-Ff-Fw5)/(deta5*m);ad5=1./a5;plot(ua1,ad1,ua2,ad2,ua3,ad3,ua4,ad4,ua5,ad5);axis([0 99 0 10]);title('汽车的加速度倒数曲线');xlabel('ua(km/h)');ylabel('1/a');gtext('1/a1');gtext('1/a2');gtext('1/a3');gtext('1/a4');gtext('1/a5');a=max(a1);af=asin(max(Ft1-Ff-Fw1)/G);C=tan(af)/(a/L+hg*tan(af)/L);disp('假设后轮驱动,最大爬坡度相应的附着率=');disp(C);假设后轮驱动,最大爬坡度相应的附着率=0.4219(4) >>clearnT=0.85;r=0.367;f=0.013;CDA=2.77;i0=5.83;If=0.218;Iw1=1.798;Iw2=3.598;L=3.2;a=1.947;hg=0.9;m=3880;g=9.8;G=m*g; ig=[5.56 2.769 1.644 1.00 0.793];nmin=600;nmax=4000;u1=0.377*r*nmin./ig/i0;u2=0.377*r*nmax./ig/i0;deta=0*ig;for i=1:5deta(i)=1+(Iw1+Iw2)/(m*r^2)+(If*(ig(i))^2*i0^2*nT)/(m*r^2);endua=[6:0.01:99];N=length(ua);n=0;Tq=0;Ft=0;inv_a=0*ua;delta=0*ua;Ff=G*f;Fw=CDA*ua.^2/21.15;for i=1:Nk=i;if ua(i)<=u2(2)n=ua(i)*(ig(2)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000)^2+40.874*(n/1000)^3-3.8445*(n/100 0)^4;Ft=Tq*ig(2)*i0*nT/r;inv_a(i)=(deta(2)*m)/(Ft-Ff-Fw(i));delta(i)=0.01*inv_a(i)/3.6;elseif ua(i)<=u2(3)n=ua(i)*(ig(3)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000)^2+40.874*(n/1000)^3-3.8445*(n/100 0)^4;Ft=Tq*ig(3)*i0*nT/r;inv_a(i)=(deta(3)*m)/(Ft-Ff-Fw(i));delta(i)=0.01*inv_a(i)/3.6;elseif ua(i)<=u2(4)n=ua(i)*(ig(4)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000)^2+40.874*(n/1000)^3-3.8445*(n/100 0)^4;Ft=Tq*ig(4)*i0*nT/r;inv_a(i)=(deta(4)*m)/(Ft-Ff-Fw(i));delta(i)=0.01*inv_a(i)/3.6;elsen=ua(i)*(ig(5)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000)^2+40.874*(n/1000)^3-3.8445*(n/100 0)^4;Ft=Tq*ig(5)*i0*nT/r;inv_a(i)=(deta(5)*m)/(Ft-Ff-Fw(i));delta(i)=0.01*inv_a(i)/3.6;enda=delta(1:k);t(i)=sum(a);endplot(t,ua);axis([0 80 0 100]);title('汽车2档原地起步换挡加速时间曲线');xlabel('时间t(s)');ylabel('速度ua(km/h)');>> ginputans =25.8223 70.073725.7467 70.0737所以汽车2档原地起步换挡加速行驶至70km/h的加速时间约为25.8s2.7已知货车装用汽油发动机的负荷特性与万有特性。
武汉理工大学matlab课设

武汉理工大学《Matlab应用课程设计》课程设计说明书课程设计任务书学生姓名:李立专业班级:电信1005班指导教师:祝立华阙大顺工作单位:信息工程学院题目:MATLAB运算与应用设计5初始条件:1.MATLAB6.5以上版本软件;2.课程设计辅导资料:“MATLAB语言基础及使用入门”、“MATLAB及在电子信息课程中的应用”等;3.先修课程:信号与系统、数字信号处理、MATLAB应用实践及信号处理类课程等。
要求完成的主要任务:(包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)1.课程设计时间:1周;2.课程设计内容:根据指导老师给定的7套题目,按规定选择其中1套完成;3.本课程设计统一技术要求:研读辅导资料对应章节,对选定的设计题目进行理论分析,针对具体设计部分的原理分析、建模、必要的推导和可行性分析,画出程序设计框图,编写程序代码(含注释),上机调试运行程序,记录实验结果(含计算结果和图表),并对实验结果进行分析和总结。
具体设计要求包括:①初步了解MATLAB、熟悉MATLAB界面、进行简单操作;②MATLAB的数值计算:创建矩阵、矩阵运算、多项式运算、线性方程组、数值统计;③基本绘图函数:plot, plot3, mesh, surf等,要求掌握以上绘图函数的用法、简单图形标注、简单颜色设定等;④使用文本编辑器编辑m文件,函数调用;⑤能进行简单的信号处理MATLAB编程;⑥按要求参加课程设计实验演示和答辩等。
4.课程设计说明书按学校“课程设计工作规范”中的“统一书写格式”撰写,具体包括:①目录;②与设计题目相关的理论分析、归纳和总结;③与设计内容相关的原理分析、建模、推导、可行性分析;④程序设计框图、程序代码(含注释)、程序运行结果和图表、实验结果分析和总结;⑤课程设计的心得体会(至少500字);⑥参考文献(不少于5篇);⑦其它必要内容等。
时间安排:1.5周(分散进行)参考文献:[1](美)穆尔,高会生,刘童娜,李聪聪.MA TLAB实用教程(第二版) . 电子工业出版社,2010.[2]王正林,刘明.精通MATLAB(升级版) .电子工业出版社,2011.[3]陈杰. MA TLAB宝典(第3版) . 电子工业出版社,2011.[4]刘保柱,苏彦华,张宏林. MATLAB 7.0从入门到精通(修订版) . 人民邮电出版社,2010.指导教师签名:年月日系主任(或责任教师)签名:年月日目录1MATLAB概述 (2)1.1MATLAB简介 (2)1.2 MATLAB的功能 (2)1.3MATLAB 的典型应用 (4)2设计题目:MATLAB运算与应用设计套题五 (4)3设计内容 (6)3.1 题一 (6)3.2 题二 (6)3.3 题三 (8)3.4 题四 (9)3.5 题五 (13)3.6 题六 (14)3.7题七 (16)3.8 题八 (17)3.9 题九 (18)3.10题十 (19)4 课程设计心得 (21)5参考文献 (22)6 本科生课程设计成绩评定表 (23)1 MATLAB概述1.1MATLAB简介MATLAB软件由美国Math Works公司于1984年推出,经过不断的发展和完善,如今己成为覆盖多个学科的国际公认的最优秀的数值计算仿真软件。
MATLAB第一章作业答案

M A T L A B第一章作业答案(共5页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第一章M A T L A B概况与基本操作1.选择题:(1)最初的MATLAB核心程序是采用A语言编写的。
(2)即将于2011年9月发布的MATLAB新版本的编号为D。
2011Ra 2011Rb R2011a R2011b(3)在默认设置中,MATLAB中的注释语句显示的颜色是D。
A.黑色B.蓝色C.红色D.绿色(4)如果要以科学计数法显示15位有效数字,使用的命令是B。
long long e long g long d(5)在命令窗口新建变量a、b,如果只查看变量a的详细信息,使用的命令为B。
a a(6)如果要清除工作空间的所有变量,使用的命令为 C 。
all C.两者都可 D.两者都不可(7)在创建变量时,如果不想立即在命令窗口中输出结果,可以在命令后加上D。
A.冒号B.逗号C.空格D.分号(8)如果要重新执行以前输入的命令,可以使用B键。
A.下箭头↓B.上箭头↑C.左箭头←D.右箭头→(9)如果要查询函数inv的相关信息,并显示在命令窗口,应使用命令A。
D.三者均可(10)如果要启动Notebook文档,下列D操作是可行的。
A.在命令窗口输入notebook命令B.在命令窗口输入notebook filename命令C.在Word中启动M-book文档D.三者均可2.填空题:(1)MATLAB是MATrix和LABoratory两个单词前三个字母的组合,意为“矩阵实验室”,它的创始人是Cleve Moler和Jack Little。
(2)在MATLAB的默认设置中,关键字显示的字体为蓝色,命令、表达式、计算结果显示的字体为黑色,字符串显示的字体为紫色,注释显示的字体为绿色,错误信息显示的字体为红色。
(3)在命令窗口中,输出结果显示为各行之间添加空行的命令为format compact,各行之间不添加空行的命令为format compact。
matlab作业题答案

MATLAB作业题答案第一章MATLAB概述1.选择题(1)在MATLAB中( C )用于括住字符串。
A、,B、;C、‘’D、“”(2)在MATLAB的命令窗口中( D )可以中断MATLAB命令运行。
A、endB、escC、backspaceD、ctrl+c(3)在MA TLAB的命令窗口中执行( B )命令,使数值 5.3显示为5.3000000000000000e+000。
A、format longB、format long eC、format shortD、format short e(4)在MA TLAB的命令窗口中执行(B )命令,将命令窗口的现实内容清空。
A、clearB、clcC、echo offD、cd2.在命令窗口中输入以下命令,写出在命令窗口中的运行结果。
a=[2+5i 5 0.2 2*3]答:a =0i 5.0000 0.2000 6.00003.使用MATLAB的‘preferences’窗口设置数据格式为有理数表示答:rational4.在命令窗口使用标点符号“%”和“;”的含义?答:%表示注释;;表示不显示运行结果。
5.用“format”命令设置数据输出格式为有理数表示,15位长格式和5位科学计数法。
答:rational long short11.在命令窗口中输入以下命令,并查看显示的图形。
a=[1 2 3 4];>> b=[5 6 7 8];>> c=a+b*i;>> plot(c)第二章 MATLAB 基本运算1. 选择题(1) 下列变量名中( A )是合法的。
A 、 char_1,i,jB 、x*y,a.1C 、x\y,a1234D 、end ,1bcx(2)下列( C )是合法常量。
A 、3*e10B 、1e500C 、-1.85e-56D 、10-2(3)x=uint8(2.3e10),则x 所占的字节是( A )个。
A 、1B 、 2C 、4D 、8(4)已知x=0:10;,则x 有( B )个元素。
武汉理工Matlab实验报告程序

1、利用zeros 和ones 函数来产生单位阶跃序列。
函数格式: zeros(1,n) ones(1,n) n 为序列长度。
程序如下: n1=-2;n2=8;k=0; n=n1:n2; nt=length(n); nk=abs(k -n1)+1;x=[zeros(1,nk -1),ones(1,nt -nk+1)]; stem(n,x)2、已知信号x1(n)=3e −0.25n (4<n<10)x2(n)=u(n+1) (-2<n<6) 求x(n)=x1(n)*x2(n),并画出对应波形。
程序如下:function[x,n]=stepseq(n1,n2,n0) n=[n1:n2]; x=[(n -n0)>=0];function [y,ny]=conv_m(x,nx,h,nh,p) nyb=nx(1)+nh(1);nyc=nx(length(x))+nh(length(h)); ny=[nyb:p:nyc]; y=conv(x,h); p=1;n1=[-4:p:10];f1=3*exp(-0.25*n1); n2=[-2:p:6];[f2,n2]=stepseq(-2,6,-1);[y,ny]=conv_m(f1,n1,f2,n2,p); subplot(3,1,1);stem(n1,f1) subplot(3,1,2);stem(n2,f2) subplot(3,1,3);stem(ny,y)图1 单位阶跃序列图2 对应波形验证线性性质:如果有两个有限长序列分别为x1(n)和x2(n),长度分别为N1和N2,且y(n)=ax1(n)+bx2(n),(a ,b 均为常数),则该y(n)的N 点DFT 为 Y(k)=DFT[y(n)]=aX1(k)+bX2(k) (0<=k<=N -1) 其中:N=max(N1,N2),X1(k)和X2(k)分别为x1(n)和x2(n)的N 点DFT 。
《电力拖动与控制系统》课程设计-异步电机矢量控制Matlab仿真实验

异步电机矢量控制Matlab仿真实验1 异步电机动态模型推导1.1 异步电机动态数学模型的性质电磁耦合是机电能量转换的必要条件,电流与磁通的乘积产生转矩,转速与磁通的乘积得到感应电动势。
无论是直流电动机,还是交流电动机均如此。
交、直流电动机结构和工作原理的不同,至使表达式差异很大。
异步电动机的动态数学模型是一个高阶、非线性、强耦合的多变量系统。
(1)变压变频调速时需要进行电压(或电流)和频率的协调控制,有电压(或电流)和频率两种独立的输入变量。
在输出变量中,除转速外,磁通也是一个输出变量。
因此异步电机是一个多变量(多输入多输出)系统。
(2)异步电动机无法单独对磁通进行控制,电流乘磁通产生转矩,转速乘磁通产生感应电动势,在数学模型中含有两个变量的乘积项。
因此即使不考虑磁路不饱和等因素,数学模型也是非线性的。
(3)三相异步电动机三相绕组存在交叉耦合,每个绕组都有各自的电磁惯性,再考虑运动系统的机电惯性,转速与转角的积分关系等,动态模型是一个高阶系统。
1.2 异步电动机的三相数学模型1.2.1 异步电机三相数学模型的前提假设在研究异步电机数学模型时,作如下的假设(1)忽略空间谐波,三相绕组对称,产生的磁动势沿气隙按正弦规律分布。
(2)忽略磁路饱和,各绕组的自感和互感都是恒定的。
(3)忽略铁心损耗。
(4)不考虑频率变化和温度变化对绕组电阻的影响。
无论异步电动机转子是绕线型还是笼型的,都可以等效成三相绕线转子,并折算到定子侧,折算后的定子和转子绕组匝数相等。
异步电动机三相绕组可以是Y连接,也可以是Δ连接。
若三相绕组为Δ连接,可先用Δ—Y变换,等效为Y 连接。
然后,按Y连接进行分析和设计。
三相异步电机的物理模型如下图1所示,定子三相绕组轴线A、B、C在空间是固定的,转子绕组轴线a、b、c随转子以角转速w旋转。
图1 三相异步电动机的物理模型1.2.2 异步电机的三相动态模型的数学表达式异步电动机的动态模型由磁链方程、电压方程、转矩方程和运动方程组成。
武汉理工大学MATLAB课设报告

课程设计任务书学生姓名:专业班级:指导教师:江雪梅工作单位:信息工程学院题目: MATLAB的基本运算与绘图初始条件:1. Matlab实验软件2. 实验程序要求完成的主要任务:1. 采用MATLAB选用适当的函数或矩阵进行如下计算(1)极限的计算、微分的计算、积分的计算、级数的计算、求解代数方程、求解常微分方程;(2)矩阵的最大值、最小值、均值、方差、转置、逆、行列式、特征值的计算、矩阵的相乘、右除、左除、幂运算;(3)多项式加减乘除运算、多项式求导、求根和求值运算、多项式的部分分式展开、多项式的拟合、插值运算。
2. MATLAB的绘图(1)绘制四个不同的一维函数y=f(x)。
把四个函数用不同曲线、不同标识符显示在同一幅图中;用同一种曲线、同一种标识符把四个函数显示在同一界面的不同窗口;要求显示网格、有图形标题、有坐标轴标志、有图形标注函数。
(2)选择合适的二维函数z= f(x,y)分别绘制其空间曲线图、三维网线图和三维曲面图(3)选择一幅图像,画出图像的频谱图。
(4)对图像加入噪声,再画出图像的频谱图。
时间安排:1.第15周排任务,分组2.16—17周设计仿真,撰写报告3.第18周完成设计,提交报告,答辩指导教师签名:年月日系主任(或责任教师)签名:年月日学号:课程设计题目 MATLAB原理与应用课程设计学院信息工程学院专业通信工程班级姓名指导教师江雪梅2016 年 1 月9 日摘要Matlab是一个高级的矩阵/阵列语言,它包含控制语句、函数、数据结构、输入和输出和面向对象编程特点。
用户可以在命令窗口中将输入语句与执行命令同步,也可以先编写好一个较大的复杂的应用程序(M文件)后再一起运行。
新版本的MATLAB语言是基于最为流行的C++语言基础上的,因此语法特征与C++语言极为相似,而且更加简单,更加符合科技人员对数学表达式的书写格式。
使之更利于非计算机专业的科技人员使用。
而且这种语言可移植性好、可拓展性极强,这也是MATLAB能够深入到科学研究及工程计算各个领域的重要原因。
武汉理工大学Matlab课设报告-PSK和DPSK信号的仿真分析

课程设计任务书学生姓名:张亚男专业班级:通信1104班指导教师:张小梅工作单位:信息工程学院题目: PSK和DPSK信号的仿真分析初始条件:在MATLAB仿真软件系统中设计并实现PSK和DPSK信号系统的仿真,并进行调试和仿真波形分析。
要求完成的主要任务: (包括课程设计工作量及技术要求,以及说明书撰写等具体要求)1、课程设计工作量:5天。
2、技术要求:调制信号:300Hz正弦信号,经过μ律PCM编码;载波频率:100kHz;要求:画出调制信号、已调信号、解调信号的波形、频谱以及误码率与输入信噪比的关系曲线3、查阅至少5篇参考文献。
按《武汉理工大学课程设计工作规范》要求撰写设计报告书。
全文用A4纸打印,图纸应符合绘图规范。
时间安排:1、2013年5 月16 日,布置课设具体实施计划与课程设计报告格式的要求说明。
2、2013年6 月27 日至2013年6 月29 日,方案选择和电路设计。
3、2013年6 月30 日至2013年7 月3 日,电路调试和设计说明书撰写。
4、2013年7 月5 日,上交课程设计成果及报告,同时进行答辩。
指导教师签名:年月日系主任(或责任教师)签名:年月日目录摘要....................................................... 错误!未定义书签。
Abstract.................................................... 错误!未定义书签。
1 方案设计................................................. 错误!未定义书签。
1.1 调制部分方案选择..................................... 错误!未定义书签。
1.2 解调部分方案选择..................................... 错误!未定义书签。
按转子磁链定向的矢量控制Matlab仿真实验(运控课设)

摘要
因为异步电动机的物理模型是一个高阶、非线性、强耦合的多变量系统,需要用一 组非线性方程组来描述,所以控制起来极为不便。异步电机的物理模型之所以复杂,关 键在于各个磁通间的耦合。如果把异步电动机模型解耦成有磁链和转速分别控制的简单 模型,就可以模拟直流电动机的控制模型来控制交流电动机。
2
(2-3) (2-4)
2.3 旋转变换
两相静止坐标系和两相旋转坐标系的变换 (简称 2s/2r 变换 ),两相静止绕组, 通以 两相平衡交流电流,产生旋转磁动势。如果令两相绕组转起来,且旋转角速度等于合成 磁动势的旋转角速度 , 则两相绕组通以直流电流就产生空间旋转磁动势。从两相静止坐标
系到两相旋转坐标系的变换 , 称为两相旋转-两相静止变换,简称 2s/2r 变换。其变换关
C2s 2r
C2r1 2s
cos sin sin cos
(2-7)
电压和磁链的旋转变换阵与电流旋转变换阵相同。
3 转子磁链计算
按转子磁链定向的矢量控制系统的关键是 r 的准确定向, 也就是说需要获得转子磁 链矢量的空间位置。根据转子磁链的实际值进行控制的方法,称作直接定向。
转子磁链的直接检测比较困难,现在实用的系统中多采用按模型计算的方法,即利
4
武汉理工大学《运动控制系统》课程设计说明书
用容易测得的电压、电流或转速等信号,借助于转子磁链模型,实时计算磁链的幅值与
空间位置。转子磁链模型可以从电动机数学模型中推导出来,也可以利用专题观测器或 状态估计理论得到闭环的观测模型。在计算模型中,由于主要实测信号的不同,又分为
iA
A
B
iB
i
C
C
i
武汉理工大学matlab实验一实验报告答案

ia=I(1);ib=I(2);ic=I(3);
i3=ia-ib
第8题程序:
t=ቤተ መጻሕፍቲ ባይዱpi:0.01:pi;
n=1;
i=0;
whilen<=10
i=i+0.88*n*t.*exp(-n*abs(t))
n=n+1;
end
plot(t,i,'r-o')
xlabel('t','FontSize',12);
'separator','on');
h_sub4=uimenu(h_menu,'label','boxoff','callback','boxoff');
h_sub5=uimenu(h_menu,'label','FigureColor','Separator','on');
h_subsub1=uimenu(h_sub5,'label','Red','ForeGroundColor','r',...
x=linspace(a,b,30);
y=linspace(a,b,30);
[xx,yy]=meshgrid(x,y);
zz=sin(sqrt(xx.^2+yy.^2))./sqrt(xx.^2+yy.^2);
mesh(xx,yy,zz)
第11题程序:
figure
h_menu=uimenu('label','Option','Position',3);
MATLAB大作业

M A T L A B大作业(总15页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--MATLAB大作业作业要求:(1)编写程序并上机实现,提交作业文档,包括打印稿(不含源程序)和电子稿(包含源程序),以班为单位交,作业提交截止时间6月24日。
(2)作业文档内容:问题描述、问题求解算法(方案)、MATLAB程序、结果分析、本课程学习体会、列出主要的参考文献。
打印稿不要求MATLAB程序,但电子稿要包含MATLAB程序。
(3)作业文档字数不限,但要求写实,写出自己的理解、收获和体会,有话则长,无话则短。
不要抄袭复制,可以参考网上、文献资料的内容,但要理解,要变成自己的语言,按自己的思路组织内容。
(4)从给出的问题中至少选择一题(多做不限,但必须独立完成,严禁抄袭)。
(5)大作业占过程考核的20%,从完成情况、工作量、作业文档方面评分。
第一类:绘制图形。
(B级)问题一:斐波那契(Fibonacci)螺旋线,也称黄金螺旋线(Golden spiral),是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线的图案,是自然界最完美的经典黄金比例。
斐波那契螺旋线,以斐波那契数为边的正方形拼成的长方形,然后在正方形里面画一个90度的扇形,连起来的弧线就是斐波那契螺旋线,如图所示。
问题二:绘制谢尔宾斯基三角形(Sierpinskitriangle)是一种分形,由波兰数学家谢尔宾斯基在1915年提出,它是一种典型的自相似集。
其生成过程为:取一个实心的三角形(通常使用等边三角形),沿三边中点的连线,将它分成四个小三角形,然后去掉中间的那一个小三角形。
接下来对其余三个小三角形重复上述操作,如图所示。
问题三:其他分形曲线或图形。
分形曲线还有很多,教材介绍了科赫曲线,其他还有皮亚诺曲线、分形树、康托(G. Cantor)三分集、Julia集、曼德布罗集合(Mandelbrot set),等等。
武汉理工大学-Matlab 课程设计1

课程设计任务书学生姓名: xxx 专业班级:信息xxx班指导教师: xxx 工作单位:信息工程学院题目:MATLAB课程设计要求完成的主要任务:1.在数字信号处理平台上(PC机﹑MATLAB仿真软件系统)进行软件仿真设计,并进行调试和数据分析。
2. 利用MATLAB仿真软件系统结合频率取样法设计一个数字高通FIR滤波器。
课程设计的目的:1.理论目的课程设计的目的之一是为了巩固课堂理论学习,并能用所学理论知识正确分析信号处理的基本问题和解释信号处理的基本现象。
2.实践目的课程设计的目的之二是通过设计具体的图像信号变换掌握图像和信号处理的方法和步骤。
时间安排:指导教师签名:年月日系主任(或责任教师)签字:年月日目录1 引言 (1)1.1MATLAB介绍 (1)1.2MATLAB信号处理工具箱函数介绍 (1)1.3滤波器的介绍 (2)2 FIR数字滤波器设计原理 (3)3 FIR数字滤波器设计方法 (4)3.1窗函数法 (4)3.2频率取样法 (5)4 频率采样法实际FIR高通滤波器 (7)4.1设计原理 (7)4.2设计步骤 (9)5 MATLAB环境下设计FIR数字高通滤波器 (9)5.1设计要求 (9)5.2 FIR数字高通滤波器程序设计 (10)5.3调试结果 (11)5.4 高通FIR数字滤波器的进一步设计 (12)6 高通FIR数字滤波器性能测试 (14)6.1高通FIR数字滤波器性能测试程序 (14)6.2 性能测试结果 (15)7 FDATOOL工具箱设计高通FIR滤波器 (16)7.1 FDATOOL工具箱 (16)7.2 FIR滤波器参数设置 (17)8心得体会 (19)参考文献 (20)附件:MATLAB程序 (21)数字滤波是语音和图象处理、模式识别、频谱分析等应用中的一个基本处理算法,数字滤波技术是信号消噪的基本方法。
根据噪声频率分量的不同,可选用具有不同滤波特性的数字滤波器。
LC并联谐振MATLAB仿真 武汉理工大学 基础强化训练
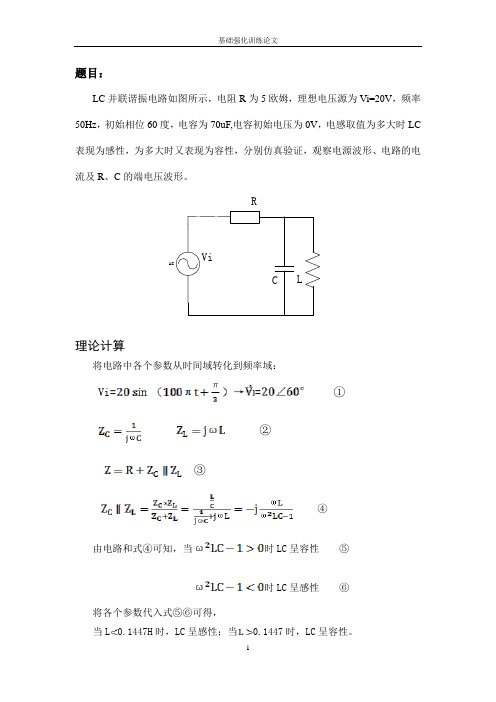
题目:LC并联谐振电路如图所示,电阻R为5欧姆,理想电压源为Vi=20V,频率50Hz,初始相位60度,电容为70uF,电容初始电压为0V,电感取值为多大时LC 表现为感性,为多大时又表现为容性,分别仿真验证,观察电源波形、电路的电流及R、C的端电压波形。
RAC理论计算将电路中各个参数从时间域转化到频率域:Vi=→=①②③④由电路和式④可知,当时LC呈容性⑤时LC呈感性⑥将各个参数代入式⑤⑥可得,当L0.1447H时,LC呈感性;当0.1447时,LC呈容性。
MATLAB电路仿真要想得到什么时候LC呈感性什么时候呈容性,必须借助电路中得示波器,或者MATLAB中得一些重要功能来观察电路中电源电压的相位和干路电流的相位的关系,如果电压超前于电流,则LC呈感性,如果电流超前于电压则LC呈容性。
仿真过程1.打开MATLAB软件2.在软件打开后的界面上点击工具栏的simulink键,弹出一个窗口如下图所示3.点击菜单栏中得File菜单新建一个模型4.在libraries中找到SinmpowerSystem,它的子菜单中可以找到电路所需的各种元件,包括正弦电压源,串联RLC电路,并联RLC电路,电压表,电流表。
示波器在Simulink的子菜单sink里面。
如图所示5.每找到一个元件将其拖到新建的模型中6. 所有的元件的参数都应该按照题目所有的条件来设定,由于电感是待求量,但又必须设定出一个确定的值才能观察电路的波形以及相位关系,所以这里我们取一系列的电感值,在理论值得附近取值稍微密一点。
6.1电源参数6.2 电阻参数6.3电容参数6.4设定初值6.5 示波器的设定由于要同时观察电源电压以及干路电流的波形,则设置双踪同时观察7. 电路参数全部设置完成后电路连接好如下图8.对电感设置不同的参数,观察波形及相位关系。
① L=0.12H时,电压超前于电流,呈感性②L=0.13H时,电压超前于电流,呈感性③L=0.14H时,电压超前于电流,呈感性④L=0.145H时,电压超前于电流,呈感性,电流波形失真⑤L=0.15H时,电压滞后于电流,呈容性⑥L=0.16H时,电压滞后于电流,呈容性为了验证公式中L趋近于0时电路呈纯阻性这一特点,另外添加两组数据如下⑦L=0.01H时,电压电流的相位比较接近,但依然是电压超前于电流,呈感性⑧ L=0.0001H时,电压电流的相位非常接近,几乎同相位,电路接近纯阻性。
