最短路径学年论文
最短路径问题网络分析毕业论文(可编辑)

最短路径问题网络分析毕业论文摘要第一章绪论二十世纪中后期,随着计算机的出现和发展,图论的研究得到广泛重视,最短路径问题是图论中的一个典范问题,它已经被应用于众多领域.最短路径问题最直接的应用当数在地理信息领域,如:GIS 网络分析、城市规划、电子导航等.在交通咨询方面,寻找交通路网中两个城市间最短的行车路线就是最短路径问题的一个典型的例子.在网络通信领域,信息包传递的路径选择问题也与最短路径问题息息相关.举个例子,OPSF开放路由选择协议,每个OPSF路由器都维护一个描述自治系统拓扑结构的数据库,通过这个数据库构建最短路径树来计算路由表,从而跟踪自治系统范围内到每个目标的最短路径.在图象分割问题中,最短路径也有直接的应用:在语音识别中,一个主要的问题就是区别同音词,例如,to、two、too.为解决这个问题,我们需要建一个图,顶点代表可能的单词,边连接相邻的单词,边上的权代表相邻的可能行大小.这样图中的最短路径,就是对句子的最好解释.由于最短路径问题的广泛应用,很多学者都对此进行了深入的研究,也产生了一些经典的算法.近些年来,对最短路径研究的热度依然不减,并且时间复杂度降得越来越低.所以在本课题中我们将提出不仅是以前我们学习过的一些经典的算法,我们还将提出一些以前没有学习过的更有应用空间的算法.以及各算法之间的比较.最后还将把这些算法在现实中的应用最一些简单的介绍.第二章网络的最短路问题的基础知识2.1 图的基本概念(1)图定义:一个(无向)图G 是一个有序二元组(V,E),其中是顶点集,是边集,且是一个无序二元组,它表示该边连接顶点与.图1就是一个图说明:在保持图的点边关系不变的情况下,图形的位置、大小、形状都是无关紧要的.若,则称连接与;点和称为的顶点,称或与关联,与是邻接的顶点;如果两条边有一个公共顶点,则称这两条边是邻接的;(2)环定义:两个顶点重合为一点的边称为环如图图1中.图1(3)重边定义:如果有两条边的顶点是同一对顶点,则称这两条边为重边(如图1中与中有两条边相连).(4)孤立点定义:不与任何边关联的点称为孤立点(如图1中);(5)无环图定义:没有环的图称为无环图;(6)简单图:定义:既没有环也没有重边的图称为简单图.设G(V,E)是一个简单图,则显然有.(7)完全图定义:若上式中等号成立,则说明该图中每对顶点间恰有一条边相连,称此图为完全图.(8)补图定义:一个简单图的补图是与有相同顶点的简单图,且中两个点相邻当且仅当它们在中不相邻.(9)二分图定义:一个图G(V,E),若存在V 的一个分划(,),使得每条边有一个顶点在中,另一个在中,则称为二分图.(10)子图、支撑子图定义:设有两个图,,如果,,则称为的支撑子图.(11)点导出子图定义:设有图G(V,E),是的非空子集,若以为点集,以两点均在中的所有边为边集的子图称为由导出的的子图,记为,简称点导出子图.(12)边导出子图定义:若是的一个非空子集,则以为边集以中边的所有顶点作为点集的子图,称为由导出的的子图,记为,简称边导出子图.(13)度:定义:图中顶点的度为与关联的边的数目(与关联的每个环算作两条边),记为.结论:设G(V,E)是一个图,则,即度数为奇数的顶点有偶数个.2.2有向图(1)有向图定义:一个有向图是一个有序二元组,其中是顶点集,称为的弧集,为一个有序二元组.称为连向的弧,为的出弧,的入弧;称为得尾,称为的头;称为的前继,称为的后继.图2就是一个有向图.图2(2)环定义:头和尾重合的弧称为环.(3)重弧定义:若两条弧有相同的头和尾,则称这两条弧为重弧.(4)简单有向图定义:没有环和重弧的有向图称为简单有向图‘(5)基图定义:把有向图中每条弧用边来代替,得到一个无向图,称为得基图.(6)完全有向图定义:设G(V,E)是一个简单有向图,则,若等号成立,则称这样的图为完全有向图.(7)出度、入度定义:有向图中顶点的出弧的数目称为的出度,记为;顶点入弧的数目称为的入度,记为.结论:设G(V,E)是一有向图,则类似地可以定义有向图的子图,支撑子图,点,边导出之子图的概念.(8)网络定义:设是一个图,若对的每一条边都赋以一个实数,称为边的权,则连同边上的权称为一个网络,记为.同样可以定义有向网络.在此主要讨论网络上的各种优化问题.无向网络可以转化为有向网络,具体做法为:把无向网络中每条边代之以一对弧()和(),且两条弧的权都等于边的权.2.3连通性途径、迹、路定义:设有图 G(V,E),如果它的某些顶点与边可以排成一个非空的有限交错序列,这里该途径中边互不相同,则称为迹;如果顶点互不相同,则称它为路.显然路必为迹,但反之未必.闭路径定义:如果某途径至少含一条边,且起点与终点重合,则称它为一条闭途径.类似可定义闭迹和回路(又称圈).注意:若为简单图,则两个顶点间边若存在必是唯一的,故由到的一条途径可以用顶点序列表示.连通图:定义:图中若存在一条从顶点到的途径,则称与是连通的.如果图中任何两个顶点都是连通的,则称是连通图.例如,完全图是连通的.二分图,,则只要,中有一个大于1,则一定不是连通图.连通子图定义:如果是的子图,且是连通的,则称为的连通子图.极大连通子图定义:如果为的连通子图,且不存在连通子图,使是的子图.图的极大连通子图又称为的连通分支.有向途径定义:设有一个有向图,中某些顶点与弧组成的非空有限序列这里,,且,则称它为从到的有向途径.类似可定义有向迹,有向路,有向闭途径,有向闭迹,有向回路(有向圈).当是简单有向图时,从到的一条有向途径可简记为().强连通定义:中若既存在一条从顶点到的有向途径,又存在从到的有向途径,则称和是强连通的.如果中任意两顶点都是强连通的,则称是强连通的.强连通分支定义:的极大强连通子图称为强连通分支.注:若强连通,则恰有一个强连通分支.结论:若为有个连通分支的简单无向图,则的邻接矩阵为准对角矩阵若为有个强连通分支的简单有向图,则的邻接矩阵为准上三角矩阵2.4割集割边定义:设有图,是的一条边,如果从中删去,使它的连通分支数量增加1,则称是的割边.显然,的一条边是割边当且仅当该边不包含在的任何闭迹中.边割定义:设是的一个非空子集,,记,如果,且从中删去这些边后,的连通分支至少增加1,则称是的一个边割.割集定义:若是一个边割,且的任何真子集都不是边割,则称它为极小边割,的极小边割又称为割集.结论:任给图,设是图的圈,是图的割集,用表示的边集.如果,那么.弧割定义:设是一个有向图,记,如果,则从中删去这些弧以后,的强连通分支数至少增加1,称它为的一个弧割.的极小弧割称为有向割集.2.5最短路问题定义:所谓最短路径是指如果从图中某一顶点称为源点到达另一顶点称为终点的路径可能不止一条,如何找到一条有向路径使得沿此路径上各弧的权值总和达到最小.第三章网络的最短路问题的算法研究3.1最短路问题的提出某旅客要从杭州乘飞机前往奥地利的萨尔斯堡,因为他害怕乘飞机,所以要选择一条航线,使得在空中飞行的时间尽可能的少.问题是如何选择航线以达到要求.为此构造一个无向网络总可以化成有向网络,故下面只讨论有向网络的最短路问题.设是一有向网络,为中一条有向路,称为路的权或路长.现寻找网络中自某一指定顶点到另一指定顶点的最短有向路.3.2 Bellman最短路方程设有一个有向网络,.若用表示自顶点到顶点的最短有向路长,用表示弧()的长度,若,则定义,则对一切有且当且仅当弧在自顶点到顶点的最短有向路上.因为所有均表示自到的最短路长,因此这些最短路必有最后一条弧(),且该有向路上自到的一段也是最短路,故有Bellman最短路方程:即自点到各点最短路长度必满足Bellman最短路方程.反过来,Bellman最短路方程的解是自点到其余各点最短路的长度.3.3无负回路网络的最短有向路的Ford算法3.3.1 Ford算法的基本思想Ford算法的思想是逐次逼近,每次逼近求出网络从到其余各顶点的带某种约束的最短路,这里的约束是路中弧数.第一次逼近是从到其他任意顶点由一条弧组成的所有路中找一条最短路,记其长度为;第二次逼近是从到由不多于两条弧组成的所有路中找一条最短路,记其长度为.一般地,第次逼近是从到由不多于条弧组成的路中找一条最短的,记其长度为.因为中自到的最短路至多含个顶点, 条弧,所以最多次逼近即可. 即为中自到的最短路长.3.3.2 Ford算法的步骤为方便起见,定义.第一步置,,.第二步令.第三步若,停止;否则令,返回第二步.3.3.3实例求如下图所示网络中从顶点到其余各点的最短路.解求解过程如下:因此从到的最短路径分别为,,,,,路长分别为1,2,-3,0,2.3.4求正权网络中有向最短路的Dijkstra算法3.4.1Dijkstra算法的基本思想对网络中每个顶点赋以一个标号,用来记录从顶点到该顶点的最短路的长度(此时称为永久标号)或最短路长度的上界(此时称为暂时标号).算法开始时,只有顶点被赋予永久标号,其它顶点被赋予暂时标号.一般地,算法在被暂时标号的顶点中寻找一个顶点,其暂时标号最小,然后将赋予永久标号,且对其余暂时标号的顶点按方式修正其标号.算法在所有顶点均被赋予永久标号终止.3.4.2Dijkstra算法的理论依据对于中任一顶点,其永久标号是从顶点到该顶点的最短路的长度.对于中任一顶点,其暂时标号是从顶点出发,只经过中顶点到达该顶点的最短路的长度.3.4.3 Dijkstra算法的算法步骤最短路径问题是指在一个赋权图的两个指定节点和之间找出一条具有最小权的路.Dijkstra 算法是一个解最短路径问题的算法,这个算法不仅可以找到最短的,路径而且可以给出从到图中所有节点的最短路径.其基本步骤如下:1 设,对所有的节点来说,设,并将标号为0, ,为和w之间的权值距离.2按照每个未标号的节点w计算, ,表示点t 到点w 之间的权值距离 .若被修改了说明在当前得到的到w 的最优路径上t 和w 相邻用记录下来在所有中选择一个最小的即,未标号.将s 标号为, 表示节点到s的最优路径的长度为且与s 相邻.3 若终点v 已标号,则停止.得到一条从到v 的最优路径,否则,转向2再计算.3.4.4 Dijkstra算法的应用举例以具体实例说明Dijkstra 算法的具体应用.例 1. 利用Dijkstra 算法求图1 中节点A 到其它各节点的最优路径 202.9 3.218 4.4 3.5 3.2 4.516 Y 4.1 2.2 14 4.22 3.4 4.512 5.62.9 3 4.22.2 10 3.4 3.5 4 2.23 8 0 24 6 X 8 图1 101214相应的权值为:根据Dijkstra 算法的实现步骤其计算过程可归纳为表1 所示.从表1 中可以看出从到的最短路径为且到的距离为18.3 在求到最短路径的过程中到其余各点的最短路径也相应求出.若以计算一次为计算单位,则利用Dijkstra算法计算到最短路径时所需的计算次数15+14+13+ +2 119次表1采用Dijkstra 算法求解A到其他各节点最优路径的过程序号 A B C D E F G H I J K L M N O P1 - 4.2 3.42 - 4.2 3.4/A9.0 6.93 - 4.2/A - 8.6 8.3 6.94 - - - 8.6 8.3 6.9/C 11.9 10.95 - - - 8.5 8.3/B -10.3 11.2 10.96 - - - 8.6/B - - 11.5 10.3 11.2 10.97 - - - - - - 11.5 10.3/D 11.2 10.9 13.513.78 - - - - - - 11.5 - 11.2 10.9/F 13.5 13.713.19 - - - - - - 11.5 - -11.2/E - 13.5 13.713.110 - - - - - - 11.5/D - - - 13.5 13.713.111 - - - - - - - - - - 13.5 13.713.1/J16.112 - - - - - - - - - - 13.5/H 13.7 -18.0 16.113 - - - - - - - - - - - 13.7/H - 15.916.114 - - - - - - - - - - - - - 15.9/L16.1 18.715 - - - - - - - - - - - - - - 16.1/M18.33.4.5 Dijkstra算法的不足在现行电子地图中,网络模型的规模常常较大,节点数多达上千或上万,并且对网络模型的查询也要求实时性,因此Dijkstra 算法虽然在理论上是可行的,但在实际应用中不尽人意,当网络模型中节点数和边数较多的情况下,算法的计算量较大时间花费较多效率非常低.3.4.6 改进Dijkstra 算法的基本思想及实现表1 中的数值大多数是,都是无用运算,如果节点数量很大,将极其浪费运算时间.由于,节点是否在上次已经被计算出最短路径未知,当前节点是否与节点是否相连也未知,也就是未知,这时是已知的,故本次计算的到底是不是,取决于上一步数值和的数值,从表达式可以看出,只要这两个数值不都是,本次计算的就不会是,所以在上面Dijkstra 算法的实现步骤第2 步时,先判断一下,只要原来的, 的数值中至少有一个不是,才进行下面的计算,这样就保证了当预见是时,不对它进行计算,避免了大量无效的计算,提高了搜索效率.下面仍以一个具体实例来说明改进的Dijkstra算法的具体应用.例2 利用改进的Dijkstra 算法求图1中节点A到其他各节点的最优路径,此例的计算过程和Dijkstra 算法基本一致,只是表 1 中所有标记的部分在改进Dijkstra 算法中被省去了,利用改进的Dijkstra 算法计算到最短路径时所需计算次数为次,由此可见,改进的Dijkstra 算法确实减小了计算量在程序设计中,判断语句所花费的时间可以忽略,并不增大计算量.3.4.7 实验对比为了更好地说明改进的Dijkstra 算法的有效性,利用C语言自行编制了最短路径搜索程序并进行了仿真实验,采用自绘制的地图,共5 张,第一张图16个节点,共24条弧;第二张图32个节点,共55条弧;第三张图43个节点,共75条弧;第四张图62个节点,共111条弧;第五张图78个节点,共139条弧,计算结果如表2 所示.从表 2 可以看出,两种算法的计算量有很大的区别,改进的Dijkstra 算法较之经典Dijkstra 算法在计算量方面有很大幅度的减少,而且这种减少的程度在节点数目增加地图更大,更复杂时,会变得越来越明显.对于实际系统,由于地图都会很大,使用改进Dijkstra 算法的改进效果将非常显著.表2 改进Dijkstra 算法和经典Dijkstra 算法计算次数比较节点数经典Dijkstra 算法改进的Dijkstra 算法16 119 4739.5%32 465 13428.8%43 861 23427.2%62 1830 44124.1%78 2926 54018.5%注:表中的百分数表示改进算法计算量与经典算法计算量的百分比3.5 算法的问题和改进3.5.1算法的基本思想算法在人工智能中是一种典型的启发式搜索算法.通过选择合适的估价函数,指导搜索朝着最有希望的方向前进,以求得最优解. 算法中关键是求估价函数:其中, 是从起点到当前节点已付出的代价, 是从当前节点到目标节点的代价估计函数,必须保证其中是从当前点到目标点的实际最小代价.3.5.2算法的步骤算法的搜索步骤如下:1给起始节点标记,对它的没有标记过的子节点进行扩展;2对每一个子节点计算评价函数值,按评价值的大小进行排列,找出评价值最小的节点,并给它作标记,如果当前节点就是目标节点,则停止搜索;3 否则,对最新被标记的节点进行第2 步处理并记录最短路径.3.5.3算法分析算法是利用对问题的了解和对问题求解过程和解的了解,寻求某种有利于问题求解的启发信息,从而利用这些启发信息去搜索最优路径.它不用遍历整个地图,而是每一步搜索都根据启发函数朝着某个方向搜索.当地图很大很复杂时,它的计算复杂度大大优于Dijkstra 算法,是一种搜索速度非常快、效率非常高的算法.但是,相应的算法也有它的缺点.启发性信息是人为加入的,有很大的主观性,直接取决于操作者的经验,对于不同的情形要用不同的启发信息和启发函数,且他们的选取难度比较大,很大程度上找不到最优路径.下面通过一个具体加以实例说明.例3 利用算法求图1 中从点出发到点的最优路径.解:在本例中将评价函数中的取为当前节点到起始节点的最短距离,而取为当前节点到目标节点的欧氏距离,在应用算法时除采用上面Dijkstra 算法所用过的拓扑结构外,还应该再给定所有节点的坐标如各点坐标为0,13, 3,16, 3,11,….根据算法的具体实现步骤可求得从到的最短路径其距离是16.6.查看表1可知,用Dijkstra 算法搜索的最优路径是, 路径长度15.9 ,很明显算法没有找到最优路径,而且通过比较两条路径可以发现:当采用算法搜索路径时,从第二个节点就把最优路径舍弃了.3.5.4 算法改进思想及实现为了克服最优路径可能被轻易舍弃的缺点,本文提出采用多次搜索的方法,用增大计算量为代价来换取尽量多的最优路径备选结果.具体的方法如下:将经典算法搜索出原始最优路径中的节点依次进行封堵后,再按照经典算法搜索在每一次封堵情况下的最优路径.最后将这些新的最优路径与原始最优路径进行对比以便确定最后的最优路径.现举例说明改进算法的具体应用.例4.利用改进的算法求图1中从点出发到点的最优路径.1 按算法寻找路径得到: ,路径长度16.6;2 封闭此路径中节点后得到的最优路径为:, 路径长度15.9;3 封闭此路径中节点后得到的最优路径为: , 路径长度17.1;4 封闭此路径中节点后得到的最优路径为: ,路径长度17.2;5 封闭此路径中节点后得到的最优路径为: ,路径长度18.7;对前面求得的5 种路径长度进行对比,得到最优路径,其长度为15.9 ,从而将此路径定为改进算法求得的最优路径.查看表1可知此路径正是采用Dijkstra算法时求得的最优路径.3.5.5 实验对比为了进一步验证改进算法的有效性利,用C 语言自行编制了最短路径搜索程序并进行了仿真实验.以78个节点含1个起始节点,77个待规划节点的地图作为对象得到的仿真结果.采用经典算法对77个节点分别进行路径规划,有45个找到了最优路径而采用改进的算法对77个节点进行路径规划时,有68个找到了最优路径,有8个节点虽未找到最优路径但得到了比经典算法更短的路径,只有1个节点和经典算法结果一致.这充分说明改进的算法较之经典的算法在搜索最优路径的成功率方面具有明显的优势.3.6 结论本文对经典Dijkstra 算法和算法进行了改进,改进后的算法具有以下特点.1改进的Dijkstra 算法能在很大程度上节省计算量,提高路径规划的速度.2改进的算法虽在一定程度上增大了计算量但远远小于Dijkstra 算法的计算量, 却大大增大了搜索到最优路径的成功率.3.7 混合步长网络漫游最短路算法3.7.1引言网络最短路问题一直是网络理论与实践的重要研究课题之一,是在工农业生产及各项经济活动中非常具有实用价值的一门计算技术,是系统工程和运筹学研究的一个重要分枝.随着图与网络理论的不断发展与完善和计算技术、计算手段的不断进步,为新的网络最短路算法的研究提供了前提和条件.经过深入的研究探索和实践,本文提出一种任意路权网络最短路的新算法??混合步长网络漫游法.3.7.2 网络漫游法原理在一个给定的任意路权网络图中,为该网络的点集合,为该网络的弧集合,为网络各弧的权数集合.确定一个点作为漫游网络的起点,并记该点的漫游路长为零 ,其余各点的漫游路长 ,以此作为初始状态.之后,每一步都以当前漫游点的路长来修正其余相关连点的路长,并选择一个新的漫游点,如此往复,直至不再有可以漫游的点为止.若从起始点到任意点的直接路长为 (为网络的顶点数,若两点和之间没有直接的弧连接,则),则以修改各点的初始漫游路长, 作为第一步各点的漫游路长,并选择所对应的点作为第一步的漫游点,称之为当前漫游点.一般而言,经过步漫游到达第点,则第点为当前漫游点,该点的当前漫游路长为 .为寻找下一步的漫游点,要计算 ,并以作为点第步的漫游路长,选择点作为第步的漫游点,如此循环,直至各能够到达的点均已漫游过且各点已不存在更短的漫游路长时,漫游终止.同时得到了从起始点到各点的最短路.3.7.3网络漫游法的特点3.7.3.1 混合步长每次从当前漫游点寻找下一漫游点时,采用了算式,所以,下一漫游点的路长不只是第步中的最短路,而且是在第步、第步、…、第1步、第0步中的最短路,是当前步长内所有步数能够到达该点的最短路.3.7.3.2路长递减性由于采用了算式作为第点的第步的路长,它小于等于步之内任一步长的路长,具有递减性.3.7.3.3条件记忆性由第k步的当前漫游点寻找下一漫游点时,是在除当前点之外的其它点中寻找.其余的点分为两类,一类是还没有漫游过的点,它自然属于寻找的范围;另一类是已经漫游过的点,这类点分为两种情况,其一是该点记录的步步长之内的最短路值是该点作为漫游点时的路长,则该点不在寻找之列,即该点已漫游过这件事是在记忆之中的,其二是该点虽然已漫游过,但在其后的漫游中更新了该点漫游时的路长值,则该点在寻找范围之列,即对该点已漫游过这一事实失去记忆,如同没有漫游过的点一样.也就是说,若该点作为漫游点时的路长值一直保持为该点的最短漫游路长,则对该点保持记忆;若该点作为漫游点时的路长值已发生变化,则对该点的漫游失去记忆.3.7.4 网络漫游法的算法对于给定的任意路权网络,按照如下步骤进行网络漫游,只要网络中不含负回路,最终总可以求得从起始点到其所能到达的所有点的最短路.当然,也可以从终点反向漫游,以求得从网络的任意一点到终点的最短路.3.7.4.1 确定漫游起始状态若求从某点到其它各点的最短路,则以作为漫游的起始点(当前漫游点),并记该点的起始漫游路长为零,其余各点的漫游路长为无穷大(注:若求其它各点到终点的最短路,则以作为漫游起点,进行反向漫游即可).3.7.4.2 从当前漫游点向外探索计算从当前漫游点走到其它各点所产生的路长3.7.4.3确定各点新的漫游路长将各点的与其当前的最短路长进行比较,选取较小者作为该点新的漫游路长,即.3.7.4.4 作漫游标记当从本漫游点向外探索之后则对其作一标记,表示此点已漫游过.在以后的漫游中保持此标记,直到该点有更短的漫游路长出现时,则除去该点的漫游标志.3.7.4.5 确定新的漫游点在当前没有作漫游标记的点中,选取所对应的点作为新的漫游点.返回3.2继续漫游.。
迪克斯屈拉最短路径算法图论论文

计算机网络中迪克斯屈拉最短路径算法的程序实现及应用沈敬红 S140131109重庆邮电大学通信与信息工程学院摘要:本文首先介绍了图论的发展历程,介绍了图论在实际问题中的应用。
其次,介绍了图论中最短路径的问题及相关内容,介绍了计算机网络中服务器之间存在的最短路径问题。
然后,介绍了迪克斯屈拉(Dijkstra)最短路径算法。
最后,依据算法的思想,分别实现了Dijkstra算法在求解计算网络最短路径的应用程序。
关键词:最短路径服务器Dijkstra算法程序Abstract in this paper, we firstly introduce the process of theory of graph. secondly, we give the introduction of the problem of shortest path and related content, and the application of networks which a lot of severs have to search the shortest path. And then shows the one of shortest path algorithms: The Dijkstra algorithm. Finally, according to the ideas of this algorithm, we put forward a method to achieve the procedure using in the networks.Key word Shortest—paths Sever Dijkstra Program1、引言图论(Graph Theory)是数学的一个分支。
它以图为研究对象。
图论中的图是由若干给定的点及连接两点的线所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系,用点代表事物,用连接两点的线表示相应两个事物间具有这种关系。
最短路径算法的研究毕业论文绝对精品

本科毕业设计论文题目名称:最短路径算法的研究学院:计算机科学技术专业年级:计算机科学与技术(师范)级学生姓名:班级学号:2 班 13 号指导教师:二○一二年六月八日摘要本文目的在于研究关于最短路径的算法,为研究最短路径问题在一些出行问题、管理问题、工程问题及实际生活问题中的应用,为企业和个人提供方便的选择方法。
同时,也为其他的同学提供一些解题的思路与方法,为他们提供有利的资源。
最后应用蚁群算法来解决浙江旅行商问题。
通过应用最短路径算法中的蚁群算法来解决浙江旅行商问题,以各城市经纬度作为初始条件,通过 MATLAB 程序计算最短路径,并画出最短路线图。
关键词:最短路径算法;最短路径应用;蚁群算法;浙江旅行商精品毕业论文Abstract In this paper the purpose is to collect the shortest path algorithmabout common for the shortest path problem in some travel problemsmanagement engineering problems and practical application of life forenterprise and individual with convenient selection method. At the sametime the students for the mathematical modeling provide some ideas andmethods for problem solving provide favorable resources for the game.At last by use of ant colony algorithm to solve the zhejiang travelingsalesman problem. Through the application of the shortest path algorithm of ant colonyalgorithm to solve the zhejiang traveling salesman problem in the cityas the coordinates of initial conditions through the MATLAB calculationshortest paths and draw the shortest route map Key words:The shortest path algorithm The shortest path applicationant colony algorithm Zhejiang traveling salesma 精品毕业论文目录摘要 ........................................................................................................................................... IAbstract................................................................................................................................. ..........II第1章绪论...............................................................................................................................1 1.1 选题的意义及目的. (1)1.1.1 选题的意义 (1)1.1.2 选题的目的...........................................................................................................1 1.2 选题经过及国内外动态. (1)1.2.1 选题经过 (1)1.2.2选题的国内外动态...............................................................................................2第2章最短路径算法的介绍...................................................................................................3 2.1 Dijkstra 算法. (3)2.1.1 算法介绍及适用条件和范围 (3)2.1.2 算法描述和算法实现 (3)2.1.3 具体算法分析.......................................................................................................4 2.2A 算法 (8)2.2.1 算法介绍及适用条件和范围 (8)2.2.2 算法描述和算法实现 (9)2.2.3 具体算法分析.......................................................................................................9 2.3 Bellman-Ford 算法 (11)2.3.1 算法介绍及适用条件和范围 (11)2.3.2 算法描述和算法实现 (11)2.3.3 具体算法设计.....................................................................................................12 2.4 Topological Sort 算法 ..............................................................................................15 2.4.1算法介绍及适用条件和范围.............................................................................15 2.4.2算法描述和算法实现.........................................................................................16 2.4.3具体算法设计.....................................................................................................16 2.5 SSSP On DAG 算法 .. (20)2.5.1 算法介绍及适用条件和范围 (20)2.5.2 算法描述和算法实现.........................................................................................21 2.6 Floyd 算法 (21)2.6.1 算法介绍及适用条件和范围 (21)2.6.2 算法描述和算法实现 (21)2.6.3 算法具体分析.....................................................................................................22第3 章最短路径算法的比较 ................................................................................................26第 4 章最短路径算法的应用 (28)4.1 TSP问题的介绍 ............................................................................................................28 4.2 TSP 问题算法的介绍. (28)4.2.1 贪心算法 (28)4.2.2 模拟退火算法 (29)4.2.3 遗传序列算法 (29)精品毕业论文 4.2.4蚁群算法.............................................................................................................30 4.3算法应用 (31)4.3.1 解决浙江旅行商问题时算法描述 (31)4.3.2 蚁群算法的算法描述 (31)4.3.3 蚁群算法解决浙江旅行商问题.........................................................................34第5 章最短路径算法的展望 (36)绪论 (38)致谢 (39)参考文献 ............................................................................................................................... ........40 精品毕业论文第1章绪论1.1 选题的意义及目的1.1.1 选题的意义随着计算机科学的发展,人们生产生活经济利润的提高,最短路径问题逐渐成为计算机科学、运筹学、地理信息科学等学科的一个研究热点。
数模论文公园内道路有条件限制的设计最短路径

装订线公园内道路设计最优问题摘要对于题中所给的道路设计问题,即研究在约束条件下最小生成树问题。
题中所给三个问题,研究在不同现实背景下的最优道路设计问题,根据所给限制条件的增加,层层深入。
本文针对题中所述的矩形公园,利用图论中各种成熟的相关算法,对道路和最短的设计方案进行建模求解:对问题一,分为两个步骤进行建模求解。
步骤一利用kruskal算法生成总道路和的最小树,步骤二用Dijkstra算法对步骤一生成的道路用是否满足“任意两入口间最短道路长小于二者连线的1.4倍”这一条件进行验算,对于个别不满足的道路进行微调和修改。
最终方案中得到的道路总长度为394.5米。
对问题二,在问题一的基础上,我们采用求解欧式距离的斯坦纳点最小树的逐步调优法,根据相应理论通过离散概率随机抽取相应的斯坦纳点进行扰动,直到得到最优解。
经验算确定,最终方案得到的道路总长度为362.1米。
对问题三,我们利用题中的限制条件,分析了所给的人工湖位置与入口的坐标的数据特点,先确定了在不加道路交叉点情况下,仅利用湖四周的道路,即可满足任意入口间最短路径1.4倍条件的可利用的最短道路,再利用问题二中的方法添加了一个斯坦纳点,并在其邻域内进行扰动后得到最优解。
经验算确定,最终方案得到的道路总长度为324.6米。
最后本文还结合实际情况,对模型的优缺点进行了分析与评价,并提出了改进和推广方向。
关键词:最小生成树;约束条件;kruskal算法;Dijkstra算法;求解欧式距离的斯坦纳点最小树的逐步调优法;二叉堆目录1.问题重述 (1)1.1.问题背景 (1)1.2.问题要求 (1)1.3.问题提出 (1)2.问题分析 (2)2.1.问题一的分析 (2)2.2.问题二的分析 (2)2.3.问题三的分析 (3)3.模型假设 (3)4.符号说明及名词解释 (3)4.1.基本符号 (3)5.模型建立与求解、检验 (4)5.1.问题一 (4)5.1.1.问题解析 (4)5.1.2. 模型建立与求解、检验 (7)5.2. 问题二 (11)5.2.1. 问题解析 (11)5.2.2. 模型建立与求解、检验 (14)5.3. 问题三 (14)5.3.1. 问题解析 (14)5.3.2. 模型建立与求解、检验 (15)6.结果表示 (15)6.1.问题一 (15)6.2.问题二 (16)6.3.问题三 (16)7.模型的评价、优化及推广 (17)7.1.模型的评价 (17)7.2.模型的优化 (18)7.3.模型的推广 (19)8.参考文献 (19)9.附件清单 (20)1. 问题重述1.1. 问题背景西安某大学计划建一个形状为矩形或其他不规则图形的公园,不仅为了美化校园环境,也是想为其学生提供更的生活条件。
校园最短路径问题研究

2009年西北民族大学本科生数学建模竞赛承诺书我们仔细阅读了西北民族大学本科生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): B我们的参赛的论文题目是:校园最短路径问题研究校园最短路径问题研究——以西北民族大学榆中校区为例摘要:本文以西北民族大学榆中校区为例,分析了其道路分布的特点,提出了如何选择最短路径的问题,并应用图与网络分析中的Dijskra算法和动态规划中的解决旅行售货员问题的方法,通过建立合适的数学模型,并适当的应用matlab软件,给出了实际问题中的最短路径和最佳路线,为大家提供参考。
建议在学习生活中选择合适的路线。
关键词:Dijskra算法最短路径旅行售货员AbstractIn this paper we use Northwest University for Nationalities YuZhong campus as an example, it analyzes the characteristics of the distribution of the road, and raise a question about how to choose the shortest path, and apply to Graph Theory and Network Analysis with Dijskra algorithm and Dynamic Programming in the Traveling Salesman Problem solving methods, through establish proper mathematical model, and appropriate application of matlab software, present a practical problem the shortest path and the best route, provide the reference for everyone. The suggestion is that we should choose the appropriate route in the study life .Key words: Dijskra algorithm the shortest path Traveling Salesman Problem1、问题的提出西北民族大学榆中校区是一个占地面积十分庞大的大学校园,由于其中仍有一些主体建筑正在建设过程中,导致校园内道路星罗棋布,错综复杂。
图论论文--最短路径算法应用

课程论文课程名称图论及其应用题目最短路径算法应用--最短路径游览校园姓名学号专业计算机技术摘要:重邮是个美丽的学校,我们考入重邮后,都喜欢上了学校。
而且经常有同学来找我玩,作为他们的导游,在带领他们游览学校时候,遇到了一个问题:怎样走最短路径来游览学校最多的景点。
当学完图论后,我找到了答案,运用图论中的一些知识,找到一个最短最有效的路径从而迅速到达某个地点。
本文运用了图论中的最短路径算法,邻接矩阵,赋权图等知识,把学校里面我们经常去的地方选了出来,画出平面图,建模赋权图,模拟了在任意两点之间的最短路径的实现以及编程显示。
关键词:数据结构;最短路径;迪杰斯特拉算法; 一:背景介绍设计学校的校园平面图,所含景点不少于8个(中心食堂、信科、图书馆……) 1) 带领同学们从新大门开始利用最短路径游览学校的几个景点。
2) 为来访同学提供图中任意景点的问路查询,即查询任意两个景点之间的一条最短的简单路径。
3) 在社会生活中,最短距离的运用相当广泛。
除了该课题外,还有于此相关的城市道路的设计,交通线路的设计,旅游景点的设计等等。
除了路径长度方面外,到两地花费的最少、时间的最短等等都是同样的道理。
二:最短路径知识点边上有数的图称为加权图,在加权图中我们经常找到两个指定点间最短路径,称为最短路径问题。
在最短路问题中,给出的是一有向加权图G=(V,E),在其上定义的加权函数W:E →R 为从边到实型权值的映射。
路径P=(v 0, v 1,……, v k )的权是指其组成边的所有权值之和:11()(,)ki i i w p w vv -==∑定义u 到v 间最短路径的权为{}{}min ():)w p u v u v v δυ→(,=∞如果存在由到的通路如果不存在从结点u 到结点v 的最短路径定义为权())w p v δυ=(,的任何路径。
①边的权常被解释为一种度量方法,而不仅仅是距离。
它们常常被用来表示时间、金钱、罚款、损失或任何其他沿路径线性积累的数量形式。
最短路径问题设计论文

目录第1章绪论 (1)1.1 问题描述 (1)1.2 问题分析 (1)1.3 相关标识(名词定义) (1)1.4 本文主要研究内容 (2)第2章算法设计与实现 (3)2.1 穷举法 (3)2.1.1穷举法描述 (3)2.1.2穷举法设计 (3)2.1.3 穷举法分析 (6)2.2 回溯法 (6)2.2.1 回溯法描述 (6)2.2.2 回溯法设计 (6)2.2.3 回溯法分析 (9)2.3 贪心法 (10)2.3.1 贪心法描述 (10)2.3.2 贪心法设计 (10)2.3.3 贪心法分析 (12)2.4 动态规划法 (12)2.4.1 动态规划法描述 (12)2.4.2 动态规划法设计 (12)2.4.3 动态规划法分析 (14)第3章实验结果分析与算法对比 (15)3.1 输入数据 (15)3.2 实验结果与分析 (15)3.3 算法分析与对比 (17)第4章总结与展望 (18)参考文献 (1)第1章 绪论1.1 问题描述最短路径问题是图论理论的一个经典问题。
寻找最短路径就是在指定网络中两结点间找一条距离最小的路。
最短路不仅仅指一般地理意义上的距离最短,还可以引申到其它的度量,如时间、费用、线路容量等。
最短路径算法的选择与实现是通道路线设计的基础,最短路径算法是计算机科学与地理信息科学等领域的研究热点,很多网络相关问题均可纳入最短路径问题的范畴之中。
经典的图论与不断发展完善的计算机数据结构及算法的有效结合使得新的最短路径算法不断涌现。
本文主要解决的问题是:给定带权有向图G =(V , E),对任意顶点i v ,j v ∈V (i ≠j ),求顶点i v 到顶点j v 的最短路径。
即给定一个有向图,再给出任意2个不相邻的顶点,求2个顶点之间的最短距离。
1.2 问题分析给定一个带权有向图G =(V , E )中的各个顶点之间的权值,对任意输入2个顶点i v ,j v ∈V (i ≠j ),求出从i v 到j v 的最短路径。
浅谈初中数学教学中的最短路径问题

浅谈初中数学教学中的最短路径问题摘要:最短路问题是一类具有代表性的中学数学问题,其研究与解决要求对数学知识进行灵活运用。
因此,数学的教学与实践必须密切结合,因为数学来源于生活,对生活有指导作用。
在此基础上,作者根据以往的教学实践,提出了一种新的解决方案。
关键字:初中数学;最短路径;策略引言初中数学的最短路问题,涉及到了“最短垂线”和“轴对称”的概念,这些概念在实际生活中是很常见的。
比如,一个人想要游到另一个人的身边,问他从哪里走到另一个人的身边,是最短的一条路,这就是一个最短路径问题。
从这一点来看,本论文所提出的最短路问题是一项很有意义的研究工作。
在中学数学习题中,最常出现的是最短路问题。
这是一道很常见的题目,也是近年来各省市中考中的热门题目。
所以,在教学中,教师应指导学生如何正确地解决这类问题,从而更好地了解问题的实质,并培养学生的思维。
老师既要让学生分析和总结“最短路径问题”,又要让学生明确各种问题的解法,让学生去感受和体会这些问题中所包含的数学哲学,从而让学生在求解“最短路径问题”的过程中寻找到关键信息,将问题变得简单,让学生在读完文章后,就可以理解所求问题的数学实质。
一、设置具体情境,激发学生主动思考最短路径所牵扯到的内容通常都是与生活现实紧密相关的,在进行最短路线问题的教学时,老师应该创设一个特定的生活情景,让学生快速地融入到课堂,并调动他们的积极性。
比如,在教授最短路问题时,老师可以这么安排:“学生,最短路问题在现实生活中被大量使用,比如:在希腊的亚历山大利亚,有一名名叫海伦的学生,一名将领去见海伦,他向她提问:从 A点到 L点,和一匹马,从 B点到 A点,怎样才能最快地到达 B点?现在,你们可以将这个问题变成一个算术问题,并且想一想,怎样才能找到最小的路径。
”在个案中,老师利用特定的情景来让学生快速的融入到教学中,利用特定的情景来提高学生对数学课堂的参与性,使他们对数学知识的意义有更深的认识。
运筹学论文最短路问题
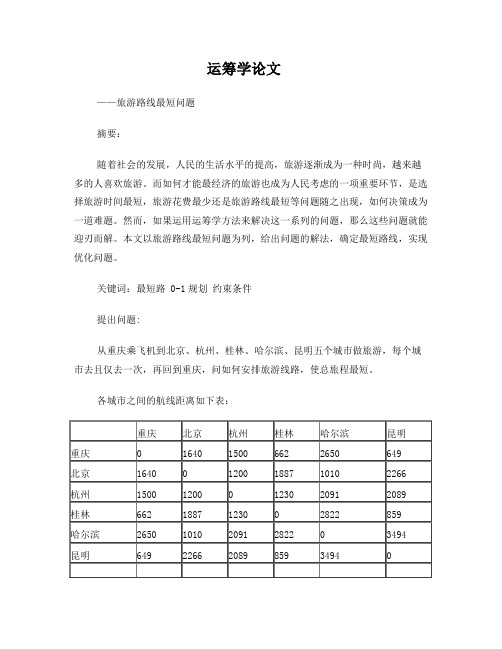
运筹学论文——旅游路线最短问题摘要:随着社会的发展,人民的生活水平的提高,旅游逐渐成为一种时尚,越来越多的人喜欢旅游。
而如何才能最经济的旅游也成为人民考虑的一项重要环节,是选择旅游时间最短,旅游花费最少还是旅游路线最短等问题随之出现,如何决策成为一道难题。
然而,如果运用运筹学方法来解决这一系列的问题,那么这些问题就能迎刃而解。
本文以旅游路线最短问题为列,给出问题的解法,确定最短路线,实现优化问题。
关键词:最短路 0-1规划约束条件提出问题:从重庆乘飞机到北京、杭州、桂林、哈尔滨、昆明五个城市做旅游,每个城市去且仅去一次,再回到重庆,问如何安排旅游线路,使总旅程最短。
各城市之间的航线距离如下表:问题分析:1.这是一个求路线最短的问题,题目给出了两两城市之间的距离,而在最短路线中,这些城市有的两个城市是直接相连接的(即紧接着先后到达的关系),有些城市之间就可能没有这种关系,所以给出的两两城市距离中有些在最后的最短路线距离计算中使用到了,有些则没有用。
这是一个0-1规划的问题,也是一个线性规划的问题。
2.由于每个城市去且仅去一次,最终肯定是形成一个圈的结构,这就导致了这六个城市其中有的两个城市是直接相连的,另外也有两个城市是不连接的。
这就可以考虑设0-1变量,如果两个城市紧接着去旅游的则为1,否则为0。
就如同下图3.因为每个城市只去一次,所以其中任何一个城市的必有且仅有一条进入路线和一条出去的路线。
LINGO解法:为了方便解题,给上面六个城市进行编号,如下表(因为重庆是起点,将其标为1)重庆北京杭州桂林哈尔滨昆明1 2 3 4 5 6假设:设变量x11。
如果x11=1,则表示城市i与城市j直接相连(即先后紧接到达关系),否则若x11=0,则表示城市i与城市j不相连。
特别说明:xij和xji是同一变量,都表示表示城市i与城市j是否有相连的关系。
这里取其中xij (i<j)的变量。
模型建立:由于这是一个最短路线的问题,且变量已经设好。
最短路径毕业论文

本科毕业论文(设计) 论文题目:交通咨询系统的最短路径算法与实现****:**学号: **********专业:信息管理与信息系统班级:信管0201****:***完成日期:2015年 5月 5日目录序言 (1)一、绪论 (2)(一)课题的背景和意义 (2)(二)研究现状 (2)1.最短路径算法研究现状 (2)2.最短路径算法分类 (3)3.算法时间复杂度 (3)(三)研究内容 (4)(四)论文结构 (4)二、最短路径算法相关原理 (4)(一)D IJKSTRA算法 (4)1.算法思想分析 (5)2.实现思路 (5)3.计算步骤 (5)(二)F LOYD算法 (7)1.算法思想原理: (8)2.算法描述: (8)3.Floyd算法过程矩阵的计算----十字交叉法 (8)三、开发工具与环境 (10)(一)J AVA技术 (10)1. Java简介 (10)2.Java的处理流程 (11)四、交通咨询系统的实现 (11)(一)系统分析 (11)1.系统的设计内容: (11)2.系统的设计思想 (12)3.系统设计流程 (12)(二)系统功能结构 (12)1. 系统构架设计 (12)2.系统详细设计 (14)3. 测试数据及分析 (26)五、设计总结 (28)致谢 (29)参考文献 (29)交通咨询系统的最短路径算法与实现内容摘要目前在交通咨询领域,最短路径算法的研究和应用越来越多,其中最短路径算法的效率问题是普遍关注并且在实际应用中迫切需要解决的问题。
随着现代生活节奏的加快,以及城市汽车数量的不断增加,交通网络也越来越发达,在交通工具和交通方式不断更新的今天,人们在旅游、出差或者其他出行时,不仅会关心费用问题,而且对里程和所需要的时间等问题也特别感兴趣。
为了能够更方便人们的出行,我们就应该以最短路径问题建立一个交通咨询系统。
这样的一个交通系统可以回答人们提出的有关交通的所有问题,比如任意一个城市到其他城市的最短路径,或者任意两个城市之间的最短路径问题。
GPS车载导航中最短路径算法设计与实现论文

1。2 最短路径算法的应用与发展
1。2。1
最短路径问题在交通网络结构的分析,交通运输线路(公路、铁路、河流航运线、航空线、管道运输线路等)的选择,通讯线路的建造与维护,运输货流的最小成本分析,城公共交通网络的规划等,都有直接应用的价值.
最短路径问题在实际中还常用于汽车导航系统以及各种应急系统等(如110报警、119火警以及120医疗救护系统)这些系统一般要求计算出到出事地点的最佳路线的时间应该在15一35内,在行车过程中还需要实时计算出车辆前方的行驶路线,这就决定了最短路径问题的实现应该是高效率的。
关键词GPS导航最短路径算坐标差预设点
1。
自20世纪后期以来,随着全球经济的深入发展,世界各国城市(尤其是大城市)的人口和车辆持续增长,由于交通拥挤而造成的损失随之逐年增加。因而各国竞相投资修建交通设施,试图解决这一问题。但是车辆的增长速度远远高于道路和其他交通设施的增长速度,由此带来的有目共睹的事实是道路交通系统的复杂性和拥挤度的与日俱增[1]。近年来人们已经逐渐认识到单纯依靠增加道路基础设施建设不可能从根本上解决车辆的快速增长与交通设施滞后之间的突出矛盾.只有在计算机、信息和通讯等高科技手段的辅助下充分利用现有的道路基础设施,才是合理可行的方法。由此出现了建设智能交通系统(Intelligent Transportation System,ITS)的热潮。事实上,建立现代化的交通系统,已经成为国家现代化的重要标志之一。与此相关的一系列方法与技术也成为当今计算机科学、地理信息科学等相关学科中的研究重点和热点。
物流论文-配送中心车辆最短路径问题的研究

刘孝配:配送中心车辆最短路径问题的研究
参考文献...................................................................................................................... 31 附录 A........................................................................................................................... 32 附录 B........................................................................................................................... 33
II
山东交通学院毕业设计(论文)
目 录
前 言.............................................................................................................................. 1 1 绪论............................................................................................................................ 2 1.1 研究的背景及意义......................................................................................... 2 1.2 论文研究现状................................................................................................. 3 1.3 论文研究的内容.............................................................................................. 4 2 配送中心车辆最短路径问题概述............................................................................ 5 2.1 配送中心概述................................................................................................. 5 2.1.1 配送中心的概念................................................................................... 5 2.1.2 配送中心的功能................................................................................... 5 2.2 最短路径问题介绍......................................................................................... 5 2.3 最短路径问题的相关概念.............................................................................. 6 2.3.1 图论相关定义...................................................................................... 6 2.3.2 最短路径.............................................................................................. 7 2.4 最短路径问题的常用解决方法——Dijkstra 算法................................... 10 2.4.1 介绍..................................................................................................... 10 2.4.2 Dijkstra 算法思想.......................................................................... 10 2.4.3 Dijkstra 算法步骤.......................................................................... 10 2.4.4 Dijkstra 算法缺陷........................................................................... 11 3 配送中心车辆最短路径算法的实现...................................................................... 13 3.1 SPFA 算法解决最短路径问题...................................................................... 13 3.1.1 SPFA 算法介绍................................................................................... 13 3.1.2 SPFA 算法的理论基础....................................................................... 13 3.2 lingo 软件解决最短路径问题.................................................................... 17 3.2.1 软件概述............................................................................................ 17 3.2.2 利用 lingo 软件解决最短路径问题................................................. 18 4 案例分析及其结果分析.......................................................................................... 21 4.1 案例................................................................................................................ 21 4.1.1 案例说明............................................................................................ 22 4.1.2 案例分析............................................................................................ 23 4.2 SPFA 算法计算.............................................................................................. 23 4.3 Lingo 软件运行............................................................................................ 26 结 论............................................................................................................................ 29 致 谢............................................................................................................................ 30
最短路径最少费用数学建模论文

摘要现今社会网络越来越普及,网购已成为一种常见的消费方式,随之物流行业也渐渐兴盛,每个工厂为了自身的发展需要以最快的速度及时将产品送达所需单位,即高质量高速度的完成送货任务,针对本案例,我们采用了大量的科学分析方法,并进行了反复验证,得出如下结果:问题1:根据所给问题与数据,我们将题目中给出的城市,及其之间的线路可看成一个赋权连通简单无向图,采用了求这个图最小生成树的办法,求出最优线路.在此基础上,我们通过观察分析计算对上述结果进行修正,然后我们再采用穷举法对问题结果进行验证,结果相吻合。
最终得到如下路线:北京→香港→湖南→海南→广西→重庆→河南→云南→西藏→新疆→青海→甘肃→宁夏→江苏→福建→上海→台湾→上海→黑龙江→内蒙古→黑龙江→吉林→北京。
(最短时间为61小时)问题2:由于题中有货物重量与体积限制,货机一次最多只能载50件产品,考虑19个城市的总需求为114,这就估算出至少需要返回2次,采用逆向求解的方法,相当于3架货机同时送货,要设计线路使总共花费的时间最短,尽量使送货任务均衡,最大限度不超过50件货物,最后得出结果为:北京→吉林→黑龙江→内蒙古→新疆→西藏→云南→河南→北京→重庆→广西→海南→湖南→香港→北京→重庆→青海→甘肃→宁夏→江苏→福建→上海→台湾→上海→北京。
(总的时间为71.77777)(其中红色表示只路过不送货)问题3:要求问题1,2的花费最少,只需对前两个模型做进一步优化即可,经过优化计算我们得到如下结果:问题1的最少花费为584250(元),路线如下:北京→香港→湖南→海南→广西→重庆→河南→云南→西藏→新疆→青海→甘肃→宁夏→江苏→福建→上海→台湾→上海→黑龙江→内蒙古→黑龙江→吉林→北京问题2的最少花费为711750(元),线路如下:北京→吉林→黑龙江→内蒙古→新疆→西藏→云南→河南→北京→重庆→广西→海南→湖南→香港→北京→重庆→青海→甘肃→宁夏→江苏→福建→上海→台湾→上海→北京。
基于随机点集最短路径算法的研究与实现——毕业论文

毕业设计中文题目基于随机点集最短路径算法的研究与实现英文题目The Research and Implementation of the Shortest Path Algorithm Based on the Stochastic Set院系:计算机与信息工程学院年级专业:金融服务姓名:学号:指导教师:职称:年月摘要最短路径的研究属于网络优化领域,它也是图论的重要内容,涉及现实生活诸多方面。
该算法可应用于交通规划、旅游安排、城市建设等,至今仍然是业界研究热点。
本文着重研究的是图网中任意若干顶点之间的最短路径最优规划。
本课题通过使用matlab实现4个经典的随机最短路径派生算法,并将其应用在纽约等6个城市路网数据集上,进行随机规划最优最短路径的模拟,来研究算法各项性能指标,对比其优劣。
案例研究结果表明,本课题所采用的算法,大幅度减少了冗余节点,减轻了复杂度的操作,提高了算法的性能和效率,并且确保课精确度。
该算法可以有效应用在多种路径规划类现实应用中,提高工作效率。
关键词:最短路径;网络规划ABSTRACTShortest patch belongs to network optimization,also the important content in graph theory. It is widely used in different fields in the real life. At present, these research theories can be used in application fields such as traffic planning, tourism arrangement, urban construction and so on. The shortest path algorithm is still a hot research topic now.The paper will study the randomly processed four modern classical derived shortest path algorithms in urban road network dataset respectively. The subject will analyze the impact of these four algorithms on different performance. And applies these algorithms in New York City road network data set, data sets are six such cities. For the simulation of stochastic programming optimal shortest path algorithm to research the performance indexes, compared the advantages and disadvantages.Case study results show that this topic by the algorithm, greatly reduces the redundant nodes and reduces the complexity of the operation,Not only the performance and efficiency of this algorithm is improved, and to ensure accuracy. The algorithm can be effectively applied in a variety of path planning in the practical application, improve the work efficiency.Key Words: shortest patch; network optimization目录第1章引言 (1)1.1 课题研究背景及意义 (1)1.2 本文的研究内容 (1)第2章最短路径问题与随机概念 (3)2.1 最短路径概述 (3)2.1.1 最短路径研究发展历史 (4)2.1.2 国内外研究现状 (5)2.2 图的相关定义 (6)2.2.1 图 (6)2.2.2 赋权图 (7)2.2.3 无向图和有向图 (7)2.2.4 顶点的度数 (7)2.2.5 路径 (7)2.2.6 随机定义 (7)2.3 本章小结 (8)第3章求解最短路径的相关算法 (9)3.1 Dijkstra 算法 (9)3.2 Floyd 算法 (11)3.3 SPFA 算法 (11)3.4 Bellman-Ford 算法 (13)3.5 本章小结 (16)第4章随机最短路径的矩阵算法 (17)4.1 问题引出 (17)4.2 相关描述 (17)4.3 算法原理 (18)4.4 算法思想 (18)4.5 实验及性能分析 (19)4.5.1 单源点最短路径算法实验 (19)4.5.2 全源最短路径算法实验 (22)4.6 可行性分析 (23)4.7 算法实例 (23)4.8 本章小结 (27)第5章随机点的最短路径算法应用 (28)5.1 真实模型假设 (28)5.2 问题分析 (29)5.3 问题求解 (29)5.4 本章小结 (30)第6章总结与展望 (31)6.1 总结 (31)6.2 展望 (31)参考文献 (33)致谢 (35)第1章引言1.1课题研究背景及意义最短路径问题不仅是业界研究的重点在国内外仍然占有重要地位。
最短路径学年论文

摘要:主要介绍最短路径问题中的经典算法——迪杰斯特拉(Dijkstra)算法和弗洛伊德(Floyd)算法,以及在实际生活中的运用。
关键字:Dijkstra算法、Floyd算法、赋权图、最优路径、Matlab目录摘要··11引言··12最短路··22.1 最短路的定义·22.2最短路问题常见算法··23 Dijkstra算法··23.1 Dijkstra算法描述··23.2 Dijkstra算法举例··33.3算法的正确性和计算复杂性··53.3.1贪心选择性质··53.3.2最优子结构性质··63.3.3 计算复杂性··74 Floyd算法··74.1Floyd算法描述··84.2 Floyd算法步骤··114.3 Floyd算法举例··115 Dijkstra算法和Floyd算法在求最短路的异同··116 利用计算机程序模拟算法··117 附录··118 论文总结··139 参考文献··131 引言最短路问题是图论理论的一个经典问题。
寻找最短路径就是在指定网络中两结点间找一条距离最小的路。
最短路不仅仅指一般地理意义上的距离最短,还可以引申到其它的度量,如时间、费用、线路容量等。
最短路径算法的选择与实现是通道路线设计的基础,最短路径算法是计算机科学与地理信息科学等领域的研究热点,很多网络相关问题均可纳入最短路径问题的范畴之中。
经典的图论与不断发展完善的计算机数据结构及算法的有效结合使得新的最短路径算法不断涌现。
最短路径算法在线路抢修中的应用论文

最短路径算法在线路抢修中的应用论文最短路径算法在线路抢修中的应用论文从某顶点出发,沿图的边到达另一顶点所经过的路径中,各边上权值之和最小的一条路径叫做最短路径。
下面是小编为大家整理的最短路径算法在线路抢修中的应用论文,欢迎阅读。
摘要:配电网结构越来越复杂,电力设备日益增加,配电网故障定位及最佳路径选择的问题是电力部门的研究热点,也是提高抢修效率和供电质量的关键。
文章首先分析了配电网使用最短路径算法进行线路抢修的重要意义,其次阐述了最短路径算法的基本原理、优化算法流程,最后对优化算法效率进行分析,以便能实现最短抢修路径的有效选择。
关键词:最短路径;配电网;线路抢修随着国民经济的迅猛发展,电力系统与工农业生产、居民生活息息相关,人们对配电网的稳定性和可靠性提出了更高要求。
配电网不仅是供电与用电的连接,也承担着管理的角色,一旦配电网出现电力故障,配电管理要在尽可能短的时间内恢复供电,而要最短时间内恢复供电,对故障进行准确定位、隔离及抢修是确保配电网高效运行的关键,其中对故障准确定位是最为关键的,能否准确对故障进行定位直接影响恢复供电时间。
虽然配电网自动化程度不断提高,隔离开关可以解决部分电力故障,对于隔离开关难以解决的'故障,就必须派出专门人员去解决故障。
在实际抢修过程中,最短路径选择成为影响抢修效率的关键要素,能够有利于确保抢修的及时性和高效性。
基于此,笔者对基于空间方向的最短路径优化算法在配电网线路抢修进行研究。
1.线路抢修使用最短路径算法的重要意义配电线路一旦发生电力故障,要及时进行维护,而配电网线路复杂、电力设备众多,维修路径的选择如果仅依靠实践经验,就难以提高工作效率,也失去了灵活性,若能寻找一种耗时较短、路径也短的线路选择方式,不仅能够尽快恢复供电,确保供电可靠性,还能缩短维修时间,有效降低电力部门的运营成本,提高经济效益和社会效益,对整个社会来说意义深远。
2.最短路径优化算法的基本原理根据几何原理可知,两点之间直线距离最短,然而在实际的配电网线路中,两点之间直线作为一段道路的概率很小,但沿着两点之间的直线代表抢修线路的趋势,在沿着这个方向上存在某条道路最短路径可能性较大。
单源最短路径问题 徐林林2

哈尔滨师范大学学年论文题目单源最短路径问题学生徐林林指导教师马瑞华讲师年级 2008级专业计算机科学与技术系别计算机系学院计算机科学与信息工程哈尔滨师范大学2011年06 月论文提要最短路径算法是图论中应用最广的算法之一。
许多实际问题只需要简单的数学模型转换,它就成为一个最短路径问题。
例如,从城市甲到城市乙,需要经过许多站点和不同路径、怎样选择行走路线。
使从甲城市到乙城市所经过的路径最短;如果是乘公交车,那么又有怎样选择乘车方法,使费用最少或时间最短以到达目的地等。
这些都是一些典型而又直接的最短路径问题。
本文对实际应用中的单源最短路径问题给出了一种贪心解法。
文中首先介绍单源最短路径问题,然后对其进行分析和讨论,并证明了该问题具有贪心选择性质和最优子结构性质,并在此基础上给出了该问题的贪心算法。
请用分页符实现分页!在这个文件中修改之后再发给我!单源最短路径问题徐林林摘要:本文对实际应用中的单源最短路径问题给出了一种贪心解法。
文中首先介绍单源最短路径问题,然后对其进行分析和讨论,并证明了该问题具有贪心选择性质和最优子结构性质,并在此基础上给出了该问题的贪心算法。
关键词:单源最短路径贪心算法一、问题描述标题应该单独一行。
所谓单源最短路径问题是指,已知图G=(V,E),我们希望找出从某给定的源结点S ∈V到V中的每个结点的最短路径。
我们可以发现有这样一个事实:如果P是G中从vs到vj的最短路,vi是P中的一个点,那么,从vs沿P到vi的路是从vs到vi的最短路。
请不要使用这样口语化的语句。
二、概要设计对于图G,如果所有Wij≥0的情形下,目前公认的最好的方法是由Dijkstra于1959年提出来的。
例 1 已知如下图所示的单行线交通网,每弧旁的数字表示通过这条单行线所需要的费用,现在某人要从v1出发,通过这个交通网到v8去,求使总费用最小的旅行路线。
Dijkstra方法的基本思想是从vs出发,逐步地向外探寻最短路。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
摘要:主要介绍最短路径问题中的经典算法——迪杰斯特拉(Dijkstra)算法和弗洛伊德(Floyd)算法,以及在实际生活中的运用。
关键字:Dijkstra算法、Floyd算法、赋权图、最优路径、Matlab目录摘要 (1)1引言 (1)2最短路 (2)2.1 最短路的定义 (2)2.2最短路问题常见算法 (2)3 Dijkstra算法 (2)3.1Dijkstra算法描述 (2)3.2 Dijkstra算法举例 (3)3.3算法的正确性和计算复杂性 (5)3.3.1贪心选择性质 (5)3.3.2最优子结构性质 (6)3.3.3 计算复杂性 (7)4 Floyd算法 (7)4.1Floyd算法描述 (8)4.2 Floyd算法步骤 (11)4.3 Floyd算法举例 (11)5 Dijkstra算法和Floyd算法在求最短路的异同 (11)6 利用计算机程序模拟算法 (11)7 附录 (11)8 论文总结 (13)9 参考文献 (13)1 引言最短路问题是图论理论的一个经典问题。
寻找最短路径就是在指定网络中两结点间找一条距离最小的路。
最短路不仅仅指一般地理意义上的距离最短,还可以引申到其它的度量,如时间、费用、线路容量等。
最短路径算法的选择与实现是通道路线设计的基础,最短路径算法是计算机科学与地理信息科学等领域的研究热点,很多网络相关问题均可纳入最短路径问题的范畴之中。
经典的图论与不断发展完善的计算机数据结构及算法的有效结合使得新的最短路径算法不断涌现。
2 最短路2.1 最短路的定义对最短路问题的研究早在上个世纪60年代以前就卓有成效了,其中对赋权图 的有效算法是由荷兰著名计算机专家E.W.Dijkstra 在1959年首次提出的,该算法能够解决两指定点间的最短路,也可以求解图G 中一特定点到其它各顶点的最短路。
后来海斯在Dijkstra 算法的基础之上提出了海斯算法。
但这两种算法都不能解决含有负权的图的最短路问题。
因此由Ford 提出了Ford 算法,它能有效地解决含有负权的最短路问题。
但在现实生活中,我们所遇到的问题大都不含负权,所以我们在的()0ij w ≥的情况下选择Dijkstra 算法。
定义1若图G=G(V,E)中各边e 都赋有一个实数W(e),称为边e 的权,则称这种图为赋权图,记为G=G(V,E,W)。
定义2若图G=G(V,E)是赋权图且()0W e ≥,()e E G ∈,假设[i,j] 的权记为()i j W ,,若i 与j 之间没有边相连接,那么()i j =W ∞,。
路径P 的定义为路径中各边的长度之和,记W (P )。
图G 的结点u 到结点v 距离记为d(u,v),则u 、v 间的最短路径可定义为{()min P 0d(u,v)=,u v W =∞(),不可达时。
2.2 最短路问题常见算法在求解网络图上节点间最短路径的方法中,目前国内外一致公认的较好算法有迪杰斯特拉(Dijkstra)及弗罗伊德(Floyd)算法。
这两种算法中,网络被抽象为一个图论中定义的有向或无向图,并利用图的节点邻接矩阵记录点间的关联信息。
在进行图的遍历以搜索最短路径时,以该矩阵为基础不断进行目标值的最小性判别,直到获得最后的优化路径。
Dijkstra 算法是图论中确定最短路的基本方法,也是其它算法的基础。
为了求出赋权图中任意两结点之间的最短路径,通常采用两种方法。
一种方法是每次以一个结点为源点,重复执行Dijkstra 算法n 次。
另一种方法是由Floyd 于1962年提出的Floyd 算法,其时间复杂度为()3O n ,虽然与重复执行Dijkstra 算法n 次的时间复杂度相同,但其形式上略为简单,且实际运算效果要好于前者。
3 Dijkstra 算法 3.1 Dijkstra 算法描述Dijkstra 算法是解但愿最短路径问题的一个贪心算法。
其基本思想是,设置顶点集合S 并不断地做贪心选择来扩充这个集合。
一个顶点属于集合S 当且仅当从源到该顶点的最短路径长度已知。
初始时,S 中仅含有源。
设u 是图G 的某一顶点,把从源到u 且中间只经过S 中顶点的路称为源到u 的特殊路径,并记录当前每个顶点所对应的特殊路径长度。
Dijkstra 算法每次从V —S 中取出具有最短路径长度的顶点u ,将u 添加到S 中,同时对短路径进行修改。
一旦S 包含了所有V 中顶点,那么最后记录的最短路径就是源到所有其他顶点之间的最短路径长度。
算法要点如下:(1) 把V 分为两个子集S 和T 。
初始时,S={a},T=V-S ,其中a 为源点; (2) 对T 中每一个元素t 计算D (t ),根据D (t )值找出T 中距a 最短的一结点x ,写出a 到x 的最短路径长度D (x );(3) 更新S ,置S 为S {x},更新T ,置T 为T-{x},判断条件:若T=∅,则终止,否则再重复(2)。
3.2 Dijkstra 算法举例问题的提出,给定一个带权有向图(既有向网)G 和源点Vo ,求Vo 到G 中其他每个顶点的最短路径。
限定各边上的权值必须不小于0.如下图所示:图1 公路网络赋权图为了方便计算,先作出该网络的距离邻接矩阵,如下:12345612345605250159A 21081058025910202520v v v v v v v v v v v v ⎡⎤⎢⎥∞∞∞⎢⎥⎢⎥∞⎢⎥=∞⎢⎥⎢⎥∞⎢⎥∞⎢⎥⎢⎥∞∞∞⎣⎦设()(){}1234560,,,,,,j W v T v v s v v v v v -==∞∈=,第一次迭代①计算(),2,3,4,5,6j T v j =如下()()(){}{}22112min ,min ,055T v T v W v w =+=∞+= ()()(){}{}33113min ,min ,022T v T v W v w =+=∞+= ()()(){}{}44114min ,min ,0T v T v W v w =+=∞+∞=∞ ()()56,T v T v =∞=∞②取(){}()32min j jv sT v T v ∈==,令()()332W v T v ==③由于()36k n =≠=,令{}2456,,,,3s v v v v i -==转(1) 第二次迭代:①算(),2,4,5,6j T v j =如下()()(){}{}22323min ,min 5,213T v T v W v w =+=+= ()()(){}{}44334min ,min 8,288T v T v W v w =+=+= ()()(){}{}55335min ,min 10,21010T v T v W v w =+=+= ()()(){}{}66336min ,min ,2T v T v W v w =+=∞+∞=∞②取(){}()2min 3j jv sT v T v -∈==令()()223W v T v ==③由于()26k n =≠=,令{}456,,2s v v v i -==转(1) 第三次迭代:①算(),4,5,6j T v j =如下()()(){}{}44224min ,min 8,358T v T v W v w =+=+= ()()(){}{}55225min ,min 10,3910T v T v W v w =+=+= ()6T v =∞②取(){}()()()444min 8,8j jv sT v T v W v T v -∈====③由于()46k n =≠=,令{}56,4s v v i -==转(1) 第四次迭代:①算(),5,6j T v j =如下()()(){}{}55445min ,min 10,2810T v T v W v w =+=+= ()()(){}{}66446min ,min ,8513T v T v W v w =+=∞+=②取(){}()()()555min 10,10j jv sT v T v W v T v -∈====③由于()56k n =≠=,令{}6s v -=转(1) 第五次迭代:①算(),6j T v j =如下()()(){}{}66556min ,min 13,10212T v T v W v w =+=+=②由于6k n ==。
因此已找到1v 到6v 的最短距离为12。
计算结束。
对应的迭代表格如下:找最短路线:逆向追踪得132456v v v v v v →→→→→ 最短距离为12,即从城市1v 到城市6v 的距离最短,即费用最省。
3.3算法的正确性和计算复杂性 3.3.1贪心选择性质Dijkstra 算法是贪心算法策略的一个典型例子。
它所做的贪心选择是从V —S 中选择具有最短特殊路径的顶点u ,从而确定从源到u 的最短路径长度dist[u]。
这种贪心选择导致最优解在于如果存在一条源到u 且长度比dist[u]更短的路,设这条路初次走出S 之外到达的顶点x V S ∈—,然后徘徊于S 内外若干次,最后离开S 到达u ,如图2所示。
在这条路径上,分别标记d(v,x),d(x,u)和d(v,u)为顶点v 到顶点x ,顶点x 到顶点u 和顶点v 到顶点u 的路长,那么有:dist[x]d(v,x)≤d(v,x)+d(x,u)=d(v,u)<dist[u]利用权边的非负性,可知d(v,x)0≥,从而推出dist[x]dist[u]≤。
此为矛盾。
这就证明了dist[u]是从源点到u 的最短路径长度。
图2 从源到u 的最短路径3.3.2最优子结构性质要完成Dijkstra 算法正确性的证明,还必须证明最优子结构性质,即算法中确定的dist[u]确实是当前从源到顶点u 的最短特殊路径长度。
为此,只要考察算法在添加u 到S中后,dist[u]的值所起的变化。
将添加u 之前的S 成为老S 。
当添加了u 之后,可能出现一条到顶点i 的新的特殊路。
如果这条新特殊路是先经过老S 到达顶点u ,然后从u 经一条边直接到达顶点i ,则这种路的最短的长度是dist[u]+c[u][i]。
此时如果dist[u]+c[u][i]<dist[i],则计算中用dist[u]+c[u][i]作为dist[i]的新值。
如果这条新特殊路径经过老S 到达u 后,不是从u 经过一条边直接到达i ,而是像图3那样,回到老S 中某个顶点x ,最后才到达顶点i ,那么由于x 在老S 中,因此x 比u 先加入S ,所以图3中从源到x 的路的长度比从源到u ,再从u 到x 的路的长度小。
于是当前dist[i]的值小于从源经x 到i 的路的长度,也小于图中从源经u 和x ,最后到达i 的路的长度。
