层次分析法及Excel求解实验
1.层次分析法使用excel设计绩效考核
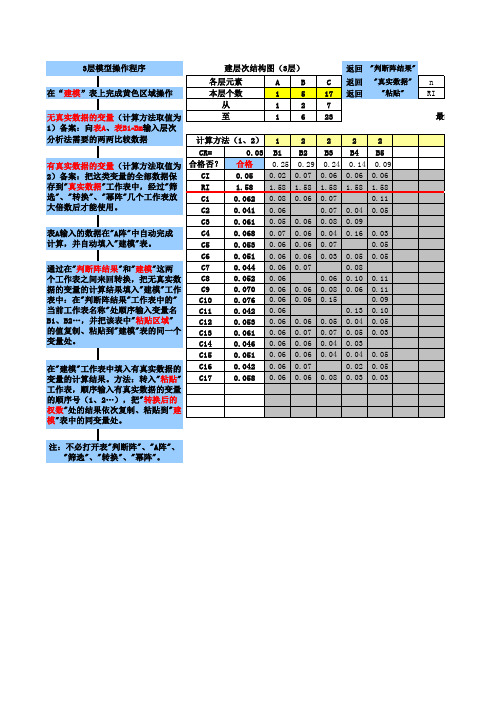
在“建模”表上完成黄色区域操作
无真实数据的变量(计算方法取值为 1)备案:向表A、表B1~Bm输入层次 分析法需要的两两比较数据
有真实数据的变量(计算方法取值为 2)备案:把这类变量的全部数据保 存到"真实数据"工作表中,经过"筛 选"、"转换"、"幂阵"几个工作表放 大倍数后才能使用。
0.05 0.05 0.03
n RI
最终计算表(灰色
注:不必打开表"判断阵"、"A阵"、 "筛选"、"转换"、"幂阵"。
2 0.50
3 0.58
4 0.90
5 1.12
随机一致性表
6
7
8
9
1.24 1.32 1.41 1.45
10 1.49
11 1.52
12 1.54
13 1.56
14 1.58
最终计算表(灰色区域粘贴而来)
0.06 0.07 0.06 0.06 0.07 0.06
C 17 7 23
2 B3 0.24 0.06 1.58 0.07 0.07 0.08 0.04 0.07 0.03
0.06 0.08 0.15
0.05 0.07 0.04 0.04
0.08
返回 返回 返回
2 B4 0.14 0.06 1.58
C11 0.042 0.06
C12 0.053 0.06
C13 0.061 0.06
C14 0.046 0.06
C15 0.051 0.06
C16 0.042 0.06
C17 0.058 0.06
用excel作层次分析法

2005-05-04
用 Excel 求解层次分析法(AHP)问题
一、 层次分析法(AHP)简介
层次分析法(AHP)的由来
美国运筹学家 A.L.Saaty 于本世纪 70 年代提出的层次分析法
(Analytical Hierar-chy Process,简称 AHP 方法),是一种定性
与定量相结合的决策分析方法。它是一种将决策者对复杂系统的决策
欢迎访问我的个人主页
第 6 页 共 15 页
/jhgk1983
用 Excel 求解层次分析法(AHP)问题
2005-05-04
p2
1
1
2
4
1
1/2
p3
1
1/2
1
5
3
1/2
p4
1/4
1/4
1/5
1
1/3
1/3
p5
1
1
1/3
3
1
1
p6
2
2
2
3
1
1
组织部门给三个人,甲、乙、丙对每个目标的层性打分。
版权所有——京华孤客
欢迎访问我的个人主页
第 2 页 共 15 页
/jhgk1983
用 Excel 求解层次分析法(AHP)问题
2005-05-04
…… … ………
…… … ………
pn bn1 bn2 … … bnn
在层次分析法中,为了使判断定量化,关键在于设法使任意 两个方案对于某一准则的相对优越程度得到定量描述。一般对单 一准则来说,两个方案进行比较总能判断出优劣,层次分析法采 用 1-9 标度方法,对不同情况的评比给出数量标度。
2005-05-04
层次分析法确定评价指标权重及Excel计算

江苏科技信息February 2012表2判断矩阵摘要:文章介绍了层次分析法确定评价指标权重的过程和计算方法,建立的Excel 计算模板操作简单,方便推广,具有较强的实用性。
关键词:决策分析法;层次分析法;权重;Excel ;计算模板作者简介:曹茂林,扬州市环境监测中心站,高级工程师;研究方向:环境监测技术与环境科技管理。
■曹茂林层次分析法确定评价指标权重及Excel 计算层次分析法(Analytic hierarchy process ,简称AHP 法)是美国运筹学家T.L.Saaty 等人在20世纪70年代中期提出了一种定性和定量相结合的,系统性、层次化的多目标决策分析方法。
在环境科研实践中,AHP 法广泛应用于生态安全[1]、环境规划[2]、区域承载力[3]、化学品环境性能评价[4]等众多领域。
AHP 法的核心是将决策者的经验判断定量化,增强了决策依据的准确性,在目标结构较为复杂且缺乏统计数据的情况下更为实用。
应用AHP 法确定评价指标的权重,就是在建立有序递阶的指标体系的基础上,通过比较同一层次各指标的相对重要性来综合计算指标的权重系数。
具体步骤如下:1.构造判断矩阵同一层次内n 个指标相对重要性的判断由若干位专家完成。
依据心理学研究得出的“人区分信息等级的极限能力为7±2”的结论,AHP 法在对指标的相对重要性进行评判时,引入了九分位的比例标度,见表1。
判断矩阵A 中各元素a ij 为i 行指标相对j 列指标进行重要性两两比较的值。
显然,在判断矩阵A 中,a ij >0,a ii =1,a ij =1/a ji (其中i ,j=1,2,…,n )。
因此,判断矩阵A 是一个正交矩阵,左上至右下对角线位置上的元素为1,其两侧对称位置上的元素互为倒数。
每次判断时,只需要作n(n-1)/2次比较即可。
表2是一个7阶判断矩阵,本文以此为例介绍应用Excel 计算指标权重并进行一致性检验的方法。
层次分析法及求解实验讲课文档

值便越小。
一般来说只要 CI≤0.10 ,判断矩阵的一致性是可以接受的,
否则需要重新进行两两比较判断。
判断矩阵的维数 n越大,判断的一致性越差,故应放宽对高维
判断矩阵的一致性要求,于是提出了平均随机一致性指标的修正值
RI,并取合理的CR为衡量判断矩阵一致性的指标。
W 0 . 105
0 . 258
1 5 3
1
1 0.637 1.936
AW 1 0.105 0.318
3 0.258 0.785
5
1 3 1
3
11
.936
0
.318
0
.785
[
]
3
.037
PPT 9
层次分析法(AHP)的具体步骤
(1)明确问题
在分析社会、经济的以及科学管理等领域的问题时,首先
要对问题有明确的认识,弄清问题的范围,了解问题所包含的
因素,确定出因素之间的关联关系和隶属关系。
(2) 递阶层次结构的建立
根据对问题分析和了解,将问题所包含的因素,按照是否共
有某些特征进行归纳成组,并把它们之间的共同特性看成是系统
2022年1月16日星期日
2022年1月16日星期日
第二十二页,共46页。
n
b
j 1
PPT 22
ij
对向量W=( W1, W2…… Wn)t归一化处理:
Wi
Wi
n
W
j 1
j
计算判断矩阵最大特征根λmax
用电子表格(Excel)实现层次分析法(AHP)的简捷计算

用电子表格(Excel)实现层次分析法(AHP)的简捷计算先锋(华南农业大学林学院,广东广州510640)摘要:传统的层次分析法算法具有构造判断矩阵不容易、计算繁多重复且易出错、一致性调整比较麻烦等缺点。
层次分析法Excel 算法利用常用的办公软件电子表格(Excel)的运算功能,设置简明易懂的计算表格和步骤,使得判断矩阵的构造、层次单排序和层次总排序的计算以及一致性检验和检验之后对判断矩阵的调整变得十分简单。
从而可以为层次分析法的学习、应用、推广和改进探讨提供方便。
关键词:层次分析法Excel1 层次分析法(AHP)的应用难点层次分析法(Analytical Hierarchy Process,简称AHP)是美国匹兹堡大学教授A.L.Saaty ,于20 世纪70 年代提出的一种系统分析方法,它综合了定性与定量分析,模拟人的决策思维过程,具有思路清晰、方法简便、适用面广、系统性强等特点,是分析多目标、多因素、多准则的复杂大系统的有力工具。
层次分析法的基本原理简单说就是用下一层次因素的相对排序来求得上一层次因素的相对排序。
应用层次分析法解决问题的思路是:首先把要解决的问题分出系列层次,即根据问题的性质和要达到的目标将问题分解为不同的组成因素,按照因素之间的相互影响和隶属关系将各层次各因素聚类组合,形成一个递阶的有序的层次结构模型;然后对模型中每一层次每一因素的相对重要性,依据人们对客观现实的判断给予定量表示(也可以先进行定性判断,再予赋值量化),再利用数学方法确定每一层次全部因素相对重要性次序的权值;最后通过综合计算各层因素相对重要性的权值,得到最低层(方案层)相对于较高层(分目标或准则层)和最高层(总目标)的相对重要性次序的组合权值,以此进行进行方案排序,作为评价和选择方案的依据。
层次分析法在多个领域得到广泛应用,但在应用中也是确实存在着不少难点。
1.1 构造一个合适的判断矩阵不容易建立层次结构模型和构造判断矩阵是层次分析法的主要基本工作,构造判断矩阵是关键之关键。
层次分析法Excel演算实验

0.066666667 0.405480133 0.104729434
1
1 0.258284994
3.871692207
1
Awi/Wi 1.9354877 3.038511091 0.3182215 3.038511091 0.7848018 3.038511091
3.038511091
按行相乘
开3次方
年份 成分 2004 2005 2006 2007 2008 2009 2010 2011
人员成本 36% 35% 30% 28% 30% 28% 26% 23%
2004 2004 2004 2004 2004 2004 2004 2004
45% 40% 35% 30% 25% 20% 15% 10% 5% 0%
3.003694598
按行相乘
开3次方
权重Wi
Awi
15 2.466212074 0.648329014
0.1 0.464158883 0.122020192
0.666666667 0.873580465 0.229650794
3.803951422
1
Awi/Wi 1.94738 3.003694598 0.36651 3.003694598 0.68980 3.003694598
2002
2004
2006
成本A与其他6个因素比较
A,B
对于A:
A,C
对于A:
A,D
对于A:
A,E
对于A:
A,F
对于A:
A,G
对于A:
质量A与其他5个因素比较
A,B
对于A:
A,C
对于A:
9*1/5 28*1/3 20*1/4 25*1 17*5 29*1/2
用电子表格(Excel)实现层次分析法(AHP)的简捷计算
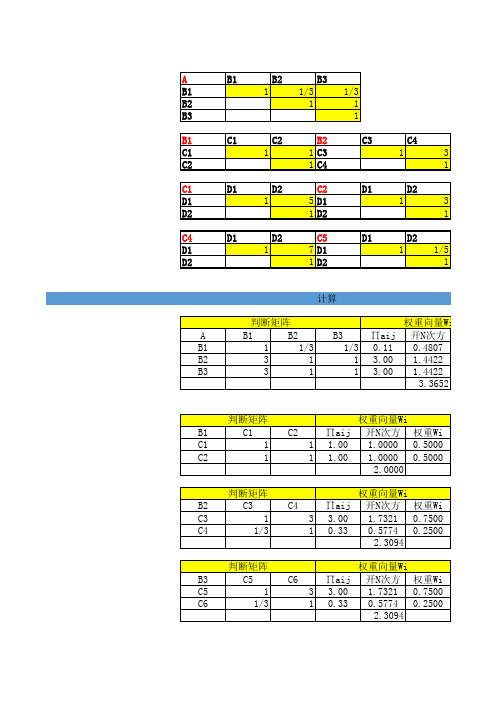
计算 判断矩阵 B1 B2 1 1/3 3 1 3 1 权重向量Wi 开N次方 0.4807 1.4422 1.4422 3.3652
A B1 B2 B3
B3 1/3 1 1
∏aij 0.11 3.00 3.00
B1 C1 C2
判断矩阵 C1 1 1
C2 1 1
权重向量Wi ∏aij 开N次方 权重Wi 1.00 1.0000 0.5000 1.00 1.0000 0.5000 2.0000 权重向量Wi 开N次方 权重Wi 1.7321 0.7500 0.5774 0.2500 2.3094 权重向量Wi 开N次方 权重Wi 1.7321 0.7500 0.5774 0.2500 2.3094
D1
D1
权重向量Wi 权重Wi 0.1429 0.4286 0.4286
λ max 一致性检验 (AW)i (AW)i/Wi C.I. R.I. C.R. 0.4286 3.0000 0.0000 0.5149 0.0000 1.2857 3.0000 1.2857 3.0000
λ max= 3.0000
λ max= 1.3333
λ max 一致性检验 (AW)i (AW)i/Wi C.I. R.I. C.R. 0.5000 2.0000 -0.8333 0.0000 0.0000 1.5000 2.0000
λ max= 1.3333
B2 C3 C4 CR
Wi
0.7500 0.2500 0.0000
λ max= 1.3333
λ max 一致性检验 (AW)i (AW)i/Wi C.I. R.I. C.R. 1.5000 2.0000 -0.8333 0.0000 0.0000 0.5000 2.0000
《系统工程》实验——层次分析参考实例

系统工程实验——层次分析法参考实例交通是关系到我们每一个人的事情,在交通工具选择中,如果按经济比较方法,由于定性和定量因素之间没有统一的度量尺度,也未考虑定性、定量因素间的相对重要性,因此难以判断,而应用层次分析法能够较好地弥补这些不足。
层次分析法需要大量的运算过程,如果没有合理工具的支持也将是一个繁琐复杂的过程,而简单通用的软件系统(如EXCEL)就能够灵活地应用于层次分析法的运算中,大大简化计算时间,提高分析效率。
本实验将结合个人的具体情况,在EXCEL系统中,应用层次分析法选择你回家时最优的交通工具。
1.明确问题,建立系统的递阶层次结构模型。
常用的交通工具有汽车、火车、飞机和轮船。
根据对交通工具选择因素进行分析,各种备选方案的影响因素主要包括安全、快捷、方便、经济、舒适等几个方面。
具体构建交通工具选择的递阶层次结构模型。
2.建立各层次判断矩阵。
依据个人的具体情况和个人主观判断,比较每一层次内阁因素对上一层次有关因素的相对重要性,各因素之间逐对地进行两两比较判断,再根据实验原理中给出的九级标度法将这些结果定量化,从而构建比较判断矩阵。
本实验共构建6个判断矩阵。
把每个判断矩阵表示在EXCEL中。
步骤举例如下:(1)新建EXCEL文档,取名为“层次分析法应用实验”。
(2)输入判断矩阵,为使画面清晰,可设置单元格格式。
把工作表中网格去掉。
工具→选项,打开选项窗口,取消“网格线”,如下图:选择判断矩阵所在单元格,设置单元格边框。
选择判断矩阵数值所在单元格,设置单元格数字类型为分数。
如下图:依据以上的方法建立本实验中的六个判断矩阵,并输入到EXCEL 系统中。
各方案针对“安全”指标的判断矩阵举例如下:3.层次单排序。
对各判断矩阵进行计算,求解各判断矩阵的特征向量,即为层次单排序。
以最高层的判断矩阵为例,在EXCEL中计算过程如下(“和积法”和“方根法”选其一)。
其他各判断矩阵的层次单排序计算过程相同。
层次分析法excel

层次分析法(AnalytioHieacrrhyProcess,AHP),是一种定性与定量相结合的多目标决策方法,在许多工程领域都有应用。
利用层次分析法进行风险识别的基本思路是:把复杂的风险问题分解为各个组成因素,将这些因素按支配关系分组形成有序的递阶层次结构,通过两两比较判断的方式确定每一层次中各因素相对于上一层或最高层总目标的相对重要性,并加以排序,从而判断出系统主要风险模式和风险因素。
AHP体现了人们的决策思维的基本特征,即分解、判断、综合。
对于AHP的进一步定义、优缺点就不多说了,网上有很多的介绍。
今天主要探讨一下如何用Excel来进行层次分析法的核心步骤——判断矩阵特征值与特征向量的计算。
首先,来看一下计算方法。
这种计算方法来自同济大学巩春领博士的学位论文《大跨度斜拉桥施工风险分析与对策研究》。
数据分析你最喜欢的软件是哪个?可以说我最喜欢的是是Excel么~好多事情都可以用这个随处可以找到的方便快捷的工具完成,还可以与更多的人分享源文件,简直是人生一大快事。
AHP有很多计算工具,比如matlab(这个我也做了,稍后完善一下也分享出来),还有其他各种小软件。
不喜欢黑箱软件,不能调整算法,还是先研究一下excel的实现吧。
上面的系列公式,正好适合用excel做。
第一步,输入判断矩阵,拉出列和继续地,根据上面的公式,先后按次序作出归一化后的矩阵、求行和、求归一化后的权重、计算矩阵乘积、矩阵对应元素与权重向量元素求商,最后得到最大特征值——话说这也是普通矩阵得到最大特征值的一种方式。
这里要介绍一个Excel命令:MMULT:求矩阵相乘矩阵相乘,矩阵A乘以矩阵B=矩阵C,需要用命令指定两个矩阵,和一个结果矩阵的位置。
MMULT(array1,array2)函数介绍:返回两个数组的矩阵乘积。
结果矩阵的行数与数组array1的行数相同,矩阵的列数与数组array2的列数相同。
语法MMULT(array1,array2)Array1, array2是要进行矩阵乘法运算的两个数组。
层次分析法中用方根法计算权重在Excel中的具体操作
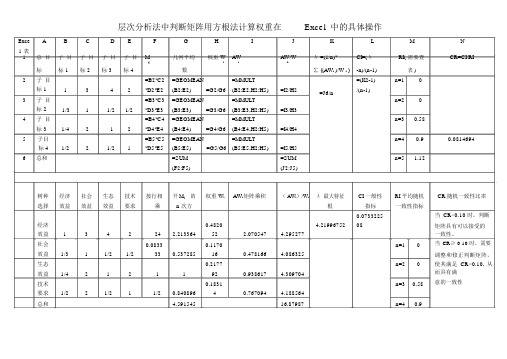
层次分析法中判断矩阵用方根法计算权重在Excel 中的具体操作Exce A B C D E F G H I J K L M Nl 表1总目子目子目子目子目M几何平均权重 W AW AW/Wλ =(1/n)*CI=(λRI( 需要查CR=CI/RIij i i ii标标 1标 2标 3标 4数∑ {(AW i )/W i }-n)/(n-1)表 )2子目=B2*C2=GEOMEAN=MMULT=(K2-1)n=10标 11342*D2*E2(B2:E2)=G2/G6(B2:E2,H2:H5)=I2/H2=J6/n/(n-1)3子目=B3*C3=GEOMEAN=MMULT n=20标 21/311/21/2*D3*E3(B3:E3)=G3/G6(B3:E3,H2:H5)=I3/H34子目=B4*C4=GEOMEAN=MMULT n=30.58标 31/4212*D4*E4(B4:E4)=G4/G6(B4:E4,H2:H5)=I4/H45子目=B5*C5=GEOMEAN=MMULT n=40.90.0814694标 41/221/21*D5*E5(B5:E5)=G5/G6(B5:E5,H2:H5)=I5/H56总和=SUM=SUM n=5 1.12(F2:F5)(J2:J5)树种经济社会生态技术按行相开 M ij的权重 W i AW i矩阵乘积( AW i)/W iλ 最大特征CI 一般性RI 平均随机选择效益效益效益要求乘n 次方根指标一致性指标0.0733225经济0.4820 4.2199675208效益134224 2.21336452 2.070547 4.295277社会0.08330.1170n=10效益1/311/21/2330.537285160.478166 4.086325生态0.2177n=20效益1/421211920.938617 4.309704技术0.1831n=30.58要求1/221/211/20.84089640.767094 4.188564总和 4.59154516.87987n=40.9CR随机一致性比率当CR<0.10 时,判断矩阵具有可以接受的一致性。
用电子表格(Excel)实现层次分析法(AHP)的简捷计算

D1
D1
权重向量Wi 权重Wi 0.1429 0.4286 0.4286
λ max 一致性检验 (AW)i (AW)i/Wi C.I. R.I. C.R. 0.4286 3.0000 0.0000 0.5149 0.0000 1.2857 3.0000 1.2857 3.0000
λ max= 3.0000
λ max= 1.3333
λ max 一致性检验 (AW)i (AW)i/Wi C.I. R.I. C.R. 1.5000 2.0000 -0.8333 0.0000 0.0000 0.5000 2.0000
λ max= 1.3333
λ max 一致性检验 (AW)i (AW)i/Wi C.I. R.I. C.R. 1.6667 2.0000 -0.8333 0.0000 0.0000 0.3333 2.0000
D1 D2 CR
0.7500 0.2500 0.0000
C5 D1 D2 CR
Wi
0.1667 0.8333 0
C6 D1 D2 CR 总排序
Wi
0.2500 0.7500 0.0000
B层次总排序(CR = 0.0000) B1 B2 B3 0.1429 0.4286 0.4286 C层次总排序(CR = 0.0000)
C2 D1 D2
判断矩阵 D1 1 1/3
D2 3 1
∏aij 3.00 0.33
C3 D1 D2
判断矩阵 D1 1 5
D2 1/5 1
∏aij 0.20 5.00
C4 D1 D2
判断矩阵 D1 1 1/7
D2 7 1
∏aij 7.00 0.14
C5 D1 D2
判断矩阵 D1 1 5
excel表格在层次分析法的实际应用(包括计算过程)
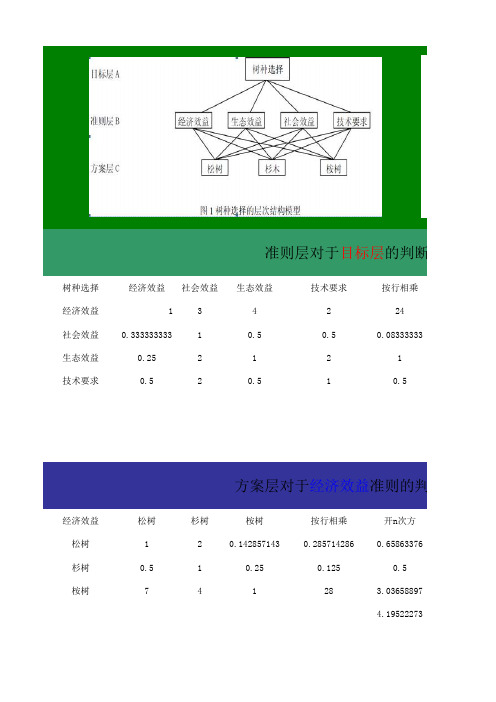
树种选择经济效益社会效益生态效益技术要求按行相乘经济效益134224社会效益0.33333333310.50.50.08333333生态效益0.252121技术要求0.520.510.5经济效益松树杉树桉树按行相乘开n次方松树120.1428571430.2857142860.65863376杉树0.510.250.1250.5桉树741283.036588974.19522273准则层对于目标层的判断矩阵及单排方案层对于经济效益准则的判断矩阵及单方案层对于社会效益准则的判断矩阵及单社会效益松树杉树桉树按行相乘开n次方松树10.50.2杉树210.3333桉树531方案层对于生态效益准则的判断矩阵及单生态效益方案层对于社会效益准则的判断矩阵及单社会效益松树0.1569961360.07568031杉树0.1191831830.0574525桉树0.7238206810.34891925层次分析总排序CI0.088464121RI0.514910.514910.514910.51491CR0.171805016开n次方权重WiAwiAwi/Wi2.2133638390.482052 2.0705473 4.2952770.5372849660.1170160.4781661 4.08632510.2177920.9386173 4.3097040.8408964150.183140.7670943 4.1885644.5915452214.2199680.0733225080.082448761符合CR <0.1权重Wi AwiAwi/Wi0.1569961360.498765 3.17692820.1191831830.378636 3.17692820.7238206812.2995263.17692823.17692820.0884641210.171805016不符合RI <0.1层的判断矩阵及单排和一致性检验CI=(λ-n)/(n-1)CR=CI/RI(RI=0.8931)准则的判断矩阵及单排序和一致性检验CI=(λ-n)/(n-1)CR=CI/RI(RI=0.51491)准则的判断矩阵及单排序和一致性检验权重Wi Awi Awi/Wi准则的判断矩阵及单排序和一致性检验准则的判断矩阵及单排序和一致性检验析总排序计算总排序ai*bi∑ai*bi总排序一致性检验CI=∑ai*Cii RI CR=CI/RI0.51491。
用excel作层次分析法

版权所有——京华孤客
欢迎访问我的个人主页
第 10 页 共 15 页
/jhgk1983
用 Excel 求解层次分析法(AHP)问题
2005-05-04
二、层次分析法(AHP)的具体步骤 9 明确问题 在分析社会、经济的以及科学管理等领域的问题时,首先要 对问题有明确的认识,弄清问题的范围,了解问题所包含的因素, 确定出因素之间的关联关系和隶属关系。 9 递阶层次结构的建立 根据对问题分析和了解,将问题所包含的因素,按照是否共 有某些特征进行归纳成组,并把它们之间的共同特性看成是系统 中新的层次中的一些因素,而这些因素本身也按照另外的特性组 合起来,形成更高层次的因素,直到最终形成单一的最高层次因 素。 o 最高层是目标层 o 中间层是准则层 o …….. o 最低层是方案层或措施层 9 建立两两比较的判断矩阵 判断矩阵表示针对上一层次某单元(元素),本层次与它有 关单元之间相对重要性的比较。一般取如下形式: Cs p1 p2 … … pn p1 b11 b12 … … b1n p2 b21 b22 … … b2n
标 度 定义与说明
1
两个元素对某个属性具有同样重要性
3
两个元素比较,一元素比另一元素稍微重要
5
两个元素比较,一元素比另一元素明显重要
7
两个元素比较,一元素比另一元素重要得多
9
两个元素比较,一元素比另一元素极端重要
2,4,6,8 表示需要在上述两个标准之间拆衷时的标度
1/bij bii = 1
两个元素的反比较 判断矩阵 B 具有如下特征:
