角的大小比较
角的大小比较及直角、锐角和钝角的认识

角的各部分名称:
( 顶点 )
玩调皮猴
怎样比较角的大小呢?
怎样比较角的大小呢?
首页
末页
怎样比较角的大小呢?
首页
末页
角的大小与边的长短无关。
红角与蓝角:大小之争
角的大小与边的长短无关 角的大小与边的开叉有关
练习本
你知道
分别是什么角吗?
是锐角
是钝角
小朋友,你能给我们分一分类么?
如果在直角另 一边的外面,
就是钝角。
小朋友们,你们能很快地说出下面 各角的名称吗?
直锐
钝钝 锐
钝
角角
角角 角
角
我是小法官。
1、直角比钝角( B)
A.大 B.小 C.一样大
2、 这个角是钝角。(B )
A.对 B.不对
1. 说一说有哪些角。
2.
钝角
锐角
直角
3.
我画了个锐角。
钝角。
4. 用三角板拼一拼。
①
②
③
④
⑤
比直角小 锐角
直角
比直角大 钝角
直角 比直角小的角叫做锐角 比直角大的角叫做钝角
钝角
直角
锐角
这个角你能一眼看出是什么角吗? 如果不能,可以请谁来帮忙?
锐角ห้องสมุดไป่ตู้
顶点与直角的顶点重合,一条边与直 角的一条边重合,看另一条边。
如果在直角另 一边的里面,
就是锐角。
如果与直角的 另一边重合,
就是直角。
4.5角的大小比较

解析 经过仔细观察分析你会发现∠BOC=∠COD-∠BOD=∠BOA-∠AOC=90°+90°-135°=45°.
解 45
点拨 也可以先求出∠BOD,因为∠BOD=∠AOD-∠AOB=135°-90°=45°.再求∠BOC,∠BOC=∠COD-∠BOD=90°-45°=45°.
如图4—5—5所示,∠AOB与∠COD都是直角,则∠AOC=∠BOD.
<img src=c:\全科学习\初一\数学\4.5角的大小比较\6.bmp>
这是因为∠AOC与∠BOD是同一个角∠BOC的余角,根据同角的余角相等,所以∠AOC=∠BOD.
如图4—5—6所示,CD⊥AB且∠1=∠2则∠EDC=∠CDF.
<img src=c:\全科学习\初一\数学\4.5角的大小比较\5.bmp>
∠1与∠2互为补角,可用数学语言表示为:
∠1+∠2=180°,∠1=180°-∠2或∠2=180°-∠1.
5.余角和补角的性质
(1)同角或等角的余角相等.
(2)同角或等角的补角相等.
注意:同角或等角的余角相等包含两方面内容:一是同一个角的余角相等,二是相等的角的余角相等.
∠1与∠2互为余角,可以用数学语言表示为:
∠1+∠2=90°,∠1=90°-∠2或∠2=90°-∠1.
4.互为补角
如果两个角的和是平角,那么称这两个角互为补角.
如图4—5—4,∠AOB是一个平角,所以∠1与∠2互为补角,这是两个角互为补角的特殊情形,通常又称为互为邻补角,二者有一条公共边.
角的大小比较

怎样比较角的大小呢?
怎样比较角的大小呢?
你知道
分别是什么角吗?
是锐角
你知道
分别是什么角吗?
是钝角
√
○
√
○
( 3)
(6)
( 5 )( 4 )
角的两边张口越大,角就越大。
1、先点底边的“移”字。 2、“移”字重复点击,绿色角重பைடு நூலகம்左右移动。 3、“长”字重复点击,角的两边重复延长收回 4、“文字”配合使角。
角的大小与两边的长短无关
移 长 文字
角
• 我是一个小小角
• 一个顶点两条边 • 想知我的大与小 • 要看张口不看边
填一填
• (1)一个角有( 一 )个顶点,( 两 )条 边。 • (2)△内有( 三 )个角,□内有( 四 ) 个角,☆内有( 五 )个角
火眼金睛
1.角有无数条边。( ×) 2.角有一个顶点,两条边。( √ ) 3.角的边越长,这个角就越大。( × ) 4.一个角的两边叉开的越大,这个角就越大。 (√ ) 5.角的大小跟边的长短无关,跟两边张口的 大小也无关。( ×)
喜欢我就动手画我吧!
试一试
锐角
试一试
试一试
钝角
试一试
锐角
钝角
角的比较与排序

角的比较与排序角是几何学中一个基本的概念,广泛应用于各个领域。
在几何学中,角是由两条射线共享一个公共端点所形成的图形。
本文将探讨角的比较和排序方法,从而更好地理解角的性质和应用。
一、角的定义和性质角的定义:两条射线共享一个公共端点所形成的图形称为角。
通常用大写字母表示角,如∠ABC。
角的性质:1. 角可以顺时针或逆时针方向进行度量,度量以度或弧度为单位。
2. 角外部的两条射线连起来可以形成一条直线,即角的外部。
3. 角的内部是由角的两条射线所包围的区域。
4. 角可以分为锐角(小于90度)、直角(等于90度)、钝角(大于90度)和平角(等于180度)四种类型。
二、角的比较角的比较是指根据角的大小关系进行排序或确定其相等性。
下面介绍几种角的比较方法。
1. 角的度数比较法:根据角度的度数大小进行比较。
角度度数越大,角度越大。
2. 角的尺规比较法:通过利用尺规来测量角的大小。
将尺规放在角的一条边上,另一条边对应的尺规刻度即为该角的度数。
通过比较尺规刻度来确定角的大小关系。
3. 角的三角函数比较法:利用三角函数的性质来比较角的大小。
常用的三角函数有正弦、余弦和正切函数,它们可以通过计算角的边长比例来比较角大小。
4. 角的图示比较法:通过将待比较的角绘制在坐标系中,观察它们的图形位置和形状,进而判断角的大小。
三、角的排序根据角的大小关系,可以将角进行排序。
下面介绍几种常见的角的排序方法。
1. 比较度数大小排序:将角的度数进行比较,按照角度度数从小到大或从大到小进行排序。
2. 比较尺规大小排序:使用尺规来测量每个角的大小,将角的度数按照从小到大或从大到小进行排序。
3. 比较三角函数大小排序:通过计算每个角的三角函数值,将角按照三角函数值的大小进行排序。
4. 根据图示进行排序:将角绘制在坐标系中,根据它们的位置和形状进行排序。
一般来说,角的大小与对应射线在坐标系中的位置有关。
四、角的应用角的性质和排序方法在各个领域都有重要的应用,如以下几个例子:1. 角度测量和方向判断:通过角的度数,可以测量和判断物体的方向,比如导航系统中的方向指示。
二年级下册数学-角的大小比较北师大版

1
2
把两个角重合在一起,就能看出哪个角更大。 通过比较,∠2更大一些。
二年级下册数学-角的大小比较北师大 版
二年级下册数学-角的大小比较北师大 版
知识讲解
如图,比较两个三角板的角的大小,你发现了什么?
二年级下册数学-角的大小比较北师大 版
二年级下册数学-角的大小比较北师大 版
知识讲解
如图,比较两个三角板的角的大小,你发现了什么?
二年级下册数学-角的大小比较北师大 版
二年级下册数学-角的大小比较北师大 版
知识总结
01
角的大小与角的边的长度没有关系。
02
角的大小和角张开的大小有学-角的大小比较北师大 版
北师大版小学数学二年级下册
角的大小比较
> 12 3
激趣导入
同学们,我们已经认识了角,知道了角的组成部分。今 天我们一起来学习关于角的大小知识,你们准备好了吗?
知识讲解
下面两个角哪个角更大呢?剪下附页3中图1的两个角,比一 比。
1
2
二年级下册数学-角的大小比较北师大 版
知识讲解
说一说你是怎样比较的?
答:把淘气做的角张口弄小些,就能变成一个更小的角。
二年级下册数学-角的大小比较北师大 版
二年级下册数学-角的大小比较北师大 版
练习巩固
这是淘气做的活动角。
(1)怎样把淘气做的角变成一个更小的角? 做一做,说一说。 (2)怎样把淘气做的角变成一个更大的角? 做一做,说一说。
答:把淘气做的角张口弄大些,就能变成一个更大的角。
二年级下册数学-角的大小比较北师大 版
二年级下册数学-角的大小比较北师大 版
知识讲解
如图,比较两个三角板的角的大小,你发现了什么?
角的比较重难点题型

角的比较--重难点题型【知识点1 角的比较与运算】【题型1 角的大小比较】∠COD=50°;小丽用叠合法比较,将两个角的顶点重合,边OB与OD重合,边OA 和OC置于重合边的同侧,则边OA.(填序号:①“在∠COD的内部”;②“在∠COD的外部”;③“与边OC重合”)【变式1-1】(2021春•呼和浩特期末)如图,∠AOB=∠COD,则∠AOC与∠DOB的大小关系是()A.∠AOC>∠DOBB.∠AOC<∠DOBC.∠AOC=∠DOBD.∠AOC与∠DOB无法比较大小【变式1-2】(2021秋•开封期末)如图所示,其中最大的角是,∠DOC,∠DOB,∠DOA的大小关系是.【变式1-3】(2021秋•门头沟区期末)如图所示的网格是正方形网格,点A,B,C,D,O 是网格线交点,那么∠AOB∠COD.(填“>”,“<”或“=”)【题型2 角的和差】【例2】(2021秋•安庆期末)如图,已知∠BOC=2∠AOC,OD平分∠AOB,且∠COD=20°,求∠AOB的度数.【变式2-1】(2021秋•五常市期末)用一副三角板不能画出的角是()A.75°B.105°C.110°D.135°【变式2-2】2021秋•北碚区期末)将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕.若∠ABE=30°,则∠DBC为度.【变式2-3】(2021秋•荔湾区期末)把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、D、B三点在同一直线上,BM为∠ABC的平分线,BN为∠CBE的平分线,则∠MBN的度数是()A.30°B.45°C.55°D.60°【题型3 n等分线】【例3】(2021秋•罗湖区校级期末)如图,已知O为直线AB上一点,过点O向直线AB 上方引三条射线OC、OD、OE,且OC平分∠AOD,∠2=3∠1,∠COE=70°,求∠2的度数.【变式3-1】(2021秋•奉化区校级期末)OB是∠AOC内部一条射线,OM是∠AOB平分线,ON是∠AOC平分线,OP是∠NOA平分线,OQ是∠MOA平分线,则∠POQ:∠BOC=()A.1:2B.1:3C.2:5D.1:4【变式3-2】(2021秋•江汉区期末)如图,射线OB、OC在∠AOD内部,其中OB为∠AOC 的三等分线,OE、OF分别平分∠BOD和∠COD,若∠EOF=14°,请直接写出∠AOC 的大小.【变式3-3】(2021秋•越秀区校级月考)如图1,已知∠AOB=120°,∠COD=60°,OM在∠AOC内,ON在∠BOD内,∠AOM=13∠AOC,∠BON=13∠BOD.(本题中所有角均大于0°且小于等于180°)(1)∠COD从图1中的位置绕点O逆时针旋转到OC与OB重合时,如图2,则∠MON =°;(2)∠COD从图2中的位置绕点O逆时针旋转n°(0<n<120且n≠60),求∠MON 的度数;(3)∠COD从图2中的位置绕点O顺时针旋转n°(0<n<180且n≠60a,其中a为正整数),直接写出所有使∠MON=2∠BOC的n值.【题型4 角平分线】【例4】(2021秋•武都区期末)如图所示,点O是直线AB上一点,OE,OF分别平分∠AOC和∠BOC,若∠AOC=68°,则∠BOF和∠EOF是多少度?【变式4-1】(2021秋•南山区期末)已知三条不同的射线OA、OB、OC,有下列条件,其中能确定OC平分∠AOB的有()①∠AOC=∠BOC②∠AOB=2∠AOC③∠AOC+∠COB=∠AOB④∠BOC=12∠AOBA.1个B.2个C.3个D.4个【变式4-2】(2021秋•曲阳县期末)已知将一副三角板(直角三角板OAB和直角板OCD,∠AOB=90°,∠ABO=45°,∠CDO=90°,∠COD=30°)(1)如图1摆放,点O、A、C在一条直线上,∠BOD的度数是;(2)如图2,变化摆放位置将直角三角板COD绕点O逆时针方向转动,若要OB恰好平分∠COD,则∠AOC的度数是;(3)如图3,当三角板OCD摆放在∠AOB内部时,作射线OM平分∠AOC.射线ON 平分∠BOD,如果三角板OCD在∠AOB内绕点O任意转动,∠MON的度数是否发生变化?如果不变,求其值;如果变化,说明理由.【变式4-3】(2021秋•裕华区校级期中)如图1,∠AOB=40°,∠AOB的一边OB与射线OM重合,现将∠AOB绕着点O按顺时针方向旋转180°.在旋转过程中,当射线OA、OB或者直线MN是某一个角(小于180°)的平分线时,旋转角的度数为.【题型5 余角与补角的定义】【例5】(2021春•金山区期末)如果一个角的补角的2倍减去这个角的余角恰好等于这个角的4倍,求这个角的度数.【变式5-1】(2021•寻乌县模拟)已知∠A是锐角,∠A与∠B互补,∠A与∠C互余,则∠B﹣∠C的值等于()A.45°B.60°C.90°D.180°【变式5-2】(2020秋•麦积区期末)一个角的补角加上10°后,等于这个角的余角的3倍,求这个角以及它的余角和补角的度数.【变式5-3】(2021秋•沂水县期末)如图,已知∠AOB=130°,画∠AOB的平分线OC,画射线OD,使∠COD和∠AOC互余,并求∠BOD的度数.【题型6 利用余角或补角的性质得角相等】【例6】(2021秋•鹿邑县期末)如图,O为直线AB上一点,∠DOE=90°,OD是∠AOC 的角平分线,若∠AOC=70°.(1)求∠BOD的度数.(2)试判断OE是否平分∠BOC,并说明理由.【变式6-1】(2021秋•旌阳区期末)如图,两个直角∠AOC和∠BOD有公共顶点O,下列结论:①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠AOD+∠BOC=180°;④若OB平分∠AOC,则OC平分∠BOD;⑤∠AOD的平分线与∠BOC的平分线是同一条射线,其中正确的有.(填序号)【变式6-2】(2021秋•芮城县期末)综合与实践已知直线AB 经过点O ,∠COD =90°,OE 是∠BOC 的平分线.(1)如图1,若∠AOC =30°,求∠DOE ;(2)如图1,若∠AOC =α,求∠DOE ;(用含α的式子表示)(3)将图1中的∠COD 绕顶点O 顺时针旋转到图2的位置,其它条件不变,(2)中的结论是否还成立?试说明理由;(4)将图1中的∠COD 绕顶点O 逆时针旋转到图3的位置,其它条件不变,直接用含α的式子表示∠DOE .【变式6-3】(2019秋•东西湖区期末)如图1,平面内一定点A 在直线EF 的上方,点O 为直线EF 上一动点,作射线OA 、OP 、OA ',当点O 在直线EF 上运动时,始终保持∠EOP =90°、∠AOP =∠A 'OP ,将射线OA 绕点O 顺时针旋转60°得到射线OB .(1)如图1,当点O 运动到使点A 在射线OP 的左侧,若OA '平分∠POB ,求∠BOF 的度数;(2)当点O 运动到使点A 在射线OP 的左侧,且∠AOE =3∠A 'OB 时,求∠AOF ∠AOP 的值;(3)当点O 运动到某一时刻时,∠A 'OB =130°,请直接写出∠BOP = 度.【题型7 求几何图形中互余或互补角的个数】【例7】(2021•娄星区模拟)如图,C 是直线AB 上一点,CD 是∠ACB 的平分线. ② 图中互余的角有 ;②图中互补的角有 ;③图中相等的角有 .【变式7-1】(2021秋•南开区期末)如图所示,已知O 是直线AB 上一点,∠BOE =∠FOD =90°,OB 平分∠COD .(1)图中与∠DOE 相等的角有 ;(2)图中与∠DOE 互余的角有 ;(3)图中与∠DOE 互补的角有 .【变式7-2】(2021秋•成都期中)如图,O 是直线AB 上的一点,∠AOD =120°,∠AOC =90°,OE 平分∠BOD .写出图中所有互补的角和互余的角.【变式7-3】(2021春•吴中区月考)如果∠α和∠β互补,且∠α>∠β,则下列式子中:①90°﹣∠β;②∠α﹣90°;③12(∠α+∠β);④12(∠α﹣∠β).可以表示∠β的余角的有( )A .①②B .①②③C .①②④D .①②③④【题型8 数学思想方法与角】【例8】(2021秋•河东区期末)已知∠AOB=90°,OC为一射线,OM,ON分别平分∠BOC和∠AOC,则∠MON是()A.45°B.90°C.45°或135°D.90°或135°【变式8-1】(2021秋•成华区期中)(1)如图1,射线OC、OD在∠AOB的内部,射线OM、ON分别平分∠AOD、∠BOC、且∠BON=50°,∠AOM=40°,∠COD=30°,求∠AOB的度数;(2)如图2,射线OC、OD在∠AOB的内部,射线OM、ON分别平分∠AOD、∠BOC、且∠AOB=150°,∠COD=30°,求∠MON的度数【变式8-2】(2021秋•无锡期末)如图,∠AOB=150°,∠COD=40°,OE平分∠AOC,则2∠BOE﹣∠BOD=°.【变式8-3】(2021秋•镇海区期末)新定义问题如图①,已知∠AOB,在∠AOB内部画射线OC,得到三个角,分别为∠AOC、∠BOC、∠AOB.若这三个角中有一个角是另外一个角的2倍,则称射线OC为∠AOB的“幸运线”.(本题中所研究的角都是大于0°而小于180°的角.)【阅读理解】(1)角的平分线这个角的“幸运线”;(填“是”或“不是”)【初步应用】(2)如图①,∠AOB=45°,射线OC为∠AOB的“幸运线”,则∠AOC的度数为;【解决问题】(3)如图②,已知∠AOB=60°,射线OM从OA出发,以每秒20°的速度绕O点逆时针旋转,同时,射线ON从OB出发,以每秒15°的速度绕O点逆时针旋转,设运动的时间为t秒(0<t<9).若OM、ON、OA三条射线中,一条射线恰好是以另外两条射线为边的角的“幸运线”,求出所有可能的t值.。
认角、比较角的大小、画角

画角要记住:先画 顶点再画边。
别忘了让我来 帮助你呀!
五、课堂作业
作业:第39页“做一做”第1题。 第43页练习八,第3题。
角的初步认识
认角、比较角的 大小、画角
一、联系生活,揭示课题
(一)寻找生活中的角
今天我们一起学习 角的初步认识。
(二)揭示课题
二、认识角及各部分名称
一个角有几个顶点? 这些物品中都有角。 有几条边?
一个角有一个顶 点,有两条边。 两条边是直直的, 都从顶点出发。
二、认识角及各部分名称
1. 指一指哪里有角。
二、认识角及各部分名称
2. 下面的图形哪些是角,哪些不是角?
(
(
×)
三、比较角的大小
我发现角的两边 张开得越大,角 就越大。
比的时候要注意两个 角顶点对齐,一条边 也对齐。
三、比较角的大小
3. 打开折扇,看看角有什么变化。
4. 在两个三角尺上各选一个角, 比一比它们的大小。
四、画角
角的比较大小 角的比较

角的比较大小角的比较教学建议一、知识结构二、重点、难点分析本节教学的重点是角的大小比较,角平分线的意义,两个角的和、差、倍、分的意义.难点是空间观念,几何识图能力的培养.角的比较的相关知识是进一步学习角的度量和画法,以及进一步研究平面几何图形的基础.1﹒角的大小的比较有两种方法:(1)重合法:即把要比较的两个角的顶点和一条边重合,再比较另一条边的位置;(2)度量法;即比较两个角的度数.两种方法的比较结果是一致的.2.利用比较角大小的上述两种方法,就可以画出角的和、差、倍、分,并进而比较角的和、差、倍、分的大小.3.对于角平分线的概念,要注意以下两点:(1)它是角的内部的一条射线,并且是一条特殊的射线,它把角分成了相等的两部分.(2)要掌握角平分线的数学表达式:若OC 是的平分线,则或4.在比较角的大小时,应注意角的大小只与开口的大小有关,而与角的边画出部分的长短无关.这是因为角的边是射线而非线段.若用射线旋转成角的定义,也可以说转得较多的角较大.三、教法建议1.本节教材,完全可以对照线段的比较,线段的和差倍分,以及中点的意义来进行.两者是十分相似的.2.比较两个角的大小时,把角叠合起来,一定要使两个角的顶点及一边重合,另一边落在第一条边的同旁,否则不能进行比较.这可以通过叠合两块三角尺比较角的大小的实例来说明.这和线段大小比较十分相似.3.由于前面学过线段的大小比较和线段的和、差、倍、分.本课教学的指导思想就是运用类比联想的思维方法,引导学生利用旧知识,解决新问题.4.在本课的练习中,在可能的情况下,将以后经常遇到的图形,提前让学生见到,为以后的学习奠定了基础.5.在角的和、差、倍、分的计算中,由于度、分、秒的四则运算还没有讲到,因此只进行度的加、减.教学设计示例一、素质教育目标(一)知识教学点1.理解两个角的和、差、倍、分的意义.2.掌握角平分线的概念3.会比较角的大小,会用量角器画一个角等于已知角.(二)能力训练点1.通过让学生亲自动手演示比较角的大小,画一个角等于已知角等,培养训练学生的动手操作能力.2.通过角的和、差、倍、分的意义,角平分线的意义,进一步训练学生几何语言的表达能力及几何识图能力,培养其空间观念.(三)德育渗透点通过具体实物演示,对角的大小进行比较这一由感性认识上升到理性认识的过程,培养学生严谨的科学态度,对学生进行辩证唯物主义思想教育.(四)美育渗透点通过对角的大小比较,提高学生的鉴赏力,通过学生自己作角及角平分线,使学生进一步体会几何图形的形象直观美.二、学法引导1.教师教法:直观演示、尝试、指导相结合.2.学生学法:主动参与、积极思维、动手实践相结合.三、重点·难点·疑点及解决办法(一)重点角的大小比较,角平分线的意义,两个角的和、差、倍、分的意义.(二)难点空间观念,几何识图能力的培养.(三)疑点角的和、差、倍、分的意义.(四)解决办法通过学生主动参与,在自觉与不自觉中掌握知识点,再经过练习,解决难点和疑点.四、课时安排1课时五、教具学具准备投影仪或电脑、一副三角板、自制胶片(软盘)、量角器.六、师生互动活动设计七、教学步骤(一)明确目标通过教学,使学生在角的比较中掌握方法,理解相应概念,并掌握角平分线的概念.(二)整体感知通过现代化教学手段与学生的画图相结合,完成本节教学任务.(三)教学过程创设情境,引出课题师:请同学们拿出你的一副三角板,你能说出这几个角的大小吗?学生基本知道一副三角板各角的度数,他们可能利用度数比较,也可能通过观察,也会有同学用叠合法.这里可以让学生讨论,说出采用的比较方法,但叙述可能不规范.教师既不给予肯定也不否定,只是再提出新问题.投影显示:两个度数相差1度以内的角,不标明度数,只凭眼观察不能确定两个角的大小.师:对于这两个角你能说出它们哪一个大?哪一个小吗?(学生困惑时教师点出课题.)这节课我们就学习角的比较.同学们提出的比较一副三角板各角的方法有些很好,但不规范.希望同学们认真学习本节内容,掌握角的比较等知识,为以后的学习打好基础.(板书课题)[板书] 1.5 角的比较【教法说明】由学生熟知的三角板各角的比较入手,把学生带入比较角的大小的意境.但问题一转,出现了不标度数,观察又不能确定大小的角,当学生束手无策时,教师提出这就是我们要学习的新内容,调动学生的积极性,吸引其注意力.探究新知1.角的比较(1)叠合法教师通过活动投影演示:两个角设计成不同颜色,三种情况:,,,如图1所示.图1演示:移动,使其顶点与的顶点重合,一边和重合,出现以下三种情况,如图2所示.图2师:请同学们观察的另一边的位置情况,你能确定出两个角的大小关系吗?学生活动:观察教师演示后,同桌也可以利用两副三角板演示以上过程,帮助理解比较两角的大小,回答教师提出的问题.教师根据学生回答整理板书.[板书]① 与重合,等于,记作.② 落在的内部,小于,记作.③ 落在的外部,大于,记作.【教法说明】通过直观的实物演示和投影(电脑)显示,既加强了角的比较的直观性,又可提高学生的兴趣.注意再次强调角的大小只与开口大小有关,与边的长短无关,以及角的符号与小于号、大于号书写时的区别.(2)测量法师:小学我们学过用量角器测量一个角,角的大小也可以按其度数比较.度数大的角则大,度数小的则小.反之,角大度数大,角小度数小.学生活动:请同桌分别画两个角,然后交换用量角器测量其度数,比较它们的大小.【教法说明】测量前教师可提问使用量角器应注意的问题.即三点:对中;重合;读数.让学生动手操作,培养他们动手能力.反馈练习:课本第32页习题1.3A组第3题,用量角器测量、、的大小,同桌交换结果看是否准确.2.角的和、差、倍、分投影显示:如图1,、.图1提出问题:如图1,,把移到上,使它们的顶点重合,一边重合,会有几种情况?请同学们在练习本上画出.你如何把移到上,才能保证的大小不变呢?学生活动:讨论如何移到上,移动后有几种情况,在练习本上画出图形.(有小学测量的基础,学生不会感到困难,可放手让学生自己动手操作.)教师根据学生回答小结:量角器可起移角的作用,先测量的度数,然后以的顶点为顶点,其中一边为作作一个角等于,出现两种情况.如图2及图3所示:(1)在内部时,如图2,是与的差,记作:.(2)在外部时,如图3,是与的和,记作:.【教法说明】在以上教学过程中,一定要注意训练学生的看图能力和几何语句表达能力,如与的和差所得到的两个图形中,还可让学生观察得到图2中是与的差,记作:,或与的和等于,记作:,图3中是与的差,记作:等进行看图能力的训练.图2 图3反馈练习:学生在练习本上完成画图.已知如图4,,画,使.师:两个的和是,那么是的2倍,记作,或是的,记作:.同样,有角的3倍和等等.角的和、差、倍、分的度数等于它们的度数的和、差、倍、分.图43.角平分线学生观察以上反馈练习中的图形,,也就是把分成了两个相等的角,这条射线叫的平分线.[板书]定义:一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.几何语言表示:是的平分线,(或).说明:若,则是的平分线,同样有两条三等分线,三条四等分线,等等.变式训练,培养能力投影显示:1.如图1填空:图1①②2.是的平分线,那么,①②图23.如图2:是的平分线,是的平分线①若,则② ,,则度【教法说明】练习中的第1、2题可口答,第3题在教师引导下写出过程,初步渗透推理过程,培养学生的逻辑推理能力,推理过程由已知入手,联想得出结论.(四)总结、扩展找学生回答:今天学习了哪些内容?教师归纳得出以下知识结构:八、布置作业课本第33页B组第1、2题.作业答案1.解:,若,那么,2.解:∵ 是的平分线,∴ .又∵ 是的平分线,∴ .又∵ ,∴ .说明:学生作业或回答问题,尽量要求用“∵ ∴”的形式,为以后解证明题打好基础.九、板书设计同七、(四)的格式.。
初一几何:角的大小比较与画相等的角
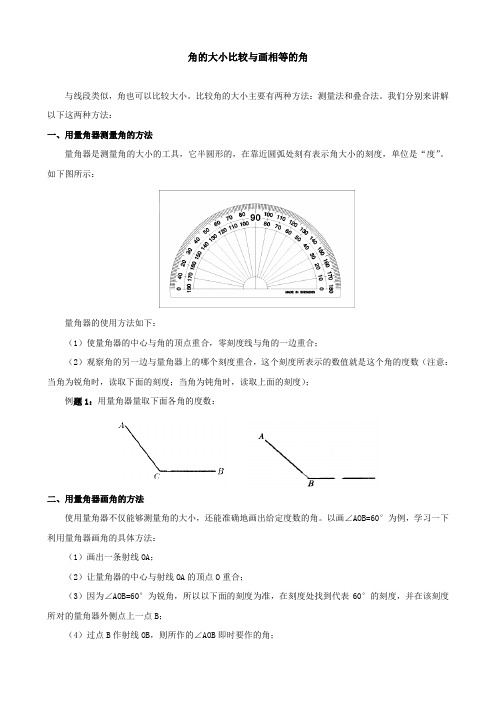
角的大小比较与画相等的角与线段类似,角也可以比较大小。
比较角的大小主要有两种方法:测量法和叠合法。
我们分别来讲解以下这两种方法:一、用量角器测量角的方法量角器是测量角的大小的工具,它半圆形的,在靠近圆弧处刻有表示角大小的刻度,单位是“度”。
如下图所示:量角器的使用方法如下:(1)使量角器的中心与角的顶点重合,零刻度线与角的一边重合;(2)观察角的另一边与量角器上的哪个刻度重合,这个刻度所表示的数值就是这个角的度数(注意:当角为锐角时,读取下面的刻度;当角为钝角时,读取上面的刻度);例题1:用量角器量取下面各角的度数:二、用量角器画角的方法使用量角器不仅能够测量角的大小,还能准确地画出给定度数的角。
以画∠AOB=60°为例,学习一下利用量角器画角的具体方法:(1)画出一条射线OA;(2)让量角器的中心与射线OA的顶点O重合;(3)因为∠AOB=60°为锐角,所以以下面的刻度为准,在刻度处找到代表60°的刻度,并在该刻度所对的量角器外侧点上一点B;(4)过点B作射线OB,则所作的∠AOB即时要作的角;例题1:用量角器画出∠AOB=120°、∠DEF=∠=45°、∠HGI=135°。
(只写一个角的作图过程)三、角的大小比较(叠合法)如下图所示,我们以∠AOB与∠DEF为例,来学习一如何用叠合法比较角的大小。
叠合法法比较角的大小的步骤如下:(1)移动∠DEF,使其顶点E与∠AOB的顶点O叠合,边ED与∠AOB的边OA叠合,让另一边EF与边OB处于同一侧;(2)这时另一边EF对于∠AOB而言,有以下三种可能位置关系:图①图②图③①边EF在∠AOB的内部,此时∠DEF<∠AOB,如图①所示:②边EF与边OB重合,此时∠DEF=∠AOB,如图②所示:③边EF在∠AOB的外部,此时∠DEF>∠AOB,如图③所示:在使用叠合法比较两角大小时要注意以下问题:1)使两个角的顶点重合;2)使两个角的一条边重合;3)让两个角的另一条边落在重合边的同一侧;4)两个角的大小有大于、小于和相等三种情况,具体比较时结论只能是三种情况中的一种。
角与角的大小比较

α
O
1
C
比一比,赛一赛
一、选择题(每题10分)
1、下列说法正确的是( B ) A,角的边越长,则角越大。 B,角的大小与边的长短无关。 C,角的大小与顶点的位置有关。 D,角的大小决定于始边旋转的方向。 2、把图中以A为顶点,AB,AC为两条边的角表示成 ∠ABC, ∠CAB,∠BCA, ∠A,∠α,∠BAC,其中表示方法正确 的有( B )个。 A,2 B,3 C,4 D,5
B C D
α
A
练习2
将图中的角用不同的方法表示出来,并填写下表
B
5
4
3
2
1
E
D
A
C
∠1
∠BCE
∠2 ∠ACB
∠3
∠BAC
∠4
∠DAB
∠5
∠ABC
3、下图一组角,其大小顺序正确的是( D ) A, ∠1< ∠2< ∠3< ∠4 B, ∠1< ∠4< ∠2< ∠3 C, ∠1< ∠4< ∠3< ∠2 D, ∠1< ∠3< ∠2<∠4
有101条,那么以O为顶 点的角有几个? 5050个
O
B
如果以O为顶点的射线共有n条,那么以O为顶点 的角有几个? n n 1
2
个
想一想
利用一副三角板,你能 画出哪些度数的角?
飞
天 高 任 鸟
欢迎
遨游
数学 海洋!
跃
海 阔 凭 鱼
角与角的大小比较
B 终边 O 顶点 始边 A
B
O
A
一、角的定义
①一条射线绕着它的端点旋转到另一位置时 所形成的图形叫角 (angle)。 射线的端点(如O点)叫角的顶点.射线原来所在的 位置(如OA)叫角的始边。旋转后的位置(如OB) 叫角的终边,统称角的边(side). 从始边旋转到终边所扫过的区域叫角的内部。
角的大小比较

B
C
E
F
2、叠合法比较
D
A
B
DE边在∠ABC的外部,则
C
E
F
∠ABC<∠DEF
2、叠合法比较
A D
B
DE与AB边重合,则
C
E
F
∠ABC=∠DEF
2、叠合法比较
A D
B
C
E
F
DE边在∠ABC的内部,则
∠ABC>∠DEF
2、叠合法比较 D
∠ABC<∠DEF
B (E)
C A
(F) (D)
∠ABC=∠DEF
C B A
图中∠AOB是∠AOC和∠BOC的差, 记作∠AOB=∠AOC-∠BOC
那么,图中∠AOC-∠AOB=
∠BOC
填空
∠AOC =∠____ + ∠ __ AOB BOC ∠AOC= ∠____-∠ __ AOD DOC ∠BOD - ∠COD= ∠ __ BOC D
C
B
O
A
∠BOC= ∠AOC - ∠ __ = ∠BOD - ∠ COD __ AOB ∠AOB= ∠____ - ∠____ - ∠____ AOD BOC COD ∠AOD = ∠____+ ∠ BOC ∠____ __+ AOB COD
1 2
AOC
AOB BOC COD
1 3
AOD
AO C 2 AO B 2 BO C
A O D 3 A O B 3 B O C 3 C O D
OB是 AOC 的 角 平 分 线
O B、 O C 是 A O D 的三等分线
120°
角的大小比较方法有

角的大小比较方法有
以下是角的大小比较方法:
1. 用度数表示。
角度越大,角就越大。
例如,一个90度的角比一个45度的角大。
2. 用弧长表示。
如果两个角在同一圆周上,它们的弧长也可以用来比较大小。
弧长越长,角就越大。
3. 用三角函数表示。
三角函数(如正弦、余弦、正切等)可以用来比较不同角度的大小关系,例如sin30<sin60<sin90。
4. 用向量表示。
如果两个角的向量大小相等,但方向不同,则它们的角度相等。
如果一个向量比另一个更长,那么它所对应的角度就更大。
5. 用比例表示。
两个角度之间的大小比例可以用分数表示,例如,比较150度和45度,可以将它们都化为最简分数:150/360和45/360,然后比较它们的大小。
第31课 角的大小比较(教师版)

第30课 角的大小比较学习目标1.理解角的大小的概念,会用度量法比较两个角的大小,了解比较两个角的大小的叠合方法.2.理解角的分类.3.会用量角器作一个角等于已知角.A .B .C .D .知识点01 角的大小比较角的大小比较:(1)度量法:如果两个角的度数相等,那么我们就说这两个角相等.如果两个角的度数不相等,度数较大的角较大(2)叠合法:A .B .C .D .知识点02 角的分类α锐角直角钝角平角周角范围0°<α<90°α=90°90°<α<180°α=180°α=360°考点01 角的大小比较【典例1】如图,用同样大小的三角板比较∠A 和∠B 的大小,下列判断正确的是( )A .∠A >∠B B .∠A <∠BC .∠A =∠BD .没有量角器,无法确定【思路点拨】由图知∠A >45°,∠B <45°,故可比较大小.【解析】解:∵图中三角尺为等腰直角三角形,∴∠A >45°,∠B <45°,∴∠A >∠B ,故选:A .【点睛】本题主要考查角的大小比较,熟练利用中间角比较角的大小是解题的关键.【即学即练1】已知∠α与∠β都小于平角,在平面内把这两个角的一条边重合,若∠α的另一条边恰好落在∠β的内部,则( )A .∠α<∠βB .∠α=∠βC .∠α>∠βD .不能比较∠α与∠β的大小【思路点拨】如果两个角的顶点重合,且有一边重合,如果另两边也重合,说明两角相等;如果两边不重合,另一条边在里面的小,在外面的大;再结合“若∠α的另一条边恰好落在∠β的内部”即可比较出∠α与∠β的大小.【解析】解:∵∠α与∠β的一条边重合,且∠α的另一条边恰好落在∠β的内部,∴∠α<∠β.故选:A .【点睛】本题考查角的大小比较,熟练掌握比较角大小的方法是解题关键.考点02 角的分类【典例2】把一副三角尺按如图所示的方式拼在一起.(1)写出图中∠A ,∠B ,∠BCD ,∠D 的度数;(2)用“<”将上述各角连接起来;(3)指出∠A ,∠B ,∠BCD ,∠D中的锐角、钝角和直角.能力拓展【思路点拨】(1)一副三角尺一个是等腰直角三角形,另一个是一个角为30°的直角三角形,看图写出各个角的度数,(2)按角的大小顺序连接;(3)根据锐角、钝角和直角的定义判定即可.【解析】解:(1)∠A =30°,∠B =90°,∠BCD =150°,∠D =45°;(2)∠A <∠D <∠B <∠BCD ;(3)∠A ,∠D 是锐角;∠B 是直角;∠BCD 是钝角.【点睛】本题主要考查角的比较与运算,熟记一副三角尺的各个角的度数是解答本题的关键.【即学即练2】如图,AOE 是一条直线,图中小于平角的角共有( )A .4个B .8个C .9个D .10个【思路点拨】根据角的定义分别表示出各角即可.【解析】解:图中小于平角的角共有:∠AOB ,∠AOC ,∠AOD ,∠BOC ,∠BOD ,∠BOE ,∠COD ,∠DOE ,∠COE ,共9个.故选:C .【点睛】此题主要考查了角的定义,熟练掌握角定义是解题关键.题组A 基础过关练1.在∠AOB 内部任取一点C ,作射线OC ,则一定存在( )A .∠AOB >∠AOC B .∠AOC >∠BOC C .∠BOC >∠AOCD .∠AOC =∠BOC 分层提分【思路点拨】利用角的大小进行比较即可得出结论.【解析】解:∵射线OC在∠AOB的内部,那么∠AOC在∠AOB的内部,且有一公共边;∴一定存在∠AOB>∠AOC.故选:A.【点睛】本题考查角的大小比较,解答的关键是明确题意,得出角之间的关系.2.若∠1=50°5',∠2=50.5°,则∠1与∠2的大小关系是( )A.∠1=∠2B.∠2>∠1C.∠1>∠2D.无法确定【思路点拨】把两个度数统一即可判断.【解析】解:50.5°=50°30′,则∠1<∠2.故选:B.【点睛】本题考查了角的度数的表示,正确记忆度、分、秒是60进制是解题关键.3.下面所标注的四个角中最大的角是( )A.B.C.D.【思路点拨】根据直角,锐角,钝角,平角的定义进行角的大小比较.【解析】解:A:图中标注的角为钝角,钝角大于90°;B:图中标注的角为锐角,锐角大于0°而小于90°;C:图中标注的角为直角,直角等于90°;D:图中标注的角为平角,平角等于180°.∴锐角<直角<钝角<平角.故选:D.【点睛】本题考查直角,锐角,钝角,平角的定义及角的大小比较.钝角大于90°,锐角大于0°而小于90°,直角等于90°,平角等于180°.4.如图,在正方形网格中有∠α和∠β,则∠α和∠β的大小关系是( )A.∠α>∠βB.∠α<∠βC.∠α=∠βD.无法确定【思路点拨】将两个角叠合在一起,通过观察比较,即可得出答案.【解析】解:使∠α和∠β顶点和一边重合,,由图直观可得∠α>∠β,故选:A.【点睛】本题主要考查两个角的大小比较,掌握角大小的比较方法是解题的关键.6.如图,若∠AOC=∠BOD,那么∠AOD与∠BOC的关系是( )A.∠AOD>∠BOC B.∠AOD<∠BOC C.∠AOD=∠BOC D.无法确定【思路点拨】根据题意∠AOC=∠BOD,再根据图得知∠COD为∠AOD与∠BOC的公共角,从而得出答案.【解析】解:∵∠AOC=∠BOD,∠COD为∠AOD与∠BOC的公共角,∴∠AOC+∠COD=∠BOD+∠COD,∴∠AOD=∠BOC,故选:C.【点睛】本题考查了角的大小比较,解题的关键是根据图得知∠COD为∠AOD与∠BOC的公共角,再解题就容易了.7.如图,在此图中小于平角的角的个数是( )A.9B.10C.11D.12【思路点拨】根据角的定义,找出图中小于平角的角.【解析】解:由图可知:∠CAB、∠CAE、∠BAE、∠AEB、∠CED、∠D、∠DCE、∠DCA、∠ECA、∠EBA、∠ABC小于平角,共11个.故选:C.【点睛】除了注意角要小于平角外,还要注意同一顶点处的角要全部找出来.8.下列角度中,比20°小的是( )A.19°38′B.20°50′C.36.2°D.56°【思路点拨】根据角的大小比较方法分别与20°进行比较,即可得出答案.【解析】解:∵19°38′<20°,20°50′>20°,36.2°>20°,56°>20°,∴比20°小的是19°38,故选:A.【点睛】此题考查了角的大小比较,根据角的比较方法进行比较,是一道基础题,比较简单.9.比较∠1与∠2的大小,下列放置方法正确的是( )A.B.C.D.【思路点拨】运用叠合法直接对比观察即可.【解析】解:根据两个角比较大小,一般用叠合法,即顶点和一条边重合且另外的一条边在同侧,通过观察D选项符合题意.故选:D.【点睛】本题考查角的大小比较,灵活运用叠合法是解答本题的关键.10.已知∠A=20°24′,∠B=20.4°.比较大小:∠A = ∠B(填“>或<或=”).【思路点拨】根据1°=60′对∠B进行换算即可得出答案.【解析】解:∵20.4°=20°24′,∴∠A=∠B,故答案为:=.【点睛】本题考查了角的大小比较,度分秒的换算,掌握1°=60′是解题的关键.11.如图,已知三个角α,β,γ,将这三个角按从大到小的顺序排列: β , γ , α .【思路点拨】根据图形观察比较即可比较角的大小.【解析】解:由图可得,β>γ>α.∴三个角按从大到小的顺序排列为:β,γ,α.故答案为:β,γ,α.【点睛】本题主要考查了角的大小比较,比较角的大小有两种方法:①测量法,即用量角器量角的度数,角的度数越大,角越大.②叠合法,即将两个角叠合在一起比较,使两个角的顶点及一边重合,观察另一边的位置.12.已知∠α是直角,∠β是钝角,∠γ是锐角,则用“<”号将三个角连接起来是 ∠γ<∠α<∠β .【思路点拨】根据直角、顿角及锐角的定义进行解答即可.【解析】解:∵等于90°的角叫直角;大于90°的角叫钝角;小于90°的角叫锐角,∴∠γ<∠α<∠β.故答案为:∠γ<∠α<∠β.【点睛】本题考查的是角的大小比较,熟知直角、钝角及锐角的定义是解答此题的关键.13.如图所示,∠AOF是平角、请你比较∠AOB,∠AOC,∠AOD,∠AOE四个角的大小.【思路点拨】根据一个角在另一个角的内部,则这个角小于另一个角.【解析】解:由题意可得:∠AOB<∠AOC<∠AOD<∠AOE.【点睛】此题考查了角的大小比较,掌握角与角之间的关系是本题的关键,比较角的大小,就是比较角的开口大小,比较的方法是需要熟记的.题组B 能力提升练14.如图,射线OC、OD分别在∠AOB的内部、外部,下列各式中错误的是( )A.∠AOB<∠AOD B.∠BOC<∠AOB C.∠COD>∠AOD D.∠AOD>∠AOC【思路点拨】结合图形分析角与角之间的关系即可判断.【解析】解:A.∵∠AOB在∠AOD的内部,∴∠AOB<∠AOD,故A正确;B.∵∠BOC在∠AOB的内部,∴∠BOC<∠AOB,故B正确;C.∵∠COD在∠AOD的内部,∴∠COD<∠AOD,故C错误;D.∵∠AOC在∠AOD的内部,∴∠AOD>∠AOC,故D正确;故选:C.【点睛】本题考查了角的大小比较,结合图形去分析是解题的关键.15.若∠A=32°18′,∠B=32°15′30″,∠C=32.25°,则( )A.∠A>∠B>∠C B.∠B>∠A>∠C C.∠A>∠C>∠B D.∠C>∠A>∠B【思路点拨】将三个角的度数都转化成度分秒的形式后,即可得到三个角的大小关系.【解析】解:∵1°=60′;∴0.25°=60′×0.25=15′;∴∠C=32°15′;∴32°18′>32°15′30″>32°15′;∴∠A>∠B>∠C.故选:A.【点睛】本题主要考查角的大小比较,需要熟练掌握度数与度分秒形式之间的转化.16.分别记以下三个时刻3:30,6:40,9:00时针和分针所成角的大小为α,β,γ,请比较α,β,γ的大小 β<α<γ .(用“<”号连结)【思路点拨】首先求得三个时刻的时针与分针所成的角的度数,然后比较大小即可.【解析】解:∵3:30时,钟表的时针与分针形成的夹角的度数α=75°;6:40时,钟表的时针与分针形成的夹角的度数β=40°;9:00时,钟表的时针与分针形成的夹角的度数γ=90°;∴β<α<γ.故答案为:β<α<γ.【点睛】本题考查了钟面角,求出每个时刻时针与分针所成的角的大小是解题的关键.17.如图,AOB为一直线,OC,OD,OE是射线,则图中大于0°小于180°的角有 9 个.【思路点拨】大于0°小于180°的角有∠AOE,∠AOD,∠AOC,∠EOD,∠EOC,∠EOB,∠DOC,∠DOB,∠COB.共9个.【解析】解:大于0°小于180°的角有∠AOE,∠AOD,∠AOC,∠EOD,∠EOC,∠EOB,∠DOC,∠DOB,∠COB.共9个.故答案为:9.【点睛】此题主要考查了角的定义,即由一个顶点射出的两条射线组成一个角.18.如图,回答下列问题:(1)比较∠FOD与∠FOE的大小;(2)借助三角板比较∠DOE与∠BOF的大小;(3)借助量角器比较∠AOE与∠DOF的大小.【思路点拨】(1)根据OD边在∠FOE内部,即可得出∠FOD<∠FOE.(2)用量角器量∠DOE大于45゜,∠DOF小于45゜,即可得出∠DOE>∠DOF.(3)用量角器量出角的度数,再比较大小即可.【解析】解:(1)∵OD在∠FOE的内部,∴FOD<∠FOE.(2)用含有45゜角的三角板比较,可得∠DOE>45゜,∠BOF<45゜,则∠DOE>∠BOF.(3)用量角器度量得∠AOE=30゜,∠DOF=30゜,则∠AOE=∠DOF.【点睛】此题考查了角的大小比较,解题的关键是会用量角器估算角的大小,是一道基础题.题组C 培优拔尖练19.如图,如果∠CAE>∠BAD,那么下列说法中一定正确的是( )A.∠BAC>∠CAD B.∠DAE>∠CADC.∠CAE<∠BAC+∠DAE D.∠BAC<∠DAE【思路点拨】先由∠CAE>∠BAD,根据角的和差可得∠CAD+∠DAE>∠BAC+∠CAD,再利用不等式的性质得出∠DAE>∠BAC,即∠BAC<∠DAE.【解析】解:∵∠CAE>∠BAD,∴∠CAD+∠DAE>∠BAC+∠CAD,∴∠DAE>∠BAC,即∠BAC<∠DAE.故选:D.【点睛】本题考查了角的大小比较,角的和差,不等式的性质,根据角的和差结合图形得出∠CAE=∠CAD+∠DAE,∠BAD=∠BAC+∠CAD是解题的关键.20.如图,点A,O,B在同一条直线上,OC,OE分别是∠AOD,∠BOD的平分线.(1)试比较∠AOC,∠COD,∠AOD,∠AOE的大小;(2)若∠BOD=72°,求∠COD,∠COE的度数;(3)写出图中所有的锐角、直角、钝角与平角.【思路点拨】(1)根据角平分线定义判断∠AOC和∠COD,再根据角的一边重合,比较另一边的张开幅度即可;(2)先求出∠AOD,再根据角平分线定义求∠COD,然后根据∠COE=∠COD+∠DOE,并结合角平分线的定义解答.对于(3),根据角的分类解答即可.【解析】解:(1)由题意与图形可知,∠AOC=∠COD<∠AOD<∠AOE.(2)因为∠AOD=180°﹣∠BOD=180°﹣72°=108°,所以∠COD=∠AOD=54°.∠COE=∠COD+∠DOE=∠AOD+∠BOD=(∠AOD+∠BOD)=∠AOB=90°.(3)锐角:∠AOC,∠COD,∠DOE,∠DOB,∠BOE;直角:∠COE;钝角:∠AOD,∠AOE,∠COB;平角:∠AOB.【点睛】本题主要考查了角的基础知识,掌握角平分线定义是解题的关键.21.有公共顶点的两个角,∠AOB=∠COD,且OE为∠BOC的角平分线.(1)如图1,请探索∠AOE和∠DOE的大小关系,并说明理由;(2)如图2,∠AOE和∠DOE是否仍然满足(1)中关系?请说明理由;(3)若∠AOB=90°,∠AOC=64°,求出∠BOE的度数.【思路点拨】(1)根据角平分线的定义,由OE为∠BOC的角平分线,得∠BOE=∠COE,进而推断出∠AOE=∠DOE.(2)与(1)同理.(3)根据角的和差关系,由∠AOB=90°,∠AOC=64°,得∠AOB﹣∠AOC=26°.根据角平分线的定义,由OE为∠BOC的角平分线,得∠BOE=.【解析】解:(1)∠AOE=∠DOE,理由如下:∵OE为∠BOC的角平分线,∴∠BOE=∠COE.∵∠AOB=∠COD,∴∠AOB+∠BOE=∠COD+∠COE.∴∠AOE=∠DOE.(2)∠AOE=∠DOE,理由如下:∵OE为∠BOC的角平分线,∴∠BOE=∠COE.∵∠AOB=∠COD,∴∠AOB﹣∠BOE=∠COD﹣∠COE.∴∠AOE=∠DOE.(3)∵∠AOB=90°,∠AOC=64°,∴∠AOB﹣∠AOC=26°.∵OE为∠BOC的角平分线,∴∠BOE=.【点睛】本题主要考查角的和差关系、角平分线的定义,熟练掌握角的和差关系、角平分线的定义是解决本题的关键.。
角的度量与比较

角的度量与比较角是几何学中的重要概念,它是由两条射线共同组成的一部分平面。
角的度量和比较是我们在几何学中经常要进行的操作,下面将详细介绍角的度量方法以及如何比较不同角的大小。
一、角的度量方法在角的度量中,我们通常使用度和弧度两种单位进行表示。
度是最常见的单位,用符号°来表示。
它将一圆分为360等份,每份为1°。
而弧度是数学家们更常用的单位,用符号rad来表示。
弧度的度量方式是以圆的半径为1所对应的圆心角所对应的弧长为1.1. 度的度量方法度是角度的度量单位,我们可以通过直接读数的方式来表示角的度量大小。
例如,一个直角对应的角度为90°,一个平角对应的角度为180°。
2. 弧度的度量方法弧度是角度的另一种度量方式,通过弧长与半径的比值来表示。
当弧长等于半径时,对应的角度为1弧度。
弧度与度之间的转换关系为:1弧度约等于57.3°。
二、角度比较角度的比较可以分为两种情况进行讨论,即两个角的度量单位相同和不同的情况。
1. 相同度量单位的角比较当两个角的度量单位相同时,我们可以直接通过数值大小来比较它们的大小。
例如,角A的度量为60°,角B的度量为45°,可以得出角A比角B更大。
2. 不同度量单位的角比较当两个角的度量单位不同时,我们需要通过将其转换为同一种度量单位来进行比较。
例如,角C的度量为2弧度,角D的度量为90°,我们可以将角C转换为180°进行比较,从而得出角D比角C更大。
三、角度的常见分类除了比较角的大小,我们还经常遇到需要对角进行分类的情况。
以下是一些常见的角度分类:1. 锐角锐角是指度量小于90°的角。
锐角的特点是两条射线之间形成的夹角较小,弧度不超过1.5708 rad。
2. 直角直角是指度量等于90°的角。
直角的特点是两条射线之间形成的夹角为90°,弧度约为1.5708 rad。
角的大小比较教案

角的大小比较教案教案标题:角的大小比较教案教学目标:1. 理解角的概念和特征。
2. 能够比较不同角的大小。
3. 运用所学知识解决与角大小比较相关的问题。
教学准备:1. 教师准备:投影仪、白板、马克笔、角度模型(如角度计、角度模型图等)。
2. 学生准备:课本、笔记本、铅笔、直尺。
教学过程:引入活动:1. 利用投影仪或白板展示一些日常生活中的角,如直角、锐角、钝角等,并引导学生观察并讨论这些角的特征。
知识讲解与示范:2. 介绍角的概念:角是由两条射线共同起点形成的图形,起点称为角的顶点,两条射线称为角的边。
3. 解释角的大小比较方法:a. 角的大小可以通过比较两条边之间的夹角来判断,夹角越大,角就越大。
b. 使用角度计或角度模型图来测量和比较角的大小。
4. 示范如何使用角度计或角度模型图来测量和比较角的大小。
练习与讨论:5. 学生个别或小组合作完成以下练习:a. 观察给定的角,判断它们的大小关系,如:比较两个角的大小,判断它们是否相等。
b. 给出一些角的度数,让学生按照从小到大或从大到小的顺序进行排序。
c. 给出一些角的度数,让学生用角度计或角度模型图进行测量和比较。
6. 引导学生讨论他们的答案和解决问题的方法,并给予肯定和指导。
巩固与拓展:7. 给学生提供更多的角大小比较问题,让他们运用所学知识解决,如:判断一个角是否是直角、锐角或钝角,比较不同角的大小关系等。
8. 鼓励学生在日常生活中观察和发现角的应用,如:家具的角、建筑物的角等,并思考它们的大小关系。
总结与评价:9. 对本节课所学内容进行总结,并强调角的大小比较方法。
10. 针对学生的学习情况进行评价,鼓励他们积极参与课堂活动,并提供必要的指导和帮助。
拓展活动:11. 布置角度计算和角度比较的作业,让学生在家中继续巩固和拓展所学内容。
12. 鼓励学生使用在线学习资源或角度模拟软件进行角度比较的练习。
教学反思:本节课通过引入活动、知识讲解与示范、练习与讨论、巩固与拓展等环节,帮助学生理解角的概念和特征,并学会比较不同角的大小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
比较角的大小
新马集中心学校 齐平超
教学目标:
知识与技能:
1、会用叠合法比较两个角的大小,会用“=”、“<”、“>”表示两个角的大小关系;
2、了解角的和、差、倍、分,会用图形和符号语言表示角的和、差、倍、分;
3、理解角的平分线的概念。
培养学生用类比的学习方法和数形结合的能力。
4、熟练应用图形分析角的和与差以及准确表达角平分线的三种关系式,能够为以后的证明做好准备。
通过类比学习,体会数学学习的智慧美、图形的对称美。
过程与方法:
通过实际观察、操作、体会角的大小,并简单说理,培养学生的观察思维能力及合情推理能力。
情感、态度与价值观:
通过角的度量和折叠,体验数、符号和图形是描述现实世界的重要手段。
教学重点及难点
重点:角的大小比较,角平分线的意义,两个角的和、差、倍、分的意义。
难点:角平分线的几何语言的表达方式的选择.,空间观念,几何识图能力的培养。
教学方法与手段:
1、教学方法:直观演示验证法,自主、合作、探究式
2、教学手段:借助于多媒体课件演示及学生动手操作确认发现新知。
教学流程设计:
教学过程:
课前准备
(1)比较两条线段长短的方法有_________和________。
(2)角的度量单位是什么?你会用量角器度量角吗? 课内探究
探究1:角的比较方法。
(1)度量法:角的值越大,角就越______。
(2)叠合法:把一个角放在另一个角上,使____________________,并将_________________,使这两个角的另一边_______________________________,就可以明显看出两个角的大小。
课前
延伸
自主探究
合作交流
教师点拨
有效训练
反馈矫正 课堂小结 课后延伸
如图∠AOB 与∠COD 的大小。
①∠AOB_____∠COD ②∠AOB_____∠COD ③∠AOB_____∠COD
探究2:角的和、差、倍、分。
1、如图1,如果将∠α与∠β的顶点重合,再将∠α的一边与∠β的一边重合,并使两角的另一边分别在重合边的两侧,这时它们不重合的两边组成∠AOB 。
那么∠AOB 与∠α、∠β有什么关系?
答案:这时∠AOB 叫做∠α与∠β的 。
记作: 或 。
2、如图2,是取两张硬纸片叠合作一起,在其中一张上任意画出一个∠α,然后剪下并分开得到的,它们的大小有什么关系?
如上图2,则∠AOB=______+______=2∠___=2∠___。
探究3:角的平分线
1、已知∠1,你能用量角器画出∠AOB ,使它的度数是∠1的2倍吗?则∠AOB=______+______=2∠___=2∠___,∠1=______-_____。
2、角的平分线是______________________________________________。
如课本P 148页图4—28,如果OC 是∠AOB 的角平分线,
则∠______=∠______=2
1
∠______;
如果∠AOC=∠BOC=2
1
∠AOB,则射线OC 是_________________。
有效训练
1,如上图3,在∠AOC 的内部画射线OB ,在∠AOC 的外部画射线OD 。
∠AOC 是那两个角的和?∠BOD 是哪两个角的和?当∠AOB=∠COD 时,你能找出其他相等的角吗?
2、课本第150页练习2题 课堂小结:
这节课你学到了哪些知识,最大的收获是什么?还有哪些困惑? 课堂检测:
1、射线OC 在∠AOB 内部,下列给出的条件中不能得到OC 为∠AOB 的平
分线的是()
A、2∠AOC=∠BOA
B、∠AOB=2∠BOC
C、∠AOC+∠BOC=∠AOB
D、∠AOC=∠BOC
2、如图1-33,若∠AOB=∠COB=∠DOC,进行下列填空。
(1)∠AOD=( )+( )+( );
(2)∠AOB=( )∠AOD;
(3)∠AOD=( )∠COB;
(4)∠DOB=( )=( )+( )。
课后提升:
配套同步作业第102、103页。
教学反思
本课的学习,我主要是通过引导学生通过自主学习和合作探究的途径,学习了角的大小比较的两种方法,通过学习培养学生由自主探究认识角的比较方法,结合小组交流,学习角平分线性质,加强了学生对知识的理解和应用。
整节课学生探究有目的,交流有效果,真正是在教师的点拨下快乐的学习,并不断得到锻炼和提升。
不足之处是对于学生能力拓展方面不够,需在以后设计与教学中大力改进。
