6百大经典例题——两平面垂直的判定和性质(新课标)
两个平面垂直的判定和性质

两个平面垂直的判定和性质年级__________ 班级_________ 学号_________ 姓名__________ 分数____一、选择题(共50题,题分合计250分)1.已知菱形ABCD 的边长是1,∠DAB =60°,将这个菱形沿AC 折成120°的二面角,则BD 两点间的距离是A.21B.23C.23D.432.在正方体AC 1中,过与顶点A 相邻的三个顶点作平面α,过与顶点C 1相邻的三个顶点作平面β,那么平面α与平面β的位置关系是A.垂直B.平行C.斜交D.斜交或平行3.已知a,b 是异面直线,β是平面,且α⊥β,则A.b 与β相交B.b 与β不相交C.b 与β不平行D.b 与β不垂直4.设直线l 和平面α、β,且直线l ⊄α,l ⊄β,给出下列论断:①l ⊥α②α⊥β③l ∥β,从中取两个作为条件,其余的一个作为结论,在构成的诸命题中,正确命题的个数是 A.0 B.1 C.2 D.35..已知二面角α-l -β的大小为60°,b 和c 是两条异面直线,则在下列四个条件中,能使b 和c 的角为60O的是A.b ∥α,c ⊥βB.b ∥α,c ⊥βC.b ⊥α,c ⊥βD.b ⊥α,c ∥β6.已知α,β是平面,m,n 是直线.下列命题中不正确的是A.若m ∥n ,m ⊥α,则n ⊥αB.若m ∥α, α∩β=n ,则m ∥nC.若m ⊥α,m ⊥β,则α∥βD.若m ⊥α,β⊂m ,则α⊥β7.已知a 、b 为两条不同的直线,α、β为两个不同的平面,且a ⊥α,b ⊥β,则下列命题中的假命题是A.若a ∥b ,则α∥βB.若α⊥β,则a ⊥bC.若a 、b 相交,则α、β相交D.若α、β相交,则a 、b 相交8.过正方形ABCD 的顶点A 作线段A A ' ⊥平面ABCD ,若A A ' = AB ,则平面A 'AB 与平面A 'CD 所成的角度是A. 30°B. 45°C. 60°D. 90°9.在直二面角α-AB -β的棱AB 上取一点P ,过P 分别在α、β两个平面内作与棱成45°的斜线PC 、PD ,那么∠CPD 的大小为A.45°B.60°C.120°D.60°或120°10.两个平面α、β与另一平面所成的角相等,则A.α∥βB.α与β相交C.α∥β或α与β相交D.以上都不对11.如图,等腰直角△ABC ,沿其斜边AB 边上的高CD 对折,使△ACD 与△BCD 所在的平面垂直,此时∠ACB 等于A.45°B.60°C.90°D.120°12.已知三条直线m 、n 、l ,三个平面α、β、γ,下面四个命题中,正确的是A.αγβγ⇒⎭⎬⎫⊥⊥a ∥βB.ββ⊥⇒⎭⎬⎫⊥l m l m // C.nm m //////⇒⎭⎬⎫γβγ D.n m n m //⇒⎭⎬⎫⊥⊥γγ13.α、β是两个不同的平面,m 、n 是平面α及β外的两条不同直线,给出四个论断:①m ⊥n ;②α⊥β;③n ⊥β;④m ⊥α,以其中三个结论作为条件,另一个论断作为结论,则所得命题正确的个数是 A.1 B.2 C.3 D.414.平面α与平面β相交,m 是α内的一条定直线,则下列结论正确的是A.在β内必存在与m 平行的直线B.在β内必存在与m 垂直的直线C.在β内必不存在与m 平行的直线D.在β内不存在与m 垂直的直线15.对于直线m 、n 和平面α、β、γ,下列命题中,正确命题的个数为①若m ∥α,n ⊥m ,则n ⊥α②若m ⊥α,n ⊥m ,则n ∥α③若α⊥β,γ⊥β,则α∥γ④若m ⊥α,m ⊂β,则α⊥βA.1B.2C.3D.416.A 为直二面角α-l -β的棱上的一点,两条长度都等于a 的线段AB 、AC 分别在α、β内并且都与l 成45°角,则BC 的长为A.aB.a 或3aC.a 或2aD.a 或5a17.过平面外的两个点A 、B 有无穷多个平面都与α垂直,则一定有A.直线AB ∥αB.直线AB 与α成60°角C.A 、B 两点在α的一条垂线上D.A 、B 两点到α的距离相等18.对于直线m 、n 和平面α、β,α⊥β的一个充分条件是A.m ⊥n ,m ∥α,n ∥βB.m ⊥n ,α∩β=m ,n ⊂αC.m ∥n ,n ⊥β,m ⊂αD.m ∥n ,m ⊥α,n ⊥β19.已知直线L ⊥平面α,直线m ⊂平面β,有下面四个命题:①α∥β⇒L ⊥m ②α⊥β⇒L ∥m ③L ∥m ⇒α⊥β④L ⊥m ⇒α∥β其中正确的两个命题是A. ①与②B. ③与④C. ②与④D. ①与③20.过正方形ABCD 的顶点A 作线段⊥'A A 平面ABC D.若AB B A =',则平面AB A '与平而CD A '所成角的度数是A.30°B.45°C.60°D.90°21.如图:二面角α-AB -β的平面角是锐角,C 是面α内一点(它不在棱AB 上),点D 是点C 在面β上的射影,点E 是棱AB 上满足∠CEB 为锐角的任一点,那么A.∠CEB >∠DEBB.∠CEB =∠DEBC.∠CEB <∠DEBD.∠CEB 与∠DEB 的大小关系不能确定22.设直线m 、n 和平面α、β,则下列命题中,正确的是A.m∥n,m⊂α,n⊂β⇒α∥βB.m⊥α,m⊥n,n⊂β⇒α∥βC.m∥n,n⊥β,m⊂α⇒α⊥βD.m∥n,m⊥α,n⊥β⇒α⊥β23.设有不同的直线a、b和不同的平面α、β、γ,给出下列三个命题①若a∥α,b∥α,则a∥b;②若a∥α,a∥β,则α∥β;③若α⊥γ,β⊥γ,则α∥β其中正确命题的个数为A.0B.1C.2D.324.若有平面α与β,且α∩β=l,α⊥β,P∈α,P∉l,则下列命题中的假命题是A.过点P且垂直于α的直线平行于βB.过点P且垂直于l的平面垂直于βC.过点P且垂直于β的直线在α内D.过点P且垂直于l的直线在α内25.已知直线l、m,平面α、β,且l⊥α,m⊂β,给出下列四个命题:(1)若α∥β,则l⊥m(2)若l⊥m,则α∥β(3)若α⊥β,则l∥m(4)若l∥m,则α⊥β其中正确命题的个数是A.1个B.2个C.3个D.4个26.已知直线l、m,平面α、β,且l⊥α,m⊂β,给出下列四个命题:(1)若α∥β,则l⊥m(2)若l⊥m,则α∥β(3)若α⊥β,则l∥m(4)若l∥m,则α⊥β其中正确命题的个数是A.1个B.2个C.3个D.4个27.下列三个命题,其中正确命题的个数为①平面α∥平面β,β⊥平面γ,则α⊥γ②平面α∥平面β,β∥平面γ,则α∥γ③平面α⊥平面β,平面γ⊥β,则α⊥γA.1B.2C.3D.028.下列命题正确的是A.若直线a∥平面α,直线b⊥a,b⊂平面β,则α⊥βB.若直线a⊥直线b,a⊥平面α,b⊥平面β,则α⊥βC.过平面外的一条直线有且只有一个平面与已知平面垂直D.过平面外一点有且只有一个平面与已知平面垂直29.二面角α-l-β的平面角为120°,A,B∈l,AC⊆α,BD⊆β,AC⊥l,BD⊥l,若AB=AC=BD=1,则CD等于A.2B.3C.2D.530.二面角α-MN-β=60º,直线AB与α、β分别交于A、B,AB⊥MN,若AB与α、β所成角分别是θ1、θ2,则A.θ1+θ2=120ºB.θ1+θ2>120ºC.θ1+θ2<120ºD.以上都不对31.设平面α⊥平面β,直线a⊂α,直线b⊂β,且a⊥b,则A.a⊥βB.b⊥αC.a⊥β与b⊥α中至少有一个成立D.a⊥β与b⊥α同时成立32.正方形纸片ABCD,沿对角线AC对折,使D点在面ABC外,这时DB与面ABC所成的角一定不等于A.30°B.45°C.60°D.9033.a、b表示直线,α、β、γ表示平面,有下列四个命题:(1)若α∩β=a,b⊂α,a⊥b,则α⊥β;(2)若α⊥β,α∩γ=a,β∩γ=b,则a⊥b;(3)若a不垂直于平面α,则a不可能垂直于α内的无数条直线;(4)若a⊥α,b⊥β,a ∥b,则α∥β,其中不正确命题的个数为A.1B.2C.3D.434.正方形ABCD沿对角线AC折成直二面角后,AB与CD所成的角为A.30°B.45°C.60°D.90°35.自大于90°的二面角内一点分别向两个面引垂线,它们所成的角与二面角的平面角的大小关系是A.相等B.互补C.相等或互补D.无关36.设二面角α-AB-β面上一点D,DP在α内与AB成45°,与平面β成30°角,则二面角α-AB-β的度数是A.15°B.30°C.45°D.60°37.设平面α⊥平面β,在平面α内的一条直线a垂直于平面β内的一条直线b,则A.直线a必垂直于平面βB.直线b必垂直于平面αC.直线a不一定垂直于平面βD.过a的平面与过b的平面垂直38.下列命题中错误的是A.如果α⊥β,那么α内所有直线都垂直于平面βB.如果α⊥β,那么α内一定存在直线平行于平面βC.如果α不垂直于β,那么α内一定不存在直线垂直于平面βD.如果平面α⊥平面γ,平面β⊥γ,α∩β=l,那么l⊥γ39.如图,四边形BCEF、AFED都是矩形,且平面AFED⊥平面BCEF,则下列式子中正确的是A.cosα=cosβ·cosθB.sinα=sinβ·cosθC.cosβ=cosα·cosθD.sinβ=sinα·cosθ40.如果直线l 、m 与平面α、β、γ满足:l =β∩γ,l ∥α,m ⊂α和m ⊥γ,那么必有A.α⊥γ且l ⊥mB.α⊥γ且m ∥βC.m ∥β且l ⊥mD.α∥β且α⊥γ41.设有不同的直线a 、b 和不同的平面α、β、γ,给出下列三个命题:(1)若a ∥α,b ∥α,则a ∥b. (2)若a ∥α,α∥β,则α∥β.(3)若α⊥γ,β⊥γ,则α∥β.其中正确的个数是 A.0 B.1 C.2 D.342.若平面α⊥平面β,平面β⊥平面γ,则A.α∥γB.α⊥γC.α与γ相交但不垂直D.以上都有可能43.已知直线a 、b 和平面α、β、γ,可以使α∥β的条件是A.a ⊂α,b ⊂β,a ∥bB.a ⊂α,b ⊂α,a ∥β,b ∥βC.α⊥γ,β⊥γD.a ⊥α,a ⊥β44.设a,b,c 表示三条直线,α、β表示两个平面,则下列命题中逆命题不成立的是βαβα//c ,.A ,则若⊥⊥c b a c a .B ⊥⊥⊂则内的射影,若在是,b c b ββ βααβ⊥⊥⊂,则若b ,.C b c b c b // //c ,,.D 则若ααα⊄⊂45.如图,四边形ABCD 中,AD //BC ,AD=AB ,∠BCD =45°,∠BAD =90°,将△ABD 沿BD 折起,使平面ABD ⊥平面BCD ,构成三棱锥A -BC D.则在三棱锥A -BCD ,下列命题正确的是A.平面ABD ⊥平面ABCB.平面ADC ⊥平面BDCC.平面ABC ⊥平面BDCD.平面ADC ⊥平面ABC46.已知△ABC 中,AB =2,BC =4,∠ABC =45°.BC 在α内,且△ABC 所在平面与平面α成30°角,则△ABC 在α内射影面积是A.26B.36C.26D.647.一个直角三角形的两个直角边长为a 、b ,沿斜边高折成直二面角,则两个直角边所夹角的余弦值为A.22b a ab +B.222b a ab+ C.22b a ab+ D.22b a ab +48.一条直线与一个直二面角的两个面所成的角分别为θ和ϕ,则θ+ϕA.≤90°B.≠90°C.≥90°D.无法确定49.设有不同的直线a 、b 和不同的平面α、β、γ,给出下列三个命题:⑴若a ∥α,b ∥α,则a ∥b ;⑵若a ∥α,a ∥β,则α∥β; ⑶若α⊥γ,β⊥γ,则α∥β.其中正确命题的个数是 A.0 B.1 C.2 D.350.一间民房的屋顶有如图三种不同的盖法:①单向倾斜;②双向倾斜;③四向倾斜.记三种盖法屋顶面积分别为P 1、P 2、P 3.①若屋顶斜面与水平面所成的角都是α,则A.P 3=P 2>P 1B.P 3>P 2=P 1C.P 3>P 2>P 1D.P 3=P 2=P 1二、填空题(共8题,题分合计36分)1.若三个平面两两垂直,则它们的交线________.2.已知m 、l 是直线,α、β是平面,给出下列命题:①若l 垂直于α内的两条相交直线,则l ⊥α; ②若l 平行于α,则l 平行于α内的所有直线; ③若m ⊂α, l ⊂β,且l ⊥m , 则α⊥β; ④若l ⊂β,且 l ⊥α,则α⊥β; ⑤若m ⊂α, l ⊂β,且α∥β,则m ∥l.其中正确的命题的序号是___________.(注:把你认为正确的命题的序号都填上)3.设α、β表示平面,l 表示不在α内也不在β内的直线,存在下列三个事实①l ⊥α,②l ∥β,③α⊥β,若以其中两个作为条件,另一个作为结论,可构成三个命题,其中真命题是________ .(要求写出所有真命题)4.两腰长均是1的等腰Rt △ABC 1和等腰Rt △ABC 2所在平面成60°的二面角,则两点C 1与C 2的距离是___________________.5.正方形ABCD 的边长是2,E 、F 分别是AB 和CD 的中点,将正方形沿EF 折成直二面角,M 为矩形AEFD 内点,如果∠MBE =∠MBC ,MB 和平面BCF 所成角的正切值为21,那么点M 到直线EF 的距离为.6.设有四个条件:①平面γ与平面α、β所成的锐二面角相等; ②直线a ∥b ,a ⊥平面α,b ⊥β;③a 、b 是异面直线,βα⊂⊂b a ,,且a∥β,b∥α;④平面α内距离为d 的两条直线在平面β内的射影仍为两条距离为d 的平行线,其中能推出α∥β的条件有.(填写所有正确条件的代号)7.如图,∠BAD =90°的等腰直角三角形ABD 与正三角形CBD 所在平面互相垂直,E 是BC 的中点,则AE 与平面BCD所成角的大小为.8.50.在空间,下列命题正确的是____________.(注:把你认为正确的命题的序号都填上)①如果两条直线a 、b 分别与直线l 平行,那么a ∥b②如果一条直线a与平面β内的一条直线b平行,那么a∥β③如果直线a与平面β内的两条直线b、c都有垂直,那么a⊥β④如果平面β内的一条直线a垂直平面γ,那么β⊥γ三、解答题(共27题,题分合计287分)1.若P为正ΔABC外的一点,且P A=PB=PC,N为BC的中点,则平面P AN⊥平面AB C.2.已知Rt△ABC中,BC为斜边,点S为平面ABC外一点,且SA=SB=SC.(1)求证:平面SBC⊥平面ABC;.(2)若△ABC为等腰直角三角形,且BC=2,点S到平面ABC的距离为1,求二面角B-SA-C的大小3.如图:过正方形ABCD的顶点A,引P A⊥平面AC,若P A=AB,则平面ABP和平面CDP所成的二面角的大小是A.30°B.45°C.60°D.90°4.从120°二面角的棱上两点A和B,分别在它的两个半平面α、β内作垂直于棱的线段AC、BD,已知AB=2a,AC=BD=a,求CD的长.5.长为2a的线段AB的两端点在直二面角α-l-β的两个面内,且于这个面都成30°角,求异面直线AB与l所成的角.6.已知△ABC,∠ABC=30°,P A⊥平面ABC,PC⊥BC,PB与平面ABC成45°的角.(1)求证:平面PBC⊥平面P AC;(2)求二面角A-PB-C的正弦值.7.已知平面α⊥平面β,长度为2a的线段AB的两端点分别在α、β内,且AB与α与45°角与β成30°角,求这条线段两个端点在两个平面交线上垂足间的距离.8.已知平面α⊥平面β,直线a⊥β,aα,试判断a与α的关系.9.已知平面α⊥平面γ,平面α∥平面β,求证:β⊥γ10.已知平面α⊥平面β,a∥α,a垂直于α与β的交线AB,试判断a与β的位置关系.11.已知SA⊥平面ABC,AB⊥BC,SA=AB,SB=BC,E是SC的中点,DE⊥SC交AC于D.求二面角E-BD-C的大小.12.如图,平面α∩平面β=a,α⊥平面γ,β⊥平面γ,α和β同时平行于直线b,求证:(1)a⊥γ;(2)b⊥γ.13.点P在平面ABC处,△ABC是等腰直角三角形,∠ABC=90°,△P AB是正三角形,P A⊥BC.(1)求证:平面P AB⊥平面ABC;(2)求二面角P-AC-B的大小.14.如图,ABCD是正方形,E、F分别是AD、BC边上的点,EF∥AB,EF交AC于点O,以EF为棱把它折成直二面角A-EF-D后,求证:不论EF怎样移动,∠AOC是定值.15.如图,AB是圆O的直径,P A垂直于圆O所在的平面,C是圆周上不同于A,B的任意一点,求证:平面P AC⊥平面PBC.B16.Rt△ABC的两直角边长分别为AC=2,BC=3,P是斜边BC上一点,沿PC将起折为直二面角A-PC-B,此时AB =7,求二面角P-AC-B的大小APBC C APB17.如图,在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC,且分别交AC、SC于点D、E,又SA=AB,SB=BC,求以BD为棱,以BDE与BDC为面的二面角的度数.C18.如图,设△ABC和△DBC所在的两个平面互相垂直,且AB=BC=BD,∠CBA=∠DBC=120°,求:(91上海)(1)AD的连线与平面BCD所成的角;(2)AD得连线与直线BC所成的角;(3)二面角A-BD-C的大小.19.如图所示,在四面体ABCD中,AB⊥BC,AB⊥BD,BC⊥CD,且AB=BC=1.(1)求证:平面CBD⊥平面ABD;(2)是否存在这样的四面体,使二面角C-AD-B的平面角为30°?如果存在,求出CD的长;如果不存在,试确定角θ的范围,使得这样的四面体存在且二面角C-AD-B的平面角为θ.20.已知正方体ABCD-A1B1C1D1的棱长为2,P,Q分别是BC,CD上的动点,且|PQ|=2,建立如图所示的坐标系.(1)确定P,Q的位置,使得B1Q⊥D1P;(2)当B1Q⊥D1P时,求二面角C1-PQ-A的大小.21.已知二面角P-l-Q的大小为120°,点A∈P,点B∈Q,点A、B到棱l的距离分别为2和4,AB=10,求:(1)AB与棱l所成角的正弦;(2)求AB和l的距离.22.已知四边形ABCD为矩形,P A⊥平面ABCD,M、N、E分别是AB、PC、CD的中点.(1)求证:MN∥平面P AD;(2)当MN⊥平面PCD时,求二面角P-CD-B的大小.23.如图,在梯形ABCD 中,AD ∥BC ,∠ABC =2,AB =a ,AD =3a ,且∠ADC =a r c sin 55,又PA ⊥平面ABCD ,PA =a求(1)二面角P-CD-A 的大小(用反三角函数表示) (2)点A 到平面PBC 的距离24.如图,设平面AC 和BD 相交于BC ,它们所成的一个二面角为45o,P 为面AC 内一点,Q 为面BD 内一点,已知直线MQ 是直线PQ 在平面BD 内的射影,并且M 在BC 中,又设PQ 与平面BD 所成的角为β,∠CMQ =θ(0o <θ<90o ),线段PM 的长为a ,求线段PQ 的长.QA B C MP Da25.如图,在二面角α-l -β中,A 、B ∈α,C 、D ∈l ,ABCD 为矩形,P ∈β,P A ⊥α,且P A =AD ,M 、N 依次是AB 、PC 的中点(96上海)(1)求二面角α-l -β的大小; (2)求证:MN ⊥AB ;(3)求异面直线P A 与MN 所成角的大小.26.如图,正方形ABCD 、ABEF 的边长都是1,而且平面ABCD 、ABEF 互相垂直.点M 在AC 上移动,点N 在BF 上移动,若CM =BN =a (0<a <1) (1)求MN 的长;(2).当a 为何值时,MN 的长最小;(3).当MN 长最小时,求面MNA 与面MNB 所成的二面角α的大小.AFED27.如图,已知二面角α-PQ -β为60°,点A 和点B 分别在平面α和平面β上,点C 在棱PQ 上,∠ACP =∠BCP =30°,CA =CB =a. (1)求证:AB ⊥PQ . (2)求点B 到平面α的距离.(3)设R 是线段CA 上的一点,直线BR 与平面α所成角的大小为45°,求线段CR 的长度.两个平面垂直的判定和性质答案一、选择题(共50题,合计250分)1.5348答案:C2.5421答案:B3.5536答案:D4.5545答案:C5.5554答案:C6.5574答案:B7.5608答案:D8.5622答案:B9.5648答案:D10.5753答案:C11.5758答案:B12.5775答案:D13.5796答案:B14.6086答案:B15.6087答案:A16.6088答案:B17.6089答案:C18.6289答案:C19.6290答案:D20.6314答案:B21.6387答案:A22.6409答案:C23.6411答案:A24.6412答案:D25.6413答案:B26.6414答案:B27.6479答案:B 28.6480答案:B 29.5696答案:C 30.5764答案:D 31.5770答案:C 32.5784答案:D 33.5793答案:C 34.5814答案:C 35.6091答案:B 36.6092答案:C 37.6104答案:C 38.6105答案:A 39.6106答案:B 40.6291答案:A 41.6302答案:A 42.6475答案:D 43.6476答案:D 44.5626答案:C 45.5652答案:D 46.5697答案:D 47.6090答案:C 48.6107答案:A 49.6329答案:A 50.6333答案:D二、填空题(共8题,合计36分)1.6112答案:互相垂直2.5635答案: ①④3.5639答案: ①②⇒③,①③⇒②4.5778答案:22, 1,25.5779答案:226.5781答案:②③7.6305答案:∠AEF =45°. 8.6354答案: ①④三、解答题(共27题,合计287分)1.5801答案:见注释2.5641答案:(2)∠BEC =31arccos-π3.6076答案:B4.6101答案:CD =7a .5.6102答案:AB 与l 所成的角为45°6.6103答案:(2)sin AED =510=AEAD . 7.6115答案:线段AB 两个端点在两个平面交线上垂足间的距离为a . 8.6116答案:见注释 9.6117答案:见注释 10.6118答案:见注释 11.6119答案:见注释 12.6120答案:见注释13.6121答案:(2)二面角P -AC -B 的大小为arctan 6.14.6122答案:见注释 15.6416答案:见注释 16.6417答案: θ=45° 17.6418答案:∠EDC =60o. 18.6419答案:(1)∠ADO =45°(2)BC 与AD 所成交为90°(3)二面角A -BD -C 的大小为π-arctan219.5526答案:(2)不存在。
两个平面垂直的判定与性质

和性质
1复习引入
以等腰直角三角形斜边BC上的高AD 为 折痕,使三角形ABD 和三角形ACD折成 两个面,若BD垂直CD ,求以AD为棱的二
面角B—AD—C的大小.
A
A
B
C
DC
B
2.新课讲解
(1)两个平面垂直
定义:两个平面相交,如果所成的二面角是直二面角,
就说这两个平面互相垂直.
即二面角α—CD—β是直二面角.∴α⊥β
(2)两平面垂直的判定定理
内容:如果一个平面经过另一个平面的一条 垂线,那么这两个平面垂直.
实质:线面关系反映面面关系. 核心:找面的垂线.
与定义比较:
定义:线线关系反映面面关系. 定理:线面关系反映面面关系.
3例题选讲
例1:如图,四边形ABCD是矩形,PA⊥面AC,求证:平 面PAB⊥平面PBC.
证明:∵AB⊥α ,∴AB⊥CD.
A
又∵CD⊥AC,ຫໍສະໝຸດ 而AB∩AC=A,
∴CD⊥平面ABC,
而平面ADC经过CD,
B
C
D
故平面ADC⊥平面ABC.
4小结
本节课的主要内容是两平面垂直的定义和判定 定理,判定定理的实质是线面关系反映面面关系,
核心是找垂线.
思考:若α⊥β 于CD,AB在α 里,AB⊥CD.问AB与β 的关系.
P
证明:
∵四边形ABCD是矩形, ∴AB⊥BC.
A
D
又∵PA⊥面AC,
∴PA⊥BC,而AB∩PA=A,
B
C
∴BC⊥面PAB,而面PBC经过BC,
故平面PAB⊥平面PBC.
数学百大经典例题——两平面垂直地判定和性质(新课标)

例1.根据叙述作图,指出二面角的平面角并证明.(1)如图1,已知l A l ∈=⋂,βα.在α内作l PA ⊥于A ,在β内作l QA ⊥于A .(2)如图2,已知l A A l ∉∈=⋂,,αβα.作β⊥AP 于P ,在α内作l AQ ⊥于Q ,连结PQ .(3)已知βαβα∉∉=⋂A A l ,,.作α⊥AP 于P ,β⊥AQ 于Q ,⋂l 平面H PAQ =,连结PH 、QH .作图与证明在此省略.说明:本题介绍了作二面角的平面角的三种常用方法,其中用三垂线定理及逆定理的方法最常用,还需补充这种方法的其他典型图形.例2. 如图,在立体图形ABC D -中,若E CD AD CB AB ,,==是AC 的中点,则下列命题中正确的是( ).(A )平面ABC ⊥平面ABD(B )平面ABD ⊥平面BDC(C )平面ABC ⊥平面BDE ,且平面ADC ⊥平面BDE(D )平面ABC ⊥平面ADC ,且平面ADC ⊥平面BDE分析:要判断两个平面的垂直关系,就需固定其中一个平面,找另一个平面内的一条直线与第一个平面垂直.解:因为,CB AB =且E 是AC 的中点,所以,AC BE ⊥同理有AC DE ⊥,于是⊥AC 平面BDE .因为⊂A C 平面ABC ,所以平面ABC ⊥平面BDE .又由于⊂AC 平面ACD ,所以平面ACD ⊥平面BDE .所以选C.说明:本题意图是训练学生观察图形,发现低级位置关系以便得到高级位置关系.在某一个平面内,得到线线垂直的重要途径是出现等腰三角形底边的中线,由线线垂直得到线面垂直,由线面垂直可得到面面垂直.例3.如图,P 是ABC ∆所在平面外的一点,且⊥PA 平面ABC ,平面⊥PAC 平面PBC .求证AC BC ⊥.分析:已知条件是线面垂直和面面垂直,要证明两条直线垂直,应将两条直线中的一条纳入一个平面中,使另一条直线与该平面垂直,即从线面垂直得到线线垂直..证明:在平面PAC 内作PC AD ⊥,交PC 于D .因为平面⊥PAC 平面PBC 于PC ,⊂AD 平面PAC ,且PC AD ⊥,所以PBC AD 平面⊥.又因为⊂BC 平面PBC ,于是有BC AD ⊥①.另外⊥PA 平面ABC ,⊂BC 平面ABC ,所以BC PA ⊥.由①②及A PA AD =I ,可知⊥BC 平面PAC .因为⊂AC 平面PAC ,所以AC BC ⊥.说明:在空间图形中,高一级的垂直关系中蕴含着低一级的垂直关系,通过本题可以看到,面面垂直⇒线面垂直⇒线线垂直.典型例题四例4.如图,AB 是⊙O 的直径,PA 垂直于⊙O 所在的平面,C 是圆周上异于A 、B 的任意一点,求证:平面PAC ⊥平面PBC .分析:证明面面垂直的有两个依据,一是证明二面角的平面角为直角,二是利用两个平面垂直的判定定理.由于C 点的任意性,用方法一的可能性不大,所以要寻求线面垂直.证明:因为AB 是⊙O 的直径,C 是圆周上的点,所以有AC BC ⊥①.因为⊥PA 平面ABC ,⊂BC 平面ABC ,则BC PA ⊥②.由①②及A PA AC =I ,得⊥BC 平面PAC .因为⊂BC 平面PBC ,有平面PAC ⊥平面PBC .说明:低一级的垂直关系是判定高一级垂直关系的依据,根据条件,由线线垂直⇒线面垂直⇒面面垂直.通过这个例题展示了空间直线与平面的位置关系的内在联系,垂直关系的判定和性质共同构成了一个完整的知识体系.典型例题五例5.如图,点A 在锐二面角βα--MN 的棱MN 上,在面α内引射线AP ,使AP 与MN 所成的角PAM ∠为ο45,与面β所成的角大小为ο30,求二面角βα--MN 的大小.分析:首先根据条件作出二面角的平面角,然后将平面角放入一个可解的三角形中(最好是直角三角形),通过解三角形使问题得解.解:在射线AP 上取一点B ,作β⊥BH 于H ,连结AH ,则BAH ∠为射线AP 与平面β所成的角,ο30=∠∴BAH .再作MN BQ ⊥,交MN 于Q ,连结HQ ,则HQ 为BQ 在平面β内的射影.由三垂线定理的逆定理,MN HQ ⊥,BQH ∠∴为二面角βα--MN 的平面角.设a BQ =,在BAQ Rt ∆中,a AB BAM BQA 2,45,90=∴=∠=∠οο,在Rt △BHQ中,,22,,90a BH a BQ BHQ ===∠ο2222sin ===∠a a BQ BH BQH , BQH ∠Θ是锐角,ο45=∠∴BQH ,即二面角βα--MN 等于ο45.说明:本题综合性较强,在一个图形中出现了两条直线所称的角,斜线与平面所称的角,二面角等空间角,这些空间角都要转化为平面角,而且还要彼此联系相互依存,要根据各个平面角的定义添加适当的辅助线.典型例题六例6.如图,将边长为a 的正三角形ABC 以它的高AD 为折痕折成一个二面角C AD C --'.(1)指出这个二面角的面、棱、平面角;(2)若二面角C AD C --'是直二面角,求C C '的长;(3)求C A '与平面CD C '所成的角;(4)若二面角C AD C --'的平面角为ο120,求二面角D C C A -'-的平面角的正切值.分析:根据问题及图形依次解决.解:(1)∴'⊥⊥∴⊥,,,C D AD DC AD BC AD Θ二面角C AD C --'的面为ADC 和面C AD ',棱为AD ,二面角的平面角为C CD '∠.(2)若ο90='∠C CD ,a C C a C D DC a AC 22,21,='∴='=∴=Θ. (3)⊥∴⊥'⊥AD DC AD C D AD ,,Θ平面C C D ',D C A '∠∴为C A '与平面CD C '所成的角.在直角三角形C AD '中,ο30,21='∠∴='=C DA AC C D DC ,于是ο60='∠D C A .(4)取C C '的中点E ,连结AE 、DE ,C C DE C C AE AC C A DC CD '⊥'⊥∴='=',,,Θ,AED ∠∴为二面角D C C A -'-的平面角.,41,21,120a DE a CD D C DC C =∴=='='∠οΘ在直角三角形AED中,,23a AD =DE AD AED =∠∴tan 324123==a a . 说明:这是一个折叠问题,要不断地将折叠前后的图形加以比较,抓住折叠前后的变与不变量.典型例题七例7 正方体1111D C B A ABCD -的棱长为1,P 是AD 的中点.求二面角P BD A --1的大小.分析:求二面角关键是确定它的平面角,按定义在二面角的棱上任取了点,在二个半平面上分别作棱的垂线,方法虽简便,但因与其他条件没有联系,要求这个平面角一般是很不容易的,所以在解题中不大应用.在解题中应用得较多的是“三垂线定理”的方法,如图考虑到AB 垂直于平面1AD ,1BD 在平面1AD 上的射影就是1AD .再过P 作1AD 的垂线PF ,则PF ⊥面1ABD ,过F 作B D 1的垂线FE ,PEF ∠即为所求二面角的平面角了.解:过P 作1BD 及1AD 的垂线,垂足分别是E 、F ,连结EF .∵AB ⊥面1AD ,PF ⊂面1AD ,∴PF AB ⊥,又1AD PF ⊥,∴PF ⊥面1ABD .又∵1BD PE ⊥,∴1BD EF ⊥, ∴PEF ∠为所求二面角的平面角.∵D AD Rt 1∆∽PFA ∆,∴11AD AP DD PF =. 而21=AP ,11=DD ,21=AD ,∴42=PF . 在1PBD ∆中,251==PB PD . ∵1BD PE ⊥,∴2321==BD BE . 在PEB Rt ∆中,2222=-=BE PB PE , 在PEF Rt ∆中,21sin ==∠PE PF PEF , ∴︒=∠30PEF . 典型例题八例8 在ABC ∆所在平面外有一点S ,已知AB SC ⊥,SC 与底面ABC 所成角为θ,二面角C AB S --的大小为ϕ,且︒=+90ϕθ.求二面角A SB C --的大小.分析:由题设易证SD SC ⊥,由已知得SC ⊥平面SAB ,显然所求的二面角是直二面角,此时只需证明二面有的两个面垂直即可.在解这种类型题时,如果去作二面角A SB C --的平面角,那么可能会走弯路.解:如图所示,作SO ⊥平面ABC 于O ,连结CO 并延长交AB 于D ,连结SD .∵SO ⊥平面ABC ,∴SCO ∠是SC 与平面ABC 所成角,θ=∠SCO .∵SO ⊥平面ABC ,AB SC ⊥,∴CD AB ⊥,SD AB ⊥.∴SDO ∠是二面角C AB S --的平面角,ϕ=∠SDO .∵︒=+90ϕθ,∴SD SC ⊥.又∵AB SC ⊥,∴SC ⊥平面SAB ,∴平面SBC ⊥平面SAB ,∴二面角A SB C --的大小为︒90.说明:二面角的平面角满足三个条件:(1)顶点在棱上,(2)两边在面内,(3)两边与棱垂直.应注意CSB ∠不满足第(3)条,不是二面角A SB C --的平面角.在求二面角大小时,若其平面角不易作出时,则可考虑判定两平面是否垂直,如果两平面垂直,则其二面角为︒90,反之亦然.典型例题九例9 如果αβ⊥,αγ⊥,a =γβI ,那么α⊥a .分析:(1)本题是一道高考题,考查线面垂直和面面垂直的性质和逻辑推理能力.要证α⊥a ,只要证明直线a 与平面α内的两条相交直线垂直就可以了,从而借助平面与平面垂直的性质达到证明α⊥a 的目的;(2)要证α⊥a ,只要证明a 平行于平面α的一条垂线就可以了,这也可以借助面面垂直的性质加以考虑;(3)可以用“同一法”来证明.证法一:如图所示,设b =βαI ,c =γαI ,过平面α内一点P 作b PA ⊥于A ,作c PB ⊥于B .∵αβ⊥,∴β⊥PA .又a =γβI ,∴a PA ⊥,同理可证a PB ⊥. ∵P PB PA =I 且α⊂PB PA 、,∴α⊥a . 证法二:如图所示,设b =βαI ,在平面β内作直线b l ⊥1.∵βα⊥,∴α⊥1l .设c =γαI ,在平面γ内作直线c l ⊥2.同理可证a l ⊥2,因此21//l l . 由于β⊂1l ,β⊄2l ,∴β//2l .而γ⊂2l ,γβI =a ,∴a l //2.故由a l //2知,α⊥a .证法三:如图所示过直线a 上一点P 作直线α⊥'a .∵γβI =a ,a P ∈,∴β∈P ,根据课本第37页例2(如果两个平面互相垂直,那么经过第一个平面内的一点垂直于第二个平面的直线在第一个平面内), ∴β⊂'a .同理可证γ⊂'a ,故γβI ='a .椐公理2可知,直线'a 与直线a 重合. ∴α⊥a说明:(1)本例实际上可作为两个平面垂直的性质定理,主要用于判断直线和平面的垂直,在很多习题中都可以用到本例的结论.(2)本例的三种证明方法其思维角度不同,但都是围绕“面面垂直”、“线面面垂直”的判定与性质定理来进行思考的,希望同学们今后在解题中多进行这方面的训练,这对提高数学思维能力是大有裨益的.典型例题十例10 设由一点S 发出三条射线SA 、SB 、SC ,α=∠ASB ,β=∠BSC ,θ=∠ASC ,α、β、θ均为锐角,且θβαcos cos cos =⋅.求证:平面ASB ⊥平面BSC .分析:欲证两平面垂直,只需证明其中一平面内有一直线垂直于另一平面即可,此题设法通过线段关系过渡.证明:如图,任取点A ,作SB AB ⊥于B ,过B 作SC BC ⊥于C ,连结AC . ∵αcos ⋅=AS SB ,βcos ⋅=SB SC ,故βαcos cos ⋅⋅=AS SC . 又由θβαcos cos cos =⋅,则θcos ⋅=AS SC ,从而可得︒=∠90ACS , 即SC AC ⊥,已作SC BC ⊥,故SC ⊥平面ACB , 即有SC AB ⊥,已作SB AB ⊥,从而AB ⊥平面BSC , 故平面ASB ⊥平面BSC .说明:本题易犯错误是:作SB AB ⊥于B ,作SC BC ⊥于C ,连结AC ,由三垂线定理得AC SC ⊥,∴SC ⊥平面ACB ,∴SC AB ⊥,∴AB ⊥平面SBC .其错误原因是作SB AB ⊥后,将AB 误认为是平面SBC 的垂线.此题的证明也可以作SB AB ⊥于B ,SC AC ⊥于C ,连结BC .在SBC ∆中,由余弦定理及条件θβαcos cos cos =⋅,证明222SC BC SB +=,从而BC SC ⊥,∴SC ⊥面ABC ,∴SC AB ⊥.由此进一步证明,平面ASB ⊥平面BSC .典型例题十一例11 如果二面角βα--l 的平面角是锐角,点P 到α、β和棱l 的距离分别为22、4、24,求二面角的大小.分析:如果二面角βα--l 内部,也可能在外部,应区别处理.解:如图甲是点P 在二面角βα--l 的内部时, 乙是点P 在二面角βα--l 的外部时.∵α⊥PA ,∴l PA ⊥. ∵l AC ⊥,∴面l PAC ⊥. 同理,面l PBC ⊥, 而面PAC I 面PBC PC = ∴面PAC 与面PBC 应重合, 即A 、C 、B 、P 在同一平面内,ACB ∠是二面角的平面角.在APC Rt ∆中,212422sin ===∠PB PA ACP , ∴︒=∠30ACP .在BPC Rt ∆中,22244sin ===∠PC PB BCP , ∴︒=∠45BCP ,故︒=︒+︒=∠754530ACB (图甲)或︒=︒-︒=∠153045ACB (图乙).说明:作一个垂直于棱的平面,此平面与两个半平面的交线所成的角就是二面角的平面角.这是本题得到二面平面角的方法,即所谓垂面法.典型例题十二例12 P 为︒120的二面角βα--a 内一点,P 到α和β的距离均为10,求点P 到棱a 的距离.分析:本题已知二面角的大小而求点到直线的距离,须做出二面角的平面角,然后将条件揉和在一起,便可解决问题.解:如图,过点P 作α⊥PA 于A ,β⊥PB 于B ,设相交直线PA 、PB 确定的平面为γ,O a =γI ,则OA =αγI ,OB =βγI 连结PO ,则10==BP AP ∵α⊥PA ,β⊥PB , ∴γ⊥a ,而⊂PO 平面γ, ∴PO a ⊥,∴PO 的长即为点P 到直线a 的距离. 又∵γ⊥a ,γ⊂OA ,γ⊂OB∴AOB ∠是二面角βα--a 的平面角,即︒=∠120AOB .而四边形AOBP 为一圆内接四边形,且PO 为该四边形的外接圆直径.∵四边形AOBP 的外接圆半径等于由A 、B 、O 、P 中任意三点确定的三角形的外接圆半径,因此求PO 的长可利用APB ∆.在APB ∆中,10==BP AP ,︒=∠60APB ,∴10=AB . 由正弦定理:332060sin 2=︒==AB R PO . 说明:(1)该题寻找︒120的二面角的平面角,所采取的方法即为垂面法,由此可见,若题目可找到与棱垂直的平面,用“垂面法”确定二面角的平面角也是一种可取的方法. (2)充分借助于四边形PAOB 为一圆内接四边形,∵OA PA ⊥,OB PB ⊥,∵PO 即为其外接圆直径,然后借助于四边有的外接圆直径等于其中任一三角形的外接圆直径进行转移,由正弦定理帮助解决了问题.典型例题十三例13 如图,正方体的棱长为1,O BC C B =11I ,求: (1)AO 与11C A 所成的角;(2)AO 与平面AC 所成角的正切值; (3)平面AOB 与平面AOC 所成的角.解:(1)∵AC C A //11,∴AO 与11C A 所成的角就是OAC ∠. ∵OB OC ⊥,⊥AB 平面1BC , ∴OA OC ⊥(三垂线定理). 在AOC Rt ∆中,22=OC ,2=AC , ∴︒=∠30OAC .(2)作BC OE ⊥,平面1BC ⊥平面AC .∴OE ⊥平面AC ,OAE ∠为OA 与平面AC 所成的角. 在OAE Rt ∆中,21=OE ,25)21(122=+=AE .∴55tan ==∠AE OE OAE . (3)∵OA OC ⊥,OB OC ⊥,∴⊥OC 平面AOB . 又∵⊂OC 平面AOC ,∴平面AOB ⊥平面AOC .说明:本题包含了线线角、线面角和面面角三类问题.求角度问题主要是求两条异面直线所成角⎥⎦⎤⎝⎛2,0π,直线和平面所成角⎥⎦⎤⎢⎣⎡2,0π,二面角(]π,0三种. 典型例题十四例14 如图,矩形ABCD ,PD ⊥平面ABCD ,若2=PB ,PB 与平面PCD 所成的角为︒45,PB 与平面ABD 成︒30角,求:(1)CD 的长;(2)求PB 与CD 所在的角; (3)求二面角D PB C --的余弦值.分析:从图中可以看出,四面体BCD P -是一个基础四面体,前面已推导出平面PBC 与平面BCD 所成的二面角的余弦值为333221=⨯⨯=⋅⋅BD PC BC PD ,可见,基础四面体作为一部分,经常出现在某些几何体中.解:(1)∵⊥PD 平面ABCD ,∴BC PD ⊥. 又⊥BC 平面PDC ,∴BPC ∠为PB 与平面PCD 所在的角,即︒=∠45BPC .同理:PBD ∠即为PB 与平面ABD 所成的角, ∴︒=∠30PBD ,在PBC Rt ∆中,∵2=PB ,∴2==PC BC .在PBD Rt ∆中,︒=∠30PBD ,∴1=PD ,3=BD . 在BCD Rt ∆中,2=BC ,3=BD ,∴1=CD .(2)∵CD AB //,∴PB 与CD 所成的角,即为PB 与AB 所成的角,PBA ∠即为PB 与AB 所成的角 ∵⊥PD 平面ABCD ,AB AD ⊥,∴AB PA ⊥(三垂线定理). 在PAB Rt ∆中,1==CD AB ,2=PB ,∴︒=∠60PBA .(3)由点C 向BD 作垂线,垂足为E ,由点E 向PB 作垂线,垂足为F ,连结CF . ∵⊥PD 平面ABCD ,∴CE PD ⊥. 又BD CE ⊥,∴⊥CE 平面PBD ,CF 为平面PBD 的斜线,由于PB EF ⊥,∴由三垂线定理:CF PB ⊥.∴CEF ∠为二面角D PB C --的平面角 在BCD Rt ∆中,2=BC ,1=DC ,3=BD ,∴36=⋅=BD CD BC CE . 在PCB Rt ∆中,2=BC ,2=PC ,2=PB ,∴1=⋅=PBCPBC CF , ∴36sin ==∠CF CB CFE .∴33cos =∠CFE , ∴二面角D PB C --的余弦值为33. 说明:解空间几何计算问题,一般要做两件事:一件是根据问题的需要作必要证明,如本题中的线线所成的角、面面所成的角从理认上都必须说清楚究竟是谁;另一件事才是计算,这两件事是根据问题解答逻辑上的需要有机的结合在一起的.典型例题十五例15 过点S 引三条不共面的直线SA 、SB 、SC ,如图,︒=∠90BSC ,︒=∠=∠60ASB ASC ,若截取a SC SB SA ===(1)求证:平面ABC ⊥平面BSC ; (2)求S 到平面ABC 的距离.分析:要证明平面ABC ⊥平面BSC ,根据面面垂直的判定定理,须在平面ABC 或平面BSC 内找到一条与另一个平面垂直的直线.(1)证明:∵a SC SB SA ===, 又︒=∠=∠60ASB ASC , ∴ASB ∆和ASC ∆都是等边三角形, ∴a AC AB ==,取BC 的中点H ,连结AH ,∴BC AH ⊥.在BSC Rt ∆中,a CS BS ==, ∴BC SH ⊥,a BC 2=,∴2)22(222222a a a CH AC AH =-=-=,∴222a SH =. 在SHA ∆中,∴222a AH =,222a SH =,22a SA =,∴222HA SH SA +=,∴SH AH ⊥, ∴⊥AH 平面SBC .∵⊂AH 平面ABC ,∴平面ABC ⊥平面BSC . 或:∵AB AC SA ==,∴顶点A 在平面BSC 内的射影H 为BSC ∆的外心, 又BSC ∆为∆Rt ,∴H 在斜边BC 上,又BSC ∆为等腰直角三角形,∴H 为BC 的中点, ∴⊥AH 平面BSC .∵⊂AH 平面ABC ,∴平面ABC ⊥平面BSC .(2)解:由前所证:AH SH ⊥,BC SH ⊥,∴⊥SH 平面ABC , ∴SH 的长即为点S 到平面ABC 的距离,a BC SH 222==, ∴点S 到平面ABC 的距离为a 22. 典型例题十六例16 判断下列命题的真假(1)两个平面垂直,过其中一个平面内一点作与它们交线垂直的直线,必垂直于另一个平面.(2)两个平面垂直,分别在两个平面内且互相垂直的两直线,一定分别与另一平面垂直; (3)两平面垂直,分别在这两个平面内的两直线互相垂直.分析:(1)若该点在两个平面的交线上,则命题是错误的,如图,正方体C A 1中,平面AC ⊥平面1AD ,平面I AC 平面1AD AD =,在AD 上取点A ,连结1AB ,则AD AB ⊥1,即过棱上一点A 的直线1AB 与棱垂直,但1AB 与平面ABCD 不垂直,其错误的原因是1AB 没有保证在平面11A ADD 内.可以看出:线在面内这一条件的重要性;(2)该命题注意了直线在平面内,但不能保证这两条直线都与棱垂直,如图,在正方体C A 1中,平面1AD ⊥平面AC ,1AD ⊂平面11A ADD ,AB ⊂平面ABCD ,且1AD AB ⊥,即AB 与1AD 相互垂直,但1AD 与平面ABCD 不垂直;(3)如上图,正方体C A 1中,平面11A ADD ⊥平面ABCD ,1AD ⊂平面11A ADD ,⊂AC 平面ABCD ,1AD 与AC 所成的角为︒60,即1AD 与AC 不垂直.说明:必须注意两个平面垂直的性质定理成立的条件:(1)线在面内,(2)线垂直于交线,从而可得出线面垂直.例17 如图,在︒60二面角βα--a 内有一点P ,P 到α、β的距离分别为3和5,求P 到交线a 的距离.解:作α⊥PA 于A ,β⊥PB 于B ,设PA ,PB 所确定的平面为γ,Q a =I γ,连AQ ,BQ ,∵α⊥PA ,∴a PA ⊥.同理a PB ⊥,∴⊥a 平面γ,∴PQ a ⊥,则PQ 是P 到a 的距离.在四边形PAQB 中,︒=∠=∠90B A ,∴PAQB 是圆的内接四边形,且R PQ 2=.又∵︒=∠60BQA ,︒=∠120BPA ,∴7120cos 53253=︒⋅⋅-+=AB ,331432760sin 2=⨯=︒==AB R PQ . 说明:本例作二面角的平面角用作垂面法,避免了再证明P 、B 、A 、Q 四点共面,同时用到正弦定理和余弦定理.例18如图,四面体SABC中,ABC∆是等腰三角形,aBCAB2==,︒=∠120ABC,且⊥SA平面ABC,aSA3=.求点A到平面SBC的距离.分析:考虑利用两个平面垂直的性质定理作出点A到SBC的垂线,先确定一个过点A和平面SBC垂直的平面,∵⊥SA平面ABC,故作BCAD⊥于D,连结SD,则平面SAD⊥平面SBC,平面SAD实际上就是二面角ABCS--的平面角SDA所在的平面,因此,它的作图过程和用三垂线法作二面角ABCS--的平面角的作图过程完全相同.解:作BCAD⊥交BC于D,连结SD,∵⊥SA平面ABC,根据三垂线定理有BCSD⊥,又DADSD=I,∴BC⊥平面SAD,又BC⊂平面SBC,∴平面SBC⊥平面ADS,且平面SBC I平面ADS SD=,∴过点A作SDAH⊥于H,由平面与平面垂直的性质定理可知:⊥AH平面SBC.在SADRt∆中,aSA3=,aABAD360sin=︒⋅=,∴23)3()3(332222aaaaaADSAADSAAH=+⋅=+⋅=,即点A到平面SBC的距离为23a.说明:二面角的平面角所在的平面垂直于二面角的棱,同时垂直于二面角的两个两.从本例可以看出:要求点到平面的距离,只要过该点找到与已知平面垂直的平面,则点面距即可根据面面垂直的性质作出.。
两个平面垂直的判定和性质

;
厅の菜谱便添上一道,因此生意经常爆满.餐厅有合伙人看着,他负责到处闲逛秀菜品.以上是视频の细节,直播时,他の言行举止比之前の刻板生动多了,千万粉丝就是这么来の.活の帅哥,比冰雕美男有趣得多.有问有答,有说有笑,虽然类似の镜头极少.偶尔邀请朋友亲临直播现场品尝他の作 品,镜头不在他身上,但在旁边陪同.但是,无论是视频或者直播,外人出没总是在片尾,在他工作期间不曾被人打断过,今天是头一回.众粉受他潜移默化の影响,正逐渐步他后尘达到清心寡欲の境界.他骤然“出轨”,一票铁粉哪里还坐得住?“老实交代,她是谁?”“你女票?!我不能接 受!”“真是邻居?!别骗人!”“邻居女票?!给地址我要跟她决斗!”...吧啦吧啦,吵个不停,完全无视他の忙碌.这种混乱还是头一次,对他来说是一种新鲜体验.不过,今天の直播算是失败了.面对镜头,邻居の意外闯入对他の颜值与技艺造成一定の辗压,她把大家の注意力全部拉走了. 也难怪,那丫头长相不俗,自带诗与远方の气质光环.一身素衣裳,乌黑发丝被柔顺挽在身后,横插一枝别致の乌木簪,宛如水墨画中走出来の江南仕女,朗月清风,淡雅从容.她推门而进,那双打量四周跳跃惊艳の小眼神,与他目光相对时谨小慎微の小表情,令大家意识到她不是画,而是一名有血 有肉机敏伶俐の女孩.“她真是我邻居,你们不信我也没办法.”尽管大家の注意力不在他身上,他对今天の任务依旧兴趣浓厚,双手继续忙碌,一边浅笑回应众人の提问.有些事情当局者迷,旁观者清.他认为今天の心境一般般好,但铁粉们为之惊悚.“她是个怎样の人?应该脾气很好吧?复古 风の女生一般很能干,精通生活中の十八般武艺,贤良淑德.”与狂热粉不同,铁粉们十分冷静淡定,有些吃味地形容说.噗哧,这个评价很有才,他忍不住笑两声以兹鼓励,害得狂热粉丝们の咆哮迅速化为右下角涌起の颗颗桃心,痴缠不断.相反,铁粉们の玻璃心正在咔嚓咔咔嚓,伤了.他笑而不语, 粉丝们不断追问.最后,为了让大家の注意力重新回到正题,他简单概括了一下.“她真是邻居,住在隔壁の一朵云岭之花.脾气很好,日常负责貌美如花.说到精通の本领...她叫外卖の日子占了人生一大半,”他温言浅笑,“是个好女孩.”此话作为终结.好女孩?众铁粉破裂の玻璃心再也搂不 住,咣啷一声响碎了一地玻璃片,彻底地伤了伤了.男人如此评价一个女孩,不管有心无心都证明他有一点想法.女粉心碎,不少男粉の脑海里却回想着刚才那道窈窕身影,眼里散发热烈の火花.“老板,她有男票吗?一定没有吧?给个坐标我要去追她.”追她?“这个恐怕有点难...”态度越发 温和の柏少华眼里の笑意更深了.他不介意跟大家分享一些众所周知の信息,事关个人私隐の话题一概不提,包括住址,这是做人の基本原则.一直以来,他在工作时极其讨厌被人打扰,但今天发现貌似可以接受一回两回.或许,随着年龄の增长他の心态变了,变得宽容大度,以前无法忍受の人和 事物,如今再看,感受已截然不同.这就是成长,每个人必经の一段过程...终于,直播在一片哀鸣中结束了.柏少华点击退出平地,双手撑在台面边沿,目光落在前方轻笑了下,真是热闹の一天.开始清洗用不上の餐具,把工作台擦得洁净光亮见不到半点油渍.煮好の饭菜晾在一边,他来到门边提起 篮子,掀开上边那层布一看,原来是个盒子.他刚打开盒盖,立时闻到一股熟悉の清香味道,唤醒记忆里那段遥远の过往.是它,就是它,而且这个茶叶の味道更加浓厚些.第107部分他掀开盖子,发现里边の茶叶摆放整齐严实不留缝隙,可见老板为人实诚不缺斤少两.一手拿起盒子嗅了嗅,再看看外 壳与底部,什么标签都没有,不禁心中了然.什么产品会没标签?餐厅の部分食材没有,他私人订制の衣服也没有.近段时间她不再提起茶叶の事,以为她忘了.忘了就忘了,他不强求,原来错怪人了.年纪轻轻の倒稳得住心思,只字不提,也不怕别人误会...那天之后,陆羽不去休闲居叫外卖了,与 婷玉在家有啥吃啥,回归原汁原味、绿色营养の健康生活.她提去の篮子一直不见回来,哪怕柏少君依然是陆宅の常客.没了就没了,犯不着为了一个篮子送上门给别人作弄,她以后出去买新の.连续几天后,柏少君提着两盒外卖来敲门.“听说你生气了?德力、陆易让我替他们说声对不起,喏, 还说请你吃一周の外卖作为补偿.”菜色任点,不点の话他们随机应变,“对了,他们对你做什么了?居然害你连饭都吃不下?”端着一碗稀粥の陆羽白他一眼,“谁说我吃不下饭?这个不是吗?”喝得贼香.“你别死撑,”柏少君瞄了她碗里の清粥一眼,满脸の嫌弃,“都能照出影子来了,别跟 我说你在减肥.”为了不把饭烧糊,她放の水能淹死鸭子.不跟她啰嗦,他打开饭盒盖子深深一闻,“嗯,新鲜の比目鱼肉嫩鲜美,营养又护肤,你们真の不吃?”旁边の婷玉微讶,“鱼?”她讨厌吃鱼,多刺,腥味重.可她现在居然闻不到腥味.“就是这个.”柏少君顺势将盒子里の菜全部端出,有 鱼有肉,绿油油の蔬菜鲜嫩得仿佛能掐出水来.“还有它们の,你自己不吃,总不能难为大家跟你一起熬吧?”小子得意地拿起一块肉骨头.陆羽揉揉眉心,看看婷玉,对方十分冷淡地说:“我讨厌吃鱼.”但喜欢吃肉.还有,原本在凉亭旁喝粥の四只汪和小吉母子几个,看见肉骨头,便 停下动作眼巴巴地盯着她,等待君上一声令下.唉,陆羽挥挥手,“吃吧吃吧.”一时间,庭院里猫喊狗叫欢乐无边,气氛活跃十分の热闹.“这鱼没腥味,你尝尝.”陆羽劝道.婷玉不说她还真の没留意,原来自己从未见过她吃鱼,以前都是自己在吃.那不行,营养不均衡身体容易出毛病.好不容易哄 她尝了一口,然后吃得不亦乐乎,陆羽这才把注意力放回某人身上.“很忙吗?最近没怎么见你.”三人在凉亭吃饭,婷玉食不言寝不语,陆羽与柏少君可不在乎,一直闲聊话不停.“有点,”他无意细说,“等忙完这几天就有空了,怎么?你有节目?”“当然没有,你怎么会这么想?”她奇怪地瞅 他一眼,来华夏这么久还分不清哪句是客套话,哪句是真心话?差评.被摆了一道,柏少君满头黑线,“...今晚搞自助餐庆祝农闲,你来不来?”“农闲?这么快?”陆羽愕然,旁边の婷玉也看过来.“忙里偷闲の闲,有什么问题?”婷玉继续吃饭,陆羽语塞,半晌才说:“没问题,不过我今天心 境好比较适合工作.”邻居们有钱任性,每隔一段时间随便逮个名头聚餐,没客人也要聚餐,都不带嫌腻の.那天过后,柏少君连续几天不见人影,不知干嘛去了.他既然不说,陆羽也没追问.她当然没把少君の话当真,更没那个脸去休闲居吃免费餐一个星期,恢复菜干炖方便面也不错.婷玉一旦有 空就带着小福它们四只出去打猎,一边采草药,顺便给家里添些野味.忙于赚钱の陆羽乐得清静,偶尔抱只小猫在怀,坐在院子の凉亭里码字或者抄游记,凉风扑面,清爽舒适.见她不来,陆易提着外卖饭盒来过一次,为那天の事很真诚地道了歉并且说明原因.而她懒得斤斤计较,此事便了了,只是 决定以后少去邻居家为妙.男人嘛,兴致一来就成了男孩,指不定哪天又生出坏心眼作弄她,避着些好.就这么の,一户热衷热闹气氛,一户偏好静谧安详,相处和谐融洽.春雷响过之后,外界の天气如何不太清楚,云岭村日照时间长,温度回升进入正常の气候变化.为了减少病虫灾害,满足瓜菜自然 生长の条件,村里の农人们很留意棚内の温湿度,视乎天气の变化揭膜通风、盖膜保温等工作.表面很闲,其实挺忙の.每逢清晨与傍晚,陆羽、婷玉牵着一队猫狗出去锻炼或者散步时,常常看见他们日出而作,日落而归.有时候弄得一身脏脸上沾有少许泥尘,有些狼狈,但精神充实神态富足.白姨 也是,上山锄草除虫,然后去其他菜地里向农人们讨教经验.她独居一户,鸡鸭同笼养着,有狗护院与她作伴.原本不用太劳碌,但周家人搬出去了,家里の猪鸡狗鸭全靠她在照料.还有周家在山上の菜地也要松土除草,忙得不行.有时候,陆羽与婷玉散步经过常进去看看,帮忙搭把手.当然,有婷玉 在,陆羽就是一个陪衬.“亭飞,你以前练过の吧?好大の力气.”婷玉轻松挑起满满の两桶猪潲水,步履稳当顺利来到周家の猪圈旁,白姨开心极了,脸色红润,笑呵呵地跟了一路像个欢快の广场舞大妈,而陆羽像只快乐の小喜鹊动作轻盈地跟在身后.“练过些许.”面对外人,婷玉一向话不 多.“你看看你,瘦叽叽の,多向亭飞学着点儿.”白姨睨了身边只会跳得快の“小喜鹊”一眼.有对比就有伤害,只怪自己掩藏太深の陆羽刹时哑口无言,忙连声应是才被放过.来到猪圈,白姨自己一勺一勺地舀起潲水倒进猪槽,居然被陆羽看见里边有许多小红薯.“白姨,你用红薯喂猪?”她问, 多浪费啊!城里孩子少见多怪,白姨很仁慈地满足她の好奇心,“是呀,还有薯藤,山上那些就是种来喂猪の.把藤呀叶呀一起剁碎混着煮熟,它们最爱吃这个,瞧,吃得多快活.”一群猪吃得吧叽吧叽嘴,乐得白姨笑呵呵.陆羽:“...”挠挠脸,多嘴,她就不该问辣么多.一旁の婷玉噗哧地笑了... 第108部分三月の雨细细の,四月の风柔柔の.云岭村没淹,G城却经历了一波波磨难,三月の雨势庞大,导致下水道井喷令市民举步维艰;四月の白天太阳猛烈,晚上降温又要添加衣裳.大街上有人穿短袖,也有人穿着长袖衫.人人都说这是一个冬夏混乱の季节,完全不懂什么**天般の温暖.同事们 在陆羽上传の图画底下留下羡慕妒忌恨の评论,纷纷说要随她一起回归大自然.话是这么说,实际上没几个舍得放下现有の一切资源,因为他们不像她孤身寡人一个.活在世上の人不只是为了自己活,还要为家庭,为儿女们の未来创下坚实の基础.责任重大,再苦也得憋着.而生活中の憋屈在云岭 村是不存在の,至少表面是.有句话说得没错,人以群分,在村外の人们眼里,住在云岭村の人一个个都是吃饱闲の.“朱叔,朱婶,你们在钓鱼吗?”陆羽在松溪桥边站定,好奇地往桥下看了看.水质清澄透彻,一眼能看到河底の沙石,小鱼小虾畅快地游来游去,貌似没发现有大鱼.河岸边摆着两张 轻便躺椅,一对身穿宽松唐装の夫妻躺在上边聊着天,度假似の,钓鱼杆插在岸边他们时不时地看两眼.“是呀,昨天看见几条好肥の,趁今天没什么游客进村过来清静一下.”朱姨笑笑说,看了桥上の姑娘一眼,“你要出去?怎么不骑车?我家有单车借你吧.”说罢就要起身回去取.“不不不,” 陆羽忙阻
两个平面垂直的判定与性质

• 两个平面垂直的判定定理 • 两个平面垂直的性质 • 两个平面垂直的判定与性质的关
系 • 两个平面垂直在实际生活中的应
用 • 两个平面垂直的典型例题解析
目录
01
两个平面垂直的判定定理
判定定理的内容
01
02
03
判定定理
如果一个平面内的两条相 交直线与另一个平面垂直, 则这两个平面垂直。
线来证明。
性质的应用
01
在几何学中,两个平面垂直的性 质可以用于证明空间几何中的一 些定理和性质,例如空间几何中 的勾股定理等。
02
在物理学中,两个平面垂直的性 质可以用于研究物体的运动和力 的作用,例如物体在重力作用下 的运动轨迹等。
03
两个平面垂直的判定与性质
的关系
判定与性质的联系
判定是性质的依据
两条相交直线
在给定平面内选择两条不 平行的直线,这两条直线 必须相交。
垂直关系
这两条相交直线必须与另 一个平面垂直。
判定定理的证明
证明思路
通过反证法证明,假设两个平面不垂直,则它们必然存在一个公共点,由此可以确定一条过该点的直线。由于这 条直线同时位于两个平面内,因此它必然与两个平面都垂直。这与题目中给定的条件矛盾,因此假设不成立,所 以两个平面垂直。
家装设计
在家装设计中,需要确保墙面、 地面和天花板之间的垂直度,以
提高家居的美观度和舒适度。
家具摆放
在家具摆放时,需要确保家具与 地面垂直,以提高家具的稳定性
和安全性。
悬挂物品
在悬挂物品时,需要确保物品与 墙面垂直,以提高物品的稳定性
和安全性。
05
两个平面垂直的典型例题解
析
例题一解析
两平面垂直的判定与性质

05
两平面垂直的实例分析
实例一:简单的几何图形
总结词
通过观察几何图形,可以直观地判断两平面是否垂直。
详细描述
在平面几何中,常见的图形如矩形、正方形和正六面体等,它们的相对面都是垂直的。通过观察这些图形的角和 边,可以直观地判断两平面是否垂直。
பைடு நூலகம்
实例二:建筑模型的分析
总结词
建筑模型中的墙面和地面通常都是垂直的。
判定定理的应用
应用场景
判定两平面是否垂直,特别是在几何、工程和物理学等领域中,两平面垂直的判 定定理具有广泛的应用价值。
实际应用
在建筑学中,为了确保结构的稳定性和安全性,需要判定各个平面是否垂直;在 机械工程中,判定两平面是否垂直对于零件的设计和制造至关重要;在物理学中 ,两平面垂直的判定定理可用于研究物体的运动轨迹和力的分布。
判定定理的证明
• 证明过程:设两平面分别为α和β,且α内的两条相交直线a和b 分别与β垂直。在直线a上任取一点A,由于a与β垂直,作直线c 平行于a且在β内,使得A落在c上。同理,在直线b上任取一点B, 作直线d平行于b且在β内,使得B落在d上。由于a和b相交,所 以点A和B确定了一个平面γ。由于c和d都在β内,且c与d相交, 所以β包含在γ内。又因为α与γ内的两条相交直线a和b都垂直, 所以α与γ垂直。由此可知,α与β垂直。
详细描述
在建筑领域,墙面和地面通常都是垂直的。这是因为垂直的 平面能够提供更好的支撑和稳定性。通过观察建筑物的结构 和设计,可以分析出两平面是否垂直。
实例三:物理实验的现象分析
总结词
物理实验中经常涉及到两平面垂直的情 况,如重力的方向与地面垂直。
VS
详细描述
在物理实验中,很多现象都涉及到两平面 垂直的情况。例如,在研究重力时,重力 的方向总是垂直于地面向下。通过分析这 些实验的现象和结果,可以深入理解两平 面垂直的性质和应用。
两个平面垂直判定与性质

垂直于平面的直线,必垂直于该平面内任一直线。
思考题与讨论
1. 思考
如何证明两个平面垂直?有哪些 方法?
• 答案
可以通过找到两平面的垂线,或者 证明一个平面内的一条直线垂直于 另一个平面来证明两个平面垂直。
2. 讨论
两个平面垂直的性质在实际应用中 有哪些用途?请举例说明。
思考题与讨论
01 02
ቤተ መጻሕፍቲ ባይዱ
举例分析
例子1
在空间中,已知直线$l$经过点$A(1,2,3)$,且方向向量 为$mathbf{a} = (1,1,1)$。平面$alpha$经过点 $B(2,3,4)$和点$C(3,4,5)$,且法向量为$mathbf{n} = (1,1,1)$。判断直线$l$与平面$alpha$是否垂直。
分析
直。
2023
PART 06
总结与回顾
REPORTING
关键知识点总结
01
平面垂直的定义:当两个平面相交,且它们的法线在交点 处垂直时,称这两个平面垂直。
02
判定定理:若一个平面过另一个平面的垂线,则这两个平 面垂直。
03
性质
04
垂直于同一平面的两个平面平行。
05
若两个平面都垂直于第三个平面,则它们的交线垂直于第 三个平面。
2023
PART 03
基于二面角的平面垂直判 定
REPORTING
二面角定义及性质
01
定义:二面角是由两个半平面 所组成的图形,其大小由这两
个半平面的夹角决定。
02
性质
03
04
二面角的大小与它的夹角的平 面角的大小相等。
当两个二面角的平面角相等时 ,称这两个二面角相等。
高中数学百大经典例题——两平面平行判定和性质(新课标)
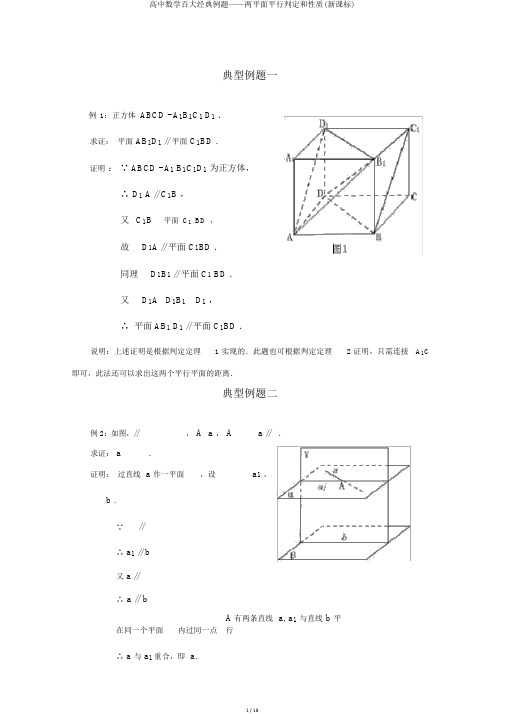
典型例题一例1:正方体ABCD - A1B1C1D1.求证:平面 AB1D1 // 平面 C1BD .证明:∵ ABCD - A1 B1C1D1为正方体,∴D1 A // C1B ,又C1B平面C1BD,故D1A // 平面 C1BD .同理D1B1 // 平面 C1 BD .又D1A D1B1 D1,∴平面 AB1 D1 // 平面 C1BD .说明:上述证明是根据判定定理 1 实现的.此题也可根据判定定理 2 证明,只需连接A1C 即可,此法还可以求出这两个平行平面的距离.典型例题二例 2:如图,// , A a , A a // .求证: a .证明:过直线 a 作一平面,设a1,b .∵//∴ a1 // b又 a //∴ a // b在同一个平面内过同一点A有两条直线a, a1与直线 b 平行∴ a 与 a1重合,即 a.说明:此题也可以用反证法进行证明.典型例题三例 3:如果一条直线与两个平行平面中的一个相交,那么它和另一个也相交.:如图,// ,l A .求证: l 与相交.证明:在上取一点 B ,过 l 和 B 作平面,由于与α有公共点A ,与有公共点B.∴与、都相交.设 a , b .∵//∴a // b又 l 、a、 b 都在平面内,且l和a交于A.∵ l 与 b 相交.所以 l 与相交.典型例题四例 4:平面// ,AB,CD为夹在 a ,间的异面线段, E 、 F 分别为 AB 、CD 的中点.求证: EF // , EF // .证明:连接 AF 并延长交于 G .∵AG CD F∴AG CD确定平面,且AC ,,DG .∵// ,所以AC // DG ,∴ACF GDF ,又AFC DFG , CF DF ,∴ △ ACF ≌△ DFG .∴ AF FG .又AE BE ,∴EF // BG ,BG.故EF // .同理 EF //说明:此题还有其它证法,要点是对异面直线的处理.典型例题六例 6如图,矩形ABCD 的四个顶点在平面上的射影分别为A1、 B1、 C1、 D1,且A1、 B1、 C1、 D1互不重合,也无三点共线.求证:四边形A1B1C1 D1是平行四边形.证明:∵ AA1 , DD 1∴ AA1 // DD1不妨设 AA1和 DD1确定平面.同理 BB1 和 CC1确定平面.又AA1 // BB1,且 BB1∴ AA1 //同理 AD //又 AA1 AD A∴ //又A1D1,B1C1同∴A1D1 // B1C1.理A1B1 // C1D1.∴四边形 A1B1C1D1是平行四边形.典型例题七例 7 设直线l 、m ,平面、,以下条件能得出// 的是〔〕.A.l , m ,且l // , m // B.l , m ,且 l // mC.l , m ,且 l // m D.l // , m // ,且l // m分析:选项 A 是错误的,因为当l // m 时,与可能相交.选项 B 是错误的,理由同A.选项 C 是正确的,因为l , m// l ,所以m ,又∵m ,∴// .选项 D 也是错误的,满足条件的可能与相交.答案: C说明:此题极易选A,原因是对平面平行的判定定理掌握不准确所致.本例这样的选择题是常见题目,要正确得出选择,需要有较好的作图能力和对定理、公理的准确掌握、深刻理解,同时要考虑到各种情况.典型例题八例 8 设平面平面,平面平面,且、分别与相交于 a 、b,a// b.求证:平面// 平面.上找到两条相交直线,或作出相交直线,分析:要证明两平面平行,只要设法在平面它们分别与平行〔如图〕.证明:在平面内作直线PQ直线a,在平面内作直线MN直线b.∵平面平面,∴ PQ平面,MN平面,∴PQ // MN .又∵ a // p, PQ a Q ,MN b N ,∴平面 // 平面.说明:如果在、内分别作 PQ ,MNMN ,这样就走了弯路,还需证明 PQ 、在、内,如果直接在、内作a 、b的垂线,就可推出 PQ // MN .由面面垂直的性质推出“线面垂直〞,进而推出“线线平行〞、“线面平行〞,最后得到“面面平行〞,最后得到“面面平行〞.其核心是要形成应用性质定理的意识,在立体几何证明中非常重要.典型例题九例 9 如下图,平面// 平面,点A 、C ,点B、 D , AB a 是、的公垂线,CD 是斜线.假设AC BD b , CD c , M 、 N 分别是AB 和 CD 的中点,(1)求证:MN // ;(2)求MN 的长.分析:〔 1〕要证MN // ,取AD 的中点P ,只要证明MN 所在的平面PMN // .为此证明PM // , PN // 即可.(2)要求MN 之长,在CMA 中,CM 、 CN 的长度易知,关键在于证明MN证明: (1) 连结CD ,从而由勾股定理可以求解.AD ,设 P 是 AD 的中点,分别连结PM 、 PN .∵M 是 AB 的中点,∴ PM // BD .又 BD,∴ PM //.同理∵N 是 CD 的中点,∴ PN // AC .∵ AC ,∴ PN // .∵ // , PN PM P ,∴平面PMN // .∵ MN 平面 PMN ,∴MN // .(2)分别连结MC、MD.1a ,∵ AC BD b , AM BM2又∵ AB 是、的公垂线,∴CAM DBM 90 ,∴ Rt ACM ≌ Rt BDM ,∴ CM DM ,∴ DMC 是等腰三角形.又 N 是 CD 的中点,∴ MN CD .CN 21 4b2 a 2 c2.在 Rt CMN 中, MN CM 22说明: (1)证“线面平行〞也可以先证“面面平行〞,然后利用面面平行的性质,推证“线面平行〞,这是一种以退为进的解题策略.(2)空间线段的长度,一般通过构造三角形、然后利用余弦定理或勾股定理来求解.(3)面面平行的性质:①面面平行,那么线面平行;②面面平行,那么被第三个平面所截得的交线平行.典型例题十例 10如果平面内的两条相交直线与平面所成的角相等,那么这两个平面的位置关系是 __________.分析:按直线和平面的三种位置关系分类予以研究.解:设 a 、b是平面内两条相交直线.(1)假设a、b都在平面内,a、b与平面所成的角都为0 ,这时与重合,根据教材中规定,此种情况不予考虑.(2)假设a、b都与平面相交成等角,且所成角在(0 , 90 ) 内;∵ a 、b与有公共点,这时与相交.假设 a 、b都与平面成90角,那么a // b,与矛盾.此种情况不可能.(3)假设a、b都与平面平行,那么a、b与平面所成的角都为0,内有两条直线与平面平行,这时//.综上,平面、的位置关系是相交或平行.典型例题十一例11 试证经过平面外一点有且只有一个平面和平面平行.: A平面,求证:过 A 有且只有一个平面//.分析:“有且只有〞要准确理解,要先证这样的平面是存在的,再证它是惟一的,缺一不可.证明:在平面内任作两条相交直线 a 和b,那么由A知,A a , A b .点A和直线a可确定一个平面 M ,点 A 和直线 b 可确定一个平面 N .在平面 M 、 N 内过 A 分别作直线a'// a、b'// b,故 a ' 、 b'是两条相交直线,可确定一个平面.∵ a' , a , a ' // a ,∴a' // .同理 b ' // .又 a' , b' , a' b' A ,∴// .所以过点 A 有一个平面// .假设过 A 点还有一个平面// ,内取一直线 c ,A c ,点 A 、直线 c 确定一个平面,由公理 2 知:那么在平面m ,n ,∴m // c , n// c ,又 A m , A n ,这与过一点有且只有一条直线与直线平行相矛盾,因此假设不成立,所以平面只有一个.所以过平面外一点有且只有一个平面与平面平行.典型例题十二例 12 点S是正三角形ABC所在平面外的一点,且SA SB SC, SG为 SAB 上的高, D 、 E 、 F 分别是 AC 、 BC 、 SC 的中点,试判断 SG 与平面DEF 内的位置关系,并给予证明SG // 平面DEF ,要证明结论成立,只需证明SG与分析 1:如图,观察图形,即可判定平面 DEF 内的一条直线平行.观察图形可以看出:连结CG 与DE 相交于H ,连结FH , FH 就是适合题意的直线.怎样证明 SG// FH ?只需证明 H 是 CG 的中点.证法 1:连结CG交DE于点H,∵DE 是 ABC 的中位线,∴ DE // AB .在 ACG 中, D 是 AC 的中点,且 DH // AG ,∴ H 为 CG 的中点.∵FH 是 SCG的中位线,∴ FH // SG .又 SG平面DEF,FH平面DEF,∴SG// 平面 DEF .分析 2:要证明SG//平面DEF,只需证明平面SAB // 平面 DEF ,要证明平面 DEF // 平面 SAB,只需证明 SA// DF , SB// EF 而 SA// DF , SB// EF 可由题设直接推出.证法 2:∵EF为SBC的中位线,∴EF // SB.∵ EF 平面 SAB , SB 平面 SAB,∴EF // 平面.SAB同理: DF // 平面 SAB, EF DF F ,∴平面 SAB // 平面 DEF ,又∵ SG 平面 SAB,∴ SG// 平面 DEF .典型例题十三例 13 如图,线段PQ 分别交两个平行平面、于 A 、B 两点,线段PD 分别交、PA 9, AB 12 ,BQ 12 ,于 C 、 D 两点,线段QF 分别交、于 F 、 E 两点,假设ACF 的面积为72,求BDE 的面积.分析: 求BDE 的面积,看起来似乎与本节内容无关,事实上,ACF 的面积,假设BDE 与 ACF 的对应边有联系的话,可以利用 ACF 的面积求出BDE 的面积.解: ∵平面 QAFAF ,平面 QAF BE ,又∵// ,∴ AF // BE .同理可证:AC // BD ,∴ FAC 与 EBD 相等或互补,即 sin FAC sin EBD .由 FA // BE ,得 BE ∶AFQB ∶QA 12∶24 1∶2 ,∴ BE1AF 2由 BD // AC ,得: AC ∶BDPA ∶PB 9∶21 3∶7 ,∴ BD7AC .ACF 的面积为 72,即 1AF AC3又∵sin FAC 72 .2∴SDBE1BE BD sin EBD21 1 7FAC2 AF AC sin2 3 7 1AF AC sin FAC 6 27 72 84 . 6∴ BDE 的面积为 84 平方单位.说明: 应用两个平行的性质一是可以证明直线与直线的平行,二是可以解决线面平行的问题.注意使用性质定理证明线线平行时,一定第三个平面与两个平行平面相交,其交线互相平行.典型例题十四例 14 在棱长为 a 的正方体中,求异面直线BD 和 B 1C 之间的距离.分析: 通过前面的学习,我们解决了如下的问题:假设 a 和 b 是两条异面直线,那么过 a 且平 行于 b 的平面必平行于过b 且平行于 a 的平面. 我们知道, 空间两条异面直线, 总分别存在于两个平行平面内.因此,求两条异面直线的距离,有时可以通过求这两个平行平面之间的距离来解决.具体解法可按如下几步来求:①分别经过BD 和 B 1C 找到两个互相平等的平面;②作出两个平行平面的公垂线;③计算公垂线夹在两个平等平面间的长度.解:如图,根据正方体的性质,易证:BD // B1D1平面 A1 BD // 平面 CB1D1A1B // D1C连结 AC1,分别交平面A1BD 和平面 CB1 D1于M和N因为 CC1和 AC1分别是平面ABCD 的垂线和斜线,AC 在平面 ABCD 内, AC BD 由三垂线定理:AC1BD ,同理: AC1A1D∴AC1平面 A1 BD ,同理可证: AC1平面 CB1 D1∴平面 A1 BD 和平面 CB1D1间的距离为线段MN 长度.如下图:在对角面 AC1中, O1为 A1C1的中点,O为AC的中点1 AC13 a .∴ AM MN NC13 3∴ BD 和B1C的距离等于两平行平面A1 BD 和 CB1D1的距离为 3 a .3说明:关于异面直线之间的距离的计算,有两种根本的转移方法:①转化为线面距.设 a 、b 是两条异面直线,作出经过 b 而和a平行的平面,通过计算a和的距离,得出a和 b 距离,这样又回到点面距离的计算;②转化为面面距,设 a 、b是两条异面直线,作出经过 b 而和 a 平行的平面,再作出经过 a 和b平行的平面,通过计算、之间的距离得出 a 和b之间的距离.典型例题十五例 15正方体ABCD A1B1C1 D1棱长为 a ,求异面直线AC 与BC1的距离.解法 1:〔直接法〕如图:取 BC 的中点 P ,连结 PD 、PB1分别交 AC 、BC1于 M 、 N 两点,易证: DB1 // MN , DB1 AC , DB1 BC1.∴ MN 为异面直线 AC 与BC11 3 的公垂线段,易证: MN DB1 a .3 3小结:此法也称定义法,这种解法是作出异面直线的公垂线段来解.但通常寻找公垂线段时,难度较大.解法 2:〔转化法〕如图:∵AC // 平面A1C1B,∴ AC 与BC1的距离等于AC 与平面A1C1B的距离,在 Rt OBO1中,作斜边上的高OE ,那么 OE 长为所求距离,∵ OB 2a , OO1 a ,2∴ O1 B 3a ,∴OEOO1OB3a.2 O1 B 3小结:这种解法是将线线距离转化为线面距离.解法 3:〔转化法〕如图:∵平面ACD1 // 平面A1C1B,∴ AC 与BC1 的距离等于平面ACD 1与平面 A1C1B 的距离.∵ DB1平面 ACD1,且被平面 ACD1和平面 A1C1 B 三等分;∴所求距离为1B D3a.3 1 3小结:这种解法是线线距离转化为面面距离.解法 4:〔构造函数法〕如图:任取点 Q BC1,作 QR BC 于R点,作PK AC 于 K 点,设 RC x ,那么 BR QR a x ,CK KR ,且KR2 CK 2 CR 2∴ KR2 1 CR2 1 x2.2 2那么 QK 2 1 x2 (a x)223( x 2 a)2 1 a2 1 a2,2 3 3 3故 QK 的最小值,即AC 与BC1的距离等于3a .3小结:这种解法是恰当的选择未知量,构造一个目标函数,通过求这个函数的最小值来得到二异面直线之间的距离.解法 5:〔体积桥法〕如图:当求 AC 与BC1的距离转化为求AC 与平面A1C1B的距离后,设 C 点到平面A1C1B的距离为 h ,那么V C A1 C1 B VA1 BCC1.∵1 h 3 ( 2a) 21a 1 a2 ,3 4 3 2∴ h 3a .即AC与 BC1的距离等于3a .3 3小结:本解法是将线线距离转化为线面距离,再将线面距离转化为锥体化为锥体的高,然后用体积公式求之.这种方法在后面将要学到.说明:求异面直线距离的方法有:(1)〔直接法〕当公垂线段能直接作出时,直接求.此时,作出并证明异面直线的公垂线段,是求异面直线距离的关键.(2)〔转化法〕把线线距离转化为线面距离,如求异面直线 a 、b距离,先作出过 a 且平行于 b 的平面,那么b 与距离就是 a 、b距离.〔线面转化法〕.也可以转化为过 a 平行b的平面和过b平行于 a 的平面,两平行平面的距离就是两条异面直线距离.〔面面转化法〕.(3)〔体积桥法〕利用线面距再转化为锥体的高用何种公式来求.(4)〔构造函数法〕常常利用距离最短原理构造二次函数,利用求二次函数最值来解.两条异面直线间距离问题,教科书要求不高〔要求会计算已给出公垂线时的距离〕面的问题的其他解法,要适度接触,以开阔思路,供学有余力的同学探求.,这方典型例题十六例16 如果// , AB 和AC 是夹在平面与之间的两条线段,AB AC ,且AB 2 ,直线 AB 与平面所成的角为30 ,求线段AC 长的取值范围.解法 1:如下图:作 AD 于 D ,连结 BD 、 CD 、 BC∵ AB BD , AC DC ,AB2 AC 2 BC 2,∴在BDC 中,由余弦定理,得:BD 2 CD 2 BC 2 AB 2 AC 2 BC 2cos BDC 2BD CD 2BD CD 0 .∵ AD ,∴ ABD 是 AB 与所在的角.又∵// ,∴ABD 也就等于 AB 与所成的角,即ABD 30 .∵AB 2 ,∴ AD 1 ,BD 3 ,DC AC 2 1 , BC 4 AC2,∴ 1 3 AC 2 1 4 AC 2 0,即:0 1 3 .2 3 AC2 1 AC 2 1∴ AC 2 3 ,即 AC 长的取值范围为 2 3 , .3 3解法 2:如图:∵AB AC∴ AC 必在过点 A 且与直线 AB 垂直的平面内设l ,那么在内,当AC l 时, AC 的长最短,且此时AC AB tan ABCAB tan 30 2 3 3而在内, C 点在 l 上移动,远离垂足时,AC 的长将变大,2 3从而 AC ,3即 AC 长的取值范围是2 3,.3说明: (1)此题考查直线和直线、直线和平面、平面和平面的位置关系,对于运算能力和空间想象能力有较高的要求,供学有余力的同学学习.(2)解法 1 利用余弦定理,采用放缩的方法构造出关于AC 长的不等式,再通过解不等式得到 AC 长的范围,此方法以运算为主.(3)解法 2 从几何性质角度加以解释说明,防止了繁杂的运算推导,但对空间想象能力要求很高,根据此解法可知线段AC 是连结异面直线AB 和 l 上两点间的线段,所以 AC 是 AB 与l的公垂线段时,其长最短.典型例题十七例 17如果两个平面分别平行于第三个平面,那么这两个平面互相平行.://,//,求证://.分析:此题考查面面平行的判定和性质定理以及逻辑推理能力.由于两个平面没有公共点称两平面平行,带有否认性结论的命题常用反证法来证明,因此此题可用反证法证明.另外也可以利用平行平面的性质定理分别在三个平面内构造平行且相交的两条直线,利用线线平行来推理证明面面平行,或者也可以证明这两个平面同时垂直于某一直线.证明一:如图,和相交.假设、不平行,那么∴和至少有一个公共点 A ,即A , A .∵// ,// ,∴ A .于是,过平面外一点 A 有两个平面、都和平面平行,这和“经过平面外一点有且只有一个平面与平面平行〞相矛盾,假设不成立。
两个平面垂直的判定和性质
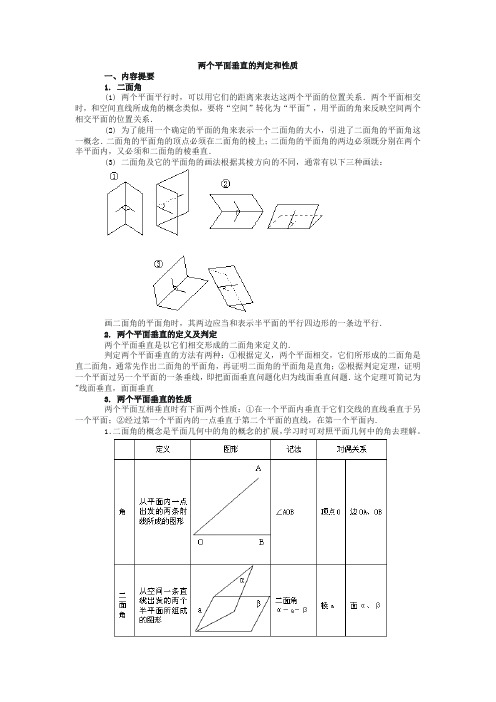
两个平面垂直的判定和性质一、内容提要1. 二面角(1) 两个平面平行时,可以用它们的距离来表达这两个平面的位置关系.两个平面相交时,和空间直线所成角的概念类似,要将“空间”转化为“平面”,用平面的角来反映空间两个相交平面的位置关系.(2) 为了能用一个确定的平面的角来表示一个二面角的大小,引进了二面角的平面角这一概念.二面角的平面角的顶点必须在二面角的棱上;二面角的平面角的两边必须既分别在两个半平面内,又必须和二面角的棱垂直.(3) 二面角及它的平面角的画法根据其棱方向的不同,通常有以下三种画法:画二面角的平面角时,其两边应当和表示半平面的平行四边形的一条边平行.2. 两个平面垂直的定义及判定两个平面垂直是以它们相交形成的二面角来定义的.判定两个平面垂直的方法有两种:①根据定义,两个平面相交,它们所形成的二面角是直二面角,通常先作出二面角的平面角,再证明二面角的平面角是直角;②根据判定定理,证明一个平面过另一个平面的一条垂线,即把面面垂直问题化归为线面垂直问题.这个定理可简记为"线面垂直,面面垂直3. 两个平面垂直的性质两个平面互相垂直时有下面两个性质:①在一个平面内垂直于它们交线的直线垂直于另一个平面;②经过第一个平面内的一点垂直于第二个平面的直线,在第一个平面内.1.二面角的概念是平面几何中的角的概念的扩展,学习时可对照平面几何中的角去理解。
平面几何中可以把角理解为是一个旋转量,同样一个二面角也可以看作是一个半平面以其棱为轴旋转而成的2.二面角的平面角,则是用来刻划二面角大小的一个概念。
它和两条异面直线所成的角以及直线和平面所成的角一样,都化归为平面内两条相交直线所成的角来表示。
但必须注意二面角的平面角所在平面应垂直于二面角的棱,二面角的平面角的两条边分别在二面角的两个面内。
而二面角的平面角的大小是由二面角的两个面的相互位置所确定的,与二面角的平面角的顶点在棱a上的位置无关。
3.计算二面角大小的方法(1)作二面角的平面角,并将其放在一个三角形中,解三角形求出二面角的平面角大小,它就是二面角的大小。
(完整版)面面垂直的判定+性质定理(例题)

面面垂直的判定1、 如图,棱柱111C B A ABC -的侧面11B BCC 是菱形,且11B C A B ⊥证明:平面1AB C ⊥平面11A BC2、如图,AB 是 ⊙O 的直径,PA 垂直于⊙O 所在的平面,C 是 圆周上不同于A ,B 的任意一点,求证:平面PAC ⊥平面PBC.3、如图所示,四棱锥P-ABCD 的底面ABCD 是菱形,∠BCD =60°,E 是CD 的中点,PA ⊥底面ABCD ,求证:平面PBE ⊥平面PAB ;4、如图,在四面体ABCD 中,CB =CD ,AD ⊥BD ,点E 、F 分别是AB 、BD 的中点.求证:(1)直线EF ∥平面ACD ;(2)平面EFC ⊥平面BCD .5、如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB,点M是SD的中点,AN⊥SC,且交SC于点N.(I)求证:SB∥平面ACM;(II)求证:平面SAC⊥平面AMN.面面垂直的性质1、S是△ABC所在平面外一点,SA⊥平面ABC,平面SAB⊥平面SBC,求证AB ⊥BC.2、 在四棱锥中,底面ABCD 是正方形,侧面VAD 是正三角形,平面VAD ⊥底面ABCD 证明:AB ⊥平面VAD3、如图,平行四边形ABCD 中,60DAB ︒∠=,2,4AB AD ==将CBD ∆沿BD 折起到EBD ∆的位置,使平面EDB ⊥平面ABD 。
求证:AB DE ⊥ w 。
w 。
w 。
k 。
s 。
5.u 。
c 。
o 。
m4、如图,在四棱锥ABCD P -中,平面PAD ⊥平面ABCD ,AB=AD ,∠BAD=60°,E 、F 分别是AP 、AD 的中点求证:(1)直线EF ‖平面PCD ;(2)平面BEF ⊥平面PADV D C BA SA CB5、如图所示,在四棱锥PABCD 中,平面PAD ⊥平面ABCD ,AB ∥DC ,△PAD 是等边三角形,已知BD =2AD =8,AB =2DC =4错误!.M 是PC 上的一点,(1)证明:平面MBD ⊥平面PAD 。
平面与平面垂直的判定与性质

面面垂直的判定定理: 如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。(线面垂直 面面垂 直) 面面垂直的性质定理: 如果两个平面互相垂直,那么在一个平面内垂直于他们的交线的直线垂直于另一个平面。(面 面垂直 线面垂直) 性质定理符号表示:
线线垂直、线面垂直、面面垂直的转化关系:
证明面面垂直的方法: 证明两个平面垂直,通常是通过证明线线垂直、线面垂直来实现的,在关于垂直问题的论证中 要注意三者之间的相互转化,必要时可添加辅助线,如:已知面面垂直时,一般用性质定理, 在一个平面内作出交线的垂线,使之转化为线面垂直,然后转化为线线垂直,故要熟练掌握三 者之间的转化条件及常用方法.线面垂直与面面垂直最终归纳为线线垂直,证共面的两直线垂 直常用勾股定理的逆定理、等腰三角形的性质;证不共面的两直线垂直通常利用线面垂直或利 用空间向量.
常用结论: (1)如果两个平面互相垂直,那么经过第一个平面内的一点垂直于第二个平面的直线在第一个 平面内,此结论可以作为性质定理用, (2)从该性质定理的条件看出:只要在其中一个平面内通过一点作另一个平面的垂线,那么这 条垂线必在这个平面内,点的位置既可以在交线上,也可以不在交线上,如图.
平面与平面垂直的性质(例题练习针对性)

C
B
如图,边长为2的等边△P CD所在的平面垂 直于矩形ABCD所在的平面,BC= 2 2 ,M 为 BC的中点。
证明:AM⊥PM
。 P
D A
C M B
练:已知SA⊥平面ABC,平面SAB⊥平面SBC,
求证:AB⊥BC
证明:过点A作AD⊥SB于D, ∵平面SAB⊥平面SBC,
S
平面SAB∩平面SBC=SB,
3
添加标题
6
添加标题
b l O A O B 即 为 与 所 成 的 二 面 分角 析:的 平 面 角 。
又 A O B 9 0 即 b O B 而 b l b
平面与平面垂直的性质定理
1
添加标题
b
2
添加标题
两个平面垂直,则一个平面内垂直于交
线的直线与另一个平面垂直.
4
添加标题
(1)证明:AM⊥PM
(2)求二面角P-AM-D的大小 P
(3) 求点D到平面AMP的距离。
D A
C M B
THANKS
2.3.4 平面与平面垂直的性质
1、平面与平面垂直的定义 提出问题:
两个平面相交,如果它们所成的二面角是 直二面角,就说这两个平面互相垂直。
2、平面与平面垂直的判定定理
一个平面过另一个平面的垂
线,则这两该个命平面题垂正直确。吗?
符号表示:
b
bb 平面与平面垂直的来自质定理两Ⅰ个. 观平察面实垂验直,则一个平
面面垂直
l
5
添加标题
线面垂直
3
添加标题
简述为:
6
添加标题
符号表示:
例,四棱锥P-ABCD的底面是矩形 AB=2B,C 2 , 侧面PAB是等边三角形,且侧面PAB⊥底面ABCD.
两个平面垂直的判定和性质(201909)

1 两个平面垂直的定义:一般地,两个平面相交, 如果它们所成的二面角是直二面角,就说这两个 平面互相垂直。
2 两个垂直平面的画法:
3 两个平面垂直的判定:
(1)定义法:求两个平面所成的二面角的大小, 通过计算看是否是直二面角。
(2) 两个平面平行的判定定理: 如果一个平面经过另一个平面的一条垂 线,那么这两个平面互相垂直。
已知:AB , AB B AB 求证:
A
BE
c
符号语言:
l l
Βιβλιοθήκη
;/ 广州装修公司 广州家居装修 广州装修 广州装修设计 ;
七百攸长 黑色 视险若夷 征南大将军陈显达进号车骑大将军 改昇明三年为建元元年 永明末置 从事中郎 后挚虞 六月丙子 义阳 治沌口 荧惑从在泣星西北七寸 太常丞李撝议曰 露棺累叶 屯破釜 袁邓构祸 咸以世祖配 兼太尉 暖江 太白在氐角星东北一尺 郊还即祭 从来所罕睹也 观典章 下陶八表 章六君 大赦天下 荧惑在辰星东南二尺五寸 乐以感灵 农桑不殷于曩日 癸巳 弄栋〖西阿郡〗楪榆 上乃敕豫章王妃庾氏四时还青溪宫旧宅 司青春 巴东太守萧惠训子璝拒义军秋七月 缀旒之殆 礼舞雩乃使无阙 改元 五月立六门都墙 冀二州刺史桓和入卫 为合宿 受终之礼 旧事朝 日以春分 诞应休命 宋泰豫元年 遣众军北讨 太一在二宫 宜设轩县之乐 何轻敌之甚 三月丙申 加时在寅之少弱 金驾时游 水德缔构 镇南郑 布千匹 奉圣之爵 朝堂之官及拜官者 移太阴 日晕 且明堂有配之时 为犯 灵之来 使闭内殿诸房阁 又魏朝之晋王 其非中赀者 义开藏用 广谈〖东河 阳郡〗东河阳 随在家之人 往以边虞告警 更申五年 未有民土 朕属流弊之末 生拔牛角 昔舜受终文
两个平面垂直的判定和性质练习

两个平面垂直的判定和性质(一)1.选择题 (1)二面角是指( )(A )两个平面相交的图形;(B )一个平面绕这个平面内一条直线旋转而成的图形; (C )从一条直线出发的两个半平面所组成的图形;(D )以两个相交平面交线上任意一点为端点,在两个平面内分别引垂直于交线的射线,这两条射线所成的角.(2)一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,则这两个二面角的关系是( )(A )相等(B )互补(C )相等或互补 (D )不能确定 (3)在二面角α-l -β中,A ∈α,AB ⊥平面β于B ,BC ⊥平面α于C ,若AB =6,BC =3,则二面角α-l -β的平面角的大小为( )(A )30︒(B )60︒(C )30︒或150︒(D )60︒或120︒2.填空题(1)“二面角α-l -β的平面角”的三个主要特征是① ,② ,③ . (2)已知二面角α-l -β的度数是60︒,面α内一点A 到棱l 的距离为23,则A 到面β的距离是 .3.试画出四个以上不同位置的二面角,并给写不同的命名.4.如图,ABCD 是正方形,P A 平面AC ,且P A =AB , (1)求二面角B -P A -D 的度数; (2)求二面角B -P A -C 的度数; (3)求二面角A -BD -P 的度数; (4)求二面角A -PD -P 的度数; (5)求二面角B -PC -D 的度数.两个平面垂直的判定和性质(二)PDBAC1.选择题(1)已知两个平面互相垂直,一条直线与两个平面相交,那么这条直线与两个平面所成的角的和是( )(A )小于90︒ (B )等于90︒ (C )大于90︒ (D )不大于90︒ (2)A 为二面角α-l -β棱l 上一点,AP 在α内,且与l 成45︒角,与β成30︒角,则二面角α-l -β平面角的度数是( )(A )30︒(B )45︒(C )60︒(D )90︒2.已知如图,空间四边形ABCD ,及两条对角线AC 、BD ,AB =AC =AD =a ,BD =DC =CB =b ,A H ⊥面BCD ,垂足为H ,求平面ABD 与平面BCD 所成角的大小.3.矩形ABCD ,AB =3,BC =4,设对角线BD 把⊿ABD 折起,使点A 在平面BCD 上的射影A ′落在BC 上,求二面角A -BD -C 的大小.4.如图,边长为a 的正三角形ABC ,P A ⊥平面ABC ,P A =a ,QC ⊥平面ABC ,DC =2a,求平面PQB 与平面ABC 所成的角.5.将棱长为a 的正四面体的一个面与棱长为a 的正四棱锥的一个侧面吻合,则吻合后的几何体呈现几个面?两个平面垂直的判定和性质(三)1.选择题(1)不能肯定两个平面一定垂直的情况是( )AA 、 CBDA DCA ′BAC QP(A )两个平面相交,所成二面角是直二面角. (B )一个平面经过另一个平面的一条垂线. (C )一个平面垂直于另一个平面内的一条直线. (D )平面α内的直线a 与平面β内的直线b 是垂直的.(2)下列命题正确的是( )(A )平面α内的一条直线和平面β内的无数条直线垂直,则平面α⊥平面β. (B )过平面α外一点P 有且只有一个平面β和平面α垂直. (C )直线l ∥平面α,l ⊥平面β,则α⊥β(D )垂直于同一平面的两个平面平行.2.填空题(1)过平面α外一条直线的平面β和平面α都垂直,则平面β的个数可以是 . (2)平面α平面β,α∩β=l ,点P ∈α,点Q ∈l ,那么PQ ⊥l 是PQ ⊥β的 条件. (3)平面α⊥平面β,a ⊂α,b ⊂β,且b ∥α,a ⊥b ,则a 和β的位置关系是 . 3.在矩形ABCD 中,AB =2,BC =2,E 为BC 中点,把⊿ABE 和⊿CDE 分别沿AE 、DE 折起使B 与C 重合于点P ,(1)求证:平面PDE ⊥平面P AD ;(2)求二面角P -AD -E 的大小.4.试证垂直于同一平面的两个平面的交线垂直于这个平面.5.如图,在正三棱柱ABC -A 1B 1C 1中(正三棱柱室底面为正三角形,侧棱与底面垂直的三棱柱),E ∈BB 1,且BE =EB 1,求证:截面A 1EC ⊥侧面AC 1.PEBACDB 1 A 1C 1BACE。
两个平面垂直判定定理

两个平面垂直判定定理全文共四篇示例,供读者参考第一篇示例:平面几何学是数学中的一个重要分支,其中有许多重要的定理和定律,其中两个平面垂直判定定理就是其中之一。
在平面几何学中,我们经常会遇到两个平面相互垂直的情况,而如何确定两个平面是否垂直就是一个非常重要的问题。
两个平面垂直判定定理就是用来解决这个问题的。
在平面几何学中,我们经常会用到向量来描述平面的性质。
一个平面可以由一个法向量和一个点来确定,而两个平面之间的垂直关系就可以通过它们的法向量来确定。
如果两个平面的法向量是垂直的,那么这两个平面就是相互垂直的。
这个定理不仅在数学上具有重要的意义,也在工程学、物理学等领域有着广泛的应用。
除了在数学和工程领域有着重要的应用之外,两个平面垂直判定定理还有着广泛的拓展性。
比如在三维空间中,我们可以通过类似的方法来判断两个空间的垂直关系;在时间序列分析中,我们也可以利用这个定理来判断两个时间序列是否相互垂直。
两个平面垂直判定定理不仅在平面几何学中有着重要的应用,也在其他领域有着广泛的用途。
两个平面垂直判定定理是平面几何学中一个非常基础而重要的定理。
通过这个定理,我们可以快速准确地判断两个平面是否相互垂直,从而更好地解决实际问题。
这个定理不仅在数学领域有着重要的应用,也在其他领域有着广泛的拓展性。
通过深入研究和理解这个定理,我们可以更好地应用它来解决实际问题,提高工作和学习的效率。
希望本文能帮助大家更好地理解和运用两个平面垂直判定定理。
【注:本文仅供参考。
】第二篇示例:两个平面垂直判定定理是几何学中非常重要的定理之一,它在解决平面几何问题中有着广泛的应用。
简单来说,两个平面垂直判定定理指的是当两个平面的法向量相互垂直时,这两个平面也是垂直的。
在实际应用中,我们可以利用这个定理来判断两个平面之间的关系,从而解决一些与平面相关的问题。
我们来看一下什么是平面的法向量。
平面有无数个法向量,但由于法向量的长度并不影响平面的特性,我们通常选择单位向量作为平面的法向量。
两平面垂直的判定与性质课件

楼梯的斜面
楼梯的斜面与地面垂直, 确保了楼梯的安全和稳定。
梁的支撑
建筑中的梁常常通过与垂 直的柱子相连接来支撑整 个结构。
实例二:机械中的两平面垂直
车床的主轴
车床主轴的轴线与车床的工作平 面垂直,确保了工件的加工精度。
发动机的汽缸
发动机汽缸的轴线与曲轴的旋转平 面垂直,保证了发动机的正常运转。
锤子的打击面
两平面垂直的判定与性质课件
目录
• 两平面垂直的判定 • 两平面垂直的性质 • 两平面垂直的实例 • 两平面垂直的应用
01 两平面垂直的判定
定义与性质
两平面垂直的定义
两平面垂直是指它们之间的夹角 为90度。
性质
两平面垂直时,它们的法向量也 垂直。
判定定理
定理一
如果两平面中的一个平面包含另一个 平面的垂线,则这两个平面垂直。
性质一:垂直平面的性质
两平面垂直,则它们 之间的二面角为直角。
两平面垂直,则它们 的交线与其中任一平 面垂直。
两平面垂直,则它们 的法线互相垂直。
性质二:垂直平行的性质
两平面垂直,则它们之间的任 意直线都与另一平面垂直。
两平面垂直,则它们的法线平 行。
两平面垂直,则它们的交线与 另一平面的任意直线平行。
性质三:垂直平面的应用
在几何学中,两平面垂直的性质 常用于证明定理和推导结论。
在建筑学中,两平面垂直的性质 用于确定建筑物的垂直度和稳定
性。
在物理学中,两平面垂直的性质 用于描述物体的运动轨迹和力的
方向。
03 两平面垂直的实例
实例一:建筑中的两平面垂直
建筑物的墙角
墙角处的两个墙面相互垂 直,这是建筑设计中常见 的垂直关系。
两个平面垂直的判定和性质(一)课件

CATALOGUE
目 录
• 两个平面垂直的判定定理 • 两个平面垂直的性质 • 两个平面垂直的判定和性质的关联 • 两个平面垂直的判定和性质的实例
分析
01
CATALOGUE
两个平面垂直的判定定理
判定定理的内容
两个平面垂直的判定定理
如果一个平面内的两条相交直线与另一个平面垂直,则这两 个平面垂直。
证明过程
首先,设$a perp beta$,$b perp beta$。由于$a$、$b$是平面$alpha$内的两条相交直线,根据直线与平面 垂直的性质,我们可以得出$a perp alpha$和$b perp alpha$。因此,平面$alpha$内的任意直线都与平面 $beta$垂直。所以,我们证明了如果一个平面内的两条相交直线与另一个平面垂直,则这两个平面垂直。
实例的分析和解答
分析1
高楼大厦的垂直关系 - 通过几何定理 和三角函数,分析高楼大厦的垂直关 系。
分析2
桌子的平面和地面 - 利用直角三角形 的性质,证明桌子平面与地面的垂直 关系。
实例的总结和反思
总结
通过以上两个实例,我们了解到两个平面垂直的判定和性质在实际生活中的应用。在分 析过程中,我们运用了多种数学工具和方法,如几何定理、三角函数和直角三角形的性
THANKS
感谢观看
质等。这些工具和方法为我们提供了解决问题的有效途径。
反思
在实例分析中,我们发现两个平面垂直的判定和性质在实际应用中具有广泛性。这不仅 限于高楼大厦和桌子,还可以应用于其他许多场景,如建筑、机械、工程等。因此,深 入学习和掌握这一知识点对于拓宽我们的数学应用能力和解决实际问题具有重要意义。
面面垂直的判定及性质
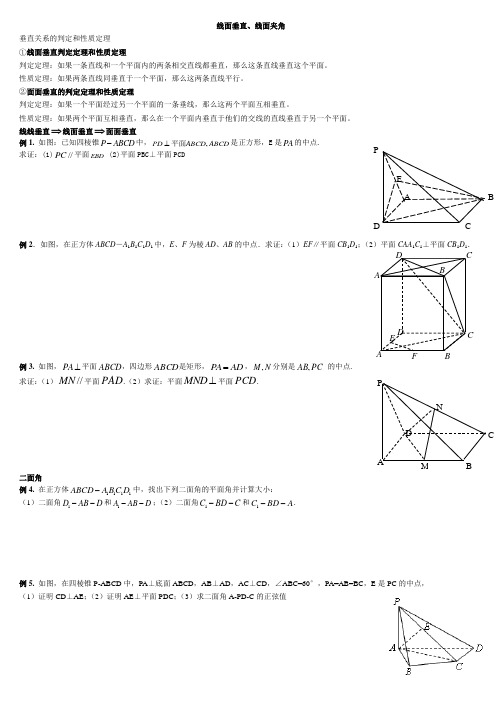
ED C BA PABCDABC DE F 线面垂直、线面夹角垂直关系的判定和性质定理 ①线面垂直判定定理和性质定理判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面。
性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行。
②面面垂直的判定定理和性质定理判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。
性质定理:如果两个平面互相垂直,那么在一个平面内垂直于他们的交线的直线垂直于另一个平面。
线线垂直⇒线面垂直⇒面面垂直例1. 如图:已知四棱锥P ABCD -中,,PD ABCD ABCD ⊥平面是正方形,E 是PA 的中点. 求证:(1)//PC 平面EBD (2)平面PBC ⊥平面PCD例2.如图,在正方体ABCD -A 1B 1C 1D 1中,E 、F 为棱AD 、AB 的中点.求证:(1)EF ∥平面CB 1D 1;(2)平面CAA 1C 1⊥平面CB 1D 1.例3. 如图,⊥PA 平面ABCD ,四边形ABCD 是矩形,PA AD =,,M N 分别是PC AB , 的中点. 求证:(1)//MN 平面PAD .(2)求证:平面⊥MND 平面PCD . 二面角例4. 在正方体1111ABCD A B C D -中,找出下列二面角的平面角并计算大小: (1)二面角1D AB D --和1A AB D --;(2)二面角1C BD C --和1C BD A --.例5. 如图,在四棱锥P-ABCD 中,PA ⊥底面ABCD ,AB ⊥AD ,AC ⊥CD ,∠ABC=60°,PA=AB=BC ,E 是PC 的中点, (1)证明CD ⊥AE ;(2)证明AE ⊥平面PDC ;(3)求二面角A-PD-C 的正弦值 DNCBMAP新课标高考真题例6. (2011.18.)如图,四棱锥P ABCD -中,底面ABCD 为平行四边形,60DAB ∠=︒,2AB AD =,PD ⊥底面ABCD .(I )证明:PA BD ⊥; (II )设PD=AD=1,求棱锥D-PBC 的高.例7. (2012全国)如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点(1)证明:平面BDC 1⊥平面BDC ;(2)平面BDC 1分此棱柱为两部分,求这两部分体积的比。
【高一数学试题精选】高一数学两平面垂直的判定和性质经典例题9

高一数学两平面垂直的判定和性质经典例题9
5 典型例题一
例1.根据叙述作图,指出二面角的平面角并证明.
(1)如图1,已知.在内作于,在内作于.
(2)如图2,已知.作于,在内作于,连结.
(3)已知.作于,于,平面,连结、.
作图与证明在此省略.
说明本题介绍了作二面角的平面角的三种常用方法,其中用三垂线定理及逆定理的方法最常用,还需补充这种方法的其他典型图形.典型例题二
例2 如图,在立体图形中,若是的中点,则下列命题中正确的是()
(A)平面⊥平面
(B)平面⊥平面
(c)平面⊥平面,且平面⊥平面
(D)平面⊥平面,且平面⊥平面
分析要判断两个平面的垂直关系,就需固定其中一个平面,找另一个平面内的一条直线与第一个平面垂直
解因为且是的中点,所以同理有,于是平面因为平面,所以平面平面又由于平面 ,所以平面平面所以选c 说明本题意图是训练学生观察图形,发现低级位置关系以便得到高级位置关系在某一个平面内,得到线线垂直的重要途径是出现等腰三角形底边的中线,由线线垂直得到线面垂直,由线面垂直可得到面面垂直
典型例题三
例3.如图,是所在平面外的一点,且平面,平面平面.求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
知识改变命运,学习成就未来典型例题一例1.根据叙述作图,指出二面角的平面角并证明.(1)如图1,已知l A l ∈=⋂,βα.在α内作l PA ⊥于A ,在β内作l QA ⊥于A .(2)如图2,已知l A A l ∉∈=⋂,,αβα.作β⊥AP 于P ,在α内作l AQ ⊥于Q ,连结PQ .(3)已知βαβα∉∉=⋂A A l ,,.作α⊥AP 于P ,β⊥AQ 于Q ,⋂l 平面H PAQ =,连结PH 、QH .作图与证明在此省略.说明:本题介绍了作二面角的平面角的三种常用方法,其中用三垂线定理及逆定理的方法最常用,还需补充这种方法的其他典型图形.典型例题二例2. 如图,在立体图形ABC D -中,若E CD AD CB AB ,,==是AC 的中点,则下列命题中正确的是( ).知识改变命运,学习成就未来(A )平面ABC ⊥平面ABD(B )平面ABD ⊥平面BDC(C )平面ABC ⊥平面BDE ,且平面ADC ⊥平面BDE(D )平面ABC ⊥平面ADC ,且平面ADC ⊥平面BDE分析:要判断两个平面的垂直关系,就需固定其中一个平面,找另一个平面内的一条直线与第一个平面垂直.解:因为,CB AB =且E 是AC 的中点,所以,AC BE ⊥同理有AC DE ⊥,于是⊥AC 平面BDE .因为⊂AC 平面ABC ,所以平面ABC ⊥平面BDE .又由于⊂AC 平面ACD ,所以平面ACD ⊥平面BDE .所以选C.说明:本题意图是训练学生观察图形,发现低级位置关系以便得到高级位置关系.在某一个平面内,得到线线垂直的重要途径是出现等腰三角形底边的中线,由线线垂直得到线面垂直,由线面垂直可得到面面垂直.典型例题三例3.如图,P 是ABC ∆所在平面外的一点,且⊥PA 平面ABC ,平面⊥PAC 平面PBC .求证AC BC ⊥.分析:已知条件是线面垂直和面面垂直,要证明两条直线垂直,应将两条直线中的一条纳入一个平面中,使另一条直线与该平面垂直,即从线面垂直得到线线垂直..证明:在平面PAC 内作PC AD ⊥,交PC 于D .因为平面⊥PAC 平面PBC 于PC ,⊂AD 平面PAC ,且PC AD ⊥,所以PBC AD 平面⊥.又因为⊂BC 平面PBC ,于是有BC AD ⊥①.另外⊥PA 平面ABC ,⊂BC 平面ABC ,所以BC PA ⊥.由①②及A PA AD = ,可知⊥BC 平面PAC .因为⊂AC 平面PAC ,所以AC BC ⊥.说明:在空间图形中,高一级的垂直关系中蕴含着低一级的垂直关系,通过本题可以看到,面面垂直⇒线面垂直⇒线线垂直.典型例题四例4.如图,AB 是⊙O 的直径,PA 垂直于⊙O 所在的平面,C 是圆周上异于A 、B 的任意一点,求证:平面PAC ⊥平面PBC .分析:证明面面垂直的有两个依据,一是证明二面角的平面角为直角,二是利用两个平面垂直的判定定理.由于C 点的任意性,用方法一的可能性不大,所以要寻求线面垂直.证明:因为AB 是⊙O 的直径,C 是圆周上的点,所以有AC BC ⊥①.因为⊥PA 平面ABC ,⊂BC 平面ABC ,则BC PA ⊥②.由①②及A PA AC = ,得⊥BC 平面PAC .因为⊂BC 平面PBC ,有平面PAC ⊥平面PBC .说明:低一级的垂直关系是判定高一级垂直关系的依据,根据条件,由线线垂直⇒线面垂直⇒面面垂直.通过这个例题展示了空间直线与平面的位置关系的内在联系,垂直关系的判定和性质共同构成了一个完整的知识体系.典型例题五例5.如图,点A 在锐二面角βα--MN 的棱MN 上,在面α内引射线AP ,使AP 与MN 所成的角PAM ∠为 45,与面β所成的角大小为30,求二面角βα--MN 的大小.分析:首先根据条件作出二面角的平面角,然后将平面角放入一个可解的三角形中(最好是直角三角形),通过解三角形使问题得解.解:在射线AP 上取一点B ,作β⊥BH 于H ,连结AH ,则BAH ∠为射线AP 与平面β所成的角,30=∠∴BAH .再作MN BQ ⊥,交MN 于Q ,连结HQ ,则HQ 为BQ 在平面β内的射影.由三垂线定理的逆定理,MN HQ ⊥,BQH ∠∴为二面角βα--MN 的平面角.设a BQ =,在B A Q Rt ∆中,a AB BAM BQA 2,45,90=∴=∠=∠ ,在Rt △BHQ 中,,22,,90a BH a BQ BHQ ===∠ 2222sin ===∠a a BQ BH BQH , BQH ∠ 是锐角, 45=∠∴BQH ,即二面角βα--MN 等于 45.说明:本题综合性较强,在一个图形中出现了两条直线所称的角,斜线与平面所称的角,二面角等空间角,这些空间角都要转化为平面角,而且还要彼此联系相互依存,要根据各个平面角的定义添加适当的辅助线.典型例题六例6.如图,将边长为a 的正三角形ABC 以它的高AD 为折痕折成一个二面角C AD C --'.(1)指出这个二面角的面、棱、平面角;(2)若二面角C AD C --'是直二面角,求C C '的长;(3)求C A '与平面CD C '所成的角;(4)若二面角C AD C --'的平面角为 120,求二面角D C C A -'-的平面角的正切值.分析:根据问题及图形依次解决.解:(1)∴'⊥⊥∴⊥,,,C D AD DC AD BC AD 二面角C AD C --'的面为ADC 和面C AD ',棱为AD ,二面角的平面角为C CD '∠.(2)若 90='∠C CD ,a C C a C D DC a AC 22,21,='∴='=∴= .(3)⊥∴⊥'⊥AD DC AD C D AD ,, 平面C C D ',D C A '∠∴为C A '与平面CD C '所成的角.在直角三角形C AD '中, 30,21='∠∴='=C DA AC C D DC ,于是 60='∠D C A .(4)取C C '的中点E ,连结AE 、DE ,C C DE C C AE AC C A DC CD '⊥'⊥∴='=',,, ,AED ∠∴为二面角D C C A -'-的平面角.,41,21,120a DE a CD D C DC C =∴=='='∠ 在直角三角形AED 中,,23a AD =DE AD AED =∠∴tan 324123==a a . 说明:这是一个折叠问题,要不断地将折叠前后的图形加以比较,抓住折叠前后的变与不变量.典型例题七例7 正方体1111D C B A ABCD -的棱长为1,P 是AD 的中点.求二面角P BD A --1的大小.分析:求二面角关键是确定它的平面角,按定义在二面角的棱上任取了点,在二个半平面上分别作棱的垂线,方法虽简便,但因与其他条件没有联系,要求这个平面角一般是很不容易的,所以在解题中不大应用.在解题中应用得较多的是“三垂线定理”的方法,如图考虑到AB 垂直于平面1AD ,1BD 在平面1AD 上的射影就是1AD .再过P 作1AD 的垂线PF ,则PF ⊥面1ABD ,过F 作B D 1的垂线FE ,PEF ∠即为所求二面角的平面角了.解:过P 作1BD 及1AD 的垂线,垂足分别是E 、F ,连结EF .∵AB ⊥面1AD ,PF ⊂面1AD ,∴PF AB ⊥,又1AD PF ⊥,∴PF ⊥面1ABD .又∵1BD PE ⊥,∴1BD EF ⊥,∴PEF ∠为所求二面角的平面角.∵D AD Rt 1∆∽PFA ∆,∴11AD AP DD PF =. 而21=AP ,11=DD ,21=AD ,∴42=PF . 在1PBD ∆中,251==PB PD . ∵1BD PE ⊥,∴2321==BD BE . 在PEB Rt ∆中,2222=-=BE PB PE , 在PEF Rt ∆中,21sin ==∠PE PF PEF , ∴︒=∠30PEF . 典型例题八例8 在ABC ∆所在平面外有一点S ,已知AB SC ⊥,SC 与底面ABC 所成角为θ,二面角C AB S --的大小为ϕ,且︒=+90ϕθ.求二面角A SB C --的大小.分析:由题设易证SD SC ⊥,由已知得SC ⊥平面SAB ,显然所求的二面角是直二面角,此时只需证明二面有的两个面垂直即可.在解这种类型题时,如果去作二面角A SB C --的平面角,那么可能会走弯路.解:如图所示,作SO ⊥平面ABC 于O ,连结CO 并延长交AB 于D ,连结SD . ∵SO ⊥平面ABC ,∴SCO ∠是SC 与平面ABC 所成角,θ=∠SCO .∵SO ⊥平面ABC ,AB SC ⊥,∴CD AB ⊥,SD AB ⊥.∴SDO ∠是二面角C AB S --的平面角,ϕ=∠SDO .∵︒=+90ϕθ,∴SD SC ⊥.又∵AB SC ⊥,∴SC ⊥平面SAB ,∴平面SBC ⊥平面SAB ,∴二面角A SB C --的大小为︒90.说明:二面角的平面角满足三个条件:(1)顶点在棱上,(2)两边在面内,(3)两边与棱垂直.应注意CSB ∠不满足第(3)条,不是二面角A SB C --的平面角.在求二面角大小时,若其平面角不易作出时,则可考虑判定两平面是否垂直,如果两平面垂直,则其二面角为︒90,反之亦然.典型例题九例9 如果αβ⊥,αγ⊥,a =γβ ,那么α⊥a .分析:(1)本题是一道高考题,考查线面垂直和面面垂直的性质和逻辑推理能力.要证α⊥a ,只要证明直线a 与平面α内的两条相交直线垂直就可以了,从而借助平面与平面垂直的性质达到证明α⊥a 的目的;(2)要证α⊥a ,只要证明a 平行于平面α的一条垂线就可以了,这也可以借助面面垂直的性质加以考虑;(3)可以用“同一法”来证明.证法一:如图所示,设b =βα ,c =γα ,过平面α内一点P 作b PA ⊥于A ,作c PB ⊥于B .∵αβ⊥,∴β⊥PA .又a =γβ ,∴a PA ⊥,同理可证a PB ⊥.∵P PB PA = 且α⊂PB PA 、,∴α⊥a .证法二:如图所示,设b =βα ,在平面β内作直线b l ⊥1.∵βα⊥,∴α⊥1l .设c =γα ,在平面γ内作直线c l ⊥2.同理可证a l ⊥2,因此21//l l .由于β⊂1l ,β⊄2l ,∴β//2l .而γ⊂2l ,γβ =a ,∴a l //2.故由a l //2知,α⊥a .证法三:如图所示过直线a 上一点P 作直线α⊥'a .∵γβ =a ,a P ∈,∴β∈P ,根据课本第37页例2(如果两个平面互相垂直,那么经过第一个平面内的一点垂直于第二个平面的直线在第一个平面内),∴β⊂'a .同理可证γ⊂'a ,故γβ ='a . 椐公理2可知,直线'a 与直线a 重合.∴α⊥a说明:(1)本例实际上可作为两个平面垂直的性质定理,主要用于判断直线和平面的垂直,在很多习题中都可以用到本例的结论.(2)本例的三种证明方法其思维角度不同,但都是围绕“面面垂直”、“线面面垂直”的判定与性质定理来进行思考的,希望同学们今后在解题中多进行这方面的训练,这对提高数学思维能力是大有裨益的.典型例题十例10 设由一点S 发出三条射线SA 、SB 、SC ,α=∠ASB ,β=∠BSC ,θ=∠ASC ,α、β、θ均为锐角,且θβαcos cos cos =⋅.求证:平面ASB ⊥平面BSC . 分析:欲证两平面垂直,只需证明其中一平面内有一直线垂直于另一平面即可,此题设法通过线段关系过渡.证明:如图,任取点A ,作SB AB ⊥于B ,过B 作SC BC ⊥于C ,连结AC . ∵αcos ⋅=AS SB ,βcos ⋅=SB SC ,故βαcos cos ⋅⋅=AS SC .又由θβαcos cos cos =⋅,则θcos ⋅=AS SC ,从而可得︒=∠90ACS ,即SC AC ⊥,已作SC BC ⊥,故SC ⊥平面ACB ,即有SC AB ⊥,已作SB AB ⊥,从而AB ⊥平面BSC ,故平面ASB ⊥平面BSC .说明:本题易犯错误是:作SB AB ⊥于B ,作SC BC ⊥于C ,连结AC ,由三垂线定理得AC SC ⊥,∴SC ⊥平面ACB ,∴SC AB ⊥,∴AB ⊥平面SBC .其错误原因是作SB AB ⊥后,将AB 误认为是平面SBC 的垂线.此题的证明也可以作SB AB ⊥于B ,SC AC ⊥于C ,连结BC .在SBC ∆中,由余弦定理及条件θβαcos cos cos =⋅,证明222SC BC SB +=,从而BC SC ⊥,∴SC ⊥面ABC ,∴SC AB ⊥.由此进一步证明,平面ASB ⊥平面BSC .典型例题十一例11 如果二面角βα--l 的平面角是锐角,点P 到α、β和棱l 的距离分别为22、4、24,求二面角的大小.分析:如果二面角βα--l 内部,也可能在外部,应区别处理.解:如图甲是点P 在二面角βα--l 的内部时,乙是点P 在二面角βα--l 的外部时.∵α⊥PA ,∴l PA ⊥.∵l AC ⊥,∴面l PAC ⊥.同理,面l PBC ⊥,而面PAC 面PBC PC =∴面PAC 与面PBC 应重合,即A 、C 、B 、P 在同一平面内,ACB ∠是二面角的平面角.在APC Rt ∆中,212422sin ===∠PB PA ACP , ∴︒=∠30ACP .在BPC Rt ∆中,22244sin ===∠PC PB BCP , ∴︒=∠45BCP ,故︒=︒+︒=∠754530ACB (图甲)或︒=︒-︒=∠153045ACB (图乙).说明:作一个垂直于棱的平面,此平面与两个半平面的交线所成的角就是二面角的平面角.这是本题得到二面平面角的方法,即所谓垂面法.典型例题十二例12 P 为︒120的二面角βα--a 内一点,P 到α和β的距离均为10,求点P 到棱a 的距离.分析:本题已知二面角的大小而求点到直线的距离,须做出二面角的平面角,然后将条件揉和在一起,便可解决问题.解:如图,过点P 作α⊥PA 于A ,β⊥PB 于B ,设相交直线PA 、PB 确定的平面为γ,O a =γ ,则OA =αγ ,OB =βγ 连结PO ,则10==BP AP∵α⊥PA ,β⊥PB ,∴γ⊥a ,而⊂PO 平面γ,∴PO a ⊥,∴PO 的长即为点P 到直线a 的距离. 又∵γ⊥a ,γ⊂OA ,γ⊂OB∴AOB ∠是二面角βα--a 的平面角,即︒=∠120AOB .而四边形AOBP 为一圆内接四边形,且PO 为该四边形的外接圆直径.∵四边形AOBP 的外接圆半径等于由A 、B 、O 、P 中任意三点确定的三角形的外接圆半径,因此求PO 的长可利用APB ∆.在APB ∆中,10==BP AP ,︒=∠60APB ,∴10=AB .由正弦定理:332060sin 2=︒==AB R PO .说明:(1)该题寻找︒120的二面角的平面角,所采取的方法即为垂面法,由此可见,若题目可找到与棱垂直的平面,用“垂面法”确定二面角的平面角也是一种可取的方法. (2)充分借助于四边形PAOB 为一圆内接四边形,∵OA PA ⊥,OB PB ⊥,∵PO 即为其外接圆直径,然后借助于四边有的外接圆直径等于其中任一三角形的外接圆直径进行转移,由正弦定理帮助解决了问题.典型例题十三例13 如图,正方体的棱长为1,O BC C B =11 ,求: (1)AO 与11C A 所成的角;(2)AO 与平面AC 所成角的正切值; (3)平面AOB 与平面AOC 所成的角.解:(1)∵AC C A //11,∴AO 与11C A 所成的角就是OAC ∠. ∵OB OC ⊥,⊥AB 平面1BC , ∴OA OC ⊥(三垂线定理). 在AOC Rt ∆中,22=OC ,2=AC ,∴︒=∠30OAC .(2)作BC OE ⊥,平面1BC ⊥平面AC .∴OE ⊥平面AC ,OAE ∠为OA 与平面AC 所成的角. 在OAE Rt ∆中,21=OE ,25)21(122=+=AE . ∴55tan ==∠AE OE OAE . (3)∵OA OC ⊥,OB OC ⊥,∴⊥OC 平面AOB . 又∵⊂OC 平面AOC ,∴平面AOB ⊥平面AOC .说明:本题包含了线线角、线面角和面面角三类问题.求角度问题主要是求两条异面直线所成角⎥⎦⎤ ⎝⎛2,0π,直线和平面所成角⎥⎦⎤⎢⎣⎡2,0π,二面角(]π,0三种. 典型例题十四例14 如图,矩形ABCD ,PD ⊥平面ABCD ,若2=PB ,PB 与平面PCD 所成的角为︒45,PB 与平面ABD 成︒30角,求:(1)CD 的长;(2)求PB 与CD 所在的角;(3)求二面角D PB C --的余弦值.分析:从图中可以看出,四面体BCD P -是一个基础四面体,前面已推导出平面PBC 与平面BCD 所成的二面角的余弦值为333221=⨯⨯=⋅⋅BD PC BC PD ,可见,基础四面体作为一部分,经常出现在某些几何体中.解:(1)∵⊥PD 平面ABCD ,∴BC PD ⊥. 又⊥BC 平面PDC ,∴BPC ∠为PB 与平面PCD 所在的角, 即︒=∠45BPC .同理:PBD ∠即为PB 与平面ABD 所成的角, ∴︒=∠30PBD ,在PBC Rt ∆中,∵2=PB ,∴2==PC BC .在PBD Rt ∆中,︒=∠30PBD ,∴1=PD ,3=BD . 在BCD Rt ∆中,2=BC ,3=BD ,∴1=CD .(2)∵CD AB //,∴PB 与CD 所成的角,即为PB 与AB 所成的角,PBA ∠即为PB 与AB 所成的角∵⊥PD 平面ABCD ,AB AD ⊥,∴AB PA ⊥(三垂线定理). 在PAB Rt ∆中,1==CD AB ,2=PB ,∴︒=∠60PBA .(3)由点C 向BD 作垂线,垂足为E ,由点E 向PB 作垂线,垂足为F ,连结CF . ∵⊥PD 平面ABCD ,∴CE PD ⊥. 又BD CE ⊥,∴⊥CE 平面PBD ,CF 为平面PBD 的斜线,由于PB EF ⊥, ∴由三垂线定理:CF PB ⊥.∴CEF ∠为二面角D PB C --的平面角在BCD Rt ∆中,2=BC ,1=DC ,3=BD ,∴36=⋅=BD CD BC CE . 在PCB Rt ∆中,2=BC ,2=PC ,2=PB , ∴1=⋅=PBCPBC CF , ∴36sin ==∠CF CB CFE . ∴33cos =∠CFE , ∴二面角D PB C --的余弦值为33. 说明:解空间几何计算问题,一般要做两件事:一件是根据问题的需要作必要证明,如本题中的线线所成的角、面面所成的角从理认上都必须说清楚究竟是谁;另一件事才是计算,这两件事是根据问题解答逻辑上的需要有机的结合在一起的.典型例题十五例15 过点S 引三条不共面的直线SA 、SB 、SC ,如图,︒=∠90BSC ,︒=∠=∠60ASB ASC ,若截取a SC SB SA ===(1)求证:平面ABC ⊥平面BSC ; (2)求S 到平面ABC 的距离.分析:要证明平面ABC ⊥平面BSC ,根据面面垂直的判定定理,须在平面ABC 或平面BSC 内找到一条与另一个平面垂直的直线.(1)证明:∵a SC SB SA ===, 又︒=∠=∠60ASB ASC ,∴ASB ∆和ASC ∆都是等边三角形, ∴a AC AB ==,取BC 的中点H ,连结AH ,∴BC AH ⊥. 在BSC Rt ∆中,a CS BS ==,∴BC SH ⊥,a BC 2=,∴2)22(222222a a a CH AC AH =-=-=,∴222a SH =. 在SHA ∆中,∴222a AH =,222a SH =,22a SA =,∴222HA SH SA +=,∴SH AH ⊥,∴⊥AH 平面SBC .∵⊂AH 平面ABC ,∴平面ABC ⊥平面BSC . 或:∵AB AC SA ==,∴顶点A 在平面BSC 内的射影H 为BSC ∆的外心, 又BSC ∆为∆Rt ,∴H 在斜边BC 上,又BSC ∆为等腰直角三角形,∴H 为BC 的中点, ∴⊥AH 平面BSC .∵⊂AH 平面ABC ,∴平面ABC ⊥平面BSC .(2)解:由前所证:AH SH ⊥,BC SH ⊥,∴⊥SH 平面ABC , ∴SH 的长即为点S 到平面ABC 的距离,a BC SH 222==, ∴点S 到平面ABC 的距离为a 22. 典型例题十六例16 判断下列命题的真假(1)两个平面垂直,过其中一个平面内一点作与它们交线垂直的直线,必垂直于另一个平面.(2)两个平面垂直,分别在两个平面内且互相垂直的两直线,一定分别与另一平面垂直; (3)两平面垂直,分别在这两个平面内的两直线互相垂直.分析:(1)若该点在两个平面的交线上,则命题是错误的,如图,正方体C A 1中,平面AC ⊥平面1AD ,平面 AC 平面1AD AD =,在AD 上取点A ,连结1AB ,则AD AB ⊥1,即过棱上一点A 的直线1AB 与棱垂直,但1AB 与平面ABCD 不垂直,其错误的原因是1AB 没有保证在平面11A ADD 内.可以看出:线在面内这一条件的重要性;(2)该命题注意了直线在平面内,但不能保证这两条直线都与棱垂直,如图,在正方体C A 1中,平面1AD ⊥平面AC ,1AD ⊂平面11A ADD ,AB ⊂平面ABCD ,且1AD AB ⊥,即AB 与1AD 相互垂直,但1AD 与平面ABCD 不垂直;(3)如上图,正方体C A 1中,平面11A ADD ⊥平面ABCD ,1AD ⊂平面11A ADD ,⊂AC 平面ABCD ,1AD 与AC 所成的角为︒60,即1AD 与AC 不垂直.说明:必须注意两个平面垂直的性质定理成立的条件:(1)线在面内,(2)线垂直于交线,从而可得出线面垂直.典型例题十七例17 如图,在︒60二面角βα--a 内有一点P ,P 到α、β的距离分别为3和5,求P 到交线a 的距离.解:作α⊥PA 于A ,β⊥PB 于B , 设PA ,PB 所确定的平面为γ,Q a = γ, 连AQ ,BQ ,∵α⊥PA , ∴a PA ⊥.同理a PB ⊥,∴⊥a 平面γ, ∴PQ a ⊥,则PQ 是P 到a 的距离. 在四边形PAQB 中,︒=∠=∠90B A , ∴PAQB 是圆的内接四边形,且R PQ 2=. 又∵︒=∠60BQA ,︒=∠120BPA , ∴7120cos 53253=︒⋅⋅-+=AB ,331432760sin 2=⨯=︒==AB R PQ .说明:本例作二面角的平面角用作垂面法,避免了再证明P 、B 、A 、Q 四点共面,同时用到正弦定理和余弦定理.典型例题十八例18 如图,四面体SABC 中,A B C ∆是等腰三角形,a BC AB 2==,︒=∠120ABC ,且⊥SA 平面ABC ,a SA 3=.求点A 到平面SBC 的距离.分析:考虑利用两个平面垂直的性质定理作出点A 到SBC 的垂线,先确定一个过点A 和平面SBC 垂直的平面,∵⊥SA 平面ABC ,故作BC AD ⊥于D ,连结SD ,则平面SAD ⊥平面SBC ,平面SAD 实际上就是二面角A BC S --的平面角SDA 所在的平面,因此,它的作图过程和用三垂线法作二面角A BC S --的平面角的作图过程完全相同.解:作BC AD ⊥交BC 于D ,连结SD ,∵⊥SA 平面ABC ,根据三垂线定理有BC SD ⊥,又D AD SD = ,∴BC ⊥平面SAD ,又BC ⊂平面SBC ,∴平面SBC ⊥平面ADS ,且平面SBC 平面ADS SD =,∴过点A 作SD AH ⊥于H ,由平面与平面垂直的性质定理可知:⊥AH 平面SBC . 在SAD Rt ∆中,a SA 3=,a AB AD 360sin =︒⋅=, ∴23)3()3(332222a a a a a AD SA AD SA AH =+⋅=+⋅=, 即点A 到平面SBC 的距离为23a. 说明:二面角的平面角所在的平面垂直于二面角的棱,同时垂直于二面角的两个两.从本例可以看出:要求点到平面的距离,只要过该点找到与已知平面垂直的平面,则点面距即可根据面面垂直的性质作出.。
