数学作业4

合集下载

数学作业4

一、解方程
12.6（x+4.8）÷2=63 x÷2+x÷4=7.5 7.4x-5.6=10+5.4x
三、列式计算
1. 1.16与1.24的和被5个4.8的和除，商是多少
2.一个数除以6.3，再减去2.5的差等于6.5，求这个数
二、应用题
1.摩托车厂要装配1128台摩托车，甲乙两组同时装配，甲组每天装配69台，
乙组每天装配72台，多少天能完成装配任务？
2.在平行四边形ABCD中，AD比EC长6厘米，三角形ABE的面积是36
平方厘米，求AE的长度.
3.在一场羽毛球赛上，男球迷比女球迷的人数的3倍还多156元，且男球迷
的人数比女球迷多504人，男女球迷各有多少人？
4.儿童节当天，影院安排了两场儿童电影，放映时间一共是150分钟，第一
场电影放映的时间比第二场多30分钟，这两场电影放映的时间分别是多少分钟？
5.两辆汽车同时从AB两地相对开出，甲车行了165千米时与乙车相遇，这
时甲车距离两地中点还有15千米，已知乙车每小时行78千米，相遇时乙车行了多少小时？AB两地相距多少千米？。

数学作业练习4

爸爸买了596元钱的东西，给了售货员600元，可是售货员没有零钱找补，爸爸就又给了售货员6元，这时应找多少元钱？
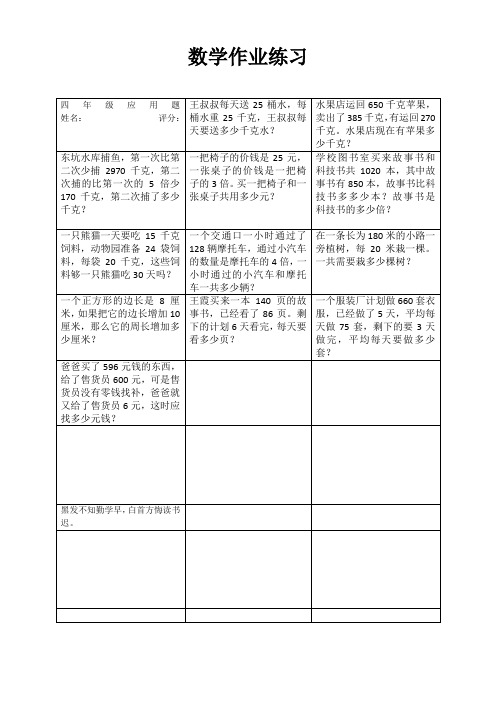
黑发不知勤学早，白首方悔读书迟。
学校图书室买来故事书和科技书共1020本，其中故事书有850本，故事书比科技书多多少本？故事书是科技书的多少倍？
一只熊猫一天要吃15千克饲料，动物园准备24袋饲料，每袋20千克，这些饲料够一只熊猫吃30天吗？
一个交通口一小时通过了128辆摩托车，通过小汽车的数量是摩托车的4倍，一小时通过的小汽车和摩托车一共多少辆？
在一条长为180米的小路一旁植树，每20米栽一棵。一共需要栽多少棵树？
一个正方形的边长是8厘米，如果把它的边长增加10厘米，那么它的周长增加多少厘米？
王霞买来一本140页的故事书，已经看了86页。剩下的计划6天看完，每天要看多少页？
一个服装厂计划做660套衣服，已经做了5天，平ቤተ መጻሕፍቲ ባይዱ每天做75套，剩下的要3天做完，平均每天要做多少套？
数学
四年级应用题姓名：评分：
王叔叔每天送25桶水，每桶水重25千克，王叔叔每天要送多少千克水？
水果店运回650千克苹果，卖出了385千克，有运回270千克。水果店现在有苹果多少千克？
东坑水库捕鱼，第一次比第二次少捕2970千克，第二次捕的比第一次的5倍少170千克，第二次捕了多少千克？
一把椅子的价钱是25元，一张桌子的价钱是一把椅子的3倍。买一把椅子和一张桌子共用多少元？

五年级数学暑假作业4

1 1 13 9 151 －——+ ——+ —5 7 14 8 161 1 1 13 + ——－——－0.1256 2 6 8二、脱式计算（能简算的要简算）。

1 1 1 9 1 1—+ —+ ——－—－—2 5 2 8 2 25 1 1 8 1 55 －—－—－——－—+ —6 3 6 9 6 4三、解方程。

1 5 3X + —＝——+ X ＝ 25 6 4四、解决问题。

打印同样一份稿件，甲打字员用了6/5小时完成，乙打字员用了0.4小时完成，哪位打字员的速度快些？3 1 7 1 131 －——+ ——+ —4 3 6 3 62 6 1 13 －——－——－0.1253 7 5 8二、脱式计算（能简算的要简算）。

1 4 6 5 1 1—+ —+ ——－—－—7 3 7 4 2 25 1 1 5 1 65 －—－—－——－—+ —6 4 6 6 5 7三、解方程。

1 7 3X －—＝——+ X ＝ 67 8 4四、解决问题。

一个长方体，如果高增加4cm，就变成了棱长是7cm的正方体。

表面积和体积各增加了多少？1 9 11 1 171 －——+ ——+ —4 8 16 8 161 2 1 98 －——+ ——－ 1.84 3 2 5二、脱式计算（能简算的要简算）。

1 2 12 6 7 1—+ —+ ——－—－—13 3 13 5 8 84 1 1 8 1 24 －—－—－——+ —+ —5 4 5 9 4 3三、解方程。

1 8 1X －—＝——+ X ＝ 36 7 7四、解决问题。

一个长方体玻璃容器，从里面量长为6分米，宽为3分米，高5分米。

向容器中倒入9升水，再把一个苹果放入水中，这时测得容器内的水面的高度是11厘米。

这个苹果的体积是多少？4 7 13 1 111 －——+ ——+ —5 6 12 6 123 1 1 13 + ——+ ——－0.1254 25 8二、脱式计算（能简算的要简算）。

1 6 11 10 4 1—+ —+ ——－—－—12 7 12 9 5 53 1 14 1 92 －—－—－——－—+ —4 2 45 3 8三、解方程。

小学二年级数学暑假作业4

10÷2＝10÷2＝7700－400＝5×9＝1×6＝7600－3000＝80＋70＝27＋6＝500＋100＝二、填空我能行。

填上合适的单位。

小强的体重是34（）两袋加碘盐重1100（）一袋方便面124（）一车煤重4000（）三、竖式计算。

59 ÷ 7 ＝42 ÷ 3 ＝________ ________7 )59 3 )42267 ＋ 247 ＝994 － 121 ＝267 994＋ 247 － 121————————四、脱式计算。

12÷6＋15 8×(8－4)五、解决问题。

面包师傅做了55个面包，小明买走了19个，小红买走了26个还可以买几个？32÷4＝27÷3＝9700－400＝3×9＝3×6＝9900－2400＝20＋30＝51＋8＝300＋900＝二、填空我能行。

一台电脑的价格是1997元，大约是（）元；一辆电动车的价格是2006元，比一台电脑大约便宜（）元。

三、竖式计算。

57 ÷ 7 ＝20 ÷ 4 ＝________ ________7 )57 4 )20176 ＋ 419 ＝917 － 183 ＝176 917＋ 419 － 183————————四、脱式计算。

60＋4×3 27＋8×7五、解决问题。

停车场有卡车35辆，有轿车23辆。

开走了12辆，现在有多少辆车？56÷7＝18÷3＝1100＋800＝9×3＝3×6＝7400－3400＝40＋100＝39＋6＝200＋400＝二、填空我能行。

把20平均分成4份，每份是（）。

三、竖式计算。

65 ÷ 9 ＝82 ÷ 5 ＝________ ________9 )65 5 )82126 ＋ 267 ＝733 － 204 ＝126 733＋ 267 － 204————————四、脱式计算。

四年级下册数学假期作业(4)

把每天的练习题目都写在大演草上（抄题）。

日期：时间：家长签字：1、竖式计算（带★的要验算）234×46 ★613×482、脱式计算，能简便的要简便125×25×32 600－9520÷28 3500÷ 25 ÷43.《故事大王》每本12元，《十万个为什么》每本25元，买8本《故事大王》和8本《十万个为什么》一共需要多少钱4．四二班有男生38人，女生26人。

每8人一组参加清理小广告的活动，一共可以分成多少组日期：时间：家长签字：1、竖式计算（带★的要验算）★ 240×38 7300÷902、脱式计算，能简便的要简便1880-(59+21)×12 (75+240)÷(20-5)33×13-993．李大爷带了250元买化肥，买了5袋化肥后还剩下25元。

每袋化肥的价钱是多少元4．一个修路队修一条公路，每天修 24米，修了15天后，还剩下130米。

这条公路长多少日期：时间：家长签字：1、竖式计算（带★的要验算）320×25 285÷152、脱式计算，能简便的要简便546×(210－195) (6130－5960)×40 (4361－716)÷813．张老是带了200元钱，想买2个排球和4根跳绳，每个排球48元，每根跳绳12元，还剩多少元4．一台电冰箱2400元，一台彩色电视3500元，一台洗衣机1650元。

买三种家电各一台，一共需要多少元日期：时间：家长签字：1、竖式计算（带★的要验算）★ 125×48 376÷842、脱式计算，能简便的要简便88×225＋225×12 36×19-19×26 75+360÷(20-5)3．春季同学们植树，四年级同学植树88棵，五年级同学植树96棵，六年级同学植树104棵，三个年级的学生一共植树多少棵4．小红上学期期末考试，语文、数学、自然、社会、英语的成绩分别是88分、96分、94分、90分、82分。

九年级上册数学作业本 (4)

九年级上册数学作业本1. 课程概述本文档是九年级上册数学作业本的概述和目录。

本学期数学课程将涵盖数论、代数、几何和概率等主题。

通过这些课程，学生将培养数学思维能力，提高解决问题的能力，以及应用数学知识解决实际问题的能力。

2. 目录单元一：数论•作业1：整数的性质•作业2：公因数和最大公约数•作业3：最小公倍数•作业4：整除性质与带余除法•作业5：素数与合数•作业6：整数的应用单元二：代数•作业7：代数式与函数•作业8：多项式•作业9：因式分解•作业10：分式•作业11：分式方程•作业12：代数方程与不等式•作业13：代数方程的应用单元三：几何•作业14：平面几何基础•作业15：相似与全等•作业16：三角形•作业17：圆的性质•作业18：立体几何单元四：概率•作业19：概率基本概念•作业20：事件的概率•作业21：概率计算•作业22：统计与概率注：每个单元共有4～5个作业，每个作业有若干小题。

3. 作业要求•作业本可以打印并用作电子表格填写。

•每个作业都有截止日期，请按时完成并提交作业。

•若有任何问题，请及时向老师请教。

4. 评分标准•每个题目将根据正确性、详尽性和解决问题的能力进行评分。

•作业将在提交后尽快批改和回馈。

•作业的总评分将根据每个单元作业的得分累计计算。

5. 作业提交方式•作业可以通过纸质版或者电子版提交。

•若选择电子版，请将作业以PDF文件形式发送给老师。

•若选择纸质版，请按时交给老师。

6. 注意事项•完成作业时，请务必认真思考每个问题并用清晰的方法解决。

•如果遇到困难，请主动寻求帮助，不要抄袭他人答案。

•目前无论选择在线提交还是纸质提交，都需要保留好自己的作业，以备后续学习和复习使用。

希望大家在这个学期里能够努力学习数学，提高自己的思维能力和解决问题的能力。

祝大家学业进步！。

高中数学必修二A版作业4

课时作业(四)1．若3x －2(x －a )＝0，则向量x 等于( ) A ．2a B ．－2a C ．25a D ．－25a答案 B解析由题知3x －2x ＋2a ＝0，∴x ＝－2a . 2．下列结论正确的是( )A ．若向量b 与a 共线，则存在唯一的实数λ使b ＝λaB ．若b ＝λa ，则a 与b 共线C ．若λa ＝0，则a ＝0D ．|λa |＝λ|a | 答案 B3．设e 是与向量AB →共线的单位向量，AB →＝3e ，又向量BC →＝－5e ，若AB →＝λAC →，则λ＝( ) A.23 B.32 C ．－32D ．－23答案 C解析 AC →＝AB →＋BC →＝3e －5e ＝－2e ，由AB →＝λAC →得3e ＝λ·(－2e )，∴λ＝－32.4．在四边形ABCD 中，AB →＝a ＋2b ，BC →＝－4a －b ，CD →＝－5a －3b ，其中a ，b 不共线，则四边形ABCD 为( ) A ．梯形 B ．平行四边形 C ．菱形 D ．矩形答案 A解析 AB →＝a ＋2b ，CD →＝－5a －3b ，因为a 与b 不共线，所以AB →与CD →不共线，所以AB 与CD 不平行．又AD →＝AB →＋BC →＋CD →＝－8a －2b ，显然AD →＝2BC →，所以AD ∥BC ，所以四边形ABCD 为梯形．故选A.5．已知向量a ，b 不共线，c ＝k a ＋b (k ∈R )，d ＝a －b ，如果c ∥d ，那么( ) A ．k ＝1且c 与d 同向 B ．k ＝1且d 与c 反向C ．k ＝－1且c 与d 同向D ．k ＝－1且d 与c 反向答案 D解析由c ∥d ，得c ＝λd ，∴k a ＋b ＝λ(a －b )，即⎩⎪⎨⎪⎧k ＝λ1＝－λ，∴⎩⎪⎨⎪⎧k ＝－1λ＝－1，即c ＝－a ＋b 且c ＝－d . 6．如图，在△ABC 中，D 是边BC 的中点，AG →＝2GD →，则用向量AB →，AC →表示BG →为( )A.BG →＝－23AB →＋13AC →B.BG →＝－13AB →＋23AC →C.BG →＝23AB →－13AC →D.BG →＝23AB →＋13AC →答案 A解析由题意可得BG →＝BA →＋AG →＝BA →＋23AD →＝BA →＋23×12(AB →＋AC →)＝BA →＋13AB →＋13AC →＝13AC→－23AB →.故选A. 7．已知O 是△ABC 所在平面内一点，D 为BC 边中点，且2OA →＋OB →＋OC →＝0，那么( ) A.AO →＝OD → B.AO →＝2OD → C.OA →＝3OD → D ．2AO →＝OD → 答案 A解析如图，延长OD 至E ，使|DE →|＝|OD →|，连接BE ，EC ，则四边形OBEC 为平行四边形，∴OB →＋OC →＝OE →＝2OD →，∴2OA →＋OB →＋OC →＝2OA →＋2OD →＝0. ∴OA →＋OD →＝0.∴OD →＝－OA →＝AO →.故选A.8．(a ＋9b －2c )＋(b ＋2c )＝________．答案 a ＋10b9．点C 在线段AB 上，且AC CB ＝32，则AC →＝________AB →，BC →＝________AB →.答案 35 －2510．已知△OBC 中，点A 是线段BC 的中点，点D 是线段OB 的一个三等分点(靠近点B )，设AB →＝a ，AO →＝b .(1)用向量a 与b 表示向量OC →；(2)若OE →＝35OA →，判断C ，D ，E 是否共线，并说明理由．解析 (1)∵AB →＝a ，AO →＝b ，点A 是BC 的中点， ∴AC →＝－a .∴OC →＝OA →＋AC →＝－a －b . (2)假设存在实数λ，使CE →＝λCD →. ∵CE →＝CO →＋OE →＝a ＋b ＋35(－b )＝a ＋25b ，CD →＝CB →＋BD →＝CB →＋13BO →＝CB →＋13(BA →＋AO →)＝2a ＋13(－a ＋b )＝53a ＋13b ，∴a ＋25b ＝λ⎝⎛⎭⎫53a ＋13b ， ∴⎩⎨⎧53λ＝113λ＝25，此方程组无解，∴不存在实数λ，满足CE →＝λCD →. ∴C ，D ，E 三点不共线．11．已知向量a ∥b ，且|a |>|b |>0，则向量a ＋b 的方向( ) A ．与向量a 方向相同 B ．与向量a 方向相反 C ．与向量b 方向相同 D ．与向量b 方向相反答案 A解析因为a ∥b 且|a |>|b |>0，所以当a ，b 同向时，a ＋b 的方向与a 相同，当a ，b 反向时，∵|a |>|b |，∴a ＋b 的方向仍与a 相同．12．【多选题】若点D ，E ，F 分别为△ABC 的边BC ，CA ，AB 的中点，且BC →＝a ，CA →＝b ，则下列结论正确的是( ) A.AD →＝－12a －bB.BE →＝a ＋12bC.CF →＝－12a ＋12bD.EF →＝12a答案 ABC解析在△ABC 中，AD →＝AC →＋CD →＝－CA →＋12CB →＝－b －12a ，故A 正确；BE →＝BC →＋CE →＝BC→＋12CA →＝a ＋12b ，故B 正确；AB →＝AC →＋CB →＝－b －a ，CF →＝CA →＋AF →＝CA →＋12AB →＝b ＋12(－b －a )＝－12a ＋12b ，故C 正确；EF →＝12CB →＝－12a ，故D 不正确．故选ABC.13．如图，圆O 是等边三角形ABC 的外接圆，点D 为劣弧AC 的中点，则OD →＝( )A.23BA →＋13AC →B.23BA →－13AC →C.13BA →＋23AC →D.43BA →＋23AC → 答案 A解析连接BO ，易知B ，O ，D 三点共线，设OD 与AC 的交点为E ，则OD →＝BO →＝23BE →＝23×12(BA →＋BC →)＝13(BA →＋BA →＋AC →)＝23BA →＋13AC →.故选A. 14.向量a ，b ，c 在正方形网格中的位置如图所示．若向量λa ＋b 与c 共线，则实数λ＝( )A ．－2B ．－1C ．1D ．2答案 D解析由题图易得2a ＋b ＝c .因为向量λa ＋b 与c 共线，所以λ＝2.故选D.15．在△ABC 中，已知D 是AB 边上一点，若AD →＝2DB →，CD →＝13CA →＋λCB →，则λ＝( )A.23B.13 C ．－13D ．－23答案 A解析 ∵CD →＝CA →＋AD →＝CA →＋2DB →＝CA →＋2(CB →－CD →)＝CA →＋2CB →－2CD →， ∴3CD →＝CA →＋2CB →. ∴CD →＝13CA →＋23CB →.∴λ＝23.故选A.设a 是任一向量，e 是单位向量，且a ∥e ，则下列表示形式中正确的是( ) A ．e ＝a|a |B ．a ＝|a |eC ．a ＝－|a |eD ．a ＝±|a |e 答案 D解析对于A ，当a ＝0时，a|a |没有意义，错误；对于B 、C 、D ，当a ＝0时，选项B 、C 、D 都对；当a ≠0时，由a ∥e 可知，a 与e 同向或反向．故选D.。

三年级数学暑假作业4

一、填空题。

（画图后解答）1、生产队养公鸡、母鸡共404只，其中公鸡是母鸡的3倍，公鸡养了——只，母鸡养了————只。

2、A、B两人同时从学校出发相背而行，2小时共行48千米，A的速度是B的2倍，A 的速度是每小时——千米，B的速度是每小时————千米。

3、甲乙两个冷藏库原来共存肉92吨，从甲库运出28吨后，乙库存肉比甲库的4倍少6吨，甲库原来存肉——吨，乙库原来存肉——吨。

4、甲乙两个粮仓共存粮2200千克，由乙仓运出210千克，甲仓存的粮食是乙仓的2倍少380千克，甲仓库原来存粮食——千克，乙仓库原来存粮食——千克。

5、姐姐有320元钱，弟弟有180元钱，弟弟给姐姐——钱后，姐姐的钱比弟弟的钱多3倍？6、甲、乙两个粮仓存粮320吨，后来从甲仓运出40吨，给乙仓运进20吨，这时甲仓存粮是乙仓的2倍，甲仓库原来存粮食——吨，乙仓库原来存粮食——吨。

7、学校买了4个足球和2个排球，共用去162元，每个足球比每个排球贵3元，每个足球————元，每个排球————元。

8、有两层书架，共有书173本。

从第一层拿走38本书后，第二层的书是第一层的2倍还多6本，则第二层有————本书。

9、甲、乙、丙三数之和是100，甲数除以乙数，丙数除以甲数，商都是5，余数都是1，乙数是——————。

10、小利的科技书比故事书少16本，故事书是科技书的3倍。

小利有科技书————本，故事书————本。

11、甲、乙两个数，如果甲数加上50，就等于乙数。

如果乙数加上350就等于甲数的3倍，问甲————，乙—————。

12、小明、小丽做题，如果小明再做4道就和小丽做的一样多。

如果小丽再做6道就是小明的3倍，小明做———道题，小丽做——道题。

13、小丽和小荣集邮，小丽邮票的张数是小荣的5倍。

如果小丽把自已的邮票给小荣100张，她俩邮票的数正好相等。

小丽和小荣各有————张、————张。

14、两筐桃的个数相等，如果第一筐卖出150个，第二筐卖出194个，那么剩下的桃第一筐是第二筐的3倍，第一筐——个，第二筐——个。

人教版八年级数学寒假作业-作业四

人教版八年级数学寒假作业-作业四学校:___________姓名：___________班级：___________考号：___________一、填空题1．各条边都相等的多边形是正多边形．（____） 2．n 边形内角和等于2180()n ⨯︒－ .（____） 3．n 边形的外角和等于360︒ .（____） 4．n 边形共有(3)2n n - 条对角线．（____） 5．一个多边形增加一条边，内角和就增加180°.（____）6．已知一个多边形的每一个外角都相等，一个内角与一个外角的度数之比为7:2，则这个多边形的边数为_________.7．如图，平面上两个正方形与正五边形都有一条公共边，则∠α等于 °.8．活动课上，小华从点O 出发，每前进1米，就向右转体a°(0＜a ＜180)，照这样走下去，如果他恰好能回到O 点，且所走过的路程最短，则a 的值等于_ ．9．一个多边形从一个顶点出发可引3条对角线，这个多边形的内角和等于________．二、单选题10．随着多边形的边数n 的增加，它的外角和( ) A ．增加 B ．减小 C ．不变D ．不定11．一个多边形的内角和比它的外角和的2倍还大180°，这个多边形的边数是（） A ．5B ．6C ．7D ．812．已知多边形内角和与外角和的总和为2160︒ ，则这个多边形的对角线共有( ) A ．54条 B ．65条 C ．60条D ．55条13．如果一个多边形的每个内角都等于144︒ ，那么它的内角和为( ) A ．1260︒ B ．1440︒ C ．1620︒D ．1800︒14．从一个多边形的一个顶点出发，可引12条对角线，则这个多边形的边数为( )A ．12B ．13C ．14D ．1515．四边形ABCD 中，∠A +∠C=∠B +∠D ，∠A 的外角为120°，则∠C 的度数为（） A ．36° B ．60°C ．90°D ．120°三、解答题16．已知：如图，AB ∥CD ，求图形中的x 的值．17．如图所示，90A C ∠∠︒＝＝，直线BE DF ，分别平分ABC ∠ 和ADC BE ∠，和DF 平行吗？说明你的理由．18．如图，清晨小明沿着一个五边形广场周围的小路，按逆时针方向跑步．(1)小明每从一条街道转下一条街道时，身体转过的角是哪个角，在图上标出； (2)他每跑一圈，身体转过的角度之和是多少？ (3)你是怎么得到的？(4)如果广场是六边形、八边形的形状，那么还有类似的结论吗？参考答案1．×【解析】【分析】根据正多边形的判定定理即可解答.【详解】例如菱形，各边相等但不是正多边形，平面内各边相等，各角也相等的多边形叫做正多边形.故答案为：×【点睛】此题考查正多边形的判定，解题关键在于掌握判定定理.2．√【分析】从四边形的一个顶点出发可以画1条对角线，把四边形分成两个三角形，所以四边形内角和为：（4-2）×180°，从五边形的一个顶点出发可以画2条对角线，把五边形分成三个三角形，所以四边形内角和为：（5-2）×180°，从n边形的一个顶点出发可以画（n-3）条对角线，把四边形分成（n-2）个三角形，所以n边形内角和为：（n-2）×180°．【详解】因为三角形的内角和是180°，四边形的内角和是360°，五边形的内角和是540°，∴n边形的内角的和公式：（n-2）×180°.故答案为：√.【点睛】此题考查多边形，多边形内角与外角，解题关键在于掌握运算公式.3．√【分析】本题比较简单，需要识记“任意多边形的外角和等于360°”，直接解答．【详解】由已学定理可知：任意多边形的外角和等于360°，故答案为：√．【点睛】此题考查多边形内角（和）与外角（和），解题关键在于掌握其性质定义.4．√【分析】正多边形的定义：各边相等，各角也相等的多边形叫做正多边形.熟悉多边形中对角线条数的计算公式：n边形过一个顶点有(n−3)条对角线，共有(3)2n n-条对角线(n≥3，且n为整数).即可解答. 【详解】n边形共有(3)2n n-条对角线，故答案为：√.【点睛】此题考查对角线，解题关键在于掌握运算公式.5．√【分析】利用n边形的内角和公式（n-2）•180°（n≥3）且n为整数），多边形外角和为360°即可解决问题．【详解】根据n边形的内角和可以表示成（n-2）•180°，可以得到增加一条边时，边数变为n+1，则内角和是（n-1）•180°，因而内角和增加：（n-1）•180°-（n-2）•180°=180°．故答案为：√.【点睛】此题考查多边形的内角和公式和外角和，解题关键在于熟练掌握运算公式．6．9【解析】试题分析：设多边形的一个内角为7x度，则一个外角为2x度，先根据多边形的内角和外角的关系，求出一个外角．再根据外角和是固定的360°，从而可代入公式求解．设多边形的一个内角为7x度，则一个外角为2x度，依题意得7x+2x=180解得x=20，2x=40，则则这个多边形的边数为考点：本题考查的是多边形的内角与外角关系，多边形的外角和点评：解答本题的关键是熟练掌握多边形的一个内角与外角互补，任意多边形的外角和均是360度，与边数无关．7．72【分析】先分别求出正五边形的一个内角为108°，正方形的每个内角是90°，再根据圆周角是360度求解即可．【详解】正五边形的一个内角为108°，正方形的每个内角是90°，所以∠α=360°-108°-90°-90°=72°，故答案为72.【点睛】本题考查了多边形的内角和，熟练掌握多边形内角和公式：（n-2）•180°是解题的关键. 8．120【解析】解：根据题意，小华所走过的路线是正多边形，∴边数，走过的路程最短，则n最小，a最大，n最小是3，a°最大是120°．9．720【分析】首先确定出多边形的边数，然后利用多边形的内角和公式计算即可．【详解】∵从一个顶点可引对角线3条，∴多边形的边数为3+3=6.多边形的内角和=(n−2)×180°=4×180°=720°故答案为：720°.【点睛】此题考查多边形内角（和）与外角（和），多边形的对角线，解题关键在于掌握计算公式.【分析】所有多边形的外角和是360度，这个数值与边数的大小无关．【详解】若一个多边形的边数增加,它的外角和是360°，保持不变.故选：C.【点睛】此题考查多边形内角与外角，解题关键在于掌握其性质定义.11．C【解析】解：设这个多边形的边数是n，根据题意得，（n-2）•180°=2×360°+180°，n=7．故选C．点睛：本题考查了多边形的内角和与外角，熟记多边形的内角和公式与外角和定理是解题的关键，需要注意，任何多边形的外角和都是360°，与边数无关．12．A【分析】已知一个多边形的内角和与外角和的差为2160°，外角和是360度，因而内角和是1800度．n 边形的内角和是（n-2）•180°，代入就得到一个关于n的方程，就可以解得边数n，从而得到这个多边形的对角线的条数．【详解】设这是n边形，则（n-2）×180°=2160°-360°，n-2=10，n=12．这个多边形的对角线的条数=12×（12-3）÷2=54．故选A.【点睛】此题考查多边形内角（和）与外角（和），解题关键在于掌握计算公式.13．B【分析】多边形的每一个内角都等于144°，则每个外角是180-144=36度．外角和是360度，则可以求得这个多边形的边数，再根据边数即可求得内角和．这个多边形的边数是360°÷(180°−144°)=360°÷36°=10，则内角和是(10−2)×180°=1440°；故选B.【点睛】此题考查多边形内角与外角，解题关键在于掌握计算公式.14．D【分析】n边形有n个顶点，从其中的一个顶点出发，除了自身以及相邻的两个顶点，与其余顶点连线是这个多边形的对角线.即从一个顶点可引出(n-3)条对角线，这些对角线将多边形分成(n-2)个三角形.【详解】由题意提n-3=12，解得n=15.故选：D.【点睛】此题考查多边形的对角线，解题关键在于掌握计算公式.15．D【解析】【分析】根据四边形的内角和是360度，以及∠A+∠C=∠B+∠D就可求得：∠A+∠C=180°，根据∠A 的外角为120°就可求得∠A的度数，即可求得∠C的度数．【详解】∠A=180°﹣120°=60°，∵四边形ABCD中，∠A+∠C+∠B+∠D=360°，且∠A+∠C=∠B+∠D，∴∠A+∠C=180°，∴∠C=180﹣60=120°，故选D．【点睛】本题考查了四边形的内角和定理，以及多边形的内角与相邻的外角的关系，熟练掌握相关知识是解题的关键.【分析】先根据平行线的性质求得∠B的度数，再利用多边形的内角和定理进行求解即可.【详解】∵AB∥CD，∠C=60°，∴∠B=180°-60°=120°，∴（5-2）×180°=x+150°+125°+60°+120°，∴x=85°．BE DF，理由见解析17．//【分析】由四边形的内角和为360度求出∠ADC+∠ABC度数，由DF、BE分别为角平分线，利用角平分线定义及等量代换得到∠ABE+∠FDC为90度，再由直角三角形ADF两锐角互余及∠ADF=∠FDC，利用等量代换得到一对同位角相等，利用同位角相等两直线平行即可得出BE与DF平行．【详解】BE∥DF，理由如下：四边形ABCD中,∠A=∠C=90°，∴∠ADC+∠ABC=180°，∵BE平分∠ABC交CD于E，DF平分∠ADC交AB于F，∴∠ADF=∠FDC，∠ABE=∠CBE，∴∠ABE+∠FDC=90°，∵∠AFD+∠ADF=90°，∠ADF=∠FDC，∴∠AFD=∠ABE，∴BE∥DF.【点睛】此题考查平行线的判定，多边形内角与外角，解题关键在于掌握平行线的判定定理. 18．(1) ∠1，∠2，∠3，∠4，∠5；(2)360︒；(3)因为五边形外角和为360︒；(4)有【分析】（1）由已知条件，小强按逆时针方向跑步，可得出小强转过的角度；要求他跑完一圈身体转过的度数，就是五边形外角和的度数，根据多边形外角和计算公式即可得出（2）的答案；由“多边形的外角和为360°”，可得到（3）的答案，同理，六边形、八边形的形状，同样有类似的结论得到（4）的答案，据此即可完成解答.【详解】(1)∠1，∠2，∠3，∠4，∠5；(2)∵各角是五边形的外角，∴身体转过的角度之和是360°；(3)∠1+∠2+∠3+∠4+∠5=360°，因为各角是五边形的外角；(4)有，多边形外角和为360度.【点睛】此题考查多边形内角与外角，解题关键在于掌握其定义.。

预初(上)数学周末作业四

预初（上）数学周末作业四班级___________姓名___________学号___________成绩___________ 一、填空题：（每空2分，共36分）1、按从小到大顺序排列的第12个素数为___________；2、两个两位数，它们的最大的公约数是8，最小公倍数是96，这两个数的和是___________；3、一堆沙土重1516吨，用去了全部的23，则用去了_______吨，还剩总数的_______；（几分之几）4、4米长的绳子，先截下14米，则还剩___________米； 5、()37()16219105-==-；6、在分数1325，4210，15354，747，93155中，最简分数有___________； 7、约成最简分数：185481=___________；8、一个分数是分子与分母之和为96，化成最简分数为35，这个分数为___________；9、比较大小：28162619________63361912⋅；10、11519化为假分数为___________，14611化为带分数为___________；11、一袋大米重25千克，先吃去这袋大米的15，又吃去这袋大米的15千克，两次一共吃去___________千克；12、工厂食堂第一季度用煤13吨，第二季度比第一季度少用了124吨；第三季度比第二季度多用了315吨，则第二季度用煤___________吨；13、六年级的男生人数是女生人数的115倍，那么男生人数占全年级人数的___________； 14、右图是一堆圆片，如果将其中的34涂成红色，那就需要涂红___________个圆片；如果拿走4个圆片，将剩下圆片的34涂成红色，那就需要涂红___________个圆片.二、选择题：（每题3分，共15分） 1、下列说法中，正确的个数有（）①正整数可能分为素数，合数与1 ②两个素数的乘积一定是合数 ③互素的两个数没有公因数 ④除2外，所有的素数都是奇数 A 、1个 B 、2个 C 、3个 D 、4个 2、下列结论错误的个数是（）（1）如果a 和b 的最小公倍数是ab ，那么a 和b 是素数（2）一个正整数的倍数一定比这个数的任何因数都大（3）一个正整数的因数至少有两个（4）边长是正整数的正方形的周长一定是合数 A 、1个 B 、2个 C 、3个 D 、4个 3、如果分数2xy的分子加上4x ，为了保持分数的大小不变，分母应（） A 、加上4x B 、加上4yC 、加上5yD 、加上8yA 、223B 、233C 、123D 、1334、下列说法中，有多少个是正确的？（） ①最简分数必须是真分数。

七年级数学寒假作业4

寒假作业4学校:___________姓名：___________班级：___________考号：___________一、单选题1．有理数a 、b 、c 满足a+b+c ＞0，且abc ＜0，则a 、b 、c 中正数有（）个．A ．0B ．1C ．2D ．32．A ，B ，C 三点在同一直线上，线段AB ＝5cm ，BC ＝4cm ，那么A ，C 两点的距离是（）A ．1cmB ．9cmC ．1cm 或9cmD ．以上答案都不对3．下列说法：（1）两点之间线段最短；（2）两点确定一条直线；（3）同一个锐角的补角一定比它的余角大90°；（4）A 、B 两点间的距离是指A 、B 两点间的线段；其中正确的有（）A ．一个B ．两个C ．三个D ．四个 4．下列方程为一元一次方程的是（）A ．30y +=B ．23x y +=C ．112+=D ．12y y+= 5．某商人在一次买卖中均以120元卖出两件衣服，一件赚25%，一件赔25%，在这次交易中，该商人（）A ．赚16元B ．赔16元C ．不赚不赔D ．无法确定二、填空题6．如图，OE 平分AOC ∠，OF 平分BOC ∠，124EOF ︒∠=，则AOB ∠的度数为________．7．如果x =2是关于x 的方程x –a =3的解，则a =__________．8．方程2(52)314a x x -++=是一元一次方程，则=a ________．三、解答题9．公园门票价格规定如下表：某校初一（1）、（2）两个班共104人去游公园，其中（1）班人数较少，不足50人．经估算，若两个班都以班为单位购票，则一共应付1240元，问：(1)两班各有多少学生？(2)如果两班联合起来，作为一个团体购票，可省多少钱？(3)如果初一（1）班单独组织去游公园，作为组织者的你将如何购票才最省钱？10．如图，C 为线段AD 上一点，点B 为CD 的中点，且9cm,2cm AD BD ==．(1)图中共有条线段．(2)求AC 的长．(3)若点E 在直线AD 上，且3cm EA =，求BE 的长．11．探究：有一长6cm ，宽4cm 的矩形纸板，现要求以其一组对边中点所在直线为轴，旋转180°，得到一个圆柱，现可按照两种方案进行操作：方案一：以较长的一组对边中点所在直线为轴旋转，如图①；方案二：以较短的一组对边中点所在直线为轴旋转，如图①．(1)请通过计算说明哪种方法构造的圆柱体积大；(2)若将此长方形绕着它的其中一条边所在的直线为轴旋转360°，则得到的圆柱体积为多少？参考答案：1．C【分析】利用有理数的加法，乘法法则判断即可．【详解】∵有理数a、b、c满足a+b+c＞0，且abc＜0，①a，b，c中负数有1个，正数有2个．故选C．【点睛】本题考查了有理数的乘法，加法，以及正数与负数，熟练掌握运算法则是解答本题的关键．2．C【分析】由已知条件知A，B，C三点在同一直线上，做本题时应考虑到A、B、C三点之间的位置，分情况可以求出A，C两点的距离．【详解】第一种情况：C点在线段AB上时，故AC=AB－BC=1cm；第二种情况：当C点在线段AB的延长线上时，AC=AB+BC=9cm，故选C．【点睛】本题考查两点间的距离，渗透了分类讨论的思想，体现了思维的严密性，在今后解决类似的问题时，要防止漏解．3．C【分析】（1）根据线段的性质即可求解；（2）根据直线的性质即可求解；（3）余角和补角一定指的是两个角之间的关系，同角的补角比余角大90°；（4）根据两点间的距离的定义即可求解．【详解】（1）两点之间线段最短是正确的；（2）两点确定一条直线是正确的；（3）同一个锐角的补角一定比它的余角大90°是正确的；（4）A、B两点间的距离是指A、B两点间的线段的长度，原来的说法是错误的．故选C．【点睛】本题考查了补角和余角、线段、直线和两点间的距离的定义及性质，是基础知识要熟练掌握．4．A【分析】只含有一个未知数（元），并且未知数的指数是1（次）的整式方程叫做一元一次方程，它的一般形式是ax ＋b ＝0（a ，b 是常数且a≠0），据此判断即可．【详解】解：A 、是一元一次方程，正确；B 、含有2个未知数，不是一元一次方程，错误；C 、不含有未知数，不是一元一次方程，错误；D 、不是整式方程，故不是一元一次方程，错误．故选：A ．【点睛】本题主要考查了一元一次方程的定义，只含有一个未知数，且未知数的指数是1，一次项系数不是0，这是这类题目考查的重点．5．B【分析】要知道赔赚，就要算出两件衣服的进价，再用两件衣服的进价和两件衣服的售价作比较，即可得出答案．【详解】解：设此商人赚钱的那件衣服的进价为x 元，则(125%)120x ，得96x =；设此商人赔钱的那件衣服进价为y 元，则(125%)120y ，解得160y =；所以他一件衣服赚了24元，一件衣服赔了40元，所以卖这两件衣服总共赔了4024=16（元）．故选B ．【点睛】本题考查了一元一次方程的应用，正确理解题意，计算出两件物品的原价是解题的关键．6．112︒【分析】根据角平分线的性质计算出2AOC COE ∠=∠，2BOC COF ∠=∠，再根据角的关系，即可求解．【详解】①OE 平分AOC ∠，OF 平分BOC ∠，①2AOC COE ∠=∠，2BOC COF ∠=∠，①2()2248AOC BOC COE COF EOF ︒∠+∠=∠+∠=∠=，①360248112AOB ︒︒︒∠=-=．【点睛】本题考查了角的平分线定义及性质，熟练掌握角平分线的意义是解本题的关键．7．-1【分析】把2x =代入方程计算即可求出a 的值.【详解】把2x =代入方程得：23a -=，解得：1a =-，故答案为：1-.【点睛】此题考查了一元一次方程的解，方程的解即为能使方程左右两边相等的未知数的值.8．25【分析】根据一元一次方程的定义得出520a -=，求出即可．【详解】由题意，得520a -=．所以25a =．故答案为：25．【点睛】本题考查了一元一次方程的定义，能熟记一元一次方程的定义的内容是解此题的关键．9．(1)初一（1）班有48人，则初一（2）班有56人(2)304元(3)48人买51张票可以更省钱【分析】（1）若设初（1）班有x 人，则初一（2）班有（104-x ）人，根据初一（2）班的人数是否超过100张，分类讨论并根据总价钱即可列方程；（2）由题意可得购买104张票只有9元一张，列式计算即可得到答案；（3）应尽量设计的能够享受优惠，购买51张票时只有11元一张，计算即可得出答案．【详解】（1）解：设初一（1）班有x 人，则初一（2）班有（104-x ）人，根据题意得，()131********x x +-=或()1391041240x x +-=，解得：x 48=或x 76=（不合题意，舍去）所以初一（1）班有48人，则初一（2）班有56人；（2）可省钱：12401049304-⨯=（元），所以可省304元钱；（3）要想享受优惠，由（1）可知初一（1）班有48人，4813624⨯=元，但若多买3张票，需要花费5111561⨯=元，①561624＜，①48人买51张票可以更省钱．【点睛】本题考查的是最优化设计问题，一元一次方程的应用，掌握利用一元一次方程解决分段费用问题是本题的关键．10．(1)图中共有6条线段(2)5cm AC =(3)线段BE 的长为10cm 或4cm【分析】（1）固定A 为端点，数线段，依次类推，最后求和即可；（2）根据2AC AD CD AC BC =-=-，计算即可；（3）分点E 在点A 左边和右边两种情形求解．【详解】（1）以A 为端点的线段为：,,AC AB AD ；以C 为端点的线段为：,CB CD ；以B 为端点的线段为：BD ；共有3216++=（条）；故答案为：6．（2）①点B 为CD 的中点．①2CD BD =．①2cm BD =，①4cm CD =．①9cm,4cm AD CD ==，①5cm AC AD CD =-=；（3）①点B 为CD 的中点， 2cm BD =，①2cm BC BD ==，①5cm AC =，①7cm AB AC BC =+=，当E 在点A 的左边时，则BE BA EA =+且7cm,3cm BA EA ==，①10cm BE =．当E 在点A 的右边时，则BE AB EA =-，且7cm,3cm AB EA ==，①4cm BE =．①线段BE 的长为10cm 或4cm【点睛】本题考查了数线段，线段的中点，线段的和（差），熟练掌握线段的中点，灵活运用线段的和，差是解题的关键．11．(1)按方案一方法构造的圆柱体积大；(2)将此长方形绕着它的其中一条边所在的直线为轴旋转360°，则得到的圆柱体积为为144 cm 3或96 cm 3【分析】（1）分别按方案一，方案二转法，根据体积公式找出半径与高，代入计算即可；（2）分两种情况，按长方形长边所在的直线为轴旋转360°，绕长方形的短边所在的直线为轴旋转360°，确定半径与高代入体积公式计算即可．【详解】（1）解：方案一：以较长的一组对边中点所在直线为轴旋转，旋转半径为r =3cm ，体积为：223436r h πππ=⨯⨯=cm 3，方案二：以较短的一组对边中点所在直线为轴旋转，旋转半径为r =2cm ，体积为：222624r h πππ=⨯⨯=cm 3，按方案一方法构造的圆柱体积大；（2）解：分两种情况绕长方形的短边所在的直线为轴旋转360°，得到的圆柱体积为2264144r h πππ=⨯⨯=cm 3; 绕长方形绕长边所在的直线为轴旋转360°，则得到的圆柱体积为224696r h πππ=⨯⨯=cm 3，综合将此长方形绕着它的其中一条边所在的直线为轴旋转360°，则得到的圆柱体积为为144 cm 3或96 cm 3．【点睛】本题考查基本图形旋转得到的体积问题，掌握解决旋转半径与圆柱体的高是解题关键．。

八下数学作业4

一元二次方程的应用——篱笆问题1、用一条长为40cm的绳子围成一个面积为acm2的长方形，a的值不可能为（）A．20B．40C．100D．1202、如图所示，在一边靠墙（墙足够长）空地上，修建一个面积为672m2的长方形临时仓库，仓库一边靠墙，另三边用总长为76m的栅栏围成，若设栅栏AB的长为xm，则下列各方程中，符合题意的是（）A．x（76﹣x）＝672B．x（76﹣2x）＝672C．x（76﹣2x）＝672D．x（76﹣x）＝6723、如图，空地上（空地足够大）有一段长为20m的旧墙MN，小敏利用旧墙和木栏围成一个长方形菜园ABCD，已知木栏总长100m，长方形菜园ABCD的面积为900m2．若设AD＝X m，则可列方程（）A．（50﹣）x＝900B．（60﹣x）x＝900C．（50﹣x）x＝900D．（40﹣x）x＝9004、某兴趣小组想借助如图所示的直角墙角DA和DC（两边足够长），再用28m长的篱笆围成一个面积为192m2长方形花园ABCD（篱笆只围AB、BC两边），在P处有一棵树与墙CD、AD的距离分别是15m和6m，现要将这棵树也围在花园内（含边界，不考虑树的粗细），则AB的长为（）A．8或24B．16C．12D．16或125、用10米长的铝材制成一个长方形窗框，使它的面积为6平方米．若设它的一条边长为x米，则根据题意可列出关于x的方程为．6、如图，EF是一面长18米的墙，用总长为32米的木栅栏（图中的虚线）围一个矩形场地ABCD，中间用栅栏隔成同样三块．若要围成的矩形面积为60平方米，试求AB，BC的长。

（1）若设BC为x米，则AB=米，可列方程为．（2）若设AB为y米，则BC=米，可列方程为．（3）通过以上方法，可求得AB=米,BC=米.7、如图，有一块长方形的土地，宽为120m，建筑商把它分成甲、乙、丙三部分，甲和乙均为正方形，现计划甲建住宅区，乙建商场，丙地开辟成面积为3200m2的公园．若设这块长方形的土地长为X m．那么根据题意列出的方程是．（将答案写成ax2+bx+c＝0（a≠0）的形式）8、如图，某农场要建一个长方形的养鸡场，鸡场的一边靠墙，墙长25m，另外三边用木栏围着，木栏长40m．（1）若养鸡场面积为200m2，求鸡场平行于墙的一边长．（2）养鸡场面积能达到250m2吗？如果能，请给出设计方案，如果不能，请说明理由．9、如图，一农户要建一个矩形猪舍，猪舍的一边利用长为12m的住房墙，另外三边用25m长的建筑材料围成，为方便进出，在垂直于住房墙的一边留一个1m 宽的门，所围矩形猪舍的长、宽分别为多少时，猪舍面积为80m2？10、如图，有长为22米的篱笆，一面利用墙（墙的最大可用长度为14米），围成中间隔有一道篱笆的长方形花圃，为了方便出入，在建造篱笆花圃时，在BC 上用其他材料造了宽为1米的两个小门．（1）设花圃的宽AB为x米，请你用含x的代数式表示BC的长米；（2）若此时花圃的面积刚好为45m2，求此时花圃的宽．11、为了节省材料，某水产养殖户利用水库的岸堤（岸堤足够长）为一边，用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域，而且这三块矩形区域的面积相等．设BC的长度为xm，矩形区域ABCD的面积为ym2．（1）求AE的长（用x的代数式表示）；（2）当y＝108m2时，求x的值．。

九年级数学寒假作业(4)

九年级数学寒假作业（4）1、如图，AB 是⊙O 的直径，C ，D 为圆上两点∠AOC =130°，则∠D 等于（）A ．25°B ．30°C ．35°D ．50°2、图中圆与圆之间不同的位置关系有（）A ．2种 B ．3种 C ．4种 D ．5种3、一个钢管放在V 形架内，右图是其截面图，O 为钢管的圆心．如果钢管的半径为25 cm ∠MPN = 60︒，则OP =( )A ．50 cm B ．253cm C ．3350cm D ．503cm4、如图，圆锥的底面半径为3cm ，母线长为5cm ，则它的侧面积为（）A. 60πcm 2B. 45πcm 2C. 30πcm 2 D15πcm 25、如图，在Rt ABC △中，C ∠=90°，AB =10，若以点C 为圆心，CB 长为半径的圆恰好经过AB 的中点D ，则AC 的长等于（）A．B ．5 C． D ．66、如图，两同心圆的圆心为O ，大圆的弦AB 切小圆于P ，两圆的半径分别为6，3，则图中阴影部分的面积是（）A．π B．π C．3πD．2π7、.以正方形ABCD 的BC 边为直径作半圆O ，过点D 作直线切半圆于点F ，交AB 边于点E ，则三角形ADE 和直角梯形EBCD 周长之比为（）A .34∶B . 45∶C . 56∶D .67∶8、庆祝祖国六十华诞，某单位排练的节目需用到如图所示的扇形布扇，布扇完全打开后，外侧两竹条AB 、AC 夹角为120°，AB 的长为30cm ，贴布部分BD 的长为20cm ，则贴布部分的面积约为____________2cm ．（π取3）9、如图，AB 是⊙O 的直径，AE 平分∠BAF ，交⊙O 于点E ，过点E 作直线E D ⊥AF ，交AF 的延长线于点D ，交AB 的延长线于点C ．（1）求证：CD 是⊙O 的切线；（2）若CB=2，CE=4，求AE 的长E10、如图，AB是⊙O的直径，AD是弦，∠DAB=22.5°，延长AB到点C，使得∠ACD=45°．（1）求证：CD是⊙O的切线；（2）若AB BC的长．11、如图，在平面直角坐标系中，点O1的坐标为（-4，0），以点O1为圆心，8为半径的圆与x轴交于A，B两点，过A作直线l与x轴负方向相交成60°的角，且交y轴于C点，以点O2（13，5）为圆心的圆与x轴相切于点D．（1）求直线l的解析式；（2）将⊙O2以每秒1个单位的速度沿x轴向左平移，当⊙O2第一次与⊙O1外切时，求⊙O2平移的时间．。

一年级数学暑假作业四

一、填一填。

(每空1分，共14分)1．长方形有( )条边，( )边相等，正方形的( )条边都相等。

2．把长方形、正方形上下对折，就把它们分成了( )两部分。

3．至少用( )个同样的正方形能拼成一个长方形，至少用( )个同样的正方形能拼成一个大正方形。

4．两个一样的可以拼成一个( )，也可以拼成一个( )，还可以拼成一个( )。

5．至少用( )根同样的小棒能摆一个正方形，至少用( )根同样的小棒能摆一个长方形。

6．七巧板是由( )个图形组成，其中有( )个正方形，( )个三角形。

二、认一认，连一连。

(8分)三、选一选。

(把正确答案的序号填在括号里)(每题2分，共10分)1．下面的图形中，( )是长方形。

①②③2．每个面都是长方形的是( )。

①②③3．用下面物体( )可以画圆。

①②③4．右面的图形沿虚线剪开得到( )。

① 4个三角形② 4个长方形③ 4个正方形5．左边的图形和右边的图形( )能拼成一个长方形。

四、找规律，接着画。

(每题3分，共9分)1．______ ______ ______2．______ ______ ______3．______ ______ ______五、涂一涂。

(8分)六、数一数，填一填。

(8分)七、画一画，分一分。

(每题3分，共12分) 1．分成两个大小相同的长方形。

2．分成两个大小相同的正方形。

3．分成四个大小相同的三角形。

4．分成三个三角形。

八、从右边的图形中圈出两个能拼成左边的图形。

(每题4分，共8分)1．2．九、在点子图上画一个长方形、一个正方形和一个三角形。

(9分)△有（）个， □有（）个， ○有（）个，▭有（）个。

十、下面的墙上各缺几块？(6分)缺了( )块。

缺了( )块。

十一、用下面的小棒摆一摆。

(填序号)(每题4分，共8分) 1．用其中的4根摆一个正方形，可以选( )。

2．用其中的4根摆一个长方形，可以选( )。

一、填空题。

1. 按要求把算式填在相应的圈里。