习题 4

合集下载

《随机过程及其在金融领域中的应用》习题四答案

3
e 2
解法二：
平均每小时有30人到达
= 30 =0.5人/分钟
60
根据齐次 Poisson 过程的到达时间间隔Xn, n 1, 2, 是独立同分布于均值
为 1 的指数分布的，故可有：
相继到达的顾客的时间间隔大于 2 分钟的概率为： P Xn 2 et e1
PNt n
n

k

PNs

k PNts PNt n
nk
sk es
k!
t snk n k!

t n et
ets
s k nk t s nk
tk tnk
n!
k !n k !

不妨设 t s 则
E
M 2 T
1 T2
T 0
T 0
E

Nt
Ns
dsdt

1 T2
T 0
T 0
t 2ts dsdt
1
T2
T 0

Tt

1 2

2T
2t

dt

T 2

2T 2 4
Var M T E M 2 T E M T 2 T 2
0!
1!
2!
e2 2e2 2e2 5e2
P N1 1, N2 3 P N1 1, N21 3 1 P N1 1 P N1 2 2e2 2e2 4e4
P
N1

2
N1
1

P
N1 2, N1
P N0,s1 0, Ns1,s1h 1, Ns1h,s2 0, Ns2 ,s2 h 1, Ns2 h,s3 0, Ns3 ,s3 h 1

临床医学练习4

临床医学病原生物学阶段练习题4姓名学号人体寄生虫学绪论一、名词解释中间宿主终宿主转续宿主保虫宿主寄生虫的生活史伴随免疫二、填空题1. 寄生虫感染人体的途径包括、、、、、。

2. 寄生虫对人体造成的三大危害是、、。

三、选择题一、A1型题1. 寄生是指两种生物生活在一起的利害关系是（）A．一方受益，另一方无害 B．一方受益，另一方受害C．双方都有利 D．双方都无利 E．双方无利也无害2. 感染期是指寄生虫生活史中：（）A．对人具有感染性的阶段 B．对动物具有感染性的阶段C．感染人体的日期D．发育到具有感染性的日期 E.对人具有致病性的时期3. 中间宿主是指（）A．寄生虫的成虫或无性生殖阶段寄生的宿主B．寄生虫的幼虫或无性生殖阶段寄生的宿主C．寄生虫成虫或有性生殖阶段寄生的宿主D．寄生虫的幼虫或有性生殖阶段寄生的宿主E．寄生虫的成虫寄生的宿主4. 有些寄生虫的成虫除能寄生于人体外，还可寄生于某些脊椎动物体内，这些动物可成为人体寄生虫病传播的来源，故称这些动物为（）A．终宿主 B．中间宿主 C．保虫宿主D．转续宿主E. 传播媒介5．某些寄生虫的感染期，被非正常宿主吞食后，孵出的幼虫虽可在这种非正常宿主体内长期生活，但不能发育为成虫，这种非正常宿主称为：( )A．终宿主 B．中间宿主 C．保虫宿主 D．转续宿主 E．贮存宿主6. 寄生虫的生活史是指（）A．寄生虫的繁殖方式 B．寄生虫的取食来源C．寄生虫生长、发育、繁殖的全过程D．寄生虫宿主的种类E．寄生虫寄生于宿主的部位7．人体寄生虫包括三大类（）A．线虫、吸虫、绦虫B．线虫、原虫、绦虫C．蠕虫、原虫、医学节肢动物D．原虫、线虫、医学节肢动物E．蠕虫、吸虫、医学节肢动物8．寄生虫病的传染源应包括（）A．病人B．病人和保虫宿主C．带虫者和保虫宿主D．病人和带虫 E．病人、带虫者、保虫宿主9．在宿主体内，寄生虫使宿主产生获得性免疫力，这种免疫力对成虫不发生影响，但可作用于入侵的早期童虫，这种免疫力称为：( )A．带虫免疫 B．伴随免疫 C．保护性免疫D．消除性免疫 E．缺乏有效的获得性免疫10．有些寄生虫感染后，引起宿主对重复感染有一定免疫力，但宿主体内还有低密度的虫体存在，这种免疫状态称为：( )A．消除性免疫 B．缺少有效的获得性免疫C．保护性免疫 D．带虫免疫 E．伴随免疫11．人感染疟原虫后的免疫类型多属于: ( )A. 带虫免疫B. ADCC获得性免疫C. 消除性免疫D. 伴随免疫E. 先天性免疫12. 带虫者是指（）A．病人B．感染了寄生虫而未出现临床症状的人C．无免疫力的人D．易感者E．以上都不是二、X型题1．寄生虫对宿主的致病作用有：( )A．夺取营养B．机械性损伤作用C．毒性损伤D．免疫反应性损伤 E. 以上都对2. 寄生虫病流行的主要因素有（）A. 自然因素B. 生物因素C. 社会因素D. 历史原因E. 以上都对3. 寄生虫病流行特点为：（）A．地方性B．季节性C．自然疫源性D．隐性 E. 以上都对4. 建国初期我国重点防治的五大寄生虫疾病为（）A. 疟疾B.血吸虫病C.丝虫病D.黑热病E.钩虫病参考答案一、名词解释中间宿主：寄生虫幼虫或无性生殖阶段所寄生的宿主。

中财会计习题 (4)

第二部分存货一、单项选择题1．某股份有限公司对期末存货采用成本与可变现净值孰低计价。

2006年12月31日库存自制半成品的实际成本为20万元，预计进一步加工所需费用为8万元，预计销售费用及税金为4万元。

该半成品加工完成后的产品预计销售价格为30万元。

2006年12月31日该项存货应计提的跌价准备为( )万元。

A、0B、10 C．8 D．22．在出借包装物采用一次摊销的情况下，出借包装物报废时收回的残料价值应冲减的是( )。

A．管理费用 B．其他业务支出 C．包装物成本 D．销售费用3．在物价持续上涨的情况下，下列各种计价方法中，使期末存货价值最大的是( )。

A先进先出法 B．个别认定法 C．加权平均法 D．移动加权平均法4．某商场采用毛利率法对商品的发出和结存进行日常核算。

2001年l0月．甲类商品期初库存余额为20万元。

该类商品本月购进为60万元．本月销售收入为92万元，本月销售折让为2万元；上月该类商品按扣除销售折让后计算的毛利率为30％。

假定不考虑相关税费，2001年10月该类商品月末库存成本为( )万元。

A．15．6 B．17 C．52．4 D．535．某企业采用计划成本法进行材料的日常核算。

2001年12月，月初结存材料计划成本为300万元．本月收人材料计划成本为700万元；月初结存材料成本差异为超支2万元．本月收人材料成本差异为节约10万元；本月发出材料计划成本为800万元。

本月结存材料的实际成本为( )万元。

A．197．6 B．202．4 C．201．6 D．198．46．甲工业企业为增值税一般纳税企业，适用的增值税税率为17％。

本期购入原材料100公斤，价款为57000元(不含增值税额)。

验收人库时发现短缺5％，经查属于运输途中合理损耗。

该批原材料入库前的挑选整理费用为380元。

该批原材料的实际单位成本为每公斤( )元。

A．545．3 B．573．8 C．604 D．7067．下列各项业务中，不会引起期末存货账面价值发生增减变动的是( )。

微生物学习题与答案4

第四章微生物的营养和培养基A部分习题一、选择题1. 大多数微生物的营养类型属于：（）A. 光能自养B. 光能异养C. 化能自养D. 化能异养2. 蓝细菌的营养类型属于：（）A．光能自养 B. 光能异养C．化能自养 D. 化能异养3. 碳素营养物质的主要功能是：（）A. 构成细胞物质B. 提供能量C. A，B 两者4. 占微生物细胞总重量70%-90% 以上的细胞组分是：（）A. 碳素物质B. 氮素物质C. 水5. 能用分子氮作氮源的微生物有：（）A. 酵母菌B. 蓝细菌C. 苏云金杆菌6. 腐生型微生物的特征是：（）A. 以死的有机物作营养物质B. 以有生命活性的有机物作营养物质C. A，B 两者7. 自养型微生物和异养型微生物的主要差别是：（）A. 所需能源物质不同B. 所需碳源不同C. 所需氮源不同8. 基团转位和主动运输的主要差别是：（）A. 运输中需要各种载体参与B. 需要消耗能量C. 改变了被运输物质的化学结构9. 单纯扩散和促进扩散的主要区别是：（）A. 物质运输的浓度梯度不同B. 前者不需能量，后者需要能量C. 前者不需要载体，后者需要载体10. 微生物生长所需要的生长因子（生长因素）是：（）A. 微量元素B. 氨基酸和碱基C. 维生素D. B，C二者11. 培养基中使用酵母膏主要为微生物提供：（）A. 生长因素B. C 源C. N 源12. 细菌中存在的一种主要运输方式为：（）A. 单纯扩散B. 促进扩散C. 主动运输D. 基团转位13. 微生物细胞中的C素含量大约占细胞干重的：（）A. 10%B. 30%C. 50%D.70%14. 用牛肉膏作培养基能为微生物提供：（）A. C 源B. N 源C. 生长因素D. A，B，C 都提供15. 缺少合成氨基酸能力的微生物称为：（）A. 原养型B. 野生型C. 营养缺陷型二、是非题1. 最常用的固体培养基的凝固剂是琼脂。

2. 大多数微生物可以合成自身所需的生长因子，不必从外界摄取。

惯性技术习题答案(4)

4.1说明惯性导航的基本原理及特点惯性导航是一种利用惯性原理的自主式的导航方式。

它完全依靠机载惯性设备自主地完成导航任务，是航天、航空和航海领域中的一种广泛使用的主要导航方法。

惯性导航具有以下优点（1）由于它是不依赖于任何外部信息．也不向外部辐射能量的自主式系统．故隐蔽性好且不受外界电磁干扰的影响；（2）可全天候、全球、全时间地工作于空中、地球表面乃至水下．（3）能提供位置、速度、航向和姿态角数据，所产生的导航信息连续性好而且噪声低．（4）数据更新率高、短期精度和稳定性好。

4.2导航平台的主要性能指标有哪些？说明其意义导航平台的主要性能指标主要包括稳定性及精度问题等，要提高其稳定性可以设置阻尼器等，要提高精度则可在回路中加上校正装置等。

4.3说明指北方位、自由方位、游移方位三种导航系统的异同。

三种导航系统异同：4.4说明纯惯导高度通道为什么是不稳定的？在精确导航中，g 不是常值而是高度H 的函数，当R H >>时)21(0RH g g -=。

由此，纯惯导高度通道的特征方程式为：)2()2(22=-+=-Rg s Rg s Rg s因此该系统虽然是一个闭环系统，但特征式有一个正根，说明系统是不稳定的，计算高度H 误差是扩散的。

4.5说明高度通道阻尼回路的作用。

由于纯惯导高度通道是不稳定的，因此不能直接采用纯惯性的高度通道，而必须引入外部高度信息（气压高度表、无线电高度表、大气数据系统等）对高度通道构成阻尼回路，这种阻尼回路有时也叫互补滤波器，使两种高度住处起互补作用，这样两方面可以取长补短，得到动态品质好而误差不随时间发散的组合高度系统。

4.6结合第一章的知识，进一步说明舒勒摆的概念。

如何使导航平台具有舒勒特性？舒勒摆指单摆长度L 正好等于地球半径R 时，其自然振荡周期等于84.4min 能指示垂线的这样一个装置，此装置不会受支点加速度的干扰，它的重要意义还在于，任何装置只要能使它的振动周期满足等于84.4min ，它就具有摆长等于地球半径R 单摆的抗干扰能力。

国际法习题及答案4

A破坏和平罪
B战争罪
C违反人道罪
D侵略罪
13.1998年的《国际刑事法院罗马规约》“对整个国际社会关注的最严重犯罪具有管辖权”，而所谓“整个国际社会关注的最严重犯罪”一般被统称为是“核心罪行”，该“核心罪行”包括：（ABCD）
A灭绝种族罪
B危害人类罪
C战争罪
D侵略罪
14.庇护的对象有：AC
4.国家法上国家债务是指一国对其他国或国际组织所承担的任何财政义务，下列
哪几项属于国家应继承的债务？（AB）
A.国债
B.以国家名义所借用于兴建该国某一大型水利工程的债务
C.一国某省所借用于兴建该省自来水净化的债务
D.战争债务及征服债务
5.甲国与乙国相邻，为谋求共同发展，多年来，两国间签署了若干个双边协议，协定。后甲国分立为东甲，西甲两国。现问，如果所涉各方之间尚没有新的相关协议达成，那么，根据国际法中有关国家继承的规则，对于东甲，西甲两国，下列哪几项条约需要继承？（ABD）
B.该油田位于甲乙两国各自底土中的部分分属甲国和乙国各自所有
C.该油田的开发应在联合国托管理事会监督下进行
D.无论哪一方对该油田进行开发，都必须与另一方分享所获得的油气收益
16. 风光秀丽的纳列温河是甲国和乙国的界河，两国的边界线确定为该河流的主航道中心线。甲乙两国间没有其他涉及界河制度的条约。现甲国提议开发纳列温河的旅游资源，相关旅行社也设计一系列界河水上旅游项目。根据国际法的相关原则和规则，下列哪一项活动不需要经过乙国的同意，甲国就可以合法从事？(D)
A边沁
B苏文
C格劳秀斯
D孟德斯鸠
24.根据国际法原理，（D）是国际法的基础
A核不扩散原则

四年级上册第4单元第3课时《积的变化规律》精选习题+详细解析

四年级上册第4单元第3课时《积的变化规律》精选习题+详细解析积的变化规律在四年级上册数学课程中，我们学习了很多关于数学运算的知识。

在第4单元的第3课时中，我们将探索积的变化规律。

在本文中，我们将提供一些精选习题，并对其进行详细解析，以帮助大家更好地理解和掌握积的变化规律。

1. 习题1小明有7个小袋子，每个袋子里有3颗糖果。

请问小明一共有多少颗糖果？解析：我们可以使用乘法来解决这个问题。

因为小明有7个小袋子，每个袋子有3颗糖果，所以需要计算7乘以3。

答案：7 × 3 = 21所以，小明一共有21颗糖果。

2. 习题2花园里有6排花盆，每排花盆有4盆花。

请问花园里一共有多少盆花？解析：同样地，我们可以使用乘法来解决这个问题。

花园有6排花盆，每排有4盆花，所以需要计算6乘以4。

答案：6 × 4 = 24所以，花园里一共有24盆花。

3. 习题3一个竹筐装满了8扎花。

每个扎花有5朵。

请问竹筐里一共有多少朵花？解析：继续使用乘法来解决这个问题。

竹筐里有8扎花，每扎花有5朵，所以需要计算8乘以5。

答案：8 × 5 = 40所以，竹筐里一共有40朵花。

4. 习题4一面墙上有9行书架，每行书架上有6本书。

请问这面墙上一共有多少本书？解析：同样使用乘法来解决这个问题。

墙上有9行书架，每行书架上有6本书，所以需要计算9乘以6。

答案：9 × 6 = 54所以，这面墙上一共有54本书。

5. 习题5小明用金币堆成了一个9层的金塔。

每一层金塔上的金币数量依次递增，第1层是1枚金币，第2层是2枚金币，以此类推。

请问小明一共用了多少个金币？解析：这道题需要我们计算1+2+3+4+5+6+7+8+9的和，即求这9个数的总和。

答案：1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45所以，小明一共用了45个金币。

通过以上的习题和解析，我们可以看到积的变化规律很常见，并且可以通过乘法来解决。

《面向对象程序设计》习题四答案

面向对象程序设计习题4
(3) 下列程序中，基类base和派生类d1、d2中都含有私有、保护和公有成员，d1类是base的派生类，d2是d1问属性的变化
面向对象程序设计习题4 #include <iostream.h> #include <iostream.h> class base class base {{private: int n1; private: int n1; protected: int k1; protected: int k1; public: public: base(){n1=0;k1=1;} base(){n1=0;k1=1;} void fun1(){cout<<n1<<k1<<endl;} }; void fun1(){cout<<n1<<k1<<endl;} }; class d1:public base class d1:public base {{ int n2; int n2; protected: protected: int k2; int k2; public: public: d1(){n2=10;k2=11;} d1(){n2=10;k2=11;} void fun2(){cout<<n1<<k1<<endl; cout<<n2<<k2<<endl;} }; void fun2(){cout<<n1<<k1<<endl; cout<<n2<<k2<<endl;} }; class d2:public d1 class d2:public d1 {{ int n3; int n3; protected: protected: int k3; int k3; public: public: d2(){n3=20;k3=21;} d2(){n3=20;k3=21;} void fun3() void fun3()

城市园林绿地规划习题四答案

城市园林绿地规划习题四答案(总4页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--《城市园林绿地规划》习题（四）一、填空题1、居住区用地按照功能来分，可以分为_公共绿地_、宅旁绿地_、__公共服务设施所属绿地_、__道路绿地_四类。

20~30m②二级，居住小区级道路，（非城市级道路，无红线），居住区的次要道路，建筑控制线宽10~14m（采暖地区14m，费采暖地区10m），车道不小于6~9m。

③三级，组团级道路，居住区内支路，建筑控制线宽8~10米（采暖10m，不采暖8m），车道3~5m.④四级，宅间小路，通向但愿门前小路，~3m3、一般可以分为___________、___________、___________、___________等四级。

4、宅间绿化布置形式包括（1）底层行列式空间绿化；周边式居住建筑群、中部空间的绿化；庭院绿化；5、住宅建筑旁的绿化；多单元式住宅四周绿化；生活杂务用场地的绿化_6种类型。

6、工厂绿化的意义主要表现在以下（1）生态环境保护功能；（2）精神财富创造功能；（3）物质财富创造功能三个方面。

7、工厂企业的组成部分包括__厂前区、生产区、露天堆料场及仓库区、绿化美化地段_四部分。

8、工厂企业的绿化有以下_选择适应性强，具有抗御有害污染性能的树种、满足绿化的主要功能要求、_适地适树，满足植物生态要求、选择病虫害较少的树种，易于管理四个特点。

9、工厂中的植物在构成视觉空间中的作用有__点缀衬托、替代、分隔、遮盖、围合等四方面。

10、园林绿化植物选择要遵循___适地适树、植物多样性_、__市花市树、珍贵树种、古树名木五个基本原则。

10、城市道路绿化有构成城市绿地系统的线性因素、环境保护功能、安全功能、景观功能四方面的作用。

11、行道树的种植方式有_树带式_和___树池式__两种。

12、安全视距计算公式是：_D=a+tv+b汽车停车后与危险带之间的安全距离，a-汽车停车后与危险带的安全距离，一般采用4m;t-驾驶员发现必须刹车的时间，一般用;v-规定行车速度（m/s）b-刹车距离（m）b=v2/2qø;q=s_______________________。

国际金融习题与答案 (4)

第七章国际直接投资(练习)一、本章要义练习说明：请结合学习情况在以下段落空白处填充适当的文字，使上下文合乎逻辑。

国际直接投资是指投资者跨越（1）——，通过（2）——等手段，以掌握和控制国外企业经营活动从而谋取利润的一种投资活动。

国际直接投资的基本方式有两种：合营（资）和独资，每一种方式又可细分出不同的组织形式来。

合营方式主要有两种：（3）——和（4）——。

在我国，通常将前者称为合营企业，而将后者称为合作企业。

（5）——企业是国际上通行的现代企业模式，包括（6）——和（7）——两种形式。

前者是指注册资本由（8）——股份构成，通过发行（9）——（或股权证）等筹集资本，股东以其所认购的（10）——对公司承担（11）——责任，公司以其全部资本对其债务承担（12）——责任的企业法人。

后者是指由两个以上的股东，以其所认缴的（13）——对公司承担（14）——责任，公司以其全部资产对其债务承担（15）——责任的企业法人。

契约式合营是对外直接投资中一种重要的方式。

在我国。

（16）——具体是指由中国企业或其他经济组织与外国企业、其他经济组织或个人在中国境内以实施联合经营为目的，双方以平等的地位通过签订合约，明确双方权利和义务、履行合同规定条款而产生的经济组织。

中外合作企业既可以作为企业法人、负有限责任，也可以不是法人，类似于国外的合伙企业。

独资企业是指一国投资者（公司、企业、其他经济组织或个人）按照东道国法律，经政府批准，在境内单独投资、独立经营、自负盈亏的一种国际直接投资方式。

独资企业基本形式主要有两种：一种是（17）——，另外一种为（18）——。

后一种分支机构在法律上、经济上没有独立性，仅仅是母公司的附属机构。

选择合营方式还是合作方式，或者是独资方式，对于跨国投资者、东道国政府与企业而言，各有利弊。

各国政府对国际直接投资的态度迥然不同。

发展中国家在保护民族工业、核心资源的前提下，引导外资进入到一些鼓励发展的行业。

西方经济学习题习题第 4-5

西方经济学习题习题第 4-5 章一、判断题1．在生产函数中，只要有?种投入不变，便是短期生产函数。

（√）2．如果平均变动成本等于边际成本，则边际产量等于平均产量。

（√）3．当平均产量最高时，平均成本最低。

（×）4．当 SMC=LMC，并且小于 LAC 时，LAC 曲线处于下降阶段。

（√）5．若生产函数 q= 4 L 9 K ，且 L，K 价格相同，则为实现利润最大化，企业应投入较多的劳动和较少的资本。

（×）6．机会成本是企业的一种成本，它可以衡量并反映到会计帐表中。

（×）7.长期平均成本曲线是短期平均成本曲线的包络线，并且长期平均成本曲线与短期平均成本曲线的最低点相切。

（×）8.长、短期平均成本曲线都呈 U 形，都是由边际报酬递减规律造成的。

（×）二、选择题1、如果仅劳动是变动投入，以边际产量等于平均产量作为划分生产三阶段的标志，则 ( D )不是第Ⅱ阶段的特点。

A、边际产量报酬递减 B．平均产量不断下降 C、总产量不断提高 D．资本的平均产量递增2．若劳动与资本的投入组合处于投入产出生产函数等产量线的垂直部分，则( D )。

A、劳动与资本的边际产量都是负 B．劳动与资本的边际产量都是 0 C、劳动的边际产量为0，资本的边际产量为正 D．劳动的边际产量为正，资本的边际产量为 0 E．以上说法都不正确3．机会成本的经济含义是( B )。

A、使用一种资源的机会成本是放弃这种资源另一种用途的收入 B．使用一种资源的机会成本是放弃这种资源在其他用途中所能得到的最高收入 C、使用一种资源的机会成本是将其用于次优用途的收人 D．使用一种资源的机会成本是保证这种资源在现用途继续使用而必须支付的费用 E、以上都是机会成本的含义，只是说法不同6．如果连续增加某种生产要素，在总产量达到最大值的时候，边际产量曲线与以下哪条线相交( C )。

A．平均产量曲线 B．纵轴C．横轴 D．总产量曲线7．在总产量、平均产量和边际产量的变化过程中，下列哪一个变化首先发生( A )。

线代习题答案(4)线性代数答案北京邮电大学出版社戴斌祥主编)

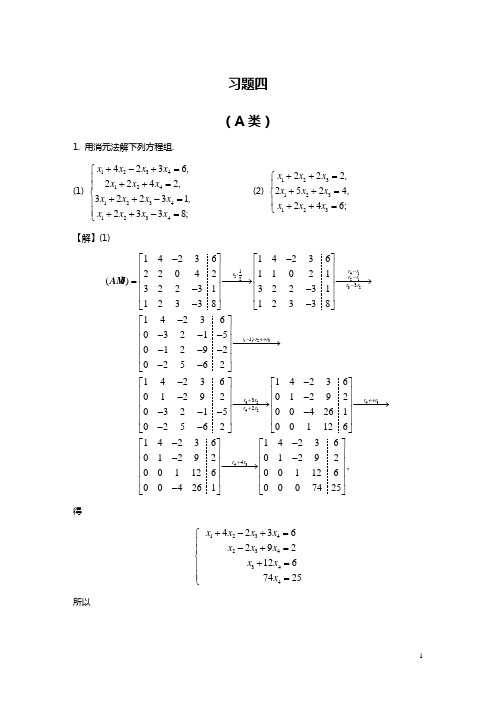
习题四（A 类）1. 用消元法解下列方程组.(1) 12341241234123442362242322312338;x x x x ,x x x ,x x x x ,x x x x +-+=⎧⎪++=⎪⎨++-=⎪⎪++-=⎩ (2) 1231231232222524246;x x x ,x x x ,x x x ++=⎧⎪++=⎨⎪++=⎩【解】(1)412213223123(1)14236142362204211021()322313223112338123381423603215012920256214236012920321502562r r r r r r r r r r -⋅---⋅↔--⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=−−−→⎢⎥⎢⎥--⎢⎥⎢⎥--⎣⎦⎣⎦-⎡⎤⎢⎥---⎢⎥−−−−→⎢⎥---⎢⎥--⎣⎦-⎡⎤⎢⎥-⎢⎥⎢⎥---⎢⎥--⎣⎦A b 32434243324142360129200426100112614236142360129201292,001126001126004261007425r r r r r r r +↔++-⎡⎤⎢⎥-⎢⎥−−−→−−−→⎢⎥-⎢⎥⎣⎦--⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥−−−→⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦得12342343444236 292 126 7425x x x x x x x x x x +-+=⎧⎪-+=⎪⎨+=⎪⎪=⎩ 所以1234187,74211,74144,7425.74x x x x ⎧=-⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩(2)解②①×2得23③① 得 2x 3=4 得同解方程组由⑥得 3=2,由⑤得 x 2=2x 3=4,由④得 x 1=22x 3 2x 2 = 10,得 (x 1,x 2,x 3)T =(10,4,2)T. 2. 求下列齐次线性方程组的基础解系.(1) 123123123 320 5 03580;x x x ,x x x ,x x x ++=⎧⎪++=⎨⎪++=⎩ (2) 12341234123412345 0 2303 8 0 3970;x x x x ,x x x x ,x x x x ,x x x x -+-=⎧⎪+-+=⎪⎨-++=⎪⎪+-+=⎩(3) 1234512341234 22702345 03568 0;x x x x x ,x x x x ,x x x x ++++=⎧⎪+++=⎨⎪+++=⎩ (4) 123451234512345 222 0 2 320247 0.x x x x x ,x x x x x ,x x x x x +-+-=⎧⎪+-+-=⎨⎪+-++=⎩【解】(1)123123123320503580.x x x ,x x x ,x x x ++=⎧⎪++=⎨⎪++=⎩ 32213123132132132151021021358042000r r r r r r +--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=−−−→−−−→--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦A得同解方程组1323123232333723,23201,202,x x x x x x x x x x x x x ⎧=--=-⎪++=⎪⎧⇒⎨⎨=-=⎩⎪⎪=⎩得基础解系为T71122⎛⎫- ⎪⎝⎭. (2) 系数矩阵为32213142413211511151112302743181027413970414811510274() 2.00000000r r r r r r r r r r r ---------⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥=−−−→−−−→⎢⎥⎢⎥--⎢⎥⎢⎥--⎣⎦⎣⎦--⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦A A∴ 其基础解系含有4()2R -=A 个解向量.1342123434342343344331225077222227400110x x x x x x x x x x x x x x x x x x x ⎡⎤⎡⎤⎡⎤---⎢⎥⎢⎥-⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-+-=-⎧⎢⎥⎢⎥⎢⎥-⎢⎥⇒==+⎨⎢⎥⎢⎥⎢⎥-+=⎢⎥⎩⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦基础解系为31272,.20110⎡⎤-⎢⎥-⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦(3)213132232112271122723450010114356800202211122701011400007r r r r r r ---⎡⎤⎡⎤⎢⎥⎢⎥=−−−→-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎡⎤⎢⎥−−−→-⎢⎥⎢⎥⎣⎦A得同解方程组12345245552270,140,700.x x x x x x x x x x ++++=⎧⎪+-=⎨⎪=⇒=⎩取3410,01x x ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦得基础解系为 (2，0，1，0，0)T,(1，1，0，1，0).(4) 方程的系数矩阵为2131322312221122211213200111247110033312221()2,0011100000r r r r r r R --+----⎡⎤⎡⎤⎢⎥⎢⎥=−−−→---⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦--⎡⎤⎢⎥−−−→=-⎢⎥⎢⎥⎣⎦A A∴ 基础解系所含解向量为n R (A )=52=3个取245x x x ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦为自由未知量 245010,,,001100x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦ 得基础解系 324010,,.101001100--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦3. 解下列非齐次线性方程组.(1) 123123121232122423442;x x x ,x x x ,x x ,x x x ++=⎧⎪-+=⎪⎨-=⎪⎪++=⎩ (2) 12341234123421422221;x x x x ,x x x x ,x x x x +-+=⎧⎪+-+=⎨⎪+--=⎩(3) 123412341234212125;x x x x ,x x x x ,x x x x -++=⎧⎪-+-=-⎨⎪-++=⎩ (4) 12345123452345123457323222623543312x x x x x ,x x x x x ,x x x x ,x x x x x .++++=⎧⎪+++-=-⎪⎨+++=⎪⎪+++-=⎩【解】（1）方程组的增广矩阵为32213142414324121121112121240322()120303224142034211211121032203220000001200240000r r r r r r r r r r r r ------↔⎡⎤⎡⎤⎢⎥⎢⎥---⎢⎥⎢⎥=−−−→−−−→⎢⎥⎢⎥---⎢⎥⎢⎥---⎣⎦⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥----⎢⎥⎢⎥−−−−→⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦A b得同解方程组3123323231232,21223222,3212 1.x x x x x x x x x x x x =⎧++=⎧⎪+⎪⎪--=⇒==-⎨⎨-⎪⎪=⎩⎪=--=-⎩ (2) 方程组的增广矩阵为312122*********()42212000102111100020r r r r ----⎡⎤⎡⎤⎢⎥⎢⎥=−−−→--⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦A b得同解方程组123444421,00,20,x x x x x x x +-+=⎧⎪⇒=-=⎨⎪-=⎩即123421,0.x x x x +-=⎧⎨=⎩令130x x ==得非齐次线性方程组的特解x T =(0，1，0，0)T .又分别取2310,01x x ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦得其导出组的基础解系为TT1211;,,1,0,0,0,1,022⎛⎫⎛⎫==- ⎪ ⎪⎝⎭⎝⎭ξξ∴ 方程组的解为121211022110.,001000x k k k k ⎡⎤⎡⎤-⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=++∈⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦R(3) 2131121111211112111000221211500004r r r r ----⎡⎤⎡⎤⎢⎥⎢⎥---−−−→--⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦()()R R ≠A A ∴ 方程组无解.(4) 方程组的增广矩阵为31413242351111171111173211320122623()01226230122623543311201226231111170122623,000000000000r r r r r r r r --+-⎡⎤⎡⎤⎢⎥⎢⎥-------⎢⎥⎢⎥=−−−→⎢⎥⎢⎥⎢⎥⎢⎥------⎣⎦⎣⎦⎡⎤⎢⎥-----⎢⎥−−−→⎢⎥⎢⎥⎣⎦A b分别令345010,,001100x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦ 得其导出组12345234502260x x x x x x x x x ++++=⎧⎨----=⎩的解为123123511622,,.010001100k k k k k k R ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥++∈⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦令3450x x x ===,得非齐次线性方程组的特解为：x T=(16,23,0,0,0)T,∴ 方程组的解为1231651123622001000010100x k k k -⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦其中123,,k k k 为任意常数.4. 某工厂有三个车间，各车间相互提供产品（或劳务），今年各车间出厂产量及对其它车间三车间0.1万元，0.2万元，0.5万元的产品；第二列，第三列类同，求今年各车间的总产量.解：根据表中数据列方程组有112321233130.10.20.4522,0.20.20.30,0.50.1255.6,x x x x x x x x x x x ---=⎧⎪---=⎨⎪--=⎩即 123123130.90.20.4522,0.20.80.30,0.50.8855.6,x x x x x x x x --=⎧⎪-+=⎨⎪-=-⎩解之 123100,70,120;x x x =⎧⎪=⎨⎪=⎩5. λ取何值时，方程组12312321231,,,x x x x x x x x x λλλλλ++=⎧⎪++=⎨⎪++=⎩ (1)有惟一解，(2)无解，(3)有无穷多解，并求解.【解】方程组的系数矩阵和增广矩阵为211111;,11111111λλλλλλλλ⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦A B|A |=2(1)(2)λλ-+.(1) 当λ≠1且λ≠2时，|A |≠0，R (A )=R (B )=3.∴ 方程组有惟一解212311(1),,.22(2)x x x λλλλλ--+===+++（2）当λ=2时，312121221111212121221111124112412121212,0333033303360003r r r r r r -↔+---⎡⎤⎡⎤⎢⎥⎢⎥=−−−→−−−→---⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦----⎡⎤⎡⎤⎢⎥⎢⎥→----⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦BR (A )≠R (B ),∴ 方程组无解.(3) 当λ=1时2131111111111111000011110000r r r r B --⎡⎤⎡⎤⎢⎥⎢⎥=−−−→⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦R (A )=R (B )<3,方程组有无穷解.得同解方程组123223 3.1,,x x x x x x x =--+⎧⎪=⎨⎪=⎩∴ 得通解为1212123111, ,.100010x x k k k k R x --⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=++∈⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦6. 齐次方程组0020x y z ,x y z ,x y z λλ++=⎧⎪+-=⎨⎪-+=⎩当λ取何值时，才可能有非零解?并求解. 【解】方程组的系数矩阵为1111211λλ⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦A|A |=(4)(1)λλ-+当|A |=0即λ=4或λ=1时，方程组有非零解.(i) 当λ=4时,21213123234215134111411411414110155211211093141141031031031000r r r r r r r r r r ↔--⋅-⋅--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=−−−→−−−→--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦--⎡⎤⎡⎤⎢⎥⎢⎥−−→−−−→--⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦A得同解方程组112322331340.13031x x x x x k k R x x x ⎡⎤-⎢⎥⎡⎤+-=⎢⎥⎡⎤⎢⎥⇒=∈⎢⎥⎢⎥⎢⎥-+=⎣⎦⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦(ii) 当λ=1时,2121312111111111111111000211211013r r r r r r ↔+------⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=−−−→−−−→---⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦A得131232323332,03,30x x x x x x x x x x x=-⎧--=⎧⎪⇒=-⎨⎨+=⎩⎪=⎩ ∴ (123,,x x x )T=k ·(2,3,1)T.k ∈R7. 当a ,b 取何值时，下列线性方程组无解，有惟一解或无穷多解？在有解时，求出其解.（1） 123412341234123423123132236x x x x x x x x x x x x a x x x bx ++-=⎧⎪+++=⎪⎨---=⎪⎪+-+=-⎩ (2) 123423423412340221(3)2321x x x x x x x x a x x b x x x ax +++=⎧⎪++=⎪⎨----=⎪⎪+++=-⎩【解】方程组的增广矩阵为(1)213132414237212311123111123101140()311207101323160172812311123110114001140003273003273006280r r r r r r r r r r a a b b a a b b -------⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥=−−−→−−−→⎢⎥⎢⎥------⎢⎥⎢⎥----+-⎣⎦⎣⎦--⎡⎤⎢⎥----⎢⎥−−→⎢⎥------⎢⎥---+⎣⎦A b .5222a ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦(i) 当b ≠52时,方程组有惟一解12344(1)326(1),,352352318(1)2(1),.35252a a a a x x b b a a a x x b b +-+=-=-++-++=-+=-++(ii) 当b =52,a ≠1时，方程组无解.(iii) 当b =52，a =1时，方程组有无穷解. 得同解方程组123423434231403274x x x x x x x x x ++-=⎧⎪--+=⎨⎪--=-⎩(*) 其导出组123423434230403270x x x x x x x x x ++-=⎧⎪--+=⎨⎪--=⎩的解为1412423434442,21313.9,91.x x x x x x k k x x x x x x =⎧⎡⎤⎡⎤⎪⎢⎥⎢⎥=⎪⎢⎥⎢⎥=∈⎨⎢⎥⎢⎥=--⎪⎢⎥⎢⎥⎪=⎣⎦⎣⎦⎩R 非齐次线性方程组（*）的特解为取x 4=1, 12345335.32331x x x x ⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎢⎥⎢⎥⎣⎦∴ 原方程组的解为5323513.3923131x k k ⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+∈⎢⎥-⎢⎥⎢⎥⎢⎥-⎣⎦⎢⎥⎢⎥⎣⎦R(2)32414231111001221()01(3)23211111100122100101012311111001221.0010100010r r r r r r a b a a b a a b a +-+⎡⎤⎢⎥⎢⎥=−−−→⎢⎥---⎢⎥-⎣⎦⎡⎤⎢⎥⎢⎥−−−→⎢⎥-+⎢⎥----⎣⎦⎡⎤⎢⎥⎢⎥⎢⎥-+⎢⎥-⎣⎦A b (i) 当a 1≠0时，R (A )=R (A )=4,方程组有惟一解.12342123.1110b a a x a b x a x b x a -+⎡⎤⎢⎥-⎡⎤⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥+⎢⎥⎢⎥⎣⎦⎢⎥-⎢⎥⎣⎦(ii) 当a 1=0时,b ≠1时，方程组R (A )=2<R (A )=3,∴ 此时方程组无解.(iii) 当a =1，b = 1时，方程组有无穷解. 得同解方程组12342340,22 1.x x x x x x x +++=⎧⎨++=⎩ 取13423433441,221,,,x x x x x x x x x x =+-⎧⎪=--+⎪⎨=⎪⎪=⎩∴ 得方程组的解为12121234111221.,100010x x k k k k x x -⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥=++∈⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦R8. 设112224336⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦A ，求一秩为2的3阶方阵B 使AB =0.【解】设B =(b 1 b 2 b 3),其中b i (i =1,2,3)为列向量,由123123()(1,2,3)i i =⇒=⇒==⇒AB A b b b Ab b b b 00为Ax =0的解.求123112224336x x x ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦=0的解.由 213123112112224000336000r r r r --⎡⎤⎡⎤⎢⎥⎢⎥=−−−→⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦A得同解方程组12322332,,,x x x x x x x =--⎧⎪=⎨⎪=⎩∴ 其解为121212312.,1001x x k k k k R x --⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=+∈⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦取123120;;,100010--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦b b b则120100010--⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦B9.已知123,,ηηη是三元非齐次线性方程组Ax =b 的解，且R (A )=1及122313111,,,011001⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥+=+=+=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ηηηηηη求方程组Ax =b 的通解.【解】Ax =b 为三元非齐次线性方程组R (A )=1⇒Ax =0的基础解系中含有3R (A )=31=2个解向量.131223121323110()(),01100110()(),110101-⎡⎤⎡⎤⎢⎥⎢⎥-=+-+==--⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦-⎡⎤⎡⎤⎢⎥⎢⎥-=+-+==-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦ηηηηηηηηηηηη由123,,ηηη为Ax=b 的解1312,⇒--ηηηη为Ax=0的解,且1312(),()--ηηηη线性无关1312,⇒--ηηηη为Ax =0的基础解系. 又[]11223131()()()211112111,011022200112ηηηηηηη=+-+++⎡⎤⎢⎥⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=-+=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦∴ 方程组Ax=b 的解为11132121212()()1002.,0101012k k k k k k =+-+-⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=++∈-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦x ηηηηηR10. 求出一个齐次线性方程组，使它的基础解系由下列向量组成.(1) 1223==;1001,-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ξξ(2) 123121232==,=021352132,.⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦ξξξ【解】(1) 1223==1001-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ξξ设齐次线性方程组为Ax =0由12,ξξ为Ax =0的基础解系，可知11121222133223231001x x k k k k x x k x x k -+-⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+=⇒=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦x令 k 1=x 2 , k 2=x 3⇒Ax =0即为x 1+2x 23x 3=0.(2) A (123ξξξ)=0⇒A 的行向量为方程组为12345121232()0021352132x x x x x ⎡⎤⎢⎥---⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥---⎣⎦的解. 即124512345123452302325302220x x x x x x x x x x x x x x -+-=⎧⎪-++-=⎨⎪-++-=⎩的解为 31212120311203123253012111212200111r r r r ------⎡⎤⎡⎤⎢⎥⎢⎥−−−→----⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦得基础解系为1η=( 5 1 1 1 0)T2η=( 1 1 1 0 1)TA =5111011101--⎡⎤⎢⎥--⎣⎦方程为1234123550,0.x x x x x x x x --++=⎧⎨--++=⎩ 11. 证明：线性方程组121232343454515x x a x x a x x a x x ax x a -=⎧⎪-=⎪⎪-=⎨⎪-=⎪-=⎪⎩有解的充要条件是510i i a ==∑.【解】215212345123415123412511000011000011000011100011100001100001100001101011100001100001100001100101r r r r a a a a a a a a a a a a a a a a a a ++-⎡⎤⎢⎥-⎢⎥⎢⎥=-−−−→⎢⎥-⎢⎥⎢⎥-⎣⎦-⎡⎤⎢⎥-⎢⎥⎢⎥-−−−→⎢⎥-⎢⎥⎢⎥-+⎣⎦-⎡⎤⎢⎥-⎢⎥⎢⎥-−−→⎢⎥-⎢⎥⎢⎥-++⎣⎦A 1234511100011000011000011001i i a a a a a =-⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦∑ 方程组有解的充要条件，即R (A )=4=R (A )510i i a =⇔=∑得证.12. 设*η是非齐次线性方程组Ax=b 的一个解，12n r ,,,-ξξξ 是对应的齐次线性方程组的一个基础解系.证明（1）1*n r ,,-,ξξ η线性无关；（2）1++***n r ,,-,ξξ ηηη线性无关. 【证明】(1) 1*n r ,,-,ξξ η线性无关⇔110*n r n r k k k --+++=ξξ η成立,当且仅当k i =0(i =1,2,…,n r ),k =01111()00*n r n r *n r n r k k k k k k ηη----+++=⇒+++=A ξξA A ξA ξ∵12n r ,,,-ξξξ 为Ax =0的基础解系0(1,2,,)i i n r ξ⇒==-A*0k ⇒=A η由于*0b =≠A η00.k b k ⇒⋅=⇒=.由于12n r ,,,-ξξξ 为线性无关112200(1,2,,)n r n r i k k k k i n r --+⋅++⋅=⇔==-ξξξ∴121*n ,,,-,ξξξ η线性无关.(2) 证1++***n r ,,-,ξξ ηηη线性无关.***11()()0n r n r k k k --⇔+++++=ξξ ηηη成立当且仅当k i =0(i =1,2,…,n r ),且k =0***11()()0n r n r k k k --+++++=ξξ ηηη即*111()0n r n r n r k k k k k ---++++++=ξξ η由(1)可知，11*n ,,-,ξξ η线性无关. 即有k i =0(i =1,2,…,n r ),且100n r k k k k -++=⇒=∴1++***n r ,,-,ξξ ηηη线性无关.（B 类）1.B2. C3. D4. C5. t= 36. R(A)=2；2；27. 设η1,η2,…,ηs 是非齐次线性方程组Ax=b 的一组解向量，如果c 1η1+c 2η2+…+c s ηs 也是该方程组的一个解向量，则c 1+c 2+…+c s = .解：因为η1, η2,…, ηs 是Ax=b 的一组解向量，则A η1=b, A η2=b,…, A ηs =b,又 C 1η1+ C 2η2+…+ C s ηs 也是Ax=b 的一解向量，所以A(C 1η1+…+ C s ηs )=b ，即C 1A η1+ CA η2+…+ C s A ηs =b,即C 1b+ C 2b+…+ C s b=b,(C1+…+C s )b=b,所以C 1+…+ C s =1.8. 设向量组1α=（1，0，2，3），2α=（1，1，3，5），3α=（1，1，a +2，1），4α=（1，2，4，a +8），β=（1，1，b +3，5）问：（1） a ，b 为何值时，β不能由1α，2α，3α，4α线性表出？（2） a ，b 为何值时，β可由1α，2α，3α， 4α惟一地线性表出？并写出该表出式. （3） a ，b 为何值时，β可由1α，2α，3α，4α线性表出，且该表出不惟一？并写出该表出式. 【解】11223344x x x x =+++βαααα (*)314132422321111101121()232433518511111111110112101121012100100225200010r r r r r r r r a b a a b a b a a ----⎡⎤⎢⎥-⎢⎥==−−−→⎢⎥++⎢⎥+⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥−−−→⎢⎥⎢⎥++⎢⎥⎢⎥-++⎣⎦⎣⎦A A b(1) β不能由1α，2α，3α，4α线性表出⇔方程组（*）无解,即a +1=0,且b ≠0.即a =1,且b ≠0.(2) β可由1α，2α，3α，4α惟一地线性表出⇔方程组(*)有惟一解，即a +1≠0，即a ≠1.(*) 等价于方程组12342343443231123121(1)(1)01011111210111121111x x x x x x x a x b a x b b a b x x x x a a a b b b x a a a b a b ba a a βααα+++=⎧⎪-+=⎪⎨+=⎪⎪+=⎩++⇒===+=+=+++⎛⎫=---=-+ ⎪+++⎝⎭++∴=-+++++(3) β可由1α，2α，3α，4α线性表出，且表出不惟一⇔方程组（*）有无数解，即有a +1=0,b =0⇒a =1,b =0.方程组（*）12112342122343142212121x k k x x x x x k k x x x x k x k =-⎧⎪+++==-+⎧⎪⇔⇒⎨⎨-+==⎩⎪⎪=⎩1234,,,k k k k 为常数.∴2111221324(2)(21)k k k k k k =-+-+++βαααα9. 设有下列线性方程组（Ⅰ）和(Ⅱ)（Ⅰ）1241234123264133x x x x x x x x x x +-=-⎧⎪---=⎨⎪--=⎩ (Ⅱ) 123423434521121x mx x x nx x x x x t +--=-⎧⎪--=-⎨⎪-=-⎩(1) 求方程组（Ⅰ）的通解；(2) 当方程组（Ⅱ）中的参数m,n,t 为何值时，（Ⅰ）与(Ⅱ)同解？解：（1）对方程组（Ⅰ）的增广矩阵进行行初等变换11026110261102641111051725001253110304162101014100120101400125 ------⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥------⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥------⎣⎦⎣⎦⎣⎦--⎡⎤⎢⎥--⎢⎥⎢⎥--⎣⎦由此可知系数矩阵和增广矩阵的秩都为3，故有解.由方程组142434020x x x x ⎪-=⎨⎪-=⎩ （*）得方程组（*）的基础解系11121⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦ξ令40x =，得方程组（Ⅰ）的特解 2450-⎡⎤⎢⎥-⎢⎥=⎢⎥-⎢⎥⎣⎦η于是方程组（Ⅰ）的通解为k =+ηξx ，k 为任意常数。

工程热力学习题解答-4

第四章热力学第二定律例题例4-1 先用电热器使 20 kg 、温度t 0=20 ℃的凉水加热到t 1=80 ℃，然后再与40 kg 、温度为 20 ℃的凉水混合。

求混合后的水温以及电加热和混合这两个过程各自造成的熵产。

水的比定压热容为 4.187 kJ/（kg·K ）；水的膨胀性可忽略。

[编题意图] 实际过程中熵产的计算是本章的重点和难点之一，本题的目的在于检测和练习电热器加热造成的熵产和不等温水混合过程中的熵产的分析计算。

[解题思路] 电加热水过程引起熵产是由于电功转变为热产，水吸收这个热后其自身温度逐渐上升，这是一个不断积累过程，需通过微元热产量g Q δ与水变化的水温T 之比这个微元熵产的积分求得。

要求凉水与热水混合造成的熵产，必须先求出20kg80℃的水放热的熵减与20℃的凉水吸热的熵增，这种内热流造成的熵产也是个逐渐积累的过程，也需积分求得。

整个加热混合造成的总熵产由二者相加得到。

[求解步骤]设混合后的温度为t ，则可写出下列能量方程：()()1120p p m c t t m c t t -=-即 ()()2041878040418720kg kJ /(kg C)C kg kJ /(kg C)C o o o o ⨯⋅⨯-=⨯⋅⨯-..t t 从而解得 t = 40 ℃ （T = 313.15 K ）电加热过程引起的熵产为1g 0g11g 10d lnT Qp p T Q m c T T S m c TTT δ===⎰⎰353.15K 20kg 4.187kJ/(kg K)ln 293.15K=⨯⋅⨯=15.593 kJ / K 混合过程造成的熵产为i 1012ig 1210d d ln lnTT p p Q p p T T m c T m c T Q T T S m c m c TT T T T δ==+=+⎰⎰⎰313.15K 20kg 4.187kJ/(kg K)ln353.15K313.15K40kg 4.187kJ/(kg K)ln293.15K10.966kJ/K 11.053kJ/K 0.987kJ/K =⨯⋅⨯+⨯⋅⨯=-+= 总的熵产S S S QQ g g g g ikJ /K kJ /K kJ /K =+=+=15593098716580...由于本例中无熵流（将使用电热器加热水看作水内部摩擦生热），根据式（4-12）可知，熵产应等于热力系的熵增。

热学教程习题参考解(第四章)

《热学教程》习题参考答案第四章习题4-1. 电子管的真空度为1.333×103-Pa,设空气分子有效直径为3.0×1010-m,求27℃时空气分子的数密度n ,平均自由程λ和碰撞频率Z .(答: 3.2×1017m 3-，7.8 m ，60s 1-) 解：由nkT P =，可得)m (1021.3317-⨯==kTP n 分子平均自由程为)m (78.7212==n d πλ碰撞频率为 )s (2.6081-===λπμλRTvZ4-2. 求氦原子在其密度2.1×102-kg/m 3,原子的有效直径=d 1.9×1010-m 的条件下的平均自由程λ.(答:1.97×106-m)解：由n N mn A μρ==，可得 )m (1016.3324-⨯==μρA N n 分子平均自由程为)m (10972.12162-⨯==nd πλ 4-3. 试估算宇宙射线中的质子在海平面附近的平均自由程.(答：约m 102.16-⨯)4-4. 测得温度15℃和压强76cmHg 时氩原子和氖原子的平均自由程分别为Ar λ=6.7×108-m 和Ne λ=13.2×108-m ，试问：(1)氩原子和氖原子的有效直径各为多少？(2) 20℃和15cmHg 时Ar λ和-40℃和75cmHg 时Ne λ多大？(答(1)101063.3-⨯m,101059.2-⨯m; (2) 71045.3-⨯m, 71080.1-⨯m)解：(1)由Pd kT n d 22221ππλ==，可得 )m (1063.321021Ar Ar -⨯=⎪⎪⎭⎫ ⎝⎛=λπP kT d)m (1059.221021Ne Ne -⨯=⎪⎪⎭⎫ ⎝⎛=λπP kT d(2)由分子平均自由程与温度及压强的关系)m (1045.3107.6288157629378Ar11212Ar2--⨯=⨯⨯⨯⨯==λλT P P T )m (1008.1102.13288757623378Ne11212Ne2--⨯=⨯⨯⨯⨯==λλT P P T 4-5. 高空的一片降雨云层,单位时间通过单位面积的降雨量为Q =10cm/hour 。

相遇问题应用题及答案

相遇问题应用题及答案相遇问题应用题及答案相遇问题【数量关系】相遇时间＝总路程÷（甲速＋乙速）总路程＝（甲速＋乙速）×相遇时间【解题思路和方法】简单的题目可直接利用公式，复杂的题目变通后再利用公式。

例1南京到上海的水路长392千米，同时从两港各开出一艘轮船相对而行，从南京开出的船每小时行28千米，从上海开出的船每小时行21千米，经过几小时两船相遇？解392÷（28＋21）＝8（小时）答：经过8小时两船相遇。

例2小李和小刘在周长为400米的环形跑道上跑步，小李每秒钟跑5米，小刘每秒钟跑3米，他们从同一地点同时出发，反向而跑，那么，二人从出发到第二次相遇需多长时间？解“第二次相遇”可以理解为二人跑了两圈。

因此总路程为400×2相遇时间＝（400×2）÷（5＋3）＝100（秒）答：二人从出发到第二次相遇需100秒时间。

例3甲乙二人同时从两地骑自行车相向而行，甲每小时行15千米，乙每小时行13千米，两人在距中点3千米处相遇，求两地的距离。

解“两人在距中点3千米处相遇”是正确理解本题题意的.关键。

从题中可知甲骑得快，乙骑得慢，甲过了中点3千米，乙距中点3千米，就是说甲比乙多走的路程是（3×2）千米，因此，相遇时间＝（3×2）÷（15－13）＝3（小时）两地距离＝（15＋13）×3＝84（千米）答：两地距离是84千米。

下面的关系式必须牢记：（1）速度和×相遇时间＝相遇路程（2）相遇路程÷速度和＝相遇时间（3）相遇路程÷相遇时间＝速度和速度和：两人或两车速度的和；相遇时间：两人或两车同时开出到相遇所用的时间。

【习题1】：两列火车同时从两地相对开出，甲列火车每小时行86千米，乙列火车每小时行102千米，经过5小时两车在途中相遇，求两地相距多少千米？【习题2】：甲、乙两人分别从相距20千米的两地同时出发相向而行，甲每小时走6千米，经过2小时后两人相遇，问乙每小时行多少千米？【习题3】：张杰和姐姐两人从相距2000米的两地相向而行，张杰每分钟行110米，姐姐每分钟行90米，如果一只狗与张杰同时同向而行，每分钟行500米，遇到姐姐后，立即回头向张杰跑去，遇到张杰再向姐姐跑去，这样不断来回，直到张杰和姐姐相遇为止。

解析几何第四章习题及解答

第4章二次曲线和二次曲面习题4.11.在直角坐标系x O y 中，以直线:43120l x y -+=为新坐标系的x '轴，取通过(1,3)A -且垂直于l 的直线为y '轴，写出点的坐标变换公式，并且求直线1:3250l x y -+=在新坐标系中的方程。

解：直线:43120l x y -+=的方向是(3,4)，与它垂直的方向是(4,3)±-，新坐标系的x '轴的坐标向量取为34(,)55，y '轴坐标向量取为43(,)55-，与直线:43120l x y -+=垂直且的直线方程可设为340x y c ++=，由于过点(1,3)A -，得到直线方程是3490x y ++=，两直线的交点(3,0)-是新坐标原点，所以点的坐标变换公式：34355.43055x x y y ⎡⎤-⎢⎥'-⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦直线1:3250l x y -+=在新坐标系中的方程：13443:3(3)2()505555l x y x y ''''---++=，化简有1:18200.l x y ''--=2.作直角坐标变换，已知点(6,5),(1,4)A B --的新坐标分别为(1,3),(0,2)-，求点的坐标变换公式。

解：设同定向的点的坐标变换公式是：cos sin .sin cos x x a y y b θθθθ'-⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎣⎦它的向量的坐标变换公式是：cos sin .sin cos u u v v θθθθ'-⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦由题意知向量(5,1) A B =-变为(1,5)A B ''=-，于是有5cos sin 1.1sin cos 5θθθθ---⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦得到125s i n ,c o s .1313θθ==于是点的坐标变换公式是：5121313.1251313x x a y y b ⎡⎤-⎢⎥'⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦将点(1,4)B -及它的像点(0,2)代入得到3713,6213a b ⎡⎤⎢⎥⎡⎤=⎢⎥⎢⎥⎣⎦⎢⎥-⎢⎥⎣⎦所以点的坐标变换公式是： 51237131313.12562131313x x y y ⎡⎤⎡⎤-⎢⎥⎢⎥'⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦设反定向的点的坐标变换公式是：cos sin .sin cos x x a y y b θθθθ'-⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎣⎦它的向量的坐标变换公式是：cos sin .sin cos u u v v θθθθ'-⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦由题意知向量(5,1)A B =-变为(1,5) A B ''=-，于是有5cos sin 1.1sin cos 5θθθθ---⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦得到s i n 1,c o s 0.θθ=-=于是点的坐标变换公式是：01.10x x a y y b '-⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'-⎣⎦⎣⎦⎣⎦⎣⎦将点(1,4B -及它的像点(0,2)代入得到3,4a b ⎡⎤⎡⎤=⎢⎥⎢⎥-⎣⎦⎣⎦所以点的坐标变换公式是： 013.104x x y y '-⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'--⎣⎦⎣⎦⎣⎦⎣⎦3.设新旧坐标系都是右手直角坐标系，点的坐标变换公式为5,3,22(1)(2) 2.3;22x x y x y y x y x y ⎛''=++ '=-+⎧⎨' =-⎩''=-+- ⎝ 其中，(,)x y 与(,)x y ''分别表示同一点的旧坐标与新坐标，求新坐标系的原点的旧坐标，并且求坐标轴旋转的角θ。

分析化学习题总汇 (4)

分析化学试卷学号：________ 姓名：________ 年级：________ 专业：________ 成绩：________第1部分填空题：（每空1分，共92分）1. 铬黑T(EBT)是一种有机弱酸，它的pK a1=6.3,pK a2=11.6，络合物Mg-EBT的lgK稳=7.0，则在pH=10时的lgK’Mg-EBT值为_________。

2. 要表示平均值的精密度，应使用________。

　3. 精密度是保证________的先决条件。

4. 考虑金属离子和EDTA的副反应，MY的条件稳定常数的对数为：_________________。

5. 0.10mol·L-1NH4HCO3溶液的pH值为_________。

6. 重量分析对称量形式的要求是_____________________________。

7. 化合物的分子中，OH基被SH基取代后，其在水中的溶解度会__________。

8. 已知CuS的K sp为6×10-36，则其在纯水中的溶解度为(忽略Cu2+的羟基配合物)________。

9. 双波长分光光度法进行定量分析的理论根据是__________________。

10. 用0.01000mol•L-1K2Cr2O7溶液滴定25.00mLFe2+溶液，耗去K2Cr2O7溶液25.00mL。

每毫升Fe2+溶液中含铁_________毫克。

11. 增加酸度，将使Cr2O2-7/Cr3+电对的电位_________。

12. 对可逆体系，n2O1 +n1R2 =n2R1 +n1O2滴定的突跃范围为____________________13. 示差分光光度法测定对比色皿的要求是___________________________。

14. 减小随机误差的方法是________。

15. 若杂质离子半径与构晶离子半径相似，形成的晶体结构相同，则它们易生成________。

习题4.1

(1)求a的值；解：(1) a=44.
(2)若新鞋号为m，旧鞋号为n，写出一个把旧鞋号
转换为新鞋号的公式. (2) m=5n+50.
课后作业
1.从教材习题中选取. 2.完成练习册本课时的习题.
第四章整式的加减 4.1 整式
习题 4.1
R ·七年级数学上册
复习巩固
1.单项式-4a2b3c的系数是__-_4__，次数是___6__.
2.写出一个系数是2，次数是3的单项式. 2xy2
（答案不唯一）
3.多项式a4-2a2b+b2的项为_a_4_,_-_2_a_2b_,_b_2_，次数是_4__.
解：立夏当日的日影长的近似值为( 10.5-6d ) 尺.
7.世界杯排球赛的积分规则为：比赛中以3-0(胜3局负0局）或者3-1取胜的球队积3分，负队积0分；比赛中以3-2取胜的球队积2分，负队积1分.若某球队以3-1胜了a场，以3-2胜了b场，以2-3负了c场，则这
支球队的积分用多项式可以表示为___3_a_+_2_b_+__c__.
拓广探索
8. 设n表示任意一个整数，用含n的代数式表示： (1)能被3整除的整数； (2)除以3余数为1的整数. 解：(1) 3n.
(2) 3n+1.
9.鞋号表明了鞋子的大小，我国1998年发布了新鞋号标准. 新鞋号标准对应于20世纪60年代后期制定的旧鞋号标准，部分鞋号对照如下
新鞋号 220 225 230 235 … 270 旧鞋号 34 35 36 37 … a
6. 我国古代数学著作《周髀算经》中提到，冬至、小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种这十二个节气中，在同一地点测量每个节气正午时同一根杆的日影长，发现每个节气与它后一个节气的日影长的差近似为定值.若这个定值为 d尺 (这里的尺是我国古代长度单位)，立春当日的日影长为10.5尺，求立夏当日日影长的近似值.