高中数学指数函数和对数函数测试题3
(完整版)指数函数对数函数专练习题(含答案).docx
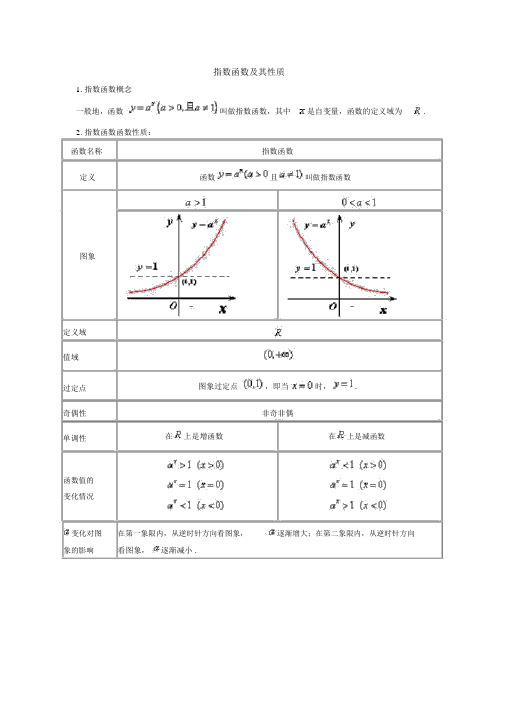
指数函数及其性质1.指数函数概念一般地,函数叫做指数函数,其中是自变量,函数的定义域为.2.指数函数函数性质:函数名称定义图象定义域值域过定点奇偶性单调性函数值的变化情况变化对图象的影响指数函数函数且叫做指数函数图象过定点,即当时,.非奇非偶在上是增函数在上是减函数在第一象限内,从逆时针方向看图象,逐渐增大;在第二象限内,从逆时针方向看图象,逐渐减小 .对数函数及其性质1.对数函数定义一般地,函数叫做对数函数,其中是自变量,函数的定义域.2.对数函数性质:函数名称定义函数对数函数且叫做对数函数图象定义域值域过定点奇偶性图象过定点,即当非奇非偶时,.单调性在上是增函数在上是减函数函数值的变化情况变化对图象的影响在第一象限内,从顺时针方向看图象,看图象,逐渐减小 .逐渐增大;在第四象限内,从顺时针方向指数函数习题一、选择题aa ≤ b,则函数 f ( x ) =1?2x 的图象大致为 ()1.定义运算 a ?b =>b a b2.函数 f ( x ) = x 2-bx + c 满足 f (1 + x ) =f (1 - x ) 且 f (0) =3,则 f ( b x ) 与 f ( c x ) 的大小关系是()xxA . f ( b ) ≤ f ( c ) x xB . f ( b ) ≥ f ( c )xxC . f ( b )> f ( c )D .大小关系随 x 的不同而不同3.函数 y = |2 x - 1| 在区间A . ( - 1,+∞ )C . ( - 1,1)( k - 1, k + 1) 内不单调,则 k 的取值范围是 ()B . ( -∞, 1)D . (0,2)4.设函数 f ( x ) =ln [( x -1)(2 -x)] 的定义域是 ,函数 ( ) = lg(x - 2x -1) 的定义域是 ,Ag xaB若 ?,则正数a 的取值范围 ()ABA . a >3B . a ≥ 3C . a > 5D . a ≥ 5.已知函数 f (x = 3- a x -3, x ≤ 7,若数列 { a n 满足 a n = f (n )(n ∈ * ,且 {a n }是递5 ) a x - 6, x >7. } N) 增数列,则实数a 的取值范围是 ()A . [ 9, 3)B . ( 9, 3) 44C . (2,3)D . (1,3)2x16.已知 a >0 且 a ≠ 1,f ( x ) = x - a ,当 x ∈ ( - 1,1) 时,均有 f ( x )< 2,则实数 a 的取值范围 是( )1 1 A . (0 , 2] ∪ [2 ,+∞ ) B . [ 4, 1) ∪ (1,4]11C . [ 2, 1) ∪ (1,2]D . (0 , 4) ∪ [4 ,+∞ )二、填空题xa7.函数 y = a ( a >0,且 a ≠ 1) 在 [1,2] 上的最大值比最小值大 2,则 a 的值是 ________.8.若曲线 | y | = 2 x + 1 与直线 y =b 没有公共点,则b 的取值范围是 ________.| x|的定义域为9. (2011 ·滨州模拟 ) 定义:区间 [x 1,x 2 ]( x 1<x 2) 的长度为 x 2- x 1. 已知函数 y = 2 [a , b] ,值域为 [1,2] ,则区间 [a , b] 的长度的最大值与最小值的差为 ________.三、解答题10.求函数y=2x2 3x 4 的定义域、值域和单调区间.11.(2011 ·银川模拟 ) 若函数y=a2x+ 2a x-1( a>0 且a≠ 1) 在x∈ [- 1,1]上的最大值为14,求a 的值.12.已知函数f (x) = 3x,(a+ 2) = 18, (x) =λ·3ax-4x的定义域为 [0,1] .f g(1)求 a 的值;(2) 若函数g( x) 在区间 [0,1] 上是单调递减函数,求实数λ的取值范围.1. 解析:由? = a a≤ b x2x x≤0,b a>b x>0 .1答案: A2. 解析:∵f (1 +x) =f (1 -x) ,∴f ( x) 的对称轴为直线x=1,由此得 b=2.又 f (0)=3,∴c=3.∴f ( x)在(-∞,1)上递减,在(1,+∞)上递增.x≥2x≥ 1,∴ (3 x) ≥(2 x) .若 x≥0,则3f f若 x<0,则3x<2x<1,∴f (3x)> f (2x).∴f (3x)≥ f (2x).答案: A3.解析:由于函数 y=|2x-1|在(-∞,0)内单调递减,在(0,+∞)内单调递增,而函数在区间 ( k- 1,k+ 1) 内不单调,所以有答案: Ck-1<0<k+1,解得-1<k<1.4.解析:由题意得: A=(1,2)x x>1x x>1在(1,2)上恒成立,即,a- 2且 a>2,由 A? B知 a- 2x x上恒成立,令x x xln a-2xln2>0 ,所以函数a-2 - 1>0 在 (1,2)u( x)=a- 2- 1,则u′( x) =au ( x ) 在 (1,2) 上单调递增,则 u ( x )> u (1) = a - 3,即 a ≥ 3.答案: B*f ( n ) 为增函数,5. 解析: 数列 { a } 满足 a = f ( n )( n ∈ N ) ,则函数nna >18- 6- ) × 7- 3,所以 3- a >0注意 a>(3,解得 2<a <3.aa8-6> 3- a × 7-3答案: C1 2x1 21 x x21的图象,6. 解析: f ( x )<? x -a < ? x - <a ,考查函数 y = a与 y =x - 2222当 a >1 时,必有 a-1≥1,即 1<a ≤ 2,21 1当 0<a <1 时,必有 a ≥ ,即 ≤a <1,2 2 1 综上, 2≤ a <1 或 1<a ≤ 2. 答案: C7. 解析: 当 a >1 时, y x在 [1,2] 上单调递增,故 2a3x= a a - a = ,得 a = . 当 0<a <1 时, y = a2 22a在 [1,2] 上单调递减,故 a -a = 2,得 a = 2. 故 a =2或 2.1131 3答案: 2或28. 解析: 分别作出两个函数的图象,通过图象的交点个数来判断参数的取值范围.x+1 与直线 y = b 的图象如图所示,由图象可得:如果x+ 1 与直线 y = b曲线 | y | = 2 | y | = 2没有公共点,则 b 应满足的条件是 b ∈ [- 1,1] .答案: [- 1,1]9. 解析: 如图满足条件的区间 [a , b] ,当 a =- 1, b = 0 或 a = 0, b = 1 时区间长度最小,最小值为 1,当 a =- 1,b = 1 时区间长度最大,最大值为2,故其差为 1.答案: 110. 解: 要使函数有意义,则只需- x 2-3x + 4≥ 0,即 x 2+ 3x -4≤ 0,解得- 4≤ x ≤ 1.∴函数的定义域为 { x | -4≤ x ≤ 1} .223225 令 t =- x - 3x + 4,则 t =- x - 3x + 4=- ( x + ) +4,2253∴当-4≤ x ≤ 1 时, t max = 4 ,此时 x =- 2, t min = 0,此时 x =- 4 或 x =1.∴0≤t ≤ 25 . ∴0≤ -x 2- 3x + 4≤ 5 .4 2∴函数 y = ( 1)x 23 x4的值域为 [ 2 , 1] .8223 225由 t =- x - 3x + 4=- ( x + )+4( - 4≤ x ≤ 1) 可知,23当- 4≤ x ≤- 2时, t 是增函数,3当- 2≤ x ≤1 时, t 是减函数.根据复合函数的单调性知:y = ( 1 )x 23 x 4在 [ - 4,- 3 3] 上是减函数,在 [ - ,1] 上是增函数.22 233∴函数的单调增区间是 [ - 2, 1] ,单调减区间是 [ - 4,- 2] . 11. 解: 令x22tt >0y= t+ 2t1= ( t+ 1)2,其对称轴为t =- 1.该二次函数a = ,∴ ,则--在[ - 1,+ ∞ ) 上是增函数.x12①若 a >1,∵x ∈ [ - 1,1] ,∴t = a ∈ [ a , a ] ,故当 t = a ,即 x =1 时, y max =a + 2a - 1=14,解得 a = 3( a =- 5 舍去 ) .②若 0<a <1,∵x ∈ [ - 1,1] ,∴ = x∈1 1=-时,a [ a , ] ,故当 t = ,即 1t a ax12y max = (a + 1) - 2= 14.11∴a =3或- 5( 舍去 ) .1综上可得 a = 3 或 3.12. 解: 法一: (1) 由已知得 a2 aa =log 32.3 += 18? 3 = 2?(2) 此时 g ( x ) = λ·2x - 4 x ,设 0≤ x 1<x 2≤ 1,因为 g ( x ) 在区间 [0,1] 上是单调减函数,所以 g ( x ) - g ( x ) = (2 x - 2x )( λ- 2x - 2x )>0 恒成立,即 λ<2x + 2x 恒成立.1 2 1 2 2 1 2 1由于 2x 2+ 2x 1>2 + 2 = 2,所以实数 λ的取值范围是λ≤ 2.法二: (1) 同法一.(2) 此时 g ( x ) = λ·2x - 4x ,因为 g ( x ) 在区间 [0,1] 上是单调减函数,所以有 g ′( x ) = λln2 ·2x - ln4 ·4x = ln2 [- 2 ·(2x )2+ λ·2x] ≤0 成立.x2 设 2 = u ∈ [1,2] ,上式成立等价于-2u+ λu ≤0 恒成立.因为 u ∈ [1,2] ,只需 λ≤2u 恒成立,所以实数 λ的取值范围是λ≤ 2.对数与对数函数同步练习一、选择题1、已知 3a2 ,那么 log3 8 2log 3 6 用 a 表示是()A 、 a 2B 、 5a2C 、 3a (1 a)2D 、 3a a 22、 2log a (M 2N ) log a Mlog a N ,则M的值为()A 、1NB 、4C 、1D 、 4 或 1413 、 已 知 x 2 y 2 1, x0, y 0 , 且 log a (1 x) m,log a n,则 log a y 等 于1 x()A 、 m nB 、 m nC 、 1m nD 、 1m n224、如果方程 lg 2 x (lg5lg 7)lgx lg5 glg 7 0 的两根是 ,,则 g的值是()A 、 lg5 glg 7B 、 lg35C 、 35D 、13515、已知 log 7[log 3 (log 2 x)] 0,那么 x2等于( )A 、1B 、13 C 、1D 、1322 2336、函数 ylg2 1 的图像关于()1 xA 、 x 轴对称B 、 y 轴对称C 、原点对称D 、直线 yx 对称7、函数 ylog (2 x 1) 3x2 的定义域是()A 、 2,1 U 1,B 、 1,1 U 1,32C 、 2,D 、 1,328、函数 ylog 1 (x 2 6x17) 的值域是()2A 、 RB 、 8,C 、, 3D 、 3,9、若 log m 9 log n 9 0 ,那么 m, n 满足的条件是( )A 、 m n 1B 、 n m 1C 、 0 n m 1D 、 0 m n 110、 log a 2 1,则 a 的取值范围是()3A 、 0, 2U 1,B 、 2,C 、 2,1D 、 0, 2U 2,3333 311、下列函数中,在 0,2 上为增函数的是()A 、 ylog 1 ( x1)B 、 y log 2 x 2 12C 、 ylog 2 1D 、 ylog 1 ( x 2 4x 5)x212、已知 g( x) log a x+1 ( a 0且a 1) 在 10, 上有 g( x)0 ,则 f ( x)a x 1 是( )A 、在 ,0上是增加的 B 、在 ,0 上是减少的C 、在, 1 上是增加的D 、在,0 上是减少的二、填空题13、若 log a 2 m,log a 3 n, a 2 m n 。
《指数函数和对数函数》单元检测试卷及答案

《指数函数和对数函数》单元检测试卷一、单选题 1.已知函数1()ln 1f x x x =--,则()y f x =的图象大致为( )A .B .C .D .2.已知函数1()3()3x xf x =-,则()f x ( )A .是奇函数,且在R 上是增函数B .是偶函数,且在R 上是增函数C .是奇函数,且在R 上是减函数D .是偶函数,且在R 上是减函数3.函数y =a x-1a(a >0,且a ≠1)的图象可能是( ) A .B .C .D .4.已知函数3,0,(),0.x x f x x x ⎧=⎨-<⎩若函数2()()2()g x f x kx xk =--∈R 恰有4个零点,则k 的取值范围是( )A .1,(22,)2⎛⎫-∞-+∞ ⎪⎝⎭B .1,(0,22)2⎛⎫-∞- ⎪⎝⎭C .(,0)(0,22)-∞ D .(,0)(22,)-∞+∞5.已知集合{|13}A x x =-<<,(){|lg 1}B x y x ==-,则()R A B =( ) A .B .()13-,C .()11-,D .(]11-,6.设函数()y f x =的图像与2x ay +=的图像关于直线y x =-对称,且(2)(4)1f f -+-=,则a =( ) A .1-B .1C .2D .47.如果方程2lg (lg 2lg 3)lg lg 2lg 30x x +++=的两根为1x 、2x ,则12x x 的值为( )A .lg 2lg3B .lg 2lg3+C .16D .6-8.若242log 42log a ba b +=+,则( )A .2a b >B .2a b <C .2a b >D .2a b <9.基本再生数R 0与世代间隔T 是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:(e )rt I t =描述累计感染病例数I (t )随时间t (单位:天)的变化规律,指数增长率r 与R 0,T 近似满足R 0 =1+rT .有学者基于已有数据估计出R 0=3.28,T =6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln2≈0.69) ( ) A .1.2天 B .1.8天 C .2.5天 D .3.5天 二、多选题10.已知函数1()3x p f x -=,2()3x p g x -=,12p p ≠,则下列四个结论中正确的是( )A .()y f x =的图象可由()y g x =的图象平移得到B .函数()()f x g x +的图象关于直线122p p x +=对称 C .函数()()f x g x -的图象关于点12,02p p +⎛⎫⎪⎝⎭对称 D .不等式()()f x g x >的解集是12,2p p +⎛⎫+∞⎪⎝⎭11.设()f x 是定义在(,)-∞+∞上的偶函数,且它在[0,)+∞上单调递增,若a f ⎛= ⎝,b f ⎛= ⎝,(2)c f =-,则a ,b ,c 的大小关系是( ) A .c a >B .a c >C .a b >D .b c >12.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数“为:设x ∈R ,用[]x 表示不超过x 的最大整数,则[]y x =称为高斯函数,例如:[ 3.5]4-=-,[2.1]2=.已知函数1()12=-+x xe f x e ,则关于函数()[()]g x f x =的叙述中正确的是( ) A .()g x 是偶函数B .()f x 是奇函数C .()f x 在R 上是增函数D .()g x 的值域是{}1,0,1-三、填空题13.函数()πcos 36f x x ⎛⎫=+ ⎪⎝⎭在[]0π,的零点个数为________.14.151lg 2lg 222-⎛⎫+- ⎪⎝⎭=______.15.函数()log 31,(0a y x a =+->且1)a ≠的图象恒过定点A ,若点A 在直线10mx ny ++=上(其中m ,n >0),则12m n+的最小值等于__________. 16.设()f x 是定义在R 且周期为1的函数,在区间[)0,1上,()2,,x x Df x x x D ⎧∈=⎨∉⎩其中集合1,n D x x n N n *⎧⎫-==∈⎨⎬⎩⎭,则方程()lg 0f x x -=的解的个数是____________ 四、解答题17.已知函数()2()log log 2(0,1)a a f x x x a a =-->≠. (1)当2a =时,求(2)f ; (2)求解关于x 的不等式()0f x >;(3)若[2,4],()4x f x ∀∈≥恒成立,求实数a 的取值范围.18.已知函数()22221log a x f x x--=(0a >且1a ≠). (1)求()f x 的解析式,再判断()f x 的奇偶性; (2)解关于x 的方程1()log 1a f x x=-.19.已知函数1()21x f x -=-.(1)作出函数()y f x =的图象;(2)若a c <,且()()f a f c >,求证:224a c +<.20.已知函数()ln f x x =.(1)若2()()4()6g x f x f x =-+的定义域为31,e e⎡⎤⎢⎥⎣⎦(e 是自然对数的底数),求函数()g x 的最大值和最小值; (2)求函数()2()||h x f x x =+的零点个数.21.如图,一个湖的边界是圆心为O 的圆,湖的一侧有一条直线型公路l ,湖上有桥AB (AB 是圆O 的直径).规划在公路l 上选两个点P 、Q ,并修建两段直线型道路PB 、QA .规划要求:线段PB 、QA 上的所有点到点O 的距离均不小于圆....O 的半径.已知点A 、B 到直线l 的距离分别为AC 和BD (C 、D 为垂足),测得AB =10,AC =6,BD =12(单位:百米).(1)若道路PB 与桥AB 垂直,求道路PB 的长;(2)在规划要求下,P 和Q 中能否有一个点选在D 处?并说明理由;(3)对规划要求下,若道路PB 和QA 的长度均为d (单位:百米).求当d 最小时,P 、Q 两点间的距离.22.已知函数121()log 21axf x x -=-,a 常数. (1)若2a =-,求证()f x 为奇函数,并指出()f x 的单调区间;(2)若对于35,22x ⎡⎤∈⎢⎥⎣⎦,不等式1221log (21)log (21)4xx m x ⎛⎫+->-- ⎪⎝⎭恒成立,求实数m的取值范围。
(精选试题附答案)高中数学第四章指数函数与对数函数真题

(名师选题)(精选试题附答案)高中数学第四章指数函数与对数函数真题单选题1、设a=log2π,b=log6π,则()A.a−b<0<ab B.ab<0<a−bC.0<ab<a−b D.0<a−b<ab答案:D分析:根据对数函数的性质可得a−b>0,ab>0,1b −1a<1,由此可判断得选项.解:因为a=log2π>log22=1,0=log61<b=log6π<log66=1,所以a>1,0<b<1,所以a−b>0,ab>0,故排除A、B选项;又1b −1a=a−bab=logπ6−logπ2=logπ3<logππ<1,且ab>0,所以0<a−b<ab,故选:D.2、若函数f(x)=x3+x2−2x−2的一个正零点附近的函数值用二分法计算,其参考数据如下:那么方程x3+x2−2x−2=0的一个近似根(精确度0.1)为().A.1.2B.1.4C.1.3D.1.5答案:B分析:根据二分法求零点的步骤以及精确度可求得结果.解:因为f(1)<0,f(1.5)>0,所以f(1)f(1.5)<0,所以函数在(1,1.5)内有零点,因为1.5−1=0.5>0.1,所以不满足精确度0.1;因为f(1.25)<0,所以f(1.25)f(1.5)<0,所以函数在(1.25,1.5)内有零点,因为1.5−1.25=0.25>0.1,所以不满足精确度0.1;因为f(1.375)<0,所以f(1.375)f(1.5)<0,所以函数在(1.375,1.5)内有零点,因为1.5−1.375=0.125>0.1,所以不满足精确度0.1;因为f(1.4375)>0,所以f(1.4375)f(1.375)<0,所以函数在(1.375,1.4375)内有零点,因为1.4375−1.375=0.0625<0.1,所以满足精确度0.1;所以方程x 3+x 2−2x −2=0的一个近似根(精确度0.05)是区间(1.375,1.4375)内的任意一个值(包括端点值),根据四个选项可知选B . 故选:B3、已知55<84,134<85.设a =log 53,b =log 85,c =log 138,则( ) A .a <b <c B .b <a <c C .b <c <a D .c <a <b 答案:A分析:由题意可得a 、b 、c ∈(0,1),利用作商法以及基本不等式可得出a 、b 的大小关系,由b =log 85,得8b =5,结合55<84可得出b <45,由c =log 138,得13c =8,结合134<85,可得出c >45,综合可得出a 、b 、c 的大小关系.由题意可知a 、b 、c ∈(0,1),a b =log 53log 85=lg3lg5⋅lg8lg5<1(lg5)2⋅(lg3+lg82)2=(lg3+lg82lg5)2=(lg24lg25)2<1,∴a <b ;由b =log 85,得8b =5,由55<84,得85b <84,∴5b <4,可得b <45; 由c =log 138,得13c =8,由134<85,得134<135c ,∴5c >4,可得c >45.综上所述,a <b <c . 故选:A.小提示:本题考查对数式的大小比较,涉及基本不等式、对数式与指数式的互化以及指数函数单调性的应用,考查推理能力,属于中等题.4、已知函数f (x )={a +a x ,x ≥03+(a −1)x,x <0(a >0 且a ≠1),则“a ≥3”是“f (x )在R 上单调递增”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件答案:A分析:先由f(x)在R 上单调递增求得a 的取值范围,再利用充分条件,必要条件的定义即得. 若f(x)在R 上单调递增, 则{a >1a −1>0a +1≥3 , 所以a ≥2,由“a ≥3”可推出“a ≥2”,但由“a ≥2”推不出 “a ≥3”, 所以“a ≥3”是“f(x)在R 上单调递增”的充分不必要条件. 故选:A.5、已知9m =10,a =10m −11,b =8m −9,则( ) A .a >0>b B .a >b >0C .b >a >0D .b >0>a 答案:A分析:法一:根据指对互化以及对数函数的单调性即可知m =log 910>1,再利用基本不等式,换底公式可得m >lg11,log 89>m ,然后由指数函数的单调性即可解出. [方法一]:(指对数函数性质) 由9m =10可得m =log 910=lg10lg9>1,而lg9lg11<(lg9+lg112)2=(lg992)2<1=(lg10)2,所以lg10lg9>lg11lg10,即m >lg11,所以a =10m −11>10lg11−11=0.又lg8lg10<(lg8+lg102)2=(lg802)2<(lg9)2,所以lg9lg8>lg10lg9,即log 89>m ,所以b =8m −9<8log 89−9=0.综上,a >0>b . [方法二]:【最优解】(构造函数) 由9m =10,可得m =log 910∈(1,1.5).根据a,b 的形式构造函数f(x)=x m −x −1(x >1) ,则f ′(x)=mx m−1−1, 令f ′(x)=0,解得x 0=m11−m,由m =log 910∈(1,1.5) 知x 0∈(0,1) .f(x)在(1,+∞)上单调递增,所以f(10)>f(8),即a>b,又因为f(9)=9log910−10=0,所以a>0>b .故选:A.【整体点评】法一:通过基本不等式和换底公式以及对数函数的单调性比较,方法直接常用,属于通性通法;法二:利用a,b的形式构造函数f(x)=x m−x−1(x>1),根据函数的单调性得出大小关系,简单明了,是该题的最优解.6、已知函数f(x)={2,x>mx2+4x+2,x≤m,若方程f(x)−x=0恰有三个根,那么实数m的取值范围是()A.[−1,2)B.[−1,2]C.[2,+∞)D.(−∞,−1]答案:A分析:由题意得,函数y=f(x)与函数y=x有三个不同的交点,结合图象可得出结果.解:由题意可得,直线y=x与函数f(x)=2(x>m)至多有一个交点,而直线y=x与函数f(x)=x2+4x+2(x≤m)至多两个交点,函数y=f(x)与函数y=x有三个不同的交点,则只需要满足直线y=x与函数f(x)=2(x>m)有一个交点直线y=x与函数f(x)=x2+4x+2(x≤m)有两个交点即可,如图所示,y=x与函数f(x)=x2+4x+2的图象交点为A(−2,−2),B(−1,−1),故有m≥−1.而当m≥2时,直线y=x和射线y=2(x>m)无交点,故实数m的取值范围是[−1,2).故选:A.7、已知x ,y ,z 都是大于1的正数,m >0,log x m =24,log y m =40,log xyz m =12,则log z m 的值为( ) A .160B .60C .2003D .320答案:B分析:根据换底公式将log x m =24,log y m =40,log xyz m =12,化为log m x =124,log m y =140,log m xyz =112,再根据同底数的对数的加减法运算即可得解. 解:因为log x m =24,log y m =40,log xyz m =12, 所以log m x =124,log m y =140,log m xyz =112,即log m x +log m y +log m z =112,∴log m x =112−log m y −log m z =112−124−140=160, ∴log z m =60. 故选:B .8、下列函数中是增函数的为( )A .f (x )=−xB .f (x )=(23)xC .f (x )=x 2D .f (x )=√x 3答案:D分析:根据基本初等函数的性质逐项判断后可得正确的选项. 对于A ,f (x )=−x 为R 上的减函数,不合题意,舍. 对于B ,f (x )=(23)x为R 上的减函数,不合题意,舍. 对于C ,f (x )=x 2在(−∞,0)为减函数,不合题意,舍.对于D,f(x)=√x3为R上的增函数,符合题意,故选:D.9、已知函数f(x)={a x,x<0(a−3)x+4a,x≥0满足对任意x1≠x2,都有(x1-x2)[f(x1)-f(x2)]<0成立,则a的取值范围为()A.(0,14]B.(0,1)C.[14,1)D.(0,3)答案:A分析:根据给定不等式可得函数f(x)为减函数,再利用分段函数单调性列出限制条件求解即得.因对任意x1≠x2,都有(x1-x2)[f(x1)-f(x2)]<0成立,不妨令x1<x2,则f(x1)>f(x2),于是可得f(x)为R上的减函数,则函数y=a x在(−∞,0)上是减函数,有0<a<1,函数y=(a−3)x+4a在[0,+∞)上是减函数,有a−3<0,即a<3,并且满足:a0≥f(0),即4a≤1,解和a≤14,综上得0<a≤14,所以a的取值范围为(0,14].故选:A10、如图所示,函数y=|2x−2|的图像是()A.B.C.D.答案:B分析:将原函数变形为分段函数,根据x=1及x≠1时的函数值即可得解.∵y=|2x−2|={2x−2,x≥12−2x,x<1,∴x=1时,y=0,x≠1时,y>0. 故选:B.填空题11、化简:(1+1232)(1+1216)(1+128)(1+124)(1+122)(1+12)=________.答案:2−1263分析:分析式子可以发现,若在结尾乘以一个(1−12),则可以从后到前逐步使用平方差公式进行计算,为保证恒等计算,在原式末尾乘以(1−12)×2即可﹒原式=(1+1232)(1+1216)(1+128)(1+124)(1+122)(1+12)×(1−12)×2=(1+1232)(1+1216)(1+128)(1+124)(1+122)×(1−122)×2 =(1+1232)(1+1216)(1+128)(1+124)×(1−124)×2=(1+1232)(1+1216)(1+128)×(1−128)×2=(1+1232)(1+1216)×(1−1216)×2=(1+1232)×(1−1232)×2=(1−1264)×2=2−1263所以答案是:2−1263﹒12、不等式log4x≤12的解集为___________.答案:(0,2]分析:根据对数函数的单调性解不等式即可. 由题设,可得:log 4x ≤log 4412,则0<x ≤412=2, ∴不等式解集为(0,2]. 所以答案是:(0,2].13、在用二分法求函数f (x )的零点近似值时,若第一次所取区间为[−2,6],则第三次所取区间可能是______.(写出一个符合条件的区间即可) 答案:[−2,0]或[0,2]或[2,4]或[4,6](写一个即可). 分析:根据二分法的概念,可求得结果.第一次所取区间为[−2,6],则第二次所取区间可能是[−2,2],[2,6];第三次所取区间可能是[−2,0],[0,2],[2,4],[4,6].所以答案是:[−2,0]或[0,2]或[2,4]或[4,6](写一个即可).14、设函数f(x)={2x +1,x ≤0|lgx |,x >0,若关于x 的方程f 2(x )−af (x )+2=0恰有6个不同的实数解,则实数a 的取值范围为______. 答案:(2√2,3)分析:作出函数f(x)的图象,令f(x)=t ,结合图象可得,方程t 2−at +2=0在(1,2]内有两个不同的实数根,然后利用二次函数的性质即得;作出函数f(x)={2x +1,x ≤0|lgx |,x >0的大致图象,令f (x )=t ,因为f 2(x )−af (x )+2=0恰有6个不同的实数解, 所以g (t )=t 2−at +2=0在区间(1,2]上有2个不同的实数解,∴{Δ=a 2−8>01<a2<2g (1)=3−a >0g (2)=6−2a ≥0 , 解得2√2<a <3,∴实数a 的取值范围为(2√2,3). 所以答案是:(2√2,3).15、函数y =log a (kx −5)+b (a >0且a ≠1)恒过定点(2,2),则k +b =______. 答案:5分析:根据对数函数的图象与性质,列出方程组,即可求解. 由题意,函数y =log a (kx −5)+b 恒过定点(2,2),可得{2k −5=1b =2 ,解得k =3,b =2,所以k +b =3+2=5.所以答案是:5. 解答题16、(1)计算:(1100)−12−√(1−√2)2−8×(√5−√3)0+816;(2)已知x +x −1=4,求x 12+x −12. 答案:(1)3;(2)x 12+x −12=√6.分析:(1)根据指数幂的运算法则进行计算,求得答案; (2)先判断出x >0,然后将x 12+x −12平方后结合条件求得答案. (1)原式=[(100)−1]−12−(√2−1)−8+(23)16,=10012−√2+1−8+212=10+1−8=3.(2)由于x +x−1=4>0,所以x >0,(x 12+x −12)2=x +x −1+2=6,所以x 12+x −12=√6.17、(1)证明对数换底公式:log b N =log a N log a b(其中a >0且a ≠1,b >0且b ≠1,N >0)(2)已知log 32=m ,试用m 表示log 3218. 答案:(1)证明见解析;(2)log 3218=2+m 5m.分析:(1)将对数式转化为指数式,然后两边取对数,利用对数函数的应算法则,即可证明. (2)利用换底公式将等号左边化为以3为底的对数,然后根据对数运算法则化简即得. (1)设log b N =x ,写成指数式b x =N . 两边取以a 为底的对数,得xlog a b =log a N .因为b >0,b ≠1,log a b ≠0,因此上式两边可除以log a b ,得x =log a N log a b.所以,log b N =log a N log a b.(2)log 3218=log 318log 332=log 332+log 32log 325=2+log 325log 32=2+m 5m.小提示:本题考查换底公式的证明和应用,属基础题,关键是将对数式转化为指数式,然后两边取对数,利用对数函数的应算法则,即可证明. 18、已知函数f (x )=a x −1a x +1(a >0,且a ≠1). (1)若f (2)=35,求f (x )解析式; (2)讨论f (x )奇偶性.答案:(1)f (x )=2x −12x +1;(2)奇函数.分析:(1)根据f (2)=35,求函数的解析式;(2)化简f (−x ),再判断函数的奇偶性. 解:(1)∵f (x )=a x −1a x +1,f (2)=35.即a 2−1a 2+1=35,∴a =2.即f (x )=2x −12x +1.(2)因为f (x )的定义域为R ,且f (−x )=a −x −1a −x +1=1−a x1+a x =−f (x ),所以f (x )是奇函数.19、如图,某中学准备在校园里利用院墙的一段,再砌三面墙,围成一个矩形花园ABCD ,已知院墙MN 长为25米,篱笆长50米(篱笆全部用完),设篱笆的一面AB 的长为x 米.(1)当AB 的长为多少米时,矩形花园的面积为300平方米?(2)若围成的矩形ABCD 的面积为 S 平方米,当 x 为何值时, S 有最大值,最大值是多少?答案:(1)15米;(2)当 x 为12.5米时, S 有最大值,最大值是312.5平方米.分析:(1)设篱笆的一面AB 的长为 x 米,则BC =(50−2x)m ,根据“矩形花园的面积为300平方米”列一元二次方程,求解即可;(2)根据题意,可得S =x(50−2x),根据二次函数最值的求法求解即可.(1)设篱笆的一面AB 的长为 x 米,则BC =(50−2x)m ,由题意得,x(50−2x)=300,解得x 1=15,x 2=10,∵50−2x ≤25,∴x ≥12.5,∴x=15,所以,AB的长为15米时,矩形花园的面积为300平方米;(2)由题意得,S=x(50−2x)=−2x2+50x=−2(x−12.5)2+312.5,12.5≤x<25∴x=12.5时,S取得最大值,此时,S=312.5,所以,当x为12.5米时,S有最大值,最大值是312.5平方米.。
深圳文成学校必修一第三单元《指数函数和对数函数》检测题(含答案解析)

一、选择题1.设a ,b ,c 为正数,且3a =4b =6c ,则有( ) A .111c a b=+ B .221c a b=+ C .122c a b=+ D .212c a b=+ 2.函数()212()log 23f x x x =--+单调减区间为( )A .(,1]-∞-B .(3,1]--C .[)1,1-D .[)1-+∞, 3.若x ,y ,z 是正实数,满足2x =3y =5z ,试比较3x ,4y ,6z 大小( ) A .3x >4y >6z B .3x >6z >4y C .4y >6z >3xD .6z >4y >3x4.已知函数||()2x f x =,记131(())4a f =,37(log )2b f =,13(log 5)c f =,则a ,b,c 的大小关系为( )A .c b a >>B .b a c >>C .a b c >>D .c a b >>5.已知函数3()22x f x =+,则111357(1)432234f f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++++= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭( ) A .212 B .214C .7D .1526.函数1()1x f x a +=-恒过定点( )A .(1,1)B .(1,1)-C .(1,0)-D .(1,1)--7.如图是指数函数①y =x a ;②y =x b ;③y =c x ;④y =d x 的图象,则a ,b ,c ,d 与1的大小关系是( )A .a <b <1<c <dB .b <a <1<d <cC .1<a <b <c <dD .a <b <1<d <c8.已知235log log log 0x y z ==<,则2x 、3y 、5z的大小排序为A .235x y z <<B .325y x z<<C .523z x y <<D .532z y x<<9.已知函数()sin 2f x x x =-,且()0.3231ln ,log ,223a f b f c f ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,则以下结论正确的是 A .c a b >>B .a c b >>C .a b c >>D .b a c >>10.函数()log (2)a f x ax =-(0a >且1a ≠)在[]0,3上为增函数,则实数a 的取值范围是( )A .2,13⎛⎫⎪⎝⎭B .(0,1)C .20,3⎛⎫ ⎪⎝⎭D .[)3,+∞ 11.设0.512a ⎛⎫= ⎪⎝⎭,0.50.3b =,0.3log 0.2c =,则a 、b 、c 的大小关系( ). A .b a c <<B .a b c <<C .a b c >>D .a c b <<12.如果函数(0,1)x y a a a =>≠的反函数是增函数,那么函数log (1)a y x =-+的图象大致是( )A .B .C .D .二、填空题13.现有下列四个结论:①若25a b m ==且a b =时,则1m =; ②若236log log log a b c ==,则c ab =;③对函数()3xf x =定义域内任意的1x ,都存在唯一的2x ,使得()()121f x f x ⋅=成立;④存在实数a ,使得函数()()2ln g x x ax a =++的定义域和值域均为R .其中所有正确结论的序号是_________.14.()()2lg 45f x x x =--+的单调递增区间为______.15.函数()()12log 13y x x =-+的递增区间为______.16.给定函数y =f (x ),设集合A ={x |y =f (x )},B ={y |y =f (x )}.若对于∀x ∈A ,∃y ∈B ,使得x +y =0成立,则称函数f (x )具有性质P .给出下列三个函数:①1y x =;②12xy ⎛⎫= ⎪⎝⎭;③y =lgx .其中,具有性质P 的函数的序号是_____. 17.给出下列命题:①函数2x y =与2log y x =互为反函数,其图象关于直线y x =对称; ②已知函数2(1)21f x x x -=-+,则(5)26f =;③当0a >且1a ≠时,函数()log (2)3a f x x =--的图像必过定点(3,3)-; ④用二分法求函数()ln 26f x x x =+-在区间(2,3)内的零点近似值,至少经过3次二分后精确度达到0.1;⑤函数2()2x f x x =-的零点有2个. 其中所有正确命题....的序号是______ 18.已知1a b >>,若10log log 3a b b a +=,b a a b =,则ab =___________. 19.已知3(1)4,1()1,1a a x a x f x og x x -+<⎧=⎨≥⎩是R 上的减函数,那么a 的取值范围是__________.20.若函数1log 12a y x ⎛⎫=+⎪⎝⎭在区间3,62⎡⎤-⎢⎥⎣⎦有最小值-2,则实数a =_______.三、解答题21.已知函数()2221log 2m x f x x-=-(0m >且1m ≠) (1)求()f x 的解析式;(2)判断函数()f x 的奇偶性,并说明理由;(3)若关于x 的方程()1log m f x x =+有解,求m 的取值范围. 22.已知函数()3lg3xf x x+=-. (1)求函数()f x 的定义域;(2)判断函数()f x 的奇偶性,并说明理由. 23.已知函数()22x x f x k -=+. (1)若()f x 为偶函数,求实数k 的值;(2)若()4f x 在2[log x m ∈,2log (2)](m m +为大于0的常数)上恒成立,求实数k 的最小值.24.分别计算下列数值:(1)1lg3lg94lg81lg 27+--;(2)已知()1401x xx -+=<<,求221122x x x x---+.25.已知函数210(),22,01xx ax a x f x a a x ⎧+--≤<=⎨-≤≤⎩,其中a >0且a ≠1. (1)当12a =时,求f (x )的值域; (2)函数y =f (x )能否成为定义域上的单调函数,如果能,则求出实数a 的范围;如果不能,则给出理由;(3)()2f x -在其定义域上恒成立,求实数a 的取值范围. 26.已知函数()f x 是定义在R 上的奇函数,当0x 时,()121xaf x =++. (1)求实数a 的值及()f x 的解析式; (2)求方程4|(1)|5f x -=的解.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】首先根据指对互化求出,,a b c ,再根据换底公式表示111,,a b c,最后根据对数运算法则化简. 【详解】设3a =4b =6c =k , 则a =log 3k , b =log 4k , c =log 6k , ∴311log 3log k a k ==, 同理1log 4k b =,1log 6k c=, 而11log 2,log 3log 22k k k b c ==+, ∴1112c a b =+,即221c a b =+. 故选:B 【点睛】本题考查指对数运算,换底公式,以及对数运算的性质,关键是灵活应用对数运算公式,公式1log log a b b a=是关键. 2.B解析:B【分析】根据复合函数的单调性可知,()()212log 23f x x x =--+的单调减区间为223t x x =--+在定义域上的单调增区间.再根据一元二次函数的单调性求单调增区间即可. 【详解】解:函数()()212log 23f x x x =--+的定义域为()3,1-令223t x x =--+,则()12log g t t =为单调递减函数,由复合函数的单调性可知:()f x 的单调递减区间为223t x x =--+在()3,1-上的单调增区间.()222314t x x x =--+=-++,对称轴为1x =-,开口向下,所以223t x x =--+的单调增区间为(]3,1--. 故选:B. 【点睛】本题考查复合函数的单调性,属于中档题. 方法点睛:(1)先求出函数的定义域; (2)判断外层函数的单调性;(3)根据复合函数同增异减的原则,判断要求的内层函数的单调性; (4)求出单调区间.3.B解析:B 【分析】令235x y z t ===,则1t >,lg lg 2t x =,lg lg 3t y =,lg lg 5tz =,利用作差法能求出结果. 【详解】∵x 、y 、z 均为正数,且235x y z ==, 令235x y z t ===,则1t >, 故2lg log lg 2t x t ==,3lg log lg 3t y t ==,5lg log lg 5tz t ==, ∴()3lg lg5lg 4lg 2lg 3630lg 2lg5lg 2lg5t t t x z -⎛⎫-=-=>⎪⋅⎝⎭,即36x z >; ()2lg lg 27lg 253lg 2lg 6420lg5lg3lg3lg5t t t z y -⎛⎫-=-=> ⎪⋅⎝⎭,即64z y >, 即364x z y >>成立,故选:B. 【点睛】关键点点睛:(1)将指数式转化为对数式; (2)利用作差法比较大小.4.A解析:A 【分析】首先判断函数()f x 的性质,再比较133317,log ,log 542⎛⎫ ⎪⎝⎭的大小关系,从而利用单调性比较a ,b ,c 的大小关系. 【详解】()2xf x =是偶函数,并且当0x >时,2x y =是增函数,()133log 5log 5c f f ⎛⎫== ⎪⎝⎭,因为1310()14<<,3371log log 52<<,即1333170log log 542⎛⎫<<< ⎪⎝⎭ 又因为()y f x =在()0,∞+是增函数,所以a b c <<. 故选:A. 【点睛】关键点点睛:本题考查利用函数的单调性和奇偶性比较函数值的大小,本题的关键是判断函数()2xf x =的性质,后面的问题迎刃而解.5.B解析:B 【分析】先利用解析式计算3()(2)2f x f x +-=,再计算和式即可得到结果. 【详解】 因为3()22xf x =+, 所以2332(2)22224xx x f x -⋅-==+⋅+,()3323()(2)222222x x x f x f x ⋅+-=+=++. 故1113573321(1)34322342224f f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++++=⨯+=⎪ ⎪ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭. 故选:B. 【点睛】本题解题关键是通过指数式运算计算3()(2)2f x f x +-=,再配对求和即解决问题.解析:C 【分析】根据指数函数性质求定点. 【详解】因为01a =,所以()011f a -=-=0,因此过定点()1,0-,选C.【点睛】本题考查指数函数性质以及定点问题,考查基本分析求解能力,属于基础题.7.B解析:B 【分析】根据指数函数的图象与性质可求解. 【详解】根据函数图象可知函数①y =x a ;②y =x b 为减函数,且1x =时,②y =1b <①y =1a , 所以1b a <<,根据函数图象可知函数③y =c x ;④y =d x 为增函数,且1x =时,③y =c 1>④y =d 1, 所以1c d >> 故选:B 【点睛】本题主要考查了指数函数的单调性,指数函数的图象,数形结合的思想,属于中档题.8.A解析:A 【解析】x y z ,, 为正实数,且235log log log 0x y z ==<,111235235k k k x y z ---∴===,,,可得:1112352131,51k kk x y z ---=>=>=>,. 即10k -> 因为函数1kf x x -=() 单调递增,∴235x y z<<.故选A.9.D解析:D 【解析】因为()cos 20f x x '=-<,所以函数()sin 2f x x x =-的单调递减函数,又因为0.3213log 0,ln ln 1,12232e <<=<<,即0.3213log ln 232<<,所以由函数的单调性可得:0.3213(log )(ln )(2)32f f f >>,应选答案D .解析:C 【分析】根据对数函数性质与复合函数的单调性求解. 【详解】因为0a >且1a ≠,令2t ax =-,所以函数2t ax =-在[]0,3上为减函数, 所以函数log a y t =应是减函数,()f x 才可能是增函数, ∴01a <<,因为函数()f x 在[]0,3上为增函数, 由对数函数性质知230a ->,即23<a , 综上023a <<. 故选:C . 【点睛】本题考查复合函数的单调性,掌握对数函数性质是解题关键,考查逻辑思维能力和计算能力,属于常考题.11.A解析:A 【分析】利用对数函数,幂函数的单调性比较大小即可. 【详解】解:因为12y x =在[0,)+∞上单调递增,110.32>>所以0.50.50.5110.32⎛⎫> ⎪⎝⎭>,即0.50.5110.32⎛⎫>> ⎪⎝⎭因为0.30.3log 0.2log 0.31>= 所以b a c << 故选:A 【点睛】本题主要考查了利用对数函数,幂函数的单调性比较大小,是中档题.12.C解析:C 【分析】由题意求得1a >,再结合对数函数的图象与性质,合理排除,即可求解. 【详解】因为函数(0,1)xy a a a =>≠的反函数是增函数,可得函数xy a =为增函数,所以1a >,所以函数log (1)a y x =-+为减函数,可排除B 、D ; 又由当0x =时,log (01)0a y =-+=,排除A. 故选:C. 【点睛】本题主要考查了指数函数和对数函数的图象与性质的应用,其中解答中熟记指数函数和对数函数的图象与性质,以及指数函数与对数的关系是解答的关键,着重考查推理与运算能力.二、填空题13.①②③【分析】利用换底公式结合求得的值可判断①的正误;设利用对数与指数的互化以及指数的运算性质可判断②的正误;由求得可判断③的正误;求出函数的定义域值域分别为时对应的实数的取值范围可判断④的正误【详解析:①②③ 【分析】利用换底公式结合a b =,求得m 的值,可判断①的正误;设236log log log a b c t ===,利用对数与指数的互化以及指数的运算性质可判断②的正误;由()()121f x f x ⋅=求得21x x =-,可判断③的正误;求出函数()g x 的定义域、值域分别为R 时,对应的实数a 的取值范围,可判断④的正误. 【详解】对于①,由于250a b m ==>,可得2lg log lg 2m a m ==,5lg log lg 5mb m ==, 由于a b =可得lg lg lg 2lg 5m m=,则lg 0m =,解得1m =,①正确; 对于②,设236log log log a b c t ===,可得2t a =,3t b =,6t c =,则236t t t ab c =⋅==,②正确;对于③,对任意的1x R ∈,则()()1212123331xxx x f x f x +⋅=⋅==,120x x ∴+=,可得21x x =-,③正确;对于④,若函数()()2ln g x x ax a =++的定义域为R ,对于函数2y x ax a =++,240a a ∆=-<,解得01a <<;若函数()()2ln g x x ax a =++的值域为R ,则函数2y x ax a =++的值域包含()0,∞+,则240a a ∆=-≥,解得0a ≤或1a ≥.所以,不存在实数a ,使得函数()()2ln g x x ax a =++的定义域和值域均为R ,④错误.故答案为:①②③.【点睛】关键点点睛:解本题第④问的关键点在于找到函数()()2ln g x x ax a =++的定义域为R的等价条件∆<0;函数()()2ln g x x ax a =++的值域为R 的等价条件0∆≥.14.【分析】由复合函数的单调性只需求出的增区间即可【详解】令则由与复合而成因为在上单调递增且在上单调递增所以由复合函数的单调性知在上单调递增故答案为:【点睛】本题主要考查了复合函数的单调性对数函数的单调 解析:(]5,2--【分析】由复合函数的单调性,只需求出245t x x =--+的增区间即可. 【详解】令245t x x =--+,则()()2lg 45f x x x =--+由lg y t =与245t x x =--+复合而成,因为lg y t =在(0,)t ∈+∞上单调递增,且245(0)t x x t =--+>在(5,2]x ∈--上单调递增,所以由复合函数的单调性知,()()2lg 45f x x x =--+在(5,2]x ∈--上单调递增.故答案为:(]5,2-- 【点睛】本题主要考查了复合函数的单调性,对数函数的单调性,二次函数的单调性,属于中档题.15.【分析】首先求出函数的定义域再根据复合函数的单调性计算可得【详解】解:则解得即函数的定义域为令则因为在上单调递增在上单调递减;在定义域上单调递减根据复合函数的单调性同增异减可知函数在上单调递增故答案 解析:()1,1-【分析】首先求出函数的定义域,再根据复合函数的单调性计算可得. 【详解】 解:()()12log 13y x x =-+则()()130x x -+>解得31x -<<即函数的定义域为()3,1- 令()()()()21314t x x x x =-+=-++,()3,1x ∈-,则12logy t =因为()t x 在()3,1--上单调递增,在()1,1-上单调递减;12log y t =在定义域上单调递减根据复合函数的单调性“同增异减”可知函数()()12log 13y x x =-+在()1,1-上单调递增故答案为:()1,1-【点睛】本题考查复合函数的单调区间的计算,属于基础题.16.①③【分析】A 即为函数的定义域B 即为函数的值域求出每个函数的定义域及值域直接判断即可【详解】对①A =(﹣∞0)∪(0+∞)B =(﹣∞0)∪(0+∞)显然对于∀x ∈A ∃y ∈B 使得x+y =0成立即具有性解析:①③【分析】A 即为函数的定义域,B 即为函数的值域,求出每个函数的定义域及值域,直接判断即可.【详解】对①,A = (﹣∞,0)∪ (0,+∞),B = (﹣∞,0)∪ (0,+∞),显然对于∀x ∈A ,∃y ∈B ,使得x +y =0成立,即具有性质P ;对②,A =R ,B = (0,+∞),当x >0时,不存在y ∈B ,使得x +y =0成立,即不具有性质P ;对③,A = (0,+∞),B =R ,显然对于∀x ∈A ,∃y ∈B ,使得x +y =0成立,即具有性质P ; 故答案为:①③.【点睛】本题以新定义为载体,旨在考查函数的定义域及值域,属于基础题.17.①③【分析】①求解出的反函数再根据反函数的特点进行判断;②采用换元法求解出的解析式由此计算出的值并进行判断;③分析当对数式的真数为时此时的值由此确定出函数所过定点并进行判断;④根据每经过一次操作区间 解析:①③【分析】①求解出2x y =的反函数,再根据反函数的特点进行判断;②采用换元法求解出()f x 的解析式,由此计算出()5f 的值并进行判断;③分析当对数式的真数为1时,此时,x y 的值,由此确定出函数所过定点并进行判断; ④根据每经过一次操作区间长度变为原来的一半,由此列出关于次数的不等式,求解出次数的范围并进行判断;⑤根据()()2,4f f 的值以及零点的存在性定理进行判断.【详解】①令2y x =,所以2log y x =,所以函数2x y =与2log y x =互为反函数,则图象关于y x =对称,故正确;②令1x t -=,则1x t =+,所以()()()221211f t t t t =+-++=,所以()2f x x =,所以()525f =,故错误;③令21x -=,所以3x =,所以()3log 133a f =-=-,所以()f x 过定点()3,3-,故正确;④因为区间()2,3的长度为1,经过n 次操作过后区间长度变为12n ,所以10.12n ≤,所以4n ≥,故错误;⑤因为()()22422220,4240f f =-==-=,且()()()21011210,020102f f --=--=-<=-=>, 所以()f x 在()1,0-上有零点,所以()f x 的零点至少有3个,故错误;故答案为:①③.【点睛】结论点睛:(1)同底数的指数函数和对数函数互为反函数,图象关于y x =对称;(2)形如()()()log 0,1a f x g x b a a =+>≠的图象过定点问题,可考虑令()1g x =,由此求解出x 的值,从而对应的()f x 的值可求,则定点坐标可求;(3)利用二分法求解函数零点的近似值时,每进行一次操作,区间长度会变为原来的一半. 18.9【分析】由对数的运算性质解并整理得由可求出的值【详解】解:整理得解得或因为所以则即因为所以所以解得或因为所以所以所以故答案为:9【点睛】关键点睛:本题主要考查对数运算和指数运算解题的关键是由得出再 解析:9【分析】 由对数的运算性质解10log log 3a b b a +=并整理得3a b =,由b a a b =可求出,a b 的值. 【详解】 解:110log log log log 3a b b b b a a a +=+=,整理得()23log 10log 30b b a a -+=, 解得log 3b a =或13,因为1a b >>,所以log 1b a >,则log 3b a =,即3a b =,因为b a a b =,所以33b b b b =,所以33b b =,解得b =0,因为1b >,所以b =所以3a ==,所以9ab ==.故答案为:9.【点睛】 关键点睛:本题主要考查对数运算和指数运算,解题的关键是由10log log 3a b b a +=得出3a b =,再根据指数运算求解.19.【分析】由在R 上单调减确定a3a-1的范围再根据单调减确定在分界点x=1处两个值的大小从而解决问题【详解】因为是上的减函数所以解得故答案为:【点睛】本题考查分段函数单调性问题关键根据单调性确定在分段 解析:3,17⎡⎫⎪⎢⎣⎭【分析】由()f x 在R 上单调减,确定a , 3a -1的范围,再根据单调减确定在分界点x =1处两个值的大小,从而解决问题.【详解】因为3(1)4,1()1,1a a x a x f x og x x -+<⎧=⎨≥⎩是R 上的减函数, 所以10013(1)4log 10a a a a a -<⎧⎪<<⎨⎪-+≥=⎩, 解得317a ≤<, 故答案为:3,17⎡⎫⎪⎢⎣⎭【点睛】本题考查分段函数单调性问题,关键根据单调性确定在分段点处两个值的大小,属于中档题.20.或2【分析】根据复合函数的单调性及对数的性质即可求出的值【详解】当时在为增函数求得即;当时在为减函数求得即故答案为:或【点睛】本题考查复合函数单调性对数方程的解法难度一般 解析:12或2 【分析】 根据复合函数的单调性及对数的性质即可求出a 的值.【详解】当1a >时, 1log 12a y x ⎛⎫=+⎪⎝⎭在3,62⎡⎤-⎢⎥⎣⎦为增函数,min 33log 1-224a y f ⎛⎫⎛⎫=-=-+= ⎪ ⎪⎝⎭⎝⎭,求得-214a =,即=2a ; 当01a <<时, 1log 12a y x ⎛⎫=+ ⎪⎝⎭在3,62⎡⎤-⎢⎥⎣⎦为减函数,()()min 6log 31-2a y f ==+=,求得-24a =,即1=2a .故答案为:12或2. 【点睛】 本题考查复合函数单调性,对数方程的解法,难度一般.三、解答题21.(1)()1log 1mx f x x +=-;(2)()f x 为奇函数,理由见解析;(3)3m ≥+. 【分析】(1)令21t x =-,采用换元法求解函数解析式;(2)先确定函数的定义域,再由函数奇偶性的定义判断即可;(3)由条件可转化为()11x m x x +=-在()0,1x ∈上有解问题即可. 【详解】 (1)令21t x =-,则21x t =+,则()()11log log 211m m t t f t t t ++==-+-, 所以()1log 1mx f x x +=-; (2)由101x x+>-得11x -<<, 又()()()11log log 11m m x x f x f x x x---===---+,所以()f x 为定义域上的奇函数; (3)由110x x -<<⎧⎨>⎩得01x <<, 又1log 1log log 1m m m x x mx x +=+=-,11x mx x+=-在()0,1x ∈上有解, ()11x m x x +=-,令()11,2u x =+∈,2132323t m u u u u ==≥=+-+-⎛⎫-++ ⎪⎝⎭,当且仅当u =,所以3m ≥+.【点睛】易错点睛: (1)判断函数的奇偶性一定不要忘记先判断定义域是否关于原点对称;(2)利用基本不等式求解范围,一定要注意满足“一正二定三相等”的条件.22.(1)()3,3-;(2)()f x 为奇函数,证明见解析.【分析】(1)利用对数式的真数大于零求解出不等式的解集即为定义域;(2)先判断定义域是否关于原点对称,若定义域关于原点对称,分析()(),f x f x -之间的关系,由此判断出()f x 的奇偶性.【详解】(1)因为303x x+>-,所以()()330x x -+<, 所以{}33x x -<<,所以()f x 的定义域为()3,3-;(2)()f x 为奇函数,证明:因为()f x 的定义域为()3,3-关于原点对称, 且()()1333lg lg lg 333x x x f x f x x x x --++⎛⎫-===-=- ⎪+--⎝⎭, 所以()()f x f x -=-,所以()f x 为奇函数.【点睛】思路点睛:判断函数()f x 的奇偶性的步骤如下:(1)先分析()f x 的定义域,若()f x 定义域不关于原点对称,则()f x 为非奇非偶函数,若()f x 的定义域关于原点对称,则转至(2);(2)若()()f x f x =-,则()f x 为偶函数;若()()f x f x -=-,则()f x 为奇函数. 23.(1)1k =;(2)当02m <<时,k 的最小值为4,当2m 时,k 的最小值为24m m -+.【分析】(1)根据函数是偶函数,利用偶函数的定义求解.(2)将()4f x ,转化为2(2)42x x k -+⨯,令2[x t m =∈,2]m +,构造函数2()4g t t t =-+,利用二次函数的性质求得其最大值即可..【详解】(1)()f x 为偶函数,()()f x f x ∴=-,2?22?2x x x x k k --∴+=+,即(1)(22)0x xk ---=,对任意的x 恒成立, 1k ∴=.(2)由()4f x ,可得2?24x x k -+,即2(2)42x x k-+⨯,令2[x t m =∈,2]m +, 2()4g t t t ∴=-+,当02m <<时,对称轴2[t m =∈,2]m +,则()max g t g =(2)4244=-+⨯=,当2m 时,对称轴2t m =,则2()()4max g t g m m m ==-+,故当02m <<时,k 的最小值为4,当2m 时,k 的最小值为24m m -+.【点睛】本题主要考查函数的奇偶性的和不等式恒成立的问题,还考查了分类讨论的思想和运算求解的能力,属于中档题.24.(1)32;(2)-. 【分析】(1)利用对数的运算性质化简可求得所求代数式的值;(2)由已知条件可求得1x x --的值,可求得22x x -+,并求得1122x x -+的值,代入计算可求得所求代数式的值.【详解】 (1)原式11lg3lg3lg3111lg3322lg5lg 2lg1081222lg32lg 27+-=++=+=; (2)因为()()()221114x xx x x x x x -----=+-=-, 所以()()2211412x x x x ---=+-=, 因为01x <<,则1x x -<,所以1x x --=-22x x --=-, 又因为21112226x x x x --⎛⎫+=++= ⎪⎝⎭,所以1122x x -+=所以221122x x x x ---=-+【点睛】本题考查指数式与对数式的计算,考查了平方关系以及对数运算性质的应用,考查计算能力,属于基础题.25.(1)()f x 的值域为9[16-,1];(2)能,a 的取值集合为{2};(3)232a -. 【分析】(1)由二次函数和指数函数的值域求法,可得()f x 的值域;(2)讨论1a >,01a <<,结合指数函数的单调性和二次函数的单调性,即可得到所求范围;(3)讨论x 的范围和a 的范围,结合参数分离和对勾函数的单调性、指数函数的单调性,计算可得所求范围.【详解】(1)当10x -<时,21122y x x =+-,对称轴为1[14x =-∈-,0), 可得y 的最小值为916-,y 的最大值为0; 当01x 时,12?()1[02x y =-∈,1];综上()f x 的值域为9[16-,1]; (2)当1a >时,函数22x y a a =-在[0,1]递增,故二次函数2y x ax a =+-在[1-,0]也要递增, 1222a a a⎧--⎪⎨⎪--⎩,故只有2a =符合要求; 当01a <<时,函数22xy a a =-在[0,1]递减,故二次函数2y x ax a =+-在[1-,0]也要递减, 0222a a a⎧-⎪⎨⎪--⎩,无解. 综上,a 的取值集合为{2};(3)①当[1x ∈-,0]时,22x ax a +--恒成立,即有2(1)2a x x ---,即221x a x +-, 由221x y x+=-,令1t x =-,[1t ∈,2], 可得32232y t t=+--,当且仅当t =时,取得等号, 可得232a -;②当[0x ∈,1]时,①当1a >时,22x y a a =-,222x a a --,即有222a -,求得2a ,故12a <;②当01a <<时,成立,综上可得a 的范围为232a -.【点睛】本题考查分段函数的值域和单调性的判断和运用,考查分类讨论思想方法和化简运算能力,以及不等式恒成立问题解法,属于中档题.26.(1) 2a =-,()2121x x f x -=+;(2) 212log 3x =+或212log 3x =- 【分析】(1)根据奇函数(0)0f =求解a ,再根据奇函数的性质求解()f x 的解析式即可.(2)根据(1)可得()2121x x f x -=+为奇函数,可先求解4|()|5f t =的根,再求解4|(1)|5f x -=即可. 【详解】(1)因为()f x 是定义在R 上的奇函数,且当0x ≥时,()121x a f x =++,故0(0)1021a f =+=+,即102a +=,解得2a =-.故当0x ≥时,()22112121x x x f x -=-=++. 所以当0x < 时, ()()211221211221x x x x x x f x f x -----=--=-=-=+++. 故()2121x x f x -=+ (2) 先求解4|()|5f t =,此时()214215t t f t -==±+. 当()()214421521215t t t t -=⇒+=-+,即29t =解得22log 92log 3t ==. 因为()2121x x f x -=+为奇函数,故当214215t t -=-+时, 22log 3t =-. 故4|(1)|5f x -=的解为212log 3x -=或212log 3x -=-, 解得212log 3x =+或212log 3x =-【点睛】本题主要考查了根据奇函数求解参数的值以及解析式的方法,同时也考查了根据函数性质求解绝对值方程的问题,属于中档题.。
高中数学-指数函数与对数函数检测题及答案

高中数学-指数函数与对数函数检测题第I 卷 选择题一、选择题(每小题5分,共60分)。
1.0.70.60.7log 6,6,0.7a b c ===,则,,a b c 的大小关系为( )A. a b c >>B. c a b >>C. b a c >>D. b c a >> 2、实数a =20.2,b =log20.2,c =(2)0.2的大小关系正确的是( )A .a <c <bB .a <b <cC .b <a <cD .b <c <a3、已知 1.2 2.333,2log 0.3,0.8a b c ===,则,,a b c 的大小关系为( )A .c b a <<B .c a b <<C .b a c <<D .b c a <<4、函数()log 1xa f x a x =-有两个不同的零点,则实数a 的取值范围是( )A .()1,10B .()1,+∞C .()0,1D .()10,+∞5、设函数2log 1y x =-与22x y -=的图象的交点为()00,x y ,则0x 所在的区间是( )A .()0,1B .()1,2C .()2,3D .()3,46、已知函数()2log 23a y x x =+-,当2x =时,0y >,则此函数的单调递减区间为( )A .(),3-∞-B .()1,+∞C .(),1-∞-D .()1,-+∞7、已知函数()()2,log x a f x a g x x -==(其中0a >且1a ≠),若()()044<-g f ,则()(),f x g x 在同一坐标系内的大致图象是( )8、函数()ln xf x x e =+的零点所在的区间是( )A .()B .()C .(1,e )D .(e ,∞)9、函数22log (32)y x x =-+的递减区间是( )A .(,1)-∞B .(2,)+∞C .3(,)2-∞D .3(,)2+∞10、已知456log 28,log 35,log 42a b c ===,则,,a b c 的大小关系为( ) A . b c a << B . c b a << C . a c b << D . a b c <<11、已知函数()22x f x =-,()(2)g x ax x a =-同时满足条件:①,()0x R f x ∀∈<或()0g x <;②(,4)x ∃∈-∞-,使得()()0f x g x <,则实数a 的取值范围是( )A .(2,0)-B .(,2)-∞-C .(8,0)-D .(0,2)12、已知函数21()(0)2xf x x e x =+-<与2()ln()g x x x a =++的图象上存在关于y 轴对称的点,则a 的取值范围是( ) A.(e -∞ B.(,e e C.()e eD.()e -∞ 第II 卷 非选择题二、填空题(每小题5分,共20分) 13、计算 =+⨯+2lg 5lg 2lg )5(lg 2________.14、若表示,a b 两数中的最大值,若{}2()max ,x x f x e e -=,则()f x 的最小值为 ,若{}()max ,x x t f x e e -=关于2015x =对称,则t = 。
高中数学对数函数指数函数经典题型练习(有答案)

高中数学对数函数指数函数经典题型练习一、选择题1.(多选题)设a,b,c为实数且a>b,则下列不等式一定成立的是()A.1a >1bB.2020a-b>1C.lna>lnb D.a(c²+1)>b(c²+1)2.已知函数f(x)=ln(x+√x²+1)+1,若正实数a,b满足分f(4a)+f(b-1)=2,则1a+1b的最小值为()A.4 B.8C.9 D.133.已知函数,g(x)=f(x)- x+a,若g(x)恰有3个零点,则实数a的取值范围是()A.a<-1 B.a>0C.-1<a<0 D.a>14.(多选题)已知a>b>0,且a+b=1,则()A.loga b>logba B.2a+1b>6C.ab<ba D.2a-2b>2-b-2-a5.下列函数中,其图象与函数y=ln(x+1)的图象关于直线x=1对称的是()A.y=ln(1-x) B.y=ln(3-x)C.y=ln(1+x) D.y=ln(3+x)6.已知a=243,b=e13ln3 ,c=323,则()A. c<b<aB. b<c<aC. c<a<bD. b<a<c7.若t=log2x=log3y=log5z ,且t<-2则()A.5z<2x<3yB.5z<3y<2xC.3y<2x<5zD. 2x<3y<5z8.已知函数f(x)=log 13(-x²+2x+3),则f(x)的递减区间是()A.(-∞,1) B.(-3,-1)C.(-1,1)D.(1,﹢∞)9.已知x=20.2,y=log20.2,z=0.20.3则下列结论正确的是()A.x<y<zB.y<z<xC.z<y<xD.z<x<y10函数f(x)=2x +log12x -3的零点所在区间()A.(0,1)B.(1,2)C. (2,3)D.(3,4)11.已知函数f(x)={|log2x|,0<x≤8−12x+5, x>8,若a、b、c互不相等,且f(a)=f(b)=f(c),则abc的取值范围是()A. (5,10)B. (5,8)C. (6,8)D. (8,10)12.若,,,则三个数的大小关系是A. B.C. D.13已知,则之间的大小关系是()A. B.C. D.14.设,,,则()A. B.C. D.15.函数的定义域是( )A. B.C. D.16.计算(lg2)2+(lg5)2+lg4•lg5等于()A. 0B. 1C. 2D. 317.函数的单调递减区间为()A. B.C. D.18.函数(a>0且a≠1)一定经过的定点是( )A.(0,1)B.(1,3)C.(1,2)D.(1,1)19.已知是定义在上的奇函数,且当时,,则()20.已知,,,则的大小关系是()A. B.C. D.二、填空题1..2.函数的值域是________.3.已知函数,则______.4.———.5.函数的单调递增区间为______________.三、计算题1.化简、计算:(1)(2)2.求的值.四、解答题1.计算下列各式的值:(1);(2).2.已知函数,且.(1)求使成立的的值;(2)若,试判断函数的奇偶性.参考答案一、选择题1、【答案】BD【解】对于,若,则,所以错误;对于,因为,所以,故正确;对于,函数的定义域为,而,不一定是正数,所以错误;对于,因为,所以,所以正确.故选:BD2、【答案】C【解】解:由函数,设,知,所以是奇函数,则,又因为正实数,满足,,所以,,当且仅当,时取到等号.故选:C.3、【答案】D【解】由恰有个零点,即方程恰有个实数根.即函数的图像与的图像有三个交点,如图.与函数的图像恒有一个交点,即函数与有两个交点.设与函数相切于点,由所以,得,所以切点为,此时,切线方程为将向下平移可得与恒有两个交点,所以故选:D4、【答案】ABD【解】A.由已知可得,由对数函数性质可知y=logax,y=logbx为单调递减函数,因为a>b>0,,,所以logab>logba,正确;B. 由a>b>0,a+b=1,所以,正确;C. 由已知可得,由指数函数性质可知都是单调递减函数,幂函数是单调递减函数,因为a>b>0,,错误;D.令,由知为偶函数,当时,令,,,,所以,所以当时,是单调递增函数,因为a>b>0,所以. 2a+2-a >2b +2-b,即2a-2b>2-b-2-a,正确.故选:A B D.5、【答案】B【解】设为所求曲线上一点,关于对称点,,与关于对称,故选:B.6、【答案】B【解】由题意,,因为函数在上单调递增,所以,即.故选:B.7、【答案】B【解】,,,,单调递减,,.故选:.8、【答案】C【解】令,则是上的减函数,而的递增区间是,根据复合函数的同增异减原则知,的递减区间是,故选C.9、【答案】B【解】∵x=20.2>20=1,=0,,∴y<z<x.故选:B.10、【答案】B【解】由题意,可得函数在定义域上为增函数,,,所以,根据零点存在性定理,的零点所在区间为故选B.11、【答案】D【解】函数的图像如图所示:不相等,令,因为,由图知:,解得.又因为,所以.故选12、【答案】C13、【答案】D14、【答案】A15、【答案】D【解】:可因式分解为,则或解得或,所以函数的定义域为.16、【答案】B17、【答案】A18、【答案】B19、【答案】C20、【答案】B二、填空题1、2、3、解:. 4、5、三、计算题1、(1)π(2)52、原式.四、解答题1、解:(1)(2)2、(1)由可求得,再由可得,进一步求解即可;(2)先判断函数的定义域,再结合奇偶函数的判定性质证明即可;【详解】(1)由,∴可化,∴或,均符合.(2)∵,定义域关于原点对称,∴,因此是奇函数.。
高中数学第四章指数函数与对数函数典型例题(带答案)

高中数学第四章指数函数与对数函数典型例题单选题1、已知a=lg2,10b=3,则log56=()A.a+b1+a B.a+b1−aC.a−b1+aD.a−b1−a答案:B分析:指数式化为对数式求b,再利用换底公式及对数运算性质变形. ∵a=lg2,0b=3,∴b=lg3,∴log56=lg6lg5=lg2×3lg102=lg2+lg31−lg2=a+b1−a.故选:B.2、函数f(x)=|x|⋅22−|x|在区间[−2,2]上的图象可能是()A.B.C.D.答案:C分析:首先判断函数的奇偶性,再根据特殊值判断即可;解:∵f(−x)=|x|⋅22−|x|=f(x),∴f(x)是偶函数,函数图象关于y轴对称,排除A,B选项;∵f(1)=2=f(2),∴f(x)在[0,2]上不单调,排除D选项.故选:C3、式子√m⋅√m 43√m 56m >0)的计算结果为( )A .1B .m 120C .m 512D .m 答案:D分析:由指数运算法则直接计算可得结果.√m⋅√m 43√m 56=m 12⋅m 43m 56=m 12+43−56=m .故选:D.4、若f(x)={(6−a)x −a,x <1log a x +3,x ≥1是定义在R 上的增函数,实数a 的取值范围是( )A .[1,5]B .[32,5) C .(32,5)D .(1,5) 答案:B分析:由题意得{6−a >1a >1log a 1+3≥(6−a)−a ,解不等式组可求得答案因为f(x)={(6−a)x −a,x <1log a x +3,x ≥1是定义在R 上的增函数,所以{6−a >1a >1log a 1+3≥(6−a)−a ,解得32≤a <5,故选:B5、函数f (x )=√3−x +log 13(x +1)的定义域是( )A .[−1,3)B .(−1,3)C .(−1,3]D .[−1,3] 答案:C分析:由题可得{3−x ≥0x +1>0,即得.由题意得{3−x ≥0x +1>0,解得−1<x ≤3, 即函数的定义域是(−1,3].故选:C.6、下列函数中是增函数的为( )A .f (x )=−xB .f (x )=(23)xC .f (x )=x 2D .f (x )=√x 3答案:D分析:根据基本初等函数的性质逐项判断后可得正确的选项. 对于A ,f (x )=−x 为R 上的减函数,不合题意,舍. 对于B ,f (x )=(23)x为R 上的减函数,不合题意,舍.对于C ,f (x )=x 2在(−∞,0)为减函数,不合题意,舍. 对于D ,f (x )=√x 3为R 上的增函数,符合题意, 故选:D.7、下列计算中结果正确的是( ) A .log 102+log 105=1B .log 46log 43=log 42=12C .(log 515)3=3log 515=−3D .13log 28=√log 283=√33答案:A分析:直接根据对数的运算性质及换底公式计算可得;解:对于A :log 102+log 105=log 10(2×5)=log 1010=1,故A 正确; 对于B :log 46log 43=log 36,故B 错误;对于C :(log 515)3=(log 55−1)3=(−log 55)3=−1,故C 错误; 对于D :13log 28=13log 223=13×3log 22=1,故D 错误; 故选:A8、荀子《劝学》中说:“不积跬步,无以至千里;不积小流,无以成江海.”所以说学习是日积月累的过程,每天进步一点点,前进不止一小点.我们可以把(1+1%)365看作是每天的“进步”率都是1%,一年后是1.01365≈37.7834;而把(1−1%)365看作是每天“退步”率都是1%,一年后是0.99365≈0.0255.若“进步”的值是“退步”的值的100倍,大约经过(参考数据:lg101≈2.0043,lg99≈1.9956) ( )天.A .200天B .210天C .220天D .230天 答案:D分析:根据题意可列出方程100×0.99x =1.01x ,求解即可.设经过x 天“进步”的值是“退步”的值的100倍,则100×0.99x=1.01x,即(1.010.99)x =100,∴x =log 1.010.99100=lg lg 1.010.99=lg lg 10199=2lg−lg≈22.0043−1.9956=20.0087≈230.故选:D . 多选题9、已知函数f(x)=1−2x 1+2x,则下面几个结论正确的有( )A .f(x)的图象关于原点对称B .f(x)的图象关于y 轴对称C .f(x)的值域为(−1,1)D .∀x 1,x 2∈R ,且x 1≠x 2,f (x 1)−f (x 2)x 1−x 2<0恒成立答案:ACD分析:利用奇函数的定义和性质可判断AB 的正误,利用参数分离和指数函数的性质可判断CD 的正误. 对于A ,f(x)=1−2x1+2x ,则f(−x)=1−2−x1+2−x =2x −11+2x =−f(x), 则f(x)为奇函数,故图象关于原点对称,故A 正确.对于B ,计算f(1)=−13,f(−1)=13≠f(1),故f(x)的图象不关于y 轴对称,故B 错误. 对于C ,f(x)=1−2x1+2x =−1+21+2x ,1+2x =t,t ∈(1,+∞),故y =f(x)=−1+2t ,易知:−1+2t ∈(−1,1),故f(x)的值域为(−1,1),故C 正确. 对于D ,f(x)=1−2x1+2x =−1+21+2x ,因为y =1+2x 在R 上为增函数,y =−1+21+t 为(1,+∞)上的减函数, 由复合函数的单调性的判断法则可得f (x )在R 上单调递减,故∀x 1,x 2∈R ,且x 1≠x 2,f(x 1)−f(x 2)x 1−x 2<0恒成立,故D 正确.故选:ACD.小提示:方法点睛:复合函数的单调性的研究,往往需要将其转化为简单函数的复合,通过内外函数的单调性结合“同增异减”的原则来判断.10、设函数f (x )=ax 2+bx +c (a,b,c ∈R,a >0),则下列说法正确的是( ) A .若f (x )=x 有实根,则方程f(f (x ))=x 有实根 B .若f (x )=x 无实根,则方程f(f (x ))=x 无实根 C .若f (−b 2a)<0,则函数y =f (x )与y =f(f (x ))都恰有2个零点D .若f (f (−b 2a))<0,则函数y =f (x )与y =f(f (x ))都恰有2零点答案:ABD分析:直接利用代入法可判断A 选项的正误;推导出f (x )−x >0对任意的x ∈R 恒成立,结合该不等式可判断B 选项的正误;取f (x )=x 2−x ,结合方程思想可判断C 选项的正误;利用二次函数的基本性质可判断D 选项的正误.对于A 选项,设f (x )=x 有实根x =x 0,则f(f (x 0))=f (x 0)=x 0,A 选项正确; 对于B 选项,因为a >0,若方程f (x )=x 无实根,则f (x )−x >0对任意的x ∈R 恒成立, 故f(f (x ))>f (x )>x ,从而方程f(f (x ))=x 无实根,B 选项正确;对于C 选项,取f (x )=x 2−x ,则f (12)=−14<0,函数y =f (x )有两个零点, 则f(f (x ))=[f (x )]2−f (x )=0,可得f (x )=0或f (x )=1,即x 2−x =0或x 2−x =1. 解方程x 2−x =0可得x =0或1,解方程x 2−x −1=0,解得x =1±√52. 此时,函数y =f(f (x ))有4个零点,C 选项错误;对于D 选项,因为f (f (−b2a ))<0,设t =f (−b2a ),则t =f (x )min , 因为f (t )<0且a >0,所以,函数f (x )必有两个零点,设为x 1、x 2且x 1<x 2, 则x 1<t <x 2,所以,方程f (x )=x 1无解,方程f (x )=x 2有两解,因此,若f(f(−b))<0,则函数y=f(x)与y=f(f(x))都恰有2零点,D选项正确.2a故选:ABD.小提示:思路点睛:对于复合函数y=f[g(x)]的零点个数问题,求解思路如下:(1)确定内层函数u=g(x)和外层函数y=f(u);(2)确定外层函数y=f(u)的零点u=u i(i=1,2,3,⋯,n);(3)确定直线u=u i(i=1,2,3,⋯,n)与内层函数u=g(x)图象的交点个数分别为a1、a2、a3、⋯、a n,则函数y=f[g(x)]的零点个数为a1+a2+a3+⋯+a n.11、(多选题)某市出租车收费标准如下:起步价为8元,起步里程为3km(不超过3km按起步价付费);超过3km 但不超过8km时,超过部分按每千米2.15元收费;超过8km时,超过部分按每千米2.85元收费,另每次乘坐需付燃油附加费1元.下列结论正确的是()A.出租车行驶4km,乘客需付费9.6元B.出租车行驶10km,乘客需付费25.45元C.某人乘出租车行驶5km两次的费用超过他乘出租车行驶10km一次的费用D.某人乘坐一次出租车付费22.6元,则此次出租车行驶了9km答案:BCD分析:根据题意分别计算各个选项的情况,即可得答案.对于A选项:出租车行驶4km,乘客需付费8+1×2.15+1=11.15元,故A错误;对于B选项:出租车行驶10 km,乘客需付费8+2.15×5+2.85×(10-8)+1=25.45元,故B正确;对于C选项:乘出租车行驶5km,乘客需付费8+2×2.15+1=13.30元,乘坐两次需付费26.6元,26.6>25.45,故C正确;对于D选项:设出租车行驶x km时,付费y元,由8+5×2.15+1=19.75<22.6,知x>8,因此由y=8+2.15×5+2.85(x-8)+1=22.6,解得x=9,故D正确.故选:BCD.小提示:本题考查函数模型的应用,解题要点为认真审题,根据题意逐一分析选项即可,属基础题.12、若log2m=log4n,则()A.n=2m B.log9n=log3mC.lnn=2lnm D.log2m=log8(mn)答案:BCD分析:利用对数运算化简已知条件,然后对选项进行分析,从而确定正确选项.依题意log2m=log4n,所以m>0,n>0,log2m=log22n=12log2n=log2n12,所以m=n 12,m2=n,A选项错误.log9n=log32m2=22log3m=log3m,B选项正确.lnn=lnm2=2lnm,C选项正确.log8(mn)=log23m3=33log2m=log2m,D选项正确.故选:BCD13、在平面直角坐标系中,我们把横纵坐标相等的点称之为“完美点”,下列函数的图象中存在完美点的是()A.y=﹣2x B.y=x﹣6C.y=3xD.y=x2﹣3x+4答案:ACD分析:横纵坐标相等的函数即y=x,与y=x有交点即存在完美点,依次计算即可.横纵坐标相等的函数即y=x,与y=x有交点即存在完美点,对于A,{y=xy=−2x,解得{x=0y=0,即存在完美点(0,0),对于B,{y=xy=x−6,无解,即不存在完美点,对于C,{y=xy=3x,解得{x=√3y=√3或{x=−√3y=−√3,即存在完美点(√3,√3),(−√3,−√3)对于D,{y=xy=x2−3x+4,x2−3x+4=x,即x2−4x+4=0,解得x=2,即存在完美点(2,2).故选:ACD.填空题14、化简(√a−1)2+√(1−a)2+√(1−a)33=________.答案:a-1分析:根据根式的性质即可求解.由(√a−1)2知a-1≥0,a≥1.故原式=a-1+|1-a|+1-a=a-1.所以答案是:a-115、对数型函数f(x)的值域为[0,+∞),且在(0,+∞)上单调递增,则满足题意的一个函数解析式为______.答案:f(x)=|log2(x+1)|(答案不唯一,满足f(x)=|log a(x+b)|,a>1,b≥1即可)分析:根据题意可利用对数函数的性质和图像的翻折进行构造函数.∵函数f(x)的值域为[0,+∞),且在(0,+∞)上单调递增,∴满足题意的一个函数是f(x)=|log2(x+1)|.所以答案是:f(x)=|log2(x+1)|(答案不唯一)16、函数y=log a(x+1)-2(a>0且a≠1)的图象恒过点________.答案:(0,-2)分析:由对数函数的图象所过定点求解.解:依题意,x+1=1,即x=0时,y=log a(0+1)-2=0-2=-2,故图象恒过定点(0,-2).所以答案是:(0,-2)解答题17、(1)计算0.027−13−(−16)−2+810.75+(19)0−3−1;(2)若x 12+x−12=√6,求x 2+x −2的值.答案:(1)-5;(2)14.分析:(1)由题意利用分数指数幂的运算法则,计算求得结果. (2)由题意两次利用完全平方公式,计算求得结果. (1)0.027−13−(−16)−2+810.75+(19)0−3−1=0.3﹣1﹣36+33+1−13=103−36+27+1−13=−5.(2)若x 12+x −12=√6,∴x +1x +2=6,x +1x =4,∴x 2+x ﹣2+2=16,∴x 2+x ﹣2=14.18、已知函数f (x )=2x −12x +1.(1)判断并证明f (x )在其定义域上的单调性;(2)若f (k ⋅3x )+f (3x −9x +2)<0对任意x ≥1恒成立,求实数k 的取值范围. 答案:(1)f (x )在R 上单调递增;证明见解析 (2)(−∞,43)分析:(1)设x 2>x 1,可整理得到f (x 2)−f (x 1)=2(2x 2−2x 1)(2x 2+1)(2x 1+1)>0,由此可得结论;(2)利用奇偶性定义可证得f (x )为奇函数,结合单调性可将恒成立的不等式化为k <g (x )=3x −23x −1,由g (x )单调性可求得g (x )≥43,由此可得k 的取值范围.(1)f (x )在R 上单调递增,证明如下: 设x 2>x 1,∴f (x 2)−f (x 1)=2x 2−12x 2+1−2x 1−12x 1+1=(2x 2−1)(2x 1+1)−(2x 2+1)(2x 1−1)(2x 2+1)(2x 1+1)=2(2x 2−2x 1)(2x 2+1)(2x 1+1);∵x 2>x 1,∴2x 2−2x 1>0,又2x 2+1>0,2x 1+1>0,∴f (x 2)−f (x 1)>0, ∴f (x )在R 上单调递增. (2)∵f (−x )=2−x −12−x +1=1−2x1+2x =−f (x ),∴f (x )为R 上的奇函数,由f(k⋅3x)+f(3x−9x+2)<0得:f(k⋅3x)<−f(3x−9x+2)=f(9x−3x−2),由(1)知:f(x)在R上单调递增,∴k⋅3x<9x−3x−2在[1,+∞)上恒成立;当x≥1时,3x≥3,∴k<3x−23x−1在[1,+∞)上恒成立;令g(x)=3x−23x−1,∵y=3x在[1,+∞)上单调递增,y=23x在[1,+∞)上单调递减,∴g(x)在[1,+∞)上单调递增,∴g(x)≥g(1)=3−23−1=43,∴k<43,即实数k的取值范围为(−∞,43).。
(压轴题)高中数学必修一第三单元《指数函数和对数函数》检测题(包含答案解析)

一、选择题1.下列各组函数中,表示同一个函数的是( )A .211x y x -=-与1y x =+B .y x =与log xa y a =(0a >且1a ≠)C.y =1y x =-D .lg y x =与21lg 2y x =2.2017年5月,世界排名第一的围棋选手柯洁0:3败给了人工智能“阿法狗”.为什么人类的顶尖智慧战胜不了电脑呢?这是因为围棋本身也是一个数学游戏,而且复杂度非常高.围棋棋盘横竖各有19条线,共有1919361⨯=个落子点.每个落子点都有落白子、落黑子和空白三种可能,因此围棋空间复杂度的上限3613M ≈.科学家们研究发现,可观测宇宙中普通物质的原子总数8010N ≈.则下列各数中与MN最接近的是( )(参考数据:lg30.48≈) A .3310B .5310C .7310D .93103.已知0.20.33log 0.2,3,0.2a b c ===,则( )A .a b c <<B .a c b <<C .c a b <<D .b c a <<4.已知函数||()2x f x =,记131(())4a f =,37(log )2b f =,13(log 5)c f =,则a ,b,c 的大小关系为( )A .c b a >>B .b a c >>C .a b c >>D .c a b >>5.已知函数222,1()log (1),1x x f x x x ⎧-≤=⎨->⎩,则52f f ⎡⎤⎛⎫= ⎪⎢⎥⎝⎭⎣⎦( ) A .12-B .-1C .-5D .126.已知函数3131()(),()log ,()(0)2xf x xg x x xh x x x x =-=-=->的零点分别为,,a b c ,则,,a b c 的大小顺序为( )A .a b c >>B .c a b >>C .b c a >>D .b a c >>7.已知函数 ()lg 2x xe ef x --=,则f (x )是( )A .非奇非偶函数,且在(0,+∞)上单调递增B .奇函数,且在R 上单调递增C .非奇非偶函数,且在(0,+∞)上单调递减D .偶函数,且在R 上单调递减8.若一系列函数的解析式和值域相同,但其定义域不同,则称这些函数为“同族函数”,例如函数2y x =,x ∈[1,2]与函数.2y x =,[]2,1x ∈--即为同族函数,下面函数解析式中也能够被用来构造“同族函数”的是( )A .y =xB .1y x x=+ C . 22x x y -=- D .y =log 0.5x 9.如图是指数函数①y =x a ;②y =x b ;③y =c x ;④y =d x 的图象,则a ,b ,c ,d 与1的大小关系是( )A .a <b <1<c <dB .b <a <1<d <cC .1<a <b <c <dD .a <b <1<d <c10.已知3log 2a =,那么33log 82log 6-用a 表示是( ) A .52a - B .2a -C .23(1)a a -+D .231a a --11.函数()22x xxf x -=+的大致图象为( ) A . B .C .D .12.已知函数()2,01,0x x f x x x >⎧=⎨+≤⎩,若()()10f a f +=,则实数a 的值等于( )A .-3B .-1C .1D .3二、填空题13.函数12()log (2)f x x =-的定义域为______.14.已知()f x 是定义在R 上的奇函数,且当0x 时,2log (1),01,()31,1,x x f x x x +<⎧=⎨--⎩则方程1()2f x =的所有实根之和为________. 15.已知函数log (3)a y ax =-在(1,2)上单调递减,则实数a 的取值范围为___________. 16.已知函数22()log ()f x ax x a =++的值域为R ,则实数a 的取值范围是_________ 17.若函数11x y a+=+()0,1a a >≠恒过点(,)P m n ,则函数()11142x xf x ⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭在[],m n 上的最小值是_____.18.函数()()212log 56f x x x =-+的单调递增区...间是__________. 19.设函数()f x =,则()()()()()()543456f f f f f f -+-+-++++=_____.20.已知奇函数()()y f x x R =∈满足:对一切x ∈R ,()()11f x f x +=-且[]0,1x ∈时,()1xf x e =-,则()2019f f =⎡⎤⎣⎦__________.三、解答题21.已知函数2()46f x ax x =-+.(1)若函数2log ()y f x =的值域为R ,求实数a 的取值范围;(2)若函数log ()a y f x =在区间(1,3)上单调递增,求实数a 的取值范围. 22.设131()log 1axf x x -=-为奇函数,a 为常数. (1)求a 的值.(2)若[2,4]x ∀∈,不等式1()3xf x x m ⎛⎫+>+ ⎪⎝⎭恒成立,求实数m 的取值范围.23.设函数()()1xxf x a k a -=--,(0a >且1a ≠)是定义域为R 的奇函数,且()312f =. (1)求k ,a 的值;(2)求函数()f x 在[)1,+∞上的值域; (3)设()()222xx g x a a m f x -=+-⋅,若()g x 在[)1,+∞上的最小值为2-,求m 的值;(4)对于(3)中函数()g x ,如果()0g x >在[)1,+∞上恒成立,求m 的取值范围. 24.(1)已知12x y +=,9xy =,且x y <,求11221122x y x y-+值;(2)求值:2(lg 2)lg5lg 20+⋅.25.已知函数()442xx f x =+;(1)若01a <<,求()()1f a f a +-的值; (2)求12320202021202120212021f f f f ⎛⎫⎛⎫⎛⎫⎛⎫+++⋅⋅⋅+⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭的值. 26.已知函数()21log 1x f x x +=-, (1)求函数()y f x =的定义域; (2)证明:()y f x =是奇函数; (3)设()()()14h x f x f x =+,求函数()y h x =在[]3,7内的值域;【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】分析各个选项中每组函数的定义域和对应关系,若定义域和对应关系均相同则为同一个函数,由此判断出正确选项. 【详解】A .211x y x -=-的定义域为{}1x x ≠,1y x =+的定义域为R ,所以不是同一个函数;B .y x =与log xa y a =的定义域均为R ,且log xa y a =即为y x =,所以是同一个函数;C .y =(][),11,-∞-+∞,1y x =-的定义域为R ,所以不是同一个函数;D .lg y x =的定义域为()0,∞+,21lg 2y x =的定义域为{}0x x ≠,所以不是同一个函数, 故选:B. 【点睛】思路点睛:同一函数的判断步骤:(1)先判断函数定义域,若定义域不相同,则不是同一函数;若定义域相同,再判断对应关系;(2)若对应关系不相同,则不是同一函数;若对应关系相同,则是同一函数.2.D解析:D 【分析】设36180310M x N ==,两边取对数,结合对数的运算性质进行整理,即可求出M N . 【详解】解:设36180310M x N ==,两边取对数36136180803lg lg lg3lg10361lg38093.2810x ==-=⨯-=,所以93.2810x =,故选:D . 【点睛】 关键点睛:本题考查了对数的运算,关键是结合方程的思想令36180310x =,两边取对数后进行化简整理.3.B解析:B 【分析】根据指数函数的单调性以及对数函数的单调性分别判断出,,a b c 的取值范围,从而可得结果 【详解】因为33log 0.2log 10<=,0.20331>=,...030002021<<=,a cb ∴<<. 故选:B . 【点睛】比较大小问题,常见思路有两个:一是利用中间变量;二是利用函数的单调性直接解答4.A解析:A 【分析】首先判断函数()f x 的性质,再比较133317,log ,log 542⎛⎫ ⎪⎝⎭的大小关系,从而利用单调性比较a ,b ,c 的大小关系. 【详解】()2xf x =是偶函数,并且当0x >时,2x y =是增函数,()133log 5log 5c f f ⎛⎫== ⎪⎝⎭,因为1310()14<<,3371log log 52<<,即1333170log log 542⎛⎫<<< ⎪⎝⎭ 又因为()y f x =在()0,∞+是增函数,所以a b c <<. 故选:A. 【点睛】关键点点睛:本题考查利用函数的单调性和奇偶性比较函数值的大小,本题的关键是判断函数()2xf x =的性质,后面的问题迎刃而解.5.A解析:A 【分析】根据分段函数解析式,依次计算255log 122f ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭,23log 2f ⎛⎫ ⎪⎝⎭,即可得选项.【详解】因为函数222,1()log (1),1x x f x x x ⎧-≤=⎨->⎩,所以2253log log 2122f ⎛⎫=<= ⎪⎝⎭,23log 2531222222f f⎡⎤⎛⎫∴=-=-=- ⎪⎢⎥⎝⎭⎣⎦. 故选:A. 【点睛】本题考查根据分段函数求解函数值,关键在于根据解析式分段求解,由内到外,准确认清自变量的所在的范围和适用的解析式.6.B解析:B 【分析】将函数3131()(),()log ,()(0)2xf x xg x x xh x x x x =-=-=->的零点,转化为函数y x =的图象分别与函数3131(),log ,(0)2xy y x y x x ===>的图象交点的横坐标,利用数形结合法求解. 【详解】函数3131()(),()log ,()(0)2x f x x g x x x h x x x x =-=-=->的零点,即为函数y x =的图象分别与函数3131(),log ,(0)2xy y x y x x ===>的图象交点的横坐标, 如图所示:由图象可得:c a b >>, 故选:B 【点睛】本题主要考查函数的零点以及指数函数,对数函数和幂函数的图象的应用,还考查了数形结合的思想方法,属于中档题.7.A解析:A 【分析】本题考查函数的奇偶性和和单调性的概念及简单复合函数单调性的判定. 【详解】要使函数有意义,需使0,2x x e e -->即21,1,x xx e e e >∴>解得0;x >所以函数()f x 的为(0,);+∞定义域不关于原点对称,所以函数()f x 是非奇非偶函数;因为1,xxx y e y ee-==-=-是增函数,所以2x xe e y --=是增函数,又lg y x =是增函数,所以函数()lg 2x xe ef x --=在定义域(0,)+∞上单调递增.故选:A 【点睛】本题考查对数型复合函数的奇偶性和单调性,属于中档题.8.B解析:B 【分析】由题意,能够被用来构造“同族函数”的函数必须满足在其定义域上不单调,由此判断各个函数在其定义域上的单调性即可.【详解】对A :y x =在定义域R 上单调递增,不能构造“同族函数”,故A 选项不正确;对B :1y x x=+在(),1-∞-递增,在()1,0-递减,在()0,1递减,在()1,+∞递增,能构造“同族函数”,故B 选项正确; 对C :22xxy -=-在定义域上递增,不能构造“同族函数”,故C 选项不正确; 对D :0.5log y x =在定义域上递减,不能构造“同族函数”,故D 选项不正确. 故选:B. 【点睛】本题给出“同族函数”的定义,要求我们判断几个函数能否被用来构造“同族函数”,考查基本初等函数的单调性的知识点,属于基础题.9.B解析:B 【分析】根据指数函数的图象与性质可求解. 【详解】根据函数图象可知函数①y =x a ;②y =x b 为减函数,且1x =时,②y =1b <①y =1a , 所以1b a <<,根据函数图象可知函数③y =c x ;④y =d x 为增函数,且1x =时,③y =c 1>④y =d 1, 所以1c d >> 故选:B 【点睛】本题主要考查了指数函数的单调性,指数函数的图象,数形结合的思想,属于中档题.10.B解析:B 【解析】试题分析:33333333log 82log 6log 22log 233log 22(log 2log 3)-=-⨯=-+3log 222a =-=-,所以答案选B .考点:指数对数的计算11.B解析:B 【分析】根据函数为奇函数排除C ,取特殊值排除AD 得到答案. 【详解】 当()22x xx f x -=+,()()22x x xf x f x ---==-+,函数为奇函数,排除C ; 2221(2)22242f -=<=+,排除A ;3324(3)22536f -==+,4464(4)224257f -==+,故()()34f f >,排除D. 故选:B. 【点睛】 本题考查了函数图象的识别,意在考查学生的计算能力和识图能力,取特殊值排除是解题的关键.12.A解析:A 【分析】先求得()1f 的值,然后根据()f a 的值,求得a 的值. 【详解】由于()1212f =⨯=,所以()()20,2f a f a +==-,22a =-在()0,∞+上无解,由12a +=-解得3a =-,故选A.【点睛】本小题主要考查分段函数求函数值,考查已知分段函数值求自变量,属于基础题.二、填空题13.【分析】根据二次根式和对数式有意义的条件得到不等式组求解函数的定义域即可得结果【详解】根据题意可得:解得所以函数的定义域为故答案为:【点睛】该题考查的是有关求函数的问题涉及到的知识点有求给定函数的定 解析:(2,3]【分析】根据二次根式和对数式有意义的条件,得到不等式组求解函数的定义域即可得结果. 【详解】根据题意可得:1220log (2)0x x ->⎧⎪⎨-≥⎪⎩,解得23x <≤,所以函数()f x =(2,3],故答案为:(2,3]. 【点睛】该题考查的是有关求函数的问题,涉及到的知识点有求给定函数的定义域,在解题的过程中,注意二次根式和对数式需要满足的条件即可得结果.14.【分析】画出分段函数的图像根据图像结合解析式进行求解【详解】根据分段函数的解析式以及函数为奇函数作图如下:由图容易知因为在区间上关于对称且在区间上关于对称故其与直线的所有交点的横坐标之和为0故所有根解析:21-【分析】画出分段函数的图像,根据图像,结合解析式,进行求解. 【详解】根据分段函数的解析式,以及函数为奇函数,作图如下:由图容易知,因为31y x =--在区间[)1,+∞上,关于3x =对称, 且31y x =---+在区间(],1-∞上,关于3x =-对称, 故其与直线12y =的所有交点的横坐标之和为0. 故1()2f x =所有根之和,即为当()0,1x ∈时的根, 此时()21log 12x +=,解得21x =. 21. 【点睛】本题考查函数图像的交点,涉及函数图像的绘制,函数奇偶性的应用,属函数综合题.15.【分析】由复合函数的单调性:同增异减由于递减因此必须递增即有还要考虑函数定义域即在时恒成立【详解】∵∴是减函数又在上是减函数所以且∴故答案为:【点睛】本题考查对数型复合函数的单调性掌握复合函数单调性 解析:3(1,]2【分析】由复合函数的单调性:同增异减,由于3u ax =-递减,因此log a y u =必须递增,即有1a >,还要考虑函数定义域,即在(1,2)x ∈时,30ax ->恒成立.【详解】∵0a >,∴3u ax =-是减函数,又log (3)a y ax =-在(1,2)上是减函数,所以1a >, 且320a -≥,∴312a <≤. 故答案为:3(1,]2.【点睛】本题考查对数型复合函数的单调性,掌握复合函数单调性是解题关键,同时要考虑函数的定义域.16.【分析】设值域为根据题意对分类讨论结合根的判别式即可求解【详解】设值域为函数的值域为当时值域为满足题意;当时须解得综上实数a 的取值范围是故答案为:【点睛】本题考查对数函数的性质复合函数的性质二次函数 解析:10,2⎡⎤⎢⎥⎣⎦【分析】设2()u x ax x a =++值域为A ,根据题意(0,)A +∞⊆,对a 分类讨论,结合根的判别式,即可求解. 【详解】设2()u x ax x a =++值域为A ,函数22()log ()f x ax x a =++的值域为,(0,)R A +∞⊆,当0a =时,2()log f x x =值域为R ,满足题意;当0a ≠时,须20140a a >⎧⎨∆=-≥⎩,解得102a <≤, 综上,实数a 的取值范围是10,2⎡⎤⎢⎥⎣⎦.故答案为:10,2⎡⎤⎢⎥⎣⎦.【点睛】本题考查对数函数的性质,复合函数的性质,二次函数的取值和根的判别式的关系,属于中档题.17.【分析】先利用指数型函数恒过定点问题求定点得到换元令利用二次函数的单调性即可求解【详解】函数恒过点则区间变为由函数令则利用二次函数的单调性当时则函数在上的最小值是故答案为:【点睛】关键点睛:把指数型解析:34【分析】先利用指数型函数恒过定点问题求定点,得到1,2m n =-=,换元,令11,224xt t ⎛⎫=≤≤ ⎪⎝⎭,利用二次函数的单调性,即可求解. 【详解】 函数11x y a+=+()0,1a a >≠恒过点()1,2-,则1,2m n =-=,区间[],x m n ∈变为[]1,2x ∈-,由函数()11142x xf x ⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭, 令11,224xt t ⎛⎫=≤≤ ⎪⎝⎭, 则()2213124f t t t t ⎛⎫=-+=-+ ⎪⎝⎭, 利用二次函数的单调性,当12t =时,()min 34f t =,则函数()11142xxf x ⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭在[],m n 上的最小值是34.故答案为:34. 【点睛】关键点睛:把指数型复合函数求最值问题转化为二次函数求最值问题是解决本题的关键.18.【分析】求出函数的定义域利用复合函数法可求得函数的单调递增区间【详解】对于函数有解得或所以函数的定义域为内层函数在区间上单调递减在区间上单调递增外层函数为减函数所以函数的单调递增区间为故答案为:【点 解析:(),2-∞【分析】求出函数()f x 的定义域,利用复合函数法可求得函数()()212log 56f x x x =-+的单调递增区间. 【详解】对于函数()()212log 56f x x x =-+,有2560x x -+>,解得2x <或3x >.所以,函数()()212log 56f x x x =-+的定义域为()(),23,-∞+∞,内层函数256u x x =-+在区间(),2-∞上单调递减,在区间()3,+∞上单调递增, 外层函数12log y u =为减函数,所以,函数()f x 的单调递增区间为(),2-∞.故答案为:(),2-∞. 【点睛】复合函数()y f g x ⎡⎤=⎣⎦的单调性规律是“同则增,异则减”,即()y f u =与()u g x =.若具有相同的单调性,则()y f g x ⎡⎤=⎣⎦为增函数,若具有不同的单调性,则()y f g x ⎡⎤=⎣⎦必为减函数.19.【分析】根据指数的运算律计算出的值由此可计算出所求代数式的值【详解】因此故答案为【点睛】本题考查指数幂的化简计算解题的关键在于观察代数式结构并计算出为定值考查计算能力属于中等题解析:【分析】根据指数的运算律计算出()()1f x f x +-=的值,由此可计算出所求代数式的值. 【详解】()f x =()1122xx f x ∴-====, ()()12x x x f x f x ∴+-=+===,因此,()()()()()()5434566f f f f f f -+-+-++++==.故答案为 【点睛】本题考查指数幂的化简计算,解题的关键在于观察代数式结构并计算出()()1f x f x +-为定值,考查计算能力,属于中等题.20.【分析】根据题意求得的周期性则可求再结合函数解析式求得函数值即可【详解】由题可知:因为对一切故关于对称;又因为是奇函数则可得故可得故函数是周期为的函数则又当故则故答案为:【点睛】本题考查利用函数周期 解析:31e e --【分析】根据题意,求得()f x 的周期性,则()2019f 可求,再结合函数解析式,求得函数值即可. 【详解】由题可知:因为对一切x R ∈,()()11f x f x +=-, 故()f x 关于1x =对称; 又因为()f x 是奇函数,则可得()()()()()21111f x f x f x f x f x +=++=--=-=-, 故可得()()()()4222f x f x f x f x +=++=-+=, 故函数()f x 是周期为4的函数. 则()()()201911f f f =-=-,又当[]0,1x ∈,()1x f x e =-,故()()201911f f e =-=-,则()()()()()320191131eff f e f e f e e-=-=--=--=-.故答案为:31e e --. 【点睛】本题考查利用函数周期性求函数值,属综合中档题;难点在于求得函数的周期.三、解答题21.(1)20,3⎡⎤⎢⎥⎣⎦;(2)[)2,+∞.【分析】(1)根据条件分析出2()46f x ax x =-+的值域包含()0,∞+,由此根据a 与0的关系分类讨论,求解出结果;(2)根据1,01a a ><<两种情况结合复合函数单调性的判断方法进行分类讨论,然后求解出a 的取值范围. 【详解】(1)因为()22log 46y ax x =-+的值域为R ,所以246y ax x =-+的值域包含()0,∞+,当0a =时,246y ax x =-+即46y x =-+,此时46y x =-+的值域为R ,满足; 当0a ≠时,则有016240a a >⎧⎨∆=-≥⎩,所以203a <≤,综上可知:20,3a ⎡⎤∈⎢⎥⎣⎦;(2)当1a >时,log a y x =在()0+∞,上单调递增,所以2()46f x ax x =-+在()1,3上递增,所以()2110a f ⎧≤⎪⎨⎪>⎩,所以2a ≥,当01a <<时,log a y x =在()0+∞,上单调递减,所以2()46f x ax x =-+在()1,3上递减,所以()2330a f ⎧≥⎪⎨⎪>⎩,此时a 无解,综上可知:[)2,a ∈+∞. 【点睛】思路点睛:形如()()()2lg 0f x ax bx ca =++≠的函数,若函数的定义域为R ,则有0a >⎧⎨∆<⎩; 若函数的值域为R ,则有0a >⎧⎨∆≥⎩. 22.(1)1a =-;(2)89m <. 【分析】(1)由奇函数的性质()()0f x f x ,代入运算后可得1a =±,代入验证即可得解;(2)转化条件为131log 113xx x m x +<⎛⎫- ⎝+⎪⎭-对于[2,4]x ∀∈恒成立,令()[]131log ,2,4113xx g x x x x ⎛⎫-+=+⎝⎭∈- ⎪,结合函数的单调性求得()min g x 即可得解.【详解】(1)因为131()log 1axf x x -=-为奇函数, 则1113331111()()log log log 1111ax ax ax ax f x f x x x x x +-⎡+-⎤⎛⎫⎛⎫-+=+= ⎪⎪⎢⎥------⎝⎭⎝⎭⎣⎦ ()21231log 01ax x-==-, 则()22111ax x -=-,所以21a =即1a =±, 当1a =时,()11331()log log 11xf x x -==--,不合题意; 当1a =-时,131()log 1x f x x +=-,由101xx +>-可得1x >或1x <-,满足题意; 故1a =-;(2)由1()3xf x x m ⎛⎫+>+ ⎪⎝⎭可得131log 113xx x m x ⎛⎫>+ +⎪⎭+⎝-,则131log 113xx x m x +<⎛⎫- ⎝+⎪⎭-对于[2,4]x ∀∈恒成立,令()[]131log ,2,4113xx g x x x x ⎛⎫-+=+⎝⎭∈- ⎪,因为函数12111x y x x +==+--在[2,4]上单调递减,所以函数131log 1xy x +=-在[2,4]上单调递增, 所以()g x 在[2,4]上单调递增,所以()()1min 32log 182993g x g -===+, 所以89m <. 【点睛】关键点点睛:解决本题的关键是将恒成立问题转化为求函数的最值. 23.(1)2a =,2k =;(2)3,2⎡⎫+∞⎪⎢⎣⎭;(3)2m =;(4)17,12⎛⎫-∞ ⎪⎝⎭. 【分析】(1)由奇函数性质求得k ,由3(1)2f =可求得a ; (2)利用函数的单调性得值域;(3)换元,设22x x t -=-,则3,2t ⎡⎫∈+∞⎪⎢⎣⎭,()g x 转化为()222k t t mt =-+,3,2t ⎡⎫∈+∞⎪⎢⎣⎭,由二次函数的性质求得最小值,再由最小值为2-可得m , (4)在(3)基础上,由()k t 的最小值大于0可得m 的取值范围.【详解】解:(1)∵函数()()1xxf x a k a -=--,(0a >且1a ≠)是定义域为R 的奇函数,∴()00f =,即()110k --=,2k =, ∵()312f =.∴132a a -=,2a =, ∴2a =,2k =, (2)1()2222xxx x f x -=-=-是增函数,∴1≥x 时,13()222f x ≥-=,即值域中3,2⎡⎫+∞⎪⎢⎣⎭; (3)()()2222222xx x x g x m --=+--,设22xxt -=-,[)1,x ∈+∞,3,2t ⎡⎫∈+∞⎪⎢⎣⎭, ∴()222k t t mt =-+,3,2t ⎡⎫∈+∞⎪⎢⎣⎭,∵若()g x 在[)1,+∞上的最小值为2-,∴()222k t t mt =-+,3,2t ⎡⎫∈+∞⎪⎢⎣⎭的最小值为2-,∴23222m m ⎧≥⎪⎨⎪-+=-⎩或3293224m m ⎧<⎪⎪⎨⎪-+=-⎪⎩ 即2m =,或2512m =(舍去), 故2m =;(4)()222k t t mt =-+,3,2t ⎡⎫∈+∞⎪⎢⎣⎭, ∵()0g x >在[)1,+∞上恒成立, ∴()0k t >在3,2t ⎡⎫∈+∞⎪⎢⎣⎭上恒成立,∴23220m m ⎧≥⎪⎨⎪-+>⎩或3293204m m ⎧<⎪⎪⎨⎪-+>⎪⎩, 解不等式得出x ∈∅或1712m <, ∴m 的取值范围为17,12⎛⎫-∞ ⎪⎝⎭.【点睛】方法点睛:本题考查指数函数的性质,考查奇偶性,由奇偶性同函数解析式,由单调性是函数的值域,在求函数()g x 的最值问题,不等式恒成立问题时,解题方法是换元法,即设22x x t -=-,把指数函数转化为二次函数,然后利用二次函数性质求解.24.(1)2)1. 【分析】(1)求出x y -的值,再化简11221122x y x y-+即得解;(2)利用对数的运算法则化简求解. 【详解】(1)因为222()()41249108x y x y xy -=+-=-⨯=,又x y <,所以x y -=-所以1111222221122()3x y x yx yx y--====--+.(2)原式22(lg2)lg5(1lg2)(lg2)lg5lg2lg5=+⋅+=+⋅+lg2(lg2lg5)lg5lg2lg51=++=+=.【点睛】关键点点睛:解答指数对数运算题的关键是通过观察式子的特点,再熟练利用指数对数的运算法则和性质求解.25.(1)1;(2)1010.【分析】(1)根据4()42xxf x=+的表达式,求出()(),1f a f a-的表达式,再进行分式通分运算,可得()()11f a f a+-=.(2)设12320202021202120212021S f f f f⎛⎫⎛⎫⎛⎫⎛⎫=+++⋅⋅⋅+⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,再把S的表达式运用加法交换律改写成20201202120212021202321S f f f f⎛⎫⎛⎫⎛⎫⎛⎫=++++⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,把两式相加利用()(1)1f x f x+-=求出S的值.【详解】(1)4()42xxf x=+,x∈R.∴()()1f a f a+-1144444442424224a a a aa a aa--=+=+++++4214224aa a=+=++,(2)设12320202021202120212021S f f f f⎛⎫⎛⎫⎛⎫⎛⎫=+++⋅⋅⋅+⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,则20201202120212021202321S f f f f⎛⎫⎛⎫⎛⎫⎛⎫=++++⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,两式相加得:12[][][]92022020220120201202120212022120211021S f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=++++++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭由(1)得:202022011 09211,1,,221202120212021202120220101f f f f f f⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+=+=+=⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,∴220201010S S=⇒=.【点睛】本题考查指数幂运算,分式运算,利用函数的性质进行式子求值,考查运算求解能力. 26.(1)见解析;(2)见解析;(3)[]4,5 【分析】 (1)由不等式101x x +>-即可求出()f x 的定义域; (2)证明()()f x f x -=-可得()f x 为奇函数;(3)先求出()f x 在[]3,7上的值域,令()t f x =,求()14h t t t=+的值域. 【详解】 (1)由101x x +>-得:1x >或1x <-, ()f x ∴的定义域为()(),11,-∞-+∞;(2)()()222111log log log 111x x x f x f x x x x -+-+-===-=---+-, ()f x ∴为奇函数;(3)()22log 11f x x ⎛⎫=+ ⎪-⎝⎭在[]3,7上单调递减,令()t f x =,则24log ,13t ⎡⎤∈⎢⎥⎣⎦, 而()14h t t t=+在10,2⎛⎤ ⎥⎝⎦单调递减,在1,12⎡⎤⎢⎥⎣⎦上单调递增,又()2411log 15,4342h h h h ⎛⎫⎛⎫⎛⎫<=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, ∴函数()h x 在[]3,7内的值域为[]4,5.【点睛】本题主要考查了对数型函数的定义域,奇偶性,考查了复合函数的单调性,值域求解,属于中档题.。
(必考题)高中数学必修一第三单元《指数函数和对数函数》测试题(含答案解析)

一、选择题1.下列各组函数中,表示同一个函数的是( )A .211x y x -=-与1y x =+B .y x =与log xa y a =(0a >且1a ≠)C .21y x =-与1y x =-D .lg y x =与21lg 2y x =2.函数12xy ⎛⎫= ⎪⎝⎭的大致图象是( ). A . B .C .D .3.我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微:数形结合百般好,隔离分家万事休”.在数学学习中和研究中,常用函数的图象来研究函数的性质,页常用函数的解析式来琢磨函数图象的特征,如函数()22xy xx R =-∈的大致图象是( )A .B .C .D .4.已知函数()()3,<1log ,1a a x a x f x x x ⎧--=⎨≥⎩的值域..是R ,那么实数a 的取值范围是( ) A .31,2⎛⎤ ⎥⎝⎦B .()1,+∞C .()()0,11,3D .3,32⎡⎫⎪⎢⎣⎭5.已知函数22()lg[(1)(1)1]f x a x a x =-+++的值域为R .则实数a 的取值范围是( ) A .5[1,]3B .5(1,]3C .(]5,1(,)3-∞-⋃+∞D .()5,1[1,)3-∞-6.已知:23log 2a =,42log 3b =,232c -⎛⎫= ⎪⎝⎭,则a ,b ,c 的大小关系是( )A .b c a <<B .b a c <<C .c b a <<D .c a b <<7.函数()212()log 4f x x =-的单调递增区间为( ). A .(0,+∞)B .(-,0)C .(2,+∞)D .(-,-2)8.已知函数()f x 是定义在R 上的单调递增的函数,且满足对任意的实数x 都有[()3]4x f f x -=,则()()f x f x +-的最小值等于( ).A .2B .4C .8D .129.函数1()1x f x a +=-恒过定点( )A .(1,1)B .(1,1)-C .(1,0)-D .(1,1)--10.如图是指数函数①y =x a ;②y =x b ;③y =c x ;④y =d x 的图象,则a ,b ,c ,d 与1的大小关系是( )A .a <b <1<c <dB .b <a <1<d <cC .1<a <b <c <dD .a <b <1<d <c11.函数2()ln(43)f x x x =+-的单调递减区间是( )A .32⎛⎤-∞ ⎥⎝⎦,B .3,42⎡⎫⎪⎢⎣⎭C .3,2⎡⎫+∞⎪⎢⎣⎭D .31,2⎛⎤- ⎥⎝⎦12.已知函数()2,01,0x x f x x x >⎧=⎨+≤⎩,若()()10f a f +=,则实数a 的值等于( )A .-3B .-1C .1D .3二、填空题13.下列命题中所有正确的序号是_____________.①函数1()3x f x a -=+(0a >且1)a ≠的图像一定过定点(1,4)P ; ②函数(1)f x -的定义域是(1,3),则函数()f x 的定义域为(2,4); ③若1log 12a>,则a 的取值范围是112⎛⎫⎪⎝⎭,; ④若22ln ln()x y x y -->-- (0x >,0y <),则0x y +<.14.函数()log 31a y x =+-.(0a >且1a ≠)的图像恒过定点A ,若点A 在直线10mx ny ++=上(其中m ,0n >),则12m n+的最小值等于__________. 15.设函数2()ln(1)f x x x =+,若()23(21)0f a f a +-<,则实数a 的取值范围为_____.16.函数()()cos1log sin f x x =的单调递增区间是____________. 17.函数()()212log 56f x x x =-+的单调递增区...间是__________. 18.已知奇函数()()y f x x R =∈满足:对一切x ∈R ,()()11f x f x +=-且[]0,1x ∈时,()1xf x e =-,则()2019f f =⎡⎤⎣⎦__________.19.设函数122,1()1log ,1x x f x x x -⎧≤=⎨->⎩,则满足()2f x ≤的x 的取值范围是_______________.20.如果()231log 2log 9log 64x x x f x =-+-,则使()0f x <的x 的取值范围是______.三、解答题21.已知函数()log (1)log (1)a a f x x x =+--,(0a >且1a ≠) (1)求()f x 的定义域;(2)判断()f x 的奇偶性,并予以证明; (3)求使()0f x >的x 取值范围. 22.已知函数122()log 2xf x x-=+. (1)求函数()f x 的定义域,并判断其奇偶性;(2)判断()f x 在其定义域上的单调性,并用单调性定义证明. 23.已知函数()421()x x f x a a R =-+⋅-∈. (1)当1a =时,求()f x 的值域; (2)若()f x 在区间[]1,0-的最大值为14-,求实数a 的值. 24.已知函数35()log 5xf x x-=+. (1)求函数()f x 的定义域;(2)判断函数()f x 奇偶性,并证明你的结论.25.已知集合(){}2log 33A x x =+≤,{}213B x m x m =-<≤+. (1)若2m =-,求AB ;(2)若A B A ⋃=,求实数m 的取值范围.26.已知函数()f x 是定义在R 上的奇函数,当0x 时,()121xaf x =++. (1)求实数a 的值及()f x 的解析式; (2)求方程4|(1)|5f x -=的解.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】分析各个选项中每组函数的定义域和对应关系,若定义域和对应关系均相同则为同一个函数,由此判断出正确选项. 【详解】A .211x y x -=-的定义域为{}1x x ≠,1y x =+的定义域为R ,所以不是同一个函数;B .y x =与log xa y a =的定义域均为R ,且log xa y a =即为y x =,所以是同一个函数; C.y =(][),11,-∞-+∞,1y x =-的定义域为R ,所以不是同一个函数;D .lg y x =的定义域为()0,∞+,21lg 2y x =的定义域为{}0x x ≠,所以不是同一个函数, 故选:B. 【点睛】思路点睛:同一函数的判断步骤:(1)先判断函数定义域,若定义域不相同,则不是同一函数;若定义域相同,再判断对应关系;(2)若对应关系不相同,则不是同一函数;若对应关系相同,则是同一函数.2.A解析:A 【分析】去绝对值符号后根据指数函数的图象与性质判断. 【详解】由函数解析式可得:1,022,0xx x y x ⎧⎛⎫≥⎪ ⎪=⎨⎝⎭⎪<⎩可得值域为:01y <≤,由指数函数的性质知:在(),0-∞上单调递增;在()0,∞+上单调递减. 故选:A. 【点睛】思路点睛:函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置. (2)从函数的单调性,判断图象的变化趋势; (3)从函数的奇偶性,判断图象的对称性; (4)从函数的特征点,排除不合要求的图象.3.A解析:A 【分析】分析函数()()22xf x xx R =-∈的奇偶性,结合()01f =可得出合适的选项.【详解】令()22=-xf x x ,该函数的定义域为R ,()()()2222xxf x x x f x --=--=-=,函数()22=-xf x x 为偶函数,排除B 、D 选项;又()010f =>,排除C 选项. 故选:A. 【点睛】函数图象的辨识可从以下方面入手: (1)从函数的定义域,判断图象的左右位置; (2)从函数的值域,判断图象的上下位置. (3)从函数的单调性,判断图象的变化趋势; (4)从函数的奇偶性,判断图象的对称性; (5)从函数的特征点,排除不合要求的图象.4.A解析:A 【分析】当0<a <1时,当1≥x 时,log 0a y x =≤,则当1x <时,()3y a x a =--的值域必须要包含()0,+∞,,当1a >时,当1≥x 时,[)log 0a y x =∈+∞,,则当1x <时,()3y a x a =--的值域必须要包含()0-∞,,从而可得答案. 【详解】由题意,()f x 的值域为R ,当0<a <1时,当1≥x 时,log 0a y x =≤,所以当1x <时,()3y a x a =--的值域必须要包含()0,+∞,当1x <时,()3y a x a =--单调递增,()332y a x a a =--<- 所以不满足()f x 的值域为R .当1a >时,当1≥x 时,[)log 0a y x =∈+∞,, 所以当1x <时,()3y a x a =--的值域必须要包含()0-∞,, 若3a =时,当1x <时,3y a =-=-,不满足()f x 的值域为R .若3a >时,当1x <时,()3y a x a =--单调递减,()332y a x a a =-->- 所以不满足()f x 的值域为R .若13a <<时,当1x <时,()3y a x a =--单调递增,()332y a x a a =--<- 要使得()f x 的值域为R ,则320a -≥,即32a ≤ 所以满足条件的a 的取值范围是:312a <≤, 故选:A .【点睛】关键点睛:本题考查根据函数的值域求参数的范围,解答本题的关键是当0<a <1时,当1≥x 时,log 0a y x =≤,则当1x <时,()3y a x a =--的值域必须要包含()0,+∞,,当1a >时,当1≥x 时,[)log 0a y x =∈+∞,,则当1x <时,()3y a x a =--的值域必须要包含()0-∞,,属于中档题. 5.A解析:A 【分析】当函数的值域为R 时,命题等价于函数()()22111y a x a x =-+++的值域必须包含区间()0+∞,得解 【详解】22()lg[(1)(1)1]f x a x a x =-+++的值域为R令()()22111y a x a x =-+++,则()()22111y a x a x =-+++的值域必须包含区间()0+∞,当210a -=时,则1a =± 当1a =时,21y x =+符合题意; 当1a =-时,1y =不符合题意;当1a ≠±时,()()222101410a a a ⎧->⎪⎨∆=+--≥⎪⎩,解得513a <≤ 513a ∴≤≤,即实数a 的取值范围是5[1,]3故选:A 【点睛】转化命题的等价命题是解题关键.6.A解析:A 【分析】由换底公式和对数函数的性质可得112b a <<<,再由指数函数的性质可得102c <<,即可得解. 【详解】23ln3ln12log =02ln 2ln 2a ==>,4212ln ln 2ln1323log =03ln 4ln 2ln 2b ====<, a b ∴>22223231log log 410,239222a c -⎛⎫⎛⎫<===< ⎪ ⎪⎭=⎝>⎭=⎝,b c a ∴<<, 故选:A 【点睛】方法点睛:本题考查了对数式、指数式的大小比较,比较大小的常用方法为同底的对数式和指数式利用其单调性进行比较,也可以借助于中间值0和1进行比较,考查了运算求解能力与逻辑推理能力,属于常考题.7.D解析:D 【分析】求出函数的定义域,根据对数型复合函数的单调性可得结果. 【详解】函数()212()log 4f x x =-的定义域为()(),22,-∞-+∞,因为函数()f x 是由12log y u =和24u x =-复合而成,而12log y u =在定义域内单调递减,24u x =-在(),2-∞-内单调递减,所以函数()212()log 4f x x =-的单调递增区间为(),2-∞-, 故选:D. 【点睛】易错点点睛:对于对数型复合函数务必注意函数的定义域.8.B解析:B 【分析】根据()3x f x -为定值,可假设()3xf x m =+,然后计算()()f x f x +-,并计算m 的值,然后使用基本不等式,可得结果. 【详解】由题可知:()3xf x -为定值故设()3xf x m -=,即()3xf x m =+又[()3]4xf f x -=,所以()341mf m m m =+=⇒= 则()31xf x =+()()3131x x f x f x -+-=+++则1()()32243x x f x f x +-=++≥= 当且仅当133xx =时,取等号 所以()()f x f x +-的最小值为:4故选:B 【点睛】本题考查基本不等式的应用,还考查镶嵌函数的应用,难点在于()3xf x -为定值,审清题意,细心计算,属中档题.9.C解析:C 【分析】根据指数函数性质求定点. 【详解】因为01a =,所以()011f a -=-=0,因此过定点()1,0-,选C.【点睛】本题考查指数函数性质以及定点问题,考查基本分析求解能力,属于基础题.10.B解析:B 【分析】根据指数函数的图象与性质可求解. 【详解】根据函数图象可知函数①y =x a ;②y =x b 为减函数,且1x =时,②y =1b <①y =1a , 所以1b a <<,根据函数图象可知函数③y =c x ;④y =d x 为增函数,且1x =时,③y =c 1>④y =d 1, 所以1c d >> 故选:B 【点睛】本题主要考查了指数函数的单调性,指数函数的图象,数形结合的思想,属于中档题.11.B解析:B 【分析】先求函数的定义域,再利用复合函数的单调性同增异减,即可求解. 【详解】由2430x x +->得2340x x --<,解得:14x -<<,2()ln(43)f x x x =+-由ln y t =和234t x x =-++复合而成,ln y t =在定义域内单调递增,234t x x =-++对称轴为32x =,开口向下, 所以 234t x x =-++在31,2⎛⎫- ⎪⎝⎭ 单调递增,在3,42⎡⎫⎪⎢⎣⎭单调递减, 所以2()ln(43)f x x x =+-的单调减区间为3,42⎡⎫⎪⎢⎣⎭,故选:B 【点睛】本题主要考查了利用同增异减求复合函数的单调区间,注意先求定义域,属于中档题12.A解析:A 【分析】先求得()1f 的值,然后根据()f a 的值,求得a 的值. 【详解】由于()1212f =⨯=,所以()()20,2f a f a +==-,22a =-在()0,∞+上无解,由12a +=-解得3a =-,故选A.【点睛】本小题主要考查分段函数求函数值,考查已知分段函数值求自变量,属于基础题.二、填空题13.①③④【分析】由指数函数的图象函数的定义域对数函数的性质判断各命题①令代入判断②利用函数的定义求出的定义域判断③由对数函数的单调性判断④引入新函数由它的单调性判断【详解】①令则即图象过点①正确;②则解析:①③④ 【分析】由指数函数的图象,函数的定义域,对数函数的性质判断各命题.①,令1x =代入判断,②利用函数的定义求出()f x 的定义域判断,③由对数函数的单调性判断,④引入新函数1()ln 2ln 2xxg x x x -⎛⎫=-=- ⎪⎝⎭,由它的单调性判断.【详解】①令1x =,则(1)4f =,即()f x 图象过点(1,4),①正确; ②13x <<,则012x <-<,∴()f x 的定义域是(0,2),②错;③1log 1log 2a a a ,∴0112a a <<⎧⎪⎨>⎪⎩,∴112a <<.③正确;④由22ln ln()x y x y -->-- (0x >,0y <),得ln 2ln()2x y x y --<--, 又1()ln 2ln 2xx g x x x -⎛⎫=-=- ⎪⎝⎭是(0,)+∞上的增函数, ∴由ln 2ln()2x y x y --<--,得x y <-,即0x y +<,④正确. 故答案为:①③④【点睛】关键点点睛:本题考查指数函数的图象,对数函数的单调性,函数的定义域问题,定点问题:(1)指数函数(0x y a a =>且1)a ≠的图象恒过定点(0,1);(2)对数函数log (0a y x a =>且1)a ≠的图象恒过定点(1,0),解题时注意整体思想的应用.14.8【分析】根据函数平移法则求出点得再结合基本不等式即可求解【详解】由题可知恒过定点又点在直线上故当且仅当时取到等号故的最小值等于8故答案为:8【点睛】本题考查函数平移法则的使用基本不等式中1的妙用属 解析:8【分析】根据函数平移法则求出点A ()2,1--,得21m n +=,再结合基本不等式即可求解【详解】由题可知,()log 31a y x =+-恒过定点()2,1--,又点A 在直线 10mx ny ++=上,故21m n +=,()121242448n m m n m n m n m n ⎛⎫+=++=++≥+= ⎪⎝⎭,当且仅当122n m ==时取到等号,故12m n+的最小值等于8 故答案为:8【点睛】本题考查函数平移法则的使用,基本不等式中“1”的妙用,属于中档题15.【分析】根据已知可得为奇函数且在上单调递增不等式化为转化为关于自变量的不等式即可求解【详解】的定义域为是奇函数设为增函数在为增函数在为增函数在处连续的所以在上单调递增化为等价于即所以实数的取值范围为 解析:1(1,)3- 【分析】根据已知可得()f x 为奇函数且在R 上单调递增,不等式化为()23(12)f a f a <-,转化为关于自变量的不等式,即可求解.【详解】()f x 的定义域为R ,()()))ln10f x f x x x +-=+==,()f x ∴是奇函数,设,[0,)()x u x x =∈+∞为增函数,()f x 在[0,)+∞为增函数,()f x 在(,0)-∞为增函数,()f x 在0x =处连续的,所以()f x 在R 上单调递增,()23(21)0f a f a +-<,化为()23(12)f a f a <-,等价于2312a a <-,即213210,13a a a +-<-<<, 所以实数a 的取值范围为1(1,)3-.故答案为: 1(1,)3-【点睛】本题考查利用函数的单调性和奇偶性解不等式,熟练掌握函数的性质是解题的关键,属于中档题. 16.【分析】根据对数型复合函数单调性列不等式再根据正弦函数性质得结果【详解】单调递增区间为单调递减区间且所以故答案为:【点睛】本题考查对数型复合函数单调性以及正弦函数性质考查基本分析求解能力属基础题 解析:[2,2),()2k k k Z ππππ++∈ 【分析】根据对数型复合函数单调性列不等式,再根据正弦函数性质得结果.【详解】()()cos1cos1(0,1)log sin f x x ∈∴=单调递增区间为sin y x =单调递减区间且sin 0x >, 所以22,()2k x k k Z ππππ+≤<+∈, 故答案为:[2,2),()2k k k Z ππππ++∈【点睛】 本题考查对数型复合函数单调性以及正弦函数性质,考查基本分析求解能力,属基础题. 17.【分析】求出函数的定义域利用复合函数法可求得函数的单调递增区间【详解】对于函数有解得或所以函数的定义域为内层函数在区间上单调递减在区间上单调递增外层函数为减函数所以函数的单调递增区间为故答案为:【点 解析:(),2-∞【分析】求出函数()f x 的定义域,利用复合函数法可求得函数()()212log 56f x x x =-+的单调递增区间.【详解】对于函数()()212log 56f x x x =-+,有2560x x -+>,解得2x <或3x >. 所以,函数()()212log 56f x x x =-+的定义域为()(),23,-∞+∞,内层函数256u x x =-+在区间(),2-∞上单调递减,在区间()3,+∞上单调递增, 外层函数12log y u =为减函数,所以,函数()f x 的单调递增区间为(),2-∞. 故答案为:(),2-∞.【点睛】复合函数()y f g x ⎡⎤=⎣⎦的单调性规律是“同则增,异则减”,即()y f u =与()u g x =.若具有相同的单调性,则()y f g x ⎡⎤=⎣⎦为增函数,若具有不同的单调性,则()y f g x ⎡⎤=⎣⎦必为减函数.18.【分析】根据题意求得的周期性则可求再结合函数解析式求得函数值即可【详解】由题可知:因为对一切故关于对称;又因为是奇函数则可得故可得故函数是周期为的函数则又当故则故答案为:【点睛】本题考查利用函数周期 解析:31e e --【分析】根据题意,求得()f x 的周期性,则()2019f 可求,再结合函数解析式,求得函数值即可.【详解】由题可知:因为对一切x R ∈,()()11f x f x +=-,故()f x 关于1x =对称;又因为()f x 是奇函数,则可得()()()()()21111f x f x f x f x f x +=++=--=-=-,故可得()()()()4222f x f x f x f x +=++=-+=,故函数()f x 是周期为4的函数.则()()()201911f f f =-=-,又当[]0,1x ∈,()1x f x e =-,故()()201911f f e =-=-, 则()()()()()320191131e f f f e f e f e e -=-=--=--=-.故答案为:31e e --.【点睛】本题考查利用函数周期性求函数值,属综合中档题;难点在于求得函数的周期. 19.【分析】根据分段函数分段解不等式最后求并集【详解】当时因为解得:∴当时解得:所以综上原不等式的解集为故答案为:【点睛】本题主要考查了解分段函数不等式涉及指数与对数运算属于基础题解析:[0,)+∞【分析】根据分段函数,分段解不等式,最后求并集.【详解】当1x ≤时,1()2x f x -=,因为11x -≤,解得:0x ≥,∴01x ≤≤ ,当1x >时,2()1log 2f x x =-≤,2log 1x ≥-,解得:12x ≥,所以1x >, 综上,原不等式的解集为[)0,+∞.故答案为:[)0,+∞.【点睛】 本题主要考查了解分段函数不等式,涉及指数与对数运算,属于基础题.20.【分析】可结合对数化简式将化简为再解对数不等式即可【详解】由由得即当时故;当时无解综上所述故答案为:【点睛】本题考查对数化简公式的应用分类讨论求解对数型不等式属于中档题 解析:81,3⎛⎫ ⎪⎝⎭【分析】可结合对数化简式将()f x 化简为()1log 2log 3log 4x x x f x =-+-,再解对数不等式即可【详解】由()2323231log 2log 9log 641log 2log 3log 4x x x x x x f x =-+-=-+- 31log 2log 3log 41log 8x x x x =-+-=+,由()0f x <得81log 03x -<, 即8log log 3x x x >, 当1x >时,83x <,故81,3x ⎛⎫∈ ⎪⎝⎭;当()0,1x ∈时,83x >,无解 综上所述,81,3x ⎛⎫∈ ⎪⎝⎭ 故答案为:81,3⎛⎫ ⎪⎝⎭【点睛】本题考查对数化简公式的应用,分类讨论求解对数型不等式,属于中档题三、解答题21.(1){|11}x x -<<;(2)函数()f x 是奇函数,证明见解析;(3)当1a >时,01x <<;当01a <<时,10x -<<【分析】(1)根据对数的真数为正数列式可解得结果;(2)函数()f x 是奇函数,根据奇函数的定义证明即可;(3)不等式化为log (1)log (1)a a x x +>-后,分类讨论底数a ,根据对数函数的单调性可解得结果.【详解】(1)要使函数数()f x 有意义,则必有1010x x +>⎧⎨->⎩,解得11x -<<, 所以函数()f x 的定义域是{|11}x x -<< .(2)函数()f x 是奇函数,证明如下:∵(1,1)x ∈-,(1,1)x -∈-,()log (1)log (1)a a f x x x -=--+[]log (1)log (1)a a x x =-+--()f x =-,∴函数()f x 是奇函数(3)使()0f x >,即log (1)log (1)a a x x +>-当1a >时,有111010x x x x +>-⎧⎪->⎨⎪+>⎩,解得01x <<,当01a <<时,有111010x x x x +<-⎧⎪->⎨⎪+>⎩,解得10x -<<.综上所述:当1a >时,01x <<;当01a <<时,10x -<<.【点睛】方法点睛:已知函数解析式,求函数定义域的方法:有分式时:分母不为0;有根号时:开奇次方,根号下为任意实数,开偶次方,根号下大于或等于0;有指数时:当指数为0时,底数一定不能为0;有根号与分式结合时,根号开偶次方在分母上时:根号下大于0;有指数函数形式时:底数和指数都含有x ,指数底数大于0且不等于1;有对数函数形式时,自变量只出现在真数上时,只需满足真数上所有式子大于0,自变量同时出现在底数和真数上时,要同时满足真数大于0,底数要大0且不等于1.22.(1)定义域为(2,2)-,奇函数(2)函数()f x 在(2,2)-上为增函数,证明见解析【分析】(1)根据真数大于0可得定义域,根据奇函数的定义可得函数为奇函数;(2)设1222x x -<<<,根据对数函数的单调性可得12()()f x f x <,再根据定义可证函数()f x 在(2,2)-上为增函数.【详解】(1)由函数有意义得202x x->+,解得22x -<<, 所以函数的定义域为(2,2)-, 因为1112222()log log ()22x x f x f x x x -+-⎛⎫-===- ⎪-+⎝⎭, 所以函数为奇函数.(2)因为124()log 12f x x ⎛⎫=-+⎪+⎝⎭,所以函数()f x 在(2,2)-上为增函数, 证明:设1222x x -<<<,则120224x x <+<+<,则1244122x x >>++,则124411022x x -+>-+>++, 因为1012<<,所以12()()f x f x <,所以函数()f x 在(2,2)-上为增函数, 【点睛】思路点睛:判断函数的奇偶性的思路:①求出定义域,并判断其是否关于原点对称;②若定义域不关于原点对称,则函数为非奇非偶函数,若定义域关于原点对称,再判断()f x -与()f x 的关系,若()()f x f x -=-,则函数为奇函数;若()()f x f x -=,则函数为偶函数.23.(1)3,4⎛⎤-∞- ⎥⎝⎦;(2)a =【分析】(1)令()20,xt =∈+∞,可得21y t t =-+-,利用二次函数的性质可求出; (2)令12,12x t ⎡⎤=∈⎢⎥⎣⎦,可得21y t at =-+-,讨论对称轴2a t =的取值范围结合二次函数的性质即可求出.【详解】(1)()2()421221x x x x f x a a =-+⋅-=-+⋅-.令()20,xt =∈+∞,21y t at =-+-,1a =时,2213124y t t t ⎛⎫=-+-=--- ⎪⎝⎭在10,2⎛⎫ ⎪⎝⎭上单调递增,在1,2⎛⎫+∞ ⎪⎝⎭上单调递减. ∴当12t =时,max 34y =-,∴3,4y ⎛⎤∈-∞- ⎥⎝⎦, 所以()f x 的值域为3,4⎛⎤-∞- ⎥⎝⎦. (2)令12,12x t ⎡⎤=∈⎢⎥⎣⎦,22211124a y t at t a ⎛⎫=-+-=---+ ⎪⎝⎭, 其图象的对称轴为2a t =. ①当122a ≤,即1a ≤时,函数y 在区间1,12⎡⎤⎢⎥⎣⎦上单调递减, 当12t =时,max 1111424y a =-+-=-,解得2a =,与1a ≤矛盾; ②当12a ≥,即2a ≥时,函数y 在区间1,12⎡⎤⎢⎥⎣⎦上单调递增, 当1t =时,max 1114y a =-+-=-,解得74a =,与2a ≥矛盾, ③当1122a <<,即12a <<时,函数y 在1,22a ⎡⎤⎢⎥⎣⎦上单调递增,在,12a ⎡⎤⎢⎥⎣⎦上单调递减.当2a t =时,2max 11144y a =-=-,解得a =,舍去a =综上,a =【点睛】思路点睛:求二次函数在闭区间[],a b 的最值的思路;(1)二次函数开口向上时,求函数的最大值,讨论对称轴和2a b +的大小求解; (2)二次函数开口向上时,求函数的最小值,讨论对称轴在(]()[),,,,,a a b b -∞+∞三个区间的范围求解.24.(1)(5,5)- (2)奇函数,见解析【分析】(1)若()f x 有意义,则需满足505x x->+,进而求解即可; (2)由(1),先判断定义域是否关于原点对称,再判断()f x -与()f x 的关系即可.【详解】(1)由题,则505x x->+,解得55x -<<,故定义域为()5,5-(2)奇函数,证明:由(1),()f x 的定义域关于原点对称,因为()()33355log log log 1055x x f x f x x x +--+=+==-+,即()()f x f x -=-, 所以()f x 是奇函数【点睛】本题考查具体函数的定义域,考查函数的奇偶性的证明.25.(1){}31A B x x ⋂=-<≤;(2)[][)1,24,m ∈-+∞ 【分析】(1)计算{}35A x x =-<≤,{}51B x x =-<≤,再计算交集得到答案.(2)A B A ⋃=,故B A ⊆,讨论B =∅和B ≠∅,计算得到答案.【详解】(1)(){}{}2log 3335A x x x x =+≤=-<≤,{}51B x x =-<≤, 故{}31A B x x ⋂=-<≤.(2){}35A x x =-<≤,A B A ⋃=,故B A ⊆, 当B =∅时,213m m -≥+,解得4m ≥;当B ≠∅时,4m <,故21335m m -≥-⎧⎨+≤⎩,解得12m -≤≤. 综上所述:[][)1,24,m ∈-+∞.【点睛】本题考查交集运算,根据集合的包含关系求参数,意在考查学生的计算能力和综合应用能力. 26.(1) 2a =-,()2121x x f x -=+;(2) 212log 3x =+或212log 3x =- 【分析】(1)根据奇函数(0)0f =求解a ,再根据奇函数的性质求解()f x 的解析式即可.(2)根据(1)可得()2121x x f x -=+为奇函数,可先求解4|()|5f t =的根,再求解4|(1)|5f x -=即可. 【详解】(1)因为()f x 是定义在R 上的奇函数,且当0x ≥时,()121x a f x =++,故0(0)1021a f =+=+,即102a +=,解得2a =-.故当0x ≥时,()22112121x x x f x -=-=++. 所以当0x < 时, ()()211221211221x x x x x x f x f x -----=--=-=-=+++.故()2121x x f x -=+ (2) 先求解4|()|5f t =,此时()214215t t f t -==±+. 当()()214421521215t t t t -=⇒+=-+,即29t =解得22log 92log 3t ==. 因为()2121x x f x -=+为奇函数,故当214215t t -=-+时, 22log 3t =-. 故4|(1)|5f x -=的解为212log 3x -=或212log 3x -=-, 解得212log 3x =+或212log 3x =-【点睛】本题主要考查了根据奇函数求解参数的值以及解析式的方法,同时也考查了根据函数性质求解绝对值方程的问题,属于中档题.。
2023-2024学年高考数学指数函数与对数函数专项练习题(含答案)

2024....二、多选题.函数,若对任意实数、,,则下列结论错误的是()(32log f x x x =++a b 0a b +>A .方程有且只有6个不同的解B .方程()()0f g x =解C .方程有且只有5个不同的解D .方程()()0f f x =解的零点个数为 .()4log =-y f x x16.已知函数,若方程有4个不同的实根,,,22log (1),13()1357,322x x f x x x x ⎧-<≤⎪=⎨-+>⎪⎩()34f x =1x 2x 3x 且,则.4x 1234x x x x <<<()341211x x x x ⎛⎫++=⎪⎝⎭答案:1.C【分析】根据函数的单调性,借助中间值比较大小.【详解】因为函数在单调递增,且,所以,即,2log y x =()0,∞+π2>22log π>log 21=1a >因为函数在单调递减,且,所以,即,0.5log y x =()0,∞+π1>0.50.5log π<log 1=00b <因为函数在单调递增,且,所以,即,πxy =(),-∞+∞20-<200<ππ1-<=01c <<所以,a c b >>故选:C 2.A【分析】由提供的数据知,描述西红柿种植成本与上市时间的变化关系函数不可能是单Q t 调函数,故选取二次函数进行描述,将表格所提供的三组数据代入,即得函2Q at bt c =++Q 数解析式,进而求解.【详解】因为随着时间的增加,种植成本先减少后增加,所以函数不单调,所以选取,且开口向上,2Q at bt c =++将表格中的三组数据分别代入,2Q at bt c =++得解得116360060,8410000100,11632400180,a b c a b c a b c =++⎧⎪=++⎨⎪=++⎩0.01,2.4,224,a b c =⎧⎪=-⎨⎪=⎩即,对称轴,开口向上,20.01 2.4224Q t t =-+ 2.412020.01t -=-=⨯在对称轴处即120天时函数取最小值.∴t =西红柿种植成本最低时的上市天数是120天.∴故选:A.3.C【分析】由指数函数的性质分别对和的情况讨论单调性并求值域,从而列方程组01a <<1a >即可得到答案.【详解】函数(且)的值域为,2x y a =-0a >1,11a x ≠-≤≤5,13⎡⎤-⎢⎥⎣⎦又由指数函数的单调性可知,当时,函数在上单调递减,值域是01a <<2xy a =-[]1,1-12,2a a -⎡⎤--⎣⎦所以有,即,解得;110152321a a a -<<⎧⎪⎪-=-⎨⎪-=⎪⎩101133a a a -<<⎧⎪⎪=⎨⎪=⎪⎩13a =当时,函数在上单调递增,值域是1a >2x y a =-[]1,1-12,2a a -⎡⎤--⎣⎦所以有,即 ,解得.11152321a a a ->⎧⎪⎪-=-⎨⎪-=⎪⎩11133a a a ->⎧⎪⎪=⎨⎪=⎪⎩3a =综上所述,或.13a =3a =故选:C.4.B【分析】结合已知条件,利用抽象函数的定义域以及对数、分式的定义域求法求解即可.【详解】因为函数的定义域是,()f x [1,2022]所以对于有:,(1)()lg f x g x x +=1120220lg 0x x x ≤+≤⎧⎪>⎨⎪≠⎩解得:且,02021x <≤1x ≠故函数的定义域是,()()1ln f x g x x+=(01)(1],,2021⋃故选:B .5.A【分析】根据题意,求得,得到,结合零点的存在性定理,3()0,(2)02f f >>3(1)()02f f ⋅<即可求解.【详解】由函数,且,可得,()348f x x x =+-()()10,30f f <>3()70,(2)2602f f =>=>所以,根据零点的存在性定理,3(1)()02f f ⋅<可得方程的近似解落在区间为.3480x x +-=31,2⎛⎫⎪⎝⎭故选:A.6.C【分析】根据给定条件,可得函数在R 上单调递增,再利用分段函数及对数函数单调性()f x 列出不等式求解即得.【详解】函数的定义域为R ,(2)1,1()log ,1a a x x f x x x --≤⎧=⎨>⎩由对任意,都有,得函数在R 上单调递增,12x x ≠1212()()f x f x x x ->-()f x 于是,解得,20130a a a ->⎧⎪>⎨⎪-≤⎩23a <≤所以实数的取值范围为.a (]2,3故选:C 7.B【分析】利用对数的换底公式和运算法则即可得解.【详解】,,,230x y k ==>Q 23log ,log x k y k ==∴11log 2,log 3k k x y ∴==,,则.12log 2log 3log 61k k k x y ∴=+=+=∴26k =6k =故选:B.8.A【分析】由函数的定义域排除C ,由函数的奇偶性排除D ,由特殊的函数值排除B ,结合奇偶性和单调性判断A.【详解】由得,则函数的定义域为,排除选项C ;30x ->33x -<<()ln 3y x =-()3,3-又,所以为偶函数,则图象关于y 轴对称,排除选项D ;()()ln 3ln 3x x --=-()ln 3y x =-当时,,排除选项B ,52x =1ln 02y =<因为为偶函数,且当时,函数单调递减,()ln 3y x =-30x >>()()ln 3ln 3y x x =-=-选项A 中图象符合.故选:A 9.ACD【分析】分析函数的奇偶性与单调性,由已知可得出,结合函数的奇偶性()f x a b >-()f x与单调性可得出合适的选项.【详解】令,对任意的,,即,()()22log 1g x x x =++x ∈R 21x x x+>≥-210x x ++>所以,函数的定义域为,()g x R 则.()()()()2222221log 1log 1log1g x x x x x g x x x⎛⎫-=+--=+-==- ⎪⎝⎭++所以,函数是定义域为的奇函数,()g x R 因为函数、为上的增函数,1u x =221u x =+[)0,∞+所以,内层函数在上为增函数,21u x x =++[)0,∞+外层函数在上为增函数,2log y u =()0,∞+所以,函数在上为增函数,()()22log 1g x x x =++[)0,∞+由于函数是定义域为的奇函数,则该函数在上为增函数,()g x R (],0-∞所以,函数在上单调递增,()()22log 1g x x x =++R 因为的定义域为,则,()f x R ()()()()()33f x x g x x g x f x -=-+-=--=-所以,函数为奇函数,()f x 又因为函数为上的增函数,所以,函数在上单调递增.3y x =R ()f x R 因为,所以,则,即,A 错B 对,0a b +>a b >-()()()f a f b f b >-=-()()0f a f b +>又、的大小不确定,故CD 错.a b 故选:ACD.方法点睛:函数的三个性质:单调性、奇偶性和周期性,在高考中一般不会单独命题,而是常将它们综合在一起考查,其中单调性与奇偶性结合、周期性与抽象函数相结合,并结合奇偶性求函数值,多以选择题、填空题的形式呈现,且主要有以下几种命题角度;(1)函数的单调性与奇偶性相结合,注意函数的单调性及奇偶性的定义,以及奇、偶函数图象的对称性.(2)周期性与奇偶性相结合,此类问题多考查求值问题,常利用奇偶性及周期性进行交换,将所求函数值的自变量转化到已知解析式的函数定义域内求解;(3)周期性、奇偶性与单调性相结合,解决此类问题通常先利用周期性转化自变量所在的区间,然后利用奇偶性和单调性求解.10.ABC【分析】根据题意,由函数的定义,只需满足集合中的每一个元素在集合中都有唯一一P Q 个元素与之对应即可,再结合选项逐一分析,即可得到结果.【详解】选项A ,,集合中的每一个元素在集合中都有唯一一个元素与之1:2f x y x→=P Q 对应,故A 正确;选项B ,,集合中的每一个元素在集合中都有唯一一个元素与之对应,故13:f x y x →=P Q B 正确;选项C ,,集合中的每一个元素在集合中都有唯一一个元素与之对应,1:2xf x y ⎛⎫→= ⎪⎝⎭P Q 故C 正确;选项D ,,集合中的1,在集合中没有元素与之对应,故D 错误;:ln f x y x →=P Q 故选:ABC 11.ABD【分析】根据奇偶性的定义即可判断A,根据基本函数的单调性即可判断BC ,根据反函数的性质即可判断D.【详解】对于A ,定义域为,关于原点对称,又由于()f x R ()()e e e e ,,22x x x xf x f x --++=-=,所以为偶函数,A 正确,()()=f x f x -()f x 对于B ,,由于函数在单调递增,所以在()e 121e 1e 1x x x f x -==-++e 1xy =+x ∈R 1e 1x y =+单调递减,因此在单调递增,B 正确,x ∈R ()21e 1xf x =-+x ∈R 对于C ,由于函数为定义域上的偶函数,当时,在区间上单调递lg y x=0x >lg y x =()0,∞+增,故C 错误,对于D ,由于函数与互为反函数,所以两者图象关于,D 正13xy ⎛⎫= ⎪⎝⎭133log log y x x ==-y x =确,故选:ABD 12.ACD【分析】令,结合图象可得有3个不同的解,,,不妨设,()t x g =()0f t =1t 2t 3t 123t t t <<则可知,,,令,结合图象可得有2个不同的解121t -<<-2t =312t <<()m f x =()0g m =,,不妨设,则可知,,再数形结合求出复合函数的解的1m 2m 12m m <121m -<<-201m <<个数.【详解】A 选项,令,结合图象可得有3个不同的解,,,()t x g =()0f t =1t 2t 3t 不妨设,则可知,,,123t t t <<121t -<<-20t =312t <<由图可知有2个不同的解,有2个不同的解,有2个不同的解,()1g x t =()2g x t =()3g x t =即有6个不同的解,A 正确;()()0f g x =B 选项,令,结合图象可得有2个不同的解,,()m f x =()0g m =1m 2m 不妨设,则可知,,12m m <121m -<<-201m <<由图可知有1个解,有3个不同的解,()1f x m =()2f x m =即有4个不同的解,B 错误;()()0g f x =C 选项,令,结合图象可得有3个不同的解,,()m f x =()0f m =1m 2m 3m 且,,,121m -<<-20m =312m <<由图可知有1个解,有3个不同的解,有1个解,()1f x m =()2f x m =()3f x m =即有5个不同的解,C 正确;()()0f f x =D 选项,令,结合图象可得有两个不同的解,()t x g =()0g t =1t2t 不妨设,则可知,,12t t <121t -<<-201t <<由图可知有2个不同的解,有2个不同的解,()1g x t =()2g x t =即有4个不同的解,D 正确.()()0g g x =故选:ACD .13.193【分析】利用位数的定义,结合对数运算法则即可得解.k故答案为.14。
2020-2021学年高中数学必修第一册第四章《指数函数与对数函数》测试卷及答案解析

③b>a>1
④0<a<b<1
⑤a=b
其中不可能成立的关系有( )
A.1 个
B.2 个
C.3 个
D.4 个
【解答】解:∵实数 a,b 满足 th a th b,
hh 即
h
hᵎ
hh
,∴
h
h
hᵎ
hh
,∴
h
h
hᵎ ;
h
h 对于①,当 a=3,b=2 时, h
h h ,即 th 3
th 2,∴①不成立;
对于②,当 a ,b 时, th
∴
;
使
∴使
使
使
x=y=3 时取等号.
故选:B.
使 使
使
,当且仅当
,即
使
6.已知 3m=2n=k 且
,则 k 的值为( )
A.15
B.
C.
【解答】解:∵3m=2n=k,∴m=log3k,n=log2k,
D.6
∴
th
th
th
th logk6=2,
∴k2=6,∴
,
故选:C.
7.设 a=30.7,b=( )﹣0.8,c=log0.70.8,则 a,b,c 的大小关系为( )
第6页共9页
∴ thh
,
∴f(6t)﹣f(3t)=loga6t﹣loga3t=loga2 .
故答案为: . 四.解答题(共 6 小题)
14.(1)计算: ୠ
⺁
ୠ;
(2)已知 x+x﹣1=4,求 x2﹣x﹣2 的值.
【解答】解:(1) ୠ
⺁
ୠ
ୠ
⺁
;
ୠ
(2)由 x+x﹣1=4,两边平方并整理得 x2+x﹣2=14,
苏教版高中数学必修第一册第6章幂函数、指数函数和对数函数测试卷(含答案)

苏教版高中数学必修第一册第6章幂函数、指数函数和对数函数测试卷(满分150分,时间120分钟)班级姓名评价一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.函数f (x )2(3x +1)的定义域为()A.-13,+∞B.-∞,C.-13D.-13,12.设a =log 42.4,b =log 32.9,c =log 32.4,则a ,b ,c 的大小关系为()A.b >c >aB.b >a >cC.c >b >aD.a >c >b3.已知0<m <n <1,则指数函数①y =m x 和②y =n x 的图象为()A.B. C. D.4.已知函数f (x )=log 3(x -1),若f (a )=2,则实数a 的值为()A.3B.8C.9D.105.函数y 2+2的增区间为()A.(-∞,0)B.(-∞,-1]C.[-1,+∞)D.[-2,+∞)6.不论a 为何值,函数y =(a -1)2x-2恒过一定点,则这个定点为()A.1,B.1C.-1,D.-17.已知函数f (x )=log a x (0<a <1),则函数y =f (|x |+1)的图象大致是()A. B. C. D.8.春末夏初,南京玄武湖公园荷花池中的荷花枝繁叶茂,已知每天新长出的荷叶覆盖水面的面积是前一天的两倍,若荷叶20天可以完全长满荷花池水面,则当荷叶刚好覆盖水面面积18时,荷叶已生长了()A.4天B.15天C.17天D.18天二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合要求.全部选对的得5分,部分选对的得3分,有选错的得0分.9.下列函数中定义域和值域相同的是()A.y = 23B.y = 15C.y =-xD.y =3x10.已知函数f (x )=log 3( -2), >2,3 -1, ≤2,则下列各式正确的是()A.f (5)=1B.f (f (5))=1C.f (3)=9D.f (f (3))=1311.设函数f (x )=(3-2 ) -1, ≤1,, >1,其中a >0且a ≠1,下列关于函数f (x )的说法正确的是()A.若a =2,则f (log 23)=3B.若f (x )在R 上是增函数,则1<a <32C.若f (0)=-1,则a =32D.函数f (x )为R 上的奇函数12.已知函数f (x )=lo g 12x ,下列四个命题正确的是()A.函数f (|x |)为偶函数B.若f (a )=|f (b )|,其中a >0,b >0,a ≠b ,则ab =1C.函数f (-x 2+2x )在(1,3)上为增函数D.若0<a <1,则|f (1+a )|<|f (1-a )|三、填空题:本题共4小题,每小题5分,共20分.其中第15题第一个空2分,第二个空3分.13.若幂函数y =f (x 2,则f .14.设函数f (x )=lg x ,若f (2x )<f (2),则实数x 的取值范围是.15.函数f (x )=a 2-x-1(a >0,a ≠1)恒过定点,当0<a <1时,f (x 2)的增区间为.16.已知函数f (x )=x 2+log 2|x |,则不等式f (x -1)-f (1)<0的解集为.四、解答题:本题共6小题,共70分.解答时应写出文字说明、证明过程或演算步骤.17.(10分)比较下列各组数的大小:(1)1.8,2.2;(2)0.70.8,0.80.7.18.(12分)已知关于x 的方程5x=15- 有负根,求实数a 的取值范围.19.(12分)已知函数f (x )=log a (-x 2+2x +3)(其中a >0且a ≠1)的值域为[-2,+∞).(1)求实数a 的值;(2)求函数f (x )的单调区间.20.(12分)已知函数f (x )=(a 2-a +1)x a +1为幂函数,且为奇函数.(1)求实数a 的值;(2)求函数g (x )=f (x )+1-2 ( )在0.21.(12分)设函数f (x )=lg (ax )·lg2.(1)当a =0.1时,求f (1000)的值;(2)若f (10)=10,求实数a 的值;(3)若对一切正实数x 恒有f (x )≤98,求实数a 的取值范围.22.(12分)为了预防流感,某学校对教室用药薰消毒法进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y (单位:mg )与t 时间(单位:h )成正比,药物释放完毕后,y 与t之间的函数关系式为y 2+0.9 +(a 为常数),其图象如图所示,根据图中提供的信息回答下列问题:(1)从药物释放开始,求每立方米空气中的含药量y 与时间t 之间的函数关系式.(2)据测定,当空气中每立方米的含药量降低到116mg 以下时,学生方可进入教室,那么从药物释放开始至少需要经过多少小时,学生才可以回到教室?(第22题)参考答案1.D2.A3.C4.D5.B6.C7.A8.C9.BC 10.ABD 11.AB 12.ABD 13.-214.(0,1)15.(2,0)[0,+∞)16.(0,1)∪(1,2)17.(1)1.82.2(2)0.70.8<0.80.718.方程5x=15- 有负根,即0<15-<1,解得a <4,即a ∈(-∞,4)19.(1)a =12(2)函数f (x )的减区间为(-1,1],增区间为[1,3)20.(1)a =0(2)g (x )=x +1-2 ,x ∈0t =1-2 ,t ∈[0,1],则g (t )=t +1- 22=-12(t -1)2+1,所以12≤g (t )≤121.(1)f (1000)=-14(2)f (10)=lg (10a )·lg 100=(1+lg a )(lg a -2)=(lg a )2-lg a -2=10,即(lg a )2-lg a -12=0,解得lg a =4或-3,即a =104或10-3(3)因为对一切正实数x 恒有f (x )≤98,所以lg (ax )·lg 2≤98在(0,+∞)上恒成立,即(lg a +lg x )(lg a -2lg x )≤98,即2(lg x )2+lg a ·lg x -(lg a )2+98≥0在(0,+∞)上恒成立.因为x >0,所以lg x ∈R .由二次函数的性质可知,Δ=(lg a )2-8-(lg )2+,所以(lg a )2≤1,则-1≤lg a ≤1,所以110≤a ≤1022.(1)当0≤t ≤1时,设y =kt ,将点(0.1,1)代入得k =10,所以y =10t ,再将点(0.1,1)代入y 2+0.9 +,得a =-0.1,所以y 0≤ ≤1,2+0.9 -0.1, >1(2)2+0.9 -0.1≤116,所以( 2+0.9 -0.1),所以5(t 2+0.9t -0.1)≥4,所以10t 2+9t -9≥0,所以t ≥35或t ≤-32(舍去),所以学生要在0.6h 后才可以进入教室。
指数函数和对数函数练习题

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载指数函数和对数函数练习题地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容第三章指数函数和对数函数§1正整数指数函数§2指数扩充及其运算性质1.正整数指数函数函数y=ax(a>0,a≠1,x∈N+)叫作________指数函数;形如y=kax(k∈R,a>0,且a≠1)的函数称为________函数.2.分数指数幂(1)分数指数幂的定义:给定正实数a,对于任意给定的整数m,n(m,n互素),存在唯一的正实数b,使得bn=am,我们把b叫作a的 eq \f(m,n) 次幂,记作b=;(2)正分数指数幂写成根式形式:= eq \r(n,am) (a>0);(3)规定正数的负分数指数幂的意义是:=__________________(a>0,m、n∈N+,且n>1);(4)0的正分数指数幂等于____,0的负分数指数幂__________.3.有理数指数幂的运算性质(1)aman=________(a>0);(2)(am)n=________(a>0);(3)(ab)n=________(a>0,b>0).一、选择题1.下列说法中:①16的4次方根是2;② eq \r(4,16) 的运算结果是±2;③当n为大于1的奇数时, eq \r(n,a) 对任意a∈R都有意义;④当n 为大于1的偶数时, eq \r(n,a) 只有当a≥0时才有意义.其中正确的是( )A.①③④ B.②③④ C.②③ D.③④2.若2<a<3,化简 eq \r(2-a2) + eq \r(4,3-a4) 的结果是( )A.5-2a B.2a-5 C.1 D.-13.在(- eq \f(1,2) )-1、、、2-1中,最大的是( )A.(- eq \f(1,2) )-1 B. C. D.2-14.化简 eq \r(3,a\r(a)) 的结果是( )A.a B. C.a2 D.5.下列各式成立的是( )A. eq \r(3,m2+n2) = B.( eq \f(b,a) )2=C. eq \r(6,-32) =D. eq \r(\r(3,4)) =6.下列结论中,正确的个数是( )①当a<0时,=a3;② eq \r(n,an) =|a|(n>0);③函数y=-(3x-7)0的定义域是(2,+∞);④若100a=5,10b=2,则2a+b=1.A.0 B.1C.2 D.3二、填空题7. eq \r(6\f(1,4)) - eq \r(3,3\f(3,8)) + eq \r(3,0.125) 的值为________.8.若a>0,且ax=3,ay=5,则=________.9.若x>0,则(2+)(2-)-4·(x-)=________.三、解答题10.(1)化简: eq \r(3,xy2·\r(xy-1)) · eq \r(xy) ·(xy)-1(xy≠0);(2)计算:+ eq \f(-40,\r(2)) + eq \f(1,\r(2)-1) - eq \r(1-\r(5)0) ·.11.设-3<x<3,求 eq \r(x2-2x+1) - eq \r(x2+6x+9) 的值.12.化简:÷(1-2 eq \r(3,\f(b,a)) )× eq \r(3,a) .13.若x>0,y>0,且x- eq \r(xy) -2y=0,求 eq \f(2x-\r(xy),y +2\r(xy)) 的值.§3指数函数(一)1.指数函数的概念一般地,________________叫做指数函数,其中x是自变量,函数的定义域是____.2.指数函数y=ax(a>0,且a≠1)的图像和性质一、选择题1.下列以x为自变量的函数中,是指数函数的是( )A.y=(-4)x B.y=πxC.y=-4x D.y=ax+2(a>0且a≠1) 2.函数f(x)=(a2-3a+3)ax是指数函数,则有( )A.a=1或a=2 B.a=1C.a=2 D.a>0且a≠13.函数y=a|x|(a>1)的图像是( )4.已知f(x)为R上的奇函数,当x<0时,f(x)=3x,那么f(2)的值为( )A.-9 B. eq \f(1,9)C.- eq \f(1,9) D.95.如图是指数函数①y=ax;②y=bx;③y=cx;④y=dx的图像,则a、b、c、d与1的大小关系是( )A.a<b<1<c<dB.b<a<1<d<cC.1<a<b<c<dD.a<b<1<d<c6.函数y=( eq \f(1,2) )x-2的图像必过( )A.第一、二、三象限 B.第一、二、四象限C.第一、三、四象限 D.第二、三、四象限二、填空题7.函数f(x)=ax的图像经过点(2,4),则f(-3)的值为________.8.若函数y=ax-(b-1)(a>0,a≠1)的图像不经过第二象限,则a,b必满足条件________.9.函数y=8-23-x(x≥0)的值域是________.三、解答题10.比较下列各组数中两个值的大小:(1)0.2-1.5和0.2-1.7;(2)和;(3)2-1.5和30.2.11.2000年10月18日,美国某城市的日报以醒目标题刊登了一条消息:“市政委员会今天宣布:本市垃圾的体积达到50 000 m3”,副标题是:“垃圾的体积每三年增加一倍”.如果把3年作为垃圾体积加倍的周期,请你根据下面关于垃圾的体积V(m3)与垃圾体积的加倍的周期(3年)数n的关系的表格,回答下列问题.(1)设想城市垃圾的体积每3年继续加倍,问24年后该市垃圾的体积是多少?(2)根据报纸所述的信息,你估计3年前垃圾的体积是多少?(3)如果n=-2,这时的n,V表示什么信息?(4)写出n与V的函数关系式,并画出函数图像(横轴取n轴).(5)曲线可能与横轴相交吗?为什么?能力提升12.定义运算a⊕b= eq \b\lc\{\rc\(\a\vs4\al\co1(a a≤b,b a>b)) ,则函数f(x)=1⊕2x的图像是( )13.定义在区间(0,+∞)上的函数f(x)满足对任意的实数x,y都有f(xy)=yf(x).(1)求f(1)的值;(2)若f( eq \f(1,2) )>0,解不等式f(ax)>0.(其中字母a为常数).§3指数函数(二)1.下列一定是指数函数的是( )A.y=-3x B.y=xx(x>0,且x≠1)C.y=(a-2)x(a>3) D.y=(1- eq \r(2) )x 2.指数函数y=ax与y=bx的图像如图,则( )A.a<0,b<0 B.a<0,b>0C.0<a<1,b>1 D.0<a<1,0<b<13.函数y=πx的值域是( )A.(0,+∞) B.[0,+∞)C.R D.(-∞,0)4.若( eq \f(1,2) )2a+1<( eq \f(1,2) )3-2a,则实数a的取值范围是( )A.(1,+∞) B.( eq \f(1,2) ,+∞) C.(-∞,1) D.(-∞, eq \f(1,2) ) 5.设 eq \f(1,3) <( eq \f(1,3) )b<( eq \f(1,3) )a<1,则( ) A.aa<ab<ba B.aa<ba<abC.ab<aa<ba D.ab<ba<aa6.若指数函数f(x)=(a+1)x是R上的减函数,那么a的取值范围为( )A.a<2 B.a>2C.-1<a<0 D.0<a<1一、选择题1.设P={y|y=x2,x∈R},Q={y|y=2x,x∈R},则( )A.QP B.QPC.P∩Q={2,4} D.P∩Q={(2,4)}2.函数y= eq \r(16-4x) 的值域是( )A.[0,+∞) B.[0,4] C.[0,4) D.(0,4)3.函数y=ax在[0,1]上的最大值与最小值的和为3,则函数y=2ax-1在[0,1]上的最大值是( )A.6 B.1 C.3 D. eq\f(3,2)4.若函数f(x)=3x+3-x与g(x)=3x-3-x的定义域均为R,则( ) A.f(x)与g(x)均为偶函数 B.f(x)为偶函数,g(x)为奇函数C.f(x)与g(x)均为奇函数 D.f(x)为奇函数,g(x)为偶函数5.函数y=f(x)的图像与函数g(x)=ex+2的图像关于原点对称,则f(x)的表达式为( )A.f(x)=-ex-2 B.f(x)=-e-x+2C.f(x)=-e-x-2 D.f(x)=e-x+26.已知a=,b=,c=,则a,b,c三个数的大小关系是( )A.c<a<b B.c<b<aC.a<b<c D.b<a<c二、填空题7.春天来了,某池塘中的荷花枝繁叶茂,已知每一天新长出荷叶覆盖水面面积是前一天的2倍,若荷叶20天可以完全长满池塘水面,当荷叶刚好覆盖水面面积一半时,荷叶已生长了________天.8.已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=1-2-x,则不等式f(x)<- eq \f(1,2) 的解集是________________.9.函数y=的单调递增区间是________.三、解答题10.(1)设f(x)=2u,u=g(x),g(x)是R上的单调增函数,试判断f(x)的单调性;(2)求函数y=的单调区间.11.函数f(x)=4x-2x+1+3的定义域为[- eq \f(1,2) , eq\f(1,2) ].(1)设t=2x,求t的取值范围;(2)求函数f(x)的值域.能力提升12.函数y=2x-x2的图像大致是( )13.已知函数f(x)= eq \f(2x-1,2x+1) .(1)求f[f(0)+4]的值;(2)求证:f(x)在R上是增函数;(3)解不等式:0<f(x-2)< eq \f(15,17) .习题课1.下列函数中,指数函数的个数是( )①y=2·3x;②y=3x+1;③y=3x;④y=x3.A.0 B.1 C.2 D.32.设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b(b为常数),则f(-1)等于( )A.-3 B.-1 C.1 D.33.对于每一个实数x,f(x)是y=2x与y=-x+1这两个函数中的较小者,则f(x)的最大值是( )A.1 B.0C.-1 D.无最大值4.将 eq \r(2\r(2)) 化成指数式为________.5.已知a=40.2,b=80.1,c=( eq \f(1,2) )-0.5,则a,b,c的大小顺序为________.6.已知+=3,求x+ eq \f(1,x) 的值.一、选择题1.的值为( )A. eq \r(2) B.- eq \r(2) C. eq\f(\r(2),2) D.- eq \f(\r(2),2)2.化简 eq \r(3,a-b3) + eq \r(a-2b2) 的结果是( ) A.3b-2a B.2a-3bC.b或2a-3b D.b3.若0<x<1,则2x,( eq \f(1,2) )x,(0.2)x之间的大小关系是( ) A.2x<(0.2)x<( eq \f(1,2) )x B.2x<( eq\f(1,2) )x<(0.2)xC.( eq \f(1,2) )x<(0.2)x<2xD.(0.2)x<( eq \f(1,2) )x<2x4.若函数则f(-3)的值为( )A. eq \f(1,8)B. eq\f(1,2)C.2 D.85.函数f(x)=ax-b的图像如图所示,其中a,b均为常数,则下列结论正确的是( )A.a>1,b>0B.a>1,b<0C.0<a<1,b>0D.0<a<1,b<06.函数f(x)= eq \f(4x+1,2x) 的图像( )A.关于原点对称B.关于直线y=x对称C.关于x轴对称D.关于y轴对称二、填空题7.计算:-(- eq \f(1,4) )0+160.75+=________________.8.已知10m=4,10n=9,则=________.9.函数y=1-3x(x∈[-1,2])的值域是________.三、解答题10.比较下列各组中两个数的大小:(1)0.63.5和0.63.7;(2)( eq \r(2) )-1.2和( eq \r(2) )-1.4;(3)和;(4)π-2和( eq \f(1,3) )-1.311.函数f(x)=ax(a>0,且a≠1)在区间[1,2]上的最大值比最小值大 eq \f(a,2) ,求a的值.能力提升12.已知f(x)= eq \f(a,a2-1) (ax-a-x)(a>0且a≠1),讨论f(x)的单调性.13.根据函数y=|2x-1|的图像,判断当实数m为何值时,方程|2x-1|=m无解?有一解?有两解?§4对数(一)1.对数的概念如果ab=N(a>0,且a≠1),那么数b叫做______________,记作__________,其中a叫做__________,N叫做________.2.常用对数与自然对数通常将以10为底的对数叫做__________,以e为底的对数叫做__________,log10N可简记为________,logeN简记为________.3.对数与指数的关系若a>0,且a≠1,则ax=N⇔logaN=____.对数恒等式:=____;logaax=____(a>0,且a≠1).4.对数的性质(1)1的对数为____;(2)底的对数为____;(3)零和负数________.一、选择题1.有下列说法:①零和负数没有对数;②任何一个指数式都可以化成对数式;③以10为底的对数叫做常用对数;④以e为底的对数叫做自然对数.其中正确命题的个数为( )A.1 B.2C.3 D.42.有以下四个结论:①lg(lg10)=0;②ln(ln e)=0;③若10=lg x,则x=100;④若e=ln x,则x=e2.其中正确的是( )A.①③ B.②④C.①② D.③④3.在b=log(a-2)(5-a)中,实数a的取值范围是( )A.a>5或a<2 B.2<a<5 C.2<a<3或3<a<5 D.3<a<44.方程= eq \f(1,4) 的解是( )A.x= eq \f(1,9) B.x= eq\f(\r(3),3)C.x= eq \r(3) D.x=95.若loga eq \r(5,b) =c,则下列关系式中正确的是( )A.b=a5c B.b5=acC.b=5ac D.b=c5a6.的值为( )A.6 B. eq \f(7,2)C.8 D. eq \f(3,7)二、填空题7.已知log7[log3(log2x)]=0,那么=________.8.若log2(logx9)=1,则x=________.9.已知lg a=2.431 0,lg b=1.431 0,则 eq \f(b,a) =________.三、解答题10.(1)将下列指数式写成对数式:①10-3= eq \f(1,1 000) ;②0.53=0.125;③( eq \r(2) -1)-1= eq \r(2) +1.(2)将下列对数式写成指数式:①log26=2.585 0;②log30.8=-0.203 1;③lg 3=0.477 1.11.已知logax=4,logay=5,求A=的值.能力提升12.若loga3=m,loga5=n,则a2m+n的值是( )A.15 B.75C.45 D.22513.(1)先将下列式子改写成指数式,再求各式中x的值:①log2x=- eq \f(2,5) ;②logx3=- eq \f(1,3) .(2)已知6a=8,试用a表示下列各式:①log68;②log62;③log26.§4对数(二)1.对数的运算性质如果a>0,且a≠1,M>0,N>0,则:(1)loga(MN)=________________;(2)loga eq \f(M,N) =________;(3)logaMn=__________(n∈R).2.对数换底公式logbN= eq \f(logaN,logab) (a,b>0,a,b≠1,N>0);特别地:logab·logba=____(a>0,且a≠1,b>0,且b≠1).一、选择题1.下列式子中成立的是(假定各式均有意义)( )A.logax·logay=loga(x+y) B.(logax)n=nlogaxC. eq \f(logax,n) =loga eq \r(n,x)D. eq \f(logax,logay) =logax-logay2.计算:log916·log881的值为( )A.18 B. eq \f(1,18) C. eq \f(8,3) D. eq \f(3,8)3.若log5 eq \f(1,3) ·log36·log6x=2,则x等于( )A.9 B. eq \f(1,9) C.25D. eq \f(1,25)4.已知3a=5b=A,若 eq \f(1,a) + eq \f(1,b) =2,则A等于( )A.15 B. eq \r(15) C.± eq \r(15)D.2255.已知log89=a,log25=b,则lg 3等于( )A. eq \f(a,b-1)B. eq \f(3,2b-1)C. eq\f(3a,2b+1) D. eq \f(3a-1,2b)6.若lg a,lg b是方程2x2-4x+1=0的两个根,则(lg eq\f(a,b) )2的值等于( )A.2 B. eq \f(1,2) C.4 D. eq\f(1,4)二、填空题7.2log510+log50.25+( eq \r(3,25) - eq \r(125) )÷ eq\r(4,25) =______________.8.(lg 5)2+lg 2·lg 50=________.9.2008年5月12日,四川汶川发生里氏8.0级特大地震,给人民的生命财产造成了巨大的损失.里氏地震的等级最早是在1935年由美国加州理工学院的地震学家里特判定的.它与震源中心释放的能量(热能和动能)大小有关.震级M= eq \f(2,3) lg E-3.2,其中E(焦耳)为以地震波的形式释放出的能量.如果里氏6.0级地震释放的能量相当于1颗美国在二战时投放在广岛的原子弹的能量,那么汶川大地震所释放的能量相当于________颗广岛原子弹.三、解答题10.(1)计算:lg eq \f(1,2) -lg eq \f(5,8) +lg 12.5-log89·log34;(2)已知3a=4b=36,求 eq \f(2,a) + eq \f(1,b) 的值.11.若a、b是方程2(lg x)2-lg x4+1=0的两个实根,求lg(ab)·(logab+logba)的值.能力提升12.下列给出了x与10x的七组近似对应值:假设在上表的各组对应值中,有且仅有一组是错误的,它是第________组.( )A.二 B.四C.五 D.七13.一种放射性物质不断变化为其他物质,每经过一年的剩余质量约是原来的75%,估计约经过多少年,该物质的剩余量是原来的 eq \f(1,3) ?(结果保留1位有效数字)(lg 2≈0.301 0,lg 3≈0.477 1)§5对数函数(一)1.对数函数的定义:一般地,我们把______________________________叫做对数函数,其中x是自变量,函数的定义域是________.________为常用对数函数;y=________为自然对数函数.2.对数函数的图像与性质3.反函数对数函数y=logax(a>0且a≠1)和指数函数____________________互为反函数.一、选择题1.函数y= eq \r(log2x-2) 的定义域是( )A.(3,+∞) B.[3,+∞) C.(4,+∞) D.[4,+∞)2.设集合M={y|y=( eq \f(1,2) )x,x∈[0,+∞)},N={y|y=log2x,x∈(0,1]},则集合M∪N是( )A.(-∞,0)∪[1,+∞) B.[0,+∞)C.(-∞,1] D.(-∞,0)∪(0,1)3.已知函数f(x)=log2(x+1),若f(α)=1,则α等于( )A.0 B.1 C.2 D.3 4.函数f(x)=|log3x|的图像是( )5.已知对数函数f(x)=logax(a>0,a≠1),且过点(9,2),f(x)的反函数记为y=g(x),则g(x)的解析式是( )A.g(x)=4x B.g(x)=2x C.g(x)=9x D.g(x)=3x6.若loga eq \f(2,3) <1,则a的取值范围是( )A.(0, eq \f(2,3) ) B.( eq \f(2,3) ,+∞) C.( eq \f(2,3) ,1) D.(0, eq \f(2,3) )∪(1,+∞)二、填空题7.如果函数f(x)=(3-a)x,g(x)=logax的增减性相同,则a的取值范围是________.8.已知函数y=loga(x-3)-1的图像恒过定点P,则点P的坐标是________.9.给出函数,则f(log23)=________.三、解答题10.求下列函数的定义域与值域:(1)y=log2(x-2);(2)y=log4(x2+8).11.已知函数f(x)=loga(1+x),g(x)=loga(1-x),(a>0,且a≠1).(1)设a=2,函数f(x)的定义域为[3,63],求函数f(x)的最值.(2)求使f(x)-g(x)>0的x的取值范围.能力提升12.已知图中曲线C1,C2,C3,C4分别是函数y=x,y=x,y=x,y=x 的图像,则a1,a2,a3,a4的大小关系是( )A.a4<a3<a2<a1 B.a3<a4<a1<a2 C.a2<a1<a3<a4D.a3<a4<a2<a113.若不等式x2-logmx<0在(0, eq \f(1,2) )内恒成立,求实数m的取值范围.§5对数函数(二)1.函数y=logax的图像如图所示,则实数a的可能取值是( )A.5 B. eq \f(1,5)C. eq \f(1,e)D. eq \f(1,2)2.下列各组函数中,表示同一函数的是( )A.y= eq \r(x2) 和y=( eq \r(x) )2B.|y|=|x|和y3=x3C.y=logax2和y=2logaxD.y=x和y=logaax3.若函数y=f(x)的定义域是[2,4],则y=f(x)的定义域是( )A.[ eq \f(1,2) ,1] B.[4,16]C.[ eq \f(1,16) , eq \f(1,4) ] D.[2,4]4.函数f(x)=log2(3x+1)的值域为( )A.(0,+∞) B.[0,+∞)C.(1,+∞) D.[1,+∞)5.函数f(x)=loga(x+b)(a>0且a≠1)的图像经过(-1,0)和(0,1)两点,则f(2)=________.6.函数y=loga(x-2)+1(a>0且a≠1)恒过定点________________________________________________________________________.一、选择题1.设a=log54,b=(log53)2,c=log45,则( )A.a<c<b B.b<c<aC.a<b<c D.b<a<c2.已知函数y=f(2x)的定义域为[-1,1],则函数y=f(log2x)的定义域为( )A.[-1,1] B.[ eq \f(1,2) ,2]C.[1,2] D.[ eq \r(2) ,4]3.函数f(x)=loga|x|(a>0且a≠1)且f(8)=3,则有( )A.f(2)>f(-2) B.f(1)>f(2)C.f(-3)>f(-2) D.f(-3)>f(-4)4.函数f(x)=ax+loga(x+1)在[0,1]上的最大值与最小值之和为a,则a的值为( )A. eq \f(1,4)B. eq \f(1,2) C.2 D.45.已知函数f(x)=lg eq \f(1-x,1+x) ,若f(a)=b,则f(-a)等于( )A.b B.-bC. eq \f(1,b) D.- eq \f(1,b)6.函数y=3x(-1≤x<0)的反函数是( )A.y=x(x>0) B.y=log3x(x>0)C.y=log3x( eq \f(1,3) ≤x<1) D.y=x( eq\f(1,3) ≤x<1)二、填空题7.函数f(x)=lg(2x-b),若x≥1时,f(x)≥0恒成立,则b应满足的条件是________.8.函数y=logax当x>2时恒有|y|>1,则a的取值范围是________.9.若loga2<2,则实数a的取值范围是______________.三、解答题10.已知f(x)=loga(3-ax)在x∈[0,2]上单调递减,求a的取值范围.11.已知函数f(x)= eq \f(1-ax,x-1) 的图像关于原点对称,其中a 为常数.(1)求a的值;(2)若当x∈(1,+∞)时,f(x)+(x-1)<m恒成立.求实数m的取值范围.能力提升12.若函数f(x)=loga(x2-ax+ eq \f(1,2) )有最小值,则实数a的取值范围是( )A.(0,1) B.(0,1)∪(1, eq \r(2) ) C.(1, eq \r(2) ) D.[ eq \r(2) ,+∞)13.已知logm4<logn4,比较m与n的大小.习题课1.已知m=0.95.1,n=5.10.9,p=log0.95.1,则这三个数的大小关系是( )A.m<n<p B.m<p<nC.p<m<n D.p<n<m2.已知0<a<1,logam<logan<0,则( )A.1<n<m B.1<m<n C.m<n<1 D.n<m<13.函数y= eq \r(x-1) + eq \f(1,lg2-x) 的定义域是( ) A.(1,2) B.[1,4]C.[1,2) D.(1,2]4.给定函数①y=,②y=(x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数序号是( )A.①② B.②③ C.③④ D.①④5.设函数f(x)=loga|x|,则f(a+1)与f(2)的大小关系是________________.6.若log32=a,则log38-2log36=________.一、选择题1.下列不等号连接错误的一组是( )A.log0.52.7>log0.52.8 B.log34>log65 C.log34>log56 D.logπe>logeπ2.若log37·log29·log49m=log4 eq \f(1,2) ,则m等于( )A. eq \f(1,4)B. eq \f(\r(2),2)C. eq \r(2) D.43.设函数若f(3)=2,f(-2)=0,则b等于( )A.0 B.-1 C.1 D.24.若函数f(x)=loga(2x2+x)(a>0,a≠1)在区间(0, eq \f(1,2) )内恒有f(x)>0,则f(x)的单调递增区间为( )A.(-∞,- eq \f(1,4) ) B.(- eq \f(1,4) ,+∞) C.(0,+∞) D.(-∞,- eq \f(1,2) )5.若函数若f(a)>f(-a),则实数a的取值范围是( )A.(-1,0)∪(0,1) B.(-∞,-1)∪(1,+∞)C.(-1,0)∪(1,+∞) D.(-∞,-1)∪(0,1)6.已知f(x)是定义在R上的奇函数,f(x)在(0,+∞)上是增函数,且f( eq \f(1,3) )=0,则不等式f(x)<0的解集为( )A.(0, eq \f(1,2) ) B.( eq\f(1,2) ,+∞)C.( eq \f(1,2) ,1)∪(2,+∞) D.(0, eq\f(1,2) )∪(2,+∞)二、填空题7.已知loga(ab)= eq \f(1,p) ,则logab eq \f(a,b) =________.8.若log236=a,log210=b,则log215=________.9.设函数若f(a)= eq \f(1,8) ,则f(a+6)=________.三、解答题10.已知集合A={x|x<-2或x>3},B={x|log4(x+a)<1},若A∩B=∅,求实数a的取值范围.11.抽气机每次抽出容器内空气的60%,要使容器内的空气少于原来的0.1%,则至少要抽几次?(lg 2≈0.301 0)能力提升12.设a>0,a≠1,函数f(x)=loga(x2-2x+3)有最小值,求不等式loga(x-1)>0的解集.13.已知函数f(x)=loga(1+x),其中a>1.(1)比较 eq \f(1,2) [f(0)+f(1)]与f( eq \f(1,2) )的大小;(2)探索 eq \f(1,2) [f(x1-1)+f(x2-1)]≤f( eq \f(x1+x2,2) -1)对任意x1>0,x2>0恒成立.§6指数函数、幂函数、对数函数增长的比较1.当a>1时,指数函数y=ax是________,并且当a越大时,其函数值增长越____.2.当a>1时,对数函数y=logax(x>0)是________,并且当a越小时,其函数值________.3.当x>0,n>1时,幂函数y=xn是________,并且当x>1时,n越大,其函数值__________.一、选择题1.今有一组数据如下:现准备了如下四个答案,哪个函数最接近这组数据( )A.v=log2t B.v=t C.v= eq \f(t2-1,2) D.v=2t-22.从山顶到山下的招待所的距离为20千米.某人从山顶以4千米/时的速度到山下的招待所,他与招待所的距离s(千米)与时间t(小时)的函数关系用图像表示为( )3.某公司为了适应市场需求对产品结构做了重大调整,调整后初期利润增长迅速,后来增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润y与时间x的关系,可选用( )A.一次函数 B.二次函数 C.指数型函数 D.对数型函数4.某自行车存车处在某天的存车量为4 000辆次,存车费为:变速车0.3元/辆次,普通车0.2元/辆次.若当天普通车存车数为x辆次,存车费总收入为y元,则y关于x的函数关系式为( )A.y=0.2x(0≤x≤4 000) B.y=0.5x(0≤x≤4 000)C.y=-0.1x+1 200(0≤x≤4 000) D.y=0.1x+1 200(0≤x≤4000)5.已知f(x)=x2-bx+c且f(0)=3,f(1+x)=f(1-x),则有( )A.f(bx)≥f(cx) B.f(bx)≤f(cx) C.f(bx)<f(cx)D.f(bx),f(cx)大小不定6.某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为l1=5.06x-0.15x2和l2=2x,其中x为销售量(单位:辆).若该公司在这两地共销售15辆车,则可能获得的最大利润是( )A.45.606 B.45.6 C.45.56 D.45.51二、填空题7.一种专门侵占内存的计算机病毒,开机时占据内存2KB,然后每3分钟自身复制一次,复制后所占内存是原来的2倍,那么开机后经过________分钟,该病毒占据64MB内存(1MB=210KB).8.近几年由于北京房价的上涨,引起了二手房市场交易的火爆.房子几乎没有变化,但价格却上涨了,小张在2010年以80万元的价格购得一套新房子,假设这10年来价格年膨胀率不变,那么到2020年,这所房子的价格y(万元)与价格年膨胀率x之间的函数关系式是________.三、解答题9.用模型f(x)=ax+b来描述某企业每季度的利润f(x)(亿元)和生产成本投入x(亿元)的关系.统计表明,当每季度投入1(亿元)时利润y1=1(亿元),当每季度投入2(亿元)时利润y2=2(亿元),当每季度投入3(亿元)时利润y3=2(亿元).又定义:当f(x)使[f(1)-y1]2+[f(2)-y2]2+[f(3)-y3]2的数值最小时为最佳模型.(1)当b= eq \f(2,3) ,求相应的a使f(x)=ax+b成为最佳模型;(2)根据题(1)得到的最佳模型,请预测每季度投入4(亿元)时利润y4(亿元)的值.10.根据市场调查,某种商品在最近的40天内的价格f(t)与时间t满足关系f(t)=,销售量g(t)与时间t满足关系g(t)=- eq \f(1,3) t+ eq\f(43,3) (0≤t≤40,t∈N).求这种商品的日销售额(销售量与价格之积)的最大值.11.某商品在近30天内每件的销售价格p(元)与时间t(天)的函数关系是p=该商品的日销售量Q(件)与时间t(天)的函数关系式为Q=-t+40(0<t≤30,t∈N),求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天?能力提升12.某种商品进价每个80元,零售价每个100元,为了促销拟采取买一个这种商品,赠送一个小礼品的办法,实践表明:礼品价值为1元时,销售量增加10%,且在一定范围内,礼品价值为(n+1)元时,比礼品价值为n元(n∈N+)时的销售量增加10%.(1)写出礼品价值为n元时,利润yn(元)与n的函数关系式;(2)请你设计礼品价值,以使商店获得最大利润.13.已知桶1与桶2通过水管相连如图所示,开始时桶1中有a L水,t min后剩余的水符合指数衰减函数y1=ae-nt,那么桶2中的水就是y2=a-ae-nt,假定5 min后,桶1中的水与桶2中的水相等,那么再过多长时间桶1中的水只有 eq \f(a,4) L?第三章章末检测一、选择题(本大题共12小题,每小题5分,共60分)1.已知函数f(x)=lg(4-x)的定义域为M,函数g(x)= eq \r(0.5x-4) 的值域为N,则M∩N等于( )A.M B.NC.[0,4) D.[0,+∞)2.函数y=3|x|-1的定义域为[-1,2],则函数的值域为( )A.[2,8] B.[0,8]C.[1,8] D.[-1,8]3.已知f(3x)=log2 eq \r(\f(9x+1,2)) ,则f(1)的值为( )A.1 B.2 C.-1 D. eq\f(1,2)4.等于( )A.7 B.10 C.6 D. eq\f(9,2)5.若100a=5,10b=2,则2a+b等于( )A.0 B.1C.2 D.36.比较、23.1、的大小关系是( )A.23.1<< B.<23.1<C.<<23.1 D.<<23.17.式子 eq \f(log89,log23) 的值为( )A. eq \f(2,3)B. eq \f(3,2)C.2 D.38.已知ab>0,下面四个等式中:①lg(ab)=lg a+lg b;②lg eq \f(a,b) =lg a-lg b;③ eq \f(1,2) lg( eq \f(a,b) )2=lg eq \f(a,b) ;④lg(ab)= eq \f(1,logab10) .其中正确的个数为( )A.0 B.1 C.2 D.39.为了得到函数y=lg eq \f(x+3,10) 的图像,只需把函数y=lg x 的图像上所有的点( )A.向左平移3个单位长度,再向上平移1个单位长度B.向右平移3个单位长度,再向上平移1个单位长度C.向左平移3个单位长度,再向下平移1个单位长度D.向右平移3个单位长度,再向下平移1个单位长度10.函数y=2x与y=x2的图像的交点个数是( )A.0 B.1C.2 D.311.设偶函数f(x)满足f(x)=2x-4(x≥0),则{x|f(x-2)>0}等于( ) A.{x|x<-2或x>4} B.{x|x<0或x>4}C.{x|x<0或x>6} D.{x|x<-2或x>2}12.函数f(x)=a|x+1|(a>0,a≠1)的值域为[1,+∞),则f(-4)与f(1)的关系是( )A.f(-4)>f(1) B.f(-4)=f(1)C.f(-4)<f(1) D.不能确定二、填空题(本大题共4小题,每小题5分,共20分)13.已知函数f(x)= eq \b\lc\{\rc\ (\a\vs4\al\co1(\f(1,2)x,x≥4f x+1, x<4)) ,则f(2+log23)的值为______.14.函数f(x)=loga eq \f(3-x,3+x) (a>0且a≠1),f(2)=3,则f(-2)的值为________.15.函数y=(x2-3x+2)的单调递增区间为______________.16.设0≤x≤2,则函数y=-3·2x+5的最大值是________,最小值是________.三、解答题(本大题共6小题,共70分)17.(10分)已知指数函数f(x)=ax(a>0且a≠1).(1)求f(x)的反函数g(x)的解析式;(2)解不等式:g(x)≤loga(2-3x).18.(12分)已知函数f(x)=2a·4x-2x-1.(1)当a=1时,求函数f(x)在x∈[-3,0]的值域;(2)若关于x的方程f(x)=0有解,求a的取值范围.19.(12分)已知x>1且x≠ eq \f(4,3) ,f(x)=1+logx3,g(x)=2logx2,试比较f(x)与g(x)的大小.20.(12分)设函数f(x)=log2(4x)·log2(2x), eq \f(1,4) ≤x≤4,(1)若t=log2x,求t的取值范围;(2)求f(x)的最值,并写出最值时对应的x的值.21.(12分)已知f(x)=loga eq \f(1+x,1-x) (a>0,a≠1).(1)求f(x)的定义域;(2)判断f(x)的奇偶性并予以证明;(3)求使f(x)>0的x的取值范围.22.(12分)已知定义域为R的函数f(x)= eq \f(-2x+b,2x+1+2) 是奇函数.(1)求b的值;(2)判断函数f(x)的单调性;(3)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.。
(压轴题)高中数学必修一第三单元《指数函数和对数函数》测试题(包含答案解析)(3)

一、选择题1.设a ,b ,c 为正数,且3a =4b =6c ,则有( )A .111c a b =+ B .221c a b =+ C .122c a b =+ D .212c a b =+ 2.设()|lg |f x x =,且0a b c <<<时,有()()()f a f c f b >>,则( )A .(1)(1)0a c -->B .1ac >C .1ac =D .01ac <<3.已知1311531log ,log ,363a b c π-===,则,,a b c 的大小关系是( )A .b a c <<B .a c b <<C .c b a <<D .b c a <<4.函数()212()log 4f x x =-的单调递增区间为( ). A .(0,+∞)B .(-,0)C .(2,+∞)D .(-,-2)5.一种放射性元素最初的质量为500g ,按每年10%衰减.则这种放射性元素的半衰期为( )年.(注:剩余质量为最初质量的一半,所需的时间叫做半衰期),(结果精确到0.1,已知lg 20.3010=,lg30.4771=)A .5.2B .6.6C .7.1D .8.36.若函数ya >0,a ≠1)的定义域和值域都是[0,1],则log a 56+log a 485=( ) A .1B .2C .3D .47.设52a -=,5log 2b =,8log 5c =,则( ) A .a b c <<B .b c a <<C .c b a <<D .c a b <<8.在数学史上,一般认为对数的发明者是苏格兰数学家——纳皮尔(Napier ,1550-1617年).在纳皮尔所处的年代,哥白尼的“太阳中心说”刚刚开始流行,这导致天文学成为当时的热门学科.可是由于当时常量数学的局限性,天文学家们不得不花费很大的精力去计算那些繁杂的“天文数字”,因此浪费了若干年甚至毕生的宝贵时间.纳皮尔也是当时的一位天文爱好者,为了简化计算,他多年潜心研究大数字的计算技术,终于独立发明了对数.在那个时代,计算多位数之间的乘积,还是十分复杂的运算,因此纳皮尔首先发明了一种计算特殊多位数之间乘积的方法.让我们来看看下面这个例子:这两行数字之间的关系是极为明确的:第一行表示2的指数,第二行表示2的对应幂.如果我们要计算第二行中两个数的乘积,可以通过第一行对应数字的和来实现. 比如,计算64×256的值,就可以先查第一行的对应数字:64对应6,256对应8,然后再把第一行中的对应数字加和起来:6+8=14;第一行中的14,对应第二行中的16384,所以有:64×256=16384,按照这样的方法计算:16384×32768=( )A .134217728B .268435356C .536870912D .5137658029.已知()243,1log 2,1a x ax x f x x a x ⎧-+<=⎨+≥⎩满足对任意12x x ≠,都有()()12120f x f x x x -<-成立,那么a 的取值范围是( )A .10,2⎛⎤ ⎥⎝⎦B .1,12⎡⎫⎪⎢⎣⎭C .12,23⎡⎤⎢⎥⎣⎦D .2,13⎡⎫⎪⎢⎣⎭10.函数()22x xxf x -=+的大致图象为( ) A . B .C .D .11.如果函数(0,1)x y a a a =>≠的反函数是增函数,那么函数log (1)a y x =-+的图象大致是( )A .B .C .D .12.实数,a b 满足2510a b ==,则下列关系正确的是( ) A .212a b+= B .111a b+= C .122a b+= D .1212a b += 二、填空题13.设函数123910()lg 10x x x x x af x +++++=,其中a 为实数,如果当(,1]x ∈-∞时()f x 有意义,则a 的取值范围是________.14.定义{},,max ,,x x y x y y x y≥⎧=⎨<⎩,设{}()max ,log xa f x a a x=--(),1x R a +∈>.则不等式()2f x ≥的解集是_____________.15.若函数()()20.2log 1f x kx kx =-+的定义域是R ,则实数k 的取值范围是______.16.设log c a 、log c b 是方程2530x x +-=的两个实根,则log b ac =______.17.若幂函数()2()57m f x m m x =-+在R上为增函数则1log 2log 2lg5lg4mm m+-=_____.18.设实数x 满足01x <<,且2log 4log 1x x -=,则x =______.19.设函数122,1()1log ,1x x f x x x -⎧≤=⎨->⎩,则满足()2f x ≤的x 的取值范围是_______________.20.设函数()122,12log ,1x x f x x x +⎧≤=⎨->⎩,若()()04f f x =则0x ______.三、解答题21.已知函数()x x f x a k a -=-⋅(0a >且1a ≠)是定义域为R 的奇.函数,且3(1)2f =. (1)求k 的值,并判断()f x 的单调性(不要求证明); (2)是否存在实数()2,3mm m >≠,使函数()()22(2)log 1x xm g x a a mf x --⎡⎤=+-+⎣⎦在[]1,2上的最大值为0?如果存在,求出实数m 所有的值;如果不存在,请说明理由.22.已知函数22()log (23).f x x x =-++(1)求函数()f x 的定义域和值域;(2)写出函数()f x 的单调增区间和减区间(不要求证明). 23.已知函数()()()ln 1ln 1f x x k x =++-,0k ≠. (1)当()f x 分别为奇函数和偶函数时,求k 的值;(2)若()f x 为奇函数,证明:对任意的m 、()1,1n ∈-,()()1m n f m f n f mn +⎛⎫+=⎪+⎝⎭.24.(1)已知12x y +=,9xy =,且x y <,求11221122x y x y-+值;(2)求值:2(lg 2)lg5lg 20+⋅.25.已知函数()2()log log 2(0,1)a a f x x x a a =-->≠.(1)当2a =时,求(2)f ; (2)求解关于x 的不等式()0f x >;(3)若[2,4],()4x f x ∀∈≥恒成立,求实数a 的取值范围.26.已知函数()442xx f x =+;(1)若01a <<,求()()1f a f a +-的值; (2)求12320202021202120212021f f f f ⎛⎫⎛⎫⎛⎫⎛⎫+++⋅⋅⋅+⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭的值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】首先根据指对互化求出,,a b c ,再根据换底公式表示111,,a b c,最后根据对数运算法则化简. 【详解】设3a =4b =6c =k , 则a =log 3k , b =log 4k , c =log 6k , ∴311log 3log k a k ==, 同理1log 4k b =,1log 6k c=, 而11log 2,log 3log 22k k k b c ==+, ∴1112c a b =+,即221c a b =+. 故选:B 【点睛】本题考查指对数运算,换底公式,以及对数运算的性质,关键是灵活应用对数运算公式,公式1log log a b b a=是关键. 2.D解析:D 【分析】作出()f x 的图象,利用数形结合即可得到结论. 【详解】∵函数()|lg |f x x =,作出()f x 的图象如图所示,∵0a b c <<<时,有()()()f a f c f b >>,∴0<a <1,c >1,即f (a )=|lga |=﹣lga ,f (c )=|lgc |=lgc ,∵f (a )>f (c ),∴﹣lga >lgc ,则lga +lgc =lgac <0,则01ac <<. 故选:D .【点睛】关键点点睛:利用对数函数的图象和性质,根据条件确定a ,c 的取值范围.3.D解析:D 【分析】根据指数函数和对数函数性质,借助0和1进行比较. 【详解】由对数函数性质知151log 16>,13log 03π<,由指数函数性质知13031-<<,∴b c a <<. 故选:D . 【点睛】方法点睛:本题考查指数式、对数式的大小比较,比较指数式大小时,常常化为同底数的幂,利用指数函数性质比较,或化为同指数的幂,利用幂函数性质比较,比较对数式大小,常常化为同底数的对数,利用对数函数性质比较,如果不能化为同底数或同指数,或不同类型的数常常借助中间值如0或1比较大小.4.D解析:D 【分析】求出函数的定义域,根据对数型复合函数的单调性可得结果. 【详解】函数()212()log 4f x x =-的定义域为()(),22,-∞-+∞,因为函数()f x 是由12log y u =和24u x =-复合而成,而12log y u =在定义域内单调递减,24u x =-在(),2-∞-内单调递减,所以函数()212()log 4f x x =-的单调递增区间为(),2-∞-,故选:D. 【点睛】易错点点睛:对于对数型复合函数务必注意函数的定义域.5.B解析:B 【分析】先根据题意列出关于时间的方程,然后利用指对互化以及对数换底公式并结合所给数据可计算出半衰期. 【详解】设放射性元素的半衰期为x 年,所以()500110%250x-=, 所以()1110%2x-=,所以0.91log 2x =,所以109log 2x =, 所以lg 2lg10lg9x =-,所以lg 212lg 3x =-,所以0.3010120.4771x =-⨯,所以 6.6x ≈,故选:B. 【点睛】思路点睛:求解和对数有关的实际问题的思路: (1)根据题设条件列出符合的关于待求量的等式;(2)利用指对互化、对数运算法则以及对数运算性质、对数换底公式求解出待求量的值.6.C解析:C 【分析】先分析得到a >1,再求出a =2,再利用对数的运算求值得解. 【详解】由题意可得a -a x ≥0,a x ≤a ,定义域为[0,1], 所以a >1,y [0,1]上单调递减,值域是[0,1],所以f (0)1,f (1)=0, 所以a =2, 所log a 56+log a 485=log 256+log 2485=log 28=3. 故选C 【点睛】本题主要考查指数和对数的运算,考查函数的单调性的应用,意在考查学生对这些知识的理解掌握水平,属于基础题.7.A【分析】由551112,2332log -<<<,8152log >,即可得出a ,b ,c 的大小关系. 【详解】52112243--<=<,11325551152532log log log =<<=,12881582log log >=,a b c ∴<<.故选:A 【点睛】本题主要考查了指数函数、对数函数的单调性,对数的运算性质,还考查了转化求解问题的能力,属于中档题.8.C解析:C 【分析】先找到16384与32768在第一行中的对应数字,进行相加运算,再找和对应第二行中的数字即可. 【详解】由已知可知,要计算16384×32768,先查第一行的对应数字: 16384对应14,32768对应15,然后再把第一行中的对应数字加起来:14+15=29,对应第二行中的536870912, 所以有:16384×32768=536870912, 故选C. 【点睛】本题考查了指数运算的另外一种算法,关键是认真审题,理解题意,属于简单题.9.C解析:C 【分析】判断函数的单调性.利用分段函数解析式,结合单调性列出不等式组求解即可. 【详解】解:243,1log 2,1a x ax x f x x a x ⎧-+<=⎨+≥⎩()满足对任意12x x ≠,都有()()12120f x f x x x --<成立, 所以分段函数是减函数,所以:0121442a a a a<<⎧⎪≥⎨⎪-≥⎩,解得12,23a ⎡⎤∈⎢⎥⎣⎦.故选C . 【点睛】本题考查分段函数的单调性的应用,函数的单调性的定义的理解,考查转化思想以及计算10.B解析:B 【分析】根据函数为奇函数排除C ,取特殊值排除AD 得到答案. 【详解】当()22x xx f x -=+,()()22x x xf x f x ---==-+,函数为奇函数,排除C ; 2221(2)22242f -=<=+,排除A ;3324(3)22536f -==+,4464(4)224257f -==+,故()()34f f >,排除D.故选:B. 【点睛】本题考查了函数图象的识别,意在考查学生的计算能力和识图能力,取特殊值排除是解题的关键.11.C解析:C 【分析】由题意求得1a >,再结合对数函数的图象与性质,合理排除,即可求解. 【详解】因为函数(0,1)xy a a a =>≠的反函数是增函数,可得函数xy a =为增函数,所以1a >, 所以函数log (1)a y x =-+为减函数,可排除B 、D ; 又由当0x =时,log (01)0a y =-+=,排除A. 故选:C. 【点睛】本题主要考查了指数函数和对数函数的图象与性质的应用,其中解答中熟记指数函数和对数函数的图象与性质,以及指数函数与对数的关系是解答的关键,着重考查推理与运算能力.12.B解析:B 【分析】根据指数式与对数的互化公式,求得11lg2,lg5a b==,再结合对数的运算公式,即可求解. 【详解】因为2510a b ==,可得25log 10,log 10a b ==,所以11lg2,lg5a b==,则11lg 2lg5lg101a b +=+==. 故选:B. 【点睛】本题主要考查指数式与对数的互化,以及对数的运算公式的化简、求值,其中解答中熟记指数式与对数的互化公式,以及对数的运算公式,准确运算是解答的关键,着重考查运算与求解能力.二、填空题13.【分析】由题意可得对任意的恒成立分离变量后利用函数的单调性求得在上的范围即可得解【详解】根据题意对任意的恒成立即恒成立则因为函数在上为增函数所以故答案为:【点睛】本题考查对数函数的定义域指数函数的单 解析:[ 4.5,)-+∞【分析】由题意可得对任意的(,1]x ∈-∞,10210x x a ⋅+⋯++>恒成立,分离变量a 后利用函数的单调性求得981()101010x x xg x ⎛⎫⎛⎫⎛⎫=---⋯- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭在(,1]x ∈-∞上的范围,即可得解. 【详解】根据题意对任意的(,1]x ∈-∞,123910010x x x x x a+++++>恒成立,即10210x x a ⋅+⋯++>恒成立,则981101010x x xa ⎛⎫⎛⎫⎛⎫>---⋯- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 因为函数981()101010xxxg x ⎛⎫⎛⎫⎛⎫=---⋯- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭在(,1]x ∈-∞上为增函数,所以111981 4.5101010a ⎛⎫⎛⎫⎛⎫---=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故答案为:[ 4.5,)-+∞【点睛】本题考查对数函数的定义域,指数函数的单调性,不等式恒成立问题,属于基础题.14.【分析】利用分段函数列出不等式求解即可【详解】解:在上为单调递增函数又当时当时不等式或解得或故答案为:【点睛】本题考查分段函数的应用函数值的求法考查转化思想以及计算能力 解析:21(0,][log (2),)a a a++∞ 【分析】利用分段函数列出不等式求解即可.【详解】解:()log log xxa a a a x a a x ---=-+,1a >,()log xa g x a a x =-+在()0,∞+上为单调递增函数,又1(1)log 10a g a a =-+=, 当()0,1x ∈时,log 0xa a a x -+<,当()1,x ∈+∞时,log 0xa a a x -+>,,1()log ,01x a a a x f x x x ⎧->∴=⎨-<<⎩不等式()2f x ≥,21x a a x ⎧-≥∴⎨>⎩或log 201a x x -≥⎧⎨<<⎩,解得log (2)a x a ≥+或210x a <≤, 故答案为:21(0,][log (2),)a a a ++∞. 【点睛】本题考查分段函数的应用,函数值的求法,考查转化思想以及计算能力.15.【分析】由题可知恒成立再分情况讨论即可【详解】由题可知恒成立当时成立当时当时不等式不恒成立故实数k 的取值范围是故答案为:【点睛】本题主要考查了对数的定义域以及二次函数恒成立问题属于中等题型 解析:[)0,4【分析】由题可知210kx kx -+>恒成立.再分情况讨论即可. 【详解】由题可知210kx kx -+>恒成立.当0k =时成立.当0k >时,24004k k k ∆=-<⇒<<. 当k 0<时,不等式不恒成立. 故实数k 的取值范围是[)0,4. 故答案为:[)0,4 【点睛】本题主要考查了对数的定义域以及二次函数恒成立问题.属于中等题型.16.【分析】根据题意由韦达定理得进而得再结合换底公式得【详解】解:因为、是方程的两个实根所以由韦达定理得所以所以所以故答案为:【点睛】本题解题的关键在于根据韦达定理与换底公式进行计算其中两个公式的转化是解析:37±【分析】根据题意由韦达定理得log log 5c c a b +=-,log log 3c c a b ⋅=-,进而得()2log log 37c c a b -=,再结合换底公式得1log log b acc b a==【详解】解:因为log c a 、log c b 是方程2530x x +-=的两个实根, 所以由韦达定理得log log 5c c a b +=-,log log 3c c a b ⋅=-, 所以()()22log log log log 4log log 37c c c c c c a b a b a b -=+-⋅=,所以log log c c b a -=所以11log log log log b c c acc b b a a===-故答案为: 【点睛】本题解题的关键在于根据韦达定理与换底公式进行计算,其中()()22log log log log 4log log c c c c c c a b a b a b -=+-⋅,1log log b acc b a=两个公式的转化是核心,考查运算求解能力,是中档题.17.3【分析】利用幂函数的定义与性质求得将代入利用对数的运算法则化简得解【详解】在上为增函数解得(舍去)故答案为:3【点睛】正确理解幂函数的定义求得的值和熟练运用对数恒等式是关键解析:3 【分析】利用幂函数的定义与性质求得3m =,将3m =代入,利用对数的运算法则化简得解. 【详解】()()257m f x m m x =-+在R 上为增函数,25710m m m ⎧-+=∴⎨>⎩,解得3,2m m ==(舍去),1log 2log 2lg 5lg 4mm m∴+-=31log 23l l og 3g1003+=故答案为:3.【点睛】正确理解幂函数的定义求得m 的值和熟练运用对数恒等式是关键.18.【分析】利用换底公式和对数运算法则可将方程转化为解方程求得或进而结合的范围求得结果【详解】即解得:或或故答案为:【点睛】本题考查对数方程的求解问题涉及到对数运算法则和换底公式的应用;考查基础公式的应解析:14【分析】利用换底公式和对数运算法则可将方程转化为222log 1log x x-=,解方程求得2log 2x =-或2log 1x =,进而结合x 的范围求得结果.【详解】22log 42log 2log x x x ==2222log 4log log 1log x x x x∴-=-= 即()222log log 20x x +-=,解得:2log 2x =-或2log 1x = 14x ∴=或2x = 01x << 14x ∴=故答案为:14【点睛】本题考查对数方程的求解问题,涉及到对数运算法则和换底公式的应用;考查基础公式的应用能力.19.【分析】根据分段函数分段解不等式最后求并集【详解】当时因为解得:∴当时解得:所以综上原不等式的解集为故答案为:【点睛】本题主要考查了解分段函数不等式涉及指数与对数运算属于基础题 解析:[0,)+∞【分析】根据分段函数,分段解不等式,最后求并集. 【详解】当1x ≤时,1()2xf x -=,因为11x -≤,解得:0x ≥,∴01x ≤≤ ,当1x >时,2()1log 2f x x =-≤,2log 1x ≥-,解得:12x ≥,所以1x >, 综上,原不等式的解集为[)0,+∞. 故答案为:[)0,+∞. 【点睛】本题主要考查了解分段函数不等式,涉及指数与对数运算,属于基础题.20.或2【分析】已知复合函数值求自变量从外层求出里层设求出对应的的值再由求出即可【详解】令则当若若当(舍去)故答案为:或【点睛】本题考查由函数值求自变量涉及到简单指数和对数方程考查分类讨论思想和数学计算解析:1-或2 【分析】已知复合函数值求自变量,从外层求出里层,设0()t f x =,求出()4f t =对应的t 的值,再由0()t f x =求出0x 即可. 【详解】令0()t f x =,则()4f t =,当11,24,1tt t +≤==,若010001,()21,1x x f x x +≤===-,若00202001,()2log 1,log 1,2x f x x x x >=-===, 当2211,()2log 4,log 2,4t f t t t t >=-==-=(舍去) 故答案为:1-或2. 【点睛】本题考查由函数值求自变量,涉及到简单指数和对数方程,考查分类讨论思想和数学计算能力,属于中档题.三、解答题21.(1)1k =;()f x 为R 上的增函数;(2)存在,176m =. 【分析】(1)根据奇函数的性质和()312f =,代入求函数的解析式,并判断单调性;(2)由(1)可知()()2(2)2log 22221xx x x m g x m ---=+--+⎡⎤⎣⎦,并通过换元22x x t -=-,转化为()()()22log 3m g t t mt -=-+,讨论底数21m ->,和021m <-<两种情况,并讨论内层函数的对称轴和定义域的关系,结合外层函数的单调性,确定内层函数的最值,最后确定函数的最大值求m . 【详解】(1)∵函数()x xf x a k a -=-⋅(0a >且1a ≠)是定义域为R 的奇函数,0R ∈,∴(0)0f =,10k -=,∴1k =. 因为3(1)2f =,∴132a a -=,22320a a --=,2a =或12a =-, ∵0a >,∴2a =,()22x x f x -=-,因为2x 为增函数,2x -为减函数,所以()f x 为R 上的增函数.(Ⅱ)()()22(2)log 1xx m g x aa mf x --⎡⎤=+-+⎣⎦()22(2)log 22221x x x x m m ---=+--+⎡⎤⎣⎦()()2(2)log 22223x x x x m m ---⎡⎤=---+⎢⎥⎣⎦, 设22x x t -=-,则()()22222233x x x x m t mt -----+=-+,∵[]1,2x ∈,∴315,24⎡⎤∈⎢⎥⎣⎦t ,记()23h t t mt =-+, (1)当021m <-<,即23m <<时,要使()g x 最大值为0,则要min ()1h t =,∵22()()(3)24m m h t t =-+-,312m <<,315,24⎡⎤∈⎢⎥⎣⎦t ,∴()h t 在315,24⎡⎤⎢⎥⎣⎦上单调递增,∴min 3213()()242h t h m ==-,由min ()1h t =,得176m =,因17(2,3)6∈,所以176m =满足题意. (2)当21m ->,即3m >时,要使()g x 最大值为0,则要max ()1h t =,且min ()0h t >. ∵322m >, ①若321228m <≤ ,则max 1522515()()314164h t h m ==-+=,25760m =,又2min ()()3024m m h t h ==->,∴3m <<25760>∴25760m =不合题意. ②若2128m > ,即214m >,则max 32132132121()()02424248h t h m ==-<-⨯=-<,max ()1h t ≠,综上所述,只存在176m =满足题意. 【点睛】关键点点睛:本题考查对数型复合函数根据最值,求参数的取值范围,属于中档题型,本题的第一个关键点是换元化简函数,设22x x t -=-,则()()22222233x x x x m t mt -----+=-+,第二个关键点是需分析外层函数的单调性,并讨论内层函数的对称轴和定义域的关系.22.(1)定义域为(1,3)-,值域为(,2]-∞(2)递增区间为(1,1)-,递减区间为[1,3) 【分析】(1)由2230x x -++>解得结果可得定义域,根据二次函数知识求出真数的值域,根据对数函数的单调性可求得()f x 的值域;(2)在定义域内求出真数的单调区间,根据底数大于1可得函数()f x 的单调区间.【详解】(1)由函数有意义可得2230x x -++>,即2230x x --<, 解得13x ,所以函数()f x 的定义域为(1,3)-, 因为13x,所以2223(1)4x x x -++=--+(0,4]∈,所以()(,2]f x ∈-∞,即函数()f x 的值域为(,2]-∞.(2)因为函数()f x 的定义域为(1,3)-,且函数2y x 2x 3=-++在(1,1)-上递增,在(1,3)上递减,又对数函数的底数为21>,所以函数()f x 的递增区间为(1,1)-,递减区间为[1,3). 【点睛】方法点睛:已知函数解析式,求函数定义域的方法: 有分式时:分母不为0;有根号时:开奇次方,根号下为任意实数,开偶次方,根号下大于或等于0; 有指数时:当指数为0时,底数一定不能为0;有根号与分式结合时,根号开偶次方在分母上时:根号下大于0; 有指数函数形式时:底数和指数都含有x ,指数底数大于0且不等于1;有对数函数形式时,自变量只出现在真数上时,只需满足真数上所有式子大于0,自变量同时出现在底数和真数上时,要同时满足真数大于0,底数要大0且不等于1. 23.(1)()f x 为奇函数时,1k =-,()f x 为偶函数时,1k =;(2)证明见解析. 【分析】(1)求出函数的定义域,利用函数的奇偶性的定义列等式即可求得k 的值; (2)根据函数解析式分别求得()()+f m f n ,1m n f mn +⎛⎫⎪+⎝⎭,即可证明结论.【详解】(1)由1010x x +>⎧⎨->⎩,解得11x -<<,得函数()f x 的定义域为()1,1-,当()f x 为奇函数时,()()0f x f x +-=,即()()()()ln 1ln 1ln 1ln 10x k x x k x ++-+-++=, 整理可得()()()1ln 1ln 10k x x +-++=⎡⎤⎣⎦, 因为上式恒成立,所以10k +=,所以1k =-; 当()f x 为偶函数时,()()0f x f x --=,即()()()()ln 1ln 1ln 1ln 10x k x x k x ++----+=, 整理得()()()1ln 1ln 10k x x -+--=⎡⎤⎣⎦, 因为上式恒成立,所以10k -=,所以1k =.综上,当()f x 为奇函数时,1k =-,当()f x 为偶函数时,1k =;(2)由(1)知,1k =-,()()()1ln 1ln 1ln1xf x x x x+=+--=-, ()()()()()()1111ln ln ln 1111m n m nf m f n m n m n +++++=+=----,()()()()11111ln ln ln 111111m nm n m n mn m n mn f m n mn mn m n m n mn++++++++⎛⎫+=== ⎪+++----⎝⎭-+, 所以()()1m n f m f n f mn +⎛⎫+= ⎪+⎝⎭.【点睛】方法点睛:已知函数的奇偶性求参数值一般思路是:(1)利用函数的奇偶性的定义转化为()()f x f x -=(偶函数)或()()f x f x -=-(奇函数),从而建立方程,使问题获得解决;(2)取一对互为相反数的自变量的函数值,建立等式求出参数的值,但同时要对此时函数的奇偶性进行验证. 24.(1)3-2)1. 【分析】(1)求出x y -的值,再化简11221122x y x y-+即得解;(2)利用对数的运算法则化简求解. 【详解】(1)因为222()()41249108x y x y xy -=+-=-⨯=,又x y <,所以x y -=-所以1111222221122()3x y x y x y x y--====--+. (2)原式22(lg 2)lg5(1lg 2)(lg 2)lg5lg 2lg5=+⋅+=+⋅+lg2(lg2lg5)lg5lg2lg51=++=+=.【点睛】关键点点睛:解答指数对数运算题的关键是通过观察式子的特点,再熟练利用指数对数的运算法则和性质求解.25.(1)2-;(2)当1a >时,()0f x >的解集为()210,,a a ⎛⎫+∞ ⎪⎝⎭,当01a <<时;()210,,a a ⎛⎫+∞ ⎪⎝⎭(3)(31,2⎫⎤⎪⎦⎪⎣⎭.【分析】(1)将2a =直接代入解析式计算即可.(2)将()2()log log 20a a f x x x =-->整理为()()log 2log 10a a x x -+>,解得log 1<-a x 或log 2a x >,再对a 讨论即可解不等式.(3)将问题转化为min ()4f x ≥,分别分1a >和01a <<讨论,求()f x 最小值,令其大于4,即可求解.【详解】(1)当2a =时,()()222log log 2f x x x =--()21122f ∴=--=-(2)由()0f x >得:()()()2log log 2log 2log 10a a a a x x x x --=-+>log 1a x ∴<-或log 2a x >当1a >时,解不等式可得:10x a<<或2x a > 当01a <<时,解不等式可得:1x a>或20x a << 综上所述:当1a >时,()0f x >的解集为()210,,a a ⎛⎫+∞ ⎪⎝⎭;当01a <<时,()0f x >的解集为()210,,aa ⎛⎫+∞ ⎪⎝⎭(3)由()4f x ≥得:()()()2log log 6log 3log 20a a a a x x x x --=-+≥log 2a x ∴≤-或log 3a x ≥①当1a >时,()max log log 4a a x =,()min log log 2a a x =2log 42log a a a -∴≤-=或3log 23log a a a ≥=,解得:1a <≤②当01a <<时,()max log log 2a a x =,()min log log 4a a x =2log 22log a a a -∴≤-=或3log 43log a a a ≥=1a ≤<综上所述:a 的取值范围为(3,11,22⎫⎤⎪⎦⎪⎣⎭【点睛】本题主要考查了复合函数的单调性、考查函数的最值和恒成立问题、考查分类讨论的思想,属于中档题. 26.(1)1;(2)1010. 【分析】(1)根据4()42xx f x =+的表达式,求出()(),1f a f a -的表达式,再进行分式通分运算,可得()()11f a f a +-=. (2)设12320202021202120212021S f f f f ⎛⎫⎛⎫⎛⎫⎛⎫=+++⋅⋅⋅+⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,再把S 的表达式运用加法交换律改写成20201202120212021202321S f f f f ⎛⎫⎛⎫⎛⎫⎛⎫=++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,把两式相加利用()(1)1f x f x +-=求出S 的值.【详解】 (1)4()42xxf x =+,x ∈R . ∴()()1f a f a +-1144444442424224aaaa a a a a--=+=+++++4214224a a a=+=++,(2)设12320202021202120212021S f f f f ⎛⎫⎛⎫⎛⎫⎛⎫=+++⋅⋅⋅+⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,则 20201202120212021202321S f f f f ⎛⎫⎛⎫⎛⎫⎛⎫=++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 两式相加得:12[][][]92022020220120201202120212022120211021S f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=++++++⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭由(1)得:20202201109211,1,,221202120212021202120220101f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+=+=+= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭, ∴220201010S S =⇒=.【点睛】本题考查指数幂运算,分式运算,利用函数的性质进行式子求值,考查运算求解能力.。
指数函数对数函数专练习题(含答案)

一、填空题1.函数y =a x(a >0,且a ≠1)在[1,2]上的最大值比最小值大a2,则a 的值是________.2.若曲线|y |=2x+1与直线y =b 没有公共点,则b 的取值范围是________.三、解答题3.求函数y =24.(2011·银川模拟)若函数y =a 2x +2a x-1(a >0且a ≠1)在x ∈[-1,1]上的最大值为14,求a 的值.对数与对数函数同步练习一、选择题1、已知32a =,那么33log 82log 6-用a 表示是( )A 、2a -B 、52a -C 、23(1)a a -+D 、 23a a -2、2log (2)log log a a a M N M N -=+,则NM的值为( ) A 、41B 、4C 、1D 、4或1 3、已知221,0,0x y x y +=>>,且1log (1),log ,log 1y a aa x m n x+==-则等于( ) A 、m n + B 、m n - C 、()12m n + D 、()12m n -4、如果方程2lg (lg5lg7)lg lg5lg70x x +++= 的两根是,αβ,则αβ 的值是( )A 、lg5lg 7B 、lg 35C 、35D 、3515、已知732log [log (log )]0x =,那么12x -等于( )A 、13 B 、 C D6、函数2lg 11y x ⎛⎫=- ⎪+⎝⎭的图像关于( )A 、x 轴对称B 、y 轴对称C 、原点对称D 、直线y x =对称7、函数(21)log x y -= )A 、()2,11,3⎛⎫+∞ ⎪⎝⎭B 、()1,11,2⎛⎫+∞ ⎪⎝⎭C 、2,3⎛⎫+∞ ⎪⎝⎭D 、1,2⎛⎫+∞ ⎪⎝⎭8、函数212log (617)y x x =-+的值域是( )A 、RB 、[)8,+∞C 、(),3-∞-D 、[)3,+∞ 9、若log 9log 90m n <<,那么,m n 满足的条件是( )A 、 1 m n >>B 、1n m >>C 、01n m <<<D 、01m n <<<10、2log 13a <,则a 的取值范围是( )A 、()20,1,3⎛⎫+∞ ⎪⎝⎭B 、2,3⎛⎫+∞ ⎪⎝⎭C 、2,13⎛⎫ ⎪⎝⎭D 、220,,33⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭11、下列函数中,在()0,2上为增函数的是( )A 、12log (1)y x =+ B 、2log y =C 、21log y x = D 、2log (45)y x x =-+ 12、已知()log x+1 (01)a g x a a =>≠且在()10-,上有()0g x >,则1()x f x a +=是( ) A 、在(),0-∞上是增加的 B 、在(),0-∞上是减少的 C 、在(),1-∞-上是增加的 D 、在(),0-∞上是减少的 二、填空题13、若2log 2,log 3,m n a a m n a +=== 。
(典型题)高中数学必修一第三单元《指数函数和对数函数》检测题(答案解析)

一、选择题1.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设x ∈R ,用[]x 表示不超过x 的最大整数,则[]y x =称为高斯函数,例如:35]4[--.=,[]2.12=,已知函数21()12x x e f x e =++,()[()]g x f x =,则下列叙述正确的是( ) A .()g x 是偶函数 B .()f x 在R 上是增函数C .()f x 的值域是1,2⎛⎫-+∞ ⎪⎝⎭D .()g x 的值域是{1,0,1}-2.已知函数()()2log 23a f x x x =--+,若()00f <,则此函数的单调递增区间是( ) A .(],1-∞-B .[)1,-+∞C .[)1,1-D .(]3,1--3.函数()212()log 4f x x =-的单调递增区间为( ).A .(0,+∞)B .(-,0)C .(2,+∞)D .(-,-2)4.已知函数3131()(),()log ,()(0)2xf x xg x x xh x x x x =-=-=->的零点分别为,,a b c ,则,,a b c 的大小顺序为( )A .a b c >>B .c a b >>C .b c a >>D .b a c >>5.已知函数()()2ln f x ax bx c =++的部分图象如图所示,则a b c -+的值是( )A .1-B .1C .5-D .56.设函数()21xf x =-,c b a <<,且()()()f c f a f b >>,则22a c +与2的大小关系是( ) A .222a c +> B .222a c +≥ C .222a c +≤D .222a c +<7.已知3log 2a =,那么33log 82log 6-用a 表示是( ) A .52a -B .2a -C .23(1)a a -+D .231a a --8.已知函数()2,01,0x x f x x x >⎧=⎨+≤⎩,若()()10f a f +=,则实数a 的值等于( )A .-3B .-1C .1D .39.若函数()()212log 45f x x x =-++在区间()32,2m m -+内单调递增,则实数m 的取值范围为( ) A .4,33⎡⎤⎢⎥⎣⎦B .4,23⎡⎤⎢⎥⎣⎦C .4,23⎡⎫⎪⎢⎣⎭D .4,3⎡⎫+∞⎪⎢⎣⎭10.函数()log (3)a f x ax =-在[]13,上单调递增,则a 的取值范围是( ) A .()1+∞, B .()01,C .103⎛⎫ ⎪⎝⎭,D .()3+∞, 11.函数()log 1a f x x =+(且).当(1,0)x ∈-时,恒有()0f x >,有( ).A .()f x 在(,0)-∞+上是减函数B .()f x 在(,1)-∞-上是减函数C .()f x 在(0,)+∞上是增函数D .()f x 在(,1)-∞-上是增函数12.函数2ln 8x y x =-的图象大致为( )A .B .C .D .二、填空题13.已知()(3),1log ,1aa x a x f x x x --<⎧=⎨≥⎩的值域为R ,那么实数a 的取值范围是_________.14.已知常数0a >,函数()22xx f x ax =+的图象经过点65P p ⎛⎫ ⎪⎝⎭,,15Q q ⎛⎫- ⎪⎝⎭,.若236p q pq +=,则a =______.15.函数x )是_________(奇、偶)函数.16.定义{},,max ,,x x y x y y x y≥⎧=⎨<⎩,设{}()max ,log x a f x a a x =--(),1x R a +∈>.则不等式()2f x ≥的解集是_____________.17.函数()()()212log 24f x ax x a R =-+∈,若()f x 的值域为(],1-∞,则a 的值为______.18.对于函数()f x 定义域中任意的1x 、()212x x x ≠,有如下结论: ①()()()1212f x x f x f x +=⋅;②()()()1212f x x f x f x ⋅=+;③()()()12120x x f x f x -⋅-<⎡⎤⎣⎦;④()()121222f x f x x x f ++⎛⎫<⎪⎝⎭. 当()2xf x =时;上述结论正确的是__________.(写出所有正确的序号)19.设函数()f x 的定义域为D ,若存在0x D ∈,使得00(1)()(1)f x f x f +=+,则称0x 为函数()f x 的“可拆点”.若函数22()log 1af x x =+在(0,)+∞上存在“可拆点”,则正实数a 的取值范围为____________.20.若函数1log 12a y x ⎛⎫=+ ⎪⎝⎭在区间3,62⎡⎤-⎢⎥⎣⎦有最小值-2,则实数a =_______. 三、解答题21.已知函数()421()x x f x a a R =-+⋅-∈. (1)当1a =时,求()f x 的值域; (2)若()f x 在区间[]1,0-的最大值为14-,求实数a 的值. 22.已知函数()ln(32)f x x =+,()ln(32)g x x =-.设函数()()()F x f x g x =-. (1)求函数()F x 的定义域; (2)判断()F x 奇偶性并证明; (3)若()0F x >成立,求x 的取值范围.23.设函数()()22()log 4log 2f x x x =⋅的定义域为1,44⎡⎤⎢⎥⎣⎦.(1)求()y f x =的最大值和最小值,并求出最值时对应的x 值; (2)解不等式()60f x ->.24.已知函数()log (0,1)a f x x a a =>≠,且(4)(2)1f f -=. (1)求函数()f x 的表达式;(2)判断函数()(2)(2)g x f x f x =++-的奇偶性,并说明理由.25.已知函数210(),22,01xx ax a x f x a a x ⎧+--≤<=⎨-≤≤⎩,其中a >0且a ≠1. (1)当12a =时,求f (x )的值域;(2)函数y =f (x )能否成为定义域上的单调函数,如果能,则求出实数a 的范围;如果不能,则给出理由;(3)()2f x -在其定义域上恒成立,求实数a 的取值范围.26.已知222log ()log log x y x y +=+,则x y +的取值范围是__________.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】计算(2),(2)g g -得出()()22g g ≠-判断选项A 不正确;通过分离常数结合复合函数的单调性,可得出()f x 在R 上是增函数,判断选项B 正确;由x y e =的范围,利用不等式的关系,可求出15()22f x <<,进而判断选项CD 不正确,即可求得结果. 【详解】对于A ,根据题意知,2152()1221x x xe f x e e =+=-++. ∵252(2)[(2)]221g f e ⎡⎤==-=⎢⎥+⎣⎦, 2222121(2)[(2)]01212e g f e e --⎡⎤⎡⎤-=-=+=+=⎢⎥⎢⎥++⎣⎦⎣⎦, (2)(2)g g ∴≠-,∴函数()g x 不是偶函数,故A 错误;对于B ,1x y e =+在R 上是增函数,则21xy e =+在R 上是减函数,则52()21xf x e =-+在R 上是增函数,故B 正确; 对于C ,0xe >,11x e ∴+>,2202,20,11x x e e <<-<-<++ 15()22f x ∴<<,即()f x 的值域是15,22⎛⎫⎪⎝⎭,故C 错误;对于D ,()f x 的值域是15,22⎛⎫⎪⎝⎭,则()g x 的值域是{0,1,2},故D 错误. 故选:B. 【点睛】本题要注意对函数的新定义的理解,研究函数的单调性和值域常用分离常数,属于较难题.2.C解析:C 【分析】由()00f <求得01a <<,求出函数()f x 的定义域,利用复合函数法可求得函数()f x 的单调递增区间. 【详解】由题意可得()0log 30log 1a a f =<=,01a ∴<<.对于函数()()2log 23a f x x x =--+,2230x x --+>,可得2230x x +-<,解得31x -<<.所以,函数()f x 的定义域为()3,1-.由于内层函数223u x x =--+在区间(]3,1--单调递增,在区间[)1,1-单调递减. 外层函数log a y u =单调递减,由复合函数法可知,函数()f x 的单调递增区间为[)1,1-. 故选:C. 【点睛】方法点睛:函数单调性的判定方法与策略:(1)定义法:一般步骤:设元→作差→变形→判断符号→得出结论;(2)图象法:如果函数()f x 是以图象的形式给出或者函数()f x 的图象易作出,结合图象可得出函数的单调区间;(3)导数法:先求出函数的导数,利用导数值的正负确定函数的单调区间; (4)复合函数法:先将函数()y f g x ⎡⎤=⎣⎦分解为内层函数()u g x =和外层函数()y f u =,再讨论这两个函数的单调性,然后根据复合函数法“同增异减”的规则进行判定. 3.D解析:D 【分析】求出函数的定义域,根据对数型复合函数的单调性可得结果. 【详解】函数()212()log 4f x x =-的定义域为()(),22,-∞-+∞,因为函数()f x 是由12log y u =和24u x=-复合而成,而12log y u =在定义域内单调递减,24u x =-在(),2-∞-内单调递减,所以函数()212()log 4f x x =-的单调递增区间为(),2-∞-, 故选:D. 【点睛】易错点点睛:对于对数型复合函数务必注意函数的定义域.4.B解析:B 【分析】将函数3131()(),()log ,()(0)2x f x x g x x x h x x x x =-=-=->的零点,转化为函数y x =的图象分别与函数3131(),log ,(0)2xy y x y x x ===>的图象交点的横坐标,利用数形结合法求解. 【详解】函数3131()(),()log ,()(0)2x f x x g x x x h x x x x =-=-=->的零点,即为函数y x =的图象分别与函数3131(),log ,(0)2x y y x y x x ===>的图象交点的横坐标, 如图所示:由图象可得:c a b >>,故选:B 【点睛】本题主要考查函数的零点以及指数函数,对数函数和幂函数的图象的应用,还考查了数形结合的思想方法,属于中档题.5.D解析:D 【分析】由图中函数的单调性可得方程20ax bx c ++=的两根为2和4,利用根与系数的关系结合(1)0f =列式求得,,a b c 的值,则答案可求.【详解】解:由图可知,函数()f x 的减区间为(,2)-∞,增区间为(4,)+∞, ∴内层函数2t ax bx c =++的减区间为(,2)-∞,增区间为(4,)+∞, ∴方程20ax bx c ++=的两根为2和4, 又(1)0f =,68ln()0ba ca abc ⎧-=⎪⎪⎪∴=⎨⎪++=⎪⎪⎩,解得13283a b c ⎧=⎪⎪=-⎨⎪⎪=⎩. 182533a b c ∴-+=++=.故选:D. 【点睛】本题考查函数的图象与图象变换,考查复合函数的单调性,考查数学转化思想方法,是中档题.6.D解析:D 【分析】运用分段函数的形式写出()f x 的解析式,作出()21xf x =-的图象,由数形结合可得0c <且0a >,21c <且21a >,且()()0f c f a ->,去掉绝对值,化简即可得到结论.【详解】()21,02112,0x xxx f x x ⎧-≥=-=⎨-<⎩, 作出()21xf x =-的图象如图所示,由图可知,要使c b a <<且()()()f c f a f b >>成立, 则有0c <且0a >, 故必有21c <且21a >,又()()0f c f a ->,即为()12210c a--->,∴222a c +<. 故选:D . 【点睛】本题考查指数函数单调性的应用,考查用指数函数单调性确定参数的范围,本题借助函数图象来辅助研究,由图象辅助研究函数性质是函数图象的重要作用,以形助数的解题技巧必须掌握,是中档题.7.B解析:B 【解析】试题分析:33333333log 82log 6log 22log 233log 22(log 2log 3)-=-⨯=-+3log 222a =-=-,所以答案选B .考点:指数对数的计算8.A解析:A 【分析】先求得()1f 的值,然后根据()f a 的值,求得a 的值. 【详解】由于()1212f =⨯=,所以()()20,2f a f a +==-,22a =-在()0,∞+上无解,由12a +=-解得3a =-,故选A.【点睛】本小题主要考查分段函数求函数值,考查已知分段函数值求自变量,属于基础题.9.C解析:C 【分析】求得函数()y f x =的定义域,利用复合函数法求得函数()y f x =的单调递增区间,根据题意可得出区间的包含关系,由此可求得实数m 的取值范围. 【详解】解不等式2450x x -++>,即2450x x --<,解得15x -<<,内层函数245u x x =-++在区间()1,2-上单调递增,在区间()2,5上单调递减, 而外层函数12log y u =在定义域上为减函数,由复合函数法可知,函数()()212log 45f x x x =-++的单调递增区间为()2,5, 由于函数()()212log 45f x x x =-++在区间()32,2m m -+上单调递增,所以,32232225m m m m -≥⎧⎪-<+⎨⎪+≤⎩,解得423m ≤<.因此,实数m 的取值范围是4,23⎡⎫⎪⎢⎣⎭. 故选:C. 【点睛】本题考查利用对数型复合函数在区间上的单调性求参数,考查计算能力,属于中等题.10.D解析:D 【分析】由题意可得可得1a >,且30a ->,由此求得a 的范围. 【详解】解:函数()log (3)a f x ax =-在[]13,上单调递增,而函数()3t x ax =-在[]13,上单调递增,根据复合函数的单调性可得1a >,且30a ->,解得3a >,即()3a ∈+∞,故选:D . 【点睛】本题主要考查对数函数的定义域、单调性,复合函数的单调性,属于基础题.11.D解析:D 【解析】试题分析:根据题意,当(1,0)x ∈-时,1(0,1)x +∈,而此时log 10a x +>,所以有01a <<,从而能够确定函数在(,1)-∞-上是增函数,在区间(1,)-+∞上是减函数,故选D .考点:函数的单调性.12.D解析:D 【分析】先根据偶函数性质排除B ,再考虑当0x >且0x →时,y →+∞,排除A.再用特殊值法排除C ,即可得答案. 【详解】解:令()2ln 8x f x y x ==-,则函数定义域为{}0x x ≠ ,且满足()()f x f x -=,故函数()f x f (x )为偶函数,排除选项B ; 当0x >且0x →时,y →+∞,排除选项A ;取特殊值x =1ln 1ln 0y e =-<-=,排除选项C. 故选:D. 【点睛】本题考查利用函数解析式选函数图象问题,考查函数的基本性质,是中档题.二、填空题13.【分析】分类讨论和结合已知和对数函数及一次函数的单调性得a 的不等式组求解即可【详解】解:若当时当时此时的值域不为R 不符合题意;若当时当时要使函数的值域为R 需使解得综上所述故答案为:【点睛】本题考查分解析:31,2⎛⎤⎥⎝⎦【分析】分类讨论01a <<和1a >,结合已知和对数函数及一次函数的单调性,得a 的不等式组求解即可. 【详解】 解:若01a <<, 当1≥x 时,log 0a x ≤,当1x <时,()3332a x a a a a --<--=-,此时f x ()的值域不为R ,不符合题意;若1a >,当1≥x 时,log 0a x ≥,当1x <时,要使函数f x ()的值域为R ,需使30log 13a a a a ->⎧⎨≤--⎩,解得332a a <⎧⎪⎨≤⎪⎩,312a ∴<≤, 综上所述,312a <≤,故答案为:31,2⎛⎤ ⎥⎝⎦.【点睛】本题考查分段函数的值域及对数函数的性质,考查分类讨论思想与数学运算能力,是中档题.14.6【分析】直接利用函数的关系式利用恒等变换求出相应的a 值【详解】函数f (x )=的图象经过点P (p )Q (q )则:整理得:=1解得:2p+q=a2pq 由于:2p+q=36pq 所以:a2=36由于a >0故解析:6 【分析】直接利用函数的关系式,利用恒等变换求出相应的a 值. 【详解】函数f (x )=22xx ax+的图象经过点P (p ,65),Q (q ,15-).则:226112255p q pq ap aq +=-=++, 整理得:22222222p q p q p qp qp q aq ap aq ap a pq+++++++++=1, 解得:2p+q =a 2pq , 由于:2p+q =36pq , 所以:a 2=36, 由于a >0, 故:a=6. 故答案为6 【点睛】本题考查的知识要点:函数的性质的应用,代数式的变换问题的应用.15.奇【解析】又所以函数f(x)是奇函数点睛:判断函数的奇偶性其中包括两个必备条件:(1)定义域关于原点对称这是函数具有奇偶性的必要不充分条件所以首先考虑定义域;(2)判断f(x)与f(-x)是否具有等解析:奇 【解析】210x x x x x x R +->=-≥∴∈又()()))lglglg10f x f x x x -+=+==所以函数f(x) 是奇函数.点睛: 判断函数的奇偶性,其中包括两个必备条件:(1)定义域关于原点对称,这是函数具有奇偶性的必要不充分条件,所以首先考虑定义域;(2)判断f (x )与f (-x )是否具有等量关系.在判断奇偶性的运算中,可以转化为判断奇偶性的等价关系式f (x )+f (-x )=0(奇函数)或f (x )-f (-x )=0(偶函数)是否成立.16.【分析】利用分段函数列出不等式求解即可【详解】解:在上为单调递增函数又当时当时不等式或解得或故答案为:【点睛】本题考查分段函数的应用函数值的求法考查转化思想以及计算能力 解析:21(0,][log (2),)a a a++∞ 【分析】利用分段函数列出不等式求解即可. 【详解】解:()log log xxa a a a x a a x ---=-+,1a >,()log x a g x a a x =-+在()0,∞+上为单调递增函数,又1(1)log 10a g a a =-+=, 当()0,1x ∈时,log 0xa a a x -+<,当()1,x ∈+∞时,log 0xa a a x -+>,,1()log ,01x a a a x f x x x ⎧->∴=⎨-<<⎩不等式()2f x ≥,21x a a x ⎧-≥∴⎨>⎩或log 201a x x -≥⎧⎨<<⎩,解得log (2)a x a ≥+或210x a <≤, 故答案为:21(0,][log (2),)a a a ++∞. 【点睛】本题考查分段函数的应用,函数值的求法,考查转化思想以及计算能力.17.【分析】根据对数的性质可知且最小值为即可求得的值【详解】因为的值域为所以函数的最小值为即解得故答案为:【点睛】本题考查对数函数的值域考查对数的性质合理转化是解题的关键考查了运算能力属于中档题 解析:27【分析】根据对数的性质可知2240y ax x =-+>,且最小值为1,即可求得a 的值. 【详解】因为()()()212log 24f x ax x a R =-+∈的值域为(],1-∞,所以2240ax x -+>,函数224y ax x =-+的最小值为12,即()20442142a a a >⎧⎪⎨⨯--=⎪⎩,解得27a =,故答案为:27【点睛】本题考查对数函数的值域,考查对数的性质,合理转化是解题的关键,考查了运算能力,属于中档题.18.①④【分析】根据指数幂的运算法则判断①;采用举例子的方法判断②;根据指数函数的单调性判断③;利用指数幂的运算并采用作差法判断④【详解】对于①:因为所以故①正确;对于②:取所以所以不恒成立故②错误;对解析:①④ 【分析】根据指数幂的运算法则判断①;采用举例子的方法判断②;根据指数函数的单调性判断③;利用指数幂的运算并采用作差法判断④. 【详解】对于①:因为()()()12121212122,222x x x x x x f x x f x f x +++=⋅=⋅=,所以()()()1212f x x f x f x +=⋅,故①正确;对于②:取121,2x x ==,所以()()()()121224,246f x x f f x f x ⋅==+=+=,所以()()()1212f x x f x f x ⋅=+不恒成立,故②错误;对于③:因为()2xf x =是R 上的增函数,所以()()()12120x x f x f x -⋅->⎡⎤⎣⎦,故③错误;对于④:因为()()121212122222,=222x x x x f x f x x x f ++++⎛⎫= ⎪⎝⎭,且12121212121222222222222422220242x x x x x x x x x x x x ++++⎛⎫⎛⎫⎛⎫++⋅-⋅--==> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 所以()()121222f x f x x x f ++⎛⎫<⎪⎝⎭,故④正确, 所以正确的有:①④, 故答案为:①④. 【点睛】结论点睛:可直接判断函数单调性的几种变形形式:(1)已知12,x x D ∀∈(D 为函数定义域),且12x x ≠,都有()()()()12120x x f x f x -->或()()12120f x f x x x ->- 成立,则()f x 为单调递增函数;(2)已知12,x x D ∀∈(D 为函数定义域),且12x x ≠,都有()()()()12120x x f x f x --<或()()12120f x f x x x -<- 成立,则()f x 为单调递增函数.19.【分析】首先根据定义列出的等式转化为再根据分离常数和换元法求的取值范围【详解】函数为可分拆函数存在实数使得且设当时等号成立即故答案为:【点睛】思路点睛:本题是一道以新定义为背景的函数性质的综合应用题解析:[3【分析】首先根据定义,列出()()()0011f x f x f +=+的等式,转化为()()20202111x a x +=++,再根据分离常数和换元法,求a 的取值范围. 【详解】 函数()22log 1af x x =+为“可分拆函数”,∴存在实数00x >,使得()2222200log log log 1211aa a x x =++++且0a >,()()222002111a a x x ∴=+++,()()()2220000002222000000021*********222222211x x x x x x a x x x x x x x +++--++∴====-++++++++, 设0422x t +=>,024t x -∴=, 2161622204204t a t t t t∴=-=-++++ ,20444t t ++≥=,当t =即32a <. 故答案为:)32⎡⎣ 【点睛】思路点睛:本题是一道以新定义为背景的函数性质的综合应用题型,首先正确利用新定义,并正确表示()()20202111x a x +=++,利用01x >,转化为求函数的值域,即求a 的取值范围.20.或2【分析】根据复合函数的单调性及对数的性质即可求出的值【详解】当时在为增函数求得即;当时在为减函数求得即故答案为:或【点睛】本题考查复合函数单调性对数方程的解法难度一般解析:12或2 【分析】根据复合函数的单调性及对数的性质即可求出a 的值. 【详解】当1a >时, 1log 12a y x ⎛⎫=+ ⎪⎝⎭在3,62⎡⎤-⎢⎥⎣⎦为增函数,min 33log 1-224a y f ⎛⎫⎛⎫=-=-+= ⎪ ⎪⎝⎭⎝⎭,求得-214a=,即=2a ; 当01a <<时, 1log 12a y x ⎛⎫=+ ⎪⎝⎭在3,62⎡⎤-⎢⎥⎣⎦为减函数,()()min 6log 31-2a y f ==+=,求得-24a =,即1=2a . 故答案为:12或2. 【点睛】本题考查复合函数单调性,对数方程的解法,难度一般.三、解答题21.(1)3,4⎛⎤-∞- ⎥⎝⎦;(2)a =【分析】(1)令()20,xt =∈+∞,可得21y t t =-+-,利用二次函数的性质可求出;(2)令12,12xt ⎡⎤=∈⎢⎥⎣⎦,可得21y t at =-+-,讨论对称轴2at =的取值范围结合二次函数的性质即可求出. 【详解】(1)()2()421221x x xx f x a a =-+⋅-=-+⋅-.令()20,xt =∈+∞,21y t at =-+-,1a =时,2213124y t t t ⎛⎫=-+-=--- ⎪⎝⎭在10,2⎛⎫ ⎪⎝⎭上单调递增,在1,2⎛⎫+∞ ⎪⎝⎭上单调递减. ∴当12t =时,max 34y =-,∴3,4y ⎛⎤∈-∞- ⎥⎝⎦,所以()f x 的值域为3,4⎛⎤-∞- ⎥⎝⎦.(2)令12,12xt ⎡⎤=∈⎢⎥⎣⎦,22211124a y t at t a ⎛⎫=-+-=---+ ⎪⎝⎭, 其图象的对称轴为2at =. ①当122a ≤,即1a ≤时,函数y 在区间1,12⎡⎤⎢⎥⎣⎦上单调递减, 当12t =时,max 1111424y a =-+-=-,解得2a =,与1a ≤矛盾;②当12a ≥,即2a ≥时,函数y 在区间1,12⎡⎤⎢⎥⎣⎦上单调递增, 当1t =时,max 1114y a =-+-=-,解得74a =,与2a ≥矛盾, ③当1122a <<,即12a <<时,函数y 在1,22a ⎡⎤⎢⎥⎣⎦上单调递增,在,12a ⎡⎤⎢⎥⎣⎦上单调递减.当2at =时,2max 11144y a =-=-,解得a =,舍去a =综上,a = 【点睛】思路点睛:求二次函数在闭区间[],a b 的最值的思路; (1)二次函数开口向上时,求函数的最大值,讨论对称轴和2a b+的大小求解; (2)二次函数开口向上时,求函数的最小值,讨论对称轴在(]()[),,,,,a a b b -∞+∞三个区间的范围求解. 22.(1)33,22⎛⎫- ⎪⎝⎭;(2)奇函数,证明见解析;(3)302x <<【分析】(1)由320320x x +>⎧⎨->⎩可解得结果;(2)()F x 是奇函数,根据奇函数的定义可证结论正确; (3)根据对数函数的单调性可解得结果. 【详解】(1)由320320x x +>⎧⎨->⎩,解得3322x -<<,所以函数()F x 的定义域为33(,)22-.(2)()F x 是奇函数. 证明如下:x ∀∈33(,)22-,都有x -∈33(,)22-,因为 ()ln(32)ln(32)()F x x x F x -=--+=-, ∴()F x 是奇函数.(3)由()0F x >可得()()0f x g x ->,得ln(32)ln(32)0x x +-->, 即ln(32)ln(32)x x +>-, 由对数函数的单调性得32320x x ,解得302x <<. 【点睛】易错点点睛:利用对数函数的单调性解对数不等式时,容易忽视函数的定义域.23.(1)当x =时,()f x 取得最小值14-;当4x =时,()f x 取得最大值12;(2){}24x x <≤【分析】(1)令2log t x =,可得[]2,2t ∈-,从而()()22log 4log 2x x ⋅232t t =++,结合二次函数的性质,可求出最大值和最小值,及取得最值时对应的x 值;(2)由(1)知,2()32f x t t =++,[]2,2t ∈-,则不等式可化为2340t t +->,可求出t 的范围,结合2log t x =,可求出x 的范围. 【详解】 (1)由题意,()()()()222222log 4log 2log 4log log 2log x x x x ⋅=+⋅+=()()222log 1log x x +⋅+,令2log t x =,∵1,44x ⎡∈⎤⎢⎥⎣⎦,∴[]2log 2,2t x =∈-则()()22132y t t t t =++=++,根据二次函数的性质,可得当32t =-,即322x -==232y t t =++取得最小值,最小值为233132224⎛⎫⎛⎫-+-+=- ⎪ ⎪⎝⎭⎝⎭; 当2t =时,即224x ==时,232y t t =++取得最大值,最大值为2232212+⨯+=. (2)由(1)知,2()32f x t t =++,[]2,2t ∈-, 则()60f x ->可化为2340t t +->,解得1t >或4t <-, 因为[]2,2t ∈-,所以12t <≤, 则222log 2log log 4x <≤,即24x <≤, 故不等式()60f x ->的解集为{}24x x <≤. 【点睛】关键点点睛:本题考查求复合函数的最值,及函数不等式的解.解决本题的关键是利用换元法,令2log t x =,可将()f x 转化为关于t 的二次函数232y t t =++,进而可求出最值,并解不等式即可,注意不要漏掉[]2,2t ∈-.考查学生的逻辑推理能力,计算求解能力,属于中档题.24.(1)2()log f x x =(2)偶函数.见解析 【分析】(1)根据(4)(2)1f f -=,代入到函数的解析式中可求得2a =,可求得函数()f x 的解析式; (2)由函数()f x 的解析式,求得函数()g x 的解析式,先求得函数()g x 的定义域,再由函数的奇偶性的判断方法证得函数的奇偶性. 【详解】(1)因为()log (0,1)a f x x a a =>≠,且(4)(2)1f f -=,所以log 4log 21a a -=,即log 21a =.,解得2a =,所以2()log f x x =;(2)因为()log a f x x =,所以22()log (2)log (2)g x x x =++-,由2020x x +>⎧⎨->⎩,得22x -<<,所以()g x 的定义域为()22-,, 又因为22()log (2)log (2)()g x x x g x -=-++=, 所以22()log (2)log (2)g x x x =++-为偶函数. 【点睛】本题考查对数函数的函数解析式的求解,函数的奇偶性的证明,属于基础题. 25.(1)()f x 的值域为9[16-,1];(2)能,a 的取值集合为{2};(3)232a -. 【分析】(1)由二次函数和指数函数的值域求法,可得()f x 的值域;(2)讨论1a >,01a <<,结合指数函数的单调性和二次函数的单调性,即可得到所求范围;(3)讨论x 的范围和a 的范围,结合参数分离和对勾函数的单调性、指数函数的单调性,计算可得所求范围. 【详解】(1)当10x -<时,21122y x x =+-,对称轴为1[14x =-∈-,0), 可得y 的最小值为916-,y 的最大值为0; 当01x 时,12?()1[02xy =-∈,1];综上()f x 的值域为9[16-,1];(2)当1a >时,函数22x y a a =-在[0,1]递增, 故二次函数2y x ax a =+-在[1-,0]也要递增,1222aa a⎧--⎪⎨⎪--⎩,故只有2a =符合要求; 当01a <<时,函数22x y a a =-在[0,1]递减, 故二次函数2y x ax a =+-在[1-,0]也要递减,0222aa a⎧-⎪⎨⎪--⎩,无解. 综上,a 的取值集合为{2};(3)①当[1x ∈-,0]时,22x ax a +--恒成立,即有2(1)2a x x ---,即221x a x+-,由221x y x+=-,令1t x =-,[1t ∈,2],可得32232y t t=+--,当且仅当t = 可得232a -;②当[0x ∈,1]时,①当1a >时,22x y a a =-,222x a a --,即有222a -,求得2a ,故12a <; ②当01a <<时,成立, 综上可得a 的范围为232a -. 【点睛】本题考查分段函数的值域和单调性的判断和运用,考查分类讨论思想方法和化简运算能力,以及不等式恒成立问题解法,属于中档题.26.[4,)+∞【分析】利用对数式的运算性质把给出的等式变形,去掉对数符号后利用基本不等式转化为关于(x +y )的二次不等式,求解后即可得到x +y 的取值范围. 【详解】222log ()log log x y x y +=+,x y xy ∴+=,0,0x y >>,2()2x y x y xy +∴+=≤,当且仅当2x y ==时,等号成立。
高中数学 第四章 指数函数、对数函数与幂函数综合测试训练(含解析)新人教B版必修第二册-新人教B版高

第四章综合测试(时间:120分钟 满分150分)一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若n ∈N ,a ∈R ,给出下列式子:①4-42n;②4-42n +1;③5a 4;④4a 5.其中恒有意义的式子的个数是( B )A .1B .2C .3D .4 [解析] 根据根指数是偶数时,被开方数非负,可知②无意义;当a <0时,④无意义;恒有意义的是①③.故选B .2.函数y =log 12x -3的定义域为( C )A .(-∞,18]B .[18,+∞)C .(0,18]D .(0,8][解析] 要使函数y =log 12x -3有意义,应满足log 12x -3≥0, ∴log 12x ≥3,∴⎩⎪⎨⎪⎧x >0x ≤⎝ ⎛⎭⎪⎫123=18,∴0<x ≤18,故选C .3.下列不等式中正确的是( C ) A .lg 0.1>lg 0.2 B .0.20.1<0.20.2C .0.20.1>lg 0.1D .0.10.2<lg 0.2[解析] lg 0.1<0,0.20.1>0,∴0.20.1>lg 0.1,故选C . 4.已知函数f (x )=⎩⎪⎨⎪⎧log 3x x >0⎝ ⎛⎭⎪⎫12xx ≤0,则f ⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫127=( D ) A .-18B .18C .-8D .8[解析] f ⎝ ⎛⎭⎪⎫127=log 3127=log 33-3=-3,f ⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫127=f (-3)=⎝ ⎛⎭⎪⎫12-3=8,故选D .5.若a >b >1,0<c <1,则( C ) A .a c<b cB .ab c <ba cC .a log b c <b log a cD .log a c <log b c[解析] 令a =4,b =2,c =12,则a c =412 =2,b c =212 =2,∴a c >b c,排除A ;ab c =42,ba c =4,∴ab c >ba c ,排除B ;log a c =log 412=-12,log b c =log 212=-1,∴log a c >log b c ,排除D ,故选C .6.已知f (x )是函数y =log 2x 的反函数,则y =f (1-x )的图像是( C )[解析] 因为函数y =log 2x 的反函数是y =2x ,所以f (x )=2x .故f (1-x )=21-x,因为此函数在R 上是减函数,且过点(0,2).因此选C .7.下列函数中,满足“f (x +y )=f (x )f (y )”的增函数是( B ) A .f (x )=x 3B .f (x )=3xC .f (x )=x 12D .f (x )=⎝ ⎛⎭⎪⎫12x[解析] 对于函数f (x )=x 3,f (x +y )=(x +y )3,f (x )f (y )=x 3·y 3,而(x +y )3≠x 3y 3,所以f (x )=x 3不满足f (x +y )=f (x )f (y ),故A 错误; 对于函数f (x )=3x,f (x +y )=3x +y=3x ·3y =f (x )f (y ),因此f (x )=3x满足f (x +y )=f (x )f (y ),且f (x )=3x是增函数,故B 正确;对于函数f (x )=x 12 ,f (x +y )=(x +y )12 ,f (x )f (y )=x 12 y 12 =(xy )12 ,而(x +y )12 ≠(xy )12 ,所以f (x )=x 12 不满足f (x +y )=f (x )f (y ),故C错误;对于函数f (x )=⎝ ⎛⎭⎪⎫12x ,f (x +y )=⎝ ⎛⎭⎪⎫12x +y =⎝ ⎛⎭⎪⎫12x ·⎝ ⎛⎭⎪⎫12y=f (x )·f (y ),因此f (x )=⎝ ⎛⎭⎪⎫12x 满足f (x +y )=f (x )f (y ),但f (x )=⎝ ⎛⎭⎪⎫12x不是增函数,故D 错误.8.设函数f (x )=⎩⎪⎨⎪⎧3x -1x <12xx ≥1,则满足f [f (a )]=2f (a )的a 的取值X 围是( C )A .[23,1]B .[0,1]C .[23,+∞)D .[1,+∞)[解析] 由f [f (a )]=2f (a )可得f (a )≥1,故有⎩⎪⎨⎪⎧a <13a -1≥1或⎩⎪⎨⎪⎧a ≥12a≥1,二者取并集即得a 的取值X 围是⎣⎢⎡⎭⎪⎫23,+∞,故选C .二、多项选择题(本大题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项是符合题目要求的.全部选对的得5分,选对但不全的得3分,有选错的得0分)9.已知实数a ,b 满足等式3a=6b,给出下列四个关系式:①a =b ;②0<b <a ;③a <b <0;④b <0<A .其中可能成立的是( ABC )A .①B .②C .③D .④[解析] 在同一个坐标系中画出函数y =3x,y =6x的图象如图所示.由图像,可知当a =b =0时,3a=6b,故①可能成立;作出直线y =k ,如图所示,当k >1时,若3a=6b,则0<b <a ,故②可能成立;当0<k <1时,若3a=6b,则a <b <0,故③可能成立.故选ABC .10.对于0<a <1,下列四个不等式中成立的是( BD )A .log a (1+a )<log a ⎝⎛⎭⎪⎫1+1a B .log a (1+a )>log a ⎝ ⎛⎭⎪⎫1+1aC .a1+a<a1+1aD .a1+a>a1+1a[解析] 因为0<a <1,所以a <1a ,从而1+a <1+1a,所以log a (1+a )>log a ⎝ ⎛⎭⎪⎫1+1a .又因为0<a <1,所以a1+a>a1+1a.11.设函数f (x )=2x,对于任意的x 1,x 2(x 1≠x 2),下列命题中正确的是( ACD ) A .f (x 1+x 2)=f (x 1)·f (x 2)B .f (x 1·x 2)=f (x 1)+f (x 2) C .f x 1-f x 2x 1-x 2>0D .f ⎝ ⎛⎭⎪⎫x 1+x 22<f x 1+f x 22[解析] 2x 1·2x 2=2x 1+x 2,所以A 成立,2x 1+2x 2≠2x 1·x 2,所以B 不成立,函数f (x )=2x,在R 上是单调递增函数,若x 1>x 2则f (x 1)>f (x 2),则f x 1-f x 2x 1-x 2>0,若x 1<x 2,则f (x 1)<f (x 2),则f x 1-f x 2x 1-x 2>0,故C 正确;f ⎝⎛⎭⎪⎫x 1+x 22<f x 1+f x 22说明函数是凹函数,而函数f (x )=2x是凹函数,故ACD 正确.12.关于函数f (x )=|ln |2-x ||,下列描述正确的有( ABD ) A .函数f (x )在区间(1,2)上单调递增 B .函数y =f (x )的图像关于直线x =2对称 C .若x 1≠x 2,但f (x 1)=f (x 2),则x 1+x 2=4 D .函数f (x )有且仅有两个零点[解析] 函数f (x )=|ln |2-x ||的图像如图所示:由图可得:函数f (x )在区间(1,2)上单调递增,A 正确;函数y =f (x )的图像关于直线x =2对称,B 正确;若x 1≠x 2,但f (x 1)=f (x 2),则当x 1,x 2>2时,x 1+x 2>4,C 错误;函数f (x )有且仅有两个零点,D 正确.三、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中的横线上) 13.设函数f (x )=x -a (其中a 为常数)的反函数为f -1(x ),若函数f -1(x )的图像经过点(0,1),则方程f -1(x )=2的解为__1__.[解析] 由y =f (x )=x -a ,得x -a =y 2(y ≥0)把点(0,1)代入得a =1. 所以f -1(x )=x 2+1(x ≥0).由f -1(x )=2,得x 2+1=2,即x =1.14.设f (x )=⎩⎪⎨⎪⎧2e x -1,x <2log 32x-1,x ≥2,则f [f (2)] =__2__.[解析] 因为f (2)=log 3(22-1)=1, 所以f [f (2)]=f (1)=2e1-1=2.15.已知函数f (x )=b -2x2x +1为定义在区间[-2a,3a -1]上的奇函数,则a =__1__,f ⎝ ⎛⎭⎪⎫12=__22-3__.[解析] 因为f (x )是定义在[-2a,3a -1]上的奇函数. 所以定义域关于原点对称, 即-2a +3a -1=0,所以a =1, 因为函数f (x )=b -2x2x +1为奇函数, 所以f (-x )=b -2-x 2-x +1=b ·2x -11+2x =-b -2x1+2x ,即b ·2x-1=-b +2x,所以b =1, 所以f (x )=1-2x1+2x ,所以f ⎝ ⎛⎭⎪⎫12=1-212 1+212 =1-21+2=22-3.16.下列说法中,正确的是__①④__. ①任取a >0,均有3a >2a, ②当a >0,且a ≠1,有a 3>a 2, ③y =(3)-x是增函数,④在同一坐标系中,y =2x与y =2-x的图像关于y 轴对称. [解析] ∵幂函数y =x a ,当a >0时, 在(0,+∞)上是增函数, ∵3>2,∴3a>2a,故①正确;当a =0.1时,0.13<0.12,故②错; 函数y =(3)-x=⎝⎛⎭⎪⎫33x是减函数,故③错; 在同一坐标系中,y =2x 与y =2-x=(12)x 的图像关于y 轴对轴,故④正确.四、解答题(本大题共6个小题,共70分,解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分10分)计算下列各式的值. (1)⎝ ⎛⎭⎪⎫23-2+(1-2)0+⎝ ⎛⎭⎪⎫27823 ; (2)2lg 2+lg 31+12lg 0.36+13lg 8.[解析] (1)⎝ ⎛⎭⎪⎫23-2+(1-2)0+⎝ ⎛⎭⎪⎫27823 =94+1+94=112.(2)2lg 2+lg 31+12lg 0.36+13lg 8=lg 4+lg 31+lg 0.6+lg 2=lg 12lg 12=1.18.(本小题满分12分)已知函数f (x )=2x -1+a (a 为常数,且a ∈R )恒过点(1,2).(1)求a 的值;(2)若f (x )≥2x,求x 的取值X 围.[解析] (1)f (1)=20+a =1+a =2,解得a =1. (2)由f (x )=2x -1+1=2x 2+1≥2x ,得2x2≤1,即2x -1≤1=20,即x -1≤0,解得x ≤1,因此,实数x 的取值X 围是(-∞,1].19.(本小题满分12分)求函数y =(2x )2-2×2x+5,x ∈[-1,2]的最大值和最小值. [解析] 设2x=t ,因为x ∈[-1,2],所以2x=t ∈⎣⎢⎡⎦⎥⎤12,4则y =t 2-2t +5为二次函数,图像开口向上,对称轴为t =1, 当t =1时,y 取最小值4,当t =4时,y 取最大值13.20.(本小题满分12分)已知幂函数y =f (x )的图像过点(8,m )和(9,3). (1)求m 的值;(2)若函数g (x )=log a f (x )(a >0,a ≠1)在区间[16,36]上的最大值比最小值大1,某某数a 的值.[解析] (1)由题意,y =f (x )是幂函数,设f (x )=x α,图像过点(8,m )和(9,3)可得9α=3,所以α=12,故f (x )=x 12 ,所以m =f (8)=22,故m 的值为22.(2)函数g (x )=log a f (x ),即为g (x )=log a x , 因为x 在区间[16,36]上,所以x ∈[4,6], ①当0<a <1时,g (x )min =log a 6,g (x )max =log a 4, 由log a 4-log a 6=log a 23=1,解得a =23.②当a >1时,g (x )min =log a 4,g (x )max =log a 6,由log a 6-log a 4=log a 32=1,解得a =32,综上可得,实数a 的值为23或32.21.(本小题满分12分)一片森林原来的面积为a ,计算每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到森林面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的14,已知到今年为止,森林剩余面积为原来的22.(1)求每年砍伐面积的百分比;(2)到今年为止,该森林已被砍伐了多少年? (3)今后最多还能砍伐多少年?[解析] (1)设每年砍伐面积的百分比为x (0<x <1),则a (1-x )10=12a ,即(1-x )10=12,解得x =1-(12)110 .(2)设经过m 年剩余面积为原来的22, 则a (1-x )m=22a , 即(12)m 10 =(12)12 ,m 10=12,解得m =5, 故到今年为止,该森林已被砍伐5年. (3)设从今年开始,以后最多能砍伐n 年,则n 年后剩余面积为22a (1-x )n . 令22a (1-x )n ≥14a ,即(1-x )n ≥24, (12)n 10 ≥(12)32 ,n 10≤32,解得n ≤15. 故今后最多还能砍伐15年.22.(本小题满分12分)已知函数f (x )=log 2⎝ ⎛⎭⎪⎫12x +a .(1)若函数f (x )是R 上的奇函数,求a 的值;(2)若函数f (x )的定义域是一切实数,求a 的取值X 围;(3)若函数f (x )在区间[0,1]上的最大值与最小值的差不小于2,某某数a 的取值X 围. [解析] (1)函数f (x )是R 上的奇函数,则f (0)=0,求得a =0. 又此时f (x )=-x 是R 上的奇函数,所以a =0为所求. (2)函数f (x )的定义域是一切实数,则12x +a >0恒成立.即a >-12x 恒成立,由于-12x ∈(-∞,0).故只要a ≥0即可.(3)由已知函数f (x )是减函数,故f (x )在区间[0,1]上的最大值是f (0)=log 2(1+a ).最小值是f (1)=log 2⎝ ⎛⎭⎪⎫12+a .由题设log 2(1+a )-log 2⎝ ⎛⎭⎪⎫12+a ≥2⇒⎩⎪⎨⎪⎧a +12>0a +1≥4a +2.故-12<a ≤-13为所求.。
2023-2024学年高一上数学《指数函数与对数函数》测试卷及答案解析

2023-2024学年高一数学《指数函数与对数函数》一.选择题(共12小题)1.(2022春•鼓楼区校级期中)设,则a,b,c的大小顺序为()A.a<c<b B.c<a<b C.a<b<c D.b<a<c 2.(2022春•鼓楼区校级期中)关于x的不等式e x≤ax(x﹣lnx)只有唯一实数解,则实数a的取值范围是()A.{e}B.[e,+∞)C.{1}D.(0,1] 3.(2022春•福州期中)已知a=lg2,b=log23,c=log34,则a,b,c的大小关系为()A.a>b>c B.a<b<c C.a<c<b D.c<a<b 4.(2022•福州模拟)折纸是我国民间的一种传统手工艺术.现有一张长10cm、宽8cm的长方形的纸片,将纸片沿着一条直线折叠,折痕(线段)将纸片分成两部分,面积分别为S1,S2.若S1:S2=1:3,则折痕长的最大值为()A .cm B.10cm C.2cm D.2cm 5.(2021秋•福州期末)已知函数f(x)=(x+3)(x﹣e)+(x﹣e)(x﹣π)+(x﹣π)(x+3)的零点x1,x2(x1<x2),则()A.x1x2>0B .<﹣C.x2﹣x1<e D.x1+x2<π6.(2021秋•福州期末)设a=0.123,b=30.4,c=log0.40.12,则a,b,c的大小关系为()A.a<b<c B.b<a<c C.a<c<b D.c<a<b 7.(2021秋•仓山区校级期末)若方程x2+2x+m2+3m=m cos(x+1)+7有且仅有1个实数根,则实数m的值为()A.2B.﹣2C.4D.﹣4 8.(2021秋•鼓楼区校级期中)某科技有限公司为了鼓励员工创新,打破发达国家的芯片垄断,计划逐年增加研发资金投入,若该公司2018年全年投入的研发资金为200万元,在此基础上,每年投入的研发资金比上一年增加10%,则该公司全年投入的研发资金开始超过400万元的年份是()(参考数据:1.16=1.77,1.17=1.95,1.18=2.14,1.19=2.36)第1页(共23页)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
指数函数和对数函数·换底公式·例题
例1-6-38log34·log48·log8m=log416,则m 为 [ ]
解 B 由已知有
[ ]
A.b>a>1
B.1>a>b>0
C.a>b>1
D.1>b>a>0
解 A 由已知不等式得
故选A.
[ ]
故选A.
[ ]
A.[1,+∞] B.(-∞,1] C.(0,2) D.[1,2)
2x-x2>0得0<x<2.又t=2x-x2=-(x-1)2+1在[1,+∞)上是减函数,
[ ]
A.m>p>n>q
B.n>p>m>q
C.m>n>p>q
D.m>q>p>n
例1-6-43 (1)若log a c+log b c=0(c≠0),则ab+c-abc=____;
(2)log89=a,log35=b,则log102=____(用a,b表示).
但c≠1,所以lga+lgb=0,所以ab=1,所以ab+c-abc=1.
例1-6-44函数y=f(x)的定义域为[0,1],则函数f[lg(x2-1)]的定义域是____.
由题设有0≤lg(x2-1)≤1,所以1≤x2-1≤10.解之即得.
例1-6-45已知log1227=a,求log616的值.
例1-6-46比较下列各组中两个式子的大小:
例1-6-47已知常数a>0且a≠1,变数x,y满足
3log x a+log a x-log x y=3
(1)若x=a t(t≠0),试以a,t表示y;
(2)若t∈{t|t2-4t+3≤0}时,y有最小值8,求a和x的值.
解 (1)由换底公式,得
即 log a y=(log a x)2-3log a x+3
当x=a t时,log a y=t2-3t+3,所以
y=a r2-3t+3
(2)由t2-4t+3≤0,得1≤t≤3.
值,所以当t=3时,u max=3.即a3=8,所以a=2,与0<a<1矛盾.此时满足条件的a值不存在.。
