逻辑斯蒂方程
逻辑斯蒂公式计算拐点

逻辑斯蒂公式计算拐点
逻辑斯蒂函数(Logistic function)也称为Sigmoid函数,其公式表示如下:
f(x) = 1 / (1 + e^(-x))
其中,e表示自然对数的底 (约等于2.71828)。
拐点(Inflection point)是指函数曲线上由凹转凸或由凸转凹的点。
在逻辑斯蒂函数中,拐点就是函数曲线从增长趋势到减少趋势或从减少趋势到增长趋势的位置。
为了找到逻辑斯蒂函数的拐点,我们需要解方程 f''(x) = 0,即求逻辑斯蒂函数的二阶导数关于x的解。
首先,我们计算逻辑斯蒂函数的一阶导数f'(x) 和二阶导数f''(x):
f'(x) = (e^(-x)) / (1 + e^(-x))^2 f''(x) = (e^(-x))/(1 + e^(-x))^2 - 2(e^(-x))^2/(1 + e^(-x))^3
将 f''(x) = 0 代入上述方程,并进行简化运算,可得:
(e^(-x)) - 2(e^(-x))^2 = 0
然后,将 (e^(-x)) 因式分解为公因式,得到:
(e^(-x))(1 - 2e^(-x)) = 0
由于 (e^(-x)) 不可能为零,因此我们解方程 1 - 2e^(-x) = 0,得到:
e^(-x) = 1/2
取对数,得到:
-x = ln(1/2)
最后,解方程得到:
x = ln(2)
所以逻辑斯蒂函数的拐点为 x = ln(2)。
逻辑斯蒂增长模型
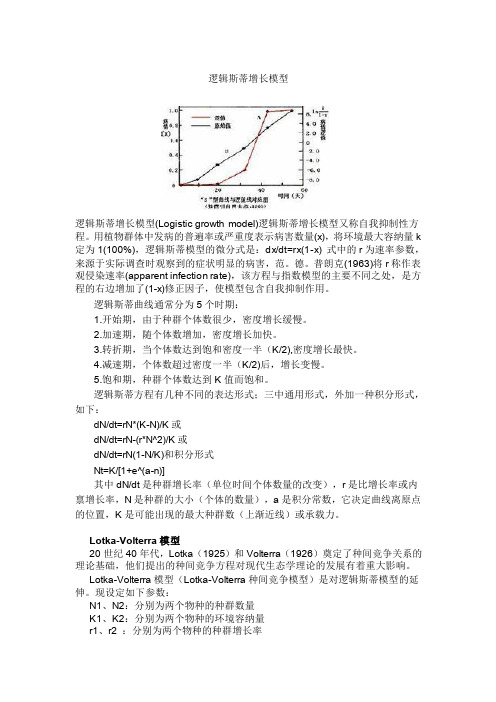
逻辑斯蒂增长模型逻辑斯蒂增长模型(Logistic growth model)逻辑斯蒂增长模型又称自我抑制性方程。
用植物群体中发病的普遍率或严重度表示病害数量(x),将环境最大容纳量k 定为1(100%),逻辑斯蒂模型的微分式是:dx/dt=rx(1-x) 式中的r为速率参数,来源于实际调查时观察到的症状明显的病害,范。
德。
普朗克(1963)将r称作表观侵染速率(apparent infection rate),该方程与指数模型的主要不同之处,是方程的右边增加了(1-x)修正因子,使模型包含自我抑制作用。
逻辑斯蒂曲线通常分为5个时期:1.开始期,由于种群个体数很少,密度增长缓慢。
2.加速期,随个体数增加,密度增长加快。
3.转折期,当个体数达到饱和密度一半(K/2),密度增长最快。
4.减速期,个体数超过密度一半(K/2)后,增长变慢。
5.饱和期,种群个体数达到K值而饱和。
逻辑斯蒂方程有几种不同的表达形式;三中通用形式,外加一种积分形式,如下:dN/dt=rN*(K-N)/K或dN/dt=rN-(r*N^2)/K或dN/dt=rN(1-N/K)和积分形式Nt=K/[1+e^(a-n)]其中dN/dt是种群增长率(单位时间个体数量的改变),r是比增长率或内禀增长率,N是种群的大小(个体的数量),a是积分常数,它决定曲线离原点的位置,K是可能出现的最大种群数(上渐近线)或承载力。
Lotka-Volterra模型20世纪40年代,Lotka(1925)和Volterra(1926)奠定了种间竞争关系的理论基础,他们提出的种间竞争方程对现代生态学理论的发展有着重大影响。
Lotka-Volterra模型(Lotka-Volterra种间竞争模型)是对逻辑斯蒂模型的延伸。
现设定如下参数:N1、N2:分别为两个物种的种群数量K1、K2:分别为两个物种的环境容纳量r1、r2 :分别为两个物种的种群增长率依逻辑斯蒂模型有如下关系:dN1 / dt = r1 N1(1 - N1 / K1)其中:N/K可以理解为已经利用的空间(称为“已利用空间项”),则(1-N/K)可以理解为尚未利用的空间(称为“未利用空间项”)当两个物种竞争或者利用同一空间时,“已利用空间项”还应该加上N2种群对空间的占用。
logistic方程

logistic方程Logistic方程,也被称为逻辑回归方程,是一种广泛应用于机器学习和统计学的有用工具。
其基本原理是,利用一系列的自变量(称为预测变量)x1,x2,…,xn来预测一个因变量(称为响应变量)y的概率。
它的公式可以用数学表达为:p = 1/(1+ e^-(-θ^T X))其中p代表响应变量y取正类(即“1”)的概率,而e是自然常数,θ是一组参数,X是自变量向量。
Logistic方程以贝叶斯概率论为基础,它是从一个因变量(y)和一些自变量(X)中建立联系的模型,称为回归模型。
这种模型的主要目的是建立在一组自变量的基础上来预测一个因变量的取值,特别是一个类别型变量(如果该变量有两个可能的取值,如“正类”或“负类”)。
Logistic方程最初是用来拟合二元逻辑回归模型的,它便于理解,因为它是基于概率模型来表达因变量与自变量之间的关系的,其所拟合出来的曲线称为Logistic函数曲线。
Logistic函数曲线非常好用,因为它提供了在某一特定点处响应变量发生的概率,当选择了它作为响应变量的算法时,它可以极大的简化计算。
另外,Logistic函数曲线具有S字形,它比较容易让人理解,并可以容易地用于模型分析。
Logistic方程还有另外一些优点,它可以让计算任务更加容易,从而加快计算速度。
此外,Logistic方程能够提供准确的预测结果,它所生成的输出结果可以使预测准确率达到90%以上,从而可以减少错误的决策,提高决策的准确性。
但Logistic方程也有一些不足,其中最明显的是它对输入数据的要求高,需要把输入数据整理成规范的格式,以便将其输入到Logistic方程中进行分析。
另外,它也要求输入数据量是足够大,以便能够准确地预测结果。
此外,Logistic方程也不能处理非线性关系,以及多重共线性(multicollinearity)的情况。
总之,Logistic方程是一种强大的机器学习工具,能够提供准确且可靠的预测结果,在机器学习领域得到了广泛的应用,如在分类问题上,在计算统计学上、在决策树上以及在生物信息学等领域得到了广泛的应用。
logistic回归模型

Logistic回归模型
• 列联表中的数据是以概率的形式把属性变量联系 起来的,而概率p的取值在0与1之间,因此,要把
概率 p (x)与 x 之间直接建立起函数关系是不合
适的。即 (x) x
Logistic回归模型
• 因此,人们通常把p的某个函数f(p)假设为变量的 函数形式,取 f ( p) ln (x) ln p
1 (x) 1 p
• 称之为logit函数,也叫逻辑斯蒂变换。 • 因此,逻辑斯蒂变换是取列联表中优势的对数。
当概率在0-1取值时,Logit可以取任意实数,避免 了线性概率模型的结构缺陷。
Logistic回归模型
假设响应变量Y是二分变量,令 p P(Y 1) ,影响Y
的因素有k个 x1, xk,则称:
多项logit模型
• 前面讨论的logit模型为二分数据的情况,有时候 响应变量有可能取三个或更多值,即多类别的属 性变量。
• 根据响应变量类型的不同,分两种情况:
–响应变量为定性名义变量; –响应变量为定性有序变量;
• 当名义响应变量有多个类别时,多项logit模型应 采取把每个类别与一个基线类别配成对,通常取 最后一类为参照,称为基线-类别logit.
• 为二分数据的逻辑斯ln 1蒂pp回归g(模x1,型,,xk简) 称逻辑斯蒂 回归模型。其中的k个因素称为逻辑斯蒂回归模型 的协变量。
• 最重要的逻辑斯蒂回归模型是logistic线性回归模 型,多元logit模型的形式为:
ln
p 1 p
0
1x1
k xk
Logistic回归模型
• 其中,0, 1, , k 是待估参数。根据上式可以得到
多项logit模型
逻辑斯谛增长曲线的形成过程及各阶段的特征

逻辑斯蒂增长模型
逻辑斯蒂增长模型又称自我抑制性方程。用植物群体中发 病的普遍率或严重度表示病害数量(x),将环境最大容纳 量k定为1(100%)。
具体来说就是:
1.指数增长是在无限环境中表现 出来的。 2.指数增长只能在短期内表现出 来。 3.在自然界空间和资源都是有限 的,种群的增长表现为S型,称
之为逻辑斯谛增长。
(1)逻辑斯谛增长的条件和模型: 条件(假定):
种群增长有一个环境条件所允许的最大值,称 为环境容量或承载力,记作K。当种群大小增至 K时,种群不再增长。
随着种群密度上升,种群增长率逐渐按比例降 低,即每增加一个个体的影响是1/K(种群增 长受密度的制约)。
dN rN ( K N )
饱和期,种群个体数达到K值而饱和。
当种群的增长达到环境条件所允许的最大值时, 即达到了饱和期,种群个体数达到K值而饱和, 种群数量很难再有所增长了。
返回
加速期:随个体数增加,密度增长加快。
经历过开始期后,生物种群对所处的生态环境有了 一定的适应后,各方面的条件都比刚开始的时候优 越了很多,于是生物种群的生长会进入一个加速期。 而随着加速期生物个体数量的增加,其密度增长也 会随之加快。
转折期,当个体数达到饱和密度一半(K/2),密度增长最快
当生物个体数达到饱和密度一半(K/2)时,表明生物种群 已经充分利用生态资源进行自我生长,这时生物种群发展 到转折期,这个时期也是生物种群密度增长最快的时期。
dt
K
Nt
1
K e
-rt
1
K e-r(t-/r)
逻辑斯蒂曲线的各个阶段和特征:
减速期
种群逻辑斯谛方程

实验一 昆虫种群逻辑斯蒂增长模型(验证性实验)一、 实验目的逻辑斯蒂曲线是一条S 型曲线,它是生物种群在有限资源环境中(空间和食物)增长到一定程度时,环境阻力逐渐增大,致使种群的最大数量限制在一个固定水平之下,种群将不再继续增长而稳定在环境负荷量K 值左右。
实验已证明S 形曲线是生物界中普遍存在的一种规律,具有广泛的应用价值。
通过实验熟悉种群S 形增长的特点及曲线拟合的方法。
二、 实验原理由逻辑斯蒂增方程 N=erta K -+1取自然对数得a-rt=ln(NNK -) ---Y 则 Y=a-rt首先求得环境负荷量K 值后,再将各N 值换算为ln[(k-n)/n]。
K 值求法有多种,如将接近饱和点附近的n 点N 值平均,而得一个值,或用三等距计算法。
应用三点测定K 值常受所选点位置的影响,因此本实验采用直线回归计算K 值。
该方法是对N n 与N n /N a+1进行回归,得直线回归式:N n /N a+1=A+BN n利用最小二乘法求得A 、B 。
令N n /N a+1=1,代入直线回归式,即表N n =N a+1时,种群个体数不在增加,那么N n 值就视为环境负荷K 值,显然K=BA-1。
A 、B 值求得后,确定K 值,可根据Y=a-rt 回归式,确定参数a 和r 。
三、 实验方法为100克经轻压而裂开的麦粒(约2000粒)中数入5对小谷蠹成虫开始实验,每周把麦粒筛出,弃去粉末状粪物质,并补充以新鲜的经碾压的麦粒,使其重新维持100克,并每两周计算一次成虫数,实验可设3~5个重复。
四、实验结果小谷蠹种群增长结果见表1。
1. K值的确定:设N n/N a+1=Y,N=XK值确定按表2进行。
2. 参数a , r 的确定:K值确定后,表1中ln(N NK-) 可统计出。
设Y= ln(N NK-),X=t参数a , r的确定按表3进行。
表1 小谷蠹种群增长结果时间t 种群个数N Nn /Nn+1Y=ln((K-N)/N)0 10 0.546448087 4.1632351951 18.3 0.631034483 3.5459227072 29 0.61440678 3.0685202213 47.2 0.663853727 2.5518116434 71.1 0.372056515 2.1018527665 191.1 1.094501718 0.8820998976 174.6 0.678585309 1.0075134717 257.3 0.733675506 0.4298863768 350.7 0.795238095 -0.1492014679 441 0.859146698 -0.73344294810 513.3 0.917098446 -1.30285736811 559.7 0.940988568 -1.79381889312 594.8 0.94502701 -2.32793012713 629.4 0.9834375 -3.29239764914 640 0.982951928 -3.91269345615 651.1 0.993287567 -5.95309417116 655.5 0.99378411217 659.6 0.99667573318 661.8 0.9977385819 663.3表2 N n/N a+1~N n线性回归统计表统计项统计值统计项统计值∑x 7155.5 SSx(SSv) 1227374.369 ∑X23922173.33 SSy(SST) 0.697440815 X376.6052632 SP 762.5136429 y 15.73993636 r 0.824148389 ∑y213.73668274 A 0.594449439 y0.828417703 B 0.000621256∑XY 6690.256518 K=B A-1652.7914211 表中各值的计算公式:SS X=∑X2 -( 1/n)(∑X)2SS Y=∑Y2 –( 1/n)(∑Y)2SP=∑XY–( 1/n)(∑X)(∑Y)r=SP/( SS X * SS Y)1/2B=SP/ SS XA=y-B X表3 ln(N NK-)~t 线性回归统计表统计项统计值统计项统计值∑x 120 SSx(SSv) 340∑X21240 SSy(SST) 124.5577615X7.5 SP -203.2955841y -1.7145938 r( 相关系数) -0.987877489 ∑y2124.7124895 a(A) 4.377299301y-0.107162113 B -0.597928188 ∑XY -216.1550376 r( 参数)=-B 0.597928188 表中各值的计算公式:SS X=∑X2 -( 1/n)(∑X)2SS Y=∑Y2 –( 1/n)(∑Y)2SP=∑XY–( 1/n)(∑X)(∑Y)r(相关系数)=SP/( SS X * SS Y)1/2B=SP/ SS Xa=y-B X五、作业1. 完成表1、2、3的计算。
origin逻辑斯蒂方程拟合步骤

origin逻辑斯蒂方程拟合步骤
用逻辑斯蒂回归进行数据拟合一般需要以下步骤:
1. 数据准备:首先需要准备好用于拟合的数据集。
数据集应包含两个关键列:自变量(X)和因变量(Y)。
自变量可以是单个变量或多个变量,而因变量应为二元变量(0或1)。
2. 模型建立:使用逻辑斯蒂回归模型建立拟合模型。
逻辑斯蒂回归模型是一个用于描述二分类问题的回归模型,通过将线性函数的输出值通过S形函数(逻辑斯蒂函数)转换为概率值。
3. 参数估计:使用最大似然估计方法来估计逻辑斯蒂回归模型的参数。
最大似然估计方法是一种通过最大化观测到的数据的概率来估计模型参数的统计方法。
4. 模型拟合:使用估计出的参数对逻辑斯蒂回归模型进行拟合。
将自变量输入模型,计算输出的概率值。
5. 拟合评估:对拟合结果进行评估,常用的评估指标包括准确率、精确率、召回率、F1分数等。
可以使用交叉验证等方法进一步评估模型的性能。
6. 预测应用:使用拟合完成的逻辑斯蒂回归模型进行新样本的分类预测。
将新的自变量输入模型,根据模型输出的概率值进行分类。
以上是逻辑斯蒂回归模型的拟合步骤,需要注意的是,不同的软件和编程环境可能会有些差异,具体的步骤和实现方法可以根据所使用的工具进行适当调整。
论述逻辑斯蒂增长模型

论述逻辑斯蒂增长模型逻辑斯蒂增长模型(Logistic Growth Model)是一种描述种群增长的数学模型。
它基于种群生物学的基本原理,通过考虑种群的出生率、死亡率和迁移率,来预测种群在未来的增长趋势。
逻辑斯蒂增长模型最早由比利时数学家皮埃尔·弗朗索瓦·鲁韦(Pierre François Verhulst)于19世纪提出,并被广泛应用于生态学、经济学等领域。
该模型的基本假设是种群的增长率与种群数量成正比,但增长速度会随着种群数量的增加而减缓。
在逻辑斯蒂增长模型中,种群的增长速率由两个因素决定:出生率和死亡率。
出生率表示新个体的产生速度,通常与种群的繁殖能力相关;而死亡率表示个体的死亡速度,通常与种群的寿命和环境条件相关。
这两个因素共同决定了种群的增长速度。
逻辑斯蒂增长模型的数学表达形式为:dN/dt = rN(1 - N/K)其中,dN/dt表示时间t上种群数量N的变化率,r表示增长率,K 表示环境容量。
这个方程的含义是,种群数量的变化率与种群数量N和环境容量K之间的关系成正比,但随着种群数量接近或超过环境容量,增长率会逐渐减小,最终趋于稳定。
逻辑斯蒂增长模型的一个重要特点是S形曲线。
当种群数量较小时,增长率较高;当种群数量接近环境容量时,增长率逐渐减小;当种群数量超过环境容量时,增长率变为负数,种群数量开始减少。
逻辑斯蒂增长模型的应用非常广泛。
在生态学中,它可以用来研究动植物种群的增长和衰退趋势,帮助科学家预测和管理自然资源。
在经济学中,它可以用来研究市场的供需关系和消费行为,帮助决策者制定合理的政策和规划。
然而,逻辑斯蒂增长模型也有一些局限性。
首先,它假设种群的增长率只受到出生率、死亡率和迁移率的影响,而忽略了其他可能的影响因素,如环境变化、天敌的存在等。
其次,逻辑斯蒂增长模型无法预测种群数量的具体数值,只能描述其增长趋势。
最后,该模型需要准确的数据作为输入,而在实际应用中往往存在数据获取的困难和不确定性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在自然界来和人类社会上存在大量的S型变化的现象,逻辑斯蒂模型几乎是描述s型增长的唯一数学模型。这是一条连续的、单调递增的、但参数k为上渐近线的s型曲线,其变化速度一看是增长较慢,中间段增长速度加快,以后增长速度下降并且趋于稳定。利用它我们可以表征种群的数量动态,描述客观事物的增长过程,同时也作为其它复杂模型的理论基础如Lotka-Volterra两种群竞争模型。
二、逻辑斯蒂方程的产生和发展
在提出逻辑斯蒂模型之前,最早给出种群生态学经典数学模型是Malthus模型,由英国统计学家Malthus(1766-1834)在1798《人口原理》一书中,提出了闻名于世的Malthus人口模型。设t0时刻的人口总数为N0,t时刻人口总数为N(t),则:
但是这个模型有很大的局限性:只考虑出生率和死亡率,而没有考虑环境因素。实际上人类所生存的环境中资源并不是无限的,因而人口的增长也不可能是无限的,实践证明Malthus人口模型只符合人口的过去而不能用来预测未来人口总数。比利时数学家P.F.Verhulst对Malthus模型中关于人口增长率为常数这一假设修改为
解得t=6,即6小时后,全市有75%的人了解这一通知。
3.商品销售预测问题
例如,某种商品的销售,开始时,知道的人很少,销售量也很小。当这种商品信息传播出去后,销售量大量增加,到接近饱和时销售量增加极为缓慢。比如,这种商品饱和量估计a=500(百万件),大约5年可达饱和,常数b经测定为b=lnl0,B=100。下面我们来预测一下第3年末的销售量是多少。
逻辑斯蒂方程
出自MBA智库百科(/)
逻辑斯蒂方程(Logistic Equation)
[编辑]
逻辑斯蒂方程的推导
当一种新产品刚面世时,厂家和商家总是采取各种措施促进销售。他们都希望对这种产品的推销速度做到心中有数,这样厂家便于组织生产,商家便于安排进货。怎样建立数学模型描述新产品推销速度呢?
S型曲线 当Y值为最大值的一半时增长率最大
人口限制增长问题
人口的增长不是呈指数型增长的,这是由于环境的限制、有限的资源和人为的影响,最终人口的增长将减慢下来。实际上,人口增长规律满足逻辑斯蒂方程。
提问人的追问2010-06-02 19:58
逻辑斯谛曲线的特征
团队的补充2010-06-02 20:06
...................(3)
例如,当某种商品调价的通知下达时,有10%的市民听到这一通知,2小时以后,25%的市民知道了这一信息,由逻辑斯蒂方程可算出有75%的市民了解这一情况所需要的时间。
在方程(3)中,由t=0时,P=10%可得B=9;再由t=2时,P=25%可得, 。
当P=75%时,有:
逻辑斯蒂方程的基本性质
1.当t=O时,x(t)的值为: ;
2.x(t)的增长率 ,因此,x(t)是增函数;
3.当B值较大而t较小时, 将很大, ,于是
x(t)近似于依指数函数增大,销售速度不断增大;
4.当t增大以后, 越来越接近于零,分母越来越接近于1,销售速度开始下降,x(t)的值接近于a(饱和值)。
当x=0.5时,逻值(ln(x/(1-x))等于0;x<0.5时,逻值为负值;x>0.5时,逻值为正值。S型曲线的直线化,就是将病情(x)百分率转换成逻值后,用普通坐标纸以逻值为纵坐标对时间(t)作图,则病情进展曲线就成为一条直线,也称逻值线(图中B)。逻值线与纵轴相交的截点,为初始病害数量(x0),逻值线的斜率就是病害的流行速度,即表观侵染速率
由 ,有:
(百万件)
所以第三年末的市场销售量大约为454.5百万件,这样可以做到有计划地生产。
逻辑斯蒂方程的应用比较广泛。如果问题的基本数量特征是:在时间t很小时,呈指数型增长,而当t增大时,增长速度就下降,且越来越接近于一个确定的值,这类问题可以用逻辑斯蒂方程加以解决。
浅评逻辑斯蒂方程
宋波玄玉仁卢凤勇崔启武
其中r,k成为生命系数,是最早的逻辑斯蒂方程模型。"
S型
起初增长率越来越大 超过一半后 增长率就会越来越小
当Y值为最大值的一半时 增长率最大
逻辑斯蒂增长模型又称自我抑制性方程。用植物群体中发病的普遍率或严重度表示病害数量(x),将环境最大容纳量k定为1(100%),逻辑斯蒂模型的微分式是:
dx/dt=rx(1-x)
其线性方程为:
式中:ln(x/(1-x))称作x的逻辑斯蒂转换值,通常简称逻值(logit(x));
【摘要】:正一、一个重要而被滥加引用的方程1838年Verhulst提出的逻辑斯蒂方程,被人们广泛地引用。不仅在自然科学中,甚至在社会科学中亦如此。Deevey认为这种增长型可能是最普遍的,在生态学上,由于逻辑斯蒂方程与因种群密度制约因素而形成的负反馈机制有联系,因而有人说,逻辑斯蒂方程是种群生态学中的核心理论之一,可见,逻辑斯蒂方程处于十分重要地位。(1)利用逻辑斯蒂方程表征种群数量动态:著名的经典实验有Pearl(1927)的果蝇;chapman(1931)的拟谷盗;Gause(1934)
[编辑]
逻辑斯蒂方程的应用
1.人口限制增长问题
人口的增长不是呈指数型增长的,这是由于环境的限制、有限的资源和人为的影响,最终人口的增长将减慢下来。实际上,人口增长规律满足逻辑斯蒂方程。
2.信息传播问题
所谓信息传播可以是一则新闻,一条谣言或市场上某种新商品有关的知识,在初期,知道这一信息的人很少,但是随时间的推移,知道的人越来越多,到一定时间,社会上大部分人都知道了这一信息.这里的数量关系可以用逻辑斯蒂方程来描述。若以t表示从信息产生算起的时间,P表示已知信息的人口比例,则逻辑斯蒂方程变为:
首先要考虑社会的需求量.社会对产品的需求状况一般依如下两个特性确定:
1.对产品的需求有一个饱和水平.当产品需求量达到一定数量时,对这种产品的需求也饱和了,设饱和水平为a;
2.假设在时刻t,社会对产品的需求量为x=x(t),需求的增长速度dx/dt正比于需求量x(t)与需求接近饱和水平的程度a-x(t)之乘积,记比例系数为k;
根据上述实际背景的两个特征,可.......(1)
分离变量,得:
两边积分,得:
其中:
从而,通解为:
......(2)
其中 ,B和b为正常数,可由初始条件确定。式(1)称为逻辑斯蒂方程(1ogistic equation),式(2)称为逻辑斯蒂曲线。
[编辑]
