MATLAB 练习(含代码)
Matlab的操作练习

(5)
5 s,t 5
2、编写程序,绘制右 边图形并加上相应标 注。
3、编写程序,绘制右 边螺旋线图形并加上 相应标注。
4、编写程序,绘制右 边图形并加上相应标 注。
5、绘制下列图形 (1)分别利用ezplot函数和plot函数绘制曲线
x2/3 y2/3 1
(2)分别利用ezplot函数和plot函数绘制曲线
练习2、阅读程序 if A then x= 1 else x=0 end
(a)当A取下面旳数组时,程序输出旳成 果是什么? (1)A=ones(3) (2)A=eye(3) (3)A=inf (4)A=rand(3)>0.5
(b)假如程序中旳A换成any(A)或者all(A) 呢?
在matalb旳程序编写中,假如能够利用数组运算、矩阵运算替代循环 旳点运算,计算效率会大大提升。
x2 y4 0
(3)分别利用ezplot3函数和plot3函数绘制曲线
x cos(t)2 sin(t); y sin(t)2 cos(t); 0 t 2
z t2 *(2 t)2
6、选择合适旳函数绘制图形 (1) 双扭线 = co(s 2) (2)在复平面上绘制函数图形
z cos t i sin(2t)
(3) z1 cos t i sin(2t) z 2 sin(t) icos(2 t)
绘制图形 z=z1*z2
7、分别利用mesh和ezmesh函数绘制网线图
(1)
z x2 y
(2)
z x2 y2
(3)
z2 x2 2y2
符号运算旳练习
1、利用符号运算解下列方程和方程组
(1)x4-1=0旳实根
(1) 100阶矩阵A=(aij), 其中aij=ij
MATLAB编程练习(含答案很好的)

001双峰曲线图:z=peaks(40);mesh(z);surf(z)002解方程:A=[3,4,-2;6,2,-3;45,5,4];>> B=[14;4;23];>> root=inv(A)*B003傅里叶变换load mtlb ;subplot(2,1,1);plot(mtlb);>> title('原始语音信息');>> y=fft(mtlb);>> subplot(2,1,2);>> yy=abs(y);>> plot(yy);>> title('傅里叶变换')004输入函数:a=input('How many apples\n','s')005输出函数a=[1 2 3 4 ;5 6 7 8;12 23 34 45;34 435 23 34]a =1 2 3 45 6 7 812 23 34 4534 435 23 34disp(a)a =1 2 3 45 6 7 812 23 34 4534 435 23 34b=input('how many people\n' ,'s')how many peopletwo peopleb =two people>> disp(b)two people>>006求一元二次方程的根a=1;b=2;c=3;d=sqrt(b^2-4*a*c);x1=(-b+d)/(2*a)x1 =-1.0000 + 1.4142i>> x2=(-b-d)/(2*a)x2 =-1.0000 - 1.4142i007求矩阵的相乘、转置、存盘、读入数据A=[1 3 5 ;2 4 6;-1 0 -2;-3 0 0];>> B=[-1 3;-2 2;2 1];>> C=A*BC =3 142 20-3 -53 -9>> C=C'C =3 2 -3 314 20 -5 -9>> save mydat C>> clear>> load mydat C008编写数学计算公式:A=2.1;B=-4.5;C=6;D=3.5;E=-5;K=atan(((2*pi*A)+E/(2*pi*B*C))/D) K =1.3121009A=[1 0 -1;2 4 1;-2 0 5];>> B=[0 -1 0;2 1 3;1 1 2];>> H=2*A+BH =2 -1 -26 9 5-3 1 12>> M=A^2-3*BM =3 3 -62 13 -2-15 -3 21>> Y=A*BY =-1 -2 -29 3 145 7 10>> R=B*AR =-2 -4 -1-2 4 14-1 4 10>> E=A.*BE =0 0 04 4 3-2 0 10>> W=A\BW =0.3333 -1.3333 0.66670.2500 1.0000 0.25000.3333 -0.3333 0.6667 >> P=A/BP =-2.0000 3.0000 -5.0000-5.0000 3.0000 -4.00007.0000 -9.0000 16.0000>> Z=A.\BWarning: Divide by zero.Z =0 -Inf 01.0000 0.2500 3.0000-0.5000 Inf 0.4000>> D=A./BWarning: Divide by zero.D =Inf 0 -Inf1.0000 4.0000 0.3333-2.0000 0 2.5000010a=4.96;b=8.11;>> M=exp(a+b)/log10(a+b)M =4.2507e+005011求三角形面积:a=9.6;b=13.7;c=19.4;>> s=(a+b+c)/2;>> area=sqrt(s*(s-a)*(s-b)*(s-c))area =61.1739012逻辑运算A=[-1 0 -6 8;-9 4 0 12.3;0 0 -5.1 -2;0 -23 0 -7]; >> B=A(:,1:2)B =-1 0-9 40 00 -23>> C=A(1:2,:)C =-1.0000 0 -6.0000 8.0000 -9.0000 4.0000 0 12.3000>> D=B'D =-1 -9 0 00 4 0 -23>> A*Bans =1.0000 -184.0000-27.0000 -266.90000 46.0000 207.0000 69.0000>> C<Dans =0 0 1 01 0 0 0>> C&Dans =1 0 0 00 1 0 1>> C|Dans =1 1 1 11 1 0 1>> ~C|~Dans =0 1 1 11 0 1 0013矩阵运算练习:A=[8 9 5;36 -7 11;21 -8 5]A =8 9 536 -7 1121 -8 5>> BB =-1 3 -22 0 3-3 1 9>> RT=A*BRT =-5 29 56-83 119 6-52 68 -21>> QW=A.*BQW =-8 27 -1072 0 33-63 -8 45>> ER=A^3ER =6272 3342 294415714 -856 52608142 -1906 2390 >> BF=A.^3BF =512 729 12546656 -343 13319261 -512 125 >> A/Bans =3.13414.9634 -0.4024-1.2561 12.5244 -3.2317-1.9878 6.4512 -2.0366>> EKV=B\AEKV =10.7195 -1.2683 3.52449.4756 1.5854 3.71954.8537 -1.4878 1.3171>> KDK=[A,B]KDK =8 9 5 -1 3 -236 -7 11 2 0 321 -8 5 -3 1 9 >> ERI=[A;B]ERI =8 9 536 -7 1121 -8 5-1 3 -22 0 3-3 1 9014一般函数的调用:A=[2 34 88 390 848 939];>> S=sum(A)S =2301>> min(A)ans =2>> EE=mean(A)EE =383.5000>> QQ=std(A)QQ =419.3794>> AO=sort(A)AO =2 34 88 390 848 939 >> yr=norm(A)yr =1.3273e+003>> RT=prod(A)RT =1.8583e+012>> gradient(A)ans =32.0000 43.0000 178.0000 380.0000 274.5000 91.0000 >> max(A)ans =939>> median(A)ans =239>> diff(A)ans =32 54 302 458 91>> length(A)ans =6>> sum(A)ans =2301>> cov(A)ans =1.7588e+005>>015矩阵变换:A=[34 44 23;8 34 23;34 55 2]A =34 44 238 34 2334 55 2>> tril(A)ans =34 0 08 34 034 55 2>> triu(A)ans =34 44 230 34 230 0 2>> diag(A)ans =34342norm(A)ans =94.5106>> rank(A)ans =3>> det(A)ans =-23462>> trace(A)ans =70>> null(A)ans =Empty matrix: 3-by-0>> eig(A)ans =80.158712.7671-22.9257>> poly(A)ans =1.0e+004 *0.0001 -0.0070 -0.1107 2.3462>> logm(A)Warning: Principal matrix logarithm is not defined for A with nonpositive real eigenvalues. A non-principal matrixlogarithm is returned.> In funm at 153In logm at 27ans =3.1909 + 0.1314i 1.2707 + 0.1437i 0.5011 - 0.2538i0.4648 + 0.4974i 3.3955 + 0.5438i 0.1504 - 0.9608i0.2935 - 1.2769i 0.8069 - 1.3960i 3.4768 + 2.4663i>> fumn(A)Undefined command/function 'fumn'.>> inv(A)ans =0.0510 -0.0502 -0.0098-0.0326 0.0304 0.02550.0305 0.0159 -0.0343>> cond(A)ans =8.5072>> chol(A)Error using ==> cholMatrix must be positive definite.>> lu(A)ans =34.0000 44.0000 23.00000.2353 23.6471 17.58821.0000 0.4652 -29.1816>> pinv(A)ans =0.0510 -0.0502 -0.0098-0.0326 0.0304 0.02550.0305 0.0159 -0.0343>> svd(A)ans =94.510622.345611.1095>> expm(A)ans =1.0e+034 *2.1897 4.3968 1.93821.31542.6412 1.16431.8782 3.7712 1.6625>> sqrtm(A)ans =5.2379 + 0.2003i 3.4795 + 0.2190i 1.8946 - 0.3869i0.5241 + 0.7581i 5.1429 + 0.8288i 2.0575 - 1.4644i3.0084 - 1.9461i4.7123 - 2.1276i 2.1454 + 3.7589i >>016多项式的计算:A=[34 44 23;8 34 23;34 55 2]A =34 44 238 34 2334 55 2>> P=poly(A)P =1.0e+004 *0.0001 -0.0070 -0.1107 2.3462>> PPA=poly2str(P,'X')PPA =X^3 - 70 X^2 - 1107 X + 23462017多项式的运算:p=[2 6 8 3];w=[32 56 0 2];>> m=conv(p,w)m =64 304 592 548 180 16 6 >> [q,r]=deconv(w,p)q =16r =0 -40 -128 -46>> dp=polyder(w)dp =96 112 0>> [num,den]=polyder(w,p)num =80 512 724 312 -16den =4 24 68 108 100 48 9>> b=polyfit(p,w,4)Warning: Polynomial is not unique; degree >= number of data points. > In polyfit at 74b =-0.6704 9.2037 -32.2593 0 98.1333>> r=roots(p)r =-1.2119 + 1.0652i-1.2119 - 1.0652i-0.5761018求多项式的商和余p=conv([1 0 2],conv([1 4],[1 1]))p =1 5 6 10 8>> q=[1 0 1 1]q =1 0 1 1>> [w,m]=deconv(p,q)w =1 5m =0 0 5 4 3>> cq=w;cr=m;>> disp([cr,poly2str(m,'x')])5 x^2 + 4 x + 3>> disp([cq,poly2str(w,'x')])x + 5019将分式分解a=[1 5 6];b=[1];>> [r,p,k]=residue(b,a)r =-1.00001.0000p =-3.0000-2.0000k =[]020计算多项式:a=[1 2 3;4 5 6;7 8 9];>> p=[3 0 2 3];>> q=[2 3];>> x=2;>> r=roots(p)r =0.3911 + 1.0609i0.3911 - 1.0609i-0.7822>> p1=conv(p,q)p1 =6 9 4 12 9>> p2=poly(a)p2 =1.0000 -15.0000 -18.0000 -0.0000 >> p3=polyder(p)p3 =9 0 2>> p4=polyval(p,x)p4 =31021求除式和余项:[q,r]=deconv(conv([1 0 2],[1 4]),[1 1 1])022字符串的书写格式:s='student's =student>> name='mary';>> s1=[name s]s1 =marystudent>> s3=[name blanks(3);s]s3 =marystudent>>023交换两个数:clearclca=[1 2 3 4 5];b=[6 7 8 9 10];c=a;a=b;b=c;ab24If语句n=input('enter a number,n=');if n<10nend025 if 双分支结构a=input('enter a number ,a=');b=input('enter a number ,b=');if a>bmax=a;elsemax=b;endmax026三个数按照由大到小的顺序排列:A=15;B=24;C=45;if A<BT=A;A=B;B=T;elseif A<CT=A;A=C;C=T;elseif B<CT=B;B=C;C=T;endABC027建立一个收费优惠系统:price=input('please jinput the price : price=') switch fix(price/100)case[0,1]rate =0;case[2,3,4]rate =3/100;case num2cell(5:9)rate=5/100;case num2cell(10:24)rate=8/100;case num2cell(25:49)rate=10/100;otherwiserate=14/100;endprice=price*(1-rate)028:while循环语句i=0;s=0;while i<=1212s=s+i;i=i+1;ends029,用for循环体语句:sum=0;for i=1:1.5:100;sum=sum+i;endsum030循环的嵌套s=0;for i=1:1:6;for j=1:1:8;s=s+i^j;end;end;s031continue 语句的使用:for i=100:120;if rem(i,7)~=0;continue;end;iend032x=input ('输入X的值x=')if x<1y=x^2;elseif x>1&x<2y=x^2-1;elsey=x^2-2*x+1;endy033求阶乘的累加和sum=0;temp=1;for n=1:10;temp=temp*n;sum=sum+temp;endsum034对角线元素之和sum=0;a=[1 2 3 4;5 6 7 8;9 10 11 12;13 14 15 16]; for i=1:4;sum=sum+a(i,i);endsum035用拟合点绘图A=[12 15.3 16 18 25];B=[50 80 118 125 150.8];plot(A,B)036绘制正玄曲线:x=0:0.05:4*pi;y=sin(x);plot(x,y)037绘制向量x=[1 2 3 4 5 6;7 8 9 10 11 12;13 14 15 16 17 18] plot(x)x=[0 0.2 0.5 0.7 0.6 0.7 1.2 1.5 1.6 1.9 2.3]plot(x)x=0:0.2:2*piy=sin(x)plot(x,y,'m:p')038在正弦函数上加标注:t=0:0.05:2*pi;plot(t,sin(t))set(gca,'xtick',[0 1.4 3.14 56.28])xlabel('t(deg)')ylabel('magnitude(v)')title('this is a example ()\rightarrow 2\pi')text(3.14,sin(3.14),'\leftarrow this zero for\pi')039添加线条标注x=0:0.2:12;plot(x,sin(x),'-',x,1.5*cos(x),':');legend('First','Second',1)040使用hold on 函数x=0:0.2:12;plot(x,sin(x),'-');hold onplot(x,1.5*cos(x),':');041一界面多幅图x=0:0.05:7;y1=sin(x);y2=1.5*cos(x);y3=sin(2*x);y4=5*cos(2*x);subplot(221);plot(x,y1);title('sin(x)')subplot(222);plot(x,y2);title('cos(x)')subplot(223);plot(x,y3);title('sin(2x)')subplot(224);plot(x,y4);title('cos(2x)')042染色效果图x=0:0.05:7;y1=sin(x);y2=1.5*cos(x);y3=sin(2*x);y4=5*cos(2*x);subplot(221);plot(x,y1);title('sin(x)');fill(x,y1,'r') subplot(222);plot(x,y2);title('cos(x)');fill(x,y2,'b') subplot(223);plot(x,y3);title('sin(2x)');fill(x,y3,'k') subplot(224);plot(x,y4);title('cos(2x)');fill(x,y4,'g')043特殊坐标图clcy=[0,0.55,2.5,6.1,8.5,12.1,14.6,17,20,22,22.1] subplot(221);plot(y);title('线性坐标图');subplot(222);semilogx(y);title('x轴对数坐标图');subplot(223);semilogx(y);title('y轴对数坐标图');subplot(224);loglog(y);title('双对数坐标图')t=0:0.01:2*pi;r=2*cos(2*(t-pi/8));polar(t,r)044特殊函数绘图:fplot('cos(tan(pi*x))',[-0.4,1.4])fplot('sin(exp(pi*x))',[-0.4,1.4])045饼形图与条形图:x=[8 20 36 24 12];subplot(221);pie(x,[1 0 0 0 1]);title('饼图');subplot(222);bar(x,'group');title('垂直条形图');subplot(223);bar(x,'stack');title('累加值为纵坐标的垂直条形图'); subplot(224);barh(x,'group');title('水平条形图');046梯形图与正弦函数x=0:0.1:10;y=sin(x);subplot(121);stairs(x);subplot(122);stairs(x,y);047概率图x=randn(1,1000);y=-2:0.1:2;hist(x,y)048向量图:x=[-2+3j,3+4j,1-7j];subplot(121);compass(x);rea=[-2 3 1];imag=[3 4 -7];subplot(122);feather(rea,imag);049绘制三维曲线图:z=0:pi/50:10*pi;x=sin(z);y=cos(z);plot3(x,y,z)x=-10:0.5:10;y=-8:0.5:8;[x,y]=meshgrid(x,y);z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2); subplot(221);mesh(x,y,z);title('普通一维网格曲面');subplot(222);meshc(x,y,z);title('带等高线的三维网格曲面'); subplot(223);meshz(x,y,z);title('带底座的三维网格曲面'); subplot(224);surf(x,y,z);title('充填颜色的三维网格面')050 带网格二维图x=0:pi/10:2*pi;y1=sin(x);y2=cos(x);plot(x,y1,'r+-',x,y2,'k*:')grid onxlabel('Independent Variable x') ylabel('Dependent Variable y1&y2') text(1.5,0.5,'cos(x)')051各种统计图y=[18 5 28 17;24 12 36 14;15 6 30 9]; subplot(221);bar(y)x=[4,6,8];subplot(222);bar3(x,y)subplot(223);bar(x,y,'grouped') subplot(224);bar(x,y,'stack')052曲面图x=-2:0.4:2;y=-1:0.2:1;[x,y]=meshgrid(x,y);z=sqrt(4-x.^2/9-y.^2/4); surf(x,y,z)grid on053创建符号矩阵e=[1 3 5;2 4 6;7 9 11];m=sym(e)符号表达式的计算问题因式分解:syms xf=factor(x^3-1)s=sym('sin(a+b)'); expand(s)syms x tf=x*(x*(x-8)+6)*t; collect(f)syms xf=sin(x)^2+cos(x)^2; simplify(f)syms xs=(4*x^2+8*x+3)/(2*x+1); simplify(s)通分syms x yf=x/y-y/x;[m,n]=numden(f)嵌套重写syms xf=x^4+3*x^3-7*x^2+12; horner(f)054求极限syms x a;limit(exp(-x),x,0,'left')求导数syms xdiff(x^9+x^6)diff(x^9+x^6,4)055求不定积分与定积分syms x ys=(4-3*x^2)^2;int(s)int(x/(x+y),x)int(x^2/(x+2),x,1,3) double(ans)056函数的变换:syms x ty=exp(-x^2);Ft=fourier(y,x,t)fx=ifourier(Ft,t,x)057求解方程syms a b c xs=a*x^2+b*x+c;solve(s)syms x y zs1=2*x^2+y^2-3*z-4;s2=y+z-3;s3=x-2*y-3*z;[x,y,z]=solve(s1,s2,s3)058求微分方程:y=dsolve('Dy-(t^2+y^2)/t^2/2','t')059求级数和syms x ksymsum(k)symsum(k^2-3,0,10)symsum(x^k/k,k,1,inf)060泰勒展开式syms xs=(1-x+x^2)/(1+x+x^2);taylor(s)taylor(s,9)taylor(s,x,12)taylor(s,x,12,5)061练习syms x a;s1=sin(2*x)/sin(5*x);limit(s1,x,0)s2=(1+1/x)^(2*x);limit(s2,x,inf)syms xs=x*cos(x);diff(s)diff(s,2)diff(s,12)syms xs1=x^4/(1+x^2);int(s1)s2=3*x^2-x+1int(s2,0,2)syms x y zs1=5*x+6*y+7*z-16;s2=4*x-5*y+z-7;s3=x+y+2*z-2;[x,y,z]=solve(s1,s2,s3)syms x yy=dsolve('Dy=exp(2*x-y)','x')y=dsolve('Dy=exp(2*x-y)','y(0)=0','x')n=sym('n');s=symsum(1/n^2,n,1,inf)x=sym('x');f=sqrt(1-2*x+x^3)-(1-3*x+x^2)^(1/3);taylor(f,6)062求于矩阵相关的值a=[2 2 -1 1;4 3 -1 2;8 5 -3 4;3 3 -2 2]adet=det(a)atrace=trace(a)anorm=norm(a)acond=cond(a)arank=rank(a)eiga=eig(a)063矩阵计算A=[0.1389 0.6038 0.0153 0.9318;0.2028 0.2772 0.7468 0.4660;0.1987 0.1988 0.4451 0.4186]B=var(A)C=std(A)D=range(A)E=cov(A)F=corrcoef(A)064求根及求代数式的值P=[4 -3 2 5];x=roots(P)x=[3 3.6];F=polyval(P,x)065多项式的和差积商运算:f=[1 2 -4 3 -1]g=[1 0 1]g1=[0 0 1 0 1]f+g1f-g1conv(f,g)[q,r]=deconv(f,g)polyder(f)066各种插值运算:X=0:0.1:pi/2;Y=sin(X);interp1(X,Y,pi/4)interp1(X,Y,pi/4,'nearest')interp1(X,Y,pi/4,'spline')interp1(X,Y,pi/4,'cubic')067曲线的拟合:X=0:0.1:2*pi;Y=cos(X);[p,s]=polyfit(X,Y,4)plot(X,Y,'K*',X,polyval(p,X),'r-')068求函数的最值与0点x=2:0.1:2;[x,y]=fminbnd('x.^3-2*x+1',-1,1) [x,y]=fzero('x.^3-2*x+1',1)069求多项式的表达式、值、及图像y=[1 3 5 7 19]t=poly(y)x=-4:0.5:8yx=polyval(t,x)plot(x,yx)070数据的拟合与绘图x=0:0.1:2*pi;y=sin(x);p=polyfit(x,y,5);y1=polyval(p,x)plot(x,y,'b',x,y1,'r')071求代数式的极限:syms xf=sym('log(1+2*x)/sin(3*x)');b=limit(f,x,0)072求导数与微分syms xf=sym('x/(cos(x))^2');y1=diff(f)y2=int(f,0,1)078划分网格函数[x,y]=meshgrid(-2:0.01:2,-3:0.01:5); t=x.*exp(-x.^2-y.^2);[px,py]=gradient(t,0.05,0.1);td=sqrt(px.^2+py.^2);subplot(221)imagesc(t)subplot(222)imagesc(td)colormap('gray')079求多次多项方程组的解:syms x1 x2 a ;eq1=sym('x1^2+x2=a')eq2=sym('x1-a*x2=0')[x1 x2]=solve(eq1,eq2,x1,x2)v=solve(eq1,eq2)v.x1v.x2an1=x1(1),an2=x1(2)an3=x2(1),an4=x2(2)080求解微分方程:[y]=dsolve('Dy=-y^2+6*y','y(0)=1','x')s=dsolve('Dy=-y^2+6*y','y(0)=1','x')[u]=dsolve('Du=-u^2+6*u','u(0)=1')w=dsolve('Du=-u^2+6*u','z')[u,w]=dsolve('Du=-w^2+6*w,Dw=sin(z)','u(0)=1,w(0)=0','z') v=dsolve('Du=-w^2+6*w,Dw=sin(z)','u(0)=1,w(0)=0','z')081各种显现隐含函数绘图:f=sym('x^2+1')subplot(221)ezplot(f,[-2,2])subplot(222)ezplot('y^2-x^6-1',[-2,2],[0,10])x=sym('cos(t)')y=sym('sin(t)')subplot(223)ezplot(x,y)z=sym('t^2')subplot(224)ezplot3(x,y,z,[0,8*pi])082极坐标图:r=sym('4*sin(3*x)')ezpolar(r,[0,6*pi])083多函数在一个坐标系内:x=0:0.1:8;y1=sin(x);subplot(221)plot(x,y1)subplot(222)plot(x,y1,x,y2)w=[2 3;3 1;4 6]subplot(223)plot(w)q=[4 6:3 5:1 2]subplot(224)plot(w,q)084调整刻度图像:x=0:0.1:10;y1=sin(x);y2=exp(x);y3=exp(x).*sin(x);subplot(221)plot(x,y2)subplot(222)loglog(x,y2)subplot(223)plotyy(x,y1,x,y2)085等高线等图形,三维图:t=0:pi/50:10*pi;subplot(2,3,1)plot3(t.*sin(t),t.*cos(t),t.^2) grid on[x,y]=meshgrid([-2:0.1:2])z=x.*exp(-x.^2-y.^2)subplot(2,3,2)plot3(x,y,z)box offsubplot(2,3,3)meshz(x,y,z)subplot(2,3,4)surf(x,y,z)contour(x,y,z)subplot(2,3,6)surf(x,y,z)subplot(2,3,5)contour(x,y,z)box offsubplot(2,3,6)contour3(x,y,z)axis off086统计图Y=[5 2 1;8 7 3;9 8 6;5 5 5;4 3 2]subplot(221)bar(Y)box offsubplot(222)bar3(Y)subplot(223)barh(Y)subplot(224)bar3h(Y)087面积图Y=[5 1 2;8 3 7;9 6 8;5 5 5;4 2 3];subplot(221)area(Y)grid onset(gca,'Layer','top','XTick',1:5)sales=[51.6 82.4 90.8 59.1 47.0];x=90:94;profits=[19.3 34.2 61.4 50.5 29.4];subplot(222)area(x,sales,'facecolor',[0.5 0.9 0.6], 'edgecolor','b','linewidth',2) hold onarea(x,profits,'facecolor',[0.9 0.85 0.7], 'edgecolor','y','linewidth',2) hold offset(gca,'Xtick',[90:94])set(gca,'layer','top')gtext('\leftarrow 销售量') gtext('利润')gtext('费用')xlabel('年','fontsize',14)088函数的插值:x=0:2*pi;y=sin(x);xi=0:0.1:8;yi1=interp1(x,y,xi,'linear')yi2=interp1(x,y,xi,'nearest') yi3=interp1(x,y,xi,'spline')yi4=interp1(x,y,xi,'cublic')p=polyfit(x,y,3)yy=polyval(p,xi)subplot(3,2,1)plot(x,y,'o')subplot(3,2,2)plot(x,y,'o',xi,yy)subplot(3,2,3)plot(x,y,'o',xi,yi1)subplot(3,2,4)plot(x,y,'o',xi,yi2)subplot(3,2,5)plot(x,y,'o',xi,yi3)subplot(3,2,6)plot(x,y,'o',xi,yi4)089二维插值计算:[x,y]=meshgrid(-3:0.5:3);z=peaks(x,y);[xi,yi]=meshgrid(-3:0.1:3); zi=interp2(x,y,z,xi,yi,'spline') plot3(x,y,z)hold onmesh(xi,yi,zi+15)hold offaxis tight090函数表达式;function f=exlin(x)if x<0f=-1;elseif x<1f=x;elseif x<2f=2-x;elsef=0;end091:硬循环语句:n=5;for i=1:nfor j=1:nif i==ja(i,j)=2;elsea(i,j)=0;endendendwhile 循环语句:n=1;while prod(1:n)<99^99;n=n+1endn:092 switch开关语句a=input('a=?')switch acase 1disp('It is raning') case 0disp('It do not know')case -1disp('It is not ranging')otherwisedisp('It is raning ?')end093画曲面函数:x1=linspace(-3,3,30)y1=linspace(-3,13,34)[x,y]=meshgrid(x1,y1);z=x.^4+3*x.^2-2*x+6-2*y.*x.^2+y.^2-2*y; surf(x,y,z)。
matlab编程实例100例

1-32是:图形应用篇33-66是:界面设计篇67-84是:图形处理篇85-100是:数值分析篇实例1:三角函数曲线(1)function shili01h0=figure('toolbar','none',...'position',[198 56 350 300],...'name','实例01');h1=axes('parent',h0,...'visible','off');x=-pi:0.05:pi;y=sin(x);plot(x,y);xlabel('自变量X');ylabel('函数值Y');title('SIN( )函数曲线');grid on实例2:三角函数曲线(2)function shili02h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例02');x=-pi:0.05:pi;y=sin(x)+cos(x);plot(x,y,'-*r','linewidth',1);grid onxlabel('自变量X');ylabel('函数值Y');title('三角函数');实例3:图形的叠加function shili03h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例03');x=-pi:0.05:pi;y1=sin(x);y2=cos(x);plot(x,y1,...'-*r',...x,y2,...'--og');grid onxlabel('自变量X');ylabel('函数值Y');title('三角函数');实例4:双y轴图形的绘制function shili04h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例04');x=0:900;a=1000;b=0.005;y1=2*x;y2=cos(b*x);[haxes,hline1,hline2]=plotyy(x,y1,x,y2,'semilogy','plot'); axes(haxes(1))ylabel('semilog plot');axes(haxes(2))ylabel('linear plot');实例5:单个轴窗口显示多个图形function shili05h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例05');t=0:pi/10:2*pi;[x,y]=meshgrid(t);subplot(2,2,1)plot(sin(t),cos(t))axis equalsubplot(2,2,2)z=sin(x)-cos(y);plot(t,z)axis([0 2*pi -2 2])subplot(2,2,3)h=sin(x)+cos(y);plot(t,h)axis([0 2*pi -2 2])subplot(2,2,4)g=(sin(x).^2)-(cos(y).^2);plot(t,g)axis([0 2*pi -1 1])实例6:图形标注function shili06h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例06');t=0:pi/10:2*pi;h=plot(t,sin(t));xlabel('t=0到2\pi','fontsize',16);ylabel('sin(t)','fontsize',16);title('\it{从0to2\pi 的正弦曲线}','fontsize',16) x=get(h,'xdata');y=get(h,'ydata');imin=find(min(y)==y);imax=find(max(y)==y);text(x(imin),y(imin),...['\leftarrow最小值=',num2str(y(imin))],...'fontsize',16)text(x(imax),y(imax),...['\leftarrow最大值=',num2str(y(imax))],...'fontsize',16)实例7:条形图形function shili07h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例07');tiao1=[562 548 224 545 41 445 745 512];tiao2=[47 48 57 58 54 52 65 48];t=0:7;bar(t,tiao1)xlabel('X轴');ylabel('TIAO1值');h1=gca;h2=axes('position',get(h1,'position'));plot(t,tiao2,'linewidth',3)set(h2,'yaxislocation','right','color','none','xticklabel',[]) 实例8:区域图形function shili08h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例08');x=91:95;profits1=[88 75 84 93 77];profits2=[51 64 54 56 68];profits3=[42 54 34 25 24];profits4=[26 38 18 15 4];area(x,profits1,'facecolor',[0.5 0.9 0.6],...'edgecolor','b',...'linewidth',3)hold onarea(x,profits2,'facecolor',[0.9 0.85 0.7],...'edgecolor','y',...'linewidth',3)hold onarea(x,profits3,'facecolor',[0.3 0.6 0.7],...'edgecolor','r',...'linewidth',3)hold onarea(x,profits4,'facecolor',[0.6 0.5 0.9],...'edgecolor','m',...'linewidth',3)hold offset(gca,'xtick',[91:95])set(gca,'layer','top')gtext('\leftarrow第一季度销量')gtext('\leftarrow第二季度销量')gtext('\leftarrow第三季度销量')gtext('\leftarrow第四季度销量')xlabel('年','fontsize',16);ylabel('销售量','fontsize',16);实例9:饼图的绘制function shili09h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例09');t=[54 21 35;68 54 35;45 25 12;48 68 45;68 54 69];x=sum(t);h=pie(x);textobjs=findobj(h,'type','text');str1=get(textobjs,{'string'});val1=get(textobjs,{'extent'});oldext=cat(1,val1{:});names={'商品一:';'商品二:';'商品三:'};str2=strcat(names,str1);set(textobjs,{'string'},str2)val2=get(textobjs,{'extent'});newext=cat(1,val2{:});offset=sign(oldext(:,1)).*(newext(:,3)-oldext(:,3))/2; pos=get(textobjs,{'position'});textpos=cat(1,pos{:});textpos(:,1)=textpos(:,1)+offset;set(textobjs,{'position'},num2cell(textpos,[3,2]))实例10:阶梯图function shili10h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例10');a=0.01;b=0.5;t=0:10;f=exp(-a*t).*sin(b*t);stairs(t,f)hold onplot(t,f,':*')hold offglabel='函数e^{-(\alpha*t)}sin\beta*t的阶梯图'; gtext(glabel,'fontsize',16)xlabel('t=0:10','fontsize',16)axis([0 10 -1.2 1.2])实例11:枝干图function shili11h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例11');x=0:pi/20:2*pi;y1=sin(x);y2=cos(x);h1=stem(x,y1+y2);hold onh2=plot(x,y1,'^r',x,y2,'*g');hold offh3=[h1(1);h2];legend(h3,'y1+y2','y1=sin(x)','y2=cos(x)') xlabel('自变量X');ylabel('函数值Y');title('正弦函数与余弦函数的线性组合');实例12:罗盘图function shili12h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例12');winddirection=[54 24 65 84256 12 235 62125 324 34 254];windpower=[2 5 5 36 8 12 76 14 10 8];rdirection=winddirection*pi/180;[x,y]=pol2cart(rdirection,windpower); compass(x,y);desc={'风向和风力','气象台','10月1日0:00到','10月1日12:00'};gtext(desc)实例13:轮廓图function shili13h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例13');[th,r]=meshgrid((0:10:360)*pi/180,0:0.05:1); [x,y]=pol2cart(th,r);z=x+i*y;f=(z.^4-1).^(0.25);contour(x,y,abs(f),20)axis equalxlabel('实部','fontsize',16);ylabel('虚部','fontsize',16);h=polar([0 2*pi],[0 1]);delete(h)hold oncontour(x,y,abs(f),20)实例14:交互式图形function shili14h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例14');axis([0 10 0 10]);hold onx=[];y=[];n=0;disp('单击鼠标左键点取需要的点'); disp('单击鼠标右键点取最后一个点'); but=1;while but==1[xi,yi,but]=ginput(1);plot(xi,yi,'bo')n=n+1;disp('单击鼠标左键点取下一个点');x(n,1)=xi;y(n,1)=yi;endt=1:n;ts=1:0.1:n;xs=spline(t,x,ts);ys=spline(t,y,ts);plot(xs,ys,'r-');hold off实例14:交互式图形function shili14h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例14');axis([0 10 0 10]);hold onx=[];y=[];n=0;disp('单击鼠标左键点取需要的点'); disp('单击鼠标右键点取最后一个点'); but=1;while but==1[xi,yi,but]=ginput(1);plot(xi,yi,'bo')n=n+1;disp('单击鼠标左键点取下一个点');x(n,1)=xi;y(n,1)=yi;endt=1:n;ts=1:0.1:n;xs=spline(t,x,ts);ys=spline(t,y,ts);plot(xs,ys,'r-');hold off实例15:变换的傅立叶函数曲线function shili15h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例15');axis equalm=moviein(20,gcf);set(gca,'nextplot','replacechildren') h=uicontrol('style','slider','position',...[100 10 500 20],'min',1,'max',20) for j=1:20plot(fft(eye(j+16)))set(h,'value',j)m(:,j)=getframe(gcf);endclf;axes('position',[0 0 1 1]);movie(m,30)实例16:劳伦兹非线形方程的无序活动function shili15h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例15');axis equalm=moviein(20,gcf);set(gca,'nextplot','replacechildren') h=uicontrol('style','slider','position',...[100 10 500 20],'min',1,'max',20) for j=1:20plot(fft(eye(j+16)))set(h,'value',j)m(:,j)=getframe(gcf);endclf;axes('position',[0 0 1 1]);movie(m,30)实例17:填充图function shili17h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例17');t=(1:2:15)*pi/8;x=sin(t);y=cos(t);fill(x,y,'r')axis square offtext(0,0,'STOP',...'color',[1 1 1],...'fontsize',50,...'horizontalalignment','center') 例18:条形图和阶梯形图function shili18h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例18');subplot(2,2,1)x=-3:0.2:3;y=exp(-x.*x);bar(x,y)title('2-D Bar Chart')subplot(2,2,2)x=-3:0.2:3;y=exp(-x.*x);bar3(x,y,'r')title('3-D Bar Chart')subplot(2,2,3)x=-3:0.2:3;y=exp(-x.*x);stairs(x,y)title('Stair Chart')subplot(2,2,4)x=-3:0.2:3;y=exp(-x.*x);barh(x,y)title('Horizontal Bar Chart')实例19:三维曲线图function shili19h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例19');subplot(2,1,1)x=linspace(0,2*pi);y1=sin(x);y2=cos(x);y3=sin(x)+cos(x);z1=zeros(size(x));z2=0.5*z1;z3=z1;plot3(x,y1,z1,x,y2,z2,x,y3,z3)grid onxlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure1:3-D Plot')subplot(2,1,2)x=linspace(0,2*pi);y1=sin(x);y2=cos(x);y3=sin(x)+cos(x);z1=zeros(size(x));z2=0.5*z1;z3=z1;plot3(x,z1,y1,x,z2,y2,x,z3,y3)grid onxlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure2:3-D Plot')实例20:图形的隐藏属性function shili20h0=figure('toolbar','none',...'position',[200 150 450 300],...'name','实例20');subplot(1,2,1)[x,y,z]=sphere(10);mesh(x,y,z)axis offtitle('Figure1:Opaque')hidden onsubplot(1,2,2)[x,y,z]=sphere(10);mesh(x,y,z)axis offtitle('Figure2:Transparent') hidden off实例21PEAKS函数曲线function shili21h0=figure('toolbar','none',...'position',[200 100 450 450],...'name','实例21');[x,y,z]=peaks(30);subplot(2,1,1)x=x(1,:);y=y(:,1);i=find(y>0.8&y<1.2);j=find(x>-0.6&x<0.5);z(i,j)=nan*z(i,j);surfc(x,y,z)xlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure1:surfc函数形成的曲面') subplot(2,1,2)x=x(1,:);y=y(:,1);i=find(y>0.8&y<1.2);j=find(x>-0.6&x<0.5);z(i,j)=nan*z(i,j);surfl(x,y,z)xlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure2:surfl函数形成的曲面')实例22:片状图function shili22h0=figure('toolbar','none',...'position',[200 150 550 350],...'name','实例22');subplot(1,2,1)x=rand(1,20);y=rand(1,20);z=peaks(x,y*pi);t=delaunay(x,y);trimesh(t,x,y,z)hidden offtitle('Figure1:Triangular Surface Plot'); subplot(1,2,2)x=rand(1,20);y=rand(1,20);z=peaks(x,y*pi);t=delaunay(x,y);trisurf(t,x,y,z)title('Figure1:Triangular Surface Plot'); 实例23:视角的调整function shili23h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例23');x=-5:0.5:5;[x,y]=meshgrid(x);r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;subplot(2,2,1)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure1')view(-37.5,30)subplot(2,2,2)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure2')view(-37.5+90,30)subplot(2,2,3)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure3')view(-37.5,60)subplot(2,2,4)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure4')view(180,0)实例24:向量场的绘制function shili24h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例24');subplot(2,2,1)z=peaks;ribbon(z)title('Figure1')subplot(2,2,2)[x,y,z]=peaks(15);[dx,dy]=gradient(z,0.5,0.5); contour(x,y,z,10)hold onquiver(x,y,dx,dy)hold offtitle('Figure2')subplot(2,2,3)[x,y,z]=peaks(15);[nx,ny,nz]=surfnorm(x,y,z);surf(x,y,z)hold onquiver3(x,y,z,nx,ny,nz)hold offtitle('Figure3')subplot(2,2,4)x=rand(3,5);y=rand(3,5);z=rand(3,5);c=rand(3,5);fill3(x,y,z,c)grid ontitle('Figure4')实例25:灯光定位function shili25h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例25');vert=[1 1 1;1 2 1;2 2 1;2 1 1;1 1 2;12 2;2 2 2;2 1 2];fac=[1 2 3 4;2 6 7 3;4 3 7 8;15 8 4;1 2 6 5;5 6 7 8];grid offsphere(36)h=findobj('type','surface');set(h,'facelighting','phong',...'facecolor',...'interp',...'edgecolor',[0.4 0.4 0.4],...'backfacelighting',...'lit')hold onpatch('faces',fac,'vertices',vert,...'facecolor','y');light('position',[1 3 2]);light('position',[-3 -1 3]); material shinyaxis vis3d offhold off实例26:柱状图function shili26h0=figure('toolbar','none',...'position',[200 50 450 450],...'name','实例26');subplot(2,1,1)x=[5 2 18 7 39 8 65 5 54 3 2];bar(x)xlabel('X轴');ylabel('Y轴');title('第一子图');subplot(2,1,2)y=[5 2 18 7 39 8 65 5 54 3 2];barh(y)xlabel('X轴');ylabel('Y轴');title('第二子图');实例27:设置照明方式function shili27h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例27');subplot(2,2,1)sphereshading flatcamlight leftcamlight rightlighting flatcolorbaraxis offtitle('Figure1')subplot(2,2,2)sphereshading flatcamlight leftcamlight rightlighting gouraudcolorbaraxis offtitle('Figure2')subplot(2,2,3)sphereshading interpcamlight rightcamlight leftlighting phongcolorbaraxis offtitle('Figure3')subplot(2,2,4)sphereshading flatcamlight leftcamlight rightlighting nonecolorbaraxis offtitle('Figure4')实例28:羽状图function shili28h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例28');subplot(2,1,1)alpha=90:-10:0;r=ones(size(alpha));m=alpha*pi/180;n=r*10;[u,v]=pol2cart(m,n);feather(u,v)title('羽状图')axis([0 20 0 10])subplot(2,1,2)t=0:0.5:10;x=0.05+i;y=exp(-x*t);feather(y)title('复数矩阵的羽状图')实例29:立体透视(1)function shili29h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例29');[x,y,z]=meshgrid(-2:0.1:2,...-2:0.1:2,...-2:0.1:2);v=x.*exp(-x.^2-y.^2-z.^2);grid onfor i=-2:0.5:2;h1=surf(linspace(-2,2,20),...linspace(-2,2,20),...zeros(20)+i);rotate(h1,[1 -1 1],30)dx=get(h1,'xdata');dy=get(h1,'ydata');dz=get(h1,'zdata');delete(h1)slice(x,y,z,v,[-2 2],2,-2)hold onslice(x,y,z,v,dx,dy,dz)hold offaxis tightview(-5,10)drawnowend实例30:立体透视(2)function shili30h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例30');[x,y,z]=meshgrid(-2:0.1:2,...-2:0.1:2,...-2:0.1:2);v=x.*exp(-x.^2-y.^2-z.^2); [dx,dy,dz]=cylinder;slice(x,y,z,v,[-2 2],2,-2)for i=-2:0.2:2h=surface(dx+i,dy,dz);rotate(h,[1 0 0],90)xp=get(h,'xdata');yp=get(h,'ydata');zp=get(h,'zdata');delete(h)hold onhs=slice(x,y,z,v,xp,yp,zp);axis tightxlim([-3 3])view(-10,35)drawnowdelete(hs)hold offend实例31:表面图形function shili31h0=figure('toolbar','none',...'position',[200 150 550 250],...'name','实例31');subplot(1,2,1)x=rand(100,1)*16-8;y=rand(100,1)*16-8;r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;xlin=linspace(min(x),max(x),33); ylin=linspace(min(y),max(y),33); [X,Y]=meshgrid(xlin,ylin);Z=griddata(x,y,z,X,Y,'cubic'); mesh(X,Y,Z)axis tighthold onplot3(x,y,z,'.','Markersize',20)subplot(1,2,2)k=5;n=2^k-1;theta=pi*(-n:2:n)/n;phi=(pi/2)*(-n:2:n)'/n;X=cos(phi)*cos(theta);Y=cos(phi)*sin(theta);Z=sin(phi)*ones(size(theta));colormap([0 0 0;1 1 1])C=hadamard(2^k);surf(X,Y,Z,C)axis square实例32:沿曲线移动的小球h0=figure('toolbar','none',...'position',[198 56 408 468],...'name','实例32');h1=axes('parent',h0,...'position',[0.15 0.45 0.7 0.5],...'visible','on');t=0:pi/24:4*pi;y=sin(t);plot(t,y,'b')n=length(t);h=line('color',[0 0.5 0.5],...'linestyle','.',...'markersize',25,...'erasemode','xor');k1=uicontrol('parent',h0,...'style','pushbutton',...'position',[80 100 50 30],...'string','开始',...'callback',[...'i=1;',...'k=1;,',...'m=0;,',...'while 1,',...'if k==0,',...'break,',...'end,',...'if k~=0,',...'set(h,''xdata'',t(i),''ydata'',y(i)),',...'drawnow;,',...'i=i+1;,',...'if i>n,',...'m=m+1;,',...'i=1;,',...'end,',...'end,',...'end']);k2=uicontrol('parent',h0,...'style','pushbutton',...'position',[180 100 50 30],...'string','停止',...'callback',[...'k=0;,',...'set(e1,''string'',m),',...'p=get(h,''xdata'');,',...'q=get(h,''ydata'');,',...'set(e2,''string'',p);,',...'set(e3,''string'',q)']); k3=uicontrol('parent',h0,...'style','pushbutton',...'position',[280 100 50 30],...'string','关闭',...'callback','close');e1=uicontrol('parent',h0,...'style','edit',...'position',[60 30 60 20]);t1=uicontrol('parent',h0,...'style','text',...'string','循环次数',...'position',[60 50 60 20]);e2=uicontrol('parent',h0,...'style','edit',...'position',[180 30 50 20]); t2=uicontrol('parent',h0,...'style','text',...'string','终点的X坐标值',...'position',[155 50 100 20]); e3=uicontrol('parent',h0,...'style','edit',...'position',[300 30 50 20]); t3=uicontrol('parent',h0,...'style','text',...'string','终点的Y坐标值',...'position',[275 50 100 20]);实例33:曲线转换按钮h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例33');x=0:0.5:2*pi;y=sin(x);h=plot(x,y);grid onhuidiao=[...'if i==1,',...'i=0;,',...'y=cos(x);,',...'delete(h),',...'set(hm,''string'',''正弦函数''),',...'h=plot(x,y);,',...'grid on,',...'else if i==0,',...'i=1;,',...'y=sin(x);,',...'set(hm,''string'',''余弦函数''),',...'delete(h),',...'h=plot(x,y);,',...'grid on,',...'end,',...'end'];hm=uicontrol(gcf,'style','pushbutton',...'string','余弦函数',...'callback',huidiao);i=1;set(hm,'position',[250 20 60 20]);set(gca,'position',[0.2 0.2 0.6 0.6])title('按钮的使用')hold on实例34:栅格控制按钮h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例34');x=0:0.5:2*pi;y=sin(x);plot(x,y)huidiao1=[...'set(h_toggle2,''value'',0),',...'grid on,',...];huidiao2=[...'set(h_toggle1,''value'',0),',...'grid off,',...];h_toggle1=uicontrol(gcf,'style','togglebutton',...'string','grid on',...'value',0,...'position',[20 45 50 20],...'callback',huidiao1);h_toggle2=uicontrol(gcf,'style','togglebutton',...'string','grid off',...'value',0,...'position',[20 20 50 20],...'callback',huidiao2);set(gca,'position',[0.2 0.2 0.6 0.6])title('开关按钮的使用')实例35:编辑框的使用h0=figure('toolbar','none',...'position',[200 150 350 250],...'name','实例35');f='Please input the letter';huidiao1=[...'g=upper(f);,',...'set(h2_edit,''string'',g),',...];huidiao2=[...'g=lower(f);,',...'set(h2_edit,''string'',g),',...];h1_edit=uicontrol(gcf,'style','edit',...'position',[100 200 100 50],...'HorizontalAlignment','left',...'string','Please input the letter',...'callback','f=get(h1_edit,''string'');',...'background','w',...'max',5,...'min',1);h2_edit=uicontrol(gcf,'style','edit',...'HorizontalAlignment','left',...'position',[100 100 100 50],...'max',5,...'min',1);h1_button=uicontrol(gcf,'style','pushbutton',...'string','小写变大写',...'position',[100 45 100 20],...'callback',huidiao1);h2_button=uicontrol(gcf,'style','pushbutton',...'string','大写变小写',...'position',[100 20 100 20],...'callback',huidiao2);实例36:弹出式菜单h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例36');x=0:0.5:2*pi;y=sin(x);h=plot(x,y);grid onhm=uicontrol(gcf,'style','popupmenu',...'string',...'sin(x)|cos(x)|sin(x)+cos(x)|exp(-sin(x))',...'position',[250 20 50 20]);set(hm,'value',1)huidiao=[...'v=get(hm,''value'');,',...'switch v,',...'case 1,',...'delete(h),',...'y=sin(x);,',...'h=plot(x,y);,',...'grid on,',...'case 2,',...'delete(h),',...'y=cos(x);,',...'h=plot(x,y);,',...'grid on,',...'case 3,',...'delete(h),',...'y=sin(x)+cos(x);,',...'h=plot(x,y);,',...'grid on,',...'case 4,',...'y=exp(-sin(x));,',...'h=plot(x,y);,',...'grid on,',...'end'];set(hm,'callback',huidiao)set(gca,'position',[0.2 0.2 0.6 0.6])title('弹出式菜单的使用')实例37:滑标的使用h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例37');[x,y]=meshgrid(-8:0.5:8);r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;h0=mesh(x,y,z);h1=axes('position',...[0.2 0.2 0.5 0.5],...'visible','off');htext=uicontrol(gcf,...'units','points',...'position',[20 30 45 15],...'string','brightness',...'style','text');hslider=uicontrol(gcf,...'units','points',...'position',[10 10 300 15],...'min',-1,...'max',1,...'style','slider',...'callback',...'brighten(get(hslider,''value''))');实例38:多选菜单h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例38');[x,y]=meshgrid(-8:0.5:8);r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;h0=mesh(x,y,z);hlist=uicontrol(gcf,'style','listbox',...'string','default|spring|summer|autumn|winter',...'max',5,...'min',1,...'position',[20 20 80 100],...'callback',[...'k=get(hlist,''value'');,',...'switch k,',...'case 1,',...'colormap default,',...'case 2,',...'colormap spring,',...'case 3,',...'colormap summer,',...'case 4,',...'colormap autumn,',...'case 5,',...'colormap winter,',...'end']);实例39:菜单控制的使用h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例39');x=0:0.5:2*pi;y=cos(x);h=plot(x,y);grid onset(gcf,'toolbar','none')hm=uimenu('label','example');huidiao1=[...'set(hm_gridon,''checked'',''on''),',...'set(hm_gridoff,''checked'',''off''),',...'grid on'];huidiao2=[...'set(hm_gridoff,''checked'',''on''),',...'set(hm_gridon,''checked'',''off''),',...'grid off'];hm_gridon=uimenu(hm,'label','grid on',...'checked','on',...'callback',huidiao1);hm_gridoff=uimenu(hm,'label','grid off',...'checked','off',...'callback',huidiao2);实例40:UIMENU菜单的应用。
matlab练习有程序超全
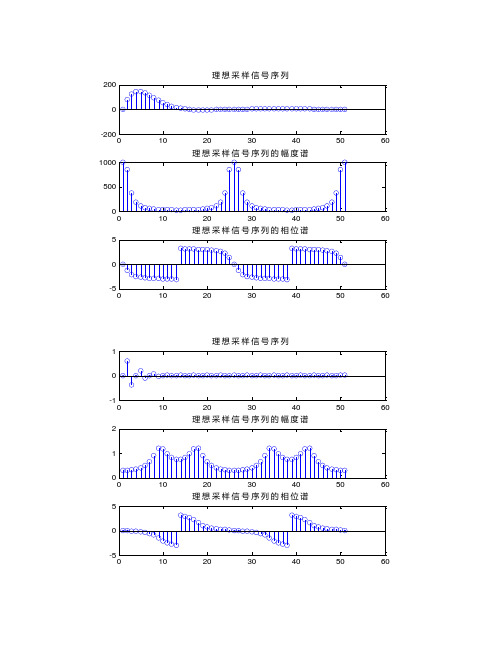
0102030405060-2000200理想采样信号序列05001000理想采样信号序列的幅度谱0102030405060-505理想采样信号序列的相位谱0102030405060-101理想采样信号序列0102030405060012理想采样信号序列的幅度谱0102030405060-505理想采样信号序列的相位谱00.51单位冲击信号序列0102030405060012单位冲击信号的幅度谱0102030405060-505单位冲击信号的相位谱00.51单位冲击信号序列0510单位冲击信号的幅度谱0102030405060-505单位冲击信号的相位谱特定冲击串卷积24单位冲击信号序列510单位冲击信号的幅度谱0102030405060 -55单位冲击信号的相位谱24系统hb[n]05101520253035404550-200200输入信号x[n]0102030405060708090100 -10001000输出信号y[n]204060输入信号的幅度谱204060输入信号的相位谱系统响应的幅度谱0204060系统响应的相位谱输出信号的幅度谱050100输出信号的相位谱246810121416012302402460246810121416-0.50.5102468101214161234123402468101214165101520程序一 for a=1:3 kk(a)=4-a; end for a=4:7 kk(a)=a-3; end for a=8:15 kk(a)=0; end123402468101214165101520close all;subplot(2,1,1);stem(kk);subplot(2,1,2);stem(abs(fft(kk,16)))程序二n=0:15; %定义序列的长度是15 a=0.1;f=0.0625;x=exp(-a*n).*sin(2*pi*f*n); close all;subplot(2,1,1);stem(x);subplot(2,1,2);stem(abs(fft(x)))程序三n=0:15; %定义序列的长度是15 p=8;q=2;x=exp(-1*(n-p).^2/q);close all;subplot(3,1,1);stem(abs(fft(x)))p=8;q=4;x=exp(-1*(n-p).^2/q); subplot(3,1,2);stem(abs(fft(x)))p=8;q=8;x=exp(-1*(n-p).^2/q);subplot(3,1,3);stem(abs(fft(x)))程序四n=1:50; %定义序列的长度是50hb=zeros(1,50); %注意:MATLAB中数组下标从1开始hb(1)=1;hb(2)=2.5;hb(3)=2.5;hb(4)=1;close all;subplot(3,1,1);stem(hb);title('系统hb[n]');m=1:50; %定义序列的长度是50A=444.128; %设置信号有关的参数a=50*sqrt(2.0)*pi;T=0.001; %采样率w0=50*sqrt(2.0)*pi;x=A*exp(-a*m*T).*sin(w0*m*T); %pi是MATLAB定义的π,信号乘可采用“.*”subplot(3,1,2);stem(x);title('输入信号x[n]');y=conv(x,hb);subplot(3,1,3);stem(y);title('输出信号y[n]');k=-25:25;X=x*(exp(-j*pi/12.5)).^(n'*k);magX=abs(X); %绘制x(n)的幅度谱subplot(3,2,1);stem(magX);title('输入信号的幅度谱');angX=angle(X); %绘制x(n)的相位谱subplot(3,2,2);stem(angX) ; title ('输入信号的相位谱')Hb=hb*(exp(-j*pi/12.5)).^(n'*k);magHb=abs(Hb); %绘制hb(n)的幅度谱subplot(3,2,3);stem(magHb);title('系统响应的幅度谱'); angHb=angle(Hb); %绘制hb(n)的相位谱subplot(3,2,4);stem(angHb) ; title ('系统响应的相位谱')n=1:99;k=1:99;Y=y*(exp(-j*pi/12.5)).^(n'*k);magY=abs(Y); %绘制y(n)的幅度谱subplot(3,2,5);stem(magY);title('输出信号的幅度谱'); angY=angle(Y); %绘制y(n)的相位谱subplot(3,2,6);stem(angY) ; title ('输出信号的相位谱')程序五n=1:50; %定义序列的长度是50x=zeros(1,50); %注意:MATLAB中数组下标从1开始x(1)=1;x(2)=2.5;x(3)=2.5;x(4)=1;close all;subplot(3,1,1);stem(x);title('单位冲击信号序列');k=-25:25;X=x*(exp(-j*pi/12.5)).^(n'*k);magX=abs(X); %绘制x(n)的幅度谱subplot(3,1,2);stem(magX);title('单位冲击信号的幅度谱'); angX=angle(X); %绘制x(n)的相位谱subplot(3,1,3);stem(angX) ; title ('单位冲击信号的相位谱')程序六n=1:50x=sign(sign(10-n)+1);close all;subplot(3,1,1);stem(x);title('单位冲击信号序列');k=-25:25;X=x*(exp(-j*pi/25)).^(n'*k);magX=abs(X); %绘制x(n)的幅度谱subplot(3,1,2);stem(magX);title('单位冲击信号的幅度谱'); angX=angle(X); %绘制x(n)的相位谱subplot(3,1,3);stem(angX) ; title ('单位冲击信号的相位谱') 程序7n=1:50; %定义序列的长度是50x=zeros(1,50); %注意:MATLAB中数组下标从1开始x(1)=1;close all;subplot(3,1,1);stem(x);title('单位冲击信号序列');X=x*(exp(-j*pi/12.5)).^(n'*k);magX=abs(X); %绘制x(n)的幅度谱subplot(3,1,2);stem(magX);title('单位冲击信号的幅度谱'); angX=angle(X); %绘制x(n)的相位谱subplot(3,1,3);stem(angX) ; title ('单位冲击信号的相位谱') 程序8n=0:50; %定义序列的长度是50A=1; %设置信号有关的参数a=0.4;T=1; %采样率w0=2.0734;x=A*exp(-a*n*T).*sin(w0*n*T); %pi是MATLAB定义的π,信号乘可采用“.*”close all %清除已经绘制的x(n)图形subplot(3,1,1);stem(x); %绘制x(n)的图形title('理想采样信号序列');k=-25:25;W=(pi/12.5)*k;X=x*(exp(-j*pi/12.5)).^(n'*k);magX=abs(X); %绘制x(n)的幅度谱subplot(3,1,2);stem(magX);title('理想采样信号序列的幅度谱');angX=angle(X); %绘制x(n)的相位谱subplot(3,1,3);stem(angX) ; title ('理想采样信号序列的相位谱')程序9n=0:50; %定义序列的长度是50A=444.128; %设置信号有关的参数a=50*sqrt(2.0)*pi;T=0.001; %采样率w0=50*sqrt(2.0)*pi;x=A*exp(-a*n*T).*sin(w0*n*T); %pi是MATLAB定义的π,信号乘可采用“.*”close all %清除已经绘制的x(n)图形subplot(3,1,1);stem(x); %绘制x(n)的图形title('理想采样信号序列');k=-25:25;W=(pi/12.5)*k;X=x*(exp(-j*pi/12.5)).^(n'*k);magX=abs(X); %绘制x(n)的幅度谱subplot(3,1,2);stem(magX);title('理想采样信号序列的幅度谱'); angX=angle(X); %绘制x(n)的相位谱subplot(3,1,3);stem(angX) ; title ('理想采样信号序列的相位谱')。
MATLAB--练习(含代码)

MATLAB 练习实验一常见分布的概率密度、分布函数生成[实验目的]1. 会利用MATLAB软件计算离散型随机变量的概率,连续型随机变量概率密度值。
2.会利用MATLAB软件计算分布函数值,或计算形如事件。
3.会求上分位点以及分布函数的反函数值。
[实验要求]1.掌握常见分布的分布律和概率密度的产生命令,如binopdf,normpdf2. 掌握常见分布的分布函数命令,如binocdf,normcdf3. 掌握常见分布的分布函数反函数命令,如binoinv,norminv[实验内容]1 事件A在每次试验中发生的概率是0.3,计算(1)在10次试验中A恰好发生6次的概率;(2)在10次试验中A至多发生6次的概率.binopdf(6,10,0.3)>> binocdf(6,10,0.3)2设随机变量X服从参数是3的泊松分布,求概率poisspdf(6,3)3设随机变量X服从区间[2,6]上的均匀分布,求(1)X=4时的概率密度值;(2).unifpdf(4,2,6)>> unifcdf(5,2,6)4设随机变量X服从参数是6的指数分布,求(1)X=0,1,2,3,4,5,6时的概率密度值;(2).exppdf(0:6,6)>> expcdf(5,6)5设随机变量X服从均值是6,标准差是2的正态分布,求(1) X=3,4,5,6,7,8,9时的概率密度值;(2)X=3,4,5,6,7,8,9时的分布函数值;(3)若=0.345,求x;(4)求标准正态分布的上0.05分位数。
normpdf(3:9,6,2)normcdf(3:9,6,2)norminv(0.345,6,2)norminv(0.95,0,1)6设随机变量X服从自由度是6的t分布,求(1)X=-3,-2,-1,0,1,2,3时的概率密度值; (2)X=-3,-2,-1,0,1,2,3时分布函数值; (3)若=0.345,求x;(4)求t分布的上0.05分位数.tpdf(-3:3,6)tcdf(-3:3,6)tinv(0.345,6)tinv(0.95,6)7设随机变量X服从自由度是6的2χ分布,求(1) X=0,1,2,3,4,5,6时的概率密度值;(2) X=0,1,2,3,4,5,6时的分布函数值;(3) 若=0.345,求x;(4) 求2χ分布的上0.05分位数.chi2pdf(0:6,6)chi2cdf(0:6,6)chi2inv(0.345,6)chi2inv(0.95,6)8设随机变量X服从第一自由度是2,第,二自由度是6的F分布,求(1) X=0,1,2,3,4,5,6时的概率密度值;(2) X=0,1,2,3,4,5,6时的分布函数值;(3) 若=0.345,求x;(4) 求F分布的上0.05分位数.fpdf(0:6,2,6)fcdf(0:6,2,6)finv(0.345,2,6)finv(0.95,2,6)实验二概率作图[实验目的]1.熟练掌握MATLAB软件的关于概率分布作图的基本操作2.会进行常用的概率密度函数和分布函数的作图3.会画出分布律图形1.掌握MATLAB画图命令plot2.掌握常见分布的概率密度图像和分布函数图像的画法[实验内容]9事件A在每次试验中发生的概率是0.3,记10次试验中A发生的次数为X.(1)画出X的分布律图形;x=0:10;>> y=binopdf(x,10,0.3);>> plot(x,y,'.')>>(2)画出X的分布函数图形;x=0:0.01:10;>> y=binocdf(x,10,0.3);>> plot(x,y)10设随机变量X服从参数是6的指数分布,(1)画出X的概率密度图形x=0:0.01:10;>> y=exppdf(x,6);>> plot(x,y)(2)画出X的分布函数图形x=-1:0.01:10;>> y=expcdf(x,6);>> plot(x,y)11设随机变量X服从参数是3的泊松分布。
Matlab 编程练习

Matlab 编程练习
1、 对于B AX =,如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ,⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡=282637B ,求解X 。
2、 将矩阵4257a ⎡⎤=⎢⎥⎣⎦
、⎥⎦⎤⎢⎣⎡=3817b 和⎥⎦⎤⎢⎣⎡=2695c 组合成两个新矩阵: (1)组合成一个4⨯3的矩阵,第一列为按列顺序排列的a 矩阵元素,第二列为按列顺序排列的b 矩阵元素,第三列为按列顺序排列的c 矩阵元素,即
⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎣⎡237912685574 (2) 按照a 、b 、c 的列顺序组合成一个行矢量,即
[]296531877254
3、 绘制曲线13++=x x y ,x 的取值范围为[-5,5],并加注图例横坐标“x”、纵坐标“Y”、题
目“曲线”。
4、 22y x xe z --=,当x 和y 的取值范围均为-2到2时,绘制出三维线图、曲面图和网格曲面。
5、 编制一个解数论问题的函数文件:取任意整数,若是偶数,则用2除,否则乘3加1,
重复此过程,直到整数变为1。
Lingo 编程练习
与课后题3类似,但更简单:
某昼夜服务的公共交通系统每天各时间段(每4小时为一个时间段)所需的值班人数如表所示,这些值班人员在某一时段开始上班后要连续工作8个小时(包括轮流用膳时间),问该公交系统至少需要多少名工作人员才能满足值班的需要?
班 次
时 间 段 所 需 人 数 1
6:00—10:00 60 2
10:00—14:00 70 3
14:00—18:00 60 4
18:00—22:00 50 5
22:00—2:00 20 6
2:00—6:00 10。
Matlab基本操作练习

实验一Matlab基本操作练习一、实验目的(1)了解和学会使用matlab平台的命令窗口、帮助窗口、编辑窗口、工作空间。
(2)学会使用matlab的.m文件、.mat文件(3)学会基本的矩阵赋值、运算和查找等操作(4)了解for循环、while循环的执行过程(5)掌握函数的定义和调用的基本方法二、实验内容1、了解save命令和load命令的使用。
操作步骤:(1)在命令窗口输入如下命令:clear ;savefile = 'TestFile.mat';p = rand(1, 4);q = ones(10);r = ones(10,2);save(savefile, 'p', 'q', 'r')(2)观察并记录下当前工作空间中的变量;(3)输入如下命令:clear;(4)观察当前工作空间中的变量;(5)在命令窗口输入如下命令:load TestFile(6)观察当前工作空间中的变量;2、练习基本的数学运算(1)逐句输入并运行以下命令,观察每一步的运行结果,弄明白每一条语句的含义。
(2)计算A*inv(C),将结果与divrAC比较计算A*inv(C),将结果与divrAC比较3、练习矩阵定位函数find的使用逐句输入并运行以下命令,观察每一步的运行结果,弄明白每一条语句的含义。
clear;X = [1 0 4 -3 0 0 0 8 6]Indices1 = find(X)indices2=find(X>=6)clear;A=[3 2 0; -5 0 1]Indices3=find(A)[row,col,value]=find(A)4、练习for循环和while循环的使用操作步骤:(1)在命令窗口输入如下命令clear ;clc;(2)在命令窗口输入如下命令,并观察s1的值:a=1:100;s1=0;for k=1:100s1=s1+k;end(3)在命令窗口输入如下命令,并观察s2的值:s2=0;k=1;while k<=100s2=s2+k;k=k+1;end(4)在命令窗口输入如下命令,并观察s3的值:s3=sum(a);[s1 s2 s3]5、练习函数的定义和调用;定义和调用一个连续求和的函数SumOfN,能实现功能:给一个参数n,求出从1到n连续求和的结果。
matlab习题及答案

matlab习题及答案《Matlab习题及答案:提升编程技能,解决实际问题》Matlab是一种强大的数值计算和数据分析工具,它被广泛应用于工程、科学和其他领域的计算和模拟。
为了帮助大家提升编程技能,解决实际问题,我们为大家准备了一些Matlab习题及答案,希望能够帮助大家更好地掌握Matlab的使用。
1. 习题一:编写一个Matlab程序,计算斐波那契数列的前20个数字,并将结果打印出来。
答案:下面是一个简单的Matlab程序,用于计算斐波那契数列的前20个数字。
```matlaba = 0;b = 1;fib = zeros(1, 20);fib(1) = a;fib(2) = b;for i = 3:20fib(i) = fib(i-1) + fib(i-2);enddisp(fib);```2. 习题二:编写一个Matlab程序,求解一个二次方程ax^2 + bx + c = 0的根。
答案:下面是一个简单的Matlab程序,用于求解二次方程的根。
```matlaba = 1;b = -3;c = 2;delta = b^2 - 4*a*c;if delta > 0x1 = (-b + sqrt(delta))/(2*a);x2 = (-b - sqrt(delta))/(2*a);disp(['The roots are ', num2str(x1), ' and ', num2str(x2)]);elseif delta == 0x = -b/(2*a);disp(['The root is ', num2str(x)]);elsedisp('The equation has no real roots');end```通过以上两个习题及答案的示例,我们可以看到Matlab的强大功能和灵活性。
通过练习这些习题,我们可以更好地掌握Matlab的基本语法和常用函数,从而在实际问题中更快更准确地解决数值计算和数据分析的挑战。
matlab简单编程21个题目及答案
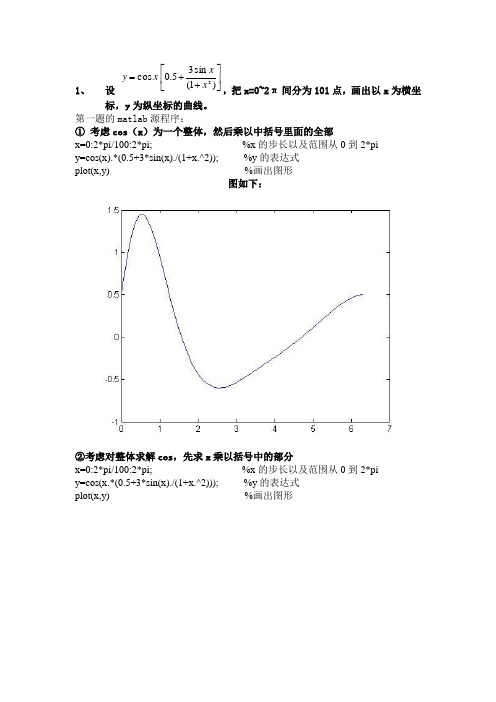
1、设⎥⎦⎤⎢⎣⎡++=)1(sin35.0cos2xxxy,把x=0~2π间分为101点,画出以x为横坐标,y为纵坐标的曲线。
第一题的matlab源程序:①考虑cos(x)为一个整体,然后乘以中括号里面的全部x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x).*(0.5+3*sin(x)./(1+x.^2)); %y的表达式plot(x,y)%画出图形图如下:②考虑对整体求解cos,先求x乘以括号中的部分x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x.*(0.5+3*sin(x)./(1+x.^2))); %y的表达式plot(x,y) %画出图形图如下:2、产生8×6阶的正态分布随机数矩阵R1, 求其各列的平均值和均方差。
并求该矩阵全体数的平均值和均方差。
第二题的matlab源程序如下:R1=randn(8,6) %产生正态分布随机矩阵R1 =1.0933 -0.7697 1.5442 -0.1924 1.4193 0.21571.1093 0.3714 0.0859 0.8886 0.2916 -1.1658-0.8637 -0.2256 -1.4916 -0.7648 0.1978 -1.14800.0774 1.1174 -0.7423 -1.4023 1.5877 0.1049-1.2141 -1.0891 -1.0616 -1.4224 -0.8045 0.7223-1.1135 0.0326 2.3505 0.4882 0.6966 2.5855-0.0068 0.5525 -0.6156 -0.1774 0.8351 -0.66691.5326 1.1006 0.7481 -0.1961 -0.2437 0.1873aver=(sum(R1(1:end,1:end)))./8 %产生各行的平均值aver =0.0768 0.1363 0.1022 -0.3473 0.4975 0.1044a=std(R1(1:end,1:end)) %产生各行的均方差也就是标准差a =1.0819 0.8093 1.3456 0.8233 0.8079 1.2150aver1=(sum(R1(:)))./48 %全体数的平均值aver1 =0.0950b=std(R1(:)) %全体数的均方差即标准差b =1.01033、设x=rcost+3t,y=rsint+3,分别令r=2,3,4,画出参数t=0~10区间生成的x~y 曲线。
(完整版)matlab基础练习题(带答案)

Matlab 基础练习题常量、变量、表达式1、 MATLAB 中,下面哪些变量名是合法的?( )(A )_num (B )num_ (C )num- (D )-num 2、 在MA TLAB 中,要给出一个复数z 的模,应该使用( )函数。
(A )mod(z) (B )abs(z) (C )double(z) (D )angle(z) 3、 下面属于MATLAB 的预定义特殊变量的是?( )(A )eps (B )none (C )zero (D )exp4、 判断:在MA TLAB 的内存工作区中,存放一个英文字符 'a' 需要占用1个字节,存放一个中文字符‘啊’需要占用2个字节。
( 错,都是2个字节 )5、 判断:MA TLAB 中,i 和j ( 对 )6、 判断:MA TLAB 中,pi 代表圆周率,它等于3.14。
( 错,后面还有很多位小数 )7、 在MA TLAB 中,若想计算的51)3.0sin(21+=πy 值,那么应该在MA TLAB 的指令窗中输入的MA TLAB 指令是__y1=2*sin(0.3*pi)/(1+sqrt(5))_。
8、 在MA TLAB 中,a = 1,b = i ,则a 占_8__个字节,b 占_16_个字节,c 占________字节。
9、 在MA TLAB 中,inf 的含义是__无穷大__,nan 的含义是__非数(结果不定)___。
数组1、 在MA TLAB 中,X 是一个一维数值数组,现在要把数组X 中的所有元素按原来次序的逆序排列输出,应该使用下面的( )指令。
(A )X[end:1] (B )X[end:-1:1] (C )X (end:-1:1) (D )X(end:1) 2、 在MA TLAB 中,A 是一个字二维数组,要获取A 的行数和列数,应该使用的MATLAB的命令是( )。
(A )class(A) (B )sizeof(A) (C )size(A) (D )isa(A)3、 在MATLAB 中,用指令x=1:9生成数组x 。
matlab期末作业_附源代码

clc f=[-11,-9]'; A=[6,5;10,20]; B=[60,150]; Ae=[]; Be=[]; xm=[0,0]; xM=[8,Inf]; [x,f_opt]=linprog(f,A,B,Ae,Be,xm,xM)
6
③结果如下:
Optimization terminated. x= 8.0000 2.4000 f_opt = -109.6000
⑤结果分析: 生产甲800箱,生产乙240箱,获利最多为109.6万元。 显然应该是要改变生产计划的,改变计划获利增加。
7
②编写 m 文件
function y = myodefun(t,x ) y=[-x(1)^3-x(2);x(1)-x(2)^3]; end
0<t<30
③在 command 窗口中输入:
>> tspan=[0,30]; >> x0=[1;0.5]; >> [t,x]=ode45('myodefun',tspan,x0); >> plot(t,x(:,1),'g*',t,x(:,2),'b-.');
②Matlab源代码
clc f=[-10,-9]'; A=[6,5;10,20]; B=[60,150]; Ae=[]; Be=[]; xm=[0,0]; xM=[8,Inf]; [x,f_opt]=linprog(f,A,B,Ae,Be,xm,xM)
③结果如下:
Optimization terminated. x= 6.4286 4.2857 f_opt = -102.8571
1
1.求解微分方程组,画出解函数图。
MATLAB部分课后习题代码

习题1.6.2 第5题clearclcA=[1 4 7 10;2 5 8 11;3 6 9 12]B=flipud(A') %将A左旋90度C=fliplr(A') %将A右旋90度习题2.6 第6题clearclcx=input('输入10个两位整数')b=mean(x);for i=1:10if x(i) < b & rem(x(i),2)~=0x(i)endend习题2.6 第7题clearclcx=input('请输入一个正整数')for i=2:xif rem(x,i)==0breakendendif i < x & i > 1disp('不是素数')elsedisp('是素数')end3.4.2 自己练第6题clearclcx=-3:0.01:3;y=exp(-x.^2);plot(x,y)3.4.2 自己练第8题clearclcx=-2:0.1:2;y=-1:0.05:1;[x,y]=meshgrid(x,y);z=sqrt(5-x.^3/3-y.^2/7);surf(x,y,z)grid on3.5习题第1题(1)clearclcx=-1:0.01:1;y=log((1-x)./(1+x));plot(x,y)(2)clearclcx=-pi/2:pi/100:pi/2;y=sqrt(cos(x));plot(x,y)(3)clearclcx=-1:0.03:1;y=sin(1./x);plot(x,y)(4)clearclcx=-0.5:0.01:0.5;y=sin(x)./x;plot(x,y)3.5习题第2题clearclcx=-2*pi:pi/100:2*pi;y1=x;y2=x.^2;y3=-y2;y4=x.*sin(x);plot(x,y1,x,y2,x,y3,x,y4)3.5习题第3题clearclcx1=-10:0.01:1;x2=1:0.01:4;x3=4:0.01:10;y1=x1;y2=(x2).^2;y3=exp(x3);plot(x1,y1,x2,y2,x3,y3)3.5习题第4题clearclct=-2*pi:pi/1000:2*pi;y1=cos(t).^3-1;y2=sin(2*t)/2;y3=2*t.^2+1;subplot(131);polar(t,y1);title('cos(t)^3 - 1'); subplot(132);polar(t,y2);title('cos(t)sin(t)'); subplot(133);polar(t,y3);title('2t^2 + 1');3.5习题第5题clearclct=0:0.05:3*pi;a=3;b=1;n=2;r=a*sin(b+n*t);polar(t,r)3.5习题第6题clearclcx=-2*pi:pi/100:2*pi;y=sin(1./x);subplot(121);plot(x,y,'r')subplot(122);fplot('sin(1./x)',2*pi*[-1 1])3.5习题第7 (1)题clearclct=0:0.1:2*pi;x=sin(t);y=cos(t);[x,y]=meshgrid(x,y);z=x.^2/4 + y.^2/9;meshc(x,y,z);3.5习题第7 (2)题clearclcx=0:0.45:10;y=0:0.45:10;[x,y]=meshgrid(x,y);z=x.* y;meshc(x,y,z)view(-154,12)3.5习题第7 (3)题clearclcx=-5:0.05:5;y=-5:0.05:5;[x,y]=meshgrid(x,y);z=sin(x.*y);meshc(x,y,z)view(-60,50)3.5习题第8 题clearclcx=-5:0.2:5;y=-5:0.2:5;[x,y]=meshgrid(x,y);z=(1/(2*pi))*exp((-1/2)*(x.^2+y.^2)); meshc(x,y,z)3.5习题第9 题clearclcx=-1.5*pi:pi/100:1.5*pi;y1=2*exp(-0.5*x);y2=sin(2*pi*x);plot(x,y1,'r')hold onplot(x,y2,'b')3.5习题第10题clearclcx=-2:0.01:2;y=-1:0.01:1;[x,y]=meshgrid(x,y);z=y./(1+x.^2+y.^2);mesh(x,y,z)view(-96,16)第五章部分课件5.1 数据处理和分析5.1.2 最大值和最小值MATLAB提供的求数据序列的最大值和最小值的函数分别为max和min,两个函数的调用格式和操作过程类似。
matlab习题与答案

matlab习题与答案MATLAB习题与答案MATLAB是一种强大的数学软件,被广泛应用于科学、工程和金融等领域。
它不仅提供了丰富的数学函数和工具,还具备强大的数据可视化能力。
在学习和使用MATLAB的过程中,习题与答案的练习是非常重要的一部分。
本文将介绍一些常见的MATLAB习题,并给出相应的答案。
1. 习题:计算一个数组的平均值和标准差。
答案:```matlabA = [1, 2, 3, 4, 5];mean_A = mean(A);std_A = std(A);```2. 习题:生成一个10x10的随机矩阵,并计算其中每一行的和。
答案:```matlabA = rand(10, 10);row_sum = sum(A, 2);```3. 习题:计算两个数组的点积。
答案:```matlabA = [1, 2, 3];B = [4, 5, 6];dot_product = dot(A, B);```4. 习题:将一个字符串数组中的所有元素连接起来。
答案:```matlabstr_array = ["Hello", "World"];joined_str = strjoin(str_array);```5. 习题:计算一个数组中每个元素的平方根。
答案:```matlabA = [1, 4, 9, 16];sqrt_A = sqrt(A);```6. 习题:将一个数组中的所有负数替换为0。
答案:```matlabA = [-1, 2, -3, 4];A(A < 0) = 0;```7. 习题:计算一个矩阵的转置矩阵。
答案:```matlabA = [1, 2, 3; 4, 5, 6];transpose_A = A';```8. 习题:计算一个数组中的最大值和最小值。
答案:```matlabA = [1, 2, 3, 4, 5];max_A = max(A);min_A = min(A);```9. 习题:计算一个矩阵的行列式。
Matlab上机题代码及结果4题

例1下图描述了六个城市之间的航空航线图,其中1、2、......、6表示六个城市,带箭头线段表示两个城市之间的航线。
用MATLAB软件完成以下操作:(1)构造该图的邻接矩阵A;(2)若某人连续乘坐五次航班,那么他从哪一个城市出发到达哪一个城市的方法最多?(3)若某人可以乘坐一次、二次、三次或四次航班,那么他从哪一个城市出发总是不能达到哪一个城市?航空航线图(六城市)解:(1)构造邻接矩阵;(2)计算矩阵可达矩阵,找出该矩阵的最大元素,并确定它所在的位置;(3)计算可达矩阵,找出该矩阵中零元素的位置。
在MATLAB软件的M编辑器中编写m文件:% 图与矩阵clearA=[0,1,0,0,0,1;0,0,1,1,0,0;0,0,0,1,1,0;0,1,0,0,0,0;1,0,1,0,0,0;0,1,0,0,1,0]; % 构造邻接矩阵B=A^5;C=A+A^2+A^3+A^4;disp('邻接矩阵A为:');disp(A);disp('矩阵A^5为:');disp(B);m=max(max(B)); % 计算矩阵B的最大值[m_i,m_j]=find(B==m); % 寻找矩阵B中元素等于m的位置fprintf('矩阵A^5最大值%d的位置在:\n',m);disp([m_i,m_j]);disp('矩阵A+A^2+A^3+A^4为:');disp(C);[z_i,z_j]=find(C==0); % 寻找矩阵C中零元素的位置disp('矩阵A+A^2+A^3+A^4零元素的位置在:');disp([z_i,z_j]);在MATLAB命令窗口中输入m文件名称,计算结果为:邻接矩阵A为:0 1 0 0 0 10 0 1 1 0 00 0 0 1 1 00 1 0 0 0 01 0 1 0 0 00 1 0 0 1 0矩阵A^5为:2 5 5 53 12 4 43 2 02 3 5 5 2 10 2 1 3 2 12 6 4 5 4 11 4 4 7 4 2矩阵A^5最大值7的位置在:6 4矩阵A+A^2+A^3+A^4为:2 6 5 6 4 21 4 4 6 3 12 5 4 5 4 11 3 3 3 1 03 5 6 64 23 6 6 54 1矩阵A+A^2+A^3+A^4零元素的位置在:4 6从计算结果中可以看出,矩阵A^5最大值出现在矩阵的第六行第四列,说明:这个人如果从城市6出发连续乘坐五次航班后到达城市4,他可以选择的乘机路线最多,共有7种不同的方法。
MATLAB题目和答案

MATLAB题目和答案题目1编写一个MATLAB函数,该函数可以计算一个矩阵的逆矩阵。
解答1function invMatrix = calculateInverse(matrix)invMatrix = inv(matrix);end题目2编写一个MATLAB函数,该函数可以计算两个矩阵的乘积。
解答2function productMatrix = calculateProduct(matrix1, matrix2)productMatrix = matrix1 * matrix2;end编写一个MATLAB函数,该函数可以计算一个向量中的最大值和最小值。
解答3function [maxValue, minValue] = calculateMinMa x(vector)maxValue = max(vector);minValue = min(vector);end题目4编写一个MATLAB函数,该函数可以计算一个向量的平均值和标准差。
解答4function [average, stdDev] = calculateAverageA ndStdDev(vector)average = mean(vector);stdDev = std(vector);end编写一个MATLAB函数,该函数可以生成一个指定长度的斐波那契数列。
解答5function fibonacciSequence = generateFibonacci Sequence(length)fibonacciSequence = zeros(1, length);fibonacciSequence(1) = 0;fibonacciSequence(2) = 1;for i = 3:lengthfibonacciSequence(i) = fibonacciSequence (i-1) + fibonacciSequence(i-2);endend题目6编写一个MATLAB函数,该函数可以计算一个向量的累积和。
matlab练习程序(多圆交点)

matlab练习程序(多圆交点)最近总是对计算⼏何⽅⾯的程序⽐较感兴趣。
多圆求交点,要先对圆两两求交点。
有交点的圆分为相切圆和相交圆。
相切圆求法: 1.根据两圆⼼求直线 2.求公共弦直线⽅程 3.求两直线交点即两圆切点。
相交圆求法: 1.求公共弦⽅程直线。
2.公共弦直线⽅程和其中⼀个圆⽅程联⽴求解即可。
公共弦直线⽅程就是两圆⽅程的差。
结果如下:matlab代码如下:main.m:clear all;close all;clc;n=20;cic=rand(n,3); %(x,y,r)hold on;for i=1:n-1for j=i+1:ncic1=cic(i,:);cic2=cic(j,:);p=circleCross(cic1,cic2);if ~isempty(p)plot(p(:,1),p(:,2),'.');endendendfor i=1:ntheta=0:0.001:2*pi;x=cic(i,1)+cic(i,3)*cos(theta);y=cic(i,2)+cic(i,3)*sin(theta);plot(x,y,'-');endaxis equalcircleCross.m:function p=circleCross(cic1,cic2)x0=cic1(1);y0=cic1(2);r0=cic1(3);x1=cic2(1);y1=cic2(2);r1=cic2(3);d=sqrt((x0-x1)^2+(y0-y1)^2); %两圆⼼距离k1=(y0-y1)/(x0-x1); %连接两圆⼼直线b1=y1-k1*x1;k2=-1/k1; %公共弦⽅程直线b2=(r0^2-r1^2-x0^2+x1^2-y0^2+y1^2)/(2*(y1-y0));p=[];if d==abs(r1-r0) || d==r1+r0 %相切时的交点xx=-(b1-b2)/(k1-k2);yy=-(-b2*k1+b1*k2)/(k1-k2);p=[xx yy];elseif abs(r1-r0)<d && d<r1+r0 %相交时的交点%公共弦⽅程与其中⼀个圆的交点xx1=(-b2* k2 + x1 + k2 *y1 - sqrt(-b2^2 + r1^2 + k2^2 *r1^2 - 2 *b2* k2* x1 - k2^2* x1^2 + 2*b2*y1 + 2*k2*x1*y1 - y1^2))/(1 + k2^2); yy1=k2*xx1+b2;xx2=(-b2* k2 + x1 + k2 *y1 + sqrt(-b2^2 + r1^2 + k2^2 *r1^2 - 2 *b2* k2* x1 - k2^2* x1^2 + 2*b2*y1 + 2*k2*x1*y1 - y1^2))/(1 + k2^2); yy2=k2*xx2+b2;p=[xx1 yy1;xx2 yy2];endend多圆求交点我只能两两⽐较了,不知道有没有什么快速的⽅法。
matlab练习程序(求灰度图像最大灰度,最小灰度,平均灰度)

matlab练习程序(求灰度图像最⼤灰度,最⼩灰度,平均灰度)clearclc;img = imread('124.jpg'); % Read image from graphics file[m n t] = size(img); % 获取图型⼤⼩max = 0;min = 256;avg = 0;for i =1:1:mfor j = 1:1:nif img(i,j)<minmin = img(i,j);endif img(i,j) >maxmax = img(i,j);endavg = avg +double(img(i, j));endendavg = uint8(avg/(m*n));mntmaxminavg在Matlab中如何读出、写⼊图像⽂件以及对图像进⾏简单处理Matlab图像处理⼯具箱⽀持四种基本图像类型:索引图像、灰度图像、⼆进制图像和RGB图像。
MATLAB直接公图像⽂件中读取的图像为RGB图像,它存储在三维数组中,这个三维数组有三个⾯,依次对应红(Red)、绿(Green)、蓝(Blue)三种颜⾊,⽽⾯中的数据则分别是这三种颜⾊的强度值,⾯中的元素对应于图像中的像素点。
设所得矩阵为A三维矩阵(256,256,3),A(:,:,1)代表红颜⾊的2维矩阵,A(:,:,2)代表绿颜⾊的2维矩阵,A(:,:,3)代表蓝颜⾊的2维矩阵。
imread -图像读取指令imshow - 图像显⽰指令rgb2ind - RGB格式图像变为索引格式im2bw - 索引格式变为⼆值图像格式ind2gray - 索引格式变为灰度格式。
matlab代码练习

第一篇:十分钟学会GUI系列视频教程%hf得到figure的句柄 color设定当前图形界面的背景颜色Menu设定当前的菜单栏hf = figure('Units','Normalized',...'Position',[0.2 0.2 0.5 0.5],...'Color','w','Menu','none');%ha得到axes的句柄属性有Uints,Position,Box ,NextPlotha=axes(...'Parent',hf,...'Units','Normalized',...'Position',[0.1 0.1 0.6 0.8],...'Box','on',...'NextPlot','Add');%uicontrol可以设置按钮等控件其通过style进行区分不同的属性%相关属性有Position ,callback回调函数位置设定等,%第三行的代码可以没有 callback函数中Plot函数的步长必须一致,否则%不一致的话坐标轴就会不搭配hb1 =uicontrol(...'Parent',hf,...'Units','Normalized',...'Style','pushbutton',...'Callback','plot(sin([0:0.01:2*pi]),''g'')',...'String','sinx',...'Units','Normalized',...'Position', [0.75 0.1 0.15 0.1]);hb2 = uicontrol(...'Parent',hf,...'Units','Normalized',...'Style','pushbutton',...'Callback','plot(cos([0:0.01:2*pi]),''r'')',...'String','cosx',...'Units','Normalized',...'Position', [0.75 0.2 0.15 0.1]);hb3 = uicontrol(...'Parent',hf,...'Units','Normalized',...'Position',[0.75 0.3 0.15 0.1],...'Style','pushbutton',...'Callback','try delete(allchild(ha));end',...%注意此处的用法'String','delete');hf=figure(); %()可没有get(hf);set(hf,'Color','y');set(hf,'Menu','none'); %或者使用set(hf,'Menubar','none');set(hf,'NumberTitle','off','Name','示例'); %设置标题pause(1); %停下1秒set(hf,'visible','off'); %设置窗口不可见pause(1);set(hf,'visible','on'); %设置窗口可见set(hf,'WindowKeyPressFcn','Closereq'); %按键关闭窗口set(hf,'WindowButtonDownFcn','Closereq');%按下鼠标关闭窗口hb=uicontrol(...'parent',hf,... %这句可有可无'Style','PushButton',...'Callback','closereq');%axes 注意下面的两种方式创建一个坐标轴%①在原来父对象的基础上创建新的坐标对象ha=axes('Parent',hf,...'Box','on',...'NextPlot','add');%②与原来的图形对象没有关系,直接创建一个坐标轴ha=axes; %可有();set(ha,'NextPlot','add'); %注意set函数的使用,(对象,属性名,属性值,属性名,属性值,...)plot([0:200]);plot(sin([0:0.01:3]));%坐标轴的设定ha=axes();set(ha,'NextPlot','add');%line对象的使用hll=ezplot('cos(x)'); %ezplot('函数名');hl2=ezplot('sin(x)');set(hl2,'Color','r',...'Marker','p',... %设置标记为五角星符号'MarkerEdgeColor','g',... %设置符号的边沿颜色为green'MarkerFaceColor','k'); %设置里面的颜色为blackset(hll,'Color','r',...'Marker','p',...'MarkerEdgeColor','g',...'MarkerFaceColor','k');%line对象的xData,yData的使用hl1=ezplot('sin(x)');hl_x=get(hl1,'XData');hl_y=get(hl1,'YData');plot(hl_x,hl_y);% textha=axes;ht=text(1,0.5,'示例'); %其中的前两个参数是指示例这两个字的位置坐标(1,0.5)%源程序中的代码,不懂????text('String','\int_0^x dF(x)','Position',[0.5 0.5]);text('Interpreter','latex','String','$$ \int_0^x dF(x) $$','Position',[0.2 0.2]);% 原始的语句写出来plot(x);% 在原始语句两边加上单引号'plot(x)';% 当原始语句中含有引号,那么将原始的单引号都改为两个单引号,然后在最外层加上一对单引号'plot(x,y,''r'')';uigetfile%uigetfile的返回值【文件名,文件路径,点击“是”还是“否”】[a,b,c]=uigetfile;%规定打开文件的类型uigetfile('*.m');uiputfile%输出参数的意义[e,f,g]=uiputfile;%补充一些uicontrol的用法% handle = uicontrol('Name,Value,...)% handle = uicontrol(parent,'Name,Value,...)%uisetcolor 设置颜色uisetcolorhl = plot([1:10]);a = uisetcolor(hl); %将plot所绘制的曲线的颜色设置的值给a,方面后续的操作例如:%注意以下三种写法的区别(三种效果都不一样)%① callback 可以跟多个语句,算法为:选择一种颜色,把这种颜色给buttonb=uicontrol('Parent',gcf,'Style','pushbutton','String','颜色设置',...'callback','c=uisetcolor;set(b,''BackgroundColor'',c);');%②参照下面字体的设置,可见直接操作button对象的句柄,默认操作的是string b=uicontrol('Parent',gcf,'Style','pushbutton','String','颜色设置',...'callback','uisetcolor(b)');%③将背景和字体都进行了设置b=uicontrol('Parent',gcf,'Style','pushbutton','String','颜色设置',...'callback','c=uisetcolor(b);set(b,''BackgroundColor'',c);');%uisetfont 设置字体S=uisetfont;figure;hb=uicontrol('Parent',gcf,'Style','Pushbutton','String','字体设置',...'callback','d=uisetfont(hb)','Position',[0.2,0.2,0.5,0.5],'Units','Normalized');%普通对话框dialogh=dialog('name','关于...','Position',[200,300,500,200]);%下面这两种方式都可以关闭对话框%①uicontrol('Parent',h,'Style','PushButton','Position',[20,30,50,20],...'String','确定','Callback','closereq');%closereq:Default figure close request function%②uicontrol('Parent',h,'Style','PushButton','Position',[20,30,50,20],...'String','确定','Callback','delete(gcbf)');%这里的gcbf是返回所被回调函数执行的对象的所有句柄%Handle of figure containing object whose callback is executingerrordlg('this is a errordlg');warndlg('this is a warndlg');%输入对话框inputdlg%inputdlg的语法 nswer = inputdlg(prompt,dlg_title,num_lines)inputdlg('请输入姓名','please input the name')inputdlg('请留言','留言',4);%输入多个文本框时,可以使用元胞数组name=inputdlg({'请输入姓名','请输入性别'},'实例');%列表对话框% listdlg [Selection,ok] = listdlg('ListString',S)[select,ok]=listdlg(... %这里的字母不区分大小写'Name','选择列表',...'ListString',{'a','b','c','d'},...'OKString','确定',...'CancelString','取消',...'SelectionMode','Single'...);第二篇:GUI设计笔记hb=figure('toolbar','none','menubar','none','numbertitle','off','units','normalized',... 'position',[0.2 0.2 0.5 0.5],'name','moving');close allclearhf=figure;%movegui(hf,'center'); %不懂ha=axes('units','normalized','position',[0 0 1 1])% imshow('B.bmp') 利用imshow(file)无法使得图像铺满整个坐标轴CData=imread('B.bmp');image(CData);axis offstrcell={'二二更健康','哈哈','呵呵','嘻嘻'};for i=0:numel(A)strtemp=strcell{i};str=str(:)';text('string',str,'position',[700-100*i 300],'Horizoontal','right',...'fontname','华文行楷','fontsize',12,'fontwight','bold');endA=[2,3;3,5;2 0];size(A)length(A)numel(A) %获取数组的元素的数目number of element in the array%figure(1) %创建句柄值为1的图形界面figure(1);set([0,1],'units','normalized'); %将root 和figure 的uints(单位)设置为normalized(归一化,按着比例缩放)get([0,1],'units');%gca 当前坐标轴的句柄gcf 当前图形界面的句柄%窗口figure的设置h=figure('units','pixels','Position',[200 300 400 200],'menubar', 'none','name','恭喜','numbertitle','off');%也可以用结构体来设置一个窗口fig.units = 'pixels';fig.position=[200 300 400 200];fig.nemubar='none';='恭喜';fig.numbertitle='off';%delete()hf=figure;t=0:0.001:2*pi;x=sin(t);hp=plot(t,x);pause(2);delete(hp); %删除该句柄,图形被删除pause(2);delete(hf);%findall 查找findall(gcf) %查找当前窗口的所有的子对象h=findall(0,'type','figure');delete(h); %删除当前的窗口,窗口将会被关闭%delete 将删除一个对象hf=figure();pause(1);delete(hf);%clf 清空当前figure窗口对象hf=figure;ha=axes;pause(1);clf;%cla 清空当前的坐标轴hf=figure();ha=axes();hl=ezplot('sin(x)');pause(1);cla;%close 关闭窗口hf=figure('units','normalized','Position',[0.2 0.5 0.5 0.4],'menubar','none','numbertitle','off','name','close'); pause(3);close(hf); %参数可以为句柄值hf=figure('units','normalized','Position',[0.2 0.5 0.50.4],'menubar','none','numbertitle','off','name','close');pause(3);close('close'); %参数也可以是figure的name%close all force 强行关闭无法关闭的窗口hf=figure('units','normalized','Position',[0.2 0.5 0.50.4],'menubar','none','numbertitle','off','name','close');pause(3);close force%程序控制执行uiwait()等待 uiresume() 继续执行%uiwait(h)等待figure对象h被删除之后才继续执行/uiwait(h,timeout) 等待被删除或者时间溢出(单位为s)%uiresume 继续执行由uiwait之后的语句%组合键ctrl+c可以退出死循环%visible on/off 可以设定figure是否可见figureaxespausehf=figure('visible','off');%closerequestfcnfigure;ezplot('sin(x)');CloseRequestFcn;hq=questdlg('if you close current windows','close now?','yes','no','cancel');switch hqcase 'yes'delete(gcf);case 'no'returnend%文件I/O操作a=ls %查看该目录下的所有文件b=dir('*.gif'); %查找该目录下所有的gif图片M=[2 4 5 7 5 34]; %将某个数组存入到xls表格中xlswrite('a1',M);%图像的操作imread/imwriteM=imread('1380412466870_mh1392209058037.jpg'); %读取一个图像imwrite(M,'b.bmp'); %另存为一个图像(该函数没有返回值)imwrite(M,'B.png'); %注意:该函数不能讲次图片内存为一个gif的图像%将一个图像读取到坐标轴上面imshow imageimshow('B.png'); %坐标轴会自适应图片坐标轴隐藏了ColorData=imread('b.bmp'); %iamge()图片自适应坐标轴(图像会变形失真)image(ColorData); %这两句共同显示一张图片,其实是先读取一个图片变为数组%在将数组转化为一个一个图片(个人感觉imshow才是真正的读取图片)%音频的操作wavread audioplayer%[data,Fs,nBits]=wavread('回应.wav');%player=audioplayer(data,Fs);%play(player);%A=ones(1000);%player=audioplayer(A,7400,8);%play(player)%[data,Fs,nBites]=wavread('music.wav');%ao=analogoutput('winsound');%nChannel=size(data,2);%addChannel(ao,1:nChannel);%set(ao,'sampleRate',Fs);%set(ao,'BitsPerSample',nBites);%putdata(ao,data);%start(ao);%stop(ao);%文件I/O操作a=ls %查看该目录下的所有文件b=dir('*.gif'); %查找该目录下所有的gif图片M=[2 4 5 7 5 34]; %将某个数组存入到xls表格中xlswrite('a1',M);%图像的操作imread/imwriteM=imread('1380412466870_mh1392209058037.jpg'); %读取一个图像imwrite(M,'b.bmp'); %另存为一个图像(该函数没有返回值)imwrite(M,'B.png'); %注意:该函数不能讲次图片内存为一个gif的图像%将一个图像读取到坐标轴上面imshow imageimshow('B.png'); %坐标轴会自适应图片坐标轴隐藏了ColorData=imread('b.bmp'); %iamge()图片自适应坐标轴(图像会变形失真)image(ColorData); %这两句共同显示一张图片,其实是先读取一个图片变为数组%在将数组转化为一个一个图片(个人感觉imshow才是真正的读取图片)%音频的操作wavread audioplayer[data,fs,bits]=wavread('回应.wav');player=audioplayer(data,fs,bits);play(player);%核心图像对象%image的核心属性是CData 它定义了一个图像的数据%line的核心属性石Xdata,Ydata,Zdata%text的核心属性是string%图像对象A=rand(120);%方式1%h=image(A);%方式2h=image; %创建一个图像对象axis tight %设置坐标轴自适应图像set(h,'CData',A); %将图像对象的核心属性CData大小设置为A%line 画一条线x=0:0.001:2*pi;y=sin(x);line(x,y,'marker','o');x=[2,4];y=[2,4];line(x,y,'markerfacecolor','r'); %从(2,2)开始到(4,4)结束% 动态改变线宽t=0:0.002:2*pi;x=0.5*sin(t);y=0.5*cos(t);hl=plot(x,y,'marker','o','markersize',2)axis equalpausei=0;for i=1:100set(hl,'markersize',i);i=i+1;pause(0.002);end%line绘制一个点figure;axes;x=0;y=1;line(x,y,'marker','o','markersize',12,'markerfacecolor','r');%或者plot(x,y,'o');%可以设定x,y在坐标轴的位置figureaxeshold online('xData',1,'yData',1,'marker','o','markersize',12);%text对象%属性有:string fontsize fontweight fontname(字体的名称)color%color position(不是像素或者比例定的位置,而是坐标点'position',[2 1]表示在(2,1)显示该字符)figure('toolbar','none','numbertitle','off','menubar','none','name','picture'); %图像ha=axes('units','normalized','position',[0 0 1 1]); %轴CData=imread('B.bmp'); %读一张图片image(CData);axis offstr={'二','二','更','健','康'};for i=1:numel(str)strtemp=str(i);text('string',strtemp,'fontsize',25,'fontname','华文行楷','fontweight','bold',...'position',[210+30*i 50],'color','g');pause(0.5);end%text的简单用法,也可以用下面的语句axestext(0.5,1,'sinx')%uicontrol 属性有backgroundcolor (对象的背景颜色) CData(对象图案) Position%type、visual、uints,string,fontsize(string的大小)h=uicontrol; %默认是一个按钮M=imread('b.bmp'); %读取一张图像%imshow(M);uicontrol('style','pushbutton','backgroundcolor','g',...'CData',M,'units','normalized','position',[0.2 0.4 0.5 0.3],...'string','photo','fontsize',12) %'CData作为字符串M是数据,不需要加%通过uicontrol(h)设置h为当前的操作对象实现自动聚焦的功能hf=figure('menubar','none','toolbar','none','units','normalized','position',[0.2 0.2 0.5 0.5],...'visible','off');ht=uicontrol('style','edit','string','请输入一个参数',...'fontsize',12,'units','normalized','position',[0.2 0.4 0.5 0.1]);uicontrol('style','pushbutton','string','设置','fontsize',12,'units','normalized','position',[0.4 0.2 0.1 0.1],...'callback','uicontrol(ht)');set(hf,'visible','on');%uicontrol的应用hf=figure('toolbar','none','menubar','none','numbertitle','off');ha=axes;axis([0 8 -1.5 1.5]);xlabel('x');ylabel('y');x=0:0.002:2*pi;y=sin(x);hl=line(x,y);set(0,'defaultuicontrolfontsize',12);uicontrol('style','pushbutton','string','加号','units','normalized','position',[0.1 0 0.08 0.07],'callback',...'set(hl,''marker'',''+'')');uicontrol('style','pushbutton','string','虚线','units','normalized','position',[0.2 0 0.08 0.07],'callback',...'set(hl,''linestyle'',''--'')');uicontrol('style','pushbutton','string','蓝色','units','normalized','position',[0.3 0 0.08 0.07],'callback',...' set(hl,''color'',''y'')');figureaxesaxis equalaxis([-2 2 -2 2]);axis manual %固定坐标轴hold ont=0:0.02:2*pi;x=sin(t);y=cos(t);for i=1:numel(t)line('xdata',x(i),'ydata',y(i));pause(0.0002);end%同时画图figureaxesaxis equalaxis([0 8 -1 1]);axis manual %固定坐标轴hold ont=0:0.02:2*pi;x=sin(t);y=cos(t);for i= 1:numel(t)plot(t(i),x(i),'g');plot(t(i),y(i),'r');pause(0.0002);hold onend%定时器的操作%创建一个定时器t=timer('Tag','t1','name','timer1');%利用tag属性或者name属性可以查找该定时器timerfind(t,'tag','t1');timerfind(t,'name','timer1');%采用running属性查找timerfind(t,'running','off');%定时器的操作步骤% 1.创建定时器%①period 定时周期%②TimeFcn 定时执行的回调函数%③BusyMode 闲忙状态%④ExecutionMode 执行模式用于精确定时%另外常用:在延时时可以设置startdelay属性,当需要该定时器时可以用name/tag查找t=timer('period',1,'TimerFcn',@timeupdate,'busymode','queue',...'ExecutionMode','fixedRate');start(t);%2. 编写回调函数% callback函数的声明和使用% h为定时器对象的句柄func 是用户自定义函数StartFcn是定时器的属性set(h,'StartFcn','func');set(h,'StartFcn',@func);set(h,'StartFcn',{'func',3,5});set(h,'StartFcn',{@func,3,5});%3. 启动定时器对象% 采用start或者startat函数启动定时器%4.停止定时器对象%1.stop 函数停上%2.执行完TimerFcn%3.产生错误时,先调用ErrorFcn 再调用StopFcn%5删除定时器对象delete(t)%预定义对话框%颜色设置对话框uisetcolor%字体设置对话框uisetfont%提问对话框questdlg%警告对话框warndlg%错误对话框errordlg%帮助对话框helpdlg%普通对话框diadlg%输入对话框inputdlg%进度条对话框waitbar%uisetcolorc=uisetcolor(h,'colortitle');c=uisetcolor('colortitle') %它里面的参数一般是颜色对话框的tilte%返回值为选的颜色%uisetfont%返回值s是一结构体s=uisetfont(h,'fonttitle');%h是设置对象的句柄s=uisetfont('fonttitle');%其结果如下:% FontName: 'Arial Unicode MS'% FontWeight: 'bold'% FontAngle: 'italic'% FontSize: 24% FontUnits: 'points'%如果要设置某一个量,可以利用结构体的访问s.FontNamehf=figure('toolbar','none','numbertitle','off','menubar','none','name','font/color set');ha=axes('units','normalized');hte=text(0.5,0.5,'sinx');hti=title('哈哈');%title和text都有color,fontsize,fontweight,fontname属性%回调函数是多个语句的时候,可以用;隔开uicontrol('style','pushbutton','units','normalized','position',[0.2 0.2 0.1 0.1],...'callback','set(hte,''color'',uisetcolor(''请选择颜色''))','string','颜色选择');uicontrol('style','pushbutton','units','normalized','position',[0.2 0.1 0.1 0.1],...'callback',...'s=uisetfont(''请选择字体'');set(hte,''fontsize'',s.FontSize);set(hti,''fontweight'',s.FontWeight);set(hti,''FontName'',s.FontNam e)',...'string','字体选择');%waitbar(x,'title') x是完成的进度,0~1之间gca; %设置当前坐标轴用于绘制曲线h2=waitbar(0,'开始绘图...','windowstyle','modal');t=0:0.001:pi;for i=0:10plot(t,sin(2*pi*i*t));waitbar(i/10,h2,['已完成',num2str(10*i)]);pause(0.5);endclose(h2);%错误对话框errordlg('string','title')errordlg('输入的参数有误','提示')%警告对话框warndlg('string','title')warndlg('范围已超出','警告');%帮助对话框helpdlg('string','title')helpdlg('单击右键选择界面','提示');%提问对话框questdlg('question string','title')questdlg('你确定这么做吗','提问');%输入对话框inputdlg('prompt','title') prompt是提示信息可以是字符串也可以是数组inputdlg('请输入参数','输入提醒');inputdlg({'用户名','密码'},'登陆框');%inputdlg('string','title',max_line) %max_line是最大输入行数inputdlg('留言','留言框',3)%subplot的其他用法subplot(3,2,4)subplot(3,2,5)subplot(3,2,6);subplot(3,2,[5 6])subplot(3,2,[1 3])subplot(3,2,[1 6])subplot(3,2,[2 6])subplot(3,2,[3 4 5])subplot 324%绘图工具%axis 设置坐标轴的范围%box 显示或者隐藏坐标轴的边框 box on/off%grid 设置网格线 grid on/off/minor(次网格线)%例如:subplot 221plot(sin(0:2*pi/1000:2*pi));box off %注意:必须先画图,在设置坐标轴边框subplot 222plot(sin(0:2*pi/1000:2*pi));subplot(2,2,[3 4]);plot(sin(0:2*pi/1000:2*pi));grid minor %画出次网格线%axis的设置axis[xmin xmax ymin ymax] %设置坐标轴的范围axis manual %保持当前坐标轴的范围不变即为冻结坐标轴axis auto %将数据的范围自动适应坐标轴的范围axis tight %将坐标轴的范围设置为数据值的范围axis equal %坐标轴等刻度axis square %坐标轴等长,坐标轴的刻度自适应图像,使图像保持原状% axis equal /squaret=0:2*pi/1000:2*pi;x=sin(t);plot(t,x);axis equalt=0:2*pi/1000:2*pi;x=sin(t);plot(t,x);axis squareaxis off %只显示图像其他的什么也不显示对应axis on%绘图注释%legend 创建数据图例%title 创建标题%xlabel ylabel 两个方向上的坐标标签% legend('string','string');t=0:2*pi/1000:2*pi;x=sin(t);y=cos(t);plot(t,x,t,y,'m-');legend ('正弦','余弦');%title('string','fontmame','字体'); 后两个可以不要t=0:2*pi/1000:2*pi;x=sin(t);y=cos(t);plot(t,x,t,y,'m-');title('正弦,余弦曲线','fontname','楷体');axis equal%绘制一个圆(体会axis equal和axis square的用法)t=0:0.001:2*pi;x=3*cos(t);y=3*sin(t);plot(x,y);axis equal %axis square也行%绘制一个矩形(体会plot的真实含义)x=[1,4,4,1,1];y=[1,1,4,4,1];plot(x,y);title('矩形','fontname','楷体');grid onbox onlegend('矩形');axis([0 5 0 5]);%体会fill和plot的不同x=[1,4,4,1]; %不需要五个,四个就行了y=[1,1,4,4];fill(x,y,'g'); %最后一个参数必须有title('矩形','fontname','楷体');grid onbox onlegend('矩形');axis([0 5 0 5]);function chang_color()k=input('please input a number to change the color','s')switch kcase 1set(gcf,'color','g');case 2set(gcf,'color','k');case 3set(gcf,'color','m');otherwiseset(gcf,'color','y');endend% 波形的合成产生60hz和150hz的信号x=0:0.0002:0.06;y=sin(2*pi*60*x);z=sin(2*pi*150*x);t=z+y;plot(x,y,'r');hold onplot(x,z,'g');plot(x,t)% 产生60hz和150hz的带有噪声的信号% plot()如果是需要画出某些点的值而不是连成的先,可以t(1:50)这种写法% plot() 如果是多个点的话,会自动连成线,如果单个点的话,会打印一个点t=0:0.0002:0.06;x=sin(2*pi*60*t)+sin(2*pi*150*t);y=x+2*randn(size(t));%plot(t,y,'y');hold onplot(1000*t(1:50),1000*y(1:50),'g+'); %50个点%也可以这样代替%x=linspace(0,2*pi,30);%y=sin(x);%for i = 1:30%plot(x(i),y(i),'r+');%hold on%end%plot(1000*t,y,'m-');xlabel('time(ms)')grid onY=fft(y,512);x=-pi:0.02:pi;y=sin(x);plot(x,y);line([-5 5],[0 0]); %第一个参数为x坐标的变化第二个参数为y坐标的变化%数据拟合%多项式拟合ployfit()x=0:0.1:1;y=[-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.3 11.2];n=2;p=polyfit(x,y,n);xi=linspace(0,1,100);yi=polyval(p,xi);plot(x,y,'m',xi,yi,'g');xlabel('x');ylabel('y');x=0:0.01:2*pi;y=sin(x);y1=y-1;n=12;p=polyfit(x,y1,n);xi=linspace(0,2*pi,100);yi=polyval(p,xi);plot(x,y,'m',xi,yi,'r');for i=1:20x=0:0.02:2*pi;y=sin(5000*x).*cos(5000*x);sound(y);pause(0.8);y=sin(2000*x).*cos(2000*x);sound(y);pause(0.4);y=sin(1000*x).*cos(1000*x);sound(y);pause(2);endx=-pi:0.02:pi;y=sin(x);plot(x,y);title('正弦曲线');axis equalxlabel('x值');ylabel('y值');text(0.8,0.5,'正弦曲线','sc')%line([-pi,pi],[0,0]);grid on %打开网格线pause(3);grid offgtext('正弦曲线'); %将鼠标点到哪儿哪儿就会出现要显示的字符t=0:0.02:10*pi;x=sin(t);y=cos(t);z=t;plot3(x,y,z);xlabel('x');ylabel('y');zlabel('z');title('螺旋线')t=0:0.02:10*pi;subplot(2,2,1);x=sin(t);plot(t,x);axis equalsubplot(2,2,2);y=cos(t);plot(t,y);axis equalsubplot(2,2,4);z=tan(t);z=plot(t,z);axis equalf='sin(x)';a=diff(sym(f)); %求微分b=int(sym(f)); %求积分% ax^2+bx+ceq='a*x^2+b*x+c=0';rh0=(1+sqrt(5))/2;sym(rh0,'f');a=input('a=');w=input('w=');r=input('r=');x=a*cos(wt+r);dx=diff(x,t);plot(t,dx);%微分的应用syms a x b c %使用符号变量之前需要声明一下f=sym('a*x^2+b*x+c');df=diff(f);df2=diff(f,2);df22=diff(f,x,2);df3=diff(f,a);df33=diff(f,a,2);%积分的应用syms a xf=sym('a*cos(x)');sf=int(f,x,1);syms a b;s=a*cos(b*x);int(s,x,cos(a),sin(b));syms x1s=x1*(log(2*x1));int(s,x1,2)%定积分的应用%求x1*log(x1+1)从0到1的积分syms x1s=x1*log(x1+1);si=int(s,x1,0, 1);%偏微分的应用syms x yf=x*sin(y);dfdxdy=diff(diff(f,x),y)%两重积分% f=x*exp(-x*y)f=x*exp(-x*y);sf=int(int(f,x),y)% simple函数的应用syms a x b cf=c*cos(a*x+b);sf=int(f,x);df=diff(sf,x);dff=simple(df);%微积分的求解实例syms xf=1/(5+4*cos(x));ezplot(f)f1=diff(f);ezplot(f1)f2=diff(f,2);ezplot(f2);s1=int(f2,x);%s2 = int(int(f2,1),1) 注意这里的没有积分的重数这个参数,二重积分写成int(int(f)) s = int(int(f2,x),x);ezplot(s2)ezplot(sin(x),[-pi pi]) %ezplot() 后面的两个参数是x的范围,用一个数组表示x=t*sin(t);y=t*cos(t);ezplot(x,y,[0 4*pi]);hold onx2=t*sin(t);ezplot(x2,y2);%小球绕轨迹运动ha=axes('units','normalized','position',[0.1 0.1 0.7 0.7]);axis equalhold on%产生一个圆t=0:0.008:2*pi;x=2*sin(t);y=2*cos(t);line(x,y,'linewidth',2);%创建一个小球 %line 对象后marker,markerfacecolor(填充颜色)标记的大小hbobble=line('xData',0,'yData',1,'marker','o','markerfacecolor','r','markersize',15)%初始化设置npos=length(t);ipos=1;delt=0.0001;isforward=true;while ishandle(hf)set(hbobble,'xdata',x(ipos),'ydata',y(ipos));drawnow; %刷新屏幕pause(delt);ipos=ipos-(-1)^isforward; % isforward 是控制旋转方向的等价于ipos=ipos+1;ipos=ipis-1;if ipos == npos %这是正这走(ipos增大一直到最大长度)ipos = 1;elseif ipos == 0 %这是逆着走(ipos先减小到0 然后赋值为最大值,让其一直减小ipos=npos;endend%小球在环套里运动ha=axes('units','normalized','position',[0.1 0.1 0.7 0.7]);axis equal%axis offhold ont=0:0.01:2*pi;%内径y1=1.65*cos(t);line(x1,y1,'linewidth',2,'color','g');%外径x2=1.95*sin(t);y2=1.95*cos(t);line(x2,y2,'linewidth',2,'color','m');%小球的轨迹x=1.8*sin(t);y=1.8*cos(t);line(x,y,'linewidth',2,'color','w');%创造一个小球ball=line('xData',0,'yData',1.8,'marker','o','markersize',18,'markerfacecolor','k') %参数初始化ipos=1;delay_time=0.002;npos=length(t); %npos=numel(t)也可以%转动while 1if ipos == npos%ipos=1;break;endset(ball,'xData',x(ipos),'yData',y(ipos));drawnow;ipos=ipos+1;pause(delay_time);end%先画出螺旋线t=linspace(0,10*pi,3000);x=40*sin(t);y=40*cos(t);z=t;plot3(x,y,z);%下面是comet的示例%t=linspace(0,2*pi,3000);%x=sin(t);%y=cos(t);%comet(x,y,0);%斜下抛vx=20;vy=20;t=0:0.02:30;x=vx*t;y=vy*t-9.8*t.^2/2;comet(x,y);%斜上抛因为由于速度的合成:vx.^2+vy.^2=定值vx = 100*cos(1/4*pi);vy = 100*sin(1/4*pi);t = 0:0.001:15;x = vx*t;y = vy*t-9.8*t.^2/2;comet(x,y)%一般的过程%擦除重绘模式动画%选择一个擦除模式set(h,'erasemode',erasemode);%h由plot或者line生成%刷新数据for i=1:nset(h,'Xdata',xdata,'Ydata',ydata); %h由plot或者line生成drownnow;endobj=videoinput('winvideo'); set(obj,'IriggerRepeat',inf); set(obj,'Framesperirigger',1); preview(obj);。
matlab编程训练

matlab训练建立一个脚本文件,用于两个变量值的互相交换。
x=input('输入变量x=');y=input('输入变量y=');z=x;x=y;y=z;xy比较从键盘输入的两个数的大小,输出其中较大的数。
(扩展,输出两个同型矩阵中对应位置较大的数)function [ y ] = ex2( x )a=input('输入数字x=');b=input('输入数字y=');if a>bfprintf('较大数为%d\n',a)elseif a<bfprintf('较大数为%d\n',b)elseendend编写一个函数求一元二次方程的根,并编写测试脚本文件测试结果。
function ex3a = input('请输入二次项系数: ');b = input('请输入一次项系数: ');c = input('请输入常数项: ');discriminant = b^2 - 4 * a * c;if discriminant > 0x1 = (-b + sqrt(discriminant)) / (2*a);x2 = (-b - sqrt(discriminant)) / (2*a);fprintf('x1 = %f\n', x1);fprintf('x2 = %f\n', x2);elseif discriminant == 0x1 = ( -b ) / (2*a);fprintf('x1 = x2 = %f\n', x1);elsereal_part = (-b) / (2*a);imag_part = sqrt( abs(discriminant)) / (2*a);disp('此方程无实根:');fprintf('x1 = %f + i %f \n',real_part, imag_part);fprintf('x1 + %f - i %f \n', real_part, imag_part);end编写一个函数求圆的面积与周长,并编写测试脚本文件测试结果。
matlab练习程序(旋转矩阵、欧拉角、四元数互转)

%旋转矩阵转四元数 t=sqrt(1+R(1,1)+R(2,2)+R(3,3))/2; q=[t (R(3,2)-R(2,3))/(4*t) (R(1,3)-R(3,1))/(4*t) (R代码如下:
clear all; close all; clc;
%欧拉角 x = 0.5; y = 0.6; z = 0.7; Ang1 = [x y z];
%欧拉角转旋转矩阵 Rx = [1 0 0;
0 cos(x) -sin(x); 0 sin(x) cos(x)]; Ry = [cos(y) 0 sin(y); 0 1 0; -sin(y) 0 cos(y)]; Rz = [cos(z) -sin(z) 0; sin(z) cos(z) 0; 0 0 1]; R = Rz*Ry*Rx; R1 = R;
Ang1 Ang2 Ang3
R1 R2
Q1 Q2
参考:
%欧拉角转四元数 q = [cos(x/2)*cos(y/2)*cos(z/2) + sin(x/2)*sin(y/2)*sin(z/2) ...
sin(x/2)*cos(y/2)*cos(z/2) - cos(x/2)*sin(y/2)*sin(z/2) ... cos(x/2)*sin(y/2)*cos(z/2) + sin(x/2)*cos(y/2)*sin(z/2) ... cos(x/2)*cos(y/2)*sin(z/2) - sin(x/2)*sin(y/2)*cos(z/2)]; Q2 = q;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
>> pro(2)=poisscdf(1,0.8); >> pro(3)=poisscdf(4,0.8)-pro(2); >> pro(1)=1-pro(2)-pro(X~N(1,9),Y~N(0,16) , 且 X 与 Y 的相关系数为, 令 Z=X/3+Y/2.求 (1) E(Z) ,D(Z) ; (2) 求 X 与 Z 的相关系数 。 解 根据题意,有 E(X)=1,D(X)=9,E(y)=0 ,D(y)=16 由 E(Z)=E(X/3)+E(y/2)=E(X)/3+E(Y)/2 得 E(Z)=1/3+0=1/3 由 ,cov(X,Y)= 有 Cov(X,Y)=0.5=6 D(Z)=D(X/3+Y/2)=D(X/3)+D(Y/2)+2cov(X/3,Y/2) 得到 D(Z)=D(X)/9+D(Y)/4+2cov((X,Y) =9/9+16/4+2=3 得 cov(X,Z)=cov(X,X/3)+cov(X,Y/2) =1/3cov(X,X)+1/2cov(X,Y) =9/3+(-6)=0
MATLAB 练习 实验一 常见分布的概率密度 、分布函数生成 [实验目的] 1. 会利用 MATLAB 软件计算离散型随机变量的概率,连续型随机变量概率密度值。 2.会利用 MATLAB 软件计算分布函数值,或计算形如事件。 3.会求上分位点以及分布函数的反函数值。 [实验要求] 1.掌握常见分布的分布律和概率密度的产生命令,如 binopdf,normpdf 2. 掌握常见分布的分布函数命令,如 binocdf,normcdf 3. 掌握常见分布的分布函数反函数命令,如 binoinv,norminv [实验内容] 1 事件 A 在每次试验中发生的概率是 0.3,计算 (1)在 10 次试验中 A 恰好发生 6 次的概率; (2)在 10 次试验中 A 至多发生 6 次的概率. binopdf(6,10,0.3) >> binocdf(6,10,0.3) 2 设随机变量 X 服从参数是 3 的泊松分布,求概率 poisspdf(6,3) 3 设随机变量 X 服从区间[2,6]上的均匀分布,求 (1)X=4 时的概率密度值; (2). unifpdf(4,2,6) >> unifcdf(5,2,6) 4 设随机变量 X 服从参数是 6 的指数分布,求 (1)X=0,1,2,3,4,5,6 时的概率密度值; (2). exppdf(0:6,6) >> expcdf(5,6) 5 设随机变量 X 服从均值是 6,标准差是 2 的正态分布,求 (1) X=3,4,5,6,7,8,9 时的概率密度值; (2)X=3,4,5,6,7,8,9 时的分布函数值; (3)若=0.345,求 x; (4)求标准正态分布的上 0.05 分位数。 normpdf(3:9,6,2) normcdf(3:9,6,2) norminv(0.345,6,2) norminv(0.95,0,1) 6 设随机变量 X 服从自由度是 6 的 t 分布 ,求
[实验要求] 1.掌握 MATLAB 画图命令 plot 2.掌握常见分布的概率密度图像和分布函数图像的画法 [实验内容] 9 事件 A 在每次试验中发生的概率是 0.3,记 10 次试验中 A 发生的次数为 X. (1)画出 X 的分布律图形; x=0:10; >> y=binopdf(x,10,0.3); >> plot(x,y,'.') >> (2)画出 X 的分布函数图形; x=0:0.01:10; >> y=binocdf(x,10,0.3); >> plot(x,y) 10 设随机变量 X 服从参数是 6 的指数分布, (1)画出 X 的概率密度图形 x=0:0.01:10; >> y=exppdf(x,6); >> plot(x,y) (2)画出 X 的分布函数图形 x=-1:0.01:10; >> y=expcdf(x,6); >> plot(x,y) 11 设随机变量 X 服从参数是 3 的泊松分布。 (1)画出 X 的分布律图形; x=0:10; >> y=poisspdf(x,3); >> plot(x,y,'.') (2)画出 X 的分布函数图形; >> x=0:0.01:10; >> y=poisscdf(x,3); >> plot(x,y) 12 设随机变量 X 服从区间[2,6]上的均匀分布。 (1)画出 X 的概率密度图形 x=0:0.01:10; >> y=unifpdf(x,2,6); >> plot(x,y,'*') (2)画出 X 的分布函数图形 >> x=0:0.01:10; >> y=unifcdf(x,2,6);
[实验要求] 两个正态总体的区间估计理论知识 [实验内容] 25 为比较甲乙两种型号步枪子弹的枪口速度, 随机地取甲种型号子弹 10 发, 得到枪口速度 的平均值为 500(m/s),标准差 1.10(m/s) ;乙种型号子弹 20 发,得到枪口速度的平均值 为 496(m/s),标准差 1.20(m/s) 。两个总体都近似服从正态分布,且方差相等。求两个总 体均值差的置信水平为 0.95 的置信区间。 t=tinv(0.975,28); >> s=sqrt((9*1.10^2+1.20^2)/28); >> d1=(500-496)-t*s*sqrt(1/10+1/20) >> d2=(500-496)+t*s*sqrt(1/10+1/20) 26 从甲乙两个蓄电池厂生产的产品中,分别抽取 10 个产品,测得它们的电容量(单位: Ah)为: 甲厂:146 141 138 142 140 143 138 137 142 137 乙厂:141 143 139 139 140 141 138 140 142 136 若蓄电池的电容量服从正态分布, 求两个工厂生产的蓄电池的电容量方差之比的置信水平为 0.90 的置信区间。 x1=[146 141 138 142 140 143 138 137 142 137]; >> x2=[141 143 139 139 140 141 138 140 142 136]; >> s1=var(x1); >> s2=var(x2); >> f1=finv(0.95,9,9); >> f2=finv(0.05,9,9); >> d1=s1/s1*(1/f1) >> d2=s1/s2*(1/f2) 实验六 假设检验 [实验目的] 1 会用 MATLAB 进行单个正态总体均值及方差的假设检验 2 会用 MATLAB 进行两个正态总体均值差及方差比的假设检验 [实验要求] 熟悉 MATLAB 进行假设检验的基本命令与操作 [实验内容] 27 某工厂生产 10
(1)X=-3,-2,-1,0,1,2,3 时的概率密度值; (2)X=-3,-2,-1,0,1,2,3 时分布函数值; (3)若=0.345,求 x; (4)求 t 分布的上 0.05 分位数. tpdf(-3:3,6) tcdf(-3:3,6) tinv(0.345,6) tinv(0.95,6) 7 设随机变量 X 服从自由度是 6 的 (1) X=0,1,2,3,4,5,6 时的概率密度值; (2) X=0,1,2,3,4,5,6 时的分布函数值; (3) 若=0.345,求 x; (4) 求
[Ex,Dx]=normstat(1,sqrt(9)); >> [Ey,Dy]=normstat(0,sqrt(16)); >> rxy=-0.5; >> syms x y z >> z=x/3+y/2; >> covxy=rxy*sqrt(Dx)*sqrt(Dy); >> Ez=Ex/3+Ey/2 >> Dz=Dx/9+Dy/4+2*1/3*1/2*(covxy) >> covxz=Dx/3+covxy/2 实验四 统计中的样本数字特征 23 随机生成 4 组 10 个整数数据,求每组数据的平均值。 > X=fix(20*rand(10,4)) >> M=mean(X) 24 随机生成服从标准正态分布的 6 组 10 个数据,求每组数据的极差、样本方差、样本标准 差。 X=normrnd(0,1,10,6) M1=range(X) M2=var(X) M3=std(X) 实验五 两个正态总体均值差,方差比的区间估计 [实验目的] 1 掌握两个正态总体均值差,方差比的区间估计方法 2 会用 MATLAB 求两个正态总体均值差,方差比的区间估计
>> plot(x,y) 13 设随机变量 X 服从均值是 6,标准差是 2 的正态分布。 (1) 画出 X 的概率密度图形 x=-10:0.01:10; >> y=normpdf(x,6,2); >> plot(x,y) (2) 画出 X 的分布函数图形 > x=-10:0.01:10; >> y=normcdf(x,6,2); >> plot(x,y) (3) 在同一个坐标系中画出均值是 6,标准差是 1,,3 的正态分布概率密度图形 x=0:0.01:13; >> y1=normpdf(x,6,1); >> y2=normpdf(x,6,2); >> y3=normpdf(x,6,3); >> plot(x,y1,x,y2,x,y3) 14 设随机变量 X 服从自由度是 6 的 t 分布 (1)画出 X 的概率密度图形 x=-10:0.01:10; >> y=tpdf(x,6); >> plot(x,y) (2)画出 X 的分布函数图形 x=-10:0.01:10; >> y=tcdf(x,6); >> plot(x,y) 15 设随机变量 X 服从自由度是 6 的 (1) 画出 X 的概率密度图形 x=0:0.01:10; >> y=chi2pdf(x,6); >> plot(x,y) (2)画出 X 的分布函数图形 x=0:0.01:10; >> y=chi2cdf(x,6); >> plot(x,y) 16 设随机变量 X 服从第一自由度是 2,第,二自由度是 6 的 F 分布 (1)画出 X 的概率密度图形 x=0:0.001:10; >> y=fpdf(x,2,6); >> plot(x,y) (2)画出 X 的分布函数图形 x=0:0.001:10; >> y=fcdf(x,2,6);
