数学物理方法答案梁昆淼编(第四版)
数学物理方法第一章

(或微商),以 f '(z) 或 df/dz 表示
讨论:
1、从形式上看,复变函数导数的定义与实变函数的定义相同,
因而实变函数论中关于导数的规则和公式往往可以适用于实变 函数。
则
x cos y sin
z (cos i sin )
z e
i
指数式
讨论:i)复数的辐角不能唯一地确定。如果 0 是其中一个辐角, 则
0 2k (k 0,1,2,) 也是其辐角,把属于 [0,2 ) 的辐角称为主值辐角,记为arg z .
存在,且连续,并
且满足柯西-黎曼条件。 证明:由于这些偏导数连续,二元函数 u 和 v 的增量可分别写为
各 个
,于是有
根据柯西-黎曼条件,上式即
这一极限是与 z 0 无关的有限值。证毕。
讨论:复变函数与实变函数的导数有本质上的差别,复变函数 可微,不但要求复变函数的实部与虚部可微,而且还要求其实 部与虚部满足柯西-黎曼条件。
单连通区域:在区域 B 做任何简单的闭曲线,曲线包围 的点全属于 B。否则为多连通区域。
三、复变函数例
多项式
a0 a1 z a2 z an z
2
n
n 为正整数
有理分式
a0 a1 z a2 z 2 an z n b0 b1 z b2 z 2 bm z m
ii)当 1时,z cos i sin ei 称为单位复数。
iii)复数 z 的共轭复数
z x iy (cos isin ) e
梁昆淼力学答案-第一章.docx

力学(梁昆淼版)习题分析与解答大王物理教研团编著蠢大王物理考研序言本习题指导主要配合梁昆淼教授所著《力学》(第四版上册)的学习而编写。
梁昆淼教授的《力学》在国内享有极高的声誉。
是国内众多高校的力学本科教材。
梁教授的力学在讲解清楚数学计算的同时,十分注重物理图像。
能够让学生形成更加具体的物理模型。
国内有一部分教材过于执着于数学的计算反而忽略的对物理模型的训练,而梁教授的书则是将大部分精力花在对物理模型的构建上。
因此梁教授的力学是国内最适合物理学考研的力学教材。
梁教授的《力学》题量适中,是一本适合反复研究的经典题集。
国内很多教材每一章的题目动辄五六十题,这类教材题目众多,但是难度又偏低,导致很多考生在训练的过程中耗费了大量时间在无意义的题目上,最终折戟沉沙。
并且很多同学在刷题的过程中,还往往发现不了这些问题。
所以笔者极其不推荐这种量大且没有意义的刷题。
最有效的刷题,永远是在精而不在多。
梁教授的《力学》难度足以应该国内的所有985高校的研究生试题。
而且习题的难度选择的恰到好处。
一方面习题的难度足以让你掌握力学的所有知识点及其变化,另一方面又不会过于执着于物理之外的奇技淫巧。
并且梁教授的习题集是命题的一个重要参考,大量高校的考研试题中也会出现习题集中的类似题目。
这是第一章习题的答案,本题集的答案完全免费,以任何手段买卖罪过无边!接下来几章的答案会在接下来的几个月的时间里陆续更新,同学们可以扫描下方二维码添加婷婷学姐微信领取!大王物理考研•教研团队1.1小球从竖直标尺的零点无初速地自由落下,用照相机拍摄小球下落情况.在底片上,小球的路径呈现为从毫米刻度到电毫米刻度的一段直线.求拍摄时的曝光时间.【解】设小球到达72]处耗时勺,712处耗时-gtf = Hi mm:g後=n2 mmAt = t2_tl =丄.8 : 103(帀一而)s1.2电车停在十字路口.绿灯一亮,电车立刻以2m/s2的匀加速开动,在其启动时恰有一"车以10m/s的匀速追上并驶过.问电车将在何处追上卡车?【解】电车与卡车运动距离相同1 ?S — Vgt + ~ G.2S = V r t其中% = 0 m/s a = 2 m/s2 = 10 m/s 解得t = 10 sS = 100 m1.3在刹车作用下,汽车通过某段10m长度用了2.2s,而通过紧接的10m长度所用时间延长为3 s,设汽车速度的减慢是匀速的.求汽车的加速度.【解】汽车做匀减速运动v o ti +-atl = s1 ?v0t2 + 2at2 = 2s其中Zt] = 2.2 s t2 = 5.2 s s = 10 m 解得a = —0.47 m/s21.4雪橇无初速度的从力点匀加速滑下斜坡48,随后沿水平面匀减速运动到。
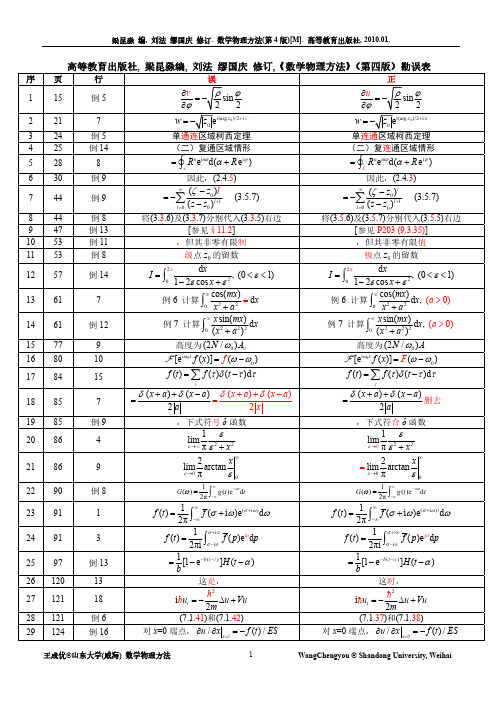
王成优_“数学物理方法”(第4版)勘误表
1 d d 1 dx d d (sin ) ( sin 2 ) sin d d sin d dx dx d d (1 x 2 ) dx dx
d m2 2 d (1 x ) [ l ( l 1) ] 0 dx d 1 x2
2π
[ei x f ( x)] f ( 0 )
0
f (t ) f ( ) (t )d
r
[ei x f ( x)] F ( 0 )
0
f (t ) f ( ) (t )d
( x a) ( x a)
2a
( x a) ( x a)
2x
( x a) ( x a)
2a
删去
,下式符号 δ 函数 1 lim π 2 x 2
,下式符合 δ 函数 1 lim 0 π 2 x 2
2 x lim arctan 0 π 0
G ( )
(1 2rx r 2 ) lr l 1Pl ( x)
l 0
(1 2rx r 2 ) lr l 1Pl ( x)
王成优©山东大学(威海) 数学物理方法
2
WangChengyou © Shandong University, Weihai
梁昆淼 编, 刘法 缪国庆 修订. 数学物理方法(第 4 版)[M]. 高等教育出版社, 2010.01.
F ( )
1
2
[ xJ1 ( x) x] 0
F ( )
1
2
[ xJ1 ( x)] 0
渐进
渐近
a k cos a, b k sin a eikp cos( a )
数学物理方法梁昆淼答案

数学物理方法梁昆淼答案【篇一:第五章傅里叶变换数学物理方法梁昆淼】>?t1.函数 f(t)???0?12. 函数 f(t)???03.设(|t|?1)(|t|?1)的傅里叶变换为2(?cos??sin?/?)/(??)(|t|?1)(|t|?1)的傅里叶变换为f(?)?2sin?/??。
的傅立叶变换像函数,的傅立叶变换像函数为 _______________________ 。
4.?2012?2011excosx??(x??) dx?[sinx??(x??e??。
5. ?12009?6 ?2008) ]dx? 6.?xsinx?(x? ?1?3) dx?。
7. ?xsinx?(x?) dx? ?128.?[(x2?1)tan(sinx)??(x?)] dx? 。
?201038?911??9.?x3 ?(x?3) dx?-27 。
?tf(t)?10.函数 ??0(|t|?1)(|t|?1)的傅里叶变换为2(?cos??sin?/?)/(??)。
(0?t?1)?1?(?1?t?0)的傅里叶变换为。
11. f(t)???1?0(|t|?1)?12. 在(??,?)这个周期上,f(x)?x。
其傅里叶级数展开为?k?1?2sinkx k13.当0?x?2时,f(x)??1;当?2?x?0时,f(x)?1;当|x|?2时,f(x)?0。
则函数的f(x)傅里叶变换为b(?)?2??(1?cos2?)1?14已知函数f(x)的傅里叶变换为f(?),试证明f(ax)的傅里叶变换为f()。
af[f(ax)]?1?2????f(ax)e?i?xdx【令x?y/a】?1?2????f(y)e?i?aydya【令y?x】?1?f(x) ?i?ax2????aedx?1?af(a)a---(2分) ---(2分) ---(2分) ---(2分) 证明:【篇二:8000份课程课后习题答案与大家分享~~】> 还有很多,可以去课后答案网(/bbs)查找。
第四章 留数定理 习题梁昆淼数学物理方法

第四章 留数定理1. 函数z ze z f /1)(=在0=z 的奇点类型为 本性奇点 ,其留数为 1/2 。
2. 设n m ,为整数,则=⋅⎰-dx nx mx )cos (sin ππ0 。
3.函数23)(22+++=z z z z z f 有____1___个极点,为_____1____阶极点,在极点处的留数为____________-2____________。
4.为的单极点,则为__________________。
5.函数sin /()z z f z e =在0=z 的奇点类型为 可去奇点 ,其留为 06.函数43)(22-+-=z z zz z f 有________个极点,为__________阶极点;在极点处的留数 为________________________。
7.为的 。
A) 单极点 B) 二阶极点C) 三阶极点 D) 四阶极点8.已知函数,试判断是的几阶极点,然后计算、和在的留数,再利用所得结果给出在的邻域上洛朗展开级数的前三项。
(注意:此题亦可用的泰勒展开直接求出的洛朗展开的前几项,然后利用所得结果求出留数。
)9.求函数的奇点所在的位置,然后计算积分。
10.用留数定理计算复积分⎰=-+=2/3||22)2)(1(z z z dzI 。
解: 回路内有两个一阶极点.,21i z i z -== (2分)其留数为分)(350/)34(])2(2/[1])2)(/[(1lim )]()[(lim )(Re 22221i i i z i z z f i z z sf iz iz -=-=-+=-=→→分)(350/)34(])2(2/[1])2)(/[(1lim )]()[(lim )(Re 22222i i i z i z z f i z z sf iz iz +=---=--=+=→-→25/8))(Re )((Re 221i z sf z sf i I ππ=+= (2分)。
数学物理方法第四版梁昆淼期末总结86页PPT

25、学习是劳动,是充满思想的劳动。——乌申斯基
谢谢!
45、法律的制定是为了保证每一个人 自由发 挥自己 的才能 ,而不 是为了 束缚他 的才能 。—— 罗伯斯 庇尔
21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
数学物理方法第四版梁昆淼 期末总结
41、实际上,我们想要的不是针对犯 罪的法 律公民,就 像影子 跟随着 身体一 样。— —贝卡 利亚 43、法律和制度必须跟上人类思想进 步。— —杰弗 逊 44、人类受制于法律,法律受制于情 理。— —托·富 勒
数学物理方法第1章复变函数-2016解答

【解】 设方根为 w k ,根据上面公式有
wk
1 e n
i 2kπ n
k 0,1,2,…,n 1
当 n=2 时,其根为 1. 对应于单位圆与实轴
的两交点.
22
当 n 3 时,各根分别位于单位圆 z 1的内接正多边
形的顶点处,其中一个顶点对应着主根: w0 1 , (k 0 ) .
面上的一个矢量, 为矢量长度,
为幅角 。记
z ei
z=x+iy=2k 幅角主值:0 Arg z 2 , Arg z ,
(z 0, ; k 0,1,2,...)
注:arg :argument (幅角、宗量,自变量)
数学物理方程(方法)
共60学时,3学分.
(以课堂讲授为主,加强课前和课后练习)
考试时间:暂定11月30日下午 考核方式:30%作业+70%期末考试
主要参考书目:
1. 梁昆淼 《数学物理方法》(第四版)高等教育出版社. 2. 吴崇试,《数学物理方法》,北京大学出版社 3. 冉扬强,《数学物理方法》, 科学出版社。 4. 王友年等《数学物理方法》,大连理工大学出版社
等式,对于 x 0 ,其辐角不满足要求.
24
1.2 复变函数 (一) 复变函数的定义
在复平面上一点集 E 中每一点z ,都有一个或几个 复数w与之对应,称w为 z 的函数,E 为定义域,记 w =f(z),z E 。z有时称为宗量(argument) 或自变量。 实函数: y=f(x)= ± x^(1/2), x>=0 多值
17
N
A’
A
S
球的南极与复数平面的原 点相切,平面上任意点 A 与球的北极由一条直线相 连,直线与球相交于 A’ 。 由此,每一有限的复数 投 影到球上一点 。这个投影 叫测地投影,这个球叫复 数球。
数理方法题解 梁昆淼
∂u ∂ρ
=
1 ρ
∂v ∂ϕ
1
ρ
∂u ∂ϕ
=
−
∂v ∂ρ
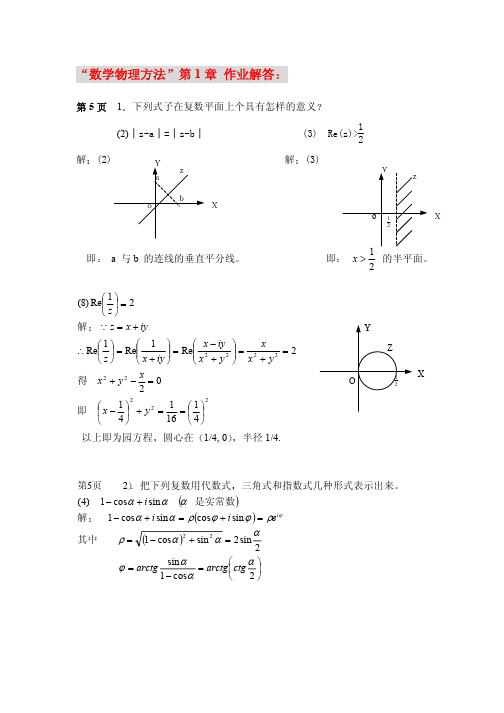
第18页 2 .已知解析函数f (z)的实部u(x, y)或虚部v(x, y), 求该解析函数 以下题目可以有多种解法 这里只列其中之一
(1) u(x, y) = e x sin y
解 已知实部或虚部 一般意味它们已经是调和函数 可以验证
=
x2
x +
y2
=2
得
x2
+
y2
−
x 2
=
0
即
x −
1 4
2
+
y2
=
1 16
=
1 4
2
以上即为园方程 圆心在 1/4, 0 半径 1/4.
o1
2
即
x
>
1 2
的半平面
Y Z
O
1
X
2
第5页 2 . 把下列复数用代数式 三角式和指数式几种形式表示出来
(4) 1 − cosα + i sinα (α 是实常数)
其中
ρ = x2 + y2
ϕ
=
arctg
y x
(6) e1−i
解 e1+i = e × ei = e(cos1 + i sin1)
第9页 2 .计算下列数值 a和b为实常数 x为实变数
(3) ln(−1)
[ ] 解 ln(−1) = ln 1ei(π +2nπ ) = ln1 + i(2n + 1)π = i(2n + 1)π
解 1 − cosα + i sinα = ρ(cosϕ + i sinϕ ) = ρeiϕ
数学物理方法第四版(梁昆淼)期末总结

常见函数的泰勒展开式:
1) e z z k k0 k !
2)
1
zk
1 z k0
3)
1
(1)k zk
1z k0
(z ) (z 1) (z 1)
4)sinz (1)k
z2k1
k0
(2k1)!
(z )
5)cosz (1)k
z2k
(z )
k0
(2k)!
例 3 .把 f ( z ) a r c t g z 在 z 0 0 邻 域 展 成 泰 勒 级 数 .
解: arctgz 11z2 dz
1
1z2
(1)kz2k,
k0
z
1
arctg
(1)k
z2k1c
k0 2k1
arc0tg0
c0
arctgz(1)k z2k1,z1
k02k1
1
(1)ktk,
t 1
1t k0
例 4 .把 f(z ) z 2 (z 1 i)在 圆 环 1 z i 展 成 幂 级 数 .
Arg arzz g2k k0,1,
例1:已知 z23i ,则 z z 1 3
。
zz2x2y2 1 3
例2:复数ez 的模为 e x ,辐角为 y2k, k0,1,2,
.
ez exiy e x eiy
三、解析函数 f(z) u (x ,y ) i(v x ,y ) 1、柯西-黎曼方程
u
f(z) dz2i f(n)()
l(z)n1
n!
来计算积分.
sin( z)
例 1.
4 dz, 其 中 c:(x1)2y21
c z21
sin( z)
4 dz
