2014公务员考试行测备考:巧解青蛙跳井问题
2014年河北公务员面试:言语表达5

2014年河北公务员面试:言语表达51、漫画:一个人在井里打水,突然青蛙跳了出来。
以“机遇”为题做演讲。
【参考要点】从题干出发,引出主题:做好准备,把握机遇;理论和事例论证,论述机遇的重要性,我们要善于抓住机遇,更要善于创造和把握住机遇;总结,结合历史形势,表明我们要努力做好工作,同时审时度势,抓住发展的大好机遇成就自己的事业。
【参考答案】大家好!我今天演讲的题目是“机遇”。
漫画中井底的青蛙想要逃出牢笼,走向更广阔的天地。
而伸入井底的水桶正好给青蛙一个机会,因此它毫不犹豫地把握住了机会,走向了新生。
这幅漫画告诉我们,要做好准备,把握机遇。
古今中外,凡是在事业上取得成功的人,对机会的重要性都有非常深刻的理解和感悟。
柏拉图说:“一个人不论干什么事,失掉恰当的时节、有利的时机就会前功尽弃。
”而宋代文学家苏轼说:“来而不可失者,时也,蹈而不可失者,机也。
”这些都强调了机会的重要性。
因此,对于个人而言,不仅要做好准备,等待机会,更要善于创造和把握机会。
当机会来临时,我们要有能力去把握;当机遇不佳时,我们要耐得住寂寞,潜心积蓄能量,主动寻求突破。
胡锦涛同志曾深刻指出:“在历史发展的关键时期,把握住了机遇,落后的国家和民族就有可能实现超越式发展,成为时代发展的弄潮儿;而丧失了机遇,原本强盛的国家和民族也会不进则退,成为时代发展的落伍者。
”我们国家现在迎来了大发展的关键时期,正处于百年难得的大好机遇中,因此,我们需要抓住这一大好机会,实现中华民族的伟大复兴。
而这个任务,主要还是要靠我们年轻人来完成。
重任在肩,我们当不辱使命。
当前,我们河北省和全国很多地方一样,正处于快速发展的大好时机。
作为年轻人的我们更要审时度势,顺应历史发展的潮流,把握这次良好的机遇,积极响应国家政策的号召,勇敢地担负起建设家乡的任务,用我们的青春、知识和汗水扎根基层,为家乡的发展做出贡献。
我相信,只要我们善于抓住机会,我们一定会在建设家乡的事业中找到个人发展的舞台,现在国家为我们提供了广阔的平台,我们需要抓住这次机会,燃烧我们的激情,成就自己的一番事业,为家乡的发展贡献一份力量。
2014广西公务员考试行测备考用不等式1分钟解决青蛙跳井题
2014广西公务员考试行测备考:用不等式1分钟解决青蛙跳井题在行测考试数学运算中,青蛙跳井问题是困扰我们很多考生的难题,同时,青蛙跳井问题灵活多变,可以与行程问题、工程问题相结合,增加了题目难度,常使很多考生无从下手,下面中公教育专家结合具体的例子给大家做一详细的讲解,让大家掌握该题型的解题方法,一分钟内即可解决青蛙跳井问题。
一、基本青蛙跳井问题我们先由一道简单的例题认识一下青蛙跳井问题。
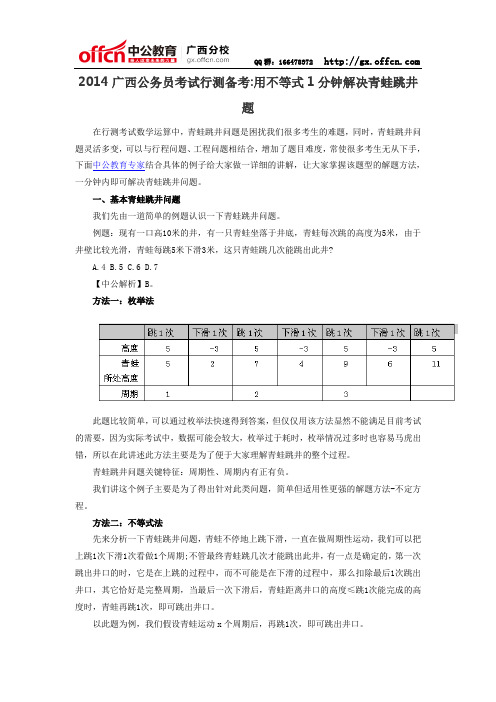
例题:现有一口高10米的井,有一只青蛙坐落于井底,青蛙每次跳的高度为5米,由于井壁比较光滑,青蛙每跳5米下滑3米,这只青蛙跳几次能跳出此井?A.4B.5C.6D.7【中公解析】B。
方法一:枚举法此题比较简单,可以通过枚举法快速得到答案,但仅仅用该方法显然不能满足目前考试的需要,因为实际考试中,数据可能会较大,枚举过于耗时,枚举情况过多时也容易马虎出错,所以在此讲述此方法主要是为了便于大家理解青蛙跳井的整个过程。
青蛙跳井问题关键特征:周期性、周期内有正有负。
我们讲这个例子主要是为了得出针对此类问题,简单但适用性更强的解题方法-不定方程。
方法二:不等式法先来分析一下青蛙跳井问题,青蛙不停地上跳下滑,一直在做周期性运动,我们可以把上跳1次下滑1次看做1个周期;不管最终青蛙跳几次才能跳出此井,有一点是确定的,第一次跳出井口的时,它是在上跳的过程中,而不可能是在下滑的过程中,那么扣除最后1次跳出井口,其它恰好是完整周期,当最后一次下滑后,青蛙距离井口的高度≤跳1次能完成的高度时,青蛙再跳1次,即可跳出井口。
以此题为例,我们假设青蛙运动x个周期后,再跳1次,即可跳出井口。
青蛙每运动1周期能上移2m,运动x个周期后,上移(2x)m,此时距离井口的高度为10-2x≤5,解得x≥2.5,所以x=3,也就是青蛙运动3个周期后,再跳1次,即可跳出井口,与我们前面枚举法做出来的结果相同,但就通过解不等式,就省却了枚举的过程,计算量小,用时短,不易出错。
国家公务员行测:爬井问题

爬井问题
【例1】
青蛙在井底向上爬,井深10米,青蛙每次跳上5米,又滑下来4米,象这样青蛙需跳几次方可出井?
A.6次
B.5次
C.9次
D.10次
解答:答案为A。
考生不要被题中的枝节所蒙蔽,每次上5米下4米实际上就是每次跳1米,因此10米花10次就可全部跳出。
这样想就错了。
因为跳到一定时候,就出了井口,不再下滑。
【例2】蜗牛沿着15米高的柱子往上爬,每天从清晨道傍晚向上爬6米,夜间又滑下来4米,像这样从某天清晨开始,第几天爬到柱顶?()
A10 B5 C6 D9
解析:第5天结束后,蜗牛应在10米处。
第6天白天它还可以向上爬5米,所以就可以登顶不再下滑。
故选C。
本文来源:浙江中公教育。
2014河北公务员考试行测:青蛙跳井解算术题

2014河北公务员考试行测:青蛙跳井解算术题青蛙跳井问题是公务员考试行测比较经典的一种题型,有具体的解决思路和方法,可以算作是一种模型,只要能判断出是属于这种模型,就可以快速计算出。
尤其它可以解决比较复杂的行程、工程问题,大家知道行程问题和工程问题是公务员考试行测考试的重要考查题型,也是许多考生感觉很难的两种题型。
因此,中公教育专家在这里就提供一种快速解决复杂的行程、工程问题的方法—青蛙跳井模型,希望对参加公务员考试尤其是对即将参加2014年省考公务员的考生的考生有所帮助。
上面所给的公式是解决标准的青蛙跳井问题,针对所求的时间为整天,这类问题比较简单若今后在公考中出现直接用公式就可以快速做出选项,而比较复杂的“青蛙跳井问题”即后面所讲的复杂行程、工程问题,则是以后公考行测考试的一大趋势。
在解决这样的问题时,所要求的时间可以是小数,这样就需要对公式进行灵活改进,具体见后面解析。
二、青蛙跳井模型解决行程问题:例2、甲乙两人计划从A地步行去B地,乙早上7∶00出发,匀速步行前往,甲因事耽搁,9∶00才出发。
为了追上乙,甲决定跑步前进,跑步的速度是乙步行速度的2.5倍,但每跑半小时都需要休息半小时,那么甲什么时候才能追上乙?A. 10∶20B. 12∶10C. 14∶30D. 16∶10河北公务员考试网:/秦皇岛公务员考试网:/石家庄公务员考试网:/三、青蛙跳井模型解决工程问题:在工程问题中有一种题型比较难即是交替合作问题,尤其是出现“负效率”的题型中更是好多考生感觉很困惑的,而这类问题用青蛙跳井模型来解决确实非常简单的。
解决这类问题的关键是:预留最大的效率,找出最小的循环周期和一个循环周期的效率和。
下面通过例子来详细讲解:例3、有一个水池,装有甲、乙、丙三根水管,其中甲、乙为进水管,丙为出水管。
单开甲管需15 小时注满空水池,单开乙管需10 小时注满空水池,单开丙池需9 小时把满池的水放完,现按甲、乙、丙的顺序轮流开,每次1 小时,问几小时才能注满空水池?A.47B.38C.50D.46河北公务员考试网:/秦皇岛公务员考试网:/石家庄公务员考试网:/。
公务员、银行校招笔试行测技巧:数量关系常见10大题型及快速解题公式

公务员、银行校招笔试行测技巧数量关系常见10大题型及快速解题公式题型一、和倍问题问题描述:已知两数之和及倍数关系,可快速得出这两数。
大+小=和;大=倍×小,则:小=和÷(倍+1);大=倍×小=和-小。
题型二、差倍问题问题描述:已知两数之差及倍数关系,可快速得出这两数大-小=差;大=倍×小,则:小=差÷(倍-1);大=倍×小=差+小。
题型三、和差问题问题描述:已知两数之和及两数之差,可快速得出这两数大+小=和;大-小=差;则:大=(和+差)÷2;小=(和-差)÷2题型四、日期问题问题描述:若2017年7月10日星期三,则2018年8月10日星期几?平年:365=52×7+1平过1;闰年:366=52×7+2闰过2。
题型五、植树问题问题描述:在一个路段上植树,植树方式不同,棵数和段数的关系不同。
①不封闭路段:两端植:棵数=段数+1;一端植:棵数=段数,②两端都不植:棵数=段数-1;③封闭路线:棵数=段数题型六:方阵问题问题描述:已知每一边上的数量,求方阵一圈的个数;已知每一圈的数量,求方阵一边上的个数。
若一圈个数m,一边个数为n。
则m=4n-4;n=(m+4)÷4题型七:火车过桥问题问题描述:在火车车长和桥长已知时,根据车速求时间。
在火车车长和桥长已知时,根据时间求车速完全过桥:车速=(桥长+车长)÷过桥时间完全在桥:车速=(桥长车长)÷过桥时间过大小桥:车速=(大桥小桥)÷时间差题型八:青蛙跳井问题问题描述:已知青蛙每次向上跳5米,向下滑4米,则10米深的井,需要跳几次才能跳出井口?次数=(总长-单长)÷(实际单长)+1解释:总长是指10米;单长是指青蛙的一次跳几米,也就是5米;实际单长是指青蛙实际向上滑了几米,指1米。
题型九:空瓶换水问题问题描述:已知4个空瓶可以换一瓶饮料,则若买36瓶饮料,最多喝多少瓶?N空瓶换1瓶水,相当于买(N-1)喝N瓶。
国考行测数量关系考前指导:青蛙跳井问题

国考行测数量关系考前指导:青蛙跳井问题一、标准青蛙跳井问题1、模型:现有一口高10米的井,有一只青蛙坐落于井底,青蛙每次跳的高度为5米,由于井壁比较光滑,青蛙每跳5米下滑3米,这只青蛙几次能跳出此井?(1)分析青蛙跳井问题:我们明显发现,青蛙在运动过程中一直是上跳下滑,具有周期性、循环性,在每一个周期之中,青蛙都会先向上跳跃5米,再向下滑动3米,所以在完整的一个循环周期内,青蛙实际向上跳跃运动了2米。
(2)我们可以想到,青蛙在跳出井口的一瞬间一定是在向上运动的过程,而不是先跳出到空中再回落到井口。
所以我们要首先将向上运动过程的5米距离预留出来,此处5米就称作预留量。
(3)剩余的预留高度五米需要几个周期才能达到呢?我们可以用5÷2=2.5个周期达到,向上取整为3个周期。
(4)在3个周期之后,这只青蛙到达了6米的高度。
再跳一次,就可以跳出井口了。
通过上述分析,我们知道青蛙跳井问题有两个关键特征:2、关键特征:(1)周期性;(2)周期内工作效率有正有负。
经过上面的学习,我们可以通过练习一道变形题目来加以巩固。
例:单杠上挂着一条4米长的爬绳,小赵每次向上爬1米又滑下半米,问小赵几次才能爬上单杠?(1)一周期中,小赵先先向上1米,再下滑0.5米。
所以一个完整的周期小赵会向上运动0.5米。
(2)小赵上单杠一定是在向上运动过程,所以预留峰值一米长度。
(3)剩余三米,需要留个完整周期达到。
(4)最后一米再爬一次,故共七次到达单杠。
二、青蛙跳井与工程问题结合----有负效率的交替合作这类工程问题当中,由于存在了负效率,就类似于先向上爬又下滑的青蛙跳井问题。
我们用一道经典模型题目来进行了解:一水池有甲和乙两根进水管,丙一根排水管。
空池时,单开甲水管,5小时可将水池注满水;单开乙水管,6小时可将水池注满水;满池水时单开丙管,4小时可排空水池。
如果按甲、乙、丙......的顺序轮流各开1小时,要将水池注满水需要多少小时?(1)此题目所求为乘除关系,且对应量未知,可以先设特殊值从而简化运算。
2014重庆公务员考试行测:过河爬井问题

2014重庆公务员考试行测:过河爬井问题
8月8号公务员精品班开课
根据以往重庆市人力资源和社会保障网发布的公告,2014年重庆下半年公务员考试公告预计8月上中旬发布,考试初步确定2014年9月!笔试考试科目为:行测+申论!面试形式为结构化+无领导面试!
2014重庆下半年公务员考试:过河爬进问题最常见于公务员考试中,属于趣味杂题中的一种,学习这种题只要把核心公式记下来直接套用即可。
公式:M个人过河,船能载N个人。
需要A个人划船,共需过河(M-A)/ (N-A)次
【真题】32名学生需要到河对岸去野营,只有一条船,每次最多载4人(其中需1人划船),往返一次需5分钟,如果9时整开始渡河,9时17分时,至少有( )人还在等待渡河。
A. 15
B. 17
C. 19
D. 22
【解析】由于9时开始渡河,往返一次需要5分钟,9点0分、9点5分、9点10分、9点15分,船各运一批人过河,所以一共运了4次(其中第四次还在路上)。
运用公式:(M-1)/(4-1)=4求出M=13。
因此,共有13人已经离开了出发点,因此至少有32-13=19人等待过河。
【青蛙爬井问题】。
国家公务员考试行测指导:青蛙跳井类问题的快速解题方法

答案:C
二、包含负效率的交替完工问题
例3:一水池有甲和乙两根进水管,丙一根排水管。空池时,单开甲水管,5个小时可将水池注满;单开乙水管,6个小时可将水池注满;满池水时单开丙水管,4个小时可将水池排空。如果按照甲、乙、丙、甲、乙、丙……的顺序轮流各开一个小时,要将水池注满需要多少个小时?
A19小时B19小时36分钟C18小时48分钟D18小时
答案:B
青蛙跳井问题是在工程类问题中常见的一类题型,这种解题方法其实也可以运用到行程类问题当中的走停追及问题,那么什么样的题目可以用此方法解决?又怎么样去快速解决这类问题?中公教育专家带大家一起10米的井,有一只青蛙坐落于井底,青蛙每次跳的高度为5米,由于井壁比较光滑,青蛙每跳5米,下滑3米,这只青蛙跳几次能跳出此井?
国家公务员考试行测指导:青蛙跳井类问题的快速解题方法
公务员考试行政职业能力测验主要测查与公务员职业密切相关的、适合通过客观化纸笔测验方式进行考查的基本素质和能力要素,包括言语理解与表达、数量关系、判断推理、资料分析和常识判断等部分。行政职业能力测验涉及多种题目类型,试题将根据考试目的、报考群体情况,在题型、数量、难度等方面进行组合。了解公务员成绩计算方法,可以让你做到心中有数,认真备考。
(完整版)公务员考试行测数量关系50个常见问题公式法巧解

公务员考试行测数量关系50个常见问题公式法巧解一、页码问题对多少页出现多少1或2的公式如果是X千里找几,公式是1000+X00*3 如果是X百里找几,就是100+X0*2,X有多少个0 就*多少。
依次类推!请注意,要找的数一定要小于X ,如果大于X就不要加1000或者100一类的了,比如,7000页中有多少3 就是1000+700*3=3100(个)20000页中有多少6就是2000*4=8000 (个)友情提示,如3000页中有多少3,就是300*3+1=901,请不要把3000的3忘了二、握手问题N个人彼此握手,则总握手数S=(n-1){a1+a(n-1)}/2=(n-1){1+1+(n-2)}/2=『n^2-n』/2 =N×(N-1)/2 例题:某个班的同学体育课上玩游戏,大家围成一个圈,每个人都不能跟相邻的2个人握手,整个游戏一共握手152次,请问这个班的同学有( )人A、16B、17C、18D、19【解析】此题看上去是一个排列组合题,但是却是使用的多边形对角线的原理在解决此题。
按照排列组合假设总数为X人则Cx取3=152 但是在计算X 时却是相当的麻烦。
我们仔细来分析该题目。
以某个人为研究对象。
则这个人需要握x-3次手。
每个人都是这样。
则总共握了x×(x-3)次手。
但是没2个人之间的握手都重复计算了1次。
则实际的握手次数是x×(x-3)÷2=152 计算的x=19人三,钟表重合公式钟表几分重合,公式为:x/5=(x+a)/60 a时钟前面的格数四,时钟成角度的问题设X时时,夹角为30X ,Y分时,分针追时针5.5,设夹角为A.(请大家掌握)钟面分12大格60小格每一大格为360除以12等于30度,每过一分钟分针走6度,时针走0.5度,能追5.5度。
1.【30X-5.5Y】或是360-【30X-5.5Y】【】表示绝对值的意义(求角度公式)变式与应用2.【30X-5.5Y】=A或360-【30X-5.5Y】=A (已知角度或时针或分针求其中一个角)五,往返平均速度公式及其应用(引用)某人以速度a从A地到达B地后,立即以速度b返回A地,那么他往返的平均速度v=2ab/(a+b )。
青蛙跳井问题

答:这支队伍长29米。
例4 时钟4点钟敲4下,12秒钟敲完,那么6点钟敲6下,几秒钟敲完?
分析 如果盲目地计算:12÷4=3(秒), 3×6=18(秒),认为敲6下需要18秒钟就错了.请看下图:
时钟敲4下,其间有3个间隔,每个间隔是:12÷3=4(秒);时钟敲6下,其间共有5个间隔,所用时间为:
还需要的时间:16×4=64(秒)
答:还需要64秒才能到达8层。
例6 晶晶上楼,从1楼走到3楼需要走36级台阶,如果各层楼之间的台阶数相同,那么晶晶从第1层走到第6层需要走多少级台阶?
分析 要求晶晶从第1层走到第6层需要走多少级台阶,必须先求出每一层楼梯有多少台阶,还要知道从一层走到6层需要走几层楼梯。
可以从中发现规律:切的次数总比切的段数少1.因此,在24秒内切了4段,实际只切了3次,这样我们就可以求出切一次所用的时间了,又由于用同样的速度切成5段;实际上切了4次,这样切成5段所用的时间就可以求出来了。
解:切一次所用的时间:24÷(4-1)=8(秒)
切5段所用的时间:8×(5-1)=32(秒)
注:例1~例4所叙述的问题虽然不是上楼梯,但它和上楼梯有许多相似之处,请同学们自己去体会.爬楼梯问题的解题规律是:所走的台阶数=每层楼梯的台阶数×(所到达的层数减起点的层数)。
4×5=20(秒)。
解:每次间隔时间为:12÷(4-1)=4(秒)
敲 6下共用的时间为:4×(6-1)=20(秒)
答:时钟敲6下共用20秒。
例5.某人要到一座高层楼的第8层办事,不巧停电,电梯停开,如从1层走到4层需要48秒,请问以同样的速度走到八层,还需要多少秒?
为什么是3分钟而不是4分钟呢?原来从一层上到四层,只要上三层楼梯,而不是四层楼梯。
(完整版)公务员考试数量关系经典类型问题

交替合作问题:交替合作问题与合作问题有很大的区别体现在“交替”两个字,合作效率为各部分效率的加和;交替合作,也叫轮流工作,顾名思义即是每个人按照一定的顺序轮流进行工作。
解决交替合作问题关键:(1)已知工作量一定,设出特值。
(2)找出各自的工作效率,找出一个周期持续的时间及工作量;(3)在出现有剩余工作量的情况需要根据工作顺序认真计算,确定到最后工作完成。
例1:一条隧道,甲单独挖要20天完成,乙单独挖要10天完成。
如果甲先挖1天,然后乙接替甲挖1天,再由甲接替乙挖1天,两人如此交替工作。
那么挖完这条隧道共用多少天?A.13B.13.5C.14D.15.5【答案】 B【解析】:典型的关于交替合作的问题,题目体现出已知工作总量一定和两人工作时间,可以设特值,假设总的工作量为20,则甲的工作效率为1,乙的工作效率为2,因为1个周期持续的时间为2天,一个周期可以完成总的工作量为1+2=3;所以20÷3=6..........2就代表前面需要6个周期,对应6×2=12天,之后剩下2的工作量需要甲先做1天,剩下乙工作半天,所以整个过程需要13.5天,故答案为B。
以上为正效率交替合作的问题,还有一个涉及到负效率交替合作例2、有一个水池,装有甲、乙、丙三根水管,其中甲、乙为进水管,丙为出水管。
单开甲管需15小时注满空水池,单开乙管需10小时注满空水池,单开丙池需9小时把满池的水放完,现按甲、乙、丙的顺序轮流开,每次1小时,问几小时才能注满空水池?A.47B.38C.50D.46【答案】 B【解析】:典型的关于交替合作的问题,题目体现出已知工作总量一定和两人工作时间,可以设特值,假设总的工作量为90,则甲的工作效率为6,乙的工作效率为9,丙的工作效率为-10,所以1个周期持续的时间为3天,一个周期可以完成总的工作量为6+9-10=5,此种最大效率6+9=15,所以(90-15)÷5=15,就代表共需要15个周期,对应15×3=45天,之后剩下15的工作量需要甲先做1天,乙再工作1天就可以完成,故答案为B。
2015国家公务员考试行测备考:“青蛙跳井”如何应对?

2015国家公务员考试行测备考:“青蛙跳井”如何应对?
近年来,工程问题中的交替合作问题在公务员考试中频频出现,对于这类问题的解答,广大考生基本上能够做到游刃有余。
但随着公务员考试难度的增加,交替合作问题中出现了负效率的参与,也就是我们通常所说的“青蛙跳井”,对于这类问题我们该怎么去思考解答,这就是中公教育专家在本文中要给出的答案。
一、交替合作问题的一般解题思路
对于交替合作而言,我们的解题过程有以下四个步骤:
①设特值,确定工作总量和工作效率
②计算一个周期内的工作量之和
③做除法,确定整周期数及剩余工作量
④分析剩余工作量确定最终结论
对于全是正效率参与的交替合作问题而言,正周期数的确定直接用工作总量除以周期工作量,将所得结果取整即可。
但是对于负效率参与的问题,我们会发现在整个工作过程中,周期的工作量之和并不一定是周期工作过程中所完成工作量的最大值,所以关于正周期数的确定就不能简简单单的做除法了,事实上,对于负效率参与的工程问题而言,周期数的确定是难点也是关键点,只要这个问题解决了,该类问题也就变得很简单了。
行测数量关系技巧:青蛙跳井问题你跳出来了吗?

⾏测数量关系技巧:青蛙跳井问题你跳出来了吗? 做了许多⾏测模拟题还是没有有效的提升⾃⼰的分数?那是你没有掌握⼀些技巧和重点,下⾯由店铺⼩编为你精⼼准备了“⾏测数量关系技巧:青蛙跳井问题你跳出来了吗?”,持续关注本站将可以持续获取更多的考试资讯!⾏测数量关系技巧:青蛙跳井问题你跳出来了吗? 在公务员⾏测考试中数量关系相对来说难度较⼤,但是近⼏年数量关系常考的题型基本上没有太⼤变化,所以⼤家在考场上⼀定要放在最后做数量关系,放在最后做不是不做也不是全做,⽽是先要保证⼀些常见的、对你来说⽐较题型的分数拿到,还有剩余时间在做其他题⽬。
对于常见题型的解题⽅法需要在考前掌握,那么今天给各位考⽣介绍技巧性⽐较强的⼀种题型:青蛙跳井问题。
⼀、基本模型 例如:现有⼀⼝深10⽶的井,有⼀只青蛙在井底,青蛙每次往上跳的⾼度为5⽶,由于井壁⽐较光滑,青蛙跳⼀次就会往下滑3⽶,问这只青蛙经过⼏次才能跳出之⼝井? 【解析】阅读题⼲,假设青蛙往上跳5⽶做正功,往下滑3⽶做负功,⼀正⼀负的交替上的上升,⼀正⼀负作为⼀个周期,则⼀个周期内升5+(-3)=2⽶,⼀个周期内上跳1次,这个时候有的同学认为共需要5个周期,跳5次就可以出井,事实上并不是这样,不管青蛙⼏次跳出井,有⼀点是确定的,青蛙是在上跳的过程中出井,⽽不可能是在下滑的过程中,那么就要在井⼝预留⼀个⼀下能跳出的距离,也就是青蛙⼀次上跳的⾼度5⽶,此处5⽶被称作预留量,所以当青蛙跳到预留量之内再跳⼀次就可以跳出井。
那么问题来了,需要⼏个周期?再跳⼏次才能到达预留量之内呢?总⾼度是10⽶,⼀个周期前进2⽶,因此需经过个周期实现距离井⼝5⽶的⾼度(⌈⌉为向上取整符号),⼀个周期需要跳⼀次,三个周期即跳三次,此时青蛙再上跳⼀次即可跳出井⼝,即⼀共需要3+1=4次跳出井⼝。
这时候⼤家是不是⼜有疑惑,计算周期的时候为啥向上取整?咱们刚才5⽶的预留量为⼀个周期内最⼤的⾼度,也叫做周期峰值,只要跳到预留量之内再跳⼀次就可以跳出井⼝,⽽我们拿总⾼度减去周期峰值的差再除以⼀个周期值得到商为刚好为预留点上,如果低于这个商就没有办法跳到预留量之内,跳的次数没有说出现⼩数次的情况,即周期数都为整数,所以必须向上取整。
国考行测数量关系考前指导:青蛙跳井问题

国考行测数量关系考前指导:青蛙跳井问题一、标准青蛙跳井问题1、模型:现有一口高10米的井,有一只青蛙坐落于井底,青蛙每次跳的高度为5米,由于井壁比较光滑,青蛙每跳5米下滑3米,这只青蛙几次能跳出此井?(1)分析青蛙跳井问题:我们明显发现,青蛙在运动过程中一直是上跳下滑,具有周期性、循环性,在每一个周期之中,青蛙都会先向上跳跃5米,再向下滑动3米,所以在完整的一个循环周期内,青蛙实际向上跳跃运动了2米。
(2)我们可以想到,青蛙在跳出井口的一瞬间一定是在向上运动的过程,而不是先跳出到空中再回落到井口。
所以我们要首先将向上运动过程的5米距离预留出来,此处5米就称作预留量。
(3)剩余的预留高度五米需要几个周期才能达到呢?我们可以用5÷2=2.5个周期达到,向上取整为3个周期。
(4)在3个周期之后,这只青蛙到达了6米的高度。
再跳一次,就可以跳出井口了。
通过上述分析,我们知道青蛙跳井问题有两个关键特征:2、关键特征:(1)周期性;(2)周期内工作效率有正有负。
经过上面的学习,我们可以通过练习一道变形题目来加以巩固。
例:单杠上挂着一条4米长的爬绳,小赵每次向上爬1米又滑下半米,问小赵几次才能爬上单杠?(1)一周期中,小赵先先向上1米,再下滑0.5米。
所以一个完整的周期小赵会向上运动0.5米。
(2)小赵上单杠一定是在向上运动过程,所以预留峰值一米长度。
(3)剩余三米,需要留个完整周期达到。
(4)最后一米再爬一次,故共七次到达单杠。
二、青蛙跳井与工程问题结合----有负效率的交替合作这类工程问题当中,由于存在了负效率,就类似于先向上爬又下滑的青蛙跳井问题。
我们用一道经典模型题目来进行了解:一水池有甲和乙两根进水管,丙一根排水管。
空池时,单开甲水管,5小时可将水池注满水;单开乙水管,6小时可将水池注满水;满池水时单开丙管,4小时可排空水池。
如果按甲、乙、丙......的顺序轮流各开1小时,要将水池注满水需要多少小时?(1)此题目所求为乘除关系,且对应量未知,可以先设特殊值从而简化运算。
公务员考试行测趣味题讲解之青蛙跳井

东莞中公教育公务员考试行测趣味题讲解之青蛙跳井近期,盆友圈里突然间兴起了养青蛙的热潮,一款画风清奇,规则简单名为“旅行青蛙”的游戏火了起来。
这个游戏,让玩家沉浸在一只青蛙身上,盼着他吃饱穿暖。
游戏中,玩家需要给青蛙准备好食物和行囊,接下来他便会出远门,在途中会给玩家带特产或者寄明信片。
但令人心酸的是,大部分时间青蛙都不会在家。
那么如此佛系玩家,如此孤独的青蛙是一个公考生正确的打开方式么?今天中公教育专家就蹭着“旅行青蛙”的热度,跟大家讲讲同样的青蛙问题----青蛙跳井问题,又称含有负效率的交替合作问题。
先简单介绍一下含有负效率的交替合作问题,此问题的基础是建立在工程问题中的,完成某项工程,除了存在正效率之外,还存在着阻碍工程的负效率,同时正负效率并不是同时工作,而是交替进行。
例如一个水池,有进水管和出水管两根水管分别工作一小时交替进行,求多长时间可以将水池注满?不要觉得这种问题设计的不合理,也不要觉得这种问题没有实际意义。
青蛙跳井问题:现有一口高20米的井,有一只青蛙坐落于井底,青蛙每次跳的高度为5米,由于井壁比较光滑,青蛙每跳5米下滑2米,请问,这只青蛙几次能跳出此井?拿到这道题,很多同学就会思考,青蛙跳5米滑2米那就意味着青蛙一次只能跳3米呀,直接用20除以3得出几次就是几次呗。
嗯,如果你是这样做的题,那也就活该你的青蛙不回家了。
大家思考一个问题,如果青蛙已经跳了15米,那它是不是下次一次就可以跳出去了,不需要考虑下滑的过程了。
那是几次能跳到15米呢?5次之后再跳一次就可以跳出井了,即总共跳了6次可以跳出井。
这道题虽然做出来了,但是我们不能就题论题,我们要从这个题目中总结出做题的规律。
在分析题目的过程中,是不是只要达到了15米,那青蛙通过一次最高跳出的5米,就可以成功实现他越狱的目的了。
所以我们在做题的过程中,需要看做工者最多一次能做多少工作量,我们称这个最多工作量为周期峰值,在总工作量除去这个周期峰值后,看做工者经过几个循环可以到达,之后在经过不到一个循环的周期峰值,就能够完成工作。
公务员考试行测:巧解青蛙跳井问题

行测考试的工程类题中经常会考正负效率交替的合作问题,通常我们称此类题目为青蛙跳井问题。
本文中公教育专家将通过详细讲解典型例题,为考生总结此类题目的解题技巧。
例:一只青蛙想从一口10米深的井中跳出,一天跳,可以跳3m,一天休息,由于井壁比较滑,会下滑1m,如此交替进行。
请问这只青蛙几天能跳出这口井?中公解析:在此类问题中我们知道,两天构成一个循环,一个循环的效率为+3-1=+2m,周期为两天。
很多人会觉得青蛙跳出来正好需要5个循环,共计10天。
但是实际上并不是,如下图所示中.公教育版权:从图中可以看出,实际在8天多,青蛙就已经跳出这口井了。
所以在做题过程中要树立一种预留思想。
当青蛙经过几个整循环后只要大于10-3=7m,青蛙就能跳出去,所以我们要把3m作为预留量。
首先我们要判断有多少个整循环和剩余的量,不管是均为正效率的交替合作,还是正负交替的交替合作,主要的关键在于剥离整循环和剩余量。
可得:2×[N]≥10-3,[N]=4注:[N]为能取的最小整数即经过4个整循环,剩余量10-4×2=2m剩余量时间:2/3天,整循环时间:4×2=8天共计:8+2/3=8.67天判断有几个整循环的关键在于找预留量,实际上预留量为一个循环效率能达到的最大值,我们把这个值叫做循环效率最大增量,比如说下面这几组效率能达到循环效率最大增量为:+3 +5 -7 +9 循环效率最大增量+10+12 -7 +6 - 7 循环效率最大增量+12注:循环效率最大增量就是从第一个数字开始加,不一定全部加完,能加出的最大值中.公教育版权。
综上所述,青蛙跳井问题的解题方法为:(1)找一个循环量的效率和,同时计算出循环周期(2)找循环效率最大增量作为预留量(3)找整循环:循环量×[N]≥总量-最大增量,[ N]为满足不等式的最小正整数(4) 计算整循环时间=[N]x周期(5)计算剩余量=总量-循环量×[N](6)计算剩余量时间(7)计算总时间中公教育专家提醒考生,解决青蛙跳井问题,要掌握以上方法,并加以练习,便可快速正确的解答此类问题。
行测技巧:浅析数量中的青蛙跳井问题

浅析数量中的青蛙跳井问题工程问题在行测考试中占据着重要的位置,常见的题型有普通工程、多者合作、交替合作等,今天我们一起来看看交替合作中的一种题型,叫做“青蛙跳井”。
交替合作大家都应该很熟悉了,就是几个人在合作完成某项工程的时候按一定的顺序轮流去做。
这类题目考查的形式主要有两种:一种是只有正效率的交替合作,另一种是正负效率交替合作,也就是大家熟悉的青蛙跳井问题。
这类题出题形式相似,在学习的过程中掌握好题型特征,并能运用好特值法,那么这类题目将成为大家得分的一类题目。
一、题目展示:有一口井,深20米,井底有只青蛙,每天都会向上跳5米,由于壁滑,又会下滑3米。
问第几天可以跳出井口?【中公解析】青蛙向上跳5米,再下滑3米,这个过程看作一个周期,这个周期内总共向上跳了2米(即为周期任务量),同时向上跳的最大高度为5米(即为周期峰值)。
由于青蛙最后一定是在向上跳时跳出井的,同时为了更快的跳出,为了保证最后无论剩余多少都能保证一次跳出,所以预留最大高度5米。
然后求需要的整周期数82520=⎥⎦⎤⎢⎣⎡=-n 个整周期后,剩余的高度为20-2×8=4米,再需要1次就可以跳出井口,所以总共需要9次即可。
二、解题步骤:1.设工作总量为“时间们”的最小公倍数,反算工作效率;2.找出一个周期的工作效率(周期内效率累积的总任务)、时间和周期峰值(周期内效率累积的最大值);3.预留周期峰值,求出工作的周期数(有余数时向上取整)和剩余工作量,并分配剩余工作量;4.算出总时间。
三、例题解析:【例题】一温泉池有甲丙两个进水管和乙丁两个排水管,单开进水管向空池注水,甲需3小时,丙需5小时;单开排水管将满池的水放空,乙需4小时,丁需6小时,现池内有61的水,如果按照甲、乙、丙、丁的顺序轮流各开一个小时,那么经过多少小时后水池的水开始溢出?A.20小时15分钟B.20小时45分钟C.10小时45分钟D.5小时45分钟【中公解析】设工作总量为60;则甲、丙、乙、丁的效率分别为20、12、-15、-10;一个循环周期内时间T=4,周期效率P=7,周期峰值为17;预留周期峰值,求出周期数并向上取整,(60-10-17)÷7=4……5,取整为5个周期;求出剩余工作量,50-5×7=15;所以开始溢水共需时间t=5×4+43=20h45min ;故本题选B 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014公务员考试行测备考:巧解青蛙跳井问题
行测考试的工程类题中经常会考正负效率交替的合作问题,通常我们称此类题目为青蛙跳井问题。
本文中公教育专家将通过详细讲解典型例题,为考生总结此类题目的解题技巧。
例:一只青蛙想从一口10米深的井中跳出,一天跳,可以跳3m,一天休息,由于井壁比较滑,会下滑1m,如此交替进行。
请问这只青蛙几天能跳出这口井?
中公解析:在此类问题中我们知道,两天构成一个循环,一个循环的效率为+3-1=+2m,周期为两天。
很多人会觉得青蛙跳出来正好需要5个循环,共计10天。
但是实际上并不是,如下图所示中.公教育版权:
从图中可以看出,实际在8天多,青蛙就已经跳出这口井了。
所以在做题过程中要树立一种预留思想。
当青蛙经过几个整循环后只要大于10-3=7m,青蛙就能跳出去,所以我们要把3m作为预留量。
首先我们要判断有多少个整循环和剩余的量,不管是均为正效率的交替合作,还是正负交替的交替合作,主要的关键在于剥离整循环和剩余量。
可得:
2×[N]≥10-3,[N]=4
注:[N]为能取的最小整数
即经过4个整循环,剩余量10-4×2=2m
剩余量时间:2/3天,整循环时间:4×2=8天
共计:8+2/3=8.67天
判断有几个整循环的关键在于找预留量,实际上预留量为一个循环效率能达到的最大值,我们把这个值叫做循环效率最大增量,比如说下面这几组效率能达到循环效率最大增量为:
+3 +5 -7 +9 循环效率最大增量+10
+12 -7 +6 - 7 循环效率最大增量+12
注:循环效率最大增量就是从第一个数字开始加,不一定全部加完,能加出的最大值中.公教育版权。
综上所述,青蛙跳井问题的解题方法为:
(1)找一个循环量的效率和,同时计算出循环周期
(2)找循环效率最大增量作为预留量
(3)找整循环:循环量×[N]≥总量-最大增量,[ N]为满足不等式的最小正整数
(4) 计算整循环时间=[N]x周期
(5)计算剩余量=总量-循环量×[N]
(6)计算剩余量时间
(7)计算总时间
中公教育专家提醒考生,解决青蛙跳井问题,要掌握以上方法,并加以练习,便可快速正确的解答此类问题。
