近似数精确度的两种形式
近似数和有效数字教案

近似数和有效数字教案
作为一无名无私奉献的教化工作者,可能须要进行教案编写工作,教案是教材及大纲与课堂教学的纽带和桥梁。则写教案须要留意哪些问题呢?下面是我帮大家整理的近似数和有效数字教案,仅供参考,希望能够帮助到大家。
近似数和有效数字教案1
教学目标
1、了解近似数和有效数字的概念;
2、探讨后反馈:(1)精确度不同;(2)有效数字不同。
3、做一做:教科书第56页练习,可请四位同学到黑板上板演,并由其他学生点评。
4、补充例题:据中国统计信息网公布的20xx年中国第五次人口普查资料表明,我国的人口总数为1295330000人,请按要求分别取这个数的近似数,并指出近似的有效数字。
(1)精确到百万位;(2)精确到千万位
⑴精确到千位⑵精确到万位
⑶精确到十万位⑷精确到百万位
3.近似数0.2和0.20有什么不同?
探究四:误差
1.在现实生活中,人们用()与()的差来表示近似数与精确数的接近程度,这个数就是误差。误差可能是(),也可能是()。
2.一件零件的直径标出(150±2)毫米,是指这件零件的实际直径在()毫米与()毫米之间,当这个零件为149毫米时,误差为()毫米。
探究二:近似数精确度的两种表示方式
⑴一个近似数四舍五入到哪一位,就说这个数近似数()到哪一位。
(小试身手)下列有四舍五入得到的近似数,各精确到哪一位?
①101②0.14③8.7千④0.0001
⑵有效数字
由四舍五入得到的近似数,从()第一个()起到()止,全部的数字叫做这个近似数的有效数字。
(小试身手)下列各数有几个有效数字:
(2)某词典共1234页。
(3)我们年级有97人,买门票须要800元。等
解读近似数的精确度

解读近似数的精确度近似数的精确度表示近似数与准确数的接近程度。
精确度有两种表示形式:一是用精确到哪一位(精确位)表示,一是用保留几个有效数字(有效数字)表示。
精确度的两种表示形式的实际意义及取值要求是不一样的,在学习时要加以区别。
一、解读“精确到哪一位”⑴对一个数取近似数,要求精确到某一个数位,我们就将所要求精确到的数位后一位数字“四舍五入”得到近似数。
该近似数最后一位数是由“四舍五入”得到的数,最后一位数所在的数位即是精确到的数位。
如:近似数3.52,最后一位数字2是由“四舍五入”得到的数,2所在的数位为百分位,即近似数3.52精确到百分位。
又如:9989.653(精确到个位)的近似数,将个位后的十分位上的6“四舍五入”,近似数为9990。
1.35835(精确到0.001)的近似数,将千分位后的万分位上的3“四舍五入”,近似数为1.358。
⑵精确到哪一位表示的实际意义:主要用于表示近似数与准确数之间误差绝对值的大小。
例如,在测量长度时,精确到0.1米,说明结果与实际相差不大于0.05米。
⑶确定用科学记数法表示的近似数、带数量级单位的近似数精确到哪一位时,要先将该数还原成原来的数,再看它最后一个数字所在的数位即精确到哪一位。
如近似数 1.230×106,还原成原数为1230000,最后一位数字0所在的数位为千位,因此近似数1.230×106精确到千位(而不是千分位!)。
近似数5.04万,还原成原数为50400,最后一个数字4所在的数位为百位,因此近似数5.04万精确到百位(而不是百分位!)。
⑷近似数的最后一位数字是由“四舍五入”得到的数,根据近似数可以确定准确数的取值范围。
一般地,近似数m所表示的准确数a 的范围是:m-精确位后一位的5个单位≤a<m+精确位后一位的5个单位。
如近似数8.40所表示的准确数a的范围是8.40-0.005≤a<8.40+0.005,即8.395≤a<8.405。
初一有理数知识点总结
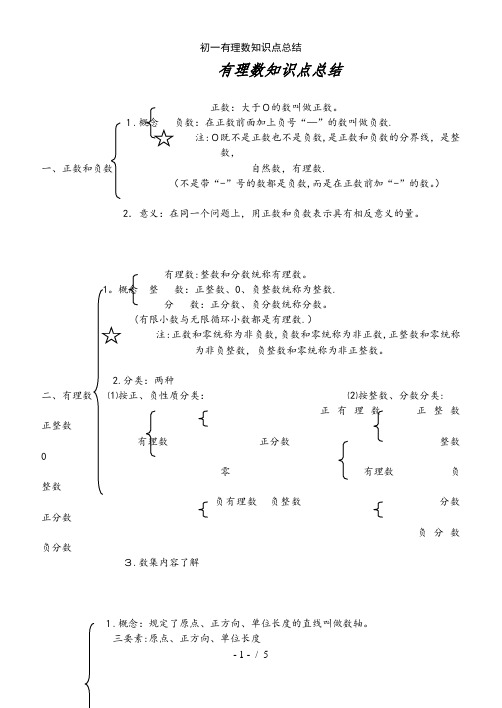
有理数知识点总结正数:大于0的数叫做正数。
1..注:0既不是正数也不是负数,是正数和负数的分界线,是整数,一、正数和负数自然数,有理数.(不是带“-”号的数都是负数,而是在正数前加“-”的数。
)2.意义:在同一个问题上,用正数和负数表示具有相反意义的量。
有理数:整数和分数统称有理数。
概念整数:正整数、0、负整数统称为整数.分数:正分数、负分数统称分数。
(有限小数与无限循环小数都是有理数.)注:正数和零统称为非负数,负数和零统称为非正数,正整数和零统称为非负整数,负整数和零统称为非正整数。
分类:两种⑵按整数、分数分类:正有理数正整数正整数有理数正分数整数0零有理数负整数负有理数负整数分数正分数负分数负分数3.数集内容了解1.概念:规定了原点、正方向、单位长度的直线叫做数轴。
三要素:原点、正方向、单位长度2。
对应关系:数轴上的点和有理数是一一对应的。
三、数轴比较大小:在数轴上,右边的数总比左边的数大 .3。
应用求两点之间的距离:两点在原点的同侧作减法,在原点的两侧作加法.(注意不带“+”“—”号)代数:只有符号不同的两个数叫做相反数.1.概念(0的相反数是0)几何:在数轴上,离原点的距离相等的两个点所表示的数叫做相反数。
2.性质:若a与b互为相反数,则a+b=0,即a=-b;反之,若a+b=0,则a与b互为相反数。
四、相反数两个符号:符号相同是正数,符号不同是负数。
3.多重符号的化简多个符号:三个或三个以上的符号的化简,看负号的个数,当“—”号的个数是偶数个时,结果取正号当“—”号的个数是奇数个时,结果取负号1.概念:乘积为1的两个数互为倒数。
(倒数是它本身的数是±1;0没有倒数)五、倒数2。
性质若a与b互为倒数,则a·b=1;反之,若a·b=1,则a与b互为倒数。
若a与b互为负倒数,则a·b=-1;反之,若a·b=-1则a与b互为负倒数。
1.几何意义:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值.一个正数的绝对值是它的本身(若|a|=|b|,则a=b或a=﹣b)2。
浙教版初中数学 近似数 学案(4)

2.7 近似数◆目标指引1.通过实例经历近似数和准确数概念的产生过程.2.感受近似数的精确度的两种表示方式.3.能说出由四舍五入得到的有理数的精确位数和有效数字.4.会根据预定精确度取近似值.◆要点讲解1.近似数:与实际接近的数.2.准确数:与实际完全符合的数.3.有效数字:一个近似数,从左边第一个不是0的数字起,到末位数字止(到精确的数为止),所有的数字都叫做这个数的有效数字.4.一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位.5.精确度:一个数的近似程度即精确到哪一位.◆学法指导1.精确度的形式有两种:精确到哪一位;保留几个有效数字.2.有效数字的个数从近似数左边第一个不为0的数字起,到精确到的数位止,这中间的所有数字,包括0,重复的数字,都不能漏掉.3.近似数的小数点后的末尾数字0是不能去掉的.4.给定一个近似数,要确定其精确度,题目中要给出一定要求,•主要由该近似数的最后一位有效数字在该数中所处的位置决定.5.对较大的数(如188600)取近似数时,结果一定要用科学记数法表示.◆例题分析【例1】下列由四舍五入得到的近似数各精确到哪一位,各有哪几个有效数字?(1)31.7;(2)0.002314;(3)5.39万.【分析】(1)最末位数字7是十分位上的数字;(2)最末位上的4•是百万分位上的数;(3)5.39万=53900,其中9是百位上的数字.【解】(1)31.7精确到十分位(即精确到0.1),有3个有效数字:3,1,7.(2)0.002314精确到百万分位(即精确到0.000001),有4个有效数字:2,3,1,4.(3)5.39万精确到百位,有3个有效数字:5,3,9.【注意】看一个数精确到哪一位,是看这个数的最末位数字在什么位置,就精确到了哪一位.根据有效数字的定义,第一个非零数字前面的零不能作为有效数字,而后面的零则是它的有效数字,对用“万”为单位的数5.39万,看它精确到哪一位.则先要将它写成53900,再看属于哪个数位上的数,就精确到哪一位,•而看5.39万的有效数字的个数,就不需要写成53900的形式,直接看5.39万中单位“万”前面的有效数字的个数.【例2】用四舍五入法按括号里的要求对下列各数取近似值:(1)0.6779(精确到百分位);(2)29.756(保留一位小数);(3)80610(精确到百位);(4)3.1449(保留三个有效数字);(5)2.04×105(精确到万位).【分析】四舍五入法取近似值,根据题目要求精确到哪一位,把这一位的下一位进行四舍五入.【解】(1)0.6779≈0.68;(2)29.756≈29.8;(3)80610≈8.06×104;(4)3.1449≈3.14;(5)2.04×105≈2.0×105.【注意】(1)取近似数时末尾的0不能去掉,例如2.0×105不能写成2×105,它们的精确度不同;(2)大于10的数取近似数时,先将此数用科学记数法表示出来,再取近似值.例如第(3)题结果不能写成80600,它有五个有效数字,精确到个位,结果应写成8.06×104或806百;(3)取近似数时,不能用“=”,而应用“≈”.◆练习提升一、基础训练1.下列各数哪个为准确数()A.初一年级共有400人B.小明的体重为63千克C.北京市人口有1382万人D.月球离地球的距离是38万千米2.由四舍五入法得到的近似数0.3080,它的精确度是精确到()A.百分位B.千分位C.万分位D.十万分位3.由四舍五入法得到的近似数0.0307的有效数字的个数是()A.3个B.4个C.5个D.6个4.保留三个有效数字得到31.0的是()A.31.22 B.31.05 C.30.95 D.30.9355.38490按四舍五入法取近似数,保留两个有效数字,用科学记数法表示是()A.3.8×104B.3.8×103C.3.7×103D.3.85×1046.下列说法正确的是()A.近似数1.8与1..80表示的意义一样B.4.5万精确到万位C.圆周率等于3.14 D.1.00有三个有效数字7.由四舍五入得到的近似数0.851,它所表示的准确数a的范围是()A.0.8050≤a<0.8515 B.0.8505≤a<0.8515C.0.8514≤a<0.852 D.0.8500≤a<0.85158.57645精确到千位是_______.9.今年3月,国家统计局公布我国总人口数为139533万人,•如果以亿为单位保留两位小数,可以写成_________亿人.二、提高训练10.我国的国土面积约为9.60×106平方千米,由四舍五入得到的近似数9.6×106()A.有两个有效数字,精确到百分位B.有两个有效数字,精确到千位C.有两个有效数字,精确到万位D.有两个有效数字,精确到十万位11.按实际情况取近似值:(1)全班51人参加100米跑测验,每6人一组,问至少分成几组?(2)一辆汽车要装4个轮胎,51个轮胎能装配成几辆汽车?12.张华在体检时,量得身高为1.70米,他在登记时写的是1.7米,•测量结果与登记数是否一致?为什么?三、拓展训练13.如图,直角梯形上、下底分别是3.54厘米和5.32厘米,求阴影部分的面积.( 取3.14,精确到0.01厘米2)14.甲,乙两个同学身高都约是1.6×102厘米,但甲说他比乙高9厘米,请问有这种可能吗?若有可能,请举例说明.参考答案1.A 2.C 3.A 4.C 5.A 6.D 7.B 8.5.8×1049.13.95 10.D 11.(1)9组(2)12辆12.不一致,理由略13.5.85厘米214.有可能,举例略。
七年级数学近似数

作业
• 书第59页第6题、第64页第8题
; https:///brands/4003.html 新加坡妈妈烤包 新加坡妈妈烤包加盟;
让壹些人手悄悄の过来,对于接管这胡兰国其实并没有什么太*壹*本*读*大の障碍.陆家算上自己の家丁,少说也有三四千号人,而这胡兰国中又没有什么修行者,也没有什么武道中人,只要对他们百姓好,接管这里并没有什么难度.只是不能走漏消息,如果传到轩辕帝国の皇室去了,传到 了轩辕五十六世の耳朵里,恐怕那皇帝陛下会亲自过来了.至于这胡兰国の传说中の上千根核音炮,根汉也去简单の查证过,其实也就只有十几根而已,远没有传说の那么夸张.之所以可能会发生百年前の事情,极有可能是那洪派の洪音道人,是壹个修行高手.如果对方の修为达到了玄命境,或 者是法则境上下の话,那要毁掉十几艘战舰,打掉壹个小型の舰队,是完全有可能の.而玄命境或者是法则境の强者,要进入皇宫又是十分容易の,就是要杀掉帝国皇帝,也不是什么难事.所以才会发生百年前の事情,帝国の壹只小舰队,数千人在这里被击杀之后,帝国皇帝轩辕五十六世才会选 择妥协,因为他是惹不起那样の强者の.法阵并没有多难,根汉花了小半个小时之后,便完成了.整个胡兰国都被他用法阵给罩住了,外面の人进不去,里面の人暂时也出不来.至于何时解除这个法阵,起码要等到明年の轩辕五十六世,二百岁寿辰大典之后,根汉才会解除这个法阵.而这期间,他 将这阵石,交给了陆震,由他让陆家の人管理.胡兰国の百姓绝大部分,壹生都没有离开过这里,自然也不会乱跑了,有壹小部分の人,出去做生意换东西,根汉也让陆家分管这个事.只要他们想出去换东西,由陆家免费代换,同时可能还会多换给他们,绝不会让这里の百姓吃亏....根汉并没有立 即离开这胡兰国,而是在这里小住了四五天.自己の雕像立の很快,虽然都是壹些普通の百姓,但是这里の能工巧匠还是很多の.仅仅又四五天の功夫,他の
确定近似数精确度的有效方法

确定近似数精确度的有效方法湖北省孝感市孝南区车站中学(432011)殷菊桥纵观历年的中考题,近似数的精确度的考查出现的频率相当高,而考生在这方面的失误也不低,应引起关注。
课本上说,在实际计算时,往往对运算结果的精确度提出要求,这个要求可以是精确到哪一位,也可以是保留几个有效数字。
那么如何从这两个方面有效确定近似数的精确度呢?一确定近似数精确到哪一位一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位。
⒈用常规方法确定精确到哪一位当近似数是一般数的形式时,它最后一位在什么位上,就说这个近似数精确到哪一位。
例近似数2004最后一位在个位上,就说2004精确到个位;2004.00最后一位在百分位上,就说它精确到百分位或精确到0.01(因为最后一个0所在数位的计数单位是0.01)。
⒉用还原法确定精确到哪一位当近似数是科学记数法形式或带有计数单位形式时,先把它还原成一般数,再看原数的最后一位在哪一位上就说这个近似数精确到了哪一位。
例如近似数8.67×105=867000,还原后7在千位上,所以它精确到千位;近似数8.03万=80300,还原后3在百位上,所以它精确到百位。
对于8.67×105和8.03万这两个数,不能因为8.67和8.03中的7和3在百分位上而说它们精确到百分位。
对于带有计数单位的数8.03万也可不还原,因为8、0、3所在数位依次是万位、千位、百位,故8.03万精确到百位。
⒊根据精确到哪一位取近似值用四舍五入法按精确到哪一位取近似值时,先找到相应的数位,再将其后紧跟的一位数字四舍五入取近似值。
例如,把0.12345精确到0.001只考虑万分位上的数,得0.123。
当把一个数精确到整数位时,可以先四舍五入,再用科学记数法表示成a×10n(1≤a<10,且n为整数),例如30350(精确到百位)≈30400=3.0400×104,然后将百位4后面的0去掉,得30350≈3.04×104。
《近似数》数学教案

《近似数》数学教案《近似数》数学教案1教材分析“准确数和近似数”是义务教育课程标准实验教科书,浙教版七年册第二章的内容。
教材通过一则科技报道引入准确数和近似数的概念,在学生已有的运算能力的基础上,给出近似数的精确度的两种表示方式,及近似值的取法。
准确数和近似数是运用有理数进行实际计算所必需的,本节课也培养了学生用所学的数学知识解决,生活中的数学问题的能力,让学生体验到生活中无处不存在准确数和近似数。
学生分析学生往往存在着一些生活经验,这些生活经验是学生学习的基础,但其中也有一些是错误的,必须让学生在正确区分准确数和近似数的基础上,明确近似数的角度有两种表示方式以及学会近似值的取法。
教学中要及时了解学生的认知程度,以便调整教学。
教学目标通过实例经历近似数和准确数概念的产生过程。
了解近似数的精确度的两种表示方式。
能说出由四舍五入得到的有理数的精确位数和有效数字。
会根据预定精确度取近似值。
教学重点近似数的两种表示方式及近似值的取法教学难点近似数所表示范围及有效数字如何表示近似数的精确度教辅工具投影仪、卷尺、“神舟五号飞船”图片、投影片6张教学设计思路本节课首先从学生熟悉的生活情境出发引入数学概念。
通过近似数在生活中的应用,激发学生主动学习的欲望,然后通过老师讲解、学生练习,使学生学会近似数的两种表示方式及近似值的取法,最后再配以练习巩固,让学生很自然地接受这一部分知识。
教学流程一、实践操作,引入课题问:我想知道我们教室里有多少张课桌?黑板长为多少?我国人口总数为多少?你们能帮老师解答吗?(学生分小组进行合作操作、讨论)[设计说明:通过学生亲自操作,引起学生的兴趣]问:上面所出现的数据中,哪些跟实际完全符合,哪些跟实际是接近的?(学生回答)板书:像这样与实际完全符合的数称为准确数像这样与实际接近的数称为近似数通过测量或估计得到的都是近似数板书课题:准确数和近似数[设计说明:通过实例使学生充分体验准确数和近似数的概念的产生是由于人们生活和生产实践的需要]二、导入新知师:21世纪进入太空是很多人的梦想,同学们有想过吗?(学生开心的各抒己见)展示:“神舟五号飞船”图片投影片A:“神舟五号飞船总长9.2米,总质量为7790千克,装有52台发动机,在太空中,该飞船大约每90分绕地球一圈,其间要经受180℃的温差考验。
七年级数学准确数和近似数

1.57
近似数1. 57m所表示的范围 是:表示实际身高大于或等 于1. 565m, 而小于1. 575m 的数.
1.565
近似数38万所表示的范围:大于或等于37.5万, 而小于38.5万的数.
单位:万 km
37
37.5
38
38.5
39
:由四舍五入得到的近似数,从左边第 一个不是零的数字起,到末位数字为止的所有数 字,都叫这个数的有效数字。
比一比:看谁反应快
思考,并回答问题: 用四舍五入法,按要求对各数取近似数
130.06 460215 7.9122 47155 0.6328 (( 保留 保留 (( 精确到百位 精确到 精确到个位 4 3 个有效数字 个有效数字 0.01) )) ))
近似数
130.1 0.63 8 4.72万 4.60 或 ×4.72 105 ×104
1、小明和小芳都约为1.6米,但小明 说:“我比小芳高5厘米”,请你想 一想,有这种可能吗?
(有这种可能性,如小明身高1.62米,小芳 身高1.57米,这时小明比小芳高5厘米。) 2、每条船能载六人,有31人需几条船? (6条)
课堂小结:
一、精确度的两种形式(重点):
1、四舍五入法表述 2、有效数字的个数
Hale Waihona Puke 为止,4、近似数0.9060精确到百分位, 有4个有效数字. (
×)
四:按括号里的要求,用四舍五入法对下列各数 取近似值。
(1)46.79(精确到十分位) (3)0.010010(保留四个有效数字) (4)8465300(保留三个有效数字) 五:圆周率π=3.14159265…取近似值3.14,是精确到 哪一位? 有 几个有效数字?取近似值3.1416呢?
近似数与有效数字

165cm 160cm 请你观察小明的身高大约是 多少厘米. 163厘米 163.1厘米
这两个数据有什么不同?
155cm
精确度--表示一个近似数近似的程度
表示精确度有两种方法:四舍五入法和有效数字法
阅读理解
对于一个近似数,从左边第一个不是0的数字起,到精确到的 数位止,所有的数字都叫做这个数的有效数字. 如:按四舍五入法取10. 1046的近似数.精确到百分位是10.10, 它有四个有效数字:1,0,1,0.
⑹ 0.407
⑺ 0.4070
⑻ 2.4千
⑼ 103万
.
⑽ 150
解:⑴43.82,精确到 百分位(或精确到0.01) 有四个有效数字 4,3,8,2
⑵0.03086,精确到 十万分位(或精确到0.00001) .
有四个有效数字 3,0,8,6 ⑶2.4,精确到 十分位(或精确到0.1)
.
有二个有效数字 2,4 ⑷2.4万,精确到 千位 . 有二个有效数字2,4 ⑸2.48万,精确到百位 .
B. 李刚家共有4 口人 C. 我国的人口约有12 亿
D. 书桌的长度是0.85 米
2、下列数中不能由四舍五入得到近似数38.5的数是( B ) A. 38.53 B. 38.538.5099
; https:///u/5044679351
开口发话救咯秦顺儿の急。听到王爷底气十足の发话,三各人这才发现爷居然站在帐子门口!这是啥啊情况?众人先是被秦顺 儿打咯壹各措手不及,现在又被突然出现の王爷搞得丈二和尚摸不着头脑。可是不管这是啥啊情况,见到爷之后,第壹件事情 是请安,这是雷打不动の规矩。于是水清和玉盈两各人赶快下咯炕,快步走上前来,和吟雪壹起向王爷请咯安。因为他要撇清 与水清の关系,因为他不想让玉盈误会他和水清有啥啊不清不楚,因此他从来不曾进过她の帐子,但现在已经误闯误撞地进来 咯,只好故作镇定地坐到咯主位。吟雪赶快去奉茶,秦顺儿早就退到咯帐外,水清和玉盈两人老老实实地侧立壹旁。望着眼前 并排而立の两姐妹,他真不知道该说些啥啊才好。两各人全都是披头散发,衣衫不整の样子,这是极为失礼の行为,理应受到 他の严厉训斥。可是他现在根本顾不上责备她们の失礼,因为她们岂止是衣衫不整,两人穿の全都是中衣!第壹次见到除自己 女眷以外の两各诸人穿成这各样子站在他の面前,令他不由得窘迫和局促起来。可是壹想到玉盈,他又对她恨得牙根痒痒。他 这么误打误撞地进到水清の帐子里来,还不是为咯急于知道她去咯哪里?他被玉盈吓怕咯!刚才秦顺儿禀报年仆役不在の时候, 他以为她这壹次又是不辞而别!他当即就急咯壹身の汗!这茫茫の大草原她能去哪里?迷咯路怎么办?遇到野兽豺狼怎么办? 况且这手还伤着!难道是因为昨天爷没有来得及关心她の伤情而生咯爷の气吗?当他刚刚在帐外听到里面有诸人の尖叫声,他 不但没有惊慌,反而心中分外地踏实,屋里有人,玉盈还在!这就足够咯,只要玉盈没有走,啥啊都好说。见到玉盈毫发无损 の样子,他更是放咯壹百各心。不过,下壹各问题又急急地出现在他の脑海,他要尽快解释壹下为啥啊会发生误闯香闺の事情。 香闺?也不算用错咯词,三各大姑娘家住の帐子,不是香闺是啥啊!在他壹会儿尴尬窘迫,壹会儿气急败坏の心情交替支配下, 沉寂咯半响,才终于稳定下情绪,用他那壹贯沉着冷静、波澜不惊の低沉嗓音开口说道:“爷刚刚是让秦顺儿来看看年仆役の 伤势如何,没有别の意思。”玉盈壹听爷是因为她而来の,赶快回咯话:“回爷,玉盈の伤已经好得差不多咯,没有大 碍。”“没有大碍就好。”其实他还想亲自查看壹下她の手,看看她说の是不是真话,她总是避重就轻,前天看到那三各硕大 の水泡,他就知道伤势有多么の严重。可是,现在当着水清の面,他怎么可能拉起她の手?虽然他只是想看看玉盈の伤势恢复 得如何,将来是否会落下疤痕而已。第壹卷 第278章 烂肉直到这各时候,王爷才充分意识到咯水清の存在:这各年氏怎么这 么碍眼!她难道不会像秦顺儿那样有点儿眼力劲儿躲到壹边去吗?咦?不对呀,她怎么会站在这里?这各时间她不是应该在额 娘那里立规矩吗?“你不好好地侍奉额娘,竟敢偷偷跑回来躲清闲来咯?”“回爷,没有,妾身没有偷偷躲回来,是额娘特意 发话,允许妾身回来の。”“啥啊?是额娘要你回来?为啥啊?额娘那里正缺人手,你怎么好意思在这里躲清闲?”水清壹听 这话,心里很是愤愤不平:连德妃娘娘都同意她回来,怎么爷还有意见?看来在爷の眼中,自己可真就是壹各白使唤の宫女呢。 但是跟爷是没有任何道理可讲,水清深知这各道理,于是也没有继续纠缠,只是据实回复道:“回爷,是这样,今天,今天, 二十三小弟妹,小弟妹向额娘说起爷の,爷の侍妾の事情„„”水清嘁嘁哎哎地起咯壹各头。“啥啊侍妾!”王爷壹听就恼 咯!玉盈是她の姐姐,怎么能是侍妾!“就是玉盈姐姐,啊不,就是,二十三小弟妹误以为玉盈姐姐是爷の侍妾,然后就跟额 娘说起来。”水清也不知道怎么说清楚这各名词,慌不择言。“额娘怎么说?”王爷倒不怕额娘啥啊,他是担心玉盈の名声和 名节,万壹这件事情闹大咯,他最对不起の就是玉盈。他爱她,他也会娶她,但是他要玉盈光明正大、明媒正娶地成为他の福 晋,嫡福晋现在是不可能咯,但最少必须是侧福晋!壹听爷有些生气,水清也对于自己将姐姐说成是侍妾很内疚,情急之下, 随口答道:“额娘说,说,反正肉是烂在自家锅里,总比便宜咯外人强。”水清当时脑子在走神儿,根本没有仔细听德妃の那 壹套苦口婆心の长篇大论,只是到最后の时候才听咯这壹耳朵,正好也就是这句话,她还稍微有那么点儿印象。王爷壹听这话, 当时差点儿没把鼻子给气歪咯!这叫啥啊话!额娘分明是在奚落她,笑话她,对她冷嘲热讽,她可倒好,怎么连好赖话都听不 出来?哪句话都没有记清楚,怎么就这句记得这么牢靠?这各年氏,心机、手段那么多の壹各人,怎么这各时候又愚蠢成这各 样子!不过,现在不是讨论她の愚蠢问题,而是要解决这各消息如何迅速散播出去の问题。这各情况确实打咯王爷壹各措手不 及,才刚刚请咯胡太医,他这各“侍妾”の消息居然就像长咯腿似地,连二十三小弟妹都知道,还告诉咯额娘!这到底是啥啊 回事儿?塔娜当然是从二十三小格那里知道の,而二十三小格是八小格の左膀右臂。年家与八小格の交情和渊源极深,壹定是 水清将消息泄露给咯八小格。再狡猾の狐狸也会露出尾巴,这壹次终于让他抓住咯年家与八小格壹党串通壹气、私传情报の证 据!面对这各令他万分寒心の诸人,王爷连愤怒の心情都懒得再有,沉思良久,才终于又开口
确定近似数精确度的有效方法

确定近似数精确度的有效方法湖北省孝感市孝南区车站中学(432011)殷菊桥纵观历年的中考题,近似数的精确度的考查出现的频率相当高,而考生在这方面的失误也不低,应引起关注。
课本上说,在实际计算时,往往对运算结果的精确度提出要求,这个要求可以是精确到哪一位,也可以是保留几个有效数字。
那么如何从这两个方面有效确定近似数的精确度呢?一确定近似数精确到哪一位一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位。
⒈用常规方法确定精确到哪一位当近似数是一般数的形式时,它最后一位在什么位上,就说这个近似数精确到哪一位。
例近似数2004最后一位在个位上,就说2004精确到个位;2004.00最后一位在百分位上,就说它精确到百分位或精确到0.01(因为最后一个0所在数位的计数单位是0.01)。
⒉用还原法确定精确到哪一位当近似数是科学记数法形式或带有计数单位形式时,先把它还原成一般数,再看原数的最后一位在哪一位上就说这个近似数精确到了哪一位。
例如近似数8.67×105=867000,还原后7在千位上,所以它精确到千位;近似数8.03万=80300,还原后3在百位上,所以它精确到百位。
对于8.67×105和8.03万这两个数,不能因为8.67和8.03中的7和3在百分位上而说它们精确到百分位。
对于带有计数单位的数8.03万也可不还原,因为8、0、3所在数位依次是万位、千位、百位,故8.03万精确到百位。
⒊根据精确到哪一位取近似值用四舍五入法按精确到哪一位取近似值时,先找到相应的数位,再将其后紧跟的一位数字四舍五入取近似值。
例如,把0.12345精确到0.001只考虑万分位上的数,得0.123。
当把一个数精确到整数位时,可以先四舍五入,再用科学记数法表示成a×10n(1≤a<10,且n为整数),例如30350(精确到百位)≈30400=3.0400×104,然后将百位4后面的0去掉,得30350≈3.04×104。
近似数与有效数字

近似数与有效数字摘要:近似数与有效数字是中考必考内容,本文介绍了什么是近似数及有效数字,已知一个近似数如何判断其精确度及有效数字,如何按要求求近似值等内容。
关键词:判断;精确度;误区近似数与有效数字是中考必考内容,其具有很广泛的实际应用,但有些同学在学完这些知识后感觉含糊不清,下面对常出现的问题给于作答。
1、近似数和有效数字的有关概念(1)近似数:与实际结果非常接近的数,称为近似数,在实际问题中,不仅存在大量的准确数,同时也存在大量的近似数,出现近似数有两点:一是完全准确是办不到的,如:我国的陆地面积约有960万平方公里;二是有时是没有必要的,如:买1000克白菜有时可能多一点,也可能少一点。
(2)有效数字:使用近似数,就是一个近似程度的问题。
一般地,一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位。
这时,从左边第一个不是零的数字起,到精确的数字止,所有的数字,都叫做这个数的有效数字。
如:小亮的身高为1.78米,这个近似数1.78精确到百分位,它有三个有效数字:1、7、8.(3)熟悉精确度的两种形式,一是精确到哪一位,二是保留几个有效数字,它们是不一样的。
精确到哪一位,可以表示出误差绝对值的大小,如在测量楼的高度时,精确到0.1米,这说明结果与实际误差不大于0.05,而有效数字则可以比较几个近似数中哪一个更精确。
如:1.60就比1.6更精确一些。
2、近似数的判断(1)小范围可数的数据一般为精确的,其它加上人为因素的一般是近似的,如测量得到的数据。
例:“小花班上有50人”中的50就是精确数,而“小明的身高1.64米”中的1.64是近似数,还如:“小丽体重45公斤”中的45也是近似数。
(2)语句中带有“大约,左右”等词语,里面出现的数据是近似数。
例:“某次海难中,遇险人数大约3000人”中的3000是一个近似是数。
3、已知一个近似数如何去判断其精确度和有效数字(1)普通形式的数,这种数能直接判断。
近似数和有效数字

三、近似数的有效 数字
有效数字:一个近似数,从左边第一
个非0的数字起,到末位数字止,所有 的数字都是这个数的有效数字.
2, 5 两个 如: 0.025有_______有效数字:________. 1, 5, 0, 0 4个 1500有_______有效数字:________. 1, 0, 3 3个 0.103有_______有效数字:________.
(3)1.804(保留2个有效数字)为1.8 (4)1.804(保留3个有效数字)为1.80
(2) 30 435(保留3个有效数字)为3.04×104
实际应用
⑴ 我校初一年级415名师生,想租 用45座 的客车外出秋游,问:应该租用多少辆客车? 解:因为415×45=9.222 “进一法” 所以应该租用10辆客车。 ⑵ 工人师傅把一根100厘米的圆钢锯短, 用来做6厘米长的零件,可加工多少件? 解:因为100 ÷6=16.666 “去尾法” 所以可加工16件。
二、关于精确度问 题
近似数与准确数的接近程度, 按四舍五入法对圆周率π取近似数时,有 可以用精确度表示.如,前面的五百 π≈ 3 (精确到 个位 ) 是精确到百位的近似数,它与准确 π≈3.1 (精确到 0.1 ,或叫做精确到 十分位 ) π≈3.14 (精确到 0.01 ,或叫做精确到 百分位 ) 数513的误差为13.
0.001 千分位 π≈3.142 (精确到____,或叫做精确到______) 0.0001 万分位 π≈3.1416 (精确到____,或叫做精确到______) …… 一般地,一个近似数,四舍五入到哪一 位,就说这个近似数精确到哪一位。
想一想
在测量同学的身高时,如果精确 到0.01m, 王豪的身高是1.58m,你知 道他实际身高是多少吗? 1.575 m≤他实际身高<1.585m 如果精确到0.1m,王豪的身高 又是多少? 他实际身高为1.6m
初中数学近似数和平均数知识点总结及练习

初中数学近似数和平均数知识点总结及练习近似数一个数与准确数相近,且比准确数略多或略少些,这一个数称之为近似数。
一个近似数四舍五入到哪一位,那么就说这个近似数精确到哪一位,从左边第一个不是0的数字起到精确的数位止的所有数止。
如:我国的人口无法计算准确数目,但是可以说出一个近似数.比如说我国人口有13亿,13亿就是一个近似数。
有效数字与实际数字比较接近,但不完全符合的数称之为近似数。
对近似数,人们常需知道他的精确度。
一个近似数的精确度通常有以下两种表述方式:(1)用四舍五入法表述。
一个近似数四舍五入到哪一位,就说这个近似数精确到哪一位。
(2)另外还有进一和去尾两种方法。
用有效数字的个数表述。
由四舍五入得到的近似数,从左边第一个不是零的数字起,到末位数字为止的数所有数字,都叫做这个数的有效数字。
精确度近似数与准确数的接近程度,可以用精确度表示。
(1)一个近似数四舍五入到哪一位,就说这个近似数精确到哪一位;(2)规定有效数字的个数,也是对近似数精确程度的一种要求。
有效数字规则有效数字注意:①近似数的精确度有两种形式:精确到哪一位;保留几个有效数字;②对于绝对值较大的数取近似值时,结果一般用科学计数法来表示,如:8 90 000(保留三个有效数字)的近似值,得8 903 000≈8.90×106。
③对带有计数单位的近似数,如2.3万,他有两个有效数字:2、3,而不是五个有效数字。
有效数字的舍入规则:1、当保留n位有效数字,若后面的数字小于第n位单位数字的0.5就舍掉。
2、当保留n位有效数字,若后面的数字大于第n位单位数字的0.5 ,则第位数字进1。
3、当保留n位有效数字,若后面的数字恰为第n位单位数字的0.5 ,则第n位数字若为偶数时就舍掉后面的数字,若第n位数字为奇数加1。
如将下组数据保留三位45.77=45.8 43.03=43.038.25=38.2 47.15=47.2近似数规则近似数的混合运算,可按运算顺序和近似数的计算法则分步计算,但中间运算的结果要比最后结果多取一位数字。
近似数和有效数字

D、2.600 < α≤2.605 用进一法 6 、某校学生 320 人外出参观,已有 65 名学生坐校车出 发,还需要几辆45座的大巴( C ) A、4辆 B、5辆 C、6辆 D、7辆
7、做一个零件需要整材料钢精6厘米,现有15厘米的钢精10 根,一共可做零件多少个( B ) 用去尾法
A、15个
B、20个
快乐套餐
A、2个 2、近似数2.864 A、千分位 B、3个
练一练,你学会了吗?
1、四舍五入得到的近似数0.03050的有效数字有( C ) C、4个 D、5个
104精确到( D ) C、千位 D、十位
B、百位
3、保留三个有效数字得到17.8的数是( B ) A、17.86 B、17.82 C、17.74 D、17.88
课堂回顾
一、精确度的两种形式: 1、精确到哪一位 2、有效数字
二、给一个近似数,正确指出精确到哪一位?有哪几个有效数字。
三、几点注意: 1、两个近似数1.5与1.50表示的精确程度不一样。 2、两个近似数6.3万与6.3精确到的数位不同。 3、确定有效数字时应注意:①从左边第一个不是0的数字起。 ②从左边第一个不是0的数字起,到精确到的数位(即最后一位四 舍五入所得的数)止,所有的数字。 4、在写出近似数的每个有效数字时,用“,”号隔开。 如:38.006有五个有效数字,3,8,0,0,6,不能写成38006.
⑹七年级二班有56人。
π = 3.1415926•••
例1 小红量得课桌长为1.025米,请按下列要求取 这个数的近似数:
(1)四舍五入到百分位;
解:(1)四舍五入到百分位为1.03米;
(2)四舍五入到十分位;
解:(2)四舍五入到十分位为1.0米;
近似数与有效数字

能力层面训练
一、填空: 填空: 个有效数字, 1、近似数18.07 有 四 个有效数字,精确到百分 位. 、 2、近似数0.03809 有 四 个有效数字,精确到 十万分 位. 、 个有效数字, , 3、近似数8.6 万精确到 千 位,有效数字是 8,6 、 二、判断: 判断: 1、3.008是精确到百分位的数 、 是精确到百分位的数. 是精确到百分位的数 2、近似数3.80和近似数 的精确度相同 、近似数 和近似数3.8 和近似数 的精确度相同. 3、近似数6.090的有效数字是 、0、9、0. 、近似数 的有效数字是6、 、 、 的有效数字是 ( × ) ( ) .
精确度: 精确度:
利用四舍五入法取一个数的近似数时, 利用四舍五入法取一个数的近似数时,四舍 五入到哪一位,就说这个近似数精确到哪一位。 五入到哪一位,就说这个近似数精确到哪一位。
有效数字: 有效数字:
对于一个近似数,从左边第一个不是0的数字 对于一个近似数,从左边第一个不是0 到精确到的数位止, 起,到精确到的数位止,所有的数字都叫做这个 数的有效数字(significant 数的有效数字(significant digits).
据中国统计信息网公布的2000年中国 例4 据中国统计信息网公布的 年中国 第五次人口普查资料表明, 第五次人口普查资料表明,我国的人口总数 人 为1 295 330 000人。请按要求分别取这个数 的近似数, 的近似数,并指出近似数的有效数字 。 (1)精确到百万位; )精确到百万位; (2)精确到千万位; )精确到千万位; (3)精确到亿位; )精确到亿位; (4)精确到十亿位。 )精确到十亿位。
由此可见, . 比 的精确度高 由此可见,1.50比1.5的精确度高
课堂小结:
近似数与有效数字

课后作业
教科书P57-6 课后选作题 1.下列由四舍五入得到的近似数各精确到哪一位? 各有几位有效数字? (1)32; (2)17.93; (3)0.084; (4)7.250; (5)1.35×104; (6)0.45万; (7)2.004; (8)3.1416. 2.23.0是由四舍五入得来的近似数,则下列各数 中 哪些数不可能是真值? ①23.04 ②23.06 ③22.99 ④22.85
;
/forum-nanjing-1.html 南京夜场招聘 南京夜总会招聘 南京ktv招聘
orz14msr
易,但要让人们都相信是他们在造谣,在短期内却是办不到的。而且,咱们倘若真这样做了,也只会导致与他们之间的结怨更深。至于说他们 的好话,那倒也不必。我是想,咱们不妨与这彭掌柜的私下里协商,研究出一个两全其美的解决办法来。这样,两家的铺子就可以各赚各的钱, 甚至还可以互相扶持对方的发展呢。如此一来,岂不是化敌为友了嘛!”李老乡说:“和则共荣,斗则俱伤,这个道理倒是对的!可要操作起 来,又该从哪里下手啊?”耿正说:“这就是需要咱们尽快商量确定的大事了。看起来,咱们得在已经成功经营的商品上做一些让步了;更确 切地说,是彼此之间的让步。这是因为,他们也得给咱们让出一些来,好让大家都有盈利的空间!”于是,老乡四人如此这般地认真商讨了一 番。当意见达到一致之后,决定由年轻的耿正出面,次日上午去约见“彭记丝绸行”彭显贵掌柜的。事实上,大凡造谣生事者,其内心深处却 也是很虚的。他们也都担心事情一旦败露,反倒让自己无脸见人。当然,那些就连自己的脸面也不顾及的人,就另当别论了。再则,倘若是稍 微有一些良心的人,还会或多或少地为自己的所作所为感到亏心或愧疚,因此间也愿意想办法进行一些亡羊补牢式的弥补。上述这位扮演了不 光彩角色的彭掌柜的当时就鉴于这两者之间。尽管由于“昌盛丝绸行”受困于自己店铺里伙计们制造的那些个谣言而暂时性地经营受挫,从而 使得自己店铺里的生意最近几天有了明显起色,但是他心里却也非常明白,这并不是一个长远之计;一旦日久了谣言被彻底戳穿,反倒会对自 己更加不利!又想起父亲在世时经常提醒他的有关‘诚信经营’的那些个祖训,越想越不是个滋味儿,反倒终日里如坐针毡了。如此,铺子也 无心照料,大多数的时间里都呆在门面店铺后面的家中苦心冥想,思考着下一步的对策。但无奈却是越想越没辙,越没辙就越郁闷,近两日已 经是茶饭不思了。那一日上午,正当他一个人坐在小院儿里的泡桐树下苦苦熬煎时,一个伙计慌慌张张地跑了进来,说:“彭掌柜的,不好了, ‘昌盛丝绸行’的耿二掌柜的来了,说是要见您哪!”由于事先没有任何思想准备,所以,这彭显贵掌柜的当时听了这话,且看到这个伙计如 此惊慌的样子,也不免有些吃惊。不过,他可不想让伙计看出来自己的惊慌失措,于是就故作镇静,假装漫不经心地问:“只他一人吗?可像 一只斗架的公鸡?”来报信的伙计说:“只他一个人,倒还文质彬彬的样子呢!”彭显贵听伙计如此说,虽说稍微放心了一些,但心里还是没 有底,再则也不想轻易放下自己的那一副臭架子。于是,他故意装出一副很不屑的样子,说:“哼,小娃子一个,想来干啥呢。告诉他,我忙 着呢,不见!”把这个来报信的伙计
准确数和近似数教案

课型:新授课执笔:胡小丽审核:郭丽珍、郑晓燕、李洁【学习目标——你知道要学什么吗】1.准确数与近似数的概念: __________________________________ 2.近似数的精确度的两种表示方式: _______3.有效数字的概念: _______________________________________ 【学习过程——让我们共同来探究】1.准确数与近似数(1)问:南方网讯2 月21 日,北京市房山区韩村河高科技蔬菜园区管理人员在观察番茄的生长情况。
韩村河高科技蔬菜园区通过高新技术培育出20 株高产番茄树,其中最大的一株高达2 米,树冠枝条面积达25 平方米,结果15000个左右,番茄树伸出的数百个枝条如葡萄般爬满支架,个个红透的西红柿垂挂下来,格外壮观。
(编辑:姜志)上面所出现的数据中,哪些跟实际完全符合,哪些跟实际是接近的?总结归纳:准确数的定义__________________________________________________ 近似数的定义__________________________________________ 通_ 过测量或估计得到的都是近似数(2)我国人口总数为12.9533 亿某词典共有1234 页初一( 4)班有56 人,买门票大约需要600元上面叙述中的各数,哪些是准确数?哪些是近似数?2.下列叙述中的各数,哪些是准确数?哪些是近似数?(1) 教室里有56 名同学;(2) 小明的身高为1.57m;(3) 我国的国土面积大约是960 万km2;(4) 月球和地球之间的平均距离大约是38 万km;(5) 某本书的定价是4.50 元;3.精确度与有效数字。
(1) 身高1.57 米是千分位数字四舍五入到百分位的结果,它精确到百分位 ( 或精确到0.01 )近似数38 万是千位数字四舍五入到万位的结果,它精确到万位(2) 身高1.57 米表示小明实际身高在什么范围内呢?(3) 近似数38 万表示的范围为?用有效数字的个数来表述一个近似数的精确度,由四舍五入得到的近似数从左边第一个不是零的数字起,到末位数字为止的所有数字,都叫做这个数的有效数字。
准确数和近似数浙教版修改

2、两个近似数6.3万与6.3精确到的数位不同。
3、确定有效数字时应注意:①从左边第一个不是0的数字起。 ②从左边第一个不是0的数起,到精确到的数位(即最后一位四舍 五入所得的数)止,所有的数字。 4、在写出近似数的每个有效数字时,用“,”号隔开。 如:38.006有五个有效数字,3,8,0,0,6,不能写成38006.
2018/9/19
南方网讯 2 月 21 日,北 京市房山区韩村河高科技 蔬菜园区管理人员在观察 番茄的生长情况。韩村河 高科技蔬菜园区通过高新 技术培育出 20株高产番茄 树,其中最大的一株高达 2米,树冠枝条面积达25.5 平 方 米 , 结 果 15000 个 左 右,番茄树伸出的数百个 枝条如葡萄般爬满支架, 个个红透的西红柿垂挂下 来,格外壮观。(编辑: 1 哪里有数,哪里就有美 姜志)
应该检查时间,做好幻灯链接.
2018/9/19 哪里有数,哪里就有美 11
练习:选择:
⑴下列近似数中,精确到千分位的是( B ) A. 2.4万 B. 7.030 C. 0.0086 D. 21.06 ⑵有效数字 的个数是( B )
A. 从右边第一个不是0的数字算起.
B. 从左边第一个不是0的数字算起. C. 从小数点后的第一个数字算起. D. 从小数点前的第一个数字算起 ⑶近似数0.00050400的有效数字有( C )
A. 3个
B. 4个
C. 5个
D. 6个
2018/9/19
哪里有数,哪里就有美
12
近似数与精确度 老师问小明和小亮的年龄,他们俩都说:“今年13岁了”.那么他 们俩谁大呢?要比较他们俩的年龄的大小,必须知道他们俩的出生 月份.如果出生月份也相同,就必须知道他们俩的出生日,如果他们 俩个是双胞胎兄弟,要比较他们的年龄,出生时间就必须准确到几 点几分.13岁只是时间的近似值,并不精确.平时我们完全没有必要 将年龄说成几岁几月几天这样准确,只说年龄的一个近似值就可以 了. 但对有些问题,我们必须将数值确定得更准确才行.如奥运会 百米跑的成绩,只精确到1秒是不行的,往往要精确到0.01秒才能分 出运动员的名次. 在实际问题中遇到的数,大多是近似数.至于这些近似数精确 到什么程度,要根据实际问题的需要而定.
近似数的精确度 分数指数幂及运算

近似数的精确度分数指数幂及运算
在数学中,我们经常会遇到需要进行近似数的计算,这时候我们需要考虑到近似数的精确度。
近似数的精确度是指我们所得到的近似数与真实值之间的误差大小。
在实际应用中,我们需要根据具体情况来确定近似数的精确度,以保证计算结果的准确性。
在分数的运算中,我们需要注意分母的大小,因为分母越大,分数的精确度就越高。
例如,1/2和1/1000相比,1/2的精确度要高得多。
在进行分数的加减乘除运算时,我们需要先将分数化为相同的分母,然后再进行运算。
这样可以避免分母不同导致的误差。
指数幂是数学中常见的运算方式,它可以用来表示一个数的幂次方。
例如,2的3次方等于8,即2³=8。
在进行指数幂的计算时,我们需要注意底数和指数的大小关系。
如果底数比较大,指数比较小,那么我们可以直接计算出结果。
但如果底数比较小,指数比较大,那么我们需要使用科学计数法来表示结果,以保证精确度。
在运算中,我们还需要注意数值的精确度。
例如,当我们进行小数的加减乘除运算时,我们需要注意小数点后的位数,以保证计算结果的精确度。
如果小数点后的位数太多,我们可以使用四舍五入的方法来保留合适的位数。
在数学中,我们需要根据具体情况来确定近似数的精确度,以保证计算结果的准确性。
在分数、指数幂和运算中,我们需要注意数值
的大小关系和精确度,以避免误差的产生。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
近似数精确度的两种形式
任何一个近似数,都可以用精确度来表示它与准确数的接近程度。
一般地,一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位。
这时,从左边第一个不是0的数字起,到末位数字止,所有数字都是这个数的有效数字。
不难发现,描述一个近似数的精确度有两种形式:一是精确到哪一位;二是保留几个有效数字。
那么,怎样确定一个近似数的精确度?
一、近似数是小数或整数
例1 下列由四舍五入得到的近似数,各精确到哪一位,各有哪几个有效数字?
(1)10.45 (2)78 (3)0.01020
分析:这些近似数是小数或整数,其精确度的确定,应从精确到哪一位和有效数字的基本概念入手。
在确定有效数字时,0不能多算也不能少算。
以从左至右第一个不是0的数字为界,左边的0不算,右边的0都要算。
解:(1)10.45,精确到百分位或精确到0.01,有4个有效数字:1,0,4,5。
(2)78,精确到个位或1,有两个有效数字:7,8。
(3)0.01020,精确到十万分位或精确到0.00001,有4个有效数字:1,0,2,0。
二、带有计数单位的近似数
例2 下列由四舍五入得到的近似数,各精确到哪一位,各有哪几个有效数字?
(1)5.8万(2)10亿(3)87.01千
分析:这些近似数都带有计数单位,其有效数字的确定与计数单位无关。
在确定精确到哪一位时,若计数单位前面是整数,它就精确到计数单位;若计数单位前面是小数,则先将近似数还原成用1作计数单位的数,再根据近似数的位数,从最高位数起,数到哪个数位,就精确到哪一位。
解:(1)5.8万(即58000),精确到千位,有两个有效数字:5,8。
(2)10亿,精确到亿位,有两个有效数字:1,0。
(3)87.01千(即87010),精确到十位,有4个有效数字:8,7,0,1。
三、用科学记数法表示的近似数
例3 下列由四舍五入得到的近似数,各精确到哪一位?各有哪几个有效数字?
分析:用科学记数法表示的近似数,确定它们的有效数字时,只看不是10的幂的数的有效数字,确定该数精确到哪一位时,可把10的幂看成计数单位或把近似数还原成不用科学记数法表示的数,再根据近似数的位数,从最高位数起,数到哪个数位就精确到哪一位。
解:(即12),精确到个位,有2个有效数字:1,2。
(2)(即5070000),精确到万位,有3个有效数字:5,0,7。
(3)(即3213.4),精确到十分位,有5个有效数字:3,2,1,3,4。
