专题:对勾函数(汇编)
对勾函数绝对经典
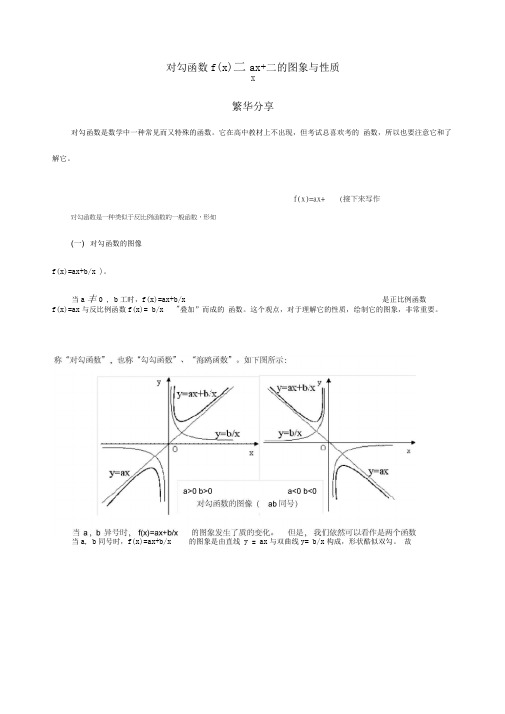
对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+ (接下来写作对勾函数f(x)二ax+二的图象与性质X繁华分享对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像f(x)=ax+b/x )。
当a丰0 , b工时,f(x)=ax+b/x 是正比例函数f(x)=ax与反比例函数f(x)= b/x "叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a, b同号时,f(x)=ax+b/x 的图象是由直线y = ax与双曲线y= b/x构成,形状酷似双勾。
故加”而成。
(请自己在图上完成:他是如何叠加而成的。
ab异号)般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二)对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,g = 是2耐当且黯心扌时取等号),此时卞=卡。
当x<0时,f(£ = 3龙十g玉一2耳旺律且尽当= £时IR等号卜此时耳=-皆。
即对勾函数的定点坐标:ulr2,-2 vabA;(三)对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
定义域:図£ = 0% 值域;{y|y >厶飯或v< -2VaS)(四)对勾函数的单调性对于函数f(x)= ax-1-单调增区间’fl U 卡卄);单调减2>(五)对勾函数的渐进线由图像我们不难得到:对于函它的渐进线有两離"Xiy = is;F =0;X(六)对勾函数的奇偶性对勾函数在定义域内是奇函数,利用对号函数以上性质,在解某些数学题时很简便,下面举例说明:1、求函数yx2 2x 4 .x22x 的最小值。
对勾函数详细分析

对勾函数详细分析对勾函数,又称为Heaviside函数或者单位阶跃函数,是一种常见的数学函数。
它在控制系统、信号处理和电路分析等领域具有广泛的应用。
在数学上,对勾函数可以通过以下方式定义:H(x)=0,x<0H(x)=1/2,x=0H(x)=1,x>0其中,H(x)表示对勾函数,x为自变量。
从定义可以看出,对勾函数在x小于0时取0,在x等于0时取1/2,在x大于0时取1对勾函数在数学上的精确定义可以依赖于Laplace变换或者Fourier 变换等数学工具,用于解决微积分和微分方程等问题。
在实际应用中,对勾函数通常以数学形式存在,用于描述信号的开关行为。
在控制系统中,对勾函数可以表示系统的阶跃响应。
阶跃响应是指当输入信号为一个单位阶跃函数时,系统所产生的响应。
对勾函数可以帮助分析系统的稳定性、零极点和频率响应等性质。
在信号处理中,对勾函数可以用于描述数字信号的采样和量化过程。
当对一个连续信号进行采样时,可以将采样函数表示为对勾函数。
对勾函数在离散时间中具有单位阶跃响应的特性,可以用于分析信号的频谱和滤波等问题。
在电路分析中,对勾函数可以用于描述开关电路的动态响应。
开关电路通常包含开关元件和电容、电感等被控元件。
对勾函数可以帮助确定电路的稳态和暂态响应,并且可以用于分析电路中的信号传输、噪声和功耗等问题。
此外,对勾函数在概率论和统计学中也有应用。
例如,对勾函数可以用于计算累积分布函数(CDF)和概率密度函数(PDF)。
对勾函数可以将离散随机变量转化为连续随机变量,以进行概率计算和数值模拟等工作。
对勾函数具有一些重要的性质。
首先,它是一个连续函数,但不是光滑函数。
它在x=0处的导数不存在,即导数不连续。
其次,对勾函数是一个奇函数,即H(-x)=1-H(x)。
此外,对勾函数是一个分布函数,满足概率的基本性质,即0≤H(x)≤1总结起来,对勾函数是一个常用的数学函数,具有广泛的应用。
它可以表示系统的阶跃响应,在信号处理和电路分析等领域发挥重要作用。
对勾函数讲解与例题解析
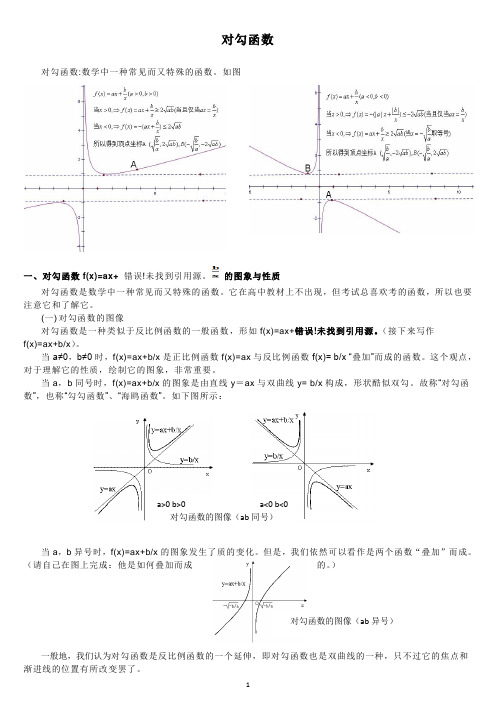
对勾函数对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+错误!未找到引用源。
的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+错误!未找到引用源。
(接下来写作f(x)=ax+b/x )。
当a≠0,b≠0时,f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a ,b 同号时,f(x)=ax+b/x 的图象是由直线y =ax 与双曲线y= b/x 构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:当a ,b 异号时,f(x)=ax+b/x 的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
a>0 b>0 a<0 b<0 对勾函数的图像(ab 同号)对勾函数的图像(ab 异号)接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,错误!未找到引用源。
当x<0时,错误!未找到引用源。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性(五) 对勾函数的渐进线 由图像我们不难得到: (六)对勾函数的奇偶性 :对勾函数在定义域内是奇函数, 二、均值不等式(基本不等式) 对勾函数性质的研究离不开均值不等式。
对勾函数表达式

对勾函数表达式
摘要:
1.对勾函数的定义和基本形式
2.对勾函数的性质和特点
3.对勾函数的应用领域
4.对勾函数的符号和意义
5.对勾函数的简史
正文:
对勾函数,也被称为双勾函数,是一种常见的数学函数表达式。
它的基本形式为y=ax^2+bx+c,其中a、b、c 为常数,且a≠0。
这个函数图像的形状就像一个对勾,因此得名对勾函数。
对勾函数具有许多有趣的性质和特点。
例如,它的图像具有对称性,即以直线x=-b/2a 为对称轴。
此外,对勾函数的顶点坐标为(-b/2a, c -
b^2/4a),这也是函数的最小值(当a>0)或最大值(当a<0)所在的位置。
对勾函数在许多领域都有广泛的应用。
在物理学中,它可以描述简谐振动的位移时间关系;在经济学中,它可以描述生产和消费的关系;在生物学中,它可以描述种群数量随时间的变化关系。
对勾函数的符号和意义也值得我们关注。
一般来说,我们用y 表示函数的输出,x 表示函数的输入。
而a、b、c 则分别表示函数的三个参数,决定了函数的形状和位置。
对勾函数的简史也很有趣。
尽管对勾函数在现代数学中有着广泛的应用,但它的起源可以追溯到古代希腊。
在古希腊,对勾函数被认为是一种神秘的符号,象征着生命和死亡的循环。
对勾函数

对勾函数对勾函数,又称为符号函数,是一种常见的数学函数,其定义如下:$$f(x) = \begin{cases}1, & x>0 \\0, & x= 0 \\-1, & x<0 \\\end{cases}$$对勾函数是一个以0为界限,将实数轴分为三个区间的函数。
当$x>0$时,对勾函数的输出为1;当$x=0$时,对勾函数的输出为0;当$x<0$时,对勾函数的输出为-1。
对勾函数在数学和应用领域都有广泛的应用。
在数学上,它常被用来描述分段函数的行为或定义符号。
在实际应用中,对勾函数可以用来表示正负号、描述一些变化的特征等。
首先,让我们来看一下对勾函数的一些基本性质。
对勾函数是一个分段函数,其图像可以用一条竖直的线段来表示。
当$x>0$时,对勾函数的取值为1,表示正号;当$x=0$时,对勾函数的取值为0;当$x<0$时,对勾函数的取值为-1,表示负号。
这一特性使得对勾函数在描述正负关系时非常方便,例如在表示数轴上的正负数时,我们可以使用对勾函数。
其次,对勾函数还可以用来描述一些变化的特征。
在某些数学问题中,我们需要考虑某个变量的增减性或者是一个函数在不同区间的取值情况。
对勾函数可以帮助我们简洁地描述这些特征。
以$x$为自变量的函数$f(x)$为例,如果我们想要描述$f(x)$在不同区间的增减性,我们可以将$x$的取值范围分为多个区间,并在每个区间里使用对勾函数来表示该区间内$f(x)$的增减性。
这样一来,我们可以更加清晰地描述函数的特性。
此外,对勾函数在数学问题的解法中也有一定的应用。
在某些问题中,我们需要考虑多个条件的约束,而对勾函数可以帮助我们将这些条件转化为可计算的形式。
例如,在一些最优化问题中,我们希望找到一个变量的取值范围,在这个范围内函数取得最大或最小值。
这时,我们可以将这个范围用对勾函数表示出来,然后通过对这个函数进行求导、分析等数学方法来求解问题。
对勾函数

对勾函数图象性质对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x )。
当a≠0,b≠0时,f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a ,b 同号时,f(x)=ax+b/x 的图象是由直线y =ax 与双曲线y= b/x 构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:当a ,b 异号时,f(x)=ax+b/x 的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
a>0 b>0 a<0 b<0 对勾函数的图像(ab 同号) 对勾函数的图像(ab 异号)(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到: 当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性(五) 对勾函数的渐进线由图像我们不难得到:(六) 对勾函数的奇偶性 :对勾函数在定义域内是奇函数, 二、类耐克函数性质探讨 函数xbax y +=,在时或00==b a 为简单的单调函数,不予讨论。
(完整版)对勾函数详细分析

对勾函数的性质及应用一、对勾函数b y ax x =+)0,0(>>b a 的图像与性质:1. 定义域:),0()0,(+∞⋃-∞2. 值域:),2[]2,(+∞⋃--∞ab ab3. 奇偶性:奇函数,函数图像整体呈两个“对勾”的形状,且函数图像关于原点呈中心对称,即0)()(=-+x f x f 4. 图像在一、三象限, 当0x >时,by ax x=+≥ab 2(当且仅当b x a ,即)(x f 在x=a b 时,取最小值ab 2由奇函数性质知:当x<0时,)(x f 在x=ab -时,取最大值ab 2-5. 单调性:增区间为(∞+,ab ),(a b -∞-,),减区间是(0,a b ),(a b -,0)二、对勾函数的变形形式 类型一:函数by ax x=+)0,0(<<b a 的图像与性质 1.定义域:),0()0,(+∞⋃-∞ 2.值域:),2[]2,(+∞⋃--∞ab ab3.奇偶性:奇函数,函数图像整体呈两个“对勾”的形状.4.图像在二、四象限, 当x<0时,)(x f 在x=ab 时,取最小值ab 2;当0x >时,)(x f 在x=ab -时,取最大值ab 2-5.单调性:增区间为(0,a b ),(a b -,0)减区间是(∞+,ab ),(a b -∞-,),类型二:斜勾函数by ax x =+)0(<ab①0,0<>b a 作图如下1.定义域:),0()0,(+∞⋃-∞2.值域:R3.奇偶性:奇函数4.图像在二、四象限,无最大值也无最小值.5.单调性:增区间为(-∞,0),(0,+∞).②0,0><b a 作图如下:1.定义域:),0()0,(+∞⋃-∞2.值域:R3.奇偶性:奇函数4.图像在二、四象限,无最大值也无最小值.5.单调性:减区间为(-∞,0),(0,+∞).类型三:函数)0()(2>++=ac xcbx ax x f 。
专题:对勾函数

基本不等式与对勾函数之答禄夫天创作创作时间:二零二一年六月三十日 二、 对勾函数by ax x=+)0,0(>>b a 的图像与性质 性质:1.界说域:),0()0,(+∞⋃-∞2. 值域:),2()2,(+∞⋃--∞ab ab3.奇偶性:奇函数, 函数图像整体呈两个“对勾”的形状, 且函数图像关于原点呈中心对称, 即0)()(=-+x f x f4.图像在一、三象限那时0x >, 由基本不等式知b y ax x=+≥ab 2(当且仅当b x a=取等号),即)(x f 在x=ab 时, 取最小值ab 2由奇函数性质知: 当x<0时, )(x f 在x=a b -时, 取最年夜值ab 2-5.单调性:增区间为(∞+,a b ), (ab -∞-,)减区间是(0,ab ), (ab -,0)一、对勾函数的变形形式类型一:函数b y ax x=+)0,0(<<b a 的图像与性质此函数与对勾函数xb x a y )()(-+-=关于原点对称, 故函数图像为 性质:类型二:斜勾函数b y ax x=+)0(<ab①,0<>b a 作图如下性质: ②0,0><b a 作图如下: 类型三:函数)0()(2>++=ac xc bx ax x f此类函数可变形为b x c ax x f ++=)(, 则)(x f 可由对勾函数xc ax y +=上下平移获得 例1作函数xx x x f 1)(2++=的草图解:11)(1)(2++=⇒++=xx x f x x x x f 作图如下:类型四:函数)0,0()(≠>++=k a kx ax x f 此类函数可变形为kkx ak x x f -+++=)()(, 则)(x f 可由对勾函数xax y +=左右平移, 上下平移获得 例2作函数21)(-+=x x x f 的草图解:2212)(21)(+-+-=⇒-+=x x x f x x x f 作图如下: 例3作函数x x x x f +++=23)(的作图: 解:1212211212)(23)(-+++=+++=++++=⇒+++=x x x x x x x x f x x x x f 练习:1.求函数421)(-+=x x x f 在),2(+∞上的最低点坐标2. 求函数1)(-+=x xx x f 的单调区间及对称中心类型五:函数)0,0()(2>≠+=b a b x axx f此类函数界说域为R , 且可变形为x b x axbx a x f +=+=2)(a.若0>a , 则)(x f 的单调性和对勾函数xb x y +=的单调性相反, 图像如下:性质:1.界说域:),(+∞-∞ 2. 值域:)21,21(ba ba ⋅⋅-3. 奇偶性:奇函数, 函数图像整体呈两个倒着的“对勾”的形状, 且函数图像关于原点呈中心对称, 即0)()(=-+x f x f4. 图像在一、三象限那时0x >, 由基本不等式知ba xb x a x f 22)(=⋅≤(当且仅当b x =取等号),即)(x f 在b x =时, 取最年夜值ba 2由奇函数性质知:当x<0时, )(x f 在x=b -时, 取最小值ba2-5. 单调性:减区间为(∞+,b ), (b -∞-,)增区间是],[b b -例4作函数1)(2+=x xx f 的草图 解:x x xx x f x xx f 1111)(1)(22+=+=⇒+=b.若0<a , 作出函数图像: 例5作函数42)(2+-=x xx f 的草图 类型六:函数)0()(2≠+++=a mx c bx ax x f此类函数可变形为)0()()()()(2>++++=+++++=at s mx t m x a m x t m x s m x a x f ,则)(x f 可由对勾函数xtax y +=左右平移, 上下平移获得 例6说明函数11)(2+++=x x x x f 由对勾函数x x y 1+=如何变换而来解:111111)1()1()(2-+++=+++-+=x x x x x x f故 此函数)(x f 可由对勾函数xx y 1+=向(填“左”、“右”)平移单元, 向(填“上”、“下”)平移单元.草图如下:练习:1.已知1->x , 求函数1107)(2+++=x x x x f 的最小值1<x , 求函数1109)(2--+=x x x x f 的最年夜值类型七:函数)0()(2≠+++=a cbx ax mx x f 例7求函数21)(2++-=x x x x f 在区间),1(+∞上的最年夜值解:那时1=x , 0)1(=f 那时1≠x , 3141114)1(3)1(14)1(3)1(1)(22+-+-=-+-+-=+-+--=x x x x x x x x x f问:若区间改为),4[+∞则)(x f 的最年夜值为 练习232)(22++++=x x x x x f 在区间),0[+∞上的最年夜值类型八:函数ax b x x f ++=)(此类函数可变形为标准形式:)0()(>-+-++=+-++=a b ax a b a x ax ab a x x f例8求函数13)(-+=x x x f 的最小值解:141141)(-+-=-+-=x x x x x f练习:1.求函数15)(++=x x x f 的值域2.求函数32)(++=x x x f 的值域类型九:函数)0()(22>++=a ax b x x f此类函数可变形为标准形式:)()()(22222o a b ax a b a x ax ab a x x f >-+-++=+-++=例9求函数45)(22++=x x x f 的最小值解:45)(22++=x x x f 414414)(2222+++=+++=⇒x x x x x f练习:1. 求函数171)(22++=x x x f 的值域 例10已知20,a >求函数.解:2令t ),则1t t +y=11a ≥时, min y101a <<时, 2min y =。
对勾函数讲解与例题解析
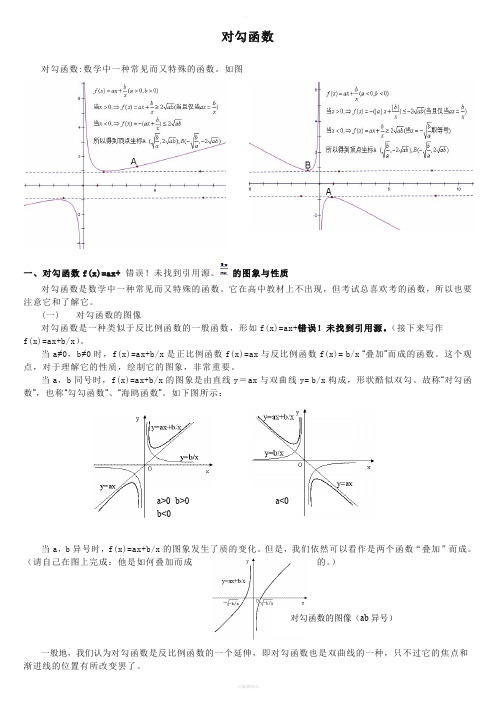
对勾函数对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+错误!未找到引用源。
的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+错误!未找到引用源。
(接下来写作f(x)=ax+b/x )。
当a ≠0,b ≠0时,f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a ,b 同号时,f(x)=ax+b/x 的图象是由直线y =ax 与双曲线y= b/x 构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:当a ,b 异号时,f(x)=ax+b/x 的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
a>0 b>0 a<0 b<0 对勾函数的图像(ab 同号)对勾函数的图像(ab 异号)接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,错误!未找到引用源。
当x<0时,错误!未找到引用源。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性(五) 对勾函数的渐进线 由图像我们不难得到: (六) 对勾函数的奇偶性 :对勾函数在定义域内是奇函数,二、均值不等式(基本不等式) 对勾函数性质的研究离不开均值不等式。
对勾函数的性质及图像

对勾函数的性质及图像一、引言在数学中,对勾函数是一种常见的函数类型,其性质和图像具有一定的特点。
本文将探讨对勾函数的定义、性质以及绘制其图像的方法。
通过深入研究对勾函数,我们可以更好地理解其在数学中的应用和意义。
二、对勾函数的定义对勾函数通常用符号\( y = \sin(x) \) 表示,其中\( \sin \) 代表正弦函数。
正弦函数是周期性函数的一种,其定义域为实数集,值域在区间\([-1, 1]\)内取值。
对勾函数具有以下几个重要的特点:1.周期性:对勾函数以\( 2\pi \)为一个完整的周期,在每个周期内函数值重复。
2.奇函数性质:对勾函数关于原点对称,即\( \sin(-x) = -\sin(x) \),这是因为正弦函数是奇函数。
3.连续性:对勾函数在其定义域内是连续的。
三、对勾函数的性质对勾函数具有许多重要的性质,包括但不限于:1.基本性质:对勾函数在整个实轴上都有定义,且处处可导。
2.最值点:对勾函数在\( x = \frac{\pi}{2} + 2k\pi \)和\( x = -\frac{\pi}{2} + 2k\pi \)处取得极值,其中\( k \)为整数。
3.周期性:对勾函数的周期为\( 2\pi \),即\( \sin(x) = \sin(x + 2k\pi)\),其中\( k \)为整数。
4.导数性质:对勾函数的导数为余弦函数,即\( y’ = \cos(x) \)。
5.零点:对勾函数在\( x = k\pi \)处取零点,其中\( k \)为整数。
四、对勾函数的图像为了更直观地理解对勾函数的性质,我们可以通过绘制其图像来观察其特点。
下面是一些绘制对勾函数图像的方法:markdown python import numpy as np import matplotlib.pyplot as pltx = np.linspace(-2np.pi, 2np.pi, 1000) y = np.sin(x)plt.plot(x, y, label=’y = sin(x)’) plt.axhline(0, color=’black’,linewidth=0.5)plt.axvline(0, color=’black’,linewidth=0.5) plt.grid(color = ‘gray’, linestyle = ‘–’, linewidth = 0.5)plt.xlabel(’x’) plt.ylabel(’y’) plt.title(’Graph of sin(x)’) plt.legend() plt.show()通过上述代码,我们可以生成对勾函数\( y = \sin(x) \)的图像。
对勾函数讲解与例题解析

对勾函数对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+ 的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它与了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x )。
当a≠0,b≠0时,f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a ,b 同号时,f(x)=ax+b/x 的图象是由直线y =ax 与双曲线y= b/x 构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:当a ,b 异号时,f(x)=ax+b/x 的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点与渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
a>0 b>0对勾函数的图像(ab(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到: 当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性 (五) 对勾函数的渐进线由图像我们不难得到:(六) 对勾函数的奇偶性 :对勾函数在定义域内是奇函数,二、均值不等式(基本不等式)对勾函数性质的研究离不开均值不等式。
说到均值不等式,其实也是根据二次函数得来的。
我们都知道,(a-b)^2≥0,展开就是a^2-2ab+b^2≥0,有a^2+b^2≥2ab,两边同时加上2ab ,整理得到(a+b)^2≥4ab,同时开根号,就得到了均值定理的公式:a+b≥2sqrt(ab)。
数学对勾函数(详细分析“函数”共8张)

性质一
➢ 函数y=ax+b/x的性质 ➢ Ⅰ当a、b均大于零时,性质 : ➢ ⑴定义域:x≠0 ➢ ⑵值 域:〔-∞,-2 根号ab〕∪〔2根号ab ,
+∞〕 ⑶奇偶性:奇函数 ➢ ⑷单调性:当x﹥0时,当0﹤x﹤根号b/a 时,
y为减函数 当x﹥根号b/a 时,y为增函 数 当x﹤0时,当- 根号b/a﹤x﹤0时,y 为减函数 当x﹤根号b/a- 时,y为增函 数
第7页,共8页。
图像三
第8页,共8页。
数学对勾函数
第1页,共8页。
简介对Biblioteka 函数:图像,性质,单调性对勾函数是数学中一种常见而又特殊的函数,见图示。 对勾函数是一种类似于反比例函数的一般函数,
又被称为“双勾函数〞、"勾函数"等。也被形象称 为“耐克函数〞
所谓的对勾函数〔双曲线函数〕,是形如 f(x)=ax+b/x的函数。由图像得名。
当x>0时,f(x)=ax+b/x有最小值〔这里为了研究方 便,规定a>0,b>0〕,也就是当x=sqrt(b/a)的时候 〔sqrt表示求二次方根〕
第6页,共8页。
图象二
Ⅰ当a、b均大于零时,性质 : 当a、b>0时,图像分布在第一、三象限两条渐近线的锐角之间局部,由于其对称性,只讨论第一象限中的情形。 ⑷单调性:当x﹥0时,当0﹤x﹤根号b/a 时,y为减函数 当x﹥根号b/a 时,y为增函数 当x﹤0时,当- 根号b/a﹤x﹤0时,y为减函数 当 x﹤根号b/a- 时,y为增函数 对号函数是双曲线旋转得到的,所以也有渐近线、焦点、顶点等等 对勾函数是数学中一种常见而又特殊的函数,见图示。 ⑷单调性:当x﹥0时,当0﹤x﹤根号b/a 时,y为减函数 当x﹥根号b/a 时,y为增函数 当x﹤0时,当- 根号b/a﹤x﹤0时,y为减函数 当 x﹤根号b/a- 时,y为增函数 Ⅰ当a、b均大于零时,性质 : ⑷单调性:当x﹥0时,当0﹤x﹤根号b/a 时,y为减函数 当x﹥根号b/a 时,y为增函数 当x﹤0时,当- 根号b/a﹤x﹤0时,y为减函数 当 x﹤根号b/a- 时,y为增函数 当a、b>0时,图像分布在第一、三象限两条渐近线的锐角之间局部,由于其对称性,只讨论第一象限中的情形。 ⑷单调性:当x﹥0时,当0﹤x﹤根号b/a 时,y为减函数 当x﹥根号b/a 时,y为增函数 当x﹤0时,当- 根号b/a﹤x﹤0时,y为减函数 当 x﹤根号b/a- 时,y为增函数 对号函数永远是奇函数,关于原点呈中心对称 ⑵值 域:〔-∞,-2 根号ab〕∪〔2根号ab ,+∞〕 ⑶奇偶性:奇函数 当x>0时,f(x)=ax+b/x有最小值〔这里为了研究方便,规定a>0,b>0〕,也就是当x=sqrt(b/a)的时候〔sqrt表示求二次方根〕 ⑹对称性:图像关于原点对称 利用平均值不等式〔a>0,b>0且ab的值为定值时,a+b≥2√ab〕可知最小值是2倍根号ab,在x=根号下b/a的时候取得,所以在〔0,负根号下b/a〕 上单调递减,在〔根号下b/a,正无穷〕上单调递增
对勾函数讲解与例题解析

对勾函数对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+ 的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x )。
当a≠0,b≠0时,f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a ,b 同号时,f(x)=ax+b/x 的图象是由直线y =ax 与双曲线y= b/x 构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:当a ,b 异号时,f(x)=ax+b/x 的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和a>0 b>0 a<0 b<0 对勾函数的图像(ab 同号)对勾函数的图像(ab 异号)渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性(五) 对勾函数的渐进线 由图像我们不难得到: (六)对勾函数的奇偶性 :对勾函数在定义域内是奇函数, 二、均值不等式(基本不等式) 对勾函数性质的研究离不开均值不等式。
高中数学对勾函数练习题精编版

对勾函数练习题
1.若x>2.求 的值域。
2.若x>1.求 的最小值。
3.若x>0.求 的最小值。
4.”(1)求 。
(2)若对任意x∈[1,+∞],f(x)>0恒成立,求a范围。
5.函数 的最小值为____________;
6.
7.2003年,上海市总人口达到1464万人,上海是全国第一个出现人口负增长的地区。函数 的最大值为。
但这些困难并非能够否定我们创业项目的可行性。盖茨是由一个普通退学学生变成了世界首富,李嘉诚是由一个穷人变成了华人富豪第一人,他们的成功表述一个简单的道理:如果你有能力,你可以从身无分文变成超级富豪;如果你无能,你也可以从超级富豪变成穷光蛋。
为此,装潢美观,亮丽,富有个性化的店面环境,能引起消费者的注意,从而刺激顾客的消费欲望。这些问题在今后经营中我们将慎重考虑的。11.
“碧芝”最吸引人的是那些小巧的珠子、亮片等,都是平日里不常见的。店长梁小姐介绍,店内的饰珠有威尼斯印第安的玻璃珠、秘鲁的陶珠、奥利的施华洛世奇水晶、法国的仿金片、日本的梦幻珠等,五彩缤纷,流光异彩。按照饰珠的质地可分为玻璃、骨质、角质、陶制、水晶、仿金、木制等种类,其造型更是千姿百态:珠型、圆柱型、动物造型、多边形、图腾形象等,美不胜收。全部都是进口的,从几毛钱一个到几十元一个的珠子,做一个成品饰物大约需要几十元,当然,还要决定于你的心意。“碧芝”提倡自己制作:端个特制的盘子到柜台前,按自己的构思选取喜爱的饰珠和配件,再把它们串成成品。这里的饰珠和配件的价格随质地而各有同,所用的线绳价格从几元到一二十元不等,如果让店员帮忙串制,还要收取10%~20%的手工费。
8.若 ,则 的最值是。
对勾函数讲解与例题解析

对勾函数讲解与例题解析对勾函数是一种常见而特殊的函数,虽然在高中教材中不常出现,但在考试中却经常被考到。
对勾函数的图像由直线和双曲线组成,当a,b同号时,形状类似双勾,因此被称为“对勾函数”、“勾勾函数”、“海鸥函数”。
当a,b异号时,图像会发生质的变化,但仍可看作是两个函数叠加而成。
对勾函数认为是反比例函数的一种延伸,其顶点坐标可以通过均值不等式求得。
对勾函数的定义域、值域也可根据顶点坐标得出,且在定义域内是奇函数。
对勾函数的单调性和渐进线也可以从图像中得到。
研究勾函数性质需要用到均值不等式。
均值不等式是根据二次函数推导而来的。
二次函数展开后可以得到a^2+b^2≥2ab,整理后得到(a+b)^2≥4ab,开根号后得到a+b≥2√ab。
将ax+b/x套用这个公式,可以得到ax+b/x≥2√ab,当且仅当ax=b/x时取到最小值,此时x=sqrt(b/a),对应的f(x)=2√ab。
均值不等式可以写成(a+b)/2≥√ab,其中前面的式子是算术平均数,后面的式子是几何平均数,总结起来就是算术平均数不小于几何平均数。
要求函数y=x+1/x的最小值,可以用均值不等式来解。
因为x>0,所以y=x+1/x≥2√x/x=2,当且仅当x=1时取到最小值,此时y=2.另一种解法是用二次函数的方法,将y=x+1/x表示为y=x^2+1/x^2+2,然后用求根公式求出当y取最小值时对应的x=1,此时y=2.单调性定义是指函数在一定区间内单调递增或单调递减。
如果对于任意的x1,x2,只有x1,x2∈(a,b)时,f(x1)-f(x2)>0,则函数在(a,b)内单调递增;如果对于任意的x1,x2,只有x1,x2∈(a,b)时,f(x1)-f(x2)<0,则函数在(a,b)内单调递减。
因为y=x+1/x在(0,1)内单调递增,在(1,∞)内单调递减,所以当x=1时取到最小值,y=2.复合函数的单调性是指由两个单调递增或单调递减的函数组成的复合函数在一定区间内也具有相同的单调性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本不等式与对勾函数
一、 对勾函数b
y ax x
=+)0,0(>>b a 的图像与性质 性质:
1. 定义域:),0()0,(+∞⋃-∞
2. 值域:),2()2,(+∞⋃--∞ab ab
3. 奇偶性:奇函数,函数图像整体呈两个“对勾”
的形状,且函数图像关于原点呈中心对称,即
0)()(=-+x f x f
4. 图像在一、三象限
当0x >时,由基本不等式知
b
y ax x
=+
≥ab 2(当且仅当x =, 即)(x f 在x=a b 时,取最小值ab 2 由奇函数性质知:当x<0时,)(x f 在x=a
b
-
时,取最大值ab 2- 5. 单调性:增区间为(∞+,a b ),(a b -∞-,) 减区间是(0,a
b ),(a b -,0) 一、对勾函数的变形形式 类型一:函数b
y ax x
=+
)0,0(<<b a 的图像与性质 此函数与对勾函数x
b x a y )
()(-+-=关于原点对称,故函数图像为
性质:
类型二:斜勾函数b
y ax x
=+
)0(<ab ①0,0<>b a 作图如下 性质:
②0,0><b a 作图如下:
类型三:函数)0()(2>++=
ac x
c
bx ax x f 此类函数可变形为b x c ax x f ++
=)(,则)(x f 可由对勾函数x
c
ax y +=上下平移得到 例1作函数x
x x x f 1
)(2++=的草图
解:11
)(1)(2++=⇒++=
x
x x f x x x x f 作图如下:
类型四:函数)0,0()(≠>++=k a k
x a
x x f 此类函数可变形为k k x a k x x f -+++=)()(,则)(x f 可由对勾函数x
a
x y +=左右平移,上下平移得到
例2作函数21
)(-+=x x x f 的草图
解:22
1
2)(21)(+-+-=⇒-+
=x x x f x x x f 作图如下:
例3作函数x x x x f +++=2
3
)(的作图:
解:12
1
2211212)(23)(-+++=+++=++++=⇒+++=x x x x x x x x f x x x x f
练习: 1.求函数4
21
)(-+=x x x f 在),2(+∞上的最低点坐标
2. 求函数1
)(-+=x x
x x f 的单调区间及对称中心
类型五:函数)0,0()(2>≠+=
b a b
x ax
x f 此类函数定义域为R ,且可变形为x b x a
x
b
x a x f +
=+=
2
)( a.若0>a ,则)(x f 的单调性和对勾函数x
b
x y +
=的单调性相反,图像如下:
性质:
1.定义域:),(+∞-∞ 2. 值域:)21,21(b
a b
a ⋅
⋅
-
3. 奇偶性:奇函数,函数图像整体呈两个倒着的“对勾”的形状,且函数图像关于原点呈中心对称,即
0)()(=-+x f x f
4. 图像在一、三象限
当0x >时,由基本不等式知b
a x
b x a x f 22)(=
⋅
≤
(当且仅当b x =取等号),
即)(x f 在b x =时,取最大值
b
a 2
由奇函数性质知:
当x<0时,)(x f 在x=b -时,取最小值b
a 2-
5. 单调性:减区间为(∞+,b ),(b -∞-,)
增区间是],[b b -
例4作函数1
)(2
+=x x
x f 的草图 解:x x x
x x f x x
x f 111
1)(1)(22+
=+=⇒+=
b. 若0<a ,作出函数图像: 例5作函数4
2)(2+-=x x
x f 的草图
类型六:函数)0()(2≠+++=
a m
x c
bx ax x f 此类函数可变形为)0()()()()(2>++++=+++++=
at s m
x t
m x a m x t m x s m x a x f , 则)(x f 可由对勾函数x
t
ax y +
=左右平移,上下平移得到 例6说明函数11)(2+++=x x x x f 由对勾函数x
x y 1
+=如何变换而来
解: 11
1
111)1()1()(2-+++=+++-+=
x x x x x x f 故 此函数)(x f 可由对勾函数x
x y 1
+
=向 (填“左”、“右”)平移 单位,向 (填“上”、“下”)平移 单位.草图如下:
练习:1.已知1->x ,求函数1
10
7)(2+++=x x x x f 的最小值
2.已知1<x ,求函数1
10
9)(2--+=x x x x f 的最大值
类型七:函数)0()(2
≠+++=a c
bx ax m
x x f 例7求函数2
1
)(2
++-=
x x x x f 在区间),1(+∞上的最大值 解:当1=x 时,0)1(=f 当1≠x 时,3
1411
1
4
)1(3)1(14)1(3)1(1)(22+-+-=-+-+-=+-+--=
x x x x x x x x x f
问:若区间改为),4[+∞则)(x f 的最大值为
练习:1.求函数2
3
2)(22++++=x x x x x f 在区间),0[+∞上的最大值
类型八:函数a
x b x x f ++=
)(
此类函数可变形为标准形式:)0()(>-+-+
+=+-++=
a b a
x a b a x a
x a
b a x x f
例8求函数1
3)(-+=
x x x f 的最小值
解: 1
411
41)(-+
-=-+-=x x x x x f
练习: 1.求函数1
5)(++=x x x f 的值域
2.求函数3
2
)(++=x x x f 的值域
类型九:函数)0()(2
2>++=a a
x b x x f
此类函数可变形为标准形式:)()()(2
22
22o a b a
x a b a x a
x a
b a x x f >-+-+
+=+-++=
例9求函数4
5)(2
2++=x x x f 的最小值
解:4
5)(2
2++=x x x f 4
144
14)(2
22
2++
+=+++=
⇒x x x x x f
练习:1. 求函数17
1
)(22++=x x x f 的值域
例10已知
2
0,
a>求函数的最小值。
解:2
=
令t≥则
1 t
t
+ y=
1即1
a≥时,
min
y
1即01
a
<<时,2
min
y=。
