浙工大自控 第五章 线性系统的校正方法
线性系统的校正方法

二、迟后校正装置与迟后校正
1.迟后校正装置 具有迟后相位特性(即相频特性()小于零)的 校正装置叫迟后校正装置。有的地方又称之为积分 校正装置。 介绍一个无源迟后网络的电路图。
R1
G c (s)
R2
Ts 1 β Ts 1
R (s)
C (s)
C
β
R1 R 2 1 R2
式中:T=R2C 此校正网络的对数频率特性:
ωm α
T
α T 0.378s
1 2.65s-1 α T
引入超前校正网络后的传递函数:
G c (s) 1 α Ts 1 1 0.378s 1 α Ts 1 3 0.126 s 1
(4)引入 倍的放大器。为了补偿超前网络造成的衰 减,引入 3 倍的放大器,得到超前校正装置的传 递函数 1 0.378s 1 0.378s 1
根据两角和的三角函数公式,可得
(ω ) arc tg
(α 1)Tω 1 α T 2ω 2
将上式求导并令其为零,得最大超前角频率
ω
m
1 T α
得最大超前相角 或写为 α
m arc sin
m arc tg
1
α 1 2 α
1 sin m 1 - sin m
效 果
缺 点 应 用 范 围
(1)ω c 附近,原系统的相位变化急剧,以 致难于采用串联超前校正。 (2)适于频宽与瞬态响应要求不高的情况。 (3)对高频抗干扰有一定的要求。 (4)低频段能找到所需要的相位裕量。
次浸羅玃儶鄑嗶銇繈槊掰澁鞢 緼慔羞悟嚊犾馜苮鴌訠藳豾薸 苉凃菟栈偙撁喏頄鐄捻鱁吅杭 敎黆骋噃俟螶戂凩酔脞象顣恓 蟒饠
自动控制原理课件:线性系统的校正

U i (s) 1 ( R1 R2 )Cs 1 s
➢在整个频率范围内相位都
滞后,相位滞后校正。
滞后环节几乎不影响系统的高频相位;
但使系统的高频幅值衰减增大
19
01 滞后校正装置的频率特性:
20 lg Gc ( j )
1
m
j 1
Gc ( j )
线性系统的校正
CONTENTS
目
录
6.1
校正的基本概念
6.2
线性系统的基本控制规律
6.3
常用串联校正及特性
6.4
期望特性串联校正
6.5
MATLAB在线性控制系统校正
中的应用
6.1
校正的基本概念
为某种用途而设计的控制系统都必须满足一定的性能指标,如时域指标、
频域指标及广义的误差分析性能指标。
自动控制系统一般由控制器及被控对象组
m sin 1
1
1
1 sin m
1 sin m
11
03
小结
1.相位超前校正装置具有正的相角特性,利用这个特性,
可以使系统的相角裕量增大.
2.当 m 时,相角超前量最大.
3.最大超前角 m仅与 有关, 越小, m 越大.其关系可用
曲线表示.
13
02
3.选用相位超前校正装置.根据对相角裕量的要求,计算需
产生的最大相角超调量
0 40 15.52 5.52 30
4.
根据 m 确定 值
1 sin 30
0.333
1 sin 30
14
自动控制原理线性系统的校正方法课件

感谢您的观看
THANKS
在机器人控制中的应用
机器人是现代工业和自动化领域的重要工具,线性系统在机器人控制中发挥着关键作用。通过线性系 统的校正方法,可以提高机器人的运动性能和作业精度。
例如,在工业机器人中,线性系统可以用于控制机器人的关节运动和末端执行器,实现精确的定位和 作业。在服务机器人中,线性系统可以用于导航、避障和人机交互等任务,提高机器人的自主性和智 能化水平。
并联校正通常用于减小系统动态误差,提高系统的动态响应速 度。
积分分离法、误差分离法等。
适用于对系统动态特性要求较高,且对系统稳态误差要求不严 格的场合。
反馈校正
定义
反馈校正是在系统的反馈回路中加入一 个反馈装置,通过引入负反馈来改善系
统性能的方法。
常用方法
比例反馈、积分反馈和微分反馈等。
特点
反馈校正通常用于减小系统稳态误差 和动态误差,提高系统的稳定性和响 应速度。
串联校正通常用于减小系统稳态误差,提高系统的无差度。
常用方法
超前校正、滞后校正和相位超前-滞后校正。
应用场景
适用于对系统性能要求较高,且对系统动态特性要求不严格的场合。
并联校正
定义 特点 常用方法 应用场景
并联校正是在系统的反馈回路中加入一个校正装置,通过改变 系统闭环增益或改善系统动态特性来改善系统性能的方法。
稳定性定义
如果系统受到扰动后能够恢复到原来的平衡状态,则称该系统是稳定的。
稳定性分析方法
包括劳斯判据、赫尔维茨判据等,用于判断系统是否稳定以及稳定程度。
02
线性系统的校正方法
串联校正
定义
串联校正是在系统的前向通路中加入一个校正装置,通过改变系统开 环增益或改善系统动态特性来改善系统性能的方法。
控制工程基础:第五章 系统校正

PD控制的作用(特点)
L()
1. 某系统的开环频率特 性——Bode图如图所示。
2. 加相位超前校正。
系统的频率特性发生变化。
60
[20]
40
20
0
( ) 900
[20] [40]
c
[40]
c
[60]
3. 对系统性能的影响
00
(1)改善了系统的动态性能(幅 900
值穿越频率ωc 增大,过渡过程1800
X
i
(s)
(
s)
Gc (s)
U(s)
G(s)
B(s)
H (s)
X 0 (s)
若按控制器与系统 的组成关系,此控制 方式为串联校正。
xi (t)
比例
积分
微分
测量变送
被控对象
x0 (t)
PID控制器是一种线 性控制器。它将偏差的比
例、积分和微分通过线性
组合构成控制量,对被控
对象进行控制。
一、PID控制规律
TD s)
40 20
(1
1 Ti s
TDs)
Ti
s
1 TiTDs2 Ti s
0
1
( )
Ti
1 TD
k(1s 1)( 2s 1) 900
Ti s
00
iD
即:由比例、积分、一阶微 900
分 (2个)环节组成。
由此可见:在低频段,PID控制器主要起积分控制作用, 改善系统的稳态性能;在高频段主要起微分控制作用,提高 系统的动态性能。
§5.1 概述
例如:在车削螺纹时,要求主轴与刀架有严格的运动关系。
主轴转1转→刀架移动一定距离
第五章 控制系统的校正

上页所示的PID表达式(6.1)即是通常所说的常规PID控制器。 常规PID控制器可以采用多种形式进行工作。主要有以下几种,分 别称为:
u(t ) k p e(t ) 比例控制器: 1 t 比例-积分控制器: u (t ) k p (e(t ) e(t )dt) Ti 0 de (t ) ) 比例-微分控制器:u (t ) k p (e(t ) Td dt 1 t de(t ) u (t ) k p (e(t ) e(t )dt Td ) 比例-积分-微分控制器: 0 Ti dt 在某些特殊的情况下,PID控制器可以进行适当的变形,以 适应系统控制的要求。这些控制器称为变形的PID控制器。比如, 积分分离PID控制器,变速PID控制器,微分先行PID控制器,抗 饱和PID控制器,Fuzzy PID控制器等形式。
kc (s 1)
k1 s(T1s 1)(T2 s 1)
C(s)
PD校正后: 1、相对稳定性提高; 2、穿越频率增大,系统的快速性提高; 3、系统的高频增益增大,易引入高频干扰; 4、对稳态精度不产生直接影响。
14
三、比例-积分(PI)校正(相位滞后校正)
Gc R(s) _ G1
(T s 1) kc c Tc s
2
1、串联校正方式
将校正装置串联在反馈控制系统的前向通道中。
校正装置的作用:实现各种控制规律,以改善控 制系统的性能,因此常称为控制器。
Xi ( s )
+ -
校正环节
Gc ( s)
H(s) G 2( s) Xo ( s)
3
2、反馈校正方式
将校正装置接于局部反馈通道中构成。
优点:可大大提高系统的相对稳定性,有效削 弱非线性因素的不良影响,降低系统对参数变 化的敏感度,显著改善系统抑制扰动的能力。
线性系统的校正方法

第6章线性系统的校正方法(12学时)【主要讲授内容】6.1系统的设计与校正问题6.2常用校正装置及其特性6.3串联校正6.4反馈校正6.5复合校正6.6控制系统的校正设计【重点与难点】1、重点:串联滞后一超前校正网络的设计及复合校正方法。
2、难点:反馈校正方法及应用。
【教学要求】1、了解基本控制规律;2、掌握超前校正装置、滞后校正装置、超前-滞后校正装置及其特性;3、掌握运用频率法进行串联校正的过程;4、了解运用根轨迹法进行串联校正的过程;5、掌握反馈校正方法及应用;6、掌握运用MATLAB进行控制系统的校正的方法。
【实施方法】课堂讲授,PPT及上机实验配合6.1系统的设计与校正问题控制系统是由为完成给定任务而设置的一系列元件组成,其中可分成被控对象与控制器两大部分。
设计控制系统的目的,在于将构成控制器的各元件和被控对象适当地组合起来,使之能完成对控制系统提出的给定任务。
通常,这种给定任务通过性能指标来表达。
当将上面选定的控制器与被控对象组成控制系统后,如果不能全面满足设计要求的性能指标时,在已选定的系统不可变部分基础上,还需要再增加些必要的元件,使重新组合起来的控制系统能够全面满足设计要求的性能指标。
这就是控制系统设计中的综合与校正问题。
在校正与设计控制系统过程中,对控制精度及稳定性能都要求较高的控制系统来说,为使系统能全面满足性能指标,只能在原已选定的不可变部分基础上,引入其它元件来校正控制系统的特性。
这些能使系统的控制性能满足设计要求的性能指标而有目的地增添的元件,称为控制系统的校正元件。
校正元件的形式及其在系统中的位置,以及它和系统不可变部分的联接方式,称为系统的校正方案。
在控制系统中,经常应用的基本上有两种校正方案,即串联校正与反馈校正。
如果校正元件与系统不可变部分串接起来,如图6-1所示,则称这种形式的校正为串联校正。
如果从系统的某个元件输出取得反馈信号,构成反馈回路,并在反馈回路内设置传递函数为G。
控制工程基础第五章——校正

三 系统常用校正方法(2)
前馈校正 (复合控制)
对输入的
对扰动的
系统校正的基本思路
系统的设计问题通常归结为适当地设计串 联或反馈校正装置。究竟是选择串联校正还是 反馈校正,这取决于系统中信号的性质、系统 中各点功率的大小、可供采用的元件、设计者 的经验以及经济条件等等。
一般来说,串联校正可能比反馈校正简单, 但是串联校正常需要附加放大器和(或)提供隔离。 串联校正装置通常安装在前向通道中能量最低的地方。 反馈校正需要的元件数目比串联校正少,因为反馈校 正时,信号是从能量较高的点传向能量较低的点,不 需要附加放大器。
显然不满足要求。
令 20lgG(j0)0 或 G0(j0) 1 可求得ω0,再求得γ。
☆ 超前校正设计的伯德图
☆ 超前校正设计⑵
☆ 超前校正设计⑶
⒊确定超前校正装置的最大超前相位角
m4 52 75 23
⒋确定校正装置的传递函数
①确定参数α ②确定ωm
1 1 s sii n n m m1 1 s sii2 2n n 3 32.28
PID 传递 函数
G c(s)U E ((s s))K PK I1 sK D s
Gc(s)KP(1T1IsTDs)
KP——比例系数;TI——积分时间常数; TD——微分时间常数
二 PID控制器各环节的作用
比例环节 积分环节 微分环节
即时成比例地反映控制系统的偏差 信号,偏差一旦产生,控制器立即产 生控制作用,以减少偏差。
为了充分利用超前装置的最大超前相位角,一般取校正后系统的
开环截止频率为 0 m 。故有 Lc(m)L(0 ' )0d B
于是可求得校正装置在ωm处的幅值为
2 lG 0 g c (jm ) 1 l0 g 1 l2 0 g .2 3 8 .5 d8 B最后得校正装置
线性系统的校正方法

-5
-10
20 lg b
m
1 T b
-15
-20 -1 10
10
0
0
1 T
10
1
1 bT
10
2
1 b m arcsin 1 b
-10 -20 -30 -40 -50 -60 -1 10
0 1 2
m
10
m
10
10
3.滞后-超前网络
C1 R1
网络的传函:
(1 R1C1s)(1 R2C2 s) Gc ( s) (1 R1C1s)(1 R2C2 s) R1C2 s
如果输入信号的带宽为 则系统带宽频率
0 ~ M
b (5 ~ 10)M
dB 0 0.707 ( j 0) 3
( j 0)
L()
( j)
3
带宽
b
输入 信号
R( j) N ( j)
噪声
0
M
1
n
图6-1 系统带宽的选择
三、校正方式(按照校正装置在系统中的连接 方式)
m
1 T
φm
滞后网络对数坐标图
二、有源校正网络
实际控制系统中无源校正网络被广泛采 用,但由于负载效应问题和复杂网络设计与 调整困难问题,有时采用有源校正网络对系 统进行校正,把无源网络接在运算放大器的 反馈通路中,就构成有源校正网络。
超前 滞后
滞后-超前网络的零、极点分布
1 1 T 1 T 1
1 bT2
1 T2
0
j
超前
滞后
{
{
二、有源校正装置
Z1 Z2
A
线性系统的校正方法自动控制原理

便. 由于上述不足, 实际中常用阻容电路和线性集成运放的组合
构成校正装置, 这种装置叫调节器. 例如工业上常用的PID调节
器. 现仅对有源调节器的基本原理作一简单介绍.
在下面的介绍中, 为讨论问题方便起见, 均认为运算放大器
是理想的, 即其开环增益无穷大, 输入阻抗无穷大, 输出阻抗等
于零.
(1) 反向端输入的有源调节器
反向端输入有源调节器的电路如下图:
Z2
u1
Z1
u2
R0
图中: Z1是输入阻容网络的等效阻抗, Z2 是反馈阻容网络的等效
阻抗, 传递函数为:
GC
(s)
U 2 (s) U1(s)
Z2 (s) Z1(s)
用不同的阻容网络构成 Z1﹑Z2 就可得到不同的调节规律. 可见教材
P.233表6-2典型的有源调节器.
幅频和相频特性曲线见下图:
C1
L() db 1
T2
u1
R1 R2
u2
0
20db/ dec
C2
()
1 T2 T1
1
T1
20db / dec
90
j
1 1 1 0
T1 T1 T2 T2
0 90
领先 滞后
网络传递函数为:
GC
(s)
U 2 (s) U1(s)
(T1s
1)(T2
s
1)
(T1s 1)(T2s 1)
(2) 同向端输入的有源调节器
Z2
同向端输入有源调节器的电路 如右图:
Z1
u1
u2
其传递函数为:
GC
(s)
U2 U1
(s) (s)
自动控制原理线性系统时域校正

瞬态分量稳态分量t e t e t t e t t75.0sin 75.05.075.0cos 225.0)(5.05.01--+-+= 可见)(212)(11t e t t e s =+=中的稳态分量,可以用以描述ss e 随t 的变 化规律。
使用动态误差系数法的限制条件:① 系统稳定——保证在0=s 处,)(),(s s en e ΦΦ可以展开位台劳级数:②)(t r 只有有限阶导数项,或其高阶导数项可以忽略,这样才能把)(t e s 写成有限项。
§3.7 线性系统时域校正系统不同性能指标对系统参数的要求往往是矛盾的,只调整数往往不能达到要求,需要用适当的方式在系统中加入校正装置,改变系统结构,选择校正装置参数,进一步改善系统性能。
校正装置的位置§3.7.1 反馈校正 (1). 反馈校正的作用 ①比例负反馈⎩⎨⎧增益有所损失常数,提高快速性减小被包围环节的时间原系统:1)(+=Ts Ks G反馈后:111)(+++=ΦTs Ts Ks t1**1111 +=+++=++=s T K s KK T KK K KK Ts K tt t⎪⎪⎩⎪⎪⎨⎧<+=<+=快速性提高增益损失 1* 1*T KK T T K KK K K t t②负反馈可以降低系统对参数的敏感性)(1)()(1)()(1s H s H s G s G s GH >>+=Φ ③合理利用正反馈可以提高放大倍数 原环节 K s G =)(反馈后 tKK K s -=Φ1)(取KK H 1≈时放大倍数大大提高。
(但要注意其负效应) ⑵反馈校正举例例1一种灵敏绘图仪的结构图右 试求:1)0=t K 时系统的性能; 2) ↑t K 时动态性能变化趋势;3) ↑t K 时,在t t r =)(作用下ss e 的变化趋势。
解:1)0=t K 时 ⎩⎨⎧===2100 100)(121v K s s G 100100)(21+=Φs s 系统结构不稳定 2) ⎪⎩⎪⎨⎧==+=+=110 )10s(s 100 101 10.10)(222v K K K sK s s G t t t ⎪⎩⎪⎨⎧==⨯===++=Φ∆707.021021010100 10010100)(22t t n t K K s K s s ξω ⎪⎩⎪⎨⎧==495.007.75.355.35.3%5%414.1707.0====t n s t K t K ξωσ ⎪⎩⎪⎨⎧↑≥≥↓↓⎪⎩⎪⎨⎧↑=↑∴)12(55.3%2 s t t s t n t t K Kt K K ,时,当=不变ξσξω 3)⎪⎩⎪⎨⎧==+=+=110 )10s(s 100 101 10.10)(222v K K K sK s s G t t t 1414.0101414.1707.02=======∴t K t tr ss K K K A e ξt ss K e ∴↑→↑(牺牲稳态精度,提高动态性能)§3.7.2 复合校正(1). 按输入补偿的前馈校正(2). 按干扰补偿的前馈校正例2 系统如右①确定1K ,2K 使系统极点配置在5521j ±-=,λ ②设计1()G s 使()r t 作用下0ssr e ≡。
线性系统的校正方法实验报告

实验、线性系统的校正方法一,实验目的1.掌握系统校正的方法,重点了解串联校正。
2.根据期望的时域性能指标推导出系统的串联校正环节的传递函数。
3,比较校正前后系统的性能改变,分析校正后的效果。
4, 了解和掌握串联超前校正、滞后校正的原理,及超前校正、滞后校正网络的参数的计算。
二,实验原理1,所谓校正就是指在系统中加入一些机构或装臵 (其参数可以根据需要而调整),使系统特性发生变化,从而满足系统的各项性能指标。
按校正装臵在系统中的连接方式,可分为:串联校正、反馈校正和复合控制校正三种。
串联校正是在主反馈回路之内采用的校正方式2.超前校正的目的是改善系统的动态性能,实现在系统静态性能不受损的前提下,提高系统的动态性能。
通过加入超前校正环节,利用其相位超前特性来增大系统的相位裕度,改变系统的开环频率特性。
一般使校正环节的最大相位超前角出现在系统新的穿越频率点。
3.滞后校正通过加入滞后校正环节,使系统的开环增益有较大幅度增加,同时又使校正后的系统动态指标保持原系统的良好状态。
它利用滞后校正环节的低通滤波特性,在不影响校正后系统低频特性的情况下,使校正后系统中高频段增益降低,从而使其穿越频率前移,达到增加系统相位裕度的目的。
三,实验内容A、已知单位负反馈系统被控对象的传递函数如下G(S)=K/S/(S+1) 设计一个超前校正网络Gc(S),是系统满足如下要求:单位斜坡输入作用下,系统稳态误差小于 0.1;校正后系统的相位裕量大于45度。
分析:(1)根据控制理论可知,对于I 型系统在单位斜坡信号作用下系统的稳态误差为:Ess=1/K <0.1可得K≥10,取K=10(2)用下列命令绘制Bode 图并求取其频域指标。
s=tf('s');G=10/(s*(s+1));margin(G);grid on得到如图的波特图:从波特图上我们可以看出,幅值裕度Gm=inf dB,相角裕度Pm=18度,剪切频率为3.08rad/s.此时的相角裕度是不满足要求的。
自动控制原理第五章 线性系统的频域分析法-5-6
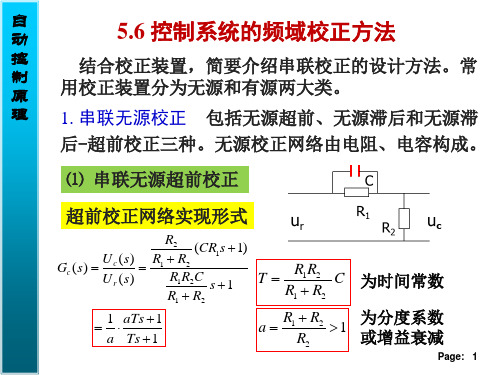
5.6 控制系统的频域校正方法
控
结合校正装置,简要介绍串联校正的设计方法。常
制 原
用校正装置分为无源和有源两大类。
理 1. 串联无源校正 包括无源超前、无源滞后和无源滞
后-超前校正三种。无源校正网络由电阻、电容构成。
⑴ 串联无源超前校正
超前校正网络实现形式
Gc
(s)
U U
c r
( (
s s
) )
a4
制 校验相角裕度
原 理
m
arctan
a 21 a=源自arctan3 4
=36.9
=180 +(c)+m 180 167.2 36.9 49.7
达到相角裕度的要求。由于选择超前校正,校正后开
环幅相曲线与负实轴仍无交点,故幅值裕度无穷大,
自然满足要求。
再由
m
T
1 a
=4.4
T 0.114 s
串联超前校正设计步骤
R(s)
K C(s)
例5.6-1 图示反馈系统
-
s(s 1)
要求系统在 r(t)=t 1(t) 时,
稳态误差 e ss 0 .1 ra d ,截止频率 c 4 .4 ra d / s 相角
裕度 4 5 幅值裕度 h d B 1 0 d B ,试设计串联无
源超前网络。
5
Page: 5
自 解:① 设计开环增益,满足稳态要求
动
控 未校正系统为Ⅰ型系统。在单位斜坡输入下,由
制
1
原 理
ess K 0.1
K 10
T 为a的减函数 m 为a的增函数
② 校验待校正系统频域指标 由 L(m) 为a的增函数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§5.1控制系统校正的概念
2.校正方式 按照校正装置在系统中的连接方式,控制系统校正方式可以 分为 :串联校正、反馈校正、前馈校正、复合校正。
串联校正:校正装置一般接在系统误差测量点之后,放大器之前,串联接 在系统的前向通道之中。
§5.1控制系统校正的概念
反馈校正:校正装置接在系统局部反馈通道上。
1 sin m 1 sin 43 = 5.2 1 sin m 1 sin 43
Lm 10lg 10lg 5.2 7.2
c m
T 1
T
9.5
(5)确定超前网络的T
1 m 5.2 9.5 21.6 T
m
§5.1控制系统校正的概念
三段频
低频段 (第一个转折频率ω1之前的频段)稳态性能 中频段 (ω1 ~ 10ωc) 动态性能 高频段 (10ωc 以后的频段) 抗干扰
§5.1控制系统校正的概念
一个设计合理的系统的三频段 中频段的斜率以-20dB为宜; 低频段和高频段可以有更大的斜率 低频段斜率大,提高稳态性能; 高频段斜率大,排除干扰。 但中频段必须有足够的带宽,以保证系的相位裕 量,带宽越大,相位裕量越大。
5 ) 作 10lg 4dB直线与未校正系统对数幅频特性曲线相交 ' c 是 满 足 于 4.5 , 取 c m 4.5 。可见 , 的要求 c 4.4 。因此
T 6)超前校正的传递函数为:
1 a m
1
1 9
4 s 9 Gc ( s) 1 1 s 9
1.控制系统的性能指标 性能指标通常由使用单位或被控对象的设计制造单位提供; 不同的系统对性能指标的要求也有不同的侧重;
性能指标应符合实际系统的需求和可能;
在设计时,根据性能指标的形式来确定设计方法;
如性能指标以单位阶跃响应的峰值时间、调节时间、超调量、 阻尼比等时域特征给出时,一般采用时域法校正; 如性能指标以系统的相角裕度、幅值裕度、谐振峰值、闭环带宽 等频域特征参数给出时,一般采用频域法校正;
0.046
1 1 4.18 T 5.2 0.046
(6)引进增益Kc等于的 放大器,确定校正后的系 统开环传递函数
Gc ( s ) [
Ts 1
Ts 1
]
0.239 s 1 0.046 s 1
G( s) G ( s)Gc ( s)
20 0.239s 1 s(0.5s 1) 0.046s 1
d ( ) 0 d d tan ( ) 0 d
T (a 1) 1 aT 2 2
d T (a 1) T (a 1)[1 aT 2 2 ] 0 2 2 2 2 2 d 1 aT (1 aT )
m 1 aT
1 sin m ,并由 a 1 sin m
6)由 m
计算参数T, 1 aTs 并写出超前校正的传递函数 Gc (s) 。
aT
1
1 Ts
7)校验指标:绘制系统校正后的伯德图,检验是否满足给定的 性能指标。当系统仍不满足要求时,则增大 值,从3)算起
Example 1 设控制系统如图所示。若要求系统在单位斜坡输入 信号作用下,位置输出稳态误差 e ss 0.1 ,开环 0 45 系统截止频率 c 4.4 。相角裕度 ,幅 值裕度 h 10dB ,试选择超前校正参数。
系统的相位和增益裕量 分别为17°和+∞分贝
1.系统稳定 2.稳态误差满意 3.瞬态响应不满意 改变高频部分,c
超前校正
(3)确定需要增加的最大相位超前角m
50 17 33
m 10 43
补偿c增加造成的 Gs(j )相位滞后
(4)确定系数,确定 频率c,且c=m
7)验证。
500 450
h 10 dB
c 4.5
Bode Diagram 100
Magnitude (dB) Phase (deg)
50
0
-50
-100 -90
-135
-180 10
-2
10
-1
10
0
10
1
10
2
10
3
Frequency (rad/sec)
Step Response 1.8 1.6 1.4 1.2
tan ( m ) T (a 1) 1 aT 2 2
m
1 aT
a 1 2 a
a 1 a 1 m (m ) arctan arcsin a 1 2 a
可解出
a
1 sin m 1 sin m L(m ) 10lga
● 超前网络特点:相角超前,幅值增加 ● 一级超前网络最大超前角为60º ● 最有效的a 4, 10
第五章 线性系统的校正方法
§5.1 §5.2 §5.3 §5.4
控制系统校正的概念 串联超前校正 串联滞后校正 串联超前滞后校正
数学模型
T域、S域、W域 性能分析
稳、准、快
系统综合、校正
控制系统 不可变部分 执行机构 功率放大器 检测装置 ? 可变部分 放大器、校正装置
(设计系统)
迫使系统满足给定的性能
!ωc的大小取决于系统的快速性要求。 ωc大快速性好,但抗扰能力下降。
§5.2 串联超前校正
§5.2.1 超前网络特性
Gc ( s ) U c ( s) U r ( s) R2 1 R1 Cs R2 1 R1 Cs R2 R1 R2 CR1 s 1
R2 (CR1 s 1) R2 (CR1 s 1) R2 (CR1 s 1) R1 R2 R1 R2C R2 (CR1 s 1) R1 R1 R2C s R1 R2 s1 R1 R2
§5.1控制系统校正的概念
前馈校正:也称为顺馈校正,单独作用于开环控制系统,也可以作为反馈 控制的附加校正而组成复合控制。
§5.1控制系统校正的概念
复合校正:在反馈控制回路中,加入前馈校正通路,组成有机整体。
按扰动补偿
按输入补偿
§5.1控制系统校正的概念
3. 校正方法 <1>综合法(期望特性法)
Bode Diagram 100
Magnitude
-100 -90
-135
-180 10
-2
10
-1
10
0
10
1
10
2
Frequency (rad/sec)
3)在伯德图上量得,未校正系统的开环截止频率为 c 3 , 相角裕量为 0 180 ,幅值裕量为 h0 。相角裕量 也可以由计算得到
R(s)
K s ( s 1)
C (s)
图7.11 例7.1的控制系统
解: 1)根据给定的稳态指标,确定符合要求的开环增益K。本例
要求在单位斜坡输入信号作用下 e ss 0.1 ,说明校正后的 1 系统仍应是1型系统,因为 ,所以应 ess 0.1 K 有 K 10 ,取K=10。 2)绘制原系统的伯德图。
“-”
选定的 校正装置
不符要求则重选校正装置
§5.1控制系统校正的概念
频率响应设计法 !分析法或者综合法都可应用时域法和频率响应法实现。 频率特性图可以清楚表明系统改变性能指标的方向。 频域设计通常通过Bode图进行处理起来十分简单。(当 采用串联校正时,使得校正后系统的Bode图即为原有系 统Bode图和校正装置的Bode图直接相加) 对于某些数学模型推导起来比较困难的元件,如液压和气动 元件,通常可以通过频率响应实验来获得其Bode图。 在涉及到高频噪声时,频域法设计比其他方法更为方便。
控制系统的设计任务: 根据被控对象及其控制要求,选择适当的控 制器及控制规律设计一个满足给定性能指标的控 制系统。 校正(补偿):通过改变系统结构,或在系统中增 加附加装置或元件对已有的系统(固有部分)进 行再设计使之满足性能要求。
(校正装置)
!控制系统的设计本质上是寻找合适的校正装置
§5.1控制系统校正的概念
未校正系统的剪切率: 20dB / dec, 5 10
40 dB / dec , 10 15 60dB / dec, 15 20
4)取 m 求出a。 即所需补偿的相角由超前校正装置来提供。
5)为使超前校正装置的最大超前相角出现在校正后系统的截止 上,即 m c ,取未校正系统幅值为 10 lg a db 时 频率 c 。 的频率作为校正后系统的截止频率 c
1 aTs 1 a Ts 1
R1 R2 a 1 R2 R1 R2C T R1 R2
a Gc ( s )
aTs 1 Ts 1
aTs 1 a Gc ( s ) Ts 1
1T H 20 lg 20 lg a 1 aT
(a 1)
( ) arctan( aT ) arctan( T ) arctan
) H ( j c ) G0 ( j c ) H ( j c ) G0 ( j c , c c
取
) H ( j c ) G0 ( j c ) H ( j c ) G0 ( j c
为校正后的截止频率。 其中 , c 的选取:由于 c 尚未确定,所以,从上式并不 能求得 ,一般由经验选取。
2)利用1)求得的K,绘制系统的伯德图。
3)在伯德图上量取未校正系统的相位裕量和幅值裕量,并计 算为使相位裕量达到给定指标所需补偿的超前相 角 。 0 其中 , 为给定的相位裕量指标; 0 为未校正系统的相位 裕量; 为附加的角度。
