中考数学总复习专题训练(三)
九年级中考复习数学考点专题训练——专题三:一次函数

中考数学考点专题训练——专题三:一次函数1.在学习一元一次不等式与一次函数中,小明在同一个坐标系中分别作出了一次函数y=k1x+b1和y=kx+b 的图象,分别与x轴交于点A、B,两直线交于点C.已知点A(﹣1,0),B(2,0),观察图象并回答下列问题:(1)关于x的方程k1x+b1=0的解是;关于x的不等式kx+b<0的解集是;(2)直接写出关于x的不等式组的解集;(3)若点C(1,3),求关于x的不等式k1x+b1>kx+b的解集和△ABC的面积.2.为让更多的学生学会游泳,少年宫新建一个游泳池,其容积为480m3,该游泳池有甲、乙两个进水口,注水时每个进水口各自的注水速度保持不变.同时打开甲、乙两个进水口注水,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图象如图所示.(1)根据图象求游泳池的蓄水量y(m3)与注水时间t(h)之间的函数关系式,并写出同时打开甲、乙两个进水口的注水速度;(2)现将游泳池的水全部排空,对池内消毒后再重新注水.已知单独打开甲进水口注满游泳池所用时间是单独打开乙进水口注满游泳池所用时间的倍.求单独打开甲进水口注满游泳池需多少小时?3.规定:若直线l与图形M有公共点,则称直线l是图形M的关联直线.已知:矩形ABCD的其中三个顶点的坐标为A(t,0),B(t+2,0),C(t+2,3)(1)当t=1时,如图以下三个一次函数y1=x+4,y2=﹣x+2,y3=x+2中,是矩形ABCD的关联直线;(2)已知直线l:y=x+2,若直线l是矩形ABCD的关联直线,求t的取值范围;(3)如果直线m:y=tx+2(t>0)是矩形ABCD的关联直线,请直接写出t的取值范围.4.如图,直线y=﹣与x轴相交于点A,与直线y=x相交于点B.(1)求点A,点B的坐标;(2)动点C从原点O出发,以每秒1个单位的速度在线段OA上向点A做匀速运动,连接BC,设运动时间为t秒,△BCA的面积为S,求出S关于t的函数关系式;(3)若点P是坐标平面内任意一点,以O,A,B,P为顶点的四边形是平行四边形,请直接写出点P的坐标.5.已知:在平面直角坐标系中,点O为坐标原点,直线AB与x轴的正半轴交于点A,与y轴的负半轴交于点B,OA=OB,过点A作x轴的垂线与过点O的直线相交于点C,直线OC的解析式为y=x,过点C作CM⊥y轴,垂足为M,OM=9.(1)如图1,求直线AB的解析式;(2)如图2,点N在线段MC上,连接ON,点P在线段ON上,过点P作PD⊥x轴,垂足为D,交OC于点E,若NC=OM,求的值;(3)如图3,在(2)的条件下,点F为线段AB上一点,连接OF,过点F作OF的垂线交线段AC于点Q,连接BQ,过点F作x轴的平行线交BQ于点G,连接PF交x轴于点H,连接EH,若∠DHE=∠DPH,GQ﹣FG =AF,求点P的坐标.6.如图:在平面直角坐标系xOy中,过点A(﹣2,0)的直线l1和直线l2:y=2x相交于点B(2,m).(1)求直线l1的表达式;(2)过动点P(n,0)(n<0)且垂直于x轴的直线与l1、l2的交点分别为C,D.横、纵坐标都是整数的点叫做整点.①当n=﹣1时,直接写出△BCD内部(不含边上)的整点个数;②若△BCD的内部(不含边上)恰有3个整点,直接写出n的取值范围.7.如图,在平面直角坐标系中,点O为坐标原点,直线l分别交x轴、y轴于A.B两点,OA<OB,且OA、OB的长分别是一元二次方程x2﹣14x+48=0的两根.(1)求直线AB的解析式;(2)点C从点A出发沿射线AB方向运动,运动的速度为每秒2个单位,设△OBC的面积为S,点C运动的时间为t,写出S与t的函数关系式,并直接写出自变量的取值范围;(3)点P是y轴上的点,点Q是第一象限内的点,若以A、B、P、Q为顶点的四边形是菱形请求出点Q的坐标.8.团结奋战,众志成城,齐齐哈尔市组织援助医疗队,分别乘甲、乙两车同时出发,沿同一路线赶往绥芬河.齐齐哈尔距绥芬河的路程为800km,在行驶过程中乙车速度始终保持80km/h,甲车先以一定速度行驶了500km,用时5h,然后再以乙车的速度行驶,直至到达绥芬河(加油、休息时间忽略不计).甲、乙两车离齐齐哈尔的路程y(km)与所用时间x(h)的关系如图所示,请结合图象解答下列问题:(1)甲车改变速度前的速度是km/h,乙车行驶h到达绥芬河;(2)求甲车改变速度后离齐齐哈尔的路程y(km)与所用时间x(h)之间的函数解析式,不用写出自变量x的取值范围;(3)甲车到达绥芬河时,乙车距绥芬河的路程还有km;出发h时,甲、乙两车第一次相距40km.9.如图,已知直线y=kx+b与直线y=﹣x﹣9平行,且y=kx+b还过点(2,3),与y轴交于A点.(1)求A点坐标;(2)若点P是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON 上分别截取:PC=MP,MB=OM,OE=ON,ND=NP,试证:四边形BCDE是平行四边形;(3)在(2)的条件下,在直线y=kx+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,直接写出所有符合的点P的坐标;若不存在,请说明理由.10.小碚向某校食堂王经理建议食堂就餐情况,经调查发现就餐时,有520人排队吃饭就餐,就餐开始后仍有学生继续前来排队进食堂.设学生按固定的速度增加,食堂打饭窗口打饭菜的速度也是固定的.若每分钟该食堂新增排队学生数12人,每个打饭窗口1每分钟打饭菜10人.已知食堂的前a分钟只开放了两个打饭窗口;某一天食堂排队等候的学生数y(人)与打饭菜时间x(分钟)的关系如图所示.(1)求a的值;(2)求排队到第16分钟时,食堂排队等候打饭菜的学生人数;(3)若要在开始打饭菜后8分钟内让所有排队的学生都能进食堂后来到食堂窗口的学生随到随吃,那么小碚应该建议食堂王经理一开始就需要至少同时开放几个打饭窗口?11.如图,在平面直角坐标系中,直线y1=kx+b与x轴交于点A(4,0),与y轴交于点B(0,3),点C是直线y2=﹣x+5上的一个动点,连接BC,过点C作CD⊥AB于点D.(1)求直线y1=kx+b的函数表达式;(2)当BC∥x轴时,求BD的长;(3)点E在线段OA上,OE=OA,当点D在第一象限,且△BCD中有一个角等于∠OEB时,请直接写出点C的横坐标.12.在平面直角坐标系xOy中,点A(t﹣1,1)与点B关于过点(t,0)且垂直于x轴的直线对称.(1)以AB为底边作等腰三角形ABC,①当t=2时,点B的坐标为;②当t=0.5且直线AC经过原点O时,点C与x轴的距离为;③若△ABC上所有点到y轴的距离都不小于1,则t的取值范围是.(2)以AB为斜边作等腰直角三角形ABD,直线m过点(0,b)且与x轴平行,若直线m上存在点P,△ABD 上存在点K,满足PK=1,直接写出b的取值范围.13.笛卡尔是法国数学家、科学家和哲学家,他的哲学与数学思想对历史的影响是深远的.1637年,笛卡尔发表了《几何学》,创立了直角坐标系.其中笛卡尔的思想核心是:把几何学的问题归结成代数形式的问题,用代数的方法进行计算、证明,从而达到最终解决几何问题的目的.某学习小组利用平面直角坐标系在研究直线上点的坐标规律时,发现直线y=kx+b(k≠0)上的任意三点A (x1,y1),B(x2,y2),C(x3,y3)(x1≠x1≠x3),满足===k,经学习小组查阅资料得知,以上发现是成立的,即直线y=kx+b(k≠0)上任意两点的坐标M(x1,y1)N(x2,y2)(x1≠x2),都有的值为k,其中k叫直线y=kx+b的斜率.如,P(1,3),Q(2,4)为直线y=x+2上两点,则k PQ==1,即直线y=x+2的斜率为1.(1)请你直接写出过E(2,3)、F(4,﹣2)两点的直线的斜率k EF=.(2)学习小组继续深入研究直线的“斜率”问题,得到如下正确结论:不与坐标轴平行的任意两条直线互相垂直时,这两条直线的斜率之积是定值.如图1,直线GH⊥GI于点G,G(1,3),H(﹣2,1),I(﹣1,6).请求出直线GH与直线GI的斜率之积.(3)如图2,已知正方形OKRS的顶点S的坐标为(6,8),点K,R在第二象限,OR为正方形的对角线.过顶点R作RT⊥OR于点R.求直线RT的解析式.14.定义:在平面直角坐标系中,O为坐标原点,对于任意两点P(m,y)、Q(x,y0),m为任意实数,若,则称点Q是点P的变换点,例如:若点P(m,y)在直线y=x上,则点P的变换点Q在函数的图象上,设点P(m,y)在函数y=x2﹣2x的图象上,点P的变换点Q所在的图象记为G.(1)直接写出图象G对应的函数关系式.(2)当m=3,且﹣2≤x≤3时,求图象G的最高点与最低点的坐标.(3)设点A、B的坐标分别为(m﹣1,﹣2)、(2m+2,﹣2),连结AB,若图象G与线段AB有交点,直接写出m的取值范围.(4)若图象G上的点Q的纵坐标y0的取值范围是y0≥k或y0≤n,其中k>n,令s=k﹣n,求s与m之间的函数关系式,并写出m的取值范围.15.如图,把矩形OABC放入平面直角坐标系xOy中,使OA、OC分别落在x、y轴的正半轴上,对角线AC所在直线解析式为y=﹣x+15,将矩形OABC沿着BE折叠,使点A落在边OC上的点D处.(1)求点E的坐标;(2)在y轴上是否存在点P,使△PBE为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.16.如图,直线与x、y轴交于点A、B,过点B作x轴的平行线交直线y=x+b于点D,直线y=x+b交x、y轴于点E、K,且DK=.(1)如图1,求直线DE的解析式;(2)如图2,点P为AB延长线上一点,把线段BP绕着点B顺时针旋转90°得到线段BF,若点F刚好落在直线DE上,求点P的坐标;(3)如图3,在(2)的条件下,点M为ED延长线上一点,连接PM和AM,AM交线段BD于点N,若PM+MN =AN,求线段PM的长.17.在平面上,对于给定的线段AB和点C,若平面上的点P(可以与点C重合)满足,∠APB=∠ACB.则称点P为点C关于直线AB的联络点.在平面直角坐标系xOy中,已知点A(2,0),B(0,2),C(﹣2,0).(1)在P1(2,2),P(1,0),R(1+,1)三个点中,是点O关于线段AB的联络点的是.(2)若点P既是点O关于线段AB的联络点,同时又是点B关于线段OA的联络点,求点P的横坐标m的取值范围;(3)直线y=x+b(b>0)与x轴,y轴分交于点M,N,若在线段BC上存在点N关于线段OM的联络点,直接写出b的取值范围.18.已知直线y=x+b与x轴交于点A,与y轴交于点B,(1)如图1,求∠BAO的度数;(2)如图2,点D在第三象限,连接BD,将线段BD以B为旋转中心逆时针旋转90°得到BE且点E在第四象限,连接DE、OE,若DE=2OE,求证:S△ADE=2S△AOE;(3)如图3,点C为点A关于y轴的对称点,点D在第二象限,连接BD,将线段BD以B为旋转中心逆时针旋转90°得到BE,点E在第四象限,连接OE且OE∥BC,过点A作AP⊥BE交BC于点P,点Q在AB上,BQ=BP,过点Q作QG⊥AP交x轴于点G.若OF=,CG=7,求S△AOE.19.如图,在平面直角坐标系xOy中,直线y=x+4与y=kx+4分别交x轴于点A、B,两直线交于y轴上同一点C,点D的坐标为(﹣,0),点E是AC的中点,连接OE交CD于点F.(1)求点F的坐标;(2)若∠OCB=∠ACD,求k的值;(3)在(2)的条件下,过点F作x轴的垂线1,点M是直线BC上的动点,点N是x轴上的动点,点P是直线l上的动点,使得以B,P,M、N为顶点的四边形是菱形,求点P的坐标.20.在平面直角坐标系中,O为坐标原点,直线y=x+4分别交y轴和x轴于点A、B两点,点C在x轴的正半轴上,AO=2OC,连接AC.(1)如图1,求直线AC的解析式;(2)如图2,点P在线段AB上,点Q在BC的延长线上,满足:AP=CQ,连接PQ交AC于点D,过点P作PE⊥AC于点E,设点P的横坐标为t,△PQE的面积为S,求S与t的函数关系式(不要求写出自变量t的取值范围);(3)如图3,在(2)的条件下,PQ交y轴于点M,过点A作AN⊥AC交QP的延长线于点N,过点Q作QF ∥AC交PE的延长线于点F,若MN=DQ,求点F的坐标.备战2021中考数学考点专题训练——专题三:一次函数参考答案1.在学习一元一次不等式与一次函数中,小明在同一个坐标系中分别作出了一次函数y=k1x+b1和y=kx+b 的图象,分别与x轴交于点A、B,两直线交于点C.已知点A(﹣1,0),B(2,0),观察图象并回答下列问题:(1)关于x的方程k1x+b1=0的解是;关于x的不等式kx+b<0的解集是;(2)直接写出关于x的不等式组的解集;(3)若点C(1,3),求关于x的不等式k1x+b1>kx+b的解集和△ABC的面积.【答案】解:(1)∵一次函数y=k1x+b1和y=kx+b的图象,分别与x轴交于点A(﹣1,0)、B(2,0),∴关于x的方程k1x+b1=0的解是x=﹣1,关于x的不等式kx+b<0的解集,为x>2,故答案为x=﹣1,x>2;(2)根据图象可以得到关于x的不等式组的解集﹣1<x<2;(3)∵AB=3,∴S△ABC=•y C==.2.为让更多的学生学会游泳,少年宫新建一个游泳池,其容积为480m3,该游泳池有甲、乙两个进水口,注水时每个进水口各自的注水速度保持不变.同时打开甲、乙两个进水口注水,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图象如图所示.(1)根据图象求游泳池的蓄水量y(m3)与注水时间t(h)之间的函数关系式,并写出同时打开甲、乙两个进水口的注水速度;(2)现将游泳池的水全部排空,对池内消毒后再重新注水.已知单独打开甲进水口注满游泳池所用时间是单独打开乙进水口注满游泳池所用时间的倍.求单独打开甲进水口注满游泳池需多少小时?【答案】解:(1)设y与t的函数解析式为y=kt+b,,解得,,即y与t的函数关系式是y=140t+100,同时打开甲、乙两个进水口的注水速度是:(380﹣100)÷2=140(m3/h);(2)∵单独打开甲进水口注满游泳池所用时间是单独打开乙进水口注满游泳池所用时间的倍.∴甲进水口进水的速度是乙进水口进水速度的,∵同时打开甲、乙两个进水口的注水速度是140m3/h,∴甲进水口的进水速度为:140÷(+1)×=60(m3/h),480÷60=8(h),即单独打开甲进水口注满游泳池需8h.3.规定:若直线l与图形M有公共点,则称直线l是图形M的关联直线.已知:矩形ABCD的其中三个顶点的坐标为A(t,0),B(t+2,0),C(t+2,3)(1)当t=1时,如图以下三个一次函数y1=x+4,y2=﹣x+2,y3=x+2中,是矩形ABCD的关联直线;(2)已知直线l:y=x+2,若直线l是矩形ABCD的关联直线,求t的取值范围;(3)如果直线m:y=tx+2(t>0)是矩形ABCD的关联直线,请直接写出t的取值范围.【答案】解:(1)当t=1时,A(1,0),B(3,0),C(3,3),D(1,3),则三个一次函数y1=x+4,y2=﹣x+2,y3=x+2中,y2=﹣x+2,y3=x+2是矩形ABCD的关联直线;故答案为:y2=﹣x+2,y3=x+2;(2)由矩形的性质得D(t,3),当y=3时,t+2=3,解得t=1;当y=0时t+2+2=0,解得t=﹣4.故t的取值范围为﹣4≤t≤1;(3)由矩形的性质得D(t,3),当y=3时,t2+2=3,解得t=±1(负值舍去).故t的取值范围为0<t≤1.4.如图,直线y=﹣与x轴相交于点A,与直线y=x相交于点B.(1)求点A,点B的坐标;(2)动点C从原点O出发,以每秒1个单位的速度在线段OA上向点A做匀速运动,连接BC,设运动时间为t秒,△BCA的面积为S,求出S关于t的函数关系式;(3)若点P是坐标平面内任意一点,以O,A,B,P为顶点的四边形是平行四边形,请直接写出点P的坐标.【答案】解:(1)当y=0时,0=﹣,解得x=4;则A(4,0);联立两直线的解析式得,解得.则B(2,2);(2)∵A(4,0),∴OA=4,∴S=(OA﹣t)×2=(4﹣t)×2=4﹣t(0≤t<4);(3)如图,当OA为平行四边形的边时,∵OA=4,∴P1(6,2),P2(﹣2,);当OA为对角线时,P3(2,﹣2).综上所示,点P的坐标为:P1(6,2),P2(﹣2,2),P3(﹣2,2).5.已知:在平面直角坐标系中,点O为坐标原点,直线AB与x轴的正半轴交于点A,与y轴的负半轴交于点B,OA=OB,过点A作x轴的垂线与过点O的直线相交于点C,直线OC的解析式为y=x,过点C作CM⊥y轴,垂足为M,OM=9.(1)如图1,求直线AB的解析式;(2)如图2,点N在线段MC上,连接ON,点P在线段ON上,过点P作PD⊥x轴,垂足为D,交OC于点E,若NC=OM,求的值;(3)如图3,在(2)的条件下,点F为线段AB上一点,连接OF,过点F作OF的垂线交线段AC于点Q,连接BQ,过点F作x轴的平行线交BQ于点G,连接PF交x轴于点H,连接EH,若∠DHE=∠DPH,GQ﹣FG =AF,求点P的坐标.【答案】解:(1)∵CM⊥y轴,OM=9,∴y=9时,9=x,解得x=12,∴C(12,9),∵AC⊥x轴,∴A(12,0),∵OA=OB,∴B(0,﹣12),设直线AB的解析式为y=kx+b,则有,解得,∴直线AB的解析式为y=x﹣12.(2)如图2中,∵∠CMO=∠MOA=∠OAC=90°,∴四边形OACM是矩形,∴AO=CM=12,∵NC=OM=9,∴MN=CM﹣NC=12﹣9=3,∴N(3,9),∴直线ON的解析式为y=3x,设点E的横坐标为4a,则D(4a,0),∴OD=4a,把x=4a,代入y=x中,得到y=3a,∴E(4a,3a),∴DE=3a,把x=4a代入,y=3x中,得到y=12a,∴P(4a,12a),∴PD=12a,∴PE=PD﹣DE=12a﹣3a=9a,∴=.(3)如图3中,设直线FG交CA的延长线于R,交y轴于S,过点F作FT⊥OA于T.∵GF∥x轴,∴∠OSR=∠MOA=90°,∠CAO=∠R=90°,∠BOA=∠BSG=90°,∠OAB=∠AFR,∴∠OFR=∠R=∠AOS=∠BSG=90°,∴四边形OSRA是矩形,∴OS=AR,AR=OA=12,∵OA=OB,∴∠OBA=∠OAB=45°,∴∠FAR=90°﹣45°=45°,∴∠FAR=∠AFR,∴FR=AR=OS,∵OF⊥FQ,∴∠OSR=∠R=∠OFQ=90°,∴∠OFS+∠QFR=90°,∵∠QFR+∠FQR=90°,∴∠OFS=∠FQR,∴△OFS≌△FQR(AAS),∴SF=QR,∵∠SFB=∠AFR=45°,∴∠SBF=∠SFB=45°,∴SF=SB=QR,∵∠SGB=∠QGR,∠BSG=∠R,∴△BSG≌△QRG(AAS),∴SG=GR=6,设FR=m,则AR=m,AF=m,QR=SF=12﹣m,∵GQ﹣FG=AF,∴GQ=×m+6﹣m=m+6,∵GQ2=GR2+QR2,∴(m+6)2=62+(12﹣m)2,解得m=4,∴FS=8,AR=4,∵∠OAB=∠FAR,FT⊥OA,FR⊥AR,∴FT=FR=AR=4,∠OTF=90°,∴四边形OSFT是矩形,∴OT=SF=8,∵∠DHE=∠DPH,∴tan∠DHE=tan∠DPH,∴=,由(2)可知DE=3a,PD=12a,∴=,∴DH=6a,∴tan∠PHD===2,∵∠PHD=∠FHT,∴tan∠FHT==2,∴HT=2,∵OT=OD+DH+HT,∴4a+6a+2=8,∴a=,∴OD=,PD=12×=,∴P(,).6.如图:在平面直角坐标系xOy中,过点A(﹣2,0)的直线l1和直线l2:y=2x相交于点B(2,m).(1)求直线l1的表达式;(2)过动点P(n,0)(n<0)且垂直于x轴的直线与l1、l2的交点分别为C,D.横、纵坐标都是整数的点叫做整点.①当n=﹣1时,直接写出△BCD内部(不含边上)的整点个数;②若△BCD的内部(不含边上)恰有3个整点,直接写出n的取值范围.【答案】解:(1)将点B的坐标代入y=2x得,m=2×2=4,故点B(2,4),设直线l1的表达式为y=kx+b,将点A、B的坐标代入上式并解得:,解得,故直线l1的表达式为:y=x+2;(2)①当n=﹣1时,如下图,从图中可以看出,整点个数为1,即点(0,1);②如上图,当n=﹣2时,△BCD的内部(不含边上)恰有3个整点,故﹣2≤n<﹣1.7.如图,在平面直角坐标系中,点O为坐标原点,直线l分别交x轴、y轴于A.B两点,OA<OB,且OA、OB的长分别是一元二次方程x2﹣14x+48=0的两根.(1)求直线AB的解析式;(2)点C从点A出发沿射线AB方向运动,运动的速度为每秒2个单位,设△OBC的面积为S,点C运动的时间为t,写出S与t的函数关系式,并直接写出自变量的取值范围;(3)点P是y轴上的点,点Q是第一象限内的点,若以A、B、P、Q为顶点的四边形是菱形请求出点Q的坐标.【答案】解:(1)x2﹣14x+48=0,则x=6或8,故点A、B的坐标分别为(6,0)、(0,8),则AB=10;设直线AB的表达式为:y=kx+b,则,解得,故直线AB的表达式为:y=﹣x+8;(2)过点C作CM⊥y轴于点M,则,即,解得:CM=|10﹣2t|,S=×BO×CM=×8×|10﹣2t|=|10﹣2t|,故S=;(3)点A、B的坐标分别为(6,0)、(0,8),设点P、Q的坐标分别为(0,s)、(m,n),①当AB是菱形的边时,点A向上平移8个单位向左平移6个单位得到点B,同样点Q向上平移8个单位向左平移6个单位得到点P,即0﹣8=m,s+6=n且BP=BA=10,解得:m=﹣8,n=24,故点Q的坐标为(﹣8,24);②当AB是菱形的对角线时,由中点公式得:6+0=m+0,8+0=s+n且BP=BQ,即(s﹣8)2=m2+(n﹣8)2,解得:m=6,m=,故点Q的坐标为(6,);综上,点Q的坐标为(﹣8,24)或(6,).8.团结奋战,众志成城,齐齐哈尔市组织援助医疗队,分别乘甲、乙两车同时出发,沿同一路线赶往绥芬河.齐齐哈尔距绥芬河的路程为800km,在行驶过程中乙车速度始终保持80km/h,甲车先以一定速度行驶了500km,用时5h,然后再以乙车的速度行驶,直至到达绥芬河(加油、休息时间忽略不计).甲、乙两车离齐齐哈尔的路程y(km)与所用时间x(h)的关系如图所示,请结合图象解答下列问题:(1)甲车改变速度前的速度是km/h,乙车行驶h到达绥芬河;(2)求甲车改变速度后离齐齐哈尔的路程y(km)与所用时间x(h)之间的函数解析式,不用写出自变量x的取值范围;(3)甲车到达绥芬河时,乙车距绥芬河的路程还有km;出发h时,甲、乙两车第一次相距40km.【答案】解:(1)甲车改变速度前的速度为:500出5=100(km/h),乙车达绥芬河是时间为:800÷80=10(h),故答案为:100;10;(2)∵乙车速度为80km/h,∴甲车到达绥芬河的时间为:,甲车改变速度后,到达绥芬河前,设所求函数解析式为:y=kx+b(k≠0),将(5,500)和(,800)代入得:,解得,∴y=80x+100,答:甲车改变速度后离齐齐哈尔的路程y(km)与所用时间x(h)之间的函数解析式为y=80x+100();(3)甲车到达绥芬河时,乙车距绥芬河的路程为:800﹣80×=100(km),40÷(100﹣80)=2(h),即出发2h时,甲、乙两车第一次相距40km.故答案为:100;2.9.如图,已知直线y=kx+b与直线y=﹣x﹣9平行,且y=kx+b还过点(2,3),与y轴交于A点.(1)求A点坐标;(2)若点P是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON 上分别截取:PC=MP,MB=OM,OE=ON,ND=NP,试证:四边形BCDE是平行四边形;(3)在(2)的条件下,在直线y=kx+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,直接写出所有符合的点P的坐标;若不存在,请说明理由.【答案】解:(1)∵直线y=kx+b与y=﹣x﹣9平行,且过点A(2,3),则,解得,∴一次函数解析式为y=﹣x+4,当x=0时,y=4,∴A点坐标是(0,4);(2)证明:∵PM⊥x轴,PN⊥y轴,∴∠M=∠N=∠O=90°,∴四边形PMON是矩形,∴PM=ON,OM=PN,∠M=∠O=∠N=∠P=90°.∵PC=MP,MB=OM,OE=ON,ND=NP,∴PC=OE,CM=NE,ND=BM,PD=OB,在△OBE和△PDC中,OB=PD,∠O=∠CPD,OE=PC,∴△OBE≌△PDC(SAS),∴DC=BE,同理可证△MBC≌△NDE(SAS),∴DE=BC.∴四边形BCDE是平行四边形;(3)存在这样的点P,理由:设点P(m,﹣m+4),则CM=PC=|(4﹣m)|=|﹣m|,PD=m,当四边形BCDE为正方形时,则∠DCB=90°,DC=BC,而∠CBM+∠MCB=90°,∠MCB+∠DCP=90°,∴∠CBM=∠DCP,而∠DPC=∠CMB=90°,∴△DPC≌△CMB(AAS),∴CM=PD,即=|﹣m|=m,解得:m=或﹣8,故P点坐标是(,)或(﹣8,8).10.小碚向某校食堂王经理建议食堂就餐情况,经调查发现就餐时,有520人排队吃饭就餐,就餐开始后仍有学生继续前来排队进食堂.设学生按固定的速度增加,食堂打饭窗口打饭菜的速度也是固定的.若每分钟该食堂新增排队学生数12人,每个打饭窗口1每分钟打饭菜10人.已知食堂的前a分钟只开放了两个打饭窗口;某一天食堂排队等候的学生数y(人)与打饭菜时间x(分钟)的关系如图所示.(1)求a的值;(2)求排队到第16分钟时,食堂排队等候打饭菜的学生人数;(3)若要在开始打饭菜后8分钟内让所有排队的学生都能进食堂后来到食堂窗口的学生随到随吃,那么小碚应该建议食堂王经理一开始就需要至少同时开放几个打饭窗口?【答案】解:(1)由图象知,520+12a﹣2×10a=424,∴a=12;(2)设当12≤x≤20时,y与x之间的函数关系式为y=kx+b,由题意,得,解得:,∴y=﹣53x+1060,当x=16时,y=212,即排队到第16分钟时,食堂排队等候打饭菜的学生有212人.(3)设需同时开放n个打饭窗口,由题意知10n×8≥520+12×8解得:n≥7.7,∵n为整数,∴n最小=8.答:至少需要同时开放8个打饭窗口.11.如图,在平面直角坐标系中,直线y1=kx+b与x轴交于点A(4,0),与y轴交于点B(0,3),点C 是直线y2=﹣x+5上的一个动点,连接BC,过点C作CD⊥AB于点D.(1)求直线y1=kx+b的函数表达式;(2)当BC∥x轴时,求BD的长;(3)点E在线段OA上,OE=OA,当点D在第一象限,且△BCD中有一个角等于∠OEB时,请直接写出点C的横坐标.【答案】解:(1)把A(4,0),B(0,3)代入y1=kx+b,得到,解得:,∴y1=﹣x+3.(2)∵BC∥x轴,∴点C的纵坐标为3,当y=3时,3=﹣x+5,解得x=,∴C(,3),∵CD⊥AB,∴直线CD的解析式为y=x+,由,解得,∴D(,),∴BD==.(3)如图,当∠BCD=∠BEO时,过点A作AM⊥BC交BC的延长线于M,点M作MN⊥x轴于N.∵OB=3,OE=OA=,∴tan∠BEO==2,∵CD⊥AB,AM⊥AB,∴CD∥AM,∴∠AMB=∠BCD=∠BEO,∴tan∠AMB==2,∵AB===5,∴AM=AB=,∵∠AOB=∠ANM=∠BAM=90°,∴∠BAO+∠ABO=90°,∠BAO+∠MAN=90°,∴∠MAN=∠ABO,∴△ABO∽△MAN,∴==,∴==,∴AN=,MN=2,∴M(,2),∴直线BM的解析式为y=﹣x+3,由,解得x=,∴点C的横坐标为当∠CBD=∠BEO时,同法可得点C的横坐标为.12.在平面直角坐标系xOy中,点A(t﹣1,1)与点B关于过点(t,0)且垂直于x轴的直线对称.(1)以AB为底边作等腰三角形ABC,①当t=2时,点B的坐标为;②当t=0.5且直线AC经过原点O时,点C与x轴的距离为;③若△ABC上所有点到y轴的距离都不小于1,则t的取值范围是.(2)以AB为斜边作等腰直角三角形ABD,直线m过点(0,b)且与x轴平行,若直线m上存在点P,△ABD 上存在点K,满足PK=1,直接写出b的取值范围.【答案】解:(1)①如图1中,由题意A(1,1),A,B关于直线x=2对称,∴B(3,1).故答案为(3,1).②如图2中,由题意A(﹣0.5,1),直线l:x=0.5,∵直线AC的解析式为y=﹣2x,∴C(0.5,﹣1),∴点C到x轴的距离为1,故答案为1.③由题意A(t﹣1,0),B(t+1,0),∵△ABC上所有点到y轴的距离都不小于1,∴t﹣1≥1或t+1≤﹣1,解得t≥2或t≤﹣2.故答案为t≥2或t≤﹣2.(2)如图3中,∵A(t﹣1,0),B(t+1,0),∴AB=t+1﹣(t﹣1)=2,∵△ABD是以AB为斜边的等腰直角三角形,∴点D到AB的距离为1,,∴当点D在AB上方时,若直线m上存在点P,△ABD上存在点K,满足PK=1,则0≤b≤3.当点D在AB下方时,若直线m上存在点P,△ABD上存在点K,满足PK=1,则﹣1≤b≤2.13.笛卡尔是法国数学家、科学家和哲学家,他的哲学与数学思想对历史的影响是深远的.1637年,笛卡尔发表了《几何学》,创立了直角坐标系.其中笛卡尔的思想核心是:把几何学的问题归结成代数形式的问题,用代数的方法进行计算、证明,从而达到最终解决几何问题的目的.某学习小组利用平面直角坐标系在研究直线上点的坐标规律时,发现直线y=kx+b(k≠0)上的任意三点A (x1,y1),B(x2,y2),C(x3,y3)(x1≠x1≠x3),满足===k,经学习小组查阅资料得知,以上发现是成立的,即直线y=kx+b(k≠0)上任意两点的坐标M(x1,y1)N(x2,y2)(x1≠x2),都有的值为k,其中k叫直线y=kx+b的斜率.如,P(1,3),Q(2,4)为直线y=x+2上两点,则k PQ==1,即直线y=x+2的斜率为1.(1)请你直接写出过E(2,3)、F(4,﹣2)两点的直线的斜率k EF=.(2)学习小组继续深入研究直线的“斜率”问题,得到如下正确结论:不与坐标轴平行的任意两条直线互相垂直时,这两条直线的斜率之积是定值.如图1,直线GH⊥GI于点G,G(1,3),H(﹣2,1),I(﹣1,6).请求出直线GH与直线GI的斜率之积.(3)如图2,已知正方形OKRS的顶点S的坐标为(6,8),点K,R在第二象限,OR为正方形的对角线.过顶点R作RT⊥OR于点R.求直线RT的解析式.【答案】解:(1)∵E(2,3)、F(4,﹣2),∴k EF==﹣,故答案为﹣.(2)∵G(1,3),H(﹣2,1),I(﹣1,6),∴k GH==,k GI==﹣,∴k GH•k GI=﹣1.(3)如图2中,过点K作KM⊥x轴于M,过点S作SN⊥x轴于N,连接KS交OR于J.∴S(6,8),∴ON=6,SN=8,∵四边形OKRS是正方形,∴OK=OS,∠KPS=∠KMO=∠SNO=90°,KJ=JS,JR=JO,∴∠KOM+∠SON=90°,∠SON+∠OSN=90°,∴∠KOM=∠OSN,∴△OMK≌△SNO(AAS),∴KM=ON=6,OM=SN=8,∴K(﹣8,6),∵KJ=JS,∴J(﹣1,7),∵JR=OJ,∴R(﹣2,14),∵k OR==﹣7,∵RT⊥OR,∴k RT=﹣=,设直线RT的解析式为y=x+b.把(﹣2,14)代入可得14=﹣+b,∴b=,∴直线RT的解析式为y=x+14.定义:在平面直角坐标系中,O为坐标原点,对于任意两点P(m,y)、Q(x,y0),m为任意实数,若,则称点Q是点P的变换点,例如:若点P(m,y)在直线y=x上,则点P的变换点Q在函数的图象上,设点P(m,y)在函数y=x2﹣2x的图象上,点P的变换点Q所在的图象记为G.(1)直接写出图象G对应的函数关系式.(2)当m=3,且﹣2≤x≤3时,求图象G的最高点与最低点的坐标.(3)设点A、B的坐标分别为(m﹣1,﹣2)、(2m+2,﹣2),连结AB,若图象G与线段AB有交点,直接写出m的取值范围.(4)若图象G上的点Q的纵坐标y0的取值范围是y0≥k或y0≤n,其中k>n,令s=k﹣n,求s与m之间的函数关系式,并写出m的取值范围.【答案】解:(1)图象G对应的函数关系式y=;(2)当m=3时,图象G对应的函数关系式y=,当x=3时,y=9﹣6﹣1=2.当﹣2≤x≤3时,y=﹣x2+x+1=﹣(x﹣1)2+,当x=1时,y取得最大值为;当x=﹣2时,y取得最小值为﹣3.故图象G的最高点的坐标为(3,2),最低点的坐标为(﹣2,﹣3).(3)当y=﹣2时,﹣x2+x+1=﹣2,解得x1=1﹣,x2=1+,∵点P的变换点Q在函数的图象上,∴m的取值范围为1﹣<m≤2﹣或﹣≤m≤1或1+≤m≤2+;(4)当m>1时,x=m左侧的最高点的坐标为(1,),x=m右侧的最低点的坐标为(m,m2﹣2m﹣1),∵点Q的纵坐标y0的取值范围是y0≥k或y0≤n,∴y0≥m2﹣2m﹣1或y0≤,∴k=m2﹣2m﹣1,n=,当k=时,m2﹣2m﹣1=,解得m1=1+,m2=1﹣(舍去),∵k>n,∴当m>1+时,s=m2﹣2m﹣1﹣=m2﹣2m﹣;当m≤1时,x=m左侧图象无最高点,x=m右侧的最低点的坐标为(1,﹣2),没有符合点Q的纵坐标y0的取值范围是y0≥k或y0≤n.综上所述,求s与m之间的函数关系式为s=m2﹣2m﹣(m>1+).15.如图,把矩形OABC放入平面直角坐标系xOy中,使OA、OC分别落在x、y轴的正半轴上,对角线AC 所在直线解析式为y=﹣x+15,将矩形OABC沿着BE折叠,使点A落在边OC上的点D处.(1)求点E的坐标;(2)在y轴上是否存在点P,使△PBE为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.【答案】解:(1)∵AC所在直线解析式为y=﹣x+15,∴令x=0,y=15,令y=0.则﹣,解得x=9.∴A(9,0),C(0,15),B(9,15),。
2021年中考数学复习专题之三角形03-【三角形的面积】基础训练

2021中考数学复习专题之三角形03【三角形的面积】基础训练一.选择题1.△ABC中,BC=10,AC﹣AB=4.过C作∠BAC的角平分线的垂线,垂足为D,连结BD,CD,则S的最大值为()△BDCA.10B.15C.12D.142.如图,在四边形ABCD中,对角线AC,BD交于点O,∠CBD=90°,BC=4,OB=OD=3,AC=10,则四边形ABCD的面积为()A.48B.36C.24D.123.在平面直角坐标系中,由点A(a,3),B(a+4,3),C(b,﹣3)组成的△ABC的面积是()A.6B.12C.24D.不确定4.如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为6、7、8,四边形DHOG面积为()A.6B.7C.8D.95.如图,在△ABC中,AG=BG,BD=DE=EC,CF=4AF,若四边形DEFG的面积为14,则△ABC的面积为()A.24B.28C.35D.306.如图,点P在直线m上移动,A,B是直线n上的两个定点,且直线m∥n.对于下列各值:①点P到直线n的距离;②△PAB的周长:③△PAB的面积:④∠APB的大小.其中不会随点p 的移动而变化的是()A.①②B.①③C.②④D.③④7.如图,△ABC中,AD是BC上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是20,则△ABE的面积是()A .10B .6C .5D .48.活动课上,小华将两张直角三角形纸片如图放置,已知AC =8,O 是AC 的中点,△ABO 与△CDO 的面积之比为4:3,则两纸片重叠部分即△OBC 的面积为( )A .4B .6C .2D .29.如图,已知△ABC 中,CN =3BN ,AM =CM ,AN 交BM 于O .若S △ABC =40,则下列正确的是( )①S △ABO =2;②BO :MO =2:3;③AO :NO =4;④S △AMO =12:⑤S △CMO =13.A .①②④B .②③④C .②③④⑤D .①②③④10.已知点A (1,2a +1),B (﹣a ,a ﹣3),若线段AB ∥x 轴,则三角形AOB 的面积为( ) A .21B .28C .14D .10.5二.填空题11.如图,点E 、F 都在线段AB 上,分别过点A 、B 作AB 的垂线AD 、BC ,连接DE 、DF 、CE 、CF ,DF 交CE 于点G ,已知AD =BE =7.5,AE =BF =CB =2.5.如果△DEG 的面积为S 1,△CFG 的面积为S 2,则S 1﹣S 2= .12.如图,在△ABC 中,∠BAC =90°,AD 是高,BE 是中线,CF 是角平分线,CF 交AD 于点G ,交BE 于点H ,下面说法中正确的序号是 .①△ABE 的面积等于△BCE 的面积;②∠AFG =∠AGF ;③∠FAG =2∠ACF ;④BH =CH .13.如图,△ABC 中,D 是AB 的中点,且AE :CE =3:1,S △CEP =1,则S △BPC = .14.如图,已知△ABC 中,∠BAC =120°,点D 在边BC 上,且AD =4.BD :CD =3:2.当△ABD 面积最大时,AB 的长为 .15.如图,AD 是△ABC 的中线,G 是AD 上的一点,且AG =2GD ,连结BG ,若S △ABC =12,则S △ABG 为 .三.解答题16.在平面直角坐标系中,已知点A,B,C的坐标分别为A(﹣1,0),B(3,﹣2),C(a,b),且+|a+2b﹣7|=0.(1)求点C的坐标;(2)画出△ABC并求△ABC的面积;(3)若BC与x轴交点为点M,求点M坐标.17.如图,长方形ABCD中,AB=10cm,BC=8cm,点E是CD的中点,动点P从A点出发,以每秒2cm的速度沿A→B→C→E运动,最终到达点E.若点P运动的时间为x秒,那么当x为何值时,△APE的面积等于32cm2?(提醒:同学们,要分类讨论哦!)18.如图,在△ABC中,AD是BC边上的中线,AE是BC边上的高线,已知AE=4,△ABD的面积是6,求BC的长.19.在平面直角坐标系中,已知以A(﹣1,0)或以B(3,0)为直角顶点的直角三角形ABC的面积为6,求顶点C的坐标.20.已知A(0,2),B(4,0),C(6,6)(1)在图中的直角坐标系中画出△ABC;(2)求△ABC的面积.参考答案一.选择题1.解:如图:延长AB ,CD 交点于E ,∵AD 平分∠BAC ,∴∠CAD =∠EAD ,∵CD ⊥AD ,∴∠ADC =∠ADE =90°,在△ADE 和△ADC 中,,∴△ADE ≌△ADC (ASA ),∴AC =AE ,DE =CD ;∵AC ﹣AB =4,∴AE ﹣AB =4,即BE =4;∵DE =DC ,∴S △BDC =S △BEC ,∴当BE ⊥BC 时,S △BDC 面积最大,即S △BDC 最大面积=××10×4=10.故选:A .2.解:在Rt△OBC中,由勾股定理,得CO===5.∵AC=10,∴AO=5,∴OA=OC,∵OB=OD=3,∴四边形ABCD是平行四边形.四边形ABCD的面积为BC•BD=4×(3+3)=24,故选:C.3.解:∵点A(a,3),B(a+4,3),∴AB=4,∵C(b,﹣3),∴点C在直线y=﹣3上,∵AB :y =3与直线y =﹣3平行,且平行线间的距离为6, ∴S =×4×6=12,故选:B .4.解:连接OC ,OB ,OA ,OD ,∵E 、F 、G 、H 依次是各边中点,∴△AOE 和△BOE 等底等高,所以S △OAE =S △OBE , 同理可证,S △OBF =S △OCF ,S △ODG =S △OCG ,S △ODH =S △OAH , ∴S 四边形AEOH +S 四边形CGOF =S 四边形DHOG +S 四边形BFOE , ∵S 四边形AEOH =6,S 四边形BFOE =7,S 四边形CGOF =8, ∴6+8=7+S 四边形DHOG ,解得S 四边形DHOG =7.故选:B .5.解:连接EG ,CG ,∵BD =DE =EC ,∴BD =BC ,∵AG =BG =AB ,∴S △BDG =S △BCG =S △ABC =S △ABC ,同理S △ECF =S △ABC =S △ABC ,S △AFG =×S △ABC =S △ABC ,∴S 四边形DEFG =S △ABC ﹣S BDG ﹣S △CEF ﹣S △AGF =S △ABC =14,∴S △ABC =30.故选:D .6.解:①∵直线m ∥n ,∴点P 到直线n 的距离不变;②∵PA 、PB 的长度随点P 的移动而变化,∴△PAB 的周长会随点P 的移动而变化;③∵点P 到直线n 的距离不变,AB 的大小,∴△PAB 的面积不变;④直线m 、n 之间的距离不随点P 的移动而变化,∠APB 的大小随点P 的移动而变化; 故不会随点p 的移动而变化的是①③,故选:B .7.解:∵AD 是BC 上的中线,∴S △ABD =S △ACD =S △ABC ,∵BE 是△ABD 中AD 边上的中线,∴S △ABE =S △BED =S △ABD ,∴S △ABE =S △ABC ,∵△ABC 的面积是20,∴S △ABE ==5. 故选:C .8.解:∵点O 是直角△ABC 斜边AC 的中点,∴S △ABO =S △CBO ,OB =OA =OC ,∵△ABO 与△CDO 的面积之比为4:3,∴△CBO 与△CDO 的面积之比为4:3,∴OB :OD =4:3,设OB =4x ,则OD =3x ,∴OA =OC =4x ,∵AC =8,∴4x +4x =8,解得x =1,在Rt △ODC 中,OD =3,OC =4,∴CD ==,∴S △ODC =×3×=,而△CBO 与△CDO 的面积之比为4:3,∴S △OBC =×=2.故选:D .9.解:过M 点作MD ∥BC ,交AN 于点N ,连接OC ,则△DOM ∽△NOB ,∴DM :BN =DO :ON =MO :BO ,∵AM =CM ,∴DM 为△ANC 的中位线,∴AD =DN ,BC =2DM ,∵CN =3BN ,∴DM :BN =3:2,BN :BC =1:4,∴DO :ON =MO :BO =3:2,∴BO :MO =2:3,故②正确;AO :NO =4:1,故③正确;AO :AN =4:5,OM :BM =3:5,∵S △ABC =40,AM =CM ,BN :BC =1:4,∴S △ABN =10,S △ABM =20,∵S △ABO :S △ABN =AO :AN =4:5,S △AMO :S △ABM =MO :BM =3:5,∴S △ABO =8,故①错误;S △AMO =12,故④正确;∵AM =CM ,∴S △CMO =S △AMO =12,故⑤错误.故选:B .10.解:∵AB ∥x 轴,∴2a +1=a ﹣3.解得a =﹣4.∴A (1,﹣7),B (4,﹣7).∴AB =3.∴△AOB 的面积为:×3×7=10.5,故选:D .二.填空题11.解:∵AD =BE =7.5,AE =BF =CB =2.5.∴AF =BE ,∴AD =AF =7.5,在△ADE 和△BEC 中,,∴△ADE ≌△BEC (SAS ),∴S △DAE =S △CBE ,∵S 1=S △DAF ﹣S △DAE ﹣S △EFG ,S 2=S △CBE ﹣S △EFG ﹣S △CBF ,∴S 1﹣S 2=S △DAE +S △CBF =+=.故答案为.12.解:∵BE是中线,∴AE=CE,∴△ABE的面积=△BCE的面积(等底等高的三角形的面积相等),故①正确;∵CF是角平分线,∴∠ACF=∠BCF,∵AD为高,∴∠ADC=90°,∵∠BAC=90°,∴∠ABC+∠ACB=90°,∠ACB+∠CAD=90°,∴∠ABC=∠CAD,∵∠AFG=∠ABC+∠BCF,∠AGF=∠CAD+∠ACF,∴∠AFG=∠AGF,故②正确;∵AD为高,∴∠ADB=90°,∵∠BAC=90°,∴∠ABC+∠ACB=90°,∠ABC+∠BAD=90°,∴∠ACB=∠BAD,∵CF是∠ACB的平分线,∴∠ACB=2∠ACF,∴∠BAD=2∠ACF,即∠FAG =2∠ACF ,故③正确;根据已知条件不能推出∠HBC =∠HCB ,即不能推出BH =CH ,故④错误;故答案为:①②③.13.解:连接PA ,∵D 是AB 的中点,∴S △ADC =S △BCD ,S △PAD =S △PBD ,∴S △BPC =S △APC ,∵AE :CE =3:1,S △CEP =1,∴S △AEP =3S △CEP =3,∴S △APC =4,∴S △BPC =4,故答案为4.14.解:作DE ⊥AB 于E ,∴S △ABD =AB •DE ,∵DE ⊥AB ,∴DE ≤AD .当DA ⊥AB 时,DE 与DA 重合,此时,DE 取得最大值4,△ABD 面积最大,作CF ⊥AB ,交BA 的延长线于F ,∴DE ∥CF ,∴△BDE ∽△BCF , ∴=,即=, ∴=,∴CF =,∵∠BAC =120°,∴∠CAF =60°,∴∠ACF =30°∴AF =tan30°•CF =×=,∵AD ∥CF , ∴==,∴AB =. 故答案为.15.解:∵AD 是△ABC 的中线,S △ABC =12,∴S △ABD =S △ABC =×12=6,∵AG =2GD ,∴S △ABG =S △ABD =×6=4,故答案为:4.三.解答题16.解:(1)∵+|a +2b ﹣7|=0, ∴, 解得:,∴C (1,3);(2)如图,△ABC 为所作,如图,分别过点B ,点C 作x 轴的平行线BF ,DE ,过点A ,点B 作y 轴的平行线DF ,EB , ∴S △ABC =S 四边形DFBE ﹣S △ADC ﹣S △BCE ﹣S △ABF ,=4×5﹣﹣﹣,=8;(3)设点M 的坐标为(m ,0),∵S△ABC =S△AMC+S△ABM,S△ABC=8,∴,∴AM=,∴m﹣(﹣1)=,∴m=,∴M(,0).17.解:①如图1,当P在AB上时,∵△APE的面积等于32,∴×2x•8=32,解得:x=4;②当P在BC上时,∵△APE的面积等于32,∴S 矩形ABCD ﹣S △CPE ﹣S △ADE ﹣S △ABP =32,∴10×8﹣(10+8﹣2x )×5﹣×8×5﹣×10×(2x ﹣10)=32, 解得:x =6.6;③当P 在CE 上时,∴(10+8+5﹣2x )×8=32,解得:x =7.5<(10+8+5),x =7.5时2x =15,P 在BC 边,∴舍去;答:4或6.6.18.解:∵AD 为△ABC 的中线,∴S △ABC =2S △ABD =2×6=12, ∴×AE •BC =12,即4•BC =12,∴BC =6.19.解:设C 点的纵坐标为t ,∵A (﹣1,0),B (3,0),∴AB =4,∵S=×4×|t|=6,解得|t|=3,△ABC∴点C的坐标为(﹣1,3)或(3,3)或(﹣1,﹣3)或(3,﹣3).20.解:(1)在平面直角坐标系中画出△ABC如图所示:(2)△ABC的面积=6×6﹣×4×2﹣﹣=36﹣4﹣6﹣12=14.21 / 21。
3、2020重庆中考复习数学几何最值专题训练三(含答案解析)
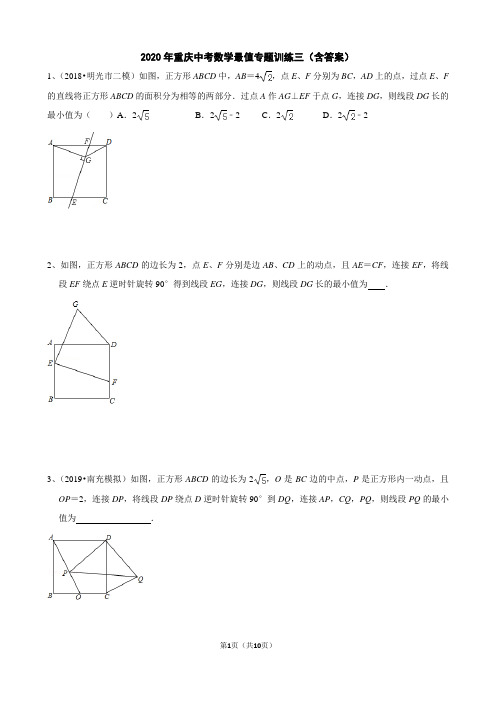
2020年重庆中考数学最值专题训练三(含答案)1、(2018•明光市二模)如图,正方形ABCD中,AB=4,点E、F分别为BC,AD上的点,过点E、F 的直线将正方形ABCD的面积分为相等的两部分.过点A作AG⊥EF于点G,连接DG,则线段DG长的最小值为()A.2B.2﹣2C.2D.2﹣22、如图,正方形ABCD的边长为2,点E、F分别是边AB、CD上的动点,且AE=CF,连接EF,将线段EF绕点E逆时针旋转90°得到线段EG,连接DG,则线段DG长的最小值为.3、(2019•南充模拟)如图,正方形ABCD的边长为2,O是BC边的中点,P是正方形内一动点,且OP=2,连接DP,将线段DP绕点D逆时针旋转90°到DQ,连接AP,CQ,PQ,则线段PQ的最小值为.4、如图,平行四边形ABCD中,∠B=60°,BC=12,AB=10,点E在AD上,且AE=4,点F是AB上一点,连接EF,将线段EF绕点E逆时针旋转120°得到EG,连接GD,则线段GD长度的最小值为.5、(2019•惠山区一模)如图,正方形ABCD中,AB=2,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF,OF.则线段OF长的最小值()A.2B.+2C.2﹣2 D.56、如图,在边长为2的正方形ABCD中,点O为AB中点,以AB为直径在正方形ABCD内部作半圆,E为半圆上任意一点(不与A.B重合),连接CE,将线段CE绕点C逆时针旋转90°得列CF,连接DE、BF,OF.则线段OF长的最小值为.7、(2019秋•颍州区校级月考)如图,正方形ABCD的边长为5,O是AB边的中点,点E是正方形内一动点,OE=2,将线段CE绕C点逆时针旋转90°得CF,连OF,线段OF的最小值为.8、(2019•太原二模)如图,在Rt△ABC中,∠ABC=90°,∠BAC=30°,BC=2,点D是AC边的中点,E是直线BC上一动点,将线段DE绕点D逆时针旋转90°得到线段DF,连接AF、EF,在点E的运动过程中线段AF的最小值为.9、(2019秋•锡山区期中)已知:如图,△ABC是边长为6的等边三角形,直线AF⊥BC于F,点D是直线AF上一动点,以BD为边在BD的右侧作等边△BDE,连接EF,则EF的最小值为.10、(2019•台州模拟)如图,四边形ABCD是矩形,AB=4,BC=a(a>1),E是BC上的一点,且BE=1,点F是边AB上的任意一点.连接EF,将线段EF绕点E顺时针旋转90°,得到线段EG.在点F从点B运动到点A的过程中,若要点G能落在对角线AC上,则a的最大值为.11、如图1,四边形ABCD是矩形,AB=2,BC=4,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE、BG,则2BG+BE的最小值为.2020年重庆中考数学最值专题训练三(含答案)1、(2018•明光市二模)如图,正方形ABCD中,AB=4,点E、F分别为BC,AD上的点,过点E、F 的直线将正方形ABCD的面积分为相等的两部分.过点A作AG⊥EF于点G,连接DG,则线段DG长的最小值为()A.2B.2﹣2C.2D.2﹣2解:连接AC,BD交于O,∵过点E、F的直线将正方形ABCD的面积分为相等的两部分,∴EF过点O,∵AG⊥EF,∴∠AGO=90°,∴点G在以AO为直径的半圆弧上,设AO的中点为M,连接DM交半圆弧于G,则此时,DG最小,∵四边形ABCD是正方形,AB=4,∴AC=8,AC⊥BD,∴AO=OD=AC=4,∴AM=OM=AO=2,∴DM==2,∴DG=2﹣2,故选:B.2、如图,正方形ABCD的边长为2,点E、F分别是边AB、CD上的动点,且AE=CF,连接EF,将线段EF绕点E逆时针旋转90°得到线段EG,连接DG,则线段DG长的最小值为.解:如图,过点F作FM⊥AB于M,过点G作GH⊥AD于H,GN⊥AB于N,∵四边形ABCD是正方形,∴AB=BC=AD=CD=2,∠B=∠C=∠BAD=90°,且FM⊥AB,GH⊥AD,GN⊥AB,∴四边形BCFM,四边形AHGN是矩形,∴BM=CF,NG=AH,AN=GH,MF=BC=2,∵将线段EF绕点E逆时针旋转90°得到线段EG,∴EG=EF,∠GEF=90°,∴∠NEG+∠FEM=90°,且∠NGE+∠NEG=90°,∴∠FEM=∠NGE,且∠N=∠FME=90°,EF=EG,∴△EGN≌△EFM(AAS)∴NE=MF=2,EM=NG,设AE=CF=a,∴EM=2﹣2a=NG=AH,AN=2﹣a=GH,∴HD=AD﹣AH=2﹣(2﹣2a)=2a,∵GD==∴当a=时,GD有最小值为,3、(2019•南充模拟)如图,正方形ABCD的边长为2,O是BC边的中点,P是正方形内一动点,且OP=2,连接DP,将线段DP绕点D逆时针旋转90°到DQ,连接AP,CQ,PQ,则线段PQ的最小值为.解:连接OD,如图所示:∵DQ=DP,∠PDQ=90°,∴PQ=DP,OD===5,∵OP+DP≥OD,∴DP≥OD﹣OP=5﹣2=3,∴PQ≥3,∴线段PQ的最小值为3.4、如图,平行四边形ABCD中,∠B=60°,BC=12,AB=10,点E在AD上,且AE=4,点F是AB上一点,连接EF,将线段EF绕点E逆时针旋转120°得到EG,连接GD,则线段GD长度的最小值为2.解:将线段AE绕点E逆时针旋转120°得到EH,连接HG,过点H作HM⊥AD,∵四边形ABCD是平行四边形,∴∠A+∠B=180°,∴∠A=120°,∵将线段AE绕点E逆时针旋转120°得到EH,将线段EF绕点E逆时针旋转120°得到EG,∴EF=EG=4,AE=EH,∠AEH=∠FEG=120°,∴∠DEH=60°,∠AEF=∠HEG,且EF=EG,AE=EH,∴△AEF≌△HEG(SAS)∴∠A=∠EHG=120°=∠AEH,∴AD∥HG,∴点G的轨迹是过点H且平行于AD的直线,∴当DG⊥HG时,线段GD长度有最小值,∵∠HEM=60°,EH=4,HM⊥AD,∴EM=2,MH=EM=2,∴线段GD长度的最小值为2,5、(2019•惠山区一模)如图,正方形ABCD中,AB=2,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF,OF.则线段OF长的最小值()A.2B.+2C.2﹣2 D.5解法一:如图,连接DO,将线段DO绕点D逆时针旋转90°得DM,连接OF,FM,OM,∵∠EDF=∠ODM=90°,∴∠EDO=∠FDM,∵DE=DF,DO=DM,∴△EDO≌△FDM(SAS),∴FM=OE=2,∵正方形ABCD中,AB=2,O是BC边的中点,∴OC=,∴OD=,∴OM=,∵OF+MF≥OM,∴OF≥.故选:D.解法二:如图,由于OE=2,所以E点可以看作是以O为圆心,2为半径的半圆上运动,延长BA到P 点,使得AP=OC,连接PE,∵AE=CF,∠P AE=∠OCF,∴△P AE≌△OCF,∴PE=OF,当O、E、P三点共线时,PE最小,OP===5,∴PE=OF=OP﹣OE=5﹣2,∴OF的最小值是5﹣2.6、如图,在边长为2的正方形ABCD中,点O为AB中点,以AB为直径在正方形ABCD内部作半圆,E为半圆上任意一点(不与A.B重合),连接CE,将线段CE绕点C逆时针旋转90°得列CF,连接DE、BF,OF.则线段OF长的最小值为.解:由于OE=2,所以E点可以看作是以O为圆心,2为半径的半圆上运动,延长BA到P点,使得AP=OC,连接PE,∵AE=CF,∠P AE=∠OCF,∴△P AE≌△OCF(SAS),∴PE=OF,当PE最小时,为O、E、P三点共线,OP===5,∴PE=OF=OP﹣OE=5﹣2,∴OF的最小值是5﹣2.7、(2019秋•颍州区校级月考)如图,正方形ABCD的边长为5,O是AB边的中点,点E是正方形内一动点,OE=2,将线段CE绕C点逆时针旋转90°得CF,连OF,线段OF的最小值为.解:如图,连接CO,将线段CO绕点C逆时针旋转90°得CM,连接FM,OM,则∠ECF=∠OCM=90°,∴∠ECO=∠FCM,∵CE=CF,CO=CM,∴△ECO≌△FCM(SAS),∴FM=OE=2,∵正方形ABCD中,AB=5,O是AB边的中点,∴OB=2.5,∴OC==,∴OM=OC=,∵OF+MF≥OM,∴OF≥﹣2.∴线段OF的最小值为﹣2.8、(2019•太原二模)如图,在Rt△ABC中,∠ABC=90°,∠BAC=30°,BC=2,点D是AC边的中点,E是直线BC上一动点,将线段DE绕点D逆时针旋转90°得到线段DF,连接AF、EF,在点E的运动过程中线段AF的最小值为+1.解:如图,作DM⊥BC于M,FJ⊥DM于J交AB于N.∵Rt△ABC中,∠ABC=90°,∠BAC=30°,BC=2,∴AC=2BC=4,AB=BC=2,∵AD=DC.DM∥AB,∴DM=AB=,BM=CM=1,易证四边形BMJN是矩形,∴JN=BM=1,∵∠FDJ+∠EDM=90°,∠EDM+∠DEM=90°,∴∠FDJ=∠DEM,∵∠FJD=∠DME=90°,∴△FJD≌△DME(AAS),∴FJ=DM=,∴FN=FJ+JN=1+,∴点F在直线l上运动(直线l与直线AB之间的距离为+1),根据垂线段最短可知,当AF⊥直线l时,AF的值最短,最小值为+1,9、(2019秋•锡山区期中)已知:如图,△ABC是边长为6的等边三角形,直线AF⊥BC于F,点D是直线AF上一动点,以BD为边在BD的右侧作等边△BDE,连接EF,则EF的最小值为.解:如图,取AB中点H,连接DH,∵△ABC,△BDE都是等边三角形,∴AB=BC,BD=BE,∠DBE=∠ABC=60°,∴∠ABD=∠EBC,∵△ABC是等边三角形,AF⊥BC,∴BF=BC=AB=3,∠BAF=30°,∵H是AB中点,∴AH=BH=AB=BF=3,且∠ABD=∠EBC,BD=BE,∴△BHD≌△BFE(SAS)∴EF=DH,∴当DH取最小值时,EF有最小值,当DH⊥AF时,DH有最小值,∴DH=AH=,∴EF的最小值为,10、(2019•台州模拟)如图,四边形ABCD是矩形,AB=4,BC=a(a>1),E是BC上的一点,且BE=1,点F是边AB上的任意一点.连接EF,将线段EF绕点E顺时针旋转90°,得到线段EG.在点F从点B运动到点A的过程中,若要点G能落在对角线AC上,则a的最大值为.解:如图,当点G落在对角线AC上,过点G作GH⊥BC于点H,∵△EFB≌△GEH,∴GH=BE=1,EH=BF,∴CH=BC﹣BE﹣EH=a﹣1﹣BF,∵△CHG∽△CBA,∴,∴,∴BF=∵点F是边AB上的任意一点,∴0≤BF≤AB,∴0≤≤4,∴≤a≤∴a的最大值为11、如图1,四边形ABCD是矩形,AB=2,BC=4,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE、BG,则2BG+BE的最小值为4.解:延长BE、GD相交于点H.∵矩形ECGF、矩形ABCD,∴∠ECG=∠BCD=90°,∴∠DCG=∠BCE∵CD:CB=2:4=1:2,CG:CE=1:2,∴CD:CB=CG:CE,∵∠DCG=∠BCE∴△DCG∽△BCE,∴,∠BEC=∠DGC,∴DG=BE作EN⊥BC于N,GM⊥BC交BC的延长线于M.易证△ECN∽△CGM,∴==2,∵EN=AB=2,∴CM=1,∴点G的运动轨迹是直线MG,作点D关于直线GM的对称点G′,连接BG′交GM于G,此时BG+GD的值最小,最小值=BG′∵DG=BE,∴BE=2DG,∴2BG+BE=2BG+2DG=2(BG+DG)∴2BG+BE的最小值就是2(BG+DG)的最小值.∵BG′==2,∴2BG+BE的最小值为4。
2020年中考数学专题训练(三)与角平分线有关的全等证明的三种模型

专题训练(三)与角平分线有关的全等证明的三种模型模型一过角平分线上的点向角的两边作垂线如图3-ZT-1,P是∠MON的平分线上一点,过点P作PA⊥OM于点A,PB⊥ON于点B.图3-ZT-1结论:PB=PA.1.如图3-ZT-2,∠1=∠2,∠3=∠4.求证:AP平分∠BAC.图3-ZT-22.感知:如图3-ZT-3①,AD平分∠BAC,∠B+∠C=180°,∠B=90°.易知:DB=DC.探究:如图3-ZT-3②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°.求证:DB=DC.图3-ZT-33.如图3-ZT-4,P为∠ABC的平分线上的一点,点D和点E分别在AB和BC上,且BD<BE,PD=PE,试探究∠BDP与∠BEP的数量关系,并给予证明.图3-ZT-44.如图3-ZT-5,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40°,求∠PAC 的度数.图3-ZT-5模型二截取构造对称全等(截长补短)如图3-ZT-6,P是∠MON的平分线上一点,A是射线OM上任意一点,在ON上截取OB=OA,连接PB.图3-ZT-6结论:△OPB≌△OPA.5.如图3-ZT-7所示,在△ABC中,AD是△ABC的外角平分线,P是AD上异于点A的任意一点,试比较PB+PC 与AB+AC的大小,并说明理由.图3-ZT-76.如图3-ZT-8所示,AD是△ABC的内角平分线,P是AD上异于点A的任意一点,试比较PC-PB与AC-AB 的大小,并说明理由.图3-ZT-87.如图3-ZT-9所示,在△ABC中,∠A=100°,∠ABC=40°,AB=AC,BD是∠ABC的平分线,延长BD至点E,使ED=AD.求证:BC=AB+CE.图3-ZT-9模型三角平分线+垂线(延长法)如图3-ZT-10,P是∠MON的平分线上的一点,AP⊥OP于点P,延长AP交ON于点B.图3-ZT-10结论:OA=OB.8.如图3-ZT-11,在△ABC中,AD是∠BAC的平分线,BE⊥AD于点E.探究∠ABE,∠DBE,∠C之间的数量关系.图3-ZT-119.如图3-ZT-12,已知等腰直角三角形ABC中,∠A=90°,AB=AC,BD平分∠ABC,CE⊥BD交BD的延长线于点E.求证:BD=2CE.图3-ZT-12教师详解详析1.证明:如图,过点P作PQ⊥AB于点Q,PN⊥BC于点N,PM⊥AC于点M.∵∠1=∠2,∠3=∠4,∴PQ=PN,PN=PM.∴PQ=PM.又∵PQ⊥AB,PM⊥AC,∴AP平分∠BAC.2.证明:如图,过点D分别作DE⊥AB于点E,DF⊥AC于点F.∵AD平分∠BAC,DE⊥AB,DF⊥AC,∴∠F=∠DEB=90°,DE=DF.∵∠ABD+∠ACD=180°,∠ACD+∠FCD=180°,∴∠ABD=∠FCD.在△DFC和△DEB中,{∠F=∠DEB,∠FCD=∠EBD, DF=DE,∴△DFC≌△DEB.∴DC=DB.3.解:∠BDP+∠BEP=180°.证明:过点P作PM⊥AB于点M,PN⊥BC于点N,则∠PMD=∠PNE=90°.∵BP平分∠ABC,∴PM=PN.在Rt△DPM和Rt△EPN中,{PD=PE,PM=PN,∴Rt△DPM≌Rt△EPN(HL).∴∠ADP=∠BEP.∵∠BDP+∠ADP=180°,∴∠BDP+∠BEP=180°.4.解:如图,过点P作PN⊥BD,PF⊥BA,PM⊥AC,垂足分别为N,F,M.设∠PCD=x °.∵CP 平分∠ACD ,∴∠ACP=∠PCD=x °,PM=PN. ∵BP 平分∠ABC , ∴∠ABP=∠PBC ,PF=PN. ∴PF=PM. ∵∠BPC=40°,∴∠ABP=∠PBC=∠PCD-∠BPC=(x-40)°.∴∠BAC=∠ACD-∠ABC=2x °-(x °-40°)-(x °-40°)=80°. ∴∠CAF=100°.在Rt △PFA 和Rt △PMA 中,{PA =PA,PF =PM,∴Rt △PFA ≌Rt △PMA (HL). ∴∠FAP=∠PAC=50°.5.解:PB+PC>AB+AC.理由如下:如图,在BA 的延长线上截取一点F ,使AF=AC ,连接PF.在△ACP 和△AFP 中,{AC =AF,∠CAP =∠FAP,AP =AP,∴△ACP ≌△AFP (SAS). ∴AC=AF ,PC=PF. ∵PB+PF>BF , ∴PB+PC>AB+AC.6.解:PC-PB<AC-AB.理由如下:如图,在AC上截取一点F,使AF=AB,连接PF.在△ABP和△AFP中,{AB=AF,∠BAP=∠FAP, AP=AP,∴△ABP≌△AFP(SAS).∴PB=PF.∵AF=AB=AC-CF,∴CF=AC-AB.∵PC-PF<CF,∴PC-PB<AC-AB.7.证明:如图,在BC上截取一点F,使得FB=AB,连接DF.∵BD是∠ABC的平分线,∠ABC=40°,∴∠ABD=∠FBD=20°.在△ABD和△FBD中,{AB=FB,∠ABD=∠FBD, BD=BD,∴△ABD≌△FBD(SAS).∴AD=FD,∠BDF=∠BDA=180°-∠A-∠ABD=60°.∴∠FDC=∠BDA=∠EDC=60°.又∵ED=AD,∴ED=FD.在△EDC和△FDC中,{ED =FD,∠EDC =∠FDC,DC =DC,∴△EDC ≌△FDC (SAS). ∴CE=CF.∴BC=FB+CF=AB+CE.8.解:如图,延长BE 交AC 于点F.在△ABE 和△AFE 中,{∠BAE =∠FAE,AE =AE,∠AEB =∠AEF =90°,∴△ABE ≌△AFE (ASA). ∴∠ABE=∠AFE. ∵∠AFB=∠DBE+∠C , ∴∠ABE=∠DBE+∠C.9.证明:如图,延长CE ,BA 交于点F.在△BEF 和△BEC 中,{∠FBE =∠CBE,BE =BE,∠BEF =∠BEC,∴△BEF ≌△BEC (ASA). ∴FE=CE=12CF ,即CF=2CE.∵∠ABD+∠ADB=90°,∠EDC+∠DCE=90°,∠ADB=∠EDC , ∴∠ABD=∠DCE.在△ABD 和△ACF 中,{∠ABD =∠DCE,AB =AC,∠BAD =∠CAF =90°,∴△ABD≌△ACF(ASA).∴BD=CF.∴BD=2CE.。
专题3分式与二次根式含答案解析2023年江西省中考数学一轮复习专题训练

专题3 分式与二次根式一、单选题1.下列计算一定正确的是( )A .2a 2b ⋅a 3=2a 5bB .2a 2+a 3=2a 5C .a a−1−1a−1=0D .3a −a =32.计算 a+1a −1a 的结果为( )A .1B .-1C .a+2aD .a−2a3.分式 x+5x−2的值是零,则 x 的值为( )A .5B .-5C .-2D .24.(2021·章贡模拟)下列运算中,正确的是( )A .(a 2)3=a 5B .(12)−1=−2 C .(2021−√5)0=1D .a 3•a 3=2a 65.下列计算错误的是( )A .a 2ab =a b(ab≠0 )B .ab 2÷ 12b =2ab 3(b≠0)C .2a 2b+3ab 2=5a 3b 3D .(ab 2)3=a 3b 66.(2020·吉安模拟)下列计算正确的是( )A .3x 2y +5xy =8x 3y 2B .(x +y)2=x 2+y 2C .(−2x)2÷x =4xD .y x−y +xy−x =17.下列说法正确的是( )A .若A 、B 表示两个不同的整式,则 A B一定是分式B .(a 4)2÷a 4=a 2C .若将分式 xyx+y 中,x 、y 都扩大 3 倍,那么分式的值也扩大 3 倍 D .若 3m =5,3n =4 则 32m−n =528.2019新型冠状病毒,因武汉病毒性肺炎病例而被发现,2020年1月12日被世界卫生组织命名“2019-nCoV”.冠状病毒是一个大型病毒家族,借助电子显微镜,我们可以看到这些病毒直径约为125纳米(1纳米=1 × 10-9米),125纳米用科学记数法表示等于( )米 A .1.25 × 10-10 B .1.25 × 10-11 C .1.25 × 10-8D .1.25 × 10-79.下列各等式中,正确是( )A .- √(−3)2 =-3B .± √32 =3C .( √−3 )2=-3D .√32 =±310.(2020·抚州模拟)下列计算正确的是( )A .-(x -y )2=-x 2-2xy -y 2B .(- 12 xy 2)3=- 16x 3y 6C .x 2y÷ 1y =x 2(y≠0)D .(- 13 )-2÷ 94=4二、填空题11.(2022·玉山模拟)计算12x −13x的结果是 .12.(2022·石城模拟)已知 a ,b(a ≠b) 满足 a 2−2a −1=0 , b 2−2b −1=0 ,则 ab +ba =. 13.(2022·瑞金模拟)使式子√x+3x−5有意义的x 的取值范围是 .14.(2022·新余模拟)2021年10月11日,联合国《生物多样性公约》缔约方大会第十五次会议(COP15)在昆明正式拉开帷幕.在多彩的生物界,科学家发现世界上最小的开花结果植物是澳洲的出水浮萍,其质量仅有0.000000076克,0.000000076用科学记数法表示是 .15.(2021·江西模拟)若二次根式 √2021−x 有意义,则x 的取值范围是 .16.(2020·安源模拟)今年世界各地发现新冠肺炎疫情,疫情是由一种新型冠状病毒引起的,疫情发生后,科学家第一时间采集了病毒样本进行研究.研究发现这种病毒的直径约85纳米(1纳米=0.000000001米).数据85纳米用科学记数法可以表示为 米.17.(2020·石城模拟)一种细菌的半径约为0.000045米,用科学记数法表示为 米.18.(2020·抚州模拟)对于任意不相等的两个数a ,b ,定义一种运算※如下:a※b= √a+b a−b,如3※2= √3+23−2=√5 .那么4※8= . 19.(2020七上·景德镇期中)已知: a =√5+√3 , b =√5−√3,则 a 2−ab +b 2= . 20.(2020八下·高安期末)计算: (2√13)⋅(13√27)= . 三、计算题21.(2022七下·南康期末)计算下列各式的值:(1)√2(√2+2);(2)√3(√31√3.22.(2022八下·新余期末)计算:(1)√28−|1−√7|−(√2022−1)0(2)(√3+2)2−√48+√8×√1223.(2022·瑞金模拟)(1)计算:(π−3)0+(13)−1−√12+2sin60° (2)化简:(1x+2−1)÷x 2−1x+224.(2022·高安模拟)计算:(1)(−12)0+|√3−2|+tan60°; (2)2m−4m 2−4÷m−1m+2−1m−125.(2022·赣州模拟)先化简,再求值:5a +a 2−4a−1÷a 2+2a a−1,其中a =3.答案解析部分1.【答案】A【解析】【解答】2a 2b ⋅a 3=2a 5b ,故A 符合题意;2a 2+a 3不能合并同类项,故B 不符合题意;a a−1−1a−1=a−1a−1=1,故C 不符合题意; 3a −a =2a ,故D 不符合题意; 故答案为:A .【分析】根据合并同类项,单项式乘单项式,分式的加减分别计算,再判断即可.2.【答案】A【解析】【解答】解:a+1a−1a =a+1−1a =aa =1 . 故答案为:A .【分析】利用分式的基本性质计算求解即可。
2020初中数学中考专题复习——四边形中的线段最值问题专项训练3(附答案详解)

(1)如图①,当点 落在 边上时,求点 的坐标;
(2)如图②,当点 落在线段 上时, 与 交于点 .求点 的坐标;
(3)记 为矩形 对角线的交点, 为 的面积,求 的取值范围(直接写出结果即可).
A. B. C. D.
3.线段AB上有一动点C(不与A,B重合),分别以AC,BC为边向上作等边△ACM和等边△BCN,点D是MN的中点,连结AD,BD,在点C的运动过程中,有下列结论:①△ABD可能为直角三角形;②△ABD可能为等腰三角形;③△CMN可能为等边三角形;④若AB=6,则AD+BD的最小值为 .其中正确的是( )
【详解】
解:如图所示,作以BD为对称轴作N的对称点N',连接PN',MN',
根据轴对称性质可知,PN=PN',
∴PM-PN=PM-PN'≤MN',
当P,M,N'三点共线时,PM-PN'= MN',
∵正方形边长为4,
∴AC= AB=4 ,
∵O为AC中点,
∴AO=OC=2 ,
∵N为OA中点,
∴ON= ,
7.A
【解析】
【分析】
连接BD、BF,延长AC交GE于H,连接BH,证明四边形BNHM是矩形,得出MN=BH,由直角三角形的性质得出GH,AH的长,当BH⊥AG时,BH最小,由直角三角形的性质得出BH的长,即可得出答案.
【详解】
连接BD、BF,延长AC交GE于H,连接BH,如图所示:
∵四边形ABCD和四边形BEFG是菱形,∠DAB=60°,∴AD∥BC∥GF,AC⊥BD,BF⊥GE,BE=BG,AM=CM,EN=GN,∴∠GAH=30°,∠EBG=∠DAB=60°,∴△BEG是等边三角形,∴∠BGE=60°,∴∠AHG=90°,∴四边形BNHM是矩形,GH AG=4,AH GH=4 ,∴MN=BH,当BH⊥AG时,BH最小.
中考数学专题复习阅读思考题强化练习(三)

【详解】
解:(1)在Rt△AFE中,tan∠AFE= ,∠AFE=37°,
∴ ,
∵∠HCD=90°,∠FDC=90°,
∴HC∥FD,
又∵HC=FD,
∴四边形HCDF是矩形,
∴HF=CD=32m.
在Rt△AHE中,tan∠AHE= = ≈0.45,
(2)根据三角形的三边关系;三角形两边之和大于第三边,由于每段的长为不小于1的整数,所以设最小的是1,又由于其中任意三段都不能拼成三角形,所以每段长是:1,1,2,3,5,然后依此类推,最后每段的总和要不大于15即可.
【详解】
解:(1)填表如下:
项
第2项
第3项
第4项
第5项
第6项
第7项
第8项
第9项
…
这一项的平方
问题解答:
(1)根据柏拉图的研究,当 时,请直接写出一组勾股数;
(2)若 表示大于1的整数,试证明 是一组勾股数;
(3)请举出一个反例(即写出一组勾股数),说明柏拉图给出的勾股数公式不能构造出所有的勾股数.
6.阅读下列材料,并完成相应任务:
黄金分割
天文学家开普勒把黄金分割称为神圣分割,并指出毕达哥拉斯定理(勾股定理)和黄金分割是几何中的双宝,前者好比黄金,后者堪称珠宝,历史上最早正式在书中使用“黄金分割”这个名称的是欧姆,19世纪以后“黄金分割”的说法逐渐流行起来,黄金分割被广泛应用于建筑等领域.黄金分割指把一条线段分为两部分,使其中较长部分与线段总长之比等于较短部分与较长部分之比,该比值为 .用下面的方法(如图①)就可以作出已知线段 的黄金分割点 :
解得IF=
故S△ABI= AB•FI= ×9× = .
2021年九年级数学中考复习分类专题练习:等边三角形的判定与性质(三)

2021年九年级数学中考复习分类专题:等边三角形的判定与性质(三)一.选择题1.如图,等边△ABC中,D、E分别为AC、AB上两点,下列结论:①若AD=AE,则△ADE是等边三角形;②若DE∥BC,则△ADE是等边三角形,其中正确的有()A.①B.②C.①②D.都不对2.如图,D是等边△ABC的边AC上的一点,E是等边△ABC外一点,若BD=CE,∠1=∠2,则对△ADE的形状最准确的是()A.等腰三角形B.直角三角形C.等边三角形D.不等边三角形3.设M,N,P分别是等边三角形ABC各边上的点,AM=BN=CP,则△MNP是()A.等边三角形B.等腰三角形C.直角三角形D.不等边三角形4.已知:如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD、CE相交于点N,则下列五个结论:①AD=BE;②∠BMC=∠ANC;③∠APM=60°;④AN=BM;⑤△CMN是等边三角形.其中,正确的有()A.2个B.3个C.4个D.5个5.如图,在△ABC中,D、E在BC上,且BD=DE=AD=AE=EC,则∠BAC的度数是()A.30°B.45°C.120°D.15°6.如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于()A.25°B.30°C.45°D.60°7.如图,已知△ABC是等边三角形,点D,E,F分明是边AB,BC,AC的中点,则图中等边三角形的个数是()A.2个B.3个C.4个D.5个8.如图,等边三角形ABC中,AD是BC上的高,∠BDE=∠CDF=60°,图中与BD相等的线段有()A.5条B.6条C.7条D.8条9.如图,已知∠ABC=120°,BD平分∠ABC,∠DAC=60°,若AB=2,BC=3,则BD的长是()A.5 B.7 C.8 D.910.如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论错误的是()A.△BPQ是等边三角形B.△PCQ是直角三角形C.∠APB=150°D.∠APC=135°二.填空题11.已知∠AOB=30°,点P在OA上,且OP=2,点P关于直线OB的对称点是Q,则PQ=.12.在△ABC 中,AB =AC =8cm ,∠B =60°,则BC = cm .13.如图,△ABC 是等边三角形,D ,E ,F 分别是AB ,BC ,CA 边上一点,且AD =BE =CF .则△DEF 的形状是 .14.两块完全一样的含30°角的三角板重叠在一起,若绕长直角边中点M 转动,使上面一块的斜边刚好过下面一块的直角顶点.如图,∠A =30°,AC =8,则此时两直角顶点C ,C ′间的距离是 .15.如图,已知△ABC 中高AD 恰好平分边BC ,∠B =30°,点P 是BA 延长线上一点,点 O 是线段AD 上一点且OP =OC ,下面的结论:①∠APO +∠DCO =30°;②△OPC 是等边三角形;③AC =AO +AP ;④S △ABC =S 四边形AOCP .其中正确的为 .(填序号)16.如图所示是两块完全一样的含30°角的三角板,分别记作△ABC 和△A 1B 1C 1,现将两块三角板重叠在一起,设较长直角边的中点为M ,绕中点M 转动三角板ABC ,使其直角顶点C 恰好落在三角板A 1B 1C 1的斜边A 1B 1上,当∠A =30°,AC =10时,两直角顶点C ,C 1的距离是 .三.解答题17.如图,已知:边长相等的等边△ABC和等边△DEF重叠部分的周长是6.(1)求证:△FGH和△CHL和△LEK和△KBJ和△JDI和△IAG都是等边三角形.(或证明∠AGF=∠FHC=∠CLE=∠EKB=∠BJI=∠DIA=120°)(2)求等边△ABC的边长.18.如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,且BE=8cm.(1)求∠D的度数;(2)若BC=10cm,求ED的长.19.如图,△ABC是等边三角形,O为△ABC内一点,且∠AOB=120°,∠BOC=120°.求证:由线段AO、BO、CO构成的一个三角形是等边三角形.证明过程如下,请仔细阅读并将证明继续下去:证明:将△ABO绕点A逆时针旋转60°,此时B点与C点重合,O落在O′,连接AO′、OO′、CO′,∴AO=AO′,∠OAO′=60°∴△AOO′是一个等边三角形∴AO=OO′又∵OB=O′C∴线段OA、OB、OC构成了△OCO′请继续:20.如图,等边△ABC中,点D、E、F分别同时从点A、B、C出发,以相同的速度在AB、BC、CA上运动,连结DE、EF、DF.(1)证明:△DEF是等边三角形;(2)在运动过程中,当△CEF是直角三角形时,试求的值.21.已知,在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC.(1)【特殊情况,探索结论】如图1,当点E为AB的中点时,确定线段AE与DB的大小关系,请你直接写出结论:AE DB(填“>”、“<”或“=”).(2)【特例启发,解答题目】如图2,当点E为AB边上任意一点时,确定线段AE与DB的大小关系,请你直接写出结论,AE DB(填“>”、“<”或“=”);理由如下,过点E作EF∥BC,交AC 于点F.(请你完成以下解答过程).(3)【拓展结论,设计新题】在等边三角形ABC中,点E在直线AB上,点D在线段CB的延长线上,且ED=EC,若△ABC的边长为1,AE=2,求CD的长(请你画出相应图形,并直接写出结果).参考答案一.选择题1.解:∵△ABC为等边三角形,∴∠A=60°,∵AD=AE,∴△ADE是等边三角形;所以①正确;∵△ABC为等边三角形,∴∠C=∠B=60°,∵DE∥BC,∴∠ADE=∠C=∠B=∠AED=60°,∴△ADE是等边三角形,所以②正确.故选:C.2.解:∵三角形ABC为等边三角形,∴AB=AC,∵BD=CE,∠1=∠2,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴AD=AE,∠BAD=∠CAE=60°,∴△ADE是等边三角形.故选:C.3.解:∵△ABC是等边三角形,∴AB=BC=AC,∠A=∠B=∠C=60°,∵AM=BN=CP,∴BM=CN=AP,在△AMP,△BNM和△CPN中,,∴△AMP≌△BNM≌△CPN(SAS),∴PM=MN=NP,∴△MNP是等边三角形.4.解:∵△ABC和△DEC都是等边三角形,∴AC=BC,CD=CE,∠ACB=∠ECD=60°,∴∠ACB+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD,∴△BCE≌△ACD(SAS),∴AD=BE,故选项①正确;∵∠ACB=∠ACE=60°,由△BCE≌△ACD得:∠CBE=∠CAD,∴∠BMC=∠ANC,故选项②正确;由△BCE≌△ACD得:∠CBE=∠CAD,∵∠ACB是△ACD的外角,∴∠ACB=∠CAD+∠ADC=∠CBE+∠ADC=60°,又∠APM是△PBD的外角,∴∠APM=∠CBE+∠ADC=60°,故选项③正确;在△ACN和△BCM中,,∴△ACN≌△BCM,∴AN=BM,故选项④正确;∴CM=CN,∴△CMN为等腰三角形,∵∠MCN=60°,∴△CMN是等边三角形,故选项⑤正确;故选:D.5.解:设∠B=x∵BD=AD则∠B=∠BAD=x,∠ADE=2x,∵AD=AE∴∠AED=∠ADE=2x,∵AE=EC,∠AED=∠EAC+∠C∴∠EAC=∠C=x又BD=DE=AD,由直角三角形斜边的中线等于斜边的一半,知∠BAE=90°,则∠B+∠AED=x+2x=90°得x=30°∴∠BAC=180°﹣2x=120°故选:C.6.解:△ABC沿CD折叠B与E重合,则BC=CE,∵E为AB中点,△ABC是直角三角形,∴CE=BE=AE,∴△BEC是等边三角形.∴∠B=60°,∴∠A=30°,故选:B.7.解:∵D,E,F分明是边AB,BC,AC的中点,∴AD=BD=BE=EC=CF=FA=DF=DE=EF=AB=AC=∴等边三角形有:△ABC、△ADF、△BDE、△CEF、△DEF共5个,故选:D.8.解:如图,连接EF.∵等边△ABC中,AD是BC边上的高,∴∠BAD=∠CAD=30°,∵∠BDE=∠CDF=60°,∴∠ADE=∠ADF=30°,△AEF、△BDE、△CDF、△DEF都是全等的等边三角形,∴∴BD=DC=DE=BE=AE=AF=FC=FD,即图中与BD相等的线段有7条.故选:C.9.解:在CB的延长线上取点E,使BE=AB,连接AE,∵∠ABC=120°,∴∠ABE=180﹣∠ABC=60°,∵BE=AB,∴△ABE为等边三角形,∴AE=AB,∠BAE=∠E=60°,∵∠DAC=60°,∴∠DAC=BAE,∵∠BAD=∠BAC+∠DAC,∠EAC=∠BAC+∠BAE,∴∠BAD=∠EAC,∵BD平分∠ABC,∴∠ABD=∠ABC=60°,∴∠ABD=∠E,在△ABD和△AEC中,,∴△ABD≌△AEC(ASA),∴BD=CE,∵CE=BE+BC=AB+BC=3+2=5,∴BD=5,故选:A.10.解:∵△ABC是等边三角形,∴∠ABC=60°,∵△BQC≌△BPA,∴∠BPA=∠BQC,BP=BQ=4,QC=PA=3,∠ABP=∠QBC,∴∠PBQ=∠PBC+∠CBQ=∠PBC+∠ABP=∠ABC=60°,∴△BPQ是等边三角形,∴PQ=BP=4,∵PQ2+QC2=42+32=25,PC2=52=25,∴PQ2+QC2=PC2,∴∠PQC=90°,即△PQC是直角三角形,∵△BPQ是等边三角形,∴∠BOQ=∠BQP=60°,∴∠BPA=∠BQC=60°+90°=150°,∴∠APC=360°﹣150°﹣60°﹣∠QPC=150°﹣∠QPC,∵∠PQC=90°,PQ≠QC,∴∠QPC≠45°,即∠APC≠135°,∴选项A、B、C正确,选项D错误.故选:D.二.填空题(共6小题)11.解:如图,连OQ,∵点P关于直线OB的对称点是Q,∴OB垂直平分PQ,∴∠POB=∠QOB=30°,OP=OQ,∴∠POQ=60°,∴△POQ为等边三角形,∴PQ=PO=2.故答案为2.12.解:∵在△ABC中,AB=AC=8cm,∠B=60°,∴△ABC是等边三角形,∴BC=8cm.故答案为:8.13.解:∵△ABC为等边三角形,且AD=BE,∴AF=BD,∠A=∠B=60°,∴在△ADF与△BED中,,∴△ADF≌△BED(SAS).同理证得△ADF≌△CFE(SAS),∴△ADF≌△BED≌△CFE(SAS),∴DF=ED=EF,∴△DEF是一个等边三角形.故答案是:等边三角形.14.解:如图,连接CC',∵点M是AC中点,∴AM=CM=AC=4,∵旋转,∴CM=C'M,AM=A'M∴A'M=MC=C'M=4,∴∠A'=∠A'CM=30°∴∠CMC'=∠A'+∠MCA'=60°,且CM=C'M∴△CMC'是等边三角形∴C'C=CM=4故答案为:415.解:①连接OB,如图1,∵△ABC中高AD恰好平分边BC,即AD是BC垂直平分线,∴AB=AC,BD=CD,∴OB=OC=OP,∴∠APO=∠ABO,∠DBO=∠DCO,∵∠ABC=∠ABO+∠DBO=30°,∴∠APO+∠DCO=30°.故①正确;②△OBP中,∠BOP=180°﹣∠OPB﹣∠OBP,△BOC中,∠BOC=180°﹣∠OBC﹣∠OCB,∴∠POC=360°﹣∠BOP﹣∠BOC=∠OPB+∠OBP+∠OBC+∠OCB,∵∠OPB=∠OBP,∠OBC=∠OCB,∴∠POC=2∠ABD=60°,∵PO=OC,∴△OPC是等边三角形,故②正确;③如图2,在AC上截取AE=PA,∵∠PAE=180°﹣∠BAC=60°,∴△APE是等边三角形,∴∠PEA=∠APE=60°,PE=PA,∴∠APO+∠OPE=60°,∵∠OPE+∠CPE=∠CPO=60°,∴∠APO=∠CPE,∵OP=CP,在△OPA和△CPE中,,∴△OPA≌△CPE(SAS),∴AO=CE,∴AC=AE+CE=AO+AP;故③正确;④如图3,作CH⊥BP,∵∠HCB=60°,∠PCO=60°,∴∠PCH=∠OCD,在△CDO和△CHP中,,∴△CDO≌△CHP(AAS),∴S△OCD =S△CHP∴CH=CD,∵CD=BD,∴BD=CH,在Rt△ABD和Rt△ACH中,,∴Rt△ABD≌Rt△ACH(HL),∴S △ABD =S △AHC ,∵四边形OAPC 面积=S △OAC +S △AHC +S △CHP ,S △ABC =S △AOC +S △ABD +S △OCD∴四边形OAPC 面积=S △ABC .故④正确.故答案为:①②③④.16.解:如图,连接CC 1,∵两块三角板重叠在一起,较长直角边的中点为M ,∴M 是AC 、A 1C 1的中点,AC =A 1C 1,∴CM =A 1M =C 1M =AC =5,∵∠A =30°,∴∠A 1=∠A 1CM =30°,∴∠CMC 1=60°,∴△CMC 1为等边三角形,∴CC 1=CM =5,∴CC 1长为5.故答案为5.三.解答题(共5小题)17.解:(1)∵△ABC和△DEF都是等边三角形,∴∠F=60°,FG=FH,FD=BC,∴△FGH是等边三角形,同理△CHL、△LEK、△KBJ、△JDI、△TAG都是等边三角形;(2)∵△FGH是等边三角形,∴GH=FG.同理,IJ=ID,HL=CL,JK=KB,∴重叠部分的周长为:FD+BC=6,∴FD=BC=3,即等边△ABC的边长是 3.18.解:(1)延长ED交BC于点F,延长AD交BC于H,如图.∵∠EBC=∠E=60°,∴△BEF是等边三角形,∴EF=BF=BE=8,∠EFB=60°.∵AB=AC,AD平分∠BAC,∴AH⊥BC,即∠AHC=90°,∴∠HDF=30°,∴∠ADE=∠HDF=30°;(2)∵BC=10,∴FC=2.∵AB=AC,AD平分∠BAC,∴BH=CH=BC=5,∴HF=5﹣2=3.在Rt△DHF中,∵∠HDF=30°,∴DF=2HF=6,∴DE=8﹣6=2.∴ED的长为2cm.19.证明:将△ABO绕点A逆时针旋转60°,此时B点与C点重合,O落在O′,连接AO′、OO′、CO′,∴AO=AO′,∠OAO′=60°,∴△AOO′是一个等边三角形,∴AO=OO′,又∵OB=O′C,∴线段OA、OB、OC构成了△OCO′,∵∠AOB=120°,∠BOC=120°.∴∠AOC=120°,∠AO′C=120°∵△AOO′是一个等边三角形,∴∠AOO′=∠AO′O=60°,∴∠O′OC=∠OO′C=60°,∴△OCO′是等边三角形,∴线段AO、BO、CO构成的一个三角形是等边三角形.20.(1)证明:∵△ABC是等边三角形,∴∠A=∠B=∠C=60°,AB=BC=CA,∵AD=BE=CF,∴BD=EC=AF,在△ADF、△BED和△CFE中∴△ADF≌△BED≌△CFE,∴DE=EF=FD,∴△DEF是等边三角形;(2)解:∵△ABC和△DEF是等边三角形,∴△DEF∽△ABC,∵DE⊥BC,∴∠BDE=30°,∴BE=BD,即BE=BC,CE=BC,∵EF=EC•sin60°=BC•=BC,∴=()2=()2=.21.解:(1)当E为AB的中点时,AE=DB;(2)AE=DB,理由如下,过点E作EF∥BC,交AC于点F,证明:∵△ABC为等边三角形,∴△AEF为等边三角形,∴AE=EF,BE=CF,∵ED=EC,∴∠D=∠ECD,∵∠DEB=60°﹣∠D,∠ECF=60°﹣∠ECD,∴∠DEB=∠ECF,在△DBE和△EFC中,,∴△DBE≌△EFC(SAS),∴DB=EF,则AE=DB;(3)点E在AB延长线上时,如图所示,同理可得△DBE≌△EFC,∴DB=EF=2,BC=1,则CD=BC+DB=3.故答案为:(1)=;(2)=。
中考数学复习专题训练《圆的综合》(3)

中考数学复习专题训练《圆的综合》(3)1.如图,在3×3的正方形网格中,每个小正方形的边长都为1,O、A、B三点都在格点处,线段OA绕点O顺时针旋转至OB.(1)求线段OA的长;(2)画出旋转过程中点A经过的路径,且求出该路径的长.2.如图,网格中每个小正方形的边长为1,△OAB的顶点都在格点上,以O为坐标原点,OA所在直线为x轴建立平面直角坐标系.(1)将△OAB绕点O按逆时针方向旋转,使A点初次落在点A1上,请在图中画出△OAB 旋转后所得的像△OA1B1;(2)将△OA1B1向左平移三个单位得到△O2A2B2,请在图中画出平移后所得的像△O2A2B2;(3)求两次变换后B点所经过的路径总长.3.如图,点O、B的坐标分别为(0,0),(3,0),将△OAB绕点O按逆时针方向旋转90°到△OA′B′.(1)画出△OA′B′;(2)点A′的坐标为;(3)求在旋转过程中,点B所经过的路线的长度.4.如图,在正三角形网格中,每一个小三角形都是边长为1的正三角形,解答下列问题:(1)网格中每个小三角形的面积为;(2)将顶点在格点上的四边形ABOC绕点O顺时针旋转120°两次,画出所得到的两个图形,并写出点A所经过的路线为.(结果保留π).5.如图,边长为a的正方形ABCD沿直线l向右滚动.(1)当正方形滚动一周时,正方形中心O经过的路程为,此时点A经过的路程为;(2)当点A经过的路程为时,中心O与初始位置的距离为;(3)将正方形在滚动中转了180°时点A的位置记为A1,正方形转了360°时点B的位置记为B1,请你猜想∠AA1B1的大小,并请你利用三角函数中正切的两角和公式来验证你的猜想.6.如图,⊙O的半径为10cm.(1)如果∠AOB=100°,求扇形AOB的面积;(2)已知弧BC长为25cm,求∠COB的度数.(结果保留整数)7.如图,点C,D是半圆O上的三等分点,直径AB=8,连接AD,AC,作DE⊥AB,垂足为E,DE交AC于点F.(1)求证:AF=DF.(2)求阴影部分的面积(结果保留π和根号).8.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABO的三个顶点A,B,O都在格点上.(1)画出△ABO绕点O逆时针旋转90°后得到的三角形;(2)求△ABO在上述旋转过程中所扫过的面积.9.如图,P A、PB是半径为1的⊙O的两条切线,点A、B分别为切点,∠APB=60°,OP 与弦AB交于点C,与⊙O交于点D.(1)在不添加任何辅助线的情况下,写出图中所有的全等三角形;(2)求阴影部分的面积(结果保留π).10.如图,在半径为,圆心角等于45°的扇形AOB内部作一个正方形CDEF,使点C 在OA上,点D、E在OB上,点F在弧AB上.(1)求正方形CDEF的边长;(2)求阴影部分的面积(结果保留π).11.如图,已知△ABC,若将△ABC绕点C按顺时针方向旋转90°后得到△A1B1C1.①请在图中画出△A1B1C1;②写出A点的对应点A1的坐标;③求出线段CB在旋转过程中扫过的面积.12.如图,⊙O交x轴于A,B两点(点A在点B的左侧),交y轴的正半轴于点C,点D 为第一象限内⊙O上的一点,连接AD,OD,CD,已知∠DAB=15°,CD=2.(1)∠OCD=.(2)⊙O的半径为.(3)S扇形COD=.13.如图,⊙O是等边三角形ABC的外接圆,已知△ABC的边长为a,求图中阴影部分的面积.14.如图,点P在圆O外,P A与圆O相切于A点,OP与圆周相交于C点,点B与点A关于直线PO对称,已知OA=4,P A=.求:(1)∠POA的度数;(2)弦AB的长;(3)阴影部分的面积.15.如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,过点C作DC⊥OA,交AB于点D,(1)求证:∠CDO=∠BDO;(2)若∠A=30°,⊙O的半径为4,求阴影部分的面积.(结果保留π)16.如图,在△ABC中,AB=AC,∠B=30°,O是BC上一点,以点O为圆心,OB长为半径作圆,恰好经过点A,并与BC交于点D.(1)判断直线CA与⊙O的位置关系,并说明理由;(2)若AB=2,求图中阴影部分的面积(结果保留π).17.如图,扇形OAB的半径OA=4,圆心角∠AOB=90°,点C是弧AB上异于A、B的一点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,过点C作弧AB所在圆的切线CG交OA的延长线于点G.(1)求证:∠CGO=∠CDE;(2)若∠CGD=60°,求图中阴影部分的面积.18.如图,已知A为⊙O外一点,连接OA,交⊙O于P,AB是⊙O的切线,B是切点,且PO=2cm,AB=2cm,求阴影部分的面积.19.如图,已知菱形ABCD的边长为1.5cm,B,C两点在扇形AEF的上,求的长度及扇形ABC的面积.20.如图所示,在⊙O中,=,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.(1)求证:AC2=AB•AF;(2)若⊙O的半径长为2cm,∠B=60°,求图中阴影部分面积.21.在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10m,拴住小狗的10m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2).(1)如图1,画出小狗活动的区域,并求出当BC=2m时S的值.(结果保留π)(2)如图2,现考虑在(1)中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其他条件不变,设BC=xm,①写出面积S与x的关系式;②在BC的变化过程中,当S取得最小值时,求边BC的长及S的最小值.(结果保留π)22.如图,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°.正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动.(1)请在所给的图中,用尺规画出点A在正方形整个翻滚过程中所经过的路线图;(2)求正方形在整个翻滚过程中点A所经过的路线与梯形MNPQ的三边MN、NP、PQ 所围成图形的面积S.23.如图,在⊙O中,弦BC垂直于半径OA,垂足为E,D是优弧BC上一点,连接BD,AD,OC,∠ADB=30°.(1)求∠AOC的度数;(2)若弦BC=8cm,连结OB,求图中扇形BOC的面积.24.如图,点A是游乐场上方25m处安装的一盏照明灯,灯光以圆锥形式照射地面.若圆锥的母线AB与AC的夹角为60°,求此灯光照射地面的面积.25.如图,在△ABC中,∠BAC=90°,请用尺规作图法作经过A、B、C三点的⊙O.(不写作法,保留作图痕迹)26.如图,点E,C在BF上,BE=FC,∠ABC=∠DEF=45°,∠A=∠D=90°.(1)求证:AB=DE;(2)若AC交DE于M,且AB=,ME=,将线段CE绕点C顺时针旋转,使点E旋转到AB上的G处,求旋转角∠ECG的度数.27.如图,四边形ABCD内接于以BC为直径的圆,圆心为O,且AB=AD,延长CB、DA 交于P,过C点作PD的垂线交PD的延长线于E,且PB=BO,连接OA.(1)求证:OA∥CD;(2)求线段BC:DC的值;(3)若CD=18,求DE的长.28.如图,在四边形ABCD中,∠A=∠D=90°,AD=AB,以BC为直径的半⊙O与边AD相切于点E.(1)求证:∠BCE=∠DCE;(2)若,求DE的长.29.如图,四边形ABCD内接于⊙O,直径AC与弦BD的交点为E,OB∥CD,BH⊥AC,垂足为H,且∠BF A=∠DBC.(1)求证:BF是⊙O的切线;(2)若BH=3,求AD的长度;(3)若sin∠DAC=,求△OBH的面积与四边形OBCD的面积之比.30.如图,AD是△ABC的角平分线,以点C为圆心,CD为半径作圆交BC的延长线于点E,交AD于点F,交AE于点M,且∠B=∠CAE,EF:FD=4:3.(1)求证:点F是AD的中点;(2)求cos∠AED的值;(3)如果BD=10,求半径CD的长.。
中考数学总复习专题三解答题重难点题型突破题型二几何图形探究题类型与三角形、四边形有关的探究题课件

(2)如图②,过点 F 作 FG⊥AB 于 G,连接 FE.∵AF=BE,AF∥BE,∴ 四边形 ABEF 是平行四边形,∵AF+BE=16,∴AB=AF=BE=8,∵32 3= 8×FG,∴FG=4 3,在 Rt△FAG 中,AF=8,∴∠FAG=60°,当点 G 在 线段 AB 上时,∠FAB=60°,当点 G 在线段 BA 延长线时,∠FAB=120°,
解:(1)原命题不成立,新结论为:∠APB=90°, AF+BE=2AB(或 AF=BE=AB),证明:∵AM∥BN, ∴∠MAB+∠NBA=180°,∵AE,BF 分别平分∠MAB,∠NBA,
∴∠EAB=12∠MAB,∠FBA=12∠NBA,
∴∠EAB+∠FBA=12(∠MAB+∠NBA)=90°, ∴∠APB=90°,∵AE 平分∠MAB,∴∠MAE=∠BAE, ∵AM∥BN,∴∠MAE=∠BAE,∴∠BAE=∠BEA, ∴AB=BE,同理:AF=AB,∴AF+BE=2AB(或 AF=BE=AB);
辽宁专用
专题三 解答题重难点题型突破
题型二 几何图形探究题 类型1 与三角形、四边形有关的探究题
【例1】 (2016·抚顺)如图,在△ABC中,BC >AC,点E在BC上,CE=CA, 点D在AB上,连接DE,∠ACB+∠ADE=180°,作CH⊥AB,垂足为H.
(1)如图①,当∠ACB=90°时,连接CD,过点C作CF⊥CD交BA的延长线于点F. ①求证:FA=DE; ②请猜想三条线段DE、AD、CH之间的数量关系,直接写出结论; (2)如图②,当∠ACB=120°时,三条线段DE、AD、CH之间存在怎样的数量关 系?请证明你的结论.
(3)成立.∵四边形 ABCD 是正方形,∴BC=CD,∠FBC=∠ECD=90 °,
中考数学专题复习几何探究练习(三)

中考数学专题复习几何探究练习(三)学校:___________姓名:___________班级:___________考生__________评卷人得分一、解答题1.【感知】如图①,点C是AB中点,CD⊥AB,P是CD上任意一点,由三角形全等的判定方法“SAS”易证△P AC≌△PBC,得到线段垂直平分线的一条性质“线段垂直平分线上的点到线段两端的距离相等”【探究】如图①,在平面直角坐标系中,直线y=-13x+1分别交x轴、y轴于点A和点B,点C是AB中点,CD⊥AB交OA于点D,连结BD,求BD的长【应用】如图①(1)将线段AB绕点A顺时针旋转90°得到线段AB′,请在图①网格中画出线段AB;(2)若存在一点P,使得P A=PB′,且∠APB′≠90°,当点P的横、纵坐标均为整数时,则AP长度的最小值为______.2.如图,在正方形ABCD中,点E是边BC上任意一点(点E不与点B、C重合),连结DE,点C关于DE的对称点为C1,连结AC1并延长交DE的延长线于点M,F是AC1的中点,连结DF.【猜想】如图①,①FDM的大小为度.【探究】如图①,过点A作AM1①DF交MD的延长线于点M1,连结BM.求证:△ABM①①ADM1.【拓展】如图①,连结AC,若正方形ABCD的边长为2,则△ACC1面积的最大值为.3.问题呈现:下图是小明复习全等三角形时遇到的一个问题并引发的思考,请帮助小明完成以下学习任务.请根据小明的思路,结合图①,写出完整的证明过程.结论应用:(1)如图①,在四边形ABCD中,AB AD BC=+,DAB∠的平分线和ABC∠的平分线交于CD边上点P.求证:PC PD=;(2)在(1)的条件下,如图①,若10AB=,1tan2PAB∠=.当PBC有一个内角是45︒时,PAD△的面积是.4.【教材呈现】如图是华师版八年级下册数学教材第117页的部分内容.结合图①,补全证明过程.【应用】如图①,直线EF分别交矩形ABCD的边AD、BC于点E、F,将矩形ABCD 沿EF翻折,使点C的对称点与点A重合,点D的对称点为D′,若AB=3,BC=4,则四边形ABFE的周长为.【拓展】如图①,直线EF分别交▱ABCD的边AD、BC于点E、F,将▱ABCD沿EF翻折,使点C的对称点与点A重合,点D的对称点为D′,若AB=22,BC=4,①C=45°,则EF的长为.5.在等腰直角三角形纸片ABC中,点D是斜边AB的中点,10,AB=点E为BC上一点,将纸片沿DE折叠,点B的对应点为点B'.()1如图①,连接,CD则CD的长为;()2如图①,'B E与AC交于点,//F DB BC'.①求证:四边形'BDB E为菱形;①连接',B C则'B FC的形状为;()3如图①,则CEF∆的周长为;6.【教材呈现】数学课上,赵老师用无刻度的直尺和圆规按照华师版教材八年级上册87页完成角平分线的作法,方法如下:【问题1】赵老师用尺规作角平分线时,用到的三角形全等的判定方法是.【问题2】小明发现只利用直角三角板也可以作①AOB的角平分线,方法如下:步骤:①利用三角板上的刻度,在OA、OB上分别截取OM、ON,使OM=ON.①分别过点M、N作OM、ON的垂线,交于点P.①作射线OP,则OP为①AOB的平分线.(1)请写出小明作法的完整证明过程.(2)当tan①AOB=43时,量得MN=4cm,直接写出MON△的面积.7.教材呈现:如图是华师版九年级上册数学教材第77页的部分内容.定理证明:请根据教材内容,结合图①,写出证明过程.定理应用:在矩形ABCD中,AB=2AD,AC为矩形ABCD的对角线,点E在边AB上,且AE=3BE.(1)如图①,点F在边CB上,连结EF.若13BFCF,则EF与AC的关系为.(2)如图①,将线段AE绕点A旋转一定的角度α(0°<α<360°),得到线段AE',连结CE′,点H为CE'的中点,连结BH.设BH的长度为m,若AB=4,则m的取值范围为.8.在等腰直角三角形纸片ABC中,点D是斜边AB的中点,AB=10,点E为BC上一点,将纸片沿DE折叠,点B的对应点为点B'.(1)如图①,连接CD,则CD的长为;(2)如图①,B'E与AC交于点F,DB'①BC.①求证:四边形BDB'E为菱形;①连接B'C,则①B'FC的形状为;(3)如图①,则①CEF的周长为.9.如图,在ABC中,中线BD,CE相交于点O,F,G分别是OB,OC的中点.(1)求证:四边形DEFG是平行四边形;(2)当四边形DEFG的形状为矩形时,ABC为______三角形;(3)连接OA,当OA BC时,四边形DEFG的形状为______.10.如图1,正方形ABCD的边长为8cm,点F从点B出发,沿射线AB方向以1cm/秒的速度移动,点E从点D出发,向点A以1cm/秒的速度移动(不与点A重合).设点E,F同时出发移动t秒.(1)基础探究:如图1,在点E、F移动过程中,连接CE、CF、EF,判断CE与CF的数量与位置关系,并说明理由.(2)应用拓展:如图2,点G、H分别在边AD、BC上,且217cmGH=,连接EF,当EF与GH交于点P,且45GPE∠=︒,若点P为EF的中点,则CF的长度为________,AP的长度为________.参考答案:1.探究:BD 的长为53;应用:(1)见解析;(2)5.【解析】 【分析】探究:根据直线解析式,求出点A 、B 坐标,得到BO 、AO 的长,设BD 的长为a ,根据勾股定理列方程可求出BD ;应用:(1)根据旋转的性质作图即可;(2)根据题意可知P 点坐标在AB’线段垂直平分线上,如图所示,点P’是垂直平分线上最近的格点,但是此时'’90AP B ∠=︒,不符合题意,根据网格特点可知垂直平分线上下一个格点位置,由网格特点和勾股定理可得符合题意的AP=5. 【详解】 解:探究: 由题意得:当x 0=时,y 1=;当y 0=时,x 3=;()A 3,0∴,()B 0,1. AO 3∴=,BO 1=.设BD 的长为a .①点C 是AB 中点,CD AB ⊥交OA 于点D ,DA DB a ∴==,OD 3a =-.在Rt BOD 中,BOD 90∠=︒,222BD BO DO ∴=+,()22213a a +-=,5a 3∴=,5BD 3=. BD ∴的长为53.应用:(1)如图,线段'AB 即为所求.(2)根据题意可知P点坐标在AB’线段垂直平分线上,如图所示,点P’是垂直平分线上最近的格点,但是此时'’90AP B∠=︒,不符合题意,根据网格特点可知垂直平分线上下一个格点位置,由网格特点和勾股定理可得符合题意的AP=5.【点睛】本题主要考查了线段垂直平分线的性质,熟知线段垂直平分线上的点到线段两端点的距离相等是解题关键.2.(1)45°;(2)证明见解析;(3)22﹣2.【解析】【分析】(1)证明①CDE=①C1DE和①ADF=①C1DF,可得①FDM=12①ADC=45°;(2)先判断出①DAM1=①BAM,由(1)可知:①FDM=45°,进而判断出①AMD=45°,得出AM=AM1,即可得出结论;(3)先作高线C1G,确定①ACC1的面积中底边AC为定值2,根据高的大小确定面积的大小,当C1在BD上时,C1G最大,其①AC1C的面积最大,并求此时的面积.【详解】(1)由对称得:CD=C1D,①CDE=①C1DE,在正方形ABCD中,AD=CD,①ADC=90°,①AD=C1D,①F是AC1的中点,①DF①AC1,①ADF=①C1DF,①①FDM=①FDC1+①EDC1=12①ADC=45°;故答案为:45;(2)①DF①AC1,①①DFM=90°,①①MAM'=90°,在正方形ABCD中,DA=BA,①BAD=90°,①①DAM1=①BAM,由(1)可知:①FDM=45°①①DFM=90°①①AMD=45°,①①M1=45°,①AM=AM1,在:△ABM和△ADM1中,①11BA DABAM DAMAH AM=⎧⎪∠=∠⎨⎪=⎩,①①ABM①①ADM1(SAS);(3)如图,过C1作C1G①AC于G,则1AC CS=12AC•C1G,在Rt△ABC中,AB=BC=2,①AC=2222+=22,即AC为定值,当C1G最大值,△AC1C的面积最大,连接BD交AC于O,当C1在BD上时,C1G最大,此时G与O重合,①CD=C1D=2,OD=12AC=2,①C1G=C1D﹣OD=2﹣2,①1AC CS=12AC•C1G=12×22(2﹣2)=22﹣2,故答案为:22﹣2.此题是四边形综合题,主要考查了正方形的性质、等腰直角三角形的判定和性质、全等三角形的判定和性质等知识,解题的关键是①AMD=45°.3.问题呈现:见解析;结论应用:(1)见解析;(2)403或8 【解析】【分析】问题呈现:由“SAS ”可证△MOP ≌△NOP ,可得PM =PN ;结论应用:(1)在AB 上截取AE =AD ,连接PE ,由“SAS ”可证△ADP ≌△AEP ,△BPC ≌△BPE ,可得PD =PE =PC ;(2)延长AP ,BC 交于点H ,由“ASA ”可证△ADP ≌△HCP ,可得CP =DP ,AD =CH ,S △ADP =S △CPH ,分三种情况讨论,由角平分线的性质和锐角三角函数可求解.【详解】问题呈现:证明:①OC 平分AOB ∠,①AOC BOC ∠=∠.在POM 和PON △中,OP OP POM PON OM ON =⎧⎪∠=∠⎨⎪=⎩.①POM PON △≌△.结论应用:在AB 上截取AE AD =,①AP 平分DAB ∠,①DAP BAP ∠=∠,①AP AP =,①ADP AEP △≌△.①PE PD=.①AB AD BC=+,①BE BC=,①BP平分ABC∠,①ABP CBP ∠=∠.①BP BP=.①PBE PBC△≌△.①PE PC=.①PC PD=.(2)由(1)可证∠D=∠AEP,∠PCB=∠PEB,∵∠AEP+∠PEB=180°,∴∠PCB+∠D=180°,∴AD∥BC,∵AB=10,tan∠P AB=PBPA=12,∴P A=2PB,∵P A2+PB2=AB2,∴PB=25,P A=45,如图③,延长AP,BC交于点H,∵AD∥BC,∴∠DAP=∠H,∴∠H=∠BAP,∴AB=BH=10,又∵PB平分∠ABC,∴BP⊥AP,AP=PH=45,∵∠DAP=∠H,AP=PH,∠DP A=∠CPH,∴△ADP≌△HCP(ASA),∴CP=DP,AD=CH,S△ADP=S△CPH,若∠PBC=45°时,则∠PBC=∠H=45°,∴PB=PH(不合题意舍去),若∠BPC=45°时,则∠HPC=∠BPC=45°,如图④,过点C作CN⊥BP于N,CM⊥PH于M,∴CM=CN,∵S△PBH=12×BP×PH=12×BP×CN+12×PH×CM,∴CM=CN=453,∴S△PCH=12×45×453=403=S△ADP;若∠PCB=45°时,如图⑤,过点P作PF⊥BC于F,∵∠P AB=∠H,∴tan H=tan∠P AB=12,∴12 PFFH,∴FH=2PF,∵PF2+FH2=PH2=80,∴PF=4,FH=8,∵PF⊥BC,∠BCP=45°,∴∠PCB=∠FPC=45°,∴CF=PF=4,∴CH=4,∴S△ADP=S△CPH=12×4×4=8,故答案为:8或403.【点睛】本题是三角形综合题,考查了全等三角形的判定和性质,角平分线的性质,勾股定理,锐角三角函数等知识,添加恰当辅助线构造全等三角形是本题的关键.4.【教材呈现】证明见解析;【应用】434;【拓展】2103;【解析】【分析】教材呈现:由“ASA”可证①AOE①①COF,可得OE=OF,由对角线互相平分的四边形是平行四边形可证四边形AFCE是平行四边形,即可证平行四边形AFCE是菱形;应用:过点F作FH①AD于H,由折叠的性质可得AF=CF,①AFE=①EFC,由勾股定理可求BF的长,EF的长,拓展:过点A作AN①BC,交CB的延长线于N,过点F作FM①AD于M,由等腰直角三角形的性质可求AN=BN=2,由勾股定理可求AE=AF=103,再利用勾股定理可求EF的长.【详解】解:【教材呈现】①四边形ABCD是矩形,①AE①CF,①①EAO=①FCO,①EF垂直平分AC,①AO=CO,①AOE=①COF=90°,①①AOE①①COF(ASA)①OE=OF,又①AO=CO,①四边形AFCE是平行四边形,①EF①AC,①平行四边形AFCE是菱形;【应用】如图,过点F作FH①AD于H,①将矩形ABCD沿EF翻折,使点C的对称点与点A重合,①AF=CF,①AFE=①EFC,①AF2=BF2+AB2,①(4﹣BF)2=BF2+9,①BF=78,①AF=CF=258,①AD①BC,①①AEF=①EFC=①AFE,①AE=AF=258,①①B=①BAD=①AHF=90°,①四边形ABFH是矩形,①AB=FH=3,AH=BF=78,①EH=94,①EF=22EH FH+=81916+=154,①四边形ABFE的周长=AB+BF+AE+EF=3+78+258+154=434,故答案为:434.【拓展】如图,过点A作AN①BC,交CB的延长线于N,过点F作FM①AD于M,①四边形ABCD是平行四边形,①C=45°,①①ABC=135°,①①ABN=45°,①AN①BC,①①ABN=①BAN=45°,①AN=BN=22AB=2,①将▱ABCD沿EF翻折,使点C的对称点与点A重合,①AF=CF,①AFE=①EFC,①AD①BC,①①AEF=①EFC=①AFE,①AE=AF,①AF2=AN2+NF2,①AF2=4+(6﹣AF)2,①AF=103,①AE=AF=103,①AN①MF,AD①BC,①四边形ANFM是平行四边形,①AN①BC,①四边形ANFM是矩形,①AN =MF =2,①AM =22AF MF -=10049-=83, ①ME =AE ﹣AM =23,①EF =22MF ME +=449+=2103, 故答案为:2103. 【点睛】本题是四边形综合题,考查了平行四边形的性质,菱形的性质,折叠的性质,全等三角形的判定和性质,勾股定理等知识,添加恰当辅助线构造直角三角形是本题的关键. 5.(1)5;(2)①见解析;①等腰三角形;(3)52【解析】【分析】(1)利用直角三角形斜边上的中线等于斜边的一半即可求解;(2)①由翻折可知','45DB DB B B =∠=∠=︒,进而证得'//,B E AB 则有∴四边形'BDB E 为平行四边形,由',BD B D =即可得证;①连接CD,易证得','45DB DC DB E DCA =∠=∠=︒进而证得''FB C FCB ∠=∠,则有'FB FC =,即可得出结论;(3)由'FB FC =和'B E BE =得CEF ∆的周长=''CE FC EF CE B F EF CE B E CE BE BC ++=++=+=+=,由等腰直角三角形的性质可求得BC ,即可求得CEF ∆的周长.【详解】解:(1)①①ABC 是等腰直角三角形,D 为斜边AB 的中点,AB=10,①152CD AB ==, 故答案为:5;()2①证明:由翻折可知','45DB DB B B =∠=∠=︒'DB ①BC''45,B EC B ∴∠=∠=︒①'45,B EC B ∠=∠=︒①'EB ①BD∴四边形'BDB E 为平行四边形.又',BD B D =∴四边形'BDB E 为菱形;②如图2,连接CD ,则有CD=BD=AD,由翻折可知','45DB DB DB E B =∠=∠=︒①','45DB DC DB E DCA A =∠=∠=∠=︒,①''DB C DCB ∠=∠①DB E CB F DCA FCB ∠+∠=∠+∠'''①''CB F FCB ∠=∠①'FB FC =,①'B FC 的形状为等腰三角形;故答案为:等腰三角形;(3)如图3,由(2)知'FB FC =,'B E BE =,①CEF ∆的周长=''CE FC EF CE B F EF CE B E CE BE BC ++=++=+=+=,①①ABC 是等腰直角三角形,AB=10,①222100BC AB ==,解得:52BC =,①CEF ∆的周长为52,故答案为:52.【点睛】本题考查等腰直角三角形的性质、直角三角形斜边中线性质、折叠性质、菱形的判定与性质、等腰三角形的判定,解得的关键是认真审题,从图形中分析相关联信息,借助辅助线,利用基本图形的性质进行推理、计算.6.【问题1】SSS ;【问题2】(1)见解析;(2)8.【解析】【分析】问题1:根据SSS证明三角形全等即可.问题2:(1)根据HL证明三角形全等即可解决问题.(2)作MH①OB于H,连接MN.想办法求出ON,MH即可解决问题.【详解】解:问题1:由作图可知:OE=OD,EC=DC,OC=OC,①EOC DOC≌△△(SSS),故答案为SSS.问题2:(1)证明:由作图可知:OM=ON,①①ONP=①OMP=90°,OP=OP,①Rt ONP≌Rt OMP△(HL),①①PON=①POM,即OP平分①AOB.(2)解:作MH①OB于H,连接MN.①tan①AOB=4,3MHOH=①可以假设MH=4k,OH=3k,则OM=ON=5k,①HN=2k,在Rt MNH△中,①222,MN HN MH=+①()()222442,k k=+①255k=(负根已经舍弃),①ON=5k=25,MH=4k=855,①1185258.225MNO S ON MH ==⨯⨯= 【点睛】本题考查的是角平分线的作图与作图原理,三角形全等的判定与性质,锐角三角函数的应用,勾股定理的应用,掌握以上知识是解题的关键.7.定理证明:见解析;定理应用:(1)EF ∥AC ,EF =14AC ;(2)5﹣32≤BH ≤5+32 【解析】【分析】定理证明:延长DE 到F ,使FE =DE ,连接CF ,易证①ADE ①①CFE ,再根据全等三角形的性质,进一步可得出CF ①AB ,从而可证明四边形BCFD 是平行四边形,最后根据平行四边形的性质即可得证;定理应用:(1)取AB ,BC 的中点M ,N ,连接MN .再根据题目中的线段关系,可得出AM =BM ,CN =BN ,ME =EB ,FN =FB ,根据三角形的中位线定理即可得出答案; (2)如图①中,延长CB 到T ,连接AT ,TE ′.根据题意得出BH =12TE ′,再根据矩形的性质可求得AT 的值,结合题意求得AE 的值,最后根据三角形三边关系即可得出答案.【详解】 解:定理证明:如图①中,延长DE 到F ,使FE =DE ,连接CF ,在△ADE 和△CFE 中,AE EC AED CEF DE EF =⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△CFE (SAS ),∴∠A =∠ECF ,AD =CF ,∴CF ∥AB ,又∵AD =BD ,∴CF=BD,∴四边形BCFD是平行四边形,∴DF∥BC,DF=BC,∴DE∥BC,DE=12BC.定理应用:(1)如图①中,取AB,BC的中点M,N,连接MN.∵AE=3BE,BF:CF=1:3,∴AM=BM,CN=BN,ME=EB,FN=FB,∴MN∥AC,MN=12AC,EF∥MN,EF=12MN,∴EF∥AC,EF=14AC.故答案为:EF∥AC,EF=14AC.(2)如图①中,延长CB到T,连接AT,TE′.∵CH=HE′,CB=BT,∴BH=12TE′,∵四边形ABCD是矩形,∴∠ABC=∠ABT=90°,∵AB=4,BC=AD=BT=2,∴AT=22224225AB BT+=+=,∵AE=3BE,AB=4,∴AE=AE′=3,∴25﹣3≤TE′≤25+3,∴5﹣32≤BH≤5+32.故答案为:5﹣32≤BH≤5+32.【点睛】本题考查了矩形的性质、三角形三边关系、平行四边形的判定及性质、三角形中位线性质、旋转的性质、全等三角形的判定及性质,综合性比较强,添加合适的辅助线,是解题的关键.8.(1)5;(2)①见解析;①等腰三角形;(3)52.【解析】【分析】(1)由直角三角形斜边上的中线性质即可得出答案;(2)①由折叠的性质得B'D=BD,B'E=BE,①B'DE=①BDE,证出B'D=BE,得四边形BDB'E是平行四边形,进而得出结论;①证出CD=B'D,得①DCB'=①DB'C,证出DB'①AC,则①ACB'=90°-①DB'C,证出CD①B'E,则①EB'C=90°-①DCB',得①ACB'=①EB'C,即可得出结论;(3)连接B'C,由等腰直角三角形的性质得BC=22AB=52,①B=45°,CD=12AB=BD,①ACD=12①ACB=45°,证出CF=B'F,进而得出答案.【详解】(1)解:①①ABC是等腰直角三角形,点D是斜边AB的中点,AB=10,①CD=12AB=5,故答案为:5;(2)①证明:由折叠的性质得:B'D=BD,B'E=BE,①B'DE=①BDE,①DB'①BC,①①B'DE=①BED,①①BDE=①BED,①BD=BE,①B'D=BE,①四边形BDB'E是平行四边形,又①B'D=BD,①四边形BDB'E为菱形;①解:①①ABC是等腰直角三角形,点D是斜边AB的中点,AB=BD,①CD=12由折叠的性质得:B'D=BD,①CD=B'D,①①DCB'=①DB'C,①①ACB=90°,①AC①BC,①DB'①BC,①DB'①AC,①①ACB'=90°﹣①DB'C,由①得:四边形BDB'E为菱形,①AB①B'E,①CD①AB,①CD①B'E,①①EB'C=90°﹣①DCB',①①ACB'=①EB'C,①FB'=FC,即①B'FC为等腰三角形;故答案为:等腰三角形;(3)解:连接B'C,如图①所示:①①ABC 是等腰直角三角形,点D 是斜边AB 的中点,AB =10,①BC =22AB =52,①B =45°,CD =12AB =BD ,①ACD =12①ACB =45°, 由折叠的性质得:B 'D =BD ,①B '=①B =45°,①CD =B 'D ,①①DCB '=①DB 'C ,①①FCB '=①FB 'C ,①CF =B 'F ,①①CEF 的周长=EF +CF +CE =EF +B 'F +CE =B 'E +CE =BE +CE =BC =52;故答案为:52.【点睛】 本题是四边形综合题目,考查了菱形的判定与性质、平行四边形的判定与性质、等腰直角三角形的性质、折叠的性质、等腰三角形的判定与性质、直角三角形斜边上的中线性质等知识;本题综合性强,熟练掌握菱形的判定与性质和等腰三角形的判定与性质是解题的关键.9.(1)见解析;(2)等腰;(3)菱形.【解析】【分析】(1)由中线BD ,CE 相交于点O ,可得DE 是ABC 的中位线,可得//DE BC ,12DE BC =,由F 、G 分别是OB ,OC 的中点,可得FG 是OBC 的中位线,可得//FG BC ,12FG BC =,可推出//DE FG ,DE FG =即可; (2)由四边形DEFG 的形状为矩形,可得FD=EG ,OE=OF=OG=OD ,EF①ED ,①EOF=①DOG ,由F 、G 分别是OB ,OC 的中点,可得BO=CO ,,由中线CE ,E 为中点,F 是OB 的中点,可得EF①OA ,可推出OA①ED ,由等腰三角形性质可得OA 平分①EOD ,可证△AOB①①AOC (SAS ),可得AB=AC 即可;(3)连接OA ,由(1)知四边EFGD 为平行四边形,由中位线性质可得AO=2EF ,2BC FG =,由OA BC =,可得EF=FG 即可.【详解】证明:(1)①中线BD ,CE 相交于点O ,①E 、D 分别为AB 、AC 中点,①DE 是ABC 的中位线,①//DE BC ,12DE BC =, 又①F 、G 分别是OB ,OC 的中点,①FG 是OBC 的中位线,①//FG BC ,12FG BC =, ①//DE FG ,DE FG =,①四边形DEFG 是平行四边形;(2)连接OA ,如图①四边形DEFG 的形状为矩形,①FD=EG ,OE=OF=OG=OD ,EF①ED ,①EOF=①DOG , ①F 、G 分别是OB ,OC 的中点,①BO=CO ,①中线CE ,E 为中点,F 是OB 的中点,①EF①OA ,①OA①ED ,①OA 平分①EOD ,①①EOA=①DOA ,①①BOA=①EOF+①EOA=①DOG+①DOA=①COA ,①AO=AO ,①①AOB①①AOC (SAS ),①AB=AC ,①①ABC 为等腰三角形,故答案为:等腰;(3)当OA BC =时,四边形DEFG 的形状为菱形.由(1)知四边EFGD 为平行四边形,①中线CE ,E 为中点,F 是OB 的中点,①EF 为①ABO 的中位线,①AO=2EF ,又①F 、G 分别是OB ,OC 的中点,①FG 是OBC 的中位线,①2BC FG =,①OA BC =,①2EF=2FG ,①EF=FG ,①四边形DEFG 是菱形,故答案为:菱形.【点睛】本题考查平行四边形的判定与性质,等腰三角形的判定,菱形的判定,掌握平行四边形的判定方法与性质,等腰三角形的判定,菱形的判定定理,细心观察图形,利用数形结合从图形中分析线段之间和角之间关系是解题关键.10.(1)CE CF =,CE CF ⊥,理由见解析;(2)217,34;【解析】【分析】 (1)根据正方形的性质和运动的距离可证明()EDC FBC SAS ≌△△,可得CE CF =,再利用角之间的关系可证CE CF ⊥;(2)连接EC ,证明四边形GECH 是平行四边形,即可求出CF ,再利用直角三角形斜边上的中线等于斜边的一半即可求出AP .(1)解:①四边形ABCD为正方形,①CD CB=,90EDC ABC BCD∠=∠=∠=︒,①90FBC EDC∠=∠=︒,①ED FB t==,在EDC△和FBC中,90CD CBFBC EDCED FB=⎧⎪∠=∠=︒⎨⎪=⎩①()EDC FBC SAS≌△△,①CE CF=,ECD BCF=∠∠,①90ECD BCE∠+∠=︒,①90BCF BCE∠+∠=︒,即:90ECF∠=︒,①CE CF=,CE CF⊥,(2)解:连接CE,如图①CE CF=,CE CF⊥,①45CEF∠=︒,①45GPE∠=︒,①CEF GPE∠=∠,①CE GH∥,①GE CH∥,①四边形GECH是平行四边形,①217CE GH==,①CE CF =,①217CF =,①2234EF CF ==,①P 是EF 的中点,AFE △是直角三角形,①1342AP EF ==. 【点睛】本题考查正方形的性质,全等三角形的判定以及性质,平行四边形的判定及性质,直角三角形斜边上的中线等于斜边的一半.(1)的关键是证明()EDC FBC SAS ≌△△,(2)的关键是证明四边形GECH 是平行四边形.。
2021年中考数学复习专题3 方程、函数思想 - 副本(教学课件)

精讲释疑
重重点点题题型型
题组训练
题 型 一 用方程思想解决实际问题
例1.欣欣服装店某天用相同的价格a(a>0)卖出了两件服装,其中 一件盈利20%,另一件亏损20%,那么该服装店卖出这两件服 装的盈利情况是( B )
A.盈利
B.亏损
C.不盈不亏
D.与售价a有关
重重点点题题型型
题组训练
【解析】列一元一次方程求出两件衣服的进价,进而求出总盈 亏.设第一件衣服的进价为x元,依题意得:x(1+20%)=a,设 第二件衣服的进价为y元,依题意得:y(1-20%)=a,得出x(1 +20%)=y(1-20%),整理得:3x=2y,该服装店卖出这两件 服装的盈利情况为:0.2x-0.2y=0.2x-0.3x=-0.1x,即赔了 0.1x元.
重重点点题题型型
题组训练
解:(1)根据题意,得y与x的解析式为:y=22+2(x-1)=2x+ 20(1≤x≤12); (2)设当天的销售利润为w元,则当1≤x≤6时,w=(1200-800)(2x +20)=800x+8000,∵800>0,∴w随x的增大而增大,∴当x =6时,w最大值=800×6+8000=12800.
重重点点题题型型
题组训练
题 型 二 用方程思想解决几何问题
例 3.(温州一模)如图,在△ABC 中,分别以 AB,AC 为边向外 作正方形 ABED,ACGF.若点 E,A,G 在同一直线上,EG=8 2 ,
15 BC=7,则△ABC 的面积为__4__.
重重点点题题型型
题组训练
【解析】设 AB=x,AC=y,∵EG=8 2 ,BC=7,∴x2 +y2=72, 2 x+ 2 y=8 2 ,∴x+y=8,∴(x+y)2=x2+y2 +2xy=64,∴2xy=15,∴xy=125 ,∴△ABC 的面积=12 AB·AC =12 xy=145 .
人教版数学中考复习训练专题三 函数图象与性质综合题 附答案

专题三 函数图象与性质综合题类型一 交点问题典例精析例 在平面直角坐标系xOy 中,已知点A (-1,2),点B (3,2),点C (-2,-3)是平面内3个点.(1)连接AB ,若直线y =34x +b 与线段AB 有交点,求b 的取值范围;(2)连接BC ,若直线y =34x +b 与线段BC 在第三象限内有交点,求b 的取值范围;(3)若直线y =kx +3与直线BC 无交点,求k 的值;(4)若直线AB 、直线y =kx +3与直线BC 能够围成三角形,求k 的取值范围;(5)若双曲线y =k x 过点A 且与直线y =34x +b 在(-5≤x ≤-1)有交点,求b 的取值范围;(6)连接AB ,若抛物线y =x 2+c 与线段AB 有公共点,求c 的取值范围;(7)若抛物线y =x 2+c (-2≤x ≤2)与直线BC 有一个交点,求c 的取值范围;(8)连接AB ,若抛物线y =(x -k )2与线段AB 有公共点,求k 的取值范围;(9)若双曲线y =k x过点B 且与抛物线y =x 2 +c 在2≤x ≤6有交点,求c 的取值范围.1. (2020河北24题10分)表格中的两组对应值满足一次函数y =kx +b ,现画出了它的图象为直线l ,如图.而某同学为观察k ,b 对图象的影响,将上面函数中的k 与b 交换位置后得另一个一次函数,设其图象为直线l ′.(1)求直线l 的解析式;(2)请在图上画出..直线l ′(不要求列表计算),并求直线l ′被直线l 和y 轴所截线段的长; (3)设直线y =a 与直线l ,l ′及y 轴有三个不同的交点,且其中两点关于第三点对称,直接..写出a 的值.第1题图2. (2016河北26题12分)如图,抛物线L :y =-12(x -t )(x -t +4)(常数t >0)与x 轴从左到右的交点为B ,A ,过线段OA 的中点M 作MP ⊥x 轴,交双曲线y =k x(k >0,x >0)于点P ,且OA ·MP =12. (1)求k 值;(2)当t =1时,求AB 长,并求直线MP 与L 对称轴之间的距离;(3)把L 在直线MP 左侧部分的图象(含与直线MP 的交点)记为G ,用t 表示图象G 最高点的坐标;(4)设L 与双曲线有个交点的横坐标为x 0,且满足4≤x 0≤6,通过L 位置随t 变化的过程,直接..写出t的取值范围.第2题图针对演练3. (2020承德二模)如图,在平面直角坐标系中,点A,B,C三点的坐标分别为(2,0),(1,2),(4,3),直线l的解析式为y=kx+4-3k(k≠0).(1)当k=1时,直线l与x轴交于点D,则点D的坐标为________,S△ABD=________;(2)小明认为点C也在直线l上,他的判断是否正确,请说明理由;(3)若线段AB与直线l有交点,求k的取值范围.第3题图4. 如图,在平面直角坐标系中,边长为2的正方形ABCD 位于第二象限,且AB ∥x 轴,点B 在点C的正下方,双曲线y =1-2m x(x <0)经过点C. (1)求m 的取值范围;(2)若点B (-1,1),判断双曲线是否经过点A ;(3)设点B (a ,2a +1).①若双曲线经过点A ,求a 的值;②若直线y =2x +2交AB 于点E ,双曲线与线段AE 有交点,求a 的取值范围.第4题图5.(2020石家庄模拟)如图,已知点A(0,2),B(2,2),C(-1,-2),抛物线F:y=x2-2mx+m2-2与直线x=-2交于点P.(1)当抛物线F经过点C时,求它的表达式;(2)设点P的纵坐标为y p,求y p的最小值,此时抛物线F上有两点(x1,y1),(x2,y2),且x1<x2≤-2,比较y1与y2的大小;(3)当抛物线F与线段AB有公共点时,直接写出m的取值范围.第5题图6. 如图,已知抛物线y =ax 2-2x +3a (a >0)与x 轴相交于不同的两点A (x 1,0),B (x 2,0),且x 1<x 2.点P 为双曲线y =k x(1≤x ≤4)上的任意一点,过点P 作x 轴的垂线,交x 轴于点C ,交抛物线y =ax 2-2x +3a (a >0)于点Q .(1)若△POC 的面积为6,求k 值;(2)若k =3.①当a =12时,求点A 、B 的坐标,并求当点P 到抛物线对称轴的距离最大时,PQ 的值; ②若抛物线与双曲线有一个交点,直接写出a 的取值范围.第6题图7. (2020唐山开平区一模)已知,如图,二次函数L ∶y =mx 2+2mx +k (其中m ,k 是常数,k 为正整数),(1)若L 经过点(1,k +6),求m 的值;(2)当m =2,若L 与x 轴有公共点时且公共点的横坐标为非零的整数,确定k 的值;(3)在(2)的条件下,将L ∶y =mx 2+2mx +k 的图象向下平移8个单位,得到函数图象M ,求M 的解析式;(4)在(3)的条件下,将M 的图象在x 轴下方的部分沿x 轴翻折,图象的其余部分保持不变,得到一个新的图象N ,请结合新的图象解答问题,若直线y =12x +b 与N 有两个公共点时,请直接写出b 的取值范围.第7题图8.如图①,二次函数y=ax2-3ax+c的图象与x轴交于点A、B,与y轴交于点C,直线y=-x+4经过点B、C.(1)求抛物线的表达式;(2)过点A的直线y=kx+k交抛物线于点M,交直线BC于点N,连接AC,当直线y=kx+k平分△ABC 的面积时,求点M的坐标;(3)如图②,把抛物线位于x轴上方的图象沿x轴翻折,当直线y=kx+k与翻折后的整个图象只有三个交点时,求k的取值范围.第8题图类型二整点问题例我们把横,纵坐标都是整数的点叫作整点.在平面直角坐标系中,点A(5,0),B(0,5),C(-1,0).(1)若直线l过点A,B,求直线l与坐标轴围成的区域W1内(含边界)整点的个数;(2)连接AB,BC,AC,求△ABC所围成的区域W2内(不含边界)整点的个数;(3)若直线y=a、线段AB与y轴所围成的三角形区域W3内(含边界)恰有6个整点,求a的取值范围;(4)若直线y=x+b与直线AB及y轴所围成的三角形区域W4内(不含边界)恰有4个整点,求b的取值范围;(5)若直线y=kx+2与直线BC及x轴所围成的区域W5内(不含边界)恰有4个整点,求k的取值范围;(6)若双曲线y =4x (x >0)与线段AB 交于D ,E 两点(点D 在点E 的上方),求曲线DE 与线段DE 所围成的区域W 6内(含边界)整点的个数;(7)在(6)的条件下,若直线y =x +b 与双曲线y =4x 交于点F ,与y 轴交于点G ,连接DG ,若线段DG ,FG ,曲线DF 所围成的区域W 7内(含边界)恰有5个整点,求b 的取值范围;(8)若抛物线y =x 2-2x +m -2与过点B 的直线y =5所围成的区域W 8内(不含边界)有4个整点,求m 的取值范围;(9)若抛物线y =x 2-2x +m -2与直线y =-x +2交于M ,N 两点(点M 在点N 的左侧),将曲线MN 与线段MN 所围成的区域记为W 9,若W 9内(不含边界)恰好有4个整点,求m 的取值范围.1.(2019河北26题12分)如图,若b是正数..,直线l:y=b与y轴交于点A;直线a:y=x-b与y轴交于点B;抛物线L:y=-x2+bx的顶点为C,且L与x轴正半轴的交点为D.(1)若AB=8,求b的值,并求此时L的对称轴与a的交点坐标;(2)当点C在l下方时,求点C与l距离的最大值;(3)设x0≠0,点(x0,y1),(x0,y2),(x0,y3)分别在l,a和L上,且y3是y1,y2的平均数,求点(x0,0)与点D间的距离;(4)在L和a所围成的封闭图形的边界上..写出b...,把横、纵坐标都是整数的点称为“美点”,分别直接=2019和b=2019.5时“美点”的个数.第1题图针对演练2.在平面直角坐标系xOy中,直线x=5与直线y=3,x轴分别交于点A,B,直线y=kx+b(k≠0)经过点A且与x轴交于点C(9,0).(1)求直线y=kx+b的表达式;(2)横、纵坐标都是整数的点叫做整点.记线段AB,BC,CA围成的区域(不含边界)为W.①结合函数图象,直接写出区域W内的整点个数;②将直线y=kx+b向下平移n个单位,当平移后的直线与区域W没有公共点时,请结合图象直接写出n的取值范围.第2题图3. 已知点A (4,1),若直线y 1=14x +b 与双曲线y 2=4x(x >0)交于点B ,与y 轴交于点C.探究:由双曲线y 2=4x (x >0)与线段OA ,OC ,BC 围成的区域M 内(不含边界)整点的个数(点的横、纵坐标都是整数的点称为整点).(1)当b =-1时,如图,求区域M 内的整点的个数;(2)当b <0时,若区域M 内恰好有4个整点,求b 的取值范围.第3题图4. 如图,函数y 1=-x 2+12x +c (-2020≤x ≤1)的图象记为L 1,最大值为M 1;函数y 2=-x 2+2cx +1(1≤x≤2020) 的图象记为L 2,最大值为M 2.L 1的右端点为A ,L 2的左端点为B ,L 1,L 2合起来的图形记为L .(1)当c =1时,求M 1,M 2的值;(2)若把横、纵坐标都是整数的点称为“美点”,当点A ,B 重合时,求L 上“美点”的个数; (3)若M 1,M 2的差为4716,直接写出c 的值.第4题图5. 如图,在平面直角坐标系中,设抛物线y =-x 2+bx +b -1为L 1,A (-5,-2),B (5,-2). (1)若L 1经过原点,求抛物线L 1的解析式,并求出此时抛物线的顶点坐标;(2)无论b 取何值,L 1总经过一个定点M ,随着b 的变化,抛物线L 1的顶点总在另一条抛物线上运动,且这条抛物线的顶点为M ,若设另一条抛物线为L 2.①求点M 的坐标; ②求出抛物线L 2的解析式;(3)若把抛物线L 1:y =-x 2+bx +b -1经过线段AB 端点时与线段AB 所围成的封闭图形称为C ,图形C 边界上横、纵坐标都是整数的点为“理想点”,求图形C 上“理想点”的个数.第5题图专题三 函数图象与性质综合题类型一 交点问题例 解:(1)∵直线y =34x +b 与线段AB 有交点,即直线y =34x +b 与线段AB 两端点交点为临界点,如解图①②,将A (-1,2)代入y =34x +b ,得b =114,将B (3,2)代入y =34x +b ,得b =-14,∴b 的取值范围为-14≤b ≤114;例题解图①例题解图②(2)设线段BC 的解析式为y =kx +m (k ≠0),将B (3,2),C (-2,-3)代入,得⎩⎪⎨⎪⎧3k +m =2-2k +m =-3,解得⎩⎪⎨⎪⎧k =1m =-1,∴线段BC 的解析式为y =x -1(-2≤x ≤3), ∴线段BC 与y 轴的交点为(0,-1). 当y =34x +b 过点(0,-1),如解图③,∴即b =-1,当y =34x +b 过点C (-2,-3),如解图④,∴-3=-32+b ,∴b =-32,∴当直线y =34x +b 与线段BC 在第三象限内有交点,b 的取值范围为-32≤b <-1;例题解图③例题解图④(3)由(2)知,直线BC 的解析式为y =x -1, 若y =kx +3与直线BC 无交点,∴直线y =kx +3与直线BC 平行,如解图⑤, ∴当k =1时,直线y =kx +3与直线BC 无交点;例题解图⑤(4)由(2)知直线BC 的解析式为y =x -1, 由题可知直线AB 的解析式为y =2,若直线AB ,直线y =kx +3与直线BC 能够围成三角形, 即直线y =kx +3与直线AB 、直线BC 都有交点, ∴k ≠1,k ≠0.∵直线AB 与直线BC 交于点B ,∴当直线y =kx +3过点B (3,2)时,直线AB 、直线y =kx +3与直线BC 交于一点,不能围成三角形.∴将B (3,2)代入y =kx +3,得3k +3=2,∴k =-13.综上所述,k ≠-13,0,1;(5)∵双曲线y =kx 过点A (-1,2),∴k =-2,∴双曲线的解析式为y =-2x .∵-5≤x ≤-1. ∴令x =-5,则y =25.当直线y =34x +b 与双曲线y =-2x 相切时,如解图⑥,∴34x +b =-2x ,整理得34x 2+bx +2=0, ∴b 2-6=0,∴b =6或b =-6(舍去).当直线y =34x +b 过点(-5,25),如解图⑦,∴25=-5×34+b , ∵b =8320.由解图可知,b 的取值范围为6≤b ≤8320;例题解图⑥例题解图⑦(6)由题可知A (-1,2),B (3,2), 抛物线y =x 2+c 的对称轴为直线x =0,∴当抛物线顶点在线段AB 上时,如解图⑧, ∴c =2.当抛物线过点B 时,如解图⑨, ∴2=9+c ,∴c =-7, ∴c 的取值范围为-7≤c ≤2;例题解图⑧例题解图⑨(7)联立⎩⎪⎨⎪⎧y =x -1y =x 2+c ,整理得x 2-x +c +1=0,如解图○10, ∴(-1)2-4(c +1)=0, ∴c =-34.例题解图○10对于抛物线y=x2+c,当x=2时,y=4+c,当点(2,4+c)在直线BC上时,如解图⑪,此时抛物线与直线BC有两个交点,将(2,4+c)代入直线BC解析式y=x-1,得2-1=4+c,解得c=-3;例题解图⑪当x=-2时,y=4+c,当点(-2,4+c)在直线BC上时,如解图⑫,此时抛物线与直线BC有一个交点,将(-2,4+c)代入直线BC解析式y=x-1,得-2-1=4+c,解得c=-7;例题解图⑫综上所述,抛物线y=x2+c(-2≤x≤2)与直线BC有一个交点,c的取值范围为-7≤c<-3,或c=-34;(8)∵A(-1,2),B(3,2),抛物线y=(x-k)2与线段AB有公共点,则当y=(x-k)2过点A(-1,2),如解图⑬,∴2=(-1-k)2,∴k=-1-2或k=-1+2(舍).当y=(x-k)2过点B(3,2),如解图⑭,∴2=(3-k)2,∴k=3+2或k=3-2(舍).∴k 的取值范围为-1-2≤k ≤3+2;例题解图⑬ 例题解图⑭(9)∵双曲线y =kx 过点B (3,2),∴2=k 3,∴k =6,∴双曲线的解析式为y =6x .∵2≤x ≤6, ∴当x =2时,y =3, 当x =6时,y =1,当抛物线过点(2,3)时,如解图⑮,将(2,3)代入y =x 2+c , 即3=4+c , ∴c =-1,同理当抛物线过点(6,1)时,将(6,1)代入y =x 2+c , 即1=36+c ,∴c =-35, ∴c 的取值范围为-35≤c ≤-1.例题解图⑮1. 解:(1)∵(-1,-2),(0,1)在函数y =kx +b 的图象上,∴⎩⎪⎨⎪⎧-2=-k +b 1=b ,解得⎩⎪⎨⎪⎧k =3b =1.∴直线l 的解析式为y =3x +1;(3分) (2)依题意,直线l ′的解析式为y =x +3, ∴直线l ′的图象如解图,第1题解图联立方程组⎩⎪⎨⎪⎧y =3x +1,y =x +3,解得⎩⎪⎨⎪⎧x =1,y =4,(5分)∴直线l 与直线l ′的交点坐标为(1,4). 又∵直线l ′与y 轴的交点坐标为(0,3),∴直线l ′被直线l 和y 轴所截得的线段长为(1-0)2+(4-3)2=2;(7分) (3)a 的值为52或175或7.(10分)2. 解:(1)设点P (x ,y ),则MP =y ,由OA 的中点为M ,知OA =2x ,代入OA ·MP =12,得2x ·y =12,即xy =6, ∵点P 在双曲线y =kx (k >0,x >0)上,∴k =xy =6;(3分)(2)当t =1时,令y =0,则0=-12(x -1)(x +3),解得x 1=1,x 2=-3,∵点B 在点A 左边, ∴B (-3,0),A (1,0), ∴AB =4.(5分)∴L 的对称轴为直线x =-1,∵点M 的坐标为(12,0),∴MP 与L 对称轴的距离为32;(6分)(3)∵A (t ,0),B (t -4,0), ∴L 的对称轴为直线x =t -2.(7分) 又∵点M 的横坐标为t2,∴当t -2≤t2,即t ≤4时,顶点(t -2,2)就是G 的最高点;当t -2>t 2,即t >4时,L 与MP 的交点(t 2,-18t 2+t )就是G 的最高点;(10分)(4)5≤t ≤8-2或7≤t ≤8+ 2.(12分)第2题解图3. 解:(1)(-1,0),3;4. 解:(1)∵双曲线y =1-2mx (x <0)位于第二象限,∴1-2m <0, ∴m >12;(2)∵点B (-1,1), ∴A (-3,1),C (-1,3), ∵双曲线y =1-2mx (x <0)经过点C ,∴双曲线的解析式为y =-3x ,∵-3×1=-3, ∴双曲线经过点A ; (3)①∵点B (a ,2a +1),∴A (a -2,2a +1),C (a ,2a +3).∵双曲线y =1-2mx (x <0)经过点A 、C ,∴(a -2)(2a +1)=a (2a +3), 解得a =-13;②∵点E 在AB 上, ∴点E 的纵坐标为2a +1, 代入y =2x +2得,x =a -12,∴E (a -12,2a +1),∵C (a ,2a +3),双曲线y =1-2mx(x <0)经过点C , ∴双曲线为y =a (2a +3)x,把E (a -12,2a +1)代入得,2a +1=a (2a +3)a -12,解得a =-16,由①知,双曲线过点A 时,a =-13.∴双曲线与线段AE 有交点,a 的取值范围是-13≤a ≤-16.5. 解:(1)∵抛物线F 经过点C (-1,-2), ∴-2=1+2m +m 2-2. ∴m =-1.∴抛物线F 的表达式是y =x 2+2x -1;(2)当x =-2时,y P =4+4m +m 2-2=(m +2)2-2. ∴当m =-2时,y P 的最小值为-2. 此时抛物线F 的表达式是y =(x +2)2-2. ∴当x ≤-2时,y 随x 的增大而减小. ∵x 1<x 2≤-2, ∴y 1>y 2;(3)-2≤m ≤0或2≤m ≤4. 6. 解:(1)∵△POC 的面积为6,∴12x P ·y P =6. ∴x P ·y P =12. ∴k =12; (2)①∵a =12,∴抛物线的解析式为y =12x 2-2x +32.当y =0时,12x 2-2x +32=0,解得x 1=1,x 2=3.∵x 1<x 2,∴A (1,0),B (3,0).∵抛物线的解析式为y =12x 2-2x +32,∴抛物线的对称轴为直线x =2, ∵k =3,∴y =3x(1≤x ≤4).当点P 位于(4,34)时,点P 到x =2的距离最大,当x =4时,y =12×42-2×4+32=32,∴PQ =32-34=34;②3576≤a ≤54. 7. 解:(1)将点(1,k +6)代入y =mx 2+2mx +k 中,得m =2; (2)y =mx 2+2mx +k =2x 2+4x +k ,由题意得:b 2-4ac =16-8k ≥0,解得k ≤2, ∵k 为正整数, ∴k =1或2.当k =1时,方程2x 2+4x +0没有整数解,故舍去, 则k =2;(3)由(2)得m =2,k =2,∴y =2x 2+4x +2,向下平移8个单位,平移后的表达式为y =2x 2+4x +2-8=2x 2+4x -6;(4)-12<b <32或b >27332.第7题解图8. 解:(1)由直线y =-x +4知,点B 、C 的坐标分别为(4,0)、(0,4), 把点B 、C 的坐标分别为(4,0)、(0,4), 代入y =ax 2-3ax +c 中,得⎩⎪⎨⎪⎧c =416a -12a +c =0, 解得⎩⎪⎨⎪⎧a =-1c =4,∴抛物线的表达式为y =-x 2+3x +4; (2)由y =-x 2+3x +4,得A (-1,0). 如解图,过点N 作NG ⊥AB 于点G ,第8题解图∵直线y =kx +k 平分△ABC 的面积, ∴NG =12OC =2,∴当y =2时,2=-x +4,∴x =2, ∴N (2,2).把N (2,2)代入y =kx +k ,得k =23,∴直线AM 的解析式为k =23x +23,联立⎩⎪⎨⎪⎧y =23x +23y =-x 2+3x +4,解得⎩⎨⎧x 1=103y 1=269,⎩⎪⎨⎪⎧x 2=-1y 2=0.∴M (103,269);(3)翻折后的整个图象包括两部分:分别是抛物线y =x 2-3x -4(-1≤x ≤4)与y =-x 2+3x +4(x >4或x <-1).①当直线y =kx +k 与抛物线y =x 2-3x -4=(x -32)2-254(-1≤x ≤4)相交时,由⎩⎪⎨⎪⎧y =kx +ky =x 2-3x -4,得x 2-3x -4=kx +k , 整理,得x 2-(k +3)x -(k +4)=0, 解得x 1=-1,x 2=k +4. ∴y 1=0,y 2=k 2+5k . ∴两个函数图象有两个交点,其中一个交点为A (-1,0),另一个交点坐标为(k +4,k 2+5k ).观察图象可知:另一个交点在x 轴下方,横坐标在-1与4之间,纵坐标在-254与0之间.∴-1<k +4<4,解得-5<k <0. -254<k 2+5k <0,整理,得 4k 2+20k +25>0且k 2+5k <0, 解得,(2k +5)2>0且-5<k <0. k 为任意实数,(2k +5)2>0恒成立, ∴-5<k <0;②当直线y =kx +k 与图象y =-x 2+3x +4(x >4或x <-1)相交时, -x 2+3x +4=kx +k , 整理得x 2+(k -3)x +(k -4)=0 解得x 1=-1,x 2=4-k ,∴y 1=0,y 2=5k -k 2. ∴两个函数图象有两交点,其中一个是点A (-1,0),另一个交点坐标为(4-k ,5k -k 2). 观察图象可知:另一个交点的横坐标大于4,纵坐标小于0, 即4-k >4,解得k <0. 5k -k 2<0,∴k (5-k )<0, ∵k <0,∴5-k >0,∴k <5. ∴k <0.∴综上所述,当直线y =kx +k 与翻折后的整个图象只有三个交点时,k 的取值范围是-5<k <0.类型二 整点问题例 解:(1)如解图①,设直线l 的解析式为y =px +q , 将A (5,0),B (0,5)代入得,⎩⎪⎨⎪⎧5p +q =0,q =5,解得⎩⎪⎨⎪⎧p =-1,q =5. ∴直线l 的解析式为y =-x +5.结合图象可知,线段OA 上共有6个整点,线段OB (不含原点)上共有5个整点,线段AB 上(不含端点)共有4个整点,△AOB 内部共有6个整点,∴直线l 与坐标轴围成的区域W 1内(含边界)整点的个数为6+5+4+6=21个;例题解图①(2)如解图②,设直线BC 的解析式为y =p 1x +q 1, 将B (0,5),C (-1,0)代入得,⎩⎪⎨⎪⎧q 1=5,-p 1+q 1=0,解得⎩⎪⎨⎪⎧p 1=5,q 1=5, ∴直线BC 的解析式为y =5x +5,结合图象,△BOC(不含边界)所围成的区域内无整点,由(1)知,△AOB(不含边界)所围成的区域内有6个整点,∴△ABC所围成的区域W2内(不含边界)整点的个数等于线段OB(不含端点)上的整点个数加上△AOB 内部的整点个数为4+6=10个;例题解图②(3)如解图③,当a=3时,直线y=3,线段AB与y轴所围成的三角形区域W3内(含边界)恰好有6个整点,∴结合图象可知,当2<a≤3时,直线y=a,线段AB与y轴所围成的三角形区域W3内(含边界)恰好有6个整点;例题解图③(4)如解图④,当b=0时,y=x,此时y=x与直线AB及y轴所围成的三角形区域W4内(不含边界)有2个整点,当b=-1时,y=x-1,此时y=x-1与直线AB及y轴所围成的三角形区域W4内(不含边界)有4个整点,结合图象可知,-1≤b<0;例题解图④(5)如解图⑤,x <时当直线y =kx +2过(-5,1)时,直线y =kx +2与直线BC 及x 轴所围成的三角形区域W 5内(不含边界)有4个整点,将(-5,1)代入y =kx +2得k =15,当直线y =kx +2过(-4,1)时,直线y =kx +2与直线BC 及x 轴所围成的三角形区域W 5内(不含边界)有3个整点,将(-4,1)代入y =kx +2得k =14,结合图象可知,15≤k <14;同理,x >0时,当直线y =kx +2过(3,1)时,直线y =kx +2与直线BC 及x 轴所围成的三角形区域W 5内(不含边界)有3个整点,将(3,1)代入y =kx +2得k =-13,当直线y =kx +2过(4,1)时,直线y =kx +2与直线BC 及x 轴所围成的三角形区域W 5内(不含边界)有4个整点,将(4,1)代入y =kx +2得k =-14,∴-13≤k <-14,综上可得,15≤k <14或-13≤k <-14;例题解图⑤(6)如解图⑥,由图象可知曲线DE 上有(1,4)(2,2),(4,1)共3个整点,线段DE (不含端点)上有(2,3),(3,2)共2个整点,曲线DE 与线段DE 围成的区域内部无整点,∴曲线DE 与线段DE 所围成的区域W 6内(含边界)有5个整点;例题解图⑥(7)如解图⑦,当G 点与原点重合时,此时线段DG ,FG 与曲线DF 所围成的区域W 7内(含边界)有6个整点,此时b=0,如解图⑧,当点G的纵坐标在0与-1之间时,此时线段DG,FG与曲线DF所围成的区域W7内(含边界)有5个整点,如解图⑨,当G点与过(0,-1)时,此时线段DG,FG与曲线DF所围成的区域W7内(含边界)有8个整点,此时b=-1,∴-1<b<0;例题解图⑦例题解图⑧例题解图⑨(8)由抛物线y=x2-2x+m-2可得,抛物线的对称轴为直线x=1,且抛物线恒过点(0,m-2),如解图○10,当抛物线的顶点为(1,2)时,此时抛物线与直线y=5所围成的区域W8内(不含边界)有4个整点,分别为(1,3),(0,4),(1,4),(2,4),将(1,2)代入抛物线解析式得,1-2+m-2=2,解得m=5,当抛物线的顶点为(1,3)时,此时抛物线与直线y=5所围成的区域W8内(不含边界)有1个整点(1,4),将(1,3)代入抛物线解析式得,1-2+m-2=3,解得m=6,结合图象可知,5≤m<6.例题解图○10(9)由抛物线y=x2-2x+m-2可得,抛物线的对称轴为直线x=1,且抛物线恒过点(0,m-2),如解图⑪,当抛物线的顶点为(1,-2)时,此时抛物线与直线y=-x+2所围成的区域W9内(不含边界)有4个整点,分别为(0,0),(0,1),(1,0),(1,-1),将(1,-2)代入抛物线解析式得,1-2+m-2=-2,解得m=1,当抛物线的顶点为(1,-1)时,此时抛物线与直线y=-x+2所围成的区域W9内(不含边界)有2个整点,分别为(0,1),(1,0),将(1,-1)代入抛物线解析式得,1-2+m-2=-1,解得m=2,∴综上所述,1≤m<2.例题解图⑪1.解:(1)当x=0时,y=x-b=-b,∴B(0,-b),∵AB=8,A(0,b),∴b-(-b)=8.∴b=4;(2分)∴L 的解析式为y =-x 2+4x , ∴L 的对称轴为直线x =2,将x =2代入直线a 的解析式中得y =2-4=-2, ∴L 的对称轴与a 的交点坐标为(2,-2);(4分) (2)∵y =-x 2+bx =-(x -b 2)2+b 24, ∴L 的顶点C 的坐标为(b 2,b 24).∵点C 在l 下方,∴点C 与l 的距离为b -b 24=-14(b -2)2+1≤1,∴点C 与l 距离的最大值为1;(7分)(3)由题意可得,y 1=b ,y 2=x 0-b ,y 3=-x 20+bx 0, ∵y 3是y 1,y 2的平均数, ∴y 3=y 1+y 22,即-x 20+bx 0=x 02, 化简得x 0(2x 0-2b +1)=0, 解得x 0=0或x 0=b -12,∵x 0≠0, ∴x 0=b -12,对于L ,当y =0时,0=-x 2+bx ,即0=-x (x -b ).解得x 1=0,x 2=b , ∵b >0,∴D 点坐标为(b ,0),∴点(x 0,0)与点D 间的距离为b -(b -12)=12;(10分)(4)当b =2019时,“美点”的个数为4040;(11分) 当b =2019.5时,“美点”的个数为1010.(12分) 2. 解:(1)如解图,则点A 的坐标为(5,3), ∵直线y =kx +b 过点A (5,3),点C (9,0),∴⎩⎪⎨⎪⎧5k +b =39k +b =0,解得⎩⎨⎧k =-34b =274, 即直线y =kx +b 的表达式是y =-34x +274;(2)①3个;第2题解图3. 解:(1)∵A (4,1), ∴直线OA 的解析式为y =14x .∵直线y 1=14x +b ,∴直线y 1与OA 平行,当b =-1时,直线解析式为y 1=14x -1,解方程4x =14x -1得x 1=2-25(舍去),x 2=2+25,则B (2+25,5-12),∵C (0,-1),∴区域M 内的整点为(1,0),(2,0),(3,0),共3个;(2)当直线y 1在OA 的下方时,当直线y 1=14x +b 过点(1,-1)时,b =-54,则直线y 1=14x +b 经过(5,0),∴区域M 内恰有4个整点,则b 的取值范围是-54≤b <-1.当直线l 在OA 的上方时,∵点(2,2)在函数y 2=4x(x >0)的图象上,当直线y 1=14x +b 过(1,2)时,b =74,此时区域M 内有3个整点.当直线y 1=14x +b 过(1,3)时,b =114,∴区域M 内恰有4个整点时,b 的取值范围是74<b ≤114.综上所述,区域M 内恰有4个整点时,b 的取值范围是-54≤b <-1或74<b ≤114.4. 解:(1)当c =1时,y 1=-x 2+ 12x +c =-x 2+ 12x +1=-(x -14)2+1716 .又∵-2020≤x ≤1,∴M 1=1716. y 2=-x 2+2cx +1=-x 2+2x +1=-(x -1)2+2. 又∵1≤x ≤2020, ∴M 2=2;(2)当x =1时,y 1=-x 2+12x +c =c -12;y 2=-x 2+2cx +1=2c .若点A ,B 重合,则c -12=2c ,解得c =-12.∴L 1∶y 1=-x 2+12 x -12(-2020≤x ≤1);L 2∶y 2=-x 2-x +1(1≤x ≤2020).在L 1上,x 为奇数的点是“美点”,则L 1上有1011个“美点”, 在L 2上,x 为整数的点是“美点”,则L 2上有2020个“美点”. 又∵点A ,B 重合,则L 上“美点”的个数是1011+2020-1=3030; (3)c =-238或2.5. 解:(1)∵L 1:y =-x 2+bx +b -1经过原点, ∴将(0,0)代入得b =1,∴抛物线L 1的解析式为y =-x 2+x , 将y =-x 2+x 配方得y =-(x -12)2+14,∴顶点坐标为(12,14);(2)①对于抛物线L 1:y =-x 2+bx +b -1=(x +1)b -x 2-1,当x =-1时,y =-2,故抛物线y =-x 2+bx +b -1总经过一个定点M (-1,-2);②∵抛物线L 2的顶点为M , ∴设它的解析式为y =a (x +1)2-2, 又∵抛物线L 1的顶点总在抛物线L 2上, ∴将点(12,14)代入解得a =1,∴抛物线L 2的解析式为y =(x +1)2-2,即y =x 2+2x -1;(3)当抛物线L 1经过点B 时,将B (5,-2)代入抛物线L 1解析式y =-x 2+bx +b -1得b =4, ∴抛物线L 1的解析式为y =-x 2+4x +3,令y =-2,得-2=-x 2+4x +3,解得x 1=-1,x 2=5,∴抛物线L 1与线段AB 交于(-1,-2),(5,-2)两点,由解析式可以得出,只要x 取整数,则抛物线L 1上点的纵坐标也一定是整数.∴抛物线L 1经过端点B 时形成的封闭图形C 上的“理想点”个数为12个;当抛物线L 1经过点A 时,将A (-5,-2)代入抛物线L 1解析式y =-x 2+bx +b -1得b =-6, ∴抛物线L 1的解析式为y =-x 2-6x -7,从解析式可以得出,只要x 取整数,则抛物线L 1上点的纵坐标也一定是整数,令y =-2,得-2=-x 2-6x -7,解得x 1=-5,x 2=-1, ∴抛物线L 1与线段AB 交于(-5,-2),(-1,-2)两点,故当抛物线L 1经过端点A 时形成的封闭图形C 上的“理想点”的个数为8个; 综上所述,封闭图形C 上的“理想点”的个数为8个或12个.。
2021年九年级数学中考复习——几何小专题:三角形综合之解答题专项(三)

2021年九年级数学中考复习——几何小专题:三角形综合之解答题专项(三)练习一1.在△ABC中,AB=AC,点D是直线BC上一点(不与B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=度;(2)如图2,如果∠BAC=60°,则∠BCE=度;(3)设∠BAC=α,∠BCE=β.①如图3,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;②当点D在直线BC上移动,请直接写出α,β之样的数量关系,不用证明.2.在△ABC中,∠ACB=90°,AC=BC.点D是直线AB上一点(点D与点A、B不重合),以CD为直角边作等腰直角三角形DCE,使∠DCE=90°,连结AE.(1)如图①,当点D在线段AB上,点E与点A在CD同侧.求证:AE=BD.(2)如图②,当点D在AB的延长线上,点E与点A在CD同侧.若AE=1,AB=4,则AD=.(3)如图③,当点D在BA的延长线上,点E与点A在CD的两侧时,直接写出线段AB、AD、AE三者之间的数量关系:.3.如图,在Rt△ABC中,∠ACB=90°,AC=20,BC=15,动点P从点A出发(动点P不与△ABC的顶点重合),沿折线AC﹣CB以每秒5个单位的速度向终点B运动,过点P作PD⊥AB于点D,以点P为直角顶点作Rt△PDE,使DE与点P所在的直角边平行,设点P的运动时间为t(秒).(1)求AB的长;(2)当点E落在△ABC的直角边上时,求t的值;(3)当△PDE的两条直角边所在的直线截△ABC所得的三角形全等时,求△PDE与△ABC重叠部分图形的周长;(4)设Q为边DE的中点,作射线CQ,当CQ将△PDE分成面积比为1:3两部分时,直接写出t的值.4.如图,在△ABC中,AB=AC=3,∠B=50°,点D在线段BC上运动(不与B、C 重合),连接AD,作∠ADE=50°,DE交线段AC于E.(1)当∠BDA=105°时,∠BAD=°,∠DEC=°;(2)若DC=AB,求证:△ABD≌△DCE;(3)在点D的运动过程中,是否存在△ADE是等腰三角形?若存在,请直接写出此时∠BDA的度数;若不存在,请说明理由.5.已知△ABC是等边三角形,点P,Q分别为边AB,BC上的动点(端点除外)点P,Q 以相同的速度,同时从点A,点B出发,直线AQ,CP相交于点M.(Ⅰ)如图①,求证:△ABQ≌△CAP;(Ⅱ)如图①,当点P,Q分别在AB,BC边上运动时,∠QMC的大小是否变化?若变化,请说明理由;若不变,求出它的大小;(Ⅲ)如图②,当点P,Q分别在AB,BC的延长线上运动时,∠QMC的大小是否变化?若变化,请说明理由;若不变,求出它的度数.练习二6.在Rt△ABC中,∠ACB=90°,AC=BC,点D、F是线段AB上两点,连结CD,过A作AE⊥CD于点E,过点F作FM⊥CD于点M.(1)如图1,若点E是CD的中点,求∠CAE的大小;(2)如图2,若点D是线段BF的中点,求证:CE=FM;(3)如图3,若点F是线段AB的中点,AE=,CE=1,求FM的值.7.在△ABC中,∠A=90°,AB=AC=+1.且AD=AE=1.(1)如图1,点D,E分别在边AB,AC上,连接DE.直接写出DE的值,BC的值;(2)现将△ADE如图2放置,连接CE,BE,CD,求证:CD=BE;(3)现将△ADE如图3放置,使C,A,E三点共线,延长CD交BE于点F,求证:CF垂直平分BE.8.在等腰直角△ABC中,AB=AC,∠A=90°,过点B作BC的垂线l.点P为直线AB上的一个动点(不与点A,B重合),将射线PC绕点P顺时针旋转90°交直线l 于点D.(1)如图l,点P在线段AB上,依题意补全图形.①求证:∠BDP=∠PCB;②用等式表示线段BC,BD,BP之间的数量关系,并证明.(2)点P在线段AB的延长线上,直接写出线段BC,BD,BP之间的数量关系.9.定义:点P是△ABC内部的一点,若经过点P和△ABC中的一个顶点的直线把△ABC 平分成两个面积相等的图形,则称点P是△ABC关于这个顶点的均分点,例如图1中,点P是△ABC关于顶点A的均分点.(1)下列图形中,点D一定是△ABC关于顶点B的均分点的是;(填序号)(2)在△ABC中,BC=2,AB=AC且AB>BC,点P是△ABC关于顶点A的均分点,且≤BP≤2,直接写出∠BPC的范围;(3)如图2,在△ABC中,∠BAC=90°,BC=10,点P是△ABC关于顶点A的均分点,直线AP与BC交于点D,当BP⊥AD时,BP=4,求CP的长.10.在△ABC和△DBE中,CA=CB,EB=ED,点D在AC上.(1)如图1,若∠ABC=∠DBE=60°,求证:∠ECB=∠A;(2)如图2,设BC与DE交于点F.当∠ABC=∠DBE=45°时,求证:CE∥AB;(3)在(2)的条件下,若tan∠DEC=时,求的值.练习三11.如图,△AOB是等边三角形,以直线OA为x轴建立平面直角坐标系,若B(a,b)且a、b满足+(b﹣5)2=0,D为y轴上一动点,以AD为边作等边△ADC,CB交y轴于E.(1)如图1,求A点坐标;(2)如图2,D为y正半轴上一点,C在第二象限,CE的延长线交x轴于M,当D 点在y轴正半轴上运动时,M点坐标是否变化,若不变,求M点的坐标,若变化,说明理由;(3)如图3,D在y轴负半轴上,以DA为边向右构造等边△DAC,CB交y轴于E 点,如果D点在y轴负半轴上运动时,仍保持△DAC为等边三角形,连BE,试求CE,OD,AE三者的数量关系,并证明你的结论.12.【教材呈现】数学课上,胡老师用无刻度的直尺和圆规按照华师版教材八年级上册87页完成角平分线的作法,方法如下:【试一试】如图1,∠AOB为已知角,试按下列步骤用直尺和圆规准确地作出∠AOB的平分线.第一步:在射线OA、OB上,分别截取OD、OE,使OD=OE;第二步:分别以点D和点E为圆心、适当长(大于线段DE长的一半)为半径作圆弧,在∠AOB内,两弧交于点C;第三步:作射线OC.射线OC就是所要求作的∠AOB的平分线.【问题1】胡老师用尺规作角平分线时,用到的三角形全等的判定方法是.【问题2】小萱同学发现只利用直角三角板也可以作∠AOB的角平分线,方法如下(如图2):步骤:①利用三角板上的刻度,在OA、OB上分别截取OM、ON,使OM=ON.②分别过点M、N作OM、ON的垂线,交于点P.③作射线OP,则OP为∠AOB的平分线.(1)请写出小萱同学作法的完整证明过程.(2)当∠MON=60°时,量得MN=4cm,则△MON的面积是cm2.13.某校组织数学兴趣探究活动,爱思考的小实同学在探究两条直线的位置关系查阅资料时发现,两条中线互相垂直的三角形称为“中垂三角形”.如图1、图2、图3中,AF、BE是△ABC的中线,AF⊥BE于点P,像△ABC这样的三角形均称为“中垂三角形”.【特例探究】(1)如图1,当∠PAB=45°,AB=6时,AC=,BC=;如图2,当sin∠PAB=,AB=4时,AC=,BC=;【归纳证明】(2)请你观察(1)中的计算结果,猜想AB2、BC2、AC2三者之间的关系,用等式表示出来,并利用图3证明你的结论.【拓展证明】(3)如图4,在△ABC中,AB=4,BC=2,D、E、F分别是边AB、AC、BC的中点,连结DE并延长至G,使得GE=DE,连结BG,当BG⊥AC于点M时,求GF的长.14.如图,△ABC为等边三角形,直线l经过点C,在l上位于C点右侧的点D满足∠BDC =60°.(1)如图1,在l上位于C点左侧取一点E,使∠AEC=60°,求证:△AEC≌△CDB;(2)如图2,点F、G在直线l上,连AF,在l上方作∠AFH=120°,且AF=HF,∠HGF=120°,求证:HG+BD=CF;(3)在(2)的条件下,当A、B位于直线l两侧,其余条件不变时(如图3),线段HG、CF、BD的数量关系为.15.阅读材料:小明遇到这样一个问题:如图1,在△AC中,∠A=2∠B,CD平分∠ACB,AD=2.2,AC=3.6,求BC的长.小明的想法:因为CD平分∠ACB,所以可利用“翻折”来解决该问题.即在BC边上取点E,使EC=AC,并连接DE(如图2).(1)如图2,根据小明的想法,回答下面问题:①△DEC和△DAC的关系是,判断的依据是;②△BDE是三角形;③BC的长为.(2)参考小明的想法,解决下面问题:已知:如图3,在△ABC中,AB=AC,∠A=20°,BD平分∠ABC,BD=2.3,BC =2,求AD的长.参考答案1.解:(1)∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,∵∠DAE=∠BAC,∴∠BAD=∠CAE,且AB=AC,AD=AE,∴△BAD≌△CAE(SAS)∴∠ABC=∠ACE=45°,∴∠BCE=∠ACB+∠ACE=90°,故答案为:90;(2)∵∠BAC=60°,AB=AC,∴△ABC为等边三角形,∴∠ABD=∠ACB=60°,∵∠BAC=∠DAE,∴∠BAD=∠CAE,在△ABD和△ACE中,∵∠BAD=∠CAE,且AB=AC,AD=AE,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE=60°,∴∠BCE=∠ACE+∠ACB=60°+60°=120°,故答案为:120.(3)①α+β=180°,理由:∵∠BAC=∠DAE,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC.即∠BAD=∠CAE.在△ABD与△ACE中,,∴△ABD≌△ACE(SAS),∴∠B=∠ACE.∴∠B+∠ACB=∠ACE+∠ACB.∵∠ACE+∠ACB=β,∴∠B+∠ACB=β,∵α+∠B+∠ACB=180°,∴α+β=180°.②如图1:当点D在射线BC上时,α+β=180°,连接CE,∵∠BAC=∠DAE,∴∠BAD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,在△ABC中,∠BAC+∠B+∠ACB=180°,∴∠BAC+∠ACE+∠ACB=∠BAC+∠BCE=180°,即:∠BCE+∠BAC=180°,∴α+β=180°,如图2:当点D在射线BC的反向延长线上时,α=β.连接BE,∵∠BAC=∠DAE,∴∠BAD=∠CAE,且AB=AC,AD=AE,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,∴∠ABD=∠ACE=∠ACB+∠BCE,∴∠ABD+∠ABC=∠ACE+∠ABC=∠ACB+∠BCE+∠ABC=180°,∵∠BAC=180°﹣∠ABC﹣∠ACB,∴∠BAC=∠BCE.∴α=β;综上所述:点D在直线BC上移动,α+β=180°或α=β.2.(1)证明:如图①,∵∠ACB=90°,∠DCE=90°,∴∠BCD+∠ACD=90°,∠ACE+∠ACD=90°,∴∠BCD=∠ACE,在△BCD和△ACE中,,∴△BCD≌△ACE(SAS),∴AE=BD;(2)解:如图②,∵∠ACB=90°,∠DCE=90°,∴∠BCD+∠BCE=90°,∠ACE+∠BCE=90°,∴∠BCD=∠ACE,在△BCD和△ACE中,,∴△BCD≌△ACE(SAS),∴AE=BD,∴AD=AB+BD=AB+AE=5,故答案为:5;(3)解:同(2)的证明方法可得,△BCD≌△ACE(SAS),∴AE=BD,∴AB+BD=BD=AE,故答案为:AB+AD=AE.3.解:(1)在Rt△ABC中,∠ACB=90°,AC=20,BC=15,∴AB===25;(2)如图1,P在AC上时,点E在BC上,DE∥AC,∵DE∥AC,∴∠CPE=∠DEP,∵PD⊥AB,∴∠ADP=90°,由题意得:AP=5t,sin A=,即,∴PD=3t,∴AD=4t,BD=25﹣4t,∵∠DPE=90°,∴∠APD+∠CPE=90°=∠APD+∠A,∴∠CPE=∠A=∠DEP,∴sin∠DEP=,∴DE=5t,∵DE∥AC,∴,即,解得:t=;如图2,P在BC上时,点E在AC上,DE∥BC,由题意得:CP=5t﹣20,PB=15﹣(5t﹣20)=35﹣5t,∵∠EPD=∠PDB=90°,∴EP∥AB,∵DE∥BC,∴四边形EPBD是平行四边形,∴DE=PB=35﹣5t,∵∠CEP=∠A=∠PDE,∴sin∠CEP=sin∠PDE,∴=,即,∴EP=,∴=,解得:t=;综上,t的值是或;(3)如图3,P在AC上,△PDE与△ABC重叠部分图形是△PDE,设直线PE与BC 交于点F,∵AP∥DE,AD∥PE,∴四边形APED是平行四边形,∴DE=AP=5t,AD=PE=4t,∵△ADP≌△PCF,∴PC=AD=4t,∵AC=AP+CP,即20=5t+4t,∴t=,∴△PDE的周长=PD+PE+DE=3t+4t+5t=12t=12×=,即△PDE与△ABC重叠部分图形的周长是;如图4,P在BC上,△PDE与△ABC重叠部分的图形是△PDE,设直线PE与AC交于点G,同理得:四边形DEPB是平行四边形,∴DE=PB,∵△GCP≌△PDB,∴PC=BD=5t﹣20,Rt△PDB中,cos B==,∴=,解得:t=,∴PB=35﹣5×=,∵∠C=∠PDB=90°,∠B=∠B,∴△PDB∽△ACB,∴=,∴△PDB的周长=×(15+20+25)=,∴△PDE的周长=,即△PDE与△ABC重叠部分图形的周长是;综上,△PDE与△ABC重叠部分图形的周长为或;(4)分两种情况:①如图5,P在AC上,设PE与CQ交于点O,连接PQ,∵Q是DE的中点,∴DQ=EQ=t,∴S△PDQ=S△PQE,Rt△PDE中,PD=3t,PE=4t,DE=5t,∵==,∴=,∴=,∴=1,∵DE∥CP,∴,即=1,解得:t=;②如图6,P在BC上,=,同理得:=1,∵CP=5t﹣20,PB=35﹣5t,由上题知:四边形DEPB是平行四边形,∴DE=PB=35﹣5t,∴EQ=,∵ED∥PC,∴=1,∴EQ=CP,∴=5t﹣20,解得:t=5;综上,t的值是或5.4.解:(1)∵在△BAD中,∠B=∠50°,∠BDA=105°,∴∠BAD=180°﹣∠B﹣∠BDA=180°﹣50°﹣105°=25°;∵AB=AC,∴∠B=∠C=50°,∴∠DEC=180°﹣∠C﹣∠EDC=180°﹣50°﹣25°=105°,故答案为:25,105;(2)∵∠B=∠C=50°,∴∠DEC+∠EDC=130°,又∵∠ADE=50°,∴∠ADB+∠EDC=130°,∴∠ADB=∠DEC,在△ABD和△DCE中,,∴△ABD≌△DCE(AAS).(3)当∠BDA的度数为100°或115°时,△ADE的形状是等腰三角形,①∠BDA=100°时,则∠ADC=80°,∵∠C=50°,∴∠DAC=50°,∴∠DAC=∠ADE,∴△ADE的形状是等腰三角形;②∠BDA=115°时,则∠ADC=65°,∵∠C=50°,∴∠DAC=65°,∵∠ADE=50°,∴∠AED=65°,∴∠DAC=∠AED,∴△ADE的形状是等腰三角形.5.解:(1)证明:如图1,∵△ABC是等边三角形∴∠ABQ=∠CAP=60°,AB=CA,又∵点P、Q运动速度相同,∴AP=BQ,在△ABQ与△CAP中,,∴△ABQ≌△CAP(SAS);(2)点P、Q在AB、BC边上运动的过程中,∠QMC不变.理由:∵△ABQ≌△CAP,∴∠BAQ=∠ACP,∵∠QMC是△ACM的外角,∴∠QMC=∠ACP+∠MAC=∠BAQ+∠MAC=∠BAC,∵∠BAC=60°,∴∠QMC=60°;(3)如图2,点P、Q在运动到终点后继续在射线AB、BC上运动时,∠QMC不变.理由:同理可得,△ABQ≌△CAP,∴∠BAQ=∠ACP,∵∠QMC是△APM的外角,∴∠QMC=∠BAQ+∠APM,∴∠QMC=∠ACP+∠APM=180°﹣∠PAC=180°﹣60°=120°,即若点P、Q在运动到终点后继续在射线AB、BC上运动,∠QMC的度数为120°.6.(1)解:∵AC=BC,∠ACB=90°,∴∠CAB=∠B=45°,∵AE⊥CD,EC=ED,∴AC=AD,∴∠CAE=∠DAE=22.5°,∴∠CAE=22.5°.(2)证明:过点B作BN⊥CD交CD的延长线于点N.∴∠BNC=90°,∵AE⊥CD,∴∠CEA=∠BNC=90°,∴∠CAE+∠ACD=90°,∵∠ACB=90°,∴∠ACD+∠BCN=90°,∴∠CAE=∠BCN,在△AEC和△CNB中,,∴△AEC≌△CNB(AAS),∴CE=BN,∵FM⊥CD,BN⊥CD,∴∠FMD=∠BND=90°,∵点D是线段BF的中点,∴FD=BD,在△FMD和△BND中,,∴△FMD≌△BND(AAS),∴FM=BN,∴CE=FM.(3)解:在线段AE上取点G,使得AG=CE,连结CF、EF,如图3所示:∵AF=FB,AC=BC,∠ACB=90°,∴CF⊥AB,CF=AF,∵∠FAG+∠ADE=90°,∠ADE+∠FCE=90°,∴∠GAF=∠ECF,在△AGF和△CEF中,,∴△AGF≌△CEF(SAS),∴FG=EF,∠AFG=∠CFE,∴∠EFG=∠AFC=90°∴△EFG是等腰直角三角形,∴EG=EF,∠GEF=45°,∴∠MEF=90°﹣45°=45°,∴△EFM是等腰直角三角形,∴EF=FM,∴AE﹣CE=AE﹣AG=EG=EF=2FM=﹣1,∴FM=.7.(1)解:在Rt△ADE中,∠A=90°,AD=AE=1,∴DE===,同理,BC==2+,故答案为:;2+;(2)证明:∵∠CAB=∠DAE=90°,∴∠CAB﹣∠DAB=∠DAE﹣∠DAB,即∠CAD=∠BAE,在△CAD和△BAE中,,∴△CAD≌△BAE(SAS),∴CD=BE;(3)证明:∵C,A,E三点共线,∴CE=CA+AE=+2,∴CE=CB,∴点C在线段BE的垂直平分线上,∵BD=AB﹣AD=,DE=,∴BD=DE,∴点D在线段BE的垂直平分线上,∴CF垂直平分BE.8.解:(1)①补全图形如图1,证明:如图1,设PD与BC的交点为点E,根据题意可知,∠CPD=90°,∵BC⊥l,∴∠DBC=90°,∴∠BDP+∠BED=∠PCB+∠PEC=90°,∴∠BDP=∠PCB;②BC﹣BD=BP.证明:如图2,过点P作PF⊥BP交BC于点F,∵AB=AC,∠A=90°,∴∠ABC=45°,∴BP=BF,∠PFB=45°,∴∠PBD=∠PFC=135°,又∵∠BDP=∠PCF,∴△BPD≌△FPC(AAS),∴BD=FC,在等腰直角△BPF中,BF=BP,∴BC﹣BD=BP.(2)BD﹣BC=BP.证明:如图3,过点P作PM⊥PB交BD于点M,由(1)可知∠ABC=∠PBM=45°,∴∠PBM=∠PMB=45°,∴PB=PM,∠PBC=∠PCB=135°,同(1)可得∠PDB=∠PCB,∴△PMD≌△PBC(AAS),∴DM=BC,∵PB=PM,∠BPM=90°,∴BM=PB,∴BD﹣DM=BM=BD﹣BC=PB.9.解:(1)在图①中,∵∠BAE=∠CAE,∴点D不一定是△ABC关于顶点B的均分点;在图②中,∵BE=CE,∴点D一定是△ABC关于顶点A的均分点,但点D不一定是△ABC关于顶点B的均分点.在③中,∵∠ABE=∠CBE,AB≠BC,∴点D不一定是△ABC关于顶点B的均分点;④∵AE=CE,∴点D一定是△ABC关于顶点B的均分点.故答案为:④.(2)60°≤∠BPC≤90°.如图1,点P是△ABC关于顶点A的均分点,∵AB=AC,点P是△ABC关于顶点A的均分点,∴BD=CD,∴AD⊥BC,∵BC=2,∴BD=1,∴当∠BED=45°时,BE=,当∠BFD=30°时,BF=2BD=2,∵点P在AD上运动,且≤BP≤2,∴60°≤∠BPC≤90°.(3)解:如图2,过C点作CE⊥AP,交直线AP于点E.∵点P是△ABC关于顶点A的均分点,BC=10,∴BD=CD=5.在Rt△BPD中,∵∠BPD=90°,∴BP2+PD2=BD2.∵BP=4,BD=5,∴PD=3.∵BP⊥AP,CE⊥AP,∴∠BPD=∠CED=90°.∵∠BDP=∠CDE,∴△BPD≌△CDE(AAS).∴PD=DE,PB=CE=4.∴PE=2PD=6.在Rt△PEC中,∵∠PEC=90°,∴PE2+CE2=CP2.∴CP===.10.(1)证明:∵CA=CB,EB=ED,∠ABC=∠DBE=60°,∴△ABC和△DBE都是等边三角形,∴AB=BC,DB=BE,∠A=60°.∵∠ABC=∠DBE=60°,∴∠ABD=∠CBE,∴△ABD≌△CBE(SAS).∴∠A=∠ECB;(2)证明:∵∠ABC=∠DBE=45°,CA=CB,EB=ED,∴△ABC和△DBE都是等腰直角三角形,∴∠CAB=45°,∴,∴,∵∠ABC=∠DBE,∴∠ABD=∠CBE,∴△ABD∽△CBE,∴∠BAD=∠BCE=45°,∵∠ABC=45°,∴∠ABC=∠BCE,∴CE∥AB;(3)解:过点D作DM⊥CE于点M,过点D作DN∥AB交CB于点N,∵∠ACB=90°,∠BCE=45°,∴∠DCM=45°,∴∠MDC=∠DCM=45°,∴DM=MC,设DM=MC=a,∴a,∵DN∥AB,∴△DCN为等腰直角三角形,∴DN=DC=2a,∵tan∠DEC=,∴ME=2DM,∴CE=a,∴,∵CE∥DN,∴△CEF∽△NDF,∴.11.解:(1)如图1中,作BF⊥AO于F.∵+(b﹣5)2=0,∴a=﹣5,b=5,∴B(﹣5,5),∵BA=BO,BF⊥OA,∴FA=FO=5,∴OA=10,∴A(﹣10,0).(2)点M的坐标不发生变化.理由:如图2中,∵△ABO,△ADC都是等边三角形,∴∠OAB=∠DAC,OA=OB,AD=AC,∴∠OAD=∠BAC,∴△OAD≌△BAC,∴∠AOD=∠CBA=90°,在Rt△ABM中,∵∠ABM=90°,AB=OA=10,∠BAM=60°,∴AM=2AB=20,∴OM=AM﹣OA=10,∴M(10,0).(3)结论:OD=CE+AE.理由:如图3中,取AE的中点R,连接BR、OR.∵∠ABE=∠AOE=90°,AR=ER,∴BR=AR=RE=OR,∴A、B、E、O四点共圆,∴∠BAE=∠BOE=90°﹣60°=30°,∴BE=AE,∵△ABO,△ADC都是等边三角形,∴∠OAB=∠DAC,OA=OB,AD=AC,∴∠OAD=∠BAC,∴△OAD≌△BAC,∴OD=BC=CE+BE=CE+AE.即OD=CE+AE.12.解:【问题1】胡老师用尺规作角平分线时,用到的三角形全等的判定方法是SSS,故答案为:SSS;【问题2】(1)在Rt△OPN和Rt△OPM中,,∴Rt△OPN≌Rt△OPM(HL),∴∠NOP=∠MOP,∴OP为∠AOB的平分线;(2)∵∠MON=60°,OM=ON,∴△MON为等边三角形,∴OM=ON=MN=4(cm),∵OM=ON,OP为∠AOB的平分线,∴NH=HM=MN=2(cm),由勾股定理得,OH===2(cm),∴△MON的面积=×MN×OH=×4×2=4(cm2),故答案为:4.13.(1)解:如图1,∵AF⊥BE,∴∠APB=∠APE=∠BPF=90°,∵∠PAB=45°,AB=6,∴AP=PB=6,如图1,连接EF,∵AF,BE是△ABC的中线,∴EF是△ABC的中位线,∴EF∥AB.且EF=AB,∴,∴PE=PF=3,由勾股定理得:AE=BF===3,∴AC=BC=2AE=6,如图2,∵sin∠PAB=,AB=4,AF⊥BE,∴∠PAB=30°,∴BP=AB=2,AP=2,∵AF、BE是△ABC的中线,∴PE=PB=1,PF=AP=,由勾股定理得:AE===,BF===,∴AC=2AE=2,BC=2BF=2,故答案为:6,6,2,2;(2)解:猜想:AB2、BC2、AC2三者之间的关系是:AC2+BC2=5AB2,证明:如图3,设PF=m,PE=n则AP=2m,PB=2n,在Rt△APB中,(2m)2+(2n)2=AB2①,在Rt△APE中,(2m)2+n2=()2②,在Rt△BPF中,m2+(2n)2=()2③,由①得:m2+n2=,由②+③得:5(m2+n2)=,∴AC2+BC2=5AB2;(3)解:如图4,连接CG,EF,过点F作FN∥BG交CG于点N,FG与AC交于点Q,∵FN∥BG,BG⊥AC,∴FN⊥AC,∵F是BC的中点,∴N是CG的中点,∵D、E分别是AB、AC的中点,∴DE=FC,DE∥FC,∵ED=EG,∴EG=FC,EG∥FC,∴四边形EFCG是平行四边形,∴Q是FG的中点,∴△FCG是中垂三角形,∵AB=4,BC=2,∴CG=EF=BD=2,FC=,由(2)中结论可知:5FC2=CG2+FG2,即5×5=(2)2+FG2,∴GF=.14.(1)证明:如图1,∵△ABC是等边三角形,∴AC=BC,∠ACB=60°,∴∠BCD+∠ACE=120°,∵∠AEC=60°,∴∠ACE+∠EAC=120°,∴∠BCD=∠EAC,∵∠AEC=∠BDC=60°,∴△AEC≌△CDB(AAS);(2)证明:如图2,在l上位于C点左侧取一点E,使∠AEC=60°,连接AE,由(1)知:△AEC≌△CDB,∴BD=CE,∵∠AEF=∠AFH=60°,∴∠AFE+∠FAE=∠AFE+∠GFH=60°,∴∠FAE=∠GFH,∵∠HGF=∠AEF=120°,AF=FH,∴∠HGF≌△FEA(AAS),∴GH=EF,∴CF=EF+CE=HG+BD;(3)解:HG=CF+BD,理由是:如图3,在l上位于C点右侧取一点E,使∠AED=60°,连接AE,在l上取一点M,使BM=BD,∵∠BDC=60°,∴△BDM是等边三角形,∴∠DBM=60°,∴∠CBM+∠ABM=∠ABM+∠ABD,∴∠ABD=∠CBM,∵∠CAB=∠BDC=60°,∠ANC=∠DNB,∴∠ACE=∠ABD=∠CBM,∵∠ACE+∠BCE=∠ACE+∠CAE=60°,∴∠CAE=∠BCE,∵AC=BC,∴△ACE≌△CBM(ASA),∴CE=BM=BD,∵∠AFH=120°,∴∠AFC+∠GFH=∠AFC+∠FAE=60°,∴∠GFH=∠FAE,∵∠HGF=∠AEF=120°,AF=FH,∴△HGF≌△FEA(AAS),∴GH=FE,∵EF=CF+CE∴HG=CF+BD.故答案为:HG=CF+BD.15.解:(1)如答图1,①在△ACD与△ECD中,,∴△ACD≌△ECD(SAS);②由①知,△ACD≌△ECD,∴AD=DE,∠A=∠DEC,∵∠A=2∠B,∴∠DEC=2∠B,∴∠B=∠EDB,∴BE=DE,∴△BDE是等腰三角形;③由①知,△ACD≌△ECD,则EC=AC=3.6,DE=AD=2.2.又∵BE=DE,∴BE=AD=2.2.∴BC=BE+EC=2.2+3.6=5.8.故答案是:①△ACD≌△ECD;SAS;②等腰;③5.8;(2)∵△ABC中,AB=AC,∠A=20°,∴∠ABC=∠C=80°,∵BD平分∠B,∴∠1=∠2=40°∠BDC=60°,如答图2,在BA边上取点E,使BE=BC=2,连接DE,则△DEB≌△DBC,∴∠BED=∠C=80°,∴∠4=60°,∴∠3=60°,在DA边上取点F,使DF=DB,连接FE,则△BDE≌△FDE,∴∠5=∠1=40°,BE=EF=2,∵∠A=20°,∴∠6=20°,∴AF=EF=2,∵BD=DF=2.3,∴AD=BD+BC=4.3.。
河南省中考数学专题复习专题三几何图形的折叠与动点问题训练

专题三几何图形的折叠与动点问题类型一与特殊图形有关(2018·河南)如图.∠MAN=90°.点C在边AM上.AC=4.点B为边AN上一动点.连接BC.△A′BC与△ABC关于BC所在直线对称.点D.E分别为AC.BC的中点.连接DE并延长交A′B所在直线于点F.连接A′E.当△A′EF为直角三角形时.AB的长为________.【分析】当△A′EF为直角三角形时.存在两种情况:①∠A′EF=90°.②∠A′FE=90°进行讨论.【自主解答】当△A′EF为直角三角形时.存在两种情况:①当∠A′EF=90°时.如解图①.∵△A′BC与△ABC关于BC所在直线对称.∴A′C=AC=4.∠ACB=∠A′CB.∵点D.E分别为AC.BC的中点.∴D、E是△ABC的中位线.∴DE∥AB.∴∠CDE=∠MAN=90°.∴∠CDE=∠A′EF.∴AC∥A′E.∴∠ACB=∠A′EC.∴∠A′CB=∠A′EC.∴A′C=A′E=4.在Rt△A′CB中.∵E是斜边BC的中点.∴BC=2A′E=8.由勾股定理.得AB2=BC2-AC2.∴AB=82-42=43;②当∠A′FE=90°时.如解图②.∵∠ADF=∠A=∠DFB=90°.∴∠ABF=90°.∵△A′BC与△ABC关于BC所在直线对称.∴∠ABC=∠CBA′=45°.∴△ABC是等腰直角三角形.∴AB=AC=4;综上所述.AB的长为43或4.图①图②1.如图.四边形ABCD是菱形.AB=2.∠ABC=30°.点E是射线DA上一动点.把△CDE沿CE折叠.其中点D 的对应点为D′.连接D′B. 若使△D′BC为等边三角形.则DE=________________.2.如图.在Rt△ABC中.∠ACB=90°.AB=5.AC=4.E、F分别为AB、AC上的点.沿直线EF将∠B折叠.使点B恰好落在AC上的D处.当△ADE恰好为直角三角形时.BE的长为______.3.(2017·河南)如图.在Rt△ABC中.∠A=90°.AB=AC.BC=2+1.点M.N分别是边BC.AB上的动点.沿MN所在的直线折叠∠B.使点B的对应点B′始终落在边AC上.若△MB′C为直角三角形.则BM的长为__________.4.(2018·新乡一模)菱形ABCD的边长是4.∠DAB=60°.点M、N分别在边AD、AB上.且MN⊥AC.垂足为P.把△AMN沿MN折叠得到△A′MN.若△A′DC恰为等腰三角形.则AP的长为____________.5.(2017·三门峡一模)如图.在Rt△ABC中.∠ACB=90°.AB=5.AC=3.点D是BC上一动点.连接AD.将△ACD沿AD折叠.点C落在点C′.连接C′D交AB于点E.连接BC′.当△BC′D是直角三角形时.DE的长为______.6.(2018·盘锦)如图.已知Rt△ABC中.∠B=90°.∠A=60°.AC=23+4.点M、N分别在线段AC、AB 上.将△ANM沿直线MN折叠.使点A的对应点D恰好落在线段BC上.当△DCM为直角三角形时.折痕MN的长为__________.7.(2018·乌鲁木齐)如图.在Rt△ABC中.∠C=90°.BC=2 3.AC=2.点D是BC的中点.点E是边AB上一动点.沿DE所在直线把△BDE翻折到△B′DE的位置.B′D交AB于点F.若△AB′F为直角三角形.则AE的长为________.8.(2017·洛阳一模)在菱形ABCD 中.AB =5.AC =8.点P 是对角线AC 上的一个动点.过点P 作EF 垂直AC 交AD 于点E.交AB 于点F.将△AEF 折叠.使点A 落在点A′处.当△A′CD 为等腰三角形时.AP 的长为______.9.(2018·濮阳一模)如图.在Rt△ABC 中.∠C=90°.AC =3.BC =4.点D.E 为AC.BC 上两个动点.若将∠C 沿DE 折叠.点C 的对应点C′恰好落在AB 上.且△ADC′恰好为直角三角形.则此时CD 的长为__________.类型二 点的位置不确定(2016·河南)如图.已知AD∥BC .AB⊥BC .AB =3.点E 为射线BC 上一个动点.连接AE.将△ABE 沿AE折叠.点B 落在点B′处.过点B′作AD 的垂线.分别交AD.BC 于点M.N.当点B′为线段MN 的三等分点时.BE 的长为________.【分析】 根据勾股定理.可得EB′.根据相似三角形的性质.可得EN 的长.根据勾股定理.可得答案.【自主解答】 由翻折的性质.得AB =AB′.BE =B′E.①当MB′=2.B′N=1时.设EN =x.得B′E=x 2+1.由△B′EN~△AB′M .EN B′M =B′E AB′.即x 2=x 2+13.x 2=45.BE =B′E=45+1=355; ②当MB′=1.B′N=2时.设EN =x.得B′E=x 2+22.△B′EN∽△AB′M .EN B′M =B′E AB′.即x 1=x 2+43.解得x 2=12.BE =B′E=12+4=322.故答案为:322或355.1.如图.正方形ABCD 的边长为9.将正方形折叠.使D 点落在BC 边上的点E 处.折痕为GH.若点E 是BC 的三等分点.则线段CH 的长是_______.2.(2018·林州一模)在矩形ABCD中.AB=4.BC=9.点E是AD边上一动点.将边AB沿BE折叠.点A的对应点为A′.若点A′到矩形较长两对边的距离之比为1∶3.则AE的长为__________.3.(2015·河南)如图.矩形ABCD中.AD=5.AB=7.点E为DC上一个动点.把△ADE沿AE折叠.当点D的对应点D′落在∠ABC的平分线上时.DE的长为______.4.(2017·商丘模拟)如图.在矩形ABCD中.AD=5.AB=8.点E为射线DC上一个动点.把△ADE沿直线AE 折叠.当点D的对应点F刚好落在线段AB的垂直平分线上时.则DE的长为__________.5.如图.在矩形ABCD中.BC=6.CD=8.点P是AB上(不含端点A.B)任意一点.把△PBC沿PC折叠.当点B 的对应点B′落在矩形ABCD对角线上时.BP=________.6.(2018·河南模拟)如图.△ABC中.AB= 5.AC=5.tan A=2.D是BC中点.点P是AC上一个动点.将△BPD 沿PD折叠.折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半.则AP的长为____________.7.在矩形ABCD中.AB=6.BC=12.点E在边BC上.且BE=2CE.将矩形沿过点E的直线折叠.点C.D的对应点分别为C′.D′.折痕与边AD交于点 F.当点 B.C′.D′恰好在同一直线上时.AF的长为__________________.类型三根据图形折叠探究最值问题如图.在矩形纸片ABCD中.AB=2.AD=3.点E是AB的中点.点F是AD边上的一个动点.将△AEF沿EF所在直线翻折.得到△A′EF.则A′C的长的最小值是________.【分析】以点E为圆心.AE长度为半径作圆.连接CE.当点A′在线段CE上时.A′C的长取最小值.根据折叠的性质可知A′E=1.在Rt△BCE中利用勾股定理可求出CE的长度.用CE-A′E即可求出结论.例3题解图【自主解答】以点E为圆心.AE长度为半径作圆.连接CE.当点A′在线段CE上时.A′C的长取最小值.如解图所示.根据折叠可知:A′E=AE=12AB=1.在Rt△BCE中.BE=12AB=1.BC=3.∠B=90°.∴CE=BE2+BC2=10.∴A′C的最小值=CE-A′E=10-1.故答案为10-1.1.(2019·原创)如图.在边长为10的等边三角形△ABC中.D是AB边上的动点.E是AC边的中点.将△ADE 沿DE翻折得到△A′DE.连接BA′.则BA′的最小值是__________.2.在矩形ABCD中.AD=12.E是AB边上的点.AE=5.点P在AD边上.将△AEP沿EP折叠.使得点A落在点A′的位置.如图.当A′与点D的距离最短时.△A′PD的面积为________.3.如图.在边长为4的正方形ABCD中.E为AB边的中点.F是BC边上的动点.将△EBF沿EF所在直线折叠得到△EB′F.连接B′D.则当B′D取得最小值时.tan∠BEF的值为__________.4.(2017·河南模拟)如图.在Rt△ABC中.∠ACB=90°.AC=4.BC=6.点D是边BC的中点.点E是边AB上的任意一点(点E不与点B重合).沿DE翻折△DBE使点B落在点F处.连接AF.则线段AF的长取最小值时.BF 的长为_________.参考答案类型一针对训练1.3+1或23-2 【解析】(1)当点E在边AD上时.过点E作EF⊥CD于F.如解图①.设CF=x.第1题解图①∵∠ABC=30°.∴∠BCD=150°.∵△BCD′是等边三角形.∴∠DCD′=90°.由折叠可知.∠ECD=∠D′CE=45°.∵EF=CF=x.在直角三角形DEF中.∠D=30°.∴DE=2x.∴DF=3x.∴CD=CF+DF=x+3x=2.解得x=3x-1.∴DE=2x=23-2.(2)当E在DA的延长线上时.如解图②.第1题解图②过点B作BF⊥DA于点F.根据折叠可知.∠ED′C=∠D=30°.又∵三角形BD′C是等边三角形.∴D′E垂直平分BC.∵AD∥BC.∴D′E⊥AD.∵∠ABC=30°∴∠BAF=30°.又∵AB=2.∴AF= 3.令D′E与BC的交点为G.则易知EF =BG =12BC =1.∴AE=3-1.∴DE=3+1.综上所述.DE 的长度为3+1或23-2. 2.158或157【解析】在Rt△ABC 中.∵∠C=90°.AB =5.AC =4.∴BC=3.沿直线EF 将∠B 折叠.使点B 恰好落在BC 上的D 处.当△ADE 恰好为直角三角形时.根据折叠的性质:BE =DE.设BE =x.则DE =x.AE =5-x.①当∠ADE=90°时.则DE∥BC .∴DE CB =AE AB .∴x 3=5-x 5.解得x =158;②当∠AED=90°时.则△AED∽△ACB .∴DE BC=AE AC .∴x 3=5-x 4.解得x =157.故所求BE 的长度为:158或157. 3.122+12或1 【解析】①如解图①.当∠B′MC=90°.B′与A 重合.M 是BC 的中点.∴BM=12BC =122+12;②如解图②.当∠MB′C=90°.∵∠A=90°.AB =AC.∴∠C=45°.∴△CMB′是等腰直角三角形.∴CM=2MB′.∵沿MN 所在的直线折叠∠B.使点B 的对应点为B′.∴BM=B′M .∴CM=2BM.∵BC=2+1.∴CM +BM =2BM +BM =2+1.∴BM=1.综上所述.若△MB′C 为直角三角形.则BM 的长为122+12或1.图①图②第3题解图 4.433或23-2 【解析】①如解图①.当A′D=A′C 时.∠A′DC=∠A′CD=30°.∴∠AA′D=60°.又∵∠CAD=30°.∴∠ADA′=90°.在Rt△ADA′中.AA′=AD cos 30°=432=833.由折叠可得AP =12AA′=433;图①图②第4题解图②如解图②.当CD =CA′=4时.连接BD 交AC 于O.则Rt△COD 中.CO =CD×cos 30°=4×32=2 3.∴AC =4 3.∴AA′=AC -A′C=43-4.由折叠可得AP =12AA′=23-2;故答案为433或23-2. 5 .32或34【解析】如解图①所示.点E 与点C′重合时.在Rt△ABC 中.BC =AB 2-AC 2=4.由翻折的性质可知;AE =AC =3、DC =DE.则EB =2.设DC =ED =x.则BD =4-x.在Rt△DBE 中.DE 2+BE 2=DB 2.即x 2+22=(4-x)2.解得x =32.∴DE=32.图①图②第5题解图如解图②所示:∠EDB=90°时.由翻折的性质可知:AC =AC′.∠C=∠AC′D=90°.∵∠C=∠AC′D =∠CDC′=90°.∴四边形ACDC′为矩形.又∵AC=AC′.∴四边形ACDC′为正方形.∴CD=AC =3.∴DB=BC -DC =4-3=1.∵DE∥AC .∴△BDE∽△BCA.∴DE AC =DB CB =14.即ED 3=14.解得DE =34.点D 在CB 上运动.∠DBC′<90°.故∠DBC′不可能为直角.故答案为:32或34. 6.23+43或 6 【解析】分两种情况:①如解图①.当∠CDM=90°.△CDM 是直角三角形.∵在Rt△ABC 中.∠B=90°.∠A=60°.AC =23+4.∴∠C=30°.AB =12AC =3+2.由折叠可得.∠MDN=∠A=60°.∴∠BDN=30°.∴BN=12DN =12AN.∴BN=13AB =3+23.∴AN=2BN =233+43.∵∠DNB=60°.∴∠ANM =∠DNM=60°.∴∠ANM=60°.∴AN=MN =23+43.②如解图②.当∠CMD=90°时.△CDM 是直角三角形.由题可得∠CDM=60°.∠A=∠MDN=60°.∴∠BDN=60°.∠BND=30°.∴BD=12DN =12AN.BN =3BD.又∵AB=3+2.∴AN=2.BN = 3.过N 作NH⊥AM 于H.则∠ANH=30°.∴AH=12AN =1.HN = 3.由折叠可得∠AMN=∠DMN=45°.∴△MNH 是等腰直角三角形.∴HM=HN = 3.∴MN= 6.故答案为23+43或 6.图①图②第6题解图7.3或145 【解析】∴∠C=90°.BC =2 3.AC =2.∴tan B=AC BC =223=33.∴∠B=30°.∴AB=2AC =4.∵点D 是BC 的中点.沿DE 所在直线把△BDE 翻折到△B′D′E 的位置.B′D 交AB 于点F.∴DB=DC = 3.EB′=EB.∠DB′E=∠B=30°.设AE =x.则BE =4-x.EB′=4-x.当∠AFB′=90°时.在Rt△BDF 中.cos B =BF BD .∴BF=3cos 30°=32.∴EF=32-(4-x)=x -52.在Rt△B′EF 中.∵∠EB′F=30°.∴EB′=2EF. 则4-x =2(x -52).解得x =3.此时AE 为3;第7题解图当∠FB′A=90°时.作EH⊥AB′于H.连接AD.如解图.∵DC=DB′.AD =AD.∴Rt△ADB′≌Rt△ADC .∴AB′=AC =2.∵∠AB′E=∠AB′F+∠EB′F=90°+30°=120°.∴∠EB′H=60°.在Rt△EHB′中.B′H=12B ′E =12(4-x).EH =3B′H=32(4-x).在Rt△AEH 中.∵EH 2+AH 2=AE 2.∴34(4-x)2+[12(4-x)+2]2=x 2.解得x =145.此时AE 为145.综上所述.AE 的长为3或145. 8.32或3916【解析】∵四边形ABCD 是菱形.∴AB=BC =CD =AD =5.∠DAC=∠BAC.∵EF⊥AA′.∴∠EPA=∠FPA′=90°.∴∠EAP+∠AEP=90°.∠FAP+∠AFP=90°.∴∠AEP=∠AFP .∴AE=AF.∵△A′EF 是由△AEF 翻折.∴AE=EA′.AF =FA′.∴AE=EA′=A′F=FA.∴四边形AEA′F 是菱形.∴AP=PA′.①当CD=CA′时.∵AA′=AC -CA′=3.∴AP =12AA′=32.②当A′C =A′D 时.∵∠A′CD =∠A′DC =∠DAC .∴△A′CD∽△DAC.∴A′C AD =DC AC .∴A′C=258.∴AA′=8-258=398.∴AP=12AA′=3916.故答案为32或3916. 9.127或43【解析】①如解图①.当∠ADC′=90°时.∠ADC′=∠C .第9题解图①∴DC′∥CB .∴△ADC′∽△ACB.又∵AC=3.BC =4.∴AD DC′=34.设CD =C′D=x.则AD =3-x.∴3-x x =34.解得x =127.经检验:x =127是所列方程的解.∴CD=127;②如解图②.当∠DC′A=90°时.∠DCB=90°.第9题解图②由折叠可得.∠C =∠DC′E =90°.∴C′B 与CE 重合.由∠C =∠AC′D =90°.∠A =∠A .可得△ADC′∽△ABC .在Rt △ABC 中.AB =5.∴AD C′D =AB CB =54.设CD =C′D=x.则AD =3-x.∴3-x x =54.解得x =43.∴CD=43.综上所述.CD 的长为127或43. 类型二针对训练1.4或52 【解析】设CH =x.则DH =EH =9-x.当BE∶EC=2∶1时.BC =9.∴CE=13BC =3.在Rt△ECH 中.EH 2=EC 2+CH 2.即(9-x)2=32+x 2.解得x =4.即CH =4.当BE∶EC=1∶2时.CE =23BC =6.在Rt△ECH 中.EH 2=EC 2+CH 2.即(9-x)2=62+x 2.解得:x =52.即CH =52.故CH 的长为4或52. 2.477或4155【解析】如解图.过点A′作A′M⊥AD 于M 交BC 于N.则四边形ABNM 是矩形.∴AB=MN =4.∵若点A′到矩形较长两对边的距离之比为1∶3.∴A′M=1.A′N=3或A′M=3.A′N=1.①当A′M=1.A′N =3时.在Rt△BA′N 中.BN =42-32=7.∴AM =BN =7.由△A′EM~△BA′N .∴EM A′N =A′M BN .∴EM 3=17.∴EM=377.∴AE=477;②当A′M=3.A′N=1时.同理可得AE =4155.,第2题解图)第3题解图3.52或53【解析】如解图.连接BD′.过D′作MN⊥AB .交AB 于点M.CD 于点N.作D′P⊥BC 交BC 于点P.∵点D 的对应点D′落在∠ABC 的平分线上.∴MD′=PD′.设MD′=x.则PD′=BM =x.∴AM=AB -BM =7-x.又由折叠图形可得AD =AD′=5.∴x 2+(7-x)2=25.解得x =3或4.即MD′=3或4.在Rt△END′中.设ED′=a.①当MD′=3时.AM =7-3=4.D′N=5-3=2.EN =4-a.∴a 2=22+(4-a)2.解得a =52.即DE =52;②当MD′=4时.AM =7-4=3.D′N=5-4=1.EN =3-a.∴a 2=12+(3-a)2.解得a =53.即DE =53.综上所述.DE 的长为52或53. 4.52或10 【解析】分两种情况:①如解图①.当点F 在矩形内部时.∵点F 在AB 的垂直平分线MN 上.∴AN =4.∵AF=AD =5.由勾股定理得FN =3.∴FM=2.设DE 为x.则EM =4-x.FE =x.在△EMF 中.由勾股定理.得x 2=(4-x)2+22.∴x=52.即DE 的长为52;图①图②第4题解图②如解图②.当点F 在矩形外部时.同①的方法可得FN =3.∴FM=8.设DE 为y.则EM =y -4.FE =y.在△EMF 中.由勾股定理.得y 2=(y -4)2+82.∴y=10.即DE 的长为10.综上所述.点F 刚好落在线段AB 的垂直平分线上时.DE 的长为52或10. 5.3或92【解析】①点A 落在矩形对角线BD 上.如解图①.∵在矩形ABCD 中.AB =8.BC =6∴∠ABC=90°.AC =BD.∴AC=BD =62+82=10.根据折叠的性质.得PC⊥BB′.∴∠PBD=∠BCP .∴△BCP∽△ABD .∴BP AD =BC AB.即BP 6=68.解得BP =92;②点A 落在矩形对角线AC 上.如解图②.根据折叠的性质.得BP =B′P .∠B=∠PB′C =90°.∴∠AB′A=90°.∴△APB′∽△ACB .∴B′P BC =AP AC .即BP 6=8-BP 10.解得BP =3.故答案为:3或92.图①图②第5题解图6.2或5- 5 【解析】分两种情况:①当点B′在AC 的下方时.如解图①.∵D 是BC 中点.∴S △BPD =S △PDC .∵S △PDF =12S △BPD .∴S △PDF =12S △PDC .∴F 是PC 的中点.∴DF 是△BPC 的中位线.∴DF∥BP .∴∠BPD=∠PDF .由折叠得:∠BPD=∠B′PD .∴∠B′PD=∠PDF .∴PB′=B′D .即PB =BD.过B 作BE⊥AC 于E.在Rt△ABE中.tan A =BE AE=2.∵AB= 5.∴AE=1.BE =2.∴EC=5-1=4.由勾股定理.得BC =BE 2+EC 2=22+42=2 5.∵D 为BC 的中点.∴BD= 5.∴PB=BD = 5.在Rt△BPE 中.PE =1.∴AP=AE +PE =1+1=2;图①图②第6题解图②当点B′在AC 的上方时.如解图②.连接B′C .同理得:F 是DC 的中点.F 是PB′的中点.∴DF=FC.PF =FB′.∴四边形DPCB′是平行四边形.∴PC=B′D=BD= 5.∴AP=5- 5.综上所述.AP的长为2或5-5.7.8+23或8-2 3 【解析】由折叠的性质得.∠EC′D′=∠C=90°.C′E=CE.∵点B、C′、D′在同一直线上.∴∠BC′E=90°.∵BC=12.BE=2CE.∴BE=8.C′E=CE=4.在Rt△BC′E中.BE C′E=2.∴∠C′BE=30°.①当点C′在BC的上方时.如解图①.过E作EG⊥AD于G.延长EC′交AD于H.则四边形ABEG是矩形.∴EG=AB=6.AG=BE=8.∵∠C′BE=30°.∠BC′E=90°.∴∠BEC′=60°.由折叠的性质得.∠C′EF=∠CEF=60°.∵AD∥BC.∴∠HFE=∠CEF=60°.∴△EFH是等边三角形.∴在Rt△EFG 中.EG=6.∴GF=23.∴AF=8+23;②当点C′在BC的下方时.如解图②.过F作FG⊥AD于G.D′F交BE于H.同①可得.四边形ABGF是矩形.△EFH是等边三角形.∴AF=BG.FG=AB=6.∠FEH=60°.在Rt△EFG 中.GE=23.∵BE=8.∴BG=8-2 3.∴AF=8-2 3.图①图②第7题解图类型三针对训练1.53-5 【解析】如解图.连接BE.第1题解图∵AB=BC=AC=10.∴∠C=60°.∵AB=BC.E是AC的中点.∴BE⊥AC.∴BE=BC2-EC2=102-52=53.∵AC=10.E是AC边的中点.∴AE=5.由翻折的性质可知A′E=AE=5.∵BA′+A′E≥BE.∴当点B、A′、E在一条直线上时.BA′有最小值.最小值=BE-A′E=53-5.2.403【解析】连接DE.DE=52+122=13.∵将△AEP沿FP折叠.使得点A落在点A′的位置.∴EA′=EA=5.∵A′D≥DE-EA′第2题解图(当且仅当A′点在DE 上时.取等号).∴当A′与点D 的距离最短时.A′点在DE 上.∴DA′=13-5=8.设PA′=x.则PA =x.PD =12-x.在Rt△DPA′中.x 2+82=(12-x)2.解得x =103.∴△A′PD 的面积=12×8×103=403. 3.1+52【解析】在Rt△ADE 中.DE =22+42=2 5.当B′在ED 上时.B′D 最小.在ED 上截取EB′=EB =2.连接B′F .FD.则B′D=ED -EB′=25-2.设BF =x.则B′F=x.CF =4-x.在Rt△B′FD 和Rt△FCD 中.利用勾股定理.可得DB′2+B′F 2=DF 2=CF 2+DC 2.即(25-2)2+x 2=(4-x)2+42.解得x =5+1.∴Rt△BEF 中.tan∠BEF=BF BE =1+52.第3题解图4.1255【解析】由题意得:DF =DB.第4题解图∴点F 在以D 为圆心.BD 为半径的圆上.作⊙D; 连接AD 交⊙D 于点F.此时AF 值最小.∵点D 是边BC 的中点.∴CD=BD =3;而AC =4.由勾股定理得:AD 2=AC 2+CD 2.∴AD=5.而FD =3.∴FA=5-3=2.即线段AF长的最小值是2.连接BF.过F 作FH⊥BC 于H.∵∠ACB=90°.∴FH∥AC .∴△DFH∽△DAC .∴DF AD =DH CD =HF AC.即35=DH 3=HF 4.∴HF=125.DH =95.∴BH=245.∴BF=BH 2+HF 2=1255.。
2021重庆中考复习数学几何最值问题专题训练三(含答案)
2021年重庆中考复习最值问题专题训练三1、如图,在▱ABCD中,AB=2,AB AC,∠D=60°,点P、Q分别是AC和BC上的动点,在点P和点Q运动的过程中,PB+PQ的最小值为2、如图,在正方形ABCD中,AB=6,E是BC边的中点,F是CD边上的一点,且DF=2,若M、N分别是线段AD、AE上的动点,则MN+MF的最小值为 .3、如图,在正方形ABCD中,动点E、F分别从D、C两点同时出发,以相同的速度在直线DC、CB上移动,连接AE和DF交于P,若AD=6,则线段CP的最小值为.4、如图,矩形ABCD中,AB=4,AD=6,点E,F分别是AB,BC边上的两动点,且EF=2,点G为EF的中点,点H为AD边上一动点,连接CH,GH,则GH+CH的最小值为5、如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=5,AC =,CB的反向延长线上有一动点D,以AD为边在右侧作等边三角形,连CE,CE最短为.6、如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),则四边形AEPQ的周长的最小值是 .7、如图,正方形ABCD中,AB=2,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF,OF.则线段OF长的最小值.8、如图,矩形ABCD中,AB=5,AD=10,点E,F,G,H分别在矩形各边上,点F,H为不动点,点E,G为动点,若要使得AF=CH,BE=DG,则四边形EFGH周长的最小值为9、如图,△ABC中,∠A=45°,∠ABC=60°,AB=3+,点D是边AB上任意一点,以CD 为边在AD的右侧作等边△DCE,连接BE,则△BDE面积的最大值为.10、如图,菱形ABCD的边长为3,∠BAD=60°,点E、F在对角线AC上(点E在点F的左侧),且EF=1,则DE+BF最小值为11、如图,正方形ABCD边长为3,点E、F是对角线AC上的两个动点(点E在点F的左侧),且EF=1,则DE+BF的最小值是 .12、如图,正方形ABCD的边长为3,E、F是对角线BD上的两个动点,且EF =,连接AE、AF,则AE+AF的最小值为13、如图,已知正方形ABCD的边长为6,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点P是AB边上一动点,连接PD,PE,则PD+PE的长度最小值为 .14、如图,Rt△ABC中.∠BAC=90°,AB=1,AC=2.点D,E分别是边BC,AC上的动点,则DA+DE的最小值为15、如图,M、N是正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为6,则线段CF的最小值是 .16、如图,菱形ABCD的边长为4,∠B=120°,E是BC的中点,F是对角线AC上的动点,连结EF,将线段EF绕点F按逆时针旋转30°,G为点E对应点,连结CG,则CG的最小值为 .2021年重庆中考复习最值问题专题训练三1、如图,在▱ABCD中,AB=2,AB AC⊥,∠D=60°,点P、Q分别是AC和BC上的动点,在点P和点Q运动的过程中,PB+PQ的最小值为B解:作点B关于AC的对称点F,连接CF,作FQ BC⊥交AC于点P,则FQ的长即为PB+PQ的最小值(垂线段最短),易知△BCF是等边三角形,∴BP+PQ的最小值为2.2、如图,在正方形ABCD中,AB=6,E是BC边的中点,F是CD边上的一点,且DF=2,若M、N分别是线段AD、AE上的动点,则MN+MF的最小值为 .解:作点F关于AD的对称点G,过G作GN⊥AE与N,交AD于M,则GN的长度等于MN+MF的最小值,∵△DGM≌△DGF,∴∠DMF=∠GMD,∵∠GMD=∠AMN,∠AMN+∠MAN=∠MAN+∠BAE=90°,∴∠FMD=∠BAE=∠AMN,∴△ABE∽△DMF∽△AMN,∴,∵AB=6,∴BE=3,∵DF=2,∴DM=4,∴AM=2,∵,∴MN=,∵GM=2,∴GN =GM+MN=MN+MF=+2=.∴MN+MF的最小值为.3、如图,在正方形ABCD中,动点E、F分别从D、C两点同时出发,以相同的速度在直线DC、CB上移动,连接AE和DF交于P,若AD=6,则线段CP的最小值为.解:由题意得:AD=CD,DE=FC,∠ADC=∠DCF=90°,∴△DCF≌△ADE(SAS),∴∠DAE=∠FDC,∴∠APD=90°,即:相当于点P始终在以AD为直径的圆上,取AD的中点Q,当Q、P、C三点共线时,PC最小,PC=CQ﹣PQ=﹣3=3﹣3.4、如图,矩形ABCD中,AB=4,AD=6,点E,F分别是AB,BC边上的两动点,且EF=2,点G为EF的中点,点H为AD边上一动点,连接CH,GH,则GH+CH的最小值为解:由已知,点G在以B圆心,1为半径的圆在与长方形重合的弧上运动.作C关于AD的对称点C′,连接C ′B,交AD于H,交以D为圆心,以1为半径的圆于G由两点之间线段最短,此时C′B的值最小为,则GH+CH的最小值C′G=10﹣1=9.5、如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=5,AC=,CB的反向延长线上有一动点D,以AD为边在右侧作等边三角形,连CE,CE最短为.解:在AC的右侧作等边△ACF,连接EF,则AC=AF=CF=AC=5,∠CAF=∠AFC═60°,∵△ADE是等边三角形,∴AD=AE,∠DAE=60°=∠CAF,∴∠CAD=∠FAE,在△DAC和△EAF 中,,∴△DAC≌△EAF(SAS),∴∠ACD=∠AFE ∵∠ACB=90°,∴∠ACD=90°,∴∠AFE=90°,∴∠CFE=90°﹣60°=30°,当CE⊥EF时,CE有最小值,∴CE的最小值=CF =.6、如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),则四边形AEPQ的周长的最小值是 .解:如图所示,作E关于BC的对称点E′,点A关于DC的对称点A′,连接A′E′,四边形AEPQ的周长最小,∵AD=A′D=3,BE=BE′=1,∴AA′=6,AE′=4.∴A′E′==2,∴四边形AEPQ的周长最小值=2+2.7、如图,正方形ABCD中,AB=2,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF,OF.则线段OF长的最小值.解:如图,连接DO,将线段DO绕点D逆时针旋转90°得DM,连接OF,FM,OM,∵∠EDF=∠ODM=90°,∴∠EDO=∠FDM,∵DE=DF,DO=DM,∴△EDO≌△FDM (SAS),∴FM=OE=2,∵正方形ABCD中,AB=2,O是BC边的中点,∴OC =,∴OD =,∴OM=,∵OF+MF≥OM,∴OF ≥.故选:D.8、如图,矩形ABCD中,AB=5,AD=10,点E,F,G,H分别在矩形各边上,点F,H为不动点,点E,G为动点,若要使得AF=CH,BE=DG,则四边形EFGH周长的最小值为解:作点F关于CD的对称点F′,连接F′H交CD于点G,此时四边形EFGH周长取最小值,过点H作HH′⊥AD于点H′,如图所示.∵AF=CH,DF=DF′,∴H′F′=AD=10,∵HH′=AB=5,∴F′H ==5,∴C四边形EFGH=2F′H=10.9、如图,△ABC中,∠A=45°,∠ABC=60°,AB=3+,点D是边AB上任意一点,以CD 为边在AD的右侧作等边△DCE,连接BE,则△BDE面积的最大值为.解:作CM⊥AB于M,作EN⊥AB于N,如图所示:∵∠A=45°,∠ABC=60°,∴△ACM是等腰直角三角形,∠BCM=30°,∴AM=CM,CM =BM,设BM=x,则AM=CM =x,∴AB=x +x=3+,解得:x =,∴BM =,CM=AM=3,设AD=y,则DM=3﹣y,BD=3+﹣y,∵△CDE是等边三角形,∴∠DCE=60°CD=CE,∴∠DCM+∠BCE=30°=∠BCM,在MB上截取MH=MD=3﹣y,连接CH,则CD=CH=CE,∵CM⊥DH,∴∠DCM=∠HCM,∴∠BCH=∠BCE,在△BCH和△BCE 中,,∴△BCH≌△BCE(SAS),∴∠CBH=∠CBE=60°,BH=BE=3+﹣y﹣2(3﹣y)=y +﹣3,∴∠EBN=60°,∵EN⊥AB,∴∠BEN=30°,∴BN=BE,EN=BN=BE =(y +﹣3),∵△BDE的面积=BD×EN=×(3+﹣y )×(y +﹣3)=(﹣y2+6y﹣6)=﹣(y﹣3)2+,∴当y=3,即AD=3时,△BDE面积的最大值为.10、(2019•蓝田县一模)如图,菱形ABCD的边长为3,∠BAD=60°,点E、F在对角线AC上(点E在点F的左侧),且EF=1,则DE+BF最小值为解:如图,作DM∥AC,使得DM=EF=1,连接BM交AC于F,∵DM=EF,DM∥EF,∴四边形DEFM是平行四边形,∴DE=FM,∴DE+BF=FM+FB=BM,根据两点之间线段最短可知,此时DE+FB最短,∵四边形ABCD是菱形,AB=3,∠BAD=60°∴AD=AB,∴△ABD是等边三角形,∴BD=AB=3,在Rt△BDM中,BM ==,∴DE+BF的最小值为.11、(2019春•仪征市期中)如图,正方形ABCD边长为3,点E、F是对角线AC上的两个动点(点E在点F的左侧),且EF=1,则DE+BF的最小值是.解:如图,作DM∥AC,使得DM=EF=1,连接BM交AC于F,∵DM=EF,DM∥EF,∴四边形DEFM是平行四边形,∴DE=FM,∴DE+BF=FM+FB=BM,根据两点之间线段最短可知,此时DE+FB最短,∵四边形ABCD是正方形,AB=3,∠BAD=90°∴AD=AB,∴△ABD是等腰直角三角形,∴BD=AB=3,在Rt△BDM 中,BM ==,∴DE+BF的最小值为.12、(2019春•梁溪区期末)如图,正方形ABCD的边长为3,E、F是对角线BD上的两个动点,且EF=,连接AE、AF,则AE+AF的最小值为( )A.2B.3C.D .解:如图作AH∥BD,使得AH=EF =,连接CH交BD于F,则AE+AF的值最小.∵AH=EF,AH∥EF,∴四边形EFHA是平行四边形,∴EA=FH,∵F A=FC,∴AE+AF=FH+CF=CH,∵四边形ABCD是正方形,∴AC⊥BD,∵AH∥DB,∴AC⊥AH,∴∠CAH=90°,在Rt△CAH中,CH ==2,∴AE+AF的最小值2,故选:A13、如图,已知正方形ABCD的边长为6,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点P是AB边上一动点,连接PD,PE,则PD+PE的长度最小值为 .解:∵四边形ABCD是正方形,∴∠ABC=90°,∴∠ABE+∠CBE=90°,∵∠ABE=∠BCE,∴∠BCE+∠CBE=90°,∴∠BEC=90°,∴点E在以BC为直径的半圆上移动,如图,设BC的中点为O,作正方形ABCD关于直线AB对称的正方形AFGB,则点D的对应点是F,连接FO交AB于P,交半圆O于E,则线段EF的长即为PD+PE的长度最小值,∵∠G=90°,FG=BG=AB=6,∴OG=9,∴OF==3,∴EF=3﹣3,故PD+PE的长度最小值为3﹣3,14、如图,Rt△ABC中.∠BAC=90°,AB=1,AC=2.点D,E分别是边BC,AC上的动点,则DA+DE的最小值为解:作A关于BC的对称点A',连接AA',交BC于F,过A'作A'E⊥AC于E,交BC于D,则AD=A'D,此时AD+DE的值最小,就是A'E的长;Rt△ABC中,∠BAC=90°,AB=1,AC =2,∴BC=,S△ABC =AB•AC =BC•AF,∴1×2=3AF,AF=,∴AA'=2AF=,∵∠A'FD=∠DEC=90°,∠A'DF=∠CDE,∴∠A'=∠C,∵∠AEA'=∠BAC=90°,∴△AEA'∽△BAC ,∴,∴,∴A'E =,即AD+DE 的最小值是;故选:B.15、如图,M、N是正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为6,则线段CF的最小值是 .解:如图,在正方形ABCD中,AD=BC=CD,∠ADC=∠BCD,∠DCE=∠BCE,在Rt△ADM和Rt△BCN中,,∴Rt△ADM≌Rt△BCN(HL),∴∠DAM=∠CBN,在△DCE和△BCE 中,,∴△DCE≌△BCE(SAS),∴∠CDE=∠CBE ∴∠DAM=∠CDE,∵∠ADF+∠CDE=∠ADC=90°,∴∠DAM+∠ADF=90°,∴∠AFD=180°﹣90°=90°,取AD的中点O,连接OF、OC,则OF=DO =AD=3,在Rt△ODC中,OC ==3根据三角形的三边关系,OF+CF>OC,∴当O、F、C三点共线时,CF的长度最小,最小值=OC﹣OF=3﹣3.16、如图,菱形ABCD的边长为4,∠B=120°,E是BC的中点,F是对角线AC上的动点,连结EF,将线段EF绕点F按逆时针旋转30°,G为点E对应点,连结CG,则CG的最小值为.解:如图取CD的中点K,连接FK,KG,EK,延长KG交BC于J,作CH⊥JK于H.∵四边形ABCD是菱形,∴∠FCE=∠FCK,CE=CK,AB∥CD,∴∠DCB+∠B=180°,∵∠B=120°,∴∠DCB=60°,∵BE=EC,CK=KD,∴CK=CE,∴△ECK是等边三角形,∵CF=CF,∠FCK=∠FCE,CK=CE,∴△FCK≌△FCE(SAS),∴FK=FE,∵FG=FE,∴FE=FG=FK,∴∠EKG=∠EFG=15°,∵∠CKE=60°,∴∠CKJ=45°,∴点G在直线KJ上运动,根据垂线段最短可知,当点G 与H重合时,CG的值最小,在Rt△CKH中,∵∠CKH=45°,∠CHK=90°,CK=CD=2,∴CH=KH=,∴CG的最小值为.。
2020重庆中考复习数学几何最值专题训练三(含答案解析)
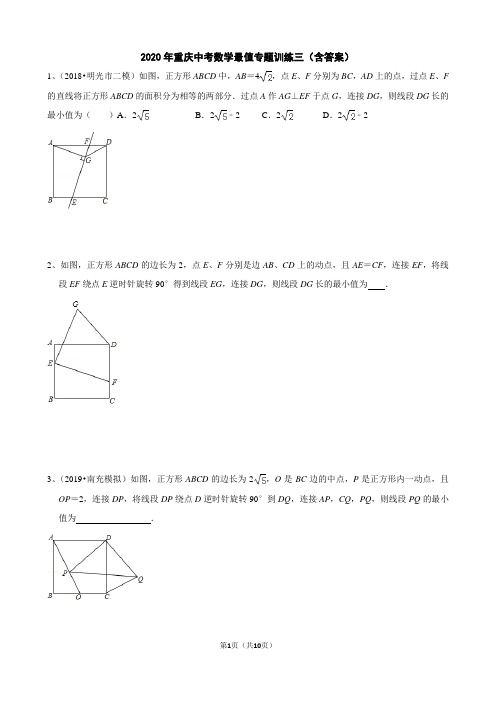
2020年重庆中考数学最值专题训练三(含答案)1、(2018•明光市二模)如图,正方形ABCD中,AB=4,点E、F分别为BC,AD上的点,过点E、F 的直线将正方形ABCD的面积分为相等的两部分.过点A作AG⊥EF于点G,连接DG,则线段DG长的最小值为()A.2B.2﹣2C.2D.2﹣22、如图,正方形ABCD的边长为2,点E、F分别是边AB、CD上的动点,且AE=CF,连接EF,将线段EF绕点E逆时针旋转90°得到线段EG,连接DG,则线段DG长的最小值为.3、(2019•南充模拟)如图,正方形ABCD的边长为2,O是BC边的中点,P是正方形内一动点,且OP=2,连接DP,将线段DP绕点D逆时针旋转90°到DQ,连接AP,CQ,PQ,则线段PQ的最小值为.4、如图,平行四边形ABCD中,∠B=60°,BC=12,AB=10,点E在AD上,且AE=4,点F是AB上一点,连接EF,将线段EF绕点E逆时针旋转120°得到EG,连接GD,则线段GD长度的最小值为.5、(2019•惠山区一模)如图,正方形ABCD中,AB=2,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF,OF.则线段OF长的最小值()A.2B.+2C.2﹣2 D.56、如图,在边长为2的正方形ABCD中,点O为AB中点,以AB为直径在正方形ABCD内部作半圆,E为半圆上任意一点(不与A.B重合),连接CE,将线段CE绕点C逆时针旋转90°得列CF,连接DE、BF,OF.则线段OF长的最小值为.7、(2019秋•颍州区校级月考)如图,正方形ABCD的边长为5,O是AB边的中点,点E是正方形内一动点,OE=2,将线段CE绕C点逆时针旋转90°得CF,连OF,线段OF的最小值为.8、(2019•太原二模)如图,在Rt△ABC中,∠ABC=90°,∠BAC=30°,BC=2,点D是AC边的中点,E是直线BC上一动点,将线段DE绕点D逆时针旋转90°得到线段DF,连接AF、EF,在点E的运动过程中线段AF的最小值为.9、(2019秋•锡山区期中)已知:如图,△ABC是边长为6的等边三角形,直线AF⊥BC于F,点D是直线AF上一动点,以BD为边在BD的右侧作等边△BDE,连接EF,则EF的最小值为.10、(2019•台州模拟)如图,四边形ABCD是矩形,AB=4,BC=a(a>1),E是BC上的一点,且BE=1,点F是边AB上的任意一点.连接EF,将线段EF绕点E顺时针旋转90°,得到线段EG.在点F从点B运动到点A的过程中,若要点G能落在对角线AC上,则a的最大值为.11、如图1,四边形ABCD是矩形,AB=2,BC=4,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE、BG,则2BG+BE的最小值为.2020年重庆中考数学最值专题训练三(含答案)1、(2018•明光市二模)如图,正方形ABCD中,AB=4,点E、F分别为BC,AD上的点,过点E、F 的直线将正方形ABCD的面积分为相等的两部分.过点A作AG⊥EF于点G,连接DG,则线段DG长的最小值为()A.2B.2﹣2C.2D.2﹣2解:连接AC,BD交于O,∵过点E、F的直线将正方形ABCD的面积分为相等的两部分,∴EF过点O,∵AG⊥EF,∴∠AGO=90°,∴点G在以AO为直径的半圆弧上,设AO的中点为M,连接DM交半圆弧于G,则此时,DG最小,∵四边形ABCD是正方形,AB=4,∴AC=8,AC⊥BD,∴AO=OD=AC=4,∴AM=OM=AO=2,∴DM==2,∴DG=2﹣2,故选:B.2、如图,正方形ABCD的边长为2,点E、F分别是边AB、CD上的动点,且AE=CF,连接EF,将线段EF绕点E逆时针旋转90°得到线段EG,连接DG,则线段DG长的最小值为.解:如图,过点F作FM⊥AB于M,过点G作GH⊥AD于H,GN⊥AB于N,∵四边形ABCD是正方形,∴AB=BC=AD=CD=2,∠B=∠C=∠BAD=90°,且FM⊥AB,GH⊥AD,GN⊥AB,∴四边形BCFM,四边形AHGN是矩形,∴BM=CF,NG=AH,AN=GH,MF=BC=2,∵将线段EF绕点E逆时针旋转90°得到线段EG,∴EG=EF,∠GEF=90°,∴∠NEG+∠FEM=90°,且∠NGE+∠NEG=90°,∴∠FEM=∠NGE,且∠N=∠FME=90°,EF=EG,∴△EGN≌△EFM(AAS)∴NE=MF=2,EM=NG,设AE=CF=a,∴EM=2﹣2a=NG=AH,AN=2﹣a=GH,∴HD=AD﹣AH=2﹣(2﹣2a)=2a,∵GD==∴当a=时,GD有最小值为,3、(2019•南充模拟)如图,正方形ABCD的边长为2,O是BC边的中点,P是正方形内一动点,且OP=2,连接DP,将线段DP绕点D逆时针旋转90°到DQ,连接AP,CQ,PQ,则线段PQ的最小值为.解:连接OD,如图所示:∵DQ=DP,∠PDQ=90°,∴PQ=DP,OD===5,∵OP+DP≥OD,∴DP≥OD﹣OP=5﹣2=3,∴PQ≥3,∴线段PQ的最小值为3.4、如图,平行四边形ABCD中,∠B=60°,BC=12,AB=10,点E在AD上,且AE=4,点F是AB上一点,连接EF,将线段EF绕点E逆时针旋转120°得到EG,连接GD,则线段GD长度的最小值为2.解:将线段AE绕点E逆时针旋转120°得到EH,连接HG,过点H作HM⊥AD,∵四边形ABCD是平行四边形,∴∠A+∠B=180°,∴∠A=120°,∵将线段AE绕点E逆时针旋转120°得到EH,将线段EF绕点E逆时针旋转120°得到EG,∴EF=EG=4,AE=EH,∠AEH=∠FEG=120°,∴∠DEH=60°,∠AEF=∠HEG,且EF=EG,AE=EH,∴△AEF≌△HEG(SAS)∴∠A=∠EHG=120°=∠AEH,∴AD∥HG,∴点G的轨迹是过点H且平行于AD的直线,∴当DG⊥HG时,线段GD长度有最小值,∵∠HEM=60°,EH=4,HM⊥AD,∴EM=2,MH=EM=2,∴线段GD长度的最小值为2,5、(2019•惠山区一模)如图,正方形ABCD中,AB=2,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF,OF.则线段OF长的最小值()A.2B.+2C.2﹣2 D.5解法一:如图,连接DO,将线段DO绕点D逆时针旋转90°得DM,连接OF,FM,OM,∵∠EDF=∠ODM=90°,∴∠EDO=∠FDM,∵DE=DF,DO=DM,∴△EDO≌△FDM(SAS),∴FM=OE=2,∵正方形ABCD中,AB=2,O是BC边的中点,∴OC=,∴OD=,∴OM=,∵OF+MF≥OM,∴OF≥.故选:D.解法二:如图,由于OE=2,所以E点可以看作是以O为圆心,2为半径的半圆上运动,延长BA到P 点,使得AP=OC,连接PE,∵AE=CF,∠P AE=∠OCF,∴△P AE≌△OCF,∴PE=OF,当O、E、P三点共线时,PE最小,OP===5,∴PE=OF=OP﹣OE=5﹣2,∴OF的最小值是5﹣2.6、如图,在边长为2的正方形ABCD中,点O为AB中点,以AB为直径在正方形ABCD内部作半圆,E为半圆上任意一点(不与A.B重合),连接CE,将线段CE绕点C逆时针旋转90°得列CF,连接DE、BF,OF.则线段OF长的最小值为.解:由于OE=2,所以E点可以看作是以O为圆心,2为半径的半圆上运动,延长BA到P点,使得AP=OC,连接PE,∵AE=CF,∠P AE=∠OCF,∴△P AE≌△OCF(SAS),∴PE=OF,当PE最小时,为O、E、P三点共线,OP===5,∴PE=OF=OP﹣OE=5﹣2,∴OF的最小值是5﹣2.7、(2019秋•颍州区校级月考)如图,正方形ABCD的边长为5,O是AB边的中点,点E是正方形内一动点,OE=2,将线段CE绕C点逆时针旋转90°得CF,连OF,线段OF的最小值为.解:如图,连接CO,将线段CO绕点C逆时针旋转90°得CM,连接FM,OM,则∠ECF=∠OCM=90°,∴∠ECO=∠FCM,∵CE=CF,CO=CM,∴△ECO≌△FCM(SAS),∴FM=OE=2,∵正方形ABCD中,AB=5,O是AB边的中点,∴OB=2.5,∴OC==,∴OM=OC=,∵OF+MF≥OM,∴OF≥﹣2.∴线段OF的最小值为﹣2.8、(2019•太原二模)如图,在Rt△ABC中,∠ABC=90°,∠BAC=30°,BC=2,点D是AC边的中点,E是直线BC上一动点,将线段DE绕点D逆时针旋转90°得到线段DF,连接AF、EF,在点E的运动过程中线段AF的最小值为+1.解:如图,作DM⊥BC于M,FJ⊥DM于J交AB于N.∵Rt△ABC中,∠ABC=90°,∠BAC=30°,BC=2,∴AC=2BC=4,AB=BC=2,∵AD=DC.DM∥AB,∴DM=AB=,BM=CM=1,易证四边形BMJN是矩形,∴JN=BM=1,∵∠FDJ+∠EDM=90°,∠EDM+∠DEM=90°,∴∠FDJ=∠DEM,∵∠FJD=∠DME=90°,∴△FJD≌△DME(AAS),∴FJ=DM=,∴FN=FJ+JN=1+,∴点F在直线l上运动(直线l与直线AB之间的距离为+1),根据垂线段最短可知,当AF⊥直线l时,AF的值最短,最小值为+1,9、(2019秋•锡山区期中)已知:如图,△ABC是边长为6的等边三角形,直线AF⊥BC于F,点D是直线AF上一动点,以BD为边在BD的右侧作等边△BDE,连接EF,则EF的最小值为.解:如图,取AB中点H,连接DH,∵△ABC,△BDE都是等边三角形,∴AB=BC,BD=BE,∠DBE=∠ABC=60°,∴∠ABD=∠EBC,∵△ABC是等边三角形,AF⊥BC,∴BF=BC=AB=3,∠BAF=30°,∵H是AB中点,∴AH=BH=AB=BF=3,且∠ABD=∠EBC,BD=BE,∴△BHD≌△BFE(SAS)∴EF=DH,∴当DH取最小值时,EF有最小值,当DH⊥AF时,DH有最小值,∴DH=AH=,∴EF的最小值为,10、(2019•台州模拟)如图,四边形ABCD是矩形,AB=4,BC=a(a>1),E是BC上的一点,且BE=1,点F是边AB上的任意一点.连接EF,将线段EF绕点E顺时针旋转90°,得到线段EG.在点F从点B运动到点A的过程中,若要点G能落在对角线AC上,则a的最大值为.解:如图,当点G落在对角线AC上,过点G作GH⊥BC于点H,∵△EFB≌△GEH,∴GH=BE=1,EH=BF,∴CH=BC﹣BE﹣EH=a﹣1﹣BF,∵△CHG∽△CBA,∴,∴,∴BF=∵点F是边AB上的任意一点,∴0≤BF≤AB,∴0≤≤4,∴≤a≤∴a的最大值为11、如图1,四边形ABCD是矩形,AB=2,BC=4,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE、BG,则2BG+BE的最小值为4.解:延长BE、GD相交于点H.∵矩形ECGF、矩形ABCD,∴∠ECG=∠BCD=90°,∴∠DCG=∠BCE∵CD:CB=2:4=1:2,CG:CE=1:2,∴CD:CB=CG:CE,∵∠DCG=∠BCE∴△DCG∽△BCE,∴,∠BEC=∠DGC,∴DG=BE作EN⊥BC于N,GM⊥BC交BC的延长线于M.易证△ECN∽△CGM,∴==2,∵EN=AB=2,∴CM=1,∴点G的运动轨迹是直线MG,作点D关于直线GM的对称点G′,连接BG′交GM于G,此时BG+GD的值最小,最小值=BG′∵DG=BE,∴BE=2DG,∴2BG+BE=2BG+2DG=2(BG+DG)∴2BG+BE的最小值就是2(BG+DG)的最小值.∵BG′==2,∴2BG+BE的最小值为4。
中考数学专题训练-尺规作图 (3)(原卷版)

中考数学专题训练-尺规作图 (3)1.尺规作图的定义:只用不带刻度的直尺和圆规通过有限次操作,完成画图的一种作图方法.尺规作图可以要求写作图步骤,也可以要求不一定要写作图步骤,但必须保留作图痕迹。
2.尺规作图的五种基本情况 (1)作一条线段等于已知线段; (2)作一个角等于已知角; (3)作已知线段的垂直平分线; (4)作已知角的角平分线; (5)过一点作已知直线的垂线。
3.对尺规作图题解法写出已知,求作,作法(不要求写出证明过程)并能给出合情推理。
4.中考要求(1)能完成以下基本作图:作一条线段等于已知线段,作一个角等于已知角,作角的平分线,作线段的垂直平分线.(2)能利用基本作图作三角形:已知三边作三角形;已知两边及其夹角作三角形;已知两角及其夹边作三角形;已知底边及底边上的高作等腰三角形. (3)能过一点、两点和不在同一直线上的三点作圆.(4)了解尺规作图的步骤,对于尺规作图题,会写已知、求作和作法(不要求证明).【例题1】 如图,已知线段AB ,分别以A ,B 为圆心,大于12AB 同样长为半径画弧,两弧交于点C ,D ,连接AC ,AD ,BC ,BD ,CD ,则下列说法错误的是( )A .AB 平分∠CADB .CD 平分∠ACBC .AB ⊥CDD .AB =CD【对点练习】 如图,小红在作线段AB 的垂直平分线时,是这样操作的:分别以点A ,B 为圆心,大于线段AB 长度一半的长为半径画弧,相交于点C ,D ,则直线CD 即为所求.连结AC ,BC ,AD ,BD ,根据她的作图方法可知,四边形ADBC 一定是( )A.矩形B.菱形C.正方形D.等腰梯形【例题2】 如图,在Rt △ABC 中,∠ACB =90°,AC =2BC ,分别以点A 和B 为圆心,以大于12AB 的长为半径作弧,两弧相交于点M 和N ,作直线MN ,交AC 于点E ,连接BE ,若CE =3,则BE 的长为 . 【对点练习】 如图,BD 是矩形ABCD 的对角线,在BA 和BD 上分别截取BE ,BF ,使BE =BF ;分别以E ,F 为圆心,以大于EF 的长为半径作弧,两弧在∠ABD 内交于点G ,作射线BG 交AD 于点P ,若AP =3,则点P 到BD 的距离为 .【例题3】如图,在△ABC中,D是BC边上一点,且BD=BA.(1)尺规作图(保留作图痕迹,不写作法):①作∠ABC的角平分线交AD于点E;②作线段DC的垂直平分线交DC于点F.(2)连接EF,直接写出线段EF和AC的数量关系及位置关系.【对点练习】如图,点D在△ABC的AB边上,且∠ACD=∠A.(1)作∠BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);(2)在(1)的条件下,判断直线DE与直线AC的位置关系(不要求证明).一、选择题1.如图1,已知∠ABC,用尺规作它的角平分线.如图2,步骤如下,第一步:以B为圆心,以a为半径画弧,分别交射线BA,BC于点D,E;第二步:分别以D ,E 为圆心,以b 为半径画弧,两弧在∠ABC 内部交于点P ; 第三步:画射线BP .射线BP 即为所求. 下列正确的是( )A .a ,b 均无限制B .a >0,b >12DE 的长 C .a 有最小限制,b 无限制D .a ≥0,b <12DE 的长2. 如图,Rt △ABC 中,∠ABC =90°,根据尺规作图的痕迹判断以下结论错误的是( )A .DB =DEB .AB =AEC .∠EDC =∠BACD .∠DAC =∠C3. 如图,Rt △ABC 中,∠C =90°,利用尺规在BC ,BA 上分别截取BE ,BD ,使BE =BD ;分别以D ,E 为圆心、以大于12DE 的长为半径作弧,两弧在∠CBA 内交于点F ;作射线BF 交AC 于点G .若CG =1,P 为AB 上一动点,则GP 的最小值为( )A .无法确定B .12C .1D .24. 如图,已知△ABC (AC <BC ),用尺规在BC 上确定一点P ,使PA+PC=BC ,则符合要求的作图痕迹是( )A .B .C .D .5. 已知M 、N 是线段AB 上的两点,AM =MN =2,NB =1,以点A 为圆心,AN 长为半径画弧;再以点B 为圆心,BM 长为半径画弧,两弧交于点C ,连接AC ,BC ,则△ABC 一定是( )A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形6. 如图,Rt △ABC 中,∠C =90°,∠B =30°,分别以点A 和点B 为圆心,大于AB 的长为半径作弧,两弧相交于M 、N 两点,作直线MN ,交BC 于点D ,连接AD ,则∠CAD 的度数是( )A .20°B .30°C .45°D .60°7. 用直尺和圆规作一个角等于已知角,如图,能得出∠A ′O ′B ′=∠AOB 的依据是( )A .(SAS )B . (SSS )C . (ASA )D . (AAS )二、填空题8. 如图,已知∠MON 是一个锐角,以点O 为圆心,任意长为半径画弧,分别交OM 、ON 于点A 、B ,再分别以点A 、B 为圆心,大于12AB 长为半径画弧,两弧交于点C ,画射线OC .过点A 作AD ∥ON ,交射线OC 于点D ,过点D 作DE ⊥OC ,交ON 于点E .设OA =10,DE =12,则sin ∠MON = .9. 如图,在Rt △ABC 中,∠C =90°,以顶点B 为圆心,适当长度为半径画弧,分别交AB ,BC 于点M ,N ,再分别以点M ,N 为圆心,大于MN 的长为半径画弧,两弧交于点P ,作射线BP 交AC 于点D .若∠A =30°,则= .10. 如图, 矩形ABCD , ∠BAC =600. 以点A 为圆心,以任意长为半径作弧分别交A B.AC 于点M 、N 两点,再分别以点M 、N 为圆心,以大于21MN 的长为半径作弧交于点P ,作射线AP 交BC 于点E ,若BE =1,则矩形ABCD 的面积等于___________.三、解答题(一)11. 如图,已知△ABC ,AC >AB ,∠C =45°.请用尺规作图法,在AC 边上求作一点P ,使∠PBC =45°.(保留作图痕迹.不写作法)12. 人教版初中数学教科书八年级上册第48页告诉我们一种作已知角的平分线的方法: 已知:∠AOB .求作:∠AOB 的平分线.作法:(1)以点O 为圆心,适当长为半径画弧,交OA 于点M ,交OB 于点N .(2)分别以点M ,N 为圆心,大于12MN 的长为半径画弧,两弧在∠AOB 的内部相交于点C . (3)画射线OC ,射线OC 即为所求(如图). 请你根据提供的材料完成下面问题.(1)这种作已知角的平分线的方法的依据是 .(填序号) ①SSS ②SAS ③AAS ④ASA(2)请你证明OC为∠AOB的平分线.13.如图,C为线段AB外一点.(1)求作四边形ABCD,使得CD∥AB,且CD=2AB;(要求:尺规作图,不写作法,保留作图痕迹)(2)在(1)的四边形ABCD中,AC,BD相交于点P,AB,CD的中点分别为M,N,求证:M,P,N三点在同一条直线上.14.已知:如图,△ABC为锐角三角形,AB=AC,CD∥AB.求作:线段BP,使得点P在直线CD上,且∠ABP=12∠BAC.作法:①以点A为圆心,AC长为半径画圆,交直线CD于C,P两点;②连接BP.线段BP就是所求作的线段.(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)完成下面的证明.证明:∵CD∥AB,∴∠ABP=.∵AB=AC,∴点B在⊙A上.又∵点C,P都在⊙A上,∴∠BPC=12∠BAC()(填推理的依据).∴∠ABP=12∠BAC.15.如图,点O在∠ABC的边BC上,以OB为半径作⊙O,∠ABC的平分线BM交⊙O于点D,过点D作DE ⊥BA于点E.(1)尺规作图(不写作法,保留作图痕迹),补全图形;(2)判断⊙O与DE交点的个数,并说明理由.16.如图,在△ABC中,利用尺规作图,画出△ABC的外接圆或内切圆(任选一个.不写作法,必须保留作图痕迹)17. 请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.(1)如图①,四边形ABCD中,AB=AD,∠B=∠D,画出四边形ABCD的对称轴m;(2)如图②,四边形ABCD中,AD∥BC,∠A=∠D,画出BC边的垂直平分线n.18. 如图,在Rt △ABC 中,∠ACB =90°,AC =2,BC =3. (1)尺规作图:不写作法,保留作图痕迹. ①作∠ACB 的平分线,交斜边AB 于点D ; ②过点D 作BC 的垂线,垂足为点E . (2)在(1)作出的图形中,求DE 的长.19. 如图,在△ABC 中,点D 是AB 边上的一点.(1)请用尺规作图法,在△ABC 内,求作∠ADE .使∠ADE =∠B ,DE 交AC 于E ;(不要 求写作法,保留作图痕迹) (2)在(1)的条件下,若DB AD =2,求ECAE的值.20. 尺规作图(只保留作图痕迹,不要求写出作法):如图,已知△ABC,请根据“SAS”基本事实作出△DEF,使△DEF≌△AB C.21. 如图,BD是菱形ABCD的对角线,∠CBD=75°,(1)请用尺规作图法,作AB的垂直平分线EF,垂足为E,交AD于F;(不要求写作法,保留作图痕迹)(2)在(1)条件下,连接BF,求∠DBF的度数.22. 如图,Rt△ABC中,∠ACB=90°,一同学利用直尺和圆规完成如下操作:①以点C为圆心,以CB为半径画弧,交AB于点G;分别以点G、B为圆心,以大于GB的长为半径画弧,两弧交点K,作射线CK;②以点B为圆心,以适当的长为半径画弧,交BC于点M,交AB的延长线于点N;分别以点M、N为圆心,以大于MN的长为半径画弧,两弧交于点P,作直线BP交AC的延长线于点D,交射线CK于点E.请你观察图形,根据操作结果解答下列问题;(1)线段CD与CE的大小关系是;(2)过点D作DF⊥AB交AB的延长线于点F,若AC=12,BC=5,求tan∠DBF的值.23. 下面是小元设计的“经过已知直线外一点作这条直线的垂线”的尺规作图过程.已知:如图1,直线l和l外一点P.求作:直线l的垂线,使它经过点P.作法:如图2,(1)在直线l上任取一点A;(2)连接AP,以点P为圆心,AP长为半径作弧,交直线l于点B(点A,B不重合);(3)连接BP,作∠APB的角平分线,交AB于点H;(4)作直线PH,交直线l于点H.所以直线PH就是所求作的垂线.根据小元设计的尺规作图过程,(1)使用直尺和圆规,补全图形(保留作图痕迹);(2)完成下面的证明.证明:∵PH平分∠APB,∴∠APH= .∵PA= ,∴PH⊥直线l于H.( )(填推理的依据)24. 已知:在△ABC中,AB=A C.(1)求作:△ABC的外接圆.(要求:尺规作图,保留作图痕迹,不写作法)(2)若△ABC的外接圆的圆心O到BC边的距离为4,BC=6,则S⊙O=.25. 如图,⊙O的直径AB=10,弦AC=8,连接B C.(1)尺规作图:作弦CD,使CD=BC(点D不与B重合),连接AD;(保留作图痕迹,不写作法)(2)在(1)所作的图中,求四边形ABCD的周长.四、解答题(二)26.已知线段a 、b ,画一条线段,使其等于b a 2 .27.如下图,已知线段a 和b ,求作一条线段AD 使它的长度等于2a -b .28.求作一个角等于已知角∠MON (如图1).图(1) 图(2)29.如下图,已知∠α及线段a ,求作等腰三角形,使它的底角为α,底边为a .30.如图(1),已知直线AB 及直线AB 外一点C ,过点C 作CD ∥AB (写出作法,画出图形)图(1) 图(2)31.正在修建的中山北路有一形状如下图所示的三角形空地需要绿化.拟从点A 出发,将△ABC 分成面积相等的三个三角形,以便种上三种不同的花草,请你帮助规划出图案(保留作图痕迹,不写作法).32.已知∠AOB,求作∠AOB的平分线OC.图(1)图(2)33.如图(1)所示,已知线段a、b、h(h<b).求作△ABC,使BC=a,AB=b,BC边上的高AD=h.图(1)34.如图,已知线段a,b,求作Rt△ABC,使∠ACB=90°,BC=a,AC=b(用直尺和圆规作图,保留作图痕迹).35.如图,已知钝角△ABC,∠B是钝角.求作:(1)BC边上的高;(2)BC边上的中线(写出作法,画出图形).。
2021年中考数学复习专题-【等腰三角形的性质】考点解答题专练(三)(解析版)

2021年中考数学复习专题-【等腰三角形的性质】考点解答题专练(三)1.问题:如图,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA =EC.若∠BAE=90°,∠B=45°,求∠DAC的度数.答案:∠DAC=45°.思考:(1)如果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗?说明理由.(2)如果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数.2.如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC 于点E,过点E作EF∥BC交AB于点F.(1)若∠C=36°,求∠BAD的度数;(2)求证:FB=FE.2.如图,在△ABC中,AC<AB<BC.(1)已知线段AB的垂直平分线与BC边交于点P,连接AP,求证:∠APC=2∠B.(2)以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连接AQ.若∠AQC =3∠B,求∠B的度数.4.数学课上,张老师举了下面的例题:例1 等腰三角形ABC中,∠A=110°,求∠B的度数.(答案:35°)例2 等腰三角形ABC中,∠A=40°,求∠B的度数,(答案:40°或70°或100°)张老师启发同学们进行变式,小敏编了如下一题:变式等腰三角形ABC中,∠A=80°,求∠B的度数.(1)请你解答以上的变式题.(2)解(1)后,小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同,如果在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.5.如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.(1)判断∠ABE与∠ACD的数量关系,并说明理由;(2)求证:过点A、F的直线垂直平分线段BC.6.如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.(1)如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°①求证:AD=BE;②求∠AEB的度数.(2)如图2,若∠ACB=∠DCE=120°,CM为△DCE中DE边上的高,BN为△ABE 中AE边上的高,试证明:AE=2CM+BN.7.求证:等腰三角形的两个底角相等(请根据图用符号表示已知和求证,并写出证明过程)已知:求证:证明:8.如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O(1)求证:OB=OC;(2)若∠ABC=50°,求∠BOC的度数.9.如图,在△ABC中,AB=AC,AD是角平分线,点E在AD上,请写出图中两对全等三角形,并选择其中的一对加以证明.10.如图,已知AB=AC=AD,且AD∥BC,求证:∠C=2∠D.参考答案1.解:(1)∠DAC的度数不会改变;∵EA=EC,∴∠EAC=∠C,①,∵BA=BD,∴∠BAD=∠BDA,∵∠BAE=90°,∴∠B=90°﹣∠AED=90°﹣2∠C,∴∠BAD=(180°﹣∠B)=[180°﹣(90°﹣2∠C)]=45°+∠C,∴∠DAE=90°﹣∠BAD=90°﹣(45°+∠C)=45°﹣∠C,②由①,②得,∠DAC=∠DAE+∠CAE=45°﹣∠C+∠C=45°;(2)设∠ABC=m°,则∠BAD=(180°﹣m°)=90°﹣m°,∠AEB=180°﹣n°﹣m°,∴∠DAE=n°﹣∠BAD=n°﹣90°+m°,∵EA=EC,∴∠CAE=AEB=90°﹣n°﹣m°,∴∠DAC=∠DAE+∠CAE=n°﹣90°+m°+90°﹣n°﹣m°=n°.2.(1)解:∵AB=AC,∴∠C=∠ABC,∵∠C=36°,∴∠ABC=36°,∵BD=CD,AB=AC,∴AD⊥BC,∴∠ADB=90°,∴∠BAD=90°﹣36°=54°.(2)证明:∵BE平分∠ABC,∴∠ABE=∠CBE=∠ABC,∵EF∥BC,∴∠FEB=∠CBE,∴∠FBE=∠FEB,∴FB=FE.3.解:(1)证明:∵线段AB的垂直平分线与BC边交于点P,∴PA=PB,∴∠B=∠BAP,∵∠APC=∠B+∠BAP,∴∠APC=2∠B;(2)根据题意可知BA=BQ,∴∠BAQ=∠BQA,∵∠AQC=3∠B,∠AQC=∠B+∠BAQ,∴∠BQA=2∠B,∵∠BAQ+∠BQA+∠B=180°,∴5∠B=180°,∴∠B=36°.4.解:(1)若∠A为顶角,则∠B=(180°﹣∠A)÷2=50°;若∠A为底角,∠B为顶角,则∠B=180°﹣2×80°=20°;若∠A为底角,∠B为底角,则∠B=80°;故∠B=50°或20°或80°;(2)分两种情况:①当90≤x<180时,∠A只能为顶角,∴∠B的度数只有一个;②当0<x<90时,若∠A为顶角,则∠B=()°;若∠A为底角,∠B为顶角,则∠B=(180﹣2x)°;若∠A为底角,∠B为底角,则∠B=x°.当≠180﹣2x且180﹣2x≠x且≠x,即x≠60时,∠B有三个不同的度数.综上所述,可知当0<x<90且x≠60时,∠B有三个不同的度数.5.解:(1)∠ABE=∠ACD;在△ABE和△ACD中,,∴△ABE≌△ACD,∴∠ABE=∠ACD;(2)连接AF.∵AB=AC,∴∠ABC=∠ACB,由(1)可知∠ABE=∠ACD,∴∠FBC=∠FCB,∴FB=FC,∵AB=AC,∴点A、F均在线段BC的垂直平分线上,即直线AF垂直平分线段BC.6.(1)①证明:∵∠CAB=∠CBA=∠CDE=∠CED=50°,∴∠ACB=∠DCE=180°﹣2×50°=80°.∵∠ACB=∠ACD+∠DCB,∠DCE=∠DCB+∠BCE,∴∠ACD=∠BCE.∵△ACB和△DCE均为等腰三角形,∴AC=BC,DC=EC.在△ACD和△BCE中,有,∴△ACD≌△BCE(SAS),∴AD=BE.②解:∵△ACD≌△BCE,∴∠ADC=∠BEC.∵点A,D,E在同一直线上,且∠CDE=50°,∴∠ADC=180°﹣∠CDE=130°,∴∠BEC=130°.∵∠BEC=∠CED+∠AEB,且∠CED=50°,∴∠AEB=∠BEC﹣∠CED=130°﹣50°=80°.(2)证明:∵△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=120°,∴∠CDM=∠CEM=×(180°﹣120°)=30°.∵CM⊥DE,∴∠CMD=90°,DM=EM.在Rt△CMD中,∠CMD=90°,∠CDM=30°,∴DE=2DM=2×=2CM.∵∠BEC=∠ADC=180°﹣30°=150°,∠BEC=∠CEM+∠AEB,∴∠AEB=∠BEC﹣∠CEM=150°﹣30°=120°,∴∠BEN=180°﹣120°=60°.在Rt△BNE中,∠BNE=90°,∠BEN=60°,∴BE==BN.∵AD=BE,AE=AD+DE,∴AE=BE+DE=BN+2CM.7.解:已知:△ABC中,AB=AC,求证:∠B=∠C;证明:如图,过D作BC⊥AD,垂足为点D,∵AB=AC,AD=AD,在Rt△ABD与Rt△ACD中,,∴Rt△ABD≌Rt△ACD(HL)∴∠B=∠C.8.(1)证明:∵AB=AC,∴∠ABC=∠ACB,∵BD、CE是△ABC的两条高线,∴∠BEC=∠BDC=90°∴△BEC≌△CDB∴∠DBC=∠ECB,BE=CD在△BOE和△COD中∵∠BOE=∠COD,BE=CD,∠BEC=∠BDE=90°∴△BOE≌△COD,∴OB=OC;(2)∵∠ABC=50°,AB=AC,∴∠A=180°﹣2×50°=80°,∴∠DOE+∠A=180°∴∠BOC=∠DOE=180°﹣80°=100°.9.解:△ABE≌△ACE,△EBD≌△ECD,△ABD≌△ACD.以△ABE≌△ACE为例,证明如下:∵AD平分∠BAC,∴∠BAE=∠CAE.在△ABE和△ACE中,,∴△ABE≌△ACE(SAS).10.证明:∵AB=AC=AD,∴∠C=∠ABC,∠D=∠ABD,∴∠ABC=∠CBD+∠D,∵AD∥BC,∴∠CBD=∠D,∴∠ABC=∠D+∠D=2∠D,又∵∠C=∠ABC,∴∠C=2∠D.。
中考数学专题复习新定义阅读理解题(三)

中考数学专题复习新定义阅读理解题(三)学校:___________姓名:___________班级:___________考号:___________评卷人得分一、解答题1.对于任意一个三位正整数,十位上的数字减去个位上的数字之差恰好等于百位上的数字,则称这个三位数为“极差数”.例如:对于三位数451,5-1=4,则451是“极差数”;对于三位数110,1-0=1,则110是“极差数”.(1)求证:任意一个“极差数”一定能被11整除;(2)在一个“极差数”首位之前添加其十位的数字得到一个新的四位数M,在一个“极差能被12整除,求满足条件的数”末位之后添加数字1得到一个新的四位数N,若M N“极差数”.2.一个正整数的各位数字都相同,我们称这样的数为“称心数”,如5,44,666,2222,…对任意一个三位数n,如果n满足各数位上的数字互不相同,且都不为零,那么称这个数为“相异数”.将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和记为S(n),如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和S(123)=213+321+132=666,是一个“称心数”.(1)计算:S(432),S(617),并判断是否为“称心数”;(2)若“相异数”n=100+10p+q(其中正整数p,q满足1≤p≤9,1≤q≤9),且S(n)为最大的三位“称心数”,求n的值.3.材料:对任意一个n位正整数M(n≥3),若M与它的十位数字的p倍的差能被整数q整除,则称这个数为“p阶q级数”,例如:712是“5阶7级数”,因为712517-⨯=101;712也是“12阶10级数”,因为71212110-⨯=70.(1)若415是“5阶k级数”,且k<300,求k的最大值;(2)若一个四位数M的百位数字比个位数字大2,十位数字为1,且M既是“4阶13级数”又是“6阶5级数”,求这个四位数M.参考答案:1.(1)证明见解析;(2)满足条件的“极差数”有671或143或275.【解析】【分析】(1)设任意一个“极差数”的百位数字是a ,十位数字是b ,个位数字是c ,根据条件式子100a +10b +c =11(10b +9c ),即可求证;(2)设任意一个“极差数”的百位数字是a ,十位数字是b ,个位数字是c ,由题意可得M =1000b +100a +10b +c ,N =1000a +100b +10c +1,再根据M −N 能被12整除,可求满足条件的“极差数”.【详解】解:(1)证明:设任意一个“极差数”的百位数字是a ,十位数字是b ,个位数字是c , ∵a =b −c ,∵100a +10b +c =100b −100c +10b +c =110b −99c =11(10b −9c ),∵100a +10b +c 能被11整除,∵任意一个“极差数”一定能被11整除;(2)设任意一个“极差数”的百位数字是a ,十位数字是b ,个位数字是c ,则M =1000b +100a +10b +c ,N =1000a +100b +10c +1,则M −N =−900a +910b −9c −1=−900(b −c )+910b −9c −1=10b +891c −1,M−N 能被12整除,当c =1时,b =1,a =0(舍去);当c =1时,b =7,a =6;当c =3时,b =4,a =1;当c =5时,b =1,a =−4(舍去);当c =5时,b =7,a =2;当c =7时,b =4,a =−3(舍去).故满足条件的“极差数”有671或143或275.【点睛】本题考查了分解因式的实际运用,学生的阅读理解能力以及知识的迁移能力,解题的关键是理解“极差数”的定义.2.(432)999S =,是“称心数”;(617)1554S =,不是“称心数”;(2)n 的值为162或153或135或126.【解析】【分析】(1)根据“称心数”和“相异数”的定义即可判断;(2)根据“称心数”和“相异数”的定义可得()999S n =且19p q ++=,由此即可得出答案.【详解】(1)由题意得:(432)342234423999S =++=,(617)1677166711554S =++=,则(432)S 是“称心数”,(617)S 不是“称心数”;(2)∵“相异数”10010n p q =++(其中正整数p ,q 满足19,19p q ≤≤≤≤),n ∴是一个三位数,且百位数字为1,十位数字为p ,个位数字为q ,1p q ∴≠≠,又()S n 为最大的三位“称心数”,()999S n ∴=,19p q ∴++=,∵p 、q 的所有可能取值为62p q =⎧⎨=⎩或53p q =⎧⎨=⎩或35p q =⎧⎨=⎩或26p q =⎧⎨=⎩, n ∴的值为162或153或135或126.【点睛】本题考查了有理数的加法运算、二元一次方程的应用,理解“称心数”和“相异数”的定义是解题关键.3.(1)k 的最大值为205;(2)满足要求的M 为8311或6816.【解析】【分析】(1)根据材料中给出的“p 阶q 级数”的含义及k 的取值范围即可得出答案.(2)先设未知数表示出M ,然后根据M 既是“4阶13级数”又是“6阶5级数”列出式子并结合整除规律即可解答.【详解】(1)∵415是“5阶k 级数”,所以41551410k k -⨯=为整数, ∵k <300,∵k 的最大值为205.(2)设M 为千位数字为x ,个位数字为y ,则百位数字为y+2,∵M =1000x+100(y+2)+10+y ,(0≤y≤7)∵M 既是“4阶13级数”又是“6阶5级数”, ∵4113M -⨯与615M -⨯均为整数, ∵M ﹣4是13的整数倍,M ﹣6是5的整数倍,∵y =6或1,当y =1时,M ﹣4=1000x+307,413M -=100030713x +=77x+24﹣513x +, ∵x =8,∵M =8311.当y =6时,M ﹣4=1000x+812413M -=100081213x +=77x+63﹣713x +, ∵x =6,∵M =6816.综上所述,满足要求的M 为8311或6816.【点睛】本题以新定义的形式考查了二元一次不定方程的应用、数的整除规律.读懂材料、正确理解“p 阶q 级数”的含义是解答本题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学总复习专题训练(三(方程与不等式)考试时间:120分钟满分150分A. x 1B. x : 1C. X 2 —1D. X 「13 .如果不等式组x 2m 1的解集是x • -1,那么m 的值是()。
.X a m + 2A. 3B. 1C. -1D. -34 .不等式2x — 1 > 3x-5的正整数解的个数为()。
A. 1个B. 2个C. 3个D. 4个5.若关于x 的方程2x — 4=3m 和 x+2=m 有相同的根,贝U m 的值是()。
A. 10B.— 8C.— 10D. 86 .代数式3 - 1 与代数式-k +34 的值相等时, k 的值为()A. 7B. 8C. 9 D .101 2^Q —77.若3 m + 1与 —互为相反数,则 m 的值为()。
x + m = 48 .由方程组'可得出x 与y 的关系是( )。
j _3 = m.A. x y =1B. x y = -1C. x y=7D. x y = -73x + y = k +19.若方程组丿 丫 的解为x 、y ,且2<k<4,则x-y 的取值范围是、x+3y=3()。
1 A. 0<x-y<B. 0<x-y<1C. -3<x-y<-1D. -1<x-y<12、选择题(每小题 3分,共45 分)1 .方程x2 = x +1的根是( )。
)。
2. a :3,则不等式(a-3)x ■ a -3的解集是(4 --D3 ■4-c4 - 3-B3 ■4x v = 410. 如果中的解x、y 相同,则m的值是()。
(X —(m —1)y =6A. 1B. — 1C. 2D. —211•足球比赛的记分为:胜一场得3分,平一场得1分,负一场得0分,- 队打了14场比赛,负5场,共得19分,那么这个队胜了()。
A. 3场B. 4场C. 5场D. 6场12. 当分母解x的方程今 =-^ 时产生增根,则m的值等于()。
x —1 x —1A. —2B. —1C. 1.D. 213. 一种药品经两次降价,由每盒50元调至40.5元,平均每次降价的百分率是A. 5%B. 10 %C. 15%D. 20 %14. 如图,宽为50cm的矩形图案由10个全等的小长方形拼成,其中一个小长方形的面积为2A. 400cmB.2500cm2C. 600cmD.24 000cm15. 10年前,母亲的年龄是儿子的6倍;倍.求母子现在的年龄.设母亲现年一次方程组是(10年后,母亲的年龄是儿子的2 x 岁,儿子现年y岁,列出的二元x +10 =6(y+10 , A. ■■x -10 =2 y-10 .B.x-10 =6(y-10),x 10 =2(y 10).川+10=6(x+10), C.l y —10=2(x—10). D.y-10 = 6(x 10), y 10 = 2(x-10).二、填空题(每小题3分,共45分)1.已知方程4x+5y=8,用含x的代数式表示y为__________________2 .方程x+2y=5在正整数范围内的解是_________________________3. 已知方程3x2—19x+m=0的一个根是1,那么它的另一个根是m= ________ °4. 若方程x2+mx— 1=0的两个实数根互为相反数,那么m的值是 _________ °5. 当m ____ 时,方程x2+mx+4=0有两个相等的实数根;当m _____ 时,方程mf+4x+1=0有两个不相等的实数根;6. 方程2x(mx—4)=x2—6没有实数根,则最小的整数m= __________ 。
7. 一元二次方程x2+px+q=0两个根分别是2+ • . 3和2 — 3 ,则p= _______ , q= _________ 。
&已知方程3x+y=12有很多解,请你写出互为相反数的一组解_______________________________________________________________________ 。
2 2 x9. 若2x —3xy —20y =0,且y 工0, 则y = ________ 。
"x = 210. 写出一个以丿为解的一个二元一次方程组____________ 。
y = —311. 如果x2—2(m+1)x+m2+5是一个完全平方式,则m= __________ 。
12. 若方程x2+(a2—2)x —3=0的两根是1和一3,贝U a=________ 。
13. 若关于x的方程x2+2(m—1)x+4m2=0有两个实数根,且这两个根互为倒数,那么m的值为__________ 。
14. 如果关于x的方程x2—4x+m=0与x2—x —2m=0有一个根相同,则m的值为__________。
2 115. 已知方程2x2—3x+k=0的两根之差为2^,贝U k= __________ 。
三、解答下列各题( 第8题11分,其余每小题7分,共60分)2 2 2 21.已知a,b,c是三角形的三边长,且方程(a +b +c )x +2(a+b+c)x+3=0有两个相等的实数根,求证:这个三角形是正三角形2x 5y = -26,和方程组3x - 5y = 36的解相同,求2 •已知方程组_ax _by = -4 (bx + ay = -8(2a b)2 006的值.3 •车间里有90名工人,每人每天能隆产螺母 栓配两个螺母,那么应分配多少人生产螺栓, 和螺母正好配套?4 •用图象法解方程组2x +15•已知关于x 的方程x 2,kx-2=0的一个解与方程 3的解相同。
X — 1⑴求k 的值;⑵求方程x 2 ■ kx - 2 = 0的另一个解.6 •某商场将进货价为 30元的台灯以40元售出,平均每月能售出600个•调 查表明:这种台灯的售价每上涨 1元,其销售量就将减少 10个.为了实 现平均每月10000?元的销售利润,这种台灯的售价应定为多少?这时应 进台灯多少个?请你利用方程解决这一问题.24个或螺栓15个,若一个螺多少人生产螺母才能使螺栓7.甲、乙两地间铁路长2400 千米, 经技术改造后, 列车实现了提速. 提速后比提速前速度增加20 千米/ 时, 列车从甲地到乙地行驶时间减少 4 小时. 已知列车在现有条件下安全行驶的速度不超过140 千米/时. 请你用学过的数学知识说明这条铁路在现有条件下是否还可以再次提速?8.某工厂现有甲种原料360kg ,乙种原料290kg ,计划用这两种原料生产A, B两种产品共50件•已知生产一件A种产品,需要甲种原料9kg , 乙种原料3kg ;生产一件B 种产品,需要甲种原料4kg ,乙种原料10kg ,按要求安排A,B 两种产品的生产件数,有哪几种方案?你能设计出来吗?参考答案10、x+y=-1(不唯一);11、2; 12、土 2; 13、1 •由"=0 得(a -b)2 (b -c)2 (c - a)2 =0,所以 a = b = c 。
2x 5y - -26,3x - 5y = 36, =2'代入方程组二 一6.ax - by - -4, bx ay - -8.求得 a=1,b=-1 。
3 •设应分配x 人生产螺栓,y 人生产螺母,则x 'y=90,解得x=4。
,x15^ = 24y.、y = 50.44 •由 2x+y=4,得 y= — 2x+4。
由 4x+3y=6,得 y= x 2 。
3一4在同一坐标系内作出一次函数y= — 2x+4的图象和y= x 2的图象,32x + y = 4 如图(1),观察图象的交点坐标为(3,— 2), •••方程组丿的j4x +3y = 6x = 3解是丿。
= -2X +1 5. (1)v3, • x 1 =3x -3 , • x =2。
x —1经检验x = 2是原方程的解。
、1、B 2 、A 3、D4、D5、B6、B 10、 B 11 、 C 12 、 A 13、B14 、 A 158 -4x 52、{ x =1 { x =3y =2, y =11616;4、0;5、± 4, m K 4 且 mr^ 0; 6、2;7、一 4; 8、12 ;14、0 或3 ;15、-2。
2 •通过解方程组亠+〔x 求得yy - -6把x = 2代入方程x2• kx —2 = 0中,解得k= —1 (2)解x2-x -2 = 0,得为=2 , x2=—1 。
•••方程X2•kx-2=o的另一个解为x=—1 。
6 .设售价为x 元,则(x-30 ) [600- (x-40 )x 10]=10000 , ?解得x=50, x=80,即售价为50元时进500个;售价为80元时进200个。
7 •设提速后列车速度为x千米/时,则:2400 2400 ’4x -20 x解之得:x 1=120 x 2=—100(舍去)经检验x=120是原方程的根•/ 120<140•仍可再提速答:这条铁路在现有条件下仍可再次提速。
8 •设生产A种产品x件,则生产B种产品(50-x)件•根据提意,得”9x+4(50 —x) < 360,彳' 丿解得30 < x < 32 )。
有三种方案:(1)生产A种3x 10(50-x) < 290.产品30件,B种产品20件;(2)生产A种产品31件,B种产品19件;(3)生产A种产品32件,B种产品18件。
