比例的练习奥数1
六年级下册奥数——比和比例(一)

1.一位印度人有三个儿子,临死前对三个儿子立下遗嘱:家中19头牛,老大的21,老二得41,老三得51,千万和睦,好好商量,不要争吵。
老人死后,三个儿子商议了许久,怎么也分不开来,你能帮助他们来分配吗?2.甲、乙两班的同学人数相等,各有一些同学参加课外天文小组,甲班参加天文小组的人数恰好是乙班没有参加的人数的31,乙班参加天文小组的人数是甲班没有参加的人数的41,问甲班没有参加的人数是乙班没有参加的人数的几分之几?3.如图,四边形ABCD 被AC 和BD 分成甲、乙、丙、丁四个三角形,已知:BE=80cm ,CE=60cm ,DE=40cm ,问:丙、丁两个三角形面积之和是甲、乙两个三角形面积之和的多少倍?4.中国古代的“黑火药”配制中硝酸钾,硫磺,木炭的比例为15:2:3.今有木炭50千克,要配制“黑火药”1000千克,还需要木炭多少千克?5.如图所示,已知四边形ABCD 中,对角线AC 、BD 交于O 点,AO=1,∆ABD 的面积:∆BCD 的面积等于3:5.求OC 的长。
6.如图是一个园林的规划图,其中,正方形的43是草地;圆的76是竹林;竹林比草地多占地450平方米,问水池占地多少平方米?7.地球表面的陆地面积和海洋面积之比是29:71,其中陆地的四分之三在北半球。
那么南、北半球海洋面积之比是( )A.284:29B.284:87C.87:29 D .171:1138.五羊小学一至六年级学生人数之比为30:29:28:27:26:25,应届六年级学生毕业后,新招入一年级新生372人,其余学生全部升级,这样使得新学期开学后低年级(一、二、三年级)与高年级(四、五、六年级)学生人数之比为10:9,则这时五羊小学学生总数为多少人?9.数学奥林匹克学校某次入学考试,参加的男生与女生人数之比是4:3,结果录取91人,其中男生与女生的人数之比为8:5.在未录取的学生中,男生与女生的人数之比是3:4,那么报考的共有多少人?10.菜场运进一批蔬菜,青菜占总数的53,余下的是菠菜和萝卜,它们的重量比为3:1,萝卜比青菜少560千克,这批蔬菜一共有多少千克?11.。
宁夏固原市小学数学小学奥数系列6-2-4比例应用题专练1

宁夏固原市小学数学小学奥数系列6-2-4比例应用题专练1姓名:________ 班级:________ 成绩:________亲爱的小朋友们,这一段时间的学习,你们收获怎么样呢?今天就让我们来检验一下吧!一、比例应用题专练1 (共26题;共118分)1. (5分)一个长方体的棱长之和是90厘米,它的长、宽、高之比是4:3:2,长方体的表面积和体积各是多少?2. (5分)蔬菜批发市场周六早上批发销售了西红柿、黄瓜和辣椒共45吨,这三种蔬菜的质量比是8:2:5.这三种蔬菜各销售了多少吨?3. (5分)下面是我国石油资源区域分布情况统计表.(1)我国的石油资源主要分布在哪三种区域?(2)黄土塬的石油储量与石油资源总量的比是________.(3)你还能知道什么信息?4. (5分) (2018六下·盐田期末) 六年级三个班植树,其中一班植树棵树占总棵数的30%,二班和三班植树棵树的比是3:5,且二班比三班少植树28棵。
求一班植树多少棵?5. (5分) (2019六上·陇县期中) 学校购买了789套故事书,其中231套分给四年级,余下的按4∶5分给五、六年级。
五、六年级各分到多少套故事书?6. (5分)如图,阴影部分的面积相当于大圆面积的,相当于小圆面积的,小圆和大圆面积的比是多少?7. (5分) (2019六上·长沙期末) 米奇玩具厂接了一个紧急订单,三天赶制了840个毛绒玩具,第一天完成了总数的,第二天和第三天完成的个数比是3:4,这三天分别赶制了多少个毛绒玩具?8. (1分)(2014·衡水) 一个三角形的三个内角的比是1:2:3,其中大角的度数是________。
9. (5分) (2019六上·镇原期中) 一本书包括“地球之旅”“神秘的字宙”和“科学发现”三部分内容,共540页。
其中的页数是“地球之旅”,其余的页数按4:5分配给“神秘的宇宙”和“科学发现”。
小学奥数:比例应用题(一).专项练习及答案解析

1、比例的基本性质2、熟练掌握比例式的恒等变形及连比问题3、能够进行各种条件下比例的转化,有目的的转化;4、单位“1”变化的比例问题5、方程解比例应用题 比例与百分数作为一种数学工具在人们日常生活中处理多组数量关系非常有用,这一部分内容也是小升初考试的重要内容.通过本讲需要学生掌握的内容有: 一、比和比例的性质性质1:若a : b =c :d ,则(a + c ):(b + d )= a :b =c :d ;性质2:若a : b =c :d ,则(a - c ):(b - d )= a :b =c :d ;性质3:若a : b =c :d ,则(a +x c ):(b +x d )=a :b =c :d ;(x 为常数)性质4:若a : b =c :d ,则a ×d = b ×c ;(即外项积等于内项积)正比例:如果a ÷b =k (k 为常数),则称a 、b 成正比;反比例:如果a ×b =k (k 为常数),则称a 、b 成反比.二、主要比例转化实例① x a y b = ⇒ y b x a =; x y a b=; a b x y =; ② x a y b = ⇒ mx a my b =; x ma y mb=(其中0m ≠); ③ x a y b = ⇒ x a x y a b =++; x y a b x a--=; x y a b x y a b ++=-- ;L ④ x a y b =,y c z d = ⇒ x ac z bd=;::::x y z ac bc bd =; ⑤ x 的c a等于y 的d b ,则x 是y 的ad bc ,y 是x 的bc ad . 三、按比例分配与和差关系⑴按比例分配例如:将x 个物体按照:a b 的比例分配给甲、乙两个人,那么实际上甲、乙两个人各自分配到的物体数量与x 的比分别为():a a b +和():b a b +,所以甲分配到ax a b +个,乙分配到bx a b+个. ⑵已知两组物体的数量比和数量差,求各个类别数量的问题例如:两个类别A 、B ,元素的数量比为:a b (这里a b >),数量差为x ,那么A 的知识点拨教学目标比例应用题(一)元素数量为ax a b -,B 的元素数量为bx a b-,所以解题的关键是求出()a b -与a 或b 的比值. 四、比例题目常用解题方式和思路解答分数应用题关键是正确理解、运用单位“l ”。
奥数中的比例问题

奥数中的“比例问题”
(一)比例与和倍关系
(―)比例与差倍关系
(三)正比例、反比例的应用
应用正、反比例性质解答应用题时要注意题中某一数量是否变化,然后再确定是
成正比例,还是成反比例.找出这些具体数量相对应的分率与其他具体数量之间的正、反比例关系,就能找到更好、更巧的解题方法.
比例问题例题及答案分析1
比例问题例题及答案分析2
【例题】甲从A出发步行向B.同时,乙、丙两人从B地驾车出发,向A 行驶.甲乙两人相遇在离A地3千米的C地,乙到A地后立即调头,与丙在C地相遇.若开始出发时甲就跑步,速度提高到步行速度的2.5倍,则甲、丙相遇地点距A地7.5千米.求AB两地距离.
比例问题练习1
比例问题练习2
比例问题练习4
奥数中的“比例问题”
例题解析
一)比例与和倍关系
(二)比例与差倍关系
(三)正比例、反比例的应用
应用正、反比例性质解答应用题时要注意题中某一数量是否变化,然后再确定是成正比例,还是成反比例.找出这些具体数量相对应的分率与其他具体数量之间的正、反比例关系,就能找到更好、更巧的解题方法.
1、
2、【例题】甲从A出发步行向B.同时,乙、丙两人从B地驾车出发,向A 行驶.甲乙两人相遇在离A地3千米的C地,乙到A地后立即调头,与丙在C地相遇.若开始出发时甲就跑步,速度提高到步行速度的2.5倍,则甲、丙相遇地点距A地7.5千米.求AB两地距离.。
(完整版)六年级比和比例奥数题

(完整版)六年级⽐和⽐例奥数题六年级⽐和⽐例(1)1.4:()=()12=()÷12=0.8=()%=():()2.建筑⼯地计划运进⼀批⽔泥,第⼀次运来总数的41,第⼆次运来180吨,这时运来的与没有运来的吨数⽐是4:3,⼯地计划运进⽔泥多少吨?3.已知a:b=c:d ,现将a 扩⼤2倍,b 缩⼩到原来的21,c 不变,d 应()才能使⽐例式仍成⽴。
4.在1、2、3、4、6、8、12、16这⼋个数中,哪些数能组成⽐例。
(答案有多组,⾄少写出其中的两组,即8个⽐例式。
)5.在⼀个⽐例式⾥,第⼀个⽐是最简整数⽐,且⽐值是0.75,两个内项的乘积是60,这个⽐例式是()。
6.在⽐例尺50001的地图,量得⼀长⽅形地长3.2厘⽶,宽1.2厘⽶,这块⼟地实际的⾯积是多少?第⼀部分必做题1.(☆)两个正⽅体棱长的⽐是2:3,这两个正⽅体底⾯积的⽐是():(),体积⽐是():()。
2.(☆)甲数和⼄数的⽐是4:3,甲数与甲⼄两数和的⽐是(),甲数⽐⼄数多()(),⼄数⽐甲数少()%。
3.⼀个正⽅体的六个⾯分别是红⾊、黄⾊、绿⾊、蓝⾊、红⾊、⽩⾊,把它拿在⼿上掷回桌⾯,蓝⾊朝上的可能性⼤约是()%,红⾊⼤约是()%。
4.(☆)⑴⼀幅⾏政区域图上⽤5厘⽶表⽰实际距离100千⽶,这幅地图的⽐例尺是()。
⑵⼀个零件实际长度是3毫⽶,画在图上的长度是3厘⽶,这幅图的⽐例尺是()。
⑶在⽐例尺1:2000000的地图上,测得A、B两地是4.5厘⽶,实际距离是()千⽶。
⑷如皋、海安两城之间的实际距离是192千⽶,在⽐例尺为1:600000的图纸上,应画()厘⽶。
5.(☆)海安实⼩新建学⽣公寓楼,地基是长⽅形,长40⽶,宽15⽶,把它画在设计图上,长画80厘⽶,宽应画多少厘⽶?6.(☆☆)看下图回答下列问题:学校西⼩青家0 200 400 600⽶⼩红家a.图中⽐例尺是()。
b.⼩青家在学校的()边。
c.⼩红家到学校有()⽶。
浙江省丽水市数学小学奥数系列6-2-4比例应用题专练1

浙江省丽水市数学小学奥数系列6-2-4比例应用题专练1姓名:________ 班级:________ 成绩:________亲爱的小朋友们,这一段时间的学习,你们收获怎么样呢?今天就让我们来检验一下吧!一、比例应用题专练1 (共26题;共118分)1. (5分) (2018六上·闽侯期中) 学校跑道一圈长400米,东东和西西在跑道上散步,从同一地点出发相背而行,分钟相遇.相遇时,东东和西西走的路程比是,东东走了多少米?2. (5分)把一条长216厘米的铁丝,做成一个长方体框架,要求楼长的比是1:2:6。
如果每个面都用铁皮包上做铁盒,那么这个铁盒的体积是多少?3. (5分) (2018五上·阳江月考) 有一块260公顷的地,其中60公顷种茄子,其余的按1:4的比例种黄瓜和西红柿,这块地种黄瓜和西红柿各多少公顷?4. (5分) (2020六上·西安期末) 甲、乙、丙三个修路队合修一条45千米的公路,完工时甲队修了这条公路的,乙队和丙队所修公路长度之比为3:2,三个队各修了多少千米?5. (5分) (2019六上·滨州期中) 学校把280棵树苗按3个班的人数分配给各班,一班有48人,二班有50人,三班有42人。
3个班各应分得多少棵树苗?6. (5分)一种混凝土的水泥、黄沙和石子的比是2:3:5,如果要搅拌15吨这样的混凝土,需要水泥、黄沙和石子各多少吨?7. (5分)(2018·梁平) 学校体育室购进足球、篮球、排球共300个,已知足球个数的、篮球个数的、排球个数的是相等的,那么购进足球多少个?8. (1分)甲、乙、丙三个数的平均数是60。
甲、乙、丙三个数的比是3:2:1。
甲、乙、丙三个数分别是________、________、________。
9. (5分) (2019六上·宁津期中) 学校修整校园用的混凝土是按2份水泥、3份石子和5份沙子的标准混合成的。
(完整版)六年级奥数题:比和比例一

比例问题一、 填空题1.4:( )=2016=( )÷10=( )% 2.在3:5里,如果前项加上6,要使比值不变,后项应加 .3.12:1的图纸上,精密零件的长度为6厘米,它的实际长度是 毫米.4.某生产队有一块正方形菜地,边长120米,在总面积中种植西红柿、南瓜、茄子面积的比是25:1:21,三种蔬菜各种了 亩.5.买甲、乙两种铅笔共210支,甲种铅笔每支价值3分,乙种铅笔每支价值4分,两种铅笔用去的钱相同,甲种铅笔买了 支.6.车库中停放若干辆双轮摩托车和四轮小卧车,车的辆数与车的轮子数的比是2:5.问:摩托车的辆数与小卧车的辆数的比是 .7.自然数A 、B 满足182111=-B A ,且A :B =7:13.那么,A +B = . 8.光明小学有三个年级,一年级学生占全校学生人数的25%,二年级与三年级学生人数的比是3:4,已知一年级比三年级学生少40人,一年级有学生 人.9.水泥、石子、黄砂各有5吨,用水泥、石子、黄砂按5:3:2拌制某种混凝土,若用完石子,水泥缺 吨.黄砂多 吨.10.甲、乙两人步行的速度比是13:11.如果甲、乙分别由A 、B 两地同时出发相向而行,0.5小时后相遇,如果它们同向而行,那么甲追上乙需要 小时.11.已知甲、乙两数的比为5:3,并且它们最大公约数与最小公倍数的和是1040,那么甲数是多少,乙数是多少.12.有一块铜锌合金,其中铜与锌的比是2:3.现在加入锌6克,共得新合金36克,求在新合金内铜与锌的比.13.一段路程分成上坡、平路、下坡三段,各段路程长之比依次是1:2:3.某人走各段路所用时间之比依次是4:5:6.已知他上坡时速度为每小时3千米.路程全长50千米.问:此人走完全程用了多少时间?14.一个圆柱体的容器中,放有一个长方形铁块.现在打开一个水龙头往容器中注水,3分钟时,水恰好没过长方体的顶面,又过了18分钟,水灌满容器.已知容器的高度是50厘米.长方体的高度是20厘米,那么长方体底面积:容器底面面积等于多少?练习题1 有一个长方体,长与宽的比是2:1,宽与高的比是3:2,已知这个长方体的全部棱长之和是220cm。
比例和反比例 (奥数)

比例和反比例(奥数)一、比例和反比例1.一辆汽车在公路上行驶,行驶的时间和路程如下图。
(1)这辆车10小时行驶多少千米?(2)行驶600千米要多少时?【答案】(1)解:10x80=800(千米)答:这辆车10小时行驶800千米。
(2)解:600+80=7.5(小时)答:行驶600千米要7.5时。
【解析】【分析】(1)由时间路程图可知,1小时行驶的路程是80千米,即汽车的速度是80千米/小时,再由“路程=速度x时间〃进行计算;(2)由(1)可知汽车的速度,再由“时间=路程+速度〃进行计算。
2.两个咬合在一起的齿轮,主动轮有50个齿,每分钟转100转;从动轮有20个齿,每分钟转多少转?【答案】解:设从动轮每分钟转x转,则20x=50x10020x=5000x=250答:从动轮每分钟转250转。
【解析】【分析】由于两齿轮咬合在一起,它们必须在相同时间内转过相等的齿数,设从动齿轮每分钟转x转,则有:50x100=20x,就可解答此题.3.从甲地到乙地,小华用了5小时,小红用了3小时。
小华和小红所用的时间的比是,他们的速度比是。
【答案】5:3;3:5【解析】【解答】解:小华和小红所用的时间的比是5:3,他们的速度比是3:5。
故答案为:5:3;3:5。
【分析】路程一定,速度和时间成反比。
4.下图表示彩带的总价和购买长度之间的对应关系。
彩带总价和长度成比例关【答案】正;9.6;22.4【解析】【解答】下图表示彩带的总价和购买长度之间的对应关系。
彩带总价和长度成正比例关系,购买3米彩带需32x3=9.6元,购买7米彩带需3.2x7=22.4元。
故答案为:正;9.6;22.4o【分析】观察图可知,正比例图像是一条经过原点的直线,彩带的总价!彩带的长度=每米彩带的单价,当每米彩带的单价一定时,彩带的总价和长度成正比例;要求3米彩带需要多少钱,用每米彩带的单价x数量=彩带的总价,同样的方法可以求出7米彩带的总价,据此列式解答。
比例和反比例(奥数)(20201121064305).docx

比例和反比例 ( 奥数 )一、比例和反比例1.工人铺一条路,用边长 4 分米的方砖铺需要500 块,如果改用边长 5 分米的方砖铺,需要多少块?【答案】解:设需要x 块,4× 4× 500=5× 5×x25x= 8000x= 320答:如果改用边长 5 分米的方砖铺地,需要320 块。
【解析】【分析】此题主要考查了反比例应用题,这条路的总面积是一定的,每块砖的面积与铺的块数成反比例,据此列比例解答.2.一辆货车从甲地去相距 315 千米的乙地送货。
已知前 3 时行了 135 千米,如果用同样的速度行完剩下的路程,还要行几时?(用比例解)【答案】解:设还要行 x 时。
=x =4答:还要行 4 时。
【解析】【分析】因为速度相同即一定,故路程与时间成正比例,所以,前 3 小时行的路程: 3=剩下的路程:需要的时间,设所需时间为x 小时,则可以用这个等量关系列出比例式。
3.服装厂加工一批服装,计划每天加工120 套, 50 天可以完成。
实际每天加工了150套,多少天可以加工完?(用比例解)【答案】解:设 x 天可以加工完。
150x=120 × 50x=6000÷ 150x=40答: 40 天可以加工完。
【解析】【分析】这批服装的总数不变,每天加工的套数与加工的天数成反比例,设出未知数,根据总套数不变列出比例,解比例求出实际加工的天数即可。
4.甲乙两地相距440 千米,一辆汽车从甲地开往乙地, 3 时行了 240 千米,照这样计算,几小时可以到达乙地?(用比例解)【答案】解:设小时可以到达乙地,答: 5.5 小时可以到达乙地。
【解析】【分析】“照这样计算”的意思就是汽车的速度不变,路程与时间成正比例;设出未知数,根据速度不变列出比例,解比例求出到达乙地的速度即可。
5.给一间卧室铺地砖,每块砖的面积和砖的块数成________比例;同一个圆的半径和周长成________比例。
小学奥数教程∶比例和反比例 计算题

小学奥数教程∶比例和反比例计算题一、比例和反比例1.用一批纸张装订毕业纪念册,如果每本40页,可以装订50本。
如果现在用这批纸装订了100本,每本装订多少页?(用比例解)【答案】设每本装订x页。
100x=40×50x=20答:每本装订20页。
【解析】【分析】这批纸的总数一定,每本的页数与可以装订的本数成反比例,先设出未知数,再根据总页数一定列出比例,解比例求出每本装订的页数即可。
2.一列火车行驶720km需要3小时。
照这样计算,从甲地到乙地的铁路长约1200千米,这列火车需要行驶几小时? (用比例解答)【答案】解:设需要行驶x小时。
=x=5答:需要行驶5小时。
【解析】【分析】设这列火车需要行x小时,根据火车速度不变列出正比例关系,求出未知数,解答即可。
3.小兰看一本故事书,每天看10页,12天看完,若每天看15页,几天可以看完?【答案】解:设x天可以看完。
10×12=15x解得x=8答:8天可以看完。
【解析】【分析】已知每天看的页数×对应看完的天数=预计每天看的页数×对应预计看完的天数。
等式的性质2:等式两边同时乘(或除以)一个相同的数或式子,两边依然相等。
4.一个修路队,原计划每天修400米,15天可以修完.结果12天就完成任务,实际每天修多少米?(用比例解)【答案】解:实际每天修x米,12x=400×1512x=6000x=500答:实际每天修500米。
【解析】【分析】此题主要考查了用比例解决问题,根据题意可知,这条路的全长是不变的,设实际每天修x米,用实际每天修的米数×实际修的天数=计划每天修的米数×计划修的天数,据此列比例解答.5.一幅地图上,用3cm的线段表示实际距离900km。
一条长480km的高速公路,在这幅地图上是多少厘米?(用比例解)【答案】解:设该条公路在这幅地图上是x厘米.900km=90000000cm,480km=48000000cm,90000000x=3×48000000x=1.6答:该条公路在这幅地图上是1.6厘米.【解析】【分析】设这条公路在这幅图上是x厘米,根据图上距离与实际距离的比不变列出比例,解比例求出图上距离即可.6.为了保护环境,净化空气,六年级同学要去植树,原计划每小时植树40棵,3小时植完。
比例 (奥数)

比例 (奥数)一、比例1.下面()能和:4组成比例。
A. 5:10B.C.【答案】 C【解析】【解答】:4=÷4=;选项A,5:10=5÷10=,≠,不能组成比例;选项B,:=÷=,≠,不能组成比例;选项C,:=÷=,=,能组成比例。
故答案为:C。
【分析】表示两个比相等的式子叫比例,判断两个比是否能组成比例,用前项÷后项=比值,分别求出比值,如果比值相等,就能组成比例,否则,不能组成比例,据此解答。
2.一个零件的高是4mm,在图纸上的高是2cm.这幅图纸的比例尺是()A. 1:5B. 5:1C. 1:2D. 2:1【答案】 B【解析】【解答】解:2cm=20mm,比例尺:20:4=5:1。
故答案为:B。
【分析】把2cm换算成mm,然后写出图上距离与实际距离的比并化成后项是1的比就是这幅图的比例尺。
3.与18:15能组成比例的一个比是()A. 6:30B. :C. 0.25 :D. 5:6【答案】 A【解析】【解答】解:18:15=1.2,A、6:30=0.2,不能组成比例;B、=1.2,能组成比例;C、0.25:=0.75,不能组成比例;D、5:6=,不能组成比例。
故答案为:B。
【分析】计算出每个比的比值,与18:15的比值相等的比才能组成一个比例。
4.与∶能组成比例的是( )。
A. ∶B. 2∶5C. 5∶2【答案】 C【解析】【解答】解:,A、,不能组成比例;B、2:5=0.4,不能组成比例;C、5:2=2.5,能组成比例。
故答案为:C。
【分析】表示两个比相等的式子叫做比例,由此计算出每个比的比值,把比值相等的两个比组成比例即可。
5.如果5x=8y(x、y≠0),那么________:________=5:8.【答案】 y;x【解析】【解答】如果5x=8y(x、y≠0),那么y:x=5:8。
故答案为:y;x。
【分析】根据比例的性质:在比例里,两外项之积等于两内项之积,将相乘的两个数同时做外项或内项即可解答。
苏教版六年级小升初奥数专项训练 第九周 比例(一)

第九周比例(一)1.比例的意义和基本性质(一)【题型概述】运用比例的基本性质:内项之积等于外项之积。
可以写出很多个比例,其关键是找到两个数的积等于另外两个数的积。
下面,我们学习这方面的内容。
【典型例题】把下面的等式改写成比例。
4×15=6×10。
思路点拨由比例的基本性质,4和15可以作为比例的外项,6和10作为比例的內项。
所以4∶6=10∶15;或4∶10=6∶15, 15∶6=10∶4, 15∶10=6∶4。
也可以将6和10作为比例的外项,4和15作为比例的內项,所以6∶4=15∶10;或6∶15=4∶10,10∶4=15∶6,10∶15=4∶6。
【举一反三】1.把下面的等式改写成比例。
0.3×10=6×0.5。
2.在括号里填上适当的数。
0.35∶()=()∶103. 在括号里填上适当的数。
4()=()5.【拓展提高】从2、3、4、5、6这五个数中挑选四个数组成比例。
思路点拨我们知道,要使选择的四个数能组成比例,根据比例的基本性质,必须这四个数中某两个数的乘积等于另外两个数的乘积,接下来,就看五个数中哪四个数满足这个条件。
通过观察,不难发现:2×6=3×4。
所以2∶3 = 4∶6。
当然,大家也可以写成其他形式的比例。
【奥赛训练】4.从3、4、5、6、7、8这六个数中挑选四个数组成比例。
5.《第五次全国人口普查主要数据公报》显示,祖国大陆31个省、自治区、直辖市和现役军人的总人口为126 583万人,其中男性65 355万人,这些人口中,男性与女性人口的整数比为1000∶()。
2.比例的意义和基本性质(二) 【题型概述】运用比例的基本性质,我们可以解决一些复杂的比例问题以及生活中的实际问题。
今天,需要大家灵活运用比例的基本性质。
【典型例题】在比例“30∶20 = 48∶32”中,从30里减去18,而20、48这两项不变,要使比例成立,应在32上加上多少?思路点拨 在比例“30∶20 = 48∶32”中,两个內项没有发生变化,而两个外项都发生了变化,其中一个外项的变化时已知的,另外一个外项32的变化是未知的,所以,我们可以设32上加上的数是x ,这样就构成了一个新的比例:(30-18)∶20=48∶(32+x),用解比例的知识可以求出x 的值。
比例和反比例 (奥数)(1)
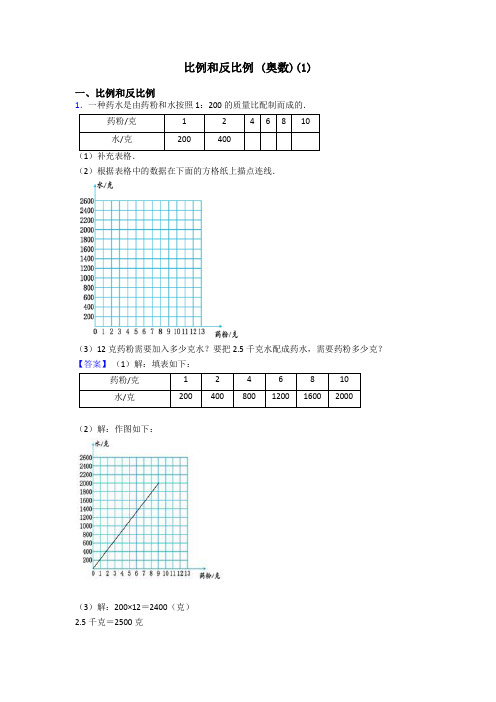
比例和反比例 (奥数)(1)一、比例和反比例1.一种药水是由药粉和水按照1:200的质量比配制而成的.药粉/克1246810水/克200400(1)补充表格.(2)根据表格中的数据在下面的方格纸上描点连线.(3)12克药粉需要加入多少克水?要把2.5千克水配成药水,需要药粉多少克?【答案】(1)解:填表如下:药粉/克1246810水/克200400800120016002000(2)解:作图如下:(3)解:200×12=2400(克)2.5千克=2500克2500× =12.5(克)答:12克药粉需要加水2400克,要把2.5千克水配成药水,需要药粉12.5克.【解析】【分析】(1)根据条件“ 一种药水是由药粉和水按照1:200的质量比配制而成的”可知,用药粉:水=1:200,据此列比例解答,然后填表即可;(2)根据统计表中的数据,在统计图中先描点,然后再连线,图中的统计图纵轴每格代表200克,据此作图;(3)根据条件可知,1克药粉要加入200克水,用药粉的质量×200=水的质量,据此用乘法计算;要把2.5千克水配成药水,需要药粉多少克,先统一单位,1千克=1000克,然后用水的质量×药粉占水的分率=药粉的质量,据此列式解答。
2.同一时间、同一地点测得的树高和它的影长如下表:树高/米2346…影长/米1.62.43.24.8…(2)树高和影长成什么比例?为什么?(3)量得一颗大树的影长是10.4米,这棵大树有多高?【答案】(1)(2)解:成正比例。
因为 =1.25, =1.25, =1.25, =0.8(一定),所以,树高和影长成正比例。
(3)解:设这棵大树的高度是x米。
=1.6x=2×10.41.6x=20.81.6x÷1.6=20.8÷1.6x=13答:这棵大树的高度是13米。
【解析】【分析】(1)观察统计图可知,横轴表示树高,竖轴表示影长,据此先描点,再连线,据此作图;(2)分别用树高:影长,求出比值,当比值一定时,成正比例,据此判断;(3)根据题意可知,设这棵大树的高度是x米,用树高:影长=树高:影长,据此列正比例解答.3.王叔叔开车从甲地到乙地,一共用了3小时,每小时行80km,原路返回每小时行100km。
比例的应用1——小学六年级奥数题

比例的应用(1)例1:甲乙两个长方形,它们的周长相等,甲的长与宽之比是3:2,乙的长与宽之比是4:3,那么,甲与乙的面积之比是多少?练习:1、甲乙两人步行的速度比是7:5,甲乙分别由A、B两地同事出发,如果相向而行,0.5小时相遇。
如果他们同时同向而行,那么甲追上乙需要多少小时?2、客车和货车从甲、乙两地同时出发,相向而行,在距中点30千米处相遇。
已知货车与客车的速度比是5:8,求甲、乙两地的距离。
例2:一种大米每千克1.08元,另一种大米每千克1.48元,把这种大米混合后,售价为每千克1.23元,求两种大米混合的重量比?练习:1、用奶糖和水果糖混合在一起酿成一种礼品糖,已知奶糖每千克5.4元,水果糖每千克3元。
现在要想配出的礼品糖每千克为4.8元,那么奶糖和水果糖应该按怎样的比例混合?2、例3:两只蜡烛长度相等,粗蜡烛可以点5小时,细蜡烛可以点4小时,同时点燃一段时间后,粗蜡烛长度是细蜡烛长度的2倍。
此时已经点燃了多少小时?练习:1、有长度相同,粗细不同的两支蜡烛,细蜡烛点完需1小时,粗蜡烛点完需2小时。
有一次停电,将这两支蜡烛同时点燃,来电时,发现粗蜡烛是细蜡烛的2 倍时,问停电多长时间?2、两支粗细,长短都不相同的蜡烛,长的一支能燃4小时,短的一支能燃6小时,将它们同时点燃2小时后,两支蜡烛剩下的长度相等。
求两支蜡烛原来的长度比。
3、两支蜡烛粗细不同,细蜡烛之长是粗蜡烛之长的2倍,细蜡烛点完要1小时,粗蜡烛点完要2小时,有一次停电,将这两支蜡烛同时点燃,来电时发现两支蜡烛所剩的长度一样。
问:停电多长时间?能力检测:1、甲和乙同时分别从A、B两站相对出发,在离中点 8千米处相遇,已知乙的速度与甲的速度比是3:4,问A、B两站相距多少千米?2、话梅糖每千克5.1元,奶糖每千克8.9元,现把这两种糖混合后,要求混合后的糖价为每千克5.4元,话梅糖和奶糖应用怎样的重量比才合适?3、一个底面直径是24厘米的圆柱形玻璃中装有水,水里放着一个底面直径12厘米,高18厘米的圆锥形铅块,当铅块从水中取出时,杯里的水面会下降多少厘米?4、一个正方体的表面积是54平方厘米,如果以这个正方体一个面的对角线为棱长做一个新的正方体,如图所示。
六年级比例奥数题及答案

六年级比例奥数题及答案六年级比例奥数题及答案 11、李明的爸爸经营个水果店,按开始的定价,每买出1千克水果,可获利0.2元。
后来李明建议爸爸降价销售,结果降价后每天的销量增加了1倍,每天获利比原来增加了50%。
问:每千克水果降价多少元?答案:设以前卖出X千克降价a元。
那么0.2X×(1+0.5)=(0.2-a)×2x则0.1X=2aXa=0.05答:每千克水果降价0.05元2、有5个小朋友,每人都从装有许多黑白围棋子的布袋中任意摸出3枚棋子.请你证明,这5个人中至少有两个小朋友摸出的棋子的颜色的配组是一样的。
解析与答案:首先要确定3枚棋子的颜色可以有多少种不同的情况,可以有:3黑,2黑1白,1黑2白,3白共4种配组情况,看作4个抽屉。
把每人的3枚棋作为一组当作一个苹果,因此共有5个苹果。
把每人所拿3枚棋子按其颜色配组情况放入相应的抽屉。
由于有5个苹果,比抽屉个数多,所以根据抽屉原理,至少有两个苹果在同一个抽屉里,也就是他们所拿棋子的颜色配组是一样的。
六年级比例奥数题及答案 2猎狗发现在离它10米的前方有一只奔跑着的兔子,马上追上去,兔跑9步的路程狗只需跑5步,但狗跑2步的时间,兔却跑3步。
问狗追上兔时,共跑了多少米路程?答案与解析:60米对于追及问题,我们知道:10米=速度差×追及时间狗追上兔时,所跑路程应为:总路程=狗的速度×追及时间这就是要弄清狗的速度与兔的速度差之间的倍数关系。
另一方面,在分析速度时,一定是相同时间内狗与兔的速度之间的倍数,而不是相同的步数或相同的路程。
只要分析清楚这些,就可以解出本题了。
详解1:为了看相同时间的路程关系,也就是速度关系,我们进行如下处理:狗跑2步的时间兔跑3步,则狗跑6步的时间兔子跑了9步,也就是兔子跑了狗的5步,那么在这段时间内,狗追上了兔子,狗的一步或狗兔间的距离缩短了狗的1步,而狗跑了6步,所以狗的速度是速度差的6倍。
奥数系列训练-比例问题(含答案)

奥数系列训练-比例问题(含答案)【奥数系列训练】(含答案)——比例问题请填入正确答案:【题目1】在3:5里,如果前项加上6,要使比值不变,后项应加多少?【题目2】12:1的图纸上,精密零件的长度为6公分,则他的实际长度是多少公厘?【题目3】小明、小青和小华做红花,小明比小青多做16朵,小华与小青做的朵数的比是5:6,小青和小华做的总朵数与小明做的朵数的比是11:8,小明做多少朵?【题目4】五年级举行数学竞赛,一班占参加比赛总人数的1/3,二班与三班参加比赛人数的比是11:13,二班比三班少8人,则三班有多少人参加比赛?【题目5】买甲、乙两种铅笔共210支,甲种铅笔每支价值3元,乙种铅笔每支价值4元,两种铅笔用去的钱相同,甲种铅笔买多少支?【题目6】自然数A、B满足1/A-1/B = 1/182,且A:B = 7:13,那么A+B得多少?【题目7】光明小学有三个年级,一年级学生占全校学生人数的25%,二年级与三年级学生人数的比是3:4,已知一年级比三年级学生少40人,一年级有学生多少人?【题目8】甲、乙两人步行的速度比是13:11,如果甲、乙由A、B两地同时出发相向而行,0.5小时后相遇,如果它们同向而行,那么甲追上乙需要多少小时?【题目9】鸡、鸭、鹅的只数比是3:2:1,画成扇形统计图,表示鸡的只数的扇形的圆心角是多少度?【题目10】已知甲、乙两数的比为5:3,并且他们最大公约数与最小公倍数的和是1040,那么甲数是多少?【参考答案】1.【解答】在3:5里,如果前项加6,前项为3+6=9,即扩大了9÷3=3倍。
要使比值不变,后项也应扩大3倍。
即为5×3=15,后项应增加15-5=10。
2.【解答】实际距离=图上距离÷比例尺。
可得6÷(12:1)=0.5(公分)=5(公厘)。
3.【解答】小华、小青和小明所有朵数之比5:6:8,将他们做的朵数看出5份、6份和8份,小明比小青多2份是16朵,故每份是8朵。
【精品】比例 (奥数)

【精品】比例 (奥数)一、比例1.已知a:b=c:d,若将b乘5,使比例不成立的条件是( )。
A. a乘5B. c除以5C. d除以5【答案】 C【解析】【解答】因为 a:b=c:d ;所以bc=ad;bx5xc=ax5xd;bx5xc÷5=bc=ad故答案为:C【分析】由比例的基本性质可知,bc=ad,若将b乘5,等式左边扩大到原来的5倍,若d 除以5,等式的右边缩小到原来的.因此,等式不成立,即比例也不成立。
2.图上2厘米代表实际距离60千米,甲、乙两地相距120千米,画在这幅图上,应画()厘米。
A. 4B. 6C. 8D. 10【答案】 A【解析】【解答】解:120÷60=2,2×2=4(厘米),应画4厘米。
故答案为:A。
【分析】可以计算出两地的距离是60千米的多少倍,那么图上距离也就是2厘米的多少倍。
3.一幅中国地图上,量得西安到我国钓鱼岛的距离是34cm,西安到钓鱼岛的实际距离是17000千米,这幅地图的比例尺是________。
【答案】 1:50000000【解析】【解答】解:17000千米=1700000000厘米,比例尺:34:1700000000=1:50000000。
故答案为:1:50000000。
【分析】把实际距离换算成厘米,然后写出图上距离与实际距离的比,并把这个比化成前项是1的比就是这幅图的比例尺。
4.在比例尺是1:10000000的地图上,北京到秦皇岛的实际距离是300km,那么两地的图上距离是________ cm。
若在这幅地图上量得甲地到乙地的距离是6cm,则甲地到乙地的实际距离是________km。
【答案】 3;600【解析】【解答】300km=300×100000=30000000cm;30000000×=3(cm);6÷=60000000(cm)=600(km).故答案为:3;600.【分析】已知比例尺和实际距离,要求图上距离,用实际距离×比例尺=图上距离,据此列式解答;已知比例尺和图上距离,要求实际距离,用图上距离÷比例尺=实际距离,据此列式解答,注意:计算时,要把单位化统一.5.从12的约数中任选四个数组成比例是________.【答案】 1:2=3:6【解析】【解答】解:12的约数有1、2、3、4、6、12,组成的比例是1:2=3:6。
【精品】比例 (奥数)

【精品】比例 (奥数)一、比例1.一个零件的高是4mm,在图纸上的高是2cm.这幅图纸的比例尺是()A. 1:5B. 5:1C. 1:2D. 2:1【答案】 B【解析】【解答】解:2cm=20mm,比例尺:20:4=5:1。
故答案为:B。
【分析】把2cm换算成mm,然后写出图上距离与实际距离的比并化成后项是1的比就是这幅图的比例尺。
2.下面各比中,能与:6组成比例的是()A. 2.5:16B. 0.1:C. 3:2.4D. :4【答案】 D【解析】【解答】解:;A、2.5:16=2.5÷16=0.15625,不能组成比例;B、,不能组成比例;C、3:2.4=1.25,不能组成比例;D、,能组成比例。
故答案为:D。
【分析】比例是表示两个比相等的式子,因此比值相等的两个比才能组成比例。
3.下面各比中与:组成比例的比是()。
A. 3:4B. 4:3C. 1:12【答案】 B【解析】【解答】:=÷=,选项A,3:4=3÷4=,≠,不能组成比例;选项B,4:3=4÷3=,=,能组成比例;选项C,1:12=1÷12=,≠,不能组成比例。
故答案为:B.【分析】判断两个比是否能组成比例,可以求出比值,用前项÷后项=比值,如果比值相等,就能组成比例,否则不能组成比例.4.如果5x=8y(x、y≠0),那么________:________=5:8.【答案】 y;x【解析】【解答】如果5x=8y(x、y≠0),那么y:x=5:8。
故答案为:y;x。
【分析】根据比例的性质:在比例里,两外项之积等于两内项之积,将相乘的两个数同时做外项或内项即可解答。
5.一幅地图的比例尺是1:400000,把它改成线段比例尺是________,已知AB两地的实际距离是24千米,在这幅地图上应画________厘米。
【答案】;6【解析】【解答】400000厘米=4千米,图上1厘米代表实际4千米,线段比例尺为:, 24÷4=6(厘米).故答案为:;6.【分析】先把400000厘米化为4千米,比例尺就是图上1厘米表示实际4千米;实际距离×比例尺=图上距离,据此解答.6.在3,15,12,5,9,30,20把可以组成的比例写出两组________、________。
小学奥数教程∶比例和反比例 计算题(1)

小学奥数教程∶比例和反比例计算题(1)一、比例和反比例1.工人铺一条路,用边长4分米的方砖铺需要500块,如果改用边长5分米的方砖铺,需要多少块?【答案】解:设需要x块,4×4×500=5×5×x25x=8000x=320答:如果改用边长5分米的方砖铺地,需要320块。
【解析】【分析】此题主要考查了反比例应用题,这条路的总面积是一定的,每块砖的面积与铺的块数成反比例,据此列比例解答.2.妈妈有一辆自行车,A和B是自行车的两个齿轮(如图),骑车时用脚驱动A带动B,从而使自行车前进。
(1)这辆自行车,齿轮A有50个齿,齿轮B有20个齿。
当齿轮A转动1圈时,齿轮B 转动多少圈?(2)这辆自行车的车轮直径约是60cm,妈妈每天上班的路程大约是3000m。
妈妈骑车上班大约要置多少圈(即齿轮A转动的圈数)?(计算时π取3,最后结果保留整数)【答案】(1)解:50×1÷20=2.5(圈)答:齿轮B转动2.5圈。
(2)解:60cm=0.6m3000÷(0.6×3×2.5)≈667(圈)答:妈妈骑车上班大约要置667圈。
【解析】【分析】(1)根据题意可知,用齿轮A的齿数×转动的圈数÷齿轮B的齿数=齿轮B转动的圈数,据此列式解答;(2)根据题意可知,先求出自行车齿轮B每圈走过的路程,用周长公式:C=πd,然后根据齿轮A转1圈,齿轮B转2.5圈,可以求出齿轮A每圈走过的路程,用齿轮B每圈走过的路程×齿轮B转动的圈数=齿轮A每圈走过的路程,最后用上班的总路程÷齿轮A每圈走过的路程=齿轮A转动的圈数,据此列式解答,结果保留整数.3.乐乐买了一个军舰模型,包装盒上写着“按1:400制作”,他量了一下,模型长45cm。
这艘军舰实际有多长?【答案】解:设这艘军舰实际长xcm.x=45×400x=1800018000cm=180m答:这艘军舰实际长180米.【解析】【分析】先设出未知数,然后根据1:400的比列出比例,解比例求出实际的长度,注意换算单位.4.用边长15厘米的方砖给房间铺地需要2000块,如果改用边长为25厘米的方砖铺地,需要多少块?【答案】解:设需要x块。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.如果2a = 7b, 那么 a: b=( ):( ) 7.把8×125= 25×40改写成四个比值不同的 比例是 • ( ) • ( ) • ( ) • ( )
3.甲、乙、丙三人进行100米赛跑(假设他们 的速度保持不变),甲到终点时,乙还差20 米,丙离终点还有25米,问乙到达终点时, 丙还差几米?
4.甲、乙两人进行百米赛跑,当甲到达终点时, 乙在甲后面20米,如果两人各自的速度不变, 要使甲、乙两人同时到达终点,甲的起跑线应 比原起跑线后移多少米?
1.甲、乙两种电话机的价格之比是7:3,如 果它们的价格分别上涨70元后,价格之比是7 :4。这两种商品原来的价格是多少元? • • • •
• • •
2.甲乙两位老师本月收入的钱数之比是8:5 ,开支的钱数之比是4:3,甲老师结余152 元,乙老师结余69元。问甲、乙二位老师本 月各收入多少元?
8.将 2、3、4三个数再配上一个数组成比例, 这个数可以是( ),( )或( )。 • 9.有两个比,它们的比值都是0.625,第一个 比的前项和第二个比的后项都是40,把这两 个比组成比例是( )
Байду номын сангаас
拓展提高:
24的因数有哪些?从这些因数中选择 4个数组成的比例是( )
24的因数有哪些?从这些因数中选择 4个数组成比值最小的比例是 ( )。
5如图,一张扇形薄铁片,弧长18.84分米, 它能够围成一个高4分米的圆锥, 试求圆锥的容积(接缝处忽略不计)。
