宁夏银川九中2018届高三上学期第一次月考数学理试题Word版含答案

合集下载

2018届宁夏银川九中高三下学期第一次模拟考试理科数学试题及答案

银川九中2018届高三年级第一次模拟数学(理科)试卷（时间：120分钟满分：150分）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，其中第Ⅱ卷第22～24题为选考题，其它题为必考题。

考生作答时，将答案答在答题卡上，在本试卷上答题无效。

考试结束后，将本试卷和答题卡一并交回。

注意事项：1．答题前，考生务必先将自己的姓名、准考证号填写在答题卡上，认真核对条形码上的姓名、准考证号，并将条形码粘贴在答题卡的指定位置上。

2．选择题答案使用2B 铅笔填涂,如需改动，用橡皮擦干净后，再选涂其他答案的标号；非选择题答案使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚。

3．请按照题号在各题的答题区域(黑色线框)内作答，超出答题区域书写的答案无效。

4．保持卡面清洁，不折叠，不破损。

5．做选考题时，考生按照题目要求作答，并用2B 铅笔在答题卡上把所选题目对应的题号涂黑。

参考公式：样本数据n x x x ,,21的标准差锥体体积公式其中x 为样本平均数其中S 为底面面积，h 为高柱体体积公式球的表面积，体积公式V Sh = 24S R π=343V R π= 其中S 为底面面积，h 为高其中R 为球的半径第Ⅰ卷（选择题，共60分）一、选择题：（本大题共12小题，每题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．复数1a i i+-为纯虚数，则它的共轭复数是( ) A. 2i B. 2i - C. iD. i -2. 下列函数中，同时具有性质：(1)图象过点(0,1)；(2)在区间(0，＋∞)上是减函数；(3)是偶函数.这样的函数是 ( )A. y ＝x 3＋1B. y ＝log 2(|x|＋2)C. y ＝(12)|x| D. y ＝2|x|3．在各项都为正数的等比数列{a n }中，首项a 1=3，前三项和为21，则a 3+a 4+a 5= （）A.33B.72C.84D.1894．角α的终边经过点A ()a ，且点A 在抛物线214y x =-的准线上，则sin α=（）5．某程序框图如图所示，该程序运行后，输出的x 值为31，则a 等于（）A ．1-B ．0C ．2D ．16.—个几何体的三视图及其尺寸如右图所示，其中正（主)视图是直角三角形,侧(左)视图是半圆，俯视图是等腰三角形，则这个几何体的体积是(单位cm 3)（）A ．B ．C ．D ．7．已知实数m 是2，8的等比中项，则圆锥曲线22y x m +＝1的离心率为（）D ．以上都不对8．曲线y=11x x -+在点（0，一1）处的切线与两坐标轴围成的封闭图形的面积为（）A ．41 B ．－12 C ．43 D ．189.为了测算如图所示的阴影部分的面积，作一个边长为3的正方形将其包含在内，并向正方形内随机投掷600个点.已知恰有200个点落在阴影部分内，据此，可估计阴影部分的面积是（）A.4B.3C.2D.110．设函数())sin(2)(||)2f x x x πϕϕϕ=+++<，且其图象关于直线0x =对称，则（）A ．()y f x =的最小正周期为π，且在(0,)2π上为增函数 B ．()y f x =的最小正周期为π，且在(0,)2π上为减函数 C ．()y f x =的最小正周期为2π，且在(0,)4π上为增函数 D ．()y f x =的最小正周期为2π，且在(0,)4π上为减函数 11.已知正方形ABCD 的边长为2，点P,Q 分别是边AB ，BC 边上的动点且,AQ DP ⊥ ，则QP CP ⊥的最小值为（）A ．1B ．2C ．3D ．412. 已知⎩⎨⎧>-≤-=0,230,2)(2x x x x x f ,若ax x f ≥|)(|在]1,1[-∈x 上恒成立,则实数a 的取值范围是( )A.),0[]1(+∞--∞B.]0,1[-C.]1,0[D.)0,1[-第Ⅱ卷（非选择题，共90分）二、填空题：本大题共4小题，每题5分，共20分．各题答案必须填写在答题卡上（只填结果，不要过程）13.已知点P 在抛物线y 2=4x 上，那么点P 到点Q （2，-1）的距离与点P 到抛物线焦点距离之和取得最小值时，点P 的坐标为 .14. 已知圆C ：x 2+y 2-6x-4y+8=0.以圆C 与坐标轴的交点分别作为双曲线的一个焦点和顶点，则适合上述条件的双曲线的标准方程为 .15．如图,为了测得河的宽度CD ，在一岸边选定两点A 、B ，使A 、B 、D 在同一直线上.现测得∠CAB=30°,∠CBA=75°,AB=120 m ，则河的宽度是 .16.球内接正六棱锥的侧棱长与底面边长分别为22和2，则该球的体积为；三、解答题：本大题共解答5题，共60分．各题解答必须答在答题卡上（必须写出必要的文字说明、演算步骤或推理过程）．17.（本小题满分12分）已知函数22()2(1)57f x x n x n n =-+++-．（Ⅰ）设函数()=的图像的顶点的纵坐标构成数列{}n a，求证：{}n ay f x为等差数列；（Ⅱ）设函数()=的图像的顶点到x轴的距离构成数列{}n b，求{}n by f x的前n项和S．n18. （本小题满分12分）为了解某商场旅游鞋的日销售情况，现抽取部分顾客购鞋的尺码，将所得数据绘成如图所示频率分布直方图，已知图中从左到右前三组的频率之比为1：2：3，第二组的频数为10.（1）用频率估计概率，求尺码落在区间（37.5，43.5】的概率约是多少？（2）从尺码落在区间（37.5，43.5】和（43.5，45.5】的顾客中任意选取两人，记在区间（43.5，45.5】内的人数为X，求X的分布列及数学期望EX。

宁夏银川市高三数学上学期第一次月考试题文

宁夏银川市2018届高三数学上学期第一次月考试题文（注：班级.姓名.学号.座位号一律写在装订线以外规定的地方，卷面不得出现任何标记）一、选择题（本大题共12小题，每小题5分） 11．已知集合(){}lg 3A x y x ==+，{}2B x x =≥，则AB =（）A. (3,2]-B.(3,)-+∞C.[2,)+∞D.[3,)-+∞ 22．已知命题p ：1≤∈x cos R x ，有对任意，则A ．1≥∈⌝x cos R x p ，使：存在B ．1≥∈⌝x cos R x p ，有：对任意C ．1>∈⌝x cos R x p ，使：存在D ．1>∈⌝x cos R x p ，有：对任意33．已知向量()x ,1=，()3,x =，若与=（）2.A3.B 2.C4.D4．曲线324y x x =-+在点(1,3)处的切线的倾斜角为（） A ．30° B ．45° C ．60° D ．120° 5．若角α的终边在直线y ＝2x 上，则ααααcos 2sin cos sin 2+-的值为( )A ．0 B. 34 C ．1 D. 546．把函数)6sin(π+=x y 图象上各点的横坐标缩短到原来的21倍（纵坐标不变），再将图象向右平移3π个单位，那么所得图象的一条对称轴方程为（）。

A ．8π=x B ．4π-=x C ． 4π=x D ．2π-=x7．下列说法错误．．的是（） A ．命题“若0xy =，则,x y 中至少有一个为零”的否定是：“若0xy ≠，则,x y 都不为零”． B ．对于命题:p R x ∃∈，使得210x x ++<；则p ⌝是:R x ∀∈，均有210x x ++≥． C ．命题“若0m >，则方程20x x m +-=有实根”的逆否命题为：“若方程2x x m +-=无实根，则0m ≤”． D “1x =”是“2320x x -+=”的充分不必要条件． 8．已知向量()1,3a =，()3,b m =.若向量,a b 的夹角为π6，则实数m =（）（A ）（B （C ）0 （D ）9．已知,,a b c 分别是△ABC 的三个内角,,A B C 所对的边长，若1a =，b =，2A C B +=，则sin C =（A ）1 （B ）21（C ）22 （D ）2310．函数2()21log f x x x =-+的零点所在的一个区间是A. (18，14)B. (14，12)C. (12，1) D. (1，2)11．函数πsin 23y x ⎛⎫=- ⎪⎝⎭在区间ππ2⎡⎤-⎢⎥⎣⎦，的简图是（）124．设函数()log (2)a f x x a =-+在区间(1,)+∞上恒为正值，则实数a 的取值范围是A ．(1,2]B ．(1,2)C ．(0,1)(1,2)⋃D ．5(1,)2二、填空题（本大题共4小题，每小题5分）13．已知向量(),1a λ=，()2,1b λ=+，若a b a b +=-，则实数λ的值为＝________.145．已知函数f (x )＝ln(1＋x )－ax 的图象在x ＝1处的切线与直线x ＋2y －1＝0平行，则实数a 的值为______.156．若sin cos θθ+=tan 3πθ⎛⎫+ ⎪⎝⎭的值是 ___________. 167．函数f (x )＝sin ⎝ ⎛⎭⎪⎫2x －π3(x ∈R)的图象为C ，以下结论正确的是________．(写出所有正确结论的编号)xＡ．Ｂ．Ｃ．Ｄ．①图象C 关于直线x ＝11π12对称； ②图象C 关于点⎝ ⎛⎭⎪⎫2π3，0对称；③ 函数f (x )在区间⎝ ⎛⎭⎪⎫－π12，5π12内是增函数；④由y ＝sin 2x 的图象向右平移π3个单位长度可以得到图象C .三、解答题（解答应写出文字说明、证明过程或求解演算步骤） 17．（本题满分12分）设向量()()3sin ,sin ,cos ,sinx ,0,.2a x x b x x π⎡⎤==∈⎢⎥⎣⎦（I ）若a b =，求x 的值；（II ）设函数()f x a b =⋅，求()x f 的最大值。

(优辅资源)宁夏银川九中高三上学期第一次月考数学(理)试题Word版含答案

优秀文档银川九中 2017-2018 学年度第一学期第一次月考试卷高三年级数学（理科）试卷（本试卷满分 150 分）命题人：杨世暄本试卷分第 I 卷（选择题）和第 II 卷（非选择题）两部分，全部为必考题。

考生作答时，将答案答在答题卡上，在本试卷上答题无效。

第Ⅰ卷（选择题）一、选择题（本题共 12 小题，每题 5 分，共 60 分）1．已知全集 U=R ， A= { x| x 2＜ 16} ， B= { x| y=log 3（ x ﹣4） } ，则以下关系正确的选项是（）A ． A ∪ B=RB ． A R B=RC ． A ∩ R B ） =RD ．（? R A ）∪ B=R∪（ ? ）（ ?2. 以下四个函数中 , 与 y=x 表示同一函数的是 ( )A ． y=( ) 2B.y=C.y=D.y=3．给定以下结论：其中正确的个数是（）①用 20cm 长的铁丝折成的矩形最大面积是 25 cm 2；②命题“全部的正方形都是矩形”的否定是“全部的正方形都不是矩形” ；③函数 y2 x 与函数 y log 1 x 的图象关于直线 yx 对称．2A ． 0B ． 1C ． 2D ． 34．函数 ylog 1 (3x2) 的定义域是（）．2A ． [1,)B ．(2,)C ．[2,1]D ． (2,1]3335．三个数60 .7 ， 0.76 ， log 0.7 6 的大小序次是（）A ． 0.76log 0. 7 660.7B ． 0.7660.7 log 0.7 6C ． log 0.7 660 .70.76D ． log 0.7 6 0.7660.76. 已知函数 f(x) 的定义域为 (-1,0), 则函数 f(2x+1)的定义域为 ()(A)(-1,1)(B)(-1,-1 ) (C)(-1,0) ( D)( 1,1)227.函数 f x e xx 2 的零点所在的一个区间是()A ． (2, 1)B ． (－ 1,0)C ．(0,1)D ． (1,2) 8．函数 y log a (| x | 1)( a 1) 的大体图像是（）9. 已知 f (x) 是定义域为 R 的偶函数，且 f (2 x) f (2 x) ，当 x[ 0,2] 时，f ( x) x 22x ，则 f ( 5) （）A, －1B, 0 C, 1 D,3510．定义在 R 上的函数 f （ x ），若是存在函数 g （x ） =kx +b （ k ， b 为常数）使得 f （ x ）≥ g （x ）对一的确数 x 都建立，则称 g （x ）为 f （ x ）的一个承托函数，现在以下函数：①f （ x ） =x 3 ；② f （ x ） =2 x ；③ f （x ） = ；则存在承托函数的 f （ x ）的序号为（）A ．①B ．②C ．①②D ．②③11．已知函数f (x 1) 是定义在 R 上的奇函数，若关于任意给定的不等实数 x 1 、 x 2 ，不等式( x 1x 2 )[ f (x 1 ) f (x 2 )] 0f (1 x) 0 的解集为（）恒建立，则不等式A ． 1,B ． 0,C ．,0D ．,112．当 0x1时， 4xlog a x ，则 a 的取值范围是（）2A ．（0， 2 ）B ．（2，1）C ．（1， 2 ）D ．（ 2 ，2）22二、填空题（本大题共 4 个小题，每题5 分，共 20 分）1113. 计算（ lg-lg 25 ）÷ 100 2 =.41，则 f f14,已知函数 fx5 x, x 3 =．log 4 x, x15．设函数 f ( x) 是定义在 R 上的偶函数，且关于任意的 x R 恒有 f ( x 1)f ( x) ，已知当 x[0,1] 时， f ( x) 3x ．则① 2 是 f (x) 的周期；②函数 f ( x) 在（ 2， 3）上是增函数；③函数 f ( x) 的最大值为 1，最小值为 0；④直线 x2 是函数 f ( x) 图象的一条对称轴．其中全部正确命题的序号是 .．．16.已知 f(x) ＝ (3 a 1) x 4a, x ，a 的取值范围是.1 是 R 上的减函数，那么log a x ,x ≥ 1.三、解答题（本大题共 6 小题，共 70 分）17. （本小题满分 12 分）设有两个命题， p ：关于 x 的不等式 ax1 （ a>0，且 a ≠1）的解集是 {x|x<0} ；q ：函数 y lg( ax 2x a )的定义域为 R 。

宁夏银川市2018届高三数学上学期第一次月考试题理

宁夏银川市2018届高三数学上学期第一次月考试题理试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，其中第Ⅱ卷第22～23题为选考题，其它题为必考题。

考生作答时，将答案答在答题卡上，在本试卷上答题无效。

考试结束后，将本试卷和答题卡一并交回。

3．请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。

4．保持卡面清洁，不折叠，不破损。

5．做选考题时，考生按照题目要求作答，并用2B 铅笔在答题卡上把所选题目对应的题号涂黑。

第I 卷一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项1{}Z k k x x ∈+==,2，则（）C ．N MD ．φ=⋂N M 2 ）6<x D 10>x3 ）．若21x ≠，则1x ≠且1x ≠- C ．若1x ≠且1x ≠-，则21x ≠D ．若1x ≠或1x ≠-，则21x ≠4．函数xx x y 2-4)ln(2+-=的定义域为（）A. -01∞+∞（，）（，）B. -012]∞（，）（，C. ），（0-∞D.]2-，（∞ 5．下列函数中，既是偶函数又在区间),0(+∞上单调递减的是（） A ．12+-=x yB ．||lg x y =C ．x y 1=D ．xe y -=⊂ ≠6．幂函数()()226844mm f x m m x -+=-+在()0,+∞为增函数，则m 的值为（）A ．1或3B ． 1C ．3D ．27．已知函数⎩⎨⎧<+≥=4)2(42)(x x f x x f x ，则)3log 1(2+f 的值为 ( )A ．6B ．11C ．24D ．368．函数x x x f 2ln )(-= 的零点所在的大致区间是（）A ．)2,1(B ．)3,2(C ．1(,1)(3,4)e和 D ．),(+∞e 9．设a ＝log 0.50.8，b ＝log 1.10.8，c ＝1.10.8，则a ，b ，c 的大小关系为( )．A ．a <b <cB ．a <c <bC ．b <c <aD ． b <a <c10.函数f (x )的图象向右平移1个单位长度，所得图象与曲线y ＝e x关于y 轴对称，则f (x )＝( ) A ．ex ＋1B ．ex －1C ．e－x ＋1D ．e－x －111．定义在R 上的函数f (x )满足f (x ＋6)＝f (x )．当－3≤x ＜－1时，f (x )＝－(x ＋2)2，当－1≤x ＜3时，f (x )＝x .则f (1)＋f (2)＋f (3)＋…＋f (2 017)＝( )A ．335B ．337C ．1 678D ．2 017若a ，b ，c 互不相等，且()()()f a f b f c ==，则．()10,12 D ．()20,24第Ⅱ卷题～第21题为必考题，每个试题考生都必须做答．第二．填空题：本大题共4小题，每小题5分。

宁夏银川九中高三上学期第一次月考试题数学(理) Word版含答案

银川九中阶段性适应性摸底检测考试高三数学试卷（理科）命题：李晓鹏一、选择题：（每题5分，共60分）1．若集合A ＝{x ||x |>1，x ∈R }，B ＝{y |y ＝2x 2，x ∈R }，，则(∁R A )∩B ＝ ( ) A ．{x |－1≤x ≤1} B ．{x |x ≥0} C ．{x |0≤x ≤1} D ．Ø 2．xxx f --=11)(的定义域是（）A ．(1]-∞，B ．)1,0()0,(⋃-∞C ．(001-∞⋃，）（，]D ．[1+∞，）3．已知函数⎪⎩⎪⎨⎧>-≤=-)1( )23(log )1( 2)(2x x x x f x ，若4)(=a f ，则实数=a （）A ．2-或6B ．2-或310C ．2-或2D ．2或3104．若直线的参数方程为12()23x tt y t =+⎧⎨=-⎩为参数，则直线的斜率为（）A ．23B ．23-C ．32D ．32-5．把方程1xy =化为以t 为参数的参数方程是（）A ．1212x t y t -⎧=⎪⎨⎪=⎩B ．sin 1sin x t y t =⎧⎪⎨=⎪⎩C ．cos 1cos x t y t =⎧⎪⎨=⎪⎩D ．tan 1tan x ty t =⎧⎪⎨=⎪⎩6.不等式｜5x-x 2｜<6的解集为 ( )(A){x ｜x<2或x>3} (B){x ｜-1<x<2或3<x<6} (C){x ｜-1<x<6} (D){x ｜2<x<3}7．已知函数bx ax y +=2和xbay =|)| || ,0(b a ab ≠≠在同一直角坐标系中的图象不可能．．．是（）8．极坐标方程cos 2sin 2ρθθ=表示的曲线为（）A ．一条射线和一个圆B ．两条直线C ．一条直线和一个圆D ．一个圆9．直线112()x t t y ⎧=+⎪⎪⎨⎪=-⎪⎩为参数和圆2216x y +=交于,A B 两点，则AB 的中点坐标为（）10.不等式 |x-5|+|x+3|≥10的解集是 ( ) (A)［-5,7］ (B)［-4,6］(C)(-∞,-5］∪［7,+∞) (D)(-∞,-4］∪［6,+∞) 11.已知:命题：“是的充分必要条件”；命题：“”．则下列命题正确的是（） A ．命题“∧”是真命题B ．命题“（┐）∧”是真命题C ．命题“∧（┐）”是真命题D ．命题“（┐）∧（┐）”是真命题 12. ABC ∆中，角,,A B C 成等差数列是sin sin )cos C A A B =+成立的（） A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件二、填空题：（每题5分，共20分）13．设全集{,,,}U a b c d =,集合{,}A a b =,{,,}B b c d =,则U U C A C B =（）（）_________． 14.将点的直角坐标错误！未找到引用源。

宁夏银川市2018届高三数学上学期第一次月考试题理2017092002123

宁夏银川市 2018届高三数学上学期第一次月考试题理试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，其中第Ⅱ卷第 22～23题为选考题，其它题为必考题。

考生作答时，将答案答在答题卡上，在本试卷上答题无效。

考试结束后，将本试卷和答题卡一并交回。

2．选择题答案使用 2B 铅笔填涂,如需改动，用橡皮擦干净后，再选涂其他答案的标号；非选择题答案使用 0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚。

3．请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。

4．保持卡面清洁，不折叠，不破损。

5．做选考题时，考生按照题目要求作答，并用 2B 铅笔在答题卡上把所选题目对应的题号涂黑。

第 I 卷一、选择题:本大题共 12小题,每小题 5分,共 60分,在每小题给出的四个选项中,只有一项是符合题目要求的． 1．设集合 Mx x 2k 1, k Z，Nx x k 2, k Z，则（）A ．M NB ． M NC ．N MD ． M N≠≠2． “x 5”的一个必要不充分条件是（）A x6B x3 C x6D x 10x 21x1 x 13．命题“，则或”的逆否命题为（）x 2 1 x1 x 1x 2 1x 1x 1 A ．若，则且B ．若，则且 C ．若 x 1且 x1，则 x 21 D ．若 x 1或 x1，则 x 2 1y ln(x 2x ) 4 - 2x4．函数的定义域为（）A.（-，0）（1，） B.（-，0）（1，2] C.（-，0） D.（- ，2]5．下列函数中，既是偶函数又在区间(0,)上单调递减的是（）1yy lg | x |y xx2yy lg | x |y xA ．1ye xB．C．D．12f x m m x0,m244m6m86．幂函数在为增函数，则的值为（）A．1或3 B．1 C．3 D．2x2x47．已知函数，则的值为( )f(x)f(1log3)f(x2)x42A．6B．11 C．24D．362f(x)ln x8．函数x的零点所在的大致区间是（）A．(1,2)B．(2,3)C．(1,1)和(3,4)D．(e,)e9．设a＝log0.50.8，b＝log1.10.8，c＝1.10.8，则a，b，c的大小关系为()．A．a<b<c B．a<c<b C．b<c<a D．b<a<c10.函数f(x)的图象向右平移1个单位长度，所得图象与曲线y＝e x关于y轴对称，则f(x)＝()A．e x＋1 B．e x－1 C．e－x＋1 D．e－x－111．定义在R上的函数f(x)满足f(x＋6)＝f(x)．当－3≤x＜－1时，f(x)＝－(x＋2)2，当－1≤x＜3时，f(x)＝x.则f(1)＋f(2)＋f(3)＋…＋f(2 017)＝()A．335 B．337 C．1 678 D．2 017lg x,0＜x10,f x12.已知函数若a，b，c互不相等，且，则abcf a f b f c1x6,x＞102的取值范围是（）A．1,10B．5,6C．10,12D．20,24第Ⅱ卷本卷包括必考题和选考题两部分．第13题～第21题为必考题，每个试题考生都必须做答．第22题～第23题为选考题，考生根据要求做答二．填空题：本大题共4小题，每小题5分。

宁夏银川一中高三第一次月考数学(理).pdf

九年级上册单元课时当堂训练 Unit 3 Period 2（Reading1）1.怎样处理它________________________2.熬夜_______________________________________3. 值得做某事_______________________4.保持清醒___________________________________5._____________________6.对某人严格_________________________________ 7. 我的问题的原因____________________8.在________________ 9. 给我一些建议______________________10. 期盼_____________________________________ 二、词汇运用 1. Our English teacher is very s____________ with us. He’s a good teacher. 2. He often o___________ me some help with my English, so I can learn English well. 3. The film provided us with a______(value)record of the earthquake. 4. Tom is confident that he has made a good_____________(choose) . 5. Jim speaks in such a low voice that we can h hear him. 6.. It’s very nice of you to offer me so many good (建议). 7. I think this book is very important. It is w___________ reading and will help you a lot. 8.You’d better write to the famous youth worker about how to d___________ with your problem. 9. There is no d__________ that Millie will come on time. 10. No one can (获得) success without hard work. 三、翻译。

宁夏回族自治区银川市2018届高三数学上学期第一次月考试题文

宁夏回族自治区银川市2018届高三数学上学期第一次月考试题文第Ⅰ卷 (选择题共60分)一、选择题：本大题共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1．已知集合⎭⎬⎫⎩⎨⎧≥+-=021A x x x，{}13B >=x x 则A ．{}2B A ->=⋃x x B ．{}2B A -≥=⋃x x C ．{}002-B A ><<=⋃x x x 或 D ．{}10B A ≤<=⋃x x2．“x>1”是“)2(log 21<+x ”的A ．充要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件 3．函数2cos2y x x =+的一个对称轴为 A ．x=4π B ．x=π2 C ．x=2π3 D ．x=65π4．设0.6 1.50.60.60.6 1.5a b c ===，，，则a b c ，，的大小关系是 A ．a b c ＜＜B ． a c b ＜＜C ．b a c ＜＜D ．b c a ＜＜5．函数()cos 6f x x πω⎛⎫=+ ⎪⎝⎭（0ω>）的最小正周期为π，则()f x 满足A ．在0,3π⎛⎫⎪⎝⎭上单调递增B ．图象关于直线6x π=对称C．3f π⎛⎫=⎪⎝⎭D ．当512x π=时有最小值1- 6．函数()cos2sin 2f x x x π⎛⎫=++ ⎪⎝⎭的最小值是 A ．2-B ．89-C ．87-D ．07．函数2()ln(28)f x x x =--的单调递减区间是 A ．(,2)-∞-B ．(,1)-∞-C ．(1,)+∞D ．(4,)+∞8．在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,且满()C b B c a cos cos 2=-,则A 的取值范围⎪⎭⎫ ⎝⎛320.A π， ()π，0.B ⎪⎭⎫ ⎝⎛323.C ππ， ⎪⎭⎫ ⎝⎛ππ,32.D9．已知函数1222,1()log (1),1x x f x x x -⎧-≤=⎨-+>⎩ ，且4)a (-=f ，则=-)14(a fA ．74-B ．54-C ．34-D ．14-10．当210≤<x 时，有x a xlog 4<，则a 的取值范围是 ⎪⎪⎭⎫⎝⎛220A.，⎪⎪⎭⎫⎝⎛1,22B. ()21C.， ()22D.， 11．已知函数)sin()(ϕω+=x A x f 的图象如图所示，则该函数的解析式可能是)623sin(43)(.A π+=x x f )5154sin(54)(.B +=x x f )665sin(54)(.C π+=x x f )5132sin(54)(.D -=x x f 12. 设函数a ax x e x f x +--=)12()(其中1<a ,若存在唯一的整数0x ,使得0)(0<x f ,则a 的取值范围是⎪⎭⎫⎢⎣⎡1,23-A.e ⎪⎭⎫⎢⎣⎡-43,23B.e ⎪⎭⎫⎢⎣⎡43,23C.e ⎪⎭⎫⎢⎣⎡1,23D.e 第Ⅱ卷（非选择题共90分）本卷包括必考题和选考题两部分．第13题～第21题为必考题，每个试题考生都必须做答．第22题～第23题为选考题，考生根据要求做答．二、填空题：本大题共4小题，每小题5分．13．对于任意的两个正数m ，n ，定义运算⊙：当m 、n 都为偶数或都为奇数时，m ⊙n ＝2nm +；当m 、n 为一奇一偶时，m ⊙n ＝mn ，设集合A ＝{(a ，b )|a ⊙b ＝4，a ，b ∈N*}，则集合A 的子集个数为________．14．如图，某工程中要将一长为100 m ，倾斜角为75°的斜坡改造成倾斜角为30°的斜坡，并保持坡高不变，则坡底需加长________m .15．已知命题p ：关于x 的不等式)10(1≠>>a a a x 且的解集是{}0>x x ，命题q ：函数)lg(2a x ax y +-=的定义域为R ，如果p ∨q 为真命题，p∧q 为假命题，则实数a 的取值范围为________________．16．设函数))((R x x f ∈满足 x x f x f sin )()(+=+π当π<≤x 0时，0)(=x f则=)623(πf ________ . 三、解答题：本大题共6小题，共70分。

银川一中2018届高三数学第一次月考试题理科有答案

银川一中2018届高三数学第一次月考试题（理科有答案）银川一中2018届高三年级第一次月考数学试卷（理）命题人：吕良俊第Ⅰ卷(选择题共60分)一、选择题：本大题共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．若集合，则有A．B．C．D．2．设，则“”是“为偶函数”的A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．即不充分也不必要条件3．下列命题中，真命题是（）A．B．C．的充要条件是D．是的充分条件4．已知函数在区间[]上的最大值是，最小值是，则A．2B．1C．0D．5．下列四个命题：(1)函数在时是增函数，也是增函数，所以是增函数；(2)若函数与轴没有交点，则且；(3)的递增区间为；(4)和表示相等函数.其中正确命题的个数是A．B．C．D．6．若函数的定义域为,值域为，则的取值范围是A．B．C．D．7．若函数分别是上的奇函数、偶函数，且满足，则有A．B．C．D．8．在同一平面直角坐标系中，函数的图象与的图象关于直线对称.而函数的图象与的图象关于轴对称，若，则的值是A．B．C．D．9．函数的图象大致是10．已知实数满足等式，下列五个关系式：①②③④⑤.其中不可能成立的是A．①③B．②④C．①④D．②⑤11．直线（）与函数，的图象分别交于、两点，当最小时，值是A．B．C．D．12．设函数满足，，是的导函数，当时，；当且时，，则函数在上的零点个数为（）A．5B．6C．7D．8第Ⅱ卷（非选择题共90分）本卷包括必考题和选考题两部分．第13题～第21题为必考题，每个试题考生都必须做答．第22题～第23题为选考题，考生根据要求做答．二、填空题：本大题共4小题，每小题5分．13．已知函数（为常数）.若在区间上是增函数，则的取值范围是.14．里氏地震级数M的计算公式为：，其中A是测震仪记录的地震曲线的最大振幅，是相应的标准地震的振幅.假设在一次地震中，测震仪记录的最大振幅是1000，此时标准地震的振幅为0.001，则此次地震的震级为级；9级地震的最大振幅是5级地震最大振幅的倍.15．设函数则实数的取值范围是.16．设函数,已知则.三、解答题:共70分.解答应写出文字说明，证明过程或演算步骤.17.（本小题满分12分）已知集合,,,（1）当时，试判断是否成立？（2）若,求的取值范围.18．（本小题满分12分）已知函数若对于都有，且在轴上截得的弦长为4.（1）试求的解析式；（2）设函数求在区间[2,5]上的最值.19.（本小题满分12分）已知,.（1）若函数与有相同的单调区间，求值；（2）x∈,,求的取值范围.20.（本小题满分12分）已知两条直线和，与函数的图象从左至右相交于点A，B，与函数的图象从左至右相交于点C,D.记线段AC和BD在x 轴上的投影长度分别为.（1）当变化时，试确定的表达式；（2）求出的最小值.21．（本小题满分12分）已知函数，曲线在点（）处的切线方程是（1）求的值；（2）设若当时，恒有，求的取值范围.请考生在第22、23两题中任选一题做答，如果多做．则按所做的第一题记分．做答时请写清题号。

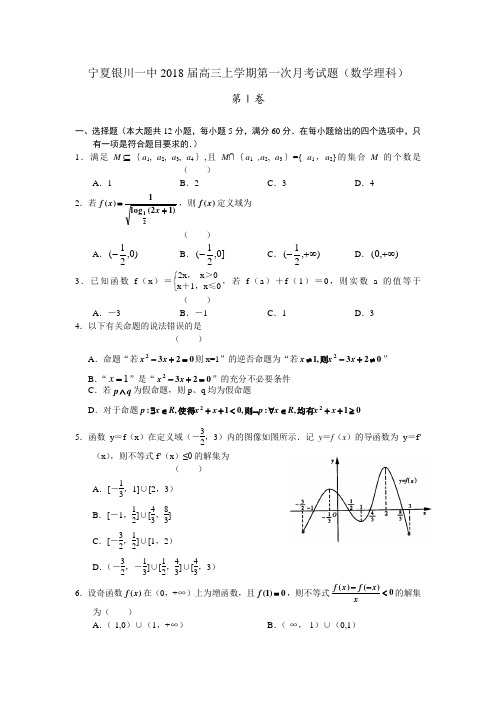
宁夏银川一中2018届高三上学期第一次月考数学试卷(理科)Word版含解析

2017-2018学年宁夏银川一中高三（上）第一次月考数学试卷（理科）一、选择题：本大题共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）若集合M={（x，y）|x+y=0}，N={（x，y）|x2+y2=0，x∈R，y∈R}，则有（）A．M∪N=M B．M∪N=N C．M∩N=M D．M∩N=∅【分析】据集合的表示法知两个集合一个表示直线一个表示一个点且点在直线上，得到两集合的并集．【解答】解：∵M={（x，y）|x+y=0}表示的是直线x+y=0又N={（x，y）|x2+y2=0}表示点（0，0）∵（0，0）在直线x+y=0上∴M∪N=M故选项为A【点评】本题考查集合的表示法及两个集合的并集的定义、据定义求并集．2．（5分）设φ∈R，则“φ=0”是“f（x）=cos（2x+φ）（x∈R）为偶函数”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．即不充分也不必要条件【分析】f（x）=cos（2x+φ）（x∈R）为偶函数，由f（﹣x）=f（x）可得：cosφ=±1，即可得出．【解答】解：f（x）=cos（2x+φ）（x∈R）为偶函数，由f（﹣x）=f（x）可得：cosφ=±1，解得φ=kπ，k∈Z．∴“φ=0”是“f（x）=cos（2x+φ）（x∈R）为偶函数”的充分不必要条件．故选：A．【点评】本题考查了函数的奇偶性、三角函数求值、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．3．（5分）下列命题中，真命题是（）A．∃x0∈R，≤0 B．∀x∈R，2x＞x2C．a+b=0的充要条件是=﹣1 D．a＞1，b＞1是ab＞1的充分条件【分析】利用指数函数的单调性判断A的正误；通过特例判断，全称命题判断B的正误；通过充要条件判断C、D的正误；【解答】解：因为y=e x＞0，x∈R恒成立，所以A不正确；因为x=﹣5时2﹣5＜（﹣5）2，所以∀x∈R，2x＞x2不成立．a=b=0时a+b=0，但是没有意义，所以C不正确；a＞1，b＞1是ab＞1的充分条件，显然正确．故选D．【点评】本题考查必要条件、充分条件与充要条件的判断，全称命题，特称命题，命题的真假判断与应用，考查基本知识的理解与应用．4．（5分）已知函数f（x）=在区间[a，b]上的最大值是，最小值是﹣3，则a+b=（）A．2 B．1 C．0 D．﹣1【分析】先判断函数f（x）区间[a，b]上的单调性，再代值计算即可．【解答】解：函数f（x）===2+，∴f（x）在（﹣∞，2）或（2，+∞）上单调递减，∵在区间[a，b]上的最大值是，最小值是﹣3，∴函数f（x）在[a，b]上单调递减，∴，解得a=﹣1，b=1，∴a+b=0，故选：C．【点评】本题考查了函数的单调性的应用，考查了转化能力和运算能力，属于中档题5．（5分）下列四个命题：（1）函数f（x）在x＞0时是增函数，x＜0也是增函数，所以f（x）是增函数；（2）若函数f（x）=ax2+bx+2与x轴没有交点，则b2﹣8a＜0且a＞0；（3）y=x2﹣2|x|﹣3的递增区间为[1，+∞）；（4）y=1+x和y=表示相等函数．其中正确命题的个数是（）A．0 B．1 C．2 D．3【分析】举出反例函数f（x）=，可判断（1）；举出反例函数f（x）=2，即a=b=0，可判断（2）；求出函数的单调区间，可判断（3）；化简第二个函数的解析式，可判断（4）．【解答】解：（1）函数f（x）=在x＞0时是增函数，x＜0也是增函数，但f （x）不是增函数，故错误；（2）当a=b=0时，函数f（x）=ax2+bx+2与x轴没有交点，故错误；（3）y=x2﹣2|x|﹣3的递增区间为[1，+∞）和[﹣1，0]，故错误；（4）y=1+x和y==|1+x|不表示相等函数，故错误．故正确的命题个数为0，故选：A．【点评】本题考查的知识点是命题的真假判断与应用，函数的单调性，函数的图象和性质，相等函数，难度中档．6．（5分）若函数y=x2﹣3x+4的定义域为[0，m]，值域为[，4]，则m的取值范围是（）A．（0，4]B．[，4] C．[，3] D．[，+∞）【分析】先配方利用定义域值域，分析确定m的范围．【解答】解：y=x2﹣3x+4=x2﹣3x++=（x﹣）2+，定义域为〔0，m〕=4，那么在x=0时函数值最大，即y最大又值域为〔，4〕，根据二次函数的对称性，≤m≤3，故选：C．【点评】本题考查函数的定义域值域的求法，是一道基础题．7．（5分）若函数f（x），g（x）分别是R上的奇函数、偶函数，且满足f（x）﹣g（x）=e x，则有（）A．f（2）＜f（3）＜g（0）B．g（0）＜f（3）＜f（2）C．f（2）＜g （0）＜f（3）D．g（0）＜f（2）＜f（3）【分析】因为函数f（x），g（x）分别是R上的奇函数、偶函数，所以f（﹣x）=﹣f（x），g（﹣x）=g（x）．用﹣x代换x得：f（﹣x）﹣g（﹣x）=﹣f（x）﹣g（x）=e﹣x，又由f（x）﹣g （x）=e x联立方程组，可求出f（x），g（x）的解析式进而得到答案．【解答】解：用﹣x代换x得：f（﹣x）﹣g（﹣x）=e﹣x，即f（x）+g（x）=﹣e ﹣x，又∵f（x）﹣g（x）=e x∴解得：，，分析选项可得：对于A：f（2）＞0，f（3）＞0，g（0）=﹣1，故A错误；对于B：f（x）单调递增，则f（3）＞f（2），故B错误；对于C：f（2）＞0，f（3）＞0，g（0）=﹣1，故C错误；对于D：f（x）单调递增，则f（3）＞f（2），且f（3）＞f（2）＞0，而g（0）=﹣1＜0，D正确；故选D．【点评】本题考查函数的奇偶性性质的应用．另外还考查了指数函数的单调性．8．（5分）在同一平面直角坐标系中，函数y=g（x）的图象与y=e x的图象关于直线y=x对称．而函数y=f（x）的图象与y=g（x）的图象关于y轴对称，若f （m）=﹣1，则m的值是（）A．﹣e B． C．e D．【分析】由函数y=g（x）的图象与y=e x的图象关于直线y=x对称，则y=g（x）的图象与y=e x互为反函数，易得y=g（x）的解析式，再由函数y=f（x）的图象与y=g（x）的图象关于y轴对称，进而可以得到函数y=f（x）的解析式，由函数y=f（x）的解析式构造方程f（m）=﹣1，解方程即可求得m的值．【解答】解：∵函数y=g（x）的图象与y=e x的图象关于直线y=x对称∴函数y=g（x）与y=e x互为反函数则g（x）=lnx，又由y=f（x）的图象与y=g（x）的图象关于y轴对称∴f（x）=ln（﹣x），又∵f（m）=﹣1∴ln（﹣m）=﹣1，故选B．【点评】互为反函数的两个函数图象关于线y=x对称，有f（x）的图象上有（a，b）点，则（b，a）点一定在其反函数的图象上；如果两个函数图象关于X轴对称，有f（x）的图象上有（a，b）点，则（a，﹣b）点一定在函数g（x）的图象上；如果两个函数图象关于Y轴对称，有f（x）的图象上有（a，b）点，则（﹣a，b）点一定在函数g（x）的图象上；如果两个函数图象关于原点对称，有f（x）的图象上有（a，b）点，则（﹣a，﹣b）点一定在函数g（x）的图象上．9．（5分）函数y=e|lnx|﹣|x﹣1|的图象大致是（）A．B．C． D．【分析】根据函数y=e|lnx|﹣|x﹣1|知必过点（1，1），再对函数进行求导观察其导数的符号进而知原函数的单调性，得到答案．【解答】解：由y=e|lnx|﹣|x﹣1|可知：函数过点（1，1），当0＜x＜1时，y=e﹣lnx﹣1+x=+x﹣1，y′=﹣+1＜0．∴y=e﹣lnx﹣1+x为减函数；若当x＞1时，y=e lnx﹣x+1=1，故选D．【点评】本题主要考查函数的求导与函数单调性的关系．10．（5分）已知实数a，b满足等式log2017a=log2018b，下列五个关系式：①0＜a ＜b＜1；②0＜b＜a＜1；③1＜a＜b；④1＜b＜a；⑤a=b．其中不可能成立的是（）A．①③B．②④C．①④D．②⑤【分析】在同一坐标系中做出y=log2017x和y=log2018x两个函数的图象，结合图象求解即可【解答】解：实数a，b满足等式log2017a=log2018b，即y=log2017x在x=a处的函数值和y=log2018x在x=b处的函数值相等，由下图可知②③⑤均有可能成立，不可能成立的是①④．故选：C．【点评】本题考查命题真假的判断，考查对数函数等基础知识，考查化归与转化思想、数形结合思想，是中档题．11．（5分）直线x=t（t＞0）与函数f（x）=x2+1，g（x）=lnx的图象分别交于A、B两点，当|AB|最小时，t值是（）A．1 B． C．D．【分析】将两个函数作差，得到函数y=f（x）﹣g（x），再求此函数的最小值对应的自变量x的值．【解答】解：设函数y=f（x）﹣g（x）=x2﹣lnx+1，求导数得y′=2x﹣=当0＜x＜时，y′＜0，函数在（0，）上为单调减函数，当x＞时，y′＞0，函数在（，+∞）上为单调增函数所以当x=时，所设函数的最小值为+ln2，所求t的值为．故选B．【点评】可以结合两个函数的草图，发现在（0，+∞）上x2＞lnx恒成立，问题转化为求两个函数差的最小值对应的自变量x的值．12．（5分）设函数f（x）（x∈R）满足f（﹣x）=f（x），f（π﹣x）=f（x），f′（x）是f（x）的导函数，当x∈[0，π]时，0≤f（x）≤1；当x∈（0，π）且x时，（x﹣）f′（x）＞0，则函数y=f（x）﹣|lg（x+1）|在（﹣1，2π]上的零点个数为（）A．5 B．6 C．7 D．8【分析】以分界点进行讨论，确定函数的单调性，利用函数的图形，画出草图进行求解，即可得到结果．【解答】解：∵f（x）（x∈R）满足f（﹣x）=f（x），∴f（x）为偶函数，∵f（π﹣x）=f（x），∴f（x﹣π）=f（x），∴f（x）是以π为周期的周期函数，当x∈[0，π]时，0≤f（x）≤1，∵x∈（0，π）且x≠时，（x﹣）f′（x）＞0，∴当x∈（0，）时，f′（x）＜0，f（x）单调递减；当x∈（，π）时，f′（x）＞0，f（x）单调递增，分别画出y=f（x）与y=|lg（x+1）|的草图如图，由图象可得函数y=f（x）﹣|lg（x+1）|在（﹣1，2π]上的零点个数为5个，故选：A．【点评】本题考查函数的单调性，考查函数的零点，考查函数的周期性与奇偶性，利用数形结合的思想来求解，会化难为易．二、填空题：本大题共4小题，每小题5分．13．（5分）已知函数f（x）=e|2x+a|（a为常数）．若f（x）在区间[1，+∞）上是增函数，则a的取值范围是[﹣2，+∞）．【分析】令t=|2x+a|，根据外函数为增函数，要使f（x）在区间[1，+∞）上是增函数，只需内函数t=|2x+a|在区间[1，+∞）上是增函数，由此求得a的取值范围．【解答】解：令t=|2x+a|，则外函数y=e t为增函数，要使f（x）在区间[1，+∞）上是增函数，则内函数t=|2x+a|在区间[1，+∞）上是增函数，∴a≥﹣2．∴a的取值范围是[﹣2，+∞）故答案为：[﹣2，+∞）．【点评】本题考查与指数函数有关的复合函数的单调性，复合函数的单调性满足同增异减的原则，是基础题．14．（5分）里氏震级M的计算公式为：M=lgA﹣lgA0，其中A是测震仪记录的地震曲线的最大振幅，A0是相应的标准地震的振幅，假设在一次地震中，测震仪记录的最大振幅是1000，此时标准地震的振幅A0为0.001，则此次地震的震级为6 级；9级地震的最大的振幅是5级地震最大振幅的10000 倍．【分析】根据题意中的假设，可得M=lgA﹣lgA0=lg1000﹣lg0.001=6；设9级地震的最大的振幅是x，5级地震最大振幅是y，9=lgx+3，5=lgy+3，由此知9级地震的最大的振幅是5级地震最大振幅的10000倍．【解答】解：根据题意，假设在一次地震中，测震仪记录的最大振幅是1000，此时标准地震的振幅为0.001，则M=lgA﹣lgA0=lg1000﹣lg0.001=3﹣（﹣3）=6．设9级地震的最大的振幅是x，5级地震最大振幅是y，9=lgx+3，5=lgy+3，解得x=106，y=102，∴．故答案为：6，10000．【点评】本题考查对数的运算法则，解题时要注意公式的灵活运用．15．（5分）设函数f（x）=，若f（a）＞a，则实数a的取值范围是（﹣∞，﹣1）∪（1，+∞）．【分析】根据分段函数的解析式，分段求解即可．【解答】解：函数f（x）=，则f（a）=，∵f（a）＞a，∴或解得：a＞1或a＜﹣1．∴实数a的取值范围是（﹣∞，﹣1）∪（1，+∞）．故答案为：（﹣∞，﹣1）∪（1，+∞）．【点评】本题考查了分段函数的不等式的求解，主要分段函数各自的定义域范围．属于基础题．16．（5分）设函数f（x）=，已知f（2）=5，则f（﹣2）= ﹣3 ．【分析】将函数f（x）分离，把x=2带入的值等于5，利用奇偶性找出关系式即可得答案．【解答】解：f（x）===1+．∵f（2）=5，∴=4．那么：f（﹣2）=1﹣=﹣3．故答案为：﹣3．【点评】本题考查了函数的化解和奇偶性的灵活运用．属于基础题．三、解答题：共70分.解答应写出文字说明，证明过程或演算步骤.17．（12分）已知集合A={x|﹣2≤x≤a}（a＞0），B={y|y=2x+3，x∈A}，C={z|z=x2，x∈A}，（1）当a=1时，试判断C⊆B是否成立？（2）若C⊆B，求a的取值范围．【分析】（1）将a=1代入，分别求出集合A，B，C，进而可判断出C⊆B成立（2）由已知可得B={y|y=2x+3，x∈A}=[﹣1，2a+3]，当0＜a≤2时，C={z|z=x2，x∈A}=[0，4]，当a＞2时，C={z|z=x2，x∈A}=[0，a2]，结合C⊆B，可得满足条件的a的取值范围．【解答】（本小题满分12分）解：（1）当a=1时，∵集合A={x|﹣2≤x≤1}=[﹣2，1]，B={y|y=2x+3，x∈A}=[﹣1，5]，C={z|z=x2，x∈A}=[0，4]，∴C⊆B成立（2）∵集合A={x|﹣2≤x≤a}（a＞0），B={y|y=2x+3，x∈A}=[﹣1，2a+3]，当0＜a≤2时，C={z|z=x2，x∈A}=[0，4]，而C⊆B，则2a+3≥4，解得：a≥，故≤a≤2；当a＞2时，C={z|z=x2，x∈A}=[0，a2]，而C⊆B，则2a+3≥a2，解得：﹣1≤a ≤3，故2＜a≤3；∴a的取值范围为≤a≤3．【点评】本题考查的知识点是集合的包含关系判断及应用，分类讨论思想，难度中档．18．（12分）已知函数f（x）=x2+bx+c若对于∀x∈R都有f（2﹣x）=f（x），且在x轴上截得的弦长为4．（1）试求f（x）的解析式；（2）设函数g（x）=，求g（x）在区间[2，5]上的最值．【分析】（1）利用二次函数的对称轴，以及在x轴上截得的弦长为4，列出方程求解即可．（2）化简函数的解析式，利用函数的单调性求解函数的最值即可．【解答】（本小题满分12分）解：（1）函数f（x）=x2+bx+c，∵对于∀x∈R都有f（2﹣x）=f（x），∴x=1是函数的对称轴，即b=﹣2．又∵在x轴上截得的弦长为4，∴x1=﹣1，x2=3，f（x）的解析试：f（x）=x2﹣2x﹣3．（2）函数g（x）====x﹣1﹣．则g（x）在区间[2，5]上单调递增，g（x）min=g（2）=﹣3．g（x）max=g（5）=3．【点评】本题考查二次函数的解析式的求法，函数的单调性的应用，考查计算能力．19．（12分）已知f（x）=m（x﹣2m）（x+m+3）（m≠0），g（x）=2x﹣2．（1）若函数y=|g（x）|与y=f（x）有相同的单调区间，求m值；（2）∃x∈（﹣∞，﹣4），f（x）g（x）＜0，求m的取值范围．【分析】（1）求得y=|g（x）|的单调区间，以及二次函数的对称轴和零点，即可得到m的方程，解方程可得m的值；（2）由x∈（﹣∞，﹣4）时，g（x）＜0，则∃x∈（﹣∞，﹣4），f（x）＞0．考虑其否定，结合二次函数的性质，得到m的不等式组，解不等式可得m的范围．【解答】解：（1）函数y=|g（x）|=，|g（x）|在（﹣∞，1）上是减函数，在（1，+∞）是增函数．对于f（x），m≠0时为二次函数，两个零点2m，﹣m﹣3，其对称轴为x=即x=，则=1，可得m=5；（2）x∈（﹣∞，﹣4）时，g（x）＜0，则∃x∈（﹣∞，﹣4），f（x）＞0．考虑其否定：∀x∈（﹣∞，﹣4），f（x）≤0，对于f（x），m≠0时为二次函数，两个零点2m，﹣m﹣3，则有，解得﹣2≤m≤0．∃x∈（﹣∞，﹣4），f（x）＞0，则m＜﹣2或m＞0．【点评】本题考查二次函数和指数函数的单调性，考查不等式的性质及应用，考查运算能力，属于中档题．20．（12分）已知两条直线l1：y=m和l2：y=（m＞0），l1与函数y=|log2x|的图象从左至右相交于点A，B，l2与函数y=|log2x|的图象从左至右相交于点C，D．记线段AC和BD在x轴上的投影长度分别为a，b．（1）当m变化时，试确定=f（m）的表达式；（2）求出=f（m）的最小值．【分析】（1）首先设出点的坐标，然后结合对数的运算法则得到函数的解析式即可；（2）结合（1）的结论和均值不等式的性质整理计算即可求得最终结果．【解答】解：（1）设A（x1，y1），B（x2，y2），C（x3，y3），D（x4，y4），由题意知：，又因为log2x2=m，∴，∴．则：．（2）由（1）可知：，当且仅当，即时取得最小值．【点评】本题考查对数的运算法则，均值不等式求最值等，重点考查学生对基础概念的理解和计算能力，属于中等题．21．（12分）已知函数，曲线y=f（x）在点（1，f（1））处的切线方程是5x﹣4y+1=0．（Ⅰ）求a，b的值；（Ⅱ）设g（x）=2ln（x+1）﹣mf（x），若当x∈[0，+∞）时，恒有g（x）≤0，求m的取值范围．【分析】（Ⅰ）求导函数，利用曲线y=f（x）在点（1，f（1））处的切线方程是5x﹣4y+1=0，建立方程组，即可求a，b的值；（Ⅱ）由（Ⅰ）知：，，求导函数，构建新函数h（x）=﹣mx2+（2﹣2m）x+2﹣2m，分类讨论，确定g（x）在[0，+∞）上的单调性，即可得到结论．【解答】解：（Ⅰ）求导函数，可得．∵曲线y=f（x）在点（1，f（1））处的切线方程是5x﹣4y+1=0．∴，∴，∴﹣﹣﹣﹣﹣﹣﹣（4分）（Ⅱ）由（Ⅰ）知：，∴，则，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（6分）令h（x）=﹣mx2+（2﹣2m）x+2﹣2m，当m=0时，h（x）=2x+2，在x∈[0，+∞）时，h（x）＞0，∴g′（x）＞0，即g（x）在[0，+∞）上是增函数，则g（x）≥g（0）=0，不满足题设．当m＜0时，∵且h（0）=2﹣2m＞0∴x∈[0，+∞）时，h（x）＞0，g′（x）＞0，即g（x）在[0，+∞）上是增函数，则g（x）≥g（0）=0，不满足题设．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（8分）当0＜m＜1时，则△=（2﹣2m）2+4m（2=2m）=4（1﹣m2）＞0，由h（x）=0得；则x∈[0，x2）时，h（x）＞0，g′（x）＞0即g（x）在[0，x2）上是增函数，则g（x2）≥g（0）=0，不满足题设．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（10分）当m≥1时，△=（2﹣2m）2+4m（2=2m）=4（1﹣m2）≤0，h（x）≤0，g′（x）≤0，即g（x）在[0，+∞）上是减函数，则g（x）≤g（0）=0，满足题设．综上所述，m∈[1，+∞）﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（12分）【点评】本题考查导数知识的运用，考查导数的几何意义，考查函数的单调性，考查分类讨论的数学思想，正确求导，合理分类是关键．请考生在第22、23两题中任选一题作答，如果多做．则按所做的第一题记分．作答时请写清题号．[选修4-4：极坐标系与参数方程]22．（10分）在直角坐标系中，曲线C1的参数方程为（α为参数），M是曲线C1上的动点，点P满足=2（1）求点P的轨迹方程C2；（2）以O为极点，x轴正半轴为极轴的极坐标系中，射线与曲线C1、C2交于不同于极点的A、B两点，求|AB|．【分析】（1）首先设P（x，y），由题意知M与P的关系，再由M是曲线C1上的动点，求出点P的参数方程，即：（α为参数），从而得到C2的轨迹方程为：（x﹣4）2+y2=16．（2）为了求出线段AB的长度，首先把把曲线C1的方程转化为极坐标方程为：ρ=4cosθ，再把曲线C2方程转化为的极坐标方程为：ρ=8cosθ，最后利用射线与C1的交点A的极径为，射线与C2的交点B的极径为．，最终求出线段AB的长度．【解答】解：（1）设P（x，y），由题意知M（，），M是曲线C1上的动点，所以：（α为参数），整理得：（α为参数），从而C2的轨迹方程为：（x﹣4）2+y2=16．（2）依题意把曲线C1的方程转化为极坐标方程为：ρ=4cosθ，曲线C2方程转化为的极坐标方程为：ρ=8cosθ，射线与C1的交点A的极径为，射线与C2的交点B的极径为．，所以：|AB|=|ρ1﹣ρ2|=2．【点评】本题考查的知识点，参数方程及极坐标方程与普通方程的互化，利用极径求线段的长度，属于基础题型．[选修4-5：不等式选讲]23．设函数f（x）=|x﹣a|．（1）当a=2时，解不等式f（x）≥7﹣|x﹣1|；（2）若f（x）≤2的解集为[﹣1，3]，=a（m＞0，n＞0），求证：m+4n．【分析】（1）把原不等式去掉绝对值，转化为与之等价的三个不等式组，分别求得每个不等式组的解集，再取并集，即得所求．（2）由题意求得+=1，再根据m+4n=（m+4n）•（+），利用基本不等式证得结论成立．【解答】解：（1）当a=2时，不等式f（x）≥7﹣|x﹣1|，即|x﹣2|+|x﹣1|≥7，∴①，或②，或③．解①求得x≤﹣2，解②求得x∈∅，解③求得x≥5，∴不等式的解集为（﹣∞﹣2]∪[5，+∞）．（2）f（x）≤2，即|x﹣a|≤2，解得a﹣2≤x≤a+2，而f（x）≤2解集是[﹣1，3]，∴，解得a=1，∴ +=1 （m＞0，n＞0）．∴m+4n=（m+4n）•（+）=3++≥3+2，当且仅当=，即m=+1，n=时，取等号．【点评】本题主要考查绝对值不等式的解法，基本不等式的应用，属于中档题．。

宁夏回族自治区银川市2018届高三数学上学期第一次月考试题文2017090502127

宁夏回族自治区银川市 2018届高三数学上学期第一次月考试题文第Ⅰ卷 (选择题共 60分)一、选择题：本大题共 12小题，每小题 5分，满分 60分.在每小题给出的四个选项中，只有一项是符合题目要求的.x1Ax x B31x1．已知集合，则2xA ． A Bx x2B ． ABx x2C ． ABx - 2 x0或xD ． ABx 0 x12．“x>1”是“ log (2) 0 ”的1 x2A ．充要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件 3．函数 y3 sin 2x cos 2x 的一个对称轴为π2π5 A ．x=B ．x=C ．x=D ．x=42364．设 a 0.60.6，b 0.61.5，c1.50.6，则 a ，b ，c 的大小关系是A ． a ＜b ＜cB ． a ＜c ＜bC ．b ＜a ＜cD ．b ＜c ＜af x x 5．函数cos5．函数cos6（0 ）的最小正周期为，则 fx满足A ．在 0,上单调递增B ．图象关于直线3x对称6C ． f3 3 2D ．当 x5时有最小值 1 12的最小值是6．函数cos2sinf x x x297A．-2B．-C．-D．0887．函数f(x)ln(x22x8)的单调递减区间是A．(,2)B．(,1)C．(1,)D．(4,) 8．在△ABC中,角A,B,C的对边分别是a,b,c,且满2a c cos B b cos C,则A的取值范围222, A.0 C.，D.， B.0，3333x1x22,1f(x)f(a)4f(14a)9．已知函数，且，则log(x1),x127531A．B．C．D．4444110 x4x log x10．当时，有，则 a 的取值范围是a22 2A. ，,1B. C.1，2D.2，22 211．已知函数 f (x ) A sin(x) 的图象如图所示，则该函数的解析式可能是A. f 3 3 (x )sin( x 4 2) 64 4 B. f (x ) sin( x5 5 1 5 )C. f (x ) 4 5sin( x 5 6) 64 2 D. f (x ) sin( x5 3 1 5 )12. 设函数 f (x ) e x (2x 1) ax a 其中 a 1,若存在唯一的整数 x 0 ,使得 f (x 0 ) 0 ,则 a 的取值范围是A. -3 2e,1B.3 2e , 343 C.2e,343 D. 2e,1第Ⅱ卷（非选择题共 90分）本卷包括必考题和选考题两部分．第 13题～第 21题为必考题，每个试题考生都必须做答．第 22题～第 23题为选考题，考生根据要求做答．二、填空题：本大题共 4小题，每小题 5分．m n13．对于任意的两个正数 m ，n ，定义运算⊙：当 m 、n 都为偶数或都为奇数时，m ⊙n ＝；2当 m 、n 为一奇一偶时，m ⊙n ＝ mn ，设集合 A ＝{(a ，b )|a ⊙b ＝4，a ，b ∈N*}，则集合 A 的子集个数为________．14．如图，某工程中要将一长为100 m，倾斜角为75°的斜坡改造成倾斜角为30°的斜坡，并保持坡高不变，则坡底需加长________m.15．已知命题p：关于x的不等式a x1(a0且a1)的解集是x x0，命题q：函数lg()的定义域为R，如果p∨q为真命题，p∧qy ax2x a为假命题，则实数a的取值范围为________________．16．设函数f(x)(x R)满足f(x)f(x)sin x当0x时，f(x)0则2f23(6)________ .三、解答题：本大题共6小题，共70分。

2018届宁夏银川九中高三上学期期中考试理科数学试题及答案精品

宁夏银川九中高三年级期中试卷理科数学本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分．第II 卷第22—24题为选考题，其他题为必考题．考生作答时，将答案答在答题卡上，在本试卷上答题无效．注意事项：1．答题前，考生先将自己的姓名、准考证号填写在答题卡上． 2．选择题答案使用2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其他答案标号；非选择题答案使用0.5毫米的黑色中性（签字）笔或炭素笔书写，字体工整，笔迹清楚．3．请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效．4．保持卡面清洁，不折叠，不破损．5．作选考题时，考生按照题目要求作答，并用2B 铅笔在答题卡上把所选题目对应的标号涂黑．第I 卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．函数23log (21)y x =-的定义域是（）A ．[1，2]B ．[1,2)C ．1(,1]2D ．1[,1]22. 已知命题p ：“x ∈R，x 2＋1>0”；命题q ：“x ∈R，e x＝1-”则下列判断正确的是 ( )MNU A. p ∨q 为真命题， ⌝p 为真命题 B. p ∨q 为真命题，⌝p 为假命题C. p ∧q 为真命题， ⌝p 为真命题D. p ∧q 为真命题，⌝p 为假命题3.设全集U 是实数集R ，M={x|x 2＞4}，N={x|1＜x ＜3}，则图中阴影部分所表示的集合是（） A.{x|-2≤x＜1} B. {x|-2≤x≤2}C.{x|1＜x≤2}D.{x|x ＜2} 4．函数2()2(,)f x x x m x m R =++∈的最小值为1-，则21()f x dx⎰等于（） A ．2B ．163C ．6D ．75．已知,,a b ∈R 则“33log log a b >”是“11()()22ab<”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件6．已知函数)(x f 是奇函数，当0>x 时，)10()(≠>=a a a x f x 且 , 且3)4(log 5.0-=f ，则a 的值为（）A.3 B. 3 C. 9 D.237．函数1()()sin 2xf x x π=-在区间[0,2]上的零点个数为（）A ．1个B ．2个C ．3个D ．4个8．下面是函数f(x)在区间[1，2]上的一些点的函数值x 1 1.251.375 1.4065 1.438 1.5 1.61 1.875 2f(x )-2 -0.984 0.260 -0.052 0.165 0.625-0.315 4.356由此可判断：方程f(x)=0在[1，2]解的个数（）A.至少5个B.5个C.至多5个D.4个9.△ABC 中，a,b,c 分别是内角A ，B ，C 所对的边，且cos 2B+3cos(A+C)+2=0,b=3,则c ∶sin C 等于（）A.3∶ 1B.3∶ 1 C.2∶ 1D.2∶1 10、下图是函数y ＝A sin(ωx ＋φ)(x ∈R)在区间⎣⎢⎢⎡⎦⎥⎥⎤－π6，5π6上的图象，为了得到这个函数的图象，只要将y ＝sin x (x ∈R)的图象上所有的点( )A ．向左平移π3个单位长度，再把所得各点的横坐标缩短到原来的12倍，纵坐标不变B ．向左平移π3个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变C ．向左平移π6个单位长度，再把所得各点的横坐标缩短到原来的12倍，纵坐标不变 D ．向左平移π6个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变11．当210≤<x 时，x a x log 4<，则a 的取值范围是（）A. (0，22)B. (22，1) C. (1，2) D. (2，2)12. 锐角△ABC 中，B=2A ，则b a的取值范围是（）A.(-2,2)B.(0,2）C.(2,2)D.(2,3)第II 卷本卷包括必考题和选考题两部分，第13题－第21题为必考题，每个试题考生都必须做答，第22—24题为选考题，考生根据要求做答．二、填空题：本大题共4小题，每小题5分． 13．设函数x x e e x f -+=)(，若曲线)(x f y =上在点))(,(00x f x P 处的切线斜率为32，则=0x .14．若命题“存在实数x ，使210x ax ++<”的否定．．是假命题，则实数a的取值范围为。

宁夏银川一中2017-2018学年高三上学期第一次月考数学理试卷 Word版含解析

2017-2018学年宁夏银川一中高三（上）第一次月考数学试卷（理科）一、选择题：本大题共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．设U=R，A={x|x2﹣3x﹣4＞0}，B={x|x2﹣4＜0}，则（∁U A）∩B=（）A．{x|x≤﹣1，或x≥2}B．{x|﹣1≤x＜2}C．{x|﹣1≤x≤4}D．{x|x≤4} 2．设i为虚数单位，复数（2﹣i）z=1+i，则z的共轭复数在复平面中对应的点在（）A．第一象限 B．第二象限 C．第三象限 D．第四象限3．若“x＞a”是“x＞1或x＜﹣3”的充分不必要条件，则a的取值范围是（）A．a≥1 B．a≤1 C．a≥﹣3 D．a≤﹣34．下列函数中，既是偶函数又在（﹣∞，0）上单调递增的是（）A．y=x2 B．y=2|x|C．y=log2D．y=sinx5．当0＜x＜1时，则下列大小关系正确的是（）A．x3＜3x＜log3x B．3x＜x3＜log3x C．log3x＜x3＜3x D．log3x＜3x＜x36．f（x）=﹣+log2x的一个零点落在下列哪个区间（）A．（0，1）B．（1，2）C．（2，3）D．（3，4）7．已知f（x）=，则不等式x+2xf（x+1）＞5的解集为（）A．（1，+∞）B．（﹣∞，﹣5）∪（1，+∞）C．（﹣∞，﹣5）∪（0，+∞）D．（﹣5，1）8．函数f（x）的图象向右平移1个单位长度，所得图象与曲线y=e x关于y轴对称，则f（x）=（）A．e x+1B．e x﹣1C．e﹣x+1 D．e﹣x﹣19．已知函数f（x）=e|x|+x2，（e为自然对数的底数），且f（3a﹣2）＞f（a﹣1），则实数a 的取值范围是（）A． B．C．D．10．函数y=2x2﹣e|x|在[﹣2，2]的图象大致为（）A．B．C．D．11．已知定义在R上的函数y=f（x）满足：函数y=f（x﹣1）的图象关于直线x=1对称，且当x∈（﹣∞，0），f（x）+xf′（x）＜0（f′（x）是函数f（x）的导函数）成立．若，b=（ln2）•，则a，b，c的大小关系是（）A．a＞b＞c B．b＞a＞c C．c＞a＞b D．a＞c＞b12．已知函数f（x）=，若方程f（x）=a有四个不同的解x1，x2，x3，x4，且x1＜x2＜x3＜x4，则x3（x1+x2）+的取值范围是（）A．（﹣1，+∞）B．（﹣1，1] C．（﹣∞，1）D．[﹣1，1）二、填空题：本大题共4小题，每小题5分．13．f（x）=的定义域为．14．已知函数y=f（x﹣1）是奇函数，且f （2）=1，则f （﹣4）=．15．已知f（x）为偶函数，当x＜0时，f（x）=ln（﹣x）+3x，则曲线y=f（x）在点（1，﹣3）处的切线方程是．16．已知函数f（x）=，若关于x的方程f2（x）﹣af（x）=0恰有5个不同的实数解，则a的取值范围是．三、解答题：本大题共5小题，共74分．解答应写出文字说明，证明过程或演算步骤．17．（12分）有两个命题，p：关于x的不等式a x＞1（a＞0，且a≠1）的解集是{x|x＜0}；q：函数y=lg（ax2﹣x+a）的定义域为R．如果p∨q为真命题，p∧q为假命题，求实数a的取值范围．18．（12分）某厂生产某种产品的年固定成本为250万元，每生产x万件，需另投入的成本为C（x）（单位：万元），当年产量小于80万件时，C（x）=x2+10x；当年产量不小于80万件时，C（x）=51x+﹣1450．假设每万件该产品的售价为50万元，且该厂当年生产的该产品能全部销售完．（1）写出年利润L（x）（万元）关于年产量x（万件）的函数关系式；（2）年产量为多少万件时，该厂在该产品的生产中所获利润最大？最大利润是多少？19．（12分）已知函数f（x）的图象与函数h（x）=x++2的图象关于点A（0，1）对称．（Ⅰ）求f（x）的解析式；（Ⅱ）若g（x）=x2•[f（x）﹣a]，且g（x）在区间[1，2]上为增函数，求实数a的取值范围．20．（12分）已知f（x）═ax﹣﹣51nx，g（x）=x2﹣mx+4（1）若x=2是函数f（x）的极值点，求a的值；（2）当a=2时，若∃x1∈（0，1），∀x2∈[1，2]都有f（x1）≥g（x2）成立，求实数m的取值范围．21．（12分）已知函数f（x）=﹣x2+alnx（a∈R）．（Ⅰ）当a=2时，求函数f（x）在点（1，f（1））处的切线方程；（Ⅱ）若函数g（x）=f（x）﹣2x+2x2，讨论函数g（x）的单调性；（Ⅲ）若（Ⅱ）中函数g（x）有两个极值点x1，x2（x1＜x2），且不等式g（x1）≥mx2恒成立，求实数m的取值范围．[选修4-1：几何证明选讲]22．（10分）如图所示，已知PA与⊙O相切，A为切点，PBC为割线，弦CD∥AP，AD、BC相交于E点，F为CE上一点，且DE2=EF•EC．（Ⅰ）求证：∠P=∠EDF；（Ⅱ）求证：CE•EB=EF•EP．[选修4-4：坐标系与参数方程]23．在平面直角坐标系xOy中，已知曲线C1：（θ为参数），以平面直角坐标系xOy的原点O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线l：ρ（2cosθ﹣sinθ）=6．（1）将曲线C1上的所有点的横坐标伸长为原来的倍，纵坐标伸长为原来的2倍后得到曲线C2，试写出直线l的直角坐标方程和曲线C2的参数方程；（2）在曲线C2上求一点P，使点P到直线l的距离最大，并求出此最大值．[选修4-5：不等式选讲]24．已知函数f（x）=|x+a|+|2x﹣1|（a∈R）．（l）当a=1，求不等式f（x）≥2的解集；（2）若f（x）≤2x的解集包含[，1]，求a的取值范围．2016-2017学年宁夏银川一中高三（上）第一次月考数学试卷（理科）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（2016秋•临猗县校级月考）设U=R，A={x|x2﹣3x﹣4＞0}，B={x|x2﹣4＜0}，则（∁U A）∩B=（）A．{x|x≤﹣1，或x≥2}B．{x|﹣1≤x＜2}C．{x|﹣1≤x≤4}D．{x|x≤4}【考点】交、并、补集的混合运算．【专题】集合思想；综合法；集合．【分析】分别求出集合A、B，从而求出A的补集，再求出其和B的交集即可．【解答】解：A={x|x2﹣3x﹣4＞0}={x|x＞4或x＜﹣1}，B={x|x2﹣4＜0}={x|﹣2＜x＜2}，则（∁U A）∩B=[﹣1，4]∩（﹣2，2）=[﹣1，2），故选：B．【点评】本题考查了集合的运算，考查解不等式问题，是一道基础题．2．（2016•海南校级三模）设i为虚数单位，复数（2﹣i）z=1+i，则z的共轭复数在复平面中对应的点在（）A．第一象限 B．第二象限 C．第三象限 D．第四象限【考点】复数代数形式的乘除运算．【专题】转化思想；综合法；数系的扩充和复数．【分析】利用复数的运算法则、共轭复数的定义、几何意义即可得出．【解答】解：复数（2﹣i）z=1+i，∴（2+i）（2﹣i）z=（2+i）（1+i），∴z=则z的共轭复数=﹣i在复平面中对应的点在第四象限．故选：D．【点评】本题考查了复数的运算法则、共轭复数的定义、几何意义，考查了推理能力与计算能力，属于基础题．3．（2016•杭州校级模拟）若“x＞a”是“x＞1或x＜﹣3”的充分不必要条件，则a的取值范围是（）A．a≥1 B．a≤1 C．a≥﹣3 D．a≤﹣3【考点】必要条件、充分条件与充要条件的判断．【专题】数形结合；转化思想；不等式的解法及应用；简易逻辑．【分析】根据“x＞a”是“x＞1或x＜﹣3”的充分不必要条件即可得出．【解答】解：∵“x＞a”是“x＞1或x＜﹣3”的充分不必要条件，如图所示，∴a≥1，故选：A．【点评】本题考查了简易逻辑的判定方法、不等式的性质，考查了推理能力与计算能力，属于基础题．4．（2013秋•洛阳期末）下列函数中，既是偶函数又在（﹣∞，0）上单调递增的是（）A．y=x2 B．y=2|x|C．y=log2D．y=sinx【考点】函数单调性的判断与证明；函数奇偶性的判断．【专题】函数的性质及应用．【分析】利用基本初等函数的性质逐一判断得出结论．【解答】解：对于A，由二次函数性质可知，函数又在（﹣∞，0）上单调递减，故排除A；对于B，由在（﹣∞，0）上y=得函数又在（﹣∞，0）上单调递减，故排除B；对于C，当x∈（﹣∞，0）时，y=，由复合函数的单调性可知，函数在（﹣∞，0）上单调递增，且由偶函数的定义可知函数为偶函数，故正确；对于D，由正弦函数的性质可知为奇函数，故排除D．故选C．【点评】考查学生对基本初等函数的性质单调性、奇偶性的掌握运用能力，可用排除法．5．（2014•钟祥市校级模拟）当0＜x＜1时，则下列大小关系正确的是（）A．x3＜3x＜log3x B．3x＜x3＜log3x C．log3x＜x3＜3x D．log3x＜3x＜x3【考点】不等关系与不等式；对数值大小的比较．【专题】函数的性质及应用．【分析】因为0＜x＜1，所以可选取中间数0，1，利用对数函数、幂函数、指数函数的单调性即可比较出其大小．【解答】解：∵0＜x＜1，∴log3x＜log31=0，0＜x3＜1，1=30＜3x，∴，故选C．【点评】掌握对数函数、指数函数、幂函数的单调性是解题的前提．6．（2012•市中区校级一模）f（x）=﹣+log2x的一个零点落在下列哪个区间（）A．（0，1）B．（1，2）C．（2，3）D．（3，4）【考点】函数零点的判定定理．【专题】计算题．【分析】根据函数的实根存在定理，要验证函数的零点的位置，只要求出函数在区间的两个端点上的函数值，得到结果．【解答】解：根据函数的实根存在定理得到f（1）•f（2）＜0．故选B．【点评】本题考查函数零点的判定定理，本题解题的关键是做出区间的两个端点的函数值，本题是一个基础题．7．（2016秋•荆州校级月考）已知f（x）=，则不等式x+2xf（x+1）＞5的解集为（）A．（1，+∞）B．（﹣∞，﹣5）∪（1，+∞）C．（﹣∞，﹣5）∪（0，+∞）D．（﹣5，1）【考点】一元二次不等式的解法．【专题】分类讨论；转化法；不等式的解法及应用．【分析】根据分段函数f（x）的解析式，讨论x的取值，解对应的不等式即可．【解答】解：由f（x）=知，当x+1＞1，即x＞0时，不等式x+2xf（x+1）＞5可化为x+2•2x＞5，解得x＞1；当x+1≤1，即x≤0时，不等式x+2xf（x+1）＞5可化为x﹣2x＞5，解得x＜﹣5；综上，不等式的解集为（﹣∞，﹣5）∪（1，+∞）．故选：B．【点评】本题考查了分段函数与不等式的解法和应用问题，也考查了分类讨论思想的应用问题，是基础题目．8．（2013•北京）函数f（x）的图象向右平移1个单位长度，所得图象与曲线y=e x关于y轴对称，则f（x）=（）A．e x+1B．e x﹣1C．e﹣x+1 D．e﹣x﹣1【考点】函数解析式的求解及常用方法；函数的图象与图象变化．【专题】函数的性质及应用．【分析】首先求出与函数y=e x的图象关于y轴对称的图象的函数解析式，然后换x为x+1即可得到要求的答案．【解答】解：函数y=e x的图象关于y轴对称的图象的函数解析式为y=e﹣x，而函数f（x）的图象向右平移1个单位长度，所得图象与曲线y=e x的图象关于y轴对称，所以函数f（x）的解析式为y=e﹣（x+1）=e﹣x﹣1．即f（x）=e﹣x﹣1．故选D．【点评】本题考查了函数解析式的求解与常用方法，考查了函数图象的对称变换和平移变换，函数图象的平移遵循“左加右减，上加下减”的原则，是基础题．9．（2014•江岸区校级模拟）已知函数f（x）=e|x|+x2，（e为自然对数的底数），且f（3a﹣2）＞f（a﹣1），则实数a的取值范围是（）A． B．C．D．【考点】函数单调性的性质．【专题】计算题．【分析】先判定函数的奇偶性和单调性，然后将f（3a﹣2）＞f（a﹣1）转化成f（|3a﹣2|）＞f（|a﹣1|），根据单调性建立不等关系，解之即可．【解答】解：∵f（x）=e|x|+x2，∴f（﹣x）=e|﹣x|+（﹣x）2=e|x|+x2=f（x）则函数f（x）为偶函数且在[0，+∞）上单调递增∴f（﹣x）=f（x）=f（|﹣x|）∴f（3a﹣2）=f（|3a﹣2|）＞f（a﹣1）=f（|a﹣1|），即|3a﹣2|＞|a﹣1|两边平方得：8a2﹣10a+3＞0解得a＜或a＞故选A．【点评】本题主要考查了函数的单调性和奇偶性的综合应用，绝对值不等式的解法，同时考查了转化的思想和计算能力，属于属于基础题．10．（2016春•厦门校级期末）函数y=2x2﹣e|x|在[﹣2，2]的图象大致为（）A．B．C．D．【考点】函数的图象．【专题】图表型；分析法；函数的性质及应用．【分析】根据已知中函数的解析式，分析函数的奇偶性，最大值及单调性，利用排除法，可得答案．【解答】解：∵f（x）=y=2x2﹣e|x|，∴f（﹣x）=2（﹣x）2﹣e|﹣x|=2x2﹣e|x|，故函数为偶函数，当x=±2时，y=8﹣e2∈（0，1），故排除A，B；当x∈[0，2]时，f（x）=y=2x2﹣e x，∴f′（x）=4x﹣e x=0有解，故函数y=2x2﹣e|x|在[0，2]不是单调的，故排除C，故选：D【点评】本题考查的知识点是函数的图象，对于超越函数的图象，一般采用排除法解答．11．（2015秋•韶关期末）已知定义在R上的函数y=f（x）满足：函数y=f（x﹣1）的图象关于直线x=1对称，且当x∈（﹣∞，0），f（x）+xf′（x）＜0（f′（x）是函数f（x）的导函数）成立．若，b=（ln2）•，则a，b，c的大小关系是（）A．a＞b＞c B．b＞a＞c C．c＞a＞b D．a＞c＞b【考点】对数值大小的比较．【专题】计算题；转化思想；综合法；函数的性质及应用．【分析】由导数性质推导出当x∈（﹣∞，0）或x∈（0，+∞）时，函数y=xf（x）单调递减．由此能求出结果．【解答】解：∵函数y=f（x﹣1）的图象关于直线x=1对称，∴y=f（x）关于y轴对称，∴函数y=xf（x）为奇函数．∵[xf（x）]'=f（x）+xf'（x），∴当x∈（﹣∞，0）时，[xf（x）]'=f（x）+xf'（x）＜0，函数y=xf（x）单调递减，当x∈（0，+∞）时，函数y=xf（x）单调递减．∵，，，，∴a＞b＞c．故选：A．【点评】本题考查三个数的大小的比较，是基础题，解题时要认真审题，注意导数性质、函数性质的合理运用．12．（2015•郴州模拟）已知函数f（x）=，若方程f（x）=a有四个不同的解x1，x2，x3，x4，且x1＜x2＜x3＜x4，则x3（x1+x2）+的取值范围是（）A．（﹣1，+∞）B．（﹣1，1] C．（﹣∞，1）D．[﹣1，1）【考点】函数的零点与方程根的关系．【专题】计算题；作图题；函数的性质及应用．【分析】作函数f（x）=的图象如下，由图象可得x1+x2=﹣2，x3x4=1；1＜x4≤2；从而化简x3（x1+x2）+，利用函数的单调性求取值范围．【解答】解：作函数f（x）=，的图象如下，由图可知，x1+x2=﹣2，x3x4=1；1＜x4≤2；故x3（x1+x2）+=﹣+x4，其在1＜x4≤2上是增函数，故﹣2+1＜﹣+x4≤﹣1+2；即﹣1＜﹣+x4≤1；故选B．【点评】本题考查了分段函数的应用，属于中档题．二、填空题：本大题共4小题，每小题5分．13．（2016秋•襄城区校级月考）f（x）=的定义域为（0，2）．【考点】函数的定义域及其求法．【专题】计算题；函数思想；数学模型法；函数的性质及应用．【分析】由分母中根式内部的代数式大于0，然后求解对数不等式得答案．【解答】解：由1﹣log2x＞0，得log2x＜1，解得0＜x＜2．∴f（x）=的定义域为（0，2）．故答案为：（0，2）．【点评】本题考查函数的定义域及其求法，考查了对数不等式的解法，是基础题．14．已知函数y=f（x﹣1）是奇函数，且f （2）=1，则f （﹣4）=﹣1．【考点】函数奇偶性的性质．【专题】综合题；转化思想；演绎法；函数的性质及应用．【分析】先推得函数y=f（x）的图象关于点（﹣1，0）中心对称，由此得出恒等式：f（x）+f（﹣2﹣x）=0，再令x=2代入即可解出f（﹣4）．【解答】解：因为函数y=f（x﹣1）是奇函数，所以y=f（x﹣1）的图象点（0，0）中心对称，而f（x﹣1）的图象向左平移一个单位，即得f（x）的图象，所以，y=f（x）的图象关于点（﹣1，0）中心对称，因此，对任意的实数x都有，f（x）+f（﹣2﹣x）=0，令x=2代入上式得，f（2）+f（﹣4）=0，由于f（2）=1，所以，f（﹣4）=﹣1，故答案为：﹣1．【点评】本题主要考查了抽象函数的图象和性质，涉及奇偶性的应用，函数图象对称中心的性质，属于中档题．15．（2016春•德宏州校级期末）已知f（x）为偶函数，当x＜0时，f（x）=ln（﹣x）+3x，则曲线y=f（x）在点（1，﹣3）处的切线方程是2x+y+1=0．【考点】利用导数研究曲线上某点切线方程．【专题】方程思想；函数的性质及应用；导数的概念及应用．【分析】由偶函数的定义，可得f（﹣x）=f（x），即有x＞0时，f（x）=lnx﹣3x，求出导数，求得切线的斜率，由点斜式方程可得切线的方程．【解答】解：f（x）为偶函数，可得f（﹣x）=f（x），当x＜0时，f（x）=ln（﹣x）+3x，即有x＞0时，f（x）=lnx﹣3x，f′（x）=﹣3，可得f（1）=ln1﹣3=﹣3，f′（1）=1﹣3=﹣2，则曲线y=f（x）在点（1，﹣3）处的切线方程为y﹣（﹣3）=﹣2（x﹣1），即为2x+y+1=0．故答案为：2x+y+1=0．【点评】本题考查导数的运用：求切线的方程，同时考查函数的奇偶性的定义和运用，考查运算能力，属于中档题．16．（2016•绍兴二模）已知函数f（x）=，若关于x的方程f2（x）﹣af（x）=0恰有5个不同的实数解，则a的取值范围是（0，1）．【考点】根的存在性及根的个数判断．【专题】作图题；函数的性质及应用．【分析】作f（x）的图象，从而由f2（x）﹣af（x）=f（x）（f（x）﹣a）=0可得f（x）=a 有三个不同的解，从而结合图象解得．【解答】解：作f（x）的图象如下，，f2（x）﹣af（x）=f（x）（f（x）﹣a）=0，∴f（x）=0或f（x）=a；∵f（x）=0有两个不同的解，故f（x）=a有三个不同的解，故a∈（0，1）；故答案为：（0，1）．【点评】本题考查了函数的零点与方程的根的关系应用．三、解答题：本大题共5小题，共74分．解答应写出文字说明，证明过程或演算步骤．17．（12分）（2016秋•庄浪县校级月考）有两个命题，p：关于x的不等式a x＞1（a＞0，且a≠1）的解集是{x|x＜0}；q：函数y=lg（ax2﹣x+a）的定义域为R．如果p∨q为真命题，p∧q为假命题，求实数a的取值范围．【考点】复合命题的真假．【专题】函数的性质及应用；不等式的解法及应用；简易逻辑．【分析】对于命题p：利用指数函数的单调性可得：0＜a＜1．对于命题q：函数y=lg（ax2﹣x+a）的定义域为R．等价于∀x∈R，ax2﹣x+a＞0．对a分类讨论，利用函数的图象与性质即可得出．如果p∨q为真命题，p∧q为假命题，则p真q假，或p假q真，即可得出．【解答】解：p：关于x的不等式a x＞1（a＞0，且a≠1）的解集是{x|x＜0}，∴0＜a＜1．q：函数y=lg（ax2﹣x+a）的定义域为R．等价于∀x∈R，ax2﹣x+a＞0．如果p∨q为真命题，p∧q为假命题，求实数a的取值范围．（i）a=0 不成立．（ii）a≠0 时，，解得，即q：a．如果p∨q为真命题，p∧q为假命题，则p真q假，或p假q真，∴或，解得，或a≥1．∴实数a的取值范围是，或a≥1．【点评】本题考查了不等式的解法、简易逻辑的判定方法、函数的性质，考查了推理能力与计算能力，属于中档题．18．（12分）（2016春•德州期末）某厂生产某种产品的年固定成本为250万元，每生产x万件，需另投入的成本为C（x）（单位：万元），当年产量小于80万件时，C（x）=x2+10x；当年产量不小于80万件时，C（x）=51x+﹣1450．假设每万件该产品的售价为50万元，且该厂当年生产的该产品能全部销售完．（1）写出年利润L（x）（万元）关于年产量x（万件）的函数关系式；（2）年产量为多少万件时，该厂在该产品的生产中所获利润最大？最大利润是多少？【考点】函数模型的选择与应用；函数解析式的求解及常用方法．【专题】应用题；函数的性质及应用．【分析】（1）分两种情况进行研究，当0＜x＜80时，投入成本为（万元），根据年利润=销售收入﹣成本，列出函数关系式，当x≥80时，投入成本为，根据年利润=销售收入﹣成本，列出函数关系式，最后写成分段函数的形式，从而得到答案；（2）根据年利润的解析式，分段研究函数的最值，当0＜x＜80时，利用二次函数求最值，当x≥80时，利用基本不等式求最值，最后比较两个最值，即可得到答案．【解答】解：（1）∵每件商品售价为0.005万元，∴x千件商品销售额为0.005×1000x万元，①当0＜x＜80时，根据年利润=销售收入﹣成本，∴=；②当x≥80时，根据年利润=销售收入﹣成本，∴=．综合①②可得，．（2）由（1）可知，，①当0＜x＜80时，=，∴当x=60时，L（x）取得最大值L（60）=950万元；②当x≥80时，=1200﹣200=1000，当且仅当，即x=100时，L（x）取得最大值L（100）=1000万元．综合①②，由于950＜1000，∴当产量为10万件时，该厂在这一商品中所获利润最大，最大利润为1000万元．【点评】本题主要考查函数模型的选择与应用．解决实际问题通常有四个步骤：（1）阅读理解，认真审题；（2）引进数学符号，建立数学模型；（3）利用数学的方法，得到数学结果；（4）转译成具体问题作出解答，其中关键是建立数学模型．本题建立的数学模型为分段函数，对于分段函数的问题，一般选用分类讨论和数形结合的思想方法进行求解．属于中档题．19．（12分）（2013•合肥二模）已知函数f（x）的图象与函数h（x）=x++2的图象关于点A（0，1）对称．（Ⅰ）求f（x）的解析式；（Ⅱ）若g（x）=x2•[f（x）﹣a]，且g（x）在区间[1，2]上为增函数，求实数a的取值范围．【考点】函数单调性的性质；函数解析式的求解及常用方法；奇偶函数图象的对称性．【专题】函数的性质及应用．【分析】（I）先设f（x）的图象上任一点P（x，y），再由点点对称求出对称的坐标，由题意把对称点的坐标代入h（x）的解析式，进行整理即可；（II）由（I）求出g（x）的解析式，再求出导数，将条件转化为：3x2﹣2ax+1≥0在区间[1，2]上恒成立，再分离出常数a，利用函数y=在区间[1，2]上的单调性求出函数的最小值，再求出a的范围．【解答】解：（I）设f（x）的图象上任一点P（x，y），则点P关于点A（0，1）对称P′（﹣x，2﹣y）在h（x）的图象上，∴2﹣y=﹣x﹣+2，得y=，即f（x）=，（II）由（I）得，g（x）=x2•[f（x）﹣a]=x2•[﹣a]=x3﹣ax2+x，则g′（x）=3x2﹣2ax+1，∵g（x）在区间[1，2]上为增函数，∴3x2﹣2ax+1≥0在区间[1，2]上恒成立，即a≤（）在区间[1，2]上恒成立，∵y=在区间[1，2]上递增，故此函数的最小值为y=4，则a≤4=2．【点评】本题考查了利用轨迹法求函数解析式，导数与函数单调性、最值问题，以及恒成立问题，考查了转化思想．20．（12分）已知f（x）═ax﹣﹣51nx，g（x）=x2﹣mx+4（1）若x=2是函数f（x）的极值点，求a的值；（2）当a=2时，若∃x1∈（0，1），∀x2∈[1，2]都有f（x1）≥g（x2）成立，求实数m的取值范围．【考点】利用导数求闭区间上函数的最值；利用导数研究函数的极值．【专题】综合题；转化思想；演绎法；导数的概念及应用．【分析】（1）利用x=2是函数f（x）的极值点，求出f′（2）=0，即可求出a的值；（2）对g（x）进行配方，讨论其最值问题，根据题意∃x1∈（0，1），∀x2∈[1，2]，总有f（x1）≥g（x2）成立，只要要求f（x）max≥g（x）max，即可，从而求出m的范围．【解答】解：（1）∵f（x）═ax﹣﹣51nx，∴f′（x）═a+﹣，∵x=2是函数f（x）的极值点，∴f′（2）═a+﹣=0，∴a=2，经检验a=2，x=2是函数f（x）的极值点；（2）当a=2时，f（x）=2x﹣﹣5lnx，g（x）=x2﹣mx+4=+4﹣，∃x1∈（0，1），∀x2∈[1，2]，总有f（x1）≥g（x2）成立，∴要求f（x）的最大值大于g（x）的最大值即可，f′（x）=，令f′（x）=0，解得x1=，x2=2，当0＜x＜，x＞2时，f′（x）＞0，f（x）为增函数；当＜x＜2时，f′（x）＜0，f（x）为减函数．∵x1∈（0，1），∴f（x）在x=出取得极大值，也是最大值，∴f（x）max=f（）=1﹣4+5ln2=5ln2﹣3，∵g（x）=x2﹣mx+4=+4﹣，若m≤3，g max（x）=g（2）=4﹣2m+4=8﹣2m，∴5ln2﹣3≥8﹣2m，∴m≥，∵＞3，故m不存在；若m＞3时，g max（x）=g（1）=5﹣m，∴5ln2﹣3≥5﹣m，∴m≥8﹣5ln2．【点评】本题考查了利用导数研究函数的单调性极值与最值、通过构造函数研究函数的单调性解决问题的方法，考查了转化能力、推理能力与计算能力，属于难题．21．（12分）（2016•抚顺一模）已知函数f（x）=﹣x2+alnx（a∈R）．（Ⅰ）当a=2时，求函数f（x）在点（1，f（1））处的切线方程；（Ⅱ）若函数g（x）=f（x）﹣2x+2x2，讨论函数g（x）的单调性；（Ⅲ）若（Ⅱ）中函数g（x）有两个极值点x1，x2（x1＜x2），且不等式g（x1）≥mx2恒成立，求实数m的取值范围．【考点】利用导数研究函数的极值；利用导数研究函数的单调性；利用导数研究曲线上某点切线方程．【专题】综合题；转化思想；综合法；导数的概念及应用．【分析】（Ⅰ）求当a=2时，函数的导数，求得切线的斜率和切点，由点斜式方程即可得到切线方程；（Ⅱ）求出g（x）的导数，分类讨论，令导数大于0，得增区间，令导数小于0，得减区间；（Ⅲ）不等式g（x1）≥mx2恒成立即为≥m，求得=1﹣x1++2x1lnx1，令h（x）=1﹣x++2xlnx（0＜x＜），求出导数，判断单调性，即可得到h（x）的范围，即可求得m的范围．【解答】解：（Ⅰ）因为当a=2时，f（x）=﹣x2+2lnx，所以f′（x）=﹣2x+．因为f（1）=﹣1，f'（1）=0，所以切线方程为y=﹣1；（Ⅱ）g（x）=x2﹣2x+alnx的导数为g′（x）=2x﹣2+=，a≤0，单调递增区间是（，+∞）；单调递减区间是（0，）；0＜a＜，单调递增区间是（0，），（，+∞）；单调递减区间是（，）；a≥，g（x）的单调递增区间是（0，+∞），无单调递减区间；（Ⅲ）由（II）函数g（x）有两个极值点x1，x2（x1＜x2），0＜a＜，x1+x2=1，0＜x1＜，＜x2＜1=1﹣x1++2x1lnx1，令h（x）=1﹣x++2xlnx（0＜x＜），h′（x）=+2lnx，由0＜x＜，则＜0，又2lnx＜0，则h′（x）＜0，即h（x）在（0，）递减，即有h（x）＞h（）=﹣﹣ln2，即m≤﹣﹣ln2，即有实数m的取值范围为（﹣∞，﹣﹣ln2]．【点评】本题考查导数的运用：求切线方程和单调区间，主要考查导数的几何意义，同时考查函数的单调性的运用，以及不等式恒成立问题转化为求函数的最值或范围，属于中档题．[选修4-1：几何证明选讲]22．（10分）（2015•海南模拟）如图所示，已知PA与⊙O相切，A为切点，PBC为割线，弦CD∥AP，AD、BC相交于E点，F为CE上一点，且DE2=EF•EC．（Ⅰ）求证：∠P=∠EDF；（Ⅱ）求证：CE•EB=EF•EP．【考点】与圆有关的比例线段．【专题】证明题．【分析】（1）根据所给的乘积式和对应角相等，得到两个三角形相似，由相似得到对应角相等，再根据两直线平行内错角相等，角进行等量代换，得到要证的结论．（2）根据第一问所得的结果和对顶角相等，得到两个三角形相似，根据三角形相似得到对应线段成比例，把比例式转化为乘积式，再根据相交弦定理得到比例式，等量代换得到结果．【解答】证明：（1）∵DE2=EF•EC，∴DE：CE=EF：ED．∵∠DEF是公共角，∴△DEF∽△CED．∴∠EDF=∠C．∵CD∥AP，∴∠C=∠P．∴∠P=∠EDF．（2）∵∠P=∠EDF，∠DEF=∠PEA，∴△DEF∽△PEA．∴DE：PE=EF：EA．即EF•EP=DE•EA．∵弦AD、BC相交于点E，∴DE•EA=CE•EB．∴CE•EB=EF•EP．【点评】本题考查三角形相似的判定和性质，考查两条直线平行的性质定理，考查相交弦定理，是一个比较简单的综合题目．[选修4-4：坐标系与参数方程]23．（2016春•宁夏校级期末）在平面直角坐标系xOy中，已知曲线C1：（θ为参数），以平面直角坐标系xOy的原点O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线l：ρ（2cosθ﹣sinθ）=6．（1）将曲线C1上的所有点的横坐标伸长为原来的倍，纵坐标伸长为原来的2倍后得到曲线C2，试写出直线l的直角坐标方程和曲线C2的参数方程；（2）在曲线C2上求一点P，使点P到直线l的距离最大，并求出此最大值．【考点】参数方程化成普通方程；简单曲线的极坐标方程．【专题】方程思想；转化思想；坐标系和参数方程．【分析】（1）直线l：ρ（2cosθ﹣sinθ）=6．把x=ρcosθ，y=ρsinθ代入可得直角坐标方程．由曲线C1：（θ为参数），将曲线C1上的所有点的横坐标伸长为原来的倍，纵坐标伸长为原来的2倍后得到曲线C2的参数方程：（α为参数）．（2）设P，点P到直线l的距离d==，利用三角函数的单调性与值域即可得出．【解答】解：（1）直线l：ρ（2cosθ﹣sinθ）=6．可得：直线l的直角坐标方程为：2x﹣y﹣6=0．由曲线C1：（θ为参数），将曲线C1上的所有点的横坐标伸长为原来的倍，纵坐标伸长为原来的2倍后得到曲线C2的参数方程：（α为参数）．（2）设P，点P到直线l的距离d==．∴当=﹣1时，d取得最大值=2，此时P．【点评】本题考查了参数方程化为普通方程、极坐标方程化为直角坐标方程、点到直线的距离公式、三角函数的值域，考查了推理能力与计算能力，属于中档题．[选修4-5：不等式选讲]24．（2014•河南模拟）已知函数f（x）=|x+a|+|2x﹣1|（a∈R）．（l）当a=1，求不等式f（x）≥2的解集；（2）若f（x）≤2x的解集包含[，1]，求a的取值范围．【考点】绝对值不等式的解法．【专题】不等式．【分析】对第（1）问，利用零点分段法，令|x+1|=0，|2x﹣1|=0，获得分类讨论的标准，最后取各部分解集的并集即可；对第（2）问，不等式f（x）≤2x的解集包含[，1]，等价于f（x）≤2x在[，1]内恒成立，由此去掉一个绝对值符号，再探究f（x）≤2x的解集与区间[，1]的关系．【解答】解：（1）当a=1时，由f（x）≥2，得|x+1|+|2x﹣1|≥2，①当x≥时，原不等式可化为（x+1）+（2x﹣1）≥2，得x≥，∴x≥；②当﹣1≤x＜时，原不等式可化为（x+1）﹣（2x﹣1）≥2，得x≤0，∴﹣1≤x≤0；③当x＜﹣1时，原不等式可化为﹣（x+1）﹣（2x﹣1）≥2，得x≤，∴x＜﹣1．综上知，原不等式的解集为{x|x≤0，或}．（2）不等式f（x）≤2x的解集包含[，1]，等价于f（x）≤2x在[，1]内恒成立，从而原不等式可化为|x+a|+（2x﹣1）≤2x，即|x+a|≤1，∴当x∈[，1]时，﹣a﹣1≤x≤﹣a+1恒成立，∴，解得，故a的取值范围是[﹣]．【点评】1．本题考查了含两个绝对值不等式的解法，一般有零点分段法，函数图象法等．2．第（2）问的关键是将条件转换成不等式恒成立问题，这也是本题的难点所在．。

宁夏银川九中2020届高三上学期第一次月考数学理试题Word版含答案

银川九中2017-2018学年度第一学期第一次月考试卷高三年级数学（理科）试卷（本试卷满分150分）命题人：杨世暄本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，全部为必考题。

考生作答时，将答案答在答题卡上，在本试卷上答题无效。

第Ⅰ卷（选择题）一、选择题（本题共12小题，每小题5分，共60分）1．已知全集U=R ，A={x |x 2＜16}，B={x |y=log 3（x ﹣4）}，则下列关系正确的是（） A ．A ∪B=R B ．A ∪（∁R B ）=R C ．A ∩（∁R B ）=R D ．（∁R A ）∪B=R 2.下列四个函数中,与y=x 表示同一函数的是( ) A ．y=()2B.y=C.y=√x 2D.y=3．给定下列结论：其中正确的个数是（）①用20cm 长的铁丝折成的矩形最大面积是252cm ；②命题“所有的正方形都是矩形”的否定是“所有的正方形都不是矩形”； ③函数2xy -=与函数12log y x =的图象关于直线y x =对称．A ．0B ．1C ．2D ．34．函数12log (32)y x =-的定义域是（）．A ．[1,)+∞B ．2(,)3+∞ C ．2[,1]3 D ．2(,1]35．三个数7.06，67.0，6log 7.0的大小顺序是（）A ．7.07.0666log 7.0<<B ．6log 67.07.07.06<<C ．67.07.07.066log << D ．7.067.067.06log <<6.已知函数f(x)的定义域为(-1,0),则函数f(2x+1)的定义域为( )(A)(-1,1) (B)(-1,-) (C)(-1,0) (D)(,1)7.函数()2x f x e x =+-的零点所在的一个区间是()A ．(2,1)--B ．(－1,0)C ．(0,1)D ．(1,2) 8．函数log (||1)(1)a y x a =+>的大致图像是（）9.已知)(x f 是定义域为R 的偶函数，且)2()2(x f x f -=+，当]2,0[∈x 时，x x x f 2)(2-=，则=-)5(f （）A, －1 B, 0 C, 1 D,3510．定义在R 上的函数f （x ），如果存在函数g （x ）=kx +b （k ，b 为常数）使得f （x ）≥g （x ）对一切实数x 都成立，则称g （x ）为f （x ）的一个承托函数，现在如下函数：①f （x ）=x 3；②f （x ）=2x ；③f （x ）=；则存在承托函数的f （x ）的序号为（） A ．①B ．②C ．①②D ．②③11．已知函数(1)f x +是定义在R 上的奇函数，若对于任意给定的不等实数1x 、2x ，不等式1212()[()()]0x x f x f x --<恒成立，则不等式(1)0f x -<的解集为（）A ．()1,+∞ B ．()0,+∞ C ．(),0-∞ D ．(),1-∞12．当102x <≤时，4log xa x <，则a 的取值范围是（） A ．（0，22） B ．（22，1） C ．（12） D ．2，2）二、填空题（本大题共4个小题，每小题5分，共20分）13.计算（lg 14-lg 25）÷12100-= .14,已知函数()41,05log ,0x f x x x x ⎧≤⎪=-⎨⎪>⎩，则()3f f -⎡⎤⎣⎦= ．15．设函数()f x 是定义在R 上的偶函数，且对于任意的x ∈R 恒有(1)()f x f x +=-，已知当[0,1]x ∈时，()3xf x =．则①2是()f x 的周期；②函数()f x 在（2，3）上是增函数； ③函数()f x 的最大值为1，最小值为0； ④直线2x =是函数()f x 图象的一条对称轴．其中所有正确．．命题的序号是 . 16.已知f (x )＝(31)4,1log ,1.a a x a x x x -+<⎧⎨⎩，≥是R 上的减函数，那么a 的取值范围是 . 三、解答题（本大题共6小题，共70分）17. （本小题满分12分）设有两个命题，p ：关于x 的不等式1>xa （a>0，且a ≠1）的解集是{x|x<0}；q ：函数)lg(2a x ax y +-=的定义域为R 。

(全优试卷)宁夏银川九中高三上学期第一次月考数学(理)试题Word版含答案

考生作答时，将答案答在答题卡上，在本试卷上答题无效。

第Ⅰ卷（选择题）一、选择题（本题共12小题，每小题5分，共60分）1．已知全集U=R ，A={x |x 2＜16}，B={x |y=log 3（x ﹣4）}，则下列关系正确的是（） A ．A ∪B=R B ．A ∪（∁R B ）=R C ．A ∩（∁R B ）=R D ．（∁R A ）∪B=R2.下列四个函数中,与y=x 表示同一函数的是( )A ．y=()2 B.y= C.y= D.y=3．给定下列结论：其中正确的个数是（） ①用20cm 长的铁丝折成的矩形最大面积是252cm ；②命题“所有的正方形都是矩形”的否定是“所有的正方形都不是矩形”；③函数2x y -=与函数12log y x =的图象关于直线y x =对称．A ．0B ．1C ．2D ．34．函数y = ）．A ．[1,)+∞B ．2(,)3+∞C ．2[,1]3D ．2(,1]35．三个数7.06，67.0，6log 7.0的大小顺序是（）A ．7.07.0666log 7.0<<B ．6log 67.07.07.06<<C ．67.07.07.066log << D ．7.067.067.06log <<6.已知函数f(x)的定义域为(-1,0),则函数f(2x+1)的定义域为( )(A)(-1,1) (B)(-1,-12) (C)(-1,0) (D)(12,1)7.函数()2x f x e x =+-的零点所在的一个区间是( )A ．(2,1)--B ．(－1,0)C ．(0,1)D ．(1,2)8．函数log (||1)(1)a y x a =+>的大致图像是（）9.已知)(x f 是定义域为R 的偶函数，且)2()2(x f x f -=+，当]2,0[∈x 时，x x x f 2)(2-=，则=-)5(f （）A, －1 B, 0 C, 1 D,3510．定义在R 上的函数f （x ），如果存在函数g （x ）=kx +b （k ，b 为常数）使得f （x ）≥g （x ）对一切实数x 都成立，则称g （x ）为f （x ）的一个承托函数，现在如下函数：①f （x ）=x 3；②f （x ）=2x ；③f （x ）=；则存在承托函数的f （x ）的序号为（） A ．① B ．② C ．①② D ．②③11．已知函数(1)f x +是定义在R 上的奇函数，若对于任意给定的不等实数1x 、2x ，不等式1212()[()()]0x x f x f x --<恒成立，则不等式(1)0f x -<的解集为（）A ．()1,+∞B ．()0,+∞C ．(),0-∞D ．(),1-∞12．当102x <≤时，4log x a x <，则a 的取值范围是（） A ．（0，2） B ．（2，1） C ．（1D ．2）二、填空题（本大题共4个小题，每小题5分，共20分） 13.计算（lg 14-lg 25）÷12100-= . 14,已知函数()41,05log ,0x f x x x x ⎧≤⎪=-⎨⎪>⎩，则()3f f -⎡⎤⎣⎦= ．15．设函数()f x 是定义在R 上的偶函数，且对于任意的x ∈R 恒有(1)()f x f x +=-，已知当[0,1]x ∈时，()3xf x =．则①2是()f x 的周期；②函数()f x 在（2，3）上是增函数；③函数()f x 的最大值为1，最小值为0；④直线2x =是函数()f x 图象的一条对称轴．其中所有正确．．命题的序号是 . 16.已知f (x )＝(31)4,1log , 1.a a x a x x x -+<⎧⎨⎩，≥是R 上的减函数，那么a 的取值范围是 . 三、解答题（本大题共6小题，共70分）17. （本小题满分12分）设有两个命题，p ：关于x 的不等式1>x a （a>0，且a ≠1）的解集是{x|x<0}；q ：函数)lg(2a x ax y +-=的定义域为R 。

2018年银川一中--高三第一次月考数学(理科)试卷答案最新

银川一中2018-2018高三第一次月考数学(理科)参考答案一、选择题：(每小题5分，共60分)二、填空题：(每小题5分，共20分)13．[)∞+-，2 14. 410 6 15. 8()()∞+⋃-，，101 16. -3三、解答题：17.（本小题满分12分）解：(1) 当1=a 时，}12|{≤≤-=x x A ，}51|{≤≤-=x x B ，}40|{≤≤=x x C ∴C B ⊆成立（2）{}|123B x x a =-≤≤+，当02a <≤时，{}|04C x x =≤≤，而C B ⊆，则1234,,22a a a +≥≥≤≤1即即2；当2a >时，{}2|0C x x a =≤≤，而C B ⊆，则223,3a a a +≥<≤即 2；∴132a ≤≤ 18．（本小题满分12分）（1）函数.)(2c bx x x f ++=对于,R x ∈∀都有)()2(x f x f =-1=∴x 是函数的对称轴，即2-=b又在x 轴上截得的弦长为4，3,121=-=∴x x)(x f 的解析试32)(2--=x x x f（2）函数()1411411321)()(22---=---=---=-=x x x x x x x x x f x g则)(x g 在区间[2,5]上单调递增()()32min -==g x g ()()35max ==g x g19. （本小题满分12分）解：(1) 函数)1()1(2222|)(|<≥⎩⎨⎧--==x x x g y xx, |)(|x g 在上)1,(-∞是减函数，在上),1(+∞是增函数.对于()f x ,0m ≠时为二次函数，两个零点2,3m m --∴其对称轴为23232-=--=m m m x ，则1123=⇒=-m m (2)(,4)x ∈-∞-时，()0g x <，(,4),()0x f x ∴∃∈-∞->.考虑其否定：(,4),()0x f x ∀∈-∞-≤.对于()f x ,0m ≠时为二次函数，两个零点2,3m m --，则有02434<⎧⎪≥-⎨⎪--≥-⎩m m m ，，，解得20m -≤≤.(,4),()0x f x ∴∃∈-∞->，则20m m <->或.20. （本小题满分12分）解：（1）设()()()()11223344,,,,,,,,A x y B x y C x y B x y ，D(x 4，y 4)，由题意知 121343241111====,;,;x x x x x x x x 又因为2122224412221+====+l o g ,;l o g ,.m m x m x x x m 82m 1+ 82122224412221+====+l o g ,;l o g ,.m m x m x xx m 4224241324|11|||||||)(x x x x x x x x x x m f a b =--=--==128128222+++==m m m m （2）由（1）)(m f 128128222+++==m m m m2124212-+++=m m 282214=≥-m ,m m 当且仅当即时，取最小值14214321222-=+==+21．(本小题满分12分)解：（1）22)1()()1)(2()(++-++='x bx ax x b ax x f .由于直线.0145=+-y x 的斜是45，且过点（23,1）， ∴⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧==⇒=+=+⇒='=21454323245)1(23)1(b a b a b a f f 即12)(2++=x xx x f -------4分（2）由（1）知：),1(12)1ln(2)(2->++-+=x x xx mx x g 则22)1(22)22()(+-+-+-='x mx m mx x g ，--------------------------6分令m x m mx x h 22)22()(2-+-+-=，当0=m 时，22)(+=x x h ，在[)+∞∈,0x 时，0)(>x h 0)(>'x g 即，)(x g 在[)+∞,0上是增函数，则0)0()(=≥g x g ，不满足题设.当0<m 时，∵011222<-=---mm m 且022)0(>-=m h ∴[)+∞∈,0x 时，0)(>x h 0)(>'x g 即，)(x g 在[)+∞,0上是增函数，则0)0()(=≥g x g ，不满足题设.----------------------------------8分当10<<m 时，则0)1(4)22(4)22(22>-==+-=m m m m ∆，由0)(=x h 得01121<---=m m m x ； 01122>-+-=mm m x则，),0[2x x ∈时，0)(>x h ，0)(>'x g 即，)(x g 在[)2,0x 上是增函数，则 0)0()(2=≥g x g ，不满足题设.--------------------------------------10分当1≥m 时，0)1(4)22(4)22(22≤-==+-=m m m m ∆，0)(≤x h 0)(≤'x g 即，)(x g 在[)+∞,0上是减函数，则0)0()(=≤g x g ，满足题设. 综上所述，),1[+∞∈m -------------------------------------------------12分选考题：共10分.请考生在第22、23题中任选一题做答，如果多做，则按所做的第一题记分.答时用2B 铅笔在答题卡上把所选题目的题号涂黑. 22. （本小题满分10分）选修4-4:极坐标系与参数方程 22.（10分）解:(I)设,则由条件知.因为M 点在上,所以为参数）ααα(sin 22cos 222⎪⎪⎩⎪⎪⎨⎧=+=y x…………2分即为参数）ααα(sin 4cos 44⎩⎨⎧=+=y x从而的轨迹方程为()16422=+-y x …………5分(Ⅱ)曲线的极坐标方程为θρcos 4=，曲线的极坐标方程为θρcos 8=射线6πθ=与的交点A 的极径为6cos 41πρ=射线6πθ=与的交点B 的极径为.6cos81πρ= ………………7分所以. ………………10分23．（本小题满分10分）解：（1）当2a =时，不等式为217x x -+-≥，∴1217x x x <⎧⎨-+-≥⎩或12217x x x ≤≤⎧⎨-+-≥⎩或2217x x x >⎧⎨-+-≥⎩，∴2x ≤-或5x ≥． ∴不等式的解集为(][),25,-∞-+∞ ．．．．．．．．．．．．．．．．．．． 5分（2）f(x)≤2即||2x a -≤，解得22a x a -≤≤+，而f(x)≤2解集是[-1，3]，．．．6分 ∴2123a a -=-⎧⎨+=⎩解得1a =，所以111(0,0)2m n m n +=>> ．．．．．．．．．．．7分∴1144(4)()3322n m m n m n m n m n+=++=++≥．（当且仅当21,4m n +==时取等号）．．．．．．．．．10分银川一中2018届高三第一次月考物理试卷答案二、选择题答案22（7分）(1)弹簧测力计 (2)23216549T a =，1.93m/s 2 ，1.18m/s23（8分）解析：(1)根据胡克定律，弹簧OC 伸长1.00 cm 时弹簧的弹力F c ＝k Δx ＝500×1.00×10－2N ＝5.00 N ；由题图可知弹簧秤a 的读数F a ＝3.00 N ，根据勾股定理，F a 2＋F b 2＝F c 2，解得F b ＝4.00 N 。

宁夏银川九中2018届高三上学期第一次月考数学理试题Word版含答案

2018届宁夏银川九中高三下学期第一次模拟考试理科数学试题及答案

宁夏银川市高三数学上学期第一次月考试题文

(优辅资源)宁夏银川九中高三上学期第一次月考数学(理)试题Word版含答案

宁夏银川市2018届高三数学上学期第一次月考试题 理

宁夏银川九中高三上学期第一次月考试题 数学(理) Word版含答案

宁夏银川市2018届高三数学上学期第一次月考试题理2017092002123

宁夏银川一中高三第一次月考数学(理).pdf

宁夏回族自治区银川市2018届高三数学上学期第一次月考试题文

银川一中2018届高三数学第一次月考试题理科有答案

最新-宁夏银川一中2018届高三上学期第一次月考试题(数

宁夏银川一中2018届高三上学期第一次月考数学试卷(理科)Word版含解析

宁夏回族自治区银川市2018届高三数学上学期第一次月考试题文2017090502127

2018届宁夏银川九中高三上学期期中考试理科数学试题及答案 精品

宁夏银川一中2017-2018学年高三上学期第一次月考数学理试卷 Word版含解析

宁夏银川九中2020届高三上学期第一次月考数学理试题Word版含答案

(全优试卷)宁夏银川九中高三上学期第一次月考数学(理)试题Word版含答案

2018年银川一中--高三第一次月考数学(理科)试卷答案 最新

宁夏银川市2018届高三数学上学期第一次月考试题理

宁夏银川九中高三上学期第一次月考试题数学(理) Word版含答案

2018届宁夏银川九中高三上学期期中考试理科数学试题及答案精品

2018年银川一中--高三第一次月考数学(理科)试卷答案最新