材料力学第07章-1应力状态分析

合集下载

材料力学第七章应力状态和强度理论

2
x y 2 a 0 2
x y x y 2
x y
2
) x
2
2
例题1: 已知:单元体各侧面应力 x=60MPa,
求: (1) = - 450斜截面上的应力,(2)主应力和主平面
dA
y

x y
2
sin 2 xy cos2
y
yx
应力圆
y
1 R 2

x
y

2
4 2 xy
x
yx xy x
y
R c

x y
2
2
x
xy
x´
dA
yx
y´
y
x y 1 2 2 2

40

x y
2 0.431MPa
sin( 80 ) xy cos(80 )

C
C

C
例题3：已知梁上的M、Q，试用单元体表示截面上1、2、
3、4点的应力状态。
1
2 0
2
1点 2点
1 2 0 3
3Q ＝ 2A
M x Wz
2 xy
x y
2 20.6 0.69 60 0
17.2
x y
2 (
6.4MPa
2 34.4
max(min)
x
17.20
x y
2
) xy
2
2
x
66.4MPa
60 0 60 0 2 ( ) 20.6 2 2 2 66.4(6.4) MPa

材料力学第07章应力状态

I象限； tan 2 0 III象限； tan 2 0
II象限； IV象限。
x y x - y cos 2 - x sin 2 2 2 x - y sin 2 x cos 2 2 1
- 2 x 0 arctan - 2 y x
3 2 1
四、应力状态的分类
单向应力状态二向应力状态 ——平面应力状态 ——简单应力状态
——复杂应力状态三向应力状态 ——空间应力状态
五、应力状态的实例
1.单向应力状态轴向拉伸杆件内的任一点

F A
F
. A
.
F
A
1 ,
2 3 0
2.二向应力状态锅炉或其它薄壁圆筒形容器壁上的任一点
F
F

F A
表示方法：围绕该点截取一单元体，并标明各面上的应力
F
A C B . .
A
A
B
B
B
C
C
MA A Wz
M B yB B Iz * FQB S z B I zb
3 FQC C 2 A
表示方法：围绕该点截取一单元体，并标明各面上的应力
F
A C B . .
用完全相似的方法可确定剪应力的极值
d ( x - y ) cos 2 - 2 x sin 2 d d 若 1 时，能使 0 d ( x - y ) cos 2 1 - 2 x sin 2 1 0
x - y tan 2 1 2 x
4
解：
F 1 FSl 4 100kN 50kN 2 2 Fl 1 Ml 4 100kN 2m 25kN m 8 8

材料力学第07章应力状态分析与强度理论

2
sin2a t xy cos2a
18/95
7.2 平面应力状态分析主应力 7.2.3 主平面的方位及极值正应力 s x s y s x s y sa cos2a t xy sin2a 2 2 s x s y ds a 上式对a 求导 2 sin2a t xy cos2a da 2 s x s y 若a a0时，导数为 0 sin2a 0 t xy cos2a 0 0 2 2t xy tan2a 0 s x s y
7.2.5 应力圆
t
sx
tyx
sy
sx txy sy
D(sx,txy) 1. 确定点 D (s ,t ) x xy
O
D'(sy,tyx)
C
s
2. 确定点D' (sy,tyx) tyx= －txy 3. 连接DD'与s 轴交于点C 4. 以 C 为圆心，CD（CD'）为半径画圆。
26/95
7.2 平面应力状态分析主应力 7.2.5 应力圆
sx sy sz
sxs1 100 MPas 2
0 MPas 3 120 MPa
11/95
7.1 一点的应力状态的概念单向、二向(平面)、三向(空间)应力状态三个主应力中仅有一个主应力不为零单向应力状态
s1
s1
F
A
F
12/95
7.1 一点的应力状态的概念单向、二向(平面)、三向(空间)应力状态
O
D'(sy,tyx)
C sx－ sx sy/2
s
27/95
7.2 平面应力状态分析主应力 7.2.5 应力圆利用应力圆确定角a 斜截面上的正应力和切应力

工程力学c材料力学部分第七章应力状态和强度理论

无论是强度分析还是刚度分析，都需要求出应力的极值，无论是强度分析还是刚度分析，都需要求出应力的极值，为了找到构件内最大应力的位置和方向需要对各点的应力情况做出分析。最大应力的位置和方向，到构件内最大应力的位置和方向，需要对各点的应力情况做出分析。
受力构件内一点处所有方位截面上应力的集合，称为一点的受力构件内一点处所有方位截面上应力的集合，称为一点的研究一点的应力状态时，应力状态。研究一点的应力状态时，往往围绕该点取一个无限小的正六面体—单元体来研究。单元体来研究的正六面体单元体来研究。
σ2
σ2
σ1
σ1
σ
σ
σ3
三向应力状态
双向应力状态
单向应力状态简单应力状态
复杂应力状态主应力符号按代数值的大小规定：主应力符号按代数值的大小规定：
σ1 ≥ σ 2 ≥ σ 3
平面应力状态的应力分析—解析法 §7−2 平面应力状态的应力分析解析法
图(a)所示平面应力单元体常用平面图形(b)来表示。现欲求 )所示平面应力单元体常用平面图形( )来表示。现欲求垂直于平面xy的任意斜截面上的应力垂直于平面的任意斜截面ef上的应力。的任意斜截面上的应力。
二、最大正应力和最大剪应力
σα =
σ x +σ y
2
+
σ x −σ y
2
cos 2α − τ x sin 2α
τα =
令
σ x −σ y
2
sin 2α + τ x cos 2α
dσ α =0 dα
σ x −σ y
2
sin 2α +τ x cos2α = 0
可见在 τ α
=0

材料力学第07章应力状态与应变状态分析

x
xy
面上的应力( ， ) 应力圆上一点( ， )
y
面的法线应力圆的半径
Ox
n D( ,
2
C
x
两面夹角两半径夹角2 ；
A(x ,xy)
且转向一致。
O
B(y ,yx)
四、在应力圆上标出极值应力
max
x
21
A(x ,xy)
OC
3 2
20 1
B(y ,yx)
m in
1 3
OCR半径
2
cos2
xy
sin 2
同理：
x
y
2
sin 2
xy
cos2
n
Ox
图2
二、极值应力
令:d
d
0
x
y
sin202 xycos200
由此得两个驻点：
01、（
01
2
）和两个极值：
tg20
2 xy x
y
y
mm
ax in
x
y ±（x
2
y
2
）2
2 xy
0 0极值正应力就是主应力！
y
O
x
A (80, 30
3、算出主应力、切应力极值
3 x
D
C
y 1
O
1 3
0C
R
10MPa 90MPa
max - min R 50MPa
B 4、算出方位角
A (80, 30
ACD arc tg AD 36.86 DC
3 y
D
2 o x 1
0
180
36.86 2
71.57

材料力学-应力状态分析

+
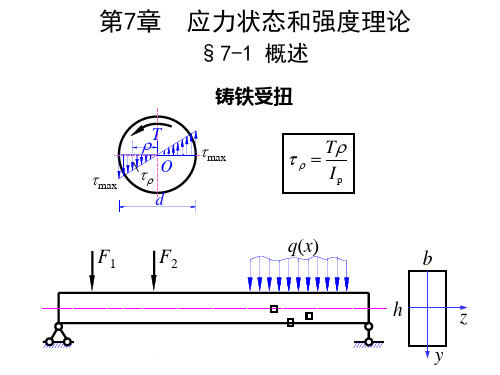
σ x σ y
2
cos 2α τ x sin 2α
sin 2α + τ x cos 2α
注意：的正负号，注意：1）σx 、σy 、τx 和 α的正负号， 2）公式中的切应力是τx ，而非τy，而非的正负号。 3）计算出的σα和τα 的正负号。
τα τ α>0
τα τ α<0
图示圆轴中，已知圆轴直径d=100mm，轴向拉例：图示圆轴中，已知圆轴直径，力 F=500kN，外力矩Me=7kNm。求 C点α = 30°截，外力矩。点 ° 面上的应力。面上的应力。 y
σy
τ
D
x
τx τy
σx
o A2
C
A1
σ
D
y
σ1 =
σ x +σ y
2
σ x +σ y + 2
2 +τ x
2
2
σ2 =
σ x +σ y
2
σ x +σ y 2 +τ x 2
σy
τ
D
x
τx τy
σx
o A2
2α0
C
A1
σ
D
y
2τ x 2α 0 = arctan σ x σ y
σ x σ y R= 2
+τ x2
2
σ x +σ y σ α 2
σy
σ x σ y 2 2 + τα = +τ x 2 τ
2 2
D
x
τx τy
σx
o
C D
y
σ
50MPa

材料力学《第七章》应力状态分析

上海交通大学
受力： sadA、 tadA 受力： sxdAcosa、 txydAcosa
受力： sydAsina、 tyxdAsina
n
sx
txy
a
sa a
a
x
ta
tyx
e
切线方向上： Σ Fτ 0
σx σy σx σy σα cos2α τ xy sin2α 2 2
b
sy
τα d A ( σ x d A cos α )sin α ( τ xy d A cos α )cos α ( σ y d A sin α )cos α ( τ yx d A sin α )sin α 0
s1
一个主应力为零，其他二个主应力不为零。
3. 三向应力状态(空间应力状态)：三个主应力均不为零。
上海交通大学
一般要找出主应力后才能确定应力状态。
四、应力状态分析步骤
s2
1. 确定构件危险截面危险点；
2. 取危险点单元体；
s3
3. 计算单元体各面应力；
4. 截面法取部分单元体； 5. 由平衡条件确定单元体斜截面上的应力。应力状态分析方法：解析法、图解法。
上海交通大学
三、应力状态的分类定义：单元体上应力为零的面称为零应力面；单元体上只有 s 而无 t 的面称为主平面。主平面上的正应力 s 称为主应力。
s2
s3
单元体在某一特殊方向上，三个互相垂直的截面上只有 s，而无 t ，即为单元体的三个主平面。用 s1 ≥ s2 ≥ s3 表示三个主应力，此单元体称为主单元体。 1. 单向应力状态：一个主应力不为零，其他二个主应力为零。如：轴向拉伸。 2. 二向应力状态(平面应力状态)：

材料力学第七章知识点总结

研究应力状态的目的：找出一点处沿不同方向应力的变化
规律，确定出最大应力，从而全面考虑构件破坏的原因，建立适当的强度条件。
材料力学
3、一点的应力状态的描述
研究一点的应力状态，可对一个包围该点的微小正六面体——单元体进行分析
在单元体各面上标上应力各边边长 dx , dy , dz
——应力单元体
三、几个对应关系
点面对应——应力圆上某一点的坐标值对应着单元体某一截面
上的正应力和切应力；
y
σy
n
τ
H (σα ,τα )
τ yxHτ xy来自αxσx
(σy ,Dτyx)
2α A (σx ,τxy)
c
σ
σx +σ y
2
转向对应——半径旋转方向与截面法线的旋转方向一致；二倍角对应——半径转过的角度是截面法线旋转角度的两倍。
α =α0
=
−2⎢⎡σ x
⎣
−σ y
2
sin 2α0
+τ xy
cos
2α
0
⎤ ⎥
⎦
=0
=
−2τ α 0
τα0 = 0
tg
2α 0
=
− 2τ xy σx −σ y
可以确定出两个相互垂直的平面——主平面，分别为
最大正应力和最小正应力所在平面。
主平面的方位
(α0 ; α0′ = α0 ± 900 )
主应力的大小
材料力学
四、在应力圆上标出极值应力
τ
τ max
x
R
O σ min
2α12α0A(σx ,τxy)
c
σ
σ
max
(σy ,τyx) D

材料力学课件第7章应力状态分析

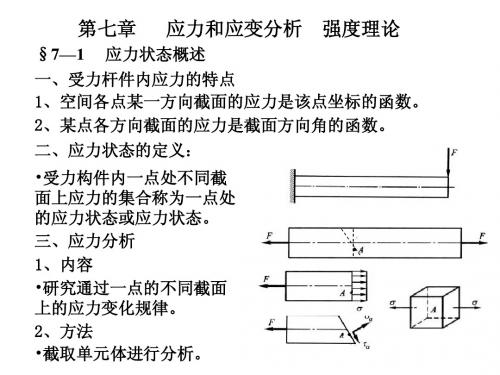
α+
2
（2）主应力值计算）方法一：方法一： σ x +σ y σ x −σ y + cos 2α 0 − τ xy sin 2α 0 σ α =
2 2 0 σ x +σ y σ x −σ y π π σ = + cos 2 α 0 + − τ xy sin 2 α 0 + α0 + π 2 2 2 2 2
2τ xy
σ x −σ y
2τ xy 1 可取：可取： α 0 = arctan − σ −σ 2 x y
1 2τ xy , arctan − σ −σ x y 2
π + 2来自3、主应力：、主应力：（1）性质：）性质： ①主应力为各截面上正应力的极值。主应力为各截面上正应力的极值。
∗ FS Sz τ= bIz
五、主平面、主应力主平面、 1、主平面、 •τ= 0的截面的截面; 的截面 •过一点有三个相过一点有三个相互垂直的主平面. 互垂直的主平面 2、主应力、 •主平面上的正应力主平面上的正应力; 主平面上的正应力 •表示符号 1 、σ2、σ3（ σ1 ≥σ2≥σ3 ）。表示符号σ 表示符号应力状态分类：六、应力状态分类： 1、单向应力状态：只有一个主应力不为零。、单向应力状态：只有一个主应力不为零。 •可用平面图形表示应力状态。可用平面图形表示应力状态。可用平面图形表示应力状态 2、二向（平面）应力状态：两个主应力不为零。、二向（平面）应力状态：两个主应力不为零。 •可用平面图形表示应力状态。可用平面图形表示应力状态。可用平面图形表示应力状态 3、三向应力状态：三个主应力都不为零。三个主应力都不为零。、 4、简单应力状态：单向应力状态。、简单应力状态：单向应力状态。 5、复杂应力状态：二向和三向应力状态。、复杂应力状态：二向和三向应力状态。

材料力学第17讲 Chapter7-1第七章应力状态(解析法)

201 78.790， 01 39.3450 02 39.3450 - 900 -50.6550
12
41MPa -61MPa
39
Thank you for your attention!
作业： Page 250: 7-1(c,d);7-2 Page 251: 7-6
下次课讲应力圆
40
- xycsc20
02
01
2
将02也限制在[-900,900 ]，取 01 0 :02 01 900 01 0 :02 01 - 900
xy 0时：
大于零的那个角（第一象限角）对应第一主应力
32
=0面上的切应力:
0
x
- y
2
sin 20
xy
x -y
2
cos 20
sin 2
x
dA
dA - x (dAcos)sin
xy
y
- xy (dAcos) cos xy (dAsin)sin
x ' y (dAsin)cos 0
x sin cos - y sin cos xy (cos2 - sin2 )
19
最后，得到以下两个方程：
x cos2 y sin2 - xy sin 2 x sin cos - y sin cos xy (cos2 - sin2 ) 引入 2 sincos sin2
27
主应力与主平面（二）
0
x
y
2
- xycsc20
1 0 y y
x
2 0 x
x
tg20
-
2 xy x -
y
(2) 若 xy 0, x y ;
tan 20 0, 0 0, csc20 0

材料力学-7-应力状态分析

y
x
yx
xy
x
y
y yx
x
y
xy
7.1 应力状态的基本概念
x
y
y
yx
x
x
xy
x
单向应力状态
( One Dimensional State of
Stresses )
纯切应力状态
( Shearing State of Stresses )
拉（压）、纯弯曲正应力
扭转
45 max xy
45 0
受扭之前，圆轴表面为正圆。
Mx
45 0
Mx
受扭后，变为一斜置椭圆，长轴方向伸长，短轴方向缩短。这是为什么？
因为：圆轴扭转时，其斜截面上存在着正应力。
第7章应力状态分析
7.3 主应力、主平面与面内最大切应力——解析法
q＝
x
2
sin 2q
q＝
x－ y
2
sin 2q xy cos2q
7.2 平面应力状态任意方向面上的应力 ——解析法例题3

n
q＝
x
2
＋
x
2
cos2q
x
x
2 3.当θ ＝45º 时，斜截面上既有正应力又有切应力，其值分别为
q＝
x
sin 2q
45 ＝
三、描述一点应力状态的基本方法
微元（Element）
围绕所考察的点截取正六面体，并使之边长足够小，趋于宏观上的 “点”。因此，微元及其各面上的应力即可描述一点的应力状态。
dz
dy dx
注意：由于微元各边长均为无穷小量，故有： 1.表面上的应力可视为均匀分布； 2.任一对平行平面上的应力相等。

材料力学第七章应力状态和应变状态分析

(设ef的面积为设的面积为的面积为dA)
σα =
τα =
σx +σ y σx σ y
+ 2
2 σx σ y
2
cos2α τ x sin2α
sin2α + τ x cos2α
τ σ
e
x
x
α
σ
α
—— 平面应力状态下任意斜截面上计算公式. 的σα和τα计算公式.
τ
y
α
b
列平衡方程: 列平衡方程:
1
0
d
y
x x
tan 2α0 =
2τ
σ
e
σe
m
F1
m a c
F2
q
y m
b d
σ
1
a
y
σ
3
σa σb τb
x
e m
σ
b
3
σ
b
α
0
x
1
y
1,梁上任一点均有两 , 个主应力, 个主应力,一个主拉应力,一个主压应力. 应力,一个主压应力. 2,主拉压应力的大 , 小从梁顶( 小从梁顶(底)到梁均连续变化. 底(顶)均连续变化.
σα +90 =
0
σx +σ y
τα +90 =
0
2 σx σ y
σx σ y
2
cos 2α + τ x sin 2α
2
sin 2α τ x cos 2α
σ α + σ α + 90 o = σ x + σ y = 常数
τ α = τ α + 90 o
——任意两个互相垂直的截任意两个互相垂直任意两个互相垂直的截面上的正应力之和为常数, 面上的正应力之和为常数, 切应力服从切应力互等定理. 切应力服从切应力互等定理.

材料力学第七章应力状态与强度理论

取三角形单元建立静力平衡方程
n 0
dA ( xdA cos ) sin ( xdA cos ) cos ( y dA sin ) cos ( y dA sin ) sin 0
t 0
dA ( xdA cos ) cos ( xdA cos ) sin ( y dA sin ) sin ( y dA sin ) cos 0
2 2

cos 2 x sin 2
2 x y 2 x y ( ) ( cos 2 x sin 2 )2
2
2

x y
sin 2 x cos 2
( 0) (
x y
2
2
sin 2 x cos 2 )
max x y x y 2 x 2 2 min
2
max
1 3
2
例7-2 试求例7-1中所示单元体的主应力和最大剪应力。
（1）求主应力的值
x 10MPa, y 30MPa, x 20MPa max x y x y 2 2 x min 2
复杂应力状态下（只就主应力状态说明）有三个主应力
1 , 2 , 3
1
E
由 1引起的线段 1应变 1
由 2引起的线段 1应变 1
2
由 3引起的线段1应变 1
3
E
E
沿主应力1的方向的总应变为：
1 1 1 1
1 42.4 1 3 2 0 MPa 由 max 3 2.4 2

材料力学第七章

2

x y
2
cos 2 x sin 2

x y
2
sin 2 x cos 2
补充例题1
T
图示圆轴中，已知：圆轴直径d=100mm，轴向拉力F=500kN，外力矩Me=7kN· m。求C点 =30°截面上的应力。
y T
y
F x
F
C
x
第7章
应力状态和强度理论
§7-1 概述
低碳钢拉伸试验
铸铁拉伸试验
低碳钢扭转试验
铸铁扭转试验
1、一点处的应力状态
构件内一点处各截面方向上的应力的情况，称为该点的应力状态。可由围绕该点的一个单元体面上的应力表示。
目的：通过应力状态分析求出该点处的 max 、 max 及其作用面，从而更好地进行强度分析。
30
在二向应力状态下，任意两个垂直面上，其σ的和为一常数。
分析轴向拉伸杆件的最大切应力的作用面，说补充例明低碳钢拉伸时发生屈服的主要原因。题3
低碳钢拉伸时，其上任意一点都是单向应力状态。
x

x y
2

x y
2
cos 2 x sin 2

x
单元体如何取？在研究点的周围，取一个由三对互相垂直的平面构成的六面体，该六面体的边长分别为无穷小量 dx、dy和dz，如下图所示。
y
dz dx dy x
z
单元体每个面上应力均布；每对相互平行面上的性质相同的应力大小相等；可用截面法求任一截面上的应力。
根据单元体的局部平衡：
y
n

y

材料力学课件第7章应力和应变分析强度理论

"
p
直径平面
FN
Ｏ
FN
d
y
D Fy 0 0 pl 2 sin d plD pD 2 l plD 0 2
π
P’
P p
y x
承受内压圆柱型薄壁容器任意点的应力状态:
二向不等值拉伸应力状态
内点P‘点的应力状态？ σ
y
σx σz=p
（续）承受内压球型薄壁容器任意点的应力状态（壁厚为t，内直径为D，t<<D，内压为p）
例题3 分析薄壁圆筒受内压时的应力状态（壁厚为δ，内直径为D，t<<D，内压为p）
L
ｐ
m
n

z
y
p
D
m
l
n
n
（1）沿圆筒轴线作用于筒底的总压力为F
πD 2 F p 4
′
p
薄壁圆筒的横截面面积
A πD
πD 2 p F pD 4 A πD 4
n
D
（2）假想用一直径平面将圆筒截分为二,并取下半环为研究对象
说明:一点处必定存在这样的一个单元体, 三个相互垂直的面均为主平面, 三个互相垂直的主应力分别记为1 ,2 , 3 且规定按代数值大小的顺序来排列, 即
1 2 3
三、应力状态的分类
1.空间应力状态三个主应力1 ,2 ,3 均不等于零 2.平面应力状态三个主应力1 ,2 ,3 中有两个不等于零 3.单向应力状态三个主应力 1 ,2 ,3 中只有一个不等于零
cos 2 xy sin 2
即两相互垂直面上的正应力之和保持一个常数
二、最大正应力及方位
2 2 x y sin 2 xy cos 2 2

材料力学第七章应力状态分析

(*)τα = Nhomakorabea2
sin 2α + τ xy cos 2α
(**)
(*) 2 + (**) 2
(σ α −
σ x +σ y
2
) + (τ α ) = (
2 2
σ x −σ y
2
2 ) 2 + τ xy
(7 - 6)
In a given problem, σx, σy, τxy are the three constants, σα,, τα are the variables. This equation is an expression for a circle of radius
σ x −α y
2
cos 2α − τ xy sin 2α
(7-1)
τα =
sin 2α + τ xy cos 2α
3. Principle Stresses in Two-dimensional Problems To find the plane for a maximum or a minimum normal stress, let σ x −α y dσ α = −2[ sin 2α + τ xy cos 2α ] = 0 = −2τ α 2 dα 2τ xy tg 2α1 = − σ x −σ y
σ'=
σ x +σ y
(7 - 5)
∴τ max = ±
min
σ1 − σ 2
2
Example 7-1 For the state of stress shown in the figure, (a) find the stresses acting on the inclined plane with θ=-22.5°; (b) find the principle stresses and shown their sense on a properly oriented element; and (c) find the maximum shear stresses with the associated normal stresses and show the results on a properly oriented element. Solution: For original state of stress σx=3 Mpa σy=1 MPa τxy= -2 Mpa (a) From Eq.(7-1)

材料力学——应力分析

,则α1
405(τx0) 405(τx0)
7-2 二向应力状态分析--解析法
例题1：一点处的平面应力状态如图所示。
已知 x 60MP，a txy 30MPa, y 40MP,a 30。
试求（1）斜面上的应力；（2）主应力、主平面；（3）绘出主应力单元体。
y t xy
x
目录
7-2 二向应力状态分析--解析法
t
ty(xdsAin)co sy(dsAin)sin0
y
Ft 0
td Atx(ydc Ao )sco sx(dc Ao )ssin ty(xdsAin)siny(dsAin)co s0
目录
7-2 二向应力状态分析--解析法
{ 利用三角函数公式
co2 s 1(1co2s)
2
sin 21(1co2s)
d d (x y)si2 n2 txc y o 2 s
设α＝α0 时，上式值为零，即
t (xy )s2 i0 n 2xc y 2 o 0 s 0
2 (x σ 2 σ y) si0n τ x 2 c yα o0s 2 2α α 0 τ 0
即α＝α0 时，切应力为零目录
2
2 s ic n o s si2 n
并注意到 t yx t xy 化简得
t 1
1
2 (xy) 2 (xy)c2 o s xs y 2 in
t1 2(xy)si2 ntxy co 2s
目录
7-2 二向应力状态分析--解析法
3. 正应力极值和方向
确定正应力极值
t 1 2 (xy ) 1 2 (xy )c2 o s xs y 2 in
（2）主平面的位置
tg2α0
2τ xy σx σy

材料力学-07-应力分析和强度理论

§7-2 平面应力状态平面应力状态--解析法平面应力状态解析法：解析法
1.斜截面上的应力 1.斜截面上的应力
y
σx
a
τ yx
τ xy
σx α
τa
n
τ xy
σa
dA
x
σy
n
τ yx
σy
t
t
∑F = 0
∑F =0
13
§7-2 平面应力状态平面应力状态--解析法平面应力状态解析法：解析法
tan 2α0 = − 2τ xy
σ x −σ y
由上式可以确定出两个相互垂直的平面，由上式可以确定出两个相互垂直的平面，分别为最大正应力和最小正应力所在平面。为最大正应力和最小正应力所在平面。所以，最大和最小正应力分别为：所以，最大和最小正应力分别为：
σmax = σ x +σ y
2 1 + 2 − 1 2
单元体
单元体——构件内的点的代表物，单元体——构件内的点的代表物，是包围被研究点的 ——构件内的点的代表物无限小的几何体。常用的是正六面体。无限小的几何体。常用的是正六面体。单元体的性质—— 平行面上，应力均布；单元体的性质——1) 平行面上，应力均布； —— 2) 平行面上，应力相等。平行面上，应力相等。
2 2
σy
τ xy
α
60 − 40 60 + 40 = + cos(−60o ) + 30 sin(−60o ) 2 2
σx
= 9.02 MPa
τα =
σ x −σ y
2 60 + 40 = sin(−60o ) − 30 cos(−60o ) 2

材料力学课件第七章应力状态分析1-2

G2 "
3.应力圆的应用
①应力圆上一点坐标代表单元体某个面上的应力；
②应力圆上半径转过2a，单元体上坐标轴转过a,且转向相同;
③圆心为平均正应力，为不变量。 ④ 半径对应极值切应力。
y yx
xy x
n
a
a x a xy
yx y
(a,a)E
B1 B O "
D' (y, yx)
G1'
D(x, xy) 2a
x
2
y
2
2 xy
②取x面，定出D( x ,xy )点；取y面，定出D'( y ,yx )点；
③连DD'交轴于C点，以C为圆心，DD1为直径作圆；
y y yx
xy x
n
a
a x x a xy
yx y
(a,a)E
B1 B O "
G1'
D(x, xy) 2a
2a0 A A1
C
'
D' (y, yx)
1. ①主平面：单元体上切应力为零的面；
②主应力：主平面上的正应力，用1、2、3 表示，有1≥2≥3。
y
z
yx
yz
xy
zy
x x
z zx xz z
x' 1
旋转
z' 3
2 y'
2.应力状态按主应力分类：
①只有一个主应力不为零称单向应力状态；
②只有一个主应力为零称两向应力状态(平面应力状态)； ③三个主应力均不为零称三向应力状态(空间应力状态)；
③主应力大小：
max min
x
y
2
x

材料力学第七章应力应变分析

x
y
2
x
2
y
cos 2
xy sin 2
x
y
2
sin 2
xy cos 2
1、最大正应力的方位
令
d d
2[
x
y sin 2
2
xy cos 2 ] 0
tg 2 0
2 xy x
y
0 0
90
0 和 0+90°确定两个互相垂直的平面，一个是最大正应力所在的平面，另一个是最小正应力所在的平面.
的方位.
m
m a
A
l
解：把从A点处截取的单元体放大如图
x 70, y 0, xy 50
A
tan 20
2 xy x y
2 50 1.429
1
3
(70) 0
0
A
x
0
27.5 62.5
3
1
因为 x < y ，所以 0= 27.5° 与 min 对应
max min
x
2
y
(
x
2
y )2
三、应力状态的分类
1、空间应力状态
三个主应力1 、2 、3 均不等于零
2、平面应力状态
三个主应力1 、2 、3 中有两个不等于零
3、单向应力状态
三个主应力 1 、2 、3 中只有一个不等于零
2 3
2
1
1
1
1
1
3 2
2
1
例题 1 画出如图所示梁S截面的应力状态单元体.
F
5
S平面
4
3
l/2
2
l/2 1
任意一对平行平面上的应力相等

材料力学 第07章-1应力状态分析