二次函数周周清
第五周二次函数周周清考试

2015—2016上学期第五周二次函数测试姓名分数一、选择题(每小题3分,共30分)1.(2015·兰州中考)下列函数解析式中,一定为二次函数的是()A.y=3x-1B.y=a+bx+cC.s=2-2t+1D.y=2.已知二次函数y=ax2+bx-1(a≠0)的图象经过点(1,1),则代数式1-a-b的值为()A.-3 B.-1 C.2 D.53.(2013·吉林中考)如图,在平面直角坐标系中,抛物线所表示的函数解析式为,则下列结论正确的是()A. B.<0,>0 C.<0,<0 D.>0,<04. 若二次函数y=(m+1)x2-mx+m2-2m-3的图象经过原点,则m的值必为( )A.-1或3 B.-1 C.3 D.-3或15.(2014·成都中考)将二次函数223y x x=-+化为2()y x h k=-+的形式,结果为()A.2(1)4y x=++ B.2(1)2y x=++ C.2(1)4y x=-+ D.2(1)2y x=-+6. 抛物线轴交点的纵坐标为()A.-3B.-4C.-5D.-17.已知二次函数,当取,(≠)时,函数值相等,则当取时,函数值为()A.B. C. D.c8.已知二次函数,当取任意实数时,都有,则的取值范围是()A.B.C.D.9.(2015·兰州中考)二次函数y=+x+c的图象与x轴有两个交点A(,0),A(,0),且,点P(m,n)是图象上一点,那么下列判断正确的是()A.当n0时,m0B.当n时,m>C.当n0时,D.当n时,m>10.(2015·贵州安顺中考)如图为二次函数+bx+c(a≠0)的图象,则下列说法:①a>0;②2a+b=0;③a+b+c>0;④当-1<x<3时,y>0.其中正确的个数为()A.1B.2C.3D.4二、填空题(每小题3分,共24分)11.二次函数y=x2+2x-4的图象的开口方向是___,对称轴是_ ___,顶点坐标是__ __.12.把抛物线的图象先向右平移3 个单位长度,再向下平移2 个单位长度,所得图象的解析式是则.13.已知抛物线的顶点为则,.14.如果函数是二次函数,那么k的值一定是.15.某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数表达式是y=60x 1.5x2,该型号飞机着陆后需滑行m才能停下来.16.二次函数的图象是由函数的图象先向(左、右)平移个单位长度,再向(上、下)平移个单位长度得到的.17.如图,已知抛物线经过点(0,-3),请你确定一个的值,使该抛物线与轴的一个交点在(1,0)和(3,0)之间,你所确定的的值是.18.如图所示,已知二次函数的图象经过(-1,0)和(0,-1)两点,则化简代数式= .三、解答题(共66分)19.(4分)已知抛物线的顶点为,与y轴的交点为求抛物线的解析式.第17题图第3题图第10题图20.(10分)已知抛物线的解析式为(1)求证:此抛物线与x轴必有两个不同的交点;(2)若此抛物线与直线的一个交点在y轴上,求m的值.21.(10分)已知二次函数y=x2+bx-c的图象与x轴两交点的坐标分别为(m,0),(-3m,0)(m ≠0).(1)求证:4c=3b2;(2)若该函数图象的对称轴为直线x=1,试求二次函数的最小值.22.(10分)已知:关于的方程(1)当取何值时,二次函数的对称轴是直线;(2)求证:取任何实数时,方程总有实数根.23.(10分)(9分)如图,矩形ABCD的两边长AB=18 cm,AD=4 cm,点P,Q分别从A,B同时出发,P在边AB上沿AB方向以每秒2 cm的速度匀速运动,Q在边BC上沿BC方向以每秒1 cm的速度匀速运动.设运动时间为x(秒),△PBQ的面积为y(cm2).(1)求y关于x的函数关系式,并写出x的取值范围;(2)求△PBQ的面积的最大值.24.(10分) 如图二次函数y=-12x2+bx+c的图象经过A(2,0),B(0,-6)两点.(1)求这个二次函数的解析式;(2)设该二次函数的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.25.(12分)如图,四边形ABCD是菱形,点D的坐标是(0,3),以点C为顶点的抛物线y=ax2+bx+c 恰好经过x轴上A,B两点.(1)求A,B,C三点的坐标;(2)求过A,B,C三点的抛物线的解析式;(3)若将上述抛物线沿其对称轴向上平移后恰好过D点,求平移后抛物线的解析式,并指出平移了多少个单位?。
实验校九上数学周周清(第10周)

1 2 C实验校九上数学周周清1.二次函数 y = x 2- mx +1的顶点在坐标轴上,则 m=.2.将二次函数 y = x 2+1的图象绕点(1,-1)旋转 180°,得到的图象的解析式为.3.一个二次函数 y=ax 2+bx+c (a >0)的图象经过五个点 A (﹣1,n ),B (3,n ),C (0,y ),D (-2,y )和 E (2.5,y 3),则下列关系正确的是( ).A .y 1>y 2>y 3B .y 2>y 3>y 1C .y 1<y 2<y 3D .y 3>y 1>y 24.如图:已知二次函数 y =ax 2+bx +c (a ≠0)过(-1,-2),对称轴所在直线为 x=2,且二次函数与 x 轴的一个交点位于 0 和 1 之间.①4a -2b+c <0, ② b <1,③ 对于任意实数 t,一定有 at 2+ bt ≤ 4a + 2b , a + b + c ④b - a的最大值为 3.上述四个判断正确的序号是.5.关于 x 的一元二次方程 - x 2+ 2x + 3 - t = 0 在- 3 ≤ x ≤ 2 范围内有两个不相等的实根,则 t 的取值范围是.6.我们把函数 y = x 2- 3x - 4 图象位于 x 轴下方的部分沿x 轴进行翻折并结合此函数图象的其它部分的组合图象记为 M ,若直线 y = 2x - b 与图象 M 有且只有三个公共点,则 b=.7.如图,将△ABC 绕点 A 逆时针旋转 98°,得到△AB 1C 1 ,若点 B 1 在线段 BC 的延长线上,则∠BB 1C 1 的度数为 .B 1C 1ABAB第 7 题图第 8 题图第 9 题图8.如图,四边形 ABCD 中,DC//AB,BC= 10 ,AB=AC=AD=5,则 BD 的长为().A . 5B . 5C . 2D . 39.△ABC 中,AB=4,∠ABC=60°,∠ACB =45°,D 为 BC 的中点, 直线l 经过点 D ,过 B 作 BF⊥ l 于 F ,过 A 作 AE⊥ l 于 E ,则 AE+BF 的最大值为 .23 10 10y -10 1 2x-234 310.如图,在正方形ABCD 中,AB=5,点 M 在 CD 的边上,且 DM=2,△AEM 与△ADM 关于 AM 所在的直线对称,将 △ADM 按顺时方向绕点 A 旋转 90°得到△ABF,连接 EF ,则线段 EF 的长为( ) .A. B. 3 C.5D. 3第 10 题第 11 题11.如图,正方形 ABCD 边长为 1,O 为正方形 ABCD 的对角线的交点,正方形 OEFG 绕点 O 旋转,GO 交 AD 于点 M , OE 交 CD 于点 N ,则线段 MN 的取值范围是 .12.如图,已知点 A(2,0),B(0,4),C(2,4),在所给的网格中完成下列任务: ⑴画线段 CD ,使 CD 与 AB 垂直且相等,并写出点 D 的坐标 ; ⑵将线段 AB 绕着某一点旋转一定角度,使其与线段 CD 重合,则这个旋转中心的坐标为 ;⑶画出以 CD 为对角线的正方形,并写出这个正方形的面积 .13.如图,在 7×7 正方形网格中的每个小正方形边长都为 1 个单位长度,我们把每个小正方形的顶点称为格点, 点 A ,B 都为格点,且点 A (-2,1),B (2,2)请分别仅用一把无刻度的直尺画图:⑴画出线段 AB 绕原点逆式针旋转 90°得到的线段 DE,点 A 的对应点为 D ,点 B 的对应点为 E.直接写出格点 D 的坐标;⑵作∠DEF,使∠DEF=45°,直接写出格点 F 的坐标;⑶作格点 M,连结 AM,使线段 AM 平行线段 DE ,直接写出 AM 与 x 轴交点的坐标.yxBAo1314.如图,在边长为 1 个单位长度的小正方形网格中,给出了△ABC ,且点 A(-1,0).仅用一把无刻度的直尺在所给的网格中画图,保留画图过程的痕迹.⑴点 B 关于 y 轴的对称点为点 B 1,描出点 B 1,并写出格点 B 1 的坐标: ; ⑵画出△ABC 绕某格点按顺时针方向旋转 n °(0< n<180)后得到的△A 1B 1C 1.且 A ,C 的对应点 A 1,C 1 都在图中的格点上,写出旋转中心的坐标 以及 n 的值 ;⑶写出线段 BC 与 B 1C 1 的关系.15.如图,有一面长为 a 米的墙,利用墙长和 30 米的篱笆,围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB 为 x 米,面积为 S 米 2. ⑴当 a=10 时:①求 S 与 x 的关系式,并写出自变量 x 的取值范围;②如果要围成面积为 48m 2的花圃,AB 的长是多少米? ⑵求长方形花圃的最大面积.16.某服装批发市场销售一种衬衫,衬衫每件进货价为 50 元,规定每件售价不低于进货价,经市场调查,每月的销售量 y(件)与每件的售价 x (元)满足一次函数关系,部分数据如下表:售价 x (元/件) 60 65 70 销售量 y (件)140013001200(2)该批发市场每月想从这种衬衫销售中获利 24000 元,又想尽量给客户实惠,该如何给这种衬衫定价? (3)物价部门规定,该衬衫的每件利润不允许高于进货价的 30% ,设这种衬衫每月的总利润为 w(元),那么售价定为多少元可获得最大利润?最大利润是多少?QABQF BAQB17.如图,抛物线 y = ax 2+ bx + c 经过 A (-1,0),B(4,0),C (0,2)三点,D 为抛物线上一个动点. ⑴求这条抛物线的函数表达式;⑵已知 E 是直线 BC 上的一动点 ,若以 A ,C ,D ,E 为顶点的四边形是平行四边形,求点 D 的坐标; ⑶在抛物线 y = ax 2+ bx + c 上,当 m ≤ x ≤ n 时, y 的取值范围是 2 ≤ y ≤25,求 m - n 的取值范围.8备用图18.已知∠POQ=60°,点 B ,C 分别在射线 OQ ,OP 上,以 BC 为边作一个等边△ABC,连接 OA. ⑴如图 1,,OB=2,OC=3,求 BC 的长; ⑵如图 2,在⑴的条件下,求 OA 的长; ⑶如图 3,过点 A 作 AE⊥OP 于 E ,作 AF⊥OQ 于 F ,若 CE=2,BF=0.5 ,则等边△ABC 的边长为.O图 1O图 2O图 32219.如图 1,抛物线y = ax 2 -2x - 3与 x 轴交于点 A ,B (3,0),交 y 轴于点 C.⑴求 a 的值;⑵连接 AC ,若点 P 为在第四象限的抛物线上的一点,且∠CAP=45°,求 P 点坐标;⑶如图 2,若点 Q 为抛物线对称轴上的一动点,AQ 交 y 轴于点 E,BQ 交 y 轴于点 F,求证:OF-3OE 是一个定值.图 1图 220.抛物线 C : y = - 1(x +1)2,将抛物线 C 向右平移 2 个单位得到抛物线 C ,再将抛物线 C 向上平移 9个单2 2位得到抛物线 C 3.⑴直接写出抛物线 C 1 的顶点坐标是 ;抛物线 C 3 解析式是 ; ⑵如图 1,点 P 是抛物线 C 3 的对称轴一点,连 PO ,将线段 PO 绕 P 点逆时针旋转 90°得到线段 PM ,且 M 点恰好在抛物线上,求此时 M 点坐标;⑶如图 2,直线 y = (k 1 +1)x 与抛物线 C 3 交于点 A 、B.直线 y = (k 2 +1)x 与抛物线 C 3 交于 C 、D 两点,且 k 1k 2 = -3, P ,Q 分别为线段 AB ,CD 的中点,求证:直线 PQ 必定经过一个定点,并求出该定点.图 1图 21 1 yO AB xPCyO AEBxQC F。
初三数学周周清(十一)

初三数学周周清(十一)命题人:李跃平时间:90分 满分:100分 姓名一、填空题(每空2分,共20分)1、若22)2(++=mx m y 是二次函数,则m =2、抛物线y=-x 2+4x +c的最大值等于3,则c=3、已知二次函数y=-x 2+2x+c 2的对称轴与x 轴交于点(m,0),则m 的值为 4、一条抛物线的对称轴是x=1,且与x 轴有唯一的公共点、开口方向向下,则这条抛物线的解析式是 (任写一个)5、抛物线c bx ax y ++=2的对称轴是x=2,且过点(3,0),则a+b+c= 6、二次函数y=x 2-2x-3与x 轴两交点之间的距离为 7、二次函数c bx ax y ++=2的图象如图所示,则一次函数y=ax+bc 的图象不过第 象限 8、将抛物线221x y -=先向右平移1个单位,再绕顶点旋转180°,所得抛物线的解析式是9、抛物线y=x 2-4x-5交x 轴于A 、B 两点,交y 轴于点C ,则△ABC 面积为 。
10、汽车刹车距离s(m)与速度v(km/h)之间的函数关系是21001v s =,在一辆车速为100km/h 的汽车前方120m 处,发现停放一辆故障车,此时刹车 有危险(填“会”或“不会”)二、选择题(每小题3分,共30分)题号 1 2 3 4 5 6 7 8 9 10 答案1、二次函数y=kx 2-3x+2k- k 2图象过原点,则k 的值: A 、2 B 、0 C 、2或0 D 、不能确定2、二次函数y=a(x-k)2+k(a 0≠)不论k 取何实数时,图象的顶点一定在OxyA 、直线y=-x 上;B 、直线y=x 上C 、x 轴上D 、y 轴上 3、若二次函数c bx ax y ++=2过原点和第一、二、三象限,则A 、a>0,b>0,c=0;B 、a>0,b<0,c=0;C 、a<0,b>0,c=0D 、a<0,b<0,c=0 4、从y=x 2的图象可看出,当-3≤x≤-1时,y的取值范围是A 、y≤0或9≥y B 、0≤y≤9 C 、0≤y≤1 D 、1≤y≤95、二次函数y=(k-1)x 2-2kx+k+3的图象与x 轴无交点,且抛物线的开口向上,则k 的取 值范围 A 、k <1 B 、k >3/2 C 、1<k<3/2 D 、k>3/2或k<1 6、已知抛物线y=kx 2-7x-7与x 轴有交点,则k 的取值范围是 A 、47->k B 、47-≤k C 、0,47≠-≥k k 且 D 、0,47≠->k k 且 7、在同一坐标系中,函数)0(2>++=+=b c bx ax y c ax y 和的图象大致是8、若一元二次方程ax 2+bx+c =0的两根是-3和1,那么二次函数y= ax 2+bx+c 的图象的对称轴是直线 A 、x=-3 B 、x=-2 C 、x=-1 D 、x=1 9、二次函数y=2x 2+bx-5(b<0)的顶点在A 、第一象限B 、第二象限C 、第三象限D 、第四象限 10、无论m 为任何实数,二次函数y=x 2+(2-m)x+m 的图象总过点A 、(-1,3)B 、(1,0)C 、(1,3)D 、(-1,0) 三、解答题1、(5分)已知矩形的周长为36cm ,矩形绕它的一边旋转形成一个圆柱,矩形的长、宽各为多少时,旋转形成的圆柱的侧面积最大?OxyDA Ox yOx yOxy2、(8分)二次函数y=-3x 2-2x+c 的顶点A 在直线313+=x y 上,且直线与x 轴的交点为B ① 求函数解析式 ② 求出△OAB 的面积3、(8分)已知二次函数y=-x 2+(m -1)x+m 与y 轴交于点(0,3) (1) 求出m 的值并画出这条抛物线; (2) 求它与x 轴的交点和抛物线顶点的坐标; (3) x 取何值时,抛物线在x 轴的上方? (4) x 取何值时,y 随x 的增大而减小?4、(6分)如图,一抛物线型拱桥,拱顶离水面高4米,水面宽度AB =10米。
12月30日(九数周周清)二次函数的图像和性质测试题

xy 0 九数周周清《二次函数的图像和性质》基础知识测验(14年12月30日)班级:_________姓名:___________得分:__________一、选择题(每小题4分,共40分):1、下列函数是二次函数的有( ).;)3(;2;12222c bx ax y D x x x y C x y B x y A ++=--==-=::::2. y=(x -1)2+2的对称轴是直线( ) A .x=-1 B .x=1 C .y=-1 D .y=13. 抛物线()12212++=x y 的顶点坐标是( )A .(2,1)B .(-2,1)C .(2,-1)D .(-2,-1)4. 函数y=-x 2-4x+3图象顶点坐标是( )A.(2,-1) B.(-2,1) C.(-2,-1) D.(2, 1)6、二次函数c bx ax y ++=2的图象如图所示,则下列结论中正确的是:( )A a>0 b<0 c>0 b 2-4ac<0B a<0 b<0 c>0 b 2-4ac>0C a<0 b>0 c<0 b 2-4ac>0D a<0 b>0 c>0 b 2-4ac>0 5.已知二次函数)2(2-++=m m x mx y 的图象经过原点,则m 的值为 ( )A . 0或2B . 0C . 2D .无法确定6、与抛物线y=-12x 2+3x -5的形状、开口方向都相同,只有位置不同的抛物线是( )(A) y = x 2+3x -5 (B) y=-12x 2+2x (C) y =12x 2+3x -5 (D) y=12x 27.正比例函数y =kx 的图象经过二、四象限,则抛物线y =kx 2-2x +k 2的大致图象是( )8、若A (-4,y 1),B (-3,y 2),C (1,y 3)为二次函数y=x 2+4x-5的图象上的三点,则y 1,y 2,y 3的大小关系是( )A 、y 1<y 2<y 3 B 、y 2<y 1<y 3 C 、y 3<y 1<y 2 D 、y 1<y 3<y 29.抛物线23y x =向右平移1个单位,再向下平移2个单位,所得到的抛物线是( ) A 23(1)2y x =-- B 23(1)2y x =+- C 23(1)2y x =++ D 23(1)2y x =-+10.在同一坐标系中,函数y mx m =+和222y mx x =-++(m 是常数,且0m ≠)的图象可能..是( ) 二、填空题:(每题4分,共32分) 1、抛物线21(2)43y x =++可以通过将抛物线y =231x 向左平移_ _ 个单位、再向 平移 个单位得到。
九年级数学下册《二次函数》周周清

九年级数学下册《二次函数》周周清(12.3)1、抛物线 y =-x 2+1 的开口向____。
2、抛物线 y =2x 2 的对称轴是____。
3、函数 y =2 (x -1)2 图象的顶点坐标为____。
4、将抛物线 y =2x 2 向下平移 2 个单位,所得的抛物线的解析式为________。
5、函数 y =x 2+bx +3 的图象经过点(-1, 0),则 b =____。
6、二次函数 y =(x -1)2+2,当 x =____时,y 有最小值。
7、函数 y =12 (x -1)2+3,当 x ____时,函数值 y 随 x 的增大而增大。
8、将 y =x 2-2x +3 化成 y =a (x -h)2+k 的形式,则 y =____。
9、若点 A ( 2, m) 在函数 y =x 2-1 的图像上,则 A 点的坐标是____。
10、抛物线 y =2x 2+3x -4 与 y 轴的交点坐标是____。
11、请写出一个二次函数以(2, 3)为顶点,且开口向上。
____________。
12、已知二次函数 y =ax 2+bx +c 的图像如图所示:则这个二次函数的解析式是 y =___。
13、在圆的面积公式 S =πr 2 中,s 与 r 的关系是( ) A 、一次函数关系 B 、正比例函数关系 C 、反比例函数关系 D 、二次函数关系14、已知函数 y =(m +2) 22-m x 是二次函数,则 m 等于( )A 、±2B 、2C 、-2D 、±2 15、已知 y =ax 2+bx +c 的图像如图所示,则 a 、b 、c 满足(A 、a <0,b <0,c <0B 、a >0,b <0,c >0C 、a <0,b >0,c >0D 、a <0,b <0,c >0 16、苹果熟了,从树上落下所经过的路程 s 与下落时间 t 满足 S =129.8),则 s 与 t 的函数图像大致是( )A B C D17、抛物线 y =-x 2 不具有的性质是( ) A 、开口向下 B 、对称轴是 y 轴 C 、与 y 轴不相交 D 、最高点是原点 18、抛物线 y =x 2-4x +c 的顶点在 x 轴,则 c 的值是( ) A 、0 B 、4 C 、-4 D 、2 19.抛物线2(1)y x m x m =-+-+与y 轴交于(03),点. (1)求出m 的值并画出这条抛物线; (2)求它与x 轴的交点和抛物线顶点的坐标; (3)x 取什么值时,抛物线在x 轴上方? (4)x 取什么值时,y 的值随x 值的增大而减小? 20.已知抛物线268y ax x =+-与直线3y x =-相交于点(1)A m ,. (1)求抛物线的解析式; (2)请问(1)中的抛物线经过怎样的平移就可以得到2y ax =的图象? ttt t x21.抛物线()2361y x =-+-的对称轴是直线( )A.6x =- B.1x =- C.1x = D.6x =22.请选择一组你喜欢的a b c ,,的值,使二次函数2(0)y ax bx c a =++≠的图象同时满足下列条件:①开口向下,②当2x <时,y 随x 的增大而增大;当2x >时,y 随x 的增大而减小.这样的二次函数的解析式可以是 ..23.已知22y x =的图象是抛物线,若抛物线不动,把x 轴,y 轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是( ).A.22(2)2y x =-+ B.22(2)2y x =+-C.22(2)2y x =-- D.22(2)2y x =++24.已知二次函数2y ax bx c =++的图象如图所示,对称轴是1x =, 下列结论中正确的是( ).A.0ac > B.0b <C.240b ac -< D.20a b +=25.小明从右边的二次函数2y ax bx c =++图象中,观察得出了下面的五条信息:①0a <,②0c =,③函数的最小值为3-,④当0x <时,0y >, ⑤当1202x x <<<时,12y y >.你认为其中正确的个数为( )A.2 B.3C.4 D.526.如图,已知抛物线2(0)y ax bx c a =++≠经过(20)(04)A B --,,,,(24)C -,三点,且与x 轴的另一个交点为E . (1)求抛物线的解析式; (2)用配方法求抛物线的顶点D 的坐标和对称轴; (3)求四边形ABDE 的面积. 27.下表给出了代数式2x bx c ++与x 的一些对应值:(1)请在表内的空格中填入适当的数; (2)设2y x bx c =++,则当x 取何值时,0y >? (3)请说明经过怎样平移函数2y x bx c =++的图象得到函数2y x =的图象. x A B C D O E x y x。
九年级上册数学第四周周清卷《二次函数》

九年级上册数学第四周周清卷《二次函数》一.选择题(每小题3分,共33分)1.下列函数中,是二次函数的是________:A 、y=2x+22B 、y=x x 221-C 、y=1+5x -x 2D 、y=(1-x)(1+x)-x 3 2..抛物线214x y -=,22x y -=,232.0x y -=的开口宽窄由小到大的顺序( )A 、1y ,2y ,3yB 、3y ,2y ,1yC 、2y ,1y ,3yD 、3y ,1y ,2y3.二次函数k k x a y ++=2)()0(≠a ,无论k 为何实数,其图像的顶点都在( )A 、x 轴上B 、y 轴上C 、直线y=x 上D 、直线y= -x 上4.与抛物线c bx ax y ++=2的对称轴的位置有关的数据是______A 、aB 、bC 、a 、bD 、a 、b 、c5.已知函数y=k x ++-2)3(3的图像上有三个点A (),251y -,B ),3(2y -,C ),5(3y -,则321,,y y y 的大小关系是( )A 、1y <2y <3yB 、3y <2y <1yC 、3y <1y <2yD 、2y <1y <3y6.、已知二次函数y=32++bx x ,当1-=x 时,y 取得最小值,则这个二次函数的顶点( )A 、第一象限B 、第二象限C 、第三象限D 、第四象限7.如图是抛物线y=c x ax +-2的图象,则下列判断正确的是( )A 、c a +>0B 、c a ->0C 、ac >0D 、ac <08.二次函数122-+=x x y ,当2-≤x ≤2时的最大值、最小值为( )A 、7,1-B 、7,2-C 、1- ,2-D 、7,09. 已知二次函数y=-x ²-2bx+c ,当x<2时,y 随x 增大而增大,b 的取值范围( )A. b ≥-1B.b ≤-1C.b ≥-2D.b ≤-210.在同一平面内,一次函数y=ax+b 与二次函数y=ax ²+bx+c 的图象可能是( )11.二.填空题(25分,每空1分)1.(1)若将抛物线y=4x 2的图像绕其顶点旋转180°,所得抛物线的解析式为______________;(2)若点A (1x ,2)、B(2x ,2)(1x ≠2x )都在抛物线2ax y =的图像上,则当221x x x +=时,y=_____.2.已知抛物线y=c x x +-62的顶点在x 轴上,则c 的值 。
初三上册数学《二次函数》周清试卷

EFD C OAB初三数学周清试卷(总用时:90分钟 总分:140分)班级__________ 姓名__________ 得分___________一、选择题(3*12=36分)1.下列方程是关于x 的一元二次方程的是( ); A.02=++c bx ax B.2112=+x xC.)1)(1(22-+=+x x x xD.)1(2)1(32+=+x x 2.二次函数y=x 2﹣x+1的图象与x 轴的交点个数是( ) A .0个 B .1个 C .2个 D .不能确定3.下列抛物线中与y =-12x 2+3x -5的形状、开口方向都相同,只有位置不同的是( )A.y =x 2+3x -5 B.y =-12x 2+2x C.y =12x 2+3x -5 D.y =12x 24. 若一次函数y=ax+b 的图象经过第二、三、四象限,则二次函数y=ax 2+bx 的图象只可能是( )5.如图,把菱形ABOC 绕点O 顺时针旋转到菱形DFOE ,则下列角中不是旋转角的是( ) A. ∠BOF B. ∠AOD C. ∠COE D. ∠COF6.关于x 的一元二次方程x²-2x+2k=0有实数根,则k 的取值范围是 ( ) A 、k<21 B 、 k≤ 21 C 、 k> 21 D 、 k≥ 217.宾馆有50间房供游客居住,当毎间房每天定价为180元时,宾馆会住满;当毎间房每天的定价每增加10元时,就会空闲一间房.如果有游客居住,宾馆需对居住的毎间房每天支出20元的费用.当房价定为多少元时,宾馆当天的利润为10890元?设房价定为x 元.则有( ) A .(180+x ﹣20)(50﹣)=10890 B .(x ﹣20)(50﹣)=10890C .x (50﹣)﹣50×20=10890D .(x +180)(50﹣)﹣50×20=108908.若方程x 2﹣8x +m=0可以通过配方写成(x ﹣n )2=6的形式,那么x 2+8x +m=5可以配成( ) A .(x ﹣n +5)2=1B .(x +n )2=1C .(x ﹣n +5)2=11D .(x +n )2=119.若二次函数y=(a ﹣1)x 2+3x +a 2﹣1的图象经过原点,则a 的值必为 ( ) A .1或﹣1 B .1C .﹣1D .010.如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是()A.B.C.D.11.若二次函数y=(a﹣1)x2+3x+a2﹣1的图象经过原点,则a的值必为()A.1或﹣1 B.1 C.﹣1 D.012.如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数).其中正确结论的有()A.①②③B.①③④C.③④⑤D.②③⑤(第10题)(第12题)(第17题)(第18题)二、填空题(3*6=18分)13.点A的坐标为(2,0),把点A绕着坐标原点顺时针旋转135º到点B,那么点B的坐标是 _________ .14.若α、β为实数且|α+β-3|+(2-αβ)2=0,则以α、β为根的一元二次方程为_______________。
九年级数学: 第22章二次函数周周清试题

23=x 23=x1.下列关系式中,属于二次函数的是(x 为自变量)( ) A.B.C.D.2. 函数y=x 2-2x+3的图象的顶点坐标是( )A. (1,-4)B.(-1,2)C. (1,2)D.(0,3) 3. 抛物线y=2(x -3)2的顶点在( )A. 第一象限B. 第二象限C. x 轴上D. y 轴上 4. 抛物线 的对称轴是( )A. x=-2B.x=2C. x=-4D. x=45. 已知二次函数y=ax 2+bx+c 的图象如图所示,则下列结论中,正确的是( ) A. ab>0,c>0B. ab>0,c<0C. ab<0,c>0D. ab<0,c<06. 二次函数y=ax 2+bx+c 的图象如图所示,则点 在第___象限( ) A. 一 B. 二 C. 三 D. 四7. 如图所示,已知二次函数y=ax 2+bx+c(a ≠0)的图象的顶点P 的横坐标是4,图象交x 轴于点A(m ,0)和点B ,且m>4,那么AB 的长是( )A. 4+mB. mC. 2m -8D. 8-2m8. 若一次函数y=ax+b 的图象经过第二、三、四象限,则二次函数y=ax 2+bx 的图象只可能是( )9. 函数y= -x 2-2x+3(x ≥0)的最大值是 ( ) A.3 B.4 C.-4 D.-3二、填空题(每题4分,共32分)11. 二次函数y=x 2-2x+1的对称轴方程是______________.12. 若将二次函数y=x 2-2x+3配方为y=(x -h)2+k 的形式,则y=________.13. 若抛物线y=x 2-2x -3与x 轴分别交于A 、B 两点,则AB 的长为_________.14. 抛物线y=x 2+bx+c ,经过A(-1,0),B(3,0)两点,则这条抛物线的解析式为_____________.15. 已知二次函数y=ax 2+bx+c 的图象交x 轴于A 、B 两点,交y 轴于C 点,且△ABC 是直角三角形,请写出一个符合要求的二次函数解析式________________.16. 在距离地面2m 高的某处把一物体以初速度v 0(m/s)竖直向上抛物出,在不计空气阻力的情况下,其上升高度s(m)与抛出时间t(s)满足: (其中g 是常数,通常取10m/s 2).若v 0=10m/s ,则该物体在运动过程中最高点距地面_________m.17. 试写出一个开口方向向上,对称轴为直线x=2,且与y 轴的交点坐标为(0,3)的抛物线的解析式为______________.18. 已知抛物线y=x 2+x+b 2经过点, 则y 1的值是_______.三、解答下列各题(19、20每题9分,21、22每题10分,共38分) 19. 若二次函数的图象的对称轴方程是 , 并且图象过A(0,-4)和B(4,0)(1)求此二次函数图象上点A 关于对称轴对称的点A ′的坐标;(2)求此二次函数的解析式;21.在直角坐标平面内,点O为坐标原点,二次函数y=x2+(k-5)x-(k+4) 的图象交x轴于点A(x1,0)、B(x2,0),且(x1+1)(x2+1)=-8.(1)求二次函数解析式;(2)将上述二次函数图象沿x轴向右平移2个单位,设平移后的图象与y轴的交点为C,顶点为P,求△POC的面积.21.已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.(1)求抛物线的解析式;(2)求△MCB的面积S△MCB 22.某商店销售一种商品,每件的进价为2.50元,根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是13.50元时,销售量为500件,而单价每降低1元,就可以多售出200件.请你分析,销售单价多少时,可以获利最大.。
一元二次方程周周清试卷

x1一元二次方程周周清试卷班级__________ 姓名____________ 分数__________一、填空题1、方程x 2+2x +m=0有两个相等实数根,则m =_______________。
2、若关于x 的二次方程kx 2+ x + 1 = 0有实数根,则k 的取值范围是____________。
3、方程x 2+9x +44=0解的情况是_____________________。
4、已知两个数的和是5,积是6,则这两个数分别是 __ 。
5、已知方程2x 2-5x -7=0的两根为x 1,x 2,则x 1+x 2 = ,x 1x 2= 。
二、选择题6、下列关于x 的方程中,是一元二次方程的是( )。
A. x 3 - 3x + 2=0B. a 2x 2 + c=0C. (k 2+1)x 2 – x - 1=0D. x 2 + = - 27、用直接开平方法解一元二次方程(x-3)2= 4时,可先把方程转化为( )。
A. x-3=2 B. x-3=4或 x-3=-4 C. x-3=-2 D. x-3=2或 x-3=-28、不解方程,判别方程2x 2+3x-4=0的根的情况( )。
A 、有两个相等的实数根 B 、有两个不相等的实数根 C 、有一个实数根 D 、无实数根 三、解答题9、解方程:x 2+2x-3=0 .10、k 为何值时,方程x 2 - 3x + k = 0 (1) 有两个不相等的实数根; (2) 有两个相等的实数根;(3) 没有实数根。
11、设x 1,x 2是方程2x 2 + 4x – 3 = 0的两个根,利用根与系数的关系,求下列各式的值。
(1)(x 1+1)(x 2+1) ; (2)11x +21x .。
度第一学期人教版九年级数学上册_第22章_二次函数_周周清测试题(含答案)-word文档资料

2019-2019学年度第一学期人教版九年级数学上册第22章_二次函数_周周清测试题考试总分: 120 分考试时间: 120 分钟学校:__________ 班级:__________ 姓名:__________ 考号:__________一、选择题(共 10 小题,每小题 3 分,共 30 分)1.下列关于的函数中,属于二次函数的是()A. B.C. D.2.抛物线的对称轴是()A. B. C. D.3.关于二次函数的图象,下列说法正确的是()A.是中心对称图形B.开口向上C.对称轴是直线D.最高点是4.已知函数的图象如图所示,则下列结论正确的是()A.,B.,C.,D.,5.关于二次函数的图象与性质,下列结论错误的是()A.抛物线开口方向向下B.当时,函数有最大值C.当时,随的增大而减小D.抛物线可由经过平移得到6.已知二次函数的图象上有三点,,,则、、的大小关系为()A. B.C. D.7.小明从右边的二次函数图象中,观察得出了下面的五条信息:① ,② ,③函数的最小值为,④当时,,⑤当时,,⑥对称轴是直线.你认为其中正确的个数为()A. B. C. D.8.若二次函数的图象的最高点在轴上,则的值为()A. B. C.或 D.无法确定9.边长为的正方形的顶点在轴的正半轴上,如图将正方形绕顶点顺时针旋转得正方形,使点恰好落在函数的图象上,则的值为()A. B. C. D.10.已知顶点为的抛物线经过点,下列结论中错误的是()A.B.若点,在抛物线上,则C.D.关于的一元二次方程的两根为和第 1 页二、填空题(共 10 小题,每小题 3 分,共 30 分)11.已知抛物线与轴的交点坐标为,,当时,的最大值为,则该抛物线的解析式为________.12.二次函数图象的顶点坐标为________.13.如图,二次函数图象的顶点为,其图象与轴的交点、的横坐标分别为,.与轴负半轴交于点,在下面五个结论中:① ;② ;③当时,;④若,且,则;⑤使为等腰三角形的值可以有三个.其中正确的结论是________.(只填序号)14.抛物线与直线交于,则________;抛物线的解析式________.15.抛物线与轴两交点的距离是________.16.如果二次函数配方后为,那么的值为________.17.若函数的图象与轴只有一个交点,则________.18.用一根长为的木条,做一个长方形的窗框,若宽为,则该窗户的面积与之间的函数关系式为________.19.试写出一个二次函数关系式,使它对应的一元二次方程的一个根为,另一个根在到之间:________.20.物体自由下落时,它所经过的距离(米)和时间(秒)之间可以用关系式来描述.建于年的上海金茂大厦高米,当时排名世界第三高楼.若从高米的观光厅上掉下一个物体,自由下落到地面约需________秒(精确到秒).三、解答题(共 6 小题,每小题 10 分,共 60 分)21.如图.已知二次函数的图象与轴的一个交点为,与轴交于点.求此二次函数关系式和点的坐标;在轴的正半轴上是否存在点.使得是以为底边的等腰三角形?若存在,求出点的坐标;若不存在,请说明理由.22.二次函数的自变量与函数值的部分对应值如下表:①表中的________;②二次函数有最________值;③若点、是该函数图象上的两点,且,,试比较大小:________;求关于的方程的根;若自变量的取值范围是,则函数值的取值范围是________.23.已知二次函数.写出它的开口方向、顶点坐标和对称轴;求它与轴的交点;画出这个二次函数图象的草图.24.某商店购进一批单价为元的日用商品,如果以单价元销售,那么每星期可售出件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高元,销售量相应减少件.设销售单价为(元)时,该商品每星期获得的利润(元).求出与之间的函数关系式及自变量的取值范围;求出销售单价为多少元时,每星期获得的利润最大?最大利润是多少?25.如图,的顶点坐标分别为,,,把沿直线翻折,点的对应点为,抛物线经过点,顶点在直线上.证明四边形是菱形,并求点的坐标;求抛物线的对称轴和函数表达式;在抛物线上是否存在点,使得与的面积相等?若存在,直接写出点的坐标;若不存在,请说明理由.26.某商品现在的售价为每件元.每天可卖出件.市场调查反映:如果调整价格.每降价元,每天可多卖出件.请你帮助分析,当每件商品降价多少元时,可使每天的销售额最大,最大销售额是多少?设每件商品降价元.每天的销售额为元.答案1.C2.B3.D4.D5.D6.D7.D8.B9.D10.B11.12.②③④14.15.16.17.或18.19.20.21.解:把点代入二次函数有:得:所以二次函数的关系式为:.当时,第 3 页∴点的坐标为.如图:作的垂直平分线交轴于点,连接,则:设,则,在直角中,即:解得:∴所以点的坐标为:综上可得点的坐标为.22.大23.解: ∵ ,∴ ,抛物线开口向下,顶点坐标,对称轴; ∵ ∴与轴交点,;画图如下:24.销售单价为元时,每星期获得的利润最大,最大利润是元.25.证明:∵ ,,,∴ ,,∴ ,由翻折可得,,,∴ ,∴四边形是菱形,∴ ,∵ ,∴点的坐标是; ∵ ,∴对称轴为直线.设的坐标为,直线的解析式为,∴ ,解得.∴ .∵点在直线上,∴ .又∵抛物线经过点和,∴ ,解得.∴抛物线的函数表达式为;存在.理由如下:由题意可知,在抛物线上,且到,所在直线距离相等,所以在二次函数与、所在的直线的夹角平分线的交点上,而、所在的直线的夹角平分线有两条:一条是所在的直线,解析式为,另外一条是过且与平行的直线,解析式为,联立,解得:(舍)或,联立,解得:(舍)或所以当与的面积相等,点的坐标为,.26.当每件商品降价元时,可使每天的销售额最大,最大销售额为元.第 5 页。
九年级数学上册 第二章 二次函数周周清 试题

二次函数制卷人:歐陽文化、歐陽理複;制卷時間:二O 二二年二月七日1.抛物线5)3(22+-=x y 的对称轴是 ,顶点坐标是 ;它是由抛物线22x y =的图象_________________________________平移得到的。
2.当_____=x ,函数322--=x x y 的函数值为5;3.假如抛物线m x x y +-=62的顶点在x 轴上,那么______=m ;4.函数322--=x x y ,那么它的顶点坐标是 ,对称轴是 ;图象与y 轴的交点为 ,与x 轴的交点为 ;5.二次函数c bx x y ++=2的顶点坐标为〔3-,1〕,那么____________,==c b ; 6.某抛物线的顶点为1(-P ,)8-且经过点0(,)6-,那么这个抛物线的解析式为 . 7、在同一直角坐标系中,一次函数c ax y +=和二次函数c ax y +=2的图象大致为〔〕8.如图,四个二次函数的图像中,分别对应的是①y = ax 2;②y = ax 2;③y = cx 2; ④y = cx 2.那么a 、b 、c 、d 的大小关系为〔 〕A.a>b>c>dB. a>b>d> cC.b > a >c>dD.b>a>d> c9.假设抛物线y = x 2+(k-1)x+(k+3)经过原点,那么k= .10.抛物线y=ax 2+bx+c 经过原点和第一、二、三象限,那么 ( )A.a>0,b>0,c>0B.a<0,b<0,c=0C.a<0,b<0,c>0D.a>0,b>0,c=0 11.假设〔2, 5〕、〔4, 5〕是抛物线y = ax 2+bx+c 上的两点,那么它的对称轴方程是 ( )A.x = -1B.x = 1C.x = 2D.x = 312.假设直线y=x-n 与抛物线y = x 2-x-n 的交点在x 轴上,那么n 的取值一定为 〔 〕13.二次函数y = ax 2+bx+c 的图像如下图,那么点〔,a b c c〕 在直角坐标系中的 〔 〕A .第一象限 B .第二象限C .第三象限D .第四象限14.假如函数y = ax 2+4x-16的图像的顶点的横坐标为l ,那么a 的值是 15.抛物线y = ax 2+12x-19的顶点的横坐标是3,那么 a= . 16.抛物线y = a(x-k)2+m 的对称轴是直线 ,顶点坐标是 .17.抛物线y = 2x 2+bx+c 的顶点坐标为〔2,-3),那么b= , c= . 18.在以下关系式中,y 是x 的二次函数的关系式是 ( )A.2xy+x 22-ax+2=0 C.y+x 22-y 2+4=019.设等边三角形的边长为x(x>0〕,面积为y ,那么y 与x 的函数关系式是( )A.212y x =B.214y x =C.232y x =D.234y x = 20.抛物线y=x 2-8x+c 的顶点在x 轴上,那么c 等于( )A.-16 B.-4 C.8 D.1621.假设直线y=ax +b (a ≠0〕在第二、四象限都无图像,那么抛物线y=ax 2+bx+c ( )xyO AxyO B xyO C xyO DA.开口向上,对称轴是y轴B.开口向下,对称轴平行于y轴C.开口向上,对称轴平行于y轴D.开口向下,对称轴是y轴22.一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标系中的图像可能是〔〕23.抛物线y=-x2+mx+n的顶点坐标是〔-1,- 3 ),那么m和n的值分别是〔〕A.2,4B.-2,-4C.2,-4D.-2,024.对于函数y=-x2+2x-2使得y随x的增大而增大的x的取值范围是 ( )≥≤0 D.x<-125.抛物线y=-2x+x2+7的开口向,对称轴是 __,顶点是 , 所在象限是 .26.假设二次函数y=mx2-3x+2m-m2的图像过原点,那么m的值是 .27.假如把抛物线y=2x2-1向左平移l个单位,同时向上平移4个单位,那么得到的新的抛物线是 .28.对于二次函数y=ax2, 当x由1增加到2时,函数值减少4,那么常数a的值是 .29.二次函数y=x2-6x+n的最小值为1,那么n的值是 .抛物线y=-2x2-1的对称轴是,顶点坐标是30、把二次函数y=-2x2+4x+3化成y=a〔x+m〕2+k的形式是,其开口方向向31、抛物线y=-2x2-x+3与y轴交点的坐标是,与x轴的交点坐标是32、函数y=2x2的图象向左平移2个单位,再向上平移3个单位得到的函数关系式是33、函数y=x2+3kx+k+1的图象过原点,那么函数的关系式是cbxaxy++=2的图象如下图,那么以下结论中正确的选项是:〔〕A a>0 b<0 c>0B a<0 b<0 c>0C a<0 b>0 c<0D a<0 b>0 c>035.以下四个函数:①(0);y kx k k=>为常数,②(,0);y kx b k b k=+>为常数,③(0);ky k kx=>为常数,④2(0);y ax a a=>为常数,其中,函数y的值随着x值得增大而减少的是 A ① B、② C、③ D、④y=x2-(12-k)x+12,当x>1时,y随着x的增大而增大,当x<1时,y随着x的增大而减小,那么k的值应取〔〕〔A〕12 〔B〕11 〔C〕10 〔D〕937.在平面直角坐标系中,抛物线21y x=-与x轴的交点的个数是〔〕A.3 B.2 C.1 D.038、以下四个函数中,y的值随着x值的增大而减小的是〔〕〔A〕xy2=〔B〕()01>=xxy〔C〕1+=xy〔D〕()02>=xxy23xy=的图象向左平移2个单位,再向上平移1个单位,所得到的图象对应的二次函数关系式是〔〕〔A〕()1232+-=xy〔B〕()1232-+=xy〔C〕()1232--=xy〔D〕()1232++=xy40、(3)抛物线y=ax2+bx,当a>0,b<0时,它的图象经过( )A.一、二、三象限B.一、二、四象限C.一、三、四象限 D.一、二、三、四象限41、假设0<b ,那么二次函数12-+=bx x y 的图象的顶点在 〔 〕 〔A 〕第一象限〔B 〕第二象限〔C 〕第三象限〔D 〕第四象限y =-4x 2-2m x +m 2与反比例函数y =xm 42+的图像在第二象限内的一个交点的横坐标是-2,那么m 的值是43.点〔a ,8〕在二次函数y =a x 2的图象上,那么a 的值是〔 〕A ,2B ,-2C ,±2D ,±2 44.抛物线y =x 2+2x -2的图象最高点的坐标是〔 〕A.〔2,-2〕B.〔1,-2〕C.〔1,-3〕D.〔-1,-3〕 45.假设y =(2-m)23m x -是二次函数,且开口向上,那么m 的值是( )A.5±5 C.5 D.046.函数y =9-4x 2,当x =_________时有最大值________.c bx ax y ++=21〔0≠a 〕与一次函数)0(2≠+=k m kx y 的图象相交于点A 〔-2,4〕,B 〔8,2〕〔如下图〕,那么能使21y y >成立的x 的取值范围是 .48.在同一直角坐标系中,函数y mx m =+和222y mx x =-++〔m 是常数,且0m ≠〕的图象可能..是〔 〕,假如抛物线y =2x 2不动,而把x 轴、y 轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是_______________________22y x x c =-++的局部图象如下图,那么c=______,当x______时,y 随x 的增大而减小.51.反比例函数y =xa(a ≠0)的图象,在每一象限内,y 的值随x 值的增大而减少,那么一次函数y =-a x +a 的图象不经过...〔 〕 A.第一象限 B.第二象限 C.第三象限 D.第四象限342++=x x y 的图像可以由二次函数2x y =的图像平移而得到,以下平移正确的选项是( )A .先向左平移2个单位,再向上平移1个单位B .先向左平移2个单位,再向下平移1个单位C .先向右平移2个单位,再向上平移1个单位D .先向右平移2个单位,再向下平移1个单位制卷人:歐陽文化、歐陽理複;制卷時間:二O 二二年二月七日第15题图xyO A.xyO xyO C.。
二次函数周周清
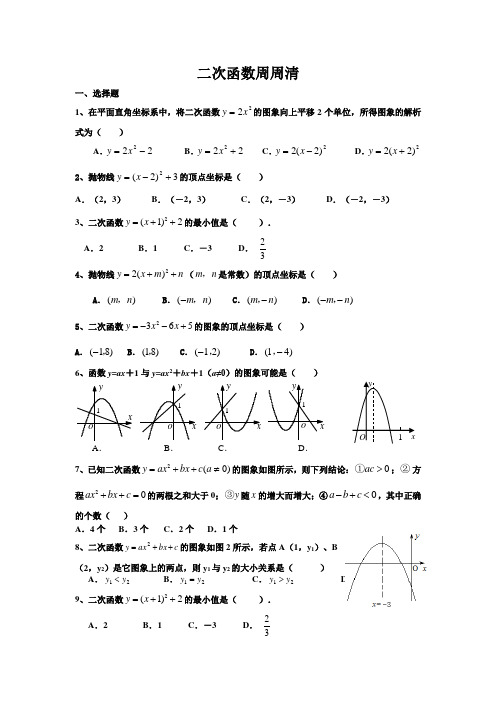
二次函数周周清一、选择题1、在平面直角坐标系中,将二次函数22x y =的图象向上平移2个单位,所得图象的解析式为( )A .222-=x yB .222+=x yC .2)2(2-=x yD .2)2(2+=x y 2、抛物线3)2(2+-=x y 的顶点坐标是( )A .(2,3)B .(-2,3)C .(2,-3)D .(-2,-3) 3、二次函数2(1)2y x =++的最小值是( ). A .2 B .1 C .-3 D .234、抛物线22()y x m n =++(m n ,是常数)的顶点坐标是( )A .()m n ,B .()m n -,C .()m n -,D .()m n --,5、二次函数2365y x x =--+的图象的顶点坐标是( ) A .(18)-, B .(18),C .(12)-,D .(14)-,6、函数y =ax +1与y =ax 2+bx +1(a ≠0)的图象可能是( )7、已知二次函数2(0)y ax bx c a =++≠的图象如图所示,则下列结论:0ac >①;②方程20ax bx c ++=的两根之和大于0;y ③随x 的增大而增大;④0a b c -+<,其中正确的个数( ) A .4个 B .3个C .2个D .1个8、二次函数c bx ax y ++=2的图象如图2所示,若点A (1,y 1)、B (2,y 2)是它图象上的两点,则y 1与y 2的大小关系是( )A .21y y <B .21y y =C .21y y >D .不能确定9、二次函数2(1)2y x =++的最小值是( ). A .2 B .1 C .-3 D .23A .B .C .D .10.把抛物线的图象向左平移2个单位,再向上平移3个单位,所得的抛物线的函数关系式是( ) A. B. C.D.11、如图,直角坐标系中,两条抛物线有相同的对称轴,下列关系不正确...的是( ) A .h m = B .k n = C .k n > D .00h k >>,12、已知二次函数2y ax bx c =++(0a ≠)的图象如图所示,有下列四个结论:20040b c b ac <>->①②③④0a b c -+<,其中正确的个数有( ) A .1个 B .2个 C .3个D .4个二、填空题1、若把代数式223x x --化为()2x m k -+的形式,其中,m k 为常数,则m k +=.2、抛物线23(1)5y x =--+的顶点坐标为__________.3、将抛物线22y x =-向上平移一个单位后,得以新的抛物线,那么新的抛物线的表达式是 .4、当x =_____________时,二次函数222y x x =+-有最小值.5、⊙O 的半径为2,C 1是函数y =12x 2的图象,C 2是函数y =-12x 2的图象,则阴影部分的面积是 .6、把抛物线y =ax+bx+c 的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y =x -3x+5,则a+b+c=__________7、(2009年本溪)如图所示,抛物线2y ax bx c =++(0a ≠)与x 轴的两个交点分别为(10)A -,和(20)B ,,当0y <时,x 的取值范围是 .8.(2009年湖州)已知抛物线2y ax bx c =++(a >0)的对称轴为直线1x =,且经过点()()212y y -1,,,,试比较1y 和2y 的大小:1y _2y (填“>”,“<”或“=”)。
九年级数学下册周周清检测内容:2.4_2.5新版北师大版

检测内容:2.4-2.5得分________ 卷后分________ 评价________一、选择题(每小题5分,共35分)1.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则关于x的方程ax2+bx+c =0的解为(A)A.x1=-1,x2=2 B.x1=-1,x2=-2C.x1=1,x2=2 D.x1=1,x2=-2第1题图第2题图2.如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集为(A)A.x<-1或x>5 B.x>5C.-1<x<5 D.无法确定3.(山西中考)竖直上抛物体离地面的高度h(m)与运动时间t(s)之间的关系可以近似地用公式h =-5t 2+v 0t +h 0表示,其中h 0(m)是物体抛出时离地面的高度,v 0(m/s)是物体抛出时的速度.某人将一个小球从距地面1.5 m 的高处以20 m/s 的速度竖直向上抛出,小球达到的离地面的最大高度为(C )A .23.5 mB .22.5 mC .21.5 mD .20.5 m4.有一拱桥洞呈抛物线形状,它的最大高度是16 m ,跨度为40 m ,现把它的示意图(如图所示)放在直角坐标系中,则这个桥洞所在抛物线的表达式为(C )A .y =125 x 2+58 xB .y =-125 x 2-125 xC .y =-125 x 2+85 xD .y =-125 x 2+85x +16第4题图第6题图5.将进价为70元的某商品按定价为100元卖出时,每天能卖出20个,若零售价每降低1元,其日销量就增加1个,为了获得最大利润,则应降价(A )A .5元B .10元C .15元D .20元6.如图,利用一个直角墙角修建一个梯形储料场ABCD ,其中∠C =120°.若新建墙BC与CD 的总长为12 m ,则该梯形储料场ABCD 的最大面积是(C )A .18 m 2B .18 3 m 2C .24 3 m 2D .4532m 27.如图,△ABC 是边长为4 cm 的等边三角形,动点P 从点A 出发,以2 cm/s 的速度沿A →C →B 运动,到达B 点即停止运动,PD ⊥AB 于点D ,则△ADP 的面积y (cm 2)与运动的时间x (s)之间的函数图象为(A )第7题图第9题图二、填空题(每小题5分,共25分)8.若抛物线y =x 2-(2k +1)x +k 2+2与x 轴有两个交点,则整数k 的最小值是2.9.如图,已知二次函数y 1=ax 2+bx +c 与一次函数y 2=kx +m 相交于A (-1,2),B (4,1)两点,则关于x 的不等式ax 2+bx +c >kx +m 的解集是x <-1或x >4.10.教练对小明推铅球的录像进行技术分析,发现铅球行进高度y (m)与水平距离x (m)之间的关系式为y =-112(x -4)2+3,由此可知铅球推出的距离是10m.11.公园里喷水池中的水柱的形状可以看成是如图所示的抛物线,若水柱上的点C ,D到地面的距离都是1.6 m ,AB =1 m ,AO =5 m ,则水柱的最大高度是7225m.第11题图第12题图12.(雅安中考) 已知函数y =⎩⎪⎨⎪⎧-x 2+2x (x >0),-x (x ≤0) 的图象如图所示,若直线y =x +m与该图象恰有三个不同的交点,则m 的取值范围为0<m <14.三、解答题(共40分)13.(8分)如图,直线y 1=-x +2和抛物线y 2=x 2+bx +c 都经过A (2,0),B (k ,2)两点.(1)求k 的值和抛物线的表达式;(2)当y 1<y 2时,求x 的取值范围.解:(1)k =0,y =x 2-3x +2(2)当y 1<y 2时,x 的取值范围是x <0或x >214.(10分)有一个抛物线型蔬菜大棚,将其截面放在如图所示的直角坐标系中,抛物线可以用函数y =ax 2+bx 来表示.已知大棚在地面上的宽度OA 为8 m ,与点O 相距2 m 处的棚高BC 为94m .(1)求该抛物线的函数表达式;(2)求蔬菜大棚离地面的最大高度;(3)若借助横梁DE 建一个门,要求门的高度不低于1.5 m ,那么横梁DE 的宽度最多是多少米?解:(1)y =-316 x 2+32x(2)y =-316 x 2+32 x =-316 (x -4)2+3,∴蔬菜大棚离地面的最大高度是3米(3)当y =-316 x 2+32x =1.5时,解得x 1=4+22 ,x 2=4-22 ,∴x 1-x 2=4+22-(4-22 )=42 ,∴横梁DE 的宽度最多是42 米15.(10分)某公司研发了一款成本为50元的新型玩具,投放市场进行试销售.其销售单价不低于成本,按照物价部门规定,销售利润不高于90%.市场调研发现,在一段时间内,每天销售数量y(个)与销售单价x(元)符合一次函数关系,如图所示,(1)根据图象,直接写出y与x的函数关系式;(2)该公司要想每天获得3 000元的销售利润,销售单价应定为多少元?(3)销售单价为多少元时,每天获得的利润最大?最大利润是多少元?解:(1)y=-2x+260(2)由题意,得(x-50)(-2x+260)=3 000,解得x1=80,x2=100.∵50≤x≤50×(1+90%)=95,∴x=80,∴销售单价应定为80元(3)设每天获得的利润为w元,由题意,得w=(x-50)(-2x+260)=-2x2+360x-13 000=-2(x-90)2+3 200,∵50≤x≤95,∴当x=90时,w有最大值,w最大=3 200.答:销售单价为90元时,每天获得的利润最大,最大利润是3 200元16.(12分)如图,排球运动员站在点O处练习发球,将球从O点正上方2 m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9 m,高度为2.43 m,球场的边界距O点的水平距离为18 m.(1)当h=2.6时,求y与x之间的函数关系式;(不要求写出自变量x的取值范围)(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;(3)若球一定能越过球网,又不出边界,求h的取值范围.解:(1)∵A(0,2),∴h=2.6时,有a(0-6)2+2.6=2,解得a=-160,∴y=-160(x-6)2+2.6(2)∵h=2.6,∴当x=9时,y=-160(9-6)2+2.6=2.45>2.43,∴排球能过球网;当y=0时,-160(x-6)2+2.6=0,解得x1=6+239,x2=6-239(舍去),而6+239>18,∴会出界(3)根据题意有⎩⎪⎨⎪⎧a (0-6)2+h =2,a (9-6)2+h ≥2.43,a (18-6)2+h ≤0,解得h ≥83。
函数与方程-幂函数与二次函数(周清+周测+方法)

函数与方程1.函数的零点(1)函数零点的定义:对于函数y=f(x),我们把使01f(x)=0的实数x叫做函数y=f(x)的零点.(2)三个等价关系:方程f(x)=0有实数根⇔函数y=f(x)的图象与x轴有交点⇔函数y=f(x)有零点.(3)函数零点的判定(零点存在定理):如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有04f(a)·f(b)<0,那么,函数y=f(x)在区间05(a,b)内有零点,即存在c∈(a,b),使得06f(c)=0,这个07c也就是方程f(x)=0的根.2.二次函数y=ax2+bx+c(a>0)的图象与零点的关系Δ>0Δ=0Δ<0二次函数y=ax2+bx+c(a>0)的图象与x轴的交点(x1,0),(x2,0)(x1,0)无交点零点个数2103.二分法(1)二分法的定义:对于在区间[a,b]上连续不断且13f(a)·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.(2)二分法求函数零点近似值的步骤给定精确度ε,用二分法求函数f(x)零点近似值的步骤如下:14f(a)·f(b)<0,给定精确度ε;②求区间(a,b)的中点c;③计算f(c)①确定区间[a,b],验证(ⅰ)若f(c)=0,则15c就是函数的零点;(ⅱ)若f(a)·f(c)<0,则令16b=c(此时零点x0∈(a,c));(ⅲ)若f(c)·f(b)<0,则令17a=c(此时零点x0∈(c,b));18|a-b|<ε,则得到零点近似值a(或b);否则重复②~④.④判断是否达到精确度ε:若函数零点结论、判断函数零点区间及个数方法有关函数零点的结论(1)若连续不断的函数f(x)在定义域上是单调函数,则f(x)至多有一个零点.(2)连续不断的函数,其相邻两个零点之间的所有函数值保持同号.(3)连续不断的函数图象通过零点时,函数值可能变号,也可能不变号.(4)函数的零点是实数,而不是点,是方程f(x)=0的实根.(5)由函数y=f(x)(图象在[a,b]上是连续不断的)在(a,b)上有零点不一定能推出f(a)·f(b)<0,如图所示,所以f(a)·f(b)<0是y=f(x)在区间(a,b)上有零点的充分不必要条件.判断函数零点所在区间的常用方法(1)定义法:利用函数零点存在定理,首先看函数y=f(x)在区间[a,b]上的图象是否连续,再看是否有f(a)·f(b)<0.若有,则函数y=f(x)在区间(a,b)内必有零点.(2)解方程法:当对应方程易解时,可通过解方程确定方程是否有根落在给定区间上.(3)数形结合法:画出相应的函数图象,通过观察图象与x轴在给定区间上是否有交点来判断,或者转化为两个函数图象在给定区间上是否有交点来判断.确定函数零点个数的方法及思路(1)解方程法:令f(x)=0,如果能求出解,则有几个解就有几个零点.(2)零点存在定理法:利用定理不仅要求函数在区间[a,b]上是连续不断的曲线,且f(a)·f(b)<0,还必须结合函数的图象与性质(如单调性、奇偶性、周期性、对称性)才能确定函数有多少个零点或零点值所具有的性质.(3)数形结合法:转化为两个函数的图象的交点个数问题.先画出两个函数的图象,看其交点的个数,其中交点的横坐标有几个不同的值,就有几个不同的零点.幂函数对点训练例1.幂函数()()22121m f x m m x -=-+在()0,∞+上为增函数,则实数m 的值为()A .2-B .0或2C .0D .2例2.已知幂函数p q y x =(p ,q ∈Z 且p ,q 互质)的图象关于y 轴对称,如图所示,则()A .p ,q 均为奇数,且0p q >B .q 为偶数,p 为奇数,且0p q<C .q 为奇数,p 为偶数,且0p q >D .q 为奇数,p 为偶数,且0p q<例3.(2022·海南·文昌中学高三阶段练习)已知幂函数()()a f x x a R =∈过点A (4,2),则f (14)=___________.例4.已知幂函数()f x 的图象过点()8,2--,且()()13f a f a +≤--,则a 的取值范围是______.例5.(2022·全国·高三专题练习)如图是幂函数i y x α=(αi >0,i =1,2,3,4,5)在第一象限内的图象,其中α1=3,α2=2,α3=1,412α=,513α=,已知它们具有性质:①都经过点(0,0)和(1,1);②在第一象限都是增函数.请你根据图象写出它们在(1,+∞)上的另外一个共同性质:___________.例7.(2022·河北石家庄·高三期末)已知实数a ,b 满足3e e 1a a a -+=+,3e e 1b b b -+=-,则a b +=()A .-2B .0C .1D .2例10.(2022·浙江·模拟预测)已知0a >,函数()(0)x a f x x a x =->的图象不可能是()A .B .C .D .例12.(2022·上海市实验学校高三阶段练习)若函数()()()3,a f x m x m a =+∈R 是幂函数,且其图象过点(,则函数()()2log 3a g x x mx =+-的单调递增区间为___________.例14.(2022·全国·高三专题练习)已知幂函数()()224222m m f x m m x -+=--在()0,∞+上单调递减.(1)求m 的值并写出()f x 的解析式;紧扣幂函数y x α=的定义、图像、性质,特别注意它的单调性在不等式中的作用,这里注意α为奇数时,x α为奇函数,α为偶数时,x α为偶函数.二次函数对点训练题型三:二次方程20(a 0)++=≠ax bx c 的实根分布及条件例15.(2022·河南·焦作市第一中学高二期中(文))设p :二次函数()()210f x ax ax a =++≠的图象恒在x轴的上方,q :关于x 的方程22210x ax a -+-=的两根都大于-1,则p 是q 的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件例16.(2022·重庆·模拟预测)已知二次函数24y x x a =-+的两个零点都在区间()1,+∞内,则a 的取值范围是()A .(),4-∞B .()3,+∞C .()3,4D .(),3-∞例17.(2022·江西省丰城中学高一开学考试)函数()3x f x =且()218f a +=,函数()34ax x g x =-.(1)求()g x 的解析式;题型四:二次函数“动轴定区间”、“定轴动区间”问题例21.(2022·贵州毕节·高一期末)已知函数2()2(0)f x x ax a =->.(1)当3a =时,解关于x 的不等式5()7f x -<<;例23.(2022·全国·高三专题练习)已知二次函数()f x 满足(1)(3)3,(1)1f f f -===-.(1)求()f x 的解析式;例24.(2022·全国·高三专题练习)设函数2()1f x ax bx =++(,a b ∈R ),满足(1)0f -=,且对任意实数x 均有()0f x ≥.(1)求()f x 的解析式;。
九下周周清2作业新版北师大版

4 =1 ×42+2-m,解得 m=6
4
15.(12 分)(平顶山二调)如图,抛物线 y=ax2+bx-3 交 x 轴于 A(-2,0),B 两点, 交 y 轴于点 C,且 a+b=0.
(1)求该抛物线的函数表达式和顶点坐标; (2)连接 AC,若将线段 AC 向右水平移动 m 个单位长度后与抛物线有交点,求 m 的 取值范围.
解:(1)y=-x2+2x+3
(2)存在,理由如下:易得点 D(2,3),设点 P(1,m),∴直线 PD 的表达式中的 k
值 kPD=32--m1
=3-m,直线 PB 的表达式中的 k 值 kPB=3--m1
=-1 2
m.当 PD⊥BP,
即 kPD·kPB=(3-m)·(-12 m)=-1 时,▱ PDNB 是矩形,解得 m=1 或 m=2,∴点 P(1,
6.如图,已知二次函数 y=-x2+4x-k 的图象与 x 轴交于 A,B 两点,与 y 轴交
于点 C,其顶点为点 D,若△ABC 与△ABD 的面积比为 1∶4,则 k 的值为( D )
A.1
B.12
C.4 3
D.4 5
7.在同一直角坐标系中,一次函数 y=ax+b 与二次函数 y=ax2+8x+b 的图象可 能是( C )
解:(1)∵点 A(4,0),点 B(0,6),∴OA=4,易得直线 AB 的表达式为 y=-3 x 2
+6,∴S△AOP=12 OA·yP=12 ·4yP=6,∴yP=3,∴-32 xP+6=3,∴xP=2,∴点 P(2, 3).又∵点 P(2,3)在抛物线 y=ax2+2 上,∴3=22a+2,∴a=1
九年级数学上册周周清3检测内容22

检测内容:22.1得分________ 卷后分________ 评价________一、选择题(每小题4分,共32分)1.下列函数中,是二次函数的有( C )①y =1- 2 x 2;②y=1x 2 ;③y=x(1-x);④y=(1-2x)(1+2x). A .1个 B .2个 C .3个 D .4个2.已知原点是抛物线y =(m +1)x 2的最低点,则m 的取值范围是( C )A .m <-1B .m <1C .m >-1D .m >-23.(攀枝花中考)抛物线y =x 2-2x +2的顶点坐标为(A)A .(1,1)B .(-1,1)C .(1,3)D .(-1,3)4.同一个坐标系中,图象不行能由函数y =2x 2+1的图象通过平移变换、轴对称变换和旋转变换得到的函数是(A)A .y =3x 2+1B .y =2x 2-1C .y =-2x 2-1D .y =2(x -1)2+15.对于抛物线y =-12(x +1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x =1;③顶点坐标为(-1,3);④x>-1时,y 随x 的增大而减小.其中正确结论的个数为( C )A .1个B .2个C .3个D .4个6.(2024·淄博)将二次函数y =x 2-4x +a 的图象向左平移一个单位长度,再向上平移一个单位长度,若得到的函数图象与直线y =2有两个交点,则a 的取值范围是(D)A .a>3B .a<3C .a>5D .a<57.(2024·宜宾)已知抛物线y =x 2-1与y 轴交于点A ,与直线y =kx(k 为随意实数)相交于B ,C 两点,则下列结论不正确的是(D)A .存在实数k ,使得△ABC 为等腰三角形B .存在实数k ,使得△ABC 的内角中有两角分别为30°和60°C .随意实数k ,使得△ABC 都为直角三角形D .存在实数k ,使得△ABC 为等边三角形8.(泸州中考)已知二次函数y =ax 2+2ax +3a 2+3(其中x 是自变量),当x≥2时,y随x 的增大而增大,且-2≤x≤1时,y 的最大值为9,则a 的值为(D)A .1或-2B .-2或2C .2D .1二、填空题(每小题4分,共24分)9.函数y =(m +2)xm 2-2+2x -1是二次函数,则m =__2__.10.(2024·宜宾)将抛物线y =2x 2的图象向左平移1个单位长度,再向下平移2个单位长度,所得函数图象的解析式为__y =2(x +1)2-2__.11.若A(-4,y 1),B(-3,y 2),C(1,y 3)为二次函数y =(x +2)2-(k +4)的图象上的三点,则y 1,y 2,y 3的大小关系是__y 2<y 1<y 3__.12.抛物线y =-2(x -h)2-h 的顶点在直线y =x +3上,抛物线的对称轴是直线__x =-32__. 13.抛物线y =-x 2+bx +c 的部分图象如图所示,若y<0,则x 的取值范围是__x<-3或x>1__. 第13题图错误!。
初中数学精品试题:九上周周清作业(3)

2020学年九年级上数学周周清错题再现练习(三)班级姓名1.当二次函数y=x2+4x+9取最小值时,x的值为()A.-2B.1C.2D.92.抛物线y=-3x2-x+4与y轴的交点坐标是.3.抛物线y=x2-5x-6与x轴的两个交点的坐标分别为.4.某校九年级共有1,2,3,4四个班,现从这四个班中随机抽取两个班进行一场篮球比赛,则恰好抽到1班和2班的概率是.5.如图,在△ABC中,∠ACB=90°,∠A=20°.将△ABC绕点C按逆时针方向旋转得到△A'B'C,且点B在A'B'上,CA'交AB于点D,则∠BDC的度数为.⏜=2CD⏜,则()6.如图,在☉O中,ABA.AB>2CDB.AB<2CDC.AB=2CDD.无法比较AB与2CD的大小⏜的度数是()7.如图所示,点A,B,C在☉O上,OA∥BC,∠OBC=40°,则ABA.10°B.20°C.40°D.70°⏜的度数为.8.如图,若∠AOB=100°,则ACB9.一个不透明的口袋中有3个小球,上面分别标有数字0,1,2,每个小球除数字外其余均相同.小华先从口袋中随机摸出1个小球,记下数字后放回并搅匀,再从口袋中随机摸出1个小球记下数字.请你用画树状图的方法,求小华两次摸出的小球上的数字之和是3的概率.10.如图,☉O的两条弦AB∥CD(AB不是直径),E为AB的中点,连结EC,ED.(1)直线EO与AB垂直吗?请说明理由;(2)求证:EC=ED.11.有一拱形桥所在弧的水上部分如图所示,∠AOB=120°,半径OA=OB=5m.一艘8m宽的船装载着一集装箱,已知箱顶宽3m,且高出水面AB2m,此船能安全过桥洞吗?请说明理由.12.某宾馆有若干间标准房,当标准房的价格为200元时,每天入住的房间数为60间.经市场调查表明,该宾馆每间标准房的价格在170~240元之间(含170元,240元)浮动时,每天入住的房间数y(间)与每间标准房的价格x(元)的数据如下表:x(元) …190 200 210 220 …y(间) …65 60 55 50 …(1)根据所给数据在坐标系中描出相应的点,并画出图象;(2)求y关于x的函数表达式和自变量x的取值范围;(3)设客房的日营业额为w(元),若不考虑其他因素,则宾馆标准房的价格定为多少元时,客房的日营业额最大?最大为多少元?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一次函数周周清
1、抛物线y=ax 2+bx+c 的图象如图,OA=OC ,则 ( )
(A ) ac+1=b (B ) ab+1=c (C )bc+1=a (D )以上都不是
2.已知点(a ,8)在二次函数y =a x 2的图象上,则a 的值是( )
A .2
B .-2
C .±2
D .±2
3、把二次函数23x y =的图象向左平移2个单位,再向上平移1个单位,所得到的图象对应的二次函数关系式是( )
(A )()1232+-=x y (B ) ()1232-+=x y (C ) ()1232--=x y (D )()1232++=x y
4、当a>0, b<0,c>0时,下列图象有可能是抛物线y=ax 2+bx+c 的是( )
5.若y=(2-m)23m x -是二次函数,且开口向上,则m 的值为( )
A .5±
B .-5
C .5
D .0
6.已知二次函数y=-1
2x 2-3x -5
2,设自变量的值分别为x 1,x 2,x 3,且-3<x 1<x 2<x 3, 则
对应的函数值y 1,y 2,y 3的大小关系是( )
A .y 1>y 2>y 3
B .y 1<y 2<y 3
C .y 2>y 3>y 1
D .y 2<y 3<y 1
二、填空题(每题3分,共24分)
7、抛物线y=-(x-L )(x-3-k)+L 与抛物线y=(x-3)2+4关于原点对称,则L+k=________
8.二次函数y=-1
22x 2+3的开口方向是_________.
9.若二次函数y=ax 2的图象经过点(-1,2),则二次函数y=ax 2的解析式是___.
C A y x
O
10、抛物线223y x x =--+与x 轴交点为 ,与y 轴交点为 .
11.抛物线()4222-++=m x x y 的图象经过原点,则=m .
12.抛物线m x x y +-=2,若其顶点在x 轴上,则=m .
三、解答题:
13.已知二次函数c bx x y ++=2的图像经过A (0,1),B (2,-1)两点.
(1)求b 和c 的值; (2)试判断点P (-1,2)是否在此函数图像上?
14、2014年度东风公司神鹰汽车改装厂开发出A 型农用车,其成本价为每辆2万元,出厂价为每辆2.4万元,年销售价为10000辆,2015年为了支援西部大开发的生态农业建设,该厂抓住机遇,发展企业,全面提高A 型农用车的科技含量,每辆农用车的成本价增长率为x ,出厂价增长率为0.75x ,预测年销售增长率为0.6x (年利润=(出厂价-成本价)×年销售量)
(1) 求2015年度该厂销售A 型农用车的年利润y (万元)与x 之间的函数关系。
(2) 该厂要是2015年度销售A 型农用车的年利润达到4028万元,该年度A 型农用车的
年销售量应该是多少辆?
15、已知函数4m m 2x )2m (y -++=是关于x 的二次函数,
求:(1)满足条件的m 值;
(2)m 为何值时,抛物线有最低点?求出这个最低点.这时当x 为何值时,y 随x 的增大
而增大?
(3)m 为何值时,函数有最大值?最大值是什么?这时当x 为何值时,y 随x 的增大而
减小?。
