二次根式的复习课导学案

合集下载

二次根式的复习课导学案

第21章《二次根式》复习导学案班级：学生姓名：导学案设计：李娅兰复习目标1. 进一步理解二次根式的意义及基本性质，并能熟练地化简含二次根式的式子；2. 熟练地进行二次根式的加、减、乘、除混合运算．复习重难点1.重点：含二次根式的式子的混合运算．2.难点：综合运用二次根式的性质及运算法则化简和计算含二次根式的式子．复习过程一、知识回顾本章知识结构()⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧≥=≥=≥≥算。

及实际问题中根式的计、二次根式的混合运算。

）进行的根式（同类二次根式把后，二次根式化为、二次根式的加减：将、二次根式的除法：；、二次根式的乘法：二次根式的运算）（）（数。

是一个），即（性质才有意义。

时，概念：当二次根式的意义二次根式432122aaaaaaaa二、例题学习例1 （1）x的取值范围是；（2）函数13--=xxy中，自变量的取值范围是；（3）若y =3-3-+xx，则y x=；例2 已知0|1|2=-++ba，那么()2012ba+的值为；例3计算：（1）312+；（2）（3）3272483÷-）（；（4）例4已知直角三角形的两条直角边分别为a和b，斜边为c（1）如果a = 12，b = 5，求c；（2）如果a = 3，c = 4，求b；（3）如果c = 10，b = 9，求a三、当堂检测1．选择题：（1）4的算术平方根是（） A. 2 B. －2 C. ±2 D. 16（2）在实数0、2-中，最小的是（）A．2- B． C．0 D（3）下列运算正确的是（）A.25=±5B.43- 27 = 1C. 18÷2=9D. 24·32=6（4）下列各式中，正确的是（）A．3- B．3- C3=± D3±（5）下列各式计算正确的是（）A； B．2=C．222-23=； D=（612a-，则（）()220130(2(1))2π-++--A ．a ＜12 B. a ≤12 C. a ＞12 D. a ≥12（7）计算75147-＋27之值为（）A ．53B ．33C ．311D ． 911 （8）下列二次根式中，最简二次根式是（）．A ．B ．C ．D ．2．填空题：（1）计算：=；计算：1)(2=_______________．（2）计算的结果是；（3）的算术平方根是；（4）有意义，则x 的取值范围是；有意义，则a 的取值范围为_____________________；（5）若0)2011(12=-++y x ，则 yx = ；（6）对于任意不相等的两个实数a 、b ，定义运算※如下：a ※b =ba ba -+，如=6※12= ． 3．解答题：（1）先化简，再求值：)12(1)1(22x x xxx --÷-+ 其中x ＝2.(2)先化简再求值：12)113(2--÷--+x x x x x x ，其中23=x .（3）先化简，再求值：111(11222+---÷-+-m m m m m m ），其中m =3．四、学习反思本节课的收获：还存在的疑惑：。

二次根式复习导学案

二次根式复习一、知识准备本章概念地图二、学习目标1．理解二次根式的意义，2()(0)a a a =≥，2a a =（重点）。

2(0,0)a b ab a b ==≥≥； (0,0)a a a b b b=≥>，并能熟练运用性质和运算法则进行化简二次根式。

（难点）3.通过对二次根式计算，化简等运算，进一步掌握有理式中因式分解，通分，约分等在二次根式计算与化简中的灵活运用，提高综合运用知识解决问题的能力。

三、学习过程 ★一、独立完成发现问题（自主学习）1.在函数23x y x+=中，自变量x 的取值范围是（） A.02≠-≥x x 且 B.02≠≤x x 且 C.0x ≠ D.2-≤x2.()23- ）A.3B.－3C.±3 D ．93.210a b ++-=，那么()2009b a + 的值为（）。

A.－1B.1C.20093D.20093-4.计算2=5.=成立的条件是 6.等式5353--=--a a a a 成立的条件是（） A.5≠a B.3≥aC.53≠≥a a 且D.5a >7.与）A ．8.若977+-+-=x x y ，则()264-xy 的算术平方根为9.计算： ①31382722--+②a a a a a 1882624--+自我总结：你对以上问题感到还有疑惑的是：，是哪个知识点没有掌握好呢？。

例1：262a a a a a a--=-+-已知求例2：化简22⎡⎤-⎢⎥⎣⎦四、知识梳理引导学生总结：（本节课我的收获主要有）1.什么叫做二次根式?你们能举出几个例子吗（注意条件）?__________________________________________________________________.2.二次根式有哪些性质？_____________________________________________________________________3.什么是最简二次根式_____________________________________同类二次根式_____________________________________4.二次根式的化简与运算：_______________________ _.五、学习检测★达标检测一（基础篇）1.已知a b <，化简二次根式b a 3-的正确结果为（） A.ab a -- B.ab a - C.ab a D.ab a -2.2) 的结果是（）A.2B.－2 D．23.在实数范围内定义运算“☆”，其规则为：22a b a b =-☆，则方程(43)13x =☆☆的解为x =（）A.6B.—6C.6±D.364.,a b a =+已知, ,a b 试求的值5.比较大小，设a b ==a b 6.x ==得7.化简：（1）8116⨯ （2）224y x x + （3）19.076.0 （4）ab ab 323÷8.计算：251256123---+⎪⎪⎭⎫ ⎝⎛-÷★达标检测二（提高篇）一、选择题。

二次根式复习导学案

《二次根式复习》导学案
学科课题名称数学年级九年级一课时二次根式复习授课时间知识技能：理解二次根式的意义，会化简二次根式，会进行二次根式的乘除、加减混合运算. 数学思考：探究二次根式概念及运算的过程，体会二次根式的解题方法. 解决问题：在解题中进行比较，寻求有效快捷的计算方法. 情感态度：培养学生良好的运算习惯和不懈的探索精神。二次根式的化简以及运算二次根式性质、法则的正确使用．二次根式的有关性质和运算法则学习过程小组合作、讨论，展示二次根式的性质和运算法则，各小组之间对比
提示：1、化简求值是常规问题，基本思想是 “先化简，再求值” 。 2、二次根式的运算是需要掌握的基本能力，关键在于如何灵活运用有关法则。
五、强化提高已知 x y 1 + x 3 =0，求 xy 的值
考虑所学过的非负数的各种形式及其性质，在此题中如何运用？
六、作业: 1．已知 a=3+2 2 ，b=3-2 2 ，则 a2b-ab2=_________．
2.
n n n 1 n3 〃（）÷ （m>0，n>0） 3 3 m 2m 2m3 m m
（1）
1 x x
(2)
Hale Waihona Puke x 3 8 x注意：求字母取值范围是中考考点，特定的形式要考虑特定的条件。
1 4 45 ）四、练一练：（1） 80 -（ 3 + 5 5
分组展示解题过程，教师典型讲解或学生分组找出对方存在的问题
（2）9 45 ÷3
3 2 1 × 2 2 3 5
学习目标
教学重点教学难点

二次根式复习导学案

二次根式复习导学案班别：姓名：小组评价等级：开始时间: 完成时间：学习目标：1、理解二次根式的有意义的条件。

2、会进行二次根式的加、减、乘、除、乘方运算。

重点：二次根式的意义与二次根式的运算。

难点：综合运用二次根式的性质及运算法则化简和计算含二次根式的式子。

一、知识点回顾1．形如的式子叫做二次根式(1)二次根式的三个性质是：性质1：a （a ≥0）是一个数；性质2：()2a = (a ≥0)；性质3：2a = (a ≥0).2.(1)当a 时，a-1有意义；(2)当x 时，2x+3.32211(2)(2)33-的值是（）． A ．0 B ．23 C ．423D ．以上都不对 4．下列二次根式能与8合并的是( )A.48B.38C.98D.285．计算：4813126927= 6. 6487.下列计算错误的是( ) (A)27714=⨯ (B)32560=÷ (C)a a a 8259=+ (D)3333=-二、方法归纳8．若12+x 与y -2互为相反数，求x y 的值．两个非负数之和一定是 .你怎样利用这个性质解决问题相关链接：9．若实数x 、y 、z 满足0412||22=+-+++-z z z y y x ，则x ＋y ＋z ＝______．三、自主演练10．下列二次根式中，最简二次根式为( ) (A)x 9 (B)32-x (C)x y x - (D)b a 2311．化简后的二次根式b 5与b 23+能合并，则－b 的值是( )(A)0 (B)1 (C)－1 (D)31 12．计算：;21448)21(2+++13．计算：);32)(32()32)(347(2-++-+课后反思：。

二次根式复习导学案

8.若，则的值为。
9．计算 =。10．的关系是。
11．化简的结果是。
12.计算：（1) (2)(＋2)－
(3) (4)
(5) (6)
三、合作交流：
学科组长组织交流，收集本组典型错例和疑惑展示在黑板上。
4、学以致用:完成书本第19至第20页复习题16.
5、收获整理
1、本节课我的收获是：（学到的知识、学会的方法、锻炼的能力等）
3．若有意பைடு நூலகம்，则m能取的最小整数值是（）
A．m=0 B．m=1 C．m=2 D．m=3
4．若x<0，则的结果是（）
A．0 B．—2 C．0或—2 D．2
5．下列二次根式中属于最简二次根式的是（）
A． B． C． D．
6．如果，那么（）
A．x≥0 B．x≥6 C．0≤x≤6 D．x为一切实数
7.① ；②
2、本节课我遗留的问题有：（不懂得知识、不同的看法、没说的意见）
六、课后拓展
已知：
襄阳市樊城区二十中八年级数学学科课堂导学案第周第课时
上课时间：年月日星期：备课组长签字：蹲点领导签字：
课题：6.2.2二次根式复习课课型：自学+展+评（复习课）设计人：任永刚复备人：
学习目标：1、在复习中巩固性质与运算。
2、通过参与教学活动,体会数学是解决实际生活问题的。
3、在学习活动中形成良好的情感、合作交流、主动参与的意识，在独立思考的同时能够倾听他人意见。
一、明确目标
（在教师的设疑、创景下，学生解读学习目标，从而基本明晰学习任务。）
二、思考探究
1.阅读书本第17页，完成活动1.活动2.
2..阅读书本第17页，完成最后3个问题.

二次根式复习导学案教案｜学案｜教学设计[人教版初三九年级]

二次根式复习学习目标：理清本章的知识结构2、通过讲与练的结合对本章所学的知识进行回想、运用重点、难点突破1、二次根式的性质（2条）2、二次根式的最简形式与同类二次根式的有关概念3、二次根式的运算步骤与方法一、课前准备：知识点1、二次根式的概念：形如的式子叫做二次根式。

知识点2、二次根式的性质： 1.=2)(a （a ≥0）,≥0)3. ⎪⎩⎪⎨⎧<=>==)0___()0___()0___(____2a a a a知识点3：二次根式的乘除： 1.计算公式：{⎪⎩⎪⎨⎧>≥=≥≥=⋅)0,0___()0,0___(b a b a b a b a 除法运算：乘法运算： 2.化简公式：⎪⎩⎪⎨⎧>≥=≥≥=⋅)0,0___()0,0___(b a b a b a b a 知识点4：二次根式的加减：1.法则：2.概念：⎩⎨⎧同类二次根式：最简二次根式：.2.1知识点5：二次根式化简求值步骤：1．“一分”：分解因数（因式）、平方数（式）；2.“二移”：根据算术平方根的概念，把根号内的平方数或者平方式移到根号外面；3.“三化”：化去被开方数中的分母。

知识点6：二次根式的加减步骤：1.化简；2.判断；3分类；4.合并。

二、例题选讲：1有意义的x 的取值范围是_____________有意义的x 的取值范围是_________________ 2、当5a等于变式题：已知x,<y,化简的结果是__________________3、计算题：（1）⎛- ⎝（2）(33变式题：（1）(33142---⎝（2）(四、练习12的整数部分为m ，小数部分为n,求3m+2n 的值变式题：若a的整数部分，b 是它的小数部分，则2b a -1=___________2、如图，数轴上表示的数2的点分别为A 、B 点，C 与A 关于B 点对称，则点C 表示的数是3、观察下列运算，完成下列各题的解答： 43（1）判断下列各式是否正确=（）=（）=（）=（）（2）根据上述判定结果你能发现什么规律？请你用含有自然数n 的式子将你发现的规律写出来，并注明n 的取值范围。

二次根式导学案(人教版全章)

二次根式导学案二次根式(1)一、学习目标1、了解二次根式的概念，能判断一个式子是不是二次根式。

2、掌握二次根式有意义的条件。

3、掌握二次根式的基本性质：)0(0≥≥a a 和)0()(2≥=a a a 二、学习重点、难点重点：二次根式有意义的条件；二次根式的性质．难点：综合运用性质)0(0≥≥a a 和)0()(2≥=a a a 。

三、学习过程（一）复习回顾：（1）已知a x =2，那么a 是x 的______;x 是a 的________, 记为______,a 一定是_______数。

（2）4的算术平方根为2，用式子表示为 =__________；正数a 的算术平方根为_______，0的算术平方根为_______；式子)0(0≥≥a a 的意义是。

（二）自主学习(1)16的平方根是；(2)一个物体从高处自由落下，落到地面的时间是t (单位：秒)与开始下落时的高度h (单位：米)满足关系式25t h =。

如果用含h 的式子表示t ，则t = ； (3)圆的面积为S ，则圆的半径是； (4)正方形的面积为3-b ，则边长为。

思考：16，5h ，πs ,3-b 等式子的实际意义.说一说他们的共同特征.定义: 一般地我们把形如a （0≥a ）叫做二次根式，a 叫做_____________1、试一试：判断下列各式，哪些是二次根式？哪些不是？为什么？3，16-，34)0(3≥a a ，12+x2、当a 为正数时a 指a 的，而0的算术平方根是，负数，只有非负数a 才有算术平方根。

所以，在二次根式a 中，字母a 必须满足 , a 才有意义。

3、根据算术平方根意义计算：(1) 2)4( (2) （3）2)5.0( （4）2)31( 根据计算结果，你能得出结论：，其中0≥a ,4、由公式)0()(2≥=a a a ，我们可以得到公式a =2)(a ,利用此公式可以把任意一个非负数写成一个数的平方的形式。

【九年级】二次根式复习导学案

【九年级】二次根式复习导学案一.学习目标：1.能熟练运用二次根式的性质进行简化；2．能够比较熟练进行二次根式的运算；3.能够利用二次根的性质和运算来解决简单的实际问题二．学习重点：二次根式的性质应用及运算．学习困难：二次根式的应用三．过程知识网络图知识点梳理一.该公式一般称为二次根式，尤其是平方数不小于二.二次根式的性质：⑴a、（a）⑵（a） 2＝a⑶a2＝。

3.二次根式乘法法则：⑴ab＝a≥0，b≥0)；⑵ab＝a≥0，b≥0).4.二次根式除法法则：⑴ab＝a≥0，b＞0）⑵ab＝a≥0，b＞0）。

5.化简二次根式实际上就是使二次根式满足：⑴；⑵；⑶.6.经过化简后，的二次根式，称为同类二次根式.7.一般来说，二次根式加减法，首先简化每个二次根式，然后8.实数中的运算律、乘法公式同样适用于二次根式的混合运算边说边练ⅰ.二次根式有意义求取值范围1.为了使X-2有意义，X的值范围为变式：若分别使1x－2，1x－2，3－xx－2有意义，那么x的取值范围又该如何？2.为了使13-x有意义，x的值范围为3.使x＋1，1x，(x－3)0三个式子都有意义的x的取值范围是.4.使x+1x-1=x2-1为真的子句；1-xx-2=1-xx-2为真5.若y=2x－5＋5－2x－3．则2xy＝.ⅱ. 二次根的非负评价1.已知a＋2＋b－1＝0，那么(a＋b)2021＝.2.假设X和y是实数，3x+4+y2-6y+9=0，那么xy=3.若4x－8＋x－y－m＝0，当y＞0时，则m的取值范围.4.如果A-3和2-B是彼此相反的数，则代数公式-1A+6b的值为5.已知△abc的三边a、b、c满足a2＋b＋c－1－2＝10a＋2b－4－22，则△abc为.ⅲ. 简化为公式A2=a1.(－7)2＝；（2）(3－π)2＝；(3)62＝2.如果已知x<1，则简化x2-2x+1=的结果；如果＜0，则简化a-3-a2=3.当a＝2时，代数式a＋1－2a＋a2＝；化简(a－1)11－a＝.5.（A-3）2=3-A为真，则A的值范围为__6.若x3＋4x2＝－xx＋4，则x的取值范围是.7.如果X-1=12，则代数公式1x-x2-2+1x2的值为8.已知实数a、b、c在数轴上的位置如图所示，试化简(a＋c)2－b－c.9.如果-3≤ 十、≤ 2.尽量简化│ X-2│ + （x+3）2+x2-10x+25ⅳ.最简与同类二次根式1.在下列表达式中，不能简化的二次根式是（）a．3a2b．23c．24d．302.在下列表达式中，最简单的二次根是（）a．8b．70c．99d．1x3.下面是一组相同类型的二次根（）a．12，－32，18b．5，75，1245c．4x3，22xd．a1a，a3b2c4.如果二次根式2a-4和6是类似的二次根式，则a的值为5.化简后，根式b－a3b和2b－a＋2是同类根式，那么a=_____，b=______.ⅴ. 二次根的运算1.化简：⑴312＝；⑵15＋16＝；⑶18a＝.2.计算：212－613+8=3.计算12(2－3)＝.4.计算（1）（2+3）（2-3）=；⑵(5－2)2022(5＋2)2022＝.5.下列各式①33＋3=63；②177=1；③2＋6=8=22；④243=22，其中错误的有（）a、 3 B.2 C.1 d.06.下列各式计算正确的是（）a、 2＋3＝5b.2＋2＝22c.33－2＝22d.12－102＝6－57.计算：⑴32－212－13－62⑵239x＋6x4－2x1x⑶(48－413)－(313－40.5)⑷(218－18)－(12＋2－213)⑸23x18x＋12xx8－x22x3⑹(32－45)2⑺(3－22)(22－3)⑻(1－23)(1＋23)－(1＋3)2⑼(3＋2－5)(3?2?5)8.如果x=5+32，y=5-32，求代数公式的值⑴x2－xy＋y2⑵xy＋yx9.遵循以下公式：32-1=2×4,42－1＝3×5,52－1＝4×6。

二次根式复习导学案(很实用)

课题：《二次根式》复习学案班级：______ 姓名：______ 时间: ______学习目标1．理解二次根式的概念，会利用概念判别二次根式、求字母的取值范围；2．掌握二次根式的性质和运算法则，会运用它们求字母的取值范围、化简和计算；3．了解最简二次根式的概念，会判别最简二次根式．专题一二次根式的三个有关概念1二次根式【温馨提示】（一）、二次根式的判别：（1）形如______（且_____）的式子叫做二次根式。

基础练习1下列各式中15、3a 、21b -、22a b +、220m +、144-，35不是二次根式的有【温馨提示】（二）、二次根式有意义的条件：如果一个代数式有意义，不仅其中的二次根式的被开方数（式），而且分母，指数为0的幂的底数。

基础练习2（1）23x x+中x 的取值范围是；（2）当__________时，212x x ++-有意义；拓展练习1（1）若等式1)23(0=-x 成立，则x 的取值范围是；（2）若3x -+3x -有意义，则x 的取值范围是_______【温馨提示】（三）、二次根式的双非负数性,即二次根式a 0，而且被开方数（式）a 0.基础练习3（1）已知1x y -++3x -=0，求x y 的值；（2）已知a 、b 为实数，且5254a a b -+-=+，求a 、b 的值．拓展练习2已知、是实数，且，求的值．2最简二次根式基础练习4化简：（1）24＝（2）29＝（3）223＝（4）0.125＝基础练习5下列二次根式中是最简二次根式的有个 25002+a 21 35 44a + 3同类二次根式【温馨提示】（五）、同类二次根式的应用把几个二次根式化为后，被开方数的二次根式叫同类二次根式。

基础练习6在8、1753a 、293a 、125、323a a、30.2、-218中，与3a 中是同类二次根式的有___ ___拓展练习3若最简二次根式22323m -与212410n m --是同类二次根式，求m 、n 的值专题二二次根式的四个性质【温馨提示】（六）、2()a = 逆用：a=基础练习6在实数内分解因式：（1）2a －2=【温馨提示】（七）二次根式的求值千万注意符号2a =基础练习7如果2(21)12a a -=-，则（）A ．a ＜12 B. a ≤12 C. a ＞12 D. a ≥12 基础练习8实数a 22(4)(11)a a --化简后为拓展练习9如果2(3)13x x -=--，则x 的取值范围是。

二次根式复习课导学案

《二次根式》复习课导学案
编写人：审核人：
温馨寄语：书山有路勤为径，学海无涯苦作舟
学习目标：
1．使学生进一步理解二次根式的意义及基本性质，并能熟练地化简含二次根式的式子；2．熟练地进行二次根式的加、减、乘、除混合运算．
学习重点：进一步理解二次根式的意义及基本性质。

学习难点：熟练地进行二次根式的加、减、乘、除混合运算．
学习过程
一.梳理知识
1．请同学回忆二次根式有哪些基本性质？用式子表示出来，并说明各式成立的条件．2．二次根式的乘法及除法的法则是什么？用式子表示出来．
3．在二次根式的化简或计算中，还常用到以下两个二次根式的关系式：
4．在含有二次根式的式子的化简及求值等问题中，常运用三个可逆的式子：
二.合作探究
1. x取什么值时，下列各式在实数范围内有意义:
2.
3.把下列各式化成最简二次根式：
三.班级展示小组代表发言
四.质疑探究听完发言，提出疑问，由其他小组解决，存在问题的，让学生再次探究五：达标测评
1．选择题：
A．a≤2B．a≥2 C．a≠2D．a＜2
A．x+2 B．－x－2 C．－x+2D．x－2
A．2x B．2a C．－2x D．－2a
2．填空题：
*4．计算：
6．x是什么值时，下列各式在实数范围内有意义？
7．把下列各式化成最简二次根式：。

二次根式复习课导学案

二次根式复习课导学案二次根式复习导学案一、学习目标1、了解二次根式、最简二次根式的概念。

2、理解二次根式的运算法则。

3、会用二次根式的概念和运算法则进行有关实数的简单四则运算（不要求分母有理化）。

二、复习过程（一）知识梳理知识点1、二次根式的概念：形如的式子叫做二次根式。

练一练：x 满足的条件是 .知识点2、二次根式的性质：1.=2. =2)(a （0a ≥）练一练：（1= （2= 知识点3：二次根式的乘除：1.= （0,0a b ≥≥）2.= （0,0a b ≥≥）练一练：（1 。

（2）化简：6a 知识点4：同类二次根式的概念几个二次根式化成最简二次根式后，如果被开方数相同，这几个二次根式叫做同类二次根式。

）.3A B C D（二）水平练习1.有意义，则x的取值范围是（）.>2 . 2 . 2 .2A xB xC xD x<≥≤2、下列各式属于最简二次根式的是（）A3、②是同类二次根式的是（） A．①和③ B．②和③ C．①和④ D．③和④4、下列各式中，正确的是（）A．3- B．3- C3± D3=± 5、下列计算正确的是（）()())()22223261.=0. =2xy020,0.x xA yB xy yy y yC x yD xy x y≠÷≠≥≥=6、比较2，的大小，正确的是（）.2.2A B C D<<<<7、下列函数中，自变量x的取值范围是3x≥的是（）1... 3 .3A yB yC y xD yx===-=-8、化简)2得（）. 2 . 2 2A B C D-9、函数1y=的自变量x的取值范围是 .10= .11是同类二次根式，则a= .12、已知10a-=，则a+b= .13、计算：（1）1822⎛⎫-⎪⎪⎭（2）22433-（3）131227234--（4）()10112283π-⎛⎫-+--+⎪⎝⎭（三）中考体验1.（2015·江苏常州·一模）若31xx--在实数范围内有意义，则x的取值范围是（）. 3 .3 1 .1 3 .31A xB x xC xD x x≥≤≠<≤≥≠且且2．（2015·广东高要市·一模）下列运算正确的是（）()()2325.2 3 =2+ 3 .=a.3=3 .33A B a C D a a+-=3.（2015·广东广州·二模）计算：1273⨯= .（四）课堂小结：本节课你有收获？。

二次根式复习导学案

3 2 1 2 1 1 2 3 1 2
2

1
。
1 1 二、已知 x ，求 x 2 x 2 的值 x x 3 2
1
2
三、先化简，再求值：
1 a2 1 a 2 2a 1 ，其中 a 。 2 a 1 a a 2 3
a
2
a a （） ② a2 a a
③ a b
④
a b
5、二次根的加减运算法则：先化简，再合并同类二次根式。二、基础训练： 1、如果
x 1
x
2

1 x x
，则 x 的取值范围是
2、比较大小： 5 6 3、计算： 27 48 ＝
6 5 ； 13 2
二次根式复习导学案
教学目标：1、掌握二次根式的概念及性质。2、能对二次根式进行化简与运算。一、知识点填空 1、形如
a (a 0) 的式子叫做二次根式，其中 a 叫被 (1)被开方数都不含分母；(2)被开方数中不含能开得尽方的因数或因式。 3、把几个二次根式化简成最简二次根式后，如果它们的被开方数相同，那么这几个二次根式叫做同类二次根式。 4、二次根式的性质及运算法则：①
四、已知 x 的值。
a
1 a
（ 0 a 1），求代数式
x2 x 6 x3 x 2 x 2 4x 2 x x 2x x 2 x 2 4x
练习：1、已知 a
1 32
，b
3 2 ，则 a 与 b 的关系是
2
2、请你观察思考下列计算过程：∵ 11 121
∴ 121 11；∵ 111 12321

二次根式复习导学案

11、若最简二次根式与是同类二次根式，求m、n的值
考点6：二次根式的性质
12、在实数内解因式：
13、如果，则 a的取值范围是;如果，则x的取值范围是。
14、已知是整数，则正整数n的最小值是；已知是整数，则自然数n可能的值是
15、当时，。
16、把(x－1) 的根号外的因式移到根号内等于
30、先阅读下列的解答过程，然后作答：
有这样一类题目：将化简，若你能找到两个数和，使且，
则可变为，即变成开方，从而使得化简。例如： = = ，∴
请仿照上例解下列问题：（1）；（2）
2、（1）中的取值范围是；（2）当时，有意义；
3、（1）若等式成立，则的取值范围是；
（2）已知、为实数，且，求、的值．
（3）已知、是实数，且，求的值．
考点3：二次根式的非负性
4、（1）当时，代数式取值最小，最小值为
（2）若与互为相反数，则
5、（1）若实数a满足，求的值；
（2）已知为实数，且，求的值。
考点4：最简二次根式
6、化简：（1）＝（2）＝（3）＝（4）＝
（5）（6）（7）（8）
7、下列二次根式中是最简二次根式的有个
8、若和都是最简二次根式，则。
9、（1）已知，，则代数式的值为
（2）计算：
考点5：同类二次根式
10、在、、、、、3 、-2 中，与中是同类二次根式的有
17、若；
18、已知，化简二次根式的正确结果为（）
A. B. C. D.
19、使等式成立的的取值范围是，能使等式成立的的取值范围是

九年级数学二次根式复习2-导学案

预习准备
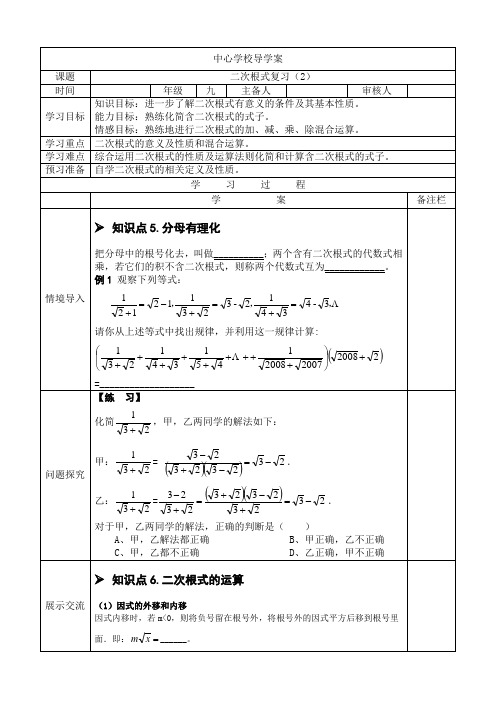
自学二次根式的相关定义及性质。
学习过程
学案
备注栏
情境导入
知识点5.分母有理化
把分母中的根号化去，叫做__________；两个含有二次根式的代数式相乘，若它们的积不含二次根式，则称两个代数式互为____________。
例1观察下列等式：
请你从上述等式中找出规律，并利用这一规律计算:
=___________________
中心学校导学案
课题
二次根式复习（2）
时间
年级
九
主备人
审核人
学习目标
知识目标：进一步了解二次根式有意义的条件及其基本性质。
能力目标：熟练化简含二次根式的式子。
情感目标：熟练地进行二次根式的加、减、乘、除混合运算。
学习重点
二次根式的意义及性质和混合运算。
学习难点
综合运用二次根式的性质及运算法则化简和计算含二次根式的式子。
问题探究
【练习】
化简，甲，乙两同学的解法如下：
甲： = ．
乙： = ．
对于甲，乙两同学的解法，正确的判断是（）
A、甲，乙解法都正确B、甲正确，乙不正确
C、甲，乙都不正确D、乙正确，甲不正确
展示交流
知识点6.二次根式的运算
（1）因式的外移和内移
因式内移时，若m<0，则将负号留在根号外，将根号外的因式平方后移到根号里面．即： ______。
因式外移时，若被开数中字母取值范围未指明时，则要进行讨论．即：
( )
= =
- ( )
（2）二次根式的加减法：先把二次根式化成最简二次根式，再合并同类二次根式。
（3）二次根式的乘除法：
乘法法则： = ，成立的条件_____________.

二次根式的复习课导学案