二次函数复习题2

合集下载

二次函数期末复习题(基础-中等)

二次函数期末复习题（基础-中等）知识导图考点精练考点一：二次函数的定义、解析式、图象及性质1．（金华）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则下列结论：①a＞0；②c＞0；③b2﹣4ac＞0，其中正确的个数是（）A．0个B．1个C．2个D．3个第1题第2题2．（凉山州）已知二次函数y＝ax2+bx+1的大致图象如图所示，那么函数y＝ax+b的图象不经过（）A．第一象限B．第二象限C．第三象限D．第四象限3．若二次函数y＝（m+1）x2+m2﹣2m﹣3的图象经过原点，则m的值必为（）A．﹣1或3B．﹣1C．3D．无法确定4．（陕西）对于抛物线y＝ax2+（2a﹣1）x+a﹣3，当x＝1时，y＞0，则这条抛物线的顶点一定在（）A．第一象限B．第二象限C．第三象限D．第四象限5．抛物线y＝3（x+2）2﹣2的顶点坐标是．6．若抛物线y＝﹣x2+bx+c经过点（﹣2，3），则2c﹣4b﹣9＝．7．（辽阳）如图，抛物线y＝x2﹣2x﹣3与y轴交于点C，点D的坐标为（0，﹣1），在第四象限抛物线上有一点P，若△PCD是以CD为底边的等腰三角形，则点P的横坐标为．考点二：二次函数的图象变换1．把抛物线y＝﹣2x2向上平移1个单位，再向右平移1个单位，得到的抛物线是（）A．y＝﹣2（x+1）2+1B．y＝﹣2（x﹣1）2+1C．y＝﹣2（x﹣1）2﹣1D．y＝﹣2（x+1）2﹣12．（山西）将抛物线y＝x2﹣4x﹣4向左平移3个单位，再向上平移5个单位，得到抛物线的函数表达式为（）A．y＝（x+1）2﹣13B．y＝（x﹣5）2﹣3C．y＝（x﹣5）2﹣13D．y＝（x+1）2﹣33．（山西）抛物线y＝﹣2x2﹣4x﹣5经过平移得到y＝﹣2x2，平移方法是（）A．向左平移1个单位，再向下平移3个单位B．向左平移1个单位，再向上平移3个单位C．向右平移1个单位，再向下平移3个单位D．向右平移1个单位，再向上平移3个单位4．如果将抛物线y＝x2﹣2x﹣1向上平移，使它经过点A（0，3），那么所得新抛物线的表达式是．5．（宁波）如图抛物线y＝ax2﹣5ax+4a与x轴相交于点A、B，且过点C（5，4）．（1）求a的值和该抛物线顶点P的坐标．（2）请你设计一种平移的方法，使平移后抛物线的顶点落在第二象限，并写出平移后抛物线的解析式．考点三：用待定系数法求二次函数解析式1．（宁波）已知抛物线y＝ax2+bx+c与x轴交于点A（1，0），B（3，0），且过点C（0，﹣3）．（1）求抛物线的解析式和顶点坐标；（2）请你写出一种平移的方法，使平移后抛物线的顶点落在直线y＝﹣x上，并写出平移后抛物线的解析式．2．（牡丹江）如图，抛物线y＝﹣x2+bx+c交x轴于A，B两点，交y轴于点C，对称轴是直线x＝﹣3，B（﹣1，0），F（0，1），请解答下列问题：（1）求抛物线的解析式；（2）写出抛物线顶点E的坐标，并判断AC与EF的位置关系．考点四：二次函数与一元二次方程、一元二次不等式的关系1．抛物线y＝x2﹣2x﹣3与x轴的交点个数是（）A．0个B．1个C．2个D．3个2．（随州）对于二次函数y＝x2﹣2mx﹣3，下列结论错误的是（）A．它的图象与x轴有两个交点B．方程x2﹣2mx＝3的两根之积为﹣3C．它的图象的对称轴在y轴的右侧D．x＜m时，y随x的增大而减小3．（2018•莱芜）函数y＝ax2+2ax+m（a＜0）的图象过点（2，0），则使函数值y＜0成立的x的取值范围是（）A．x＜﹣4或x＞2B．﹣4＜x＜2C．x＜0或x＞2D．0＜x＜24．如图，抛物线y＝ax2+bx+c的顶点为B（﹣1，3），与x轴的交点A在点（﹣3，0）和（﹣2，0）之间，以下结论：①b2﹣4ac＝0；②a+b+c＞0；③2a﹣b＝0；④c﹣a＝3；⑤（a+c）2＞b2 。

第22章《二次函数》人教版九年级上册章末复习卷(含答案)

人教版九年级上册第22章《二次函数》章末复习卷一、选择题1．函数的图象是抛物线，则的值（） A ．4 B ．-4 C ．2 D ．-22．抛物线y ＝3x 2﹣6x +4的顶点坐标是（）A ．（1，1）B ．（﹣1，1）C ．（﹣1，﹣2）D ．（1，2）3．抛物线y ＝3x 2向右平移一个单位得到的抛物线是（）A ．y ＝3x 2+1B ．y ＝3x 2﹣1C ．y ＝3（x+1）2D ．y ＝3（x ﹣1）2 4．抛物线y ＝x 2﹣5x +6与x 轴的交点情况是（）A ．有两个交点B ．只有一个交点C ．没有交点D ．无法判断5．已知,a b 是非零实数，a b >，在同一平面直角坐标系中，二次函数21y ax bx =+与一次函数2y ax b =+的大致图象不可能是（）A ．B ．C ．D ． 6．加工爆米花时，爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”．在特定条件下，可食用率p 与加工时间t （单位：分钟）满足的函数关系p ＝at 2+bt +c （a ，b ，c 是常数），如图记录了三次实验的数据．根据上述函数模型和实验数据，可得到最佳加工时间为（）A ．4.25分钟B ．4.00分钟C ．3.75分钟D ．3.50分钟7．已知二次函数y ＝ax 2+bx +c 的图象如图所示，下列结论：①ac ＜0，②b ﹣2a ＜0，③b 2﹣4ac ＜0，④a ﹣b +c ＜0，正确的是( ) www .czsx .com .cnA ．①②B ．①④C ．②③D ．②④8．对于下列结论：①二次函数y =6x 2，当x ＞0时，y 随x 的增大而增大；②关于x 的方程a （x +m ）2+b =0的解是x 1=﹣2，x 2=1（a 、m 、b 均为常数，a ≠0），则方程a （x +m +2）2+b =0的解是x 1=﹣4，x 2=﹣1；③设二次函数y =x 2+bx +c ，当x ≤1时，总有y ≥0，当1≤x ≤3时，总有y ≤0，那么c 的取值范围是c ≥3．其中，正确结论的个数是（）A ．0个B ．1个C ．2个D ．3个二、填空题9．二次函数y =－2x 2+3的开口方向是_________．10．把二次函数245y x x =-+化为()2y a x h k =-+的形式，那么h k +=_____. 11．方程ax 2+bx +c =0（a ≠0）的两根为x =﹣3和x =1，那么抛物线y =ax 2+bx +c （a ≠0）的对称轴是直线________．12．函数()2y ax bx c a 0=++≠的图象如图所示，那么ac ______0.(填“>”，“=”，或“<”)13．已知()2312y x =++，当x _______时，函数值随x 的增大而减小.14．如果A （﹣1，y 1），B （﹣2，y 2）是二次函数y =x 2+m 图象上的两个点，那么y 1________y 2（填“＜”或者“＞”）15．如图，若点B 的坐标为（3，0），则点 A 的坐标为_____．16．二次函数y＝－x2＋2x＋3的图象与x轴交于A、B两点，P为它的顶点，则S△P AB＝________．17．一根长为40cm的铁丝，把它弯成一个矩形框，设矩形的长为xcm，矩形的面积为y（cm2），试写出y与x的函数关系式：________．（注意标注自变量x的取值范围）18．抛物线的部分图象如图所示，则当y＞0时，x的取值范围是_____．三、解答题19．已知二次函数y＝(x－m)2－1（m为常数）．（1）求证：不论m为何值，该函数图象与x轴总有两个公共点；（2）请根据m的不同取值，探索该函数图象过哪些象限?（直接写出答案）（3）当1≤x≤3时，y的最小值为3，求m的值．20．已知二次函数y=﹣x2+4x．（1）写出二次函数y=﹣x2+4x图象的对称轴；（2）在给定的平面直角坐标系中，画出这个函数的图象（列表、描点、连线）；（3）根据图象，写出当y＜0时，x的取值范围．21．某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式；(2)求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？(3)如果该企业要使每天的销售利润不低于4000元，那么销售单价应控制在什么范围内？22．已知抛物线y＝ax2＋bx＋c经过A(－1，0)、B(3，0)、C(0，3)三点，直线l是抛物线的对称轴．(1)求抛物线的函数关系式；(2)设点P是直线l上的一个动点，当△P AC的周长最小时，求点P的坐标；(3)在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．23．如图，在平面直角坐标系中，抛物线y=ax2+bx+3经过A(﹣3，0)、B(1，0)两点，其顶点为D，连接AD，点P是线段AD上一个动点（不与A、D重合）．(1)求抛物线的函数解析式，并写出顶点D的坐标；(2)如图1，过点P作PE⊥y轴于点E，连接AE．求△P AE面积S的最大值；(3)如图2，抛物线上是否存在一点Q，使得四边形OAPQ为平行四边形？若存在求出Q点坐标，若不存在请说明理由．24．如图，四边形ABCD是边长为2，一个锐角等于60°的菱形纸片，小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合，按顺时针方向旋转三角形纸片，使它的两边分别交CB、BA（或它们的延长线）于点E、F，∠EDF=60°，当CE=AF时，如图1小芳同学得出的结论是DE=DF．（1）继续旋转三角形纸片，当CE≠AF时，如图2小芳的结论是否成立？若成立，加以证明；若不成立，请说明理由；（2）再次旋转三角形纸片，当点E、F分别在CB、BA的延长线上时，如图3请直接写出DE与DF的数量关系；（3）连EF，若△DEF的面积为y，CE=x，求y与x的关系式，并指出当x为何值时，y有最小值，最小值是多少？。

九年级二次函数复习 (2)

二次函数面积、线段问题1、某市化工材料经销公司购进一种化工原料若干千克，价格为每千克30元，物价部门规定其销售单价不高于每千克70元，不低于每千克30元，经市场调查发现：目前销量y （千克）是销售单价x （元）的一次函数，且当x=60时，y=80，x=50时，y=100，在销售过程中，每天还要支付其他费用450元．（1）求出y 与x 的函数关系式，并写出自变量x 的取值范围．（2）求该公司销售该原料日获利w （元）与销售单价x （元）之间的函数关系式．（3）当销售单位为多少元时，该公司日获利最大？最大获利是多少元．知识点一二次函数的易错题一、铅垂高求面积图1：S △ABC ＝ S △ACD ＋S △BCD ＝B x x －A 21×CD ；图2： S △ABC ＝S △BCD ＋S △ABD ＝c y y －A 21×BD 二、平行线转换法求面积S△ABC＝ S△BDA（过 C 点作 AB 的平行线 CD ，则两三角形同底等高）【例题精讲一】二次函数的面积问题1、抛物线y=-x2+（1-3k）x+3k与x轴交于A，B两点（A左B右），与y轴正半轴交于点C．（1）直接写出抛物线经过某个定点的坐标；（2）若k=1，点P是第二象限抛物线上的一点，连接PB交AC于D，设△PAD的面积为S1，△CBD的面积为S2，求S1-S2的最大值；2、如图，抛物线y=ax2+bx过A（4，0），B（1，3）两点，点C，B关于抛物线的对称轴对称，过点B作直线BH⊥x轴，交x轴于点H．（1）求抛物线的表达式；（2）点P是抛物线上一动点，且位于第四象限，当△ABP的面积为6时，求出点P的坐标；3、如图，抛物线21344y x x ＝－＋与x 轴交于A 、B 两点，直线l ：y ＝kx －3k ＋4与抛物线交于E 、F 两点。

（1）直线l 过定点：；（2）求BEF S △的最小值。

【课堂练习】1、如图，抛物线经过A (1，0)、B (4，0)、C (0，－4)三点，点D 是直线BC 上方的抛物线上的一个动点，连接DC 、DB ，则△BCD 的面积的最大值是___________2、已知二次函数 y ＝（m 2－2）x 2－4m x ＋n 的图象关于直线 x ＝2 对称，且最高点在直线 y ＝ 21x ＋1 上。

中考数学总复习《二次函数》专项提升练习题(附答案)

中考数学总复习《二次函数》专项提升练习题(附答案) 学校：___________班级：___________姓名：___________考号：___________一、单选题1．已知二次函数2281y x x =-+，当11x -≤≤时，函数y 的最小值是（）A ．1B ．5-C ．6-D ．7-2．把一抛物线向上平移3个单位，再向左平移1个单位得到的解析式为22y x =，则原抛物线的解析式为（） A ．()2213y x =-+B ．()2213y x =++C ．()2213y x =+-D ．()2213y x =--3．新定义：若一个点的纵坐标是横坐标的3倍，则称这个点为“三倍点”，如：()1,3A 与()2,6B --，()0,0C 等都是“三倍点”．若二次函数2y x x c =--+的图像在31x -<<的范围内，至少存在一个“三倍点”，则c 的取值范围是（）A ．45c -≤ 0c 0c >C ．0b < 0c >D ．0b < 0c < 5．把抛物线22y x =-先向右平移6个单位长度，再向下平移2个单位长度后，所得函数的表达式为（）A ．22(6)2y x =-++B ．22(6)2y x =-+-C ．22(6)2y x =--+D ．22(6)2y x =---6．如图，抛物线2y ax c =-经过正方形OACB 的三个顶点A ，B ，C ，点C 在y 轴上，则ac 的值为（）A ．1B ．2C ．3D ．47．如图，菱形ABCD 的边长为3cm ，=60B ∠︒动点P 从点B 出发以3cm /s 的速度沿着边BC CD DA --运动，到达点A 后停止运动；同时动点Q 从点B 出发，以1cm/s 的速度沿着边BA 向A 点运动，到达点A 后停止运动．设点P 的运动时间为(s)x ，BPQ 的面积为()2cm y ，则y 关于x 的函数图象为（）A ．B ．B ．C ．D ．8．已知在平面直角坐标系中，抛物线1C 的图象如图所示，对称轴为直线2x =-，将抛物线1C 向右平移2个单位长度得到抛物线2C ：2y ax bx c =++ （a 、b 、c 为常数，且0a ≠），则代数式b c a +-与0的大小关系是（）A ．0b c a +-D ．不能确定二、填空题9．若关于x 的二次函数2321y x x m =-+-的值恒为正数，则m 的取值范围为． 10．将抛物线2(1)2y x =++先向右平移3个单位，再向下平移4个单位，则所得抛物线的解析式为．11．小华酷爱足球运动一次训练时，他将足球从地面向上踢出，足球距地面的高度h （单位：m ）与足球被踢出后经过的时间t （单位：s ）之间的关系为：2412h t t =-+，则足球距离地面的最大高度为 m ．12．如图是抛物线型拱桥，当拱顶离水面2m 时，水面宽4m ，若水面下降1m ，则水面宽度增加 m ．（结果可保留根号）13．如图，抛物线()20y ax bx c a =++≠的对称轴是直线2x =-，且抛物线与x 轴交于A ，B两点，若5OA OB =，则下列结论中：①0abc >；①()220a c b +->；①50a c +=；①若m 为任意实数，则224am bm b a ++≥，正确的是 .（填序号）三、解答题 14．已知抛物线23y ax bx =++交x 轴于()()1030A B ，，，两点 (1)求抛物线的函数表达式；(2)当x 取何值时，y 随x 的增大而减小．15．如图，抛物线214y x bx c =++过点()0,0O ，()10,0E 矩形ABCD 的边AB 在线段OE 上（点B 在点A 的左侧），点C ，D 在抛物线上．设动点B 坐标为(),0t ．(1)求抛物线的函数表达式及顶点坐标；(2)当t 为何值时矩形ABCD 的周长有最大值？最大值是多少？16．“潼南柠檬”获评国家地理标志商标，被认定为全国名特优新农产品，柠檬即食片是其加工产品中非常受欢迎的一款零食．一家超市销售了净重500g 一袋的柠檬即食片，进价为每袋10元．销售过程中发现，如果以单价14元销售，那么一个月内可售出200袋．根据销售经验，提高销售单价会导致销售量减少，即销售单价每提高1元，每月销售量相应减少20袋．根据物价部门规定，这种柠檬即食片的销售单价不得低于进价且不得高于18元．(1)求每月销售量y （件）与销售单价x （元）之间的函数关系式；(2)设超市每月销售柠檬即食片获得离利润为w （元），当销售单价定为多少元时，每月可获得最大利润？最大利润是多少？(3)若超市想每月销售柠檬即食片所得利润w 稳定在900元，销售单价应定为多少元？17．如图，一名同学推铅球，铅球出手后行进过程中离地面的高度y （单位：m ）与水平距离x （单位：m ）近似满足函数关系212123y x x c =-++．已知铅球落地时的水平距离为10m ．(1)求铅球出手后水平距离与这名同学相距多远时，铅球离地面最高？(2)在铅球出手后的行进过程中，当它离地面的高度为5m 3时，此时铅球的水平距离是多少？18．我市某企业安排20名工人生产甲、乙两种产品，根据生产经验，每人每天生产2件甲产品或1件乙产品（每人每天只能生产一种产品）．甲产品生产成本为每件10元；若安排1人生产一件乙产品，则成本为38元，以后每增加1人，平均每件乙产品成本降低2元．规x x≥人生产乙产品．定甲产品每天至少生产20件．设每天安排()1(1)根据信息填表：产品种类每天工人数（人）每天产量（件）每件产品生产成本（元）甲10-乙x402x(2)为了增加利润，企业须降低成本，该企业如何安排工人生产才能使得每天的生产总成本最低？最低成本是多少？参考答案：1．B2．D3．A4．D5．D6．B7．D8．C9．43m > 10．2(2)2y x =--11．912．()264-13．③④/④③14．(1)243y x x =-+(2)当2x <，y 随x 的增大而减小15．(1)抛物线的函数表达式为21542y x x =-，顶点坐标为2554⎛⎫- ⎪⎝⎭，； (2)当1t =时，矩形ABCD 的周长有最大值，最大值为412．16．(1)()480201018y x x =-≤≤； (2)当销售单价定为17元时，每月可获得最大利润；每月获得最大利润为980元．(3)当销售单价定为15元时，每月获得利润可稳定在900元．17．(1)铅球出手后水平距离与这名同学相距3m 远时，铅球离地面最高为3m(2)此时铅球的水平距离为8m18．安排10名工人生产甲产品，10名工人生产乙产品才能使得每天的生产总成本最低，最低成本是400元。

2020重庆中考复习数学第12题二次函数专题训练二含答案

2020年重庆中考复习二次函数专题训练二1．（2020•南岸区校级模拟）如图所示，抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝1，与y 轴的一个交点坐标为（0，3），其部分图象如图所示，下列结论：①abc＜0；②4a+c＞0；③方程ax2+bx+c＝3的两个根是x1＝0，x2＝2；④方程ax2+bx+c＝0有一个实根大于2；⑤当x＜0时，y随x增大而增大．其中结论正确的个数是（）A．4个B．3个C．2个D．1个解：抛物线开口向下，a＜0，对称轴为x＝1＞0，a、b异号，因此b＞0，与y轴交点为（0，3），因此c＝3＞0，于是abc＜0，故结论①是正确的；由对称轴为x ＝﹣＝1得2a+b＝0，当x＝﹣1时，y＝a﹣b+c＜0，所以a+2a+c＜0，即3a+c ＜0，又a＜0，4a+c＜0，故结论②不正确；当y＝3时，x1＝0，即过（0，3），抛物线的对称轴为x＝1，由对称性可得，抛物线过（2，3），因此方程ax2+bx+c＝3的有两个根是x1＝0，x2＝2；故③正确；抛物线与x轴的一个交点（x1，0），且﹣1＜x1＜0，由对称轴x＝1，可得另一个交点（x2，0），2＜x2＜3，因此④是正确的；根据图象可得当x＜0时，y随x增大而增大，因此⑤是正确的；正确的结论有4个，故选：A．2．（2019秋•沙坪坝区校级月考）如图，二次函数y＝ax2+bx+c的图象经过点A（﹣3，0），其对称轴为直线x＝﹣1，有下列结论：①abc＜0；②a+b+c＜0；③5a+4c＜0；④4ac﹣b2＞0；⑤若P （﹣5，y1），Q（m，y2）是抛物线上两点，且y1＞y2，则实数m的取值范围是﹣5＜m＜3．其中正确结论的个数是（）A．1 B．2 C．3 D．4解：①观察图象可知：a＞0，b＞0，c＜0，∴abc＜0，∴①正确；②当x＝1时，y＝0，即a+b+c ＝0，∴②错误；③对称轴x＝﹣1，即﹣＝﹣1得b＝2a，当x ＝时，y＜0，即a +b+c＜0，即a+2b+4c＜0，∴5a+4c＜0．∴③正确；④因为抛物线与x轴有两个交点，所以△＞0，即b2﹣4ac＞0，∴4ac﹣b2＜0．∴④错误；⑤∵（﹣5，y1）关于直线x＝﹣1的对称点的坐标是（3，y1），∴当y1＞y2时，﹣5＜m＜3．∴⑤正确．故选：C3．如图是二次函数y＝ax2+bx+c（a，b，c是常数，且a≠0）图象的一部分，它与x轴的一个交点A在点（2，0）和点（3，0）之间，图象的对称轴是x＝1，对于下列说法：①ab＜0；②2a+b＝0；③3a+c＞0；④a+b≥m（am+b）（m为实数）；⑤当﹣1＜x＜3时，y＞0，其中正确的是（）A．①②④B．①②⑤C．②③④D．③④⑤解：①∵对称轴在y轴右侧，∴a、b异号，∴ab＜0，故正确；②∵对称轴x ＝﹣＝1，∴2a+b＝0；故正确；③∵2a+b＝0，∴b＝﹣2a，∵当x＝﹣1时，y＝a﹣b+c＜0，∴a﹣（﹣2a）+c＝3a+c＜0，故错误；④根据图示知，当x＝1时，有最大值；当m≠1时，有am2+bm+c≤a+b+c，所以a+b≥m（am+b）（m为实数）．故正确．⑤如图，当﹣1＜x＜3时，y不只是大于0．故错误．故选：A．4．（2019秋•九龙坡区校级期中）如图，抛物线y＝ax2+bx+c（a≠0）过点（3，0），且对称轴为直线x＝1．下列说法，其中正确的是（）①abc＜0 ②b2﹣4ac＞0；③a﹣b+c＜0；④b﹣c ＞2a A．①②B．①③④C．②④ D．①②④解：∵抛物线y＝ax2+bx+c（a≠0）与x轴交于点（3，0），其对称轴为直线x＝1，∴抛物线y＝ax2+bx+c（a≠0）与x轴交于点（3，0）和（﹣1，0），且b＝﹣2a，由图象知：a＜0，c＞0，b＞0，b2﹣4ac＞0，∴abc＜0故结论①②正确；∵抛物线y＝ax2+bx+c（a≠0）与x轴交于点（﹣1，0），∴a﹣b+c＝0，故结论③错误；∵a﹣b+c＝0，a＜0，∴2a﹣b+c＜0，∴b﹣c＞2a，故结论④正确；故结论正确的有①②④，故选：D．5．（2019秋•涪陵区校级月考）已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则下列结论中正确的结论有（）①abc＜0；②2a+b＝0；③b2﹣4ac＜0；④9a+3b+c＞0；⑤c+8a＜0．A．1个B．2个C．3个D．4个解：∵图象的开口向下，与y轴的交点在y轴的正半轴上，对称轴是直线x＝1，∴a＜0，c＞0，﹣＝1，即2a+b＝0，b＞0，∴abc＜0，故①②正确；∵抛物线的图象和x轴有两个交点，∴b2﹣4ac＞0，故③错误；∵抛物线的图象的对称轴是直线x＝1，和x轴的一个交点坐标是（﹣1，0），∴另一个交点坐标是（3，0），即当x＝3时，y＝a×32+b×3+c＝0，故④错误；∵2a+b＝0，即b＝﹣2a，代入解析式得：y＝ax2﹣2ax+c，当x＝3时，y＝9a﹣6a+c＝3a+c＝0，∵a＜0，∴3a+c+5a＝8a+c＜0，故⑤正确；即正确的有3个，故选：C．6．二次函数y＝ax2+bx+c（a≠0）的图象如图所示，其对称轴为直线x＝﹣1，与x轴的交点为（x1，0）、（x2，0），其中0＜x1＜1，有下列结论：①abc＞0；②﹣3＜x2＜﹣2；③4a﹣2b+c＜﹣1；④a﹣b＞am2+bm（m≠﹣1）；⑤a ＞；其中，正确的结论有（）A．5 B．4 C．3 D．2解：①对称轴在y轴左侧，则ab同号，c＜0，故abc＜0，故错误；②对称轴为直线x＝﹣1，0＜x1＜1，则﹣3＜x2＜﹣2，正确；③对称轴为直线x＝﹣1，则b＝2a，4a﹣2b+c＝c＜﹣1，故正确；④x＝﹣1时，y＝ax2+bx+c＝a﹣b+c，为最小值，故a﹣b+c＜am2+bm+c，故错误；⑤x＝1时，y＝a+b+c＝3a+c＞0，即3a＞﹣c，而c＜﹣1，故a ＞，正确；故选：C．7．（2019•重庆模拟）如图，二次函数y＝ax2+bx+c的图象与x轴交于A，B（﹣1，0）两点，与y 轴交于点C，则下列四个结论：①ac＜0；②2a+b＝0；③﹣1＜x＜3时，y＜0；④4a+c＜0．其中所有正确结论的序号是（）A．①②④B．①③④C．①②③D．②③④解：∵抛物线开口向下，∴a＜0，∵抛物线与y轴相交于正半轴，∴c＞0，则ac＜0，即①正确，该二次函数的对称轴为：x ＝﹣＝1，整理得：2a+b＝0，即②正确，∵抛物线对称轴为x＝1，点B的坐标为：（﹣1，0），则点A的坐标为：（3，0），由图象可知：当1＜x＜3时，y＞0，即③错误，由图象可知，当x＝﹣1时，函数值为0，把x＝﹣1代入y＝ax2+bx+c得：a﹣b+c＝0，∵b＝﹣2a，∴3a+c＝0，∵a＜0，∴4a+c＜0 即④正确，正确结论的序号是①②④，故选：A．8．如图，抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝1，且经过点（﹣1，0），下列四个结论：①如果点（﹣，y1）和（2，y2）都在抛物线上，那么y1＜y2；②b2﹣4ac＞0；③m（am+b）＜a+b（m≠1的实数）；④＝﹣3；其中正确的有（）A．4个B．3个C．2个D．1个解：∵对称轴为直线x＝1，∴﹣＝1，∴b＝﹣2a，∵经过点（﹣1，0），∴a﹣b+c＝0，∴c＝﹣3a，∴y＝ax2+bx+c＝a（x2﹣2x﹣3），由图象可知，a ＜0；①将点（﹣，y1）和（2，y2）分别代入抛物线解析式可得y1＝﹣a，y2＝﹣3a，∴y1＜y2；②由图象可知，抛物线与x轴有两个不同的交点，∴△＝b2﹣4ac＞0；③由图象可知，当x＝1时，函数有最大值1，∴对任意m，则有m（am+b）＜a+b；②＝＝﹣3；∴①②③④正确，故选：A．9．已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，并且关于x的一元二次方程ax2+bx+c﹣m ＝0没有实数根，下列结论：①abc＞0；②a﹣b+c＜0；③m＞﹣2；④二次函数y＝ax2+bx+c （a≠0），最小值为﹣2，其中正确的个数有（）A．1 B．2 C．3 D．4解：①对称轴在y轴右侧，则ab＜0，而c＜0，故abc＞0正确，符合题意；②当x＝﹣1时，y＝a﹣b+c＞0，故原选项错误，不符合题意；③关于x的一元二次方程ax2+bx+c﹣m＝0没有实数根，即y＝ax2+bx+c与y＝m没有交点，故m ＜﹣2，原选项错误，不符合题意；④从图象看二次函数y＝ax2+bx+c（a≠0）的最小值为﹣2，故符合题意；故选：B．10．（2019秋•曾都区期末）二次函数y＝ax2+bx+c（a≠0）的大致图象如图所示，顶点坐标为（1，﹣4a），点A（4，y1）是该抛物线上一点，若点D（x2，y2）是抛物线上任意一点，有下列结论：①4a﹣2b+c＞0；②若y2＞y1，则x2＞4；③若0≤x2≤4，则0≤y2≤5a；④若方程a（x+1）（x﹣3）＝﹣1有两个实数根x1和x2，且x1＜x2，则﹣1＜x1＜x2＜3．其中正确结论的个数是（）A．1个B．2个C．3个D．4个解：①∵二次函数y＝ax2+bx+c（a≠0）的大致图象如图所示，顶点坐标为（1，﹣4a），∴x ＝，且﹣4a＝a+b+c，∴b＝﹣2a，c＝﹣3a，∴4a﹣2b+c＝4a+4a﹣3a＝5a＞0（∵抛物线开口向上，则a＞0），于是①的结论正确；②∵点A（4，y1）关于直线x＝1的对称点为（﹣2，y1），∴当y2＞y1，则x2＞4或x2＜﹣2，于是②错误；③当x＝4时，y1＝16a+4b+c＝16a﹣8a﹣3c＝5a，∴当﹣1≤x2≤4，则﹣4a≤y2≤5a，于是③错误；④∵方程a（x+1）（x﹣3）＝﹣1有两个实数根x1和x2，且x1＜x2，∴抛物线y＝a（x+1）（x﹣3）与直线y＝﹣1交点的坐标（x1，﹣1）和（x2，﹣1），∵抛物线y＝a（x+1）（x﹣3）＝0时，x＝﹣1或3，即抛物线y＝a（x+1）（x﹣3）＝0与x轴的两个交点坐标分别为（﹣1，0）和（3，0），∴﹣1＜x1＜x2＜3，于是④正确．故选：B．11．（2020•下陆区模拟）抛物线y＝ax2+bx+c的对称轴为直线x＝﹣1，图象过（1，0）点，部分图象如图所示，下列判断中：其中正确的个数是（）①abc＞0；②b2﹣4ac＞0；③9a﹣3b+c＝0；④若点（﹣2.5，y1），（﹣0.5，y2）均在抛物线上，则y1＞y2；⑤5a﹣2b+c＜0．A．2个B．3个C．4个D．5个解：①由图象开口向上，则a＞0，故b＞0，∵c＜0，∴abc＜0，故①错误．②∵抛物线与x轴有两个交点，∴b2﹣4ac＞0，故②正确．③∵抛物线与x轴的一个交点是（1，0），对称轴是x＝﹣1，∴抛物线与x轴的另一个交点是（﹣3，0），∴9a﹣3b+c＝0，故③正确．④∵点（﹣0.5，y2）在抛物线上，对称轴为x＝﹣1，∴（﹣1.5，y2）也在抛物线上，∵﹣1.5＞﹣2.5，且（﹣1.5，y2），（﹣2.5，y1）都在对称轴的左侧，∴y1＞y2，故④正确．⑤∵抛物线对称轴x＝﹣1，经过（1，0），∴﹣＝﹣1，a+b+c＝0，∴b＝2a，c＝﹣3a，∴5a﹣2b+c＝5a﹣4a﹣3a＝﹣2a＜0，∴⑤正确．故正确的判断是②③④⑤共4个．故选：C．12．（2020•成华区模拟）已知抛物线y＝ax2+bx+c的对称轴为直线x＝2，与x轴的一个交点坐标为（4，0）其部分图象如图所示，下列结论其中结论正确的是（）①抛物线过原点；②4a+b＝0；③a﹣b+c＜0；④抛物线线的顶点坐标为（2，b）⑤当x＜2时，y随x增大而增大A．①②③B．③④⑤C．①②④D．①④⑤解：①∵抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝2，与x轴的一个交点坐标为（4，0），∴抛物线与x轴的另一交点坐标为（0，0），结论①正确；②∵抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝2，且抛物线过原点，∴﹣＝2，c＝0，∴b＝﹣4a，c＝0，∴4a+b＝0，结论②正确；③∵当x＝﹣1时，y值为正，∴a﹣b+c＞0，结论③错误；④当x＝2时，y＝ax2+bx+c＝4a+2b+c＝（4a+b+c）+b＝b，∴抛物线的顶点坐标为（2，b），结论④正确；⑤观察函数图象可知：当x＜2时，y随x增大而减小，结论⑤错误．综上所述，正确的结论有：①②④．故选：C．13．（2020•枣阳市校级模拟）已知二次函数y＝ax2+bx+c的图象如图所示，有以下结论：①a+b+c＜0；②a﹣b+c＞1；③abc＞0；④9a﹣3b+c＜0；⑤c﹣a＞1．其中所有正确结论的序号是（）A．①②B．①③④C．①②③④D．①②③④⑤解：由图象可知，a＜0，c＝1，对称轴x ＝﹣＝﹣1，∴b＝2a，①∵当x＝1时，y＜0，∴a+b+c＜0，故正确；②∵当x＝﹣1时，y＞1，∴a﹣b+c＞1，故正确；③abc＝2a2＞0，故正确；④由图可知当x＝﹣3时，y＜0，∴9a﹣3b+c＜0，故正确；⑤c﹣a＝1﹣a＞1，故正确；∴①②③④⑤正确，故选：D．14．（2020•凉山州一模）二次函数y＝ax2+bx+c的图象如图所示、则下列结论：①abc＞0；②a﹣5b+9c＞0；③3a+c＜0，正确的是（）A．①③B．①②C．①②③D．②③解：①∵抛物线的对称轴在y轴的左侧，∴ab＞0，由图象可知：c＞0，∴abc＞0，故①正确；③∵x ＝﹣＝﹣1，∴b＝2a，∴a﹣5b+9c＝9c﹣9a＝9（c﹣a）＞0，故②正确，③∵x ＝﹣＝﹣1，∴b＝2a，由图象可知：9a﹣3b+c＜0，∴9a﹣6a+c＜0，即3a+c＜0，故③正确；故选：C．15．（2020•龙岗区模拟）如图，二次函数y＝ax2+bx+c（a≠0）图象经过点（﹣1，2），下列结论中正确的有（）①4a﹣2b+c＜0；②2a﹣b＜0；③a+c＜1；④b2+8a＞4ac，A．1个B．2个C．3个D．4个解：①由函数的图象可得：当x＝﹣2时，y＜0，即y＝4a﹣2b+c＜0，故①正确；②由函数的图象可知：抛物线开口向下，则a＜0；抛物线的对称轴大于﹣1，即x ＝﹣＞﹣1，得出2a﹣b＜0，故②正确；③已知抛物线经过（﹣1，2），即a﹣b+c＝2（1），由图象知：当x＝1时，y＜0，即a+b+c＜0（2），联立（1）（2），得：a+c＜1，故③正确；④由于抛物线的对称轴大于﹣1，所以抛物线的顶点纵坐标应该大于2，即：＞2，由于a＜0，所以4ac﹣b2＜8a，即b2+8a＞4ac，故④正确，故选：D．16．（2019秋•铁锋区期末）如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于点（﹣3，0），其对称轴为直线x ＝﹣，结合图象分析下列结论：①abc＞0；②3a+c＞0；③当x＜0时，y随x的增大而增大：④若m，n（m＜n）为方程a（x+3）（x﹣2）+3＝0的两个根，则m＜﹣3且n＞2：⑤＜0，其中正确的结论有（）A．2个B．3个C．4个D．5个解：∵抛物线y＝ax2+bx+c（a≠0）与x轴交于点（﹣3，0），其对称轴为直线x ＝﹣∴抛物线y＝ax2+bx+c（a≠0）与x轴交于点（﹣3，0）和（2，0），且a＝b由图象知：a＜0，c＞0，b＜0，∴abc＞0，故结论①正确；∵抛物线y＝ax2+bx+c（a≠0）与x轴交于点（﹣3，0），∴9a﹣3b+c＝0∵a＝b，∴c＝﹣6a，∴3a+c＝﹣3a＞0，故结论②正确；∵当x ＜﹣时，y随x 的增大而增大；当﹣＜x＜0时，y随x的增大而减小，故结论③错误；∵抛物线y＝ax2+bx+c（a≠0）与x轴交于点（﹣3，0）和（2，0），∴y＝ax2+bx+c＝a（x+3）（x﹣2）∵m，n（m＜n）为方程a（x+3）（x﹣2）+3＝0的两个根∴m，n（m＜n）为方程a（x+3）（x﹣2）＝﹣3的两个根∴m，n（m＜n）为函数y＝a（x+3）（x﹣2）与直线y＝﹣3的两个交点的横坐标结合图象得：m＜﹣3且n＞2，故结论④成立；∵当x ＝﹣时，y ＝＞0，∴＜0，故结论⑤正确；故选：C．。

二次函数复习题(含参考答案)

二次函数复习题一、填空题1.已知函数y=(m+2)x m(m+1)是二次函数,则m=______________.2.二次函数y=-x2-2x的对称轴是x=_____________3.函数s=2t-t2,当t=___________时有最大值,最大值是__________.4.已知抛物线y=ax2+x+c与x轴交点的横坐标为-1,则a+c=__________.5.抛物线y=-3(x+2)2的顶点坐标是_____,若将它旋转180º后得新的抛物线,其解析式为_________.6.抛物线y=5x-5x2+m的顶点在x轴上,则m=_____________________.7.已知抛物线y=ax2+bx+c的图象与x轴有两个交点,那么一元二次方程ax2+bx+c=0的根的情况是___________________.8.已知二次函数y=x2-2x-3的图象与x轴交于A,B两点,在x轴上方的抛物线上有一点C,且△ABC的面积等于10,则点C的坐标为________.9.把抛物线y=2(x+1)2向下平移____单位后,所得抛物线在x轴上截得的线段长为5.10.如果二次函数y=x2-3x-2k,不论x取任何实数,都有y>0,则k的取值范围是________11.已知二次函数y=kx2+(2k-1)x-1与x轴交点的横坐标为x1,x2(x1<x2),则对于下列结论:(1) 当x= -2时,y=1;(2) 当x> x2时,y>0;(3)方程kx2+(2k-1)x-1=0有两个不相等的实数根x1,x2;(4) x1<-1,x2>-1;(5)x2 -x1 =k k241,其中正确的结论有__ __(只需填写序号)12.已知二次函数y=x2-2(m-1)x-1-m的图象与x轴交于A(x1,0),B(x2,0), x1<0<x2,与y轴交于点C, 且满足OC(OB-OA)=2OA·OB,则该二次函数的解析式为__________二.选择题13.抛物线y=(x-1)2+1的顶点坐标是( )(A) (1,1) (B) (-1,1) (C) (1,-1) (D) (-1,-1)14.抛物线y=-x2+x+7与坐标轴的交点个数为( )(A) 3个(B) 2个(C) 1个(D) 0个15.把抛物线y=x2+bx+c的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式是y=x2-3x+5,则有( )(A) b=3,c=7 (B) b=-9,c=-15 (C) b=3,c=3 (D) b=-9,c=2116.若二次函数y=ax2+c,当x取x1,x2(x1≠x2)时,函数值相等,则当x取x1+x2时,函数值为17.当a,b为实数，二次函数y=a(x-1)2+b的最小值为-1时有( )(A) ab (D) a≥b18.已知函数y=3x2-6x+k(k为常数)的图象经过点A(0.85,y1)，B(1.1,y2),C(2,y3),则有( )(A) y1<y2<y3(B) y1>y2>y3(C) y3>y1>y2(D) y1>y3>y219如果二次函数y=ax2+bx+c的顶点在y=2x2-x-1的图象的对称轴上，那么一定有( )(A) a=2或-2 (B) a=2b (C) a=-2b (D) a=2,b= -1,c=-120抛物线y=ax2+bx+c(a<0)经过点(-1,0)，且满足4a+2b+c>0.以下结论(1)a+b>0;(2)a+c>0;(3)-a+b+c>0;(4)b2-2ac>5a2其中正确的个数有( )(A) 1个(B) 2个(C) 3个(D) 4个三解答题：21．已知函数y=x2+bx-1的图象经过点（3，2）（1）求这个函数的解析式；（2）画出它的图象，并指出图象的顶点坐标；（3）当x>0时，求使y≥2的x的取值范围。

中考数学复习之二次函数的综合题专项训练(2)

中考数学复习之二次函数的综合题专项训练（2）1．加强劳动教育，落实五育并举．孝礼中学在当地政府的支持下，建成了一处劳动实践基地．2023年计划将其中1000m 2的土地全部种植甲乙两种蔬菜．经调查发现：甲种蔬菜种植成本y （单位；元/m 2）与其种植面积x （单位：m 2）的函数关系如图所示，其中200⩽x ⩽700；乙种蔬菜的种植成本为50元/m 2．（1）当x ＝ m 2时，y ＝35元/m 2；（2）设2023年甲乙两种蔬菜总种植成本为W 元，如何分配两种蔬菜的种植面积，使W 最小？（3）学校计划今后每年在这1000m 2土地上，均按（2）中方案种植蔬菜，因技术改进，预计种植成本逐年下降．若甲种蔬菜种植成本平均每年下降10%，乙种蔬菜种植成本平均每年下降a %，当a 为何值时，2025年的总种植成本为28920元？2．已知二次函数y ＝ax 2+bx +c （a ＞0）．（1）若a ＝1，c ＝﹣1，且该二次函数的图象过点（2，0），求b 的值；（2）如图所示，在平面直角坐标系Oxy 中，该二次函数的图象与x 轴交于点A （x 1，0），B （x 2，0），且x 1＜0＜x 2，点D 在⊙O 上且在第二象限内，点E 在x 轴正半轴上，连接DE ，且线段DE 交y 轴正半轴于点F ，∠DOF =∠DEO ，OF =32DF ．①求证：DO EO =23． ②当点E 在线段OB 上，且BE ＝1．⊙O 的半径长为线段OA 的长度的2倍，若4ac ＝﹣a 2﹣b 2，求2a +b 的值．3．综合与实践问题提出某兴趣小组开展综合实践活动：在Rt△ABC中，∠C＝90°，D为AC上一点，CD=√2，动点P以每秒1个单位的速度从C点出发，在三角形边上沿C→B→A匀速运动，到达点A时停止，以DP为边作正方形DPEF．设点P的运动时间为ts，正方形DPEF的面积为S，探究S与t的关系．初步感知（1）如图1，当点P由点C运动到点B时，①当t＝1时，S＝；②S关于t的函数解析式为．（2）当点P由点B运动到点A时，经探究发现S是关于t的二次函数，并绘制成如图2所示的图象．请根据图象信息，求S关于t的函数解析式及线段AB的长．延伸探究（3）若存在3个时刻t1，t2，t3（t1＜t2＜t3）对应的正方形DPEF的面积均相等．①t1+t2＝；②当t3＝4t1时，求正方形DPEF的面积．4．如图，已知抛物线y＝ax2﹣2ax+3与x轴交于点A（﹣1，0）和点B，与y轴交于点C，连接AC，过B、C两点作直线．（1）求a的值．（2）将直线BC向下平移m（m＞0）个单位长度，交抛物线于B′、C′两点．在直线B′C′上方的抛物线上是否存在定点D，无论m取何值时，都是点D到直线B′C′的距离最大．若存在，请求出点D的坐标；若不存在，请说明理由．（3）抛物线上是否存在点P，使∠PBC+∠ACO＝45°，若存在，请求出直线BP的解析式；若不存在，请说明理由．5．如图，抛物线y＝﹣x²+bx+c经过A（﹣1，0），C（0，3）两点，并交x轴于另一点B，点M是抛物线的顶点，直线AM与轴交于点D．（1）求该抛物线的表达式；（2）若点H是x轴上一动点，分别连接MH，DH，求MH+DH的最小值；（3）若点P是抛物线上一动点，问在对称轴上是否存在点Q，使得以D，M，P，Q为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点Q的坐标；若不存在，请说明理由．6．在平面直角坐标系中，点O 是坐标原点，抛物线y ＝ax 2+bx （a ≠0）经过点A （3，3），对称轴为直线x ＝2．（1）求a ，b 的值；（2）已知点B ，C 在抛物线上，点B 的横坐标为t ，点C 的横坐标为t +1．过点B 作x 轴的垂线交直线OA 于点D ，过点C 作x 轴的垂线交直线OA 于点E ．（i ）当0＜t ＜2时，求△OBD 与△ACE 的面积之和；（ii ）在抛物线对称轴右侧，是否存在点B ，使得以B ，C ，D ，E 为顶点的四边形的面积为32？若存在，请求出点B 的横坐标t 的值；若不存在，请说明理由． 7．如图，直线y =√52x +√5与x 轴，y 轴分别交于点A ，B ，抛物线的顶点P 在直线AB 上，与x 轴的交点为C ，D ，其中点C 的坐标为（2，0），直线BC 与直线PD 相交于点E ．（1）如图2，若抛物线经过原点O ．①求该抛物线的函数表达式；②求BE EC 的值．（2）连结PC ，∠CPE 与∠BAO 能否相等？若能，求符合条件的点P 的横坐标；若不能，试说明理由．8．已知抛物线y＝﹣x2+bx+c（b，c为常数，c＞1的顶点为P，与x轴相交于A，B两点（点A在点B的左侧），与y轴相交于点C，抛物线上的点M的横坐标为m，且−c＜m＜b 2，过点M作MN⊥AC，垂足为N．（1）若b＝﹣2，c＝3．①求点P和点A的坐标；②当MN=√2时，求点M的坐标；（2）若点A的坐标为（﹣c，0），且MP∥AC，当AN+3MN=9√2时，求点M的坐标．9．综合与探究如图，二次函数y＝﹣x2+4x的图象与x轴的正半轴交于点A，经过点A的直线与该函数图象交于点B（1，3），与y轴交于点C．（1）求直线AB的函数表达式及点C的坐标；（2）点P是第一象限内二次函数图象上的一个动点，过点P作直线PE⊥x轴于点E，与直线AB交于点D，设点P的横坐标为m．①当PD=12OC时，求m的值；②当点P在直线AB上方时，连接OP，过点B作BQ⊥x轴于点Q，BQ与OP交于点F，连接DF．设四边形FQED的面积为S，求S关于m的函数表达式，并求出S的最大值．10．如图，已知A（0，2），B（2，0）．点E位于第二象限且在直线y＝﹣2x上，∠EOD＝90°，OD＝OE，连接AB，DE，AE，DB．（1）直接判断△AOB的形状：△AOB是三角形；（2）求证：△AOE≌△BOD；（3）直线EA交x轴于点C（t，0），t＞2．将经过B，C两点的抛物线y1＝ax2+bx﹣4向左平移2个单位，得到抛物线y2．①若直线EA与抛物线y1有唯一交点，求t的值；②若抛物线y2的顶点P在直线EA上，求t的值；③将抛物线y2再向下平移2(t−1)2个单位，得到抛物线y3．若点D在抛物线y3上，求点D 的坐标．11．已知（x1，y1），（x2，y2）是抛物线C1：y=−14x2+bx（b为常数）上的两点，当x1+x2＝0时，总有y1＝y2．（1）求b的值；（2）将抛物线C1平移后得到抛物线C2：y=−14（x﹣m）2+1（m＞0）．当0≤x≤2时，探究下列问题：①若抛物线C1与抛物线C2有一个交点，求m的取值范围；②设抛物线C2与x轴交于A，B两点，与y轴交于点C，抛物线C2的顶点为点E，△ABC外接圆的圆心为点F．如果对抛物线C1上的任意一点P，在抛物线C2上总存在一点Q，使得点P、Q的纵坐标相等．求EF长的取值范围．12．在平面直角坐标系xOy中，已知点A在y轴正半轴上．（1）如果四个点（0，0）、（0，2）、（1，1）、（﹣1，1）中恰有三个点在二次函数y＝ax2（a为常数，且a≠0）的图象上．①a＝；②如图1，已知菱形ABCD的顶点B、C、D在该二次函数的图象上，且AD⊥y轴，求菱形的边长；③如图2，已知正方形ABCD的顶点B、D在该二次函数的图象上，点B、D在y轴的同侧，且点B在点D的左侧，设点B、D的横坐标分别为m、n，试探究n﹣m是否为定值．如果是，求出这个值；如果不是，请说明理由．（2）已知正方形ABCD的顶点B、D在二次函数y＝ax2（a为常数，且a＞0）的图象上，点B在点D的左侧，设点B、D的横坐标分别为m、n，直接写出m、n满足的等量关系式．13．已知抛物线y=−12x2+bx+c与x轴交于A，B（4，0）两点，与y轴交于点C（0，2）．点P为第一象限抛物线上的点，连接CA，CB，PB，PC．（1）直接写出结果；b＝，c＝，点A的坐标为，tan∠ABC＝；（2）如图1，当∠PCB＝2∠OCA时，求点P的坐标；（3）如图2，点D在y轴负半轴上，OD＝OB，点Q为抛物线上一点，∠QBD＝90°．点E，F分别为△BDQ的边DQ，DB上的动点，且QE＝DF，记BE+QF的最小值为m．①求m的值；②设△PCB的面积为S，若S=14m2−k，请直接写出k的取值范围．14．如图，在平面直角坐标系中，抛物线y＝ax2+bx+c与x轴交于B（4，0），C（﹣2，0）两点，与y 轴交于点A （0，﹣2）．（1）求该抛物线的函数表达式；（2）若点P 是直线AB 下方抛物线上的一动点，过点P 作x 轴的平行线交AB 于点K ，过点P 作y 轴的平行线交x 轴于点D ，求12PK +PD 的最大值及此时点P 的坐标；（3）在抛物线的对称轴上是否存在一点M ，使得△MAB 是以AB 为一条直角边的直角三角形；若存在，请求出点M 的坐标，若不存在，请说明理由．15．综合与实践：问题情境小莹妈妈的花卉超市以15元/盆的价格新购进了某种盆栽花卉，为了确定售价，小莹帮妈妈调查了附近A ，B ，C ，D ，E 五家花卉店近期该种盆栽花卉的售价与日销售量情况，记录如下：数据整理：（1）请将以上调查数据按照一定顺序重新整理，填写在下表中：售价（元/盆）日销售量（盆）模型建立（2）分析数据的变化规律，找出日销售量与售价间的关系．拓广应用（3）根据以上信息，小莹妈妈在销售该种花卉中，①要想每天获得400元的利润，应如何定价？②售价定为多少时，每天能够获得最大利润？16．如图，抛物线y＝ax2+bx+5与x轴交于A，B两点，与y轴交于点C，AB＝4．抛物线的对称轴x＝3与经过点A的直线y＝kx﹣1交于点D，与x轴交于点E．（1）求直线AD及抛物线的表达式；（2）在抛物线上是否存在点M，使得△ADM是以AD为直角边的直角三角形？若存在，求出所有点M的坐标；若不存在，请说明理由；（3）以点B为圆心，画半径为2的圆，点P为⊙B上一个动点，请求出PC+12P A的最小值．17．如图，二次函数y＝x2﹣6x+8的图象与x轴分别交于点A，B（点A在点B的左侧），直线l是对称轴．点P在函数图象上，其横坐标大于4，连接P A，PB，过点P作PM⊥l，垂足为M，以点M为圆心，作半径为r的圆，PT与⊙M相切，切点为T．（1）求点A，B的坐标；（2）若以⊙M的切线长PT为边长的正方形的面积与△P AB的面积相等，且⊙M不经过点（3，2），求PM长的取值范围．18．如图，已知二次函数y＝x2+bx+c图象经过点A（1，﹣2）和B（0，﹣5）．（1）求该二次函数的表达式及图象的顶点坐标．（2）当y≤﹣2时，请根据图象直接写出x的取值范围．19．如图1，抛物线y＝﹣x2+bx与x轴交于点A，与直线y＝﹣x交于点B（4，﹣4），点C （0，﹣4）在y轴上．点P从点B出发，沿线段BO方向匀速运动，运动到点O时停止．（1）求抛物线y＝﹣x2+bx的表达式；（2）当BP＝2√2时，请在图1中过点P作PD⊥OA交抛物线于点D，连接PC，OD，判断四边形OCPD的形状，并说明理由；（3）如图2，点P从点B开始运动时，点Q从点O同时出发，以与点P相同的速度沿x轴正方向匀速运动，点P停止运动时点Q也停止运动．连接BQ，PC，求CP+BQ的最小值．20．如图，在平面直角坐标系xOy中，抛物线L1：y＝x2﹣2x﹣3的顶点为P．直线l过点M （0，m）（m≥﹣3），且平行于x轴，与抛物线L1交于A、B两点（B在A的右侧）．将抛物线L1沿直线l翻折得到抛物线L2，抛物线L2交y轴于点C，顶点为D．（1）当m＝1时，求点D的坐标；（2）连接BC、CD、DB，若△BCD为直角三角形，求此时L2所对应的函数表达式；（3）在（2）的条件下，若△BCD的面积为3，E、F两点分别在边BC、CD上运动，且EF＝CD，以EF为一边作正方形EFGH，连接CG，写出CG长度的最小值，并简要说明理由．21．如图一所示，在平面直角坐标系中，抛物线y＝ax2+bx﹣8与x轴交于A（﹣4，0）、B （2，0）两点，与y轴交于点C．（1）求抛物线的函数表达式及顶点坐标；（2）点P为第三象限内抛物线上一点，作直线AC，连接P A、PC，求△P AC面积的最大值及此时点P的坐标；（3）设直线l1：y＝kx+k−354交抛物线于点M、N，求证：无论k为何值，平行于x轴的直线l2：y=−374上总存在一点E，使得∠MEN为直角．22．【建立模型】（1）如图1，点B是线段CD上的一点，AC⊥BC，AB⊥BE，ED⊥BD，垂足分别为C，B，D，AB＝BE．求证：△ACB≌△BDE；【类比迁移】（2）如图2，一次函数y＝3x+3的图象与y轴交于点A、与x轴交于点B，将线段AB绕点B逆时针旋转90°得到BC，直线AC交x轴于点D．①求点C的坐标；②求直线AC的解析式；【拓展延伸】（3）如图3，抛物线y＝x2﹣3x﹣4与x轴交于A，B两点（点A在点B的左侧），与y轴交于C点，已知点Q（0，﹣1），连接BQ，抛物线上是否存在点M，使得tan∠MBQ=13，若存在，求出点M的横坐标．23．在平面直角坐标系中，抛物线y＝ax2+bx+c（a≠0）经过点A（﹣1，0）和B（0，3），其顶点的横坐标为1．（1）求抛物线的表达式．（2）若直线x＝m与x轴交于点N，在第一象限内与抛物线交于点M，当m取何值时，使得AN+MN有最大值，并求出最大值．（3）若点P为抛物线y＝ax2+bx+c（a≠0）的对称轴上一动点，将抛物线向左平移1个单位长度后，Q为平移后抛物线上一动点．在（2）的条件下求得的点M，是否能与A、P、Q构成平行四边形？若能构成，求出Q点坐标；若不能构成，请说明理由．24．如图，抛物线y＝ax2+bx+c与x轴交于点A（﹣4，0）、B（2，0），且经过点C（﹣2，6）．（1）求抛物线的表达式；（2）在x轴上方的抛物线上任取一点N，射线AN、BN分别与抛物线的对称轴交于点P、Q，点Q关于x轴的对称点为Q′，求△APQ′的面积；（3）点M是y轴上一动点，当∠AMC最大时，求M的坐标．25．如图，在平面直角坐标系xOy中，已知抛物线y＝ax2+c经过点P（4，﹣3），与y轴交于点A（0，1），直线y＝kx（k≠0）与抛物线交于B，C两点．（1）求抛物线的函数表达式；（2）若△ABP 是以AB 为腰的等腰三角形，求点B 的坐标；（3）过点M （0，m ）作y 轴的垂线，交直线AB 于点D ，交直线AC 于点E ．试探究：是否存在常数m ，使得OD ⊥OE 始终成立？若存在，求出m 的值；若不存在，请说明理由．26．数和形是数学研究客观物体的两个方面，数（代数）侧重研究物体数量方面，具有精确性，形（几何）侧重研究物体形的方面，具有直观性．数和形相互联系，可用数来反映空间形式，也可用形来说明数量关系．数形结合就是把两者结合起来考虑问题，充分利用代数、几何各自的优势，数形互化，共同解决问题．同学们，请你结合所学的数学解决下列问题．在平面直角坐标系中，若点的横坐标、纵坐标都为整数，则称这样的点为整点．设函数y ＝（4a +2）x 2+（9﹣6a ）x ﹣4a +4（实数a 为常数）的图象为图象T ．（1）求证：无论a 取什么实数，图象T 与x 轴总有公共点；（2）是否存在整数a ，使图象T 与x 轴的公共点中有整点？若存在，求所有整数a 的值；若不存在，请说明理由．27．在平面直角坐标系中，O 为坐标原点，抛物线y =14x 2+bx +c 经过点O （0，0），对称轴过点B （2，0），直线l 过点C （2，﹣2）且垂直于y 轴．过点B 的直线l 1交抛物线于点M 、N ，交直线l 于点Q ，其中点M 、Q 在抛物线对称轴的左侧．（1）求抛物线的解析式；（2）如图1，当BM ：MQ ＝3：5时，求点N 的坐标；（3）如图2，当点Q 恰好在y 轴上时，P 为直线l 1下方的抛物线上一动点，连结PQ 、PO ，其中PO 交l 1于点E ，设△OQE 的面积为S 1，△PQE 的面积为S 2，求S 2S 1的最大值．28．在二次函数y＝x2﹣2tx+3（t＞0）中．（1）若它的图象过点（2，1），则t的值为多少？（2）当0≤x≤3时，y的最小值为﹣2，求出t的值；（3）如果A（m﹣2，a），B（4，b），C（m，a）都在这个二次函数的图象上，且a＜b ＜3．求m的取值范围．29．在平面直角坐标系中，已知抛物线y＝ax2+bx+c与x轴交于点A（﹣3，0），B（1，0）两点，与y轴交于点C（0，3），点P是抛物线上的一个动点．（1）求抛物线的表达式；（2）当点P在直线AC上方的抛物线上时，连接BP交AC于点D，如图1，当PDDB的值最大时，求点P的坐标及PDDB的最大值；（3）过点P作x轴的垂线交直线AC于点M，连结PC，将△PCM沿直线PC翻折，当点M的对应点M′恰好落在y轴上时，请直接写出此时点M的坐标．30．如图，二次函数y＝x2+bx+c的图象交x轴于点A、B，交y轴于点C，点B的坐标为（1，0），对称轴是直线x＝﹣1，点P是x轴上一动点，PM⊥x轴，交直线AC于点M，交抛物线于点N．（1）求这个二次函数的解析式；（2）若点P在线段AO上运动（点P与点A、点O不重合），求四边形ABCN面积的最大值，并求出此时点P的坐标；（3）若点P在x轴上运动，则在y轴上是否存在点Q，使以M、N、C、Q为顶点的四边形是菱形？若存在，请直接写出所有满足条件的点Q的坐标；若不存在，请说明理由．31．已知点（﹣m，0）和（3m，0）在二次函数y＝ax2+bx+3（a，b是常数，a≠0）的图象上．（1）当m＝﹣1时，求a和b的值；（2）若二次函数的图象经过点A（n，3）且点A不在坐标轴上，当﹣2＜m＜﹣1时，求n的取值范围；（3）求证：b2+4a＝0．32．如图，在平面直角坐标系中，抛物线y=14x2+bx+c与x轴交于点A，B，与y轴交于点C，其中B（3，0），C（0，﹣3）．（1）求该抛物线的表达式；（2）点P是直线AC下方抛物线上一动点，过点P作PD⊥AC于点D，求PD的最大值及此时点P的坐标；（3）在（2）的条件下，将该抛物线向右平移5个单位，点E为点P的对应点，平移后的抛物线与y轴交于点F，Q为平移后的抛物线的对称轴上任意一点．写出所有使得以QF为腰的△QEF是等腰三角形的点Q的坐标，并把求其中一个点Q的坐标的过程写出来．33．如图，已知抛物线与x轴交于A（1，0）和B（﹣5，0）两点，与y轴交于点C．直线y＝﹣3x+3过抛物线的顶点P．（1）求抛物线的函数解析式；（2）若直线x＝m（﹣5＜m＜0）与抛物线交于点E，与直线BC交于点F．①当EF取得最大值时，求m的值和EF的最大值；②当△EFC是等腰三角形时，求点E的坐标．34．某工厂计划从A，B两种产品中选择一种生产并销售，每日产销x件．已知A产品成本价m元/件（m为常数，且4≤m≤6，售价8元/件，每日最多产销500件，同时每日共支付专利费30元；B产品成本价12元/件，售价20元/件，每日最多产销300件，同时每日支付专利费y元，y（元）与每日产销x（件）满足关系式y＝80+0.01x2．（1）若产销A，B两种产品的日利润分别为w1元，w2元，请分别写出w1，w2与x的函数关系式，并写出x的取值范围；（2）分别求出产销A，B两种产品的最大日利润．（A产品的最大日利润用含m的代数式表示）（3）为获得最大日利润，该工厂应该选择产销哪种产品？并说明理由．【利润＝（售价﹣成本）×产销数量﹣专利费】35．如图，抛物线y=−43x2+bx+4与x轴交于A（﹣3，0），B两点，与y轴交于点C．（1）求抛物线解析式及B，C两点坐标；（2）以A，B，C，D为顶点的四边形是平行四边形，求点D坐标；（3）该抛物线对称轴上是否存在点E，使得∠ACE＝45°，若存在，求出点E的坐标；若不存在，请说明理由．36．如图，抛物线y＝ax2+bx+c过点A（﹣1，0），B（3，0），C（0，3）．（1）求抛物线的解析式；（2）设点P是直线BC上方抛物线上一点，求出△PBC的最大面积及此时点P的坐标；（3）若点M是抛物线对称轴上一动点，点N为坐标平面内一点，是否存在以BC为边，点B、C、M、N为顶点的四边形是菱形，若存在，请直接写出点N的坐标；若不存在，请说明理由．37．如图，在平面直角坐标系xOy中，已知抛物线y＝ax2+2x+c与坐标轴分别相交于点A，B，C（0，6）三点，其对称轴为x＝2．（1）求该抛物线的解析式；（2）点F是该抛物线上位于第一象限的一个动点，直线AF分别与y轴，直线BC交于点D，E．①当CD＝CE时，求CD的长；②若△CAD，△CDE，△CEF的面积分别为S1，S2，S3，且满足S1+S3＝2S2，求点F的坐标．38．如图1，抛物线y＝ax2+bx+3（a≠0）与x轴交于A（﹣1，0），B（3，0）两点，与y 轴交于点C．（1）求抛物线的解析式；（2）点P在抛物线上，点Q在x轴上，以B，C，P，Q为顶点的四边形为平行四边形，求点P的坐标；（3）如图2，抛物线顶点为D，对称轴与x轴交于点E，过点K（1，3）的直线（直线KD除外）与抛物线交于G，H两点，直线DG，DH分别交x轴于点M，N．试探究EM •EN是否为定值，若是，求出该定值；若不是，说明理由．39．如图，在平面直角坐标系中，抛物线y＝ax2+bx+2过点（1，3），且交x轴于点A（﹣1，0），B两点，交y轴于点C．（1）求抛物线的表达式；（2）点P是直线BC上方抛物线上的一动点，过点P作PD⊥BC于点D，过点P作y 轴的平行线交直线BC于点E，求△PDE周长的最大值及此时点P的坐标；（3）在（2）中△PDE周长取得最大值的条件下，将该抛物线沿射线CB方向平移√5个单位长度，点M为平移后的抛物线的对称轴上一点．在平面内确定一点N，使得以点A，P，M，N为顶点的四边形是菱形，写出所有符合条件的点N的坐标，并写出求解点N的坐标的其中一种情况的过程．。

中考数学总复习《二次函数》专项测试卷-附参考答案

中考数学总复习《二次函数》专项测试卷-附参考答案学校:___________姓名：___________班级：___________考号：___________一、单选题(共12题；共24分)1．二次函数y＝﹣x2+2x﹣4，当﹣1＜x＜2时，y的取值范围是（）A．﹣7＜y＜﹣4B．﹣7＜y≤﹣3C．﹣7≤y＜﹣3D．﹣4＜y≤﹣3 2．已知二次函数y=3(x−2)2+ℎ，当自变量x分别取-2，2，5时，对应的值分别为y1，y2和y 3则y1，y2和y3的大小关系正确的是()A．y3<y2<y1B．y1<y2<y3C．y2<y3<y1D．y3<y1<y23．小敏在今年的校运动会跳远比赛中跳出了满意一跳，函数ℎ=3.5t−4.9t2（的单位：秒，h的单位：米）可以描述他跳跃时重心高度的变化，则他起跳后到重心最高时所用的时间是（）A．0.71B．0.70C．0.63D．0.364．对于二次函数y=−14(x+2)2−1，下列说法正确的是（）A．当x>−2时，y随x的增大而增大B．当x=−2时，y有最大值−1C．图象的顶点坐标为(2，−1)D．图象与x轴有两个交点5．抛物线y=2x2−12x+22的顶点是（）A．(3,−4)B．(−3,4)C．(3,4)D．(2,4)6．如图，二次函数y＝ax2＋bx＋c（a≠0）的图像的顶点在第一象限，且过点（0，1）和（－1，0）下列结论：①ab＜0，②b2-4ac＞0，③a-b+c＜0，④c=1，⑤当x＞－1时，y＞0.其中正确结论的个数是（）A．2个B．3个C．4个D．5个7．如图是二次函数y＝ax2+bx+c图象的一部分，其对称轴是x＝﹣1，且过点（﹣3，0），下列说法：①abc＜0；②2a﹣b＝0；③4a+2b+c＜0；④若（﹣5，y1），（3，y2）是抛物线上两点，则y1＜y2，其中说法正确的是（）A．①②B．②③C．①②④D．②③④8．关于二次函数y=-（x -2）2＋3，以下说法正确的是（）A．当x＞-2时，y随x增大而减小B．当x＞-2时，y随x增大而增大C．当x＞2时，y随x增大而减小D．当x＞2时，y随x增大而增大9．如图，双曲线y= k x经过抛物线y=ax2+bx（a≠0）的顶点（﹣1，m）（m＞0），则下列结论中，正确的是（）A．a+b=k B．2a+b=0C．b＜k＜0D．k＜a＜010．如图，抛物线y=ax2+bx+c交x轴于(−1，0)，(3，0)两点，则下列判断中，不正确的是（）A．图象的对称轴是直线x=1B．当x>2时，y随x的增大而减小C ．当−1<x <1时D ．一元二次方程ax 2+bx +c =0的两个根是−1和311．已知点(x 1，y 1)，(x 2，y 2)(x 1<x 2)在y =−x 2+2x +m 的图象上，下列说法错误的是（）A ．当m >0时，二次函数y =−x 2+2x +m 与x 轴总有两个交点B ．若x 2=2，且y 1>y 2，则0<x 1<2C ．若x 1+x 2>2，则y 1>y 2D ．当−1≤x ≤2时，y 的取值范围为m −3≤y ≤m12．从底面竖直向上抛出一小球，小球的高度h （单位：m ）与小球运动时间t （单位：s ）之间的关系式是：h ＝30t ﹣5t 2这个函数图象如图所示，则小球从第3s 到第5s 的运动路径长为（）A ．15mB ．20mC ．25mD ．30m二、填空题(共6题；共6分)13．在二次函数 y =−x 2+bx +c 中，函数y 与自变量x 的部分对应值如下表：则m 、n 的大小关系为 m n ．（填“＜”，“＝”或“＞”）14．已知一个二次函数的图象开口向上，顶点坐标为（0，﹣1 ），那么这个二次函数的解析式可以是．（只需写一个）15．二次函数 y =ax 2+bx +c 的图象与 x 轴相交于 (−1, 0) 和 (5, 0) 两点，则该抛物线的对称轴是 .16．函数y= {x 2+2x −3(x <0)x 2−4x −3(x ≥0) 的图象与直线y=﹣x+n 只有两个不同的公共点，则n 的取值为．17．已知二次函数y ＝﹣x 2+2mx+1，当﹣2≤x≤1时最大值为4，则m 的值为． 18．若函数y=（m ﹣2）x m 2−2+3是二次函数，则m=三、综合题(共6题；共70分)19．已知抛物线 y =a(x −4)2+2 经过点 (2,−2) ．（1）求a 的值；（2）若点A(m,y1),B(n,y2)(m<n<4)都在该抛物线上，试比较y1与y2的大小．20．宁波地区最近雾霾天气频繁，使得空气净化器得以畅销，某商场代理销售某种空气净化器，其进价是500元/台，经过市场销售后发现，在一个月内，当售价是1000元/台时，可售出50台，且售价每降低20元，就可多售出5台．若供货商规定这种空气净化器售价不能低于600元/台，代理销售商每月要完成不低于60台的销售任务．（1）试确定月销售量y（台）与售价x（元/台）之间的函数关系式；并求出自变量x的取值范围；（2）当售价x（元/台）定为多少时，商场每月销售这种空气净化器所获得的利润w（元）最大？最大利润是多少？21．某服装超市购进单价为30元的童装若干件，物价部门规定其销售单价不低于每件30元，不高于每件60元.销售一段时间后发现：当销售单价为60元时，平均每月销售量为80件，而当销售单价每降低10元时，平均每月能多售出20件.同时，在销售过程中，每月还要支付其他费用450元.设销售单价为x元，平均月销售量为y件.（1）求出y与x的函数关系式，并写出自变量x的取值范围.（2）当销售单价为多少元时，销售这种童装每月可获利1800元？（3）当销售单价为多少元时，销售这种童装每月获得利润最大？最大利润是多少？22．如图，是一座古拱桥的截面图，拱桥桥洞上沿是抛物线形状，抛物线两端点与水面的距离都是1m，拱桥的跨度为10m，桥洞与水面的最大距离是5m，桥洞两侧壁上各有一盏距离水面4m 的景观灯，把拱桥的截面图放在平面直角坐标系中。

九年级-二次函数-复习-试卷(含答案)

九年级二次函数复习训练一、选择题1、二次函数y ＝(x －1)2+2的最小值是（） A.－2 C.－12、已知抛物线的解析式为y ＝(x －2)2＋1，则抛物线的顶点坐标是（） A.(－2,1)B.(2，1)C.(2，－1)D.(1，2) 3、函数2+y ax b y ax bx c =+=+与在同一直角坐标系内的图象大致是（）4、在一定条件下，若物体运动的路程s （米）与时间t （秒）的关系式为 s ＝5t 2+2t ，则当t ＝4时，该物体所经过的路程为（）米米米米5、已知二次函数y ＝ax 2+bx+c(a ≠0)的图象如图2所示，给出以下结论： ① a+b+c ＜0；② a －b+c ＜0；③ b+2a ＜0；④ abc ＞0 . 其中所有正确结论的序号是（） A. ③④B. ②③C. ①④D. ①②③6、二次函数y ＝ax 2+bx+c 的图象如图3所示，若M ＝4a+2b+c ，N ＝a －b+c ，P ＝4a+2b ，则（）＞0，N ＞0，P ＞0 B. M ＞0，N ＜0，P ＞0C. M ＜0，N ＞0，P ＞0D. M ＜0，N ＞0，P ＜07、如果反比例函数y ＝k x的图象如图4所示，那么二次函数y ＝kx 2－k 2x －1的图象大致为（）8、用列表法画二次函数y ＝x 2+bx+c 的图象时先列一个表，当表中对自变量x 的值以相等间隔的值增加时，函数y 所对应的函数值依次为：20，56，110，182，274，380，506，650.其中有一个值不正确，这个不正确的值是()A. 5069、二次函数y ＝x 2的图象向上平移2个单位，得到新的图象的二次函数表达式是（） A. y ＝x 2－2 B. y ＝(x －2)2C. y ＝x 2+2 D. y ＝(x+2)210、如图6，小敏在今年的校运动会跳远比赛中跳出了满意一跳，函数h ＝－（t 的单位：s ，h 的单位：m ）可以描述他跳跃时重心高度的变化，则他起跳后到重心最高时所用的时间是（）11．函数y=ax 2+bx+c 的图象如图7所示，那么关于一元二次方程 ax 2+bx+c-3=0的根的情况是（）A ．有两个不相等的实数根B ．有两个异号的实数根C ．有两个相等的实数根D ．没有实数根 12、当k 取任意实数时，抛物线的顶点所在曲线是（） A ．y=x 2 B ．y=-x 2 C ．y=x 2(x>0) D ．y= -x 2(x>0)13．已知a<－1，点（a －1，y 1），（a ，y 2），（a+1，y 3）都在函数y=x 2的图象上，则（） A ．y 1<y 2<y 3 B ．y 1<y 3<y 2 C ．y 3<y 2<y 1 D ．y 2<y 1<y 3 14、把抛物线y=x 2+bx+c 的图象向右平移3个单位，再向下平移2个单位，所得图象的解析式是y=x 2-3x+5，则有（） A ，3=b ，7=c B ，9-=b ，15-=cC ，3=b ，3=cD ，9-=b ，21=c15、已知函数y=ax 2+bx+c 的图像如图所示，则下列关系成立且能最精确表述的是( )A ．012b a <-0，其中所有正确结论的序号是（） A ．③④ B ．②③ C ．①④ D ．①②③ 二、填空题17，形如y ＝＿＿＿ (其中a ＿＿＿，b 、c 是_______ )的函数，叫做二次函数. 18，抛物线y ＝(x –1)2–7的对称轴是直线 .19，如果将二次函数y ＝2x 2的图象沿y 轴向上平移1个单位，那么所得图象的函数解析式是 . 20，平移抛物线y ＝x 2+2x －8，使它经过原点，写出平移后抛物线的一个解析式______ .x-11yO图2图6Oyx图7 22)(54k k x y +-=yxO图4yxOA ． yxOB ． yxOC ． yxOD ． 02xy15题16题图21，若二次函数y ＝x 2－4x ＋c 的图象与x 轴没有交点，其中c 为整数，则c ＝____(只要求写出一个). 22，现有A 、B 两枚均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6）.用小莉掷A 立方体朝上的数字为x 、小明掷B 立方体朝上的数字为y 来确定点P （x ，y ），那么它们各掷一次所确定的点P 落在已知抛物线y ＝－x 2+4x 上的概率为＿＿＿. 23，已知抛物线y ＝x 2－6x +5的部分图象如图8，则抛物线的对称轴为直线x ＝，满足y ＜0的x 的取值范围是 .24,若二次函数c bx ax y ++=2的图象经过点（-2，10），且一元二次方程02=++c bx ax 的根为21-和2，则该二次函数的解析关系式为。

专题02 二次函数解答题压轴训练(原卷版)-2020-2021学年九年级数学期末复习压轴题训练

专题02 二次函数解答题压轴训练（原卷版）1．已知二次函数y1＝ax2+4ax+4a﹣1的图象是M．（1）求M关于点R（1，0）中心对称的图象N的解析式y2；（2）当2≤x≤5时，y2的最大值为，求a的值．2．如图，在平面直角坐标系中，抛物线y＝﹣x2﹣x+与直线y＝x+b交于A、B两点，其中点A在x轴上，点P是直线AB上方的抛物线上一动点（不与点A、B重合）过P作y轴的平行线交直线于点C，连接P A、PB．（1）求直线的解析式及A、B点的坐标；（2）当△APB面积最大时，求点P的坐标以及最大面积．3．已知一次函数y1＝x﹣1，二次函数y2＝x2﹣mx+4（其中m＞4）．（1）求二次函数图象的顶点坐标（用含m的代数式表示）；（2）利用函数图象解决下列问题：①若m＝5，求当y1＞0且y2≤0时，自变量x的取值范围；②如果满足y1＞0且y2≤0时自变量x的取值范围内有且只有一个整数，直接写出m的取值范围．4．在平面直角坐标系xOy中，直线y＝2x﹣3与y轴交于点A，点A与点B关于x轴对称，过点B作y轴的垂线l，直线l与直线y＝2x﹣3交于点C．（1）求点C的坐标；（2）如果抛物线y＝nx2﹣4nx+5n（n＞0）与线段BC有唯一公共点，求n的取值范围．5．若两个二次函数图象的顶点，开口方向都相同，则称这两个二次函数为“同簇二次函数”．（1）请写出两个为“同簇二次函数”的函数；（2）已知关于x的二次函数y1＝2x2﹣4mx+2m2+1，和y2＝x2+bx+c，其中y1的图象经过点A（1，1），若y1+y2与y1为“同簇二次函数”，求函数y2的表达式，并求当0≤x≤3时，y2的取值范围．6．设二次函数y1，y2的图象的顶点分别为（a，b）、（c，d），当a＝﹣2c，b＝﹣2d，且开口方向相同时，则称y1是y2的“反倍顶二次函数”．（1）请写出二次函数y＝x2+x+1的一个“反倍顶二次函数”；（2）已知关于x的二次函数y1＝x2+nx和二次函数y2＝x2﹣2nx+1，若函数y1恰是y1+y2的“反倍顶二次函数”，求n的值．7．已知抛物线y＝ax2+bx经过点A（﹣3，﹣3）和点P（t，0），且t≠0．（1）若该抛物线的对称轴经过点A，如图，请通过观察图象，指出此时y的最小值，并写出t的值；（2）若t＝﹣4，求a、b的值，并指出此时抛物线的开口方向；（3）直接写出使该抛物线开口向下的t的一个值．8．已知：抛物线C1：y＝ax2经过点（2，），抛物线C2：y＝x2．（1）求a的值；（2）如图1，直线y＝kx（k＞0）分别交第一象限内的抛物线C2，C1于M，N两点．求证：MO＝MN．9．若二次函数的解析式为y＝（x﹣m）（x﹣1）（1≤m≤2）（1）当x分别取﹣1，0，1时对应的函数值为y1，y2，y3，请比较y1，y2，y3的大小关系．（2）对于m，当x＞k时，y随x的增大而增大，求k的最小整数值．（3）若函数过（a，b）点和（a+6，b）点，求b的取值范围．10．对a，b定义一种新运算M，规定M（a，b）＝，这里等式右边是通常的四则运算，例如：M（2，3）＝＝﹣12．（1）如果M（2x，1）＝M（1，﹣1），求实数x的值；（2）若令y＝M（x+，x﹣），则y是x的函数，当自变量x在﹣1≤x≤2的范围内取值时，函数值y为整数的个数记为k，求k的值．11．已知二次函数y＝2x2+m．（1）若点（﹣2，y1）与（3，y2）在此二次函数的图象上，则y1y2（填“＞”、“＝”或“＜”）；（2）如图，此二次函数的图象经过点（0，﹣4），正方形ABCD的顶点C、D在x轴上，A、B恰好在二次函数的图象上，求图中阴影部分的面积之和．12．已知抛物线y＝ax2+2x+3（a≠0）有如下两个特点：①无论实数a怎样变化，其顶点都在某一条直线l上；②若把顶点的横坐标减少，纵坐标增大分别作为点A的横、纵坐标；把顶点的横坐标增加，纵坐标增加分别作为点B的横、纵坐标，则A，B两点也在抛物线y＝ax2+2x+3（a≠0）上．（1）求出当实数a变化时，抛物线y＝ax2+2x+3（a≠0）的顶点所在直线l的解析式；（2）请找出在直线l上但不是该抛物线顶点的所有点，并说明理由；（3）你能根据特点②的启示，对一般二次函数y＝ax2+bx+c（a≠0）提出一个猜想吗？请用数学语言把你的猜想表达出来，并给予证明．13．对非负实数x“四舍五入”到个位的值记为＜x＞，即：当n为非负整数时，如果则＜x＞＝n．如：＜0＞＝＜0.48＞＝0，＜0.64＞＝＜1.493＞＝1，＜2＞＝2，＜3.5＞＝＜4.12＞＝4，…试解决下列问题：（1）填空：①＜π＞＝（π为圆周率）；②如果＜2x﹣1＞＝3，则实数x的取值范围为；（2）①当x≥0，m为非负整数时，求证：＜x+m＞＝m+＜x＞；②举例说明＜x+y＞＝＜x＞+＜y＞不恒成立；（3）求满足＜x＞＝的所有非负实数x的值；（4）设n为常数，且为正整数，函数的自变量x在n≤x＜n+1范围内取值时，函数值y为整数的个数记为a，满足＜＞＝n的所有整数k的个数记为b．求证：a＝b＝2n．14．已知函数y＝（m+2）x2+kx+n．（1）若此函数为一次函数；①m，k，n的取值范围；②当﹣2≤x≤1时，0≤y≤3，求此函数关系式；③当﹣2≤x≤3时，求此函数的最大值和最小值（用含k，n的代数式表示）；（2）若m＝﹣1，n＝2，当﹣2≤x≤2时，此函数有最小值﹣4，求实数k的值．15．如图，抛物线y＝ax2+bx+c的图象经过点A（﹣2，0），点B（4，0），点D（2，4），与y轴交于点C，作直线BC，连接AC、CD．（1）求抛物线的函数表达式；（2）E是抛物线上的点，求满足∠ECD＝∠ACO的点E的坐标．16．已知直线y＝kx+m与抛物线y＝﹣x2+bx+c相交于A，B两点，且点A在x轴正半轴，点B在y轴上，点O为坐标原点．（1）若点A的横坐标为2，求b﹣k的值；（2）若点A的横坐标为m，抛物线顶点的纵坐标为n，点P在线段AB上，且到两坐标轴的距离相等，当OP≤时，试比较n与b+m﹣k的大小．17．如图，抛物线y＝﹣x2+bx+c经过A（﹣1，0），C（0，3）两点，它的对称轴与x轴交于点F，过点C作CE∥x 轴交抛物线于另一点E，连结EF，AC．（1）求该抛物线的表达式及点E的坐标；（2）在线段EF上任取点P，连结OP，作点F关于直线OP的对称点G，连结EG和PG，当点G恰好落到y 轴上时，求△EGP的面积．18．直线y＝﹣x+c与x轴交于点A（4，0），与y轴交于点B，抛物线y＝﹣+bx+c经过A、B两点．（1）求抛物线表达式；（2）点P为抛物线上的一个动点，过点P作垂直于x轴的直线分别交x轴和直线AB于M、N两点，若P、M、N三点中恰有一点是其他两点所连线段的中点（三点重合除外），请求出此时点P的坐标．19．已知函数y＝．（1）|k|＝2，请画出符合条件的函数图象；（2）k的值分别取k1，k2时，得到两个函数，，其中k1＜k2且k1+k2＝0，y2的图象是由y1的图象经过怎样的变换得到的；（3）在（2）的条件下，请求出当y1＜y2时，x的取值范围．20．阅读以下材料，并解决相应问题：小明在课外学习时遇到这样一个问题：定义：如果二次函数y＝a1x2+b1x+c1（a1≠0，a1、b1、c1是常数）与y＝a2x2+b2x+c2（a2≠0，a2、b2、c2是常数）满足a1+a2＝0，b1＝b2，c1+c2＝0，则这两个函数互为“旋转函数”．求函数y＝2x2﹣3x+1的旋转函数，小明是这样思考的，由函数y＝2x2﹣3x+1可知，a1＝2，b1＝﹣3，c1＝1，根据a1+a2＝0，b1＝b2，c1+c2＝0，求出a2，b2，c2就能确定这个函数的旋转函数．请思考小明的方法解决下面问题：（1）写出函数y＝x2﹣4x+3的旋转函数．（2）若函数y＝5x2+（m﹣1）x+n与y＝﹣5x2﹣nx﹣3互为旋转函数，求（m+n）2020的值．（3）已知函数y＝2（x﹣1）（x+3）的图象与x轴交于A、B两点，与y轴交于点C，点A、B、C关于原点的对称点分别是A1、B1、C1，试求证：经过点A1、B1、C1的二次函数与y＝2（x﹣1）（x+3）互为“旋转函数”．21．如图，在平面直角坐标系中，抛物线y＝ax2+bx+c的顶点坐标为（2，9），与y轴交于点A（0，5），与x轴交于点E，B．（1）求二次函数y＝ax2+bx+c的解析式；（2）过点A作AC平行于x轴，交抛物线于点C，点P为抛物线上的一点（点P在AC上方），作PD平行于y 轴交AB于点D，问当点P在何位置时，四边形APCD的面积最大？并求出最大面积．22．设抛物线y＝的图象与x轴只有一个交点．（1）求a的值；（2）求a18+323a﹣6的值．23．已知：关于x的方程mx2﹣3（m﹣1）x+2m﹣3＝0．（1）求证：m取任何实数量，方程总有实数根；（2）若二次函数y1＝mx2﹣3（m﹣1）x+2m﹣3的图象关于y轴对称；①求二次函数y1的解析式；②已知一次函数y2＝2x﹣2，证明：在实数范围内，对于x的同一个值，这两个函数所对应的函数值y1≥y2均成立；（3）在（2）条件下，若二次函数y3＝ax2+bx+c的图象经过点（﹣5，0），且在实数范围内，对于x的同一个值，这三个函数所对应的函数值y1≥y3≥y2均成立，求二次函数y3＝ax2+bx+c的解析式．24．已知函数y＝x2+（b﹣1）x+c（b，c为常数），这个函数的图象与x轴交于两个不同的点A（x1，0）和B（x2，0）．若x1，x2满足x2﹣x1＞1；（1）求证：b2＞2（b+2c）；（2）若t＜x1，试比较t2+bt+c与x1的大小，并加以证明．25．如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（﹣1，0）和B（3，0），与y轴交于点C，C在y轴的正半轴上，S△ABC＝8；（1）求抛物线的解析式；（2）设点P是抛物线的对称轴上一动点，当△P AC的周长最小时，求点P的坐标；（3）若抛物线的顶点为D，直线CD交x轴于E．则x轴上方的抛物线上是否存在点Q，使S△QBE＝15？若存在，求出点Q的坐标，若不存在，请说明理由．26．如图，抛物线y＝﹣x2+bx+c与x轴相交于A，B两点（点A位于点B的左侧），与y轴相交于点C，M是抛物线的顶点，直线x＝1是抛物线的对称轴，且点C的坐标为（0，3）．（1）求抛物线的解析式；（2）已知P为线段MB上一个动点，过点P作PD⊥x轴于点D．若PD＝m，△PCD的面积为S．求S与m之间的函数关系式，并写出自变量m的取值范围；（3）在（2）的条件下，在线段MB上是否存在点P，使△PCD为等腰三角形？如果存在，请写出点P的坐标；如果不存在，请说明理由．27．如图，抛物线y＝x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，过点A的直线l交抛物线于点C（2，m）．（1）求抛物线的解析式．（2）点P是线段AC上一个动点，过点P作x轴的垂线交抛物线于点E，求线段PE最大时点P的坐标．（3）点F是抛物线上的动点，在x轴上是否存在点D，使得以点A，C，D，F为顶点的四边形是平行四边形？如果存在，请直接写出所有满足条件的点D的坐标；如果不存在，请说明理由．28．已知抛物线y＝﹣x2+bx+c经过点A（2，0），B（0，2），与x轴的另一个交点为C．（1）求出此抛物线的表达式及点C坐标；（2）如图1，AB的中点记为D，∠MDN＝30°，将∠MDN绕点D在AB的左侧旋转，DM与射线BO交于点E，DN与射线AO交于点F．设BE＝m，AF＝n（m＞0，n＞0），求m关于n的函数关系式．（3）当∠MDN的边经过点C时，求m，n的值（直接写出结果）．29．如图（1），抛物线y＝﹣x2+bx+c与x轴相交于点A、B，与y轴相交于点C，已知A、C两点的坐标为A（﹣1，0），C（0，3）．点P是抛物线上第一象限内一个动点．（1）求抛物线的解析式，并求出B的坐标；（2）如图1，抛物线上是否存在点P，使得△OBP≌△OCP，若存在，求点P的坐标；（3）如图2，y轴上有一点D（0，1），连结DP交BC于点H，若H恰好平分DP，求点P的坐标；（4）如图3，连结AP交BC于点M，以AM为直径作圆交AB、BC于点E、F，若E，F关于直线AP轴对称，求点E的坐标．30．如图1：在平面直角坐标系中，O为坐标原点，抛物线y＝ax2+bx+2经过A（﹣1，0），C（4，0），与y轴交于点B．（1）求抛物线的解析式；（2）如图2，点P为抛物线第四象限上一点，AP交y轴于Q，设点P的横坐标为t，求线段BQ的长d与t的函数关系（不要求写出自变量的取值范围）；（3）如图3，在（2）的条件下，D为抛物线第一象限上的一点，过D作y轴的平行线，分别交BP、AP于M、N，过P作PH⊥直线DM于H，连接AD交BP于E，若MN＝NH，∠DEP+∠ABO＝90°，求点D的坐标．31．如图，抛物线y＝x2+bx+c与x轴交于A、B两点（点A在B左边），与y轴交于点C．（1）若A（﹣1，0），B（3，0）两点，求该抛物线的解析式；（2）在（1）中位于第四象限内的抛物线上是否存在点P，使得△PBC的面积最大？若存在，求出点P的坐标及△PBC的面积最大值；若没有，请说明理由；（3）直线y＝1与抛物线y＝x2+bx+c交于抛物线对称轴右侧的点为点D，点E与点D关于x轴对称．试判断直线DB与直线AE的位置关系，并证明你的结论．32．如图，△AOB的三个顶点A、O、B分别落在抛物线C1：y＝x2+x上，点A的坐标为（﹣4，m），点B的坐标为（n，﹣2）．（点A在点B的左侧）（1）则m＝，n＝．（2）将△AOB绕点O逆时针旋转90°得到△A'OB'，抛物线C2：y＝ax2+bx+4经过A'、B'两点，延长OB'交抛物线C2于点C，连接A'C．设△OA'C的外接圆为⊙M．①求圆心M的坐标；②试直接写出△OA'C的外接圆⊙M与抛物线C2的交点坐标（A'、C除外）．。

二次函数复习2

二次函数复习
（2）
三、求抛物线解析式常用的三种方法
1、已知抛物线上的三点，通常设解析式为 y=ax2+bx+c(a≠0) 一般式 ________________ 2、已知抛物线顶点坐标（m, k），通常设 y=a(x-m)2+k(a≠0) 抛物线解析式为_______________
顶点式
②a – b + c>0 ③abc>0 ④
-1 O
m
1
x
b=2a。其中正确的结论的
个数是（ D ） A 1个 B 2个 C 3个 D 4个
13、抛物线y=ax2+bx+c如图所示，试确定a、b、c、b2-4ac的符号： y
o
x
14、抛物线y=ax2+bx+c如图所示，试确定a、b、c、 b2-4ac的符号：
＞＜ b___2a, 2a-b_____0, 2a+b_______0 ＜＞ b2-4ac_____0 ＞＜ a+b+c_____0, a-b+c____0 ＞ 4a-2b+c_____0
-2 -1
0 1
12、已知二次函数
y=ax2+bx+c的图象如图所
y
n
示,下列结论①a+ b + c<0
3、已知抛物线与x 轴的两个交点(x1,0)、 y=a(x-x1)(x-x2) (x2,0),通常设解析式为_____________ (a≠0)
交点式或两根式
1、写出一个开口向下，顶点坐标是（—2， 3）的函数解析式_________________。 2、已知二次函数的图像经过（3,0）、（2，-3）点，对称轴x=l，求这个函数的解析式． 3、已知二次函数的图像经过点（0，－4），且当x = 2，有最大值—2。求该二次函数的关系式：

《二次函数》全章复习与巩固—巩固练习(提高)

《二次函数》全章复习与巩固—巩固练习（提高）【巩固练习】一、选择题1．已知抛物线2:310C y x x =+-，将抛物线C 平移得到抛物线C '．若两条抛物线C 、C '关于直线x ＝1对称．则下列平移方法中，正确的是（）． A ．将抛物线C 向右平移52个单位 B ．将抛物线C 向右平移3个单位 C ．将抛的线C 向右平移5个单位 D ．将抛物线C 向右平移6个单位2．已知二次函数2y ax bx c =++的图象如图所示，则下列5个代数式：ac ，a+b+c ，4a-2b+c ，2a+b ，2a-b 中，其值大于0的个数为( )．A ．2B ．3C ．4D ．53．二次函数2y ax bx c =++的图象如图所示，则下列关系式不正确的是( )． A ．0a 第2题第3题4．在平面直角坐标系中，将抛物线223y x x =++绕着它与y 轴的交点旋转180°，所得抛物线的解析式是( )A ．2(1)2y x =-++ B ．2(1)4y x =--+ C ．2(1)2y x =--+ D ．2(1)4y x =-++ 5．二次函数y=ax 2+bx+c （a ≠0）的大致图象如图，关于该二次函数，下列说法错误的是（）A ．函数有最小值B ．对称轴是直线x=12 C ．当x ＜12，y 随x 的增大而减小 D ．当-1＜x ＜2时，y ＞06．（2016•梧州）如图所示，抛物线y=ax 2+bx +c （a ≠0）与x 轴交于点A （﹣2，0）、B （1，0），直线x=﹣0.5与此抛物线交于点C ，与x 轴交于点M ，在直线上取点D ，使MD=MC ，连接AC 、BC 、AD 、BD ，某同学根据图象写出下列结论： ①a ﹣b=0；②当﹣2＜x ＜1时，y ＞0； ③四边形ACBD 是菱形； ④9a ﹣3b +c ＞0你认为其中正确的是（）A ．②③④B ．①②④C ．①③④D ．①②③7．已知一次函数y ax b =+的图象过点(-2，1)，则关于抛物线23y ax bx =-+的三条叙述： ①过定点(2，1)；②对称轴可以是直线x ＝l ；③当a ＜0时，其顶点的纵坐标的最小值为3．其中所有正确叙述的有( )．A ．0个B ．1个C ．2个D ．3个8．已知二次函数24y x x a =-+，下列说法错误的是( )． A ．当x ＜1时，y 随x 的增大而减小 B ．若图象与x 轴有交点，则a ≤4C ．当a ＝3时，不等式240x x a -+>的解集是1＜x ＜3D ．若将图象向上平移1个单位，再向左平移3个单位后过点(1，-2)，则a ＝-3二、填空题9．由抛物线y ＝x 2先向左平移2个单位，再向下平移3个单位得到的抛物线的解析式为 . 10．已知一元二次方程230x bx +-=的一根为-3．在二次函数y=x 2+bx-3的图象上有三点14,5y ⎛⎫-⎪⎝⎭、25,4y ⎛⎫- ⎪⎝⎭、31,6y ⎛⎫⎪⎝⎭，y 1、y 2、y 3、的大小关系是 . 11．如图，一段抛物线y=-x （x-1）（0≤x ≤1）记为m 1，它与x 轴交点为O 、A 1，顶点为P 1；将m 1绕点A 1旋转180°得m 2，交x 轴于点A 2，顶点为P 2；将m 2绕点A 2旋转180°得m 3，交x 轴于点A 3，顶点为P 3，…，如此进行下去，直至得m 10，顶点为P 10，则P 10的坐标为( ).12．在平面直角坐标系中，如果抛物线y ＝3x 2不动，而把x 轴、y 轴分别向上，向右平移3个单位，那么在新坐标系下，此抛物线的解析式是 . 13．已知二次函数2y ax bx c =++(a ≠0)的图象如图所示，则下列结论：①a 、b 同号；②当x ＝1和x ＝3时，函数值相等；③4a+b ＝0；④当y ＝-2时，x 的值只能取0，其中正确的有 .（填序号）14．已知抛物线的顶点为125,24⎛⎫-⎪⎝⎭，与x 轴交于A 、B 两点，在x 轴下方与x 轴距离为4的点M 在抛物线上，且10AMB S =△，则点M 的坐标为．15．（2015•繁昌县一模）如图，二次函数y=ax 2+bx+c （a ≠0）的图象经过点（1，2）且与x 轴交点的横坐标分别为x 1，x 2，其中﹣1＜x 1＜0，1＜x 2＜2．下列结论：①4a+2b+c ＜0；②a ＜﹣1；③b 2+8a ＞4ac ；④2a ﹣b ＜0．其中结论正确的有．（把所有正确答案的序号都填写在横线上）16．如图所示，抛物线212y x =-+向右平移1个单位得到抛物线y 2．回答下列问题：(1)抛物线y 2的顶点坐标________．(2)阴影部分的面积S ＝________．(3)若再将抛物线y 2绕原点O 旋转180°得到抛物线y 3，则抛物线y 3的开口方向________，顶点坐标________．三、解答题17．某商品的进价为每件40元，售价为每件50元，每个月可卖出210件；如果每件商品的售价每上涨l元，则每个月少卖10件(每件售价不能高于65元)．设每件商品的售价上涨x元(x为正整数)，每个月的销售利润为y元．(1)求y与x的函数关系式并直接写出自变量x的取值范围；(2)每件商品的售价定为多少元时，每个月可获得最大利润?最大的月利润是多少元?(3)每件商品的售价定为多少元时，每个月的利润恰为2200元?根据以上结论，请你直接写出售价在什么范围时，每个月的利润不低于2200元?18．（2015•黔东南州）如图，已知二次函数y1=﹣x2+x+c的图象与x轴的一个交点为A（4，0），与y轴的交点为B，过A、B的直线为y2=kx+b．（1）求二次函数y1的解析式及点B的坐标；（2）由图象写出满足y1＜y2的自变量x的取值范围；（3）在两坐标轴上是否存在点P，使得△ABP是以AB为底边的等腰三角形？若存在，求出P的坐标；若不存在，说明理由．19. 在平面直角坐标系中，已知抛物线经过A(-4，0)、B(0，-4)、C(2，0)三点．(1)求抛物线的解析式；(2)若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S．求S关于m的函数关系式，并求出S的最大值；(3)若点P是抛物线上的动点，点Q是直线y＝-x上的动点，判断有几个位置能够使得点P、Q、B、O 为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．20. （2016•菏泽）在平面直角坐标系xOy中，抛物线y=ax2+bx+2过B（﹣2，6），C（2，2）两点．（1）试求抛物线的解析式；（2）记抛物线顶点为D，求△BCD的面积；（3）若直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC（包括端点B、C）部分有两个交点，求b的取值范围．【答案与解析】一、选择题 1.【答案】C ；【解析】22349:31024C y x x x ⎛⎫=+-=+- ⎪⎝⎭，∴ 其顶点坐标为349,24⎛⎫-- ⎪⎝⎭，设C '顶点坐标为049,4x ⎛⎫- ⎪⎝⎭，由题意得03212x ⎛⎫+- ⎪⎝⎭=， ∴ 072x =，∴ C '的解析式为274924y x ⎛⎫=-- ⎪⎝⎭．由234924y x ⎛⎫=+= ⎪⎝⎭到274924y x ⎛⎫=-= ⎪⎝⎭需向右平移5个单位，因此选C ．2.【答案】A ；【解析】由图象知，a ＜0，c ＜0，012ba<-<， ∴ b ＞0，ac ＞0，∴ 2a-b ＜0．又对称轴12ba-<，即2a+b ＜0．当x ＝1时，a+b+c ＞0；当x ＝-2时，4a-2b+c ＜0．综上知选A ． 3.【答案】C ；【解析】由抛物线开口向下知a ＜0，由图象知c ＞0，02ba-<，b ＜0，即abc ＞0，又抛物线与x 轴有两个交点，所以240b ac ->．4.【答案】B ；【解析】抛物线2223(1)2y x x x =++=++，其顶点(-1，2)绕点(0，3)旋转180°后坐标为(1，4)，开口向下．∴ 旋转后的抛物线解析式为2(1)4y x =--+．5.【答案】D ；6.【答案】C ；【解析】①∵抛物线的开口方向向上，∴a ＞0，∵对称轴为x==2＞0，又∵a ＞0，∴b ＜0，即a ，b 异号，①错误；②∵x=1和x=3关于x=2对称，∴当x=1和x=3时，函数值相等，②正确； ③∵x==2，∴b=﹣4a ，即4a+b=0，③正确；④∵y=﹣2正好为抛物线顶点坐标的纵坐标， ∴当y=﹣2时，x 的值只能取2，④正确； ⑤∵对称轴为x=2，∴x=﹣1和x=5关于x=2对称，故当﹣1＜x ＜5时，y ＜0．⑤正确. ∴②、③、④、⑤正确．故选C ． 7.【答案】D ．【解析】①∵抛物线y=ax 2+bx +c （a ≠0）与x 轴交于点A （﹣2，0）、B （1，0）， ∴该抛物线的对称轴为x=﹣=﹣0.5，∴a=b ，a ﹣b=0，①正确；②∵抛物线开口向下，且抛物线与x 轴交于点A （﹣2，0）、B （1，0）， ∴当﹣2＜x ＜1时，y ＞0，②正确； ③∵点A 、B 关于x=0.5对称， ∴AM=BM ，又∵MC=MD ，且CD ⊥AB ，∴四边形ACBD 是菱形，③正确； ④当x=﹣3时，y ＜0，即y=9a ﹣3b +c ＜0，④错误．综上可知：正确的结论为①②③．故选D ． 8．【答案】C ；【解析】二次函数24y x x a =-+的对称轴为x ＝2，由于a ＝1＞0，当x ＜2时，y 随x 增大而减小，因此A 是正确的；若图象与x 轴有交点，则△＝16-4a ≥0，∴ a ≤4．当a ＝3时，不等式为x 2-4x+3＞0，此时二次函数243y x x =-+，令y ＝0，得x 1＝1，x 2＝3，当x ＜1或x ＞3时，y ＞0，所以不等式2430x x -+>的解集为x ＜1或x ＞3．抛物线平移后得2(3)4(3)1y x x a =+-+++，即222y x x a =++-，将(1，-2)代入解得3a =-．二、填空题9．【答案】y ＝(x+2)2-3；【解析】y ＝x 2的顶点为(0，0)，y ＝(x+2)2+3的顶点为(-2，-3)，将(0，0)先向左平移2个单位，再向下平移3个单位可得(-2，-3)，即将抛物线y ＝x 2先向左平移2个单位，再向下平移3个单位得到抛物线y ＝(x+2)2-3．10．【答案】y 1＜y 2＜y 3.【解析】设x 2+bx-3＝0的另一根为x 2，则233cx a-==-，∴ x 2＝1， ∴ 抛物线的对称轴为3112x -+==-，开口向上时，到对称轴的距离越大函数值越大，所以y 1＜y 3，y 1＜y 2＜y 3，也可求出b ＝2，分别求出y 1，y 2，y 3的值再比较大小．11．【答案】（9.5，-0.25）；【解析】解：y=-x （x-1）（0≤x ≤1），OA 1=A 1A 2=1，P 2P 4=P 1P 3=2， P 2（2.5，-0.25）P 10的横坐标是1.5+2×[（10-2）÷2]=9.5， p 10的纵坐标是-0.25，故答案为（9.5，-0.25）．12．【答案】y ＝3(x+3)2-3；【解析】抛物线y ＝3x 2的顶点为(0，0)，将x 、y 轴分别向上，向右平移3个单位，逆向思考，即将(0，0)向下，向左平移3个单位，可得顶点为(-3，-3)，因此，新坐标系下抛物线的解析式是y ＝3(x+3)2-3．13．【答案】②③；【解析】由图象知，抛物线与x 轴交于点(-1，0)，(5，0)，于是可确定抛物线的对称轴为1522x -+==，则22ba-=，∴ 4a+b ＝0，故③是正确的；又∵ 抛物线开口向上，∴ a ＞0，b ＝-4a ＜0， ∴ ①是错误的；又∵1322+=，即x ＝1和x ＝3关于对称轴x ＝2对称，其函数值相等， ∴ ②是正确的；根据抛物线的对称性知，当y ＝-2时，x 的值可取0或4． ∴ ④是错误的．14．【答案】(2，-4)或(-1，-4)；【解析】∵ 1|||4|102AMB S AB =-=△，∴ |AB|＝5．又∵ 抛物线的对称轴为直线12x =，∴ A 、B 两点的坐标为(-2，0)和(3，0)．设抛物线的解析式为2y ax bx c =++，则4209301125424a b c a b c a b c ⎧⎪-+=⎪++=⎨⎪⎪++=-⎩ 解得1,1,6.a b c =⎧⎪=-⎨⎪=-⎩∴ 抛物线的解析式为26y x x =--．当y ＝-4时，246x x -=--，∴ 220x x --=，∴ x 1＝-2，x 2＝-1． ∴ M 点坐标为(2，-4)或(-1，-4)．15．【答案】①②③④；【解析】由二次函数的图象可得：当x=2时y ＜0，则有4a+2b+c ＜0（1），故①正确；∵二次函数的图象经过点（1，2），∴a+b+c=2（2），由二次函数的图象可得：当x=﹣1时，y＜0，则有a﹣b+c＜0（3），把（2）代入（1）得到2+3a+b＜0，则有a＜，把（2）代入（3）得到2﹣2b＜0，则有b＞1，则a＜﹣1，故②正确；由二次函数的图象中顶点的位置，可得：＞2（4），由抛物线开口向下，可得：a＜0，则由（4）可得4ac﹣b2＜8a，即b2+8a＞4ac，故③正确；由抛物线的对称轴的位置，可得＞0，则b＞0，又由a＜0，则有2a﹣b＜0，故④正确；故答案为：①②③④．16．【答案】 (1)(1，2)； (2)2； (3)向上； (-1，-2)；【解析】抛物线212y x=-+向右平移1个单位，则顶点由(0，2)移到(1，2)．利用割补法，阴影部分面积恰好为两个正方形的面积．若将抛物线y2绕原点O旋转180°，则抛物线y2的顶点与点(1，2)关于原点对称．三、解答题17.【答案与解析】(1)y＝(210-10x)(50+x-40)＝-10x2+110x+2100(0＜x≤15且x为整数)．(2)y＝-10(x-5.5)2+2402.5，∵ a＝-10＜0，∴当x＝5.5时，y有最大值2402.5．∵ 0＜x≤15，且x为整数．当x＝5时，50+x＝55，y＝-10(5-5.5)2+2402.5＝2400(元)；当x＝6时，50+x＝56，可求出y＝2400(元)．∴当售价定为每件55元或56元，每月利润最大，最大利润是2400元．(3)当y＝2200时，-10x2+110x+2100＝2200，解得x1＝1，x2＝10．∴当x＝1时，50+x＝51，当x＝10时，50+x＝60．∴当售价定为每件51元或60元时，每个月的利润为2200元．当售价不低于51元且不高于60元且为整数时，每个月的利润不低于2200元．18.【答案与解析】解：（1）将A点坐标代入y1，得﹣16+13+c=0．解得c=3，二次函数y1的解析式为y=﹣x2+x+3，B点坐标为（0，3）；（2）由图象得直线在抛物线上方的部分，是x＜0或x＞4，∴x＜0或x＞4时，y1＜y2；（3）直线AB的解析式为y=﹣x+3，AB 的中点为（2，） AB 的垂直平分线为y=x ﹣ 当x=0时，y=﹣，P 1（0，﹣），当y=0时，x=，P 2（，0），综上所述：P 1（0，﹣），P 2（，0），使得△ABP 是以AB 为底边的等腰三角形． 19.【答案与解析】(1)设抛物线的解析式为2y ax bx c =++(a ≠0)．∵ 抛物线经过点A(-4，0)、B(0，-4)、C(2，0)，∴ 1640,4,420,a b c c a b c -+=⎧⎪=-⎨⎪++=⎩ 解得1,21,4.a b c ⎧=⎪⎪=⎨⎪=-⎪⎩∴ 抛物线的解析式为2142y x x =+-． (2)过点M 作MD ⊥x 轴于点D ．设M 点的坐标为(m ，n)，则AD ＝m+4， MD n =-，2142n m m =+-． ∴ AMD ABO DMBO S S S S =+-△△梯形111(4)()(4)()44222m n n m =+-+-+--⨯⨯ 228n m =---2124282m m m ⎛⎫=-+---⎪⎝⎭24(40)m m m =---<<． ∴ 当2m =-时，4S =最大值． (3)满足题意的Q 点的坐标有四个，分别是：(-4，4)、(4，-4)、(225,225)-+-、(225,225)--+．20.【答案与解析】解：（1）由题意解得，∴抛物线解析式为y=x2﹣x+2．（2）∵y=x2﹣x+2=（x﹣1）2+．∴顶点坐标（1，），∵直线BC为y=﹣x+4，∴对称轴与BC的交点H（1，3），∴S△BDC=S△BDH+S△DHC=•3+•1=3．（3）由消去y得到x2﹣x+4﹣2b=0，当△=0时，直线与抛物线相切，1﹣4（4﹣2b）=0，∴b=，当直线y=﹣x+b经过点C时，b=3，当直线y=﹣x+b经过点B时，b=5，∵直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC（包括端点B、C）部分有两个交点，∴＜b≤3．。

人教版九年级上册数学试题：第22章二次函数复习题含答案

二次函数复习题一、选择题1. 二次函数y=ax 2+bx+c 的值永远为负值的条件是（） A. a ﹥0，b 2－4ac ﹤0 B. a ﹤0，b 2－4ac ﹥0 C. a ﹥0，b 2－4ac ﹥0 D .a ﹤0，b 2－4ac ﹤02.抛物线y=x 2+（2m －1）x+m 2与x 轴有两个交点，则m 的取值范围是（） A .m﹥41 B. m ﹥－41 C. m ﹤41 D .m ﹤－41 3.一次函数y=2x －3与二次函数y=x 2－2x+1的图象有（） A. 一个交点 B. 两个交点 C .无数个交点 D. 无交点 4.二次函数y=ax 2+bx+c 的最大值是零，那么代数式ab ac a 442-+的化简结果是（） A. a B. －a C. 1 D .05.把一个小球以20m/s 的速度竖直向上弹出，它在空中的高度h （m ）与时间t （s ）满足关系：h=20t －5t 2.当h=20时，小球的运动时间为（） A .20s B. 2s C. （22+2）s D .（22－2）s 6. 苹果熟了，从树上落下所经过的路线s 与下落的时间t 满足s=221gt （g 是不为0的常数），则s 与t 的函数图象大致是（）7.如图，有一抛物线形拱桥，当水线在AB 位置时，拱桥离水面2m ，水面宽4m ，水线下降1m 后，水面宽为（） A. 2m B. 3m C. 6m D. 26m二、填空题8.汽车刹车距离s （m ）与速度v （km/h ）之间的函数关系是s=21001v ，在一辆车速为100km/h 的汽车前方80m 处发现停着一辆故障车，此时刹车有危险.（填“会”或“不会”） 9.如图，一男生推铅球，铅球行进高度y （m ）与水平距离x （m ）之间的关系是(7题图)（9题图）35321212++-=xxy，则铅球推出距离为 m．三、解答题10. 已知二次函数y=ax2－2的图象经过点(1,－1).求这个二次函数的解析式,并判断该函数图象与x轴的交点的个数.11.一养鸡专业户计划用116m长的竹篱笆围成如图20－5－6所示的三间长方形鸡舍，门MN 宽2m，门PQ和RS的宽都是1m，怎样设计才能使围成的鸡舍面积最大？12.如图为某市立交桥横断面的示意图，以地面水平线为x轴，横断面的对称轴为y轴建立坐标系.已知横断面为抛物线形状，跨度为40m（即AB=40m），最高处离地面10m（即CD=10m）.问：一辆宽5m，高8m的大货车能否通过该立交桥下面？13. 已知抛物线y=x2－2x－8.（1）求证：该抛物线与x轴一定有两个交点.（2）若该抛物线与x轴的两个交点分别为A，B，且它的顶点为P，求△ABP的面积.14．有一个抛物线形的拱形桥洞，桥洞离水面的最大高度为 4m，跨度为 10m，如图所示，把它的图形放在直角坐标系中。

初三数学二次函数知识点总结及经典习题含答案 (2)

初三数学二次函数知识点总结一、二次函数概念：1．二次函数的概念：一般地，形如2y ax bx c =++（a b c ，，是常数，0a ≠）的函数，叫做二次函数。

这里需要强调：和一元二次方程类似，二次项系数0a ≠，而b c ，可以为零．二次函数的定义域是全体实数．2. 二次函数2y ax bx c =++的结构特征：⑴ 等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2． ⑵ a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项．二、二次函数的基本形式1. 二次函数基本形式：2y ax =的性质： a 的绝对值越大，抛物线的开口越小。

2. 2y ax c =+的性质：上加下减。

a 的符号开口方向顶点坐标对称轴性质0a >向上()00，y 轴0x >时，y 随x 的增大而增大；0x <时，y 随x 的增大而减小；0x =时，y 有最小值0．0a <向下()00，y 轴0x >时，y 随x 的增大而减小；0x <时，y 随x 的增大而增大；0x =时，y 有最大值0．a 的符号开口方向顶点坐标对称轴性质0a >向上()0c ，y 轴 0x >时，y 随x 的增大而增大；0x <时，y 随3. ()2y a x h =-的性质：左加右减。

4. ()2y a x h k =-+的性质：x 的增大而减小；0x =时，y 有最小值c ．0a <向下()0c ，y 轴0x >时，y 随x 的增大而减小；0x <时，y 随x 的增大而增大；0x =时，y 有最大值c ．a 的符号开口方向顶点坐标对称轴性质0a > 向上()0h ，X=hx h >时，y 随x 的增大而增大；x h <时，y 随x 的增大而减小；x h =时，y 有最小值0．0a <向下()0h ，X=hx h >时，y 随x 的增大而减小；x h <时，y 随x 的增大而增大；x h =时，y 有最大值0．a 的符号开口方向顶点坐标对称轴性质0a >向上()h k ，X=hx h >时，y 随x 的增大而增大；x h <时，y 随x 的增大而减小；x h =时，y 有最小值k ．0a < 向下()h k ，X=hx h >时，y 随x 的增大而减小；x h <时，y 随x 的增大而增大；x h =时，y 有最大值k ．三、二次函数图象的平移1. 平移步骤：⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，； ⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：向右(h >0)【或左(h <0)】平移 |k|个单位向上(k >0)【或下(k <0)】平移|k |个单位向右(h >0)【或左(h <0)】平移|k|个单位向右(h >0)【或左(h <0)】平移|k|个单位向上(k >0)【或下(k <0)】平移|k |个单位向上(k >0)【或向下(k <0)】平移|k |个单位y=a (x-h )2+ky=a (x-h )2y=ax 2+ky=ax 22. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”．概括成八个字“左加右减，上加下减”．四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭，其中2424b ac b h k a a -=-=，．六、二次函数2y ax bx c =++的性质1. 当0a >时，抛物线开口向上，对称轴为2bx a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2bx a<-时，y 随x 的增大而减小；当2bx a>-时，y 随x 的增大而增大；当2bx a=-时，y 有最小值244ac b a -．2. 当0a <时，抛物线开口向下，对称轴为2b x a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2bx a <-时，y 随x 的增大而增大；当2b x a >-时，y 随x 的增大而减小；当2bx a=-时，y 有最大值244ac b a -．七、二次函数解析式的表示方法1. 一般式：2y ax bx c =++（a ，b ，c 为常数，0a ≠）；2. 顶点式：2()y a x h k =-+（a ，h ，k 为常数，0a ≠）；3. 两根式（交点式）：12()()y a x x x x =--（0a ≠，1x ，2x 是抛物线与x 轴两交点的横坐标）. 注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x 轴有交点，即240b ac -≥时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化.八、二次函数的图象与各项系数之间的关系1. 二次项系数a⑴ 当0a >时，抛物线开口向上，a 的值越大，开口越小，反之a 的值越小，开口越大； ⑵ 当0a <时，抛物线开口向下，a 的值越小，开口越小，反之a 的值越大，开口越大． 2. 一次项系数b在二次项系数a 确定的前提下，b 决定了抛物线的对称轴．（同左异右 b 为0对称轴为y 轴） 3. 常数项c⑴ 当0c >时，抛物线与y 轴的交点在x 轴上方，即抛物线与y 轴交点的纵坐标为正； ⑵ 当0c =时，抛物线与y 轴的交点为坐标原点，即抛物线与y 轴交点的纵坐标为0； ⑶ 当0c <时，抛物线与y 轴的交点在x 轴下方，即抛物线与y 轴交点的纵坐标为负．总结起来，c 决定了抛物线与y 轴交点的位置．十、二次函数与一元二次方程：1. 二次函数与一元二次方程的关系（二次函数与x 轴交点情况）：一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况. 图象与x 轴的交点个数：① 当240b ac ∆=->时，图象与x 轴交于两点()()1200A x B x ，，，12()x x ≠，其中的12x x ，是一元二次方程()200ax bx c a ++=≠的两根．.② 当0∆=时，图象与x 轴只有一个交点； ③ 当0∆<时，图象与x 轴没有交点.1' 当0a >时，图象落在x 轴的上方，无论x 为任何实数，都有0y >； 2' 当0a <时，图象落在x 轴的下方，无论x 为任何实数，都有0y <．2. 抛物线2y ax bx c =++的图象与y 轴一定相交，交点坐标为(0，)c ；二次函数对应练习试题一、选择题1. 二次函数247y x x =--的顶点坐标是( )A.(2,－11)B.（－2，7）C.（2，11）D. （2，－3） 2. 把抛物线22y x =-向上平移1个单位，得到的抛物线是（）A. 22(1)y x =-+ B. 22(1)y x =-- C. 221y x =-+ D. 221y x =--3.函数2y kx k =-和(0)ky k x=≠在同一直角坐标系中图象可能是图中的( )4.已知二次函数2(0)y ax bx c a =++≠的图象如图所示,则下列结论: ①a,b 同号;②当1x =和3x =时,函数值相等;③40a b +=④当2y =-时, x 的值只能取0.其中正确的个数是( )A.1个B.2个C. 3个D. 4个5.已知二次函数2(0)y ax bx c a =++≠的顶点坐标（-1，-3.2）及部分图象(如图),由图象可知关于x 的一元二次方程20ax bx c ++=的两个根分别是121.3x x ==和（）Ａ．－１.３ B.-2.3 C.-0.3 D.-3.36. 已知二次函数2y ax bx c =++的图象如图所示，则点(,)ac bc 在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 7.方程222x x x-=的正根的个数为（） A.0个 B.1个 C.2个. 3 个8.已知抛物线过点A(2,0),B(-1,0),与y 轴交于点C,且OC=2.则这条抛物线的解析式为A. 22y x x =-- B. 22y x x =-++C. 22y x x =--或22y x x =-++ D. 22y x x =---或22y x x =++二、填空题9．二次函数23y x bx =++的对称轴是2x =，则b =_______。

2022年九年级数学下册专项复习2二次函数习题课件新版新人教版

– C.y2＜y3＜y1
D.y1＜y2＜y3
6.(2018·连云港)已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(Ds) 满–足A.点函火数后9表s和达点式火后h1＝3 s的－升t空2＋高度24相t同＋1，则下列说–法B.点中火正后2确4 s的火箭是落于(地面 )
– C.点火后10 s的升空高度为139 m
– D.火箭升空的最大高度为145 m
7.(2019·温州)已知二次函数y＝x2－4x
＋2，关于该函数在D－1≤x≤3的取值范围
内–，A.有下最列大值说－法1，正有最确小值的－是2 (
)
– B.有最大值0，有最小值－1
– C.有最大值7，有最小值－1
– D.有最大值7，有最小值－2
8.(2018·德州)如图，函数y＝ax2－2x＋ 1和y＝ax－a(a是常数，B 且a≠0)在同一平面直角坐标系中的图象可能是( )
1 4
，∴该抛物线
4
(2)一辆货车高4 m，宽4 m，能否从该隧道内通过？为
能.理由如下：当x＝2时，y＝－ 1 ×(2－4)2＋6＝5＞4，
什么？
4
∴该货车能通过隧道.
17.(2019·辽阳)我市某化工材料经销商
购进一种化工材料若干千克，成本价为每
千克30元，物价部门规定其销售单价不低
于(成1)求本y关价于且x的不函高数解于析成式，本并价写的出自2倍变量，x的经取试值销范围
2
16.一座隧道的截面由抛物线和矩形构成
，矩形的长为8 m，宽为2 m，隧道最高
点(解1P：)位(求1)抛设于抛物物A线线B的的的解解析中析式式央为y；＝且a(x距－h)离2＋k地.由面题意6可知m，建立如图所示的坐标系. 顶点坐标为(4，6)，∴y＝a(x－4)2＋6.∵抛物线经过点

二次函数专项复习经典试题集锦(含答案)

二次函数专项复习经典试题集锦（含答案）一、选择题：1. 抛物线3)2(2+-=x y 的对称轴是（） A. 直线3-=xB. 直线3=xC. 直线2-=xD. 直线2=x2. 二次函数c bx ax y ++=2的图象如右图，则点),(acb M 在（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. 已知二次函数c bx ax y ++=2，且0<a ，0>+-c b a ，则一定有（） A. 042>-ac bB. 042=-ac bC. 042<-ac bD. ac b 42-≤04. 把抛物线c bx x y ++=2向右平移3个单位，再向下平移2个单位，所得图象的解析式是532+-=x x y ，则有（） A. 3=b ，7=c B. 9-=b ，15-=c C. 3=b ，3=cD. 9-=b ，21=c5. 下面所示各图是在同一直角坐标系内，二次函数c x c a ax y +++=)(2与一次函数c ax y +=的大致图象，有且只有一个是正确的，正确的是（）D6. 抛物线322+-=x x y 的对称轴是直线（） A. 2-=xB. 2=xC. 1-=xD. 1=x7. 二次函数2)1(2+-=x y 的最小值是（） A. 2-B. 2C. 1-D. 18. 二次函数c bx ax y ++=2的图象如图所示，若c b a M ++=24c b a N +-=，b a P -=4，则（） A. 0>M ，0>N ，0>P B. 0<M ，0>N ，0>P C. 0>M ，0<N ，0>P D. 0<M ，0>N ，0<P 二、填空题：9. 将二次函数322+-=x x y 配方成k h x y +-=2)(的形式，则y =______________________. 10. 已知抛物线c bx ax y ++=2与x 轴有两个交点，那么一元二次方程02=++c bx ax 的根的情况是______________________.11. 已知抛物线c x ax y ++=2与x 轴交点的横坐标为1-，则c a +=_________. 12. 请你写出函数2)1(+=x y 与12+=x y 具有的一个共同性质：_______________.13. 已知二次函数的图象开口向上，且与y 轴的正半轴相交，请你写出一个满足条件的二次函数的解析式：_____________________. 14. 如图，抛物线的对称轴是1=x ，与x 轴交于A 、B 两点，若B 点坐标是)0,3(，则A点的坐标是三、解答题：1. 已知函数12-+=bx x y 的图象经过点（3，2）.（1）求这个函数的解析式；（2）当0>x 时，求使y ≥2的x 的取值范围.2、如右图，抛物线n x x y ++-=52经过点)0,1(A ，与y 轴交于点B .（1）求抛物线的解析式；（2）P 是y 轴正半轴上一点，且△PAB 是以AB 为腰的等腰三角形，试求点P 的坐标.3．如图，抛物线y 1=﹣x 2+2向右平移1个单位得到抛物线y 2，回答下列问题：（1）抛物线y 2的顶点坐标；（2）阴影部分的面积S= ；（3）若再将抛物线y 2绕原点O 旋转180°得到抛物线y 3，求抛物线y 3的解析式．4．（1999•烟台）如图，已知抛物线y=ax 2+bx+交x 轴正半轴于A ，B 两点，交y 轴于点C ，且∠CBO=60°，∠CAO=45°，求抛物线的解析式和直线BC 的解析式．O xy1-1 BA5．如图，抛物线y=x2+bx﹣c经过直线y=x﹣3与坐标轴的两个交点A，B，此抛物线与x轴的另一个交点为C，抛物线的顶点为D．（1）求此抛物线的解析式；（2）点P为抛物线上的一个动点，求使S△APC：S△ACD=5：4的点P的坐标．6．如图，抛物线y=a（x+1）2的顶点为A，与y轴的负半轴交于点B，且OB=OA．（1）求抛物线的解析式；（2）若点C（﹣3，b）在该抛物线上，求S△ABC的值．7．如图，抛物线y=x2﹣2x+c的顶点A在直线l：y=x﹣5上．（1）求抛物线顶点A的坐标及c的值；（2）设抛物线与y 轴交于点B ，与x 轴交于点C 、D （C 点在D 点的左侧），试判断△ABD 的形状．8、某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到赢利的过程，下面的二次函数图象（部分）刻画了该公司年初以来累积利润s （万元）与销售时间t （月）之间的关系（即前t 个月的利润总和s 与t 之间的关系）. （1）由已知图象上的三点坐标，求累积利润s （万元）与销售时间t （月）之间的函数关系式；（2）求截止到几月累积利润可达到30万元；（3）求第8个月公司所获利润是多少万元？参考答案一、选择题：题号 1 2 3 4 5 6 7 8 9 答案DDAADDDBD二、填空题： 1. 2)1(2+-=x y2. 有两个不相等的实数根3. 14. （1）图象都是抛物线；（2）开口向上；（3）都有最低点（或最小值）5.358512+-=x x y 或358512-+-=x x y 或178712+-=x x y 或178712-+-=x x y 6. 122++-=x x y 等（只须0<a ，0>c ） 7. )0,32(-8. 3=x ，51<<x ，1，4 三、解答题：1. 解：（1）∵函数12-+=bx x y 的图象经过点（3，2），∴2139=-+b . 解得2-=b . ∴函数解析式为122--=x x y .（2）当3=x 时，2=y . 根据图象知当x ≥3时，y ≥2.∴当0>x 时，使y ≥2的x 的取值范围是x ≥3.2. 解：（1）由题意得051=++-n . ∴4-=n . ∴抛物线的解析式为452-+-=x x y .（2）∵点A 的坐标为（1，0），点B 的坐标为)4,0(-. ∴OA =1，OB =4.在Rt △OAB 中，1722=+=OB OA AB ，且点P 在y 轴正半轴上.①当PB =PA 时，17=PB . ∴417-=-=OB PB OP . 此时点P 的坐标为)417,0(-.②当PA =AB 时，OP =OB =4 此时点P 的坐标为（0，4）.3. 解：（1）设s 与t 的函数关系式为c bt at s ++=2，由题意得⎪⎩⎪⎨⎧=++-=++-=++；5.2525,224,5.1c b a c b a c b a 或⎪⎩⎪⎨⎧=-=++-=++.0,224,5.1c c b a c b a 解得⎪⎪⎩⎪⎪⎨⎧=-==.0,2,21c b a ∴t t s 2212-=.（2）把s =30代入t t s 2212-=，得.221302t t -= 解得101=t ，62-=t （舍去）答：截止到10月末公司累积利润可达到30万元. （3）把7=t 代入，得.5.10727212=⨯-⨯=s把8=t 代入，得.16828212=⨯-⨯=s 5.55.1016=-. 答：第8个月获利润5.5万元.4. 解：（1）由于顶点在y 轴上，所以设这部分抛物线为图象的函数的解析式为1092+=ax y . 因为点)0,25(-A 或)0,25(B 在抛物线上，所以109)25(·02+-=a ，得12518-=a . 因此所求函数解析式为109125182+-=x y （25-≤x ≤25）.（2）因为点D 、E 的纵坐标为209，所以10912518209+-=，得245±=x .所以点D 的坐标为)209,245(-，点E 的坐标为)209,245(. 所以225)245(245=--=DE . 因此卢浦大桥拱内实际桥长为385227501.01100225≈=⨯⨯（米）. 5. 解：（1）∵AB =3，21x x <，∴312=-x x . 由根与系数的关系有121=+x x .∴11-=x ，22=x . ∴OA =1，OB =2，2·21-==amx x . ∵1tan tan =∠=∠ABC BAC ，∴1==OBOCOA OC . ∴OC =2. ∴2-=m ,1=a .∴此二次函数的解析式为22--=x x y .（2）在第一象限，抛物线上存在一点P ，使S △PAC =6. 解法一：过点P 作直线MN ∥AC ，交x 轴于点M ，交y 轴于N ，连结PA 、PC 、MC 、NA . ∵MN ∥AC ，∴S △MAC =S △NAC = S △PAC =6.由（1）有OA =1，OC =2. ∴6121221=⨯⨯=⨯⨯CN AM . ∴AM =6，CN =12. ∴M （5，0），N （0，10）.∴直线MN 的解析式为102+-=x y .由⎩⎨⎧--=+-=,2,1022x x y x y 得⎩⎨⎧==；4311y x ⎩⎨⎧=-=18,422y x （舍去） ∴在第一象限，抛物线上存在点)4,3(P ，使S △PAC =6. 解法二：设AP 与y 轴交于点),0(m D （m >0） ∴直线AP 的解析式为m mx y +=.⎩⎨⎧+=--=.,22m mx y x x y ∴02)1(2=--+-m x m x . ∴1+=+m x x P A ，∴2+=m x P . 又S △PAC = S △ADC + S △PDC =P x CD AO CD ·21·21+=)(21P x AO CD +. ∴6)21)(2(21=+++m m ，0652=-+m m ∴6=m （舍去）或1=m .∴在第一象限，抛物线上存在点)4,3(P ，使S △PAC =6.提高题1. 解：（1）∵抛物线c bx x y ++=2与x 轴只有一个交点，∴方程02=++c bx x 有两个相等的实数根，即042=-c b . ①又点A 的坐标为（2，0），∴024=++c b . ② 由①②得4-=b ，4=a .（2）由（1）得抛物线的解析式为442+-=x x y . 当0=x 时，4=y . ∴点B 的坐标为（0，4）. 在Rt △OAB 中，OA =2，OB =4，得5222=+=OB OA AB .∴△OAB 的周长为5265241+=++.2. 解：（1）76)34()10710710(1022++-=--⨯++-⨯=x x x x x S .当3)1(26=-⨯-=x 时，16)1(467)1(42=-⨯-⨯-⨯=最大S . ∴当广告费是3万元时，公司获得的最大年利润是16万元.（2）用于投资的资金是13316=-万元.经分析，有两种投资方式符合要求，一种是取A 、B 、E 各一股，投入资金为13625=++（万元），收益为0.55+0.4+0.9=1.85（万元）>1.6（万元）；另一种是取B 、D 、E 各一股，投入资金为2+4+6=12（万元）<13（万元），收益为0.4+0.5+0.9=1.8（万元）>1.6（万元）.3. 解：（1）设抛物线的解析式为2ax y =，桥拱最高点到水面CD 的距离为h 米，则),5(h D -，)3,10(--h B .∴⎩⎨⎧--=-=.3100,25h a h a 解得⎪⎩⎪⎨⎧=-=.1,251h a∴抛物线的解析式为2251x y -=.（2）水位由CD 处涨到点O 的时间为1÷0.25=4（小时），货车按原来速度行驶的路程为40×1+40×4=200<280， ∴货车按原来速度行驶不能安全通过此桥. 设货车的速度提高到x 千米/时，当2801404=⨯+x 时，60=x .∴要使货车安全通过此桥，货车的速度应超过60千米/时. 4. 解：（1）未出租的设备为10270-x 套，所有未出租设备的支出为)5402(-x 元. （2）54065101)5402()1027040(2++-=----=x x x x x y .∴540651012++-=x x y .（说明：此处不要写出x 的取值范围）（3）当月租金为300元时，租赁公司的月收益为11040元，此时出租的设备为37套；当月租金为350元时，租赁公司的月收益为11040元，此时出租的设备为32套.因为出租37套和32套设备获得同样的收益，如果考虑减少设备的磨损，应选择出租32套；如果考虑市场占有率，应选择出租37套.（4）5.11102)325(1015406510122+--=++-=x x x y . ∴当325=x 时，y 有最大值11102.5. 但是，当月租金为325元时，租出设备套数为34.5，而34.5不是整数，故租出设备应为34套或35套. 即当月租金为为330元（租出34套）或月租金为320元（租出35套）时，租赁公司的月收益最大，最大月收益均为11100元.16．如图，抛物线y 1=﹣x 2+2向右平移1个单位得到抛物线y 2，回答下列问题：（1）抛物线y 2的顶点坐标（1，2）；（2）阴影部分的面积S= 2 ；（3）若再将抛物线y 2绕原点O 旋转180°得到抛物线y 3，求抛物线y 3的解析式．考点：二次函数图象与几何变换．分析：直接应用二次函数的知识解决问题．解答：解：（1）读图找到最高点的坐标即可．故抛物线y 2的顶点坐标为（1，2）；（2分）（2）把阴影部分进行平移，可得到阴影部分的面积即为图中两个方格的面积=1×2=2；（6分）（3）由题意可得：抛物线y 3的顶点与抛物线y 2的顶点关于原点O 成中心对称．所以抛物线y3的顶点坐标为（﹣1，﹣2），于是可设抛物线y3的解析式为：y=a（x+1）2﹣2．由对称性得a=1，所以y3=（x+1）2﹣2．（10分）20．（1999•烟台）如图，已知抛物线y=ax2+bx+交x轴正半轴于A，B两点，交y轴于点C，且∠CBO=60°，∠CAO=45°，求抛物线的解析式和直线BC的解析式．考点：待定系数法求二次函数解析式；待定系数法求一次函数解析式．分析：根据抛物线的解析式，易求得C点的坐标，即可得到OC的长；可分别在Rt△OBC和Rt△OAC中，通过解直角三角形求出OB、OA的长，即可得到A、B的坐标，进而可运用待定系数法求得抛物线和直线的解析式．解答：解：由题意得C（0，）在Rt△COB中，∵∠CBO=60°，∴OB=OC•cot60°=1∴B点的坐标是（1，0）；（1分）在Rt△COA中，∵∠CAO=45°，∴OA=OC=∴A点坐标（，0）由抛物线过A、B两点，得解得∴抛物线解析式为y=x2﹣（）x+（4分）设直线BC的解析式为y=mx+n，得n=，m=﹣∴直线BC解析式为y=﹣x+．（6分）23．如图，抛物线y=x2+bx﹣c经过直线y=x﹣3与坐标轴的两个交点A，B，此抛物线与x轴的另一个交点为C，抛物线的顶点为D．（1）求此抛物线的解析式；（2）点P为抛物线上的一个动点，求使S△APC：S△ACD=5：4的点P的坐标．考点：二次函数综合题．专题：压轴题；动点型．分析：（1）先根据直线y=x﹣3求出A、B两点的坐标，然后将它们代入抛物线中即可求出待定系数的值．（2）根据（1）中抛物线的解析式可求出C，D两点的坐标，由于△APC和△ACD同底，因此面积比等于高的比，即P点纵坐标的绝对值：D点纵坐标的绝对值=5：4．据此可求出P点的纵坐标，然后将其代入抛物线的解析式中，即可求出P点的坐标．解答：解：（1）直线y=x﹣3与坐标轴的交点A（3，0），B（0，﹣3）．则，解得，∴此抛物线的解析式y=x2﹣2x﹣3．（2）抛物线的顶点D（1，﹣4），与x轴的另一个交点C（﹣1，0）．设P（a，a2﹣2a﹣3），则（×4×|a2﹣2a﹣3|）：（×4×4）=5：4．化简得|a2﹣2a﹣3|=5．当a2﹣2a﹣3=5，得a=4或a=﹣2．∴P（4，5）或P（﹣2，5），当a2﹣2a﹣3＜0时，即a2﹣2a+2=0，此方程无解．综上所述，满足条件的点的坐标为（4，5）或（﹣2，5）．27．如图，抛物线y=a（x+1）2的顶点为A，与y轴的负半轴交于点B，且OB=OA．（1）求抛物线的解析式；（2）若点C（﹣3，b）在该抛物线上，求S△ABC的值．考点：待定系数法求二次函数解析式；二次函数图象上点的坐标特征．专题：计算题．分析：（1）由抛物线解析式确定出顶点A坐标，根据OA=OB确定出B坐标，将B坐标代入解析式求出a的值，即可确定出解析式；（2）将C坐标代入抛物线解析式求出b的值，确定出C坐标，过C作CD垂直于x轴，三角形ABC面积=梯形OBCD面积﹣三角形ACD面积﹣三角形AOB面积，求出即可．解答：解：（1）由投影仪得：A（﹣1，0），B（0，﹣1），将x=0，y=﹣1代入抛物线解析式得：a=﹣1，则抛物线解析式为y=﹣（x+1）2=﹣x2﹣2x﹣1；（2）过C作CD⊥x轴，将C（﹣3，b）代入抛物线解析式得：b=﹣4，即C（﹣3，﹣4），则S△ABC=S梯形OBCD﹣S△ACD﹣S△AOB=×3×（4+1）﹣×4×2﹣×1×1=3．点评：此题考查了待定系数法求二次函数解析式，熟练掌握待定系数法是解本题的关键．28．如图，抛物线y=x2﹣2x+c的顶点A在直线l：y=x﹣5上．（1）求抛物线顶点A的坐标及c的值；（2）设抛物线与y轴交于点B，与x轴交于点C、D（C点在D点的左侧），试判断△ABD的形状．考点：二次函数综合题．分析：（1）先根据抛物线的解析式得出其对称轴，由此得到顶点A的横坐标，然后代入直线l的解析式中求出点A的坐标，再将点A的坐标代入抛物线的解析式y=x2﹣2x+c中，运用待定系数法即可求出c的值；（2）先由抛物线的解析式得到点B的坐标，再求出AB、AD、BD三边的长，然后根据勾股定理的逆定理即可确定△ABD是直角三角形．解答：解：（1）∵y=x2﹣2x+c，∴顶点A的横坐标为x=﹣=1，又∵顶点A在直线y=x﹣5上，∴当x=1时，y=1﹣5=﹣4，∴点A的坐标为（1，﹣4）．将A（1，﹣4）代入y=x2﹣2x+c，得﹣4=12﹣2×1+c，解得c=﹣3．故抛物线顶点A的坐标为（1，﹣4），c的值为﹣3；（2）△ABD是直角三角形．理由如下：∵抛物线y=x2﹣2x﹣3与y轴交于点B，∴B（0，﹣3）．当y=0时，x2﹣2x﹣3=0，解得x1=﹣1，x2=3，∴C（﹣1，0），D（3，0）．∵BD2=OB2+OD2=18，AB2=（4﹣3）2+12=2，AD2=（3﹣1）2+42=20，∴BD2+AB2=AD2，∴∠ABD=90°，即△ABD是直角三角形．。

中考数学复习考点题型专题练习2---《二次函数图像选择题综合》(含答案)

∴b＝2a＞0， ∵抛物线与 y 轴的交点在 x 轴的下方， ∴c＜0， ∴abc＜0，所以①正确； ∵x＝1 时，y＝0， ∴a+b+c＝0， ∴c＝﹣a﹣2a＝﹣3a， ∴c+2a＝﹣3a+2a＝﹣a＜0，所以②正确； ∵抛物线的对称轴为直线 x＝﹣1，抛物线与 x 轴的一个交点坐标为（1，0）， ∴抛物线与 x 轴的另一个交点坐标为（﹣3，0）， ∴当 x＝﹣3 时，y＝0，即 9a﹣3b+c＝0，所以③正确； ∵x＝﹣1 时，y 有最小值，
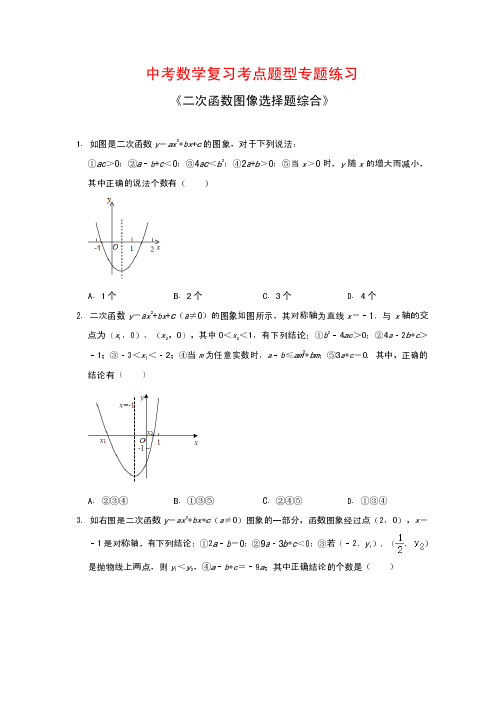
∴a﹣b+c≤ma2+bm+c（m 为任意实数）， ∴a﹣b≤m（am+b）（m 为实数），所以④错误； ∵抛物线与 x 轴有 2 个交点， ∴△＝b2﹣4ac＞0，即 4ac﹣b2＜0，所以⑤正确．故选：D． 5．解：∵抛物线开口向上， ∴a＞0， ∵抛物线的对称轴在 y 轴的右侧， ∴b＜0， ∵抛物线与 y 轴的交点在 x 轴下方， ∴c＜0， ∴abc＞0， ∴①的结论错误； ∵抛物线过点（﹣1，0）和（m，0），且 1＜m＜2，
A．2
B．3
C．4
D．5
参考答案
1．解：①由图象可知：a＞0，c＜0， ∴ac＜0，故①错误； ②由图象可知：x＝﹣1 时，y＝a﹣b+c＞0，故②错误； ③由于抛物线与 x 轴有两个交点， ∴△＝b2﹣4ac＞0，故③正确； ④由于对称轴可知：﹣ ＜1， ∴2a+b＞0，故④正确； ⑤当 x＞﹣ 时，y 随着 x 的增大而增大，故⑤错误；故选：B．
B．将（﹣1，0）代入解析式得 a﹣b+c＝0，由 x＝﹣ ＝﹣1 知 b＝2a，则 a﹣2a+c＝0，
整理得 a＝c，此选项正确；

二次函数综合训练题2

二次函数综合训练题21.如图，抛物线与x轴的交点A、B的横坐标分别为-1，-4，与y轴的交点C的纵坐标为3．（1）求抛物线的解析式；（2）如图①在抛物线的对称轴上是否存在点P，使得四边形PAOC的周长最小？若存在，求出四边形PAOC 周长的最小值；若不存在请说明理由；（3）如图②，点Q是线段OB上一动点，连接BC，在线段BC上是否存在这样的点M，使△CQM为等腰三角形，且△BQM为直角三角形？若存在，求点M的坐标，若不存在，请说明理由2.如图，已知抛物线y=ax2+bx+c与x轴交于点A、B（2，0），与直线AC：y=﹣x﹣6交y轴于点C，点D是抛物线的顶点．（1）求出抛物线的解析式及D点的坐标；（2）判断△ACD的形状，并求tan∠ADC的值；（3）直线AD 交y轴于点F，在线段AD上存在点P，使∠ADC=∠PCF，请求出点P的坐标3.已知抛物线y=（x﹣m）2﹣（x﹣m），其中m是常数．（1）求证：不论m为何值，该抛物线与x轴一定有两个公共点；（2）若该抛物线的对称轴为直线x=5／2．①求该抛物线的函数解析式；②把该抛物线沿y轴向上平移多少个单位长度后，得到的抛物线与x轴只有一个公共点4.如图，抛物线y=ax2+bx+2.5与直线AB交于点A（﹣1，0），B（4，2.5），点D是抛物线A，B两点间部分上的一个动点（不与点A，B重合），直线CD与y轴平行，交直线AB于点C，连接AD，BD．（1）求抛物线的解析式；（2）设点D的横坐标为m，△ADB的面积为S，求S关于m的函数关系式，并求出当S取最大值时的点C的坐标．5.如图，已知抛物线y=ax2+bx+3与x轴交于A（1，0），B（﹣3，0）两点，与y轴交于点C，抛物线的顶点为P，连接AC．（1）求此抛物线的解析式；（2）在抛物线上找一点D，使得DC与AC垂直，且直线DC与x轴交于点Q，求直线DC的解析式；（3）抛物线对称轴上是否存在一点M，使得S△MAP=2S△ACP？若存在，求出M点的坐标；若不存在，请说明理由6.如图，已知抛物线y=ax2+bx+3经过A（﹣3，0），B（1，0）两点，与y轴交于点C，其顶点为D，对称轴是直线l，l与x轴交于点H．（1）求该抛物线的解析式；（2）若点P是该抛物线对称轴l上的一个动点，求△PBC 周长的最小值；（3）若E是线段AD上的一个动点（E与A，D不重合），过E点作平行于y轴的直线交抛物线于F，交x轴于点G，设点E的横坐标为m，△ADF的面积为S．①求S与m的函数关系式；②S是否存在最大值？若存在，求出最大值及此时点E的坐标；若不存在，请说明理由7.如图，抛物线y=ax2+bx+4与x轴交于A（﹣2，0），D两点，与y轴交于点C，对称轴x=3交x轴交于点B．（1）求抛物线的解析式．（2）点M是x轴上方抛物线上一动点，过点M作MN⊥x轴于点N，交直线BC于点E．设点M 的横坐标为m，用含m的代数式表示线段ME的长，并求出线段ME长的最大值．（3）若点P在y轴的正半轴上，连接PA，过点P作PA垂线，交抛物线的对称轴于点Q．是否存在点P，使以点P、A、Q为顶点的三角形与△BAQ 全等？若存在，直接写出点P的坐标；若不存在，请说明理由8.已知抛物线y=ax2+bx+3，经过点M（﹣4，0），且对称轴为x=﹣2.5，交y轴于B．（1）求抛物线对应的解析式；（2）若x轴上有一点A（4，0），将△ABO沿x轴向左平移到△DCE（如图），当四边形ABCD为菱形时，试判断C，D是否在抛物线上；（3）在（2）中，若点P是抛物线上一个动点（点P不与C，D重合），经过点P作PQ∥y轴交直线CD于Q，设点P的横坐标为t，PQ的长度为d，求d与t之间的函数解析式，并直接写出当t为何值时，以P，Q，C，E为顶点的四边形是平行四边形二次函数综合训练题2答案1.解：（1）设抛物线解析式为y=ax2+bx+c（a≠0），由题意可知A（﹣1，0），B（﹣4，0），C（0，3），代入抛物线解析式可得，解得，∴抛物线解析式为y=x2+x+3；（2）∵A、B关于对称轴对称，如图1，连接BC，∴BC与对称轴的交点即为所求的点P，此时PA+PC=BC，∴四边形PAOC的周长最小值为：OC+OA+BC，∵A（﹣1，0），B（﹣4，0），C（0，3），∴OA=1，OC=3，BC==5，∴OC+AB+BC=1+3+5=9，∴在抛物线的对称轴上存在点P，使四边形PAOC的周长最小，四边形PAOC周长的最小值为9；（3）设直线BC解析式为y=kx+n，把B、C两点坐标代入可得，解得，∴直线BC的解析式为y=x+3，①当∠BQM=90°时，如图2，设M（a，b），∵∠CMQ＞90°，∴只能CM=MQ=b，∵MQ∥y轴，∴△MQB ∽△COB，∴=，即=，解得b=，代入y=x+3可得=a+3，解得a=﹣，∴M点坐标为（﹣，）；②当∠QMB=90°时，如图3，∵∠CMQ=90°，∴只能CM=MQ，设CM=MQ=m，则BM=5﹣m，∵∠BMQ=∠COB=90°，∠MBQ=∠OBC，∴△BMQ∽△BOC，∴=，解得m=，作MN∥OB，则有==，即==，∴MN=，CN=，∴ON=OC﹣CN=3﹣=，∴M点坐标为（﹣，），综上可知在线段BC上是存在这样的点M，使△CQM为等腰三角形且△BQM为直角三角形，点M的坐标为（﹣，）或（﹣，）2.解：（1）直线AC：y=﹣x﹣6，当x=0时，y=﹣6，即C（0，﹣6）．当y=0时，x=﹣6，即A（﹣6，0）．∵B（2，0），把A、B、C三点坐标代入函数解析式，得，解得，抛物线的解析式为y=x2+2x﹣6=（x+2）2﹣8，顶点D的坐标为（﹣2，﹣8）；（2）△ACD是直角三角形，理由如下：∵A（6，0），C（0，﹣6），D（﹣2，﹣8），∴由勾股定理，得AC2=62+62=72，CD2=22+（﹣8+6）2=8，AD2=（﹣2+6）2+82=80，∴AC2+CD2=AD2，∴△ACD是直角三角形，∠ACD=90°∴tan∠ADC===3；（3）设直线AD的解析式为y=mx+n．∵A（﹣6，0），D（﹣2，﹣8），，解得，∴直线AD的解析式为y=﹣2x﹣12．当x=0时，y=﹣12，即F（0，﹣12），设点P的坐标为（x，﹣2x﹣12）．∵∠ADC=∠DCF+∠DFC，∠PCF=∠DCF+∠PCD，∠ADC=∠PCF，∴∠DFC=∠PCD，在△CPD和△FPC中，，∴△CPD∽△FPC，∴=，∴=，化简，得35x2+216x+324=0，解得x1=﹣，x2=﹣（舍去）．当x=﹣时，﹣2x﹣12=﹣2×（﹣）﹣12=﹣，∴点P的坐标（﹣，﹣）3.（1）证明：y=（x﹣m）2﹣（x﹣m）=x2﹣（2m+1）x+m2+m，∵△=（2m+1）2﹣4（m2+m）=1＞0，∴不论m为何值，该抛物线与x轴一定有两个公共点；（2）解：①∵x=﹣=，∴m=2，∴抛物线解析式为y=x2﹣5x+6；②设抛物线沿y轴向上平移k个单位长度后，得到的抛物线与x轴只有一个公共点，则平移后抛物线解析式为y=x2﹣5x+6+k，∵抛物线y=x2﹣5x+6+k与x轴只有一个公共点，∴△=52﹣4（6+k）=0，∴k=，即把该抛物线沿y轴向上平移个单位长度后，得到的抛物线与x轴只有一个公共点．4. 解：（1）由题意得，解得：，∴y=﹣x2+2x+．（2）设直线AB解析式为：y=kx+b，则有，解得：，∴y=x+，则D（m，﹣m2+2m+），C（m，m+），CD=（﹣m2+2m+）﹣（m+）=﹣m2+m+2，∴S=（m+1）•CD+（4﹣m）•CD=×5×CD=×5×（﹣m2+m+2）=﹣m2+m+5∵﹣＜0，∴当m=时，S有最大值，当m=时，m+=×+=，∴点C（，）．5. 解：（1）∵抛物线与x轴交于A（1，0）、B（﹣3，0）两点，∴，解得：，∴y=﹣x2﹣2x+3，（2）∵点A（1，0），点C（0，3），∴OA=1，OC=3，∵DC⊥AC，∴∠DCO+∠OCA=90°，∵OC⊥x轴，∴∠COA=∠COQ，∠OAC+∠OCA=90°，∴∠DCO=∠OAC，∴△QOC∽△COA，∴，即，∴OQ=9，又∵点Q在x轴的负半轴上，∴Q（﹣9，0），设直线QC的解析式为：y=mx+n，则，解之得：，∴直线QC的解析式为：y=x+3，∵点D是抛物线与直线QC的交点，，解之得：或（不合题意，应舍去），∴点D（﹣，）；（3）如图，点M为直线x=﹣1上一点，连接AM，PC，PA，设点M（﹣1，y），直线x=﹣1与x轴交于点E，∴E （﹣1，0），∵A（1，0），∴AE=2，∵抛物线y=﹣x2﹣2x+3的顶点为P，对称轴为x=﹣1，∴P（﹣1，4），∴PE=4，则PM=|4﹣y|，∵S四边形AEPC=S四边形OEPC+S△AOC，=×1×（3+4）+×1×3，=×10，=5，又∵S四边形AEPC=S△AEP+S△ACP，S△AEP=AP•PE=×2×4，∴S△ACP=5﹣4=1，∵S△MAP=2S△ACP，∴×2×|y﹣4|=2×1，∴|4﹣y|=2，∴y1=2，y2=6，故抛物线的对称轴上存在点M使S△MAP=2S△ACP，点M（﹣1，2）或（﹣1，6）．6. 解：（1）由题意可知：，解得：，∴抛物线的解析式为：y=﹣x2﹣2x+3．（2）∵y=﹣x2﹣2x+3，∴C（0，3）．∵△PBC的周长为：PB+PC+BC，BC是定值，∴当PB+PC最小时，△PBC的周长最小．如答图1所示，点A、B关于对称轴l对称，连接AC交l于点P，则点P为所求的点．∵AP=BP，∴△PBC周长的最小值是：PB+PC+BC=AC+BC．∵A（﹣3，0），B（1，0），C（0，3），∴AC=，BC=．∴△PBC 周长的最小值是：+．（3）如答图2，①∵抛物线y=﹣x2﹣2x+3的顶点D坐标为（﹣1，4），A（﹣3，0），∴直线AD的解析式为：y=2x+6．∵点E的横坐标为m，∴E（m，2m+6），F（m，﹣m2﹣2m+3）∴EF=﹣m2﹣2m+3﹣（2m+6）=﹣m2﹣4m﹣3．∴S=S△AEF+S2﹣4m﹣3）×2=﹣m2﹣4m﹣3；②S=﹣m2﹣4m﹣3=﹣（m+2）2+1∴当m=﹣△DEF=EF•AG+EF•GH=EF•AH=×（﹣m2时，S最大，最大值为1．此时点E的坐标为（﹣2，2）．7. 解：（1）由题意得，点D的坐标为（8，0），把点A、D的坐标代入y=ax2+bx+4，解．故抛物线解析式为y=﹣x2+x+4．（2）由题意，点C，点B坐标分别为（0，4），（3，0），则直线CB解析式y=﹣x+4，点M坐标为（m，﹣m2+m+4），点E坐标为（m，﹣m+4），①当﹣2＜m≤0时，ME=﹣m+4﹣（﹣m2+m+4）=m2﹣m，m=﹣2时，ME=，由二次函数性质可知，ME ＜；②当0＜m＜8时，ME=﹣m2+m+4﹣（﹣m+4）=m2﹣m=﹣（m﹣）2+当m=时，ME取得最大值，最大值为．综上所述，当﹣2＜m≤0时，ME=m2﹣m，当0＜m＜8时，ME=﹣m2+m．当m=时，ME 取得最大值，最大值为．（3）存在，∵PA⊥PQ，BQ⊥x轴∴∠APQ=∠ABQ=90°，∴△APQ和△ABQ中．点P和点B是对应点，∵以点P、A、Q为顶点的三角形与△BAQ全等，只有两种情况：设点P（0，c），Q（3，n）（c＞0，∴AB=5，BQ=n，PA=，PQ=，①△PAQ≌△BAQ，∴PA=BA，PQ=BQ，∴=5，=n，∴c=或c=﹣（舍），∴P（0，），②△PQA≌△BAQ，∴PA=BQ，PQ=AB，∴=n，=5，∴c1=，d1=﹣或c2=﹣，d2=（舍）故点P坐标为P1（0，），P2（0，）8. 解：（1）∵抛物线y=ax2+bx+3，经过点M（﹣4，0），且对称轴为x=﹣，∴M关于x=﹣的对称点为（﹣1，0），∴，解得，∴抛物线的解析式：y=x2+x+3．（2）∵抛物线y=x2+x+3交y轴于B．∴B（0，3），∵A（4，0），∴OA=4，OB=3，AB==5；若四边形ABCD是菱形，则BC=AD=AB=5，∴C（﹣5，3）、D（﹣1，0）．将C（﹣5，3）代入y=x2+x+3中，得：×（﹣5）2+×（﹣5）+3=3，所以点C在抛物线上；同理可证：点D也在抛物线上．（3）设直线CD的解析式为：y=kx+b，依题意，有：，解得，∴直线CD：y=﹣x﹣．由于PQ∥y轴，设 P（t，t2+t+3），则 Q（t，﹣t﹣）；①t＜﹣5或t＞﹣1时，d=PQ=（t2+t+3）﹣（﹣t﹣）=t2+t+；②﹣5＜t＜﹣1时，d=PQ=（﹣t﹣）﹣（t2+t+3）=﹣t2﹣t﹣；若以M、N、C、E为顶点的四边形是平行四边形，由于PQ∥CE，则PQ=CE=3，则有：t2+t+=3，解得：t1=﹣3+2，t2=﹣3﹣2；﹣t2﹣t﹣=3，解得：t=﹣3；综上，当t=﹣3+2或t=﹣3﹣2或﹣3时，以P，Q，C，E为顶点的四边形是平行四边形．。

第五课时二次函数(2)复习

和点（5,0）求 x 1 时的函数值.
2.已知：直线y=-x+3交x轴于点A，交y轴于点B，抛物线y=ax2+bx+c经过A、B、C（1，0）三点. （1）求出A、B两点的坐标. （2）求抛物线的解析式. （3）若抛物线的顶点为点D，求四边形ABCD的面积.
归纳：要求出函数的解析式，先要求出关键点的坐标或从图形中找出相应点的坐标.
3、如图，点A在x轴上，OA=4，将线段OA绕点O 顺时针旋转120°至OB的位置．（1）求点B的坐标；（2）求经过点A．O、B的抛物线的解析式；
4、如图，有一个抛物线形的水泥门洞．门洞的地面宽度为8 m，两侧距地面4 m高处各有一盏灯，两灯间的水平距离为6 m．求这个门洞的高度．
归纳：要解决这种题型，相应的做法是构建适当的平面直角坐标系.
2
2
1 ∵经过点（-1，2） a(1 2) 1 2 a 3 1
∴函数解析式为： y
1
( x 2) 1 3
2
归纳：知道顶点坐标或对称轴等，一般设函数的顶点式.
练：抛物线 y ax பைடு நூலகம்x c(a 0)
2
的对称轴为直线
x 2 ，且经过点（1,4）
本节课注要复习了用待定系数法求函数的解析式，其中关键是通过适当的设出相关函数的解析式，区分什么时候采用一般式，什么时候采用顶点式，什么时候采用交点式.
归纳：解决以上这种小题的方法是：直接代入求解. 下面完成课后与综合练习1,2,3.（时间：2分钟）
1、抛物线的顶点是（2，-1），且过点（-1,2）求它的解析式. 2 解：设函数的解析式为： y a( x h) k (a 0) ∵顶点坐标是（2，-1） y a( x 2)