2017年全国统一高考数学试卷(理科)(新课标ⅲ)及参考答案

合集下载

2017年全国统一高考数学试卷(理科)(新课标ⅲ)

2017年全国统一高考数学试卷（理科）（新课标Ⅲ）一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．（5分）已知集合A={（x，y）|x2+y2=1}，B={（x，y）|y=x}，则A∩B中元素的个数为（）A．3 B．2 C．1 D．02．（5分）设复数z满足（1+i）z=2i，则|z|=（）A．B．C．D．23．（5分）某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是（）A．月接待游客量逐月增加B．年接待游客量逐年增加C．各年的月接待游客量高峰期大致在7，8月D．各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳4．（5分）（x+y）（2x﹣y）5的展开式中的x3y3系数为（）A．﹣80 B．﹣40 C．40 D．805．（5分）已知双曲线C：﹣=1 （a＞0，b＞0）的一条渐近线方程为y=x，且与椭圆+=1有公共焦点，则C的方程为（）A．﹣=1 B．﹣=1 C．﹣=1 D．﹣=16．（5分）设函数f（x）=cos（x+），则下列结论错误的是（）A．f（x）的一个周期为﹣2πB．y=f（x）的图象关于直线x=对称C．f（x+π）的一个零点为x=D．f（x）在（，π）单调递减7．（5分）执行如图的程序框图，为使输出S的值小于91，则输入的正整数N 的最小值为（）A．5 B．4 C．3 D．28．（5分）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（）A．πB． C．D．9．（5分）等差数列{a n}的首项为1，公差不为0．若a2，a3，a6成等比数列，则{a n}前6项的和为（）A．﹣24 B．﹣3 C．3 D．810．（5分）已知椭圆C：=1（a＞b＞0）的左、右顶点分别为A1，A2，且以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切，则C的离心率为（）A．B．C．D．11．（5分）已知函数f（x）=x2﹣2x+a（e x﹣1+e﹣x+1）有唯一零点，则a=（）A．﹣ B．C．D．112．（5分）在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上．若=λ+μ，则λ+μ的最大值为（）A．3 B．2 C．D．2二、填空题:本题共4小题，每小题5分，共20分。

2017高考全国3卷理科数学试题与答案

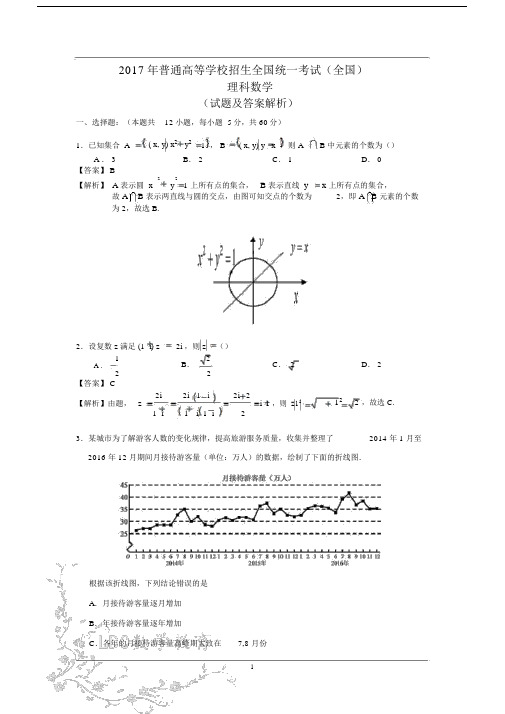
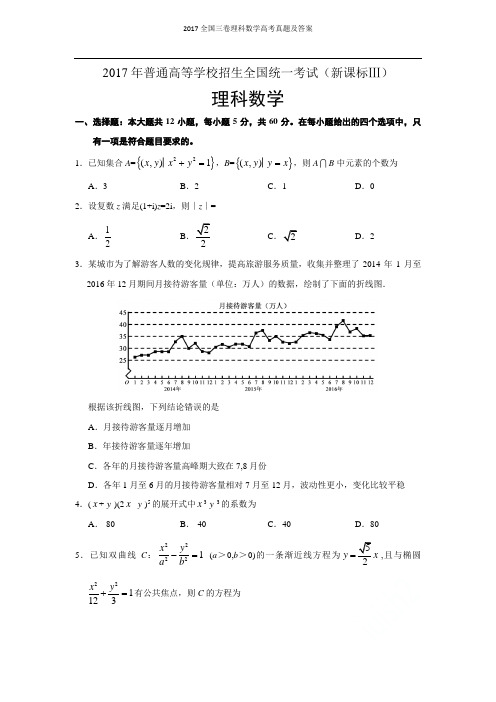
2017年普通高等学校招生全国统一考试（全国）理科数学（试题及答案解析）一、选择题：（本题共12小题，每小题 5分，共 60分）1．已知集合 A ( x, y) x 2 y 2 1 ， B( x, y) y x ，则 AB 中元素的个数为（）A ． 3B ． 2C ． 1D ． 0【答案】 B221 上所有点的集合， B 表示直线 yx 上所有点的集合，【解析】 A 表示圆 x y 故 A B 表示两直线与圆的交点，由图可知交点的个数为2，即 A B 元素的个数为2，故选 B.2．设复数 z 满足 (1 i) z 2i ，则 z （）1 B ．2 C ． 2D ． 2A ．22【答案】 C2i 2i 1 i 2i 2 122 ，故选 C.【解析】由题， z1 i 1 ii 1 ，则 z 121 i23．某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014 年 1 月至2016 年 12 月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是A ．月接待游客量逐月增加B ．年接待游客量逐年增加C ．各年的月接待游客量高峰期大致在 7,8 月份D ．各年 1 月至 6 月的月接待游客量相对 7 月至 12 月，波动性更小，变化比较平稳【答案】 A【解析】由题图可知， 2014年8月到 9月的月接待游客量在减少，则 A 选项错误，故选 A.4． ( x y)(2 x y)5 的展开式中 x 3 y 3 的系数为（）A ．B ．C ． 40D ． 80【答案】 C【解析】由二项式定理可得，原式展开中含x 3 y3的项为x 22 x 23y 33240x 333 3C 5y C 5 2xyy，则 x y 的系数为 40，故选 C.225x ，且与椭圆5．已知双曲线C ：x2y 2 1（ a 0 ， b 0 ）的一条渐近线方程为 yx 2 y 2ab21 有公共焦点．则 C 的方程为（）123A ． x 2 y 2 1B ． x 2 y 21C ． x 2 y 21D ． x 2 y 218104 55443【答案】 B【解析】 ∵双曲线的一条渐近线方程为y5 x ，则 b5 ① 又∵ 椭圆x 2y 22 a21 与双曲线有公共焦点，易知 c 3 ，则 a 2b 2 c29 ②123x2y2由①② 解得 a 2,b5 ，则双曲线 C 的方程为1，故选 B.456．设函数 f ( x)πcos(x) ，则下列结论错误的是（）38πA ． f (x) 的一个周期为2πB ． y f ( x) 的图像关于直线 x对称3C ． f ( xπ π ) 的一个零点为 xD ． f (x) 在 ( , π) 单调递减【答案】 D 62【解析】函数 fx cos xπ的图象可由 y cosx 向左平移π个单位得到，3 3 如图可知， f x在 π, π 上先递减后递增， D 选项错误，故选 D.2y- Ox67．执行右图的程序框图，为使输出S 的值小于 91，则输入的正整数N的最小值为（） A ． 5 B ．4 C ．3 D ． 2【答案】 D【解析】程序运行过程如下表所示：SM t 初始状态 0 100 1 第1次循环结束 100 10 2 第2次循环结束 90 1 3此时 S 90 91 首次满足条件，程序需在 t 3 时跳出循环，即 N2 为满足条件的最小值，故选 D.8．已知圆柱的高为 1，它的两个底面的圆周在直径为 2的同一个球的球面上，则该圆柱的体积为（）A ．πB ．3π ππ4C ．D ．【答案】 B２41 2【解析】由题可知球心在圆柱体中心，圆柱体上下底面圆半径23 ， r122则圆柱体体积 Vπ 23πrh，故选 B.49．等差数列 a n 的首项为 1，公差不为 0．若 a 2 ， a 3 ， a 6 成等比数列，则a n前 6项的和为（）A ． 24B ． 3C ． 3D ． 8【答案】 A【解析】 ∵ a n为等差数列，且 a 2 , a 3 , a 6 成等比数列，设公差为 d .则 a 32 a 2 a 6 ，即 a 12d 2a 1 d a 15d又∵ a 1 1 ，代入上式可得 d 2 2d 0又∵ d 0 ，则 d 2∴ S 66a 1 6 5 d 1 6 6 5 224 ，故选 A.2 222xya b 0A 1A 2A 1 A 210．已知椭圆 C : a 2 b 21（）的左、右顶点分别为，，且以线段为直径的圆与直线 bx ay 2ab 0 相切，则 C 的离心率为（）A ．6B ．3C ．21 33D ．３3【答案】 A【解析】 ∵ 以 A 1 A 2 为直径为圆与直线 bx ay2ab 0 相切，∴圆心到直线距离d 等于半径，∴ d2aba22又∵ a0,b0 ，则上式可化简为 a 2 3b 2 ∵ b 2 a 2c 2，可得 a 23 a2c2，即 c22a 23∴ ec 6，故选Aa311．已知函数 f ( x) x 2 2xa(e x 1e x 1 ) 有唯一零点，则a（）1 1 1A ．２B ． 3C ． 2D ． 1【答案】 C【解析】由条件，f ( x) 22xx 1e x 1x a(e) ，得：f (2x) (2 x) 2 2(2x) a(e 2 x 1e (2 x ) 1 )x 2 4 x 4 42x a(e 1 x e x 1 )22 x x 1e x 1x a(e ) ∴ f (2x) f (x) ，即 x 1 为 f (x) 的对称轴，由题意， f (x) 有唯一零点，∴ f ( x) 的零点只能为 x 1 ，即 f (1) 12 2 1 a(e 1 1e 1 1) 0 ，解得 a 1．212．在矩形 ABCD 中， AB 1， AD2 ，动点 P 在以点 C 为圆心且与 BD 相切的圆上．若APABAD ，则的最大值为（）yA ． 3B ． 2 2P gC ． 5D ． 2BC【答案】 A【解析】由题意，画出右图．设 BD 与 C 切于点 E ，连接 CE ．E以 A 为原点， AD 为 x 轴正半轴，xA(O)DAB 为y轴正半轴建立直角坐标系，则 C 点坐标为 (2,1) ． ∵|CD| 1，|BC | 2．22．∴BD 1 25 ∵ BD 切 C 于点 E ．∴CE ⊥BD ．∴ CE 是 Rt △ BCD 中斜边 BD 上的高．1 |BC| |CD|2 S △ BCD 22 2 2|EC ||BD | 5 5|BD |5即 C 的半径为 25 ．5∵P 在 C 上．∴ P 点的轨迹方程为 ( x 2)2( y 1)245 ．设 P 点坐标(x 0, y 0)，可以设出 P 点坐标满足的参数方程如下：2x 0 2 5 cos 2y 0 15 sin而 AP (x 0 , y 0 ) ， AB (0,1) ， AD (2,0) ．∵ AP AB AD (0,1) (2,0) (2 , )∴115，y 01 2 5 sin ．x 05cos52两式相加得：1 2 5sin15cos552( 2 5 )2 ( 5 )2 sin( )5 5 2 sin( ) ≤ 3(其中 sin5， cos2 5 )55当且仅当π2 k π， kZ 时，取得最大值 3．2二、填空题：（本题共4小题，每小题 5分，共 20分）x y ≥ 0,13．若 x ， y 满足约束条件xy 2 ≤ 0, 则 z 3x 4 y 的最小值为 ________．y ≥ 0,【答案】 1【解析】由题，画出可行域如图：目标函数为 z 3 x 4 y ，则直线 3 zz 值越小．yx 纵截距越大，由图可知： z 在 A 1,1 4 4处取最小值，故 z min 3 1 4 1 1 ．x y 2 0yA(1,1)B x(2,0)x y 014．设等比数列 a n满足 a 1 a 21 ， a 1 a 33 ，则 a4 ________．【答案】 8【解析】a n 为等比数列，设公比为 q ．a 1 a 2 1a 1 a 1 q 1 ① a 1 a 33 ，即 a 1 a 1 q 2 3 ② ，显然 q 1， a 1 0 ，②得 1 q3 ，即 q2 ，代入 ① 式可得 a 1 1 ，①a 4 a 1q 3 138 ．2f (x)x 1,x ≤ 0, f ( x1115．设函数 2x , x 0,则满足 f (x))的 x 的取值范围是 ________．2【答案】1 ,4【解析】fxx 1,x ≤ 0， f x f x1 1 1 1 f x2 x , x 02，即 f x2由图象变换可画出yf x1 与 y1 fx的图象如下：2yyf (x 1)2( 1,1)4 4x1 122y 1 f (x)由图可知，满足 f x1 1 1 f x 的解为,.2416． a ， b 为空间中两条互相垂直的直线，等腰直角三角形 ABC 的直角边 AC 所在直线与a ，b 都垂直，斜边①当直线 AB 与 a 成②当直线 AB 与 a 成AB 以直线 AC 为旋转轴旋转，有下列结论： 60 角时， AB 与 b 成 30 角；60 角时， AB 与 b 成 60 角；③直线 AB 与 a 所成角的最小值为45 ； ④直线 AB 与 a 所成角的最大值为60 ．其中正确的是 ________（填写所有正确结论的编号）【答案】 ②③【解析】由题意知， a 、 b 、AC 三条直线两两相互垂直，画出图形如图．不妨设图中所示正方体边长为 1，故|AC| 1， AB2，斜边 AB 以直线 AC 为旋转轴旋转，则A 点保持不变，B 点的运动轨迹是以C 为圆心， 1为半径的圆．以 C 为坐标原点，以 CD 为 x 轴正方向， CB 为 y 轴正方向，CA 为 z 轴正方向建立空间直角坐标系．则 D(1,0,0) ， A(0,0,1) ，直线 a 的方向单位向量 a(0,1,0) ， | a | 1 ．B 点起始坐标为 (0,1,0) ，直线 b 的方向单位向量 b (1,0,0) ， | b | 1 ．设 B 点在运动过程中的坐标B (cos ,sin,0) ，其中为 BC 与CD 的夹角， [0,2 π) ．那么 AB '在运动过程中的向量 AB ( cos, sin ,1) ， | AB | 2 ．设 AB 与 a 所成夹角为[0, π] ，2则cos 故设AB( cos , sin ,1) (0,1,0)2| sin| [0,2] ．a AB22π π[ ,] ，所以③正确，④错误．4 2与 b 所成夹角为π[0, ]，2AB bcosb AB(cos,sin,1) (1,0,0) .b AB2| cos |2当AB与 a 夹角为60π时，即3，sin2cos 2 cos 2 12 ．∵ cos2sin 2322 1，∴ | cos| 2 ．2∴ cos2| cos| 1 ．22π∵[0, ]． 2π∴=，此时AB与b夹角为60．3∴② 正确，①错误．三、解答题：（共70分．第 17-20题为必考题，每个试题考生都必须作答．第22， 23题为选考题，考生根据要求作答）（一）必考题：共60分．17．（ 12分）ABC 的内角A，B，C的对边分别为a，b，c，已知sin A 3 cos A 0 ，a 2 7 ，b 2．（ 1）求 c；（ 2）设D为 BC 边上一点，且AD AC ，求△ ABD 的面积．【解析】（1）由 sin A 3 cos A0 得2sin A π0 ，3即 A πkπk Z ，又A0, π，3∴ A ππ，得A2π33.1由余弦定理222.又∵a 27, b 2,cosAa b c 2 bc cos A代入并整理22得 c25 ，故c 4 .1（2）∵ AC2, BC27, AB 4 ，2 2 22 7 .由余弦定理 cosCab c2ab 7∵ AC AD ，即 △ACD 为直角三角形，则 ACCD cosC ，得 CD 7 .由勾股定理 AD CD 223 .AC 又 A2π DAB2π π π，则32 ，36 S △ ABD1AD AB sinπ3 .2618．（ 12分）某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶 4元，售价每瓶 6元，未售出的酸奶降价处理，以每瓶 2元的价格当天全部处理完．根据往年销售经验，每天需求量与当天最高气温（单位：℃）有关．如果最高气温不低于25，需求量为 500 瓶；如果最高气温位于区间 20 ，25 ，需求量为 300瓶；如果最高气温低于 20，需求量为 200瓶，为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：最高气温 10 ，1515 ，2020 ，25 25 ，3030 ，3535 ，40天数216362574以最高气温位于各区间的频率代替最高气温位于该区间的概率．（ 1）求六月份这种酸奶一天的需求量 X （单位：瓶）的分布列；（ 2）设六月份一天销售这种酸奶的利润为 Y （单位：元）．当六月份这种酸奶一天的进货量 n （单位：瓶）为多少时， Y 的数学期望达到最大值？【解析】 ⑴易知需求量 x 可取 200,300,500P X 2 16 1200 3 530 P X 36 2300 3 530 P X 25 7 4 2500 3 .30 5则分布列为：X 200 300 500P122555⑵① 当 n ≤ 200 时： Y n 6 4 2n ，此时 Y max 400 ，当 n 200 时取到 .②当 2004 2n 1 2 n 200 2 n ≤ 300 时： Y 2005 58 800 2n 6n 800n5 55此时 Y max 520 ，当 n 300 时取到 .③当 300n ≤ 500 时，Y1200 2n200223002n 30022n 25553200 2n5此时 Y 520.④当 n ≥ 500 时，易知 Y 一定小于 ③ 的情况 .综上所述：当 n 300 时， Y 取到最大值为 520 .19．（12分）如图，四面体 ABCD 中，△ABC 形．?ABD ?CBD ，AB= BD．（1）证明：平面 ACD ^ 平面 ABC ；（2）过 AC 的平面交BD于点E，若平面 AEC 把四面体 ABCD 分成体积相等的两部分．求二面角D- AE- C的余弦值．是正三角形，△ACD 是直角三角DECB【解析】⑴取 AC 中点为 O ，连接 BO ， DO ；A DABC 为等边三角形∴ BO AC E∴ AB BC CAB BCOBD BD ABDCBD .B ABDDBC∴ AD CD ,即ACD 为等腰直角三角形，ADC A为直角又 O 为底边 AC 中点∴DO AC令 AB a ，则 AB AC BC BD a易得：OD 2， OB3 a a22222∴ OD OB BD由勾股定理的逆定理可得DOB2即OD OBOD ACOD OB z AC OBO OD平面 ABC D AC平面 ABCOB平面 ABC又∵OD 平面ADC平面 ADC C E由面面垂直的判定定理可得平面 ABC ⑵由题意可知V D ACE V B ACE即B , D 到平面ACE的距离相等即E为 BD中点以 O 为原点， OA 为x轴正方向，OB 为y轴正方向， OD 为 z 轴正方向，设 AC a ，建立空间直角坐标系，则O 0,0,0 ， Aa a3,0,0 ， D 0,0,，B 0,a,0222OB yAx3 a，E 0, a,44a3a a a a易得： AE,a,， AD,0, ， OA,0,0244222设平面 AED的法向量为 n1，平面 AEC 的法向量为n2，AE n 1 03,1, 3则n 1 ，解得 n 1 ADAE n 2 0 0,1, 3OA n 2，解得 n 2若二面角 D AE C 为，易知为锐角，则 cosn 1 n 27n 1 n 272lC于 A ，B 两点，圆 M 是以2012分）已知抛物线 C : y = 2x2 0）的直线交．（，过点（，线段 AB 为直径的圆．（ 1）证明：坐标原点 O 在圆 M 上；（ 2）设圆 M 过点 P （ 4， - 2 ），求直线 l 与圆 M 的方程．【解析】 ⑴显然，当直线斜率为 0 时，直线与抛物线交于一点，不符合题意．设 l : x my 2 ， A( x 1 , y 1 ) ， B( x 2 , y 2 ) ，联立：y 22 x得 y 22my 40 ，x my24 m216 恒大于 0 ， y 1 y 22m ， y 1 y 24 ．uuruuurOA OBx 1 x 2 y 1 y 2(my 1 2)( my 2 2)(m 2 1)y 1 y 2 2m( y 1 y 2 ) 4 uur uuur 4( m 2 1) 2 m(2 m) 4∴ OA OB ，即O 在圆 M 上．uuur uur⑵若圆 M 过点 P ，则 AP BP(x 1 4)( x 2 4) ( y 1 2)( y 2 2) 0(my 1 2)( my 2 2) ( y 1 2)( y 2 2) 0(m 2 1)y 1 y 2 (2 m 2)( y 1y 2 ) 8 02m 10 解得 m 1或 1化简得 2m21①当 m时， l : 2xy4 0 圆心为 Q(x 0 , y 0 ) ，2y 0y 1y 2 1， x 01y 0 29 ，22249 22半径 r|OQ |142则圆 M : ( x 9 )2 ( y 1 )2 854 2 16②当 m 1 时， l : x y 2 0 圆心为 Q(x 0 , y 0 ) ，y 0 y 1 y 2 1 ， x 0 y 0 2 3 ， 2半径 r|OQ |32 12则圆 M : ( x 3)2 ( y 1)21021．（ 12分）已知函数 f (x)x 1 a ln x ．（ 1）若 f (x) ≥ 0 ，求 a 的值；（ 2）设 m 为整数，且对于任意正整数 n ， (1 + 1 1 1m ，求 m 的最)(1 + 2 ) 鬃?(1 n ) <2 2 2小值．【解析】 ⑴ f (x) x 1 a ln x ， x 0则 f ( x)1 a xa，且 f (1) 0当 a ≤ 0 x x上单调增，所以 0x 1时， f x 0 ， f x 在 0 ，时， f x0 ，不满足题意；当 a 0 时，当 0 x a 时， f (x) 0 ，则 f (x) 在 (0, a) 上单调递减；当 x a 时， f ( x) 0 ，则 f (x) 在 (a,) 上单调递增．①若 a 1 ， f (x) 在 (a,1) 上单调递增 ∴ 当 x (a,1) 时 f ( x) f (1) 0 矛盾 ②若 a 1 ， f (x) 在 (1,a) 上单调递减 ∴ 当 x (1,a) 时 f ( x)f (1) 0 矛盾③若 a1 ， f ( x) 在 (0,1) 上单调递减，在 (1,) 上单调递增 ∴ f (x) ≥ f (1)0 满足题意综上所述 a 1 ．⑵ 当 a 1 时 f ( x) x 1 ln x ≥ 0 即 ln x ≤ x 1则有 ln( x 1) ≤ x 当且仅当 x0 时等号成立∴ ln(11 1 ， kN *k)k22一方面： ln(11 ) ln(11 ... ln(11 1 1 ...1 1 ，2 2 )n )22n 1n 122222即 (111 1e ．)(122 )...(12 n)2另一方面： (11 11 (1 1 1 )(1 1 1352)(1 2 )...(1 2 n ) )(1 2 2 3 ) 642 2 2 2 当 n ≥3 时， (1 1 1 1 (2,e))(1 2 2 )...(12 n )2 ∵ m *(1 1 1 1 m ，N ， )(1 2 )...(1 2 n )2 2∴ m 的最小值为 3 ．22． [选修 4-4：坐标系与参数方程 ] （ 10分）在直角坐标系 xOy 中，直线 l的参数方程为x t ,（ t 为参数），直线l的参数方程ykt,xm,为m（ m 为参数），设 l 与 l 的交点为 P ，当 k 变化时， P 的轨迹为曲线 C ．y,k（ 1）写出 C 的普通方程：（ 2）以坐标原点为极点， x 轴正半轴为极轴建立极坐标系，设 l : cos( nis ) ，M 为 l 与 C 的交点，求 M 的极径．【解析】 ⑴将参数方程转化为一般方程l 1 : y k x 2⋯⋯ ① l 2 : y1 x2 ⋯⋯ ②k① ② 消 k 可得： x 2y 24即 P 的轨迹方程为 x 2 y 2 4 ； ⑵将参数方程转化为一般方程l 3 : x y 2 0⋯⋯ ③联立曲线 C 和 l 3x y2x2y24x3 22解得2y2x cos5 由sin 解得y即 M 的极半径是 5 ．23． [选修 4-5：不等式选讲 ]（10分）已知函数 f ( x) | x | | x | ．（ 1）求不等式 f ( x) 的解集；（ 2）若不等式 f ( x) x x m 的解集非空，求 m 的取值范围．3, x ≤ 1【解析】 ⑴ f x| x1| | x2| 可等价为 f x2x 1, 1x 2 .由 f x ≥ 1 可得：3,x ≥ 2①当 x ≤ 1 时显然不满足题意； ②当 1 x 2时， 2x 1≥1 ，解得 x ≥1 ；③当 x ≥ 2 时， f x 3 ≥ 1 恒成立 .综上， f x1的解集为 x | x ≥ 1 .⑵不等式 f x ≥ x 2x m 等价为 f xx 2x ≥ m ，令 g xf xx 2 x ，则 g x ≥ m 解集非空只需要g xmax ≥ m .x 2 x 3, x ≤ 1而 g xx 2 3 x 1, 1 x 2 .2x 3, x ≥ 2x①当 x ≤ 1 时， gxmaxg13 1 15 ；2②当 1 x 2 时， g xmaxg 333 3 1 5 ；222 4③当 x ≥ 2 时， g x maxg 22 22 3 1 .综上， g xmax5，故 m5 .44。

2017年全国统一高考数学试卷(理科)(新课标ⅲ)

2017年全国统一高考数学试卷（理科）（新课标Ⅲ）一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．（5分）（2017•新课标Ⅲ）已知集合A＝{（x，y）|x2+y2＝1}，B＝{（x，y）|y＝x}，则A ∩B中元素的个数为（）A．3B．2C．1D．02．（5分）（2017•新课标Ⅲ）设复数z满足（1+i）z＝2i，则|z|＝（）A．B．C．D．23．（5分）（2017•新课标Ⅲ）某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是（）A．月接待游客量逐月增加B．年接待游客量逐年增加C．各年的月接待游客量高峰期大致在7，8月D．各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳4．（5分）（2017•新课标Ⅲ）（x+y）（2x﹣y）5的展开式中的x3y3系数为（）A．﹣80B．﹣40C．40D．805．（5分）（2017•新课标Ⅲ）已知双曲线C：﹣＝1（a＞0，b＞0）的一条渐近线方程为y＝x，且与椭圆+＝1有公共焦点，则C的方程为（）A．﹣＝1B．﹣＝1C．﹣＝1D．﹣＝16．（5分）（2017•新课标Ⅲ）设函数f（x）＝cos（x+），则下列结论错误的是（）A．f（x）的一个周期为﹣2πB．y＝f（x）的图象关于直线x＝对称C．f（x+π）的一个零点为x＝D．f（x）在（，π）单调递减7．（5分）（2017•新课标Ⅲ）执行如图的程序框图，为使输出S的值小于91，则输入的正整数N的最小值为（）A．5B．4C．3D．28．（5分）（2017•新课标Ⅲ）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（）A．πB．C．D．9．（5分）（2017•新课标Ⅲ）等差数列{a n}的首项为1，公差不为0．若a2，a3，a6成等比数列，则{a n}前6项的和为（）A．﹣24B．﹣3C．3D．810．（5分）（2017•新课标Ⅲ）已知椭圆C：＝1（a＞b＞0）的左、右顶点分别为A1，A2，且以线段A1A2为直径的圆与直线bx﹣ay+2ab＝0相切，则C的离心率为（）A．B．C．D．11．（5分）（2017•新课标Ⅲ）已知函数f（x）＝x2﹣2x+a（e x﹣1+e﹣x+1）有唯一零点，则a ＝（）A．﹣B．C．D．112．（5分）（2017•新课标Ⅲ）在矩形ABCD中，AB＝1，AD＝2，动点P在以点C为圆心且与BD相切的圆上．若＝λ+μ，则λ+μ的最大值为（）A．3B．2C．D．2二、填空题:本题共4小题，每小题5分，共20分。

【数学】2017年高考真题——全国III卷(理)(解析版)

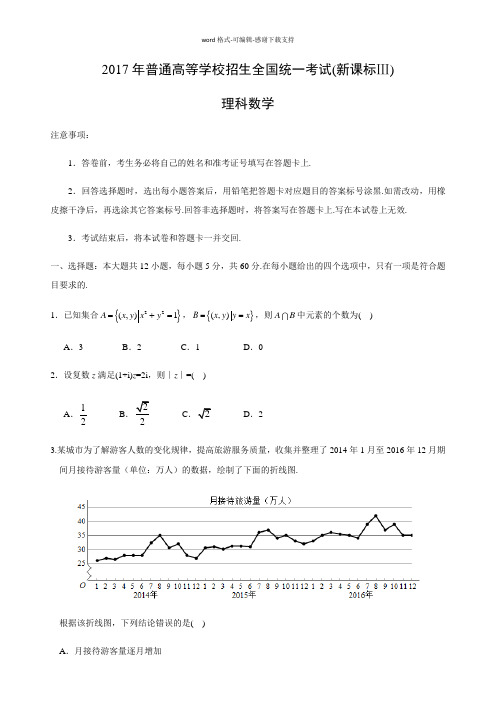
2017年普通高等学校招生全国统一考试(新课标Ⅲ)理科数学注意事项：1．答卷前，考生务必将自己的姓名和准考证号填写在答题卡上.2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其它答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.3．考试结束后，将本试卷和答题卡一并交回.一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合{}22(,)1=+=A x y x y ，{}(,)==B x y y x ，则A B 中元素的个数为( )A ．3B ．2C ．1D ．0 2．设复数z 满足(1+i)z =2i ，则∣z ∣=( )A ．12B ．22C ．2D ．23.某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图.根据该折线图，下列结论错误的是( ) A ．月接待游客量逐月增加B ．年接待游客量逐年增加C ．各年的月接待游客量高峰期大致在7,8月份D ．各年1月至6月的月接待游客量相对7月至12月，波动性更小，变化比较平稳 4. 5()(2)+-x y x y 的展开式中33x y 的系数为( ) A.-80 B.-40 C.40 D.805.已知双曲线C:22221x y a b -= (a ＞0,b ＞0)的一条渐近线方程为52y x =,且与椭圆 221123x y += 有公共焦点，则C 的方程为( ) A.221810x y -= B. 22145x y -= C. 22154x y -= D. 22143x y -= 6．设函数f (x )=cos(x +3π)，则下列结论错误的是( ) A ．f (x )的一个周期为−2π B ．y =f (x )的图像关于直线x =83π对称 C ．f (x +π)的一个零点为x =6π D ．f (x )在(2π,π)单调递减 7．执行下面的程序框图，为使输出S 的值小于91，则输入的正整数N的最小值为( )A ．5B ．4C ．3D ．28.已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( ) A.π B.3π4 C.π2 D.π49.等差数列{}n a 的首项为1，公差不为0.若a 2，a 3，a 6成等比数列，则{}n a 前6项的和为( ) A.-24 B.-3 C.3 D.810.已知椭圆C ：22221x y a b +=，（a >b >0）的左、右顶点分别为A 1，A 2，且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切，则C 的离心率为( )C.3D.1311.已知函数211()2()x x f x x x a ee --+=-++有唯一零点，则a =( )A.12-B.13C.12D.1 12. 在矩形ABCD 中，1AB =，2AD =，动点P 在以点C 为圆心且与BD 相切的圆上．若AP AB AD λμ=+，则λμ+的最大值为（）A.3C. D.2二、填空题：本题共4小题，每小题5分，共20分.13. 若x ，y 满足约束条件0,20,0,-⎧⎪+-⎨⎪⎩x y x y y ≥≤≥则34=-z x y 的最小值为________．14.设等比数列{}n a 满足121+=-a a ，133-=-a a ，则4=a ________．15.设函数10()20xx xf xx+≤⎧=⎨>⎩，，，，则满足1()()12f x f x+->的x的取值范围是_________.16.a，b为空间中两条互相垂直的直线，等腰直角三角形ABC的直角边AC所在直线与a，b都垂直，斜边AB以直线AC为旋转轴旋转，有下列结论：①当直线AB与a成60°角时，AB与b成30°角；②当直线AB与a成60°角时，AB与b成60°角；③直线AB与a所称角的最小值为45°；④直线AB与a所称角的最小值为60°；其中正确的是________.（填写所有正确结论的编号）三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.（一）必考题：60分.17.（12分）△ABC的内角A，B，C的对边分别为a，b，c，已知sin A cos A=0，a,b=2.（1）求c；（2）设D为BC边上一点，且AD⊥AC,求△ABD的面积.18.（12分）某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处学科#网理完.根据往年销售经验，每天需求量与当天最高气温（单位：℃）有关.如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间[20，25），需求量为300瓶；如果最高气温低于20，需求量为200瓶．为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：以最高气温位于各区间的频率代替最高气温位于该区间的概率.（1）求六月份这种酸奶一天的需求量X（单位：瓶）的分布列；（2）设六月份一天销售这种酸奶的利润为Y（单位：元），当六月份这种酸奶一天的进货量n（单位：瓶）为多少时，Y的数学期望达到最大值？19．（12分）如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．（1）证明：平面ACD ⊥平面ABD ；（2）过AC 的平面交BD 于点E ，若平面AEC 把四面体ABCD 分成体积相等的两部分，求二面角D –AE –C 的余弦值．20.（12分）已知抛物线C ：y 2=2x ，过点（2,0）的直线l 交C 与A ,B 两点，圆M 是以线段AB 为直径的圆. （1）证明：坐标原点O 在圆M 上；（2）设圆M 过点P （4，-2），求直线l 与圆M 的方程.21.（12分）已知函数()1ln f x x a x =--．（1）若()0f x ≥，求a 的值；（2）设m 为整数，且对于任意正整数n ，2111(1)(1)(1)222n m ，求m 的最小值．（二）选考题：共10分.请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分. 22．[选修4―4：坐标系与参数方程]（10分）在直角坐标系xOy 中，直线l 1的参数方程为2+,,x t y kt =⎧⎨=⎩（t 为参数），直线l 2的参数方程为2,,x m m m y k =-+⎧⎪⎨=⎪⎩（为参数）.设l 1与l 2的交点为P ，当k 变化时，P 的轨迹为曲线C . （1）写出C 的普通方程；（2）以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，设l 3：ρ(cos θ+sin θ， M 为l 3与C 的交点，求M 的极径.23.[选修4—5：不等式选讲]（10分）已知函数f （x ）=│x +1│–│x –2│. （1）求不等式f （x ）≥1的解集；（2）若不等式f （x ）≥x 2–x +m 的解集非空，求m 的取值范围.参考答案1.【答案】B 【解析】A 表示圆221x y +=上所有点的集合，B 表示直线y x =上所有点的集合，故A B表示两直线与圆的交点，由图可知交点的个数为2，即AB 元素的个数为22．【答案】C 【解析】由题，()()()2i 1i 2i 2i 2i 11i 1i 1i 2z -+====+++-，则22112z + 3．【答案】A 【解析】由题图可知，2014年8月到9月的月接待游客量在减少，则A 选项错误， 4．【答案】C 【解析】由二项式定理可得，原式展开中含33x y 的项为()()()()2332233355C 2C 240x x y y x y x y ⋅-+⋅-=，则33x y 的系数为40，故选C.5．【答案】B 【解析】∵双曲线的一条渐近线方程为5y =，则5b a =又∵椭圆221123x y +=与双曲线有公共焦点，易知3c =，则2229a b c +==②由①②解得2,5a b ==，则双曲线C 的方程为22145x y -=，故选B. 6．【答案】D 【解析】函数()πcos 3f x x ⎛⎫=+ ⎪⎝⎭的图象可由cos y x =向左平移π3个单位得到，如图可知，()f x 在π,π2⎛⎫⎪⎝⎭上先递减后递增，D 选项错误，故选D.7．【答案】D【解析】程序运行过程如下表所示：S Mt初始状态 0 100 1 第1次循环结束 100 10-2 第2次循环结束9013此时9091S =<首次满足条件，程序需在3t =时跳出循环，即2N =为满足条件的最小值，故选D.8．【答案】B 【解析】由题可知球心在圆柱体中心，圆柱体上下底面圆半径221312r ⎛⎫=-= ⎪⎝⎭则圆柱体体积23ππ4V r h ==，故选B.9．【答案】A 【解析】∵{}n a 为等差数列，且236,,a a a 成等比数列，设公差为d . 则2326a a a =⋅，即()()()211125a d a d a d +=++ 又∵11a =，代入上式可得220d d += 又∵0d ≠，则2d =-∴()61656561622422S a d ⨯⨯=+=⨯+⨯-=-，故选A. 10．【答案】A 【解析】∵以12A A 为直径为圆与直线20bx ay ab -+=相切，∴圆心到直线距离d 等于半径，∴222ab d a a b==+又∵0,0a b >>，则上式可化简为223a b = ∵222b ac =-，可得()2223a a c=-，即2223c a =∴63c e a ==，故选A 11．【答案】C【解析】因为f （x ）=x 2﹣2x +a （e x ﹣1+e﹣x +1）=﹣1+（x ﹣1）2+a （e x ﹣1+）=0，所以函数f （x ）有唯一零点等价于方程1﹣（x ﹣1）2=a （e x ﹣1+）有唯一解，等价于函数y =1﹣（x ﹣1）2的图象与y =a （e x ﹣1+）的图象只有一个交点．①当a =0时，f （x ）=x 2﹣2x ≥﹣1，此时有两个零点，矛盾；②当a ＜0时，由于y =1﹣（x ﹣1）2在（﹣∞，1）上递增、在（1，+∞）上递减，且y =a （e x ﹣1+）在（﹣∞，1）上递增、在（1，+∞）上递减，所以函数y =1﹣（x ﹣1）2的图象的最高点为A （1，1），y =a （e x ﹣1+）的图象的最高点为B （1，2a ），由于2a ＜0＜1，此时函数y =1﹣（x ﹣1）2的图象与y =a （e x ﹣1+）的图象有两个交点，矛盾；③当a ＞0时，由于y =1﹣（x ﹣1）2在（﹣∞，1）上递增、在（1，+∞）上递减，且y =a （e x ﹣1+）在（﹣∞，1）上递减、在（1，+∞）上递增，所以函数y =1﹣（x ﹣1）2的图象的最高点为A （1，1），y =a （e x ﹣1+）的图象的最低点为B （1，2a ），由题可知点A 与点B 重合时满足条件，即2a =1，即a =，符合条件；综上所述，a =，故选：C ． 12．【答案】A【解析】由题意，画出右图．设BD 与C 切于点E ，连接CE ．以A 为原点，AD 为x 轴正半轴，AB 为y 轴正半轴建立直角坐标系，则C 点坐标为(2,1)． ∵||1CD =，||2BC =． ∴22125BD =+=． ∵BD 切C 于点E ． ∴CE ⊥BD ．∴CE是Rt BCD△中斜边BD上的高．12||||22||||||BCDBC CDSECBD BD⋅⋅⋅====△即C∵P 在C上．∴P点的轨迹方程为224(2)(1)5-+-=x y．设P点坐标00(,)x y，可以设出P点坐标满足的参数方程如下：21xyθθ⎧=⎪⎪⎨⎪=⎪⎩而00(,)AP x y=，(0,1)AB =，(2,0)AD =．∵(0,1)(2,0)(2,)AP AB ADλμλμμλ=+=+=∴112xμθ==+，1yλθ==．两式相加得：112)2sin()3λμθθθϕθϕ+=+++=++=++≤(其中sinϕcosϕ=)当且仅当π2π2kθϕ=+-，k∈Z时，λμ+取得最大值3．二、填空题：（本题共4小题，每小题5分，共20分）13．【答案】1-【解析】由题，画出可行域如图：目标函数为34z x y =-，则直线344zy x =-纵截距越大，z 值越小．由图可知：z 在()1,1A 处取最小值，故min 31411z =⨯-⨯=-．14．【答案】8-【解析】{}n a 为等比数列，设公比为q ．121313a a a a +=-⎧⎨-=-⎩，即1121113a a q a a q +=-⎧⎪⎨-=-⎪⎩①②，显然1q ≠，10a ≠，②①得13q -=，即2q =-，代入①式可得11a =， ()3341128a a q ∴==⨯-=-．15．【答案】1,4⎛⎫-+∞ ⎪⎝⎭【解析】()1,02 ,0+⎧=⎨>⎩x x x f x x ≤，()112f x f x ⎛⎫+-> ⎪⎝⎭，即()112f x f x ⎛⎫->- ⎪⎝⎭由图象变换可画出12y f x ⎛⎫=- ⎪⎝⎭与()1y f x =-的图象如下：由图可知，满足()112f x f x ⎛⎫->- ⎪⎝⎭的解为1,4⎛⎫-+∞ ⎪⎝⎭.16．【答案】②③【解析】由题意知，a b AC 、、三条直线两两相互垂直，画出图形如图．不妨设图中所示正方体边长为1，故||1AC =，2AB =，斜边AB 以直线AC 为旋转轴旋转，则A 点保持不变，B 点的运动轨迹是以C 为圆心，1为半径的圆．以C 为坐标原点，以CD 为x 轴正方向，CB 为y 轴正方向， CA 为z 轴正方向建立空间直角坐标系．则(1,0,0)D ，(0,0,1)A ，直线a 的方向单位向量(0,1,0)=a ，||1=a ．B 点起始坐标为(0,1,0)，直线b 的方向单位向量(1,0,0)=b ，||1=b ．设B 点在运动过程中的坐标(cos ,sin ,0)B θθ'，其中θ为B C '与CD 的夹角，[0,2π)θ∈．那么'AB 在运动过程中的向量(cos ,sin ,1)AB θθ'=--，||2AB '=．设AB '与a 所成夹角为π[0,]2α∈，则(cos ,sin ,1)(0,1,0)22cos |sin |[0,]22a AB θθαθ--⋅==∈'．故ππ[,]42α∈，所以③正确，④错误．设AB '与b 所成夹角为π[0,]2β∈，cos (cos ,sin ,1)(1,0,0)|cos |2'⋅='-⋅='=βθθθAB b b AB b AB .当AB'与b 夹角为60︒时，即π3α=，sin 32πθα===． ∵22cos sin 1θθ+=，∴|cos |θ=∴1cos |cos |22βθ==． ∵π[0,]2β∈．∴π=3β，此时AB '与b 夹角为60︒． ∴②正确，①错误．三、解答题：（共70分．第17-20题为必考题，每个试题考生都必须作答．第22，23题为选考题，考生根据要求作答）（一）必考题：共60分．17．解:（1）由sin 0A A =得π2sin 03A ⎛⎫+= ⎪⎝⎭，即()ππ3A k k +=∈Z ，又()0,πA ∈， ∴ππ3A +=，得2π3A =.由余弦定理2222cos a b c bc A =+-⋅.又∵12,cos 2a b A ===-代入并整理得()2125c +=，故4c =.（2）∵2,4AC BC AB ===，由余弦定理222cos 2a b c C ab +-==∵AC AD ⊥，即ACD △为直角三角形，则cos AC CD C =⋅，得CD =由勾股定理AD 又2π3A =，则2πππ326DAB ∠=-=， 1πsin 26ABD S AD AB =⋅⋅=△18．解:(1)易知需求量x 可取200,300,500()21612003035P X +===⨯()3623003035P X ===⨯ ()257425003035P X ++===⨯.则分布列为：⑵①当200n ≤时：，此时max 400，当200n =时取到.②当200300n <≤时：()()4122002200255Y n n =⋅+⨯+-⋅-⎡⎤⎣⎦ 880026800555n n n -+=+=此时max 520Y =，当300n =时取到.③当300500n <≤时，()()()()12220022002300230022555Y n n n =⨯+-⋅-+⨯+-⋅-+⋅⋅⎡⎤⎡⎤⎣⎦⎣⎦ 320025n-=此时520Y <.④当500n ≥时，易知Y 一定小于③的情况.综上所述：当300n =时，Y 取到最大值为520.19．解:(1)取AC 中点为O ，连接BO ，DO ；ABC ∆为等边三角形∴BO AC ⊥ ∴AB BC =AB BC BD BDABD DBC =⎧⎪=⎨⎪∠=∠⎩∴∆≅∆ABD CBD . ∴AD CD =,即ACD ∆为等腰直角三角形， ADC ∠为直角又O 为底边AC 中点 ∴DO AC ⊥令AB a =，则AB AC BC BD a ====易得：22OD a =，32OB a = ∴222OD OB BD +=由勾股定理的逆定理可得2DOB π∠=即OD OB ⊥OD AC OD OB AC OB O AC ABC OB ABC⊥⎧⎪⊥⎪⎪=⎨⎪⊂⎪⊂⎪⎩平面平面OD ABC ∴⊥平面又∵OD ADC ⊂平面由面面垂直的判定定理可得ADC ABC ⊥平面平面 (2)由题意可知--=D ACE B ACE V V 即B ,D 到平面ACE 的距离相等即E 为BD 中点以O 为原点，OA 为x 轴正方向，OB 为y 轴正方向，OD 为z 轴正方向，设AC a =，建立空间直角坐标系，则()0,0,0O ，,0,02a A ⎛⎫ ⎪⎝⎭，0,0,2a D ⎛⎫ ⎪⎝⎭，30,,02B a ⎛⎫ ⎪ ⎪⎝⎭，30,,44a E a ⎛⎫ ⎪ ⎪⎝⎭ 易得：3,,244a a AE a ⎛⎫=- ⎪ ⎪⎝⎭，,0,22a a AD ⎛⎫=- ⎪⎝⎭，,0,02a OA ⎛⎫= ⎪⎝⎭ 设平面AED 的法向量为n 1，平面AEC 的法向量为n 2，则110⎧⋅=⎪⎨⋅=⎪⎩AE n AD n ，解得()13,1,3=n220⎧⋅=⎪⎨⋅=⎪⎩AE n OA n ，解得()20,1,3=-n 若二面角D AE C --为θ，易知θ为锐角，则12127cos 7⋅==⋅θn n n n20．解:(1)显然，当直线斜率为0时，直线与抛物线交于一点，不符合题意．设:2l x my =+，11(,)A x y ，22(,)B x y ，联立：222y xx my ⎧=⎨=+⎩得2240y my --=，2416m ∆=+恒大于0，122y y m +=，124y y =-． 1212OA OBx x y y ⋅=+ 12(2)(2)my my =++21212(1)2()4m y y m y y =++++24(1)2(2)4m m m =-+++0=∴OA OB ⊥，即O 在圆M 上． (2)若圆M 过点P ，则0AP BP ⋅= 1212(4)(4)(2)(2)0x x y y --+++= 1212(2)(2)(2)(2)0my my y y --+++=21212(1)(22)()80m y y m y y +--++= 化简得2210m m --=解得12m =-或1①当12m =-时，:240l x y +-=圆心为00(,)Q x y ，120122y y y +==-，0019224x y =-+=，半径||r OQ ==则圆229185:()()4216M x y -++=②当1m =时，:20l x y --=圆心为00(,)Q x y ， 12012y y y +==，0023x y =+=，半径||r OQ ==则圆22:(3)(1)10M x y -+-=21．解:(1) ()1ln f x x a x =--，0x >则()1a x af x x x-'=-=，且(1)0f = 当0a ≤时，()0f x '>，()f x 在()0+∞，上单调增，所以01x <<时，()0f x <，不满足题意；当0a >时，当0x a <<时，()0f x '<，则()f x 在(0,)a 上单调递减；当x a >时，()0f x '>，则()f x 在(,)a +∞上单调递增．①若1a <，()f x 在(,1)a 上单调递增∴当(,1)x a ∈时()(1)0f x f <=矛盾 ②若1a >，()f x 在(1,)a 上单调递减∴当(1,)x a ∈时()(1)0f x f <=矛盾③若1a =，()f x 在(0,1)上单调递减，在(1,)+∞上单调递增∴()(1)0f x f =≥满足题意综上所述1a =．(2)当1a =时()1ln 0f x x x =--≥即ln 1x x -≤则有ln(1)x x +≤当且仅当0x =时等号成立∴11ln(1)22k k+<，*k ∈N 一方面：221111111ln(1)ln(1)...ln(1)...112222222n n n ++++++<+++=-<，即2111(1)(1)...(1)e 222n +++<．另一方面：223111111135(1)(1)...(1)(1)(1)(1)222222264n +++>+++=>当3n ≥时，2111(1)(1)...(1)(2,e)222n +++∈∵*m ∈N ，2111(1)(1)...(1)222n m +++<，∴m 的最小值为3．22．解:(1)将参数方程转化为一般方程()1:2l y k x =- ……①()21:2l y x k =+ ……② ①⨯②消k 可得：224x y -=即P 的轨迹方程为224x y -=；(2)将参数方程转化为一般方程3:0l x y +-= ……③联立曲线C 和3l 2204x y x y ⎧+=⎪⎨-=⎪⎩解得2x y ⎧=⎪⎪⎨⎪=⎪⎩ 由cos sin x y ρθρθ=⎧⎨=⎩解得ρ=即M．23．解:(1)()|1||2|f x x x =+--可等价为()3,121,123,2--⎧⎪=--<<⎨⎪⎩x f x x x x ≤≥.由()1f x ≥可得：①当1-x ≤时显然不满足题意；②当12x -<<时，211-x ≥，解得1x ≥；③当2x ≥时，()31=f x ≥恒成立.综上，()1f x ≥的解集为{}|1x x ≥.(2)不等式()2-+f x x x m ≥等价为()2-+f x x x m ≥，令()()2g x f x x x =-+，则()g x m ≥解集非空只需要()max ⎡⎤⎣⎦g x m ≥.而()2223,131,123,2⎧-+--⎪=-+--<<⎨⎪-++⎩x x x g x x x x x x x ≤≥. ①当1-x ≤时，()()max 13115g x g =-=---=-⎡⎤⎣⎦； ②当12x -<<时，()2max 3335312224g x g ⎛⎫⎛⎫==-+⋅-=⎡⎤ ⎪ ⎪⎣⎦⎝⎭⎝⎭； ③当2x ≥时，()()2max 22231g x g ==-++=⎡⎤⎣⎦.综上，()max 54g x =⎡⎤⎣⎦，故54m ≤.。

2017高考数学全国卷3理(附参考答案及详解)

二填空题本大题共-小题每小题 " 分共 $# 分!把答案填在
题中横线上
,#0-*# !(!若 #- 满足约束条件+#/-0$)#则 ('(#0-- 的最小值
--*#
年普通高等学校招生全国统一考试数学理
2!*!
1
2
4
2'槡"2#
m
B+ *
'槡"2!
4h1!#"" .2(" '!*¢£-$(##%#$0(##%#
m B*".+"';!
4 mB*"'+#+"'2!
C
D
%
*
(

-#" +
022"
'!!
"# *!
$ % 3!5!
1
2
%
b
#U
-
/$#%'<9=
#.
(
* i j - "4$4&%#
为!!!!!
!-!设等比数列 !+* "满足 +! /+$ ' 0 !#+! 0+( ' 0 (#则
+-' ! ! ! ! !
! $ % !"!设函数,$#%'
#/!##)## 则满足 ,$#%/,
$# ##&##
#0
! $
&! 的 #
的取值范围是!!!!!

2017年云南省_全国统一高考数学试卷(理科)(新课标ⅲ)及解析

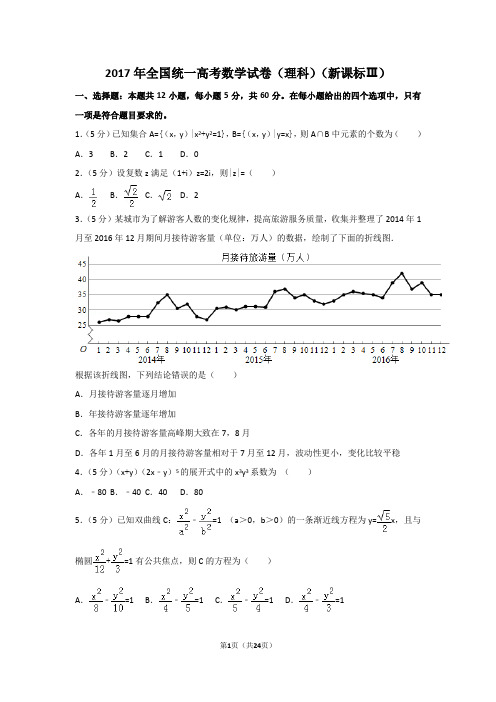
2017年全国统一高考数学试卷（理科）（新课标Ⅲ）一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．（5分）已知集合A={（x，y）|x2+y2=1}，B={（x，y）|y=x}，则A∩B中元素的个数为（）A．3 B．2 C．1 D．02．（5分）设复数z满足（1+i）z=2i，则|z|=（）A．B．C．D．23．（5分）某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是（）A．月接待游客量逐月增加B．年接待游客量逐年增加C．各年的月接待游客量高峰期大致在7，8月D．各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳4．（5分）（x+y）（2x﹣y）5的展开式中的x3y3系数为（）A．﹣80 B．﹣40 C．40 D．805．（5分）已知双曲线C：﹣=1 （a＞0，b＞0）的一条渐近线方程为y=x，且与椭圆+=1有公共焦点，则C的方程为（）A．﹣=1 B．﹣=1 C．﹣=1 D．﹣=16．（5分）设函数f（x）=cos（x+），则下列结论错误的是（）A．f（x）的一个周期为﹣2πB．y=f（x）的图象关于直线x=对称C．f（x+π）的一个零点为x=D．f（x）在（，π）单调递减7．（5分）执行如图的程序框图，为使输出S的值小于91，则输入的正整数N的最小值为（）A．5 B．4 C．3 D．28．（5分）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（）A．πB．C．D．9．（5分）等差数列{a n}的首项为1，公差不为0．若a2，a3，a6成等比数列，则{a n}前6项的和为（）A．﹣24 B．﹣3 C．3 D．810．（5分）已知椭圆C：=1（a＞b＞0）的左、右顶点分别为A1，A2，且以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切，则C的离心率为（）A．B．C．D．11．（5分）已知函数f（x）=x2﹣2x+a（e x﹣1+e﹣x+1）有唯一零点，则a=（）A．﹣B．C．D．112．（5分）在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上．若=λ+μ，则λ+μ的最大值为（）A．3 B．2C．D．2二、填空题:本题共4小题，每小题5分，共20分。

2017年全国统一高考数学试卷与解析word(理科)(新课标Ⅲ)

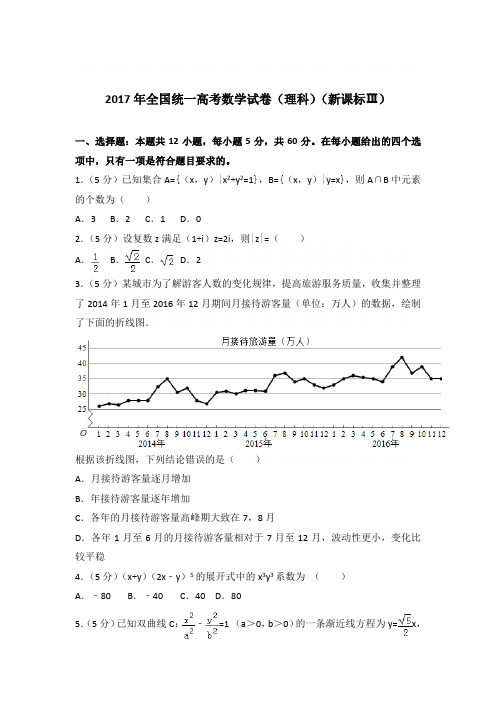
2017年全国统一高考数学试卷（理科）（新课标Ⅲ）一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

2017全国三卷理科数学高考真题及答案

2017年普通高等学校招生全国统一考试（新课标Ⅲ）理科数学一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合A ={}22(,)1x y x y +=│，B ={}(,)x y y x =│，则A B 中元素的个数为 A ．3B ．2C ．1D ．02．设复数z 满足(1+i)z =2i ，则∣z ∣= A ．12B ．22C ．2D ．23．某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是 A ．月接待游客量逐月增加 B ．年接待游客量逐年增加C ．各年的月接待游客量高峰期大致在7,8月份D ．各年1月至6月的月接待游客量相对7月至12月，波动性更小，变化比较平稳 4．(x +y )(2x -y )5的展开式中x 3y 3的系数为 A ．-80B ．-40C ．40D ．805．已知双曲线C ：22221x y a b -= (a ＞0,b ＞0)的一条渐近线方程为5y x =,且与椭圆221123x y +=有公共焦点，则C 的方程为A ．221810x y -= B ．22145x y -= C ．22154x y -= D ．22143x y -= 6．设函数f (x )=cos(x +3π)，则下列结论错误的是 A ．f (x )的一个周期为−2πB ．y =f (x )的图像关于直线x =83π对称 C ．f (x +π)的一个零点为x =6πD ．f (x )在(2π,π)单调递减 7．执行下面的程序框图，为使输出S 的值小于91，则输入的正整数N 的最小值为A ．5B ．4C ．3D ．28．已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为 A ．πB ．3π4C ．π2D ．π49．等差数列{}n a 的首项为1，公差不为0．若a 2，a 3，a 6成等比数列，则{}n a 前6项的和为 A ．-24B ．-3C ．3D ．810．已知椭圆C ：22221x y a b+=，（a >b >0）的左、右顶点分别为A 1，A 2，且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切，则C 的离心率为A 6B 3C ．23D ．1311．已知函数211()2()x x f x x x a ee --+=-++有唯一零点，则a =A．12-B．13C．12D．112．在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上．若AP=λAB+μAD，则λ+μ的最大值为A．3 B．CD．2二、填空题：本题共4小题，每小题5分，共20分。

2017年全国统一高考数学试卷(理科)(新课标ⅲ)

2017年全国统一高考数学试卷（理科）（新课标Ⅲ）一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

2017年全国统一高考真题数学试卷(理科)(新课标ⅲ)(含答案及解析)

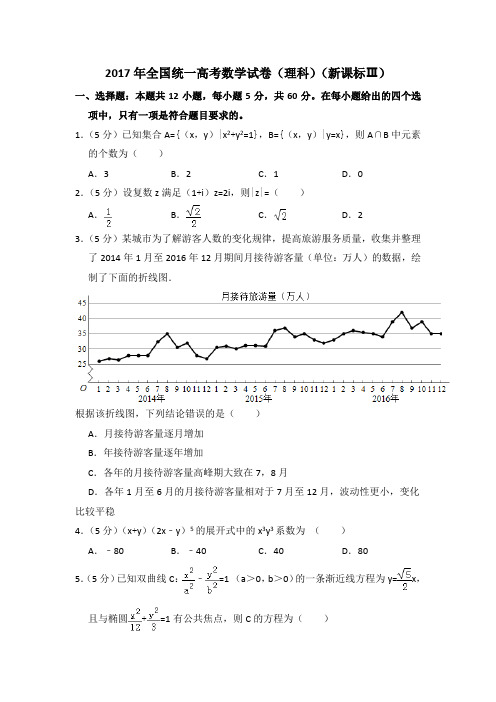
2017年全国统一高考数学试卷（理科）（新课标Ⅲ）一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．（5分）已知集合A={（x，y）|x2+y2=1}，B={（x，y）|y=x}，则A∩B中元素的个数为（）A．3B．2C．1D．02．（5分）设复数z满足（1+i）z=2i，则|z|=（）A．B．C．D．23．（5分）某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是（）A．月接待游客量逐月增加B．年接待游客量逐年增加C．各年的月接待游客量高峰期大致在7，8月D．各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳4．（5分）（x+y）（2x﹣y）5的展开式中的x3y3系数为（）A．﹣80B．﹣40C．40D．805．（5分）已知双曲线C：﹣=1 （a＞0，b＞0）的一条渐近线方程为y=x，且与椭圆+=1有公共焦点，则C的方程为（）A．﹣=1B．﹣=1C．﹣=1D．﹣=1 6．（5分）设函数f（x）=cos（x+），则下列结论错误的是（）A．f（x）的一个周期为﹣2πB．y=f（x）的图象关于直线x=对称C．f（x+π）的一个零点为x=D．f（x）在（，π）单调递减7．（5分）执行如图的程序框图，为使输出S的值小于91，则输入的正整数N 的最小值为（）A．5B．4C．3D．28．（5分）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（）A．πB．C．D．9．（5分）等差数列{a n}的首项为1，公差不为0．若a2，a3，a6成等比数列，则{a n}前6项的和为（）A．﹣24B．﹣3C．3D．810．（5分）已知椭圆C：=1（a＞b＞0）的左、右顶点分别为A1，A2，且以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切，则C的离心率为（）A．B．C．D．11．（5分）已知函数f（x）=x2﹣2x+a（e x﹣1+e﹣x+1）有唯一零点，则a=（）A．﹣B．C．D．112．（5分）在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上．若=λ+μ，则λ+μ的最大值为（）A．3B．2C．D．2二、填空题:本题共4小题，每小题5分，共20分。

2017年全国统一高考数学试卷(理科)(新课标ⅲ)

2017年全国统一高考数学试卷（理科）（新课标Ⅲ）一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

2017年全国统一高考数学试卷(理科)(新课标ⅲ)

2017年全国统一高考数学试卷（理科）（新课标Ⅲ）一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．（5分）已知集合A={（x，y）|x2+y2=1}，B={（x，y）|y=x}，则A∩B中元素的个数为（）A．3 B．2 C．1 D．02．（5分）设复数z满足（1+i）z=2i，则|z|=（）A． B． C． D．23．（5分）某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是（）A．月接待游客量逐月增加B．年接待游客量逐年增加C．各年的月接待游客量高峰期大致在7，8月D．各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳4．（5分）（x+y）（2x﹣y）5的展开式中的x3y3系数为（）A．﹣80 B．﹣40 C．40 D．805．（5分）已知双曲线C：﹣=1 （a＞0，b＞0）的一条渐近线方程为y=x，且与椭圆+=1有公共焦点，则C的方程为（）A．﹣=1 B．﹣=1 C．﹣=1 D．﹣=16．（5分）设函数f（x）=cos（x+），则下列结论错误的是（）A．f（x）的一个周期为﹣2πB．y=f（x）的图象关于直线x=对称C．f（x+π）的一个零点为x=D．f（x）在（，π）单调递减7．（5分）执行如图的程序框图，为使输出S的值小于91，则输入的正整数N 的最小值为（）A．5 B．4 C．3 D．28．（5分）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（）A．πB． C． D．9．（5分）等差数列{a n}的首项为1，公差不为0．若a2，a3，a6成等比数列，则{a n}前6项的和为（）A．﹣24 B．﹣3 C．3 D．810．（5分）已知椭圆C：=1（a＞b＞0）的左、右顶点分别为A1，A2，且以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切，则C的离心率为（）A． B． C． D．11．（5分）已知函数f（x）=x2﹣2x+a（e x﹣1+e﹣x+1）有唯一零点，则a=（）A．﹣B． C． D．112．（5分）在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上．若=λ+μ，则λ+μ的最大值为（）A．3 B．2 C． D．2二、填空题:本题共4小题，每小题5分，共20分。

【深度解析高考真题】2017年全国统一高考数学试卷(理科)(新课标ⅲ)

1.2.3.2017年全国统一高考数学试卷（理科）、选择题：本题共12小题，每小题5分，共60分。

项中，只有一项是符合题目要求的。

（X, y）|x2+y2=1｝，B=（（x，y）（5分）已知集合A=｛的个数为（）A. 3 B.C. 1（新课标m）在每小题给出的四个选| y=x｝，贝U An B中元素D. 0(1+i) z=2i,则|z|=(2（5分）设复数z满足A-寺（5分）某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理B.D. 2了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘根据该折线图，下列结论错误的是（)A.月接待游客量逐月增加B.年接待游客量逐年增加C. 各年的月接待游客量高峰期大致在7, 8月D. 各年1月至6月的月接待游客量相对于7月至12 月, 比较平稳波动性更小，变化4. (5 分)(x+y) （2x- y）5的展开式中的x3y3系数为（A.- 80B.- 40C. 40D. 805. （5分）已知双曲线C: qa孑-话=1 （a>0, b>0）的一条渐近线方程为2' 2且与椭圆号=1有公共焦点，则C的方程为（f （X ）在（卫，n ）单调递减 27. （5分）执行如图的程序框图，为使输出 S 的值小于91,8 （5分）已知圆柱的高为1，它的两个底面的圆周在直径为9. （5分）等差数列｛a n ｝的首项为1,公差不为0.若82, a 3. ｛a n ｝前6项的和为（）10. （5分）已知椭圆C:弓+話=1 （a >b >0）的左、右顶点分别为 A 1, A 2,且=1 2 2 B .丄-匚=1 2 2C 亠 Z =1D . 22 y To'45 5 443=1)6. （5分）设函数f （X ）=cos （x ^-），贝U 下列结论错误的是（ f （X ）的一个周期为-2ny=f （X ）的图象关于直线X 需匚对称■J f （X+ n ）的一个零点为x=^ 6A .B .C. A .- 24 B .- 3 C. 3D . 8 则输入的正整数NC. 3 D . 2D . 2的同一个球的球面上，则该圆柱的体积为（ B .晋A . nr 开Dpa 6成等比数列，则的最小值为（）以线段A 1A 2为直径的圆与直线bx -ay+2ab=0相切，则C 的离心率为（ A .逅B.逅C.亚33311. （5 分）已知函数 f （x ） =x 2 - 2x+a （e x -1+e -x+1）有唯一零点，贝U a=（12. （5分）在矩形ABCD 中，AB=1, AD=2,动点P 在以点的圆上.若忑=遍+应5,贝U 廿卩的最大值为（）二、填空题：本题共4小题，每小题5分，共20分。

2017年全国统一高考数学试卷(理科)(新课标Ⅲ)

2017年全国统一高考数学试卷（理科）（新课标Ⅲ）一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．(★)已知集合A={（x，y）|x 2+y 2=1}，B={（x，y）|y=x}，则A∩B中元素的个数为（）A．3 B．2 C．1 D．02．(★)设复数z满足（1+i）z=2i，则|z|=（）A． B． C． D．23．(★)某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是（）A．月接待游客量逐月增加B．年接待游客量逐年增加C．各年的月接待游客量高峰期大致在7，8月D．各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳4．(★)（x+y）（2x-y）5的展开式中的x 3y 3系数为（）A．-80 B．-40 C．40 D．805．(★★)已知双曲线C：- =1 （a＞0，b＞0）的一条渐近线方程为y= x，且与椭圆+ =1有公共焦点，则C的方程为（）A．-=1 B．-=1 C．-=1 D．-=16．(★★)设函数f（x）=cos（x+ ），则下列结论错误的是（）A．f（x）的一个周期为-2πB．y=f（x）的图象关于直线x=对称C．f（x+π）的一个零点为x=D．f（x）在（，π）单调递减7．(★★)执行如图的程序框图，为使输出S的值小于91，则输入的正整数N的最小值为（）A．5 B．4 C．3 D．28．(★★)已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（）A．π B． C． D．9．(★)等差数列{a n}的首项为1，公差不为0．若a 2，a 3，a 6成等比数列，则{a n}前6项的和为（）A．-24 B．-3 C．3 D．810．(★★)已知椭圆C：=1（a＞b＞0）的左、右顶点分别为A 1，A 2，且以线段A 1A 2为直径的圆与直线bx-ay+2ab=0相切，则C的离心率为（）A． B． C． D．11．(★★★)已知函数f（x）=x 2-2x+a（e x-1+e -x+1）有唯一零点，则a=（）A．- B． C． D．112．(★★)在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上．若=λ+μ，则λ+μ的最大值为（）A．3 B．2 C． D．2二、填空题:本题共4小题，每小题5分，共20分。

2017年高考新课标3理科数学真题及答案详解

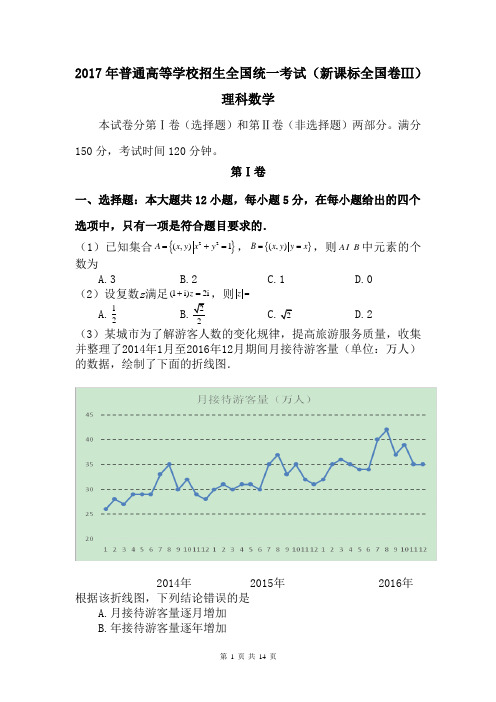
2017年普通高等学校招生全国统一考试（新课标全国卷Ⅲ）理科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

满分150分，考试时间120分钟。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．（1）已知集合{}22(,)1A x y x y =+=，{}(,)B x y y x ==，则A B 中元素的个数为A.3B.2C.1D.0 （2）设复数z 满足(1i)2i z +=，则z =A.12 D.2（3）某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．2014年 2015年 2016年根据该折线图，下列结论错误的是A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7，8月D.各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳（4）5()(2)x y x y +-的展开式中33x y 的系数为A.-80B.-40C.40D.80（5）已知双曲线22221x y C a b-=：（0a >，0b >）的一条渐近线方程为y x =，且与椭圆221123x y+=有公共焦点．则C 的方程为A.221810x y -=B.22145x y -= C.22154x y -= D.22143x y -= （6）设函数π()cos()3f x x =+，则下列结论错误的是 A.()f x 的一个周期为2π-B.()y f x =的图像关于直线8π3x =对称 C.()f x π+的一个零点为π6x = D.()f x 在π(,π)2单调递减（7）执行右图的程序框图，为使输出S 的值小于91，则输入的正整数N 的最小值为 A ．5 B ．4 C ．3 D ．2（8）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为A.πB.3π4 C.π２ D.π4 （9）等差数列{}n a 的首项为1，公差不为0．若2a ，3a ，6a 成等比数列，则{}n a 前6项的和为A.-24B.-3C.3D.8（10）已知椭圆2222:1x y C a b+=（0a b >>）的左、右顶点分别为1A ，2A ，且以线段1A 2A 为直径的圆与直线20bx ay ab -+=相切，则C 的离心率为D.13（11）已知函数211()2(e e )x x f x x x a --+=-++有唯一零点，则a = A.-12 B.13 C.12 D.1（12）在矩形ABCD 中，1AB =，2AD =，动点P 在以点C 为圆心且与BD 相切的圆上．若AP AB AD λμ=+，则λμ+的最大值为A.3B.D.2第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分. （13）若x ，y 满足约束条件0,20,0,-⎧⎪+-⎨⎪⎩x y x y y ≥≤≥则34z x y =-的最小值为________．（14）设等比数列{}n a 满足121a a +=-，133a a -=-，则4a =________．（15）设函数1,0,()2,0,+⎧=⎨>⎩x x x f x x ≤则满足1()()12f x f x +->的x 的取值范围是________．（16）a ，b 为空间中两条互相垂直的直线，等腰直角三角形ABC 的直角边AC 所在直线与a ，b 都垂直，斜边AB 以直线AC 为旋转轴旋转，有下列结论：①当直线AB 与a 成60︒角时，AB 与b 成30︒角； ②当直线AB 与a 成60︒角时，AB 与b 成60︒角； ③直线AB 与a 所成角的最小值为45︒； ④直线AB 与a 所成角的最大值为60︒．其中正确的是________（填写所有正确结论的编号）三、解答题：共70分．解答应写出文字说明、解答过程或演算步骤. （一）必考题：共60分．（17）（12分） ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c ，已知sin 0A A +=，a =，2b =．（1）求c ；（2）设D 为BC 边上一点，且AD AC ⊥，求ABD △的面积．某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完．根据往年销售经验，每天需求量与当天最高气温（单位：℃）有关．如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间[)，，需求量为300瓶；如果最高气温低于20，需求量为200瓶，2025为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数（1）求六月份这种酸奶一天的需求量X（单位：瓶）的分布列；（2）设六月份一天销售这种酸奶的利润为Y（单位：元）．当六月份这种酸奶一天的进货量n（单位：瓶）为多少时，Y的数学期望达到最大值？如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形．∠ABD=∠CBD，AB BD=．（1）证明：平面ACD⊥平面ABC；（2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分．求二面角D AE C--的余弦值．DAB CE已知抛物线2:2=，过点（2，0）的直线l交C于A，B两点，圆M是C y x以线段AB为直径的圆．（1）证明：坐标原点O在圆M上；（2）设圆M过点P（4，2-），求直线l与圆M的方程．已知函数()1ln f x x a x =--．（1）若()0f x ≥，求a 的值；（2）设m 为整数，且对于任意正整数n ，2111(1)(1)...(1)222n m+++<，求m 的最小值．（二）选做题：共10分。

2017年全国统一高考新课标版Ⅲ卷全国3卷理科数学试卷及参考答案与解析

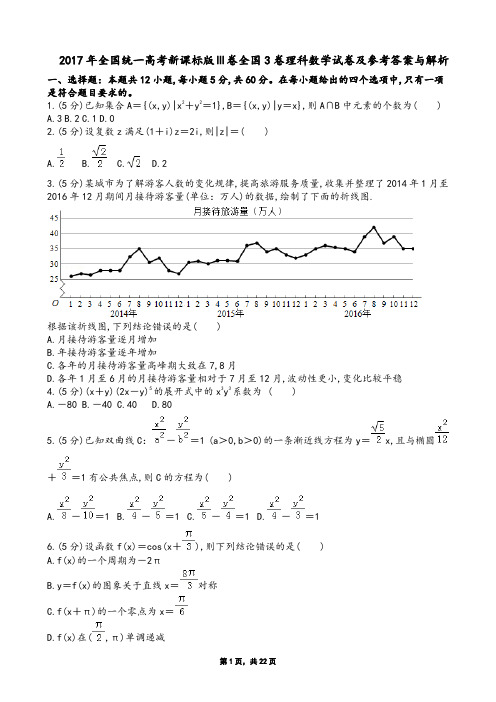
2017年全国统一高考新课标版Ⅲ卷全国3卷理科数学试卷及参考答案与解析一、选择题：本题共12小题,每小题5分,共60分。

在每小题给出的四个选项中,只有一项是符合题目要求的。

1.(5分)已知集合A＝{(x,y)|x2＋y2＝1},B＝{(x,y)|y＝x},则A∩B中元素的个数为( )A.3B.2C.1D.02.(5分)设复数z满足(1＋i)z＝2i,则|z|＝( )A. B. C. D.23.(5分)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位：万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳4.(5分)(x＋y)(2x－y)5的展开式中的x3y3系数为 ( )A.－80B.－40C.40D.805.(5分)已知双曲线C：－＝1 (a＞0,b＞0)的一条渐近线方程为y＝x,且与椭圆＋＝1有公共焦点,则C的方程为( )A.－＝1B.－＝1C.－＝1D.－＝16.(5分)设函数f(x)＝cos(x＋),则下列结论错误的是( )A.f(x)的一个周期为－2πB.y＝f(x)的图象关于直线x＝对称C.f(x＋π)的一个零点为x＝D.f(x)在(,π)单调递减7.(5分)执行如图的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为( )A.5B.4C.3D.28.(5分)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A.πB.C.D.9.(5分)等差数列{an }的首项为1,公差不为0.若a2,a3,a6成等比数列,则{an}前6项的和为( )A.－24B.－3C.3D.810.(5分)已知椭圆C：＝1(a＞b＞0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bx－ay＋2ab＝0相切,则C的离心率为( )A. B. C. D.11.(5分)已知函数f(x)＝x2－2x＋a(e x－1＋e－x＋1)有唯一零点,则a＝( )A.－B.C.D.112.(5分)在矩形ABCD中,AB＝1,AD＝2,动点P在以点C为圆心且与BD相切的圆上.若＝λ＋μ,则λ＋μ的最大值为( )A.3B.2C.D.2二、填空题:本题共4小题,每小题5分,共20分。

2017全国三卷理科数学高考真题及答案

2017年普通高等学校招生全国统一考试（新课标Ⅲ）理科数学一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合A ={}22(,)1x y x y +=│，B ={}(,)x y y x =│，则A B 中元素的个数为A ．3B ．2C ．1D ．02．设复数z 满足(1+i)z =2i ，则∣z ∣= A ．12B ．22C ．2D ．23．某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是 A ．月接待游客量逐月增加 B ．年接待游客量逐年增加C ．各年的月接待游客量高峰期大致在7,8月份D ．各年1月至6月的月接待游客量相对7月至12月，波动性更小，变化比较平稳 4．(x +y )(2x -y )5的展开式中x 3y 3的系数为A ．-80B ．-40C ．40D ．805．已知双曲线C ：22221x y a b -= (a ＞0,b ＞0)的一条渐近线方程为52y x =,且与椭圆221123x y +=有公共焦点，则C 的方程为A ．221810x y -= B ．22145x y -= C ．22154x y -= D ．22143x y -= 6．设函数f (x )=cos(x +3π)，则下列结论错误的是 A ．f (x )的一个周期为−2πB ．y =f (x )的图像关于直线x =83π对称 C ．f (x +π)的一个零点为x =6π D ．f (x )在(2π,π)单调递减 7．执行下面的程序框图，为使输出S 的值小于91，则输入的正整数N 的最小值为A ．5B ．4C ．3D ．28．已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为 A ．πB ．3π4C ．π2D ．π49．等差数列{}n a 的首项为1，公差不为0．若a 2，a 3，a 6成等比数列，则{}n a 前6项的和为A ．-24B ．-3C ．3D ．810．已知椭圆C ：22221x y a b+=，（a >b >0）的左、右顶点分别为A 1，A 2，且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切，则C 的离心率为A ．63B ．33C ．23D ．1311．已知函数211()2()x x f x x x a ee --+=-++有唯一零点，则a =A．12-B．13C．12D．112．在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上．若AP=λAB+μAD，则λ+μ的最大值为A．3 B．CD．2二、填空题：本题共4小题，每小题5分，共20分。

2017年高考理科数学全国3卷(附答案)

学校：____________________ _______年_______班姓名：____________________ 学号：________ - - - - - - - - 密封线 - - - - - - - - - 密封线 - - - - - - - - -绝密★启用前2017年普通高等学校招生全国统一考试理科数学全国III 卷（全卷共11页）(适用地区：云南、广西、贵州、四川)注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号，回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答案卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分。

在每个小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合A ={}22(,)1x y x y +=│，B ={}(,)x y y x =│，则A B 中元素的个数为 A ．3B ．2C ．1D ．02．设复数z 满足(1+i)z =2i ，则∣z ∣=A ．12B ．22C ．2D ．23．某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是A ．月接待游客量逐月增加B ．年接待游客量逐年增加C ．各年的月接待游客量高峰期大致在7,8月份D ．各年1月至6月的月接待游客量相对7月至12月，波动性更小，变化比较平稳4．(x +y )(2x -y )5的展开式中x 3y 3的系数为 A ．-80 B ．-40 C ．40D ．805．已知双曲线C ：22221x y a b -= (a ＞0,b ＞0)的一条渐近线方程为y x =,且与椭圆221123x y +=有公共焦点，则C 的方程为 A ．221810x y -=B ．22145x y -=C ．22154x y -=D ．22143x y -= 6．设函数f (x )=cos(x +3π)，则下列结论错误的是 A ．f (x )的一个周期为−2πB ．y =f (x )的图像关于直线x =83π对称 C ．f (x +π)的一个零点为x =6πD ．f (x )在(2π,π)单调递减 7．执行下面的程序框图，为使输出S 的值小于91，则输入的正整数N 的最小值为A ．5B ．4C ．3D ．28．已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为 A ．πB ．3π4C ．π2D ．π49．等差数列{}n a 的首项为1，公差不为0．若a 2，a 3，a 6成等比数列，则{}n a 前6项的和为 A ．-24B ．-3C ．3D ．810．已知椭圆C ：22221x ya b+=，（a >b >0）的左、右顶点分别为A 1，A 2，且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切，则C 的离心率为ABC．3D ．1311．已知函数211()2()x x f x x x a ee --+=-++有唯一零点，则a =A ．12-B ．13C ．12D ．112．在矩形ABCD 中，AB=1，AD=2，动点P 在以点C 为圆心且与BD 相切的圆上．若AP =λ AB +μAD ，则λ+μ的最大值为 A ．3B ．CD ．2二、填空题：本题共4小题，每小题5分，共20分。