《三角函数的有关计算》直角三角形的边角关系PPT课件四

合集下载

1.2 30度,45度,60度角的三角函数值课件4--

2 2
3 sin A 5
4 cos A 5
A
4 ┌ C (1)
3
3 3 7 tan A 7 7 3 7 sin A cos A 4 4
4 A (2)
3
┌ C
回顾与思考 1
锐角三角函数定义
直角三角形中边与角的关系: 锐角三角函数.
在直角三角形中,若一个锐角确定,那么这个角的对边,邻边和斜边之间的比值也随之确定.
BБайду номын сангаас
┌
C
D
●
2.5
2.某商场有一自动 0 扶梯,其倾斜角为30 , 高为7m,扶梯的长度是多少?
（ 1 ）计算： sin 30 cos 30
2 o 2 0
B
c
sin 2 45o cos2 450 sin 2 60o cos2 600 A
2 2
a
b ┌ C
(2)猜想：对于锐角 A， sin A cos A ？
(2) sin2600+cos2600-tan450
3 1 1 2 2
2 2
0.
3 1 1 4 4
6 随堂练习P12
计算:
(1)sin600-cos450; (2)cos600+tan600;
2 0 0 0 3. sin 45 3 sin 60 2 cos45 . 2
九年级数学(下)第一章直角三角形的边角关系
0 0 0 2.30 ,45 ,60 角的三角函数值(1)
1.如图,根据图(1)求∠A的三角函数值. 解：根据勾股定理： AB 3 4 5 B
2 2
3 tan A 4

九年级数学下册第1章直角三角形的边角关系230°,45°,60°角的三角函数值课件(新版)北师大版

◆知识导航 ◆典例导学 ◆反馈演练（ ◎第一阶 ◎第二阶 ◎第三阶）
◆知识导航 ◆典例导学 ◆反馈演练（ ◎第一阶 ◎第二阶 ◎第三阶）
◆知识导航 ◆典例导学 ◆反馈演练（ ◎第一阶 ◎第二阶 ◎第三阶）
◆知识导航 ◆典例导学 ◆反馈演练（ ◎第一阶 ◎第二阶 ◎第三阶）
◆知识导航 ◆典例导学 ◆反馈演练（ ◎第一阶 ◎第二阶 ◎第三阶）
◆知识导航 ◆典例导学 ◆反馈演练（ ◎第一阶 ◎第二阶 ◎第三阶）
◆知识导航 ◆典例导学 ◆反馈演练（ ◎第一阶 ◎第二阶 ◎第三阶）
◆知识导航 ◆典例导学 ◆反馈演练（ ◎第一阶 ◎第二阶 ◎第三阶）
◆知识导航 ◆典例导学 ◆反馈演练（ ◎第一阶 ◎第二阶 ◎第三阶）
◆知识导航 ◆典例导学 ◆反馈演练（ ◎第一阶 ◎第二阶 ◎第三阶）
◆知识导航 ◆典例导学 ◆反馈演练（ ◎第一阶 ◎第二阶 ◎第三阶）
◆知识导航 ◆典例导学 ◆反馈演练（ ◎第一阶 ◎第二阶 ◎第三阶）
◆知识导航 ◆典例导学 ◆反馈演练（ ◎第一阶 ◎第二阶 ◎第三阶）
◆知识导航 ◆典例导学 ◆反馈演练（ ◎第一阶 ◎第二阶 ◎第三阶）
◆知识导航 ◆典例导学 ◆反馈演练（ ◎第一阶 ◎第二阶 ◎第三阶）
◆知识导航 ◆典例导学 ◆反馈演练（ ◎第一阶 ◎第二阶 ◎第三阶）
◆知识导航 ◆典例导学 ◆反馈演练（ ◎第一阶 ◎第二阶 ◎第三阶）
◆知识导航 ◆典例导学 ◆反馈演练（ ◎第一阶 ◎第二阶 ◎第三阶）
◆知识导航 ◆典例导学 ◆反馈演练（ ◎第一阶 ◎第二阶 ◎第三阶）
◆知识导航 ◆典例导学 ◆反馈演练（ ◎第一阶 ◎第二阶 ◎第三阶）

新北师大版九年级数学下册《三角函数的计算》优质ppt教学课件

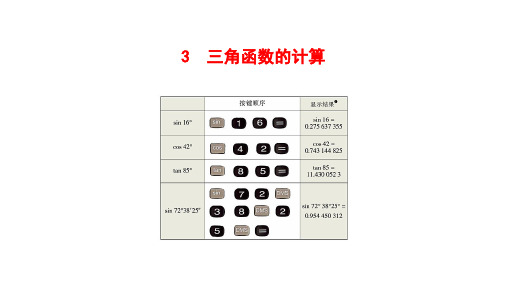
上表的显示结果是以“度”为单位的，再按 ˚ ′ ″ 键即可显示以“度、分、秒”为单位的结果.
根据上述方法你能求出问题1中∠A的大小吗？
sin A = 1 = 0.25. 按键顺序和显示结果为
4
SHIFT sin 0 · 2 5 = 14.477 512 19°
再按 ° ′ ″ 键可显示14˚28′39″，所以∠A=14˚28′39″.
正弦值随着角度的增大（或减小）而增大（或减小）；余弦值随着角度的增大（或减小）而减小（或增大）；正切值随着角度的增大（或减小）而增大（或减小）.
知识点1 利用计算器求锐角三角函数值
1.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( D )
D 39°
E
45°
C
A
【解析】（1）由题意，AC＝AB＝610 米.
（2）DE＝AC＝610米，
在Rt△BDE中，tan∠BDE＝ BE ，
DE
故BE＝DEtan39°．因为CD＝AE，
所以CD＝AB－DE·tan 39°
＝610－610×tan 39°≈116（米）. 答：大楼的高度CD约为116 米．
B．sin65°54′-sin35°54′=sin30°
C．2sin15°30′=sin31°
D．sin72°18′-sin12°18′=sin47°42′
•2. 已知sin α＝1 ，求α，若用科学计算器计算且结果以“度、分、秒
2
”为单位，最后按键(D )
•A．AC/ON
B. SHIFT
C．MODE
(4)sin18°＋cos55°－tan59°≈－0.7817.

北师大版九年级数学下册《三角函数的应用》精品课件PPT

都来当个小专家！
A
B 咋办
2 如图,水库大坝的截面是梯形
ABCD,坝顶AD=6m,坡长CD=8m.坡底
D
BC=30m,∠ADC=1350. (1)求坡角∠ABC的大小;
(2)如果坝长100m,那么修建这个 C 大坝共需多少土石方(结果精确到
0.01m3 ).
先构造直角三角形!
2020年北师大版九年级数学下册1.5《三角函数的应用》课件（共 16张pp t）
1 如图，有一斜坡AB长40m，坡顶离地面的
高度为20m,求此斜坡的倾斜角. 2.有一建筑物,在地面上A点测得其顶点 A
C的仰角为300,向建筑物前进50m至B处,又 A
测得C的仰角为450,求该建筑物的高度(结
果精确到0.1m).
B
3. 如图,燕尾槽的横断面是一个等腰梯形,其中燕尾角∠B=550,外口宽AD=180mm, 燕尾槽的尝试是70mm,求它的里口宽BC(结果精确到1mm).
北师大版九年级数学下册 2020年北师大版九年级数学下册1.5《三角函数的应用》课件（共16张ppt）
2020年北师大版九年级数学下册1.5《三角函数的应用》课件（共 16张pp t）
2020年北师大版九年级数学下册1.5《三角函数的应用》课件（共 16张pp t）
直角三角形的边角关系
看我露一手
解:要知道货轮继续向东航行途中有无触礁的危险,只
要过点A作AD⊥BC的延长线于点D,如果AD>10海里,则无
触礁的危险.根据题意可知,∠BAD=550,∠CAD=250,BC=
20海里.设AD=x,则
北
A
tan 550 BD , tan 250 CD ,

直角三角形复习课件

面积的多种计算方法
除了基本的面积公式外，还可以通过分割法、补形法等技巧来计算面积。
利用相似三角形进行计算
在某些情况下，可以利用相似三角形的性质来简化计算过程。
05
直角三角形在实际生活中的应用
测量中的应用
确定物体的高度
通过测量影子的长度，利用相似三角形的性质，可以计算出物体的高度。
计算距离
在航海、航空和地形测量中，利用直角三角形可以计算出两点之间的距离。
THANKS
感谢观看
建筑中的应用
建筑设计
在建筑设计中，直角三角形常被用于确定建筑物的比例和稳定性。
结构分析
在建筑结构分析中，利用直角三角形可以计算出结构的承载能力和稳定性。
其他应用
机械制造
在机械制造中，直角三角形被广泛应用于各种机构的设计和制造中，如齿轮、链条等。
VS
物理学
在物理学中，直角三角形被广泛应用于力的合成与分解、速度和加速度的计算等。
毕达哥拉斯定理
在直角三角形中，斜边的平方等于两直角边的平方和。
角平分线定理
在直角三角形中，角平分线将直角分为两个相等的角。
射影定理
在直角三角形中，直角边的长度等于斜边与其上高线的乘积。
判定依据
根据定义
根据角边角法
如果一个三角形有一个角为90度，则它是直角三角形。
如果两个角和它们所对的边分别相等，则它是直角三角形。
03
直角三角形的判定
判定方法
01
02
03
定义法
根据直角三角形的定义，一个三角形如果有一个角为90度，则它是直角三角形。
勾股定理法
如果一个三角形的三边满足勾股定理，即最长边的平方等于其他两边的平方和，则它是直角三角形。

解直角三角形完整版PPT课件

余弦或正切函数计算得出。
已知一边和一角求另一边
02
在直角三角形中，已知一边长和一个锐角大小可以求出另一边
长，通过正弦、余弦或正切函数计算得出。
解直角三角形的实际应用
03
例如测量建筑物高度、计算航海距离等。
三角函数在实际问题中应用
测量问题
在测量问题中，可以利用三角函数计算高度、距离等未知量。例如，利用正切函数可以计算山的高度或者河的宽度。
直角三角形重要定理
勾股定理
如上所述，勾股定理描述了直角三角形三边之间的数量关系。
射影定理
相似三角形判定定理
若两个直角三角形的对应角相等，则这两个直角三角形相似。根据此定理，可以推导出一些重要的直角三角形性质和定理。
射影定理涉及直角三角形中斜边上的高与斜边及两直角边之间的数量关系。
02
三角函数在解直角三角形中应用
• 性质：正弦、余弦函数值域为[-1,1]，正切函数值域为R；正弦、余弦函数在第一象限为正，第二象限正弦为正、余弦为负，第三象限正弦、余弦都为负，第四象限余弦为正、正弦为负；正切函数在第一、三象限为正，第二、四象限为负。
利用三角函数求边长和角度
已知两边求角度
01
在直角三角形中，已知两边长可以求出锐角的大小，通过正弦、
注意单位换算和精确度
在求解过程中，要注意单位换算和精确度的控制，避免因单位或精度问题导致答案错误。
拓展延伸：非直角三角形解法简介
锐角三角形和钝角三角形的解法
对于非直角三角形，可以通过作高线或利用三角函数等方法将其转化为直角三角形进行求解。
三角形的边角关系和面积公式
了解三角形的边角关系和面积公式，有助于更好地理解和解决非直角三角形问题。

三角函数的有关计算直角三角形的边角关系PPT优秀课件4

7.由锐角的三角函数值反求锐角
填表:已知一个角的三角函数值,求这个角的度数(逆向思维)
∠A= ∠A= ∠A= ∠A= ∠A= ∠A= ∠A= ∠A= ∠A=
1．（2010·丹东中考）计算：
24 2(2 cos 45 sin 60) 4
2 3 2 6 原式 2(2 ) 2 2 4
二、用直角三角形边和角的关系解决实际问题
例1.如图,当登山缆车的吊箱经过点A到达点B时,它走过了200m.已知缆车行驶的路线与水平面的夹角为 ∠α=160,那么缆车垂直上升的距离是多少?
如图,在Rt△ABC中, ∠C=90°,BC=ABsin160 . 你知道sin160等于多少吗? 利用科学计算器可以求得: BC=ABsin160 ≈200×0.2756≈55.12.
当缆车继续从点B到达点D时,它又走过了200m.缆车由点B到点D的行驶路线与水平面的夹角为 ∠β=420,由此你不能计算什么?
在Rt△BED中, DE=DBsin42°
BC=200sin42° 所以山高为： BC+DE=200sin42°+ 200sin16° =200(sin42°+ sin16°)
0.275635355 0.743144825 11.4300523 0.954450312
计算器的型号与功能可能不同,请按相应的说明书使用.
练一练
1 用计算器求下列各式的值: (1)sin560,(2)sin15049′, (3)cos200,(4)tan290, (5)tan44059′59″,(6)sin150+cos610+tan760.
a
A
α β
B
C A
β ┌

直角三角形的边角关系三角函数的计算讲课课件

B c a A b ┌ C
互余两角之间的三角函数关系: sinA=cosB,tanA*tanB=1.
同角之间的三角函数关系:
sin2A+cos2A=1.
sin A tan A . cos A
特殊角300,450,600角的三角函数值.
例1 小山顶上有一电视塔，在山脚C处测得塔顶A、塔底B的仰角分别为45°和30°. 若塔高AB = 40m，则山高BD ≈ m（精确到1m)；
第一章直角三角形的边角关系
1.3.1 三角函数的有关计算
回顾与思考
直角三角的边角关系
直角三角形三边的关系: 勾股定理 a2+b2=c2. A+B=900. 直角三角形两锐角的关系:两锐角互余
a sin A cos B , c
直角三角形边与角之间的关系:锐角三角函数
b cos A sin B , c
a sin A , c b cos A , c a tan A , b
a c sin A. b c cos A.
a b tan A.
a c . sin A b c . cos A a b . tan A
A
作业布置
习题1.4 1,2题;
A
B
C 图1-13
D
1 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.
A
4cm
450 300
B
C
2 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.
A
0 300 45 ┌ B 4cm C D
小结拓展直角三角形中的边角关系
已知两边求角已知一边一角已知一边一角及其三角函数求另一边求另一边 B c ┌ b C a

新浙教版九年级数学下册第一章《有关三角函数的计算》课件

D
ห้องสมุดไป่ตู้太阳光
25° A
住
宅
新
楼
楼
B
C
某居民小区有一朝向为正南方向的居民楼，该居民楼的一楼是高6米的小区超市，超市以上是居民住房.在该楼的前面要盖一栋高20米的新楼.当冬季正午的阳光与水平线的夹角为25°时.
问：若新楼的影子恰好落在超市1米高的窗台处，两楼应相距多少米？
D
太阳光
25° A
F
住宅
新
楼
w如图，在Rt△ABC中，∠C=90°， BC=ABsin16° .
w你知道sin16°等于多少吗?
对于不是30°，45°，60°这些特殊角的三角函数值，可以利用计算器来求
w怎样用科学计算器求锐角的三角函数值呢?
动手实践
知识在于积累
驶向胜利的彼岸
w用科学计算器求锐角的三角函数值，要用到三个键： w例如，求sin16°、cos42°、tan85° 和sin72°38′25″的按键盘顺序如下： sin cos tan
A
B
变式：在△ABC中，已知AB=12cm，AC=10cm
∠ A=35 °,求△ABC 的周长和面积（周长精确到 0.1cm，面积保留3个是效数字）.
模型： △ABC 的面积=1/2AC･AB ･sin ∠ A
随堂练习
行家看“门道”
驶向胜利的彼岸
w1 用计算器求下列各式的值: w(1)sin56°,(2) sin15°49′,(3)cos20°,(4)tan29°, w(5)tan44°59′59″,(6)sin15°+cos61°+tan76°.
按键的顺序
显示结果
sin16° sin 1 6 °′″ =

30°、45°、60°角的三角函数值-直角三角形的边角关系优秀PPT课件

O O 0 30 、45 、60 三角函数值
本课时学习目标
1.利用三角函数的定义求30°、45°、 60°这些特殊角的三角函数值 2.能够进行30°、45°、60°角的三角函数值计算. 3.能够根据30°、45°、60°的三角函数值说明相应的锐角的大小.
知识回顾
如图， ∠ C=900 , 求 sinA、cosA、tan，朝着梦想的方向迈进
并且毫不畏惧地，过着我理想中的生活成功，会在不期然间忽然降临！

1、你在希望中享受到的乐趣，比将来实际享受的乐趣要大得多。

1．天行健，君子以自强不息。 ——《周易》译：作为君子，应该有坚强的意志，永不止息的奋斗精神，努力加强自我修养，完成并发展自己的学业或事业，能这样做才体现了天的意志，不辜负宇宙给予君子的职责和才能。 2．勿以恶小而为之，勿以善小而不为。 ——《三国志》刘备语译：对任何一件事，不要因为它是很小的、不显眼的坏事就去做；相反，对于一些微小的。却有益于别人的好事，不要因为它意义不大就不去做它。 3．见善如不及，见不善如探汤。 ——《论语》译：见到好的人，生怕来不及向他学习，见到好的事，生怕迟了就做不了。看到了恶人、坏事，就像是接触到热得发烫的水一样，要立刻离开，避得远远的。 4．躬自厚而薄责于人，则远怨矣。 ——《论语》译：干活抢重的，有过失主动承担主要责任是“躬自厚”，对别人多谅解多宽容，是“薄责于人”，这样的话，就不会互相怨恨。 5．君子成人之美，不成人之恶。小人反是。 ——《论语》译：君子总是从善良的或有利于他人的愿望出发，全心全意促使别人实现良好的意愿和正当的要求，不会用冷酷的眼光看世界。或是唯恐天下不乱，不会在别人有失败、错误或痛苦时推波助澜。小人却相反，总是“成人之恶，不成人之美”。 6．见贤思齐焉，见不贤而内自省也。 ——《论语》译：见到有人在某一方面有超过自己的长处和优点，就虚心请教，认真学习，想办法赶上他，和他达到同一水平；见有人存在某种缺点或不足，就要冷静反省，看自己是不是也有他那样的缺点或不足。 7．己所不欲，勿施于人。 ——《论语》译：自己不想要的（痛苦、灾难、祸事……），就不要把它强加到别人身上去。 8．当仁，不让于师。 ——《论语》译：遇到应该做的好事，不能犹豫不决，即使老师在一旁，也应该抢着去做。后发展为成语“当仁不让”。 9．君子欲讷于言而敏于行。 ——《论语》译：君子不会夸夸其谈，做起事来却敏捷灵巧。 10．二人同心，其利断金；同心之言，其臭如兰。 ——《周易》译：同心协力的人，他们的力量足以把坚硬的金属弄断；同心同德的人发表一致的意见，说服力强，人们就像嗅到芬芳的兰花香味，容易接受。 11．君子藏器于身，待时而动。 ——《周易》译：君子就算有卓越的才能超群的技艺，也不会到处炫耀、卖弄。而是在必要的时刻把才能或技艺施展出来。 12．满招损，谦受益。 ——《尚书》译：自满于已获得的成绩，将会招来损失和灾害；谦逊并时时感到了自己的不足，就能因此而得益。 13．人不知而不愠，不亦君子乎？ ——《论语》译：如果我有了某些成就，别人并不理解，可我决不会感到气愤、委屈。这不也是一种君子风度的表现吗？知缘斋主人 14．言必信，行必果。 ——《论语》译：说了的话，一定要守信用；确定了要干的事，就一定要坚决果敢地干下去。 15．毋意，毋必，毋固，毋我。 ——《论语》译：讲事实，不凭空猜测；遇事不专断，不任性，可行则行；行事要灵活，不死板；凡事不以“我”为中心，不自以为是，与周围的人群策群力，共同完成任务。 16．三人行，必有我师焉，择其善者而从之，其不善者而改之。——《论语》译：三个人在一起，其中必有某人在某方面是值得我学习的，那他就可当我的老师。我选取他的优点来学习，对他的缺点和不足，我会引以为戒，有则改之。 17．君子求诸己，小人求诸人。 ——《论语》译：君子总是责备自己，从自身找缺点，找问题。小人常常把目光射向别人，找别人的缺点和不足。 18．君子坦荡荡，小人长戚戚。 ——《论语》译：君子心胸开朗，思想上坦率洁净，外貌动作也显得十分舒畅安定。小人心里欲念太多，心理负担很重，就常忧虑、担心，外貌、动作也显得忐忑不安，常是坐不定，站不稳的样子。 19．不怨天，不尤人。 ——《论语》译：遇到挫折与失败，绝不从客观上去找借口，绝不把责任推向别人，后来发展为成语“怨天尤人”。 20．不迁怒，不贰过。 ——《论语》译：犯了错误，不要迁怒别人，并且不要再犯第二次。）

《三角函数的计算》直角三角形的边角关系PPT课件

(3)cos25°18′≈0.9041；
(4)sin18°＋cos55°－tan59°≈－0.7817.
讲授新课
问题: 如图，当登山缆车的吊箱经过点A到达点B
时，它走过了200m.已知缆车行驶的路线与水平面
的夹角为∠α=16°，那么缆车垂直上升的距离是多
少？（结果精确到0.01m）在 Rt△ABC中，∠ABC=90°， BC=ABsin∠α=200sin16° 你知道sin16°是多少吗？ BC=200sin16°≈55.12（米）
BC=ABsin∠α=200sin16°
你知道sin16°是多少吗？
讲授新课
一用计算器求三角函数值 1.求sin18°．第一步：按计算器 sin 键，第二步：输入角度值18，屏幕显示结果sin18°=0.309 016 994
（也有的计算器是先输入角度再按函数名称键）.
讲授新课
2.求cos72°．第一步：按计算器 cos 键，第二步：输入角度值72，屏幕显示结果cos72°=0.309 016 994
ppt模板： . /moban/
ppt素材： . /sucai/
ppt背景： . /beijing/
ppt图表： . /tubiao/
ppt下载： . /xiazai/
ppt教程： . /powerpoint/
资料下载： . /ziliao/
范文下载： . /fanwen/
试卷下载： . /shiti/
所以，塔高DE大约是81米．
讲授新课
方法总结
解决此类问题要了解角之间的关系，找到与已知和未知相关联的直角三角形，当图形中没有直角三角形时，要通过作高或垂线构造直角三角形．
当堂练习

九年级数学《直角三角形的边角关系》课件

B.
3 2
C．1
D.32
[解析] 根据题意，两张相同的这种纸片恰好能拼成一个正三
角形，可知∠B＝60°，则sinB＝ 23.
│ 考点随堂练
6.[2010·漳州]如图25－2，当太阳光线与水平地面成30°角时，一棵树的影长为24 m，则该树高为( A )
A．8 3 m C．12 2 m
图25－2 B．12 3 m D．12 m
三角形
直角三角形的边角关系
学习目标：
1.理解并掌握锐角三角函数的定义、性质和特殊角的三角函数值，结合仰角、俯角、坡度并会熟练应用，能够熟练解决生活中的三角函数有关问题。 2.通过独立思考与小组合作，深入探究，归纳出解直角三角函数的一般步骤、数学建模的思想方法。 3.极度热情、全力以赴，提高逻辑推理能力，培养缜密的逻辑思维习惯，品味数学理性思维之美。
[解析] 设树高为x m，则斜边为2x m，由勾股定理可得
x2＋242＝(2x)2，解得x＝8 3 (m)．
点随堂练
7．一段公路路面的坡度i＝
1 3
，这段公路路面长100米，那么这
段公路升高( D )
A．30米
B．10米
C．30 10 米
D．10 10 米
[解析] 设公路升高x米，则水平距离为3x米，根据勾股定理，x2＋(3x)2＝1002，解得x＝10 10(米)．
当堂检测
1.在Rt△ABC中，∠C＝90°，∠B＝2∠A，则cosA等于( A )
3
1
A. 2
B.2
C. 3
3 D. 3
[解析] 根据三角形内角和定理，知∠A＝30°.
2．在Rt△ABC中，∠C＝90°，∠A、∠B、∠C所对的边为

304560角的三角函数值直角三角形的边角关系PPT课件4

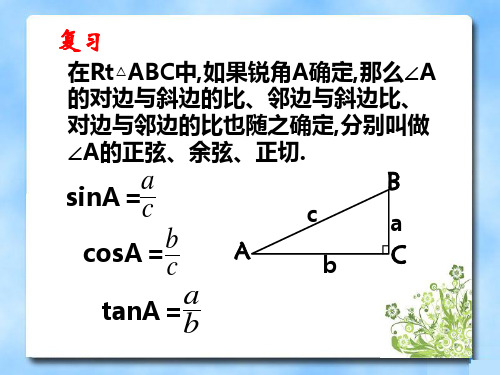
a
sin45°＝
B A
BC＝
a2a＝
2 2
cos45°＝ AA BC＝
a2a＝
2 2
tan45°＝
B A
CC＝aa＝1
B
2a 45°
a
A
45°
a
┌C
三角函数值三角函数 sinα
角α
30°
1
2
45°
2
2
60°
3
2
cosα tanα
3
3
2
3
2 2
1
1
3
2
想一想:
• 如果已知某一锐角的某种三角函数值,你能求出这一锐角吗? 比如tanA＝1,锐角A是多少度?
时间来定夺。
25、你心里最崇拜谁，不必变成那个人，而是用那个人的精神和方法，去变成你自己。 26、运气是努力的附属品。没有经过实力的原始积累，给你运气你也抓不住。上天给予每个人的都一样，但每个人的准备却不一样。不要羡
慕那些总能撞大运的人，你必须很努力，才能遇上好运气。
27、时间只是过客，自己才是主人，人生的路无需苛求，只要你迈步，路就在你的脚下延伸，只要你扬帆，便会有八面来风，启程了，人的生命才真正开始。
例题解析
例1 计算
⑴ sin30°＋cos45°; ⑵ sin260°＋cos260°－tan45°.
解: ⑴ sin30°＋cos45°
1 2 1 2 22 2
⑵sin260°＋cos260－tan45°
3 2
2
1 2
2
1
3 4
1 4
1
0
例２一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰为60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差（结果精确到0.01m）.

北师大版九年级数学下册《直角三角形的边角关系——锐角三角函数》教学PPT课件(4篇)

同理， cos
A=
AC ，cos AB
A1
=
A1C A1 B1
.
B1 B
∵AB=A1B1，
AC AB
>
A1C ，即cos A1 B1
A > cos
A1，
A A1
C
∴梯子的倾斜程度与cos A也有关系， cos A的值越小，梯子越陡.
如图：在Rt △ABC中，∠C＝90°，
sin
A
A的对边斜边
B1 B2 B3
A
C3 C2
C1
Rt△AB1C1∽Rt△AB2C2
新课学习
直角三角形的边与角的关系：
（2）BA1CC11
和B2C2
AC2
有什么关系？
B1
B2 B3
A
C3 C2
C1
B1C1 = B2C2 AC1 AC2
新课学习
直角三角形的边与角的关系：（3）如果改变B2在梯子上的位置（如B3）呢？
B2
斜边的比值、邻边与斜边的比值将怎
样变化？
C1 C2
A1
这是一个变化的过程.对边与斜边的比值、邻边与
斜边的比值都随着倾斜角的改变而改变.同时，如果给
定一个倾斜角的值，它的对边与斜边的比值、邻边与
斜边的比值是唯一确定的.
讲授新课
斜边
B ∠A的对边
A
C
∠A的邻边
定义：在Rt△ABC中，如果锐角A确定，那
∴ B1C1∥ B2C2，
C1 C2
A1
∴Rt△B1A1C1 ∽ Rt△B2A1C2.
讲授新课
想一想：如图.
（2）BA11CA11 和
A1C2 B2 A1

鲁教版九年级数学上2.4《直角三角形的边角关系》ppt(共23张PPT)

教材分析之新旧教材对比
人教版
直角三角形中，30°角所对
的直角边与斜边的比都是 1
质利
2
证用
明相直角三角形中，45°角所对
似的测猜
的直角边与斜边的比都是
2 2
性
Rt△ABC中，当锐角A的度数一定时，无论这个直角三角形的形状如何变化，A的对边与斜边的比都是一个固定的值
鲁教版
直接，但有时倾斜角不好测量角
1、单元名称的变化。降低了难度，揭示了锐角三角函数的本质意义。此外在小节的划分上更细化，具体明确。
鲁教版（九年级上册）人教版（九年级下册）
教材分析之新旧教材对比
2、对于三种锐角三角函数的引入顺序上，人教版先引入“正弦”，鲁教版先引入“正切”
教材分析之新旧教材对比
2、对于三种锐角三角函数的引入顺序上，鲁教版先引入“正切”，人教版先引入“正弦”
哪个梯子更陡？判断方法？
证明正切
正弦
余弦
引入正弦
教材分析之新旧教材对比
3、解直角三角形部分
人教版
新增一节：解一般的斜三角形
鲁教版
教材分析之新旧教材对比
4、例题更注重联系生活，显出与时俱进的创新性。
章前主题图数据简单，侧重学生自己的动手应用
更贴近学生生活
教材分析之新旧教材对比
5、更关注学生的数学活动体验。人教版的“利用三角函数测高”是出现在数学活动中，而鲁教版对于“利用三角函数测高”则出现在第6节，并且内容上更为丰富，将测量具体分为三个活动。新教材突出了解直角三角形的应用价值，更重视学生的解决实际问题的能力以及数学活动经验的积累。
实施策略
1、整合教材，重视概念的生成和理解。

直角三角形的边角关系回顾与思考演示文稿PPT课件(北师大版)

点拨：把已知条件标注在图中，发现 △DBA是等腰三角形，则可得 DB=DA=30m，用三角函数算出 BE=15m，则BC=45m；再利用三角函数
算出AC≈25.98m
9、如图，某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处，经16时的航行到达，到达后必须立即卸货，此时接到气象部门通知，一台风中心正以40海里/时的速度由A 向北偏西60°方向移动，距台风中心200海里的圆形区域（包括边界）均会受到影响。（1）问B处是否会受到影响？请说明理由。（2）为避免受到台风的影响，该船应在多长时间内卸完货物?
角三角形边角关系，此题就不难得到解决。
西
B
A
该船应在3.8时内卸完货物。
➢知识回顾
实际问题情境锐角三角函数的意义锐角三角函数的计算
30°，45°，60° 角的三角函数值
一般锐角的三角函数值
由三角函数值求锐角
利用三角函数解决实际问题
作业布置
1、复习题A组6、9题 2、复习题B组1、6题 3、选作题（附后）
角放在所构造的直角三角形中。本题已知tan∠DBA＝ 1 ，所以可以过点D作DE⊥AB于E，把∠ DBA放于Rt△DBE中，然后根5 据正切函数
的定义，即可弄清DE与BE的长度关系，再结合等腰Rt△的性质，此题就不难解答了。
7、阿雄有一块如图所示的四边形空地,求此空地的面积。 (结果精确到0.01m2).
点拨：画出图形，直观分析。结合勾股定理和三角函数知识解决。
3.已知cosA=0.6,求sinA,tanA.
点拨：画个直角三角形试一试!
复习题A组
4.如图,为了测量一条河流的宽度,一测量员在河岸边相距 180m的P和Q两点分别测定对岸一棵树T的位置,T在P的正南方向,在Q的南偏西60°的方向,求河宽(结果精确到1m).

《30°、45°、60°角的三角函数值》直角三角形的边角关系4 图文

所以，这爱情的结晶或许来得越晚越好。索性不来，也未尝不是上帝的恩赐。
一个女人，不买新衣服，不做头发，不用化妆品，不舍得吃好的，不舍得花钱看病，忽略自己的形象和健康，灰头土脸咬牙切齿地攒着钱，这样的节俭得不偿失，不算会过日子。
而不舍得出去吃饭，不舍得买花、看电影，不舍得一家人去旅游，不舍得带孩子去一次游乐场，不舍得在非基本需求方面花一分钱，这叫“不懂生活 ”，不叫“会过日子还有，路遇矿泉水瓶必须捡回家，买菜只买很便宜但烂掉了一半的，明明很忙却还为了省两块钱，去超市排队一小时买鸡蛋，这是穷怕了钻钱眼儿里了，跟会过日子挨不着边。勤俭节约是美德，穷奢极欲是恶习，这无需讨论，但这也绝不意味着花钱就可耻，省钱就光荣。在经济条件尚好、赚钱能力也不差的情况下，一味地为了省钱而节衣缩食，降低生活质量，把本来可以宽松从容的日子过得紧紧巴巴，这难道不是对自己和家人生命的浪费吗？
a
＝ 2a
＝ 21
tan60°＝ABCC＝ a3a＝ 3
30°
2a
3a
A
C 60° ┌
a
sin45°＝ABBC＝
a＝
2a
2 2
cos45°＝AABC＝
a＝
2a
2 2
tan45°＝ABCC＝aa＝1
B
2a 45°
a
A
45°
a
┌C
三角函数值三角函数 sinα
角α
30°
1
2
45°
2
2
60°

《锐角三角函数》直角三角形的边角关系PPT(第1课时)教学课件

2.sinA,cosA,tanA各是一个完整的符号,分别表示∠A的正弦、余弦和正切,记号中习惯省去“∠”；
3.sinA,cosA,tanA分别是一个比值.注意比的顺序,且在直角三角形中sinA,cosA,tanA均大于0,无单位.
4.sinA,cosA,tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则其三角函数值相等；两锐角的三角函数值相等,则这两个锐角相等.
练一练
➢ 1.在Rt△ABC中，∠C=90°，∠A、∠B、∠C的对边分别为a、b、c；
➢ ∠A的对边与斜边的比叫做∠A的正弦，即sin A=
.
➢ ∠A的邻边与斜边的比叫做∠A的余弦，即cosA=
.
➢ 2.锐角A的正弦、余弦、正切叫做∠A的
如图,当Rt△ABC中的一个锐角A确定时,它的对边与邻边的比便随之确定.此时,其它边之间的比值也确定吗?
结论: 在Rt△ABC中,如果锐角A确定,
那么∠A的对边与斜边的比、邻边与斜边的比也随之确定.
A
B
斜
边
∠A的对边
┌ ∠A的邻边 C
知识讲解
在Rt△ABC中,锐角A的对边与斜边的比叫做∠A的正弦, 记作sinA,即 sinA=A的对边
图③
图④
知识点 1 正切的定义
B
B B2 B1
A
C2 C1 C
C
如图,B1，B2是梯子AB上的点，B1C1⊥AC，垂足为点C1，
B2C2⊥AC，垂足为点C2.小明想通过测量B1C1及AC1，算出它们
的比，来说明梯子的倾斜程度；而小亮则认为，通过测量B2C2
及AC2，算出它们的比，也能说明梯子的倾斜程度.
铅直高度 A