16 分形几何(下)
欧拉的著作

19世纪伟大数学家高斯(Gauss,1777-1855年)曾说:"研究欧拉的著作永远是了解数学的最好方法."1.数论欧拉的一系列成奠定作为数学中一个独立分支的数论的基础。
欧拉的著作有很大一部分同数的可除性理论有关。
欧拉在数论中最重要的发现是二次反律。
2.代数欧拉《代数学入门》一书,是16世纪中期开始发展的代数学的一个系统总结。
3.无穷级数欧拉的《微分学原理》(Introductio calculi differentialis,1755)是有限差演算的第一部论著,他第一个引进差分算子。
欧拉在大量地应用幂级数时,还引进了新的极其重要的傅里叶三角级数类。
1777年,为了把一个给定函数展成在(0,“180”)区间上的余弦级数,欧拉又推出了傅里叶系数公式。
欧拉还把函数展开式引入无穷乘积以及求初等分式的和,这些成果在后来的解析函数一般理论中占有重要的地位。
他对级数的和这一概念提出了新的更广泛的定义。
他还提出了两种求和法。
这些丰富的思想,对19世纪末,20世纪初发散级数理论中的两个主题,即渐近级数理论和可和性的概念产生了深远影响。
4.函数概念18世纪中叶,分析学领域有许多新的发现,其中不少是欧拉自已的工作。
它们系统地概括在欧拉的《无穷分析引论》、《微分学原理》和《积分学原理》组成的分析学三部曲中。
这三部书是分析学发展的里程碑四式的著作。
5.初等函数《无穷分析引论》第一卷共18章,主要研究初等函数论。
其中,第八章研究圆函数,第一次阐述了三角函数的解析理论,并且给出了棣莫佛(de Moivre)公式的一个推导。
欧拉在《无穷分析引论》中研究了指数函数和对数函数,他给出著名的表达式(这里i表示趋向无穷大的数;1777年后,欧拉用i表示),但仅考虑了正自变量的对数函数。
1751年,欧拉发表了完备的复数理论。
6.单复变函数通过对初等函数的研究,达朗贝尔和欧拉在1747-1751年间先后得到了(用现代数语表达的)复数域关于代数运算和超越运算封闭的结论。
分形理论及其应用

X 1 : ( x1,x2,,xm )
X X
2 3
:
(
x
,
2
x
3,,
x
m
1
)
:
(
x
,
3
x
4,,
x
m
2
)
X
4
:
(
x
,
4
x5,,
x
m
3
)
把相点X1,X2,…,Xi,…,依次连起来就是一 条轨线。因为点与点之间的距空间共生成
个相点X1,X2,…,XN,给定一个数r,检查有 多少点对(Xi,Xj)之间的距离|Xi-Xj|小于r,把距离 小于r的点对数占总点对数N2的比例记作C(r),
•分形理论及其应用
Cantor集合 ,考虑多重分形,把同样的均匀质量棒
从其左端3/5处一分为二,然后把左段压缩为长度
r1=1/4,其质量P1=3/5,而右段保持原长度r2=2/5,其
质量P2=2/5;第二步按着上述的比例对两段分别进行
同样的变换就得到4段,左两段的长度分别为 r12 r1r2
质量分别为 P12 ,P1 P2 ,右两段的长度分别为 , r2 r1 r22 ,
质量分别为
, P2 P1
P
2 2
;如此操作下去就会得到一个不
均匀的Cantor集合。在这个集合中分布着众多长宽相
同的线条集合,它们构成单分形子集合。对每一个
单分形子集合,其标度指数为α,分维为f(α)。
•分形理论及其应用
最后每段线条的质量相当于二项式 (P1 P2)n展开中的
一项, n。因此可以用P1的q阶矩 Piq 取代单分形 i
第16章 分形技术———移动平均Hurst指数

于不规则现象在自然界是普遍存在的,因此分形几何又称为描述大自然的几何
学。分形几何建立以后,很快就引起了许多学科的关注,这是由于它不仅在理 论上,而且在实用上都具有重要价值。
16.1 Hurst指数简介
基于重标极差(R/S)分析方法基础上的Hurst(赫斯特)指数(H)研究是由英 国水文专家H.E.Hurst(1900—1978)在研究尼罗河水库水流量和贮存能力的关 系时,发现用有偏的随机游走(分形布朗运动)能够更好地描述水库的长期贮存能 力,并在此基础上提出了用重标极差(R/S)分析方法来建立Hurst指数,作为判断 时间序列数据遵从随机游走还是有偏的随机游走过程的指标。 Hurst指数有三种形式: ① 如果H=0.5,表明时间序列可以用随机游走来描述; ② 如果0.5<H≤1,表明黑噪声(持续性),即暗示长期记忆的时间序列; ③ 如果0≤H<0.5,表明粉红噪声(反持续性),即均值回复过程。
《金融数量分析——基于MATLAB编程 》
Hurst指数是分形技术在金融量化分析中的典型应用。分形是以非整数维形 式充填空间的形态特征。分形可以说是来自于一种思维上的理论存在。1973年,
曼德勃罗(B.B.Mandelbrot)在法兰西学院讲课时,首次提出了分维和分形几何
的设想。分形(Fractal)一词,是曼德勃罗创造出来的,其原意具有不规则、支 离破碎等意义,分形几何学是一门以非规则几何形态为研究对象的几何学。由
式中K为常数(与n无关),H即为相应的Hurst指数(与n无关)。将上式两边取对
数得到
因此对log n和log(R/S)n进行最小二乘法回归分析便可以计算出H的近似值。 注:在MATLAB中,log与ln等价。
16.3 移动平均Hurst指数计算程序
分形几何

分形几何
12
分形几何
❖ 上图是曼德布洛特集最常见的表现形式,它给我 们提供了一种理解周围世界的粗糙程度的方式。 这一以数学家贝努瓦·曼德布洛特命名的理论观察 到,不管是在物理、生物和经济等各种领域中的 许多复杂现象,都可以“以严格而有力的定量形 式逼近。”
13
分形几何
14
分形几何
15
分形几何
2
分形几何
❖ 其数学表达为: 一个二维仿射变换ω:R2→ R2
x
yБайду номын сангаас
a c
bx e
d
y
f
a,b,c,d,e,f均为实数。 这是一种最广泛的线性变换。
3
分形几何 ❖我们可以通过一系列的收缩仿射变换,使某
图形具备自相似性,从而得到分形结构。
4
分形几何
2. 科赫曲线 给定线段AB,科赫曲线可以由以下步骤生成:
27
❖ f(z) = |z2|
分形几何
28
分形几何 ❖可以看到,这一操作让模的变化更剧烈了,
等高线变得更加密集了。外面浩瀚的蓝色空 间,就对应着那些模已经相当大了的复数。
29
分形几何
❖如果对上图中的每个点再加上某个数,比如 0.3 , 那么整个图会怎样变化呢?
❖对于模相同的复数来说,给实数部分加上 0.3 , 这对实数部分本来就较大的数影响会更大一些。 因此,上图将会变得更扁,整个图形会在水平方 向上拉伸。这也就是 f(z) = |z2 + 0.3| 的等高线地 形图。见下图(为便于观察,对图像进行了旋 转)。
30
分形几何
31
分形几何
❖ 接下来,我们再对所得的 图形进行平方,继续加剧 模的变化。
分形学pdf

分形学
分形学(Fractal Geometry)是一门研究分形(fractal)对象的几何学。
分形是一种复杂的几何形态,它们在局部和整体上具有自相似性,通常无法用传统的欧几里得几何(Euclidean geometry)来描述。
分形学的研究对象包括自然界中的许多不规则形状,如云彩、山脉、河流、海岸线等,以及人工设计的分形图案。
分形学的核心概念是自相似性(self-similarity)和分数维(fractional dimension)。
自相似性意味着分形对象在不同尺度上呈现出相似的形态,而分数维则是用来描述分形对象占据空间的方式,它们通常不是整数维,如零维的点、一维的线段、二维的平面或三维的立体。
分形学的基础是分形几何学,它由法国数学家伯纳德·曼德尔布罗特(Benoît Mandelbrot)在20世纪70年代提出。
曼德尔布罗特通过研究英国海岸线的长度发现,随着测量尺度的减小,海岸线的长度会无限增长,这种现象无法用传统的几何学来解释。
他提出了分形的概念,并定义了分形的维数。
分形学在多个领域都有广泛的应用,包括物理学、化学、生物学、地理学、环境科学、计算机科学、经济学等。
在计算机图形学中,分形学用于生成复杂的自然现象和纹理。
在金融学中,分形市场理论(fractal market hypothesis)用于解释股票市场等金融现象的不规则性和复杂性。
在地质学中,分形学用于分析地貌和地质结构。
在生物学中,分形学用于研究生物体的生长和形态。
1。
第二章源头之一几何原本

《几何原本》后面各篇不再列出其它公理。这一 篇在公理之后,用48个命题讨论了关于直线和由直 线构成的平面图形的几何学,其中第47命题就是著 名的勾股定理:“在直角三角形斜边上的正方形(以 斜边为边的正方形) 等于直角边上的两个正方形。”
几何学的发展简史
几何学的发展历经了四个基本阶段:
一是经验事实的积累和初步整理
据考证西方的几何学就是起源于测地术.“几何 学”这个名词是我国明朝徐光启(1562—1633年) 译的,这个词的原义无论在拉丁文或希腊文都含“测 地术”的意思.
大约公元前1650年,埃及人阿默斯 (Ahrmes,生卒年月不详)手抄了一本书,即 后人所称的“阿默斯手册”,最早发现于埃及 底比斯的废墟中.公元1858年由英国的埃及学 者莱因德﹝A. H. Rhind﹞购得,故又名“莱因 德纸草书”.此书中载有很多关于面积的测量 法以及关于金字塔的几何问题.
第十三篇共有18个命题,主要研究五种正多面 体,并且证明了(凸的)正多面体不能多于五种。
第五公设的试证
在摆脱第五公设(也称平行公设)困扰的努力 中,第一个有影响的工作是由古希腊天文学家托 勒密完成的。在这次认真的尝试中,托勒密采取 的方式是直接证明法。他试图通过欧几里得的其 他九个公理、公设直接推导出第五公设。
第十篇是篇幅最大的一篇,包括115个
题.占全书四分之一,主要讨论无理量(与给定
的量不可通约的量),但是只涉及相当于 之类的无理量。
a b
第十一篇讨论空间的直线与平面的各种关系, 共有39个命题。
第十二篇利用穷竭法证明了“圆面积的比等于 直径平方的比”,还证明了棱锥之间、圆锥之间、 圆柱之间和球体之间的体积之比。值得指出的是: 欧几里得在任何地方都没有给出圆面积、球体积等 的计算。这并非他不知道早已存在的近似计算方法, 而是在他看来,这种计算属于实际测量而不用于理 论几何。
分形理论

分维数 -----分形几何学的数学量度
自相似维数 量度维数 盒维数
•表征形状的不同层次的比较反映出的规律。 •代表的是分形几何形状在空间中的扩张趋势。 •维数越大,就表明它在空间的扩张趋势越强。
自相似维数
自相似维数适用于人工迭代操作所形成 的分形几何形体 与每一代的单位线段数量和单位线段长 度的缩减倍数有关
量度维数
量度维数适用于类似河流或海岸线这样 的线性自然形体。 通过尽量小的单位线段累加来逼近,所 以量度维数的计算与就与用来度量的单 位长度和逼近出的总长度有关。 理论上讲,量度维数的数值加1就等于自 相似维数。
量度维数
盒维数
盒维数适用于一般的自然形状。 它用不同尺度的格网来覆盖形状,计算 形状所占据的格子数,并通过比较不同 尺度下格子数的不同来计算维数 盒维数的表达自然的本性时总是 会遇到一个难题: 它无法表现自然在不同尺度层次上 的无穷无尽的细节
自相似性
自然界的形体(如山脉、河流、云 朵等)则在局部放大后仍呈现出与整体 特征相关的丰富的细节。
自相似性
苏格兰海岸线的自相似性
自相似性
数学家眼中的分形图形
自相似性
自相似性是隐含在自然界的不同尺度 层次之间的一种广义的对称性,它使自 然造化的微小局部能够体现较大局部的 特征,进而也能体现其整体的特征。
分形几何学
1977年,曼德布罗特(Benoit Mandelbrot) 出版了《自然的分形几何学》(The Fractal Geometry of Nature) 研究对象:它们能够在不断的放大过程中,不 停地展现出自相似的、不规则变化着的细节; 不同于欧氏几何形体的一维、二维或三维形状, 它们的维数不是简单的1、2或3,而是处于它 们之间或之外的分数。
第五节 几何学的发展

5 若一直线落在两直线上所构成的同旁内角和小于两直 角,那么把两直线无限延长.它们将在同旁内角和小于 两直角的一侧相交. 欧几里得《原本》可以说是数学史上的第一座理论十 碑.它最大的功绩,是在于数学中演绎范式的确立,这 种范式要求一门学科中的每个 命题必须是在它之前已建立的一些命题的逻辑结论,而 所有这样的推理链的共同出发点,是一些基本定义和被 认为是不证白明的基本原理——公设或公理.这就是后 来所谓的公理化思想。 特点:概念清晰;定义明确;公理直观可靠而且普遍成 立;公设清楚可信且易于想象;公理数目少;引出量的 方式易于接受;证明顺序自然;
4.2 发展 德沙格(G.Desargues,1591—1661,法国) 1639年《试论圆锥与平面相交结果》 70多个射影几何术语, 无穷远点,无穷远线。 德沙格定理:“如果两个三角形对 应顶点连线共点,那么对应边的交 点共线,反之也成立” 交比不变性定理;对合;调和点组 线可以看作具有无限长半径的圆的 一部分;焦点相合的椭圆退化为圆; 焦点之一在无穷远的椭圆是一抛物 线等等。
5 非欧几何学(罗氏几何) 5.1 背景 欧几里得第五公设(平行公设):若一直线落在两直线 上所构成的同旁内角和小于两直角,那么把两直线无限 延长.它们将在同旁内角和小于两直角的一侧相交。 给定一条直线,通过此直线外的任何一点,有且只有一 条直线与之平行 证明或失败,或循环论证 萨特里(意大利)、吕格尔(德国)、兰伯特(瑞士)
第五节
几何学的发展
1 几何学简介 2 欧几里得几何学 3 解析几何 4 射影几何学 5非欧几何学 6 黎曼非欧几何 7 拓扑学 8 几何学的统一
1 几何学简介
几何学是研究空间关系的数学分支,有时简称为几何。 中文“几何”一词,为明代徐光启所创,希腊语原意为 “测地术”。 几何学的发展: 欧几里得几何学(约公元前300年); 解析几何学(17世纪); 射影几何学(18世纪); 非欧几何学(19世纪); 微分几何学(19世纪); 黎曼几何学(19世纪); 拓扑学(19世纪); 代数几何学(20世纪); 分形几何(20世纪)
学习分形形了解分形形的特点和构造方法

学习分形形了解分形形的特点和构造方法学习分形:了解分形的特点和构造方法分形(fractal)一词由波兰数学家曼德尔布罗特(Benoit Mandelbrot)于1975年引入,用于描述一类自相似的几何图形或物体。
分形具有许多独特的特点,如无穷细节、复杂性、自相似性等。
本文将介绍分形的特点和构造方法。
一、分形的特点1. 无穷细节:分形具有无穷多的细节和复杂性,无论放大或缩小图像,都能够发现新的细节。
这使得分形在数学、自然科学和艺术等领域具有广泛应用。
2. 自相似性:分形是自相似的,即整体的结构与其局部结构相似。
无论是整体还是局部的形状都能够在较小或较大的尺度上找到相似的结构。
这种自相似性是分形的重要特征。
3. 复杂性:分形的复杂性指的是其结构和形态的复杂程度。
相比于传统的几何图形,分形形状更为复杂,无法用简单的几何形状或方程式描述。
4. 维度非整:分形的维度通常是非整数维的,例如,柯赛雪垫(Koch曲线)的维度介于1和2之间。
这种非整数维度是分形与传统几何学的重要区别之一。
5. 噪声与规则性:分形能够通过噪声与规则性的结合来表现出不规则的形态。
分形结构的噪声性质使得其在模拟自然界中的山脉、云朵等不规则物体时非常逼真。
二、分形的构造方法1. 迭代函数系统(IFS):迭代函数系统是构造分形图形的一种常用方法。
它通过对函数的重复应用来生成自相似结构。
柯赛雪垫和谢尔宾斯基地毯(Sierpinski carpet)都是通过迭代函数系统构造的。
2. 分形树:分形树是用于模拟植物的分枝结构的一种方法。
通过对树干进行重复分支并在每个分支的末端再次生成分支,可以构造出栩栩如生的分形树形结构。
3. 噪声函数:噪声函数是基于随机数生成的分形图形构造方法之一。
通过使用不同频率和振幅的噪声函数叠加,可以产生具有细节丰富的分形图像。
4. 分形几何的数学公式:柯赛雪垫、曼德尔布罗特集合等分形图形可以使用数学公式进行描述和生成。
分形公式大全

分形公式大全分形公式是一种表示分形特征的数学公式,它可以描述自相似、无限细节和复杂的结构。
下面是一些常见的分形公式及其相关参考内容。
1. Mandelbrot集公式:Mandelbrot集是分形几何中最著名的一个例子,它由下面的公式定义:Z(n+1) = Z(n)² + C其中,Z(n)是一个复数,C是一个常数。
这个公式对于不同的C值会产生不同的形状,形成了Mandelbrot集的分形特征。
关于Mandelbrot集的更多内容,可以参考书籍《The Fractal Geometry of Nature》 by Benoit B. Mandelbrot。
2. Julia集公式:Julia集是类似于Mandelbrot集的分形图形,它由下面的公式定义:Z(n+1) = Z(n)² + C其中,Z(n)和C都是复数。
当给定不同的C值时,Julia集的形状也会有所不同。
关于Julia集的更多内容,可以参考书籍《The Science of Fractal Images》by Heinz-Otto Peitgen和Dietmar Saupe。
3. 分岔图公式:分岔图是描述非线性动力系统中稳定性变化的一种分形图形。
它由下面的公式定义:f(x) = r * x * (1-x)其中,r是参数,x是状态变量。
当r的值在一定范围内变化时,分岔图会展现出分形的特征。
关于分岔图的更多内容,可以参考书籍《Chaos: Making a New Science》by James Gleick。
4. 树形分形公式:树形分形是一种描述树状结构的分形图形,它由下面的公式定义:x(n+1) = r * x(n) * cos(theta) - y(n) * sin(theta)y(n+1) = r * x(n) * sin(theta) + y(n) * cos(theta)其中,x(n)和y(n)是当前点的坐标,x(n+1)和y(n+1)是下一个点的坐标,r是缩放参数,theta是旋转角度。
山东省日照市2025届高三上学期开学校际联考数学试题(含答案)

山东省日照市2025届高三上学期开学校际联考数学试题一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合M ={x∣1<x <2},N ={x∣x <3},则M ∩N =( )A. {x∣x <2}B. {x∣x <3}C. {x∣1<x <2}D. {x∣1<x <3}2.下列函数既是幂函数,又在(−∞,0)上单调递减的是( )A. y =−xB. y =x −2C. y =(12)xD. y =x 23.已知数列{a n }是公差不为0的等差数列,则“k =2”是“a 1+a 11=a k +a 10”成立的( )A. 充分必要条件 B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件4.已知sin A +cos B =23,cos A +sin B =1,则sin (A +B)=( )A. −518B. 49C. −13D. 165.已知a =log 63,b =sin π6,c =0.5−0.1,则( )A. a <b <cB. b <c <aC. c <a <bD. b <a <c6.定义在R 上的偶函数f(x)满足:对任意的x 1,x 2∈(−∞,0](x 1≠x 2),有f (x 2)−f (x 1)x 2−x 1<0,且f (2)=0,则不等式f (x )+f (−x )2x<0的解集是( )A. (−∞,−2)∪(2,+∞)B. (−2,0)∪(2,+∞)C. (−∞,−2)∪(0,2)D. (−2,0)∪(0,2)7.已知函数f(x)=sin 4ωx2+cos 4ωx2(ω>0),对任意的实数a ,f(x)在(a,a +3)上的值域是[12,1],则整数ω的最小值是( )A. 1B. 2C. 3D. 48.数列{a n }满足a 1∈Z ,a n +1+a n =2n +3,且其前n 项和为S n .若S 13=a m ,则正整数m = ( )A. 99B. 103C. 107D. 198二、多选题:本题共3小题,共15分。
计算机图形学之 分形几何

8.1 8.2 8.5 8.6
分形和分维 递归模型 本章小结 习题
8.1分形和分维
真实的世界并不规则,闪电不是直线,海 岸线不是弧线,云团不是球体,山峦也不是锥 体。自然界的许多对象是如此不规则和支离破 碎,以致欧氏几何学不能真实有效地再现大自 然。 为了再现真实世界,必须选择新的工具, 分形几何学应运而生。分形几何是以非规则物 体为研究对象的几何学。由于闪电、海岸线、 云团、山峦、海浪、野草、森林、火光等非规 则物体在自然界里比比皆是,因此分形几何学 又被称为描述大自然的几何学。
先绘制第一段直线,然后改变夹角,分别绘制其余3段直线
8.2.3 Peano-Hilbert曲线
意大利数学家皮亚诺(Peano, 1858~1932),通过对一些古代装饰图 案的研究,于1890年构造出一种奇怪的 平面曲线,这条曲线蜿蜒向前,一笔绘 成,并能充满整个平面。接着德国数学 家希尔伯特(Hilbert,1862~1943)于 1891年也构造出一种类型相同但比较简 单的曲线。这种曲线被称为PeanoHilbert曲线。
n=0 n =2 n =1
Peano-Hilbert曲线的出现,当时曾令当时的 数学界大吃一惊: 它是一条曲线,但又是一个平面; 皮亚诺曲线的方程只有一个参数,但它却能确定 了一个平面;而在欧氏几何学中,确定一条曲线需
要一个参数,确定一个平面需要两个参数。
8.2.4 Sierpinski垫片、地毯和海绵
分形山
8.1分形和分维
8.1.1 8.1.2 8.1.3 8.1.4
分形的诞生 分形的基本特征 分形的定义 分形维数的定义
8.1.1 分形的诞生
分形(Fractal)这个词,是由美籍法国 数学家曼德尔布罗特(Benoit B.Mandelbrot) 自己创造出来的,此词来源于拉丁文fractus, 意为不规则、支离破碎。1967年曼德尔布罗特 在美国《科学》杂志上发表了划时代的论文 《英国海岸线有多长?统计自相似与分数维》, 成为其分形思想萌芽的重要标志。1973年,在 法兰西学院讲学期间,曼德尔布罗特提出了分 形几何学的整体思想,并认为分数维是个可用 于研究许多物理现象的有力工具。1982年曼德 尔布罗特出版了《大自然的分形几何学》,引 起了学术界的广泛重视,曼德尔布罗特也因此 一举成名。
江苏省泰州中学高中数学选修课课件:数学史选讲-分形概述 (共55张PPT)

理 工 作 等 。 现从三 方面对 2008年 的工 作情况 如下: 一 、 一 年 来 所做的 工作
江苏省泰州中学数学选修课
Email:deyinsong@
图3 谢尔宾斯基三角形 江苏省泰州中学数学选修课
Email:deyinsong@
分形
将分形看作具有如下性质的集合:
1.F具有精细结构,即在任意小的比例尺度内包含 整体。
2.F是不规则的,以致于不能用传统的几何语言来 描述。
康托尔集F的自相似维数
由于康托尔集F中点的数目为∞,而长度为 0,因此F的维数既不是0,也不是1,而是 一个介于0与1之间的分数。
科赫曲线F的自相似维数为
dim F
ln 2 ln 3
江苏省泰州中学数学选修课
Email:deyinsong@
谢尔宾斯基地毯
波兰著名数学家谢尔宾斯基在1915-1916 年期间构造了几个典型的例子, 这些怪物 常称作“谢氏地毯”、“谢氏三角”、“谢 氏海绵” 。如今,讲分形都要提到。它们 不但有趣,而且有助于形象地理解分形。
江苏省泰州中数学选修课
Email:deyinsong@
Koch曲线的生成过程 —第4步
江苏省泰州中学数学选修课
Email:deyinsong@
Koch曲线与雪花曲线
—连接在一起的三段Koch曲线构成一个雪花曲线
江苏省泰州中学数学选修课
《数字图像处理》习题参考答案
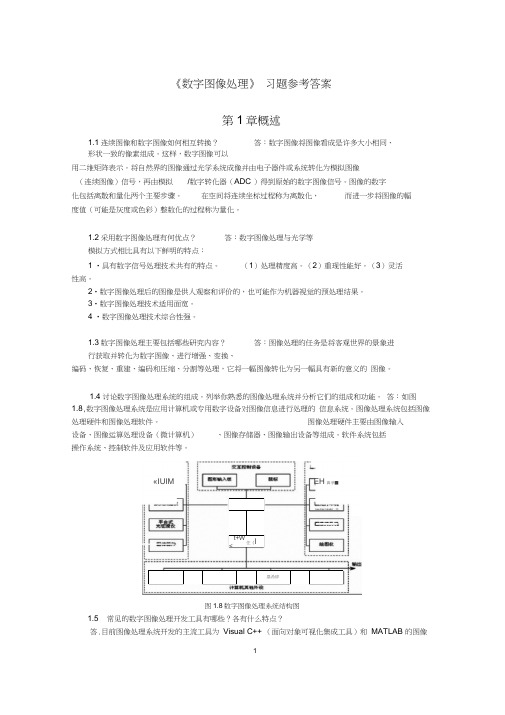
1《数字图像处理》 习题参考答案第1章概述1.1连续图像和数字图像如何相互转换?答:数字图像将图像看成是许多大小相同、形状一致的像素组成。
这样,数字图像可以用二维矩阵表示。
将自然界的图像通过光学系统成像并由电子器件或系统转化为模拟图像 (连续图像)信号,再由模拟 /数字转化器(ADC )得到原始的数字图像信号。
图像的数字化包括离散和量化两个主要步骤。
在空间将连续坐标过程称为离散化,而进一步将图像的幅度值(可能是灰度或色彩)整数化的过程称为量化。
1.2采用数字图像处理有何优点?答:数字图像处理与光学等模拟方式相比具有以下鲜明的特点:1 •具有数字信号处理技术共有的特点。
(1)处理精度高。
(2)重现性能好。
(3)灵活性高。
2•数字图像处理后的图像是供人观察和评价的,也可能作为机器视觉的预处理结果。
3•数字图像处理技术适用面宽。
4 •数字图像处理技术综合性强。
1.3数字图像处理主要包括哪些研究内容?答:图像处理的任务是将客观世界的景象进行获取并转化为数字图像、进行增强、变换、编码、恢复、重建、编码和压缩、分割等处理,它将一幅图像转化为另一幅具有新的意义的 图像。
1.4讨论数字图像处理系统的组成。
列举你熟悉的图像处理系统并分析它们的组成和功能。
答:如图1.8,数字图像处理系统是应用计算机或专用数字设备对图像信息进行处理的 信息系统。
图像处理系统包括图像处理硬件和图像处理软件。
图像处理硬件主要由图像输入设备、图像运算处理设备(微计算机) 、图像存储器、图像输出设备等组成。
软件系统包括操作系统、控制软件及应用软件等。
1.5 常见的数字图像处理开发工具有哪些?各有什么特点?答.目前图像处理系统开发的主流工具为 Visual C++ (面向对象可视化集成工具)和 MATLAB 的图像t+W<住《l 塁希碎«IUIMEH 鼻爭■图1.8数字图像处理系统结构图处理工具箱(Image Processing Tool box )。
20个有趣的数学问题

20个有趣的数学问题数学作为一门基础学科,其独特的魅力和无穷的奥秘一直吸引着无数学者和爱好者。
以下是一些有趣的数学问题,涵盖了不同领域和主题,让我们一起探索数学的奇妙世界。
1. 素数之谜:素数是只有两个正因数(1和本身)的自然数。
为什么素数的分布似乎遵循一个无规律的模式?是否有无穷多的素数?2. 分形之美:分形是具有无限精细结构的图形。
诸如科赫雪花、谢尔宾斯基垫等分形为何在视觉上如此吸引人?它们在数学上有哪些有趣的应用?3. 不可思议的数列:像斐波那契数列、卢卡斯数列等神奇的数列,它们背后的数学原理是什么?这些数列在自然界和艺术中有哪些表现?4. 概率与人生:概率论如何解释生活中的随机事件?例如,为什么足球比赛中的点球得分率不是100%?概率论如何帮助我们做出更好的决策?5. 无穷大的奇妙世界:无穷大在数学中有哪些表现形式?例如,实数集是无限大的,但可数无限和不可数无限有何不同?6. 拓扑学的魔法:拓扑学研究的是物体在变形过程中保持不变的属性。
例如,为什么一个甜甜圈和一个咖啡杯在拓扑上是等价的?7. 分形几何学:分形几何是如何揭示自然和人造对象的复杂结构的?分形几何有哪些应用,如艺术、生物学和物理学?8. 无限递归与自我相似:有些对象是自身的子对象或组成对象的组分的模式。
无限递归和自我相似在数学中有哪些例子?它们为什么有趣?9. 混沌理论与蝴蝶效应:混沌理论解释了为什么一些看似微小的变化会导致巨大的结果。
蝴蝶效应是什么?混沌理论在自然界和人类社会中有哪些应用?10. 几何学中的最短路径:在几何学中,最短路径是从一点到另一点的最直线路径。
例如,欧几里得几何中的直线段是最短路径。
但在弯曲空间中呢?黎曼几何和广义相对论如何解释最短路径?11. 无理数和超越数之谜:无理数和超越数是无限不循环的小数。
它们在数学中有哪些应用和特性?为什么它们比有理数更加神秘和有趣?12. 黄金比例与美学:黄金比例是一个特定的比率(大约等于1.618),被广泛用于艺术、建筑和设计等领域。
分形几何

度量Koch曲线(续)
现在,长度为1/3的无刻度的尺子来度量 Koch曲线。 此时Koch曲线的近似长度为 L1 = 4/3. 于是 Koch 的长度大于 4/3.
度量Koch曲线(续)
进一步,在每两个相邻的节点间加入三个 节点,这样用由16条长度为1/9的线段组成 的折线逼近Koch曲线。同样发现Koch曲线 的长度大于折线长度 L2 = 16/9 = (4/3)2.
分形几何的提出
由于不规则现象在自然界是普 遍存在的,因此分形几何又称 为描述大自然的几何学。分形 几何建立以后,很快就引起了 许多学科的关注,这是由于它 不仅在理论上,而且在实用上 都具有重要价值。
分形几何的提出
当你用一把固定长度的直尺(没有 刻度)来测量海岸线的长度时,对 海岸线上两点间的小于尺子尺寸的 曲线,只能用直线来近似。因此, 测得的长度是不精确的。
A
则称子集类
i 1 为A的一个
U
i
{U i}
―覆盖。
豪斯道夫(Hausdorff)维数
Hausdorff测度 d ) 设A是度量空间 ( R , 的任一有界子集 s≥0,对于任意的 >0,定义:
H ( A) inf{ | U i | : {U i } A的-覆盖}
分形的定义(续) 分形看作具有下列性质的集合F:
1)F具有精细结构,即在任意小 的比例尺度内着复杂的结构。 2)F是不规则的,以致于不能用 传统的几何语言来描述。
分形的定义(续)
3)F通常具有某种自相似性,或许是 近似的或许是统计意义下的。 4)F在某种方式下定义的“分维数” 通常大于F的扑维数。 5)F的定义常常是非常简单的,或许 是递归的。
Mandelbrot集(4)
GeoExpl分形数据处理

1000
100
10
1 1
126
W
10
100
C (mg/kg)
916
Pb
100
1000
C (mg/kg)
100000 10000 1000 100 10 1
1000 1 100000
10000 1000 100 10 1
10000 10 10000
尺子、盒子改为元素含量 数学关系:NC~C的关系 分形模型:
含量与频数 含量与面积 含量与周长 其实质相同(含量与个数)
含量-总量法
韩东昱,龚庆杰,向运川。区域化探数 据处理的几种分形方法。地质通报, 2004,23(7):714-719 原理: Nr~r 演变为 Nr’~r GeoExpl软件 不仅实现计算功能 而且帮助系统包含数学计算原理
D
应用实例4
适用于以下模型: 分形插值
作用: 模拟自然数据变化特征 随机性、确定性、区域结构性
李长江,麻土华,朱兴盛,等. 矿产勘查中的分形、混沌与ANN[M]. 北京:地质出版社,1999,1-140
图a 用四点插值法制作的陈蔡幅 1:5万铜含量分布图
图b 用分形插值法制作的陈 蔡幅1:5万铜含量分布图
应用实例3
适用于以下模型: 曲线分维计算 曲面分维计算
作用: 1、区分区域成矿元素与非成矿元素
按分维值D排序:一维图解 与变异系数联合:二维图解
D
分维值D
2.4 2.3 2.2 2.1 2.0
w sn mo bi ag as sb cu pb zn co ni v ti sr ba
2.5 2.4 2.3 2.2 2.1 2.0
超牛数学知识点

超牛数学知识点数学这玩意儿啊,可真是又爱又恨。
不过今天我要给大家分享一些超牛的数学知识点,保证让你对数学有新的认识。
1. 勾股定理。
这可是数学界的大明星啊。
直角三角形两直角边的平方和等于斜边的平方。
就比如说一个直角三角形,两条直角边分别是3和4,那斜边就是5啦,因为3的平方加4的平方等于9加16等于25,5的平方也等于25。
这个定理在好多实际问题里都能用得上,像建筑测量啥的。
我记得以前做几何题,只要看到直角三角形,第一反应就是勾股定理有没有用得上的地方。
2. 圆周率π。
这个神奇的数字啊,3.1415926……它表示圆的周长和直径的比值。
咱平时计算圆的周长(C = 2πr,r是半径)或者面积(S = πr²)都离不开它。
我曾经还试过背圆周率后面好多位呢,虽然最后没背多少,但感觉特别酷。
而且啊,圆周率在科学研究、工程计算里到处都是,无处不在。
3. 黄金分割比例。
这个比例大概是0.618,从美学的角度看,很多建筑、艺术作品都运用了这个比例。
比如说希腊的帕特农神庙,它的建筑比例就很接近黄金分割。
而且在人的身材比例里,如果腿长和身高的比例接近黄金分割比例,那看起来就特别好看。
我还试过用这个比例来判断一些明星的身材呢,哈哈。
4. 等差数列。
就是一组数,相邻两个数的差是固定的。
比如1,3,5,7,9……这个差就是2。
等差数列有个通项公式an = a1+(n - 1)d,其中an是第n项的数,a1是第一项的数,d就是那个公差。
以前做数列题的时候,这个公式可帮了大忙了。
5. 函数。
函数就像是一个魔法盒,给它一个输入值(自变量),就会有一个输出值(因变量)。
像一次函数y = kx + b,k是斜率,b是截距。
不同的k和b会画出不同的直线。
二次函数y = ax²+bx + c,它的图像是抛物线。
我以前学函数的时候,最开始觉得特别难,但是一旦理解了,就发现它能解决好多实际问题,比如计算利润最大的时候产量是多少之类的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题:分形几何(下)
【教学目标】了解分形几何中几个有趣的例子
【教学重点】分形几何典例
【教学过程】
引入:一类分形的典型例子有:康托尔集、谢尔宾斯基三角形和地毯、门格海绵、龙形曲线、空间填充曲线和科赫曲线。
其他的例子包括李雅普诺夫分形及克莱因群(Kleinian Group)的极限集。
1、科赫雪花曲线
要做出科赫雪花,将正三角形每边中央三分之一的线段以一对同长的线段取代,形成一个等腰的“凸角”。
再对上一步骤所形成的每一边做同样的动作。
每一次迭代,总长度增加三分之一。
科赫雪花即是无限次迭代的结果,有无限长的周长,但其面积还是有限的。
因此,科赫雪花和其他相似构造有时会被称为“怪兽曲线”。
科赫雪花曲线的构造过程局部细节图2、谢尔宾斯基三角形
谢尔宾斯基三角形构造过程(前五步)
三维版本的谢尔宾斯基三角形
3 谢尔宾斯基地毯
谢尔宾斯基地毯构造过程(前四步)
三维版谢尔宾斯基地毯(构造过程前四步)
4、康托尔集
通过考虑这个集合,康托尔和其他数学家奠
定了现代点集拓扑学的基础。
虽然康托尔自己用
一种一般、抽象的方法定义了这个集合,但是最
常见的构造是康托尔三分点集,由去掉一条线段
的中间三分之一得出。
图为构造过程的前6步。
