中考几何证明题及答案

合集下载

中考复习初中数学几何证明试题(含答案)

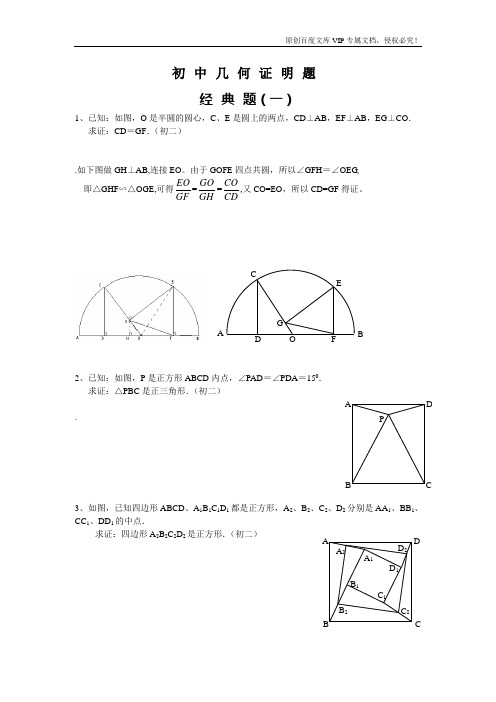
初中几何证明题经典题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）.如下图做GH ⊥AB,连接EO 。

由于GOFE 四点共圆，所以∠GFH ＝∠OEG , 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ，所以CD=GF 得证。

2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）.3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）APCDB D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 AFGCEBOD4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 及D 、E ，直线EB及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．BF求证：点P 到边AB 的距离等于AB 的一半．经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEFB 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）经典题（四）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值． A P CB P A D CB C B D A F PD E CB A APCB3、P为正方形ABCD内的一点，并且PA＝a，PB＝2a，PC＝3a，求正方形的边长．4、如图，△ABC中，∠ABC＝∠ACB＝800，D、E分别是AB、AC上的点，∠DCA＝300，∠EBA＝200，求∠BED的度数．经典题（一）1.如下图做GH⊥AB,连接EO。

几何证明练习题带答案

几何证明练习题带答案一、选择题1. 已知三角形ABC中，AB=AC，点D在BC上，且BD=DC。

求证：∠BAD=∠CAD。

A. 利用等腰三角形性质B. 利用角平分线定理C. 利用等边三角形性质D. 利用相似三角形性质答案：B2. 已知线段AB和CD平行，且M是线段AB上的一点，N是线段CD上的一点，MN与AB、CD不平行。

求证：∠AMN≠∠CNM。

A. 利用平行线性质B. 利用内错角定理C. 利用同位角定理D. 利用补角定理答案：A二、填空题1. 在三角形ABC中，若∠A=90°，AB=AC，那么∠B=∠C=______。

答案：45°2. 已知三角形ABC中，AB=5，AC=7，BC=6，根据勾股定理可知这是一个______三角形。

答案：直角三、简答题1. 如何证明三角形内角和定理？答案：在三角形ABC中，延长BC至点D，根据外角定理，∠ACD=∠A+∠B。

又因为∠ACD+∠C=180°，所以∠A+∠B+∠C=180°，证明了三角形内角和为180°。

2. 如何证明圆内接四边形的对角互补？答案：设圆内接四边形ABCD，连接对角线AC和BD，由于AC和BD 都是圆的直径，根据圆周角定理，∠A+∠C=90°，∠B+∠D=90°。

因此，对角互补。

四、证明题1. 已知三角形ABC中，AB=AC，点D在BC上，且BD=DC。

证明∠BAD=∠CAD。

证明：由于AB=AC，根据等腰三角形性质，∠ABC=∠ACB。

又因为BD=DC，根据等边三角形性质，∠ABD=∠ACD。

因此，∠BAD=∠ABC-∠ABD=∠ACB-∠ACD=∠CAD。

2. 已知圆O中，弦AB和CD相交于点P，PA=PB，PC=PD。

证明：OP垂直于AB和CD。

证明：由于PA=PB，根据圆周角定理，∠APB=∠PBA。

同理，∠CPD=∠PDC。

因为∠APB+∠CPD=180°，所以∠OPB+∠OPD=90°。

初中数学几何证明试题(含答案)

第 6 页共 15 页
4.如下图连接 AC 并取其中点 Q，连接 QN 和 QM，所以可得∠QMF=∠F，∠QNM=∠
DEN 和∠QMN=∠QNM，从而得出∠DEN＝∠F。
经典题（二）
1.(1)延长 AD 到 F 连 BF，做 OG⊥AF,
又∠F=∠ACB=∠BHD，可得 BH=BF,从而可得 HD=DF，又 AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM
BE AD
= ，即 AD•BC=BE•AC，
①
BC AC
又∠ACB=∠DCE，可得△ABC∽△DEC，既得
AB = DE ，即 AB•CD=DE•AC，
②
AC DC
由①+②可得: AB•CD+AD•BC=AC(BE+DE)= AC·BD ，得证。
第 11 页共 15 页
4.过 D 作 AQ⊥AE
(2)连接 OB，OC,既得∠BOC=1200，
从而可得∠BOM=600, 所以可得 OB=2OM=AH=AO, 得证。
第 7 页共 15 页
3.作 OF⊥CD，OG⊥BE，连接 OP，OA，OF，AF，OG，AG，OQ。由于 AD = AC = CD = 2FD = FD ， AB AE BE 2BG BG
（2）过 P 点作 BC 的平行线交 AB,AC 与点 D，F。
由于∠APD>∠ATP=∠ADP，
推出 AD>AP
①
又 BP+DP>BP
②
和 PF+FC>PC
③
又 DF=AF
④
由①②③④可得：最大 L< 2 ；

初中几何证明题五大经典(含答案)

经典题（一）1、已知：如图，O 是半圆的圆心， C、 E 是圆上的两点， CD ⊥ AB ， EF⊥ AB ，EG ⊥CO．求证： CD＝ GF．（初二）证明：过点G 作 GH⊥AB 于 H，连结 OE∵EG⊥ CO， EF⊥ AB∴∠ EGO=90 °，∠ EFO=90 °∴∠ EGO+ ∠ EFO=180 °∴ E、 G、 O、 F 四点共圆∴∠ GEO= ∠ HFG∵∠ EGO= ∠ FHG=90 °∴△ EGO∽△ FHGEO GO∴=FG HG∵GH⊥ AB ，CD ⊥AB∴GH∥ CD∴GO COHG CD∴EO COFG CD∵EO=CO∴CD=GF2、已知：如图，P 是正方形ABCD 内部的一点，∠PAD＝∠ PDA ＝ 15°。

求证：△ PBC 是正三角形．（初二）证明：作正三角形ADM ，连结 MP∵∠ MAD=60 °，∠ PAD=15 °∴∠ MAP= ∠ MAD+ ∠PAD=75 °∵∠ BAD=90 °，∠ PAD=15 °∴∠ BAP= ∠BAD- ∠PAD=90 ° -15° =75 °∴∠ BAP= ∠MAP∵MA=BA ， AP=AP∴△ MAP ≌△ BAP∴∠ BPA= ∠ MPA ，MP=BP同理∠ CPD= ∠ MPD ， MP=CP∵∠ PAD＝∠ PDA ＝ 15°∴PA=PD，∠ BAP= ∠ CDP=75 °∵BA=CD∴△ BAP ≌∠ CDP∴∠ BPA= ∠ CPD∵∠ BPA= ∠ MPA ，∠ CPD= ∠ MPD∴∠ MPA= ∠MPD=75 °∴∠ BPC=360° -75°× 4=60°∵ MP=BP ， MP=CP∴ BP=CP∴△ BPC是正三角形第1页共9页3、已知：如图，在四边形ABCD 中， AD ＝ BC ，M 、N 分别是 AB 、 CD 的中点， AD 、BC 的延伸线交MN于 E、F．求证：∠ DEN ＝∠ F．证明 :连结 AC ，取 AC 的中点 G,连结 NG 、 MG∵CN=DN ， CG=DG∴GN∥ AD ，GN= 1AD 2∴∠ DEN= ∠ GNM ∵AM=BM ， AG=CG∴GM ∥BC， GM= 1BC 2∴∠ F=∠GMN∵AD=BC∴GN=GM∴∠ GMN= ∠GNM∴∠ DEN= ∠ F经典题（二）1、已知：△ ABC 中， H 为垂心（各边高线的交点），O为外心，且OM ⊥BC 于 M ．（1）求证： AH ＝2OM ；（2）若∠ BAC ＝600，求证： AH ＝ AO ．（初二）证明：（ 1）延伸 AD 交圆于 F，连结 BF，过点 O 作 OG⊥ AD 于 G∵OG⊥ AF∴AG=FG⌒⌒∵ AB=AB ∴∠ F=∠ACB又 AD ⊥ BC， BE⊥AC∴∠ BHD+ ∠ DBH=90 °∠ACB+ ∠DBH=90 °∴∠ ACB=∠ BHD∴∠ F=∠BHD∴BH=BF 又 AD ⊥BC∴DH=DF∴ AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2（GH+DH）=2GD又 AD ⊥ BC， OM⊥ BC，OG⊥ AD∴四边形 OMDG 是矩形∴OM=GD ∴ AH=2OM（2）连结 OB 、 OC∵∠ BAC=60 ∴∠ BOC=120 °∵OB=OC ， OM ⊥ BC∴∠ BOM= 1∠ BOC=60° ∴∠ OBM=30°2∴BO=2OM由（ 1）知 AH=2OM ∴ AH=BO=AO第2页共9页2、设 MN 是圆 O 外一条直线，过O 作 OA ⊥ MN 于 A ，自 A 引圆的两条割线交圆O 于 B、 C 及 D、 E，连结 CD 并延伸交MN 于 Q，连结 EB 并延伸交MN 于 P.求证： AP ＝AQ ．证明：作点 E 对于 AG 的对称点F，连结 AF 、 CF、 QF∵ AG ⊥ PQ ∴∠ PAG= ∠ QAG=90 °又∠ GAE= ∠ GAF∴∠ PAG+∠GAE=∠ QAG+∠GAF即∠ PAE=∠ QAF∵ E、 F、 C、D 四点共圆∴∠ AEF+ ∠ FCQ=180 °∵EF⊥AG ， PQ⊥ AG∴EF∥PQ∴∠ PAF=∠ AFE∵AF=AE∴∠ AFE= ∠AEF∴∠ AEF= ∠PAF∵∠ PAF+∠QAF=180 °∴∠ FCQ= ∠QAF∴F、 C、A、Q 四点共圆∴∠ AFQ= ∠ ACQ又∠ AEP= ∠ACQ∴∠ AFQ= ∠ AEP 在△ AEP 和△ AFQ 中∠AFQ= ∠AEP AF=AE∠QAF= ∠ PAE∴△ AEP ≌△ AFQ ∴AP=AQ3、设 MN 是圆 O 的弦，过MN 的中点 A 任作两弦 BC 、DE ，设 CD 、 EB 分别交 MN 于 P、Q．求证： AP＝ AQ ．（初二）证明：作 OF⊥ CD 于 F， OG⊥ BE 于 G，连结 OP、 OQ、 OA 、 AF、 AG∵C、 D、 B、 E 四点共圆∴∠ B=∠ D ，∠ E=∠C∴△ ABE ∽△ ADC∴AB BE 2BG BGAD DC2FD DF∴△ ABG ∽△ ADF∴∠ AGB= ∠ AFD∴∠ AGE= ∠ AFC∵AM=AN ，∴OA⊥ MN又 OG⊥BE，∴∠ OAQ+ ∠ OGQ=180 °∴ O、A 、 Q、 E 四点共圆∴∠ AOQ= ∠ AGE同理∠ AOP= ∠ AFC∴∠ AOQ= ∠ AOP又∠ OAQ= ∠ OAP=90 °， OA=OA∴△ OAQ ≌△ OAP∴AP=AQ第3页共9页4、如图 ,分别以△ ABC 的 AB 和 AC 为一边 ,在△ ABC 的外侧作正方形ABFG 和正方形ACDE ，点 O 是 DF的中点， OP⊥ BC求证： BC=2OP （初二）证明：分别过F、 A 、 D 作直线 BC 的垂线，垂足分别是L 、 M 、 N∵ OF=OD ， DN ∥OP∥FL∴ PN=PL∴ OP 是梯形 DFLN 的中位线∴ DN+FL=2OP∵ ABFG 是正方形∴∠ ABM+ ∠ FBL=90 °又∠ BFL+ ∠ FBL=90 °∴∠ ABM= ∠ BFL又∠ FLB= ∠ BMA=90 °， BF=AB∴△ BFL ≌△ ABM∴ FL=BM同理△ AMC ≌△ CND∴ CM=DN∴ BM+CN=FL+DN∴ BC=FL+DN=2OP经典题（三）1、如图，四边形ABCD 为正方形， DE∥ AC ，AE ＝ AC ， AE 与 CD 订交于 F．求证： CE＝CF．（初二）证明：连结BD 交 AC 于 O。

(完整版)初中数学几何证明经典试题(含答案)

初中几何证明题经典题（一）1 已知：如图， 0是半圆的圆心， C 、E 是圆上的两点， CD 丄AB , EF 丄AB , EG 丄CO . 求证：CD = GF .（初二）2、已知：如图， P 是正方形 ABCD 内点，/ PAD =Z PDA = 150.的延长线交MN 于E 、F . 求证：/ DEN =Z F .求证：△ PBC 是正三角形.（初二）3、如图，已知四边形 ABCD 、A i B i C i D i 都是正方形, CC i 、DD i的中点.求证：四边形 A 2B 2C 2D 2是正方形.（初二）A 2、B 2、C 2、D 2 分别是 AA i 、BB i 、4、已知：如图，在四边形 ABCD 中, AD = BC , M 、N 分别是 AB 、CD 的中点, AD 、BCD经典题（二）及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证：AP = AQ .（初二） 3、如果上题把直线 MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆0的弦，过MN 的中点A 任作两弦BC 、DE , 于 P 、Q .求证：AP = AQ .（初二）4、如图，分别以厶 ABC 的AC 和BC 为一边，在△ ABC 的外侧作正方形 ACDE和正方形CBFG ，点P 是EF 的中点.求证：点P 到边AB 的距离等于1已知：△ ABC 中，H 为垂心（各边高线的交点）（1）求证：AH = 2OM ;（2）若/ BAC = 600,求证：AH = AO .（初二）,O 为外心，且0M 丄BC 于M .2、设MN 是圆0外一直线，过0作0A 丄MN 于A ，自A 引圆的两条直线，交圆于AB 的一半.（初二）HEBCM DG N BF经典题（二）1 如图，四边形 ABCD 为正方形，DE // AC , AE = AC , AE 与CD 相交于F .求证：CE = CF .（初二）4、如图，PC 切圆0于C , AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D .求证：AB = DC , BC = AD .（初三）F .E2、如图，四边形 ABCD 为正方形，DE // AC ,且CE = CA ，直线EC 交DA 延长线于求证：AE = AF .（初二）3、设ABCD 为圆内接凸四边形，求证： AB • CD + AD • BC = AC • BD .（初三）4、平行四边形 ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ,且AE = CF .求证：/ DPA =Z DPC .（初二）经典题（四）1已知：△ ABC 是正三角形，P 是三角形内一点求：/ APB的度数.（初二）2、设P 是平行四边形 ABCD 内部的一点，且/求证：/ PAB = Z PCB .（初二）C经典难题（五）1、设P是边长为1的正△ ABC内任一点,求证：一：＜L V 2.B C2、已知：P是边长为1的正方形ABCD内的一点，求PA + PB + PC的最小值.3、P为正方形ABCD内的一点，并且PA= a, PB= 2a, PC= 3a,求正方形的边长.4、如图，△ ABC 中，/ ABC =Z ACB = 80°, D、E 分别是AB、AC 上的点，/ DCA = 30°, / EBA = 20°,求/ BED 的度数.经典题（一）1•如下图做GH丄AB,连接E0。

中考数学-几何证明

2020年-春季-初三下-【入学考试】1.(初2020级BZ初三下入学测试)如图，正方形ABCD中，对角线AC, BD交于点。

，点E.点OB ,线段AB上，且AF OE ,连接AE交OF于G , 连接DG交AO于H.F分别在线段⑴如图1,若点E为线段BO中点，AE J5,求BF的长：(2)如图2,若AE平分BAC,求证：FG HG;(3)如图3,点E在线段BO (含端点)上运动，连接HE，当线段HE长度取得最大值时，直接写出cos HDO的值.2.(初2020级BS初三下入学测试)如图，平行四边形ABCD中，AB=2BC, B 60 . 曲 DC中点，连接AE . F为AD上一点，连接CF交AE与点G , CM平分FCB交AB于点M .(1)如图1,若BC 3,AF 1 求sin DCF 的值.(2)求证：EG BM CG(3)如图2, CN AB于点N ,若AG=4, MN : BN=3: 5.求CG 的长度.3.(初2020级YZ初三下入学测试)在0ABCD中BAC=90 , AB=AE,延长BE交CD 于点F . AG BE交BE于点H点，M是BC边上的点.(1)如图1,若点M与点G重合，AH 5, AD 显26 ,求CF的长：2(2)如图2.若AM是BAD的角平分线，连接MH , HMG MAH ,求证：AM 2 .2HM(3)如图3,若点M为BC的中点，作点B关于AM的对称点N，连接AN、MN、EN,请直接写出AMH、NAE、MNE之间的角度关系.4.(初2020级YZ 初三下入学测试)在正方形 ABCD 中，E 为边CD 上一点(不与点 C 、D 第4页共34重合)，垂直于BE 的一条直线 MN 分别交BC 、BE 、AD 于点M 、P 、N,正方形ABCD 的边长为6.(1)如图1,当点M 和点C 重合时，若AN =4,求线段PM 的长度;(2)如图2,当点M 在边BC 上时，判断线段AN 、MB 、EC 之间的数量关系，并说明理由;(3)如图3,当垂足P 在正方形 ABCD 的对角线 AC 上运动时，连接 NB,将^ BPN 沿着BN 翻折，点P 落在点P 处，AB 的中点为Q,直接写出PQ 的最小值.5.(万二中初2020级初三下入学测试)在4ABC与4ADF中，/BAC=/DAF=90° ,AB=AC,AD=AF, DF的延长线交BC于点E,连接DB、CF.(1)如图1,当点C、A、D三点在同一直线上，且AC=g AF, AF=超时，求CE的长；(2)如图2,当/ AFC = 90°时，求证：E是BC的中点；(3)如图3,若CF平分/ ACB,且CF的延长线与DB交于点G,请直接写出BG、DG、FG之间的数量关系.[ D6.(万中初2020级初三下入学测试) 如图，在？ABCD中，/ACB = 45° , AEXBC于点E, 过点C 作CFLAB于点F,交AE于点M.点N在边BC上，且AM = CN ,连结DN .(1)若AB= 10Q , AC = 4,求BC 的长；(2)求证：AD+AM= 22DN .(3)如图，连接EF、探究AF、EF、CF之间存在的数量关系，直接写出数量关系不需要证明.2020年-春季-初三下-【第一次诊断】1.(初2020级YW初三下第一次诊断)如图，在平行四边形ABCD中，AC为对角线，过点D作DELDC交直线AB于点E,过点E作EHXAD于点H,过点B作BFXAD于点F.(1)如图，若/ BAD=60° , AF=3, AH=2,求AC 的长.(2)如图，若BF=DH,在AC上取一点G,连接DG、GE, 若/ DGE=75° ,/CDG=45° -/CAB,求证：DG 立CG22.如图，已知ABCD中，/ B=45° , CE^AD于G,交BA延长线E, CF平分/ DCE ,连接EF, ED.(1)如果AB=5, AD = 372,求线段DE的长.(2)如果/ CFE=90° ,求证：CD 2DF 版AG .(3)如图，在(2)的条件下，若FG J5,点M、N是线段CF、CD上的动点，DM+MN 是否存在最小值，若存在，求出这个最小值；若不存在，请说明理由 ^3.(初2020级BZ初三下第一次诊断)已知△ ABC是等边三角形，CD，AB交AB于M, DBXBC, E是AC上一点，EHXBC,垂足为H, EH与CD交于点F,连接BE.(1)如图，若EC=-AC , EH=6,求BE 的长. 5(2)如图，连接AF,将AF绕点A顺时针旋转，使F点落在BD边上的G点处，AG交CD 于Q,求证：BG=CF.(3)如图，在(2)的条件下，连接FG,交BE于N,连接MN,若竺勺，4AGF的面QG 3积为49户，求MN的长.3.(万州国本中学初三下期中考试)已知，在0ABCD中，AB BD, AB BD, E为射线BC上一点，连接AE交BD于点F .(1)如图1,若点E与点C重合，且AF 2胫，求AD的长；(2)如图2,当点E在BC边上时，过点D作DG AE于G ,延长DG交BC于H ,连接FH ,求证：AF DH FH ；(3)如图3,当点E在射线BC上运动时，过点D作DG AE于G , M为AG的中点，点N在BC边上且BN 1 ,已知AB 4 J2 ,请直接写出MN的最小值.4 .（万州国本中学初三下第一次诊断）【问题背景】如图1所示，在gABC 中，AB= BC, ABC=90，点D 为直线BC 上的一个动点（不与 B 、C 重合），连结AD,将线段AD 绕点D 按顺时针方向旋转90。

中考数学经典几何证明题60例附试题分析和参考答案

中考数学经典几何证明题60例一、解答题（共60小题）1．（遵义）在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．（1）求证：△AEF≌△DEB；（2）证明四边形ADCF是菱形；（3）若AC=4，AB=5，求菱形ADCF的面积．2．（珠海）已知△ABC，AB=AC，将△ABC沿BC方向平移得到△DEF．（1）如图1，连接BD，AF，则BD AF（填“＞”、“＜”或“=”）；（2）如图2，M为AB边上一点，过M作BC的平行线MN分别交边AC，DE，DF于点G，H，N，连接BH，GF，求证：BH=GF．3．（镇江）如图，菱形ABCD的对角线AC，BD相交于点O，分别延长OA，OC到点E，F，使AE=CF，依次连接B，F，D，E各点．（1）求证：△BAE≌△BCF；（2）若∠ABC=50°，则当∠EBA=°时，四边形BFDE是正方形．4．（漳州）如图，在矩形ABCD中，点E在边CD上，将该矩形沿AE折叠，使点D落在边BC上的点F处，过点F作分、FG∥CD，交AE于点G连接DG．（1）求证：四边形DEFG为菱形；（2）若CD=8，CF=4，求的值．5．（玉林）如图，在⊙O中，AB是直径，点D是⊙O上一点且∠BOD=60°，过点D作⊙O 的切线CD交AB的延长线于点C，E为的中点，连接DE，EB．（1）求证：四边形BCDE是平行四边形；（2）已知图中阴影部分面积为6π，求⊙O的半径r．6．（永州）如图，在四边形ABCD中，∠A=∠BCD=90°，BC=DC．延长AD到E点，使DE=AB．（1）求证：∠ABC=∠EDC；（2）求证：△ABC≌△EDC．7．（营口）如图，点P是⊙O外一点，PA切⊙O于点A，AB是⊙O的直径，连接OP，过点B作BC∥OP交⊙O于点C，连接AC交OP于点D．（1）求证：PC是⊙O的切线；（2）若PD=，AC=8，求图中阴影部分的面积；（3）在（2）的条件下，若点E是的中点，连接CE，求CE的长．8．（徐州）如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，且AE=DF，∠A=∠D，AB=DC．（1）求证：四边形BFCE是平行四边形；（2）若AD=10，DC=3，∠EBD=60°，则BE=时，四边形BFCE是菱形．9．（宿迁）如图，四边形ABCD中，∠A=∠ABC=90°，AD=1，BC=3，E是边CD的中点，连接BE并延长与AD的延长线相交于点F．（1）求证：四边形BDFC是平行四边形；（2）若△BCD是等腰三角形，求四边形BDFC的面积．10．（湘西州）如图，在▱ABCD中，DE⊥AB，BF⊥CD，垂足分别为E，F．（1）求证：△ADE≌△CBF；（2）求证：四边形BFDE为矩形．11．（咸宁）已知关于x的一元二次方程mx2﹣（m+2）x+2=0．（1）证明：不论m为何值时，方程总有实数根；（2）m为何整数时，方程有两个不相等的正整数根．12．（咸宁）如图，在△ABC中，∠C=90°，以AB上一点O为圆心，OA长为半径的圆恰好与BC相切于点D，分别交AC、AB于点E、F．（1）若∠B=30°，求证：以A、O、D、E为顶点的四边形是菱形．（2）若AC=6，AB=10，连结AD，求⊙O的半径和AD的长．13．（梧州）如图，在正方形ABCD中，点P在AD上，且不与A、D重合，BP的垂直平分线分别交CD、AB于E、F两点，垂足为Q，过E作EH⊥AB于H．（1）求证：HF=AP；（2）若正方形ABCD的边长为12，AP=4，求线段EQ的长．14．（威海）如图，在△ABC中，AB=AC，以AC为直径的⊙O交AB于点D，交BC于点E．（1）求证：BE=CE；（2）若BD=2，BE=3，求AC的长．15．（铜仁市）已知，如图，点D在等边三角形ABC的边AB上，点F在边AC上，连接DF并延长交BC的延长线于点E，EF=FD．求证：AD=CE．16．（通辽）如图，四边形ABCD中，E点在AD上，其中∠BAE=∠BCE=∠ACD=90°，且BC=CE，求证：△ABC与△DEC全等．17．（铁岭）如图，矩形ABCD中，AB=8，AD=6，点E、F分别在边CD、AB上．（1）若DE=BF，求证：四边形AFCE是平行四边形；（2）若四边形AFCE是菱形，求菱形AFCE的周长．18．（天水）如图，AB是⊙O的直径，BC切⊙O于点B，OC平行于弦AD，过点D作DE⊥AB于点E，连结AC，与DE交于点P．求证：（1）AC•PD=AP•BC；（2）PE=PD．19．（泰安）如图，△ABC是直角三角形，且∠ABC=90°，四边形BCDE是平行四边形，E 为AC中点，BD平分∠ABC，点F在AB上，且BF=BC．求证：（1）DF=AE；（2）DF⊥AC．20．（随州）如图，射线PA切⊙O于点A，连接PO．（1）在PO的上方作射线PC，使∠OPC=∠OPA（用尺规在原图中作，保留痕迹，不写作法），并证明：PC是⊙O的切线；（2）在（1）的条件下，若PC切⊙O于点B，AB=AP=4，求的长．21．（绥化）如图1，在正方形ABCD中，延长BC至M，使BM=DN，连接MN交BD延长线于点E．（1）求证：BD+2DE=BM．（2）如图2，连接BN交AD于点F，连接MF交BD于点G．若AF：FD=1：2，且CM=2，则线段DG=．22．（苏州）如图，在△ABC中，AB=AC，分别以B、C为圆心，BC长为半径在BC下方画弧．设两弧交于点D，与AB、AC的延长线分别交于点E、F，连接AD、BD、CD（1）求证：AD平分∠BAC；（2）若BC=6，∠BAC=50°，求DE、DF的长度之和（结果保留π）．23．（上海）已知，如图，平行四边形ABCD的对角线相交于点O，点E在边BC的延长线上，且OE=OB，连接DE．（1）求证：DE⊥BE；（2）如果OE⊥CD，求证：BD•CE=CD•DE．24．（厦门）如图，在平面直角坐标系中，点A（2，n），B（m，n）（m＞2），D（p，q）（q＜n），点B，D在直线y=x+1上．四边形ABCD的对角线AC，BD相交于点E，且AB∥CD，CD=4，BE=DE，△AEB的面积是2．求证：四边形ABCD是矩形．25．（庆阳）如图，在正方形ABCD中，点E是边BC的中点，直线EF交正方形外角的平分线于点F，交DC于点G，且AE⊥EF．（1）当AB=2时，求△GEC的面积；（2）求证：AE=EF．26．（青海）如图，梯形ABCD中，AB∥DC，AC平分∠BAD，CE∥DA交AB于点E．求证：四边形ADCE是菱形．27．（钦州）如图，AB为⊙O的直径，AD为弦，∠DBC=∠A．（1）求证：BC是⊙O的切线；（2）连接OC，如果OC恰好经过弦BD的中点E，且tanC=，AD=3，求直径AB的长．28．（黔东南州）如图，已知PC平分∠MPN，点O是PC上任意一点，PM与⊙O相切于点E，交PC于A、B两点．（1）求证：PN与⊙O相切；（2）如果∠MPC=30°，PE=2，求劣弧的长．29．（潜江）如图，AC是⊙O的直径，OB是⊙O的半径，PA切⊙O于点A，PB与AC的延长线交于点M，∠COB=∠APB．（1）求证：PB是⊙O的切线；（2）当OB=3，PA=6时，求MB，MC的长．30．（盘锦）如图1，AB为⊙O的直径，点P是直径AB上任意一点，过点P作弦CD⊥AB，垂足为P，过点B的直线与线段AD的延长线交于点F，且∠F=∠ABC．（1）若CD=2，BP=4，求⊙O的半径；（2）求证：直线BF是⊙O的切线；（3）当点P与点O重合时，过点A作⊙O的切线交线段BC的延长线于点E，在其它条件不变的情况下，判断四边形AEBF是什么特殊的四边形？请在图2中补全图象并证明你的结论．31．（内江）如图，将▱ABCD的边AB延长至点E，使AB=BE，连接DE，EC，DE交BC 于点O．（1）求证：△ABD≌△BEC；（2）连接BD，若∠BOD=2∠A，求证：四边形BECD是矩形．32．（南通）如图，在▱ABCD中，点E，F分别在AB，DC上，且ED⊥DB，FB⊥BD．（1）求证：△AED≌△CFB；（2）若∠A=30°，∠DEB=45°，求证：DA=DF．33．（南平）如图，AB是半圆O的直径，C是AB延长线上的一点，CD与半圆O相切于点D，连接AD，BD．（1）求证：∠BAD=∠BDC；（2）若∠BDC=28°，BD=2，求⊙O的半径．（精确到0.01）34．（南京）如图，四边形ABCD是⊙O的内接四边形，BC的延长线与AD的延长线交于点E，且DC=DE．（1）求证：∠A=∠AEB；（2）连接OE，交CD于点F，OE⊥CD，求证：△ABE是等边三角形．35．（南充）如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE．求证：（1）△AEF≌△CEB；（2）AF=2CD．36．（南昌）（1）如图1，纸片▱ABCD中，AD=5，S▱ABCD=15，过点A作AE⊥BC，垂足为E，沿AE剪下△ABE，将它平移至△DCE′的位置，拼成四边形AEE′D，则四边形AEE′D 的形状为A．平行四边形B．菱形C．矩形D．正方形（2）如图2，在（1）中的四边形纸片AEE′D中，在EE′上取一点F，使EF=4，剪下△AEF，将它平移至△DE′F′的位置，拼成四边形AFF′D．①求证：四边形AFF′D是菱形．②求四边形AFF′D的两条对角线的长．37．（梅州）如图，已知△ABC，按如下步骤作图：①以A为圆心，AB长为半径画弧；②以C为圆心，CB长为半径画弧，两弧相交于点D；③连接BD，与AC交于点E，连接AD，CD．（1）求证：△ABC≌△ADC；（2）若∠BAC=30°，∠BCA=45°，AC=4，求BE的长．38．（龙岩）如图，E，F分别是矩形ABCD的边AD，AB上的点，若EF=EC，且EF⊥EC．（1）求证：AE=DC；（2）已知DC=，求BE的长．39．（柳州）如图，已知四边形ABCD是平行四边形，AD与△ABC的外接圆⊙O恰好相切于点A，边CD与⊙O相交于点E，连接AE，BE．（1）求证：AB=AC；（2）若过点A作AH⊥BE于H，求证：BH=CE+EH．40．（辽阳）如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交BC，AC于点D，E，DG⊥AC于点G，交AB的延长线于点F．（1）求证：直线FG是⊙O的切线；（2）若AC=10，cosA=，求CG的长．41．（连云港）如图，将平行四边形ABCD沿对角线BD进行折叠，折叠后点C落在点F 处，DF交AB于点E．（1）求证；∠EDB=∠EBD；（2）判断AF与DB是否平行，并说明理由．42．（莱芜）如图，△ABC是等腰直角三角形，∠ACB=90°，分别以AB，AC为直角边向外作等腰直角△ABD和等腰直角△ACE，G为BD的中点，连接CG，BE，CD，BE与CD 交于点F．（1）判断四边形ACGD的形状，并说明理由．（2）求证：BE=CD，BE⊥CD．43．（酒泉）如图，平行四边形ABCD中，AB=3cm，BC=5cm，∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连结CE，DF．（1）求证：四边形CEDF是平行四边形；（2）①当AE=cm时，四边形CEDF是矩形；②当AE=cm时，四边形CEDF是菱形．（直接写出答案，不需要说明理由）44．（荆门）已知，如图，AB是⊙O的直径，点C为⊙O上一点，OF⊥BC于点F，交⊙O 于点E，AE与BC交于点H，点D为OE的延长线上一点，且∠ODB=∠AEC．（1）求证：BD是⊙O的切线；（2）求证：CE2=EH•EA；（3）若⊙O的半径为5，sinA=，求BH的长．45．（吉林）如图①，半径为R，圆心角为n°的扇形面积是S扇形=，由弧长l=，得S扇形==••R=lR．通过观察，我们发现S扇形=lR类似于S三角形=×底×高．类比扇形，我们探索扇环（如图②，两个同心圆围成的圆环被扇形截得的一部分交作扇环）的面积公式及其应用．（1）设扇环的面积为S扇环，的长为l1，的长为l2，线段AD的长为h（即两个同心圆半径R与r的差）．类比S梯形=×（上底+下底）×高，用含l1，l2，h的代数式表示S扇环，并证明；（2）用一段长为40m的篱笆围成一个如图②所示的扇环形花园，线段AD的长h为多少时，花园的面积最大，最大面积是多少？46．（黄石）在△AOB中，C，D分别是OA，OB边上的点，将△OCD绕点O顺时针旋转到△OC′D′．（1）如图1，若∠AOB=90°，OA=OB，C，D分别为OA，OB的中点，证明：①AC′=BD′；②AC′⊥BD′；（2）如图2，若△AOB为任意三角形且∠AOB=θ，CD∥AB，AC′与BD′交于点E，猜想∠AEB=θ是否成立？请说明理由．47．（黄冈）已知：如图，在△ABC中，AB=AC，以AC为直径的⊙O交AB于点M，交BC于点N，连接AN，过点C的切线交AB的延长线于点P．（1）求证：∠BCP=∠BAN（2）求证：=．48．（湖北）如图，△ABC中，AB=AC=1，∠BAC=45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的，连接BE、CF相交于点D．（1）求证：BE=CF；（2）当四边形ACDE为菱形时，求BD的长．49．（葫芦岛）如图，△ABC是等边三角形，AO⊥BC，垂足为点O，⊙O与AC相切于点D，BE⊥AB交AC的延长线于点E，与⊙O相交于G、F两点．（1）求证：AB与⊙O相切；（2）若等边三角形ABC的边长是4，求线段BF的长？50．（呼伦贝尔）如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点，BD是对角线．（1）求证：△ADE≌△CBF；（2）若∠ADB是直角，则四边形BEDF是什么四边形？证明你的结论．51．（呼伦贝尔）如图，已知直线l与⊙O相离．OA⊥l于点A，交⊙O于点P，OA=5，AB与⊙O相切于点B，BP的延长线交直线l于点C．（1）求证：AB=AC；（2）若PC=2，求⊙O的半径．52．（贺州）如图，AB是⊙O的直径，C为⊙O上一点，AC平分∠BAD，AD⊥DC，垂足为D，OE⊥AC，垂足为E．（1）求证：DC是⊙O的切线；（2）若OE=cm，AC=2cm，求DC的长（结果保留根号）．53．（贺州）如图，将矩形ABCD沿对角线BD对折，点C落在E处，BE与AD相交于点F．若DE=4，BD=8．（1）求证：AF=EF；（2）求证：BF平分∠ABD．54．（河南）如图，AB是半圆O的直径，点P是半圆上不与点A、B重合的一个动点，延长BP到点C，使PC=PB，D是AC的中点，连接PD、PO．（1）求证：△CDP≌△POB；（2）填空：①若AB=4，则四边形AOPD的最大面积为；②连接OD，当∠PBA的度数为时，四边形BPDO是菱形．55．（桂林）如图，在▱ABCD中，E、F分别是AB、CD的中点．（1）求证：四边形EBFD为平行四边形；（2）对角线AC分别与DE、BF交于点M、N，求证：△ABN≌△CDM．56．（贵港）如图，已知AB是⊙O的弦，CD是⊙O的直径，CD⊥AB，垂足为E，且点E 是OD的中点，⊙O的切线BM与AO的延长线相交于点M，连接AC，CM．（1）若AB=4，求的长；（结果保留π）（2）求证：四边形ABMC是菱形．57．（甘南州）如图1，在△ABC和△EDC中，AC=CE=CB=CD；∠ACB=∠DCE=90°，AB与CE交于F，ED与AB，BC，分别交于M，H．（1）求证：CF=CH；（2）如图2，△ABC不动，将△EDC绕点C旋转到∠BCE=45°时，试判断四边形ACDM 是什么四边形？并证明你的结论．58．（东莞）如图，在边长为6的正方形ABCD中，E是边CD的中点，将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG．（1）求证：△ABG≌△AFG；（2）求BG的长．59．（大庆）如图，四边形ABCD内接于⊙O，AD∥BC，P为BD上一点，∠APB=∠BAD．（1）证明：AB=CD；（2）证明：DP•BD=AD•BC；（2）证明：BD2=AB2+AD•BC．60．（赤峰）如图，AB为⊙O的直径，PD切⊙O于点C，与BA的延长线交于点D，DE⊥PO 交PO延长线于点E，连接PB，∠EDB=∠EPB．（1）求证：PB是的切线．（2）若PB=6，DB=8，求⊙O的半径．中考数学经典几何证明题60例参考答案与试题解析一、解答题（共60小题）1．（遵义）在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．（1）求证：△AEF≌△DEB；（2）证明四边形ADCF是菱形；（3）若AC=4，AB=5，求菱形ADCF的面积．考点：菱形的判定与性质；全等三角形的判定与性质；直角三角形斜边上的中线；三角形中位线定理．专题：证明题．分析：（1）根据AAS证△AFE≌△DBE；（2）利用①中全等三角形的对应边相等得到AF=BD．结合已知条件，利用“有一组对边平行且相等的四边形是平行四边形”得到ADCF是菱形，由“直角三角形斜边的中线等于斜边的一半”得到AD=DC，从而得出结论；（3）由直角三角形ABC与菱形有相同的高，根据等积变形求出这个高，代入菱形面积公式可求出结论．解答：（1）证明：①∵AF∥BC，∴∠AFE=∠DBE，∵E是AD的中点，AD是BC边上的中线，∴AE=DE，BD=CD，在△AFE和△DBE中，，∴△AFE≌△DBE（AAS）；（2）证明：由（1）知，△AFE≌△DBE，则AF=DB．∵DB=DC，∴AF=CD．∵AF∥BC，∴四边形ADCF是平行四边形，∵，∠BAC=90°，D是BC的中点，E是AD的中点，∴AD=DC=BC，∴四边形ADCF是菱形；（3）解：设菱形DC边上的高为h，∴RT△ABC斜边BC边上的高也为h，∵BC==，∴DC=BC=，∴h==，菱形ADCF的面积为：DC•h=×=10．点评：本题考查了全等三角形的性质和判定，平行四边形的判定，菱形的判定的应用，菱形的面积计算，主要考查学生的推理能力．2．（珠海）已知△ABC，AB=AC，将△ABC沿BC方向平移得到△DEF．（1）如图1，连接BD，AF，则BD=AF（填“＞”、“＜”或“=”）；（2）如图2，M为AB边上一点，过M作BC的平行线MN分别交边AC，DE，DF于点G，H，N，连接BH，GF，求证：BH=GF．考点：全等三角形的判定与性质；等腰三角形的性质；平移的性质．专题：证明题．分析：（1）根据等腰三角形的性质，可得∠ABC与∠ACB的关系，根据平移的性质，可得AC与DF的关系，根据全等三角形的判定与性质，可得答案；（2）根据相似三角形的判定与性质，可得GM与HN的关系，BM与FN的关系，根据全等三角形的判定与性质，可得答案．解答：（1）解：由AB=AC，得∠ABC=ACB．由△ABC沿BC方向平移得到△DEF，得DF=AC，∠DFE=∠ACB．在△ABF和△DFB中，，△ABF≌△DFB（SAS），BD=AF，故答案为：BD=AF；（2）证明：如图：MN∥BF，△AMG∽△ABC，△DHN∽△DEF，=，=，∴MG=HN，MB=NF．在△BMH和△FNG中，，△BMH≌△FNG（SAS），∴BH=FG．点评：本题考查了全等三角形的判定与性质，利用了平移的性质，相似三角形的判定与性质，全等三角形的判定与性质．3．（镇江）如图，菱形ABCD的对角线AC，BD相交于点O，分别延长OA，OC到点E，F，使AE=CF，依次连接B，F，D，E各点．（1）求证：△BAE≌△BCF；（2）若∠ABC=50°，则当∠EBA=20°时，四边形BFDE是正方形．考点：菱形的性质；全等三角形的判定与性质；正方形的判定．专题：证明题．分析：（1）由题意易证∠BAE=∠BCF，又因为BA=BC，AE=CF，于是可证△BAE≌△BCF；（2）由已知可得四边形BFDE对角线互相垂直平分，只要∠EBF=90°即得四边形BFDE 是正方形，由△BAE≌△BCF可知∠EBA=∠FBC，又由∠ABC=50°，可得∠EBA+∠FBC=40°，于是∠EBA=×40°=20°．解答：（1）证明：∵菱形ABCD的对角线AC，BD相交于点O，∴AB=BC，∠BAC=∠BCA，∴∠BAE=∠BCF，在△BAE与△BCF中，∴△BAE≌△BCF（SAS）；（2）∵四边形BFDE对角线互相垂直平分，∴只要∠EBF=90°即得四边形BFDE是正方形，∵△BAE≌△BCF，∴∠EBA=∠FBC，又∵∠ABC=50°，∴∠EBA+∠FBC=40°，∴∠EBA=×40°=20°．故答案为：20．点评：本题考查了菱形的性质，全等三角形的判定与性质以及正方形的判定．本题关键是根据SAS证明△BAE≌△BCF．4．（漳州）如图，在矩形ABCD中，点E在边CD上，将该矩形沿AE折叠，使点D落在边BC上的点F处，过点F作分、FG∥CD，交AE于点G连接DG．（1）求证：四边形DEFG为菱形；（2）若CD=8，CF=4，求的值．考点：翻折变换（折叠问题）；勾股定理；菱形的判定与性质；矩形的性质．专题：证明题．分析：（1）根据折叠的性质，易知DG=FG，ED=EF，∠1=∠2，由FG∥CD，可得∠1=∠3，易证FG=FE，故由四边相等证明四边形DEFG为菱形；（2）在Rt△EFC中，用勾股定理列方程即可CD、CE，从而求出的值．解答：（1）证明：由折叠的性质可知：DG=FG，ED=EF，∠1=∠2，∵FG∥CD，∴∠2=∠3，∴FG=FE，∴DG=GF=EF=DE，∴四边形DEFG为菱形；（2）解：设DE=x，根据折叠的性质，EF=DE=x，EC=8﹣x，在Rt△EFC中，FC2+EC2=EF2，即42+（8﹣x）2=x2，解得：x=5，CE=8﹣x=3，∴=．点评：本题主要考查了折叠的性质、菱形的判定以及勾股定理，熟知折叠的性质和菱形的判定方法是解答此题的关键．5．（玉林）如图，在⊙O中，AB是直径，点D是⊙O上一点且∠BOD=60°，过点D作⊙O 的切线CD交AB的延长线于点C，E为的中点，连接DE，EB．（1）求证：四边形BCDE是平行四边形；（2）已知图中阴影部分面积为6π，求⊙O的半径r．考点：切线的性质；平行四边形的判定；扇形面积的计算．专题：证明题．分析：（1）由∠BOD=60°E为的中点，得到，于是得到DE∥BC，根据CD 是⊙O的切线，得到OD⊥CD，于是得到BE∥CD，即可证得四边形BCDE是平行四边形；（2）连接OE，由（1）知，，得到∠BOE=120°，根据扇形的面积公式列方程即可得到结论．解答：解：（1）∵∠BOD=60°，∴∠AOD=120°，∴=，∵E为的中点，∴，∴DE∥AB，OD⊥BE，即DE∥BC，∵CD是⊙O的切线，∴OD⊥CD，∴BE∥CD，∴四边形BCDE是平行四边形；（2）连接OE，由（1）知，，∴∠BOE=120°，∵阴影部分面积为6π，∴=6π，∴r=6．点评：本题考查了切线的性质，平行四边形的判定，扇形的面积公式，垂径定理，证明是解题的关键．6．（永州）如图，在四边形ABCD中，∠A=∠BCD=90°，BC=DC．延长AD到E点，使DE=AB．（1）求证：∠ABC=∠EDC；（2）求证：△ABC≌△EDC．考点：全等三角形的判定与性质．专题：证明题．分析：（1）根据四边形的内角和等于360°求出∠B+∠ADC=180°，再根据邻补角的和等于180°可得∠CDE+∠ADE=180°，从而求出∠B=∠CDE；（2）根据“边角边”证明即可．解答：（1）证明：在四边形ABCD中，∵∠BAD=∠BCD=90°，∴90°+∠B+90°+∠ADC=360°，∴∠B+∠ADC=180°，又∵∠CDE+∠ADC=180°，∴∠ABC=∠CDE，（2）连接AC，由（1）证得∠ABC=∠CDE，在△ABC和△EDC中，，∴△ABC≌△EDC（SAS）．点评：本题考查了全等三角形的判定与性质，等腰直角三角形的判定与性质，根据四边形的内角和定理以及邻补角的定义，利用同角的补角相等求出夹角相等是证明三角形全等的关键，也是本题的难点．7．（营口）如图，点P是⊙O外一点，PA切⊙O于点A，AB是⊙O的直径，连接OP，过点B作BC∥OP交⊙O于点C，连接AC交OP于点D．（1）求证：PC是⊙O的切线；（2）若PD=，AC=8，求图中阴影部分的面积；（3）在（2）的条件下，若点E是的中点，连接CE，求CE的长．考点：切线的判定；扇形面积的计算．专题：证明题．分析：（1）连接OC，证明△PAO≌△PCO，得到∠PCO=∠PAO=90°，证明结论；（2）证明△ADP∽△PDA，得到成比例线段求出BC的长，根据S阴=S⊙O﹣S△ABC 求出答案；（3）连接AE、BE，作BM⊥CE于M，分别求出CM和EM的长，求和得到答案．解答：（1）证明：如图1，连接OC，∵PA切⊙O于点A，∴∠PAO=90°，∵BC∥OP，∴∠AOP=∠OBC，∠COP=∠OCB，∵OC=OB，∴∠OBC=∠OCB，∴∠AOP=∠COP，在△PAO和△PCO中，，∴△PAO≌△PCO，∴∠PCO=∠PAO=90°，∴PC是⊙O的切线；（2）解：由（1）得PA，PC都为圆的切线，∴PA=PC，OP平分∠APC，∠ADO=∠PAO=90°，∴∠PAD+∠DAO=∠DAO+∠AOD，∴∠PAD=∠AOD，∴△ADP∽△ODA，∴，∴AD2=PD•DO，∵AC=8，PD=，∴AD=AC=4，OD=3，AO=5，由题意知OD为△的中位线，∴BC=6，OD=6，AB=10．∴S阴=S⊙O﹣S△ABC=﹣24；（3）解：如图2，连接AE、BE，作BM⊥CE于M，∴∠CMB=∠EMB=∠AEB=90°，∵点E是的中点，∴∠ECB=∠CBM=∠ABE=45°，CM=MB=3，BE=AB•cos45°=5，∴EM==4，则CE=CM+EM=7．点评：本题考查的是切线的判定和性质、扇形面积的计算和相似三角形的判定和性质，灵活运用切线的性质：圆的切线垂直于过切点的半径和切线的判定是解题的关键．8．（徐州）如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，且AE=DF，∠A=∠D，AB=DC．（1）求证：四边形BFCE是平行四边形；（2）若AD=10，DC=3，∠EBD=60°，则BE=4时，四边形BFCE是菱形．考点：平行四边形的判定；菱形的判定．专题：证明题．分析：（1）由AE=DF，∠A=∠D，AB=DC，易证得△AEC≌△DFB，即可得BF=EC，∠ACE=∠DBF，且EC∥BF，即可判定四边形BFCE是平行四边形；（2）当四边形BFCE是菱形时，BE=CE，根据菱形的性质即可得到结果．解答：（1）证明：∵AB=DC，∴AC=DF，在△AEC和△DFB中，∴△AEC≌△DFB（SAS），∴BF=EC，∠ACE=∠DBF∴EC∥BF，∴四边形BFCE是平行四边形；（2）当四边形BFCE是菱形时，BE=CE，∵AD=10，DC=3，AB=CD=3，∴BC=10﹣3﹣3=4，∵∠EBD=60°，∴BE=BC=4，∴当BE=4 时，四边形BFCE是菱形，故答案为：4．点评：此题考查了相似三角形的判定与性质、全等三角形的判定与性质、平行四边形的判定与性质、菱形的判定与性质以及勾股定理等知识．此题综合性较强，难度适中，注意数形结合思想的应用，注意掌握辅助线的作法．9．（宿迁）如图，四边形ABCD中，∠A=∠ABC=90°，AD=1，BC=3，E是边CD的中点，连接BE并延长与AD的延长线相交于点F．（1）求证：四边形BDFC是平行四边形；（2）若△BCD是等腰三角形，求四边形BDFC的面积．考点：平行四边形的判定与性质；等腰三角形的性质．专题：证明题．分析：（1）根据同旁内角互补两直线平行求出BC∥AD，再根据两直线平行，内错角相等可得∠CBE=∠DFE，然后利用“角角边”证明△BEC和△FCD全等，根据全等三角形对应边相等可得BE=EF，然后利用对角线互相平分的四边形是平行四边形证明即可；（2）分①BC=BD时，利用勾股定理列式求出AB，然后利用平行四边形的面积公式列式计算即可得解；②BC=CD时，过点C作CG⊥AF于G，判断出四边形AGCB 是矩形，再根据矩形的对边相等可得AG=BC=3，然后求出DG=2，利用勾股定理列式求出CG，然后利用平行四边形的面积列式计算即可得解；③BD=CD时，BC边上的中线应该与BC垂直，从而得到BC=2AD=2，矛盾．解答：（1）证明：∵∠A=∠ABC=90°，∴BC∥AD，∴∠CBE=∠DFE，在△BEC与△FED中，，∴△BEC≌△FED，∴BE=FE，又∵E是边CD的中点，∴CE=DE，∴四边形BDFC是平行四边形；（2）①BC=BD=3时，由勾股定理得，AB===2，所以，四边形BDFC的面积=3×2=6；②BC=CD=3时，过点C作CG⊥AF于G，则四边形AGCB是矩形，所以，AG=BC=3，所以，DG=AG﹣AD=3﹣1=2，由勾股定理得，CG===，所以，四边形BDFC的面积=3×=3；③BD=CD时，BC边上的中线应该与BC垂直，从而得到BC=2AD=2，矛盾，此时不成立；综上所述，四边形BDFC的面积是6或3．点评：本题考查了平行四边形的判定与性质，等腰三角形的性质，全等三角形的判定与性质，（1）确定出全等三角形是解题的关键，（2）难点在于分情况讨论．10．（湘西州）如图，在▱ABCD中，DE⊥AB，BF⊥CD，垂足分别为E，F．（1）求证：△ADE≌△CBF；（2）求证：四边形BFDE为矩形．考点：矩形的判定；全等三角形的判定与性质；平行四边形的性质．专题：证明题．分析：（1）由DE与AB垂直，BF与CD垂直，得到一对直角相等，再由ABCD为平行四边形得到AD=BC，对角相等，利用AAS即可的值；（2）由平行四边形的对边平行得到DC与AB平行，得到∠CDE为直角，利用三个角为直角的四边形为矩形即可的值．解答：证明：（1）∵DE⊥AB，BF⊥CD，∴∠AED=∠CFB=90°，∵四边形ABCD为平行四边形，∴AD=BC，∠A=∠C，在△ADE和△CBF中，，∴△ADE≌△CBF（AAS）；（2）∵四边形ABCD为平行四边形，∴CD∥AB，∴∠CDE+∠DEB=180°，∵∠DEB=90°，∴∠CDE=90°，∴∠CDE=∠DEB=∠BFD=90°，则四边形BFDE为矩形．点评：此题考查了矩形的判定，全等三角形的判定与性质，以及平行四边形的性质，熟练掌握矩形的判定方法是解本题的关键．11．（咸宁）已知关于x的一元二次方程mx2﹣（m+2）x+2=0．（1）证明：不论m为何值时，方程总有实数根；（2）m为何整数时，方程有两个不相等的正整数根．考点：根的判别式；解一元二次方程-公式法．专题：证明题．分析：（1）求出方程根的判别式，利用配方法进行变形，根据平方的非负性证明即可；（2）利用一元二次方程求根公式求出方程的两个根，根据题意求出m的值．解答：（1）证明：△=（m+2）2﹣8m=m2﹣4m+4=（m﹣2）2，∵不论m为何值时，（m﹣2）2≥0，∴△≥0，∴方程总有实数根；（2）解：解方程得，x=，x1=，x2=1，∵方程有两个不相等的正整数根，∴m=1或2，m=2不合题意，∴m=1．点评：本题考查的是一元二次方程根的判别式和求根公式的应用，掌握一元二次方程根的情况与判别式△的关系：△＞0⇔方程有两个不相等的实数根；△=0⇔方程有两个相等的实数根；△＜0⇔方程没有实数根是解题的关键．12．（咸宁）如图，在△ABC中，∠C=90°，以AB上一点O为圆心，OA长为半径的圆恰好与BC相切于点D，分别交AC、AB于点E、F．（1）若∠B=30°，求证：以A、O、D、E为顶点的四边形是菱形．（2）若AC=6，AB=10，连结AD，求⊙O的半径和AD的长．考点：切线的性质；菱形的判定与性质；相似三角形的判定与性质．专题：证明题．分析：（1）连接OD、OE、ED．先证明△AOE是等边三角形，得到AE=AO=0D，则四边形AODE是平行四边形，然后由OA=OD证明四边形AODE是菱形；（2）连接OD、DF．先由△OBD∽△ABC，求出⊙O的半径，然后证明△ADC∽△AFD，得出AD2=AC•AF，进而求出AD．解答：（1）证明：如图1，连接OD、OE、ED．∵BC与⊙O相切于一点D，∴OD⊥BC，∴∠ODB=90°=∠C，∴OD∥AC，∵∠B=30°，∴∠A=60°，∵OA=OE，∴△AOE是等边三角形，∴AE=AO=0D，∴四边形AODE是平行四边形，∵OA=OD，∴四边形AODE是菱形．（2）解：设⊙O的半径为r．∵OD∥AC，∴△OBD∽△ABC．∴，即10r=6（10﹣r）．解得r=，∴⊙O的半径为．如图2，连接OD、DF．∵OD∥AC，∴∠DAC=∠ADO，∵OA=OD，∴∠ADO=∠DAO，∴∠DAC=∠DAO，∵AF是⊙O的直径，∴∠ADF=90°=∠C，∴△ADC∽△AFD，∴，∴AD2=AC•AF，∵AC=6，AF=，∴AD2=×6=45，∴AD==3．点评：本题考查了切线的性质、圆周角定理、等边三角形的判定与性质、菱形的判定和性质以及相似三角形的判定和性质，是一个综合题，难度中等．熟练掌握相关图形的性质及判定是解本题的关键．13．（梧州）如图，在正方形ABCD中，点P在AD上，且不与A、D重合，BP的垂直平分线分别交CD、AB于E、F两点，垂足为Q，过E作EH⊥AB于H．（1）求证：HF=AP；（2）若正方形ABCD的边长为12，AP=4，求线段EQ的长．考点：正方形的性质；全等三角形的判定与性质；勾股定理．专题：证明题．分析：（1）先根据EQ⊥BO，EH⊥AB得出∠EQN=∠BHM=90°．根据∠EMQ=∠BMH得出△EMQ∽△BMH，故∠QEM=∠HBM．由ASA定理得出△APB≌△HFE，故可得出结论；（2）由勾股定理求出BP的长，根据EF是BP的垂直平分线可知BQ=BP，再根据锐角三角函数的定义得出QF=BQ的长，由（1）知，△APB≌△HFE，故EF=BP=4，再根据EQ=EF﹣QF即可得出结论．解答：（1）证明：∵EQ⊥BO，EH⊥AB，∴∠EQN=∠BHM=90°．∵∠EMQ=∠BMH，∴△EMQ∽△BMH，∴∠QEM=∠HBM．在Rt△APB与Rt△HFE中，，∴△APB≌△HFE，∴HF=AP；（2）解：由勾股定理得，BP===4．∵EF是BP的垂直平分线，∴BQ=BP=2，∴QF=BQ•tan∠FBQ=BQ•tan∠ABP=2×=．由（1）知，△APB≌△HFE，∴EF=BP=4，∴EQ=EF﹣QF=4﹣=．点评：本题考查的是正方形的性质，熟知正方形的性质及全等三角形的判定与性质是解答此题的关键．14．（威海）如图，在△ABC中，AB=AC，以AC为直径的⊙O交AB于点D，交BC于点E．（1）求证：BE=CE；（2）若BD=2，BE=3，求AC的长．考点：相似三角形的判定与性质；等腰三角形的性质；圆周角定理．专题：证明题．分析：（1）连结AE，如图，根据圆周角定理，由AC为⊙O的直径得到∠AEC=90°，然后利用等腰三角形的性质即可得到BE=CE；（2）连结DE，如图，证明△BED∽△BAC，然后利用相似比可计算出AB的长，从而得到AC的长．解答：（1）证明：连结AE，如图，∵AC为⊙O的直径，∴∠AEC=90°，∴AE⊥BC，而AB=AC，∴BE=CE；（2）连结DE，如图，∵BE=CE=3，∴BC=6，∵∠BED=∠BAC，而∠DBE=∠CBA，∴△BED∽△BAC，∴=，即=，∴BA=9，∴AC=BA=9．点评：本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形．也考查了角平分线的性质和圆周角定理．15．（铜仁市）已知，如图，点D在等边三角形ABC的边AB上，点F在边AC上，连接DF并延长交BC的延长线于点E，EF=FD．求证：AD=CE．考点：全等三角形的判定与性质；等边三角形的判定与性质．专题：证明题．分析：作DG∥BC交AC于G，先证明△DFG≌△EFC，得出GD=CE，再证明△ADG是等边三角形，得出AD=GD，即可得出结论．解答：证明：作DG∥BC交AC于G，如图所示：则∠DGF=∠ECF，在△DFG和△EFC中，，∴△DFG≌△EFC（AAS），∴GD=CE，。

初中数学-几何证明经典试题(含答案)

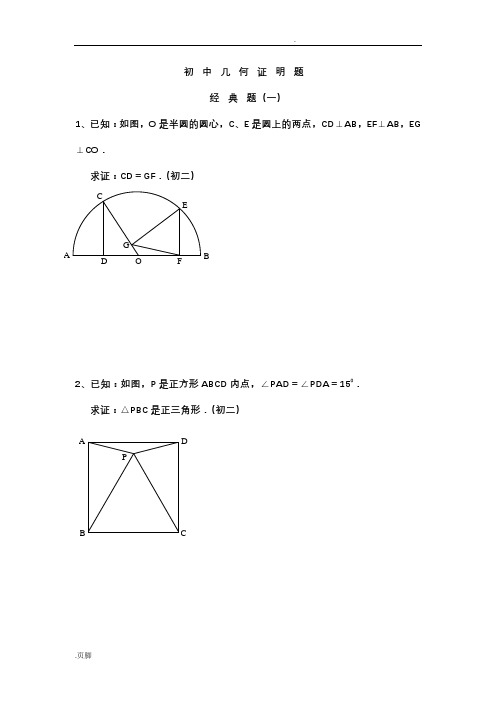
初中几何证明题经典题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）AP C DB A F GC EB O D3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）D 2C 2 B 2 A 2D 1 C 1 B 1 C BD A A 14、已知：如图，在四边形ABCD中，AD＝BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN于E、F．求证：∠DEN＝∠F．经典题（二）1、已知：△ABC中，H为垂心（各边高线的交点），O为外心，且OM⊥BC于M．（1）求证：AH＝2OM；（2）若∠BAC＝600，求证：AH＝AO．（初二）2、设MN是圆O外一直线，过O作OA⊥MN于A，自A引圆的两条直线，交圆于B、C及D、E，直线EB及CD分别交MN于P、Q．F3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．（初二）经典题（三）1、如图，四边形ABCD为正方形，DE∥AC，AE＝AC，AE与CD相交于F．2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）D4、如图，PC切圆O于C，AC为圆的直径，PEF为圆的割线，AE、AF与直线PO相交于B、D．求证：AB＝DC，BC＝AD．（初三）经典题（四）1、已知：△ABC是正三角形，P是三角形内一点，PA＝3，PB＝4，PC＝5．求：∠APB的度数．（初二）2、设P是平行四边形ABCD内部的一点，且∠PBA＝∠PDA．求证：∠PAB＝∠PCB．（初二）3、设ABCD为圆内接凸四边形，求证：AB·CD＋AD·BC＝AC·BD．（初三）4、平行四边形ABCD中，设E、F分别是BC、AB上的一点，AE与CF相交于P，且AE＝CF．求证：∠DPA＝∠DPC．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．APCBACBP D A CBPD4中，∠ABC＝∠ACB＝800，D、E分别是AB、AC上的点，∠＝200，求∠BED的度数．参考答案经典题（一）1.如下图做GH⊥AB,连接EO。

几何证明练习题及答案

几何证明练习题及答案题目1：已知三角形ABC中，AB=AC，点D在BC上，且AD垂直于BC。

证明：三角形ABD与三角形ACD全等。

答案：由于AB=AC，所以三角形ABC是等腰三角形。

根据等腰三角形的性质，角BAD等于角CAD。

又因为AD垂直于BC，所以角ADB和角ADC都是直角。

因此，我们有：- AD=AD（公共边）- ∠BAD=∠CAD（等腰三角形的性质）- ∠ADB=∠ADC=90°（直角）根据SAS（边角边）全等条件，三角形ABD与三角形ACD全等。

题目2：已知三角形ABC中，AB=AC，点E在AB上，点F在AC上，且BE=CF。

证明：三角形AEF是等腰三角形。

答案：由于AB=AC，三角形ABC是等腰三角形。

根据等腰三角形的性质，角ABC等于角ACB。

又因为BE=CF，我们可以得出：- AB=AC（已知）- BE=CF（已知）- ∠ABC=∠ACB（等腰三角形的性质）根据SSS（边边边）全等条件，三角形BEC与三角形CFB全等。

因此，角BEC等于角CFB。

由于角AEF是三角形AEF的外角，根据外角定理，角AEF等于角BEC加角CFB。

因此：- ∠AEF=∠BEC+∠CFB- ∠AEF=2∠BEC（因为∠BEC=∠CFB）由于角AEF是三角形AEF的两个相等的角，所以三角形AEF是等腰三角形。

题目3：已知四边形ABCD中，AB平行于CD，BC平行于AD，且AB=CD。

证明：四边形ABCD是平行四边形。

答案：由于AB平行于CD且BC平行于AD，根据平行四边形的定义，我们可以推断出AD也平行于BC。

因此，四边形ABCD的对边都是平行的。

又因为AB=CD，根据平行四边形的判定条件，我们可以得出四边形ABCD是平行四边形。

题目4：已知三角形ABC中，角A等于角C，点D在BC上，且AD垂直于BC。

证明：三角形ABD与三角形CBD是等腰三角形。

答案：由于角A等于角C，根据三角形内角和定理，我们可以得出角A+角C+角B=180°。

几何证明练习题带答案

几何证明练习题带答案一、选择题1. 已知三角形ABC中，AB=AC，D是BC的中点，连接AD，若∠BAC=80°，则∠ADB的度数为______。

A. 80°B. 50°C. 60°D. 40°2. 在平行四边形ABCD中，E是AB的中点，F是CD的中点，连接EF，若AB=10，BC=6，则EF的长度为______。

A. 8B. 6C. 5D. 33. 已知在三角形ABC中，AB=AC，∠BAC=90°，若AB=6，则三角形ABC的面积为______。

A. 9B. 18C. 12D. 15二、填空题1. 在三角形ABC中，若∠A=60°，AB=AC，且BC=8，则三角形ABC的面积为______。

2. 已知在直角三角形ABC中，∠C=90°，AB=10，BC=8，则AC的长度为______。

三、证明题1. 证明：在等腰三角形ABC中，若AB=AC，点D在BC上，且BD=CD，则AD平分∠BAC。

2. 证明：若四边形ABCD为平行四边形，E是AB的中点，F是CD的中点，连接EF，则EF平分对角线AC。

四、解答题1. 在三角形ABC中，AB=AC，点D在BC上，且BD=CD，求证：三角形ABD与三角形ACD全等。

2. 在平行四边形ABCD中，E是AB的中点，F是CD的中点，连接EF，求证：EF是平行四边形ABCD的对角线AC的中位线。

答案：一、选择题1. C2. A3. A二、填空题1. 16√32. 6√3三、证明题1. 证明：在等腰三角形ABC中，AB=AC，根据等腰三角形的性质，我们知道∠ABD=∠ACD。

又因为BD=CD，根据SAS（边-角-边）相似准则，我们可以证明三角形ABD与三角形ACD全等。

由于全等三角形的对应角相等，因此AD平分∠BAC。

2. 证明：因为ABCD是平行四边形，所以AB∥CD。

根据平行线的性质，我们知道∠AEB=∠DFC。

初中数学几何证明经典题(含答案)

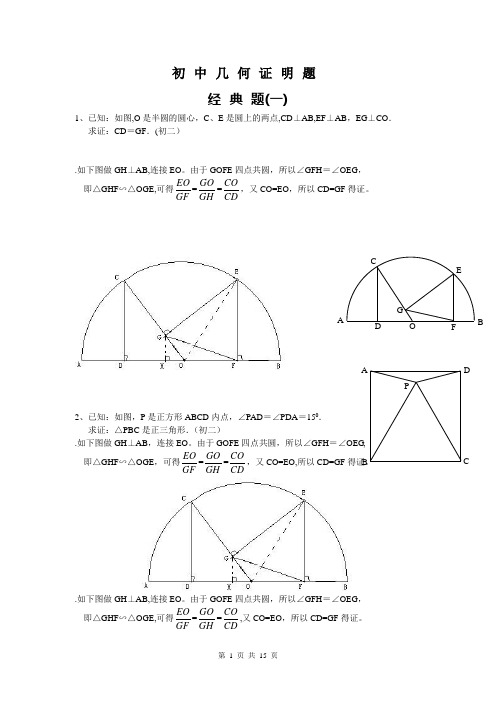
初中几何证明题经典题(一)1、已知：如图,O是半圆的圆心，C、E是圆上的两点,CD⊥AB,EF⊥AB，EG⊥CO．求证：CD＝GF．(初二）.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG，即△GHF∽△OGE,可得EOGF=GOGH=COCD，又CO=EO，所以CD=GF得证。

2、已知：如图，P是正方形ABCD内点，∠PAD＝∠PDA＝150．求证：△PBC是正三角形．（初二）.如下图做GH⊥AB，连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE，可得EOGF=GOGH=COCD，又CO=EO,所以CD=GF得证。

.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG，即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO，所以CD=GF得证。

APCDBAFGCEBOD3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．(初二）4、已知:如图，在四边形ABCD 中，AD ＝BC,M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典题(二）1、已知：△ABC 中，H 为垂心（各边高线的交点)，O 为外心，且OM ⊥BC 于M ． (1)求证：AH ＝2OM; （2）若∠BAC ＝600，求证:AH ＝AO ．（初二）D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 AN FE CDMB· A HEOF2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A,自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二)3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题:设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．(初二）4、如图,分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．经典题（三）1、如图,四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证:CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA,直线EC 交DA 延长线于F ．求证：AE ＝AF ．(初二)3、设P 是正方形ABCD 一边求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C,AC 为圆的直径,PEF 为圆的割线,AE 、证:AB ＝DC,BC ＝AD ．（初三）经典1、已知：△ABC 是正三角形,P 是三角形内一点，PA ＝3,PB ＝4,PC ＝5求：∠APB 的度数．（初二)2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证:∠PAB ＝∠PCB ．（初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD ＋AD ·BC ＝AC ·BD ．(初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P,且 AE ＝CF ．求证:∠DPA ＝∠DPC ．(初二)经典难题（五)1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC,求证：≤L ＜2．2、已知:P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点,并且PA ＝a ，PB ＝2a,PC ＝3a ，求正方形的边长．C BD A F PD E CB A APCBACPDA CBPD4、如图，△ABC中，∠ABC＝∠ACB＝800，D、E分别是AB、AC上的点，∠DCA＝300，∠EBA＝200，求∠BED的度数．经典题(一）1。

初中经典几何证明练习题集(含答案解析)

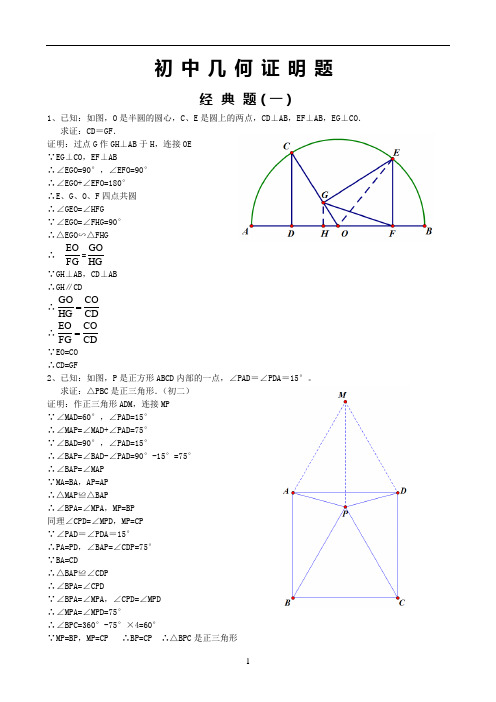
初中几何证明题经典题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．证明：过点G 作GH ⊥AB 于H ，连接OE ∵EG ⊥CO ，EF ⊥AB∴∠EGO=90°，∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ，CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知：如图，P 是正方形ABCD 内部的一点，∠PAD ＝∠PDA ＝15°。

求证：△PBC 是正三角形．（初二）证明：作正三角形ADM ，连接MP ∵∠MAD=60°，∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°，∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ，AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ，MP=BP 同理∠CPD=∠MPD ，MP=CP ∵∠PAD ＝∠PDA ＝15°∴PA=PD ，∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ，∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ，MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．证明:连接AC ，取AC 的中点G,连接NG 、MG ∵CN=DN ，CG=DG ∴GN ∥AD ，GN=21AD ∴∠DEN=∠GNM ∵AM=BM ，AG=CG ∴GM ∥BC ，GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ．（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）证明：（1）延长AD 交圆于F ，连接BF ，过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ，BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2（GH+DH ）=2GD 又AD ⊥BC ，OM ⊥BC ，OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM （2）连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ，OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由（1）知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线，过O 作OA ⊥MN 于A ，自A 引圆的两条割线交圆O 于B 、C 及D 、E ，连接CD 并延长交MN 于Q ，连接EB 并延长交MN 于P. 求证：AP ＝AQ ．证明：作点E 关于AG 的对称点F ，连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ，PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）证明：作OF ⊥CD 于F ，OG ⊥BE 于G ，连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ，∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN ， ∴OA ⊥MN 又OG ⊥BE ，∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°，OA=OA ∴△OAQ ≌△OAP在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ，点O 是DF 的中点，OP ⊥BC求证：BC=2OP （初二）证明：分别过F 、A 、D 作直线BC 的垂线，垂足分别是L 、M 、N ∵OF=OD ，DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形 ∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°，BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）证明：连接BD 交AC 于O 。

中考数学几何证明题--(专题练习答案详解)

几何证明题专题1、如图，等腰梯形ABCD中，AD∥BC，AB=DC，E为AD中点，连接BE，CE（1）求证：BE=CE；（2）若∠BEC=90°，过点B作BF⊥CD，垂足为点F，交CE于点G，连接DG，求证：BG=DG+CD．2、如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，E为AB延长线上一点，连接ED，与BC交于点H．过E作CD的垂线，垂足为CD上的一点F，并与BC交于点G．已知G 为CH的中点．（1）若HE=HG，求证：△EBH≌△GFC；（2）若CD=4，BH=1，求AD的长．3、如图，梯形ABCD中，AB∥CD，AD=DC=BC，∠DAB=60°，E是对角线AC延长线上一点，F是AD延长线上的一点，且EB⊥AB，EF⊥AF．（1）当CE=1时，求△BCE的面积；（2）求证：BD=EF+CE．4、如图．在平行四边形ABCD中，O为对角线的交点，点E为线段BC延长线上的一点，且．过点E EF∥CA，交CD于点F，连接OF．（1）求证：OF∥BC；（2）如果梯形OBEF是等腰梯形，判断四边形ABCD的形状，并给出证明．5、如图，梯形ABCD中，AD∥BC，∠ABC=90°，BF⊥CD于F，延长BF交AD的延长线于E，延长CD交BA的延长线于G，且DG=DE，AB=，CF=6．（1）求线段CD的长；（2）H在边BF上，且∠HDF=∠E，连接CH，求证：∠BCH=45°﹣∠EBC．6、如图，直角梯形ABCD中，AD∥BC，∠B=90°，∠D=45°．（1）若AB=6cm，，求梯形ABCD的面积；（2）若E、F、G、H分别是梯形ABCD的边AB、BC、CD、DA上一点，且满足EF=GH，∠EFH=∠FHG，求证：HD=BE+BF．7、已知：如图，ABCD中，对角线AC，BD相交于点O，延长CD至F，使DF=CD，连接BF交AD于点E．（1）求证：AE=ED；（2）若AB=BC，求∠CAF的度数．8、已知：如图，在正方形ABCD中，点G是BC延长线上一点，连接AG，分别交BD、CD于点E、F．（1）求证：∠DAE=∠DCE；（2）当CG=CE时，试判断CF与EG之间有怎样的数量关系？并证明你的结论．9、如图，已知正方形ABCD，点E是BC上一点，点F是CD延长线上一点，连接EF，若BE=DF，点P是EF的中点．（1）求证：DP平分∠ADC；（2）若∠AEB=75°，AB=2，求△DFP的面积．10、如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，BD=BC，E为CD的中点，交BC的延长线于F；（1）证明：EF=EA；（2）过D作DG⊥BC于G，连接EG，试证明：EG⊥AF．11、如图，直角梯形ABCD中，∠DAB=90°，AB∥CD，AB=AD，∠ABC=60度．以AD 为边在直角梯形ABCD外作等边三角形ADF，点E是直角梯形ABCD内一点，且∠EAD=∠EDA=15°，连接EB、EF．（1）求证：EB=EF；（2）延长FE交BC于点G，点G恰好是BC的中点，若AB=6，求BC的长．12、如图，在梯形ABCD中，AD∥BC，AB=DC=AD，∠C=60°，AE⊥BD于点E，F是CD的中点，DG是梯形ABCD的高．（1）求证：AE=GF；（2）设AE=1，求四边形DEGF的面积．13、已知，如图在直角梯形ABCD中，AD∥BC，∠ABC=90°，DE⊥AC于点F，交BC于点G，交AB的延长线于点E，且AE=AC，连AG．（1）求证：FC=BE；（2）若AD=DC=2，求AG的长．14、如图，直角梯形ABCD中，AD∥BC，∠ABC=90°，点E是AB边上一点，AE=BC，DE⊥EC，取DC的中点F，连接AF、BF．（1）求证：AD=BE；（2）试判断△ABF的形状，并说明理由．15、（2011•潼南县）如图，在直角梯形ABCD中，AB∥CD，AD⊥DC，AB=BC，且AE⊥BC．（1）求证：AD=AE；（2）若AD=8，DC=4，求AB的长．16、如图，已知梯形ABCD中，AD∥CB，E，F分别是BD，AC的中点，BD平分∠ABC．（1）求证：AE⊥BD；（2）若AD=4，BC=14，求EF的长．17、如图，在梯形ABCD中，AD∥BC，∠D=90°，BE⊥AC，E为垂足，AC=BC．（1）求证：CD=BE；（2）若AD=3，DC=4，求AE．18、如图，在梯形ABCD中，AD∥BC，AB⊥AC，∠B=45°，AD=1，BC=4，求DC的长．19、已知梯形ABCD中，AD∥BC，AB=BC=DC，点E、F分别在AD、AB上，且．（1）求证：BF=EF﹣ED；（2）连接AC，若∠B=80°，∠DEC=70°，求∠ACF的度数．20、如图，梯形ABCD中，AD∥BC，点E在BC上，AE=BE，且AF⊥AB，连接EF．（1）若EF⊥AF，AF=4，AB=6，求AE的长．（2）若点F是CD的中点，求证：CE=BE﹣AD．21、如图，四边形ABCD为等腰梯形，AD∥BC，AB=CD，对角线AC、BD交于点O，且AC⊥BD，DH⊥BC．（1）求证：DH=（AD+BC）；（2）若AC=6，求梯形ABCD的面积．22、已知，如图，△ABC是等边三角形，过AC边上的点D作DG∥BC，交AB于点G，在GD的延长线上取点E，使DE=DC，连接AE，BD．（1）求证：△AGE≌△DAB；（2）过点E作EF∥DB，交BC于点F，连AF，求∠AFE的度数．23、如图，梯形ABCD中，AD∥BC，DE=EC，EF∥AB交BC于点F，EF=EC，连接DF．（1）试说明梯形ABCD是等腰梯形；（2）若AD=1，BC=3，DC=，试判断△DCF的形状；（3）在条件（2）下，射线BC上是否存在一点P，使△PCD是等腰三角形，若存在，请直接写出PB的长；若不存在，请说明理由．24、如图，在梯形ABCD中，AD∥BC，∠ABC=∠BCD=60°，AD=DC，E、F分别在AD、DC的延长线上，且DE=CF．AF交BE于P．（1）证明：△ABE≌△DAF；（2）求∠BPF的度数．25、如图，在梯形ABCD中，AD∥BC，AB=AD=DC，BD⊥DC，将BC延长至点F，使CF=CD．（1）求∠ABC的度数；（2）如果BC=8，求△DBF的面积？26、如图，梯形ABCD中，AD∥BC，AB=DC=10cm，AC交BD于G，且∠AGD=60°，E、F分别为CG、AB的中点．（1）求证：△AGD为正三角形；（2）求EF的长度．27、已知，如图，AD∥BC，∠ABC=90°，AB=BC，点E是AB上的点，∠ECD=45°，连接ED，过D作DF⊥BC于F．（1）若∠BEC=75°，FC=3，求梯形ABCD的周长．（2）求证：ED=BE+FC．28、（2005•镇江）已知：如图，梯形ABCD中，AD∥BC，E是AB的中点，直线CE交DA的延长线于点F．（1）求证：△BCE≌△AFE；（2）若AB⊥BC且BC=4，AB=6，求EF的长．29、已知：如图，在梯形ABCD中，AD∥BC，BC=DC，CF平分∠BCD，DF∥AB，BF 的延长线交DC于点E．求证：（1）△BFC≌△DFC；（2）AD=DE；（3）若△DEF的周长为6，AD=2，BC=5，求梯形ABCD的面积．30、如图，梯形ABCD中，AD∥BC．∠C=90°，且AB=AD．连接BD，过A点作BD的垂线，交BC于E．（1）求证：四边形ABED是菱形；（2）如果EC=3cm，CD=4cm，求梯形ABCD的面积．参考答案1、如图，等腰梯形ABCD中，AD∥BC，AB=DC，E为AD中点，连接BE，CE（1）求证：BE=CE；（2）若∠BEC=90°，过点B作BF⊥CD，垂足为点F，交CE于点G，连接DG，求证：BG=DG+CD．证明：（1）已知等腰梯形ABCD中，AD∥BC，AB=DC，E为AD中点，∴AB=DC，∠BAE=∠CDE，AE=DE，∴△BAE≌△CDE，∴BE=CE；（2）延长CD和BE的延长线交于H，∵BF⊥CD，∠HEC=90°，∴∠EBF+∠H=∠ECH+∠H=90°∴∠EBF=∠ECH，又∠BEC=∠CEH=90°，BE=CE（已证），∴△BEG≌△CEH，∴EG=EH，BG=CH=DH+CD，∵△BAE≌△CDE（已证），∴∠AEB=∠GED，∠HED=∠AEB，∴∠GED=∠HED，又EG=EH（已证），ED=ED，∴△GED≌△HED，∴DG=DH，∴BG=DG+CD．2、如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，E为AB延长线上一点，连接ED，与BC交于点H．过E作CD的垂线，垂足为CD上的一点F，并与BC交于点G．已知G 为CH的中点．（1）若HE=HG，求证：△EBH≌△GFC；（1）证明：∵HE=HG，∴∠HEG=∠HGE，∵∠HGE=∠FGC，∠BEH=∠HEG，∴∠BEH=∠FGC，∵G是HC的中点，∴HG=GC，∴HE=GC，∵∠HBE=∠CFG=90°．∴△EBH≌△GFC；（2）解：∵ED平分∠AEF，∠A=∠DFE=90°，∴AD=DF，∵DF=DC﹣FC，∵△EBH≌△GFC，∴FC=BH=1，∴AD=4﹣1=3．3、如图，梯形ABCD中，AB∥CD，AD=DC=BC，∠DAB=60°，E是对角线AC延长线上一点，F是AD延长线上的一点，且EB⊥AB，EF⊥AF．（1）当CE=1时，求△BCE的面积；（2）求证：BD=EF+CE．（2）过E点作EM⊥DB于点M，四边形FDME是矩形，FE=DM，∠BME=∠BCE=90°，∠BEC=∠MBE=60°，△BME≌△ECB，BM=CE，继而可证明BD=DM+BM=EF+CE．（1）解：∵AD=CD，∴∠DAC=∠DCA，∵DC∥AB，∴∠DCA=∠CAB，∴，∵DC∥AB，AD=BC，∴∠DAB=∠CBA=60°，∴∠ACB=180°﹣（∠CAB+∠CBA）=90°，∴∠BCE=180°﹣∠ACB=90°，∵BE⊥AB，∴∠ABE=90°，∴∠CBE=∠ABE﹣∠ABC=30°，在Rt△BCE中，BE=2CE=2，，∴…（5分）（2）证明：过E点作EM⊥DB于点M，∴四边形FDME是矩形，∴FE=DM，∵∠BME=∠BCE=90°，∠BEC=∠MBE=60°，∴△BME≌△ECB，∴BM=CE，∴BD=DM+BM=EF+CE…（10分）4、如图．在平行四边形ABCD中，O为对角线的交点，点E为线段BC延长线上的一点，且．过点E作EF∥CA，交CD于点F，连接OF．（1）求证：OF∥BC；（2）如果梯形OBEF是等腰梯形，判断四边形ABCD的形状，并给出证明．解答：（1）证明：延长EF交AD于G（如图），在平行四边形ABCD中，AD∥BC，AD=BC，∵EF∥CA，EG∥CA，∴四边形ACEG是平行四边形，∴AG=CE，又∵，AD=BC，∴，∵AD∥BC，∴∠ADC=∠ECF，在△CEF和△DGF中，∵∠CFE=∠DFG，∠ADC=∠ECF，CE=DG，∴△CEF≌△DGF（AAS），∴CF=DF，∵四边形ABCD是平行四边形，∴OB=OD，∴OF∥BE．（2）解：如果梯形OBEF是等腰梯形，那么四边形ABCD是矩形．证明：∵OF∥CE，EF∥CO，∴四边形OCEF是平行四边形，∴EF=OC，又∵梯形OBEF是等腰梯形，∴BO=EF，∴OB=OC，∵四边形ABCD是平行四边形，∴AC=2OC，BD=2BO．∴AC=BD，∴平行四边形ABCD是矩形．5、如图，梯形ABCD中，AD∥BC，∠ABC=90°，BF⊥CD于F，延长BF交AD的延长线于E，延长CD交BA的延长线于G，且DG=DE，AB=，CF=6．（1）求线段CD的长；（2）H 在边BF 上，且∠HDF=∠E ，连接CH ，求证：∠BCH=45°﹣∠EBC ．（1）解：连接BD ，由∠ABC=90°，AD ∥BC 得∠GAD=90°，又∵BF ⊥CD ，∴∠DFE=90°又∵DG=DE ，∠GDA=∠EDF ，∴△GAD ≌△EFD ，∴DA=DF ，又∵BD=BD ，∴Rt △BAD ≌Rt △BFD （HL ），∴BF=BA=，∠ADB=∠BDF 又∵CF=6，∴BC=，又∵AD ∥BC ，∴∠ADB=∠CBD ，∴∠BDF=∠CBD ，∴CD=CB=8．（2）证明：∵AD ∥BC ，∴∠E=∠CBF ，∵∠HDF=∠E ，∴∠HDF=∠CBF ，由（1）得，∠ADB=∠CBD ，∴∠HDB=∠HBD ，∴HD=HB ，由（1）得CD=CB ，CBD CDBCBD HDF CDB CBH∴∠=∠∴∠-∠=∠-∠∠∠∴即BDH=HBDHB=HD∴△CDH ≌△CBH ，∴∠DCH=∠BCH ，∴∠BCH=∠BCD==．6、如图，直角梯形ABCD中，AD∥BC，∠B=90°，∠D=45°．（1）若AB=6cm，，求梯形ABCD的面积；（2）若E、F、G、H分别是梯形ABCD的边AB、BC、CD、DA上一点，且满足EF=GH，∠EFH=∠FHG，求证：HD=BE+BF．解：（1）连AC，过C作CM⊥AD于M，如图，在Rt△ABC中，AB=6，sin∠ACB==，∴AC=10，∴BC=8，在Rt△CDM中，∠D=45°，∴DM=CM=AB=6，∴AD=6+8=14，∴梯形ABCD的面积=•（8+14）•6=66（cm2）；（2）证明：过G作GN⊥AD，如图，∵∠D=45°，∴△DNG为等腰直角三角形，∴DN=GN，又∵AD∥BC，∴∠BFH=∠FHN，而∠EFH=∠FHG，∴∠BFE=∠GHN，∵EF=GH，∴Rt△BEF≌Rt△NGH，∴BE=GN，BF=HN，∴DA=AN+DN=AN+DG=BF+BE．7、已知：如图，▱ABCD中，对角线AC，BD相交于点O，延长CD至F，使DF=CD，连接BF交AD于点E．（1）求证：AE=ED；（2）若AB=BC，求∠CAF的度数．（1）证明：如图．∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD．∵DF=CD，∴AB∥DF．∵DF=CD，∴AB=DF．∴四边形ABDF是平行四边形，∴AE=DE．（2）解：∵四边形ABCD是平行四边形，且AB=BC，∴四边形ABCD是菱形．∴AC⊥BD．∴∠COD=90°．∵四边形ABDF是平行四边形，∴AF∥BD．∴∠CAF=∠COD=90°．8、已知：如图，在正方形ABCD中，点G是BC延长线上一点，连接AG，分别交BD、CD于点E、F．（1）求证：∠DAE=∠DCE；（2）当CG=CE时，试判断CF与EG之间有怎样的数量关系？并证明你的结论．（1）证明：在△DAE和△DCE中，∠ADE=∠CDE（正方形的对角线平分对角），ED=DE（公共边），AE=CE（正方形的四条边长相等），∴△DAE≌△DCE（SAS），∴∠DAE=∠DCE（全等三角形的对应角相等）；（2）解：如图，由（1）知，△DAE≌△DCE，∴AE=EC，∴∠EAC=∠ECA（等边对等角）；又∵CG=CE（已知），∴∠G=∠CEG（等边对等角）；而∠CEG=2∠EAC（外角定理），∠ECB=2∠CEG（外角定理），∴4∠EAC﹣∠ECA=∠ACB=45°，∴∠G=∠CEG=30°；过点C作CH⊥AG于点H，∴∠FCH=30°，∴在直角△ECH中，EH=CH，EG=2CH，在直角△FCH中，CH=CF，∴EG=2×CF=3CF．9、如图，已知正方形ABCD，点E是BC上一点，点F是CD延长线上一点，连接EF，若BE=DF，点P是EF的中点．（1）求证：DP平分∠ADC；（2）若∠AEB=75°，AB=2，求△DFP的面积．（1）证明：连接PC．∵ABCD是正方形，∴∠ABE=∠ADF=90°，AB=AD．∵BE=DF，∴△ABE≌△ADF．（SAS）∴∠BAE=∠DAF，AE=AF．∴∠EAF=∠BAD=90°．∵P是EF的中点，∴PA=EF，PC=EF，∴PA=PC．又AD=CD，PD公共，∴△PAD≌△PCD，（SSS）∴∠ADP=∠CDP，即DP平分∠ADC；（2）作PH⊥CF于H点．∵P是EF的中点，∴PH=EC．设EC=x．由（1）知△EAF是等腰直角三角形，∴∠AEF=45°，∴∠FEC=180°﹣45°﹣75°=60°，∴EF=2x，FC=x，BE=2﹣x．在Rt△ABE中，22+（2﹣x）2=（x）2解得x1=﹣2﹣2（舍去），x2=﹣2+2．∴PH=﹣1+，FD=（﹣2+2）﹣2=﹣2+4．=（﹣2+4）×=3﹣5．∴S△DPF10、如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，BD=BC，E为CD的中点，交BC的延长线于F；（1）证明：EF=EA；（2）过D作DG⊥BC于G，连接EG，试证明：EG⊥AF．（1）证明：∵AD∥BC，∴∠DAE=∠F，∠ADE=∠FCE．∵E为CD的中点，∴ED=EC．∴△ADE≌△FCE．∴EF=EA．（5分）（2）解：连接GA，∵AD∥BC，∠ABC=90°，∴∠DAB=90°．∵DG⊥BC，∴四边形ABGD是矩形．∴BG=AD，GA=BD．∵BD=BC，∴GA=BC．由（1）得△ADE≌△FCE，∴AD=FC．∴GF=GC+FC=GC+AD=GC+BG=BC=GA．∵由（1）得EF=EA，∴EG⊥AF．（5分）11、如图，直角梯形ABCD中，∠DAB=90°，AB∥CD，AB=AD，∠ABC=60度．以AD为边在直角梯形ABCD外作等边三角形ADF，点E是直角梯形ABCD内一点，且∠EAD=∠EDA=15°，连接EB、EF．（1）求证：EB=EF；（2）延长FE交BC于点G，点G恰好是BC的中点，若AB=6，求BC的长．（1）证明：∵△ADF为等边三角形，∴AF=AD，∠FAD=60°（1分）∵∠DAB=90°，∠EAD=15°，AD=AB（2分）∴∠FAE=∠BAE=75°，AB=AF，（3分）∵AE为公共边∴△FAE≌△BAE（4分）∴EF=EB（5分）（2）解：如图，连接EC．（6分）∵在等边三角形△ADF中，∴FD=FA，∵∠EAD=∠EDA=15°，∴ED=EA，∴EF是AD的垂直平分线，则∠EFA=∠EFD=30°．（7分）由（1）△FAE≌△BAE知∠EBA=∠EFA=30°．∵∠FAE=∠BAE=75°，∴∠BEA=∠BAE=∠FEA=75°，∴BE=BA=6．∵∠FEA+∠BEA+∠GEB=180°，∴∠GEB=30°，∵∠ABC=60°，∴∠GBE=30°∴GE=GB．（8分）∵点G是BC的中点，∴EG=CG∵∠CGE=∠GEB+∠GBE=60°，∴△CEG为等边三角形，∴∠CEG=60°，∴∠CEB=∠CEG+∠GEB=90°（9分）∴在Rt△CEB中，BC=2CE，BC2=CE2+BE2∴CE=，∴BC=（10分）；解法二：过C作CQ⊥AB于Q，∵CQ=AB=AD=6，∵∠ABC=60°，∴BC=6÷=4．12、如图，在梯形ABCD中，AD∥BC，AB=DC=AD，∠C=60°，AE⊥BD于点E，F是CD的中点，DG是梯形ABCD的高．（1）求证：AE=GF；（2）设AE=1，求四边形DEGF的面积．（1）证明：∵AB=DC，∴梯形ABCD为等腰梯形．∵∠C=60°，∴∠BAD=∠ADC=120°，又∵AB=AD，∴∠ABD=∠ADB=30°．∴∠DBC=∠ADB=30°．∴∠BDC=90°．（1分）由已知AE⊥BD，∴AE∥DC．（2分）又∵AE为等腰三角形ABD的高，∴E是BD的中点，∵F是DC的中点，∴EF∥BC．∴EF∥AD．∴四边形AEFD是平行四边形．（3分）∴AE=DF（4分）∵F是DC的中点，DG是梯形ABCD的高，∴GF=DF，（5分）∴AE=GF．（6分）（2）解：在Rt△AED中，∠ADB=30°，∵AE=1，∴AD=2．在Rt△DGC中∠C=60°，并且DC=AD=2，∴DG=．（8分）由（1）知：在平行四边形AEFD中EF=AD=2，又∵DG⊥BC，∴DG⊥EF，∴四边形DEGF的面积=EF•DG=．（10分）13、已知，如图在直角梯形ABCD中，AD∥BC，∠ABC=90°，DE⊥AC于点F，交BC于点G，交AB的延长线于点E，且AE=AC，连AG．（1）求证：FC=BE；（2）若AD=DC=2，求AG的长．解答：（1）证明：∵∠ABC=90°，DE⊥AC于点F，∴∠ABC=∠AFE．∵AC=AE，∠EAF=∠CAB，∴△ABC≌△AFE，∴AB=AF．∴AE﹣AB=AC﹣AF，即FC=BE；（2）解：∵AD=DC=2，DF⊥AC，∴AF=AC=AE．∴AG=CG，∴∠E=30°．∵∠EAD=90°，∴∠ADE=60°，∴∠FAD=∠E=30°，∴FC=，∵AD∥BC，∴∠ACG=∠FAD=30°，∴CG=2，∴AG=2．14、如图，直角梯形ABCD中，AD∥BC，∠ABC=90°，点E是AB边上一点，AE=BC，（1）证明：∵AD∥BC，∴∠BAD+∠ABC=180°，∵∠ABC=90°，∴∠BAD=∠ABC=90°，∵DE⊥EC，∴∠AED+∠BEC=90°∵∠AED+∠ADE=90°，∴∠BEC=∠ADE，∵∠DAE=∠EBC，AE=BC，∴△EAD≌△EBC，∴AD=BE．（2）答：△ABF是等腰直角三角形．理由是：延长AF交BC的延长线于M，∵AD∥BM，∴∠DAF=∠M，∵∠AFD=∠CFM，DF=FC，∴△ADF≌△MFC，∴AD=CM，∵AD=BE，∴BE=CM，∵AE=BC，∴AB=BM，∴△ABM是等腰直角三角形，∵△ADF≌△MFC，∴AF=FM，∴∠ABC=90°，∴BF⊥AM，BF=AM=AF，∴△AFB是等腰直角三角形．15、（2011•潼南县）如图，在直角梯形ABCD中，AB∥CD，AD⊥DC，AB=BC，且AE⊥BC．（1）求证：AD=AE；（2）若AD=8，DC=4，求AB的长．解答：（1）证明：连接AC，∵AB∥CD，∴∠ACD=∠BAC，∵AB=BC，∴∠ACB=∠BAC，∴∠ACD=∠ACB，∵AD⊥DC，AE⊥BC，∴∠D=∠AEC=90°，∵AC=AC，∴，∴△ADC≌△AEC，（AAS）∴AD=AE；（2）解：由（1）知：AD=AE，DC=EC，设AB=x，则BE=x﹣4，AE=8，在Rt△ABE中∠AEB=90°，由勾股定理得：82+（x﹣4）2=x2，解得：x=10，∴AB=10．说明：依据此评分标准，其它方法如：过点C作CF⊥AB用来证明和计算均可得分．16、如图，已知梯形ABCD中，AD∥CB，E，F分别是BD，AC的中点，BD平分∠ABC．（1）求证：AE⊥BD；（2）若AD=4，BC=14，求EF的长．（1）证明：∵AD∥CB，∴∠ADB=∠CBD，又BD平分∠ABC，∴∠ABD=∠CBD，∴∠ADB=∠ABD，∴AB=AD，∴△ABD是等腰三角形，已知E是BD的中点，∴AE⊥BD．（2）解：延长AE交BC于G，∵BD平分∠ABC，∴∠ABE=∠GBE，又∵AE⊥BD（已证），∴∠AEB=∠GEB，BE=BE，∴△ABE≌△GBE，∴AE=GE，BG=AB=AD，又F是AC的中点（已知），所以由三角形中位线定理得：EF=CG=（BC﹣BG）=（BC﹣AD）=×（14﹣4）=5．答：EF的长为5．17、如图，在梯形ABCD中，AD∥BC，∠D=90°，BE⊥AC，E为垂足，AC=BC．（1）求证：CD=BE；（2）若AD=3，DC=4，求AE．（1）证明：∵AD∥BC，∴∠DAC=∠BCE，而BE⊥AC，∴∠D=∠BEC=90°，AC=BC，∴△BCE≌△CAD．∴CD=BE．（2）解：在Rt△ADC中，根据勾股定理得AC==5，∵△BCE≌△CAD，∴CE=AD=3．∴AE=AC﹣CE=2．18、如图，在梯形ABCD中，AD∥BC，AB⊥AC，∠B=45°，AD=1，BC=4，求DC的长．解：如图，过点D作DF∥AB，分别交AC，BC于点E，F．（1分）∵AB⊥AC，∴∠AED=∠BAC=90度．∵AD∥BC，∴∠DAE=180°﹣∠B﹣∠BAC=45度．在Rt△ABC中，∠BAC=90°，∠B=45°，BC=4，∴AC=BC•sin45°=4×=2（2分）在Rt△ADE中，∠AED=90°，∠DAE=45°，AD=1，∴DE=AE=．∴CE=AC﹣AE=．（4分）在Rt△DEC中，∠CED=90°，∴DC==．（5分）19、已知梯形ABCD中，AD∥BC，AB=BC=DC，点E、F分别在AD、AB上，且．（1）求证：BF=EF﹣ED；（2）连接AC，若∠B=80°，∠DEC=70°，求∠ACF的度数．证明：∵FC=F′C，EC=EC，∠ECF'=∠BCF+∠DCE=∠ECF，∴△FCE≌△F′CE，∴EF′=EF=DF′+ED，∴BF=EF﹣ED；（2）解：∵AB=BC，∠B=80°，∴∠ACB=50°，由（1）得∠FEC=∠DEC=70°，∴∠ECB=70°，而∠B=∠BCD=80°，∴∠DCE=10°，∴∠BCF=30°，∴∠ACF=∠BCA﹣∠BCF=20°．20、如图，梯形ABCD中，AD∥BC，点E在BC上，AE=BE，且AF⊥AB，连接EF．（1）若EF⊥AF，AF=4，AB=6，求AE的长．（2）若点F是CD的中点，求证：CE=BE﹣AD．解：（1）作EM⊥AB，交AB于点M．∵AE=BE，EM⊥AB，∴AM=BM=×6=3；∵∠AME=∠MAF=∠AFE=90°，∴四边形AMEF是矩形，∴EF=AM=3；在Rt△AFE中，AE==5；（2）延长AF、BC交于点N．∵AD∥EN，∴∠DAF=∠N；∵∠AFD=∠NFC，DF=FC，∴△ADF≌△NCF（AAS），∴AD=CN；∵∠B+∠N=90°，∠BAE+∠EAN=90°，又AE=BE，∠B=∠BAE，∴∠N=∠EAN，AE=EN，∴BE=EN=EC+CN=EC+AD，∴CE=BE﹣AD．．21、如图，四边形ABCD为等腰梯形，AD∥BC，AB=CD，对角线AC、BD交于点O，且AC⊥BD，DH⊥BC．（1）求证：DH=（AD+BC）；（2）若AC=6，求梯形ABCD的面积．解：（1）证明：过D作DE∥AC交BC延长线于E，（1分）∵AD∥BC，∴四边形ACED为平行四边形．（2分）∴CE=AD，DE=AC．∵四边形ABCD为等腰梯形，∴BD=AC=DE．∵AC⊥BD，∴DE⊥BD．∴△DBE为等腰直角三角形．（4分）∵DH⊥BC，∴DH=BE=（CE+BC）=（AD+BC）．（5分）（2）∵AD=CE，∴．（7分）∵△DBE为等腰直角三角形BD=DE=6，∴．∴梯形ABCD的面积为18．（8分）注：此题解题方法并不唯一．22、已知，如图，△ABC是等边三角形，过AC边上的点D作DG∥BC，交AB于点G，在GD的延长线上取点E，使DE=DC，连接AE，BD．（1）求证：△AGE≌△DAB；（2）过点E作EF∥DB，交BC于点F，连AF，求∠AFE的度数．（1）证明：∵△ABC是等边三角形，DG∥BC，∴∠AGD=∠ABC=60°，∠ADG=∠ACB=60°，且∠BAC=60°，∴△AGD是等边三角形，AG=GD=AD，∠AGD=60°．∵DE=DC，∴GE=GD+DE=AD+DC=AC=AB，∵∠AGD=∠BAD，AG=AD，∴△AGE≌△DAB；（2）解：由（1）知AE=BD，∠ABD=∠AEG．∵EF∥DB，DG∥BC，∴四边形BFED是平行四边形．∴EF=BD，∴EF=AE．∵∠DBC=∠DEF，∴∠ABD+∠DBC=∠AEG+∠DEF，即∠AEF=∠ABC=60°．∴△AFE是等边三角形，∠AFE=60°．23、如图，梯形ABCD中，AD∥BC，DE=EC，EF∥AB交BC于点F，EF=EC，连接DF．（1）试说明梯形ABCD是等腰梯形；（2）若AD=1，BC=3，DC=，试判断△DCF的形状；（3）在条件（2）下，射线BC上是否存在一点P，使△PCD是等腰三角形，若存在，请直接写出PB的长；若不存在，请说明理由．解：（1）证明：∵EF=EC，∴∠EFC=∠ECF，∵EF∥AB，∴∠B=∠EFC，∴∠B=∠ECF，∴梯形ABCD是等腰梯形；（2）△DCF是等腰直角三角形，证明：∵DE=EC，EF=EC，∴EF=CD，∴△CDF是直角三角形（如果一个三角形一边上的中线等于这条边的一半，那么这个三角形是直角三角形），∵梯形ABCD是等腰梯形，∴CF=（BC﹣AD）=1，∵DC=，∴由勾股定理得：DF=1，∴△DCF是等腰直角三角形；（3）共四种情况：∵DF⊥BC，∴当PF=CF时，△PCD是等腰三角形，即PF=1，∴PB=1；当P与F重合时，△PCD是等腰三角形，∴PB=2；当PC=CD=（P在点C的左侧）时，△PCD是等腰三角形，∴PB=3﹣；当PC=CD=（P在点C的右侧）时，△PCD是等腰三角形，∴PB=3+．故共四种情况：PB=1，PB=2，PB=3﹣，PB=3+．（每个1分）24、如图，在梯形ABCD中，AD∥BC，∠ABC=∠BCD=60°，AD=DC，E、F分别在AD、DC的延长线上，且DE=CF．AF交BE于P．（1）证明：△ABE≌△DAF；（2）求∠BPF的度数．解答：（1）证明：∵在梯形ABCD中，AD∥BC，∠ABC=∠BCD=60°，∴AB=CD，∵AD=DC，∴BA=AD，∠BAE=∠ADF=120°，∵DE=CF，∴AE=DF，在△BAE和△ADF中，，∴△ABE≌△DAF（SAS）．（2）解：∵由（1）△BAE≌△ADF，∴∠ABE=∠DAF．∴∠BPF=∠ABE+∠BAP=∠BAE．而AD∥BC，∠C=∠ABC=60°，∴∠BPF=120°．25、如图，在梯形ABCD中，AD∥BC，AB=AD=DC，BD⊥DC，将BC延长至点F，使CF=CD．（1）求∠ABC的度数；（2）如果BC=8，求△DBF的面积？解答：解：（1）∵AD∥BC，∴∠ADB=∠DBC，∵AB=AD，∴∠ADB=∠ABD，∴∠DBC=∠ABD，∵在梯形ABCD中AB=DC，∴∠ABC=∠DCB=2∠DBC，∵BD⊥DC，∴∠DBC+2∠DBC=90°∴∠DBC=30°∴∠ABC=60°（2）过点D作DH⊥BC，垂足为H，∵∠DBC=30°，BC=8，∴DC=4，∵CF=CD∴CF=4，∴BF=12，∵∠F+∠FDC=∠DCB=60°，∠F=∠FDC∴∠F=30°，∵∠DBC=30°，∴∠F=∠DBC，∴DB=DF，∴，在直角三角形DBH中，∴，∴，∴，即△DBF的面积为．26、如图，梯形ABCD中，AD∥BC，AB=DC=10cm，AC交BD于G，且∠AGD=60°，E、F分别为CG、AB的中点．（1）求证：△AGD为正三角形；（2）求EF的长度．（1）证明：连接BE，∵梯形ABCD中，AB=DC，∴AC=BD，可证△ABC≌△DCB，∴∠GCB=∠GBC，又∵∠BGC=∠AGD=60°∴△AGD为等边三角形，（2）解：∵BE为△BCG的中线，∴BE⊥AC，在Rt△ABE中，EF为斜边AB上的中线，∴EF=AB=5cm．27、已知，如图，AD∥BC，∠ABC=90°，AB=BC，点E是AB上的点，∠ECD=45°，连接ED，过D作DF⊥BC于F．（1）若∠BEC=75°，FC=3，求梯形ABCD的周长．（2）求证：ED=BE+FC．解：（1）∵∠BEC=75°，∠ABC=90°，∴∠ECB=15°，∵∠ECD=45°，∴∠DCF=60°，在Rt△DFC中：∠DCF=60°，FC=3，∴DF=3，DC=6，由题得，四边形ABFD是矩形，∴AB=DF=3，∵AB=BC，∴BC=3，∴BF=BC﹣FC=3﹣3，∴AD=DF=3﹣3，∴C=3×2+6+3﹣3=9+3，梯形ABCD答：梯形ABCD的周长是9+3．（2）过点C作CM垂直AD的延长线于M，再延长DM到N，使MN=BE，∴CN=CE，可证∠NCD=∠DCE，∵CD=CD，∴△DEC≌△DNC，∴ED=EN，∴ED=BE+FC．28、（2005•镇江）已知：如图，梯形ABCD中，AD∥BC，E是AB的中点，直线CE交DA的延长线于点F．（1）求证：△BCE≌△AFE；（2）若AB⊥BC且BC=4，AB=6，求EF的长．（1）证明：∵AD∥BC，E是AB的中点，∴AE=BE，∠B=∠EAF，∠BCE=∠F．∴△BCE≌△AFE（AAS）．（2）解：∵AD∥BC，∴∠DAB=∠ABC=90°．∵AE=BE，∠AEF=∠BEC，∴△BCE≌△AFE．∴AF=BC=4．∵EF2=AF2+AE2=9+16=25，∴EF=5．29、已知：如图，在梯形ABCD中，AD∥BC，BC=DC，CF平分∠BCD，DF∥AB，BF 的延长线交DC于点E．（1）△BFC≌△DFC；（2）AD=DE；（3）若△DEF的周长为6，AD=2，BC=5，求梯形ABCD的面积．（1）∵DC=BC，∠1=∠2，CF=CF，∴△DCF≌△BCF．（2）延长DF交BC于G，∵AD∥BG，AB∥DG，∴四边形ABGD为平行四边形．∴AD=BG．∵△DFC≌△BFC，∴∠EDF=∠GBF，DF=BF．又∵∠3=∠4，∴△DFE≌△BFG．∴DE=BG，EF=GF．∴AD=DE．（3）∵EF=GF，DF=BF，∴EF+BF=GF+DF，即：BE=DG．∵DG=AB，∴BE=AB．∵C=DF+FE+DE=6，△DFE∴BF+FE+DE=6，即：EB+DE=6．∴AB+AD=6．又∵AD=2，∴AB=4．∴DG=AB=4．∵BG=AD=2，∴GC=BC﹣BG=5﹣2=3．又∵DC=BC=5，在△DGC中∵42+32=52∴DG2+GC2=DC2∴∠DGC=90°．=（AD+BC）•DG∴S梯形ABCD=（2+5）×430、如图，梯形ABCD中，AD∥BC．∠C=90°，且AB=AD．连接BD，过A点作BD的垂线，交BC于E．（1）求证：四边形ABED是菱形；（2）如果EC=3cm，CD=4cm，求梯形ABCD的面积．解答：解：（1）证明：∵AD∥BC，DE2=CD2+CE2=42+32=25，∴∠OAD=∠OEB，∴DE=5又∵AB=AD，AO⊥BD，∴AD=BE=5，=．∴OB=OD，∴S梯形ABCD又∵∠AOD=∠EOB，∴△ADO≌△EBO（AAS），∴AD=EB，又∵AD∥BE，∴四边形ABCD是平行四边形，又∵AB=AD∴四边形ABCD是菱形．（2）∵四边形ABCD是菱形，∴AD=DE=BE，。

中考几何证明题及答案

中考复习初中数学几何证明 试题(含答案)

几何证明练习题带答案

初中数学几何证明试题(含答案)

初中几何证明题五大经典(含答案)

(完整版)初中数学几何证明经典试题(含答案)

中考数学-几何证明

中考数学经典几何证明题60例附试题分析和参考答案

初中数学-几何证明经典试题(含答案)

几何证明练习题及答案

几何证明练习题带答案

初中数学几何证明经典题(含答案)

初中经典几何证明练习题集(含答案解析)

中考数学几何证明题--(专题练习 答案详解)

中考复习初中数学几何证明试题(含答案)

中考数学几何证明题--(专题练习答案详解)