直线,圆曲线,缓和曲线正算及反算
缓和曲线要素及计算公式

缓和曲线要素及计算公式缓和曲线:在直线与圆曲线之间加入一段半径由无穷大逐渐变化到圆曲线半径的曲线,这种曲线称为缓和曲线。
缓和曲线的主要曲线元素缓和曲线主要有ZH 、HY 、QZ 、YH 、HZ5个主点。
由此可得:q P R q T T h ++=+=2tan)(αR P R E h -+=2sec)(αs h L RL 2180)2(0+-=πβα180)2(0RL y πβα-= 式中:h T -缓和曲线切线长h E -缓和曲线外矢距 h L -缓和曲线中曲线总长 y L -缓和曲线中圆曲线长度缓和曲线与圆曲线区别:1. 因为缓和曲线起始端分别和直线与圆曲线顺滑的相接,因此必须将原来的圆曲线向内移动一段距离才能够接顺,故曲线发生了内移(即设置缓和曲线后有内移值P 产生)2. 缓和曲线的一部分在直线段,另一部分插入了圆曲线,因此有切线增长值q;3. 由于有缓和曲线的存在,因此有缓和曲线角0β。
缓和曲线角0β的计算:R L S 2/0=β(弧度)=RL Sπ90(度)内移值P 的计算:()m RL P S 242=切线增长值q的计算:)(240223m RL L q S S -=P -缓和曲线内移值 q -缓和曲线切线增长值0β-缓和曲线首或尾所采用的缓和曲线段分别的总缓和曲线角。
S L -缓和曲线两端各自的缓和曲线长.R -缓和曲线中的主圆曲线半径α-偏转角缓和曲线主点桩号:ZH 桩号=JD 桩号—h THY 桩号=ZH 桩号+S L QZ 桩号=HY 桩号+2y L YH 桩号=QZ 桩号+2y LHZ 桩号=ZH 桩号+h L另外、QZ 桩号、YH 桩号、HZ 桩号还可以用以下方式推导:QZ 桩号=ZH 桩号+2hL YH 桩号=HZ 桩号-S L HZ 桩号=YH 桩号+S L 切线支距法计算坐标: 缓和曲线段内坐标计算如式:22540SPp L R L L -=X sP RL L Y 63=进入净圆曲线段内坐标计算如式:⎥⎦⎤•⎪⎪⎭⎫- ⎝⎛⎢⎣⎡+=R L L R q X s p π1802sin⎭⎬⎫⎥⎦⎤•⎪⎪⎭⎫- ⎝⎛⎢⎣⎡-⎩⎨⎧+=R L L R P Y s p π1802cos 1上述公式还可以简化为:αsin R q X +=()αcos 1-+=R P Y+-=RL L s p πα)180(0βR L S 2/0=β(弧度)=RL Sπ90(度)。
缓和曲线和圆曲线的有关计算

缓和曲线和圆曲线的计算与测设一、缓和曲线的性质缓和曲线是直线与圆曲线间的一种过渡曲线。
它与直线分界处半径为∞,与圆曲线相接处半径与圆曲线半径R 相等。
缓和曲线上任一点的曲率半径ρ∝l1 或ρl=C式中,C 变更率。
当l =0l 时,ρ=R ,所以0Rl =C式中,0l 为缓和曲线总长。
ρl=C 是缓和曲线的必要条件,实用中能满足这一条件的曲线可以作为缓和曲线,如辐射螺旋线、三次抛物线等。
我国缓和曲线均采用辐射螺旋线。
二、缓和曲线方程式按照ρl=C 为必要条件导出的缓和曲线方程为:X=l -2540C l +493456C l +…Y=Cl 63-37336C l +51142240C l + (1)根据测设要求的精度,实际应用中可将高次项舍去,并顾及到0Rl =C ,则上式变为X=l -202540l R lY=036Rl l -3037336l R l (2)式中,x 、y 为缓和曲线上任一点的直角坐标,坐标原点为直缓点(ZH )或缓直点(HZ );通过该点的缓和曲线切线为x 轴,如图2:l 为缓和曲线上任一点P 到ZH (或HZ )的曲线长;0l 为缓和曲线总长度。
当l =0l 时,x=x 0,y=y 0,代入式(2)得:X 0=0l -23040R lY 0=Rl 62-340336Rl (3)式中,x 0 、y 0 为缓圆点(HY )或圆缓点(YH )的坐标。
三、缓和曲线常数计算β0、δ0、m 、p 、 x 0、y 0 等称为缓和曲线常数。
其物理意义及几何关系由下图,图3可得知:β0——缓和曲线的切线角,即HY (或YH )点的切线与ZH (或HZ )点切线的交角;亦即圆曲线一端延长部分所对应的圆心角。
δ0——缓和曲线的总偏角;m —切垂距,即ZH (或HZ )到由圆心O 向切线所作垂线垂足的距离; p —圆曲线内移量,为垂线长与圆曲线半径R 之差。
常数计算公式如下:X 0=0l -23040R lY 0=Rl 62-340336Rlβ0=π18020R lδ0=031β=π 18060R lm=2l -230240R lp=24R l 20-3402688Rl ≈24Rl 20 (4) 下面我们推证常数β0、δ0 、m 、p 、x 0、y 0。
圆曲线、缓和曲线计算方法

● 圆曲线方法一:sin (1cos )180i i i i i i x R y R l R ϕϕϕπ⎧⎪=⎪=-⎨⎪︒⎪=⋅⎩——i l 为待定点i P 至起点间的弧长i ϕ为i l 所对的圆心角R 为曲线半径方法二:11802l A R π︒=⋅⋅ 2sin l R A =⋅00cos(/)sin(/)x x l A y y l A =+⋅+-⎧⎨=+⋅+-⎩起点方位角左减右加起点方位角左减右加——00(,)x y 为圆曲线起点坐标方法三:180l A R π︒=⋅ 00cos(/)sin(/)x x R B A y y R B A =+⋅+-⎧⎨=+⋅+-⎩——l 为圆曲线上任意一点距起点距离00(,)x y 为圆曲线圆心坐标B 为圆心到圆曲线起点的方位角,A 为任意点对应的圆心角● 缓和曲线522030406l x l R l ly Rl ⎧=-⎪⎪⎨⎪=⎪⎩——l 为曲线上任一点至起点的曲线长R 曲线半径0l 为缓和曲线全长圆曲线、缓和曲线计算方法1、直线段:先由JD1以及JD2的坐标算出JD1到JD2的方位角,即直线段方位角A ,故可算出HZ 、ZH 坐标及其直线段各点坐标。
2、缓和曲线:以HZ 、ZH 为起点,缓和曲线上任意一点离HZ 、ZH 距离为l ,利用公式522003040()6l x l R l l R ly Rl ⎧=-⎪⎪⎨⎪=⎪⎩为缓和曲线全长,为圆曲线半径算出该点的相对起点坐标,利用arctan y x算出该点相对起点的方位角B ,再根据线路走向及直线段方位角可算出该点的方位角C (顺时针加,逆时针减),用可求出该点相对起点的距离D ,最后用00cos sin x x D C y y D C =+⎧⎨=+⎩可求出该点的坐标。
(00(,)x y 为缓和曲线起点的坐标)3、圆曲线:用上述方法求出圆曲线两端点HY 、YH 坐标,算出HY 到YH 的方位角F ,以及两点间的距离E ,用12arccos ER可算出两端点连线与起点到圆心连线的夹角G ,根据线路走向求出起点到圆心的方位角H (H=F+/-G ),00(,)x y 圆曲线为起点坐标,根据00cos sin x x R H y y R H=+⎧⎨=+⎩,求出圆心坐标。
缓和曲线要素及公式介绍

11.2.1 带缓和曲线的圆曲线的测设为了保障车辆行驶安全,在直线与圆曲线之间加入一段半径由∞逐渐变化到R的曲线,这种曲线称为缓和曲线。
目前常用的缓和曲线多为螺旋线,它有一个特性,曲率半径ρ与曲线长度l成反比。
数学表达为:ρ∝1/l 或ρ·l = k ( k为常数)若缓和曲线长度为l0,与它相连的圆曲线半径为R,则有:ρ·l = R·l0 = k目前我国公路采用k = 0.035V3(V为车速,单位为km/h),铁路采用k = 0.09808V3,则公路缓和曲线的长度为l0 = 0.035V3/R ,铁路缓和曲线的长度为:l0 = 0.09808V3/R 。
11.2.2 带缓和曲线的圆曲线的主点及主元素的计算带缓和曲线的圆曲线的主点有直缓点ZH、缓圆点HY、曲中点QZ、圆缓点YH、缓直点HZ 。
带缓和曲线的圆曲线的主元素及计算公式:切线长 T h = q+(R+p)·tan(α/2)曲线长 L h = 2l0+R·(α-2β0)·π/180°外矢距 E h = (R+p)·sec(α/2)-R切线加长 q = l0/2-l03/(240R2)圆曲线相对切线内移量 p = l02/(24R)切曲差 D h = 2T h -L h式中:α 为线路转向角;β0为缓和曲线角;其中q、p、β0缓和曲线参数。
11.2.3 缓和曲线参数推导dβ = dl/ρ = l/k·dl两边分别积分,得:β= l2/(2k) = l/(2ρ)当ρ = R时,则β =β0β0 = l0/(2R)若选用点为ZH原点,切线方向为X轴,垂直切线的方向为Y轴,建立坐标系,则:dx = dl·cosβ = cos[l2/(2k)]·dldy = dl·sinβ = si n[l2/(2k)]·dl考虑β很小,sinβ和cosβ即sin(l2/(2k))和cos(l2/(2k))可以用级数展开,等式两边分别积分,并把k = R·l0代入,得以曲线长度l为参数的缓和曲线方程式:X = l-l5/(40R2l02)+……Y = l3/(6Rl0)+……通常应用上式时,只取前一、二项,即:X = l-l5/(40R2l02)Y = l3/(6Rl0)另外,由图可知,q = X HY-R·sinβ0p = Y HY-R(1-cosβ0)以β0= l0/(2R)代入,并对sin[l0/(2R)]、cos[l0/(2R)]进行级数展开,取前一、二项整理可得:q = l0/2-l03/(240R2)p = l02/(24R)若仍用上述坐标系,对于圆曲线上任意一点i,则i点的坐标X i、Y i可以表示为:Xi = R·sinψi+qYi = R·(1-cosψi)+p11.2.4 带缓和曲线的圆曲线的主点桩号计算及检核ZH桩号 = JD桩号-T hHY桩号 = ZH桩号+l0QZ桩号 = HY桩号+L/2YH桩号 = QZ桩号+L/2 = HY桩号+L = ZH桩号+l0+LHZ桩号 = YH桩号+l0 = ZH桩号+L hJD桩号 = ZY桩号-T h+D h(检核)11.2.5 带缓和曲线的圆曲线的主点的测设过程:(1)在JD点安置经纬仪(对中、整平),用盘左瞄准直圆方向,将水平度盘的读数配到0°00′00″,在此方向量取T h,定出ZH点;(2)从JD沿切线方向量取T h-X HY,然后再从此点沿切线垂直方向量取Y HY , 定出HY点;(3)倒转望远镜,转动照准部到度盘读数为α,量取T h,定出HZ点;(4)从JD沿切线方向量取T h-X HY,然后再从此点沿切线垂直方向量取Y HY , 定出YH点;(5)继续转动照准部到度盘读数为(α+180°)/2,量取E h,定出QZ点。
【关于不同类型缓和曲线的判断及起点、终点曲率半径的计算方法

关于不同类型缓和曲线的判断及起点、终点曲率半径的计算方法目前在匝道或线路施工坐标计算中经常遇到缓和曲线,实际中相信有很多测友选择用积木法或叫线元法正反算程序进行线路坐标计算,这就牵涉到线元的起点终点曲率半径判断的问题,一般的直线元,圆曲线元的起点终点半径判断,比较容易,可能令大家感觉麻烦的就是缓和曲线起点终点半径判断问题,缓和曲线有时候判断算对了,有时候却坐标算不对,究其原因,其实问题出于该缓和曲线是否是完整缓和曲线引起的。
关于这点,相关的课本教材上没有明确的讲述,网上对此问题的解释也是散见于不同的论文著作中,对于测量新手来说,线元法程序是非常适用上手的,但却往往因为遇到不完整缓和曲线的起点或终点的半径判断计算不出来导致坐标计算错误,的确是件令人恼火的事情,在此我就把自己的判断经验做一论述,给用线元法程序的测友们一同分享,当然高手们请一笑而过,也可留下你的经验与大家一起分享交流学习。
第一:先说说完整缓和曲线和不完整缓和曲线以及不对称缓和曲线与对称缓和曲线的概念问题,以免混为一谈.1.当对于单独一段缓和曲线从其完整与否来讲是分为完整与不完整两类;当对于一个单交点内的两段缓和曲线(即常说的第一缓和曲线和第二缓和曲线而言)又有对称缓和曲线与不对称缓和曲线之分。
由此看来,完整与对称与否是针对缓和曲线两个方面来看待区分的。
2.缓和曲线我们的测量教材上讲述的其实就是完整缓和曲线,也可以知道缓和曲线上:各个点的半径是不同的,起点到终点的半径值过度是从正无穷大到所接圆曲线半径之过度如从ZH向HY方向;或者是从所接圆曲线半径值向正无穷大过度的,如从YH向HZ方向。
那么由此可以不难判断出来,完整缓和曲线就是符合上述特征的,那么不完整的缓和曲线就是不符合上述特征的,但是线路上的平曲线设计时候一般缓和曲线不单独存在的,整体上缓和曲线前或后一般都是要连接一个圆曲线的,那么不完整缓和曲线其实就是在完整缓和曲线上截取的一段,一般就是去掉了半径无穷大的那端而是从某个点开始的半径值向所接圆曲线半径值过度的。
各种曲线计算公式

一、公路平曲线坐标计算公式1、缓和曲线:Lb1 0{K,D}①T=A2/R ②L=J(K-O)+T ③B=T2 /2/A2 *180/π④M=(L-T)-(L5-T5)/40/A4+(L9-T9)/3456/A8-(L13-T13)/599040/A12+(L17-T17)/17542600/A165.N=(L3-T3)/6/A2-(L7-T7)/336/A6+(L11-T11)/42240/A10-(L15-T15) /9676800/A14+(L19-T19)/3530097000/A18⑥I=(L2-T2)*180/2/A2/π⑦X=C+Mcos(Q-ZB)-ZNsin(Q-ZB)+Dcon(Q+ZI+S)◢⑧Y=F+Msin(Q-ZB)+ZNcos(Q-ZB)+Dsin(Q+ZI+S)◢Goto 0注:A:缘和曲线参数 R:起点半径 J:曲率半径判定值(当曲率半径由小到大取1,否则取-1)(当起点半径到终点半径是由大或无穷大到小取+1,反之则取-1) K:欲求点里程 O:缘和曲线起点里程 C:缘和曲线起点X坐标Q:起始方位角(当J=-1时,方位角应+180。
) Z:偏角判定值(当J=1时,左偏为-1,右偏为1;当J=-1时,左偏为1,右偏为-1) D:距中桩的距离 S:斜交角度 F:缘和曲线起点Y坐标2、圆曲线Lb1 0{K,D}①L=K-0②X=C+R[sin(Q+L/R*180/π)-sinQ]+Dcos(Q+L/R*180/π+S)◢③Y=F-R[cos(Q+L/R*180/π)-cosQ]+Dsin(Q+L/R*180/π+S)◢ Goto 0注:K:欲求点里程 O:圆曲线起点里程 C:圆曲线起点X坐标 R:圆曲线半径 (左偏为负) Q:起始方位角 D:距中桩的距离 S:斜交角度 F:圆曲线起点Y坐标3、直线Lb1 0{K,D}①L=K-0②X=C+LcosQ+Dcos(Q+S)◢③Y=F+LsinQ+Dsin(Q+S)◢Goto 0注:K:欲求点里程 O:直线起点里程 C:直线起点X坐标 Q:起始方位角 D:距中桩的距离 S:斜交角度 F:直线起点Y坐标二、竖曲线计算公式Lb1 0①{K} ②L=K-(0-T)③H=M-IT+LI-ZL2 /2/R◢ Goto 0 注:K:欲求点里程;O:顶点里程;T:切线长;M:顶点高程;I:坡度;Z:竖曲线判定值三、预拱度计算公式Lb1 0①{K} ②H=D-(4D÷B2)×(B/2-(K-O)) 2◢ Goto 0注:D:跨中最大设计预拱度 H:要计算的预拱度 K:欲求点里程桩号(距支座的距离) O:起点桩号 B:本跨净长。
直线正反算程序

直线正、反算程序一、正算程序,(XY)(4850计算器)1、LbI 02、{KD}3、E=?:F=?:A=?:L=?:S=A+90:Q=K-L4、X=E+QcosA+DcosS:Y=F+QsinA+DsinS5、"X=":X◢"Y=":Y◢6、Goto 0二、反算程序(KD)(4850计算器)1、LbI 02、{XY}3、E=?:F=?:A=?:L=?:I=0:J=04、PoI(X-E ,Y-F):Rec(I ,(J-A)):K=L+I:D=J5、"K=":K◢"D=":D◢6、Goto 0说明:E、F:直线起点桩号坐标A:进洞方向方位角L:直线起点桩号K:所求里程D:所求里程左、右偏距,左-、右+ X、Y:所求里程坐标略图见下:E、FL A直线(正反算数据)A=193°42′25.8″L=453.5 E=11954.861 F=32887.228K D X Y500 +2 11910.159 32874.266500 -2 11909.211 32878.152550 +2 11860.639 32866.345550 -2 11861.561 32862.452正算程序输K、D:反算程序输X、Y输入(4500计算器)时, 程序中I改为V、J改为W。
I=0:J=0不用输入。
显示结果(4500计算器)输入K◢D◢X◢Y◢(4850计算器)输入"K=":K◢"X=":X◢"D=":D◢"Y=":Y◢如果有两个或两个以上隧道:正算中第3节改为, P=1=> E=?:F=?:A=?:L=?:S=A+90:Q=K-L:≠> P=2=> E=?:F=?:A=?:L=?:S=A+90:Q=K-L:≠> P=3=>……反算中第3节改为, P=1=> E=?:F=?:A=?:L=?:I=0:J=0:≠>P=2=> E=?:F=?:A=?:L=?:I=0:J=0:≠> P=3=>……△△△说明:P=1:计算1号洞数据P=2:计算2号洞数据P=3……圆曲线正、反算程序一、正算(XY)(4850计算器)1、LbI 02、{KD}3、A=?:R=?:E=?:F=?:M=?:I=0:J=04、Q=90(K-M)÷Rπ:S=A-Q:Z=A-2Q+905、Rec(2RsinQ ,S):X=E+I+DcosZ:Y=F+J+DsinZ6、"X=":X◢"Y=":Y◢7、Goto 0说明:A:1—2的方位角R:半径E,F:圆曲线起点坐标Q:圆曲线起点和曲线上任意点与切线的夹角S:圆曲线起点至曲线上任意点的方位角Z:圆心至曲线上任意点的方位角M:圆曲线起点桩号注:此程序为左转路线,如右转路线此程序中第4节改为Q=90(K-M)÷Rπ:S=A+Q:Z=A+2Q-90(如输入4500计算器程序中V变I、I变V、W变J、J变W;I=0:J=0不用输入)(程序中第6节改为X◢Y◢)一、反算(KDR)(4850计算器)1、LbI 02、{XY}3、A=?:R=?:W=?:G=?:M=?:I=0:J=04、E=A+905、PoL(X-W,Y-G):J<0=>J=J+360△6、D=I-R:K=M+Rπ(E-J)÷1807、"K=":K◢"D=":D◢8、Goto 0(,)说明:A:1—2的方位角R:半径W,G:圆心坐标M:圆曲线起点桩号序为左转路线,如右转路线此程序中第4节改为E=A-90:E<0=>E=E+360△第6节改为D=I-R:K=M+Rπ(J-E)÷180注明:如输入4500计算器程序中V变I、I变V、W变J、J变W;I=0:J=0不用输入第7节改为K◢D◢如果有两个或两个以上隧道:正算中第3节改为, P=1=> A=?:R=?:E=?:F=?:M=?:I=0:J=0:≠> P=2=> A=?:R=?:E=?:F=?:M=?:I=0:J=0:≠> P=3=>……△△△反算中第3节改为, P=1=> A=?:R=?:W=?:G=?:M=?I=0:J=0:≠>P=2=> A=?:R=?:W=?:G=?:M=?I=0:J=0:≠>: P=3=>……△△△说明:P=1:计算1号洞数据P=2:计算2号洞数据P=3……直线、圆曲线正、反算程序一、正算程序(XY)(4850计算器)1、LbI 02、{KD}3、A=?:B=?:C=?:R=?:H=?:V=?:L=?:I=0:J=04、T=Rtan(C÷2):M=L-T:N=M+RπC÷1805、Rec(T,B):E=H+I:F=V+J6、Rec(T,A-C):W=H+I:G=V+J7、Q=90(K-M)÷Rπ:S=A-Q:Z=A-2Q+90:U=A-C8、K≤M=> Rec(M-K ,B):X=E+I+Dcos(A+90):Y=F+J+Dsin(A+90):≠>K≤N=>Rec(2RsinQ ,S):X=E+I+DcosZ:Y=F+J+DsinZ:≠>K >N=>Rec(K-N ,U):X=W+I+Dcos(U+90):Y=G+J+Dsin (U+90)△△△9、"X=":X◢"Y=":Y◢10、Goto 0注:此程序为左转路线,如右转路线此程序中第6节改为Rec(T,A+C):W=H+I:G=V+J 第7节改为Q=90(K-M)÷Rπ:S=A+Q:Z=A+2Q-90:U=A+CA:1—2的方位角(,)B:2—1的方位角C:转角R:半径(H,V):转点的坐标L:转点桩号(1—2的距离+1点的桩号或者圆曲线起点桩号+切线长)(E,F):圆曲线起点坐标(W,G):圆曲线止点坐标U:2—3的方位角M:圆曲线起点N:圆曲线止点T:切线长Q:圆曲线起点和曲线上任意点与切线的夹角S:圆曲线起点至曲线上任意点的方位角Z:圆心至曲线上任意点的方位角(如输入4500计算器程序中V变I、I变V、W变J、J变W;I=0:J=0不用输入)(程序中第9节改为X◢Y◢)二、反算程序(KDR)(4850计算器)1、LbI 02、{XYZ}3、U=?:A=?:B=?:C=?:R=?:H=?:V=?:L=?:I=0:J=04、T=Rtan(C÷2):M=L-T:N=M+RπC÷1805、Q=A-C:S=B+(90-C÷2)6、Rec(R÷cos(C÷2),S):W=H+I:G=V+J7、E=A+90:E>360=>E=E-360△8、F=E-C:F<0=>F=F+360△9、PoL(X-W,Y-G):J<0=>J=J+360△10、J≤F=>D=-(X-H)sinQ+(Y-V)cosQ:K=N+(X-H)cosQ+(Y-V)sinQ-T:≠>J≤E=>D=I-R:K=M+R π(E-J)÷180:≠>J>E=>D=(X-H)sinB-(Y-V)cosB:K=L-(X-H)cosB-(Y-V)sinB△△△11、Prog"GC"12、Z-H≤1.489=>R=√((AbsD-0.9)²+(H+1.489-Z)²)-(6+U):≠> AbsD≤(U+7.5)sin36°52′12″=>R=√(D²+(Z-H-0.289)²)-(7.5+U):≠>AbsD>(U+7.5)sin36°52′12″=>R=√((AbsD-0.9)²+(Z-H-1.489)²)-(6+U)ΔΔΔ13、"K=":K◢"D=":D◢"R=":R◢14、Goto 0,)(说明:(此图为1—10节说明图)A:1—2的方位角B:2—1的方位角C:转角H,V:转点的坐标M:圆曲线起N:圆曲线止点T:切线长W,G:圆心坐标Q:2—3的方位角R:半径S:转点至圆心的方位角F:圆心至圆曲线止点方位角E:圆心至圆曲线起点方位角L:转点桩号(1—2的距离+1点的桩号或者圆曲线起点桩号+切线长)注:此程序为左转路线,如右转路线此程序中第5节改为Q=A+C:S=B-(90-C÷2)第7节改为E=B+90:E>360=>E=E-360△第8节改为F=E+C:F>360=>F=F-360△第十节改为J≤E=>D= (X-H)sinB-(Y-V)cosB:K=L-(X-H)cosB-(Y-V)sinB:≠>J≤F=>D=I-R:K=M+Rπ(J-E)÷180:≠>J>F=>D= - (X-H)sinQ+(Y-V)cosQ:K=N+(X-H)cosQ+(Y-V)sinQ-T△△△(下面图形为程序11—14节说明图)U:内空半径增大值(如测内空大小输入0;如上图所示应输入80)Z:实测高程H:路面高K:所求里程√:根号D:所求里程偏离中线距离(左-、右+)R:-为欠挖、+为超挖11、Prog"GC":把计算高程程序作为子程序带入注明:如输入4500计算器程序中V变I、I变V、W变J、J变W;I=0:J=0不用输入程序中第11节改为Prog GC 第13节改为K◢D◢R◢(以上为第一种图形、下面为第二种图形)第二种图形程序中第12节改为Z-H≥2=>R=√((Z-H-2)2+D2)-(5.46+U):≠>R=√( (H+2-Z)2+ (AbsD+2)2) -(7.46+U)△下面为第二种图形示意图:直线、圆曲线正、反算程序数据(注:子程序高程;按照高程程序中的凸行竖曲线数据输入) U=0.8 A=193°42′25.8″B=13°42′25.8″C=40°47′25.7″R=1800 H=11222.276 V=32708.546 L=1207.561K D X Y Z R450 3 11958.972 32885.143 70.294 -2.578450 -3 11957.550 32890.972 82.5 +1.895700 5 11714.617 32830.975 78.8 -0.752700 -1.3 11713.680 32837.204 82.232 +0.8701000 1 11414.857 32815.133 76.5 +0.0101000 -0.5 11414.883 32816.633 75.9 -0.6342000 5 10463.690 33090.839 58.6 +0.0572000 -4 10467.788 33098.852 58.3 -0.756如果有两个或两个以上隧道:正算中第3节改为, P=1=> A=?:B=?:C=?:R=?:H=?:V=?:L=?:I=0:J=0:≠>P=2=> A=?:B=?:C=?:R=?:H=?:V=?:L=?:I=0:J=0:≠>P=3=>……△△△反算中第3节改为, P=1=> U=?:A=?:B=?:C=?:R=?:H=?:V=?:L=?:I=0:J=0:≠>P=2=> U=?:A=?:B=?:C=?:R=?:H=?:V=?:L=?:I=0:J=0:≠> P=3=>……△△△说明:P=1:计算1号洞数据P=2:计算2号洞数据P=3……直线、曲线、缓和曲线正算程(4850计算器)文件名(X Y)1、G=?:I=0 :J=0 :2、V=?:F=?:N=?:R=?:Q=?:W=?:H=?3、LbI 04、{K,D}5、M=V÷2-V³÷240÷R²6、P=V²÷24÷R-V4÷2688÷R³7、L=πRN÷180+V8、T=M+(R+P)tan(N÷2)9、A=Q-T:B=A+V:S=A+L:C=S-V10、Rec(T,F+180)11、Z[1]=I+W12、Z[2]=J+H13、Rec(T,F+GN)14、Z[3]=I+W15、Z[4]=J+H16、K<A=>Goto 117、≠>K<B=>Goto 218、≠>K<C=>Goto 319、≠>K<S=>Goto 420、≠>K≥S=>Goto 5⊿⊿⊿⊿⊿21、LbI 122、Rec(Q-K,F+180)23、E=F+9024、X=I+W+DcosE25、Y=J+H+DsinE26、LbI 727、"X=":X◢"Y=":Y◢28、Goto 029、LbI 230、Z=K-A31、O=90Z²÷R÷V÷π32、X=Z-Z5÷40÷R²÷V²+Z9÷3456÷R4÷V433、Z=Z³÷6÷R÷V-Z7÷336÷R³÷V³+Z11÷42240÷R5÷V534、LbI 635、Rec(X,F)36、X=Z[1]+I37、Y=Z[2]+J38、Rec(Z,F+90G)39、E=F+OG+9040、X=X+I+DcosE41、Y=Y+J+DsinE42、Goto 743、LbI 344、Z=K-A45、O=90(2Z-V)÷π÷R46、X=RsinO+M47、Z=R(1-cos O)+P48、Goto 649、LbI 450、Z=S-K51、O=90Z²÷π÷R÷V52、X=Z-Z5÷40÷R²÷V²+Z9÷3456÷R4÷V453、Z=Z³÷6÷R÷V-Z7÷336÷R³÷V³+Z11÷42240÷R5÷V554、Rec(X,F+GN+180)55、X=Z[3]+I56、Y=Z[4]+J57、Rec(Z,F+GN+180-90G)58、E=F+GN-OG+9059、X=X+I+DcosE60、Y=Y+J+DsinE61、Goto 762、LbI 563、Rec(K-S+T,F+GN)64、E=F+GN+9065、X=W+I+DcosE66、Y=H+J+DsinE67、Goto 7说明:G:左转-1 右转+1V:缓和曲线长度(圆曲线输0)F:起点到转点方位角(1—2)R:半径N:转角Q:转点桩号(或者圆曲线起点桩号+切线长)W,H:转点坐标具体数据见下:G= -1 V=50 F=88°58′38″N=62°53′37″R=100 Q=706.893 W=24021.369 H=94223.502K D X Y620.157 0 24019.820 94136.780650 0 24021.238 94166.579675 0 24026.251 94191.024695 0 24034.325 94209.285705 0 24039.688 94217.721715 0 24045.866 94225.579750 0 24072.807 94247.690770 0 24090.370 94257.246注明:如输入4500计算器程序中V变I、I变V、W变J、J变W;I=0:J=0不用输入如果有两个或两个以上隧道:程序中第2节改为, P=1=> V=?:F=?:N=?:R=?:Q=?:W=?:H=?:≠>P=2=> V=?:F=?:N=?:R=?:Q=?:W=?:H=?:≠>P=3=>……△△△说明:P=1:计算1号洞数据P=2:计算2号洞数据P=3……曲线任意里程中边桩坐标正反算(CASIO fx-4800P计算器)程序一、程序功能本程序由一个主程序(TYQXJS)和两个子程——正算子程序(SUB1)、反算子程序(SUB2)序构成,可以根据曲线段——直线、圆曲线、缓和曲线(完整或非完整型)的线元要素(起点坐标、起点里程、起点切线方位角、线元长度、起点曲率半径、止点曲率半径)及里程边距或坐标,对该曲线段范围内任意里程中边桩坐标进行正反算。
铁路缓和曲线计算

、缓和曲线的作用及其几何特征行驶于曲线轨道的机车车辆,出现一些与直线运行显著不同的受力特征。
如曲线运行的离心力,外轨超高不连续形成的冲击力等。
为使上述诸力不致突然产生和消失,以保持列车曲线运行的平稳性,需要在直线与圆曲线轨道之间设置一段曲率半径和外轨超高度均逐渐变化的曲线,称为缓和曲线。
当缓和曲线连接设有轨距加宽的圆曲线时,缓和曲线的轨距是呈线性变化的。
概括起来,缓和曲线具有以下几何特征:1. 缓和曲线连接直线和半径为R的圆曲线,其曲率由零至1/R逐渐变化。
2. 缓和曲线的外轨超高,由直线上的零值逐渐增至圆曲线的超高度,与圆曲线超高相连接。
3. 缓和曲线连接半径小于350m的圆曲线时,在整个缓和曲线长度内,轨距加宽呈线性递增,由零至圆曲线加宽值。
因此,缓和曲线是一条曲率和超高均逐渐变化的空间曲线。
二、缓和曲线的几何形位条件图2-9所示为一段缓和曲线。
其始点与终点用ZH与HY表示。
要达到设置缓和曲线的目的,根据如图所取直角坐标系,缓和曲线的线形应满足以下条件:1.为了保持连续点的几何连续性,缓和曲线在平面上的形状应当是:在始点处,横坐标x= 0,纵坐标y= 0,倾角φ= 0;在终点处,横坐标x=x0,纵坐标y=y0,倾角φ=φ0。
2.列车进入缓和曲线,车体受到离心力J的作用,为保持列车运行的平稳性,应使离心力不突然产生和消失,即在缓和曲线始点处,J=0,在缓和曲线终点处Ρ=R。
3.缓和曲线上任何一点的曲率盈余外轨超高相吻合。
在纵断面上,外轨超高顺坡的形式有两种形式。
一种形式是,如图2-10(a)所示;另一种形式是曲线形,如图2-10(b)所示。
图 2-9缓和曲线坐标图列车经过直线顺坡的缓和曲线始点和终点时,对外轨都会产生冲击。
在行车速度不高,超高顺破相对平缓时,列车对外轨的冲击不大,可以采用直线形顺坡,即可满足曲率与超高相配合的要求。
当行车速度较高,为了消除列车对外轨的冲击,应采用曲线形超高顺坡。
公路缓和曲线段原理及缓和曲线计算公式

公路缓和曲线段原理及缓和曲线计算公式一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1.缓和曲线的作用1)便于驾驶员操纵方向盘2)乘客的舒适与稳定,减小离心力变化3)满足超高、加宽缓和段的过渡,利于平稳行车4)与圆曲线配合得当,增加线形美观2.缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A2/ρ(A:与汽车有关的参数)ρ=C/sC=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3.回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R,l h=s 则 l h=A2/R4.缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1)根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ρ,a s=Δa/t≤0.62)依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3)根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
4)从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5.直角坐标及要素计算1)回旋线切线角(1)缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
缓和曲线)计算公式
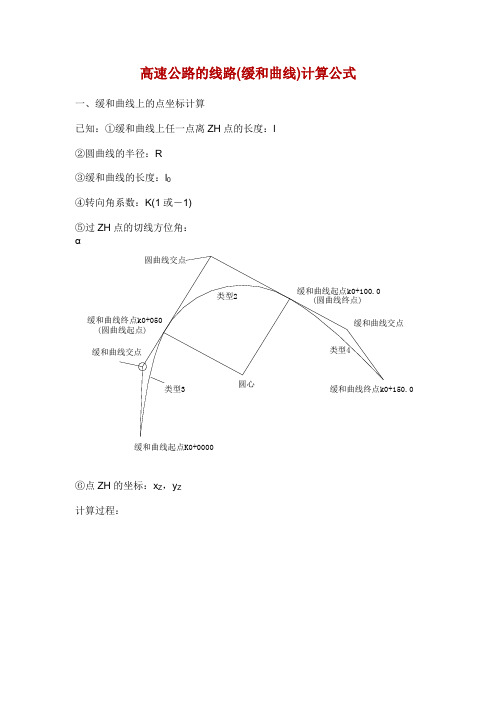
高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z,y Z为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z,y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:S Z④变坡点高程:H Z⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y ②待求点的切线方位角:αT计算过程:。
曲线计算公式及例题

一、圆曲线坐标计算公式β=180°/π×L/R(L= βπR/180°)弧长公式β为圆心角△X=sinβ×R△Y=(1-cosβ) ×RC= 弦长X=X1+cos (α±β/2)×CY=Y1+sin (α±β/2)×Cβ代表偏角,(既弧上任一点所对的圆心角)。
β/2是所谓的偏角(弦长与切线的夹角)△X 、△Y 代表增量值。
X 、Y 代表准备求的坐标。
X1、Y1代表起算点坐标值。
α代表起算点的方位角。
R 代表曲线半径二、缓和曲线坐标计算公式β= L2/2RLS ×180°/πC= L - L5/90R2L S 2X=X1+cos (α±β/3)×CY=Y1+sin (α±β/3)×C L 代表起算点到准备算的距离。
LS 代表缓和曲线总长。
X1、Y1代表起算点坐标值。
三、直线坐标计算公式X=X1+cosα×LY=Y1+sinα×LX1、Y1代表起算点坐标值α代表直线段方位角。
L 代表起算点到准备算的距离。
1)左右边桩计算方法X 边=X中+cos(α±90°) ×LY 边=Y中+sin(α±90°) ×L在计算左右边桩时,先求出中桩坐标,在用此公式求左右边桩。
如果在线路方向左侧用中桩方位角减去90°,线路右侧加90°,乘以准备算的左右宽度。
例题:直线坐标计算方法α(方位角)=18°21′47″DK184+714.029,求DK186+421.02里程坐标X1=84817.831 Y1=352.177 起始里程解:根据公式X=X1+cosα×LX=84817.831+COS18°21′47″×(86421.02—84714.029)=86437.901Y=Y1+sinα×LY=352.177+sin18°21′47″×(86421.02—84714.029)=889.943求DK186+421.02里程左右边桩, 左侧3.75m, 右侧7.05m. 解:根据公式线路左侧计算:X 边=X中+cos(α±90°) ×LX 边=86437.901+cos(18°21′47″- 90°) ×3.75=86439.082Y 边=Y中+sin(α±90°) ×LY 边=889.943+sin(18°21′47″- 90°) ×3.75=886.384线路右侧计算:X 边=X中+cos(α±90°) ×LX 边=86437.901+cos(18°21′47″+ 90°) ×7.05=86435.680Y 边=Y中+sin(α±90°) ×LY 边=889.943+sin(18°21′47″+90°) ×7.05=896.634四、例题:缓和曲线坐标计算方法α(ZH点起始方位角)=18°21′47″X1=86437.901 Y1=889.941 起始里程DK186+421.02曲线半径2500 缓和曲线长120m求HY 点坐标, 也可以求ZH 点到HY 点任意坐标解:根据公式β=L2/2RLS×180°/πβ={1202/(2×2500×120) }×(180°/π)= 1°22′30.36″C=L-L5/90R2LS2C=120-1205/(90×25002×1202)=119.997X=X1+cos(α±β/3)×CX=86437.901+cos(18°21′47″-1°22′30.36″/3)×119.997=86552.086Y=Y1+sin(α±β/3)×CY=889.941+sin(18°21′47″-1°22′30.36″/3)×119.997=926.832求DK186+541.02里程左右边桩, 左侧3.75m, 右侧7.05m. 解:根据公式线路左侧计算:X 边=X中+cos(α±90°) ×LX 边=86552.086+cos{(18°21′47″-1°22′30.36″)- 90°}×3.75=86553.182Y 边=Y中+sin(α±90°) ×LY 边=926.832+sin{(18°21′47″-1°22′30.36″)- 90°}×3.75=923.246线路右侧计算:X 边=X中+cos(α±90°) ×LX 边=86552.086+cos{(18°21′47″-1°22′30.36″)+ 90°}×7.05=86550.026Y 边=Y中+sin(α±90°) ×LY 边=926.832+sin{(18°21′47″-1°22′30.36″)+ 90°}×7.05=933.574缓和曲线方位角计算方法α=(起始方位角±β偏角)= 18°21′47″-1°22′30.36″=16°59′16.64″注:缓和曲线在计算坐标时, 此公式只能从两头往中间推, 只能从ZH 点往HY 点推,HZ 点往YH点推算, 如果YH 往HZ 点推算坐标, 公式里的β为β2/3.五、例题:圆曲线坐标计算方法α(HY点起始方位角)= 16°59′16.64″X1=86552.086 Y1=926.832曲线半径2500 曲线长748.75 起始里程DK186+541.02求YH 点坐标, 也可以求QZ 点坐标或任意圆曲线一点坐标. 解:根据公式β=180°/π×L/Rβ= 180°/π×748.75/2500=17°09′36.31″△X=sinβ×R△X=sin17°09′36.31″×2500=737.606△Y=(1-cosβ) ×R△Y=(1-cos17°09′36.31″) ×2500=111.290C= 弦长C=745.954X=X1+cos(α±β/2)×CX= 86552.086 +cos(16°59′16.64″+360°-17°09′36.31″/2) ×745.954=87290.023 Y=Y1+sin(α±β/2)×CY=926.832+ sin(16°59′16.64″+360°-17°09′36.31″/2) ×745.954=1035.905圆曲线方位角计算方法α=(起始方位角±β偏角)= 16°59′16.64″+360°-17°09′36.31″=359°49′40.33″求DK187+289.77里程左右边桩, 左侧3.75m, 右侧7.05m. 解:根据公式线路左侧计算:X 边=X中+cos(α±90°) ×LX 边=87290.023+cos(359°49′40.33″-90°) ×3.75=87290.012 Y 边=Y中+sin(α±90°) ×LY 边=1035.905+sin(359°49′40.33″-90°) ×3.75=1032.155线路右侧计算:X 边=X中+cos(α±90°) ×LX 边=87290.023+cos(359°49′40.33″+90°) ×7.05=87290.044 Y 边=Y中+sin(α±90°) ×LY 边=1035.905+sin(359°49′40.33″+90°) ×7.05=1042.955。
缓和曲线、竖曲线、圆曲线、计算

速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R 2——曲线终点处的半径P——曲线起点处的曲率1——曲线终点处的曲率P2α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i(上坡为“+”,下坡为“-”)1(上坡为“+”,下坡为“-”)②第二坡度:i2③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K③曲线终点桩号:K1④曲线起点坐标:x0,y⑤曲线起点切线方位角:α⑥曲线起点处曲率:P(左转为“-”,右转为“+”)⑦曲线终点处曲率:P(左转为“-”,右转为“+”)1求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
5800坐标计算,竖曲线缓和曲线程序

A+Q(Cos(C) +4(Cos(M)+Cos(N))+2Cos(K)+Cos(J))÷12→U:
Lbl 4: "END″
说明:QZHAO:曲中点里程(竖曲线),QDHAO:起点里程,ZDHAO:终点里程,B—HB曲中点高程,SX:上下(路面标高下多少为水稳层面),I1:第一坡度,I2:第二坡度,R:半径,T切线长,L—DQHAO:待求点里程,PY:偏移(中桩到边桩的距离),XIELV:斜率(横坡的坡度,左负右正)o-YIGAO:仪器高a
Goto 1
Lbl 2
L<G Goto 4
"HL=″:B+0.01 (L-J)C+0.01UV+Q →H
"H0=″:o-H→H
Goto 1
Lab 3
L>K Goto 4
"HL=″:B+0.01 (L-J)D+0.01UV+Q →H
"HO=:o-H→Z
Goto 1
Lbl 1
"L—DQHAO=″?L:"PY=″?U:"XIELV=″?V
If L<X:Then Goto 2:Else If L>Y:Then Goto 3:If End:I End
"HL=″:B+0.01C(L-J)+A(L-J+T) ÷(2R)+0.01UV+Q→Q
缓和曲线、 圆曲线计算方法

缓和曲线计算方法(ZH~HY)中线首先计算直线段坐标方位角(即ZH~JD坐标方位角),及ZH点坐标。
备用偏角公式:{30*L/(π*RLS)缓和曲线}1、计算待求点偏角=((L/10)2*(57296/(RLS))/60。
其中L=待求点至ZH距离、R=圆曲线半径、LS=缓和曲线长。
2、待求点方位角=直线方位角±待求点偏角。
(曲线左转-偏角,曲线右转+偏角)3、待求点至ZH点弦长=L—L5/(90*R2*LS 2),其中L=待求点至ZH距离(里程)、R=圆曲线半径。
4、待求点坐标:X=ZH点X坐标+COS(待求点方位角)*弦长Y= ZH点Y坐标+SIN(待求点方位角)*弦长缓和曲线计算左右边线坐标(ZH~HY)1、左侧方位角=(待求点方位角±2倍偏角=直线方位角±3倍偏角)—边线与中线夹角。
2、右侧方位角=(待求点方位角±2倍偏角=直线方位角±3倍偏角)+边线与中线夹角。
3、左侧边线坐标:X=该点中线X坐标+COS(左侧方位角)*边线至中线距离Y=该点中线Y坐标+SIN(左侧方位角)*边线至中线距离4、右侧边线坐标:X=该点中线X坐标+COS(右侧方位角)*边线至中线距离Y=该点中线Y坐标+SIN(右侧方位角)*边线至中线距离圆曲线计算方法(HY~YH)中线注:(ZY-YZ)同理,方位角=用直线方位角-待求点偏角首先计算直线段坐标方位角(即ZH~JD坐标方位角),及HY点坐标。
1、求出缓圆点(HY)偏角=(LS*90)/(π* R)。
2、求待求点偏角=(L*90)/(π* R)。
其中:L=待求点至HY距离(里程)、R=圆曲线半径、LS=缓和曲线长。
3、待求点至HY点弦长=2* R*SIN(待求点偏角)。
4、待求点方位角=直线方位角±HY点偏角±待求点偏角,(曲线左转-偏角,曲线右转+偏角)。
5、待求点坐标:X=HY点X坐标+COS(待求点方位角)*弦长Y=HY点Y坐标+SIN(待求点方位角)*弦长圆曲线计算左右边线坐标1、左侧方位角=(待求点方位角±偏角—边线与中线夹角)。
圆曲线和缓和曲线坐标推算公式(附带例题)

圆曲线和缓和曲线坐标推算公式(附带例题)本文为圆曲线和缓和曲线的推算公式,包括直线、缓和曲线、圆曲线上的坐标推算圆曲线和缓和曲线坐标推算公式一、直线上的坐标推算Xi=Xm Licosa0 Y=Y Lsinami0 i式中:Xm、Ym――直线段起点M坐标Li――直线段上任意点i到线路起点M的距离a0――直线段起点M到JD1的方位角二、圆曲线上任一点的坐标推算①、圆曲线上任一点i相对应的圆心角:i=180Li R式中:Li――圆曲线上任一点i离开ZY或YZ点的弧长Xi=Rsin i②、圆曲线上任一点i的直角坐标:(可不计算).Y=R(1 cos )i i本文为圆曲线和缓和曲线的推算公式,包括直线、缓和曲线、圆曲线上的坐标推算③、圆曲线ZY或YZ点到任一点i的偏角:i=i2=90Li R④、圆曲线ZY或YZ点到任一点i的弦长:Ci=2Rsin(i2) 2Rsin( i)⑤、圆曲线ZY或YZ点到任一点i的弦长的方位角:ai=azy jd或yz jd iXi=XZY或YZ Cicosai⑥、所以圆曲线上任意点i的坐标为:Y=Y CsinaiiZY或YZ i例题:已知一段圆曲线,R=3500m,Ls=553.1m,交点里程K50+154.734,ZY点到JD方向方位角为A=129°23′18.3″,右偏9°3′15.8″,ZY点里程K49+877.607,YZ点里程K50+430.707,起点坐标为x=__.196,y=__.251,求K50+200处中点坐标及左右各偏12.5m的坐标。
解:K50+200处的曲线长度为Li=322.393m180 180 Li=322.393=5 16 39.52 K50+200相对应的方位角:a=R 3500K50+200相对应的偏角:i=i2=90 90Li=322.393=2 38 19.76 R 3500K50+200到zy点的弦长:Ci=2Rsin i=2 3500 sin2 38 19.76 =322.279m zy点到K50+200中桩的方位角:ai=azy jd i=129 23 18.3 2 38 19.76 =132 1 38.06K50+200左、右偏12.5m的方位角:a左=Ai a 90 =134 39 57.82 90 =44 39 57.82 a右=Ai a 90 =134 39 57.82 90 =134 39 57.82 所以K50+200处的坐标为:.196 322.279 cos132 1 38.06 =__.4354 Xi=XZY Cicosai=__ Y=Y Csina=__.251 322.279 sin132 1 38.06 =__.6484ZYii i 本文为圆曲线和缓和曲线的推算公式,包括直线、缓和曲线、圆曲线上的坐标推算K50+200左偏12.5m的坐标为:.4354 12.5 cos44 39 57.82 =__.3256 X左=Xi 12.5cosa左=__Y=Y 12.5sina=__.6484 12.5 sin44 39 57.82 =__.4656i左左K50+200右偏12.5m的坐标为:.4354 12.5 cos134 39 57.82 =__.6482 X右=Xi 12.5cosa右=__ Y=Y 12.5sina=__.6484 12.5 sin134 39 57.82 =__.5386i右右三、缓和曲线上任一点的坐标推算L2i180=切线角:i2RLsL2i180缓和曲线上任意点i的偏角:i==36RLsi缓和曲线ZH或HZ点到任意点i的方位角为:ai=aZH jd或HZ jd iL5i xi=Li40R2L2s3缓和曲线上任意点i的坐标为:L y=ii 6RLs22缓和曲线ZH或HZ点到任意点i的弦长:Cix yXi=XZH或HZ Cicosai所以缓和曲线上任意点i的坐标为:Y=Y CsinaiiZH或HZ i本文为圆曲线和缓和曲线的推算公式,包括直线、缓和曲线、圆曲线上的坐标推算例题:已知一段缓和曲线,ZH点到JD方向方位角为A=183°17′08.9″,线路左偏43°31′02″,ZH点里程为K52+001.615,ZH点坐标x=__.927,y=__.089,R=960m,Ls=120m,求K52+100处的中点坐标及左右各偏12.5m的坐标。
公路缓和曲线计算公式讲解

公路缓和曲线计算公式讲解公路缓和曲线是指在设计公路线形时为了使车辆在曲线上能够顺利转弯而采用的一种曲线形式。
在公路设计中,缓和曲线的设计是非常重要的,因为它直接关系到车辆在曲线上的安全行驶和舒适性。
在本文中,我们将对公路缓和曲线的计算公式进行详细的讲解,希望能够帮助大家更好地理解和应用这一知识。
一、缓和曲线的类型。
在公路设计中,常见的缓和曲线类型有三种,分别是圆曲线、过渡曲线和螺旋曲线。
圆曲线是一种由圆弧组成的曲线形式,它的曲率是恒定的。
过渡曲线是一种由直线段和圆弧段组成的曲线形式,它的曲率是逐渐变化的。
螺旋曲线是一种由圆弧和直线段交替组成的曲线形式,它的曲率也是逐渐变化的。
在实际的公路设计中,我们需要根据具体的情况选择合适的缓和曲线类型,以确保车辆在曲线上的安全行驶和舒适性。
二、缓和曲线的计算公式。
1. 圆曲线的计算公式。
在公路设计中,圆曲线的计算是非常常见的。
圆曲线的计算公式如下:L = (V^2) / (127R)。
其中,L表示圆曲线的长度(单位,米),V表示车辆的设计速度(单位,公里/小时),R表示圆曲线的半径(单位,米)。
根据这个公式,我们可以计算出圆曲线的长度,从而确定圆曲线的位置和形状。
2. 过渡曲线的计算公式。
过渡曲线是一种由直线段和圆弧段组成的曲线形式,它的计算公式如下:L = (V^2) / (a)。
其中,L表示过渡曲线的长度(单位,米),V表示车辆的设计速度(单位,公里/小时),a表示过渡曲线的加速度(单位,米/秒^2)。
根据这个公式,我们可以计算出过渡曲线的长度,从而确定过渡曲线的位置和形状。
3. 螺旋曲线的计算公式。
螺旋曲线是一种由圆弧和直线段交替组成的曲线形式,它的计算公式比较复杂。
螺旋曲线的计算需要考虑曲线的曲率变化和车辆的行驶轨迹,因此通常需要借助计算机软件来进行精确计算。
三、缓和曲线的设计原则。
在公路设计中,缓和曲线的设计需要遵循一些基本原则,以确保车辆在曲线上的安全行驶和舒适性。
趋近法求算缓和曲线里程及偏距的计算原理
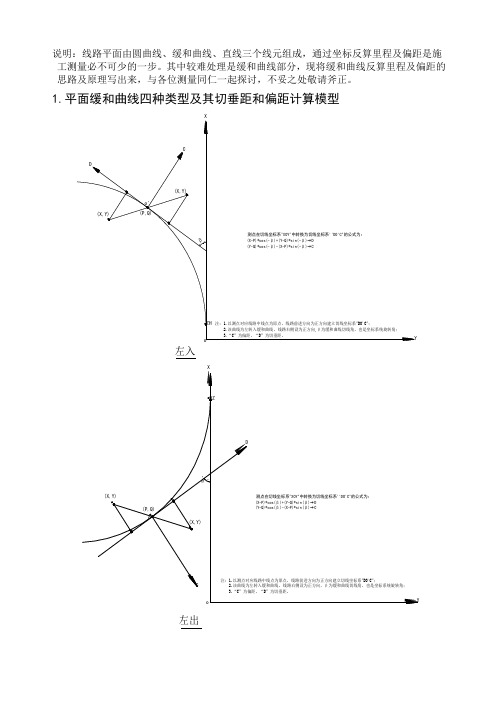
说明:线路平面由圆曲线、缓和曲线、直线三个线元组成,通过坐标反算里程及偏距是施工测量必不可少的一步。
其中较难处理是缓和曲线部分,现将缓和曲线反算里程及偏距的思路及原理写出来,与各位测量同仁一起探讨,不妥之处敬请斧正。
1.平面缓和曲线四种类型及其切垂距和偏距计算模型左入左出右入右出把以上左转曲线和右转曲线公式进行整理分析。
左转:入缓和曲线(X-P)*cos(-β)+(Y-Q)*sin(-β)→D(Y-Q)*cos(-β)-(X-P)*sin(-β)→C出缓和曲线(X-P)*cos(β)+(Y-Q)*sin(β)→D(Y-Q)*cos(β)-(X-P)*sin(β)→C右转:入缓和曲线(X-P)*cos(β)+(Y-Q)*sin(β)→D(Y-Q)*cos(β)-(X-P)*sin(β)→C出缓和曲线(X-P)*cos(-β)+(Y-Q)*sin(-β)→D(Y-Q)*cos(-β)-(X-P)*sin(-β)→C假设变量W为曲线方向判别符号,且规定W=1为右转,W=-1为左转,旋转角β=K,则以上公式简化为:入缓和曲线(X-P)×cos(W×K)+(Y-Q)×sin(W×K)→D(Y-Q)×cos(W×K)-(X-P)×sin(W×K)→C出缓和曲线(X-P)×cos(-W×K)+(Y-Q)×sin(-W×K)→D(Y-Q)×cos(-W×K)-(X-P)×sin(-W×K)→C2.趋近法求算缓和曲线里程及偏距(以上推导公式的应用)HHQX1 (计算入缓和曲线里程及偏距)程序清单:X:?Y:?W:(输入切线坐标和线路转向参数,1为左转,-1为右转X-S ZH→L:(测点对应缓和曲线长,估计值D O:S ZH+(L-L5÷(40×R2×l012)+ L9÷(3456×R4×l014))→P: W×(L3÷(6×R×l01)- L7÷(336×R3×l013))→Q:90×L2÷(π×R×l01)→K: (X-P)×cos(W×K)+(Y-Q)×sin(W×K)→D: (Y-Q)×cos(W×K)-(X-P)×sin(W×K)→C: L+D →L: LpWhile Abs(D)≥0.001: (循环语句。
公路缓和曲线段原理及缓和曲线计算公式

公路缓和曲线段原理及缓和曲线计算公式一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1.缓和曲线的作用1)便于驾驶员操纵方向盘2)乘客的舒适与稳定,减小离心力变化3)满足超高、加宽缓和段的过渡,利于平稳行车4)与圆曲线配合得当,增加线形美观2.缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A2/ρ(A:与汽车有关的参数)ρ=C/sC=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3.回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R,l h=s 则 l h=A2/R4.缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1)根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ρ,a s2)依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3)根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
4)从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5.直角坐标及要素计算1)回旋线切线角(1)缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
βx=s2/2Rl h(2)缓和曲线的总切线角β=l h2)缓和曲线直角坐标任意一点P处取一微分弧段ds,其所对应的中心角为dβxdx=dscosβxdy=dssinβx3)缓和曲线常数(1)主曲线的内移值p及切线增长值q内移值:p=Y h-R(1-cosβh)=l h2/24R切线增长值:q=X h-Rsinβh=l h/2-lh3/240R2(2)缓和曲线的总偏角及总弦长总偏角:βh=l h/2R总弦长:C h=l h-l h3/90R2O为圆曲线的圆心,圆曲线所对圆心角(等于公路偏角)。
缓和曲线的计算方法(三种)

2 s
0
距离:用曲线长l来代替弦长。放样出第1点后, 放样第2点时,用偏角和距离l交会得到。
(2)当点位于圆曲线上 方法:架仪HY (或YH),后视ZH(或HZ),拨角b0,即找
到了切线方向,再按单圆曲线偏角法进行。
b0 2 0
ls 3R
此外还有极坐标法、弦线支距法、长弦偏角 法。
3 ls 10 .00 m x0 l s 2 40 R 2 ls y 0 .17 m 0 6R
TH ( R p )tg
L H R ( 2 0 )
180
2l s 41 .96 m
E H ( R p ) sec
(2)当点位于圆曲线上,有:
x R sin q y R (1 cos ) p
2、偏角法(整桩距、短弦偏角法) 要注意:点是位于缓和曲线,还是位于圆曲线。
位于圆曲线
位于缓和曲线
2、偏角法(整桩距、短弦偏角法)
(1)当点位于缓和曲线上,有:
总偏角 (常量 ) 0 ls 6R
(3)缓和曲线的参数方程:
(4)圆曲线终点的坐标:
二.主点(major point)的测设
1、测设元素的计算
(1)内移距p 和切线增长q的计算:
24 R ls l s3 q 2 240 R 2
p
l s2
2、主点的测设
(1)里程的计算
ZH=JD-TH;HY=ZH+ls;
QZ=ZH+LH/2;HZ=ZH+LH;YH=HZ-ls
三、带有缓和曲线的圆曲线详细测设 1、切线支距法 (tangent off-set method)
公路工程测量放线圆曲线、缓和曲线(完整缓和曲线、非完整缓和曲线)计算解析

公路工程测量放线圆曲线、缓和曲线(包括完整缓和曲线、非完整缓和曲线)计算解析例:某道路桥梁中,A匝道线路。
已知交点桩号及坐标:SP,K9+000(2957714。
490,485768。
924);JD1,K9+154。
745(2957811。
298,485889.647);EP,K9+408.993(2957786。
391,486158.713)。
SP-JD1方位角:51°16′25″;转角:右44°00′54.06″;JD1—EP方位角:95°17′20″.由上面“A匝道直线、曲线及转角表”得知:K9+000—K9+116.282处于第一段圆曲线上,半径为385.75m;K9+116.282—K9+151.282处于第一段缓和曲线上,K9+151。
282的半径为300m,缓和曲线要素A1=217.335,Ls1=35m;K9+151.282-K9+216。
134处于第二段圆曲线上,半径为300m;K9+216。
134—K9+251.134处于第二段缓和曲线上,K9+251。
134的半径为1979.5,缓和曲线要素A2=111。
245,Ls2=35m;1 / 11K9+251。
134—K9+408.933处于第三段圆曲线上,半径为1979。
5m。
求:K9+130、K9+200、K9+230、K9+300的中桩坐标,切线方位角,左5米边桩的坐标,右10米边桩的坐标。
解:首先,我们知道要求一个未知点的坐标,必须知道起算点坐标,起算点至未知点的方位角,起算点至未知点的直线距离,然后利用坐标正算的计算公式,就可以直接求出未知点的坐标.那么,关于圆曲线和缓和曲线(包括完整缓和曲线和非完整缓和曲线)的计算,我们需要知道如何求出起算点至圆曲线或缓和曲线上某点的方位角和直线距离.下面,先列出关于圆曲线和缓和曲线中角度和距离计算的相关公式。
2 / 113 / 11y 轴。
过圆曲线上任意点P 的切线与ZY-JD 相交,夹角(切线角)为β,ZY-P 与ZY —JD 的夹角(弦切角)为α,ZY-P 的弧长为L ,ZY —P 的直线距离为d,圆曲线的半径为R 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
