【必考题】高中必修三数学上期末模拟试题(含答案)
【常考题】高中必修三数学上期末模拟试题(及答案)

【常考题】高中必修三数学上期末模拟试题(及答案)一、选择题1.在区间[]0,1上随机取两个数x ,y ,记P 为事件“23x y +≤”的概率,则(P = ) A .23B .12C .49 D .292.下面的程序框图表示求式子32×35×311×323×347×395的值, 则判断框内可以填的条件为( )A .90?i ≤B .100?i ≤C .200?i ≤D .300?i ≤3.执行如图的程序框图,如果输入72m =,输出的6n =,则输入的n 是( )A .30B .20C .12D .84.己知某产品的销售额y 与广告费用x 之间的关系如下表:若求得其线性回归方程为 6.5ˆˆyx a =+,其中ˆˆa y bx =-,则预计当广告费用为6万元时的销售额是( ) A .42万元B .45万元C .48万元D .51万元5.某高校大一新生中,来自东部地区的学生有2400人、中部地区学生有1600人、西部地区学生有1000人.从中选取100人作样本调研饮食习惯,为保证调研结果相对准确,下列判断正确的有( )①用分层抽样的方法分别抽取东部地区学生48人、中部地区学生32人、西部地区学生20人;②用简单随机抽样的方法从新生中选出100人; ③西部地区学生小刘被选中的概率为150; ④中部地区学生小张被选中的概率为15000A .①④B .①③C .②④D .②③6.某市委积极响应十九大报告提出的“到2020年全面建成小康社会”的目标,鼓励各县积极脱贫,计划表彰在农村脱贫攻坚战中的杰出村代表,已知A ,B 两个贫困县各有15名村代表,最终A 县有5人表现突出,B 县有3人表现突出,现分别从A ,B 两个县的15人中各选1人,已知有人表现突出,则B 县选取的人表现不突出的概率是( ) A .13B .47C .23D .567.高二某班共有学生60名,座位号分别为01, 02, 03,···, 60.现根据座位号,用系统抽样的方法,抽取一个容量为4的样本.已知03号、18号、48号同学在样本中,则样本中还有一个同学的座位号是( ) A .31号B .32号C .33号D .34号8.在半径为2圆形纸板中间,有一个边长为2的正方形孔,现向纸板中随机投飞针,则飞针能从正方形孔中穿过的概率为( ) A .4πB .3πC .2πD .1π9.在长为10cm 的线段AB 上任取一点C ,作一矩形,邻边长分別等于线段AC 、CB 的长,则该矩形面积小于216cm 的概率为( ) A .23B .34C .25D .1310.执行如图的程序框图,如果输出a 的值大于100,那么判断框内的条件为( )A .5k <?B .5k ≥?C .6k <?D .6k ≥?11.类比“赵爽弦图”,可类似地构造如图所示的图形,它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形,设D 为BE 中点,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是( )A .17B .14C .13D .41312.设数据123,,,,n x x x x L 是郑州市普通职工*(3,)n n n N ≥∈个人的年收入,若这n 个数据的中位数为x ,平均数为y ,方差为z ,如果再加上世界首富的年收入1n x +,则这1n +个数据中,下列说法正确的是( )A .年收入平均数大大增大,中位数一定变大,方差可能不变B .年收入平均数大大增大,中位数可能不变,方差变大C .年收入平均数大大增大,中位数可能不变,方差也不变D .年收入平均数可能不变,中位数可能不变,方差可能不变二、填空题13.运行如图所示的程序框图,则输出的所有y 值之和为___________.14.如图所示的程序框图,输出的S的值为()A.12B.2C.1-D.12-15.如图所示,在边长为1的正方形OABC中任取一点M.则点M恰好取自阴影部分的概率是.16.为弘扬我国优秀的传统文化,某小学六年级从甲、乙两个班各选出7名学生参加成语知识竞赛,他们取得的成绩的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83,则的值为__________.17.取一根长度为3米的绳子,拉直后在任意位置剪断,则剪出的两段的长都不小于1米(记为事件A )的概率为________18.投掷一枚均匀的骰子,则落地时,向上的点数是2的倍数的概率是_________, 19.父亲节小明给爸爸从网上购买了一双运动鞋,就在父亲节的当天,快递公司给小明打电话话说鞋子已经到达快递公司了,马上可以送到小明家,到达时间为晚上6点到7点之间,小明的爸爸晚上5点下班之后需要坐公共汽车回家,到家的时间在晚上5点半到6点半之间.求小明的爸爸到家之后就能收到鞋子的概率(快递员把鞋子送到小明家的时候,会把鞋子放在小明家门口的“丰巢”中)为 __________. 20.如图,曲线sin32xy π=+把边长为4的正方形OABC 分成黑色部分和白色部分.在正方形内随机取一点,则此点取自黑色部分的概率是__________.三、解答题21.一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1、2、3、4,现从盒子中随机抽取卡片.(Ⅰ)若一次从中随机抽取3张卡片,求3张卡片上数字之和大于或等于7的概率; (Ⅱ)若第一次随机抽取1张卡片,放回后再随机抽取1张卡片,求两次抽取的卡片中至少一次抽到数字2的概率.22.从某居民区随机抽取10个家庭,获得第i 个家庭的月收入i x (单位:千元)与月储蓄i y ,(单位:千元)的数据资料,算出101010102111180,20184,720ii i i i i i i i xy x y x ========∑∑∑∑,,附:线性回归方程1221ˆˆˆˆˆˆ,,ni ii nii x y nxyybx a b ay bx xnx ==-=+==--∑∑,其中,x y 为样本平均值. (1)求家庭的月储蓄y 对月收入x 的线性回归方程ˆˆˆybx a =+ ; (2)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.23.为了了解某省各景区在大众中的熟知度,随机从本省1565:岁的人群中抽取了n 人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该省有哪几个国家AAAAA 级旅游景区?”,统计结果如下表所示:组号 分组 回答正确的人数 回答正确的人数占本组的频率第1组 [)1525, a0.5第2组 [)2535, 18x第3组 [)3545, b 0.9 第4组 [)4555, 9 0.36第5组[)5565,3y(1)分别求出,,,a b x y 的值;(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组抽取的人数;(3)在(2)中抽取的6人中随机抽取2人,求所抽取的人中恰好没有年龄段在[)3545,的概率24.已知某校甲、乙、丙三个兴趣小组的学生人数分别为36,24,12.现采用分层抽样的方法从中抽取6人,进行睡眠质量的调查.(1)应从甲、乙、丙三个兴趣小组的学生中分别抽取多少人?(2)设抽出的6人分别用A 、B 、C 、D 、E 、F 表示,现从6人中随机抽取2人做进一步的身体检查.(i )试用所给字母列出所有可能的抽取结果;(ii )设K 为事件“抽取的2人来自同一兴趣小组”,求事件K 发生的概率.25.某机构组织语文、数学学科能力竞赛,每个考生都参加两科考试,按照一定比例淘汰后,按学科分别评出一二三等奖.现有某考场的两科考试数据统计如下,其中数学科目成绩为二等奖的考生有12人.(Ⅰ)求该考场考生中语文成绩为一等奖的人数;(Ⅱ)用随机抽样的方法从获得数学和语文二等奖的考生中各抽取5人,进行综合素质测试,将他们的综合得分绘成茎叶图(如图),求两类样本的平均数及方差并进行比较分析;(Ⅲ)已知该考场的所有考生中,恰有3人两科成绩均为一等奖,在至少一科成绩为一等奖的考生中,随机抽取2人进行访谈,求两人两科成绩均为一等奖的概率.-年网民26.随着社会的进步与发展,中国的网民数量急剧增加.下表是中国从20092018人数及互联网普及率、手机网民人数(单位:亿)及手机网民普及率的相关数据.年份网民人数互联网普及率手机网民人数手机网民普及率2009 3.828.9% 2.317.5%2010 4.534.3% 3.022.9%2011 5.138.3% 3.627.0%2012 5.642.1% 4.231.6%2013 6.245.8% 5.036.9%2014 6.547.9% 5.641.3%2015 6.950.3% 6.245.2% 20167.353.2%7.051.0% 20177.755.8%7.554.4% 20188.359.6%8.258.9%(互联网普及率=(网民人数/人口总数)×100%;手机网民普及率=(手机网民人数/人口总数)×100%)(Ⅰ)从20092018-这十年中随机选取一年,求该年手机网民人数占网民总人数比值超过80%的概率;(Ⅱ)分别从网民人数超过6亿的年份中任选两年,记X 为手机网民普及率超过50%的年数,求X 的分布列及数学期望;(Ⅲ)若记20092018-年中国网民人数的方差为21s ,手机网民人数的方差为22s ,试判断21s 与22s 的大小关系.(只需写出结论)【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【解析】 【分析】由题意结合几何概型计算公式求解满足题意的概率值即可. 【详解】如图所示,01,01x y ≤≤≤≤表示的平面区域为ABCD , 平面区域内满足23x y +≤的部分为阴影部分的区域APQ ,其中2,03P ⎛⎫ ⎪⎝⎭,20,3Q ⎛⎫⎪⎝⎭,结合几何概型计算公式可得满足题意的概率值为1222233119p ⨯⨯==⨯. 本题选择D 选项.【点睛】数形结合为几何概型问题的解决提供了简捷直观的解法.用图解题的关键:用图形准确表示出试验的全部结果所构成的区域,由题意将已知条件转化为事件A 满足的不等式,在图形中画出事件A 发生的区域,据此求解几何概型即可.2.B【解析】 【分析】根据题意可知该程序运行过程中,95i =时,判断框成立,191i =时,判断框不成立,即可选出答案。
【必考题】高中必修三数学上期末一模试卷(及答案)

【必考题】高中必修三数学上期末一模试卷(及答案)一、选择题1.将A ,B ,C ,D ,E ,F 这6个字母随机排成一排组成一个信息码,则所得信息码恰好满足A ,B ,C 三个字母连在一起,且B 在A 与C 之间的概率为( ) A .112B .15C .115D .2152.我国古代数学著作《九章算术》中,其意是:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问:米几何?右图是源于其思想的一个程序框图,若输出的2S =(单位:升),则输入k 的值为A .6B .7C .8D .93.如图所给的程序运行结果为41S =,那么判断框中应填入的关于k 的条件是( )A .7k ≥?B .6k ≥?C .5k ≥?D .6k >?4.2018年12月12日,某地食品公司对某副食品店某半月内每天的顾客人数进行统计得到样本数据的茎叶图如图所示,则该样本的中位数是( )A .45B .47C .48D .635.《九章算术》是我国古代的数学名著,体现了古代劳动人民的数学智慧,其中第六章“均输”中,有一竹节容量问题,某教师根据这一问题的思想设计了如图所示的程序框图,若输出m 的值为67,则输入a 的值为( )A .7B .4C .5D .116.下列赋值语句正确的是( ) A .s =a +1 B .a +1=s C .s -1=a D .s -a =17.预测人口的变化趋势有多种方法,“直接推算法”使用的公式是()0 1nn P P k =+(1k >-),n P 为预测人口数,0P 为初期人口数,k 为预测期内年增长率,n 为预测期间隔年数.如果在某一时期有10k -<<,那么在这期间人口数 A .呈下降趋势B .呈上升趋势C .摆动变化D .不变 8.执行如图所示的程序框图,若输入的a ,b ,c 依次为()sin sin αα,()cos sin αα,()sin cos αα,其中,42ππα⎛⎫∈⎪⎝⎭,则输出的x 为( )A .()cos cos ααB .()sin sin ααC .()cos sin ααD .()sin cos αα9.已知线段MN的长度为6,在线段MN上随机取一点P,则点P到点M,N的距离都大于2的概率为()A.34B.23C.12D.1310.如图,正方形ABNH、DEFM的面积相等,23CN NG AB==,向多边形ABCDEFGH内投一点,则该点落在阴影部分内的概率为()A.1 2B.3 4C.2 7D.3 811.赵爽是我国古代数学家、天文学家大约在公元222年赵爽为《周碑算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的一个小正方形组成的)类比“赵爽弦图”,赵爽弦图可类似地构造如图所示的图形,它是由个3全等的等边三角形与中间的一个小等边三角形组成的一个大等边三角形,设DF=2AF,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是( )A.B.C.D.12.执行如图的程序框图,若输出的4n=,则输入的整数p的最小值是()A.4B.5C.6D.15二、填空题t=,则输出的k=______.13.某程序框图如图所示,若输入的414.为长方形,,,为的中点,在长方形内随机取一点,取到的点到的距离大于1的概率为________.15.如图是某算法流程图,则程序运行后输出S的值为____.i=)满足16.已知某产品连续4个月的广告费i x(千元)与销售额i y(万元)(1,2,3,44115 iix ==∑,4112 iiy ==∑,若广告费用x和销售额y之间具有线性相关关系,且回归直线方程为^y bx a=+,0.6b=,那么广告费用为5千元时,可预测的销售额为___万元. 17.变量X与Y相对应的5组数据和变量U与V相对应的5组数据统计如表:X1011.311.812.513U1011.311.812.513 Y12345V54321用b1表示变量Y与X之间的回归系数,b2表示变量V与U之间的回归系数,则b1与b2的大小关系是___.18.如图是一个算法的流程图,则输出的a的值是__________.19.某公司的班车在8:00,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过10分钟的概率是__________20.为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,L,第五组,如图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组没有疗效的有6人,则第三组中有疗效的人数为__________.三、解答题21.一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1、2、3、4,现从盒子中随机抽取卡片.(Ⅰ)若一次从中随机抽取3张卡片,求3张卡片上数字之和大于或等于7的概率;(Ⅱ)若第一次随机抽取1张卡片,放回后再随机抽取1张卡片,求两次抽取的卡片中至少一次抽到数字2的概率.22.为了鼓励市民节约用电,某市实行“阶梯式”电价,将每户居民的月用电量分为二档,月用电量不超过200度的部分按0.5元/度收费,超过200度的部分按0.8元/度收费.某小区共有居民1000户,为了解居民的用电情况,通过抽样,获得了今年7月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图.(1)求a的值;(2)试估计该小区今年7月份用电量用不超过260元的户数;(3)估计7月份该市居民用户的平均用电费用(同一组中的数据用该组区间的中点值作代表).23.2018年中秋节到来之际,某超市为了解中秋节期间月饼的销售量,对其所在销售范围内的1000名消费者在中秋节期间的月饼购买量(单位:g)进行了问卷调查,得到如下频率分布直方图:()1求频率分布直方图中a的值;()2以频率作为概率,试求消费者月饼购买量在600g1400g~的概率;()3已知该超市所在销售范围内有20万人,并且该超市每年的销售份额约占该市场总量的5%,请根据这1000名消费者的人均月饼购买量估计该超市应准备多少吨月饼恰好能满足市场需求(频率分布直方图中同一组的数据用该组区间的中点值作代表)?24.高一某班以小组为单位在周末进行了一次社会实践活动,且每小组有5名同学,活动结束后,对所有参加活动的同学进行测评,其中A,B两个小组所得分数如下表:A组8677809488B组9183?7593其中B组一同学的分数已被污损,看不清楚了,但知道B组学生的平均分比A组学生的平均分高出1分.(1)若从B组学生中随机挑选1人,求其得分超过85分的概率;(2)从A组这5名学生中随机抽取2名同学,设其分数分别为m,n,求||8m n-≤的概率.25.甲、乙两位同学参加数学应用知识竞赛培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:(Ⅰ)分别估计甲、乙两名同学在培训期间所有测试成绩的平均分;(Ⅱ)从上图中甲、乙两名同学高于85分的成绩中各选一个成绩作为参考,求甲、乙两人成绩都在90分以上的概率;(Ⅲ)现要从甲、乙中选派一人参加正式比赛,根据所抽取的两组数据分析,你认为选派哪位同学参加较为合适?说明理由.26.某手机厂商在销售某型号手机时开展“手机碎屏险”活动.用户购买该型号手机时可选购“手机碎屏险”,保费为x元,若在购机后一年内发生碎屏可免费更换一次屏幕,为了合理确定保费x的值,该手机厂商进行了问卷调查,统计后得到下表(其中y表示保费为x元时愿意购买该“手机碎屏险”的用户比例):(1)根据上面的数据计算得()()5119.2i iix x y y=--=-∑,求出y关于x的线性回归方程;(2)若愿意购买该“手机碎屏险”的用户比例超过0.50,则手机厂商可以获利,现从表格中的5种保费任取2种,求这2种保费至少有一种能使厂商获利的概率.附:回归方程$$ˆy bx a=+中斜率和截距的最小二乘估计分别为()()()121ni iiniix x y ybx x==--=-∑∑$,$a y bx=-$【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【解析】 【分析】将A ,B ,C 三个字捆在一起,利用捆绑法得到答案. 【详解】由捆绑法可得所求概率为242466A A 1A 15P ==. 故答案为C 【点睛】本题考查了概率的计算,利用捆绑法可以简化运算.2.C解析:C 【解析】分析:执行程序框图,得到输出值4k S =,令24k=,可得8k =. 详解:阅读程序框图,初始化数值1,n S k ==,循环结果执行如下:第一次:14n =<成立,2,22k k n S k ==-=; 第二次:24n =<成立,3,263k k k n S ==-=; 第三次:34n =<成立,4,3124k k k n S ==-=; 第四次:44n =<不成立,输出24kS ==,解得8k =. 故选C.点睛:解决循环结构程序框图问题的核心在于:第一,要确定是利用当型还是直到型循环结构;第二,要准确表示累计变量;第三,要注意从哪一步开始循环,弄清进入或终止的循环条件、循环次数.3.B解析:B 【解析】 【分析】程序运行结果为41S =,执行程序,当6k =时,判断条件成立,当5k =时,判断条件不成立,输出41S =,即可选出答案. 【详解】根据程序框图,运行如下: 初始10,1k S ==,判断条件成立,得到11011S =+=,1019k =-=; 判断条件成立,得到11920S =+=,918k =-=; 判断条件成立,得到20828S =+=,817k =-=; 判断条件成立,得到28735S =+=,716k =-=; 判断条件成立,得到35641S =+=,615k =-=; 判断条件不成立,输出41S =,退出循环,即6k ≥符合题意. 故选:B. 【点睛】本题考查了程序框图的识别与判断,弄清进入循环体和跳出循环体的条件是解决本题的关键,考查了学生的推理能力,属于基础题.4.A解析:A 【解析】 【分析】由茎叶图确定所给的所有数据,然后确定中位数即可. 【详解】各数据为:12 20 31 32 34 45 45 45 47 47 48 50 50 61 63, 最中间的数为:45,所以,中位数为45. 本题选择A 选项. 【点睛】本题主要考查茎叶图的阅读,中位数的定义与计算等知识,意在考查学生的转化能力和计算求解能力.5.C解析:C 【解析】模拟程序框图的运行过程,如下:输入a ,23m a =-,1i =,()223349m a a =--=-;2i =,()2493821m a a =--=-; 3i =,()282131645m a a =--=-; 4i =,()2164533293m a a =--=-;输出3293m a =-,结束; 令329367a -=,解得5a =. 故选C.6.A解析:A【解析】赋值语句的格式为“变量=表达式”,“=”的左侧只能是单个变量,B 、C 、D 都不正确.选A.7.A解析:A 【解析】 【分析】可以通过n P 与0P 之间的大小关系进行判断. 【详解】当10k -<<时,()011011nk k <+<<+<,, 所以()001nn P P k P =+<,呈下降趋势. 【点睛】判断变化率可以通过比较初始值与变化之后的数值之间的大小来判断.8.C解析:C 【解析】 【分析】由框图可知程序的功能是输出三者中的最大者,比较大小即可. 【详解】由程序框图可知a 、b 、c 中的最大数用变量x 表示并输出, ∵,42ππα⎛⎫∈⎪⎝⎭∴0cos α12sin α<<<<, 又()y xsin α=在R 上为减函数,y sin x α=在()0∞+,上为增函数, ∴()sin sin αα<()cos sin αα,()sin cos αα<()sin sin αα故最大值为()cos sin αα,输出的x 为()cos sin αα故选:C 【点睛】本题主要考查了选择结构.算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空也是重要的考试题型,这种题考试的重点有:①分支的条件②循环的条件③变量的赋值④变量的输出.9.D解析:D 【解析】根据题意画出图形,结合图形即可得出结论.【详解】如图所示,线段MN 的长度为6,在线段MN 上随机取一点P ,则点P 到点M ,N 的距离都大于2的概率为2163P ==. 故选D .【点睛】本题考查了几何概型的概率计算问题,是基础题. 10.C解析:C【解析】【分析】由正方形ABNH 、DEFM 的面积相等,可得两正方形边长相等,设边长为3,由23CN NG AB ==,可得正方形MCNG 的边长为2,分别求出阴影部分的面积及多边形ABCDEFGH 的面积,由测度比为面积比得答案.【详解】 如图所示,由正方形ABNH 、DEFM 的面积相等,可得两正方形边长相等,设边长为3,由23CN NG AB ==,可得正方形MCNG 的边长为2, 则阴影部分的面积为224⨯=,多边形ABCDEFGH 的面积为2332214⨯⨯-⨯=.则向多边形ABCDEFGH 内投一点,则该点落在阴影部分内的概率为42147=. 故选:C.【点睛】本题主要考查了几何概型的概率的求法,关键是求出多边形ABCDEFGH 的面积,着重考查了推理与运算能力,以及数形结合的应用,属于基础题.解析:B【解析】【分析】 由题意可得,设,求得,由面积比的几何概型,可知在大等边三角形中随机取一点,则此点取自小等边三角形的概率,即可求解.【详解】 由题意可得,设,可得, 在中,由余弦定理得, 所以,,由面积比的几何概型,可知在大等边三角形中随机取一点, 则此点取自小等边三角形的概率是,故选B. 【点睛】本题主要考查了面积比的几何概型,以及余弦定理的应用,其中解答中认真审题、把在大等边三角形中随机取一点,取自小等边三角形的概率转化为面积比的几何概型是解答的关键,着重考查了推理与运算能力,属于基础题. 12.A解析:A【解析】【分析】列举出算法的每一步循环,根据算法输出结果计算出实数p 的取值范围,于此可得出整数p 的最小值.【详解】0S p =<满足条件,执行第一次循环,0021S =+=,112n =+=;1S p =<满足条件,执行第二次循环,1123S =+=,213n =+=;3S p =<满足条件,执行第二次循环,2327S =+=,314n =+=.7S p =<满足条件,调出循环体,输出n 的值为4.由上可知,37p <≤,因此,输入的整数p 的最小值是4,故选A.【点睛】本题考查算法框图的应用,解这类问题,通常列出每一次循环,找出其规律,进而对问题进行解答,考查分析问题和解决问题的能力,属于中等题.二、填空题13.【解析】【分析】根据题意执行循环结构的程序框图逐次计算即可得到答案【详解】由题意执行程序框图:可得;第一循环不满足条件;第二次循环不满足条件;第三次循环不满足条件;第四次循环不满足条件;第五次循环不 解析:【解析】【分析】根据题意,执行循环结构的程序框图,逐次计算,即可得到答案.【详解】由题意执行程序框图:可得0S =, 8k =;第一循环,不满足条件,8S =,7k =;第二次循环,不满足条件,1S =,6k =;第三次循环,不满足条件,5S =,5k =;第四次循环,不满足条件0S =,4k =;第五次循环,不满足条件4S =,3k =,第六次循环,满足条件,输出3k =.【点睛】本题主要考查了循环结构的程序框图的计算输出问题,其中解答中根据给定的程序框图,逐次循环,逐次计算,注意把握判定条件是解答的关键,着重考查了推理与运算能力,属于基础题.14.1-π12【解析】【分析】由题意得长方形的面积为S=3×2=6以O 点为原型半径为1作圆此时圆在长方形内部的部分的面积为Sn=π2再由面积比的几何概型即可求解【详解】由题意如图所示可得长方形的面积为S 解析:【解析】【分析】 由题意,得长方形的面积为,以O 点为原型,半径为1作圆,此时圆在长方形内部的部分的面积为,再由面积比的几何概型,即可求解. 【详解】 由题意,如图所示,可得长方形的面积为,以O 点为原型,半径为1作圆,此时圆在长方形内部的部分的面积为, 所以取到的点到的距离大于1的表示圆的外部在矩形内部分部分, 所以概率为.【点睛】本题主要考查了几何概型的概率的计算问题,解决此类问题的步骤:求出满足条件A 的基本事件对应的“几何度量”,再求出总的基本事件对应的“几何度量”,然后根据求解,着重考查了分析问题和解答问题的能力.15.41【解析】【分析】根据给定的程序框图计算逐次循环的结果即可得到输出的值得到答案【详解】由题意运行程序框图可得第一次循环不满足判断框的条件;第二次循环不满足判断框的条件;第三次循环不满足判断框的条件解析:41【解析】【分析】根据给定的程序框图,计算逐次循环的结果,即可得到输出的值,得到答案。
2021-2022高中数学必修三期末第一次模拟试卷(附答案)

一、选择题1.已知边长为2的正方形ABCD,在正方形ABCD内随机取一点,则取到的点到正方形四个顶点A B C D,,,的距离都大于1的概率为()A.16πB.4πC.3224π-D.14π-2.某校从高一(1)班和(2)班的某次数学考试(试卷满分为100分)的成绩中各随机抽取了6份数学成绩组成一个样本,如茎叶图所示.若分别从(1)班、(2)班的样本中各取一份,则(2)班成绩更好的概率为( )A.1636B.1736C.12D.19363.七巧板是我国古代劳动人民发明的一种智力玩具,由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成. 如图是一个用七巧板拼成的正方形,若在此正方形中任取一点,则此点取自黑色部分的概率为()A.14B.316C.38D.7164.在二项式42nxx的展开式,前三项的系数成等差数列,把展开式中所有的项重新排成一列,有理项都互不相邻的概率为()A.16B.14C.512D.135.被称为宋元数学四大家的南宋数学家秦九韶在《数书九章》一书中记载了求解三角形面积的公式,如图是利用该公式设计的程序框图,则输出的k的值为()A .4B .5C .6D .76.读下面的程序:上面的程序在执行时如果输入6,那么输出的结果为() A .6B .720C .120D .50407.若执行如图所示的程序框图,则输出S 的值为( )A .9-B .16-C .25-D .36-8.若执行如图所示的程序框图,则输出S 的值为( )A .10072015B .10082017C .10092019D .101020219.某商场为了了解毛衣的月销售量y (件)与月平均气温x (C ︒)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表: 月平均气温x C ︒171382月销售量y (件)24334055由表中数据算出线性回归方程y bx a =+中的2b =-,气象部门预测下个月的平均气温为6C ︒,据此估计该商场下个月毛衣销售量约为( )A .58件B .40件C .38件D .46件10.为了了解某同学的数学学习情况,对他的6次数学测试成绩进行统计,作出的茎叶图如图所示,则下列关于该同学数学成绩的说法正确的是( )A .中位数为83B .众数为85C .平均数为85D .方差为1911.在一段时间内,某种商品的价格x (元)和销售量y (件)之间的一组数据如下表:价格x (元) 4 6 8 10 12 销售量y (件)358910若y 与x 呈线性相关关系,且解得回归直线ˆˆˆybx a =+的斜率0.9b ∧=,则a ∧的值为( ) A .0.2 B .-0.7 C .-0.2 D .0.712.已知一组数据的茎叶图如图所示,则该组数据的平均数为( )A .85B .84C .83D .81二、填空题13.住在同一城市的甲、乙两位合伙人,约定在当天下午4.00-5:00间在某个咖啡馆相见商谈合作事宜,他们约好当其中一人先到后最多等对方10分钟,若等不到则可以离去,则这两人能相见的概率为__________.14.在棱长为2 的正方体内任取一点,则此点到正方体中心的距离不大于1的概率为_____.15.已知下列命题:①ˆ856yx =+意味着每增加一个单位,y 平均增加8个单位 ②投掷一颗骰子实验,有掷出的点数为奇数和掷出的点数为偶数两个基本事件 ③互斥事件不一定是对立事件,但对立事件一定是互斥事件④在适宜的条件下种下一颗种子,观察它是否发芽,这个实验为古典概型 其中正确的命题有__________________.16.某程序框图如图所示,则该程序运行后输出的S 的值为________.17.如图是某算法流程图,则程序运行后输出S 的值为____.18.程序如下:以上程序输出的结果是_________________19.已知一组数据:5.7,5.8,6.1,6.4,6.5,则该数据的方差是__________.20.为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,,第五组,如图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组没有疗效的有6人,则第三组中有疗效的人数为__________.三、解答题21.某校从高一年级期末考试的学生中抽出60名学生,其成绩(均为整数)的频率分布直方图如图所示.(1)估计这次考试的平均分;(2)假设分数在[90,100]的学生的成绩都不相同,且都在94分以上,现用简单随机抽样方法,从95,76,97,88,69,100这6个数中任取2个数,求这2个数恰好是两个学生的成绩的概率.22.某校高三课外兴趣小组为了解高三同学高考结束后是否打算观看2019年足球世界杯比赛的情况,从全校高三年级1500名男生、1000名女生中按分层抽样的方式抽取125名学生进行问卷调查,情况如下表:打算观看 不打算观看女生 20b男生c25(1)求出表中数据b ,c ;(2)判断是否有99%的把握认为观看2019年足球世界杯比赛与性别有关;(3)为了计算“从10人中选出9人参加比赛”的情况有多少种,我们可以发现它与“从10人中选出1人不参加比赛”的情况有多少种是一致的.现有问题:在打算观看2019年足球世界杯比赛的同学中有5名男生、2名女生来自高三(5)班,现从中推选5人接受校园电视台采访,请根据上述方法,求被推选出的5人中恰有四名男生、一名女生的概率.()20P K k ≥0.10 0.05 0.025 0.01 0.005 0K2.7063.8415.0246.6357.879附:()()()()()22n ad bc K a b c d a c b d -=++++. 23.某中学男子体育组的百米赛跑的成绩(单位:秒)如下:12.1,13.2,12.7,12.8,12.5,12.4,12.7,11.5,11.6,11.7.设计一个算法从这些成绩中搜索出小于12.1秒的成绩,画出程序框图,并编写相应程序. 24.古希腊杰出的数学家丢番图的墓碑上有这样一首诗:这是一座古墓,里面安葬着丢番图. 请你告诉我,丢番图的寿数几何? 他的童年占去了一生的六分之一, 接着十二分之一是少年时期,又过了七分之一的时光,他找到了自己的终身伴侣. 五年之后,婚姻之神赐给他一个儿子,可是儿子不济,只活到父亲寿数的一半,就匆匆离去. 这对父亲是一个沉重的打击, 整整四年,为失去爱子而悲伤, 终于告别了数学,离开了人世.试用循环结构,写出算法分析和算法程序.25.“湖广熟,天下足”,鱼米之乡的湖北是全国重要的农产品生产地.而受疫情影响,像莲藕、小龙虾等湖北很多优质农副产品近期都面临销售难题.为了让淜北尽快恢复正常,央视主持人朱广权化身直播带货官,和网红们一起为湖北产品做公益直播.在为湖北某地区的小龙虾进行带货时,需大致了解该地区小龙虾的产量,通过调查发现湖北某地区近几年的小龙虾产量统计如下表:(1)根据表中数据,建立关于t 的线性回归方程y bt a =+; (2)请你根据线性回归方程预测今年(2020年)该地区小龙虾的年产量.附:对于一组数据()11,t y ,()22,t y ,…,(),n n t y ,其回归直线y bt a =+的斜率和截距的最小二乘估计分别为:()()()121ˆniii ni i t t y y bt t ==--=-∑∑,a y bt =-.(参考数据:()()616.3ii i tty y =--=∑)26.现有某高新技术企业年研发费用投入x (百万元)与企业年利润y (百万元)之间具有线性相关关系,近5年的年科研费用和年利润具体数据如下表:(1)画出散点图;(2)求y 对x 的回归直线方程;(3)如果该企业某年研发费用投入8百万元,预测该企业获得年利润为多少?参考公式:用最小二乘法求回归方程ˆˆˆybx a =+的系数ˆˆ,a b 计算公式: 1221ˆˆˆ·,ni ii nii x y nx y bay bx xnx ==-==--∑∑【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】根据题意,作出满足题意的图像,利用面积测度的几何概型,即得解. 【详解】分别以A ,B ,C ,D 四点为圆心,1为半径作圆,由题意满足条件的点在图中的阴影部分224ABCD S =⨯=,214144ABCD S S ππ=-⨯⨯=-阴影由几何测度的古典概型,14ABCD S P S π==-阴影 故选:D 【点睛】本题考查了面积测度的几何概型,考查了学生综合分析,数形结合,数学运算的能力,属于中档题.2.C解析:C 【分析】由题意从(1)班、(2)班的样本中各取一份,(2)班成绩更好即(2)班成绩比(1)班成绩高,用列举法列出所有可能结果,由此计算出概率.根据题意,两次取出的成绩一共有36种情况;分别为()67,68、()67,72、()67,73、()67,85、()67,89、()67,93 ()76,68、()76,72、()76,73、()76,85、()76,89、()76,93 ()78,68、()78,72、()78,73、()78,85、()78,89、()78,93 ()82,68、()82,72、()82,73、()82,85、()82,89、()82,93 ()85,68、()85,72、()85,73、()85,85、()85,89、()85,93 ()92,68、()92,72、()92,73、()92,85、()92,89、()92,93满足条件的有18种,故183126p ==, 故选C 【点睛】本题考查概率的求法,考查古典概型、列举法等基础知识,考查运算求解能力,是基础题.3.B解析:B 【分析】设正方形的边长为2,计算出阴影部分区域的面积和正方形区域的面积,然后利用几何概型的概率公式计算出所求事件的概率. 【详解】设正方形的边长为2,则阴影部分由三个小等腰直角三角形构成,则正方形的对角线长为=,对应每个小等腰三角形的面积1124S ==, 则阴影部分的面积之和为13344⨯=,正方形的面积为4, 若在此正方形中任取一点,则此点取自黑色部分的概率为344631=,故选:B . 【点睛】本题考查面积型几何概型概率公式计算事件的概率,解题的关键在于计算出所求事件对应区域的面积和总区域的面积,考查计算能力,属于中等题.4.C解析:C 【分析】先根据前三项的系数成等差数列求n ,再根据古典概型概率公式求结果因为n前三项的系数为1212111(1)1,,112448n n n n n n C C C C n -⋅⋅∴=+⋅∴-= 163418118,0,1,2,82rr r r n n T C x r -+>∴=∴=⋅=,当0,4,8r =时,为有理项,从而概率为636799512A A A =,选C. 【点睛】本题考查二项式定理以及古典概型概率,考查综合分析求解能力,属中档题.5.B解析:B 【分析】模拟程序运行,依次计算可得所求结果 【详解】当4a =,3b =,2c =时,12S =<,2k =; 当5a =,4b =,3c =时,612S =<,3k =; 当6a =,5b =,4c =时,27124S =<,4k =; 当7a =,6b =,5c =时,12S =>,5k =; 故选B 【点睛】本题考查程序运算的结果,考查运算能力,需注意1k k =+所在位置6.B解析:B 【解析】 【分析】执行程序,逐次计算,根据判断条件终止循环,即可求解输出的结果,得到答案. 【详解】由题意,执行程序,可得:第1次循环:满足判断条件,1,2S i ==; 第2次循环:满足判断条件,2,3S i ==; 第3次循环:满足判断条件,6,4S i ==; 第4次循环:满足判断条件,24,5S i ==; 第5次循环:满足判断条件,120,6S i ==; 第6次循环:满足判断条件,720,7S i ==; 不满足判断条件,终止循环,输出720S =,故选B.【点睛】本题主要考查了循环结构的程序框图的计算输出,其中解答中正确理解循环结构的程序框图的计算功能,逐次计算是解答的关键,着重考查了推理与运算能力,属于基础题.7.D解析:D 【分析】执行循环结构的程序框图,逐次运算,根据判断条件终止循环,即可得到运算结果,得到答案. 【详解】由题意,执行循环结构的程序框图,可知:第一次运行时,1(1)11,0(1)1,3T S n =-=-=+-=-=•; 第二次运行时,3(1)33,1(3)4,5T S n =-=-=-+-=-=•; 第三次运行时,5(1)55,4(5)9,7T S n =-=-=-+-=-=•; 第四次运行时,7(1)77,9(7)16,9T S n =-=-=-+-=-=•; 第五次运行时,9(1)99,16(9)25,11T S n =-=-=-+-=-=•; 第六次运行时,11(1)1111,25(11)36T S =-=-=-+-=-•, 此时刚好满足9n >,所以输出S 的值为36-.故选D. 【点睛】本题主要考查了循环结构的程序框图的计算与输出问题,其中解答中熟练应用给定的程序框图,逐次运算,根据判断条件,终止循环得到结果是解答的关键,着重考查了推理与运算能力,属于基础题.8.C解析:C 【解析】 【分析】首先确定流程图的功能为计数111113355720172019S =++++⨯⨯⨯⨯的值,然后利用裂项求和的方法即可求得最终结果. 【详解】由题意结合流程图可知流程图输出结果为111113355720172019S =++++⨯⨯⨯⨯,11(2)111(2)2(2)22n n n n n n n n +-⎛⎫=⨯=- ⎪+++⎝⎭,111113355720172019S ∴=++++⨯⨯⨯⨯11111111123355720172019⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦1110091220192019⎛⎫=-=⎪⎝⎭. 本题选择C 选项. 【点睛】识别、运行程序框图和完善程序框图的思路: (1)要明确程序框图的顺序结构、条件结构和循环结构. (2)要识别、运行程序框图,理解框图所解决的实际问题. (3)按照题目的要求完成解答并验证.9.D解析:D 【解析】试题分析:由表格得(),x y 为:()10,38,因为(),x y 在回归方程y bx a =+上且2b =-,()38102a ∴=⨯-+,解得58a =∴2ˆ58yx =-+,当6x =时,26ˆ5846y=-⨯+=,故选D. 考点:1、线性回归方程的性质;2、回归方程的应用.10.C解析:C 【解析】试题分析:A 选项,中位数是84;B 选项,众数是出现最多的数,故是83;C 选项,平均数是85,正确;D 选项,方差是,错误.考点:•茎叶图的识别 相关量的定义11.C解析:C 【解析】 【分析】由题意利用线性回归方程的性质计算可得a 的值. 【详解】 由于468101285x ++++==,35891075y ++++==,由于线性回归方程过样本中心点(),x y ,故:70.98a =⨯+, 据此可得:0.2a =-. 故选C . 【点睛】本题主要考查线性回归方程的性质及其应用,属于中等题.12.A解析:A 【解析】 【分析】利用茎叶图、平均数的性质直接求解. 【详解】由一组数据的茎叶图得: 该组数据的平均数为:1(7581858995)855++++=. 故选:A . 【点睛】本题考查平均数的求法,考查茎叶图、平均数的性质等基础知识,考查运算求解能力,是基础题.二、填空题13.【分析】将甲乙到达时间设为(以为0时刻单位为分钟)则相见需要满足:画出图像根据几何概型公式得到答案【详解】根据题意:将甲乙到达时间设为(以为0时刻单位为分钟)则相见需要满足:画出图像:根据几何概型公解析:1136【分析】将甲、乙到达时间设为,x y (以4:00为0时刻,单位为分钟).则相见需要满足:10y x -≤ 画出图像,根据几何概型公式得到答案.【详解】根据题意:将甲、乙到达时间设为,x y (以4:00为0时刻,单位为分钟) 则相见需要满足:10y x -≤ 画出图像:根据几何概型公式:2500111360036P =-= 【点睛】 本题考查了几何概型的应用,意在考查学生解决问题的能力.14.【解析】【分析】以正方体的中心为球心1为半径做球若点在球上或球内时符合要求求其体积根据几何概型求概率即可【详解】当正方体内的点落在以正方体中心为球心1为半径的球上或球内时此点到正方体中心的距离不大于解析:6π 【解析】 【分析】以正方体的中心为球心,1为半径做球,若点在球上或球内时,符合要求,求其体积,根据几何概型求概率即可. 【详解】当正方体内的点落在以正方体中心为球心,1为半径的球上或球内时,此点到正方体中心的距离不大于1, 因为344133V ππ=⨯⨯=球,2228V =⨯⨯=正方体 因此正方体内点到正方体中心的距离不大于1的概率24132226V P V 球正方体ππ⨯⨯===⨯⨯, 故填6π. 【点睛】本题主要考查了几何概型,球的体积,正方体的体积,属于中档题.15.①③【分析】由回归直线的方程的意义可判断①;由基本事件的定义可判断②;由互斥事件与对立事件的定义可判断③;由古典概型的定义可判断④【详解】①由回归直线的方程的意义可知意味着每增加一个单位平均增加8个解析:①③. 【分析】由回归直线的方程的意义可判断①;由基本事件的定义可判断②;由互斥事件与对立事件的定义可判断③;由古典概型的定义可判断④. 【详解】①,由回归直线的方程的意义可知ˆ856yx =+意味着x 每增加一个单位,y 平均增加8个单位,正确;②,由于基本事件是每一个出现的基本实验结果,是不能再分的,而投掷一颗骰子实验,有掷出的点数为奇数还有1,3,5三个基本事件,故掷出的点数为奇数不是基本事件,同理掷出的点数为偶数也不是基本事件,故②是错误的;③,互斥事件不一定是对立事件,但对立事件一定是互斥事件,正确;④,古典概型要求每个基本事件出现的可能性相等,故在适宜的条件下种下一颗种子,观察它是否发芽,不是古典概型.故正确答案为:①③ 【点睛】本题主要考查回归直线的方程的意义、基本事件的定义、互斥事件与对立事件的定义、古典概型的定义,意在考查对基本定义掌握的熟练程度,属于中档题..16.【分析】根据程序框图依次计算运行结果发现输出的S 值周期变化利用终止运行的条件判断即可求解【详解】由程序框图得:;第一次运行第二次运行第三次运行故周期为4当程序运行了2019次故的值为故答案为【点睛】 解析:12【分析】根据程序框图,依次计算运行结果,发现输出的S 值周期变化,利用终止运行的条件判断即可求解 【详解】由程序框图得:1,1S k ==; 第一次运行1,2;8S k == 第二次运行1212,3;842S k =⨯=== 第三次运行121,4;2S k =⨯==故周期为4, 当2020k =,程序运行了2019次,201945043=⨯+,故S 的值为12故答案为12【点睛】本题考查程序框图,根据程序的运行功能判断输出值的周期变化是关键,是基础题17.41【分析】根据给定的程序框图计算逐次循环的结果即可得到输出的值得到答案【详解】由题意运行程序框图可得第一次循环不满足判断框的条件;第二次循环不满足判断框的条件;第三次循环不满足判断框的条件;第四次解析:41 【分析】根据给定的程序框图,计算逐次循环的结果,即可得到输出的值,得到答案. 【详解】由题意,运行程序框图,可得第一次循环,1n =,不满足判断框的条件,1415S =+⨯=;第二次循环,2n =,不满足判断框的条件,54213S =+⨯=; 第三次循环,3n =,不满足判断框的条件,134325S =+⨯=; 第四次循环,4n =,不满足判断框的条件,254441S =+⨯=; 第五次循环,5n =,满足判断框的条件,输出41S =, 故答案为41. 【点睛】本题主要考查了循环结构的程序框图的计算与输出问题,其中利用循环结构表示算法,一定要先确定是用当型循环结构,还是用直到型循环结构;当型循环结构的特点是先判断再循环,直到型循环结构的特点是先执行一次循环体,再判断;注意输入框、处理框、判断框的功能,不可混用,着重考查了分析问题和解答问题的能力,属于基础题.18.24【解析】考点:程序框图专题:图表型分析:由程序中循环的条件为i≤4我们易得到最后一次循环时i=4又由循环变量i 的初值为2故我们从2开始逐步模拟循环的过程即可得到结论解答:解:模拟程序的运行结果:解析:24 【解析】 考点:程序框图. 专题:图表型.分析:由程序中循环的条件为i≤4,我们易得到最后一次循环时i=4,又由循环变量i 的初值为2,故我们从2开始逐步模拟循环的过程,即可得到结论. 解答:解:模拟程序的运行结果: i=2时,t=2, i=3时,t=6, i=4时,t=24, 故答案为24点评:本题考查的知识点是程序框图及程序代码,在写程序运行结果时,模拟程序的运行过程是解答此类问题最常用的方法,模拟时要分析循环变量的初值,步长和终值19.1【解析】分析:先利用平均数公式求出平均数再利用方差公式即可得结果详解:的平均数为的方差为故答案为点睛:本题考查主要考查平均数公式与方差公式属于基础题样本数据的算术平均数公式;样本方差公式标准差解析:1 【解析】分析:先利用平均数公式求出平均数,再利用方差公式即可得结果. 详解:5.7,5.8,6.1,6.4,6.5的平均数为5.7+5.8+6.1+6.4+6.56.15=,5.7,5.8,6.1,6.4,6.5∴的方差为()()()()()222225.76.1+5.8 6.1+6.1 6.1+6.4 6.1+6.5 6.10.15-----=,故答案为0.1.点睛:本题考查主要考查平均数公式与方差公式,属于基础题. 样本数据的算术平均数公式12n 1(x +x +...+x )x n =;样本方差公式2222121[()()...()]n s x x x x x x n=-+-++-,标准差s =20.12【解析】分析:由频率=以及直方图可得分布在区间第一组与第二组共有20人的频率即可求出第三组中有疗效的人数得到答案详解:由直方图可得分布在区间第一组和第二组共有20人分布唉区间第一组与第二组的频率解析:12 【解析】 分析:由频率=频数样本容量,以及直方图可得分布在区间第一组与第二组共有20人的频率,即可求出第三组中有疗效的人数得到答案.详解:由直方图可得分布在区间第一组和第二组共有20人,分布唉区间第一组与第二组的频率分别为0.24,0.16,所以第一组有12人,第二组8人第三组的频率为0.36,所以第三组的人数为18人,第三组中没有疗效的有6人,第三组由疗效的有12人.点睛:1、用样本估计总体是统计的基本思想,而利用频率分布表和频率分布直方图来估计总体则是用样本的频率分布去估计总体分布的两种主要方法,分布表在数量表示上比较准确,直方图比较直观.2、频率分布表中的频数之和等于样本容量,各组中的频率之和等于1;在频率分布直方图中,各小长方形的面积表示相应各组的频率,所以,所有小长方形的面积的和等于1.三、解答题21.(1)72;(2)15. 【分析】(1)利用频率分布直方图各组的中值估计平均分.(2)这是一个古典概型,先求得从95,76,97,88,69,100这6个数中任取2个数基本事件的总数,再根据在[90,100]的人数是600.053⨯=,求得从95,97,100这3个数中任取2个数基本事件数,然后代入公式求解. 【详解】(1)平均分为:450.05+550.15+650.2+750.3+850.25+950.05=72⨯⨯⨯⨯⨯⨯;(2)从95,76,97,88,69,100这6个数中任取2个数,共有2615C =种,在[90,100]的人数是600.053⨯=,从95,97,100这3个数中任取2个数,共有233C =种,所以这2个数恰好是两个学生的成绩的概率是.31155 p==.【点睛】本题主要考查平均数的求法,古典概型的概率,还考查了运算求解的能力,属于中档题.22.(1)b=30,c=50(2)有99%的把握,(3)1021 P=【解析】试题分析:(1)由分层抽样的概念得到参数值;(2)根据公式计算得到28.66 6.635K≈>,再下结论;(3)根据古典概型的计算公式,列出事件的所有可能性,再得到4男一女的事件数目,做商即可.(1)根据分层抽样方法抽得女生50人,男生75人,所以b=50-20=30(人),c=75-25=50(人)(2)因为()()()()()22125202530508.66 6.6352030502520503025K⨯-⨯=≈>++++,所以有99%的把握认为观看2018年足球世界杯比赛与性别有关.(3)设5名男生分别为A、B、C、D、E,2名女生分别为a、b,由题意可知从7人中选出5人接受电视台采访,相当于从7人中挑选2人不接受采访,其中一男一女,所有可能的结果有A,B}A,C}A,D}A,E}A,a}A,b}B,C}B,D}B,E}B,a}B,b}C,D}C,E}C,a}C,b}D,E}D,a}D,b}E,a}E,b}a,b},共21种,其中恰为一男一女的包括,A,a}A,b}B,a}B,b}C,a}C,b}D,a}D,b}E,a}E,b},共10种.因此所求概率为1021 P=23.答案见解析【解析】试题分析:由题意,可知本题是要输出成绩小于12.1秒时的所有值,所以需要采用条件结构来画程序框图;再利用程序框图,编写出相应的程序即可.试题程序框图如图所示:程序:i=1while i <=10 Gi =input (“Gi =”); if Gi <12.1 print (%io (2),Gi ); end i =i +1; end点睛:本题考查的是算法与流程图.对算法与流程图的考查,侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环起点条件、循环次数、循环终止条件,更要通过循环规律,明确流程图研究的数学问题,是求和还是求项. 24.答案见解析 【解析】试题分析:先设丢番图的寿数为x , x 为正整数,列出方程,再用验证的方法找到方程的解,即得到丢番图的寿数.再根据算法写出算法程序. 试题设丢番图的寿数为x ,则x 为正整数,根据题意可知16x+112x+17x+5+12x+4=x ,我们可以从x=1,依次验证是不是方程的解.算法如下: S1 x=1;S2 判断16x+112x+17x+5+12x+4=x 是否成立,如果成立,则输出x ;否则,转至S3; S3 x=x+1,转至S2. 算法程序如下: x=1;while 16x+112x+17x+5+12x+4< >xx=x+1; wend x=x-1 print x end点睛:本题的难点在于写出找丢番图的寿数的算法,这里只能采取验证的方法. 25.(1)0.36 6.24y x =+;(2)8.76万吨. 【分析】(1)由题意求得知 3.5t =,7.5=y ,()62117.5i i t t =-=∑,运用公式求得b ,代入可求得y 关于t 的线性回归方程.(2)由(1)得的线性回归方程,代入年份代码7t =计算,可预测2020年该地区小龙虾的年产量.【详解】(1)由题知 3.5t =,7.5=y ,()62117.5i i t t =-=∑,()()()616216.30.3617.5ˆiii i i t t y y bt t ==--===-∑∑, 又 6.24=-=a y bt .所以,y 关于t 的线性回归方程为0.36 6.24y x =+.(2)由(1)得,当年份为2020年时,年份代码7t =,此时0.367 6.248.76=⨯+=y .所以,可预测,2020年该地区小龙虾的年产量为8.76万吨. 【点睛】本题考查线性回归方程的求解,利用线性回归方程对总体进行估计,属于中档题.26.(1)见解析(2) 1.1.7ˆ0yx =+(3)9.5百万元 【解析】试题分析:(1)根据表格中的数据,在坐标系中描出点,将点连起来,就画出了散点图;(2)根据题目中的数据计算出 1.1,0.ˆˆ7ba ==,代入平均值3,4x y ==,即可得到回归方程;(3)将8x =,代入回归方程即可得到预测值. (1)散点图(2)由题意可知,12345234473,455x y ++++++++====,51122334445771i i i x y ==⨯+⨯+⨯+⨯+⨯=∑,522222211234555i i x ==++++=∑, 根据公式,可求得2715341.1,4 1.130.ˆˆ75553ba -⨯⨯===-⨯=-⨯, 故所求回归直线的方程为 1.1.7ˆ0y x =+; (3)令8x =,得到预测值 1.1809.5ˆ.7y=⨯+=(百万元)答:如果该企业某年研发费用投入8百万元,预测该企业获得年利润为9.5百万元.。
【人教版】高中数学必修三期末模拟试卷(带答案)

一、选择题1.袋中共有15个除了颜色外完全相同的球,其中有10个白球,5个红球.从袋中任取2个球,所取的2个球中恰有1个白球,1个红球的概率为( )A.521B.1021C.1121D.12.若即时起10分钟内,甲乙两同学等可能到达某咖啡厅,则这两同学到达咖啡厅的时间间隔不超过3分钟的概率为( )A.0.3B.0.36C.0.49D.0.513.在二项式42nxx⎛+⎪⎝⎭的展开式,前三项的系数成等差数列,把展开式中所有的项重新排成一列,有理项都互不相邻的概率为()A.16B.14C.512D.134.从2017年到2019年的3年高考中,针对地区差异,理科数学全国卷每年都命了3套卷,即:全国I卷,全国II卷,全国III卷.小明同学马上进入高三了,打算从这9套题中选出3套体验一下,则选出的3套题年份和编号都各不相同的概率为()A.184B.142C.128D.1145.程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.它问世后不久便风行宇内,成为明清之际研习数学者必读的教材,而且传到朝鲜、日本及东南亚地区,对推动汉字文化圈的数学发展起了重要的作用.卷八中第33问是:“今有三角果一垛,底阔每面七个,问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为( )A.84 B.56 C.35 D.286.执行如图所示的程序框图,如果输入n=3,输出的S=()A.67B.37C.89D.497.执行如图所示的程序框图,若输入x=9,则循环体执行的次数为()A.1次B.2次C.3次D.4次8.明代数学家程大位(1533~1606年),有感于当时筹算方法的不便,用其毕生心血写出《算法统宗》,可谓集成计算的鼻祖.如图所示的程序框图的算法思路源于其著作中的“李白沽酒”问题.执行该程序框图,若输出的y的值为2,则输入的x的值为()A .74B .5627C .2D .164819.图1是某学习小组学生数学考试成绩的茎叶图,1号到16号的同学的成绩依次为1A ,216,,A A ⋯,图2是统计茎叶图中成绩在一定范围内的学生情况的程序框图,那么该程序框图输出的结果是( )A .10B .6C .7D .1610.如图是两组各7名同学体重(单位:kg )数据的茎叶图,设1、2两组数据的平均数依次为1x 和2x ,标准差依次为12s s 、,那么( )(注:标准差222121[()()...()]n s x x x x x x n=-+-++-A .1212,x x s s >>B .1212,x x s s ><C .1212,x xs s << D .1212,x x s s11.为了解某社区居民的家庭年收入所年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表: 收入x (万元)8.28.610.011.311.9支出y (万元)6.27.58.0 8.59.8根据上表可得回归直线方程ˆˆˆybx a =+,其中ˆˆˆ0.76,b a y bx ==-,据此估计,该社区一户收入为15万元家庭年支出为( ) A .11.4万元B .11.8万元C .12.0万元D .12.2万元12.已知一组数据12,,,n x x x 的平均数3x =,则数据1232,32,,32n x x x +++的平均数为( ) A .3B .5C .9D .11二、填空题13.设每门高射炮命中飞机的概率为0.06,且每一门高射炮是否命中飞机是独立的,若有一敌机来犯,则需要______门高射炮射击,才能以至少99%的概率命中它.14.北京市某银行营业点在银行大厅悬挂着不同营业时间段服务窗口个数的提示牌,如图所示. 设某人到达银行的时间是随机的,记其到达银行时服务窗口的个数为X ,则()E X =______________.15.在区间[0,2]上随机取两个数,a b ,则事件“函数()1f x bx a =+-在[0,1]内有零点”的概率为_______.16.图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入,,a b i 的值分别为6,8,0,则输出的i =________.17.将二进制数110 101(2)转为七进制数,结果为________.18.程序框图如下图所示,其输出的结果是__________________________.19.某天有10名工人生产同一零部件,生产的件数分别是:15、17、14、10、15、17、17、16、14、12,设其平均数为a,中位数为b,众数为c,则a、b、c从小到大的关系依次是________20.已知某人连续5次射击的环数分别是8,9,10,x,8,若这组数据的平均数是9,则这组数据的方差为.三、解答题21.从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:(1)求频率分布直方图中的a ,b 的值;(2)从阅读时间在[14,18)的学生中任选2人,求恰好有1人阅读时间在[14,16),另1人阅读时间在[16,18)的概率.22.在一个盒子中装有6支圆珠笔,其中3支一等品,2支二等品和1支三等品,从中任取3支.求(1)恰有1支一等品的概率; (2)恰有两支一等品的概率; (3)没有三等品的概率.23.如图,已知单位圆221x y +=与x 轴正半轴交于点P ,当圆上一动点Q 从P 出发沿逆时针旋转一周回到P 点后停止运动.设OQ 扫过的扇形对应的圆心角为xrad ,当02x π<<时,设圆心O 到直线PQ 的距离为y ,y 与x 的函数关系式()y f x =是如图所示的程序框图中的①②两个关系式.(1)写出程序框图中①②处的函数关系式; (2)若输出的y 值为12,求点Q 的坐标. 24.设计一个算法,已知函数2x y =的图象上,任意给定两点的横坐标1x 和212()x x x ≠,求过这两点的直线的斜率,并画出程序框图.25.有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表: 摄氏温度C x ︒ 5-0 5 10 15 热饮杯数y1571271077237(1)求y 关于x 的线性回归直线方程;(2)如果某天的气温是–10C ︒,预测这天卖出的热饮杯数(四舍五入,取整数).附:对于线性回归直线方程ˆˆˆybx a =+,其中1122211()()ˆ()nnii i ii i nniii i xx y y x ynx yb xx xnx ====---==--∑∑∑∑,ˆˆay bx =-, 26.某城市100户居民的月平均用水量(单位:吨),以[0,2)[2,4)[4,6)[6,8)[8,10)[10,12)[12,14)分组的频率分布直方图如图.(1)求直方图中x的值;并估计出月平均用水量的众数.(2)求月平均用水量的中位数及平均数;(3)在月平均用水量为[6,8),[8,10),[10,12),[12,14)的四组用户中,用分层抽样的方法抽取22户居民,则应在[10,12)这一组的用户中抽取多少户?(4)在第(3)问抽取的样本中,从[10,12)[12,14)这两组中再随机抽取2户,深入调查,则所抽取的两户不是来自同一个组的概率是多少?【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】由从共有15个球中任取2个球,共有215C种不同的取法,其中所取的2个球中恰有1个白球,1个红球,共有11510C C种不同的取法,再利用古典概型及其概率的计算公式,即可求解.【详解】由题意,从共有15个除了颜色外完全相同的球,任取2个球,共有215C种不同的取法,其中所取的2个球中恰有1个白球,1个红球,共有11510C C种不同的取法,所以概率为11510215501010521C CC==,故选B.【点睛】本题主要考查了排列、组合的应用,以及古典概型及其概率的应用,其中解答中认真审题,准确计算是解答的关键,着重考查了推理与运算能力,属于基础题.2.D解析:D 【分析】由几何概型中的面积型得:1277210.511010S P S ⨯⨯⨯==-=⨯阴正,即可得解.【详解】设甲、乙两同学等可能到达某咖啡厅的时间为(),x y ,则010x <≤,010y <≤,其基本事件可用正方形区域表示,如图,则甲、乙两同学等可能到达某咖啡厅的时间间隔不超过3分钟的事件为A , 则事件A 为:3x y -≤,其基本事件可用阴影部分区域表示,由几何概型中的面积型可得:1277210.511010S P S ⨯⨯⨯==-=⨯阴正.故选:D. 【点睛】本题考查了几何概型中的面积型,属于基础题.3.C解析:C 【分析】先根据前三项的系数成等差数列求n ,再根据古典概型概率公式求结果 【详解】因为42nx x 前三项的系数为1212111(1)1,,112448n n n n n n C C C C n -⋅⋅∴=+⋅∴-=163418118,0,1,2,82rr r r n n T C x r -+>∴=∴=⋅=,当0,4,8r =时,为有理项,从而概率为636799512A A A =,选C. 【点睛】本题考查二项式定理以及古典概型概率,考查综合分析求解能力,属中档题.4.D解析:D 【分析】先计算出9套题中选出3套试卷的可能,再计算3套题年份和编号都各不相同的可能,通过古典概型公式可得答案. 【详解】通过题意,可知从这9套题中选出3套试卷共有39=84C 种可能,而3套题年份和编号都各不相同共有336A =种可能,于是所求概率为61=8414.选D. 【点睛】本题主要考查古典概型,意在考查学生的分析能力,计算能力,难度不大.5.A解析:A 【分析】按照程序框图运行程序,直到满足7i ≥时输出结果即可. 【详解】按照程序框图运行程序,输入0i =,0n =,0S =, 则1i =,1n =,1S =,不满足7i ≥,循环;2i =,3n =,4S =,不满足7i ≥,循环; 3i =,6n =,10S =,不满足7i ≥,循环; 4i =,10n =,20S =,不满足7i ≥,循环;5i =,15n =,35S =,不满足7i ≥,循环; 6i =,21n =,56S =,不满足7i ≥,循环;7i =,28n =,84S =,满足7i ≥,输出84S =. 故选:A . 【点睛】本题考查根据程序框图循环结构计算输出结果的问题,属于基础题.6.B解析:B 【详解】试题分析:由题意得,输出的为数列的前三项和,而,∴,故选B.考点:1程序框图;2.裂项相消法求数列的和. 【名师点睛】本题主要考查了数列求和背景下的程序框图问题,属于容易题,解题过程中首先要弄清程序框图所表达的含义,解决循环结构的程序框图问题关键是列出每次循环后的变量取值情况,循环次数较多时,需总结规律,若循环次数较少可以全部列出.7.C解析:C 【分析】根据程序框图依次计算得到答案. 【详解】9,5x y ==,41y x -=>;115,3x y ==,413y x -=>; 1129,39x y ==,419y x -=<;结束. 故选:C . 【点睛】本题考查了程序框图的循环次数,意在考查学生的理解能力和计算能力.8.C解析:C 【分析】根据程序框图依次计算得到答案. 【详解】34y x =-,1i =;34916y y x =-=-,2i =;342752y y x =-=-,3i =;3481160y y x =-=-,4i =;34243484y y x =-=-,此时不满足3i ≤,跳出循环,输出结果为243484x -,由题意2434842y x =-=,得2x =. 故选:C 【点睛】本题考查了程序框图的计算,意在考查学生的理解能力和计算能力.9.A解析:A 【分析】先弄清楚程序框图中是统计成绩不低于90分的学生人数,然后从茎叶图中将不低于90分的个数数出来,即为输出的结果. 【详解】176A =,1i =,16i ≤成立,190A ≥不成立,112i =+=; 279A =,2i =,16i ≤成立,290A ≥不成立,112i =+=;792A =,7i =,16i ≤成立,790A ≥成立,011n =+=,718i =+=;依此类推,上述程序框图是统计成绩不低于90分的学生人数,从茎叶图中可知,不低于90分的学生数为10,故选A . 【点睛】本题考查茎叶图与程序框图的综合应用,理解程序框图的意义,是解本题的关键,考查理解能力,属于中等题.10.C解析:C 【分析】由茎叶图分别计算出两组数的平均数和标准差,然后比较大小 【详解】读取茎叶图得到两组数据分别为: (1)53565758617072,,,,,, (2)54565860617273,,,,,,()()11503678112022617x kg =+⨯++++++=,()()215046810112223627x kg =+⨯++++++=,()()()2221131653615661...726177s ⎡⎤=-+-++-=⎣⎦, ()()()2222134254625662 (736277)s ⎡⎤=-+-++-=⎣⎦, 则1212,x x s s << 故选C 【点睛】本题给出茎叶图,需要求出数据的平均数和方差,着重考查了茎叶图的认识,样本特征数的计算等知识,属于基础题.11.B解析:B 【解析】 试题分析:由题,,所以.试题 由已知,又因为ˆˆˆybx a =+,ˆˆˆ0.76,b a y bx ==- 所以,即该家庭支出为万元.考点:线性回归与变量间的关系.12.D解析:D 【解析】分析:一组数据中的每一个数加或减一个数,它的平均数也加或减这个数;;依此规律求解即可.详解::∵一组数据12,,,n x x x 的平均数为3, ∴另一组数据1232,32,,32n x x x +++的平均数121211323232[32]33211n n x x x x x x n n n=++++⋯++=++⋯++=⨯+=()(), 故选D.点睛:本题考查了平均数,平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.二、填空题13.【分析】设需要门高射炮由题意得出解出的取值范围可得出正整数的最小值【详解】设需要门高射炮则命不中的概率为由题意得出得解得而因此至少需要门高射炮故答案为:【点睛】本题考查独立事件概率乘法公式的应用在涉 解析:75【分析】设需要n 门高射炮,由题意得出()110.060.99n--≥,解出n 的取值范围,可得出正整数n 的最小值.【详解】设需要n 门高射炮,则命不中的概率为()10.06n-,由题意得出10.940.99n-≥,得0.940.01n≤,解得0.942log 0.01lg 0.94n ≥=-, 而274.43lg 0.94-≈,因此,至少需要75门高射炮.故答案为:75. 【点睛】本题考查独立事件概率乘法公式的应用,在涉及“至少”问题时,可以利用对立事件的概率公式来进行计算,考查运算求解能力,属于中等题.14.【解析】【分析】列出随机变量的分布列求解【详解】由题意知某人到达银行的概率为几何概型所以:其到达银行时服务窗口的个数为的分布列为: 5 4 3 4 2 则【点睛】本题考查几何概型及随 解析:3.5625【解析】 【分析】列出随机变量的分布列求解. 【详解】由题意知某人到达银行的概率为几何概型,所以: 其到达银行时服务窗口的个数为的分布列为:则()54342 3.56258161648E X =⨯+⨯+⨯+⨯+⨯=. 【点睛】本题考查几何概型及随机变量的分布列.15.【解析】【分析】在上任取两个数在以2为棱长的正方形内在内有零点等价于即求出可行域的面积利用几何概型概率公式求解即可【详解】在上任取两个数则在以2为棱长的正方形内因为在内有零点所以即表示如图所示的梯形 解析:38【解析】 【分析】在[]0,2上任取两个数,a b , (),a b 在以2为棱长的正方形内,()f x 在[]0,1内有零点, 等价于()()010f f ≤,即()()110a b a -+-≤,求出可行域的面积,利用几何概型概率公式求解即可. 【详解】在[]0,2上任取两个数,a b , 则(),a b 在以2为棱长的正方形内, 因为()f x 在[]0,1内有零点, 所以()()010f f ≤, 即()()110a b a -+-≤,(),a b 表示如图所示的梯形区域,由几何概型概率公式可得“函数()1f x bx a =+-在[]0,1内有零点”的概率为()112132228⨯+⨯=⨯,故答案为38. 【点睛】本题主要考查“面积型”的几何概型,属于中档题. 解决几何概型问题常见类型有:长度型、角度型、面积型、体积型,求与面积有关的几何概型问题关鍵是计算问题的总面积以及事件的面积;几何概型问题还有以下几点容易造成失分,在备考时要高度关注:(1)不能正确判断事件是古典概型还是几何概型导致错误;(2)基本事件对应的区域测度把握不准导致错误 ;(3)利用几何概型的概率公式时 , 忽视验证事件是否等可能性导致错误.16.4【解析】当输入时运算程序继续此时进而有这时输出应填答案解析:4 【解析】当输入6,8,0a b i ===时,1,,2i a b b b a =<=-=,运算程序继续,此时6,2a b ==,2,,4i a b a a b =>=-=,进而有3,,2i a b a a b =>=-=,这时2,314a b i ===+=,输出2,314a b i ===+=,应填答案4.17.【解析】试题分析:把十进制的化为七进制则所以结果为考点:进位制 解析:7104()【解析】试题分析:245(2)110101112121253=+⨯+⨯+⨯=,把十进制的53化为七进制,则53774÷=,7710÷=,1701÷=,所以结果为(7)104.考点:进位制.18.127【分析】根据题意按照程序框图的顺序进行执行然后输出结果即可【详解】解:由程序框图知循环体被执行后a的值依次为37153163127故输出的结果是127故答案为127【点睛】本题考查程序框图的识解析:127【分析】根据题意,按照程序框图的顺序进行执行,然后输出结果即可【详解】解:由程序框图知,循环体被执行后a的值依次为3、7、15、31、63、127,故输出的结果是127.故答案为127.【点睛】本题考查程序框图的识别,通过对已知框图的分析与执行,写出运算结果,属于基础题.19.【详解】分析:将数据由小到大排列好根据众数中位数平均数的概念得到相应的数据即可详解:根据提干得到中位数为b=15众数为c=17平均数为=a故故答案为点睛:这个题目考查了中位数众数平均数的概念和计算较解析:a b c<<.【详解】分析:将数据由小到大排列好,根据众数,中位数,平均数的概念得到相应的数据即可.详解:根据提干得到中位数为b=15,众数为c=17,平均数为10+12+28+30+16+51=14.710=a.故a b c<<.故答案为a b c<<.点睛:这个题目考查了中位数,众数,平均数的概念和计算,较为基础,众数即出现次数最多的数据,中位数即最中间的数据,平均数即将所有数据加到一起,除以数据个数. 20.【解析】分析:先根据平均数求x的值再求数据的方差详解:由题得所以数据的方差为故答案为点睛:(1)本题主要考查平均数和方差的计算意在考查学生对这些基础知识的掌握水平(2)方差公式为解析:4 5【解析】分析:先根据平均数求x的值,再求数据的方差.详解:由题得8+9+8109,10.5xx++=∴=所以数据的方差为22222214[(89)(99)(109)(109)(89)]55S =-+-+-+-+-=.故答案为45. 点睛:(1)本题主要考查平均数和方差的计算,意在考查学生对这些基础知识的掌握水平.(2) 方差公式为222121[()()()]n S x x x x x x n=-+-+⋅⋅⋅+-. 三、解答题21.(1)a=0.11,b=0.04;(2)23. 【分析】(1)课外阅读时间落在[6,8)的有22人,频率为0.22,由此能求出a ,课外阅读时间落在[2,4)的有8人,频率为0.08,由此能求出b ;(2)课外阅读时间落在[14,16)的有2人,设为m ,n ;课外阅读时间落在[16,18)的有2人为x ,y ,由此利用列举法能求出从课外阅读时间落在[14,18)的学生中任选2人,其中恰好有1人阅读时间在[14,16),另1人阅读时间在[16,18)的概率. 【详解】(1)课外阅读时间落在[6,8)的有22人,频率为0.22,所以0.220.112a == 课外阅读时间落在[2,4)的有8人,频率为0.08, 所以0.080.042b == (2)课外阅读时间落在[14,16)的有2人,设为m ,n ;课外阅读时间落在[16,18)的有2人为x ,y ,则从课外阅读时间落在[14,18)的学生中任选2人包含:(,)m n ,(,)m x ,(,)m y ,(,)n x ,(,)n y ,(,)x y 共6种,其中恰好有1人阅读时间在[14,16),另1人阅读时间在[16,18)的有(,)m x ,(,)m y ,(,)n x ,(,)n y 共4种, 所以所求概率为:4263p ==. 【点睛】本题考查频率直方图的求法,考查概率的求法,考查古典概型、列举法等基础知识,是基础题. 22.(1)920;(2)920;(3)12.【分析】(1)恰有一支一等品,从3支一等品中任取一支,从二、三等品种任取两支利用分布乘法原理计算后除以基本事件总数;(2)恰有两枝一等品,从3支一等品中任取两支,从二、三等品种任取一支利用分布乘法原理计算后除以基本事件总数;(3)从5支非三等品中任取三支除以基本事件总数. 【详解】(1)恰有一枝一等品的概率123336920C C P C ⋅==; (2)恰有两枝一等品的概率123336920C C P C ⋅==; (3)没有三等品的概率353612C P C ==.【点睛】本题考查古典概型及其概率计算公式,考查逻辑思维能力和运算能力,属于常考题. 23.(1)cos 2x y =,cos 2x y =-.(2) 1(,2-. 【详解】分析:(1)利用三角函数的定义与性质求出两种情况下y 与x 的函数关系式,即可得结果;(2)0x π<≤时,1cos 22x =,得23x π=,此时点Q的坐标为1,22⎛⎫- ⎪ ⎪⎝⎭;当2x ππ<<时,1cos 22x -=,得43x π=,此时点Q的坐标为1,22⎛-- ⎝⎭. 详解:(1)当0x π<≤时,cos2x y =;当2x ππ<<时,cos cos 22x x y π⎛⎫=-=- ⎪⎝⎭; 综上可知,函数解析式为()(](),0,2,,22x cos x f x x cos x πππ⎧∈⎪⎪=⎨⎪-∈⎪⎩所以框图中①②处应填充的式子分别为cos 2x y =,cos 2xy =-. (2)若输出的y 值为12,则 0x π<≤时,1cos 22x =,得23x π=,此时点Q的坐标为1,22⎛⎫- ⎪ ⎪⎝⎭;当2x ππ<<时,1cos22x -=,得43x π=,此时点Q 的坐标为13,2⎛⎫-- ⎪ ⎪⎝⎭. 点睛:本题主要考查条件语句以及算法的应用,属于中档题 .算法是新课标高考的一大热点,其中算法的交汇性问题已成为高考的一大亮,这类问题常常与函数、数列、不等式等交汇自然,很好地考查考生的信息处理能力及综合运用知识解决问題的能力,解决算法的交汇性问题的方:(1)读懂程序框图、明确交汇知识,(2)根据给出问题与程序框图处理问题即可. 24.见解析 【解析】试题分析:输入12,x x ,然后计算112x y =,222xy =和1212y y k x x -=-,最后输出,利用顺序结构的程序框图表示即可. 试题 算法如下:第一步:输入12,x x .第二步:计算112xy =. 第三步:计算222xy =.第四步:计算1212y y k x x -=-. 第五步,输出k . 程序框图下:25.(1)ˆ 5.9129.5yx =-+;(2)189杯. 【分析】(1)根据表中数据计算可得所需数据,利用最小二乘法可求得回归直线方程;(2)代入10x =-即可求得预测值. 【详解】(1)由表中数据得:505101555x -++++==,15712710772371005y ++++==,517855357205551025i ii x y==-+++=∑,5212525100225375i i x ==+++=∑,102555100ˆ 5.9375525b-⨯⨯∴==--⨯,ˆ100 5.95129.5a ∴=+⨯=,y ∴关于x 的线性回归直线方程为:ˆ 5.9129.5y x =-+.(2)令10x =-,解得:188.5189y =≈,∴如果某天的气温是–10C ︒,预测这天卖出的热饮杯数为189杯.【点睛】本题考查利用最小二乘法求解回归直线、利用回归直线求解预测值的问题;关键是熟练掌握最小二乘法,考查学生的计算能力. 26.(1) x =0.075,7;(2) 6.4,5.36;(3) 2;(4)23. 【分析】(1)根据频率和为1,列方程求出x 的值;(2)根据频率分布直方图中,每个矩形的中点横坐标与该矩形的纵坐标、组距相乘后求和可得平均值,由最高矩形的数据组中点为众数;中位数两边的频率相等,由此求出中位数;(3)求出抽取比例数,计算应抽取的户数; (4)利用列举法,由古典概型概率公式可得结果. 【详解】(1)根据频率和为1,得2×(0.02+0.095+0.11+0.125+x +0.05+0.025)=1, 解得x =0.075;由图可知,最高矩形的数据组为[6,8),所以众数为()16872+=; (2) [2,6)内的频率之和为 (0.02+0.095+0.11)×2=0.45;设中位数为y ,则0.45+(y −6)×0.125=0.5, 解得y =6.4,∴中位数为6.4;平均数为()210.0230.09550.1170.12590.075110.025 5.36⨯+⨯+⨯+⨯+⨯+⨯= (3)月平均用电量为[10,12)的用户在四组用户中所占的比例为0.0520.1250.0750.050.02511=+++,∴月平均用电量在[10,12)的用户中应抽取11×211=2(户).(4)月平均用电量在[12,14)的用户中应抽取11×111=1(户),月平均用电量在[10,12)的用户设为A、B, 月平均用电量在[12,14)的用户设为C,从[10,12),[12,14)这两组中随机抽取2户共有,,AB AC BC,3种情况,其中,抽取的两户不是来自同一个组的有,,AC BC,2种情况,所以,抽取的两户不是来自同一个组的概率为2 3 .【点睛】本题主要考查频率分布直方图的应用,属于中档题. 直方图的主要性质有:(1)直方图中各矩形的面积之和为1;(2)组距与直方图纵坐标的乘积为该组数据的频率;(3)每个矩形的中点横坐标与该矩形的纵坐标、组距相乘后求和可得平均值;(4)直方图左右两边面积相等处横坐标表示中位数.。
【人教版】高中数学必修三期末第一次模拟试卷带答案(1)

一、选择题1.盒中有形状、大小都相同的2个红色球和3个黄色球,从中取出一个球,观察颜色后放回并往盒中加入同色球4个,再从盒中取出一个球,则此时取出黄色球的概率为( ) A .35B .79C .715D .31452.已知边长为2的正方形ABCD ,在正方形ABCD 内随机取一点,则取到的点到正方形四个顶点A B C D ,,,的距离都大于1的概率为( ) A .16πB .4π C .3224π- D .14π-3.若数列{a n }满足a 1=1,a 2=1,a n +2=a n +a n +1,则称数列{a n }为斐波那契数列,斐波那契螺旋线是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线的图案,是自然界最完美的经典黄金比例.作图规则是在以斐波那契数为边的正方形拼成的长方形中画一个圆心角为90°的扇形,连起来的弧线就是斐波那契螺旋线,如图所示的7个正方形的边长分别为a 1,a 2,…,a 7,在长方形ABCD 内任取一点,则该点不在任何一个扇形内的概率为( )A .1103156π-B .14π-C .17126π-D .681237π-4.圆周率π是一个在数学及物理学中普遍存在的数学常数,它既常用又神秘,古今中外很多数学家曾研究它的计算方法.下面做一个游戏:让大家各自随意写下两个小于1的正数然后请他们各自检查一下,所得的两数与1是否能构成一个锐角三角形的三边,最后把结论告诉你,只需将每个人的结论记录下来就能算出圆周率的近似值.假设有n 个人说“能”,而有m 个人说“不能”,那么应用你学过的知识可算得圆周率π的近似值为() A .mm n+ B .nm n+ C .4mm n+ D .4nm n+ 5.二分法是求方程近似解的一种方法,其原理是“一分为二,无限逼近”.执行如图所示的程序框图,若输入11x =,22x =,0.1d =,则输出n 的值为( )A.2 B.3 C.4 D.5⨯⨯⨯⨯的值的一个程序框图,则其中判断框内应填入的6.如图给出的是计算1232018是()A .2018i <B .2018i =C .2018i ≤D .2018i >7.如图所给的程序运行结果为41S =,那么判断框中应填入的关于k 的条件是( )A .7k ≥?B .6k ≥?C .5k ≥?D .6k >?8.执行如图所示的程序框图,输出S 的值等于( )A .1111238+++⋅⋅⋅+ B .1111237+++⋅⋅⋅+ C .11111237+++++ D .11111238++++⋅⋅⋅+ 9.为了解某社区居民的家庭年收入和年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表: 收入x 万 8.3 8.6 9.9 11.1 12.1 支出y 万5.97.88.18.49.8根据上表可得回归直线方程ˆˆˆybx a =+,其中0.78b ∧=,a y b x ∧∧=-元,据此估计,该社区一户收入为16万元家庭年支出为( )A .12.68万元B .13.88万元C .12.78万元D .14.28万元10.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是 A .中位数 B .平均数 C .方差D .极差11.在一次53.5公里的自行车个人赛中,25名参赛选手的成绩(单位:分钟)的茎叶图如图所示,现将参赛选手按成绩由好到差编为125-号,再用系统抽样方法从中选取5人,已知选手甲的成绩为85分钟,若甲被选取,则被选取的其余4名选手的成绩的平均数为()A .95B .96C .97D .9812.某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y (单位:t )和年利润z (单位:千元)的影响.对近8年的年宣传费i x 和年销售量()1,2,...8i y i =数据作了初步处理,得到下面的散点图及一些统计量的值.有下列5个曲线类型:①ˆˆy bxa =+;②y x d =+;③ln y p q x =+;④21k xy k e =+;⑤212y c x c =+,则较适宜作为年销售量y 关于年宣传费x 的回归方程的是( ) A .①②B .②③C .②④D .③⑤二、填空题13.天气预报说,在今后的三天中,每一天下雨的概率均为40%.现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨;再以每三个随机数作为一组,代表这三天的下雨情况.经随机模拟试验产生了如下20组随机数: 488 932 812 458 989 431 257 390 024 556 734 113 537 569 683 907 966 191 925 271据此估计,这三天中恰有两天下雨的概率近似为__________.14.在[0,1]上随机取两个实数,a b ,则,a b 满足不等式221a b +≤的概率为________. 15.在区间[]0,2中随机地取出一个数x ,则sin6x π>的概率是__________.16.根据如图所示的伪代码可知,输出的结果为______.17.执行如图所示的程序框图,输出的S 值是__________.18.执行如图所示的算法框图,若输入的x 的值为2,则输出的n 的值为__________.19.上海市普通高中学业水平等级考成绩共分为五等十一级,各等级换算成分数如表所示: 等级A + AB + BB -C + CC -D + DE 分数 7067646158555249464340上海某高中2018届高三()1班选考物理学业水平等级考的学生中,有5人取得A +成绩,其他人的成绩至少是B 级及以上,平均分是64分,这个班级选考物理学业水平等级考的人数至少为______人. 20.已知由样本数据集合(){}11,1,2,3,...,x y i n =,求得的回归直线方程为1.2308ˆ.0y x =+,且ˆ4x =,若去掉两个数据点 (4.1,5.7)和(3.9,4.3)后重新求得的回归直线方程l 的斜率估计值为1.2,则此回归直线l 的方程为_______.三、解答题21.为了纪念五四运动100周年和建团97周年,某校团委开展“青春心向党,建功新时代”知识问答竞赛.在小组赛中,甲、乙、丙3人进行擂台赛,每局2人进行比赛,另1人当裁判,每一局的输方担任下局的裁判,由原来裁判向胜者挑战,甲、乙、丙3人实力相当. (1)若第1局是由甲担任裁判,求第4局仍是甲担任裁判的概率;(2)甲、乙、丙3人进行的擂台赛结束后,经统计,甲共参赛了6局,乙共参赛了5局而丙共担任了2局裁判.则甲、乙、丙3人进行的擂台赛共进行了多少局?若从小组赛中,甲、乙、丙比赛的所有场次中任取2场,则均是由甲担任裁判的概率是多少.22.2019年8月8日是我国第十一个全民健身日,其主题是:新时代全民健身动起来.某市为了解全民健身情况,随机从某小区居民中抽取了40人,将他们的年龄分成7段:[10,20),[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.(1)试求这40人年龄的平均数、中位数的估计值;(2)若从样本中年龄在[50,70)的居民中任取2人赠送健身卡,求这2人中至少有1人年龄不低于60岁的概率;23.设计算法输出1 000以内既能被3整除又能被5整除的所有正整数,画出程序框图. 24.已知函数2()32,(3)(5)f x x x f f =--+-求的值,设计一个算法并画出算法的程序框图.25.我国北方广大农村地区、一些城镇以及部分大中城市的周边区域,还在大量采用分散燃煤和散烧煤取暖,既影响了居民基本生活的改善,也加重了北方地区冬季的雾霾天气.推进北方地区冬季清洁取暖,是重大民生工程、民心工程,关系北方地区广大群众温暖过冬,关系雾霾天能不能减少,是能源生产和消费革命、农村生活方式革命的重要内容.2017年9月国家发改委制定了煤改气、煤改电价格扶植新政策,从而使得煤改气、煤改电用户大幅度增加,下面条形图反映了某省2018年1~7月份煤改气、煤改电的用户数量.(1)在给定坐标系中作出煤改气、煤改电用户数量y 随月份t 变化的散点图,并用散点图和相关系数说明y 与t 之间具有线性相关性;(2)建立y 关于t 的回归方程(系数精确到0.01),预测11月份该省煤改气、煤改电的用户数量. 参考数据:7772111y9.24,t 7 2.646iiii i i i y=====⋅≈≈∑∑∑(y -y ).参考公式:相关系数()()()()()()11112211niinn ni i i i i i nni i i i i i i t t y y r t ty y t y t y t ty y ======⋅--=⋅--=-⋅-⋅-∑∑∑∑∑∑.回归方程ˆy a bt=+中斜率和截距的最小二乘估计公式分别为:()()()121ˆˆˆ,nii i ni i tty y bay bt t t==⋅--==-⋅-∑∑. 26.为研究冬季昼夜温差大小对某反季节大豆新品种发芽率的影响,某校课外兴趣小组记录了5组昼夜温差与100颗种子发芽数,得到如下资料: 组号 1 2 3 4 5 温差x (C ︒) 10 11 13 12 8 发芽数y (颗)2325302616经分析,这组数据具有较强的线性相关关系,因此该小组确定的研究方案是:先从这五组数据中选取3组数据求出线性回归方程,再用没选取的2组数据进行检验.(1)若选取的是第2,3,4组的数据,求出y 关于x 的线性回归方程ˆˆˆybx a =+; (2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?(参考公式:()()()1122211ˆn ni i i i i i n n i i i i x x y y x y nxy b x x x nx====---==--∑∑∑∑,ˆˆa y bx =-)【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【分析】若取出的是红色球,再从盒中取出一个球,则此时取出黄色球的概率为:13925P =⨯,若取出的是黄色球,再从盒中取出一个球,则此时取出黄色球的概率为:23759P =⨯,由此能求出再从盒中取出一个球,则此时取出黄色球的概率. 【详解】盒中有形状、大小都相同的2个红色球和3个黄色球, 从中取出一个球,观察颜色后放回并往盒中加入同色球4个, 若取出的是红色球,再从盒中取出一个球,则此时取出黄色球的概率为:13295152P =⨯=, 若取出的是黄色球,再从盒中取出一个球,则此时取出黄色球的概率为:23775915P =⨯=, ∴再从盒中取出一个球,则此时取出黄色球的概率为:1221573155P P P =+=+=, 故选:A . 【点睛】本题考查概率的求法,考查相互独立事件概率乘法公式、互斥事件概率计算公式等基础知识,考查运算求解能力,属于中档题.2.D解析:D【分析】根据题意,作出满足题意的图像,利用面积测度的几何概型,即得解. 【详解】分别以A ,B ,C ,D 四点为圆心,1为半径作圆,由题意满足条件的点在图中的阴影部分224ABCD S =⨯=,214144ABCD S S ππ=-⨯⨯=-阴影由几何测度的古典概型,14ABCD S P S π==-阴影 故选:D 【点睛】本题考查了面积测度的几何概型,考查了学生综合分析,数形结合,数学运算的能力,属于中档题.3.D解析:D 【分析】由题意求得数列{}n a 的前8项,求得长方形ABCD 的面积,再求出6个扇形的面积和,由测度比是面积比得答案. 【详解】由题意可得,数列{}n a 的前8项依次为:1,1,2,3,5,8,13,21.∴长方形ABCD 的面积为1321273⨯=.6个扇形的面积之和为222222(1235813)684ππ+++++=.∴所求概率681273P π=-. 故选:D . 【点睛】本题考查几何概型概率的求法,考查扇形面积公式的应用,是基础题.4.C解析:C 【分析】把每一个所写两数作为一个点的坐标,由题意可得与1不能构成一个锐角三角形是指两个数构成点的坐标在圆221x y +=内,进一步得到211411+m m nπ⨯=⨯,则答案可求。
【好题】高中必修三数学上期末模拟试题及答案

【好题】高中必修三数学上期末模拟试题及答案一、选择题1.如图,一个边长为2的正方形里有一个月牙形的图案,为了估算这个月牙形图案的面积,向这个正方形里随机投入500粒芝麻,经过统计,落在月牙形图案内的芝麻有150粒,则这个月牙图案的面积约为()A.35B.45C.1D.652.某校为了解高二年级学生某次数学考试成绩的分布情况,从该年级的1120名学生中随机抽取了100 名学生的数学成绩,发现都在[80,150]内现将这100名学生的成绩按照[80,90),[90,100),[100,110),[110,120),[120,130),[130,140),[140,150]分组后,得到的频率分布直方图如图所示则下列说法正确的是()A.频率分布直方图中a的值为 0.040B.样本数据低于130分的频率为 0.3C.总体的中位数(保留1位小数)估计为123.3分D.总体分布在[90,100)的频数一定与总体分布在[100,110)的频数不相等3.已知一组数据的茎叶图如图所示,则该组数据的平均数为()A.85B.84C.83D.814.如图是把二进制的数11111化成十进制数的一个程序框图,则判断框内应填入的条件是( )A .4i >?B .5i >?C .4i ≤?D .5i ≤?5.如果数据121x +、221x +、L 、21n x +的平均值为5,方差为16,则数据:153x -、253x -、L 、53n x -的平均值和方差分别为( )A .1-,36B .1-,41C .1,72D .10-,1446.学校为了解新课程标准提升阅读要求对学生阅读兴趣的影响情况,随机抽取了100名学生进行调查.根据调查结果绘制学生周末阅读时间的频率分布直方图如图所示:将阅读时间不低于30分钟的观众称为“阅读霸”,则下列命题正确的是( ) A .抽样表明,该校有一半学生为阅读霸 B .该校只有50名学生不喜欢阅读 C .该校只有50名学生喜欢阅读 D .抽样表明,该校有50名学生为阅读霸7.某工厂对一批新产品的长度(单位:mm )进行检测,如下图是检测结果的频率分布直方图,据此估计这批产品的中位数与平均数分别为( )A .20,22.5B .22.5,25C .22.5,22.75D .22.75,22.75 8.把化为五进制数是( )A .B .C .D .9.为了解某社区居民的家庭年收入和年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:收入x 万 8.3 8.6 9.9 11.1 12.1 支出y 万5.97.88.18.49.8根据上表可得回归直线方程ˆˆˆybx a =+,其中0.78b ∧=,a y b x ∧∧=-元,据此估计,该社区一户收入为16万元家庭年支出为( ) A .12.68万元B .13.88万元C .12.78万元D .14.28万元10.按照程序框图(如图所示)执行,第3 个输出的数是( )A .6B .5C .4D .311.“微信抢红包”自2015年以来异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为8元,被随机分配为1.72元,1.83元,2.28元,1.55元,0.62元, 5份供甲、乙等5人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于3元的概率是 ( ) A .310B .25C .12D .3512.已知某班级部分同学一次测验的成绩统计如图,则其中位数和众数分别为( )A .92,94B .92,86C .99,86D .95,91二、填空题13.已知样本数据为40,42,40,a ,43,44,且这个样本的平均数为43,则该样本的标准差为_________.14.执行如图所示的程序框图若输人x 的值为3,则输出y 的值为______.15.下图给出了一个程序框图,其作用是输入x 的值,输出相应的y 值.若要使输入的x 值与输出的y 值满足关系式y=-2x+4,则这样的x 值___个.16.为调查某校学生每天用于课外阅读的时间,现从该校名学生中随机抽取名学生进行问卷调查,所得数据均在区间上,其频率分布直方图如图所示,则估计该校学生中每天用于阅读的时间在(单位:分钟)内的学生人数为____.17.玉林市有一学校为了从254名学生选取部分学生参加某次南宁研学活动,决定采用系统抽样的方法抽取一个容量为42的样本,那么从总体中应随机剔除的个体数目为__________.18.设{}{}1,3,5,7,2,4,6a b ∈∈,则函数()log a bf x x =是增函数的概率为__________.19.袋中有2个白球,1个红球,这些球除颜色外完全相同.现从袋中往外取球,每次任取1个记下颜色后放回,直到红球出现2次时停止,设停止时共取了X 次球,则(4)P X ==_______.20.使用如图所示算法对下面一组数据进行统计处理,则输出的结果为__________.数据:19.3a =,29.6a =,39.3a = 49.4a =,59.4a =,69.3a = 79.3a =,89.7a =,99.2a = 109.5a =,119.3a =,129.6a =三、解答题21.某校为了了解甲、乙两班的数学学习情况,从两班各抽出10名学生进行数学水平测试,成绩如下(单位:分):甲班:82 84 85 89 79 80 91 89 79 74 乙班:90 76 86 81 84 87 86 82 85 83 (1)求两个样本的平均数; (2)求两个样本的方差和标准差; (3)试分析比较两个班的学习情况.22.某高中为了选拔学生参加“全国高中数学联赛”,先在本校进行初赛(满分150分),随机抽取100名学生的成绩作为样本,并根据他们的初赛成绩得到如图所示的频率分布直方图.(1)求频率分布直方图中a 的值;(2)根据频率分布直方图,估计这次初赛成绩的平均数、中位数、众数.23.某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示: 等级 不合格合格得分 [)20,40[)40,60[)60,80[]80,100频数6a24b(Ⅰ)求a ,b ,c 的值;(Ⅱ)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中随机抽取10人进行座谈.现再从这10人这任选4人,记所选4人的量化总分为ξ,求ξ的分布列及数学期望()E ξ;(Ⅲ)某评估机构以指标M (()()E M D ξξ=,其中()D ξ表示ξ的方差)来评估该校安全教育活动的成效.若0.7M ≥,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(Ⅱ)的条件下,判断该校是否应调整安全教育方案? 24.一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4. (1)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;(2)先从袋中随机取一个球,该球的编号为m ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n ,求2n m <+的概率25.某中学随机抽取部分高一学生调査其每日自主安排学习的时间(单位:分钟),并将所得数据绘制成如图所示的频率分布直方图,其中自主安排学习时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].(1)求直方图中x 的值;(2)现采用分层抽样的方式从每日自主安排学习时间不超过40分钟的学生中随机抽取6人,若从这6人中随机抽取2人进行详细的每日时间安排调查,求抽到的2人每日自主安排学习时间均不低于20分钟的概率.26.设关于x 的一元二次方程2220x bx a -+=,其中,a b 是某范围内的随机数,分别在下列条件下,求上述方程有实根的概率. (1)若随机数,{1,2,3,4}a b ∈;(2)若a 是从区间[0,4]中任取的一个数,b 是从区间[1,3]中任取的一个数.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【解析】 【分析】利用与面积有关的几何概型概率计算公式求解即可. 【详解】由题可知,正方形的面积为=22=4S ⨯正,设这个月牙图案的面积为S , 由与面积有关的几何概型概率计算公式可得,向这个正方形里随机投入芝麻,落在月牙形图案内的概率为150=4500S S P S ==正,解得65S =. 故选:D 【点睛】本题考查与面积有关的几何概型概率计算公式;属于基础题、常考题型.2.C解析:C 【解析】 【分析】由频率分布直方图得的性质求出0.030a =;样本数据低于130分的频率为:0.7;[)80,120的频率为0.4,[)120,130的频率为0.3.由此求出总体的中位数(保留1位小数)估计为:0.50.41203123.30.3-+⨯≈分;样本分布在[)90,100的频数一定与样本分布在[)100,110的频数相等,总体分布在[)90,100的频数不一定与总体分布在[)100,110的频数相等. 【详解】由频率分布直方图得:()0.0050.0100.0100.0150.0250.005101a ++++++⨯=,解得0.030a =,故A 错误;样本数据低于130分的频率为:()10.0250.005100.7-+⨯=,故B 错误;[)80,120的频率为:()0.0050.0100.0100.015100.4+++⨯=, [)120,130的频率为:0.030100.3⨯=.∴总体的中位数(保留1位小数)估计为:0.50.412010123.30.3-+⨯≈分,故C 正确; 样本分布在[)90,100的频数一定与样本分布在[)100,110的频数相等, 总体分布在[)90,100的频数不一定与总体分布在[)100,110的频数相等,故D 错误.故选C . 【点睛】本题考查命题真假的判断,考查频率分布直方图的性质等基础知识,考查运算求解能力,考查数形结合思想,是基础题.因为条形分布直方图的面积表示的是概率值,中位数是位于最中间的数,故直接找概率为0.5的即可;平均数是每个长方条的中点乘以间距再乘以长方条的高,将每一个数值相加得到.3.A解析:A 【解析】 【分析】利用茎叶图、平均数的性质直接求解. 【详解】由一组数据的茎叶图得: 该组数据的平均数为:1(7581858995)855++++=. 故选:A . 【点睛】本题考查平均数的求法,考查茎叶图、平均数的性质等基础知识,考查运算求解能力,是基础题.4.C解析:C 【解析】 【分析】根据程序框图依次计算得到答案. 【详解】根据程序框图:1,1S i ==;3,2S i ==;7,3S i ==;15,4S i ==;31,5S i ==,结束. 故选:C . 【点睛】本题考查了程序框图,意在考查学生的计算能力和理解能力.5.A解析:A 【解析】 【分析】计算出数据1x 、2x 、L 、n x 的平均值x 和方差2s 的值,然后利用平均数和方差公式计算出数据153x -、253x -、L 、53n x -的平均值和方差. 【详解】设数据1x 、2x 、L 、n x 的平均值为x ,方差为2s , 由题意()()()()121221212121215n n x x x x x x x nn++++++++=+=+=L L,得2x =,由方差公式得()()()()()()22212212121212121n x x x x x x n⎡⎤⎡⎤⎡⎤+-+++-++++-+⎣⎦⎣⎦⎣⎦L ()()()2221224416n x x x x x x s n⎡⎤-+-++-⎢⎥⎣⎦===L ,24s ∴=.所以,数据153x -、253x -、L 、53n x -的平均值为()()()12535353n x x x n-+-+-L ()1235535321n x x x x n+++=-=-=-⨯=-L,方差为()()()()()()22212535353535353n x x x x x x n⎡⎤⎡⎤⎡⎤---+---++---⎣⎦⎣⎦⎣⎦L ()()()2221229936n x x x x x x s n⎡⎤-+-++-⎢⎥⎣⎦===L . 故选:A. 【点睛】本题考查平均数与方差的计算,熟练利用平均数与方差的公式计算是解题的关键,考查计算能力,属于中等题.6.A解析:A 【解析】 【分析】根据频率分布直方图得到各个时间段的人数,进而得到结果. 【详解】根据频率分布直方图可列下表:故选A. 【点睛】这个题目考查了频率分布直方图的实际应用,以及样本体现整体的特征的应用,属于基础题.7.C解析:C 【解析】 【分析】根据平均数的定义即可求出.根据频率分布直方图中,中位数的左右两边频率相等,列出等式,求出中位数即可.8.B解析:B【解析】 【分析】利用倒取余数法可得化为五进制数.【详解】 因为所以用倒取余数法得323,故选:B. 【点睛】本题考查十进制数和五进制数之间的转化,利用倒取余数法可解决此类问题.9.A解析:A 【解析】 【分析】由已知求得 x , y ,进一步求得$ a,得到线性回归方程,取16x =求得y 值即可. 【详解】8.38.69.911.1512.1 10x +++=+=, 5.97.88.18.49.858y ++++==.又 0.78b=$,∴$ 80.78100.2a y bx --⨯===$. ∴$ 0.780.2y x =+.取16x =,得$ 0.78160.212.68y ⨯+==万元,故选A .【点睛】本题主要考查线性回归方程的求法,考查了学生的计算能力,属于中档题.10.B解析:B 【解析】第一次输出1,A =第二次输出123A =+=,第三次输出325A =+= ,选B.11.D解析:D 【解析】 【分析】甲、乙二人抢到的金额之和包含的基本事件的总数2510n C ==,甲、乙二人抢到的金额之和不低于3元包含基本事件有6个,由此能求出甲、乙二人抢到的金额之和不低于3元的概率. 【详解】由题意,所发红包的总金额为8元,被随机分配为1.72元、1.83元、2.28元、1.55元、0.62元、5分,供甲、乙等5人抢,每人只能抢一次,甲乙二人抢到的金额之和包含的基本事件的总数为2510n C ==,甲乙二人抢到的金额之和不低于3元包含的基本事件有6个,分别为(1.72,1.83),(1.72,2.28),(1.72,1.55),(1.83,2.28),(1.83,1.55),(2.28,1.55)所以甲乙二人抢到的金额之和不低于3元的概率为63105p ==,故选D. 【点睛】本题主要考查了古典概型及其概率的计算问题,其中解答中正确理解题意,找出基本事件的总数和不低于3元的事件中所包含的基本事件的个数是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.12.B解析:B 【解析】由茎叶图可知,中位数为92,众数为86. 故选B.二、填空题13.【解析】【分析】由平均数的公式求得再利用方差的计算公式求得即可求解【详解】由平均数的公式可得解得所以方差为所以样本的标准差为【点睛】本题主要考查了样本的平均数与方差标准差的计算着重考查了运算与求解能解析:3【解析】 【分析】由平均数的公式,求得49a =,再利用方差的计算公式,求得2283s =,即可求解. 【详解】由平均数的公式,可得1(4042404344)436a +++++=,解得49a =, 所以方差为2222222128[(4043)(4243)(4043)(4343)(4343)(4443)]63s =-+-+-+-+-+-=,所以样本的标准差为3s =. 【点睛】本题主要考查了样本的平均数与方差、标准差的计算,着重考查了运算与求解能力,属于基础题.14.63【解析】【分析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量y的值模拟程序的运行过程分析循环中各变量值的变化情况可得答案【详解】解:模拟程序的运行可得x=3y=7不满足条件|解析:63【解析】【分析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量y的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.【详解】解:模拟程序的运行,可得x=3y=7不满足条件|x-y|>31,执行循环体,x=7,y=15不满足条件|x-y|>31,执行循环体,x=15,y=31不满足条件|x-y|>31,执行循环体,x=31,y=63此时,满足条件|x-y|>31,退出循环,输出y的值为63.故答案为63.【点睛】本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题.15.2【解析】【分析】分析程序中各变量各语句的作用再根据流程图所示的顺序可知:该程序的作用是计算分段函数的函数值并输出【详解】该题考查的是有关程序框图的问题在解题的过程中注意对框图进行分析明确框图的作用解析:2【解析】【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算分段函数2,224,251,5x xy x xxx⎧⎪≤⎪=-<≤⎨⎪⎪>⎩的函数值,并输出.【详解】该题考查的是有关程序框图的问题,在解题的过程中,注意对框图进行分析,明确框图的作用,根据题意,建立相应的等量关系式,求得结果.根据题意,可知该程序的作用是计算分段函数2,224,251,5x xy x xxx⎧⎪≤⎪=-<≤⎨⎪⎪>⎩的函数值,依题意得2224x x x ≤⎧⎨=-+⎩或252424x x x <≤⎧⎨-=-+⎩或5124x x x>⎧⎪⎨=-+⎪⎩,解得15x =-±,所以满足条件的x 的值有两个, 故答案是:2. 【点睛】该题考查的是有关程序框图的问题,在解题的过程中,注意分析框图的作用,之后建立相应的等量关系式,求得结果,从而得到满足条件的x 的个数.16.900【解析】【分析】利用频率分布直方图中频率和为1求a 值根据7080)的频率求出在此区间的人数即可【详解】由1﹣005﹣035﹣02﹣01=03故a =003故阅读的时间在7080)(单位:分钟)内 解析:【解析】 【分析】利用频率分布直方图中频率和为1求a 值,根据[70,80)的频率求出在此区间的人数即可. 【详解】由1﹣0.05﹣0.35﹣0.2﹣0.1=0.3, 故a =0.03,故阅读的时间在[70,80)(单位:分钟)内的学生人数为:0.3×3000=900, 故答案为:900. 【点睛】本题考查频率分布直方图中的有关性质的应用,考查直方图中频率和频数的求法.17.2【解析】【分析】根据系统抽样的概念结合可得最后结果为2【详解】学生总数不能被容量整除根据系统抽样的方法应从总体中随机剔除个体保证整除∵故应从总体中随机剔除个体的数目是2故答案为2【点睛】本题主要考解析:2 【解析】 【分析】根据系统抽样的概念结合2544262=⨯+,可得最后结果为2. 【详解】学生总数不能被容量整除,根据系统抽样的方法,应从总体中随机剔除个体,保证整除. ∵2544262=⨯+,故应从总体中随机剔除个体的数目是2,故答案为2. 【点睛】本题主要考查系统抽样,属于基础题;从容量为N 的总体中抽取容量为n 的样本,系统抽样的前面两个步骤是:(1)将总体中的N 个个体进行编号;(2)当Nn为整数时,抽样距即为N n ;当N n 不是整数时,从总体中剔除一些个体,使剩下的总体中的个体的个数N '能被n 整除.18.【解析】【分析】列举出所有的结果选出的所有的结果根据古典概型概率公式可求出函数是增函数的概率【详解】所有取值有:共12个值当时为增函数有共有6个所以函数是增函数的概率为故答案为【点睛】本题主要考查古 解析:12【解析】 【分析】 列举出ab所有的结果,选出1a b >的所有的结果,根据古典概型概率公式可求出函数()log a bf x x =是增函数的概率.【详解】a b 所有取值有:135713571157,,,,,,,,,,,222244446266共12个值, 当1a b >时,()f x 为增函数,有357577,,,,,222446共有6个, 所以函数()log a bf x x =是增函数的概率为61122=,故答案为12. 【点睛】本题主要考查古典概型概率公式的应用以及对数函数的性质,属于中档题. 在求解有关古典概型概率的问题时,首先求出样本空间中基本事件的总数n ,其次求出概率事件中含有多少个基本事件m ,然后根据公式mP n=求得概率. 19.【解析】【分析】由题意可知最后一次取到的是红球前3次有1次取到红球由古典概型求得概率【详解】由题意可知最后一次取到的是红球前3次有1次取到红球所以填【点睛】求古典概型的概率关键是正确求出基本事件总数解析:427 【解析】 【分析】由题意可知最后一次取到的是红球,前3次有1次取到红球,由古典概型求得概率。
【人教版】高中数学必修三期末第一次模拟试题含答案

一、选择题1.在《九章算术》中,将四个面都为直角三角形的三棱锥称为“鳖臑”.那么从长方体八个顶点中任取四个顶点,则这四个顶点组成的几何体是“鳖臑”的概率为()A.435B.635C.1235D.18352.设袋中有80个红球,20个白球,若从袋中任取10个球,则其中恰好有6个白球的概率为()A.46801010100C CC⋅B.642081010C CC⋅C.462081010C CC⋅D.64801010100C CC⋅3.将一枚质地均匀的硬币连掷三次,设事件A:恰有1次正面向上;事件B:恰有2次正面向上,则()P A B+=()A.23B.14C.38D.344.已知0.5log5a=、3log2b=、0.32c=、212d⎛⎫= ⎪⎝⎭,从这四个数中任取一个数m,使函数()32123x mx xf x=+++有极值点的概率为()A.14B.12C.34D.15.程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.它问世后不久便风行宇内,成为明清之际研习数学者必读的教材,而且传到朝鲜、日本及东南亚地区,对推动汉字文化圈的数学发展起了重要的作用.卷八中第33问是:“今有三角果一垛,底阔每面七个,问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为( )A.84 B.56 C.35 D.286.如图所示的程序框图输出的结果是()A.34 B.55 C.78 D.89 7.某程序框图如图所示,则该程序运行后输出的值是()A.3B.3C3D38.执行如下的程序框图,则输出的S是()A .36B .45C .36-D .45-9.工人月工资y (元)与劳动生产率x (千元)变化的回归直线方程为=50+80x ,下列判断不正确的是( )A .劳动生产率为1000元时,工资约为130元B .工人月工资与劳动者生产率具有正相关关系C .劳动生产率提高1000元时,则工资约提高130元D .当月工资为210元时,劳动生产率约为2000元10.某中学有学生300人,其中一年级120人,二,三年级各90人,现要利用抽样方法取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一,二,三年级依次统一编号为1,2,…,300;使用系统抽样时,将学生统一编号为1,2,…,300,并将整个编号依次分为10段.如果抽得的号码有下列四种情况:①7,37,67,97,127,157,187,217,247,277; ②5,9,100,107,121,180,195,221,265,299; ③11,41,71,101,131,161,191,221,251,281; ④31,61,91,121,151,181,211,241,271,299. 关于上述样本的下列结论中,正确的是( ) A .②④都不能为分层抽样 B .①③都可能为分层抽样 C .①④都可能为系统抽样 D .②③都不能为系统抽样11.已知某8个数的平均数为3,方差为2,现加入一个新数据3,此时这9个数的平均数为x ,方差为2s ,则( ) A .3x =,22s < B .3x =,22s > C .3x >,22s <D .3x >,22s >12.甲、乙两名同学在五次数学考试中的成绩统计如下面的茎叶图所示,若甲、乙两人的平均成绩分别是1x ,2x ,观察茎叶图,下列结论正确的是( )A .12x x <,乙比甲成绩稳定B .12x x >,乙比甲成绩稳定C .12x x <,甲比乙成绩稳定D .12x x >,甲比乙成绩稳定二、填空题13.从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为___________.14.高三某位同学参加物理、化学、政治科目的等级考,已知这位同学在物理、化学、政治科目考试中达A 的概率分别为56、78、34,这三门科目考试成绩的结果互不影响,则这位考生至少得1个A 的概率为____15.从正方体六个面的对角线中任取两条作为一对,这对对角线所成的角为60︒的概率为________16.执行下面的程序框图,如果输入的0.02t =,则输出的n =_______________.17.如图所示的程序框图的算法思路源于宋元时期数学名著《算法启蒙》中的“松竹并生”问题.若输入的a ,b 的值分别为7,3,则输出的n 的值为____________.18.执行右边的程序框图,若,则输出的________.19.下表为生产A 产品过程中产量x (吨)与相应的生产耗能y (吨)的几组相对应数据:x34 5 6y 23.55 5.5根据上表提供的数据,得到y 关于x 的线性回归方程为0.7y x a =+,则a =__________. 20.已知下列命题:①在线性回归模型中,相关指数2R 越接近于1,表示回归效果越好; ②两个变量相关性越强,则相关系数r 就越接近于1;③在回归直线方程0.52y x ∧=-+中,当解释变量x 每增加一个单位时,预报变量y ∧平均减少0.5个单位;④两个模型中残差平方和越小的模型拟合的效果越好.⑤回归直线ˆˆˆy bx a =+恒过样本点的中心(),x y ,且至少过一个样本点;⑥若2K 的观测值满足2K ≥6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;⑦从统计量中得知有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推断出现错误. 其中正确命题的序号是__________.三、解答题21.甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为15︒,边界忽略不计)即为中奖.乙商场:从装有3个白球3个红球的盒子中一次性摸出2个球(球除颜色外不加区分),如果摸到的是2个红球,即为中奖.问:购买该商品的顾客在哪家商场中奖的可能性大?22.高考的成绩不仅需要平时的积累,还与考试时的状态有关系.为了了解考前学生的紧张程度与性别是否有关系,现随机抽取某校500名学生进行了调查,结果如表所示: 心情 性别 男 女 总计 正常 30 40 70 焦虑 270 160 430 总计300200500(1)根据该校调查数据,能否在犯错误的概率不超过0.01的前提下,认为“该学校学生的考前焦虑情况与性别有关”?(2)若从考前心情正常的学生中按性别用分层抽样的方法抽取7人,再从被抽取的7人中随机抽取2人,求这两人中有女生的概率.附:22()()()()()n ad bc K a b c d a c b d -=++++,n a b c d +++=. ()20P K k ≥ 0.25 0.15 0.10 0.05 0.025 0.010 0k1.3232.0722.7063.8415.0246.63523.已知底面半径为r ,高为h 的圆柱和一正方体的体积相等,试设计一个程序分别求圆柱的表面积和正方体的表面积,并画出程序框图(π=3. 14). 24.下面给出了一个问题的算法: 第一步,输入x .第二步,若x ≥4,则执行第三步,否则执行第四步. 第三步,y =2x -1,输出y . 第四步,y =x 2-2x +3,输出y . 问题:(1)这个算法解决的问题是什么? (2)当输入的x 值为多大时,输出的数值最小?25.如表为某中学近5年被卓越大学联盟录取的学生人数.记2015年的年份序号为1,2016年的年份序号为2,…,2019年的年份序号为5.(1)求y 关于x 的线性回归方程,并估计2020年该中学被卓越大学联盟录取的学生人数.(2)若在2015年和2019年被卓越大学联盟录取的学生中分层抽样7人,再从这7人中任选2人,求这2人恰好来自同一年份的概率.参考数据:521ii x=∑=55,51i ii x y =∑=2920.参考公式:b =1221ni ii nii x ynx y xnx==--∑∑,a y bx =-26.某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);(3)若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的列联表,并根据列联表,判断是否有多少的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?附:22()()()()()n ad bc K a b c d a c b d -=++++.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】本题是一个等可能事件的概率,从正方体中任选四个顶点的选法是48C ,四个面都是直角三角形的三棱锥有4×6个,根据古典概型的概率公式进行求解即可求得. 【详解】由题意知本题是一个等可能事件的概率,从长方体中任选四个顶点的选法是4870C =,以A 为顶点的四个面都是直角三角形的三棱锥有:111111111111,,,,,A A D C A A B C A BB C A BCC A DCC DD C A ------共6个.同理以1111,,,,,,B C D A B C D 为顶点的也各有6个, 但是,所有列举的三棱锥均出现2次,∴四个面都是直角三角形的三棱锥有186242⨯⨯=个, ∴所求的概率是24127035= 故选:C . 【点睛】本题主要考查了古典概型问题,解题关键是掌握将问题转化为从正方体中任选四个顶点问题,考查了分析能力和计算能力,属于中档题.2.C解析:C 【分析】根据古典概型的概率公式求解即可. 【详解】从袋中任取10个球,共有10100C 种,其中恰好有6个白球的有468020C C ⋅种即其中恰好有6个白球的概率为4620 81010C C C⋅故选:C【点睛】本题主要考查了计算古典概型的概率,属于中档题.3.D解析:D【分析】根据题意,列举出所有的基本事件,再分别找出满足事件A与事件B的事件个数,分别求出其概率,最后再相加即可.【详解】根据题意,将一枚质地均匀的硬币连掷三次,可能出现的情况有以下8种:(正正正),(正正反),(正反正),(正反反),(反正正),(反正反),(反反正),(反反反).满足事件A:恰有1次正面向上的基本事件有(正反反),(反正反),(反反正)三种,故3()8P A=;满足事件B:恰有2次正面向上的基本事件有(正正反),(正反正),(反正正)三种,故3()8P B=;因此,3()()()4P A B P A P B+=+=.故选:D.【点睛】本题主要考查利用列举法计算基本事件的个数以及求解事件发生的概率.4.B解析:B【分析】求出函数的导数,根据函数的极值点的个数求出m的范围,通过判断a,b,c,d的范围,得到满足条件的概率值即可.【详解】f′(x)=x2+2mx+1,若函数f(x)有极值点,则f′(x)有2个不相等的实数根,故△=4m2﹣4>0,解得:m>1或m<﹣1,而a=log0.55<﹣2,0<b=log32<1、c=20.3>1,0<d=(12)2<1,满足条件的有2个,分别是a,c,故满足条件的概率p21 42 ==,故选:B.【点睛】本题考查了函数的单调性、极值问题,考查导数的应用以及对数、指数的性质,是一道中档题.5.A解析:A 【分析】按照程序框图运行程序,直到满足7i ≥时输出结果即可. 【详解】按照程序框图运行程序,输入0i =,0n =,0S =, 则1i =,1n =,1S =,不满足7i ≥,循环;2i =,3n =,4S =,不满足7i ≥,循环; 3i =,6n =,10S =,不满足7i ≥,循环;4i =,10n =,20S =,不满足7i ≥,循环; 5i =,15n =,35S =,不满足7i ≥,循环; 6i =,21n =,56S =,不满足7i ≥,循环;7i =,28n =,84S =,满足7i ≥,输出84S =. 故选:A . 【点睛】本题考查根据程序框图循环结构计算输出结果的问题,属于基础题.6.B解析:B 【分析】通过不断的循环赋值,得到临界值,即可得解. 【详解】1,1,21,2,32,3,53,5,85,8,138,13,2113,21,3421,34,55x y z x y z x y z x y z x y z x y z x y z x y z ========================不满足50z ≤,输出即可, 故选:B. 【点睛】本题考查了程序框图循环结构求输出结果,考查了计算能力,属于中当题.7.D解析:D 【分析】该框图的功能是计算:234562017sinsin sin sin sin sin sin3333333πππππππ+++++++,再根据正弦函数的周期性以及特殊角的三角函数值计算可得答案. 【详解】该框图的功能是计算:234562017sinsinsin sin sin sin sin3333333πππππππ+++++++.因为7132017sinsinsin sin 3333ππππ=====28142012sinsin sin sin33332ππππ=====, 39152013sinsin sin sin03333ππππ=====,410162014sin sin sin sin 3333ππππ=====,511172015sinsin sin sin33332ππππ=====-, 612182016sinsin sin sin 03333ππππ=====, 所以234562017sin sinsin sin sin sin sin3333333πππππππ+++++++3373363360336(336()336022222=⨯+⨯+⨯+⨯-+⨯-+⨯=. 故选:D 【点睛】本题考查了程序框图的循环结构,考查了三角函数的周期性以及特殊角的三角函数值,理解程序框图的功能是解题关键,属于基础题.8.A解析:A 【分析】列出每一步算法循环,可得出输出结果S 的值. 【详解】18i =≤满足,执行第一次循环,()120111S =+-⨯=-,112i =+=; 28i =≤成立,执行第二次循环,()221123S =-+-⨯=,213i =+=; 38i =≤成立,执行第三次循环,()323136S =+-⨯=-,314i =+=;48i =≤成立,执行第四次循环,()4261410S =-+-⨯=,415i =+=;58i=≤成立,执行第五次循环,()52i=+=;101515S=+-⨯=-,516i=≤成立,执行第六次循环,()6268S=-+-⨯=,617151621i=+=;i=+=;i=≤成立,执行第七次循环,()7278211728S=+-⨯=-,718i=≤成立,执行第八次循环,()82i=+=;88S=-+-⨯=,819281836i=≤不成立,跳出循环体,输出S的值为36,故选A.98【点睛】本题考查算法与程序框图的计算,解题时要根据算法框图计算出算法的每一步,考查分析问题和计算能力,属于中等题.9.C解析:C【解析】试题分析:根据线性回归方程=50+80x的意义,对选项中的命题进行分析、判断即可.解:根据线性回归方程为=50+80x,得;劳动生产率为1000元时,工资约为50+80×1=130元,A正确;∵=80>0,∴工人月工资与劳动者生产率具有正相关关系,B正确;劳动生产率提高1000元时,工资约提高=80元,C错误;当月工资为210元时,210=50+80x,解得x=2,此时劳动生产率约为2000元,D正确.故选C.考点:线性回归方程.10.B解析:B【分析】根据系统抽样和分层抽样的定义分别进行判断即可.【详解】若采用简单随机抽样,根据简单随机抽样的特点,1~300之间任意一个号码都有可能出现;若采用分层抽样,则1~120号为一年级,121~210为二年级,211~300为三年级.且根据分层抽样的概念,需要在1~120之间抽取4个,121~210与211~300之间各抽取3个;若采用系统抽样,根据系统抽样的概念,需要在1~30,31~60,61~90,91~ 120,121~150,151~180,181~210,211~240,241~270,271~300之间各抽一个.①项,1~120之间有 4个,121~210之间有 3个,211~300之间有 3个,并且满足系统抽样的条件,所以①项为系统抽样或分层抽样;②项,1~120之间有 4个,121~210之间有 3个,211~300之间有 3个,可能为分层抽样;③项,1~120之间有 4个,121~210之间有 3个,211~300之间有 3个,并且满足系统抽样的条件,所以③项为系统抽样或分层抽样;④项,第一个数据大于30,所以④项不可能为系统抽样,并且④项不满足分层抽样的条件.综上所述,B 选项正确. 故选:B. 【点睛】本题主要考查系统抽样和分层抽样,掌握系统抽样和分层抽样的定义是解题的关键,属于基础题.(1)系统抽样适用于总体容量较大的情况.将总体平均分成若干部分,按事先确定的规则在各部分中抽取,在起始部分抽样时采用简单随机抽样;(2)分层抽样适用于已知总体是由差异明显的几部分组成的.将总体分成互不交叉的层,然后分层进行抽取,各层抽样时采用简单随机抽样或系统抽样.11.A解析:A 【分析】由题意计算出加入新数据后的平均数,然后比较方差 【详解】()18138x x +⋯+=, ()181339x x +⋯++=, 3x ∴=,由方差的定义可知加入新数据3,样本数据会变得更加稳定 故22s < 故选A 【点睛】本题主要考查了加入数据后平均数和方差的变化,代入公式计算出结果,较为基础12.A解析:A 【解析】 【分析】根据茎叶图中的数据,即可计算出两人平均分,再根据茎叶图的分布情况可知乙成绩稳定. 【详解】 由茎叶图知, 甲的平均数是110210410511413391.65x ++++==,乙的平均数是2108115116122123116.85x ++++==,所以12x x <,从茎叶图上可以看出乙的数据比甲的数据集中,乙比甲成绩稳定故选:A.【点睛】本题考查茎叶图中两组数据的平均数和稳定程度,平均数要进行计算,稳定程度可通过计算方差或通过数据排布形状作出比较.二、填空题13.【解析】从分别写有12345的5张卡片中随机抽取1张放回后再随机抽取1张基本事件总数n=5×5=25抽得的第一张卡片上的数大于第二张卡片上的数包含的基本事件有:(21)(31)(32)(41)(42解析:2 5【解析】从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,基本事件总数n=5×5=25,抽得的第一张卡片上的数大于第二张卡片上的数包含的基本事件有:(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),共有m=10个基本事件,∴抽得的第一张卡片上的数大于第二张卡片上的数的概率p=2.5故答案为2 5 .14.【分析】先求对立事件概率:三门科目考试成绩都不是A再根据对立事件概率关系求结果【详解】这位考生三门科目考试成绩都不是A的概率为所以这位考生至少得1个A的概率为故答案为:【点睛】本题考查利用对立事件求解析:191 192【分析】先求对立事件概率:三门科目考试成绩都不是A,再根据对立事件概率关系求结果.【详解】这位考生三门科目考试成绩都不是A的概率为5731 (1)(1)(1)684192 ---=,所以这位考生至少得1个A的概率为1191 1192192 -=故答案为:191 192【点睛】本题考查利用对立事件求概率,考查基本分析求解能力,属基础题.15.【解析】【分析】正方体的面对角线共有12条能够数出每一条对角线和另外的8条构成8对直线所成角为60°得共有12×8对对角线所成角为60°并且容易看出有一半是重复的得正方体的所有对角线中所成角是60° 解析:811【解析】 【分析】正方体的面对角线共有12条,能够数出每一条对角线和另外的8条构成8对直线所成角为60°,得共有12×8对对角线所成角为60°,并且容易看出有一半是重复的,得正方体的所有对角线中,所成角是60°的有48对,根据古典概型概率公式求解即可. 【详解】如图,在正方体ABCD ﹣A 1B 1C 1D 1中,与上平面A 1B 1C 1D 1中一条对角线A 1C 1成60°的直线有:A 1D ,B 1C ,A 1B ,D 1C ,BC 1,AD 1,C 1D ,B 1A 共八对直线,总共12条对角线; ∴共有12×8=96对面对角线所成角为60°,而有一半是重复的;∴从正方体六个面的对角线中任取两条作为一对,其中所成的角为60°的共有48对. 而正方体的面对角线共有12条,所以概率为:212488C 11故答案为811【点睛】本题考查正方体面对角线的关系,考查了古典概型的概率问题,而对于本题知道96对直线中有一半是重复的是求解本题的关键.16.【解析】分析:由已知中的程序框图可知该程序的功能是利用循环结构计算并输出变量的值模拟程序运行过程分析循环变量值的变化规律即可求解答案详解:执行如图所示的程序框图:第一次循环:满足条件;第二次循环:满解析:【解析】分析:由已知中的程序框图可知,该程序的功能是利用循环结构计算并输出变量n 的值,模拟程序运行过程,分析循环变量值的变化规律,即可求解答案. 详解:执行如图所示的程序框图: 第一次循环:11,,124S m n ===,满足条件; 第二次循环:11,,248S m n ===,满足条件; 第三次循环:11,,3816S m n ===,满足条件; 第四次循环:11,,41632S m n ===,满足条件; 第五次循环:11,,53264S m n ===,满足条件; 第六次循环:11,,664128S m n ===,不满足条件,推出循环,此时输出6n =; 点睛:本题主要考查了循环结构的程序框图的运行与结果出的输出问题,解题是应模拟程序框图的运行过程,以便得出正确的计算结果,同时注意判断框的条件是解答的关键,着重考查了推理与运算能力.17.3【解析】输入进入循环不满足执行循环不满足执行循环满足输出故答案为3解析:3 【解析】输入7,3,1a b n === 进入循环,21,2622a a ab b =+===,不满足a b ≤ 执行循环,6312,,21224a n n a ab b =+==+===,不满足a b ≤ 执行循环,18913,,22428a n n a ab b =+==+===,满足a b ≤,输出3n = 故答案为318.【解析】试题分析:程序执行中的数据变化为:不成立输出考点:程序框图 解析:【解析】试题分析:程序执行中的数据变化为:17,1,0,17,2,,27,3,23p n s n s n ===<==<=⨯1111167,7,,772334233478s n s =+<==+++<⨯⨯⨯⨯⨯不成立,输出111113233478288s =+++=-=⨯⨯⨯ 考点:程序框图19.【解析】分析:首先求得样本中心点然后利用回归方程的性质求得实数a 的值即可详解:由题意可得:线性回归方程过样本中心点则:解得:点睛:本题主要考查线性回归方程的性质及其应用等知识意在考查学生的转化能力和 解析:0.85【解析】分析:首先求得样本中心点,然后利用回归方程的性质求得实数a 的值即可. 详解:由题意可得:34569==42x +++,2 3.55 5.544y +++==, 线性回归方程过样本中心点9,42⎛⎫⎪⎝⎭,则:940.72a =⨯+,解得:0.85a =.点睛:本题主要考查线性回归方程的性质及其应用等知识,意在考查学生的转化能力和计算求解能力.20.①③④⑦【分析】根据线性回归分析的概念进行分析即可【详解】在线性回归模型中相关指数越接近于1表示回归效果越好①正确;两个变量相关性越强则相关系数r 的绝对值就越接近于1②错误;③正确;两个模型中残差平解析:①③④⑦ 【分析】根据线性回归分析的概念进行分析即可. 【详解】在线性回归模型中,相关指数2R 越接近于1,表示回归效果越好,①正确;两个变量相关性越强,则相关系数r 的绝对值就越接近于1,②错误;③正确;两个模型中残差平方和越小的模型拟合的效果越好,④正确;回归直线ˆˆˆybx a =+恒过样本点的中心(),x y ,不一定过样本点,⑤错误;若2K 的观测值满足2K ≥6.635,我们有99%的把握认为吸烟与患肺病有关系,并不能说在100个吸烟的人中必有99人患有肺病,⑥错误;从统计量中得知有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推断出现错误,⑦正确.故答案为①③④⑦. 【点睛】本题考查线性回归分析的有关概念,掌握相关概念是解题基础,属于基础题.三、解答题21.乙商场中奖的可能性大. 【解析】试题分析:分别计算两种方案中奖的概率.先记出事件,得到试验发生包含的所有事件,和符合条件的事件,由等可能事件的概率公式得到. 试题如果顾客去甲商场,试验的全部结果构成的区域为圆盘的面积2R π,阴影部分的面积为224153606R R ππ⨯=, 则在甲商场中奖的概率为212166R P R ππ==; 如果顾客去乙商场,记3个白球为1a ,2a ,3a ,3个红球为1b ,2b ,3b ,记(x ,y )为一次摸球的结果,则一切可能的结果有:()12,a a ,()13,a a ,()11,a b ,()12,a b ,()13,a b ,()23,a a ,()21,a b ,()22,a b ,()23,a b ,()31,a b ,()32,a b ,()33,a b ,()12,b b ,()13,b b ,()23,b b ,共15种, 摸到的是2个红球有()12,b b ,()13,b b ,()23,b b ,共3种,则在乙商场中奖的概率为231155P ==, 又12p p <,则购买该商品的顾客在乙商场中奖的可能性大. 22.(1)能;(2)67【分析】(1)根据题意,计算可得2K 的观测值,结合独立性检验的知识分析可得答案.(2)根据题意,分析可得抽取7人,其中有3名男生,4名女生.由组合数公式计算可得”从7人中任意抽取2人”和”抽取的两人中有女生”的选法数目,由古典概型公式计算可得答案. 【详解】解:(1)根据题意,由22⨯列联表可得:2K的观测值2500(3016027040)300009.967 6.63543070300200301k ⨯⨯-⨯==≈>⨯⨯⨯ 故能在犯错误的概率不超过0.01的前提下,认为该学校学生的考前焦虑情况与性别有关. (2)根据题意,若从考前心情正常的学生中按性别用分层抽样的方法抽取7人,其中有3名男生,4名女生.从7人中任意抽取2人,有2721C =种情况.其中抽取的两人中有女生的抽法有211443+18C C C =种选法.故其概率186217P ==. 【点睛】本题考查了独立性检验,考查了古典概型.在进行独立性检验时,一般步骤为:假设无关,画列联表,求2K 的值,下结论.这里正确计算出2K 的近似值是关键.对于求古典概型概率问题,可列出所有的基本事件,也可以用排列组合的思想计算个数.23.见解析;【解析】试题分析: 先利用INPUT语句输入半径以及高的值,再分别赋值圆柱的表面积和正方体的表面积,最后输出圆柱的表面积和正方体的表面积试题程序如下:INPUT“r,h=”;r,hS=3. 14*r^2m=2*3. 14*r*hS1=2*S+mV=3. 14*r^2*ha=V^(1/3)S2=6*a^2PRINT“圆柱、正方体的表面积分别为”;S1,S2END程序框如图所示.点睛:24.(1)见解析(2)当输入的x 的值为1时,输出的数值最小. 【解析】试题分析:本题考查了一个条件分支结构的算法,可分为4x ≥和4x <,执行不同的计算,即可得到结论. 试题(1)这个算法解决的问题是求分段函数()()221x 4y x 23x 4x x ⎧-≥⎪=⎨-+<⎪⎩的函数值的问题. (2)本问的实质是求分段函数最小值的问题. 当x≥4时,y =2x -1≥7;当x<4时,y =x 2-2x +3=(x -1)2+2≥2. ∴函数最小值为2,当x =1时取到最小值. ∴当输入x 的值为1时,输出的数值最小.点睛:本题主要考查了一个条件分支结构的算法的应用问题,解答中涉及到分段函数的性质,其中程序填空是重点考查的题型,这种试题考试的重点:①分支条件;②循环的条件;③变量的赋值;④变量的输出,其中前两个是考试的重点,正确理解算法的流程,读懂题意是解答的关键.25.(1)3759y x =+;281;(2)1121. 【分析】(1)由题意计算平均数,代入公式求出回归系数,写出线性回归方程,再利用线性回归方程计算6x =时的值即可;(2)由分层抽样求出抽取的人数,再利用概率公式求出对应的概率即可. 【详解】(1)由表格可求()11234+5=35x =+++,()1100130170200+250=1705y =+++,且521i i x=∑=55,51i i i x y =∑=2920, 所以12221292053170375553n i ii n i i x y nx y xnx b ==--⨯⨯==-⨯-=∑∑,17037359a y bx =-=-⨯=, 所以y 关于x 的线性回归方程为3759y x =+,当6x =时,37659281y =⨯+=,所以2020年该中学被卓越大学联盟录取的学生人数约为281;(2)由分层抽样可知7人中有10072100250⨯=+ 人来自2015年,有25075100250⨯=+人来自2019年,从中随机抽取两人共有21种结果,抽取的两人恰好来自同一年的有11种,所以所求概率为1121P =. 【点睛】本题主要考查线性回归方程和古典概型求概率,属于中档题.26.(1)概率分别为:43100,27100,21100,9100;(2)350;(3)填表见解析;有95%的把握认为锻炼的人次与该市的空气质量有关.【分析】(1)用频率估计概率,从而得到估计该市一天的空气质量等级为1,2,3,4的概率; (2)利用频率分布直方图估计样本平均值的方法可得得答案;(3)完善列联表,由公式计算卡方的值,从而查表即可,【详解】解:(1)该市一天的空气质量等级为1的概率为:2162543100100++=; 该市一天的空气质量等级为2的概率为:5101227100100++=; 该市一天的空气质量等级为3的概率为:67821100100++=; 该市一天的空气质量等级为4的概率为:7209100100++=; (2)由题意可得:一天中到该公园锻炼的平均人次的估计值为:1000.203000.355000.45350x =⨯+⨯+⨯=;(3)根据所给数据,可得下面的22⨯列联表,由表中数据可得:2 5.820 3.841()()()()70305545K a b c d a c b d ==≈>++++⨯⨯⨯, 所以有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关.【点睛】本题考查了独立性检验与频率估计概率,估计平均值的求法,属于中档题.。
新高中必修三数学上期末模拟试题(带答案)

新高中必修三数学上期末模拟试题(带答案)一、选择题1.如图,ABC ∆和DEF ∆都是圆内接正三角形,且//BC EF ,将一颗豆子随机地扔到该圆内,用A 表示事件“豆子落在ABC ∆内”,B 表示事件“豆子落在DEF ∆内”,则(|)P B A =( )A .33B .3C .13D .232.气象意义上的春季进入夏季的标志为连续5天的日平均温度不低于022C .现有甲、乙、丙三地连续5天的日平均气温的记录数据(记录数据都是正整数):①甲地:5个数据是中位数为24,众数为22;②乙地:5个数据是中位数为27,总体均值为24;③丙地:5个数据中有一个数据是32,总体均值为26,总体方差为10.8则肯定进入夏季的地区有( )A .①②③B .①③C .②③D .①3.如果数据12,,,n x x x L 的平均数为x ,方差为28,则152x +,252x +,…,52n x +的平均数和方差分别为( )A .x ,28B .52x +,28C .52x +,2258⨯D .x ,2258⨯4.执行如图的程序框图,那么输出的S 的值是( )A .﹣1B .12C .2D .15.预测人口的变化趋势有多种方法,“直接推算法”使用的公式是()0 1n n P P k =+(1k >-),n P 为预测人口数,0P 为初期人口数,k 为预测期内年增长率,n 为预测期间隔年数.如果在某一时期有10k -<<,那么在这期间人口数A .呈下降趋势B .呈上升趋势C .摆动变化D .不变6.执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )A .4i ≤B .5i ≤C .6i ≤D .7i ≤7.执行如图的程序框图,如果输出a 的值大于100,那么判断框内的条件为( )A .5k <?B .5k ≥?C .6k <?D .6k ≥?8.已知具有线性相关的两个变量,x y 之间的一组数据如下表所示: x 01 2 3 4 y2.2 4.3 4.5 4.8 6.7若,x y 满足回归方程 1.5ˆˆyx a =+,则以下为真命题的是( ) A .x 每增加1个单位长度,则y 一定增加1.5个单位长度B .x 每增加1个单位长度,y 就减少1.5个单位长度C .所有样本点的中心为(1,4.5)D .当8x =时,y 的预测值为13.59.如图,正方形ABNH 、DEFM 的面积相等,23CN NG AB ==,向多边形ABCDEFGH 内投一点,则该点落在阴影部分内的概率为( )A .12 B .34 C .27 D .3810.要从其中有50个红球的1000个形状相同的球中,采用按颜色分层抽样的方法抽取100个进行分析,则应抽取红球的个数为( )A .5个B .10个C .20个D .45个11.从2名男生和2名女生中任意选择两人在星期六、星期日参加某公益活动,每天一人,则星期六安排一名男生、星期日安排一名女生的概率为( )A .13B .512C .12D .71212.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如40337=+.(注:如果一个大于1的整数除1和自身外无其他正因数,则称这个整数为素数.)在不超过11的素数中,随机选取2个不同的数,其和小于等于10的概率是( )A .12B .13C .14D .15二、填空题13.将函数sin 23cos 2y x x =-的图象向左平移6π个单位长度,得到函数()y g x =的图象,则5()6g π__________.14.小明通过做游戏的方式来确定接下来两小时的活动,他随机地往边长为1的正方形内扔一颗豆子,若豆子到各边的距离都大于14,则去看电影;若豆子到正方形中心的距离大于12,则去打篮球;否则,就在家写作业则小明接下来两小时不在家写作业的概率为______.(豆子大小可忽略不计) 15.已知四棱锥P ABCD -的所有顶点都在球O 的球面上,PA ⊥底面ABCD ,底面ABCD 为正方形, 2.PA AB ==现在球O 的内部任取一点,则该点取自四棱锥P ABCD -的内部的概率为______. 16.下图是华师一附中数学讲故事大赛7位评委给某位学生的表演打出的分数的茎叶图.记分员在去掉一个最高分和一个最低分后,算得平均分为91分,复核员在复核时,发现有一个数字(茎叶图中的x )无法看清,若记分员计算无误,则数字x 应该是____________.17.甲、乙二人约定某日早上在某处会面,甲在7:00~7:20内某一时刻随机到达,乙在7:05~7:20内某一时刻随机到达,则甲至少需等待乙5分钟的概率是________.18.在棱长为2 的正方体内任取一点,则此点到正方体中心的距离不大于1的概率为_____.19.在区间[]0,2中随机地取出一个数x ,则sin 6x π>的概率是__________.20.向面积为20的ABC ∆内任投一点M ,则使MBC ∆的面积小于5的概率是__________.三、解答题21.某校为了了解甲、乙两班的数学学习情况,从两班各抽出10名学生进行数学水平测试,成绩如下(单位:分):甲班:82 84 85 89 79 80 91 89 79 74乙班:90 76 86 81 84 87 86 82 85 83(1)求两个样本的平均数;(2)求两个样本的方差和标准差;(3)试分析比较两个班的学习情况.22.已知某校甲、乙、丙三个兴趣小组的学生人数分别为36,24,12.现采用分层抽样的方法从中抽取6人,进行睡眠质量的调查.(1)应从甲、乙、丙三个兴趣小组的学生中分别抽取多少人?(2)设抽出的6人分别用A 、B 、C 、D 、E 、F 表示,现从6人中随机抽取2人做进一步的身体检查.(i )试用所给字母列出所有可能的抽取结果;(ii )设K 为事件“抽取的2人来自同一兴趣小组”,求事件K 发生的概率.23.有20名学生参加某次考试,成绩(单位:分)的频率分布直方图如图所示:(Ⅰ)求频率分布直方图中m的值;(Ⅱ)分别求出成绩落在[70,80),[80,90),[90,100]中的学生人数;(Ⅲ)从成绩在[80,100]的学生中任选2人,求所选学生的成绩都落在[80,90)中的概率24.盒子里放有外形相同且编号为1,2,3,4,5的五个小球,其中1号与2号是黑球,3号、4号与5号是红球,从中有放回地每次取出1个球,共取两次.(1)求取到的2个球中恰好有1个是黑球的概率;(2)求取到的2个球中至少有1个是红球的概率.25.某医疗器械公司在全国共有100个销售点,总公司每年会根据每个销售点的年销量进行评价分析.规定每个销售点的年销售任务为一万四千台器械.根据这100个销售点的年销量绘制出如下的频率分布直方图.(1)完成年销售任务的销售点有多少个?(2)若用分层抽样的方法从这100个销售点中抽取容量为25的样本,求该五组[2,6), ,[14,18),[18,22),(单位:千台)中每组分别应抽取的销[6,10),____________售点数量.(3)在(2)的条件下,从该样本中完成年销售任务的销售点中随机选取2个,求这两个销售点不在同一组的概率.26.1766年;人类已经发现的太阳系中的行星有金星、地球、火星、木星和土星.德国的一位中学教师戴维一提丢斯在研究了各行星离太阳的距离(单位:AU,AU是天文学中计量天体之间距离的一种单位)的排列规律后,预测在火星和木星之间应该还有一颗未被发现的行星存在,并按离太阳的距离从小到大列出了如下表所示的数据:行星编号1(金星)2(地球)3(火星)4()5(木星)6(土星)(x)离太阳的距离(y ) 0.7 1.0 1.6 5.2 10.0 受他的启发,意大利天文学家皮亚齐于1801年终于发现了位于火星和木星之间的谷神星. (1)为了描述行星离太阳的距离y 与行星编号之间的关系,根据表中已有的数据画出散点图,并根据散点图的分布状况,从以下三种模型中选出你认为最符合实际的一种函数模型(直接给出结论即可);①y ax b =+;②(1)x y a b c b =⋅+>;③log (1)b y a x c b =⋅+>.(2)根据你的选择,依表中前几组数据求出函数解析式,并用剩下的数据检验模型的吻合情况;(3)请用你求得的模型,计算谷神星离太阳的距离.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【解析】如图所示,作三条辅助线,根据已知条件,这些小三角形全等,ABC ∆包含9 个小三角形,同时又在DEF ∆内的小三角形共有6 个,所以(|)P B A =6293= ,故选D. 2.B解析:B【解析】试题分析:由统计知识①甲地:5个数据的中位数为24,众数为22可知①符合题意;而②乙地:5个数据的中位数为27,总体均值为24中有可能某一天的气温低于22C o ,故不符合题意,③丙地:5个数据中有一个数据是32,总体均值为26,总体方差为10.8.若由有某一天的气温低于22C o 则总体方差就大于10.8,故满足题意,选C 考点:统计初步3.C解析:C【解析】 根据平均数的概念,其平均数为52x +,方差为2258⨯,故选C.4.B解析:B【解析】由题意可得:初如值S=2,k=2015,S=-1,k=2016<2018 S=12,k=2017<2018 2,2018S k ==输出2,选C.5.A解析:A【解析】【分析】可以通过n P 与0P 之间的大小关系进行判断.【详解】当10k -<<时,()011011nk k <+<<+<,,所以()001n n P P k P =+<,呈下降趋势.【点睛】判断变化率可以通过比较初始值与变化之后的数值之间的大小来判断. 6.B解析:B【解析】【分析】模拟执行程序框图,依次写出每次循环得到的,i S 的值,当输出的63S =时,退出循环,对应的条件为5i ≤,从而得到结果.【详解】当=11S i =,时,不满足输出条件,故进行循环,执行循环体;当1123,2S i =+==,不满足输出条件,故进行循环,执行循环体;当2327,3S i =+==,不满足输出条件,故进行循环,执行循环体;当37215,4S i =+==,不满足输出条件,故进行循环,执行循环体;当415231,5S i =+==,不满足输出条件,故进行循环,执行循环体;当313263,6S i =+==,满足输出条件,故判断框中应填入的条件为5i ≤, 故选B.【点睛】该题考查的是有关程序框图的问题,根据题意写出判断框中需要填入的条件,属于简单题目.7.C解析:C【解析】【分析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量a 的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.【详解】由题意,模拟程序的运算,可得k 1=,a 1=满足判断框内的条件,执行循环体,a 6=,k 3=满足判断框内的条件,执行循环体,a 33=,k 5=满足判断框内的条件,执行循环体,a 170=,k 7=此时,不满足判断框内的条件,退出循环,输出a 的值为170.则分析各个选项可得程序中判断框内的“条件”应为k 6<?故选:C .【点睛】本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题.8.D解析:D【解析】【分析】利用回归直线过样本点中心可求回归方程,根据该方程可得正确的选项.【详解】由$$1.5y x a=+,得x 每增一个单位长度,y 不一定增加1.5,而是大约增加1.5个单位长度,故选项,A B 错误; 由已知表格中的数据,可知0123425x ++++==,2.2 4.3 4.5 4.8 6.7 4.55y ++++==,Q 回归直线必过样本的中心点()2,4.5,故C 错误;又4.5 1.52 1.5ˆˆa a =⨯+⇒=,∴回归方程为$1.5 1.5y x =+,当8x =时,y 的预测值为1.58 1.513.5⨯+=,故D 正确,故选:D.【点睛】 本题考查线性回归方程的性质及应用,注意回归直线过(),x y ,本题属于基础题. 9.C解析:C【解析】【分析】由正方形ABNH 、DEFM 的面积相等,可得两正方形边长相等,设边长为3,由23CN NG AB ==,可得正方形MCNG 的边长为2,分别求出阴影部分的面积及多边形ABCDEFGH 的面积,由测度比为面积比得答案.【详解】 如图所示,由正方形ABNH 、DEFM 的面积相等,可得两正方形边长相等,设边长为3,由23CN NG AB ==,可得正方形MCNG 的边长为2, 则阴影部分的面积为224⨯=,多边形ABCDEFGH 的面积为2332214⨯⨯-⨯=.则向多边形ABCDEFGH 内投一点,则该点落在阴影部分内的概率为42147=. 故选:C.【点睛】本题主要考查了几何概型的概率的求法,关键是求出多边形ABCDEFGH 的面积,着重考查了推理与运算能力,以及数形结合的应用,属于基础题.10.A解析:A【解析】应抽取红球的个数为5010051000⨯= ,选A. 点睛:在分层抽样的过程中,为了保证每个个体被抽到的可能性是相同的,这就要求各层所抽取的个体数与该层所包含的个体数之比等于样本容量与总体的个体数之比,即n i ∶N i=n ∶N .11.A解析:A【解析】设2名男生记为A 1,A 2,2名女生记为B 1,B 2,任意选择两人在星期六、星期日参加某公益活动,共有(A 1,A 2),(A 1,B 1),(A 1,B 2),(A 2,B 1),(A 2,B 2),(B 1,B 2),(A 2,A 1),(B 1,A 1),(B 2,A 1),(B 1,A 2),(B 2,A 2),(B 2,B 1)12种情况,而星期六安排一名男生、星期日安排一名女生共有(A 1,B 1),(A 1,B 2),(A 2,B 1),(A 2,B 2)4种情况,则发生的概率为P=41123=, 故选:A . 12.A解析:A【解析】【分析】先列出不超过11的素数,再列举出随机选取2个不同的数的情况,进而找到和小于等于10的情况,即可求解【详解】不超过11的素数有:2,3,5,7,11,共有5个,随机选取2个不同的数可能为:()2,3,()2,5,()2,7,()2,11,()3,5,()3,7,()3,11,()5,7,()5,11,()7,11,共有10种情况, 其中和小于等于10的有:()2,3,()2,5,()2,7,()3,5,()3,7,共有5种情况, 则概率为51102P ==, 故选:A【点睛】本题考查列举法求古典概型的概率,属于基础题 二、填空题13.【解析】【分析】先利用辅助角公式将函数的解析式化简根据三角函数的变化规律求出函数的解析式即可计算出的值【详解】由题意可得因此故答案为【点睛】本题考查辅助角公式化简三角函数图象变换在三角图象相位变换的解析:【解析】【分析】先利用辅助角公式将函数sin 22y x x =-的解析式化简,根据三角函数的变化规律求出函数()y g x =的解析式,即可计算出56g π⎛⎫⎪⎝⎭的值. 【详解】sin 23cos 22sin 23y x x x π⎛⎫=-=- ⎪⎝⎭Q ,由题意可得()2sin 22sin 263g x x x ππ⎡⎤⎛⎫=+-= ⎪⎢⎥⎝⎭⎣⎦, 因此,5552sin 22sin 2sin 22sin 366333g ππππππ⎛⎫⎛⎫⎛⎫=⨯==-=-=-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 故答案为3-. 【点睛】本题考查辅助角公式化简、三角函数图象变换,在三角图象相位变换的问题中,首先应该将三角函数的解析式化为()()sin 0y A x b ωϕω=++≠(或()()cos 0y A x b ωϕω=++≠)的形式,其次要注意左加右减指的是在自变量x 上进行加减,考查计算能力,属于中等题.14.【解析】【分析】根据题意画出图形求出写作业所对应的区域面积利用得到结果【详解】由题意可知当豆子落在下图中的空白部分时小明在家写作业大正方形面积;阴影正方形面积空白区域面积:根据几何概型可知小明不在家 解析:5π4- 【解析】 【分析】根据题意画出图形,求出写作业所对应的区域面积,利用()()1P A P A =-得到结果. 【详解】由题意可知,当豆子落在下图中的空白部分时,小明在家写作业∴大正方形面积111S =⨯=;阴影正方形面积1111224S =⨯= 空白区域面积:22111244S ππ-⎛⎫=⨯-= ⎪⎝⎭根据几何概型可知,小明不在家写作业的概率为:2514S P S π-=-=本题正确结果:54π- 【点睛】本题考查几何概型中的面积型,属于基础题.15.【解析】【分析】根据条件求出四棱锥的条件和球的体积结合几何概型的概率公式进行求解即可【详解】四棱锥扩展为正方体则正方体的对角线的长是外接球的直径即即则四棱锥的条件球的体积为则该点取自四棱锥的内部的概解析:9π【解析】 【分析】根据条件求出四棱锥的条件和球的体积,结合几何概型的概率公式进行求解即可. 【详解】四棱锥P ABCD -扩展为正方体, 则正方体的对角线的长是外接球的直径,即2R =,即R =则四棱锥的条件1822233V =⨯⨯⨯=,球的体积为343π⨯=,则该点取自四棱锥P ABCD -的内部的概率8P ==,【点睛】本题主要考查几何概型的概率的计算,结合条件求出四棱锥和球的体积是解决本题的关键.本题考查了几何概型概率的求法;在利用几何概型的概率公式来求其概率时,几何“测度”可以是长度、面积、体积、角度等,其中对于几何度量为长度,面积、体积时的等可能性主要体现在点落在区域Ω上任置都是等可能的,而对于角度而言,则是过角的顶点的一条射线落在Ω的区域(事实也是角)任一位置是等可能的.16.1【解析】【分析】因为题目中要去掉一个最高分所以对进行分类讨论然后结合平均数的计算公式求出结果【详解】若去掉一个最高分和一个最低分86分后平均分为不符合题意故最高分为94分去掉一个最高分94分去掉一解析:1 【解析】 【分析】因为题目中要去掉一个最高分,所以对x 进行分类讨论,然后结合平均数的计算公式求出结果 【详解】若4x >,去掉一个最高分()90x +和一个最低分86分后,平均分为()1899291949291.65++++=,不符合题意,故4x ≤,最高分为94分,去掉一个最高分94分,去掉一个最低分86分后,平均分()18992909192915x +++++=,解得1x =,故数字x 为1 【点睛】本题考查了由茎叶图求平均值,理解题目意思运用平均数计算公式即可求出结果,注意分类讨论17.【解析】【分析】由题意知本题是一个几何概型试验包含的所有事件是Ω={(xy )|0≤x≤205≤y≤20}作出事件对应的集合表示的面积写出满足条件的事件是A ={(xy )|0≤x≤205≤y≤20y﹣x 解析:38【解析】 【分析】由题意知本题是一个几何概型,试验包含的所有事件是Ω={(x ,y )|0≤x ≤20,5≤y ≤20},作出事件对应的集合表示的面积,写出满足条件的事件是A ={(x ,y )|0≤x ≤20,5≤y ≤20,y ﹣x ≥5 },算出事件对应的集合表示的面积,根据几何概型概率公式得答案. 【详解】由题意知本题是一个几何概型,设甲和乙到达的分别为7时x 分、7时y 分, 则10≤x ≤20,5≤y ≤20,甲至少需等待乙5分钟,即y ﹣x ≥5,则试验包含的所有区域是Ω={(x ,y )|0≤x ≤20,5≤y ≤20},甲至少需等待乙5分钟所表示的区域为A ={(x ,y )|0≤x ≤20,5≤y ≤20,y ﹣x ≥5}, 如图:正方形的面积为20×15=300,阴影部分的面积为12⨯15×152252=,∴甲至少需等待乙5分钟的概率是225323008=, 故答案为38【点睛】本题主要考查“面积型”的几何概型,属于中档题. 解决几何概型问题常见类型有:长度型、角度型、面积型、体积型,求与面积有关的几何概型问题关鍵是计算问题的总面积以及事件的面积;几何概型问题还有以下几点容易造成失分,在备考时要高度关注:(1)不能正确判断事件是古典概型还是几何概型导致错误;(2)基本事件对应的区域测度把握不准导致错误 ;(3)利用几何概型的概率公式时 , 忽视验证事件是否等可能性导致错误.18.【解析】【分析】以正方体的中心为球心1为半径做球若点在球上或球内时符合要求求其体积根据几何概型求概率即可【详解】当正方体内的点落在以正方体中心为球心1为半径的球上或球内时此点到正方体中心的距离不大于解析:6π 【解析】 【分析】以正方体的中心为球心,1为半径做球,若点在球上或球内时,符合要求,求其体积,根据几何概型求概率即可. 【详解】当正方体内的点落在以正方体中心为球心,1为半径的球上或球内时,此点到正方体中心的距离不大于1, 因为344133V ππ=⨯⨯=球,2228V =⨯⨯=正方体 因此正方体内点到正方体中心的距离不大于1的概率24132226V P V 球正方体ππ⨯⨯===⨯⨯, 故填6π. 【点睛】本题主要考查了几何概型,球的体积,正方体的体积,属于中档题.19.【解析】分析:根据几何概型的概率公式即可得到结论详解:区间的两端点间距离是2在区间内任取一点该点表示的数都大于故在区间中随机地取出一个数这个数大于的概率为故答案为:点睛:本题主要考查概率的计算根据几解析:34【解析】分析:根据几何概型的概率公式即可得到结论.详解:区间[]0,2的两端点间距离是2,在区间1,22⎛⎤ ⎥⎝⎦内任取一点,该点表示的数都大于1sin62π=, 故在区间中随机地取出一个数,这个数大于12的概率为 1232.204-=- , 故答案为:34.点睛:本题主要考查概率的计算,根据几何概型的概率公式是解决本题的关键.20.【解析】分析:在内任投一点要使的面积小于5根据几何关系求解出它们的比例即可详解:记事件{的面积大于5}基本事件是的面积如图:事件A 的几何度量为图中阴影部分的面积(DE 分别是三角形的边上的四等分点)且 解析:716【解析】分析:在ABC ∆内任投一点M ,要使MBC ∆的面积小于5,根据几何关系求解出它们的比例即可.详解:记事件A ={MBC ∆的面积大于5}, 基本事件是ABC ∆的面积,如图:事件A 的几何度量为图中阴影部分的面积(D 、E 分别是三角形的边上的四等分点),ADE ABC ∆~∆Q ,且相似比为34,239416ADE ABC S S ∆∆⎛⎫∴== ⎪⎝⎭,()916ADE ABC S P A S ∆∆∴==. ∴MBC ∆的面积小于5的概率是()97111616P A -=-=. 故答案为:716. 点睛:本题考查几何概型,解答此题的关键在于明确测度比是面积比,对于几何概型常见的测度是长度之比、面积之比、体积之比、角度之比,要根据题意合理的判断和选择是哪一种测度进行求解,属于中档题.三、解答题21.(1)=83.2x 甲,=84x 乙;(2)22=26.36=13.2S S 甲乙,,=5.13S 甲,=3.63S 乙;(3)乙班的总体学习情况比甲班好 【解析】试题分析:每组样本数据有10个,求样本的平均数利用平均数公式,10个数的平均数等于这10个数的和除以10;比较平均分的大小可以看出两个班学生平均水平的高低,求样本的方差只需使用方差公式,求这10个数与平均数的差的平方方和再除以10;比较两组数据方差的大小就可得出两组数据的标准差的大小,标准差较小者成绩较稳定 。
高中必修三数学上期末模拟试卷带答案
高中必修三数学上期末模拟试卷带答案一、选择题1.在区间[]0,1上随机取两个数x ,y ,记P 为事件“23x y +≤”的概率,则(P = ) A .23B .12C .49D .292.如图阴影部分为曲边梯形,其曲线对应函数为1xy e =-,在长方形内随机投掷一颗黄豆,则它落在阴影部分的概率是( )A .23e - B .13e - C .43e- D .53e- 3.执行如图的程序框图,若输入1t =-,则输出t 的值等于( )A .3B .5C .7D .154.如图,一个边长为2的正方形里有一个月牙形的图案,为了估算这个月牙形图案的面积,向这个正方形里随机投入500粒芝麻,经过统计,落在月牙形图案内的芝麻有150粒,则这个月牙图案的面积约为( )5555.我国古代数学著作《九章算术》中,其意是:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问:米几何?右图是源于其思想的一个程序框图,若输出的2S =(单位:升),则输入k 的值为A .6B .7C .8D .96.执行如图的程序框图,如果输出a 的值大于100,那么判断框内的条件为( )A .5k <?B .5k ≥?C .6k <?D .6k ≥?7.某校从高一(1)班和(2)班的某次数学考试(试卷满分为100分)的成绩中各随机抽取了6份数学成绩组成一个样本,如茎叶图所示.若分别从(1)班、(2)班的样本中各取一份,则(2)班成绩更好的概率为( )A .1636B .1736C .12D .19368.从0,1,2,3这四个数中任取两个不同的数组成一个两位数,则这个两位数是偶数的概率为( )77999.已知统计某校1000名学生的某次数学水平测试成绩得到样本频率分布直方图如图所示,则直方图中实数a的值是()A.0.020B.0.018C.0.025D.0.0310.从2名男生和2名女生中任意选择两人在星期六、星期日参加某公益活动,每天一人,则星期六安排一名男生、星期日安排一名女生的概率为( )A.13B.512C.12D.71211.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如40337=+.(注:如果一个大于1的整数除1和自身外无其他正因数,则称这个整数为素数.)在不超过11的素数中,随机选取2个不同的数,其和小于等于10的概率是()A.12B.13C.14D.1512.有一个容量为200的样本,样本数据分组为[50,70),[70,90),[90,110),[110,130),[130,150),其频率分布直方图如图所示.根据样本的频率分布直方图估计样本数据落在区间[90,110)内的频数为()A.48B.60C.64D.72二、填空题13.若正方形ABCD的边长为4, E为四边形上任意一点,则AE的长度大于5的概率等于______14.已知2件次品和3件正品放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束,则恰好检测四次停止的概率为_____(用数字作答).15.已知四棱锥P ABCD -的所有顶点都在球O 的球面上,PA ⊥底面ABCD ,底面ABCD 为正方形, 2.PA AB ==现在球O 的内部任取一点,则该点取自四棱锥P ABCD-的内部的概率为______.16.已知某产品连续4个月的广告费i x (千元)与销售额i y (万元)(1,2,3,4i =)满足4115ii x==∑,4112i i y ==∑,若广告费用x 和销售额y 之间具有线性相关关系,且回归直线方程为^y bx a =+,0.6b =,那么广告费用为5千元时,可预测的销售额为___万元. 17.变量X 与Y 相对应的5组数据和变量U 与V 相对应的5组数据统计如表: X 10 11.3 11.8 12.5 13 U 10 11.3 11.8 12.5 13 Y12345V54321用b 1表示变量Y 与X 之间的回归系数,b 2表示变量V 与U 之间的回归系数,则b 1与b 2的大小关系是___.18.袋中有2个白球,1个红球,这些球除颜色外完全相同.现从袋中往外取球,每次任取1个记下颜色后放回,直到红球出现2次时停止,设停止时共取了X 次球,则(4)P X ==_______.19.执行下面的程序框图,如果输入的0.02t =,则输出的n =_______________.20.一组样本数据按从小到大的顺序排列为:1-,0,4,x ,y ,14,已知这组数据的平均数与中位数均为5,则其方差为__________.三、解答题21.近期,某公交公司分别推出支付宝和徽信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用x 表示活动推出的天数,y 表示每天使用扫码支付的人次(单位:十人次),统计数据如表l 所示: 表1根据以上数据,绘制了如右图所示的散点图.(1)根据散点图判断,在推广期内,(c,d均为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由);(2)根据(1)的判断结果及表1中的数据,求y关于x的回归方程,并预测活动推出第8天使用扫码支付的人次;参考数据:其中参考公式:对于一组数据,其回归直线的斜率和截距的最小二乘估计公式分别为:.22.随着智能手机的发展,各种“APP”(英文单词Application的缩写,一般指手机软件)应运而生.某机构欲对A市居民手机内安装的APP的个数和用途进行调研,在使用智能手机的居民中随机抽取100人,获得了他们手机内安装APP的个数,整理得到如图所示频率分布直方图.(Ⅰ)求a的值;(Ⅱ)从被抽取安装APP的个数不低于50的居民中,随机抽取2人进一步调研,求这2人安装APP的个数都低于60的概率;(Ⅲ)假设同组中的数据用该组区间的右端点值代替,以本次被抽取的居民情况为参考,试估计A 市使用智能手机的居民手机内安装APP 的平均个数在第几组(只需写出结论). 23.某校命制了一套调查问卷(试卷满分均为100分),并对整个学校的学生进行了测试,先从这些学生的成绩中随机抽取了50名学生的成绩,按照[)[)[]50,60,60,70,...,90,100分成5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分)(1)求频率分布直方图中的x 的值,并估计50名学生的成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表)(2)用样本估计总体,若该校共有2000名学生,试估计该校这次成绩不低于70分的人数. 24.某洗车店对每天进店洗车车辆数x 和用次卡消费的车辆数y 进行了统计对比,得到如下的表格: 车辆数x 10 18 26 36 40 用次卡消费的车辆数y710171823(Ⅰ)根据上表数据,用最小二乘法求出y 关于x 的线性回归方程;(b ∧的结果保留两位小数)(Ⅱ)试根据()I 求出的线性回归方程,预测50x =时,用次卡洗车的车辆数. 参考公式:由最小二乘法所得回归直线的方程是ˆˆˆybx a =+;其中,()1122211())()nni i i i i i nn i i i i x x y y x y nxy b x x x nx ====---==--∑∑∑∑$,a y bx =-$.25.某技术人员在某基地培育了一种植物,一年后,该技术人员从中随机抽取了部分这种植物的高度(单位:厘米)作为样本(样本容量为n )进行统计,绘制了如下频率分布直方图,已知抽取的样本植物高度在[)50,60内的植物有8株,在[]90,100内的植物有2株.(Ⅰ)求样本容量n 和频率分布直方图中的x ,y 的值;(Ⅱ)在选取的样本中,从高度在[]80,100内的植物中随机抽取3株,设随机变量X 表示所抽取的3株高度在[)80,90内的株数,求随机变量X 的分布列及数学期望;(Ⅲ)据市场调研,高度在[]80,100内的该植物最受市场追捧.老王准备前往该基地随机购买该植物50株.现有两种购买方案,方案一:按照该植物的不同高度来付费,其中高度在[]80,100内的每株10元,其余高度每株5元;方案二:按照该植物的株数来付费,每株6元.请你根据该基地该植物样本的统计分析结果为决策依据,预测老王采取哪种付费方式更便宜? 26.为研究女高中生身高与体重之间的关系,一调查机构从某中学中随机选取8名女高中生,其身高()x cm 和体重()y kg 数据如下表所示: 编号 1 2 3 4 5 6 7 8 身高/x cm164160158172162164174166体重/y kg60 46 43 48 48 50 61 52该调查机构绘制出该组数据的散点图后分析发现,女高中生的身高与体重之间有较强的线性相关关系.(1)调查员甲计算得出该组数据的线性回归方程为ˆˆ0.7yx a =+,请你据此预报一名身高为176cm 的女高中生的体重;(2)调查员乙仔细观察散点图发现,这8名同学中,编号为1和4的两名同学对应的点与其他同学对应的点偏差太大,于是提出这样的数据应剔除,请你按照这名调查人员的想法重新计算线性回归话中,并据此预报一名身高为176cm 的女高中生的体重; (3)请你分析一下,甲和乙谁的模型得到的预测值更可靠?说明理由.附:对于一组数据()()()1122,,,,,,n n x y x y x y L ,其回归方程ˆˆˆybx a =+的斜率和截距的最小二乘法估计分别为:()()()121ˆˆ,niii nii x x y y b ay bx x x ==--==--∑∑.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【解析】 【分析】由题意结合几何概型计算公式求解满足题意的概率值即可. 【详解】如图所示,01,01x y ≤≤≤≤表示的平面区域为ABCD , 平面区域内满足23x y +≤的部分为阴影部分的区域APQ ,其中2,03P ⎛⎫ ⎪⎝⎭,20,3Q ⎛⎫ ⎪⎝⎭,结合几何概型计算公式可得满足题意的概率值为1222233119p ⨯⨯==⨯. 本题选择D 选项.【点睛】数形结合为几何概型问题的解决提供了简捷直观的解法.用图解题的关键:用图形准确表示出试验的全部结果所构成的区域,由题意将已知条件转化为事件A 满足的不等式,在图形中画出事件A 发生的区域,据此求解几何概型即可.解析:D 【解析】 【分析】通过定积分可求出空白部分面积,于是利用几何概型公式可得答案. 【详解】由题可知长方形面积为3,而长方形空白部分面积为:()()11001|2x x e dx e x e -=-=-⎰,故所求概率为25133e e---=,故选D. 【点睛】本题主要考查定积分求几何面积,几何概型的运算,难度中等.3.C解析:C 【解析】 【分析】直接根据程序框图依次计算得到答案. 【详解】模拟执行程序,可得1t =-,不满足条件0t >,0t =,满足条件()()250t t +-<, 不满足条件0t >,1t =,满足条件()()250t t +-<, 满足条件0t >,3t =,满足条件()()250t t +-<,满足条件0t >,7t =,不满足条件()()250t t +-<,退出循环,输出t 的值为7. 故选:C. 【点睛】本题考查了程序框图,意在考查学生的计算能力和理解能力.4.D解析:D 【解析】 【分析】利用与面积有关的几何概型概率计算公式求解即可. 【详解】由题可知,正方形的面积为=22=4S ⨯正,设这个月牙图案的面积为S , 由与面积有关的几何概型概率计算公式可得,向这个正方形里随机投入芝麻,落在月牙形图案内的概率为150=4500S S P S ==正,解得65S =.【点睛】本题考查与面积有关的几何概型概率计算公式;属于基础题、常考题型.5.C解析:C 【解析】分析:执行程序框图,得到输出值4k S =,令24k=,可得8k =. 详解:阅读程序框图,初始化数值1,n S k ==,循环结果执行如下:第一次:14n =<成立,2,22k k n S k ==-=; 第二次:24n =<成立,3,263k k k n S ==-=; 第三次:34n =<成立,4,3124k k k n S ==-=; 第四次:44n =<不成立,输出24kS ==,解得8k =. 故选C.点睛:解决循环结构程序框图问题的核心在于:第一,要确定是利用当型还是直到型循环结构;第二,要准确表示累计变量;第三,要注意从哪一步开始循环,弄清进入或终止的循环条件、循环次数.6.C解析:C 【解析】 【分析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量a 的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案. 【详解】由题意,模拟程序的运算,可得k 1=,a 1=满足判断框内的条件,执行循环体,a 6=,k 3= 满足判断框内的条件,执行循环体,a 33=,k 5= 满足判断框内的条件,执行循环体,a 170=,k 7=此时,不满足判断框内的条件,退出循环,输出a 的值为170. 则分析各个选项可得程序中判断框内的“条件”应为k 6<? 故选:C . 【点睛】本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题.7.C解析:C【解析】【分析】由题意从(1)班、(2)班的样本中各取一份,(2)班成绩更好即(2)班成绩比(1)班成绩高,用列举法列出所有可能结果,由此计算出概率。
【典型题】高中必修三数学上期末一模试卷(带答案)(1)
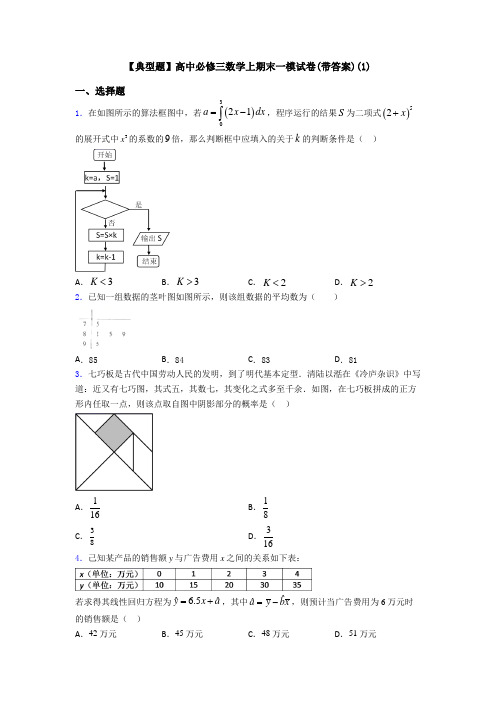
【典型题】高中必修三数学上期末一模试卷(带答案)(1)一、选择题1.在如图所示的算法框图中,若()321a x dx =-⎰,程序运行的结果S 为二项式()52x +的展开式中3x 的系数的9倍,那么判断框中应填入的关于k 的判断条件是( )A .3K <B .3K >C .2K <D .2K >2.已知一组数据的茎叶图如图所示,则该组数据的平均数为( )A .85B .84C .83D .813.七巧板是古代中国劳动人民的发明,到了明代基本定型.清陆以湉在《冷庐杂识》中写道:近又有七巧图,其式五,其数七,其变化之式多至千余.如图,在七巧板拼成的正方形内任取一点,则该点取自图中阴影部分的概率是( )A .116B .18 C .38D .3164.己知某产品的销售额y 与广告费用x 之间的关系如下表:若求得其线性回归方程为 6.5ˆˆyx a =+,其中ˆˆa y bx =-,则预计当广告费用为6万元时的销售额是( ) A .42万元B .45万元C .48万元D .51万元5.下列赋值语句正确的是( ) A .s =a +1 B .a +1=s C .s -1=a D .s -a =1 6.把化为五进制数是( ) A .B .C .D .7.执行如图所示的程序框图,若输入的a ,b ,c 依次为()sin sin αα,()cos sin αα,()sin cos αα,其中,42ππα⎛⎫∈⎪⎝⎭,则输出的x 为( )A .()cos cos ααB .()sin sin ααC .()cos sin ααD .()sin cos αα8.按照程序框图(如图所示)执行,第3 个输出的数是( )A .6B .5C .4D .39.我国古代数学著作《九章算术》中,有这样一道题目:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问:米几何?”下图是源于其思想的一个程序框图,若输出的3S =(单位:升),则输入的k =( )A .9B .10C .11D .1210.类比“赵爽弦图”,可类似地构造如图所示的图形,它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形,设2AD BD =,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是( )A .14B .13C .17D .41311.甲、乙两位同学在高一年级的5次考试中,数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是12,x x ,则下列叙述正确的是( )A .12x x >,乙比甲成绩稳定B .12x x >,甲比乙成绩稳定C .12x x <,乙比甲成绩稳定D .12x x <,甲比乙成绩稳定12.2路公共汽车每5分钟发车一次,小明到乘车点的时刻是随机的,则他候车时间不超过两分钟的概率是( )A .25B .35C .23D .15二、填空题13.在[1,1]-上随机地取一个数k ,则事件“直线y kx =与圆22(5)9x y -+=相离”发生的概率为_______。
【人教版】高中数学必修三期末模拟试题附答案

一、选择题1.七巧板是我们祖先的一项创造,被誉为“东方魔板”,它是由五块等腰直角三角形(两块全等的小三角形、一块中三角形和两块全等的大三角形)、一块正方形和一块平行四边形组成的.如图是一个用七巧板拼成的正方形,现从该正方形中任取一点,则此点取自黑色部分的概率是A.316B.38C.14D.182.袋中有白球2个,红球3个,从中任取两个,则互斥且不对立的两个事件是()A.至少有一个白球;都是白球B.两个白球;至少有一个红球C.红球、白球各一个;都是白球D.红球、白球各一个;至少有一个白球3.设袋中有80个红球,20个白球,若从袋中任取10个球,则其中恰好有6个白球的概率为()A.46801010100C CC⋅B.642081010C CC⋅C.462081010C CC⋅D.64801010100C CC⋅4.在编号分别为(0,1,2,,1)i i n=⋅⋅⋅-的n名同学中挑选一人参加某项活动,挑选方法如下:抛掷两枚骰子,将两枚骰子的点数之和除以n所得的余数如果恰好为i,则选编号为i 的同学.下列哪种情况是不公平的挑选方法()A.2n=B.3n=C.4n=D.6n=5.执行如图所示的程序框图,则输出的S=()A.1-B.2-C .2D .126.执行如图所示的程序框图,则输出的k 的值为( )A .3B .4C .5D .67.执行如下的程序框图,则输出的S 是( )A .36B .45C .36-D .45-8.执行如图的程序框图,如果输出a 的值大于100,那么判断框内的条件为( )A .5k <?B .5k ≥?C .6k <?D .6k ≥?9.2020年,一场突如其来的“新型冠状肺炎”使得全国学生无法在春季正常开学,不得不在家“停课不停学”.为了解高三学生居家学习时长,从某校的调查问卷中,随机抽取n 个学生的调查问卷进行分析,得到学生可接受的学习时长频率分布直方图(如下图所示),已知学习时长在[)9,11的学生人数为25,则n 的值为( )A .40B .50C .80D .10010.总体由编号为01,02,,29,30的30个个体组成,利用下面的随机数表选取4个个体.选取的方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出的第4个个体的编号为( ).7806 6572 0802 6314 2947 1821 98003204 9234 4935 3623 4869 6938 7481A .02B .14C .18D .2911.为了了解某社区居民是否准备收看电视台直播的“龙舟大赛”,某记者分别从社区60~70岁,40~50岁,20~30岁的三个年龄段中的128,192,x 人中,采用分层抽样的方法共抽出了30人进行调查,若60~70岁这个年龄段中抽查了8人,那么x 为( ) A .64B .96C .144D .16012.预测人口的变化趋势有多种方法,“直接推算法”使用的公式是()0 1nn P P k =+(1k >-),n P 为预测人口数,0P 为初期人口数,k 为预测期内年增长率,n 为预测期间隔年数.如果在某一时期有10k -<<,那么在这期间人口数 A .呈下降趋势B .呈上升趋势C .摆动变化D .不变二、填空题13.乒乓球赛规定:一局比赛,双方比分在10平前,一方连续发球2次后,对方再连续发球2次,依次轮换,每次发球,胜方得1分,负方得0分.设在甲、乙的比赛中,每次发球,甲发球得1分的概率为35,乙发球得1分的概率为23,各次发球的胜负结果相互独立,甲、乙的一局比赛中,甲先发球.则开始第4次发球时,甲、乙的比分为1比2的概率为________.14.在区间[2,4]-上随机地取一个实数x ,若实数x 满足||x m ≤的概率为23,则m =_______.15.设每门高射炮命中飞机的概率为0.06,且每一门高射炮是否命中飞机是独立的,若有一敌机来犯,则需要______门高射炮射击,才能以至少99%的概率命中它. 16.已知某程序框图如图所示,则该程序运行后输出S 的值为__________.17.执行如图所示的程序框图,若输入的1,7S K ==则输出的k 的值为_______.18.如果执行如图的程序框图,那么输出的S =__________.19.已知某市A社区35岁至45岁的居民有450人,46岁至55岁的居民有750人,56岁至65岁的居民有900人.为了解该社区35岁至65岁居民的身体健康状况,社区负责人采用分层抽样技术抽取若干人进行体检调查,若从46岁至55岁的居民中随机抽取了50人,试问这次抽样调查抽取的人数是________人.20.目前北方空气污染越来越严重,某大学组织学生参加环保知识竞赛,从参加学生中抽取40名,将其成绩(均为整数)整理后画出的频率分布直方图如图,若从成绩是80分以上(包括80分)的学生中选两人,则他们在同一分数段的概率为_______.三、解答题21.党的十九大报告指出,要以创新理念提升农业发展新动力,引领经济发展走向更高形态.为进一步推进农村经济结构调整,某村举办水果观光采摘节,并推出配套乡村游项目现统计了4月份200名游客购买水果的情况,得到如图所示的频率分布直方图:(1)若将购买金额不低于80元的游客称为“水果达人”,现用分层抽样的方法从样本的“水果达人”中抽取5人,求这5人中消费金额不低于100元的人数;(2)从(1)中的5人中抽取2人作为幸运客户免费参加山村旅游项目,请列出所有的基本事件,并求2人中至少有1人购买金额不低于100元的概率; (3)为吸引顾客,该村特推出两种促销方案, 方案一:每满80元可立减8元;方案二:金额超过50元但又不超过80元的部分打9折,金额超过80元但又不超过100元的部分打8折,金额超过100元的部分打7折.若水果的价格为11元/千克,某游客要购买10千克,应该选择哪种方案更优惠.22.某学校为了了解高中生的艺术素养,从学校随机选取男,女同学各50人进行研究,对这100名学生在音乐、美术、戏剧、舞蹈等多个艺术项目进行多方位的素质测评,并把调查结果转化为个人的素养指标x 和y ,制成下图,其中“*”表示男同学,“+”表示女同学. 若00.6x <<,则认定该同学为“初级水平”,若0.60.8x ≤≤,则认定该同学为“中级水平”,若0.81x <≤,则认定该同学为“高级水平”;若100y ≥,则认定该同学为“具备一定艺术发展潜质”,否则为“不具备明显艺术发展潜质”.(1)从50名女同学的中随机选出一名,求该同学为“初级水平”的概率;(2)从男同学所有“不具备明显艺术发展潜质的中级或高级水平”中任选2名,求选出的2名均为“高级水平”的概率;(3)试比较这100名同学中,男、女生指标y 的方差的大小(只需写出结论). 23.编写程序计算98246++⋅⋅⋅++的值.24.已知某算法的程序框图如图所示,若将输出的(x ,y )值依次记为(x 1,y 1),(x 2,y 2),…,(x n ,y n ),… (1)若程序运行中输出的一个数组是(9,t ),求t 的值.(2)程序结束时,共输出(x ,y )的组数为多少? (3)写出程序框图的程序语句.25.某同学在生物研究性学习中,对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究,于是他在4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下资料: 日期 4月1日 4月7日 4月15日 4月21日 4月30日 温差x C ︒ 10 11 13 12 8 发芽数y 颗2325302616(1)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另三天的数据,求出y 关于x 的线性回归方程y bx a =+;(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠? 附:回归直线的斜率和截距的最小二乘估计公式分别为:()()()1122211nniii ii i nniii i x x y y x y nx yb x x xnx====---==--∑∑∑∑,a y bx =-.26.在社会实践活动中,“求知”小组为了研究某种商品的价格x (元)和需求量y (件)之间的关系,随机统计了11月1日至11月5日该商品价格和需求量的情况,得到如下资料: 日期 11月1日 11月2日 11月3日 11月4日 11月5日 x (元) 14 16 18 20 22 y (件)1210743该小组所确定的研究方案是:先从这五天中选取2天数据,用剩下的3天数据求线性回归方程,再对被选取的2天数据进行检验.(1)若选取的是11月1日与11月5日两天数据,请根据11月2日至11月4日的数据,求出y 关于x 的线性回归方程y bx a =+;(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2件,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?参考公式:()()()1122211nniii ii i nniii i x x y y x y nx yb x x xnx====---==--∑∑∑∑,ay bx =-.【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【解析】设2AB =,则1BC CD DE EF ====. ∴1124BCI S ∆==,112242BCI EFGHS S ∆==⨯=平行四边形 ∴所求的概率为113422216P +==⨯ 故选A. 2.C解析:C 【分析】从装有3个红球和2个白球的红袋内任取两个球,所有的情况有3种:“2个白球”、“一个白球和一个红球”、“2个红球”.由于对立事件一定是互斥事件,且它们之中必然有一个发生而另一个不发生,结合所给的选项,逐一进行判断,从而得出结论. 【详解】从装有3个红球和2个白球的红袋内任取两个球,所有的情况有3种:“2个白球”、“一个白球和一个红球”、“2个红球”.由于对立事件一定是互斥事件,且它们之中必然有一个发生而另一个不发生, 对于A ,至少有1个白球;都是白球,不是互斥事件.故不符合.对于B 两个白球;至少有一个红球,是互斥事件,但也是对立事件,故不符合. 对于C 红球、白球各一个;都是白球是互斥事件,但不是对立事件,故符合. 对于D 红球、白球各一个;至少有一个白,不是互斥事件.故不符合. 故选:C .【点睛】本题主要考查互斥事件与对立事件的定义,意在考查学生对这些知识的理解掌握水平.3.C解析:C 【分析】根据古典概型的概率公式求解即可. 【详解】从袋中任取10个球,共有10100C 种,其中恰好有6个白球的有468020C C ⋅种即其中恰好有6个白球的概率为46208001010C C C ⋅ 故选:C 【点睛】本题主要考查了计算古典概型的概率,属于中档题.4.C解析:C 【分析】首先求出两枚骰子的点数之和可能的取值对应的概率,再分别讨论四个选项中n 的取值对应的余数的概率,若每一个余数的概率都相等则是公平的,若不相等则不公平,即可得正确选项. 【详解】由题意知两枚骰子的点数之和为X ,则X 可能为2,3,4,5,6,7,8,9,10,11,12,()1236P X ==, ()2336P X ==,()3436P X ==,()4536P X ==,()5636P X ==()6736P X ==,()5836P X ==,()4936P X ==,()31036P X ==,()21136P X ==,()11236P X ==, 对于选项A :2n =时,0,1,i = ()1351023636362P i ⎛⎫==++⨯= ⎪⎝⎭,()246421136363636362P i ==++++=,所以2n =是公平的,故选项A 不正确; 对于选项B :3n =时,0,1,2i =,()254110363636363P i ==+++=,()363113636363P i ==++=, ()145212363636363P i ==+++=,所以3n =是公平的,故选项B 不正确;对于选项C :4n =时,0,1,2,3i =()351103636364P i ==++=,()442136369P i ==+=, ()153123636364P i ==++=,()2625336363618P i ==++= 因为概率不相等,所以4n =不公平,故选项C 正确; 对于选项D :6n =时,0,1,2,3,4,5i =()511036366P i ==+=,()611366P i ===,()151236366P i ==+=, ()241336366P i ==+=,()331436366P i ==+=,()421536366P i ==+=,所以6n =是公平的,故选项D 不正确, 故选:C 【点睛】关键点点睛:本题解题的关键点是理解题意,对于所给n 的值的每一个余数出现的概率相等即为公平,不相等即为不公平.5.D解析:D 【分析】列举出前四次循环,可知,该算法循环是以3为周期的周期循环,利用周期性可得出输出的S 的值. 【详解】第一次循环,02020k =≤成立,1112S ==--,011k =+=; 第二次循环,12020k =≤成立,()11112S ==--,112k =+=;第三次循环,22020k =≤成立,12112S ==-,213k =+=;第四次循环,32020k =≤成立,1112S ==--,314k =+=; 由上可知,该算法循环是周期循环,且周期为3,依次类推,执行最后一次循环,20202020k =≤成立,且202036731=⨯+,此时12S =, 202012021k =+=,20212020k =≤不成立,跳出循环体,输出S 的值为12. 故选:D. 【点睛】本题考查利用程序框图计算输出结果,推导出循环的周期性是解题的关键,考查计算能力,属于中等题.6.C解析:C 【分析】根据框图模拟程序运算即可. 【详解】第一次执行程序,2111S =⨯-=,25S >-,继续循环,第二次执行程序,2k =,2121S =⨯-=-,25S >-,继续循环, 第三次执行程序,3k =,2(1)35S =⨯--=-,25S >-,继续循环, 第四次执行程序,4k =,2(5)414S =⨯--=-,25S >-,继续循环,第五次执行程序,5k =,2(14)532S =⨯--=-,25S <-,跳出循环,输出5k =,结束.故选C. 【点睛】本题主要考查了程序框图,涉及循环结构,解题关键注意何时跳出循环,属于中档题.7.A解析:A 【分析】列出每一步算法循环,可得出输出结果S 的值. 【详解】18i =≤满足,执行第一次循环,()120111S =+-⨯=-,112i =+=; 28i =≤成立,执行第二次循环,()221123S =-+-⨯=,213i =+=; 38i =≤成立,执行第三次循环,()323136S =+-⨯=-,314i =+=; 48i =≤成立,执行第四次循环,()4261410S =-+-⨯=,415i =+=; 58i =≤成立,执行第五次循环,()52101515S =+-⨯=-,516i =+=; 68i =≤成立,执行第六次循环,()62151621S =-+-⨯=,617i =+=; 78i =≤成立,执行第七次循环,()72211728S =+-⨯=-,718i =+=;88i =≤成立,执行第八次循环,()82281836S =-+-⨯=,819i =+=; 98i =≤不成立,跳出循环体,输出S 的值为36,故选A. 【点睛】本题考查算法与程序框图的计算,解题时要根据算法框图计算出算法的每一步,考查分析问题和计算能力,属于中等题.8.C解析:C 【解析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量a 的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案. 【详解】由题意,模拟程序的运算,可得k 1=,a 1=满足判断框内的条件,执行循环体,a 6=,k 3= 满足判断框内的条件,执行循环体,a 33=,k 5= 满足判断框内的条件,执行循环体,a 170=,k 7= 此时,不满足判断框内的条件,退出循环,输出a 的值为170. 则分析各个选项可得程序中判断框内的“条件”应为k 6<? 故选:C . 【点睛】本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题.9.B解析:B 【分析】由频率分布直方图的性质,求得0.25x =,再结合频率分布直方图的频率的计算方法,即可求解. 【详解】由频率分布直方图的性质,可得()20.050.150.051x +++=,解得0.25x =, 所以学习时长在[)9,11的频率2520.5x n==,解得50n =. 故选:B . 【点睛】本题主要考查了频率分布直方图性质及其应用,其中解答中熟记频率分布直方图的性质是解答的关键,着重考查了数据分析能力,以及计算能力.10.D解析:D 【解析】分析:根据随机数表法则取数:取两个数,不小于30的舍去,前面已取的舍去. 详解:从表第1行5列,6列数字开始由左到右依次选取两个数字中小于30的编号为:08,02,14,29.∴第四个个体为29. 选D .点睛:本题考查随机数表,考查对概念基本运用能力.11.D【解析】 【分析】根据60~70岁这个年龄段中128人中抽查了8人,可知分层抽样的抽样比为81=12816,因为共抽出30人,所以总人数为3016=480⨯人,即可求出20~30岁年龄段的人数. 【详解】根据60~70岁这个年龄段中128人中抽查了8人,可知分层抽样的抽样比为81=12816, 因为共抽出30人,所以总人数为3016=480⨯人,所以,20~30岁龄段的人有480128192160--=,故选D. 【点睛】本题主要考查了分层抽样,抽样,样本容量,属于中档题12.A解析:A 【分析】可以通过n P 与0P 之间的大小关系进行判断. 【详解】当10k -<<时,()011011nk k <+<<+<,, 所以()001nn P P k P =+<,呈下降趋势. 【点睛】判断变化率可以通过比较初始值与变化之后的数值之间的大小来判断.二、填空题13.【分析】先确定比分为1比2时甲乙在三次发球比赛中得分情况再分别求对应概率最后根据互斥事件概率公式求结果【详解】比分为1比2时有三种情况:(1)甲第一次发球得分甲第二次发球失分乙第一次发球得分(2)甲 解析:2875【分析】先确定比分为1比2时甲乙在三次发球比赛中得分情况,再分别求对应概率,最后根据互斥事件概率公式求结果 【详解】比分为1比2时有三种情况:(1)甲第一次发球得分,甲第二次发球失分,乙第一次发球得分(2)甲第一次发球失分,甲第二次发球得分,乙第一次发球得分(3)甲第一次发球失分,甲第二次发球失分,乙第一次发球失分所以概率为3222322212855355355375⨯⨯+⨯⨯+⨯⨯= 【点睛】本题考查根据互斥事件概率公式求概率,考查基本分析求解能力,属中档题.14.2【分析】画出数轴利用满足的概率可以求出的值即可【详解】如图所示区间的长度是6在区间上随机地取一个数若满足的概率为则有解得故答案是:2【点睛】该题考查的是有关长度型几何概型的问题涉及到的知识点有长度解析:2 【分析】画出数轴,利用x 满足||x m ≤的概率,可以求出m 的值即可. 【详解】 如图所示,区间[2,4]-的长度是6,在区间[2,4]-上随机地取一个数x , 若x 满足||x m ≤的概率为23, 则有2263m =,解得2m =, 故答案是:2. 【点睛】该题考查的是有关长度型几何概型的问题,涉及到的知识点有长度型几何概型的概率公式,属于简单题目.15.【分析】设需要门高射炮由题意得出解出的取值范围可得出正整数的最小值【详解】设需要门高射炮则命不中的概率为由题意得出得解得而因此至少需要门高射炮故答案为:【点睛】本题考查独立事件概率乘法公式的应用在涉 解析:75【分析】设需要n 门高射炮,由题意得出()110.060.99n--≥,解出n 的取值范围,可得出正整数n 的最小值.【详解】设需要n 门高射炮,则命不中的概率为()10.06n-,由题意得出10.940.99n -≥,得0.940.01n ≤,解得0.942log 0.01lg 0.94n ≥=-,而274.43lg 0.94-≈,因此,至少需要75门高射炮. 故答案为:75. 【点睛】本题考查独立事件概率乘法公式的应用,在涉及“至少”问题时,可以利用对立事件的概率公式来进行计算,考查运算求解能力,属于中等题.16.【分析】执行程序框图依次写出每次循环得到的Si 的值当i =2019时不满足条件退出循环输出S 的值为【详解】执行程序框图有S =2i =1满足条件执行循环Si =2满足条件执行循环Si =3满足条件执行循环Si解析:12-【分析】执行程序框图,依次写出每次循环得到的S ,i 的值,当i =2019时,不满足条件2018i ≤退出循环,输出S 的值为12-. 【详解】 执行程序框图,有 S =2,i =1满足条件2018i ≤ ,执行循环,S 3=-,i =2 满足条件2018i ≤ ,执行循环,S 12=-,i =3 满足条件2018i ≤ ,执行循环,S 13=,i =4 满足条件2018i ≤ ,执行循环, S =2,i =5 …观察规律可知,S 的取值以4为周期,由于2018=504*4+2,故有: S 12=-, i =2019, 不满足条件2018i ≤退出循环,输出S 的值为12-, 故答案为12-. 【点睛】本题主要考查了程序框图和算法,其中判断S 的取值规律是解题的关键,属于基本知识的考查.17.5【分析】模拟执行程序框图依次写出每次循环得到的的值当时根据题意退出循环输出结果【详解】模拟执行程序框图可得;;;;此时退出循环输出结果故答案为5【点睛】该题考查的是有关程序框图的问题涉及到的知识点解析:5 【分析】模拟执行程序框图,依次写出每次循环得到的,S K 的值,当5,58S K ==时,根据题意,退出循环,输出结果. 【详解】模拟执行程序框图,可得1,7S K ==;771,688S K =⋅==;763,5874S K =⋅==;355,5468S K =⋅==; 此时,57810<,退出循环,输出结果, 故答案为5. 【点睛】该题考查的是有关程序框图的问题,涉及到的知识点有计算循环结构程序框图输出结果的问题,属于简单题目.18.42【分析】输入由循环语句依次执行即可计算出结果【详解】当时当时当时当时当时当时故答案为42【点睛】本题主要考查了程序框图中的循环语句的运算求出输出值较为基础解析:42 【分析】输入1k =,由循环语句,依次执行,即可计算出结果 【详解】当1k =时,0212S =+⨯= 当2k =时,021226S =+⨯+⨯= 当3k =时,021222312S =+⨯+⨯+⨯= 当4k =时,021********S =+⨯+⨯+⨯+⨯= 当5k =时,0212223242530S =+⨯+⨯+⨯+⨯+⨯= 当6k =时,021222324252642S =+⨯+⨯+⨯+⨯+⨯+⨯= 故答案为42 【点睛】本题主要考查了程序框图中的循环语句的运算,求出输出值,较为基础19.【解析】根据题意可得抽样比为则这次抽样调查抽取的人数是即答案为140 解析:140【解析】根据题意可得抽样比为501,75015= 则这次抽样调查抽取的人数是()114507509002100140,1515++=⨯= 即答案为140.20.【解析】设第二组及第五组数据对应矩形的高为a 则10×(a+0015+0025+0035+a+0005)=1解得a=0010故各组的频率依次为:010015025035010005∵前三组的累积频率为 解析:715【解析】设第二组及第五组数据对应矩形的高为a , 则10×(a+0.015+0.025+0.035+a+0.005)=1, 解得a=0.010,故各组的频率依次为:0.10,0.15,0.25,0.35,0.10,0.05, ∵前三组的累积频率为:0.10+0.15+0.25=0.50, 故这次环保知识竞赛成绩的中位数为70; 成绩在[80,90)段的人数有10×0.010×40=4人, 成绩在[90,100]段的人数有10×0.005×40=2人,从成绩是80分以上(包括80分)的学生中任选两人共有15种不同的基本事件, 其中他们在同一分数段的基本事件有:7, 故他们在同一分数段的概率为7.15故答案为:7 15.三、解答题21.(1)2;(2)710;(3)应该选择方案二更优惠. 【分析】(1)由题意可求出金额在[)80,100“水果达人”的人数30人和消费金额在[]100,120“水果达人”的人数20人,然后利用分层抽样的比求出5人中消费金额不低于100元的人数为20523020⨯=+人;(2)由(1)可知抽取的5人中消费金额在[)80,100的有3人,分别记为A ,B ,C ,消费金额在[]100,120的有2人,记为a ,b ,即可列出所有的基本事件共有10种,其中满足条件的有7种,从而可求出概率;(3)由题意可得该游客要购买110元水果,分别计算两种方案所需支付金额,即可得解. 【详解】解:(1)由图可知,消费金额在[)80,100“水果达人”的人数为:200200.007530⨯⨯=人, 消费金额在[]100,120“水果达人”的人数为:200200.00520⨯⨯=人,分层抽样的方法从样本的“水果达人”中抽取5人,这5人中消费金额不低于100元的人数为:20523020⨯=+人;(2)由(1)得,消费金额在[)80,100的3个“水果达人”记为A ,B ,C , 消费金额在[]100,120的2个“水果达人”记为a ,b , 所有基本事件有:(),A B ,(),A C ,(),B C ,(),A a ,(),A b ,(),B a ,(),B b ,(),C a ,(),C b ,(),a b 共10N =种,2人中至少有1人购买金额不低于100元的有7n =种, 所求概率为710n N ==. (3)依题可知该游客要购买110元的水果, 若选择方案一,则需支付()80830102-+=元,若选择方案二,则需支付50300.9200.8100.7100+⨯+⨯+⨯=元, 所以应该选择方案二更优惠. 【点睛】此题考查了频率分布直方图,古典概型,函数等基础知识,考查了数据分析能力,运算求解能力,考查了化归与转化思想,属于中档题. 22.(I ) 310P =.(Ⅱ)15P =.(Ⅲ)这100名同学中男同学指标y 的方差大于女同学指标y 的方差. 【分析】(I )由图知,在50名参加测试的女同学中,指标x <0.6的有15人,由此能求出该同学为“初级水平”的概率;(Ⅱ)利用古典概型概率公式即可得到结果;(Ⅲ)由图可知,这100名同学中男同学指标y 的方差大于女同学指标y 的方差. 【详解】(I )由图知,在50名参加测试的女同学中,指标0.6x <的有15人, 所以,从50名女同学中随机选出一名,该名同学为“初级水平”的概率为1535010P ==. (Ⅱ)男同学“不具备明显艺术发展潜质的中级或高级水平”共有6人,其中“中级水平”有3人,分别记为1A ,2A ,3A .“高级水平”有3人,分别记为1B ,2B ,3B ,所有可能的结果组成的基本事件有:{}12,A A ,{}13,A A ,{}11,A B ,{}12,A B ,{}13,A B ,{}23,A A ,{}21,A B ,{}22,A B ,{}23,A B ,{}31,A B ,{}32,A B ,{}33,A B ,{}12,B B ,{}13,B B ,{}23,B B ,共15个,其中两人均为“高级水平”的共有3个,所以,所选2人均为“高级水平”的概率31155P ==. (Ⅲ)由图可知,这100名同学中男同学指标y 的方差大于女同学指标y 的方差. 【点睛】本题考查概率的求法,考查列举法等基础知识,考查运算求解能力,考查函数与方程思想,是基础题. 23.答案详见解析. 【解析】 【分析】根据题干要求写出循环结构的程序即可. 【详解】 程序如下: i=2 sum=0 DO sum=sum+i i=i+2LOOP UNTIL i>98 PRINT sum END 【点睛】应用循环语句编写程序时需注意: ①循环语句中的循环变量一般要设初始值.②在循环过程中需要有“结束”的语句,程序中最忌“死循环”. 24.(1)-4;(2)1009;(3)答案见解析. 【解析】 试题分析:(1)利用所给的程序框图运行程序可得当x=9时,y=-4,则t 的值为-4. (2)结合程序的算法和循环结构的特点可知共输出(x ,y )的组数为1009;(3)将所给的程序框图翻译为算法语句,利用循环语句设计相应的程序即可,注意循环语句应设计为DO 语句的形式. 试题(1)由程序框图知,当x=1时,y=0; 当x=3时,y=-2; 当x=9时,y=-4,所以t=-4.(2)当n=1时,输出一对,当n=3时,又输出一对,…,当n=2 017时,输出最后一对,共输出(x ,y )的组数为20182=1 009.(3)程序框图的程序语句如下: x =1 y =0 n =1 DOPRINT (x ,y ) n =n +2 x =3*x y =y -2LOOP UNTIL n >2 017 END点睛:程序框图的条件结构和循环结构分别对应算法语句的条件语句和循环语句,两种语句的阅读理解是复习重点.输入、输出和赋值语句是任何一个算法必不可少的语句,一个语句可以输出多个表达式.在赋值语句中,一定要注意其格式的要求,如“=”的右侧必须是表达式,左侧必须是变量;一个语句只能给一个变量赋值;变量的值始终等于最近一次赋给它的值,先前的值将被替换. 25.(1)532y x =-;(2)线性回归方程是可靠的. 【分析】(1)根据最小二乘法公式,分别将数据代入计算,即可得答案;(2)选取的是4月1日与4月30日的两组数据,即10x =和8x =代入判断即可; 【详解】解:(1)由数据得12x =,27y =,3972x y =,23432x =; 又31977i i i x y ==∑,321434i i x ==∑;97797254344322b -==-,5271232a =-⨯=-;所以y 关于x 的线性回归方程为:532y x =-. (2)当10x =时,5103222y =⨯-=,22232-<; 当8x =时,583222y =⨯-=,17162-<, 所得到的线性回归方程是可靠的. 【点睛】本题考查最小二乘法求回归直线方程及利用回归方程进行判断拟合效果,考查数据处理能力,求解时注意回归直线必过样本点中心的应用. 26.(1) 1.534y x =-+;(2)详见解析. 【分析】(1)利用表中数据,分别求得:,x y ,再利用公式求得,b a ,然后写出回归直线方程即可. (2)根据(1)中的回归直线方程,令14x =, 22x =求得相应的y 值,再与实际值结合误差要求比较即可.【详解】由表中数据得: ()()1116182018,10747,33x y =++==++= 311610187204366ii i x y ==⨯+⨯+⨯=∑, 322221161820980i i x==++=∑,313222133663187 1.59803183i ii i i x y x y b x x==--⨯⨯===--⨯-∑∑, ()7 1.51834a y bx =-=--⨯=,所以y 关于x 的线性回归方程是 1.534y x =-+.(2)当14x =时, 1.5143413y =-⨯+=,131212-=<, 当22x =时, 1.522341y =-⨯+=,1322-=≤, 所以(1)中所得到的线性回归方程是可靠的.【点睛】本题主要考查回归直线方程的求法以及应用,还考查了运算求解的能力,属于中档题.。
【人教版】高中数学必修三期末一模试卷(及答案)

一、选择题1.继刘徽之后,祖冲之为求得更精确的圆周率而作了艰苦卓绝的努力.据《惰书》记载,他已算得3.1415926 3.1415927π<<.他还得到圆周率的两个近似分数值355113和227,并称355113为密率,227为约率,他的圆周率小数值则被后世称为祖率.现用随机模拟的方法得到圆周率,从区间[0,1]随机抽取2000个数,构成1000个数对(,)x y ,其中两数的平方和小于1的数对(,)x y 共有785个,则用随机模拟的方法得到的π的近似值为( ) A .31411000B .355113C .15750D .2272.质地均匀的正四面体的四个面上分别写有数字0,1,2,3,把两个这样的四面体抛在桌面上,露在外面的6个数字为2,0,1,3,0,3的概率为( ) A .19B .164C .18D .1163.已知0.5log 5a =、3log 2b =、0.32c =、212d ⎛⎫= ⎪⎝⎭,从这四个数中任取一个数m ,使函数()32123x mx x f x =+++有极值点的概率为( ) A .14B .12C .34D .14.在编号分别为(0,1,2,,1)i i n =⋅⋅⋅-的n 名同学中挑选一人参加某项活动,挑选方法如下:抛掷两枚骰子,将两枚骰子的点数之和除以n 所得的余数如果恰好为i ,则选编号为i 的同学.下列哪种情况是不公平的挑选方法( ) A .2n =B .3n =C .4n =D .6n =5.执行如图所示的程序框图,结果是( )A.11 B.12 C.13 D.14 6.若执行如图所示的程序框图,则输出S的值是()A.63 B.15 C.31 D.32 7.执行如图所示的程序框图,若输入x=9,则循环体执行的次数为()A .1次B .2次C .3次D .4次8.如图给出的是计算1111246102+++⋅⋅⋅+的值的一个程序框图,其中判断框中应填入的是( )A .102i >B .102i ≤C .100i >D .100i ≤9.为了解一片经济树林的生长情况,随机测量了其中100株树木的底部周长(单位:cm ),根据所得数据画出样本的频率分布直方图如图所示.那么在这100株树木中,底部周长小于110cm 的株数n 是 ( )A .30B .60C .70D .8010.小明同学在做市场调查时得到如下样本数据x1 3 6 10 y 8a42他由此得到回归直线的方程为ˆ 2.115.5yx =-+,则下列说法正确的是( ) ①变量x 与y 线性负相关 ②当2x =时可以估计11.3y = ③6a = ④变量x 与y 之间是函数关系 A .①B .①②C .①②③D .①②③④11.下列说法正确的是( )①设某大学的女生体重(kg)y 与身高(cm)x 具有线性相关关系,根据一组样本数据(,)(1,2,3,,)i i x y i n =,用最小二乘法建立的线性回归方程为0.8585.71y x =- ,则若该大学某女生身高增加1cm ,则其体重约增加0.85kg ;②关于x 的方程210(2)x mx m -+=>的两根可分别作为椭圆和双曲线的离心率; ③过定圆C 上一定点A 作圆的动弦AB ,O 为原点,若1()2OP OA OB =+,则动点P 的轨迹为椭圆;④已知F 是椭圆22143x y +=的左焦点,设动点P 在椭圆上,若直线FP 的斜率大于3,则直线OP (O 为原点)的斜率的取值范围是3333(,)(,)282-∞-. A .①②③ B .①③④C .①②④D .②③④12.若某中学高二年级8个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数是( )A .90.5B .91.5C .90D .91二、填空题13.过点(0,0)O 作直线与圆22(45)(8)169x y -+-=相交,则在弦长为整数的所有直线中,等可能的任取一条直线,则弦长长度不超过14的概率为______________. 14.在区间[-1,2]上随机取一个数x,则x ∈[0,1]的概率为 .15.如图,在平放的边长为1的正方形中随机撒1000粒豆子,有380粒落到红心阴影部分上,据此估计红心阴影部分的面积为____.16.某程序框图如图所示,则该程序运行后输出的S 的值为________.17.已知某程序框图如图所示,则执行该程序后输出的结果是_____18.一个算法的程序框图如图所示,则该程序运行后输出的结果是.19.某校为了解1000名高一新生的身体生长状况,用系统抽样法(按等距的规则)抽取40名同学进行检查,将学生从1~1000进行编号,现已知第18组抽取的号码为443,则第一组用简单随机抽样抽取的号码为_________20.设一个回归方程为0.4 1.8y x =-,则当25x =时,y 的估计值是_______.三、解答题21.党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一.为坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村脱贫,坚持扶贫同扶智相结合,此帮扶单位考察了甲、乙两种不同的农产品加工生产方式,现对两种生产方式的产品质量进行对比,其质量按测试指标可划分为:指标在区间[80,100]的为优等品;指标在区间[60,80)的为合格品,现分别从甲、乙两种不同加工方式生产的农产品中,各自随机抽取100件作为样本进行检测,测试指标结果的频数分布表如下: 甲种生产方式: 指标区间 [65,70)[70,75)[75,80)[80,85)[85,90)[90,95]频数51520301515乙种生产方式: 指标区间 [70,75)[75,80)[80,85)[85,90)[90,95)[95,100]频数51520302010(1)在用甲种方式生产的产品中,按合格品与优等品用分层抽样方式,随机抽出5件产品,①求这5件产品中,优等品和合格品各多少件;②再从这5件产品中,随机抽出2件,求这2件中恰有1件是优等品的概率;(2)所加工生产的农产品,若是优等品每件可售55元,若是合格品每件可售25元.甲种生产方式每生产一件产品的成本为15元,乙种生产方式每生产一件产品的成本为20元.用样本估计总体比较在甲、乙两种不同生产方式下,该扶贫单位要选择哪种生产方式来帮助该扶贫村来脱贫?22.某市工会组织了一次工人综合技能比赛,一共有1000名工人参加,他们的成绩都分布在[]52,100内,数据经过汇总整理得到如下的频率分布直方图,规定成绩在76分及76分以上的为优秀.(1)求图中t 的值;(2)估计这次比赛成绩的平均数(同一组中的数据以这组数据所在区间中点的值作代表);(3)某工厂车间有25名工人参加这次比赛,他们的成绩分布和整体的成绩分布情况完全一致,若从该车间参赛的且成绩为优秀的工人中任选两人,求这两人成绩均低于92分的概率.23.如图,在边长为4的正方形ABCD 的边上有一点P ,沿着折线BCDA 由点B (起点)向点A (终点)运动.设点P 运动的路程为x ,APB △的面积为y ,求y 与x 之间的函数关系式,并画出程序框图.24.编写程序计算98246++⋅⋅⋅++的值.25.“湖广熟,天下足”,鱼米之乡的湖北是全国重要的农产品生产地.而受疫情影响,像莲藕、小龙虾等湖北很多优质农副产品近期都面临销售难题.为了让淜北尽快恢复正常,央视主持人朱广权化身直播带货官,和网红们一起为湖北产品做公益直播.在为湖北某地区的小龙虾进行带货时,需大致了解该地区小龙虾的产量,通过调查发现湖北某地区近几年的小龙虾产量统计如下表: 年份 2014 2015 2016 2017 2018 2019 年份代码t 1 2 3 4 5 6 年产量y (万吨)6.66.97.47.788.4(1)根据表中数据,建立关于t 的线性回归方程y bt a =+; (2)请你根据线性回归方程预测今年(2020年)该地区小龙虾的年产量.附:对于一组数据()11,t y ,()22,t y ,…,(),n n t y ,其回归直线y bt a =+的斜率和截距的最小二乘估计分别为:()()()121ˆniii ni i t t y y bt t ==--=-∑∑,a y bt =-.(参考数据:()()616.3ii i tty y =--=∑)26.某市举办了一次“诗词大赛”,分预赛和复赛两个环节,已知共有20000名学生参加了预赛,现从参加预赛的全体学生中随机地抽取100人的预赛成绩作为样本,得到如下的统计数据. 得分(百分制) [0,20) [20,40) [40,60) [60,80) [80,100] 人数1020302515(1)规定预赛成绩不低于80分为优良,若从样本中预赛成绩不低于60分的学生中随机地抽取2人,求恰有1人预赛成绩优良的概率;(2)由样本数据分析可知,该市全体参加预赛学生的预赛成绩Z 服从正态分布()2,N μσ,其中μ可近似为样本中的100名学生预赛成绩的平均值(同一组数据用该组数据的中间值代替),且2361σ=.利用该正态分布,估计全市参加预赛的全体学生中预赛成绩不低于72分的人数;(3)预赛成绩不低于91分的学生将参加复赛,复赛规则如下: ①参加复赛的学生的初始分都设置为100分;②参加复赛的学生可在答题前自己决定答题数量n ,每一题都需要“花”掉一定分数来获取答题资格(即用分数来买答题资格),规定答第k 题时“花”掉的分数为()0.21,2,k k n =; ③每答对一题得2分,答错得0分;④答完n 题后参加复赛学生的最终分数即为复赛成绩.已知学生甲答对每道题的概率均为0.75,且每题答对与否都相互独立,则当他的答题数量n 为多少时,他的复赛成绩的期望值最大?参考数据:若()2~,Z Nμσ,则() 6.827P Z μσμσ-<<+≈,()220.9545P Z μσμσ-<<+≈,()330.9973P Z μσμσ-<<+≈【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】先作出事件对应的平面区域,再利用几何概型和随机模拟求解. 【详解】由题得0101x y ≤≤⎧⎨≤≤⎩,对应的区域为图中的正方形OABC 区域,事件A :2201011x y x y ≤≤⎧⎪≤≤⎨⎪+<⎩对应的区域为图中的扇形OAC 区域,由题得2117851574==10001150ππ⋅∴⨯,. 用随机模拟的方法得到的π的近似值为15750. 故选:C 【点睛】方法点睛:几何概型的解题步骤:首先是判断事件是一维问题还是二维、三维问题(事件的结果与一个变量有关就是一维的问题,与两个变量有关就是二维的问题,与三个变量有关就是三维的问题);接着,如果是一维的问题,先确定试验的全部结果和事件A 构成的区域长度(角度、弧长等),最后代几何概型的概率公式;如果是二维、三维的问题,先设出二维或三维变量,再列出试验的全部结果和事件A 分别满足的约束条件,作出两个区域,最后计算两个区域的面积或体积代公式.2.C解析:C 【分析】露在外面的6个数字为2,0,1,3,0,3,则向下的数分别为1和2,求出所有的基本事件个数和向下数字为1和2的基本事件个数,代入概率公式即可. 【详解】抛两个正四面体,共有4416⨯=个基本事件,向下数字为1和2的基本事件共有2个,分别是1,2和()2,1, 所以向下数字为1和2的概率21168P ==, 故选:C 【点睛】本题主要考查随机事件概率的计算,难度较低.3.B解析:B 【分析】求出函数的导数,根据函数的极值点的个数求出m 的范围,通过判断a ,b ,c ,d 的范围,得到满足条件的概率值即可. 【详解】f ′(x )=x 2+2mx +1, 若函数f (x )有极值点, 则f ′(x )有2个不相等的实数根,故△=4m 2﹣4>0,解得:m >1或m <﹣1,而a =log 0.55<﹣2,0<b =log 32<1、c =20.3>1,0<d =(12)2<1, 满足条件的有2个,分别是a ,c , 故满足条件的概率p 2142==, 故选:B . 【点睛】本题考查了函数的单调性、极值问题,考查导数的应用以及对数、指数的性质,是一道中档题.4.C解析:C 【分析】首先求出两枚骰子的点数之和可能的取值对应的概率,再分别讨论四个选项中n 的取值对应的余数的概率,若每一个余数的概率都相等则是公平的,若不相等则不公平,即可得正确选项. 【详解】由题意知两枚骰子的点数之和为X ,则X 可能为2,3,4,5,6,7,8,9,10,11,12,()1236P X ==, ()2336P X ==,()3436P X ==,()4536P X ==,()5636P X ==()6736P X ==,()5836P X ==,()4936P X ==,()31036P X ==,()21136P X ==,()11236P X ==, 对于选项A :2n =时,0,1,i = ()1351023636362P i ⎛⎫==++⨯= ⎪⎝⎭,()246421136363636362P i ==++++=,所以2n =是公平的,故选项A 不正确; 对于选项B :3n =时,0,1,2i =,()254110363636363P i ==+++=,()363113636363P i ==++=, ()145212363636363P i ==+++=,所以3n =是公平的,故选项B 不正确; 对于选项C :4n =时,0,1,2,3i = ()351103636364P i ==++=,()442136369P i ==+=,()153123636364P i ==++=,()2625336363618P i ==++= 因为概率不相等,所以4n =不公平,故选项C 正确; 对于选项D :6n =时,0,1,2,3,4,5i = ()511036366P i ==+=,()611366P i ===,()151236366P i ==+=, ()241336366P i ==+=,()331436366P i ==+=,()421536366P i ==+=, 所以6n =是公平的,故选项D 不正确, 故选:C 【点睛】关键点点睛:本题解题的关键点是理解题意,对于所给n 的值的每一个余数出现的概率相等即为公平,不相等即为不公平.5.B解析:B 【分析】根据已知的程序语句可得,该程序的功能是利用循环结构计算并输出k 的值,模拟程序的运行过程,可得答案. 【详解】根据题意,模拟程序框图的运行过程,如下:17,0n k ==17不是偶数,3171=52n =⨯+,011k =+=,521≠; 52是偶数,52262n ==,112k =+=,261≠; 26是偶数,26132n ==,213k =+=,131≠; 13不是偶数,3131=40n =⨯+,314k =+=,401≠; 40是偶数,40202n ==,415k =+=,201≠; 20是偶数,20102n ==,516k =+=,101≠; 10是偶数,1052n ==,617k =+=,51≠; 5不是偶数,351=16n =⨯+,718k =+=,161≠;16是偶数,1682n ==,819k =+=,81≠; 8是偶数,842n ==,9110k =+=,41≠;4是偶数,422n ==,10111k =+=,21≠; 2是偶数,212n ==,11112k =+=,11=; 故选:B 【点睛】 关键点睛:解题的关键是要读懂程序框图,模拟程序框图的运行过程,即突破难点.6.C解析:C 【分析】根据程序框图模拟程序计算即可求解. 【详解】模拟程序的运行,可得1S =,1i =; 满足条件5i <,执行循环体,3S =,2i =; 满足条件5i <,执行循环体,7=S ,3i =; 满足条件5i <,执行循环体,15S =,4i =; 满足条件5i <,执行循环体,31S =,5i =; 此时,不满足条件5i <,退出循环,输出S 的值为31. 故选:C 【点睛】本题主要考查了程序框图,循环结构,属于中档题.7.C解析:C 【分析】根据程序框图依次计算得到答案. 【详解】9,5x y ==,41y x -=>;115,3x y ==,413y x -=>; 1129,39x y ==,419y x -=<;结束. 故选:C . 【点睛】本题考查了程序框图的循环次数,意在考查学生的理解能力和计算能力.8.B解析:B 【解析】 【分析】根据题目所求表达式1111246102+++⋅⋅⋅+中最后一个数字1102,确定填写的语句.【详解】由于题目所求是1111246102+++⋅⋅⋅+,最后一个数字为1102,即当102i =时,判断是,继续循环,2104i i =+=,判断否,退出程序输出S 的值,由此可知应填102i ≤.故选B. 【点睛】本小题主要考查填写程序框图循环条件,属于基础题.9.C解析:C 【解析】解:由图可知:则底部周长小于110cm 段的频率为(0.01+0.02+0.04)×10=0.7, 则频数为100×0.7=70人. 故选C .10.C解析:C 【解析】 【分析】根据数据和回归方程对每一个选项逐一判断得到答案. 【详解】① 2.1b =-⇒变量x 与y 线性负相关,正确 ②将2x =代入回归方程,得到11.3y =,正确 ③将(,)x y 代入回归方程,解得6a =,正确 ④变量x 与y 之间是相关关系,不是函数关系,错误 答案为C 【点睛】本题考查了回归方程的相关知识,其中中心点(,)x y 一定在回归方程上是同学容易遗忘的知识点.11.C解析:C 【分析】利用线性回归方程系数的几何意义,圆锥曲线离心率的范围,椭圆的性质,逐一判断即可. 【详解】①设某大学的女生体重y (kg )与身高x (cm )具有线性相关关系,根据一组样本数据(x i ,y i )(i =1,2,…,n ),用最小二乘法建立的线性回归方程为y ∧=0.85x ﹣85.71,则若该大学某女生身高增加1cm ,则其体重约增加0.85kg ,正确;②关于x 的方程x 2﹣mx +1=0(m >2)的两根之和大于2,两根之积等于1,故两根中,一根大于1,一根大于0小于1,故可分别作为椭圆和双曲线的离心率.正确;③设定圆C的方程为(x﹣a)2+(x﹣b)2=r2,其上定点A(x0,y0),设B(a+r cosθ,b+r sinθ),P(x,y),由12OP =(OA OB+)得22x a rcosxy b rsinyθθ++⎧=⎪⎪⎨++⎪=⎪⎩,消掉参数θ,得:(2x﹣x0﹣a)2+(2y﹣y0﹣b)2=r2,即动点P的轨迹为圆,∴故③不正确;④由22143x y+=,得a2=4,b2=3,∴1c==.则F(﹣1,0),如图:过F作垂直于x轴的直线,交椭圆于A(x轴上方),则x A=﹣1,代入椭圆方程可得32Ay=.当P为椭圆上顶点时,P(0FPk=32OAk=-,∴当直线FP时,直线OP的斜率的取值范围是32⎛⎫-∞-⎪⎝⎭,.当P为椭圆下顶点时,P(0,∴当直线FP时,直线OP的斜率的取值范围是(8,32),综上,直线OP(O为原点)的斜率的取值范围是32⎛⎫-∞-⎪⎝⎭,∪,32).故选C【点睛】本题以命题真假的判断为载体,着重考查了相关系数、离心率、椭圆简单的几何性质等知识点,属于中档题.12.A解析:A【分析】共有8个数据,中位数就是由小到大中间两数的平均数,求解即可.【详解】根据茎叶图,由小到大排列这8个数为84,85,89,90,91,92,93,95,所以中位数为90+91=90.52,故选A.【点睛】本题主要考查了中位数,茎叶图,属于中档题.二、填空题13.【分析】根据圆的性质可求得最长弦和最短弦的长度从而得到所有弦长为整数的直线条数从中找到长度不超过的直线条数根据古典概型求得结果【详解】由题意可知最长弦为圆的直径:在圆内部且圆心到的距离为最短弦长为: 解析:932【分析】根据圆的性质可求得最长弦和最短弦的长度,从而得到所有弦长为整数的直线条数,从中找到长度不超过14的直线条数,根据古典概型求得结果. 【详解】由题意可知,最长弦为圆的直径:221326r =⨯=()0,0O 在圆内部且圆心到O 12=∴最短弦长为:210=∴弦长为整数的直线的条数有:()22510232⨯-+=条其中长度不超过14的条数有:()2141019⨯-+=条∴所求概率:932p =本题正确结果:932【点睛】本题考查古典概型概率问题的求解,涉及到过圆内一点的最长弦和最短弦的长度的求解;易错点是忽略圆的对称性,造成在求解弦长为整数的直线的条数时出现丢根的情况.14.【分析】直接利用长度型几何概型求解即可【详解】因为区间总长度为符合条件的区间长度为所以由几何概型概率公式可得在区间-12上随机取一个数x 则x ∈01的概率为故答案为:【点睛】解决几何概型问题常见类型有解析:13【分析】直接利用长度型几何概型求解即可. 【详解】因为区间总长度为()213--=, 符合条件的区间长度为101-=, 所以,由几何概型概率公式可得,在区间[-1,2]上随机取一个数x,则x ∈[0,1]的概率为13, 故答案为:13. 【点睛】解决几何概型问题常见类型有:长度型、角度型、面积型、体积型,求与长度有关的几何概型问题关鍵是计算问题的总长度以及事件的长度.15.38【解析】【分析】根据几何槪型的概率意义即可得到结论【详解】正方形的面积S =1设阴影部分的面积为S ∵随机撒1000粒豆子有380粒落到阴影部分∴由几何槪型的概率公式进行估计得即S =038故答案为:解析:38 【解析】 【分析】根据几何槪型的概率意义,即可得到结论. 【详解】正方形的面积S =1,设阴影部分的面积为S , ∵随机撒1000粒豆子,有380粒落到阴影部分, ∴由几何槪型的概率公式进行估计得38011000S =, 即S =0.38, 故答案为:0.38. 【点睛】本题主要考查几何槪型的概率的计算,利用豆子之间的关系建立比例关系是解决本题的关键,比较基础.16.【分析】根据程序框图依次计算运行结果发现输出的S 值周期变化利用终止运行的条件判断即可求解【详解】由程序框图得:;第一次运行第二次运行第三次运行故周期为4当程序运行了2019次故的值为故答案为【点睛】 解析:12【分析】根据程序框图,依次计算运行结果,发现输出的S 值周期变化,利用终止运行的条件判断即可求解 【详解】由程序框图得:1,1S k ==; 第一次运行1,2;8S k == 第二次运行1212,3;842S k =⨯=== 第三次运行121,4;2S k =⨯==故周期为4, 当2020k =,程序运行了2019次,201945043=⨯+,故S 的值为12故答案为12本题考查程序框图,根据程序的运行功能判断输出值的周期变化是关键,是基础题17.-1【分析】计算的值找出周期根据余数得到答案【详解】依次计算得:…周期为32019除以3余数为0故答案为-1【点睛】本题考查了程序框图的相关知识计算数据找到周期规律是解题的关键解析:-1 【分析】计算a 的值,找出周期,根据余数得到答案. 【详解】 依次计算得:2,1a i ==1,22a i ==1,3a i =-= 2,4a i == ….周期为32019除以3余数为0,1a =- 故答案为-1 【点睛】本题考查了程序框图的相关知识,计算数据找到周期规律是解题的关键.18.4【分析】执行程序当时循环结束即可得出【详解】因为第一次进入循环后;第二次进入循环后;第三次进入循环后;第四次进入循环后循环结束所以输出的结果为4【点睛】本题主要考查了程序框图求输出的值做题时要仔细解析:4 【分析】执行程序,当4K =时循环结束,即可得出 【详解】因为第一次进入循环后1,1S K ==; 第二次进入循环后3,2S K ==; 第三次进入循环后11,3S K ==;第四次进入循环后2059,4S K ==,循环结束,所以输出的结果为4 【点睛】本题主要考查了程序框图求输出的值,做题时要仔细点,属于基础题.19.18【解析】【分析】由题意知抽样方法为系统抽样因此若第一组抽取号码为x 则第18组抽取的号码为即可解得【详解】因为抽样方法为系统抽样因此若第一组抽取号码为x 则第18组抽取的号码为解得【点睛】本题主要考解析:18【分析】由题意知,抽样方法为系统抽样,因此,若第一组抽取号码为x ,则第18组抽取的号码为1725443x +⨯=,即可解得. 【详解】因为抽样方法为系统抽样,因此,若第一组抽取号码为x ,则第18组抽取的号码为1725443x +⨯=,解得18x =. 【点睛】本题主要考查了系统抽样,属于中档题.20.2【解析】分析:直接利用回归方程将代入即可求得的估计值详解:∵回归方程为∴当时的估计值为故答案为82点睛:本题考查回归方程的运用考查学生的计算能力属于基础题解析:2 【解析】分析:直接利用回归方程,将25x =代入,即可求得y 的估计值. 详解:∵回归方程为0.4 1.8y x =-,∴当25x =时,y 的估计值为 0.425 1.88.2y =⨯-=.故答案为8.2.点睛:本题考查回归方程的运用,考查学生的计算能力,属于基础题.三、解答题21.(1)①优等品3件,合格品2件;②35;(2)选择乙生产方式. 【分析】(1)①根据频数分布表知:甲的优等品率为0.6,合格品率为0.4,即可得到抽去的件数;②记3件优等品为A ,B ,C ,2件合格品分别为a ,b ,从中随机抽2件,列举出基本事件的总数,利用古典概型及其概率的计算公式,即可求解;(2)分别计算出甲、乙种生产方式每生产100件所获得的利润为1T 元2T 元,比较即可得到结论. 【详解】(1)①由频数分布表知:甲的优等品率为0.6,合格品率为0.4,所以抽出的5件产品中,优等品3件,合格品2件.②记3件优等品为A ,B ,C ,2件合格品分别为a ,b ,从中随机抽2件,抽取方式有AB ,AC ,Aa ,Ab ,BC ,Ba ,Bb ,Ca ,Cb ,ab 共10种,设“这2件中恰有1件是优等品的事件”为M ,则事件M 发生的情况有6种,所以()63105P M ==.(2)根据样本知甲种生产方式生产100件农产品有60件优等品,40件合格品;乙种生产方式生产100件农产品有80件优等品,20件合格品. 设甲种生产方式每生产100件所获得的利润为1T 元, 乙种生产方式每生产100件所获得的利润为2T 元, 可得()()16055154025152800T =-+-=(元),()()28055202025202900T =-+-=(元),由于12T T <,所以用样本估计总体知乙种生产方式生产的农产品所获得的利润较高,该扶贫单位要选择乙生产方式来帮助该扶贫村来脱贫较好. 【点睛】本题主要考查了频率分布直方表与频率分布直方图的应用,其中解答中熟记在频率分布直方图中,各小长方形的面积表示相应各组的频率,且所有小长方形的面积的和等于1,合理利用古典概型及其概率的计算公式求解概率是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题. 22.(1)0.01;(2)69.44;(2)12. 【分析】(1)由纵坐标⨯组距=频率,以及所有组频率之和为1,即可列式求出t ; (2)根据频率分布直方图平均数公式,即可求得结果;(3)先求出25人中优秀人数为5人,再根据列举法,运用古典概型求出概率; 【详解】(1)由频率分布直方图可知:()0.250.0350.04.00581t t o +++++⨯=,解得:0.01t =(2)设这次比赛的平均数为x ,则0.0258560.0358640.04872x =⨯⨯+⨯⨯+⨯⨯0.018880.005896+⨯⨯+⨯⨯11.217.9223.04 6.47.04 3.8=+++++69.44=(3)25名工人参加比赛,优秀人数为:()250.010.010.00585⨯++⨯=人,5名优秀工人中[)76,92内有4人设为1234A A A A ,[]92,100有一人设为B ,则5人中选2人有以下情况:12A A ,13A A ,41A A ,1A B ,23A A ,24A A ,2A B ,34A A ,3A B ,4A B 共有10种情况,2人成绩均低于92分有12A A ,13A A ,41A A ,23A A ,24A A ,34A A ,共6种情况.则5人任选2人,两人成绩均低于92分的概率无63=105P =. 【点睛】本题主要考查频率分布直方图的应用,涉及到频率频数、平均数等以及古典概型求概率,同时考查对数据的处理能力.23.()()()()204848212812x xy xx x⎧≤≤⎪=≤≤⎨⎪-≤≤⎩;程序框图见解析;【解析】试题分析:根据题意可得到面积函数是一个分段函数,写出函数后,利用条件分支结构写出程序框图即可.试题由题意可得y =.程序框图如图:点睛:本题考查分段函数的算法写法,属于中档题,注意当分段函数为两段时,需要一个分支结构,如果分段函数三段时,需要两个分支结构才能完成,特别在写算法程序时,注意分支结构的连接,是与否的处理一定要细心.24.答案详见解析.【解析】【分析】根据题干要求写出循环结构的程序即可.【详解】程序如下:i=2sum=0DOsum=sum+ii=i+2LOOP UNTIL i>98PRINT sumEND【点睛】应用循环语句编写程序时需注意:①循环语句中的循环变量一般要设初始值.②在循环过程中需要有“结束”的语句,程序中最忌“死循环”.25.(1)0.36 6.24y x =+;(2)8.76万吨.【分析】(1)由题意求得知 3.5t =,7.5=y ,()62117.5i i t t =-=∑,运用公式求得b ,代入可求得y 关于t 的线性回归方程.(2)由(1)得的线性回归方程,代入年份代码7t =计算,可预测2020年该地区小龙虾的年产量.【详解】(1)由题知 3.5t =,7.5=y ,()62117.5i i t t =-=∑,()()()61621 6.30.3617.5ˆi ii i i t t y y b t t ==--===-∑∑, 又 6.24=-=a y bt .所以,y 关于t 的线性回归方程为0.36 6.24y x =+.(2)由(1)得,当年份为2020年时,年份代码7t =,此时0.367 6.248.76=⨯+=y .所以,可预测,2020年该地区小龙虾的年产量为8.76万吨.【点睛】本题考查线性回归方程的求解,利用线性回归方程对总体进行估计,属于中档题. 26.(1)2552;(2)3173;(3)当他的答题数量7n =时,他的复赛成绩的期望值最大. 【分析】(1)由表可知,样本中成绩不低于60分的学生共有40人,其中成绩优良的人数为15人,再结合排列组合与古典概型即可得解;(2)先求出样本中的100名学生预赛成绩的平均值,即为μ,从而推出~(53Z N ,219),再根据正态分布的性质即可得解;(3)以随机变量ξ表示甲答对的题数,则~B ξ(,0.75)n ,记甲答完n 题所得的分数为随机变量X ,则2X ξ=,为了获取答n 道题的资格,甲需要“花”掉的分数为20.1()n n +,设甲答完n 题后的复赛成绩的期望值为()f n ,则2()1000.1()()f n n n E X =-++,最后利用配方法即可得解.【详解】解:(1)由题意得样本中成绩不低于60分的学生共有40分,其中成绩优良的人数为15人,记“从样本中预赛成绩不低于60分的学生中随机地抽取2人,恰有1人预赛成绩优良”为事件A ,则()1125152402552C C P A C == 答:“从样本中预赛成绩不低于60分的学生中随机地抽取2人,恰有1人预赛成绩优良”的概率为2552(2)由题意知样本中的100名学生预赛成绩的平均值为:100.1300.2500.3700.25900.1533x =⨯+⨯+⨯+⨯+⨯=,则53μ=,由2361σ=得19σ=,所以()()()()17210.158652P Z P Z P Z μσμσμσ≥=≥+=--<≤+≈, 所以,估计全市参加参赛的全体学生中,成绩不低于72分的人数为20000×0.15865=3173,即全市参赛学生中预赛成绩不低于72分的人数为3173.(3)以随机变量ξ表示甲答对的题数,则()~,0.75B n ξ,且()0.75E n ξ=,记甲答完n 题所加的分数为随机变量X ,则2X ξ=,∴()()2 1.5E X E n ξ==, 依题意为了获取答n 道题的资格,甲需要“花”掉的分数为:()()20.2123...0.1n n n ⨯++++=+,设甲答完n 题后的复赛成绩的期望值为()f n ,则()()()221000.1 1.50.17104.9f n n n n n =-++=--+, 由于*n N ∈,所以当7n =时,()f n 取最大值104.9.即当他的答题数量7n =时,他的复赛成绩的期望值最大.【点睛】本题考查古典概型、正态分布的性质、二项分布的性质及数学期望的实际应用,考查学生对数据的分析与处理能力,属于中档题.。
【典型题】高中必修三数学上期末模拟试卷及答案

【典型题】高中必修三数学上期末模拟试卷及答案一、选择题1.在区间[]0,1上随机取两个数x ,y ,记P 为事件“23x y +≤”的概率,则(P = ) A .23B .12C .49 D .292.在如图所示的算法框图中,若()321a x dx =-⎰,程序运行的结果S 为二项式()52x +的展开式中3x 的系数的9倍,那么判断框中应填入的关于k 的判断条件是( )A .3K <B .3K >C .2K <D .2K >3.执行如图的程序框图,若输入1t =-,则输出t 的值等于( )A .3B .5C .7D .154.我国古代数学著作《九章算术》中,其意是:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问:米几何?右图是源于其思想的一个程序框图,若输出的2S =(单位:升),则输入k 的值为A .6B .7C .8D .95.下面的程序框图表示求式子32×35×311×323×347×395的值, 则判断框内可以填的条件为( )A .90?i ≤B .100?i ≤C .200?i ≤D .300?i ≤6.《九章算术》是我国古代的数学名著,体现了古代劳动人民的数学智慧,其中第六章“均输”中,有一竹节容量问题,某教师根据这一问题的思想设计了如图所示的程序框图,若输出m 的值为67,则输入a 的值为( )A .7B .4C .5D .117.执行如图的程序框图,那么输出的S 的值是( )A .﹣1B .12C .2D .1 8.执行如图所示的程序框图,若输入的a ,b ,c 依次为()sin sin αα,()cos sin αα,()sin cos αα,其中,42ππα⎛⎫∈⎪⎝⎭,则输出的x 为( )A .()cos cos ααB .()sin sin ααC .()cos sin ααD .()sin cos αα9.运行如图所示的程序框图,若输出的S 的值为480,则判断框中可以填( )A.60i>B.70i>C.80i>D.90i>10.从0,1,2,3这四个数中任取两个不同的数组成一个两位数,则这个两位数是偶数的概率为()A.27B.57C.29D.5911.执行如图所示的程序框图,则输出s的值为()A.10 B.17 C.19 D.3612.2路公共汽车每5分钟发车一次,小明到乘车点的时刻是随机的,则他候车时间不超过两分钟的概率是()A .25B .35C .23D .15二、填空题13.已知样本数据为40,42,40,a ,43,44,且这个样本的平均数为43,则该样本的标准差为_________.14.已知实数]9[1x ∈,,执行如图所示的流程图,则输出的x 不小于55的概率为________.15.已知某人连续5次投掷飞镖的环数分别是8,9,10,10,8,则该组数据的方差为______.16.执行如图所示的程序框图,若输入的1,7s k ==则输出的k 的值为_______.17.设{}{}1,3,5,7,2,4,6a b ∈∈,则函数()log a bf x x =是增函数的概率为__________.18.甲、乙二人约定某日早上在某处会面,甲在7:00~7:20内某一时刻随机到达,乙在7:05~7:20内某一时刻随机到达,则甲至少需等待乙5分钟的概率是________.19.在[0,1]上随机取两个实数,a b ,则,a b 满足不等式221a b +≤的概率为________.20.将红、黄、蓝、白、黑5个小球分别放入红、黄、蓝、白、黑5个盒子里,每个盒子里放且只放1个小球,则红球不在红盒内且黄球不在黄盒内的概率是______.三、解答题21.全世界越来越关注环境保护问题,某监测站点于2016年8月某日起连续n 天监测空气质量指数(AQI ),数据统计如下: 空气质量指数(3/g m μ)0-50 51-100 101-150 151-200 201-250 空气质量等级 空气优 空气良 轻度污染中度污染 重度污染 天数2040m105(1)根据所给统计表和频率分布直方图中的信息求出,n m 的值,并完成频率分布直方图;(2)在空气质量指数分别为51-100和151-200的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件A “两天空气都为良”发生的概率.22.某高中为了了解高三学生每天自主参加体育锻炼的情况,随机抽取了100名学生进行调查,其中女生有55名.下面是根据调查结果绘制的学生自主参加体育锻炼时间的频率分布直方图:将每天自主参加体育锻炼时间不低于40分钟的学生称为体育健康A 类学生,已知体育健康A 类学生中有10名女生.(Ⅰ)根据已知条件完成下面22⨯列联表,并据此资料你是否认为达到体育健康A 类学生与性别有关?非体育健康A 类学生 体育健康A 类学生 合计(Ⅱ)将每天自主参加体育锻炼时间不低于50分钟的学生称为体育健康A +类学生,已知体育健康A +类学生中有2名女生,若从体育健康A +类学生中任意选取2人,求至少有1名女生的概率. 附:()()()()()22n ad bc k a c b d c d a b -=++++23.甲,乙两人玩摸球游戏,每两局为一轮,每局游戏的规则如下:甲,乙两人均从装有4只红球、1只黑球的袋中轮流不放回摸取1只球,摸到黑球的人获胜,并结束该局. (1)若在一局中甲先摸,求甲在该局获胜的概率;(2)若在一轮游戏中约定:第一局甲先摸,第二局乙先摸,每一局先摸并获胜的人得1分,后摸井获胜的人得2分,未获胜的人得0分,求此轮游戏中甲得分X 的概率分布及数学期望.24.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:(1)求出y 关于x 的线性回归方程ˆˆˆybx a =+,并在坐标系中画出回归直线;(2)试预测加工个零件需要多少小时?(注:,,,)25.为庆祝党的98岁生日,某高校组织了“歌颂祖国,紧跟党走”为主题的党史知识竞赛。
【人教版】高中数学必修三期末一模试卷(附答案)

一、选择题1.古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:将一线段MN分为两线段MG,GN,使得其中较长的一段MG是全长MN与另一段GN GN的比例中项,即满足512MG NGMN MG-==,后人把这个数称为“黄金分割”数,把点G称为线段MN的“黄金分割”点.在矩形ABCD中,E,F是线段AB的两个“黄金分割”点.在矩形ABCD内任取一点M,则该点落在DEF内的概率为()A.524-B.514-C.522-D.512-2.七巧板是我们祖先的一项创造,被誉为“东方魔板”,它是由五块等腰直角三角形(两块全等的小三角形、一块中三角形和两块全等的大三角形)、一块正方形和一块平行四边形组成的.如图是一个用七巧板拼成的正方形,现从该正方形中任取一点,则此点取自黑色部分的概率是A.316B.38C.14D.183.如图所示,已知圆1C和2C的半径都为2,且1223C C=,若在圆1C或2C中任取一点,则该点取自阴影部分的概率为()A.233533ππ++B.233533ππ-+C.2331033ππ++D.2331033ππ-+4.据《孙子算经》中记载,中国古代诸侯的等级从低到高分为:男、子、伯、侯、公,共五级,若给获得巨大贡献的7人进行封爵,要求每个等级至少有一人,至多有两人,则伯爵恰有两人的概率为()A.310B.25C.825D.355.执行如图所示的程序框图输出的结果是()A.8B.6C.5D.36.如图给出的是计算1232018⨯⨯⨯⨯的值的一个程序框图,则其中判断框内应填入的是()A .2018i <B .2018i =C .2018i ≤D .2018i >7.若执行如图所示的程序框图,则输出S 的值为( )A .9-B .16-C .25-D .36-8.执行如图所示的程序框图,若输入的,a b 的值分别为1,2,则输出的S 是( )A.70 B.29 C.12 D.59.为了了解某社区居民是否准备收看电视台直播的“龙舟大赛”,某记者分别从社区60~70岁,40~50岁,20~30岁的三个年龄段中的128,192,x人中,采用分层抽样的方法共抽出了30人进行调查,若60~70岁这个年龄段中抽查了8人,那么x为()A.64 B.96 C.144 D.16010.某校为了提高学生身体素质,决定组建学校足球队,学校为了解报名学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如右图),已知图中从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12,则该校报名学生总人数()A.40 B.45 C.48 D.5011.在学校组织的考试中,45名学生的数学成绩的茎叶图如图所示,则该45名学生的数学成绩的中位数为()A.127 B.128 C.128.5 D.12912.有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经统计,得到一个卖出的热饮杯数与当天气温的对比表: 温度℃ -5 0 4 7 12 15 19 23 27 31 36 热饮杯数15615013212813011610489937654根据上表数据确定的线性回归方程应该是( )A .ˆ 2.352147.767yx =-+ B .ˆ 2.352127.765yx =-+ C .ˆ 2.35275.501yx =+D .ˆ 2.35263.674yx =+ 二、填空题13.如图,在长方形OABC 内任取一点(,)P x y ,则点P 落在阴影部分BCD 内的概率为________.14.如图,某建筑工地搭建的脚手架局部类似于一个223⨯⨯ 的长方体框架,一个建筑工人欲从 A 处沿脚手架攀登至B 处,则其最近的行走路线中不连续向上攀登的概率为______________.15.如图,在平放的边长为1的正方形中随机撒1000粒豆子,有380粒落到红心阴影部分上,据此估计红心阴影部分的面积为____.16.下图给出了一个程序框图,其作用是输入x的值,输出相应的y值.若要使输入的x 值与输出的y值满足关系式y=-2x+4,则这样的x值___个.t=,则输出的k=______.17.某程序框图如图所示,若输入的418.根据如图所示的程序框图,若输出的值为4,则输入的值为______________.19.福利彩票“双色球”中红色球由编号为01,02,…,33的33个个体组成,某彩民利用下面的随机数表(下表是随机数表的第一行和第二行)选取6个红色球,选取方法是从随机数表中第1行的第6列和第7列数字开始,由左到右依次选取两个数字,则选出来的第3个红色球的编号为______.20.现有10个数,其平均数为3,且这10个数的平方和是100,则这组数据的标准差是______.三、解答题21.为了解中学生课余观看热门综艺节目“爸爸去哪儿”是否与性别有关,某中学一研究性学习小组从该校学生中随机抽取了n 人进行问卷调查.调查结果表明:女生中喜欢观看该节目的占女生总人数的34,男生喜欢看该节目的占男生总人数的13.随后,该小组采用分层抽样的方法从这n 份问卷中继续抽取了5份进行重点分析,知道其中喜欢看该节目的有3人.(1) 现从重点分析的5人中随机抽取了2人进行现场调查,求这两人都喜欢看该节目的概率;(2) 若有99%的把握认为“爱看该节目与性别有关”,则参与调查的总人数n 至少为多少? 参考数据:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.22.2020年寒假期间新冠肺炎肆虐,全国人民众志成城抗疫情.某市要求全体市民在家隔离,同时决定全市所有学校推迟开学.某区教育局为了让学生“停课不停学”,要求学校各科老师每天在网上授课辅导,每天共200分钟.教育局为了了解高三学生网上学习情况,上课几天后在全区高三学生中采取随机抽样的方法抽取了80名学生(其中男女生恰好各占一半)进行问卷调查,按男女生分为两组,再将每组学生在线学习时间(分钟)分为5组[0,40],(40,80],(80,120],(120,160],(160,200]得到如图所示的频率分布直方图.全区高三学生有3000人(男女生人数大致相等),以频率估计概率回答下列问题:(1)估计全区高三学生中网上学习时间不超过40分钟的人数;(2)在调查的80名高三学生且学习时间不超过40分钟的学生中,男女生按分层抽样的方法抽取6人.若从这6人中随机抽取2人进行电话访谈,求至少抽到1名男生的概率.23.设计算法求111112233499100+++⋅⋅⋅+⨯⨯⨯⨯的值.要求画出程序框图,写出用基本语句编写的程序.24.下面给出一个用循环语句编写的程序: k =1 sum =0WHILE k <10 sum =sum +k ∧2 k =k +1 WENDPRINT sum END(1)指出程序所用的是何种循环语句,并指出该程序的算法功能; (2)请用另一种循环语句的形式把该程序写出来.25.峰谷电是目前在城市居民当中开展的一种电价类别.它是将一天24小时划分成两个时间段,把8:00—22:00共14小时称为峰段,执行峰电价,即电价上调;22:00—次日8:00共10个小时称为谷段,执行谷电价,即电价下调.为了进一步了解民众对峰谷电价的使用情况,从某市一小区随机抽取了50 户住户进行夏季用电情况调查,各户月平均用电量以[100,300),[300500),,[500700),,[700900),,[9001100),,[]11001300,(单位:度)分组的频率分布直方图如下图:若将小区月平均用电量不低于700度的住户称为“大用户”,月平均用电量低于700度的住户称为“一般用户”.其中,使用峰谷电价的户数如下表: 月平均用电量(度) [)100,300 [)300,500 [)500,700 [)700,900 [)900,1100 []11001300, 使用峰谷电价的户数3913721值作代表);(2)(i )将“一般用户”和“大用户”的户数填入下面22⨯的列联表:一般用户 大用户使用峰谷电价的用户 不使用峰谷电价的用户“使用峰谷电价”有关?()2P K k ≥0.025 0.010 0.001 k 5.0246.63510.828附:()22()()()()n ad bc K a b c d a c b d -=++++,26.某城市200户居民的月平均用电量(单位:度),以[)160,180,[)180,200,[)200,220,[)220,240,[)240,280,[)280,300分组的频率分布直方图如图:(1)求直方图中x 的值;(2)在月平均用电量为[)220,240,[)240,260,[)260,280的三组用户中,用分层抽样的方法抽取20户居民,则月平均用电量在[)220,240的用户中应抽取多少户? (3)求月平均用电量的中位数和平均数.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】分别求出对应的面积,进而求得结论. 【详解】解:设正方形ABCD 的边长为1,则AF BE ==,∴212EF AF =-=, ∴所求的概率为212DEFABCDEF ADSP S AD ⨯⨯===正方形 故选:C . 【点睛】本题主要考查几何概型,几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A 的基本事件对应的“几何度量” ()N A ,再求出总的基本事件对应的“几何度量” N ,最后根据()N A PN求解,属于中档题. 2.A解析:A 【解析】设2AB =,则1BCCD DE EF ====. ∴112224BCI S ∆=⨯⨯=,112242BCI EFGH S S ∆==⨯=平行四边形∴所求的概率为113422216P +==⨯ 故选A. 3.D解析:D 【分析】设两圆交于点,A B ,连接11,AC BC ,12,AB C C ,设12,AB C C 交于点D ,由已知的数据可得1AC B △为等边三角形,从而可求出阴影部分的面积,进而求出总面积,即可求出概率. 【详解】设两圆交于点,A B ,连接11,AC BC ,12,AB C C ,设12,AB C C 交于点D , 则112132C D C C ==,190ADC ∠=︒,所以1113cos C D AC D AC ∠==,所以130AC D ∠=︒,则160AC B ∠=︒, 所以1AC B △为等边三角形, 所以604342(4)233603S ππ⨯=-⨯=-阴, 图形的总面积42024(23)2333S πππ=⨯--=+总, 所以求概率为4232333201033233ππππ--=++,故选:D【点睛】此题考查几何概型概率的求法,关键是求阴影部分的面积,属于中档题.4.B解析:B 【分析】根据部分平均分组分配的方法可求得分法总数和伯爵恰有两人的分法数,根据古典概型概率公式可求得结果. 【详解】7人进行封爵,每个等级至少一人,至多两人,则共有2211225575327555322322C C C C C C A A A A A ⋅=种分法;其中伯爵恰有两人的分法有2211142247532247543232C C C C C A C C A A A ⋅=种分法,∴伯爵恰有两人的概率2247542257552225C C A p C C A A ==.故选:B . 【点睛】本题考查数学史与古典概型概率问题的求解,关键是能够利用排列组合中不平均分组分配的方法确定分法总数和符合题意的分法数.5.A解析:A 【分析】根据程序框图循环结构运算,依次代入求解即可. 【详解】根据程序框图和循环结构算法原理,计算过程如下:1,1,x y z x y ===+第一次循环2,1,2z x y === 第二次循环3,2,3z x y === 第三次循环5,3,5z x y ===第四次循环8z =,退出循环输一次8z =. 所以选A 【点睛】本题考查了程序框图的基本结构和运算,主要是掌握循环结构在何时退出循环结构,属于基础题.6.D解析:D 【分析】可先结合输出结果预判,满足某一条件时,输出结果s ,综合判断D 正确 【详解】由输出结果判断,显然是经过多次运算的结果,运算中i 是不断递加的,满足某一条件时,输出结果,排除A ,C ;接下来计算:设001,1s i ==,不满足判断条件,100101,12s s i i i =⋅==+=; 不满足判断条件,2112112,13s s i i i =⋅=⨯=+=; 不满足判断条件,32232123,14s s i i i =⋅=⨯⨯=+=;直到201820172017201820171232018,12019s s i i i =⋅=⨯⨯⨯=+=,此时满足判断条件,说明20192018>,故判断语句为:2018i >故选:D 【点睛】本题考查由输出值辨别判断语句,属于中档题7.D解析:D 【分析】执行循环结构的程序框图,逐次运算,根据判断条件终止循环,即可得到运算结果,得到答案. 【详解】由题意,执行循环结构的程序框图,可知:第一次运行时,1(1)11,0(1)1,3T S n =-=-=+-=-=•; 第二次运行时,3(1)33,1(3)4,5T S n =-=-=-+-=-=•; 第三次运行时,5(1)55,4(5)9,7T S n =-=-=-+-=-=•; 第四次运行时,7(1)77,9(7)16,9T S n =-=-=-+-=-=•; 第五次运行时,9(1)99,16(9)25,11T S n =-=-=-+-=-=•; 第六次运行时,11(1)1111,25(11)36T S =-=-=-+-=-•, 此时刚好满足9n >,所以输出S 的值为36-.故选D. 【点睛】本题主要考查了循环结构的程序框图的计算与输出问题,其中解答中熟练应用给定的程序框图,逐次运算,根据判断条件,终止循环得到结果是解答的关键,着重考查了推理与运算能力,属于基础题.8.B解析:B 【分析】此程序框图是循环结构图,模拟程序逐层判断,得出结果. 【详解】 解: 模拟程序:,,a b n 的初始值分别为1,2,4,第1次循环:s 1225=+⨯=,,,a 2b 5n 3===,不满足2n <; 第2次循环:s 22512=+⨯=,,,a 5b 12n 2===,不满足2n <; 第3次循环:s 521229=+⨯=,,,a 12b 29n 1===,满足2n <, 故输出29S =. 故选B. 【点睛】本题考查了程序框图的循环结构,解题的关键是要读懂循环结构的流程图,根据判断框内的条件逐步解题.9.D解析:D 【解析】【分析】根据60~70岁这个年龄段中128人中抽查了8人,可知分层抽样的抽样比为81=12816,因为共抽出30人,所以总人数为3016=480⨯人,即可求出20~30岁年龄段的人数. 【详解】根据60~70岁这个年龄段中128人中抽查了8人,可知分层抽样的抽样比为81=12816, 因为共抽出30人,所以总人数为3016=480⨯人,所以,20~30岁龄段的人有480128192160--=,故选D. 【点睛】本题主要考查了分层抽样,抽样,样本容量,属于中档题10.C解析:C 【分析】根据频数关系,求出前三段每段的频数,由直方图求出四五组的频率,进而求出前三组的频率和,从而可求该校报名学生的总人数. 【详解】从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12,∴从左到右3个小组的频数分别为6,12,18,共有36人,第4,5小组的频率之和为()0.03750.012550.25+⨯=, 则前3小组的频率之和为10.250.75-=, 则该校报名学生的总人数为360.7548÷=,故选C. 【点睛】本题主要考查频率分布直方图的应用,属于中档题. 直方图的主要性质有:(1)直方图中各矩形的面积之和为1;(2)组距与直方图纵坐标的乘积为该组数据的频率;(3)每个矩形的中点横坐标与该矩形的纵坐标相乘后求和可得平均值;(4)直观图左右两边面积相等处横坐标表示中位数.11.D解析:D 【解析】分析:由茎叶图得出45名学生的数学成绩,从而求出中位数. 详解:根据茎叶图得出45名学生的数学成绩,可知中位数为129. 故选D.点睛:本题考查了茎叶图的应用问题,解题时应根据茎叶图中的数据,进行解答,属基础题..12.A解析:A 【解析】分析:先观察表中数据的规律,确定回归系数b 的符号,再计算x 和y ,代入选项确定正确答案.详解:由表中数据规律发现:热饮杯数y 随当天气温x 升高而减少,则0b <,排除C 、D. 计算1169=(504712151923273136)1111x -++++++++++= 11228=(15615013212813011610489937654)111.641111y ++++++++++=≈ 将x 代入选项A ,得1692.352147.767111.6311ˆy=-⨯+= 将x 代入选项B ,得1692.352127.76591.6311ˆy=-⨯+= 所以选项A 正确. 故选A.点睛:本题考查线性回归方程的求法与应用,一次项系数b 符号的判断和回归直线过样本中心点(,)x y 是解题关键.二、填空题13.【分析】利用微积分基本定理先计算出阴影部分的面积根据几何概型的知识可知:阴影部分的面积与长方形面积比等于对应的概率即可计算出概率值【详解】由几何概型的知识可知:阴影部分的面积与长方形的面积之比等于所解析:1e【分析】利用微积分基本定理先计算出阴影部分的面积,根据几何概型的知识可知:阴影部分的面积与长方形面积比等于对应的概率,即可计算出概率值. 【详解】由几何概型的知识可知:阴影部分的面积与长方形OABC 的面积之比等于所求概率, 记阴影部分面积为1S ,长方形面积为2S , 所以()1110111x xS e e dx e e e e =⨯-=-=--=⎰,21S e e =⨯=,所以所求概率为121S P S e==. 故答案为:1e. 【点睛】本题考查几何概型中的面积模型以及利用微积分基本定理求解定积分的值,属于综合型问题,难度一般.几何概型中的面积模型的计算公式:()A A P =构成事件的区域面积全部试验结果所构成的区域面积.14.【解析】【分析】先求出最近路线的所有走法共有种再求出不连续向上攀登的次数然后可得概率【详解】最近的行走路线就是不走回头路不重复所以共有种向上攀登共需要3步向右向前共需要4步因为不连续向上攀登所以向解析:27 【解析】 【分析】先求出最近路线的所有走法共有77A 种,再求出不连续向上攀登的次数,然后可得概率. 【详解】最近的行走路线就是不走回头路,不重复,所以共有77A 种,向上攀登共需要3步,向右向前共需要4步,因为不连续向上攀登,所以向上攀登的3步,要进行插空,共有4345A A 种,故所求概率为43457727A A P A ==. 【点睛】本题主要考查古典概率的求解,明确事件包含的基本事件种数是求解关键,侧重考查数学建模和数学运算的核心素养.15.38【解析】【分析】根据几何槪型的概率意义即可得到结论【详解】正方形的面积S =1设阴影部分的面积为S ∵随机撒1000粒豆子有380粒落到阴影部分∴由几何槪型的概率公式进行估计得即S =038故答案为:解析:38 【解析】 【分析】根据几何槪型的概率意义,即可得到结论. 【详解】正方形的面积S =1,设阴影部分的面积为S , ∵随机撒1000粒豆子,有380粒落到阴影部分, ∴由几何槪型的概率公式进行估计得38011000S =, 即S =0.38, 故答案为:0.38. 【点睛】本题主要考查几何槪型的概率的计算,利用豆子之间的关系建立比例关系是解决本题的关键,比较基础.16.2【分析】分析程序中各变量各语句的作用再根据流程图所示的顺序可知:该程序的作用是计算分段函数的函数值并输出【详解】该题考查的是有关程序框图的问题在解题的过程中注意对框图进行分析明确框图的作用根据题意解析:2 【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算分段函数2,224,251,5x x y x x x x⎧⎪≤⎪=-<≤⎨⎪⎪>⎩的函数值,并输出.【详解】该题考查的是有关程序框图的问题,在解题的过程中,注意对框图进行分析,明确框图的作用,根据题意,建立相应的等量关系式,求得结果.根据题意,可知该程序的作用是计算分段函数2,224,251,5x x y x x x x⎧⎪≤⎪=-<≤⎨⎪⎪>⎩的函数值,依题意得2224x x x ≤⎧⎨=-+⎩或252424x x x <≤⎧⎨-=-+⎩或5124x x x>⎧⎪⎨=-+⎪⎩,解得1x =-±x 的值有两个, 故答案是:2. 【点睛】该题考查的是有关程序框图的问题,在解题的过程中,注意分析框图的作用,之后建立相应的等量关系式,求得结果,从而得到满足条件的x 的个数.17.【分析】根据题意执行循环结构的程序框图逐次计算即可得到答案【详解】由题意执行程序框图:可得;第一循环不满足条件;第二次循环不满足条件;第三次循环不满足条件;第四次循环不满足条件;第五次循环不满足条件解析:【分析】根据题意,执行循环结构的程序框图,逐次计算,即可得到答案. 【详解】由题意执行程序框图:可得0S =, 8k =; 第一循环,不满足条件,8S =,7k =; 第二次循环,不满足条件,1S =,6k =; 第三次循环,不满足条件,5S =,5k =; 第四次循环,不满足条件0S =,4k =; 第五次循环,不满足条件4S =,3k =, 第六次循环,满足条件,输出3k =.【点睛】本题主要考查了循环结构的程序框图的计算输出问题,其中解答中根据给定的程序框图,逐次循环,逐次计算,注意把握判定条件是解答的关键,着重考查了推理与运算能力,属于基础题.18.或1【解析】试题分析:根据已知中的程序框图可得:该程序的功能是计算并输出分段函数的函数值分段讨论满足y=4的x 值最后综合讨论结果可得答案考点:(1)流程图;(2)分段函数解析:或1【解析】试题分析:根据已知中的程序框图可得:该程序的功能是计算并输出分段函数的函数值,分段讨论满足y=4的x 值,最后综合讨论结果可得答案. 考点:(1)流程图;(2)分段函数.19.05【分析】根据给定的随机数表的读取规则从第一行第67列开始两个数字一组从左向右读取重复的或超出编号范围的跳过即可【详解】根据随机数表排除超过33及重复的编号第一个编号为21第二个编号为32第三个编解析:05 【分析】根据给定的随机数表的读取规则,从第一行第6、7列开始,两个数字一组,从左向右读取,重复的或超出编号范围的跳过,即可. 【详解】根据随机数表,排除超过33及重复的编号,第一个编号为21,第二个编号为32,第三个编号05,故选出来的第3个红色球的编号为05. 【点睛】本题主要考查了简单随机抽样中的随机数表法,属于容易题.20.1【解析】【分析】设这10个数为则这组数据的方差为:由此能求出这组数据的标准差【详解】现有10个数其平均数为3且这10个数的平方和是100设这10个数为则这组数据的方差为:这组数据的标准差故答案为1解析:1 【解析】 【分析】设这10个数为1x ,2x ,3x ,⋯,10x ,则12310310x x x x +++⋯+=,222212310100x x x x +++⋯+=,这组数据的方差为:()()22222222212310123101231011[()()())69101010S x x x x x x x x x x x x x x x x ⎛⎤⎤⎡=-+-+-+⋯+-=+++⋯+-+++⋯++⨯ ⎥⎥⎢⎦⎣⎝⎦,由此能求出这组数据的标准差. 【详解】现有10个数,其平均数为3,且这10个数的平方和是100,设这10个数为1x ,2x ,3x ,⋯,10x , 则12310310x x x x +++⋯+=,222212310100x x x x +++⋯+=,∴这组数据的方差为:()()22222222212310123101231011[()()())691011010S x x x x x x x x x x x x x x x x ⎛⎤⎤⎡=-+-+-+⋯+-=+++⋯+-+++⋯++⨯= ⎥⎥⎢⎦⎣⎝⎦,∴这组数据的标准差1S =.故答案为1. 【点睛】本题考查一组数据的标准差的求法,考查平均数、方差等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.三、解答题21.(1)310;(2)50n =. 【解析】分析:(1)记重点分析的5人中喜爱看该节目的为,,a b c ,不爱看的为,d e ,通过穷举法得到所有基本事件,利用古典概型公式求解即可; (2)由题意可得22⨯列联表,进而计算2256K k =,由题意得256.6356k ≥,从而得解. 详解:(1) 记重点分析的5人中喜爱看该节目的为,,a b c ,不爱看的为,d e ,从5人中随机抽取2人,所有可能的结果有()()()()()()()()()(),,,,,,,,,,,,,,,,,,,a b a c a d a e b c b d b e c d c e d e ,共10种,则这两人都喜欢看该节目的有3种, ∴310P =,即这两人都喜欢看该节目的概率为310; (2)∵进行重点分析的5份中,喜欢看该节目的有3人,故喜爱看该节目的总人数为35n ,不喜爱看该节目的总人数为25n ;设这次调查问卷中女生总人数为a ,男生总人数为b ,,*a b N ∈,则由题意可得22⨯列联表如下:解得:,2525a nb n ==, ∴正整数n 是25的倍数,设25n k =,*k N ∈,则3112,444a k a k ==, 123,633b k b k ==,则()2225126342516915106k k k k k K k k k k k ⋅-⋅==⋅⋅⋅;由题意得256.635 1.596k k ≥⇒≥,∵*k N ∈,∴2k =,故50n =. 点睛:独立性检验的一般步骤:(I )根据样本数据制成22⨯列联表;(II )根据公式()()()()()22n ad bc K a b a d a c b d -=++++计算2K 的值;(III )查表比较2K 与临界值的大小关系,作统计判断.(注意:在实际问题中,独立性检验的结论也仅仅是一种数学关系,得到的结论也可能犯错误.) 22.(1)225人;(2)1415【分析】(1)根据频率分布直方图,分别算出男生自主学习不超过40分钟的人数和女生自主学习不超过40分钟的人数求和即可.(2)根据频率分布直方图可得选4名男生,2名女生,然后利用古典概型的概率求法,先列出任选2人的基本事件的数,再找出没有男生的基本事件数,最后用对立事件的概率求解. 【详解】(1)男生自主学习不超过40分钟的人数:0.0025401500150⨯⨯=人, 女生自主学习不超过40分钟的人数:0.0012540150075⨯⨯=人, 所以估计全区高三学生网上学习时间不超过40分钟的人数为225人.(2)在80名学生中,男生网上学习不超过40分钟的人数:400.0025404⨯⨯=人, 女生网上学习不超过40分钟的人数:400.00125402⨯⨯=人, 所以选4名男生,2名女生.4名男生设为1a ,2a ,3a ,4a ,2名女生设为12,b b ,任选2人有:12a a ,13a a ,14a a ,23a a ,24a a ,34a a ,12b b ,11a b ,21a b ,31a b ,41a b ,21b a ,22b a ,23b a ,24b a ,共15种.没有男生的有12b b ,共1种.所以至少有一名男生的概率11411515P =-=. 【点睛】 本题主要考查频率分布直方图样本估计总体以及古典概型的概率,还考查了运算求解的能力,属于中档题.23.程序图见解析.【解析】【分析】这是一个累加求和问题,设计一个计数变量,一个累加变量,根据结束条件设置成直到型或当型. 最后对应改成基本语句.【详解】这是一个累加求和问题,共99项相加,可设计一个计数变量,一个累加变量,用循环结构实现这一算法.程序框图如下图所示【点睛】本题考查循环结构,考查基本分析能力.24.(1)答案见解析;(2)答案见解析.【解析】【试题分析】(1) 所用的循环语句是WHILE 循环语句,其功能是计算222129+++的值.(2)另一种循环语句就是UNTIL 型.按UNTIL 型语句改写出程序.【试题解析】(1)本程序所用的循环语句是WHILE 循环语句,其功能是计算12+22+32+…+92的值.(2)用UNTIL 语句改写程序如下:k=1sum=0DOsum=sum+k ∧2k=k+1LOOP UNTIL k>=10PRINT sumEND25.(1)众数600度,平均数640度(2)(i )见解析;(ii )不能有99%的把握认为 “用电量的高低”与“使用峰谷电价”有关.【分析】(1)由频率分布直方图计算出众数与平均数(2)完善列表联并计算出是否有关【详解】(1)根据频率分布直方图的得到100度到300度的频率为:10.0012000.00152000.00122000.00062000.00022000.1-⨯-⨯-⨯-⨯-⨯=,估计所抽取的50户的月均用电量的众数为:500+700=6002(度); 估计所抽取的50户的月均用电量的平均数为:(2000.00054000.0016000.00158000.001210000.000612000.0002)200640=⨯+⨯+⨯+⨯+⨯+⨯⨯=x (度)(2)依题意,22⨯列联表如下2K 的观测值50(2510510)400 6.349 6.6353515302063k ⨯⨯-⨯==≈<⨯⨯⨯ 所以不能有99%的把握认为 “用电量的高低”与“使用峰谷电价”有关.【点睛】本题考查了频率分布直方图,并完善列表联计算线性相关性,较为基础,需要掌握解题方法26.(1)0.0075;(2)10户;(3)224a =,225.6x =.【分析】(1)由频率和为1列出方程求解x ;(2)求出三组用户的月平均用电量的频率推出比例关系,用20乘以月平均用电量在[)220,240的用户所占比例即可得解;(3)根据中位数左边和右边的直方图面积相等列出等式估计中位数,平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.【详解】(1)由直方图的性质可得()0.0020.00950.0110.01250.0050.0025201x ++++++⨯=,解得0.0075x =,所以直方图中x 的值是0.0075.(2)因为月平均用电量为[)220,240,[)240,260,[)260,280的三组用户的频率分别为0.25、0.15、0.1,所以这三组用户的月平均用电量比例为5:3:2,所以月平均用电量在[)220,240的用户中应抽取5201010⨯=(户). (3)因为()0.0020.00950.011200.450.5++⨯=<,所以月平均用电量的中位数在[)220,240内,设中位数为a ,则()()0.0020.00950.011200.01252200.5a ++⨯+⨯-=,解得224a =.平均数 1700.041900.192100.222300.252500.152700.12900.05x =⨯+⨯+⨯+⨯+⨯+⨯+⨯ 225.6=,所以月平均用电量的中位数为224,平均数为225.6.【点睛】本题考查统计案例、分层抽样、根据频率分布直方图估计总体的数字特征,属于中档题.。
【人教版】高中数学必修三期末一模试题(附答案)(1)

一、选择题1.将曲线22x yx y +=+围成的区域记为Ⅰ,曲线1x y +=围成的区域记为Ⅱ,在区域Ⅰ中随机取一点,此点取自区域Ⅱ的概率为( ) A .12π+ B .11π+ C .22π+ D .21π+ 2.如图是一边长为8的正方形苗圃图案,中间黑色大圆与正方形的内切圆共圆心,圆与圆之间是相切的,且中间黑色大圆的半径是黑色小圆半径的2倍.若在正方形图案上随机取一点,则该点取自黑色区域的概率为( )A .8π B .16π C .18π-D .116π-3.某校从高一(1)班和(2)班的某次数学考试(试卷满分为100分)的成绩中各随机抽取了6份数学成绩组成一个样本,如茎叶图所示.若分别从(1)班、(2)班的样本中各取一份,则(2)班成绩更好的概率为( )A .1636B .1736C .12D .19364.在二项式42nx x 的展开式,前三项的系数成等差数列,把展开式中所有的项重新排成一列,有理项都互不相邻的概率为( ) A .16B .14C .512D .135.给出一个算法的程序框图如图所示,该程序框图的功能是( )A .求出,,a b c 三数中的最小数B .求出,,a b c 三数中的最大数C .将,,a b c 从小到大排列D .将,,a b c 从大到小排列6.执行如图所示的程序框图,输出S 的值为( )A .1B .0C .1D .27.执行如图所示的程序框图,若输人的n 值为2019,则S =A .B .C .D .8.执行如图所示的程序框图,若输出的结果为48,则输入k 的值可以为A .6B .10C .8D .49.根据表中提供的全部数据,用最小二乘法得出y 关于x 的线性回归方程是9944y x =+,则表中m 的值为( ) x 8 10 11 12 14 y2125m2835A .26B .27C .28D .2910.若某中学高二年级8个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数是()A.90.5 B.91.5 C.90 D.9111.甲、乙两名选手参加歌手大赛时,5名评委打的分数用如图所示的茎叶图表示,s1,s2分别表示甲、乙选手分数的标准差,则s1与s2的关系是().A.s1>s2B.s1=s2C.s1<s2D.不确定12.某校为了提高学生身体素质,决定组建学校足球队,学校为了解报名学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如右图),已知图中从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12,则该校报名学生总人数()A.40 B.45 C.48 D.50二、填空题13.将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是________.14.高三某位同学参加物理、化学、政治科目的等级考,已知这位同学在物理、化学、政治科目考试中达A的概率分别为56、78、34,这三门科目考试成绩的结果互不影响,则这位考生至少得1个A 的概率为____15.已知7个实数1,2,4,,,,a b c d -依次构成等比数列,若从这7个数中任取2个,则它们的和为正数的概率为___________.16.若45a =,则以下程序运行后的结果是_____.17.运行下边的流程图,输出的结果是__________.18.阅读如图所示的流程图,运行相应的程序,则输出n 的值为______.19.某地区共有4所普通高中,这4所普通高中参加2018年高考的考生人数如下表所示: 学校 A 高中B 高中C 高中D 高中参考人数80012001000600现用分层抽样的方法在这4所普通高中抽取144人,则应在D 高中中抽取的学生人数为_______.20.某班运动队由足球运动员18人、篮球运动员12人、乒乓球运动员6人组成(每人只参加一项),现从这些运动员中抽取一个容量为n 的样本,若分别采用系统抽样法和分层抽样法,则都不用剔除个体;当样本容量为n +1时,若采用系统抽样法,则需要剔除1个个体,那么样本容量n 为________.三、解答题21.手机支付也称为移动支付(Mobile Payment ),是当今社会比较流行的一种付款方式.某金融机构为了了解移动支付在大众中的熟知度,对15—65岁的人群作了问题为“你会使用移动支付吗?”的随机抽样调查,把回答“会”的100个人按照年龄分成5组,绘制成如图所示的频数分布表和频率分布直方图.(1)求x ,a 的值;(2)若从第1,3组中用分层抽样的方法抽取5人,求两组中分别抽取的人数; (3)在(2)抽取的5人中再随机抽取2人,求所抽取的2人来自同一个组的概率. 22.我国科学家屠呦呦教授由于在发现青蒿素和治疗疟疾的疗法上的贡献获得诺贝尔医学奖,以青蒿素类药物为主的联合疗法已经成为世界卫生组织推荐的抗疟疾标准疗法,目前,国内青蒿人工种植发展迅速,调查表明,人工种植的青蒿的长势与海拔高度、土壤酸碱度、空气湿度的指标有极强的相关性,现将这三项的指标分别记为x ,y ,z ,并对它们进行量化:0表示不合格,1表示临界合格,2表示合格,再用综合指标x y z ω=++的值评定人工种植的青蒿的长势等级:若4ω≥,则长势为一级;若23ω≤≤,则长势为二级;若01ω≤≤,则长势为三级;为了了解目前人工种植的青蒿的长势情况,研究人员随机抽取了10块青蒿人工种植地,得到如下结果: 种植地编号1A2A3A 4A 5A(),,x y z ()0,1,0 ()1,2,1 ()2,1,1 ()2,2,2 ()0,1,1(1)在这10块青蒿人工种植地中任取两地,求这两地的空气湿度的指标z 相同的概率; (2)从长势等级是一级的人工种植地中任取一地,其综合指标为m ,从长势等级不是一级的人工种植地中任取一地,其综合指标为n ,记随机变量X m n =-,求X 的分布列.23.写出一个求解任意二次函数()20y ax bx c a =++≠的最值的算法.24.某城市规定,在法定工作时间内每小时的工资是8元,在法定工作时间外每小时的加班工资为16元,某人在一周内工作60小时,其中加班20小时.编写程序,计算这个人这一周所得的工资.25.据了解,温带大陆性气候,干燥,日照时间长,昼夜温差大,有利于植物糖分积累.某课题研究组欲研究昼夜温差大小()/x ℃与某植物糖积累指数()/y GI 之间的关系,得到如下数据:下的2组数据进行检验,假设这剩下的2组数据恰好是第一组与第六组数据.(1)求y 关于x 的线性回归方程ˆˆˆybx a =+(2)若由线性回归方程得到的估计数据与所选出的检验数据的差的绝对值均不超过2.58,则认为得到的线性回归方程是理想的,试问(1)中所得线性回归方程是否理想?(参考公式:回归直线方程ˆˆˆybx a =+的斜率和截距的最小二乘估计()()()211ˆˆˆ,iii ni ni x x y y bay bx x x ==--==--∑∑ 26.经营费用指流通企业对在经营过程中发生除经营成本以外的所有费用,如管理费用、财务费用、法律费用等,这些费用没有直接用于生产产品或提供服务,但它是影响公司收益的重要因素.某创业公司从2014年开始创业到2019年每年的经营费用y (万元)、年份及其编号t ,有如下统计资料:t 1 2 3 4 5 6 y9.512.214.617.419.6m已知该公司从2014年到2019年年平均经营费用为16万元,且经营费用y 与年份编号t 呈线性相关关系.(1)求2019年该公司的经营费用;(2)y 关于t 的回归方程为 2.6y t a =+,求a ,并预测2020年所需要支出的经营费用; (3)该公司对2019年卖出的产品进行质量指标值检测,由检测结果得如图所示频率分布直方图:预计2020年生产产品质量指标值分布与上一年一致,将图表中频率作为总体的概率.当每件产品质量指标值不低于215时为优质品,指标值在185到215之间是合格品,指标值低于185时为次品.出售产品时,每件优质品可获利1.5万元,每件合格品可获利0.7万元,次品不仅全额退款,还要对客户进行赔付,所以每件次品亏损1.3万元.若2020年该公司的产量为500台,请你预测2020年该公司的总利润(总利润=销售利润-经营费用).【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C【分析】画出曲线22x y x y +=+与曲线1x y +=的图像,再根据几何概型的方法求解即可. 【详解】当0,0x y >>时,曲线22x y x y +=+、曲线1x y +=分别为2222111222x y x y x y ⎛⎫⎛⎫+=+⇒-+-= ⎪ ⎪⎝⎭⎝⎭,1x y +=.又22x y x y +=+、1x y +=均关于,x y 轴,原点对称.故两曲线围成的区域Ⅰ(正方形和四个半圆)、Ⅱ(正方形)如图:可知区域Ⅰ的面积为22222S ππ⎛⎫+⋅=+ ⎪ ⎪⎝⎭正方形;区域Ⅱ的面积为()222=;∴由几何概率公式得:22p π=+.故选:C. 【点睛】本题主要考查了几何概型的运用,需要根据题意去绝对值画出一象限的图像,再根据对称性补全图像.同时也考查了几何概型中面积型的问题.属于中档题.2.C解析:C 【分析】设黑色小圆的半径为r ,则黑色大圆的半径为2r ,由题意求得r ,进一步求出黑色区域的面积,由测度比是面积比得答案. 【详解】解:设黑色小圆的半径为r ,则黑色大圆的半径为2r , 由题意可知,88r =,即1r =.∴图中黑色区域的面积为222884412648ππππ⨯-⨯+⨯⨯+⨯=-,又正方形的面积为64.∴在正方形图案上随机取一点,则该点取自黑色区域的概率为6481648ππ-=-. 故选:C . 【点睛】本题考查几何概型的概率的求法,考查数形结合的解题思想方法,属于中档题.3.C解析:C 【分析】由题意从(1)班、(2)班的样本中各取一份,(2)班成绩更好即(2)班成绩比(1)班成绩高,用列举法列出所有可能结果,由此计算出概率. 【详解】根据题意,两次取出的成绩一共有36种情况;分别为()67,68、()67,72、()67,73、()67,85、()67,89、()67,93()76,68、()76,72、()76,73、()76,85、()76,89、()76,93 ()78,68、()78,72、()78,73、()78,85、()78,89、()78,93 ()82,68、()82,72、()82,73、()82,85、()82,89、()82,93 ()85,68、()85,72、()85,73、()85,85、()85,89、()85,93 ()92,68、()92,72、()92,73、()92,85、()92,89、()92,93满足条件的有18种,故183126p ==, 故选C 【点睛】本题考查概率的求法,考查古典概型、列举法等基础知识,考查运算求解能力,是基础题.4.C解析:C 【分析】先根据前三项的系数成等差数列求n ,再根据古典概型概率公式求结果 【详解】因为n前三项的系数为1212111(1)1,,112448n n n n n n C C C C n -⋅⋅∴=+⋅∴-= 163418118,0,1,2,82rr r r n n T C x r -+>∴=∴=⋅=,当0,4,8r =时,为有理项,从而概率为636799512A A A =,选C. 【点睛】本题考查二项式定理以及古典概型概率,考查综合分析求解能力,属中档题.5.A解析:A 【分析】对a 、b 、c 赋三个不等的值,并根据程序框图写出输出的结果,可得知该程序的功能. 【详解】令2a =,3b =,1c =,则23>不成立,21>成立,则1a =,输出的a 的值为1, 因此,该程序的功能是求出a 、b 、c 三数中的最小数,故选A . 【点睛】本题考查程序框图的功能,解题的关键就是根据题意将每个步骤表示出来,考查分析问题的能力,属于中等题.6.C解析:C 【分析】 由函数()πsin2xf x =,可求周期为4,()(1)(2)(3)40+++=f f f f ,由题意可知()(1)(2)(2021)=2021(1)1=+++==S f f f f f【详解】由函数()πsin 2x f x =的周期为2π4π2T ==, ()π1sin 12f ==,()2π2sin 02f ==,()3π3sin12f ==-,()4π4sin 02f ==,()(1)(2)(3)40+++=f f f f ()(1)(2)(2021)=2021(1)1∴=+++==S f f f f f .故选:C 【点睛】本题考查了程序框图求和,正弦型三角函数的周期等基本知识,考查了运算求解能力和逻辑推理能力,属于一般题目.7.B解析:B 【分析】根据程序框图可知,当时结束计算,此时.【详解】计算过程如下表所示:周期为6n 2019k 1 2 (2018)2019S …k<n 是是是是否【点睛】本题考查程序框图,选用表格计算更加直观,此题关键在于判断何时循环结束.8.C解析:C 【分析】执行如图所示的程序框图,逐次循环,计算其运算的结果,根据选项即可得到答案. 【详解】由题意可知,执行如图所示的程序框图,可知: 第一循环:134,2146n S =+==⨯+=; 第二循环:437,26719n S =+==⨯+=; 第三循环:7310,2191048n S =+==⨯+=, 要使的输出的结果为48,根据选项可知8k ,故选C.【点睛】本题主要考查了循环结构的计算与输出问题,其中解答中正确理解循环结构的程序框图的计算功能,逐次准确计算是解答的关键,着重考查了运算与求解能力,属于基础题.9.A解析:A 【解析】 【分析】首先求得x 的平均值,然后利用线性回归方程过样本中心点求解m 的值即可. 【详解】 由题意可得:810111214115x ++++==,由线性回归方程的性质可知:99112744y =⨯+=, 故21252835275m++++=,26m ∴=.故选:A . 【点睛】本题考查回归分析,考查线性回归直线过样本中心点,在一组具有相关关系的变量的数据间,这样的直线可以画出许多条,而其中的一条能最好地反映x 与y 之间的关系,这条直线过样本中心点.10.A解析:A 【分析】共有8个数据,中位数就是由小到大中间两数的平均数,求解即可. 【详解】根据茎叶图,由小到大排列这8个数为84,85,89,90,91,92,93,95, 所以中位数为90+91=90.52,故选A. 【点睛】本题主要考查了中位数,茎叶图,属于中档题.11.C解析:C 【分析】先求均值,再根据标准差公式求标准差,最后比较大小. 【详解】乙选手分数的平均数分别为7885848192767780949384,84,55++++++++====因此s 1<s 2,选C. 【点睛】本题考查标准差,考查基本求解能力.12.C解析:C 【分析】根据频数关系,求出前三段每段的频数,由直方图求出四五组的频率,进而求出前三组的频率和,从而可求该校报名学生的总人数. 【详解】从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12,∴从左到右3个小组的频数分别为6,12,18,共有36人,第4,5小组的频率之和为()0.03750.012550.25+⨯=, 则前3小组的频率之和为10.250.75-=, 则该校报名学生的总人数为360.7548÷=,故选C. 【点睛】本题主要考查频率分布直方图的应用,属于中档题. 直方图的主要性质有:(1)直方图中各矩形的面积之和为1;(2)组距与直方图纵坐标的乘积为该组数据的频率;(3)每个矩形的中点横坐标与该矩形的纵坐标相乘后求和可得平均值;(4)直观图左右两边面积相等处横坐标表示中位数.二、填空题13.【解析】基本事件总数为36点数之和小于10的基本事件共有30种所以所求概率为【考点】古典概型【名师点睛】概率问题的考查侧重于对古典概型和对立事件的概率的考查属于简单题江苏对古典概型概率的考查注重事件解析:5 6【解析】基本事件总数为36,点数之和小于10的基本事件共有30种,所以所求概率为305. 366=【考点】古典概型【名师点睛】概率问题的考查,侧重于对古典概型和对立事件的概率的考查,属于简单题.江苏对古典概型概率的考查,注重事件本身的理解,淡化计数方法.因此先明确所求事件本身的含义,然后一般利用枚举法、树形图解决计数问题,而当正面问题比较复杂时,往往利用对立事件的概率公式进行求解.14.【分析】先求对立事件概率:三门科目考试成绩都不是A再根据对立事件概率关系求结果【详解】这位考生三门科目考试成绩都不是A的概率为所以这位考生至少得1个A的概率为故答案为:【点睛】本题考查利用对立事件求解析:191 192【分析】先求对立事件概率:三门科目考试成绩都不是A,再根据对立事件概率关系求结果.【详解】这位考生三门科目考试成绩都不是A的概率为5731 (1)(1)(1)684192 ---=,所以这位考生至少得1个A的概率为1191 1192192 -=故答案为:191 192【点睛】本题考查利用对立事件求概率,考查基本分析求解能力,属基础题.15.【分析】根据前几项可知数列的首项为公比为由此求得的值基本事件的总数有和为正数分成两种情况一种是取出的两个数都是正数另一种是一个正数一个负数由此计算出和为正数的方法数根据古典概型概率计算公式求得概率的解析:47【分析】根据前几项可知,数列的首项为1,公比为2-,由此求得,,,a b c d 的值.基本事件的总数有27C .和为正数分成两种情况,一种是取出的两个数都是正数,另一种是一个正数一个负数,由此计算出和为正数的方法数,根据古典概型概率计算公式求得概率的值. 【详解】由题意得,这7个实数为1,2,48,16,32,64---①所选2个数均为正数:246C =(种);②所选2个数一正一负:2,4-、2,16-、2,64-、8,16-、8,64-、32,64-,共6(种)276647P C +∴==,故填4.7【点睛】本小题主要考查古典概型的概率计算,考查了等比数列的概念.在计算古典概率的过程中,首先求得分母,也即是基本事件的总数,由于抽取时没有顺序,故用组合数来计算.然后考虑分子,分子是符合题意事件的个数,要用分类加法计数原理分成两种情况来求解.中档题.16.5【分析】根据条件就是求a 除以10的整数减去a 除以10的商加上a 除以10的余数【详解】【点睛】本题考查除法与取整同余等概念考查基本求解能力解析:5 【分析】根据条件就是求a 除以10 的整数减去a 除以10 的商加上a 除以10 的余数. 【详解】4545\10/1010[]54 4.55 4.5.1010a a aMOD -+=-+=-+= 【点睛】本题考查除法与取整、同余等概念,考查基本求解能力.17.94【解析】不成立执行不成立执行成立所以输出解析:94 【解析】3,3311050a a =∴=⨯+=>不成立,执行31013150a =⨯+=>,不成立, 执行33119450a =⨯+=>,成立, 所以输出94.a =18.4【解析】不成立;不成立;不成立;成立输出故答案为【方法点睛】本题主要考查程序框图的循环结构流程图属于中档题解决程序框图问题时一定注意以下几点:(1)不要混淆处理框和输入框;(2)注意区分程序框图是解析:4 【解析】()1,0,0111,2n S S S ===+-⨯=-≥ 不成立; ()22,1121,2n S S ==-+-⨯=≥ 不成立;()33,1132,2n S S ==+-⨯=-≥ 不成立;()44,2142,2n S S ==-+-⨯=≥ 成立,输出4n = ,故答案为4 .【方法点睛】本题主要考查程序框图的循环结构流程图,属于中档题. 解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支结构还是循环结构;(3) 注意区分当型循环结构和直到型循环结构;(4) 处理循环结构的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,(6)在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可.19.24【分析】计算出高中人数占总人数的比例乘以得到在高中抽取的学生人数【详解】应在高中抽取的学生人数为【点睛】本小题主要考查分层抽样考查频率的计算属于基础题解析:24 【分析】计算出D 高中人数占总人数的比例,乘以144得到在D 高中抽取的学生人数. 【详解】应在D 高中抽取的学生人数为6001442480012001000600⨯=+++.【点睛】本小题主要考查分层抽样,考查频率的计算,属于基础题.20.6【解析】n 为18+12+6=36的正约数因为18:12:6=3:2:1所以n 为6的倍数因此因为当样本容量为时若采用系统抽样法则需要剔除1个个体所以n+1为35的正约数因此解析:6 【解析】n 为18+12+6=36的正约数,因为18:12:6=3:2:1,所以n 为6的倍数,因此6,12,18,24,30,36n =因为当样本容量为1n +时,若采用系统抽样法,则需要剔除1个个体,所以n+1为35的正约数,因此6n =三、解答题21.(1)20x,0.03a =;(2)第1组抽取的人数为2,第3组抽取的人数为3;(3)25. 【分析】(1)由频率计算出x 后可得y ,从而得频率分布图中的a ;(2)由总体比例可得各组抽取人数;(3)把抽取的人编号,用列举法写出任取2人的所有基本事件,并得出2人来自同一组的基本事件,计数后可计算概率. 【详解】(1)由题意可知,0.021010020x =⨯⨯=, 所以100(2035123)30y =-+++=, 从而11300.0310010a =⨯⨯=. (2)第1,3组共有50人,所以抽取的比例是110, 则从第1组抽取的人数为120210⨯=, 从第3组抽取的人数为130310⨯=. (3)设第1组抽取的2人为1A ,2A ,第3组抽取的3人为1B ,2B ,3B , 则从这5人中随机抽取2人有如下种情形:12(,)A A ,11(,)A B ,12(,)A B ,13(,)A B ,21(,)A B ,22(,)A B ,23(,)A B ,12(,)B B ,13(,)B B ,23(,)B B 共有10个基本事件.其中符合“抽取的2人来自同一个组”的基本事件有12(,)A A ,12(,)B B ,13(,)B B ,23(,)B B 共4个基本事件,所以抽取的2人来自同一个组的概率42105P ==. 【点睛】本题考查频率分布直方图,频数分布表,考查分层抽样和古典概型,列举法是求解古典概型的常用方法.本题考查了学生的数据处理能力,运算求解能力,属于中档题. 22.(1)25;(2)分布列见解析 【分析】()1由表可知:空气湿度指标为0的有A 1,空气湿度指标为1的有A 2,A 3,A 5,A 8,A9,A10,空气湿度指标为2的有A4,A6,A7,由此能求出这两地的空气温度的指标z 相同的概率;()2由题意得长势等级是一级()4ω≥有A2,A 3,A4,A6,A7,A9,长势等级不是一级(4)ω<的有A 1,A 5,A 8,A10,从而随机变量X 的所有可能取值为1,2,3,4,5,分别求出相应的概率,由此能求出X 的分布列和()E X . 【详解】(1)由表可以知道:空气湿度指标为0的有1A ,空气湿度指标为1的有2A ,3A ,5A ,8A ,9A ,10A ,空气湿度指标为2的有4A ,6A ,7A ,在这10块青蒿人工种植地中任取两地,基本事件总数21045n C ==,这两地的空气温度的指标z 相同包含的基本事件个数226318m C C =+=,所以这两地的空气温度的指标z 相同的概率182455m p n ===. (2)根据题意得10块青蒿人工种植的综合指标如下表:其中长势等级是一级4ω≥有2A ,3A ,4A ,6A ,7A ,9A ,共6个, 长势等级不是一级()4ω<的有1A ,5A ,8A ,10A ,共4个, 随机变量X 的所有可能取值为1,2,3,4,5,()11321164114C C P X C C ===,()1111312211647224C C C C P X C C +===, ()11111131122111647324C C C C C C P X C C ++===,()111121111164148C C C C P X C C +===, ()111111641524C C P X C C ===, 所以X 的分布列为:本题考查概率的求法,考查离散型随机变量的分布列的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用. 23.见解析 【分析】由二次函数的性质知,当0a >时,二次函数()20y ax bx c a =++≠开口方向向上,函数有最小值为244ac b a -;当0a <时, 二次函数()20y ax bx c a =++≠开口方向向下,函数有最大值为244ac b a-. 【详解】第一步,输入a ,b ,c第二步,计算244ac b m a-=;第三步,若0a >,min y m =,否则, max y m =. 【点睛】本题考查算法步骤的书写和一元二次函数的最值问题;同时让学生体会算法在解决数学问题中的作用;求解本题的关键是对一元二次函数最值情况必须熟悉;属于中档题. 24.见解析; 【解析】试题分析: 先利用INPUT 语句输入法定工作时间以及加班工作时间,再分别赋值法定工作时间工资,加班工作时间工资以及总工资,最后输出一周所得的工资. 试题 程序如下:点睛:25.(1)171277y =⨯;(2)该小组所得线性回归方程是理想的. 【分析】(1)根据数据求出ˆb与ˆa 的值,即可求出y 关于x 的线性回归方程; (2)分别计算出1月份和6月份对应的预测值,与检验数据作差取绝对值,再与2.58进行比较即可得到结论.【详解】(1)由表中2月至5月份的数据, 得11(1113128)11,(24302818)2544x y =+++==+++=,故有()()520(1)2513(3)(7)34iii x x y y =--=⨯-+⨯+⨯+-⨯-=∑,()5222222021(3)14i i x x =-=+++-=∑,34171712,251114777b a y bx ∴===-=-⨯=-, 即y 关于x 的线性回归方程为171277y =⨯; (2)由171277y =⨯,当10x =时,171215810777y =⨯-=, 1581820 2.5877-=<, 当6x =时,1712906777y =⨯=, 901515 2.5877-=<, 则该小组所得线性回归方程是理想的. 【点睛】方法点睛:该题考查的是有关回归分析的问题,解题方法如下:(1)结合题中所给的数据,根据最小二乘法系数公式起的ˆb与ˆa 的值,得到回归直线方程;(2)将相应的变量代入,得到的值域题中条件比较,得到结论. 26.(1)22.7万元;(2)6.9;25.1万元;(3)254.9万元. 【分析】(1)根据均值定义列式计算;(2)求出t ,代入方程可得a ,令7t =代入可得估计值;(3)由频率分布直方图是三种产品的概率,得三种产品的件数,根据各产品赢利可计算出总赢利,注意减去(2)中估计的经营费用. 【详解】 (1)9.512.214.617.419.6166my +++++==.解得22.7m =,即2019年该公司的经营费用为22.7万元. (2) 3.5t =,16y =,所以 2.6 6.9a y t =-=,取7t =,代入得25.1y =,预测2020年所需要支出的经营费用为25.1万元. (3)由图可得生产优质品的概率是0.1,生产合格品的概率是0.79,生产次品的概率是0.11,则预测该公司2020年的总利润为1.50.15000.70.79500 1.30.1150025.1254.9⨯⨯+⨯⨯-⨯⨯-=(万元).【点睛】本题考查线性回归方程及其应用,考查频率分布直方图及其期望,考查学生的数据处理能力,运算求解能力,属于中档题.。
高中必修三数学上期末模拟试卷(附答案)
高中必修三数学上期末模拟试卷(附答案)一、选择题1.在区间[]0,1上随机取两个数x ,y ,记P 为事件“23x y +≤”的概率,则(P = ) A .23B .12C .49 D .292.如图是把二进制的数11111化成十进制数的一个程序框图,则判断框内应填入的条件是( )A .4i >?B .5i >?C .4i ≤?D .5i ≤?3.如果数据12,,,n x x x L 的平均数为x ,方差为28,则152x +,252x +,…,52n x +的平均数和方差分别为( ) A .x ,28B .52x +,28C .52x +,2258⨯D .x ,2258⨯4.随着人民生活水平的提高,对城市空气质量的关注度也逐步增大,下图是某城市1月至8月的空气质量检测情况,图中一、二、三、四级是空气质量等级,一级空气质量最好,一级和二级都是质量合格天气,下面四种说法正确的是( ).①1月至8月空气合格天数超过20天的月份有5个 ②第二季度与第一季度相比,空气合格天数的比重下降了 ③8月是空气质量最好的一个月 ④6月的空气质量最差 A .①②③B .①②④C .①③④D .②③④5.某工厂对一批新产品的长度(单位:mm )进行检测,如下图是检测结果的频率分布直方图,据此估计这批产品的中位数与平均数分别为( )A .20,22.5B .22.5,25C .22.5,22.75D .22.75,22.756.在某地的奥运火炬传递活动中,有编号为1,2,3,L ,18的18名火炬手.若从中任选3人,则选出的火炬手的编号能组成3为公差的等差数列的概率为( ). A .151B .168C .1306D .14087.“微信抢红包”自2015年以来异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为8元,被随机分配为1.72元,1.83元,2.28元,1.55元,0.62元, 5份供甲、乙等5人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于3元的概率是 ( ) A .310B .25C .12D .358.从0,1,2,3这四个数中任取两个不同的数组成一个两位数,则这个两位数是偶数的概率为( ) A .27B .57C .29D .599.设数据123,,,,n x x x x L 是郑州市普通职工*(3,)n n n N ≥∈个人的年收入,若这n 个数据的中位数为x ,平均数为y ,方差为z ,如果再加上世界首富的年收入1n x +,则这1n +个数据中,下列说法正确的是( )A .年收入平均数大大增大,中位数一定变大,方差可能不变B .年收入平均数大大增大,中位数可能不变,方差变大C .年收入平均数大大增大,中位数可能不变,方差也不变D .年收入平均数可能不变,中位数可能不变,方差可能不变10.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如40337=+.(注:如果一个大于1的整数除1和自身外无其他正因数,则称这个整数为素数.)在不超过11的素数中,随机选取2个不同的数,其和小于等于10的概率是( ) A .12B .13C .14D .1511.执行如图的程序框图,若输出的4n =,则输入的整数p 的最小值是( )A .4B .5C .6D .1512.2路公共汽车每5分钟发车一次,小明到乘车点的时刻是随机的,则他候车时间不超过两分钟的概率是( ) A .25B .35C .23D .15二、填空题13.将函数sin 23cos 2y x x =-的图象向左平移6π个单位长度,得到函数()y g x =的图象,则5()6g π__________.14.北京市某银行营业点在银行大厅悬挂着不同营业时间段服务窗口个数的提示牌,如图所示. 设某人到达银行的时间是随机的,记其到达银行时服务窗口的个数为X ,则()E X =______________.15.已知某人连续5次投掷飞镖的环数分别是8,9,10,10,8,则该组数据的方差为______.16.某市有A 、B 、C 三所学校,各校有高三文科学生分别为650人,500人,350人,在三月进行全市联考后,准备用分层抽样的方法从所有高三文科学生中抽取容量为120的样本,进行成绩分析,则应从B 校学生中抽取______人.17.执行如图所示的伪代码,若输出的y 的值为10,则输入的x 的值是________.18.我国元朝著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,遇店添一倍,逢友饮一斗,店友经三处,没有壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的0x =,问一开始输入的x =______斗.遇店添一倍,逢友饮一斗,意思是碰到酒店就把壶里的酒加1倍,碰到朋友就把壶里的酒喝一斗,店友经三处,意思是每次都是遇到店后又遇到朋友,一共是3次.19.某校为了解1000名高一新生的身体生长状况,用系统抽样法(按等距的规则)抽取40名同学进行检查,将学生从1~1000进行编号,现已知第18组抽取的号码为443,则第一组用简单随机抽样抽取的号码为_________20.4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率是________三、解答题21.某地统计局调查了10000名居民的月收入,并根据所得数据绘制了样本的频率分布直方图如图所示.(1)求居民月收入在[3000,3500)内的频率; (2)根据频率分布直方图求出样本数据的中位数;(3)为了分析居民的月收入与年龄、职业等方面的关系,必须按月收入再从这10000中用分层抽样的方法抽出100人做进一步分析,则应从月收入在[2500,3000)内的居民中抽取多少人?22.用秦九韶算法求()543383f x x x x =+-25126x x ++-,当2x =时的值.23.某研究机构对春节燃放烟花爆竹的天数x 与雾霾天数y 进行统计分析,给出下表数据:x23578y12246(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;(2)试判断y与x之间是正相关还是负相关,并预测燃放烟花爆竹的天数为9天时的雾霾天数约为几天?(参考公式:()()()1122211n ni i i ii in ni ii ix x y y x y nx ybx x x nx====---==--∑∑∑∑$,a y bx=-$$.)24.如下图是某校高三(1)班的一次数学知识竞赛成绩的茎叶图(图中仅列出[50,60),[90,100)的数据)和频率分布直方图.(1)求分数在[50,60)的频率及全班人数;(2)求频率分布直方图中的,x y;(3)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在[90,100)之间的概率.25.读书可以使人保持思想活力,让人得到智慧启发,让人滋养浩然正气书籍是文化的重要载体,读书是承继文化的重要方式某地区为了解学生课余时间的读书情况,随机抽取了n名学生进行调查,根据调查得到的学生日均课余读书时间绘制成如图所示的频率分布直方图,将日均课余读书时间不低于40分钟的学生称为“读书之星”,日均课余读书时间低于40分钟的学生称为“非读书之星”:已知抽取的样本中日均课余读书时间低于10分钟的有10人(1)求,n p 的值;(2)根据已知条件完成下面的22⨯列联表,并判断是否有95%以上的把握认为“读书之星”与性别有关?非读书之星 读书之星 总计男女 10 55 总计(3)将上述调查所得到的频率视为概率,现从该地区大量学生中,随机抽取3名学生,每次抽取1名,已知每个人是否被抽到互不影响,记被抽取的“读书之星”人数为随机变量X ,求X 的分布列和期望()E X附:()()()()()22n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.()20P K k ≥ 0.10 0.05 0.025 0.010 0.005 0.001 0k2.7063.8415.0246.6357.87910.82826.在最强大脑的舞台上,为了与国际X 战队PK ,假设某季Dr.魏要从三名擅长速算的选手A 1,A 2,A 3,三名擅长数独的选手B 1,B 2,B 3,两名擅长魔方的选手C 1,C 2中各选一名组成中国战队.假定两名魔方选手中更擅长盲拧的选手C 1已确定入选,而擅长速算与数独的选手入选的可能性相等. (Ⅰ)求A 1被选中的概率; (Ⅱ)求A 1,B 1不全被选中的概率.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【解析】 【分析】由题意结合几何概型计算公式求解满足题意的概率值即可. 【详解】如图所示,01,01x y ≤≤≤≤表示的平面区域为ABCD ,平面区域内满足23x y +≤的部分为阴影部分的区域APQ ,其中2,03P ⎛⎫ ⎪⎝⎭,20,3Q ⎛⎫⎪⎝⎭,结合几何概型计算公式可得满足题意的概率值为1222233119p ⨯⨯==⨯. 本题选择D 选项.【点睛】数形结合为几何概型问题的解决提供了简捷直观的解法.用图解题的关键:用图形准确表示出试验的全部结果所构成的区域,由题意将已知条件转化为事件A 满足的不等式,在图形中画出事件A 发生的区域,据此求解几何概型即可.2.C解析:C 【解析】 【分析】根据程序框图依次计算得到答案. 【详解】根据程序框图:1,1S i ==;3,2S i ==;7,3S i ==;15,4S i ==;31,5S i ==,结束. 故选:C . 【点睛】本题考查了程序框图,意在考查学生的计算能力和理解能力.3.C解析:C 【解析】根据平均数的概念,其平均数为52x +,方差为2258⨯,故选C.4.A解析:A 【解析】在A 中,1月至8月空气合格天数超过20谈的月份有:1月,2月,6月,7月,8月, 共5个,故A 正确;在B 中,第一季度合格天数的比重为2226190.8462312931++≈++;第二季度合格天气的比重为1913250.6263303130++≈++,所以第二季度与第一季度相比,空气达标天数的比重下降了,所以B 是正确的;在C 中,8月空气质量合格天气达到30天,是空气质量最好的一个月,所以是正确的; 在D 中,5月空气质量合格天气只有13天,5月份的空气质量最差,所以是错误的, 综上,故选A .5.C解析:C 【解析】 【分析】根据平均数的定义即可求出.根据频率分布直方图中,中位数的左右两边频率相等,列出等式,求出中位数即可.6.B解析:B 【解析】 【分析】 【详解】分析:利用组合数列总事件数,根据等差数列通项公式确定所求事件数,最后根据古典概型概率公式求结果.详解:共有318C 17163=⨯⨯种事件数,选出火炬手编号为13(1)n a a n =+-, 由1、4、7、10、13、16,可得4种, 由2、5、8、11、14、17,可得4种, 由3、6、9、12、15、18,可得4种,4311716368p ⨯==⨯⨯.选B .点睛:古典概型中基本事件数的探求方法(1)列举法.(2)树状图法:适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目,常采用树状图法.(3)列表法:适用于多元素基本事件的求解问题,通过列表把复杂的题目简单化、抽象的题目具体化.(4)排列组合法:适用于限制条件较多且元素数目较多的题目.7.D解析:D【解析】【分析】甲、乙二人抢到的金额之和包含的基本事件的总数2510n C==,甲、乙二人抢到的金额之和不低于3元包含基本事件有6个,由此能求出甲、乙二人抢到的金额之和不低于3元的概率.【详解】由题意,所发红包的总金额为8元,被随机分配为1.72元、1.83元、2.28元、1.55元、0.62元、5分,供甲、乙等5人抢,每人只能抢一次,甲乙二人抢到的金额之和包含的基本事件的总数为2510n C==,甲乙二人抢到的金额之和不低于3元包含的基本事件有6个,分别为(1.72,1.83),(1.72,2.28),(1.72,1.55),(1.83,2.28),(1.83,1.55),(2.28,1.55)所以甲乙二人抢到的金额之和不低于3元的概率为63105p==,故选D.【点睛】本题主要考查了古典概型及其概率的计算问题,其中解答中正确理解题意,找出基本事件的总数和不低于3元的事件中所包含的基本事件的个数是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.8.D解析:D【解析】【分析】由题意列出所有可能的结果,然后结合古典概型计算公式可得概率值.【详解】能组成两位数有:10,12,13,20,21,23,30,31,32,总共有9种情况.其中偶数有5种情况,故组成的两位数是偶数的概率为59 p=.故选:D.【点睛】本题主要考查古典概型计算公式,属于中等题.9.B解析:B 【解析】∵数据x 1,x 2,x 3,…,x n 是郑州普通职工n (n ⩾3,n ∈N ∗)个人的年收入, 而x n +1为世界首富的年收入 则x n +1会远大于x 1,x 2,x 3,…,x n , 故这n +1个数据中,年收入平均数大大增大, 但中位数可能不变,也可能稍微变大,但由于数据的集中程序也受到x n +1比较大的影响,而更加离散,则方差变大. 故选B10.A解析:A 【解析】 【分析】先列出不超过11的素数,再列举出随机选取2个不同的数的情况,进而找到和小于等于10的情况,即可求解 【详解】不超过11的素数有:2,3,5,7,11,共有5个, 随机选取2个不同的数可能为:()2,3,()2,5,()2,7,()2,11,()3,5,()3,7,()3,11,()5,7,()5,11,()7,11,共有10种情况, 其中和小于等于10的有:()2,3,()2,5,()2,7,()3,5,()3,7,共有5种情况, 则概率为51102P ==, 故选:A 【点睛】本题考查列举法求古典概型的概率,属于基础题11.A解析:A 【解析】 【分析】列举出算法的每一步循环,根据算法输出结果计算出实数p 的取值范围,于此可得出整数p 的最小值. 【详解】0S p =<满足条件,执行第一次循环,0021S =+=,112n =+=; 1S p =<满足条件,执行第二次循环,1123S =+=,213n =+=; 3S p =<满足条件,执行第二次循环,2327S =+=,314n =+=. 7S p =<满足条件,调出循环体,输出n 的值为4.由上可知,37p <≤,因此,输入的整数p 的最小值是4,故选A.【点睛】本题考查算法框图的应用,解这类问题,通常列出每一次循环,找出其规律,进而对问题进行解答,考查分析问题和解决问题的能力,属于中等题.12.A解析:A 【解析】分析:根据已知中某公共汽车站每隔5分钟有一辆车通过,我们可以计算出两辆车间隔的时间对应的几何量长度为5,然后再计算出乘客候车时间不超过2分钟的几何量的长度,然后代入几何概型公式,即可得到答案 详解::∵公共汽车站每隔5分钟有一辆车通过当乘客在上一辆车开走后3分钟内到达候车时间会超过2分钟 ∴乘客候车时间不超过2分钟的概率为53255P -== . 故选A .点睛:本题考查的知识点是几何概型,其中计算出所有事件和满足条件的事件对应的几何量的值是解答此类问题的关键二、填空题13.【解析】【分析】先利用辅助角公式将函数的解析式化简根据三角函数的变化规律求出函数的解析式即可计算出的值【详解】由题意可得因此故答案为【点睛】本题考查辅助角公式化简三角函数图象变换在三角图象相位变换的解析:【解析】 【分析】先利用辅助角公式将函数sin 22y x x =-的解析式化简,根据三角函数的变化规律求出函数()y g x =的解析式,即可计算出56g π⎛⎫⎪⎝⎭的值. 【详解】sin 222sin 23y x x x π⎛⎫==- ⎪⎝⎭Q ,由题意可得()2sin 22sin 263g x x x ππ⎡⎤⎛⎫=+-= ⎪⎢⎥⎝⎭⎣⎦,因此,5552sin 22sin 2sin 22sin 66333g ππππππ⎛⎫⎛⎫⎛⎫=⨯==-=-=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭故答案为 【点睛】本题考查辅助角公式化简、三角函数图象变换,在三角图象相位变换的问题中,首先应该将三角函数的解析式化为()()sin 0y A x b ωϕω=++≠(或()()cos 0y A x b ωϕω=++≠)的形式,其次要注意左加右减指的是在自变量x 上进行加减,考查计算能力,属于中等题.14.【解析】【分析】列出随机变量的分布列求解【详解】由题意知某人到达银行的概率为几何概型所以:其到达银行时服务窗口的个数为的分布列为: 5 4 3 4 2 则【点睛】本题考查几何概型及随 解析:3.5625【解析】 【分析】列出随机变量的分布列求解. 【详解】由题意知某人到达银行的概率为几何概型,所以: 其到达银行时服务窗口的个数为的分布列为:则()54342 3.56258161648E X =⨯+⨯+⨯+⨯+⨯=. 【点睛】本题考查几何概型及随机变量的分布列.15.【解析】16.40【解析】【分析】设应从B 校抽取n 人利用分层抽样的性质列出方程组能求出结果【详解】设应从B 校抽取n 人某市有ABC 三所学校各校有高三文科学生分别为650人500人350人在三月进行全市联考后准备用分解析:40 【解析】 【分析】设应从B 校抽取n 人,利用分层抽样的性质列出方程组,能求出结果. 【详解】设应从B 校抽取n 人,Q 某市有A 、B 、C 三所学校,各校有高三文科学生分别为650人,500人,350人,在三月进行全市联考后,准备用分层抽样的方法从所有高三文科学生中抽取容量为120的样本,120n 650500350500∴=++,解得n 40=.故答案为:40.【点睛】本题考查应从B 校学生中抽取人数的求法,考查分层抽样的性质等基础知识,考查运算求解能力,是基础题.17.3【解析】【分析】分析出算法的功能是求分段函数的值根据输出的值为10分别求出当时和当时的值即可【详解】由程序语句知:算法的功能是求的值当时解得(或不合題意舍去);当时解得舍去综上的值为3故答案为3【解析:3 【解析】 【分析】分析出算法的功能是求分段函数22,31,3x x y x x <⎧=⎨+≥⎩的值,根据输出的值为10 ,分别求出当3x <时和当3x ≥时的x 值即可. 【详解】由程序语句知:算法的功能是求22,31,3x x y x x <⎧=⎨+≥⎩的值,当3x ≥时,2110y x =+=,解得3x =(或3- ,不合題意舍去); 当3x <时,210y x ==,解得5x = ,舍去, 综上,x 的值为3,故答案为3 . 【点睛】本题主要考查条件语句以及算法的应用,属于中档题 .算法是新课标高考的一大热点,其中算法的交汇性问题已成为高考的一大亮,这类问题常常与函数、数列、不等式等交汇自然,很好地考查考生的信息处理能力及综合运用知识解决问題的能力,解决算法的交汇性问题的方:(1)读懂程序框图、明确交汇知识,(2)根据给出问题与程序框图处理问题即可.18.【解析】【分析】模拟执行程序框图只要按照程序框图规定的运算方法逐次计算直到达到输出条件输出令即可得结果【详解】第一次输入执行循环体执行循环体执行循环体输出的值为0解得:故答案为【点睛】本题主要考查程 解析:78【解析】 【分析】模拟执行程序框图,只要按照程序框图规定的运算方法逐次计算,直到达到输出条件输出87x -,令870x -=即可得结果. 【详解】第一次输入x x =,1i =执行循环体,21x x =-,2i =,执行循环体,()221143x x x =--=-,3i =,执行循环体,()243187x x x =--=-,43i =>, 输出87x -的值为0,解得:78x =, 故答案为78. 【点睛】本题主要考查程序框图的循环结构流程图,属于中档题. 解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支结构还是循环结构;(3) 注意区分当型循环结构和直到型循环结构;(4) 处理循环结构的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,(6)在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可.19.18【解析】【分析】由题意知抽样方法为系统抽样因此若第一组抽取号码为x 则第18组抽取的号码为即可解得【详解】因为抽样方法为系统抽样因此若第一组抽取号码为x 则第18组抽取的号码为解得【点睛】本题主要考解析:18 【解析】 【分析】由题意知,抽样方法为系统抽样,因此,若第一组抽取号码为x ,则第18组抽取的号码为1725443x +⨯=,即可解得. 【详解】因为抽样方法为系统抽样,因此,若第一组抽取号码为x ,则第18组抽取的号码为1725443x +⨯=,解得18x =. 【点睛】本题主要考查了系统抽样,属于中档题.20.78【解析】【分析】求得4位同学各自在周六周日两天中任选一天参加公益活动周六周日都有同学参加公益活动的情况利用古典概型概率公式求解即可【详解】4位同学各自在周六周日两天中任选一天参加公益活动共有24 解析:【解析】 【分析】求得4位同学各自在周六、周日两天中任选一天参加公益活动、周六、周日都有同学参加公益活动的情况,利用古典概型概率公式求解即可. 【详解】4位同学各自在周六、周日两天中任选一天参加公益活动,共有24=16种情况, 周六、周日都有同学参加公益活动,共有24﹣2=16﹣2=14种情况, ∴所求概率为=.故答案为:.【点睛】有关古典概型的概率问题,关键是正确求出基本事件总数和所求事件包含的基本事件数:1.基本事件总数较少时,用列举法把所有基本事件一一列出时,要做到不重复、不遗漏,可借助“树状图”列举;2.注意区分排列与组合,以及计数原理的正确使用.三、解答题21.(1)0.15(2)2400(3)25人【解析】【分析】(1)由频率分布直方图计算可得月收入在[3000,3500)内的频率;(2)分别计算小长方形的面积值,利用中位数的特点即可确定中位数的值;(3)首先确定10000人中月收入在[2500,3000]内的人数,然后结合分层抽样的特点可得应抽取的人数.【详解】(1)居民月收入在[3000,3500]内的频率为0.0003(3500-3000)=0.15⨯(2)因为0.0002(15001000)0.1⨯-=,0.0004(20001500)0.2⨯-=,0.0005(25002000)0.25⨯-=,0.1+0.2+0.25=0.55>0.5,所以样本数据的中位数为0.5(0.10.2)20002000400=24000.0005-++=+.(3)居民月收入在[2500,3000]内的频率为0.0005(30002500)=0.25⨯-,所以这10000人中月收入在[2500,3000]内的人数为0.2510000=2500⨯.从这10000人中用分层抽样的方法抽出100人,则应从月收入在[2500,3000]内的居民中抽取25001002510000⨯=(人).【点睛】利用频率分布直方图求众数、中位数和平均数时,应注意三点:①最高的小长方形底边中点的横坐标即是众数;②中位数左边和右边的小长方形的面积和是相等的;③平均数是频率分布直方图的“重心”,等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和.22.238【解析】【分析】5432()3835126((((38)3)5)12)6f x x x x x x x x x x x=+-++-=+-++-,当2x=时,代入计算即可得出.【详解】根据秦九韶算法,把多项式改写成如下形式:()()()()()3835126x x x f x x x =+-++-,当2x =时.03v =,103814v v =+=,2123v v =⨯-142325=⨯-=, 3225v v =⨯+252555=⨯+=, 43212v v =⨯+55212122=⨯+=, 5426v v =⨯-12226238=⨯-=,所以当2x =时,多项式()f x 的值为238. 【点睛】本题考查了秦九韶算法,考查了推理能力与计算能力,属于基础题.23.(1)1917ˆ2626yx =-;(2)正相关,6天 【解析】 【分析】(1)利用回归直线方程计算公式,计算出回归直线方程.(2)根据回归直线方程判断出判断y 与x 之间的相关关系,令9x =,求得雾霾天数的预测值. 【详解】 (1)依题意23578122465,355x y ++++++++====,所以21515526b==-⨯$,$352626a =-⨯=-,所以ˆ2626y x =-. (2)由1917ˆ2626yx =-可知,y 与x 正相关,当9x =时,雾霾天数的预测值为19177796262613⨯-=≈天. 【点睛】 本小题主要考查回归直线方程的计算,考查利用回归直线方程进行预测,考查运算求解能力,属于基础题.24.(1)频率为0.2,人数为25人 (2)0.012x =,0.008y =(3)0.7 【解析】 【分析】(1)频率分布直方图中[)50,60所对应矩形的面积即为分数在[)50,60的频率,频数与频率比值即为总数.(2)由茎叶图得[)90,100的频数,由频数与总人数的比值得频率,从而得到y 值,再利用频率和为1可得x 值;(3)利用列举法,求出基本事件总数以及至少有一份分数在[)90,100之间的基本事件数,利用古典概型概率公式即可得出结果. 【详解】(1)分数在[)50,60的频率为0.020100.2⨯=, 由茎叶图知,分数在[)50,60之间的频数为5, ∴全班人数为5250.2=人 (2)分数在[)90,100之间的频数为2,由21025y =,得0.008y = 又()101100.0360.0240.0200.008x =-⨯+++,解得:0.012x = (3)分数在[)80,90内的人数是250.123⨯=人, 将[)80,90之间的3个分数编号为123,,a a a ,[)90,100之间的2个分数编号为12,b b ,在[)80,100之间的试卷中任取两份的基本事件为:()12,a a ,()13,a a ,()11,a b ,()12,a b ,()23,a a ,()21,a b ,()22,a b ,()31,a b ,()32,a b ,()12,b b 共10个 其中,至少有一个在[)90,100之间的基本事件有7个故至少有一份分数在[)90,100之间的概率是70.710=. 【点睛】本题考查古典概型概率公式与频率分布直方图的应用,属于基础题型.25.(1)0.01P =,n =100,(2)表见解析,没有95%以上的把握认为“读书之星”与性别有关(3)分布列见解析,()34E X = 【解析】 【分析】(1)首先根据频率和为1求P ,再根据频率,频数和样本容量的关系求n ;(2)首先计算“读书之星”的人数,然后再依次填写22⨯列联表;并根据公式计算2K 和3.841比较大小,做出判断;(3)从该地区学生中抽取一名学生是“读书之星”的概率为14,由题意可知1~3,4X B ⎛⎫ ⎪⎝⎭并求分布列和数学期望. 【详解】(1)()0.0050.0180.0200.0220.025101P +++++⨯= 解得:0.01P =, 所以100.1010n ==. (2)因为100n =,所以“读书之星”有1000.2525⨯= 从而22⨯列联表如下图所示:()2210030101545100 3.0304555752533K ⨯⨯-⨯==≈⨯⨯⨯因为3.030 3.841<,所以没有95%以上的把握认为“读书之星”与性别有关 (3)将频率视为概率,即从该地区学生中抽取一名学生是“读书之星”的概率为14. 由题意可知1~3,4X B ⎛⎫ ⎪⎝⎭所以()30301127041464P X C ⎛⎫⎛⎫⨯ ⎪ ⎪⎝⎭-=⎝⎭== ()3211271146414P X C ⎛==-=⎫⨯ ⎪⎝⎭, ()223192146414P X C ⎛⎫⎛⎫⨯ ⎪ ⎪⎝⎭⎝⎭==-=()333413641P X C ⎛⎫ ⎪⎭=⎝== 所以X 的分布列为P 27642764964164故()344E X=⨯=.【点睛】本题考查频率分布直方图的应用,独立性检验,二项分布,意在考查利用所给数据,分析问题和解决问题的能力,属于中档题型.26.(Ⅰ)13(Ⅱ)89【解析】分析:(Ⅰ)利用古典概型概率公式求出A1被选中的概率;(Ⅱ)利用对立事件概率公式求出求A1,B1不全被选中的概率.详解:(Ⅰ)从擅长速算、数独的6名选手中各选出1名与魔方选手C1组成中国战队的一切可能的结果组成集合Ω={(A1,B1,C1),(A1,B2,C1),(A1,B3,C1),(A2,B1,C1),(A2,B2,C1),(A2,B3,C1),(A3,B1,C1),(A3,B2,C1),(A3,B3,C1)},由9个基本事件组成.由题知每一个基本事件被抽取的机会均等,用M表示“A1被选中”,则M={(A1,B1,C1),(A1,B3,C1),(A1,B3,C1)},因而.(Ⅱ)用N表示“A1、B1不全被选中”这一事件,则其对立事件表示“A1、B1全被选中”,由于={(A1,B1,C1) },∴,从而点睛:古典概型中基本事件数的探求方法(1)列举法.(2)树状图法:适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目,常采用树状图法.(3)列表法:适用于多元素基本事件的求解问题,通过列表把复杂的题目简单化、抽象的题目具体化.(4)排列组合法:适用于限制条件较多且元素数目较多的题目.。
新高中必修三数学上期末模拟试卷(带答案)

新高中必修三数学上期末模拟试卷(带答案)一、选择题1.如图,ABC ∆和DEF ∆都是圆内接正三角形,且//BC EF ,将一颗豆子随机地扔到该圆内,用A 表示事件“豆子落在ABC ∆内”,B 表示事件“豆子落在DEF ∆内”,则(|)P B A =( )A .33B .3 C .13D .232.公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.小华同学利用刘徽的“割圆术”思想在半径为1的圆内作正n 边形求其面积,如图是其设计的一个程序框图,则框图中应填入、输出n 的值分别为( )(参考数据:020sin 200.3420,sin()0.11613≈≈)A .01180sin ,242S n n =⨯⨯B .01180sin ,182S n n =⨯⨯C .01360sin ,542S n n=⨯⨯D .01360sin ,182S n n=⨯⨯3.如图所给的程序运行结果为41S =,那么判断框中应填入的关于k 的条件是( )A .7k ≥?B .6k ≥?C .5k ≥?D .6k >?4.大学生小明与另外3名大学生一起分配到某乡镇甲、乙丙3个村小学进行支教,若每个村小学至少分配1名大学生,则小明恰好分配到甲村小学的概率为( ) A .112B .12C .13D .165.袋中装有红球3个、白球2个、黑球1个,从中随机摸出2个球,则与事件“至少有1个白球”互斥但不对立的事件是( ) A .没有白球 B .2个白球 C .红、黑球各1个D .至少有1个红球6.某市委积极响应十九大报告提出的“到2020年全面建成小康社会”的目标,鼓励各县积极脱贫,计划表彰在农村脱贫攻坚战中的杰出村代表,已知A ,B 两个贫困县各有15名村代表,最终A 县有5人表现突出,B 县有3人表现突出,现分别从A ,B 两个县的15人中各选1人,已知有人表现突出,则B 县选取的人表现不突出的概率是( ) A .13B .47C .23D .567.赵爽是我国古代数学家、天文学家大约在公元222年赵爽为《周碑算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的一个小正方形组成的)类比“赵爽弦图”,赵爽弦图可类似地构造如图所示的图形,它是由个3全等的等边三角形与中间的一个小等边三角形组成的一个大等边三角形,设DF =2AF ,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是( )A .B .C .D .8.已知统计某校1000名学生的某次数学水平测试成绩得到样本频率分布直方图如图所示,则直方图中实数a 的值是( )A.0.020B.0.018C.0.025D.0.039.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如40337=+.(注:如果一个大于1的整数除1和自身外无其他正因数,则称这个整数为素数.)在不超过11的素数中,随机选取2个不同的数,其和小于等于10的概率是()A.12B.13C.14D.1510.执行如图所示的程序框图,则输出s的值为()A.10 B.17 C.19 D.3611.已知某班级部分同学一次测验的成绩统计如图,则其中位数和众数分别为( )A.92,94B.92,86C.99,86D.95,9112.有一个容量为200的样本,样本数据分组为[50,70),[70,90),[90,110),[110,130),[130,150),其频率分布直方图如图所示.根据样本的频率分布直方图估计样本数据落在区间[90,110)内的频数为( )A .48B .60C .64D .72二、填空题13.我国传统的房屋建筑中,常会出现一些形状不同的窗棂,窗棂上雕刻有各种花纹,构成种类繁多的图案.如图所示的窗棂图案,是将半径为R 的圆六等分,分别以各等分点为圆心,以R 为半径画圆弧,在圆的内部构成的平面图形.现在向该圆形区域内的随机地投掷一枚飞镖,飞镖落在黑色部分(忽略图中的白线)的概率是__________.14.在[1,1]-上随机地取一个数k ,则事件“直线y kx =与圆22(5)9x y -+=相离”发生的概率为_______。
【必考题】高中必修三数学上期末一模试卷(含答案)(1)
【必考题】高中必修三数学上期末一模试卷(含答案)(1)一、选择题1.口袋里装有大小相同的5个小球,其中2个白球,3个红球,现一次性从中任意取出3个,则其中至少有1个白球的概率为( ) A .910B .710C .310D .1102.某校为了解高二年级学生某次数学考试成绩的分布情况,从该年级的1120名学生中随机抽取了100 名学生的数学成绩,发现都在[80,150]内现将这100名学生的成绩按照 [80,90),[90,100),[100,110),[110,120),[120,130),[130,140),[140,150]分组后,得到的频率 分布直方图如图所示则下列说法正确的是( )A .频率分布直方图中a 的值为 0.040B .样本数据低于130分的频率为 0.3C .总体的中位数(保留1位小数)估计为123.3分D .总体分布在[90,100)的频数一定与总体分布在[100,110)的频数不相等3.已知回归方程$21y x =+,而试验得到一组数据是(2,5.1),(3,6.9),(4,9.1),则残差平方和是( ) A .0.01 B .0.02C .0.03D .0.044.下面的程序框图表示求式子32×35×311×323×347×395的值, 则判断框内可以填的条件为( )A .90?i ≤B .100?i ≤C .200?i ≤D .300?i ≤5.如果数据121x +、221x +、L 、21n x +的平均值为5,方差为16,则数据:153x -、253x -、L 、53n x -的平均值和方差分别为( )A .1-,36B .1-,41C .1,72D .10-,1446.袋中装有红球3个、白球2个、黑球1个,从中随机摸出2个球,则与事件“至少有1个白球”互斥但不对立的事件是( ) A .没有白球 B .2个白球 C .红、黑球各1个D .至少有1个红球7.预测人口的变化趋势有多种方法,“直接推算法”使用的公式是()0 1nn P P k =+(1k >-),n P 为预测人口数,0P 为初期人口数,k 为预测期内年增长率,n 为预测期间隔年数.如果在某一时期有10k -<<,那么在这期间人口数 A .呈下降趋势B .呈上升趋势C .摆动变化D .不变8.按照程序框图(如图所示)执行,第3 个输出的数是( )A .6B .5C .4D .39.已知具有线性相关的两个变量,x y 之间的一组数据如下表所示:x0 1 2 3 4 y 2.24.34.54.86.7若,x y 满足回归方程 1.5ˆˆyx a =+,则以下为真命题的是( ) A .x 每增加1个单位长度,则y 一定增加1.5个单位长度 B .x 每增加1个单位长度,y 就减少1.5个单位长度 C .所有样本点的中心为(1,4.5) D .当8x =时,y 的预测值为13.510.甲、乙两位同学在高一年级的5次考试中,数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是12,x x ,则下列叙述正确的是( )A .12x x >,乙比甲成绩稳定B .12x x >,甲比乙成绩稳定C .12x x <,乙比甲成绩稳定D .12x x <,甲比乙成绩稳定11.执行如图的程序框图,若输出的4n =,则输入的整数p 的最小值是( )A .4B .5C .6D .1512.2路公共汽车每5分钟发车一次,小明到乘车点的时刻是随机的,则他候车时间不超过两分钟的概率是( ) A .25B .35C .23D .15二、填空题13.北京市某银行营业点在银行大厅悬挂着不同营业时间段服务窗口个数的提示牌,如图所示. 设某人到达银行的时间是随机的,记其到达银行时服务窗口的个数为X ,则()E X =______________.14.已知四棱锥P ABCD -的所有顶点都在球O 的球面上,PA ⊥底面ABCD ,底面ABCD 为正方形, 2.PA AB ==现在球O 的内部任取一点,则该点取自四棱锥P ABCD-的内部的概率为______.15.某程序框图如图所示,若输入的4t =,则输出的k =______.16.如果执行如图的程序框图,那么输出的S =__________.17.利用计算机产生0~1之间的均匀随机数a ,则使关于x 的一元二次方程20x x a -+=无实根的概率为______.18.如图,在平放的边长为1的正方形中随机撒1000粒豆子,有380粒落到红心阴影部分上,据此估计红心阴影部分的面积为____.19.如图是一个算法流程图,则输出的S 的值为______.20.把十进制数23化为二进制数是______.三、解答题21.一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1、2、3、4,现从盒子中随机抽取卡片.(Ⅰ)若一次从中随机抽取3张卡片,求3张卡片上数字之和大于或等于7的概率; (Ⅱ)若第一次随机抽取1张卡片,放回后再随机抽取1张卡片,求两次抽取的卡片中至少一次抽到数字2的概率.22.A B 两个班共有65名学生,为调查他们的引体向上锻炼情况,通过分层抽样获得了部分学生引体向上的测试数据(单位:个),用茎叶图记录如下:(1)试估计B 班的学生人数;(2)从A 班和B 班抽出的学生中,各随机选取一人,A 班选出的人记为甲,B 班选出的人记为乙,假设所有学生的测试相对独立,比较甲、乙两人的测试数据得到随机变量X .规定:当甲的测试数据比乙的测试数据低时,记1X =-;当甲的测试数据与乙的测试数据相等时,记X 0=;当甲的测试数据比乙的测试数据高时,记1X =.求随机变量X 的分布列及数学期望.(3)再从A 、B 两个班中各随机抽取一名学生,他们引体向上的测试数据分别是10,8(单位:个),这2个新数据与表格中的数据构成的新样本的平均数记1μ,表格中数据的平均数记为0μ,试判断0μ和1μ的大小.(结论不要求证明)23.2018年中秋节到来之际,某超市为了解中秋节期间月饼的销售量,对其所在销售范围内的1000名消费者在中秋节期间的月饼购买量(单位:g)进行了问卷调查,得到如下频率分布直方图:()1求频率分布直方图中a 的值;()2以频率作为概率,试求消费者月饼购买量在600g 1400g ~的概率;()3已知该超市所在销售范围内有20万人,并且该超市每年的销售份额约占该市场总量的5%,请根据这1000名消费者的人均月饼购买量估计该超市应准备多少吨月饼恰好能满足市场需求(频率分布直方图中同一组的数据用该组区间的中点值作代表)?24.为庆祝党的98岁生日,某高校组织了“歌颂祖国,紧跟党走”为主题的党史知识竞赛。
高中数学必修三期末模拟试题含答案

一、选择题1.某同学用“随机模拟方法”计算曲线ln y x =与直线,0x e y ==所围成的曲边三角形的面积时,用计算机分别产生了10个在区间[]1,e 上的均匀随机数i x 和10个区间[]0,1上的均匀随机数()*,110i y i N i ∈≤≤,其数据如下表的前两行.x 2.50 1.01 1.90 1.22 2.52 2.17 1.89 1.96 1.36 2.22 y 0.84 0.25 0.98 0.15 0.01 0.60 0.59 0.88 0.84 0.10 lnx0.900.010.640.200.920.770.640.670.310.80由此可得这个曲边三角形面积的一个近似值是 A .()215e + B .()215e - C .()315e + D .()315e - 2.中国是发现、研究和运用勾股定理最古老的国家之一,最早对勾股定理进行证明的是三国时期吴国的数学家赵爽,他创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,已知四个直角三角形的两条直角边的长度之比为12,若向大正方形中随机投入一点,则该点落入小正方形的概率为( )A .125B .19C .15D .133.甲乙两艘轮船都要在某个泊位停靠,甲停靠的时间为4小时,乙停靠的时间为6小时,假定他们在一昼夜的时间段中随机到达,则这两艘船停靠泊位时都不需要等待的概率为( ) A .916B .58C .181288D .5124.已知0.5log 5a =、3log 2b =、0.32c =、212d ⎛⎫= ⎪⎝⎭,从这四个数中任取一个数m ,使函数()32123x mx x f x =+++有极值点的概率为( )A.14B.12C.34D.15.若执行如图所示的程序框图,则输出S的值是()A.63 B.15 C.31 D.326.某程序框图如图所示,该程序运行后输出的S的值是( )A.1010 B.2019 C.2020 D.30307.《张丘建算经》中如下问题:“今有马行转迟,次日减半,疾五日,行四百六十五里,问日行几何?”根据此问题写出如下程序框图,若输出465S ,则输入m的值为()A.240 B.220 C.280 D.2608.程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.卷八中第33问:“今有三角果一垛,底阔每面七个.问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为()A.28 B.56 C.84 D.1209.某中学有学生300人,其中一年级120人,二,三年级各90人,现要利用抽样方法取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一,二,三年级依次统一编号为1,2,…,300;使用系统抽样时,将学生统一编号为1,2,…,300,并将整个编号依次分为10段.如果抽得的号码有下列四种情况:①7,37,67,97,127,157,187,217,247,277;②5,9,100,107,121,180,195,221,265,299;③11,41,71,101,131,161,191,221,251,281;④31,61,91,121,151,181,211,241,271,299.关于上述样本的下列结论中,正确的是()A.②④都不能为分层抽样B.①③都可能为分层抽样C.①④都可能为系统抽样D.②③都不能为系统抽样10.下图是某公司2018年1月至12月空调销售任务及完成情况的气泡图,气泡的大小表示完成率的高低,如10月份销售任务是400台,完成率为90%,则下列叙述不正确的是()A .2018年3月的销售任务是400台B .2018年月销售任务的平均值不超过600台C .2018年第一季度总销售量为830台D .2018年月销售量最大的是6月份11.已知变量,x y 之间的线性回归方程为0.47.6=-+y x ,且变量,x y 之间的一组相关数据如表所示,则下列说法错误的是( )A .变量,x y 之间呈现负相关关系B .m 的值等于5C .变量,x y 之间的相关系数0.4=-rD .由表格数据知,该回归直线必过点()9,412.某宠物商店对30只宠物狗的体重(单位:千克)作了测量,并根据所得数据画出了频率分布直方图如下图所示,则这30只宠物狗体重(单位:千克)的平均值大约为( )A .15.5B .15.6C .15.7D .16二、填空题13.已知某运动队有男运动员4名,女运动员3名,若现在选派3人外出参加比赛,则选出的3人中男运动员比女运动员人数多的概率是_________.14.在区间[0,2]上随机取两个数,a b ,则事件“函数()1f x bx a =+-在[0,1]内有零点”的概率为_______.15.如图,在半径为1的圆上随机地取两点,B E ,连成一条弦BE ,则弦长超过圆内接正BCD ∆边长的概率是__________.16.按下列程序框图运算:规定:程序运行到“判断结果是否大于244”为1次运算.若运算进行3次才停止,则x 的取值范围是__________.17.如下图,程序框图中,若输入4,10m n ==,则输出a 的值是________.18.右图程序框图的运行结果是____________________19.某住宅小区有居民2万户,从中随机抽取200户,调查是否安装宽带,调查结果如下表所示: 宽带租户业主已安装6042未安装3662则该小区已安装宽带的居民估计有______户.20.为弘扬我国优秀的传统文化,某小学六年级从甲、乙两个班各选出7名学生参加成语知识竞赛,他们取得的成绩的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83,则的值为__________.三、解答题21.某地区为了解群众上下班共享单车使用情况,根据年龄按分层抽样的方式调查了该地区50名群众,他们的年龄频数及使用共享单车人数分布如下表:年龄段20~2930~3940~4950~60频数1218155经常使用共享单车61251(1)由以上统计数据完成下面的22⨯列联表,并判断是否有95%的把握认为以40岁为分界点对是否经常使用共享单车有差异?年龄低于40岁年龄不低于40岁总计经常使用共享单车不经常使用共享单车总计附:()()()()()22n ad bcKa b c d a c b d-=++++,n a b c d=+++.()20P K k ≥ 0.250.15 0.10 0.050 0.025 0.010 0k 1.3232.0722.7063.8415.0246.635(2)若采用分层抽样的方式从年龄低于40岁且经常使用共享单车的群众中选出6人,再从这6人中随机抽取2人,求这2人中恰好有1人年龄在30~39岁的概率.22.绝大部分人都有患呼吸系统疾病的经历,现在我们调查患呼吸系统疾病是否和所处环境有关.一共调查了500人,患有呼吸系统疾病的350人,其中150人在室外工作,200人在室内工作.没有患呼吸系统疾病的150人,其中50人在室外工作,100人在室内工作.(1)现采用分层抽样从室内工作的居民中抽取一个容量为6的样本,将该样本看成一个总体,从中随机的抽取两人,求两人都有呼吸系统疾病的概率.(2)你能否在犯错误率不超过0.05的前提下认为感染呼吸系统疾病与工作场所有关; 附表:()20P K k ≥0.100.050.025 0K2.7063.8415.024()()()()()22n ad bc K a b c d a c b d -=++++23.从某企业生产的某种产品中抽取20件,测量这些产品的一项质量指标值,由测量得到如图1的频率分布直方图,从左到右各组的频数依次记为1A ,2A ,3A,4A ,5A .(1)求图1中a 的值;(2)图2是统计图1中各组频数的一个算法流程图,求输出的结果S .24.已知函数y=21,0,1,0,x xxx ⎧>⎪⎪⎨⎪<⎪⎩设计一个算法的程序框图,计算输入x 的值,输出y 的值.25.某同学在生物研究性学习中,对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究,于是他在4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下资料: 日期 4月1日 4月7日 4月15日 4月21日 4月30日 温差x C ︒ 10 11 13 12 8 发芽数y 颗2325302616(1)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另三天的数据,求出y 关于x 的线性回归方程y bx a =+;(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠? 附:回归直线的斜率和截距的最小二乘估计公式分别为:()()()1122211nniii i i i nniii i x x y y x y nx yb x x xnx====---==--∑∑∑∑,a y bx =-.26.某“双一流”大学专业奖学金是以所学专业各科考试成绩作为评选依据,分为专业一等奖学金(奖金额3000元)、专业二等奖学金(奖金额1500元)及专业三等奖学金(奖金额600元),且专业奖学金每个学生一年最多只能获得一次.图(1)是统计了该校2018年500名学生周课外平均学习时间频率分布直方图,图(2)是这500名学生在2018年周课外平均学习时间段获得专业奖学金的频率柱状图.(Ⅰ)求这500名学生中获得专业三等奖学金的人数;(Ⅱ)若周课外平均学习时间超过35小时称为“努力型”学生,否则称为“非努力型”学生,列22⨯联表并判断是否有99.9%的把握认为该校学生获得专业一、二等奖学金与是否是“努力型”学生有关?(Ⅲ)若以频率作为概率,从该校任选一名学生,记该学生2018年获得的专业奖学金额为随机变量X ,求随机变量X 的分布列和期望.22()()()()()n ad bc K a b c d a c b d -=++++【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【详解】 由题意可得ACB ABCD=10S nS ∆曲线矩形,n 为阴影部分的点的个数,即满足y<lnx,共6个点,即ACB ABCD6=101S S S e ∆=-曲线矩形,所以S=()315e -,选D.2.C解析:C 【分析】由已知的线段的长度比,得出两正方形的面积,运用概率公式可得选项. 【详解】设直角三角形的两直角边分别为1和222125+=5所以小正方形的边长为211-=,面积为1,大正方形的面积为2(5)5=.所以飞镖落在小正方形内的概率为1 5.故选:C.【点睛】本题考查几何概型,关键在于由长度的关系得出大正方形和小正方形的面积,属于中档题. 3.C解析:C【分析】设甲、乙到达的时间分别为,x y,列出所有基本事件的约束条件,同时列出两艘船停靠泊位时都不需要等待的约束条件,利用线性规划做出平面区域,利用几何概型概率关系转化为面积比.【详解】设甲、乙到达的时间分别为,x y,则所有基本事件的构成的区域024{|}024xxy≤≤⎧Ω=⎨≤≤⎩,则这两艘船停靠泊位时都不需要等待包含的基本事件构成的区域024024{(,)|}46xyA x yy xx y≤≤⎧⎪≤≤⎪=⎨≥+⎪⎪≥+⎩,做出Ω构成的区域,其面积为224=576,阴影部分为集合A构成的区域,面积为221(2018)3622+=,这两艘船停靠泊位时都不需要等待的概率362181()576288P A==.故选:C.【点睛】本题考查利用线性规划做出事件对应的平面区域,再利用几何概型概率公式求出事件的概率,属于中档题.4.B解析:B 【分析】求出函数的导数,根据函数的极值点的个数求出m 的范围,通过判断a ,b ,c ,d 的范围,得到满足条件的概率值即可. 【详解】f ′(x )=x 2+2mx +1, 若函数f (x )有极值点, 则f ′(x )有2个不相等的实数根, 故△=4m 2﹣4>0,解得:m >1或m <﹣1,而a =log 0.55<﹣2,0<b =log 32<1、c =20.3>1,0<d =(12)2<1, 满足条件的有2个,分别是a ,c , 故满足条件的概率p 2142==, 故选:B . 【点睛】本题考查了函数的单调性、极值问题,考查导数的应用以及对数、指数的性质,是一道中档题.5.C解析:C 【分析】根据程序框图模拟程序计算即可求解. 【详解】模拟程序的运行,可得1S =,1i =; 满足条件5i <,执行循环体,3S =,2i =; 满足条件5i <,执行循环体,7=S ,3i =; 满足条件5i <,执行循环体,15S =,4i =; 满足条件5i <,执行循环体,31S =,5i =; 此时,不满足条件5i <,退出循环,输出S 的值为31. 故选:C 【点睛】本题主要考查了程序框图,循环结构,属于中档题.6.D解析:D 【分析】模拟程序框图的运行过程,得出该程序运行后输出的算式S 是求数列的和,且数列每四项和是定值,由此得出S 的值. 【详解】模拟程序框图的运行过程,得出该程序运行后输出的算式: 由于cos,42xy T π==,且循环数为0,-1,0,1123420132014201520162017201820192020...+++++++(01210141)+...+(0+1201410120161)(01201810120201)S a a a a a a a a a a a a =++++=+-+++++-+++++++-+++++20206=30304=⨯故选:D 【点睛】本题考查了程序框图的循环结构,考查了学生逻辑推理,数学运算的能力,属于中档题.7.A解析:A 【分析】根据程序框图,依次循环计算,可得输出的S 表达式.结合465S =,由等比数列求和公式,即可求得m 的值. 【详解】由程序框图可知,0,0S i ==,1S m i ==,22mS m i =+= ,324m mS m i =++= ,4248m m mS m i =+++= ,524816m m m mS m i =++++= 此时输出S .所以46524816m m m mm ++++= 即1111146524816m ⎛⎫++++= ⎪⎝⎭由等比数列前n 项和公式可得5112465112m ⎛⎫- ⎪⎝⎭⨯=- 解得240m =故选:A 【点睛】本题考查了循环结构程序框图的应用,等比数列求和的应用,属于中档题.8.C解析:C 【分析】由已知中的程序可知:该程序的功能是利用循环结构计算并输出变量S 的值,模拟程序运行过程,分析循环中各变量值的变化情况,即可求解. 【详解】模拟程序的运行,可得:0,0,0i n S === 执行循环体,1,1,1i n S ===;不满足判断条件7i ≥,执行循环体,2,3,4i n S ===; 不满足判断条件7i ≥,执行循环体,3,6,10i n S ===; 不满足判断条件7i ≥,执行循环体,4,10,20i n S ===; 不满足判断条件7i ≥,执行循环体,5,15,35i n S ===; 不满足判断条件7i ≥,执行循环体,6,21,56i n S ===; 不满足判断条件7i ≥,执行循环体,7,28,84i n S ===; 满足判断条件7i ≥,退出循环,输出S 的值为84. 故选C. 【点睛】本题主要考查了循环结构的程序框图的计算与输出问题,其中解答中模拟程序运行的过程,通过逐次计算和找出计算的规律是解答的关键,着重考查了推理与计算能力,属于基础题.9.B解析:B 【分析】根据系统抽样和分层抽样的定义分别进行判断即可. 【详解】若采用简单随机抽样,根据简单随机抽样的特点,1~300之间任意一个号码都有可能出现;若采用分层抽样,则1~120号为一年级,121~210为二年级,211~300为三年级.且根据分层抽样的概念,需要在1~120之间抽取4个,121~210与211~300之间各抽取3个; 若采用系统抽样,根据系统抽样的概念,需要在1~30,31~60,61~90,91~ 120,121~150,151~180,181~210,211~240,241~270,271~300之间各抽一个.①项,1~120之间有 4个,121~210之间有 3个,211~300之间有 3个,并且满足系统抽样的条件,所以①项为系统抽样或分层抽样;②项,1~120之间有 4个,121~210之间有 3个,211~300之间有 3个,可能为分层抽样;③项,1~120之间有 4个,121~210之间有 3个,211~300之间有 3个,并且满足系统抽样的条件,所以③项为系统抽样或分层抽样;④项,第一个数据大于30,所以④项不可能为系统抽样,并且④项不满足分层抽样的条件.综上所述,B 选项正确. 故选:B. 【点睛】本题主要考查系统抽样和分层抽样,掌握系统抽样和分层抽样的定义是解题的关键,属于基础题.(1)系统抽样适用于总体容量较大的情况.将总体平均分成若干部分,按事先确定的规则在各部分中抽取,在起始部分抽样时采用简单随机抽样;(2)分层抽样适用于已知总体是由差异明显的几部分组成的.将总体分成互不交叉的层,然后分层进行抽取,各层抽样时采用简单随机抽样或系统抽样.10.D解析:D 【分析】根据图形中给出的数据,对每个选项分别进行分析判断后可得错误的结论. 【详解】对于选项A ,由图可得3月份的销售任务是400台,所以A 正确. 对于选项B ,由图形得2018年月销售任务的平均值为1(3245810743413)10045012⨯+++++++++++⨯=,所以B 正确. 对于选项C ,由图形得第一季度的总销售量为13002001400 1.28302⨯+⨯+⨯=台,所以C 正确.对于选项D ,由图形得销售量最大的月份是5月份,为800台,所以D 不正确. 故选D . 【点睛】本题考查统计中的识图、用图和计算,解题的关键是从图中得到相关数据,然后再根据要求进行求解,属于基础题.11.C解析:C 【解析】分析:根据线性回归方程的性质依次判断各选项即可.详解:对于A :根据b 的正负即可判断正负相关关系.线性回归方程为0.47.6y x =-+,b=﹣0.7<0,负相关.对于B :根据表中数据:x =9.可得y =4.即()16+3244m ++=,解得:m=5. 对于C :相关系数和斜率不是一回事,只有当样本点都落在直线上是才满足两者相等,这个题目显然不满足,故不正确.对于D :由线性回归方程一定过(x ,y ),即(9,4).故选:C.点睛:本题考查了线性回归方程的求法及应用,属于基础题,对于回归方程,一定要注意隐含条件,样本中心满足回归方程,再者计算精准,正确理解题意,应用回归方程对总体进行估计.12.B解析:B【分析】由频率分布直方图分别计算出各组得频率、频数,然后再计算出体重的平均值【详解】由频率分布直方图可以计算出各组频率分别为:0.10.20.250.250.15,,,,,0.05频数为:367.57.54.51.5,,,,,则平均值为:113136157.5177.519 4.521 1.515.630⨯+⨯+⨯+⨯+⨯+⨯=故选B【点睛】本题主要考查了由频率分布直方图计算平均数,需要注意计算不要出错二、填空题13.【分析】将所求事件分为两种情况:男女男这两个事件互斥然后利用古典概型的概率公式和互斥事件的概率加法公式可求出所求事件的概率【详解】事件选出的人中男运动员比女运动员人数多包含事件男女和事件男由古典概型解析:22 35.【分析】将所求事件分为两种情况:2男1女,3男,这两个事件互斥,然后利用古典概型的概率公式和互斥事件的概率加法公式可求出所求事件的概率.【详解】事件“选出的3人中男运动员比女运动员人数多”包含事件“2男1女”和事件“3男”,由古典概型概率公式和互斥事件的概率加法公式可知,事件“选出的3人中男运动员比女运动员人数多”的概率为213434372235 C C CC+=,故答案为22 35.【点睛】本题考查古典概型的概率公式和互斥事件的概率加法公式的应用,解题时要将所求事件进行分类讨论,结合相关公式进行计算,考查计算能力,属于中等题.14.【解析】【分析】在上任取两个数在以2为棱长的正方形内在内有零点等价于即求出可行域的面积利用几何概型概率公式求解即可【详解】在上任取两个数则在以2为棱长的正方形内因为在内有零点所以即表示如图所示的梯形解析:38【解析】 【分析】在[]0,2上任取两个数,a b , (),a b 在以2为棱长的正方形内,()f x 在[]0,1内有零点, 等价于()()010f f ≤,即()()110a b a -+-≤,求出可行域的面积,利用几何概型概率公式求解即可. 【详解】在[]0,2上任取两个数,a b , 则(),a b 在以2为棱长的正方形内, 因为()f x 在[]0,1内有零点, 所以()()010f f ≤, 即()()110a b a -+-≤,(),a b 表示如图所示的梯形区域,由几何概型概率公式可得“函数()1f x bx a =+-在[]0,1内有零点”的概率为()112132228⨯+⨯=⨯,故答案为38. 【点睛】本题主要考查“面积型”的几何概型,属于中档题. 解决几何概型问题常见类型有:长度型、角度型、面积型、体积型,求与面积有关的几何概型问题关鍵是计算问题的总面积以及事件的面积;几何概型问题还有以下几点容易造成失分,在备考时要高度关注:(1)不能正确判断事件是古典概型还是几何概型导致错误;(2)基本事件对应的区域测度把握不准导致错误 ;(3)利用几何概型的概率公式时 , 忽视验证事件是否等可能性导致错误.15.【解析】【分析】取圆内接等边三角形的顶点为弦的一个端点当另一端点在劣弧上时求出劣弧的长度运用几何概型的计算公式即可得结果【详解】记事件{弦长超过圆内接等边三角形的边长}如图取圆内接等边三角形的顶点为解析:1 3【解析】【分析】取圆内接等边三角形BCD的顶点B为弦的一个端点,当另一端点在劣弧CD上时,BE BC>,求出劣弧CD的长度,运用几何概型的计算公式,即可得结果.【详解】记事件A={弦长超过圆内接等边三角形的边长},如图,取圆内接等边三角形BCD的顶点B为弦的一个端点,当另一端点在劣弧CD上时,BE BC>,设圆的半径为r,劣弧CD的长度是23rπ,圆的周长为2rπ,所以()21323rP Arππ==,故答案为13.【点睛】本题主要考查“长度型”的几何概型,属于中档题. 解决几何概型问题常见类型有:长度型、角度型、面积型、体积型,求与长度有关的几何概型问题关鍵是计算问题的总长度以及事件的长度;几何概型问题还有以下几点容易造成失分,在备考时要高度关注:(1)不能正确判断事件是古典概型还是几何概型导致错误;(2)基本事件对应的区域测度把握不准导致错误;(3)利用几何概型的概率公式时 , 忽视验证事件是否等可能性导致错误. 16.【分析】根据题意得到不等式和计算得到答案【详解】根据题意知:且故故答案为:【点睛】本题考查了程序框图没有考虑完整情况是容易发生的错误解析:(]10,28【分析】根据题意得到不等式()3322244x--≤和()333222244x--->⎡⎤⎣⎦,计算得到答案.【详解】根据题意知:()332224428x x--≤∴≤且()33322224410x x--->∴>⎡⎤⎣⎦故(]10,28x∈故答案为:(]10,28【点睛】本题考查了程序框图,没有考虑完整情况是容易发生的错误.17.20【解析】模拟执行程序可得:不满足条件整除以不满足条件整除以不满足条件整除以不满足条件整除以满足条件整除以退出循环输出的值为点睛:本题主要考查的程序框图的知识点解题的关键是要读懂程序框图模拟执行程解析:20 【解析】模拟执行程序,可得:4,10m n ==,1i =,4a =不满足条件n 整除以a2i =,8a =不满足条件n 整除以a 3i =,12a =不满足条件n 整除以a4i =,16a =不满足条件n 整除以a5i =,20a =满足条件n 整除以a ,退出循环,输出a 的值为20点睛:本题主要考查的程序框图的知识点.解题的关键是要读懂程序框图.模拟执行程序,依次写出每次循环得到的i ,a 的值,当20a =的时候,满足条件n 整除以a ,退出循环,即可得到输出a 的值为20.18.120【解析】输出s=120解析:120 【解析】6,16,530,4120,34a s s a s a s a ==→==→==→==<.输出s=12019.【分析】计算出抽样中已安装宽带的用户比例乘以总人数求得小区已安装宽带的居民数【详解】抽样中已安装宽带的用户比例为故小区已安装宽带的居民有户【点睛】本小题主要考查用样本估计总体考查频率的计算属于基础题 解析:10200【分析】计算出抽样中已安装宽带的用户比例,乘以总人数,求得小区已安装宽带的居民数. 【详解】抽样中已安装宽带的用户比例为604251200100+=,故小区已安装宽带的居民有512000010200100⨯=户. 【点睛】本小题主要考查用样本估计总体,考查频率的计算,属于基础题.20.35【解析】79+78+80+80+x+85+92+967=85解得x=5根据中位数为83可知y=3故yx=35 解析:【解析】,解得,根据中位数为,可知,故.三、解答题21.(1)见解析;(2)518【分析】(1)根据题意填写列联表,由表中数据计算观测值,对照临界值得出结论; (2)用分层抽样法选出6人,利用列举法求出基本事件数,再计算所求的概率值. 【详解】(1) 根据题意填写2×2列联表如下:年龄低于40岁 年龄不低于40岁 总计 经常使用共享单车 18 6 24 不经常使用共享单车 12 14 26 总计302050222()50(1814126) 4.327 3.841()()()()30202426n ad bc K a b c d a c b d -⨯⨯-⨯===>++++⨯⨯⨯所以有95%的把握认为以40岁为分界点对是否经常使用共享单车有差异.(2) 用分层抽样法选出6人,其中20~29岁的有2人,记为A 、B ,30~39岁的有4人,记为c 、d 、e 、f,再从这6人中随机抽取2人,基本事件为: AB 、Ac 、Ad 、Ae 、Af 、Be 、Bd 、Be 、Bf 、cd 、ce 、cf 、de 、df 、ef 共15种不同取法;则抽取的这2人中恰好有1人年龄在30~39岁的基本事件为:Ac 、Ad 、Ae 、Af 、Bc 、Bd 、Be 、Bf 共8种不同取法; 故所求的概率为815P =. 【点睛】本题考查了学生运用表格求相应统计数据的能力,会运用独立性检验处理实际问题中的关联性问题,考查了分层抽样结果,以及求简单随机事件的概率,可以列举法处理,属于中档题. 22.(1)25;(2)在犯错误概率不超过0.05的前提下,能认为感染呼吸系统疾病与工作场所有关. 【分析】(1)求出6个样本中有呼吸系统疾病和无呼吸系统疾病的人数,再求得基本事件的总数,利用古典概型概率公式,即可得出结论;(2)由所给数据,得到22⨯列联表,求出观测值,同所给的临界值表进行比较,即可得出结论. 【详解】解:(1)采用分层抽样从室内工作的居民中抽取容量为6的样本,有呼吸系统疾病的抽到20064300⨯=人,无呼吸系统疾病的抽2 人.记有呼吸系统疾病的4人分别为1A 、2A 、3A 、4A ,无呼吸系统疾病的2人分别为1B 、2B ;从中随机抽取两人,则所有的可能结果有:()12,A A ,()13,A A ,()14,A A ,()11,AB ,()12,A B ,()23,A A ,()24,A A ,()21,A B ,()22,A B ,()34,A A ,()31,A B ,()32,A B ,()41,A B ,()42,A B ,()12,B B 共15个;设A = “从中随机的抽取两人,两人都有呼吸系统疾病”,则满足事件A 的基本事件有()12,A A ,()13,A A ,()14,A A ,()23,A A ,()24,A A ,()34,A A 共6个;则()62155P A ==; (2)22⨯列联表如下:计算2500(150********) 3.96831501502003003.84K ⨯⨯-⨯=≈>⨯⨯⨯, ∴在犯错误概率不超过0.05的前提下,能认为感染呼吸系统疾病与工作场所有关.【点睛】本题考查分层抽样,考查独立性检验的应用,属于中档题. 23.(1) 0.005a =. (2) 18S =. 【解析】分析:(1)由频率分布直方图中所有频率之和为1可计算出a ; (2)模拟程序运行,程序实际上是计算234A A A ++.详解:(1)由频率直方图可知()20.020.030.04101a +++⨯=, 解得0.005a =; 根据程序框图10.00510201A =⨯⨯=;20.04010208A =⨯⨯=;30.03010206A =⨯⨯=;40.02010204A =⨯⨯=;50.00510201A =⨯⨯=,所以输出的23418S A A A =++=;点睛:频率分布直方图中所有频率之和为1,即图中所有小矩形面积之和为1.24.答案见解析【解析】【试题分析】主要结构是有一个选择结构,当0x >时为1x ,当0x <时为21x ,当0x =时直接退出程序.【试题解析】根据题意,其自然语言算法如下.第一步,输入x.第二步,判断x>0是否成立.若成立,则输出y=1x,结束算法; 若不成立,则判断x<0是否成立.若成立,则输出y=21x ,结束算法;若不成立,也结束算法. 程序框图如右:【点睛】画程序框图的规则如下:(1)一个完整的程序框图必须有起止框,用来表示程序的开始和结束.(2)使用标准的图形符号表示操作,带箭头的流程线表示算法步骤的先后顺序,框图一般按从上到下、从左到右的方向画(3)算法中间要处理数据或计算,可分别写在不同的处理框中.(4)如果一个流程由于纸面等原因需要分开画.要在断开处画上连结点,并标出连结的号码.如图一.实际 上它们是同一点,只是化不才分开画.用连结点可避免流程线的交叉或过长,使流程图清晰.(5)注释框不是流程图必需的部分,只是为了提示用户 一部分框图的作用以及对某些框图的操作结果进行说明.它帮助阅读流程图的用户更好的理解流程图的来龙去脉.(6)在图形符号内用于描述的语言要非常简练清楚25.(1)532y x =-;(2)线性回归方程是可靠的. 【分析】(1)根据最小二乘法公式,分别将数据代入计算,即可得答案;(2)选取的是4月1日与4月30日的两组数据,即10x =和8x =代入判断即可;【详解】解:(1)由数据得12x =,27y =,3972xy =,23432x =;又31977ii i x y ==∑,321434i i x ==∑;97797254344322b -==-,5271232a =-⨯=-;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【必考题】高中必修三数学上期末模拟试题(含答案)一、选择题1.执行如图的程序框图,若输入1t =-,则输出t 的值等于( )A .3B .5C .7D .152.如图,ABC ∆和DEF ∆都是圆内接正三角形,且//BC EF ,将一颗豆子随机地扔到该圆内,用A 表示事件“豆子落在ABC ∆内”,B 表示事件“豆子落在DEF ∆内”,则(|)P B A =( )A .33B .3C .13D .233.一块各面均涂有油漆的正方体被锯成27个大小相同的小正方体,若将这些小正方体均匀地搅混在一起,从中任意取出一个,则取出的小正方体两面涂有油漆的概率是( ) A . B . C . D .4.某校为了解高二年级学生某次数学考试成绩的分布情况,从该年级的1120名学生中随机抽取了100 名学生的数学成绩,发现都在[80,150]内现将这100名学生的成绩按照[80,90),[90,100),[100,110),[110,120),[120,130),[130,140),[140,150]分组后,得到的频率 分布直方图如图所示则下列说法正确的是( )A .频率分布直方图中a 的值为 0.040B .样本数据低于130分的频率为 0.3C .总体的中位数(保留1位小数)估计为123.3分D .总体分布在[90,100)的频数一定与总体分布在[100,110)的频数不相等5.如果数据12,,,n x x x L 的平均数为x ,方差为28,则152x +,252x +,…,52n x +的平均数和方差分别为( )A .x ,28B .52x +,28C .52x +,2258⨯D .x ,2258⨯6.执行如图所示的程序框图,输出的S 值为( )A .1B .-1C .0D .-27.如图是某手机商城2018年华为、苹果、三星三种品牌的手机各季度销量的百分比堆积图(如:第三季度华为销量约占50%,苹果销量约占20%,三星销量约占30%).根据该图,以下结论中一定正确的是( )A .华为的全年销量最大B .苹果第二季度的销量大于第三季度的销量C .华为销量最大的是第四季度D .三星销量最小的是第四季度 8.从0,1,2,3这四个数中任取两个不同的数组成一个两位数,则这个两位数是偶数的概率为( )A .27B .57C .29D .599.设数据123,,,,n x x x x L 是郑州市普通职工*(3,)n n n N ≥∈个人的年收入,若这n 个数据的中位数为x ,平均数为y ,方差为z ,如果再加上世界首富的年收入1n x +,则这1n +个数据中,下列说法正确的是( )A .年收入平均数大大增大,中位数一定变大,方差可能不变B .年收入平均数大大增大,中位数可能不变,方差变大C .年收入平均数大大增大,中位数可能不变,方差也不变D .年收入平均数可能不变,中位数可能不变,方差可能不变10.执行如图所示的程序框图,若输入2x =-,则输出的y =( )A .8-B .4-C .4D .811.如图,边长为2的正方形有一内切圆.向正方形内随机投入1000粒芝麻,假定这些芝麻全部落入该正方形中,发现有795粒芝麻落入圆内,则用随机模拟的方法得到圆周率π的近似值为( )A .3.1B .3.2C .3.3D .3.412.小赵和小王约定在早上7:00至7:15之间到某公交站搭乘公交车去上学,已知在这段时间内,共有2班公交车到达该站,到站的时间分别为7:05,7:15,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为( )A .13B .49C .59D .23二、填空题13.若正方形ABCD 的边长为4, E 为四边形上任意一点,则AE 的长度大于5的概率等于______14.如图,在半径为1的圆上随机地取两点,B E ,连成一条弦BE ,则弦长超过圆内接正BCD ∆边长的概率是__________.15.期末考试结束后,某老师随机抽取了本班五位同学的数学成绩进行统计,五位同学平均每天学习数学的时间t (分钟)与数学成绩y 之间的一组数据如下表所示: 时间t (分钟)30 40 70 90 120 数学成绩y 35 48 m82 92 通过分析,发现数学成绩y 与学习数学的时间t 具有线性相关关系,其回归方程为0.715ˆyt =+,则表格中的m 的值是___. 16.利用计算机产生0~1之间的均匀随机数a ,则使关于x 的一元二次方程20x x a -+=无实根的概率为______.17.一只口袋中装有形状、大小都相同的6只小球,其中有3只红球、2只黄球和1只蓝球.若从中1次随机摸出2只球,则2只球颜色相同的概率为____.18.把十进制数23化为二进制数是______.19.使用如图所示算法对下面一组数据进行统计处理,则输出的结果为__________.数据:19.3a =,29.6a =,39.3a =49.4a =,59.4a =,69.3a =79.3a =,89.7a =,99.2a =109.5a =,119.3a =,129.6a =20.在四位八进制数中,能表示的最小十进制数是__________.三、解答题21.某中学高二年级的甲、乙两个班中,需根据某次数学预赛成绩选出某班的5名学生参加数学竞赛决赛,已知这次预赛他们取得的成绩的茎叶图如图所示,其中甲班5名学生成绩的平均分是83,乙班5名学生成绩的中位数是86.(1)求出x ,y 的值,且分别求甲、乙两个班中5名学生成绩的方差、,并根据结果,你认为应该选派哪一个班的学生参加决赛? (2)从成绩在85分及以上的学生中随机抽取2名.求至少有1名来自甲班的概率.22.从某居民区随机抽取10个家庭,获得第i 个家庭的月收入i x (单位:千元)与月储蓄i y ,(单位:千元)的数据资料,算出101010102111180,20184,720i i i i i i i i i xy x y x ========∑∑∑∑,,附:线性回归方程1221ˆˆˆˆˆˆ,,n i ii n ii x y nxy y bx a b ay bx x nx ==-=+==--∑∑,其中,x y 为样本平均值. (1)求家庭的月储蓄y 对月收入x 的线性回归方程ˆˆˆybx a =+ ; (2)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.23.某地统计局调查了10000名居民的月收入,并根据所得数据绘制了样本的频率分布直方图如图所示.(1)求居民月收入在[3000,3500)内的频率;(2)根据频率分布直方图求出样本数据的中位数;(3)为了分析居民的月收入与年龄、职业等方面的关系,必须按月收入再从这10000中用分层抽样的方法抽出100人做进一步分析,则应从月收入在[2500,3000)内的居民中抽取多少人?24.某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].(1)求图中a的值;(2)根据频率分布直方图,估计这100名学生语文成绩的平均数与中位数.25.某公司为研究某产品的广告投入与销售收入之间的关系,对近五个月的广告投入x (万元)与销售收入y(万元)进行了统计,得到相应数据如下表:广告投入x(万元)91081112销售收入y(万元)2123212025(1)求销售收入y关于广告投入x的线性回归方程y bx a=+$$$.(2)若想要销售收入达到36万元,则广告投入应至少为多少.参考公式:()()()121ni iiniix x y ybx x∧==--=-∑∑,ˆˆ•a yb x=-26.口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.(Ⅰ)求甲赢且编号的和为6的事件发生的概率;(Ⅱ)这种游戏规则公平吗?试说明理由.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【解析】【分析】直接根据程序框图依次计算得到答案.【详解】模拟执行程序,可得1t =-,不满足条件0t >,0t =,满足条件()()250t t +-<,不满足条件0t >,1t =,满足条件()()250t t +-<,满足条件0t >,3t =,满足条件()()250t t +-<,满足条件0t >,7t =,不满足条件()()250t t +-<,退出循环,输出t 的值为7. 故选:C.【点睛】本题考查了程序框图,意在考查学生的计算能力和理解能力.2.D解析:D【解析】如图所示,作三条辅助线,根据已知条件,这些小三角形全等,ABC ∆包含9 个小三角形,同时又在DEF ∆内的小三角形共有6 个,所以(|)P B A =6293= ,故选D. 3.C解析:C【解析】【分析】先求出基本事件总数n =27,在得到的27个小正方体中,若其两面涂有油漆,则这个小正方体必在原正方体的某一条棱上,且原正方体的一条棱上只有一个两面涂有油漆的小正方体,则两面涂有油漆的小正方体共有12个,由此能求出在27个小正方体中,任取一个其两面涂有油漆的概率.【详解】∵一块各面均涂有油漆的正方体被锯成27个大小相同的小正方体,∴基本事件总数n =27,在得到的27个小正方体中,若其两面涂有油漆,则这个小正方体必在原正方体的某一条棱上,且原正方体的一条棱上只有一个两面涂有油漆的小正方体,则两面涂有油漆的小正方体共有12个,则在27个小正方体中,任取一个其两面涂有油漆的概率P =故选:C【点睛】本题考查概率的求法,考查古典概型、正方体性质等基础知识,考查推理论证能力、空间想象能力,考查函数与方程思想,是基础题. 4.C解析:C【解析】【分析】由频率分布直方图得的性质求出0.030a =;样本数据低于130分的频率为:0.7;[)80,120的频率为0.4,[)120,130的频率为0.3.由此求出总体的中位数(保留1位小数)估计为:0.50.41203123.30.3-+⨯≈分;样本分布在[)90,100的频数一定与样本分布在[)100,110的频数相等,总体分布在[)90,100的频数不一定与总体分布在[)100,110的频数相等.【详解】由频率分布直方图得:()0.0050.0100.0100.0150.0250.005101a ++++++⨯=,解得0.030a =,故A 错误;样本数据低于130分的频率为:()10.0250.005100.7-+⨯=,故B 错误;[)80,120的频率为:()0.0050.0100.0100.015100.4+++⨯=,[)120,130的频率为:0.030100.3⨯=.∴总体的中位数(保留1位小数)估计为:0.50.412010123.30.3-+⨯≈分,故C 正确; 样本分布在[)90,100的频数一定与样本分布在[)100,110的频数相等, 总体分布在[)90,100的频数不一定与总体分布在[)100,110的频数相等,故D 错误. 故选C .【点睛】本题考查命题真假的判断,考查频率分布直方图的性质等基础知识,考查运算求解能力,考查数形结合思想,是基础题.因为条形分布直方图的面积表示的是概率值,中位数是位于最中间的数,故直接找概率为0.5的即可;平均数是每个长方条的中点乘以间距再乘以长方条的高,将每一个数值相加得到.5.C解析:C【解析】 根据平均数的概念,其平均数为52x +,方差为2258⨯,故选C.6.B解析:B【解析】【分析】由题意结合流程图运行程序,考查5i >是否成立来决定输出的数值即可.【详解】结合流程图可知程序运行过程如下:首先初始化数据:1,2i S ==,此时不满足5i >,执行循环:111,122S i i S =-==+=; 此时不满足5i >,执行循环:111,13S i i S =-=-=+=; 此时不满足5i >,执行循环:112,14S i i S =-==+=; 此时不满足5i >,执行循环:111,152S i i S =-==+=; 此时不满足5i >,执行循环:111,16S i i S=-=-=+=; 此时满足5i >,输出1S =-.本题选择B 选项.【点睛】本题主要考查循环结构流程图的识别与运行过程,属于中等题. 7.A解析:A【解析】【分析】根据图象即可看出,华为在每个季度的销量都最大,从而得出华为的全年销量最大,从而得出A 正确;由于不知每个季度的销量多少,从而苹果、华为和三星在哪个季度的销量大或小是没法判断的,从而得出选项B ,C ,D 都错误.【详解】根据图象可看出,华为在每个季度的销量都最大,所以华为的全年销量最大;每个季度的销量不知道,根据每个季度的百分比是不能比较苹果在第二季度和第三季度销量多少的,同样不能判断华为在哪个季度销量最大,三星在哪个季度销量最小;B ∴,C ,D 都错误,故选A .【点睛】本题主要考查对销量百分比堆积图的理解.8.D【解析】 【分析】由题意列出所有可能的结果,然后结合古典概型计算公式可得概率值. 【详解】能组成两位数有:10,12,13,20,21,23,30,31,32,总共有9种情况. 其中偶数有5种情况,故组成的两位数是偶数的概率为59p =. 故选:D . 【点睛】本题主要考查古典概型计算公式,属于中等题.9.B解析:B 【解析】∵数据x 1,x 2,x 3,…,x n 是郑州普通职工n (n ⩾3,n ∈N ∗)个人的年收入, 而x n +1为世界首富的年收入 则x n +1会远大于x 1,x 2,x 3,…,x n , 故这n +1个数据中,年收入平均数大大增大, 但中位数可能不变,也可能稍微变大,但由于数据的集中程序也受到x n +1比较大的影响,而更加离散,则方差变大. 故选B10.C解析:C 【解析】 【分析】执行程序框图,可得程序框图的功能是计算并输出分段函数32,0,0x x y x x ⎧>=⎨≤⎩的值,从而计算得解. 【详解】执行程序框图,可得程序框图的功能是计算并输出分段函数32,0,0x x y x x ⎧>=⎨≤⎩的值,由于20x =-<,可得2(2)4y =-=,则输出的y 等于4,故选C. 【点睛】该题考查的是有关程序框图的问题,涉及到的知识点有读取程序框图的输出的结果,在解题的过程中,需要明确框图的功能,从而求得结果.11.B解析:B 【解析】由圆的面积公式得:S π=圆,由正方形的面积公式得:4S =正,由几何概型中的面积型结合随机模拟试验可得:7951000SS =圆正,得解. 【详解】由圆的面积公式得:S π=圆, 由正方形的面积公式得:4S =正, 由几何概型中的面积型可得:7951000S S =圆正, 所以79543.21000π⨯=≈, 故选:B . 【点睛】本题考查了圆的面积公式、正方形的面积公式及几何概型中的面积型,属简单题.12.C解析:C 【解析】 【分析】设小赵到达汽车站的时刻为x ,小王到达汽车站的时刻为y ,根据条件建立二元一次不等式组,求出对应的区域面积,结合几何概型的概率公式进行计算即可. 【详解】如图,设小赵到达汽车站的时刻为x ,小王到达汽车站的时刻为y , 则0≤x≤15,0≤y≤15,两人到达汽车站的时刻(x ,y )所对应的区域在平面直角坐标系中画出(如图所示)是大正方形.将2班车到站的时刻在图形中画出,则两人要想乘同一班车, 必须满足{(x ,y )|0505x y ≤≤⎧⎨≤≤⎩,或515515x y ≤⎧⎨≤⎩<<},即(x ,y )必须落在图形中的2个带阴影的小正方形内,则阴影部分的面积S=5×5+10×10=125,则小赵和小王恰好能搭乘同一班公交车去上学的概率P=1251515⨯=59, 故选:C 【点睛】本题主要考查几何概型的概率公式的应用,根据条件求出对应区域的面积是解决本题的关键.二、填空题13.【解析】【分析】确定在正方形的位置即可求解【详解】由题时则当在上运动时的长度大于5故的长度大于5的概率等于故答案为【点睛】本题考查长度型几何概型确定的轨迹是关键是基础题解析:18【解析】 【分析】确定E 在正方形的位置即可求解 【详解】由题3BG DF ==时5AG AF ==,则当E 在,GC CF 上运动时,AE 的长度大于5 故AE 的长度大于5的概率等于111168+= 故答案为18【点睛】本题考查长度型几何概型,确定E 的轨迹是关键,是基础题14.【解析】【分析】取圆内接等边三角形的顶点为弦的一个端点当另一端点在劣弧上时求出劣弧的长度运用几何概型的计算公式即可得结果【详解】记事件{弦长超过圆内接等边三角形的边长}如图取圆内接等边三角形的顶点为解析:1 3【解析】【分析】取圆内接等边三角形BCD的顶点B为弦的一个端点,当另一端点在劣弧CD上时,BE BC>,求出劣弧CD的长度,运用几何概型的计算公式,即可得结果.【详解】记事件A={弦长超过圆内接等边三角形的边长},如图,取圆内接等边三角形BCD的顶点B为弦的一个端点,当另一端点在劣弧CD上时,BE BC>,设圆的半径为r,劣弧CD的长度是23rπ,圆的周长为2rπ,所以()21323rP Arππ==,故答案为13.【点睛】本题主要考查“长度型”的几何概型,属于中档题. 解决几何概型问题常见类型有:长度型、角度型、面积型、体积型,求与长度有关的几何概型问题关鍵是计算问题的总长度以及事件的长度;几何概型问题还有以下几点容易造成失分,在备考时要高度关注:(1)不能正确判断事件是古典概型还是几何概型导致错误;(2)基本事件对应的区域测度把握不准导致错误;(3)利用几何概型的概率公式时 , 忽视验证事件是否等可能性导致错误. 15.63【解析】回归方程过样本中心点则:即:解得:点睛:(1)正确理解计算的公式和准确的计算是求线性回归方程的关键(2)回归直线方程必过样本点中心解析:63【解析】30407090120705x++++==回归方程过样本中心点,则:0.7701564y=⨯+=,即:35488292645m++++=,解得:63m=.点睛:(1)正确理解计算$,b a$的公式和准确的计算是求线性回归方程的关键.(2)回归直线方程y bx a =+$$$必过样本点中心(),x y .16.【解析】∵方程无实根∴Δ=1-4a<0∴即所求概率为故填:解析:34【解析】∵方程无实根,∴Δ=1-4a <0,∴14a >,即所求概率为34.故填:3417.【解析】【分析】由题求得基本事件的总数15种再求得2只颜色相同包含的基本事件的个数根据古典概型及其概率的计算公式即可求解【详解】由题意一只口袋中装有形状大小都相同的6只小球其中有3只红球2只黄球和1 解析:415【解析】 【分析】由题,求得基本事件的总数15种,再求得2只颜色相同包含的基本事件的个数,根据古典概型及其概率的计算公式,即可求解。
