六年级数学下册错题难题
2020年六年级下册数学思维易错题难题训练及答案

2020年六年级下册数学思维易错题难题训练及答案一、培优题易错题1.对于实数a、b,定义运算:a▲b= ;如:2▲3=2﹣3= ,4▲2=42=16.照此定义的运算方式计算[2▲(﹣4)]×[(﹣4)▲(﹣2)]=________.【答案】1【解析】【解答】解:根据题意得:2▲(﹣4)=2﹣4= ,(﹣4)▲(﹣2)=(﹣4)2=16,则[2▲(﹣4)]×[(﹣4)▲(﹣2)]= ×16=1,故答案为:1【分析】先利用定义计算括号中的值,再进行计算即可.在利用新运算的时候需要先判断两个数的大小关系,根据其选择算式.2.如图,用相同的小正方形按照某种规律进行摆放,则第6个图形中小正方形的个数是________,第n(n为正整数)个图形中小正方形的个数是________(用含n的代数式表示).【答案】55;(n+1)2+n【解析】【解答】第1个图形共有小正方形的个数为2×2+1;第2个图形共有小正方形的个数为3×3+2;第3个图形共有小正方形的个数为4×4+3;…;则第n个图形共有小正方形的个数为(n+1)2+n,所以第6个图形共有小正方形的个数为:7×7+6=55.故答案为:55;(n+1)2+n【分析】观察图形规律,第1个图形共有小正方形的个数为2×2+1;第2个图形共有小正方形的个数为3×3+2;则第n个图形共有小正方形的个数为(n+1)2+n,找出一般规律.3.股民老黄上星期五买进某股票1000股,每股35元,下表为本周内每日该股票的涨跌情况(单位:元)(注:用正数记股价比前一日上升数,用负数记股价比前一日下降数)星期一二三四五每股涨跌+2.4﹣0.8﹣2.9+0.5+2.1(1)星期四收盘时,每股是多少元?(2)本周内最高价是每股多少元?最低价每股多少元?(3)根据交易规则,老黄买进股票时需付0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税,如果老黄在星期五收盘前将全部股票卖出,他的收益情况如何?【答案】(1)解:星期一二三四五每股涨跌+2.4﹣0.8﹣2.9+0.5+2.1实际股价37.436.633.734.236.3(2)解:本周内最高价是每股37.4元,最低价每股33.7元(3)解:买入总金额=1000×35=35000元;买入手续费=35000×0.15%=52.5元;卖出总金额=1000×36.3=36300元;卖出手续费=36300×0.15%=54.45元;卖出交易税=36300×0.1%=36.3元;收益=36300﹣(35000+52.5+54.45+36.3)=1156.75元【解析】【分析】(1)根据表中的数据,列式计算,就可求出星期四收盘时每股的价格。
六年级下册1——4单元错题

第二单元百分数错题分析错题分析:本题错误原因是只计算出了利息没有把本金加上,导致做题出错!改正措施:计算出利息后把本金加上就可以了!30000x1.30%x0.5+30000=30195(元错误原因:孩子没有认真读题,没有理解420里面有几个100,导致没有减去4个20,而只是减去了1个20,导致本题出错!改正措施:从420里边减去4个20就可以了!第一单元负数错题分析错误原因:孩子们平均数不能用整数零来表示,导致无法准确表示出比平均数大几就用正数几表示,比平均数小几就用负数几表示!改正措施:平均分是90分,美美96分记作:+6,明明80分记作-10,淘淘的100分记作+10第一单元负数错题分析错误原因:在数轴上,数轴上的三要素分不出正方向,导致方向相反!改正措施:必须认清数轴的三要素,以原点为标准,原点右边为正数,原点左边为负数!第三单元圆柱和圆锥错题分析错误原因∶该同学没有认真读题,没有分析出本题所要求的问题,要求的是圆柱和水接触的表面积,他算成了圆柱的体积!改正措施:下图是正确算法错无原因孩子们没有生活的经验,没有观察的习惯,也可以说是理论和实际练系不够紧密,没有体验到生活中处处有数学!把压路机前轮转动的一圈看成了体积,算成了体积!改正措施首先要求孩子们体验生活中处处有数学,要积累数学经验!下图是正确答案!错误原因盒子的容积至少是多少,该同学是算的圆锥形陀螺的体积!主要是实际生活经验不足!改正措施做一个底面以6为边长的正方形以5为高的长方体!列算式为6x6x5=180错误原因水面下降后,下降的水的体积是圆锥的体积,下降的水面是以圆柱形玻璃杯底面为标准,不是圆锥的底面积,圆柱也不用除以三分之一!改正措施正确答案第四单元比例错题分析错误原因没有理解比例的基本性质,两个外项的积等于两个内项的积!导致本题出错!改正措施甲比乙等于6比5错误原因孩子们没有认真读题,审题不清,问题是求少用了多少块,本题少一步!只算出来了改用后需要多少块!改正措施要求孩子们认真读题,认真审题分析数量关系!本题多加上一步就可以了!。
小学数学六年级下册错题集

小学数学六年级下册错题集一、错例目录1.负数1.1正负数的读写………………………………………………………裘迪波童栩龚荫1 1.2在直线上表示正数、0负数…………………………………………………………陈金江42.圆柱和圆锥2.1圆柱的认识…………………………………………………………裘迪波童栩龚荫62.2.1圆柱的表面积………………………………………………………………………赵国明82.2.2圆柱的表面积………………………………………………………………………赵国明102.2.3圆柱的表面积………………………………………………………………………夏春峰122.2.4圆柱的表面积………………………………………………………………………金芳132.2.5圆柱的表面积………………………………………………………………………徐琴152.2.6圆柱的表面积………………………………………………………………………石彤彤162.2.7圆柱的表面积………………………………………………………………………石彤彤172.2.8圆柱的表面积………………………………………………………………………石彤彤182.3.1圆柱的体积…………………………………………………………………………俞建栋192.3.2圆柱的体积…………………………………………………………………………厉建康202.3.3圆柱的体积…………………………………………………………………………厉建康212.3.4圆柱的体积………………………………………………………裘迪波童栩龚荫222.4.1圆锥的体积…………………………………………………………………………厉建康232.4.2圆锥的体积…………………………………………………………………………赵国明242.4.3圆锥的体积…………………………………………………………………………石彤彤252.4.4圆锥的体积…………………………………………………………………………石彤彤263.比例3.1比例的基本性质………………………………………………………………………唐彩彩273.2.1解比例………………………………………………………………………………毛敏华283.2.2解比例………………………………………………………………………………夏春峰293.3.1成反比例的量………………………………………………………………………金芳303.3.2成反比例的量……………………………………………………裘迪波童栩龚荫333.3.3成反比例的量………………………………………………………………………夏春峰353.4.1比例尺………………………………………………………………………………俞建栋363.4.2比例尺………………………………………………………………………………卢军373.4.3比例尺………………………………………………………………………………汪国祥383.4.4比例尺………………………………………………………………………………毛敏华393.4.5比例尺………………………………………………………………………………夏春峰403.5.1用比例解决问题……………………………………………………………………蔡凌燕413.5.2用比例解决问题………………………………………………………………厉建康423.5.3用比例解决问题………………………………………………………………徐琴433.5.4用比例解决问题………………………………………………………………汪国祥443.5.5用比例解决问题………………………………………………………………唐彩彩453.5.6用比例解决问题………………………………………………………………唐彩彩463.5.7用比例解决问题………………………………………………………………徐玲芬473.5.8用比例解决问题………………………………………………………………夏春峰484.整理和复习4.1.1数的认识………………………………………………………………………蔡凌燕494.1.2数的认识………………………………………………………………………陈益504.1.3数的认识………………………………………………………………………唐彩彩514.2.1数的运算………………………………………………………………………俞建栋524.2.2数的运算………………………………………………………………………俞建栋534.2.3数的运算………………………………………………………………………赵国明544.2.4数的运算………………………………………………………………………蔡凌燕564.2.5数的运算………………………………………………………………………陈益574.2.6数的运算………………………………………………………………………陈益584.2.7数的运算………………………………………………………………………金芳594.2.8数的运算………………………………………………………………………卢军604.2.9数的运算………………………………………………………………………卢军614.2.10数的运算……………………………………………………………………徐琴624.3.1常见的量………………………………………………………………………蔡凌燕634.3.2常见的量………………………………………………………………………卢军644.3.3常见的量………………………………………………………………………金芳654.3.4常见的量………………………………………………………………………唐彩彩674.4.1比和比例………………………………………………………………………蔡凌燕684.4.2比和比例………………………………………………………………………陈金江694.4.3比和比例………………………………………………………………………金芳704.4.4比和比例………………………………………………………………………厉建康724.4.5比和比例………………………………………………………………………卢军734.4.6比和比例………………………………………………………………………汪国祥744.4.7比和比例………………………………………………………………………汪国祥754.5.1图形的认识与测量……………………………………………………………俞建栋764.5.2图形的认识与测量……………………………………………………………赵国明774.5.3图形的认识与测量……………………………………………………………赵国明794.5.4图形的认识与测量……………………………………………………………赵国明814.5.5图形的认识与测量……………………………………………………………陈金江83 4.5.6图形的认识与测量………………………………………………………………陈益844.5.7图形的认识与测量…………………………………………裘迪波童栩龚荫854.5.8图形的认识与测量…………………………………………裘迪波童栩龚荫874.5.9图形的认识与测量……………………………………………………………徐琴904.5.10图形的认识与测量…………………………………………………………徐玲芬914.5.11图形的认识与测量…………………………………………………………徐玲芬944.6.1统计与可能性………………………………………………裘迪波童栩龚荫964.6.2统计与可能性…………………………………………………………………徐玲芬994.6图形与变换……………………………………………………裘迪波童栩龚荫1014.7综合应用…………………………………………………………………………徐玲芬103二、原始错例六年级下册典型错例◆典型错题错题:比较下列各组数的大小:-1和-1.2 0和32-0.1和-0.01 错解: -1<-1.2 -0.1<-0.01 ◆原因分析1、对负数概念的建构缺乏深刻地理解,没有从体会引进负数的必要性中理解负数的意义、建立负数的数感。
六年级下数学错题 难题

1.一桶色拉油,连桶重12千克,倒出一半后,连桶还重7千克,1千克油售价8.6元,这桶油能卖()元。
2、圆柱的底面直径扩大两倍,高不变。
他的底面积扩大()倍,侧面积扩大()倍,体积扩大()倍。
3、8÷14=4、6除以6/7减去6除6/7的商,差是多少?5、一个圆柱和一个圆锥的体积相等,底面半径相等。
圆柱的高是6CM,则圆锥的高是()CM。
6、在一幅地图上,用3CM的线段表示30KM的实际距离。
这幅图的比例尺是()7、工地要运一批水泥,每天运180车,需要40天完成。
现在要提前15天完成,每天应运多少车?8、看一本450页的书,两天看完90页,照这样计算,我读完这本书还需多少天?按比例解。
9、一个直角三角形,两条直角边为6CM 4CM,如果以6CM这条边为轴旋转一周,可得到一个什么形体?它的体积是多少立方厘米?10、判断——圆柱的高一定,它的底面半径和侧面积成正比。
(对)11、如上图,阴影部分面积与正方形面积的比是5:12,正方形的边长是6厘米,DE的长是()厘米。
12、设AB都是自然数,并且满足A/3+B/11=14/33 ,那么A+B=( )13、判断——刘师傅做100个零件,合格率是95%,如果再做2个合格的零件,那么合格率就达到97%。
()14、一列火车从甲开到乙需要8小时,另一列火车从乙到甲要12小时,若这两列同时从甲乙两城相对开出,多少小时可以相遇?15、男生人数是女生人数的3/5,女生人数占全班人数的()%16、钟面上,时钟转动速度是分针转动速度的()。
17、在推导圆的面积公式时,将圆等分成若干份,拼成一个近似的长方形,已知长方形的长比宽多6.42CM,这个圆的面积是()平方CM。
18、一件上衣标600元,降至60元一件,但仍然可以赚20%,如按原价出售,则这件衣服可获暴力()元。
19 一间教室的面积约是80( )。
小学六年级下册数学经典题难题专项练习含解析

小学六年级下册数学经典题难题专项练习含解析1.已知一张桌子的价钱是一把椅子的10倍,又知一张桌子比一把椅子多288元,一张桌子和一把椅子各多少元?解题思路:由已知条件可知,一张桌子比一把椅子多的288元,正好是一把椅子价钱的(10-1)倍,由此可求得一把椅子的价钱。
再根据椅子的价钱,就可求得一张桌子的价钱。
答题:解:一把椅子的价钱:288÷(10-1)=32(元)一张桌子的价钱:32×10=320(元)答:一张桌子320元,一把椅子32元。
2. 3箱苹果重45千克。
一箱梨比一箱苹果多5千克,3箱梨重多少千克?解题思路:可先求出3箱梨比3箱苹果多的重量,再加上3箱苹果的重量,就是3箱梨的重量。
答题:解:45+5×3=45+15=60(千克)答:3箱梨重60千克。
3. 甲乙二人从两地同时相对而行,经过4小时,在距离中点4千米处相遇。
甲比乙速度快,甲每小时比乙快多少千米?解题思路:根据在距离中点4千米处相遇和甲比乙速度快,可知甲比乙多走4×2千米,又知经过4小时相遇。
即可求甲比乙每小时快多少千米。
答题:解:4×2÷4=8÷4=2(千米)答:甲每小时比乙快2千米。
4. 李军和张强付同样多的钱买了同一种铅笔,李军要了13支,张强要了7支,李军又给张强0.6元钱。
每支铅笔多少钱?解题思路:根据两人付同样多的钱买同一种铅笔和李军要了13支,张强要了7支,可知每人应该得(13+7)÷2支,而李军要了13支比应得的多了3支,因此又给张强0.6元钱,即可求每支铅笔的价钱。
答题:解:0.6÷[13-(13+7)÷2]=0.6÷[13—20÷2]=0.6÷3=0.2(元)答:每支铅笔0.2元。
5.甲乙两辆客车上午8时同时从两个车站出发,相向而行,经过一段时间,两车同时到达一条河的两岸。
由于河上的桥正在维修,车辆禁止通行,两车需交换乘客,然后按原路返回各自出发的车站,到站时已是下午2点。
苏教版六年级下册数学错题难题整理
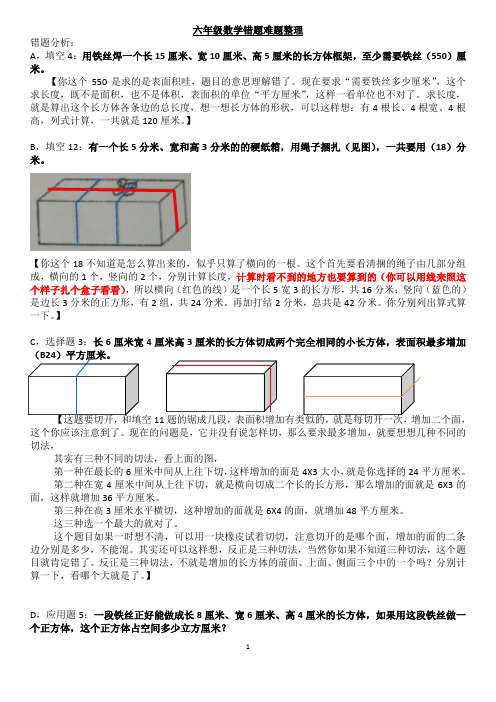
六年级数学错题难题整理错题分析:A,填空4:用铁丝焊一个长15厘米、宽10厘米、高5厘米的长方体框架,至少需要铁丝(550)厘米。
【你这个550是求的是表面积哇,题目的意思理解错了。
现在要求“需要铁丝多少厘米”,这个求长度,既不是面积,也不是体积,表面积的单位“平方厘米”,这样一看单位也不对了。
求长度,就是算出这个长方体各条边的总长度,想一想长方体的形状,可以这样想:有4根长、4根宽、4根高,列式计算,一共就是120厘米。
】B,填空12:有一个长5分米、宽和高3分米的的硬纸箱,用绳子捆扎(见图),一共要用(18)分米。
【你这个18不知道是怎么算出来的,似乎只算了横向的一根。
这个首先要看清捆的绳子由几部分组成,横向的1个,竖向的2个,分别计算长度,计算时看不到的地方也要算到的(你可以用线来照这个样子扎个盒子看看),所以横向(红色的线)是一个长5宽3的长方形,共16分米;竖向(蓝色的)是边长3分米的正方形,有2组,共24分米。
再加打结2分米,总共是42分米。
你分别列出算式算一下。
】C,选择题3:长6厘米宽4厘米高3厘米的长方体切成两个完全相同的小长方体,表面积最多增加(B24)平方厘米。
11题的锯成几段,这个你应该注意到了。
现在的问题是,它并没有说怎样切,那么要求最多增加,就要想想几种不同的切法,其实有三种不同的切法,看上面的图,第一种在最长的6厘米中间从上往下切,这样增加的面是4X3大小,就是你选择的24平方厘米。
第二种在宽4厘米中间从上往下切,就是横向切成二个长的长方形,那么增加的面就是6X3的面,这样就增加36平方厘米。
第三种在高3厘米水平横切,这种增加的面就是6X4的面,就增加48平方厘米。
这三种选一个最大的就对了。
这个题目如果一时想不清,可以用一块橡皮试着切切,注意切开的是哪个面,增加的面的二条边分别是多少,不能混。
其实还可以这样想,反正是三种切法,当然你如果不知道三种切法,这个题目就肯定错了。
六年级考试易错题

六年级考试易错题一、数学部分。
1. 题目:把5米长的绳子平均剪成8段,每段长是()米,每段是全长的()。
- 解析:- 把5米长的绳子平均剪成8段,求每段长多少米,是求具体的长度,用总长度除以段数,即5÷8 = (5)/(8)米。
- 求每段是全长的几分之几,是把全长看作单位“1”,平均分成8段,每段就是全长的1÷8=(1)/(8)。
2. 题目:一个三角形三个内角的度数比是2:3:4,这个三角形是()三角形。
- 解析:- 三角形内角和是180°。
- 三个内角分别占内角和的(2)/(2 + 3+4)=(2)/(9)、(3)/(2+3 + 4)=(3)/(9)、(4)/(2+3+4)=(4)/(9)。
- 那么三个角的度数分别为180×(2)/(9) = 40^∘,180×(3)/(9)=60^∘,180×(4)/(9) = 80^∘。
- 因为三个角都是锐角,所以这个三角形是锐角三角形。
3. 题目:甲数的(2)/(3)等于乙数的(3)/(4),甲数与乙数的最简整数比是()。
- 解析:- 根据题意可得:甲数×(2)/(3) =乙数×(3)/(4)。
- 甲数:乙数=(3)/(4):(2)/(3)。
- 化为最简整数比,(3)/(4)÷(2)/(3)=(3)/(4)×(3)/(2)=(9)/(8)=9:8。
4. 题目:从一个边长是10分米的正方形纸里剪一个最大的圆,这个圆的周长是()分米,面积是()平方分米。
- 解析:- 在正方形中剪一个最大的圆,这个圆的直径等于正方形的边长,即d = 10分米。
- 圆的周长公式C=π d,所以C = 3.14×10=31.4分米。
- 圆的半径r=(d)/(2)=5分米,面积公式S=π r^2,所以S = 3.14×5^2=3.14×25 = 78.5平方分米。
小学数学六年级数学难题(含详细答案)

小学数学六年级数学难题(含详细答案)一、分数与小数的转换1. 难题:将分数 5/8 转换为小数。
答案:将分数转换为小数的方法是将分子除以分母。
因此,5/8 转换为小数的过程是5 ÷ 8 = 0.625。
2. 难题:将小数 0.75 转换为分数。
答案:将小数转换为分数的方法是将小数部分作为分子,分母为10 的相应次幂。
因此,0.75 转换为分数的过程是 75/100,可以简化为 3/4。
二、百分数的计算1. 难题:计算 60% 的 150。
答案:计算百分数的方法是将百分数转换为分数,然后乘以相应的数值。
因此,60% 的 150 的计算过程是60/100 × 150 = 90。
2. 难题:一个数是另一个数的 120%,求这个数。
答案:计算一个数是另一个数的百分比的方法是将百分比转换为分数,然后乘以另一个数。
因此,假设另一个数是 x,那么这个数的计算过程是120/100 × x = 1.2x。
三、面积与体积的计算1. 难题:计算长方形的长为 10 厘米,宽为 5 厘米,面积是多少平方厘米?答案:计算长方形面积的方法是将长和宽相乘。
因此,长为 10 厘米,宽为 5 厘米的面积是10 × 5 = 50 平方厘米。
2. 难题:计算正方体的边长为 6 厘米,体积是多少立方厘米?答案:计算正方体体积的方法是将边长的立方。
因此,边长为 6 厘米的正方体的体积是6 × 6 × 6 = 216 立方厘米。
小学数学六年级数学难题(含详细答案)四、分数的加减法1. 难题:计算 3/4 + 2/3。
答案:分数的加法需要找到分母的公共倍数,然后将分子相加。
对于 3/4 + 2/3,我们可以将分母都转换为 12,然后相加。
计算过程如下:3/4 = 9/122/3 = 8/129/12 + 8/12 = 17/12因此,3/4 + 2/3 = 17/12,也可以表示为 1 5/12。
小学数学人教版六年级下册易错题难题

(判断题)1、行同一段路,甲用5小时,乙用4小时,甲乙速度的比是5:4。
( )2、大于90°的角都是钝角。
( )3、只要能被2除尽的数就是偶数。
( )4、每年都有365天。
( )5、圆柱的底面积扩大3倍,体积扩大3倍。
( )6、12/15不能化成有限小数。
( )7、能被3整除的数一定能被9整除。
( )8、a、b和c是三个自然数(且不等于0),在a=b×c中A、b一定是a的约数 ( )B、c一定是a和b的最大公约数. ( )C、a一定是a和b的最小公倍数. ( )D、a一定是b和c的公倍数. ( )9、两个锐角之和一定是钝角。
( )10、在比例中,如果两个内项互为倒数,那么两个外项也互为倒数。
( )11、“光明”牛奶包装盒上有“净含量:250亳升”的字样,这个250毫升是指包装盒的容积。
( )12、x+y=ky(k一定)则x、y不成比例。
( )13、正方形、长方形、平行四边形和梯形都是特殊四边形。
( )14、圆柱体积是圆锥体积的3倍,这两者一定是等底等高。
( )15、比例尺就是前项是1的比。
( )16、1千克的金属比1千克的棉花重。
( )17、1/100和1%都是分母为100的分数,它们表示的意义相同。
( )18、圆锥的体积比圆柱体积小2/3。
( )19、两条射线可以组成一个角。
( )20、把一个长方形木框拉成平行四边形后,四个角的内角和不变( )21、任何长方体,只有相对的两个面才完全相等。
( )22、周长相等的两个长方形,它们的面积也一定相等。
( )23、一个体积为1立方分米的物体,它的底面积一定是1平方分米。
( )24、一个体积为1立方分米的正方体,它的底面积一定是1平方分米( )25、工作效率和工作时间成反比例。
( )26、比的前项增加10%,要使比值不变,后项应乘1.1。
( )27、5千克盐溶解在100千克水中,盐水的含盐率是5%。
( )28、比例尺大的,实际距离也大。
六年级下学期数学 易错题汇总140题 带答案

六年级下学期易错题汇总140题1、某品牌的饮用水做活动,买四送一,小王买回了五瓶,相当于打了(八)折。
2、一件衣服原价每件50元,现价每件45元,商场正在打(九)折出售。
3、某服装店一件休闲装现价是200元,比原价降低了50元,相当于打(八)折,照这样的折扣,原价是800元的西服,现价是(640)元。
4、书店的图书凭优惠卡可打八折,小明用优惠卡买了一套书,省了9.6元。
这套书原价(48)元。
5、小明的妈妈到商场上买一个新的电风扇,电风扇的原价是120元,售货员告诉她现在降价36元出售,则这个电风扇是打(七)折出售的。
6、一件商品随季节变化降价出售,如果按现价打九折,仍可获利180元,如果打八折,就要亏损240元,这种商品的进价是( 3600 )元。
7、今年小麦产量比去年增产一成五,表示今年比去年增产( 15 )%,也就是今年的产量相当于去年的( 115 )%。
8、学校四月份的水费是2000元,五月份比四月份节约了500元,节约了(二五)成。
9、爸爸买了一台售价为7500元的笔记本电脑,还需要支付售价额20%的消费税,爸爸为此需要支付消费税(1500 )元。
10、李阿姨买了一只手表,除了按照售价支付外,还需要支付售价的20%的消费税,她一共花了7200元,他买这只手表缴纳了(1200 )元的消费税。
11、小王把1000元存入银行,两年后取出,本息共有1042元,年利率是( 2.1 )%。
12、妈妈每月工资2000元,如果妈妈把半年的工资全部存入银行,定期半年,如果年利率是1.30%,到期后她可以取回(12078 )元。
13、小新和妈妈看见商场的衬衣正在做第二件半价促销的活动,于是一人买了一200元的衬衣,相当于每件打(七五)折14、某商场做促销,推出“每满100减50”的活动,比如某顾客购买了240元的商品,只需要付款140元,若再该商场购买550元的商品,只需要支付(300)元,若用360元可以买到标价为(660)元或者(710)元的商品。
【小马虎错题本】六年级数学下册错题专练(易错知识点+分层训练)-第四单元 比例 人教版

人教版六年级数学下册错题专练第四单元 比例【错例1】判断:10:2=5是比例。
( )【错误答案】√【错误原因】本题错在没有正确理解比例的意义,5是一个数而不是一个比,它不能与10:2组成比例。
【正确答案】×【解题指导】在比例中等号的两侧必须都是一个比。
1.比例是一个( )。
A .比B .等式C .方程D .以上答案都正确2.下面的式子中,( )是比例。
A .6:32=B .1:31:3010=C .114:3:43=D .1:55:1=【错例2】判断:若5x =6y ,则x :y=5:6。
( )【错误答案】√【错误原因】这道题错在没有理解比例的基本性质。
在改写比例时,x 作外项,和x 相乘的5一定也作外项。
【正确答案】×【解题指导】把等式ax=by ( a ,b ,x ,y 均不为0)改写成比例时,相乘的2个字母必须同时作比例的外项或内项。
1.已知15×3=5×9,根据比例的基本性质写出两个比例:( )、( )。
2.已知8a =9b (a ,b 均不为0),则a ∶b = ( )∶( )。
3.把8 2.50.450⨯=⨯改写成比例是( )。
A .8:2.50.4:50=B .8:0.4 2.5:50=C .8:0.450:2.5=D .8:50 2.5:0.4=4.下面比中,能与11:23组成比例的是( )。
A .2∶3 B .3∶2 C .1∶65.下面的数中,不能与2、3、4组成比例的是( )。
A .32B .83C .3D .6【错例3】35.0=x9 【错误答案】解:x=395.0⨯ x=1.5 【错误原因】解分数形式的比例时,没有分清楚哪两个数是外项,哪两个数是内项。
【正确答案】解:0.5x=3×9x=5.093⨯ x=54【解题指导】解分数形式比例时,分子与分母交叉相乘即可。
1.解方程。
x +15x =186 5x -55612= 12∶16=14∶x 2.求未知数x 。
六年级数学错题小报

六年级数学错题小报一、计算类错题1. 题目:计算公式。
错解:有些同学可能会直接将分子分母分别相加减,得到公式。
解析:这是错误的,在进行分数加减运算时,要先通分。
分母4、6、12的最小公倍数是12。
则公式,公式,公式不变。
所以原式公式。
2. 题目:计算公式。
错解:公式(这种解法是把1.6拆错了)解析:正确的做法是把1.6拆成公式,则公式。
或者把1.6拆成公式,公式。
二、几何类错题1. 题目:一个圆柱的底面半径是2厘米,高是5厘米,求它的侧面积。
错解:有些同学可能会用公式(这是求圆柱体积的公式)来计算侧面积,得到公式平方厘米。
解析:圆柱侧面积的公式是公式,所以正确的结果是公式平方厘米。
2. 题目:一个三角形的底是8厘米,高是6厘米,求这个三角形的面积。
错解:可能会忘记除以2,直接计算成公式平方厘米。
解析:三角形面积公式是公式(其中公式是底,公式是高),所以正确结果是公式平方厘米。
三、应用题类错题1. 题目:一辆汽车从甲地到乙地,前3小时行驶了180千米,照这样的速度,又行驶了2小时到达乙地。
甲乙两地相距多少千米?错解:有些同学只计算了前3小时行驶的180千米,没有计算后面2小时行驶的路程。
解析:首先根据前3小时行驶180千米,求出速度为公式千米/小时。
总共行驶的时间是公式小时,所以甲乙两地相距公式千米。
2. 题目:一件商品原价100元,先提价10%,再降价10%,现在的价格是多少元?错解:有些同学会认为价格不变,还是100元。
解析:先提价10%后价格变为公式元,再降价10%是在110元的基础上降的,降价后的价格为公式元。
六年级下册数学思维易错题难题训练及答案含详细答案

六年级下册数学思维易错题难题训练及答案含详细答案一、培优题易错题件连衣裙的件连衣裙,针对不同的顾客,30.某儿童服装店老板以32元的价格买进301元为标准,将超过的钱数记为正,不足的钱数记为负,记录结果售价不完全相同,若以45如下表:534756售出件数21售价(元)0+2﹣+2﹣+130件连衣裙后,赚了多少钱?请问,该服装店售完这件连衣裙后,赚的钱数为:解:由题意可得,该服装店在售完这30【答案】]-2)-1)+5×((45-32)×30+[7×2+6×2+3×1+5×0+4×(]-10)-4)+(=13×30+[14+12+3+(=390+15(元),=405405元即该服装店在售完这30件连衣裙后,赚了【解析】【分析】根据表格计算售出件数与售价积的和,再以45元为标准32元的价格买.30件,求出差价,计算即可进3=2×1+3=5 ⊕b=2a+b,如1a和b,规定a⊕定义一种新运算:对于有理数2.用“⊕”)的值;⊕(﹣2(1)求2的值.,求a)]⊕=a+4(﹣(2)若[()⊕3=2)(﹣2【答案】(1)解:原式=2×2+)解:根据题意可知:2(,]+ =a+43)+(﹣)2[(a+1,+ =a+4a﹣2)2(),(a+42)+1=24(a﹣,﹣8+1=2a+84a,2a=15.a=【解析】【分析】(1)根据定义的新运算,进行计算。
(2)根据题目中定义的新运算,的值a写出算式,计算出3.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神222222,因此4,===.如:数秘”42-0 ,124-2 ,206-412,20这三个数都是神秘数.? 为什么这两个数是神秘数吗?1)28和2012((2)设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连续偶数构造的神秘数? 为什么的倍数吗?是4? 为什么是神秘数吗?)两个连续奇数的平方差(取正数)(3222222,=6 28=4×7-2-4 ,20)解:找规律:【答案】(14=4×1=2=-04×5 ,12=4×3=42222都是神秘数和2012 =504所以-50228 =8-6,,…,2012=4×503 2 2的倍数4,因此由这两个连续偶数构造的神秘数是=(2)解:(2k+2)4(2k +1)-(2 k)(3)解:由(2)知,神秘数可以表示成4(2k+1),因为2 k +1是奇数,因此神秘数是4的倍2-(2n-(2 n +1)和2 n -1,则数,但一定不是8的倍数.另一方面,设两个连续奇数为2 n +1 2=8n,即两个连续奇数的平方差是8的倍数.因此,两个连续奇数的平方差不是神秘1)数.2222,504得到-50228=4×7=828-6,2012=4×503=)根据规律得到【解析】【分析】(1这两个数是神秘数;2012和 2 2=(2k+2+2k)(2k+2-2k2)由(2k+2))=4(2k -(2k)+1),因此由这两个连续偶数构造的神秘(的倍数;数是4(3)神秘数可以表示成4(2k+1),因为2k +1是奇数,因此神秘数是4的倍数,但一定不是8的倍数;两个连续奇数的平方差是8的倍数,因此这两个连续奇数的平方差不是神秘数.4.某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西)行驶为负,一天中七次行驶纪录如下。
六年级数学下册错题难题

六年级数学下册错题难题一、填空1、在数轴上,从左到右的顺序就是数()的顺序。
2、0既不是(),也不是(),正数都()0,负数都()。
3、如果一个物体向前移动8米,记作+8米,那么这个物体向后移动8米,记作()。
4、晶晶向东走100米,记作-100米,那么她向西走100米,应记作()。
5、在数轴上与原点距离6个单位长度的点有()个,它们所表示的数分别是()。
6、如果-3表示比90小3的数,那么0表示的数是(),-5表示的数是(),+8表示的数是()。
7、如果在银行存入500元,存折上记作+500元,那么从银行取出200元,存折上应记作()。
8、在一次食品质量检查中,如果超过标准重量2克,记作+2克,那么-3克表示()。
9、当圆柱的()和()相等时,它的侧面展开是一个正方形。
10、一个圆柱的底面半径扩大到原来的2倍,底面直径扩大()倍,底面周长扩大()倍,底面积扩大()倍,高不变,体积扩大()倍;一个圆柱的底面直径和高都扩大到原来的2倍,体积就扩大到原来的()倍;一个圆柱的底面积不变,高扩大到原来的3倍,它的体积扩大到原来的()。
11、从圆锥的()到()的距离,是圆锥的高。
12、把一个27立方厘米的圆锥削成一个最大的圆锥,圆锥的体积是()立方厘米,削去了()立方厘米。
13、圆锥的体积比和它等底等高的圆柱的体积少4.2立方米,这个圆柱的体积是()立方米,圆锥的体积是()立方米。
14、一个圆柱和它等底等高的圆锥的体积之和是128立方分米,圆柱的体积是()立方分米,圆锥的体积是()立方分米。
15、把一个棱长为4厘米的正方体削成一个最大的圆柱,削去的体积是()立方厘米,削去的部分占正方体体积的()。
16、如果A÷2-B÷3=0,那么A:B=()。
17、根据2×12=8×3,写出一个比值最小的比例是()。
18、在一个比例中,两个比的比值都等于2,这个比例的外项为14和5,这个比例式是()。
六年级下册数学素材 - 错题集解析 全国版

【题目描述】0.03吨=3%吨()【典型错例】0.03吨=3%吨(√)【错因分析】百分数是“表示一个数是另一个数的百分之几的数.”它只能表示两数之间的倍数关系,不能表示某一具体数量.而学生正是由于对百分数的意义缺乏正确认识,所以导致这题判断错误.【解决对策】(1)明确百分数与分数的区别;理解百分数的意义.(2)找一找生活中哪儿见到过用百分数来表示的,从而进一步理解百分数的意义.正确解题过程0.03吨=3%吨(×)【题目描述】10克盐放入100克水中,盐水的含盐率为10%.()【典型错例】10克盐放入100克水中,盐水的含盐率为10%.(√)【错因分析】一些学生是因为对“含盐率”这一概念的不理解,所以不知该如何计算,而导致做错.一些学生比较粗心,题目当中的10克盐和100克水这样的数字也很容易使那些粗心的学生马上得出10%这样的错误答案.【解决对策】(1)理解含盐率的意义.并结合合格率、成活率等类似概念进一步理解.(2)结合求含糖率、合格率、出勤率等类似题目加强练习以达到目的.(2)教育学生做题前要养成仔细审题、认真思考的习惯.正确解题过程10克盐放入100克水中,盐水的含盐率为10%.(×)【题目描述】甲班人数比乙班多12%,乙班人数比甲班少( ).【典型错例】甲班人数比乙班多,乙班人数比甲班少().【错因分析】学生把表示具体量与表示倍数的在意义上混同了.认为甲班人数比乙班人数多就是乙班人数比甲班少.对于数量与倍数不能区分.而且一会儿把甲班人数当成单位“1”,一会儿把乙班人数当成单位“1”,概念不清楚.【解决对策】(1)区分数量与倍数的不同,(2)画线段图,建立直观、形象的模型来帮助理解.(2)明确把乙班人数看做单位“1"的量,后来又把甲班看做单位“1”的量.(3)结合类似题目加强练习以达目的.正确解题过程甲班人数比乙班多(),乙班人数比甲班少().【题目描述】将一个底面积为50平方厘米的圆锥放入一个盛有水的圆柱型容器中,水面上升了2cm,圆柱的底面积是100平方厘米,问圆锥的高是多少?【典型错例】100÷(50×2)=1;100÷50=2【错因分析】本道题目,通过询问发现部分学生将100看成是体积,认为体积除以底面积(100÷50)得到的就是高了;另一部分学生认为要将50与2进行乘法运算,利用底面积乘高得到体积,但是他们无法解释100÷(50×2)的含义.这其中一方面的原因是学生没有理解圆锥圆柱的体积计算公式,另一方面学生忽视了题中隐藏的条件,题目分析的不到位.【解决对策】放入的圆锥要占一定的体积,上升的水的体积就是圆锥的体积,明确这一点解题就很容易了;上升的水的体积是100×2,圆锥的高是100×2÷50.此外熟悉体积的计算公式是大前提.这一类型的题主要是找到“相等的量”,比如上题的体积相等,还有的题目会是高相等或者底面积相等.【题目描述】【错因分析】很多学生把这里的“等于”没理解,同时比的性质没有掌握.分数的化简有存在问题,不知道怎么化成比的形式.【解决对策】首先知道在比的性质当中,比的外项的积等于比的内项的积;其次由题目条件知道八分之五是右边的外项,十二分之五是比的内项;最后化简:=2:3【题目描述】把5/8千克的糖果平均分成5份,每份是5千克的().【错例】5/8÷5=1/8千克.【错因分析】这题要分两步来思考,先算出一份是多少千克:5/8÷5=1/8千克,然后用1/8÷5=1/40,但是好多同学都只算了第一步.【解决对策】让学生看清楚题目,明白要求什么,并在平时的教学中让学生养成仔细审题、细心算题的习惯.【题目描述】把一根米的绳子平均分成4段,每段长()米,每段占全长的().【错因分析】学生一般无法理解概念的形成,很多学生停留在死记硬背上.【解决对策】从问题本身上引导学生发现实际长度和分率的区别,可以画线段图促进理解.实际长度可以用除法算式“总长度÷段数”来计算,分率跟总长度无关只跟分成的份数有关.【题目描述】把3米长的绳子剪4次,剪成相等的长度,则().A、每段占3米的1/4B、每段是1米的3/5C、每段是全长的3/5D、每段是3/4米长度单位练习【典型错例】把3米长的绳子剪4次,剪成相等的长度,则(D).A、每段占3米的1/4B、每段是1米的3/5C、每段是全长的3/5D、每段是3/4米长度单位练习【错因分析】没有理解题目的意思,片面的理解,没有动手去操作.【解决对策】给他们演示一次.【题目描述】一个长方形周长40米,长和宽的比是4:1,长和宽各是多少【典型错例】40÷5=88×4=328×1=8【错因分析】直接就用40÷5,认为算出来的就是1份,然后分别去乘4和1,这里要让学生理解40米表示的是两条长和两条宽,而4:1只表示一条长和一条宽的比.【解决对策】40是周长,这样算出来的是两天长和宽的值,需要在进行计算.【题目描述】一杯糖水,糖与水的比是1:16,喝掉一半后,糖与水的比是().【典型错例】一杯糖水,糖与水的比是1:16,喝掉一半后,糖与水的比是(1:8).【错因分析】错误的认为喝掉一半,糖与水的比也会减少一半,缺乏生活经验,不会练习实际想问题.【解决对策】告诉学生解决问题是要联系实际,在平时上课时也要多加练习.【题目描述】一个正方形边长增加它的1/3后,则原正方形与新正方形面积的比值为_________【错误答案】16:9【正确答案】9/16【错因分析】谁是比的前项,谁是比的后项,一定要睁大眼睛看清楚!比的问题:比与比值的区别,比值是一个结果,是一个数【解决对策】用弄清题意,看看自己列的比例式是否正确,内项之积等于外向之积;比是两者之间的关系,比值是一个值,也就是一个数.【题目描述】0.52÷0.17商是(),余数不是()【错误答案】3;1【正确答案】3;0.1【错因分析】0.52÷0.17=52÷17=3……1,此处为了方便计算将被除数与除数同时扩大100倍,但是因为原式式0.52和0.17,所以余数只能是0.52-0.17×3=0.1,而不是1,那样被除数都没有余数大.【解决对策】除数×商+余数=被除数在小数化为整数做除时,记得还原【题目描述】一根长为48厘米的铁丝围成一个长方体,已知长宽高之比3:2:1,求这个这个体积这个长方体的体积?这个长方体的体积?【错误答案】48÷(3+2+1)=8(厘米)所以长:8×3=24(厘米);宽:8×2=16(厘米);高:8×1=8(厘米)体积:24×16×8=3072(立方厘米)【正确答案】48÷4÷(3+2+1)=2(厘米)所以长:2×3=6(厘米);宽:2×2=4(厘米);高:2×1=2(厘米)体积:6×4×2=48(立方厘米)【错因分析】48厘米是长方体的所有长宽高的长度总和,与其相等长度的各有4根,所以得先除以4,一开始的24,16,8是4个长、4个宽、4个高的长度.【解决对策】做题时应该脑中有图,图形结合,不可以往题目中的隐藏含义.【题目描述】甲、乙两数的比是4:5,甲数是乙数的(),乙数比甲数多().【典型错例】甲数是乙数的(45),乙数比甲数多(150).【错因分析】受整数两个量的比较影响.学生没有把握分数、百分数中两个量比较时.求谁比谁多几分之几或谁比谁少几分是几时,应找准标准量,如果标准量不同,结果也会不同.【解决对策】要让学生正确理解谁比谁多几分之几或少几分之几的含义.设计练习要有针对性,可以有一些对比练习.学会验算.【题目描述】甲乙两圆的周长比是2:3,其中一个圆的面积是18 ,另一个圆的面积可能是().,也可能是().【典型错例】①有的学生只填了一个②12,27③不会做【错因分析】学生忘记了:面积比是半径的平方比,同时也是周长的平方比.对于圆面积公式理解不透彻,思考问题不全面.【解决对策】要让学生明确:圆面积应该是圆周率乘以半径的平方.在推导圆面积公式时,让学生从各个角度来了解圆面积计算公式的推导.明确比的意义理解.【题目描述】甲班人数比乙班多2/5,乙班人数比甲班少(2/5或3/5).【错因分析】学生把表示具体量2/5与表示倍数的2/5在意义上混同了.认为甲班人数比乙班人数多2/5就是乙班人数比甲班少2/5.对于数量与倍数不能区分.而且一会儿把甲班人数当成单位“1”一会儿把乙班人数当成单位“1”概念不清楚.【解决对策】(1)区分数量与倍数的不同.(2)画线段图建立直观、形象的模型来帮助理解.(3)明确把乙班人数看做单位“1”的量,于是甲班人数是:(1+2/5)=7/5.所以乙班人数比班甲人数少(2/5÷7/5)=2/7.(4)结合类似题目加强练习以达目的.【题目描述】400÷18=22⋯⋯4,如果被除数与除数都扩大100倍,那么结果是(A )A、商22余4B、商22余400 C 、商2200余400 【错因分析】本题考查与商不变性质有关的知识.被除数、除数都扩大100倍后,商不变,但余数也扩大了100倍,想要得到原来的余数,需要缩小100倍.而学生误认为商不变,余数也不变,所以错选A,正确答案应该选B.【解决对策】(1)验算.请学生用答案A的商乘除数加余数检验是否等于被除数.从而发现选A是错误的.(2)明确商不变的性质.但是当被除数、除数都扩大100倍后商不变但余数也扩大了100倍.想要得到原来的余数,需要缩小100倍.(3)在理解商不变性质有关知识基础上加强练习以达到目的.【题目描述】两个正方体的棱长比是1:3,这两个正方体的表面积比是(1:3),体积比是(1: 5或1:9)【错因分析】这题是北师大版六年级上册第四单元《比的应用》部分的内容.目的是考查学生根据正方体的棱长比求表面积和体积的比.所以正方体的表面积和体积的计算公式是关键.学生有的是因为对正方体的表面积和体积的计算方法忘记了有的是因为对比的意义不理解认为表面积比和棱长比相同所以导致做错.【解决对策】巩固理解比的意义及求比的方法.明确正方体的表面积和体积的计算方法.结合类似的题型加以练习,进一步巩固对比的应用.【题目描述】a)比20米多1/5是()米;b)20米比()米少1/5;c)比()米多1/5是20米;【错因分析】这是一道稍加复杂的分数乘除法的辨析题,学生往往找不准单位“1”而混淆了计算方法,找不着头脑,对于理解能力欠缺的学生,根本找不着这类题的突破口.【解决对策】对于此类问题有两种方法:加强此类题的训练,找准单位“1”,发现一般“比”字后面的量是单位“1”的量.即:20×1/5=4米,20+4=24米;把“()”看成单位“1”,所以20米是(1-1/5)=4/5的长度,那么单位“1”的长度是:20÷4/5=25米;1+1/5=6/5,6/5是20的长度,所以单位“1”的长度是:20÷6/5=50/3米.可以将题目转化成“线段图”方便理解,易于做题,具体步骤及思路如下(以第一小问为例):20米【题目描述】老师把千克糖果平均分给7个班,每个班分得糖果的()/(),5个班分得()/()千克.【错因分析】第一问求的是每个班分得糖果占总量的几分之几,这是求得关系;而第二问求的是具体的数量.两者根本不同,应从不同的角度解决.【解决对策】第一问求的是“每个班级分得糖果的()/()”,和具体的数量无关,把所有的糖果看作单位“1”,把单位”1“一共分成了7份,每个班分得这样的1份,也就是1/7;第二问要求5个班分得1多少千克,先求每个班分得多少千克,再乘5即可.15÷7=15/7(千克),15/7×5=75/7(千克),5个班分得75/7千克.【题目描述】1)一根圆柱型的木材,长2米,把他横截成两段后,表面积比原来增加了25.12平方分米,这根木材原来的体积是()?错解:25.12×2=25.242)一根圆柱型的木材,长2米,沿着底面直径截成两半,表面积比原来增加了25.12平方分米,这根木材原来的体积是多少?【典型错例】25.12×2=25.243)一根圆柱型的木材,长2米,过底面圆形成十字切成四半,表面积比原来增加了25.12平方分米,这根木材原来的体积是多少?25.12×2×4=200.96【错因分析】这类型的题学生错误的形式有三种,会做的就是在计算上粗心,要不然就是不会做的,一点儿头绪也没有,或者是想当然的以为截成两段就要乘2,截成4段就要乘4,直观的想象到截成4段数量上就是4倍了.当我询问他们25.12×2也就是表面积乘以2是什么意思的时候他们却答不上来.【解决对策】这种题目首先我们要明确体积的计算公式是怎样的,避免用“表面积×2来表示体积,在学生理解了公式的基础上,从公式出发去寻找条件解题,比如这道题需要从题中去寻找底面积和高,长2米就是高,表面积比原来多25.12,表面积为什么会多?多出来的面是怎么样的?分析之后知道多出来的是两个底面,即两个底面的面积是25.12,一个底面的面积就明确了,题目也就解决了.【题目描述】写出比例尺【典型错例】【错因分析】一方面是学生没有明确比例尺的含义,它是图上距离比实际距离;另一方面是没有明确比例尺的书写规则,不如不能带上单位,要写成最简的比等.【解决对策】比例尺的含义需要学生反复记忆甚至是背诵;其他的可以采取纠错题的方式,将错误的形式与正确的形式都呈现在学生面前,让学生自己来判断,老师再加以强调.【题目描述】圆的半径、直径、周长、面积(a)圆的半径增加1cm,它的直径就增加2cm.(b)圆的半径扩大2倍,它的周长也扩大2倍.(R—2πR)(c)圆的半径扩大2倍,它的面积就扩大4倍.(R—π)(d)周长相等的两个圆,它们的面积也相等.【题目描述】百分数应用题第一类:桃树有60棵,梨树有80棵,梨树是桃树的百分之几?梨树比桃树多百分之几?第二类:一件衣服先提价10%,在降价10%,现价比原价().第三类:甲乙两数的比是80:100,甲数是乙数的百分之几?乙数是甲数的百分之几?甲数比乙数少百分之几?乙数比甲数多百分之几?【解决对策】我觉得弄清这些题的思路最重要的是理清题中的“单位1”,问题的变化就是“单位1”的变化,所以说“单位1”在分数的学习中相当重要.在辅导作业的过程中,大多数孩子在我问了“跟谁去比?谁是单位一?”等问题后就能够独立的解题.【题目描述】一项工程甲单独完成需要10天,乙单独完成需要12天,甲、乙两队合作5天后,由于甲队有新的工作任务,剩下的工作由乙队单独完成,乙队还要工作多少天才能完成?【解决对策】这种题我认为要重点理解一个词“效率”.效率是指单位时间内完成的工作量,在题目中甲一天完成的工作量1/10就是他的效率,如果说甲一个人工作了3天,那么他三天的工作量就是他一天的工作量乘以3,即:1/10×3.甲和乙合作5天的工作量就是他们合作一天的工作量乘以5,即各自的效率之和(1/8+1/10)乘以5.【题目描述】李老师有52kg,王老师的体重比李老师多1/4,王老师的体重是李老师的几分之几?【典型错例】52×1/4;1-1/4=3/4【解决对策】学生并没有完全理解题目的意思,只是为了得到答案盲目的将数字进行运算.这种情况很普遍,比如今天在课堂上学了分数的乘法,做练习题的时候就一味的用乘法;学了倒数,运算的时候就不管不顾的把分数全部倒过来运算.究其原因,一方面是学生做题的心态浮躁,另一方面是对知识不够理解.但是如果在做题之前将可能会犯的错误提出来告诉学生或让学生做纠错题情况可能会有所好转.【题目描述】把一根一米的绳子平均分成4段,每段长()米,每段占全长的().【错因分析】这是一道除法与分数关系的辨析题,也是辨别实际长度和分率的混淆题.都是求每段,学生一时无法理解概念的形成,很多学生停留在死记硬背上,无法真正的理解掌握概念内涵.【解决对策】让学生看清楚题意,从问题的本身上引导学生发现实际长度和分率的区别,可以通过画线段图帮助理解.实际长度可以通过用除法算式“总长度÷段数”来计算,分率跟总长度无关只跟分成的份数有关.【题目描述】一种油菜籽的出油率是35%,420千克的油菜籽可以榨出()千克油,要榨420千克油需()千克油菜籽.【错因分析】由于油菜籽和油的单位都是“千克”,学生往往受此疑惑而不知该选用什么计算方法.此外学生往往不能准确找出关系,不知道什么时候用乘法什么时候用除法.【解决对策】从对等的方式入手理清思路,35%中的35份表示什么,100份表示什么,引导学生用方程的思路解决,理清关系.要引导学生明白油菜籽总是比榨出来的油要多,结合生活实际经验分析题意.【题目描述】小林早晨7:30从家去学校,每分钟走50米.刚到学校门口发现数学书没有带,立即沿原路返回,每分钟走70米.到家正好是7:54.小林家离学校多少米?【典型错例】(50+70)×(54-30)÷2=1440(米)答:小林家离学校1440米.【错因分析】这是一道六年级的较难题,涉及到时间的算法,路程问题以及比值问题.算时间基本上没问题:54-30=24(分钟),但是这个时间是小林走完家—学校—家这段路程所花费的,而家—学校这段时间的速度和学校—家这段时间的速度是不同的,因此两段路程所花费的时间并不是平均的,不能用(54-30)÷2来计算.因此错误.【解决对策】去的速度:返回的速度=50:70=5:7,根据路程一定,速度和时间成反比例,所以,去的时间:返回的时间=7:5.根据往返共用24分钟,因此,去的时间(或返回的时间)可以求出,即:24×7/(5+7)=14(分钟).最后根据去的速度和时间即可求出家到学校的距离,即:50×14=700(米),答:小林家离学校700米.【题目描述】一件商品,利润是成本的20%,如果把利润提高到30%,那么售价应提高百分之几?【典型错例】30%-20%=10%答:售价应提高百分之十.【错因分析】这是一道六年级的易错题,学生容易惯性思维认为提润从百分之20%提高到百分之30%只需要将之加减,而没有正确的弄清成本、利润、售价之间的百分比关系.因此错误.【解决对策】把这件商品的成本看做单位“1”,原来利润是成本的20%,这时的售价为1+20%=120%,把利润提高到30%,这时的售价为1+30%=130%,要求售价应提高百分之几,即:[(1+30%)-(1+20%)]÷(1+20%)=10%÷120%≈8.3%,答:售价应提高8.3%.【题目描述】一座钟的时针长3厘米,它的尖端在一昼夜里走过的路程是()厘米.【典型错例】一座钟的时针长3厘米,它的尖端在一昼夜里走过的路程是(18.84 )厘米.【错因分析】这是一道六年级的较难题,不仅考察学生在平时生活中的观察能力,还在短短两句话的题干中隐藏了很多条件.根据实际观察,钟是圆形的,时针走的路程也就是以时针为半径计算周长.在这样的前提下,学生容易算出时针旋转一周走过的路程,但容易忽视一昼夜是时针走2圈,所以算出来的结果有误.【解决对策】复习钟表知识,时针走一圈是12小时,走两圈才是一昼夜,强调一昼夜的概念,在算出时针走一周的前提下,再乘以二就能得到正确的结果:18.84×2=37.68(厘米).【题目描述】两根同样长的绳子,一根剪去3/7,另一根剪去3/7米,第()根剪去的长一些.A、第一根长B、第二根长C、一样长D、无法判断【典型错例】 C【错因分析】这是一道六年级关于分数不同含义的较难题.学生看到“同样长”的字眼很容易将绳子长度设为单位“1”,一根剪去3/7,也就是1×3/7=3/7(米),恰好等于另一根剪去的3/7米,因此选C,在解题过程中,盲目设单位“1”是不可取的,假如绳子长度为2米,2米的3/7不等于3/7米,因此错误.【解决对策】虽然单设单位“1”不可取,但是可以以单位“1”的长度来判断.绳子长度<1米时,假设为1/2米长的绳子,它的3/7是1/2×3/7=3/14(米),比3/7米小,所以第二根长一些;绳子长度=1米时,一样长;绳子长度>1米时,第一根长.因此,在题干没给出绳子具体长度时,无法判断.答案选D.【题目描述】3根12分米长的铁丝围成长方形、正方形和圆形,则()面积最大.A、长方形B、正方形C、圆形【典型错例】A/BA、长方形B、正方形C、圆形【错因分析】这是一道六年级的易错题.有些学生容易忽视题干给出的已知条件,用12分米长的铁丝围成图形,那么说明图形的周长为12分米.这是个隐藏条件,不能理解的学生就看不懂题意,全凭想象认为长方形或者正方形大一些,就选错了.也不乏猜圆大一些而蒙对的例子.【解决对策】看清条件,“3根12分米长的铁丝”各围成长方形、正方形和圆形,那么三个图形的周长都是12分米.围成正方形的边长是12÷4=3(分米),面积为3×3=9(平方分米);围成长方形的长是1分米或者2分米,宽是5分米或者4分米,面积为5平方分米或者8平方分米;围成圆的半径是12÷3.14÷2≈1.9(分米),面积为1.92×3.14≈11.34(平方分米).则圆的面积最大,答案选C【题目描述】行同一段路,甲用5小时,乙用4小时,甲乙速度的比是5:4.().【典型错例】行同一段路,甲用5小时,乙用4小时,甲乙速度的比是5:4.(√).【错因分析】这是一道六年级的毕业考试易错题.在快速省题过程中,思维定势会导致学生错误地将速度之比等同于时间之比,因此错误.【解决对策】熟记路程计算公式,路程=速度×时间.“同一段路”这个条件告诉我们路程不变,那么速度和时间是呈反比的.列式5×V甲=4×V乙.甲乙速度的比应该是4 :5.答案是×.【题目描述】圆柱体积是圆锥体积的3倍,这两者一定是等底等高.().【典型错例】圆柱体积是圆锥体积的3倍,这两者一定是等底等高.(√).【错因分析】这是一道六年级的毕业考试易错题,考察学生的逆向思维能力.学生容易想到的是等底等高的圆柱体积是圆锥体积的3倍,有些学生就理所当然认为圆柱体积是圆锥的3倍,那么圆柱和圆锥就等底等高.应该由圆锥和圆柱的体积公式来推导.由圆柱和圆锥的体积公式可知,它们的体积是由底面积和高的乘积决定的,如果圆柱体积是圆锥体积的3倍,那么他们的底面积与高的乘积就相等,但不一定等底等高.因此错误.【解决对策】假设圆柱体积是12,则圆锥体积是4,圆柱底面积和高可以分别是4和3,圆锥的底面积和高可以分别是6和2,那么圆柱和圆锥就不是等底等高.所以答案是×.【题目描述】400÷18=22……4,如果被除数和除数都扩大100倍,那么结果是()A商22余4 B商22余400 C商2200余400【典型错例】(A)【错因分析】本题考查与商不变性质有关的知识.被除数、除数都扩大100倍后,商不变,但余数也扩大了100倍,想要得到原来的余数,需要缩小100倍.而学生误认为商不变余数也不变,所以错选A,正确答案应该选B.【解决对策】(1)验算.请学生用答案A的商乘除数加余数检验是否等于被除数.从而发现选A是错误的.(2)明确商不变的性质.但是当被除数、除数都扩大100倍后,商不变,但余数也扩大了100倍.想要得到原来的余数,需要缩小100倍.(3)在理解商不变性质有关知识基础上加强练习以达到目的.【题目描述】把一根米的绳子平均分成5段,每段占全长的(),每段长()【典型错例】()()【错因分析】每段与全长之间的关系是1份和5份之间的关系,即每段占全长的,÷5=米, 每段长米.本题考查分数的意义的理解和分数除法的运用,学生没有理解和掌握.所以因为分不清两个问题的含义而把两个答案混淆了.一般这类型的题目在最后一个括号后会写上单位.但我为了检查学生的细心程度,单位没写,于是有些本来会做的人因为粗心而又错了.【解决对策】(1)理解分数的意义;弄清楚两个问题各自的含义.(2)教育学生做题前要养成仔细审题、认真思考的习惯.(3)在理解了分数的意义基础上加强练习以达到目的.【题目描述】如果A是B的,那么A比B少()%.【错因分析】学生的错误往往表现在找不准单位“1”的量而发愁,且将“是字句”转换为“比字句”,理解上也有难度.【解决对策】借用假设法,把A就看成3,把B看成5,这样计算的难度就下降了;借用画图法,画出一个线段表示单位“1”,在线段上在表示出,帮助理解两者关系.【题目描述】一台碾米机每小时碾米2吨,1小时可碾米()吨,碾1吨米要()小时.【错因分析】学生往往缺乏分析数量关系的判断力,源于学生下意识地认为都是“大数除以小数”,因此拿不准到底是谁除以谁.【解决对策】从“工作效率、工作时间和工作总量”的分析入手,弄清三者之间的关系;也可以画线段图结合实际情况分析.【题目描述】。
六年级下册数学思维易错题难题训练及答案含答案

六年级下册数学思维易错题难题训练及答案含答案一、培优题易错题1.“△”表示一种新的运算符号,已知:2△3=2﹣3+4,7△2=7﹣8,3△5=3﹣4+5﹣6+7,…;按此规则,计算:(1)10△3=________.(2)若x△7=2003,则x=________.【答案】(1)11(2)2000【解析】【解答】(1)10△3=10-11+12=11;(2)∵x△7=2003,∴x-(x+1)+(x+2)-(x+3)+(x+4)-(x+5)+(x+6)=2003,解得x=2000.【分析】(1)首先弄清楚定义新运算的计算法则,从题目中给出的例子来看,第一个数表示从整数几开始,后面的数表示几个连续整数相加减,根据发现的运算规则,即可由10△3列出算式,再根据有理数加减法法则,即可算出答案;(2)根据定义新运算的计算方法,由x△7=2003,列出方程,求解即可。
2.观察下列一组图形:它们是按照一定规律排列的,依照此规律,第个图形中共有________个“★”.【答案】(3n+1)【解析】【解答】解:①为4个★,②为7个★,③ 为10个★,④为13个★,通过观察,可得第n个图形为(3n+1)个★.故答案为:(3n+1)【分析】观察图形,先写出①②③④的★的个数,通过找规律,写出第n个图形中的★个数。
3.对于实数a、b,定义运算:a▲b= ;如:2▲3=2﹣3= ,4▲2=42=16.照此定义的运算方式计算[2▲(﹣4)]×[(﹣4)▲(﹣2)]=________.【答案】1【解析】【解答】解:根据题意得:2▲(﹣4)=2﹣4= ,(﹣4)▲(﹣2)=(﹣4)2=16,则[2▲(﹣4)]×[(﹣4)▲(﹣2)]= ×16=1,故答案为:1【分析】先利用定义计算括号中的值,再进行计算即可.在利用新运算的时候需要先判断两个数的大小关系,根据其选择算式.4.列方程解应用题:(1)一个箱子,如果装橙子可以装18个,如果装梨可以装16个,现共有橙子、梨400个,而且装梨的箱子是装橙子箱子的2倍.请算一下,装橙子和装梨的箱子各多少个?(2)一群小孩分一堆苹果,每人3个多7个,每人4个少3个,求有几个小孩?几个苹果?(3)一架飞机在两城之间飞行,风速为24千米/时.顺风飞行需要2小时50分,逆风飞行需要3小时,求无风时飞机的速度和两城之间的航程.【答案】(1)解:设装橙子的箱子x个,则装梨的箱子2x个,依题意有18x+16×2x=400,解得x=8,2x=2×8=16.答:装橙子的箱子8个,则装梨的箱子16个(2)解:设有x个小孩,依题意得:3x+7=4x﹣3,解得x=10,则3x+7=37.答:有10个小孩,37个苹果(3)解:设无风时飞机的航速为x千米/小时.根据题意,列出方程得:(x+24)× =(x﹣24)×3,解这个方程,得x=840.航程为(x﹣24)×3=2448(千米).答:无风时飞机的航速为840千米/小时,两城之间的航程2448千米【解析】【分析】(1)根据梨和橙子与各自箱数分别相乘,相加为两者的总数,求出装梨和橙子的箱子数。
六下数学易错题

六下数学易错题
六下数学易错题示例如下:
1. 错误:在六下数学中,减法不能转换为加法。
这是因为在减法中,我们失去的东西比得到的东西多,而在加法中,我们得到的东西比失去的东西多。
因此,如果我们将减法转换为加法,我们将会得到一个错误的答案。
正确:在六下数学中,减法不能转换为加法,因为它们是两种不同的运算。
减法表示从一个数中减去另一个数,而加法表示将两个数相加。
因此,我们不能将减法转换为加法。
2. 错误:在六下数学中,直角三角形的两条直角边之和总是等于斜边。
正确:在六下数学中,直角三角形的两条直角边之和总是等于斜边,但这并不总是正确的。
例如,如果一个直角三角形的两条直角边长分别为 3 和 4,那么它们的和为 7,而不是斜边长 5。
因此,我们不能一概而论,认为直角三角形的两条直角边之和总是等于斜边。
拓展:在六下数学中,还有很多其他的易错题,例如分数的加减法、小数的加减法、四则运算的优先级等等。
对于这些错误,我们需要注意在学习数学的过程中及时纠正,并经常复习巩固,以免加深错误的印象。
同时,我们也需要保持耐心和细心,在做题时认真审题,仔细分析,避免粗心大意导致的错误。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级数学下册错题难题一、填空1、在数轴上,从左到右的顺序就是数()的顺序。
2、0既不是(),也不是(),正数都()0,负数都()。
3、如果一个物体向前移动8米,记作+8米,那么这个物体向后移动8米,记作()。
4、晶晶向东走100米,记作-100米,那么她向西走100米,应记作()。
5、在数轴上与原点距离6个单位长度的点有()个,它们所表示的数分别是()。
6、如果-3表示比90小3的数,那么0表示的数是(),-5表示的数是(),+8表示的数是()。
7、如果在银行存入500元,存折上记作+500元,那么从银行取出200元,存折上应记作()。
8、在一次食品质量检查中,如果超过标准重量2克,记作+2克,那么-3克表示()。
9、当圆柱的()和()相等时,它的侧面展开是一个正方形。
10、一个圆柱的底面半径扩大到原来的2倍,底面直径扩大()倍,底面周长扩大()倍,底面积扩大()倍,高不变,体积扩大()倍;一个圆柱的底面直径和高都扩大到原来的2倍,体积就扩大到原来的()倍;一个圆柱的底面积不变,高扩大到原来的3倍,它的体积扩大到原来的()。
11、从圆锥的()到()的距离,是圆锥的高。
12、把一个27立方厘米的圆锥削成一个最大的圆锥,圆锥的体积是()立方厘米,削去了()立方厘米。
13、圆锥的体积比和它等底等高的圆柱的体积少4.2立方米,这个圆柱的体积是()立方米,圆锥的体积是()立方米。
14、一个圆柱和它等底等高的圆锥的体积之和是128立方分米,圆柱的体积是()立方分米,圆锥的体积是()立方分米。
15、把一个棱长为4厘米的正方体削成一个最大的圆柱,削去的体积是()立方厘米,削去的部分占正方体体积的()。
16、如果A÷2-B÷3=0,那么A:B=()。
17、根据2×12=8×3,写出一个比值最小的比例是()。
18、在一个比例中,两个比的比值都等于2,这个比例的外项为14和5,这个比例式是()。
19、甲数的1/3等于乙数的1/2,甲数比乙数多4.2,甲数是(),乙数是()。
20、如果A÷(B×C)=1,那么A一定时,B和C成()比例;()一定时,()和()成正比例。
21、在比例中,两个外项的积是最小的合数,一个内项是0.5,另一个内项是()。
22、5A=3B,那么A:B=()。
23、如果M×N=E,当()一定时,()和()成正比例。
24、M:N=1又3/4时,那么M×()=N×()。
25、一种圆柱形状的木料,长2米,把它横截成3段后,表面积比原来增加了25.12平方厘米,原来这根木料的底面积是()平方厘米,体积是()立方厘米。
26、大于-2且小于+3的整数有()个,是()。
27、一个圆柱实心钢锭,可以铸成()个与它等底等高的实心圆锥形零件。
二、判断1、实际距离一定比图上距离大。
()2、两种相关联的量,不是成正比例,就是成反比例。
()3、在比例里,两个外项的积与两个内项的积的差是0。
()4、圆锥的体积是圆柱的1/3,那么圆锥和圆柱等底等高。
()5、一个圆锥的底面直径扩大到原来的2倍,高缩小到原来的1/2,圆锥的体积不变。
()6、圆柱的底面积扩大原来的2倍,侧面积也扩大原来的2倍。
()7、一个圆柱横截成两个小圆柱,它的表面积和体积都增加了。
()8、一个圆柱和一个圆锥的高相等,它们的底面积的比是3:2,那么它们的体积比是9:2。
()9、如果圆柱的体积是圆锥体积的3倍,那么它们一定等底等高。
()10、把两张相同的长方形纸,分别卷成两个形状不同的圆柱筒,且边缘处无重叠,并装上两个底面,那么所制的两个圆柱体的侧面积一定相等。
()11、一个数不是正数就是负数。
()12、数轴上表示-3又1/2的点在原点的左边,距离原点3又1/2个单位长度。
()三、选择1、在数轴上把3的对应点移动5个单位长度后,所得的对应点表示的数是()A、8B、-2C、8或-2D、不能确定2、有一种积分方法:以80分为准,88分记+8分,某个学生得74分,应记为()A、74分B、+6分C、-74分D、-6分3、一个圆锥和一个圆柱的体积和高分别相等,已知圆柱的底面积是 3.14平方分米,圆锥的底面积是()平方分米。
A、3.14 B、6.28 C、9.424、两个高和体积都分别相等的圆柱和圆锥,圆柱的底面积一定是圆锥底面积的()A、3倍B、1/3C、2/35、一个圆柱的体积比和它等底等高的圆锥的体积大18立方分米,那么圆锥的体积是()立方分米A、54B、6C、96、圆柱和圆锥底面半径的比是1:2,圆柱的高是圆锥高的8/9,那么圆柱和圆锥的体积比是()A、4:3B、2:3 C2:277、一个圆锥和一个圆柱等底等高,这个圆柱的体积是6.9立方米,它比圆锥的体积多()立方米。
A、2.3B、4.6C、6.98、一个圆柱和一个圆锥的高相等,它们的底面积的比是1:2,它们的体积比是()A、3:1B、2:9C、3:29、底面积和体积都分别相等的圆柱和圆锥,圆柱的高一定是圆锥高的()A、2/3B、1/3C、3倍10、下列各式中,A和B成反比例关系的是()A、A×B/3=1B、A×8=B/5C、9A=6BD、(A+7)÷10=B11、1/X=4Y,那么X和Y() A、成正比例 B、成反比例 C、不成比例四、判断下列两种量成什么比例1、报刊单价一定,报刊的份数和总价。
()2、小刚的体重和身高。
()3、小新跳高的高度和他的身高。
()4、汽车的速度一定,所行的时间和所行的路程。
()5、工厂每小时加工零件数一定,加工时间和加工的零件总数。
()6、每袋花生的质量一定,花生的总质量和袋数。
()7、三角形的面积一定,底和高。
()8、被减数一定,减数和差。
()9、正方形的边长和面积。
()10、圆柱的体积一定,圆柱的底面积和高。
()11、全班人数一定,平均每组的人数和组数。
()12、全班人数一定,出勤率和出勤人数。
()13、火车行驶的路程一定,行驶的速度和时间。
()14、正方体的棱长和体积。
()15、圆的周长与直径。
()五、解比例1/2:X=1/3:1/6 1/9:1/4=X:18 X:1.2=0.5:2 3/4:5/6=X:2/3 X:60=12:25六、解决问题1、分别写出比0小3的数,比3小2的数和比-4小2的数。
2、在数轴上表示出距离原点3个单位长度和4.5个单位长度的点,并且用“>”号将这些点所表示的数排列出来。
3、在一次数学测试中,六年级一班的平均分为87分,把高于平均分的部分记作正数。
(1)王华得了98分,(2)李刚的成绩被记作-2分,他实际得分是多少(3)张华得了83分,应记作多少?4、某蓄水池,把标准水位记为0米,如果用正数表示水面高于标准水位的高度,那么(1)+0.05米和-0.08米各表示多少(2)水面低于标准水位0.1米和高于标准水位0.12米各怎样表示。
5、有5张课桌,量得它们的高度比标准高度高0.5毫米,-1毫米,0毫米,+2.5毫米,-1.5毫米,若规定课桌的高度最高不能高于标准高度2毫米,最低不能低于标准高度2毫米,才算合格,这5张课桌有几张不合格?6、下表是六年级一般部分同学1分钟的排球成绩表如果以80个为标准,多于80个用正数表示,低于80个用负数表示,请填写下表:7、把一个棱长是6厘米的正方体木块削成一个最大的圆柱,圆柱的体积是多少?8、把一个长6厘米,宽5厘米,高4厘米的长方体削成一个最大的圆柱,圆柱的体积是多少?9、一台压路机的前轮是圆柱形的,轮宽1.8米,直径1.2米,前轮每分钟转动20周,这台压路机1分钟压过的路的面积是多少平方米?10、一对圆柱形水桶,从里面量底面直径是20厘米,底面直径的长度是高的4/5,如果给这对水桶里都装上7/10的水,每立方分米的水重1千克,这对水桶一共装了多少千克水?11、一个底面直径是40厘米的圆柱形玻璃杯,杯里装有一些水,在杯中放着一个底面直径为20厘米,高为15厘米的圆锥形铁锤,当取出铁锤后,杯里的水面下降多少厘米?12、一个圆锥形沙堆,底面积是125.6平方米,高是0.6米,把这堆沙子铺在长4.5米,宽2米的沙坑内,可以铺多厚?(得数保留两位小数)13、把一个圆锥沿高切成形状大小完全一样的两部分,结果表面积之和比原来增加48平方分米,已知圆锥的高为6分米,求原来圆锥的体积是多少立方分米?14、一个直角三角形的两条直角边长分别是4厘米和3厘米,如果以长4厘米的一边为轴旋转一周,可以得到一个圆锥,这个圆锥的体积是多少立方厘米?15、明明家有一个长方体鱼缸,长30厘米,宽20厘米,水深15厘米,爸爸又买来一个底面半径为10厘米的圆柱形的新鱼缸,如果把原鱼缸里的水全部倒入新鱼缸,新鱼缸内还有1/4的空间,这个新鱼缸的高是多少?(得数保留一位小数)16、一个棱长是6分米的正方体和一个圆柱的体积相等,已知圆柱的高是3分米,求圆柱的底面积。
17、甲乙两个仓库存粮的总数是40吨,其中甲仓库存粮的1/3与乙仓库存粮的1/4相等,两个仓库各存粮多少吨?18、甲乙两班的学生人数比是5:4,如果从一般转走9名学生,那么甲班就比乙班的人数多2/3,这时乙班有多少人?19、用98厘米长的铁丝做长和宽之比是5:2的长方形,如果把它画在比例尺是1:7的图纸上,那么这个长方形的图上面积是多少?20、在比例尺是1:3000000的地图上,量得两地的距离是6厘米,甲乙两辆汽车同时从两地相向开出,4小时后相遇,已知甲乙两车的速度比为4:5,求甲乙两车每小时各行多少千米?21、六年级学生外出活动,每6人一组,可分为40租。
如果每8人一组,可分几组?22、在比例尺是1:8000000的地图上,量得A、B两地相距6厘米。
甲乙两车分别从A、B两地同时相向开出,经过5小时两车相遇。
已知甲乙两车的速度之比是5:7,甲乙两车每小时各行多少千米?23、去年王大爷家的小麦获丰收,王大爷想把一部分小麦先储存起来,把一张长12.56米,宽6.28米的竹席,做成一个圆柱形粮囤,想一想,这个粮囤怎样做盛的粮食最多?。
