八年级数学练习题及答案百度文库
八年级数学试卷答案及答案

一、选择题(每题3分,共30分)1. 下列数中,不是有理数的是()A. 0.5B. √2C. -3D. 3/4答案:B解析:有理数是可以表示为两个整数之比的数,而√2是无理数,不能表示为两个整数之比。
2. 下列图形中,对称轴为直线y=x的是()A. 等腰三角形B. 等边三角形C. 平行四边形D. 梯形答案:B解析:等边三角形的对称轴为直线y=x。
3. 下列等式中,正确的是()A. a^2 + b^2 = (a + b)^2B. a^2 - b^2 = (a + b)(a - b)C. a^2 + 2ab + b^2 = (a + b)^2D. a^2 - 2ab + b^2 = (a - b)^2答案:B、C、D解析:根据平方差公式和完全平方公式,选项B、C、D都是正确的。
4. 下列函数中,是反比例函数的是()A. y = 2x + 3B. y = 3/xC. y = 2x^2D. y = √x答案:B解析:反比例函数的形式为y = k/x,其中k为常数。
选项B符合这个形式。
5. 下列方程中,有唯一解的是()A. 2x + 3 = 7B. 2x + 3 = 0C. 2x - 3 = 0D. 2x + 3 = 7x答案:A解析:选项A的方程为一次方程,有唯一解。
选项B、C、D的方程都至少有两个解。
二、填空题(每题5分,共25分)6. 已知a + b = 5,ab = 6,则a^2 + b^2 = __________。
答案:37解析:根据平方差公式,a^2 + b^2 = (a + b)^2 - 2ab = 5^2 - 26 = 37。
7. 已知y = kx + b,其中k和b为常数,且k < 0,b > 0,则函数图象在()A. 第一、二象限B. 第一、三象限C. 第二、三象限D. 第二、四象限答案:D解析:当k < 0时,函数图象斜率为负,因此图象在第二、四象限。
8. 已知x^2 - 5x + 6 = 0,则x的值为()A. 2B. 3C. 2或3D. 2和3答案:C解析:这是一个二次方程,可以通过因式分解或者求根公式求解。
初二数学试题训练及答案

初二数学试题训练及答案一、选择题(每题3分,共30分)1. 下列哪个数是无理数?A. √2B. 0.1010010001…C. 22/7D. π2. 如果一个数的相反数是它本身,那么这个数是:A. 0B. 1C. -1D. 23. 下列哪个选项不是单项式?A. 3xB. -5y²C. 2xyD. x/y4. 一个数的平方根是它本身,这个数可以是:A. 1B. -1C. 0D. 以上都是5. 一个等腰三角形的底角是45°,那么它的顶角是:B. 90°C. 135°D. 180°6. 一个数的绝对值是它本身,这个数可以是:A. 正数B. 负数C. 0D. 以上都是7. 下列哪个选项是二次根式?A. √3B. √(-1)C. √(2x+1)D. √(1/x)8. 一个数的立方根是它本身,这个数可以是:A. 1B. -1C. 0D. 以上都是9. 一个直角三角形的两条直角边分别是3和4,那么斜边的长度是:A. 5B. 6C. 7D. 810. 下列哪个选项是多项式?A. 2xC. 4x³D. x²+2x+1二、填空题(每题4分,共20分)1. 一个数的平方是25,那么这个数是______。
2. 如果一个数的绝对值是5,那么这个数可以是______。
3. 一个等腰三角形的顶角是70°,那么它的底角是______。
4. 一个数的立方是-8,那么这个数是______。
5. 一个直角三角形的斜边长度是5,一条直角边是3,那么另一条直角边的长度是______。
三、解答题(每题10分,共50分)1. 计算并简化:(2x+3)(x-4)。
2. 解方程:2x - 3 = 7。
3. 已知一个三角形的两边长分别为6和8,第三边长为x,且三角形的周长为20,求x的值。
4. 已知一个数的平方根是4,求这个数。
5. 一个长方形的长是10cm,宽是x cm,面积是50cm²,求x的值。
八年级数学《一次函数》经典练习题含答案

八年级数学《一次函数》经典练习题一、选择题(1)当自变量x增大时,下列函数值反而减小的是()A.B.C.D.(2)对于正比例函数,下列结论正确的是()A.B.y随x的增大而增大C.D.y随x的增大而减小(3)如果函数的图像经过(-1,8)、(2,-1)两点,那么它也必经过点()A.(1,-2)B.(3,4)C.(1,2)D.(-3,4)(4)对于一次函数,若,则函数图像不经过()A.第一象限 B.第二象限 C.第三象限 D.第四象限(5)直线与y轴交点在x轴下方,则b的取值为()A.B. C. D.(6)如图所示,函数的图像可能是()(7)已知一次函数的图像经过点,且与两坐标轴围成的三角形面积是8,则这个函数的解析式是()A.B.C.或D.或(8)已知直线如图所示,要使y的值为正,自变量x必须满足()A. B. C. D.(9)下列图像中(如图所示),不可能是关于x的一次函数的图像的是()(10)对于直线,若b减少一个单位,则它的位置将()A.向左平移一个单位B.向右平移一个单位C.向下平移一个单位D.向上平移一个单位二、填空题(1)一次函数中,k、b都是_______,且,自变量x的取值范围是_________,当,b__________时,它是正比例函数.(2)若,当时,,则.(3)直线与x轴的交点是_________,与y轴的交点是__________.(4)若函数的图像过第一、二、三象限,则,这时,y随x 的增大而________.(5)直线与x轴、y轴交于A、B两点,则的面积为_________.(6)直线若经过原点,则,若直线与x轴交于点(-1,0),则.(7)直线与直线的交点为__________.(8)已知一次函数的图像如图所示,则这个一次函数的解析式为_________.(9)已知函数,当时,有.(10)已知直线上两点和,且,当时,与的大小关系式为___________.三、解答题1.已知与成正比例(其中a、b都是常数).(1)试说明y是x的一次函数;(2)如果时,;时,,求这个一次函数的解析式.2.已知三点.试判断这三点是否在同一条直线上,并说明理由.四、应用题(1)1.将长为30cm,宽为10cm的长方形的白纸,按图所示方法粘合起来,粘合部分的宽为3cm.求5张白纸粘合后的长度;(2)设x张白纸粘合后的总长度为y cm,写出y与x之间的函数关系式,并求时,y的值.2.对于气温,有的地方用摄氏温度表示,有的地方用华氏温度表示,摄氏温度与华氏温度之间存在着某种函数关系.从温度计的刻度上可以看出,摄氏(℃)温度x与华氏(℉)温度y 有如下的对应关系:x(℃)…-10 0 10 20 30 …y(℉)…14 32 50 68 86 …(1)通过①描点连线;②猜测y与x之间的函数关系;③求解;④验证等几个步骤,试确定y与x之间的函数关系式;(2)某天,A市的最高气温是8℃,澳大利亚悉尼的最高气温是91℉,问这一天悉尼的最高气温比A市的最高气温高多少摄氏度(结果保留整数)?3.某同学将父母给的零用钱按每月相等的数额存放在储蓄盒内,准备捐给希望工程,盒内原有60元,2个月后盒内有钱80元.(1)求盒内钱数y(元)与存钱月数x之间的函数关系式;(2)按上述方法,该同学几个月能存够300元?参考答案一、(1)C (2)D (3)C (4)C (5)C(6)D (7)C (8)C (9)C (10)C二、(1)常数,,全体实数,,;(2)-4;(3),(0,-2);(4),增大;(5);(6);(7);(8);(9);(10).三、1.(1)因为与成正比例,所以(k是不等于0的常数),即.因为k是不等于0的常数,a、b都是常数,所以也是常数,所以y是x的一次函数;(2)因为时,;时,,所以有解得所以这个一次函数的解析式为.2.在同一条直线上,理由如下:设经过A、B两点的直线为,由,得解得所以经过A、B两点的直线为.当时,.所以在这条直线上.所以三点在同一条直线上.1.(1)5张白纸粘合后的长度为(cm);(2)(x为大于1的整数).当时,(cm).2.(1)①描点连线(略)②通过观察可猜测y是x的一次函数,③设,现将两对数值分别代入,得解得所以.④验证:将其余三对数值分别代入,得;;.结果等式均成立.所以y与x的函数关系式为:.(2)当时,,所以.而(℃),所以这一天悉尼的最高气温比A市的最高气温约高25℃.3.(1)设.因为当时,;当时,,所以解得所以;(2)当时,,所以.所以该同学24个月能存够300元.。
八年级数学经典练习题附答案(因式分解)

八年级数学经典练习题附答案(因式分解)因式分解练习题一、填空题:2.(a-3)(3-2a)=_______(3-a)(3-2a);12.若m2-3m+2=(m+a)(m+b),则a=______,b=______;15.当m=______时,x2+2(m-3)x+25是完全平方式.二、选择题:1.下列各式的因式分解结果中,正确的是( )A.a2b+7ab-b=b(a2+7a) B.3x2y-3xy-6y=3y(x-2)(x+1)C.8xyz-6x2y2=2xyz(4-3xy) D.-2a2+4ab-6ac=-2a(a+2b-3c)2.多项式m(n-2)-m2(2-n)分解因式等于( )A.(n-2)(m+m2) B.(n-2)(m-m2) C.m(n-2)(m+1) D.m(n-2)(m-1) 3.在下列等式中,属于因式分解的是( )A.a(x-y)+b(m+n)=ax+bm-ay+bn B.a2-2ab+b2+1=(a-b)2+1C.-4a2+9b2=(-2a+3b)(2a+3b) D.x2-7x-8=x(x-7)-84.下列各式中,能用平方差公式分解因式的是( )A.a2+b2 B.-a2+b2 C.-a2-b2 D.-(-a2)+b25.若9x2+mxy+16y2是一个完全平方式,那么m的值是( )A.-12 B.±24C.12 D.±126.把多项式a n+4-a n+1分解得( )A.a n(a4-a) B.a n-1(a3-1) C.a n+1(a-1)(a2-a+1) D.a n+1(a-1)(a2+a+1) 7.若a2+a=-1,则a4+2a3-3a2-4a+3的值为( )A.8 B.7 C.10 D.128.已知x2+y2+2x-6y+10=0,那么x,y的值分别为( )A.x=1,y=3 B.x=1,y=-3 C.x=-1,y=3 D.x=1,y=-39.把(m2+3m)4-8(m2+3m)2+16分解因式得( )A.(m+1)4(m+2)2 B.(m-1)2(m-2)2(m2+3m-2)C.(m+4)2(m-1)2 D.(m+1)2(m+2)2(m2+3m-2)210.把x2-7x-60分解因式,得( )A.(x-10)(x+6) B.(x+5)(x-12) C.(x+3)(x-20) D.(x-5)(x+12) 11.把3x2-2xy-8y2分解因式,得( )A.(3x+4)(x-2) B.(3x-4)(x+2) C.(3x+4y)(x-2y) D.(3x-4y)(x+2y) 12.把a2+8ab-33b2分解因式,得( )A.(a+11)(a-3) B.(a-11b)(a-3b) C.(a+11b)(a-3b) D.(a-11b)(a+3b)13.把x4-3x2+2分解因式,得( )A.(x2-2)(x2-1) B.(x2-2)(x+1)(x-1)C.(x2+2)(x2+1) D.(x2+2)(x+1)(x-1)14.多项式x2-ax-bx+ab可分解因式为( )A.-(x+a)(x+b) B.(x-a)(x+b) C.(x-a)(x-b) D.(x+a)(x+b)15.一个关于x的二次三项式,其x2项的系数是1,常数项是-12,且能分解因式,这样的二次三项式是( )A.x2-11x-12或x2+11x-12 B.x2-x-12或x2+x-12C.x2-4x-12或x2+4x-12 D.以上都可以16.下列各式x3-x2-x+1,x2+y-xy-x,x2-2x-y2+1,(x2+3x)2-(2x+1)2中,不含有(x-1)因式的有( )A.1个 B.2个C.3个D.4个17.把9-x2+12xy-36y2分解因式为( )A.(x-6y+3)(x-6x-3) B.-(x-6y+3)(x-6y-3)C.-(x-6y+3)(x+6y-3) D.-(x-6y+3)(x-6y+3)18.下列因式分解错误的是( )A.a2-bc+ac-ab=(a-b)(a+c) B.ab-5a+3b-15=(b-5)(a+3)C.x2+3xy-2x-6y=(x+3y)(x-2) D.x2-6xy-1+9y2=(x+3y+1)(x+3y-1)19.已知a2x2±2x+b2是完全平方式,且a,b都不为零,则a与b的关系为( )A.互为倒数或互为负倒数 B.互为相反数C.相等的数 D.任意有理数20.对x4+4进行因式分解,所得的正确结论是( )A.不能分解因式B.有因式x2+2x+2 C.(xy+2)(xy-8) D.(xy-2)(xy-8)21.把a4+2a2b2+b4-a2b2分解因式为( )A.(a2+b2+ab)2 B.(a2+b2+ab)(a2+b2-ab)C.(a2-b2+ab)(a2-b2-ab) D.(a2+b2-ab)222.-(3x-1)(x+2y)是下列哪个多项式的分解结果( )A.3x2+6xy-x-2y B.3x2-6xy+x-2y C.x+2y+3x2+6xy D.x+2y-3x2-6xy 23.64a8-b2因式分解为( )A.(64a4-b)(a4+b) B.(16a2-b)(4a2+b) C.(8a4-b)(8a4+b) D.(8a2-b)(8a4+b) 24.9(x-y)2+12(x2-y2)+4(x+y)2因式分解为( )A.(5x-y)2 B.(5x+y)2 C.(3x-2y)(3x+2y) D.(5x-2y)2 25.(2y-3x)2-2(3x-2y)+1因式分解为( )A.(3x-2y-1)2 B.(3x+2y+1)2C.(3x-2y+1)2 D.(2y-3x-1)226.把(a+b)2-4(a2-b2)+4(a-b)2分解因式为( )A.(3a-b)2 B.(3b+a)2 C.(3b-a)2 D.(3a+b)227.把a2(b+c)2-2ab(a-c)(b+c)+b2(a-c)2分解因式为( )A.c(a+b)2 B.c(a-b)2 C.c2(a+b)2 D.c2(a-b)28.若4xy-4x2-y2-k有一个因式为(1-2x+y),则k的值为( ) A.0 B.1 C.-1 D.429.分解因式3a2x-4b2y-3b2x+4a2y,正确的是( )A.-(a2+b2)(3x+4y) B.(a-b)(a+b)(3x+4y) C.(a2+b2)(3x-4y) D.(a-b)(a+b)(3x-4y) 30.分解因式2a2+4ab+2b2-8c2,正确的是( )A.2(a+b-2c) B.2(a+b+c)(a+b-c) C.(2a+b+4c)(2a+b-4c) D.2(a+b+2c)(a+b-2c) 三、因式分解:1.m2(p-q)-p+q;2.a(ab+bc+ac)-abc;3.x4-2y4-2x3y+xy3;4.abc(a2+b2+c2)-a3bc+2ab2c2;5.a2(b-c)+b2(c-a)+c2(a-b);6.(x2-2x)2+2x(x-2)+1;7.(x-y)2+12(y-x)z+36z2;8.x2-4ax+8ab-4b2;9.(ax+by)2+(ay-bx)2+2(ax+by)(ay-bx);10.(1-a2)(1-b2)-(a2-1)2(b2-1)2;11.(x+1)2-9(x-1)2;12.4a2b2-(a2+b2-c2)2;13.ab2-ac2+4ac-4a;14.x3n+y3n;15.(x+y)3+125;16.(3m-2n)3+(3m+2n)3;17.x6(x2-y2)+y6(y2-x2);18.8(x+y)3+1;19.(a+b+c)3-a3-b3-c3;20.x2+4xy+3y2;21.x2+18x-144;22.x4+2x2-8;23.-m4+18m2-17;24.x5-2x3-8x;25.x8+19x5-216x2;26.(x2-7x)2+10(x2-7x)-24;27.5+7(a+1)-6(a+1)2;28.(x2+x)(x2+x-1)-2;29.x2+y2-x2y2-4xy-1;30.(x-1)(x-2)(x-3)(x-4)-48;四、证明(求值):1.已知a+b=0,求a3-2b3+a2b-2ab2的值.2.求证:四个连续自然数的积再加上1,一定是一个完全平方数.3.证明:(ac-bd)2+(bc+ad)2=(a2+b2)(c2+d2).4.已知a=k+3,b=2k+2,c=3k-1,求a2+b2+c2+2ab-2bc-2ac的值.5.若x2+mx+n=(x-3)(x+4),求(m+n)2的值.6.当a为何值时,多项式x2+7xy+ay2-5x+43y-24可以分解为两个一次因式的乘积.7.若x,y为任意有理数,比较6xy与x2+9y2的大小.8.两个连续偶数的平方差是4的倍数.参考答案:一、填空题:7.9,(3a-1)10.x-5y,x-5y,x-5y,2a-b11.+5,-212.-1,-2(或-2,-1)14.bc+ac,a+b,a-c15.8或-2二、选择题:1.B 2.C 3.C 4.B 5.B 6.D 7.A 8.C 9.D 10.B 11.C 12.C 13.B 14.C 15.D 16.B 17.B 18.D 19.A 20.B 21.B 22.D 23.C 24.A 25.A 26.C 27.C 28.C 29.D 30.D三、因式分解:1.(p-q)(m-1)(m+1).8.(x-2b)(x-4a+2b).11.4(2x-1)(2-x).20.(x+3y)(x+y).21.(x-6)(x+24).27.(3+2a)(2-3a).四、证明(求值):2.提示:设四个连续自然数为n,n+1,n+2,n+3..6.提示:a=-18.∴a=-18.。
初二数学题库及答案

初二数学题库及答案一、整数运算1. 计算下列各式的值:a) 18 + (-7) = ?b) (-15) - (-3) = ?c) (-9) × 5 = ?d) 36 ÷ (-6) = ?2. 按要求简化下列各式:a) (-2) + 5 - 3 + (-5) = ?b) (-8) - (-3) + 6 - (-2) = ?c) 15 + 4 × (-2) - 3 × (-5) = ?d) (-7) × 3 + 5 × (-2) + 4 × (-3) = ?二、分数运算1. 将下列分数化为带分数形式:a) 21/4 = ?b) 15/2 = ?c) 7/3 = ?2. 计算下列各式的值,用最简形式表示:a) 1/2 + 3/4 = ?b) 7/8 - 3/4 = ?c) 5/6 × 2/3 = ?d) 3/5 ÷ 4/7 = ?三、数轴和坐标1. 在数轴上标出下列各点的坐标:a) A(3)b) B(-2)c) C(1/2)2. 在数轴上表示下列各个数的位置,并写出它们的坐标:a) 7b) -3/4c) -5d) 2/3四、代数式及求值1. 将下列词语转化为代数式:a) 两个数的和b) 一个数与4的积c) 一个数减去5的结果d) 一个数的三倍2. 计算下列各式的值:a) 3x + 5 - 2x, 当 x = 4 时b) 2y + 3y - 6, 当 y = -2 时c) m - 2 × 5, 当 m = 7 时d) 6n ÷ 3 + 4, 当 n = 2 时五、几何基础1. 下列图形中,哪些是多边形?哪些不是?说明原因。
2. 已知一个正方形的边长为8cm,请计算它的周长和面积。
3. 若一个三角形的底边长为6cm,高为4cm,请计算它的面积。
六、图表和数据处理1. 根据下图,回答问题:(表格描述某班的考试成绩)| 学生姓名 | 语文成绩 | 数学成绩 ||---------|---------|---------|| 张三 | 92 | 78 || 李四 | 85 | 92 || 王五 | 78 | 84 || 赵六 | 90 | 88 |a) 谁的数学成绩最好?b) 谁的语文成绩最差?c) 谁的语文和数学成绩之和最高?2. 对于以下数据,回答问题:(描述某商店每天的销售额)| 日期 | 销售额(元) ||-----|-------------|| 1号 | 1500 || 2号 | 1800 || 3号 | 2100 || 4号 | 1650 || 5号 | 1950 || 6号 | 2200 || 7号 | 2400 |a) 这些天中哪一天的销售额最低?b) 这些天中总销售额是多少?c) 这些天中销售额的平均值是多少?七、概率和统计1. 已知一副扑克牌共有52张牌,其中红桃牌有13张。
初二数学练习题加答案

初二数学练习题加答案
一、选择题:
1. 下列各数中哪个数是负数?
A. 3
B. -5
C. 2
D. 0
答案:B
2. 2的平方根是多少?
A. 2
B. 4
C. -2
D. 0
答案:A
3. 下列各组数中,哪组数中所有数字的和都是负数?
A. -1, -2, -3
B. 2, -4, -5
C. 1, 2, -3
D. -2, 3, -4
答案:D
二、填空题:
1. 已知 x + 5 = 10,那么 x 的值是___。
答案:5
2. 一根铁丝长12cm,要铸成一个长方形的边长比为2:3的铁块,则该铁块的较小边长为___cm。
答案:4
3. 一个数的2倍加3等于15,这个数是___。
答案:6
三、计算题:
1. (5 + 2) × (3 - 1) = ___。
答案:14
2. 350 ÷ (2 + 3) = ___。
答案:70
3. 如果 x = 3,那么 2x - 5 的值是___。
答案:1
四、解答题:
1. 请列举出两个互为负数的例子。
答案:-2 和 2 是互为负数的例子,因为它们的积是负数。
2. 在数轴上,-3 和 5 的位置关系是什么?请用不等式表示。
答案:-3 < 5
3. 请用运算符号填空,使得等式成立:4 ___ 2 = 8。
答案:×(乘法)。
八年级数学上册--全等三角形练习题(含答案)

八年级数学上册--全等三角形练习题(含答案)一、选择题(每题3分,共30分)1.下列判断不正确的是( )A.形状相同的图形是全等图形 B.能够完全重合的两个三角形全等C.全等图形的形状和大小都相同 D.全等三角形的对应角相等2.如图,△ABC≌△CDA,∠BAC=85°,∠B=65°,则∠CAD度数为()A.85°B.65°C.40°D.30°(第2题图) (第3题图) (第4题图) (第5题图) 3.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ 的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )A.SAS B.ASA C.AAS D.SSS4.如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB,垂足为E.若AB=10 cm,AC =6 cm,则BE的长度为( )A.10 cm B.6 cm C.4 cm D.2 cm5.如图所示,AB=CD,∠ABD=∠CDB,则图中全等三角形共有( )A.5对 B.4对 C.3对 D.2对6.点P在∠AOB的平分线上,点P到OA边的距离等于5,点Q是OB边上的任意一点,则下列选项正确的是( )A.PQ>5 B.PQ≥5 C.PQ<5 D.PQ≤57.在△ABC中,∠B=∠C,与△ABC全等的△DEF中有一个角是100°,那么在△ABC中与这100°角对应相等的角是( )A.∠A B.∠B C.∠C D.∠B或∠C8.如图所示,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,则不正确的是( )A.AB=AC B.∠BAE=∠CAD C.BE=DC D.AD=DE(第8题图) (第9题图) (第10题图) 9.如图,直线a,b,c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )A.一处 B.两处 C.三处 D.四处10.已知:如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,连接CD,C,D,E 三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )A.1 B.2 C.3 D.4二、填空题(每题3分,共30分)11.如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件是:________.(填上你认为适当的一个条件即可)12.如图,点O在△ABC内,且到三边的距离相等.若∠A=60°,则∠BOC=________°.13.在△ABC中,AB=4,AC=3,AD是△ABC的角平分线,则△ABD与△ACD的面积之比是________.(第11题图) (第12题图) (第15题图) (第16题图) 14.已知等腰△ABC的周长为18 cm,BC=8 cm,若△ABC≌△A′B′C′,则△A′B′C′的腰长等于________.15.如图,BE⊥AC,垂足为D,且AD=CD,BD=ED.若∠ABC=54°,则∠E=________°.16.如图,△ABC≌△DCB,AC与BD相交于点E,若∠A=∠D=80°,∠ABC=60°,则∠BEC 等于________.17.如图,OP平分∠MON,PE⊥OM于点E,PF⊥ON于点F,OA=OB,则图中共有________对全等三角形.18.如图,已知P(3,3),点B,A分别在x轴正半轴和y轴正半轴上,∠APB=90°,则OA+OB =________.(第17题图) (第18题图) (第19题图) (第20题图) 19.如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是________.20.如图,已知点P到BE,BD,AC的距离恰好相等,则点P的位置:①在∠DBC的平分线上;②在∠DAC的平分线上;③在∠ECA的平分线上;④恰是∠DBC,∠DAC,∠ECA的平分线的交点,上述结论中,正确的有________.(填序号)三、解答题(21,22题每题7分,23,24题每题8分,25~27题每题10分,共60分)21.如图,按下列要求作图:(1)作出△ABC的角平分线CD;(2)作出△ABC的中线BE;(3)作出△ABC的高AF.(不写作法)(第21题图)22.如图,已知△EFG≌△NMH,∠F与∠M是对应角.(1)写出所有相等的线段与相等的角;(2)若EF=2.1 cm,FH=1.1 cm,HM=3.3 cm,求MN和HG的长度.(第22题图) 23.如图,AD⊥AE,AB⊥AC,AD=AE,AB=AC.求证:△ABD≌△ACE.(第23题图)24.如图,AC∥BE,点D在BC上,AB=DE,∠ABE=∠CDE.求证:DC=BE-AC.(第24题图)25.如图所示,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB交AB于点E,点F在AC上,BD=DF.求证:(1)CF=EB;(2)AB=AF+2EB.(第25题图) 26.如图,A,B两建筑物位于河的两岸,要测得它们之间的距离,可以从点B出发在河岸上画一条射线BF,在BF上截取BC=CD,过D作DE∥AB,使E,C,A在同一直线上,则DE的长就是点A,B之间的距离,请你说明道理.(第26题图)27.如图(1),在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF,连接CF.(1)如果AB=AC,∠BAC=90°,①当点D在线段BC上时(与点B不重合),如图(2),线段CF,BD所在直线的位置关系为______,线段CF,BD的数量关系为________;②当点D在线段BC的延长线上时,如图(3),①中的结论是否仍然成立,并说明理由;(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.(第27题图)参考答案一、1.A 2.D 3.D 4.C 5.C 6.B7.A 8.D9.D 分析:如图,在△ABC内部,找一点到三边距离相等,根据到角的两边距离相等的点在角的平分线上,可知,此点在各内角的平分线上,作∠ABC,∠BCA的平分线,交于点O1,由角平分线的性质可知,O1到AB,BC,AC的距离相等.同理,作∠ACD,∠CAE的平分线,交于点O2,则O2到AC,BC,AB的距离相等,同样作法得到点O3,O4.故可供选择的地址有四处.故选D.(第9题答图)10.D二、11.∠B=∠C(答案不唯一)12.120 13. 4∶3 14. 8 cm或5 cm15.27 16. 100°17.3 分析:因为△OPE≌△OPF,△OPA≌△OPB,△AEP≌△BFP,所以共有3对全等三角形.18.6 分析:过点P作PC⊥OB于C,PD⊥OA于D,则PD=PC=DO=OC=3,可证△APD≌△BPC,∴DA=CB,∴OA+OB=OA+OC+CB=OA+OC+DA=OC+OD=6.19.50 分析:由题意易知,△AFE≌△BGA,△BGC≌△CHD.∴FA=BG=3,AG=EF=6,CG=HD=4,CH=BG=3.∴S=S梯形EFHD -S△EFA-S△AGB-S△BGC-S△CHD=1 2(4+6)×(3+6+4+3)-12×3×6×2-12×3×4×2=80-18-12=50.20.①②③④三、21.解:(1)角平分线CD如图①所示.(2)中线BE如图②所示.(3)高AF如图③所示.(第21题答图)22.解:(1)EF =MN,EG =HN,FG =MH,FH =GM,∠F =∠M,∠E =∠N,∠EGF =∠MHN,∠FHN =∠EGM.(2)∵△EFG ≌△NMH,∴MN =EF =2.1 cm,GF =HM =3.3 cm, ∵FH =1.1 cm,∴HG =GF -FH =3.3-1.1=2.2 (cm). 23.证明:∵AD ⊥AE,AB ⊥AC,∴∠CAB =∠DAE =90°. ∴∠CAB +∠CAD =∠DAE +∠CAD,即∠BAD =∠CAE. 在△ABD 和△ACE 中,⎩⎨⎧AB =AC ,∠BAD =∠CAE ,AD =AE ,∴△ABD ≌△ACE.24.证明:∵AC ∥BE,∴∠DBE =∠C.∵∠CDE =∠DBE +∠E,∠ABE =∠ABC +∠DBE,∠ABE=∠CDE,∴∠E =∠ABC.在△ABC 与△DEB中,⎩⎨⎧∠C =∠DBE ,∠ABC =∠E ,AB =DE ,∴△ABC ≌△DEB(AAS).∴BC =BE,AC =BD.∴DC =BC -BD =BE -AC.25.证明:(1)∵AD 是∠BAC 的平分线,DE ⊥AB,DC ⊥AC, ∴DE =DC. 又∵BD =DF,∴Rt △CDF ≌Rt △EDB(HL). ∴CF =EB.(2)由(1)可知DE =DC,又∵AD =AD, ∴Rt △ADC ≌Rt △ADE. ∴AC =AE.∴AB =AE +BE =AC +EB =AF +CF +EB =AF +2EB.点拨:(1)根据角平分线的性质“角平分线上的点到角的两边的距离相等”,可得点D 到AB 的距离=点D 到AC 的距离,即CD =DE.再根据Rt △CDF ≌Rt △EDB,得CF =EB.(2)利用角平分线的性质证明Rt △ADC ≌Rt △ADE,∴AC =AE,再将线段AB 进行转化. 26.解:∵DE ∥AB,∴∠A =∠E.∵E,C,A 在同一直线上,B,C,D 在同一直线上,∴∠ACB =∠ECD.在△ABC 与△EDC 中,⎩⎨⎧∠A =∠E ,∠ACB =∠ECD ,BC =CD ,∴△ABC ≌△EDC(AAS). ∴AB =DE.27.解:(1)①CF ⊥BD ;CF =BD②当点D 在线段BC 的延长线上时,①中的结论仍然成立.理由:由正方形ADEF 得AD =AF,∠DAF =90°.∵∠BAC =90°,∴∠DAF =∠BAC. ∴∠DAB =∠FAC.又∵AB =AC,∴△DAB ≌△FAC. ∴CF =BD,∠ACF =∠ABD. ∵∠BAC =90°,AB =AC,∴△ABC 是等腰直角三角形.∴∠ABC =∠ACB =45°. ∴∠ACF =45°.∴∠BCF =∠ACB +∠ACF =90°.即CF ⊥BD.(第27题答图)(2)当∠ACB =45°时,CF ⊥BC(如图).理由:过点A 作AG ⊥AC 交CB 的延长线于点G,则∠GAC =90°.∵∠ACB =45°,∠AGC =90°-∠ACB,∴∠AGC =90°-45°=45°,∴∠ACB =∠AGC =45°,∴△AGC 是等腰直角三角形,∴AC =AG.又∵∠DAG =∠FAC(同角的余角相等),AD =AF,∴△GAD ≌△CAF,∴∠ACF =∠AGC =45°,∴∠BCF =∠ACB +∠ACF =45°+45°=90°,即CF ⊥BC.。
初二数学综合练习题及答案

初二数学综合练习题及答案1. 以分数的形式写出下列小数:a. 0.6b. 0.25c. 0.75d. 0.125答案:a. 6/10b. 25/100c. 75/100d. 125/10002. 两数的和是30,差是14,求这两个数。
答案:设其中一个数为x,根据题意可得:x + (x - 14) = 302x - 14 = 302x = 30 + 142x = 44x = 22所以这两个数分别为22和8。
3. 甲、乙两人一起修一段铁轨,甲单独修完需要4天,乙单独修完需要6天。
如果两人一起修,他们需要多少天才能完成?答案:甲单独修完的工作效率是1/4,乙单独修完的工作效率是1/6,设两人一起修完的时间为x天,则他们一起的工作效率是1/x。
根据题意可得:1/4 + 1/6 = 1/x3/12 + 2/12 = 1/x5/12 = 1/x将等式两边取倒数,得:12/5 = x/1x = 12/5x = 2.4所以,甲乙两人一起修完需要2.4天。
4. 小明有5张红色的卡片,6张黄色的卡片,他从两堆卡片中分别取出一张,那么取出的两张卡片中至少有一张红色卡的概率是多少?共有5 + 6 = 11张卡片,从中任意取出两张的情况总数为C(11, 2) = 55。
取出的两张卡片中,至少有一张红色卡的情况总数为:只有一张红色卡的情况:5 * 6 = 30两张卡片都是红色卡的情况:5 * 4 = 20所以,取出的两张卡片中至少有一张红色卡的概率为(30 + 20)/55 = 50/55 = 10/11。
5. 甲、乙两数之和是65,差是15,求甲、乙两数分别是多少。
答案:设甲、乙两数分别为x和y,根据题意可得:x + y = 65x - y = 15将第二个等式两边同时加上y,得:x = y + 15将上面的表达式代入第一个等式中,得:(y + 15) + y = 652y + 15 = 652y = 65 - 152y = 50y = 50/2y = 25将y的值代入第一个等式中,得:x + 25 = 65x = 65 - 25x = 40所以,甲、乙两数分别为40和25。
八年级数学试题及答案

八年级数学试题及答案一、选择题(共10分,每题2分)1. 下列哪个数是最小的正整数?A. -3B. 0C. 1D. 2答案:C2. 计算下列哪个表达式的结果是正数?A. -1 + (-2)B. 3 - 5C. 4 × (-2)D. -3 ÷ 2答案:D3. 如果a > b > 0,那么下列哪个不等式是正确的?A. a < bB. a > bC. b > aD. a = b答案:B4. 一个数的平方根是它本身,这个数可以是:A. 0B. 1C. -1D. 2答案:A5. 下列哪个分数是最简分数?A. 6/12B. 8/16C. 5/10D. 7/3答案:D二、填空题(共10分,每题2分)6. 一个长方形的长是10厘米,宽是5厘米,它的周长是________厘米。
答案:307. 如果一个数的立方根是2,那么这个数是________。
答案:88. 一个数的绝对值是5,这个数可以是________或________。
答案:5或-59. 一个圆的半径是7厘米,它的面积是________平方厘米。
答案:153.9410. 如果一个三角形的底边长是6厘米,高是4厘米,那么它的面积是________平方厘米。
答案:12三、计算题(共30分,每题6分)11. 计算下列表达式的值:(1) (-3) × 2 + 5(2) √(16) - 4答案:(1) -6 + 5 = -1(2) 4 - 4 = 012. 解下列方程:(1) 2x + 5 = 13(2) 3y - 7 = 8答案:(1) 2x = 8,x = 4(2) 3y = 15,y = 513. 计算下列多项式的值,当x = -2时:(1) 3x^2 - 2x + 1(2) x^3 + 4x - 5答案:(1) 3 × (-2)^2 - 2 × (-2) + 1 = 12 + 4 + 1 = 17(2) (-2)^3 + 4 × (-2) - 5 = -8 - 8 - 5 = -21四、解答题(共50分,每题10分)14. 一个班级有40名学生,其中30名学生参加了数学竞赛。
八年级上册数学练习册及答案

八年级上册数学练习册及答案### 第一章:实数练习一:理解实数1. 实数的概念:实数包括有理数和无理数。
有理数可以表示为两个整数的比,而无理数则不能。
2. 实数的性质:实数具有连续性、有序性等特征。
3. 实数的运算:掌握加、减、乘、除等基本运算。
练习二:实数的运算- 例题:计算下列各数的和:- \( \sqrt{2} + \pi \)- \( \frac{1}{2} - \frac{1}{3} \)- 答案:- \( \sqrt{2} + \pi \) 的和为 \( \sqrt{2} + \pi \)。
- \( \frac{1}{2} - \frac{1}{3} = \frac{3}{6} - \frac{2}{6} = \frac{1}{6} \)。
练习三:实数的应用- 例题:如果一个数的平方是16,求这个数。
- 答案:这个数可以是 \( \sqrt{16} = 4 \) 或 \( -\sqrt{16} = -4 \)。
### 第二章:代数基础练习一:变量与表达式1. 变量的意义:变量是数学表达式中可以变化的量。
2. 表达式的构成:由变量和数字通过运算符连接而成。
练习二:代数式的简化- 例题:简化下列表达式:- \( 3x + 2y - 5x + 3y \)- 答案:\( 3x - 5x + 2y + 3y = -2x + 5y \)。
练习三:代数方程的解法- 例题:解方程 \( ax + b = c \)。
- 答案:\( x = \frac{c - b}{a} \)。
### 第三章:几何基础练习一:点、线、面1. 点:几何中最基本的元素。
2. 线:由点的连续移动形成。
3. 面:由线的连续移动形成。
练习二:角的度量- 例题:如果一个角的度数是 \( \frac{\pi}{4} \),求它的度数。
- 答案:\( \frac{\pi}{4} \) 弧度等于 \( 45^\circ \)。
练习三:三角形的性质- 例题:在一个三角形中,如果两个角分别是 \( 30^\circ \) 和\( 60^\circ \),求第三个角的度数。
初二数学题练习题含答案

初二数学题练习题含答案第一题:求下列各式的值:1. 32 × 25 + 12 × 172. 48 ÷ (3 × 4) + 25解答:1. 32 × 25 + 12 × 17 = 800 + 204 = 10042. 48 ÷ (3 × 4) + 25 = 48 ÷ 12 + 25 = 4 + 25 = 29第二题:将下列分数化为小数形式:1. 3/42. 7/8解答:1. 3/4 = 0.752. 7/8 = 0.875第三题:计算下列各式的结果,并写出计算过程:1. 1/3 + 1/52. 2/5 - 1/4解答:1. 1/3 + 1/5 = (5/15) + (3/15) = 8/152. 2/5 - 1/4 = (8/20) - (5/20) = 3/20第四题:解方程:1. 2x + 5 = 172. 3(x - 4) = 9解答:1. 2x + 5 = 172x = 17 - 52x = 12x = 62. 3(x - 4) = 93x - 12 = 93x = 9 + 123x = 21x = 7第五题:计算以下各式的值:1. 4² + 3³ ÷ 9 - 42. (3 + 4) × (6 - 2) + 12解答:1. 4² + 3³ ÷ 9 - 4 = 16 + 27 ÷ 9 - 4 = 16 + 3 - 4 = 152. (3 + 4) × (6 - 2) + 12 = 7 × 4 + 12 = 28 + 12 = 40第六题:求下列各组数的中位数:1. 3, 5, 6, 9, 122. 6, 7, 10, 12, 15, 20解答:1. 3, 5, 6, 9, 12 的中位数为 62. 6, 7, 10, 12, 15, 20 的中位数为 (10 + 12) / 2 = 11第七题:计算正方形的周长和面积,如果其中一边长为5cm。
八年级全册数学试卷及答案

一、选择题(每题3分,共30分)1. 若方程2x - 3 = 7的解为x,则x的值为()A. 5B. 2C. 1D. 02. 下列数中,有理数是()A. √2B. πC. √-1D. 0.1010010001……3. 在△ABC中,若∠A=60°,∠B=45°,则∠C的度数为()A. 75°B. 90°C. 105°D. 120°4. 下列命题中,正确的是()A. 若a > b,则a² > b²B. 若a² > b²,则a > bC. 若a² = b²,则a = bD. 若a² = b²,则a = b或a = -b5. 下列函数中,是二次函数的是()A. y = 2x + 3B. y = x² - 2x + 1C. y = x³ + 2x² + xD. y = 3x - 46. 若x + y = 5,x - y = 1,则x的值为()A. 3B. 2C. 4D. 57. 下列数中,是正比例函数的图象经过第一、二、四象限的是()A. y = 2xB. y = -3xC. y = 0.5xD. y = -0.5x8. 下列等式中,正确的是()A. a² - b² = (a + b)(a - b)B. a³ - b³ = (a - b)(a² + ab + b²)C. a³ + b³ = (a + b)(a² - ab + b²)D. a³ - b³ = (a + b)(a² + ab - b²)9. 若函数y = kx²在第一象限,则k的取值范围是()A. k > 0B. k < 0C. k ≠ 0D. k ≥ 010. 下列数中,绝对值最大的是()A. -3B. -2C. 1D. 0二、填空题(每题3分,共30分)11. 若a + b = 5,a - b = 1,则ab的值为______。
初二数学试题精选及答案

初二数学试题精选及答案一、选择题(每题3分,共30分)1. 下列哪个选项不是实数集R的子集?A. 整数集ZB. 有理数集QC. 无理数集D. 复数集C2. 如果一个三角形的两边长分别为3和4,第三边长为整数,那么第三边长可能是:A. 1B. 2C. 3D. 43. 一个数的立方根是它本身的数是:A. 0B. 1C. -1D. 以上都是4. 在直角坐标系中,点(2, -3)关于y轴的对称点的坐标是:A. (-2, -3)B. (-2, 3)C. (2, 3)D. (-2, 3)5. 一个数的绝对值是它本身,那么这个数:A. 一定是正数B. 一定是负数C. 可以是正数或0D. 可以是负数或06. 一次函数y=2x+3的图象不经过哪个象限?A. 第一象限B. 第二象限C. 第三象限D. 第四象限7. 一个数的相反数是它本身,那么这个数是:A. 正数B. 负数C. 0D. 以上都不是8. 以下哪个选项是方程2x-3=7的解?A. x=-1B. x=2C. x=5D. x=39. 一个数的平方是它本身,那么这个数是:A. 1或-1B. 0或1C. 0或-1D. 以上都不是10. 一个等腰三角形的两个底角相等,那么这个三角形的顶角可能是:A. 30°B. 45°C. 60°D. 90°二、填空题(每题3分,共30分)1. 一个数的绝对值是5,这个数可能是______。
2. 如果一个三角形的两个内角分别为30°和60°,那么第三个内角是______。
3. 一个数的立方是27,这个数是______。
4. 一个数的相反数是-8,这个数是______。
5. 一个数的平方是25,这个数是______。
6. 一次函数y=3x-2与y轴的交点坐标是______。
7. 一个等腰三角形的顶角是100°,那么它的底角是______。
8. 一个数的平方根是4,这个数是______。
八年级数学题100道(含答案)

八年级数学题100道带答案1) 66x+17y=396725x+y=1200答案:x=48 y=47(2) 18x+23y=230374x-y=1998答案:x=27 y=79(3) 44x+90y=779644x+y=3476答案:x=79 y=48(4) 76x-66y=408230x-y=2940答案:x=98 y=51(5) 67x+54y=854671x-y=5680答案:x=80 y=59(6) 42x-95y=-141021x-y=1575答案:x=75 y=48(7) 47x-40y=85334x-y=2006答案:x=59 y=48(8) 19x-32y=-1786 75x+y=4950答案:x=66 y=95 (9) 97x+24y=7202 58x-y=2900答案:x=50 y=98 (10) 42x+85y=6362 63x-y=1638答案:x=26 y=62 (11) 85x-92y=-2518 27x-y=486答案:x=18 y=44 (12) 79x+40y=2419 56x-y=1176答案:x=21 y=19 (13) 80x-87y=2156 22x-y=880答案:x=40 y=12 (14) 32x+62y=5134 57x+y=2850答案:x=50 y=57 (15) 83x-49y=8259x+y=2183答案:x=37 y=61 (16) 91x+70y=5845 95x-y=4275答案:x=45 y=25 (17) 29x+44y=5281 88x-y=3608答案:x=41 y=93 (18) 25x-95y=-4355 40x-y=2000答案:x=50 y=59 (19) 54x+68y=3284 78x+y=1404答案:x=18 y=34 (20) 70x+13y=3520 52x+y=2132答案:x=41 y=50 (21) 48x-54y=-3186 24x+y=1080答案:x=45 y=99 (22) 36x+77y=7619 47x-y=799答案:x=17 y=91 (23) 13x-42y=-2717 31x-y=1333答案:x=43 y=78 (24) 28x+28y=3332 52x-y=4628答案:x=89 y=30 (25) 62x-98y=-2564 46x-y=2024答案:x=44 y=54 (26) 79x-76y=-4388 26x-y=832答案:x=32 y=91 (27) 63x-40y=-821 42x-y=546答案:x=13 y=41 (28) 69x-96y=-1209 42x+y=3822答案:x=91 y=78 (29) 85x+67y=7338 11x+y=308答案:x=28 y=74(30) 78x+74y=12928 14x+y=1218答案:x=87 y=83 (31) 39x+42y=5331 59x-y=5841答案:x=99 y=35 (32) 29x+18y=1916 58x+y=2320答案:x=40 y=42 (33) 40x+31y=6043 45x-y=3555答案:x=79 y=93 (34) 47x+50y=8598 45x+y=3780答案:x=84 y=93 (35) 45x-30y=-1455 29x-y=725答案:x=25 y=86 (36) 11x-43y=-1361 47x+y=799答案:x=17 y=36 (37) 33x+59y=325494x+y=1034答案:x=11 y=49 (38) 89x-74y=-2735 68x+y=1020答案:x=15 y=55 (39) 94x+71y=7517 78x+y=3822答案:x=49 y=41 (40) 28x-62y=-4934 46x+y=552答案:x=12 y=85 (41) 75x+43y=8472 17x-y=1394答案:x=82 y=54 (42) 41x-38y=-1180 29x+y=1450答案:x=50 y=85 (43) 22x-59y=824 63x+y=4725答案:x=75 y=14 (44) 95x-56y=-401 90x+y=1530(45) 93x-52y=-852 29x+y=464答案:x=16 y=45 (46) 93x+12y=8823 54x+y=4914答案:x=91 y=30 (47) 21x-63y=84 20x+y=1880答案:x=94 y=30 (48) 48x+93y=9756 38x-y=950答案:x=25 y=92 (49) 99x-67y=4011 75x-y=5475答案:x=73 y=48 (50) 83x+64y=9291 90x-y=3690答案:x=41 y=92(51) 17x+62y=3216 75x-y=7350(52) 77x+67y=2739 14x-y=364答案:x=26 y=11 (53) 20x-68y=-4596 14x-y=924答案:x=66 y=87 (54) 23x+87y=4110 83x-y=5727答案:x=69 y=29 (55) 22x-38y=804 86x+y=6708答案:x=78 y=24 (56) 20x-45y=-3520 56x+y=728答案:x=13 y=84 (57) 46x+37y=7085 61x-y=4636答案:x=76 y=97 (58) 17x+61y=4088 71x+y=5609答案:x=79 y=45(59) 51x-61y=-1907 89x-y=2314答案:x=26 y=53 (60) 69x-98y=-2404 21x+y=1386答案:x=66 y=71 (61) 15x-41y=754 74x-y=6956答案:x=94 y=16 (62) 78x-55y=656 89x+y=5518答案:x=62 y=76 (63) 29x+21y=1633 31x-y=713答案:x=23 y=46 (64) 58x-28y=2724 35x+y=3080答案:x=88 y=85 (65) 28x-63y=-2254 88x-y=2024答案:x=23 y=46 (66) 43x+50y=706485x+y=8330答案:x=98 y=57 (67) 58x-77y=1170 38x-y=2280答案:x=60 y=30 (68) 92x+83y=11586 43x+y=3010答案:x=70 y=62 (69) 99x+82y=6055 52x-y=1716答案:x=33 y=34 (70) 15x+26y=1729 94x+y=8554答案:x=91 y=14 (71) 64x+32y=3552 56x-y=2296答案:x=41 y=29 (72) 94x+66y=10524 84x-y=7812答案:x=93 y=27 (73) 65x-79y=-5815 89x+y=2314答案:x=26 y=95 (74) 96x+54y=6216 63x-y=1953答案:x=31 y=60 (75) 60x-44y=-352 33x-y=1452答案:x=44 y=68 (76) 79x-45y=510 14x-y=840答案:x=60 y=94 (77) 29x-35y=-218 59x-y=4897答案:x=83 y=75 (78) 33x-24y=1905 30x+y=2670答案:x=89 y=43 (79) 61x+94y=11800 93x+y=5952答案:x=64 y=84 (80) 61x+90y=5001 48x+y=2448答案:x=51 y=21(81) 93x-19y=286x-y=1548答案:x=18 y=88 (82) 19x-96y=-5910 30x-y=2340答案:x=78 y=77 (83) 80x+74y=8088 96x-y=8640答案:x=90 y=12 (84) 53x-94y=1946 45x+y=2610答案:x=58 y=12 (85) 93x+12y=9117 28x-y=2492答案:x=89 y=70 (86) 66x-71y=-1673 99x-y=7821答案:x=79 y=97 (87) 43x-52y=-1742 76x+y=1976答案:x=26 y=55 (88) 70x+35y=829540x+y=2920答案:x=73 y=91 (89) 43x+82y=4757 11x+y=231答案:x=21 y=47 (90) 12x-19y=236 95x-y=7885答案:x=83 y=40 (91) 51x+99y=8031 71x-y=2911答案:x=41 y=60 (92) 37x+74y=4403 69x-y=6003答案:x=87 y=16 (93) 46x+34y=4820 71x-y=5183答案:x=73 y=43 (94) 47x+98y=5861 55x-y=4565答案:x=83 y=20 (95) 30x-17y=239 28x+y=1064答案:x=38 y=53 (96) 55x-12y=4112 79x-y=7268答案:x=92 y=79 (97) 27x-24y=-450 67x-y=3886答案:x=58 y=84 (98) 97x+23y=8119 14x+y=966答案:x=69 y=62 (99) 84x+53y=11275 70x+y=6790答案:x=97 y=59 (100) 51x-97y=297 19x-y=1520答案:x=80 y=39。
初中数学八年级上册 练习题(含答案)
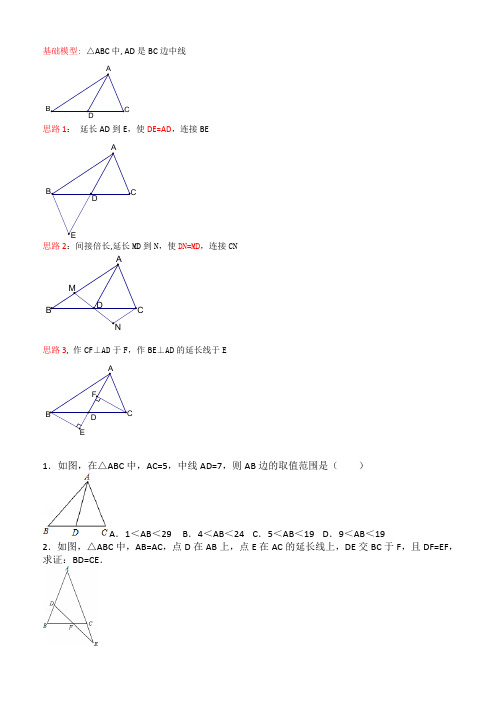
基础模型: △ABC 中, AD 是BC 边中线思路1: 延长AD 到E ,使DE=AD ,连接BE思路2:间接倍长,延长MD 到N ,使DN=MD ,连接CN思路3, 作CF ⊥AD 于F ,作BE ⊥AD 的延长线于E1.如图,在△ABC 中,AC=5,中线AD=7,则AB 边的取值范围是( )A .1<AB <29 B .4<AB <24C .5<AB <19D .9<AB <192.如图,△ABC 中,AB=AC ,点D 在AB 上,点E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE .D A B C ED A B FE DB A ND BAM3.如图,在△ABC中,AD为中线,求证:AB+AC>2AD.4.小明遇到这样一个问题,如图1,△ABC中,AB=7,AC=5,点D为BC的中点,求AD的取值范围.小明发现老师讲过的“倍长中线法”可以解决这个问题,所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法,他的做法是:如图2,延长AD到E,使DE=AD,连接BE,构造△BED≌△CAD,经过推理和计算使问题得到解决.请回答:(1)小明证明△BED≌△CAD用到的判定定理是:(用字母表示)(2)AD的取值范围是小明还发现:倍长中线法最重要的一点就是延长中线一倍,完成全等三角形模型的构造.参考小明思考问题的方法,解决问题:如图3,在正方形ABCD中,E为AB边的中点,G、F分别为AD,BC边上的点,若AG=2,BF=4,∠GEF=90°,求GF的长.5.已知:在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EF.6.已知:如图,△ABC(AB≠AC)中,D、E在BC上,且DE=EC,过D作DF∥BA交AE于点F,DF=AC.求证:AE平分∠BAC.7-10,换汤不换药(多题一解)7.如图,D是△ABC的BC边上一点且CD=AB,∠BDA=∠BAD,AE是△ABD的中线.求证:∠C=∠BAE.8.如图,已知D是△ABC的边BC上的一点,CD=AB,∠BDA=∠BAD,AE是△ABD的中线.(1)若∠B=60°,求∠C的值;(2)求证:AD是∠EAC的平分线.9.如图,已知:CD=AB,∠BAD=∠BDA,AE是△ABD的中线,求证:AC=2AE.10.已知,如图,AB=AC=BE,CD为△ABC中AB边上的中线,求证:CE=2CD.11.已知:如图,△ABC中,∠C=90°,CM⊥AB于M,AT平分∠BAC交CM于D,交BC于T,过D作DE∥AB交BC于E,求证:CT=BE.12.如图①,点O为线段MN的中点,PQ与MN相交于点O,且PM∥NQ,可证△PMO≌△QNO.根据上述结论完成下列探究活动:如图②,在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F.试探究线段AB与AF、CF之间的数量关系,并证明你的结论;(图3是原题的第2问)13.如图,在△ABC中,AD交BC于点D,点E是BC的中点,EF∥AD交CA的延长线于点F,交EF与于点G.若BG=CF,求证:AD为△ABC的角平分线.14.如图,已知在△ABC中,∠CAE=∠B,点E是CD的中点,若AD平分∠BAE.(1)求证:AC=BD;(2)若BD=3,AD=5,AE=x,求x的取值范围.15.已知在△ABC中,AD是BC边上的中线,分别以AB边、AC边为直角边各向外作等腰直角三角形,如图,求证:EF=2AD.1.解:如图,延长AD至E,使DE=AD,∵AD是△ABC的中线,∴BD=CD,在△ABD和△ECD中,,∴△ABD≌△ECD(SAS),∴AB=CE,∵AD=7,∴AE=7+7=14,∵14+5=19,14﹣5=9,∴9<CE<19,2.证明:如图,过点D作DG∥AE,交BC于点G;3.证明:4.解:(1)如图2中,延长AD到E,使DE=AD,连接BE.在△BED和△CAD中,,∴△BED≌△CAD(SAS).(2)∵△BED≌△CAD,∴BE=AC=5,∵AB=7,∴2<AE<12,∴2<2AD<12,∴1<AD<6.解决问题:如图3中,解:延长GE交CB的延长线于M.∵四边形ABCD是正方形,∴AD∥CM,∴∠AGE=∠M,在△AEG和△BEM中,,∴△AEG≌△BEM,∴GE=EM,AG=BM=2,∵EF⊥MG,∴FG=FM,∵BF=4,∴MF=BF+BM=2+4=6,∴GF=FM=6.5.证明:如图,延长AD到点G,使得AD=DG,连接BG.∵AD是BC边上的中线(已知),∴DC=DB,在△ADC和△GDB中,∴△ADC≌△GDB(SAS),∴∠CAD=∠G,BG=AC又∵BE=AC,∴BE=BG,∴∠BED=∠G,∵∠BED=∠AEF,∴∠AEF=∠CAD,即:∠AEF=∠FAE,∴AF=EF.6.证明:如图,延长FE到G,使EG=EF,连接CG.在△DEF和△CEG中,∵,∴△DEF≌△CEG.∴DF=GC,∠DFE=∠G.∵DF∥AB,∴∠DFE=∠BAE.∵DF=AC,∴GC=AC.∴∠G=∠CAE.∴∠BAE=∠CAE.即AE平分∠BAC.7.证明:延长AE到F,使EF=AE,连接DF,∵AE是△ABD的中线∴BE=ED,在△ABE与△FDE中∵,∴△ABE≌△FDE(SAS),∴AB=DF,∠BAE=∠EFD,∵∠ADB是△ADC的外角,∴∠DAC+∠ACD=∠ADB=∠BAD,∴∠BAE+∠EAD=∠BAD,∠BAE=∠EFD,∴∠EFD+∠EAD=∠DAC+∠ACD,∴∠ADF=∠ADC,∵AB=DC,∴DF=DC,在△ADF与△ADC中∵,∴△ADF≌△ADC(SAS)∴∠C=∠AFD=∠BAE.8.(1)解:∵∠B=60°,∠BDA=∠BAD,∴∠BAD=∠BDA=60°,∴AB=AD,∵CD=AB,∴CD=AD,∴∠DAC=∠C,∴∠BDA=∠DAC+∠C=2∠C,∵∠BAD=60°,∴∠C=30°;(2)证明:延长AE到M,使EM=AE,连接DM,在△ABE和△MDE中,,∴△ABE≌△MDE,∴∠B=∠MDE,AB=DM,∵∠ADC=∠B+∠BAD=∠MDE+∠BDA=∠ADM,在△MAD与△CAD,,∴△MAD≌△CAD,∴∠MAD=∠CAD,∴AD是∠EAC的平分线.9.证明:延长AE至F,使AE=EF,连接BF,在△ADE与△BFE中,,∴△AED≌△FEB,∴BF=DA,∠FBE=∠ADE,∵∠ABF=∠ABD+∠FBE,∴∠ABF=∠ABD+∠ADB=∠ABD+∠BAD=∠ADC,在△ABF与△ADC中,,∴△ABF≌△CDA,∴AC=AF,∵AF=2AE,∴AC=2AE.10.证明:取AC的中点F,连接BF;∵B为AE的中点,∴BF为△AEC的中位线,∴EC=2BF;在△ABF与△ACD中,,∴△ABF≌△ACD(SAS),∴CD=BF,∴CE=2CD.11.证明:过T作TF⊥AB于F,∵AT平分∠BAC,∠ACB=90°,∴CT=TF(角平分线上的点到角两边的距离相等),∵∠ACB=90°,CM⊥AB,∴∠ADM+∠DAM=90°,∠ATC+∠CAT=90°,∵AT平分∠BAC,∴∠DAM=∠CAT,∴∠ADM=∠ATC,∴∠CDT=∠CTD,∴CD=CT,又∵CT=TF(已证),∴CD=TF,∵CM⊥AB,DE∥AB,∴∠CDE=90°,∠B=∠DEC,在△CDE和△TFB中,,∴△CDE≌△TFB(AAS),∴CE=TB,∴CE﹣TE=TB﹣TE,即CT=BE.12.解:(1)AB=AF+CF.如图2,分别延长DC、AE,交于G点,根据图①得△ABE≌△GCE,∴AB=CG,又AB∥DC,∴∠BAE=∠G而∠BAE=∠EAF,∴∠G=∠EAF,∴AF=GF,∴AB=CG=GF+CF=AF+CF;13.解:延长FE,截取EH=EG,连接CH,∵E是BC中点,∴BE=CE,∴∠BEG=∠CEH,在△BEG和△CEH中,,∴△BEG≌△CEH(SAS),∴∠BGE=∠H,∴∠BGE=∠FGA=∠H,∴BG=CH,∵CF=BG,∴CH=CF,∴∠F=∠H=∠FGA,∵EF∥AD,∴∠F=∠CAD,∠BAD=∠FGA,∴∠CAD=∠BAD,∴AD平分∠BAC.14.(1)证明:延长AE到F,使EF=EA,连接DF,∵点E是CD的中点,∴EC=ED,在△DEF与△CEA中,,∴△DEF≌△CEA,∴AC=FD,∴∠AFD=∠CAE,∵∠CAE=∠B,∴∠AFD=∠B,∵AD平分∠BAE,∴∠BAD=∠FAD,在△ABD与△AFD中,,∴△ABD≌△AFD,∴BD=FD,∴AC=BD;(2)解:由(1)证得△ABD≌△AFD,△DEF≌△CEA,∴AB=AF,∵AE=x,∴AF=2AE=2x,∴AB=2x,∵BD=3,AD=5,∴在△ABD中,,解得:1<x<4,∴x的取值范围是1<x<4.15证明:延长AD至点G,使得AD=DG,连接BG,CG,∵AD=DG,BD=CD,∴四边形ABGC是平行四边形,∴AC=AF=BG,AB=AE=CG,∠BAC+∠ABG=180°,∵∠EAF+∠BAC=180°,∴∠EAF=∠ABG,在△EAF和△BAG中,,∴△EAF≌△BAG(SAS),∴EF=AG,∵AG=2AD,∴EF=2AD.。
初二数学练习题与答案

初二数学练习题与答案一、选择题1. 已知直线AB与直线CD相交于点O,∠AOB = 100°,那么∠AOC的度数是:A. 50°B. 100°C. 80°D. 130°答案:C. 80°2. 若一扇形的圆心角是120°,半径为6 cm,则该扇形的弧长是:A. 4π cmB. 6π cmC. 10π cmD. 12π cm答案:D. 12π cm3. 如果二次函数y = ax² + bx + c的图像与x轴有两个交点,且a > 0,那么函数的图像开口朝下。
A. 正确B. 错误答案:B. 错误4. 已知函数 f(x) = x² - 2x + 3,那么 f(1)的值为:A. -2B. 1C. 2D. 3答案:D. 35. 一件商品原价是120元,现在打8折出售,那么折后的价格是:A. 96元B. 108元C. 112元D. 124元答案:C. 112元二、填空题1. 已知20% × 25 = ______。
答案:52. 点A(2, 4)和点B(6, 9)的斜率是 ______。
答案:1.253. 一个几何图形有6个面、12个边和8个顶点,那么该图形的类型是 ______。
答案:六面体4. 2(3 + 4) - 5 × 2的值是 ______。
答案:95. 在等差数列4,7,10,13,...中,第10项的值是 ______。
答案:31三、解答题1. 设直线L1的斜率为2,过点A(-1, 3),求直线L1的方程。
解:直线的一般方程为y = kx + b,其中k为斜率,b为截距。
由已知得,直线L1的斜率为2,过点A(-1, 3),代入方程可得:3 = 2 × (-1) + b3 = -2 + bb = 5因此,直线L1的方程为y = 2x + 5。
2. 某商品原价为x元,现在打6折出售后的价格为60元,请问x的值为多少?解:打6折表示折扣为0.6,原价x元乘以折扣0.6后等于60元,可写成方程:0.6x = 60解这个方程可以得到:x = 60 ÷ 0.6 = 100因此,该商品的原价为100元。
八年级数学测试题及答案

八年级数学测试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是无理数?A. 3.14159B. πC. √2D. 0.33333…(循环小数)答案:C2. 已知a > 0,b < 0,c < 0,下列不等式成立的是:A. a + b < 0B. a - c > 0C. b - c < 0D. a × b < 0答案:D3. 若x² + 5x + 6 = 0,下列哪个是方程的解?A. x = -1B. x = -6C. x = -2 或 x = -3D. x = 2 或 x = 3答案:C4. 下列哪个是二次根式?A. √3x²C. √xD. √x²答案:B5. 函数y = 3x + 5的斜率是:A. 3B. 5C. -3D. -5答案:A6. 一个直角三角形的两条直角边分别为3和4,斜边的长度是:A. 5B. 6C. 7D. 8答案:A7. 已知一个数列1, 3, 5, 7, ...,这个数列的第10项是:A. 17B. 19C. 21D. 23答案:B8. 下列哪个是完全平方数?B. 25C. 27D. 29答案:B9. 一个圆的半径是5,那么它的周长是:A. 10πB. 20πC. 30πD. 40π答案:B10. 一个长方体的长、宽、高分别是2, 3, 4,它的体积是:A. 24B. 12C. 36D. 48答案:A二、填空题(每题4分,共20分)11. 一个数的平方根是4,这个数是________。
答案:1612. 一个数的相反数是-7,这个数是________。
答案:713. 一个数的绝对值是5,这个数可能是________或________。
答案:5 或 -514. 一个二次方程的一般形式是________。
答案:ax² + bx + c = 0(a≠0)15. 一个正数的倒数是1/8,这个正数是________。
初二数学练习题及答案

初二数学练习题及答案一、选择题1. 下列哪个数是无理数?A. -2B. √3C. 0.5D. 2.5答案:B2. 如果一个直角三角形的两条直角边分别为3和4,那么斜边的长度是多少?A. 5B. 6C. 8D. 10答案:A3. 一个数的平方根是它本身,这个数是:A. 1B. -1C. 0D. 以上都不是答案:C二、填空题4. 一个数的立方等于它本身,这个数可以是______。
答案:1 或 05. 一个数的绝对值是它本身,这个数是______。
答案:非负数6. 如果一个数的相反数是-5,那么这个数是______。
答案:5三、计算题7. 计算下列表达式的值:(1) -3²(2) (-2)³答案:(1) -9(2) -88. 计算下列方程的解:(1) 3x + 5 = 14(2) 2x - 3 = 7答案:(1) x = 3(2) x = 5四、解答题9. 一个长方形的长是10厘米,宽是5厘米,求这个长方形的周长和面积。
答案:周长= 2 × (10 + 5) = 30厘米面积= 10 × 5 = 50平方厘米10. 一个圆的半径是7厘米,求这个圆的周长和面积。
答案:周长= 2 × π × 7 ≈ 43.98厘米(π取3.14)面积= π × 7² ≈ 153.94平方厘米(π取3.14)五、应用题11. 一个班级有40名学生,其中男生占60%,女生占40%,求男生和女生各有多少人?答案:男生人数= 40 × 60% = 24人女生人数= 40 × 40% = 16人12. 一个工厂生产一批零件,合格率为98%,如果这批零件总数为1000个,求不合格的零件有多少个?答案:不合格的零件数= 1000 × (1 - 98%) = 20个本练习题旨在帮助初二学生巩固数学基础知识,提高解题能力。
希望同学们认真完成,遇到问题及时向老师或同学求助。
初二数学练习题及答案

初二数学练习题及答案初二数学练习题及答案数学是一门需要不断练习的学科,只有通过大量的练习才能真正掌握其中的知识和技巧。
对于初二的学生来说,数学练习题是非常重要的,它们不仅可以帮助学生巩固所学的知识,还可以提高他们的解题能力和思维能力。
下面是一些初二数学练习题及答案,希望能对同学们的学习有所帮助。
一、整数运算1. 计算:(-3) + 7 - (-4) - 5答案:(-3) + 7 - (-4) - 5 = -3 + 7 + 4 - 5 = 32. 计算:(-6) × 5 - (-3) ÷ 3答案:(-6) × 5 - (-3) ÷ 3 = -30 - (-1) = -30 + 1 = -29二、代数式与方程1. 计算:(2x + 3y) × 4,其中x = 2,y = 5答案:(2x + 3y) × 4 = (2 × 2 + 3 × 5) × 4 = (4 + 15) × 4 = 19 × 4 = 762. 解方程:2x + 5 = 15答案:2x + 5 = 15 → 2x = 15 - 5 → 2x = 10 → x = 10 ÷ 2 → x = 5三、几何1. 计算:一个正方形的边长为6cm,求其周长和面积。
答案:周长= 4 × 边长= 4 × 6 = 24cm,面积 = 边长× 边长= 6 × 6 = 36cm²2. 计算:一个半径为5cm的圆的周长和面积。
答案:周长= 2 × π × 半径= 2 × 3.14 × 5 = 31.4cm,面积= π × 半径² = 3.14 × 5² = 78.5cm²四、比例与百分数1. 计算:如果一辆汽车以每小时60公里的速度行驶,那么2小时行驶的距离是多少公里?答案:2小时行驶的距离 = 60公里/小时× 2小时 = 120公里2. 计算:把一个价格为100元的商品打8折,打完折后的价格是多少元?答案:打完折后的价格 = 原价× 折扣 = 100元× 0.8 = 80元五、统计与概率1. 计算:一个骰子投掷一次,出现奇数的概率是多少?答案:一个骰子有6个面,其中3个是奇数,所以出现奇数的概率 = 3/6 = 1/2 2. 计算:从1到20中,选出一个数,这个数是3的倍数的概率是多少?答案:从1到20中,有6个数是3的倍数,所以选出一个数是3的倍数的概率 = 6/20 = 3/10通过以上的练习题,我们可以发现,数学的学习并不是一件枯燥无味的事情。
八年级数学试卷全部答案

一、选择题1. 答案:B。
解析:勾股定理的公式是a² + b² = c²,其中c是斜边,a和b是两条直角边。
2. 答案:C。
解析:在等腰三角形中,底角相等,顶角为180度减去底角的度数。
3. 答案:A。
解析:正比例函数的图像是一条通过原点的直线。
4. 答案:D。
解析:一次函数的图像是一条直线,斜率k决定了直线的倾斜程度。
5. 答案:B。
解析:平行四边形的对边相等,对角线互相平分。
二、填空题6. 答案:-2。
解析:二次函数的顶点公式为(-b/2a, f(-b/2a)),将a=1, b=3代入计算得到顶点坐标为(-3/2, -1)。
7. 答案:2。
解析:三角形的外角等于不相邻的两个内角之和。
8. 答案:π。
解析:圆的周长公式为C=2πr,其中r是半径。
9. 答案:3。
解析:等差数列的通项公式为an=a1+(n-1)d,其中a1是首项,d是公差,n是项数。
10. 答案:9。
解析:勾股定理的应用,根据题目条件,a² + b² = c²,代入a=3, b=4计算得到c=5。
三、解答题11. 解答:(1)由题意知,正方形的边长为a,则对角线长度为a√2。
根据题目条件,对角线长度为8,所以a√2=8,解得a=8/√2=4√2。
(2)正方形的面积为边长的平方,所以面积为(4√2)²=32。
12. 解答:(1)由题意知,梯形的上底为a,下底为b,高为h。
根据题目条件,梯形的中位线为m=(a+b)/2,所以m=5。
(2)梯形的面积公式为S=(a+b)×h/2,代入m=5和h=4计算得到S=(5+5)×4/2=20。
13. 解答:(1)由题意知,直角三角形的两条直角边分别为a和b,斜边为c。
根据题目条件,a=3,b=4,代入勾股定理计算得到c=5。
(2)直角三角形的面积公式为S=1/2×a×b,代入a=3和b=4计算得到S=1/2×3×4=6。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级数学练习题及答案百度文库作为直角三角形的三边长的是A、7,24,B、7,12,15C、5,12,13D、3,4,52.、在长方形ABCD中AB=3cm,BC=2cm,则AB与CD 之间的距离为A. cmB. cmC. cmD. 不能确定3、如图所示,BE平分?ABC,DE//BC,图中相等的角共有A.对B.对C.对D.对、CDEC第2题图BB第4题第3题图4、如图所示,下列说法正确的是A、若AB//CD,则?1??2B、若AD//BC,则?3??C、若?1??2,则AB//CDD、若?1??2,则AD//BC5.有一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是 A.30°B.25°C.20°D.15°第8题图6.某商品的商标可以抽象为如图所示的三条线段,其中AB∥CD,∠EAB=45°,则∠FDC的度数是A.30? B.45?C.60? D.75?7、对于下列条件不能判定两直角三角形全等的是A. 两条直角边对应相等B. 斜边和一锐角对应相等C. 斜边和一直角边对应相等D. 两个锐角对应相等如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为6m和8m.按照输油中心O到三条支路的距离相等来连接管道,则O到三条支路的管道总长是A2mB.3m C.6m D.9m9、已知等腰三角形一腰上的高线为腰长的一半,那么这个等腰三角形的一个底角为A、15°或75°B、15°C、75°D、150°或30° 10. 下列说法中:其中正确的个数是①有一个角为60°的等腰三角形是等边三角形;②三边长为,,3的三角形为直角三角形;③等腰三角形的两条边长为2,4,则等腰三角形的周长为8或10;④若∠A和∠B的两边分别平行,且∠A比∠B的2倍少30°,则∠B的度数是70° A.个 B.个 C.个 D. 1个二、填一填11、如图,AB∥CD,∠1=50°,则∠2=。
12.在Rt△ABC中,∠C=90度,∠B=25度,则∠A=______度 13、等边三角形的每个内角都等于度14、如图,若AB∥CD,则∠A、∠E、∠D之间的数量关系是___________________15. 如右下图所示,小刚准备测量一条河的深度,他把一根竹竿插到离岸边1.5米远的水底,竹竿高出水面0.5米,再把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐;推断河水的深度为米. 16.现有两根木棒的长度分别为5cm和12cm,若要钉成一个直角三角形木架,则所需木棒长度为17、如图,直线a∥b,A、B为直线b上两点,C、D为直线a上两点。
请写出图中所有面积相等的三角形有对。
18、如图,△ABC是等边三角形, P是三角形内一点,将△ABP绕点A逆时针旋转后能与△ACD重合,如果AP=3,那么PD的长等于。
19.已知等边△ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点Bˊ处,DBˊ,EBˊ分别交边AC于点F,G,若∠ADF=80o ,则∠EGC的度数为第19题第20题20、有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了右图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2011次后形成的图形中所有的正方形的面积和三,解答题:50分21. 如图:已知;AB∥CD,AD∥BC,∠B与∠D相等吗?试说明理由.ADCB22. 如图,EF∥AD,∠1 =∠2,∠BAC =0°。
将求∠AGD 的过程填写完整。
解:∵EF∥ADC∴∠=又∵ ∠1 = ∠2D∴ ∠1 = ∠3∴AB∥∴∠BAC + = 180°。
AB又∵∠BAC =0°∴∠AGD =23. 如下图,正方形网格中的每个小正方形边长都是1,任意连结这些小正方形的顶点,可得到一些线段;请在图中画出CD=,EF1这样的线段.在正方形网格图①、图②中各画一个等腰三角形.要求:每个等腰三角形的一个顶点为格点A,其余顶点从格点B、C、D、E、F、G、H中选取,并且所画的两个三角形不全等.24. 已知:如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N,请说明理由.2已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC,判断△ABC的形状,并说明理由判断点O是否在∠BAC的角平分线上,并说明理由。
26. 如图是用硬纸板做成的四个全等的直角三角形,两直角边长分别是a,b,斜边长为c。
请你将它们拼成一个能证明勾股定理的图形.画出拼成的这个图形的示意图.............选择你喜欢的一种拼图来验证勾股定理的正确性.27. 已知:点ABC的两边、AC所在直线的距离相等,且OB=OC。
.O.到△........AB..............如图1,若点O在BC上,说明AB=AC;ABO 第27题图1如图2,若点O在△ABC的内部,说明:AB=AC;AOCBC第27题图2若点O在△ABC的外部,AB=AC成立吗?请画图表示。
2011学年第一学期八年级数学练习卷答案一. 选择题:每空2分 BACDB,BDCAC二:填空题:每空3分1415.10月份17. 1 1020 .201221. 相等。
理由略。
22.3.24.25. △ABC是等腰三角形。
∵OB=OC∴∠OBC=∠OCB∵BD、CE是两条高∴∠BDC=∠CEB=90° 又∵BC=CB∴△BDC≌△CEB ∴∠DBC=∠ECB∴AB=AC∴△ABC是等腰三角形。
点O是在∠BAC的角平分线上。
连结AO.∵ △BDC≌△CEB∴DC=EB, ∵OB=OC ∴ OD=OE 又∵∠BDC=∠CEB=90° AO=AO∴△ADO≌△AEO ∴∠DAO=∠EAO∴点O是在∠BAC的角平分线上。
第二学期期末检测八年级数学试卷一. 选择题1.下列式子不属于分式方程的是 A.12xx1x?12x?115??B.?C.?1?D.?x? x?1x?1x?1232x2x2y22.化简-的结果是A.-x-y B. y-xC.x-yD. x+y y?xy?x3.已知反比例函数的图象经过点P,则这个函数的图象位于A.第一、三象限B.第二、三象限C.第二、四象限D.第三、四象限4.一组数28,29.4,31.9,27,28.8,34.1,29.4的中位数,众数,极差分别是A.29.4,29.4,2.B.29.4,29.4,7.1C.27,29,4.D.28.8,28,2.55.直角三角形的斜边长为10,一直角边长是另一直角边长的3倍,则直角三角形的面积为A.1B.1C.1D.16.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是A.当AB=BC时,它是菱形B.当AC⊥BD时,它是菱形C.当∠ABC=90°时,它是矩形D.当AC=BD时,它是正方形7.菱形ABCD的∠DAB=80°,AB的垂直平分线交对角线AC于F,连DF,则A.50°B.40°C.75°D.60°8.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是A.AC=BD,AD//CD;B.AD∥BC,∠A=∠C;C.AO=BO=OC=DO; D.AO=CO=BO=DO,AB=BC9.已知函数y=kx中,y随x的增大而增大,那么函数y=D k的图像大致是 x10.为响应承办“绿色奥运”的号召,八年级班全体师生义务植树300棵.原计划每小时植树x棵,但由于参加植树的全体师生植树的积极性高涨,实际工作效率提高为原计划的1.2倍,结果提前20分钟完成任务.则下面所列方程中,正确的是A.30020300?? x601.2x B.30030030030020??20 C.?? x1.2xxx?1.2x60D.30030020?? x1.2x60二、填空题5x?3有意义;x?52212.已知x?12??y?13?与z?10z?25互为相反数,则以x、y、z为边的三角形是13.对甲、乙两台机床生产的零件进行抽样测量,其平均数、方差计算结果如下:22机床甲:甲=10,S甲=0.02;机床乙:乙=10,S乙=0.06,由此可知:_______机床性能好.k与直线y=-kx的交点的个数是 xxx?1?2与15.当x? 时,互为相反数. x?5x14.当k>0时,双曲线y?16.如图,E、F是对角线BD上的两点,请你添加一个适当的条件:______?使四边形AECF是平行四边形.17.如图,正方形ABCD中,AB=1,点P是对角线AC 上的一点,分别以AP、PC?为对角线作正方形,则两个小正方形的周长的和是________.18.某人要登上6m高的建筑物,为确保安全,梯子底端要离开建筑物2.5m,且顶端不低于建筑物顶部,则梯子长应不少于m。
三.解答题有一道题:“先化简再求值:x?12x1?2)?2,其中x=-2010”,小明做题时把“x=-”x?1x?1x?1错抄成了“x=2010”,但他的计算结果也是正确的,请你通过计算解释这是怎么回事?20.解方程21. 在压力不变的情况下,某物体承受的压强p是它的受力面积S的反比例函数,其图象如图所示.求p与S之间的函数关系式;求当S=0.m时物体承受的压强p.2x2?2?1 x?2x?4m2)22. 红星家电商场的一个柜组出售容积分别为268立升、228立升、185立升、182立升四种型号的同一品牌的冰箱,每卖出一台冰箱,售货员就在一张纸上写出它的容积作为原始记录,到月底,柜组长清点原始记录,得到一组由10个182、18个185、66个228和16个268组成的数据。
这组数据的平均数有实际意义吗?这组数据的中位数、众数分别等于多少?红星商场总经理关心的是中位数还是众数?23. 已知,如图所示,折叠长方形的一边AD,使点D落在BC边的点F?处,?如果AB=8cm,BC=10cm,求EC的长. 24. 甲、乙两同学学习计算机打字,甲打一篇3000字的文章与乙打一篇2400字的文章所用的时间相同.已知甲每分钟比乙每分钟多打12个字,问甲、乙两人每分钟各打多少个字?李明同学是这样解答的:设甲同学打印一篇000字的文章需要x分钟,根据题意,得30002400??1 xx解得:x?50.经检验x?50是原方程的解.答:甲同学每分钟打字50个,乙同学每分钟打字38个.请从、、三个步骤说明李明同学的解答过程是否正确,若有不正确的步骤改正过来.请你用直接设未知数列方程的方法解决这个问题.25.如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P?从A开始沿AD边向D以1cm/s 的速度运动,动点Q从点C开始沿CB以3cm/s的速度向点B 运动.P、Q同时出发,当其中一点到达顶点时,另一点也随之停止运动,设运动时间为ts,?问t为何值时.四边形PQCD是平行四边形.当t为何值时,四边形PQCD为等腰梯形.第二学期八年级数学参考答案及评分标准一.CACBDDDDAA二.11. x??512. 直角 13.甲14. 0 15.16. BE=FD 或AE∥FC或AF∥EC17. 18. .546或42.25三.19. 解:设所求函数解析式为p=,把代入解析式,得1000= 解得k=2500 s2.52500∴所求函数解析式为p=当s=0.5m2时,p=5000分s22. 解:这组数据的平均数没有实际意义,对商店经营也没有任何参考价值。
