【真题】2018年陕西省中考数学试卷(Word版)
2018年陕西省中考数学试题及参考答案(word解析版)
2018年陕西省中考数学试题及参考答案一、选择题(本大题共10小题,每小题3分,共30分)1.711-的倒数是()A.711B.711-C.117D.117-2.如图,是一个几何体的表面展开图,则该几何体是()A.正方体B.长方体C.三棱柱D.四棱锥3.如图,若l1∥l2,l3∥l4,则图中与∠1互补的角有()A.1个B.2个C.3个D.4个4.如图,在矩形AOBC中,A(﹣2,0),B(0,1).若正比例函数y=kx的图象经过点C,则k 的值为()A.12-B.12C.﹣2 D.25.下列计算正确的是()A.a2•a2=2a4B.(﹣a2)3=﹣a6C.3a2﹣6a2=3a2D.(a﹣2)2=a2﹣46.如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为()A B.C D.7.若直线l1经过点(0,4),l2经过点(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为()A.(﹣2,0)B.(2,0)C.(﹣6,0)D.(6,0)8.如图,在菱形ABCD中.点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、CH和HE.若EH=2EF,则下列结论正确的是()A.B.AB=2EF C.D.9.如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与⊙O相交于点D,连接BD,则∠DBC的大小为()A.15°B.35°C.25°D.45°10.对于抛物线y=ax2+(2a﹣1)x+a﹣3,当x=1时,y>0,则这条抛物线的顶点一定在()A.第一象限B.第二象限C.第三象限D.第四象限二、填空题(本大题共4小题,每小题3分,共12分)11.比较大小:“>”、“<”或“=”).12.如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为.13.若一个反比例函数的图象经过点A(m,m)和B(2m,﹣1),则这个反比例函数的表达式为.14.如图,点O是▱ABCD的对称中心,AD>AB,E、F是AB边上的点,且EF=12AB;G、H是BC边上的点,且GH=13BC,若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是.三、解答题(本大题共11小题,共78分)15.(5分)计算:((()01|52π⨯++-.16.(5分)化简:213111a a a a a a a ++⎛⎫-÷ ⎪-++⎝⎭. 17.(5分)如图,已知:在正方形ABCD 中,M 是BC 边上一定点,连接AM .请用尺规作图法,在AM 上作一点P ,使△DPA ∽△ABM .(不写作法,保留作图痕迹)18.(5分)如图,AB ∥CD ,E 、F 分别为AB 、CD 上的点,且EC ∥BF ,连接AD ,分别与EC 、BF 相交于点G ,H ,若AB=CD ,求证:AG=DH .19.(7分)对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况,他们将全部测试成绩分成A 、B 、C 、D 四组,绘制了如下统计图表:“依据以上统计信息解答下列问题: (1)求得m= ,n= ; (2)这次测试成绩的中位数落在 组;(3)求本次全部测试成绩的平均数.20.(7分)周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C、A共线.已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.21.(7分)经过一年多的精准帮扶,小明家的网络商店(简称网店)将红枣、小米等优质土特产迅速销往全国.小明家网店中红枣和小米这两种商品的相关信息如下表:根据上表提供的信息解答下列问题:(1)已知今年前五个月,小明家网店销售上表中规格的红枣和小米共3000kg,获得利润4.2万元,求这前五个月小明家网店销售这种规格的红枣多少袋;(2)根据之前的销售情况,估计今年6月到10月这后五个月,小明家网店还能销售上表中规格的红枣和小米共2000kg,其中,这种规格的红枣的销售量不低于600kg.假设这后五个月,销售这种规格的红枣为x(kg),销售这种规格的红枣和小米获得的总利润为y(元),求出y与x之间的函数关系式,并求这后五个月,小明家网店销售这种规格的红枣和小米至少获得总利润多少元.22.(7分)如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形的圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止).(1)转动转盘一次,求转出的数字是﹣2的概率;(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.23.(8分)如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC、BC交于点M、N.(1)过点N作⊙O的切线NE与AB相交于点E,求证:NE⊥AB;(2)连接MD,求证:MD=NB.24.(10分)已知抛物线L:y=x2+x﹣6与x轴相交于A、B两点(点A在点B的左侧),并与y轴相交于点C.(1)求A、B、C三点的坐标,并求△ABC的面积;(2)将抛物线L向左或向右平移,得到抛物线L′,且L′与x轴相交于A'、B′两点(点A′在点B′的左侧),并与y轴相交于点C′,要使△A'B′C′和△ABC的面积相等,求所有满足条件的抛物线的函数表达式.25.(12分)问题提出(1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为.问题探究(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.问题解决(3)如图③所示,AB、AC、BC是某新区的三条规划路,其中AB=6km,AC=3km,∠BAC=60°,BC所对的圆心角为60°,新区管委会想在BC路边建物资总站点P,在AB,AC路边分别建物资分站点E、F,也就是,分别在BC、线段AB和AC上选取点P、E、F.由于总站工作人员每天都要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷、环保和节约成本.要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值.(各物资站点与所在道路之间的距离、路宽均忽略不计)参考答案与解析一、选择题(本大题共10小题,每小题3分,共30分)1.711-的倒数是()A.711B.711-C.117D.117-【知识考点】倒数.【思路分析】根据倒数的定义,互为倒数的两数乘积为1,即可解答.【解答过程】解:711-的倒数是117-,故选:D.【总结归纳】此题主要考查倒数的概念及性质,属于基础题,注意掌握倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.2.如图,是一个几何体的表面展开图,则该几何体是()A.正方体B.长方体C.三棱柱D.四棱锥【知识考点】几何体的展开图.【思路分析】由展开图得这个几何体为棱柱,底面为三边形,则为三棱柱.【解答过程】解:由图得,这个几何体为三棱柱.故选:C.【总结归纳】考查了几何体的展开图,有两个底面的为柱体,有一个底面的为椎体.3.如图,若l1∥l2,l3∥l4,则图中与∠1互补的角有()A.1个B.2个C.3个D.4个【知识考点】余角和补角;平行线的性质.【思路分析】直接利用平行线的性质得出相等的角以及互补的角进而得出答案.【解答过程】解:∵l1∥l2,l3∥l4,∴∠1+∠2=180°,2=∠4,∵∠4=∠5,∠2=∠3,∴图中与∠1互补的角有:∠2,∠3,∠4,∠5共4个.。
陕西省2018年中考数学试题(含答案)【精品】.docx

2018年陕西省中考数学试卷一、选择题:(本大题共10题,每题3分,满分30分)1、-711的倒数是A .711B .-711C .117D .-1172、如图,是一个几何体的表面展开图,则该几何体是 A .正方体 B .长方体 C .三棱柱 D .四棱锥3、如图,若l 1∥l 2,l 3∥l 4,则图中与∠1互补的角有 A .1个 B .2个 C .3个 D .4个4、如图,在矩形ABCD 中,A (-2,0),B(0,1).若正比例函数y =kx 的图像经过点C ,则k 的取值为A.-12 B .12C .-2D .2第2题图第3题图第4题图5、下列计算正确的是A .a 2·a 2=2a 4B .(-a 2)3=-a 6C .3a 2-6a 2=3a 2D .(a -2)2=a 2-4 6、如图,在△ABC 中,AC =8,∠ABC =60°,∠C =45°,AD ⊥BC ,垂足为D ,∠ABC 的平分线交AD 于点E ,则AE 的长为A .423B .2 2C .823D .3 2第6题图第8题图第9题图7、若直线l 1经过点(0,4),l 2经过(3,2),且l 1与l 2关于x 轴对称,则l 1与l 2的交点坐标为 A .(-2,0) B .(2,0) C .(-6,0) D .(6,0)8、如图,在菱形ABCD 中,点E 、F 、G 、H 分别是边AB 、BC 、CD 和DA 的中点,连接EF 、FG 、GH 和HE .若EH =2EF ,则下列结论正确的是 A .AB =2EF B .AB =2EF C .AB =3EF D .AB =5EF9、如图,△ABC 是⊙O 的内接三角形,AB =AC ,∠BCA =65°,作CD ∥AB ,并与○O 相交于点D ,连接BD ,则∠DBC 的大小为 A .15° B .35° C .25° D .45°10、对于抛物线y =ax 2+(2a -1)x +a -3,当x =1时,y >0,则这条抛物线的顶点一定在 A .第一象限 B .第二象限 C .第三象限 D .第四象限二、填空题:(本大题共4题,每题3分,满分12分)11、比较大小:填<,>或=).12、如图,在正五边形ABCDE 中,AC 与BE 相交于点F ,则AFE 的度数为72°13、若一个反比例函数的图像经过点A (m ,m )和B (2m ,-1),则这个反比例函数的表达式为3DBy =4x14、点O 是平行四边形ABCD 的对称中心,AD >AB ,E 、F 分别是AB 边上的点,且EF =12AB ;G 、H分别是BC 边上的点,且GH =13BC ;若S 1,S 2分别表示∆EOF 和∆GOH 的面积,则S 1,S 2之间的等量关系是2S1=3S 2第12题图第14题图二、解答题(共11小题,计78分.解答应写出过程)15.(本题满分5分) 计算:(-3)×(-6)+|2-1|+(5-2π)0 解:原式=32+2-1+1=4 2 16.(本题满分5分)化简:⎝ ⎛⎭⎪⎫a +1a -1-a a +1÷3a +1a 2+a解:原式=3a +1(a +1)(a -1)×a (a +1)3a +1=aa -117.(本题满分5分)如图,已知在正方形ABCD 中,M 是BC 边上一定点,连接AM ,请用尺规作图法,在AM 上求作一点P ,使得△DPA ∽△ABM (不写做法保留作图痕迹)解:如图,P 即为所求点.18、(本题满分5分)如图,AB ∥CD ,E 、F 分别为AB 、CD 上的点,且EC ∥BF ,连接AD ,分别与EC 、BF 相交与点G 、H ,若AB =CD ,求证:AG =DH .证明:∵AB ∥CD ,∴∠A =∠D ∵CE ∥BF ,∴∠AHB =∠DGC 在∆ABH 和∆DCG 中, ∵⎩⎪⎨⎪⎧∠A =∠D∠AHB =∠DGC AB =CDBGHCADAD∴∆ABH ≌∆DCG (AAS ),∴AH =DG∵AH =AG +GH ,DG =DH +GH ,∴AG =HD 19.(本题满分7分)对垃圾进行分类投放,能有效提高对垃圾的处理和再利用减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度增强同学们的环保意识,普及垃圾分类及投放的相关知识.某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况,他们将全部测试成绩分成A 、B 、C 、D 四组,绘制了如下统计图表:(第19题图)依据以上统计信息,解答下列问题: (1)求得m =30,n =19%;(2)这次测试成绩的中位数落在B 组; (3)求本次全部测试成绩的平均数.解:测试的平均成绩=2581+5543+5100+2796200=80.1.20.(本题满分7分)周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A ,在他们所在的岸边选择了点B ,使得AB 与河岸垂直,并在B 点竖起标杆BC ,再在AB 的延长线上选择点D 竖起标杆DE ,使得点E 与点C 、A 共线.已知:CB ⊥AD ,ED ⊥AD ,测得BC =1m ,DE =1.5m ,BD =8.5m .测量示意图如图所示.请根据相关测量信息,求河宽AB .解:∵CB ⊥AD ,ED ⊥AD , ∴∠CBA =∠EDA =90° ∵∠CAB =∠EAD ∴∆ABC ∽∆ADE ∴AD AB =DE BC∴AB +8.5AB =1.51∴AB =17,即河宽为17米. 21.(本题满分7分)经过一年多的精准帮扶,小明家的网络商店(简称网店)将红枣、小米等优质土特产迅速销往A nD 、15%B 36%C 30%(1)已知今年前五个月,小明家网店销售上表中规格的红枣和小米共3000kg ,获得利润4.2万元,求这前五个月小明家网店销售这种规格的红枣多少袋;(2)根据之前的销售情况,估计今年6月到10月这后五个月,小明家网店还能销售上表中规格的红枣和小米共2000kg ,其中,这种规格的红枣的销售量不低于600kg .假设这后五个月,销售这种规格的红枣味x (kg ),销售这种规格的红枣和小米获得的总利润为y (元),求出y 与x 之间的函数关系式,并求出这后五个月,小明家网店销售这种规格的红枣和小米至少获得总利润多少元.解:(1)设前五个月小明家网店销售这种规格的红枣a 袋,销售小米b 袋,根据题意列方程得:a +2b =3000,(60-40)a +(54-38)b =42000,解得:a =1500,b =750∴前五个月小明家网店销售这种规格的红枣1500袋,销售小米750袋(2)根据题意得:y =(60-40)x +(54-38)×2000-x2=12x +16000y 随x 的增大而增大,∵x ≥600,∴当x =600时,y 取得最小值, 最小值为y =12×600+16000=23200∴小明家网店销售这种规格的红枣和小米至少获得总利润23200元.22.(本题满分7分)如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)(1)转动转盘一次,求转出的数字是-2的概率;(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.(第22题图)解:(1)由题意可知:“1”和“3”所占的扇形圆心角为120°,所以2个“-2”所占的扇形圆心角为360°-2×120°=120°,∴转动转盘一次,求转出的数字是-2的概率为120°360°=13;(2)由(1)可知,该转盘转出“1”“3”“-2”的概率相同,均为1,所有可能性如下表所示:由上表可知:所有可能的结果共9种,其中数字之积为正数的的有5种,其概率为5923.(本题满分8分)如图,在Rt △ABC 中,∠ACB =90°,以斜边AB 上的中线CD 为直径作⊙O ,分别与AC 、BC 相交于点M 、N .(1)过点N 作⊙O 的切线NE 与AB 相交于点E ,求证:NE ⊥AB ; (2)连接MD ,求证:MD =NB .1-23-223题图 23题解图(1)解:(1)如图,连接ON∵CD 是Rt △ABC 斜边AB 上的中线 ∴AD =CD =DB ∴∠DCB =∠DBC 又∵∠DCB =∠ONC ∴∠ONC =∠DBC ∴ON ∥AB∵NE 是⊙O 的切线,ON 是⊙O 的半径 ∴∠ONE =90°∴∠NEB =90°,即NE ⊥AB ;(2)如解图(1)所示,由(1)可知ON ∥AB ,O 为⊙O 的圆心,∴OC =OB ,∠CMD =90°∴CN =NB =12CB ,MD ∥CB又∵D 是AB 的中点,∴MD =12CB ∴MD =NB .24.(本题满分10分)已知抛物线L :y =x 2+x -6与x 轴相交于A 、B 两点(点A 在点B 的左侧),并与y 轴相交于点C .(1)求A 、B 、C 三点的坐标,并求出△ABC 的面积; (2)将抛物线向左或向右平移,得到抛物线L ´,且L ´与x 轴相交于A ´、B ´两点(点A ´在点B ´的左侧),并与y 轴交于点C ´,要使△A ´B ´C ´和△ABC 的面积相等,求所有满足条件的抛物线的函数表达式.解:(1)当y =0时,x 2+x -6=0,解得x 1=-3,x 2=2;当x =0时,y =-6 ∴A (-3,0),B (2,0),C (0,6)∴S △ABC =12AB ·OC =12×5×6=15; (2)将抛物线向左或向右平移时,A ´、B ´两点间的距离不变,始终为5,那么要使△A ´B ´C ´和△ABC 的面积相等,高也只能是6设A (a ,0),则B (a +5,0),y =(x -a )(x -a -5),当x =0时,y =a 2+5a当C 点在x 轴上方时,y =a 2+5a =6,a =1或a =-6,此时y =x 2-7x -6或y =x 2+7x -6; 当C 点在x 轴下方时,y =a 2+5a =-6,a =-2或a =-3,此时y =x 2-x -6或y =x 2+x -6(与圆抛物线重合,舍去);所以,所有满足条件的抛物线的函数表达式为:y =x 2-7x -6,y =x 2+7x -6,y =x 2-x -6. 25.(本题满分12分) 问题提出(1)如图①,在△ABC 中,∠A =120°,AB =AC =5,则△ABC 的外接圆半径R 的值为. 问题探究(2)如图②,⊙O 的半径为13,弦AB =24,M 是AB 的中点,P 是⊙O 上一动点,求PM 的最大值.问题解决(3)如图③所示,AB 、AC 、BC 是某新区的三条规划路其中,AB =6km ,AC =3km ,∠BAC =60°,BC 所对的圆心角为60°.新区管委会想在BC 路边建物资总站点P ,在AB 、AC 路边分别建物资分站点E 、F .也就是,分别在BC 线段AB 和AC 上选取点P 、E 、F .由于总站工作人员每天要将物资在ABB各物资站点间按P →E →F →P 的路径进行运输,因此,要在各物资站点之间规划道路PE 、EF 和FP .为了快捷环保和节约成本要使得线段PE 、EF 、FP 之和最短,试求PE +EF +FP 的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).图①图②图③解:(1)R =AB =AC =5;(2)如25题解图(2)所示,连接MO 并延长交⊙O 于N ,连接OP显然,MP ≤OM +OP =OM +ON =MN ,ON =13,OM =132-122=5,MN =18 ∴PM 的最大值为18;25题解图(2) 25题解图(3)(3)假设P 点即为所求点,分别作出点P 关于AB 、AC 的对称点P ´、P "连接PP ´、P ´E ,PE ,P "F ,PF ,PP "由对称性可知PE +EF +FP =P ´E +EF +FP "=P ´P ",且P ´、E 、F 、P "在一条直线上,所以P ´P "即为最短距离,其长度取决于P A 的长度25题解图(4)作出弧BC 的圆心O ,连接AO ,与弧BC 交于P ,P 点即为使得P A 最短的点 ∵AB =6km ,AC =3km ,∠BAC =60°,∴∆ABC 是直角三角形,∠ABC =30°,BC=3 3 BC 所对的圆心角为60°,∴∆OBC 是等边三角形,∠CBO =60°,BO =BC =3 3 ∴∠ABO =90°,AO =37,PA =37-3 3 ∠P ´AE =∠EAP ,∠P AF =∠F AP ",∴∠P ´AP "=2∠ABC =120°,P ´A =AP ",∴∠AP ´E =∠AP "F =30°∵P ´P "=2P ´A cos ∠AP ´E =3P ´A =321-9 所以PE +EF +FP 的最小值为321-9km .P''BB。
2018年陕西省中考数学试卷【word,带解析】

2018年陕西省中考数学试卷一、选择题(共 小题,每小题 分,计 分。
每小题只有一个选项是符合题意的) .( 分)﹣的倒数是()✌. . . ..( 分)如图,是一个几何体的表面展开图,则该几何体是()✌.正方体 .长方体 .三棱柱 .四棱锥 .( 分)如图,若● ∥● ,● ∥● ,则图中与∠ 互补的角有()✌. 个 . 个 . 个 . 个.( 分)如图,在矩形✌中,✌(﹣ , ), ( , ).若正比例函数⍓⌧的图象经过点 ,则 的值为()✌. . .﹣ ..( 分)下列计算正确的是()✌.♋ ❿♋ ♋ .(﹣♋ ) ﹣♋ . ♋ ﹣ ♋ ♋ .(♋﹣ ) ♋ ﹣.( 分)如图,在△✌中,✌ ,∠✌,∠ ,✌⊥ ,垂足为 ,∠✌的平分线交✌于点☜,则✌☜的长为()✌. . ...( 分)若直线● 经过点( , ),● 经过点( , ),且● 与● 关于⌧轴对称,则● 与● 的交点坐标为()✌.(﹣ , ) .( , ) .(﹣ , ) .( , ).( 分)如图,在菱形✌中.点☜、☞、☝、☟分别是边✌、 、 和 ✌的中点,连接☜☞、☞☝、 ☟和☟☜.若☜☟☜☞,则下列结论正确的是()✌.✌☜☞ .✌☜☞ .✌☜☞ .✌☜☞ .( 分)如图,△✌是⊙ 的内接三角形,✌✌,∠ ✌,作 ∥✌,并与⊙ 相交于点 ,连接 ,则∠ 的大小为()✌. . . . .( 分)对于抛物线⍓♋⌧ ( ♋﹣ )⌧♋﹣ ,当⌧ 时,⍓> ,则这条抛物线的顶点一定在()✌.第一象限 .第二象限 .第三象限 .第四象限二、填空题(共 小题,每小题 分,计 分).( 分)比较大小: (填❽>❾、❽<❾或❽❾)..( 分)如图,在正五边形✌☜中,✌与 ☜相交于点☞,则∠✌☞☜的度数为 ..( 分)若一个反比例函数的图象经过点✌(❍,❍)和 ( ❍,﹣ ),则这个反比例函数的表达式为 ..( 分)如图,点 是 ✌的对称中心,✌>✌,☜、☞是✌边上的点,且☜☞✌;☝、☟是 边上的点,且☝☟ ,若 , 分别表示△☜☞和△☝☟的面积,则 与 之间的等量关系是 .三、解答题(共 小题,计 分。
2018年陕西省中考数学试卷及答案(Word版)

2018年陕西省中考数学试卷及答案(Word版)DC80<x≤9060 5100D90<x≤100m2796(第19题图)依据以上统计信息,解答下列问题:(1)求得m=_______,n=__________;(2)这次测试成绩的中位数落在_______组;(3)求本次全部测试成绩的平均数.20.(本题满分7分)周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.21.(本题满分7分)经过一年多的精准帮扶,小明家的网络商店(简称网店)将红枣、小米等优质土特产迅速销往全国,小明家网店中红枣和小米这两种商品的相关信息如下表:商品 红枣 小米 规格 1kg /袋 2kg /袋 成本(元/袋) 40 38 售价(元/袋)6054根据上表提供的信息,解答下列问题:(1)已知今年前五个月,小明家网店销售上表中规格的红枣和小米共3000kg ,获得利润4.2万元,求这前五个月小明家网店销售这种规格的红枣多少袋;(2)根据之前的销售情况,估计今年6月到10月这后五个月,小明家网店还能销售上表中规格的红枣和小米共2000kg ,其中,这种规格的红枣的销售量不低于600kg .假设这后五个月,销售这种规格的红枣味x (kg ),销售这种规格的红枣和小米获得的总利润为y (元),求出y 与x 之间的函数关系式,并求出这后五个月,小明家网店销售这种规格的红枣和小米至少获得总利润多少元.22.(本题满分7分)如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)(1)转动转盘一次,求转出的数字是-2的概率;(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.(第22题图)-2-23123.(本题满分8分)如图,在Rt △ABC 中,∠ACB =90°,以斜边AB 上的中线CD 为直径作○O ,分别与AC 、BC 相交于点M 、N .(1)过点N 作⊙O 的切线NE 与AB 相交于点E ,求证:NE ⊥AB ; (2)连接MD ,求证:MD =NB .24.(本题满分10分)已知抛物线L :62-+=x x y 与x 轴相交于A 、B 两点(点A 在点B 的左侧),并与y 轴相交于点C . (1)求A 、B 、C 三点的坐标,并求出△ABC 的面积;(2)将抛物线向左或向右平移,得到抛物线L ’,且L ’与x 轴相交于A ’、B ’两点(点A ’在点B ’的左侧),并与y 轴交于点C ’,要使△A ’B ’C ’和△ABC 的面积相等,求所有满足条件的抛物线的函数表达式.(第23题图)ENM OD ABC25.(本题满分12分) 问题提出(1)如图①,在△ABC 中,∠A =120°,AB =AC =5,则△AC 的外接圆半径R 的值为_______. 问题探究(2)如图②,⊙O 的半径为13,弦AB =24,M 是AB 的中点,P 是⊙O 上一动点,求PM 的最大值. 问题解决(3)如图③所示,AB 、AC 、BC 是某新区的三条规划路其中,AB =6km ,AC =3km ,∠BC =60°,BC 所对的圆心角为60°.新区管委会想在BC 路边建物资总站点P ,在AB 、AC 路边分别建物资分站点E 、F .也就是,分别在BC 线段AB 和AC 上选取点P 、E 、F .由于总站工作人员每天要将物资在各物资站点间按P →E →F →P 的路径进行运输,因此,要在各物资站点之间规划道路PE 、EF 和FP .为了快捷环保和节约成本要使得线段PE 、EF 、FP 之和最短,试求PE +EF +FP 的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计)(第25题图)图③图②图①OM ABPC2018年陕西省中考数学试卷答案一、选择题1 2 3 4 5 6 7 8 9 10D C D A B C B D A C。
陕西省2018年中考数学考试及解析(word精编版)

陕西省2018年中考数学考试及解析(word精编版)————————————————————————————————作者:————————————————————————————————日期:2018年陕西省初中毕业学业考试数学试卷(满分120分,考试时间120分钟)一、选择题(共10小题,每小题3分,计30分。
每小题只有一个选项是符合题意的)1.(3分)﹣的倒数是()A. B. C. D.2.(3分)如图,是一个几何体的表面展开图,则该几何体是()A.正方体B.长方体C.三棱柱D.四棱锥3.(3分)如图,若l1∥l2,l3∥l4,则图中与∠1互补的角有()A.1个 B.2个 C.3个 D.4个4.(3分)如图,在矩形AOBC中,A(﹣2,0),B(0,1).若正比例函数y=kx 的图象经过点C,则k的值为()A.B. C.﹣2 D.25.(3分)下列计算正确的是()A.a2•a2=2a4B.(﹣a2)3=﹣a6C.3a2﹣6a2=3a2 D.(a﹣2)2=a2﹣46.(3分)如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为()A. B.2 C. D.37.(3分)若直线l1经过点(0,4),l2经过点(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为()A.(﹣2,0)B.(2,0)C.(﹣6,0) D.(6,0)8.(3分)如图,在菱形ABCD中.点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、CH和HE.若EH=2EF,则下列结论正确的是()A.AB=EF B.AB=2EF C.AB=EF D.AB=EF9.(3分)如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与⊙O相交于点D,连接BD,则∠DBC的大小为()A.15°B.35°C.25°D.45°10.(3分)对于抛物线y=ax2+(2a﹣1)x+a﹣3,当x=1时,y>0,则这条抛物线的顶点一定在()A.第一象限B.第二象限C.第三象限D.第四象限二、填空题(共4小题,每小题3分,计12分)11.(3分)比较大小:3 (填“>”、“<”或“=”).12.(3分)如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为.13.(3分)若一个反比例函数的图象经过点A(m,m)和B(2m,﹣1),则这个反比例函数的表达式为.14.(3分)如图,点O是▱ABCD的对称中心,AD>AB,E、F是AB边上的点,且EF=AB;G、H是BC边上的点,且GH=BC,若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是.三、解答题(共11小题,计78分。
陕西省2018年中考数学试题(含答案).docx
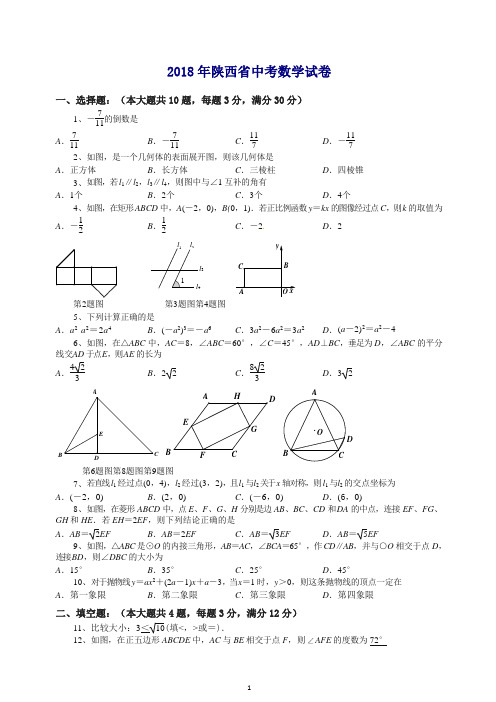
2018年陕西省中考数学试卷一、选择题:(本大题共10题,每题3分,满分30分)1、-711的倒数是A .711B .-711C .117D .-1172、如图,是一个几何体的表面展开图,则该几何体是 A .正方体 B .长方体 C .三棱柱 D .四棱锥3、如图,若l 1∥l 2,l 3∥l 4,则图中与∠1互补的角有 A .1个 B .2个 C .3个 D .4个4、如图,在矩形ABCD 中,A (-2,0),B(0,1).若正比例函数y =kx 的图像经过点C ,则k 的取值为 A.-12 B .12C .-2D .2第2题图第3题图第4题图5、下列计算正确的是A .a 2·a 2=2a 4B .(-a 2)3=-a 6C .3a 2-6a 2=3a 2D .(a -2)2=a 2-4 6、如图,在△ABC 中,AC =8,∠ABC =60°,∠C =45°,AD ⊥BC ,垂足为D ,∠ABC 的平分线交AD 于点E ,则AE 的长为A .423B .2 2C .823D .3 2第6题图第8题图第9题图7、若直线l 1经过点(0,4),l 2经过(3,2),且l 1与l 2关于x 轴对称,则l 1与l 2的交点坐标为 A .(-2,0) B .(2,0) C .(-6,0) D .(6,0)8、如图,在菱形ABCD 中,点E 、F 、G 、H 分别是边AB 、BC 、CD 和DA 的中点,连接EF 、FG 、GH 和HE .若EH =2EF ,则下列结论正确的是A .AB =2EF B .AB =2EFC .AB =3EFD .AB =5EF9、如图,△ABC 是⊙O 的内接三角形,AB =AC ,∠BCA =65°,作CD ∥AB ,并与○O 相交于点D ,连接BD ,则∠DBC 的大小为 A .15° B .35° C .25° D .45°10、对于抛物线y =ax 2+(2a -1)x +a -3,当x =1时,y >0,则这条抛物线的顶点一定在 A .第一象限 B .第二象限 C .第三象限 D .第四象限二、填空题:(本大题共4题,每题3分,满分12分)11、比较大小:填<,>或=).12、如图,在正五边形ABCDE 中,AC 与BE 相交于点F ,则AFE 的度数为72°3B13、若一个反比例函数的图像经过点A(m,m)和B(2m,-1),则这个反比例函数的表达式为y=4x14、点O是平行四边形ABCD的对称中心,AD>AB,E、F分别是AB边上的点,且EF=12AB;G、H 分别是BC边上的点,且GH=13BC;若S1,S2分别表示∆EOF和∆GOH的面积,则S1,S2之间的等量关系是2S1=3S2第12题图第14题图二、解答题(共11小题,计78分.解答应写出过程)15.(本题满分5分)计算:(-3)×(-6)+|2-1|+(5-2π)0解:原式=32+2-1+1=4 216.(本题满分5分)化简:⎝⎛⎭⎪⎫a+1a-1-aa+1÷3a+1a2+a解:原式=3a+1(a+1)(a-1)×a(a+1)3a+1=aa-117.(本题满分5分)如图,已知在正方形ABCD中,M是BC边上一定点,连接AM,请用尺规作图法,在AM上求作一点P,使得△DPA∽△ABM(不写做法保留作图痕迹)解:如图,P即为所求点.18、(本题满分5分)如图,AB∥CD,E、F分别为AB、CD上的点,且EC∥BF,连接AD,分别与EC、BF相交与点G、H,若AB=CD,求证:AG=DH.证明:∵AB∥CD,∴∠A=∠D∵CE∥BF,∴∠AHB=∠DGC在∆ABH和∆DCG中,BBCA DAD∵⎩⎪⎨⎪⎧∠A =∠D∠AHB =∠DGC AB =CD∴∆ABH ≌∆DCG (AAS ),∴AH =DG∵AH =AG +GH ,DG =DH +GH ,∴AG =HD 19.(本题满分7分)对垃圾进行分类投放,能有效提高对垃圾的处理和再利用减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度增强同学们的环保意识,普及垃圾分类及投放的相关知识.某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况,他们将全部测试成绩分成A 、B 、C 、D 四组,绘制了如下统计图表:(第19题图)依据以上统计信息,解答下列问题: (1)求得m =30,n =19%;(2)这次测试成绩的中位数落在B 组; (3)求本次全部测试成绩的平均数.解:测试的平均成绩=2581+5543+5100+2796200=80.1.20.(本题满分7分)周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A ,在他们所在的岸边选择了点B ,使得AB 与河岸垂直,并在B 点竖起标杆BC ,再在AB 的延长线上选择点D 竖起标杆DE ,使得点E 与点C 、A 共线.已知:CB ⊥AD ,ED ⊥AD ,测得BC =1m ,DE =1.5m ,BD =8.5m .测量示意图如图所示.请根据相关测量信息,求河宽AB .解:∵CB ⊥AD ,ED ⊥AD , ∴∠CBA =∠EDA =90° ∵∠CAB =∠EAD ∴∆ABC ∽∆ADE ∴AD AB =DE BC∴AB +8.5AB =1.51∴AB =17,即河宽为17米.A nD 、15%B 36%C 30%21.(本题满分7分)经过一年多的精准帮扶,小明家的网络商店(简称网店)将红枣、小米等优质土特产迅速销往全国,小明家网店中红枣和小米这两种商品的相关信息如下表:根据上表提供的信息,解答下列问题:(1)已知今年前五个月,小明家网店销售上表中规格的红枣和小米共3000kg ,获得利润4.2万元,求这前五个月小明家网店销售这种规格的红枣多少袋;(2)根据之前的销售情况,估计今年6月到10月这后五个月,小明家网店还能销售上表中规格的红枣和小米共2000kg ,其中,这种规格的红枣的销售量不低于600kg .假设这后五个月,销售这种规格的红枣味x (kg ),销售这种规格的红枣和小米获得的总利润为y (元),求出y 与x 之间的函数关系式,并求出这后五个月,小明家网店销售这种规格的红枣和小米至少获得总利润多少元.解:(1)设前五个月小明家网店销售这种规格的红枣a 袋,销售小米b 袋,根据题意列方程得:a +2b =3000,(60-40)a +(54-38)b =42000,解得:a =1500,b =750∴前五个月小明家网店销售这种规格的红枣1500袋,销售小米750袋 (2)根据题意得:y =(60-40)x +(54-38)×2000-x2=12x +16000y 随x 的增大而增大,∵x ≥600,∴当x =600时,y 取得最小值, 最小值为y =12×600+16000=23200∴小明家网店销售这种规格的红枣和小米至少获得总利润23200元.22.(本题满分7分) 如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)(1)转动转盘一次,求转出的数字是-2的概率;(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.(第22题图)解:(1)由题意可知:“1”和“3”所占的扇形圆心角为120°,所以2个“-2”所占的扇形圆心角为360°-2×120°=120°,∴转动转盘一次,求转出的数字是-2的概率为120°360°=13;(2)由(1)可知,该转盘转出“1”“3”“-2”的概率相同,均为13,所有可能性如下表所示:1-23-2由上表可知:所有可能的结果共9种,其中数字之积为正数的的有5种,其概率为5923.(本题满分8分)如图,在Rt △ABC 中,∠ACB =90°,以斜边AB 上的中线CD 为直径作⊙O ,分别与AC 、BC 相交于点M 、N .(1)过点N 作⊙O 的切线NE 与AB 相交于点E ,求证:NE ⊥AB ; (2)连接MD ,求证:MD =NB .23题图 23题解图(1)解:(1)如图,连接ON∵CD 是Rt △ABC 斜边AB 上的中线 ∴AD =CD =DB ∴∠DCB =∠DBC 又∵∠DCB =∠ONC ∴∠ONC =∠DBC ∴ON ∥AB∵NE 是⊙O 的切线,ON 是⊙O 的半径 ∴∠ONE =90°∴∠NEB =90°,即NE ⊥AB ;(2)如解图(1)所示,由(1)可知ON ∥AB ,O 为⊙O 的圆心,∴OC =OB ,∠CMD =90°∴CN =NB =12CB ,MD ∥CB又∵D 是AB 的中点,∴MD =12CB ∴MD =NB .24.(本题满分10分) 已知抛物线L :y =x 2+x -6与x 轴相交于A 、B 两点(点A 在点B 的左侧),并与y 轴相交于点C . (1)求A 、B 、C 三点的坐标,并求出△ABC 的面积; (2)将抛物线向左或向右平移,得到抛物线L ´,且L ´与x 轴相交于A ´、B ´两点(点A ´在点B ´的左侧),并与y 轴交于点C ´,要使△A ´B ´C ´和△ABC 的面积相等,求所有满足条件的抛物线的函数表达式.解:(1)当y =0时,x 2+x -6=0,解得x 1=-3,x 2=2;当x =0时,y =-6 ∴A (-3,0),B (2,0),C (0,6)∴S △ABC =12AB ·OC =12×5×6=15; (2)将抛物线向左或向右平移时,A ´、B ´两点间的距离不变,始终为5,那么要使△A ´B ´C ´和△ABC 的面积相等,高也只能是6设A (a ,0),则B (a +5,0),y =(x -a )(x -a -5),当x =0时,y =a 2+5a当C 点在x 轴上方时,y =a 2+5a =6,a =1或a =-6,此时y =x 2-7x -6或y =x 2+7x -6; 当C 点在x 轴下方时,y =a 2+5a =-6,a =-2或a =-3,此时y =x 2-x -6或y =x 2+x -6(与圆抛物线重合,舍去);所以,所有满足条件的抛物线的函数表达式为:y =x 2-7x -6,y =x 2+7x -6,y =x 2-x -6. 25.(本题满分12分) 问题提出ABB(1)如图①,在△ABC 中,∠A =120°,AB =AC =5,则△ABC 的外接圆半径R 的值为. 问题探究 (2)如图②,⊙O 的半径为13,弦AB =24,M 是AB 的中点,P 是⊙O 上一动点,求PM 的最大值. 问题解决(3)如图③所示,AB 、AC 、BC 是某新区的三条规划路其中,AB =6km ,AC =3km ,∠BAC =60°,BC 所对的圆心角为60°.新区管委会想在BC 路边建物资总站点P ,在AB 、AC 路边分别建物资分站点E 、F .也就是,分别在BC 线段AB 和AC 上选取点P 、E 、F .由于总站工作人员每天要将物资在各物资站点间按P →E →F →P 的路径进行运输,因此,要在各物资站点之间规划道路PE 、EF 和FP .为了快捷环保和节约成本要使得线段PE 、EF 、FP 之和最短,试求PE +EF +FP 的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).图①图②图③解:(1)R =AB =AC =5;(2)如25题解图(2)所示,连接MO 并延长交⊙O 于N ,连接OP显然,MP ≤OM +OP =OM +ON =MN ,ON =13,OM =132-122=5,MN =18 ∴PM 的最大值为18;25题解图(2) 25题解图(3)(3)假设P 点即为所求点,分别作出点P 关于AB 、AC 的对称点P ´、P "连接PP ´、P ´E ,PE ,P "F ,PF ,PP "由对称性可知PE +EF +FP =P ´E +EF +FP "=P ´P ",且P ´、E 、F 、P "在一条直线上,所以P ´P "即为最短距离,其长度取决于P A 的长度25题解图(4)作出弧BC 的圆心O ,连接AO ,与弧BC 交于P ,P 点即为使得P A 最短的点∵AB =6km ,AC =3km ,∠BAC =60°,∴∆ABC 是直角三角形,∠ABC =30°,BC=3 3BP''BBBC所对的圆心角为60°,∴∆OBC是等边三角形,∠CBO=60°,BO=BC=3 3∴∠ABO=90°,AO=37,PA=37-3 3∠P´AE=∠EAP,∠P AF=∠F AP",∴∠P´AP"=2∠ABC=120°,P´A=AP",∴∠AP´E=∠AP"F=30°∵P´P"=2P´A cos∠AP´E=3P´A=321-9所以PE+EF+FP的最小值为321-9km.。
(完整word版)2018陕西省中考数学试卷(附答案解析版)

2018年陕西省中考数学试卷一、选择题(共10小题,每小题3分,计30分。
每小题只有一个选项是符合题意的)1.(3.00分)(2018•陕西)﹣的倒数是()A.B.C.D.2.(3.00分)(2018•陕西)如图,是一个几何体的表面展开图,则该几何体是( )A.正方体B.长方体C.三棱柱D.四棱锥3.(3。
00分)(2018•陕西)如图,若l1∥l2,l3∥l4,则图中与∠1互补的角有( )A.1个B.2个C.3个D.4个4.(3.00分)(2018•陕西)如图,在矩形AOBC中,A(﹣2,0),B(0,1).若正比例函数y=kx 的图象经过点C,则k的值为()A.B.C.﹣2 D.25.(3。
00分)(2018•陕西)下列计算正确的是()A.a2•a2=2a4B.(﹣a2)3=﹣a6C.3a2﹣6a2=3a2D.(a﹣2)2=a2﹣46.(3。
00分)(2018•陕西)如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为()A.B.2C.D.37.(3。
00分)(2018•陕西)若直线l1经过点(0,4),l2经过点(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为( )A.(﹣2,0) B.(2,0)C.(﹣6,0) D.(6,0)8.(3.00分)(2018•陕西)如图,在菱形ABCD中.点E、F、G、H分别是边AB、BC、CD和DA 的中点,连接EF、FG、CH和HE.若EH=2EF,则下列结论正确的是()A.AB=EF B.AB=2EF C.AB=EF D.AB=EF9.(3.00分)(2018•陕西)如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与⊙O相交于点D,连接BD,则∠DBC的大小为()A.15°B.35°C.25°D.45°10.(3。
陕西省2018年中考数学试题及解析(word精编版)

2018年陕西省初中毕业学业考试数学试卷(满分120分,考试时间120分钟)一、选择题(共10小题,每小题3分,计30分。
每小题只有一个选项是符合题意的)1.(3分)﹣的倒数是()A. B. C. D.2.(3分)如图,是一个几何体的表面展开图,则该几何体是()A.正方体B.长方体C.三棱柱D.四棱锥3.(3分)如图,若l1∥l2,l3∥l4,则图中与∠1互补的角有()A.1个 B.2个 C.3个 D.4个4.(3分)如图,在矩形AOBC中,A(﹣2,0),B(0,1).若正比例函数y=kx 的图象经过点C,则k的值为()A.B. C.﹣2 D.25.(3分)下列计算正确的是()A.a2•a2=2a4B.(﹣a2)3=﹣a6C.3a2﹣6a2=3a2 D.(a﹣2)2=a2﹣46.(3分)如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为()A. B.2 C. D.37.(3分)若直线l1经过点(0,4),l2经过点(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为()A.(﹣2,0)B.(2,0)C.(﹣6,0) D.(6,0)8.(3分)如图,在菱形ABCD中.点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、CH和HE.若EH=2EF,则下列结论正确的是()A.AB=EF B.AB=2EF C.AB=EF D.AB=EF9.(3分)如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与⊙O相交于点D,连接BD,则∠DBC的大小为()A.15°B.35°C.25°D.45°10.(3分)对于抛物线y=ax2+(2a﹣1)x+a﹣3,当x=1时,y>0,则这条抛物线的顶点一定在()A.第一象限B.第二象限C.第三象限D.第四象限二、填空题(共4小题,每小题3分,计12分)11.(3分)比较大小:3 (填“>”、“<”或“=”).12.(3分)如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为.13.(3分)若一个反比例函数的图象经过点A(m,m)和B(2m,﹣1),则这个反比例函数的表达式为.14.(3分)如图,点O是▱ABCD的对称中心,AD>AB,E、F是AB边上的点,且EF=AB;G、H是BC边上的点,且GH=BC,若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是.三、解答题(共11小题,计78分。
陕西省2018年中考数学试卷及答案解析(word版)

2018年陕西省中考数学试卷一、选择题:(本大题共10题,每题3分,满分30分)1.-的倒数是A. B.- C. D.-【答案】D【解析】【分析】根据乘积为1的两个数互为倒数进行求解即可得.【详解】∵=1,∴-的倒数是-,故选D.【点睛】本题考查了倒数的定义,熟知乘积为1的两个数互为倒数是解题的关键.2.如图,是一个几何体的表面展开图,则该几何体是A.正方体B.长方体C.三棱柱D.四棱锥【答案】C【解析】根据表面展开图中有两个三角形,三个长方形,由此即可判断出此几何体为三棱柱。
【详解】观察可知图中有一对全等的三角形,有三个长方形,所以此几何体为三棱柱,故选C【点睛】本题考查了几何体的展开图,熟记常见立体图形的展开图特点是解决此类问题的关键.3.如图,若l 1∥l2,l 3∥l4,则图中与∠1互补的角有A. 1个B. 2个C. 3个D. 4个【答案】D【解析】【分析】如图根据平行线的性质可得∠2=∠4,∠1+∠2=180°,再根据对顶角的性质即可得出与∠ 1 互补的角的个数 .【详解】如图,∵l1∥l2,l3∥l4,∵∠2=∠4,∠1+∠2=180°,又∵∠2=∠3,∠4=∠5,∴与∠1互补的角有∠2、∠3、∠4、∠5共4个,故选D.【点睛】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.4.如图,在矩形ABCD中,A(-2,0),B(0,1).若正比例函数y=kx的图像经过点C,则k的取值为A.-B.C.-2D. 2【答案】A【解析】【分析】根据已知可得点C的坐标为(-2,1),把点C坐标代入正比例函数解析式即可求得k.A. a ・= 2aB. (- a )=- aC. 3a -6a = 3aD. ( a -2)=a -4【详解】 A. a ・a = a ,故 A 选项错误;B. (- a )=- a ,正确;C. 3a - 6a = -3a ,故 C 选项错误;D. (a - 2)= a - 4a+4,故 D 选项错误, ,, 【详解】∵ A(- 2,0), B(0, 1),∴ OA=2, OB=1, ∵四边形 OACB 是矩形, ∴ BC=OA=2,AC=OB=1,∵点 C 在第二象限,∴ C 点坐标为( -2, 1), ∵正比例函数 ∴ -2k=1, ∴ k=-, 故选 A.y =kx 的图像经过点C ,【点睛】本题考查了矩形的性质,待定系数法求正比例函数解析式,根据已知求得点 解题的关键 .5.下列计算正确的是C 的坐标是a2 362 2 22 2【答案】 B【解析】【分析】根据同底数幂乘法、幂的乘方、合并同类项法则、完全平方公式逐项进行计算即可得 2 2 42 3 6 2 2 2 2 2 故选 B.【点睛】本题考查了同底数幂的乘法、幂的乘方、合并同类项、完全平方公式,熟练掌握各运算.的运算法则是解题的关键.6.如图,在△ABC 中,AC = 8,∠ ABC = 60°∠ C = 45° AD ⊥ BC ,垂足为 D ,∠ABC 的平分线交 AD 于点E ,则 AE 的长为° A.B. 2C.D. 3【答案】 C【解析】【分析】由已知可知 △ADC 是等腰直角三角形,根据斜边 AC=8可得 AD=4,在 Rt △ABD 中,由∠ B=60°,可得 BD==,再由 BE 平分∠ ABC ,可得∠ EBD=30°,从而可求得 DE 长,再根据AE=AD-DE 即可 【详解】∵ AD ⊥ BC ,∴△ ADC 是直角三角形, ∵∠ C=45°, ∴∠ DAC=45, ∴ AD=DC , ∵ AC=8,∴ AD=4,在 Rt △ABD 中,∠ B=60°,∴ BD===,∵ BE 平分∠ ABC ,∴∠ EBD=30°, ∴ DE=BD?tan30°= ∴ AE=AD-DE= 故选 C.=,,【点睛】本题考查了解直角三角形的应用,熟练掌握直角三角形中边角之间的关系是解题的关键7.若直线 l 1经过点 (0,4),l 2经过 (3, 2),且 l 1与 l 2关于 x 轴对称,则 l 1与 l 2的交点坐标为.A. (- 2,0)B. (2, 0)C. (- 6,0)D. (6, 0)【答案】 B【解析】【分析】根据 l 1与 l 2关于 x 轴对称,可知l 2必经过 (0, -4), l 1必经过点 (3, -2),然后根据待定系数法分别求出 l 1、 l 2的解析式后,再联立解方程组即可得.【详解】由题意可知l 1经过点 (3,-2),( 0, 4),设 l 1的解析式为 y=kx+b ,则有,解得,所以 l 1的解析式为 y=-2x+4,由题意可知由题意可知l2经过点(3,2),(0,-4),设l 1的解析式为y=mx+n,则有,解得,所以l 2的解析式为y=2x-4,联立所以交点坐标为(故选B. ,解得:2,0),,【点睛】本题考查了两直线相交或平行问题,关于x轴对称的点的坐标特征,待定系数法等,熟练应用相关知识解题是关键.8.如图,在菱形ABCD中,点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是A. AB=EFB. AB=2EFC. AB=EFD. AB=EF【答案】D【解析】【分析】连接AC、BD交于点O,由菱形的性质可得OA= AC,OB= BD,AC⊥BD,由中位线定理可得EH= BD,EF= AC,根据EH=2EF,可得OA=EF,OB=2EF,在Rt△AOB中,根据勾股定理即可求得AB= EF,由此即可得到答案.【详解】连接AC、BD交于点O,∵四边形ABCD是菱形,∴OA= AC,OB= BD,AC⊥BD,∵E、F、G、H分别是边AB、BC、CD和DA的中点,∴EH= BD,EF= AC,∵EH=2EF,∴OA=EF,OB=2OA=2EF,在Rt△AOB中,AB=故选D.= EF,10.对于抛物线 y =ax + (2a - 1)x + a -3,当 x =1时, y > 0,则这条抛物线的顶点一定在 , °° - 【点睛】本题考查了菱形的性质、三角形中位线定理、勾股定理等,正确添加辅助线是解决问题 的关键 .9.如图,△ABC 是⊙ O 的内接三角形, AB =AC ,∠ BCA = 65°作 CD ∥AB ,并与O 相交于点 D ,连接 BD , 则∠ DBC 的大小为A. 15°B. 35°C. 25°D. 45° 【答案】 A【详解】∵ AB=AC ,∴∠ ABC=∠ ACB=65°,∴∠ A=180°-∠ ABC-∠ ACB=50°,∵ DC//AB ,∴∠ ACD=∠ A=50°, 又∵∠ D=∠ A=50°,∴∠ DBC=180 -∠ D -∠BCD=180 -50°( 65°+50°) =15°, 故选 A.【点睛】本题考查了等腰三角形的性质,圆周角定理,三角形内角和定理等,熟练掌握相关内容 是解题的关键 .2A.第一象限B.第二象限C.第三象限D.第四象限【答案】 C【详解】∵ 3 =9, 9<10,) ) 【解析】【分析】先由题意得到关于 标的取值范围,据此即可得出答案.a 的不等式,解不等式求出 a 的取值范围,然后再确定抛物线的顶点坐【详解】由题意得: ∴ 2a-1>0,a+(2a-1)+a-3>0,解得: a>1,∴<0,,∴抛物线的顶点在第三象限, 故选 C.【点睛】本题考查了抛物线的顶点坐标公式,熟知抛物线的顶点坐标公式是解题的关键二、填空题:(本大题共 4题,每题 3分,满分 12分).11.比较大小:3_________ 【答案】 <(填 <, >或= ).【解析】【分析】根据实数大小比较的方法进行比较即可得答案 2.∴ 3<,故答案为: <.【点睛】本题考查了实数大小的比较,熟练掌握实数大小比较的方法是解题的关键.12.如图,在正五边形 ABCDE 中, AC 与 BE 相交于点 F ,则 【答案】 72°AFE 的度数为 ________【解析】【分析】首先根据正五边形的性质得到AB=BC=AE ,∠ABC=∠ BAE=108°,然后利用三角形内角和定理得∠ BAC=∠ BCA=∠ ABE=∠ AEB=( 180°-108°÷2=36°,最后利用三角形的外角的性质得到 ∠ AFE=∠ BAC+∠ ABE=72°. 【详解】∵五边形ABCDE 为正五边形,∴ AB=BC=AE ,∠ABC=∠ BAE=108°,∴∠ BAC=∠ BCA=∠ ABE=∠AEB=(180°-108°÷2=36°, ∴∠ AFE=∠BAC+∠ABE=72°, 故答案为: 72°.【点睛】本题考查的是正多边形和圆,利用数形结合求解是解答此题的关键13.若一个反比例函数的图象经过点A(m , m)和 B(2m ,- 1),则这个反比例函数的表达式为______由题意得: m =2m ×(-1),【答案】【解析】【分析】根据反比例函数图象上点的横、纵坐标之积不变可得关于的值,再由待定系数法即可求得反比例函数的解析式-19.y=,【详解】设反比例函数解析式为2解得: m=-2或 m=0(不符题意,舍去), 所以点 A ( -2, -2),点 B (-4, 1), 所以 k=4,y=,所以反比例函数解析式为: 故答案为: y= .m 的方程,解方程即可求得m【点睛】本题考查了反比例函数,熟知反比例函数图象上点的横、纵坐标之积等于比例系数 解题的关键 .k 是14.点 O 是平行四边形ABCD 的对称中心, AD > AB ,E 、 F 分别是 AB 边上的点,且 EF = AB ; G 、 H 分别是 BC 边上的点,且 GH = BC ;若 S 1,S 2分别表示 ? EOF 和 ? GOH 的面积,则 S 1,S 2之间的等量关系是 ______________ 【答案】 2S 1= 3S 2【解析】【分析】过点 O 分别作 OM ⊥ BC ,垂足为 M ,作 ON ⊥AB ,垂足为 N ,根据点 O 是平行四边形ABCD的对称中心以及平行四边形的面积公式可得AB?ON=BC?OM ,再根据S 1= EF?ON ,S 2= GH?OM , EF = AB , GH = BC ,则可得到答案 . 【详解】过点O 分别作 OM ⊥ BC ,垂足为 M ,作 ON ⊥ AB ,垂足为 N ,∵点 O 是平行四边形ABCD 的对称中心,∴ S 平行四边形ABCD =AB?2ON, S 平行四边形ABCD=BC?2OM ,∴ AB?ON=BC?OM ,∵ S 1= EF?ON , S 2= GH?OM , EF = AB ,GH = BC , ∴ S 1= AB?ON , S 2= BC?OM ,∴ 2S 1= 3S 2,- 1|+ (5- 2π)( - 1|+ (5- 2π)故答案为: 2S 1= 3S 2.【点睛】本题考查了平行四边形的面积,中心对称的性质,正确添加辅助线、准确表示出图形面 积是解题的关键 .三、解答题(共 11小题,计 78分.解答应写出过程)15.计算: (-)×-)+|【答案】【解析】【分析】按顺序先分别进行二次根据的乘法运算、绝对值的化简、 序进行计算即可 .0次幂的计算,然后再按运算顺【详解】 (-= 3 = 4)×(- +.)+ |- 1+ 1【点睛】本题考查了二次根式的混合运算,熟练掌握二次根式的混合运算的法则是解题的关键16.化简: 【答案】.【解析】【分析】括号内先通分进行分式的加减运算,然后再进行分式的乘除运算即可得 【详解】= =.=.【点睛】本题考查了分式的混合运算,熟练掌握分式混合运算的顺序是解题的关键.17.如图,已知在正方形ABCD 中, M 是 BC 边上一定点,连接AM ,请用尺规作图法,在AM 上求作一点P ,使得△DPA ∽△ ABM (不写做法保留作图痕迹)【答案】作图见解析.【解析】【分析】根据尺规作图的方法过点D作AM的垂线即可得【详解】如图所示,点P即为所求作的点 .【点睛】本题考查了尺规作图——作垂线,熟练掌握作图的方法是解题的关键.18.如图,AB∥CD,E、F分别为AB、CD上的点,且EC∥BF,连接AD,分别与EC、BF相交与点G、H,若AB=CD,求证:AG=DH.【答案】证明见解析.【解析】【分析】利用AAS先证明?ABH≌?DCG,根据全等三角形的性质可得AH=DG,再根据AH=AG+GH,DG=DH+GH即可证得AG=HD.【详解】∵AB∥CD,∴∠A=∠D,∵CE∥BF,∴∠AHB=∠DGC,在?ABH和?DCG中,,∴?ABH≌?DCG(AAS),∴AH=DG,∵AH=AG+GH,DG=DH+GH,∴AG=HD.【点睛】本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键.19.对垃圾进行分类投放,能有效提高对垃圾的处理和再利用减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度增强同学们的环保意识,普及垃圾分类及投放的相关知识.某校数学兴趣小组的同学 们设计了“垃圾分类知识及投放情况 布情况,他们将全部测试成绩分成”问卷,并在本校随机抽取若干名同学进行了问卷测试.A 、B 、C 、D 四组,绘制了如下统计图表:根据测试成绩分“垃圾分类知识及投放情况”问卷测试成绩统计表依据以上统计信息,解答下列问题:(1)求得 m =, n =;(2)这次测试成绩的中位数落在组;(3)求本次全部测试成绩的平均数.【答案】(1) 30; 19%;( 2) B ;( 3) 80.1分 .【解析】【分析】( 1)根据 B 组的频数以及频率可求得样本容量,然后用样本容量乘以D 组的百分比可求得m 的值,用 A 的频数除以样本容量即可求得n 的值;( 2)根据中位数的定义进行解答即可得解; ( 3)根据平均数的定义进行求解即可得【详解】(1) 72÷36%=200, m=200× 15%=30, n=故答案为: 30, 19%;.=19%,( 2)一共有 200个数据,从小到大排序后中位数是第 中位数落在 B 组, 故答案为: B ;( 3)本次全部测试的平均成绩=100个、第 101个数据的平均数,观察可知=80.1分.【点睛】本题考查了频数分布表,扇形统计图,中位数,平均数等知识,熟练掌握相关的概念是解题的关键 .20.周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB 的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.【答案】河宽为17米.【解析】【分析】由题意先证明?ABC∽?ADE,再根据相似三角形的对应边成比例即可求得AB的长 .【详解】∵CB⊥AD,ED⊥AD,∴∠CBA=∠EDA=90°,∵∠CAB=∠EAD,∴?ABC∽?ADE,∴,又∵AD=AB+BD,BD=8.5,BC=1,DE=1.5,∴,∴AB=17,即河宽为17米.【点睛】本题考查了相似三角形的应用,熟记相似三角形的判定与性质是解题的关键.21.经过一年多的精准帮扶,小明家的网络商店(简称网店)将红枣、小米等优质土特产迅速销往全国,小明家网店中红枣和小米这两种商品的相关信息如下表:商品规格成本(元/袋)售价(元/袋)红枣1kg/袋4060小米2kg/袋3854根据上表提供的信息,解答下列问题:(1)已知今年前五个月,小明家网店销售上表中规格的红枣和小米共求这前五个月小明家网店销售这种规格的红枣多少袋;3000kg,获得利润4.2万元,(2)根据之前的销售情况,估计今年6月到10月这后五个月,小明家网店还能销售上表中规格的红枣和小米共2000 kg,其中,这种规格的红枣的销售量不低于枣味x(kg),销售这种规格的红枣和小米获得的总利润为600kg.假设这后五个月,销售这种规格的红y(元),求出y与x之间的函数关系式,并求出这后五个月,小明家网店销售这种规格的红枣和小米至少获得总利润多少元.【答案】(1)前五个月小明家网店销售这种规格的红枣店销售这种规格的红枣和小米至少获得总利润23200元.1500袋,销售小米750袋;(2)小明家网【解析】【分析】(1)设前五个月小明家网店销售这种规格的红枣a袋,销售小米b袋,根据等量关系:①销售红枣和小米共3000kg,②获得利润4.2万元,列方程组进行求解即可得;(2)根据总利润=红枣的利润+小米的利润,可得即可得答案 .y与x间的函数关系式,根据一次函数的性质【详解】(1)设前五个月小明家网店销售这种规格的红枣a袋,销售小米b袋,根据题意得:,解得:,答:前五个月小明家网店销售这种规格的红枣1500袋,销售小米750袋;(2)根据题意得:y=(60-40)x+(54-38)×∵k=12>0,∴y随x的增大而增大,∵x≥600,∴当x=600时,y取得最小值,最小值为y=12×600+16000=23200,∴小明家网店销售这种规格的红枣和小米至少获得总利润=12x+16000,23200元.【点睛】本题考查了二元一次方程组的应用,一次函数的应用,弄清题意,找出各个量之间的关”” 和所、” 系是解题的关键 .22.如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“ 1的”扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转 出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘, 直到指针指向一个扇形的内部为止)(1)转动转盘一次,求转出的数字是-2的概率;(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.【答案】(1);( 2) .【解析】【分析】(1)根据题意可求得 2个“- 2”所占的扇形圆心角的度数,再利用概率公式进行计算即可得;( 2)由题意可得转出“1、“3、“- 2”的概率相同,然后列表得到所有可能的情况,再找出符合条 件的可能性,根据概率公式进行计算即可得.【详解】(1)由题意可知:“1”“3”占的扇形圆心角为120°,所以 2个“- 2”所占的扇形圆心角为360°- 2×120°= 120°, ∴转动转盘一次,求转出的数字是-2的概率为=;( 2)由( 1)可知,该转盘转出第一次第1二次 “1”“3、“- 2”的概率相同,均为- 2,所有可能性如下表所示:31 -2 3(1, 1)(- 2, 1)(3, 1)(1,- 2)(-2,- 2)(3,- 2)(1, 3)(- 2, 3)(3, 3)由上表可知:所有可能的结果共9种,其中数字之积为正数的的有5种,其概率为., 【点睛】本题考查了列表法或树状图法求概率,用到的知识点为:概率=所求情况数与总情况数之比.23.如图,在Rt ABC 中,∠ ACB = 90°以斜边 AB 上的中线 CD 为直径作⊙ O ,分别与 AC 、BC 相交于 点 M 、 N .(1)过点 N 作⊙ O 的切线 NE 与 AB 相交于点 E ,求证: NE ⊥AB ; (2)连接 MD ,求证: MD = NB .【答案】(1)证明见解析;( 2)证明见解析 .【解析】【分析】(1)如图,连接 ON ,根据直角三角形斜边中线等于斜边的一半可得AD = CD =DB ,从而可得∠ DCB =∠ DBC ,再由∠ DCB =∠ ONC ,可推导得出 ON ∥ AB ,再结合 NE 是⊙ O 的切线,ON//AB , 继而可得到结论;( 2)如图,由( 1)可知 ON ∥AB ,继而可得 N 为 BC 中点,根据圆周角定理可知∠CMD = 90°,继而可得 MD ∥ CB ,再由 D 是 AB 的中点,根据得到【详解】(1)如图,连接 ON ,∵ CD 是 Rt △ABC 斜边 AB 上的中线, ∴ AD = CD =DB , ∴∠ DCB =∠ DBC ,又∵ OC=ON ,∴∠ DCB =∠ ONC , ∴∠ ONC =∠ DBC , ∴ ON ∥ AB ,∵ NE 是⊙ O 的切线, ON 是⊙ O 的半径, ∴∠ ONE = 90°,∴∠ NEB =90°,即 NE ⊥ AB ;( 2)如图所示,由( 1)可知 ON ∥ AB , ∵ OC = OD ,∴∴ CN = NB = CB ,MD =NB .。
2018年陕西省中考数学试卷及答案解析word版

2018年陕西省中考数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,计30分。
每小题只有一个选项是符合题意的)1.(3分)﹣的倒数是()A.B.C.D.分析:根据倒数的定义,互为倒数的两数乘积为1,即可解答.解答:解:﹣的倒数是﹣,故选:D.2.(3分)如图,是一个几何体的表面展开图,则该几何体是()A.正方体B.长方体C.三棱柱D.四棱锥分析:由展开图得这个几何体为棱柱,底面为三边形,则为三棱柱.解答:解:由图得,这个几何体为三棱柱.故选:C.3.(3分)如图,若l1∥l2,l3∥l4,则图中与∠1互补的角有()A.1个 B.2个 C.3个 D.4个分析:直接利用平行线的性质得出相等的角以及互补的角进而得出答案.解答:解:∵l1∥l2,l3∥l4,∴∠1+∠2=180°,2=∠4,∵∠4=∠5,∠2=∠3,∴图中与∠1互补的角有:∠2,∠3,∠4,∠5共4个.故选:D.4.(3分)如图,在矩形AOBC中,A(﹣2,0),B(0,1).若正比例函数y=kx 的图象经过点C,则k的值为()A.B.C.﹣2 D.2分析:根据矩形的性质得出点C的坐标,再将点C坐标代入解析式求解可得.解答:解:∵A(﹣2,0),B(0,1).∴OA=2、OB=1,∵四边形AOBC是矩形,∴AC=OB=1、BC=OA=2,则点C的坐标为(﹣2,1),将点C(﹣2,1)代入y=kx,得:1=﹣2k,解得:k=﹣,故选:A.5.(3分)下列计算正确的是()A.a2•a2=2a4B.(﹣a2)3=﹣a6C.3a2﹣6a2=3a2D.(a﹣2)2=a2﹣4分析:根据同底数幂相乘、幂的乘方、合并同类项法则及完全平方公式逐一计算可得.解答:解:A、a2•a2=a4,此选项错误;B、(﹣a2)3=﹣a6,此选项正确;C、3a2﹣6a2=﹣3a2,此选项错误;D、(a﹣2)2=a2﹣4a+4,此选项错误;故选:B.6.(3分)如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为()A.B.2 C.D.3分析:在Rt△ADC中,利用等腰直角三角形的性质可求出AD的长度,在Rt△ADB 中,由AD的长度及∠ABD的度数可求出BD的长度,在Rt△EBD中,由BD的长度及∠EBD的度数可求出DE的长度,再利用AE=AD﹣DE即可求出AE的长度.解答:解:∵AD⊥BC,∴∠ADC=∠ADB=90°.在Rt△ADC中,AC=8,∠C=45°,∴AD=CD,∴AD=AC=4.在Rt△ADB中,AD=4,∠ABD=60°,∴BD=AD=.∵BE平分∠ABC,∴∠EBD=30°.在Rt△EBD中,BD=,∠EBD=30°,∴DE=BD=,∴AE=AD﹣DE=.故选:C.7.(3分)若直线l1经过点(0,4),l2经过点(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为()A.(﹣2,0)B.(2,0) C.(﹣6,0)D.(6,0)分析:根据对称的性质得出两个点关于x轴对称的对称点,再根据待定系数法确定函数关系式,求出一次函数与x轴的交点即可.解答:解:∵直线l1经过点(0,4),l2经过点(3,2),且l1与l2关于x轴对称,∴两直线相交于x轴上,∵直线l1经过点(0,4),l2经过点(3,2),且l1与l2关于x轴对称,∴直线l1经过点(3,﹣2),l2经过点(0,﹣4),把(0,4)和(3,﹣2)代入直线l1经过的解析式y=kx+b,则,解得:,故直线l1经过的解析式为:y=﹣2x+4,可得l1与l2的交点坐标为l1与l2与x轴的交点,解得:x=2,即l1与l2的交点坐标为(2,0).故选:B.8.(3分)如图,在菱形ABCD中.点E、F、G、H分别是边AB、BC、CD和DA 的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是()A.AB=EF B.AB=2EF C.AB=EF D.AB=EF分析:连接AC、BD交于O,根据菱形的性质得到AC⊥BD,OA=OC,OB=OD,根据三角形中位线定理、矩形的判定定理得到四边形EFGH是矩形,根据勾股定理计算即可.解答:解:连接AC、BD交于O,∵四边形ABCD是菱形,∴AC⊥BD,OA=OC,OB=OD,∵点E、F、G、H分别是边AB、BC、CD和DA的中点,∴EF=AC,EF∥AC,EH=BD,EH∥BD,∴四边形EFGH是矩形,∵EH=2EF,∴OB=2OA,∴AB==OA,∴AB=EF,故选:D.9.(3分)如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与⊙O相交于点D,连接BD,则∠DBC的大小为()A.15°B.35°C.25°D.45°分析:根据等腰三角形性质知∠CBA=∠BCA=65°,∠A=50°,由平行线的性质及圆周角定理得∠ABD=∠ACD=∠A=50°,从而得出答案.解答:解:∵AB=AC、∠BCA=65°,∴∠CBA=∠BCA=65°,∠A=50°,∵CD∥AB,∴∠ACD=∠A=50°,∴∠DBC=∠CBA﹣∠ABD=15°,故选:A.10.(3分)对于抛物线y=ax2+(2a﹣1)x+a﹣3,当x=1时,y>0,则这条抛物线的顶点一定在()A.第一象限B.第二象限C.第三象限D.第四象限分析:把x=1代入解析式,根据y>0,得出关于a的不等式,得出a的取值范围后,利用二次函数的性质解答即可.解答:解:把x=1,y>0代入解析式可得:a+2a﹣1+a﹣3>0,解得:a>1,所以可得:﹣,,所以这条抛物线的顶点一定在第三象限,故选:C.二、填空题三、11.(3分)比较大小:3<(填“>”、“<”或“=”).分析:首先把两个数平方法,由于两数均为正数,所以该数的平方越大数越大.解答:解:32=9,=10,∴3<.12.(3分)如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为72°.分析:根据五边形的内角和公式求出∠EAB,根据等腰三角形的性质,三角形外角的性质计算即可.解答:解:∵五边形ABCDE是正五边形,∴∠EAB=∠ABC==108°,∵BA=BC,同理∠ABE=36°,∴∠AFE=∠ABF+∠BAF=36°+36°=72°,故答案为:72°.13.(3分)若一个反比例函数的图象经过点A(m,m)和B(2m,﹣1),则这个反比例函数的表达式为.分析:设反比例函数的表达式为y=,依据反比例函数的图象经过点A(m,m)和B(2m,﹣1),即可得到k的值,进而得出反比例函数的表达式为.解答:解:设反比例函数的表达式为y=,∵反比例函数的图象经过点A(m,m)和B(2m,﹣1),∴k=m2=﹣2m,解得m1=﹣2,m2=0(舍去),∴k=4,∴反比例函数的表达式为.故答案为:.14.(3分)如图,点O是▱ABCD的对称中心,AD>AB,E、F是AB边上的点,且EF=AB;G、H是BC边上的点,且GH=BC,若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是=.分析:根据同高的两个三角形面积之比等于底边之比得出==,==,再由点O是▱ABCD的对称中心,根据平行四边形的性质可得S△AOB =S △BOC =S ▱ABCD ,从而得出S 1与S 2之间的等量关系.解答:解:∵==,==,∴S 1=S △AOB ,S 2=S △BOC . ∵点O 是▱ABCD 的对称中心, ∴S △AOB =S △BOC =S ▱ABCD ,∴==.即S 1与S 2之间的等量关系是=.故答案为=.三、解答题15.(5分)计算:(﹣)×(﹣)+|﹣1|+(5﹣2π)0分析:先进行二次根式的乘法运算,再利用绝对值的意义和零指数幂的意义计算,然后合并即可. 解答:解:原式=+﹣1+1=3+﹣1+1=4.16.(5分)化简:(﹣)÷.分析:先将括号内分式通分、除式的分母因式分解,再计算减法,最后除法转化为乘法后约分即可得. 解答:解:原式=[﹣]÷=÷ =•=.17.(5分)如图,已知:在正方形ABCD中,M是BC边上一定点,连接AM.请用尺规作图法,在AM上作一点P,使△DPA∽△ABM.(不写作法,保留作图痕迹)分析:过D点作DP⊥AM,利用相似三角形的判定解答即可.解答:解:如图所示,点P即为所求:∵DP⊥AM,∴∠APD=∠ABM=90°,∵∠BAM+∠PAD=90°,∠PAD+∠ADP=90°,∴∠BAM=∠ADP,∴△DPA∽△ABM.18.(5分)如图,AB∥CD,E、F分别为AB、CD上的点,且EC∥BF,连接AD,分别与EC、BF相交于点G,H,若AB=CD,求证:AG=DH.分析:由AB∥CD、EC∥BF知四边形BFCE是平行四边形、∠A=∠D,从而得出∠AEG=∠DFH、BE=CF,结合AB=CD知AE=DF,根据ASA可得△AEG≌△DFH,据此即可得证.解答:证明:∵AB∥CD、EC∥BF,∴四边形BFCE是平行四边形,∠A=∠D,∴∠BEC=∠BFC,BE=CF,∴∠AEG=∠DFH,∵AB=CD,∴AE=DF,在△AEG和△DFH中,∵,∴△AEG≌△DFH(ASA),∴AG=DH.19.(7分)对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况,他们将全部测试成绩分成A、B、C、D四组,绘制了如下统计图表:“垃圾分类知识及投放情况”问卷测试成绩统计表组别分数/分频数各组总分/分A60<x≤70382581B70<x≤80725543C80<x≤90605100D90<x≤100m2796依据以上统计信息解答下列问题:(1)求得m=30,n=19%;(2)这次测试成绩的中位数落在B组;(3)求本次全部测试成绩的平均数.分析:(1)用B组人数除以其所占百分比求得总人数,再用总人数减去A、B、C 组的人数可得m的值,用A组人数除以总人数可得n的值;(2)根据中位数的定义求解可得;(3)根据平均数的定义计算可得.解答:解:(1)∵被调查的学生总人数为72÷36%=200人,∴m=200﹣(38+72+60)=30,n=×100%=19%,故答案为:30、19%;(2)∵共有200个数据,其中第100、101个数据均落在B组,∴中位数落在B组,故答案为:B;(3)本次全部测试成绩的平均数为=80.1(分).20.(7分)周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C、A共线.已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.分析:由BC∥DE,可得=,构建方程即可解决问题.解答:解:∵BC∥DE,∴△ABC∽△ADE,∴=,∴=,∴AB=17(m),经检验:AB=17是分式方程的解,答:河宽AB的长为17米.21.(7分)经过一年多的精准帮扶,小明家的网络商店(简称网店)将红枣、小米等优质土特产迅速销往全国.小明家网店中红枣和小米这两种商品的相关信息如下表:商品红枣小米规格1kg/袋2kg/袋成本(元/袋)4038售价(元/袋)6054根据上表提供的信息,解答下列问题:(1)已知今年前五个月,小明家网店销售上表中规格的红枣和小米共3000kg,获得利润4.2万元,求这前五个月小明家网店销售这种规格的红枣多少袋;(2)根据之前的销售情况,估计今年6月到10月这后五个月,小明家网店还能销售上表中规格的红枣和小米共2000kg,其中,这种规格的红枣的销售量不低于600kg.假设这后五个月,销售这种规格的红枣为x(kg),销售这种规格的红枣和小米获得的总利润为y(元),求出y与x之间的函数关系式,并求这后五个月,小明家网店销售这种规格的红枣和小米至少获得总利润多少元.分析:(1)设这前五个月小明家网店销售这种规格的红枣x袋.根据总利润=42000,构建方程即可;(2)构建一次函数,利用一次函数的性质即可解决问题;解答:解:(1)设这前五个月小明家网店销售这种规格的红枣x袋.由题意:20x+×16=42000解得x=1500,答:这前五个月小明家网店销售这种规格的红枣1500袋.(2)由题意:y=20x+×16=12x+16000,∵600≤x≤2000,当x=600时,y有最小值,最小值为23200元.答:这后五个月,小明家网店销售这种规格的红枣和小米至少获得总利润23200元22.(7分)如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形的圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止).(1)转动转盘一次,求转出的数字是﹣2的概率;(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.分析:(1)将标有数字1和3的扇形两等分可知转动转盘一次共有6种等可能结果,其中转出的数字是﹣2的有2种结果,根据概率公式计算可得;(2)列表得出所有等可能结果,从中找到乘积为正数的结果数,再利用概率公式求解可得.解答:解:(1)将标有数字1和3的扇形两等分可知转动转盘一次共有6种等可能结果,其中转出的数字是﹣2的有2种结果,所以转出的数字是﹣2的概率为=;(2)列表如下:﹣2﹣21133﹣244﹣2﹣2﹣6﹣6﹣244﹣2﹣2﹣6﹣61﹣﹣1133221﹣2﹣211333﹣6﹣633993﹣6﹣63399由表可知共有36种等可能结果,其中数字之积为正数的有20种结果,所以这两次分别转出的数字之积为正数的概率为=.23.(8分)如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC、BC交于点M、N.(1)过点N作⊙O的切线NE与AB相交于点E,求证:NE⊥AB;(2)连接MD,求证:MD=NB.分析:(1)连接ON,如图,根据斜边上的中线等于斜边的一半得到CD=AD=DB,则∠1=∠B,再证明∠2=∠B得到ON∥DB,接着根据切线的性质得到ON⊥NE,然后利用平行线的性质得到结论;(2)连接DN,如图,根据圆周角定理得到∠CMD=∠CND=90°,则可判断四边形CMDN为矩形,所以DM=CN,然后证明CN=BN,从而得到MD=NB.解答:证明:(1)连接ON,如图,∵CD为斜边AB上的中线,∴CD=AD=DB,∴∠1=∠B,∵OC=ON,∴∠1=∠2,∴∠2=∠B,∴ON∥DB,∵NE为切线,∴ON⊥NE,∴NE⊥AB;(2)连接DN,如图,∵CD为直径,∴∠CMD=∠CND=90°,而∠MCB=90°,∴四边形CMDN为矩形,∴DM=CN,∵DN⊥BC,∠1=∠B,∴CN=BN,∴MD=NB.24.(10分)已知抛物线L:y=x2+x﹣6与x轴相交于A、B两点(点A在点B的左侧),并与y轴相交于点C.(1)求A、B、C三点的坐标,并求△ABC的面积;(2)将抛物线L向左或向右平移,得到抛物线L′,且L′与x轴相交于A'、B′两点(点A′在点B′的左侧),并与y轴相交于点C′,要使△A'B′C′和△ABC的面积相等,求所有满足条件的抛物线的函数表达式.分析:(1)解方程x2+x﹣6=0得A点和B点坐标,计算自变量为0的函数值得到C点坐标,然后利用三角形面积公式计算△ABC的面积;(2)利用抛物线平移得到A′B′=AB=5,再利用△A'B′C′和△ABC的面积相等得到C′(0,﹣6)或(0,6),则设抛物线L′的解析式为y=x2+bx﹣6或y=x2+bx+6,当m+n=﹣b,mn=﹣6,然后利用|n﹣m|=5得到b2﹣4×(﹣6)=25,于是解出b 得到抛物线L′的解析式;当m+n=﹣b,mn=6,利用同样方法可得到对应抛物线L′的解析式.解答:解:(1)当y=0时,x2+x﹣6=0,解得x1=﹣3,x2=2,∴A(﹣3,0),B(2,0),当x=0时,y=x2+x﹣6=﹣6,∴C(0,﹣6),∴△ABC的面积=•AB•OC=×(2+3)×6=15;(2)∵抛物线L向左或向右平移,得到抛物线L′,∴A′B′=AB=5,∵△A'B′C′和△ABC的面积相等,∴OC′=OC=6,即C′(0,﹣6)或(0,6),设抛物线L′的解析式为y=x2+bx﹣6或y=x2+bx+6设A'(m,0)、B′(n,0),当m、n为方程x2+bx﹣6=0的两根,∴m+n=﹣b,mn=﹣6,∵|n﹣m|=5,∴(n﹣m)2=25,∴(m+n)2﹣4mn=25,∴b2﹣4×(﹣6)=25,解得b=1或﹣1,∴抛物线L′的解析式为y=x2﹣x﹣6.当m、n为方程x2+bx+6=0的两根,∴m+n=﹣b,mn=6,∵|n﹣m|=5,∴(n﹣m)2=25,∴(m+n)2﹣4mn=25,∴b2﹣4×6=25,解得b=7或﹣7,∴抛物线L′的解析式为y=x2+7x+6或y=x2﹣7x+6.综上所述,抛物线L′的解析式为y=x2﹣x﹣6或y=x2+7x+6或y=x2﹣7x+6.25.(12分)问题提出(1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为5.问题探究(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.问题解决(3)如图③所示,AB、AC、是某新区的三条规划路,其中AB=6km,AC=3km,∠BAC=60°,所对的圆心角为60°,新区管委会想在路边建物资总站点P,在AB,AC路边分别建物资分站点E、F,也就是,分别在、线段AB和AC上选取点P、E、F.由于总站工作人员每天都要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷、环保和节约成本.要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值.(各物资站点与所在道路之间的距离、路宽均忽略不计)分析:(1)设O是△ABC的外接圆的圆心,易证△ABO是等边三角形,所以AB=OA=OB=5;(2)当PM⊥AB时,此时PM最大,连接OA,由垂径定理可知:AM=AB=12,再由勾股定理可知:OM=5,所以PM=OM+OP=18,(3)设连接AP,OP,分别以AB、AC所在直线为对称轴,作出P关于AB的对称点为M,P关于AC的对称点为N,连接MN,交AB于点E,交AC于点F,连接PE、PF,所以AM=AP=AN,设AP=r,易求得:MN=r,所以PE+EF+PF=ME+EF+FN=MN=r,即当AP最小时,PE+EF+PF 可取得最小值.解答:解:(1)设O是△ABC的外接圆的圆心,∴OA=OB=OC,∵∠A=120°,AB=AC=5,∴△ABO是等边三角形,∴AB=OA=OB=5,(2)当PM⊥AB时,此时PM最大,连接OA,由垂径定理可知:AM=AB=12,∵OA=13,∴由勾股定理可知:OM=5,∴PM=OM+OP=18,(3)设连接AP,OP分别以AB、AC所在直线为对称轴,作出P关于AB的对称点为M,P关于AC的对称点为N,连接MN,交AB于点E,交AC于点F,连接PE、PF,∴AM=AP=AN,∵∠MAB=∠PAB,∠NAC=∠PAC,∴∠BAC=∠PAB+∠PAC=∠MAB+∠NAC=60°,∴∠MAN=120°∴M、P、N在以A为圆心,AP为半径的圆上,设AP=r,易求得:MN=r,∵PE=ME,PF=FN,∴PE+EF+PF=ME+EF+FN=MN=r,∴当AP最小时,PE+EF+PF可取得最小值,∵AP+OP≥OA,∴AP≥OA﹣OP,即点P在OA上时,AP可取得最小值,设AB的中点为Q,∴AQ=AC=3,∵∠BAC=60°,∴AQ=QC=AC=BQ=3,∴∠ABC=∠QCB=30°,∴∠ACB=90°,∴由勾股定理可知:BC=3,∵∠BOC=60°,OB=OC=3,∴△OBC是等边三角形,∴∠OBC=60°,∴∠ABO=90°∴由勾股定理可知:OA=3,∵OP=OB=3,∴AP=r=OA﹣OP=3﹣3,∴PE+EF+PF=MN=r=3﹣9∴PE+EF+PF的最小值为(3﹣9)km.。
【精品】2018年陕西省中考数学试卷以及答案(word解析版)

2018年陕西省中考数学试卷一、选择题(10小题,每小题3分,共30分)1.(3分)﹣711的倒数是()A.711B.−711C.117D.−1172.(3分)如图,是一个几何体的表面展开图,则该几何体是()A.正方体B.长方体C.三棱柱D.四棱锥3.(3分)如图,若l1∥l2,l3∥l4,则图中与∠1互补的角有()A.1个 B.2个 C.3个 D.4个4.(3分)如图,在矩形AOBC中,A(﹣2,0),B(0,1).若正比例函数y=kx的图象经过点C,则k的值为()A.−12B.12C.﹣2 D.25.(3分)下列计算正确的是()A.a2•a2=2a4B.(﹣a2)3=﹣a6C.3a2﹣6a2=3a2D.(a﹣2)2=a2﹣46.(3分)如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为()A.432B.22 C.832D.327.(3分)若直线l1经过点(0,4),l2经过点(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为()A.(﹣2,0)B.(2,0) C.(﹣6,0)D.(6,0)8.(3分)如图,在菱形ABCD中.点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、CH和HE.若EH=2EF,则下列结论正确的是()A.AB=2EF B.AB=2EF C.AB=3EF D.AB=5EF9.(3分)如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与⊙O相交于点D,连接BD,则∠DBC的大小为()A.15°B.35°C.25°D.45°10.(3分)对于抛物线y=ax2+(2a﹣1)x+a﹣3,当x=1时,y>0,则这条抛物线的顶点一定在()A.第一象限B.第二象限C.第三象限D.第四象限二、填空题(共4小题,每小题3分,计12分)11.(3分)比较大小:310(填“>”、“<”或“=”).12.(3分)如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为.13.(3分)若一个反比例函数的图象经过点A (m ,m )和B (2m ,﹣1),则这个反比例函数的表达式为 .14.(3分)如图,点O 是▱ABCD 的对称中心,AD >AB ,E 、F 是AB 边上的点,且EF=12AB ;G 、H 是BC 边上的点,且GH=13BC ,若S 1,S 2分别表示△EOF 和△GOH 的面积,则S 1与S 2之间的等量关系是 .三、解答题(共11小题,计78分。
陕西省2018年中考数学试题及解析(word精编版)

2018年陕西省初中毕业学业考试数学试卷(满分120分,考试时间120分钟)一、选择题(共10小题,每小题3分,计30分。
每小题只有一个选项是符合题意的)1. (3分)-的倒数是()A•丄B .丄C .吗D .尹11 11 7 72. (3分)如图,是一个几何体的表面展开图,则该几何体是()A.正方体B.长方体C.三棱柱D.四棱锥3. (3分)如图,若I1//I2, |3//|4,则图中与/ 1互补的角有()A. 1个B . 2个C . 3个D . 4个4. (3分)如图,在矩形AOB(中, A (- 2,0),B (0,1).若正比例函数y=kx 的图象经过点C,则k的值为()C1A0XA.1B1 C . - 2 D . 2225.(3 分) 下列计算正确的是()A.2c 2 c 4a ?a =2a B・( 2、36C. 3a2- 6a2=3a2 D . (a-2) 2=a2- 46. (3 分)如图,在△ ABC 中,AC=8 / ABC=60,/ C=45 , AD 丄 BC ,垂足为D,Z ABC 的平分线交AD 于点E ,则AE 的长为( )7. (3分)若直线l i 经过点(0, 4), 12经过点(3, 2),且I i 与12关于x 轴对称, 则l 1与l 2的交点坐标为( ) A.(- 2,0) B. (2,0) C.( — 6, 0) D . (6, 0)8. (3分)如图,在菱形 ABC 冲.点E 、F 、G H 分别是边AB BC CD 和 DA 的 中点,连接EF 、FG CH 和HE 若EH=2EF 则下列结论正确的是(9. (3 分)如图,△ ABC 是O 0的内接三角形,AB=AC Z BCA=65,作 CD// AB线的顶点一定在( )、填空题(共4小题,每小题3分,计12分)BD 则/ DBC 的大小为( )25°D. 45°10. (3分)对于抛物线 2y=ax + (2a - 1) x+a -3,当x=1时,y >0,则这条抛物A.第一象限B.第二象限C.第三象限D.第四象限A.D . 3 ::B . 2 二C .AB= : ; EF D . AB=〒EFC.连接.肓(填或“二”).11. (3分)比较大小:312. (3分)如图,在正五边形ABCD中, AC与BE相交于点F,则/ AFE的度数14. (3分)如图,点0是?ABCD 勺对称中心,AD >AB, E 、F 是AB 边上的点,且 EF 丄AB; G H 是BC 边上的点,且 GH=BC,若S ,S 分别表示厶EOF^P ^ GOH 23的面积,贝U S 与S2之间的等量关系是 ____ .如图,已知:在正方形 ABC 冲,M 是BC 边上一定点,连接 AM 请P ,使厶DPM A ABM (不写作法,保留作图痕迹)F 分别为AB CD 上的点,且EC// BF ,连接AD A ( m m 和 B (2m, - 1),则这个15. (5 分) 16. (5 分) (共11小题,计78分。
2018年度陕西中考数学试卷及内容答案解析word版

2018年陕西省中考数学试卷参考答案与试题解析一、选择题(共10小题,每题3分,计30分。
每题只有一个选项是符合题意的)1.(3分)﹣的倒数是()A.B.C.D.分析:依照倒数的概念,互为倒数的两数乘积为1,即可解答.解答:解:﹣的倒数是﹣,应选:D.2.(3分)如图,是一个几何体的表面展开图,那么该几何体是()A.正方体B.长方体C.三棱柱D.四棱锥分析:由展开图得那个几何体为棱柱,底面为三边形,那么为三棱柱.解答:解:由图得,那个几何体为三棱柱.应选:C.3.(3分)如图,假设l1∥l2,l3∥l4,那么图中与∠1互补的角有()A.1个B.2个C.3个D.4个分析:直接利用平行线的性质得出相等的角和互补的角进而得出答案.解答:解:∵l1∥l2,l3∥l4,∴∠1+∠2=180°,2=∠4,∵∠4=∠5,∠2=∠3,∴图中与∠1互补的角有:∠2,∠3,∠4,∠5共4个.应选:D.4.(3分)如图,在矩形AOBC中,A(﹣2,0),B(0,1).假设正比例函数y=kx的图象通过点C,那么k的值为()A.B.C.﹣2 D.2分析:依照矩形的性质得出点C的坐标,再将点C坐标代入解析式求解可得.解答:解:∵A(﹣2,0),B(0,1).∴OA=二、OB=1,∵四边形AOBC是矩形,∴AC=OB=一、BC=OA=2,那么点C的坐标为(﹣2,1),将点C(﹣2,1)代入y=kx,得:1=﹣2k,解得:k=﹣,应选:A.5.(3分)以下计算正确的选项是()A.a2•a2=2a4B.(﹣a2)3=﹣a6C.3a2﹣6a2=3a2D.(a﹣2)2=a2﹣4分析:依照同底数幂相乘、幂的乘方、归并同类项法那么及完全平方公式一一计算可得.解答:解:A、a2•a2=a4,此选项错误;B、(﹣a2)3=﹣a6,此选项正确;C、3a2﹣6a2=﹣3a2,此选项错误;D、(a﹣2)2=a2﹣4a+4,此选项错误;应选:B.6.(3分)如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,那么AE的长为()A.B.2 C.D.3分析:在Rt△ADC中,利用等腰直角三角形的性质可求出AD的长度,在Rt△ADB中,由AD的长度及∠ABD的度数可求出BD的长度,在Rt△EBD中,由BD的长度及∠EBD 的度数可求出DE的长度,再利用AE=AD﹣DE即可求出AE的长度.解答:解:∵AD⊥BC,∴∠ADC=∠ADB=90°.在Rt△ADC中,AC=8,∠C=45°,∴AD=CD,∴AD=AC=4.在Rt△ADB中,AD=4,∠ABD=60°,∴BD=AD=.∵BE平分∠ABC,∴∠EBD=30°.在Rt△EBD中,BD=,∠EBD=30°,∴DE=BD=,∴AE=AD﹣DE=.应选:C.7.(3分)假设直线l1通过点(0,4),l2通过点(3,2),且l1与l2关于x轴对称,那么l1与l2的交点坐标为()A.(﹣2,0)B.(2,0) C.(﹣6,0)D.(6,0)分析:依照对称的性质得出两个点关于x轴对称的对称点,再依照待定系数法确信函数关系式,求出一次函数与x轴的交点即可.解答:解:∵直线l1通过点(0,4),l2通过点(3,2),且l1与l2关于x轴对称,∴两直线相交于x轴上,∵直线l1通过点(0,4),l2通过点(3,2),且l1与l2关于x轴对称,∴直线l1通过点(3,﹣2),l2通过点(0,﹣4),把(0,4)和(3,﹣2)代入直线l1通过的解析式y=kx+b,则,解得:,故直线l1通过的解析式为:y=﹣2x+4,可得l1与l2的交点坐标为l1与l2与x轴的交点,解得:x=2,即l1与l2的交点坐标为(2,0).应选:B.8.(3分)如图,在菱形ABCD中.点E、F、G、H别离是边AB、BC、CD和DA的中点,连接EF、FG、GH和HE.假设EH=2EF,那么以下结论正确的选项是()A.AB=EF B.AB=2EF C.AB=EF D.AB=EF分析:连接AC、BD交于O,依照菱形的性质取得AC⊥BD,OA=OC,OB=OD,依照三角形中位线定理、矩形的判定定理取得四边形EFGH是矩形,依照勾股定理计算即可.解答:解:连接AC、BD交于O,∵四边形ABCD是菱形,∴AC⊥BD,OA=OC,OB=OD,∵点E、F、G、H别离是边AB、BC、CD和DA的中点,∴EF=AC,EF∥AC,EH=BD,EH∥BD,∴四边形EFGH是矩形,∵EH=2EF,∴OB=2OA,∴AB==OA,∴AB=EF,应选:D.9.(3分)如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与⊙O相交于点D,连接BD,那么∠DBC的大小为()A.15°B.35°C.25°D.45°分析:依照等腰三角形性质知∠CBA=∠BCA=65°,∠A=50°,由平行线的性质及圆周角定理得∠ABD=∠ACD=∠A=50°,从而得出答案.解答:解:∵AB=AC、∠BCA=65°,∴∠CBA=∠BCA=65°,∠A=50°,∵CD∥AB,∴∠ACD=∠A=50°,又∵∠ABD=∠ACD=50°,∴∠DBC=∠CBA﹣∠ABD=15°,应选:A.10.(3分)关于抛物线y=ax2+(2a﹣1)x+a﹣3,当x=1时,y>0,那么这条抛物线的极点必然在()A.第一象限B.第二象限C.第三象限D.第四象限分析:把x=1代入解析式,依照y>0,得出关于a的不等式,得出a的取值范围后,利用二次函数的性质解答即可.解答:解:把x=1,y>0代入解析式可得:a+2a﹣1+a﹣3>0,解得:a>1,因此可得:﹣,,因此这条抛物线的极点必然在第三象限,应选:C.二、填空题三、11.(3分)比较大小:3<(填“>”、“<”或“=”).分析:第一把两个数平方式,由于两数均为正数,因此该数的平方越大数越大.解答:解:32=9,=10,∴3<.12.(3分)如图,在正五边形ABCDE中,AC与BE相交于点F,那么∠AFE的度数为72°.分析:依照五边形的内角和公式求出∠EAB,依照等腰三角形的性质,三角形外角的性质计算即可.解答:解:∵五边形ABCDE是正五边形,∴∠EAB=∠ABC==108°,∵BA=BC,∴∠BAC=∠BCA=36°,同理∠ABE=36°,∴∠AFE=∠ABF+∠BAF=36°+36°=72°,故答案为:72°.13.(3分)假设一个反比例函数的图象通过点A(m,m)和B(2m,﹣1),那么那个反比例函数的表达式为.分析:设反比例函数的表达式为y=,依据反比例函数的图象通过点A(m,m)和B(2m,﹣1),即可取得k的值,进而得出反比例函数的表达式为.解答:解:设反比例函数的表达式为y=,∵反比例函数的图象通过点A(m,m)和B(2m,﹣1),∴k=m2=﹣2m,解得m1=﹣2,m2=0(舍去),∴k=4,∴反比例函数的表达式为.故答案为:.14.(3分)如图,点O是▱ABCD的对称中心,AD>AB,E、F是AB边上的点,且EF=AB;G、H 是BC边上的点,且GH=BC,假设S1,S2别离表示△EOF和△GOH的面积,那么S1与S2之间的等量关系是=.分析:依照同高的两个三角形面积之比等于底边之比得出==,==,再由点O是▱ABCD的对称中心,依照平行四边形的性质可得S△AOB =S△BOC=S▱ABCD,从而得出S1与S2之间的等量关系.解答:解:∵==,==,∴S1=S△AOB,S2=S△BOC.∵点O是▱ABCD的对称中心,∴S△AOB =S△BOC=S▱ABCD,∴==.即S1与S2之间的等量关系是=.故答案为=.三、解答题15.(5分)计算:(﹣)×(﹣)+|﹣1|+(5﹣2π)0分析:先进行二次根式的乘法运算,再利用绝对值的意义和零指数幂的意义计算,然后归并即可.解答:解:原式=+﹣1+1=3+﹣1+1=4.16.(5分)化简:(﹣)÷.分析:先将括号内分式通分、除式的分母因式分解,再计算减法,最后除法转化为乘法后约分即可得.解答:解:原式=[﹣]÷=÷=•=.17.(5分)如图,已知:在正方形ABCD中,M是BC边上必然点,连接AM.请用尺规作图法,在AM上作一点P,使△DPA∽△ABM.(不写作法,保留作图痕迹)分析:过D点作DP⊥AM,利用相似三角形的判定解答即可.解答:解:如下图,点P即为所求:∵DP⊥AM,∴∠APD=∠ABM=90°,∵∠BAM+∠PAD=90°,∠PAD+∠ADP=90°,∴∠BAM=∠ADP,∴△DPA∽△ABM.18.(5分)如图,AB∥CD,E、F别离为AB、CD上的点,且EC∥BF,连接AD,别离与EC、BF 相交于点G,H,假设AB=CD,求证:AG=DH.分析:由AB∥CD、EC∥BF知四边形BFCE是平行四边形、∠A=∠D,从而得出∠AEG=∠DFH、BE=CF,结合AB=CD知AE=DF,依照ASA可得△AEG≌△DFH,据此即可得证.解答:证明:∵AB∥CD、EC∥BF,∴四边形BFCE是平行四边形,∠A=∠D,∴∠BEC=∠BFC,BE=CF,∴∠AEG=∠DFH,∵AB=CD,∴AE=DF,在△AEG和△DFH中,∵,∴△AEG≌△DFH(ASA),∴AG=DH.19.(7分)对垃圾进行分类投放,能有效提高对垃圾的处置和再利用,减少污染,爱惜环境.为了了解同窗们对垃圾分类知识的了解程度,增强同窗们的环保意识,普及垃圾分类及投放的相关知识,某校数学爱好小组的同窗们设计了“垃圾分类知识及投放情形”问卷,并在本校随机抽取假设干名同窗进行了问卷测试.依照测试成绩散布情形,他们将全数测试成绩分成A、B、C、D四组,绘制了如下统计图表:“垃圾分类知识及投放情形”问卷测试成绩统计表组别分数/分频数各组总分/分A60<x≤70382581B70<x≤80725543C80<x≤90605100D90<x≤100m2796依据以上统计信息解答以下问题:(1)求得m=30,n=19%;(2)这次测试成绩的中位数落在B组;(3)求本次全数测试成绩的平均数.分析:(1)用B组人数除以其所占百分比求得总人数,再用总人数减去A、B、C组的人数可得m 的值,用A组人数除以总人数可得n的值;(2)依照中位数的概念求解可得;(3)依照平均数的概念计算可得.解答:解:(1)∵被调查的学生总人数为72÷36%=200人,∴m=200﹣(38+72+60)=30,n=×100%=19%,故答案为:30、19%;(2)∵共有200个数据,其中第100、101个数据均落在B组,∴中位数落在B组,故答案为:B;(3)本次全数测试成绩的平均数为=(分).20.(7分)周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C、A共线.已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=,BD=.测量示用意如下图.请依照有关测量信息,求河宽AB.分析:由BC∥DE,可得=,构建方程即可解决问题.解答:解:∵BC∥DE,∴△ABC∽△ADE,∴=,∴=,∴AB=17(m),经查验:AB=17是分式方程的解,答:河宽AB的长为17米.21.(7分)通过一年多的精准帮扶,小明家的网络商店(简称网店)将红枣、小米等优质土特产迅速销往全国.小明家网店中红枣和小米这两种商品的相关信息如下表:商品红枣小米规格1kg/袋2kg/袋成本(元/袋)4038售价(元/袋)6054依照上表提供的信息,解答以下问题:(1)已知今年前五个月,小明家网店销售上表中规格的红枣和小米共3000kg,取得利润万元,求这前五个月小明家网店销售这种规格的红枣多少袋;(2)依照之前的销售情形,估量今年6月到10月这后五个月,小明家网店还能销售上表中规格的红枣和小米共2000kg,其中,这种规格的红枣的销售量不低于600kg.假设这后五个月,销售这种规格的红枣为x(kg),销售这种规格的红枣和小米取得的总利润为y(元),求出y与x之间的函数关系式,并求这后五个月,小明家网店销售这种规格的红枣和小米至少取得总利润多少元.分析:(1)设这前五个月小明家网店销售这种规格的红枣x袋.依照总利润=42000,构建方程即可;(2)构建一次函数,利用一次函数的性质即可解决问题;解答:解:(1)设这前五个月小明家网店销售这种规格的红枣x袋.由题意:20x+×16=42000解得x=1500,答:这前五个月小明家网店销售这种规格的红枣1500袋.(2)由题意:y=20x+×16=12x+16000,∵600≤x≤2000,当x=600时,y有最小值,最小值为23200元.答:这后五个月,小明家网店销售这种规格的红枣和小米至少取得总利润23200元22.(7分)如图,能够自由转动的转盘被它的两条直径分成了四个别离标有数字的扇形区域,其中标有数字“1”的扇形的圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,那么该扇形内的数字即为转出的数字,此刻,称为转动转盘一次(假设指针指向两个扇形的交线,那么不计转动的次数,从头转动转盘,直到指针指向一个扇形的内部为止).(1)转动转盘一次,求转出的数字是﹣2的概率;(2)转动转盘两次,用树状图或列表法求这两次别离转出的数字之积为正数的概率.分析:(1)将标有数字1和3的扇形两等分可知转动转盘一次共有6种等可能结果,其中转出的数字是﹣2的有2种结果,依照概率公式计算可得;(2)列表得出所有等可能结果,从中找到乘积为正数的结果数,再利用概率公式求解可得.解答:解:(1)将标有数字1和3的扇形两等分可知转动转盘一次共有6种等可能结果,其中转出的数字是﹣2的有2种结果,因此转出的数字是﹣2的概率为=;(2)列表如下:﹣2﹣21133﹣244﹣2﹣2﹣6﹣6﹣244﹣2﹣2﹣6﹣61﹣2﹣211331﹣2﹣211333﹣6﹣633993﹣6﹣63399由表可知共有36种等可能结果,其中数字之积为正数的有20种结果,因此这两次别离转出的数字之积为正数的概率为=.23.(8分)如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,别离与AC、BC交于点M、N.(1)过点N作⊙O的切线NE与AB相交于点E,求证:NE⊥AB;(2)连接MD,求证:MD=NB.分析:(1)连接ON,如图,依照斜边上的中线等于斜边的一半取得CD=AD=DB,那么∠1=∠B,再证明∠2=∠B取得ON∥DB,接着依照切线的性质取得ON⊥NE,然后利用平行线的性质取得结论;(2)连接DN,如图,依照圆周角定理取得∠CMD=∠CND=90°,那么可判定四边形CMDN为矩形,因此DM=CN,然后证明CN=BN,从而取得MD=NB.解答:证明:(1)连接ON,如图,∵CD为斜边AB上的中线,∴CD=AD=DB,∴∠1=∠B,∵OC=ON,∴∠1=∠2,∴∠2=∠B,∴ON∥DB,∵NE为切线,∴ON⊥NE,∴NE⊥AB;(2)连接DN,如图,∵CD为直径,∴∠CMD=∠CND=90°,而∠MCB=90°,∴四边形CMDN为矩形,∴DM=CN,∵DN⊥BC,∠1=∠B,∴CN=BN,∴MD=NB.24.(10分)已知抛物线L:y=x2+x﹣6与x轴相交于A、B两点(点A在点B的左侧),并与y轴相交于点C.(1)求A、B、C三点的坐标,并求△ABC的面积;(2)将抛物线L向左或向右平移,取得抛物线L′,且L′与x轴相交于A'、B′两点(点A′在点B′的左侧),并与y轴相交于点C′,要使△A'B′C′和△ABC的面积相等,求所有知足条件的抛物线的函数表达式.分析:(1)解方程x2+x﹣6=0得A点和B点坐标,计算自变量为0的函数值取得C点坐标,然后利用三角形面积公式计算△ABC的面积;(2)利用抛物线平移取得A′B′=AB=5,再利用△A'B′C′和△ABC的面积相等取得C′(0,﹣6)或(0,6),那么设抛物线L′的解析式为y=x2+bx﹣6或y=x2+bx+6,当m+n=﹣b,mn=﹣6,然后利用|n﹣m|=5取得b2﹣4×(﹣6)=25,于是解出b取得抛物线L′的解析式;当m+n=﹣b,mn=6,利用一样方式可取得对应抛物线L′的解析式.解答:解:(1)当y=0时,x2+x﹣6=0,解得x1=﹣3,x2=2,∴A(﹣3,0),B(2,0),当x=0时,y=x2+x﹣6=﹣6,∴C(0,﹣6),∴△ABC的面积=•AB•OC=×(2+3)×6=15;(2)∵抛物线L向左或向右平移,取得抛物线L′,∴A′B′=AB=5,∵△A'B′C′和△ABC的面积相等,∴OC′=OC=6,即C′(0,﹣6)或(0,6),设抛物线L′的解析式为y=x2+bx﹣6或y=x2+bx+6设A'(m,0)、B′(n,0),当m、n为方程x2+bx﹣6=0的两根,∴m+n=﹣b,mn=﹣6,∵|n﹣m|=5,∴(n﹣m)2=25,∴(m+n)2﹣4mn=25,∴b2﹣4×(﹣6)=25,解得b=1或﹣1,∴抛物线L′的解析式为y=x2﹣x﹣6.当m、n为方程x2+bx+6=0的两根,∴m+n=﹣b,mn=6,∵|n﹣m|=5,∴(n﹣m)2=25,∴(m+n)2﹣4mn=25,∴b2﹣4×6=25,解得b=7或﹣7,∴抛物线L′的解析式为y=x2+7x+6或y=x2﹣7x+6.综上所述,抛物线L′的解析式为y=x2﹣x﹣6或y=x2+7x+6或y=x2﹣7x+6.25.(12分)问题提出(1)如图①,在△ABC中,∠A=120°,AB=AC=5,那么△ABC的外接圆半径R的值为5.问题探讨(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.问题解决(3)如图③所示,AB、AC、是某新区的三条打算路,其中AB=6km,AC=3km,∠BAC=60°,所对的圆心角为60°,新区管委会想在路边建物资总站点P,在AB,AC路边别离建物资分站点E、F,也确实是,别离在、线段AB和AC上选取点P、E、F.由于总站工作人员天天都要将物资在各物资站点间按P→E→F→P的途径进行运输,因此,要在各物资站点之间打算道路PE、EF和FP.为了快捷、环保和节约本钱.要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值.(各物资站点与所在道路之间的距离、路宽均忽略不计)分析:(1)设O是△ABC的外接圆的圆心,易证△ABO是等边三角形,因此AB=OA=OB=5;(2)当PM⊥AB时,此刻PM最大,连接OA,由垂径定理可知:AM=AB=12,再由勾股定理可知:OM=5,因此PM=OM+OP=18,(3)设连接AP,OP,别离以AB、AC所在直线为对称轴,作出P关于AB的对称点为M,P关于AC的对称点为N,连接MN,交AB于点E,交AC于点F,连接PE、PF,因此AM=AP=AN,设AP=r,易求得:MN=r,因此PE+EF+PF=ME+EF+FN=MN=r,即当AP最小时,PE+EF+PF可取得最小值.解答:解:(1)设O是△ABC的外接圆的圆心,∴OA=OB=OC,∵∠A=120°,AB=AC=5,∴△ABO是等边三角形,∴AB=OA=OB=5,(2)当PM⊥AB时,此刻PM最大,连接OA,由垂径定理可知:AM=AB=12,∵OA=13,∴由勾股定理可知:OM=5,∴PM=OM+OP=18,(3)设连接AP,OP别离以AB、AC所在直线为对称轴,作出P关于AB的对称点为M,P关于AC的对称点为N,连接MN,交AB于点E,交AC于点F,连接PE、PF,∴AM=AP=AN,∵∠MAB=∠PAB,∠NAC=∠PAC,∴∠BAC=∠PAB+∠PAC=∠MAB+∠NAC=60°,∴∠MAN=120°∴M、P、N在以A为圆心,AP为半径的圆上,设AP=r,易求得:MN=r,∵PE=ME,PF=FN,∴PE+EF+PF=ME+EF+FN=MN=r,∴当AP最小时,PE+EF+PF可取得最小值,∵AP+OP≥OA,∴AP≥OA﹣OP,即点P在OA上时,AP可取得最小值,设AB的中点为Q,∴AQ=AC=3,∵∠BAC=60°,∴AQ=QC=AC=BQ=3,∴∠ABC=∠QCB=30°,∴∠ACB=90°,∴由勾股定理可知:BC=3,∵∠BOC=60°,OB=OC=3,∴△OBC是等边三角形,∴∠OBC=60°,∴∠ABO=90°∴由勾股定理可知:OA=3,∵OP=OB=3,∴AP=r=OA﹣OP=3﹣3,∴PE+EF+PF=MN=r=3﹣9∴PE+EF+PF的最小值为(3﹣9)km.。
2018年陕西省中考数学试卷及答案解析word版

2018年陕西省中考数学试卷及答案解析word版解答:解:A、a2•a2=a4,此选项错误;B、(﹣a2)3=﹣a6,此选项正确;C、3a2﹣6a2=﹣3a2,此选项错误;D、(a﹣2)2=a2﹣4a+4,此选项错误;故选:B.6.(3分)如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为()A.B.2C.D.3分析:在Rt△ADC中,利用等腰直角三角形的性质可求出AD的长度,在Rt△ADB 中,由AD的长度及∠ABD的度数可求出BD的长度,在Rt△EBD中,由BD的长度及∠EBD的度数可求出DE的长度,再利用AE=AD﹣DE即可求出AE的长度.解答:解:∵AD⊥BC,∴∠ADC=∠ADB=90°.在Rt△ADC中,AC=8,∠C=45°,∴AD=CD,∴AD=AC=4.在Rt△ADB中,AD=4,∠ABD=60°,∴BD=AD=.∵BE平分∠ABC,∴∠EBD=30°.在Rt△EBD中,BD=,∠EBD=30°,∴DE=BD=,∴AE=AD﹣DE=.故选:C.7.(3分)若直线l1经过点(0,4),l2经过点(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为()A.(﹣2,0) B.(2,0)C.(﹣6,0) D.(6,0)分析:根据对称的性质得出两个点关于x轴对称的对称点,再根据待定系数法确定函数关系式,求出一次函数与x轴的交点即可.解答:解:∵直线l1经过点(0,4),l2经过点(3,2),且l1与l2关于x轴对称,∴两直线相交于x轴上,∵直线l1经过点(0,4),l2经过点(3,2),且l1与l2关于x轴对称,∴直线l1经过点(3,﹣2),l2经过点(0,﹣4),把(0,4)和(3,﹣2)代入直线l1经过的解析式y=kx+b,则,解得:,故直线l1经过的解析式为:y=﹣2x+4,可得l1与l2的交点坐标为l1与l2与x轴的交点,解得:x=2,即l1与l2的交点坐标为(2,0).故选:B.8.(3分)如图,在菱形ABCD中.点E、F、G、H分别是边AB、BC、CD和DA 的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是()A.AB=EF B.AB=2EF C.AB=EF D.AB=EF分析:连接AC、BD交于O,根据菱形的性质得到AC⊥BD,OA=OC,OB=OD,根据三角形中位线定理、矩形的判定定理得到四边形EFGH是矩形,根据勾股定理计算即可.解答:解:连接AC、BD交于O,∵四边形ABCD是菱形,∴AC⊥BD,OA=OC,OB=OD,∵点E、F、G、H分别是边AB、BC、CD和DA的中点,∴EF=AC,EF∥AC,EH=BD,EH∥BD,∴四边形EFGH是矩形,∵EH=2EF,∴OB=2OA,∴AB==OA,∴AB=EF,故选:D.9.(3分)如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与⊙O相交于点D,连接BD,则∠DBC的大小为()A.15°B.35°C.25°D.45°分析:根据等腰三角形性质知∠CBA=∠BCA=65°,∠A=50°,由平行线的性质及圆周角定理得∠ABD=∠ACD=∠A=50°,从而得出答案.解答:解:∵AB=AC、∠BCA=65°,∴∠CBA=∠BCA=65°,∠A=50°,∵CD∥AB,∴∠ACD=∠A=50°,又∵∠ABD=∠ACD=50°,∴∠DBC=∠CBA﹣∠ABD=15°,故选:A.10.(3分)对于抛物线y=ax2+(2a﹣1)x+a﹣3,当x=1时,y>0,则这条抛物线的顶点一定在()A.第一象限B.第二象限C.第三象限D.第四象限分析:把x=1代入解析式,根据y>0,得出关于a的不等式,得出a的取值范围后,利用二次函数的性质解答即可.解答:解:把x=1,y>0代入解析式可得:a+2a﹣1+a﹣3>0,解得:a>1,所以可得:﹣,,所以这条抛物线的顶点一定在第三象限,故选:C.二、填空题三、11.(3分)比较大小:3 <(填“>”、“<”或“=”).分析:首先把两个数平方法,由于两数均为正数,所以该数的平方越大数越大.解答:解:32=9,=10,∴3<.12.(3分)如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为72°.分析:根据五边形的内角和公式求出∠EAB,根据等腰三角形的性质,三角形外角的性质计算即可.解答:解:∵五边形ABCDE 是正五边形,∴∠EAB=∠ABC==108°,∵BA=BC ,∴∠BAC=∠BCA=36°,同理∠ABE=36°,∴∠AFE=∠ABF+∠BAF=36°+36°=72°,故答案为:72°.13.(3分)若一个反比例函数的图象经过点A (m ,m )和B (2m ,﹣1),则这个反比例函数的表达式为.分析:设反比例函数的表达式为y=,依据反比例函数的图象经过点A (m ,m )和B (2m ,﹣1),即可得到k 的值,进而得出反比例函数的表达式为.解答:解:设反比例函数的表达式为y=,∵反比例函数的图象经过点A (m ,m )和B (2m ,﹣1),∴k=m 2=﹣2m ,解得m 1=﹣2,m 2=0(舍去),∴k=4,∴反比例函数的表达式为.故答案为:.14.(3分)如图,点O 是▱ABCD 的对称中心,AD >AB ,E 、F 是AB 边上的点,且EF=AB ;G 、H 是BC 边上的点,且GH=BC ,若S 1,S 2分别表示△EOF 和△GOH的面积,则S 1与S 2之间的等量关系是= .分析:根据同高的两个三角形面积之比等于底边之比得出==,==,再由点O 是▱ABCD 的对称中心,根据平行四边形的性质可得S △AOB=S △BOC =S ▱ABCD ,从而得出S 1与S 2之间的等量关系.解答:解:∵==,==,∴S 1=S △AOB ,S 2=S △BOC .∵点O 是▱ABCD 的对称中心,∴S △AOB =S △BOC =S ▱ABCD ,∴==.即S 1与S 2之间的等量关系是=.故答案为=.三、解答题15.(5分)计算:(﹣)×(﹣)+|﹣1|+(5﹣2π)0分析:先进行二次根式的乘法运算,再利用绝对值的意义和零指数幂的意义计算,然后合并即可.解答:解:原式=+﹣1+1=3+﹣1+1=4.16.(5分)化简:(﹣)÷.分析:先将括号内分式通分、除式的分母因式分解,再计算减法,最后除法转化为乘法后约分即可得.解答:解:原式=[﹣]÷=÷=•=.17.(5分)如图,已知:在正方形ABCD中,M是BC边上一定点,连接AM.请用尺规作图法,在AM上作一点P,使△DPA∽△ABM.(不写作法,保留作图痕迹)分析:过D点作DP⊥AM,利用相似三角形的判定解答即可.解答:解:如图所示,点P即为所求:∵DP⊥AM,∴∠APD=∠ABM=90°,∵∠BAM+∠PAD=90°,∠PAD+∠ADP=90°,∴∠BAM=∠ADP,∴△DPA∽△ABM.18.(5分)如图,AB∥CD,E、F分别为AB、CD上的点,且EC∥BF,连接AD,分别与EC、BF相交于点G,H,若AB=CD,求证:AG=DH.分析:由AB∥CD、EC∥BF知四边形BFCE是平行四边形、∠A=∠D,从而得出∠AEG=∠DFH、BE=CF,结合AB=CD知AE=DF,根据ASA可得△AEG≌△DFH,据此即可得证.解答:证明:∵AB∥CD、EC∥BF,∴四边形BFCE是平行四边形,∠A=∠D,∴∠BEC=∠BFC,BE=CF,∴∠AEG=∠DFH,∵AB=CD,∴AE=DF,在△AEG和△DFH中,∵,∴△AEG≌△DFH(ASA),∴AG=DH.19.(7分)对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况,他们将全部测试成绩分成A、B、C、D四组,绘制了如下统计图表:“垃圾分类知识及投放情况”问卷测试成绩统计表依据以上统计信息解答下列问题:(1)求得m= 30 ,n= 19% ;(2)这次测试成绩的中位数落在 B 组;(3)求本次全部测试成绩的平均数.分析:(1)用B组人数除以其所占百分比求得总人数,再用总人数减去A、B、C 组的人数可得m的值,用A组人数除以总人数可得n的值;(2)根据中位数的定义求解可得;(3)根据平均数的定义计算可得.解答:解:(1)∵被调查的学生总人数为72÷36%=200人,∴m=200﹣(38+72+60)=30,n=×100%=19%,故答案为:30、19%;(2)∵共有200个数据,其中第100、101个数据均落在B组,∴中位数落在B组,故答案为:B;(3)本次全部测试成绩的平均数为=80.1(分).20.(7分)周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C、A共线.已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.分析:由BC∥DE,可得=,构建方程即可解决问题.解答:解:∵BC∥DE,∴△ABC∽△ADE,∴=,∴=,∴AB=17(m),经检验:AB=17是分式方程的解,答:河宽AB的长为17米.21.(7分)经过一年多的精准帮扶,小明家的网络商店(简称网店)将红枣、小米等优质土特产迅速销往全国.小明家网店中红枣和小米这两种商品的相关信息如下表:根据上表提供的信息,解答下列问题:(1)已知今年前五个月,小明家网店销售上表中规格的红枣和小米共3000kg,获得利润4.2万元,求这前五个月小明家网店销售这种规格的红枣多少袋;(2)根据之前的销售情况,估计今年6月到10月这后五个月,小明家网店还能销售上表中规格的红枣和小米共2000kg,其中,这种规格的红枣的销售量不低于600kg.假设这后五个月,销售这种规格的红枣为x(kg),销售这种规格的红枣和小米获得的总利润为y(元),求出y与x之间的函数关系式,并求这后五个月,小明家网店销售这种规格的红枣和小米至少获得总利润多少元.分析:(1)设这前五个月小明家网店销售这种规格的红枣x袋.根据总利润=42000,构建方程即可;(2)构建一次函数,利用一次函数的性质即可解决问题;解答:解:(1)设这前五个月小明家网店销售这种规格的红枣x袋.由题意:20x+×16=42000解得x=1500,答:这前五个月小明家网店销售这种规格的红枣1500袋.(2)由题意:y=20x+×16=12x+16000,∵600≤x≤2000,当x=600时,y有最小值,最小值为23200元.答:这后五个月,小明家网店销售这种规格的红枣和小米至少获得总利润23200元22.(7分)如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形的圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止).(1)转动转盘一次,求转出的数字是﹣2的概率;(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.分析:(1)将标有数字1和3的扇形两等分可知转动转盘一次共有6种等可能结果,其中转出的数字是﹣2的有2种结果,根据概率公式计算可得;(2)列表得出所有等可能结果,从中找到乘积为正数的结果数,再利用概率公式求解可得.解答:解:(1)将标有数字1和3的扇形两等分可知转动转盘一次共有6种等可能结果,其中转出的数字是﹣2的有2种结果,所以转出的数字是﹣2的概率为=;(2)列表如下:由表可知共有36种等可能结果,其中数字之积为正数的有20种结果,所以这两次分别转出的数字之积为正数的概率为=.23.(8分)如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC、BC交于点M、N.(1)过点N作⊙O的切线NE与AB相交于点E,求证:NE⊥AB;(2)连接MD,求证:MD=NB.分析:(1)连接ON,如图,根据斜边上的中线等于斜边的一半得到CD=AD=DB,则∠1=∠B,再证明∠2=∠B得到ON∥DB,接着根据切线的性质得到ON⊥NE,然后利用平行线的性质得到结论;(2)连接DN,如图,根据圆周角定理得到∠CMD=∠CND=90°,则可判断四边形CMDN为矩形,所以DM=CN,然后证明CN=BN,从而得到MD=NB.解答:证明:(1)连接ON,如图,∵CD为斜边AB上的中线,∴CD=AD=DB,∴∠1=∠B,∵OC=ON,∴∠1=∠2,∴∠2=∠B,∴ON∥DB,∵NE为切线,∴ON⊥NE,∴NE⊥AB;(2)连接DN,如图,∵CD为直径,∴∠CMD=∠CND=90°,而∠MCB=90°,∴四边形CMDN为矩形,∴DM=CN,∵DN⊥BC,∠1=∠B,∴CN=BN,∴MD=NB.24.(10分)已知抛物线L:y=x2+x﹣6与x轴相交于A、B两点(点A在点B 的左侧),并与y轴相交于点C.(1)求A、B、C三点的坐标,并求△ABC的面积;(2)将抛物线L向左或向右平移,得到抛物线L′,且L′与x轴相交于A'、B′两点(点A′在点B′的左侧),并与y轴相交于点C′,要使△A'B′C′和△ABC的面积相等,求所有满足条件的抛物线的函数表达式.分析:(1)解方程x2+x﹣6=0得A点和B点坐标,计算自变量为0的函数值得到C点坐标,然后利用三角形面积公式计算△ABC的面积;(2)利用抛物线平移得到A′B′=AB=5,再利用△A'B′C′和△ABC的面积相等得到C′(0,﹣6)或(0,6),则设抛物线L′的解析式为y=x2+bx﹣6或y=x2+bx+6,当m+n=﹣b,mn=﹣6,然后利用|n﹣m|=5得到b2﹣4×(﹣6)=25,于是解出b得到抛物线L′的解析式;当m+n=﹣b,mn=6,利用同样方法可得到对应抛物线L′的解析式.解答:解:(1)当y=0时,x2+x﹣6=0,解得x1=﹣3,x2=2,∴A(﹣3,0),B(2,0),当x=0时,y=x2+x﹣6=﹣6,∴C(0,﹣6),∴△ABC的面积=•AB•OC=×(2+3)×6=15;(2)∵抛物线L向左或向右平移,得到抛物线L′,∴A′B′=AB=5,∵△A'B′C′和△ABC的面积相等,∴OC′=OC=6,即C′(0,﹣6)或(0,6),设抛物线L′的解析式为y=x2+bx﹣6或y=x2+bx+6设A'(m,0)、B′(n,0),当m、n为方程x2+bx﹣6=0的两根,∴m+n=﹣b,mn=﹣6,∵|n﹣m|=5,∴(n﹣m)2=25,∴(m+n)2﹣4mn=25,∴b2﹣4×(﹣6)=25,解得b=1或﹣1,∴抛物线L′的解析式为y=x2﹣x﹣6.当m、n为方程x2+bx+6=0的两根,∴m+n=﹣b,mn=6,∵|n﹣m|=5,∴(n﹣m)2=25,∴(m+n)2﹣4mn=25,∴b2﹣4×6=25,解得b=7或﹣7,∴抛物线L′的解析式为y=x2+7x+6或y=x2﹣7x+6.综上所述,抛物线L′的解析式为y=x2﹣x﹣6或y=x2+7x+6或y=x2﹣7x+6.25.(12分)问题提出(1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为 5 .问题探究(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.问题解决(3)如图③所示,AB、AC、是某新区的三条规划路,其中AB=6km,AC=3km,∠BAC=60°,所对的圆心角为60°,新区管委会想在路边建物资总站点P,在AB,AC路边分别建物资分站点E、F,也就是,分别在、线段AB和AC 上选取点P、E、F.由于总站工作人员每天都要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷、环保和节约成本.要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值.(各物资站点与所在道路之间的距离、路宽均忽略不计)分析:(1)设O是△ABC的外接圆的圆心,易证△ABO是等边三角形,所以AB=OA=OB=5;(2)当PM⊥AB时,此时PM最大,连接OA,由垂径定理可知:AM=AB=12,再由勾股定理可知:OM=5,所以PM=OM+OP=18,(3)设连接AP,OP,分别以AB、AC所在直线为对称轴,作出P关于AB的对称点为M,P关于AC的对称点为N,连接MN,交AB于点E,交AC于点F,连接PE、PF,所以AM=AP=AN,设AP=r,易求得:MN=r,所以PE+EF+PF=ME+EF+FN=MN=r,即当AP最小时,PE+EF+PF可取得最小值.解答:解:(1)设O是△ABC的外接圆的圆心,∴OA=OB=OC,∵∠A=120°,AB=AC=5,∴△ABO是等边三角形,∴AB=OA=OB=5,(2)当PM⊥AB时,此时PM最大,连接OA,由垂径定理可知:AM=AB=12,∵OA=13,∴由勾股定理可知:OM=5,∴PM=OM+OP=18,(3)设连接AP,OP分别以AB、AC所在直线为对称轴,作出P关于AB的对称点为M,P关于AC的对称点为N,连接MN,交AB于点E,交AC于点F,连接PE、PF,∴AM=AP=AN,∵∠MAB=∠PAB,∠NAC=∠PAC,∴∠BAC=∠PAB+∠PAC=∠MAB+∠NAC=60°,∴∠MAN=120°∴M、P、N在以A为圆心,AP为半径的圆上,设AP=r,易求得:MN=r,∵PE=ME,PF=FN,∴PE+EF+PF=ME+EF+FN=MN=r,∴当AP最小时,PE+EF+PF可取得最小值,∵AP+OP≥OA,∴AP≥OA﹣OP,即点P在OA上时,AP可取得最小值,设AB的中点为Q,∴AQ=AC=3,∵∠BAC=60°,∴AQ=QC=AC=BQ=3,∴∠ABC=∠QCB=30°,∴∠ACB=90°,∴由勾股定理可知:BC=3,∵∠BOC=60°,OB=OC=3,∴△OBC是等边三角形,∴∠OBC=60°,∴∠ABO=90°∴由勾股定理可知:OA=3,∵OP=OB=3,∴AP=r=OA﹣OP=3﹣3,∴PE+EF+PF=MN=r=3﹣9∴PE+EF+PF的最小值为(3﹣9)km.第21页(共22页)第22页(共22页)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年陕西省中考数学试卷
一、选择题:(本大题共10题,每题3分,满分30分) 1.- 7
11的倒数是( )
A . 7 11
B .-
7 11
C .
11
7
D .-
11
7
2.如图,是一个几何体的表面展开图,则该几何体是( ) A .正方体 B .长方体 C .三棱柱 D .四棱锥 3.如图,若l 1∥l 2,l 3∥l 4,则图中与∠1互补的角有( )
A .1个
B .2个
C .3个
D .4个
4.如图,在矩形ABCD 中,A (1,0),B(0,1).若正比例函数y =kx 的图像经过点C ,则k 的取值为( ) A .-
1 2
B . 1 2
C .-2
D .2
(第2
题图)
l 3
l 4
(第3题图)
(第4题图)
5.下列计算正确的是( ) A .a a a 4222=•
B .a a 623
)(-=-
C .a a a 222363=-
D . 4)2(22-=-a a
6.如图,在△ABC 中,AC =8,∠ABC =60°,∠C =45°,AD ⊥BC ,垂足为D ,∠ABC 的平分线交AD 于点E ,则AE 的长为( )
A .
3
2
4 B .22 C .
3
2
8 D .23
7.若直线l 1经过点(0,4),l 2经过(3,2),且l 1与l 2关于x 轴对称,则l 1与l 2的交点坐标为( ) A .(-2,0)
B .(2,0)
C .(-6,0)
D .(6,0)
8.如图,在菱形ABCD 中,点E 、F 、G 、H 分别是边AB 、BC 、CD 和DA 的中点,连接EF 、FG 、GH 和HE .若EH =2EF ,则下列结论正确的是( )
A .A
B =EF 2
B .AB =2EF
C . EF AB 3=
D .AB =
EF 5
(第6题图)
C (第8题图)
(第9题图)
9.如图,△ABC 是⊙O 的内接三角形,AB =AC ,∠BCA =65°,作CD ∥AB ,并与○O 相交于点D ,连接BD ,则∠DBC 的大小为( )
A .15°
B .35°
C .25°
D .45°
10.对于抛物线3)12(2-+-+=a x a x a y ,当x =1时,y >0,则这条抛物线的顶点一定在( ) A .第一象限; B .第二象限 ; C 第三象限. ; D 第四象限. 二、填空题(4分×3=12分)
11、比较大小:3_____ 10(填<,>或=).
【试题解析】平方法:2
2
3910==.
12、如图,在正五边形ABCDE 中,AC 与BE 相交于点F
,则
AFE 的度数为_____
(第12题图)
B
(第14题图)
D
13、若一个反比例函数的图像经过点A (m ,m )和B (2m ,-1),则这个反比例函数的表达式为_____ 14、点O 是平行四边形ABCD 的对称中心,AD
>AB ,E ,F 分别是AB 边上的点,且EF = 1
2AB ;G ,H 分别是BC 边上的点,且GH = 1
3BC ;,若12,S S 分别表示EOF 和GOH 的面积,则12,S S 之间的等量关系是_____
三、解答题(共11小题,计18分.解答应写出过程) 15.(本题满分5分) 计算:.)25(12)6()3(0π-+-+-⨯-
16.(本题满分5分) 先化简,再求值:.1
3)111(
2a
a a a a a a ++÷+--+
17.(本题满分5分)
如图,已知在正方形ABCD 中,M 是BC 边上一定点,连接AM ,请用尺规作图法,在AM 上求作一点P ,使得△DPA ∽△ABM (不写做法保留作图痕迹)
(第17题图)
18、(本题满分5分)
如图,AB ∥CD ,E 、F 分别为AB 、CD 上的点,且EC ∥BF ,连接AD ,分别与EC 、BF 相交与点G 、H ,若AB =CD ,求证:AG =DH .
(第18题图)
A
D
19.(本题满分7分)
对垃圾进行分类投放,能有效提高对垃圾的处理和再利用减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度增强同学们的环保意识,普及垃圾分类及投放的相关知识.某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况,他们将全部测试成绩分成A 、B 、C 、D 四组,绘制了如下统计图表:
“垃圾分类知识及投放情况”问卷测试成绩统计表
(第19题图)
依据以上统计信息,解答下列问题: (1)求得m =_______,n =__________; (2)这次测试成绩的中位数落在_______组; (3)求本次全部测试成绩的平均数.
20.(本题满分7分)
周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.
请根据相关测量信息,求河宽AB.
21.(本题满分7分)
经过一年多的精准帮扶,小明家的网络商店(简称网店)将红枣、小米等优质土特产迅速销往全国,小明家网店中红枣和小米这两种商品的相关信息如下表:
商品红枣小米
规格1kg/袋2kg/袋
成本(元/袋)40 38
售价(元/袋)60 54
根据上表提供的信息,解答下列问题:
(1)已知今年前五个月,小明家网店销售上表中规格的红枣和小米共3000kg,获得利润4.2万元,求这前五个月小明家网店销售这种规格的红枣多少袋;
(2)根据之前的销售情况,估计今年6月到10月这后五个月,小明家网店还能销售上表中规格的红枣和小米共2000kg,其中,这种规格的红枣的销售量不低于600kg.假设这后五个月,销售这种规格的红枣味x(kg),销售这种规格的红枣和小米获得的总利润为y(元),求出y与x之间的函数关系式,并求出这后五个月,小明家网店销售这种规格的红枣和小米至少获得总利润多少元.
22.(本题满分7分)
如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.
23.(本题满分8分)
如图,在Rt △ABC 中,∠ACB =90°,以斜边AB 上的中线CD 为直径作○O ,分别与AC 、BC 相交于点M 、N .
(1)过点N 作⊙O 的切线NE 与AB 相交于点E ,求证:NE ⊥AB ; (2)连接MD ,求证:MD =NB .
(第23题图)
(第22题图)
24.(本题满分10分)
已知抛物线L :62-+=x x y 与x 轴相交于A 、B 两点(点A 在点B 的左侧),并与y 轴相交于点C . (1)求A 、B 、C 三点的坐标,并求出△ABC 的面积;
(2)将抛物线向左或向右平移,得到抛物线L ’,且L ’与x 轴相交于A ’、B ’两点(点A ’在点B ’的左侧),并与y 轴交于点C ’,要使△A ’B ’C ’和△ABC 的面积相等,求所有满足条件的抛物线的函数表达式.
25.(本题满分12分) 问题提出
(1)如图①,在△ABC 中,∠A =120°,AB =AC =5,则△AC 的外接圆半径R 的值为_______. 问题探究
(2)如图②,⊙O 的半径为13,弦AB =24,M 是AB 的中点,P 是⊙O 上一动点,求PM 的最大值. 问题解决
(3)如图③所示,AB 、AC 、BC 是某新区的三条规划路其中,AB =6km ,AC =3km ,∠BC =60°,BC 所对的圆心角为60°.新区管委会想在BC 路边建物资总站点P ,在AB 、AC 路边分别建物资分站点E 、F .也就是,分别在BC 线段AB 和AC 上选取点P 、E 、F .由于总站工作人员每天要将物资在各物资站点间按P →E →F →P 的路径进行运输,因此,要在各物资站点之间规划道路PE 、EF 和FP .为了快捷环保和节约成本要使得线段PE 、EF 、FP 之和最短,试求PE +EF +FP 的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计)
(第25题图)
图③
图②图①
C。
