互换的定价
第七讲互换的定价讲义.
2、互换价值的计算
（1）运用债券组合的方法
B flx :互换合约中分解出的固定利率债券的价值。 B fi :互换合约中分解出的浮动利率债券的价值。
对B公司而言，这个互换的价值就是：
V互换 B fl B fix
固定利的时间（1≤i≤n）， A： 利率互换合约中的名义本金额， ri：到期日为Ti的LIBOR连续复利即期利率， k：支付日支付的固定利息额。
6个月后的远期利率为：
现金流的价值为：
5% 0.5 4.8% 0.25 5.2% 0.25
10000 (e4.77%0.25 e5.2%0.25 )e5%0.5 10.581
9个月的远期利率为： 现金流的价值为：
5.1% 0.75 5% 0.5 5.3% 0.25
（三）利率互换的两种定价方法
1、定价思路
①将互换分解成一个债券的多头与一个债券的空头的 组合。 ②远期利率协议（FRA）的合约里事先确定将来某一时 间一笔借款的利率。在FRA执行的时候，支付的只是市场利 率与合约协定利率的利差。
举例
考虑一个2003年9月1日生效的三年期的利率互换，名
第七讲
互换的定价
一、利率互换的定价
（一）定价思路
在假设无违约风险的情况下，对利率互换进行分解 – – 分解成一个债券的多头与一个债券的空头。 分解成一个远期利率协议的组合来定价。
（二）贴现率选择
定价时现金流通常用LIBOR零息票利率贴现。
LIBOR反映了金融机构的资金成本。其隐含假设是被 定价的衍生工具的现金流的风险和银行同业拆借市场的风 险相同。
B fix 120e0.0480.25 120e0.050.5 10120e0.510.75 9975.825(万美元)
互换的定价
2、增长型互换（Accreting Swaps）、减少型互换（Amortizing Swaps）和滑道型互换（Roller－Coaster Swaps）。
3、基点互换（Basis Swaps）。 4、可延长互换（Extendable Swaps） 和可赎回互换。 5、零息互换（Zero—Coupon Swaps）。 6、后期确定互换（Back— Set Swaps） 7、差额互换（Differential Swaps） 8、远期互换（Forward Swaps） 9、互换期权（Swaption） 10、股票互换（Equity Swaps）
的优势。
生产衣料是英国的相对成本更低，而生产葡萄酒则是葡萄牙的
相对成本更低。
分工使双方的产量都提高了，两国的总产量也提高了。
由于有分工和交易，在劳动力没有增加、没有什么其他损失的情况下，
两个国家的财富都增加了。
互换的条件：
只要存在比较优势，双方就可通过适当的分工和交换使双方共同
考虑一个2003年9月1日生效的三年期的利率互换，名义
本金是1亿美元。B公司同意支付给A公司年利率为5％的利 息，同时A公司同意支付给B公司6个月期LIBOR的利息，
利息每半年支付一次。
图5.4 利率互换
表5.3
利率互换中B公司的现金流量表（百万美元）
日期 2003.9.1 2004.3.1 2004.9.1 2005.3.1 2005.9.1 2006.3.1 2006.9.1
当互换对公司而言价值为负，而且合约的另一方即将破产时，理 论上该公司面临一个意外收益，因为对方的违约将导致一项负债 的消失。 将互换合约的信用风险和市场风险区分开来是十分重要的。 市场风险可以用对冲交易来规避，信用风险则比较难规避。
互换的定价
第二，在协议签订时，一个公平的利率互换协议应 使得双方的互换价值相等。也就是说，协议签订时 的互换定价，就是选择一个使得互换的初始价值为 零的固定利率。
互换的定价与风险分析
忽略天数计算 以国际市场上的互换为例，浮动利率使用
LIBOR 贴现率也使用LIBOR
2
举例
考虑一个2005年9月1日生效的两年期利率互换， 名义本金为1亿美元。甲银行同意支付给乙公司年 利率为2.8％的利息，同时乙公司同意支付给甲银 行3个月期LIBOR的利息，利息每3个月交换一次。 利率互换中甲银行的现金流量表如表7-1所示，其 中（a）为不考虑名义本金，（b）为考虑名义本金 的情况。
净额结算 抵押和盯市 信用衍生产品
总的来看，由于国际市场上的互换协议通常涉 及资本雄厚、信用等级高的大型机构，互换违 约造成的总损失历来是较低的
28
与互换相联系的市场风险主要可分为利率风险 和汇率风险：
对于利率互换来说主要的市场风险是利率风险 对于货币互换而言市场风险包括利率风险和汇率风
3
表7-1 利率互换中甲银行的现金流量表 （百万美元） （a）不考虑名义本金
4
表7-1 利率互换中甲银行的现金流量表 （百万美元） （b）考虑名义本金
5
该利率互换由列（4）的净现金流 序列组成，这是互换的本质，即未 来系列现金流的组合
6
列（4）＝列（2）＋列（3） 在互换生效日与到期日增加1亿美元的本金
19
与利率互换类似，货币互换也可以分解为债券 的组合或远期协议的组合，只是这里的债券组 合不再是浮动利率债券和固定利率债券的组合， 而是一份外币债券和一份本币债券的组合，远 期协议也不再是FRA，而是远期外汇协议
互换定价的原理
互换定价的原理
互换定价是一种市场策略，在这种策略中，两个或多个对手方互换产品或服务的价格，以达到双方的利益最大化。
这种策略常常用于竞争激烈的市场，同时也可以作为一种谈判策略。
互换定价的原理是基于供需关系和市场竞争的基本原理。
在市场上，价格往往由供求关系决定。
如果某个产品或服务的需求量大于供应量，其价格可能会上升；反之，如果供应量大于需求量，价格可能会下降。
而互换定价则是通过调整价格来平衡供求关系，从而实现利益最大化。
在互换定价中，两个或多个对手方可以利用定价策略来实现双赢局面。
他们可以相互讨论和协商，通过调整各自的价格来达到最佳的平衡点。
通过互换产品或服务的定价，每个对手方可以在市场上获得更多的机会和竞争优势。
互换定价还可以用作谈判策略。
在商业谈判中，对手方常常试图通过互换定价来达成一致。
他们可以相互提出各自的定价要求，并在沟通和协商的过程中逐渐调整和协调双方的利益和诉求，最终达成一致意见。
总的来说，互换定价是一种通过调整价格来实现供需平衡和利益最大化的市场策略。
它可以用于竞争激烈的市场环境中，也可以作为商业谈判的一种策略手段。
【VIP专享】第04章 互换的定价
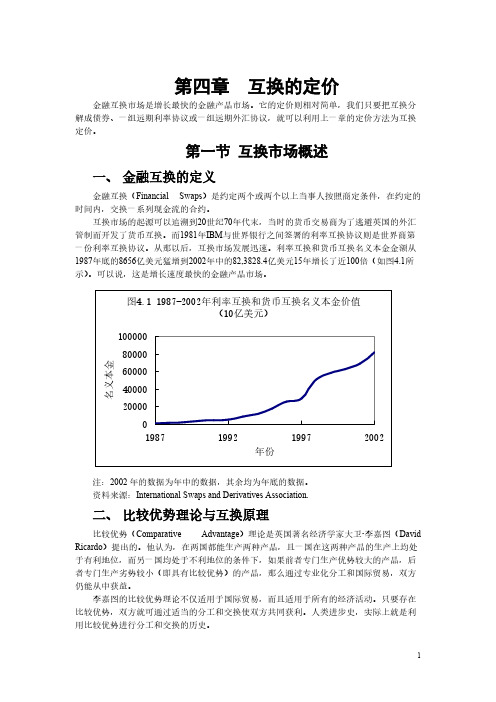
第四章互换的定价金融互换市场是增长最快的金融产品市场。
它的定价则相对简单，我们只要把互换分解成债券、一组远期利率协议或一组远期外汇协议，就可以利用上一章的定价方法为互换定价。
第一节互换市场概述一、金融互换的定义金融互换（Financial Swaps）是约定两个或两个以上当事人按照商定条件，在约定的时间内，交换一系列现金流的合约。
互换市场的起源可以追溯到20世纪70年代末，当时的货币交易商为了逃避英国的外汇管制而开发了货币互换。
而1981年IBM与世界银行之间签署的利率互换协议则是世界商第一份利率互换协议。
从那以后，互换市场发展迅速。
利率互换和货币互换名义本金金额从1987年底的8656亿美元猛增到2002年中的82,3828.4亿美元15年增长了近100倍（如图4.1所示）。
可以说，这是增长速度最快的金融产品市场。
注：2002年的数据为年中的数据，其余均为年底的数据。
资料来源：International Swaps and Derivatives Association.二、比较优势理论与互换原理比较优势（Comparative Advantage）理论是英国著名经济学家大卫 李嘉图（David Ricardo）提出的。
他认为，在两国都能生产两种产品，且一国在这两种产品的生产上均处于有利地位，而另一国均处于不利地位的条件下，如果前者专门生产优势较大的产品，后者专门生产劣势较小（即具有比较优势）的产品，那么通过专业化分工和国际贸易，双方仍能从中获益。
李嘉图的比较优势理论不仅适用于国际贸易，而且适用于所有的经济活动。
只要存在比较优势，双方就可通过适当的分工和交换使双方共同获利。
人类进步史，实际上就是利用比较优势进行分工和交换的历史。
互换是比较优势理论在金融领域最生动的运用。
根据比较优势理论，只要满足以下两种条件，就可进行互换：①双方对对方的资产或负债均有需求；②双方在两种资产或负债上存在比较优势。
金融工程第7章互换的定价与风险分析
精选ppt
15
确定利率互换的固定利率，可以令互换初始价 值为0，解方程求出k。
万美元
i=5.053%精选ppt16（三）基于远期利率的利率互换定价（用远期 利率代替各次浮动利率，有n次浮动利率的信息 分析）
设利率期限结构的利率如下（用于现金流的贴现利 率），半年复利一次：
再设各期远期利率（代替利率互换未来的浮动利 率），半年复利一次：
对以下利率互换定价。其中，互换n/2年后
到期，名义本金为NP，半年交换一次利息：
x(固定利率)
多A
B空
L（浮动利率）
精选ppt
17
17
A方（多方）收到浮动利息，每次浮动利息
用远期利息代替，再贴现求和就得到收入的现金 流现值总和；A方每次支出的固定利息为 NP*(x/2)，分别贴现求和得到支出的现金流现值 总和。令两个总和相等可解出固定利率x。
第二，求公平合理的固定利率。在协议签订 时，一个公平的利率互换协议应使得双方 的互换价值相等。也就是说，协议签订时 的互换定价，就是选择一个使得互换的初 始价值为零的固定利率。
精选ppt
10
为了说明公式（7.1）的运用，定义 i=t1i ,：2,距…,第n）i 。次 现 金 流 交 换 的 时 间 长 度 （ L ：利率互换合约中的名义本金额。 ri ：到期日为ti的LIBOR零息票利率,折现率 k ：支付日支付的固定利息额。
由二者相等，解得4K=543万美元， i=543/10000=5.43%(每3个月支付一次)
精选ppt
21
21
(五)利率互换合理的固定利率（互 换利率）的确定
互换利率（合约价值为0的固定利率）：利 率互换协议中合理的固定利率就是使得互 换价值为零的利率水平，也就是我们通常 所说的互换利率
第十章 互换定价《金融工程学》PPT课件
变量定义
第一节 利率互换的定价
第一节 利率互换的定价
一、运用债券组合给利率互换定价
第一节 利率互换的定价
一、运用债券组合给利率互换定价
第一节 利率互换的定价
一、运用债券组合给利率互换定价
角色 身份 等价
价值
互换多头
固定利率的支付者 浮动利率的收入者
互换空头
固定利率的收入者 浮动利率的支付者
出售一份名义面值的固定利率债 券
+1.20
-1.10
+1.20
-1.10
+1.20
-1.10
+16.20
-11.10
第二节 货币互换的定价
货币互换也可以分解为一份外币债券和一份本币债券的组合 ，或者远期外汇协议的组合。在协议签订时，一个公平的货 币互换协议应使得双方的互换价值相等。也就是说，协议签 订时的货币互换定价，就是选择两个使得货币互换的初始价 值为零的固定利率。
购买了一份名义面值的浮动利率 债券
ቤተ መጻሕፍቲ ባይዱ
购买一份名义面值的固定利率债 券
出售了一份名义面值的浮动利率 债券
第一节 利率互换的定价
二、运用远期利率协议给利率互换定价
第一节 利率互换的定价
三、协议签订时的利率互换定价
第二节 货币互换的定价
货币互换（Currency Swap）是在未来约定期限内将一种货币 的本金和固定利息与另一货币的等价本金和固定利息进行交 换。 在利率互换中通常无需交换本金，只需定期交换利息差额； 而在货币互换中，期初和期末须按照约定的汇率交换不同货 币的本金，期间还需定期交换不同货币的利息。
LIBOR
A
B
5%
A公司向B公司按浮动利率6个月期LIBOR支付名义本金1亿美元的利息。 B公司向A公司按固定利率5%支付名义本金1亿美元的利息。
金融工程第4章 互换的定价
固定利率 10.00% 11.20%
浮动利率 6个月期LIBOR+0.30% 6个月期LIBOR+1.00%
A公司 B公司
此表中的利率均为一年计一次复利的年利率。
在上述互换中，每隔6个月为利息支付日，因此互换协议的条款 应规定每6个月一方向另一方支付固定利率与浮动利率的差额。 假定某一支付日的LIBOR为11.00%，则A公司应付给B公司5.25 万美元[即1000万0.5（11.00%－9.95%）]。利率互换的流程图 如图5.2所示。
双方进行利率互换的主要原因是： 双方在固定利率和浮动利率市场上具有比较优势。 假定A、B公司都想借入5年期的1000万美元的借款，A想借入与 6 个月期相关的浮动利率借款，B想借入固定利率借款。但两家 公司信用等级不同，市场向它们提供的利率也不同，如表5.1所 示。
表5.1 市场提供给A、B两公司的借款利率
2005.3.1
2005.9.1 2005.3.1 2005.9.1 2006.3.1 2006.9.1
4.80
5.30 5.50 5.60 5.90 6.40
+2.10
+2.40 +2.65 +2.75 +2.80 +2.95
－2.50
－2.50 －2.50 －2.50 －2.50 －2.50
－0.40
（二）运用债券组合给利率互换定价 考虑一个2003年9月1日生效的三年期的利率互换，名义本金 是1亿美元。B公司同意支付给A公司年利率为5％的利息，同 时A公司同意支付给B公司6个月期LIBOR的利息，利息每半 年支付一次。
图5.4 利率互换
互换的定价
远期利率和FRA的价值，计算出利率互换的价值。
整理课件
9
2、互换价值的计算
（1）运用债券组合的方法
:B 互flx 换合约中分解出的固定利率债券的价值。
Bf i
:互换合约中分解出的浮动利率债券的价值。
对B公司而言，这个互换的价值就是：
V互换Bfl Bfix
整理课件
10
固定利率债券价值的计算
整理课件
15
计算步骤 计算远期利率 确定现金流 将现金流贴现
整理课件
16
举例（同前例）
假设在一笔利率互换合约中，某一金融机构支付3个月期
的LIBOR，同时收取4.8％的年利率（3个月计一次复利），名
义本金为1亿美元。互换还有9个月的期限。3个月、6个月和9
个月的LIBOR（连续复利率）分别为4.8％、5％和5.1％。试
整理课件
7
②上述利率互换也可以看成是一系列的远期利率的组合。
远期利率协议FRA可以看成一个将用事先确定的利率
交换市场利率的合约，利率互换看成是一系列用固定利率
交换浮动利率的FRA合约。
整理课件
8
（2）利率互换分解的结论
对B公司而言，该利率互换的价值就是浮动利率债券
与固定利率债券价值的差。
只要知道利率的期限结构，就可以计算出FRA对应的
在一笔货币互换中每年收入日元，利率为5％，同时付出美元，
利率为8％。两种货币的本金分别为1000万美元和120000万日
元。这笔互换还有3年的期限，即期汇率为1美元＝110日元。
试求该互换的价值。
整理课件
25
如果以美元为本币，那么： B D 0 . 8 e 0 . 0 9 1 0 . 8 e 0 . 0 9 2 1 0 . 8 e 0 . 0 9 3 $ 9 6 4 . 4 万
互换的定价与风险分析教材
互换的定价与风险分析教材引言互换（swap）是一种金融衍生品合约，用于交换不同利率或不同货币的现金流。
互换合约由于其独特的特性，在金融市场中广泛应用。
本教材将重点介绍互换的定价和风险分析。
1. 互换的基本概念1.1 互换合约的定义和要素互换合约是一种由双方达成的协议，约定在未来的某个时间段内交换一系列现金流。
互换合约包含以下基本要素：交换的利率或汇率、交换的本金和交换的支付频率。
1.2 互换的种类根据交换的内容，互换合约可以分为利率互换（interest rate swap）、货币互换（currency swap）、基差互换（basis swap）等。
2. 互换的定价方法2.1 风险中性定价原理风险中性定价原理是互换定价的基本原理之一，即在风险无法定价或无法量化的情况下，通过构建一个风险中性的投资组合，使其收益等于无风险利率，达到定价的目的。
2.2 利率曲线的构建利率曲线是互换定价的基础，可以使用不同的方法构建利率曲线，如收益率平滑法、插值法、蒙特卡洛模拟法等。
2.3 互换的定价模型互换的定价模型根据交换的内容和特性不同，可以使用不同的定价模型，如固定利率互换定价模型、浮动利率互换定价模型等。
3. 互换的风险分析3.1 利率风险分析利率风险是互换合约面临的主要风险之一，可以通过敞口分析、敏感性分析等方法进行风险评估和控制。
3.2 信用风险分析互换交易当事方的信用风险是互换交易面临的另一个重要风险，可以通过信用评级、信用保证金等方式来管理和控制。
4. 互换市场的应用案例分析4.1 利用互换进行利率风险管理利率互换是企业进行利率风险管理的一种重要工具，本节将通过案例分析展示如何利用互换合约来管理利率风险，降低债务成本。
4.2 利用互换进行外汇风险管理货币互换合约可以帮助企业进行外汇风险管理，本节将通过案例分析展示如何利用货币互换合约进行外汇风险套期保值。
4.3 利用互换进行投机和套利互换合约也可以用于投机和套利，本节将通过案例分析展示如何利用互换合约来进行投机和套利交易。
互换定价协议书
互换定价协议书甲方（出让方）：_____________________乙方（受让方）：_____________________鉴于甲方拥有某项资产或权益，乙方对甲方的资产或权益有需求，双方本着平等自愿、诚实信用的原则，经协商一致，就甲方将其资产或权益与乙方的资产或权益进行互换的定价事宜，达成如下协议：第一条互换标的1.1 甲方同意将其拥有的资产或权益（以下简称“甲方资产”）与乙方的资产或权益（以下简称“乙方资产”）进行互换。
1.2 甲方资产的具体描述为：_____________________1.3 乙方资产的具体描述为：_____________________第二条互换定价2.1 双方同意，甲方资产的定价为人民币_______元（大写：_______元整）。
2.2 双方同意，乙方资产的定价为人民币_______元（大写：_______元整）。
2.3 双方同意，互换的定价基于各自资产的公允价值，由双方协商确定。
第三条定价依据3.1 双方同意，互换定价的依据包括但不限于资产的账面价值、市场价值、专业评估机构的评估结果等。
3.2 双方同意，互换定价的依据应公平、合理，不损害任何一方的利益。
第四条互换程序4.1 双方应按照本协议约定的时间和方式完成互换资产的交付和接收。
4.2 双方应各自负责办理互换资产的过户、登记等相关手续。
第五条权利与义务5.1 甲方应保证其资产的所有权清晰，不存在任何权利瑕疵。
5.2 乙方应保证其资产的所有权清晰，不存在任何权利瑕疵。
5.3 双方应按照本协议的约定，及时履行各自的义务。
第六条违约责任6.1 如一方违反本协议的约定，应承担违约责任，向守约方支付违约金，金额为违约行为涉及金额的_______%。
6.2 因违约行为给对方造成的损失，违约方应负责赔偿。
第七条争议解决7.1 本协议在履行过程中发生的任何争议，双方应首先通过友好协商解决。
7.2 如果协商不成，任何一方均可向甲方所在地人民法院提起诉讼。
第七章 互换的定价及风险分析
二、协议签订后的利率互换定价
表7-2 运用FRA组合给利率互换定价（万美元）
二、协议签订后的利率互换定价
显然，这个结果与前面运用债券组合定出的利 率互换价值－18.52万美元是一致的，100美 元的差异源于连续复利与普通复利之间转换时 的四舍五入。
三、协议签订时的利率互换定价
假设在一笔2年期的利率互换协议中，某一金 融机构支付3个月期的LIBOR，同时每3个月收取 固定利率（3个月计一次复利），名义本金为1 亿美元。目前3个月、6个月、9个月、12个月、 15个月、18个月、21个月与2年的贴现率（连续 复利）分别为4.8％、5％、5.1％、5.2％、 5.15％、5.3％、5.3％与5.4％。第一次支付的 浮动利率即为当前3个月期利率4.8％（连续复 利）。试确定此笔利率互换中合理的固定利率。
一、利率互换定价的基本原理
2. 如果对列（4）的现金流按列进行拆分，该利 率互换可以看作由列（2）和列（3）的现金流序 列组成。假设在互换生效日与到期日增加1亿美 元的本金现金流，列（2）和列（3）转化为表71（b）的列（6）与列（7）。
一、利率互换定价的基本原理
对甲银行而言，该利率互换事实上可以看作一个 浮动利率债券多头与固定利率空头头寸的组合， 这个利率互换的价值就是浮动利率债券与固定利 率债券价值的差。由于互换为零和游戏，对于乙 公司来说，该利率互换的价值就是固定利率债券 价值与浮动利率债券价值的差。也就是说，利率 互换可以通过分解成一个债券的多头与另一个债 券的空头来定价。
第一节 利率互换的定价
考虑一个2005年9月1日生效的两年期利率互 换，名义本金为1亿美元。甲银行同意支付给乙 公司年利率为2.8％的利息，同时乙公司同意支付 给甲银行3个月期LIBOR的利息，利息每3个月交 换一次。利率互换中甲银行的现金流量表如表7-1 所示，其中（a）为不考虑名义本金，（b）为考 虑名义本金的情况。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
因此，对于该金融机构而言，此利率互换的价值为 9975.825－10000＝－24.175 万美元
利）。试确定此笔利率互换中合理的固定利率。
利率互换中合理固定利率的选择应使得利率互换的价值为零，即 Bfl Bfix 。在
这 个 例 子 中 ， Bfl 10000e0.0480.25 e0.0480.25 10000 万 美 元 ， 令
B fix
k e0.0480.25 4
k e0.050.5 4
现金流，
列（2）－列（6） 列（3）－列（7）
头寸分解
甲银行：浮动利率债券多头＋固定利率债券空 头头寸
乙公司来说：固定利率债券多头价值＋浮动利 率债券空头价值
利率互换可以通过分解成一个债券的多头与另 一个债券的空头来定价
列（4）＝行（I）＋…＋行（VIII）
除了行（I）的现金流在互换签订时就已经确 定，其他各行的现金流都类似远期利率协议 （FRA）的现金流。
LIBOR，同时每 3 个月收取固定利率（3 个月计一次复利），名义本金为 1 亿美
元。目前 3 个月、6 个月、9 个月、12 个月、15 个月、18 个月、21 个月与 2
年的贴现率（连续复利）分别为 4.8％、5％、5.1％、5.2％、5.15％、5.3％、
5.3％与 5.4％。第一次支付的浮动利率即为当前 3 个月期利率 4.8％（连续复
互换的定价与风险分析
忽略天数计算
以国际市场上的互换为例，浮动利率使用 LIBOR
贴现率也使用LIBOR
举例
考虑一个2005年9月1日生效的两年期利率互换， 名义本金为1亿美元。甲银行同意支付给乙公司年 利率为2.8％的利息，同时乙公司同意支付给甲银 行3个月期LIBOR的利息，利息每3个月交换一次。 利率互换中甲银行的现金流量表如表7-1所示，其 中（a）为不考虑名义本金，（b）为考虑名义本金 的情况。
美元无风险利率期限结构与互换收益率曲线的 差异被称为互换价差（S），主要体现了银行 间市场的信用风险与流动性风险。
互换曲线能够提供更多到期期限的利率信息
特定到期日的互换利率具有延续性，几乎每天 都可以估计出特定到期日的互换利率
互换是零成本合约，其供给是无限的，不会受 到发行量的制约和影响
对于许多银行间的金融衍生产品来说，与无风 险利率相比，互换利率由于反映了其现金流的 信用风险与流动性风险，是一个更好的贴现率 基准。
第一，在协议签订后的互换定价，是根据协议内容 与市场利率水平确定利率互换合约的价值。对于利 率互换协议的持有者来说，该价值可能是正的，也 可能是负的。
第二，在协议签订时，一个公平的利率互换协议应 使得双方的互换价值相等。也就是说，协议签订时 的互换定价，就是选择一个使得互换的初始价值为 零的固定利率。
互换多头
V互换＝B fl B fix
互换空头
V互换＝B fix B fl
固定利率债券定价
n
B fix
keriti Aerntn
i1
浮动利率债券定价
B fl ( A k * )er1t1
假设在一笔利率互换协议中，某一金融机构支付 3 个月期的 LIBOR， 同时收取 4.8％的年利率（3 个月计一次复利），名义本金为 1 亿美元。互 换还有 9 个月的期限。目前 3 个月、6 个月和 9 个月的 LIBOR（连续复 利）分别为 4.8％、5％和 5.1％。。试计算此笔利率互换对该金融机构的 价值。
题目同前
答案： 3个月计一次复利的4.8%对应的连续复利利率分别为
4
ln
1
4.8% 4
4.77%
下表列示了具体的计算过程，表中的利率均为连续复利。
这个结果与前面运用债券组合定出的利率互换价值 －18.52万美元是一致的，100美元的差异源于连续 复利与普通复利之间转换时的四舍五入。
假设在一笔 2 年期的利率互换协议中，某一金融机构支付 3 个月期的
表7-1 利率互换中甲银行的现金流量表 （百万美元） （a）不考虑名义本金
表7-1 利率互换中甲银行的现金流量表 （百万美元） （b）考虑名义本金
该利率互换由列（4）的净现金流 序列组成，这是互换的本质，即未
来系列现金流的组合
列（4）＝列（2）＋列（3） 在互换生效日与到期日增加1亿美元的本金
k e0.0510.75 4
k e0.0521 4
k e0.05151.25 4
k e0.0531.5 4
k 531.75 4
10000
k 4
e0.0542
10000万美元
可求得 k 543美元，即固定利率水平应确定为 5.43%（3 个月计一次复利）。
利率互换协议中合理的固定利率就是使得互换 价值为零的利率水平，也就是我们通常所说的 互换利率
显然，对于该金融机构的交易对手来说，此笔利率互换的价值为正，即 24.175 万美元。
运用FRA给利率互换定价
1. FRA公式：
Ae Ae e rK (T*T )
rF (T *T ) r* T * t
2. 从利率期限结构中估计出FRA对应的远期利 率与息差现值，即可得到每笔FRA的价值， 加总就可以得到利率互换的价值。
现实中的互换利率是市场以一定的计息频率为 基础、就特定期限形成的互换中间利率。以美 元为例，市场通常将每半年支付固定利息对3 个月浮动LIBOR利率的互换中间利率作为美元 互换利率。
LIBOR-互换利率－欧洲美元期货利率
“互换收益率曲线”（the Term Structure of S or the S）
利率互换可以看成是一系列用固定利率交换浮 动利率的FRA的组合。只要我们知道组成利率 互换的每笔FRA的价值，就计算出利率互换的 价值。
利率互换既可以分解为债券组合、也可以分解 为FRA的组合进行定价。由于都是列（4）现 金流的不同分解，这两种定价结果必然是等价 的。
与远期合约相似，利率互换的定价有两种情形