飞机最短航线问题
最短航线

120°E 120°W A B 40°S练习三 最短航线班级______________ 姓名______________1.从A 点去B 点,距离最短的走法可能是( )A .从A 点向东至B 点B .从A 点向西至B 点C .先向东北,再转向东南D .先向东南,再转向东北2 从A 机场到B 机场走最近路线,飞机飞行方向应是A .自西向东沿纬线飞行B .先向东南再向东北飞行C .先向北再向南沿经线圈飞行D .先向东北再向东南飞行 3. 从A 地(60°N ,90°E )到B 地(60°N ,140°E ),若不考虑地形因素,最近的走法是A .一直向东走B .一直向西走C .先向东北,再向东,最后向东南走D .先向东南,再向东,最后向东北走一架飞机从甲地(60°N ,100°W)起飞,沿最近航线匀速飞行8小时抵达乙地(60°N ,80°E)。
据此回答4-5题。
4.飞机飞行航线( )A .一直不变B .先向东北后向东南C .先向西北后向西南D .先向北后向南5.这架飞机若以同样的速度,沿60°N 纬线飞行,抵达乙地大约需要( )A .8小时B .12小时C .16小时D .20小时6.读某局部经纬网图,有关图中各点之间最短距离的说法,错误的是( )A .①到③的最短航线方向是先向东北再向东南B .①到③的最短距离是555千米C .②到④的最短航线方向是正南D .②到④的最短距离是555千米60º90º140º7.对下列甲乙两图的正确叙述是:A. 甲图中B点(90°E,0°)B.乙图表示南半球经纬网C. 甲图中 B在A 的东南方D. 乙图地球逆时针转动下图为亚洲两个国家略图,读图回答8~9题。
8.甲地在乙地的方向为()A.东北B.东南C.西南D.西北9.若一架飞机从①国的丙地飞往丁地,沿最近航线飞行,则飞行方向为()A.沿34°纬线向丁地飞行B.先向东北飞行,再向东南飞行C.先向东南飞行,再向东北飞行D.向西沿34°纬线飞行10.读右图,回答下列问题。
高三地理最短航线知识点

高三地理最短航线知识点高三地理中,最短航线是一个重要的知识点。
本文将介绍最短航线的定义、应用以及相关的地理知识,以帮助学生更好地理解和应用这一概念。
一、最短航线的定义最短航线是指两个地点之间的航线中,飞行距离最短的航线。
在地理学中,最短航线一般是指两点之间大圆弧线段的长度。
这个概念在实际应用中具有重要意义,特别是对于航空运输和航海运输来说。
二、最短航线的应用最短航线的应用主要体现在以下几个方面:1. 航空运输:航空公司在规划飞行航线时,通常会选择最短航线。
这样可以有效地减少飞行时间和燃料消耗,提高运输效率。
2. 航海运输:航海运输中的船只也会选择最短航线,以减少航行距离和节约能源。
3. 地理定位:最短航线的计算方法可以应用于地理定位相关的技术,比如全球定位系统(GPS)等。
4. 地球形状研究:最短航线的概念也可以用于研究地球的形状,例如地球是一个椭球体而非完全的球形。
三、与最短航线相关的地理知识点除了最短航线的应用,与之相关的地理知识点也是高三地理学习中需要掌握的内容。
以下是一些相关的知识点:1. 地球的形状:地球既不是完全的球形,也不是完全的扁球形,而是一个稍微扁平的椭球体。
地球的形状对最短航线的计算有一定的影响。
2. 经纬度系统:经纬度系统是用来表示地球上某一点位置的一种方法。
经度表示东西方向的位置,纬度表示南北方向的位置。
在计算最短航线时,需要使用经纬度来确定两点之间的距离。
3. 大圆弧线段:计算最短航线时,通常会使用大圆弧线段的长度来代替曲线距离。
大圆弧线段是一个圆球表面上两点间的最短弧线。
4. 不同球面距离的计算:根据地球的不同坐标系,计算最短航线的方法也不同。
常见的计算方法有球面三角法、航程计划法等。
四、实际案例应用最短航线的计算方法在实际应用中发挥着重要作用。
航空公司、航海公司以及GPS导航系统等都会使用最短航线来优化航程和节约资源。
例如,一架从纽约飞往北京的飞机,为了降低燃料消耗和飞行时间,通常会选择经过北极的最短航线。
两点间的最短航线方向问题

输入参数为大圆距离以及两个点 的经纬度,输出为最短航线方向 (以度数表示)。
优化算法以提高计算效率
为了提高计算效率,可以采用一些优 化策略。例如,使用近似算法来快速 估算大圆距离和航线方向,然后在误 差允许的范围内使用精确算法进行校 准。
还可以通过并行计算和分布式处理来 加速计算过程,特别是在处理大量数 据时。
两点间的最短航线方 向问题
• 问题定义 • 数学模型与理论 • 算法与解决方案 • 实例分析 • 结论与展望
目录
01
问题定义
什么是两点间的最短航线方向问题
两点间的最短航线方向问题,也称为“大圆航线问题”,是指确定地球上两点间最 短航线的方向。
在地球上,两点之间的最短距离并不是直线距离,而是沿着地球表面的大圆弧线 。因此,确定两点间最短航线方向的问题实际上是寻找经过这两点的大圆弧线。
大圆航线与非大圆航线的比较
总结词
大圆航线通常是最短的航线,但非大圆航线在某些情况下可能更短。
详细描述
大圆航线是指沿着地球大圆弧线的航线,通常是最短的航线。但在某些情况下,由于地球的曲率、地 形、障碍物等因素的影响,非大圆航线可能更短。例如,在穿越山脉或海峡时,选择绕过障碍物的航 线可能比直接的大圆航线更短。
03
算法与解决方案
计算大圆距离的算法
计算地球上两点A和B的大圆距离, 需要使用球面三角学中的Haversine 公式。该公式考虑了地球的曲率,能 够精确计算两点之间的大圆距离。
输入参数包括经度、纬度以及地球半 径,输出为两点之间的大圆距离确定 最短航线方向。这通常使用球面 三角学中的方位角公式来完成。
探讨不同纬度、不同经度地区最短航线方向的差异,为航空、航海等领域 提供更为精确的导航服务。
最短航线的三种判定方法

最短航线的三种判定方法以最短航线的三种判定方法为标题,写一篇文章一、最短航线的定义与重要性最短航线是指在给定的起点和终点之间选择的距离最短的航行路径。
在航空、航运和航天领域,寻找最短航线对于节省时间、燃料和资源具有重要意义。
为了确定最短航线,有三种常用的判定方法:直线距离法、曲线距离法和大圆航线法。
二、直线距离法直线距离法是最简单的判定方法,它基于两点间的直线距离。
这种方法忽略了地球的曲率和地球表面的不规则性,只考虑了两点之间的直线距离。
在实际应用中,直线距离法常用于短距离航线的计算,例如城市之间的航线。
然而,当航线跨越较大的距离时,直线距离法会引入较大的误差,因为地球的曲率不能被忽略。
三、曲线距离法曲线距离法是一种考虑地球表面曲率的判定方法。
它通过在地球表面上选择一条曲线路径来计算航线距离。
常用的曲线路径包括大圆弧和小圆弧。
大圆弧是连接两个点的最短路径,它是地球表面上的一段大圆。
小圆弧是连接两个点的路径,它不一定是最短路径,但比直线距离更接近最短航线。
曲线距离法考虑了地球的曲率,因此可以在计算较长航线时提供更准确的结果。
四、大圆航线法大圆航线法是寻找最短航线的一种常用方法,它基于大圆弧路径。
大圆弧是连接两个点的最短路径,它是地球表面上的一段大圆。
在计算大圆航线时,需要使用球面三角学公式,如球面余弦定理和球面正弦定理。
这些公式可以根据给定的起点和终点的经纬度来计算大圆航线的距离和方向。
大圆航线法是最精确的判定方法之一,广泛应用于航空和航运领域。
五、总结最短航线的判定方法有直线距离法、曲线距离法和大圆航线法。
直线距离法简单易用,适用于短距离航线的计算。
曲线距离法考虑了地球的曲率,提供了更准确的结果。
大圆航线法是最精确的判定方法之一,广泛应用于航空和航运领域。
在实际应用中,选择适当的判定方法可以帮助我们找到最短航线,节省时间和资源。
最短航线的三种判定方法

最短航线的三种判定方法以最短航线的三种判定方法为标题,写一篇文章最短航线的计算在航空领域中具有重要的意义,它能够帮助飞行员和航空公司选择最经济、最快捷的飞行路径。
本文将介绍三种常见的最短航线判定方法:大圆航线法、曲线切割法和最短时间法。
一、大圆航线法大圆航线法是一种基于球体模型的判定方法。
在地球表面,航线不是直线,而是弧线。
大圆航线法通过计算两地之间的大圆弧线来确定最短航线。
大圆航线法的计算过程相对较为简单。
首先,我们需要知道起点和终点的经纬度坐标。
然后,通过球面三角学的计算公式,计算出两地之间的大圆弧线距离。
最后,根据飞行速度和飞行时间,可以得出最短航线的飞行路径。
二、曲线切割法曲线切割法是一种基于曲线模型的判定方法。
在地球表面,航线可以近似看作是一条曲线。
曲线切割法通过将航线切割成多段小弧线,然后计算每段小弧线的长度,最后将所有小弧线长度相加得出最短航线的长度。
曲线切割法的计算相对复杂一些。
首先,我们需要将航线切割成多段小弧线。
然后,通过球面三角学的计算公式,计算每段小弧线的长度。
最后,将所有小弧线长度相加,得出最短航线的长度。
三、最短时间法最短时间法是一种基于时间模型的判定方法。
在航空领域,最短航线不仅取决于距离,还取决于飞行速度和飞行时间。
最短时间法通过计算起点和终点之间的飞行时间,并结合飞行速度,确定最短航线。
最短时间法的计算相对简单。
首先,我们需要知道起点和终点之间的距离。
然后,根据飞行速度,计算出飞行时间。
最后,比较不同航线的飞行时间,选取最短时间的航线作为最短航线。
总结起来,最短航线的判定方法有三种:大圆航线法、曲线切割法和最短时间法。
大圆航线法基于球体模型,计算两地之间的大圆弧线距离;曲线切割法将航线切割成多段小弧线,计算每段小弧线的长度;最短时间法通过计算飞行时间和飞行速度,确定最短航线。
这三种方法各有优劣,根据具体情况可选择合适的方法来计算最短航线。
无论选择哪种方法,最终的目标都是为了找到最经济、最快捷的飞行路径,提高航空运输效率。
地球上两点间的最短航线问题

图示圆弧是 否属于大圆?
判断图中 各点之间是 否为最短距 离: AB CD EF 图中甲乙两 点间的最短 距离?
甲 E 乙 A C B D F
判断图中 各点之间是 否为最短距 离: AB CD EF 图中甲乙两 点间的最短 距离?
甲 乙
1.具有地理意义的几个大圆: 经线圈 赤道 晨昏圈
D
B
70° ° 3.若图中A地点正当日
落,两个小时后,太阳 直射点的地理位置是 ( ) A.20°S,75°W B. 20°N,105°E C.23°26′N,165°E A 30° ° D.23°26′S,105°W
45° °
C
D
B
例2.飞机从②处沿图中箭头路线 飞往①的航向是( D )
D A
C B
2.在以上几条线上最短 航线方向的判断 ③晨昏圈上 在晨线上 地图上的方 向判断方法 在昏线上 分别在晨线和昏线 上 极点附近方向的 判断
D A
C B
3.其他任意点间最短航线方向的判断 ①同一纬线上 B 北半球偏北 南半球偏南
A C D
3.其他任意点间最短航线方向的判断 ①同一纬线上 ②其他任意点 B 根据地图上的 A 方向判断方法 很东北再向东 南
�
地球上两点间的最短航线方向问题
1.最短航线的判断依据:
– 数学:球面上两点间的最短距离为两点所在大 圆的劣弧. – 地理:地图上的方向
2.数学球的相关知识
– 大圆:球面上任意两点与球心所确定的平面与 球面相交所得的圆
在近年的高考地理试题中,考查地球 上两点间最短航线的方向问题经常出现, 由于很多学生对这类问题没有从本质上搞 清楚,又缺乏空间想象能力,只是机械地 背一些结论,造成解这类题目时经常出错.
15 1029地球上两点间的最短航线方向问题
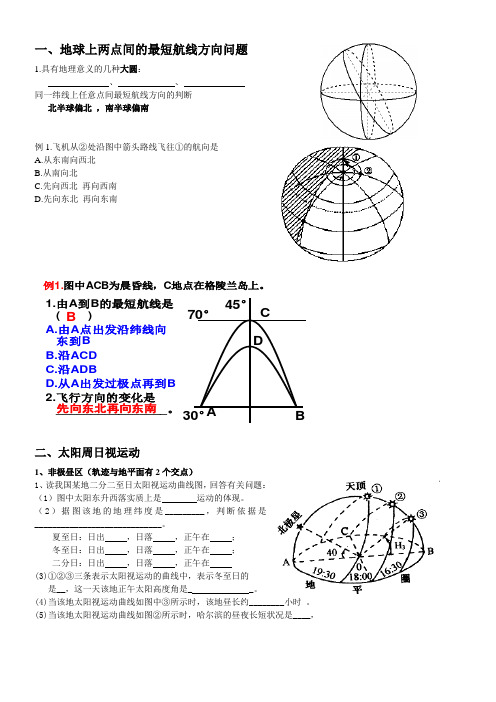
一、地球上两点间的最短航线方向问题1.具有地理意义的几种大圆:、 、 同一纬线上任意点间最短航线方向的判断北半球偏北 ,南半球偏南例1.飞机从②处沿图中箭头路线飞往①的航向是 A.从东南向西北 B.从南向北C.先向西北 再向西南D.先向东北 再向东南1、非极昼区(轨迹与地平面有2个交点) 1、读我国某地二分二至日太阳视运动曲线图,回答有关问题: (1)图中太阳东升西落实质上是 运动的体现。
(2)据图该地的地理纬度是_________,判断依据是 _____________________________。
夏至日:日出 ,日落 ,正午在 ; 冬至日:日出 ,日落 ,正午在 ; 二分日:日出 ,日落 ,正午在(3)①②③三条表示太阳视运动的曲线中,表示冬至日的 是__,这一天该地正午太阳高度角是_ _。
(4)当该地太阳视运动曲线如图中③所示时,该地昼长约________小时 。
(5)当该地太阳视运动曲线如图②所示时,哈尔滨的昼夜长短状况是____,图为某地某日某时段内的杆影轨迹示意图,O 为立杆处,虚线为杆影,曲线为杆影端点轨迹。
据此回答1—2题。
1.①----④四个杆影中最接近日落时段的是:( )A.①B. ②C.③D.④ 2.图示季节下列说法正确的是:( ) A.黑龙江河水封冻B.北极点上太阳高度逐渐增大C.北印度洋海 区海水向西流D. 夏威夷高压势力强盛逆温现象 热力环流 三圈环流 季风 突破图5是“该城市冬季近地面在不同时刻气温随高度变化过程示意图” 1. 该发电厂烟囱的设计高度应不低于A .50米B .75米C . 100米D .150米2.分布【提示注意】(1)图解低纬环流形成的方块图(以北半球为例)图1-20图7是“半球近地面风带分布示意圈”,读图回答3-4题3.图中a处的盛行风向是A.东北风B.西北风C.东南风D.西南风4.图中b处的气候特征是A.炎热干燥B.高温多雨C.温和干燥D.温和湿润5.右图为北半球大气活动中心分布示意图,读图回答(1)~(3)题。
最短航线问题

• 1.最短航线的判断依据:
– 数学:球面上两点间的最短距离为两点所在大 圆的劣弧。 – 地理:地图上的方向
• 2.数学球的相关知识
– 大圆:球面上任意两点与球心所确定的平面与 球面相交所得的圆
•
在近年的高考地理试题中,考查地球 上两点间最短航线的方向问题经常出现, 由于很多学生对这类问题没有从本质上搞 清楚,又缺乏空间想象能力,只是机械地 背一些结论,造成解这类题目时经常出错。
• 1.由A到B的最短航线 70° 是( B )
• A.由A点出发沿纬线 向东到B • B.沿ACB • C.沿ADB • D.从A出发过极点再 到B A 30° • 2.飞行方向的变化是 先向东北再向东南。 地点在格 陵兰岛上。 45°
C D
B
例.飞机从②处沿图中箭头路线飞 往①的航向是( D )
• A.从东南向西北 • B.从南向北 • C.先向西北再向西 南 • D.先向东北再向东 南
2.在以上几条线上最短 航线方向的判断 ①经线圈上 E
同一经线上:正 南或正北 经度相对:过较 近的极点
A
C
B
D
2.在以上几条线上最短 航线方向的判断 ②赤道上 正东或正西
C
B A
2.在以上几条线上最短 航线方向的判断 ③晨昏圈上 地图上的方 在晨线上 向判断方法 在昏线上 分别在晨线和昏线
上
D A
C B
2.在以上几条线上最短 航线方向的判断 ③晨昏圈上 在晨线上 地图上的方 向判断方法 在昏线上 分别在晨线和昏线
上 极点附近方向的 判断
D A
C B
3.其他任意点间最短航线方向的判断 ①同一纬线上 B 北半球偏北 南半球偏南
高中地理飞机最短航线题

高中地理飞机最短航线题在高中地理学习中,我们经常会遇到关于航线的问题。
其中一个经典的问题就是如何确定飞机的最短航线。
本文将介绍如何解决这个问题,并探讨其中的原理和应用。
首先,我们需要了解什么是最短航线。
最短航线是指两个地点之间的最短距离,通常用直线距离来表示。
然而,在实际情况中,由于地球是一个球体,直线距离并不是最短航线。
这是因为飞机在飞行过程中需要考虑地球的曲率,以及飞行高度的限制。
为了确定最短航线,我们需要使用一个叫做大圆航线的概念。
大圆航线是指连接两个地点的地球表面上的最短路径,它是一个圆周上的一段弧线。
在地理学中,大圆航线被广泛应用于航空和航海导航中。
那么,如何确定飞机的最短航线呢?首先,我们需要知道起点和终点的经纬度坐标。
然后,我们可以使用球面三角学的知识来计算大圆航线的长度和方向。
球面三角学是一种研究球面上的三角形的数学学科,它可以帮助我们解决地球表面上的航线问题。
在计算最短航线时,我们需要使用一些基本的公式和方法。
其中一个重要的公式是球面三角形的余弦定理。
根据余弦定理,我们可以计算出两个地点之间的角度,然后通过这个角度来确定大圆航线的长度。
除了长度,我们还需要确定大圆航线的方向。
在球面三角学中,方向通常用方位角来表示。
方位角是指从一个地点到另一个地点的方向,它是以北为参考的角度。
通过计算方位角,我们可以确定飞机应该朝着哪个方向飞行,以达到最短航线。
最后,我们需要考虑飞行高度的限制。
飞机在飞行过程中需要避开地球表面上的障碍物,如山脉和建筑物。
因此,我们需要根据飞机的高度限制来确定最短航线的可行性。
综上所述,确定飞机的最短航线需要使用球面三角学的知识和相关公式。
通过计算大圆航线的长度和方向,我们可以找到飞机飞行的最短路径。
这对于航空和航海导航来说非常重要,可以帮助飞机和船只节省时间和燃料。
在高中地理学习中,我们经常会遇到飞机最短航线的题目。
通过掌握球面三角学的基本原理和计算方法,我们可以轻松解决这类问题。
最短航程问题

最短航程问题(共4页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--题目某公司在六个城市C 1,C 2,C 3,C 4,C 5,C 6都有分公司,公司成员经常往来于它们之间,已知从Ci 到C j 的直达航班票价由下述矩阵的第i 行,第j 列元素给出(表示无直达航班),该公司想算出一张任意两个城市之间的最廉价路线航费表。
摘要改革开发以来,我国的经济发展迅速,人民生活水平逐渐提高,2010年,我国GDP 超越日本,排名世界第二。
我国经济的发展,使人们对交通运输提出越来越多的需求, 而民航作为航空运输工具,在交通工具中起到十分重要的作用,新型飞机(民用)快速、续航能力强、安全、便捷的特点受到越来越多的人青睐。
如果从交错复杂的飞机线路中找到最廉价的线路,不仅减少了中途时间,而且大大节省了开支费用,为企业和个人带来可观的经济效益。
本文从航班网络的实际特点出发,对航班线路网和票价进行分析,将最佳路径搜索问题转化为图论中的最短路径的问题,通过对最短路径算法的分析,实现了Floyd 算法求航班网络中的最短路径,将之建立模型,并描述了用matlab 程序进行求解的过程。
关键词:最短路 matlab Floyd 算法050402510500152025150102040201001025252010055102525550∞∞∞∞∞∞⎡⎣⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥问题提出某公司在六个城市C 1,C 2,C 3,C 4,C 5,C 6都有分公司,公司成员经常往来于它们之间,已知从Ci 到C j 的直达航班票价由下述矩阵的第i 行,第j 列元素给出(表示无直达航班),该公司想算出一张任意两个城市之间的最廉价路线航费表。
问题分析若网络中的每条边都有一个数值(长度、成本、时间等),则找出两节点(通常是源节点和阱节点)之间总权和最小的路径就是最短路问题。
最短路问题是网络理论解决的典型问题之一,可用来解决管路铺设、线路安装、厂区布局和设备更新等实际问题。
定最短航线 习题集

定“最短航线”习题集
1.天津市某校“地理社团”进行了网上模拟探究活动。
如图所示为模拟探究的区域和探险路线。
读图,完成下列问题。
若返程时从⑥地乘飞机飞往①地,则其最短航程的方向为()
A.一直向东
B.先向正北,后向正南
C.先向东北,后向东南
D.先向西北,后向西南
答案:C
解析:从⑥地飞往①地的最短航程为地球大圆劣弧的方向,因此,其飞行方向为先向东北、后向东南。
2.若飞机从图中B点飞往C点,沿最短航线飞行,合理的方向是( D )A.一直向东B.一直向西C.向东南→东→东北D.先向正南,再往正北
3.若运送物资的飞机从长城站飞往中山站,最短航线的飞行方向是______________________。
答案:先向东南,后向东北
4.若一架飞机从N点起飞,沿最短的航线到达M点,则飞机飞行的方向为( ) A.一直向东B.先西北再西南C.一直向西D.先西南再西北答案:B
5.下图为某地区经纬网局部图,图中乙地纬度为30°。
若一架飞机从丁地飞往乙地,沿最短航线的飞行方向是( )
A.向正西方向
B.向正东方向
C.先西南,后西北
D.先东南,后东北答案:D。
【真题打卡】最短航线的计算(第24天)

【真题打卡】最短航线的计算(第24天)
每天来这里
和热爱地理学习的同学们
一起刷题打卡吧
只需几分钟就能完成
一道地理高考题
日积月累,方可厚积薄发
要坚持才能看到效果哦
恭喜你
已经完成第24天的打卡任务啦
(2020年浙江省7月高考真题)图一为某飞机在甲、乙、丙间沿地球大圆周飞行轨迹示意图。
图二为飞机飞到乙地时,其垂直下方所示的经线、纬线和晨昏线位置关系图,此时丙地地方时为17点。
完成下面小题。
19.若飞机匀速、等高飞行,则在甲-乙-丙间单位时间内飞过的纬度差()A.持续变大B.先变大,后变小C.持续变小D.先变小,后变大20.当日,甲地日出的地方时为()A.5点B.6点C.7点 D.8点
参考答案【答案】19.D 20.C【解析】19.读图可知,飞机在甲-乙-丙间沿大圆周(最短航线)飞行时,是先向东北飞,再向正东飞,后向东南飞。
在由甲飞向乙时,随着纬度的升高,飞行方向越接近与纬线平行,所以,单位时间内飞过的纬度差变小;在乙点时达到最小;则飞机由乙地飞向丙地时,飞过的纬度差变大,D正确。
ABC 错误。
故选D。
20.由题干可知,此时丙地的地方时为17点,则乙地为12点,则乙地所在的经线为昼半球的中央经线;由图2可知,乙地为晨昏线与纬线相切的切点,而且“飞机在甲、乙、丙间沿地球的大圆周飞行,”可判断甲、乙、丙为晨昏线,则甲丙所在的纬线为昼弧,甲丙之间经度相差150°,则可以推出甲、丙的昼长为10小时,根据公式“日出=12-昼长/2”可以计算出甲地日出的地方时为7点,C正确。
ABD错误。
故选C。
两点间的最短航线方向问题

航线方向的判断
③晨昏圈上 在晨线上 地图上的方 在昏线上 向判断方法
D A
分别在晨线和昏线上
C B
地球上两点间的最短航线方向问题
2.在以上几条线上最短
航线方向的判断
③晨昏圈上 在晨线上 地图上的方 在昏线上 向判断方法
D A
分别在晨线和昏线上
极点附近方向的 判断
C B
地球上两点间的最短航线方向问题
3.其他任意点间最短航线方向的判断
①同一纬线上
北半球偏北
B
南半球偏南
A
C
D
地球上两点间的最短航线方向问题
3.其他任意点间最短航线方向的判断
①同一纬线上 ②其他任意点
根据地图上的 方向判断方法
B A
很少考查
例1.图中ACB为晨昏线,C地点在格陵兰岛上。
1.由A到B的最短航线是
(B )
A.由A点出发沿纬线向 东到B
地球上两点间的最短航线方向问题
1.最短航线的判断依据: 数学:球面上两点间的最短距离为两点所在 大圆的劣弧。 地理:地图上的方向
2.数学球的相关知识 大圆:球面上任意两点与球心所确定的平面 与球面相交所得的圆
在近年的高考地理试题中,考查地球上 两点间最短航线的方向问题经常出现,由于 很多学生对这类问题没有从本质上搞清楚, 又缺乏空间想象能力,只是机械地背一些结 论,造成解这类题目时经常出错。
D
B. 20°N,105°E
C.23°26′N,165°E
D.23°26′S,105°W
30°A
B
例2.飞机从②处沿图中箭头路线飞往①的航
向是( D )
A.从东南向西北 B.从南向北 C.先向西北再向西南 D.先向东北再向东南
经纬网应用小专题最短航线

② 两地都位于南半球时,最短航线向南凸出。
ⅰ 由西往东时:先向南东,再向东北。
A
B
ⅱ 由西往东时:先向西北,再向西南。
C
D
S
谢谢观赏
经纬网应用小专题最短航线
地球上两点间的最短航线方向问题
判断图中各点 之间是否为最 短距离:
AB
CD
甲
E
乙
F
EF
A
B
图中甲乙两点 间的最短距离?
C D
地球上两点间的最短航线方向问题来自判断图中各点之间是否为最
甲
短距离:
AB
乙
CD
EF
图中甲乙两点 间的最短距离?
利用经纬网确定球面两点间“最短航线”
地球上两点间的最短航线为球面最短距离,即经过两点 的大圆劣弧长度。(大圆指的是过地心的平面与地面的交线)
(1)两地在赤道上,因赤道是大圆,则最短航线沿赤道航行即可, 方向为向东或向西。(C、D两地)
N
C D
S
(2)两地不在在赤道上,最短航线的劣弧段向较高纬度凸出。
① 两地都位于北半球时,最短航线向北凸出。
ⅰ 往东时:先向东北,再向东南。(由A到B) ⅱ 往西时:先向西北,再向西南。(由 B到A )
N
例外:当给出像左图形式的非常明显的图示 或材料说明时,则根据图中信息及材料判断。
图中由A到F最短航线 一直向东北
五、利用经纬网确定球面两点间“最短航线”
地球上两点间的最短航线为球面最短距离,即经过两点 的大圆劣弧长度。(大圆指的是过地心的平面与地面的交线)
1、同一经线上的两点,其最短航线就在这条经线上,方向为正南
或正北。
(如图中A、C两地或B、D两地)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
飞机最短航线问题
GE GROUP system office room 【GEIHUA16H-GEIHUA GEIHUA8Q8-
经纬网
----------飞机最短航线问题
1、同一经线上的两点,其最短航线就在这条经线上,方向为正南或正北。
(如图中A、C两地或B、D两地)
2、若两地经度相差180°,且两地不全在赤道上时,经过两地的大圆为经线
圈,两地最短航线过极点。
(1)两地都在北半球,最短航线过北极点。
航向为先向正北,再向正南(如图中A、B两地)
(2)两地都在南半球,最短航线过南极点。
航向为先向正南,再向正北(如图中C、D两地)
(3)若一地在南半球,一地在北半球时,比较两地纬度值的大小,最短航线经过两地中纬度值较大者所在半球的极点。
由A到D时,先向南,过南极点,然后向北
由B到C时, 先向北,过北极点,然后向南
3、同一纬线上的两地(经度差不是180°)
(1)两地在赤道上,因赤道是大圆,则最短航线沿赤道航行即可,方向为向东或向西。
(C、D两地)
(2)两地不在在赤道上,最短航线的劣弧段向较高纬度凸出。
①两地都位于北半球时,最短航线向北凸出。
ⅰ往东时:先向东北,再向东南。
(由A到B)
ⅱ往西时:先向西北,再向西南。
(由 B到A )
②两地都位于南半球时,最短航线向南凸出。
ⅰ往东时:先向东南,再向东北。
(由Q到M)
ⅱ往西时:先向西南,再向西北。
(由M到Q)
4、晨昏线上的两点
由于晨昏线本身就是一个大圆,故在晨昏线上的两点最短航线就是两点之间的最短晨昏线
总结:特殊大圆---赤道、经线圈、晨昏圈
同一纬线上(非赤道、非经线圈)
1:若一架飞机从M点起飞,沿最短航线到达P点,则飞机飞行的方
向是()
A 一直向东
B 先东北再东南
C 一直向西
D 先东南再东北
读下图,N为北极点,大圆为经线圈,ACB为赤道
3假若一架飞机从A飞到B,实际最短的飞行线路是() A 弧ANB B 弧AGB
C 弧AMB
D 弧ACB
4.上图中从D点到E点的最短航线是( )
A.先西北后西南 B.先东南后东北
C.先西南后西北 D.先东北后东南
5、最短航线的特殊情况
(1)一地位于赤道,另一地不在赤道和极点上
①两地经度差≤ 90°时,最短航线方向不变。
②两地经度差> 90°时,最短航线方向变化。
由C到A时方向为向东北
由C到F时方向为向东北
由C到B时方向为先向东北,然后向东南
(2)两地同位于一个半球,并且不在同一条纬线上时,只考虑一种情况:参照同一条纬线上两地最短航线的选取方法
E到F的最短航线为 A到F最短航线。
