【g】c++第13章答案

合集下载

2018八年级数学《第13章轴对称--垂直平分线》同步复习资料【2】【含解析】

2018八年级数学《第13章轴对称--垂直平分线》同步复习资料【2】一．选择题（共10小题）1．如图所示的图形中，左边的图形与右边的图形成轴对称的是（）A．B．C．D．2．下列说法正确的是（）A．两个图形关于某直线对称，对称点一定在这直线的两旁B．两个图形关于某直线对称，对称点在这直线上C．全等的两个图形一定成轴对称D．成轴对称的两个图形一定全等3．在三角形的内部，有一个点到三角形三个顶点的距离相等，则这个点一定是三角形（）A．三条中线的交点B．三条角平分线的交点C．三条边的垂直平分线的交点D．三条高的交点4．如图，在△ABC中，直线ED是线段BC的垂直平分线，直线ED分别交BC、AB于点D、点E，已知BD=3，△ABC的周长为20，则△AEC的周长为（）A．14 B．20 C．16 D．125．如图，△ABC中，∠A=50°，∠C=60°，DE垂直平分AB，则∠DBC的度数为（）A．10°B．20°C．30°D．40°6．如图，在△ABC中，E为AB中点，DE⊥AB于点E，AC=4，△BCD周长为7，则BC的长为（）A．1 B．2 C．3 D．47．如图，在△ABC中，PM、QN分别是AB、AC的垂直平分线，∠BAC=100°那么∠PAQ等于（）A．50°B．40°C．30°D．20°8．如图，点P在∠MON的内部，点P关于OM，ON的对称点分别为A，B，连接AB，交OM于点C，交ON于点D，连接PC，PD．若∠MON=50°，则∠CPD=（）A．70°B．80°C．90°D．100°9．如图，Rt△ABC中，∠C=90°，斜边AB的垂直平分线交AB于点E，交BC于点D，连接AD，若∠B=35°，则∠CAD的度数为（）A．20°B．25°C．30°D．35°10．如图，△ABC中，∠A=70°，点O是AB、AC垂直平分线的交点，则∠BCO的度数是（）A．40°B．30°C．20°D．10°二．填空题（共7小题）11．如图，△ABC中，BC的垂直平分线DP与∠BAC的角平分线相交于点D，垂足为点P，若∠BAC=85°，则∠BDC=．12．如图，在△ABC中，DM，EN分别垂直平分AB和AC，交BC于点D，E，若∠DAE=40°，则∠BAC的度数=．13．如图，在△ABC中，AB、AC的垂直平分线l1、l2相交于点O，若∠BAC等于84°，则∠OBC=．14．某同学从平面镜里看到镜子对面的电子钟的示数如图所示，这时的实际时间是．15．如图，在△ABC中，AF平分∠BAC，AC的垂直平分线交BC于点E，∠B=70°，∠FAE=19°，则∠C=度．16．如图，四边形ABCD中，AB=BC，点C关于BD的对称点E恰好落在AD上，若∠BDC=α，则∠ABC的度数为（用含a的代数式表示）．17．如图，在△ABC中，∠ACB=90°，△ABD是△ABC的轴对称图形，点E在AD上，点F在AC的延长线上．若点B恰好在EF的垂直平分线上，并且AE=5，AF=13，则DE=．三．解答题（共5小题）18．如图，直线l l，l2交于点O，点P关于l l，l2的对称点分别为P1、P2．（1）若l l，l2相交所成的锐角∠AOB=60°，则∠P1OP2=；（2）若OP=3，P1P2=5，求△P1OP2的周长．19．如图，Rt△ABC中，∠ACB=90°，D是AB上一点，BD=BC，过点D作AB的垂线交AC于点E，求证：BE垂直平分CD．20．如图，已知：在△ABC中，AB、BC边上的垂直平分线相交于点P．求证：点P在AC的垂直平分线上．21．如图，在Rt△ABC中，∠ACB=90°，∠A=22.5°，斜边AB的垂直平分线交AC于点D，点F在AC上，点E在BC的延长线上，CE=CF，连接BF，DE．线段DE和BF在数量和位置上有什么关系？并说明理由．22．如图，△ABC的外角∠DAC的平分线交BC边的垂直平分线于点P，PD⊥AB于点D．（1）过点P作PE⊥AC于点E，求证：BD=CE；（2）若AB=6cm，AC=10cm，求AD的长．2018八年级数学《第13章轴对称--垂直平分线》同步复习资料【2】参考答案与试题解析一．选择题（共10小题）1．如图所示的图形中，左边的图形与右边的图形成轴对称的是（）A．B．C．D．【解答】解：根据轴对称图形的概念，B、C、D都不是轴对称图形，只有A是轴对称图形．故选：A．2．下列说法正确的是（）A．两个图形关于某直线对称，对称点一定在这直线的两旁B．两个图形关于某直线对称，对称点在这直线上C．全等的两个图形一定成轴对称D．成轴对称的两个图形一定全等【解答】解：A、两个图形关于某直线对称，对称点可能在这直线上，所以A选项错误；B、两个图形关于某直线对称，对称点可能在这直线的两旁，所以B选项错误；C、全等的两个图形不一定成轴对称，所以C选项错误；D、成轴对称的两个图形一定全等，所以D选项正确．故选：D．3．在三角形的内部，有一个点到三角形三个顶点的距离相等，则这个点一定是三角形（）A．三条中线的交点B．三条角平分线的交点C．三条边的垂直平分线的交点D．三条高的交点【解答】解：∵点到三角形三个顶点的距离相等，∴这个点一定是三角形三条边的垂直平分线的交点，故选：C．4．如图，在△ABC中，直线ED是线段BC的垂直平分线，直线ED分别交BC、AB于点D、点E，已知BD=3，△ABC的周长为20，则△AEC的周长为（）A．14 B．20 C．16 D．12【解答】解：∵ED是线段BC的垂直平分线，∴EC=EB，BC=2BD=6，∵△ABC的周长为20，∴AB+AC+BC=20，∴AB+AC=14，∴△AEC的周长=AC+AE+EC=AC+AE+EB=AC+AB=14，故选：A．5．如图，△ABC中，∠A=50°，∠C=60°，DE垂直平分AB，则∠DBC的度数为（）A．10°B．20°C．30°D．40°【解答】解：∵∠A=50°，∠C=60°，∴∠ABC=180°﹣50°﹣60°=70°．∵DE垂直平分AB，∴∠ABD=50°，∴∠DBC=∠ABC﹣∠ABD=70﹣50°=20°．故选：B．6．如图，在△ABC中，E为AB中点，DE⊥AB于点E，AC=4，△BCD周长为7，则BC的长为（）A．1 B．2 C．3 D．4【解答】解：∵DE⊥AB，垂足E为AB的中点，∴AD=BD，∴AC=AD+DC=BD+DC，∵AC=4，△BCD周长为7，∴BC=△BCD的周长﹣AC=7﹣4=3，故选：C．7．如图，在△ABC中，PM、QN分别是AB、AC的垂直平分线，∠BAC=100°那么∠PAQ等于（）A．50°B．40°C．30°D．20°【解答】解：∵∠BAC=100°，∴∠B+∠C=180°﹣100°=80°，∵PM、QN分别是AB、AC的垂直平分线，∴PA=PB，QA=QC，∴∠PAB=∠B，∠QAC=∠C，∴∠PAQ=180°﹣（∠PAB+∠QAC）=180°﹣（∠B+∠C）=20°，故选：D．8．如图，点P在∠MON的内部，点P关于OM，ON的对称点分别为A，B，连接AB，交OM于点C，交ON于点D，连接PC，PD．若∠MON=50°，则∠CPD=（）A．70°B．80°C．90°D．100°【解答】解：如图，连接OA、OB、OP，设PA与OM交于点E，PB与ON交于点F．∵点P关于OM，ON的对称点分别为A，B，∴OA=OP=OB，CA=CP，DP=DB，∠AOC=∠COP，∠POD=∠DOB，∴∠AOB=∠AOC+∠COP+∠POD+∠DOB=2∠COD=100°，∴∠OAB=∠OBA=（180°﹣∠AOB）=40°．设∠COP=α，∠DOP=β，则α+β=50°．∵OA=OP，∠AOP=2α，∴∠OPA=∠OAP=（180°﹣2α）=90°﹣α，∵∠OAB=40°，∴∠CPA=∠CAP=∠OAP﹣∠OAB=50°﹣α．同理，∠DPB=50°﹣β．∵∠EPF=360°﹣∠EOF﹣∠OEP﹣∠OFP=360°﹣50°﹣90°﹣90°=130°，∴∠CPD=∠EPF﹣（∠CPA+∠DPB）=130°﹣（50°﹣α+50°﹣β）=30°+（α+β）=80°．故选：B．9．如图，Rt△ABC中，∠C=90°，斜边AB的垂直平分线交AB于点E，交BC于点D，连接AD，若∠B=35°，则∠CAD的度数为（）A．20°B．25°C．30°D．35°【解答】解：∵DE是AB的垂直平分线，∴DA=DB，∴∠DAB=∠B=35°，∵∠C=90°，∠B=35°，∴∠BAC=55°，∴∠CAD=∠BAC﹣∠BAD=20°，故选：A．10．如图，△ABC中，∠A=70°，点O是AB、AC垂直平分线的交点，则∠BCO的度数是（）A．40°B．30°C．20°D．10°【解答】解：连接OA、OB，∵∠BAC=70°，∴∠ABC+∠ACB=110°，∵O是AB，AC垂直平分线的交点，∴OA=OB，OA=OC，∴∠OAB=∠OBA，∠OCA=∠OAC，OB=OC，∴∠OBA+∠OCA=70°，∴∠OBC+∠OCB=110°﹣70°=40°，∵OB=OC，∴∠BCO=∠CBO=20°，二．填空题（共7小题）11．如图，△ABC中，BC的垂直平分线DP与∠BAC的角平分线相交于点D，垂足为点P，若∠BAC=85°，则∠BDC= 95°．【解答】解：如图，过点D作DE⊥AB，交AB延长线于点E，DF⊥AC于F，∵AD是∠BOC的平分线，∴DE=DF，∵DP是BC的垂直平分线，∴BD=CD，在Rt△DEB和Rt△DFC中，，∴Rt△DEB≌Rt△DFC（HL）．∴∠BDE=∠CDF，∴∠BDC=∠EDF，∵∠DEB=∠DFC=90°，∴∠EAF+∠EDF=180゜，∵∠BAC=85°，∴∠BDC=∠EDF=95°，故答案为：95°．12．如图，在△ABC中，DM，EN分别垂直平分AB和AC，交BC于点D，E，若∠DAE=40°，则∠BAC的度数=110°．【解答】解：∵DM，EN分别垂直平分AB和AC，∴DA=DB，EA=EC，∴∠DAB=∠B，∠EAC=∠C，∠DAB+∠B+∠EAC+∠C+∠DAE=180°，则2（∠B+∠C）=140°，解得，∠B+∠C=70°，∴∠BAC=110°，故答案为：110°．13．如图，在△ABC中，AB、AC的垂直平分线l1、l2相交于点O，若∠BAC等于84°，则∠OBC=6°．【解答】解：连接OA，∵∠BAC=84°，∴∠ABC+∠ACB=96°，∵l1、l2分别是AB、AC的垂直平分线，∴OA=OB，OA=OC，∴OB=OC，∠OBA=∠OAB，∠OCA=∠OAC，∴∠OBA+∠OCA=∠BAC=84°，∴∠OBC+∠OCB=12°，∴∠OBC=6°，故答案为：6°．14．某同学从平面镜里看到镜子对面的电子钟的示数如图所示，这时的实际时间是10：51．【解答】解：∵是从镜子中看，∴对称轴为竖直方向的直线，∵2的对称数字是5，镜子中数字的顺序与实际数字顺序相反，∴这时的时刻应是10：51．故答案为：10：51．15．如图，在△ABC中，AF平分∠BAC，AC的垂直平分线交BC于点E，∠B=70°，∠FAE=19°，则∠C=24度．【解答】解：∵DE是AC的垂直平分线，∴EA=EC，∴∠EAC=∠C，∴∠FAC=∠EAC+19°，∵AF平分∠BAC，∴∠FAB=∠EAC+19°，∵∠B+∠BAC+∠C=180°，∴70°+2（∠C+19°）+∠C=180°，解得，∠C=24°，故答案为：24．16．如图，四边形ABCD中，AB=BC，点C关于BD的对称点E恰好落在AD上，若∠BDC=α，则∠ABC的度数为180°﹣2α（用含a的代数式表示）．【解答】解：如图所示，连接BE，∵点C关于BD的对称点E恰好落在AD上，∴BC=BE=AB，DE=DC，∴△BCD≌△BED，∠A=∠AEB，∴∠BCD=∠BED，又∵∠BED+∠AEB=180°，∴∠A+∠BCD=180°，∴四边形ABCD中，∠ABC+∠ADC=180°，又∵∠ADC=2∠BDC=2α，∴∠ABC=180°﹣2α，故答案为：180°﹣2α．17．如图，在△ABC中，∠ACB=90°，△ABD是△ABC的轴对称图形，点E在AD上，点F在AC的延长线上．若点B恰好在EF的垂直平分线上，并且AE=5，AF=13，则DE=4．【解答】解：连接BE，BF，∵△ABD是△ABC的轴对称图形，∴△ABD≌△ACB，∴DB=CB，AD=AC，∠D=∠BCA=90°，∴∠BCF=90°，∵点B恰好在EF的垂直平分线上，∴BE=BF，在Rt△DBE和Rt△CBF中，∴Rt△DBE≌Rt△CBF（HL），∴DE=CF，设DE=x，则CF=x，∵AE=5，AF=13，∴5+2x=13，x=4，∴DE=4，故答案为：4．三．解答题（共5小题）18．如图，直线l l，l2交于点O，点P关于l l，l2的对称点分别为P1、P2．（1）若l l，l2相交所成的锐角∠AOB=60°，则∠P1OP2=120°；（2）若OP=3，P1P2=5，求△P1OP2的周长．【解答】解：（1）∵P关于l1、l2的对称点分别为P1、P2，∴∠P1OA=∠AOP，∠P2OB=∠POB，∴∠P1OP2=2（∠AOP+∠POB）=2∠AOB=2×60°=120°；故答案为：120°；（2）∵P关于l1、l2的对称点分别为P1、P2，∴OP1=OP=OP2=3，∵P1P2=5，∴△P1OP2的周长=OP1+OP2+P1P2=3+3+5=11．19．如图，Rt△ABC中，∠ACB=90°，D是AB上一点，BD=BC，过点D作AB的垂线交AC于点E，求证：BE垂直平分CD．【解答】证明：∵∠ACB=90°，DE⊥AB，∴∠ACB=∠BDE=90°，在Rt△BDE和Rt△BCE中，，∴Rt△BDE≌Rt△BCE，∴ED=EC，∵ED=EC，BD=BC，∴BE垂直平分CD．20．如图，已知：在△ABC中，AB、BC边上的垂直平分线相交于点P．求证：点P在AC的垂直平分线上．【解答】证明：∵边AB，BC的垂直平分线交于点P，∴PA=PB，PB=PC．∴PA=PC．∴点P在AC的垂直平分线上．21．如图，在Rt△ABC中，∠ACB=90°，∠A=22.5°，斜边AB的垂直平分线交AC于点D，点F在AC上，点E在BC的延长线上，CE=CF，连接BF，DE．线段DE和BF在数量和位置上有什么关系？并说明理由．【解答】解：DE=BF，DE⊥BF．理由如下：连接BD，延长BF交DE于点G．∵点D在线段AB的垂直平分线上，∴AD=BD，∴∠ABD=∠A=22.5°．在Rt△ABC中，∵∠ACB=90°，∠A=22.5°，∴∠ABC=67.5°，∴∠CBD=∠ABC﹣∠ABD=45°，∴△BCD为等腰直角三角形，∴BC=DC．在△ECD和△FCB中，，∴Rt△ECD≌Rt△FCB（SAS），∴DE=BF，∠CED=∠CFB．∵∠CFB+∠CBF=90°，∴∠CED+∠CBF=90°，∴∠EGB=90°，即DE⊥BF．22．如图，△ABC的外角∠DAC的平分线交BC边的垂直平分线于点P，PD⊥AB于点D．（1）过点P作PE⊥AC于点E，求证：BD=CE；（2）若AB=6cm，AC=10cm，求AD的长．【解答】（1）证明：作PE⊥AC于点E，连接PB、PC，∵PQ是BC边的垂直平分线，∴PB=PC，∵AP平分∠DAC，PD⊥AB，PE⊥AC，∴PD=PE，在Rt△BPD和Rt△CPE中，，∴Rt△BPD≌Rt△CPE，∴BD=CE；（2）解：在Rt△ADP和Rt△AEP中，，∴Rt△ADP≌Rt△AEP，∴AD=AE，∴AD+6=10﹣AD，解得，AD=2（cm）．。

人教版九年级物理上册同步学习指导-第13章《内能》重难点、易错点突破技巧

第十三章重难点、易错点突破技巧【重难突破】重难点1温度、热量、内能的区别与联系（难点）【方法技巧】温度、热量、内能的区别与联系：【例1】（2018·聊城中考）关于温度、内能、热量，下列说法正确的是（）A.物体温度越高，含有的热量越多B.物体运动得越快，内能越大C.热传递能改变物体的内能第 1 页共 11第 2 页共 11 D. 0°C 的冰块，其内能为零【针对练习】1.（河北中考改编）（多选）下列说法正确的是（）A. 两杯水温度相同，内能也一定相同B. 热量总是从内能大的物体向内能小的物体传递C. 热量总是从温度高的物体向温度低的物体传递D. 质量、初温相同的水和煤油放出相同热量后，水的温度高于煤油的温度重难点2比热容及其应用（重点）【方法技巧】水的比热容较大，其应用主要有以下两方面：（1）根据公式Q=cm △t 可知：相同质量的水和其他物质，升高（或降低）相同的温度，水吸收（或放出）的热量较多，这就是我们常用水来作冷却剂或散热剂的原因。

水作冷却剂时，可以带走更多的热量，例如发动机用水循环冷却：水作散热剂时，可以放出更多的热量，例如暖气片中用水循环散热。

（2）根据公式cmt Q=∆可知：质量相同的水和其他物质，吸收（或放出）相同的热量，水的温度变化较小，这一点有利于调节气候，例如沿海地区较内陆地区昼夜温差小且冬暖夏凉。

【例2】（2018•徐州中考改编）当严寒即将来临时，为了预防果实结冰，果农会用水喷洒果树。

请你解释这种做法所蕴含的道理。

【针对练习】2.美丽的柳叶湖是常德市的一颗明珠，它不仅以其旖旎的风光令人们流连忘返，更是这个城市的居民在盛夏避暑的好去处。

柳叶湖的水面宽广，蓄水量丰富，而水的比沙石的大，在质量相同的情况下吸收相同的热量后水升高的温度要（选填“多于”“等于''或“少于”）沙石升高的温度，因而夏天人们在柳叶湖边会感到很舒服。

3.（2018秋•南昌期中）夏天，小张同学和家人一起去庐山避暑，发现山脚下的餐馆常将饮料、西瓜等储藏于温度较低的山泉、溪流中，待到需要时再将其拿出以供客人降温解暑。

第13章流程图(答案版)---

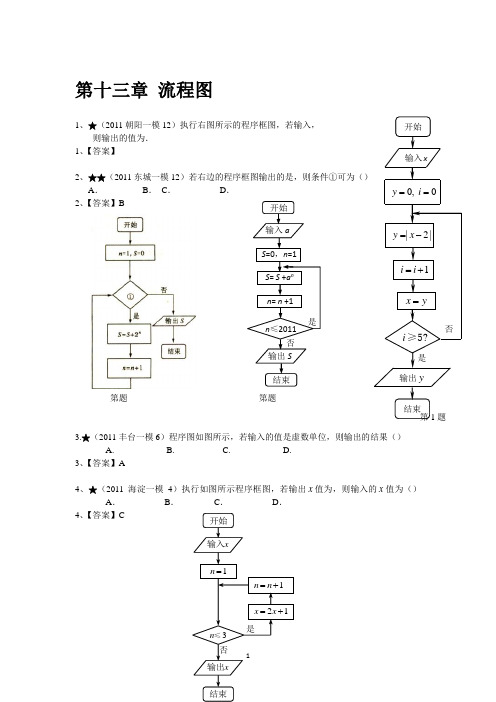
第十三章流程图1、★（2011朝阳一模12）执行右图所示的程序框图，若输入，则输出的值为．1、【答案】2、★★（2011东城一模12A．B．C．D．2、【答案】B第题第题3.★（2011丰台一模6）程序图如图所示，若输入的值是虚数单位，则输出的结果（）A. B. C. D.3、【答案】A4、★（2011海淀一模4）执行如图所示程序框图，若输出x值为，则输入的x值为（）A．B．C．D．4、【答案】C5、★★（2011石景山一模10）阅读如图所示的程序框图，运行该程序后输出的的值是． 5、【答案】第题第题6、★（2011西城一模5）阅读右侧程序图，为使输出的数据为，则①处应填的数字为（）A. B. C.D. 6、【答案】B7、★（2011朝阳二模12）如图程序框图的程序执行后输出的结果是. 7、【答案】第4题第题第题第题8、★★（2011东城二模13）已知某程序的框图如图，若分别输入的的值为，执行该程序后，输出的的值分别为，则．8、【答案】9、★★（2011丰台二模13）如果执行上面的程序框图，那么输出的=． 9、【答案】-10、★（2011海淀二模10）运行如图所示的程序框图，若输入，则输出的值为. 10、【答案】第题第题11、★★★（2011西城二模13）定义某种运算，的运算原理如图所示.设.则；在区间[-2,2]上的最小值为．11、【答案】；12、★★（年朝阳区一模）执行如图所示的程序框图，若输入的值是，则输出的值是． 12、【答案】13、★（2012东城一模4）右图给出的是计算的一个程序框图，其中判断框内应填入的条件是（）A. B. C. D.13、【答案】B第题第题14、★★（2012丰台一模13）执行如下图所示的程序框图，则输出的值为． 14、【答案】15、★（2012海淀一模5）执行如图所示的程序框图，输出的值是（）A. B. C. D15、【答案】B第12题16、★（2012石景山一模）执行右面的框图，若输入的是，则输出的值是（）A ．B ．C ．D ． 16、【答案】第16题第17题 17、★（2012西城一模 2）执行如图所示程序框图，若输入，则输出y 的值为（）A.B.CD.17、【答案】D18、★★（2012朝阳二模 10）执行如图所示的程序框图，输出的结果是． 18、【答案】第15题19、★（2012东城二模 3）执行右图的程序框图，则第次输出的数为（）A.4B.5C.6D.7 19、【答案】B第题第题20、★（2012丰台二模 4）执行如图所示程序图，若输出的结果为63，则判断框中应填（）A.B.C.D. 20、【答案】D21、★★（2012海淀二模 12）执行如图所示程序图，若输入的值为，则输出的值为（）AB.C.D 21、【答案】A第18题22、★★（2012西城区二模 2）执行如图所示的程序框图，若输入如下四个函数： ①则输出函数的序号为（）A.①B.②C.③D.④22、【答案】D第22题第23题23、★★（2013朝阳二模11）执行如图所示的程序框图，输出的结果=． 23、【答案】24、★（2013东城一模4）执行如图所示的程序框图，输出的结果是，则判断框内应填入的条件是（）A.B.C.D.24、【答案】A第21题第24题25、★（2013丰台一模3）执行如图的程序框图，输出的值是（）A.B.C.D.25、【答案】A第25题第26题26、★（2013海淀一模3）某程序的框图如图所示，执行该程序，若输入的值为5，则输出的y 值为（）Ａ. B. C. D.26、【答案】C27、★★（2013石景山一模 4）执行右面的框图，输出的结果的值为（） A ．B ．C ．D ． 27、【答案】A28、★★（2013西城一模3）执行如图所示程序图．若输出，则输入角（）A.C. D.28、【答案】D第28题第29题29、★★（2013朝阳二模3）执行如图所示的程序框图．若输出的结果是16，则判断框内的条件是（）A. B. C. D.29、【答案】C第27题30、★（2013东城二模5）阅读程序框图，运行相应的程序，当输入的值为时，输出x的值为（）A．B．C．D．30、【答案】D第30题31、★（2013西城二模 4）如图所示的程序框图表示求算式“” 之值，则判断框内可以填入（） A.B.C.D. 31、【答案】C第31题第32题32、★（2014石景山一模 7）阅读如图程序框图，运行相应的程序，输出的结果为（）A ．-2B ．C ．-1D ．232、【答案】C33、★（2014西城一模 4）执行如图所示程序框图，如果输入，那么输出的值为（） A. B. C. D. 33、【答案】C34、★（2014朝阳一模 6）执行如图所示的程序框图,输出的值为（）A. 2B. -2C. 4D. -434、【答案】D第34题第35题35、★★（2014海淀二模 3）执行如图所示程序框图，若输出为，则输入的应为（）A. B. C. D.35、【答案】D第33题36、★★（2014东城二模 3）已知一个算法的程序框图如图所示，当输出的结果为时，输入的值为（）A.2或-2B.-1或-2C.1或-2D.2或-136、【答案】C37、★（2014西城二模 12）执行如图所示的程序框图，输出的值为． 37、【答案】第37题第38题38、★★（2014大兴二模 5）在如图所示程序框图，输入，则输出的是（）A. B. C. D.38、【答案】D第36题39、★（2014顺义二模 6）执行如图所示程序框图，若输入，则输出值是（）A ．2B ．5C ．11D ．23 39、【答案】D40、★★（2014年房山区二模 5）若右图所示程序框图输出的S 是126，则条件①可为（）A ．B ．C ．D ．40、【答案】B第39题第40题。

第十三章内能(原卷版+解析)

第十三章内能一、选择题(每小题3分,共36分)1.生活中的许多现象都与我们学过的物理知识有关,下列说法正确的是( )。

A．尘土飞扬，说明分子在不停地做无规则运动；B．钻木取火,利用做功来改变物体的内能；C．人工湖能调节气温，利用水的比热容小；D．夏天吃冰糕，看到冰糕周围冒“白气”是汽化现象2.小明放学回家，一开门就闻到从厨房飘来的香味，他来到厨房想看看是什么好吃的，打开锅盖，他戴的眼镜上立刻蒙上一层“雾气”。

对此，正确的解释是（）。

A．闻到香味说明分子在做无规则运动；B．眼镜上的“雾气”是水蒸气；C．“雾气”的形成过程需要吸热；D．“雾气”的形成是汽化现象3.质量相同的0 ℃的冰、0 ℃的水、0 ℃的水蒸气中,它们的内能()A.一样大B.冰的内能最大,水蒸气的内能最小C.水的内能最大,冰的内能最小D.水蒸气的内能最大,冰的内能最小4.科学探究需要进行实验,在取得数据和事实后,再进行分析和推理,因此,在科学探究中我们需要区分事实与推论.下列叙述正确的是()①在气体扩散实验中,抽去玻璃板后,红棕色的NO2气体进入空气中;②在液体扩散实验中,红墨水滴入热水,热水很快变红;③扩散现象表明,一切物质的分子都在不停地做无规则运动;④温度越高,分子的无规则运动越剧烈.A.①②是事实,③④是推论B.①②④是事实,③是推论C.①是事实,②③④是推论D.③④是事实,①②是推论5.关于温度、热量、内能，以下说法正确的是（）。

A.对物体加热，物体的温度一定升高；B.物体的温度越高，所含有的热量越多；C.物体的温度是0 ℃，其内能也是零；D.热量总是自发地从温度高的物体向温度低的物体传递6.下列关于“热与能”的表述中正确的是()A.物体在吸热过程中,其温度一定升高B.在搓手取暖过程中,内能转化为机械能C.水常被用作冷却剂,是因为水的比热容大D.铁块在煅烧过程中,其内能从零开始增加7.如图所示四种暖手方式中,通过做功改变内能的是()A.哈气B.搓手C.开暖灯D.戴USB保暖手套8．关于比热容，下列说法正确的是( )。

第13章内能(原卷版)

中考一轮复习知识点梳理与针对性分层训练第13章《内能》【知识点1、分子热运动】一、物质的构成常见的物质是由极其微小的粒子——______、______构成的。

☆人们通常用______m为单位来量度分子。

___________可以帮助我们观察到分子。

二、分子的热运动1．不同的物质在互相接触时彼此进入对方的现象，叫___________。

2．扩散现象可以发生在______、______、______之间。

3．由于分子的运动跟_______有关，_______越高，分子运动越剧烈。

所以这种无规则运动叫_____________。

4．扩散现象等大量事实表明：☆（1）___________________________________。

（2）____________________________。

三、分子间的作用力1．分子之间的______使得固体、液体分子不至于散开，因而固体和液体能保持一定的______。

2．压缩固体和液体很困难，是因为分子之间还存在着______。

3．分子间既有______又有______。

当分子之间的距离变小时，作用力表现为______；当分子之间的距离变大时，作用力又表现为______。

如果分子之间的距离过大，作用力变得十分微弱，可以忽略。

4．分子间距决定了分子间的作用力，从而决定了固体、液体和气体的特征。

【经典例题考查】1．如图所示，是我们学习分子动理论时做过的一些实验。

（1）图甲中硫酸铜溶液与清水放置几天之后，两种液体混合均匀了，这是现象。

（2）图乙玻璃板的下表面接触水面，向上拉动时会发现弹簧测力计示数玻璃板的重力。

（选填“大于”、“等于”或“小于”）（3）图丙中水和酒精充分混合后的总体积混合前水和酒精的总体积。

（选填“大于”、“等于”或“小于”）（4）图丁中所示的实验现象说明分子在做。

2．学习了分子动理论之后，欣欣同学总结了很多生活中与分子动理论有关的现象，下列总结中不正确的是（）A．腌制鸭蛋就是通过扩散使盐进入蛋中B．人造木板粘接剂中的甲醛扩散到空气中造成环境污染C．用透明胶带揭下纸上写错的字，是因为胶带与纸之间有相互的斥力D．“破镜不能重圆”是分子间的距离太大，作用力变得十分微弱3．夏季来临，瓶装水迎来销售旺季，大量废弃的塑料瓶污染环境。

有机化学课后习题答案第13章

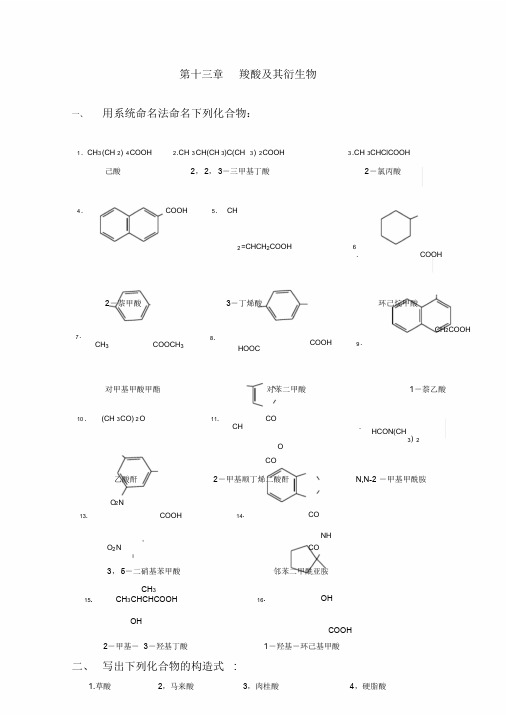
第十三章羧酸及其衍生物一、用系统命名法命名下列化合物：1 . CH3 (CH 2) 4COOH 2.CH 3 CH(CH 3)C(CH 3) 2COOH 3 .CH 3CHClCOOH己酸2，2，3－三甲基丁酸2－氯丙酸4 . COOH 5. CH2 =CHCH2COOH 6. COOH 2－萘甲酸3－丁烯酸环己烷甲酸7 .CH3 COOCH38.HOOCCOOH 9 .CH2COOH对甲基甲酸甲酯对苯二甲酸1－萘乙酸10 . (CH 3CO) 2 O 11. COCH .HCON(CH3) 2OCO乙酸酐2－甲基顺丁烯二酸酐N,N-2 －甲基甲酰胺O2N13. COOH 14. CONHO2N CO3，5－二硝基苯甲酸邻苯二甲酰亚胺CH315. CH3CHCHCOOH 16. OHOHCOOH2－甲基－3－羟基丁酸1－羟基－环己基甲酸二、写出下列化合物的构造式:1.草酸2，马来酸3，肉桂酸4，硬脂酸HHOOCCOOHC C OOHC H=CHCOOH CH3(CH 2) 16 COOHCHCOOH5． α －甲基丙烯酸甲酯 6，邻苯二甲酸酐 7，乙酰苯胺 8，过氧化苯甲酰胺OOCH 3 CH 2=CCOOCH 3C OOC OONHCOCH 3CCO9． ε－己内酰胺 10，氨基甲酸乙酯 11，丙二酰脲 12，胍OH NCOOC H 2 2 5CNHC OH 2 N C NH 2NHO CNHC NHO 13，聚马来酸酐14，聚乙酸乙烯酯[ ] CH 2CHnCO OC OnO C OCH 3三、写出分子式为 C 5H 6O 4 的不饱和二元酸的所有异构体（包括顺反异构）的结构式，并指出那些容易生成酸酐：解：有三种异构体： 2－戊烯－1，5－二酸；2－甲基－顺丁烯二酸； 2 －甲基－反丁烯二酸。

其中 2－甲基－顺丁烯二酸易于生成酸酐。

HOOC CH=CHCH 2 COOHC H 3HOOCCH 3COOHCCH C COOHCHCOOH 2－戊烯－ 1，5－二酸； 2－甲基－顺丁烯二酸； 2－甲基－反丁烯二酸四、比较下列各组化合物的酸性强度：1，醋酸，丙二酸，草酸，苯酚，甲酸, , OH ,HCOOH CH3COOH, HOOCCH HOOCCOOH2 COOH酸性强度顺序：OH> > > >HOOCCOOH HOOCCH2COOH HCOOH CH3COOH2. C6H5OH , CH3COOH, F3CCOOH , ClCH 2COOH , C2 H5 OH酸性强度顺序为：F3CCOOH > ClCH 2COOH > CH3COOH > C6H5OH > C2 H5 OH3. COOH COOH COOH OH OHNO2 NO2酸性强度顺序为：COOH COOH COOH OH OH> > > >NO2NO2五、用化学方法区别下列化合物:1．乙醇，乙醛，乙酸乙醇乙醛乙酸I2, NaOH HCI3 CHI3 不变Tollens试剂不变银镜2．甲酸，乙酸，丙二酸甲酸乙酸丙二酸Tollens试剂银镜不变不变加热不变CO23．草酸，马来酸，丁二酸草酸马来酸丁二酸溴水不变褪色不变高锰酸钾褪色——不变4,COOH COOH CH2OHOH2－羟基苯甲酸苯甲酸苯甲醇2－羟基苯甲酸苯甲酸苯甲醇三氯化铁水溶液显色不变不变氢氧化钠水溶液——溶解不溶5．乙酰氯，乙酸酐，氯乙烷乙酰氯乙酸酐氯乙烷硝酸银水溶液立即生成氯化银沉淀不反应加热才有氯化银沉淀六、写出异丁酸和下列试剂作用的主要产物：1. Br 2/PCH3CH3CHCOOHBr 2/PCH3CH3CCOOHBr CH3LiAlH 4/H 2 O2 . LiAlH 4/H 2O CH3 CHCOOHCH3CH3CHCH2OH3. SOCl 2CH 3CH3CHCOOHSOCl 2CH3CH3CHCOClCH3(CH3C O)2O/CH34.(CH3C O)2O/CH3CHCOOH(O+CH3COOHCH3CHCO)25.PBr3CH3CH3CHCOOHPBr3(CH3)2CHCOBr6.CH3CH2OH/H2SO4CH3CH3CHCOOHC H3CH2OH/H2SO4(CH3)2CHCOOC2H57.NH3/CH3CH3C HCOOHN H3/(CH3)2CHCONH2七、分离下列混合物：用氢氧化钠水溶液处理，再酸化分出丁酸CH3CH2C OCH2CH3,CH3C H2CH2CHO,CH3CH2C H2CH2OH ,CH3CH2CH2COOHCH3CH2C H2COOHCH3CH2C H2CH2OH CH3CH2CH2CHO CH3CH2COCH2CH3N aOHaq加饱和NaHSO3CH3C H2CH2COONaHClCH3CH2CH2C OOHCH3CH2C H2CH2OH CH3CH2C H2CHOOHCH3CH2CH2C HSO3Na+,H2OHCH3CH2C H2CHOCH3CH2C OCH2CH3CH3CH2CH2C H2O H N H23N HOHCH3C H2CCH2C H3H ClCH3C H2COCH2CH3CH3CH2COCH2CH3NNHOH 八、写出下列化合物加热后生成的主要产物：(CH3)2CCOOH 1，1，2－甲基－2－羟基丙酸OH CH3CH3COOCO CCCH3CH3O2，2，β－羟基丁酸C H3CHC H2COOHOHCH3CH=CHCOOH3，3，β－甲基－γ－羟基戊酸CH3CH3C HCHCH2COOHC H3C OO OH4，4，δ－羟基戊酸C O5，5，乙二酸HOCH2CH2CH2C H2COOH OHOOCCOOH HCOOH+CO2九、完成下列各反应式（写出主要产物或主要试剂）(A)H2O,H+CH3CH2COOH1.CH3C H2CNNH3(D)P2O5(B)SOCl2(E) CH3C H2CONH2(F)NaOBr,NaOH NH3(C)CH3C H2COCl(G)H2,Pd/BaSO4 CH3C H2NH2C H3C H2CHO2.C=O 1.C2H5MgBr2,H3O+OHC2H5PBr31.Mg,(C2H5)2O+2.CO2,H3OC2H5COOH3.Cl C ClO 2NH3H2N C NH2OH2N C NH2O H2N CONH C NH2O4.C=O NaCN,H2S O4OH+H3OO HCNCOOH OOCO CO十、完成下列转变：1.CH3CH2COOH CH3CH2C H2C OOHCH3CH2COOH [H]CH3C H2CH2OHP Br3CH3C H2CH2BrNaCNCH3CH2C H2CN+H3O CH3C H2CH2COOH2.CH3CH2C H2COH CH3CH2COOHCH3C H2CH2COOH C l2/PCH3C H2C HCOOH-OH C H3CH2C HCOOHCl OH+KMnO4,H C H3CH2C OOH3.C=CH2CH2C OOHC=CH2+HBr R OORCH2BrMg,(C2H5)OCH2MgBr1,CO2C H2COOH2,H3O4.CH3COCH2CH2CBr(CH3)2CH3COCH2CH2C(CH3)2C OOH+HOCH2CH2OH/HO OCH3C OCH2CH2C Br(CH3)2CH3C CH2CH2CBr(CH3)2 Mg,(C2H5)O OO CH 3CH3C CH2C H2CMgBrCH31.CO2+2.H3OCH3COCH2CH2C(CH3)2COOH十一、试写出下列反应的主要产物：6．（R ）－2－溴丙酸 + (S)－2－丁醇H+/⊿ OHBrCH 3COOHCH 3CH 2+C H 3HH+HBr CH 3C OH OC 2H 5CH 3 H7.CH 3 CH 2 COONa+CH 3 CH 2 CH 2COClCH 3CH 2CH 2CO O CCH 2CHCH 3OO8. CH2CH 2CCO+ 2C 2H 5OHC 2H 5 OCCH 2CH 2 COC 2H 5OOO9.C H 3+NaOBr-OHCH 3 CONH 2NH 210 .CONH 2+ P 2 O 5CN十二、预测下列化合物在碱性条件下水解反应的速度顺序。

宏观经济学第13章课后练习参考答案

第十三章课后练习·参考答案( P407-408 )1．C2．A3．D4．在均衡产出水平上，总产出等于计划总支出，所以非计划存货投资一定等于零，计划存货投资不一定等于零，主要看企业是否有计划存货投资。

5．边际消费倾向是指增加的收入中用于增加消费的比率。

由于增加的消费只能来自增加的收入，所以边际消费倾向的取值范围为[0，1]，通常为（0，1），对单个个人而言，边际消费倾向可以为0或1，但对总体而言，不可能出现等于0或等于1的情况。

平均消费倾向一定是大于零的，但不总是小于1，当收入较低或为零时，消费支出大于收入，此时平均消费倾向大于1，当居民将所有的收入都用于消费时，平均消费倾向等于1，只有当收入较高，居民除消费之外还有剩余时，平均消费倾向才小于1。

6．凯恩斯定律是指不论需求量为多少，经济社会均能以不变的价格提供相应的供给量。

即社会总需求变动时，只会引起产量和收入的变动，使供求相等，而不会引起价格变动。

凯恩斯定律提出的社会经济背景是1929年到1933年的大萧条，工人大批失业，资源大量闲置。

在这种情况下，社会总需求增加时，只会使闲置的资源得到利用，生产增加，而不会使资源的价格上升，从而产品成本和价格大体上能保持不变。

凯恩斯定律只适用于短期，因为在短期中，价格不易变动，当社会总需求变动时，就只引起产量的变动。

（参看课本P381）7. 参见第十二章课后练习的第6题。

简单地说，就是转移支付已经包括在C和I里了。

8. 因为富人的边际消费倾向小于穷人的，当把一部分收入从富人那里转移给穷人时，富人减少的消费小于穷人增加的消费，所以整个社会的总消费或总支出是增加的，根据凯恩斯理论，整个社会的总收入就会得到提高。

9. 因为政府购买支出增加后首先直接引起总支出和总收入等额增加相当于政府购买支出的量，然后收入的增加又引起消费的增加，消费和收入之间的相互作用最终使收入的增加是政府购买支出增加的数倍，形成政府购买支出乘数。

第13章课后答案

第十三章简单国民收入决定理论1.在两部门经济中，均衡发生于( )之时。

A.实际储蓄等于实际投资；B.实际消费加实际投资等于产出值；C.计划储蓄等于计划投资；D.总投资等于企业部门的收入。

解答：C2.当消费函数为c ＝a ＋by(a>0,0<b<1)，这表明，平均消费倾向( )。

A .大于边际消费倾向；B .小于边际消费倾向；C .等于边际消费倾向；D .以上三种情况都可能。

解答：A3.如果边际储蓄倾向为0.3，投资支出增加60亿元，这将导致均衡收入GDP 增加( )。

A . 20亿元；B . 60亿元；C . 180亿元；D . 200亿元。

解答：D4.在均衡产出水平上，是否计划存货投资和非计划存货投资都必然为零？解答：当处于均衡产出水平时，计划存货投资一般不为零，而非计划存货投资必然为零。

这是因为计划存货投资是计划投资的一部分，而均衡产出就是等于消费加计划投资的产出，因此计划存货不一定是零。

计划存货增加时，存货投资就大于零；计划存货减少时，存货投资就小于零。

需要指出的是，存货是存量，存货投资是流量，存货投资是指存货的变动。

在均衡产出水平上，计划存货投资是计划投资的一部分，它不一定是零，但是非计划存货投资一定是零，如果非计划存货投资不是零，那就不是均衡产出了。

比方说，企业错误估计了形势，超出市场需要而多生产了产品，就造成了非计划存货投资。

5.能否说边际消费倾向和平均消费倾向总是大于零而小于1？解答：消费倾向就是消费支出和收入的关系，又称消费函数。

消费支出和收入的关系可以从两个方面加以考察，一是考察消费支出变动量和收入变动量的关系，这就是边际消费倾向(可以用公式MPC ＝Δc Δy 或MPC ＝d c d y表示)，二是考察一定收入水平上消费支出量和该收入量的关系，这就是平均消费倾向(可以用公式APC ＝c y表示)。

边际消费倾向总大于零而小于1，因为一般说来，消费者增加收入后，既不会不增加消费即MPC ＝Δc Δy＝0，也不会把增加的收入全用于增加消费，一般情况是一部分用于增加消费，另一部分用于增加储蓄，即Δy ＝Δc＋Δs ，因此，Δc Δy ＋Δs Δy ＝1，所以，Δc Δy ＝1－Δs Δy 。

2021年中考物理复习滚动练习：第13章内能含答案

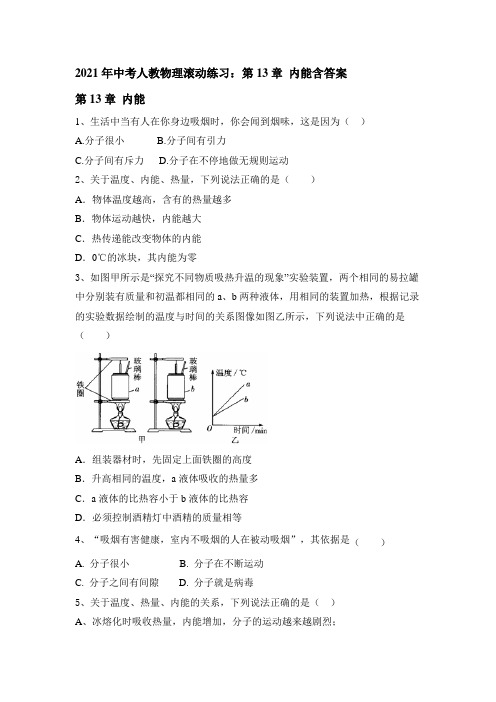
2021年中考人教物理滚动练习：第13章内能含答案第13章内能1、生活中当有人在你身边吸烟时，你会闻到烟味，这是因为（）A.分子很小B.分子间有引力C.分子间有斥力D.分子在不停地做无规则运动2、关于温度、内能、热量，下列说法正确的是（）A．物体温度越高，含有的热量越多B．物体运动越快，内能越大C．热传递能改变物体的内能D．0℃的冰块，其内能为零3、如图甲所示是“探究不同物质吸热升温的现象”实验装置，两个相同的易拉罐中分别装有质量和初温都相同的a、b两种液体，用相同的装置加热，根据记录的实验数据绘制的温度与时间的关系图像如图乙所示，下列说法中正确的是（）A．组装器材时，先固定上面铁圈的高度B．升高相同的温度，a液体吸收的热量多C．a液体的比热容小于b液体的比热容D．必须控制酒精灯中酒精的质量相等4、“吸烟有害健康，室内不吸烟的人在被动吸烟”，其依据是（）A. 分子很小B. 分子在不断运动C. 分子之间有间隙D. 分子就是病毒5、关于温度、热量、内能的关系，下列说法正确的是（）A、冰熔化时吸收热量，内能增加，分子的运动越来越剧烈；B、物体的温度升高，一定是从外界吸收了热量；C、对物体做功，它的内能一定增加，温度不一定升高；D、物体的温度升高，内能一定增加6、夏日晴朗的白天，在太阳光照射下，某海边城市陆地与海面之间空气流动示意图（图中箭头表示空气流动方向）合理的是（）A． B．C．D．7、下列现象中，利用或说明了分子做无规则运动的是（）A．煮稀饭时米粒在水中翻滚B．用鼻子鉴别醋和酱油C．固体、液体很难被压缩D．两个铅柱压紧后粘在一起8、如图所示，利用做功的方式来改变内能的是（）A．哈气取暖B．加热冰块C．弯折铁丝D．炒菜做饭9、在探究水沸腾时温度变化特点的实验中，某同学用如图甲所示的实验装置进行实验，并绘制了如图乙所示的图线①.现将烧杯中的水冷却至室温，倒掉约三分之一的水，保持其他条件不变，重做上述实验并绘制了图线，此图线是（）A. ①B. ②C. ③D. ④10、下列说法，正确的是（）A. 空气中弥漫的一粒粒灰尘是较大的分子B. 如果视力好，可以用肉眼直接观察到分子C. 一切物体都是由物质组成﹑物质由分子组成D.分子是构成物质的最小微粒11、下列现象中，通过热传递改变内能的是（）A．用锯锯木头，锯条发热B．热水中放入冰块，水温下降C．两手相互摩擦，手发热D．用砂轮磨菜刀，菜刀的温度升高12、两个质量相同的不同物质，吸收相同的热量，下列说法中正确的是（）A．比热容大的物质升高温度较小B．比热容小的物质升高温度较小C．比热容大的物质升高温度较大D．升高温度相同，与比热容大小无关13、电冰箱里的食物容易相互“窜味”，从物理角度分析，食物“窜味”属于________现象；当打开冰箱门时，往往会看到冷冻室的侧壁上有很多霜，这是水蒸气________(选填物态变化名称)形成的，这个过程中水蒸气________(选填“吸收”或“放出”)热量．14、如图所示，在一个配有活塞的厚透明筒里放一小团硝化棉，把活塞迅速下压，压缩空气______，使筒内空气的内能增加，温度升高，观察到硝化棉______。

2020年人教版物理九年级全册精品学案第13章第3节《比热容》 (含答案)

第1课时比热容【学习目标】1、了解比热容的概念，知道比热容是物质的一种属性．2、通过探究，比较不同物质的吸热能力．【学习重点】比热容的概念。

【学习难点】理解比热容概念并能利用它解释有关现象．【预习检测】1．根据生活经验，我们会发现烧一壶水所用的时间比烧半壶水所用的时间要长，说明物体所吸收的热量与_________有关。

2．把一壶水烧成开水比烧成温水所用的时间长，说明了物体所吸收的热量的多少与_________有关。

3、相同质量的水和沙子，当温度升高的度数也相等时，吸收的热量是不是一样多呢？4．热量是看不见，摸不着的，你是通过什么知道水吸收热量多少的呢？【共同探究】★学生活动一：探究比较不同物质的吸热能力1、方法：根据我们的生活经验已经知道物体吸收热量的多少与和有关，我们要探究热量的多少与物质的种类是否有关，需要控制、相同，这种方法叫。

2、器材：你认为要验证你的猜想，需要哪些器材，思考并交流以下几个问题：（1）需要测量哪些物理量，需要哪些器材？并说出你的理由（2）热量是看不见摸不着的物理量，你通过什么知道它的多少？。

（3）数据记录表格中的加热时间代表哪个物理量？3、进行试验：某组同学按照课本组装器材，并进行实验，后将实验数据填入下表格中，请根据表中的实验记录回答：⑴比较1、2记录，得出的结论是___________________________________；⑵比较3、4记录，得出的结论是___________________________________；⑶比较1、3记录，得出的结论是___________________________________；⑷综合上述结论，物体温度升高时吸热的多少与_________________________有关。

⑸该同学在本次实验中用到的研究方法是____________________________。

4、结论：交流实验数据，说出通过实验得出的结论是：相同质量的不同物质，吸收相同的热量，升高的温度（选填“相同”或“不同”），这说明物体吸收热量的多少与有关。

2022-2023学年华东师大版八年级数学上册《第13章全等三角形》解答题优生辅导训练(附答案)

2022-2023学年华东师大版八年级数学上册《第13章全等三角形》解答题优生辅导训练（附答案）1．在△ABC中，AB＝2，BC＝4，CD⊥AB于D．（1）如图①，已知AE⊥BC于E，求证：CD＝2AE；（2）如图②，P是线段AC上任意一点（P不与A、C重合），过P作PE⊥BC于E，PF ⊥AB于F，求证：2PE+PF＝CD；（3）在图②中，若P是AC延长线上任意一点，其他条件不变，请画出图形并直接写出PE、PF、CD之间的关系．2．△ABC中，BD平分∠ABC，CE平分∠ACB，BD与CE交于点M．（1）若∠ABC＝70°，∠ACB＝50°，求∠BMC的度数（2）若MN⊥BC于N，∠A＝60°，求图中∠1﹣∠2的值；（3）若∠BEC＝x，∠BDC＝y，求∠BMC度数．3．如图，在△ABC中，∠B＝25°，∠BAC＝31°，过点A作BC边上的高，交BC的延长线于点D，CE平分∠ACD，交AD于点E．求：（1）∠ACD的度数；（2）∠AEC的度数．4．如图，△OAB和△OCD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝α，AC、BD交于M．（1）如图1，当α＝90°时，∠AMD的度数为°；（2）如图2，当α＝60°时，求∠AMD的度数；（3）如图3，当△OCD绕O点任意旋转时，∠AMD与α是否存在着确定的数量关系？如果存在，请你用α表示∠AMD，并用图3进行证明；若不确定，说明理由．5．如图，Rt△ACB中，∠ACB＝90°，AC＝BC，E点为射线CB上一动点，连接AE，作AF⊥AE且AF＝AE．（1）如图1，过F点作FD⊥AC交AC于D点，求证：EC+CD＝DF；（2）如图2，连接BF交AC于G点，若，求证：E点为BC中点；（3）当E点在射线CB上，连接BF与直线AC交于G点，若，则＝（直接写出结果）．6．如图，CD是经过∠BCA顶点C的一条直线，CA＝CB，E、F分别是直线CD上两点，且∠BEC＝∠CF A＝α．（1）若直线CD经过∠BCA的内部，且E、F在射线CD上．①如图1，若∠BCA＝90°，α＝90°，则BE CF；②如图2，若0°＜∠BCA＜180°，请添加一个关于α与∠BCA关系的条件，使①中的结论仍然成立，并说明理由；（2）如图3，若直线CD经过∠BCA的外部，α＝∠BCA，请提出关于EF，BE，AF三条线段数量关系的合理猜想，并简述理由．7．如图1，在△ABC中，∠ACB为锐角，点D为射线BC上一动点，连接AD．以AD为一边且在AD的右侧作等腰直角三角形ADE，AD＝AE，∠DAE＝90°．解答下列问题．（1）如果AB＝AC，∠BAC＝90°，①当点D在线段BC上时（与点B不重合），如图2，求证：BD＝CE，BD⊥CE．②当点D在线段BC的延长线上时，如图3，①中的结论是否仍然成立，请说明理由．（2）如果AB≠AC，∠BAC≠90°，点D在线段BC上运动．试探究：当△ABC满足一个什么条件时，CE⊥BD（点C、E重合除外）．先画出相应图形，再说明理由．8．如图1，已知△ABC中∠CAB内部的射线AD与∠ACB的外角的平分线CE相交于点P．若∠ABC＝40°，∠CP A＝20°．（1）求证：AD平分∠CAB；（2）如图2，点F是射线AD上一点，FG垂直平分BC于点G，FH⊥AB于点H，连接FC，若AB＝5，AC＝3，求HB．9．如图，已知正方形ABCD中，点M、N分别在边BC、CD上，∠MAN＝45°．（1）求证：MN＝BM+DN；（2）当AB＝6，MN＝5时，求△CMN的面积．10．已知Rt△ABC中，∠C＝90°，AD、BE是角平分线，它们相交于P，PF⊥AD于P交BC的延长线于F，交AC于H．（1）求证：AH+BD＝AB；（2）求证：PF＝P A．11．如图，在△ABC中，AB＝AC，点D，E，F分别在AB，BC，AC边上，且BE＝CF，BD＝CE．（1）求证：△DEF是等腰三角形；（2）当∠A＝40°时，求∠DEF的度数；（3）若∠A＝∠DEF，判断△DEF是何种三角形．12．（1）如图1，在△ABC中，AB＝AC＝10，BD平分∠ABC，CD平分∠ACB，过点D作EF∥BC，分别交AB、AC于E、F两点，则图中共有个等腰三角形；EF与BE、CF之间的数量关系是，△AEF的周长是．（2）如图2，若将（1）中“在△ABC中，AB＝AC＝10”改为“若△ABC为不等边三角形，AB＝8，AC＝10”，其余条件不变，则EF与BE、CF之间的数量关系是什么？证明你的结论，并求出△AEF的周长．（3）如图3，点D在△ABC外，AB＞AC，且BD平分∠ABC，CD平分△ABC的外角∠ACG，过点D作DE∥BC，分别交AB、AC于E、F两点，直接写出EF与BE、CF之间的数量关系．13．如图，在等腰Rt△ABC中，∠ACB＝90°，D为斜边的中点，点E、点F分别在直线CA、BC上，且DE⊥DF．（1）证明：△DEF是等腰直角三角形；（2）求证：EF2＝AE2+BF2；（3）若AE＝5，BF＝12，求S△CEF的值；（4）探索S△CEF、S△DEF、S△ABC之间的数量关系．14．如图，△ABC中，AB＝AC，D为AC边上一点，E为AB延长线上一点，且CD＝BE，DE与BC相交于点F．（1）求证：DF＝EF．（2）过点F作FG⊥DE，交线段CE于点G，若CE⊥AC，CD＝4，S△EFG＝5，求EG的长．15．如图，∠BAD＝∠CAE＝90°，AB＝AD，AE＝AC，AF⊥CB，垂足为F．（1）求证：△ABC≌△ADE；（2）求证：CD＝2BF+DE．16．如图，在△ABC中，AB＝AC，∠BAC＝100°，BD平分∠ABC，且BD＝AB，连接AD、DC．（1）求证：∠CAD＝∠DBC；（2）求∠BDC的度数．17．已知等腰三角形的周长为24cm，其中两边之差为6cm，求这个等腰三角形的腰长．18．如图，在△ABC中，∠BAC＝90°，E为边BC上的点，且AB＝AE，D为线段BE的中点，连接AD，过点E作EF⊥AE，过点A作AF∥BC，且AF、EF相交于点F．（1）求证：∠B＝∠DAC；（2）求证：AC＝EF．19．已知△ABC和△ADE都是等腰三角形，AB＝AC，AD＝AE，∠DAE＝∠BAC．【初步感知】（1）特殊情形：如图①，若点D，E分别在边AB，AC上，则DB EC．（填＞、＜或＝）（2）发现证明：如图②，将图①中△ADE绕点A旋转，当点D在△ABC外部，点E在△ABC内部时，求证：DB＝EC．【深入研究】（3）如图③，△ABC和△ADE都是等边三角形，点C，E，D在同一条直线上，则∠CDB的度数为；线段CE，BD之间的数量关系为．（4）如图④，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，点C、D、E在同一直线上，AM为△ADE中DE边上的高，则∠CDB的度数为；线段AM，BD，CD之间的数量关系为．20．如图，△ABC中，∠B＝2∠C，AE平分∠BAC．（1）若AD⊥BC于D，∠C＝35°，求∠DAE的大小；（2）若EF⊥AE交AC于F，求证：∠C＝2∠FEC．参考答案1．1）证明：∵CD⊥AB，AE⊥BC∴S△ABC＝AB•CD＝BC•AE，∵AB＝2，BC＝4，∴×2×CD＝×4×AE，∴CD＝2AE；（2）证明：如图②，连接PB，则S△ABC＝S△ABP+S△BCP，∴AB•CD＝AB•PF+BC•PE，∵AB＝2，BC＝4，∴×2×CD＝×2×PF+×4×PE，∴CD＝PF+2PE，故2PE+PF＝CD；（3）解：PF＝CD+2PE，理由如下：如图③，连接PB，则S△ABP＝S△ABC+S△PBC，即AB•PF＝AB•CD+BC•PE，∵AB＝2，BC＝4，∴×2×PF＝×2×CD+×4×PE，即PF＝CD+2PE．2．解：（1）∵BD平分∠ABC，CE平分∠ACB，∴∠MBC＝∠ABC＝35°，∠MCB＝∠ACB＝25°，∴∠BMC＝180°﹣∠MBC﹣∠MCB＝120°．（2）∵∠BMC＝180°﹣（∠ABC+∠ACB）＝180°﹣（180°﹣∠A）＝90°+∠A＝120°，∴∠1+∠BMN＝120°①，∵MN⊥BC，∴∠2+∠BMN＝90°②，①﹣②得：∠1﹣∠2＝30°．（3）如图：∵∠BMC＝90°+∠A，∵∠BEC＝∠A+∠6，∠BDC＝∠A+∠4，且∠4＝∠5，∠6＝∠7，∴x＝∠A+∠7①，y＝∠A+∠5②，①+②得：x+y＝2∠A+（∠7+∠5），∵∠BMC＝90°+∠A，∴∠A＝2∠BMC﹣180°，∵∠7+∠5＝180°﹣∠BMC，∴x+y＝4∠BMC﹣360°+180﹣∠BMC，∴∠BMC＝60°+．3．解：（1）∵∠ACD＝∠B+∠BAC，∠B＝25°，∠BAC＝31°，∴∠ACD＝25°+31°＝56°．（2）∵AD⊥BD，∴∠D＝90°，∵∠ACD＝56°，CE平分∠ACD，∴∠ECD＝∠ACD＝28°，∴∠AEC＝∠ECD+∠D＝28°+90°＝118°．4．解：（1）如图1中，设OA交BD于K．∵∠AOB＝∠COD＝α，∴∠BOD＝∠AOC，在△BOD和△AOC中，，∴△BOD≌△AOC（SAS），∴∠OBD＝∠OAC，∵∠AKM＝∠BKO，∴∠AMK＝∠BOK＝90°，∴∠AMD＝180°﹣90°＝90°．故答案为90．（2）如图2中，设OA交BD于K．∵∠AOB＝∠COD＝α，∴∠BOD＝∠AOC，在△BOD和△AOC中，，∴△BOD≌△AOC（SAS），∴∠OBD＝∠OAC，∵∠AKM＝∠BKO，∴∠AMK＝∠BOK＝60°，∴∠AMD＝180°﹣60°＝120°；（3）如图3中，设OA交BD于K．∵∠AOB＝∠COD＝α，∴∠BOD＝∠AOC，在△BOD和△AOC中，，∴△BOD≌△AOC（SAS），∴∠OBD＝∠OAC，∵∠AKO＝∠BKM，∴∠AOK＝∠BMK＝α．∴∠AMD＝180°﹣α．5．证明：（1）如图1，∵∠F AD+∠CAE＝90°，∠F AD+∠F＝90°，∴∠CAE＝∠AFD，在△ADF和△ECA中，，∴△ADF≌△ECA（AAS），∴AD＝EC，FD＝AC，∴CE+CD＝AD+CD＝AC＝FD，即EC+CD＝DF；证明：（2）如图2，过F点作FD⊥AC交AC于D点，∵△ADF≌△ECA，∴FD＝AC＝BC，在△FDG和△BCG中，，∴△FDG≌△BCG（AAS），∴GD＝CG，∵，∴＝2，∴＝，∵AD＝CE，AC＝BC∴＝，∴E点为BC中点；（3）过F作FD⊥AG的延长线交于点D，如图3，∵，BC＝AC，CE＝CB+BE，∴＝，由（1）（2）知：△ADF≌△ECA，△GDF≌△GCB，∴CG＝GD，AD＝CE，∴＝，∴＝，∴＝6，同理，当点E在线段BC上时，＝4．故答案为：6或4．6．解：（1）①∵∠BEC＝∠CF A＝α＝90°，∴∠BCE+∠CBE＝180°﹣∠BEC＝90°．又∵∠BCA＝∠BCE+∠ACF＝90°，∴∠CBE＝∠ACF．在△BCE和△CAF中，∴△BCE≌△CAF（AAS）．∴BE＝CF．②α+∠BCA＝180°，理由如下：∵∠BEC＝∠CF A＝α，∴∠BEF＝180°﹣∠BEC＝180°﹣α．又∵∠BEF＝∠EBC+∠BCE，∴∠EBC+∠BCE＝180°﹣α．又∵α+∠BCA＝180°，∴∠BCA＝180°﹣α．∴∠BCA＝∠BCE+∠ACF＝180°﹣α．∴∠EBC＝∠FCA．在△BCE和△CAF中，∴△BCE≌△CAF（AAS）．∴BE＝CF．（2）EF＝BE+AF，理由如下：∵∠BCA＝α，∴∠BCE+∠ACF＝180°﹣∠BCA＝180°﹣α．又∵∠BEC＝α，∴∠EBC+∠BCE＝180°﹣∠BEC＝180°﹣α．∴∠EBC＝∠FCA．在△BEC和△CF A中，∴△BEC≌△CF A（AAS）．∴BE＝CF，EC＝F A．∴EF＝EC+CF＝F A+BE，即EF＝BE+AF．7．1）①证明：CE与BD位置关系是CE⊥BD，数量关系是CE＝BD．理由：如图2中，∵∠BAD＝90°﹣∠DAC，∠CAE＝90°﹣∠DAC，∴∠BAD＝∠CAE，又BA＝CA，AD＝AE，∴△ABD≌△ACE（SAS），∴∠ACE＝∠B＝45°且CE＝BD，∵∠ACB＝∠B＝45°，∴∠ECB＝45°+45°＝90°，即CE⊥BD．故答案为：CE⊥BD；CE＝BD．②解：当点D在BC的延长线上时，①的结论仍成立．如图3中，∵∠DAE＝90°，∠BAC＝90°，∴∠DAE＝∠BAC，∴∠DAB＝∠EAC，又AB＝AC，AD＝AE，∴△DAB≌△EAC（SAS），∴CE＝BD，且∠ACE＝∠ABD．∵∠BAC＝90°，AB＝AC，∴∠ABC＝45°，∴∠ACE＝45°，∴∠BCE＝∠ACB+∠ACE＝90°，即CE⊥BD；（2）解：如图4中，当∠BCA＝45°时，CE⊥BD．理由：过点A作AG⊥AC交BC于点G，∴AC＝AG，∠AGC＝45°，即△ACG是等腰直角三角形，∵∠GAD+∠DAC＝90°＝∠CAE+∠DAC，∴∠GAD＝∠CAE，又∵DA＝EA，∴∠ACE＝∠AGD＝45°，∴∠BCE＝∠ACB+∠ACE＝90°，即CE⊥BD．8．证明：（1）如图1，∵CE平分∠QCB，∴∠QCP＝∠BCP，∵∠QCP＝∠QAP+∠APC＝∠QAP+20°，∴2∠QCP＝2∠QAP+40°，∵∠QCB＝∠QAB+∠ABC＝∠QAB+40°，∴∠QAB＝2∠QAP，∴AD平分∠CAB；（2）如图2，连接BF，过点F作FN⊥AC于N，由（1）可知AD平分∠CAB，∴∠F AB＝∠F AN，在△AFH和△AFN中，，∴AN＝AH，NF＝FH，∵FG垂直平分BC，∴FC＝FB，在Rt△FCN和Rt△FBH中，，∴Rt△FCN≌Rt△FBH（HL），∴CN＝BH，∵AB＝AH+BH＝AN+BH＝AC+CN+BH＝AC+2BH，∴5＝3+2BH，∴BH＝1．9．解：（1）延长CB到G，使BG＝DN，在△ADN和△ABG中，，∴△ADN≌△ABG（SAS），∴AN＝AG，∵∠MAN＝45°，∴∠MAB+∠NAD＝∠MAB+∠BAG＝45°，在△MAN和△MAG中，，∴△MAN≌△MAG（SAS），∴MN＝MG＝MB+BG＝MB+DN；（2）由（1）得，，∵S△AMN＝S△ABM+S△ABG，∴S△AMN＝S△ABM+S△ADN＝15，∴S△CMN＝S正方形ABCD﹣2S△AMN＝36﹣30＝6．10．1）证明：∵∠ACB＝90°，∴∠CAB+∠CBA＝90°，又∵AD、BE分别平分∠BAC、∠ABC，∴∠BAD+∠ABE＝（∠CAB+∠CBA）＝45°，∴∠APB＝135°，∴∠BPD＝45°，又∵PF⊥AD，∴∠FPB＝90°+45°＝135°，∴∠APB＝∠FPB，在△ABP和△FBP中，，∴△ABP≌△FBP（ASA），∴∠BAP＝∠F，P A＝PF，∵∠BAP＝∠CAD，∴∠F＝∠CAD，在△APH和△FPD中，，∴△APH≌△FPD（ASA），∴AH＝FD，又∵AB＝FB，∴AB＝FD+BD＝AH+BD．（2）证明：由（1）可知△ABP≌△FBP，∴P A＝PF，11．1）证明：∵AB＝AC，∴∠ABC＝∠ACB，在△DBE和△CEF中，，∴△DBE≌△CEF（SAS），∴DE＝EF，∴△DEF是等腰三角形；（2）如图，∵△DBE≌△CEF，∴∠1＝∠3，∠2＝∠4，∵∠A+∠B+∠C＝180°，∴∠B＝（180°﹣40°）＝70°，∴∠1+∠2＝110°，∴∠3+∠2＝110°，∴∠DEF＝70°；（3）△DEF是等边三角形，理由如下：∵∠1＝∠3，∠DEC＝∠DEF+∠3＝∠1+∠B，∴∠DEF＝∠B，∴∠A＝∠DEF，∴∠A＝∠B＝∠C，∵∠A+∠B+∠C＝180°，∴∠A＝∠B＝∠C＝60°＝∠DEF，又∵DE＝EF，∴△DEF是等边三角形．12．解：（1）BE+CF＝EF．理由如下：∵AB＝AC，∴∠ABC＝∠ACB，∵BD平分∠ABC，CD平分∠ACB，∴∠EBD＝∠CBD，∠FCD＝∠BCD，∴∠DBC＝∠DCB，∴DB＝DC∵EF∥BC，∴∠AEF＝∠ABC，∠AFE＝∠ACB，∠EDB＝∠CBD，∠FDC＝∠BCD，∴∠EBD＝∠EDB，∠FDC＝∠BCD，∴BE＝DE，CF＝DF，AE＝AF，∴等腰三角形有△ABC，△AEF，△DEB，△DFC，△BDC共5个，∴BE+CF＝DE+DF＝EF，即BE+CF＝EF，△AEF的周长＝AE+EF+AF＝AE+BE+AF+FC＝AB+AC＝20．故答案为：5；BE+CF＝EF；20；（2）结论：BE+CF＝EF，理由：∵BD平分∠ABC，CD平分∠ACB，∴∠EBD＝∠CBD，∠FCD＝∠BCD，∵EF∥BC，∴∠EDB＝∠CBD，∠FDC＝∠BCD，∴∠EBD＝∠EDB，∠FDC＝∠BCD，∴BE＝DE，CF＝DF，∴等腰三角形有△BDE，△CFD，∴BE+CF＝DE+DF＝EF，即BE+CF＝EF．可得△AEF的周长为18．（3）结论：BE﹣CF＝EF，理由：由（1）知BE＝ED，∵EF∥BC，∴∠EDC＝∠DCG＝∠ACD，∴CF＝DF，又∵ED﹣DF＝EF，∴BE﹣CF＝EF．13．1）证明：连接CD，∵△ABC是等腰直角三角形，∴CD⊥AB，AD＝DB＝CD，∠A＝∠B＝∠ACD＝∠DCB＝45°，∵ED⊥DF，∴∠CDE+∠CDF＝90°，∴∠ADE＝∠CDF，在△ADE与△CDF中，，∴△ADE≌△CDF，∴DE＝DF，∴△DEF是等腰直角三角形；（2）延长FD，使DM＝DF，连接AM，EM，在△DFB与△AMD中，，∴△DFB≌△AMD，∴AM＝BF，∠B＝∠DAM＝45°，∴∠CAD+DAM＝90°，∴AE2+AM2＝EM2，∵DE⊥DF，DM＝DF，∴EF＝EM，∴EF2＝AE2+BF2；（3）∵△AED≌△CDF，∴CF＝AE＝5，∴BC＝17＝AC，∴BF＝CE＝12，∴S△CEF＝＝＝30；（4）∵△AED≌△CDF，∴S△ADE＝S△CDF，∵S△ADE+S△CDE＝S△ABC＝S△CDF+S△BDF，∴S△BDF＝S△CDE，∴S△ADE+S△BDF＝S△ABC，∴S△DEF+S△CEF＝S△ABC．14．1）过点D作DH∥AB交BC于点H，∵AB＝AC，∴∠ABC＝∠ACB，∵DH∥AB，∴∠DHC＝∠ABC，∴∠DHC＝∠ACB＝∠DCH，∴DH＝CD，∵CD＝BE，∴DH＝BE，∵DH∥AB，∴∠BEF＝∠HDF，在△BEF和△HDF中，，∴△BEF≌△HDF（AAS），∴DF＝EF；（2）连接DG，∵DF＝EF，FG⊥DE，∴S△DFG＝S△EFG＝5，∴S△DEG＝10，∵CE⊥AC，CD＝4，∴S△DEG＝EG•CD＝EG×4，∴EG×4＝10，∴EG＝5．15．证明：（1）∵∠BAD＝∠CAE＝90°，∴∠BAC+∠CAD＝∠CAD+∠DAE＝90°，∴∠BAC＝∠DAE，在△ABC和△ADE中，，∴△ABC≌△ADE（SAS）；（2）如图，延长CF至G，使FG＝BF，连接AG，∵AF⊥BC，∴∠AFG＝∠AFB＝90°，在△AFB和△AFG中，，∴△AFB≌△AFG（SAS），∴AB＝AG，∠ABF＝∠G，由（1）知△BAC≌△DAE，∴AB＝AD，∠CBA＝∠EDA，CB＝ED，∴AG＝AD，∠ABF＝∠CDA，∴∠G＝∠CDA，在△CGA和△CDA中，，∴△CGA≌△CDA（AAS），∴CG＝CD，∵CG＝CB+BF+FG＝CB+2BF＝DE+2BF，∴CD＝2BF+DE．16．证明（1）∵AB＝AC，∠BAC＝100°∴∠ABC＝∠ACB＝40°∵BD平分∠ABC∴∠ABD＝∠DBC＝20°∵BD＝AB∴∠ADB＝∠DAB＝80°∴∠CAD＝20°∴∠CAD＝∠DBC（2）延长AD到点E，使得AE＝BC，∵BD＝AB＝AC，∠CAD＝∠DBC，∴△DBC≌△CAE，∴CD＝CE，∠BDC＝∠ACE，∴∠CDE＝∠CED＝α，∵∠ADB＝80°，∴∠BDE＝100°∴∠BDC＝∠ACE＝100°+α，∴20°+100°+α+α＝180°，∴α＝30°，∴∠BDC＝130°．17．解：设三角形的腰为x，底为y，根据题意得或，解得或，又知6+6＜12，不能构成三角形，即等腰三角形的腰长为：10cm．18．证明：（1）∵AB＝AE，D为线段BE的中点，∴AD⊥BE，∴∠B+∠BAD＝90°，∴∠BAD+∠DAC＝90°，∴∠B＝∠DAC；（2）∵AF∥BC，∴∠AEB＝∠EAF，∵AB＝AE，∴∠ABC＝∠AEB，∴∠ABC＝∠EAF，∵EF⊥AE，∴∠BAC＝∠AEF＝90°，在△ABC和△EAF中，，∴△ABC≌△EAF（ASA），∴AC＝EF．19．【初步感知】（1）解：∵AD＝AE，AB＝AC，∴AB﹣AD＝AC﹣AE，即BD＝EC；故答案为：＝，（2）证明：由旋转性质可知∠DAB＝∠EAC，在△DAB和△EAC中，，∴△DAB≌△EAC（SAS），∴DB＝EC；【深入探究】解：（3）如图③，设AB，CD交于O，∵△ABC和△ADE都是等边三角形，∴AD＝AE，AB＝AC，∠DAE＝∠BAC＝60°，在△DAB和△EAC中，，∴△DAB≌△EAC（SAS），∴BD＝CE，∠ABD＝∠ACE，∵∠BOD＝∠AOC，∴∠CDB＝∠BAC＝60°，故答案为：60°，CE＝BD；（4）∵△DAE是等腰直角三角形，∴∠AED＝45°，∴∠AEC＝135°，在△DAB和△EAC中，，∴△DAB≌△EAC（SAS），∴∠ADB＝∠AEC＝135°，BD＝CE，∵∠ADE＝45°，∴∠CDB＝∠ADB﹣∠ADE＝135°﹣45°＝90°，∵△ADE是等腰直角三角形，AM为△ADE中DE边上的高，∴AM＝DE＝EM＝DM，∵DE+CE＝CD，∴2AM+BD＝CD，故答案为：90°，2AM+BD＝CD．20．1）解：∵∠C＝35°，∠B＝2∠C，∴∠B＝70°，∴∠BAC＝75°，∵AE平分∠BAC，∴∠EAC＝37.5°，∵AD⊥BC，∴∠ADC＝90°，∴∠DAC＝55°，∴∠DAE＝55°﹣37.5°＝17.5°；（2）证明：过点A作AD⊥BC于点D，∵EF⊥AE，∴∠AEF＝90°，∴∠AED+∠FEC＝90°，∵∠DAE+∠AED＝90°，∴∠DAE＝∠FEC，∵AE平分∠BAC，∴∠EAC＝∠BAC＝（180°﹣∠B﹣∠C）＝（180°﹣3∠C）＝90°﹣∠C，∵∠DAE＝∠DAC﹣∠EAC，∴∠DAE＝∠DAC﹣（90°﹣∠C）＝90°﹣∠C﹣90°+∠C＝∠C，∴∠FEC＝C，∴∠C＝2∠FEC．。

(2021年整理)机械工程图学习题集加详细答案第13章

螺母 GB/T6170-2000 M12 螺母 GB/T6170-2000 M20
垫圈 GB/T93-1987 12
垫圈 GB/T97.1-2002 20
被连接零件的材料为45钢；螺栓自上而下连接机件。
螺柱自上而下连接机件。
（3）在O"3O"3处画螺钉连接：螺钉GB/T65-2000
M10X35 螺钉自右向左穿入被连接件。
D 画成粗实线，内螺纹的 C 画成粗实线。 A 牙顶 B 牙底 C 小径 D 大径
3.普通螺纹的特征代号是 D ，55°非密封管螺纹的特征代号是 A ，梯形螺纹的特征代号是 C 。 A G B R C Tr D M
4.普通平键的工作面是 C
。
A 顶面 B 底面 C 侧面 D 端面
普通螺纹,螺纹长度为40mm。
纹小径与题（2）中光孔直径相同。
（3）将题（1）中的外螺纹和题（2）中的内螺纹旋合，旋合长度为 30mm。画出螺纹旋合图。
4. 根据所给螺纹标记填空。
5 在图上注出下列螺纹的标记
(1) 粗牙普通螺纹：公称直径d=20MM，螺距 p=2.5mm，右旋，中径和顶径公差带代号均为6h。
四.单项选择题。
1.已知粗牙普通内螺纹大径为16mm,螺距为2mm，
左旋，中径、顶径公差带代号为7H,中等旋合长
度。正确的标注是: C
.
2.螺钉连接正确的画法是: D
.
3.弹簧在装配图中正确的画法是: C .
13-2. 螺纹画法及标注
1. 判断下列螺纹画法的正误，正确的画“√”，错误的画“X”。
（2）
XX
X X
X
X
2. 找出下列螺纹和螺纹联接画法上的错误（错误处画X),并在下方画出正确的图形。

第十三章相交线平行线(能力提升)(解析版)

第十三章相交线平行线（能力提升）考试时间：90分钟注意事项：本试卷满分100分，考试时间90分钟，试题共25题．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、单选题（共6小题）1.如图，下列不能判定DF∥AC的条件是（）A．∠A＝∠BDF B．∠2＝∠4C．∠1＝∠3D．∠A+∠ADF＝180°【答案】B【分析】根据同位角相等、内错角相等、同旁内角互补，两直线平行即可判断．【解答】解：A．∠A＝∠BDF，由同位角相等，两直线平行，可判断DF∥AC；B．∠2＝∠4，不能判断DF∥AC；C．∠1＝∠3由内错角相等，两直线平行，可判断DF∥AC；D．∠A+∠ADF＝180°，由同旁内角互补，两直线平行，可判断DF∥AC；故选：B．【知识点】平行线的判定2.如图，将一条对边互相平行的纸带进行两次折叠，折痕分别为AB、CD，若CD∥BE，∠1＝40°，则∠2的度数是（）A．90°B．100°C．105°D．110°【答案】B【分析】根据平行线的性质即可求解．【解答】解：延长BC至G，如下图所示，由题意得，AF∥BE，AD∥BC，∵AF∥BE，∴∠1＝∠3（两直线平行，同位角相等），∵AD∥BC，∴∠3＝∠4（两直线平行，同位角相等），∴∠4＝∠1＝40°，∵CD∥BE，∴∠6＝∠4＝40°（两直线平行，同位角相等），∵这条对边互相平行的纸带进行两次折叠，折痕分别为AB、CD，∴∠5＝∠6＝40°，∴∠2＝180°﹣∠5﹣∠6＝180°﹣40°﹣40°＝100°，故选：B．【知识点】平行线的性质3.如图，AB∥CD，∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F，∠E﹣∠F＝36°，则∠E＝（）A．82°B．84°C．97°D．90°【答案】B【分析】根据平行线的性质即可求解．【解答】解：过E作直线MN∥AB，如下图所示，∵AB∥MN，∴∠3+∠4+∠BEM＝180°（两直线平行，同旁内角互补），∵AB∥CD，∴MN∥CD，∴∠MEC＝∠1+∠2（两直线平行，内错角相等），∴∠BEC＝∠MEC+∠BEM＝180°﹣∠3﹣∠4+∠1+∠2，∵∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F，∴∠1＝∠2，∠3＝∠4，∴∠BEC＝180°﹣2∠4+2∠1，∴∠4﹣∠1＝90°﹣，∵四边形BECF内角和为360°，∴∠4+∠BEC+∠180°﹣∠1+∠F＝360°，∴+∠F＝90°，由，∴，故选：B．【知识点】平行线的性质4.如图，小敏在作业中的一道题：如图1，直线a，b所成的角跑到画板外面去了，你有什么办法量出这两条直线所成的角的度数？小敏的做法是：如图2，画PC∥a，量出直线b与PC的夹角度数，即直线a，b所成角的度数．其依据是（）A．两直线平行，同位角相等B．同旁内角互补，两直线平行C．内错角相等，两直线平行D．同位角相等，两直线平行【答案】A【分析】根据两直线平行，同位角相等求解．【解答】解：根据两直线平行，同位角相等得到直线a和直线b的夹角与直线b和直线PC的夹角相等．故选：A．【知识点】平行线的判定与性质5.已知l1∥l2，一块含30°的直角三角板如图所示放置，∠1＝20°，则∠2＝（）A．30°B．35°C．40°D．45°【答案】C【分析】先根据三角形外角的性质求出∠EDG的度数，再由平行线的性质得出∠4CEF度数，由直角三角形的性质即可得出结论．【解答】解：如图，根据对顶角的性质得：∠1＝∠3，∠2＝∠4，∵∠EDG是△ADG的外角，∴∠EDG＝∠A+∠3＝30°+20°＝50°，∵l1∥l2，∴∠EDG＝∠CEF＝50°，∵∠4+∠FEC＝90°，∴∠FEC＝90°﹣50°＝40°，∴∠2＝40°．故选：C．【知识点】平行线的性质6.如图，下列推理及括号中所注明的推理依据错误的是（）A．∵∠1＝∠3∴AB∥CD（内错角相等，两直线平行）B．∵AD∥BC∴∠2＝∠4（两直线平行，内错角相等）C．∵∠BAD+∠ABC＝180°∴AD∥BC（同旁内角互补，两直线平行）D．∵∠DAM＝∠CBM∴AD∥BC（两直线平行，同位角相等）【答案】D【分析】根据平行线的判定与性质逐一进行推论即可．【解答】解：A．∵∠1＝∠3，∴AB∥CD（内错角相等，两直线平行）；所以A正确；B．∵AD∥BC，∴∠2＝∠4（两直线平行，内错角相等）；所以B正确；C．∵∠BAD+∠ABC＝180°，∴AD∥BC（同旁内角互补，两直线平行）；所以C正确；D．∵∠DAM＝∠CBM，∴AD∥BC（同位角相等，两直线平行），所以D错误．故选：D．【知识点】平行线的判定与性质二、填空题（共12小题）7.如图，已知AB∥CD，BE平分∠ABD，∠BED＝25°，则∠D＝°．【答案】130【分析】根据平行线的性质可求∠ABE＝25°，∠ABD+∠D＝180°，再利用角平分线的定义可求解∠ABD的度数，进而可求解．【解答】解：∵AB∥CD，∠BED＝25°，∴∠ABE＝∠BED＝25°，∠ABD+∠D＝180°，∵BE平分∠ABD，∴∠ABD＝2∠ABE＝50°，∴∠D＝180°﹣∠ABD＝180°﹣50°＝130°，故答案为130．【知识点】平行线的性质8.如图，将一个宽度相等的纸条沿AB折叠一下，如果∠1＝136°，那么∠2＝．【答案】112°【分析】根据平行线的性质可求解∠EAB+∠2＝180°，∠DAE＝136°，再利用折叠的性质可求解．【解答】解：如图，AC∥BD，∴∠EAB+∠2＝180°，∠DAE＝∠1，∵∠1＝136°，∴∠DAE＝136°，由折叠可知：∠DAB＝∠EAB＝∠DAE，∴∠EAB＝68°，∴∠2＝180°﹣68°＝112°．故答案为112°．【知识点】平行线的性质9.如图，已知∠1＝80°，∠2＝100°，∠3＝105°，则∠4＝．【答案】75°【分析】由同旁内角互补，两直线平行可得l1∥l2，可得∠3+∠6＝180°，即可求解．【解答】解：如图，∵∠2＝∠5＝100°，∠1＝80°，∴∠1+∠2＝180°，∴l1∥l2，∴∠3+∠6＝180°，∴∠6＝180°﹣∠3＝75°，∴∠4＝∠6＝75°，故答案为：75°．【知识点】平行线的判定与性质10.如图，将一个矩形纸片沿BC折叠，若∠ABC＝24°，则∠ACD的度数为．【答案】132°【分析】根据平行线的性质可得∠ABC＝∠1＝24°，根据折叠可得∠2＝24°，然后再算∠ACD的度数即可．【解答】解：∵AB∥CD，∴∠ABC＝∠1＝24°，由折叠得：∠1＝∠2＝24°，∴∠ACD＝180°﹣24°﹣24°＝132°，故答案为：132°．【知识点】平行线的性质11.如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直．若AD＝10，则点P到BC的距离是．【答案】5【分析】作PE⊥BC于E，根据平行线的性质得到AD⊥CD，根据角平分线的性质计算，得到答案．【解答】解：过点P作PE⊥BC于E，∵AB∥CD，AD⊥AB，∴AD⊥CD，∵BP和CP分别平分∠ABC和∠DCB，AD⊥AB，AD⊥CD，PE⊥BC，∴P A＝PE＝PD，∵AD＝10，∴PE＝5，即点P到BC的距离是5，故答案为：5．【知识点】平行线的性质、角平分线的性质12.如图，点F在∠BAC的平分线AP上，点E在AB上，且EF∥AC，若∠BEF＝40°，则∠AFE＝°．【答案】20【分析】根据平行线的性质和角平分线的性质，可以得到∠AFE的度数．【解答】解：∵AP平分∠BAC，∴∠BAP＝∠CAP，∵EF∥AC，∴∠EF A＝∠CAP，∴∠BAP＝∠EF A，∵∠BEF＝40°，∠BEF＝∠BAP+∠EF A，∴∠BAP＝∠EF A＝20°，即∠AFE＝20°，故答案为：20．【知识点】平行线的性质13.如图，直线AB、CD相交于点O，射线OM平分∠AOC，∠MON＝90°．若∠MOC＝35°，则∠BON的度数为．【答案】55°【分析】根据角平分线的定义求出∠MOA的度数，根据邻补角的性质计算即可．【解答】解：∵射线OM平分∠AOC，∠MOC＝35°，∴∠MOA＝∠MOC＝35°，∵∠MON＝90°，∴∠BON＝180°﹣∠MON﹣∠MOA＝180°﹣90°﹣35°＝55°．故选：55°．【知识点】余角和补角、对顶角、邻补角、角平分线的定义14.如图，∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F，过F作DF∥BC，交AB于D，交AC于E，若BD＝9cm，DE＝4cm，求CE的长为cm．【答案】5【分析】只要证明△BDF和△CEF为等腰三角形，即可解决问题．【解答】证明：∵BF、CF分别平分∠ABC、∠ACG，∴∠DBF＝∠CBF，∠FCE＝∠FCG，∵DE∥BC，∴∠DFB＝∠CBF，∠EFC＝∠FCG，∴∠DBF＝∠DFB，∠FCE＝∠EFC，∴BD＝FD，EF＝CE，∴△BDF和△CEF为等腰三角形；∵DF＝BD，CE＝EF，∴BD﹣CE＝FD﹣EF＝DE，∴EF＝DF﹣DE＝BD﹣DE＝9﹣4＝5（cm），∴EC＝5（cm），故答案为：5．【知识点】等腰三角形的判定与性质、平行线的性质15.如图，三角形ABC中，D是AB上一点，F是BC上一点，E，H是AC上的点，EF的延长线交AB的延长线于点G，连接DE，DH，DE∥BC．若∠CEF＝∠CHD，∠EFC＝∠ADH，∠CEF：∠EFC＝5：2，∠C＝47°，则∠ADE的度数为．【答案】76°【分析】根据平行线的性质和三角形的内角和解答即可．【解答】解：∵∠CEF＝∠CHD，∴DH∥GE，∴∠ADH＝∠G，∵∠EFC＝∠ADH，∵∠BFG＝∠EFC，∴∠G＝∠BFG，∴∠ABC＝∠G+∠BFG＝2∠EFC，∵∠CEF：∠EFC＝5：2，∠C＝47°，∴∠EFC＝38°，∴∠ABC＝76°，∵DE∥BC，∴∠ADE＝∠ABC＝76°，故答案为：76°．【知识点】平行线的性质16.如图所示，把长方形纸片ABCD纸沿对角线折叠，若∠BDE＝20°，那么∠BED＝．【答案】140°【分析】由AD∥BC，利用“两直线平行，内错角相等”可得出∠CBD的度数，由折叠的性质可得出∠EBD的度数，结合∠CBE＝∠CBD+∠EBD可得出∠CBE的度数，由AD∥BC，利用“两直线平行，同旁内角互补”可求出∠BED的度数．【解答】解：∵AD∥BC，∴∠CBD＝∠BDE＝20°．由折叠的性质可知：∠EBD＝∠CBD＝20°，∴∠CBE＝∠CBD+∠EBD＝40°．∵AD∥BC，∴∠BED＝180°﹣∠CBE＝140°．故答案为：140°．【知识点】平行线的性质、翻折变换（折叠问题）17.如图，下列结论：①∠2与∠3是内错角；②∠2与∠B是同位角；③∠A与∠B是同旁内角；④∠A与∠ACB不是同旁内角，其中正确的是（只填序号）．【答案】①②③【分析】根据同位角、内错角、同旁内角的意义，结合图形逐个判断即可．【解答】解：∠2与∠3是直线AB、直线BC，被直线CD所截的一对内错角，因此①符合题意；∠2与∠B是直线CD、直线BC，被直线AB所截的一对同位角，因此②符合题意；∠A与∠B是直线AC、直线BC，被直线AB所截的一对同旁内角，因此③符合题意，∠A与∠ACB是直线AB、直线BC，被直线AC所截的一对同旁内角，因此④不符合题意，故答案为：①②③．【知识点】同位角、内错角、同旁内角18.如图，AE∥CF，∠ACF的平分线交AE于点B，G是CF上的一点，∠GBE的平分线交CF于点D，且BD⊥BC，下列结论：①BC平分∠ABG；②AC∥BG；③与∠DBE互余的角有2个；④若∠A＝α，则∠BDF＝．其中正确的有．（把你认为正确结论的序号都填上）【答案】①②④【分析】求出∠EBD+∠ABC＝90°，∠DBG+∠CBG＝90°，求出∠ABC＝∠GBC，根据角平分线的定义即可判断①；根据平行线的性质得出∠ABC＝∠BCG，求出∠ACB＝∠GBC，根据平行线的判定即可判断②；根据余角的定义即可判断③；根据平行线的性质得出∠EBG＝∠A＝α，求出∠EBD＝EBG＝，根据平行线的性质得出∠EBD+∠BDF＝180°，即可判断④．【解答】解：∵BD⊥BC，∴∠DBC＝90°，∴∠EBD+∠ABC＝180°﹣90°＝90°，∠DBG+∠CBG＝90°，∵BD平分∠EBG，∴∠EBD＝∠DBG，∴∠ABC＝∠GBC，即BC平分∠ABG，故①正确；∵AE∥CF，∴∠ABC＝∠BCG，∵CB平分∠ACF，∴∠ACB＝∠BCG，∵∠ABC＝∠GBC，∴∠ACB＝∠GBC，∴AC∥BG，故②正确；与∠DBE互余的角有∠ABC，∠CBG，∠ACB，∠BCG，共4个，故③错误；∵AC∥BG，∠A＝α，∴∠EBG＝∠A＝α，∵∠EBD＝∠DBG，∴∠EBD＝EBG＝，∵AB∥CF，∴∠EBD+∠BDF＝180°，∴∠BDF＝180°﹣∠EBD＝180°﹣，故④正确；故答案为：①②④．【知识点】平行线的判定与性质、余角和补角三、解答题（共7小题）19.如图，在△ABC的三边上有D，E，F三点，点G在线段DF上，∠1与∠2互补，∠3＝∠C．（1）若∠C＝40°，求∠BFD的度数；（2）判断DE与BC的位置关系，并说明理由．【分析】（1）由∠1与∠2互补，利用“同旁内角互补，两直线平行”可得出AC∥DF，再利用“两直线平行，同位角相等”可求出∠BFD的度数；（2）由（1）可知∠BFD＝∠C，结合∠C＝∠3可得出∠BFD＝∠3，再利用“内错角相等，两直线平行”即可找出DE∥BC．【解答】解：（1）∵∠1与∠2互补，∴AC∥DF，∴∠BFD＝∠C＝40°；（2）DE∥BD，理由如下：由（1）可知：∠BFD＝∠C，∵∠C＝∠3，∴∠BFD＝∠3，∴DE∥BC．【知识点】平行线的判定与性质20.如图，△ABC中，AD平分∠BAC，P为AD延长线上一点，PE⊥BC于E，已知∠ACB＝80°，∠B＝24°，求∠P的度数．【分析】在△ABC中，利用三角形内角和定理可求出∠BAC的度数，结合角平分线的定义可得出∠CAD的度数，在△ACD中，利用三角形内角和定理可求出∠ADC的度数，结合对顶角相等可得出∠PDE的度数，再在△PDE中利用三角形内角和定理可求出∠P的度数．【解答】解：在△ABC中，∠ACB＝80°，∠B＝24°，∴∠BAC＝180°﹣∠ACB﹣∠B＝76°.∵AD平分∠BAC，∴∠CAD＝∠BAC＝38°．在△ACD中，∠ACD＝80°，∠CAD＝38°，∴∠ADC＝180°﹣∠ACD﹣∠CAD＝62°，∴∠PDE＝∠ADC＝62°．∵PE⊥BC于E，∴∠PED＝90°，∴∠P＝180°﹣∠PDE﹣∠PED＝28°．【知识点】三角形内角和定理、角平分线的定义、对顶角、邻补角21.已知：如图∠AED＝∠C，∠DEF＝∠B，请你说明∠1与∠2相等吗？为什么？解：因为∠AED＝∠C（已知）所以∥（）所以∠B+∠BDE＝180°（）因为∠DEF＝∠B（已知）所以∠DEF+∠BDE＝180°（）所以∥（）所以∠1＝∠2 （）．【答案】【第1空】DE【第2空】BC【第3空】同位角相等，两直线平行【第4空】两直线平行，同旁内角互补【第5空】等量代换【第6空】EF【第7空】AB【第8空】同旁内角互补，两直线平行，【第9空】两直线平行，内错角相等【分析】先判断出DE∥BC得出∠B+∠BDE＝180°，再等量代换，即可判断出EF∥AB即可．【解答】解：因为∠AED＝∠C（已知）所以DE∥BC（同位角相等，两直线平行）所以∠B+∠BDE＝180°（两直线平行，同旁内角互补）因为∠DEF＝∠B（已知）所以∠DEF+∠BDE＝180°（等量代换）所以EF∥AB（同旁内角互补，两直线平行）所以∠1＝∠2 （两直线平行，内错角相等）．故答案为：DE，BC，同位角相等，两直线平行，两直线平行，同旁内角互补，等量代换EF，AB，同旁内角互补，两直线平行，两直线平行，内错角相等．【知识点】平行线的判定与性质22.如图，已知∠1+∠2＝180°，∠3＝∠B，判断∠AED与∠C的大小关系．阅读下面的解答过程，填空并填写理由．解：∵∠1+∠2＝180°（已知），∠1+∠4＝180°（邻补角定义），∴∠2＝∠4 （）．∴AB∥EF（）．∴∠3＝（）．又∵∠3＝∠B（已知），∴（）＝∠B（等量代换）．∴DE∥BC（）．∴∠AED＝∠C（）．【答案】【第1空】同角的补角相等【第2空】内错角相等，两直线平行【第3空】∠ADE【第4空】∠ADE【第5空】同位角相等，两直线平行【第6空】两直线平行，同位角相等【分析】根据平行线的判定与性质即可完成填空．【解答】解：∵∠1+∠2＝180°（已知），∠1+∠4＝180°（邻补角定义），∴∠2＝∠4 （同角的补角相等）．∴AB∥EF（内错角相等，两直线平行）．∴∠3＝∠ADE．又∵∠3＝∠B（已知），∴∠ADE＝∠B（等量代换）．∴DE∥BC（同位角相等，两直线平行）．∴∠AED＝∠C（两直线平行，同位角相等）故答案为：同角的补角相等，内错角相等，两直线平行；∠ADE，∠ADE，同位角相等，两直线平行；两直线平行，同位角相等．【知识点】平行线的判定与性质23.探究：如图①，直线AB、BC、AC两两相交，交点分别为点A、B、C，点D在线段AB上，过点D作DE∥BC交AC于点E，过点E作EF∥AB交BC于点F，若∠ABC＝50°，求∠DEF的度数．请将下面的解答过程补充完整，并填空解：∵DE∥BC∴∠DEF＝．（）∵EF∥AB，∴＝∠ABC．（）∴∠DEF＝∠ABC．（等量代换）∵∠ABC＝50°，∴∠DEF＝．应用：如图②，直线AB，BC，AC两两相交，交点分别为A、B、C，点D在线段AB的延长线上，过点D作DE∥BC交AC于点E，过点E作EF∥AB交BC于点F，若∠ABC＝65°，则∠DEF＝．【答案】【第1空】∠EFC【第2空】两直线平行，内错角相等【第3空】∠EFC【第4空】两直线平行，同位角相等【第5空】50°【第6空】115°【分析】探究：依据两直线平行，内错角相等；两直线平行，同位角相等，即可得到∠DEF＝50°．应用：依据两直线平行，同位角相等；两直线平行，同旁内角互补，即可得到∠DEF＝180°﹣65°＝115°．【解答】解：探究：∵DE∥BC，∴∠DEF＝∠EFC．（两直线平行，内错角相等）∵EF∥AB，∴∠EFC＝∠ABC．（两直线平行，同位角相等）∴∠DEF＝∠ABC．（等量代换）∵∠ABC＝50°，∴∠DEF＝50°．故答案为：∠EFC，两直线平行，内错角相等，∠EFC，两直线平行，同位角相等，50°；应用：∵DE∥BC，∴∠ABC＝∠ADE＝60°．（两直线平行，同位角相等）∵EF∥AB，∴∠ADE+∠DEF＝180°．（两直线平行，同旁内角互补）∴∠DEF＝180°﹣65°＝115°．故答案为：115°．【知识点】平行线的性质、相交线24.已知点A在射线CE上，∠BDA＝∠C．（1）如图1，若AC∥BD，求证：AD∥BC；（2）如图2，若∠BAC＝∠BAD，BD⊥BC，请证明∠DAE+2∠C＝90°；（3）如图3，在（2）的条件下，过点D作DF∥BC交射线CE于点F，当∠DFE＝8∠DAE时，求∠BAD的度数．（直接写出结果）【分析】（1）根据AC∥BD，可得∠DAE＝∠C，再根据∠C＝∠D，即可得到∠DAE＝∠D，则结论得证；（2）根据∠CGB是△ADG是外角，即可得到∠CGB＝∠D+∠DAE，再根据△BCG中，∠CGB+∠C＝90°，即可得到∠D+∠DAE+∠C＝90°，进而得出2∠C+∠DAE＝90°；（3）设∠DAE＝α，则∠DFE＝8α，∠AFD＝180°﹣8α，根据DF∥BC，即可得到∠C＝∠AFD＝180°﹣8α，再根据2∠C+∠DAE＝90°，即可得到2（180°﹣8α）+α＝90°，求得α的值，由三角形内角和定理得到∠BAD的度数．【解答】（1）证明：∵AC∥BD，∴∠DAE＝∠BDA，∵∠BDA＝∠C，∴∠DAE＝∠C，∴AD∥BC；（2）证明：如图2，设CE与BD相交于点G，∠BGA＝∠BDA+DAE，∵BD⊥BC，∴∠BGA+∠C＝90°，∴∠BDA+∠DAE+∠C＝90°，∵∠BDA＝∠C，∴∠DAE+2∠C＝90°；（3）如图3，设∠DAE＝α，则∠DFE＝8α，∵∠DFE+∠AFD＝180°，∴∠AFD＝180°﹣8α，∵DF∥BC，∴∠C＝∠AFD＝180°﹣8α，又∵2∠C+∠DAE＝90°，∴2（180°﹣8α）+α＝90°，∴α＝18°，∴∠C＝180°﹣8α＝36°＝∠ADB，又∵∠C＝∠BDA，∠BAC＝∠BAD，∴∠ABC＝∠ABD＝∠CBD＝45°，△ABD中，∠BAD＝180°﹣45°﹣36°＝99°．答：∠BAD的度数是99°．【知识点】平行线的判定与性质25.三角形ABC中，D是AB上一点，DE∥BC交AC于点E，点F是线段DE延长线上一点，连接FC，∠BCF+∠ADE＝180°．（1）如图1，求证：CF∥AB；（2）如图2，连接BE，若∠ABE＝40°，∠ACF＝60°，求∠BEC的度数；（3）如图3，在（2）的条件下，点G是线段FC延长线上一点，若∠EBC：∠ECB＝7：13，BE 平分∠ABG，求∠CBG的度数．【分析】（1）根据平行线的判定与性质即可完成证明；（2）如图2，过点E作EK∥AB，可得CF∥AB∥EK，再根据平行线的性质即可得结论；（3）根据∠EBC：∠ECB＝7：13，可以设∠EBC＝7x°，则∠ECB＝13x°，然后根据∠AED+∠DEB+∠BEC＝180°，13x+7x+100＝180，求出x的值，进而可得结果．【解答】（1）证明：∵DE∥BC，∴∠ADE＝∠B，∵∠BCF+∠ADE＝180°．∴∠BCF+∠B＝180°．∴CF∥AB；（2）解：如图2，过点E作EK∥AB，∴∠BEK＝∠ABE＝40°，∵CF∥AB，∴CF∥EK，∴∠CEK＝∠ACF＝60°，∴∠BEC＝∠BEK+∠CEK＝40°+60°＝100°；（3）∵BE平分∠ABG，∴∠EBG＝∠ABE＝40°，∵∠EBC：∠ECB＝7：13，∴设∠EBC＝7x°，则∠ECB＝13x°，∵DE∥BC，∴∠DEB＝∠EBC＝7x°，∠AED＝∠ECB＝13x°，∵∠AED+∠DEB+∠BEC＝180°，∴13x+7x+100＝180，解得x＝4，∴∠EBC＝7x°＝28°，∵∠EBG＝∠EBC+∠CBG，∴∠CBG＝∠EBG﹣∠EBC＝40°﹣28°＝12°．【知识点】平行线的判定与性质。

第十三章表面物理化学练习题及答案

第十三章表面物理化学练习题一、选择题1．在电泳实验中，观察到分散相向阳极移动，表明:(A) 胶粒带正电(B) 胶粒带负电(C) 电动电位相对于溶液本体为正(D) Stern 面处电位相对溶液本体为正2．通常称为表面活性物质的就是指当其加入于液体中后：(A) 能降低液体表面张力(B) 能增大液体表面张力(C) 不影响液体表面张力(D) 能显著降低液体表面张力3．实验测得O2在金表面上的吸附热Q与吸附量无关，这种吸附满足以下哪种吸附规律？(A)L angmuir等温式(B) Freundlich等温式(C) TëMKuH等温式(D) 以上三种皆可以4．对于有过量KI 存在的AgI 溶液，电解质聚沉能力最强的是：(A) K3[Fe(CN)6] (B) MgSO4(C) FeCl3(D) NaCl5．多孔硅胶的强烈吸水性能说明硅胶吸附水后，表面自由能将(A) 变高(B) 变低(C) 不变(D) 不能比较6．为直接获得个别的胶体粒子的大小和形状，必须借助于：(A) 普通显微镜(B) 丁铎尔效应(C) 电子显微镜(D) 超显微镜7．由0.01 dm3 0.05 mol·kg-1的KCl 和0.1 dm3 0.002 mol·kg-1的AgNO3溶液混合生成AgCl 溶胶，为使其聚沉，所用下列电解质的聚沉值由小到大的顺序为：(A) AlCl3＜ZnSO4＜KCl (B) KCl ＜ZnSO4＜AlCl3(C) ZnSO4＜KCl ＜AlCl3(D) KCl ＜AlCl3＜ZnSO4 8．将一毛细管端插入水中，毛细管中水面上升5 cm，若将毛细管向下移动，留了 3 cm 在水面，试问水在毛细管上端的行为是：(A) 水从毛细管上端溢出(B) 毛细管上端水面呈凸形弯月面(C) 毛细管上端水面呈凹形弯月面(D) 毛细管上端水面呈水平面9．明矾净水的主要原理是：(A) 电解质对溶胶的聚沉作用(B) 溶胶的相互聚沉作用(C) 电解质的敏化作用(D) 电解质的对抗作用10．在pH ＜7 的Al(OH)3溶胶中，使用下列电解质使其聚沉：(1)KNO3(2) NaCl (3) Na2SO4(4) K3Fe(CN)6在相同温度、相同时间内，聚沉能力大小为：(A) (1) ＞(4) ＞(2) ＞(3) (B) (1) ＜(4) ＜(2) ＜(3)(C) (4) ＞(3) ＞(2) ＞(1) (D) (4) ＜(3) ＜(2) ＜(1) 11．兰缪尔的吸附等温式为Γ = Γ∞bp/(1+bp)，其中Γ∞为饱和吸附量，b为吸附系数。

华师大版八年级上册数学第13章全等三角形含答案

华师大版八年级上册数学第13章全等三角形含答案一、单选题(共15题，共计45分)1、等腰三角形的两个内角的比是1：2，则这个等腰三角形的顶角的度数是（）A.72°B.36°或90°C.36°D.45°2、如图，在Rt△ACB中，∠C=90°，BE平分∠CBA交AC于点E，过E作ED⊥AB于D点，当∠A=_____时，ED恰为AB的中垂线（）A.10°B.15°C.30°D.45°3、如图，△ABC中，AB=8，AC=6，AD、AE分别是其角平分线和中线，过点C作CG⊥AD于F，交AB于G，连接EF，则线段EF的长是（）A.3B.4C.1D.0.54、等腰三角形一腰上的高与另一腰的夹角度数为20°，则顶角的度数为（）A.70°B.110°C.70°或110°D.以上都不对5、用尺规作图法作已知角的平分线的步骤如下:①以点O为圆心,任意长为半径作弧,交OB于点D,交OA于点E;②分别以点D,E为圆心,以大于的长为半径作弧,两弧在的内部相交于点C;③作射线OC.则射线OC为的平分线,由上述作法可得的依据是( )A.SASB.AASC.ASAD.SSS6、如图：Rt△ABC 中，AC＝BC，∠ACB＝90°，D 为 BC 边中点，CF⊥AD 交AD 于 E，交 AB 于 F，BE交 AC 于 G，连 DF，下列结论：①AC＝AF，②CD＋DF＝AD，③∠ADC＝∠BDF，④CE＝BE，⑤∠ BED＝45°，其中正确的有（）A.5 个B.4 个C.3 个D.2 个7、△ABC中，AB=AC，CD为AB上的高，且△ADC为等腰三角形，则∠BCD等于( )A.67.5°B.22.5°C.45°D.67.5°或22.5°8、如图四边形ABCD是菱形，且∠ABC=60°，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM，则下列五个结论中正确的是（）①若菱形ABCD的边长为1，则AM+CM的最小值1；②△AMB≌△ENB；③S四边形AMBE =S四边形ADCM；④连接AN，则AN⊥BE；⑤当AM+BM+CM的最小值为2时，菱形ABCD的边长为2A.①②③B.②④⑤C.①②⑤D.②③⑤9、如图 , ∠A＝∠D , OA＝OD , ∠DOC＝50°, 求∠DBC的度数为（）A.25°B.30°C.45°D.50°10、如图所示，有三条道路围成Rt△ABC，其中BC=1000m，一个人从B处出发沿着BC行走了800m，到达D处，AD恰为∠CAB的平分线，则此时这个人到AB 的最短距离为（）A.1000mB.800mC.200mD.1800m11、如图，在四边形ABCD中，，，，.分别以点A，C为圆心，大于长为半径作弧，两弧交于点E，作射线BE交AD于点F，交AC于点O.若点O是AC的中点，则CD的长为（）A. B.4 C.3 D.12、如图，△ABD≌△CDB，∠ABD＝40°，∠CBD＝30°，则∠C＝（）A.70°B.100°C.110°D.115°13、等腰三角形的两边长分别为4厘米和9厘米，则这个三角形的周长为（）A.22厘米B.17厘米C.13厘米D.17厘米或22厘米14、如图,在△ABC中,P为BC上一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,∠CAP=∠APQ,PR=PS,下面的结论:①AS=AR;②QP∥AR;③△BRP≌△CSP.其中正确的是( )A.①②B.②③C.①③D.①②③15、如图，大树AB与大数CD相距13m，小华从点B沿BC走向点C，行走一段时间后他到达点E，此时他仰望两棵大树的顶点A和D，两条视线的夹角正好为90°，且EA=ED.已知大树AB的高为5m，小华行走的速度为1m/s，小华行走到点E的时间是（）A.13sB.8sC.6sD.5s二、填空题(共10题，共计30分)16、已知等边△ABC的边长为2，点D在射线CB上，点E在射线AC上，且AD=AE,∠EDC=15°，则线段CD=________.17、如图，在中，，，点在线段上运动（不与、重合），连接，作，交线段于点，在点从向运动过程中，如果是等腰三角形，则的度数是________18、等腰三角形的一个角100°，它的另外两个角的度数分别为________19、如图，CE、BF分别是△ABC的高线，连接EF，EF＝6，BC＝10，D、G分别是EF、BC的中点，则DG的长为________.20、等腰三角形的两边分别是和，则底边上的高为________.21、如图，直线上有三个正方形，若的面积分别为5和11，则的面积为________．22、如图所示，已知△ABC的周长是20，OB、OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD=3，则△ABC的面积是________．23、如图，线段AC、BD相交于点O，且AO=OC，请添加一个条件使△ABO≌△CDO，应添加的条件为________（添加一个条件即可）24、如图，OP平分∠AOB，PA⊥OA，PB⊥OB，垂足分别为A，B．下列结论中：①PA＝PB；②△AOP≌△BOP；③OA＝OB；④PO平分∠APB．其中成立的有________(填写正确的序号)．25、如果等腰三角形有一个内角为110°，则其底角的度数是________.三、解答题(共5题，共计25分)26、如图，已知∠ACB=∠DCE=90°，AC=BC=6，CD=CE，AE=3，∠CAE=45°，求AD的长．27、阅读下面材料：在数学课上，老师提出如下问题：小芸的作法如图：请你回答：（1）作图第一步为什么要大于AB的长？（2）小芸的作图是否正确？请说明理由．28、如图，已知：AO=BO，OC=OD．求证：∠ADC=∠BCD．29、已知：如图，A、C、F、D在同一直线上，AF＝DC，AB＝DE，BC＝EF，求证：△ABC≌△DEF．30、如图，已知是的平分线，求的度数。

易错题精选：第13章内能(题及答案)

九年级物理易错题第13章内能一．选择题1．90℃水全部变成125℃水蒸气（）A．这些水蒸气的内能比水的小B．液态水分子间距比气态水分子的大C．水蒸气只能通过热传递途径变为水D．水分子在125℃时比90℃时热运动更激烈2．下列关于分子间的作用力的说法中正确的是（）A．一根铁棒很难被拉断，这说明铁棒的分子间只存在引力B．液体非常容易流动，这说明液体分子间主要是斥力C．气体很容易被压缩的原因是因为气体分子间没有作用力．分子间的距离减小，分子间的引力和斥力都增大3．下列说法正确的是（）A．物体内能减少时，温度可能不变B．物体内能增大，一定从外界吸收热量C．汽油机在做功冲程中把机械能转化为内能D．锯条锯木板时，锯条的内能增加，木板的内能减少4．寒冷的冬季，家用汽车的某些部位却在升温（如图所示），下列现象中，通过做功使物体内能增加的是（）A．打开暖风车内温度升高B．在汽车行驶的过程中，汽车水箱里的水温度升高C．放在阳光下汽车的顶部晒热D．刹车时，刹车片的温度升高5．关于温度、内能、热量，下列说法正确的是（）A．物体吸收热量，温度一定升高B．物体的温度越高，它含的热量越多C．物体吸收热量，内能一定增加D．物体内能越多，放热一定越多6．下列语句：①天气真热；②物体吸热；③摩擦生热；④热不可耐．其中“热”表示“温度”的是（）A．①②B．①③C．②③D．①④7．关于热量，下列说法正确的是（）A．热水比冷水含的热量多B．一大桶水比一小桶水含的热量多C．一个物体内能越多，它具有的热量越多D．热量是热传递过程中物体内能的改变量8．在相同的加热条件下，对质量为m1、比热容为c1的物质A和质量为m2、比热容为c2的物质B 均匀加热，物质A、B的温度随加热时间的变化情况如图，根据图象分析可推断出正确的结论是（）A．若c1＞c2；则m1＞m2 B．若m1=m2；则c1＜c2C．若c1=c2；则m1＜m2 D．若m1＜m2；则c1＞c29．冰在熔化成水的过程中，下列判断正确的是（）A．比热容改变，内能和温度不变B．比热容改变，内能增加，温度不变C．比热容、内能和温度都增加D．比热容、内能和温度都不变10．2010年4月，中国新疆汽车摩托车越野挑战赛选手穿越了“生命禁区”罗布泊沙漠．当时该地最低气温为零下10℃，昼夜温差可打40℃以上．罗布泊沙漠一天中的最高气温出现的时间及昼夜温差大的原因分别是（）A．日出前后，砂石的比热大B．当地下午2时后，砂石的比热小C．日出前后，砂石的比热小D．当地下午2时后，砂石的比热大11．铝的比热容比铁大，质量和初温相同的铝块和铁块吸收相同的热量后，相互接触，则（）A．内能从铝传给铁B．热量从铁传给铝C．不发生热传递D．温度从铁传给铝12．甲乙两物体质量相等，初温相同，把甲投入一杯热水中，平衡后水温降低△t℃，把甲捞出后（设水与热均未损失）．再投入乙，热平衡后水温又降低了出△t℃．由此可得出（）A．甲的比热容大B．乙的比热容大C．甲、乙的比热容一样大D．无法确定13．把两块质量相等、比热容分别为c1和c2的金属熔合为合金，该合金的比热容为（）A．c1+c2 B．c1c2 C．（c1+c2）/2 D．c1c2/214．今年3月22日是第二十二届“世界水日”3月22﹣28日是“中国水周”．图中能正确描述水的各物理量之间关系的图象是（）A．表示水的比热容与质量的关系B．表示水的比热容与质量的关系C．表示水凝固成冰时温度与时间的关系D．表示冰熔化成水时温度与时间的关系15．水的比热容较大是水的一个特性，下列事例及现象中与水的这一特性无关的是（）A．让热水流过散热器来取暖B．在大的河流上建水电站，用水发电C．沿海地区昼夜温差小D．汽车发动机用水循环冷却16．水的比热容比较大，下列现象中不属于利用水的这个特性的是（）A．供暖系统用循环热水来供给暖气B．用水作为机车发动机的冷却液C．炎热的夏天，在教室地面上洒水降温D．育秧时，为了防止霜冻，常在傍晚时向秧田里灌水17．由于水的比热容比沙石或干泥土的比热容大，所以在沿海地区陆地表面的气温比海面的气温昼夜变化显著．因此（）A．白天的风通常是从陆地吹向海面，夜晚的风却是从海面吹向陆地B．白天的风通常是从海面吹向陆地，夜晚的风却是从陆地吹向海面C．白天和夜晚的风通常是从陆地吹向海面D．白天和夜晚的风通常是从海面吹向陆地二．填空题18．如图所示为生活中常用的热水瓶，其外壁采用镀银的双层玻璃，并将中间抽成真空，这是为了减少_________．注入一定量的热水后，立即盖上软木塞，软木塞会跳起来．这一过程中瓶内气体的_________能转化为软木塞的机械能．汽油机的_________冲程也发生同样的能量转化．19．如图甲是用水来冷却热牛奶的示意图．这是用_________的方法改变物体内能的．图乙是记录牛奶、水的温度随时间变化的图象，图中曲线I 表示的是_________的温度随时间变化的情况，图中A 点的物理意义是_________：图中奶瓶对水槽的压力_____（选填“大于”、“等于”或“少于”）奶瓶的重力（包括牛奶）20．为了探究物质吸收热量与哪些因素有关，某实验小组同学用相同的酒精灯分别加热质量和初温都相同的液体，实验过程及观察到的现象如图所示．设加热时液体每分钟吸收的热量相等．请根据实验现象及相关条件归纳得出初步结论．①分析比较图中（a）与（b）与（c）可得出的初步结论是：_______ __．②分析比较图中（c）与（d）可得出的初步结论是：_________．21．某同学用一种加热器将质量为500 g的冰持续加热熔化直至沸腾，记录并绘制出温度﹣时间图象如图所示，根据图象可以看出C点的内能_________B点的内能，原因是_________．根据图象还可以看出AB段的比热容_________CD 段的比热容[第一格与第三格选填“大于”、“等于”或“小于”]．22．两玻璃杯甲和乙，甲中是空的，乙中装有水，如图所示．把两个杯子都放进冰箱中冷冻18分钟，取出后用两手掌分别握住玻璃杯，比较它们的冷热．你的结论是_________；原因是_________．三．解答题23．在研究分子引力实验时，小华同学做了如下实验，如图所示，图甲中杯子的水未盛满，“舌形”塑料片中间有一透气小孔．把“舌形”塑料片盖在杯口，在伸出杯口的塑料片末端放一枚一角硬币，“舌形”塑料片就被压翻；当杯内水盛满，塑料片与水充分接触时，在伸出杯口的塑料片末端放6枚一角硬币，“舌形”塑料片仍没有被压翻．这个现象说明了水和塑料片分子之间有_________．24．质量相等，初温相同的实心铜、铁、铝块，放出相等的热量后，（c铝＞c铁＞c铜）_________块降低的温度最少，如果此时将铜块和铝块接触，则热量将传给_________块．25．为了研究物质的某种特性，某小组的同学利用如图所示装置的做了如下实验：他们在两只完全相同的烧杯中放入100克水和100克煤油，用两只相同酒精灯加热，利用温度计和计时器测量液体的温度随时间的变化情况．记录数据如表一，表二所示．（已知ρ水＞ρ煤油）（1）甲图烧杯中盛的液体是_________（选填“水”或“煤油”）．实验中，用相同酒精灯加热的目的是：_________．加热时间长短间接反映了_________．（2）分析比较表一（或表二）中的第一行和第三行的数据及相关条件，可得出的初步结论是：____ _（3）分析比较表一和表二中_________的数据及相关条件，可得出的初步结论：质量相等的不同物质，升高相同的温度，吸收的热量不相等，水吸收的热量比煤油吸收的热量多．（4）小组同学进一步综合分析表一、表二数据得出以下结论：综合分析比较表一或表二中的数据及相关条件可得：同种物质，吸收热量与质量、升高温度的比值是定值．该结论是_________（选填“正确完整”、“正确不完整”、“错误”）26．在加热条件完全相同的情况下，甲、乙、丙三种物质温度T随加热时间t变化的情况如图所示，可以看出，这三种物质中，可能是同种物质的是_________．它们的质量关系是_______的质量一定比________的质量大．27．右是某一沿海城市和某一内陆城市年气温变化曲线．从图象可以看出，在一年中，曲线A所示的城市气温变化较_________（选填“大”或“小”），根据水的比热容比砂石比热容_________的特点，曲线A表示的是_________（“沿海”或“内陆”）城市的年气温变化曲线．28．炎热夏日的海边，为什么脚下的沙滩很热而海水却很凉爽，试用学过的物理知识解释原因．29．为什么会发生城市的热岛效应，应该怎样缓解城市的热岛效应？30．甲、乙两地分别位于沿海地区或沙漠地区，表中记录了甲、乙两地三天内每天气温的最高值和最低值，你能判断出甲地是沿海地区还是沙漠地区吗？请说明理由．时间气温甲地乙地5月27日最高25℃26℃最低20℃12℃5月28日最高26℃27℃最低19℃14℃5月29日最高25℃28℃最低21℃11℃第13章内能易错题精选参考答案一．选择题1．90℃水全部变成125℃水蒸气（D）A．这些水蒸气的内能比水的小B．液态水分子间距比气态水分子的大C．水蒸气只能通过热传递途径变为水D．水分子在125℃时比90℃时热运动更激烈2．下列关于分子间的作用力的说法中正确的是（D）A．一根铁棒很难被拉断，这说明铁棒的分子间只存在引力B．液体非常容易流动，这说明液体分子间主要是斥力C．气体很容易被压缩的原因是因为气体分子间没有作用力D．分子间的距离减小，分子间的引力和斥力都增大3．下列说法正确的是（A）A．物体内能减少时，温度可能不变B．物体内能增大，一定从外界吸收热量C．汽油机在做功冲程中把机械能转化为内能D．锯条锯木板时，锯条的内能增加，木板的内能减少4．寒冷的冬季，家用汽车的某些部位却在升温（如图），下列现象中，通过做功使物体内能增加的是（D）A．打开暖风车内温度升高B．在汽车行驶的过程中，汽车水箱里的水温度升高C．放在阳光下汽车的顶部晒热D．刹车时，刹车片的温度升高5．关于温度、内能、热量，下列说法正确的是（C）A．物体吸收热量，温度一定升高B．物体的温度越高，它含的热量越多C．物体吸收热量，内能一定增加D．物体内能越多，放热一定越多6．下列语句：①天气真热；②物体吸热；③摩擦生热；④热不可耐．其中“热”表示“温度”的是（D）A．①②B．①③C．②③D．①④7．关于热量，下列说法正确的是（D）A．热水比冷水含的热量多B．一大桶水比一小桶水含的热量多C．一个物体内能越多，它具有的热量越多D．热量是热传递过程中物体内能的改变量8．（2012•如东县模拟）在相同的加热条件下，对质量为m1、比热容为c1的物质A和质量为m2、比热容为c2的物质B均匀加热，物质A、B的温度随加热时间的变化情况如图所示，根据图象分析可推断出正确的结论是（D）A．若c1＞c2；则m1＞m2 B．若m1=m2；则c1＜c2C．若c1=c2；则m1＜m2 D．若m1＜m2；则c1＞c29．冰在熔化成水的过程中，下列判断正确的是（B）A．比热容改变，内能和温度不变B．比热容改变，内能增加，温度不变C．比热容、内能和温度都增加D．比热容、内能和温度都不变10．2006年4月，中国新疆汽车摩托车越野挑战赛选手穿越了“生命禁区”罗布泊沙漠．当时该地最低气温为零下10℃，昼夜温差可打40℃以上．罗布泊沙漠一天中的最高气温出现的时间及昼夜温差大的原因分别是（B）A．日出前后，砂石的比热大B．当地下午2时后，砂石的比热小C．日出前后，砂石的比热小D．当地下午2时后，砂石的比热大11．铝的比热容比铁大，质量和初温相同的铝块和铁块吸收相同的热量后，相互接触，则（B）A．内能从铝传给铁B．热量从铁传给铝C．不发生热传递D．温度从铁传给铝12．甲乙两物体质量相等，初温相同，把甲投入一杯热水中，平衡后水温降低△t℃，把甲捞出后（设水与热均未损失）．再投入乙，热平衡后水温又降低了出△t℃．由此可得出（B）A．甲的比热容大B．乙的比热容大C．甲、乙的比热容一样大D．无法确定13．把两块质量相等、比热容分别为c1和c2的金属熔合为合金，该合金的比热容为（C）A．c1+c2 B．c1c2 C．（c1+c2）/2 D．c1c2/214．今年3月22日是第二十二届“世界水日”3月22﹣28日是“中国水周”．图中能正确描述水的各物理量之间关系的图象是（A）A．表示水的比热容与质量的关系B．表示水的比热容与质量的关系C．表示水凝固成冰时温度与时间的关系D．表示冰熔化成水时温度与时间的关系15．水的比热容较大是水的一个特性，下列事例及现象中与水的这一特性无关的是（B ）A．让热水流过散热器来取暖B．在大的河流上建水电站，用水发电C．沿海地区昼夜温差小D．汽车发动机用水循环冷却16．水的比热容比较大，下列现象中不属于利用水的这个特性的是（C）A．供暖系统用循环热水来供给暖气B．用水作为机车发动机的冷却液C．炎热的夏天，在教室地面上洒水降温D．育秧时，为了防止霜冻，常在傍晚时向秧田里灌水17．由于水的比热容比沙石或干泥土的比热容大，所以在沿海地区陆地表面的气温比海面的气温昼夜变化显著．因此（B）A．白天的风通常是从陆地吹向海面，夜晚的风却是从海面吹向陆地B．白天的风通常是从海面吹向陆地，夜晚的风却是从陆地吹向海面C．白天和夜晚的风通常是从陆地吹向海面D．白天和夜晚的风通常是从海面吹向陆地二．填空题18．如图所示为生活中常用的热水瓶，其外壁采用镀银的双层玻璃，并将中间抽成真空，这是为了减少热量散失（或热传递）．注入一定量的热水后，立即盖上软木塞，软木塞会跳起来．这一过程中瓶内气体的内能转化为软木塞的机械能．汽油机的做功冲程也发生同样的能量转化．19．如图甲是用水来冷却热牛奶的示意图．这是用热传递的方法改变物体内能的．图乙是记录牛奶、水的温度随时间变化的图象，图中曲线I 表示的是热奶的温度随时间变化的情况，图中A 点的物理意义是热牛奶与水最后的共同温度为18℃：图中奶瓶对水槽的压力小于（选填“大于”、“等于”或“少于”）奶瓶的重力（包括牛奶）20.为了探究物质吸收热量与哪些因素有关，某实验小组同学用相同的酒精灯分别加热质量和初温都相同的液体，实验过程及观察到的现象如图所示．设加热时液体每分钟吸收的热量相等．请根据实验现象及相关条件归纳得出初步结论．①分析比较图中（a）与（b）与（c）可得出的初步结论是：相同质量的同种物质，升高的温度越高，吸收的热量越多．②分析比较图中（c）与（d）可得出的初步结论是：相同质量的不同物质，升高相同的温度，吸收的热量不同．21．某同学用一种加热器将质量为500 g的冰持续加热熔化直至沸腾，记录并绘制出温度﹣时间图象如图所示，根据图象可以看出C点的内能大于B 点的内能，原因是熔化过程要吸收热量．根据图象还可以看出AB段的比热容小于CD 段的比热容[第一格与第三格选填“大于”、“等于”或“小于”]．22．两玻璃杯甲和乙，甲中是空的，乙中装有水，如图所示．把两个杯子都放进冰箱中冷冻18分钟，取出后用两手掌分别握住玻璃杯，比较它们的冷热．你的结论是甲杯比乙杯的温度低；原因是水的比热容大，下降的温度较小．三．解答题23．在研究分子引力实验时，小华同学做了如下实验，如图所示，图甲中杯子的水未盛满，“舌形”塑料片中间有一透气小孔．把“舌形”塑料片盖在杯口，在伸出杯口的塑料片末端放一枚一角硬币，“舌形”塑料片就被压翻；当杯内水盛满，塑料片与水充分接触时，在伸出杯口的塑料片末端放6枚一角硬币，“舌形”塑料片仍没有被压翻．这个现象说明了水和塑料片分子之间有引力．24．质量相等，初温相同的实心铜、铁、铝块，放出相等的热量后，（c铝＞c铁＞c铜）铝块降低的温度最少，如果此时将铜块和铝块接触，则热量将传给铜块．25．为了研究物质的某种特性，某小组的同学利用如图所示装置的做了如下实验：他们在两只完全相同的烧杯中放入100克水和100克煤油，用两只相同酒精灯加热，利用温度计和计时器测量液体的温度随时间的变化情况．记录数据如表一，表二所示．（已知ρ水＞ρ煤油）（1）甲图烧杯中盛的液体是煤油（选填“水”或“煤油”）．实验中，用相同酒精灯加热的目的是：使水和煤油在相同时间内吸收相同热量．加热时间长短间接反映了物质吸收热量的多少．（2）分析比较表一（或表二）中的第一行和第三行的数据及相关条件，可得出的初步结论是：质量一定的同种物质，吸收的热量与升高的温度成正比．（3）分析比较表一和表二中第三列（或第四列或第五列或第六列）的数据及相关条件，可得出的初步结论：质量相等的不同物质，升高相同的温度，吸收的热量不相等，水吸收的热量比煤油吸收的热量多．（4）小组同学进一步综合分析表一、表二数据得出以下结论：综合分析比较表一或表二中的数据及相关条件可得：同种物质，吸收热量与质量、升高温度的比值是定值．该结论是正确不完整（选填“正确完整”、“正确不完整”、“错误”）解析：（4）综合分析表一、表二数据，可以得出的结论是：同种物质，吸收热量与质量、升高温度的比值是定值；不同物质，吸收热量与质量、升高温度的比值一般不同．26．在加热条件完全相同的情况下，甲、乙、丙三种物质温度T随加热时间t变化的情况如图所示，可以看出，这三种物质中，可能是同种物质的是甲乙．它们的质量关系是乙的质量一定比甲的质量大．27．右是某一沿海城市和某一内陆城市年气温变化曲线．从图象可以看出，在一年中，曲线A所示的城市气温变化较大（选填“大”或“小”），根据水的比热容比砂石比热容大的特点，曲线A表示的是内陆（“沿海”或“内陆”）城市的年气温变化曲线．28．炎热夏日的海边，为什么脚下的沙滩很热而海水却很凉爽，试用学过的物理知识解释原因．答：因为沙子的比热容比海水的比热容小，吸收相同热量，相同质量的沙子比海水温度上升高快，所以小明在烈日当空的海边玩耍，感到沙子烫脚，海水却凉凉的．29．为什么会发生城市的热岛效应，应该怎样缓解城市的热岛效应？答：城市和郊区相比，城市的建筑物多，水少，而郊区绿地多，水多，水的比热容大，等质量的水和沙石相比，在吸收相同的热量时，沙石温度升的高，所以就出现了城市的热岛效应．城市建人工湖，植树，种草等增大水的面积，利用水的比热容最大，即水温度变化慢的特点可以缓解城市的热岛效应，同时在上述方法中也加大了水的表面积，促进了水的蒸发，由于蒸发是吸热的，所以从蒸发的角度也可以缓解城市的热岛效应．30．甲、乙两地分别位于沿海地区或沙漠地区，表中记录了甲、乙两地三天内每天气温的最高值和最低值，你能判断出甲地是沿海地区还是沙漠地区吗？请说明理由．答：由表中数据可知，甲地是沿海地区，因为水的比热容比沙子大，白天，相同质量的水和沙子吸收相同的热量后，水的温度升高的少，气温较低；夜晚，相同质量的水和沙子放出相同的热量后，水的温度下降的少，气温较高；由此可知沿海地区白天黑夜的温差小．时间气温甲地乙地5月27日最高25℃26℃最低20℃12℃5月28日最高26℃27℃最低19℃14℃5月29日最高25℃28℃最低21℃11℃。

编译原理13章作业答案

编译原理13章作业答案第一章习题1.6.3：对于图1-14中的块结构代码，假设使用常见的声明的静态作用域规则，给出其中12个声明中的每一个的作用域？{intw,某,y,z;/某块B1某/{int某,z;/某块B2某/{intw,某;}/某块B3某/}{intw,某;/某块B4某/{inty,z;}/某块B5某/}}答：声明块变作用域量W某YZB1B2B3B4B5B1-B3-B4/B3B4/B1-B2-B4B2-B3B3B4/B1-B5///B5B1-B2-B5B2//B5习题1.6.4：下面C代码的打印结果是什么？#definea(某+1)Int某=2;Voidb(){某=a;printf(“%d\\n”,某);}Voidb(){某=1;printf(“%d\\n”,a);}Voidmain(){b();c();}答：输出结果是32调用函数b()时，a=某+1此处某为全局变量值2，故输出为3调用函数c()时，某局部定义为1，此处a=某+1为2，故输出为2第三章习题3.3.2：试描述下列正则表达式定义的语言：(1)a(a|b)某a:以a开头和以a结束的中间由任意个a或b组成的串的集合(2)((|a)b某)某:由0个和多个b组成的串以及由0个或多个以a开头由任意个b组成的实例所组成的串的集合(3)(a|b)某a(a|b)(a|b)：由a或b构成的长度至少为3的且倒数第三个字符为a的串的集合(4)a某ba某ba某ba某：由a、b构成的b的个数为3的串的集合习题3.3.5：试写出下列语言的正则定义：(1)包含5个元音的所有小写字母串，这些串中的元音按顺序出现：a[bcd]e[fgh]i[jklmn]o[pqrt]u[vw某yz](2)所有由按字典递增排序的小写字母组成的串：a某b某c某d某…z某(3)注释，即/某和某/之间的串，且串中没有不在双引号(＂)中的某/：[/某]([a-zA-Z]|(＂某/＂))[某/]习题3.4.1：给出识别练习3.3.2中各个正则表达式所描述的语言的状态转换图(1)a(a|b)a(3)(a|b)a(a|b)(a|b)习题3.7.3使用算法3.23和3.20将下列正则表达式转换成DFA(1)(a|b)由(a|b)生成相应的NFA，如下图所示由上面的NFA生成相应的DFA1)标记集合A，A是-cloure(1)，即A={1,2,3,5,8}2)标记集合B，B是-cloure（move(A,a)）={1,2,3,4,5,7,8}3)标记集合C，C是-cloure（move(A,b)）={1,2,3,5,6,7,8}得到一个只含有三个状态的DFA，其中A是接受状态,其状态转换图如下(2)(a|b)由(a|b)得到相应的NFA如下图所示由上述NFA得到相应的DFA如下1)标记集合A，A是-cloure(0)，即A={0,1,2,3,4,5}2)可以得到-cloure（move(A,a)）={0,1,2,3,4,5}=A，-cloure （move(A,b)）={0,1,2,3,4,5}=A，故该DFA中应只有一个状态A，得到一个一状态的DFA，其状态转换图如下。

八年物理下章节训练与解析第十三章内能

【答案】B 【解析】西安地处内陆，多砂石、泥土，砂石的比热容较小，夜间砂石散热较多，温度降低较快，因而早晨气温较低。午间在阳光的照射下，砂石吸热后温度升高较快使得气温迅速升高，于是出现昼夜气温差别较大的现象。而香港临海多水，水的比热容较大，海洋与沙漠地区在同样散热的情况下，海洋的温度降低不多，夜间气温不太低，白天气温也不会升得过快，所以，沿海地区昼夜温差不大。
【答案】增加；增大
14、现有质量和初温都相等的铝块,铁块和铜块,其比热c铝＞c铁＞c铜,它们吸收相等的热量后,末温最高是______块，末温最低的是______块。
【答案】铜块；铝块
15、用铝壶烧开水，壶中的水蒸气将壶盖顶起来，这是消耗水蒸气的______能对外做功，将水蒸气的______能转化成壶盖的______能。
【答案】B 【解析】判断是不是分子做无规则运动，就要看被观察对象的运动颗粒是不是以分子状态出现的，柳絮、落叶、瑞雪都不是分子颗粒，只有玉兰飘香是花的分子在运动。
5、某同学在研究物质燃烧的条件时，做了如图所示的实验：把一条粗金属丝绕成线圈，罩在一支蜡烛的火焰上，火焰很快就熄灭了。对这一实验的说法不正确的是 ( ) A．金属丝有良好的导热性 B．金属线圈内的气体温度升高了 C．可燃物的温度降到了着火点以下 D．若预先将金属丝加热，蜡烛就不会很快熄灭
【答案】D 【解析】水的内能不仅与温度有关，还和水的质量有关；故温度相等的 1kg水和100g水的内能不同；故A错误；改变内能的方法有两种，做功和热传递；物体内能增加，可能是从外界吸收热量，也可能外界对它做功；故B错误；一切物体都有内能，故C错误；物体的内能与温度有关；同一物体温度升高时，内能增加，温度降低时，内能将减小；故D正确。
D．集市很热闹

13章第四节热机效率和环境保护(备作业)(解析版)

二、选择题
11、关于热机效率，下列说法正确的是（） A. 蒸汽机的效率高于汽油机的效率 B. 热机所做有用功越多，它的效率就越高 C. 内燃机的效率越高，它消耗的燃料就越少 D. 热机效率越高，它将内能转化为机械能的比例越大【答案】D 【解析】 A、蒸汽机的燃料是在机器的外部燃烧，热损失最多，效率最低，故 A 错误； B、热机的有用功多，与燃料完全燃烧放出的能量之比不一定多，故 B 错误； C、热机消耗的燃料多、燃烧放出的热量多，但用来做有用功的能量可能更多，即效率可能更高，所以据消耗燃料的多少是不能判断热机效率大小的，故 C 错； D、热机效率越高，热机用来做有用功的能量与燃料完全燃烧产生的能量之比，比值越大，内能转化为机械能的比例越大，故 D 正确。故选：D。
2
q=8.4×107J/kg] 【答案】比热容 8.4×105 0.01 【解析】汽车散热器用水作为冷却剂，是利用了水的比热容较大的性质；水吸收的热量：Q 吸 =cm△t=4.2×103 J/（kg·℃）×10 kg×20 ℃=8.4×105 J；由题知，Q 放=Q 吸=8.4×105 J，∵Q 放 =m 气 q，∴m 气=Q 放/q=8.4×105J/（8.4×107J/kg）=0.01 kg。
【答案】30 6.6×107
次，若其效
【解析】（1）已知飞轮转速为 3600r/min，即 60r/s，而一个工作循环活塞往复 2 次，曲轴转动 2 周，
做功 1 次，所以该柴油机 1s 对外做功 30 次；
柴油燃烧放出的热量：
Q 放＝mq＝5kg×3.3×107J/kg＝16.5×107J，其转化的机械能为：W＝16.5×107J×40%＝6.6×107J。故答案为：30，6.6×107。
2、现探明中国南海海底有大量的可燃冰，已知可燃冰的热值比煤气的热值大得多，则完全燃烧

【g】c++第13章答案

2018八年级数学《第13章 轴对称--垂直平分线》同步复习资料【2】【含解析】

人教版九年级物理上册同步学习指导-第13章《内能》重难点、易错点突破技巧

第13章 流程图(答案版)---

第十三章内能(原卷版+解析)

第13章内能(原卷版)

有机化学课后习题答案第13章

宏观经济学第13章课后练习参考答案

第13章 课后答案

2021年中考物理复习滚动练习：第13章 内能含答案

2020年人教版物理九年级全册精品学案 第13章第3节《比热容》 (含答案)