首先可绘制矩阵散点图

合集下载

人力资源回归预测法

人力资源回归预测法人力资源管理对于企业的发展起着至关重要的作用。

为了合理规划和调配人力资源，预测人力资源需求是一项必不可少的工作。

而人力资源回归预测法是一种常用的预测方法，可以通过对历史数据的分析，利用回归模型来预测未来的人力资源需求。

人力资源回归预测法基于统计学原理，通过对过去的数据进行分析和建模，来预测未来的人力资源需求。

这种方法的核心思想是，人力资源需求与一系列相关因素之间存在着一定的线性关系，通过建立回归模型，可以利用这些相关因素的变化来预测人力资源的需求量。

在进行人力资源回归预测之前，首先需要确定一些相关的自变量。

这些自变量可以包括企业的规模、行业的发展状况、经济的增长率、劳动力市场的供求情况等。

通过对这些自变量的收集和整理，可以建立起一个完整的数据集。

接下来，需要对数据进行处理和分析。

首先，可以通过绘制散点图来观察变量之间的关系，判断是否存在线性关系。

如果存在线性关系，可以进一步计算相关系数，来评估变量之间的相关程度。

然后，可以利用多元线性回归模型来建立预测模型，通过最小二乘法来估计模型的参数。

在建立好回归模型之后，可以利用该模型来进行人力资源需求的预测。

根据预测的目标，可以设置不同的自变量的取值，来预测不同时间段的需求量。

同时，也可以通过模型的拟合优度来评估模型的准确性和可靠性。

人力资源回归预测法的优点在于可以利用历史数据来进行预测，具有一定的科学性和可靠性。

同时，该方法也可以帮助企业进行人力资源的合理规划和调配，减少人力资源的浪费和闲置。

然而，该方法也存在一些局限性，如对于外部环境的变化较为敏感，需要不断更新和调整模型。

人力资源回归预测法是一种常用的预测方法，可以通过对历史数据的分析和建模，来预测未来的人力资源需求。

通过合理利用该方法，企业可以更好地规划和调配人力资源，提高企业的竞争力和效益。

但同时也需要注意该方法的局限性，及时更新和调整模型，以适应外部环境的变化。

excel怎么做直角坐标系散点图

Excel如何绘制直角坐标系散点图
Excel是一款强大的办公软件，除了表格处理和数据计算外，还具备绘制图表的功能。

直角坐标系散点图是一种常见的数据可视化方式，在Excel中制作起来也非常简单。

下面将介绍如何在Excel中绘制直角坐标系散点图。

步骤一：准备数据
首先，打开Excel并准备要绘制散点图所需的数据。

通常情况下，数据应该包含两列：一列用于X轴数据，一列用于Y轴数据。

确保数据以合适的格式组织，这样绘制起来会更加方便。

步骤二：选择数据
在Excel中选中包含数据的范围。

可以同时选中X轴和Y轴的数据，也可以先选中其中一列，再按住Ctrl键选中另一列。

步骤三：插入散点图
在Excel的菜单栏中选择“插入”选项卡，然后选择“散点图”功能。

在弹出的菜单中，选择合适的散点图类型，通常选择标准散点图即可。

步骤四：调整图表样式
一般来说，Excel会自动绘制散点图，但有时需要对图表进行一些调整以使其更清晰易读。

可以修改标题、坐标轴标签、数据点的形状和颜色等，以及添加图例来帮助解读数据。

步骤五：保存和分享
完成散点图的制作后，记得保存Excel文件。

可以将图表导出为图片或PDF格式，也可以直接在Excel中将文件分享给其他人。

通过以上步骤，你可以在Excel中轻松制作直角坐标系散点图，将数据直观地呈现出来，帮助你更好地分析和理解数据。

希望这个简单的教程对你有所帮助！。

(完整版)Stata学习笔记和国贸理论总结

Stata学习笔记一、认识数据（一）向stata中导入txt、csv格式的数据1．这两种数据可以用文本文档打开，新建记事本，然后将相应文档拖入记事本即可打开数据，复制2．按下stata中的edit按钮，右键选择paste special3．*.xls/*.xlsx数据仅能用Excel打开，不可用记事本打开，打开后会出现乱码，也不要保存，否则就恢复不了。

逗号分隔的数据常为csv数据。

（二）网页数据网页上的表格只要能选中的，都能复制到excel中；网页数据的下载可以通过百度“国家数据”进行搜索、下载二、Do-file 和log文件打开stata后，第一步就要do-file，记录步骤和历史记录，方便日后查看。

Stata处理中保留的三种文件：原始数据(*.dta)，记录处理步骤(*.do)，以及处理的历史记录(*.smcl)。

三、导入StataStata不识别带有中文的变量，如果导入的数据第一行有中文就没法导入。

但是对于列来说不会出现这个问题，不分析即可（Stata不分析字符串，红色文本显示；被分析的数据，黑色显示）；第一行是英文变量名，选择“Treat first row as variable names”在导入新数据的时候，需要清空原有数据，clear命令。

导入空格分隔数据：复制——Stata中选择edit按钮或输入相应命令——右键选择paste special——并选择，确定；导入Excel中数据，复制粘贴即可；逗号分隔数据，选择paste special后点击comma，然后确定。

Stata数据格式为*.dta，导入后统一使用此格式。

四、基本操作（几个命令）（一）use auto，clear 。

在清空原有数据的同时，导入新的auto数据。

（二）browse 。

浏览数据。

（三）describe 和list。

查看数据，describe 和list 使用list命令能使我们根据自己的需要选择数据（例如其与in/if语句的结合使用）。

SPSS实验7-曲线估计

SPSS作业7：曲线估计为研究居民家庭教育支出和消费性支出之间的关系，收集到1990年到2002年全国人均消费性支出和教育支出的数据。

首先绘制教育支出和消费性支出的散点图，如下所示：（一）教育支出的相关因素分析曲线估计的基本操作：（1）选择菜单Analyz e－Regression―Curve Estimation;（2）选择被解释变量到Dependent框中，再选择菜单Graph s―Scatter;分别作简单散点图，矩阵散点图，结果如下：Graph教育支出和年人均消费性支出的散点图分析：观察散点图发现两变量之间呈非线性关系，其中，教育支出为被解释变量，消费性支出为解释变量，分析结果如下：教育支出的曲线估计结果MODEL: MOD_2.Dependent variable.. X5 Method.. QUADRATIListwise Deletion of Missing DataMultiple R .99353R Square .98710Adjusted R Square .98452Standard Error 45.70690Analysis of Variance:DF Sum of Squares Mean SquareRegression 2 1598766.0 799383.00Residuals 10 20891.2 2089.12F = 382.64096 Signif F = .0000-------------------- Variables in the Equation -------------------- Variable B SE B Beta T Sig TX2 -.147527 .025041 -1.134958 -5.892 .0002 X2**2 2.46018091E-05 2.2722E-06 2.085797 10.827 .0000 (Constant) 252.697890 57.792248 4.373 .0014Dependent variable.. X5 Method.. CUBICListwise Deletion of Missing DataMultiple R .99711R Square .99422Adjusted R Square .99230Standard Error 32.23848Analysis of Variance:DF Sum of Squares Mean SquareRegression 3 1610303.3 536767.78Residuals 9 9353.9 1039.32F = 516.46087 Signif F = .0000-------------------- Variables in the Equation -------------------- Variable B SE B Beta T Sig T X2 .075378 .069194 .579897 1.089 .3043 X2**2 -1.98768467E-05 1.3446E-05 -1.685204 -1.478 .1734 X2**3 2.59626300E-09 7.7924E-10 2.112252 . . (Constant) -41.313805 97.204131 -.425 .6808Dependent variable.. X5 Method.. COMPOUNDListwise Deletion of Missing DataMultiple R .99737R Square .99476Adjusted R Square .99428Standard Error .09002Analysis of Variance:DF Sum of Squares Mean SquareRegression 1 16.905289 16.905289Residuals 11 .089131 .008103F = 2086.35111 Signif F = .0000-------------------- Variables in the Equation -------------------- Variable B SE B Beta T Sig T X2 1.000420 9.1977E-06 2.711154 108768.23 .0000 (Constant) 20.955019 1.226139 17.090 .0000Dependent variable.. X5 Method.. POWERListwise Deletion of Missing DataMultiple R .97687R Square .95428Adjusted R Square .95012Standard Error .26578Analysis of Variance:DF Sum of Squares Mean SquareRegression 1 16.217387 16.217387Residuals 11 .777033 .070639F = 229.58009 Signif F = .0000-------------------- Variables in the Equation --------------------Variable B SE B Beta T Sig TX2 1.845988 .121832 .976871 15.152 .0000(Constant) 3.5781705054E-05 3.7164E-05 .963 .3563分析：由表可知：三次曲线和二次曲线的拟合优度都比较高，可参见下图。

高维数据可视化的主要方法

高维数据可视化的主要方法随着科技的发展和数据的爆炸式增长，我们面临的数据越来越高维。

高维数据的特点是维度多、样本稀疏，给数据分析和可视化带来了巨大的挑战。

为了更好地理解和分析高维数据，研究人员提出了许多高维数据可视化的方法。

本文将介绍几种主要的高维数据可视化方法。

1. 散点矩阵图散点矩阵图是一种常用的高维数据可视化方法。

它通过绘制数据集中每两个维度之间的散点图，可以直观地展示出各个维度之间的关系。

每个散点代表一个样本，不同的颜色可以表示不同的类别。

散点矩阵图可以帮助我们找出高维数据中存在的规律和异常值。

2. 平行坐标图平行坐标图是一种常用的高维数据可视化方法，它可以显示多个维度之间的关系。

在平行坐标图中，每个维度表示为垂直于坐标轴的一条直线，每个样本则表示为连接各个维度的折线。

通过观察这些折线的形状和走势，我们可以发现高维数据中的模式和异常。

3. t-SNEt-SNE是一种降维算法，可以将高维数据映射到二维或三维空间中进行可视化。

t-SNE通过计算样本之间的相似度，然后在低维空间中保持相似度关系，将高维数据映射到低维空间。

这样一来，我们可以通过观察降维后的数据点在二维或三维空间中的分布情况，来了解高维数据中的结构和聚类情况。

4. 主成分分析（PCA）主成分分析是一种常用的降维方法，可以将高维数据映射到低维空间中。

主成分分析通过线性变换将原始数据的维度降低，同时保留最大方差的特征。

这样一来，我们可以用较低维度的数据来表示高维数据，方便可视化和分析。

5. 矩阵散点图矩阵散点图是一种可视化高维数据的方法，适用于数据之间存在复杂关系的情况。

在矩阵散点图中，每个维度都用一个坐标轴表示，每个样本则表示为一个散点。

通过绘制不同维度之间的散点图，我们可以观察到高维数据的内在结构和规律。

6. 树状图树状图是一种将高维数据可视化为树状结构的方法。

在树状图中，每个节点代表一个维度，树的根节点代表整个数据集。

通过观察树状图的结构和分支情况，我们可以发现高维数据中的聚类和相似性。

智慧树知到《SPSS应用》章节测试答案

智慧树知到《SPSS应用》章节测试答案绪论1、学习《SPSS应用》可以有效提高你的统计思维能力。

A:对B:错正确答案：对第一章1、SPSS软件是20世纪60年代末，由（）大学的三位研究生最早研制开发的。

A.哈佛大学B.斯坦福大学C.波士顿大学D.剑桥大学正确答案：斯坦福大学2、（）文件格式是SPSS独有的，一般无法通过Word，Excel等其他软件打开。

A.savB.txtC.mp4D.flv正确答案：sav3、Spss输出结果保存时的文件扩展名是（）。

A.savB.spvC.mp4D.flv正确答案：spv4、数据编辑窗口的主要功能有（）。

A.定义SPSS数据的结构B.录入编辑和管理待分析的数据C.结果输出D.A和B正确答案：A和B5、数据编辑窗口中的一行称为一个（）。

A.变量B.个案C.属性D.元组正确答案：个案第二章1、SPSS中无效的变量名有（）。

A.@a1B.abc1#C.homeD.cd_1正确答案：@a1,home2、SPSS软件的编辑窗口能打开的文件类型有（）。

A..stB..docC..xlsD..mat正确答案：*.xls3、变量的起名规则一般：变量名的字符个数不多于（）。

A.6B.7C.8D.9正确答案：84、SPSS默认的字符型变量的对齐方式是（）。

A.右对齐B.中间对齐C.左对齐D.以上说法都不对正确答案：中间对齐5、SPSS的主要变量类型不包括（）。

A.数值型B.字符型C.日期型正确答案：英镑型第三章1、关于利用Sort by对数据排序的描述错误的有（）。

A.排序变量可以是多个B.排序变量最多一个C.排序变量为多个时先按第一个排序，取值相同的再按第二个排，以此类推D.观测个体所有变量的值都变到新位置正确答案：B2、在横向合并数据文件时，两个数据文件都必须事先按关键变量值（）。

A.升序排序B.降序排序C.不排序D.可升可降正确答案：A3、通过（）可以达到将数据编辑窗口中的计数数据还原为原始数据的目的。

采用散点图气泡图三种方案轻松制作波士顿矩阵

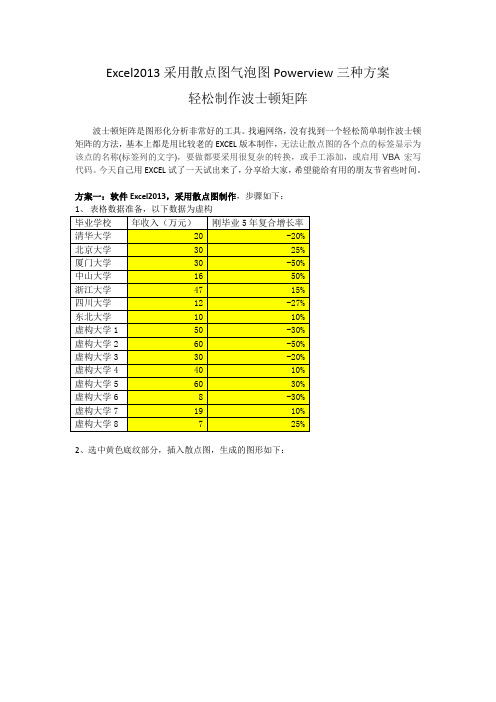
Excel2013采用散点图气泡图Powerview三种方案轻松制作波士顿矩阵波士顿矩阵是图形化分析非常好的工具。

找遍网络，没有找到一个轻松简单制作波士顿矩阵的方法，基本上都是用比较老的EXCEL版本制作，无法让散点图的各个点的标签显示为该点的名称(标签列的文字)，要做都要采用很复杂的转换，或手工添加，或启用VBA宏写代码。

今天自己用EXCEL试了一天试出来了，分享给大家，希望能给有用的朋友节省些时间。

方案一：软件Excel2013，采用散点图制作，步骤如下：2、选中黄色底纹部分，插入散点图，生成的图形如下：把表中图拉伸放大，方便大家查看，如下：把图表标题改成波士顿矩阵，生成的图形如下：-60%-40%-20%0%20%40%60%010203040506070图表标题-60%-40%-20%0%20%40%60%010203040506070波士顿矩阵4、右键选中图上小点点，再点左键，调出菜单，选生成数据标签，过程图和生成的图形如下：-20%25%-50%50%15%-27%10%-30%-50%-20%10%30%-30%10%25%-60%-40%-20%0%20%40%60%010203040506070波士顿矩阵5、右键选中图上小点点，再点左键，调出菜单，选设置数据标签格式，过程图和生成的图形如下：6、右键选中单元格中的值前的勾，在新跳出的数据标签区域栏选中毕业大学那列，再点确定，然后把Y值前的勾去掉，过程图和生成的图形如下：7、右键点图中网络线，在右上角新出来设置主要网格线格式的菜单中，选无线条去掉横的网格线，然后用同样的方法去掉竖的网格线，过程图和生成的图形如下：8、右键点图中横坐标，在右上角新出来设置坐标轴格式的菜单中，把纵坐标交叉由自动调成坐标轴值为35，过程图和生成的图形如下：9、右键点图中横坐标、纵坐标，和方框进行美化和处理，过程图和生成的图形如下：10、好了，大功告成，如下：方案二：软件Excel2013，采用气泡图制作，步骤如下：1、选中下表格所有部分，插入气泡图，生成的图形一步步如下，由于气泡图的过程与散点图非常类似，除了多了一个气泡大小（我是用年收入体现气泡大小差异）外，中间过程我不毕业学校年收入（万元）刚毕业5年复合增长率清华大学20 -20%北京大学30 25%厦门大学30 -50%中山大学16 50%浙江大学47 15% 四川大学12 -27% 东北大学10 10% 虚构大学1 50 -30% 虚构大学2 60 -50% 虚构大学3 30 -20% 虚构大学4 40 10% 虚构大学5 60 30% 虚构大学6 8 -30% 虚构大学7 19 10% 虚构大学8 7 25%好了，是不是超级简单。

矩阵的散布图解原理和应用

矩阵的散布图解原理和应用1. 引言散布图（Scatter plot）是一种常用的数据可视化工具，用于展示两个变量之间的关系。

矩阵的散布图是指将多个变量两两组合，生成多个散布图的图表。

本文将介绍矩阵的散布图的原理和应用。

2. 矩阵的散布图的原理矩阵的散布图的原理基于散布图的原理，即通过绘制变量之间的点来显示它们之间的关系。

对于矩阵的散布图，我们需要选择两个或多个变量，并将它们两两组合。

对于每个组合，我们绘制一个散布图来显示它们之间的关系。

3. 矩阵的散布图的应用矩阵的散布图在数据分析中有广泛的应用。

下面列举了一些常见的应用场景：•探索变量之间的相互关系：通过生成矩阵的散布图，我们可以快速了解多个变量之间的关系，从而帮助我们发现变量之间的模式和趋势。

•识别异常值和离群点：矩阵的散布图可以帮助我们发现变量之间的异常值和离群点。

通过观察散布图中的点分布情况，我们可以发现那些与其他变量不一致的数据点。

•比较不同变量的分布：通过生成矩阵的散布图，我们可以直观地比较不同变量的分布情况。

例如，我们可以将人口数量和GDP进行组合，从而探索人口数量和GDP之间的关系。

4. 生成矩阵的散布图的步骤以下是生成矩阵的散布图的基本步骤：•选择要比较的变量：首先，我们需要选择要比较的变量。

这些变量可以是连续变量或分类变量。

•组合变量：根据选择的变量，我们需要将它们两两组合。

如果我们选择了n个变量，将会生成n * (n-1)个散布图。

•绘制散布图：对于每个变量组合，我们绘制一个散布图来显示它们之间的关系。

散布图可以使用散点图的形式，其中横轴和纵轴分别表示两个变量的值。

•分析结果：根据生成的矩阵的散布图，我们可以分析变量之间的关系。

我们可以观察点的分布情况，找出异常值和离群点，并比较不同变量的分布情况。

5. 矩阵的散布图的示例下面是一个示例，展示了如何生成矩阵的散布图：变量1 变量2 变量3变量1 散布图散布图变量2 散布图变量3在这个示例中，我们选择了3个变量进行比较。

第六章spss相关分析和回归分析

第六章SPSS相关分析和回归分析第六章SPSS相关分析与回归分析6.1相关分析和回归分析概述客观事物之间的关系大致可归纳为两大类，即,函数关系:指两事物之间的一种一一对应的关系，如商品的销售额和销售量之间的关系。

,相关关系（统计关系）：指两事物之间的一种非一一对应的关系，例如家庭收入和支出、子女身高和父母身高之间的关系等。

相关关系乂分为线性相关和非线性相关。

相关分析和回归分析都是分析客观事物之间相关关系的数量分析方法。

6. 2相关分析相关分析通过图形和数值两种方式，有效地揭示事物之间相关关系的强弱程度和形式。

6.2. 1散点图它将数据以点的的形式画在直角坐标系上，通过观察散点图能够直观的发现变量间的相关关系及他们的强弱程度和方向。

6.2.2相关系数利用相关系数进行变量间线性关系的分析通常需要完成以下两个步骤：第一，计算样本相关系数r;,+1之间，相关系数r的取值在-1,R>0表示两变量存在正的线性相关关系;r〈0表示两变量存在负的线性相关关系,R,1表示两变量存在完全正相关;r, -1表示两变量存在完全负相关;r, 0表示两变量不相关,|r|>0.8表示两变量有较强的线性关系；r <0.3表示两变量之间的线性关系较弱第二，对样本来自的两总体是否存在显著的线性关系进行推断。

对不同类型的变量应采用不同的相关系数来度量，常用的相关系数主要有Pearson 简单，相关系数、Spearman等级相关系数和Kendall相关系数等。

6. 2. 2. 1 Pearson简单相关系数(适用于两个变量都是数值型的数据)(,)(,)yy, ixxi,r 22(,), (,) yy,, ixxiPearson简单相关系数的检验统计量为：rn, 22t,6. 2. 2. 2 Spearman等级相关系数Spearman等级相关系数用来度量定序变量间的线性相关关系，设计思想与Pearson 简1, r(,)xyii单相关系数相同，只是数据为非定距的，故计算时并不直接采用原始数据，而是利(,)xy(,)UViiii用数据的秩，用两变量的秩代替代入Pearson简单相关系数计算公式中，于是xyii其中的和的取值范禺被限制在1和n之间，且可被简化为:2nn6D, i22,,,,,其中rDUV1 (),, iii,, 2, nn(l)iillnn22DUV,, (),, iii,, llii,如果两变量的正相关性较强，它们秩的变化具有同步性，于是的值较小，r趋向于1；nn22DUV,, (),, iii,, Uii,如果两变量的正相关性较弱,它们秩的变化不具有同步性，于是的值较大，r趋向于0;,在小样本下，在零假设成立时，Spearman等级相关系数服从Spearman分布; 在大样本下，Spearman等级相关系数的检验统计量为Z统计•量，定义为：Zrn,, 1Z统计量近似服从标准正态分布。

Excel中的图表散点图使用指南

Excel中的图表散点图使用指南Excel作为一款功能强大的办公软件，被广泛应用于数据处理和分析。

其中，图表是Excel中常用的功能之一，而散点图作为图表的一种，可以帮助我们更直观地观察和分析数据。

在本文中，我们将为大家介绍Excel中散点图的使用指南，帮助读者更好地利用Excel进行数据可视化。

一、散点图的基本概念和用途散点图是通过将数据点以点的形式绘制在坐标系上，用来表示两个变量之间的关系。

其中，横坐标表示一个变量，纵坐标表示另一个变量，通过观察数据点的分布情况，我们可以推断出两个变量之间的关系。

散点图在数据分析中具有广泛的用途。

它可以用来观察变量之间的相关性，例如，我们可以通过绘制散点图来观察销售额和广告投入之间的关系，从而帮助我们确定广告投入对销售额的影响程度。

此外，散点图还可以用来发现异常值和趋势，帮助我们更好地理解数据。

二、如何创建散点图在Excel中创建散点图非常简单。

首先，我们需要准备好数据，将需要绘制的数据放在一个表格中。

然后，选中需要绘制散点图的数据范围，包括横坐标和纵坐标的数据。

接下来，点击Excel菜单栏中的“插入”选项卡，然后选择“散点图”按钮。

在弹出的菜单中，选择合适的散点图类型，例如，散点图、带有趋势线的散点图等。

最后，Excel会自动在工作表中创建散点图，并将选中的数据绘制在图表中。

三、如何优化散点图的显示效果为了使散点图更具有可读性和美观性，我们可以对散点图进行一些优化。

首先，我们可以添加图表标题和坐标轴标题，以便更清晰地表达图表的含义。

其次，我们可以调整散点图的大小和位置，使其更好地适应工作表的布局。

此外，我们还可以调整数据点的形状、颜色和大小，以突出显示不同的数据特征。

另外，我们还可以添加趋势线，帮助我们更好地观察数据的趋势和变化。

四、如何解读散点图在观察散点图时，我们应该注意以下几个方面。

首先，我们可以通过观察数据点的分布情况来判断两个变量之间的关系。

如果数据点呈现出一定的规律性，例如，呈现出直线状、曲线状或聚集状等，那么我们可以认为两个变量之间存在一定的相关性。

matlab画三维散点图

matlab画三维散点图MATLAB是一种非常强大的数值计算和可视化软件，广泛用于科学、工程、统计学等领域的数据分析和可视化。

其中之一的功能是绘制三维散点图，这种图形能够帮助我们直观地观察和理解数据的分布情况。

本文将介绍如何使用MATLAB绘制三维散点图。

一、准备数据在绘制三维散点图之前，我们首先需要准备数据。

在MATLAB中，数据可以以不同的形式输入，如矩阵、向量或数据文件。

这里，我们假设我们已经有了一个包含三个列的矩阵，每一列代表一个维度的数据。

例如，我们有一个矩阵A，其中第一列代表x坐标，第二列代表y坐标，第三列代表z坐标。

二、绘制三维散点图在MATLAB中，我们可以使用scatter3函数来绘制三维散点图。

该函数的语法如下：scatter3(x, y, z)其中，x、y和z分别是包含数据的向量或矩阵。

例如，我们可以使用下面的代码来绘制散点图：scatter3(A(:,1), A(:,2), A(:,3))三、设置图形属性除了绘制三维散点图，我们还可以通过设置不同的属性来适应数据的特点和需求。

下面是一些常用的属性设置：1. 颜色：可以使用Color参数来定义散点的颜色。

例如，可以使用'b'来表示蓝色散点、'r'表示红色散点。

如果想要为每个散点指定不同的颜色，可以使用RGB值或提供一个与数据大小相同的向量来表示颜色。

2. 标记：可以使用Marker参数来指定散点的标记。

例如，可以使用'o'表示圆形标记、'+'表示十字标记。

3. 大小：可以使用Size参数来调整散点的大小。

默认情况下，散点的大小是基于数据的相对大小确定的。

4. 标签：可以使用Text参数来为散点添加文本标签。

使用Text中的文本来指定标签的内容。

下面是一个例子，演示如何使用属性设置：scatter3(A(:,1), A(:,2), A(:,3), 'Marker', 'o', 'Size', 50, 'Color', 'b')四、添加标题和坐标轴标签为了进一步提高图形的可读性，我们还可以添加标题和坐标轴标签。

中级绘图--散点图（散点图矩阵、高密度散点图、（旋转）三维散点图、气泡图）

中级绘图--散点图（散点图矩阵、⾼密度散点图、（旋转）三维散点图、⽓泡图）1 散点图散点图可⽤来描述两个连续型变量间的关系。

R中创建散点图的基础函数是plot(x, y)，其中，x和y是数值型向量，代表着图形中的(x, y)点。

下⾯展⽰了⼀个例⼦。

attach(mtcars)plot(wt, mpg, main="Basic Scatter plot of MPG vs. Weight", xlab="Car Weight (lbs/1000)",ylab="Miles Per Gallon ", pch=19)abline(lm(mpg~wt), col="red", lwd=2, lty=1)lines(lowess(wt,mpg), col="blue", lwd=2, lty=2)结果分析：使⽤的是mtcars数据框，创建了⼀幅基本的散点图，wt和mpg之间的关系是⽤实⼼圆圈来表⽰的，abline()函数⽤来添加最佳拟合的线性直线，如图中红⾊实线所⽰，lowess()函数则⽤来添加⼀条平滑曲线，如图中蓝⾊虚线所⽰。

结果表⽰，随着车重的增加，每加仑英⾥数减少。

1.1 散点图矩阵R中有很多创建散点图矩阵的实⽤函数。

pairs()函数可以创建基础的散点图矩阵,下⾯的代码⽣成了⼀个散点图矩阵，包含mpg、disp、drat和wt四个变量：pairs(~mpg+disp+drat+wt, data=mtcars, main="Basic Scatter Plot Matrix")结果分析：看到所有指定变量间的⼆元关系，主对⾓线的上⽅和下⽅的六幅散点图是相同的，可以发现是关于主对⾓线对称。

通过调整参数，可以只展⽰下三⾓或者上三⾓的图形。

例如，选项upper.panel = NULL将只⽣成下三⾓的图形。

散点图矩阵的概念

散点图矩阵的概念散点图矩阵是一种数据可视化技术，用于展示多个变量之间的关系。

它将数据集中的每个变量与其他所有变量进行组合，并在一个二维平面上绘制散点图。

这样一来，矩阵的每个小格子里都有一个散点图，可以直观地了解所有变量之间的相关性和分布情况。

散点图矩阵通常用于研究多变量之间的线性和非线性关系，以及了解变量之间是否存在相关性。

通过矩阵的图表，我们可以快速查看数据集中的所有变量，发现其中的规律和趋势。

在大数据处理和数据挖掘中，散点图矩阵可以帮助我们理解数据，发现异常情况，并为进一步的分析和建模提供依据。

散点图矩阵的绘制通常是通过程序代码实现的。

首先，我们需要准备一个包含多个变量的数据集，每个变量都可以用数字来表示。

接下来，我们使用绘图库或图表工具，将数据集中的每个变量都与其他变量进行组合。

最后，我们将每个组合在一个矩阵中进行可视化展示。

在散点图矩阵中，每个小格子代表两个变量之间的关系，横轴和纵轴分别表示这两个变量的取值范围。

每个散点图通常用圆点、正方形或其他符号来表示数据点的位置。

数据点的形状、颜色、大小等特征可以进一步表示其他变量的信息。

通过观察散点图矩阵，我们可以观察到以下几个重要的信息：首先，散点图的分布情况可以告诉我们变量之间的相关性。

如果一个散点图呈线性分布，那么这两个变量之间可能存在线性关系。

如果散点图没有特定的分布规律，可能意味着这两个变量之间没有明显的关系。

其次，我们可以通过散点图的形态来识别异常情况。

如果散点图中有极端值或离群点，可能表示数据集中存在异常值或错误测量。

最后，通过观察整个矩阵，我们可以在变量之间发现更复杂的关系。

例如，我们可以发现一些变量与其他变量相关，形成类似“簇”的分布。

散点图矩阵在许多领域中都有广泛的应用。

在统计学和数据挖掘中，散点图矩阵常用于探索数据集，发现新的特征和变量之间的关系。

在金融和经济学中，散点图矩阵可以用来分析不同经济变量之间的关系，研究市场波动和走势。

初中数学什么是数据的散点矩阵如何绘制数据的散点矩阵图

初中数学什么是数据的散点矩阵如何绘制数据的散点矩阵图数据的散点矩阵是一种用于可视化多个变量之间关系的图表。

它通过在一个矩阵中绘制多个散点图，将每个变量与其他变量进行比较和分析。

散点矩阵图能够帮助我们观察和分析多个变量之间的相关性、分布以及可能存在的模式。

以下是如何绘制数据的散点矩阵图的步骤：1. 收集数据：首先，收集包含多个变量的数据集。

确保数据集中的每个变量都具有相同的观测数量。

2. 数据准备：对于每个变量，进行必要的数据清洗和处理。

确保数据的格式正确，缺失值得到处理，并进行必要的标准化或归一化。

3. 绘制散点矩阵图：通过使用绘图工具（如Python中的Matplotlib库、R语言中的ggplot2包等），将每个变量与其他变量进行组合，绘制散点矩阵图。

4. 确定矩阵的大小和排列：根据数据集中的变量数量，确定矩阵的大小和排列方式。

通常，散点矩阵图是一个方阵，其中每个单元格都是一个散点图。

5. 绘制散点图：在每个单元格中，绘制两个变量之间的散点图。

横坐标代表一个变量，纵坐标代表另一个变量。

可以使用不同的符号、颜色或大小来表示不同的类别或分组。

6. 添加轴标签和标题：为整个图表添加轴标签和标题，以使图表更具可读性和可理解性。

7. 解读图表：观察每个散点图，分析变量之间的关系。

可以观察数据点的分布、线性或非线性关系、异常值等。

需要注意的是，散点矩阵图适用于变量较少的情况下，当变量数量较多时，矩阵图可能显得过于拥挤，不易于解读。

在这种情况下，可以选择绘制子集或使用其他可视化方法，如相关矩阵图等。

总结起来，数据的散点矩阵是一种用于可视化多个变量之间关系的图表。

绘制散点矩阵图的步骤包括收集数据、数据准备、绘制散点矩阵图、确定矩阵的大小和排列、绘制散点图、添加轴标签和标题以及解读图表。

散点矩阵图可以帮助我们观察和分析多个变量之间的相关性、分布以及可能存在的模式。

数据描述与散点图

数据描述与散点图散点图是一种常用的统计图表，用于表示两个变量之间的关系。

它通常使用点的位置来表示两个变量的数值，从而直观地展示它们之间的相关性。

本文将介绍如何进行数据描述并绘制散点图。

1. 数据描述在进行数据描述之前，首先需要明确所研究的两个变量，并收集相关数据。

例如，我们研究某个地区的温度与冰淇淋销量之间的关系，需要收集一段时间内的温度和冰淇淋销量数据。

数据描述可以包括以下几个方面：（1）变量的定义：明确要研究的两个变量是什么，例如温度和冰淇淋销量。

（2）数据采集方法：描述数据是如何收集的，例如通过气象站记录温度，店铺销售记录冰淇淋销量。

（3）数据的范围与样本量：说明数据的时间范围以及样本数量，例如某地区一年内的温度和冰淇淋销量数据。

（4）数据的基本统计特征：描述数据的基本统计特征，如平均值、中位数、最大值和最小值等。

2. 绘制散点图绘制散点图可以使用各种统计软件或数据可视化工具，如Excel、Python的Matplotlib库等。

以下是散点图的绘制步骤：（1）准备数据：将收集到的温度和冰淇淋销量数据整理为两列。

（2）选择合适的坐标系：根据数据的特点选择合适的坐标系，如希望横轴表示温度，纵轴表示冰淇淋销量。

（3）绘制散点图：根据坐标系，将每组温度和冰淇淋销量数据绘制为一个点。

可以使用不同的颜色或形状来区分不同的数据组。

（4）添加标签和标题：根据需要，添加横轴和纵轴的标签，以及图表的标题，用于说明数据的含义。

（5）美化图表：根据需要，可以对图表进行美化，如调整点的大小、颜色和形状，添加网格线等。

3. 解读散点图散点图可以直观地展示两个变量之间的关系，并帮助我们进行数据的解读和分析。

下面是一些解读散点图的常见方法：（1）趋势判断：观察散点图中点的分布趋势，可以判断两个变量之间的关系是正相关、负相关还是无关。

如果散点图呈现出一个明显的上升或下降趋势，表示两个变量之间存在一定的相关性。

（2）异常点分析：查找散点图中的异常点，即偏离其他点较远的数据点。

二级市场股票价格影响因素辨析

多元回归分析方法应用于股票定价逻辑剖析的思路，源于传统定价理论中的多因素定价模型，该模型在发展过程中多是基于实证观点建立起来的。

实证分析研究经济状态“是什么”，它侧重研究经济系统如何运作，分析经济活动的过程、结果和发展方向。

实证分析在一定的假定条件下，描述、解释或说明已观察到的事实，对将会出现的情况或现象进行预测。

客观事实是检验由实证分析方法得出结论的唯一标准。

有学者指出，实证分析的基本特征：以对经济现象分析归纳出的基本前提假设为起点，并基于这些假设进行逻辑演绎，推导出一系列结论，再逐步放松一些假设，使结论更接近具体事实。

1 研究方法1.1 从企业价值研究开始上市公司的整体价值由其股权资本价值和债务价值两部分组成。

为了方便，我们将占比较小的优先股暂时忽略，以普通股价值作为企业资本的衡量标准；债务违约风险一般较小，其市场价格的变动也不会很大。

由此，在企业资本结构不变的前提下，企业的整体价值越大，其股权资本的价值就越高，股票价格也就越高。

一般投资者都认可股价是由企业的内在价值决定的，但“内在价值”是财报中的哪些指标及怎样的权重决定的？如果这种定价逻辑在二级市场的行业板块中是普遍适用的，那么我们可以用截面数据拟合出定价的回归方程，从而揭示二级市场行业板块的定价逻辑。

1.2 多元线性回归模型多元线性回归模型(multivariable linear regression model)中，当预测对象y同时受到多个解释变量1x，2x，…，mx影响，且各个解释变量都与预测对象有线性相关时，可以建立多元线性回归模型进行预测和分析，模型为：01122ˆˆm m iy x x xββββε=+++⋅⋅⋅++对(1,2,,)i i n=⋅⋅⋅个样本均可写出：01122,1,2,,m m iy x x x i nββββε=+++⋅⋅⋅++=⋅⋅⋅(1)其中：m为解释变量的数目；mβ为回归系数(regression coefficient)；ε为随机干扰误差。

第32讲绘制(散点绘制)

第32讲绘制(散点绘制)散点绘制是一种用于可视化数据的方法，通过在坐标系中绘制离散的数据点来展示它们的分布和关系。

本文档将介绍如何进行散点绘制以及如何解读散点图。

散点绘制的步骤散点绘制通常需要以下几个步骤：1. 准备数据：首先，你需要选择要绘制的数据，并准备好它们的数值。

这些数据可以是一组相关的数据，比如两个变量之间的关系，或者是一组独立的数据，比如样本的分布。

2. 创建坐标系：在绘制散点图之前，你需要创建一个合适的坐标系。

坐标系通常由两个轴组成，分别代表数据的两个维度。

例如，x轴可以表示一个变量的取值，y轴可以表示另一个变量的取值。

3. 绘制数据点：一旦坐标系准备好，你可以开始绘制数据点了。

根据数据的具体取值，在坐标系中标出每一个数据点。

你可以使用不同的符号或颜色来表示不同的数据点，以区分它们的属性或类别。

4. 添加标签和标题：为了增加图表的可读性，你可以在数据点附近添加标签，以显示数据的具体值。

此外，还可以添加一个标题，说明图表的主题或目的。

散点图的解读散点图可以提供以下信息：- 数据的分布：通过观察散点图中的点的分布情况，你可以了解数据的分布模式。

例如，如果数据点趋向于聚集在一起，可能表示存在某种相关性或趋势。

- 变量之间的关系：散点图可以显示两个变量之间的关系。

如果数据点呈现出一种特定的形态，比如线性、曲线或聚集，那么可以得出这两个变量之间存在一种关联关系。

- 异常值的检测：通过观察散点图，你可以发现是否存在异常值。

异常值是与其他数据点明显不同的值，可能是由于测量错误或异常情况引起的。

总结散点绘制是一种用于展示数据分布和变量关系的方法。

通过遵循准备数据、创建坐标系、绘制数据点以及添加标签和标题的步骤，你可以轻松地绘制散点图。

通过解读散点图，你可以获得关于数据的分布、变量关系和异常值的有用信息。

> 注意：本文档提供了散点绘制的基本概念和步骤，但在实际应用中可能需要根据具体情况进行调整和进一步的学习。

GDP增长与城乡居民收入差距的SPSS分析1

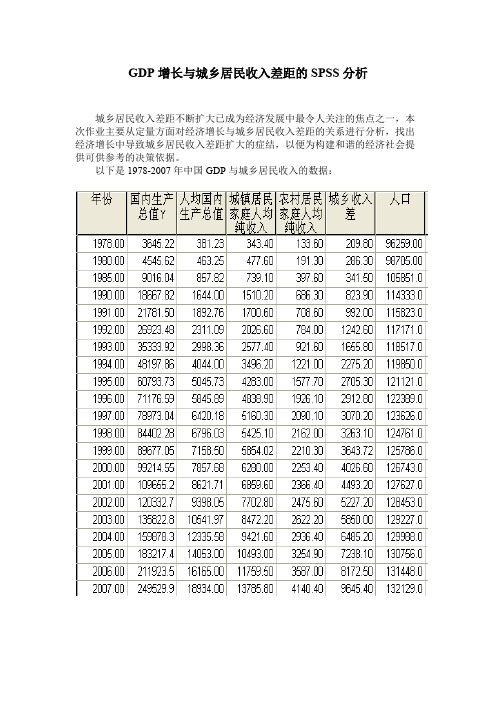
GDP增长与城乡居民收入差距的SPSS分析城乡居民收入差距不断扩大已成为经济发展中最令人关注的焦点之一，本次作业主要从定量方面对经济增长与城乡居民收入差距的关系进行分析，找出经济增长中导致城乡居民收入差距扩大的症结，以便为构建和谐的经济社会提供可供参考的决策依据。

以下是1978-2007年中国GDP与城乡居民收入的数据：1、相关分析：用SPSS绘制矩阵散点图如下所示：通过上图的观测值的分布情况可以看出人均GDP、城镇居民年收入、农村居民年收入和城乡差距绝对数之间呈现强正线性相关。

为了精确的反映两个变量间线性相关的强弱程度，我们利用相关系数来进行变量间线性关系的分析：由上表可知四者之间的简单相关系数都接近1。

所以通过相关分析可知人均GDP受其它三者的正向影响。

但是通过观察上述数据发觉人均GDP受农村居民收入的影响相对较小。

为了把握人均GDP受三个变量影响程度的强弱，下面要通过偏相关分析来描述和反映：2、偏相关分析：三、回归分析：输出结果：P值均显著小于显著性水平α=0.01，说明被解释变量与解释变量全体的线性关系是显著的，可建立线性模型。

建立回归方程Y=1.936X-29.023 (Y:人均国内生产总值；X：城乡收入差)结果分析：显而易见我国GDP的增长大大促进了城镇居民的收入，而对农村居民收入的促进作用并不是很大，经济的增长加剧了收入的不平等。

可以说我国经济的增长是以加剧收入分配的不平等为前提的。

但是在经济社会发展过程中产生这种差距是不可避免的，城乡居民收入差距是市场经济的本质要求，是在居民总体收入水平提高的基础上产生的，也就是说，是在共同富裕目标下产生的差距，是相对差距而非绝对差距。

尽管一定收入差距的扩大会促进资源的优化配置和经济效率的提高，最终会促进经济的增长，但是，如果这种差距过大，就不可避免地会影响整个经济的发展速度和质量，不利于和谐社会的构建。

面对不断扩大的城乡居民收入差距，必须采取有效的政策措施，迅速且较大幅度地提高农村居民收入，不断缩小城乡居民收入差距。

Stata学习笔记和国贸理论总结

Stata 学习笔录一、认识数据（一）向 stata 中导入 txt 、 csv 格式的数据1．这两种数据能够用文本文档翻开，新建记事本，而后将相应文档拖入记事本即可翻开数据，复制2 ．按下 stata中的edit按钮，右键选择paste special3． *.xls/*.xlsx数据仅能用Excel翻开，不行用记事本翻开，翻开后会出现乱码，也不要保存，不然就恢复不了。

逗号分开的数据常为csv 数据。

（二）网页数据网页上的表格只需能选中的，都能复制到excel 中；网页数据的下载能够经过百度“国家数据”进行搜寻、下载二、 Do-file和log文件翻开 stata后，第一步就要do-file，记录步骤和历史记录，方便往后查看。

Stata 办理中保存的三种文件：原始数据(*.dta)，记录办理步骤(*.do)，以及办理的历史记录(*.smcl)。

三、导入 StataStata不辨别带有中文的变量，假如导入的数据第一行有中文就无法导入。

可是关于列来说不会出现这个问题，不剖析即可（Stata 不剖析字符串，红色文本显示；被剖析的数据，黑色显示）；第一行是英文变量名，选择“ Treat first row as variable names”在导入新数据的时候，需要清空原有数据，clear 命令。

导入空格分开数据：复制—— Stata 中选择 edit按钮或输入相应命令——右键选择 paste special ——并选择，确立；导入Excel 中数据，复制粘贴即可；逗号分开数据，选择paste special后点击comma，而后确立。

Stata数据格式为 *.dta，导入后一致使用此格式。

四、基本操作（几个命令）（一） use auto ，clear。

在清空原有数据的同时，导入新的auto 数据。

（二） browse 。

阅读数据。

（三）describe和list。

查察数据，describe和list使用list命令能使我们依据自己的需要选择数据（比如其与in/if语句的联合使用）。