动点问题解析优秀课件
合集下载
动点问题公开课课件.ppt

等边三角形,质点P从点A沿AB—BD作匀速运动,
质点Q从点D同时出发沿DC—CB—BA作匀速运动. (1)如果质点P、Q运动的速度
Q
(分2)别如是果4厘问米题/(秒1、)5中厘的米质/秒点,P、 Q的为分请类速a厘别说三度米同出角不时/经形变秒沿过?,,原(1质经2路按秒点过返角后Q3回的秒的△,速后大AP质度,小Q是点改P分、哪变P类Q一)
3a B
3a
F
分别到达E、F两点,若△BEF与
E
题(1)中的△APQ相似,试求a
的值.
3a
F
1: 12-3a=6 解得: a=2
A
(P)
24
(P)
D (Q)
2: 3a-12=6 解得: a=6
3: 3a-12=24 解得: a=12
(F) C
1、用运动的眼光观察和研究,把握运动变化的全过程。
2、善于探索各量之间的关系,利用几何知识,方程,函数 等帮助解决问题。
(1)当t为何值时,四边形APQD为矩形;
1cm/s Q
D
C
4m/s)
4t=20-t
解得:t=4
3、如图,在矩形ABCD中,AB=20厘米,BC=4厘米,⊙P从点A开始沿折线 A—B—C—D以4厘米/秒的速度移动,⊙Q从点C开始沿CD以1厘米/秒 的速度移动,如果⊙P和⊙Q分别从点A、C同时出发,当其中一个圆心 到达D点时,另一圆也随之停止运动.设运动时间为t(秒).
动点问题的探究
杨村中学 徐慧瑶
解题策略
• 用运动的眼光观察和研究,把握运动变化 的全过程。
1、如图,已知正三角形
ABC的高为9厘米,⊙O的
半径为r厘米,当圆心O
A
从点A出发,沿线路AB—
中考常见动点问题解题方法(共29张PPT)

AE
10-2t
t
30o
2t
30o
B
F
D
C
(3)当t为何值时,△DEF为直角三角形?请说明理由.
1单位/s
解析:
2单位/s
②当∠DEF=90o时
30o
由(2)知EF∥AD
5
∴∠ADE=∠DEF=90o
∵∠A=90o-∠C=60o
1
∴AD= AE
2
1
2
即10-2t= t
A
E 10-2t
60o
t
2t
则t=4
10、阅读一切好书如同和过去最杰出的人谈话。01:48:2201:48:2201:488/23/2021 1:48:22 AM
11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。21.8.2301:48:2201:48Aug-2123-Aug-21
最小值时,△APD中AP边上的高为 _________
3、如图,⊙O的半径为2,点A、B、C
在⊙O上,OA⊥OB, ∠AOC=60°,P是OB上
的一动点,则PA+PC的最小值是________
两个动点(一)
例、如图,∠AOB=45°,P是∠AOB内一
特点:已知一个定点位于平面内两相交直线之间,
点,PO=10,Q、R分别是OA、OB上的动点,
∵点D'和点D关于x轴对称,
∴点D'的坐标为(0,-2).
设直线CD'的解析式为y=kx+b,
∵直线CD'过点C(-3,2),D'(0,-2),
4
2 = -3 + ,
人教版八年级数学下册专题 动点问题(几何)优质课件.ppt

专题 动点问题(几何)
一、学习目标
1.掌握运动型的几何问题的解 法; 2.找出图形中发生变化与不发 生变化的元素.
二、经典范例引路
范例:如图,在长方形ABCD中,AB=12厘米, BC=6厘米.点P沿AB边从点A开始向点B以2厘米/ 秒的速度移动;点Q沿DA边从点D开始向点A以1 厘米/秒的速度移动. 如果P、Q同时出发,用t(秒)表示移动的时间, 那么:
二、经典范例引路
v=1 cm/s v=2 cm/s
(1)如图1,当t=____秒时,线段AQ=AP (即△QAP为等腰直角三角形).
二、经典范例引路
vv==11cmc/sm/s vv==22cmc/sm/s
当t秒时,DQ=t , AQ=6-t, AP=2t,由6-t=2t建立方程求 出其解即可;
CONTENTS
目录
01 教学目标 03 教学准备 02 教学内容 04 教学过程
第一节
教学目标
输入你的文本 根据你所需的内容输入你想要的文本 点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解,
请根据您的具体内容酌情修改。
MORE THAN TEMPLATE
点击此处添加副标题
您的内容打在这里,或者通过复制您的文本后, 在此框中选择粘贴,并选择只保留文字。 。
MORE THAN TEMPLATE
点击此处添加副标题
STRENGTHS
S
Lorem Ipsum simply dummy text of the printing.
Lorem Ipsum simply
dummy text of the printing.
O
OPPORTUNITIE S
Lorem Ipsum simply dummy text of the printing. Lorem Ipsum simply dummy text of the printing.
一、学习目标
1.掌握运动型的几何问题的解 法; 2.找出图形中发生变化与不发 生变化的元素.
二、经典范例引路
范例:如图,在长方形ABCD中,AB=12厘米, BC=6厘米.点P沿AB边从点A开始向点B以2厘米/ 秒的速度移动;点Q沿DA边从点D开始向点A以1 厘米/秒的速度移动. 如果P、Q同时出发,用t(秒)表示移动的时间, 那么:
二、经典范例引路
v=1 cm/s v=2 cm/s
(1)如图1,当t=____秒时,线段AQ=AP (即△QAP为等腰直角三角形).
二、经典范例引路
vv==11cmc/sm/s vv==22cmc/sm/s
当t秒时,DQ=t , AQ=6-t, AP=2t,由6-t=2t建立方程求 出其解即可;
CONTENTS
目录
01 教学目标 03 教学准备 02 教学内容 04 教学过程
第一节
教学目标
输入你的文本 根据你所需的内容输入你想要的文本 点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解,
请根据您的具体内容酌情修改。
MORE THAN TEMPLATE
点击此处添加副标题
您的内容打在这里,或者通过复制您的文本后, 在此框中选择粘贴,并选择只保留文字。 。
MORE THAN TEMPLATE
点击此处添加副标题
STRENGTHS
S
Lorem Ipsum simply dummy text of the printing.
Lorem Ipsum simply
dummy text of the printing.
O
OPPORTUNITIE S
Lorem Ipsum simply dummy text of the printing. Lorem Ipsum simply dummy text of the printing.
中考总复习动点问题精品PPT教学课件

E
(P)
D (Q)
F两点,若△BEF与题
(1)中的△APQ相似, 试求a的值.
2020/12/8
(F) C 综上:当a=2或6或12时,
△BEF与△APQ相似 4
3、如图,在矩形ABCD中,AB=20厘米,BC=4厘米,点P从点A开 始沿折线A—B—C—D以4厘米/秒的速度移动,点Q从点C开 始沿CD以1厘米/秒的速度移动,如果点P和Q分别从点A、C 同时出发,当其中一个点到达D点时,另一点也随之停止运 动.设运动时间为t(秒).
厘米的等边三角形,质点P从点A沿AB—
A
BD作匀速运动,质点Q从点D同时出发沿
DC—CB—BA作匀速运动.
3a
Q
(P)
(21)如果问质点题(P、1) Q运中 3a
的 动的质速点度P、分Q别分是别同4厘时米沿/ B F
原 秒路、返5厘回米,/质秒点,请P的说速出 度 经不过变12,秒质后点△QA的PQ速是度哪 3a F 改 一类变三为角a厘形米?/(秒按,角经的过 3大秒小后分,类P)、Q分别到达E、
2020/12/8
1
1、如图,已知正三角形
ABC的高为9厘米,⊙O的
半径为r厘米,当圆心O
A
从点A出发,沿线路AB—
BC—CA运动,回到点A时,
⊙O随着点O的运动而停
止.
B
C
(1)当r=9厘米时,⊙O
在移动过程中与△ABC三
边有几个切点?
当r=9厘米时,⊙O在移动过程
中与△ABC三边有三个切点.
2020/12/8
温馨提示:本文内容皆为可修改式文档,下载后,可根据读者的需求 作修改、删除以及打印,感谢各位小主的阅览和下载
第35讲动点问题专题PPT课件
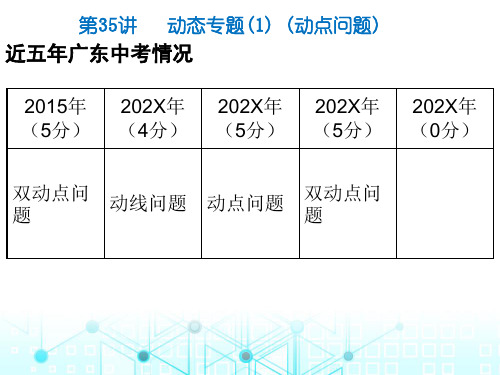
③如答图2-35-10,当4≤x<6时,CD=6-x, ∵∠BCE=90°,∠PDC=60°,
④当x≥6时,y=0.
②如答图2-35-5,作DH⊥AB于点H. 在Rt△ADH中,∵AD=x,∠DAH=∠ACO=30°,
在Rt△BDH中, ∴矩形BDEF的面积为
∴当x=3时,y有最小值为
分层训练
A组
3.(202X衢州)如图2-35-3,正方形ABCD的边长为4,点
E是AB的中点,点P从点E出发,沿E→A→D→C移动至终
第35讲 动态专题(1) (动点问题)
近五年广东中考情况
2015年 202X年 202X年 202X年 202X年 (5分) (4分) (5分) (5分) (0分)
双动点问 题
动线问题
的运动中,一些图 形位置、数量关系的“变”与“不变”的问题.常用 的数学思想是方程思想、数学建模思想、函数思想、 转化思想等;常用的数学方法有分类讨论法、数形 结合法等.
(3)在直线l移动过程中,l上是否存在一点Q,使以B, C,Q为顶点的三角形是等腰直角三角形?若存在,直 接写出Q点的坐标;若不存在,请说明理由.
解:(1)在Rt△BOC中,OB=3,
设CO=4k,则BC=5k, ∵BC2=CO2+OB2,∴25k2=16k2+9, ∴k=1或-1(不符,舍去).∴BC=5,OC=4. ∵四边形ABCD是菱形,∴CD=BC=5.∴D(5,4). (2)①如答图2-35-6,当0≤t≤2时,直线l扫过的图形 是四边形OCQP,S=4t.
②如图2-35-2②,当点E在OC的延长线上时, △DCE是等腰三角形,则只有CD=CE, ∠DBC=∠DEC=∠CDE= ∠ACO=15°, ∴∠ABD=∠ADB=75°.∴AB=AD= 综上所述,满足条件的AD的值为2或
④当x≥6时,y=0.
②如答图2-35-5,作DH⊥AB于点H. 在Rt△ADH中,∵AD=x,∠DAH=∠ACO=30°,
在Rt△BDH中, ∴矩形BDEF的面积为
∴当x=3时,y有最小值为
分层训练
A组
3.(202X衢州)如图2-35-3,正方形ABCD的边长为4,点
E是AB的中点,点P从点E出发,沿E→A→D→C移动至终
第35讲 动态专题(1) (动点问题)
近五年广东中考情况
2015年 202X年 202X年 202X年 202X年 (5分) (4分) (5分) (5分) (0分)
双动点问 题
动线问题
的运动中,一些图 形位置、数量关系的“变”与“不变”的问题.常用 的数学思想是方程思想、数学建模思想、函数思想、 转化思想等;常用的数学方法有分类讨论法、数形 结合法等.
(3)在直线l移动过程中,l上是否存在一点Q,使以B, C,Q为顶点的三角形是等腰直角三角形?若存在,直 接写出Q点的坐标;若不存在,请说明理由.
解:(1)在Rt△BOC中,OB=3,
设CO=4k,则BC=5k, ∵BC2=CO2+OB2,∴25k2=16k2+9, ∴k=1或-1(不符,舍去).∴BC=5,OC=4. ∵四边形ABCD是菱形,∴CD=BC=5.∴D(5,4). (2)①如答图2-35-6,当0≤t≤2时,直线l扫过的图形 是四边形OCQP,S=4t.
②如图2-35-2②,当点E在OC的延长线上时, △DCE是等腰三角形,则只有CD=CE, ∠DBC=∠DEC=∠CDE= ∠ACO=15°, ∴∠ABD=∠ADB=75°.∴AB=AD= 综上所述,满足条件的AD的值为2或
九年级数学动点问题ppt课件

动点问题
!
图形中的点、线运动,构成了数学中的一个新问题---动态几何。它通常分为三种类型:动点问题、动线问题、 动形问题。在解这类问题时,要充分发挥空间想象的能力 ,不要被“动”所迷惑,而是要在“动”中求“静”,化“动”为“ 静”,抓住它运动中的某一瞬间,寻找确定的关系式,就能 找到解决问题的途径。
C
5、等腰梯形
思
化动为静
分类讨论
路
构建函数模型、方程模型
3、求面积
A
M
D
P
Q
B
C
6、直角三角形
A
B' B
A
B'
B
P D
E' E
P
C
D
E'
E
C
数形结合
小结:
积累就是知识
动点问题 动点题是近年来中考的的一个热点问题,解这类题目要“以静制动”, 即把动态问题,变为静态问题来解。一般方法:首先根据题意理清题目中两个变量X、Y 及相关常量。第二找关系式。把相关的量用一个自变量的表达式表达出来,再解出。 第三,确定自变量范围,画相应的图象。
tD
Q
B
A
4
3 2t
∟G
P
C
∵点D在线段PQ的中垂线上 ∴DQ=DP
DQ 2 DP 2
t242(2t3)2
3 t2 1t2 2 5 0
∵ △ = —156<0
.
∴方程无解。
即点D都不可能在线段QP的中垂线 上。
4. ( 2009 中 考 ) 例 1 、 如 图 , 已 知 在 直 角 梯 形 ABCD 中 ,
比为7︰15?若存在,求出相应的t的值;不存在说明理由。
!
图形中的点、线运动,构成了数学中的一个新问题---动态几何。它通常分为三种类型:动点问题、动线问题、 动形问题。在解这类问题时,要充分发挥空间想象的能力 ,不要被“动”所迷惑,而是要在“动”中求“静”,化“动”为“ 静”,抓住它运动中的某一瞬间,寻找确定的关系式,就能 找到解决问题的途径。
C
5、等腰梯形
思
化动为静
分类讨论
路
构建函数模型、方程模型
3、求面积
A
M
D
P
Q
B
C
6、直角三角形
A
B' B
A
B'
B
P D
E' E
P
C
D
E'
E
C
数形结合
小结:
积累就是知识
动点问题 动点题是近年来中考的的一个热点问题,解这类题目要“以静制动”, 即把动态问题,变为静态问题来解。一般方法:首先根据题意理清题目中两个变量X、Y 及相关常量。第二找关系式。把相关的量用一个自变量的表达式表达出来,再解出。 第三,确定自变量范围,画相应的图象。
tD
Q
B
A
4
3 2t
∟G
P
C
∵点D在线段PQ的中垂线上 ∴DQ=DP
DQ 2 DP 2
t242(2t3)2
3 t2 1t2 2 5 0
∵ △ = —156<0
.
∴方程无解。
即点D都不可能在线段QP的中垂线 上。
4. ( 2009 中 考 ) 例 1 、 如 图 , 已 知 在 直 角 梯 形 ABCD 中 ,
比为7︰15?若存在,求出相应的t的值;不存在说明理由。
八年级数学动点问题专题通用课件

在研究波动现象时,动点 问题可以用来描述波的传 播和振动。
日常生活中的应用
行车路线规划
在日常生活中,动点问题 可以用于解决行车、骑车 或步行的最短路径问题。
物流配送
在物流领域,动点问题常 用于优化配送路线和时间 ,降低成本和提高效率。
时间安排
在日程安排和时间管理中 ,动点问题可以帮助我们 找到最优的时间分配方案 。
科学实验中的应用
化学反应速率
在化学反应中,动点问题可以用 来描述反应速率和反应机理。
生物种群动态
在生态学中,动点问题可以用来研 究生物种群的动态变化和演化。
天文观测
在天文学中,动点问题可以用于描 述行星、恒星的运动轨迹和观测数 据的处理。
04
动点问题的练习题和解析
基础练习题
总结词:这些题目是解决动点问 题的基础,适合初学者练习。
注意事项
在建立函数模型时,需要准确理解问题的条件和要求,并注意函数的 正确性和可解性。
03
动点问题的实际应用
物理问题中的应用
01
02
03
运动学问题
动点问题在物理运动学中 有着广泛的应用,如速度 、加速度和位移的计算。
力学问题
在力学领域,动点问题可 用于解决力的合成与分解 、牛顿运动定律等问题。
波动问题
题的效率和精确度。
注重培养学生的创新思维和实 践能力,通过解决动点问题培
养数学创新人才。
THANKS
感谢观看
注意事项
在利用几何法解决问题时,需 要准确理解几何图形的性质和 定理,并注意图形的合理性和
美观性。
函数法
总结词
通过建立函数模型,解决动点问题。
详细描述
在动点问题中,常常需要建立函数模型来表示动点的运动规律或变化 趋势,然后通过求解函数来找到动点的位置或相关参数。
日常生活中的应用
行车路线规划
在日常生活中,动点问题 可以用于解决行车、骑车 或步行的最短路径问题。
物流配送
在物流领域,动点问题常 用于优化配送路线和时间 ,降低成本和提高效率。
时间安排
在日程安排和时间管理中 ,动点问题可以帮助我们 找到最优的时间分配方案 。
科学实验中的应用
化学反应速率
在化学反应中,动点问题可以用 来描述反应速率和反应机理。
生物种群动态
在生态学中,动点问题可以用来研 究生物种群的动态变化和演化。
天文观测
在天文学中,动点问题可以用于描 述行星、恒星的运动轨迹和观测数 据的处理。
04
动点问题的练习题和解析
基础练习题
总结词:这些题目是解决动点问 题的基础,适合初学者练习。
注意事项
在建立函数模型时,需要准确理解问题的条件和要求,并注意函数的 正确性和可解性。
03
动点问题的实际应用
物理问题中的应用
01
02
03
运动学问题
动点问题在物理运动学中 有着广泛的应用,如速度 、加速度和位移的计算。
力学问题
在力学领域,动点问题可 用于解决力的合成与分解 、牛顿运动定律等问题。
波动问题
题的效率和精确度。
注重培养学生的创新思维和实 践能力,通过解决动点问题培
养数学创新人才。
THANKS
感谢观看
注意事项
在利用几何法解决问题时,需 要准确理解几何图形的性质和 定理,并注意图形的合理性和
美观性。
函数法
总结词
通过建立函数模型,解决动点问题。
详细描述
在动点问题中,常常需要建立函数模型来表示动点的运动规律或变化 趋势,然后通过求解函数来找到动点的位置或相关参数。
课件--动点问题
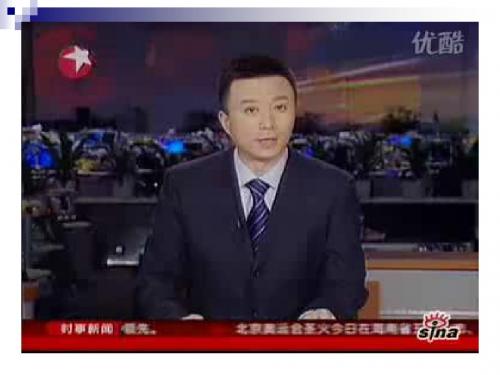
防风暴指挥中心发现在O处的热带风暴中心正以100 千米/时的速度沿北偏东30°的OC方向运动,风暴中 心周围200千米内要受影响,现知在O处正北方向320 千米有一城市A,你能否帮指挥中心预测一下:A市 受影响吗?若受影响,受影响的时间为多长 ?
A
C
O
Hale Waihona Puke 中考专题之——动态问题探究(一)
铜陵市第四中学
2抓住图形在变化过程中不变的东西,找准图 形的代数表达式,正确分析变量与其它量之间 的内在联系,建立它们之间的关系。
例2 如图,已知直角梯形ABCD中,AD∥BC, ∠B=90º,AB=12cm,BC=8cm,DC=13cm,动点P沿 A→D→C线路以2cm/s速度向C运动,动点Q沿B→C 线路以1cm/s的速度向C运动。P、Q两点分别从A、 B同时出发,当其中一点到达C点时,另一点也随 之停止。设运动时间为t秒, P D A △PQB的面积为y c㎡. (1)求AD长及t取值范围; (2)求y关于t函数关系式; (3)在动点P、Q运动过程中, 求△PQB面积最大值。
B P A 解(1)点P在AB上 y=5x (0≤x≤10) 综合: D A D (2)点P在BC上 y=50(10<x≤20) A C B P C B C P D
(3)点P在CD上 y=150-5x(20<x≤30)
解题方法: 1“动静结合”处理问题。要弄清楚图形的变 化过程,充分地发挥自己的空间想象力,动态 地分析图形运动的特点和规律,必要时多画几 个草图分析也可。在分析后得到的每种情况中, 则要“化动为静”,用静态的观点去求出所求 的问题。
解:当点P在AD边上时 y=6t (0≤t≤1.5) 12 13
B
t
Q
C
例2 如图,已知直角梯形ABCD中,AD∥BC,∠B=90º, AB=12cm,BC=8cm,DC=13cm,动点P沿A→D→C线路以 2cm/s速度向C运动,动点Q沿B→C线路以1cm/s的速度 向C运动。P、Q两点分别从A、B同时出发,当其中一点 到达C点时,另一点也随之停止。设运动时间为t秒, 3 2t △PQB的面积为y c㎡。 A D (2)求y关于t函数关系式;
A
C
O
Hale Waihona Puke 中考专题之——动态问题探究(一)
铜陵市第四中学
2抓住图形在变化过程中不变的东西,找准图 形的代数表达式,正确分析变量与其它量之间 的内在联系,建立它们之间的关系。
例2 如图,已知直角梯形ABCD中,AD∥BC, ∠B=90º,AB=12cm,BC=8cm,DC=13cm,动点P沿 A→D→C线路以2cm/s速度向C运动,动点Q沿B→C 线路以1cm/s的速度向C运动。P、Q两点分别从A、 B同时出发,当其中一点到达C点时,另一点也随 之停止。设运动时间为t秒, P D A △PQB的面积为y c㎡. (1)求AD长及t取值范围; (2)求y关于t函数关系式; (3)在动点P、Q运动过程中, 求△PQB面积最大值。
B P A 解(1)点P在AB上 y=5x (0≤x≤10) 综合: D A D (2)点P在BC上 y=50(10<x≤20) A C B P C B C P D
(3)点P在CD上 y=150-5x(20<x≤30)
解题方法: 1“动静结合”处理问题。要弄清楚图形的变 化过程,充分地发挥自己的空间想象力,动态 地分析图形运动的特点和规律,必要时多画几 个草图分析也可。在分析后得到的每种情况中, 则要“化动为静”,用静态的观点去求出所求 的问题。
解:当点P在AD边上时 y=6t (0≤t≤1.5) 12 13
B
t
Q
C
例2 如图,已知直角梯形ABCD中,AD∥BC,∠B=90º, AB=12cm,BC=8cm,DC=13cm,动点P沿A→D→C线路以 2cm/s速度向C运动,动点Q沿B→C线路以1cm/s的速度 向C运动。P、Q两点分别从A、B同时出发,当其中一点 到达C点时,另一点也随之停止。设运动时间为t秒, 3 2t △PQB的面积为y c㎡。 A D (2)求y关于t函数关系式;
动点问题专题课优质课件
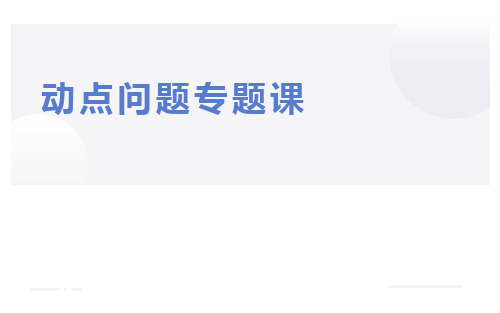
假设存在符合条件的点P,设点P的横坐标是x
△PAB的铅垂高为h, 则h(﹣x2+2x+3)﹣(﹣x+3) =﹣x2+3x
由S△PAB= S△CAB 得:
解得 P点坐标为
P(x ﹣x2+2x+3) E ( x ﹣﹣xx++3)
3)
2013•保定二模)如图,矩形AOCD的顶点A的坐标是(0,4).动点 P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度 匀速向点C运动,同时动点Q从点C出发沿线段CD(不包括端点C,D) 以每秒1个单位长度的速度匀速向点D运动.当其中一点到达终点时,另 一点也停止运动.设运动时间为t(秒),当t=2(秒)时, PQ=2√5.解答下列问题: (1)求点D的坐标; (2)直接写出t的取值范围. (3)连接AQ并延长交x轴于点E,把AQ沿AD翻折,点Q落在CD延长 线上点F处,连接EF. ①t为何值时,PQ∥AF; ②△AEF的面积S是否随t的变化而变化?若变化,求出S与t的函数关系 式;若不变化,求出S的值.
当P点到达D点时,动点P、Q同时停止运动,设点P、Q同时出发,并
运动了t秒,回答下列问题:
(1)BC= _________ cm;
(2)当t为多少时,四边形PQCD成为平行四边形?
(3)当t为多少时,四边形PQCD为等腰梯形?
(4)是否存在t,使得△DQC是等腰三角形?若存在,请求出t的值;若
不存在,说明理由.
A
P
D
B
Q
C
②当DQ=DC时, ∴3t=12;
A
D
B
C
Q
③当QD=QC时, ∴t=
A
D
B
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D
C
2
A
B
P
7 6
7
t 1 t 13
t
2.在Rt△ABC中,∠C=90°,AC=6cm, BC=8cm, 点P由点A出发 ,沿AC向C运动,速度为2cm/s,同时 点Q由AB中点D出发,沿DB向B运动,速度为1cm/s, 连接PQ,若设运动时间为t(s)
(1)当t为何值时, (0<t ≤3) PQ∥BC?
(3)求x为何值时,△APD的面积为 5 3 2y
C
P
A D 图1
B
C1
C2
O
4.5 F x
图2
1、如图:已知 ABCD中,AB=7,BC=4,∠A=30° (1)点P从点A沿边AB向点B运动,速度为1cm/s,时间为t(s).
当t为何值时,△PBC为等腰三角形?
D
A 30°
7-t B
P
7
若△PBC为等腰三角形
B
C
∴ QN = 8
5+t 10
三角函数法
∴QN=4+4 t 5
∴ y = 1 × 2t 4 + 4 t
2
5
∴ y = 4 t 2 + 4t 5
2.(3)在Rt△ABC中,∠C=90°,点P由点A出发 ,沿AC向C运动,速度为
2cm/s,同时 点Q由AB中点D出发,沿DB向B运动,速度为1cm/s, 连接PQ,若设运动时间为t(s)若点P由点A出发,沿AC向C运动到C点停止后,点Q继 续沿DB向B运动到B点后继续向CB方向运动到C点停止。 若设运动时间为t(s),设△ APQ的面积为y(cm ),求y与t之间的函数关系。
(2)设△ APQ的面积为y(cm 2 ),求y与t之间的函数关系。 (0<t ≤3)
A
A
M
D
P
D
P
Q
Q
∟
N
B
CB
C
2.(2)
M
A
D
P
Q
B
C
相似法
∵△APM∽ △ABC
∴ PM = AP BC AB
∴ PM = 2t 8 10
∴PM = 8 t 5
∴ y = 1 × (5 + t ) 8 t
2
5
∴ y = 4 t 2 + 4t 5
动点问题解析优秀课件
图形中的点、线运动,构成了数学中的一个 新问题----动态几何。它通常分为三种类型:动点 问题、动线问题、动形问题。
在解这类问题时,要充分发挥空间想象的能力, 不要被“动”所迷惑,而是要在“动”中求“静”, 化“动”为“静”,---找出切入点,充分利用图中 条件,建立模型(方程和函数),这样就能找到解 决问题的途径。
2.(2)
D
Q
B
相似法
∟
A
∵△AQN∽ △ABC
P
∴QN = AQ BC AB
N
∴QN= 5+t
C
8
10
∴QN=4+4 t
5
∴ y = 1 × 2t 4 + 4 t
2
5
∴ y = 4 t 2 + 4t 5
2.(2)
D
Q
∟
A 在 R A t 中 BC C , 90
SinA= 8 10
P
N
∴ QN = 8 AQ 10
【丽水市小中考】
23.如图1,在Rt△ABC中,∠C=Rt∠,∠A= 30°,D为AB上一个动点,过 点D作DP⊥AB交折线A—C—B于点P,设AD的长为x,△APD的面 积为y, y关于x的函数图象由C1,C2两段组成,如图2所示.
(1)当x=4.5时,求AP的长;
(2)求图2中图象C2段的函数解析式;
y = 4 t 2 +4t 5
y =12+12 t 5
y39-3t
A
10
D
Q
B
Q8
∟
6
N
C
P
35
13 t
积累就是知识
收获一:化动为静找切入点 收获二:分类讨论 收获三:数形结合充分利用图形和条件 收获四:构建函数模型、方程模型
2.(4)是否存在某一时刻t,使△ APQ的面积与△ ABC的面积
比为7︰15?若存在,求出相应的t的值;不存在说明理由。
(0<t ≤3)
A
SΔABC =1 2×8×6=24
D
Q
P
∴ y =7
SΔABC
15
B
C
∴4t2+4t = 7 ×24
5
15
计算要仔细
∴ t2+ 5t -1= 40
∴ (t+ 7)t(-2)= 0
∴ t= -7(舍去 ,t=) 2
∴当t=2时, △ APQ的面积与△ ABC的面积比为7︰15
C
则PB=BC
4
∴7-t=4
∴t=3
如图:已知 ABCD中,AB=7,BC=4,∠A=30° (2)若点P从点A沿射线AB运动,速度仍是1cm/s。
当t为何值时,△PBC为直角三角形?
D
C
4
A
7Leabharlann B 23 p∟D
C
4
A
7
B
p
1.如图:已知 ABCD中,AB=7,BC=4,∠A=30°
(3)是否存在某一时刻t,使得△PBC面积为6cm 2 ?
若PQ∥BC
A 则△ AQP~△ABC
5+t D
2t ∴ AQ = AP AB AC
Q
B
P ∴5+t = 2t
C
10
6
∴ t = 15 7
2.在Rt△ABC中,∠C=90°,AC=6cm, BC=8cm, 点P由点A出发 ,沿AC向C运动,速度为2cm/s,同时 点Q由AB中点D出发,沿DB向B运动,速度为1cm/s, 连接PQ,若设运动时间为t(s) (0<t ≤3)
