广东省增城中学2010届高中毕业班高三数学第二次综合测试
广东省增城中学2010届高三第三次综合测试

2010年增城中学普通高中毕业班综合测试(三)英语试题 2009.11本试卷共12页,满分为150分,考试时间120分钟。
注意事项:1.答卷前,考生务必将自己的姓名,考号填写在答题卷和答题卡上。
2.选择题每小题选出答案后,用2B铅笔将答题卡上,对应题目的答案标号涂写,如写改动,用橡皮擦干净后,再选涂其它答案标号,答在试题卷上无效。
3.非选择题用0.5毫米的黑色墨水签字笔答在答题卷上每题对应的答题区域内,答在试题卷上或不在指定区域无效。
4、考试结束,请将答题卡和答题卷上交一、听力(共两节,满分35分)第一节:听独白或对话(共15小题;每小题2分,满分30分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置,听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第1段材料,回答第1—3题。
1. What is Sandy Paris' telephone number?A. 6518935.B. 3613759.C. 3617395.2. Why does Sandy make the call?A. To give the address to Wendy.B. To invite Wendy to the party.C. To make sure whether Wendy is going to the party.3. What is true about Wendy?A. She knows where the party will be held.B. She hasn't told Sandy whether she is going.C. She is not likely to go to the party.听第2段材料,回答第4—6题。
2010广州高三二模数学试题及答案(理科)

试卷类型:A2010年广州市普通高中毕业班综合测试(二)数 学(理科)2010.4 本试卷共4页,21小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上.将条形码横贴在答题卡右上角“条形码粘贴处”. 2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案.答案不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题组号对应的信息点,再作答.漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回. 参考公式:如果事件A 、B 互斥,那么()()()P A B P A P B +=+. 如果事件A 、B 相互独立,那么()()()P A B P A P B ∙=∙.如果事件A 在一次试验中发生的概率是p ,那么n 次独立重复试验中事件A 恰好发生k 次的概率()n P k =C ()1n kkk np p --()0,1,2,,k n =.两数立方差公式: ()()3322a b a b a ab b -=-++.一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知i 为虚数单位,若复数()()11a a -++i 为实数,则实数a 的值为 A .1- B .0 C .1 D .不确定 2. 已知全集U =AB 中有m 个元素,()()U U A B 痧中有n 个元素.若A B I 非空, 则A B I 的元素个数为A .mnB .m n +C .m n -D . n m -3. 已知向量a ()sin ,cos x x =,向量b (=,则+a b 的最大值为A. 13 D.94. 若,m n 是互不相同的空间直线, α是平面, 则下列命题中正确的是A. 若//,m n n α⊂,则//m αB. 若//,//m n n α,则//m αC. 若//,m n n α⊥,则m α⊥D. 若,m n n ⊥5. 在如图1所示的算法流程图, 若()()32,x f x g x x ==, 则()2h 的值为(注:框图中的赋值符号“=”也可以写成“←” 或“:= A. 9 B. 8 C. 6D. 46. 已知点(),P x y的坐标满足10,30,2.xy x y x -+≥⎧⎪+-≥⎨⎪≤⎩O 为坐标原点, 则PO 的最小值为A.2 B. 2图1 7. 已知函数()sin f x x x =, 若12,,22x x ππ⎡⎤∈-⎢⎥⎣⎦且()()12f x f x <, 则下列不等式中正确的是 A. 12x x > B. 12x x < C. 120x x +< D. 2212x x <8. 一个人以6米/秒的匀速度去追赶停在交通灯前的汽车, 当他离汽车25米时交通灯由红变绿, 汽车开始作变速直线行驶 (汽车与人的前进方向相同), 汽车在时刻t 的速度为()v t t =米/秒, 那么, 此人A. 可在7秒内追上汽车B. 可在9秒内追上汽车C. 不能追上汽车, 但其间最近距离为14米D. 不能追上汽车, 但其间最近距离为7米二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9~13题) 9.若函数()()()cos cos 02f x x x π⎛⎫=ω-ωω>⎪⎝⎭的最小正周期为π,则ω的值为 .图310.已知椭圆C 的离心率2e =且它的焦点与双曲线2224x y -=的焦点重合, 则椭圆C 的方 程为 .11.甲、乙两工人在一天生产中出现废品数分别是两个随机变量ξ、η,其分布列分别为:若甲、乙两人的日产量相等,则甲、乙两人中技术较好的是 . 12.图2是一个有n 层()2n ≥的六边形点阵.它的中心是一个点, 算作第一层, 第2层每边有2个点,第3层每边有3个点 ,…, 第n 层每边有n 个点, 则这个点阵的点数共有 个.13. 已知2nx ⎫⎪⎭的展开式中第5项的系数与第3项的系数比为56 则该展开式中2x 的系数为 .(二)选做题(14~ 15题,考生只能从中选做一题)14.(坐标系与参数方程选做题)已知直线l 的参数方程为1,42.x t y t =+⎧⎨=-⎩(参数t ∈R ),圆C 的参数方程为2cos 2,2sin .x y θθ=+⎧⎨=⎩(参数[]0,2θπ∈),则直线l 被圆C 所截得的弦长为 .15.(几何证明选讲选做题)如图3, 半径为5的圆O 的两条弦 AD 和BC 相交于点P , ,OD BC P ⊥为AD 的中点, 6BC =, 则弦AD 的长度为 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤,16. (本小题满分12分)已知1 tan2,tan42παβ⎛⎫+==⎪⎝⎭.(1) 求tanα的值; (2) 求()()sin2sin cos2sin sin cosαβαβαβαβ+-++的值.D B CAEPBCA 如图4, 在直角梯形ABCD 中, 90,30,1,ABC DAB CAB BC AD CD ︒︒∠=∠=∠===, 把△DAC 沿对角线AC 折起后如图5所示(点D 记为点P ), 点P 在平面ABC 上的正投影E 落在线段AB 上, 连接PB .(1) 求直线PC 与平面PAB 所成的角的大小;(2) 求二面角P AC B --的大小的余弦值. 图4 图5一射击运动员进行飞碟射击训练, 每一次射击命中飞碟的概率p 与运动员离飞碟的距离s (米)成反比, 每一个飞碟飞出后离运动员的距离s (米)与飞行时间t (秒)满足()()15104s t t =+≤≤, 每个飞碟允许该运动员射击两次(若第一次射击命中,则不再进行第二次射击).该运动员在每一个飞碟飞出0.5秒时进行第一次射击, 命中的概率为45, 当第一次射击没有命中飞碟, 则在第一次射击后 0.5秒进行第二次射击,子弹的飞行时间忽略不计.(1) 在第一个飞碟的射击训练时, 若该运动员第一次射击没有命中, 求他第二次射击命中飞碟 的概率;(2) 求第一个飞碟被该运动员命中的概率;(3) 若该运动员进行三个飞碟的射击训练(每个飞碟是否被命中互不影响), 求他至少命中两个飞碟的概率.已知抛物线C :22x py=()0p >的焦点为F ,A 、B 是抛物线C 上异于坐标原点O 的不同两点,抛物线C 在点A 、B 处的切线分别为1l 、2l ,且12l l ⊥,1l 与2l 相交于点D . (1) 求点D 的纵坐标;(2) 证明:A 、B 、F 三点共线;(3) 假设点D 的坐标为3,12⎛⎫- ⎪⎝⎭,问是否存在经过A 、B 两点且与1l 、2l 都相切的圆, 若存在,求出该圆的方程;若不存在,请说明理由.已知函数()32f x x x ax b =-++(a,b ∈R )的一个极值点为1x =.方程20ax x b ++=的两个实根为,αβ()αβ<, 函数()f x 在区间[],αβ上是单调的.(1) 求a 的值和b 的取值范围;(2) 若[]12,,x x αβ∈, 证明:()()121f x f x -≤.21. (本小题满分14分)已知数列{}n a 和{}n b 满足11a b =,且对任意n ∈N *都有1n n a b +=,121n n n na ba a +=-. (1) 求数列{}n a 和{}nb 的通项公式; (2) 证明:()31324122341123ln 1n nn na a aa a a a a nb b b b b b b b ++++++<+<++++.2010年广州市普通高中毕业班综合测试(二)数学(理科)试题参考答案及评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分. 一、选择题:本大题主要考查基本知识和基本运算.共8小题,每小题5分,满分40分.二、填空题:本大题主要考查基本知识和基本运算.本大题共7小题,考生作答6小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题.9.1 10. 22182x y += 11. 乙 12. 2331n n -+ 13. 180 14 15. 三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分)(本小题主要考查两角和与差的三角公式等知识, 考查化归与转化的数学思想方法和运算求解能力)(1)解法1:∵tan 24πα⎛⎫+=⎪⎝⎭, ∴tantan 421tantan 4+=-παπα. …2分∴1tan 21tan αα+=-. 解得1tan 3α=. …4分解法2:∵tan 24πα⎛⎫+=⎪⎝⎭, ∴tan tan 44ππαα⎡⎤⎛⎫=+-⎪⎢⎥⎝⎭⎣⎦tan tan441tan tan44ππαππα⎛⎫+- ⎪⎝⎭=⎛⎫++ ⎪⎝⎭…2分 21121-=+⨯13=. …4分(2)解:()()sin 2sin cos 2sin sin cos αβαβαβαβ+-++sin cos cos sin 2sin cos 2sin sin cos cos sin sin αβαβαβαβαβαβ+-=+- …6分cos sin sin cos cos cos sin sin αβαβαβαβ-=+()()sin cos βαβα-=- …8分()tan βα=- tan tan 1tan tan -=+βαβα…10分112311123-=+⨯ 17=. …12分17. (本小题满分12分)(本小题主要考查空间线面关系、空间角等知识, 考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力) 方法一:(1) 解:在图4中,∵90,30,1,ABC DAB CAB BC ︒︒∠=∠=∠==DBCA图 5FEPBCA∴tan 30BC AB ︒===, 121sin302BC AC ︒===, 60DAC ︒∠=. ∵AD CD =,∴△DAC 为等边三角形. ∴2AD CD AC ===. …2分 在图5中,∵点E 为点P 在平面ABC 上的正投影,∴PE ⊥平面ABC . ∵BC ⊂平面ABC , ∴PE ⊥BC .∵90CBA ︒∠=, 图4 ∴BC AB ⊥. ∵,PEAB E PE =⊂平面PAB , AB ⊂平面PAB ,∴BC ⊥平面PAB .∴CPB ∠为直线PC 与平面PAB 所成的角. …4分 在Rt △CBP 中, 1,2BC PC DC ===, ∴1sin 2BC CPB PC ∠==. ∵090CPB ︒︒<∠<, ∴30CPB ︒∠=.∴直线PC 与平面PAB 所成的角为30︒. …6分 (2) 解:取AC 的中点F , 连接PF ,EF .∵ =PA PC , ∴ ⊥PF AC .∵PE ⊥平面ABC ,AC ⊂平面ABC , ∴PE AC ⊥. ∵,=⊂PFPE P PF 平面PEF , PE ⊂平面PEF ,DBCA∴AC ⊥平面PEF . ∵⊂EF 平面PEF , ∴⊥EF AC .∴PFE ∠为二面角P AC B --的平面角. …8分 在R t △EFA 中,11302︒==∠=AF AC ,FAE , ∴=EF AF tan30︒⋅3=3==AE . 在R t △PFA 中,==PF 在R t △PEF中,1cos 3∠===EF PFE PF .∴二面角P AC B --的大小的余弦值为13. …12分 方法二: 解:在图4中,∵90,30,1,ABC DAB CAB BC ︒︒∠=∠=∠==∴tan 30BC AB ︒===, 12sin302BC AC ︒===, 60DAC ︒∠=. ∵AD CD =,∴△DAC 为等边三角形. ∴2AD CD AC ===. …2分 在图5中,∵点E 为点P 在平面ABC 上的射影,∴PE ⊥平面ABC . ∵BC ⊂平面ABC , ∴PE ⊥BC .∵90CBA ︒∠=, 图4 ∴BC AB ⊥.图5C∵,PE AB E PE =⊂平面PAB , AB ⊂平面PAB ,∴BC ⊥平面PAB . …4连接EC ,在R t △PEA 和R t △PEC 中,2,PA PC PE PE ===, ∴R t △PEA ≅R t △PEC . ∴EA EC =.∴30ECA EAC ︒∠=∠=.∴60CEB ︒∠=.在R t △CBE中,tan 60BC EB ︒===∴AE AB EB =-=在R t △PEA中,PE ==3. …6分 以点E 为原点,EB 所在直线为x 轴,与BC 平行的直线为y 轴,EP 所在直线为z 轴,建立空间直角坐标系E xyz -,则()0,0,0E,A ⎛⎫ ⎪ ⎪⎝⎭,B ⎫⎪⎪⎝⎭,C ⎫⎪⎪⎝⎭, 0,0,3P ⎛ ⎝⎭. ∴()0,1,0BC =,0,0,3EP ⎛= ⎝⎭,()3,1,0AC =,333PC ⎛=- ⎝⎭.(1)∵cos ,BC PC BC PC BC PC==12, ∴,30BC PC ︒=.∴ 直线PC 与平面PAB 所成的角为30︒. …9分 (2) 设平面PAC 的法向量为n (),,x y z =,由0,0.⎧=⎪⎨=⎪⎩n AC n PC得0,0y x y z +=+-=. 令1x =,得y ==z . ∴n 1,⎛= ⎝⎭为平面PAC 的一个法向量.∵EP ⎛= ⎝⎭为平面ABC 的一个法向量, ∴cos ,=n EP n EPn EP13=-.∵二面角P AC B --的平面角为锐角, ∴二面角P AC B --的平面角的余弦值为13. …12分 18. (本小题满分14分)(本小题主要考查古典概型、二项分布等知识, 考查或然与必然的数学思想方法,以及数据处理能力、运算求解能力和应用意识) (1)解:依题意设(kp k s=为常数),由于()()15104s t t =+≤≤, ∴ ()()04151kp t t =≤≤+. …2分当0.5t =时, 145p =, 则()45150.51k =⨯+,解得18k =. ∴()()()1860415151p t t t ==≤≤++. …4分当1t =时, 263525p ==⨯. ∴该运动员第二次射击命中飞碟的概率为35. …6分 (2) 解:设“该运动员第一次射击命中飞碟”为事件A ,“该运动员第二次射击命中飞碟”为事 件B ,则“第一个飞碟被该运动员命中”为事件:A AB +. …7分 ∵()()43,55P A P B ==,∴()()()()P A AB P A P A P B +=+44323155525⎛⎫=+-⨯=⎪⎝⎭. ∴第一个飞碟被该运动员命中的概率为2325. …10分 (3) 解:设该运动员进行三个飞碟的射击训练时命中飞碟的个数为ξ, 则23325B ,ξ⎛⎫ ⎪⎝⎭.∴至少命中两个飞碟的概率为()()23P P P ξξ==+= …12分=C ()2231p p -+ C 333p23232233252525⎛⎫⎛⎫=⨯⨯+ ⎪⎪⎝⎭⎝⎭=1534115625. …14分19. (本小题满分14分)(本小题主要考查直线、圆、抛物线、曲线的切线等知识, 考查数形结合、化归与转化、函数与方程的数学思想方法,以及推理论证能力和运算求解能力) (1) 解:设点A 、B 的坐标分别为()11,x y 、()22,x y , ∵ 1l 、2l 分别是抛物线C 在点A 、B 处的切线, ∴直线1l 的斜率1'11x x x k y p ===,直线2l 的斜率2'22x x x k y p===. ∵ 12l l ⊥,∴ 121k k =-, 得212x x p =-. ① …2分 ∵A 、B 是抛物线C 上的点,∴ 221212,.22x x y y p p==∴ 直线1l 的方程为()21112x x y x x p p -=-,直线2l 的方程为()22222x xy x x p p-=-.由()()21112222,2,2x x y x x p p x x y x x p p ⎧-=-⎪⎪⎨⎪-=-⎪⎩解得12,2.2x x x p y +⎧=⎪⎪⎨⎪=-⎪⎩ ∴点D 的纵坐标为2p-. …4分 (2) 证法1:∵ F 为抛物线C 的焦点, ∴ 0,2p F ⎛⎫ ⎪⎝⎭. ∴ 直线AF 的斜率为21221111122202AFx p p y x p p k x x px ---===-, 直线BF 的斜率为22222222222202BFx p p y x p p k x x px ---===-. ∵ 2222121222AF BFx p x p k k px px ---=-…6分 ()()22222112122x x p x x p px x ---=()()2121212122x x x x p x x px x -+-=()()221212122p x x p x x px x --+-=0=. ∴AF BF k k =.∴A 、B 、F 三点共线. …8分 证法2:∵ F 为抛物线C 的焦点, ∴ 0,2p F ⎛⎫ ⎪⎝⎭. ∴2221111,,222x p x p AF x x p p ⎛⎫⎛⎫-=--=- ⎪ ⎪⎝⎭⎝⎭,2222222,,222x p x p BF x x p p ⎛⎫⎛⎫-=--=- ⎪ ⎪⎝⎭⎝⎭.∵ 22122211211222222212222p x p x x x x x pp x p x x x x p----===----, …6分 ∴ //AF BF .∴A 、B 、F 三点共线. 证法3:设线段AB 的中点为E , 则E 抛物线C 的准线为:2pl y =-. 作11,AA l BB l ⊥⊥, 垂足分别为11,A B . ∵ 由(1)知点D 的坐标为12,22x x p +⎛⎫- ⎪⎝⎭∴DE l ⊥.∴DE 是直角梯形11AA B B 的中位线. ∴()1112DE AA BB =+. …6分 根据抛物线的定义得:11,AA AF BB BF ==, ∴()()111122DE AA BB AF BF =+=+. ∵AD DB ⊥,E 为线段AB 的中点,∴12DE AB =. ∴()1122AB AF BF =+,即AB AF BF =+. ∴A 、B 、F 三点共线. …8分 (3)解: 不存在. 证明如下:假设存在符合题意的圆,设该圆的圆心为M , 依题意得,MA AD MB BD ⊥⊥,且MA MB =, 由12l l ⊥,得AD BD ⊥. ∴ 四边形MADB 是正方形.∴ AD BD =. …10分∵点D 的坐标为3,12⎛⎫- ⎪⎝⎭, ∴12-=-p,得2p =. 把点D 3,12⎛⎫- ⎪⎝⎭的坐标代入直线1l , 得211131422x x x ⎛⎫--=⨯- ⎪⎝⎭解得14x =或11x =-,∴点A 的坐标为()4,4或11,4⎛⎫- ⎪⎝⎭.同理可求得点B 的坐标为()4,4或11,4⎛⎫- ⎪⎝⎭.由于A 、B 是抛物线C 上的不同两点,不妨令11,4A ⎛⎫- ⎪⎝⎭,()4,4B .∴AD == BD ==. …13分∴AD BD ≠, 这与AD BD =矛盾.∴经过A 、B 两点且与1l 、2l 都相切的圆不存在. …14分 20. (本小题满分14分)(本小题主要考查函数和方程、函数导数、不等式等知识, 考查函数与方程、化归与转化的数学思想方法,以及抽象概括能力、推理论证能力和运算求解能力) (1) 解:∵()32f x x x ax b =-++,∴()'232fx x x a =-+.∵()32f x x x ax b =-++的一个极值点为1x =, ∴()'2131210f a =⨯-⨯+=.∴ 1a =-. …2分 ∴()()()'2321311fx x x x x =--=+-,当13x <-时, ()'0f x >;当113x -<<时, ()'0f x <;当1x >时, ()'0f x >; ∴函数()f x 在1,3⎛⎤-∞- ⎥⎝⎦上单调递增, 在1,13⎡⎤-⎢⎥⎣⎦上单调递减,在[)1,+∞上单调递增.∵方程20ax x b ++=的两个实根为,αβ, 即20x x b --=的两根为,αβ()αβ<,∴αβ==. ∴1,b αβαβ+==-,αβ-=…4分 ∵ 函数()f x 在区间[],αβ上是单调的,∴区间[],αβ只能是区间1,3⎛⎤-∞- ⎥⎝⎦,1,13⎡⎤-⎢⎥⎣⎦,[)1,+∞之一的子区间.由于1,αβ+=αβ<,故[]1,,13αβ⎡⎤⊆-⎢⎥⎣⎦. 若0α<,则1αβ+<,与1αβ+=矛盾. ∴[][],0,1αβ⊆.∴方程20x x b --=的两根,αβ都在区间[]0,1上. …6分令()2g x x x b =--, ()g x 的对称轴为[]10,12x =∈, 则()()00,10,140.g b g b b =-≥⎧⎪=-≥⎨⎪∆=+>⎩解得104b -<≤.∴实数b 的取值范围为1,04⎛⎤-⎥⎝⎦. …8分 说明:6分至8分的得分点也可以用下面的方法.∵1111,2222αβ+=≤=≥且函数()f x 在区间[],αβ上是单调的,∴[]1,,13αβ⎡⎤⊆-⎢⎥⎣⎦.由1,31,140.b αβ⎧≥-⎪⎪≤⎨⎪∆=+>⎪⎩即11,231,140.b ⎧-≥-⎪≤⎪+>⎪⎪⎪⎩…6分 解得104b -<≤. ∴实数b 的取值范围为1,04⎛⎤-⎥⎝⎦. …8分 (2)证明:由(1)可知函数()f x 在区间[],αβ上单调递减, ∴函数()f x 在区间[],αβ上的最大值为()f α, 最小值为()f β.∵[]12,,x x αβ∈,∴()()()()12f x f x f f αβ-≤-()()3232b b αααβββ=--+---+ ()()()3322αβαβαβ=-----()()()21αβαβαβαβ⎡⎤=-+--+-⎣⎦()1b =-()1b =-. …10分令t =则()2114b t =-()1b -()3154t t =-. 设()()3154h t t t =-, 则()()'21534h t t =-.∵104b -<≤,∴01t <≤.∴()()'21534h t t =-0>. ∴函数()()3154h t t t =-在(]0,1上单调递增. …12分∴()()11h t h ≤=.∴ ()()121f x f x -≤. …14分 21. (本小题满分14分)(本小题主要考查导数及其应用、数列、不等式等知识, 考查化归与转化、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和创新意识) (1)解:∵对任意n ∈N *都有1n n a b +=,121n n n na ba a +=-, ∴12211111n n n n n n na b a a a a a +-===--+. ∴1111n na a +=+,即1111n n a a +-=. …2分∴数列1n a ⎧⎫⎨⎬⎩⎭是首项为11a ,公差为1的等差数列. ∵11a b =, 且111a b +=, ∴11a b =12=. ∴()1211nn n a =+-=+. …4分 ∴ 11n a n =+, 11n n n b a n =-=+. …6分 (2)证明: ∵11n a n =+, 1n n b n =+, ∴1n n a b n=. ∴所证不等式()31324122341123ln 1n nn na a aa a a a a nb b b b b b b b ++++++<+<++++, 即()1111111ln 11234123n n n++++<+<+++++. ① 先证右边不等式: ()111ln 1123n n +<++++.令()()ln 1f x x x =+-, 则()'1111x f x x x=-=-++. 当0x >时, ()'0fx <,所以函数()f x 在[)0,+∞上单调递减.∴当0x >时,()()00f x f <=, 即()ln 1x x +<. …8分分别取1111,,,,23x n=. 得()111111ln 11ln 1ln 1ln 112323n n⎛⎫⎛⎫⎛⎫++++++++<++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 即()111111ln 1111112323n n⎡⎤⎛⎫⎛⎫⎛⎫++++<++++⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦. 也即341111ln 212323n n n+⎛⎫⨯⨯⨯⨯<++++ ⎪⎝⎭. 即()111ln 1123n n +<++++. …10分 ② 再证左边不等式: ()1111ln 12341n n ++++<++. 令()()ln 11x f x x x =+-+, 则()()()'2211111xf x x x x =-=+++. 当0x >时, ()'0fx >,所以函数()f x 在[)0,+∞上单调递增.∴当0x >时,()()00f x f >=, 即()ln 11xx x+>+. …12分 分别取1111,,,,23x n=. 得()111111ln 11ln 1ln 1ln 123231n n⎛⎫⎛⎫⎛⎫++++++++>+++⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭. 即()111ln 1111123n ⎡⎤⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦111231n>++++. 也即341111ln 223231n n n+⎛⎫⨯⨯⨯⨯>+++⎪+⎝⎭. 即()111ln 1231n n+>++++. ∴()31324122341123ln 1n nn na a aa a a a a nb b b b b b b b ++++++<+<++++. …14分。
2010年广州市高三二模数学试题及答案(文科word版)

2010年广州市普通高中毕业班综合测试一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 设全集{}1,2,3,4,5U =,集合{}2,3,4A =,{}2,5B =,则()U B A ð=A.{}5B. {}125,,C. {}12345,,,,D.∅2. 已知i 为虚数单位,若复数()()211a a -++i 为实数,则实数a A .1- B .0 C .13. 在长为3m 的线段AB 上任取一点P , 则点P 与线段两 端点A 、B 的距离都大于1m 的概率是A.14 B.13 C. 12 D.234. 如图1的算法流程图, 若()()32,xf xg x x ==,则()2h 的值为(注:框图中的赋值符号“=”也可以写成“←” 或“:=”)A. 9B. 8C. 6 5. 命题“若,x y 都是偶数,则x y +也是偶数”的逆否命题是A .若x y +是偶数,则x 与y 不都是偶数B .若x y +是偶数,则x 与y 都不是偶数C .若x y +不是偶数,则x 与y 不都是偶数D .若x y +不是偶数,则x 与y 都不是偶数6. 设变量,x y 满足约束条件2,, 2.x y x x y ≤⎧⎪≤⎨⎪+≥⎩则目标函数2z x y =+的最小值为A. 6B. 4C. 3D. 2 7. 若0x <且1xxa b >>, 则下列不等式成立的是A. 01b a <<<B. 01a b <<<C. 1b a <<D. 1a b << 8. 函数()cos sin 44f x x x ππ⎛⎫⎛⎫=+- ⎪ ⎪⎝⎭⎝⎭12-是 A. 最小正周期为2π的偶函数 B. 最小正周期为π的偶函数 C. 最小正周期为2π的奇函数 D. 最小正周期为π的奇函数图39. 高8m 和4m 的两根旗杆笔直地竖在水平地面上, 且相距10m , 则地面上观察两旗杆顶端仰角相等的点的轨迹为A. 圆B. 椭圆C. 双曲线D. 抛物线 10. 已知函数()sin f x x x =-,若12,,22x x ππ⎡⎤∈-⎢⎥⎣⎦且()()120f x f x +>,则下列不等式中 正确的是A. 12x x >B. 12x x <C. 120x x +>D. 120x x +< 二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分.(一)必做题(11~13题)11.已知向量a ,b 满足1=a ,b =2, a b 1=, 则a 与b 的夹角大小是 .12. 已知双曲线C :()2222100x y a ,b a b-=>>的离心率2e =, 且它的一个顶点到相应焦点的距离为1, 则双曲线C 的方程为 . 13.图2是一个有n 层()2n ≥的六边形点阵.它的中心是一个点,算作第一层, 第2层每边有2个点,第3层每边有3个点 ,…,第n 层每边有n 个点,则这个点阵的点数共有 个(二)选做题(14~ 15题,考生只能从中选做一题)14.(坐标系与参数方程选做题)已知直线l 的参数方程为1,42.x t y t =+⎧⎨=-⎩(参数t ∈R ),圆C 的参数方程为2cos 2,2sin .x y θθ=+⎧⎨=⎩(参数[]0,2θπ∈),则直线l 被圆C 所截得的弦长为 .15.(几何证明选讲选做题)如图3, 半径为5的圆O 的两条弦 AD 和BC 相交于点P , ,OD BC P ⊥为AD 的中点, 6BC =, 则弦AD 的长度为 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤, 16. (本小题满分12分)已知1sin 0,,tan 23⎛⎫=∈= ⎪⎝⎭πααβ.(1) 求tan α的值; (2) 求()tan 2+αβ的值. 17. (本小题满分12分)某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:若单科成绩85分以上(含85分),则该科成绩为优秀. (1)根据上表完成下面的2×2列联表(单位:人):关系?(3)若从这20个人中抽出1人来了解有关情况,求抽到的学生数学成绩与物理成绩至少有一门 不优秀的概率. 参考数据:① 假设有两个分类变量X 和Y ,它们的值域分别为{}12,x x 和{}12,y y ,其样本频数列联表(称 为22⨯列联表)为: 则随机变量()()()()()22n ad bc K a b c d a c b d -=++++,其中n a b c d =+++为样本容量;②独立检验随机变量2K 的临界值参考表:NMB 1C 1D 1A 1DCBA18. (本小题满分14分)在长方体1111ABCD A BC D -中, 11,2AB BC AA ===, 点M 是BC 的中点,点N 是1AA 的中点. (1) 求证: //MN 平面1ACD ; (2) 过,,N C D 三点的平面把长方体1111ABCD A BC D -截成 两部分几何体, 求所截成的两部分几何体的体积的比值.19. (本小题满分14分)我国是水资源比较贫乏的国家之一,各地采用价格调控等手段以达到节约用水的目的. 某市用水收费标准是:水费=基本费+超额费+定额损耗费,且有如下三条规定:① 若每月用水量不超过最低限量m 立方米时,只付基本费9元和每户每月定额损耗费a 元;② 若每月用水量超过m 立方米时,除了付基本费和定额损耗费外,超过部分每立方米付n 元的超额费; ③ 每户每月的定额损耗费a 不超过5元.(1) 求每户每月水费y (元)与月用水量x (立方米)的函数关系; (2) 该市一家庭今年第一季度每月的用水量和支付的费用如下表所示:试分析该家庭今年一、二、三各月份的用水量是否超过最低限量,并求m,n,a 的值. 20. (本小题满分14分)已知椭圆22122:1(0)x y C a b a b+=>>的右焦点2F 与抛物线22:4C y x =的焦点重合,椭圆1C 与抛物线2C 在第一象限的交点为P ,25||3PF =.圆3C 的圆心T 是抛物线2C 上的动点, 圆3C 与y 轴交于,M N 两点,且||4MN =.(1)求椭圆1C 的方程;(2)证明:无论点T 运动到何处,圆3C 恒经过椭圆1C 上一定点. 21. (本小题满分14分)已知数列{}n a 和{}n b 满足11a b =,且对任意n ∈N *都有1n n a b +=,121n n n na ba a +=-. (1) 判断数列1n a ⎧⎫⎨⎬⎩⎭是否为等差数列, 并说明理由; (2) 证明: ()111n nn n a b ++> .一选择题:2213y x -=11.3π12.13. 2331n n -+14.15.16.(本小题满分12分) (1) 解:∵sin 0,,2⎛⎫=∈ ⎪⎝⎭παα ∴cos ===α. …2分∴sin 1tan cos 25===ααα. …4分 (2)解法1:∵1tan 3=β, ∴22tan tan 21tan βββ=- …6分 2123113⨯=⎛⎫- ⎪⎝⎭34=. …8分 ∴()tan tan 2tan 21tan tan 2++=-αβαβαβ…10分132413124+=-⨯2=. …12分 解法2: ∵1tan 3=β, ∴()tan tan tan 1tan tan ++=-αβαβαβ…6分112311123+=-⨯1=. …8分∴()()()tan tan tan 21tan tan +++=-+αββαβαββ …10分1131113+=-⨯2=. …12分17.(本小题满分12分)(1)解:2×2列联表为(单位:人):…4分 (2)解:提出假设0H :学生数学成绩与物理成绩之间没有关系.根据列联表可以求得22121214720(5)8.8027.879136K ⨯-⨯⨯⨯⨯⨯=≈>. …6分 当0H 成立时,2(7.879)0.005P K >=.(数学驿站 )所以我们有99.5%的把握认为:学生的数学成绩与物理成绩之间有关系. …8分 (3)解:由(1)可知数学成绩与物理成绩都优秀的学生的人数为5人,则数学成绩与物理成绩至少有一门不优秀的学生人数为15人. …10分P NMB 1C 1D 1A 1DCBAPNMB 1C 1D 1A 1DCBAD 1A 1故从20名学生中抽出1名,抽到的学生数学成绩与物理成绩至少有一门不优秀的概率为153204=. …12分 18. (本小题满分14分)(本小题主要考查空间线面关系、几何体的体积等知识, 考查数形结合、化归与转化的数学思想方法, 以及空间想象能力、推理论证能力和运算求解能力) (1)证法1:设点P 为AD 的中点,连接,MP NP .∵ 点M 是BC 的中点,∴ //MP CD .(数学驿站 ) ∵ CD ⊂平面1ACD ,MP ⊄平面1ACD , ∴ //MP 平面1ACD . …2分 ∵ 点N 是1AA 的中点, ∴ 1//NP A D .∵ 1A D ⊂平面1ACD ,NP ⊄平面1ACD , ∴ //NP 平面1ACD . …4分 ∵ MP NP P = ,MP ⊂平面MNP ,NP ⊂平面MNP , ∴ 平面//MNP 平面1ACD . ∵ MN ⊂平面MNP ,∴//MN 平面1ACD . …6分 证法2: 连接AM 并延长AM 与DC 的延长线交于点P , 连接1A P , ∵ 点M 是BC 的中点, ∴ BM MC =.∵ BMA CMP ∠=∠, 90MBA MCP ︒∠=∠=, ∴ Rt MBA ≅Rt MCP . …2分∴ AM MP =.∵ 点N 是1AA 的中点,∴ 1MN //A P . …4分∵ 1A P ⊂平面1ACD ,MN ⊄平面1ACD , ∴ //MN 平面1ACD . …6分(2) 解: 取1BB 的中点Q , 连接NQ ,CQ , ∵ 点N 是1AA 的中点, ∴ //NQ AB . ∵ //AB CD , ∴ //NQ CD .∴ 过,,N C D 三点的平面NQCD 把长方体1111ABCD A BC D -截成两部分几何体,其中一部分几何体为直三棱柱QBC -NAD , 另一部分几何体为直四棱柱1111B QCC A NDD -. …8分 ∴ 11111222QBC S QB BC ∆==⨯⨯= , ∴ 直三棱柱QBC -NAD 的体积112QBC V S AB ∆==, …10分 ∵ 长方体1111ABCD A BC D -的体积112V =⨯⨯2=, ∴直四棱柱1111B QCC A NDD -体积2132V V V =-=. …12分 ∴ 12V V =1232=13.∴ 所截成的两部分几何体的体积的比值为13. …14分(说明:213V V =也给分) 19.(本小题满分14分)(本小题主要考查函数和方程、分段函数等知识, 考查函数与方程、分类与整合的数学思想方法,以及抽象 概括能力、推理论证能力、运算求解能力和应用意识) (1)解:依题意,得()()()909a,x m,y n x m a,x m.+<≤*⎧⎪=⎨+-+>**⎪⎩ 其中05a <≤. …2分 (2)解:∵05a <≤,∴9914a <+≤.由于该家庭今年一、二月份的水费均大于14元,故用水量4立方米,5立方米都大于最低限量m 立方米. …4分将417x ,y =⎧⎨=⎩和523x ,y =⎧⎨=⎩分别代入()**,得()()1794,2395.n m a n m a =+-+⎧⎪⎨=+-+⎪⎩…6分两式相减, 得6n =.代入()1794n m a,=+-+得616a m =-. …8分 又三月份用水量为2.5立方米, 若25m .<,将2511x .,y =⎧⎨=⎩代入()**,得613a m =-,这与616a m =-矛盾. …10分 ∴25m .≥,即该家庭三月份用水量2.5立方米没有超最低限量. 将 2.5,11x y =⎧⎨=⎩代入()*,得119a =+,由616119a m ,a.=-⎧⎨=+⎩ 解得23a ,m .=⎧⎨=⎩ …13分答:该家庭今年一、二月份用水超过最低限量,三月份用水没有超过最低限量,且362m ,n ,a ===. …14分 20.(本小题满分14分)(本小题主要考查直线、圆、抛物线、椭圆等知识, 考查数形结合、化归与转化、特殊与一般、函数与方程的数学思想方法,以及推理论证能力、运算求解能力和创新意识)(1)解法1:∵抛物线22:4C y x =的焦点坐标为(1,0), …1分∴点2F 的坐标为(1,0).∴椭圆1C 的左焦点1F 的坐标为1(1,0)F -,抛物线2C 的准线方程为1x =-. 设点P 的坐标为11(,)x y ,由抛物线的定义可知211PF x =+,∵253PF =,(数学驿站 ) ∴1513x +=,解得123x =.由211843y x ==,且10y >,得1y =∴点P的坐标为23,⎛⎝. …3分 在椭圆1C :22221(0)x y a b a b+=>>中,1c =.122||||4a PF PF =+=+=.∴2,a b === ∴椭圆1C 的方程为22143x y +=. …6分 解法2:∵抛物线22:4C y x =的焦点坐标为(1,0), …1分 ∴点2F 的坐标为(1,0).∴ 抛物线2C 的准线方程为1x =-.设点P 的坐标为11(,)x y ,由抛物线的定义可知211PF x =+,∵253PF =, ∴1513x +=,解得123x =.由211843y x ==,且10y >得1y =∴点P的坐标为2(3. …3分 在椭圆1C :22221(0)x y a b a b+=>>中,1c =.由222221424199c ,a b c ,.ab ⎧⎪=⎪=+⎨⎪⎪+=⎩解得2,a b == ∴椭圆1C 的方程为22143x y +=. …6分 (2)证法1: 设点T 的坐标为00(,)x y ,圆3C 的半径为r ,∵ 圆3C 与y 轴交于,M N 两点,且||4MN =, ∴||4MN ==.∴r =∴圆3C 的方程为222000()()4x x y y x -+-=+.()* …8分∵ 点T 是抛物线22:4C y x =上的动点,∴ 2004y x =(00x ≥).∴20014x y =. 把20014x y =代入()* 消去0x 整理得:22200(1)2()024x y yy x y +---+=.()** …10分方程()**对任意实数0y 恒成立,∴2210,220,40.xy x y ⎧-=⎪⎪-=⎨⎪+-=⎪⎩解得2,0.x y =⎧⎨=⎩…12分 ∵点(2,0)在椭圆1C :22143x y +=上, ∴无论点T 运动到何处,圆3C 恒经过椭圆1C 上一定点()2,0. …14分 证法2: 设点T 的坐标为00(,)x y ,圆3C 的半径为r , ∵ 点T 是抛物线22:4C y x =上的动点,∴ 2004y x =(00x ≥). …7分∵ 圆3C 与y 轴交于,M N 两点,且||4MN =, ∴||4MN ==. ∴r =∴ 圆3C 的方程为222000()()4x x y y x -+-=+.()*** …9分令00x =,则2004y x =0=,得00y =.此时圆3C 的方程为224x y +=. …10分由22224,1,43x y x y⎧+=⎪⎨+=⎪⎩解得2,0.x y =±⎧⎨=⎩ ∴圆3C :224x y +=与椭圆1C 的两个交点为()2,0、()2,0-. …12分 分别把点()2,0、()2,0-代入方程()***进行检验,可知点()2,0恒符合方程()***,点()2,0-不恒符合方程()***.∴无论点T 运动到何处,圆3C 恒经过椭圆1C 上一定点()2,0. …14分 21.(本小题满分14分) (1) 解: 数列1n a ⎧⎫⎨⎬⎩⎭为等差数列. …1分 理由如下:∵对任意n ∈N *都有1n n a b +=,121n n n na ba a +=-, ∴12211111n n n n n n na b a a a a a +-===--+. ∴1111n na a +=+,即1111n n a a +-=. …3分∴数列1n a ⎧⎫⎨⎬⎩⎭是首项为11a ,公差为1的等差数列. …4分(2) 证明: ∵11a b =, 且111a b +=, ∴11a b =12=. 由(1)知()1211nn n a =+-=+.∴ 11n a n =+, 11n n n b a n =-=+. …6分 所证不等式()111n nn n a b ++> ,即111111n nn n n +⎛⎫⎛⎫+> ⎪ ⎪++⎝⎭⎝⎭ ,也即证明111111n nn n +⎛⎫⎛⎫+>+ ⎪⎪+⎝⎭⎝⎭. 令()()ln 11xf x x x =>-, 则()'21ln (1)x xx f x x --=-. 再令()1ln x g x x x-=-, 则()'211g x x x =-21x x-=. …8分当1x >时, ()'0g x <,∴函数()g x 在[)1,+∞上单调递减. ∴当1x >时,()()10g x g <=,即1ln 0x x x--<. ∴当1x >时, ()'21ln (1)x xx f x x --=-0<. ∴函数()ln 1xf x x =-在()1,+∞上单调递减. …10分 ∵111111n n<+<++, ∴11111f f n n ⎛⎫⎛⎫+>+ ⎪ ⎪+⎝⎭⎝⎭. ∴11ln 1ln 111111111n n n n⎛⎫⎛⎫++ ⎪ ⎪+⎝⎭⎝⎭>+-+-+. …12分∴111ln 1ln 11n n n n +⎛⎫⎛⎫+>+ ⎪⎪+⎝⎭⎝⎭.∴111111n nn n +⎛⎫⎛⎫+>+ ⎪⎪+⎝⎭⎝⎭. ∴()111n n n n a b ++> 成立. …14分。
增城中学学年度第一学期高三年级综合测试(二).docx

高中数学学习材料鼎尚图文*整理制作增城中学2015--2016学年度第一学期高三年级综合测试(二)数学(理科)命题人:钟康生 审题人:李勋说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟。
第Ⅰ卷一、选择题:共12小题,每小题5分,共60分.1. 已知b 是实数,若12bii+-是纯虚数,则b =( )A .2B .2-C .21D .21-2. 设cos(α+ππ<α<23π),那么sin(2)πα-的值为( )A .12-B. 12C .2-D .23. 由直线6x π=-,曲线cos y x =,x 轴和y 轴所围成的封闭图形的面积是( )A.2πC. 2D. 124. 已知两向量a 、b 满足1a =,2b =,3a b +=,则a 与b 的夹角为( )A. 45oB. 60oC. 120oD. 90o5. 执行右边的程序框图,若p =0.8,则输出的n =( )A .4B .5C .6D .36. “lg ,lg ,lg x y z 成等差数列”是“2y xz =”成立的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件7. 设已知数列{}n a 对任意的N n m ∈,,满足n m n m a a a +=+,且12=a ,那么10a 等于( )A.3B.5C.7D.98. 设变量x ,y 满足约束条件:4,,20,x y x x ⎧⎪⎨⎪+≥⎩+y ≤≥则21z x y =-+的最大值为( )A .2B .1-C .4D .39.某几何体的三视图如下图所示,图中的四边形都是边长为4的正方形,其中正视图、侧视图中的两条虚线互相垂直,则该几何体的表面积是( )A .96B .80 C.80 D.9210.函数2()sin ln(1)f x x x =⋅+的大致图象是( )Ox O yx O yx.Ox .C D11.球O 的球面上有四点S 、A 、B 、C ,其中O 、A 、B 、C 四点共面,O 为球心,ABC ∆是边长为2的正三角形,S 不在ABC ∆所在的平面上,则棱锥S ABC -的体积的最大值为( )A .23B .43CD . 12.若a 满足4lg =+x x ,b 满足410=+xx ,函数⎩⎨⎧>≤+++=0202)()(2x x x b a x x f ,,,则关于x 的方程x x f =)(解的个数是( )A .1B .2C .3D .4第Ⅱ卷本卷包括必考题和选考题两部分。
广东省增城中学高三数学第三次综合测试(文) 全国通用
增城中学2010届普通高中毕业班综合测试(三)数学(文科)2009.11.本试卷共4页.共21小题,满分150分.考试用时120分钟.一、选择题:本大题共10 小题,每小题5分,满分50分.每小题给出的四个选项中,只有一项是符合题目要求. 1.复数2ii+-等于( ). A .12i -+ B.12i - C. i 21+ D. 12i --2.集合{}20,2,A a =,{}1,B a =,若{}1AB =,则a 的值为( )A. 0B. 1C.-1D. 1±3.已知0AB AC ⋅=uu u r uu u r , ||3,||2AB AC ==u u u r u u u r ,则||BC uu u r=( )A 5B.C. 13D.4.设a b <,函数2()()y a x x b =--的图象可能是( )5.曲线1xy x =+在2x =-处的切线方程为( ) A .40x y ++= B.40x y -+= C. 0x y -= D. 40x y --=6. 圆222440x y x y +-+-=与直线220()tx y t t R ---=∈的位置关系( )A .相离B .相切C .相交D .以上都有可能7.已知等比数列}{n a 中1n n a a +>,且37283,2a a a a +=⋅=,则117a a =( ) A. 21B. 23C. 32D. 28.将函数sin y x =的图象向左..平移(02)ϕϕπ≤<个单位后,得到函数sin()6y x π=-的图象,则ϕ等于( )ADA .6π B .116π C. 76π D. 56π9.椭圆22:12x C y +=的右焦点为F,右准线l ,点A l ∈,线段AF 交C 于点B .若3FA FB =,则AF =( ) A .B . 2C .D .310.已知函数2log (1),0,()(1)1,0.x x f x f x x -≤⎧=⎨-+>⎩则(2010)f =( )A .2008B .2009C .2010D .2011二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分. (一)必做题(11-13题)11.已知某商场新进3000袋奶粉,为检查其三聚氰胺是否超标,现采用系统抽样的方法从中抽取150袋检查,若第一组抽出的号码是11,则第六十一组抽出的号码为 . 12.已知抛物线C 的顶点坐标为原点,焦点在x 轴上,直线y=x 与抛物线C 交于A ,B 两点,若()2,2P 为AB 的中点,则抛物线C 的方程为 .13.一个算法的程序框图如右图所示,若该程序输出的结果为45,则判断框中应填入的条件是 .(二)选做题(14、15题,考生只能从中选做一题,两题全答的,只以第一小题计分)14.(坐标系与参数方程选做题)若直线sin()42πρθ+=,与直线31x ky +=垂直,则常数k = .15.(几何证明选讲选做题)如图,过点D 做圆的切线切于B 点,作割线交圆于,A C 两点,其中3,4,BD AD == 2AB =,则BC = .(第13题图)三、解答题,本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分13分) 设函数2()2sin cos cos sin sin (0)2f x x x x ϕϕφπ=+-<<在π=x 处取最小值.(Ⅰ)求ϕ的值;(Ⅱ)在∆ABC 中,c b a ,,分别是角A,B,C 的对边,已知,2,1==b a 23)(=A f ,求角C . 17.(本小题满分12分)某公司在过去几年内使用某种型号的灯管1000支,该公司对这些灯管的使用寿命(单位:小(II )根据上述统计结果,计算灯管使用寿命不足1500小时的频率;(III )该公司某办公室新安装了这种型号的灯管2支,若将上述频率作为概率,试求恰有1支灯管的使用寿命不足1500小时的概率.18.(本小题满分13分)如图,在四棱锥S ABCD -中,2SA AB ==,SB SD ==ABCD 是菱形,且60ABC ∠=︒,E 为CD 的中点. (Ⅰ)证明:CD ⊥平面SAE ;(Ⅱ)侧棱SB 上是否存在点F ,使得//CF 平面SAE ?并证明你的结论.19.(本小题满分14分) 如图,椭圆2222:1x y C a b+=(a >b >0)的一个焦点为F (1,0),且过点(2,0).(Ⅰ)求椭圆C 的方程;(Ⅱ)若AB 为垂直于x 轴的动弦,直线:4l x =与x 轴交于点N ,直线AF 与BN 交于 点M .求证:点M 恒在椭圆C 上.20.(本小题满分14分)已知{}n a 是一个公差大于0的等差数列,且满足3655a a ⋅=, 2716a a +=. (Ⅰ)求数列{}n a 的通项公式:(Ⅱ)若数列{}n a 和数列{}n b 满足等式:31223(*)2222nn nb b b b a n N =++++∈, 求数列{}n b 的前n 项和n S . 21.(本小题满分14分)已知函数3()3.f x x x =-(Ⅰ)求曲线()y f x =在点2x =处的切线方程;(Ⅱ)若过点(1,)(2)A m m ≠-可作曲线()y f x =的三条切线,求实数m 的取值范围.增城中学2010届高中毕业班综合测试(三)数学试题(文科)答案一、选择题:本大题共10 小题,每小题5分,满分50分.每小题给出的四个选项中,只有一项符合题目要求.1.解析:2(2)2112()1i i i i i i i i ++-===-+--,故选A. 2.解析:∵{}20,2,A a =,{}1,B a =,{}1A B =∴211a a ⎧=⎨≠⎩∴1a =-,故选C. 3.解析: 0AB AC ⋅=uu u r uu u r ,∴AB AC ⊥uu u r uu u r。
广东省增城中学2010届高中毕业班第二次综合测试(英语)

广东省增城中学2010届高中毕业班第二次综合测试(英语)2009.9 试卷共12面,4大题,满分150分。
考试用时120分钟。
I 听力(共两节,满分35分)第一节听力理解(5段共15小题;每小题2分,满分30分)每段播放两遍。
各段后有几个小题,各段播放前每小题有5秒钟的阅题时间。
请根据各段播放内容及其相关小题,在5秒钟内从题中所给的A、B、C三个选项中,选出最佳选项,并在答题卡上将该项涂黑。
听第一段对话,回答第1-3题1. What are they mainly talking about?A. Going out for food.B. Going shopping.C. Going for a picnic.2. When will they go?A. This Sunday.B. Next Saturday.C. Next Sunday.3. What will the man most probably do the day before they go?A. Prepare the car.B. Buy some food.C. Write the report.听第二段对话,回答第4-6题4. Why is Simon at home?A. He has a serious cold.B. He hurt his leg.C. He doesn’t want to climb the mountain.5. Where does Janet most probably speak to Simon?A. At Simon’s home.B. At Simon’s school.C. In the hospital.6. What will Simon do next?A. Go to see the doctor.B. Call his teacher.C. Take his medicine.听第三段对话,回答第7-9题7. What language may not be learned by the man?A. ChineseB. SpanishC. Japanese8. What language is the man learning?A. ChineseB. EnglishC. French9. What does the woman think of language learning?A. In language learning only a few languages are difficult to learn.B. The language similar to one’s native language is easier to learn.C. The sound system is the hardest part of a language.听第四段对话,回答第10-12题10. What is the possible relationship between the two speakers?A. Colleagues.B. Schoolmates.C. Landlady and tenant(佃户).11. How much does the man need to pay for one month?A. 1,200 dollars.B. 700 dollars.C. 500 dollars.12. What does the man think of his room in the apartment?A. It’s very bright.B. It’s quite big.C. It’s comfortable.听第五段独白,回答第13-15题13. What does the speaker most probably do?A. A book seller.B. A camera seller.C. A photography teacher.14. How can people take a great picture according to the speaker?A. They must obey some rules of photography.B. They must try new ways of photography.C. They must use the digital cameras to take pictures.15. Which of the following is mainly talked about in the book?A. All good pictures come from digital cameras.B. There are some best ways to make a wonderful picture.C. How to improve the photography skill.第二节:听取信息:(共5小题;每小题1分,满分5分)听下面一段独白。
2010年广州市增城中学普通高中毕业班综合测试

2010年广州市增城中学普通高中毕业班综合测试(四)文科综合试题2009.12校对:柳文本试卷共10页,41小题,满分300分。
考试用时150分钟。
第Ⅰ卷(选择题共140分)本卷共35小题,每小题4分,共140分。
在每小题给出的四个选项中,只有一项符合题目要求。
1.读某山区公路规划设计图,图中公路沿线甲、乙、丙、丁四地中,海拔最高的是A.甲B.乙C.丙D.丁某城市一中学地理兴趣小组研究出该市的“热岛效应”现象如下图所示。
据图回答2~3题。
2.若甲图的纵坐标代表城区与郊区温度差,则横坐标不可能代表A.建筑物面积 B.C02排放量C.工业化程度 D.街道数量3.同学们在研究中发现:不同季节、时段城区与郊区的温差有所不同(如乙图所示)。
从图中可看出城区与郊区A.夏季温差总体小于冬季温差B.午后温差大于夜晚温差C.冬、夏季的差异在午夜最大 D.温差变化冬、夏季同步近日我们又迎来了西方国家的除夕—圣诞节,世界各地开展了一系列活动庆祝圣诞节,图中横坐标表示地球自转的线速度,纵坐标表示年降水量,数码表示广州、乌鲁木齐、圣地亚哥(南美洲智利的首都,纬度约33°S)、吉隆坡(马来西亚的首都,纬度3°N)四个城市。
依据下图完成4~5小题。
4.四个城市中,7月气温低于1月气温的是A.① B.②C.③ D.④5.四个城市中在圣诞节这天的天气描述正确是A.①处夜降暴雪,过了个白色的圣诞节B.②城市举行大型花卉展,过了个五彩缤纷的圣诞节C.③地阴雨连绵,过了个灰色的圣诞节D.④城市炎热干燥,冰激凌制成的圣诞老人十分畅销下图为“我国东部春、夏季节降水量占全年降水量的百分比示意图”。
读图回答6~7题。
6.图中甲地夏季降水占全年的比例小于乙地的原因是A.甲地位于山地背风坡,乙地位于山地迎风坡B.甲地夏季受副热带高气压带控制,乙地夏季受锋面雨带影响C.甲地距海远,乙地距海近 D.甲地台风雨少,乙地台风雨多7.以下有关图中乙地的错误说法是A.冬季降水比例偏少B.夏季低洼地区易形成内涝C.春季降水比例偏少D.夏季易受风沙影响8.分析下面海洋表面等温线和洋流分布示意图(左下图),表示北半球副热带大陆东岸的是图为陆地环境主要构成要素的相互关联图(右上图),读图完成第9题。
《精编》广东省增城中学高三数学上学期第二次月考 理 新人教A版.doc

广东省增城中学届高三上学期第二次月考数学〔理〕试卷第I 卷〔选择题,共40分〕试题分第I 卷〔选择题〕和第II 卷〔非选择题〕两局部.共150分,考试时间120分钟.本卷须知:1.第I 卷〔选择题〕每题选出答案后,用铅笔把答题卷上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案. 2.第II 卷〔非选择题〕答案写在答题卷上.第I 卷〔选择题,共40分〕一、选择题〔本大题共有8小题,每题5分,共40分.在每题给出的四个选项中,只有一项为哪一项符合题目要求的.〕1. 16sin 3π⎛⎫-= ⎪⎝⎭〔 〕.A. 2B. 2- C. 12 D. 12-2.以下函数中()f x 与()g x 相等的是〔 〕.A. ()1f x x =-,()21x g x x=- B. ()2f x x =,()g x = C. ()2f x x = ,()4g x =D. ()f x =()g x =()2sin()26x f x π=-的最小正周期是〔 〕.A. πB. 2πC. 4πD. 2π()f x =的定义域是〔 〕. A. 3{|}4x x > B. {|01}x x <≤ C. {|1}x x ≥ D. 3{|1}4x x <≤ 5.如图,在平行四边形ABCD 中,假设,OA a =,OB b =那么以下各表述是正确的为〔 〕.A .OA OB AB += B .OC OD AB += C .CD a b =-+ D .()BC a b =-+ 6. 函数2sin 2xy x =-xA. 12-B. 122-C.14-428. 如以以下图,()(1,2,3,4)i f x i =是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的1x 和2x ,任意1212[0,1],[(1)]()(1)()f x x f x f x λλλλλ∈+-≤+-恒成立〞的只有〔 〕A .1()f x 和3()f xB .2()f xC .2()f x 和3()f xD .4()f x第II 卷〔非选择题,共110分〕二、填空题〔本大题共7小题,考生作答6题,每题5分,共30分.〕 〔一〕必做题〔9~13题〕()|sin |f x x =的最小正周期为 .10.化简()()()()()11sin 2cos cos cos 229cos sin 3sin sin 2πππαπαααππαπαπαα⎛⎫⎛⎫-++- ⎪ ⎪⎝⎭⎝⎭⎛⎫----+ ⎪⎝⎭= .11. 函数()248f x x kx =--在[5,20]上具有单调性,那么实数k 的取值范围为_________ .12.函数()2tan f x x x =的导函数()'f x =____________. 13.如下几个式子: 〔1〕1sin 2cos 2tan 1sin 2cos 2θθθθθ++=+-; 〔2〕tan()tan 2tan 2424x x x ππ⎛⎫++-= ⎪⎝⎭;〔3〕134sin10︒=; 〔4〕在△ABC 中,()22cos cos c a B b A a b -=-. 上述式子成立的是_________________.〔请填写序号〕〔二〕选做题〔14~15题,只能做一题.....,两题全答的,只计算前一题得分〕. 14. 〔几何证明选讲选做题〕如图,点P 在圆O 直 径AB 的延长线上,且2PB OB ==,PC 切圆O 于C 点,CD AB ⊥于D 点,那么PC = ,CD = .ABCD O P()1f x ()2f x ()3f x ()4f x15. 〔坐标系与参数方程选做题〕参数方程224sin =⎪⎭⎫⎝⎛+πθρ表示的曲线的普通方程是 .三、解答题〔本大题共6小题,共80分.解容许写出文字说明、证明过程或演算步骤.〕16.〔此题总分值12分〕函数()sin sin cos 66f x x x x a ππ⎛⎫⎛⎫=++-++ ⎪ ⎪⎝⎭⎝⎭的最大值为1.〔1〕求常数a 的值; 〔2〕求()f x 的单调增区间.17.〔此题总分值12分〕抛物线C :214y x =的焦点为F . 〔1〕抛物线C 上点A 的横坐标为1,求在点A 处抛物线C 的切线方程;〔2〕斜率为1的直线l 过点F ,与抛物线C 相交于M 、N 两点,求线段MN 的长.18.〔此题总分值14分〕如图,平面PAD ⊥平面ABCD ,四边形ABCD 为正方形, △PAD 是直角三角形,且2PA AD ==,E 、F 、G 分别是线段PA 、PD 、CD 的中点. 〔1〕求证:EF ⊥平面PAB ;〔2〕求异面直线EG 与BD 所成的角的余弦值.19.〔此题总分值14分〕如图,OPQ 是半径为为1,圆心角为3π的扇形,C 是扇形弧上的动点,ABCD 是扇形的内接矩形.记COP α∠=,矩形ABCD 的面积为S . 〔1〕请找出S 与α之间的函数关系〔以α为自变量〕;〔2〕求当α为何值时,矩形ABCD 的面积最大?并求出这个最大面积.G AB C DE FP ABCDPQO20.〔此题总分值14分〕函数x x x f sin )(-=. 〔1〕假设[0,]x π∈,试求()f x 的值域;〔2〕假设()[0,],0,x πθπ∈∈,求证:2()()2()33f f x xf θθ++≥;〔3〕假设[,(1)],(,(1)),x k k k k k Z ππθππ∈+∈+∈,猜测2()()2()33f f x xf θθ++与的大小关系〔不必写出比拟过程〕.21.〔此题总分值14分〕函数211()ln()22f x ax x ax =++-.〔a 为常数,0a >〕 〔1〕假设12x =是函数()f x 的一个极值点,求a 的值; 〔2〕求证:当02a <≤时,()f x 在1[, )2+∞上是增函数;〔3〕假设对任意..的(1, 2)a ∈,总存在..01[, 1]2x ∈,使不等式20()(1)f x m a >-成立,求实数m 的取值范围.增城中学届高三综合测试〔二〕二.填空题(本大题共6小题,每题5分,共30分.)〔一〕必做题〔9~13题〕 9 10 11 12 13 〔二〕选做题〔14~15题〕 14 15 三.解答题(本大题共6 小题,共80分.解容许写出文字说明,证明过程或演算步骤.) 16.〔本小题总分值12分〕17.〔本小题总分值12分〕班级 姓名 学号AE FP18.〔本小题总分值14分〕19.〔本小题总分值14分〕ABCDPQO20.〔本小题总分值14分〕2.必修一P24 T2与P18 例2改编3.必修四P35例2〔3〕4. 必修一P74 T7(2)5. 必修四P86 例4 改编6. 年山东高考理科数学T97.选修2-2 P60 B 组T2(2)8.必修一P45 T5改编9. 必修四P60例211.必修一P44 T912.选修2-2 P65 T2〔1〕 13.〔1〕必修四P143 T1(8);〔2〕必修四P143 T1(3); 〔3〕必修四P146 T5(1);〔4〕必修五P20 T14; 二.填空题:本大题共6小题,每题5分,共30分.9.π 10.tan α- 11.{|40,160}k k k ≤≥或 12.()22sin 2cos x x x+13.〔2〕〔3〕〔4〕 14. 15.1=+y x 三.解答题: 16.〔本小题总分值12分〕必修四P147例12改编 解:〔1〕()(sin coscos sin )(sin cos cos sin )cos 6666f x x x x x x a ππππ=++-++…………4分cos x x a =++2sin()6x a π=++…………………………………6分∴max ()21f x a =+=,∴1a =-.………………………………………8分 〔2〕由22,262k x k k Z πππππ-<+<+∈……………………………………10分得222,33k x k k Z ππππ-<<+∈ 所以()f x 的单调增区间为2[2,2],33k k k Z ππππ-+∈. …………………12分 17.〔本小题总分值12分〕选修2-1 P69例4与选修2-2 P18T6改编解:〔1〕当1x =时,211144y =⨯=,即11,4A ⎛⎫⎪⎝⎭.………………………1分 1'2y x =,………………3分 所求切线的斜率1'|x k y ===11122⨯=.………5分所求切线方程为()11142y x -=⨯-,即2410x y --=.…………………………6分〔2〕抛物线C :24x y =,焦点()0,1F ……………………………………………7分∴直线l 的方程为1y x =+. ………………………………………………………8分联立241x y y x ⎧=⎨=+⎩,解得222322x y ⎧=+⎪⎨=+⎪⎩,或222322x y ⎧=-⎪⎨=-⎪⎩.…………………………10分∴()()()()22||[222222][322322]MN =+--++--=8.所以,线段MN 的长为8. ………………………………………………………12分 18.〔本小题总分值14分〕解法一:〔1〕证明:∵ABCD 为正方形,△PAD 是直角三角形,且PA=AD=2,∴AD ⊥AB ,AD ⊥PA 又AB ∩PA=A ,………………………………………2分 ∴AD ⊥面PAB.∵E 、F 分别是线段PA 、PD 的中点,∴EF ∥AD ,∴EF ⊥面PAB.………6分〔2〕解:取BC 的中点M ,连结GM 、AM 、EM ,那么GM//BD ,…………………8分 ∴∠EGM 〔或其补角〕就是异面直线EG 与BD 所成的角. ……………10分 在Rt △MAE 中, 622=+=AM EA EM ,同理6=EG ,又221==BD GM , ∴在△MGE 中,632626262cos 222=⋅-+=⋅-+=∠GM EG ME GM EG EGM ………… 故异面直线EG 与BD 所成的角的余弦值为63. ……14分 解法二:建立如以以下图的空间直角坐标系A -xyz ,那么A 〔0,0,0〕,B 〔2,0,0〕,C 〔2,2,0〕,D 〔0,2,0〕, P 〔0,0,2〕,E 〔0,0,1〕,F 〔0,1,1〕,G 〔1,2,0〕. (1) 证明:∵EF =〔0,1,0〕,AP =〔0,0,2〕, AB =〔2,0,0〕,∴EF ·AP =0×0+1×0+0×2=0, EF ·AB =0×2+1×0+0×0=0,∴EF ⊥AP ,EF ⊥AB.又∵AP 、AB ⊂面PAB ,且PA ∩AB=A ,∴EF ⊥平面PAB. 又EF ⊂面EFG ,∴平面EFG ⊥平面PAB.〔2〕解:∵)0,2,2(),1,2,1(-=-=BD EG ,6322642||||,cos =⋅+-=⋅>=<∴BD EG BDEG BD EG , 故异面直线EG 与BD 所成的角的余弦值为63. 19.〔本小题总分值14分〕必修四例4解:在RT OBC 中,cos cos OB OC αα=⋅=,sin sin BC OC αα=⋅=在RT OAD 中,tan 60DA OA︒==2分∴333OA DA BC α===,∴cos 3AB OB OA αα=-=-,……4分矩形ABCD 的面积2cos sin sin sin cos 33S AB BC αααααα⎛⎫=⋅=-=- ⎪ ⎪⎝⎭)11sin 21cos 2sin 2222αααα=--=12cos 2226πααα⎫⎛⎫=+-=+⎪ ⎪⎪⎝⎭⎭………………………8分 〔2〕由03πα<<,得52666πππα<+<,………………………………………10分 所以当262ππα+=,即6πα=时, ……………………………………………12分=66S -最大所以,当6πα=时,矩形ABCD .………………14分 20.〔本小题总分值14分〕选修2-2 P32 T1〔1〕改编解:〔1〕当(0,)x π∈时,()1cos 0f x x '=->,∴()f x 在()0,π单调递增∵()()00,sin f f ππππ==-= ∴()0f x π≤≤所以()f x 的值域为[0,]π.……………………………4分〔2〕设2()()2()()33f f x x g x f θθ++=-,2sin sin 2()sin 33x x g x θ++=--即 )32cos cos (31)(x x x g ++-='θ……6分2[0,],(0,)(0,)3x x θπθππ+∈∈∴∈ 由()0g x '=,得x θ=,∴当(0,)x θ∈时,()0g x '>,∴()g x 在()0,π上单调递增……………………………………8分∴对[0,]x π∈,有()()0g x g θ≥=, 因而2()()2()33f f x x f θθ++≥.…10分 〔3〕在题设条件下,当k 为偶数时)32(3)()(2x f x f f +≥+θθ 当k 为奇数时)32(3)()(2x f x f f +≤+θθ.……14分 21.解:2212()22()211122a ax x a a f x x a ax ax --'=+-=++. 〔1〕由,得 1()02f '=且2202a a-≠,∴220a a --=,解得2a =或1a =- 0a >,∴2a =.………………………………………………………………4分 〔2〕当02a <≤时,22212(2)(1)02222a a a a a a a a ----+-==≤,∴21222a a-≥, ∴当12x ≥时,2202a x a--≥.又201ax ax >+,∴()0f x '≥, 故()f x 在1[, )2+∞上是增函数. ………………………………………………9分 〔3〕(1, 2)a ∈时,由〔2〕知,()f x 在1[,1]2上的最大值()111ln 122f a a ⎛⎫=++-⎪⎝⎭ 于是问题等价于:对任意的(1, 2)a ∈,不等式()211ln 11022a a m a ⎛⎫++-+-> ⎪⎝⎭()()211ln 1122g a a a m a ⎛⎫=++-+- ⎪⎝⎭,()12a << 那么()()1'12[212]11a g a ma ma m a a =-+=--++,当0m =时,()'01a g a a -=<+ ∴()g a 在区间()1,2上递减,此时,()()10g a g <=由于210a ->,∴0m ≤时不可能使()0g a >恒成立,故必有0m >∴()21'[1]12ma g a a a m ⎛⎫=-- ⎪+⎝⎭假设1112m ->,可知()g a 在区间1(1, min{2, 1})2m-上递减, 在此区间上,有()(1)0g a g <=,与()0g a >恒成立矛盾, 故1112m-≤,这时,()0g a '>,()g a 在(1, 2)上递增,恒有()(1)0g a g >=, 满足题设要求,∴01112m m>⎧⎪⎨-≤⎪⎩,即14m ≥, 所以,实数m 的取值范围为1[, )4+∞.……14分。
广州市增城市2010届高中毕业班调研测试(文科综合)试卷 精品

广东省增城市2011届高中毕业班调研测试文科综合能力测试本试卷共41小题,满分300分,考试用时150分钟注意事项:1.答卷前,考生务必用2B铅笔在“考生号”外填涂考生号,用黑色字迹的钢笔或签字笔填写学校、姓名、试室号和座位号。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑。
修改时须用橡皮擦干净。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目规定的区域。
一、选择题:本题共35小题,每小题4分,共140分。
每小题给出的四个选取项中,只有一个选项符合题目要求。
1.读下面的“经纬网和中国省级行政中心叠加图”,下列叙述正确的是()纬度①②③④⑤经度A.①地比④地的日出时间早B.④地的自转线速度比③地小C.夏至日②地昼长比⑤地昼长要长D.任何时候⑤地的正午太阳高度角都比②地小2.下图为某内陆国家等高线地形图,以下叙述与图中信息相符的是()A B C DA.该国地势北高南低B.该国的农业地域类型为季风水田农业C.该国的地形多陡崖D.该国地形以高原和山地为主3.素有“亚洲花都”之称的云南在2009年末遭遇了60年不遇的大旱。
关于云南干旱,下列说法正确的是()A.云南多伏旱B.云南是否会发生干旱与季风势力的强弱密切相关C.云南位于非季风区,降水少D.云南海拔高,气温低,降水少4.下面的图A是某地气候特征图,该地应位于图B中的()图A 图BA.a地B.b地C.c地D.d地5.今年4月中旬,受强冷空气的持续影响,本该是春暖花开的我国北方地区却出现“倒春寒”,暴雪降温严重影响了当地人们的生活和工作。
下列能反映我国这次强冷空气的天气系统是()6.右图为欧洲部分地区略图,图中甲线为一月0℃等温线。
影响该等温线分布的主要原因是()A.盛行风、洋流B.纬度、地形C.经度、地形D.盛行风、纬度7读下图,下列叙述正确的是()海洋海洋大西洋甲乙丁丙A .①处地貌为三角洲,是由流水侵蚀形成的B .①处地貌为冲积扇,是由流水的搬运堆积形成的C .②处地质构造为褶皱,是由板块相互挤压形成的D .②处地质构造为断层,是由外力作用形成的8.近年我国南方河流频频出现咸潮入侵现象,该现象多出现在海平面高于常年平均值的时期。
广东省增城中学高三数学第二次综合测试 理 【会员独享】

增城中学2011届高三级第二次阶段综合测试数学(理科)试卷一、选择题:本大题共8小题,每小题5分,共40分.每小题给出的四个选项中,只有一个选项是符合题目要求的. 1.函数x y sin 2=的定义域为A ,值域为B ,则A B ⋂=( )A .AB .BC .]1,1[-D .A 22.)(x f y =过点(,)a b ,则其反函数一定经过点( )A .(,)a bB .(,)b aC .(,)a aD .(,)b b3.已知向量a 、b 满足1,4,a b ==,且2a b ⋅= ,则a 与b 的夹角为( )A .6πB .4πC .3πD .2π4. 已知3(,),sin ,25παπα∈=则tan()4πα+等于( )A .17B .7C .17- D .7-5.函数)(x f 的定义域为开区间),(b a ,导函数)(x f ¢在),(b a 内的图象如图所示,则函数)(x f 在开区间),(b a 内有极大值点( )A .1个B .2个C .3个D .4个6.在1,2,3,4,5这五个数字组成的没有重复数字的三位数中,各位数字之和为奇数的共有( )A .36个B .24个C .18D .6个 7.关于直线m 、n 与平面α、β,有下列四个命题:①βα//,//n m 且βα//,则n m //; ②βα⊥⊥n m ,且βα⊥,则n m ⊥; ③βα//,n m ⊥且βα//,则n m ⊥; ④βα⊥n m ,//且βα⊥,则n m //. 其中正确命题的个数是( )A .1B .2C .3D .48.抛物线2y x =-上的点到直线4380x y +-=距离的最小值是( )A .43 B .75 C .85D .3 二、、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分。
(一)必做题(9~13题) 9.22(1)i =+10.6(x -的展开式中的常数项是a ,则a = 11. 不等式13x x a -++≥恒成立,则a 的取值范围是 . 12.已知()f x =sin()A wx ϕ+, (),()0f A f αβ==,||παβ-的最小值为3,则正数w =13.如图所示,四个正方体图形中,B A ,为正方形的两个顶点,P N M ,,分别为其所在棱的中点,能得出//AB 面MNP 的图形的序号是 .(写出所有符合要求的图形序号)(二)选做题(14~15题,考生只能从中选做一题)14.直角坐标系下的(1,1)化成极坐标系下的坐标为 . 15.如图,点C B A ,,是圆O 上的,且,4=AB ,30ACB ∠=o ,则圆O 的面积等于三、解答题:本大题共6小题,满分80分. 解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分) 已知函数()1cos 2cos 2xf x x x a +=++(a 为常数). (1)求函数()x f 的最小正周期,并指出其单调减区间; (2)若函数()x f 在⎥⎦⎤⎢⎣⎡20π, 上的最大值是2,试求实数a 的值.17. (本小题满分12分)从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件A :“取出的2件产品都是二等品”的概率04.0)(=A PA B M N P ② D C A B M N P ① D C A B M N P ③ C D AC M NP ④ B D(1)求从该批产品中任取1件是二等品的概率p ;(2)若该批产品共10件,从中任意抽取2件,ξ表示取出的2件产品中二等品的件数,求ξ的分布列.18. (本小题满分14分)如图,在三棱锥S ABC -中,侧面SAB 与侧面SAC 均为等边三角形,90BAC ∠=°, O 为BC 中点.(1)证明:SO ⊥平面ABC ; (2)求二面角A SC B --的余弦值.19.(本小题满分14分)设函数∈+++-=a ax x a x x f 其中,86)1(32)(23R . (1)若3)(=x x f 在处取得极值,求常数a 的值; (2)若)0,()(-∞在x f 上为增函数,求a 的取值范围.20.(本小题满分14分)已知数列3021,,,a a a ,其中1021,,,a a a 是首项为1,公差为1的等差数列;201110,,,a a a 是公差为d 的等差数列;302120,,,a a a 是公差为2d 的等差数列(0≠d ).OS BC(1)若4020=a ,求d ;(2)试写出30a 关于d 的关系式,并求30a 的取值范围;(3)续写已知数列,使得403130,,,a a a 是公差为3d 的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论? 21.(本小题满分14分)如图,直线y kx b =+与椭圆2214x y +=交于A B ,两点,记AOB △的面积为S .(I )求在0k =,01b <<的条件下,S 的最大值;(II )当2AB =,1S =时,求直线AB 的方程.(第21题)三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤16. (本小题满分12分)(Ⅰ)∵()1cos 222xf x x a +=++ 1sin 262x a π⎛⎫=+++ ⎪⎝⎭ …………2分 , ∴ 最小正周期22T ππ== ………4分 单调递减区间为2,63k k ππππ⎡⎤++⎢⎥⎣⎦()k ∈Z .………6分 (Ⅱ)令26u x π=+………7分,则()1sin 2g u u a =++,7,66u ππ⎡⎤∈⎢⎥⎣⎦………9分. ()x f 的最大值为32a +=2 ……11分. 解得a=12…12分17. (本小题满分12分)解:(1)设任取一件产品是二等品的概率为P ,依题意有………1分 2()P A P ==0.04 …………3分解得120.20.2p p ==-,(舍去).…………5分故该批产品中任取1件是二等品的概率为0.2. ………6分(2)ξ的可能取值为012,,.………7分 若该批产品共10件,由(1)知其二等品有100.22⨯=件,………8分18. (本小题满分14分) (Ⅰ)由题设AB AC SB SC ====SA ,连结OA ,ABC △为等腰直角三角形,所以OA OB OC SA ===,且AO BC ⊥,又SBC △为等腰三角形,故SO BC ⊥,………2分且SO =,从而222OA SO SA +=.所以SOA △为直角三角形, SO AO ⊥.……4分又AO BO O = .所以SO ⊥平面ABC .……6分(Ⅱ)解法一:取SC 中点M ,连结AM OM ,,由(Ⅰ)知SO OC SA AC ==,,得OM SC AM SC ⊥⊥,.OMA ∠∴为二面角A SC B --的平面角.……9分 由AO BC AO SO SO BC O ⊥⊥= ,,得AO ⊥平面SBC .……11分所以AO OM ⊥,又AM =,故sin AO AMO AM ∠===…13分 所以二面角A SC B --…14分 解法二:以O 为坐标原点,射线OB OA ,分别为x 轴、y 轴的正半轴,建立如图的空间直角坐标系O xyz -.设(100)B ,,,则(100)(010)(001)C A S -,,,,,,,,.OSBCSC 的中点11022M ⎛⎫- ⎪⎝⎭,,,111101(101)2222MO MA SC ⎛⎫⎛⎫=-=-=-- ⎪ ⎪⎝⎭⎝⎭,,,,,,,,.00MO SC MA SC ==,∴··.故,MO SC MA SC MO MA ⊥⊥>,,<等于二面角A SC B --的平面角.cos MO MA MO MA MO MA<>==,·· 所以二面角A SC B --.20. (本小题满分14分)(1)1010.a = ……2分 20101040,3a d d =+=∴=……4分 (2)())0(11010222030≠++=+=d d d d a a …… 6分当),0()0,(∞+∞-∈ d 时,[)307.5,10)(10a ∈⋃+∞. ……8分(3)所给数列可推广为无穷数列{}n a ,其中1021,,,a a a 是首项为1,公差为1的等差数列,当1≥n 时,数列)1(1011010,,,++n n n a a a 是公差为n d 的等差数列. ……10 分研究的问题可以是:试写出)1(10+n a 关于d 的关系式,并求)1(10+n a 的取值范围.……12分 研究的结论可以是:由()323304011010d d d d a a +++=+=, 依次类推可得 ()⎪⎩⎪⎨⎧=+≠--⨯=+++=++.1),1(10,1,11101101)1(10d n d d d d d a n nn 当0>d 时,)1(10+n a 的取值范围为),10(∞+等. ……14分(Ⅱ)解:由2214y kx b x y =+⎧⎪⎨+=⎪⎩,,……7分 得22212104k x kbx b ⎛⎫+++-= ⎪⎝⎭,2241k b ∆=-+,①……8分11||||AB x x =-2==.② …9分 设O 到AB 的距离为d ,则21||S d AB ==,又因为d =, 所以221b k =+,……10分 代入②式并整理,得42104k k -+=,解得212k =,232b =,代入①式检验,0∆>, 故直线AB 的方程是y x =或y x =或y x =+,或y x =14分(一条直线1分)。
《精编》广东省增城市高三数学毕业班调研测试题 理新人教A版.doc

届增城市高中毕业班调研测试理科数学试题分第I 卷〔选择题〕和第II 卷〔非选择题〕两局部。
共150分,考试时间120分钟。
本卷须知:1.第I 卷〔选择题〕每题选出答案后,用铅笔把答卷上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题上; 2.第II 卷〔非选择题〕答案写在答卷上。
参考公式:24R S π=球,3114,,(),333V Sh V Sh V S S h V R π'===+=柱锥台球 如果事件A 、B 互斥,那么P 〔A+B 〕=P 〔A 〕+P 〔B 〕.如果事件A 、B 相互独立,那么)()()(B P A P B A P =⋅.第I 卷〔选择题,共40分〕一、选择题:本大题共有8小题,每题5分,共40分。
在每题给出的四个选项中,只有一项为哪一项符合题目要求的。
{24},{3782},P x x Q x x x =≤<=-≥-集合那么=⋂Q P〔A 〕 {34x x ≤<} 〔B 〕 {34x x <<} 〔C 〕 {24x x ≤<} 〔D 〕 {2x x ≥}1i= 〔A 〕2i (B) 2i- (C) i (D) i -()f x =(A) [2,)+∞ (B) [1,)+∞ (C) (0,)+∞ (D) (0,1] 4.以下命题中正确的个数是〔1〕假设直线l 上有无数个点不在平面α内,那么l ∥α.〔2〕假设直线l 与平面α平行,那么l 与平面α内的任意一条直线都平行. 〔3〕如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行. 〔4〕假设直线l 与平面α平行,那么l 与平面α内的任意一条直线都没有公共点. (A) 0 (B) 1 (C) 2 (D) 35.直线12:(3)453,:2(5)8l m x y m l x m y ++=-++=平行,那么实数m 的值为 〔A 〕 -7 〔B 〕 -1 〔C 〕 -1或-7 〔D 〕 1336.假设3log 1(0,1)4aa a <>≠,那么实数a 的取值范围是 〔A 〕〔0,1〕 〔B 〕 〔1,+∞〕 〔C 〕3(0,)(1,)4⋃+∞ 〔D 〕3(,1)(1,)4⋃+∞7.设等比数列{}n a 的各项均为正数,且564718a a a a +=,那么3132310log log log a a a +++=〔A 〕 12 〔B 〕 10 〔C 〕 8 〔D 〕 32log 5+8.点P 是椭圆221625400x y +=上一点,且在x 轴上方,1F 、2F 分别是椭圆的左、右焦点,直线2PF的斜率为-,那么12PF F ∆的面积是〔A 〕〔B 〕〔C 〕〔D 〕第II 卷〔非选择题,共110分〕4~15题是选做题,只能做一题,两题全答的,只计算前一题得分. 〔一〕必做题〔9~13题〕9.向量(2,3),(,6)a b x ==-共线,那么x = . 10.有一问题的算法是 第一步,令1,0.i S ==第二步,假设100i ≤成立,那么执行第三步;否那么,输出S ,结束算法. 第三步,.S S i =+第四步,1i i =+,返回第二步. 那么输出的结果是 .31031(2)2x x-的展开式中的常数项是 . 12.以初速度40ms,垂直向上抛一物体,ts 时刻的速度〔v 的单位是ms〕为4010v t =-,那么该物体到达最大高度为 .、B 、C 三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:今需要A,B,C 三种规格的成品分别为15、18、27块,要使所用钢板张数最少,第一、第二种钢板的张数各是 . 〔二〕选做题〔14、15题〕14〔几何证明选讲选做题〕圆的直径13AB cm =,C 为圆上一点,CD AB ⊥,垂足为D ,且6CD cm =,那么AD = cm .15〔坐标系与参数方程选做题〕直线的极坐标方程为sin()4πρθ+=0,0〕到这条直线的距离是 .三、解答题:本大题共6小题,共80分.解容许写出文字说明、证明过程或演算步骤. 16〔14分〕22()(sin cos )2cos f x x x x =++-2〔1〕求()f x 的最大值及相应的x 值;VAB C〔2〕当(0,)2πα∈时,()28f απ-=()f α的值. 17〔14分〕从5名男生和4名女生中选出4人去参加辩论比赛.〔1〕求参加辩论比赛的4人中有2名女生的概率; 〔2〕设ξ为参加辩论比赛的女生人数,求ξ的分布列及数学期望.18〔14分〕如图,在三棱锥V ABC -中,AB =1,2VC VA VB AC BC =====〔1〕求证:AB VC ⊥; 〔2〕求V ABC V -19〔12分〕数列{}n a 满足121,2a a ==,且当1n >时,112n n n a a a -+=+恒成立. 〔1〕求{}n a 的通项公式; 〔2〕设12n n S a a a =+++,求证121112nS S S +++<. 20〔14分〕设()ln ()af x x a x=+为常数 〔1〕求()f x 的单调区间;〔2〕判断()f x 在定义域内是否有零点?假设有,有几个?21〔12分〕点(1,0),(1,0)A B -,直线,AM BM 相交于点M ,且直线BM 的斜率与直线AM 的斜率的差为1.〔1〕求点M 的轨迹C 的方程;〔2〕假设过点(0,0)F 作直线交轨迹C 于,P Q 两点,证明以PQ 为直径的圆与直线:1l y =-相切.。
增城市2010届广州市高三“二模”数学试题分析及教学建议
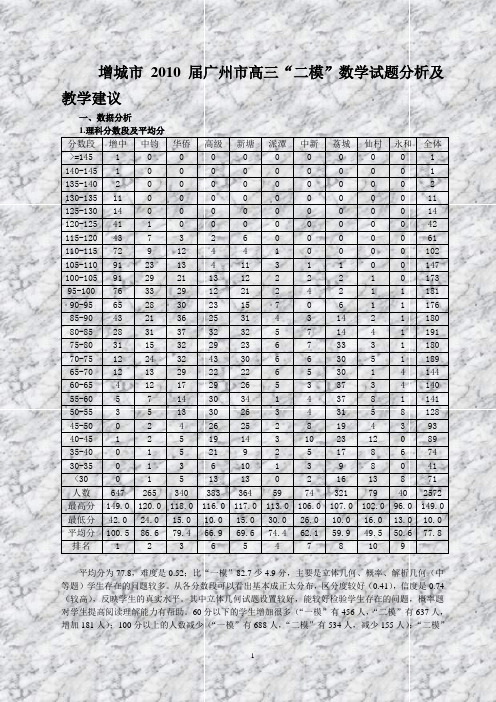
增城市2010届广州市高三“二模”数学试题分析及教学建议一、数据分析1.理科分数段及平均分分数段增中中钧华侨高级新塘派潭中新荔城仙村永和全体>=145 1 0 0 0 0 0 0 0 0 0 1 140-145 1 0 0 0 0 0 0 0 0 0 1 135-140 2 0 0 0 0 0 0 0 0 0 2 130-135 11 0 0 0 0 0 0 0 0 0 11 125-130 14 0 0 0 0 0 0 0 0 0 14 120-125 41 1 0 0 0 0 0 0 0 0 42 115-120 43 7 3 2 6 0 0 0 0 0 61 110-115 72 9 12 4 4 1 0 0 0 0 102 105-110 91 23 13 4 11 3 1 1 0 0 147 100-105 91 29 21 13 12 2 2 2 1 0 173 95-100 76 33 29 12 21 2 4 2 1 1 181 90-95 65 28 30 23 15 7 0 6 1 1 176 85-90 43 21 36 25 31 4 3 14 2 1 180 80-85 28 31 37 32 32 5 7 14 4 1 191 75-80 31 15 32 29 23 6 7 33 3 1 180 70-75 12 24 32 43 30 6 6 30 5 1 189 65-70 12 13 29 22 22 6 5 30 1 4 144 60-65 4 12 17 29 26 5 3 37 3 4 140 55-60 5 7 14 30 34 1 4 37 8 1 141 50-55 3 5 13 30 26 3 4 31 5 8 128 45-50 0 2 4 26 25 2 8 19 4 3 93 40-45 1 2 5 19 14 3 10 23 12 0 89 35-40 0 1 5 21 9 2 5 17 8 6 74 30-35 0 1 3 6 10 1 3 9 8 0 41<30 0 1 5 13 13 0 2 16 13 8 71人数647 265 340 383 364 59 74 321 79 40 2572 最高分149.0 120.0 118.0 116.0 117.0 113.0 106.0 107.0 102.0 96.0 149.0 最低分42.0 24.0 15.0 10.0 15.0 30.0 26.0 10.0 16.0 13.0 10.0 平均分100.5 86.6 79.4 66.9 69.6 74.4 62.1 59.9 49.5 50.6 77.8 排名 1 2 3 6 5 4 7 8 10 9平均分为77.8,难度是0.52;比“一模”82.7少4.9分,主要是立体几何、概率、解析几何(中等题)学生存在的问题较多。
广东省增城中学高三数学普通高中毕业班综合测试(二)(文) 新人教版【会员独享】

2010年增城中学普通高中毕业班综合测试(二)数学(文) 本试卷共4页,21小题,满分150分.考试用时120分钟.一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知全集,U R =且{}{}2|12,|680,A x x B x x x =->=-+<则()U C A B 等于A .[1,4)-B .(2,3)C .(2,3]D .(1,4)-2.下列函数中,在其定义域内既是奇函数又是减函数的是 A. R x x y ∈-=,3 B. R x x y ∈=,sin C. R x x y ∈=, D. R x x y ∈=,)21(3.3x >”是24x >“的A .必要不充分条件B .充分不必要条件C .充分必要条件D .既不充分也不必要条件4.已知向量),2,1(),,2(==b t a 若1t t =时,a ∥b ;2t t =时,b a ⊥,则A .1,421-=-=t t B. 1,421=-=t tC. 1,421-==t tD. 1,421==t t5.若,,l m n 是互不相同的空间直线,,αβ是不重合的平面,则下列命题中为真命题的是A .若//,,l n αβαβ⊂⊂,则//l nB .若,l αβα⊥⊂,则l β⊥C. 若,l n m n ⊥⊥,则//l m D .若,//l l αβ⊥,则//αβ6.若等差数列{n a }的前三项和93=S 且11=a ,则2a 等于A .3 B.4 C. 5 D. 67.已知a 是实数,2a i i-+是纯虚数,则a =A.12B.12-8.某校共有学生2000名,各年级男、女生人数表1,已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19. 现用分层抽样的方法在全校抽取64名学生,则应在初三年A.24B.18C.16D.129.曲线313y x x =+在点413⎛⎫ ⎪⎝⎭,处的切线与坐标轴围成的三角形面积为 A.19 B.29 C.13 D.2310.设函数()y f x =在(,)-∞+∞内有定义,对于给定的正数K ,定义函数(),(),(),().K f x f x K f x K f x K ≤⎧=⎨>⎩取函数()2x f x -=.当K =12时,函数()K f x 的单调递增区间为 A .(,0)-∞ B .(0,)+∞ C .(,1)-∞- D .(1,)+∞二、填空题(本大题共5小题,考生作答4小题,每小题5分,满分20分)(一)必做题(11~13题)11.在ABC △中,5cos 13B =-,4cos 5C =. 则sin A 的值是 . 12.若变量,x y 满足240,250,0,0,x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩则32z x y =+的最大值是 .13.执行右边的程序框图1,若p =0.8,则输出的n = .(二)选做题(14、15题,考生只能从中选做一题)14.(几何证明选讲选做题)如图所示,圆O 的直径,6=AB ,C 为圆周上一点,3=BC ,过C 作圆的切线l ,过A 作l 的垂线AD ,AD 分别与直线l 、圆交于点D 、E ,则∠DAC = , 线段AE 的长为 .15.(坐标系与参数方程选做题) 已知曲线12,C C 的极坐标方程分别为cos 3,4cos ρθρθ==0,0,2πρθ⎛⎫≥≤<⎪⎝⎭则曲线1C 与2C 交点的极坐标为 .三、解答题(本大题共6小题,满分80分.解答须写出文字说明,证明过程或演算步骤)16.(本小题满分12分)已知函数1)4()cos x f x xπ-=, (Ⅰ)求()f x 的定义域及最小正周期; 图1(Ⅱ)设α是第四象限的角,且4tan 3α=-,求()f α的值.17.(本小题满分12分)为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6名学生进行问卷调查,6人得分情况如下:5,6,7,8,9,10.把这6名学生的得分看成一个总体.(I )求该总体的平均数;(II )用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过0.5的概率.18.(本小题满分14分)如图,在Rt AOB △中,π6OAB ∠=,斜边4AB =.Rt AOC △可以通过Rt AOB △以直线AO 为轴旋转得到,且二面角B AOC --的直二面角.D 是AB 的中点.(I )求证:平面COD ⊥平面AOB ;(II )求异面直线AO 与CD 所成角的大小.(Ⅲ)求三棱锥A OCD -的体积.19.(本小题满分14分)已知椭圆C 的中心为直角坐标系xOy 的原点,焦点在x 轴上,它的一个项点到两个焦点的距离分别是7和1.(I)求椭圆C 的方程;(II)若P 为椭圆C 的动点,M 为过P 且垂直于x 轴的直线上的点,OP e OM =(e 为椭圆C的离心率),求点M 的轨迹方程,并说明轨迹是什么曲线. OC A DB20.(本小题满分14分)设函数.0),1ln()1()(>++-=a x a ax x f 其中(1)求函数)(x f 的单调区间;(2)当x>0时,证明不等式;)1ln(1x x x x <+<+ (3)设)(x f 的最小值为(),g a 证明不等式:1()0g a a -<<.21.(本小题满分14分)设向量b a b a ⋅=∈-+==+y N n x n x x 函数),)(12,(),2,(在[0,1]上的最大值与最小值的和为a n ,又数列}{n b 满足:.1109)109()109(2)1(21121++++=+++-+--- n n n n b b b n nb (1)求证:1+=n a n ;(2)求n b 的表达式;(3)}{,n n n n c b a c 试问数列⋅-=中,是否存在正整数k ,使得对于任意的正整数n ,都有k n c c ≤成立?证明你的结论.2010年增城中学普通高中毕业班综合测试(二)数学(文科)本试卷共4页,21小题,满分150分.考试用时120分钟.一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知全集,U R =且{}{}2|12,|680,A x x B x x x =->=-+<则()U C A B 等于A .[1,4)-B .(2,3)C .(2,3]D .(1,4)-2.下列函数中,在其定义域内既是奇函数又是减函数的是 A. R x x y ∈-=,3 B. R x x y ∈=,sin C. R x x y ∈=, D. R x x y ∈=,)21(3.3x >”是24x >“的A .必要不充分条件B .充分不必要条件C .充分必要条件D .既不充分也不必要条件4.已知向量),2,1(),,2(==b t a 若1t t =时,a ∥b ;2t t =时,b a ⊥,则A .1,421-=-=t t B. 1,421=-=t tC. 1,421-==t tD. 1,421==t t5.若,,l m n 是互不相同的空间直线,,αβ是不重合的平面,则下列命题中为真命题的是A .若//,,l n αβαβ⊂⊂,则//l nB .若,l αβα⊥⊂,则l β⊥C. 若,l n m n ⊥⊥,则//l m D .若,//l l αβ⊥,则//αβ6.若等差数列{n a }的前三项和93=S 且11=a ,则2a 等于A .3 B.4 C. 5 D. 67.已知a 是实数,2a i i-+是纯虚数,则a =A.12B.12-8.某校共有学生2000名,各年级男、女生人数表1,已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19. 现用分层抽样的方法在全校抽取64名学生,则应在初三年A.24B.18C.16D.129.曲线313y x x =+在点413⎛⎫ ⎪⎝⎭,处的切线与坐标轴围成的三角形面积为 A.19 B.29 C.13 D.2310.设函数()y f x =在(,)-∞+∞内有定义,对于给定的正数K ,定义函数(),(),(),().K f x f x K f x K f x K ≤⎧=⎨>⎩取函数()2x f x -=.当K =12时,函数()K f x 的单调递增区间为 A .(,0)-∞ B .(0,)+∞ C .(,1)-∞- D .(1,)+∞二、填空题(本大题共5小题,考生作答4小题,每小题5分,满分20分)(一)必做题(11~13题)11.在ABC △中,5cos 13B =-,4cos 5C =. 则sin A 的值是 . 12.若变量,x y 满足240,250,0,0,x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩则32z x y =+的最大值是 .13.执行右边的程序框图1,若p =0.8,则输出的n = .(二)选做题(14、15题,考生只能从中选做一题)14.(几何证明选讲选做题)如图所示,圆O 的直径,6=AB ,C 为圆周上一点,3=BC ,过C 作圆的切线l ,过A 作l 的垂线AD ,AD 分别与直线l 、圆交于点D 、E ,则∠DAC = , 线段AE 的长为 .15.(坐标系与参数方程选做题) 已知曲线12,C C 的极坐标方程分别为cos 3,4cos ρθρθ==0,0,2πρθ⎛⎫≥≤<⎪⎝⎭则曲线1C 与2C 交点的极坐标为 .三、解答题(本大题共6小题,满分80分.解答须写出文字说明,证明过程或演算步骤)16.(本小题满分12分)已知函数1)4()cos x f x xπ-=,(Ⅰ)求()f x 的定义域及最小正周期;(Ⅱ)设α是第四象限的角,且4tan 3α=-,求()f α的值.17.(本小题满分12分)为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6名学生进行问卷调查,6人得分情况如下:5,6,7,8,9,10.把这6名学生的得分看成一个总体. 图1(I )求该总体的平均数;(II )用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过0.5的概率.18.(本小题满分14分)如图,在Rt AOB △中,π6OAB ∠=,斜边4AB =.Rt AOC △可以通过Rt AOB △以直线AO 为轴旋转得到,且二面角B AOC --的直二面角.D 是AB 的中点.(I )求证:平面COD ⊥平面AOB ;(II )求异面直线AO 与CD 所成角的大小.(Ⅲ)求三棱锥A OCD -的体积.19.(本小题满分14分)已知椭圆C 的中心为直角坐标系xOy 的原点,焦点在x 轴上,它的一个项点到两个焦点的距离分别是7和1.(I)求椭圆C 的方程;(II)若P 为椭圆C 的动点,M 为过P 且垂直于x 轴的直线上的点,OP e OM =(e 为椭圆C的离心率),求点M 的轨迹方程,并说明轨迹是什么曲线.20.(本小题满分14分)设函数.0),1ln()1()(>++-=a x a ax x f 其中(1)求函数)(x f 的单调区间; (2)当x>0时,证明不等式;)1ln(1x x x x <+<+ (3)设)(x f 的最小值为(),g a 证明不等式:1()0g a a -<<.OC A DB21.(本小题满分14分)设向量b a b a ⋅=∈-+==+y N n x n x x 函数),)(12,(),2,(在[0,1]上的最大值与最小值的和为a n ,又数列}{n b 满足:.1109)109()109(2)1(21121++++=+++-+--- n n n n b b b n nb (1)求证:1+=n a n ;(2)求n b 的表达式;(3)}{,n n n n c b a c 试问数列⋅-=中,是否存在正整数k ,使得对于任意的正整数n ,都有k n c c ≤成立?证明你的结论.。
增城市2010届高三级十月测试(文数)

2010届高三级十月测试文科数学试卷试题分第1卷(选择题)和第II 卷(非选择题)两部分。
共150分,考试时间120分钟。
注意事项:1.第1卷(选择题)每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如 需改动,用橡皮擦干净后,再选涂其它答案,不能答在试卷上;2.第11卷(非选择题)答案用黑色笔或签字笔写在答题卡上,参考公式:24R S π=球,,Sh V =柱,,31Sh V =锥h S S S S V )''(31++=台,334R V π=球 如果事件A 、B 互斥,那么P(A+B)=P(A)+P(B).如果事件A ,B 相互独立,那么P(A ⋅B)=P (A )P(B ).第1卷(选择题,共50分)一、选择题:本走题共有10小题,每小题5分,共50分,在每小题给出的四个选项中,只 有一项是符合题目要求的.1.设A={3,5,6,8},B={4,5,7,8},则B A =A.{5,8}B.{5,6,7}C.{3.4,6,7}D.(3,4,5,6,7,8} 2.=)(x f x x -⋅-42的定义域是A.[2,+∞)B.(-∞,4]C.[2,4]D.(2,4)3.复数i-2的共轭复数是A.i+2B.-2+iC.-2-iD.2-i4.已知向量)3,2(=→a ,)6,(-=→x b 共线,则x=A. 3B. -4C. -3D. 25.函数)32sin()(π+=x x f )62cos(π-+x 是 A .周期为π的奇函数 B .周期为π的非奇非偶函数C .周期为2π的奇函数D .周期为2π的非奇非偶函数6.已知两个平面垂直,下列命题:①一个平面内已知直线必垂直于另一个平面内的任意一条直线;②一个平面内的已知直线必垂直于另一个平面内的无数条直线;③一个平面内的任意一条直线必垂直于另一个平面;④过一个平面内任意一点(此点不在交线上)作交线的垂线,则此垂线必垂直于另一个平面,其中正确命题的个数是( )A .3B .2C .1 D.O7.有两个等差数列2,6,10,…190,及2,8,14,…,200,由这两个等差数列的公共项按从小到大的顺序组成一个新数列,则这个数列的各项的和为A. 4608B.3434C.1472D.13808.双曲线32822=-y x 的离心率是A .414 B. 7142 C. 423 D. 322 9.在某年的足球甲A 联赛上,一队每场比赛平均失球数是1.5,全年比赛失球个数的标准差为1.1:二队每场比赛平均失球数是2.1,全年失球个数标准差为0.4.有下列四种说法: ①平均说来一队比二队防守技术好;②二队比一队技术水平更稳定;③一队有时表现很差,有时表现又非常好;④二队很少不失球。
广州市高三数学综合测试(二)试题.pdf

广州市高三数学综合测试(二)试题
说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共 150 分.考试时间 120
分钟.
参考公式:
三角函数的和差化积公式
sinθ+sin =2sin + cos −
2
2
sinθ-sin =2cos + sin −
2
2
cosθ+cos =2cos + cos −
室,其中 G、M 分别在 AB 和 AD 上,H 在 EF 上.设矩形 AGHM 的面积为 S,∠HCF=θ,请将 S 表示为θ的函数,并指出当点
H 在 EF 的何处时,该健身室的面积最大,最大面积是多少?
21.(本小题满分 14 分) 已知定点 Q(6,0)和抛物线 y2=8x 上的两个动点 A(x1,y1)、B(x2,y2),其中 A、B 的横 坐标 x1、x2 满足 x1≠x2 且 x1+x2=4. (Ⅰ)证明线段 AB 的垂直平分线过定点 Q; (Ⅱ)当 A、B 两点的距离为何值时,△AQB 的面积最大? 22.(本小题满分 14 分) 已知二次函数 f(x)=ax2+bx+c 满足 f(1)=0.
A.(0, 1 ) 2
B.(0,1 ]
C.(0,+∞)
D.[1,+∞ )
学无 止 境
6.在极坐标系中,点(3, )到直线ρcos(θ- )=2 的距离为
3
3
A.0
B.1
C.2
D.3
7.已知函数 f(x)的图象与函数 g(x)=2x-1 的图象关于直线 y=x 对称,则函数 f(x)的解
析式为 f(x)等于
AB∶BC=1∶ 2 ,O、F 分别为 CD、BC 的中点,且 EO⊥底面
增城中学第一学期高三年级综合测试(二).docx

马鸣风萧萧马鸣风萧萧高中数学学习材料马鸣风萧萧*整理制作增城中学2015-2016学年度第一学期高三年级综合测试(二)数学(文科)命题人:党红亮 审题人:倪华梁说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟。
第Ⅰ卷一.选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集{0,1,2,3,4,5}U =,集合{2,4}A =,2{|540,}B x x x x U =-+<∈,则集合()()U U C A C B ⋂=( )(A ){0,4,5,2} (B ){0,4,5} (C ){2,4,5} (D ){0,1,5}2.复数122ii+-的共轭复数是( ) (A )35i (B )35i -(C )i (D )—i3.“0ab <”是“0a >且0b <”的( ) (A )必要不充分条件 (B )充要条件(C )充分不必要条件 (D )既不充分也不必要条件4.执行如图所示的程序框图,若输入3x =,则输出y 的值为( ) (A )5 (B )7(C )15(D )315.为了得到函数sin(2)2y x π=-的图像,只需把函数sin 2y x =的图像( )(A )向左平移4π个单位 (B )向右平移4π个单位 (C )向左平移2π个单位 (D )向右平移2π个单位 6.已知双曲线221x ky -=的一个焦点是(5,0),则其渐近线的方程为( )(A )14y x =± (B )4y x =± (C )12y x =± (D )2y x =±7.如图2,三棱锥A BCD -中,AB ⊥平面BCD ,BC CD ⊥,若2AB BC CD ===,则该三棱锥的侧视图(投影线平行于BD )的面积为( ) (A )2 (B )2 (C )22 (D )238.在ABC ∆中,,,A B C 所对的边分别为c b a ,,,若060=A ,3=a ,3=+c b ,则ABC ∆的面积为( ) (A )34 (B )32(C )3 (D )2 9.若实数x ,y 满足条件0,10,01,x y x y x +≥⎧⎪-+≥⎨⎪≤≤⎩则3y x -的最大值为( )(A )6(B )5(C )4(D )310.已知函数()=sin ()cos()22f x x x ππ+-,其中正确说法为( ) (A )若)()(21x f x f -=,则21x x -=(B ))(x f 在区间3[,]44ππ--上是增函数 (C ))(x f 的最小正周期是2π(D ))(x f 的图象关于直线43π=x 对称 11.若[0,1],[0,1]a b ∈∈,则函数322y x ax bx =+++为增函数的概率为( )(A )56 (B )23 (C )13 (D )1612.已知22(0)()(1)(0)a x x x f x f x x ⎧--<=⎨-≥⎩,且函数()y f x x =-恰有3个不同的零点,则a 的取值范围是( )马鸣风萧萧(A )[1,)-+∞ (B )[1,0)- (C) (0,)+∞ (D) [2,)-+∞第Ⅱ卷二.填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分.13.圆22430x y x +-+=的圆心到直线30x y -=的距离是_____.14.已知向量(1,2)=a ,(,2)λ=-b .若向量,-a b a 夹角为90︒,则实数λ=_____.15.已知矩形ABCD 的顶点都在半径为R 的球O 的球面上,6AB =,23BC =,棱锥O-ABCD 的体积为83,则球O 的表面积为___________.16.海事救护船A 在基地的北偏东60o ,与基地相距1003海里,渔船B 被困海面,已知B 距离基地100海里,而且在救护船A 正西方,则渔船B 与救护船A 的距离是___________海里.三.解答题:本大题共6小题,满分70分.解答须写出文字说明、证明过程和演算步骤.17.(本小题满分12分)设{}n a 是等差数列,{}n b 是各项都为正数的等比数列,且111a b ==,3521a b +=,5313a b +=(I )求{}n a ,{}n b 的通项公式; (II )求数列n n a b ⎧⎫⎨⎬⎩⎭的前n 项和n S .18(本小题满分共12分)如图5,在四棱锥S ABCD -中,底面ABCD 是平行四边形,侧面SBC 是正三角形,点E 是SB 的中点,且AE ⊥平面CBS (I )证明:BS AC ⊥;(II )若AS AB ⊥,2=BC ,求点S 到平面ABC 的距离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年增城中学普通高中毕业班综合测试(二)数学 2009.9本试卷共4面,21小题,满分150分,考试用时120分钟。
一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.若复数iia 213++(a ∈R ,i 为虚数单位位)是纯虚数,则实数a 的值为( ) A .6-B .6C .4D .-22.命题“x ∀∈R ,221x x -+≥0”的否定是( )A .x ∃∈R ,221x x -+≥0B .x ∃∈R ,2210x x -+>C .x ∃∈R ,2210x x -+<D .x ∀∈R ,2210x x -+<3.设函数))((R x x f ∈为奇函数,3)()2(-=+x f x f ,则=-)4(f ( )A .3B .6-C .3-D .64.已知等差数列}{n a 的前13项之和为39,则876a a a ++等于( )A .6B .9C .12D .185.已知向量(,1),(4,),//,a x b x a b ==且则x 的值为( )A. 0B. 2C. 4 或-4D. 2或-26.已知椭圆22221(0)x y a b a b+=>>的左焦点为F ,右顶点为A ,点B 在椭圆上,且BF x⊥轴,直线AB 交y 轴于点P .若2AP PB =,则椭圆的离心率是( )A .2 B .2C .13D .127.设A 、B 是非空集合,定义{}A B x x A B x A B ⨯=∈⋃∉⋂且,已知A={|x y =,B={|2,0}xy y x =>,则A ×B 等于( )A .[)0,+∞B .[][)0,12,+∞C .[)[)0,12,+∞D .[]0,1(2,)+∞8.定义在R 上的偶函数()f x 满足:对任意的1212,(,0]()x x x x ∈-∞≠,有2121()(()())0x x f x f x -->.则当*n N ∈时,有( )A .()(1)(1)f n f n f n -<-<+B .(1)()(1)f n f n f n -<-<+C .(1)()(1)f n f n f n +<-<-D .(1)(1)()f n f n f n +<-<- 二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9-12题)9. (4的展开式中33x y 的系数为 .10.如右图是一个算法的程序框图,当输出值y 的范围大于1时, 则输入值x 的取值范围是 ____________ .11.甲、乙两人从4门课程中各选修2门。
则甲、乙所选的课程中至少有1门不相同的选法共有 种12.已知函数()f x 满足:()()()f p q f p f q +=, (1)3f =,则)7()8()4()5()6()3()3()4()2()1()2()1(2222f f f f f f f f f f f f +++++++=(二)选做题(13-15题,考生只能从中选做两题)13.(不等式选讲选做题)若b a 、为正实数,3=+b a ,则b a +++11的最大值是______ 14.(几何证明选讲选做题)如图所示,AC 和AB 分别是圆O 的切线,B 、C 为切点,且OC =3,AB =4,延长AO 到D 点,则△ABD 的面积是___________. 15.(坐标系与参数方程选做题)设(,)P x y 是曲线2cos :sin x C y =-+θ⎧⎨=θ⎩ (θ为参数)上任意一点, 则yx的取值范围是 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明,证明过程或演算步骤. 16.(本小题满分12分)已知函数()sin(),f x A x x R ωϕ=+∈(其中0,0,02A πωϕ>><<)的图象与x 轴的交点中,相邻两个交点之间的距离为2π,且图象上一个最低点为2(,2)3M π-. (Ⅰ)求()f x 的解析式;(Ⅱ)当[,]122x ππ∈,求()f x 的值域.17、(本小题满分12分)已知||2,||2x y ≤≤,点P 的坐标为(,)x y . (I )求当,x y R ∈时,P 满足22(2)(2)4x y -+-≤的概率; (II )求当,x y Z ∈时,P 满足22(2)(2)4x y -+-≤的概率.18.(本小题满分14分)如图,矩形ABCD 中,AD ABE ⊥平面,2AE EB BC ===,F 为CE 上的点,且BF ACE ⊥平面,AC BDG = .(Ⅰ)求证:AE ⊥平面BCE ; (Ⅱ)求证://AE 平面BFD ;(Ⅲ)求三棱锥C BGF -的体积.AD19.(本小题满分14分)已知,椭圆C 过点A 3(1,)2,两个焦点为(-1,0),(1,0)。
(Ⅰ)求椭圆C 的方程;(Ⅱ)E,F 是椭圆C 上的两个动点,如果直线AE 的斜率与AF 的斜率互为相反数,证明直线EF 的斜率为定值,并求出这个定值。
20.(本小题满分14分)已知函数22()(23)(),x f x x ax a a e x R =+-+∈其中a R ∈(Ⅰ)当0a =时,求曲线()(1,(1))y f x f =在点处的切线的斜率; (Ⅱ)当23a ≠时,求函数()f x 的单调区间与极值。
21.(本小题满分14分)设函数()f x 满足1)0(=f ,且对任意R y x ∈,,都有2)()()()1(+--⋅=+x y f y f x f xy f .(Ⅰ)求)(x f 的解析式;(Ⅱ)若数列{}n a 满足:13()1n n a f a +=-(*n N ∈),且11a =, 求数列{}n a 的通项;(Ⅲ)求证:(1)3112,().22(1)f n n N f n -*⎛⎫≤+<∈ ⎪-⎝⎭2010年增城中学普通高中毕业班综合测试(二)数学试卷参考答案一.选择题二、填空题.9.6; 10.()()+∞-∞-,101, ; 11.30 ; 12.24;13.10; 14.548; 15.[-33 ,33 ].三.解答题.16.(本小题满分12分)解:(1)由最低点为2(,2)3M π-得A=2. ………(1分) 由x 轴上相邻的两个交点之间的距离为2π得2T =2π,即T π=,222T ππωπ===…(3分) 由点2(,2)3M π-在图像上的242sin(2)2,)133ππϕϕ⨯+=-+=-即sin( 故42,32k k Z ππϕπ+=-∈ 1126k πϕπ∴=- 又(0,),,26∈∴=ππϕϕ ……(5分) ()2sin(2)6f x x =+故π……(6分)(2)7[,],2[,]122636x x πππππ∈∴+∈ ……(7分)当26x π+=2π,即6x π=时,()f x 取得最大值2; ……(9分)当7266x ππ+=,即2x π=时,()f x 取得最小值-1, ……(11分)故()f x 的值域为[-1,2] ……(12分)17.(本小题满分12分)解:(Ⅰ)点P 所在的区域为正方形ABCD 的内部(含边界),满足22(2)(2)4x y -+-≤的点的区域为以(2,2)为圆心,2为半径的圆面(含边界). ………………………(3分)∴所求的概率211244416P ππ⨯==⨯. …………………………………………………(5分) (II )满足,x y ∈Z ,且||2,||2x y ≤≤的点有25个, ………………………………(8分)满足,x y ∈Z ,且22(2)(2)4x y -+-≤的点有6个, ………………………………(11分)∴所求的概率2625P =. …………………………………………………………………(12分) 18.(本小题满分14分) 解:(Ⅰ)证明: AD ⊥平面ABE ,//AD BC .∴BC ⊥平面ABE ,则AE BC ⊥. …… (2分)又 BF ⊥平面ACE ,则AE BF ⊥. …… (3分) BC BF B = …… (4分)∴AE ⊥平面BCE . ……………… (5分) (Ⅱ)证明:依题意可知:G 是AC 中点. BF ⊥平面ACE ,则CE BF ⊥,而BC BE =.∴F 是AC 中点. ……………………………………(7分)在AEC ∆中,//FG AE ,∴//AE 平面BFD . …………………(9分) (Ⅲ)解法一: //AE 平面BFD ,∴//AE FG ,而AE ⊥平面BCE .∴FG ⊥平面BCE ,∴FG ⊥平面BCF . …………………………………(10分)G 是AC 中点,∴F 是CE 中点.∴FG //AE 且112FG AE ==. BF ⊥平面ACE ,∴BF CE ⊥. ……………………………………(11分) ∴Rt BCE ∆中,12BF CF CE ===∴112C F B S ∆=⋅. ……(13分) ∴1133C BFG G BCF CFB V V S FG --∆==⋅⋅=. …………………………………(14分)解法二:111111444323C BFG C ABE A BCE V V V BC BE AE ---==⋅=⋅⋅⋅⋅⋅=. …(14分)19.(本小题满分14分)解:(Ⅰ)由题意,c=1,可设椭圆方程为2219114b b+=+,解得23b =,234b =-(舍去) 所以椭圆方程为22143x y +=。
……………4分 (Ⅱ)设直线AE 方程为:3(1)2y k x =-+,代入22143x y +=得 2223(34)4(32)4()1202k x k k x k ++-+--=设(x ,y )E E E ,(x ,y )F F F ,因为点3(1,)2A 在椭圆上,所以2234()122x 34F k k --=+ 32E E y kx k =+- ………9分又直线AF 的斜率与AE 的斜率互为相反数,在上式中以—K 代K ,可得AD2234()122x 34F k k+-=+ 32E E y kx k =-++所以直线EF 的斜率()212F E F E EF F E F E y y k x x k K x x x x --++===--即直线EF 的斜率为定值,其值为12。
……14分 20.(本小题满分14分)(I )解:.3)1(')2()(')(022e f e x x x f e x x f a x x =+===,故,时,当.3))1(,1()(e f x f y 处的切线的斜率为在点所以曲线= ……2分(II )[].42)2()('22x e a a x a x x f +-++=解:.2232.220)('-≠-≠-=-==a a a a x a x x f 知,由,或,解得令……4分以下分两种情况讨论。
