江苏省扬州中学2018届高三5月第四次模拟考试数学 Word版含答案

合集下载

2018届高三数学5月份第四次模拟考试

2018届高三数学5月份第四次模拟考试文科数学注意事项：1.答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目填涂在答题卡规定的位置上。

2.第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应的答案标号涂黑。

第Ⅰ卷（选择题共60分）一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.（1）已知集合{}{}3,x log 1P x x N Q x =∈=<，则P Q ⋂= （） A.{}0,1,2B.{}1,2C.(]0,2D.()0,3（2）若复数1z ，2z 在复平面内对应的点关于虚轴对称，且112z i =-，则12z z = （） A.3455i +B.3455i -+C.3455i -- D.3455i - （3）在等差数列{}n a 中，若14739a a a ++=，36927a a a ++=，则9S = （）A.66B.99C.144D.297（4）如图所示，网格纸上小正方形的边长为1，粗线画出的是某三棱锥的三视图，则此三棱锥的最长的棱为（）A.B.4D.3（5）《孙子算经》是中国古代重要的数学著作，书中有一问题：“今有方物一束，外周一匝有三十二枚，问积几何？“该著作中提出了一种解决此问题的方法：“重置二位，左位减八，余加右位，至尽虚减一，即得.”通过对该题的研究发现，若一束方物外周一匝的枚数n 是8的整数倍时，均可采用此方法求解，右图是解决这类问题的程序框图，若输入n=24，则输出的结果为（）A.23B.49C.24D.48（6）若正实数x ，y 满足4x+y=xy ，则x+4y 取最小值时，y 的值为（）A.1B.2C.3D.5（7）函数[]2cos ()(-2,2)1x xf x x x =∈+的大致图像是（）ABCD（8）将函数2sin 3y x =的图像向右平移12π个单位长度，得到函数(x)y f =的图像，则下列说法不正确的是（） A.函数()f x 的图像关于直线4x π=对称B.函数()f x 的一个零点为012x π=C.函数()f x 在区间,66ππ⎡⎤-⎢⎥⎣⎦上单调递增 D.函数()f x 的最小正周期为23π（9）若02πα<<，02πβ-<<，1cos 43πα⎛⎫+= ⎪⎝⎭，cos()423πβ-=，则c o s ()2βα+=（）A.9B.3-C.27D.9-（10）已知在四棱锥P-ABCD 中，平面PAB ⊥平面ABCD ，且△PAB底面ABCD（）A.74πB.4πC.16πD.7π（11）已知1F ，2F 为双曲线222:102x y C b b-=>（）的左右焦点，点A 为双曲线C 右支上一点，1AF 交左支于点B,2AF B ∆是等腰直角三角形，22AF B π∠=，则双曲线C 的离心率为（） A.4B.C.2（12）若对于任意的正实数x ，y 都有y 2ln y xx e x me⎛⎫-≤ ⎪⎝⎭成立，则实数m 的取值范围为（） A.1,1e ⎛⎫ ⎪⎝⎭B.21,1e ⎛⎫⎪⎝⎭C.21,e e ⎛⎫⎪⎝⎭D.510,e ⎛⎫ ⎪⎝⎭第Ⅱ卷（非选择题共90分）二、填空题：本大题共4个小题，每小题5分，共20分.（13）已知向量a=（1,2），b=（1,1），c=2a+kb ，若b ⊥c ，则a c =_______.（14）在圆224x y +=上任取一点，则该点到直线0x y +-=的距离[0,1]d ∈的概率为_______.（15）已知实数x ，y 满足2202401x y x y y x +-≥⎧⎪+-≤⎨⎪≤+⎩，且341x y m x ++=+，则实数m 的取值范围为_______.（16）已知数列{}n a ，令()()112122n n n P a a a n N n-+=+++∈，则称{}n P 为{}n a 的“伴随数列”，若数列{}n a 的“伴随数列”{}n P 的通项公式为()12n n P n N ++=∈，记数列{}n a kn -的前n 项和为n S ，若4n S S ≤对任意的正整数n 恒成立，则实数k 的取值范围为_______.三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤. （17）（本小题满分12分）已知△ABC 内接于半径为R 的圆，a ，b ，c 分别是角A ，B ，C 的对边，且()()222sin sin sin R B A b c C -=-，c=3，（Ⅰ）求角A 的大小；（Ⅱ）若AD 是BC边上的中线，2AD =,求△ABC 的面积.（18）（本小题满分12分）旅游公司规定：若一个导游一年内为公司挣取的旅游总收入不低于40（单位：百万元），则称为优秀导游.经验表明，如果公司的优秀导游率越高，则该公司的影响度越高.已知甲、乙两家旅游公司各有导游100名，统计他们一年内旅游总收入，分别得到甲公司的频率分布直方图和乙公司的频数分布表如下：（Ⅰ）求a ，b 的值，并比较甲、乙两家旅游公司，哪家的影响度高？（Ⅱ）若一个导游的奖金y （单位：万元）与其一年内旅游总收入x （单位：百万元）之间的关系为12022040340x y x x <⎧⎪=≤<⎨⎪≥⎩，求甲公司导游的年平均奖金；（Ⅲ）从甲、乙两家公司旅游收入在[50,60)的总人数中，用分层抽样的方法随机抽取6人进行表彰，其中有两名导游代表旅游行业去参加座谈，求参加座谈的导游中有乙公司导游的概率.（19）（本小题满分12分）如图，在三棱柱111ABC A B C -中，平面11A B C ⊥平面11AACC ,90ABC ∠=. （Ⅰ）证明：1AC CA ⊥；（Ⅱ）若11A B C ∆是边长为2的等边三角形，求点1B 到平面ABC 的距离.（20）（本小题满分12分）已知椭圆2222:1(0)x y C a b a b +=>>的离心率为2，且过点1,2⎛ ⎝⎭. （Ⅰ）求椭圆C 的方程；（Ⅱ）过椭圆C 的左焦点的直线1l 与椭圆C 交于A ，B 两点，直线2l 过坐标原点且斜率与直线1l 的斜率互为相反数.若直线2l 与椭圆交于E ，F 两点且均不与点A ，B 重合，试证明直线AE 的斜率与直线BF 的斜率之和为零.（21）（本小题满分12分）已知函数()1ln f x a x x x ⎛⎫=-- ⎪⎝⎭，其中a R ∈. （Ⅰ）若a=1，求曲线()y f x =在点()()1,f 1P 处的切线方程；（Ⅱ）若对任意1x ≥，都有()0f x ≥恒成立，求实数a 的取值范围.请考生在第22题和第23题中任选一题作答，并用2B 铅笔将所选题号涂黑，多涂、错涂、漏涂均不给分，如果多做，则按所做的第一题记分. （22）[选修4-4：坐标系与参数方程]（本小题满分10分）平面直角坐标系中，直线l的参数方程为11x t y =+⎧⎪⎨=+⎪⎩（t 为参数）.以原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 的极坐标方程为22cos 1cos θρθ=-.（Ⅰ）写出直线l 的极坐标方程与曲线C 的直角坐标方程；（Ⅱ）已知与直线l 平行的直线l '过点M （2,0），且与曲线C 交于A ，B 两点，试求AB .（23）[选修4-5：不等式选讲]（本小题满分10分）已知函数()12f x x x =+--，()2g x x x a =--.（Ⅰ）当a=5时，求不等式()()f x g x ≥的解集；（Ⅱ）若不等式()()f x g x ≥的解集包含[2,3]，求a 的取值范围.濮阳市2018届第三次模拟考试文科数学参考答案一、选择题（每小题5分，共60分）1.B 由题意，可得{}0,1,2P =，()0,3Q =，所以{}1,2PQ =,选B2.A 复数1z ，2z 在复平面内对应的点关于虚轴对称，且112z i =- ∴212z i =--∴()()()()121212124334121212555i i z ii i z i i i ---+==-==+--+- 故选A. 3.B 设公差为d ，()()36914727391262a a a a a a d ++-++=-=-=⇒-.14711393919a a a a d a ++=+=⇒=，根据等差数列的求和公式：91989992S a d ⨯=+⨯=。

江苏省扬州中学高三数学5月卷(四模卷)

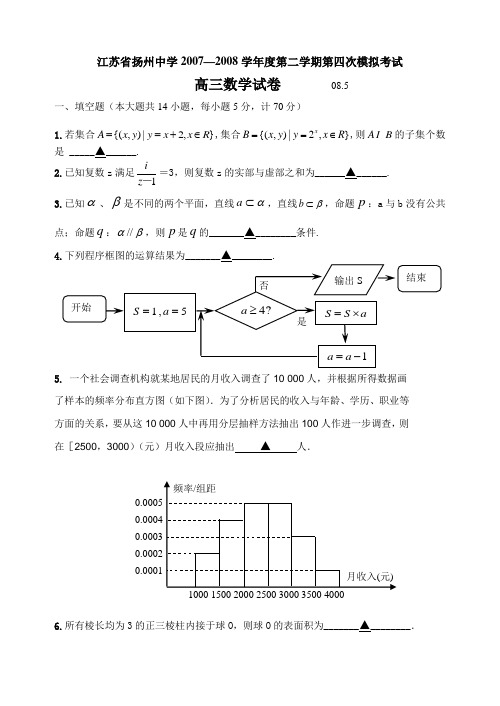
江苏省扬州中学2007—2008学年度第二学期第四次模拟考试高三数学试卷 08.5一、填空题（本大题共14小题，每小题5分，计70分）1.若集合{(,)|2,}A x y y x x R ==+∈,集合{(,)|2,}x B x y y x R ==∈,则A B 的子集个数是 _____▲______. 2.已知复数z 满足1iz －＝3，则复数z 的实部与虚部之和为______▲______. 3.已知α、β是不同的两个平面，直线α⊂a ，直线β⊂b ，命题p ：a 与b 没有公共点；命题q ：βα//，则p 是q 的_______▲________条件.4.下列程序框图的运算结果为_______▲________.5. 一个社会调查机构就某地居民的月收入调查了10 000人，并根据所得数据画了样本的频率分布直方图（如下图）．为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10 000人中再用分层抽样方法抽出100人作进一步调查，则在［2500，3000）（元）月收入段应抽出 ▲ 人．6.所有棱长均为3的正三棱柱内接于球O ，则球O 的表面积为_______▲________．7.函数y ＝f(x)定义域为(a ，b)，y ＝f '(x)在(a ，b)上的图象如图，则y ＝f(x)在区间(a ，b)上极大值点的个数为_____▲____.8.在坐标平面内，由不等式组123y x y x ⎧≥--⎪⎨≤-+⎪⎩ 所确定的平面区域的面积为_____▲______．9. 已知等差数列{}n a 的前n 次和为n s ，且2510,55S S ==，则过点),(n a n P 和),2(2++n a n Q （*N n -∈）的直线方向向量的坐标可以是_______▲_______．10. 已知函数⎩⎨⎧≥+-<=)0(4)3(),0()(x a x a x a x f x 满足对任意121212()(),f x f x x x x x -≠-都有0<成立，则a 的取值范围是_______▲_______．11. 在数列{}n a 中，已知11a =, 2a =, 21n n n a a ++=-,则2008a 等于_______▲_______．12.已知ABC k Z k ∆≤==∈则若,4||),4,2(),1,(,是直角三角形的概率是 ▲ ．13. ω是正实数，设{|()S f x ωθ==cos[()]x ωθ+是奇函数}，若对每个实数a ，)1,(+⋂a a S ω的元素不超过2个，且有a 使)1,(+⋂a a S ω含2个元素，则ω的取值范围是 ▲ .14. 一只球放在桌面上，桌面上一点A 的正上方有一点光源O ，OA 与球相切，让A 在桌面上运动，OA 始终与球相切，OA 形成一个轴截面顶角为45O的圆锥，则点A 的轨迹椭圆的离心率为 ▲ .二、解答题（本大题共6小题，计90分）15. （本小题14分）已知向量a =(cos α,sin α)，求b =(cos β,sin β)， |a -b |=552（1）求cos(α-β)的值；（2）若202π<α<<β<π-,且sin β=-135,求sin α的值.．16. （本小题14分）在正三角形ABC 中，E 、F 分别是AB 、 AC 边上的点，满足AE EB =12CF FA =（如图1）. 将△AEF 沿EF 折起到EF A 1∆的位置，使二面角A 1－EF －B 成直二面角，连结A 1B 、A 1C. （如图2）（1）求证：A 1E⊥平面BEC ；（2）求直线A 1E 与平面A 1BC 所成角的大小.17. （本小题15分）运货卡车以每小时x 千米的速度匀速行驶130千米(60≤100)x ≤．假设汽油的价格是每升2元，而汽车每小时耗油)3602(2x +升，司机的工资是每小时14元.（1）求这次行车总费用y 关于x 的表达式；（2）当x 为何值时，这次行车的总费用最低，并求出最低费用的值．18. （本小题15分）在平面直角坐标系xOy 中，过定点),0(p C 作直线与抛物线)0(22>=p py x 相交于A 、B 两点．（1）若点N 是点C 关于坐标原点O 的对称点，求△ANB 面积的最小值；（2）是否存在垂直于y 轴的直线l ，使得l 被以AC 为直径的圆截得的弦长恒为定值？若存在，求出l 的方程;若不存在，说明理由． 19．（本小题16分）已知数列{}n a 的前n 项和n S 满足2(1),1n n n S a n =+-≥.（1）写出数列{}n a 的前两项12,a a ；（2）求数列{}n a 的通项公式. （3）证明：对任意的整数4>m ,有4511178ma a a +++<.20. （本小题16分）已知函数()ln()x f x e a =+(a 为常数)是实数集R 上的奇函数,函数()()sin g x f x x λ=+是区间[1,1]-上的减函数. （1）求()g x 在[1,1]x ∈-上的最大值；（2）若2()1g x t t λ≤++对[1,1]x ∀∈-及(],1λ∈-∞-恒成立,求t 的取值范围；（3）讨论关于x 的方程2ln ()2x f x x ex m =-+的根的个数.命题：张福俭校对：唐一良图2图1B A BFC理科附加题1．一个袋子里装有大小相同的3个红球和2个黄球，从中同时取出2个，求其中含红球个数的数学期望与标准差分别是多少?2．曲线C 的极坐标方程是1cos ρθ=+，点A 的极坐标是（2，0），求曲线C 在它所在的平面内绕点A 旋转一周而形成的图形的周长考场号_____ 考试号________________ 学号_____ 班级___________座位号__________ 姓名_____________………………密……………封……………线……………内……………不……………要……………答……………题………………3．（Ⅰ）过曲线2(0)y x x =≥上某一点A 作一切线l ，使之与曲线以及x 轴所围成的图形的面积为112，试求： ⑴切点A 的坐标；⑵过切点A 的切线l 的方程；⑶上述所围成的平面图形绕x 轴旋转一周所得旋转体的体积4．若兔子和狐狸的生态模型为111 1.1.10.3,0.20.4n n n n n n R R F F R F ----=-⎧⎨=+⎩(1)n ≥对初始群00010050R F α⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭，讨论第n 年种群数量n α及当n 越来越大时，种群数量n α的变化趋势命题、校对：张春琦、侯绪兵高三数学第四次模拟试卷答题纸一、填空题：（本大题共14小题，每小题5分，计70分）1． 2． 3． 4．5． 6． 7． 8． 9．10． 11． 12． 13． 14．三、解答题（本大题共6小题，计90分） 15．解：16．解：17．解：考场号_____ 考试号________________ 学号_____ 班级___________座位号__________ 姓名_____________………………密……………封……………线……………内……………不……………要……………答……………题………………18．解：第19、20题做在反面高三数学第四次模拟试卷参考答案1. 42.433.必要不充分4. 205.256. 21π7. 28. 169. 2 10. ⎥⎦⎤ ⎝⎛41,0 11.0 12. 7313. 2πωπ<≤1-15. 解：（I ）∵|a -b |=552,∴a 2-2a ·b +b 2=54，又a =(cos α,sin α), b =(cos β,sin β),∴a 2=b 2=1, a ·b =cos αcos β+sin αsin β=cos(α-β).∴cos(α-β)=532542=-. （II ）∵-202π<α<<β<π,∴0<α-β<π,由（1）得cos(α-β)=53, ∴sin(α-β)=54. 又sin β=-135,∴cos β= 1312. ∴sin α=sin ［(α-β)+β］=sin(α-β)cos β+cos(α-β)sin β=54×6533)135(531312=-⨯+16.解不妨设正三角形ABC 的边长为3，则（1）在图1中，取BE 中点D ，连结DF ，则∵12AE CF EB FA ==, ∴1AE =,2AF =而060A ∠=，∴EF AE ⊥∴在图2中有1A E EF ⊥,BE EF ⊥, ∴1A EB ∠为二面角1A EF B --的平面角 ∵二面角1A EF B --为直二面角, ∴1A E BE ⊥ 又∵BEEF E =, ∴1A E ⊥平面BEC .（2）建立坐标系，则不妨设平面A 1BP 的法向量1(,,)n x y z =，则1110A B n BC n ⎧⋅=⎪⎨⋅=⎪⎩,得1n =∴111111cos ,||||14n EA n EA n EA ⋅<>===⋅⨯ 故直线A 1E 与平面A 1BP 所成角的大小为3π. 或：过E 作EH BC ⊥于H ，连A 1H ，作EO 1A H ⊥于O ，证明EO 1A BC ⊥平面，在直角三角形A 1EH 中求得直线A 1E 与平面A 1BP 所成角的大小为3π. 17. 解：（1）设行车所用时间为)(130h xt = ,2130141302(2),[60,100]360x y x x x⨯=⨯⨯++∈ 所以，这次行车总费用y 关于x 的表达式是234013([60,100])18y x x x=+∈（2）,2234013018y x=-+>所以234013([60,100])18y x x x=+∈为增函数.所以，当60x =时，这次行车的总费用最低，最低费用为2473元18．（1）依题意，点N 的坐标为(0)N p -，，可设1122()()A x y B x y ，，，，直线AB 的方程为y kx p =+，与22x py =联立得22x py y kx p ⎧=⎨=+⎩，．消去y 得22220x pkx p --=．由韦达定理得122x x pk +=，2122x x p =-．于是12122AMN BCN ACN S S S p x x =+=-△△△·12p x x =-=2p==，∴ 当0k =，2min ()ABN S =△．（2）假设满足条件的直线l 存在，其方程为y a =，设AC 的中点为O '，l 与AC 为直径的圆相交于点P ，Q PQ ，的中点为H ，则O H PQ '⊥，Q '点的坐标为1122x y p +⎛⎫⎪⎝⎭，．12O P AC '===∵ 111222y p O H a a y p +'=-=--， 222PH O P O H ''=-∴2221111()(2)44y p a y p =+--- 1()2p a y a p a ⎛⎫=-+- ⎪⎝⎭，22(2)PQ PH =∴14()2p a y a p a ⎡⎤⎛⎫=-+- ⎪⎢⎥⎝⎭⎣⎦．令02p a -=，得2pa =，此时PQ p =为定值，故满足条件的直线l 存在，其方程为2py =，即抛物线的通径所在的直线．19．解（１）由111121,1;a S a a ==-=得由2122222(1),0;a a S a a +==+-=得（２）当2≥n 时，有,)1(2)(211n n n n n n a a S S a -⨯+-=-=--即有 ,)1(2211---⨯+=n n na a 从而,)1(22221----⨯+=n n n a a32322(1),n n n a a ---=+⨯- …….2212-=a a接下来，逐步迭代就有122111)1(2)1(2)1(22-----⨯++-⨯+-⨯+=n n n n n a a].)1(2[323])2(1[2)1(2)]2()2()2[()1(21211211--------+=----=-++-+--+=n n n nn n n n n经验证a 1也满足上式，故知 .1],)1(2[3212≥-+=--n a n n n或：对1122(1)n n n a a --=+⨯-的两边同除以(1)n-，便得122(1)(1)nn a a -=-⋅---．令,(1)nn n a b =-就有122nn b b -=--，于是1222()33n n b b -+=-+，这说明数列23n b ⎧⎫+⎨⎬⎩⎭是等比数列，公比2,q =- 首项11b =-，从而，得111221()(2)()(2)333n n n b b --+=+⋅-=-⋅-，即 121()(2)(1)33n n n a -+=-⋅--，故有.1],)1(2[3212≥-+=--n a n n n（３）由通项公式得.24=a当3≥n 且n 为奇数时， ]121121[2311121-++=+--+n n n na a).2121(232222312222223123221213221----------+=+⨯<--++⨯=n n n n n n n n n n当m m 且4>为偶数时，m a a a 11154+++ )212121(2321)11()11(14431654--++++<+++++=m m m a a a a a .878321)211(4123214=+<-⨯⨯+=-m 当m m 且4>为奇数时，1m +为偶数，可以转化为上面的情景 .87111111115454<++++<++++m m m a a a a a a a故任意整数m>4，有.8711154<+++m a a a20.（1）)ln()(a e x f x+=是奇函数，则)ln()ln(a e a ex x+-=+-恒成立. .1))((=++∴-a e a e xx .0,0)(,112=∴=++∴=+++--a a e e a a ae ae x x x x又)(x g 在[－1，1]上单调递减，,1sin )1()(max --=-=∴λg x g（2）2sin11t t λλ--≤++只需在(],1λ∈-∞-上恒成立,(]2(1)sin1101.t t λλ∴++++≥∈∞在－，－恒成立令),1(11sin )1()(2-≤++++=λλλt t h 则⎩⎨⎧≥+++--≤+,011sin 1012t t t221sin10,sin10t t t t t ≤-⎧∴-+≥⎨-+≥⎩而恒成立1-≤∴t . （3）由（1）知,2ln ,)(2m ex x xxx x f +-=∴=方程为令m ex x x f x xx f +-==2)(,ln )(221， 21ln 1)(x xx f -=' ，当],0()(,0)(,),0(11e x f x f e x 在时∴≥'∈上为增函数； ),0[)(,0)(,),[11e x f x f e x 在时∴≤'+∞∈上为减函数，当e x =时，.1)()(1max 1ee f x f ==而222)()(e m e x x f -+-=，)(1x f 函数∴、)(2x f 在同一坐标系的大致图象如图所示，∴①当e e m e e m 1,122+>>-即时，方程无解.②当e e m e e m 1,122+==-即时，方程有一个根.③当ee m e e m 1,122+<<-即时，方程有两个根.[附加题]1.解：设其中含红球个数为X ，则X=0，1或2，11223232222555133(0),(1),(2)10510C C C C P X P X P X C C C ⋅=========故含红球个数的数学期望为1336012105105⨯+⨯+⨯= 含红球个数的方差为2226163639(0)(1)(2)5105551025-⨯+-⨯+-⨯=35， 2．解：设(,)P ρθ是曲线C 上的任意一点，则||1cos OP ρθ==+，由余弦定理，得 22222||||||2||||cos (1cos )2AP OP OA OP OA θθ=+-⋅=++21614(1cos )cos 3(cos )33θθθ-+=-+,当1cos 3θ=-时，||APA （2，0）代入曲线C 的极坐标方程，是满足的，知点A 在曲线C 上，所以曲线C 在它所在的平面内绕点A 旋转一周而形成的图形是以点A为圆心、||AP =23．解：⑴设点A 的坐标为2(,)a a ，过点A 的切线的斜率为'|2x a k y a ===，故过点A 的切线l 的方程为22()y a a x a -=-，即22y ax a =-，令0y =，得2ax =，则321224ABC a a S a ∆=⋅⋅=，33200|33a a ABO x a S x dx ∆===⎰，∴311212ABO ABC a S S S ∆∆====∴1a =或解：232220112[()222430a a y y S a dy ay y a a =+=+-⎰3111212a ==，∴1a = ∴切点A 的坐标为（1，1）⑵直线方程为21y x =-⑶l 与x 轴的交点为1(,0)2，故1142510211(21)05V x dx x dx x πππ=--=⎰⎰311(21)162x π--130=π 4．解：,n n n R M F α⎡⎤==⎢⎥⎣⎦ 1.10.30.20.4-⎡⎤⎢⎥⎣⎦，2n 1220M ()n n n n M M M M ααααα---=====M 的特征值11λ=对应的特征向量123,0.51αλ⎡⎤==⎢⎥⎣⎦对应的特征向量020*******,301025012R F αα⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤====+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦=12011223010,3010n n n n M ααααλαλα+==+319010(0.5)3010(0.5)123020(0.5)n n n ⎡⎤+⨯⎡⎤⎡⎤=+⨯=⎢⎥⎢⎥⎢⎥+⨯⎢⎥⎣⎦⎣⎦⎣⎦，当n 越来越大时，(0.5)n 趋向于0，n α趋向于9030⎡⎤⎢⎥⎣⎦，即兔子和狐狸的数量趋于稳定在90和30。

2018届江苏省扬州中学高三上学期月考数学试题及答案

江苏省扬州中学2018学年第一学期月考高三数学试卷一、填空题：1. 已知集合⎭⎬⎫⎩⎨⎧∈==R x y y A x ,21|，{}R x x y y B ∈-==),1(log |2，则=⋂B A ▲ ．2．已知ss :p “若b a =，则||||b a =”，则ss p 及其逆ss 、否ss 、逆否ss 中，正确ss 的个数是 ▲ ．3.设x 是纯虚数，y 是实数，且y x i y y i x +--=+-则,)3(12等于 ▲ ．4. 已知⎩⎨⎧>+-≤=0,1)1(0,cos )(x x f x x x f π，则4()3f 的值为 ▲ ．5. 在等差数列{}n a 中，若7893a a a ++=，则该数列的前15项的和为 ▲ ．6. 已知直线 ⊥平面α，直线m ⊂平面β，有下面四个ss ：①α∥β⇒ ⊥m ；②α⊥β⇒ ∥m ；③ ∥m ⇒α⊥β；④ ⊥m ⇒α∥β 其中正确ss 序号是 ▲ ． 7. 已知||1a = ，||2b =，a 与b 的夹角为120︒，0a c b ++= ，则a 与c 的夹角为▲ ．8. 设y x ,均为正实数，且33122x y+=++，则xy 的最小值为 ▲ ．9.已知方程2x +θtan x －θsin 1=0有两个不等实根a 和b ，那么过点),(),,(22b b B a a A 的直线与圆122=+y x 的位置关系是 ▲ ．10．若动直线)(R a a x ∈=与函数())()cos()66f x xg x x ππ=+=+与的图象分别交于NM ,两点，则||MN 的最大值为 ▲ ．11. 设12()1f x x =+，11()[()]n n f x f f x +=，且(0)1(0)2n n n f a f -=+，则2014a = ▲ ．12. 函数32()f x x bx cx d =+++在区间[]1,2-上是减函数,则c b +的最大值为 ▲ ．13．已知椭圆与x 轴相切，左、右两个焦点分别为)25(1,1(21，），F F ，则原点O 到其左准线的距离为 ▲ ．14. 设13521A ,,,,2482n nn -⎧⎫=⎨⎬⎩⎭(),2n N n *∈≥，A n 的所有非空子集中的最小元素的和为S ，则S = ▲ ．二、解答题：15．(本小题满分14分)设向量),cos ,(sin x x a =),sin 3,(sin x x b =x ∈R ，函数)2()(b a a x f +⋅=. （1）求函数)(x f 的单调递增区间；（2）求使不等式()2f x '≥成立的x 的取值集合． 16．(本小题满分14分)如图，在四棱锥ABCD P -中，底面为直角梯形，//,90AD BC BAD ︒∠=，PA 垂直于底面ABCD ，N M BC AB AD PA ,,22====分别为PB PC ,的中点．（1）求证：DM PB ⊥；（2）求点B 到平面PAC 的距离．17．(本小题满分14分)某种商品原来每件售价为25元，年销售8万件．（1）据市场调查，若价格每提高1元，销售量将相应减少2000件，要使销售的总收入不低于原收入，该商品每件定价最多为多少元？（2）为了扩大该商品的影响力，提高年销售量．公司决定明年对该商品进行全面技术革新和营销策略改革，并提高定价到．x 元．公司拟投入21(600)6x -万元作为技改费用，投入50万元作为固定宣传费用，投入15x 万元作为浮动宣传费用．试问：当该商品明年的销售量a 至少应达到多少万件时，才可能使明年的销售收入不低于原收入．．．与总投入．．．之和？并求出此时商品的每件定价．18．(本小题满分16分)已知函数()21f x x =-，设曲线()y f x =在点(),n n x y 处的切线与x 轴的交点为()1,0n x +，其中1x 为正实数. （1）用n x 表示1n x +；（2）12x =,若1lg1n n n x a x +=-，试证明数列{}n a 为等比数列，并求数列{}n a 的通项公式；（3）若数列{}n b 的前n 项和()12n n n S +=，记数列}{n n b a ⋅的前n 项和n T ，求n T ．.19. (本小题满分16分)如图所示，已知圆M A y x C ),0,1(,8)1(:22定点=++为圆上一动点，点P 是线段AM 的垂直平分线与直线CM 的交点．（1）求点P 的轨迹曲线E 的方程；（2）设点00(,)P x y 是曲线E 上任意一点，写出曲线E 在点00(,)P x y 处的切线l 的方程；（不要求证明）（3）直线m 过切点00(,)P x y 与直线l 垂直，点C 关于直线m 的对称点为D ，证明：直线PD 恒过一定点，并求定点的坐标．20. (本小题满分16分)设0a >，两个函数()axf x e =，g()ln x b x =的图像关于直线y x =对称. （1）求实数b a ,满足的关系式；（2）当a 取何值时，函数()()()h x f x g x =-有且只有一个零点；（3）当1=a 时，在),21(+∞上解不等式2)()1(x x g x f <+-．高三___________ 姓名_____________ 学号………………密……………封……………线……………内……………不……………要……………答……………题………………数学(附加题)21．B ．(本小题满分10分)已知二阶矩阵M 有特征值8λ=及对应的一个特征向量111⎡⎤=⎢⎥⎣⎦e ，并且矩阵M 对应的变换将点(1,2)-变换成(2,4)-, 求矩阵M ．.C ．(本小题满分10分)在直角坐标系中，参数方程为为参数）t t y t x (21232⎪⎪⎩⎪⎪⎨⎧=+=的直线l ，被以原点为极点， x 轴的正半轴为极轴，极坐标方程为θρcos 2=的曲线C 所截，求截得的弦长．22． (本小题满分10分)设函数()(,n)1nf x x =+,()n N *∈．（1）求(,6)f x 的展开式中系数最大的项；（2）若(,n)32f i i =（i 为虚数单位）,求13579n n n n nC C C C C -+-+．23． (本小题满分10分)电子蛙跳游戏是: 青蛙第一步从如图所示的正方体1111D C B A ABCD -顶点A 起跳，每步从一顶点跳到相邻的顶点．（1）求跳三步跳到1C 的概率P ；（2）青蛙跳五步，用X 表示跳到过1C 的次数，求随机变量X 的概率分布及数学期望)(X E ．1A12一、填空题1. ()+∞,0 2．2 3. i 251-- 4. 325.156. ①③7. 90︒8.169. 相切 10．2 11. 201512⎛⎫- ⎪⎝⎭ 12.152- 13⎪⎩⎪⎨⎧∈≥-=*2,3,212,47N n n n n二、解答题15．解：(1) )2()(b a a x f +⋅=222sin cos 2(sin cos )x x x x x =++111cos 2222(sin 2cos 2)2x x x x =+-+=+-⋅ 22(sin 2coscos 2sin )22sin(2)666x x x πππ=+-=+-. …………5′由222262k x k πππππ-≤-≤+，得63k x k ππππ-≤≤+()k ∈Z ，∴()f x 的单调递增区间为[,]63k k ππππ-+()k ∈Z . …………8′(2) 由()22sin(2)6f x x π=+-，得()4cos(2)6f x x π'=-.由()2f x '≥，得1cos(2)62x π-≥，则222363k x k πππππ-≤-≤+，即124k x k ππππ-≤≤+()k ∈Z . ∴使不等式()2f x '≥成立的x 的取值集合为,124x k x k k ππππ⎧⎫-≤≤+∈⎨⎬⎩⎭Z .……14′16．解：（1）因为N 是PB 的中点，PA=AB ，所以AN ⊥PB,因为AD ⊥面PAB ，所以AD ⊥PB,又因为AD ∩AN=A 从而PB ⊥平面ADMN,因为平面ADMN ，所以PB ⊥DM. …………7′(2) 连接AC ，过B 作BH ⊥AC ，因为PA ⊥底面ABCD ，所以平面PAB ⊥底面ABCD ，所以BH 是点B 到平面PAC 的距离.在直角三角形ABC 中，BH＝AB BC AC ⋅ ……………14′17．解：（1）设每件定价为x 元，依题意，有25(80.2)2581x x --⨯≥⨯，整理得26510000x x -+≤，解得2540x ≤≤．∴ 要使销售的总收入不低于原收入，每件定价最多为40元．………7′高三数学月考试卷参考答案（2）依题意，25>x 时，不等式21125850(600)65ax x x ≥⨯++-+有解, 等价于25>x 时，1501165a x x ≥++有解, ()150110306x x x +≥==当且仅当时，等号成立 , 10.2a ∴≥.∴当该商品明年的销售量a 至少应达到10.2万件时，才可能使明年的销售收入不低于原收入与总投入之和，此时该商品的每件定价为30元．……14′ 18．解：（1）由题可得()2f x x '=，所以在曲线上点()(),n n x f x 处的切线方程为()()()n n n y f x f x x x '-=-，即()()212n n n y x x x x --=-令0y =，得()()2112n n n n x x x x +--=-，即2112nn n x x x ++= 由题意得0n x ≠，所以2112n n nx x x ++=………………5′（2）因为2112n n n x x x ++=，所以2211221111221lg lg lg 112112n n n n n n n n n n nx x x x x a x x x x x ++++++++===+--+- ()()2211lg 2lg211nn n n n x x a x x ++===--即12n n a a +=，所以数列{}n a 为等比数列故11111112lg22lg 31n n n n x a a x ---+==⋅=- ………10′ （3）当1n =时，111b S ==，当2n ≥时，()()11122n n n n n n n b S S n -+-=-=-= 所以数列{}n b 的通项公式为n b n =，故数列{}n n a b 的通项公式为12lg 3n n n a b n -=⋅()21122322lg 3n n T n -∴=+⨯+⨯++⋅ ①①2⨯的()2212322lg 3n n T n =⨯+⨯++⋅ ②①-②得()2112222lg 3n n n T n --=++++-⋅故()221lg 3n nn T n =⋅-+ ………………16′19.解：（1）点P 是线段AM 的垂直平分线,∴PA PM ＝PA PC PM PC AC 2＋＝＋＝＝，∴动点N 的轨迹是以点C （－1，0），A （1，0）为焦点的椭圆. 椭圆长轴长为,222=a 焦距2c=2. .1,1,22===∴b c a∴曲线E 的方程为.1222=+y x ………5′（2）曲线E 在点00(,)P x y 处的切线l 的方程是0012x xy y +=.………8′（3）直线m 的方程为0000()2()x y y y x x -=-，即000020y x x y x y --= .设点C 关于直线m 的对称点的坐标为()D ,m n ,则0000001212022x nm y x n m y x y ⎧=-⎪+⎪⎨-⎪⋅--=⎪⎩，解得320002043200002002344424482(4)x x x m x x x x x n y x ⎧+--=⎪-⎪⎨+--⎪=⎪-⎩ ∴直线PD 的斜率为4320000032000042882(34)n y x x x x k m x y x x -++--==---+ 从而直线PD 的方程为： 432000000320004288()2(34)x x x x y y x x y x x ++---=---+ 即3200043200002(34)14288y x x x y x x x x --+=+++--, 从而直线PD 恒过定点(1,0)A .………16′ 20.解：（1）设P()axx e ，是函数()axf x e =图像上任一点，则它关于直线y x =对称的点P ()axe x ，，在函数g()ln x b x =的图像上，ln ax x b e abx ∴==，1ab ∴=.（2）当0a >时，函数()()()h x f x g x =-有且只有一个零点，两个函数的图像有且只有一个交点，两个函数关于直线y x =对称，∴两个函数图像的交点就是函数()ax f x e =，的图像与直线y x=的切点.设切点为00A()ax x e，，00=ax x e ()ax f x ae =，，0=1ax ae ∴，0=1ax ∴，00==ax x e e ∴, ∴当011a x e==时，函数()()()h x f x g x =-有且只有一个零点x e =；（3）当a =1时，设 ()2()(1)+g r x f x x x =--1x e -=2ln x x +-，则()r x ，112x e x x -=-－＋，当1,12x ⎛⎫∈ ⎪⎝⎭时，112211,1x x e x --<-=<-－，()0r x ，＜，当[)1,+x ∈∞时，112121,0x x e x--≤-=<－－，()0r x ，＜．()r x ∴在1,2⎛⎫+∞ ⎪⎝⎭上是减函数.又(1)r ＝0，∴不等式()2(1)+g f x x x -<解集是()1,+∞．21．B ．解：设M=ab cd ⎡⎤⎢⎥⎣⎦，则a b c d ⎡⎤⎢⎥⎣⎦11⎡⎤⎢⎥⎣⎦=811⎡⎤⎢⎥⎣⎦=88⎡⎤⎢⎥⎣⎦，故8,8.a b c d +=⎧⎨+=⎩a b c d ⎡⎤⎢⎥⎣⎦12-⎡⎤⎢⎥⎣⎦=24-⎡⎤⎢⎥⎣⎦，故22,2 4.a b c d -+=-⎧⎨-+=⎩联立以上两方程组解得a=6，b=2，c=4，d=4，故M=6244⎡⎤⎢⎥⎣⎦．………10′ C ．解：由题意知，直线l 的倾斜角为 30，并过点A （2，0）；曲线C 是以（1，0）为圆心、半径为1的圆，且圆C 也过点A （2，0）；设直线l 与圆C 的另一个交点为B ，在OAB Rt ∆中，330cos 2== AB ．…………10′22．解：（1）展开式中系数最大的项是第4项＝()333620C x x =；………5′（2）由已知，n(1)32i i =＋，两边取模，得n 32=，所以10n =.所以13579n n n n n C C C C C -+-+=135791010101010C C C C C -+-+ 而1001229910101010101010(1)i C C i C i C i C i =+++++ ＋()()0246810135791010101010101010101010C C C C C C C C C C C i =++++－－－－＋－32i =所以.32910710510310110=+-+-C C C C C …………10′23．解：将A 标示为0，A 1、B 、D 标示为1，B 1、C 、D 1标示为2，C 1标示为3，从A 跳到B 记为01，从B 跳到B 1再跳到A 1记为121，其余类推.从0到1与从3到2的概率为1，从1到0与从2到3的概率为13，从1到2与从2到1的概率为23. （1）P ＝P （0123）＝1⨯23⨯13＝29； ………4′（2）X ＝0,1，2. P （X ＝1）＝P （010123）＋P （012123）＋P （012321）＝1⨯13⨯1⨯23⨯13＋1⨯23⨯23⨯23⨯13＋1⨯23⨯13⨯1⨯23 ＝2681，P （X ＝2）＝P （012323）＝1⨯23⨯13⨯1⨯13＝681， P （X ＝0）＝1－P （X ＝1）－P （X ＝2）＝4981或P （X ＝0）＝P （010101）＋P （010121）＋P （012101）＋P （012121）＝1⨯13⨯1⨯13⨯1＋1⨯13⨯1⨯23⨯23＋1⨯23⨯23⨯13⨯1＋1⨯23⨯23⨯23⨯23＝4981， ∴ E （X ）＝1⨯2681＋2⨯681＝3881.…………10′。

江苏省扬州中学2018届高三5月第四次模拟考试化学试卷(附答案)

2018年普通高等学校招生全国统一考试（扬州中学冲刺卷）化学2018.5注意事项考生在答题前请认真阅读本注意事项及各题答题要求1．本卷满分为120分，考试时间为100分钟。

考试结束后，请将本试卷和答题卡一并交回。

2．答题前，请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。

3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符。

4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案。

作答非选择题，必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效。

5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗。

可能用到的相对原子质量：H-1 C-12 N-14 O-16 Na-23 S-32 Cu-64 Ba-137 V-51选择题单项选择题：本题包括10小题，每小题2分, 共计20分。

每小题只有一个．．．．选项符合题意。

1. 2018年是“2025中国制造”启动年，而化学与生活、人类生产、社会可持续发展密切相关，下列有关化学知识的说法错误．．的是A．高纯度的二氧化硅广泛用于制作光导纤维，光导纤维遇强碱会“断路”B．我国发射“嫦娥三号”卫星所使用的碳纤维，是一种非金属材料C．用聚氯乙烯代替木材，生产快餐盒，以减少木材的使用D．碳纳米管表面积大，可用作新型储氢材料2. 化学需要借助化学专用语言描述，下列有关化学用语表示正确的是A.碳铵的化学式: NH4HCO3B. 次氯酸的结构式：H—Cl—OC. 中子数为145、质子数为94的钚(Pu)原子：145 94PuD. S2﹣的结构示意图：3. 下列家庭化学实验不能达到预期目的的是A. 用灼烧并闻气味的方法区别纯棉织物和纯羊毛织物B. 用湿润的淀粉-KI 试纸检验 HCl 气体中是否混有 Cl 2C. 向 Ca(ClO)2 溶液中加入硫酸溶液，来证明 S 、Cl 的非金属性强弱D. 将一片铝箔用火灼烧，铝箔熔化但不滴落，证明铝箔表面致密Al 2O 3薄膜的熔点高于Al 4. 下列实验装置设计不能．．达到目的的是A ．实验I ：所示装置可制备氨气B ．实验II ：检验电解饱和食盐水的产物C12C ．实验III ：制取并观察Fe(OH)2沉淀D ．实验IV ：吸收SO 25. A 、B 、C 是原子序数依次增大的短周期主族元素，三种元素原子序数之和为35，且C 的原子序数是A 的2倍。

江苏省扬州树人学校2018届高三模拟考试(四)数学试题(解析版)

树人学校2017-2018第二学期高三模拟考试（四）数学Ⅰ第Ⅰ卷（共70分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合，，则__________．【答案】.【解析】分析：解不等式求得集合，然后再求出．详解：由题意得，∴．点睛：本题考查二次不等式的解法和集合交集的运算，考查学生的运算能力，属容易题．2. 在复平面内，复数（为虚数单位）对应的点位于第__________象限．【答案】三.【解析】分析：由复数的除法运算将复数化为代数形式，然后再根据复数的几何意义进行判断．详解：由题意得，∴复数对应的点为，位于第三象限．点睛：复数与复平面内的点和向量之间建立了一一对应的关系，这是复数几何意义的表现．3. 设，则“”是“”的__________条件．（填“充分不必要”、“必要不充分”、“充要”或“既不充分也不必要”）【答案】充分不必要.【解析】分析：解不等式和，然后根据解集间的关系进行判断即可得到结论．详解：解不等式不等式，得；不等式即为，解得或．∵或，∴“”是“”的充分不必要条件．点睛：利用集合间的包含关系判断充分必要条件时常用的结论：①若A⊆B，则A是B的充分条件或B是A的必要条件；②若A＝B，则A是B的充要条件．4. 为了了解一批产品的长度（单位：毫米）情况，现抽取容量为400的样本进行检测，如图是检测结果的频率分布直方图，根据产品标准，单件产品长度在区间的一等品，在区间和的为二等品，其余均为三等品，则样本中三等品的件数为__________．【答案】100.【解析】分析：根据频率分布直方图得到三等品的频率，然后可求得样本中三等品的件数．详解：由题意得，三等品的长度在区间，和内，根据频率分布直方图可得三等品的频率为，∴样本中三等品的件数为.点睛：频率分布直方图的纵坐标为，因此每一个小矩形的面积表示样本个体落在该区间内的频率，把小矩形的高视为频率时常犯的错误．5. 运行如图所示的算法流程图，输出的的值为__________．【答案】9.【解析】分析：逐次运行程序框图中的程序可得输出结果．详解：依次运行程序框图中的程序，可得①，不满足条件，继续运行；②，不满足条件，继续运行；③，不满足条件，继续运行；④，满足条件，输出9．点睛：判断程序框图的输出结果时，一般采用的方法是依次运行框图给出的程序，逐步得到输出结果即可。

扬州市2017—2018学年度高三第四次调研测试参考答案

2
6 2k 3 3k 2 1
2k 2 2 (k 0) ，解得 k
6 , 0) . 3
3 ， 3
……15 分 ……16 分
所以所以点 M 的坐标为 (
方法 2：设 M (m,0)(m 0) ，则 k AM 所以直线 AN 的方程为 y
2 m ，又 AM⊥AN，所以 k AN ， m 2
③当 0 a
数学参考答案第 3 页（共 6 页）
所以 f x 极大值 f 1 ae 1 ， f x 极小值 f ( x1 )
ae x1 ln x1 x1 1 ln a x1
15 分
f x 极小值 f ( x2 )
综上得：
ae x2 ln x2 x2 1 ln a . x2
……3 分
……5 分

方法 1：因为 M 为 x 轴正半轴上一点，所以直线 AM 的斜率存在且小于 0，又 AN AM ，所以 AN 的斜率存在且大于 0，设直线 AN 的方程为 y kx 2 (k 0) ，则直线 AM 的方程为 y
1 x 2 k
……6 分
x2 y 2 1 6 2k 由 6 消去 y 可得 (3k 2 1) x 2 6 2kx 0 ，解得 xN 2 3k 2 1 y＝kx＋ 2
m ……6 分 x 2， 2 x2 y 2 m 12m 1 得(2＋3m2)x2＋12mx＝0，所以 xN 联列 y ……10 分 x 2与 6 2 3m2 2 2
2 m2 12m 2 所以 AN 3m 2 2 在直角 AMN 中，由 AMN 60 得 AN 3 AM ，
6. 6

江苏省扬州市2018届高三5月第四次模拟考试数学试题及答案

扬州市2018届高三考前调研测试试题数学2018．5一、填空题（本大题共14小题，每小题5分，共70分，请将答案填写在答题卷相应的位置上）1．已知集合{1,2,3},{|(3)0}A B x x x =-=-<，则A B = ___ ▲ ．2．在复平面内，复数12i z i-=（i 为虚数单位）对应的点位于第 ▲ 象限． 3．设x R ∈，则“22>x ” 是“11x <”的 ▲ 条件．（填“充分不必要”、“必要不充分”、“充要”或“既不充分也不必要”）4．为了了解一批产品的长度（单位：毫米）情况，现抽取容量为400的样本进行检测，下图是检测结果的频率分布直方图，根据产品标准，单件产品长度在区间[25,30)的为一等品，在区间[20,25)和[30,35)的为二等品，其余均为三等品，则样本中三等品的件数为 ▲ ．5．运行如图所示的算法流程图，输出的k 的值为 ▲ ．6．在平面直角坐标系xOy 中，若抛物线22(0)=>y px p 上横坐标为1的点到焦点的距离为4，则该抛物线的焦点到准线的距离 ▲ ．7．书架上有5本书，其中语文书2本，数学书3本，从中任意取出2本，则取出的两本书都是数学书的概率为 ▲ ．8．已知等差数列{}n a 的前n 项和为,n S 且136S =，则91032a a -= ▲ ．9．记棱长都为1的正三棱锥的体积为1V ，棱长都为1的正三棱柱的体积为2V ，则12=V V ▲ ．10．若将函数()()cos 2(0)ϕϕπ=+<<f x x 的图象向左平移12π个单位所得到的图象关于原点对称，则ϕ= ▲ ．11．在ABC ∆中，AH 是底边BC 上的高，点G 是三角形的重心，若2,4,30AB AC BAH ==∠= ，则()AH BC AG +⋅= ▲ ．12．已知函数()21=+-+f x x b （,a b 为正实数）只有一个零点，则121a a b ++的最小值为 ▲ ．13．已知等边ABC ∆的边长为2，点P 在线段AC 上，若满足210PA PB λ⋅-+= 的点P 恰有两个，则实数λ的取值范围是 ▲ ．14．已知函数2|||1|,0()2,0x a x x f x x ax x ++->⎧=⎨-+≤⎩ 的最小值为a ，则实数a 的取值集合为 ▲ ．二、解答题：（本大题共6小题，计90分．解答应写出必要的文字说明、证明过程或演算步骤）15．（本小题满分14分）在ABC ∆中，角A,B,C 的对边分别为a,b,c ，已知cos A b c === （1）求a ；（2）求cos()B A -的值．16．（本小题满分14分）如图，在三棱锥P ABC -中，平面PAB ⊥平面,,,PAC AB BP M N ⊥分别为,PA AB 的中点．（1）求证：//PB 平面CMN ；（2）若AC PC =，求证：AB ⊥平面CMN ．17．（本小题满分14分）M N P如图所示，已知,A B是东西方某市为改善市民出行，准备规划道路建设.规划中的道路--向主干道边两个景点，且它们距离城市中心O的距离均为，C是正北方向主干道边上的一个景点，且距离城市中心O的距离为4km，线路MN段上的任意一点到景点A的距离比到景点B 的距离都多16km，其中道路起点M到东西方向主干道的距离为6km，线路NP段上的任意一点到O的距离都相等.以O为原点、线段AB所在直线为x轴建立平面直角坐标系xOy.M N P的曲线方程；（1）求道路--M N P上建一站点Q，使得Q到景点C的距离最近，问如何设置站点Q的位（2）现要在道路--置（即确定点Q的坐标）？在平面直角坐标系x O y 中，椭圆C ：22221x y a b +=(0)a b >>的短轴长为3（1）求椭圆C 的方程；（2）已知A 为椭圆C 的上顶点，点M 为x 轴正半轴上一点，过点A 作AM 的垂线AN 与椭圆C 交于另一点N ，若60 AMN ∠=，求点M 的坐标.已知函数()ln xae f x x x x=-+，()x x g x e =，（其中a 为参数）（1）若对任意x R ∈，不等式()0g x b -<恒成立，求实数b 的取值范围；（2）当1a e=时，求函数()f x 的单调区间；（3）求函数()f x 的极值.已知无穷数列{}n a 的各项都不为零，其前n 项和为n S ，且满足1n n n a a S +⋅= *()n N ∈，数列{}n b 满足n n n a b a t=+，其中t 为正整数．（1）求2018a ；（2）若不等式2211n n n n a a S S +++<+对任意*n N ∈都成立，求首项1a 的取值范围；（3）若首项1a 是正整数，则数列{}n b 中的任意一项是否总可以表示为数列{}n b 中的其他两项之积？若是，请给出一种表示方式；若不是，请说明理由．扬州市2018届高三考前调研测试数学第二部分（加试部分）（总分40分，加试时间30分钟）注意事项：答卷前，请考生务必将自己的学校、姓名、考试号等信息填写在答卷上规定的位置．解答过程应写在答题卷的相应位置，在其它地方答题无效．21．B ．选修4-2：矩阵与变换（本小题满分10分）已知,a b R ∈，若点(1,1)P -在矩阵41a b ⎡⎤=⎢⎥⎣⎦A 对应的变换作用下得到点(2,2)Q -． ⑴求,a b 的值；⑵求矩阵A 的特征值．21．C ．选修4-4：坐标系与参数方程（本小题满分10分）在极坐标系中，直线cos()πρθ+=C ，求以点C 为圆心且半径为1的圆的极坐标方程．22．（本小题满分10分）在正四棱柱1111ABCD A BC D -中，12,AB AA ==8个顶点中任取3个点构成三角形，记三角形的面积为X ． ⑴求(4)P X =的值；⑵求X 的分布列和数学期望.23．（本小题满分10分）在数列{}n a 中，*111,1,()n a a n N +==∈． ⑴求23,a a 的值；⑵证明：①01n a ≤≤； ②22114n n a a +<<．。

江苏省扬州市高三数学第四次模拟考试试卷-人教版高三全册数学试题

扬州市2014—2015学年度第四次调研测试试题高三数学参考答案第一部分1．已知集合{1,2,4},{2,3,4,5}A B ==，则AB =．{2，4}2．设复数z 满足()132i z i +=-+，则z ＝____________．13i -3．命题“2,10x R x ∀∈+>”的否定是．2,10x R x ∃∈+≤ 4．已知α为第三象限角，且tan 2α=，则sin 2α= ．455．从3名男同学，2名女同学中任选2人参加体能测试，则选到的2名同学中至少有一名男同学的概率是．9106．已知向量(1,3)=a ，(2,1)=-b ，(3,2)=c .若向量c 与向量k +a b 共线，则实数k = －17．锐角ABC △中角,,A B C 的对边分别是,,a b c ，4,5a b ==, ABC △的面积为53则c．218．用半径为6的半圆形铁皮卷成一个圆锥的侧面，则此圆锥的体积是．93π 9．已知等比数列{}n a 的前n 项和为n S ，若2244a S a S =，则12015S S 等于．110．若函数()cos f x k x =⋅的图象过点(,1)3P π，则该函数图象在P 点处的切线倾斜角等于．23π析：∵函数()cos f x k x =⋅的图象经过点(,1)3P π，∴()cos 1233f k k ππ==⇒=，∴x x f cos 2)(=，()2sin f x x '=-，()2sin333k f ππ'==-=-11．若直线30x y m ++=截半圆225y x =-8，则m = ．310-12．平面内四点,,,O A B C 满足4,25,5,0OA OB OC OB OC ===⋅=，则ABC ∆面积的最大值为．1513．已知椭圆E ：22221(0)x y a b a b +=>>的右焦点为F ，离心率为32，过原点O 且倾斜角为3π的直线l 与椭圆E 相交于A 、B 两点，若△AFB 的周长为13413+，则椭圆方程为．2214x y += 析：由已知2a b =，椭圆方程可化为：2224x y a +=，将:3l y x =代入得13||A x =，DB由椭圆对称性，△AFB 的周长=2||24||A a AB a x +=+，可得2a =． 14．已知函数||()()xx f x x R e=∈，12()421()x x g x a a a a R +=-+⋅++-∈，若{|(g())}R A x f x e =>=，则a 的取值范围是．[1,0]- 析：当0x ≥时，1'()xxf x e -=，得()f x 在[)0,1上是增函数，在()1,+∞上是减函数，当1x =时有极大值1e ；当0x <时，1'()0x x f x e-=<恒成立，()f x 是减函数，且(1)f e -=．设()g x t =，由()f t e >得1t <-，即()1g x <-对x R ∈恒成立，22()(2)21x g x a a a =--++-，当0a >时，2()21g x a a ≤+-，而2211a a +->-，不合题意；当0a ≤时，2()(,1)g x a a ∈-∞+-，∴211a a +-≤-，得10a -≤≤． 15．如图，三棱锥A BCD -中，侧面ABC 是等边三角形，M 是ABC ∆的中心． ⑴若DM BC ⊥，求证AD BC ⊥；⑵若AD 上存在点N ，使//MN 平面BCD ，求AN ND的值．证⑴连AM 并延长交BC 于E ，连DE因为M 是等边ABC ∆的中心，所以E 是BC 的中点，AE BC ⊥ ……………2分又因为DM BC ⊥，AE DM M =，,AE DM ⊂平面ADE ，所以BC ⊥平面ADE ， ……………5分因为AD ⊂平面ADE ，所以AD BC ⊥； ……………7分 ⑵,M AE AE ∈⊂平面ADE ，所以M ∈平面ADE ，因为AD 上存在点N ，所以N ∈平面ADE ，所以MN ⊂平面ADE ， ……………9分又//MN 平面BCD ，平面ADE平面BCD DE =，所以//MN DE ， ……………12分在ADE ∆中，因为12AM ME =，所以12AN ND =． ……………14分16．ABC ∆的内角,A B 满足2cossin 22A B A Ba i j +-=+(单位向量,i j 互相垂直)，且6||2a =． ⑴求tan tan A B 的值； ⑵若sin A =，边长2a =，求边长c ．解⑴因为2223||2cossin 222A B A B a +-=+=，即1cos()31cos()22A B A B --+++=， ……………3分所以cos cos sin sin cos cos sin sin 02A B A BA B A B +--=，化简整理，得13tan tan 022A B-=，故tan tan A B =13. ……………7分(2)由(1)可知,A B 为锐角．因为sin A =，所以2tan 3A =，1tan 2B =，tan tan 7tan tan()1tan tan 4A B C A B AB +=-+=-=--，sin C =……………12分因为正弦定理sin sin a cA C=，所以227c =，所以边长c =． ……………14分 17．一件要在展览馆展出的文物近似于圆柱形，底面直径为0.8米，高1.2米，体积约为0.6立方米．为保护文物需要设计各面是玻璃平面的正四棱柱形无底保护罩，保护罩底面边长不少于1.2米，高是底面边长的2 倍．保护罩内充满保护文物的无色气体，气体每立方米500元．为防止文物发生意外，展览馆向保险公司进行了投保，保险费用与保护罩的占地面积成反比例，当占地面积为1平方米时，保险费用为48000元． ⑴若保护罩的底面边长为2.5米，求气体费用与保险费用的和； ⑵为使气体费用与保险费用的和最低，保护罩应如何设计？解⑴2248000500(2.550.6)230052.5⨯-+=； ……………4分 ⑵保护罩的底面边长为x 米，底面积为S 平方米，体积为V 立方米，总费用为y 元，则 48000500(0.6)y V S =-+=2248000500(20.6)x x x ⋅-+32480001000300x x=+-，（ 1.2x ≥）……9分 52339600032'30003000x y x x x-=-=，令'0y =得2x =，当1.22x ≤<时'0y <，y 递减；当2x >时'0y >，y 递增∴当2x =时，y 有极小值即最小值．答：为了使这两项总费用最低，保护罩的底面边长应设计为2米． ……………14分18．已知椭圆22221(0)x y a b a b+=>>的左顶点为A ，右焦点为F ，右准线为l ，l 与x 轴相交于点T ，且F 是AT 的中点．⑴求椭圆的离心率；⑵过点T 的直线与椭圆相交于,M N 两点，,M N 都在x 轴上方，并且M 在,N T 之间，且2NF MF =．①记,NFM NFA ∆∆的面积分别为12,S S ，求12S S ； ②若原点O 到直线TMN 的距离为4141，求椭圆方程．解⑴因为F 是AT 的中点，所以22a a c c-+=，即(2)()0a c a c -+=，又a 、0c >，所以2a c =，所以12c e a ==； ……………4分 ⑵①解法一：过,M N 作直线l 的垂线，垂足分别为11,M N ，依题意，11NF MFe NN MM ==，又2NF MF =，故112NN MM =，故M 是NT 的中点，∴12MNF TNF S S ∆∆= 又F 是AT 中点，∴ANF TNF S S ∆∆=，∴1212S S =； ……………8分解法二：∵2a c =，∴3b c =，椭圆方程为2222143x y c c+=，(,0)F c ，(4,0)T c设11(,)M x y ，22(,)N x y ，点M 在椭圆2222143x y c c +=上，即有22211334y c x =-，∴2222211113()()34MF x c y x c c x =-+=-+-22111111124|2|2422x cx c x c c x =-+=-=-同理2122NF c x =-，又2NF MF =，故1224x x c -=得M 是,N T 的中点，∴12MNF TNF S S ∆∆=，又F 是AT 中点，∴ANF TNF S S ∆∆=，∴1212S S =； ……………8分 ②解法一：设(,0)F c ，则椭圆方程为2222143x y c c+=，由①知M 是,N T 的中点，不妨设00(,)M x y ，则00(24,2)N x c y -，又,M N 都在椭圆上，即有⎧⎪⎨⎪⎩220022220022143(24)4143x y c c x c y c c +=-+=即⎧⎪⎨⎪⎩220022220022143(2)1434x y c c x c y c c +=-+=两式相减得：220022(2)3444x x c c c --=，解得074x c =， ……………10分可得0y =，故直线MN的斜率为8744k c c ==-， ……………13分直线MN的方程为4)y x c =-60y +-= 原点O 到直线TMN的距离为d ==，41=，解得c = 故椭圆方程为2212015x y +=． ……………16分解法二：设(,0)F c ，则椭圆方程为2222143x y c c+=，由①知M 是,N T 的中点，故1224x x c -=，直线MN 的斜率显然存在，不妨设为k ，故其方程为(4)y k x c =-，与椭圆联立，并消去y 得：22222(4)143x k x c c c-+=，整理得：222222(43)3264120k x ck x k c c +-+-=，（*）设11(,)M x y ，22(,)N x y ，依题意：⎧⎪⎨⎪⎩21222221223243641243ck x x k k c c x x k +=+-=+ 由⎧⎨⎩212212324324ck x x k x x c +=+-=解得：⎧⎨⎩2122221644316443ck c x k ck c x k +=+-=+所以222222221641646412434343ck c ck c k c c k k k +--⨯=+++，解之得：2536k =，即k =．直线MN的方程为(4)6y x c =--60y +-= 原点O 到直线TMN的距离为d ==，41=，解得c =，故椭圆方程为2212015x y +=． ……………16分19．设m 个正数m a a a ,...,,21()*4,m m N ≥∈依次围成一个圆圈．其中1231,,,...,,k k a a a a a -*(,)k m k N <∈ 是公差为d 的等差数列，而111,,,...,,m m k k a a a a a -+是公比为2的等比数列． ⑴若12a d ==，8k =，求数列m a a a ,...,,21的所有项的和m S ； ⑵若12a d ==，2015m <，求m 的最大值； ⑶是否存在正整数k ，满足1211213()k k k k m m a a a a a a a a -++-++++=++++？若存在，求出k 值；若不存在，请说明理由．解⑴依题意16k a =，故数列m a a a ,...,,21即为2，4，6，8，10，12，14，16，8，4共10个数，此时10m =，84m S =， ……………4分 ⑵由数列1231,,,...,,k k a a a a a -是首项为2、公差为2的等差数列知，2k a k =，而111,,,...,,m m k k a a a a a -+是首项为2、公比为2的等比数列知，22m kk a +-=，故有222m kk +-=，12m kk +-=，即k 必是2的整数次幂，由122km k +⋅=知，要使m 最大，k 必须最大，又2015k m <<，故k 的最大值102，从而1010241222m +⋅=，m 的最大值是1033． ……………9分⑶由数列1231,,,...,,k k a a a a a -是公差为d 的等差数列知，1(1)k a a k d =+-，而111,,,...,,m m k k a a a a a -+是公比为2的等比数列112m k k a a +-=⋅，故1(1)a k d +-112m k a +-=⋅，11(1)(21)m kk d a +--=- 又121113()k k k k m m a a a a a a a a -+-+++=++++，12m a a =则11112(1)32212m k ka k k d a --+-=⨯⨯-，即11111[(21)]32(21)2m km k ka k a a +--+-=⨯-，则11126(21)22m k m k k k +--⋅+=-，即1126212m k m k k k +-+-⋅+=⨯-，显然6k ≠，则112182166m k k k k+-+==-+-- 所以6k <，将12345k =，，，，一一代入验证知，当4k =时，上式右端为8，等式成立，此时6m =，综上可得：当且仅当6m =时，存在4k =满足等式． ……………16分20．设函数1()1f x x =-，()1x g x ax =+(其中a R ∈，e 是自然对数的底数）． ⑴若函数()()()F x f x g x =-没有零点，求实数a 的取值范围；⑵若函数(),()f x g x 的图象有公共点P ，且在点P 有相同的切线，求实数a 的值；⑶若()()xf eg x ≤在x ∈[0,)+∞恒成立，求实数a 的取值范围．解⑴由()()()0F x f x g x =-=得2(1)(1)10a x a x ----=，显然0x =，1x a=-都不是此方程的根，当1a =时，没有实根，则1a ≠，由2(1)4(1)0a a -+-<得：31a -<<，故当(3,1]a ∈-时，函数()()()F x f x g x =-没有零点； ……………3分⑵21'()f x x=，21'()(1)g x ax =+，设它们的公共点为(,)P P P x y ，则有⎧⎪⎨⎪⎩()()'()'()P P P P P P y f x y g x f x g x ===即⎧⎨⎩()()'()'()P P P P f x g x f x g x ==也就是⎧⎪⎨⎪⎩2211111()(1)P P P P Px x ax x ax -=+=+当1P P ax x +=时111P x -=，无解；当1P P ax x +=-时111P x -=-，12P x =，3a =-；…………8分 ⑶由题得111xx e ax -≤+在[0,)+∞上恒成立，因为0x ≥，故1[0,1)xe --∈，所以110x e -≥在[0,)+∞上恒成立，故01xax ≥+在[0,)+∞上恒成立，所以，0a ≥. ……………10分解法一：不等式11x x e ax --≤+恒成立等价于(1)(1)0xax e x -+--≤在[0,)+∞上恒成立，令1()(1)(1)1x x ax h x ax e x ax x e -+=+--=-+--，则1'()1x ax a h x a e -+=+-，再设()'()m x h x =，则21'()xax a m x e-+-=，同时，'(0)21m a =-，'(0)0h =，(0)0h =， ①当0a =时，1'()0,x m x e=-<，则()'()m x h x =在[0,)+∞上单调递减，∴ '()'(0)=0h x h ≤，∴()h x 在[0,)+∞上单减，∴ ()(0)=0h x h ≤，即()()xf eg x ≤在[0,)+∞上恒成立，②当102a <≤时，21()'()xa a x a m x e ---=，因为210a a-->，所以'()0m x <，则()'()m x h x =在[0,)+∞上单调递减，∴'()'(0)=0h x h ≤，∴ ()h x 在[0,)+∞上单减， ∴()(0)=0h x h ≤，即()()xf eg x ≤在[0,)+∞上恒成立，③当12a >时，21()'()xa a x a m x e ---=，210a a->若210a x a-<<，则'()0m x >，即()'()m x h x =在21(0,)a a -上单调递增，所以'()'(0)0h x h >=即()h x 在21(0,)a a-上也单调递增，∴()(0)=0h x h >，即()()xf eg x ≥，不满足条件.综上，()()xf eg x ≤在[0,)+∞上恒成立时，实数a 的取值范围是1[0,]2. (16)分解法二：不等式11x x e ax --≤+恒成立等价于(1)(1)0x xax e e x +--≤在[0,)+∞上恒成立，设()(1)(1)=(1)(1)xxxh x ax e e x e ax x ax =+---+-+，则'()()xh x e ax x a a =-+-，再设()'()()xm x h x e ax x a a ==-+-，则'()[(1)(21)]xm x e a x a =-+- 同时，'(0)21m a =-，(0)'(0)0m h ==，(0)0h =，①当1a ≥时，'(0)210m a =->，故函数'()h x 是(0,)+∞上的增函数所以'()'(0)0h x h >=，所以函数()h x 是(0,)+∞上的增函数，所以当(0,)x ∈+∞时，()(0)0h x h >=，即()()xf eg x ≤，与()()x f e g x ≤在[0,)+∞上恒成立不符，②当102a ≤≤时2101a a -≥-，21'()(1)()01x a m x a e x a -=-+<-，故函数'()h x 是(0,)+∞上的减函数所以'()'(0)0h x h <=，函数()h x 是(0,)+∞上的减函数，所以当(0,)x ∈+∞时，()(0)0h x h ≤=，即()()f x g x ≤在[0,)+∞上恒成立，③当112a <<时，2101a a -<-，21'()(1)()1x a m x a e x a -=-+-当21(0,)1a x a -∈--时，'()0m x >，故函数'()h x 是21(0,)1a a ---上的增函数所以在21(0,)1a x a -∈--上，'()'(0)0h x h >=，所以函数()h x 是21(0,)1a a ---上的增函数，所以当21(0,)1a x a -∈--时，()(0)0h x h >=，即()()xf eg x ≥，与()()xf eg x ≤在[0,)+∞上恒成立不符，综上可得，使()()xf eg x ≤在[0,)+∞上恒成立实数a 的取值范围是1[0,]2．第二部分21B ．已知矩阵213,125M β ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦，计算2M β．解法一：矩阵M 的特征多项式为221()4312f λλλλλ- -==-+- -，令()0f λ=，解得1,3λλ==，对应的一个特征向量分别为1211,11αα⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦， ……………5分令12m n βαα=+，得1,4m n =-=，22221212(4)()4()M M M M βαααα=-+=-+22113511431137⎡⎤⎡⎤⎡⎤=-⨯+⨯=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦． ……………10分解法二：因为221211212M 5 4⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥ 4 5⎣⎦⎣⎦⎣⎦， ……………5分所以2335537M β5 4⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥4 5⎣⎦⎣⎦⎣⎦． ……………10分 21C ．已知圆C 的极坐标方程是4sin ρθ=，以极点为平面直角坐标系的原点，极轴为x 轴的正半轴，建立平面直角坐标系，直线l的参数方程是2(12x t t y t m ⎧=⎪⎪⎨⎪=+⎪⎩是参数）．若直线l 与圆C 相切，求正数m 的值．解：由4sin ρθ=，得24sin ρρθ=，所以2240x y y +-=，即圆C 方程为22(2)4x y +-= ……………4分又由212x t y t m ⎧=⎪⎪⎨⎪=+⎪⎩，消t得0x +=， ……………8分因为直线l 与圆C相切，所以||22-=得23m =±，又0m >，所以323m =+． ……………10分 22．如图，平行四边形ABCD 所在平面与直角梯形ABEF 所在平面互相垂直，且11,//2AB BE AF BE AF ===，,,2,3AB AF CBA BC P π⊥∠==为 DF 中点．⑴求异面直线DA 与PE 所成的角；⑵求平面DEF 与平面ABCD 所成的二面角（锐角）的余弦值．解：在ABC ∆中，1,,23AB CBA BC π=∠==，所以2222cos 3AC BA BC BA BC CBA =+-⨯∠=所以222AC BA BC +=，所以AB AC ⊥又因为平面ABCD ⊥平面ABEF ，平面ABCD 平面ABEF AB =， AC ⊂平面ABCD ，所以AC ⊥平面ABEF如图，建立空间直角坐标系{,,}AB AF AC ，则13(0,0,0),(1,0,0),3),(3),(1,1,0),(0,2,0),(2A B C D E F P -- ⑴33(1,0,3),(,0,22DA PE =-=- 设异面直线DA 与PE 所成的角为α，则3cos |||2||||23DA PE DA PE α⋅===⨯⨯ 所以异面直线DA 与PE 所成的角为6π； ……………5分 ⑵(0,2,0)AF =是平面ABCD 的一个法向量，设平面DEF 的一个法向量(,,)n x y z =，(2,1,3),(1,2,3)DE DF =-=则(,,)(2,1,3)230(,,)(1,2,3)230n DE x y z x y z n DF x y z x y z ⎧⋅=⋅=+-=⎪⎨⋅=⋅=+=⎪⎩，得33z x ==，取1x =，则1,3y z ==故(1,1,3)n =是平面DEF 的一个法向量，设平面DEF 与平面ABCD 所成的二面角（锐角）为β，则2cos |||||||2AF n AF n β⋅===⨯⨯． ……………10分 23．设集合{1,0,1}M =-，集合123{(,,)|,1,2,,}n n i A x x x x x M i n =∈=，，，集合n A 中满足条件“121||||||n x x x m ≤+++≤”的元素个数记为n m S ．⑴求22S 和42S 的值；⑵当m n <时，求证：n m S 111322n m n +++<+-．解⑴228S =，4232S =； ……………3分 ⑵设集合{0}P =，{1,1}Q =-．若12||||||1n x x x +++=，即123,,n x x x x ，，中有1n -个取自集合P ，1个取自集合Q ，故共有112n n C -种可能，即为112n C ，同理，12||||||2n x x x +++=，即123,,n x x x x ，，中有2n -个取自集合P ，2个取自集合Q ，故共有222n nC -种可能，即为222n C ， ……若12||||||n x x x m +++=，即123,,n x x x x ，，中有n m -个取自集合P ，m 个取自集合Q ，故共有2n m m n C -种可能，即为2m m n C ，所以1122222n m m m n n n S C C C =++⋅⋅⋅+，因为当0k n ≤≤时，1k n C ≥，故10k n C -≥所以1122222n m m m n n n S C C C =+++001122112(222)(1)2(1)2m m m m n n n n n n n n C C C C C C ++<+++++-++- 0011221112(222222)(222)m m m m n n m m n n n n n n n C C C C C C ++++=+++++++-++11(12)(22)n n m ++=+--11322n n m ++=-+． ……………10分。

高考数学试题-江苏省扬州中学2018年高三第四次模试题(数学) 最新

江苏省扬州中学2018年高三第四次模试题数学试卷 2018.5一、填空题：（本大题共14小题，每小题5分，计70分）1. 集合{}{}{}3,2,,,2aM N a b M N ==⋂=若，则M N ⋃= ．2.在复平面内，复数21i-对应的点到直线1y x =+的距离是． 3.已知函数2log (0)()3(0)x x x f x x >⎧=⎨≤⎩，则⎥⎦⎤⎢⎣⎡)41(f f 的值为_____________． 4. 在ABC ∆，60A =︒，2BC =，AC =，则ABC ∆的形状为． 5.若方程ln 2100x x +-=的唯一解为0x ，且0(,1),x k k k N ∈+∈，则k = ． 6.已知a 、b 、c 是直线，α是平面，给出下列命题：①若//a b ，b c ⊥，则a c ⊥； ②若a b ⊥，b c ⊥，则//a c ；③若//a α，b α⊂，则//a b ；④若a α⊥，b α⊂，则a b ⊥；⑤若a 与b 异面，则至多有一条直线与a 、b 都垂直．其中真命题是．（把符合条件的序号都填上）7. 设)2,1(-=，)1,(-=a ，)0,(b -=，0,0>>b a ,O 为坐标原点，若A 、B 、C 三点共线，则ab 的最大值是．8.若数列{}n a 的通项公式21(1)n a n =+，记12()2(1)(1)(1)n f n a a a =--⋅⋅⋅-，试通过计算(1)f 、(2)f 、(3)f 的值，推测出()f n = ．9. 在同一平面直角坐标系中，已知函数()y f x =的图象与xy e =的图象关于直线y x =对称，则函数()y f x =对应的曲线在点（,()e f e ）处的切线方程为． 10. 如图，在ABC ∆中，30=∠=∠CBA CAB ，AC 、BC 边上的高分别为BD 、AE ，则以A 、B 为焦点，且过D 、E的椭圆与双曲线的离心率的倒数和为 .11.如果执行下面的程序框图，那么输出的S 值为 .B12.定义：关于x 的两个不等式()0<x f 和()0<x g 的解集分别为()b a ,和⎪⎭⎫ ⎝⎛a b 11，，则称这两个不等式为对偶不等式.如果不等式022cos 342<+-θx x 与不等式012sin 422<++θx x 为对偶不等式，且,2πθπ⎛⎫∈ ⎪⎝⎭，则=θ .13. 已知函数bx ax x x f -+=2331)(（R b a ∈,），若)(x f y =在区间[]2,1-上是单调减函数，则b a +的最小值为 .14. 已知连续*21()n n N +∈个正整数总和为a ，且这些数中后n 个数的平方和与前n 个数的平方和之差为b ．若1160a b =，则n 的值为．二、解答题：（本大题共6小题，计90分）15.某校从参加高一年级期中考试的学生中随机抽取60名学生，将其数学成绩（均为整数）分成六段[)50,40，[)60,50…[]100,90后得到如下部分频率分布直方图.观察图形的信息，回答下列问题：(Ⅰ)求分数在[)70,80内的频率，并补全这个频率分布直方图；(Ⅱ）统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计本次考试的平均分； (Ⅲ）用分层抽样的方法在分数段为[)80,60的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任取2人，求至多有1人在分数段[)80,70的概率.16. 已知向量(s i n,c o s a αα=，(6sin cos ,7sin 2cos )b αααα=+-，设函数()f a b α=⋅．（1）求函数()f α的最大值；（2）在锐角三角形ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，()6f A =，且ABC ∆的面积为3，2b c +=+a 的值．17. 如图，棱柱ABCD-A 1B 1C 1D 1的底面ABCD 为菱形，平面AA 1C 1C ⊥平面ABC D ．（1）证明：BD ⊥AA 1；（2）证明：平面AB 1C//平面DA 1C 1（3）在直线CC 1上是否存在点P ，使BP//平面DA 1C 1？若存在，求出点P 的位置；若不存在，说明理由．18.如图，已知圆22:2O x y +=交x 轴于A 、B 两点，P 在圆O 上运动（不与A 、B 重合），过P 作直线1l ，OS 垂直于1l 交直线2:3l x =-于点S ．（1）求证：“如果直线1l 过点(1,0)T -，那么1OP PS ⋅=”为真命题；（2）写出（1）中命题的逆命题，判断它是真命题还是假命题，并说明理由．19. 已知等比数列{}n a 的前n 项和为n S ，且点*1(,)()n n n P a S n N +∈在函数()1f x x =+的图象上．（1）求1a 的值；（2）若数列{}n b 满足：124444(1)n n b bb b n n S ⋅⋅⋅⋅⋅⋅⋅=-，且25b =．求数列{}n b 的通项公式．20.设2()(f x x bx c b =++、)c R ∈．（1）若()f x 在[2,2]-上不单调，求b 的取值范围；（2）若()||f x x ≥对一切x R ∈恒成立，求证：214b c +≤；（3）若对一切x R ∈，有1()0f x x +≥，且2223()1x f x ++的最大值为1，求b 、c 满足的条件．加试部分21．[选做题]A ．选修4—1：几何证明选讲如图，设AB 为⊙O 的任一条不与直线l 垂直的直径，P 是⊙O 与l 的公共点，AC ⊥l ，BD ⊥l ，垂足分别为C ，D ，且PC=PD ，求证：（1）l 是⊙O 的切线；（2）PB 平分∠ABD ．B ．选修4—2：矩阵与变换二阶矩阵M 对应的变换将点(1,1)-与(2,1)-分别变换成点(1,1)--与(0,2)-．求矩阵M ；C ．选修4—4：坐标系与参数方程若两条曲线的极坐标方程分别为ρ =l 与ρ =2cos(θ+π3)，它们相交于A ，B 两点，求线段AB 的长．D ．选修4—5：不等式选讲求函数()f x =[必做题]22．（本小题10分）口袋中有)(*N ∈n n 个白球，3个红球．依次从口袋中任取一球，如果取到红球，那么继续取球，且取出的红球不放回；如果取到白球，就停止取球．记取球的次数为X ．若307)2(==X P ，求：（1）n 的值；（2）X 的概率分布与数学期望．23．（本小题10分）已知曲线1:(0)C y x x=>，过1(1,0)P 作y 轴的平行线交曲线C 于1Q ，过1Q 作曲线C 的切线与x 轴交于2P ，过2P 作与y 轴平行的直线交曲线C 于2Q ，照此下去，得到点列12,,P P ⋅⋅⋅，和12,,Q Q ⋅⋅⋅，设||n n n P Q a =*1|()n n nQ Q b n N +=∈．（1）求数列{}n a 的通项公式；（2）求证：1222n n n b b b -++⋅⋅⋅+>-；（3）求证：曲线C 与它在点n Q 处的切线，以及直线11n n P Q ++所围成的平面图形的面积与正整数n 的值无关．2018届高三数学模拟试卷参考答案 2018.51.{1,2,3}2. 23. 914. 直角三角形5.46. ①④7. 188.21n n ++ 9.1y x e =. 10.3 11.20462047 12. 56π 13. 2314.515. （Ⅰ）分数在[)70,80内的频率为：1(0.0100.0150.0150.0250.005)10-++++⨯10.70.3=-=，故0.30.0310=，如图所示：（Ⅱ）平均分为：450.1550.15650.15750.3850.25950.0571x =⨯+⨯+⨯+⨯+⨯+⨯=．（Ⅲ）由题意，[)60,70分数段的人数为：0.15609⨯=人；[)70,80分数段的人数为：0.36018⨯=人；∵在[)80,60的学生中抽取一个容量为6的样本，∴[)60,70分数段抽取2人，分别记为,m n ；[)70,80分数段抽取4人，分别记为,,,a b c d ；设从样本中任取2人，至多有1人在分数段[)80,70为事件A ，则基本事件空间包含的基本事件有：(,)m n 、(,)m a 、(,)m b 、(,)m c 、(,)m d 、……、(,)c d 共15种，则事件A 包含的基本事件有：(,)m n 、(,)m a 、(,)m b 、(,)m c 、(,)m d 、(,)n a 、(,)n b 、(,)n c 、(,)n d 共9种， ∴93()155P A ==． 16. （1）2；（217. 证明：⑴连BD ，∵ 面ABCD 为菱形，∴BD ⊥AC 由于平面AA 1C 1C ⊥平面ABCD ，则BD ⊥平面AA 1C 1C 故： BD ⊥AA 1 ⑵连AB 1，B 1C ，由棱柱ABCD-A 1B 1C 1D 1的性质知AB 1//DC 1，AD//B 1C ，AB 1∩B 1C=B 1,A 1D ∩DC 1=D 由面面平行的判定定理知：平面AB 1C//平面DA 1C 1⑶存在这样的点P 因为A 1B 1∥AB ∥DC ，∴四边形A 1B 1CD 为平行四边形． ∴A 1D//B 1C 在C 1C 的延长线上取点P ，使C 1C=CP ，连接BP ，因B 1B ∥CC 1，∴BB 1∥CP ，∴四边形BB 1CP 为平行四边形则BP//B 1C ，∴BP//A 1D ∴BP//平面DA 1C 1 18. （1）设000(,)(0)P x y y ≠，则22002x y +=．当01x =-时，直线1l 过点(1,0)T -，(3,0)S ∴-，即00(3,)PS x y =---，2200031OP PS x x y ∴⋅=---=．当01x ≠-时，直线1l 过点(1,0)T -，∴直线1l 的斜率0101y k x =+，∴直线OS 的斜率001x k y +=-，其方程为001x y x y +=-，0033(3,)x S y +∴-，即000033(3,)x PS x y y +=---． 220000333321OP PS x x x y ∴⋅=--++-=-=．故“如果直线1l 过点(1,0)T -，那么1OP PS ⋅=”为真命题．（2）逆命题为：如果1OP PS ⋅=，那么直线1l 过点(1,0)T -．逆命题也为真命题，以下给出证明：设000(3,),(,)(0)S t P x y y -≠，则00(3,)PS x t y =---，1OP PS ⋅=，22000031x x ty y ∴--+-=，又22002x y +=，033=x t y +∴．当01x =-时，直线1l 的方程为1x =-，显然过点(1,0)-；当01x ≠-时，直线OS 的斜率001x k y +=-，∴直线1l 的方程为0000()1y y y x x x -=-+，令0y =，得1x =-，∴直线1l 过定点(1,0)-．综上，直线1l 恒过定点(1,0)-．19. 解（1）因为点1(,)n n n P a S +在函数()1f x x =+的图象上，所以*11()n n S a n N +=+∈，因为1121S a a ==+，211a a =-，12231a a S a +==+，3122a a =-．又数列{}n a 为等比数列，所以2213a a a =，即2111(1)(22)a a a -=-，故11a =-，或11a =（舍去）．（2）由（1）知数列{}n a 是以11a =-为首项，2q =为公比的等比数列．所以1(12)12n n S --=-12n =-，12n n S -=．由121244444(1)n n n b b b b b b b n n S ++⋅⋅⋅+⋅⋅⋅⋅⋅⋅⋅==- 22222n n nb n nb n +=⋅=，得122()2n n b b b n nb ++⋅⋅⋅+=+对*n N ∈成立． ①则12112()2(1)(1)n n n b b b b n n b ++++⋅⋅⋅++=+++对*n N ∈成立． ②②-①，得1122(1)n n n b n b nb ++=++-，即1(1)2n n n b nb +-+=对*n N ∈成立． ③ 则有212(1)n n nb n b +++=+对*n N ∈成立． ④④－③，得211(1)(1)n n n n nb n b n b nb +++--=+-，21()2n n n n b b nb +++=，即212n n n b b b +++=对*n N ∈成立．由等差数列定义，知{}n b 为等差数列．当1n =时，由①式得1122b b =+，12b =，则公差213d b b =-=，所以*23(1)31()n b n n n N =+-=-∈． 20.（1）由题意222b--≤≤，44b ∴-≤≤；（2）须2x bx c x ++≥与2x bx c x ++≥-同时成立，即22(1)40(1)40b c b c ⎧--≤⎪⎨+-≤⎪⎩，2+14b c ∴≤；（3）因为1||2x x+≥，依题意，对一切满足||2x ≥的实数x ，有()0f x ≥． ①当()0f x =有实根时，()0f x =的实根在区间[2,2]-内，设2()f x x bx c =++，所以(2)0(2)0222f f b ⎧⎪-≥⎪≥⎨⎪⎪-≤-≤⎩，即42042044b c b c b -+≥⎧⎪++≥⎨⎪-≤≤⎩，又2222312(2,3]11x x x +=+∈++，于是，2223()1x f x ++的最大值为(3)1f =，即931b c ++=，从而38c b =--．故423804238044b b b b b ---≥⎧⎪+--≥⎨⎪-≤≤⎩，即45444b b b ⎧≤-⎪⎪≤-⎨⎪-≤≤⎪⎩，解得4,4b c =-=． ②当()0f x =无实根时，240b c ∆=-<，由二次函数性质知，2()f x x bx c =++在(2,3]上的最大值只能在区间的端点处取得，所以，当(2)(3)f f >时，2223()1x f x ++无最大值．于是，2223()1x f x ++存在最大值的充要条件是(2)(3)f f ≤，即4293b c b c ++≤++，所以，5b ≥-．又2223()1x f x ++的最大值为(3)1f =，即931b c ++=，从而38c b =--．由240b c ∆=-<，得212320b b ++<，即84b -<<-．所以b 、c 满足的条件为380b c ++=且54b -≤<-．综上：380b c ++=且5 4.b -≤≤-加试部分21A ．证明：（1）连结OP ，因为AC ⊥l ，BD ⊥l ，所以AC//BD ．又OA=OB ，PC=PD ，所以OP//BD ，从而OP ⊥l ．因为P 在⊙O 上，所以l 是⊙O 的切线．（2）连结AP ，因为l 是⊙O 的切线，所以∠BPD=∠BAP ．又∠BPD+∠PBD=90°，∠BAP+∠PBA=90°，所以∠PBA=∠PBD ，即PB 平分∠ABD ．21B.1234M ⎡⎤=⎢⎥⎣⎦；21C ．由1ρ=得221x y +=，又22cos()cos ,cos sin 3πρθθθρρθθ=+=∴=220x y x ∴+-=，由222210x y x y x ⎧+=⎪⎨+-=⎪⎩得1(1,0),(,2A B -,AB ∴==． 21D.由柯西不等式，()f x=≤==1=76x =时，()f x22.（1）由题知,307)2)(3(3)2(23113=++=⨯==+n n n A A A X P n n 2*755420,(76)(7)0.,7.n n n n n N n -+=--=∈=即即因所以为（2）由题知，X 的可能取值为1，2，3，4，所以,120112073071071)4(,1207)3(,307)2(,107)1(310172311017=---==========X P A A A X P X P A A X P所以，X 的概率分布表为所以.811120141207330721071)(=⨯+⨯+⨯+⨯=X E 答X 的数学期望是.81123.（1）/211,y y x x=∴=-．设(,)n n n Q x y ，则直线1n n Q P +的方程为21()n n n y y x x x -=--，令0y =，得21n n n nx x x y +=+，11,2n n n n x y x x +=∴=，则数列{}n x 是首项为1，公比为2的等比数列，于是12n n x -=．从而____ 姓名_____________ 学内……………不……………要……………答……………题………………111||2n n n n n n a P Q y x -====．（2）11111(,),(,)n n n n n n Q a Q a a a +++， 1|n n n b Q Q +∴====．利用2222()()(0,0)a b ab a b +≥+>>，当且仅当a b =时取等号，得1122n n n b -=>+．于是121111(1)(2)(2)222n n i n i b -=>++++⋅⋅⋅++∑12111(122)(+)222n n -=++⋅⋅⋅+++⋅⋅⋅+11(1)121222112212nn n n --=+=---．（3）曲边三角形11n n n Q P Q ++是由曲线1y x=与直线11n n P Q ++、切线1n n Q P +所围成的图形．于是1212[()]n nx x n n x S dx x x x +=--+⎰2212()n n x x n n x dx x x x =+-⎰2222[ln ]2nn x x n nx x x x x =+- 1(ln 224)(ln 2)2n n x x =+--+-1ln 22=-，与n 无关，为定值．江苏省扬州中学2018届高三数学模拟试卷答题纸一、填空题：（本大题共14小题，每小题5分，共70分．）1． 2． 3． 4． 5． 6． 7． 8． 9． 10． 11． 12． 13． 14．二、解答题：（本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤．）15．第15题图16．17．Array18．19．____ 座位号_____ 班级___________ 姓名_____________ 学………封……………线……………内……………不……………要……………答……………题………………（20题请写在反面答题纸上）江苏省扬州中学2018届高三模拟考试数学附加题答题纸1． 2． 3．4．。

扬州市2017—2018学年度高三第四次调研测试参考答案(1)

2 m
，又
AM⊥AN，所以 kAN
m， 2
所以直线 AN 的方程为 y m x 2 ， 2
……6 分
联列 y m x 2
2
与
x2 6
y2 2
1得(2＋3m2)x2＋12mx＝0，所以 xN
12m ……10 3m2 2
分
所以 AN
2 m2 12m 2 3m2 2
……12 分
在直角 AMN 中，由 AMN 60 得 AN 3AM ，
10
10
在 ABC 中， a b ，即 3 2 ，所以 sin B 5 ，
sin A sin B 3 10 sin B
5
10
……8 分 ……10 分
又 A ( , ) ，所以 B (0, ) ，所以 cos B 1 sin2 B 1 ( 5 )2 2 5
2
2
5
5
所以 cos(B A) cos B cos A sin B sin A 2 5 ( 10 ) 5 3 10 2 ． 14 分
……5 分
令 f () 0 ，则 1 2, 2 3 ．
21．C．解：直线 cos( ) 2 的直角坐标系方程为 x y 2 ，
4
令 y 0，所以 C(2, 0) ，
……10 分 ……5 分
所以以点 C 为圆心且半径为1的圆的直角坐标系方程为 (x 2)2 y2 1，
即 x2 y2 4x 3 0 ，所以所求的的极坐标方程为 2 4 cos 3 0 ．
a1
1 2
5
；
综合①②得： 0 a1
1 2
5
（3）由数列{a2n}是首项为1 、公差为1 的等差数列；数列 {a2n1}是首项为正整数 a1 、公差为1 的等差数列知，

(全优试卷)江苏省扬州中学高三5月第四次模拟考试数学Word版含答案

扬州中学高三数学试卷 2018.5.18必做题部分一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置．．．．．．．上．． 1、已知集合{1,0,2},{21,},A B x x n n Z =-==-∈则A B ⋂= ▲ ．2、已知复数1212,2z i z a i =-=+（其中i 是虚数单位，a R ∈），若12z z ⋅是纯虚数，则a 的值为 ▲ ．3、从集合{1,2,3}中随机取一个元素，记为a ，从集合{2,3,4}中随机取一个元素，记为b ，则a b ≤的概率为 ▲ ．4、对一批产品的长度（单位:毫米）进行抽样检测，样本容量为400，右图为检测结果的频率分布直方图，根据产品标准，单件产品长度在区间[25,30)的为一等品，在区间[20,25) 和[30,35)的为二等品，其余均为三等品，则样本中三等品的件数为 ▲ ．5、运行右面的算法伪代码，输出的结果为S= ▲ ．6、若双曲线2222:1(0,0)x y C a b a b-=>>的离心率为10，则双曲线C 的渐近线方程为 ▲ ．7、正三棱柱ABC -A 1B 1C 1的底面边长为2，侧棱长为3，D 为BC 中点，则三棱锥A -B 1DC 1的体积为 ▲ ．8、函数cos(2)()y x ϕπϕπ=+-≤≤的图象向右平移2π个单位后，与函数sin(2)3y x π=+的图象重合，则ϕ= ▲ ．S 011011(1)Pr int For i From To Step S S i i End For S←←++9a= ▲ ．1011▲ ．12M 为BC 的中点，D 为以AC 为直径的圆上一动点，的最小值是 ▲ ．13数恰有4的取值范围是▲ ．14、的取值范围为 ▲ ．二、解答题：本大题共6小题，共计90分．请在答题卡指定区域．．．．．．．内作答．解答时应写出文字说明、证明过程或演算步骤．15、全优试卷且1m n ⋅=u r r.(1)求角A 的大小；(2)若223b c a +==，求sin()π-4B 的值16、如图，四棱锥P —ABCD 中，四边形ABCD 为菱形，P A ⊥平面ABCD ，BD 交AC 于点E ，F 是线段PC 中点，G 为线段EC 中点．（1）求证：FG//平面PBD ；（2）求证：BD ⊥FG ．17、已知椭圆)0(1:2222>>=+b a b y a x C 的左焦点为F ，上顶点为A ，直线AF 与直线023=-+y x 垂直，垂足为B ，且点A 是线段BF 的中点.（1）求椭圆C 的方程；（2）若M ，N 分别为椭圆C 的左，右顶点，P 是椭圆C 上位于第一象限的一点，直线MP 与直线4=x 交于点Q ，且9MP NQ =u u u r u u u rg ，求点P 的坐标.18、中国古建筑中的窗饰是艺术和技术的统一，给人以美的享受．如图为一花窗中的一部分，呈长方形，长30 cm ，宽26 cm ，其内部窗芯（不含长方形边框）用一种条形木料做成，由两个菱形和六根支条构成，整个窗芯关于长方形边框的两条对称轴成轴对称．设菱形的两条对角线长分别为x cm 和y cm ，窗芯所需条形木料的长度之和为L ．（1）试用x ，y 表示L ；（2）如果要求六根支条的长度均不小于2 cm ，每个菱形的面积为130 cm 2，那么做这样一个窗芯至少需要多长的条形木料（不计榫卯及其它损耗）？19、已知函数2()=x x f x e，（1）求函数()f x 的单调区间；（2）当240m e <<时，判断函数2(),(0)x xg x m x e=-≥有几个零点，并证明你的结论；（3）设函数21111()+()()22⎡⎤=-----⎢⎥⎣⎦h x x f x x f x cx x x ，若函数()h x 在()0,+∞为增函数，求实数c 的取值范围．20、.（1（2）若数列”，整数，试问：是否存在数使得可能值，如果不存在，请说明理由。

【2018-2019】2018届江苏省扬州中学高考数学模拟试卷及答案-实用word文档 (9页)

本文部分内容来自网络整理，本司不为其真实性负责，如有异议或侵权请及时联系，本司将立即删除！== 本文为word格式，下载后可方便编辑和修改！ ==2018届江苏省扬州中学高考数学模拟试卷及答案备考高考数学最简单有效的方法就是多做数学模拟试卷题，多做高考数学模拟试卷题能够帮助我们熟悉解题技巧和思路，下面是小编为大家精心推荐的2018届江苏省扬州中学高考数学模拟试卷，希望能够对您有所帮助。

2018届江苏省扬州中学高考数学模拟试卷题目一.填空题：1.已知全集U={1，2，3，4，5，6}，A={1，3，5}，B={1，2，3，5}，则∁U(A∩B)=.2.“ ”是“ ”的条件.(填：充分不必要、必要不充分、充要、既不充分又不必要)3.如图所示，该伪代码运行的结果为 .4. 已知一组数据为8,12,10,11,9.则这组数据方差为____________.5. 已知实数x,y满足条件，为虚数单位)，则的最小值等于 .6.已知向量夹角为45°，且，则 = .7.函数在处的切线方程为 .8.在区间内随机地取出一个数，则恰好使1是关于的不等式的一个解的概率大小为_____ __.9.已知正四棱锥的体积是48cm3，高为4cm，则该四棱锥的侧面积是 cm2.10.若，则的最大值为__________ ____.11.由直线上的点向圆引切线，则切线长的最小值为 .直角的三边满足，则面积的最大值是13.设数列满足，且对任意的，满足则 =____________ __.14.如图，直角梯形中，∥ ， .在等腰直角三角形中，，点分别为线段上的动点，若，则的取值范围是 _____________.二.解答题：15. (本小题14分) 已知均为锐角,且 , .(1)求的值; (2)求的值.16. (本小题14分)如图，四棱锥中，底面是菱形，，，为的中点， .(1)求证： ;(2)若菱形的边长为，，求四面体的体积;17. (本小题14分)如图，某生态园将一块三角形地的一角开辟为水果园，已知角为，的长度均大于200米，现在边界处建围墙，在处围竹篱笆.(1)若围墙、总长度为200米，如何可使得三角形地块面积最大?(2)已知竹篱笆长为米，段围墙高1米，段围墙高2米，造价均为每平方米100元，求围墙总造价的取值范围.18.(本小题16分)已知椭圆的离心率为，左、右焦点分别为圆，是上一点，，且 .(1)求椭圆的方程;(2)当过点的动直线与椭圆相交于不同两点时，线段上取点，且满足，证明点总在某定直线上，并求出该定直线的方程.19. (本小题16分)已知函数 ( 为自然对数的底数).(1)当时，直接写出的值域(不要求写出求解过程);(2)若，求函数的单调区间;(3)若，且方程在内有解，求实数的取值范围.20. (本小题16分) 若数列和的项数均为，则将定义为数列和的距离.(1) 已知 , ， ,求数列和的距离 .(2) 记为满足递推关系的所有数列的集合，数列和为中的两个元素，且项数均为 .若，，数列和的距离大于201X ，求的最小值.(3) 若存在常数M>0,对任意的，恒有则称数列和的距离是有界的.若与的距离是有界的，求证：与的距离是有界的.第Ⅱ卷(共40分)21B.矩阵与变换(本小题满分10分)若点A(2，2)在矩阵M= 对应变换的作用下得到的点为B(一2，2)，求矩阵M的逆矩阵.21C.坐标系与参数方程(本小题满分10分)在直角坐标系中，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为，直线的参数方程为 ( 为参数).(1)求曲线的普通方程;(2)若直线与曲线交于两点，点的坐标为，求的值.22. (本题满分10分)如图，在棱长为3的正方体ABCD﹣A1B1C1D1中，A1E=CF=1.(1)求两条异面直线AC1与D1E所成角的余弦值;(2)求直线AC1与平面BED1F所成角的正弦值.23.(本小题满分10分)已知非空有限实数集S的所有非空子集依次记为S1，S2，S3，……，集合Sk中所有元素的平均值记为bk.将所有bk组成数组T：b1，b2，b3，……，数组T中所有数的平均值记为m(T).(1)若S={1，2}，求m(T);(2)若S={a1，a2，…，an}(n∈N*，n≥2)，求m(T).2018届江苏省扬州中学高考数学模拟试卷答案。

优质金卷：江苏省扬州树人学校2018届高三模拟考试(四)数学试题(考试版)

绝密★启用前江苏省扬州树人学校2018届高三模拟考试（四）数学试题考试范围：高考范围（不含选讲内容）；考试时间：120分钟；【名师解读】本卷难度中等，全卷梯度设置合理．命题内容符合考试说明命题要求，全卷覆盖面广，涵盖了高考数学内容，无偏难怪出现，命题所占比例基本符合教章所占比例，重点内容重点考查.全卷突出基础知识、基本运算能力及推理论证能力的考查，选题贴近高考.一、填空题1．已知集合错误！未找到引用源。

，错误！未找到引用源。

，则错误！未找到引用源。

__________．2．在复平面内，复数错误！未找到引用源。

（错误！未找到引用源。

为虚数单位）对应的点位于第__________象限．3．设错误！未找到引用源。

，则“错误！未找到引用源。

”是“错误！未找到引用源。

”的__________条件．（填“充分不必要”、“必要不充分”、“充要”或“既不充分也不必要”）4．为了了解一批产品的长度（单位：毫米）情况，现抽取容量为400的样本进行检测，如图是检测结果的频率分布直方图，根据产品标准，单件产品长度在区间错误！未找到引用源。

的一等品，在区间错误！未找到引用源。

和错误！未找到引用源。

的为二等品，其余均为三等品，则样本中三等品的件数为__________．5．运行如图所示的算法流程图，输出的错误！未找到引用源。

的值为__________．6．在平面直角坐标系错误！未找到引用源。

中，若抛物线错误！未找到引用源。

上横坐标为1的点到焦点的距离为4，则该抛物线的焦点到准线的距离为__________．7．书架上有5本书，其中语文书2本，数学书3本，从中任意取出2本，则取出的两本书都是数学书的概率为__________．8．已知等差数列错误！未找到引用源。

的前错误！未找到引用源。

项和为错误！未找到引用源。

，且错误！未找到引用源。

，则错误！未找到引用源。

__________．9．记棱长为1的正三棱锥的体积为错误！未找到引用源。

2018届江苏省扬州中学高三下学期周练数学试题及答案

2018届扬州中学高三数学周练卷第I 卷(必做题共160分)一、填空题：本大题共14小题，每小题5分，共70分．把答案填在题中横线上．1．已知复数i zz=-+11，则z 的虚部为 ▲ ．2．为了检查某超市货架上的奶粉是否含有三聚氰胺，要从编号依次为01到50的袋装奶粉中抽取5袋进行检验，现将50袋奶粉按编号顺序平均分成5组，用每组选取的号码间隔一样的系统抽样方法确定所选取的5袋奶粉的编号，若第4组抽出的号码为36，则第1组中用抽签的方法确定的号码是 ▲ .3．右图是一个算法的伪代码，输出结果是 ▲ ．4．已知函数2()log f x x =．在区间122⎡⎤⎢⎥⎣⎦，上随机取一0x ，则使得0()0f x ≥的概率为 S ←0a ←1For I From 1 to 3 a ←2×a S ←S ＋a End For Print S（第3题）▲ ．5．若直线()2210a a x y +-+=的倾斜角为钝角，则实数a 的取值范围是 ▲ ． 6．若直线2y x m =+是曲线ln y x x =的切线，则实数m 的值为 ▲ ．7．将函数⎪⎭⎫⎝⎛+=42sin 2)(πx x f 的图像向右平移)0(>ϕϕ个单位，再将图像上每一点横坐标缩短到原来的21倍，所得图像关于直线4π=x 对称，则ϕ的最小正值为▲ ．8．已知m ，n 是空间中两条不同的直线，α，β，γ是空间中三个不同的平面，则下列命题正确的序号是 ▲ ．①若//m n ，m β⊥，则n β⊥； ②若//m n ，//m β，则//n β； ③若//m α，//m β，则//αβ； ④若αγ⊥，βγ⊥，则//αβ．9．若中心在原点、焦点在坐标轴上的双曲线的一条渐近线方程为30x y +=，则此双曲线的离心率为 ▲ ；10.若c b a ,,为正实数，,0111,=++==zyxc b a z y x 则=abc ▲ ．11．已知b a ,为不共线的向量，设条件M ： )(b a b -⊥；条件N ：对一切x ∈R ，不≥-M 是N 的 ▲ 条件．12. 已知0x >，0y >，1x y +=，则2221x y x y +++的最小值为 ▲ ．13．对任意x ∈R ，函数()f x 满足1(1)2f x +=，设)()]([2n f n f a n -=，数列}{n a 的前15项的和为3116-，则(15)f = ▲ ． 14. 集合{}22(,)(cos )(sin )1x y x r y r θθ-+-≤其中01,0r θπ≤≤≤≤，对应图形的面积为 ▲ ．二、解答题：本大题6小题，共90分 15．(本题满分14分)已知函数)()2cos sin 222xx xf x =-．（1）设ππ22θ⎡⎤∈-⎢⎥⎣⎦，，且()1f θ=，求θ的值；（2）在△ABC 中，AB =1，()1f C ，且△ABC，求sin A +sin B的值．16．(本题满分14分)如图，在四棱锥P －ABCD 中，PD ⊥平面ABCD ，四边形ABCD 是菱形，AC ＝6，BD＝8，E 是PB 上任意一点，△AEC 面积的最小值是3．（Ⅰ）求证：AC ⊥DE ；（Ⅱ）求四棱锥P －ABCD 的体积．17．(本题满分14分) 在平面直角坐标系xOy 中，如图，已知椭圆E ：22221(0)y x a b a b +=>>的左、右顶点分别为1A 、2A ，上、下顶点分别为1B 、2B ．设直线11A B 的倾斜角的正弦值为13，圆C 与以线段2OA （1）求椭圆E 的离心率；（2）判断直线11A B 与圆C 的位置关系，并说A（第16题）CDE PFB明理由；（3）若圆C 的面积为π，求圆C 的方程．18．(本题满分16分) 一个如图所示的不规则形铁片，其缺口边界是口宽4分米，深2分米（顶点至两端点,A B 所在直线的距离）的抛物线形的一部分，现要将其缺口边界裁剪为等腰梯形．（1）若保持其缺口宽度不变，求裁剪后梯形缺口面积的最小值；（2）若保持其缺口深度不变，求裁剪后梯形缺口面积的最小值．19．（本小题共16分）已知数列{}n a ，{}n b 满足12a =，121n n n a a a +=+，1n n b a =-，数列{}n b 的前n 项和为n S ，2n n n T S S =-.（1）求数列{}n b 的通项公式；（2）求证：1n n T T +>；（3）求证：当2n ≥时，271112nn S +≥．20．（本小题共16分）已知函数12()416mxf x x =+，m x x f -=)21()(2，其中m ∈R ．（1）若0<m ≤2，试判断函数f (x )=f 1 (x )+f 2 (x )()[2,)x ∈+∞的单调性，并证明你的结论；（2）设函数12(),2,()(), 2.f x xg x f x x ⎧=⎨<⎩≥ 若对任意大于等于2的实数x 1，总存在唯一的小于2的实数x 2，使得g (x 1) = g (x 2) 成立，试确定实数m 的取值范围．高三数学附加题 0421．已知矩阵13213A⎡⎤⎢⎥=⎢⎥⎢⎥-⎢⎥⎣⎦，点()1,1M-，()0,2N．求线段MN在矩阵1A-对应的变换作用下得到线段M N''的长度．22.在直角坐标系xOy 中，曲线C 的参数方程为⎩⎨⎧=+=θθθ2sin cos sin y x (θ为参数)，若以直角坐标系xOy 的O 点为极点，x 轴正方向为极轴，且长度单位相同，建立极坐标系，得直线l 的极坐标方程为16cos 2=⎪⎭⎫⎝⎛+πθρ．求直线l 与曲线C 交点的极坐标．23.如图所示的几何体中，面CDEF CD AB //，BC AB 2=，60ABC ∠= ，且平面CDEF ⊥平面ABCD ．(1)求BC 与平面EAC 所成角的正弦值；(2)线段ED 上是否存在点Q ，使平面EAC ⊥平面证明你的结论．24．对有()4n n ≥个元素的总体{}n ,,3,2,1 进行抽样，先将总体分成两个子总体{}m ,,3,2,1 和{}n m m ,,2,1 ++(m 是给定的正整数，且22m n -≤≤)，再从每个子总体中各随机抽取2个元素组成样本．用ij P 表示元素i 和j 同时出现在样本中的概率． (1)求n P 1的表达式(用n m ,表示)； (2)求所有)1(n j i P ij ≤<≤的和．4.26参考答案：一、填空题1．1．2．06 3．14． 4。

江苏省扬州中学2018届高三5月第四次模拟考试化学

考试结束后，请将本试卷和答题卡一并交回。

2．答题前，请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。

3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符。

4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案。

作答非选择题，必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效。

5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗。

可能用到的相对原子质量：H-1 C-12 N-14 O-16 Na-23 S-32 Cu-64 Ba-137 V-51选择题单项选择题：本题包括10小题，每小题2分, 共计20分。

每小题只有一个．．．．选项符合题意。

1. 2018年是“2025中国制造”启动年，而化学与生活、人类生产、社会可持续发展密切相关，下列有关化学知识的说法错误．．的是A．高纯度的二氧化硅广泛用于制作光导纤维，光导纤维遇强碱会“断路”B．我国发射“嫦娥三号”卫星所使用的碳纤维，是一种非金属材料C．用聚氯乙烯代替木材，生产快餐盒，以减少木材的使用D．碳纳米管表面积大，可用作新型储氢材料2. 化学科学需要借助化学专用语言描述，下列有关化学用语表示正确的是A.碳铵的化学式: NH4HCO3B. 次氯酸的结构式：H—Cl—OC. 中子数为145、质子数为94的钚(Pu)原子：145 94PuD. S2﹣的结构示意图：3. 下列家庭化学实验不能达到预期目的的是A. 用灼烧并闻气味的方法区别纯棉织物和纯羊毛织物B. 用湿润的淀粉-KI 试纸检验 HCl 气体中是否混有 Cl 2C. 向 Ca(ClO)2 溶液中加入硫酸溶液，来证明 S 、Cl 的非金属性强弱D. 将一片铝箔用火灼烧，铝箔熔化但不滴落，证明铝箔表面致密Al 2O 3薄膜的熔点高于Al4. 下列实验装置设计不能．．达到目的的是A ．实验I ：所示装置可制备氨气B ．实验II ：检验电解饱和食盐水的产物C12C ．实验III ：制取并观察Fe(OH)2沉淀D ．实验IV ：吸收SO 25. A 、B 、C 是原子序数依次增大的短周期主族元素，三种元素原子序数之和为35，且C 的原子序数是A 的2倍。

届扬州市高三数学模拟试卷及答案

届扬州市高三数学模拟试卷及答案2018届扬州市高三数学模拟试卷及答案高考即将到来，们高考数学复习的怎么样呢，不如让我们做套高考模拟试卷来看看吧，以下是店铺为你整理的2018届扬州市高考数学模拟试卷，希望能帮到你。

2018届扬州市高考数学模拟试卷题目一、填空题(本大题共14小题，每小题5分，共70分，请将答案填写在答题卷相应位置)1.已知，则▲ .2.若复数满足，则复数在复平面上对应的点在第▲ 象限.3.随着社会的发展，食品问题渐渐成为社会关注的热点，为了提高学生的食品安全意识，某学校组织全校学生参加食品安全知识竞赛，的频率分布直方图如下图所示，数据的分组依次为，，，，若该校的学生总人数为3000，则成绩不超过60分的学生人数大约为▲ .4.在区间内任取一个实数 , 则满足的概率为▲ .5.如图是一个算法流程图，则输出的值为▲ .6.函数的定义域为▲ .7.已知双曲线的一条渐近线方程为，则该双曲线的焦距为▲ .8.已知，则▲ .9.已知圆锥的侧面展开图是半径为4，圆心角等于的扇形，则这个圆锥的体积是▲10.已知圆为常数)与直线相交于两点，若，则实数▲ .11、设等差数列的前项和为，若，，则的最小值为▲ .12.若动直线与函数，的图象分别交于两点，则线段长度的最大值为▲ .13.在中，、分别是、的中点，是直线上的动点.若的面积为2，则的最小值为▲ .14.已知函数有两个不相等的零点，则的最大值为▲ .二、解答题(本大题共6小题，共90分.解答应写出必要的文字说明、证明过程或演算步骤)15.(本小题满分14分)在中，角A,B,C的对边分别为a,b,c，若， .⑴求的值;⑵若，求的面积.16.(本小题满分14分)如图，在四棱锥P-ABCD中，底面ABCD为梯形，CD∥AB，AB=2CD，AC交BD于O，锐角PAD所在平面⊥底面ABCD，PA⊥BD，点Q在侧棱PC上，且PQ=2QC.求证：⑴PA∥平面QBD;⑵BD AD.17.(本小题满分14分)如图是一座桥的截面图，桥的路面由三段曲线构成，曲线和曲线分别是顶点在路面、的抛物线的一部分，曲线是圆弧，已知它们在接点、处的切线相同，若桥的.最高点到水平面的距离米，圆弧的弓高米，圆弧所对的弦长米.(1)求弧所在圆的半径;(2)求桥底的长.18.(本小题满分16分)如图，已知椭圆的左顶点，且点在椭圆上，、分别是椭圆的左、右焦点。

江苏省扬州中学2018届高三5月第四次模拟考试 数学 Word版含答案

2018届高三数学5月份第四次模拟考试

江苏省扬州中学高三数学5月卷(四模卷)

2018届江苏省扬州中学高三上学期月考数学试题及答案

江苏省扬州中学2018届高三5月第四次模拟考试化学试卷(附答案)

江苏省扬州树人学校2018届高三模拟考试(四)数学试题(解析版)

扬州市2017—2018学年度高三第四次调研测试参考答案

江苏省扬州市2018届高三5月第四次模拟考试数学试题及答案

江苏省扬州市高三数学第四次模拟考试试卷-人教版高三全册数学试题

高考数学试题-江苏省扬州中学2018年高三第四次模试题(数学) 最新

扬州市2017—2018学年度高三第四次调研测试参考答案(1)

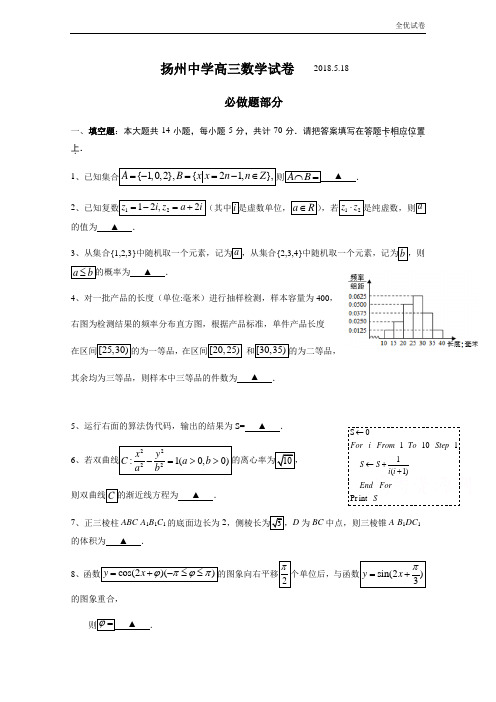
(全优试卷)江苏省扬州中学高三5月第四次模拟考试数学Word版含答案

【2018-2019】2018届江苏省扬州中学高考数学模拟试卷及答案-实用word文档 (9页)

优质金卷：江苏省扬州树人学校2018届高三模拟考试(四)数学试题(考试版)

2018届江苏省扬州中学高三下学期周练数学试题及答案

江苏省扬州中学2018届高三5月第四次模拟考试化学

届扬州市高三数学模拟试卷及答案

江苏省扬州中学2018届高三5月第四次模拟考试数学 Word版含答案