Lingo在优化水文地质参数估值中的应用

合集下载

关于介绍lingo的推文

关于介绍lingo的推文-概述说明以及解释1.引言1.1 概述Lingo是一种智能语音识别技术，它基于人工智能和自然语言处理技术，能够将语音转换为文本。

随着智能语音助手和语音交互技术的快速发展，Lingo在多个领域得到了广泛的应用。

通过使用Lingo，我们可以实现语音转文字的功能，从而提高工作效率和便利性。

在这篇文章中，我们将会介绍Lingo的特点、应用领域以及它的优势和劣势。

首先，我们将详细解释什么是Lingo以及它的工作原理。

接着，我们将探讨Lingo在各个领域中的应用，比如智能音箱、智能助手和语音识别系统等。

我们将阐述Lingo在提供便捷的语音输入和与计算机进行语音交互方面的独特优势。

然而，正如任何一项技术都有其优势和劣势一样，Lingo也不例外。

我们将探讨Lingo的优点，比如高准确性、快速响应和便捷性。

同时，我们也会分析其劣势，如对口音和背景噪音的敏感性以及隐私安全问题。

了解这些优势和劣势将有助于我们更好地了解Lingo的实际应用场景，以及在使用中需要注意的问题。

最后，在结论部分，我们将总结Lingo的重要性并展望其未来的发展。

我们将探讨Lingo在语音识别技术中的前景以及其对人们日常生活和工作的影响。

同时，我们也会提出一些问题和建议，以希望进一步推动Lingo 技术的发展和改进。

通过本文的阅读，读者将对Lingo有一个全面的了解，包括其概念和工作原理，以及在各个领域的应用和其带来的优势和劣势。

同时，读者也可以进一步思考Lingo未来的发展方向，以及如何更好地将其运用到我们的生活和工作中。

1.2 文章结构:本文将按照以下方式展开对Lingo的介绍。

首先，在引言部分我们会概述本文的主题和目的，并对文章整体结构进行说明。

接下来，我们将进入正文部分，详细探讨Lingo的定义、特点、应用领域以及其优势和劣势。

在结论部分，我们会总结Lingo的重要性，并展望其未来的发展。

最后，我们会以一个简短的结束语结束全文，并提出一些关于Lingo的问题或建议。

数学建模中的优秀软件——LINGO

第９卷第３期２００７年６月黄山学院学报ＪＯｕｒｎａｌ０ｆＨｕａｎｇｓｈａｎＵｎｉＶｅｆｓｉｔｙＶｏ】．９．ＮＯ．３Ｊｕｎ．２００７数学建模中的优秀软件——ＬＩＮＧＯ周甄川（黄山学院数学系，安徽黄山２４５０４１）摘要：介绍了数学建模的相关概念、数学建模竞赛概况，探讨了ＬＩＮＧｏ系统的功能与特点，以及它在数学建模中的应用。

关键词：数学模型；数学建模；ＬｌＮＧｏ系统中图分类号：ＴＰ３１９：０１４１．４文献标识码：Ａ文章编号：１６７２—４４７ｘ（２００７）０３—０１１２—０３在对自然科学与社会科学许多课题的研究中，科学工作者常将事物的变化规律用特定的数学表达式的形式加以描述。

将寻求这种确定事物变化规律的过程称为“数学建模”。

而在数学建模以及全国大学生数学建模竞赛中，最常碰到的是一类决策问题，即在一系列限制条件下，寻求使某个或多个指标达到最大或最小，这种决策问题通常称为最优化问题【１】。

最优化理论是近几十年发展和形成的一门新兴的应用性学科。

它主要解决最优生产计划、最优分配、最优设计、最优决策、最佳管理等最优化问题。

主要研究方法是定量化、系统化和模型化方法，特别是运用各种数学模型和技术来解决问题。

它主要由决策变量、目标函数、约束条件三个要素组成。

当遇到的实际问题时即使建立了模型，找到了解的方法，对于较大的计算量也是望而却步，ＬＩＮＧｏ系列优化软件包就给我们提供了理想的选择。

１什么是数学建模数学建模（ＭａｔｈｅＩｍｔｉｃａｌＭｏｄｅｌｉｎ曲‘１１顾名思义就是建立数学模型以解决实际问题的过程。

它利用数学和计算机对实际问题进行分析研究，抽象出反映事物内在活动规律的数学关系表达式，通过对这些数学关系表达式的求解和反复验证，最终解决实际问题。

数学是所有自然科学的基础，随着计算机软硬件技术的迅速发展，数学建模和与之相伴的计算已逐渐成为工程设计的关键工具，并在人类社会实践活动中的众多领域内发挥着越来越重要的作用。

那么，什么是数学模型？如何建立数学模型？如何用数学模型解决实际问题呢？模型就是对事物的一种抽象。

Lingo软件的应用

Lingo软件的应用颜宁生（北京服装学院）本人有一个“杜撰”课程对联的爱好，有一位同学在参加我的数学建模培训班后，给我写了一幅对联，表达了他对练好Lingo软件的决心。

上联：有心栽花花可以不开下联：无心插柳柳必须成荫横批：感悟拎购时间：2012，7，21地点：华南理工大学内容一、数学建模案例二、适合学生学习Lingo软件的两类入门题三、练会Lingo后的同学能帮老师做什么四、一份《数学建模》试卷模板一、数学建模案例上联：数学建模融入到现实生活当中下联：拎购软件嵌入到衣可晒单元格横批：嵌入技术嵌入技术过滤器的作用，把有用的信息过滤出来，从而求解的界面更生动和友好。

1.1、2012年北京工业大学数学建模C题1.1.1、假设为了简化模型的求解，假设每辆货车进入生产线后，其糖份就不再流失。

1.1.2、数学模型首先，将剩余时间分成4个时间段，设x（i，j）为0‐1变量，若第j辆货车在第i个时间段进入生产线，则x（i，j）=1，否则取0，（i=1，2，3，4；j=1，2，……，11），设a ij表示第j辆货车在第i个时间段进入生产线时能够加工出的蔗糖的百分比。

根据表C.1，得到a ij 值如下：aijj1234567891011i 111111111111 20.32490.547600.51840.75690.21160.14440.26010.65610.51840.49 30.10560.299900.268700.04480.02090.06770.43050.26870.2401 40.01110.089900.072200.0020.00040.00460.18530.07220.0576i=j=111max =a i j x i j st: x i j 3,1,2,3,4x i j (1,2,3,4;1,2, (11)j i i j =≤===∑∑∑41111（，）（，）（，）（，）=0或11.1.3、数学模型求解的Lingo 程序1.1.3.1、获取数据的Lingo 程序sets:h/1..2/;l/1..11/;hl(h,l):bg7;endsets data:bg7=@ole('C 题.xls','_bg7');@ole('C 题.xls','_g7')=bg7;enddata1.1.3.2、自动求解的Lingo 程序sets:h/1..4/;l/1..11/;hl(h,l):a,x;minimum/1/:h22;endsets data:a =@ole('C 题.xls','_g11');@ole('C 题.xls','_g17')=x;@ole('C 题.xls','h22')=h22;enddatamax=@sum(hl:a*x);@for(h(i):@sum(l(j):x(i,j))<=3);@for(l(j):@sum(h(i):x(i,j))=1);h22(1)=@sum(hl:a*x);@for(hl:@bin(x));End1.1.3.3、自动判解的Lingo 程序sets:h/1..4/;l/1..11/;hl(h,l):a,x;minimum/1/:y10;endsets data:a =@ole('C 题.xls','_g11');x=@ole('C题.xls','_g17');h22=@ole('C题.xls','h22');@ole('C题.xls','y10')=y10;enddatay10(1)=@if(@abs(h22-@sum(hl:a*x))#lt#0.01,100,0);end1.1.3.4、随机方案求甘蔗糖产量的Lingo程序sets:h/1..4/;l/1..11/;hl(h,l):a,x;minimum/1/:h23;endsetsdata:a=@ole('C题.xls','_g11');x=@ole('C题.xls','_g17');@ole('C题.xls','h23')=h23;enddatah23(1)=@sum(hl:a*x);end1.1.4、结果最优方案为：j1234567891011i 100100110000 200001000011 301010000100 410000001000即：第3辆、第6辆和第7辆第1批进入生产线；第5辆、第10辆和第11辆第2批进入生产线；第2辆、第4辆和第9辆第9批进入生产线；第1辆和第8辆第4批进入生产线；最优值为5.78009124，即能将11车甘蔗加工出5.78车甘蔗糖。

LINGO在工程优化设计中的应用

1. 引言
在工程项目中，如何统筹安排人力,物力，财力，达到最大限度降低工程造价的目的，具有重要的经济意义。这就要求运用运筹学中数学规划的方法和理论，但是工程问题的复杂性(主要是决策变量较多)决定了必须依靠计算机来达到求解的高效率。工程问题中的优化设计的一般方法，首先要将工程中的各个影响因素抽象为决策变量，并据此将问题转化为合理的数学模型，用数学语言来描述工程优化问题，主要的研究方法是定量化，模型化。然后，根据数学模型的特点来确定合适的优化方法和计算程序，最终获得最优设计方案。
Ix = µl dh + 2bt
Iy dh + 2bt
(刚度条件)
d > 0.004，t > 0.004，h > 0,b > 0
程序如下：
min=78000*15*(d*h+2*b*t);
d*h^3/12+b*t^3/6+(h+t)^2*b*t/2=t*b^3/6+d^3*h/12;
d*h+2*b*t>=1/215;
LINGO 模型主要由以下 5 个段构成：目标与约束短、集合段、数据段、初始段和计算段。模型主要组成部分包括决策变量，目标函数和约束条件。常用的语言有集合语言和变量语言。使用集合语言时，LINGO 模型以“MODEL：”语句开始，以“END”语句结束。语句一般以“；” 结束。LINGO 本身带有大量的内部函数，引用时均以“@”号开头。默认变量均为非负，可以用函数“@FREE（Viberal name）”取消默认设置。注释部分用“!”开始。集合语言实际上是一种建模语言，能够方便的定义变量和输入约束条件。使用变量语言时，操作相当简单，只需要将数学模型的目标函数和约束条件输入模型窗口中即可运行求解，目标函数以“MAX=” 或“MIN=”开始，目标函数与约束条件之间的语序没有要求，求解时会自动寻找目标函数，系数和变量之间使用运算符“*”。该语言缺点是变量较多或约束较多时，输入效率较低[1]。其它有关使用方法可参考文献[1]和版本自带的帮助文档。

优化软件LinGo的使用

5、模型中使用的参数数量级要适当 (如小于103)
•LINGO软件的使用
需要掌握的几个重要方面
正确阅读求解报告（尤其要掌握灵敏性分
析的求解选项
掌握与外部文件的基本接口方法
模型
min或max f(x)
S.T. G(x)≤或≥或＝0 L ≤x≤U
例题2
数学模型：
min
s.t.
其中：
ij ij
c x
i 1 j 1
3
4
xl＝5 2 4 6 cl= 4 9 4
c = 10 6 7 12
16 10 5 9 5 4 10 10
x
i 1 4
j 1
3
ij
xl j , j 1 4
cli , i 13
x
ij
xij 0, i 13, j 1 4
优化(Optimization), 规划(Programming)
无约束优化线性规划非线性规划
整数规划
组合优化
不确定规划
多目标规划
目标规划
网络优化
动态规划
优化问题的一般形式
优化问题三要素：决策变量；目标函数；约束条件
min s.t.
其中SI {1,, n}，SJ ={1,, m}
Lingo表示：
SI/1..n/； SJ/1..m/； IJ(I,J)：x,c；
集合的类型
setname(parent_set_list) [/member_list/] [: attribute_list];
集合
setname [/member_list/] [: attribute_list];

lingo基本用法

lingo基本用法以下是 9 条关于“lingo 基本用法”的内容：1. 嘿，你知道吗，lingo 里的变量定义可简单啦！就像给东西起个名字一样自然。

比如说，咱要算一堆苹果的数量，那就可以设个变量叫apple_num 呀，这不就清楚明白啦！2. 哇塞，lingo 的约束条件就像是给问题加上规矩。

就好比说，规定一个房间最多能进 10 个人，这就是个约束呀。

比如限制某种资源不能超过多少，lingo 就能很好地处理呢！3. 哎呀呀，lingo 的目标函数那可重要了！这就好比是你要去追求的目标。

比如你想让利润最大化，那目标函数就是让利润相关的表达式达到最大呀！像算怎么卖东西能赚最多钱，lingo 就能帮你找到答案哟！4. 嘿，lingo 的表达式书写也不难呢！就像写个数学式子一样。

比如 2x +3y 这么简单明了。

要计算一些关系，用它来写表达式再合适不过了！5. 哇哦，lingo 里的集合定义多有意思啊！像是把一群相关的东西归到一起。

比如把不同类型的商品归成一个集合，然后对它们进行统一的处理呀，是不是很方便呀？6. 哎呀，lingo 的求解命令一敲，就等着答案出来啦！就像你按下按钮，机器就开始工作一样。

你看，多神奇啊，一下子就知道结果了呢！7. 嘿，lingo 还能处理复杂的数据呢！就像一个聪明的小助手，不管多乱的数据它都能理清楚。

比如算一大堆乱七八糟数字的关系，lingo 绝对能应付得来呀！8. 哇，lingo 的模型建立虽然要动点脑筋，但一旦建好了，那可太好用啦！就跟盖房子一样，辛苦一点，盖好了住着就舒服啦。

你想想，自己建的模型能用起来，多有成就感呀！9. 哎呀呀，掌握了 lingo 的基本用法，那真的是能解决好多问题呢！不管是算数量还是优化方案，都不在话下。

所以呀，还不赶紧去学学，让它为你服。

LINGO软件在优化模型中的应用

羊羽lingo是linearinteractivegeneraloptimizer的缩写即交互式的线性和通用优化求解器由美国lindo系统公司推出的可以用于求解非线性规划也可以用于一些线性和非线性方程组的求解等功能十分强大是求解优化模型的最佳选择
LINGO软件 ——在优化模型中的应用
腾讯微博：羊羽
LINGO软件在优化模型中的应用
LINGO软件在优化模型中的应用
解：设每天用x1 桶牛奶在甲车间生产，用x2 桶牛奶在乙车间生产，可获利z 元。
则该问题的数学模型为： max z=72x1+64x2 s.t x1+x2≤50 12x1+8x2≤480 3x1≤100 x1,x2≥0
LINGO软件在优化模型中的应用
结果：
这个线性规划的最优解为x1=20，x2=30，最优值为z=3360，即用20 桶牛奶在甲车间生产，30 桶牛奶在乙车间生产，可获最大利润3360 元。
优点
3）强大的求解器 LINGO拥有一整套快速的，内建的求解器用来求解线性、非线性、二次约束和整数优化问题。
LINGO软件在优化模型中的应用
优点
4）交互式模型在LINGO内可以直接创建和求解模型，也可以从自己编写的应用程序中直接调用 LINGO。对于开发交互式模型，LINGO提供了一整套建模环境，用来求解和分析构建的模型。
从该问题的求解我们可以看到用LINGO 软件求解线性规划是非常方便、快捷的，比单纯形法人工计算效率高很多。
LINGO软ห้องสมุดไป่ตู้在优化模型中的应用
附加问题：
1）若用35元可以买到1桶牛奶，应否作这项投资？若投资，每天最多购买多少桶牛奶？ 2）若可以聘用临时工人以增加劳动时间，付给临时工人的工资最多是每小时几元？ 3）由于市场需求变化，甲车间奶制品的获利增加到30元，应否改变生产计划？

Lingo的基本使用方法

1. LINGO入门
内容提要
2.在LINGO中使用集合
3. 运算符和函数
4. LINGO的主要菜单命令
5. LINGO命令窗口
6.习题
1. LINGO入门
1. LINGO入门 2.在LINGO中使用集合 3. 运算符和函数 4. LINGO的主要菜单命令 5. LINGO命令窗口 6.习题
LINGO软件的主要特色
运行状态窗口
扩展的求解器 (求解程序) 状态框
使用的特殊求解程序 : B-and-B (分枝定界算法) Global (全局最优求解程序) Multistart(用多个初始点求解的程序)
目前为止找到的可行解的最佳目标函数值
有效步数
目标函数值的界
特殊求解程序当前运行步数：分枝数(对B-and-B程序)；子问题数(对Global程序)；初始点数(对Multistart程序)
INV (0) 10
加上变量的非负约束
注：LINGO中没有数组，只能对每个季度分别定义变量，如正常产量就要有RP1，RP2，RP3，RP4 4个变量等。写起来就比较麻烦，尤其是更多(如1000个季度)的时候。
记四个季度组成的集合QUARTERS={1，2，3，4}，它们就是上面数组的下标集合，而数组DEM,RP,OP, INV对集合QUARTERS中的每个元素1，2，3，4分别对应于一个值。LINGO正是充分利用了这种数组及其下标的关系，引入了“集合”及其“属性”的概念，把QUARTERS={1，2，3，4}称为集合，把DEM,RP,OP, INV 称为该集合的属性(即定义在该集合上的属性)。
两种命令模式
Windows模式：通过下拉式菜单命令驱动LINGO运行（多数

Lingo软件在运筹学中的应用

Lingo软件在运筹学中的应用Lingo软件在运筹学中的应用随着信息技术的不断发展，计算机软件在各个领域中的应用越来越广泛，尤其是在运筹学领域。

运筹学是研究在复杂决策环境下，如何高效地进行决策的学科。

Lingo软件作为一款运筹学建模和求解工具，为运筹学的研究和应用带来了很大的便利和效率。

本文将介绍Lingo软件在运筹学中的应用，并通过实例来说明其实际效果。

首先，Lingo软件在线性规划问题中的应用非常广泛。

线性规划是一种数学优化技术，用于在给定的约束条件下最大化或最小化线性目标函数。

Lingo软件提供了直观的图形用户界面，使得用户可以轻松地建立线性规划模型，并通过内置的求解器进行求解。

用户只需输入决策变量、约束条件和目标函数，Lingo就能自动找到最优解。

这对于一些复杂的决策问题，如生产规划、资源调度和供应链优化等，提供了很大的帮助。

其次，Lingo软件在整数规划和混合整数规划问题中也有着广泛的应用。

整数规划是在线性规划的基础上，将决策变量限制为整数解的优化问题。

混合整数规划在整数规划的基础上，允许部分决策变量取非整数解。

这种类型的决策问题在实际中很常见，如生产工作安排、旅行路线规划和仓储优化等。

Lingo软件提供了强大的分支定界算法和割平面算法，能够有效地求解整数规划和混合整数规划问题。

用户只需调整问题的参数，Lingo就能快速找到最优解，大大减少了优化问题的求解时间。

此外，Lingo软件还可以用于非线性规划问题的建模和求解。

非线性规划是在线性规划的基础上，将决策变量限制为非线性函数的优化问题。

非线性规划在许多实际问题中都有着广泛的应用，如投资组合优化、工程设计和市场定价等。

Lingo软件提供了多种求解算法，如牛顿法、拟牛顿法和遗传算法等，能够有效地求解非线性规划问题。

用户只需选择合适的算法和调整参数，Lingo就能找到最优解或是近似最优解。

最后，Lingo软件还具有灵活的扩展性和集成性。

它可以与其他优化软件和模拟软件进行集成，提供更强大的求解能力和模型分析能力。

lingo用法

lingo用法Lingo是一种俚语，既可以指代一种特定的语言，也可以是特定领域内的术语或俚语。

它的用法相对灵活，可以根据具体情境进行调整。

首先，lingo这个词最初源自英语，其最常见的意思是指一种特定的语言或方言。

在这个意义上，lingo可以代表任何一种特定的语言，不论是国际语言还是地方方言。

例如，可以说某人操流利的英语，或者他会说多种方言和lingo。

此外，lingo还可以指代特定领域内的术语或俚语。

在不同的行业或社群中，有许多专业术语和俚语，这些术语和俚语通常被认为是该领域或社群的lingo。

举几个例子，医学界有一些特定的术语，如"CT scan"（计算机断层扫描）和"gastroenterologist"（胃肠科医生）；IT界有一些俚语，如"bug"（故障）和"hack"（黑客）。

此外，在不同的地区，也会有一些特定的领域内的俚语或术语，这些也被称为lingo。

例如，在美国，有一些特定的俚语和术语仅仅在某个地区或某个人群中使用，这些俚语和术语可以被称为该地区或人群的lingo。

比如，美国西海岸特定的俚语使用频繁，如"hella"（非常）和"gnarly"（厉害）。

在交流中，使用lingo可以增进彼此的亲近感和凝聚力，因为使用者之间共享相同的术语和俚语。

此外，了解并正确运用lingo也可以帮助与特定群体或领域的人进行更有效的沟通。

然而，值得注意的是，使用lingo时应该遵守适当的场合和人群。

在正式场合或与不熟悉的人交流时，过度使用lingo可能造成误解或隔阂。

因此，在不同的沟通环境中，应根据具体情况灵活运用lingo。

总而言之，lingo是一种俚语，可以指代特定的语言或领域内的术语和俚语。

它的使用范围广泛，可以根据具体情境进行调整。

通过运用正确的lingo，可以增进与特定群体和领域内的人的沟通，并提升彼此的凝聚力。

Theis井函数计算方法及井模型参数优化计算研究

N n
由于 Theis 井函数为指数积分式, 数学上无法直
W (u)=
i -ln(u)+ða• i u i=0 4
5
式中：γ =0.5772156649015329，是欧拉常数；N 理论上趋近于无穷㊂展开项 N㊂国内绝大多数研究者都是采用的这种方似数值计算方法会因为级数项的取舍而导致实际应 5~11 时的 u-W (u)图，可以很明显地看出当 u 大于 2 时大,其后果是模型参数最终求解结果出现较大误差㊂
数 W (u)的方法,其替代公式如下：的误差㊂
2 • (1-G ) ,h = (1-G ) • (G 2-6 • G +12) ɕ G• (2-G ) 3 • G• (2-G )2 • b
如图 2 示,拟合式(6)当 u 大于 2 时 W (u)出现明显笔者基于最小二乘原理 , 得出如下井函数 W (u)替
⎧ | | | | ⎨ | | | | ⎩
解几乎完全重合： W (u)=
代公式,具体系数见表 2,效果图见图 2,和高精度数值 b 1+b 2 • ub 3+b 4 • ln(u)+b 5 • exp(b 6 • u)
p
系数如表 1㊂
Srivastava 于 1998 年提出的方法如公式(4)示,其
4.156969E-6 -2.624277E-5 4.156478E-6 4.156969E-6 4.156969E-6 4.112166E-6 0.7894027 100.17575
10
9.835525E-11 -52247.83580 4027.53816
程先云 1，郑凡东 2，杨

LINGO在水力计算中的应用

１．２在多项求和公式方面的应用
堕：ｆ一＿，
凼
（３）
将其用差分格式离散化为：
Ｅ１一巨，，＝＋－￣ｐ（ｉ — ），ｐ１，２ …”
又
：
（４）
ｈ＋垡２ｇＡ
（５）
多项求和公式通常可以由求和符号 ∑简单地表达出来，然而进行求解时却非常困难，计算量大，耗时费力。多项求和公式在水力计算中也是经常出现，比如管网中枝状管网和环状管网的水力计算、分水闸中有压流圆形涵管式分水闸流量系数的计算、河道恒定流水面曲线计算中的复式断面动能修正系数的计算、裁弯工程中引河和老河道的河道特征数的计算、以及普通完全井的井群计算等等，加大了水力计算的工作量。ＬＩＮＧＯ软件却可以简单地求解此类问题，只需要将求和项以求和符号∑的方式输入进去，即可以快速地得到正确结果。
（４）明渠恒定非均匀流水面曲线的计算明渠恒定渐变流的微分方程为：
在水力计算中，常常会遇到一些商次的隐函数方程和微分方程，对于这些方程，水力学中经通常采用试算法和迭代法。试算法概念简单，方法直观，易于理解。但是该方法往往带有一定的盲目性，若要达到给定的精度，有时需经过多次试凑，才能完成。而若采用数值分析中的迭代法则可以避免盲目性，准确的解出正确的答案，并且此方法适合用计算机编程求解，尤其用ＬＩＮＯ软件求解非常方便。Ｇ
＝
（
譬嘞＋壶）
（６）（７）故综Fra bibliotek方程可表示为：
＋
器菇。＋器～Ａｓｐ

LINGO使用说明(比较简单)

Lingo介绍Lingo是美国LINDO系统公司（Lindo Symtem Inc）开发的求解数学规划系列软件中的一个（其他软件为LINGDO,GINO,What’s Best等），它的主要功能是求解大型线性、非线性和整数规划问题，目前的版本是lingo11.0。

lingo分为Demo、solve suite、hyper、industrial、extended等六类不同版本，只有Demo版本是免费的，其他版本需要向LINDO系统公司（在中国的代理商）购买，Lingo的不同版本对模型的变量总数、非线性变量个数、整型变量个数和约束条件的数量做出不同的限制（其中extended版本无限制）。

Lingo的主要功能特色为：（1）既能求解线性规划，也有较强的求解非线性规划的能力；（2）输入模型简练直观；（3）运行速度快、计算能力强；（4）内置建模语言，提供几十种内部函数，从而能以较少语句，较直观的方式描述较大规模的优化模型；（5）将集合的概念引入编程语言，很容易将实际问题转换为Lingo语言；（6）能方便地与excel、数据库等其他软件交换数据。

学校图书馆40本《lingo和excel在数学建模中的应用》，袁新生、邵大宏、郁时炼主编，科学出版社Lingo程序设计简要说明在数学建模中会遇到如规划类的题型，在这种模型中总存在着一个目标，并希望这个目标的取值尽可能的大或小，同时与这个目标有关的一系列变量之间存在一些约束。

在构造出目标函数和约束条件的表达式后，我们需要对求出这个最值和各变量的取值。

一般我们用LINGO来对模型进行求解，本文将通过举一个简单的例子，围绕这个例子逐步学习LINGO 的使用。

LINGO只是一个求解工具，我们主要的任务还是模型的建立！当你在windows下开始运行LINGO系统时，会得到类似下面的一个窗口：外层是主框架窗口，包含了所有菜单命令和工具条，其它所有的窗口将被包含在主窗口之下。

在主窗口内的标题为LINGO Model –LINGO1的窗口是LINGO的默认模型窗口，建立的模型都都要在该窗口内编码实现。

基于LINGO的优化算法在运筹管理中的应用

基于LINGO的优化算法在运筹管理中的应用优化算法作为一种高效的数据处理方法，已经被广泛应用于各行各业。

在运筹管理领域中，基于LINGO的优化算法已经成为了一种不可替代的分析工具。

在实际应用中，我们可以通过LINGO优化算法，有效地优化生产流程、物流配送、供应链管理等方面的问题，使得整个企业的经营效益得到明显提升。

一、LINGO优化算法的基本原理LINGO是一种专业的优化算法语言，其主要目的是快速地解决复杂的优化问题。

LINGO主要利用线性规划、整数规划、非线性规划等方法，通过数学模型来优化决策问题。

基于LINGO的优化算法的基本原理就是通过建立数学模型，将现实问题转换成为数学问题。

将整个问题转换成一个标准的数学形式后，LINGO可以更加高效地运用各类优化算法将其求解。

这种方法可以大大提高解决问题的准确性和效率。

二、LINGO优化算法在企业生产流程优化中的应用生产流程是企业生产过程中最为核心的环节，一般来讲，生产流程中存在许多可以优化的环节。

例如，生产调度问题、零部件的优化选配、库存管理等。

这些问题的优化都可以运用基于LINGO的优化算法进行求解。

例如，对于生产调度问题，我们可以通过LINGO建立一个优化模型，考虑生产过程中的资源利用率、时间效率等因素，系统地推导出生产调度的最优方案。

通过模型计算结果，我们可以得到最适合企业生产排程的生产方案，并在实践中应用。

三、LINGO优化算法在物流配送中的应用物流配送是企业供应链管理中非常重要的一环。

通过LINGO优化算法，我们可以对物流配送过程中的问题进行求解。

例如，考虑如何优化物流线路、改善配送效率、降低运输成本等。

对于物流配送中的问题，我们可以运用LINGO算法建立一个数学模型，通过模拟尝试，优化各环节，获得最合理的运输方案，进一步优化企业运营成本，并为企业提高利润效益。

四、LINGO优化算法在供应链管理中的应用供应链管理是现代企业运营活动中不可缺少的环节。

LINGO使用大全

10由于开市场需求变化每千克a1的获利增加到30元是否应该改变生产计这个优化问题的目标是使每天的获利最大要作的决策是生产计划即每天用多少桶奶生产a1用多少桶牛奶生产a2当然不潮湿策变量也可以取每天生产多少年千克a1多少千克a2得到的模型不会有本质区别决策受到3个条件的条件的限制
目
录
第一章引言 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 1.1 优化模型的基本概念· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 1.1.1 优化模型的一般形式· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 1.1.2 可行解与最优解· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 1.1.3 优化模型的基本类型· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 1.2 优化问题的建模实例· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 1.2.1 线性规划模型· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 1.2.2 二次规划模型· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 1.2.3 非线性规划模型· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 1.2.4 整数规划模型· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 1.2.5 其他优化模型· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 1.3 LINDO/LINGO 软件简介· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 1.3.1 LINDO/LINGO 软件的基本功能· · · · · · · · · · · · · · · · · · · · · · · · · · · 1.3.2 LINDO/LINGO 软件的求解过程· · · · · · · · · · · · · · · · · · · · · · · · · · · 1.3.3 建立 LINDO/LINGO 优化模型需要注意的几个基本问题· · · · · · · 习题 1· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 第二章 LINDO 软件的基本使用方法· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 2.1 LINDO 入门· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 2.1.1 LINDO 软件的安装过程· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 2.1.2 编写一个简单的 LINDO 程序· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 2.1.3 一些注意事项· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 2.2 敏感性分析· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 2.3 整数线性规划的求解· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · *2.4 二次规划的求解· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · *2.5 LINDO 的主要菜单命令· · · · · · · · · · · · · · · · · · · · · · · · · · · · 2.5.1 文件主菜单· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 2.5.2 编辑主菜单· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 2.5.3 求解主菜单· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 2.5.4 报告主菜单· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · *2.6 LINDO 命令窗口· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 2.6.1 INFORMATION（信息类命令） · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 2.6.2 INPUT（输入类命令） · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 2.6.3 DISPLAY（显示类命令） · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 2.6.4 OUTPUT（输出类命令） · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 2.6.5 SOLUTION（求解类命令） · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 2.6.6 PROBLEM EDITING（编辑类命令） · · · · · · · · · · · · · · · · · · · · · · · 2.6.7 QUIT（退出类命令） · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 2.6.8 INTEGER，QUADRATIC，AND PARAMETRIC PROGRAMS （整数，二次与参数规划命令） · · · · · · · · · · · · · · · · · · · · · · · · · · · · 2.6.9 CONVERSATIONAL PARAMETERS（对话类命令） · · · · · · · · · · 2.6.10 USER SUPPLIED ROUTINES（用户过程类命令） · · · · · · · · · 2.6.11 MISCELLANEOUS（其他命令） · · · · · · · · · · · · · · · · · · · · · · · · · · ·

第四讲 LINGO在环境系统优化中的应用

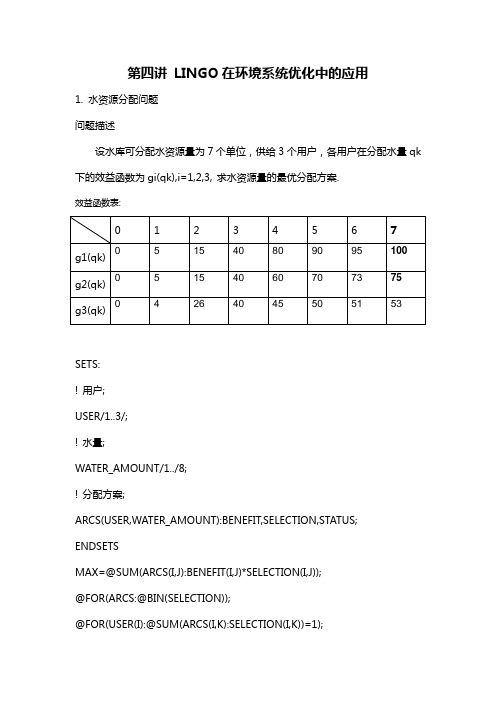
第四讲 LINGO在环境系统优化中的应用1. 水资源分配问题问题描述设水库可分配水资源量为7个单位，供给3个用户，各用户在分配水量qk 下的效益函数为gi(qk),i=1,2,3,求水资源量的最优分配方案.SETS:!用户;USER/1..3/;!水量;WATER_AMOUNT/1../8;!分配方案;ARCS(USER,WATER_AMOUNT):BENEFIT,SELECTION,STATUS;ENDSETSMAX=@SUM(ARCS(I,J):BENEFIT(I,J)*SELECTION(I,J));@FOR(ARCS:@BIN(SELECTION));@FOR(USER(I):@SUM(ARCS(I,K):SELECTION(I,K))=1);@SUM(ARCS(I,J):STATUS(I,J)*SELECTION(I,J))=7;DATA:!效益;BENEFIT=0 5 15 40 80 90 95 1000 5 15 40 60 70 73 750 4 26 40 45 50 51 53;!待定分配量;STATUS=0 1 2 3 4 5 6 70 1 2 3 4 5 6 70 1 2 3 4 5 6 7;ENDDATA2.大气污染物排放的控制问题问题描述在一个小区内有三个排放总悬浮颗粒物(TSP)的点源,其中两个是燃煤发电厂,另一个是水泥厂.发电厂每烧1t煤排放95kg总悬浮颗粒物,而水泥厂每生厂每烧1t煤排放85kg总悬浮颗粒物.两个发电厂燃煤量分别为400 000t/a 和300 000t/a, 水泥厂产量为250 000t/a.当前, 这三个总悬浮颗粒物排放源没有控制措施.现在,每个点源可以选择的控制方法的去除效率和费用见下表.此问题的目标是以最小的费用把水泥厂和两个发电厂的总悬浮颗粒物总排放量削减80%.现在排放量总计为67 750 000kg/a.由于要求总排放量削减80%,则最大允许排放量应为17 550 000kg/a.根据题意,建立如下数学模型:Min Z=X11+2X14+2.8X15+1.4X21+2.2X24+3X25+1.1X31+1.2X32+1.5X33+3X34S.TX10+X11+X14+X15=400000X20+X21+X24+X25=300000X30+X31+X32+X33+X34=25000095X10+39X11+5.7X14+2.9X15+95X20+39X21+5.7X24+2.9X25+85X30+34.9X31+22.1X32+13.6X33+5.1X34<=17550000 Xij>=0式中:i--污染源,1表示发电厂1, 2表示发电厂2, 3表示水泥厂3;j--控制方法, 0表示不控制, 1表示隔板沉淀槽, 2表示多级除尘器, 3表示长锥除尘器, 4表示喷雾洗涤器, 5表示静电除尘器;Xij--点源i采用控制方法j的生产量,t/a.LINGO模型:SETS:POLUTION/ELEC1 ELEC2 CEMENT/:COAL,DISCHARGE; CONTROLS/CON0..CON5/:EFFECT;ARCS(POLUTION, CONTROLS):PRODUCTION, FARE, INCLUDE; ENDSETSMIN=@SUM(ARCS(I,J):FARE(I,J)*PRODUCTION(I,J)*INCLUDE(I,J)); @SUM(POLUTION(I):@SUM(CONTROLS(J):DISCHARGE(I)*(1-EFFECT(J))*PRODUCTION(I,J)*INCLUDE(I,J))) <=@SUM(POLUTION(I):COAL(I)*DISCHARGE(I))*0.2;@FOR(POLUTION(I):@SUM(CONTROLS(J):PRODUCTION(I,J)*INCLUDE(I,J))=COAL(I));@FOR(ARCS(I,J):INCLUDE(I,J)=@IF(FARE(I,J)#EQ#0,0,1));@FOR(ARCS:@GIN(PRODUCTION));DATA:COAL=400000,300000,250000;DISCHARGE=95,95,85;EFFECT=0,0.59,0.74,0.84,0.94,0.97;FARE=0 1 0 0 2 2.80 1.4 0 0 2.2 30 1 1.2 1.5 3 0;ENDDATA3.固体废弃物处置问题问题描述有两个城市要建设一个区域固体废弃物处置系统.城市1有40000人, 固体废弃物量是700t/周;城市2有65000人, 固体废弃物量是1200t/周.现在有三种可能的方案,即焚烧、排海、掩埋.针对这三种方案有三个处理场地,场地处理系统情况如下表.已知运输费用为0.5美元/(t*km),试确定最优固体废弃物处置方案,使整个系统的费用最低.LINGO模型(程序需要修改，自己完成)SETS:CITY/A,B/:WASTE;PLANT/FIRE,OCEAN,BURY/:MATCH,FIX,CHANGE,ABILITY;PLAN(CITY,PLANT):PRODUCE,DISTANCE;ENDSETSMIN=@SUM(PLANT:MATCH*FIX)+@SUM(PLAN(I,J):(PRODUCE(I,J)*CHANGE(J)+PRODUCE(I,J)*DISTANCE(I,J)*0.5));@FOR(CITY(I):SUM(PLAN(I,J):PRODUCE(I,J))=WASTE(I));@FOR(PLANT(J):@SUM(PLAN(I,J):PRODUCE(I,J))<=MATCH(J)*ABILITY(J));@FOR(PLANT:@BIN(MATCH));DATA:FIX=3850 1150 1920;CHANGE=12 16 6;ABILITY=1000 500 1300;DISTANCE=15 5 3010 15 25;WASTE=700 1200;ENDDATA。

Lingo软件在最优化问题中的应用

• endsets
• 这里allowed定义为product,machine,week的派生集，其组成成员如下：
（A,M,1),(A,M,2),(A,N,1),(A,N,2)
(B,M,1),(B,M,2),(B,N,1),(B,N,2) 三、模型的数据部分；数据部分以关键字“data:”开始，以关键字"enddata"结束。在这里，可以指定集成员、集的属性。其语法如下：
在Lingo模型中使用集之前，必须事先定义。集以关键字“sets:”开始，以“endsets”结束。
• 1、原始集的定义 • 用下面的语法定义一个原始集： • setname[/member_list][:attribute_list]; • （1）若要一列出集成员：则用显式罗列成员，中间用空格或逗号隔开，也可混合使用。如： • set: • students/Mike Peter,Rose,Carl/:sex,age;
• 2、派生集的定义 • 定义一个派生集，用如下语法： • setname(parent_set_list)[/member_list/][:attribute_list]; • 其中parent_set_list是已定义集的列表，多个时必须用逗号隔开。如： • set:
product/A B/; machine/M N/; • week/1..2/; • allowed(product,machine,week):x;
• X=1,2,3; • Y=4,5,6; • enddata
• 四、Lingo软件使用的注意事项。 • （1）LINGO中不区分大小写字母，变量（和行名）可以使用不超过32个字符表示，且必须以字母开头。 • （2）在命令方式下（Command Window中），必须先输入MODEL：表示开始输入模型。LINGO中模型以 “MODEL:”开始，以“END”结束。对简单的模型，这两个语句也可以省略。 •