第3章 MATLAB程序设计
最优化 马昌凤 第三章作业

最优化方法及其Matlab程序设计习题作业暨实验报告学院:数学与信息科学学院班级:12级信计一班姓名:李明学号:1201214049第三章 最速下降法和牛顿法一、上机问题与求解过程1、用最速下降法求212221216423),(x x x x x x f --+=的极小值。
解:仿照书上编写最速下降法程序如下:function [x,val,k]=grad(fun,gfun,x0) %功能:用最速下降法求解无约束化问题:min f(x) %输入:x0是初始点,fun,gfun 分别是目标函数和梯度 %输出:x,val 分别是近似嘴有点和最优值,k 是迭代次数 maxk=5000;rho=0.5;sigma=0.4;%一开始选择时选择的rho 和sibma 选择的数据不够合理,此处我参照书上的数据编写数据 k=0;epsilon=1e-5; while (k<maxk)g=feval(gfun,x0); %计算梯度 d=-g;%计算搜索方向if (norm(d)<epsilon),break ;end m=0;mk=0; while (m<20)%Armijo 搜索if (feval(fun,x0+rho^m*d)<feval(fun,x0)+sigma*rho^m*g'*d) mk=m;break ;%直接利用Armijo 搜索公式,一开始的时候没有记住公式编写出现错误 end m=m+1; endx0=x0+rho^mk*d; k=k+1; end x=x0;val=feval(fun,x0) %求得每一个的函数值然后仿照书上建立两个目标函数和梯度的M 文件:function f=fun(x)f=3*x(1)^2+2*x(2)^2-4*x(1)-6*x(2); function g=gfun(x) g=[6*x(1)-4,4*x(2)-6]';选取初始点为']0,0[,调用函数程序,得出最小极值点为']500.1,6667.0[,极小值为8333.5-,在界面框中输入的程序如下:[x,val,k]=grad('fun','gfun',x0) val = -5.8333 x =0.6667 1.5000 val =-5.8333 k = 10从结果可以看出迭代次数为10次,如果选取不同的初值点则迭代次数不一样,但是极小值相同。
matlab编程2

第二节 程序控制结构
选择结构
选择结构 是根据给定的条件成立或不成立,分别执 行不同的语句. Matlab 用于实现选择结构的语句有 if -end语句 和 switch-end 语句
19
第二节 程序控制结构
if -end条件语句
单分支结构
if 条件表达式 语句组 end
双分支结构
If 条件表达式
例
input应用时,注意:
输入字符串时必须带单引号 单引号的输出:两个连续的单引号 若输入的是数、数学表达式,则in不能出现
11
第二节 程序控制结构
disp
数据的输出:disp
disp(X)
输出变量 X 的值,X 可以是数值矩阵或字符串
一次只能输出一个变量
例
>> A='Hello, Tom!'; >> disp(A) >> B=[1 2 3; 4 5 6; 7 8 9]; >> disp(B)
x=input(‘输入初值x=’);
n=input(‘输入迭代次数=’);
y(1)=x ; for k=1:n x=1/(x+1); y(k)=x;
function y=dd2(x,n) y(1)=x ; for k=1:n x=1/(x+1); y(k)=x; end
end
y
解:程序如下: function y=f(x)
是
语句组2
……
K=值m? 否 语句组n
是
语句组m
switch-end语句的 下一句
第二节 程序控制结构
switch-end 语句
关于 switch-end 语句的几点注解:
matlab第一讲

·
1.2 MATLAB 集成开发环境
如果一个命令行很长,一个物理行之内写不下,可以在第1个物理行之 后加上3个小黑点并按下回车键,然后接着下一个物理行继续写命令的 其他部分。3个小黑点称为续行符,即把下面的物理行看作该行的“逻 辑”继续。 例如:
z=1+1/(1*2)+(1*2*3)+1/(1*2*3*4)+…
系统科学研究所
1.2 MATLAB 集成开发环境
MATLAB的工具栏提供了一些命令按钮和一个当前路径列表框。
2.命令窗口
一般来说,在命令编辑区的一个命令行输入一条命令,命令行以回车 结束。但一个命令行可以输入若干条命令,各命令之间以逗号分隔, 若前一命令后带有分号,则逗号可以省略。例如:
x=720,y=68 x= 720 y=86 x=720;y=86 y=86
1.3MATLAB 的帮助功能
1.3.1帮助界面
进入MATLAB帮助界面可以通过以下3种方法。 单击MATLAB主窗口工具栏中的Help按钮。
在命令窗口中输入”helpwin”、”helpdesk”或“doc”命令。
选择Help菜单中的”MATLAB Help”选项。 1.3.2帮助命令
1.help命令
系统科学研究所
1.2 MATLAB 集成开发环境
检查该命令是否为MATLAB 搜索路径中其他目录下的M文件。 2.设置搜索路径
用户可以将自己的工作目录列入MATLAB搜索路径,从而将用户目录
纳入MATLAB系统统一管理。 (1)用path命令设置搜索路径 (2)用对话框设置搜索路径
·
系统科学研究所
统程序设计语言一样进行程序设计,而且结合MATLAB的数值计算和
matlab第三章课后部分答案

matlab第三章课后部分答案习题三3-2 从键盘输入一个三位整数,将它反向输出。
如输入639,输出为936程序如下:m=input('请输入一个三位整数:');m1=fix(m/100);%求m的百位整数m2=rem(fix(m/10),10);%求m的十位数字m3=rem(m,10);%求m的个位数字m=m3*100+m2*10+m1%反向输出m3-3 输入一个百分制成绩,要求输出成绩等级A,B,C,D,E。
其中90~100分为A,80~89分为B,70~79分为C,60~69分为D,60分以下为E。
要求:(1)分别用if语句和switch语句实现。
(2)输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
程序如下:(1)if语句c=input('请输入成绩:');if c>=90&c<=100disp('A 成绩合理');elseif c>=80&c<=89disp('B 成绩合理');elseif c>=70&c<=79disp('C 成绩合理'); elseif c>=60&c<=69disp('D 成绩合理'); elseif c<60disp('E 成绩合理');elsedisp('成绩错误');end(2)switch语句c=input('请输入成绩:'); switch fix(c)case num2cell(90:100)disp('A 成绩合理'); case num2cell(80:89)disp('B 成绩合理'); case num2cell(70:79)disp('C 成绩合理'); case num2cell(60:69)disp('D 成绩合理'); case num2cell(0:59)disp('E 成绩合理');x=fix(rand(1,20)*89)+10;x1=fix(sum(x)/20);disp(['平均数是:',num2str(x1)])m=(rem(x,2)==0&x<x1);n=find(m);disp(['小于平均数的数是:',num2str(x(n))]); 3-6 输入20个数,求其中最大数和最小数。
matlab 教程 第三章Matlab 绘图与例题

机动 目录 上页 下页 返回 结束
二、三维网格图命令mesh
• mesh(X,Y,Z) 生成网格曲面,X,Y,Z是同维数的矩阵 • mesh(x,y,Z) x,y是向量,而Z是矩阵。等价于
机动 目录 上页 下页 返回 结束
三、三维表面图命令surf
• surf的调用格式与mesh相同,不同之处是surf绘的是曲面 而不是网格。
• 三维表面图可以用shading命令修饰其显式形式。
Matlab还提供了waterfall(x,y,z)及contour3(x,y,z)等命 令绘制三维图形。
3
2
在[0,4π]间的图形。
解:syms t
ezplot(‘2/3*exp(-t/2)*cos(3/2*t)’,[0,4*pi])
第二节 Matlab二维特殊图形
Matlab提供了许多其他的二维绘图指令, 大大扩充了Matlab的曲线作图指令,可以满足 用户的不同需要。
注 目录 上页 下页 返回 结束
axis equal 使坐标轴在三个方向上刻度增量相同
axis square 使坐标轴在三个方向上长度相同
axis
返回表示当前图形坐标轴的范围
机动 目录 上页 下页 返回 结束
第四节 Matlab空间曲面绘图
二元函数 z f (x, y) 的图形是三维空间曲面,函
数图形在了解二元函数的特性上帮助很大。
第3章 Matlab 绘图与例题
第一节
第3章
Matlab二维曲线绘图
一、基本绘图指令plot
MATLAB使用教程

2.2 变量和赋值
2.2.1 变量的命名 在MATLAB中,变量名是以字母开头, 后接字母、数字或下划线的字符序列, 最多19个字符。 在MATLAB中,变量名区分字母的大小 写。MATLAB提供的标准函数名以及命 令名必须用小写字母。
目录 21
2.2.2 赋值语句 MATLAB赋值语句有两种格式: (1) 变量=表达式 (2) 表达式 一般地,运算结果在命令窗口中显示出来。如 果在语句的最后加分号,那么,MATLAB仅仅 执行赋值操作,不再显示运算的结果。 在MATLAB语句后面可以加上注释,注释以% 开头,后面是注释的内容。
目录 22
例2.1 计算表达式的值,并将结果赋给变量x, 然后显示出结果。 在MATLAB命令窗口输入命令:
x=(5+cos(47*pi/180))/(1+sqrt(7)-2*i) %计算表达式的值
目录 23
2.2.3 数据的输出格式 MATLAB用十进制数表示一个常数,具体可 采用日常记数法和科学记数法两种表示方法。 数据输出时用户可以用format命令设置或改 变 数 据 输 出 格 式 。 format 命 令 的 格 式 为 : format 格式符 注意,format命令只影响数据输出格式,而 不影响数据的计算和存储。
17
例1.4 设有常微分方程初值问题,试求 其数值解,并与精确解相比较。 (1)建立函数文件funt.m: function yp=funt(t,y) yp=(y^2-t-2)/4/(t+1); (2)求解微分方程: t0=0;tf=10;y0=2; [t,y]=ode23('funt',[t0,tf],y0); y1=sqrt(t+1)+1; t'
最优化马昌凤第三章作业

最优化方法及其Matlab程序设计习题作业暨实验报告学院:数学与信息科学学院班级:12级信计一班姓名:李明学号:49第三章 最速下降法和牛顿法一、上机问题与求解过程1、用最速下降法求212221216423),(x x x x x x f --+=的极小值。
解:仿照书上编写最速下降法程序如下:function [x,val,k]=grad(fun,gfun,x0)%功能:用最速下降法求解无约束化问题:min f(x)%输入:x0是初始点,fun,gfun分别是目标函数和梯度%输出:x,val分别是近似嘴有点和最优值,k是迭代次数maxk=5000;rho=;sigma=;%一开始选择时选择的rho和sibma选择的数据不够合理,此处我参照书上的数据编写数据k=0;epsilon=1e-5;while(k<maxk)g=feval(gfun,x0);%计算梯度d=-g;%计算搜索方向if(norm(d)<epsilon),break;endm=0;mk=0;while(m<20)%Armijo搜索if(feval(fun,x0+rho^m*d)<feval(fun,x0)+sigma*rho^m*g'*d)mk=m;break;%直接利用Armijo搜索公式,一开始的时候没有记住公式编写出现错误endm=m+1;endx0=x0+rho^mk*d;k=k+1;endx=x0;val=feval(fun,x0)%求得每一个的函数值然后仿照书上建立两个目标函数和梯度的M文件:function f=fun(x)f=3*x(1)^2+2*x(2)^2-4*x(1)-6*x(2);function g=gfun(x)g=[6*x(1)-4,4*x(2)-6]';选取初始点为']0,0[,调用函数程序,得出最小极值点为']6667.0[,极小值为8333500.1,,在界面框中输入的程序如下:.5[x,val,k]=grad('fun','gfun',x0)val =x =k =10从结果可以看出迭代次数为10次,如果选取不同的初值点则迭代次数不一样,但是极小值相同。
MATLAB第三章

第三章微积分问题的计算机求解一、实验内容:题目1.试求出如下极限。
①limx→∞(3x +9x )1/ x,②lim x→∞[(x+2)x+2(x+3)x+3 ]/(x+5)2x+5【分析】:该题为单变量函数的极限。
极限问题可以用limit()函数直接求出。
要注意该函数的调用格式为:L=limit(fun,x,x0)(求极限),L=limit(fun,x,x0,’left’或’right’)(求极限)。
还需注意一开始要对函数的字符进行申明。
【解答】:(1)输入如下语句:>> syms x;f=(3^x+9^x)^(1/x);L=limit(f,x,inf)语句运行后显示如下:L =9(2)输入如下语句:>>syms x;f=(x+2)^(x+2)*(x+3)^(x+3)/(x+5)^(2*x+5);>> L=limit(f,x,inf)语句运行后显示如下:L =exp(-5)题目2.试求下面的双重极限。
①lim x→−1y→2 (x2y+xy3)/(x+y) 3,②limx→0 y→0 xy /√(xy+1)−1,③limx→0y→0 [1−cos(x2+y2)]/(x2+y2)e x2+y2。
【分析】:该题为多变量函数的极限问题。
他可以用嵌套使用limit()函数来解决。
在MATLAB上可以用L=limit(limit(f,x,x0),y,y0)或者L=limit(f,y,y0),x,x0)来解决。
其思想是所有的先关于X求导,再所有的关于y求导。
【解答】:(1)输入如下语句:>> syms x y>> f=(x^2*y+x*y^3)/(x+y)^3;>> L=limit(limit(f,x,-1),y,2)语句运行后显示如下:L =-6(2)输入如下语句:>> syms x yf=(x*y)/(sqrt(x*y+1)-1);L=limit(limit(f,x,0),y,0)按ENTER键,语句运行后显示如下:L =2(3)输入如下语句:>> syms x yf=(1-cos(x^2+y^2))/(sqrt(x^2+y^2)*exp(x^2+y^2));L=limit(limit(f,x,0),y,0)按ENTER键,语句运行后显示如下:L =题目3.求出下面函数的导数。
第三章 四连杆之MATLAB程式
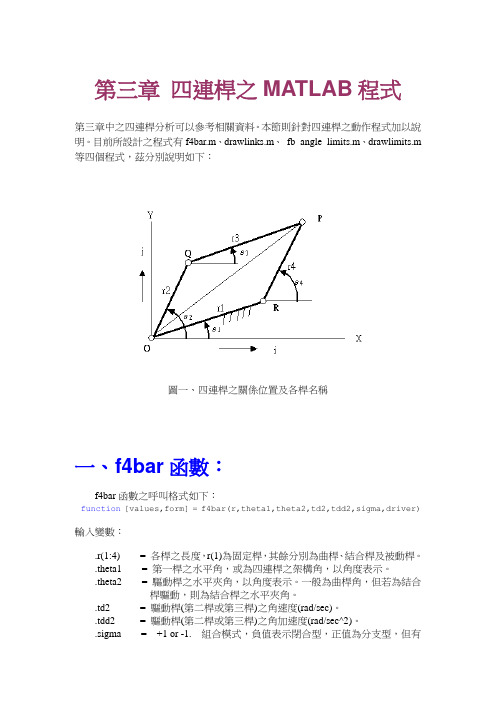
第三章四連桿之MATLAB程式第三章中之四連桿分析可以參考相關資料。
本節則針對四連桿之動作程式加以說明。
目前所設計之程式有f4bar.m、drawlinks.m、fb_angle_limits.m、drawlimits.m 等四個程式,茲分別說明如下:圖一、四連桿之關係位置及各桿名稱一、f4bar函數:f4bar函數之呼叫格式如下:function [values,form] = f4bar(r,theta1,theta2,td2,tdd2,sigma,driver)輸入變數:.r(1:4) = 各桿之長度,r(1)為固定桿,其餘分別為曲桿、結合桿及被動桿。
.theta1 = 第一桿之水平角,或為四連桿之架構角,以角度表示。
.theta2 = 驅動桿之水平夾角,以角度表示。
一般為曲桿角,但若為結合桿驅動,則為結合桿之水平夾角。
.td2 = 驅動桿(第二桿或第三桿)之角速度(rad/sec)。
.tdd2 = 驅動桿(第二桿或第三桿)之角加速度(rad/sec^2)。
.sigma = +1 or -1. 組合模式,負值表示閉合型,正值為分支型,但有時需視實際情況而定。
.driver = 0 (驅動桿為第二桿); 1 (驅動桿為第三桿)輸出變數:.form = 組合狀態,0 :表示無法組合;1:可以正確組合.values = 輸出矩陣,其大小為 4 X 7,各行之資料分配如下:其中第一行之連桿位置向量,屬於單桿的位置向量。
第二行為各桿之水平夾角,第三及第四行為各桿之角度速度及角加速度。
第五至七行則為P點與Q點之速度與加速度量,第五行為向量,第六行為絕對量,第七行為夾角。
值得一提的是第一行、三行、四行及五行之向量表示法屬於複數之型式。
故若要得到其絕對值僅需在MATLAB指令檔中,以abs()這一個函數指令即可求得,而以函數angle()則可求得其夾角,雖然第二行與第七行之輸出亦有相對應之夾角。
例一:為第二桿為驅動桿[val,form]=f4bar([3 2 4 2],0,60,10,0,-1,0)val = Columns 1 through 33 0 01 + 1.7321i 60 103.8682 - 1.0182i -14.7465.40781.8682 + 0.71389i 20.913 16.549 Columns 4 through 60 1 + 1.7321i 20 1.8682 + 0.71389i 2-127.58 173.21 - 100i 200-236.27 364.19 - 953.09i 1020.3 Column 76020.913-30-69.087form = 1 (表示可以組合)本例中,有框線者表示其為輸入值。
第三章MATLAB有限元分析与应用

第三章MATLAB有限元分析与应用有限元分析(Finite Element Analysis, FEA)是一种工程计算方法,用于解决结构力学和流体力学等问题。
它将一个复杂的结构分割成多个简单的离散单元,通过建立数学模型和求解方程组,得到结构的力学、热力学和流体力学等性能参数。
MATLAB是一种功能强大的数学计算软件,具有直观的用户界面和丰富的工具箱,可以方便地进行有限元分析。
本章将介绍在MATLAB中进行有限元分析的基本步骤和方法,以及一些常见的应用例子。
首先,进行有限元分析需要将结构进行离散化。
常用的离散化方法有节点法和单元法。
节点法是将结构的几何形状划分为小的节点,并在节点上进行计算。
单元法是将结构划分为多个小的单元,并在每个单元内进行计算。
在MATLAB中,可以通过创建节点和单元的矩阵来描述结构和单元的关系。
例如,创建一个2D结构形式的节点矩阵:nodes = [0 0; 1 0; 0 1; 1 1];然后,通过创建描述节点连接关系的矩阵,来定义结构的单元:elements = [1 2 3; 2 4 3];这里的每一行代表一个单元,数字表示节点的编号。
接下来,需要定义材料的力学参数和边界条件。
材料的力学参数包括弹性模量、泊松比等。
边界条件包括支座约束和加载条件。
在MATLAB中,可以通过定义力学参数和边界条件的向量来描述。
例如,定义弹性模量和泊松比的向量:E=[200e9200e9];%弹性模量nu = [0.3 0.3]; % 泊松比定义支座约束的向量(1表示固定,0表示自由):constraints = [1 1; 0 0; 0 1; 0 1];定义加载条件的向量(包括点力和面力):最后,通过求解方程组得到结构的应力和位移等结果。
在MATLAB中,可以利用有限元分析工具箱中的函数进行计算。
例如,可以使用“assem”函数将节点和单元的信息组装成方程组,并使用“solveq”函数求解方程组。
第3章用MATLAB进行控制系统时域分析

第3章用MATLAB进行控制系统时域分析MATLAB是一种功能强大的计算机软件,被广泛用于进行控制系统分析和设计。
在控制系统领域,时域分析是一种常用的方法,它可以用来评估和改进系统的性能及稳定性。
在MATLAB中,有几个重要的函数可以用于进行控制系统时域分析,包括step、impulse、lsim和initial等。
这些函数可以帮助我们了解系统的响应和行为。
首先,我们可以使用step函数来绘制系统的阶跃响应。
阶跃响应表示系统对输入信号的反应。
通过分析阶跃响应曲线的特性,我们可以评估系统的稳定性和性能。
例如,我们可以从阶跃响应曲线中获取系统的超调量、上升时间和峰值时间等信息。
step函数的使用方法如下:```step(sys)```其中,sys是一个控制系统的传递函数或状态空间模型。
调用step 函数后,MATLAB会自动绘制系统的阶跃响应曲线,并且返回一个包含系统响应数据的结构体。
另一个常用的时域分析函数是impulse,它可以用来绘制系统对冲击输入的响应。
冲击响应是系统对于单位冲击信号的输出。
通过分析冲击响应曲线,我们可以了解系统的固有特性,例如共振频率和阻尼比。
impulse函数的使用方法与step函数类似:```impulse(sys)```同样,调用impulse函数后,MATLAB会绘制系统的冲击响应曲线,并且返回一个包含系统响应数据的结构体。
除了阶跃响应和冲击响应外,我们还可以使用lsim函数来绘制系统对任意输入信号的响应。
lsim函数可以接受用户自定义的输入信号,并给出系统的输出响应。
通过分析系统的输出信号,我们可以更加全面地了解系统的性能和行为。
lsim函数的使用方法如下:```lsim(sys,u,t)```其中,sys是一个控制系统的传递函数或状态空间模型,u是输入信号,t是时间向量。
调用lsim函数后,MATLAB会根据输入信号和时间向量绘制系统的输出响应曲线,并返回一个包含系统响应数据的结构体。
《Matlab语言基础》教学大纲-通信工程

《Matlab语言基础》教学大纲一、课程基本信息课程名称:Matlab语言基础课程编码:58082014课程类别:专业选修课适用专业:通信工程开课学期:2-1课程学时:32学时课程学分:2学分先修课程:C语言、高等数学、线性代数并修课程:课程简介:MATLAB是矩阵实验室(Matrix Laboratory)的简称,是美国MathWorks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析及数值计算的高级技术计算语言和交互式环境,应用于工程计算、控制设计、信号处理与通信、图像处理、信号检测、金融建模设计与分析等各个领域。
Matlab语言在高校与研究单位起着重大的作用,是通用的科学计算、数值仿真和可视化及动态仿真的重要工具。
二、课程教育目标了解Matlab 的特点;理解Matlab 的数值计算、程序设计、绘图功能及在通信工程的科学计算和建模中的应用;掌握Matlab语言的基本编程思想和方法。
三、课程教学内容、要求及学时安排第一章 MATLAB概述【教学内容】1.Matlab 的特点、绪论;2.Matlab 快速入门;【教学要求】1.熟悉MATLAB命令窗口及文件管理,MATLAB帮助系统。
2.掌握命令行的输入及编辑,用户目录及搜索路径的设置。
3.了解MATLAB的主要功能。
【教学方法】采用多媒体教学方式,结合Matlab仿真软件进行课堂演示。
【学时】2第二章 MATLAB数据和数值计算【教学内容】1. MATLAB数据类型;2. 基本运算符;3.矩阵运算;4.数组运算;【教学要求】1.熟悉MATLAB变量的命名,赋值语句,数据的输出格式。
熟悉傅立叶分析,常微分方程的数值求解,非线性方程度数值求解。
2.掌握矩阵的建立、拆分及冒号表达式,MATLAB运算,结构数据和单元数据,字符串;掌握矩阵分析,数据处理。
3.了解MATLAB数据的特点。
【教学方法】采用多媒体教学方式,结合Matlab仿真软件进行课堂演示。
有限元方法与MATLAB程序设计 第3章 桁架和刚架

Fe keUe
Ue TUe
结构坐标系下的 单元刚度方程
9
结构坐标系下单元刚度矩阵 ke T TkeT
c cos s sin
y
Fe keUe
y
i (xi , yi )
(xj, yj ) x j
x
结构坐标系
cos sin 0
0 1 0 1 0 e cos sin 0
0
ke
EA sin
Fyi
Fxj Fyj
EA l
0
1
0
0 0 0
0 1 0
0
vi
0 0
u v
j j
单元坐标系下的 1 0 1 0
单元刚度矩阵
ke
EA l
0
1
0 0
0 1
0 0
0
0
0
0
7
§3.1.3 整体坐标系下的单元刚度方程
Fxi Fxi cos Fyi sin Fyi Fxi sin Fyi cos Fxj Fxj cos Fyj sin
是结构坐标系x轴正方 向至单元坐标轴x 的角度
y
x
y Fxi i
Fxi Fyi Fyi
x
结构(整体)坐标系
Fyj Fxj sin Fyj cos
Fxi Fyi
Fxj
Fyj
e
cos
sin
0
0
sin cos
0 0
0 0
cos sin
0
e
Fxi
e0Fyi源自sin cosFxj
Fyj
Fe TFe Ue TUe
cos
T sin
0
0
sin cos
第三章 matlab图形绘制

指定
grid 图形中加网格
例3.在同一坐标系下画出sinx和cosx的图形,并适当加 标注.
x=linspace(0,2*pi,30);y=[sin(x);cos(x)]; plot(x,y);grid;xlabel (‘x’);ylabel (‘y’); title(‘sine and cosine curves’); text(3*pi/4,sin(3*pi/4),’\leftarrowsinx’); text(2.55*pi/2,cos(3*pi/2),’cos\rightarrow’)
结果见下图.
4.多幅图形
subplot(m,n,p)可以在同一个图形窗口中画出多个图 形,用法见下例.
x=linspace(0,2*pi,30);y=sin(x);z=cos(x);u=2*sin(x).* cos(x);v=sin(x)./cos(x); subplot(2,2,1),plot(x,y),title(‘sin(x)’) subplot(2,2,2),plot(x,z),title(‘cos(x)’) subplot(2,2,3),plot(x,u),title(‘2sin(x)cos(x)’) subplot(2,2,4),plot(x,v),title(‘sin(x)/cos(x)’)
plot(x1,y1,x2,y2, …) 在此格式中,每对x,y必须符合 plot(x,y)中的要求,不同对之间没有影响,命令对每 一对x,y绘制曲线.
例1.做出y=sinx在[0,2π]上的图形,结果见下图.
x=linspace(0,2*pi,30); sin(x);plot(x,y)
例2.在同一坐标系下做出两条曲线y=sinx和y=cosx 在[0,2π]上的图形.结果见下图.
matlab自学经典

Matlab Main Toolbox——matlab主工具箱
功
Control System Toolbox——控制系统工具箱 Communication Toolbox——通讯工具箱
能 Financial Toolbox——财政金融工具箱
性
System Identification Toolbox——系统辨识工具箱 Fuzzy Logic Toolbox——模糊逻辑工具箱
X1I=0.0
过程化“让某物怎么样去干事X2情I=0”.0
34 WRITE (6,6)A,B,C,X1R,X1I,X2R,X2I X0=X
6 FORMAT (1X,7(F7.4,3X))
printf("Input a,b,c:");
GOTO 4
scanf("%f%f%f",&a,&b,&c);
STOP。
其中 c ij a i1 b 1j a i2 b 2j ... a itb tj
精选课件
12
1.1 MATLAB发展历史 Matlab——Matrix Laboratory
美国新墨西哥大学Cleve Moler 在70年代后期设计 矩阵运算语言.
1983年, Cleve Moler到Standford大学讲学,Jack Little等C语言开发了第二代专业版。
精选课件
13
Matlab 的发行
1984年,Matlab 1.0 (操作系统 DOS,数值计算及数据图形化) 1993年,Matlab 4.0 (93年推出Windows版,加入 simulink) 1993年,Matlab 4.1(符号运算工具箱) Maple 1994年,Matlab 4.2(广泛重视和应用) 1997年,Matlab 5.3(真正实现32位运算) 2002年,Matlab 6.5(采用JIT加速器) 2004年,Matlab 7.0
第3章MATLAB程序设计3.1 M文件3.2 程序控制结构3.3 函数文...

例3-3 求一元二次方程ax2 +bx+c=0 的根。
程序如下: a=input('a=?'); b=input('b=?'); c=input('c=?'); d=b*b-4*a*c; x=[(-b+sqrt(d))/(2*a),(-b-sqrt(d))/(2*a)]; disp(['x1=',num2str(x(1)),',x2=',num2str(x(2))]);
2.数据的输出
MATLAB提供的命令窗口输出函 数主要有disp函数,其调用格式为 disp(输出项) 其中输出项既可以为字符串,也可 以为矩阵。
例3-2 输入x,y的值,并将它们的 值互换后输出。
程序如下: x=input('Input x please.'); y=input('Input y please.'); z=x; x=y; y=z; disp(x); disp(y);
程序如下: A=[1,2,3;4,5,6]; B=[7,8,9;10,11,12]; try C=A*B; catch C=A.*B; end C lasterr %显示出错原因
3.2.3 循环结构
1.for语句 for语句的格式为: for 循环变量=表达式1:表达式2:表达式3 循环体语句 end 其中表达式1的值为循环变量的初值,表达式 2的值为步长,表达式3的值为循环变量的 终值。步长为1时,表达式2之间第一个能 被21整除的整数。
程序如下: for n=100:200 if rem(n,21)~=0 continue end break end n
4.循环的嵌套: 如果一个循环结构的循环体又包括一
MATLAB程序设计知到章节答案智慧树2023年广西科技大学

MATLAB程序设计知到章节测试答案智慧树2023年最新广西科技大学第一章测试1.当在命令行窗口执行命令时,如果不想立即在命令行窗口中输出结果,可以在命令后加上()。
参考答案:分号(;)2.MATLAB命令行窗口中提示用户输入命令的符号是()。
参考答案:>> ;3.fix(264/100)+mod(264,10)*10的值是()。
参考答案:424.下列可作为MATLAB合法变量名的是()。
参考答案:xyz_2a。
5.在命令行窗口输入下列命令后,x的值是()。
>> clear>> x=i*j参考答案:-1;6.建立矩阵时,不同行的元素之间用()分隔。
参考答案:分号;7.输入字符串时,要用()将字符序列括起来。
参考答案:' ';8.最初的MATLAB核心程序是采用()语言编写的。
参考答案:FORTRAN;9.下列选项中能反应MATLAB特点的是()。
参考答案:编程效率高。
10.如果要重新执行以前输入的命令,可以使用()。
参考答案:上移光标键(↑)。
11.plot(x,y)是一条()命令。
参考答案:绘图;12.以下两个命令行的区别是()。
>> x=5,y=x+10>> x=5,y=x+10;参考答案:第一个命令行同时显示x和y的值,第二个命令行只显示x的值;13.下列选项中,不是MATLAB帮助命令的是()。
参考答案:search;14.下列数值数据表示中错误的是()。
参考答案:2e;15.下列语句中错误的是()。
参考答案:x=y=3;16.已知s='显示"hello"',则s的元素个数是()。
参考答案:9;17.建立矩阵时,同一行的元素之间用()分隔。
参考答案:空格;;逗号;18.在当前文件夹和搜索路径中都有fpp.m文件,那么在命令行窗口输入fpp时,下列说法错误的是()。
参考答案:先执行当前文件夹的fpp.m文件,再执行搜索路径中的fpp.m文件;;先执行搜索路径中的fpp.m文件,再执行当前文件夹的fpp.m文件;;执行搜索路径中的fpp.m文件;19.内存变量文件是二进制格式文件,扩展名为.mat。
MATLAB基础与编程入门(第二版)(张威)-第3章

第三章 数 据 类 型
注意:
MATLAB和C语言在处理数据类型和变量时不同。在C语言 中,任何变量在使用之前都必须声明,然后赋值,在声明变量时 就指定了变量的数据类型。但是在MATLAB中,任何数据变量都不 需要预先的声明,MATLAB将自动地将数据类型设置为双精度类型, 若需要使用其他类型的数据,则必须通过数据类型的转换完成。 MATLAB的数据类型名称同样就是数据类型转换的函数,利用这些 函数来完成相应的数据类型转化的工作。
第三章 数 据 类 型
第三章 数 据 类 型
3.1 概述 3.2 MATLAB基本数值类型 3.3 逻辑类型和关系运算 3.4 字符串 3.5 元胞数组 3.6 结构 3.7 本章小结
第三章 数 据 类 型 3.1 概 述
MATLAB的早期版本只有非常简单的二维数组和字符类型 的数据,目前的MATLAB版本中不仅有多达十几种的基本数据类型, 在不同的专业工具箱中还有特殊的数据类型,并且MATLAB还支持 面向对象的编程技术,支持用户自定义的数据类型。
关于数据类型转换函数的使用可以参阅相应的在线帮助。
第三章 数 据 类 型
例子3-2 使用不同的数据类型。
在MATLAB命令行窗体中键入下面的指令:
>> A = [1 2 3];
>> B = [4 5 6];
>> C = A + B;
>> whos
Name
Size
Bytes Class
A
1x3
24 double
MATLAB支持的基本数据类型见图3-1。
第三章 数 据 类 型
MATLAB数据类型
基本数值类型
字符串
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.打开已有的M文件 打开已有的M文件,也有3种方法: (1) 菜单操作。从MATLAB主窗口的File菜 单中选择Open命令,则屏幕出现Open对话 框,在Open对话框中选中所需打开的M文 件。在文档窗口可以对打开的M文件进行编 辑修改,编辑完成后,将M文件存盘。 (2) 命令操作。在MATLAB命令窗口输入命 令:edit 文件名,则打开指定的M文件。 (3) 命令按钮操作。单击MATLAB主窗口工 具栏上的Open File命令按钮,再从弹出的 对话框中选择所需打开的M文件。
3.4 程序举例 例3-19 猜数游戏。首先由计算机产生 [1,100]之间的随机整数,然后由用户 猜测所产生的随机数。根据用户猜测 的情况给出不同提示,如猜测的数大 于产生的数,则显示“High”,小于则 显示“Low”,等于则显示“You won”, 同时退出游戏。用户最多可以猜7次。
(3) 多分支if语句: if 条件1 语句组1 elseif 条件2 语句组2 …… elseif 条件m 语句组m else 语句组n end 语句用于实现多分支选择结构。
例3-5 输入一个字符,若为大写字母,则输出其对 应的小写字母;若为小写字母,则输出其对应的 大写字母;若为数字字符则输出其对应的数值, 若为其他字符则原样输出。 c=input('请输入一个字符','s'); if c>='A' & c<='Z' disp(setstr(abs(c)+abs('a')-abs('A'))); elseif c>='a'& c<='z' disp(setstr(abs(c)- abs('a')+abs('A'))); elseif c>='0'& c<='9' disp(abs(c)-abs('0')); else disp(c); end
例3-9 已知 ,当n=100时,求y的值。 程序如下: y=0; n=100; for i=1:n y=y+1/(2*i-1); end y
在实际MATLAB编程中,采用循环语句会 降低其执行速度,所以前面的程序通常由 下面的程序来代替: n=100; i=1:2:2*n-1; y=sum(1./i); y
例3-3 求一元二次方程ax2 +bx+c=0的根。 程序如下: a=input('a=?'); b=input('b=?'); c=input('c=?'); d=b*b-4*a*c; x=[(-b+sqrt(d))/(2*a),(-b-sqrt(d))/(2*a)]; disp(['x1=',num2str(x(1)),',x2=',num2str(x(2))]);
例3-1 分别建立命令文件和函数文件,将华 氏温度f转换为摄氏温度c。 程序1: 首先建立命令文件并以文件名f2c.m存盘。 clear; %清除工作空间中的变量 f=input('Input Fahrenheit temperature:'); c=5*(f-32)/9 然后在MATLAB的命令窗口中输入f2c,将会 执行该命令文件,执行情况为: Input Fahrenheit temperature:73 c= 22.7778
2.数据的输出 MATLAB提供的命令窗口输出函 数主要有disp函数,其调用格式为 disp(输出项) 其中输出项既可以为字符串,也可 以为矩阵。
例3-2 输入x,y的值,并将它们的值互换后输出。 程序如下: x=input('Input x please.'); y=input('Input y please.'); z=x; x=y; y=z; disp(x); disp(y);
(2) 双分支if语句: if 条件 语句组1 else 语句组2 end 当条件成立时,执行语句组1,否则执行语 句组2,语句组1或语句组2执行后,再执行 if语句的后继语句。
例3-4 计算分段函数的值。 程序如下: x=input('请输入x的值:'); if x<=0 y= (x+sqrt(pi))/exp(2); else y=log(x+sqrt(1+x*x))/2; end Y
3.程序的暂停 暂停程序的执行可以使用pause函数, 其调用格式为: pause(延迟秒数) 如果省略延迟时间,直接使用pause, 则将暂停程序,直到用户按任一键后 程序继续执行。 若要强行中止程序的运行可使用 Ctrl+C命令。
3.2.2 选择结构 1.if语句 在MATLAB中,if语句有3种格式。 (1) 单分支if语句: if 条件 语句组 end 当条件成立时,则执行语句组,执行完之后继续执 行if语句的后继语句,若条件不成立,则直接执行 if语句的后继语句。
程序2: 首先建立函数文件f2c.m。 function c=f2c(f) c=5*(f-32)/9 然后在MATLAB的命令窗口调用该函数文件。 clear; y=input('Input Fahrenheit temperature:'); x=f2c(y) 输出情况为: Input Fahrenheit temperature:70 c= 21.1111 x= 21.1111
3.3.2 函数调用 函数调用的一般格式是: [输出实参表]=函数名(输入实参表) 要注意的是,函数调用时各实参出现 的顺序、个数,应与函数定义时形参 的顺序、个数一致,否则会出错。函 数调用时,先将实参传递给相应的形 参,从而实现参数传递,然后再执行 函数的功能。
例3-15 利用函数文件,实现直角坐标(x,y)与极坐 标(ρ,θ)之间的转换。 函数文件tran.m: function [rho,theta]=tran(x,y) rho=sqrt(x*x+y*y); theta=atan(y/x); 调用tran.m的命令文件main1.m: x=input('Please input x=:'); y=input('Please input y=:'); [rho,the]=tran(x,y); rho the 在MATLAB中,函数可以嵌套调用,即一个函数 可以调用别的函数,甚至调用它自身。一个函数 调用它自身称为函数的递归调用。
for语句更一般的格式为: for 循环变量=矩阵表达式 循环体语句 end 执行过程是依次将矩阵的各列元 素赋给循环变量,然后执行循环体 语句,直至各列元素处理完毕。
例3-10 写出下列程序的执行结果。 s=0; a=[12,13,14;15,16,17;18,19,20;21,22,23]; for k=a s=s+k; end disp(s');
例3-16 利用函数的递归调用,求n!。 n!本身就是以递归的形式定义的: 显然,求n!需要求(n-1)!,这时可采用递归调用。递 归调用函数文件factor.m如下: function f=factor(n) if n<=1 f=1; else f=factor(n-1)*n; %递归调用求(n-1)! end
3.2 程序控制结构 3.2.1 顺序结构 1.数据的输入 从键盘输入数据,则可以使用input函数来进 行,该函数的调用格式为: A=input(提示信息,选项); 其中提示信息为一个字符串,用于提示用户 输入什么样的数据。 如果在input函数调用时采用's'选项,则允 许用户输入一个字符串。例如,想输入一 个人的姓名,可采用命令: xm=input('What''s your name?','s');
例3-12 求[100,200]之间第一个能被21整除的整数。 程序如下: for n=100:200 if rem(n,21)~=0 continue end break end n
4.循环的嵌套 如果一个循环结构的循环体又包括一个循环结构,就称为 循环的嵌套,或称为多重循环结构。 例3-13 若一个数等于它的各个真因子之和,则称该数为完 数,如6=1+2+3,所以6是完数。求[1,500]之间的全部完数。 for m=1:500 s=0; for k=1:m/2 if rem(m,k)==0 s=s+k; end end if m==s disp(m); end end
3.3 函数文件 3.3.1 函数文件的基本结构 函数文件由function语句引导,其基本结构 为: function 输出形参表=函数名(输入形参表) 注释说明部分 函数体语句 其中以function开头的一行为引导行,表示该 M文件是一个函数文件。函数名的命名规则 与变量名相同。输入形参为函数的输入参 数,输出形参为函数的输出参数。当输出 形参多于一个时,则应该用方括号括起来。
2.while语句 while语句的一般格式为: while (条件) 循环体语句 end 其执行过程为:若条件成立,则执行 循环体语句,执行后再判断条件是否 成立,如果不成立则跳出循环。
例3-11 从键盘输入若干个数,当输入0时结束输入,求这 些数的平均值和它们之和。 程序如下: sum=0; cnt=0; val=input('Enter a number (end in 0):'); while (val~=0) sum=sum+val; cnt=cnt+1; val=input('Enter a number (end in 0):'); end if (cnt > 0) sum mean=sum/cnt end
