九年级数学与圆有关的位置关系
九年级点与圆的位置关系知识点

九年级点与圆的位置关系知识点我们生活中到处都是点和圆,而点与圆之间的位置关系是数学中非常重要的一个知识点。
在九年级的数学课程中,我们将学习点与圆的位置关系,探索它们之间的奥妙。
1. 点在圆内:当一个点位于一个圆的内部时,我们称它为圆的内点。
圆的内点与圆心之间的距离小于半径的长度。
这意味着,无论内点与圆的任何一点相连,线段的长度都小于半径。
这个性质对于我们判断几何图形的位置关系尤为重要。
2. 点在圆外:当一个点位于一个圆的外部时,我们称它为圆的外点。
圆的外点与圆心之间的距离大于半径的长度。
同样地,我们可以利用这个特性来推断几何图形的位置关系。
3. 点在圆上:当一个点位于一个圆上时,我们称它为圆的边点。
边点与圆心之间的距离等于半径的长度。
这意味着边点与圆心之间的连线就是圆的半径。
此外,边点还有一个特殊的性质,就是任何通过边点的直径都可以被边点所分成两段相等的弧。
4. 内切圆和外切圆:在九年级,我们还将学习内切圆和外切圆这两个重要的概念。
内切圆是指一个圆恰好与多边形的边相切,且圆的圆心位于多边形的内部。
外切圆则是指一个圆恰好与多边形的边相切,且圆的圆心位于多边形的外部。
通过这些概念,我们不仅可以研究多边形与圆的位置关系,还能够解决一些实际问题。
例如,我们可以利用内切圆和外切圆来设计最大面积或最小周长的形状。
5. 点与圆的判定问题:在九年级的数学课程中,我们还会学习如何判定一个点与一个已知圆的位置关系。
这需要我们掌握一些重要的定理和方法。
例如,切线定理可以帮助我们判断一个直线与圆的位置关系,弦切角定理则可以用来判断两条弧的位置关系。
此外,我们还可以使用勾股定理和三角形相似性来解决一些点与圆的位置关系问题。
在学习点与圆的位置关系时,我们不仅仅停留在理论层面,更要加强实际应用。
数学在现实生活中的应用非常广泛,点与圆的位置关系也不例外。
例如,我们可以利用圆与点的位置关系来设计游乐场、车辆行驶轨迹等等。
通过深入理解点与圆的位置关系,我们可以更好地认识和应用数学知识。
九年级数学直线和圆的位置关系

高档题型解析及思路拓展
例题3
解析
思路拓展
已知直线$l_{1}$和圆$O_{1}$相切于点 $P$,直线$l_{2}$过点$P$且与圆 $O_{1}$相交于另一点$Q$,求直线 $l_{2}$的方程。
由于直线$l_{1}$和圆$O_{1}$相切于点 $P$,因此点$P$是切点,且直线 $l_{1}$在点$P$处的切线斜率与直线 $l_{2}$的斜率相等。我们可以通过求 出点$P$的坐标和切线斜率,再利用点 斜式求出直线$l_{2}$的方程。
若直线与圆相切,则直线到圆心的距 离等于半径,由此可求出切线方程。
直线与圆的交点坐标
联立直线方程和圆方程求解,可得交 点坐标。若有两个交点,则它们关于 圆心对称。
02
直线与圆的位置关系分类
相离关系
定义
直线与圆没有公共点,称为相离。
判定方法
通过比较圆心到直线的距离与圆的 半径大小来判断。若圆心到直线的 距离大于圆的半径,则直线与圆相 离。
直线与圆的交点个数
通过观察图形或计算,确定直线与圆的交点个数。若有两个交点,则直线与圆 相交;若有一个交点,则直线与圆相切;若没有交点,则直线与圆相离。
综合应用举例
解法一
联立直线l和圆C的方程,消去一 个未知数得到一个一元二次方程 。根据判别式的值判断位置关系 。
解法二
计算圆心(a,b)到直线l的距离d,根 据d与半径r的大小关系判断位置关 系。
圆的性质
圆上任意一点到圆心的距 离等于半径;圆的任意弦 所对的圆周角等于弦所对 圆心角的一半。
圆的切线
与圆有且仅有一个交点的 直线称为圆的切线,切线 与半径垂直。
直线与圆的交点问题
直线与圆的位置关系
直线与圆的切线问题
初三数学直线和圆的位置关系

初三数学直线和圆的位置关系一.直线和圆的位置关系:①相交:直线和圆有两个公共点,这时说这条直线和圆相交;这条直线叫做圆的割线;②相切:直线和圆有唯一公共点,这时说这条直线和圆相切;这条直线叫做圆的切线,这个点叫做切点.③相离:直线和圆没有公共点,这时说这条直线和圆相离.二.直线和圆的位置关系的判定:(1)定理:若⊙O的半径为R,圆心到直线l 的距离为d. 则直线l与⊙O相交d﹤R;直线l与⊙O相切 d =R;直线l与⊙O相离d﹥R;(2)“圆心到直线的距离d和半径R的数量关系”与“直线和圆的位置关系”之间的对应与等价关系列表如下:例1、1.在Rt△ABC中,∠C=,AC=3cm,AB=6cm,以点C为圆心,与AB边相切的圆的半径为_________cm.2.如图,⊙O的半径OD为5cm,直线l⊥OD,垂足为O,则直线l沿射线OD方向平移_________cm时与⊙O相切.3.已知⊙O的直径为6cm,如果直线l上的一点C到圆心的距离为3cm,则直线l与⊙O的位置关系是_________.4.⊙O的半径为R,圆心O到直线l的距离d与R是方程x2-6x+9=0的两个实数根,则直线l和⊙O的位置关系是_________.三.切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线;2.切线的性质:①切线垂直于过切点的半径;②切线和圆心的距离等于半径;③经过圆心且垂直于切线的直线必过切点;④经过切点垂直于切线的直线必过圆心.综上所述,在解决有关圆的切线的问题,连接圆心和切点的线段是最常见的辅助线.四、切线长的定义及切线长定理过圆外一点作圆的切线,这点和切点之间的线段长叫做这点到圆的切线长,如图所示,PA,PB 是⊙O的两条切线,A,B为切点,线段PA,PB的长即为点P到⊙O的切线长.切线长定理:过圆外一点所画的圆的两条切线长相等.例2、如图,AB是⊙O的直径,BC切⊙O于点B,AD∥CO.求证:CD是⊙O的切线.1、⊙O的半径为R,直线l和⊙O有公共点,若圆心到直线l的距离是d,则d与R的大小关系是()A.d>RB.d<RC.d≤RD.d≥R2、点A为直线l上任一点,过A点与直线l相切的圆有()个.A.1 B.2C.不存在 D.无数个3、在Rt△ABC中,∠A=,BA=12,CA=5,若以A为圆心,5为半径作圆,则斜边BC与⊙A的位置关系是()A.相交 B.相离C.相切 D.不确定4、等边△ABC的边长为6,点O为△ABC的外心,以O为圆心,为半径的圆与△ABC的三边()A.都相交B.都相离C.都相切D.不确定5、两个同心圆的半径分别为3cm和5cm,作大圆的弦MN=8cm,则MN与小圆的位置关系是()A.相交 B.相切C.相离D.无法判断6、如图,在直角坐标系中,⊙O的半径为1,则直线与⊙O的位置关系是()A.相离 B.相交C.相切 D.以上三种情形都有可能7、下列说法正确的是()A.垂直于切线的直线必过切点B.垂直于半径的直线是圆的切线C.圆的切线垂直于经过切点的半径D.垂直于切线的直线必经过圆心8、已知Rt△ABC的直角边AC=BC=4cm,若以C为圆心,以3cm的长为半径作圆,则这个圆与斜边所在的直线的位置关系是()A.相交 B.相切C.相离 D.不能确定9、如右上图,在△ABC中,AB=2,AC=1,以AB为直径的圆与AC相切,与边BC交于点D,则AD的长为()10、如下图,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=25°,∠D=__________.11、如图,⊙O的半径为1,圆心O在正三角形的边AB上沿图示方向移动,当⊙O移动到与AC相切时,OA=__________.12、设⊙O的半径为R,⊙O的圆心到直线的距离为d,若d、R是方程x2-6x+m=0的两根,则直线l 与⊙O相切时,m的值为__________.13、已知∠ABC=60°,点O在∠ABC的平分线上,OB=5cm,以O为圆心,2cm为半径作⊙O,则⊙O与BC的位置关系是__________.14、如图,Rt△ABC中,∠B=90°,∠A的平分线交BC于D,E为AB上一点,DE=DC,以D为圆心,DB的长为半径作⊙D.求证:(1)AC是⊙D的切线;(2)AB+EB=AC.15、如图,以边长为4的正△ABC的BC边为直径作⊙O与AB相交于点D,⊙O的切线DE交AC于E,EF⊥BC,点F是垂足,求EF的长.16、如图,PA是⊙O的切线,切点是A,过点A作AH⊥OP于点H,交⊙O于点B.求证:PB是⊙O的切线.17、如图,已知AB是⊙O的直径,AB=2,∠BAC=30°,点C在⊙O上,过点C与⊙O相切的直线交AB 的延长线于点D,求线段BD的长.1.弧长公式:n°的圆心角所对的弧长l公式不要死记硬背,可依比例关系很快地随手推得:2.扇形面积公式:(1)和含n°圆心角的扇形的面积公式同样不要死记硬背,可依比例关系很快地随手推得:.(2)将弧长公式代入扇形面积公式中,立即得到用弧长和半径表示的扇形面积公式:。
初中数学——(54)直线与圆的位置关系

初中数学——(54)直线与圆的位置关系一、直线与圆的位置关系(一)相交:直线与圆有两个公共点,d<r(二)相切:直线与圆有一个公共点,d=r1、切线:垂直于半径且与圆相切的直线就是切线2、切线垂直于过切点的半径3、过切点垂直于切线的直线必过圆心(三)相离:直线与圆有没有公共点,d>r二、切线长定理从圆外一点引圆的两条切线,它们的切线长相等,这点和圆心的连线平分两条切线的夹角,即:PA,PB是两条切线,且PA=PB,那么OP平分∠BAP三、圆幂定理定理图形结论相交弦定理PA·PB=PC·PD相交弦定理推论PC2=PA·PB 切割线定理PT2=PA·PB切割线定理推论PA·PB=PC·PD圆幂定理P'C·P'D=r2-OP'2 PA·PB=OP2-r2四、圆柱计算(一)S 表 = S 侧+2S 底 = 2πrh +2πr 2 (二)V 体 = πr 2h五、圆锥计算(一)S 表 = S 侧+S 底 = πRr +πr 2(二)V 体 =31πr 2h六、练习题(一)以等边三角形ABC 的BC 边为直径画半圆,分别交AB 、AC 于点E 、D ,DF 是圆的切线,过点F 作BC 的垂线交BC 于点G .若AF 的长为2,则FG 的长为多少?B1RrCBO(二)AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连结AC交⊙O于D,∠C=38°。
点E在AB右侧的半圆上运动(不与A、B重合),求∠AED的大小(三)如图,AB为⊙O的直径,弦CD⊥AB于点E,若CD=,且AE:BE =1:3,求AB的长(四)已知AB是⊙O的直径,AD⊥l于点D1、如图①,当直线l与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;2、如图②,当直线l与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小(五)如图,AB为的直径,点C在⊙O上,点P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q。
初中数学 公切线与圆的位置关系是什么

初中数学公切线与圆的位置关系是什么
公切线与圆的位置关系主要有三种情况:外公切线、内公切线和不相交。
1. 外公切线:
-外公切线是指一条直线与圆相切,且位于圆的外部。
-外公切线与圆的切点位于圆上,且与切点连线垂直于圆的半径。
-外公切线与圆的切点构成的线段与圆的半径之差相等。
-外公切线与圆的位置关系是切点位于圆的外部,切线与圆的位置关系是切线与圆只有一个切点。
2. 内公切线:
-内公切线是指一条直线与圆相切,且位于圆的内部。
-内公切线与圆的切点位于圆上,且与切点连线垂直于圆的半径。
-内公切线与圆的切点构成的线段与圆的半径之和相等。
-内公切线与圆的位置关系是切点位于圆的内部,切线与圆的位置关系是切线与圆只有一个切点。
3. 不相交:
-当两个圆之间的距离大于两个圆的半径之和时,它们没有公共切点,也就是不存在公切线。
-不相交的圆之间有两种情况:一个圆在另一个圆的内部或两个圆完全分离。
需要注意的是,公切线与圆的位置关系是由两个因素决定的:切点的位置和切线与圆的关系。
公切线的切点位于圆上,且与切点连线垂直于圆的半径。
切线与圆的位置关系是切线与圆只有一个切点。
希望以上内容能够满足你对公切线与圆的位置关系的了解。
中考数学复习之与圆有关的位置关系,考点过关与基础练习题
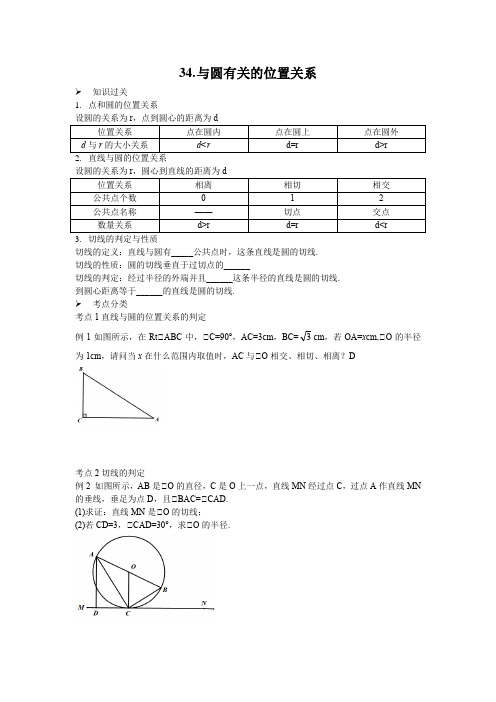
34.与圆有关的位置关系➢知识过关1.点和圆的位置关系2.直线与圆的位置关系3.切线的判定与性质切线的定义:直线与圆有_____公共点时,这条直线是圆的切线.切线的性质:圆的切线垂直于过切点的______切线的判定:经过半径的外端并且______这条半径的直线是圆的切线.到圆心距离等于______的直线是圆的切线.➢考点分类考点1直线与圆的位置关系的判定例1如图所示,在Rt△ABC中,△C=90°,AC=3cm,BC=3cm,若OA=x cm,△O的半径为1cm,请问当x在什么范围内取值时,AC与△O相交、相切、相离?D考点2切线的判定例2 如图所示,AB是△O的直径,C是O上一点,直线MN经过点C,过点A作直线MN 的垂线,垂足为点D,且△BAC=△CAD.(1)求证:直线MN是△O的切线;(2)若CD=3,△CAD=30°,求△O的半径.考点3 切线的性质 例3 如图所示,在△O 中,点C 是直径AB 延长线上一点,过点C 作△O 的切线,切点为D ,连接BD.(1)求证:△A=△BDC(2)若CM 平分△ACD ,且分别交AD 、BD 于点M 、N ,当DM=1时,求MN 的长.➢ 真题演练1.如图,A 、P 、B 、C 是⊙O 上的四点,∠APC =∠BPC =60°,P A =2,PC =4,则△ABC 的面积为( )A .43√3B .32√3C .2√3D .3√32.如图,四边形ABCD 是⊙O 的内接四边形,∠B =90°,∠BCD =120°,AB =4,BC =2,则AD 的长为( )A .2√3B .4−√3C .√3+1D .2+√33.如图,P A 、PB 、CE 分别与⊙O 相切于点A 、B 、D 点,若圆O 的半径为6,OP =10,则△PCE 的周长为( )A .10B .12C .16D .204.如图所示,点P 是⊙O 的半径OC 延长线上的一点,过点P 作⊙O 的切线,切点为A ,AB 是⊙O 的弦,连接AC ,BC ,若∠P AB =70°,则∠ACB 的大小为( )A .70°B .110°C .120°D .140°5.如图,在△ABC 中,∠A =60°,BC =12,若⊙O 与△ABC 的三边分别相切于点D ,E ,F ,且△ABC 的周长为32,则DF 的长为( )A .2B .3C .4D .66.如图,已知DC 是⊙O 的直径,点B 为CD 延长线上一点,AB 是⊙O 的切线,点A 为切点,且∠BAD =35°,则∠ADC =( )A .75°B .65°C .55°D .50°7.如图,PC 、PB 是⊙O 的切线,AB 是⊙O 的直径,延长PC ,与BA 的延长线交于点E ,过C 点作弦CD ,且CD ∥AB ,连接DO 并延长与圆交于点F ,连接CF ,若AE =2,CE =4,则CD 的长度为( )A .3B .4C .185D .2458.如图,四边形ABCD 内接于⊙O ,AE ⊥CB ,交CB 的延长线于点E .若BA 平分∠DBE ,AD =7,CE =√13,则AE 的长度为 .9.如图,四边形ABCD 内接于⊙O ,AB 为直径,AD =CD ,过点D 作DE ⊥AB 于点E ,连接AC 交DE 于点F .若sin ∠CAB =35,DF =5,则AB 的长为 .10.如图,P A、PB分别与⊙O相切于A、B两点,C为⊙O上一点连接AC、BC,若∠C=55°,则∠P的度数是°.11.如图,AB为圆O直径,∠DAB=∠ABC=90°,CD与圆O相切于点E,EF⊥AB于点F,EF交BD于点G,若AD=2,BC=6.(1)求CD的长度.(2)求EG的长度.(3)求FB的长度.12.如图,P A、PB、CD是⊙O的切线,点A、B、E为切点.(1)如果△PCD的周长为10,求P A的长;(2)如果∠P=40°,①求∠COD;②连AE,BE,求∠AEB.13.如图,P A、PB分别与⊙O相切于点A、B,PO的延长线交⊙O于点C,连接BC,OA.(1)求证:∠POA=2∠PCB;(2)若OA=3,P A=4,求tan∠PCB的值.➢ 课后练习1.如图,P A ,PB 是⊙O 的两条切线,A ,B 是切点,过半径OB 的中点C 作CD ⊥OB 交P A 于点D ,若PD =3,AD =5,则⊙O 的半径长为( )A .2√7B .4√2C .3√3D .2√52.如图,等边三角形ABC 的边长为4,⊙C 的半径为√3,P 为AB 边上一动点,过点P 作⊙C 的切线PQ ,切点为Q ,则PQ 的最小值为( )A .12B .√3C .2√3D .33.如图,点O 是矩形ABCD 对角线BD 上的一点,⊙O 经过点C ,且与AB 边相切于点E ,若AB =4,BC =5,则⊙O 的半径长为( )A .165B .258C .5√419D .44.如图,在△ABC 中,∠ACB =90°,AC =BC =√2,点D 是AB 边上一个动点,以点D 为圆心r 为半径作⊙D ,直线BC 与⊙D 切于点E ,若点E 关于CD 的对称点F 恰好落在AB 边上,则r 的值是( )A .√2−1B .1C .√2D .√2+15.如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,如果∠D=30°,AB=4,那么线段CD的长是.6.如图,△ABD内接于⊙O,AD为直径,CD为⊙O的切线,连接BC,若CD=AD,AB =2,BC=2√13,则BD=.7.已知菱形ABCD的边长为4,∠BAD=60°,M是线段AD的中点,点P是对角线AC 上的动点,连接PM,以P为圆心,PM长为半径作⊙P,当⊙P与菱形ABCD的边相切时,AP的长为.8.如图,已知△ABC,以AB为直径的⊙O交AC于点E,交BC于点D,且BD=CD,DF ⊥AC于点F.给出以下四个结论:̂=DÊ;④∠A=2∠FDC.①DF是⊙O的切线;②CF=EF;③AE其中正确结论的序号是.9.如图,在Rt△ABC中,AC=BC=6,点O为边BC上一动点,连接OA.以O为圆心,OB为半径作圆,交OA于D,过D作⊙O的切线,交AC于点E.当⊙O与边AC相切时,CE的长为.10.如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交AB于点D,点Q为CA延长线上一点,延长QD交BC于点P,连接OD,∠ADQ=12∠DOQ.若AQ=AC,AD=4时,写出BP的长为.11.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆交于点D.(1)如图1,连接DB,求证:DB=DE;(2)如图2,若∠BAC=60°,求证:AB+AC=√3AD.12.如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F.(1)若∠ABC=50°,∠ACB=75°,求∠BOC的度数;(2)若AB=13,BC=11,AC=10,求AF的长.➢冲击A+。
九年级数学直线与圆的位置关系

点和圆的位置关系有几种?
A B C
点到圆心的距离为d, 圆的半径为r,则: 点在圆外 点在圆上 点在圆内 d>r; d=r; d<r.
直线与圆的位置关系
(地平线)
● ● ●
O
● ●
O
O
a(地平线)
O
O
一、直线与圆的位置关系
(用公共点的个数来区分)
特点: 直线和圆没有公共点, 叫直线和圆相离 特点: 直线和圆有惟一的公共点, 叫做直线和圆相切。 C
C
x
A
图形 直线与圆的 位置关系
.O r d ┐ l
.o d r ┐ l .
A
. B
.O d r ┐ . lC
相离
0 d>r
相切
1 d=r
相交பைடு நூலகம்
2 d<r
公共点的个数
圆心到直线的距离 d 与半径 r 的关系
公共点的名称 直线名称
切点
切线
已知⊙O的半径r=7cm,直线l1 // l2, 且l1与⊙O相切,圆心O到l2的距离为9cm. 求l1与l2的距离m.
.A
.A
.B
这时的直线叫切线
惟一的公共点叫切点。 特点: 直线和圆有两个公共点, 叫做直线和圆相交。
a(地平线)
观察太阳落山的照片,在太阳落山的过程中,太阳与 地平线(直线a)经历了哪些位置关系的变化?
看图判断直线l与 ⊙O的位置关系
(1) (2)
· O · O
l
(3) l l
· O
相离
相交
相切
课堂练习:
2、已知⊙O的半径为5cm, 圆心O与直线AB的距 离为d, 根据条件填写d的范围: 1)若AB和⊙O相离, 则 d > 5cm ; ; 2)若AB和⊙O相切, 则 d = 5cm
初中数学知识点精讲精析 圆和圆的位置关系

3·6圆和圆的位置关系1.圆与圆的五种位置关系:(1)外离:两个圆没有公共点,并且每一个圆上的点都在另一个圆的外部;(2)外切:两个圆有唯一公共点,除公共点外一个圆上的点都在另一个圆的外部;(3)相交:两个圆有两个公共点,一个圆上的点有的在另一个圆的外部,有的在另一个圆的内部;(4)内切:两个圆有一个公共点,除公共点外,⊙O2上的点在⊙O1的内部;(5)内含:两个圆没有公共点,⊙O2上的点都在⊙O1的内部.外离和内含都没有公共点;外切和内切都有一个公共点,相交有两个公共点.因此只从公共点的个数来考虑,可分为相离、相切、相交三种.(2)相交2.两圆相内切或外切时,两圆的连心线一定经过切点,都是轴对称图形,对称轴是它们的连心线.3.在图(1)中,两圆相外切,切点是A.因为切点A在连心线O1O2上,所以O1O2=O1A+O2A =R+r,即d=R+r:反之,当d=R+r时,说明圆心距等于两圆半径之和,O1、A、O2在一条直线上,所以⊙O1与⊙O2只有一个交点A,即⊙O1与⊙O2外切.在图(2)中,⊙O1与⊙O2相内切,切点是B.因为切点B在连心线O1O2,所以O1O2=O1B-O2B,即d=R-r:反之,当d=R-r时,圆心距等于两半径之差,即O1O2=O1B-O2B,说明O1、O2、B在一条直线上,B既在⊙O1上,又在⊙O2上,所以⊙O1与⊙O2内切.当两圆相外切时,有d=R+r,反过来,当d=R+r时,两圆相外切,即两圆相外切 d=R+r当两圆相内切时,有d=R-r,反过来,当d=R-r时,两圆相内切,即两圆相内切d =R-r.设两圆半径分别为R和r,圆心矩为d,那么(1)两圆外离d>R+r(2)两圆外切d=R+r(3)两圆相交R-r<d<R=r(R≥r)(4)两圆内切d=R-r(R>r)(5)两圆内含d<R-r(R>r)同心圆d=04.定理:相交两圆的连心线垂直平分两圆的公共弦.1.两个同样大小的肥皂泡黏(点O,O′是圆心),分隔两个肥皂泡的肥皂膜PQ成一条直线,TP、NP分别为两圆的切线,求∠TPN的大小.分析:因为两个圆大小相同,所以半径OP=O′P=OO′,又TP、NP分别为两圆的切线,所以PT⊥OP,PN⊥O′P,即∠OPT=∠O′PN=90°,所以∠TPN等于360°减去∠OPT+∠O′PN+∠OPO°即可.【解析】∵OP =OO′=PO′,∴△PO′O是一个等边三角形.∴∠OPO′=60°.又∵TP与NP分别为两圆的切线,∴∠TPO=∠NPO′=90°.∴∠TPN=360°-2× 90°-60°=120°.2.如图⊙O的半径为5cm,点P是⊙O外一点,OP=8cm.求:(1)以P为圆心作⊙P与⊙O外切,小圆⊙P的半径是多少?(2)以P为圆心作⊙P与⊙O内切,大圆⊙P的半径是多少?【解析】(1)设⊙O与⊙P外切于点A.∴ PA=OP-OA=8-5,∴ PA=3cm.(2)设⊙O与⊙p内切于点B.∴ PB=OP+OB=8+5,∴ PB=13cm.(3)如图7-101,⊙O2与以O1为圆心的同心圆相交于A、B、C、D.3.求证:四边形ABCD是等腰梯形.分析:欲证明四边形ABCD是等腰梯形,只需证明AB∥CD,AD=BC且AB≠CD即可.【解析】证明:连结O1O2,∵⊙O2与以O1为圆心的圆相交于A、B、C、D,∴ AB⊥O1O2,DC⊥O1O2.∴ AB∥CD.在⊙O2中,∵AB∥CD,又∵ AB≠CD,∴四边形ABCD是等腰梯形.4.已知:如图7-102,A是⊙O1、⊙O2的一个交点,点P是O1O2的中点.如果过A的直线MN垂直于PA,交⊙O1于M,交⊙O2于N.那么AM与AN有什么关系呢?是O1O2中点,由平行线等分线段定理可得AC=AD,而得结论.【解析】证明:过点O1、O2分别作O1C⊥MN,O2D⊥MN,垂足为C、D,又∵ PA⊥MN,∴ PA∥O1C∥O2D,∵O1P=O2P,∴ AC=AD.∴ AM=AN.。
九年级数学 点与圆、直线与圆、圆与圆的位置关系

九年级数学 点与圆、直线与圆、圆与圆的位置关系1、点与圆的位置关系有 种,若圆的半径为r ,点P 到圆心的距离为d 。
则:点P 在圆内⇔ ;点P 在圆上⇔ ;点P 在圆外⇔ 。
2、过三点的圆:⑴过同一直线上三点 作圆,过 三点,有且只有一个圆;⑵三角形的外接圆:经过三角形各顶点的圆叫做三角形的 ,外接圆的圆心叫做三角形的 ,这个三角形叫做这个圆的 。
⑶三角形外心的形成:三角形 的交点, 相等。
1、直线与圆的位置关系有 种:○1当直线和圆有两个公共点时,叫做直线和圆 ,这时直线叫圆的 线,; ○2当直线和圆有唯一公共点时,叫做直线和圆 ,这时直线叫圆的 线; ○3当直线和圆没有公共点时,叫做直线和圆 ,这时直线叫圆的 线。
2、设⊙O 的半径为r ,圆心O 到直线l 的距离为d ,则:直线l 与⊙O 相交r d _____⇔直线l 与⊙O 相切r d _____⇔直线l 与⊙O 相离r d _____⇔3、 切线的性质和判定:⑴性质定理:圆的切线垂直于经过切点的 。
【谈重点】根据这一定理,在圆中遇到切线时,常常连接圆心和切点,即可得垂直关系。
⑵判定定理:经过半径的 且 这条半径的直线是圆的切线。
【谈重点】在切线的判定中,当直线和圆的公共点标出时,用判定定理证明。
当公共点未标出时,一般可证圆心到直线的距离d=r 来判定相切。
4、 切线长定理:⑴切线长定义:在经过圆外一点的圆的切线上,这点和切点之间 的长叫做这点到圆的切线长。
⑵切线长定理:从圆外一点引圆的两条切线,它们的 相等,并且圆心和这一点的连线平分 的夹角5、 三角形的内切圆:⑴与三角形各边都 的圆,叫做三角形的内切圆,内切圆的圆心叫做三角形的 ;⑵三角形内心的形成:是三角形 的交点;(3)内心的性质:到三角形各 的距离相等,内心与每一个顶点的连接线平分 。
【谈重点】三类三角形内心都在三角形若△ABC三边为a、b、c面积为s,内切圆半径为r,则s= ,若△ABC为直角三角形,则r=考点一:切线的性质例题1已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.(1)若⊙O的半径为8,求CD的长;(2)证明:PE=PF;(3)若PF=13,sinA=513,求EF的长.对应训练1.如图,△ABC内接于⊙O,弦AD⊥AB交BC于点E,过点B作⊙O的切线交DA的延长线于点F,且∠ABF=∠ABC.(1)求证:AB=AC;(2)若AD=4,cos∠ABF=45,求DE的长.考点二:切线的判定例题2如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=63cm.(1)求证:AC是⊙O的切线;(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)对应训练2.如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.(1)求证:AC是⊙O的切线:(2)若BF=8,DF=40,求⊙O的半径r.知识点三、圆和圆的位置关系圆和圆的位置关系有种,若⊙O1半径为R,⊙O 2半径为r,圆心距为d;○1当⊙O 1 与⊙O 2 外离⇔;○2当⊙O 1 与⊙O 2 外切⇔;○3当⊙O 1 与⊙O2相交⇔;○4当⊙O 1 与⊙O2内切⇔;○5当⊙O 1 与⊙O 2内含⇔。
人教版圆和圆的位置关系

内含:两圆没有公共点时,并且一个圆的 点都在另一个圆的内部,称这两圆内含
圆和圆的位置关系
1个公共点
外切 内切
相切
圆和圆的位置关系
外切
内切
相切:两圆有一个公共点时,称这两圆相
定 义
切 这个唯一 的公共点称为切点。
外切:两圆有一个公共点时,并且除了这
个公共点外,一个圆的点都在另一个圆的
外部,称这两圆外切。
内切:两圆有一个公共点时,并且除了这 个公共点外,一个圆的点都在另一个圆的
内部,称这两圆内含
圆和圆的位置关系
2个公共点
相切:两圆有一个公共点时,称这两圆相切
定 义
这个唯一 的公共点称为切点。
圆和圆的位置关系
外离
外切
相交
内切
内含
圆和圆的位置关系
请说一说图中所反映的圆和圆有哪些位置关系?
外离
圆和圆的位置关系
请说一说图中所反映的圆和圆有哪些位置关系?
内切
圆和圆的位置关系
请说一说图中所反映的圆和圆有哪些位置关系?
内含
圆和圆的位置关系
请说一说图中所反映的圆和圆有哪些位置关系?
外切
动手操作:请用半径不同的两圆摆一摆
圆和圆有几种不同的位置关系,每种位置 关系中两圆有多少个公共点?
两圆的位置关系
讨论:
如果两圆的半径分别为r和R(设
R>r),圆心距(两圆圆心的距离)
为d,那么圆和圆的五种位置关系 中,d与R+r和R-r之间有什么数量 关系?
几何画板展示圆和圆的五种位置关系
圆O1和圆O2的半径分别为3厘米和4厘米, 下列情况下两圆的位置关系是怎样?
( 1 ) O1O2=8厘米 外离
九年级数学圆与圆的位置关系

九年级数学圆与圆的位置关系在我们学习数学的过程中,有些知识总是能让人拍案叫绝,比如说圆与圆之间的位置关系。
你想啊,两个圆就像两个好朋友,有时候紧紧相拥,有时候则是形同陌路。
今天咱们就来聊聊这些圆的“社交”动态,保准让你听了哈哈大笑,边学边乐。
首先呢,咱们得知道圆和圆之间的基本关系。
两个圆如果能够相交,形成两个交点,那就叫做“相交”。
这就好比是两位朋友在某个聚会上聊得火热,结果发现两个人的兴趣爱好还真是有那么一点点相似,嘿嘿,意外的发现吧。
如果这两个圆的距离刚刚好,让它们只轻轻碰了一下,那就叫做“相切”。
就像两个朋友在街上偶遇,点头致意一下,心照不宣,继续各自的旅程,既亲密又有些距离。
哦,对了,记得咱们的圆心距离和半径的关系。
圆心距小于半径之和,那就能相交;等于半径之和,那就相切;大于半径之和,嘿,那就各自飞了。
咱们得聊聊“相离”这种情况。
两圆如果完全不相交,远得像两个恋人各自生活在两个城市,联系得少之又少,那就是“相离”。
你想啊,两个圆心的距离大于半径之和,真是远得像是天涯海角,不同的生活方式,不同的爱好,没啥交集,生活就这么各自精彩。
想象一下,两个圆在画纸上悄悄地待着,互不干扰,彼此就是那种“风马牛不相及”的感觉。
再来看看特殊的情况。
比如,当两个圆的圆心重合,但半径不同,那就有点意思了。
想象一下,有个圆在外面转来转去,另一个圆在它的“肚子”里悄悄待着。
这个时候,内圆完全被外圆包裹住了,像极了朋友间的包容。
总有那么一个人,给你无条件的支持,虽然不总是被看到,但心里永远有那么一个位置。
可惜,这种情况可不是每个人都能理解的。
说到这里,咱们再来琢磨一下这些圆之间的关系的意义。
生活中,朋友之间的关系也好,爱人之间的互动也罢,都是那么复杂又简单。
有人总是希望彼此相交,有人则想要独立。
相交的朋友就像是在一起打游戏,总是能碰撞出各种火花,而相切的朋友则是在适当的时候给予彼此空间,既能相互支持,又能保留个人的独特性。
九年级数学第三十三课 圆与圆的位置关系

第33课圆与圆的位置关系知识点:圆和圆的位置关系、两圆的连心线的性质、两圆的公切线大纲要求:1.了解两圆公切线的求法,掌握圆和圆的位置关系;2.了解两圆位置关系与公共点个数、外公切线条数、内公切线条数以及d、R、r之间的关系;3.掌握相交两圆的性质和相切两圆的性质;4.注意 (1)圆与圆的五种位置关系相交和相切是重点;(2)在解题中把两个圆中有关问题利用圆的性质和直线圆的位置关系的定理和性质转化为一般圆的问题;(3)涉及相交两圆的问题常可作出公共弦,利用圆周角定理及其推论或连心线垂直乎分公共弦。
公共弦可沟通两个圆的角之间关系,有了连心线,公共弦不仅可取应用相交两圆的性质定理且还能沟通两圆半径、公切线等之间的关系;(4)涉及相切两圆问题主要可从以下几个方面考虑;①过切点作两圆的公切线,利用弦切角定理或切线长定理;②作出连心线,利用连心线过切点的性质;③利用两圆的圆心距等于两圆半径之和或之差;④当两圆外切时,利用连心线、外公切线及过公切线切点的两条毕径组成的直角梯形,将有关圆的间题转化为直线形间题,把梯形问题转化为直角三角形问题,通过解直角三角形来解决有关两圆公切线等问题。
考查重点与常甩题型:1.判断基本概念、基本定理等的正误。
在中考题申常以选择题或填空题的形式考查学生对基本概念和基本定理的正确理解,如:已知两圆的半径分别为2、5,且圆心距等于3,则两圆位置关系是 ( )(A)外离 (B)外切 (C)相交 (D) 内切2.考查两圆位置关系中的相交及相切的性质,可以以各种题型形式出现,多见于选择题或填空题,有时在证明、计算及综合题申也常有出现。
预习练习:1.已知两圆的半径分别是2和4,圆心距是3,那么这两圆的位置是()(A)内含 (B)内切 (C)相交 (D) 外切2.已知半径为R和r的两个圆相外切。
则它的外公切线长为()(A)R+r (B)R2+r2 (C) R+r (D) 2Rr3.已知⊙O1半径为3cm,⊙O2半径为4cm,并且⊙O1与⊙O2相切,则这两个圆的圆心距为()(A)1cm (B)7cm (C) 10cm (D) 1cm或7cm4.两圆半径为5和r,圆心距为8,当两圆相交时,r取值范围是5.两圆直径分别为6、8,圆心距为10,则这两圆的最多公切线条数是考点训练:1.已知半径为R和r的两个圆外切,R=2+ 3 ,r=2- 3 ,两圆的一条公切线与连心线的夹角为α,则角α的度数为()(A)30 ° (B)45 ° (C) 60 ° (D) 无法确定2.如图,两个同心圆,点A在大圆上,ABC为小圆的割线,若AB·AC=8,则圆环的面积为()(A)8π(B)12π(C) 4π(D) 16π。
(中考考点梳理)圆的性质及与圆有关的位置关系-中考数学一遍过

考点18 圆的性质及与圆有关的位置关系一、圆的有关概念1.与圆有关的概念和性质(1)圆:平面上到定点的距离等于定长的所有点组成的图形.(2)弦与直径:连接圆上任意两点的线段叫做弦,过圆心的弦叫做直径,直径是圆内最长的弦.(3)弧:圆上任意两点间的部分叫做弧,小于半圆的弧叫做劣弧,大于半圆的弧叫做优弧.(4)圆心角:顶点在圆心的角叫做圆心角.(5)圆周角:顶点在圆上,并且两边都与圆还有一个交点的角叫做圆周角.(6)弦心距:圆心到弦的距离.2.注意(1)经过圆心的直线是该圆的对称轴,故圆的对称轴有无数条;(2)3点确定一个圆,经过1点或2点的圆有无数个.学-科网(3)任意三角形的三个顶点确定一个圆,即该三角形的外接圆.二、垂径定理及其推论1.垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.关于垂径定理的计算常与勾股定理相结合,解题时往往需要添加辅助线,一般过圆心作弦的垂线,构造直角三角形.2.推论(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧.三、圆心角、弧、弦的关系1.定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.圆心角、弧和弦之间的等量关系必须在同圆等式中才成立.2.推论在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.四、圆周角定理及其推论1.定理一条弧所对的圆周角等于它所对的圆心角的一半.2.推论(1)在同圆或等圆中,同弧或等弧所对的圆周角相等.(2)直径所对的圆周角是直角.圆内接四边形的对角互补.在圆中求角度时,通常需要通过一些圆的性质进行转化.比如圆心角与圆周角间的转化;同弧或等弧的圆周角间的转化;连直径,得到直角三角形,通过两锐角互余进行转化等.五、与圆有关的位置关系1.点与圆的位置关系设点到圆心的距离为d.(1)d<r⇔点在⊙O内;(2)d=r⇔点在⊙O上;(3)d>r⇔点在⊙O外.判断点与圆之间的位置关系,将该点的圆心距与半径作比较即可.2.直线和圆的位置关系位置关系相离相切相交图形公共点个数0个1个2个数量关系d>r d=r d<r 由于圆是轴对称和中心对称图形,所以关于圆的位置或计算题中常常出现分类讨论多解的情况.六、切线的性质与判定1.切线的性质(1)切线与圆只有一个公共点.(2)切线到圆心的距离等于圆的半径.(3)切线垂直于经过切点的半径.利用切线的性质解决问题时,通常连过切点的半径,利用直角三角形的性质来解决问题.2.切线的判定(1)与圆只有一个公共点的直线是圆的切线(定义法).(2)到圆心的距离等于半径的直线是圆的切线.(3)经过半径外端点并且垂直于这条半径的直线是圆的切线.切线判定常用的证明方法:①知道直线和圆有公共点时,连半径,证垂直;②不知道直线与圆有没有公共点时,作垂直,证垂线段等于半径.七、三角形与圆1.三角形的外接圆相关概念经过三角形各顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.外心是三角形三条垂直平分线的交点,它到三角形的三个顶点的距离相等.2.三角形的内切圆与三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.内心是三角形三条角平分线的交点,它到三角形的三条边的距离相等.考向一圆的基本认识1.在一个圆中可以画出无数条弦和直径.2.直径是弦,但弦不一定是直径.3.在同一个圆中,直径是最长的弦.4.半圆是弧,但弧不一定是半圆.弧有长度和度数,规定半圆的度数为180°,劣弧的度数小于180°,优弧的度数大于180°.5.在同圆或等圆中能够互相重合的弧是等弧,度数或长度相等的弧不一定是等弧.典例1下列命题中正确的有①弦是圆上任意两点之间的部分;②半径是弦;③直径是最长的弦;④弧是半圆,半圆是弧.A.1个B.2个C.3个D.4个【答案】A【解析】①弦是圆上任意两点之间所连线段,所以①错误;②半径不是弦,所以②错误;③直径是最长的弦,正确;④只有180°的弧才是半圆,所以④错误,故选A.1.把圆的半径缩小到原来的14,那么圆的面积缩小到原来的A.12B.14C.18D.1162.半径为5的圆的一条弦长不可能是A.3 B.5 C.10 D.12考向二垂径定理1.垂径定理中的“弦”为直径时,结论仍然成立.2.垂径定理是证明线段相等、弧相等的重要依据,同时也为圆的计算和作图问题提供了理论依据.典例2把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16 cm,则球的半径为A.cm B.10 cmC.cm D.cm【答案】B【点睛】解本题的关键是作辅助线弦心距,构造直角三角形,这个直角三角形的斜边是半径,另两条边分别为弦心距和弦的一半,再根据解直角三角形解题.典例3 如图,将半径为2 cm 的圆形纸片折叠后,圆弧恰好经过圆心O ,则折痕AB 的长为A .2 cmB cmCD 【答案】C【解析】在图中构建直角三角形,先根据勾股定理得AD 的长,再根据垂径定理得AB 的长. 作OD ⊥AB 于D ,连接OA .根据题意得OD =12OA =1cm ,再根据勾股定理得:AD cm ,根据垂径定理得AB . 故选C .3.如图,⊙O 的直径为10,圆心O 到弦AB 的距离OM 的长为4,则弦AB 的长是A .3B .6C.4 D.84.如图,某菜农在蔬菜基地搭建了一个横截面为圆弧形的蔬菜大棚,大棚的跨度弦AB 大棚顶点C离地面的高度为2.3米.(1)求该圆弧形所在圆的半径;(2)若该菜农的身高为1.70米,则他在不弯腰的情况下,横向活动的范围有几米?考向三弧、弦、圆心角、圆周角1.圆心角的度数等于它所对弧的度数,把顶点在圆心的周角等分成360份,每一份的圆心角是1°的角,1°的圆心角对着1°的弧.2.圆周角要具备两个特征:①顶点在圆上;②角的两边都和圆相交,二者缺一不可.典例4如图,AB和CD是⊙O的两条直径,弦DE∥AB,若弧DE为40°的弧,则∠BOC=A.110° B.80°C.40° D.70°【答案】A【解析】连接OE,如图所示:∵弧DE 为40°的弧,∴∠DOE =40°.∵OD =OE ,∴∠ODE =180402︒-︒=70°. ∵弦DE ∥AB ,∴∠AOC =∠ODE =70°,∴∠BOC =180°–∠AOC =180°–70°=110°.故选A .【点睛】本题考查的是圆心角、弧、弦的关系,根据题意作出辅助线,构造出等腰三角形是解答此题的关键. 典例5 如图,在⊙O 中,圆心角∠AOB =120°,P 为弧AB 上一点,则∠APB 度数是A .100°B .110°C .120°D .130°【答案】C【解析】如图,在优弧AB 上取点C ,连接AC 、BC ,由圆周角定理得由圆内接四边形的性质得到,180120APB ACB ∠=︒-∠=︒,故选C . 【点睛】在同圆或等圆中,同弧所对的圆周角等于圆心角的一半.5.如图,AB 为⊙O 的直径,点C 在⊙O 上,若∠OCA =50°,AB =4,则 BC的长为A .103π B .109π C .59π D .518π 6.如图,AB 是⊙O 的直径, =BCCD DE =,∠COD =38°,则∠AEO 的度数是A.52° B.57° C.66° D.78°考向四点、直线与圆的位置关系1.点和圆的位置关系:①在圆上;②在圆内;③在圆外.2.直线和圆的位置关系:相交、相切、相离.典例6 已知⊙O的半径是5,点A到圆心O的距离是7,则点A与⊙O的位置关系是A.点A在⊙O上B.点A在⊙O内C.点A在⊙O外D.点A与圆心O重合【答案】C【解析】∵O的半径是5,点A到圆心O的距离是7,即点A到圆心O的距离大于圆的半径,∴点A在⊙O外.故选C.【点睛】直接根据点与圆的位置关系的判定方法进行判断.典例7 在△ABC中,AB=AC=2,∠A=150°,那么半径长为1的⊙B和直线AC的位置关系是A.相离B.相切C.相交D.无法确定【答案】B【解析】过B作BD⊥AC交CA的延长线于D,∵∠BAC=150,∴∠DAB=30°,∴BD=11222AB=⨯=1,即B到直线AC的距离等于⊙B的半径,∴半径长为1的⊙B和直线AC的位置关系是相切,故选B.【点睛】本题考查了直线与圆的位置关系的应用,过B作BD⊥AC交CA的延长线于D,求出BD和⊙B的半径比较即可,主要考查学生的推理能力.7.如图,⊙O的半径为5cm,直线l到点O的距离OM=3cm,点A在l上,AM=3.8cm,则点A与⊙O的位置关系是A.在⊙O内B.在⊙O上C.在⊙O外D.以上都有可能8.如图,⊙O的半径OC=5cm,直线l⊥OC,垂足为H,且l交⊙O于A、B两点,AB=8cm,则l沿OC所在直线向下平移__________cm时与⊙O相切.学_科网考向五切线的性质与判定有圆的切线时,常常连接圆心和切点得切线垂直半径,这是圆中作辅助线的一种方法.典例8 如图,已知BC是⊙O的直径,AB是⊙O的弦,切线AD交BC的延长线于D,若∠D=40°,则∠B 的度数是A.40° B.50°C.25° D.115°【答案】C【解析】连接OA,根据切线的性质得到OA⊥AD,由三角形的内角和得到∠AOC=50°,根据等腰三角形的性质得到∠B=∠OAB,根据圆周角定理可得到结论.连接OA,∵AD是⊙O的切线,∴OA⊥AD,∴∠D=40°,∴∠AOC=50°,∵BO=OA,∴∠B=∠BAO,∴∠B+∠BAO=∠AOC=50°,∴∠B=∠BAO=12∠AOC=25°.故选C.【点睛】本题考查了切线的性质,三角形内角和,圆周角定理,正确的作出辅助线是解题的关键.典例9 如图,Rt△ABC中,∠C=90°,AB=5,AC=3,点E在中线AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径为A.78B.67C.56D.1【答案】B9.已知四边形ABCD是梯形,且AD∥BC,AD<BC,又⊙O与AB、AD、CD分别相切于点E、F、G,圆心O在BC上,则AB+CD与BC的大小关系是A.大于B.等于C.小于D.不能确定10.如图,以等腰△ABC的腰AB为⊙O的直径交底边BC于D,DE AC于E.;(2)DE为⊙O的切线.求证:(1)DB DC1.下列关于圆的叙述正确的有①圆内接四边形的对角互补;②相等的圆周角所对的弧相等;③正多边形内切圆的半径与正多边形的半径相等;④同圆中的平行弦所夹的弧相等.A.1个B.2个C.3个D.4个2.如图所示,△ABC的三个顶点在⊙O上,D是 AB上的点,E是 AC上的点,若∠BAC=50°,则∠D+∠E=A.220° B.230°C.240° D.250°3.如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD =180°,则弦BC 的长等于A BC .8D .64.如图,在平面直角坐标系中,过格点A ,B ,C 作一圆弧,则圆心坐标是A .点(1,0)B .点(2,1)C .点(2,0)D .点(2.5,1)5.如图,点O 是△ABC 的内心,∠A =62°,则∠BOC =A .59°B .31°C .124°D .121°6.如图,一圆内切四边形ABCD ,且BC =10,AD =7,则四边形的周长为A .32B .34C .36D .387.已知在⊙O 中,AB =BC ,且 34AB AMC ∶∶,则∠AOC =__________.8.如图,A 、B 、C 、D 都在⊙O 上,∠B =130°,则∠AOC 的度数是__________.9.如图,PA 、PB 分别切⊙O 于A 、B ,并与圆O 的切线DC 分别相交于D 、C .已知△PCD 的周长等于14cm ,则PA =__________cm .10.如图,在⊙O 的内接四边形ABCD 中,AB AD =,120C ∠=︒,点E 在弧AD 上.若AE 恰好为⊙O 的内接正十边形的一边, DE的度数为__________.11.如图,在圆内接四边形ABCD 中,若∠A ,∠B ,∠C 的度数之比为4∶3∶5,则∠D 的度数是__________°.12.如图,AB 为⊙O 的直径,C 、F 为⊙O 上两点,且点C 为弧BF 的中点,过点C 作AF 的垂线,交AF的延长线于点E,交AB的延长线于点D.(1)求证:DE是⊙O的切线;学_科网(2)如果半径的长为3,tan D=34,求AE的长.13.如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.(1)判断直线DE与⊙O的位置关系,并说明理由;(2)若AC=6,BC=8,OA=2,求线段DE的长.14.如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D 点,连接BD并延长至F,使得BD=DF,连接CF、BE.(1)求证:DB=DE;(2)求证:直线CF为⊙O的切线.1.(2018•张家界)如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=A.8cm B.5cmC.3cm D.2cm2.(2018•甘孜州)如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是A.AC=AB B.∠C=12∠BODC.∠C=∠B D.∠A=∠BOD3.(2018•乐山)《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆柱形木材的直径是多少?”如图所示,请根据所学知识计算:圆柱形木材的直径AC是A.13寸B.20寸C.26寸D.28寸4.(2018•日照)如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠BED 的正切值等于A BC.2 D.1 25.(2018•常州)某数学研究性学习小组制作了如下的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺CA的0刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出sin∠AOB的值是A.58B.78C.710D.456.(2018•襄阳)如图,点A,B,C,D都在半径为2的⊙O上,若OA⊥BC,∠CDA=30°,则弦BC的长为A.4 B.C D .7.(2018•邵阳)如图所示,四边形ABCD 为⊙O 的内接四边形,∠BCD =120°,则∠BOD 的大小是A .80°B .120°C .100°D .90°8.(2018•宜宾)在△ABC 中,若O 为BC 边的中点,则必有:AB 2+AC 2=2AO 2+2BO 2成立.依据以上结论,解决如下问题:如图,在矩形DEFG 中,已知DE =4,EF =3,点P 在以DE 为直径的半圆上运动,则PF 2+PG 2的最小值为A B .192C .34D .109.(2018•牡丹江)如图,△ABC 内接于⊙O ,若sin ∠BAC =13,BC ,则⊙O 的半径为A .B .C .D .10.(2018•湘西州)已知⊙O 的半径为5cm ,圆心O 到直线l 的距离为5cm ,则直线l 与⊙O 的位置关系为 A .相交 B .相切 C .相离D .无法确定11.(2018•常州)如图,AB 是⊙O 的直径,MN 是⊙O 的切线,切点为N ,如果∠MNB =52°,则∠NOA 的度数为A.76° B.56°C.54° D.52°12.(2018•广元)如图是一块测环形玉片的残片,作外圆的弦AB与内圆相切于点C,量得AB=8cm、点C 与 AB的中点D的距离CD=2cm.则此圆环形士片的外圆半径为__________cm.13.(2018•毕节市)如图,AB是⊙O的直径,C、D为半圆的三等分点,CE⊥AB于点E,∠ACE的度数为__________.14.(2018•牡丹江)如图,在⊙O中, AB=2 AC,AD⊥OC于D.求证:AB=2AD.15.(2018•湖北)如图,在⊙O中,AB为直径,AC为弦.过BC延长线上一点G,作GD⊥AO于点D,交AC于点E,交⊙O于点F,M是GE的中点,连接CF,CM.(1)判断CM与⊙O的位置关系,并说明理由;(2)若∠ECF=2∠A,CM=6,CF=4,求MF的长.16.(2018•黄石)如图,已知A、B、C、D、E是⊙O上五点,⊙O的直径BE,∠BCD=120°,A为 BE的中点,延长BA到点P,使BA=AP,连接PE.(1)求线段BD的长;(2)求证:直线PE是⊙O的切线.17.(2018•贺州)如图,AB是⊙O的弦,过AB的中点E作EC⊥OA,垂足为C,过点B作直线BD交CE 的延长线于点D,使得DB=DE.(1)求证:BD是⊙O的切线;(2)若AB=12,DB=5,求△AOB的面积.1.【答案】D【解析】设原来的圆的半径为r ,则面积S 1=πr 2,∴半径缩小到原来的14后所得新圆的面积22211ππ416S r r ⎛⎫== ⎪⎝⎭,∴22211π116π16rS S r ==.故选D . 2.【答案】D【解析】∵圆的半径为5,∴圆的直径为10,又∵直径是圆中最长的弦,∴圆中任意一条弦的长度10l ≤.故选D . 3.【答案】B【解析】如图,连接OA ,∵O 的直径为10,5OA ∴=, ∵圆心O 到弦AB 的距离OM 的长为4, 由垂径定理知,点M 是AB 的中点,12AM AB =, 由勾股定理可得,3AM =,所以6AB =.故选B .4.【解析】(1)如图所示:CO ⊥AB 于点D ,设圆弧形所在圆的半径为xm,根据题意可得:DO2+BD2=BO2,则(x–2.3)2+12)2=x2,解得x=3.答:圆弧形所在圆的半径为3米;(2)如图所示:当MN=1.7米,则过点N作NF⊥CO于点F,可得:DF=1.7米,则FO=2.4米,NO=3米,故FN=1.8(米),故该菜农身高1.70米,则他在不弯腰的情况下,横向活动的范围有3.6米.5.【答案】B【解析】根据题意可知:∠OAC=∠OCA=50°,则∠BOC=2∠OAC=100°,则弧BC的长度为故选B.7.【答案】A【解析】如图,连接OA,则在直角△OMA中,根据勾股定理得到OA5=<.∴点A与⊙O的位置关系是:点A在⊙O内.故选A.8.【答案】2【解析】连接OA.∵直线和圆相切时,OH=5,又∵在直角三角形OHA中,HA=AB÷2=4,OA=5,∴OH=3.∴需要平移5–3=2(cm).故答案是:2.【点睛】本题考查垂径定理及直线和圆的位置关系.注意:直线和圆相切,应满足d=R.9.【答案】B【解析】如图,连接OF,OA,OE,作AH⊥BC于H.∵AD是切线,∴OF⊥AD,易证四边形AHOF是矩形,∴AH=OF=OE,∵S△AOB=12•OB•AH=12•AB•OE,∴OB=AB,同理可证:CD=CO,∴AB+CD=BC,故选B.【点睛】本题考查了切线的性质,切线垂直于过切点的半径,正确作出辅助线是关键. 10.【解析】(1)如图,连AD ,∵AB 是直径,∴90ADB ∠=︒,AD BC ⊥, 又AB AC =,∴D 为BC 中点,DB DC =; (2)连OD ,∵D 为BC 中点,OA OB =, ∴OD 为ABC △中位线,OD AC ∥, 又DE AC ⊥于,E ∴90ODE DEC ∠=∠=︒, ∴DE 为⊙O 的切线.学科_网1.【答案】B【解析】①圆内接四边形的对角互补;正确;②相等的圆周角所对的弧相等;错误;③正多边形内切圆的半径与正多边形的半径相等;错误;④同圆中的平行弦所夹的弧相等;正确; 正确的有2个,故选B . 2.【答案】B【解析】如图,连接OA 、OB 、OC ,由圆心角、弧、弦的关系定理得出∠BOC =100°,得出∠AOB +∠AOC =260°,由圆周角定理得出∠D =12(∠BOC +∠AOC ),∠E =12(∠BOC +∠AOB ),即可得出∠D+∠E=12(∠BOC+∠AOC+∠BOC+∠AOB)=12(260°+100°+100°)=230°.故选B.3.【答案】C【解析】如图,延长CA,交⊙A于点F,∵∠BAC+∠BAF=180°,∠BAC+∠EAD=180°,∴∠BAF=∠DAE,∴BF=DE=6,∵CF是直径,∴∠ABF=90°,CF=2×5=10,∴BC8=.故选C.4.【答案】C【解析】根据勾股定理可知A、B、C点到(2,0,然后可知圆心为(2,0)或者通过AB、BC的垂直平分线求解也可以.故选C.5.【答案】D【解析】∵∠BAC=62°,∴∠ABC+∠ACB=180°–62°=118°,∵点O是△ABC的内心,∴∠OBC=12∠ABC,∠OCB=12∠ACB,∴∠OBC+∠OCB=12(∠ABC+∠ACB)=12×118°=59°,∴∠BOC=180°–59°=121°.故选D.6.【答案】B【解析】由题意可得圆外切四边形的两组对边和相等,所以四边形的周长=2×(7+10)=34.故选B.7.【答案】144°【解析】根据AB =BC 可得:弧AB 的度数和弧BC 的度数相等,则弧AMC 的度数为:(360°÷10)×4=144°,则∠AOC =144°. 8.【答案】100°【解析】∵∠B =130°,∴∠D =180°-130°=50°,∴∠AOC =2∠D =100°.故答案为100°. 9.【答案】7【解析】如图,设DC 与⊙O 的切点为E ;∵PA 、PB 分别是⊙O 的切线,且切点为A 、B ,∴PA =PB ; 同理,可得:DE =DA ,CE =CB ;则△PCD 的周长=PD +DE +CE +PC =PD +DA +PC +CB =PA +PB =14(cm ); ∴PA =PB =7cm ,故答案是:7. 10.【答案】84︒【解析】如图,连接BD ,OA ,OE ,OD ,∵四边形ABCD 是圆的内接四边形,∴180BAD C ∠+∠=︒, ∵120C ∠=︒,∴60BAD ∠=︒,∵AB AD =,∴ABD △是正三角形,∴60ABD ∠=︒,2120AOD ABD ∠=∠=︒, ∵AE 恰好是⊙的内接正十边形的一边,∴3603610AOE ︒∠==︒, ∴1203684DOE ∠=︒-︒=︒,∴ DE的度数为84°.故答案为:84°.11.【答案】120【解析】∵∠A ,∠B ,∠C 的度数之比为4∶3∶5, ∴设∠A =4x ,则∠B =3x ,∠C =5x .∵四边形ABCD是圆内接四边形,∴∠A+∠C=180°,即4x+5x=180°,解得x=20°,∴∠B=3x=60°,∴∠D=180°–60°=120°.故答案为:120.13.【解析】(1)直线DE与⊙O相切,理由如下:如图,连接OD,∵OD=OA,∴∠A=∠ODA,∵EF是BD的垂直平分线,∴EB=ED,∴∠B=∠EDB,∵∠C=90°,∴∠A+∠B=90°,∴∠ODA+∠EDB=90°,∴∠ODE=180°–90°=90°,∴直线DE与⊙O相切;(2)连接OE,设DE=x,则EB=ED=x,CE=8–x,∵∠C=∠ODE=90°,∴OC2+CE2=OE2=OD2+DE2,∴42+(8–x)2=22+x2,解得:x=4.75,则DE=4.75.14.【解析】(1)∵E是△ABC的内心,∴∠BAE=∠CAE,∠EBA=∠EBC,∵∠BED=∠BAE+∠EBA,∠DBE=∠EBC+∠DBC,∠DBC=∠EAC,∴∠DBE=∠DEB,∴DB=DE.(2)如图,连接CD.∵AD平分∠BAC,∴∠DAB=∠DAC,∴ BD= CD,∴BD=CD,∵BD=DF,∴CD=DB=DF,∴∠BCF=90°,∴BC⊥CF,∴CF是⊙O的切线.1.【答案】A【解析】∵弦CD⊥AB于点E,CD=8cm,∴CE=12CD=4cm.在Rt△OCE中,OC=5cm,CE=4cm,∴OE=3cm,∴AE=AO+OE=5+3=8cm.故选A.2.【答案】B【解析】A、根据垂径定理不能推出AC=AB,故A选项错误;B、∵直径CD⊥弦AB,∴ AD= BD,∵ AD对的圆周角是∠C, BD对的圆心角是∠BOD,∴∠BOD=2∠C,故B选项正确;C、不能推出∠C=∠B,故C选项错误;D、不能推出∠A=∠BOD,故D选项错误;故选B.3.【答案】C【解析】设⊙O的半径为r.在Rt△ADO中,AD=5,OD=r–1,OA=r,则有r2=52+(r–1)2,解得r=13,∴⊙O的直径为26寸,故选C.4.【答案】D【解析】∵∠DAB=∠DEB,∴tan∠DAB=tan∠DEB=12.故选D.5.【答案】D【解析】如图,连接AD.∵OD是直径,∴∠OAD=90°,∵∠AOB+∠AOD=90°,∠AOD+∠ADO=90°,∴∠AOB=∠ADO,∴sin∠AOB=sin∠ADO=810=45,故选D.6.【答案】D【解析】如图,∵OA⊥BC,∴CH=BH, AC= AB,∴∠AOB=2∠CDA=60°,∴BH=OB•sin∠AOB BC=2BH D.7.【答案】B【解析】∵四边形ABCD为⊙O的内接四边形,∴∠A=180°–∠BCD=60°,由圆周角定理得,∠BOD=2∠A=120°,故选B.8.【答案】D【解析】如图,设点M为DE的中点,点N为FG的中点,连接MN交半圆于点P,此时PN取最小值.∵DE=4,四边形DEFG为矩形,∴GF=DE,MN=EF,∴MP=FN=12DE=2,∴NP=MN–MP=EF–MP=1,∴PF2+PG2=2PN2+2FN2=2×12+2×22=10.故选D.9.【答案】A【解析】如图:连接OB ,O C .作OD ⊥BC 于D∵OB =OC ,OD ⊥BC ,∴CD =12BC ,∠COD =12∠BOC ,又∵∠BOC =2∠A ,BC ,∴∠COD =∠A ,CD ,∵sin ∠BAC =13,∴sin ∠COD =CD OC =13,∴OC ,故选A . 10.【答案】B【解析】∵圆心到直线的距离5cm=5cm ,∴直线和圆相切.故选B . 11.【答案】A【解析】∵MN 是⊙O 的切线,∴ON ⊥NM ,∴∠ONM =90°,∴∠ONB =90°–∠MNB =90°–52°=38°,∵ON =OB ,∴∠B =∠ONB =38°,∴∠NOA =2∠B =76°.故选A . 12.【答案】5【解析】如图,连接OA ,∵CD =2cm ,AB =8cm , ∵CD ⊥AB ,∴OD ⊥AB ,∴AC =12AB =4cm ,∴设半径为r ,则OD =r –2, 根据题意得:r 2=(r –2)2+42,解得:r =5. ∴这个玉片的外圆半径长为5cm .故答案为:5.13.【答案】30°【解析】如图,连接OC .∵AB是直径, AC= CD= BD,∴∠AOC=∠COD=∠DOB=60°,∵OA=OC,∴△AOC是等边三角形,∴∠A=60°,∵CE⊥OA,∴∠AEC=90°,∴∠ACE=90°–60°=30°.故答案为30°.14.【解析】如图,延长AD交⊙O于E,∵OC⊥AD,∴ AE=2 AC,AE=2AD,∵ AB=2 AC,∴ AE= AB,∴AB=AE,∴AB=2AD.15.【解析】(1)CM与⊙O相切.理由如下:连接OC,如图,∵GD⊥AO于点D,∴∠G+∠GBD=90°,∵AB为直径,∴∠ACB=90°,∵M点为GE的中点,∴MC=MG=ME,∴∠G=∠1,∵OB=OC,∴∠B=∠2,∴∠1+∠2=90°,∴∠OCM=90°,∴OC⊥CM,∴CM为⊙O的切线;16.【解析】(1)连接DE,如图,∵∠BCD+∠DEB=180°,∴∠DEB=180°–120°=60°,∵BE为直径,∴∠BDE=90°,在Rt △BDE 中,DE =12BE =12×,BD DE ; (2)连接EA ,如图, ∵BE 为直径,∴∠BAE =90°,∵A 为 BE的中点,∴∠ABE =45°, ∵BA =AP ,而EA ⊥BA , ∴△BEP 为等腰直角三角形, ∴∠PEB =90°,∴PE ⊥BE , ∴直线PE 是⊙O 的切线.17.【解析】(1)∵OA =OB ,DB =DE ,∴∠A =∠OBA ,∠DEB =∠DBE ,∵EC ⊥OA ,∠DEB =∠AEC ,∴∠A +∠DEB =90°, ∴∠OBA +∠DBE =90°,∴∠OBD =90°, ∵OB 是圆的半径,∴BD 是⊙O 的切线;(2)如图,过点D 作DF ⊥AB 于点F ,连接OE , ∵点E 是AB 的中点,AB =12, ∴AE =EB =6,OE ⊥AB ,又∵DE =DB ,DF ⊥BE ,DB =5,DB =DE ,∴EF =BF =3,∴DF =4, ∵∠AEC =∠DEF ,∴∠A =∠EDF ,∵OE ⊥AB ,DF ⊥AB ,∴∠AEO =∠DFE =90°,∴△AEO ∽△DFE ,∴EO AE FE DF =,即634EO =,得EO =4.5, ∴△AOB 的面积是:12 4.522AB OE ⋅⨯==27.。
初中数学九年级《圆与圆的位置关系》-完整版PPT课件

关 置
与 圆
的 位
2008 新北京新奥运
认真观察 观察结果
外离:两圆无公共点,并且每个圆上的点都在另 一个圆的外部时,叫两圆外离
切点
外切:两圆有一个公共点,并且除了公共点外, 每个圆上的点都在另一个圆的外部时,叫两 圆外切
相交:两圆有两个公共点时,叫两圆相交 切点
内切:两圆有一个公共点,并且除了公共点外,一个 圆上的点都在另一个圆的内部时,叫两圆内切
已知:⊙O1和⊙O2的半径分别2cm和4cm,当圆心 距O1O2分别为下列数值时,判断两圆位置关系.
(1)0cm (2)8 cm
特例
内含:两圆无公共点,并且一个圆上的点都在另一 个圆的内部时,叫两圆内含
圆心距:两圆心之间的距离
外离
外切
相交
内切
内含同心圆
圆
外离
与
相离
圆 的
内含
位
外切
置
相切
关
系
内切
相交
两圆位置关系的性质与判定:
演示
0
两圆外离
位置关系
R―r
性质
d 和R、 r关系
Rr
d >R+ r
两圆外切
d =R+ r
两圆相交
判断: 1 两圆无公共点,两圆一定外离 ( )
已知:⊙O1和⊙O2的半径分别2cm和4cm,当圆心距O1O2 分别为下列数值时,判断两圆位置关系.
(1)2cm (2)4 cm 3 6 cm
判断: 2 当两圆圆心距大于半径之差 时,两圆相交( )
判断: 3 已知两圆相切R=7, r=2则圆心距等于9 ( )
同 心 圆 两圆内切 内
含;R+ r
九年级数学下册第28章圆28.2与圆有关的位置关系4圆与圆的位置关系课件华东师大版 (2)

1 86 2
24
cm2.
3.(2012·六盘水中考)已知两圆的半径分别为2和3,两圆的圆 心距为4,那么这两圆的位置关系是______. 【解析】∵3-2<4<3+2,∴两圆相交. 答案:相交
4.(2011·绍兴中考) 如图,相距2 cm的两个点A,B在直线l上,它 们分别以2 cm/s和1 cm/s的速度在l上同时向右平移,当点A,B分 别平移到点A1,B1的位置时,半径为1 cm的⊙A1与半径为BB1的 ⊙B相切,则点A平移到点A1所用的时间为______s.
6.如图,要在直径为50厘米的圆形木板上截出 四个大小相等的圆形凳面,问怎样截才能截出 直径最大的凳面,最大的凳面直径是多少厘米?
【解析】截法如图所示, 根据圆的对称性可知:O1,O3都在⊙O的直径AB上, 设所截出的凳面的最大直径为d厘米. 则O1O2=d,O2O3=d,O12Od3;= 又∵O1O3=AB-(O1A+O3B)=50-d, ∴ 2=d50-d, ( 2 1)d 50, ∴d=50( 2-1)(厘米). ∴最大的直径是50( -21)厘米 .
【解析】连结OA,OC, ∵AB是小圆的切线,∴OC⊥AB. ∵OA=5 cm,OC=3 cm, ∴ AC OA2 OC2 52 32 4 cm. ∵AB是大圆的弦,OC过圆心,OC⊥AB, ∴AB=2AC=2×4=8 (cm). 答案:8
5.如图,两个等圆⊙O与⊙O′外切,过点 O作⊙O′的两条切线OA,OB, A,B是 切点,则∠AOB=_______. 【解析】连结OO′和O′A, 根据切线的性质,得O′A⊥OA, 根据题意得OO′=2O′A,则∠AOO′=30°, 再根据切线长定理得 ∠AOB=2∠AOO′=60°. 答案:60°
最新中考数学-一轮复习:与圆有关的位置关系

与圆有关的位置关系基础知识知识点一、点与圆的位置关系1. 点和直线有三种位置关系:①点在圆外,即这个点到圆心的距离大于半径;②点在圆上,即这个点到圆心的距离等于半径;③点在圆内,即这个点到圆心的距离小于半径.2. 用数量关系表示位置关系:⊙O的半径为r,点P到圆心的距离OP=d,则有①点P在⊙O外d>r;②点P在⊙O上d=r;③点P在⊙O内d<r.知识点二、直线和圆的位置关系1.直线和圆的三种位置关系:(1)相离:直线和圆没有公共点,这时我们说这条直线和圆相离.(2)相切:直线和圆只有一个公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.(3)相交:直线和圆有两个公共点,这时我们说这条直线和圆相交.2、直线和圆的位置关系的性质与判断:设圆的半径为r,圆心到直线的距离为d,则:①直线和圆相离 d < r②直线和圆相切 d = r③直线和圆相交 d > r.知识点三、切线的判定定理1.切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.在应用定理时,必须先弄清两个条件:一是经过半径的外端;二是垂直于这条半径,两者缺一不可.2. 切线的判定方法有以下几种:①可以直接应用定义:直线与圆有一个公共点时,直线是圆的切线.②圆心到直线的距离等于半径的直线是圆的切线.③切线的判定定理.当已知条件中没有指出圆与直线的公共点时,常运用方法②进行判定;当已知条件中明确指出圆与直线有公共点时,常运用判定定理进行判定.证题方法“有点连半径,无点作垂线”.知识点四、切线的性质定理与切线长定理1. 切线的性质定理:圆的切线垂直于过切点的半径.当已知圆的切线时,常常连接过切点的半径,得两线垂直关系. 2.切线长定理(1)切线长的定义:过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长. (2)切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等. 知识点五、三角形的外接圆与外心1. 三角形的外接圆:经过三角形的三个顶点的圆叫做三角形的外接圆.2. 三角形的外心:三角形外接圆的圆心,是三角形三条边垂直平分线的交点.这个点叫做三角形的外心.3. 三角形外心的性质:①三角形的外心是外接圆的圆心,它到三角形各顶点的距离相等;②三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的;但一个圆的内接三角形却有无数个,这些三角形的外心重合.知识点六、三角形的内切圆与内心1.三角形的内切圆是指与三角形各边都相切的圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.任意一个三角形都有且只有一个内切圆.但一个圆的外切三角形有无数个.2. 三角形的内心:三角形内切圆的圆心,是三角形三条角平分线的交点,到三角形三边的距离相等. 常见结论:(1)Rt △ABC 的三条边分别为:a 、b 、c (c 为斜边),则它的内切圆的半径2ab cr ; (2)△ABC 的周长为l ,面积为S ,其内切圆的半径为r ,则12S lr . 知识点七、正多边形与圆的关系1. 正多边形的概念:各边相等,各角也相等的多边形叫做正多边形.2. 正多边形与圆的关系可以这样表述:把圆分成n (n≥3)等份,依次连接各分点所得的多边形就是这个圆的内接正n 边形.利用这一关系可以判定一个多边形是否是正多边形或作出一个正多边形.这个圆是这个正多边形的外接圆.正多边形的外接圆的圆心叫做这个正多边形的中心.外接圆的半径叫做这个正多边形的半径.正多边形每一边所对的圆心角叫做正多边形的中心角.3. 对称性:①正多边形的轴对称性:正多边形都是轴对称图形,一个正n 边形共有n 条对称轴,每条对称轴都通过正n 边形的中心.②正多边形的中心对称性:边数为偶数的正多边形是中心对称图形,它的中心是对称中心. ③正多边形的旋转对称性:正多边形都是旋转对称图形,最小的旋转角等于中心角. 典型例题解析例1. 已知点P到⊙O上的点的最短距离为3cm,最长距离为5cm,则⊙O的半径为cm.例2. 已知⊙O的半径长为2cm,如果直线l上有一点P满足PO=2cm,那么直线l与⊙O的位置关系是()A.相切B.相交C.相离或相切D.相切或相交例3. Rt△ABC中,∠C=90°,AC=5,BC=12,如果以点C为圆心,r为半径,且⊙C与斜边AB仅有一个公共点,那么半径r的取值范围是.例4. (朝阳)如图,△MBC中,∠B=90°,∠C=60°,MB=23,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为()A.2B.3C.2 D.3例5. (葫芦岛)如图,边长为a的正六边形内有一边长为a的正三角形,则SS阴影空白()A.3 B.4 C.5 D.6例6. 如图:⊙I是Rt△ABC的内切圆,∠C=90°,AC=6,BC=8,则⊙I的半径是.例7. (锦州)已知,⊙O为∆ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE 的延长线上,且GA=GE.(1)求证:AG与⊙O相切.(2)若AC=6,AB=8,BE=3,求线段OE的长.(2)过点O作OH⊥AB,垂足为H,例8. (来宾)如图,AB为⊙O的直径,BF切⊙O于点B,AF交⊙O于点D,点C在DF上,BC交⊙O 于点E,且∠BAF=2∠CBF,CG⊥BF于点G.连接AE.(1) 直接写出AE与BC的位置关系;(2) 求证:△BCG∽△ACE ;(3) 若∠F=60°,GF=1,求⊙O得半径.巩固训练1. (青岛)直线l与半径为r的⊙O相交,且点O到直线l的距离为6,则r的取值范围是()A.r<6 B.r=6 C.r>6 D.r≥62. 在⊙O中,圆心O在坐标原点上,半径为210,点P的坐标为(4,5),那么点P与⊙O的位置关系是()A.点P在⊙O外B.点P在⊙O上C.点P在⊙O内D.不能确定3. 已知正三角形外接圆半径为3,这个正三角形的边长是()A.2 B.3 C.4 D.54. (天津)如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠B=25°,则∠C的大小等于()A.20°B.25°C.40°D.50°△放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,用一个圆面5. 如下图,将ABC△,能够完全覆盖这个三角形的最小圆面的半径是________.去覆盖ABC6. (曲靖)如图,正六边形ABCDEF的边长为2,则对角线AE的长是.7. (莱芜)如图,正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,下列说法不正确的是()A. △CDF的周长等于AD+CDB. FC平分∠BFDC. AC2+BF2=4CD2D. DE2=EF·CE8. (广安)如图,矩形ABCD的长为6,宽为3,点O1为矩形的中心,⊙O2的半径为1,O1O2⊥AB于点P,O1O2=6,若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边只有一个公共点的情况一共出现()A.3次B.4次C.5次D.6次9. (日照)如图,在Rt△OAB中,OA=4,AB=5,点C在OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数kyx(k≠0)的图象经过圆心P,则k= .10. (德州)如图,⊙O的直径AB为10cm,弦BC为6cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.(1)求AC,AD的长;(2)试判断直线PC与⊙O的位置关系,并说明理由.11. (河南)如图,CD是⊙O的直径,且CD=2cm,点P为CD的延长线上一点,过点P作⊙O的切线P A、PB,切点分别为点A、B.(1)连接AC,若∠APO=30°,试证明△ACP是等腰三角形;(2)填空:①当DP= cm时,四边形AOBD是菱形;②当DP=cm时,四边形AOBP是正方形.12. (抚州)如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A,B两点,连接AP 并延长分别交⊙P、x轴于点D、点E,连接DC并延长交y轴于点F,若点F的坐标为(0,1),点D的坐标为(6,-1).(1)求证:DC=FC.(2)判断⊙P与x轴的位置关系,并说明理由.(3)求直线AD的解析式.中考预测1. 在直角坐标平面内,点A的坐标为(1,0),点B的坐标为(a,0),圆A的半径为2.下列说法中不正确的是()A.当a=-1时,点B在圆A上B.当a<1时,点B在圆A内C.当a<-1时,点B在圆A外D.当-1<a<3时,点B在圆A内2. 如图,△ABC的边AC与⊙O相交于C,D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A =30°,则∠C的大小是( )A.30°B.45°C.60°D.40°3. 如图,在平面直角坐标系xOy中,半径为2的⊙P的圆心P的坐标为(-3, 0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为()A.1 B.1或5 C.3 D.54. 如图,P为⊙O的直径BA延长线上一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD. 已知PC=PD=BC. 下列结论:(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°. 其中正确的个数为()A. 4个B. 3个C. 2个D. 1个5. ⊙O的半径为R,点O到直线l的距离为d,R,d是方程x2-4x+m=0的两根,当直线l与⊙O相切时,m的值为.6. 直角三角形的两边长分别为16和12,则此三角形的外接圆半径是.7. 已知∠BAC=45°,一动点O在射线AB上运动(点O与点A不重合),设OA=x,如果半径为1的⊙O与射线AC只有一个公共点,那么x的取值范围是.8. 如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=8,则图中阴影部分的面积是__________.(结果保留π)9. 如图,正方形ABCD的边长为2,⊙O的直径为AD,将正方形沿EC折叠,点B落在圆上的F点,则BE的长为.10. 如图,Rt△ABC中,∠ABC=90°.以AB的中点O为圆心、OA长为半径作半圆,交AC于点D.点E为BC的中点,连接DE.(1)求证:DE是该半圆的切线;(2)若∠BAC=30°,DE=2,求AD的长.11.如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE AC,垂足为E.(1)证明:DE为⊙O的切线;(2)连接OE,若BC=4,求△OEC的面积.12. 如图,AB 是⊙O 的直径,点C 在⊙O 上,与⊙O 相切, BD ∥AC . (1)图中∠OCD =_______°,理由是_____________________; (2)⊙O 的半径为3,AC =4,求OD 的长.13. 阅读材料:已知,如图(1),在面积为S 的△ABC 中, BC =a ,AC =b , AB =c ,内切圆O 的半径为r.连接OA 、OB 、OC ,△ABC 被划分为三个小三角形. ∵r c b a r AB r AC r BC S S S S OAB OAC OBC )(21212121++=⋅+⋅+⋅=++=△△△.. ∴cb a Sr ++=2.(1)类比推理:若面积为S 的四边形ABCD 存在内切圆(与各边都相切的圆),如图(2),各边长分别为AB =a ,BC =b ,CD =c ,AD =d ,求四边形的内切圆半径r ;(2)理解应用:如图(3),在等腰梯形ABCD 中,AB ∥DC ,AB =21,CD =11,AD =13,⊙O 1与⊙O 2分别为△ABD 与△BCD 的内切圆,设它们的半径分别为r 1和r 2,求21r r 的值.参考答案:巩固训练∵∠ODE=∠DEA=90°,∴OD∥AC,∴11313222 OCES CE DE∆=⨯⨯=⨯=.13. 【解析】 (1)连接OA 、OB 、OC 、OD. ∵AOD COD BOC AOB S S S S S △△△△+++=dr cr br ar 21212121+++=r d c b a )(21+++=。
中考数学专题特训第二十四讲:与圆有关的位置关系(含详细参考答案)

中考数学专题复习第二十四讲与圆有关的位置关系【基础知识回顾】一、点与圆的位置关系:1、点与圆的位置关系有种,若圆的半径为r点P到圆心的距离为d则:点P在圆内<=> 点P在圆上<=>点P在圆外<=>2、过三点的圆:⑴过同一直线上三点作用,过三点,有且只有一个圆⑵三角形的外接圆:经过三角形各顶点的圆叫做三角形的外接圆的圆心叫做三角形的这个三角形叫做这个圆的⑶三角形外心的形成:三角形的交点,外心的性质:到相等【赵老师提醒:1、锐角三角形外心在三角形直角三角形的外心是锐角三角形的外心在三角形】一、直线与圆的位置关系:1、直线与圆的位置关系有种:当直线和圆有两个公共点时,叫做直线和圆直线叫圆的线,这的直线叫做圆的直线和圆没有公共点时,叫做直线和圆2、设Qo的半径为r,圆心o到直线l的距离为d,则:直线l与Qo相交<=>d r,直线l与Qo相切<=>d r直线l与Qo相离<=>d r3、切线的性质和判定:⑴性质定理:圆的切线垂直于经过切点的【赵老师提醒:根据这一定理,在圆中遇到切线时,常用连接圆心和切点,即可的垂直关系】⑵判定定理:经过半径的且这条半径的直线式圆的切线【赵老师提醒:在切线的判定中,当直线和圆的公共点标出时,用判定定理证明。
当公共点未标出时,一般可证圆心到直线的距离d=r来判定相切】4、切线长定理:⑴切线长定义:在经过圆外一点的圆的切线上,这点和切点之间的长叫做这点到圆的切线长。
⑵切线长定理:从圆外一点到圆的两条切线,它们的相等,并且圆心和这一点的连线平分的夹角5、三角形的内切圆:⑴与三角形各边都的圆,叫做三角形的内切圆,内切圆的圆心叫做三角形的⑵三角形内心的形成:是三角形的交点内心的性质:到三角形各的距离相等,内心与每一个顶点的连接线平分【赵老师提醒:三类三角形内心都在三角形若△ABC三边为a、b、c面积为s,内切圆半径为r,则s= ,若△ABC为直角三角形,则r= 】二、圆和圆的位置关系:圆和圆的位置关系有种,若Qo1半径为R,Qo2半径为r,圆心距外,则Qo1 与Qo2 外距<=> Qo1 与Qo2 外切<=>两圆相交<=> 两圆内切<=>两圆内含<=>【赵老师提醒:两圆相离无公共点包含和两种情况,两圆相切有唯一公共点包含和两种情况,注意题目中两种情况的考虑圆心同是两圆此时d= 】三、反证法:假设命题的结论,由此经过推理得出由矛盾判定所作的假设从而得到原命题成立,这种证明命题的方法叫反证法【赵老师提醒:反证法正题的关键是提出即假设所证结论的反面成立,择推理论证得出的矛盾可以与相矛盾,也可以与相矛盾,从而肯定原命题成立】【典型例题解析】考点一:切线的性质线,证明:AB=4PD.考点:切线的性质;等边三角形的判定与性质;含30度角的直角三角形;圆心角、弧、弦的关系;圆周角定理.专题:几何综合题.分析:(1)PO与BC的位置关系是平行;(2)(1)中的结论成立,理由为:由折叠可知三角形APO与三角形CPO全等,根据全等三角形的对应角相等可得出∠APO=∠CPO,再由OA=OP,利用等边对等角得到∠A=∠APO,等量代换可得出∠A=∠CPO,又根据同弧所对的圆周角相等得到∠A=∠PCB,再等量代换可得出∠COP=∠ACB,利用内错角相等两直线平行,可得出PO与BC平行;(3)由CD为圆O的切线,利用切线的性质得到OC垂直于CD,又AD垂直于CD,利用平面内垂直于同一条直线的两直线平行得到OC与AD平行,根据两直线平行内错角相等得到∠APO=∠COP,再利用折叠的性质得到∠AOP=∠COP,等量代换可得出∠APO=∠AOP,再由OA=OP,利用等边对等角可得出一对角相等,等量代换可得出三角形AOP三内角相等,确定出三角形AOP为等边三角形,根据等边三角形的内角为60°得到∠AOP为60°,由OP 平行于BC,利用两直线平行同位角相等可得出∠OBC=∠AOP=60°,再由OB=OC,得到三角形OBC为等边三角形,可得出∠COB为60°,利用平角的定义得到∠POC也为60°,再加上OP=OC,可得出三角形POC为等边三角形,得到内角∠OCP为60°,可求出∠PCD为30°,在直角三角形PCD中,利用30°所对的直角边等于斜边的一半可得出PD为PC的一半,而PC等于圆的半径OP等于直径AB的一半,可得出PD为AB的四分之一,即AB=4PD,得证.解答:解:(1)PO与BC的位置关系是PO∥BC;(2)(1)中的结论PO∥BC成立,理由为:由折叠可知:△APO≌△CPO,∴∠APO=∠CPO,又∵OA=OP,∴∠A=∠APO,∴∠A=∠CPO,又∵∠A与∠PCB都为PB所对的圆周角,∴∠A=∠PCB,∴∠CPO=∠PCB,对应训练1.(2012•玉林)如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.(1)求证:AE平分∠CAB;(2)探求图中∠1与∠C的数量关系,并求当AE=EC时,tanC的值.考点:切线的性质;特殊角的三角函数值.专题:探究型.分析:(1)连接OE,则OE⊥BC,由于AB⊥BC,故可得出AB∥OE,进而可得出∠2=∠AEO,由于OA=OE,故∠1=∠AEO,进而可得出∠1=∠2;(2)由三角形外角的性质可知∠1+∠AEO=∠EOC,,因为∠1=∠AEO,∠OEC=90°,所以2∠1+∠C=90°;当AE=CE时,∠1=∠C,再根据2∠1+∠C=90°即可得出∠C的度数,由特殊角的三角函数值得出tanC即可.解答:(1)证明:连接OE,∵⊙O与BC相切于点E,∴OE⊥BC,∴∠OBP+∠ABP=90°,∠ACP+∠APC=90°,∵OP=OB,∴∠OBP=∠OPB,∵∠OPB=∠APC,∴∠ACP=∠ABC,∴AB=AC;(2)延长AP交⊙O于D,连接BD,∵设圆半径为r,则OP=OB=r,PA=5-r,∴AB2=OA2-OB2=52-r2,AC2=PC2-PA2=(25)2-(5-r)2,∴52-r2=(25)2-(5-r)2,解得:r=3,∴AB=AC=4,∵PD是直径,∴∠PBD=90°=∠PAC,∵∠DPB=∠CPA,∴△DPB∽△CPA,∴CP AP PD BP=,∴2553 33BP-=+,解得:PB=655.考点二:切线的判定(2)解:作BG⊥CD,垂足是G,在Rt△ABD中∵AB=10,sin∠DAB=35,又∵sin∠DAB=BD AB,∴BD=6∵C是弧AB的中点,∴∠ADC=∠CDB=45°,∴BG=DG=BDsin45°=6×22=32,∵∠DAB=∠DCB∴tan∠DCB=BGCG=34,∴CG=42,∴CD=CG+DG=42+32=72,∴S△CBD=12CD•BG=7232212⨯=.点评:本题考查的是切线的判定定理,涉及到圆周角定理、解直角三角形及三角形的面积公式,根据题意作出辅助线,构造出直角三角形是解答此题的关键.对应训练考点三:三角形的外接圆和内切圆例4 (2012•阜新)如图,在△ABC中,BC=3cm,∠BAC=60°,那么△ABC能被半径至少为cm的圆形纸片所覆盖.考点:三角形的外接圆与外心;圆周角定理;锐角三角函数的定义.专题:计算题.分析:作圆O的直径CD,连接BD,根据圆周角定理求出∠D=60°,根据锐角三角函数的定义得出sin∠D= BCCD,代入求出CD即可.解答:解:作圆O的直径CD,连接BD,∵弧BC对的圆周角有∠A、∠D,∴∠D=∠A=60°,∵直径CD,A.r B.2r C.2r D.2r考点:三角形的内切圆与内心;矩形的判定;正方形的判定;切线长定理.专题:计算题.分析:连接OD、OE,求出∠ODB=∠DBE=∠OEB=90°,推出四边形ODBE是正方形,得出BD=BE=OD=OE=r,根据切线长定理得出MP=DM,NP=NE,代入MB+NB+MN得出BD+BE,求出即可.解答:解:连接OD、OE,∵⊙O是Rt△ABC的内切圆,∴OD⊥AB,OE⊥BC,∵∠ABC=90°,∴∠ODB=∠DBE=∠OEB=90°,∴四边形ODBE是矩形,∵OD=OE,∴矩形ODBE是正方形,∴BD=BE=OD=OE=r,∵⊙O切AB于D,切BC于E,切MN于P,∴MP=DM,NP=NE,∴Rt△MBN的周长为:MB+NB+MN=MB+BN+NE+DM=BD+BE=r+r=2r,故选C.点评:本题考查的知识点是矩形的判定、正方形的判定、三角形的内切圆和内心、切线长定理等,主要考查运用这些性质进行推理和计算的能力,题目比较好,难度也适中.对应训练4.(2012•台州)已知,如图1,△ABC中,BA=BC,D是平面内不与A、B、C重合的任意一点,∠ABC=∠DBE,BD=BE.(1)求证:△ABD≌△CBE;∴sin∠D=BCCD=45,∴CD=25 4,答:三角形ABC外接圆的直径是254.(2)解:连接IC、BI,且延长BI交AC于F,过I作IE⊥AB于E,∵AB=BC=5,I为△ABC内心,∴BF⊥AC,AF=CF,∵sin∠A=45=BFAB,∴BF=4,在Rt△ABF中,由勾股定理得:AF=CF=3,AC=2AF=6,∵I是△ABC内心,IE⊥AB,IF⊥AC,IG⊥BC,∴IE=IF=IG,设IE=IF=IG=R,∵△ABI、△ACI、△BCI的面积之和等于△ABC的面积,∴12AB×R+12BC×R+12AC×R=12AC×BF,即5×R+5×R+6×R=6×4,∴R=32,在△AIF中,AF=3,IF=32,由勾股定理得:AI=352.答:AI的长是352.点评:本题考查了三角形的面积公式,三角形的内切圆和内心,勾股定理,等腰三角形的性质,圆周角定理等知识点的应用,主要考查学生运用性质进行推理和计算的能力,题目综合性比较强,有一定的难度.考点三:圆与圆的位置关系例6(2012•毕节地区)第三十奥运会将于2012年7月27日在英国伦敦开幕,奥运会旗图案有五个圆环组成,如图也是一幅五环图案,在这个五个圆中,不存在的位置关系是()A.外离B.内切C.外切D.相交考点:圆与圆的位置关系.分析:根据两圆的位置关系易得到它们的位置关系有外切、外离、相交.解答:解:观察图形,五个等圆不可能内切,也不可能内含,并且有的两个圆只有一个公共点,即外切;有的两个圆没有公共点,即外离;有的两个圆有两个公共点,即相交.故选B.点评:本题考查了圆与圆的位置关系:若两圆的半径分别为R,r,圆心距为d,若d>R+r,两圆外离;若d=R+r,两圆外切;若R-r<d<R+r(R≥r),两圆相交;若d=R-r(R>r),两圆内切;若0≤d<R-r(R>r),两圆内含.对应训练6.(2012•德阳)在平面直角坐标系xOy中,已知点A(0,2),⊙A的半径是2,⊙P的半径是1,满足与⊙A及x轴都相切的⊙P有个.6.4考点:圆与圆的位置关系;坐标与图形性质;直线与圆的位置关系.分析:分两圆内切和两圆外切两种情况讨论即可得到⊙P的个数.解答:解:如图,满足条件的⊙P有4个,故答案为4.点评:本题考查了圆与圆的位置关系、坐标与图形的性质及直线与圆的知识,能充分考虑到分内切和外切是解决本题的关键.【聚焦山东中考】1.(2012•济南)已知⊙O1和⊙O2的半径是一元二次方程x2-5x+6=0的两根,若圆心距O1O2=5,则⊙O1和⊙O2的位置关系是()A.外离B.外切C.相交D.内切考点:圆与圆的位置关系.分析:先根据一元二次方程根与系数的关系,可知圆心距=两圆半径之和,再根据圆与圆的位置关系即可判断.解答:解:∵⊙O1和⊙O2的半径是一元二次方程x2-5x+6=0的两根,∴两根之和=5=两圆半径之和,又∵圆心距O1O2=5,∴两圆外切.故选B.点评:此题综合考查一元二次方程根与系数的关系及两圆的位置关系的判断.圆和圆的位置与两圆的圆心距、半径的数量之间的关系:①两圆外离⇔d>R+r;②两圆外切⇔d=R+r;③两圆相交⇔R-r<d<R+r(R≥r);④两圆内切⇔d=R-r(R>r);⑤两圆内含⇔d<R-r(R>r).2.(2012•青岛)已知,⊙O1与⊙O2的半径分别是4和6,O1O2=2,则⊙O1与⊙O2的位置关系是()A.内切B.相交C.外切D.外离考点:圆与圆的位置关系.分析:由⊙O1与⊙O2的半径分别是4和6,O1O2=2,根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系即可得出两圆位置关系.解答:解:∵⊙O1与⊙O2的半径分别是4和6,O1O2=2,∴O1O2=6-4=2,∴⊙O1与⊙O2的位置关系是内切.故选A.点评:此题考查了圆与圆的位置关系.此题比较简单,注意掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系是解此题的关键.3.(2012•泰安)如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则BC的长为()A.π B.2πC.3π D.5π考点:切线的性质;弧长的计算.分析:连接OB,由于AB是切线,那么∠ABO=90°,而∠ABC=120°,易求∠OBC,而OB=OC,那么∠OBC=∠OCB,进而求出∠BOC的度数,在利用弧长公式即可求出BC的长.解答:解:连接OB,∵AB与⊙O相切于点B,∴∠ABO=90°,∵∠ABC=120°,∴∠OBC=30°,∵OB=OC,∴∠OCB=30°,∴∠BOC=120°,∴ BC 的长为nπr 180 =120×π×3 180 =2π,故选B.点评:本题考查了切线的性质、弧长公式,解题的关键是连接OB,构造直角三角形.4.(2012•潍坊)已知两圆半径r1、r2分别是方程x2-7x+10=0的两根,两圆的圆心距为7,则两圆的位置关系是()A.相交B.内切C.外切D.外离考点:圆与圆的位置关系;解一元二次方程-因式分解法.分析:首先解方程x2-7x+10=0,求得两圆半径r1、r2的值,又由两圆的圆心距为7,根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系即可得出两圆位置关系.解答:解:∵x2-7x+10=0,∴(x-2)(x-5)=0,∴x1=2,x2=5,即两圆半径r1、r2分别是2,5,∵2+5=7,两圆的圆心距为7,∴两圆的位置关系是外切.故选C.点评:此题考查了圆与圆的位置关系与一元二次方程的解法.此题比较简单,注意掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系是解此题的关键.5.(2012•济南)如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,以其三边为直径向三角形外作三个半圆,矩形EFGH的各边分别与半圆相切且平行于AB或BC,则矩形EFGH的周长是.5.4848考点:切线的性质;勾股定理;矩形的性质.分析:首先取AC的中点O,过点O作MN∥EF,PQ∥EH,由题意可得PQ⊥EF,PQ⊥GH,MN⊥EH,MN⊥FG,PL,KN,OM,OQ分别是各半圆的半径,OL,OK是△ABC的中位线,又由在Rt△ABC中,∠B=90°,AB=6,BC=8,即可求得个线段长,继而求得答案.解答:解:取AC的中点O,过点O作MN∥EF,PQ∥EH,∵四边形EFGH是矩形,∴EH∥PQ∥FG,EF∥MN∥GH,∠E=∠H=90°,∴PQ⊥EF,PQ⊥GH,MN⊥EH,MN⊥FG,∵AB∥EF,BC∥FG,∴AB∥MN∥GH,BC∥PQ∥FG,∴AL=BL,BK=CK,∴OL=12BC=12×8=4,OK=12AB=12×6=3,∵矩形EFGH的各边分别与半圆相切,∴PL=12AB=12×6=3,KN=12BC=12×8=4,在Rt△ABC中,AC= ,∴OM=OQ=12AC=5,∴EH=FG=PQ=PL+OL+OQ=3+4+5=12,EF=GH=MN=OM+OK+NK=5+3+4=12,∴矩形EFGH的周长是:EF+FG+GH+EH=12+12+12+12=48.故答案为:48.点评:此题考查了切线的性质、矩形的性质,三角形中位线的性质以及勾股定理等知识.此题难度较大,解题的关键是掌握辅助线的作法,注意数形结合思想的应用.6.(2012•菏泽)如图,PA,PB是⊙O是切线,A,B为切点,AC是⊙O的直径,若∠P=46°,则∠BAC= 度.6.23考点:切线的性质.专题:计算题.分析:由PA、PB是圆O的切线,根据切线长定理得到PA=PB,即三角形APB为等腰三角形,由顶角的度数,利用三角形的内角和定理求出底角的度数,再由AP为圆O的切线,得到OA与AP垂直,根据垂直的定义得到∠OAP为直角,再由∠OAP-∠PAB即可求出∠BAC 的度数.解答:解:∵PA,PB是⊙O是切线,∴PA=PB,又∠P=46°,∴∠PAB=∠PBA=180-462=67°,又PA是⊙O是切线,AO为半径,∴OA⊥AP,∴∠OAP=90°,∴∠BAC=∠OAP-∠PAB=90°-67°=23°.故答案为:23。
圆九年级数学《与圆的位置关系》课件

4、如图,圆O1、圆O2相交于点A、B,过点A的 作CD⊥AB交两圆于点C、D,求证:CD=2O1O2
C
A
D
O2
O1
B
圆与圆的位置关系
新课引入
O1
O2
圆O1沿直线O1O2向右运动,它与 圆O2的交点数有何变化情况?
学习目标
了解圆与圆的五种位置关系,会根据圆 心距判断圆与圆的位置关系
自学探究
自学课本45~46页,回答下列问题 1、圆与圆有几种位置关系?如何判断? 2、当两圆相交、外切、内切时连心线有何性 质?
疑探交流
当圆心O1和圆心O2重合时,即d=0时,两圆 是同心圆
A
O1 C
O2
B
定理:两圆相交时, 连心线垂直平分两 圆的公共弦
O1
C
O2
定理:两圆 相切时,连 心线过切点
当堂检测 1、圆O1、圆O2的半径分别为3cm、4cm.若设: (1)O1O2=8cm,(2)O1O2=7cm,(3)O1O2=5cm, (4)O1O2=1cm,(5)O1O2=0cm,(6)O1O2=0.5cm 2、已知:两圆的圆心距为6cm,其中一个圆的半 径为1cm,在下列条件下,求另一个圆的半径r或 取值范围 (1)两圆外切 (2)两圆内切 (3)两圆内含 3、三角形三边分别为2、3、4,以各顶点作圆, 三个圆两两外切,求这三个圆的半径.
针对上述问题,组内交流合作,先对议, 再组议
学教新课
O1
O2
外离
Hale Waihona Puke O1O2外切
O1
O2
O1
O2
O1 O2
相交
内切
内含
连接O1O2,上述五种位置关系中,圆心距d与 两圆半径R、r有何关系?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)设⊙O与⊙P内切 B 于点B,则 PB=OP+OB ∴ PB=13 cm.
.
0
A
.
P
变式:已知⊙A ⊙B相切,圆心距为10cm,
其中⊙A的半径为4cm,求⊙B的半径?
练习2
定圆0的半径是4cm,动圆P的半径是1cm, (1) 设⊙ P和⊙ 0相外切,那么点P与点O的距离 是多少?点P可以在什么样的线上运动? (2) 设⊙ P 和 ⊙O 相内切,情况又怎样?
课堂小结
名称 公共点 两圆位置 圆心距和半径的关系
相离 外切
0 1
一圆在另一 圆的外部
一圆在另一 圆的外部
d>R+r d=R+r R-r<d<R+r d=R-r d<R-r
相交
内切 内含
2
1 0
两圆相交 一圆在另一 圆的内部
一圆在另一 圆的内部
思考题 已知⊙01和⊙02的半径分别为R和r(R>r), 圆心距为d,若两圆相交,试判定关于x的方 程x2-2(d-R)x+r2=0的根的情况。
布置作业
P课本
2 3 4
T
P N
· ·
0 `
0`
Q
练习3 两个圆的半径的比为2 : 3 ,内切时圆心距等 于 8cm,那么这两圆相交时,圆心距d的取值 范围是多少?
解 设大圆半径 : 3x-2x=8 x=8 ∴ R=24 cm r=16cm ∵ 两圆相交 R-r<d<R+r ∴ 8cm<d<40cm
观察图,可以发现,当两圆的半径一定 时,两圆的位置关系与两圆圆心的距离 的大小有关。设两圆的半径分别为R和r (R>r),圆心距为d ,那么: (1)两圆外离 (2)两圆外切 (3)两圆相交 (4)两圆内切 (5)两圆内含 d>R+r d=R+r R-r<d<R+r d=R-r d<R-r
演示
练习1 ⊙01和⊙ 02 的半径分别为3cm 和 4 cm ,设 (1) 0102= 8cm (2) 0102 = 7cm (3) 0102 =5cm (4) 0102 = 1cm (5) 0102=0.5cm (6) 01和02重合 ⊙0和⊙02的位置关系怎样?
复习引入
1。直线和圆的位置关系有几种?
直线和圆相离<=> d > r 直线和圆相切<=> d = r
直线和圆相交<=> d < r
演示
如果把月亮和太阳抽象成两个圆,在发生 日食过程中,这两个圆具有不同的位置关系。 今天我们就来学习——
圆和圆的位置关系
观察演示,考察两圆的位置关 系并观察两圆公共点的个数。
(1) 解:∵⊙0和⊙P相外切 ∴OP= R + r ∴OP=5cm ∴ P点在以O点为圆心,以5cm 为半径的圆上运动 (2) 解: ∵⊙0和⊙P相内切 ∴ OP=R-r ∴OP=3cm ∴ P点在以O点为圆心,以3cm 为半径的圆上运动
演示
例2: 两个同样大小的肥皂泡黏在一起,其剖面如图所 示(点o,o`是圆心,)分隔两个肥皂泡的肥皂膜PQ成 一条直线(线段PQ称为两圆的公共弦),TP,NP分别 为两圆的切线, (1)图中两圆的位置关系是什么? (2)求∠TPN的大小? (3)Oo`与PQ有什么位置关系?
演示
圆 和 圆 的 位 置 关 系
外离 内含 外切 内切 相交
没 有 公 共 点
相 离
一 个 公 共 点 两 个 公 共 点
相 切
相 交
1)两个圆没有公共点,并且每个圆上的点都 在另一个圆的外部时,叫做这两圆外离。 2)两个圆有唯一的公共点,并且除了这个公 共点以外,每个圆上的点都在另一个圆的外 部时,叫做这两个外切。这个唯一的公共点 叫做切点。 3)两个圆有两个公共点时,叫做这两个圆相 交 4)两个圆有唯一的公共点,并且除了这个公 共点以外,一个圆上的点都在另一个圆的内 部时,叫做这两个圆内切。这个唯一的公共 点叫做切点。 5)两个圆没有公共点,并且一个圆上的点都 在另一个圆的内部时,叫做这两个圆内含。 两圆同心是两圆内含的一种特例。
答: (1)两圆相离
(3)两圆相交
(2)两圆外切
(4)两圆内切
(5)两圆内含
(6)两圆同心
淋浴房 http://www.linyufang.so/ 整体淋浴房 0 圬罔牁
例1:如图⊙O的半径为5cm,点P是⊙O外一点, OP=8cm。 求:(1)以P为圆心作⊙P与⊙O外切,小圆⊙P 的半径是多少? (2)以P为圆心作⊙P与⊙O内切,大圆⊙P 的半径是多少?
解 ∵两圆相交 ∴R- r<d<R+r △ =b2-4ac=[-2(d-R)]2-4r2 =4(d-R)2-4r2 =4(d-R+r)(d-R-r) =4[d-(R-r)][d-(R+r)] ∵d-(R-r)>0 d-(R+r)<0 ∴ 4[d-(R-r)][d-(R+r)]<0 ∴ 方程没有实数根
